Preprint
Article
Application of Microfracture Analysis to Prevent Fatigue Fractures in Materials through Non-destructive Tests
Altmetrics
Downloads
82
Views
22
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
30 November 2023
Posted:
01 December 2023
You are already at the latest version
Alerts
Abstract
Fatigue fractures in materials are the main cause of approximately 80% of all material failures, and it is believed that such failures can be predicted and mathematically calculated in a reliable manner. It is possible to establish prediction modalities in cases of fatigue fracture, according to three fundamental variables in fatigue, such as volume, number of fracture cycles, as well as applied stress, with the integration of Weibull constants (length characteristic). This investigation was carried out mechanical fatigue tests on specimens smaller than 4 mm2 in section of different industrial materials for their subsequent analysis through precision computed tomography in search of microfractures. The measurement of these microfractures, along with their metrics and classifications, was recorded. A convolutional neural network trained with deep learning was used to achieve the detection of microfractures in image processing. The detection of microfractures in images with 480x854 or 960x960 pixels is the primary objective of this network, and its accuracy is above 95%. Images that have microfractures and those that do not are classified by the network. Subsequently, by means of image processing, the microfracture is isolated. Finally, the images that do contain this feature are interpreted by image processing to obtain their area, perimeter, characteristic length, circularity, orientation, and type microfracture metrics. All values will be obtained in pixels and converted to metric units (μm) through a conversion factor based on image resolution.
Keywords:
Subject: Engineering - Mechanical Engineering
1. Introduction
A fatigue fracture is defined as a “partial or complete fracture due to its inability to withstand non-visible stresses applied rhythmically, repeatedly and below the threshold” (Guten, 1997). Fatigue fractures occur due to the accumulation of stress-induced microfractures. They begin as microfractures and become more extensive with repetitive stresses until reaching a macrofracture size of approximately 1 mm, this being the size necessary to result in a true fracture through the structure of a material (Presbitero et al., 2012 and 2017). Fatigue fractures involve approximately 80% of all material failures (Pang et al., 2008). In human bones, fatigue fractures often occur in military recruits, 0.91% of male recruits and 1.09% of female recruits suffer fatigue fractures. Between 4.7% and 15.6% of all runners’ injuries are stress fractures (Currey, 2012).
Recent studies on the detection of fractures in materials through computer vision by deep learning in neural networks have obtained results with precision of up to 98% (Ramirez et al., 2011). Likewise, image processing techniques can be used for gradient detection, which varies and is analyzed to determine the most appropriate value (Kim et al., 2018). In a recent study of 2020 (Rezaie et al., 2020), both methods were compared for detecting cracks in concrete walls. It was found that the deep learning method, using the TernausNet network, is more effective, obtaining an accuracy of 81.9% compared to the threshold change method (Wang et al., 2020).
The main objective of this project is to determine, establish and verify methodologies and fields of study towards precise prediction procedures for the prevention of fatigue fractures in industrial materials, through the development of microfractures and the use of non-destructive testing. There are studies in the literature based on the analysis of microfractures different types of materials, however, a wide field of research is still open for studies to clarify how microfractures are generated, grow and cause the fracture of the material in each case. We have implemented a methodology for analyzing microfractures, which we consider can be quantified and compared with other same or similar materials in relation to their generation and growth due to the external fatigue stresses applied to the material in each specific case to study and analyze.
Our studies have been implemented mainly in cortical bone structures, although it is important to determine that bone is a composite material and this methodology can be executed in the analysis of the development of microfractures in different types of industrial materials (Diab et al., 2005), such as aerospace industry, metallurgy, composite materials, historical buildings, monuments, as well as earthquakes, among others.
It is possible to implement prediction modalities in instances of fatigue fracture, according to three fundamental variables in fatigue, such as the volume, the number of cycles to fracture, as well as the applied stress, with the integration of the Weibull distribution constants of two parameters (characteristic length). Therefore, the implementation of a broad area of study and innovation is studied, which will be based on the performance of mechanical tests through application of fatigue stress and characterization of properties in materials through non-destructive testing, in prevention, comparison and evaluation of fractures in different types of industrial materials due to fatigue.
2. Methodology
To establish comparisons in the determination of Weibull constants, specimens measuring 2x2x3 mm were made, in order to establish compression tests under fatigue. Cyclic axial compression forces will be applied to the samples, under a frequency of 3 Hz with an applied stress of 80 MPa, with cycles between 11 and 91 MPa. This constant stress range will be applied until fracture.
Once the fatigue tests were developed, the specimens were analyzed using X-ray computed tomography, in the facilities of the Center for Industrial Engineering and Development (CIDESI), belonging to the National Council of Humanities, Science and Technology (CONAHCYT), Mexico, where microfractures will be identified and isolated from the rest of the reconstructed specimen volume, to proceed to calculate the corresponding Weibull constants.
Therefore, through these fatigue tests and the use of the study of microfracture accumulation, based on the concept of characteristic length through the Weibull distribution, the implementation of new methodologies will be allowed, as well as new areas of study within of fracture mechanics in materials, based on precise models towards the prevention of the development of fractures of industrial materials due to fatigue.
As the first material, there is bone tissue, on which fatigue tests have already been carried out previously in a past investigation. This material gave way to start this research, as it already had computed tomography images (Figure 1) that allowed the neural network to be trained, as well as to be used in the simulation stage. Additionally, for image processing, images of metallic materials, nylon-based materials, ultra-high molecular weight polyethylene composite materials, and granite are available.
The fatigue tests on the specimens were carried out following the aforementioned characteristics in fatigue machines with cyclic loading for laboratory use, this load being compressed. Each specimen is fatigued or near complete failure for about 4,000 cycles. Once the specimen has been fatigued, each one is extracted and sent to the next process, obtaining computed tomography images of between 800 and 1700 slices.
The specimens are placed in a laboratory-grade tomograph (phoenix v|tome|x m from General Electric), at a distance of between 7 and 10 mm, as appropriate, to perform the tomography and obtain an image of each slice in a high resolution. 2014x2024 pixels. Approximately 1,700 cuts are made in the section of the specimen and processed with the definition required for the correct identification of the microfractures. To obtain correct cuts of the specimen, a power of 6W was assigned to the tomograph, a voltage of 60 kV and a current of 100μA was used.
Previously, the detection of microfractures in test tubes was done individually, that is, a person analyzed each of the images, marking which and where microfractures were found. In this study, modern tools are used, such as image processing and the use of neural networks. The detection of microfractures is done jointly through two paths, as shown in Figure 2, one image analysis and processing and the other by semantic segmentation. Matlab, its machine learning and image processing tools, was used as a software for both cases, and codes were generated to put everything together.
The route that was followed as a methodology for the detection of microfractures and their analysis is described in Figure 3, which consists of 5 main stages.
It was decided to create a new neural network, which was designed specifically for the detection of microfractures. Said neural network should be able to read, as an input image, any resolution and take it to a resolution of 480x854 or 960x960 pixels with 3 color channels; translated to Matlab, a vector example [960 960 3] as Input Layer or to a color channel (grayscale). The neural network was generated, following the considerations, with 15 processing layers, in addition to integrating the SGDM (Stochastic Gradient Descent with Momentum) technique into its vectors. The results of the neural network allow us to classify, as a first instance, the images that do have microfracture and those that do not, dividing them into two classes.
Due to the small database of tomography images, both with and without microfractures, the Data Augmentation tool was used to train the neural network. Using this technique allows you to significantly increase the amount of training data for the neural network in a synthetic way. In addition to this, semantic segmentation was used, which requires five stages: labeling images, training (Deep Learning), convolutional neural network, automatic detection and data extraction.
Figure 4.
a) Original CT image; b) Binarized image; c) Image after removing isolated regions and filling gaps; d) Image after applying a Canny filter; e) Detection of interior (green) and exterior (red) edges.
Figure 4.
a) Original CT image; b) Binarized image; c) Image after removing isolated regions and filling gaps; d) Image after applying a Canny filter; e) Detection of interior (green) and exterior (red) edges.

In addition to the analysis of the isolated microfractures from the tomography scans, the model of the test tube is reconstructed based on the images obtained with isolated microfractures, generating a 3D element that presents only the characteristics sought in this research, such as: number of total microfractures, volume total microfractures, microfracture volumetric density and microfracture properties.
The 3D model of the test tube is reconstructed using the FIJI software (Image J), for which the folder containing the images obtained from automatic identification is taken. It is important to generate the model and carry out a series of comparisons between automatic models and manually generated models, in order to find the accuracy of the automatic identification software.
The mesoscale model of microstructure in OOF2 software was developed from a cross-sectional image of a microstructure obtained by computed tomography. The tomography image was previously digitized using Image J software to differentiate the phases present in the bone cortical tissue. The bone cortical microstructure was separated into osteonal tissue and interstitial lamellae. Subsequently, using OOF2, the mechanical properties were assigned to the previously differentiated phases. Finally, a finite element model was implemented to determine the effect of the deformation generated by the differences between the mechanical properties of each of the cortical bone phases. The differences in mechanical properties are based on the constituent elements of cortical bone, these being: collagen with an E = 800 MPa and hydroxyapatite with an E = 22.1 GPa.
Figure 5 shows the meshing of the structure in the digitized image of the bone tissue. For the finite element model, the movement was restrained at the bottom and a tensile stress of 100 MPa was applied.
As a comparison, the commonly used software SolidWorks was used, which is based on the ANSYS methodology for its finite element calculations. When comparing both methods, two main factors are taken into account: processing time and the number of nodes.
For the mechanical simulation analysis with isolated microfracture, the resulting image from the automatic microfracture detection software is used, which is a binary image that includes only the microfractures and empty the rest, Figure 6. It is important to take into account that, when be a square image and not the actual shape of the specimen, the microfracture analysis will be affected.
3. Results and discussion
For the mechanical simulation analysis with isolated microfracture, the image resulting from the automatic microfracture detection software is used, which is a binary image that includes only the microfractures and empty the rest. The image is entered into the SolidWorks software to generate the drawing that simulates the microfractures. This process is done automatically with the Autotrace function. Once the figure is generated, the previously determined thickness of 2.35 μm is added and the material (Figure 6), which is a mixture of collagen and hydroxyapatite, of which its mechanical characteristics are described in this same section. Microfractures are taken as hollow sections. The corresponding mesh is generated with the greatest possible precision by the software, which has a maximum edge dimension of 69 μm and a minimum of 1.4 μm, according to its equivalence in image pixels. The specimen is analyzed with the load equivalent to the corresponding section of 100 MPa, that is, the load is divided among the 1277 sections, resulting in a load of 0.078 MPa. Once the fixed point and load variables has been adjusted, the analysis is carried out to obtain results of total displacements, in each axis, normal, shear and von Mises forces.
Figure 7 shows the analysis process carried out for the cortical bone microstructure. Figure 7a represents an X-ray computed tomography image of a bone segment. This image makes it possible to differentiate osteons from the matrix. Figure 7b shows the digitization of the image using Image J software. Finally, Figure 7c shows the meshing of the phases, as well as the assignment of properties (red for osteons and white for the matrix).
Figure 8 shows the simulation results. In the microstructure of cortical bone, there is a rigid phase (hydroxyapatite phase) and a ductile phase (collagen phase). This difference in mechanical behavior produces an irregularity in its deformation. Figures 8a,b show the deformation field of the composite microstructure. In this case, collagen is more ductile than hydroxyapatite; Fractures are centered in the matrix and stop growing when they reach the osteon.
The simulations of the specimens in SolidWorks were done in two different ways: with unisulated microfracture and with isolated microfracture. This methodology was used to compare the development of microfractures, not only between finite element methods, but also between elements that affect the material.
The results of the main stresses in the microfractures (Figure 9 and Figure 10) showed a growth trend in the areas where they are thinner, likewise, in the areas where two microfractures converge, becoming one and generating a larger one, the which leads to the material fracturing completely. The principal stresses do not represent a value even close to the maximum stress supported by the material, however, being subjected to fatigue means that the energy cannot be dissipated elastically and generates microfractures. Compression stress values in the upper area of the specimen made it possible to simulate the physical fatigue analyzes to which they were subjected.
Like simulation studies with isolated microfractures, the generation of the digital model of the tomography in its mechanical analysis determines the concentration of stress on the microfractures. In this case, two types of models were made: thickness of the cross section of the tomography (Figure 11) and total thickness of the specimen if it were the same throughout its section (Figure 4.11). For the cross section of the tomography, the thickness of 2.35 μm was used. Being a specimen with a microfracture on the edge, this resulted in a section fracture. Furthermore, it was found that hydroxyapatite osteons absorb the main stresses in the specimen, moving through the ductile collagen tissue.
Figure 11.
Material displacement in cross section simulation (units in mm).
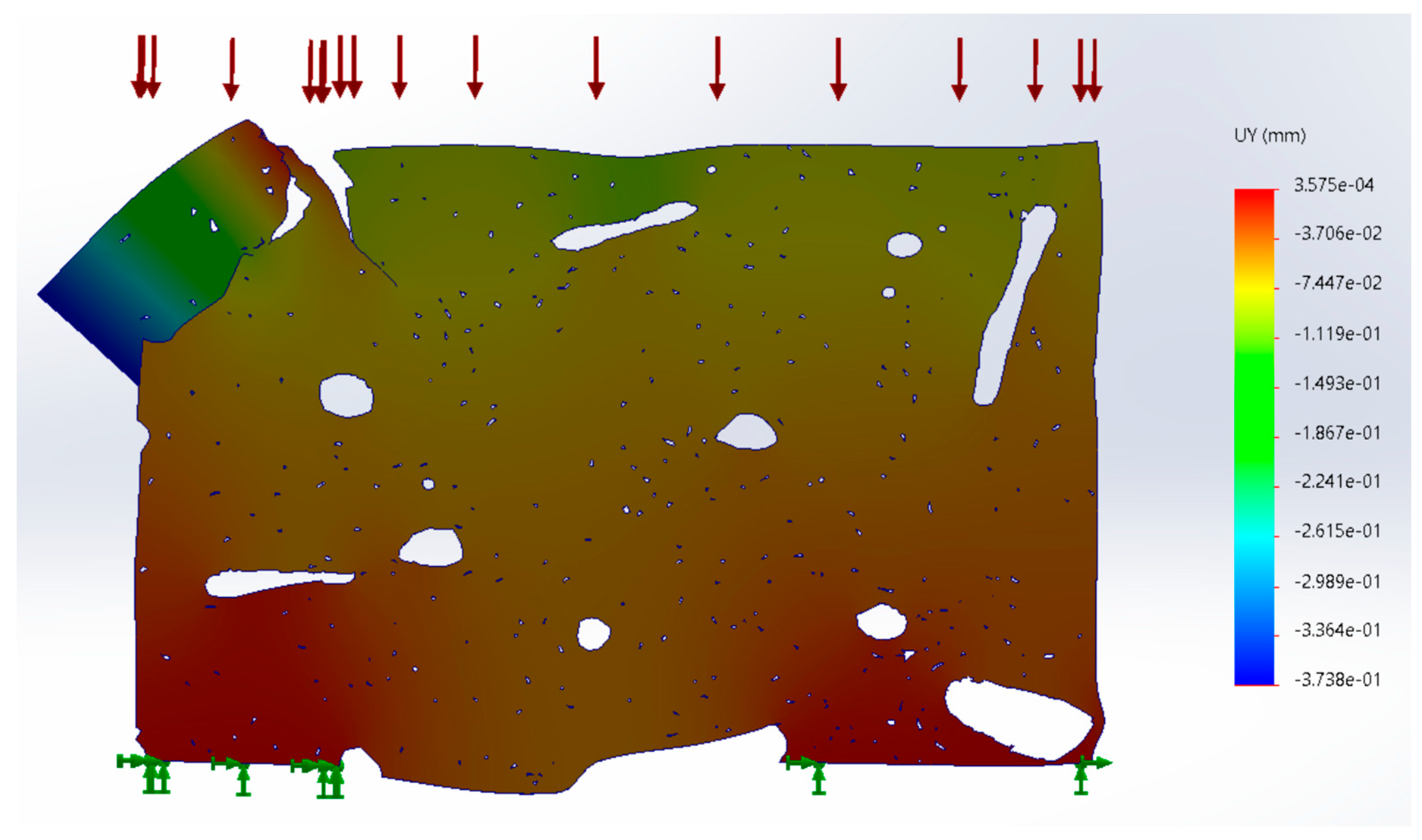
Figure 12.
Meshing for full section simulation.
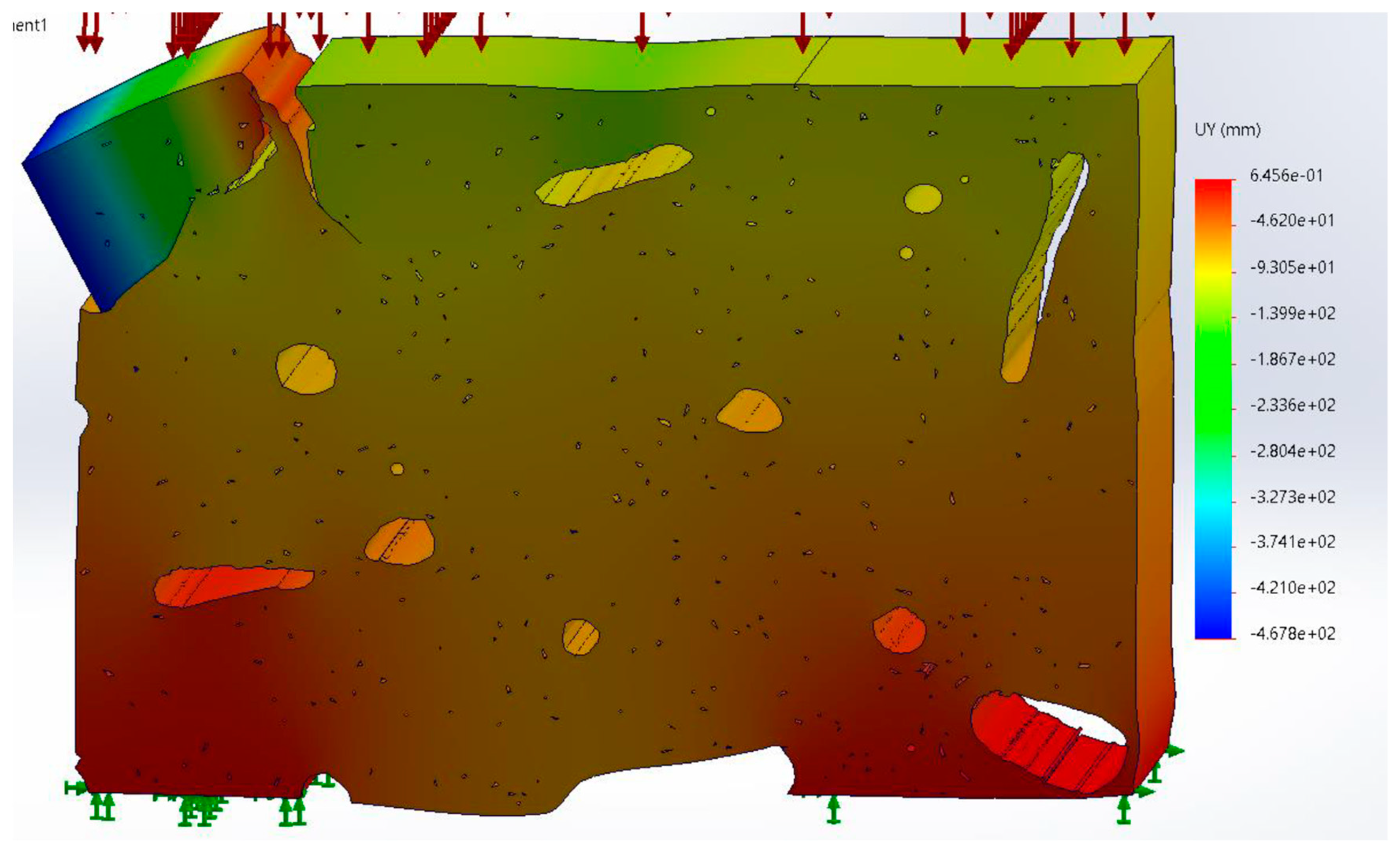
Figure 13.
Displacement for full section simulation (units in mm).
In the first instance, the neural network was designed to read 640x640 pixel images, however, very low precision results were obtained (Figure 14). It was decided to reduce the resolution of the image to facilitate training. The different previous stages in which the network was trained are described in Table 1.
Throughout the time in which this research has been carried out, modifications, updates and new training have been made to the neural network. Staying with the version that worked best for the classification of microfracture images. The processing time has also been improved depending on the training iterations, despite the greater number of images available to train the network, being 3028 with microfracture and 687 without microfracture. As the last training stage, it was decided to use the data augmentation technique only for images without microfracture and thus equalize the distribution of the classes. However, the results obtained were not satisfactory (Figure 15) and it was decided to use previous training.
Several stages and several iterations of the detection software were generated to find a correct result of each type of material. An example is shown in Figure 16, which is from a group of scans that turned out to complicate the development of the software.
Figure 17, Figure 18 and Figure 19 show the results of the identification software in its previous stages until reaching very precise results in its final stage.
All the necessary modifications were made to the automatic detection model until reaching the current model, in which the greatest number of microfractures with their greatest extension are identified, no unwanted elements are included and there is a detection precision of 5 pixels up to the total dimensions of the image, in addition to not modifying its morphology (Figure 20).
It is important to give the software user the possibility of changing parameters to be able to find the microfracture in the image, which is why the resolution of the tomography, the number of images to be processed, the material and the folders where they are included as input data; images are read and saved. However, despite having powerful software, there are microfractures that cannot be detected due to their size in pixels, which is independent of the resolution in μm/pixel, due to the characteristic of circularity or eccentricity of the figure; which is a calculated parameter to a certain extent in image processing. The minimum extension to detect microfractures is 5 pixels, which translates to an extension in microns of between 7 μm and 20 μm, depending on the tomography. An artificial increase in the resolution of the images is proposed in order to be detected.
The mechanical analysis of finite elements was carried out through the comparison of ANSYS and ABAQUS methodologies, both being conclusive in studies with similar results. Due to the complexity of the research study, the mechanical simulation analyzes were carried out in two different blocks. In the first instance, manual image processing for phase isolation and meshing was performed in the OOF2 software. As a second part, we worked with the images obtained from the microfracture identification software, as well as the manually processed images. The objective of working with the methodology of both sections was to determine how much precision existed in the automatic identification software and the feasibility of using the resulting images for mechanical simulations.
Based on the advances in the automatic identification of microfractures, the aim is to validate the precision of the neural network to identify these microfractures in new materials that are awarded by research institutions and private companies. We are working on the identification of microfractures in materials for food use, granite and composites with high precision, thanks to the higher resolution tomography obtained. Likewise, the mentioned materials are added to the database to feed back to the neural network.
The subsequent fatigue tests, as well as their corresponding computed tomography scans, will allow us to continue working to identify microfractures and, once detected, carry out simulations that allow us to compare their development physically with computerized analyses. Within the simulation stage, it is necessary to continue processing images with microfractures to generate finite element analysis, vibration modes and loads in both software, which will allow a broader perspective of the behavior of microfractures. The conclusion of the identification software is of great support to obtain the images that must be worked within simulations, as well as the generation of the 3D model for finite element analysis in total volume. Following the objective of the project and the extension granted to it, the mathematical model that describes the microfractures and how they lead to a total fracture of the material must be developed, as well as finding methodologies for predicting the extension of the microfracture.
4. Conclusions
The sequence of the methodology, as well as its parts, was constantly updated. As a main change, within the identification of microfractures, the segmentation stage was eliminated to carry out image processing based on morphological operations, which provided shorter processing time and more precise identification results. The processing time for the automatic identification software met the overall goal of this part, which was to reduce detection time. It was possible to identify and isolate the microfractures from a series of more than 1,200 images in an approximate time of 3 minutes, which is infinitely less than the identification, isolation and processing of the images manually, which can take months.
The simulations, both from ANSYS and ABAQUS, resulted in an advance in understanding the development of microfractures, by indicating that they tend to join together to form one of greater length. It was important to make a comparison between both finite element methods to confirm the results of both or determine if there were differences. Making a comparison between results from ABAQUS and ANSYS, it is very evident that they converge on the same point: The hydroxyapatite fabric gives the material rigidity to withstand the loads, moving through the collagen fabric, which provides a field material that dissipates the stresses.
It is of utmost importance to generate various simulations with different types of microfractures to determine their general behavior, which would help generate the generalized mathematical model for the materials. Due to the extension of the research project and the inconveniences generated in the instrumentation necessary for the fatigue analyzes and computed tomography, the objective of generating a general methodology for the prediction of fractures has not been fulfilled to its full extent. However, the advances in the sections described in this document are conclusive and provide the necessary material to achieve the general objectives.
In the next stage of the research, it is intended to present results that lead to the implementation of the mathematical model that describes the behavior of microfractures and generates a field of predictive study for fractures in industrial materials, as well as inorganic materials.
References
- Guten, G. (1997). Running Injuries. Philadelphia: W.B. Saunders Company.
- Presbitero G., O’Brien FJ, Lee TC., Taylor D (2012). Distribution of microcrack lengths in bone in vivo and in vitro. J Theor Biol. [CrossRef]
- Presbítero G., Gutiérrez D., Taylor D. (2017). Osteoporosis and Fatigue fracture prevention by analysis of bone microdamage. In: TMS 2017 146th annual meeting & exhibition supplemental proceedings. [CrossRef]
- Presbítero G, Hernández M, Contreras Susarrey O, Gutiérrez D (2017). Microdamage distribution in fatigue fractures of bone allografts following gamma-ray Exposure. Acta Bioeng Biomech 19:4. [CrossRef]
- Pang HT, Reed PAS (2008). Effects of microstructure on room temperature fatigue crack initiation and short crack propagation in Udimet 720Li Ni base superalloy. Int. J. Fatigue 30:2009–2020. [CrossRef]
- Currey JD (2012). The structure and mechanics of bone. J. Mater. Sci. [CrossRef]
- Ramírez J, Chacón M (2011). Redes neuronales artificiales para el procesamiento de imágenes, una revisión de la última década. Revista de ingeniería eléctrica, electrónica y computación 9:1.
- Kim JJ., Nam J., Jang IG. (2018). Computational study of estimating 3D trabecular bone microstructure for the volume of interest from CT scan data. Int. J. Numer Methods Biomed Eng. [CrossRef]
- Rezaie, A., Achanta, R., Godio, M., & Beyer, K. (2020). Comparison of crack segmentation using digital image correlation measurements and deep learning. Construction and Building Materials, 261. [CrossRef]
- Wang M, Li S., Scheidt A., Qwamizadeh M., Busse B., Silberschmidt VV. (2020). Numerical study of crack initiation and growth in human cortical bone: effect of micro-morphology. Eng. Fract. Mech. [CrossRef]
- Diab T., Vashishth D. (2005). Effects of damage morphology on cortical bone fragility. Bone 37(1):96–102. [CrossRef]
Figure 1.
Computed tomography of specimens of a) bone tissue; b) nylon with 5% hollow microspheres; c) Sigma food material; d) ultra-high molecular weight polyethylene and b) granite.
Figure 1.
Computed tomography of specimens of a) bone tissue; b) nylon with 5% hollow microspheres; c) Sigma food material; d) ultra-high molecular weight polyethylene and b) granite.

Figure 2.
Microfracture detection methods.
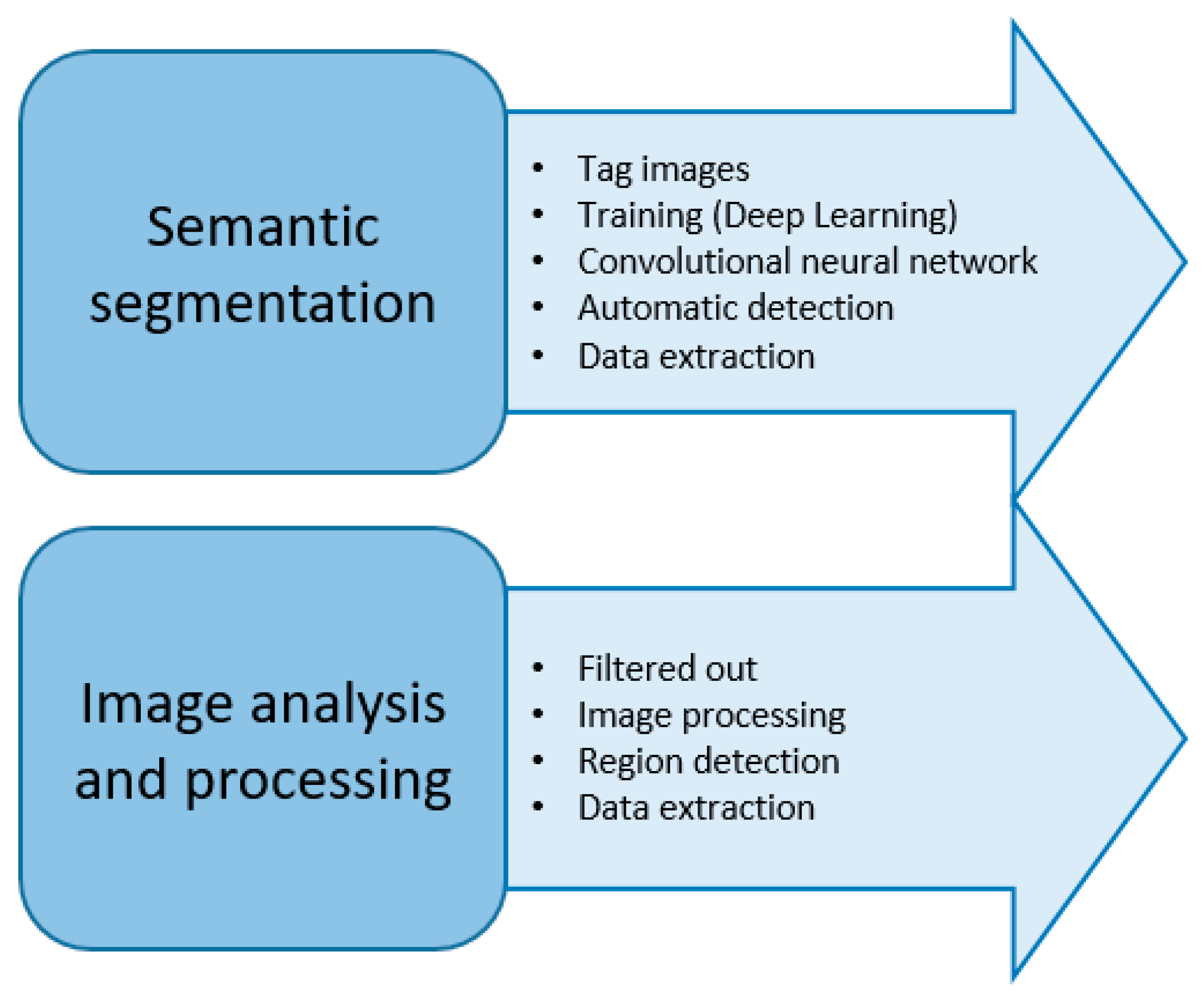
Figure 3.
Methodology for detecting microfractures.
Figure 5.
Meshing in the cortical bone structure. Boundary conditions are shown.
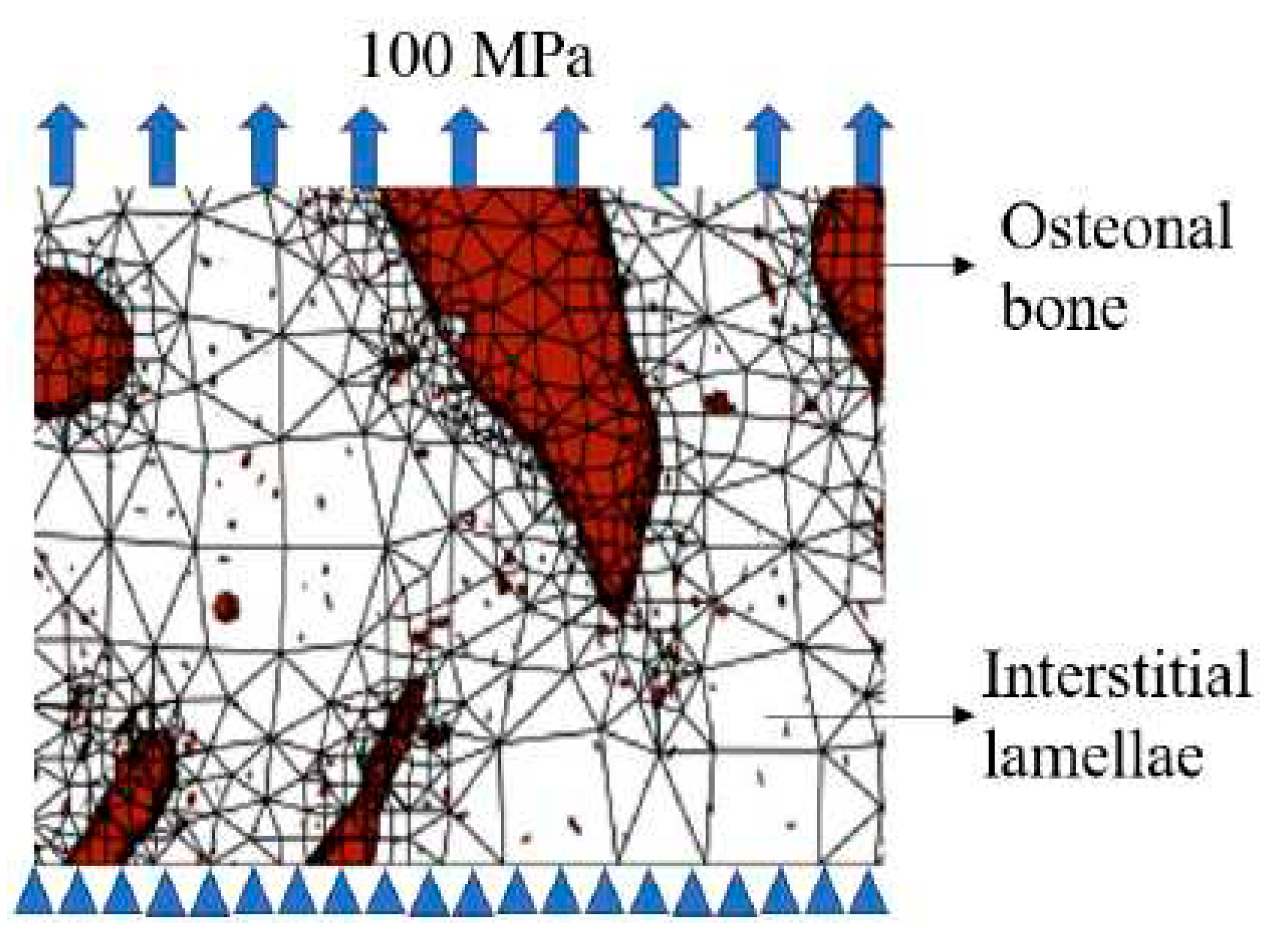
Figure 6.
a) Original binarized image; b) Drawing on the binarized image; c) Section of the digitized test tube; d) Meshing, loads and fixings for the test piece section; e) Study carried out under the conditions of microfracture in edges.
Figure 6.
a) Original binarized image; b) Drawing on the binarized image; c) Section of the digitized test tube; d) Meshing, loads and fixings for the test piece section; e) Study carried out under the conditions of microfracture in edges.
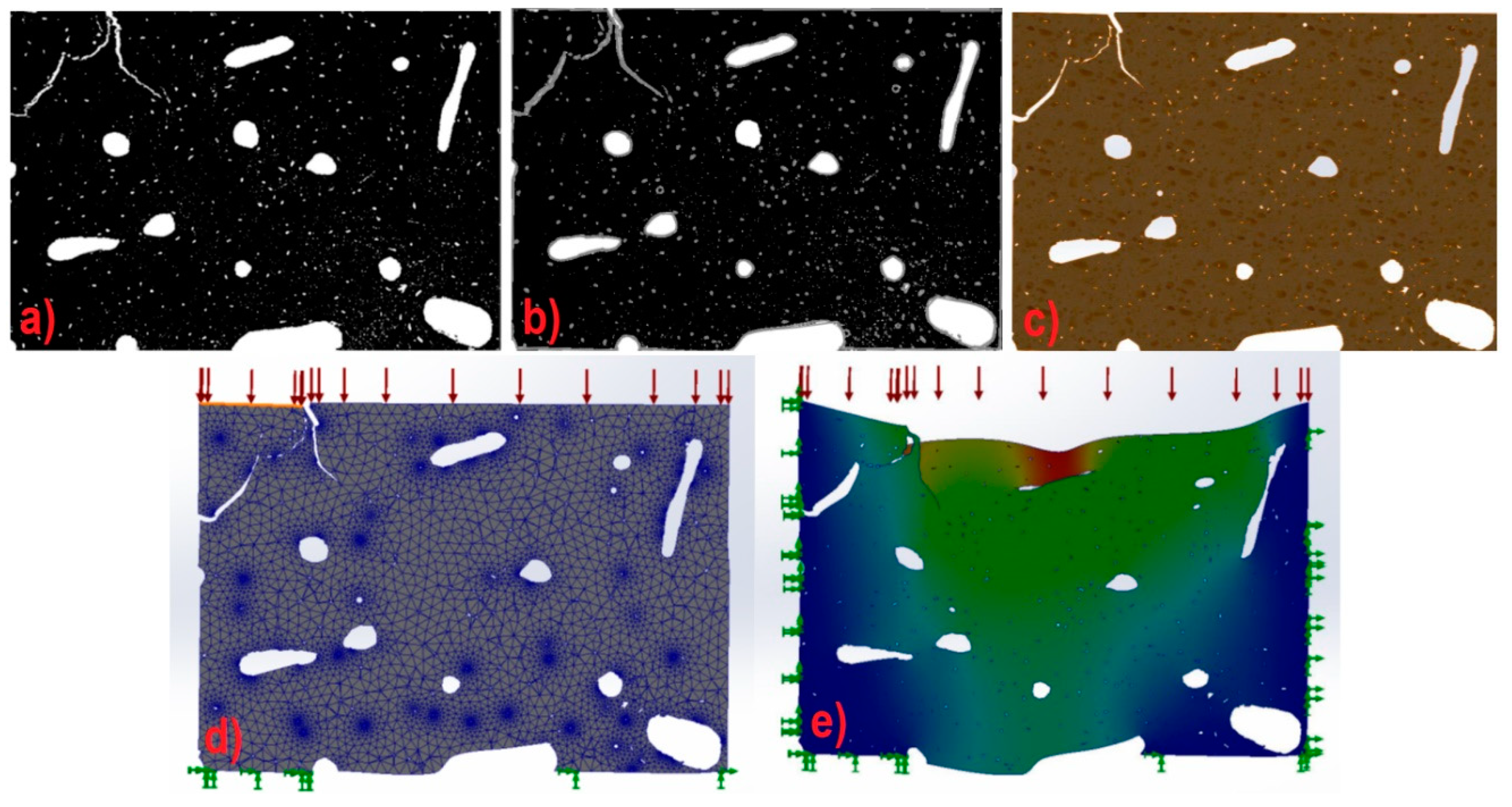
Figure 7.
a-g) Original tomography images. b-h) Digitization of images for phase separation. c-i) Meshing of the microstructure.
Figure 7.
a-g) Original tomography images. b-h) Digitization of images for phase separation. c-i) Meshing of the microstructure.

Figure 8.
Displacement field generated in the cortical bone structure. a) Mesh displacement. b) Displacement of osteonal tissue. (Units in mm).
Figure 8.
Displacement field generated in the cortical bone structure. a) Mesh displacement. b) Displacement of osteonal tissue. (Units in mm).
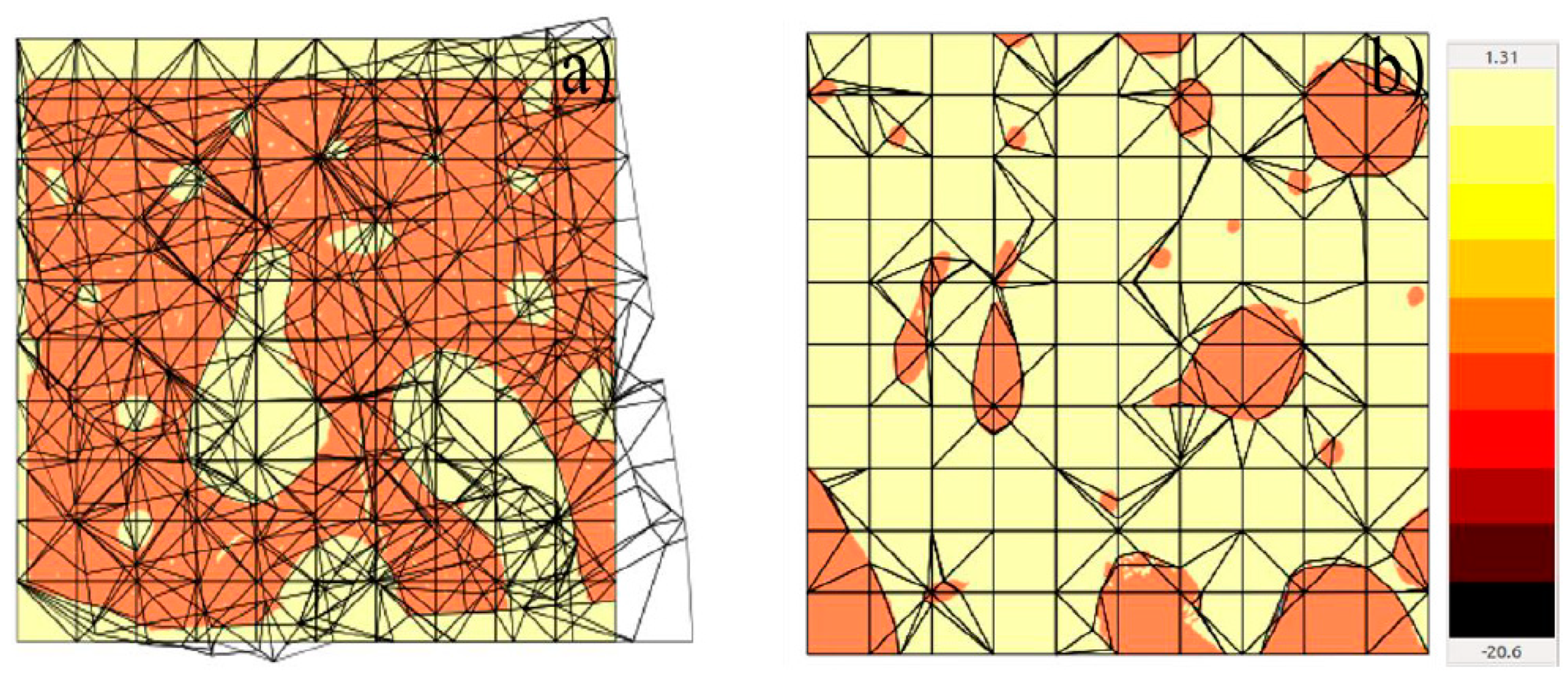
Figure 9.
First principal stress in the region of interest of the specimen (units in MPa).

Figure 10.
Principal stress in the Z axis; the values indicate that the material supports the main load, however, there are areas between microfractures that promote their conjunction (units in MPa).
Figure 10.
Principal stress in the Z axis; the values indicate that the material supports the main load, however, there are areas between microfractures that promote their conjunction (units in MPa).

Figure 14.
Training statistics for net with a resolution of 640x640 pixels.
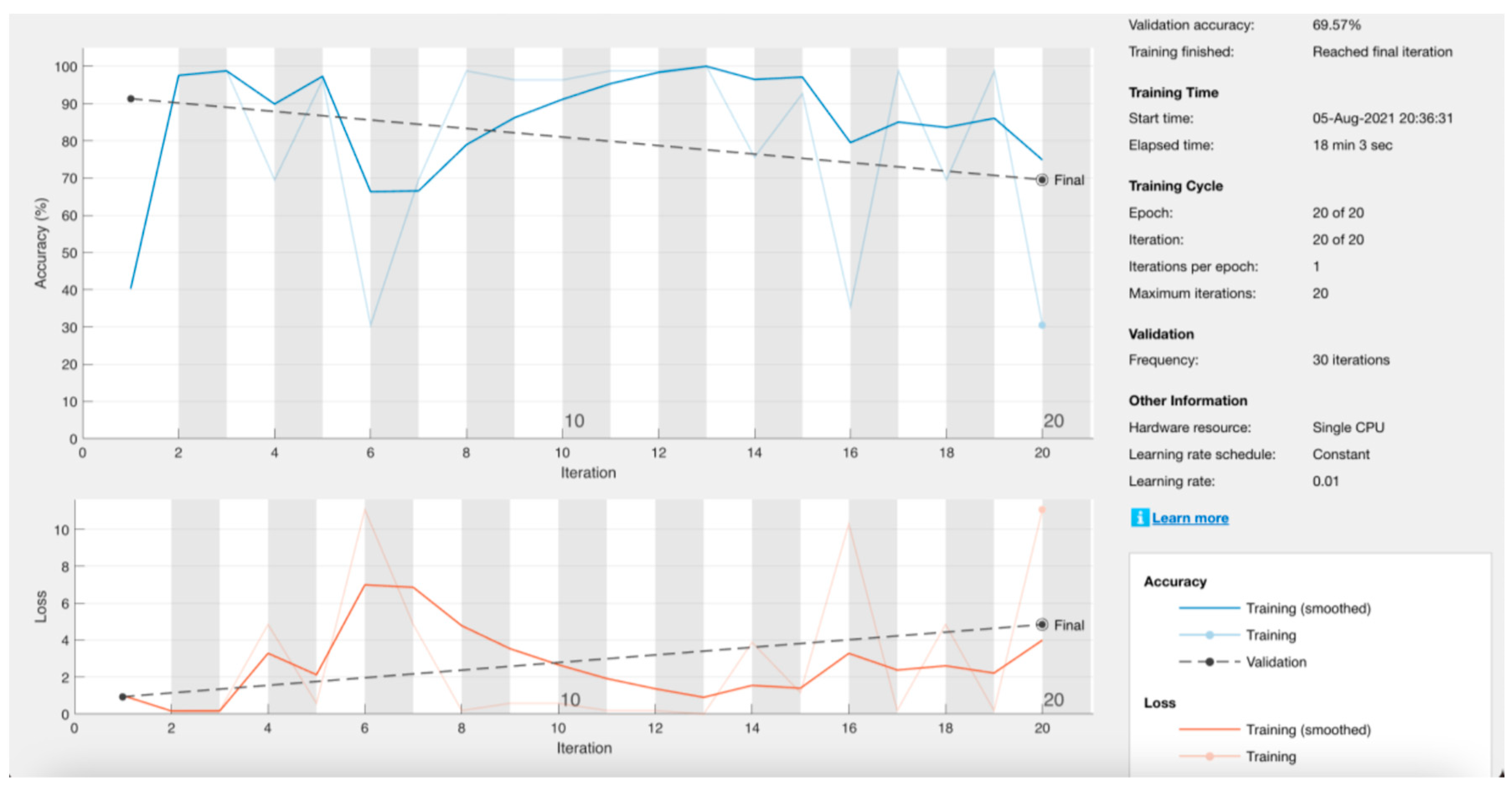
Figure 15.
Results of training the neural network with data augmentation for images without microfractures.
Figure 15.
Results of training the neural network with data augmentation for images without microfractures.
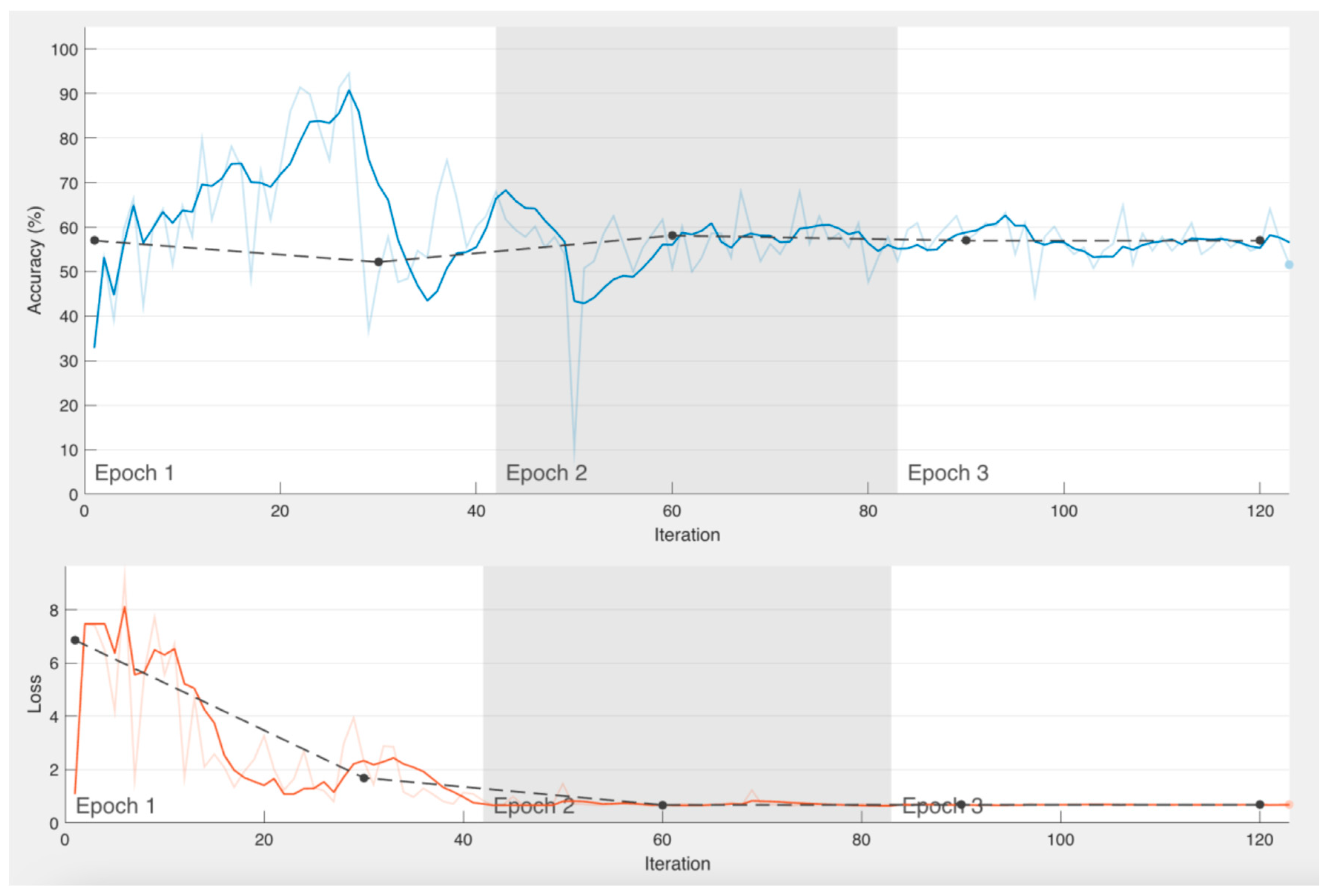
Figure 16.
Computed tomography and its process of identifying microfractures until they are isolated.
Figure 16.
Computed tomography and its process of identifying microfractures until they are isolated.

Figure 17.
Detection in the previous stage of automatic identification. Unwanted items are displayed.
Figure 17.
Detection in the previous stage of automatic identification. Unwanted items are displayed.

Figure 18.
Detection in the previous stage of automatic identification. Elements that do not correspond to microfractures are shown.
Figure 18.
Detection in the previous stage of automatic identification. Elements that do not correspond to microfractures are shown.
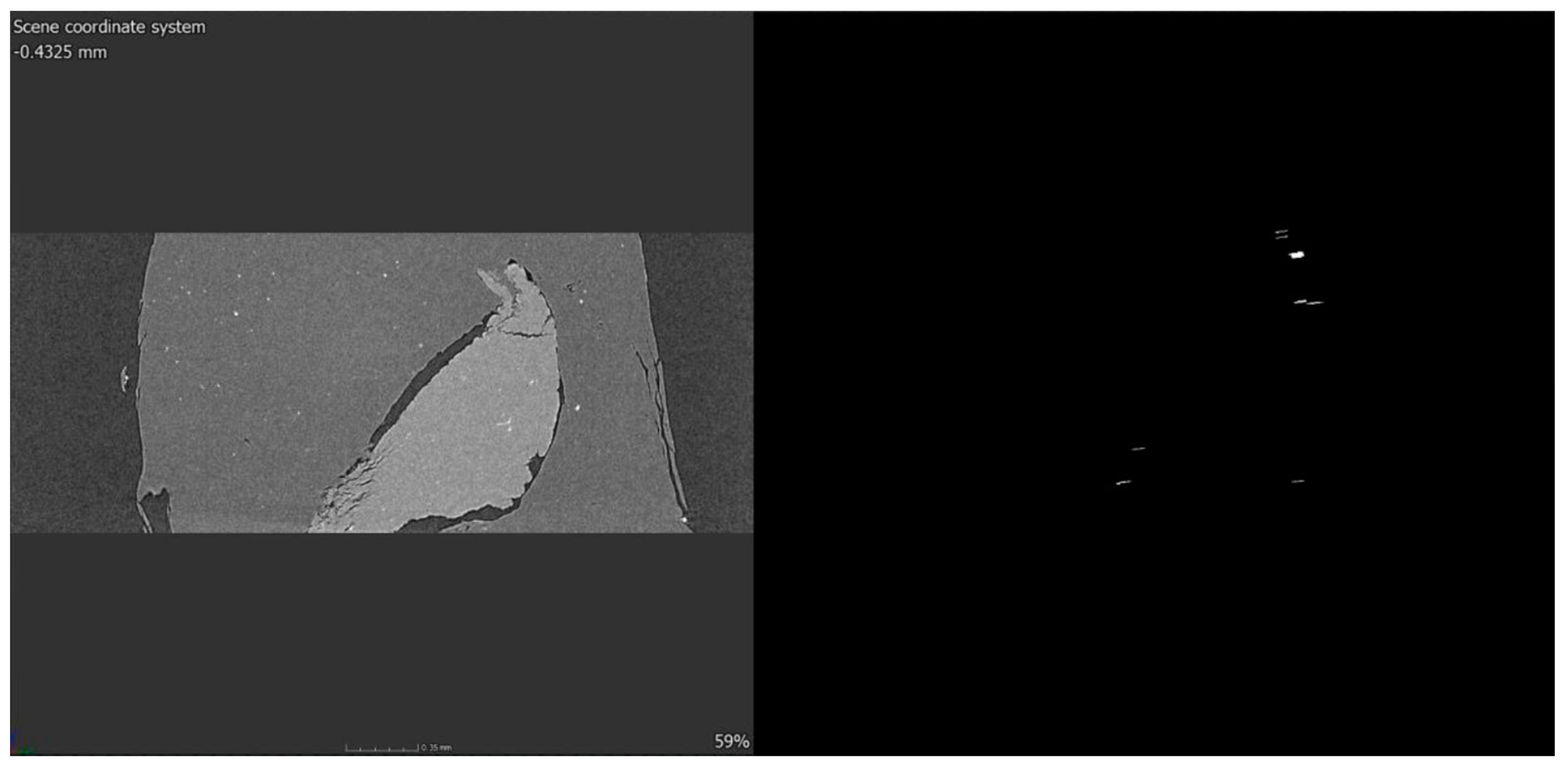
Figure 19.
Detection in the previous stage of automatic identification. The largest microfractures are shown, however, the smallest ones are not detected.
Figure 19.
Detection in the previous stage of automatic identification. The largest microfractures are shown, however, the smallest ones are not detected.
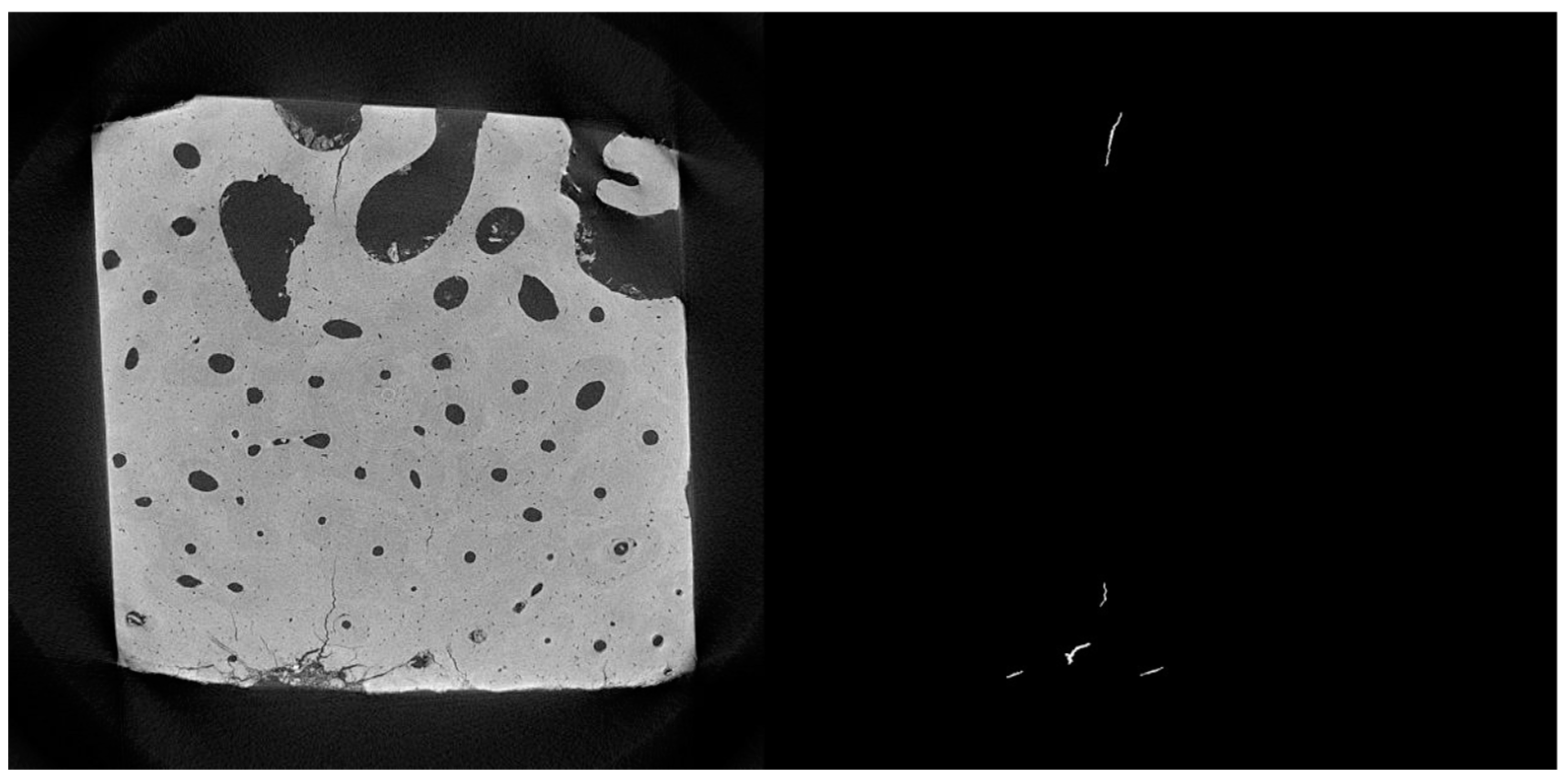
Figure 20.
Automatic identification current detection. All microfractures larger than 5 pixels are detectable.
Figure 20.
Automatic identification current detection. All microfractures larger than 5 pixels are detectable.
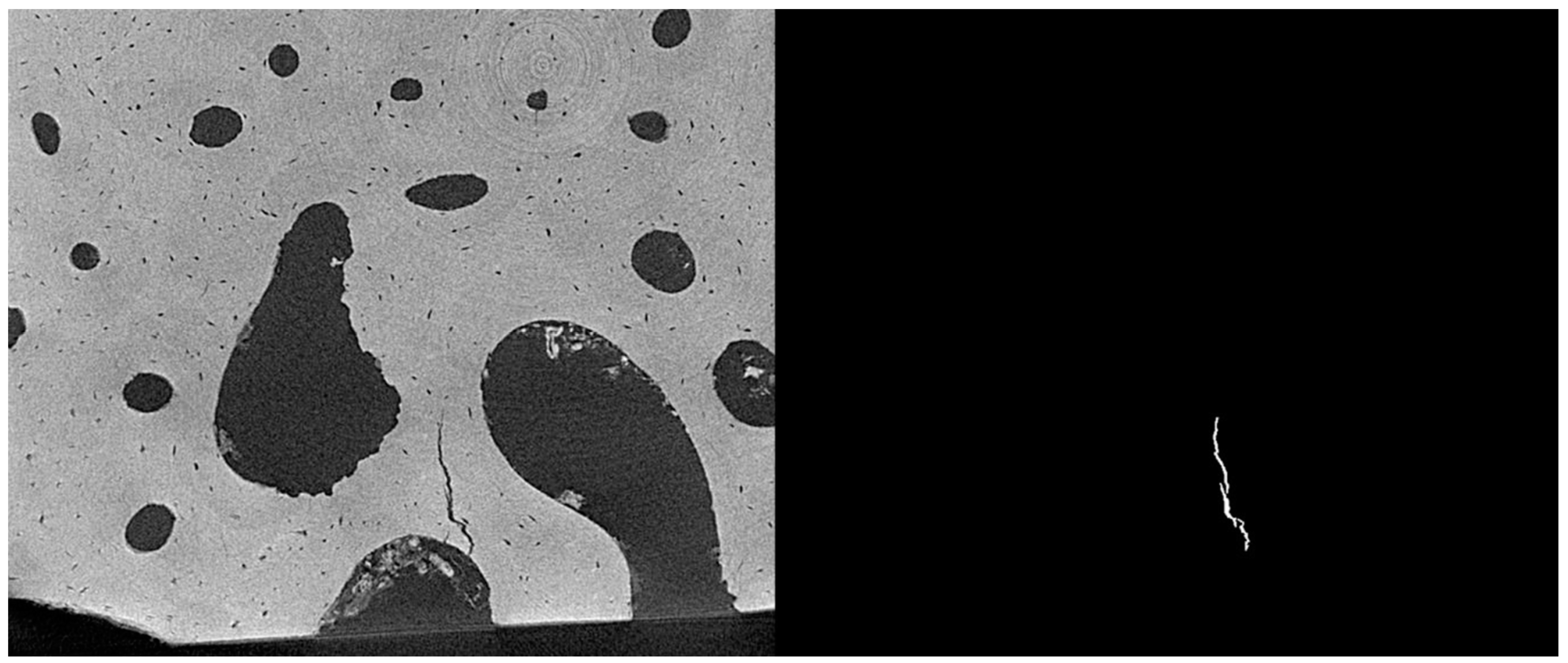
Table 1.
Previous iterations of the net neural network with their summarized values. Data obtained directly from Matlab except for approximate precision.
Table 1.
Previous iterations of the net neural network with their summarized values. Data obtained directly from Matlab except for approximate precision.
| Interaction | Microfracture entry images | Entry images without microfracture | Resolution in pixels | Processing time | Theoretical precision | Data loss | Approximate precision |
| 1 | 81 | 36 | 640x640 | 18 min 03 seg | 69.57% | 4% | 70% |
| 2 | 81 | 36 | 480x480 | 08 min 08 seg | 95.65% | 0% | 80% |
| 3 | 301 | 290 | 480x480 | 48 min 14 seg | 49.15% | 1% | 95% |
| 4 | 1505 | 1450 | 480x480 | 52 min 49 seg | 50.85% | 0.5% | 90% |
| 5 | 1505 | 1450 | 480x480 | 46 min 12 seg | 86.55% | 0% | 90% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






