Prerpints.org logo
Preprint
Article

LSTM-based Virtual Load Sensor for Heavy-Duty Vehicles

Altmetrics

Downloads

83

Views

26

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

30 November 2023

Posted:

01 December 2023

You are already at the latest version

Alerts
Abstract
In this paper, a special recurrent neural network (RNN) called \emph{Long Short-Term Memory (LSTM)} is used to design a virtual load sensor that estimates the mass of heavy vehicles. The estimation algorithm consists of a two-layer LSTM network, with the two layers based on sequence-to-sequence and sequence-to-one logic, respectively. The network estimates the vehicle mass based on the vehicle speed, longitudinal acceleration, engine speed, engine torque, and the accelerator pedal position. The network is trained and tested with a data set collected in a high-fidelity simulation environment called Truckmaker. Training data is generated in acceleration maneuvers in a range of speeds whereas test data is obtained by simulating the vehicle in a Worldwide harmonized light vehicles test cycle (WLTC). Preliminary results show that, with the proposed approach, the heavy-vehicle mass can be estimated as accurately as commercial load sensors in a range of load mass as wide as four tons.
Keywords: 
Subject: Engineering  -   Automotive Engineering

1. Introduction

The accurate knowledge of the vehicle mass is important in all types of heavy vehicles for both energy efficiency and safety, as explained next. The operation of the powertrain like in, e.g., automatic gear shifting can be optimized by algorithms relying on the knowledge of the vehicle mass [1]. Such information can also be used to provide truck drivers with recommendations aiming at adapting their driving style to the current vehicle mass and road profile. Similar recommendations can help improve vehicle safety by, e.g., estimating the braking distance based on the current mass [2]. In buses, mass estimation can be used to estimate the number of passengers for various purposes ranging from resource planning and bus scheduling to adjustment of the air conditioning, based on the number of passengers [3]. The mass information can be used for determining the vehicle ordering within a platoon. For example, the heaviest truck might be leading a platoon as its braking distance is larger than others and it may cause rear-end collisions while following at close distance lighter vehicles. On the other hand, heavier trucks should be placed at the platoon tail while traveling uphill, in order not to excessively limit other trucks’ speed. Mass information, along with inertia, could be effectively used by active safety systems to prevent rollover [4].
It must be pointed out that load sensors exist [5], which are reliable (same lifespan as the vehicle), affordable, and are calibrated with fairly simple procedures. Nevertheless, in truck and trailer combinations, the presence of such sensors depends on the trailer’s manufacturer. Hence, load sensors cannot be assumed available on every trailer. In such situations, estimating the vehicle mass rather than measuring it with a sensor is definitely preferable. Finally, even in the presence of a load sensor, a mass estimation algorithm could be used to detect any sensor failure, malfunctioning, or need for recalibration.
One of the most common algorithms that is used for mass estimation is recursive least square (RLS) [6,7,8,9,10,11]. RLS is also used to jointly estimate mass and road grade if road grade is not available. In [6], an RLS mass estimation algorithm updates the mass estimate according to a set of rules: the absolute value of longitudinal acceleration is more than 0.1 m / s 2 , the engine torque percentage is between 40 and 90%, lateral acceleration is less than 5 m / s 2 , the absolute engine torque gradient is less than 1000 N m / s . Finally, the mass estimate is updated only if the brake pedal is not pressed and if specific gears are engaged. Such rules are defined according to the vehicle operation where the vehicle model the RLS estimation algorithm is built upon is more accurate and so is the mass estimate. In general, defining such rules might be impractical and time-consuming. The mass, drag coefficient and rolling resistance are jointly estimated in [7], by using a RLS estimation algorithm built upon the vehicle longitudinal dynamics. First, road grade is estimated and then the mass is estimated by filtering engine torque, road grade, vehicle speed, and acceleration by second order Butterworth low pass filter. In [8], an RLS mass estimation algorithm is fed with data extracted from the measured signals by a supervisory algorithm, that searches for maneuvers dominated by inertial dynamics (e.g., acceleration maneuvers). A RLS with multiple forgetting factors is proposed in [9], for mass and road grade, respectively, a single forgetting factor for both has proven not to be beneficial. In [10] show how a nonlinear road grade and mass estimator can be designed by initializing the estimates with initial guesses of mass and road grade calculated by an adaptive least square while assuming they are both constant. The RLS mass estimator in [11] builds upon the longitudinal and roll vehicle dynamics.
Model-based (e.g., RLS) estimation methods are very convenient as they also provide a measure of the estimate accuracy depending on the measurement noise. On the other hand, the estimate is as accurate as the system model, and obtaining accurate system mathematical models can be a lengthy and expensive process. In fact, the RLS-based vehicle mass estimation algorithm available in the literature must be coupled with additional logic that enables the mass update in conditions where the vehicle model is accurate. Such logic can be difficult and impractical to be tuned.
Learning-based methods can also be used for mass estimation of heavy vehicles. In [12], the authors used a shallow neural network with rectified linear unit (ReLU) activation function for mass and road grade estimation whereas [13] proposes a Deep Neural Network (DNN) with 15 fully connected layers with leaky ReLU activation function to estimate the trailer mass. The first layer has 140 neurons and the number of neurons in each layer dwindles down by 10, with the exception of the output layer which has one neuron that outputs the mass estimate.
In [14], the mass of heavy-duty vehicles is estimated by using Gaussian Belief Propagation with k-nearest factors (kNF-GBP), such that the effect of noisy data is attenuated without resorting to any additional sensors. Vehicle velocity and acceleration, fuel consumption, engine load, and speed, reference torque, GPS location are used as measurements. Such approach provides the mean and variance of the mass estimate. The work in [15] proposes a Random Forest method for mass estimation in passenger weight on e-scooters. The algorithm is used for classification rather than regression since there is limited data. In [16], RLS is combined with machine learning approach by using fuzzy logic. The estimates from the RLS and ML methods are weighted based on longitudinal acceleration, acceleration rate, and vehicle speed. An additional weight is assigned to the previous mass estimate that is used when both ML and RLS methods are not reliable. The ML approach relies on a two-layer neural network with 1024 and 256 neurons.
The automotive industry has also contributed to the development of vehicle mass estimators. In [17], an RLS mass estimator is built upon the longitudinal dynamics and the measurements of wheel speeds, engine torque, gearbox data, brake pressures, and longitudinal acceleration. The initial mass estimate is calculated based on the seat belt sensors and fuel level information. If one of the doors is opened, RLS is reset. In [18] the RLS algorithm estimates the vehicle mass from the vehicle center of gravity height variations, measured by a lidar. The work in [19] estimates the mass in three steps. When the engine starts, the last estimated vehicle mass is used. After a certain time or when the vehicle reaches a defined velocity, the mass is estimated based on the longitudinal dynamics if the vehicle is moving on a straight line. Then when the vehicle reaches the set velocity a second time such as it accelerates and then decelerates, mass is calculated based on total force difference divided by the difference of acceleration values when the vehicle reaches the set velocity the first and second time. The reason why this last step is used is to decrease error due to the noise of longitudinal acceleration and vehicle speed measurements. In [20] the vehicle mass is estimated from inertial sensor measurements that measure the vertical acceleration. As the unladen mass of the truck is usually known, if the longitudinal and lateral accelerations are negligible, the load mass can be estimated from the vertical acceleration using an RLS approach. In [21], a mass estimation method is proposed for vehicle platoons. The mass difference between adjacent vehicles can be estimated based on the longitudinal dynamics and the information exchanged by the trucks, including torque, brake, and gap information.
This paper explores the use of Long Short Term Memory networks for mass estimation in heavy vehicles. Our objective is to understand the necessary training effort, in terms of training data set size and training time, to achieve a mass estimate that is as accurate as the measurement obtained from the available commercial load sensors [5]. Our choice of a type of RNN is motivated by the objective of achieving the target accuracy with as shallow as possible networks. Furthermore, LSTM networks, compared to standard RNNs, alleviate gradient vanishing issues.
The paper is structured as follows. In Section 2, the longitudinal vehicle dynamics model is presented. Section 3 gives information about the background of neural networks and methodology. NN is firstly described in Section 3.1 and then RNN is explained in Section 3.2. Then, LSTM is shown in Section 3.3. In Section 3.4, how data is used to train and test a neural network is described. In Section 4, we proposed a data driven mass estimation algorithm. In Section 5, how data is collected is explained. Experimental validation is done in Section 6 and results are discussed here. In Section 7, the conclusion and future work are written.

2. Longitudinal Vehicle Dynamics

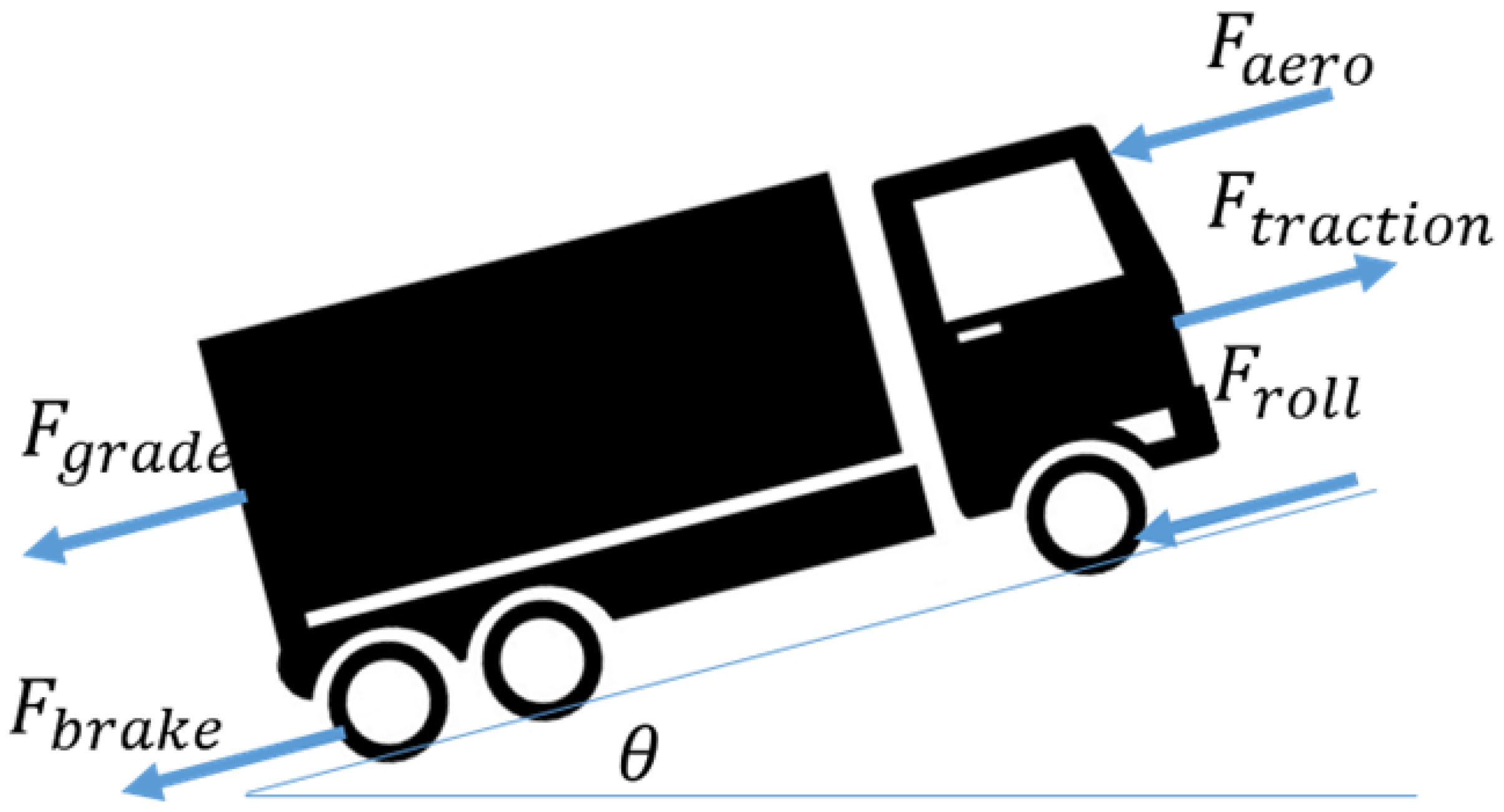
Before presenting the vehicle mass estimation algorithm, it is convenient to recall the longitudinal vehicle dynamics shown in Figure 1. The vehicle longitudinal velocity can be found as the solution of the differential equation
m v ˙ = F t r a c t i o n − F b r a k e − F a e r o − F r o l l − F g r a d e .
In equation (1), F a e r o is the air drag force, which can be modeled as in (2).
F a e r o = 0.5 ρ c d A f ( v + v w i n d ) 2 , = f a e r o ( ρ , c d , A f , v , v w i n d ) ,
where ρ is the air density, c d is the aerodynamic drag coefficient, A f is the area of the front side of the vehicle, v and v w i n d are the speeds of the truck and the wind, respectively [22]. For the sake of simplicity, braking maneuvers are not considered in this paper. F r o l l is the rolling resistance force calculated as in (3).
F r o l l = μ m g c o s ( θ ) , = f r o l l ( μ , m , θ ) ,
with θ the road gradient, μ the rolling resistance coefficient, m the mass of the truck and g is gravitational acceleration. F g r a d e is the force introduced by the road grade as in (4).
F g r a d e = m g s i n ( θ ) , = f g r a d e ( m , θ ) ,
and F t r a c t i o n is the traction or propulsive force (5) where
F t r a c t i o n = T e n g i n e − J e q ω ˙ r w h e e l g r g f i n a l , = f t r a c t i o n ( T e n g i n e , J e q , ω , r w h e e l , g r , g f i n a l ) ,
T e n g i n e is the engine torque which can be estimated with various methods, J e q is the equivalent inertia, ω is the engine crankshaft speed, g r and g f i n a l are gear ratio and final drive ratio respectively whereas r w h e e l is the radius of the wheel. From equation (1), the vehicle mass m can be expressed as in (6).
m = F t r a c t i o n − F b r a k e − F a e r o − F r o l l − F g r a d e v ˙ , = f ( u ( t ) , τ ) ,
where u ( t ) = ( T e n g i n e , ω , θ , v, v ˙ ) is the input vector of the model (6), which includes the onboard sensors measurements, and τ = ρ , c d , A f , μ , g , J e q , r w h e e l , g r , g f i n a l that contains the physical parameters of the vehicle model. In principle, a mathematical model f ^ could be built for the function f based on a vehicle mathematical model. In practice, such a function f ^ rarely enables a sufficiently accurate estimate of the vehicle mass m. Hence, in this paper, we show how the function f ^ can be built based on input ( u ( t ) ) and output (m) data samples.

3. Background on Artificial Neural Networks and Methodology

Consider a system
y = f ( u ) ,
where u , y are the system input and output vectors, respectively. In Section 3.1, we recall how Artificial Neural Networks (ANNs) can be used to formulate a mathematical model
y ^ = f ^ ( x ) ,
of the system (7), starting from samples of input and output, u , y , respectively. Note that, in general, the input vectors u and x of the functions f and f ^ , respectively, are different. Indeed, the input vector x may include all, or part of, the signals in u and additional signals as well. We then illustrate in Section 4 how NNs are used in this paper to design a mass estimation algorithm.

3.1. Neural Networks

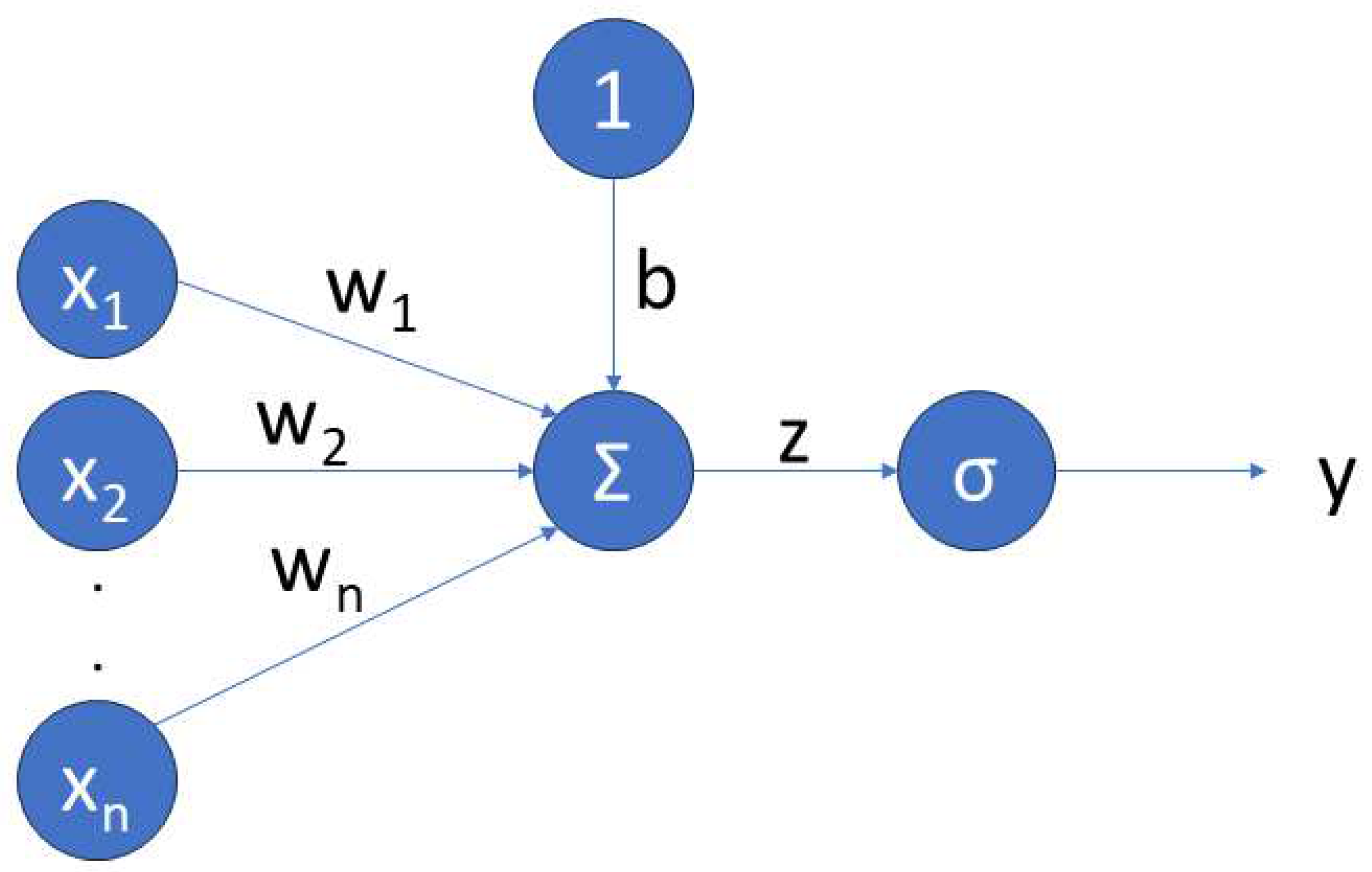
ANNs are nonlinear functions, where a vector x ( t ) of inputs is mapped into an output y ^ . In the simplest ANN, which is called single layer neural network or perceptron shown in Figure 2, all input signals are directly connected to an output node which is called neuron and maps the input to the output signals through an activation function. In an ANN, the output signal is expressed as
y ^ = σ ∑ i = 1 n w i x i + b , = f ^ ( x , W , b ) ,
where x ( t ) = x 1 ( t ) , … , x n ( t ) is the input vector containing the features of the network, W = w 1 , … , w n and b = b 1 , … , b n are the network weights and biases, n is the number of inputs, y ^ is the model output, σ is the activation function. For the sake of readability, with a slight abuse of notation, the same symbol f ^ as in (8) has been used in (9) although the two functions have a different number of arguments.
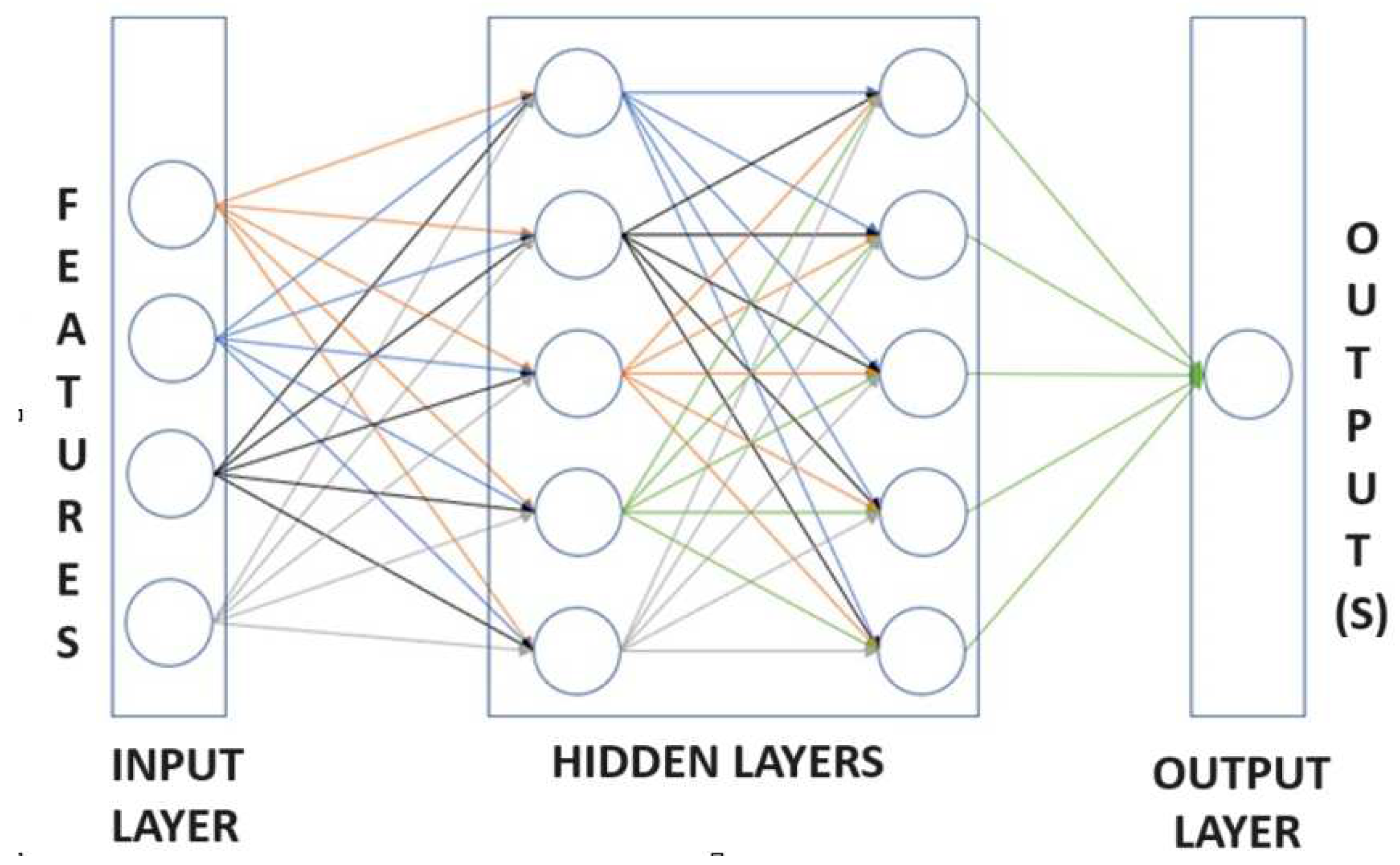
A network where the inputs are mapped to the output with interconnected layers or neurons, rather than a single neuron, is called feed-forward neural network (FFNN) or Multilayer Perceptron (MLP) as shown in Figure 3. If a FFNN has two hidden layers or more, this is called deep neural network (DNN).
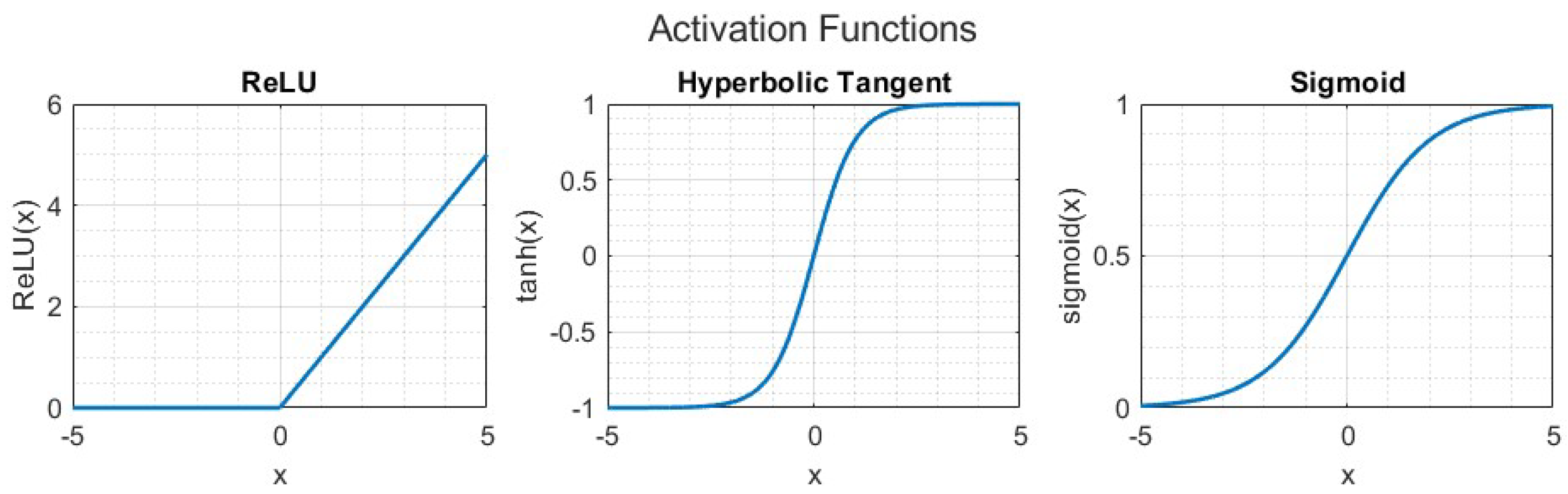
Various activation functions σ can be used in the definition of an ANN, such as hyperbolic tangent (tanh), sigmoid or rectified linear unit (ReLU) as shown in Figure 4. The choice of the activation functions depends, among other things, on the efficiency of the resulting training algorithms used to calibrate the network weights and biases on the input and output data. For example, ReLU is often used as an activation function in FFNNs, as the training phase is much faster than hyperbolic tangent or sigmoid functions.
Once the number of layers and neurons and activation functions have been chosen for a NN, its weights and biases must be found (NN must be trained), based on input and output data samples. A NN is trained by solving the following problem
[ W * , b * ] = argmin W , b L ( u , x , W , b ) ,
L ( u , x , W , b ) = 1 N ∑ i = 1 N y ^ ( x ) − y ( u ) 2 ,
where N is the number of output samples. The cost (10b) builds on the error between measured y and predicted outputs y ^ . A solution of the problem (10a) can be found with the backpropagation method [23]. In backpropagation the weights and biases are iteratively updated [24] through a standard Newton’s iteration
W + b + = W b − α ∇ L ,
where α is the learning rate and ∇ L is the gradient of the cost (10b). If the learning rate is large, the updated weights and bias may diverge from the optimal solution. On the other hand, a small learning rate may result in slower convergence of the learning algorithm [25]. The iterative parameters update procedure (11) requires the initialization of the vector W b T . Such initialization is crucial as it may result in a learning procedure converging to a local minimum. Unfortunately, there are no systematic procedures to initialize the iteration (11) such that local minima are avoided.

3.2. Recurrent Neural Networks

Recurrent Neural Networks can be used to model systems with memory, e.g., dynamical systems. RNNs are obtained by adding cyclical connections to feedforward neural networks. That is, previous values of the predicted output signal are fed into the network as in
y ^ t = g t ( y ^ t − 1 , y ^ t − 2 , … , x t , … )
Alternatively, the following recursive structure [26,27] can be adopted
h t = σ ( W h x x t + W h h h t − 1 + b h ) ,
y ^ t = W y h h t + W y x x t + b y ,
where x t and h t are the current inputs and hidden states, b h and b y are the biases, W are weights, σ is the activation function which can be sigmoid function or tanh since they are both differentiable. While DNN can also be used to model time series, previous values of the same feature need to be used as separate inputs, thus increasing the number of parameters since each input has separate weights. This is not the case in RNNs, where different time steps of the same feature (i.e., input) share the same weight.
The weights W and biases b in (13) are learned by optimizing the fit to a dataset, as explained in Section 3.1. Such a learning process is affected by two well-known problems. The gradient of the loss function in (11) may exponentially decrease and shrink or exponentially increase and blow up. These phenomena are known as the vanishing and exploding gradient problems, respectively. Exploding gradient can be solved by gradient clipping [28]. The gradient is scaled down if it exceeds a predefined limit. However, gradient vanishing is more complex to solve. The Gated Recurrent Unit [29] and Long Short-Term Memory [30] methods are proven effective in preventing vanishing and exploding gradient problems. The latter is recalled in Section 3.3 since it is used for mass estimation in Section 4.

3.3. Long-Short Term Memory

In LSTM networks, the gradient vanishing problem is attacked at the training stage, by introducing gates in each cell of the network. Such gates, consisting of weights and sigmoid functions, selectively let the input signals to a cell in the LSTM network to be stored, outputted or forgotten [31]. The introduction of such gates allows control of the propagation of the state of each cell. As a result, it can be shown that, as opposed to classic (or “vanilla”) RNN, the gradient depends on the weights of the forget gates that, at the training stage, can be updated to avoid the gradient vanishing. However, such a mechanism does not prevent the gradient from exploding.
The structure of a LSTM cell [32] is
f t = σ ( W f x x t + W f h h t − 1 + b f )
i t = σ ( W i x x t + W i h h t − 1 + b i )
o t = σ ( W o x x t + W o h h t − 1 + b o )
c t = f t ⊙ c t − 1 + i t ⊙ t a n h ( W c x x t + W c h h t − 1 + b c )
h t = o t ⊙ t a n h ( c t )
where f , i , and o are the forget, input, and output gates, respectively, defined as in (14), (15) and (16), respectively, W * x and W * h can be referred to as input and recurrent weights, respectively. σ is the sigmoid function. The cell state c t and hidden state h t are shown in (17) and (18). The symbol ⊙ denotes the element-wise multiplication. The final hidden state is used as an estimated output.

3.4. Training, validation and testing

The design of a NN is an iterative procedure, which consists of the following phases:
  • Design. In this phase a network structure is chosen in terms of the number of hidden layers, the number of units (neurons or cells based on the network architecture) in each layer and activation functions. The choice of the network architecture results in a set of biases and weights W , b to be learned.
  • Learning. The weights and biases W , b are found (learnt) as the solution W * , b * of the optimization problem (10), where the deviation of the model output y ^ from the system output measurements y is minimized, in the sense of cost (10b). In this phase, a set of hyperparameters [33] must be chosen to make the learning process fast and accurate. Such parameters include dropout probability, epoch number, weight initialization, batch size, and validation patience, which are explained next in this section.
  • Testing. The learnt model y ^ = f ^ ( x , W * , b * ) is evaluated by comparing its output y ^ against the output y of the actual system. If the model accuracy, that is the error y − y ^ , is not satisfactory in the RMS sense, then the design procedure restarts from the design phase, with a new network structure.
The training process of a neural network is affected by the range of the input signals (i.e., the features) values. The unbalanced magnitude of the features may flaw the training process thus making some features completely or partially irrelevant. Such an undesired issue can be avoided by normalizing the features.
The design and learning phases rely on two disjoint data sample sets that we refer to as training and validation data sets. The training data set is used to build the cost function (10b) that is minimized in (10), through the iterative procedure (11) that requires an initialization. That is, an initial guess of the values of weights and biases needs to be provided. Such an initialization has an enormous impact on the training process of the neural network.
If a network has been designed with more weights and biases than necessary, in the training phase the “unnecessary” parameters are exploited to learn the noise, which unavoidably affects the measurements of the system output y. Such phenomenon is known as overfitting and can be detected by evaluating the learned model y ^ = f ^ ( x , W * , b * ) on the validation data set that has not been used to build the function (10b). In case of overfitting, the error y − y ^ , calculated on the validation data set, is much larger than the error calculated with the training data set. The detection of overfitting suggests adopting a network structure with fewer parameters at the design stage. Also, in order to prevent overfitting, dropout which consists of temporarily and randomly removing neurons can be used [34]. In dropout, with a tunable probability, neurons are removed, along with all their connections, at each weight update iteration. It should be pointed out that dropout occurs during training only.
Depending on the availability of hardware, the extensiveness of the dataset, and network complexity, training a neural network on an entire dataset may be prohibitive. In such a case, the dataset can be partitioned into smaller equal-sized datasets which are called mini-batches. In each iteration of the training process, weights and biases of a mini-batch are updated.
To clearly describe the complexity of the training process, an epoch number is defined as the multiplication of the number of iterations by the number of mini-batches. Typically, a maximum epoch number is set to limit the duration of the training. Such a maximum, epoch number should be chosen large enough to adequately train the network. As mentioned in Section 3.1, if the learning rate is small, more epoch number is necessary to reach the convergence. The learning rate also depends on the chosen optimization method to train the neural network. The learning rate can be a fixed value or it can be decreased after some iterations. On the other hand, if the cost L in (10b) does not decrease for more than a chosen number of iterations then training can be stopped regardless of maximum epoch number. This training option is called validation patience.
In the testing phase, the learned model is tested on “fresh” test data. That is data that is not included in the training and validation data sets. If the error is not satisfactory, the procedures continue with a design phase where a new network structure is chosen with different hyperparameters.

4. LSTM-based Mass Estimation

The estimation of a vehicle mass is a regression problem, where the parameter to be estimated depends on the engine torque and speed, the vehicle speed and acceleration, and a number of physical parameters, as explained in equation (6).
Min-max normalization is used to scale features before choosing the network. For example, if the minimum and maximum values of the vehicle velocity v are v m i n and v m a x , respectively, then the normalized velocity v n o r m is calculated by normalization as shown in (19).
v n o r m = v − v m i n v m a x − v m i n .
In this study, an LSTM network is used to estimate the mass of a heavy vehicle because of its more efficient training, compared to standard RNNs. The LSTM network designed in this paper has two hidden layers with 16 LSTM cells each. The outputs of the first layer cells are fed into the cells of the second layer. Such a layer is referred to as sequence-to sequence model. The second layer is referred to as a sequence-to-one, as the sequence of outputs from the first layer is processed, thus resulting in a single output (i.e., the mass). More than 3000 parameters (weights and biases) are used to train the network.
Such a structure is the result of a trial-and-error procedure that led to an acceptably accurate mass estimate, that is, an accuracy comparable to a commercial load sensor. Such a trial-and-error procedure is driven by the evaluation of the network made with the validation data set, as explained in Section 3.4.
It is worth pointing out that simpler networks (e.g., only one layer or two layers with fewer LSTM cells per layer) lead to underfitting with an accuracy of the estimate in the validation phase lower than the accuracy goal. On the other hand, more complex LSTM networks have led to overfitting. That is, part of the network structure and parameters are used to learn the measurement noise. For this reason, overfitting also leads to poorly estimated mass.
In particular, a few hyperparameters must be set that affect the training procedure. Such hyperparameters, along with their values are shown in Table 1.
Various initialization methods can be used for starting the training phase. One of them is Glorot (Xavier) initializer [36], which is a method where the parameters to be learned are sampled from a uniform distribution between ± 6 / ( n i + n o ) where n i and n o are numbers of inputs and outputs, respectively. Another method is orthogonal initialization [37], where an orthogonal matrix Q and upper triangular matrix R are obtained from QR decomposition of a randomly generated matrix.
However, validation patience is not limited in this study and the training process is not stopped until the end of the training. Instead of it, the set of computed weights and biases for training data which results in minimum error on validation data is stored whereas all other set of weights and biases of training data that belongs to other iterations are deleted.

5. Data Collection

Artificial data is generated by simulating, in the TruckMaker simulation environment, a truck while executing a number of maneuvers. Engine torque, engine speed, longitudinal vehicle acceleration, vehicle speed, and accelerator pedal position are used as features in this study.
The training data set is built by extracting data samples from the generated artificial data, according to the following criteria.
  • Engaged clutch. Data samples are selected if the clutch is engaged. This criterion is meant to exclude from the training data set those samples containing transients that would need extra parameters to achieve a good fit, yet are unnecessary to correctly estimate the vehicle mass.
  • Fixed gear. The training data contains data samples collected when the same gear, as training over the whole gear range would require additional parameters without increasing the mass estimation accuracy.
  • Limited speed. Data samples are used for training for vehicle speeds in the range 60 to 95 kph. This limitation is introduced to avoid the need for additional parameters to capture speed phenomena like, e.g., wind drag, over a wide range of speeds, without increasing the estimate accuracy.
  • No braking. The brake pedal is not used in the data samples used for training and this feature is also eliminated since information related to braking is not as reliable as information related to propulsion in heavy-duty vehicles. E.g., the braking force resulting from a brake pedal value may significantly vary due to the heating of the brake pads.
  • Straight driving. Data is collected while driving straight, as only longitudinal motion is considered.
  • Flat roads. There is no downhill or uphill in order not to increase complexity by adding road grade as another feature.
  • No wind. Wind effect is neglected since there is no labeled data for wind in reality.
The data samples used for training the designed LSTM-based mass estimator are collected for 9 various vehicle masses ranging from 6.8 to 7.8 tons with increments of 125 kg to curb mass. After 1 ton load is added to the curb mass of the vehicle, the procedure is repeated for 0-2 ton load with increments of 250 kg, 0-3 ton load with increments of 375 kg, and 0-4 ton load with increments of 500 kg.
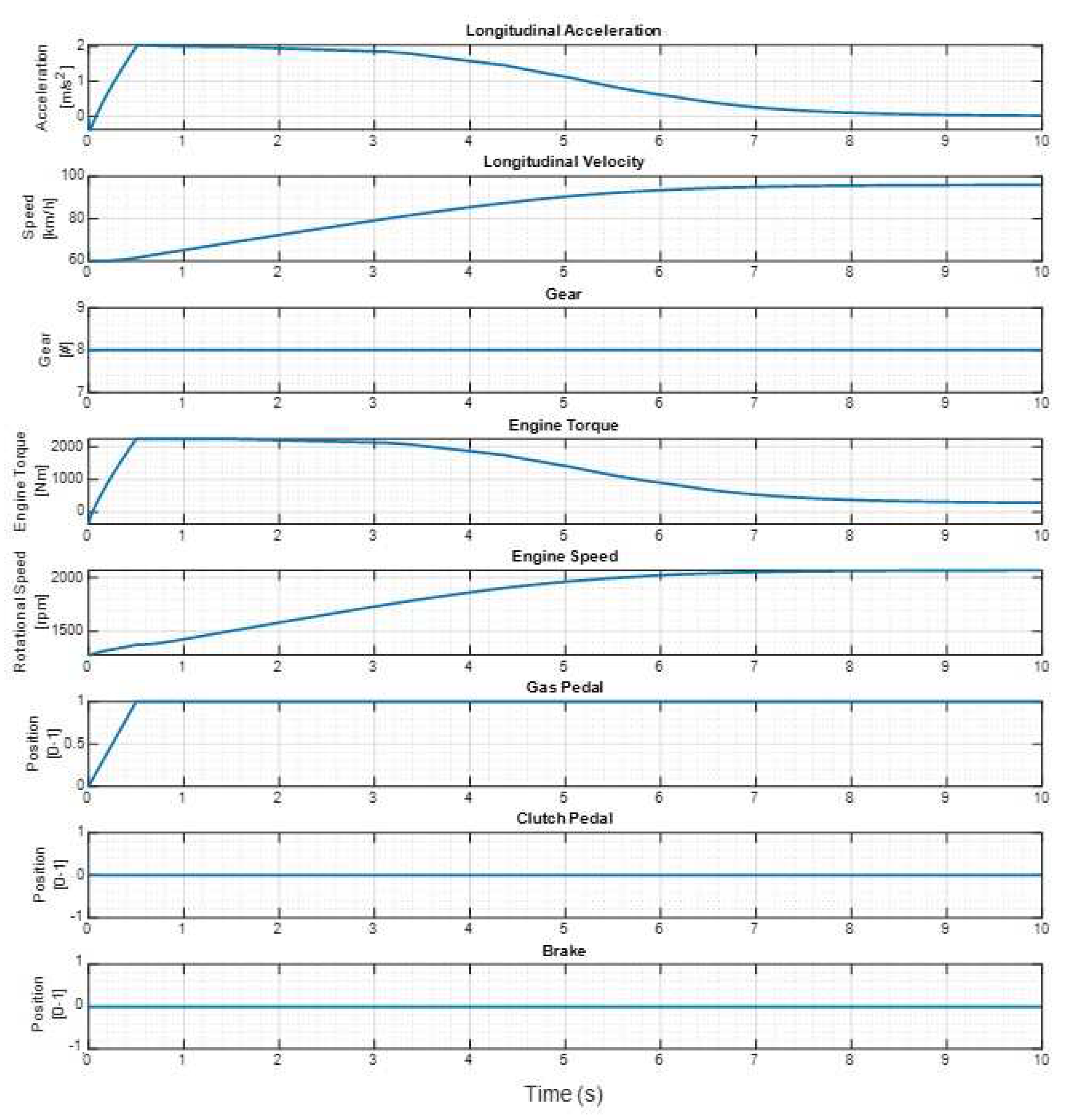
Maneuvers are simulated and last 10 seconds each. In each simulation, the initial speed is chosen that belongs to the set {60, 70, 80, 90} kph. For each initial speed, two initial accelerator pedal position percentages are chosen which are 0 and 100%. 55 scenarios are defined for these 8 combinations of initial vehicle speed and accelerator pedal position. One of such 55 scenarios is shown in Figure 5. 11 final pedal position percentages are chosen from 0 to 100% with 10% increments and times to reach these percentages are defined as { 0.5 , 1 , 2 , 5 , 10 } seconds in order to have constant pedal positions and accelerations. Such combinations result in 3960 different simulations corresponding to 11 hours of driving time in total. The validation data set consists of 495 such simulations, while the training data set contains the rest.
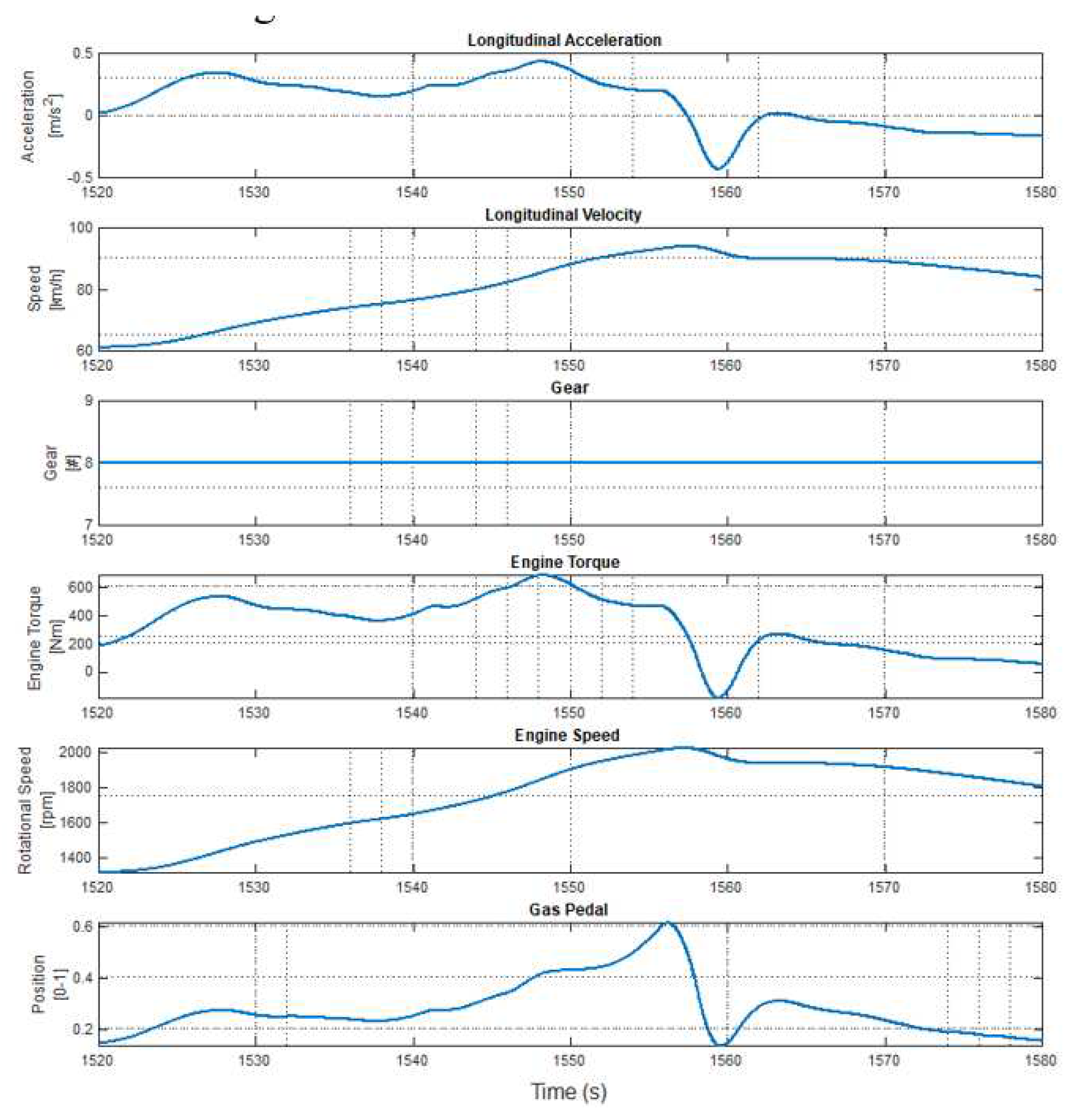
TruckMaker is also used to generate testing data, which consists of data samples obtained by simulating the truck in maneuvers on a flat, straight road. 21 values of masses are used by adding 200 kg to curb mass until the maximum load is 4 tons. A vehicle speed profile is generated that resembles the Worldwide harmonized Light vehicles Test Cycle (WLTC) class 2 driving cycle. In particular, since WLTC driving cycle is for passenger cars, in our tailored-WLTC the cycle chunks with a velocity higher than the maximum truck velocity are clipped, and the remaining cycle chunks are merged. The learned model is tested only in the highest gear. Therefore, features between 1520 s and 1580 s are used as testing data with 10 s intervals. As a result, the first 3 tests contain only acceleration, 4th test has both acceleration and deceleration parts whereas 5th test can be accepted as a constant speed test and 6th test is a deceleration test as shown in Figure 6.
To sum up, training and validation data are collected based on excitation (various gas pedal positions and rates) whereas test data is collected based on realistic driving cycle WLTC.

6. Experimental Validation

The LTSM-based vehicle mass estimation algorithm, designed as explained in Section 4, has been trained with the training and validation data sets, described in Section 5, using the MatLab R2022a Deep Learning toolbox and an NVIDIA A100 Tensor Core 40 GB GPU.
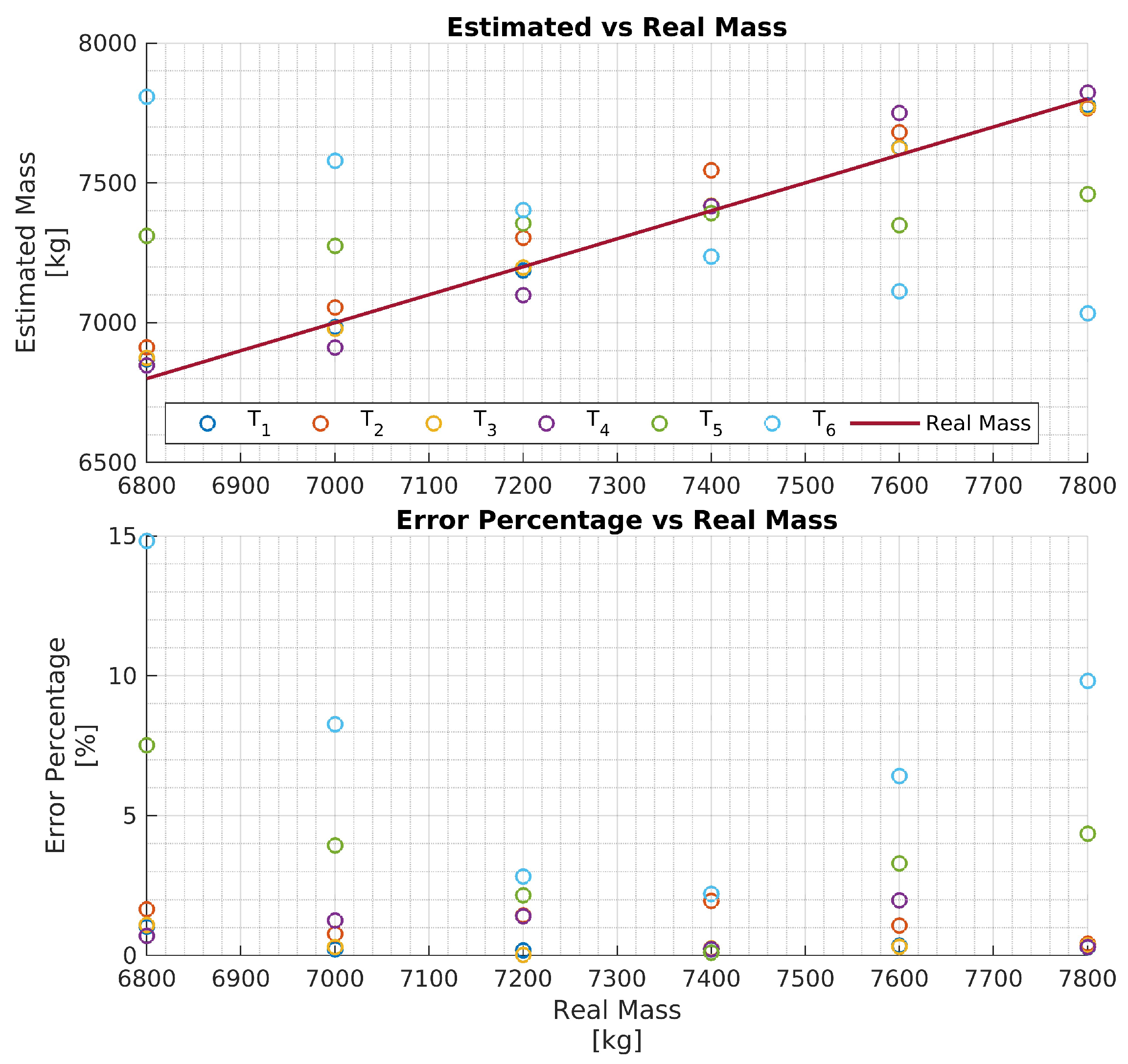
In particular, four networks N i , i ∈ { 1 , 2 , 3 , 4 } have been trained on four training data sets, each consisting of 11 hrs of driving data obtained by varying the vehicle mass in the ranges R i = [ 6.8 , 6.8 + i ] , i = { 1 , 2 , 3 , 4 } , respectively. That is, each network N i is trained to estimate the vehicle mass over the mass range R i . 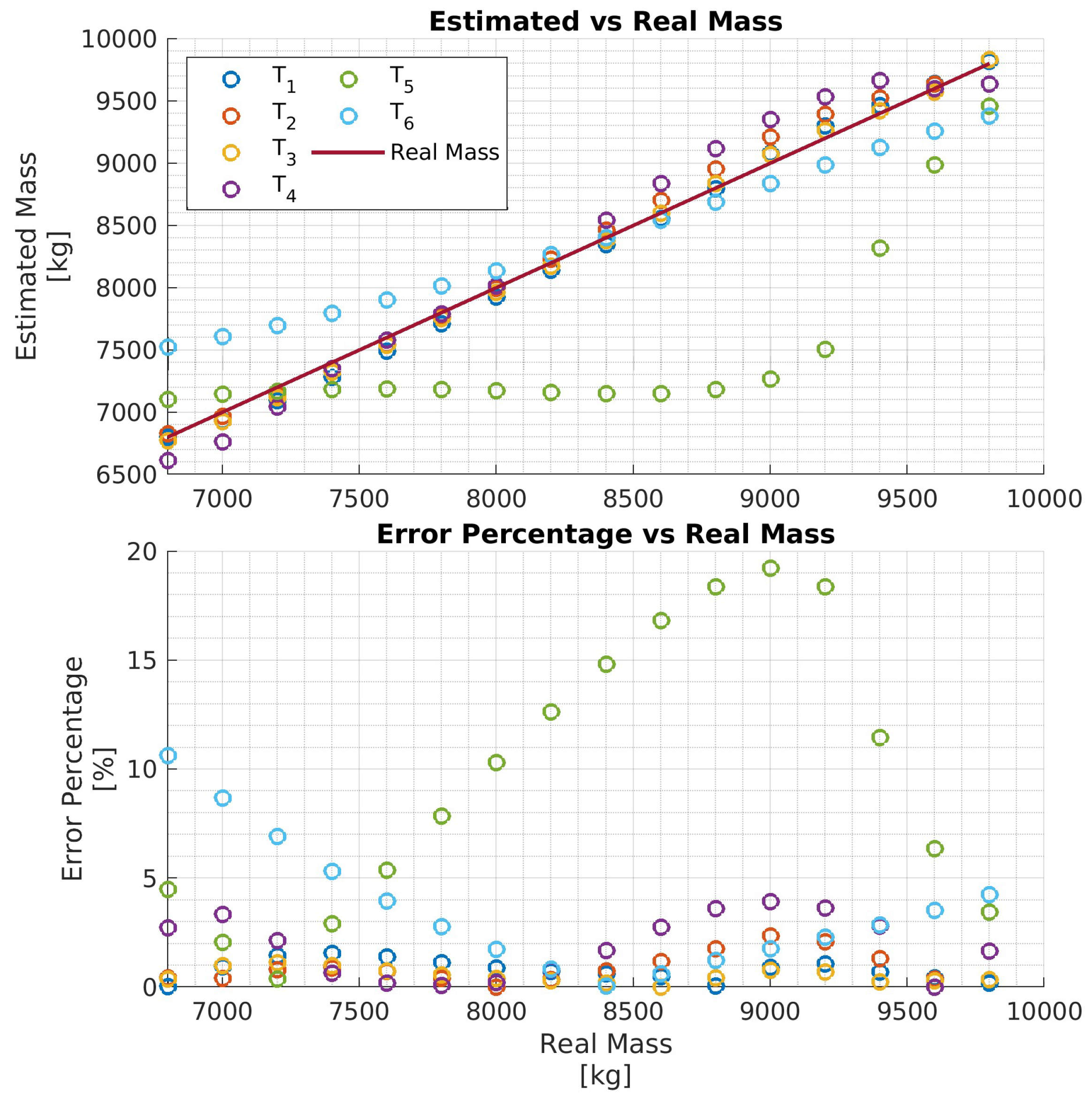The four networks are then evaluated with test data and the results are reported in Figure 7, Figure 8, Figure 9 and Figure 10, respectively. To better evaluate the performance of the four networks, the test data set has been partitioned into six 10-second time intervals T j , j ∈ { 1 , 2 , … , 6 } . For each network N i , the maximum mass estimation error in each T j is reported for vehicle masses selected in the range R i . For example, Figure 7 shows the evaluation of the network N 1 trained in the vehicle mass range R 1 = [ 6.8 , 7.8 ] tons. The six different colors show the mass estimation errors in the time intervals T j , j ∈ { 1 , 2 , … , 6 } . It can be clearly seen that the estimation errors are lower in the time intervals T 1 , T 2 , T 3 of the test data, corresponding to acceleration maneuvers, while the estimation error grows in T 4 , T 5 , T 6 where the gas pedal (lowest plot in Figure 6) is released and the engine brake is used. Although, in principle, training data could be generated containing more samples in the braking maneuver, this may unnecessarily decrease the accuracy of the estimate in the acceleration phase. Indeed, from the distribution of the estimation error w.r.t. the acceleration and/or the gas pedal signals, it could be derived a very simple logic to activate the network and achieve an accurate mass estimate. 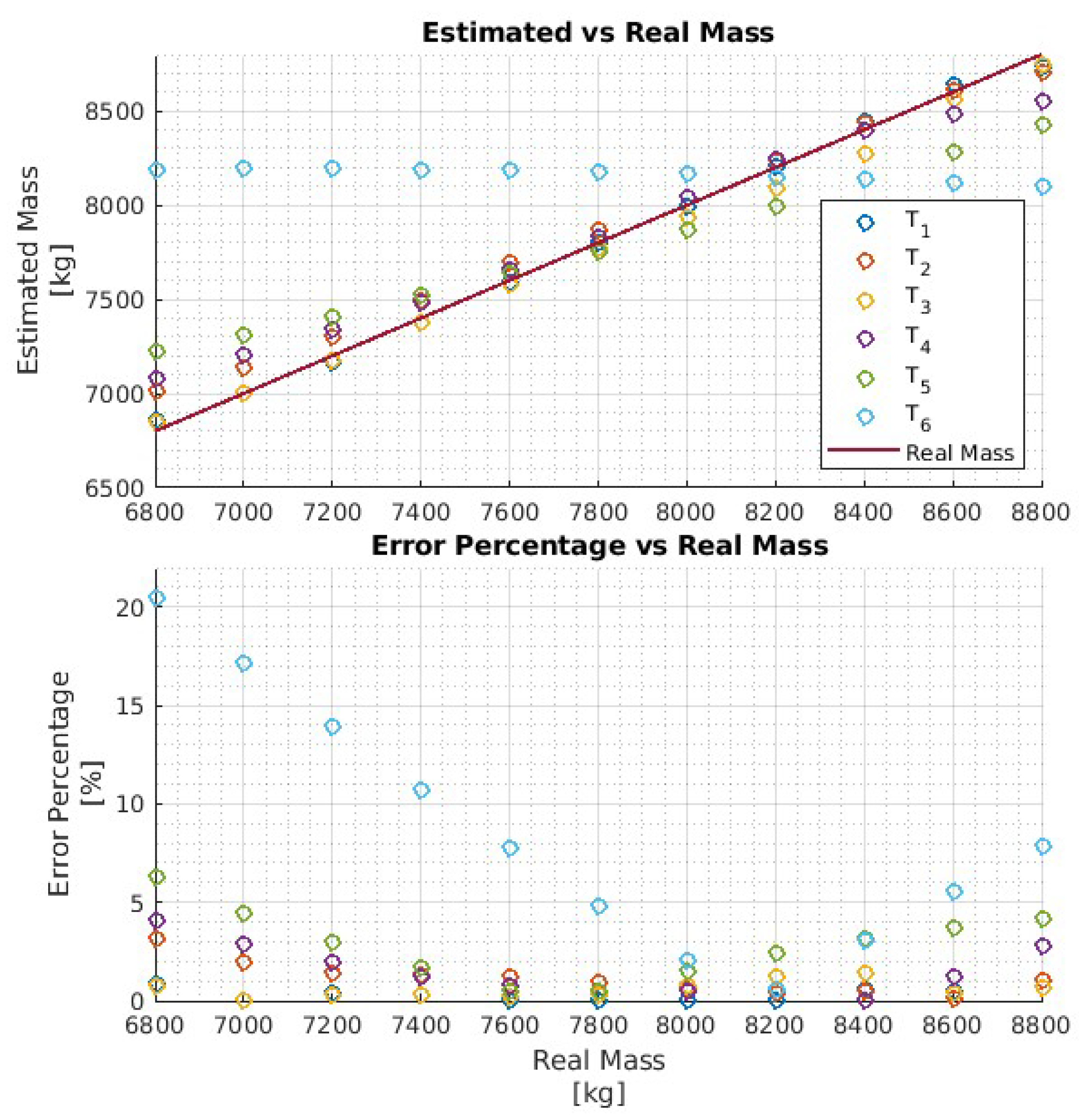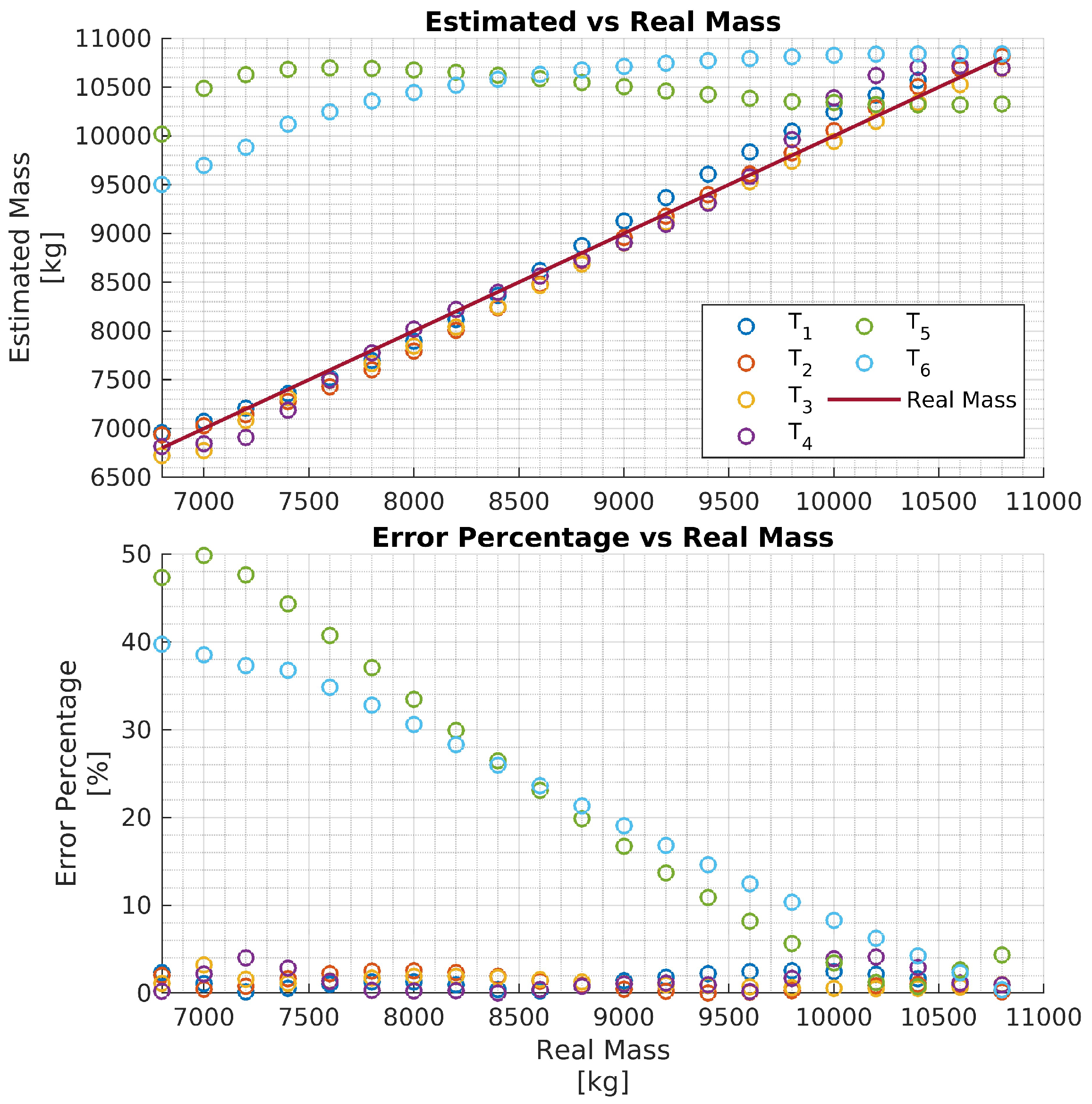The Figure 8, Figure 9 and Figure 10 report the evaluation of the networks N 2 , N 3 , N 4 on the same test data set in Figure 6. We recall that such networks, compared to N 1 , are trained over wider mass ranges of 2, 3, and 4 tons, respectively. As expected, the estimation errors of the networks increase as the mass range is increased. Nevertheless, while all networks exhibit an estimation error below 5% in T 1 , T 2 , T 3 , in the rest of the test data set the estimation error increases significantly. As remarked for network N 1 , while it could be possible to decrease the estimation error in the braking phases ( T 4 to T 6 ), this seems to be unnecessary as also for wider ranges of vehicle mass, the networks accurately estimate the mass in acceleration maneuvers.

7. Conclusion and Future Work

In this paper, a virtual load sensor is designed based on Long Short-Term Memory neural networks, which estimate the mass of heavy vehicles. As the load’s mass varies within wide ranges in heavy vehicles, our objective is to evaluate how the estimation error scales with the load mass range, while maintaining constant the size of the training data (11 hours of driving data) set and the network complexity (approximately 3000 parameters). That is, since producing training data has a cost, we are interested in understanding how the estimation accuracy varies over wider mass ranges while keeping constant the training cost. Our results show that, as long as the proposed LSTM-based virtual load sensor is used in accelerating maneuvers, an accuracy comparable to commercial axle load sensors can be achieved in 4-ton wide load mass ranges. While such a result should be confirmed with wider (up to 10 tons) load mass ranges, this is a good starting point that helps to understand the feasibility of such an approach w.r.t. the training cost (i.e., the amount of training data).
The paper shows how the experiments can be designed to collect training and validation data that leads to mass estimation accuracy comparable to that of commercial load sensors. The proposed approach is evaluated on test data obtained by generating speed profiles that resemble Worldwide harmonized Light vehicles Test Cycle (WLTC).
While the used data in this paper has been generated by the high-fidelity vehicle model TruckMaker, the training and test should be repeated with experimental data collected in experiments with real trucks.

Acknowledgments

The work of Abdurrahman Isbitirici is supported by the Ministry of National Education of the Republic of Turkiye. The authors would like to thank IPG Automotive for providing TruckMaker license. The authors also would like to thank Volvo Trucks for providing some technical information. The authors also would like to thank the University of Modena and Reggio Emilia for providing hardware and giving access to the GPUs cluster.

References

  1. Xu, C.; Geyer, S.; Fathy, H.K. Formulation and comparison of two real-time predictive gear shift algorithms for connected/automated heavy-duty vehicles. IEEE Transactions on Vehicular Technology 2019, 68, 7498–7510. [Google Scholar] [CrossRef]
  2. Chen, Y.L.; Shen, K.Y.; Wang, S.C. Forward collision warning system considering both time-to-collision and safety braking distance. In Proceedings of the 2013 IEEE 8th Conference on Industrial Electronics and Applications (ICIEA). IEEE; 2013; pp. 972–977. [Google Scholar] [CrossRef]
  3. Ritter, A. Optimal Control of Battery-Assisted Trolley Buses. PhD thesis, ETH Zurich, 2021. [Google Scholar]
  4. Kober, W.; Hirschberg, W. On-board payload identification for commercial vehicles. In Proceedings of the 2006 IEEE International Conference on Mechatronics. IEEE; 2006; pp. 144–149. [Google Scholar] [CrossRef]
  5. Technoton. Axle Load Sensors, 2023. Accessed on November 26, 2023.
  6. Paulsson, E.; Åsman, L. Vehicle Mass and Road Grade Estimation using Recursive Least Squares. Master’s thesis, Lund University, Lund, Sweden, 2016. [Google Scholar]
  7. Bae, H.S.; Ryu, J.; Gerdes, J.C. Road grade and vehicle parameter estimation for longitudinal control using GPS. In Proceedings of the Proceedings of the IEEE Conference on Intelligent Transportation Systems. Citeseer; 2001; pp. 25–29. [Google Scholar]
  8. Fathy, H.K.; Kang, D.; Stein, J.L. Online vehicle mass estimation using recursive least squares and supervisory data extraction. In Proceedings of the 2008 American control conference. IEEE; 2008; pp. 1842–1848. [Google Scholar] [CrossRef]
  9. Vahidi, A.; Stefanopoulou, A.; Peng, H. Recursive least squares with forgetting for online estimation of vehicle mass and road grade: theory and experiments. Vehicle System Dynamics 2005, 43, 31–55. [Google Scholar] [CrossRef]
  10. McIntyre, M.L.; Ghotikar, T.J.; Vahidi, A.; Song, X.; Dawson, D.M. A two-stage Lyapunov-based estimator for estimation of vehicle mass and road grade. IEEE Transactions on vehicular Technology 2009, 58, 3177–3185. [Google Scholar] [CrossRef]
  11. Kim, D.; Choi, S.B.; Oh, J. Integrated vehicle mass estimation using longitudinal and roll dynamics. In Proceedings of the 2012 12th International Conference on Control, Automation and Systems. IEEE; 2012; pp. 862–867. [Google Scholar]
  12. Torabi, S.; Wahde, M.; Hartono, P. Road grade and vehicle mass estimation for heavy-duty vehicles using feedforward neural networks. In Proceedings of the 2019 4th international conference on intelligent transportation engineering (ICITE). IEEE; 2019; pp. 316–321. [Google Scholar] [CrossRef]
  13. Korayem, A.H.; Khajepour, A.; Fidan, B. Trailer mass estimation using system model-based and machine learning approaches. IEEE Transactions on Vehicular Technology 2020, 69, 12536–12546. [Google Scholar] [CrossRef]
  14. Eagon, M.; Fakhimi, S.; Pernsteiner, A.; Northrop, W.F. Mass Detection for Heavy-Duty Vehicles using Gaussian Belief Propagation. In Proceedings of the 2022 IEEE Intelligent Vehicles Symposium (IV). IEEE; 2022; pp. 1655–1661. [Google Scholar] [CrossRef]
  15. Leoni, J.; Strada, S.; Tanelli, M.; Savaresi, S.M. Real Time Passenger Mass Estimation for e-scooters. In Proceedings of the 2023 American Control Conference (ACC). IEEE; 2023; pp. 1741–1746. [Google Scholar] [CrossRef]
  16. Yu, Z.; Hou, X.; Leng, B.; Huang, Y. Mass estimation method for intelligent vehicles based on fusion of machine learning and vehicle dynamic model. Autonomous Intelligent Systems 2022, 2, 4. [Google Scholar] [CrossRef]
  17. Mittal, A.; Fairgrieve, A. Vehicle Mass Estimation. US-20180245966-A1, 2018. [Google Scholar]
  18. Rezaeian, A.; Li, D. Vehicle Center of Gravity Height Detection and Vehicle Mass Detection Using Light Detection and Ranging Point Cloud Data. US-20220144289-A1, 2022. [Google Scholar]
  19. Huang, X. Method for Real-Time Mass Estimation of a Vehicle System. US-20190186985-A1, 2019. [Google Scholar]
  20. Jundt, O.; Juhasz, G.; Weis, R.; Skrabak, A. System and Method for Identifying a Change in Load of a Commercial Vehicle. US-20220041172-A1, 2022. [Google Scholar]
  21. Switkes, J.P.; Erlien, S.M.; Schuh, A.B. Applications for Using Mass Estimations for Vehicles. US-20220229446-A1, 2022. [Google Scholar]
  22. Rajamani, R. Vehicle dynamics and control; Springer Science & Business Media, 2011. [Google Scholar]
  23. Schmidhuber, J. Deep learning in neural networks: An overview. Neural networks 2015, 61, 85–117. [Google Scholar] [CrossRef]
  24. LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
  25. Li, F.F.; Karpathy, A.; Johnson, J. Lecture Notes in Convolutional Neural Networks for Visual Recognition. Stanford University.
  26. Goodfellow, I.; Bengio, Y.; Courville, A. Deep learning; MIT press, 2016. [Google Scholar]
  27. Rodriguez, P.; Wiles, J.; Elman, J.L. A recurrent neural network that learns to count. Connection Science 1999, 11, 5–40. [Google Scholar] [CrossRef]
  28. Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. In Proceedings of the International conference on machine learning. Pmlr; 2013; pp. 1310–1318. [Google Scholar]
  29. Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv preprint 2014, arXiv:1412.3555. [Google Scholar]
  30. Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural computation 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
  31. Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. Neural computation 2000, 12, 2451–2471. [Google Scholar] [CrossRef]
  32. Greff, K.; Srivastava, R.K.; Koutník, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A search space odyssey. IEEE transactions on neural networks and learning systems 2016, 28, 2222–2232. [Google Scholar] [CrossRef]
  33. Chowdhury, K. 10 Hyperparameters to Keep an Eye on for your LSTM Model—and other Tips. 2023. [Google Scholar]
  34. Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: a simple way to prevent neural networks from overfitting. The journal of machine learning research 2014, 15, 1929–1958. [Google Scholar]
  35. Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv preprint 2014, arXiv:1412.6980. [Google Scholar]
  36. Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In the Proceedings of the thirteenth international conference on artificial intelligence and statistics. JMLR Workshop and Conference Proceedings; 2010; pp. 249–256. [Google Scholar]
  37. Hu, W.; Xiao, L.; Pennington, J. Provable benefit of orthogonal initialization in optimizing deep linear networks. arXiv preprint 2020, arXiv:2001.05992. [Google Scholar]
Preprints 91899 g001
Figure 1. Longitudinal Vehicle Dynamics.
Figure 1. Longitudinal Vehicle Dynamics.
Preprints 91899 g001
Preprints 91899 g002
Figure 2. Perceptron.
Figure 2. Perceptron.
Preprints 91899 g002
Preprints 91899 g003
Figure 3. Feedforward neural network.
Figure 3. Feedforward neural network.
Preprints 91899 g003
Preprints 91899 g004
Figure 4. Activation Functions: ReLU, tanh, sigmoid.
Figure 4. Activation Functions: ReLU, tanh, sigmoid.
Preprints 91899 g004
Preprints 91899 g005
Figure 5. Training Data with 60 kph initial velocity, 0% initial accelerator pedal percentage, 100% final accelerator pedal percentage in 0.5s.
Figure 5. Training Data with 60 kph initial velocity, 0% initial accelerator pedal percentage, 100% final accelerator pedal percentage in 0.5s.
Preprints 91899 g005
Preprints 91899 g006
Figure 6. Inputs for test data.
Figure 6. Inputs for test data.
Preprints 91899 g006
Preprints 91899 g007
Figure 7. Performance of the network N 1 with the test data set.
Figure 7. Performance of the network N 1 with the test data set.
Preprints 91899 g007
Preprints 91899 g008
Figure 8. Performance of the network N 2 with the test data set.
Figure 8. Performance of the network N 2 with the test data set.
Preprints 91899 g008
Preprints 91899 g009
Figure 9. Performance of the network N 3 with the test data set.
Figure 9. Performance of the network N 3 with the test data set.
Preprints 91899 g009
Preprints 91899 g010
Figure 10. Performance of the network N 4 with the test data set.
Figure 10. Performance of the network N 4 with the test data set.
Preprints 91899 g010
Table 1. Hyperparameters and Training Options.
Table 1. Hyperparameters and Training Options.
Hyperparameter Value or name
# of hidden layers 2
# of neurons in the hidden layers 16,16
Output mode of Lstm layers sequence,last
Dropout probability 0.5
Solver adam [35]
Execution environment gpu
# of epoch 5000
Initial learning rate 0.0025
Sequence length longest
Output network best-validation-loss
Gradient threshold 1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated