A Data-Driven Approach to Team Formation in Software Engineering Based on Personality Traits

Preprint

Article

A Data-Driven Approach to Team Formation in Software Engineering Based on Personality Traits

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

30 November 2023

Posted:

01 December 2023

You are already at the latest version

Alerts

Abstract

Collaboration among individuals with diverse skills and personalities is crucial in producing high-quality software. The success of any software project depends on the team’s cohesive functionality and mutual complementation. This study introduces a data-centric methodology for forming Software Engineering (SE) teams centred around personality traits. Our study analyzed data from an SE course where 157 students in 31 teams worked through four project phases and were evaluated based on deliverables and instructor feedback. Using the Five Factor Model (FFM) and a variety of statistical tests, we determined that teams with higher levels of extraversion and conscientiousness and lower neuroticism consistently performed better. We examined team member interactions and developed a predictive model using extreme gradient boosting. The model achieved a 74% accuracy rate in predicting inter-member satisfaction rankings. Through graphical explainability, it underscored incompatibilities among members, notably those with differing levels of extraversion. Based on our findings, we introduce a team formation algorithm using Simulated Annealing (SA), built upon the insights from our predictive model and additional heuristics.

Keywords:

Subject: Computer Science and Mathematics - Computer Science

1. Introduction

Team formation (TF) is critical in many domains, including business, sports, and academia [1,2]. In Software Engineering (SE), however, TF assumes a unique and pivotal role. SE, an engineering discipline encompassing all aspects of software production [3], is deeply rooted in collaboration. The complexity of software projects often necessitates a team of engineers with diverse specializations, making these teams’ efficiency, communication, and synergy crucial for project success. This study aims to bridge the gap in TF by integrating psychological metrics with machine learning techniques to optimize team composition in SE.

Historically, TF has relied heavily on empirical metrics, but recent trends have shifted towards incorporating psychological aspects to enhance team dynamics, and performance [4]. The dynamics of how team members interact and engage with each other are crucial in SE. Research has consistently shown a strong correlation between positive team dynamics and the success of high-performing teams [5,6,7,8]. However, despite its recognized importance, integrating psychological traits into automated TF systems, particularly in SE, still needs to be explored.

This gap is particularly evident when considering the subtler yet influential factor of team members’ psychological and personality traits. These traits can profoundly impact how individuals approach problems, interact with colleagues, and respond to stress or success. There has been a growing interest in using personality frameworks, such as the Big Five personality traits, to build technically proficient and psychologically compatible teams.

In the following section, we review the current literature and identify gaps and limitations, which lead to the introduction of our proposed solution. In the subsequent sections, we outline our methodologies, describe the data collection process, detail the models employed, and provide an initial overview of the data. This is followed by a presentation of our results, including the trained model and the newly proposed team formation algorithm. The paper concludes with a discussion of our findings and considerations for future research.

2. Related work and proposed solution

The interaction between individual personality traits and team performance has been extensively studied, especially in situations that require collaboration and specialized skills. A hierarchical model developed by [9] categorizes key personality facets vital for team performance, offering a detailed understanding of how broad personality traits correlate with specific team requirements. This model utilizes specific facets of higher-level dimensions, such as adjustment, flexibility, and dependability, to predict team adaptability, interpersonal cohesion, and decision-making.

A study by [10] investigated the impact of personality traits on the performance of product design teams comprising undergraduate engineering students. The findings indicated a significant positive correlation between conscientiousness, openness, and team performance. In the study, groups of three students were tasked with building a bridge using limited resources, emphasizing the profound influence of personality traits over other factors, including cognitive ability and demographic diversity.

The research by [11] delved into the predictive capacity of conscientiousness facets within engineering student project teams over a 6.5-month-long task. The primary conclusion was that conscientiousness effectively forecasted team performance. However, it was noted that other traits, such as agreeableness, extraversion, and neuroticism, did not have a significant predictive impact on team performance.

In the realm of SE, [12] assessed the impact of personality traits on SE team effectiveness using the Myers-Briggs Type Indicator (MBTI). They highlighted the significant role of personality clashes in software project failures and pointed out a gender-based variance in MBTI traits among programmers. Suggestions for optimal trait balances for male and female team members are presented.

The research [13] undertook a systematic literature review from 1970 to 2010, centring on individual personalities in SE. This review offers an extensive overview of the field’s current understanding, notably highlighting the diversity of results.

The study [14] provided direct evidence of the impact of specific personality traits in a SE context, emphasizing the significance of extraversion in promoting effective team dynamics. It also found that Openness to Experience positively correlates with team performance, though not with team climate. However, the limited sample size of respondents might limit the generalizability of these findings.

In their research, [15] mapped the job requirements of various SE roles to the Big Five Personality Traits, suggesting specific personality traits beneficial for different SE roles. This mapping includes the need for extraversion and agreeableness in system analysts, openness and conscientiousness in software testers, and a combination of extraversion, openness, and agreeableness in programmers.

Authors in [16] extended the application of personality traits in team dynamics to an educational perspective, focusing on team dynamics within the context of student programming projects. This study addresses the gap between academic projects and real-world software development, offering insights into managing and facilitating student projects that closely mimic professional environments.

Building on previous research, it is evident that personality traits significantly influence team performance. However, existing literature in SE lacks a comprehensive framework that integrates psychological metrics into team formation (TF) and is inconclusive about the most beneficial traits, except for conscientiousness. Notably, most studies have focused on the impact of personality traits on team performance without delving into TF dynamics, analyzing groups as cohesive units rather than individual team members.

Our study aims to bridge this gap in SE by examining inter-member dynamics, employing traditional statistical analysis and machine learning techniques for deeper insights. Furthermore, we introduce a simulated annealing-based TF algorithm to incorporate these findings effectively. This approach contributes to the SE field by proposing a framework for TF that includes psychological metrics to enhance individual and team efficacy. The methodologies we used and the proposed framework are depicted in Figure 1.

3. Materials and Methods

3.1. Data Acquisition and Description

Data for this study was sourced from the mandatory course Software Engineering at the Faculty of Computer and Information Science, University of Ljubljana. The study encompassed 157 third-year undergraduates, divided into 31 teams of five to six, whose contributions were anonymized for analysis. The course’s curriculum was segmented into four stages: project proposal, requirement gathering, solution design, and implementation. The project phases spanned three months, each lasting 2-3 weeks.

Before the project began, students completed a 41-item psychometric questionnaire based on the Five-Factor Model (FFM), utilizing a 5-point Likert scale to gauge personality traits for insights into team dynamics. Following each phase, surveys were collected to assess team satisfaction, focusing on performance, communication, and individual contributions.

Version control was managed via Git within a GitHub organization, allowing for the extraction of commit data, including the number of commits and lines of code. After each stage, teaching assistants (TAs) evaluated the teams’ deliverables using a 0-100 scale.

3.2. Five Factor Model

The Five-Factor Model (FFM), also known as the OCEAN model, is a prominent psychological framework for evaluating human personality along five key dimensions: Openness (O), Conscientiousness (C), Extraversion (E), Agreeableness (A), and Neuroticism (N) [17]. In our study, participants underwent a standardized test to measure these dimensions. Each questionnaire item aligns with a specific dimension and carries an "influence value," denoted by

I (q)

, reflecting the question’s framing.

Particularly, when a question negatively correlates with the trait it assesses, the corresponding response,

R (q)

, is inverted to represent the trait accurately. To quantify the dimension score S for a set of related questions Q, we calculate S as the weighted sum of the responses

R (q)

and their respective influence values

I (q)

, normalized by the maximum possible score for that set,

\max_score (Q)

. Mathematically, this is represented as

S = \frac{\sum_{q \in Q} R (q) \times I (q)}{\max_score (Q)}

Despite some criticism, such as not fully accounting for all variances in human personality [18] or the lack of complete independence among variables [19], the FFM is a reliable and valid model for measuring personality traits in SE domains [20].

3.3. XGBoost and Shapley Additive EXplanations

To create a predictive model focusing on the assessment of inter-member satisfaction, we employed the Extreme Gradient Boosting algorithm, widely recognized as XGBoost. XGBoost is an open-source machine learning framework known for its computational efficiency and robust performance metrics. As a type of ensemble learning, it is an optimized version of gradient-boosted decision trees tailored for speed and accuracy. Noteworthy features of XGBoost include its built-in capacity to handle missing data, support for parallel processing, and its versatility in addressing a diverse range of predictive problems [21].

In addition to model prediction, interpretability is crucial when dealing with large "black box" machine learning models. This research uses Shapley Additive EXplanations (SHAP) to provide a detailed understanding of feature influence on predictions [22].

3.4. Simulated Annealing

To address the NP-hard challenge of TF, we employed Simulated Annealing (SA) [23], a heuristic optimization algorithm. The algorithm was designed to optimize the composition of student teams by using heuristics from the FFM and the XGBoost predictive model. SA initiates with a solution

S_{init}

and, in each iteration, generates a new candidate solution

S^{'}

from the neighbourhood

N (S)

of S. The acceptance of

S^{'}

over S is dictated by the Metropolis criterion, which considers the change in objective function

Δ E = E (S^{'}) - E (S)

. A solution

S^{'}

is accepted if

Δ E \leq 0

or if a randomly generated number between 0 and 1 is less than

exp (- Δ E / T)

, where T is the current temperature. The algorithm iterates for a fixed number of iterations

N_{stop}

and returns the most optimized solution found.

3.5. Data overview

3.5.1. Phase results

After each project phase, students were evaluated and graded by TAs. The grading criteria were based on quantifiable aspects such as the volume of work completed, project deliverables, and the overall quality of the work. Rather than team grades, individual grades were assigned on a scale from 0 to 100. These grades were communicated to each student during a meeting with the TA and their respective team. The distribution of these grades across different phases is illustrated in the histogram shown in Figure 2.

The average grades for the first two phases were relatively consistent, with

μ_{1} = 77.7

for the first phase and

μ_{2} = 77.8

for the second. However, the third phase proved more challenging, reflected in a drop in the average grade to

μ_{3} = 73.0

. The average grade increased again in the fourth phase to

μ_{4} = 84.0

. This pattern aligns with student feedback, which indicated that the third and fourth phases were the most difficult. The improved performance in the fourth phase can be attributed to its focus on project implementation, a task with which the students were the most familiar.

3.5.2. FFM data

Aggregate data of the distribution of students is depicted in Table 1. We compared the results to a study on the effect of teammate personality on team production [24]. Our observed average for conscientiousness stands at 0.69, exceeding the 0.59 reported in the referenced study. This disparity can be attributable to our participants being in their third academic year, suggesting a more developed work ethic than first-year undergraduates. Our dataset displayed slightly higher averages for openness (0.67) and agreeableness (0.61). In contrast, extraversion averaged at 0.54, a significant deviation from the 0.75 cited in the comparative study. Neuroticism showcased consistency across both datasets, with our average resting at 0.37 compared to 0.38 in the reference study.

To measure the linear relationship between each pair of traits, we constructed a correlation matrix utilizing the PCCs. The values in this matrix span the interval

[- 1, 1]

. A value approaching 1 indicates a strong positive relationship, while a value nearing -1 signifies a pronounced negative relationship. Conversely, values proximate to 0 indicate minimal to non-existent correlations.

Key insights derived from the correlation matrix, presented in Table 2, are as follows:

Conscientiousness and Neuroticism: A moderate negative correlation ( $r = - 0.33$ ) is observed between Conscientiousness and Neuroticism. This suggests that individuals scoring higher in conscientiousness tend to exhibit fewer neurotic traits.
Extraversion and Openness: The data indicate a positive correlation ( $r = 0.20$ ) between Extraversion and Openness.
Conscientiousness and Extraversion: A notable correlation exists between Conscientiousness and Extraversion, evidenced by a coefficient of $r = 0.23$ .

The observed relationships in the first two points are consistent with prior research [25,26]. The third point, however, presents an ambiguous relationship, which could be attributed to the limited sample size or the specific demographic characteristics of the student population studied.

3.5.3. Repository Commit Data

Git data was collected from each team’s repository, into which students committed their code and documentation. The initial dataset comprised 59305 commits harvested from the git repositories of student teams. Several filtering steps were implemented to ensure relevance and accuracy. Commits outside the project deadlines were excluded to align with the grading period. Additionally, commits with erroneous timestamps—attributable to misconfigured git clients—were removed. Non-source-code elements like tool-generated directories (for example node_modules generated by a package manager) and build artefacts, which do not represent a developer’s effort, were also omitted.

Furthermore, commits that merely consisted of minified CSS files within documentation directories—often a byproduct of wireframe creation—were considered non-essential and excluded. A noticeable pattern of commits with large but equal counts of line additions and deletions was attributed to code formatting tools. To address this, commits were filtered using a heuristic that targeted those with line modifications exceeding 50, ensuring that trivial style changes did not inflate the data.

After these preprocessing steps, the commit count was refined to 28466, representing approximately 48% of the initial volume. A visual representation of the filtered commit activity across teams is shown in Figure 3. The vertical dashed orange lines represent the deadlines for individual phases.

4. Results

4.1. Team Performance and FFM Dimensions

We define team performance as the arithmetic mean of grades in each project phase. Using the median performance as the separation criterion, teams were classified as high-performing or low-performing, as depicted in Figure 4. The variations in FFM dimensions between these groups were statistically significant and aligned with previous research, confirming the following:

Openness and Agreeableness don’t have a meaningful effect on team performance. Contrary to the assumption that teams with open or agreeable members would perform better, the data doesn’t support this claim.
Conscientiousness is confirmed by past research [24] to have a positive association with team performance. Teams with organized, dependable, and hardworking members tend to outperform others.
Neuroticism hurts how teams fare, which aligns with previous findings [12]. High neuroticism in individuals can lead to challenges within the team, affecting overall effectiveness.
Extraversion plays a complex role. Although it has its advantages and disadvantages, it positively influences team performance in our dataset. Since computer science students may generally be more introverted, extroverted members can be advantageous. Their engagement can counterbalance any issues like dominating conversations.

Before assessing the significance of our findings, we checked if the conditions for a parametric t-test were met. Levene’s test confirmed that the variances between the two groups were equal. However, the Shapiro-Wilk test revealed that only the extraversion and conscientiousness dimensions were normally distributed. Considering these points, we opted for the non-parametric Mann-Whitney U test to examine the mean differences across the dimensions. The test highlighted significant differences between high-performing and low-performing teams in the following dimensions: Conscientiousness (

p = 0.005

), Extraversion (

p = 0.0001

) and Neuroticism (

p = 0.004

4.2. Analysis of Team Satisfaction Metrics

In evaluating team satisfaction during post-project phases, two distinct metrics were employed. The first, a rating scale

R_{1} \in [- 2, 2]

, measured individual satisfaction levels, with

- 2

indicating very low satisfaction and 2 denoting high satisfaction with team members’ contributions. Each team member received a non-unique score from their peers. The second metric, a ranking system

R_{2} \in [1, len (teams)]

, assigned each member a unique rank, with 1 representing the highest satisfaction level.

Team satisfaction was quantified as the normalized sum of all inter-member satisfaction scores, calculated using the formula:

T = \frac{\sum_{i = 1}^{n} \sum_{j = 1, j \neq i}^{n} \frac{s_{i j}}{n - 1}}{n}

(1)

Here,

s_{i j}

is the satisfaction score assigned by member i to member j, which could be either

R_{1}

R_{2}

, and n is the total number of team members. The condition

j \neq i

excludes self-assessment scores.

Using

R_{1}

s_{i j}

, team satisfaction was calculated for each project phase, with the results depicted in Figure 5. Phases 2 and 4 showed a notable positive correlation between team satisfaction and performance, with correlation coefficients of

r = 0.39

and

r = 0.32

. However, Phase 1 exhibited a weak or non-existent relationship, possibly due to initial adjustment among team members. Phase 3’s average scores were 5 points lower than the first two phases, leading to reduced satisfaction levels, particularly when outcomes did not meet expectations.

While

R_{1}

correlates with performance, its suitability for our team formation method is questionable due to potential data skewness, defined as:

Skewness (g 1) = \frac{n}{(n - 1) (n - 2)} \sum {(\frac{x_{i} - \bar{x}}{s})}^{3}

(2)

Our dataset’s skewness was

- 1.22

, indicating strong negative skewness. The ICC test [27] further revealed inconsistencies in the data, possibly due to biased evaluations by students concerned about peer grades.

Consequently, we will use the ranked work contribution score

R_{2}

for further analysis. ICC(3,k) tests on

R_{2}

showed adequate consistency, with 61 out of 108 groups (56.48%) achieving an ICC over 0.5, and 72 groups (66.67%) exceeding 0.4. These thresholds were based on varied interpretations of the ICC value [28,29]. The chosen threshold is deemed good by both standards. This indicates a general agreement on top contributors, though not unanimous.

A hypothesis for subsequent investigation is that a significant portion of these rankings could be explained by tangible metrics like commit counts and lines of code, with the remaining variance potentially linked to distinct personality traits within the teams.

4.2.1. Work contribution

To effectively measure individual contributions during different project phases, we introduce a metric denoted as

work_{ratio}_{n}

, with n representing the project phase. This metric is derived from Git data, following a specific preprocessing approach.

The calculation of

work_{ratio}_{n}

involves several steps:

The number of lines each member adds m is normalized by taking the square root. This adjustment favours smaller, frequent commits instead of larger, sporadic ones. Lines removed are not considered, as they do not reliably indicate work contribution.
The normalized line additions for each member m are summed up.
The total normalized line additions for the team t are calculated.
The expected work ratio r per student is determined as $r = \frac{1}{len (team)}$ . For example, in a five-member team, the expected ratio is 0.2.
The individual contribution proportion p is computed as $p = \frac{m}{t}$ .
Finally, the work ratio for phase n is calculated by $work_{ratio}_{n} = \frac{p}{r}$ .

The

work_{ratio}_{n}

metric provides insights into a student’s relative contribution:

A value above 1 indicates contributions exceeding expectations.
A value below 1 suggests contributions falling short of expectations.
A value around 1 implies contributions meeting expectations.

The relationship between work contribution and ranking is examined through regression plots (Figure 6). It’s important to interpret these findings correctly:

A lower work contribution suggests that the student contributed more than expected.
A higher work contribution indicates that the student contributed less than expected.

The correlation coefficients for each project phase are as follows:

r_{1} = - 0.44

r_{2} = - 0.39

r_{3} = - 0.38

, and

r_{4} = - 0.60

. These values indicate a moderate negative correlation between work contribution and ranking. However, the correlation is not strong enough to fully explain the variance in rankings. The following section will explain the remaining variance using gradient boosting.

4.3. Binary Classification of Inter-Member Satisfaction

We want to predict whether two members will successfully collaborate based on their personality traits. We will use the

R_{2}

metric as the target variable to achieve this and employ the XGBoost algorithm to create a binary classifier that predicts whether two members will be satisfied with each other. To train this classifier, we will use the following features:

Features 1...5: OCEAN scores of the ranker member.
Features 6...10: OCEAN scores of the target member.
Feature 11: The ${work}_{n}$ ratio of the target member.

The ranker is designated as the student responsible for assessing the target student. In our approach, rather than both ratios, we incorporate solely the

{work}_{n}

ratio of the target. This decision is based on our strategy to set this variable as a constant during the prediction phase. While adding a second variable might potentially enhance the model’s accuracy in the training phase, it is anticipated that it could diminish the accuracy in the practical application within the team formation algorithm we will introduce later.

A dataset of 3108 data points was constructed by pairing each member with another team member. The dataset was split into a training set of 2486 data points and a test set of 622 data points following an 80:20 train-test split. The model was trained using a grid search with cross-validation to identify the best hyperparameters. The optimal model configuration required 300 estimators, a max depth of 12, and a learning rate of 0.1. The model yielded an accuracy of 0.74, a precision of 0.69, and an ROC-AUC score of 0.79.

To explain how the model works, we utilized SHAP. The beeswarm summary plot, shown in Figure 7, displays the feature importance of the XGBoost model. The most important feature is the

{work}_{n}

ratio of the target member, followed by the target member’s OCEAN scores, and finally, the ranker member’s OCEAN scores.

Two SHAP waterfall plots in Figure 8 were created to assess how the model works. In the negative classification example, we can see that the low amount of work (5x less than expected) done by the target student was the main reason for the negative classification, but above-average neuroticism also contributed. In the positive classification example, we can see that the high amount of work nudges the classification to be positive. At the same time, the interplay between Raters’ and Target’s FFM dimensions cancels out.

The dependence plot in Figure 9 suggests that team satisfaction is positively influenced when Rater and Target have similar extraversion levels. High extraversion in both tends to skew predictions positively while diverging levels yield adverse outcomes. Similar trends were observed for conscientiousness and neuroticism, reinforcing the model’s validity.

4.4. Team Formation Algorithm

Based on prior observations, the following heuristics were established for effective team formation:

Maximize inter-team $R_{2}$ to enhance team performance.
Teams should exhibit high levels of conscientiousness ( $Q_{c}$ ) and extraversion ( $Q_{e}$ ).
Aim for low levels of neuroticism ( $Q_{n}$ ) within teams.
Maintain minimal standard deviation across teams for each dimension: $Q_{c}$ , $Q_{e}$ , and $Q_{n}$ .
Incorporate at least one student with high conscientiousness ( ${student}_{max (c)}$ ) in each team, as suggested by [24]. This approach triggers a beneficial "conscientiousness shock," improving team dynamics.

The Simulated Annealing (SA) algorithm was implemented with the following parameters:

Initial Solution ( $S_{init}$ ): Teams are formed randomly considering team size distributions, with the constraint that each team includes a student with high conscientiousness. This is achieved by selecting the top N students, where N equals the number of teams. These students are given a locked status to prevent team swaps.
Generation of New Solution ( $S^{'}$ ): A candidate solution is formed by exchanging two students between different teams while ensuring that students with the locked status remain fixed.
Evaluation Function ( $E (S)$ ): The function $E (S) = w_{inter} \times Q T_{inter} + w_{c} \times Q_{c} + w_{e} \times Q_{e} + w_{n} \times {NQ}_{n}$ integrates various dimensions such as interpersonal satisfaction ( $Q T_{inter}$ ), conscientiousness ( $Q_{c}$ ), extraversion ( $Q_{e}$ ), and neuroticism ( ${NQ}_{n}$ ). Weights $w_{inter}$ , $w_{c}$ , $w_{e}$ , and $w_{n}$ allow adjustment of each dimension’s influence.

Inter-member Satisfaction (

{QT}_{inter}

): For a team

T_{k}

, the average satisfaction

μ_{T_{k}}

is calculated using the binary classifier’s predictions

p (f_{i, j})

for each student pair. The global average and standard deviation across all teams are computed to derive

{QE}_{inter} = μ - σ

Scores for Q and

N Q

: For each dimension, the team average

μ_{T_{k}}

and global averages

μ

and

σ

are computed. The resulting scores are defined as

Q = μ - σ

for

Q_{c}

and

Q_{e}

, and

N Q = (1 - μ) - σ

for

Q_{n}

4.: Stopping Condition: The algorithm stops after $I_{stop} = 710 N - 1740$ iterations, where N is the number of teams. This formula is based on a linear regression model, with a minimum threshold of 6000 iterations for $N < 10$ .

We evaluated the proposed algorithm by comparing it with other methodologies and dimensions, as detailed below:

Shuffled: Teams were formed randomly from a predefined set of students.
Course: Teams as they existed during the course. Although this data point might appear similar to the Shuffled method, it was included separately as the students’ choices could have influenced team compositions.
Sorted by conscientiousness: Students were ranked according to their conscientiousness scores and then assigned to teams in a round-robin fashion. This method was employed to contrast the SA algorithm’s performance with a basic heuristic.

Figure 10 illustrates the operation of the SA algorithm and its comparison with the aforementioned methodologies. The first scenario (left) displays the application of the algorithms on the original dataset, whereas the second scenario (right) applies them to a synthetic dataset. This synthetic dataset was generated by calculating the mean and standard deviation for each dimension of the original dataset and then creating a new dataset with an equivalent number of students and teams. Random values from a normal distribution, based on the mean and standard deviation of the original data, were used to populate this new dataset. This approach aimed to test the algorithm’s robustness and confirm that the peculiarities of the original dataset did not bias the results. In the SA algorithm, the weights applied were

w_{c} = 2

w_{e} = 1

w_{c} = 1

, and

w_{inter} = 0.75

. These were chosen to underscore the importance of the conscientiousness dimension while ensuring balanced representation across other dimensions.

In the analysis of the original data, the Sorted by conscientiousness method yielded the lowest score, with

E (s) = 1.66

, followed by the Shuffled and Course methods, each scoring

E (s) = 1.70

. In contrast, the SA algorithm consistently outperformed these approaches, achieving an average score of

E (s) = 2.14

. Notably, the conscientiousness dimension, evaluated separately, matched the performance of the third method, with

E {(s)}_{c} = 0.67

. This indicates that the SA algorithm effectively sorts students based on conscientiousness and maintains a balanced distribution across the other dimensions.

To contextualize the computational efficiency of our algorithm, one can consider the total number of unique team configurations that would be examined in an exhaustive combinatorial search. Utilizing the formula

(\binom{number of students}{number of teams})

, an exhaustive evaluation for selecting just one team of 5 from a pool of 150 participants would necessitate investigating 591600030 distinct combinations. In stark, the SA algorithm substantially mitigates this computational demand. Specifically, it required searching only

710 \times 30 - 1740 = 19560

configurations to achieve the results presented in Figure 10.

5. Discussion and conclusion

This study explored the impact of the Five-Factor Model of personality traits on team dynamics, analyzing data from 157 third-year undergraduates formed into 31 teams. The results showed that teams typically perform better with more extroverted and conscientious members but less neurotic. Using an XGBoost model, we successfully predicted team satisfaction with 74% accuracy and 69% precision. We also introduced an innovative method for automatically forming teams based on the FFM. By applying a simulated annealing technique, we developed an efficient algorithm that effectively groups participants according to specific criteria. This method ensures a well-balanced distribution of personality traits among teams and enhances overall member satisfaction.

We recommend enlarging the dataset for future studies to encompass more participants and a more comprehensive range of projects. This expansion would help refine the XGBoost model’s accuracy and further examine how personality traits influence team performance. We also propose integrating technical skills as a factor in the algorithm to enhance its effectiveness and address the tendency of technically proficient members to contribute more to projects.

Author Contributions

Conceptualization, Dejan Lavbič and Jan Vasiljević; methodology, Dejan Lavbič; software, Jan Vasiljević; validation, Jan Vasiljević and Dejan Lavbič; formal analysis, Jan Vasiljević and Dejan Lavbič; investigation, Jan Vasiljević and Dejan Lavbič; data curation, Jan Vasiljević and Dejan Lavbič; writing—original draft preparation, Jan Vasiljević and Dejan Lavbič; writing—review and editing, Dejan Lavbič and Jan Vasiljević; visualization, Jan Vasiljević; supervision, Dejan Lavbič; project administration, Dejan Lavbič. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

The data that supports the findings of this study are not publicly available due to privacy restrictions. The participants in this research self-reported their answers regarding personality traits, and ensuring the confidentiality and privacy of their responses is of utmost importance. To protect the identity and sensitive information of the participants, we are unable to share the raw data.

Acknowledgments

Sincere gratitude to everyone who has contributed to completing this research, including the participating students and especially teaching assistants Marko Poženel and Aljaž Zrnec, for their dedicated assistance and support during the course Software Engineering.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:

TF	Team Formation
SE	Software Engineering
MBTI	Myers-Briggs Type Indicator
FFM	Five-Factor Model
TA	Teaching Assistant
O	Openness
C	Conscientiousness
E	Extraversion
A	Agreeableness
N	Neuroticism
ICC	Intraclass Correlation Coefficient

References

Zainal, D.; Razali, R.; Mansor, Z. Team Formation for Agile Software Development: A Review 2020. 10, 555. [CrossRef]
Budak, G.; Kara, I.; Ic, Y.; Kasimbeyli, R. New mathematical models for team formation of sports clubs before the match 2019. 27. [CrossRef]
Sommerville, I. Software Engineering, 9 ed.; Addison-Wesley, 2010.
Costa, A.; Ramos, F.; Perkusich, M.; Dantas, E.; Dilorenzo, E.; Chagas, F.; Meireles, A.; Albuquerque, D.; Silva, L.; Almeida, H.; et al. Team Formation in Software Engineering: A Systematic Mapping Study 2020. 8, 145687–145712. [CrossRef]
Fiore, S.; Salas, E.; Cuevas, H.; Bowers, C. Distributed coordination space: Toward a theory of distributed team process and performance 2003. 4. [CrossRef]
Mathieu, J.E.; Rapp, T.L. Laying the foundation for successful team performance trajectories: The roles of team charters and performance strategies. 2009. 94 1, 90–103. [CrossRef]
Burke, S. Is there a “Big Five” in Teamwork? 2005. 36, 555 – 599. [CrossRef]
Fiore, S.M.; Schooler, J.W. Process mapping and shared cognition: Teamwork and the development of shared problem models. 2004.
Driskell, J.E.; Goodwin, G.F.; Salas, E.; O’Shea, P.G. What makes a good team player? Personality and team effectiveness. 10, 249–271. [CrossRef]
Gilal, A.; Jaafar, J.; Omar, M.; Basri, S.; Izzatdin, A. Balancing the Personality of Programmer: Software Development Team Composition 2016. 29. [CrossRef]
O’Neill, T.A.; Allen, N.J. Personality and the Prediction of Team Performance. 25, 31–42. [CrossRef]
Kichuk, S.L.; Wiesner, W.H. The big five personality factors and team performance: implications for selecting successful product design teams 1997. 14, 195–221. [CrossRef]
Cruz, S.; Da Silva, F.; Monteiro, C.; Santos, C.; Dos Santos, M. Personality in software engineering: preliminary findings from a systematic literature review. In Proceedings of the 15th Annual Conference on Evaluation & Assessment in Software Engineering (EASE 2011). IET, pp. 1–10. [CrossRef]
Soomro, A.B.; Salleh, N.; Nordin, A. How personality traits are interrelated with team climate and team performance in software engineering? A preliminary study. In Proceedings of the 2015 9th Malaysian Software Engineering Conference (MySEC). IEEE; pp. 259–265. [CrossRef]
Rehman, M.; Mahmood, A.K.; Salleh, R.; Amin, A. Mapping job requirements of software engineers to Big Five Personality Traits. In Proceedings of the 2012 International Conference on Computer & Information Science (ICCIS). IEEE; pp. 1115–1122. [CrossRef]
Scott, T.J.; Tichenor, L.H.; Bisland, R.B.; Cross, J.H. Team dynamics in student programming projects. 26, 111–115. [CrossRef]
Costa, P.; McCrae, R. The Five-Factor Model, Five-Factor Theory, and Interpersonal Psychology 2012. pp. 91–104. ISBN 9780470471609. [CrossRef]
John, O.P.; Srivastava, S. The Big Five Trait taxonomy: History, measurement, and theoretical perspectives. 1999.
Ashton, M.; Lee, K.; Goldberg, L.; de Vries, R. Higher Order Factors of Personality: Do They Exist? 2009. 13, 79–91. [CrossRef]
Jia, J.; Zhang, P.; Zhang, R. A comparative study of three personality assessment models in software engineering field. In Proceedings of the 2015 6th IEEE International Conference on Software Engineering and Service Science (ICSESS), 2015; pp. 7–10. [CrossRef]
Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; ACM, 2016; pp. 785–794. [Google Scholar] [CrossRef]
Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the Advances in Neural Information Processing Systems; Guyon, I.; Luxburg, U.V.; Bengio, S.; Wallach, H.; Fergus, R.; Vishwanathan, S.; Garnett, R., Eds. Curran Associates, Inc., 2017, Vol. 30.
Luke, S. Essentials of Metaheuristics, second ed.; Lulu, 2013.
Hancock, S.A.; Hill, A.J. The effect of teammate personality on team production 2022. 78, 102248. [CrossRef]
Linden, D.v.d.; Nijenhuis, J.t.; Bakker, A.B. The General Factor of Personality: A meta-analysis of Big Five intercorrelations and a criterion-related validity study 2010. 44, 315–327. [CrossRef]
ICERI 2015: 8th International Conference of Education Research and Innovation, Seville (Spain), 16-18 November 2015 : proceedings; Iated Academy, 2015. OCLC: 992764949.
Liljequist, D.; Elfving, B.; Roaldsen, K.S. Intraclass correlation: A discussion and demonstration of basic features 2019. 14. [CrossRef]
Cicchetti, D. Guidelines, Criteria, and Rules of Thumb for Evaluating Normed and Standardized Assessment Instrument in Psychology 1994. 6, 284–290. [CrossRef]
Koo, T.K.; Li, M.Y. A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research 2016. 15, 155–163. [CrossRef]

Figure 1. Overview of the proposed approach.

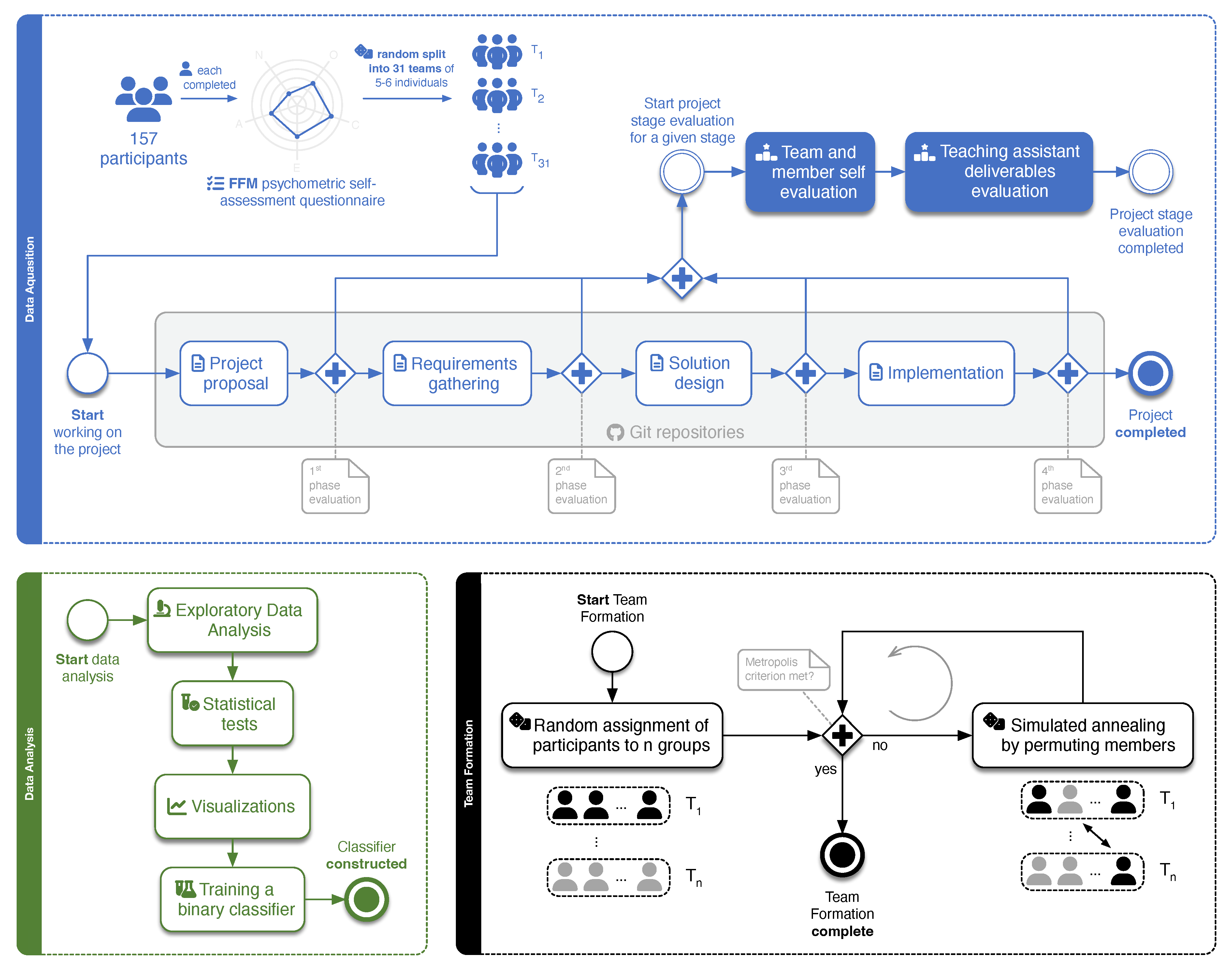
Figure 2. Histograms of grades assigned to individual students in each phase.

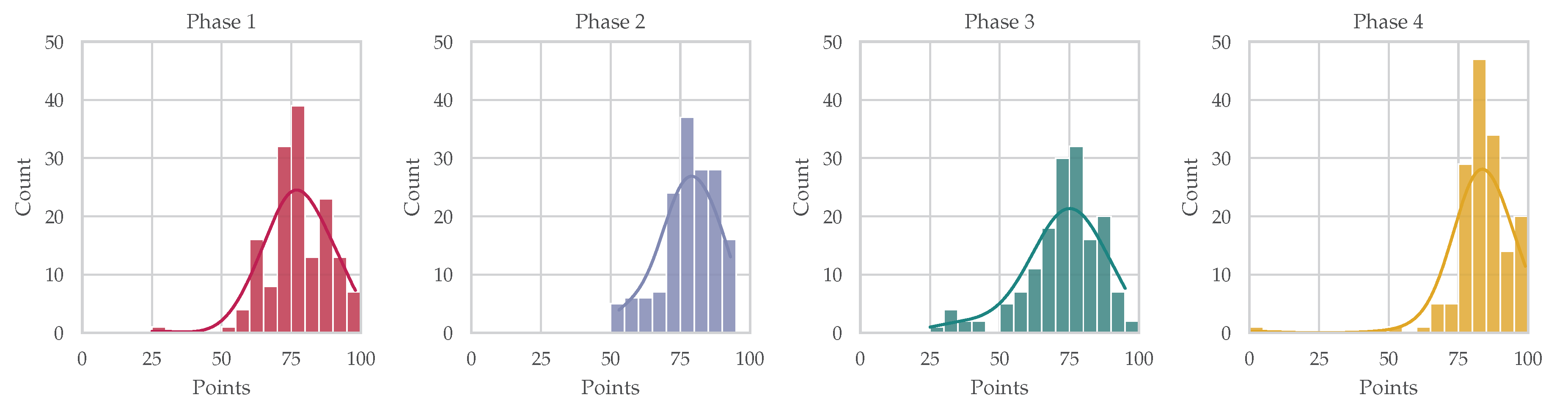
Figure 3. Stripplot of filtered out commits by various groups. The vertical dashed orange lines represent the deadlines for individual phases.

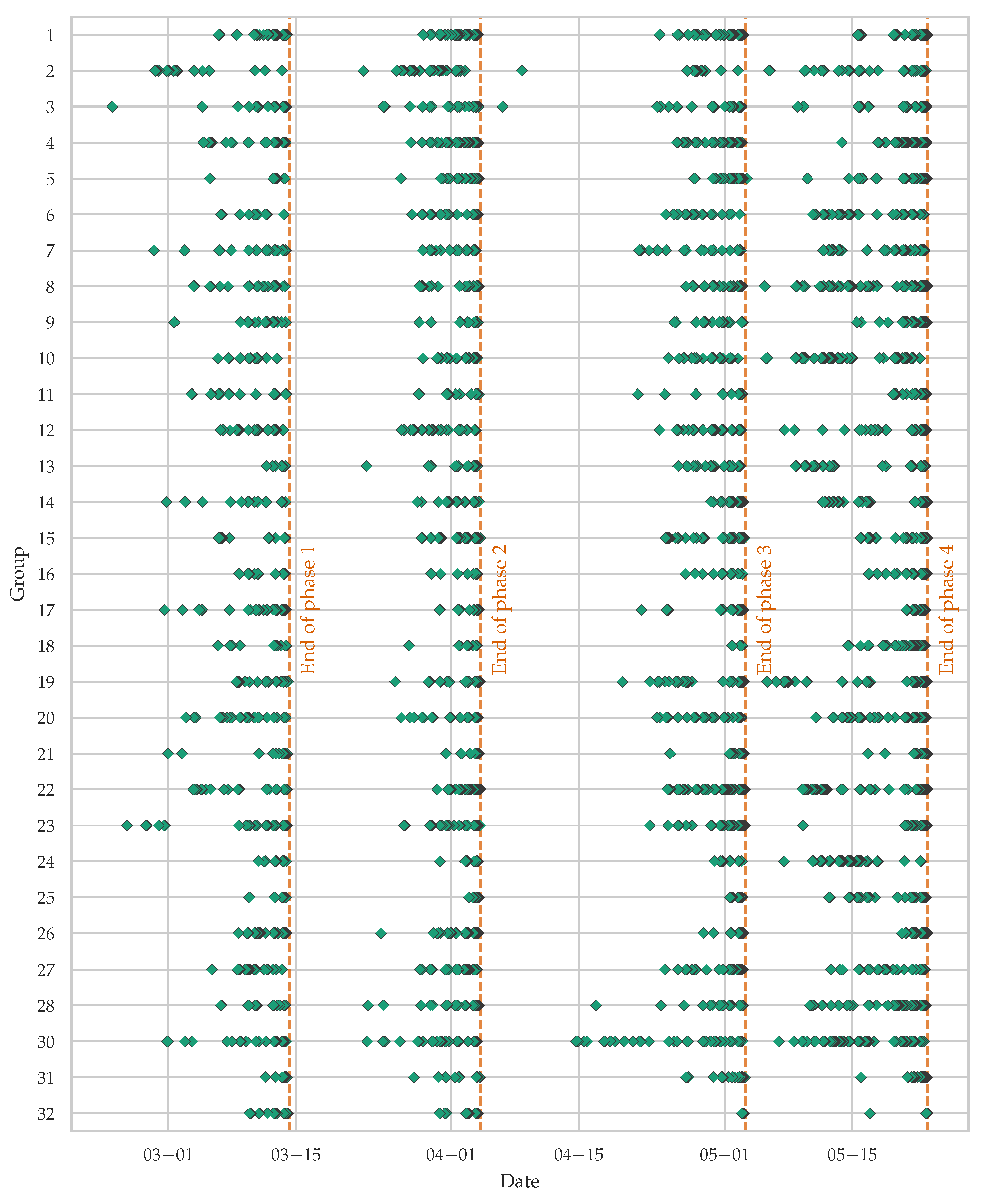
Figure 4. Plots of the FFM dimensions.

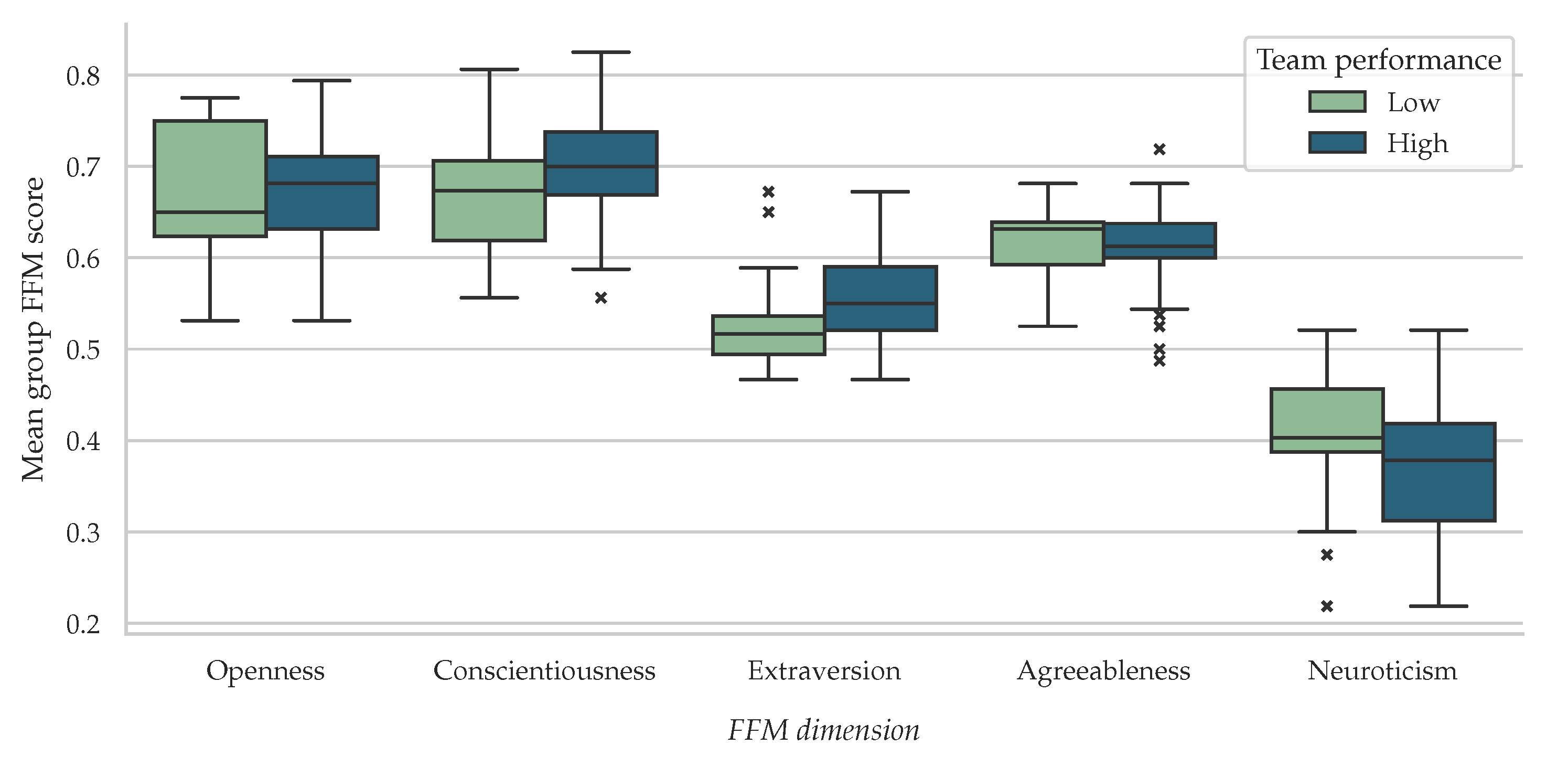
Figure 5. Relationship between team satisfaction and performance across project phases.

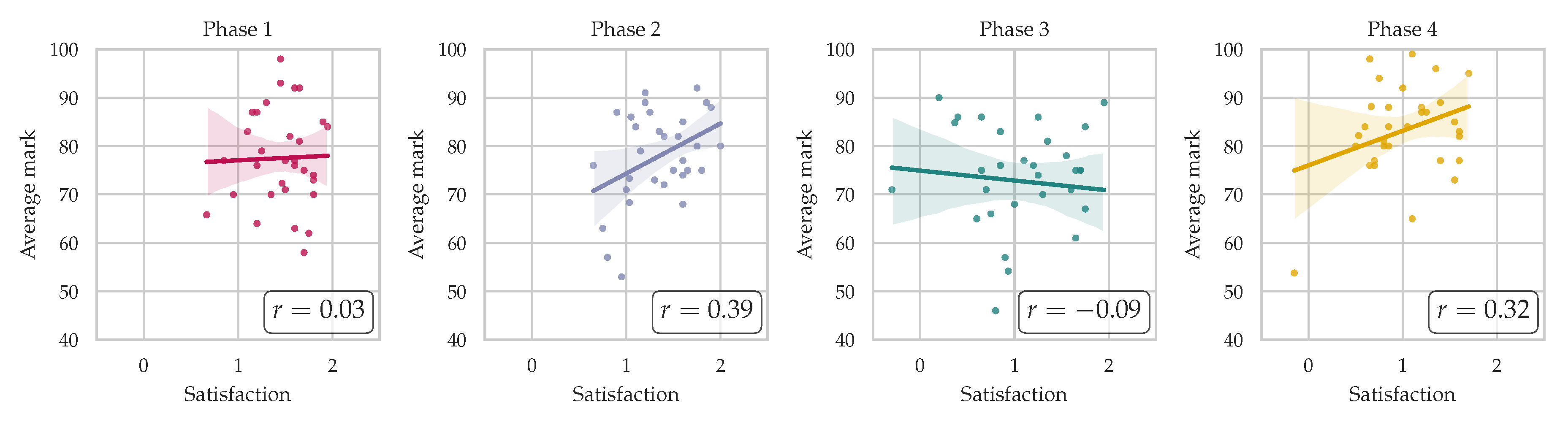
Figure 6. Regression plot of work contribution versus work ratio for each project phase.

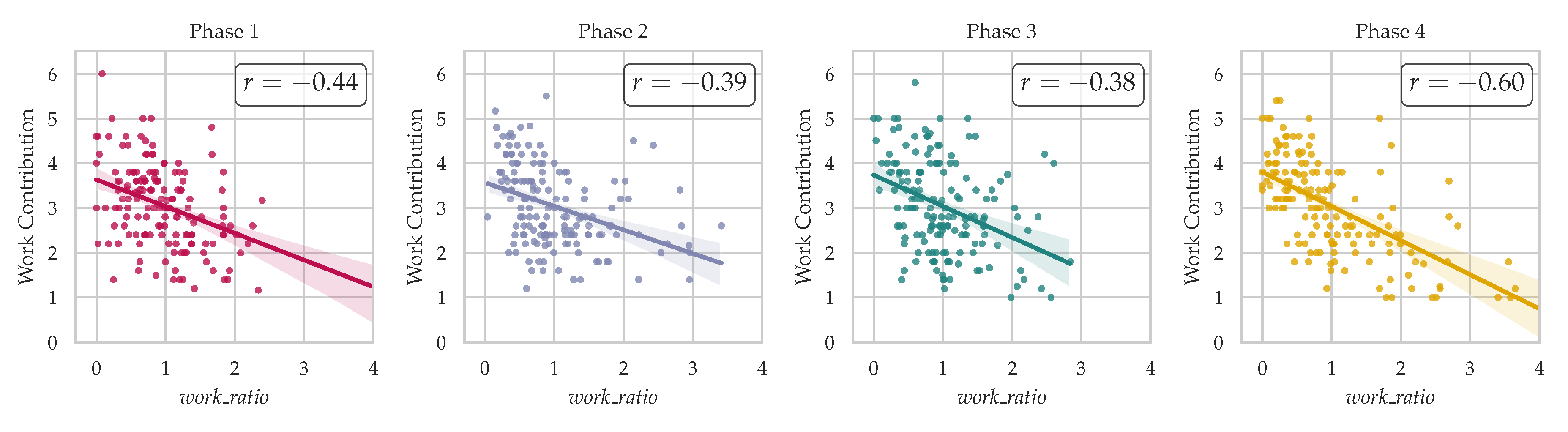
Figure 7. SHAP beeswarm plot of the XGBoost model displaying feature importance.

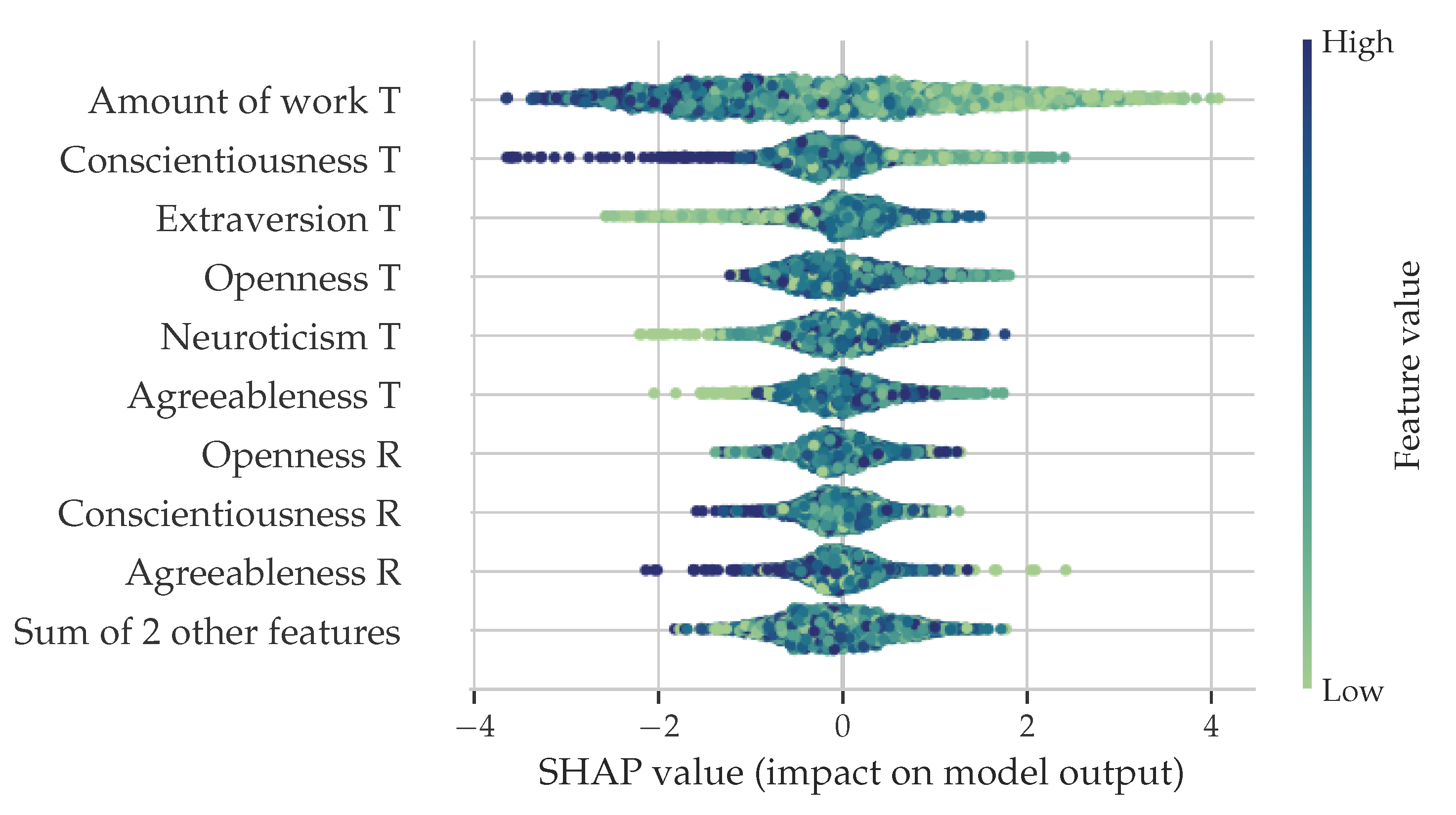
Figure 8. Waterfall plots of SHAP values for the XGBoost model. a) A positive classification. b) A negative classification.

Figure 9. SHAP dependance plot of Raters and Targets extraversion

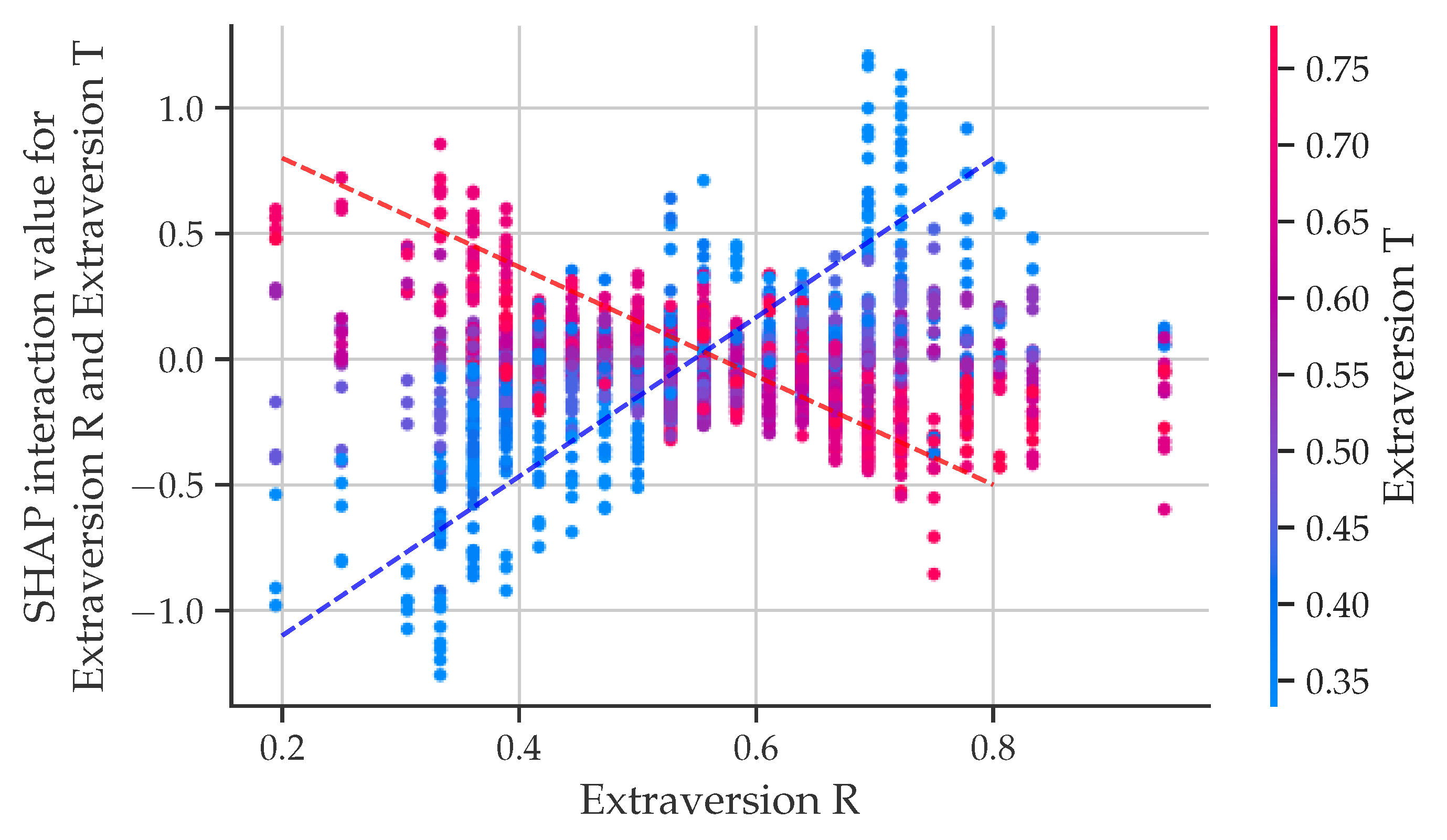
Figure 10. Distribution of scores before and after SA algorithm using 10000 iterations, with

w_{c} = 2

w_{e} = 1

w_{c} = 1

and

w_{inter} = 0.75

Figure 10. Distribution of scores before and after SA algorithm using 10000 iterations, with

w_{c} = 2

w_{e} = 1

w_{c} = 1

and

w_{inter} = 0.75

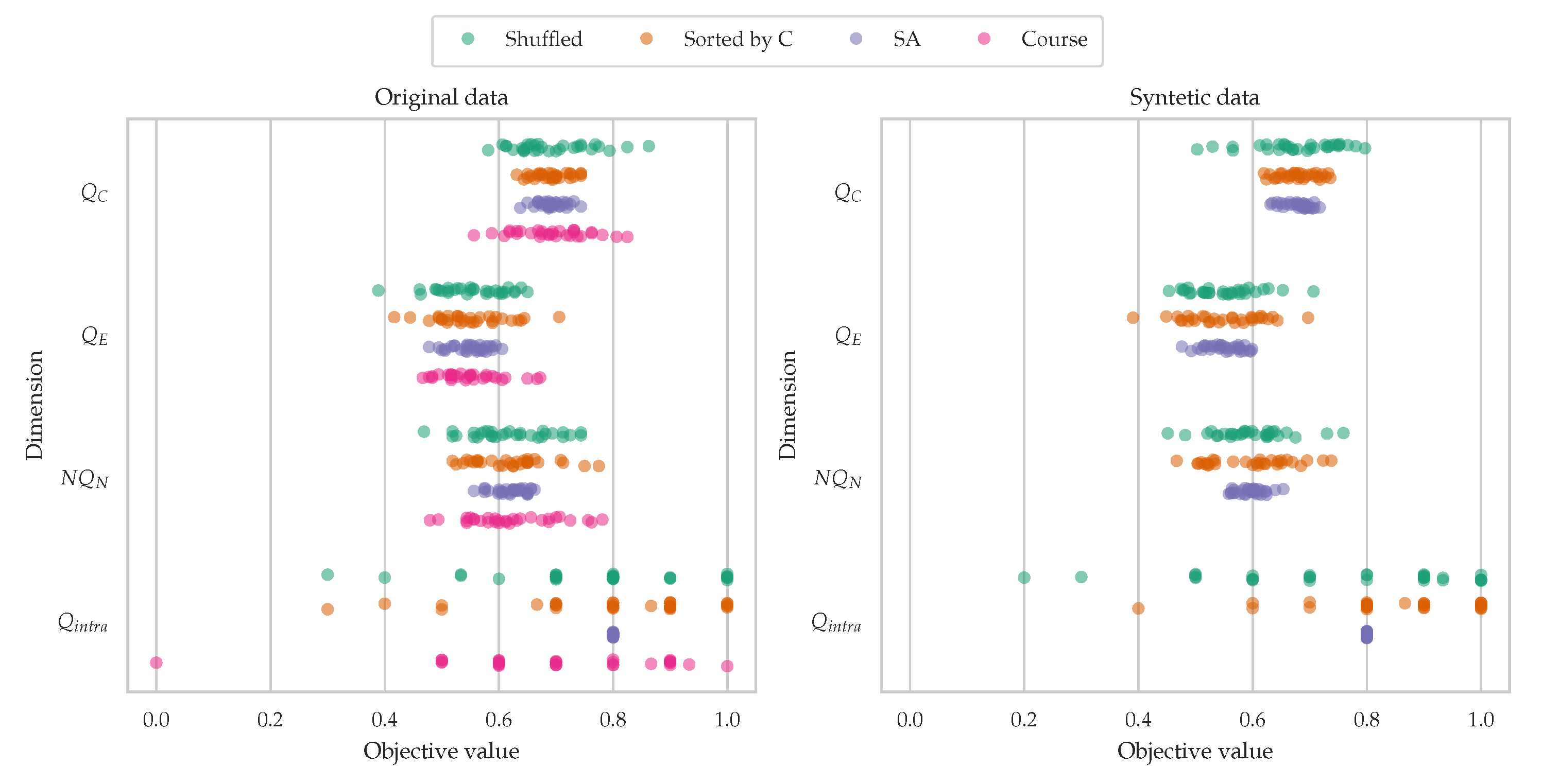
Table 1. Mean and standard deviation of the FFM personality traits.

	Openness	Conscientiousness	Extraversion	Agreeableness	Neuroticism
mean	0.67	0.69	0.55	0.61	0.38
std	0.15	0.14	0.14	0.13	0.16

Table 2. Correlation matrix of FFM dimensions among students. Symbols denote significance levels: *

p < 0.05

, **

p < 0.01

, ***

p < 0.001

Table 2. Correlation matrix of FFM dimensions among students. Symbols denote significance levels: *

p < 0.05

, **

p < 0.01

, ***

p < 0.001

	O	C	E	A	N
O (Openness)	-
C (Conscientiousness)	0.18*	-
E (Extraversion)	0.20*	0.23**	-
A (Agreeableness)	0.18*	0.00	-0.01	-
N (Neuroticism)	-0.07	-0.33***	-0.17*	-0.08	-

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Data-Driven Approach to Team Formation in Software Engineering Based on Personality Traits

Abstract

1. Introduction

2. Related work and proposed solution

3. Materials and Methods

3.1. Data Acquisition and Description

3.2. Five Factor Model

3.3. XGBoost and Shapley Additive EXplanations

3.4. Simulated Annealing

3.5. Data overview

3.5.1. Phase results

3.5.2. FFM data

3.5.3. Repository Commit Data

4. Results

4.1. Team Performance and FFM Dimensions

4.2. Analysis of Team Satisfaction Metrics

4.2.1. Work contribution

4.3. Binary Classification of Inter-Member Satisfaction

4.4. Team Formation Algorithm

5. Discussion and conclusion

Author Contributions

Funding

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe