Prerpints.org logo
Preprint
Article

Oscillation Resynchronization in a Photosensitive Reaction-Diffusion System

Altmetrics

Downloads

117

Views

43

Comments

0

This version is not peer-reviewed

Submitted:

25 November 2023

Posted:

01 December 2023

You are already at the latest version

Alerts
Abstract
: Oscillation synchronization through diffusion-based communication of active materials can lead to emergence of diverse patterns and collective behaviors. A detailed general description of the formation process of synchronization or resynchronization dynamics is a challenging task. We employ a photosensitive Belousov-Zhabotinsky reaction-diffusion model (within a gel media) to investigate the recovery process of oscillation synchronization between a pair of gel patches. The recovery time for oscillation resynchronization can be modulated by patch-distance, species of signaling molecules, intensity and duration of illumination. Analysis reveals that the “switch effect” of the gel-distance and the “promotion effect” from illumination on the oscillation resynchronization originate from the competition between processes of photo-promotion of oscillation, diffusion of signaling molecules (HBrO2 and Br-) and disproportionation of HBrO2. These results will benefit studies on bio-inspired active materials and soft motors.
Keywords: 
Subject: Chemistry and Materials Science  -   Physical Chemistry

1. Introduction

Active matter with communicating elements is an integrated system in which its elements can consume energy to perform mechanical work or to moves, including living organisms and active artificial systems. Communicating in some way and achieving synchrony between these elements to generate collective behaviors is a key issue for the active matter [1,2,3,4]. In living systems, elements communicate with each other through the diffusion of signal molecules [5], electronic signals [6], and stress signals [7,8] at various levels including sub-cellular, cellular, tissues, individual, and colony levels. This communication allows for the achievement of synchrony or asynchrony states and subsequently leads to the generation of self-replicating, self-healing, self-organizing and self-driving processes [2,4,5,6,7]. For examples, embryogenesis [9], the organization of myosin motor and actin filaments in the muscle elements [10], neural networks organized into memory media [11], organ development [12], weak synchronization of collective oscillation in bacterial colony [13], synchronization of rhythmic cilia [14,15], synchronization of metabolic of yeast cells [16], shallow gradients sensing of cell colony [17], synchronization of firefly fluorescence [18] and Mexican waves in stadium [19]. The elements of active matter interact with each other through various type of communication to produce emergent collective behaviors.
The emergent mechanism and systematic control of this process are important scientific issues [20]. The research findings in this field have been utilized for designing artificial systems, including functional active materials and soft robots. For examples, Huygens’ synchrony of coupled liquid crystalline oscillators [21], particle robots [22], bio-inspired Central pattern generator [23], Interactive Materials [24], synchronized pattern in active materials [25].
In the previous report, researchers explored how the synchrony state of the system changes with environment and system parameters. They discovered the mechanism that governs the final synchrony state and transitions between different synchrony states based on these parameters. Additionally, they proposed design criteria for various functions based on these laws. However, one challenge that has yet to be elucidated in this scientific field is understanding the general mechanism behind the evolution process of synchronous states, rather than solely studying stable synchronous states. From a research operability perspective, this problem can be expressed as finding a general mechanism for the system recovering from a damaged synchrony state. E.g., How can the dynamics of resynchronization in the reaction-diffusion system (RDS) of a disarranged living organism [5] be described in general?
The synchronization between different sub-RDS through molecular diffusion-based communication is ubiquitous in nature, also serves as a universal model system for bioinspired synchronization [5,6,7,23,24,25]. In this work, a widely studied photosensitive active polymer gel that hosts the tris(bipyridine)ruthenium [Ru(bipy)]-catalyzed Belousov-Zhabotinsky reaction (BZR) is used to study the resynchronization behavior. It is a reaction-diffusion-force coupling system, which can transform chemical energy into mechanical work autonomously [26] and can be controlled by illumination. Balazs and coworkers simulated and analyzed chemical-mechanical co-oscillatory behavior within am anisotropic BZ gel medium via gLSM [27,28,29], stress-modulated synchronized oscillation [30], geometrical parameter modulated collective oscillation of multiple gels [31], synchronized waves modulated by the asymmetric size of media [32], mechanical-chemical effect on the synchronized oscillation [33] and materials with BZ gel that compute [34]. The BZ gel system is also one of the important research systems for bionic directed motion [35,36,37,38,39,40,41] and collective behavior [28,42,43], both of which are closely related to oscillation synchronization.
To simplify, we simulate the oscillation synchronization process between inert BZ gel samples immersed in the BZ reaction solution (a pair of circular gel samples), where illumination induces the destruction of an initially synchronized state. Where the “inert” refers to a nondeformable BZ gel with a highly crosslinked polymer [44]. The catalyst for the BZ reaction exists only inside the gel patch, therefore BZR occurs only inside the gel. The communication between patches can be achieved through the diffusion of the intermediate products of BZR [45]. In this work, we characterize the recovery process of oscillation synchronization by measuring time it takes for two gel blocks to resynchronize (recovery time). We explore the effect of the light intensity, the spacing of the gel patches and other factors on the recovery time. Finally, we propose a mechanism of the resynchronization between the gel patches.

2. Results and discussion

2.1. Model and schematic of the system

In this work, we employ a modified version of Amimiya’s photosensitive BZ reaction model (in its four-variable form [46]) to investigate a reaction-diffusion system, specifically the synchronized oscillation reaction between gel patches in a two-dimensional thin-solution condition. Note that oscillation denotes periodic changes of concentration versus time. For a solution system that is sufficiently thin, the hydrodynamic effect can be disregarded, implying that it can be described by a reaction-diffusion equation. Notably, this four-variable model enables us to explore the roles of the intermediate products HBrO2, Br-, and BrMA in the process of communication and synchronization between gel patches. It also helps us to determine which substance plays a significant role in the communication process and acts as a signaling molecule. The differential expression reads
∂x/∂t = (x - x2 + y(q -x) + IP2) /ε1 + Dx∇2x
∂v/∂t = (-qy + 2xy +0.5x2 – vz – rv – IP1) /ε2 + Dv∇2v
∂y/∂t = (-qy - xy + vz + IP1) /ε3 + Dy∇2y
∂z/∂t = x – z - nvz + I (0.5P1+P2)
Where x, v, y and z denote dimensionless concentration of HBrO2, BrMA, Br- and Ru3+, respectively. x=X/X0, v=V/V0, y=Y/Y0, z=Z/Z0, X, V, Y, Z, H and X0, V0, Y0, Z0, H0 are dimensional concentration and initial concentration of HBrO2, BrMA, Br-, Ru3+, H+ respectively. A0 and B0 are dimensional concentration of BrO3- and MA. q, ε1, ε2, ε3, n, P1 and P2 are parameters of the Amimiya model. q=1×10-4, ε1=3.1×10-3, ε2=1.8×10-5, ε3=3.5×10-4, n=12.23, P1=0.124, P2=0.77. I is dimensionless illumination intensity. Dimensionless diffusion coefficients Dx, Dv, and Dy are set at 1.0 (serving as the default value), which corresponds to a diffusion coefficient value of 1.5×10-5 cm2/s for the substance in solution (Dreal). The absence of a diffusion process for the catalyst substance (z variable) is attributed to its binding with the gel chains. The unit time T0 = 1/(k5B0), the unit length L0 = (Dreal T0)0.5. The time step is set at 1.0×10-4. The governing partial differential equation were numerically integrated using an explicit fourth-order Runge-Kutta method and utilizing nine-point central-difference approximations for 2D Laplacian operators. Our simulation of the 2D system employs 1024×1024 grid points, and zero-flux boundary condition were used at all ends.
As shown in Figure 1a, two circular gels are positioned and fixed in the center of the rectangular area with a distance dx. The remaining area (excluding the gels) contains the catalyst-free BZ solution. A pair of samples consists of gel patch 1 and 2, which are placed on the left and right sides of the space, respectively. The default concentration of reactants enables autonomous oscillation reactions to occurs in the gel. The diffusion of intermediate products (HBrO2, Br-, and BrMA) continues throughout all regions of the system. Note that BZ reaction take place in the gel patches; while only the disproportionation of HBrO2 occurs in the solution part. The reactants bromate, acidity, and malonate of BZR are uniformly distributed throughout the space and are assumed to satisfy the Pool approximation, which ensures that their concentrations remain constant.
The background light intensity (I0) illuminates both gel patch 1 and 2, serves as the default value for environmental illumination. Starting at a specific moment (uniformly 625s), a sustaining light intensity I is initiated and only illuminate to the gel patch 1. Photoreaction process in the BZR enables the system to produces various products, such as Br-, Ru3+ and HBrO2. On the one hand, this process obeys a nonmonic relationship between oscillation frequency and light intensity (the F-I relationship) [46], that is, with increasing illumination, the oscillation frequency undergoing a fast rise and a slow drop, namely photo-promoting (I = 0.0 ~ 5.0×10-5) and photo-inhibiting (I = 5.0×10-5~1.28×10-4) of oscillation frequency, respectively, as shown in Figure 1b. On the other hand, it modulates various type of diffusion-based communication through signal molecules. Here, the light intensity is dimensionless parameter. In this paper, the destruction of oscillation-synchrony is carried out based on the F-I relationship (the frequency of oscillation modulated by illumination intensity). Initially, the two gel patches have the same oscillation frequency under the background illumination (I0=1.0×10-5). When the light intensity is applied solely to the gel patch 1, it changes the oscillation frequency and generates a transient state of asynchronous oscillation between the gel pair. Then, the recovery process from oscillation synchronous can be observed and analyzed.

2.2. Recovery of synchrony oscillation between gel patches

Firstly, we analysis the recovery process of oscillation synchrony between the gel patches just after applying light I (2.0×10-5) only to the patch 1. As shown in Figure 1b, the illumination I =2.0×10-5 is located at the photo-promotion region of the F-I relationship. As shown in Figure 2a–d, the simulated spatiotemporal plot of each intermediate products enables us to analyze the process of resynchronized oscillation intuitively. Each space-time plot consists of 3000 concentration data for (a) HBrO2, (b) Ru3+, (c) Br-, and (d) BrMA scan along the center line crossing the pair gels (see dashed line in Figure 1a) at 3 s intervals. The left and right areas of each plot, representing patches 1 and 2, are separated by respective gaps. The gap in the middle of each plot represents the space between the gel pair, where variables x, v, and y can diffuse and fill due to their nature of diffusion. Note that the gap shown in Figure 2 represents the shortest distance between the two circular gels, however, the average distance between them is greater. When the system is in an initial synchronized state (time<625 s), the pair gel has the same oscillation phase and frequency due to identical details on both patches (in the time region above the dashed line in Figure 2a–d). When the gel patch 1 is illuminated at time= 625 s (indicated by the dashed line), sustained changes occur in the spatiotemporal pattern within the patches (asynchrony state) until 1060 s, when two patches oscillate with the same frequency, implying the resynchronized oscillation. Note that the oscillation frequency of patch 2 changes only due to the communication between the gel, without any other impact on it. Figure 2e shows the local value of the variable v at the center of both patches versus time, revealing noticeable variations in oscillation amplitude at time points (625 s and 1060 s), respectively. At around 1060 s, the oscillation period of gel patch 2 is the same as that in patch 1 but with a phase delay due to a photo-promotion effect (I=2.0×10-5) on oscillation frequency in the gel patch 1, resulting in wave propagation from patch 1 to patch 2. Note that intermediate HBrO2 will gradually decompose during diffusion, which limits its communication distance as a signaling molecule. In previous studies, it is regards as the main signaling molecule for diffusion-based communication between the BZ gels [28]. The effect of different signaling molecules on the synchrony-recovery will be discussed later in order to identify the dominate signaling molecule.
Real-time oscillation frequencies in the center of two patches are shown in Figure 3, respectively. The real-time frequency refers to the reciprocal of current period of these oscillations. Figure 3 demonstrates a clear increase in oscillation frequency when the gel patch 1 is illuminated with I=2.0×10-5, which aligns accord with the F-I relationship (refer to Figure 1b). Compared to Figure 2, Figure 3 clearly illustrates the time points when illumination starts and the recovery of synchrony. Moreover, Figure 3 demonstrates that the oscillation frequency of the pair patches ultimately matches that of the illuminated one (the gel patch 1).

2.3. Recovery time of synchronization modulated by illumination

It is clear that the recovery time can server as a dynamic characteristic of the synchronization recovery. The effect of parameters on the resynchronization, specifically in terms of recovery time, is currently under investigation. The parameters include the light intensity of I, the distance between patches and the duration of illumination. Furthermore, studying diffusion-limited schemes help to identify signaling molecules. The mechanics of resynchronization can be discussed based on this.
As shown in Figure 4, there are five scenarios with I set at 1.2×10-5, 1.4×10-5, 1.6×10-5, 1.8×10-5 and 2.0×10-5, respectively. The time series of frequency for each scenario eventually achieve a resynchronized state with different frequency, that is, high intensity of I for high frequency which dominated by photo-promotion effect as shown in Figure 1b. Keeping the start time of irradiating fixed at 625 s, the recovery time of oscillation synchronization between two gel patches decreasing from 1082 s, 732 s, 575, 520 s to 516 s, with increasing light intensity (I) from 1.2×10-5, 1.4×10-5, 1.6×10-5, 1.8×10-5 to 2.0×10-5, respectively. Note that when I is greater than 1.6×10-5, the decreasing trend of the recovery time gradually slows down. Why is fasting recovery with illumination used for generating synchronization? According to the Amimiya’s photosensitive BZR model [46], our work on the F-I relationship [46], and a general viewpoint of HBrO2 diffusion-based communication [28], at low light intensity, photoreaction generates HBrO2 which not only promotes oscillation frequency but also increases diffusion-based communication due to a high concentration of photo-generated HBrO2, thereby shorting the recovery time. However, at high light intensity, the photo-generation effect on HBrO2 approaches saturation [45,46], where the photo effect on the recovery time changes little with light intensity.

2.4. Recovery time of synchronization modulated by the patches-distant

Another crucial factor that influences the communication process is the distance separating the communicated pair. As shown in Figure 5, here are five schemes with the distance dx set at 0.04 mm, 0.06 mm, 0.08 mm, 0.10 mm, and 0.12 mm, respectively. In the initial state, each scheme has the same oscillation frequency until the gel patch 1 is exposed to the irradiated light intensity (I = 1.4×10-5). It is evident from the Figure 5 (e.g., at the marking of gel patch 1) that the oscillation frequency of gel patch 1 increases rapidly in all the systems after application and then stabilizes. After the “light on” (time > 625 s), the oscillation frequency of gel patch 1 suddenly increases to 0.014 s-1, while the frequency of gel patch 2 undergoes changes based on the value of dx. Specifically, when dx ≤ 0.08 mm, resynchronization between the pair is successful with almost identical recovery time (732 s). However, when dx > 0.08 mm, the gel pair experiences an asynchronous state. In particular, new frequency of the oscillation frequency occurs when dx = 0.10 mm, which is represented as a period change of frequency versus time (see Figure 5). The results suggest that the synchronous state can only occur when the distance is small enough (dx ≤ 0.08 mm).

2.5. Effect of illumination-duration on the recovery time

In the above schemes, there is only “switch on” option for the irradiation on the patch 1. As shown in Figure 6, the effect of I-duration on the resynchronization is discussed, with options for both “switch on” and “switch off” irradiation. The I-duration for three schemes is 250 s, 500 s, and 875 s, respectively. For the gel patch 1, all schemes shown a fast decrease of oscillation frequency. In the photosensitive BZR, the critical concentration of Br- ([Br-]cr) in photo-promotion state (I=1.4×10-5) is high than that in the low light intensity (I0=1.4×10-5), thus, when the illumination changes from I to I0 (switch off), the reaction requires more time to reach [Br-]cr, resulting in a prolonged period of oscillation and a decrease in frequency [46]. For gel patch 2, there is no change in frequency 2 when the duration is short (Figure 6a). However, when the duration equals 500 s, a critical state of resynchronization occurs (see Figure 6b). When the I-duration is large enough, clear resynchronization takes place until “switch off”. This suggests that the diffusion-based communication of signaling molecules in response to light intensity can only be effective if the new state of patch 1 is maintained for a certain duration. In other words, the resynchronization requires sufficient time for the diffusion of signaling molecules through the gap while the patch 1 remains in its current state (illuminated by I).

2.6. Signal molecules for the synchrony recovery

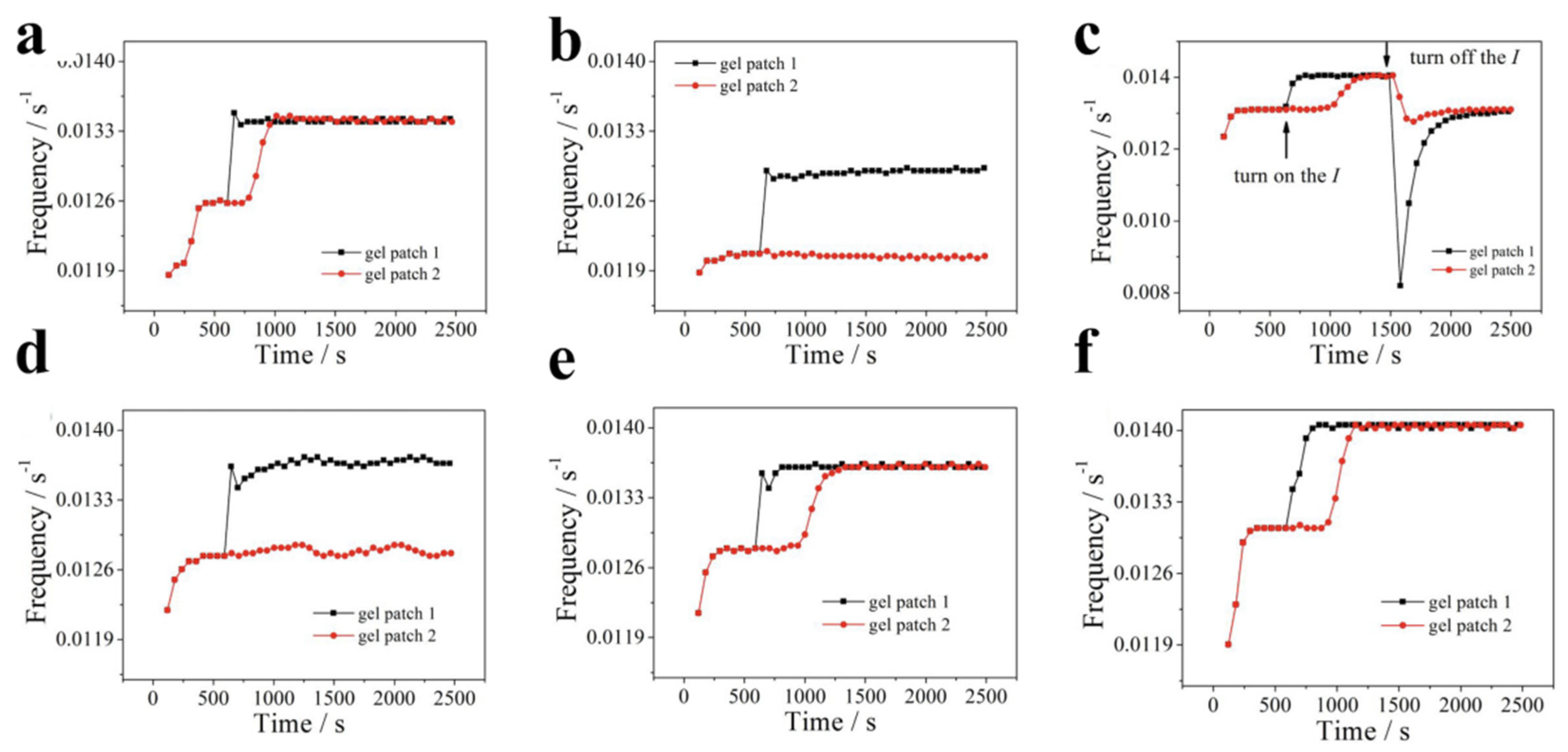
Another fundamental question remains unanswered: what is the effect of diffusive molecules (HBrO2, BrMA and Br-) of BZR on the resynchronization. Here, numerical sim-ulations are conducted for ideal schemes with limited diffusion. These schemes involve variables x, v and y, which correspond to HBrO2, BrMA and Br- in the system with or without diffusion. Some conclusions can be drawn from these six schemes based on the data in Figure 7. Firstly, in all schemes, the resynchronization will fail where the diffusion of HBrO2 is totally prohibited, which indicate the diffusion of HBrO2 is the sufficient and necessary condition for the resynchronization. Secondly, by comparing Figure 6a,e, it is clear that the diffusion of y (Br-) prolongs the recovery time of resynchronization pro-cess, indicating an inhibition effect of Br- on the recovery. Thirdly, by comparing Figure 6 (a) with (f), the diffusion of BrMA have a promotion effect on the basic oscillation frequency (without regard to illumination) but have little effect on the recovery time. In addition to HBrO2, the prolonging effect of Br- on the resynchronization is due to its inhibition of BZR autocatalysis. The promotion effect of BrMA diffusion on the basic oscillation frequency originates from a decrease in concentration of BrMA within the gel patch 1 induced by diffusion, which indirectly reduces the production of Br-, as demonstrated in our previous work [46]. As shown in Figure 7, it is evident that the presence of Br- inhibits the recovery process, indicating its role as a signaling molecule for communication in our system. As far as we know, this is the first time that a second signaling molecule has been identified in the synchronization of the BZR system.

3. Conclusions

Using a modified Amimiya’s photosensitive BZR model for studying resynchronization oscillation between a pair gel patch, we found that recovery process of the synchronization can be modulated by distance between the pair, the intensity and the duration of illumination. The results revealed that photo-promotion effect of the F-I relationship shorting the oscillation resynchronization with one patch-illuminated, while both the pair distance and the illumination-duration manifest as a “switch effect” on the oscillation resynchronization. Moreover, besides HBrO2, we found the inhibitor of oscillation BZR (Br-) have an obvious delay effect on the resynchronization process, which indicate oth HBrO2 and Br- are signaling molecules for such diffusion-based communication. To sum up, our results indicate that a “switch effect” of pair-distance which modulate by photo-promotion of the F-I relationship of the photosensitive BZR on the oscillation resynchronization of the pair gel patches, which originate from the competition between photo-generation while diffusion of signaling molecules (HBrO2 and Br-) and disproportionation of HBrO2.
Furthermore, new experimental efforts should be conducted under the guidance of these simulations. The size of gel with a circular shape may significantly impact the distance effect on resynchronization. Therefore, further research should be carried out using pairs of rectangle gels or other shaped samples. Another important issue is how the new frequency generation occurs during the transition from resynchronization to asynchronization via a state of periodic changes in oscillation frequency. Moreover, based on our results in the inert system, exploration into various types of directional locomotion and collective behavior of active gel with diffusion-based communication can proceed further.

Author Contributions

Conceptualization, L.R. and D.S.; methodology, L.R.; formal analysis, D.S.; investigation, Y.T.; data curation, Q. Z.; writing—original draft preparation, D.S.; writing—review and editing, L.R.; visualization, D.S.; project administration, L.R.; funding acquisition, L.R. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China grant number 21972165 and 22372122.

Institutional Review Board Statement

Not applicable

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Balanov, A.; Janson, N.; Postnov, D.; Sosanovtseva, O. Synchronization from simple to complex. Springer, 2008, pp. 1-19.
  2. Winfree, A. T. The Geometry of Biological Time. Springer, 1980, pp. 347-366.
  3. Bechinger, C.; Leonardo, R. D.; Löwen, H. Active particles in complex and crowded environments. Rev. Mod. Phys. 2016, 88, 045006. [CrossRef]
  4. Merindol, R.; Walther. A. Materials learning from life: concepts for active adaptive and autonomous molecular systems. Chem. Soc. Rev. 2017, 46, 5588-5619. [CrossRef]
  5. Soh, S.; Byrska, M.; Kandere-Grzybowska, K.; Grzybowski, B. A. Reaction-Diffusion Systems in Intracellular Molecular Transport and Control. Angew. Chem. Int. Ed. 2010, 49, 4170-4198. [CrossRef]
  6. Alexander, R. M. Principles of Animal Locomotion. Princeton, 2002, pp. 21-48.
  7. Pollard, T. D.; Earnshaw, W. C.; Lippincott-Schwartz, J.; Johnson, G. Cell biology. Elsevier Health Sciences, 2016, pp. 24-56.
  8. Ji, F. T.; Wu, Y. L.; Pumera, M.; Zhang, L. Collective Behaviors of Active Matter Learning from Natural Taxes Across Scales. Adv. Mater. 2022, 35, 202203959. [CrossRef]
  9. Oates, A. C.; Morelli, L. G.; Ares, S. Patterning embryos with oscillations: structure, function and dynamics of the vertebrate segmentation clock. Development 2012, 139, 625–639. [CrossRef]
  10. Squire, J. M. In muscle sarcomeres, myosin are threaded in thick-filaments interdigitized with actin fibrils. Curr. Opin. Struct. Biol. 1997, 7, 247–257. [CrossRef] [PubMed]
  11. Umbach, G.; Tan, R.; Jacobs, J.; Pfeiffer, B. E.; Lega, B. Flexibility of functional neuronal assemblies supports human memory. Nat. Commun. 2022, 13. 6162. [CrossRef]
  12. He, L.; Wang, X.; Tang, H. L; Montell, D. J. Tissue elongation requires oscillating contractions of a basal actomyosin network. Nat. Cell Biol. 2012, 12, 1133–1142. [CrossRef]
  13. Chen, C.; Liu, S.; Shi, X. Q.; Chate, H.; Wu, Y. L. Weak synchronization and large-scale collective oscillation in dense bacterial suspensions. Nature 2017, 542, 210-214. [CrossRef] [PubMed]
  14. Tu, H. Q.; Li, S.; Xu, Y. L.; Zhang, Y. C.; Li, P. Y.; Liang, L. Y. Rhythmic cilia changes support SCN neuron coherence in circadian clock. Science 2023, 380, 972-979. [CrossRef]
  15. Gilpin, W.; Bull, M. S.; Prakash, M. The multiscale physics of cilia and flagella. Nat. Rev. Phys. 2020, 2, 74–88. [CrossRef]
  16. Ghosh, A. K.; Chance, B.; Pye, E. K. Metabolic coupling and synchronization of NADH oscillations in yeast cell populations. Arch. Biochem. Biophys. 1971, 145, 319-331. [CrossRef]
  17. Ellison, D.; Mugler, A.; Brennan, M. D.; Lee, S. H.; Huebner, R. J.; Dhamir, E. R.; Woo, L. A. Cell-cell communication enhances the capacity of cell ensembles to sense shallow gradients during morphogenesis. Proc. Natl. Acad. Sci. USA. 2016, 113, E679-E688. [CrossRef] [PubMed]
  18. Smith, H. M. Synchronous flashing of fireflies. Science 1935, 82, 151-152. [CrossRef] [PubMed]
  19. Farkas, I.; Helbing, D.; Vicsek, T. Mexican waves in an excitable medium. Nature 2002, 419, 131–132. [CrossRef]
  20. Andersan, P.W. More is different. Science 1972, 4, 393-396. [CrossRef] [PubMed]
  21. Vantomme, G.; Elands, L.; Gelebart, A. H. Coupled liquid crystalline oscillators in Huygens’ synchrony. Nat. Mater. 2021, 20, 1702–1706. [CrossRef]
  22. Li, S. G.; Batra, R.; Brown, D.; Chang, H. D.; Ranganathan, N.; Hoberman, C.; Rus, D.; Lipson, H. Particle robotics based on statistical mechanics of loosely coupled components. Nature 2019, 567, 361-365. [CrossRef]
  23. Litschel, T.; Norton, M. M.; Tserunyan, V.; Fraden, S. Engineering reaction–diffusion networks with properties of neural tissue. Lab. Chip 2018, 18, 714-722. [CrossRef]
  24. Lerch, M. M.; Grinthal, A.; Aizenberg, J. Viewpoint Homeostasis as Inspiration Toward Interactive Materials. Adv. Mater. 2020, 32, 1905554. [CrossRef]
  25. Totz, J. F. Synchronization and Waves in Active Media. Springer, 2019, pp. 37-52.
  26. Yoshida, R.; Takahashi, T.; Yamaguchi. T.; Ichijo, H. Self-Oscillating Gel. J. Am. Chem. Soc. 1996, 118, 5134–5135. [CrossRef]
  27. Kim, Y. S.; Tamate, R.; Akimoto, A. M. Recent developments in self-oscillating polymeric systems as smart materials: from polymers to bulk hydrogels. Mater. Horiz. 2017, 4, 38-54. [CrossRef]
  28. Kuksenok, O.; Dayal, P.; Bhattacharya, A. Chemo-responsive, self-oscillating gels that undergo biomimetic communication. Chem. Soc. Rev. 2013, 42, 7257-7277. [CrossRef]
  29. Osypova, A.; Dubner, M.; Panzarasa, G. Oscillating reactions meet polymers at interfaces. Materials 2020, 13, 2957. [CrossRef]
  30. Yashin, V. V.; Balazs, A. C. Chemomechanical synchronization in heterogeneous self-oscillating gels. Phys. Rev. E 2008, 77, 046210. [CrossRef] [PubMed]
  31. Yashin, V. V.; Balazs, A. C. Controlling chemical oscillations in heterogeneous Belousov-Zhabotinsky gels via mechanical strain. Phys. Rev. E 2009, 79, 046214. [CrossRef]
  32. Yashin, V. V.; Suzuki, S.; Yoshida, R.; Balazs, A. C. Controlling the dynamic behavior of heterogeneous self-oscillating gels. J. Mater. Chem. 2012, 22, 13625. [CrossRef]
  33. Tateyama, S.; Shibuta, Y.; Yoshida, R. Direction Control of Chemical Wave Propagation in Self-Oscillating Gel Array. J. Phys. Chem. B 2008, 112, 1777. [CrossRef] [PubMed]
  34. Ito, K.; Ezaki, T.; Suzuki. S.; Kobayashi, R.; Hara, Y.; Nakatra, S. Synchronization of Two Self-Oscillating Gels Based on Chemo-Mechanical Coupling. J. Phys. Chem. B 2016, 120, 2977. [CrossRef]
  35. Fang, Y.; Yashin, V. V.; Levitan, S. P.; Balazs, A. C. Pattern recognition with “materials that compute”. Sci. Adv. 2016, 2, e1601114. [CrossRef] [PubMed]
  36. Lu, X.; Ren, L.; Gao, Q.; Zhao, Y.; Wang, S.; Yang, J.; Epstein, I. R. Photophobic and phototropic movement of a self-oscillating gel. Chem. Commun. 2013, 49, 7690-7692. [CrossRef] [PubMed]
  37. Ren, L.; She, W.; Gao, Q.; Pan, C.; Ji, C.; Epstein, I. R. Retrograde and Direct Wave Locomotion in a Photosensitive Self-Oscillating Gel. Angew. Chem. Int. Ed. 2016, 55, 14301-14305. [CrossRef]
  38. Ren, L.; Wang, M.; Pan, C.; Gao, Q.; Liu, Y.; Epstein, I. R. Autonomous reciprocating migration of an active material. Proc. Nati. Acad. Sci. USA. 2017, 114, 8704-8709. [CrossRef]
  39. Ren, L.; Wang, L.; Gao, Q.; Teng, R.; Xu, Z.; Wang, J.; Pan, C.; Epstein, I. R. Programmed Locomotion of an Active Gel Driven by Spiral Waves. Angew. Chem. Int. Ed. 2020, 59, 7106 -7112. [CrossRef]
  40. Ren, L.; Yuan, L.; Gao, Q.; Teng, R.; Wang, J.; Epstein, I. R. Chemomechanical Origin of Directed Locomotion Driven by Internal Chemical Signals. Sci. Adv. 2020, 6, eaaz9125. [CrossRef] [PubMed]
  41. Wang, J.; Ren, L.; Teng, R.; Epstein, I. R.; Wang, H.; Zhang, M.; Yuan, L.; Gao, Q. Y. Rotational Locomotion of an Active Gel Driven by Internal Chemical Signals. J. Phys. Chem. Lett. 2021. 12. 11987-11991. [CrossRef] [PubMed]
  42. Teng, R.; Gao, Q. Y; Yuan, L.; Ren, L.; Wang, J.; Wang, Y. J.; Epstein, I. R.; Heterogeneity-driven collective-motion patterns of active gels. Cell Rep. Phys. Sci. 2022, 3, 100933. [CrossRef]
  43. Teng, R.; Li, Y.; Ren, L.; Epstein, I. R.; Gao, Q. Y. Transitions of Collective Motions Driven by Phase Resetting. Chem. Phys. Chem. 2023, 24, e202300336. [CrossRef] [PubMed]
  44. Lu, X. J.; Ren, L.; Gao, Q. Y.; Yang, Y. Y.; Zhao, Y. M.; Huang, J.; Lu. X. L.; Epstein, I. R. Multiple Length Scale Instabilities of Unidirectional Pulse propagation in a diffusion-fed gel. J. Phys. Chem. Lett. 2013, 4, 3891–3896. [CrossRef]
  45. Ren, L.; Fan, B.; Gao, Q.; Zhao, Y.; Luo, H.; Xia, Y.; Lu, X.; Epstein, I. R. Experimental, numerical, and mechanistic analysis of the nonmonotonic relationship between oscillatory frequency and photointensity for the photosensitive Belousov–Zhabotinsky oscillation. Chaos 2015, 25, 064607. [CrossRef]
  46. Amemiya, T.; Ohmori, T.; Yamaguchi, T. An Oregonator-Class Model for Photoinduced Behavior in the Ru(bpy)32+-Catalyzed Belousov-Zhabotinsky Reaction. J. Phys. Chem. A 2000, 104, 336-344. [CrossRef]
Preprints 91458 g001
Figure 1. Schematic of simulated system and the illumination-modulated oscillation frequency. (a) for oscillation synchronization between the gel patches. The distance between two fixed gel patches is set at dx. Color denotes the value of z variable, with white indicating catalyst-free BZ solution. (b) Simulated nonmonotonic relationship between the oscillation frequency and the light intensity by using the modified four-variable Amimiya’s model. Model concentrations: [BrO3-] = 0.1M, [H+] = 0.6M, [MA] = 0.06M, which serve as default parameter values for our simulations.
Figure 1. Schematic of simulated system and the illumination-modulated oscillation frequency. (a) for oscillation synchronization between the gel patches. The distance between two fixed gel patches is set at dx. Color denotes the value of z variable, with white indicating catalyst-free BZ solution. (b) Simulated nonmonotonic relationship between the oscillation frequency and the light intensity by using the modified four-variable Amimiya’s model. Model concentrations: [BrO3-] = 0.1M, [H+] = 0.6M, [MA] = 0.06M, which serve as default parameter values for our simulations.
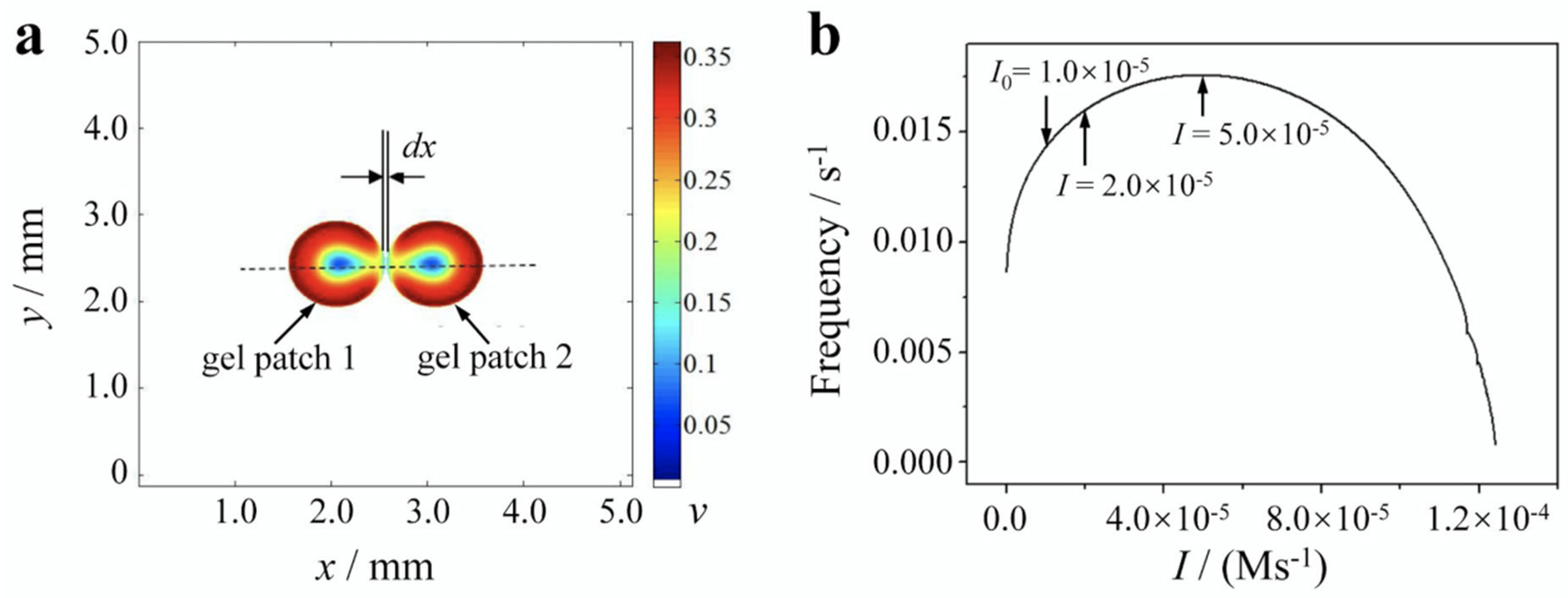
Preprints 91458 g001
Preprints 91458 g002
Figure 2. Spatiotemporal plots of a pair of the gel patches. Data are read from the location which is denoted by a dash line as shown in Figure 1 (recording from 500 s to 1500 s with 3000 data in total). A dash line in (a) to (d) indicates the start time of illumination (I=2.0×10-5) to irradiate the gel patch 1 only, besides both gels are irradiated by background illumination (I0=1.0×10-5). (e) Time series of z-variable oscillations at the center point of the two gel patches.
Figure 2. Spatiotemporal plots of a pair of the gel patches. Data are read from the location which is denoted by a dash line as shown in Figure 1 (recording from 500 s to 1500 s with 3000 data in total). A dash line in (a) to (d) indicates the start time of illumination (I=2.0×10-5) to irradiate the gel patch 1 only, besides both gels are irradiated by background illumination (I0=1.0×10-5). (e) Time series of z-variable oscillations at the center point of the two gel patches.
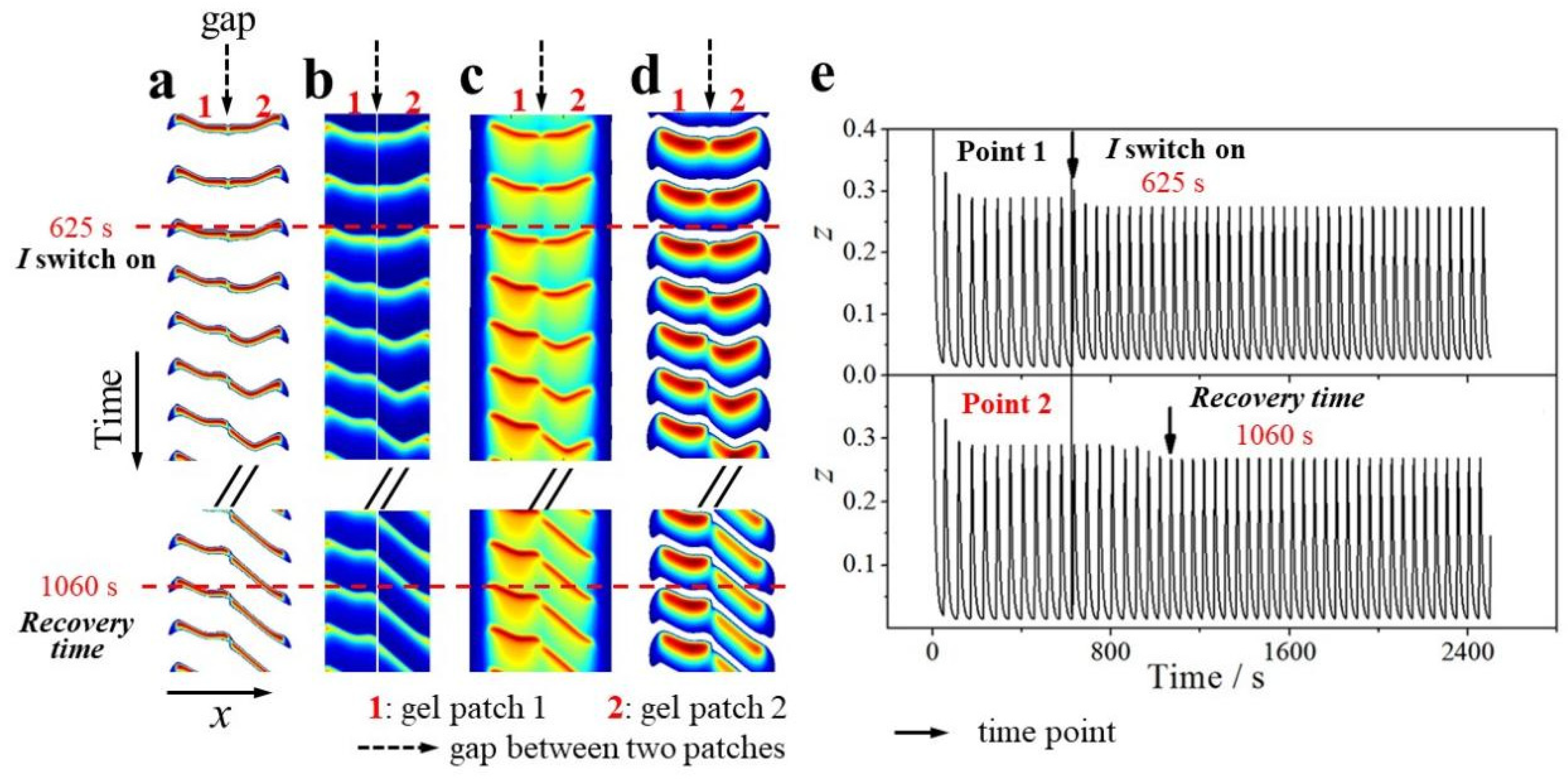
Preprints 91458 g002
Preprints 91458 g003
Figure 3. Time series of real-time oscillation frequency at the center of gel patches 1 and 2, respectively. Arrows indicate the moment when starts irradiating (I=2.0×10-5). The time point of synchronization recovery is denote by (×).
Figure 3. Time series of real-time oscillation frequency at the center of gel patches 1 and 2, respectively. Arrows indicate the moment when starts irradiating (I=2.0×10-5). The time point of synchronization recovery is denote by (×).
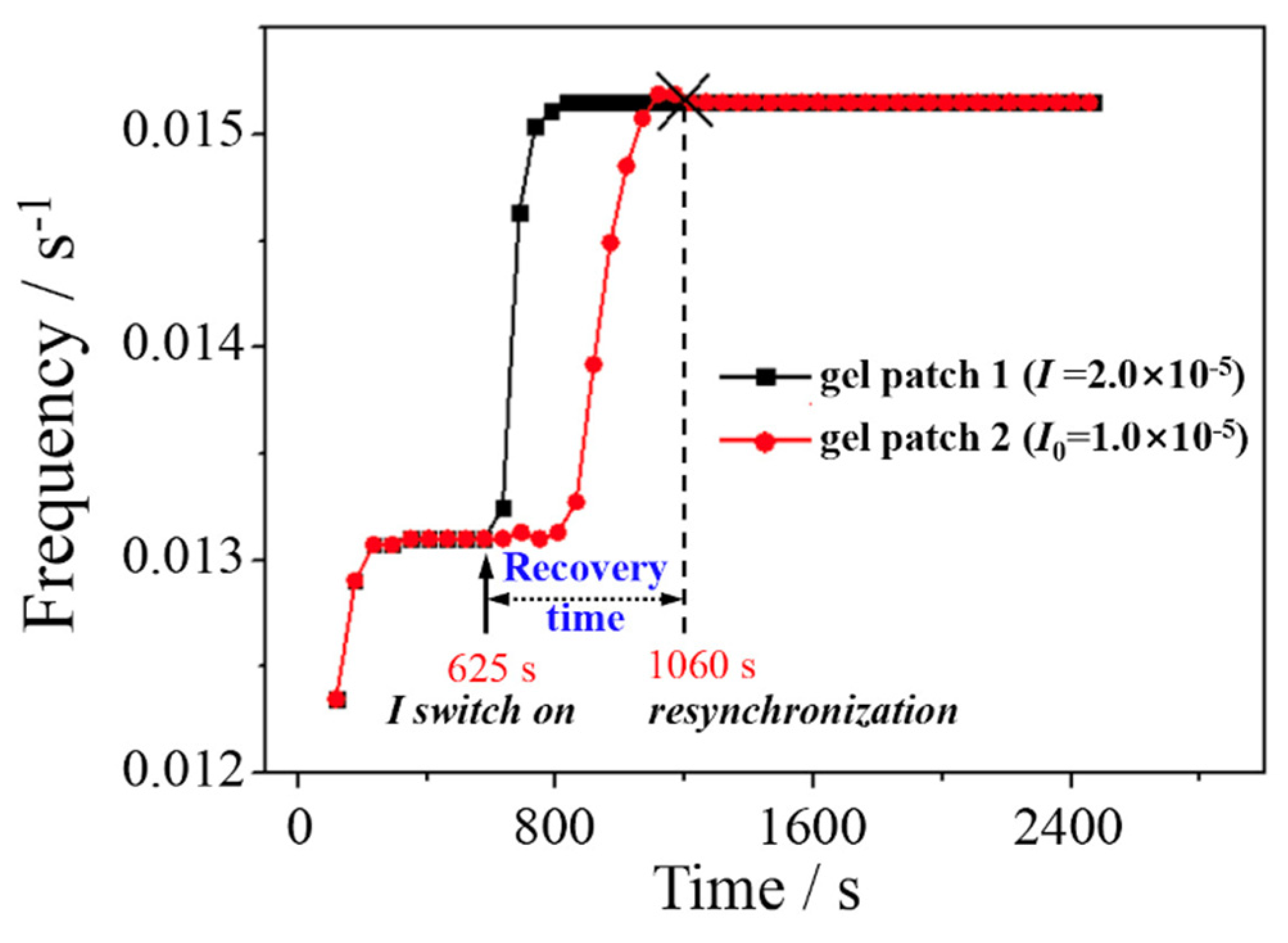
Preprints 91458 g003
Preprints 91458 g004
Figure 4. Recovery of synchronization for scenarios of gel patches with different I. The start time for irradiating the gel patch 1 is the same for all scenarios, at time point 625 s as arrow indicated. I0=1.0×10-5. The moments of recovered synchronization are marked as (×) on curves, respectively.
Figure 4. Recovery of synchronization for scenarios of gel patches with different I. The start time for irradiating the gel patch 1 is the same for all scenarios, at time point 625 s as arrow indicated. I0=1.0×10-5. The moments of recovered synchronization are marked as (×) on curves, respectively.
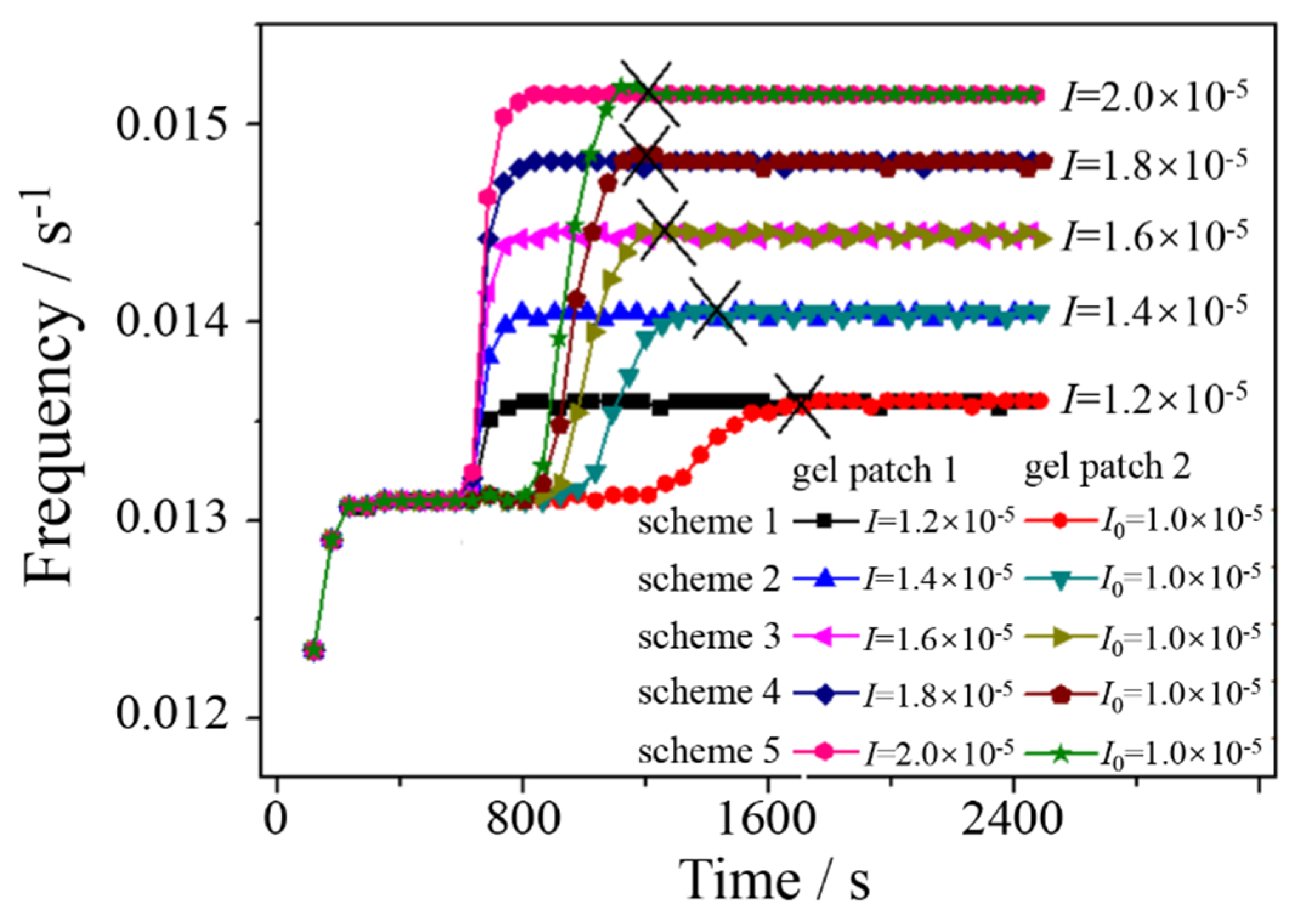
Preprints 91458 g004
Preprints 91458 g005
Figure 5. The recovery time of synchronization versus the distant between the two patches. I = 1.4×10-5.
Figure 5. The recovery time of synchronization versus the distant between the two patches. I = 1.4×10-5.
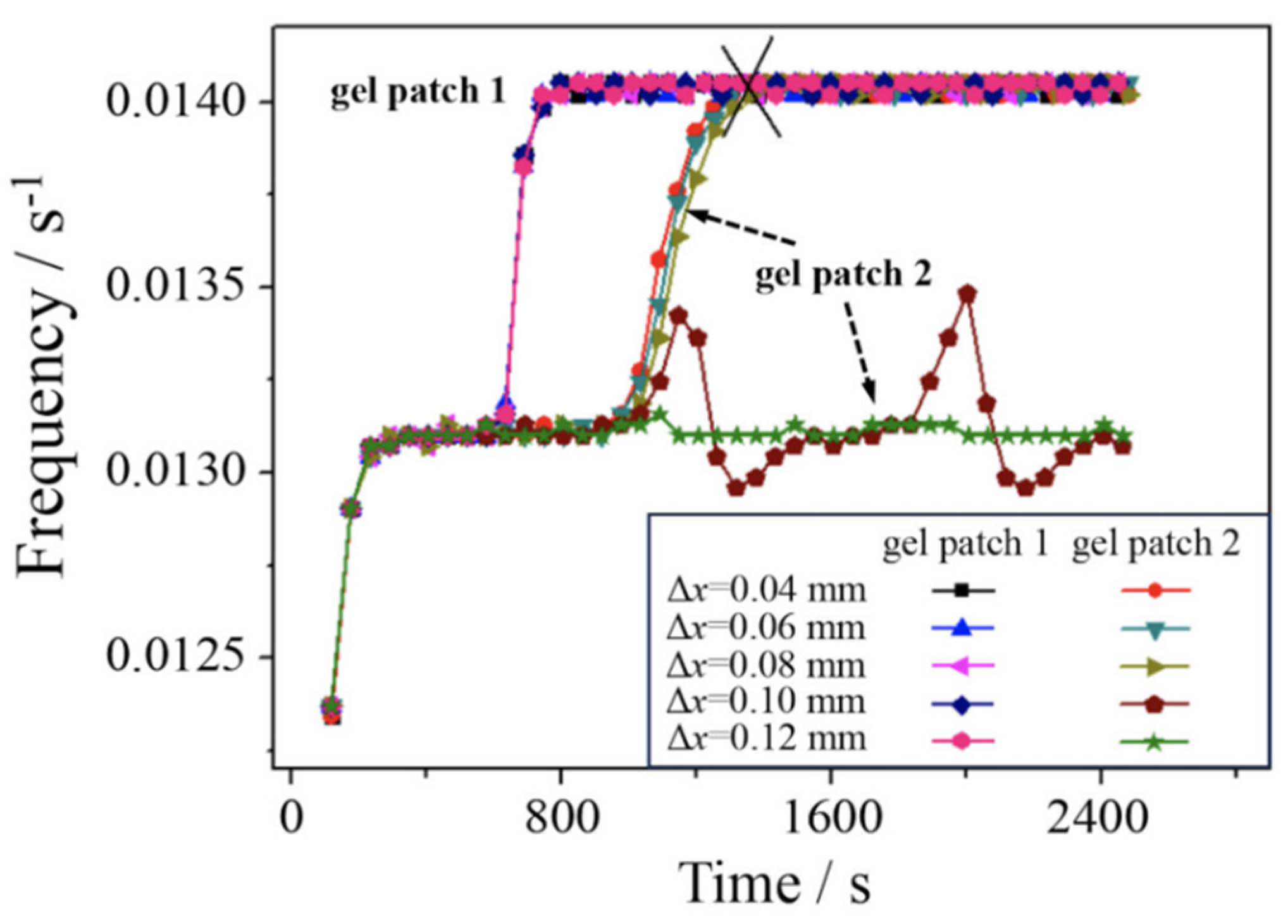
Preprints 91458 g005
Preprints 91458 g006
Figure 6. The relationship between the duration of I and the synchronization recovery. I = 1.4×10-5. The start time of I for all scenarios are the same. The duration time of I respectively are: (a) 250s; (b) 500s; (c) 875s, respectively.
Figure 6. The relationship between the duration of I and the synchronization recovery. I = 1.4×10-5. The start time of I for all scenarios are the same. The duration time of I respectively are: (a) 250s; (b) 500s; (c) 875s, respectively.
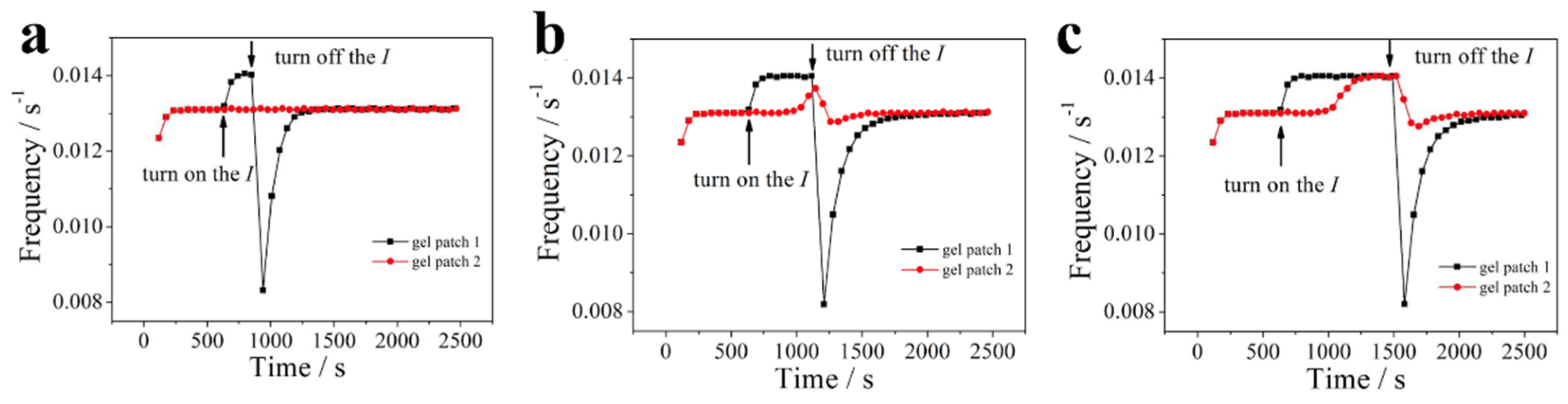
Preprints 91458 g006
Preprints 91458 g007
Figure 7. Recovery of synchronization for various diffusion limited systems. I=1.4×10-5. Only variable (a) x, (b) v, or (c) y with diffusion (D=1.0), respectively. Only variable (d) x, (e) v, or (f) y without diffusion (D=0.0), respectively. Other variables are the same as the default setting.
Figure 7. Recovery of synchronization for various diffusion limited systems. I=1.4×10-5. Only variable (a) x, (b) v, or (c) y with diffusion (D=1.0), respectively. Only variable (d) x, (e) v, or (f) y without diffusion (D=0.0), respectively. Other variables are the same as the default setting.
Preprints 91458 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated