Preprint
Article
Assessing Recession Constant Sensitivity and Its Interaction with Data Adjustment Parameters in Continuous Hydrological Modeling in Data Scarce Basins: A Case Study Using the Xinanjiang Model
Altmetrics
Downloads
95
Views
84
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
30 November 2023
Posted:
01 December 2023
You are already at the latest version
Alerts
Abstract
While considering the sensitivity over the parameter optimization, it is essential to determine which parameters have the most significant implications on model performance. This study focuses on the baseflow recession constant as one of the independent basin parameters to forecast low flows, perform hydrograph analysis, and calibrate rainfall-runoff models for significant improvement. Prior studies examined that the optimization of data adjustment parameters can improve the hydrological model performance and determine the minimum acceptable data length for data scarce regions using the Xinanjaing model. However, it is essential to pay special attention to the sensitivity of the recession constant, which can also impact the model performance during the data scarcity. Therefore, this study extends the research to comprehend the recession constant sensitivity over data adjustment parameters in the shorter datasets leading to more reliable parameter estimation. In terms of that, this study explores how recession constant affects hydrological parameter estimation on annual scale while keeping data adjustment parameters constant in continuous hydrological modeling, employing the Xinanjiang (XAJ) model as a case study. This study considered two approaches of recession constant (cg); (i) assessing the relationship between cg and the data adjustment parameter (Cep), for the 28-year datasets, (ii) investigating the significant impacts of the sensitivity of cg over Cep in shorter datasets which can affect the estimation of the acceptable minimum data length in the data scarce basins. The study underscores the importance of the recession constant sensitivity for reliable continuous hydrological model predictions, especially in data-scared areas. The study’s outcomes enhance the understanding of the importance of parameter sensitivity and its relationship in conceptual hydrological modeling during the data limitations.
Keywords:
Subject: Environmental and Earth Sciences - Water Science and Technology
1. Introduction
Hydrological models have been regarded as a powerful and essential tool for handling water and environmental resources as the magnitude of harm they inflict are increasing in both financial and social aspects[1]. In this context, hydrological modeling methods are advanced tremendously in terms of complexities with a wide range of application areas, including the study of the climate change and land use paradigm, flood forecasting, and rainfall-runoff modeling [2,3,4,5]. Assessing the modeling process’s uncertainty and quantifying it contributes in assessing how reliable the predictions remain. To make reliable decisions, model users and decision-makers need to be aware of the possible range of outcomes. Uncertainties within hydrological modeling play the vital role in many regions, especially in developing countries, where the data scarcity and data limitations can impact the model calibration predictions. Consequently, the importance of understanding the uncertainties within hydrological modeling has grown significantly [6,7,8].
In the domain of hydrological study, modeling uncertainties can be categorized into three major groups, known as: (i) data uncertainty, (ii) model structure uncertainty, and (iii) parameter uncertainty [9,10,11,12]. Among these, parameter uncertainties arising from the challenges of optimizing model parameters and model estimation are frequently identified in recent studies. Since the majority of model parameters are difficult to predict precisely, they need to be evaluated through a calibration procedure using the available data. Addressing the issues associated with parameter uncertainties in hydrological modeling has been a major focus in recent studies [13,14,15]. However, identifying suitable parameter values to manage uncertainty in parameter estimation becomes challenging due to limited data availability in hydrological modeling, especially in many developing and underdeveloped countries [6,7,8,16]. Parameter estimation during data scarcity can lead to inadequate model performance, overparameterization, and poor model robustness. In addition, recent literature on hydrological model calibration demonstrates that improvements are needed in the existing calibration approaches’ process representation, spatial prediction, and runtime efficiency in the case of data scarcity [17].To address the above identified issues, it is crucial to detect the sensitive parameters in model calibration and parameter optimization in the data scarce basins.
Conceptual hydrological models are one example of how actual process models continuously improve to effectively represent the underlying uncertainties associated with inputs, parameters, and the presumed model validation [18,19,20,21,22,23,24,25]. In addition, conceptual models specialize in minimal data requirements and broad applicability in real-world hydrology [26].In this context, this study utilized the XAJ, a widely used probability-distributed model for hydrological studies, to evaluate the most influential parameters [27,28].Given the data adjustment and linear reservoir recession are common parts in many widely used hydrological models, e.g., the NWS River Forecast System - Catchment Modeling and TANK Model [29], the results of this study are of general applicability and not limited to the XAJ model.According to recent studies, Lu and Li (2014) examined parameter sensitivities within the Xinanjiang (XAJ) model using global sensitivity analysis techniques across different timescales for model calibration improvement. Their work notably highlighted the increased sensitivity of the recession constant on an annual timescale while data adjustment parameters remained constant.
Through this research initiative, we aim to validate the relationship between the data adjustment parameter (Cep) and the recession constant (cg) while only limited datasets are available, highlighting the critical role of recession constant sensitivity. As inaccurate parameter estimation due to data scarcity can lead to poor model calibration and performance, current research initially aims to prove the interaction of the data adjustment parameter (Cep) with the recession constant (cg) in 28-year dataset to highlight the importance of the sensitivity of the recession constant in hydrological modeling. Next, it offers valuable insights into the significant impact of cg on Cep within shorter subsets, seeking to address the constraints posed by these influences on parameter estimation and the determination of the acceptable minimum data length, particularly in data-scarce regions. This approach can identify which parameters influence the model’s calibration and performance without over-parameterization [30].
2. Materials and Methods
2.1. Study Basins
Five river basins in the USA (MOPEX ID: 903504000, MOPEX ID: 902387500, MOPEX ID: 902472000, MOPEX ID: 903443000, and MOPEX ID: 911532500) are investigated during this research including the same two basins from the recent study [31]. According to the study, these basins possess robust datasets, and the XAJ model could accurately estimate their runoff. Assessing to include the same two basin permits comparing the parameter optimization and the minimum data length estimation from two different approaches. Furthermore, it provided a way to correlate the relationship between parameter sensitivity with model performance. Table 1 illustrates a brief overview of the physical characteristics of the researched basins.
2.2. Data Description
The U.S. MOPEX dataset [32] was used to develop the basin scale daily precipitation, P (daily mean aerial precipitation calculated from ground-based gauge precipitation), potential evaporation, Ep (developed from NOAA Evaporation Atlas), and discharge, Q (developed from USGS hydro-climatic data) information utilized in this research openly available at ftp://hydrology.nws.noaa.gov/ (accessed on 19 October 2013). Table 2 provides comprehensive descriptive data statistics of the examined basins.
Considering the lack of data and limitations in practical modelling research, the XAJ model is calibrated using 28-year datasets and subsets from each basin to highlight the model’s effectiveness. For subsets, 28-year datasets are divided into shorter data lengths with different year intervals starting from 6-year to 28-year subsets[31].
Here, we defined the input datasets In,m including P and Ep, and as the observed runoff, where n is the length of datasets and m is the number of subsets ().
2.3. XAJ Model and Parameter Description
In this study, we used the Xinanjiang model, a conceptual hydrological model, designed by the Flood Forecast Research Institute of the East Chinese Technical University of Water Resources [33]. This model is utilized for humid and semiarid areas of China to estimate runoff generation within a basin [33,34]. The physical meaning of the model is robust. The simulated XAJ model utilized in this research comprises fifteen parameters as referred in Table 3 [33,35,36]. The complexity of the connections and interactions among the numerous parameters required in calibration can be minimized by the level of parameter estimation.
Here, the estimation of data adjustment parameter, Cep, is detailed through the aridity index method[37] while the calculation of the recession constant parameter, cg, employs the time constant, T.
denote the pre-optimized parameter vector as in Table 2 .
Let the function specify the XAJ model calibration, X and let the input datasets comprise the vector In,m where n is the length of datasets and m is the number of subsets. Let the simulated runoff by the XAJ model calibration for In,m be specified by the following equation:
where Cep represents the adjustment parameter (the most sensitive parameter at the annual scale in the XAJ model), cg is the recession constant (sensitive at the annual scale when the adjustment parameters are kept constant), represents the application of 13 pre-optimized parameter values, a subset of all 15 parameters in the XAJ model. These parameters are fixed in this study. As these parameter values are not inferred through the calibration process, will be excluded from the following equation for clarity.
Table 2.
Descriptive statistics of studied basins
| MOPEX ID | Mean precipitation (mm/year) |
Median precipitation (mm/year) |
Minimum precipitation (mm/year) |
Maximum precipitation (mm/year) |
Standard Deviation |
|---|---|---|---|---|---|
| 903504000 | 1890 | 2051.98 | 1427.09 | 4424.72 | 571.450 |
| 902387500 | 1480 | 1481.05 | 1046.53 | 1930.67 | 228.240 |
| 902472000 | 1492 | 1550.62 | 1135.21 | 4615.13 | 674.880 |
| 903443000 | 2156 | 2064.90 | 1349.55 | 6646.70 | 1018.10 |
| 911532500 | 2687 | 2718.04 | 1644.96 | 7172.92 | 1176.72 |
2.4. Relationship Between Data Adjustment Parameter (Cep) and the Recession Constant (cg)
According to the general water balance equation for vertical water flux, the relationship between the adjustment parameter and the recession constant parameter can be observed as shown in the following equation,
where Pg is the actual rainfall calculated from a ground-based rain gauge, Epan is the annual evaporation, R is the annual runoff depth, and S is the changes in water storage.
However, in this study, we considered that the baseflow storage can be affected by the recession constant cg at the beginning and end of the year under certain circumstances. To resolve this approach, must be taken into consideration, which is a highly subjective task that might have significant effects on the close relationship between Cep and cg.
2.5. Assessment of Recession Constant, (cg)
Three runoff components of surface runoff, interflow, and baseflow, are routed using three linear reservoirs as follows:
where subscript x indicates runoff component, s for surface flow,i for interflow, and g for baseflow cs, ci and cg are their recession coefficients.Usually,
According to [34], among 15 parameters, the most sensitive parameter at the annual scale while keeping Cp and Cep constants is cg. In this study, the values of cg were calculated using the time constant not to exceed the limits between 0 and 1. T is related to cg by the following expression,
whereas T is the time constant constant of the baseflow system in days, cg is the recession constant in t dimensionless quantity whose value depends on the time unit chosen.
2.6. Assessment of Data Adjustment Parameter, (Cep)
Li and Lu [37] emphasize that this study predominantly uses the aridity index method. Correlating runoff coefficient and data aridity could support the reduction of parameter space for Cp and Cep rather than separate assessments. To reduce such inaccuracy and improve the efficiency of parameter estimation, the interaction between the runoff coefficient and the data aridity index is applied to parameter estimation.
- Within the limitations of the pan aridity index and annual runoff coefficient, the values of Cp and Cep might be determined.
In the logarithm form,
Here, estimation for 28-year datasets and subsets is outlined by function Y, represent the estimated Cep values for subsets, In,m. The subsequent equation explains data adjustment parameter estimation in subsets, In,m.
2.7. Evaluation of Model Performance Using Nash-Sutcliffe Efficiency
The Nash and Sutcliffe (1970) coefficient of efficiency is widely used in the evaluation of hydrological modelling [38,39,40,41,42,43]. Simulated runoff information is derived utilizing well-known Nash-Sutcliffe efficiency [44].
The definition of Nash-Sutcliffe efficiency is as follows;
where Qcal is the simulated runoff, Qobs is the observed runoff, and is the mean value of observed runoff.
This study calculates the observed and simulated runoff from the XAJ model driven by 28-year datasets and subsets, In,m. It can be expressed as follows:
where are the daily observed runoff.
At an annual scale, the parameters affecting the are mainly Cep and cg. Equation (9) can also be written in the following function:
2.8. Application of Data Adjustment Parameter and Recession Constant in Model Calibration
The simulated recession constant, cg,ref, is initially estimated using the linear polynomial regression analysis. The values of cg,ref were selected based on the cg values with the best model performance in the longest datasets.
where refers to the estimated adjustment parameter value using a 28-year data length.
Table 3.
Description of the parameters in the Xinanjiang model.
| Parameter | Physical meaning | Range | Pre-optimized values, ϕ0 | ||||
|---|---|---|---|---|---|---|---|
| MOPEX ID | |||||||
| 903504000 | 902387500 | 902472000 | 903443000 | 911532500 | |||
| Group I | |||||||
| Cp | Ratio of measured precipitation to actual precipitation | 0.8–1.2 | 1 | 1 | 1 | 1 | 1 |
| Cep | Ratio of potential evaporation to pan evaporation | 0.8–1.2 | 0.7908 | 1.25 | 1.2806 | 0.9865 | 0.7184 |
| Group II | |||||||
| SM | Areal mean free water capacity of the surface soil layer (mm) | 1–50 | 40 | 30 | 50 | 40 | 30 |
| EX | Areal mean of the free water capacity of the surface soil layer (mm) | 0.5–2.5 | 1.2 | 0.5 | 0.5 | 1.2 | 0.5 |
| KI | Outflow coefficients of the free water storage to interflow | 0–0.7; KI + KG = 0.7 | 0.1 | 0.3 | 0.55 | 0.1 | 0.3 |
| KG | Outflow coefficients of the free water storage to groundwater | 0–0.7; KI + KG = 0.7 | 0.6 | 0.4 | 0.15 | 0.6 | 0.4 |
| cs | Recession constant of the lower interflow storage | 0.5–0.9 | 0.6 | 0.85 | 0.75 | 0.6 | 0.4 |
| ci | Recession constant for the lower interflow storage | 0.5–0.9 | 0.9 | 0.75 | 0.8 | 0.9 | 0.75 |
| cg | Recession constant of the groundwater storage | 0.9835–0.998 | 0.98 | 0.987 | 0.983 | 0.98 | 0.983 |
| Group III | |||||||
| b | Exponent of the tension water capacity curve | 0.1–0.3 | 0.3 | 0.15 | 0.15 | 0.3 | 0.15 |
| imp | Ratio of the impervious to the total area of the basin | 0–0.005 | 0.02 | 0.01 | 0.01 | 0.02 | 0.01 |
| WUM | Water capacity in the upper soil layer (mm) | 5–20 | 5–20 | 20 | 20 | 20 | 20 |
| WLM | Water capacity in the lower soil layer (mm) | 60–90 | 60–90 | 80 | 80 | 80 | 80 |
| WDM | Water capacity in the deeper soil layer (mm) | 10–100 | 10–100 | 60 | 160 | 160 | 160 |
| C | Coefficient of deep evapotranspiration | 0.1–0.3 | 0.1–0.3 | 0.15 | 0.15 | 0.15 | 0.15 |
Note: ϕ0 indicates the pre-optimized parameter values.
To highlight the sensitivity impact of the recession constant in shorter datasets, the data adjustment parameter values for subsets are essential to optimize the recession constant values for subsets. To compare the impacts of parameter sensitivity in shorter data length, we first identify the estimated Cep values for subsets based on three conditions: maximum, minimum and median annual model results, NSE. Let , and be the maximum, minimum and median values in subsets (In,m), when running the model using cg,ref.
- The maximum, minimum and median annual NSE, can be specified using and cg,ref in subsets using by the following equations,
For the comparison of the sensitivity influence of recession constants over the parameter estimation in shorter data length, we apply the maximum, minimum and median calibrated data adjustment parameter values (, and ) in model calibration to receive the maximum, minimum and median recession constant values (, and ) in subsets. Finally, the maximum, minimum and median annual NSE results using , and are estimated by comparing NSE results with cg,ref using the following equations.
where , and are calculated based on the maximum, minimum and median model outputs while running with , and with cg,ref.
2.9. Application of Linear Polynomial Regression Analysis for Data Comparison
3. Results and Discussions
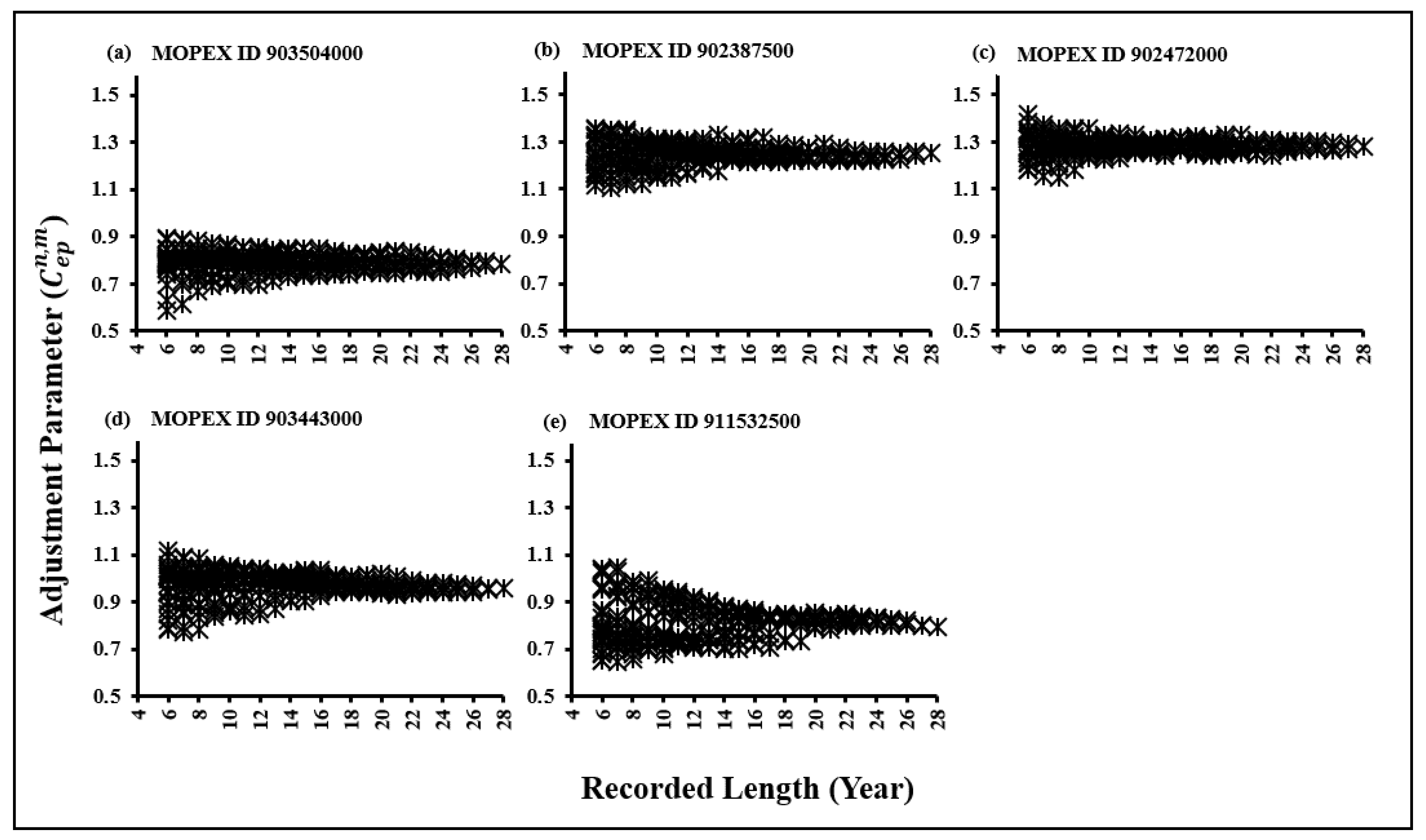
The effect of data scarcity on parameter estimation plays as one of the most important factors which influences the model’s reliability and precision. Therefore, in designing long-term hydrological models, the time-related character of sensitivity should be considered [48]. In this research, the performance of the data adjustment parameter estimation is improved with the longer datasets. According to the Figure 1, it can be seen clealry that the variation of the data adjustment values is large in the shorter datasets. In this research, variables impacting runoff generation (cg) appears sensitive yet again on an annual scale in the XAJ model while maintaining Cp and Cep constant [34]. Therefore, this study tried to analyse the sensitiviy of recession constant estimation in accordance with the data adjustment parameter during the data scarcity. In order to prove that, the consideration of the sensitivity of recession constant over the model performance became critical.
To highlight the recession constant sensitivity, the XAJ model calibration was performed in two approach as discussed in Section 2.8. Firstly, the model is simulated using the recession constant values (cg,ref) optimized with longer datasets. Secondly, the model performance was checked using the recession constant for subsets ().
3.1. Reference cg for 28-Year Datasets
The pre-optimized recession constant values, , in five MOPEX studied basins were initially computed based on the time constant, T, as in Equation (7), to achieve in the interval of [0,1].These cg values were applied in the XAJ model calibration alongside with the remaining pre-optimized parameters,.Relying on the annual Nash results, the estimation of simulated cg for each basin can be assessed by using the polynomila regression analysis.
To be able to attain better calibration, model users typically employ the longest accessible data series.This study considered the simulated recession constant as the reference, as it was estimated using 28-year of datasets. However, the real issue is the information included in the datasets and how effectively that information is extracted, not the length of the dataset itself [23,49]. Therefore, estimating the Cep values () for shorter datasets is essential to analyze the impact of the recession constant in subsets. Figure 2 reveals the best connection values, cg,ref, comparing the annual Nash, NSE, and the pre-optimized cg values.
Figure 2.
Estimation of reference cg (cg,ref) from annual Nash NSE results using 28-year of datasets in MOPEX ID (a) 903504000 (b)902387500 (c) 902472000 (d) 903443000 (e) 911532500.
Figure 2.
Estimation of reference cg (cg,ref) from annual Nash NSE results using 28-year of datasets in MOPEX ID (a) 903504000 (b)902387500 (c) 902472000 (d) 903443000 (e) 911532500.
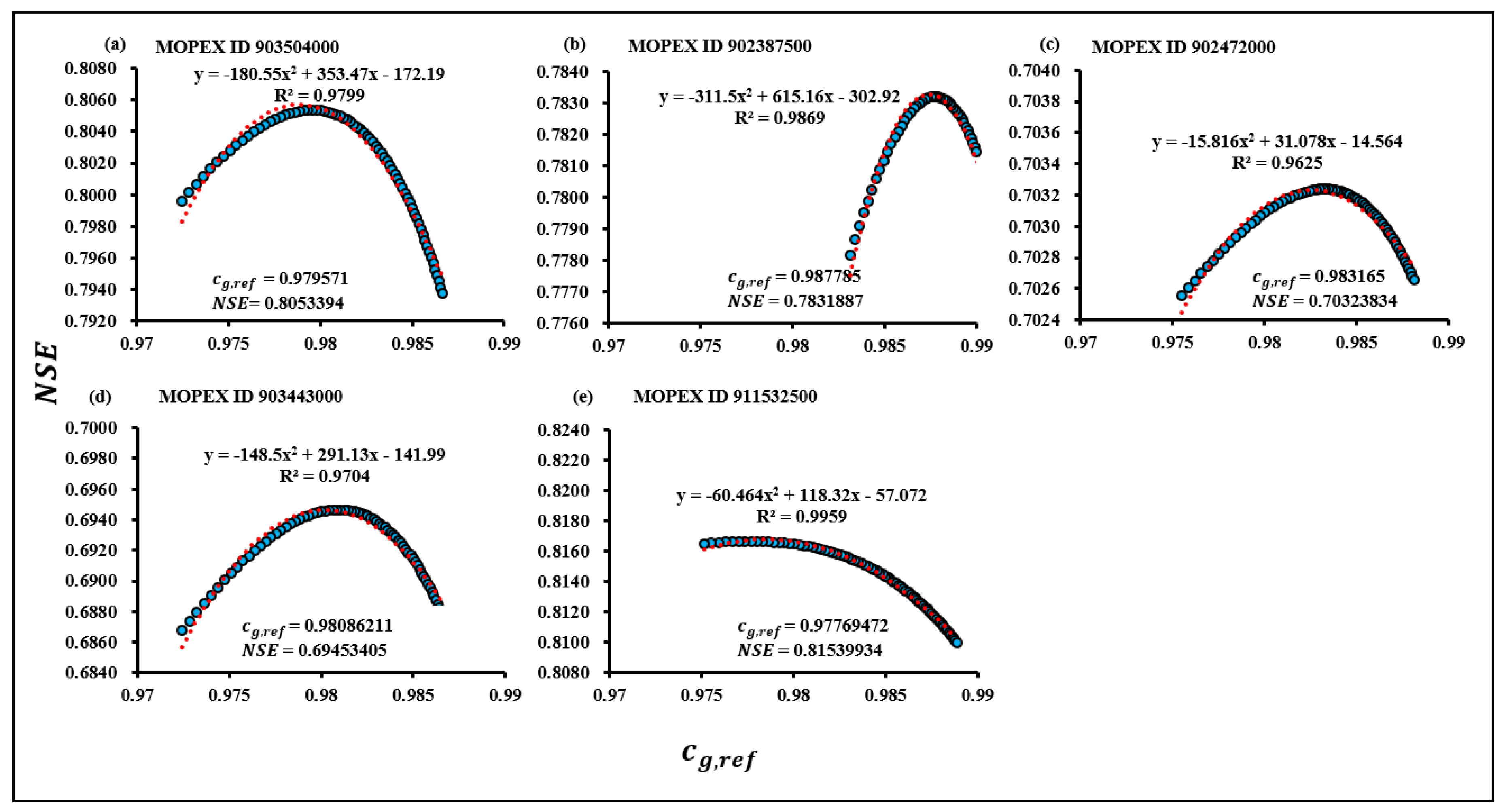
Figure 3.
Estimation of Cep for subsets in MOPEX ID (a) 903504000 (b)902387500 (c) 902472000 (d) 903443000 (e) 911532500.
Figure 3.
Estimation of Cep for subsets in MOPEX ID (a) 903504000 (b)902387500 (c) 902472000 (d) 903443000 (e) 911532500.
3.2. Derivation of Data Adjustment Parameter ()
To compare the sensitivity of the recession constant over the data adjustment parameter for consecutive subsets (In,m) it was essential to evaluate the initial model performance values of NSE applying with and cg,ref.
Firstly, the value of is classified into three categories based on the model (NSE) values calibrated using the reference cg,ref in each subset, In,m :
- (i)
- (selected when the annual Nash values,NSE, are highest after the model calibration with cg,ref in each subset, In,m);
- (ii)
- (selected when the annual Nash values,NSE, are median after the model calibration with cg,ref in each subset, In,m) and
- (iii)
- (selected when the annual Nash values,NSE, are lowest after the model calibration with cg,ref in each subset, In,m)
3.3. Comparative Evaluation of Annual Nash Results, NSE, using and in Subsets
After the model calibration using the reference cg, the Cep () resulted from the highest annual Nash results were selected for each subsets as shown in Table 4.
Firstly,it is observed that as the data length increases, the NSE values derived from both cg,ref and exhibit a declining trend. As indicated in Table, this implies that longer datasets might struggle to align with the model’s best performance. In the contrary, the 6-year subsets display the most significant upward trends in NSE results, attributed to shorter datasets being more compatible with . Beyond this trend pattern, a comparison was conducted between NSE values in subsets when using cg,ref and as shown in Figure 3.
Figure 4.
Estimation of for subsets by using linear polynomial regression analysis in MOPEX ID (a) 903504000 (b)902387500 (c) 902472000 (d) 903443000 (e) 911532500.
Figure 4.
Estimation of for subsets by using linear polynomial regression analysis in MOPEX ID (a) 903504000 (b)902387500 (c) 902472000 (d) 903443000 (e) 911532500.
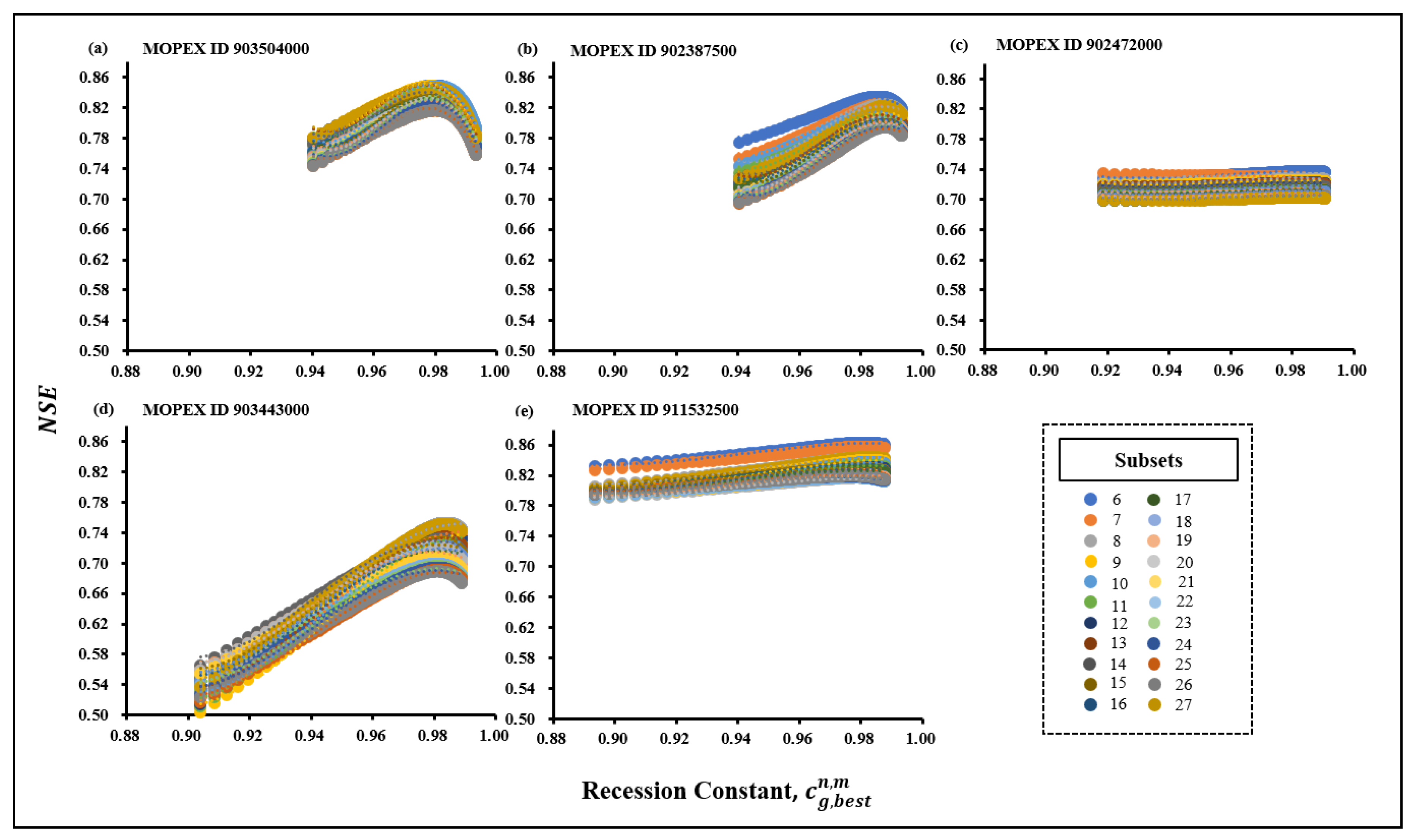
According to Figure , the NSE curves in each subset showed a relative increase while running the model with . However, no significant difference between the curves of NSE resulted from the model calibration using both cg,ref and . In other words, the results suggest little space for improving the model performance while running the model with . Therefore, the impact of the sensitivity of over Cep in parameter estimation can be considered limited. Consequently, the potential impact of the sensitivity of can also be limited to the performance of the model as well as the minimum data length estimation. On the other hand, the recent estimation of the minimum data length remains consistent while considering the sensitivity of parameter estimation with cg considering best parameter optimization scenario in subsets.
Figure 5.
Comparison of Nash values using cg,ref and for subsets in MOPEX ID (a) 903504000 (b)902387500 (c) 902472000 (d) 903443000 (e) 911532500.
Figure 5.
Comparison of Nash values using cg,ref and for subsets in MOPEX ID (a) 903504000 (b)902387500 (c) 902472000 (d) 903443000 (e) 911532500.
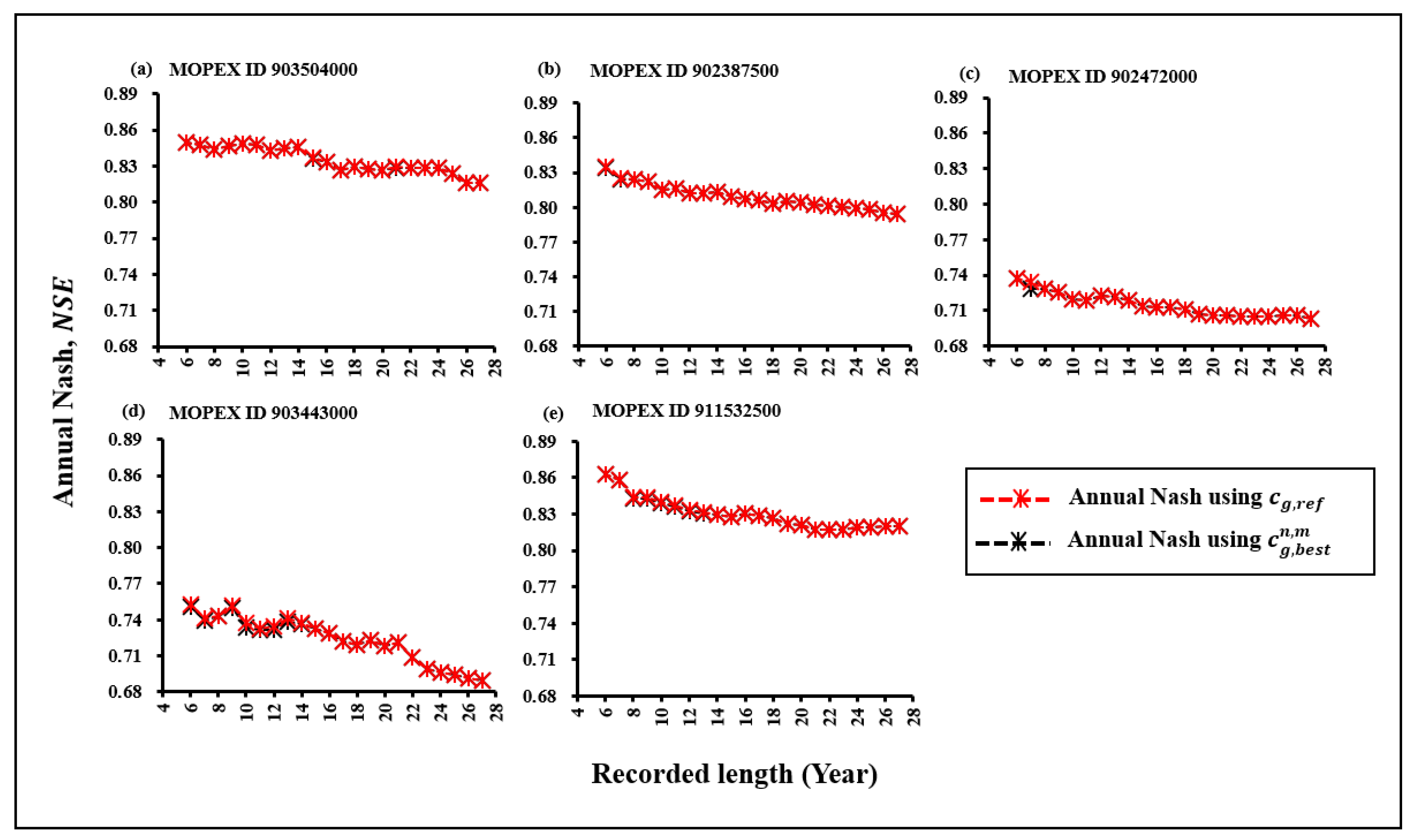
Figure 6.
Estimation of for subsets by using linear polynomial regression analysis in MOPEX ID (a) 903504000 (b)902387500 (c) 902472000 (d) 903443000 (e) 911532500.
Figure 6.
Estimation of for subsets by using linear polynomial regression analysis in MOPEX ID (a) 903504000 (b)902387500 (c) 902472000 (d) 903443000 (e) 911532500.
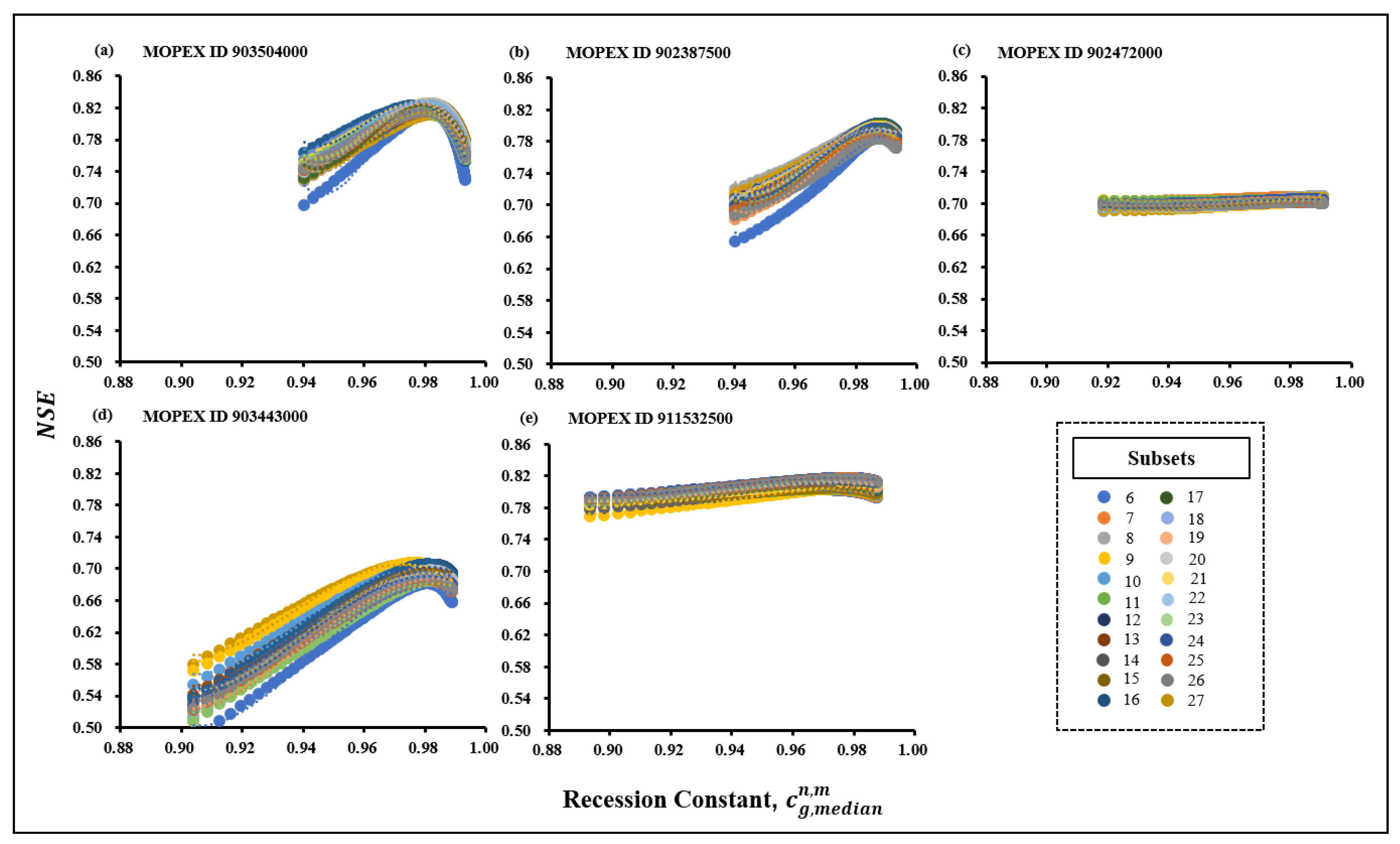
Figure 7.
Comparison of Nash reulsts using cg,ref and for subsets in MOPEX ID (a) 903504000 (b)902387500 (c) 902472000 (d) 903443000 (e) 911532500.
Figure 7.
Comparison of Nash reulsts using cg,ref and for subsets in MOPEX ID (a) 903504000 (b)902387500 (c) 902472000 (d) 903443000 (e) 911532500.
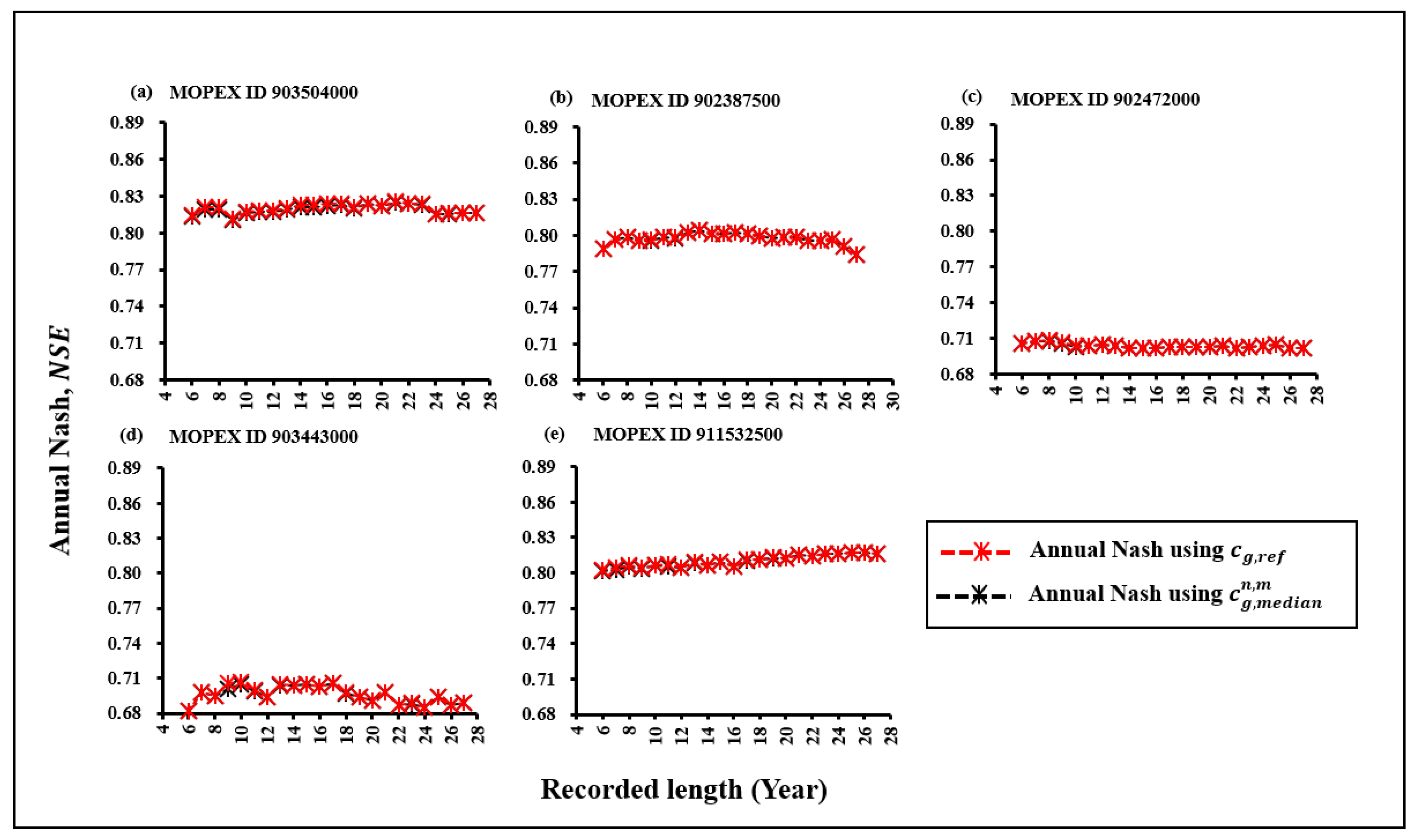
Table 4.
Detail Description of and values in MOPEX ID (a) 903504000 (b)902387500 (c) 902472000 (d) 903443000 (e) 911532500.
Table 4.
Detail Description of and values in MOPEX ID (a) 903504000 (b)902387500 (c) 902472000 (d) 903443000 (e) 911532500.
| MOPEX ID | ||||||||||
| Subsets | 9903504000 | 9902387500 | 9902472000 | 9903443000 | 9911532500 | |||||
| Cep,best | Cep,best | cg,best | Cep,best | cg,best | Cep,best | cg,best | Cep,best | cg,best | ||
| 6 | 0.8189 | 0.979725 | 1.3559 | 0.98548 | 1.3108 | 0.98496 | 1.1154 | 0.98386 | 0.8562 | 0.98106 |
| 7 | 0.7970 | 0.979725 | 1.3500 | 0.98644 | 1.2181 | 0.91861 | 1.0891 | 0.98411 | 0.8353 | 0.98122 |
| 8 | 0.7810 | 0.978669 | 1.3524 | 0.98728 | 1.2805 | 0.98333 | 1.0831 | 0.98318 | 0.9835 | 0.98197 |
| 9 | 0.7937 | 0.978669 | 1.2974 | 0.98791 | 1.3074 | 0.98300 | 1.037 | 0.98359 | 0.9933 | 0.98253 |
| 10 | 0.7883 | 0.979033 | 1.3009 | 0.98791 | 1.3065 | 0.98333 | 1.0529 | 0.98460 | 0.9504 | 0.98293 |
| 11 | 0.8095 | 0.980980 | 1.2574 | 0.98597 | 1.2712 | 0.98411 | 1.0226 | 0.98260 | 0.9298 | 0.98293 |
| 12 | 0.8043 | 0.978669 | 1.2611 | 0.98644 | 1.2699 | 0.98365 | 1.0405 | 0.98411 | 0.9108 | 0.98212 |
| 13 | 0.7763 | 0.978669 | 1.2684 | 0.98687 | 1.2688 | 0.98300 | 1.0123 | 0.98411 | 0.8969 | 0.98226 |
| 14 | 0.7737 | 0.978669 | 1.2394 | 0.98728 | 1.2874 | 0.98282 | 0.991 | 0.98245 | 0.8732 | 0.97894 |
| 15 | 0.7666 | 0.978292 | 1.2292 | 0.98687 | 1.2843 | 0.98333 | 0.972 | 0.98060 | 0.8548 | 0.97791 |
| 16 | 0.7783 | 0.979725 | 1.2559 | 0.98728 | 1.2673 | 0.98365 | 0.96 | 0.98131 | 0.8634 | 0.97875 |
| 17 | 0.7955 | 0.979385 | 1.2197 | 0.98741 | 1.2666 | 0.98317 | 0.9566 | 0.98165 | 0.846 | 0.97952 |
| 18 | 0.7864 | 0.980054 | 1.2253 | 0.98741 | 1.2847 | 0.98349 | 0.9615 | 0.98131 | 0.8394 | 0.97970 |
| 19 | 0.7810 | 0.980054 | 1.2428 | 0.98754 | 1.2462 | 0.98191 | 0.9463 | 0.98149 | 0.8321 | 0.97875 |
| 20 | 0.7959 | 0.980054 | 1.2398 | 0.98766 | 1.2638 | 0.98229 | 0.9451 | 0.97982 | 0.8267 | 0.97894 |
| 21 | 0.7880 | 0.980681 | 1.2324 | 0.98741 | 1.3095 | 0.98454 | 0.932 | 0.98022 | 0.8095 | 0.97875 |
| 22 | 0.7959 | 0.980980 | 1.2268 | 0.98754 | 1.3090 | 0.98454 | 0.9377 | 0.98041 | 0.8475 | 0.97769 |
| 23 | 0.8087 | 0.981270 | 1.2249 | 0.98766 | 1.2804 | 0.98468 | 0.941 | 0.98060 | 0.8403 | 0.97701 |
| 24 | 0.8115 | 0.981270 | 1.2335 | 0.98791 | 1.2863 | 0.98482 | 0.9436 | 0.98096 | 0.8083 | 0.97629 |
| 25 | 0.8059 | 0.980681 | 1.2315 | 0.98802 | 1.3000 | 0.98454 | 0.9405 | 0.98096 | 0.7995 | 0.97552 |
| 26 | 0.7897 | 0.980054 | 1.2492 | 0.98802 | 1.2984 | 0.98426 | 0.9702 | 0.98198 | 0.8064 | 0.97629 |
| 27 | 0.7931 | 0.980054 | 1.2606 | 0.98791 | 1.2888 | 0.98396 | 0.9505 | 0.98096 | 0.7972 | 0.97701 |
3.4. Comparative Evaluation of Median () Results with Annual Nash (NSE) in Subsets
In this section, the values of Cep () were selected based on the median values of model output (NSE) after the model calibration with cg,ref for 28-year of datasets, as shown in Table 5. After the selection with the model outputs using cg,ref, the calibration of the model was performed in order to achieve the relationship between NSE with results. In Figure 6, the can be assumed by the model output (NSE) using the linear polynomial regression analysis. Here, while taking the cg values in the median range, the trend of the NSE values in all subsets for all studied basins has slightly increased as the data length increased.
While considering cg values within the median parameter optimization performance scenario, NSE values show a slight upward trend across all subsets as data length increases. Furthermore, NSE values when utilizing are slightly higher than those with cg,ref. Despite this minor difference, it is reasonable to conclude that model outcomes using median values did not indicate any limitations over the model performance while calibrating during the data scarcity as indicated in Figure 7.
Figure 8.
Estimation of for subsets by using linear polynomial regression analysis in MOPEX ID (a) 903504000 (b)902387500 (c) 902472000 (d) 903443000 (e) 911532500.
Figure 8.
Estimation of for subsets by using linear polynomial regression analysis in MOPEX ID (a) 903504000 (b)902387500 (c) 902472000 (d) 903443000 (e) 911532500.
3.5. Comparative Assessment of Annual Nash results, NSE, Using and in Subsets
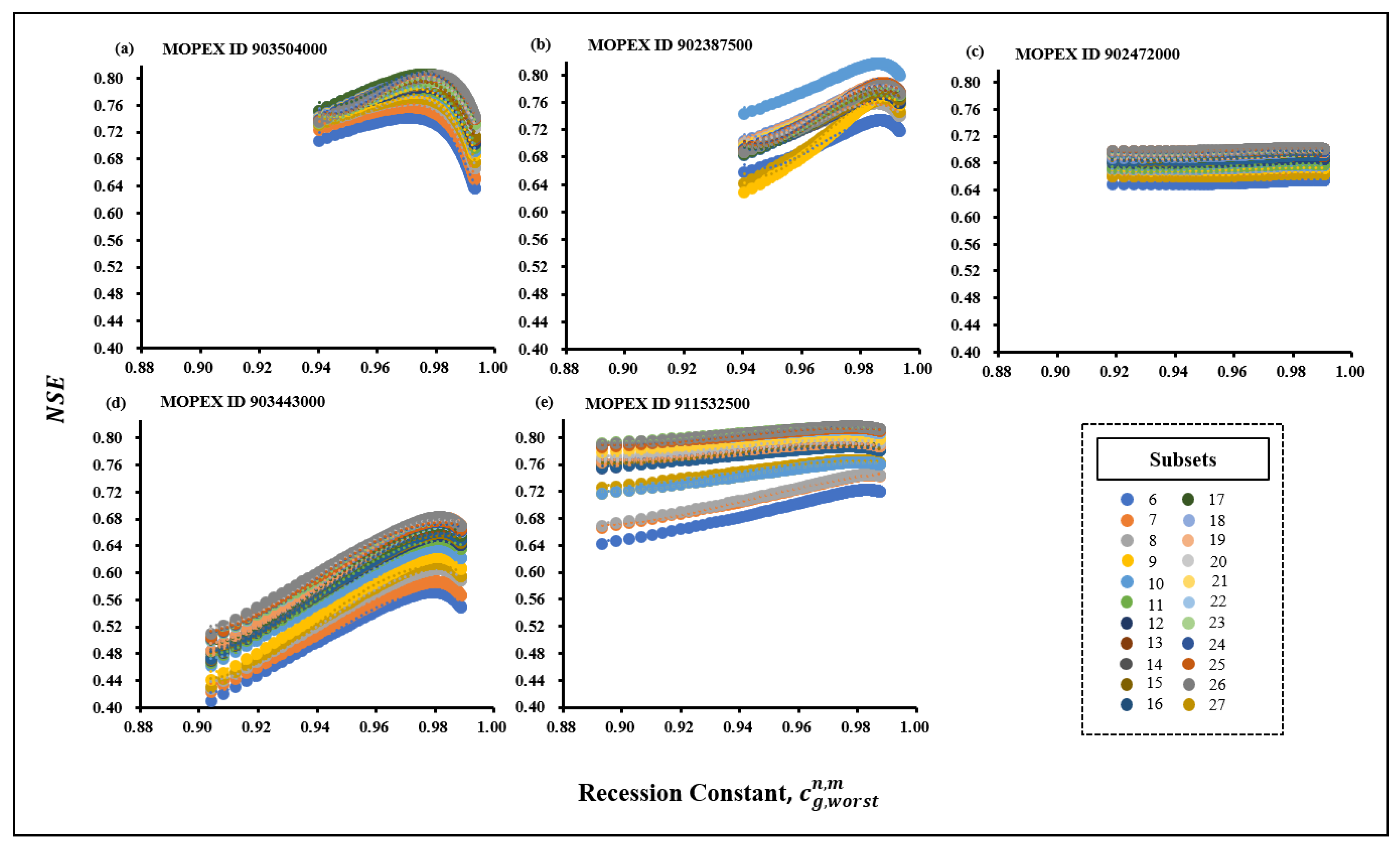
According to [50], to estimate the most sensitive parameter, it can be considered both the best and worse condition for the sensitivity analysis for the parameter optimization. However, to expect good model performance, the worst condition for the parameter optimization is essential to take into consideration.This approach achieving strong model performance under challenging conditions is imperative.A significant difference is evident when comparing NSE values obtained from the two categories (best and median) with those from and cg,ref. This result showed the significant impact over the model performance by utilizing NSE values with . Unlike the previously mentioned categories, the influence of cg on the estimation of Cep becomes pronounced in the worst-case scenario (Figure 4). Additionally, the sensitivity of cg further magnifies its impact on model performance under these conditions. The insight provided by Figure 9 clearly illustrates the variations in NSE values among the three categories across all studied basins.
Table 6.
Detail Description of and values in MOPEX ID (a) 903504000 (b)902387500 (c) 902472000 (d) 903443000 (e) 911532500.
Table 6.
Detail Description of and values in MOPEX ID (a) 903504000 (b)902387500 (c) 902472000 (d) 903443000 (e) 911532500.
| MOPEX ID | ||||||||||
| Subsets | 903504000 | 902387500 | 902472000 | 903443000 | 911532500 | |||||
| Cep,worst | cg,worst | Cep,worst | cg,worst | Cep,worst | cg,worst | Cep,worst | cg,worst | Cep,worst | cg,worst | |
| 6 | 0.5869 | 0.98155 | 1.1664 | 0.98673 | 1.3523 | 0.98702 | 0.9408 | 0.97941 | 0.9584 | 0.98318 |
| 7 | 0.6114 | 0.98235 | 1.1331 | 0.98548 | 1.2522 | 0.98411 | 0.9662 | 0.98022 | 0.9644 | 0.98413 |
| 8 | 0.6705 | 0.98235 | 1.1894 | 0.98548 | 1.2689 | 0.98381 | 0.9467 | 0.98096 | 0.9351 | 0.98413 |
| 9 | 0.6877 | 0.98182 | 1.2826 | 0.98728 | 1.2907 | 0.98426 | 0.952 | 0.98060 | 0.8556 | 0.97952 |
| 10 | 0.6992 | 0.98098 | 1.2653 | 0.98825 | 1.3156 | 0.98522 | 0.9688 | 0.98096 | 0.8752 | 0.98058 |
| 11 | 0.6954 | 0.98182 | 1.2574 | 0.98597 | 1.2822 | 0.98547 | 0.9863 | 0.98114 | 0.8559 | 0.98058 |
| 12 | 0.6940 | 0.98155 | 1.1682 | 0.98687 | 1.311 | 0.98496 | 0.9907 | 0.98131 | 0.8166 | 0.97678 |
| 13 | 0.7099 | 0.98209 | 1.1957 | 0.98715 | 1.3273 | 0.98559 | 0.9997 | 0.98165 | 0.8366 | 0.97791 |
| 14 | 0.7289 | 0.98235 | 1.1779 | 0.98741 | 1.3046 | 0.98534 | 1.0104 | 0.98165 | 0.7986 | 0.97653 |
| 15 | 0.7337 | 0.98209 | 1.2303 | 0.98754 | 1.3123 | 0.98702 | 0.9983 | 0.98214 | 0.815 | 0.97701 |
| 16 | 0.7322 | 0.98260 | 1.2374 | 0.98754 | 1.3199 | 0.98692 | 0.9905 | 0.98182 | 0.8059 | 0.97653 |
| 17 | 0.7379 | 0.97750 | 1.2769 | 0.98754 | 1.3247 | 0.98672 | 0.9973 | 0.98198 | 0.8224 | 0.97747 |
| 18 | 0.7377 | 0.98182 | 1.2919 | 0.98741 | 1.3103 | 0.98692 | 1.0057 | 0.98198 | 0.8428 | 0.97724 |
| 19 | 0.7517 | 0.97972 | 1.2381 | 0.98715 | 1.3158 | 0.98712 | 1.014 | 0.98317 | 0.8347 | 0.97653 |
| 20 | 0.7450 | 0.98037 | 1.2190 | 0.98741 | 1.2928 | 0.98454 | 0.9987 | 0.98275 | 0.8278 | 0.97701 |
| 21 | 0.7474 | 0.98155 | 1.2240 | 0.98754 | 1.2918 | 0.98454 | 0.9687 | 0.98165 | 0.805 | 0.97678 |
| 22 | 0.7543 | 0.98005 | 1.2330 | 0.98754 | 1.265 | 0.98349 | 0.9558 | 0.98198 | 0.7971 | 0.97578 |
| 23 | 0.7510 | 0.98037 | 1.2326 | 0.98766 | 1.2587 | 0.98265 | 0.9592 | 0.98182 | 0.8002 | 0.97604 |
| 24 | 0.7526 | 0.97938 | 1.2303 | 0.98766 | 1.2779 | 0.98349 | 0.9655 | 0.98198 | 0.8067 | 0.97653 |
| 25 | 0.7591 | 0.98037 | 1.2255 | 0.98754 | 1.2717 | 0.98282 | 0.9467 | 0.98131 | 0.8231 | 0.97791 |
| 26 | 0.7672 | 0.98037 | 1.2239 | 0.98766 | 1.2755 | 0.98426 | 0.9531 | 0.98149 | 0.8193 | 0.97813 |
| 27 | 0.7797 | 0.98005 | 1.2413 | 0.98766 | 1.2699 | 0.98349 | 0.9608 | 0.98149 | 0.801 | 0.97791 |
4. Conclusion
This study presents an overview of the crucial role of recession constant sensitivity with the data adjustment parameter in parameter estimation using the XAJ model. Linear polynomial regression analysis is tested, utilizing 28-year U.S. MOPEX datasets and subsets from five river basins. The objective of this paper was to identify the recession constant sensitivity in parameter estimation can result the poor model performance during the data scarcity. The data analysis results revealed that the potential impact of recession constant and its interaction with data adjustment parameter are limited in longer datasets. While recession constant sensitivity moderately impacts model performance in shorter datasets, a significant difference in model performance is observed while calibrating the model in the worst scenario. This analysis indicates that the recession constant parameter and the data adjustment parameter relationship remains robust across different data lengths even though the data adjustment parameters showed the large parameter variations in shorter datasets. Overall, in basins with limited data, it is crucial to consider the interaction of the recession constant as it can impact the model performance during the worst case scenario.
Understanding recession constant sensitivity enhances parameter estimation, improving more accurate and reliable conceptual hydrological model predictions and facilitating precise, acceptable minimum data length estimation in data scarce basins. This study can be mainly used in areas where data availability is limited to consider the recession constant sensitivity in the longer time scales. In summary, this study bridges a gap in understanding the complex interrelationships of hydrological model parameters, facilitating more precise water resource management and planning decisions.
Author Contributions
Conceptualization, T.T.Z. and M.L.; methodology, T.T.Z. and M.L.; software, T.T.Z.; validation, T.T.Z.; formal analysis, T.T.Z.; investigation, T.T.Z. and M.L.; resources, M.L.; data curation, T.T.Z. and M.L.; writing—original draft preparation, T.T.Z.; writing—review and editing, T.T.Z. and M.L.; visualization, T.T.Z.; supervision, M.L.; project administration, M.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Information on all the data applied in this research is shown in Section 2
Conflicts of Interest
Regarding this paper and the research, the authors state that they have no conflicts of interest.
References
- Devia, G.K.; Ganasri, B.P.; Dwarakish, G.S. A review on hydrological models. Aquatic procedia 2015, 4, 1001–1007. [Google Scholar] [CrossRef]
- Peel, M.C.; Blöschl, G. Hydrological modelling in a changing world. Progress in Physical Geography 2011, 35, 249–261. [Google Scholar] [CrossRef]
- Birkholz, S.; Muro, M.; Jeffrey, P.; Smith, H.M. Rethinking the relationship between flood risk perception and flood management. Science of the total environment 2014, 478, 12–20. [Google Scholar] [CrossRef] [PubMed]
- Adikari, Y.; Yoshitani, J. Global trends in water-related disasters: an insight for policymakers. World Water Assessment Programme Side Publication Series, Insights. The United Nations, UNESCO. International Centre for Water Hazard and Risk Management (ICHARM), 2009; 1–24. [Google Scholar]
- Modarres, R.; Ouarda, T.B. Modeling rainfall–runoff relationship using multivariate GARCH model. Journal of Hydrology 2013, 499, 1–18. [Google Scholar] [CrossRef]
- Loucks, D.P.; Van Beek, E. Water resource systems planning and management: An introduction to methods, models, and applications; Springer, 2017.
- Refsgaard, J.C.; Knudsen, J. Operational validation and intercomparison of different types of hydrological models. Water resources research 1996, 32, 2189–2202. [Google Scholar] [CrossRef]
- Ramos, M.H.; Mathevet, T.; Thielen, J.; Pappenberger, F. Communicating uncertainty in hydro-meteorological forecasts: mission impossible? Meteorological Applications 2010, 17, 223–235. [Google Scholar] [CrossRef]
- Raje, D.; Krishnan, R. Bayesian parameter uncertainty modeling in a macroscale hydrologic model and its impact on Indian river basin hydrology under climate change. Water Resources Research 2012, 48. [Google Scholar] [CrossRef]
- Zhao, F.; Wu, Y.; Qiu, L.; Sun, Y.; Sun, L.; Li, Q.; Niu, J.; Wang, G. Parameter uncertainty analysis of the SWAT model in a mountain-loess transitional watershed on the Chinese Loess Plateau. Water 2018, 10, 690. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, S.; Huang, Z.; Yan, W. Parameter optimization, sensitivity, and uncertainty analysis of an ecosystem model at a forest flux tower site in the United States. Journal of Advances in Modeling Earth Systems 2014, 6, 405–419. [Google Scholar] [CrossRef]
- Bárdossy, A.; Singh, S. Robust estimation of hydrological model parameters. Hydrology and earth system sciences 2008, 12, 1273–1283. [Google Scholar] [CrossRef]
- Renard, B.; Kavetski, D.; Kuczera, G.; Thyer, M.; Franks, S.W. Understanding predictive uncertainty in hydrologic modeling: The challenge of identifying input and structural errors. Water Resources Research 2010, 46. [Google Scholar] [CrossRef]
- Muleta, M.K.; Nicklow, J.W. Sensitivity and uncertainty analysis coupled with automatic calibration for a distributed watershed model. Journal of hydrology 2005, 306, 127–145. [Google Scholar] [CrossRef]
- Jeremiah, E.; Sisson, S.A.; Sharma, A.; Marshall, L. Efficient hydrological model parameter optimization with Sequential Monte Carlo sampling. Environmental Modelling & Software 2012, 38, 283–295. [Google Scholar]
- Celeux, G.; Hurn, M.; Robert, C.P. Computational and inferential difficulties with mixture posterior distributions. Journal of the American Statistical Association 2000, 95, 957–970. [Google Scholar] [CrossRef]
- Arnold, J.G.; Youssef, M.A.; Yen, H.; White, M.J.; Sheshukov, A.Y.; Sadeghi, A.M.; Moriasi, D.N.; Steiner, J.L.; Amatya, D.M.; Skaggs, R.W.; et al. Hydrological processes and model representation: impact of soft data on calibration. Transactions of the ASABE 2015, 58, 1637–1660. [Google Scholar]
- Bates, B.C.; Campbell, E.P. A Markov chain Monte Carlo scheme for parameter estimation and inference in conceptual rainfall-runoff modeling. Water resources research 2001, 37, 937–947. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Ter Braak, C.J.; Clark, M.P.; Hyman, J.M.; Robinson, B.A. Treatment of input uncertainty in hydrologic modeling: Doing hydrology backward with Markov chain Monte Carlo simulation. Water Resources Research 2008, 44. [Google Scholar] [CrossRef]
- Gottschalk, F.; Sun, T.; Nowack, B. Environmental concentrations of engineered nanomaterials: review of modeling and analytical studies. Environmental pollution 2013, 181, 287–300. [Google Scholar] [CrossRef] [PubMed]
- Kuczera, G.; Parent, E. Monte Carlo assessment of parameter uncertainty in conceptual catchment models: the Metropolis algorithm. Journal of hydrology 1998, 211, 69–85. [Google Scholar] [CrossRef]
- Micevski, T.; Kuczera, G. Combining site and regional flood information using a Bayesian Monte Carlo approach. Water Resources Research 2009, 45. [Google Scholar] [CrossRef]
- Sorooshian, S.; Gupta, V.K. Automatic calibration of conceptual rainfall-runoff models: The question of parameter observability and uniqueness. Water resources research 1983, 19, 260–268. [Google Scholar] [CrossRef]
- Thyer, M.; Renard, B.; Kavetski, D.; Kuczera, G.; Franks, S.W.; Srikanthan, S. Critical evaluation of parameter consistency and predictive uncertainty in hydrological modeling: A case study using Bayesian total error analysis. Water Resources Research 2009, 45. [Google Scholar] [CrossRef]
- Wagener, T.; McIntyre, N.; Lees, M.; Wheater, H.; Gupta, H. Towards reduced uncertainty in conceptual rainfall-runoff modelling: Dynamic identifiability analysis. Hydrological processes 2003, 17, 455–476. [Google Scholar] [CrossRef]
- Bergström, S. Principles and confidence in hydrological modelling. Hydrology Research 1991, 22, 123–136. [Google Scholar] [CrossRef]
- Beven, K.J. Rainfall-runoff modelling: the primer; John Wiley & Sons, 2011.
- Lu, M. Recent and future studies of the Xinanjiang Model. J. Hydraul. Eng 2021, 52, 432–441. [Google Scholar]
- Singh, V.P.; et al. Computer models of watershed hydrology; Vol. 1130, Water resources publications Highlands Ranch, CO, 1995.
- Gan, Y.; Duan, Q.; Gong, W.; Tong, C.; Sun, Y.; Chu, W.; Ye, A.; Miao, C.; Di, Z. A comprehensive evaluation of various sensitivity analysis methods: A case study with a hydrological model. Environmental modelling & software 2014, 51, 269–285. [Google Scholar]
- Zin, T.T.; Lu, M. Influence of Data Length on the Determination of Data Adjustment Parameters in Conceptual Hydrological Modeling: A Case Study Using the Xinanjiang Model. Water 2022, 14, 3012. [Google Scholar] [CrossRef]
- Schaake, J.; Cong, S.; Duan, Q. US MOPEX data set. Technical report, Lawrence Livermore National Lab.(LLNL), Livermore, CA (United States), 2006.
- Ren-Jun, Z. The Xinanjiang model applied in China. Journal of hydrology 1992, 135, 371–381. [Google Scholar] [CrossRef]
- Lu, M.; Li, X. Time scale dependent sensitivities of the XinAnJiang model parameters. Hydrological Research Letters 2014, 8, 51–56. [Google Scholar] [CrossRef]
- Hapuarachchi, H.; Li, Z.; Wang, S. Application of SCE-UA method for calibrating the Xinanjiang watershed model. Journal of Lake Sciences 2001, 13, 304–314. [Google Scholar]
- Zhao, R.; Liu, X. The Xinanjiang Model, Computer Models of Watershed Hydrology; Singh, VP, Ed, 1995.
- Li, X.; Lu, M. Application of aridity index in estimation of data adjustment parameters in the Xinanjiang model. 土木学会論文集B1 (水工) 2014, 70, I_163–I_168. [Google Scholar] [CrossRef] [PubMed]
- Garrick, M.; Cunnane, C.; Nash, J. A criterion of efficiency for rainfall-runoff models. Journal of Hydrology 1978, 36, 375–381. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. Journal of hydrology 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H. On typical range, sensitivity, and normalization of Mean Squared Error and Nash-Sutcliffe Efficiency type metrics. Water Resources Research 2011, 47. [Google Scholar] [CrossRef]
- Houghton-Carr, H. Assessment criteria for simple conceptual daily rainfall-runoff models. Hydrological Sciences Journal 1999, 44, 237–261. [Google Scholar] [CrossRef]
- McCuen, R.H.; Knight, Z.; Cutter, A.G. Evaluation of the Nash–Sutcliffe efficiency index. Journal of hydrologic engineering 2006, 11, 597–602. [Google Scholar] [CrossRef]
- Schaefli, B.; Gupta, H.V. Do Nash values have value? Hydrological processes 2007, 21, 2075–2080. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. Journal of hydrology 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Kutner, M.H. Applied linear statistical models. (No Title), 2005. [Google Scholar]
- Burden, R.L.; Faires, J.D.; Burden, A.M. Numerical analysis; Cengage learning, 2015.
- Ostertagová, E. Modelling using polynomial regression. Procedia Engineering 2012, 48, 500–506. [Google Scholar] [CrossRef]
- McCuen, R.H. The role of sensitivity analysis in hydrologic modeling. Journal of hydrology 1973, 18, 37–53. [Google Scholar] [CrossRef]
- Li, C.z.; Wang, H.; Liu, J.; Yan, D.h.; Yu, F.l.; Zhang, L. Effect of calibration data series length on performance and optimal parameters of hydrological model. Water Science and Engineering 2010, 3, 378–393. [Google Scholar]
- Li, X.; Lu, M. Multi-step optimization of parameters in the Xinanjiang model taking into account their time scale dependency. Journal of Japan Society of Civil Engineers, Ser. B1 (Hydraulic Engineering) 2012, 68, I_145–I_150. [Google Scholar] [CrossRef] [PubMed]
Figure 1.
Box plot with Cep values using 75th percentile and 25th percentile in MOPEX ID (a) 903504000 (b)902387500 (c) 902472000 (d) 903443000 (e) 911532500.
Figure 1.
Box plot with Cep values using 75th percentile and 25th percentile in MOPEX ID (a) 903504000 (b)902387500 (c) 902472000 (d) 903443000 (e) 911532500.
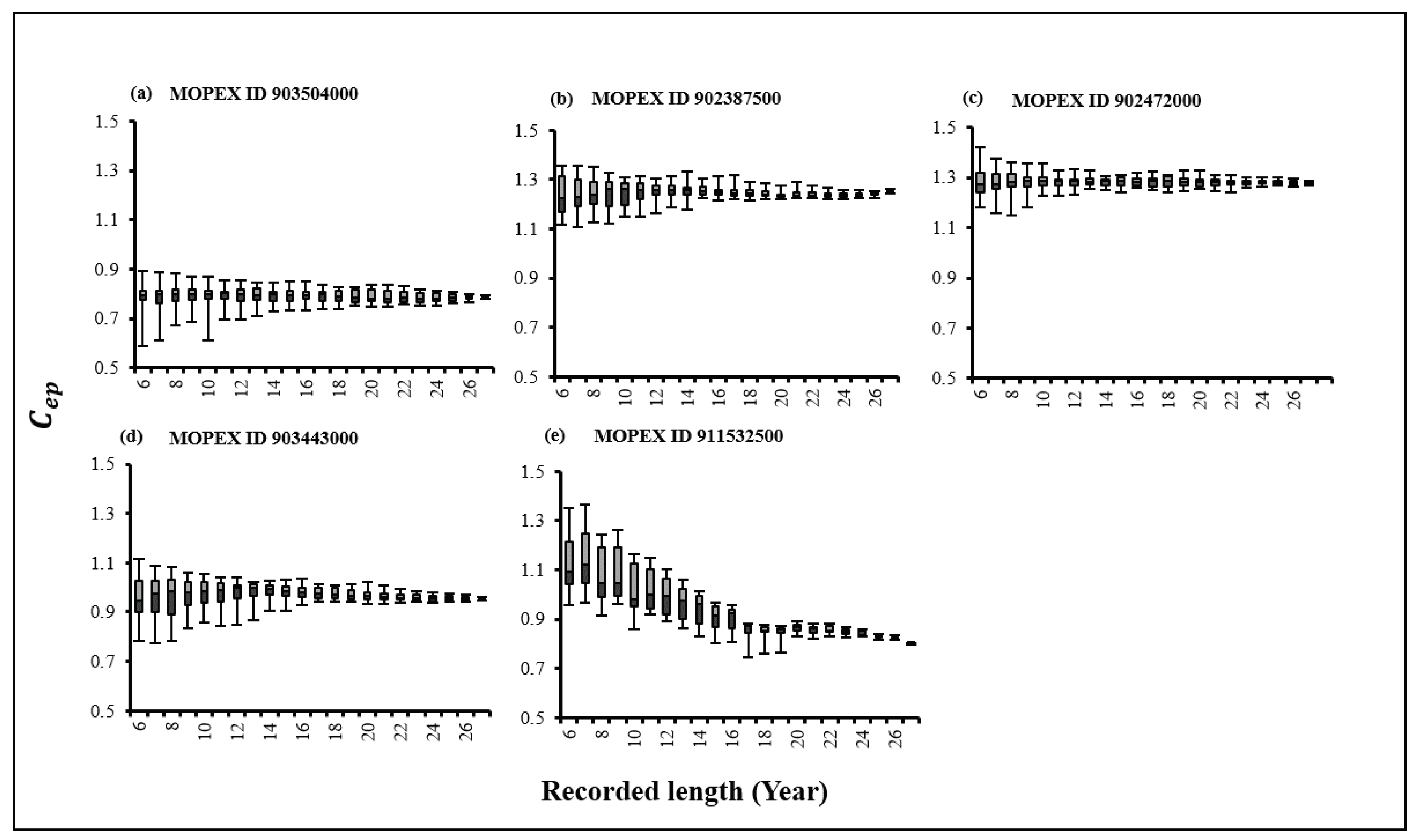
Figure 9.
Comparison of Nash using and for subsets in MOPEX ID (a) 903504000 (b)902387500 (c) 902472000 (d) 903443000 (e) 911532500.
Figure 9.
Comparison of Nash using and for subsets in MOPEX ID (a) 903504000 (b)902387500 (c) 902472000 (d) 903443000 (e) 911532500.
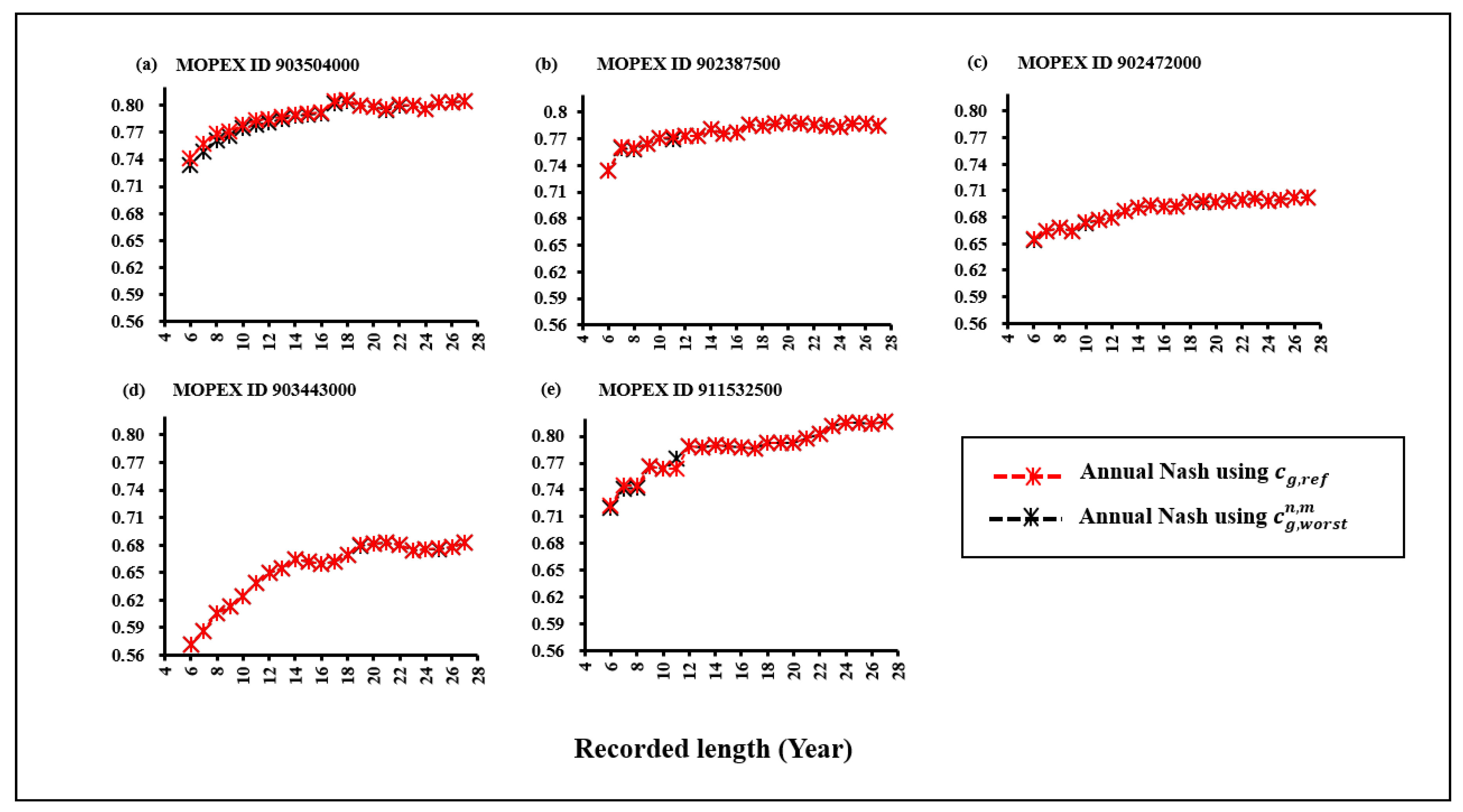
Figure 10.
Comparison of annual Nash in subsets based on all three categories (, and ) in MOPEX ID (a) 903504000 (b)902387500 (c) 902472000 (d) 903443000 (e) 911532500.
Figure 10.
Comparison of annual Nash in subsets based on all three categories (, and ) in MOPEX ID (a) 903504000 (b)902387500 (c) 902472000 (d) 903443000 (e) 911532500.
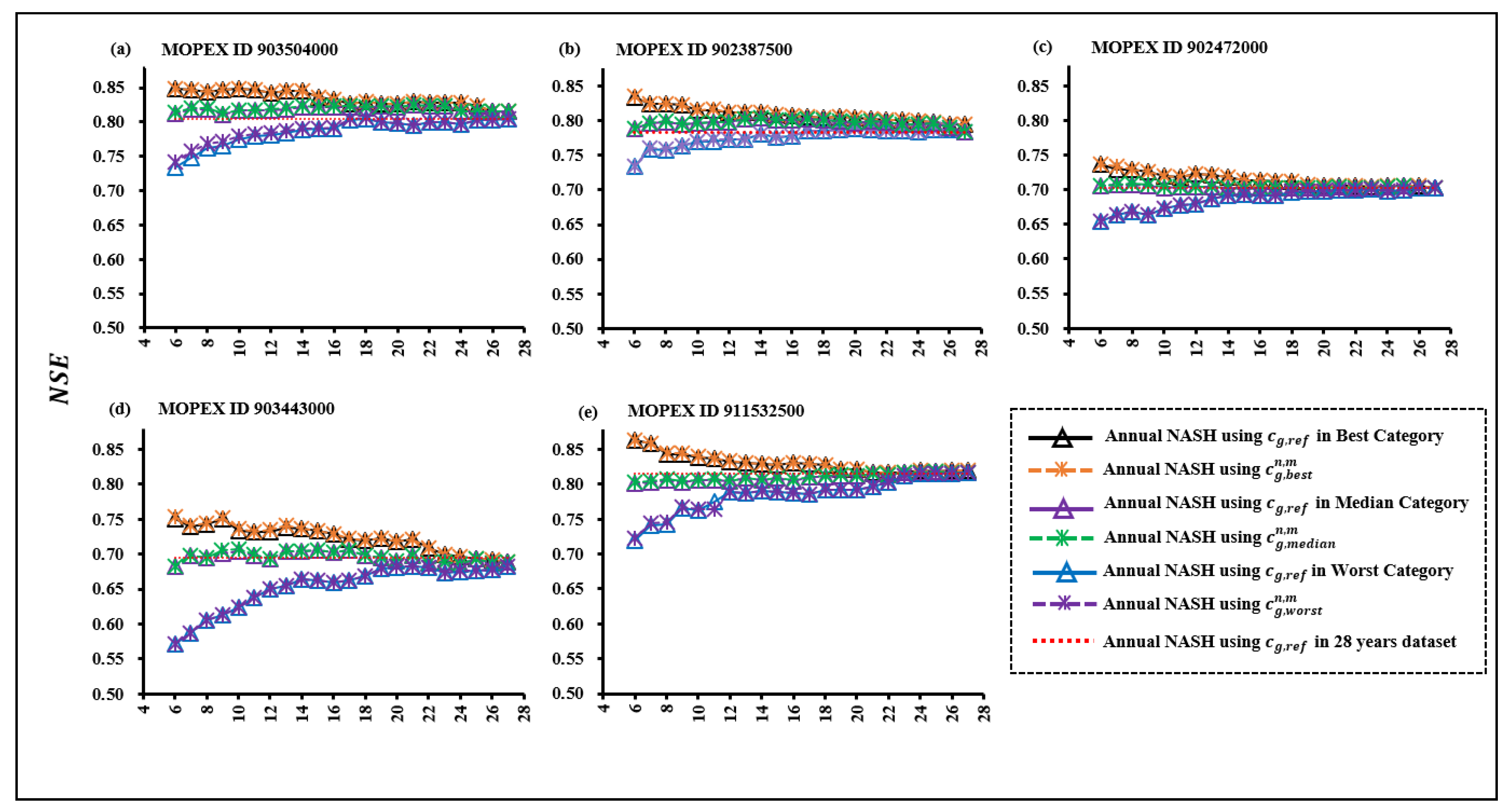
Table 1.
Studied MOPEX basins, locations and basin characteristics.
| Location | |||||||
| MOPEX ID | Long | Lat | State | Drainage area (Sq.km) | Data length (year) | MP(mm/year) | MPE(mm/year) |
| 903504000 | -83.62 | 35.13 | NC | 135.00 | 28 | 1893 | 762.00 |
| 902387500 | -84.94 | 34.58 | GA | 4144.0 | 28 | 1480 | 901.00 |
| 902472000 | -89.41 | 31.71 | MS | 1924.0 | 28 | 1492 | 1060.0 |
| 903443000 | -83.62 | 35.29 | NC | 740.00 | 28 | 2156 | 817.00 |
| 911532500 | -124.05 | 41.79 | CA | 1577.0 | 28 | 2687 | 740.00 |
* indicates the selected basins in Alabama, USA; including Mean Precipitation (MP) and Mean Potential
Table 5.
Detail Description of and values in MOPEX ID (a) 903504000 (b)902387500 (c) 902472000 (d) 903443000 (e) 911532500.
Table 5.
Detail Description of and values in MOPEX ID (a) 903504000 (b)902387500 (c) 902472000 (d) 903443000 (e) 911532500.
| MOPEX ID | ||||||||||
| Subsets | 903504000 | 902387500 | 902472000 | 903443000 | 911532500 | |||||
| Cep,median | cg,median | Cep,median | cg,median | Cep,median | cg,median | Cep,median | cg,median | Cep,median | cg,median | |
| 6 | 0.8852 | 0.97116 | 1.2602 | 0.98937 | 1.2648 | 0.98229 | 1.0093 | 0.98078 | 0.6528 | 0.96957 |
| 7 | 0.8840 | 0.97116 | 1.2397 | 0.98644 | 1.2654 | 0.98229 | 1.0336 | 0.98022 | 0.6465 | 0.96640 |
| 8 | 0.8811 | 0.97182 | 1.1995 | 0.98673 | 1.3409 | 0.98904 | 0.8624 | 0.97941 | 0.7498 | 0.97037 |
| 9 | 0.8167 | 0.97306 | 1.2783 | 0.98673 | 1.3468 | 0.98852 | 0.836 | 0.97509 | 0.7287 | 0.97254 |
| 10 | 0.8079 | 0.97364 | 1.2863 | 0.98728 | 1.2288 | 0.97604 | 0.8684 | 0.97654 | 0.9082 | 0.97914 |
| 11 | 1.0000 | 0.97419 | 1.2478 | 0.98779 | 1.2429 | 0.98152 | 0.8674 | 0.97782 | 0.7455 | 0.96829 |
| 12 | 0.8000 | 0.97472 | 1.2394 | 0.98728 | 1.2321 | 0.98022 | 0.9259 | 0.98096 | 0.7268 | 0.97350 |
| 13 | 0.8379 | 0.97572 | 1.1886 | 0.98802 | 1.2627 | 0.98396 | 1.006 | 0.98304 | 0.7081 | 0.97075 |
| 14 | 0.8302 | 0.97572 | 1.2704 | 0.98825 | 1.273 | 0.98426 | 0.9633 | 0.98096 | 0.7092 | 0.97254 |
| 15 | 0.8182 | 0.97619 | 1.2547 | 0.98814 | 1.2608 | 0.98426 | 0.9652 | 0.98131 | 0.8439 | 0.97791 |
| 16 | 0.8486 | 0.97619 | 1.3136 | 0.98802 | 1.2845 | 0.98559 | 0.962 | 0.98149 | 0.7697 | 0.97350 |
| 17 | 0.7506 | 0.97619 | 1.2419 | 0.98791 | 1.2926 | 0.98583 | 0.9467 | 0.98078 | 0.708 | 0.97185 |
| 18 | 0.8241 | 0.97664 | 1.2386 | 0.98802 | 1.2902 | 0.98411 | 0.9685 | 0.98165 | 0.7311 | 0.97254 |
| 19 | 0.7801 | 0.97708 | 1.2414 | 0.98741 | 1.258 | 0.98426 | 0.965 | 0.98198 | 0.735 | 0.97319 |
| 20 | 0.7816 | 0.97750 | 1.2764 | 0.98847 | 1.2874 | 0.98468 | 0.967 | 0.98230 | 0.8224 | 0.97701 |
| 21 | 0.8303 | 0.97790 | 1.2425 | 0.98791 | 1.2762 | 0.98396 | 0.9548 | 0.98182 | 0.8302 | 0.97769 |
| 22 | 0.7824 | 0.97790 | 1.2532 | 0.98741 | 1.2884 | 0.98522 | 0.9438 | 0.98131 | 0.8179 | 0.97834 |
| 23 | 0.7902 | 0.97829 | 1.2389 | 0.98802 | 1.2877 | 0.98509 | 0.9827 | 0.98182 | 0.8161 | 0.97701 |
| 24 | 0.7694 | 0.97867 | 1.2558 | 0.98754 | 1.3018 | 0.98482 | 0.9566 | 0.98182 | 0.8304 | 0.97854 |
| 25 | 0.7933 | 0.97867 | 1.2567 | 0.98754 | 1.2852 | 0.98454 | 0.9405 | 0.98096 | 0.8137 | 0.97724 |
| 26 | 0.7965 | 0.97903 | 1.2511 | 0.98754 | 1.2637 | 0.98317 | 0.9441 | 0.98078 | 0.8039 | 0.97791 |
| 27 | 0.7931 | 0.97938 | 1.2413 | 0.98766 | 1.2699 | 0.98349 | 0.9505 | 0.98096 | 0.801 | 0.97791 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






