Preprint
Review
Topology of Saliva
Altmetrics
Downloads
132
Views
94
Comments
0
This version is not peer-reviewed
Submitted:
02 December 2023
Posted:
04 December 2023
You are already at the latest version
Alerts
Abstract
Physical properties like shape, volume and size affect the dynamics of biological systems. Along these lines, we focus on the topological properties of biological fluids and their biochemical and physiological outcomes. We take as a paradigmatic example the salivary fluid and describe how its topological features may affect the physiopathology of the oral cavity. Topological approaches assess the general properties of saliva, ignoring small-scale physical details such as density, flow rate, stiffness, viscosity. Specifically, the mucin aggregates scattered in the salivary fluid can be tackled in terms of topological holes, i.e., vortical clusters that modify the direction, flow, impulse, local rate-of-change and velocity of saliva. While the current methodological approaches are inclined to remove the effects of impurities assessing systems as homogeneous structures, we argue that the occurrence of mucins breaks up the salivary fluid’s homogeneity, leading to unexpected biophysical modifications. We suggest that every collected salivary sample is not reliable for accurate clinical and experimental investigation, since it displays highly local as well as variable chemical, physical and biological features, not reflecting the current physiological state of the oral cavity. Therefore, the assessment of a single salivary sample is not fully reproducible and cannot provide information about the biophysical, enzymatic and microbiological content of the whole saliva. In sum, the very topological features of the saliva - such as volume, shape, antipodal cells, vortex area, whirling fluid mass, segmentation, discretization, triangulation, node numbering - produce unnoticed biological consequences and network connectivity features with intriguing operational implications.
Keywords:
Subject: Biology and Life Sciences - Biophysics
INTRODUCTION
From the allometric studies of Otto Snell and D’Arcy Wentworth Thompson (Thompson 1942) onwards, there has been a growing interest towards the physical and topological properties of biophysical systems that influence physiological responses (Bull et al., 2021). Changes in cellular shape, size, volume, polarity, charge, heat, particle transport and extracellular medium drive numerous biological activities at different coarse-grained scales, from protein folding (Oroguchi et al., 2016; Lella and Mahalakshmi, 2017) to endoplasmic reticulum reorganization (Parlakgül et al., 2022), and nuclear pore shaping (Zheng and Xie, 2019; Schuller et al., 2021), from presynaptic transmission (Ucar et al., 2021) to enveloped viruses’ evolution (Twarock and Luque, 2019; Christensen et al., 2020) from tissue morphogenesis (Bailles et al., 2019) to extensibility of plants (Zhang et al., 2021) and engineered intestinal organoids (Gjorevski et al., 2022).
Here we analyze on the topological properties of organic fluids and their biochemical and physiological consequences, focusing on the salivary gel. We opted for saliva as paradigmatic example of an organic fluid because of methodological and operational advantages. The oral fluid is easily available to investigators for diagnostic and monitoring purposes via noninvasive, fast, economical, standardized and reproducible methods of collection. Saliva is a mucinous-serous secretion containing 99.5% water and inorganic/organic substances (Ben-Aryeh et al., 1990; Davis et al., 2020; Zarrin et al., 2020). Forming a selective barrier for transport of water and nutrients through the mucosal surface (Meldrum et al., 2018; Faruqueet al., 2022), saliva provides protection for oral tissues against mechanical, thermal, chemical and biological injuries (Kubala et al., 2018) and contributes in flavor perception and food acceptance (Méjean et al., 2015). The salivary fluid is involved in metabolic processes to such a point that one hundred ninety-six salivary metabolites have been mapped into 49 metabolic pathways (Bessonneau et al., 2017).
Looking for topological features in biophysical settings, we will examine the occurrence of “topological holes”, e.g., nucleations, aggregates and impurities that encode information about the structural complexity of the system in which they are contained. Specifically, we will discuss the mucin aggregates scattered in the salivary medium. We will argue that, apart from the specific physical changes in density, stiffness and viscosity, the increases in number of mucin aggregates (namely, increases in number of topological holes) produces general changes in the topological features of the whole salivary fluid. Once the salivary homogeneity is broken by the very occurrence of mucin aggregates, unexpected biophysical consequences occur.
SALIVARY MUCINS AND TOPOLOGICAL HOLES
The salivary mucus is a dynamic hydrogel lining the luminal surfaces of oral cells. It displays a unique set of rheological properties including low solubility, high viscosity, elasticity, spinnbarkeit, stiffness, adhesiveness (Kumar et al., 2017). The rheological properties of saliva are critical to fulfill chewing, swallowing and vocalization (Marcinkowska-Gapińska et al., 2018; Rereddy et al., 2023), affecting lubrication and coating of oral surfaces, consistency of ingested foods and taste sensitivity (Schwarz 1987; Pushpass et al., 2019).
The main responsible for the peculiar properties of saliva are the mucins, that account for 20–30% of the total amount of salivary proteins (Inoue et al., 2008). Changes in pH and calcium concentration drive the physiological transition of mucins from a condensed form to an expanded linear conformation (Meldrum et al., 2018). The intact mucin molecule consists of a linear polymer of high molecular weight arranged in a network-like formation, where globular domains are punctuated by domains characterized by unordered protein backbone (Kesimer et al, 2008). Mucin polymers display marked length heterogeneity (from ≈670 nm of the monomers and ≈10 μm of the polymers) that is responsible for flexibility and stiffness (Hughes et al., 2019).
We will see that the occurrence of patches of mucins in organized structures can be formulated and compared in the topological terms of their proximities, local similarities and variations.
We will take the salivary mucins as a paradigmatic example of the occurrence of topological holes in biophysical fluids. The hole (aka vortex) is one of the hallmarks of the mathematical branch of topology. The holes are mathematical entities that prevent objects from being continuously shrunken to a point. Holes allow differentiation and classification of the various shapes in such a way that two shapes can be distinguished by examining their holes (Tozzi et al., 2017). The holes can be described in terms of genus: for instance, the sphere does not contain holes and has genus 0, a donut contains a hole and has genus 1, the shape of the number 8 contains two holes and has genus 2, and so on.
The appraisal of topological holes is a methodological and operational approach (Afriat 2012) that has already been fruitful in the investigation of cavities and impurities in physical systems, including cosmic microwave background radiation (Pranav et al., 2019), skyrmions’ ultrafast polarization (Li et al., 2021), quasiparticles superposition (Dai et al., 2020), Berezinskii–Kosterlitz–Thouless phase transitions (Beekman et al., 2017; Bighin et al., 2019; Padavić et al., 2020), nanocrystals nucleation (Jeon et al., 2021). Likewise, many biological processes can be described in terms of holes, from the backbone chains’ conformation of biomolecules, to the DNA modifications during the cell cycle phases (Achar et al., 2020) and the ciliary field defects in simple organisms (Bull et al., 2021). Likewise, the brain, rather than being homogeneous, is punctured by countless, uniformly placed anatomical and functional “cavities” (Don et al., 2020; Tozzi et al., 2021).
In the following, we will suggest that mucins aggregates can be described in terms of holes embedded in surfaces affecting the features of the salivary fluid envisioned as a topological manifold. We will argue that the occurrence of topological holes in saliva produces experimentally detectable effects that can be assessed at the macroscopic scale of the fluid.
SALIVARY HOMOGENEITY AND CONTINUITY ARE DISRUPTED BY MUCINS
By a topological standpoint, a pure fluid like the distilled water does not contain holes and can be therefore defined as a finite, closed manifold equipped with topological genus 0. A pure fluid stands for a uniform topological object that might be mathematically considered as homogeneous three-dimensional space (Williamson and Janos, 1987). According to the continuum assumption of fluid mechanics, fluids can be modeled as a continuous mass even though they are composed of discrete molecules on a microscopic scale (Murphy et al., 2022). A continuously distributed fluid fills the entire space it occupies, regardless of the microscopic occurrence of particles, cracks and impurities. It is no coincidence that the many macroscopic quantities in fluid mechanics like density, velocity, pressure, etc. are assumed to vary continuously from point to point within the flow (Colin 2014). The continuum assumption is very useful by a methodological perspective since it averages the microscopic quantities on a small sampling volume, wiping out molecular discontinuities and abrupt changes in values (Colin 2014). The operational approaches based on the continuum assumption regard holes as a route toward failure and tend to remove unwanted factors like e.g., swelling instabilities and compartment alterations (Bertoldi 2017).
Here we argue that the occurrence of impurities modifies systems’ topological features. In biological settings, the presence of holes encodes remarkable information about a given structure and its three-dimensional structural complexity. We suggest that the occurrence of holes leads to increases in genus, so that the more the impurities, the higher the genus of the fluid. When dealing with topological spaces of genus ≥1, retraction is banned and dysconnectivity starts to catch on. In mathematical jargon, dysconnectivity can be treated in terms of disjoint sets. Two sets are disjoint if they have no elements in common, or in other words, if their intersection is an empty set such that such that a ∩ b = Ø (Cormen et al., 2001). In topological spaces of genus ≥1, the production of disjoint subsets impairs manifold connectedness such that continuity gets lost. Therefore, increases in the number of mucins (namely, increases in the number of topological holes) should modify the functional features of the whole salivary fluid. Apart their chemical effects, mucins may be conceptually assimilated to physical particles that disrupt the continuity of the salivary medium. Since manifolds of genus ≥1 must contain at least some disconnected elements, the very existence of salivary mucins rules out the possibility of indivisibility inside the salivary fluid. Once its homogeneity and connectivity get lost, the salivary medium can no longer be studied taking into account the continuous assumption. The occurrence of mucins requires that the salivary fluid must be operationally split in subsets that are different from each other and must be treated just by discrete operational approaches.
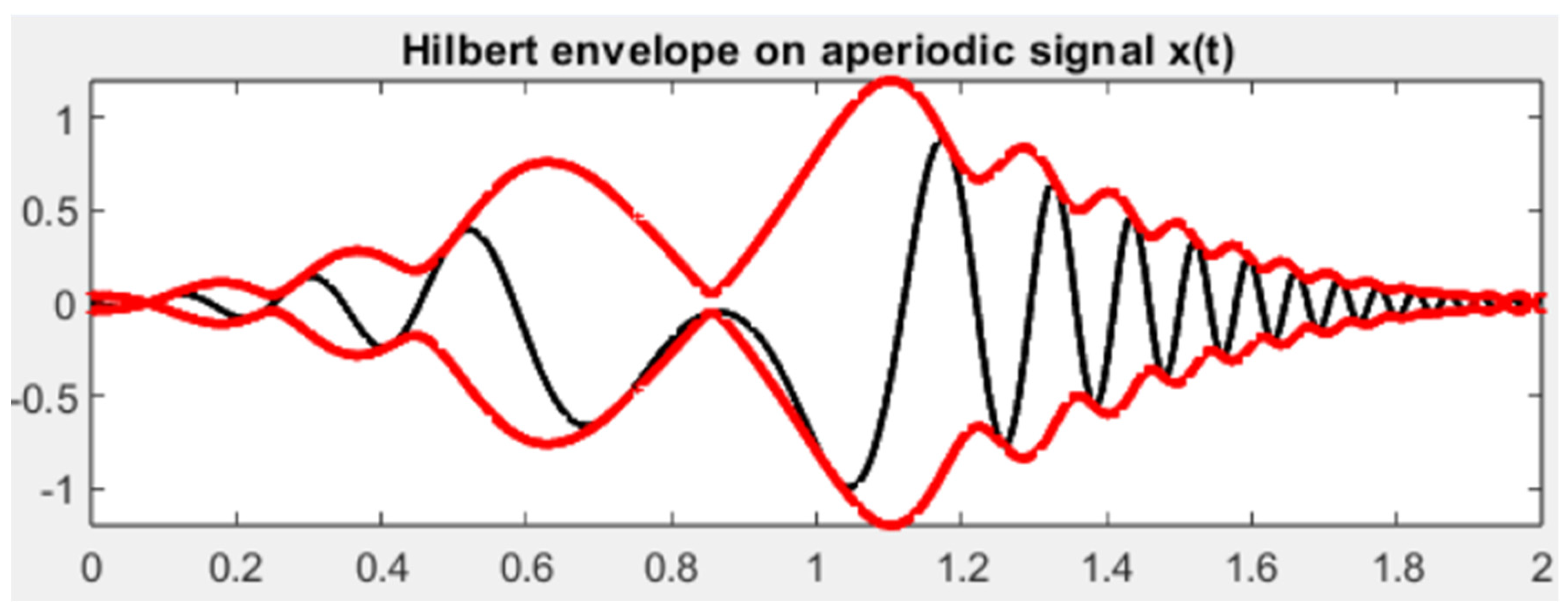
The topological relationships between mucin aggregates and salivary fluid can be tackled in terms of topological nerve structures including intersecting surface islands, intersecting saliva subsets (Figure 1), intersecting cell complexes or ribbon complexes, inherent surface curvature antipodes, islands, centroids and amenable vortexes (Peters, 2020; Peters and Vergili, 2021; Peters et al., 2023). Topology concerns not just mathematical shapes, but also physical features such as functions, vectors and energies (for a survey, see Tozzi et al., 2017). To provide an example of physical features that can be treated in terms of topological approaches, the signals detected from samples of collected saliva can be described as temperature variation curves (Figure 2), length of light penetration curves, proximities of saliva vortexes, envelopes on the signals’ curves. These signals from collected saliva can be represented by Hilbert transforms and Fourier transforms (Figure 2). The quantification, interpretation and comparison of salivary signals x(t) at time t can be analyzed via a Fourier transform such as:
This means that, inside biophysical fluids provided with topological holes, the regions surrounding the holes must display at least some inhomogeneous signal (e.g., differences in temperature, fluid velocity, vortexes, proximities of surface curves, enzymatic activity, etc.). Based on the above topological framework, we argue that modifications of the salivary fluid, such as changes in density, temperature spikes, fluid velocity variation, viscosity, stiffness, bacterial binding capacity, etc., must be strictly local and cannot be generalized to whole saliva. Since the signal under investigation cannot be homogeneous throughout the whole saliva, single measurements of salivary fluid are not reliable. The practical outcome is that every collected salivary sample displays a variable number of features, so that the assessment of a single sample is not fully reproducible and cannot provide information about the physical, chemical, enzymatic and microbiological content of the whole saliva.
In conclusion, the occurrence of mucins deeply modifies the topology of the salivary medium, providing researchers with remarkable methodological weapons for salivary dynamics evaluation.
CONCLUSIONS
Topological approaches provide tools for measuring the large-scale properties of spaces and metrics, ignoring the small-scale details. In our case, a topological approach provides tools for measuring the general properties of the salivary fluid, leaving apart single parameters like stiffness, viscosity, etc. We argue that topological modifications, correlated with the very mathematical structure of the subtending manifold, can modify the physiology of the salivary gel, altering location, number and connectivity of nodes and compartments.
To analyse system’s large-scale properties, scientists overlook small-scale details such as holes and impurities and tend to encourage coarse-grained methodological approaches based on the continuum assumption. We argue that the continuum assumption does not hold for salivary fluid, due to the presence of mucin aggregates. This leads us to speculate about unusual methodological approaches to the study of the salivary fluid. Approaches to biological fluids based on the occurrence of holes permit the assessment of systems dynamics not just from the standpoint of Euclidean metric spaces, but also from the more refined standpoint of algebraic manifolds. This means that the occurrence of topological holes permits the theoretical possibility to assess living systems’ dynamics in terms of Hilbert spaces equipped with their own algebras, groups, operators and metric structure.
The occurrence of holes causes the failure of the continuum assumption-based theorems that have been proven useful to investigate a large array of physical and biophysical issues. Amongst them, the hairy ball theorem (colloquially stating that “whenever one attempts to comb a hairy ball flat, there will always be at least one tuft of hair at one point on the ball”), the Brouwer fixed point theorem (“no matter how you slosh the coffee, some point is always in the same position that it was before the sloshing began”) and the Borsuk-Ulam theorem (“at any moment, there is always a pair of antipodal points on the Earth’s surface with equal temperatures and barometric pressures”) should be mentioned (Tozzi and Papo, 2020). Describe genus-0 convex spheres, all these theorems cannot be used to treat manifolds of genus ≥1. Therefore, the occurrence of salivary mucins (namely, topological holes) forbids the use of these topological theorems for the evaluation of salivary properties. To provide an example of their failure, the well-known capability of the Borsuk-Ulam theorem to evaluate living beings’ symmetries (Tozzi et al., 2017) is lost under the circumstances of a biological fluid filled with topological holes. One might be tempted to speculate that the occurrence of countless aggregates of salivary mucins might give rise to open manifolds of almost infinite number of topological holes. This would pave the way to use the powerful mathematical approaches related to infinite-genus manifolds, such as the Loch Ness monster surface (Valdez 2009; Arredondo and Ramírez Maluendas, 2017), the Jacob’s ladder, i.e., a surface with two ends (Ghys 1995), or to groups with no planar ends and with self-similar end spaces (Aougab et al., 2021), the Weierstrass’ one-ended, periodic minimal surfaces (Edward 1995), Veech groups of tame translation surfaces (Ramírez Maluendas and Valdez 2017), blooming Cantor trees with infinite number of handles and wild translation surfaces (Randecker 2018).
Biological flows are widespread phenomena that occur at different levels of biological systems’ organization, from the intracytoplasmic streaming to the horizontal gas-liquid flow of microorganisms living in water columns (Chang and Zhou, 2019; Mogre et al., 2020; Vutukuri et al. 2020). Topological considerations lead us to hypothesize that mucins could be able to affect the dynamics of salivary flows (Syed Musa, 2021). The occurrence of high amounts of mucins, leading to failure in manifold homogeneity, could be capable of impairing the salivary flows. Mucin aggregates might function as micrometric “obstacles” that generate inertial elastic instability and increase the overall flow resistance of saliva. When the continuum assumption of fluid mechanics is no longer a good approximation, statistical mechanics might come into play (Barber and Emerson 2002). Therefore, intra-salivary flows could be treated in terms of statistical approaches, leaving apart the continuum assumption. In the Hamiltonian formulation of classical mechanics, the phase space of certain classical systems with internal flows takes on the structure of a topological manifold. By an operational standpoint, every phase space of Lagrangian manifolds contains a minimum number of loops, i.e., configurations in which the system returns to the starting point (Frauenfelder 2004). The Arnold conjecture suggests that this minimum number of loops is at least equal to the number of closed orbits (i.e., of holes) in the overall phase space (Abbondandolo. 2001; Abouzaid and Blumberg, 2021). This implies that the Hamiltonian motion of the salivary flows could be correlated with the number of holes, namely, of salivary mucin aggregates.
It is widely known that the flow rate and composition of the salivary fluid is rather inconstant and deeply modified by environmental toxicants and physiological states such as chemical, mechanical and pharmacologic stimuli, age, stress, as well as pathological conditions (Sivakumar et al., 2009; Cabras et al., 2010; Wu et al., 2018; Hurley et al., 2019; Hardy et al., 2022). By an operational standpoint, our topological approach provides a mathematical explanation for this annoying phenomenon that impacts the quantitative evaluation of collected salivary samples. In touch with the empirical findings, our framework predicts that every collected salivary sample is not homogeneous, rather displays a highly variable number of features. We conclude that the assessment of a single salivary sample is not fully reproducible, therefore it cannot provide information about the physical, chemical, enzymatic and microbiological features of the whole saliva.
STATEMENT
The Authors warrant that the article is original, does not infringe on any copyright or other proprietary right of any third part, is not under consideration by another journal, and has not been previously published.
The Authors do not have any known or potential conflict of interest including any financial, personal or other relationships with other people or organizations within three years of beginning the submitted work that could inappropriately influence, or be perceived to influence, their work.
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
This research does not contain any studies with human participants or animals performed by the Author.
The Authors had full access to all the data in the study and take responsibility for the integrity of the data and the accuracy of the data analysis. Both the Authors performed: study concept and design, acquisition of data, analysis and interpretation of data, drafting of the manuscript, critical revision of the manuscript for important intellectual content, statistical analysis, obtained funding, administrative, technical, and material support, study supervision.
References
- Abbondandolo, A. 2001. The Arnold conjectures for sympletic fixed points. Morse Theory for Hamiltonian Systems. Chapman and Hall. pp. 153–172. ISBN 1-58488-202-6.
- Abouzaid M, Blumberg AJ. 2021. Arnold Conjecture and Morava K-theory. arXiv:2103.01507.
- Achar, Y.J.; Adhil, M.; Choudhary, R. et al. 2020. Negative supercoil at gene boundaries modulates gene topology. Nature 577, 701–705 (2020). [CrossRef]
- Afriat, A. 2012. Topology, holes and sources. International journal of theoretical physics, 52 (3). pp. 1007-1012.
- Aougab, T. , Patel P, Vlamis NG. 2021. Isometry groups of infinite-genus hyperbolic surfaces. Math. Ann. 381, 459–498. [CrossRef]
- Arredondo JA, Ramírez Maluendas, C. 2017. On the Infinite Loch Ness monster. Commentationes Mathematicae Universitatis Carolinae, 58 (4): 465–479. [CrossRef]
- Bailles, A.; Collinet, C.; Philippe, JM. et al. 2019. Genetic induction and mechanochemical propagation of a morphogenetic wave. Nature 572, 467–473. [CrossRef]
- Barber RW, Emerson DR. 2002. The influence of knudsen number on the hydrodynamic development length within parallel plate micro-channels. WIT Transactions on Engineering Sciences. Volume 36.
- Beekman AJ, Nissinen J, Wu K, Liu K, Slager R-J, et al. 2017. Dual gauge field theory of quantum liquid crystals in two dimensions. Physics Reports. Volume 683, 18 April 2017, Pages 1-110. [CrossRef]
- Ben-Aryeh, H. ; M. Fisher, R. Szargel, D. Laufer. 1990. Composition of whole unstimulated saliva of healthy children: Changes with age. Archives of Oral Biology Volume 35, Issue 11, 1990, Pages 929-931. [CrossRef]
- Bertoldi, K. 2017. Harnessing Instabilities to Design Tunable Architected Cellular Materials. Annual Review of Materials Research. Vol. 5: 47. [CrossRef]
- Bessonneau, Vincent; Janusz Pawliszyn,Stephen, M. Rappaport. 2017. The Saliva Exposome for Monitoring of Individuals’ Health Trajectories. Environ Health Perspect. 2017 Jul; 125(7): 077014. [CrossRef]
- Bighin G, Defenu N, Nándori I, Salasnich L, Trombettoni, A. 2019. Berezinskii-Kosterlitz-Thouless Paired Phase in Coupled XY Models. Phys. Rev. Lett. 123, 100601.
- Bull MS, Prakash, M. 2021a. Mobile defects born from an energy cascade shape the locomotive behavior of a headless animal. arXiv:2107.02940.
- Cabras, Tiziana; Elisabetta Pisano, Andrea Mastinu, Gloria Denotti, Pietro Paolo Pusceddu, et al. 2010. Alterations of the Salivary Secretory Peptidome Profile in Children Affected by Type 1 Diabetes. Mol Cell Proteomics. 2010 Oct; 9(10): 2099–2108. Published online 2010 Jun 28. [CrossRef]
- Christensen DE, Ganser-Pornillos BK, Johnson JS, Pornillos O, Sundquist WI. 2020. Reconstitution and visualization of HIV-1 capsid-dependent replication and integration in vitro. Science. Vol 370, Issue 6513. [CrossRef]
- Chang BSH, Zhou Y-L. 2019. Flow Regime Recognition and Dynamic Characteristics Analysis of Air-Water Flow in Horizontal Channel under Nonlinear Oscillation Based on Multi-Scale Entropy. Entropy 2019, 21(7), 667. [CrossRef]
- Colin, S. 2014. Chapter 2 – Single-phase gas flow in microchannels. in Heat Transfer and Fluid Flow in Minichannels and Microchannels (Second Edition). [CrossRef]
- Cormen TH, Leiserson CE, Rivest RL, Stein, C. 2001. Data structures for Disjoint Sets. In: Introduction to Algorithms, MIT Press, 498–524. ISBN 0-262-03293-7.
- Dai, Y.; Zhou, Z.; Ghosh, A. et al. Plasmonic topological quasiparticle on the nanometre and femtosecond scales. Nature 588, 616–619 (2020). [CrossRef]
- Davis, E.; Bakulski, K.M.; Goodrich, J.M. et al. 2020. Low levels of salivary metals, oral microbiome composition and dental decay. Sci Rep 10, 14640 (2020). [CrossRef]
- Don AP, Peters JF, Ramanna S, Tozzi, A. 2020. Topological View of Flows inside the BOLD Spontaneous Activity of the Human Brain. Front. Comput. Neurosci. [CrossRef]
- Faruque, Mouri; Melène Wanschers, Antoon, J.; Ligtenberg, Marja, L.; Laine, Floris, J. Bikker. 2022. A review on the role of salivary MUC5B in oral health. Journal of Oral Biosciences. Volume 64, Issue 4, December 2022, Pages 392-399. [CrossRef]
- Ferri, M.; Gagliardi, C. & Grasselli, L. 1986. A graph-theoretical representation of PL-manifolds — A survey on crystallizations. Aeq. Math. 31, 121–141 (1986). [CrossRef]
- Frauenfelder, U. 2004. The Arnold–Givental conjecture and moment Floer homology. International Mathematics Research Notices, 2004 (42): 2179–2269. [CrossRef]
- Ghys, É. 1995. Topologie des feuilles génériques. Annals of Mathematics, Second Series, 141 (2): 387–422. [CrossRef]
- Gjorevski N, Nikolaev M, Brown E, Mitrofanova O, Brandenberg N, et al. 2022. Tissue geometry drives deterministic organoid patterning. Science, Vol 375, Issue 6576. [CrossRef]
- Hardy, Mike; Liam Kelleher, Paulo de Carvalho Gomes, Emma Buchan Hin On Martin Chu, Pola Goldberg Oppenheimer. 2022. Methods in Raman spectroscopy for saliva studies – a review. Applied Spectroscopy Reviews, Volume 57, 2022 - Issue 3. Pages 177-233 | Published online: 30 Aug 2021. [CrossRef]
- Holmes, CC; N. M. Adams. 2003. Likelihood Inference in Nearest-Neighbour Classification Models. Biometrika, 90, 2003 pp. 99–112. [CrossRef]
- Hughes, Gareth W; Caroline Ridley, Richard Collins, Alan Roseman, Robert Ford, David J Thornton. 2019. The MUC5B mucin polymer is dominated by repeating structural motifs and its topology is regulated by calcium and pH. Sci Rep. 2019 Nov 22;9(1):17350. [CrossRef]
- Hurley, E.; Barrett, M.P.J.; Kinirons, M. et al. 2019. Comparison of the salivary and dentinal microbiome of children with severe-early childhood caries to the salivary microbiome of caries-free children. BMC Oral Health 19, 13 (2019). [CrossRef]
- Inoue, Hiroko; Kentaro Ono, Wataru Masuda, Tomohiro Inagaki, Makoto Yokota, Kiyotoshi Inenaga. 2008. Rheological Properties of Human Saliva and Salivary Mucins. Journal of Oral Biosciences Volume 50, Issue 2, 2008, Pages 134-141. [CrossRef]
- Jeon S, Heo T, Hwang S-Y, Ciston, J., Bustillo KC, et al. 2021. Reversible disorder-order transitions in atomic crystal nucleation. Science. Vol 371, Issue 6528, pp. 498-503. [CrossRef]
- Kesimer, Mehmet; John K Sheehan. 2008. Analyzing the functions of large glycoconjugates through the dissipative properties of their absorbed layers using the gel-forming mucin MUC5B as an example. Glycobiology, Volume 18, Issue 6, June 2008, Pages 463–472. [CrossRef]
- Kubala, Elżbieta; Paulina Strzelecka, Marta Grzegocka, Danuta Lietz-Kijak, Helena Gronwald, et al. 2018. A Review of Selected Studies That Determine the Physical and Chemical Properties of Saliva in the Field of Dental Treatment. Biomed Res Int. 2018 May 9:2018:6572381. [CrossRef]
- Kumar, Brij; Nilotpol Kashyap, Alok Avinash, Ramakrishna Chevvuri, Mylavarapu Krishna Sagar, Kumar Shrikant. 2017. The composition, function and role of saliva in maintaining oral health: A review. International Journal of Contemporary Dental and Medical Reviews (2017), Article ID 011217, 6 Pages.
- Lella M, Mahalakshmi, R. 2017. Metamorphic Proteins: Emergence of Dual Protein Folds from One Primary Sequence. Biochemistry. 2017, 56, 24, 2971–2984. [CrossRef]
- Li, S. , Deng, B., Grinthal, A. et al. Liquid-induced topological transformations of cellular microstructures. Nature 592, 386–391 (2021). [CrossRef]
- Li, Q.; Stoica, V.A.; Paściak, M. et al. Subterahertz collective dynamics of polar vortices. Nature 592, 376–380 (2021). [CrossRef]
- Lipsky, O.; Porat, E. 2008. Approximated Pattern Matching with the L 1, L 2 and L∞ Metrics. In: Amir, A.; Turpin, A.; Moffat, A. (eds) String Processing and Information Retrieval. SPIRE 2008. Lecture Notes in Computer Science, vol 5280. Springer, Berlin, Heidelberg. [CrossRef]
- Marcinkowska-Gapińska A, Linkowska-Świdzińska K, , Świdziński T, , Surdacka, A. 2018. Rheological parameters of saliva in comparison with taste examination. Biorheology, 01 Jan 2018, 55(1):51-60. [CrossRef]
- Meldrum, Oliver W; Gleb E Yakubov, Mauricio R Bonilla, Omkar Deshmukh, Michael A McGuckin, Michael J Gidley. 2018. Mucin gel assembly is controlled by a collective action of non-mucin proteins, disulfide bridges, Ca2+-mediated links, and hydrogen bonding. Sci Rep. 2018 Apr 11;8(1):5802. [CrossRef]
- Méjean, Caroline; Martine Morzel, Eric Neyraud, Sylvie Issanchou, Christophe Martin, et al. 2015. Salivary Composition Is Associated with Liking and Usual Nutrient Intake. PLOS One. [CrossRef]
- Mogre SS, Brown AI, Koslover EF. 2020. Getting around the cell: physical transport in the intracellular world. Physical Biology, Volume 17, Number 6. [CrossRef]
- Murphy MA, Horstemeyer MF, Prabhu RK. 2022. Chapter 4 - Modeling nanoscale cellular structures using molecular dynamics. Multiscale Biomechanical Modeling of the Brain, Pages 53-76. [CrossRef]
- Oroguchi, T.; Nakasako, M. 2016. Changes in hydration structure are necessary for collective motions of a multi-domain protein. Sci Rep 6, 26302. [CrossRef]
- Padavić K, Sun K, Lannert C, Vishveshwara, S. 2020. Vortex-antivortex physics in shell-shaped Bose-Einstein condensates. arXiv:2005.13030. [CrossRef]
- Parlakgül, G. , Arruda AP, Pang, S. et al. 2022. Regulation of liver subcellular architecture controls metabolic homeostasis. Nature 603, 736–742. [CrossRef]
- Perez-Tanoira, Ramón; Antti Aarnisalo, Aaro Haapaniemi, Riitta Saarinen, Pentti Kuusela, Teemu J Kinnari. 2019. Bacterial biofilm in salivary stones. Eur Arch Otorhinolaryngol. 2019 Jun;276(6):1815-1822. [CrossRef]
- Peters JF 2020 Ribbon complexes & their approximate descriptive proximities. Ribbon & vortex nerves, Betti numbers and planar divisions, Bull. Allahabad Math. Soc. 35, no. 1, 31-53.
- Peters JF, Vergili, T 2021 Fixed point property of amenable planar vortexes, Applied Gen. Topology 22, no. 2, 385-397.
- Peters JF, Alfano R, Smith P, Tozzi A, Vergili, T. 2023. Geometric realizations of homotopic paths over curved surfaces. Filomat 38(3):793-802.
- Pranav P, Adler RJ, Buchert T, Edelsbrunner, H., Jones BJT, et al. 2019. Unexpected topology of the temperature fluctuations in the cosmic microwave background. Astronomy & Astrophysics. Volume 627, Article Number A163. [CrossRef]
- Pushpass, Rose-Anna Grace ; Blánaid Daly, Charles Kelly, Gordon Proctor, Guy Howard Carpenter. 2019. Altered Salivary Flow, Protein Composition, and Rheology Following Taste and TRP Stimulation in Older Adults. Front. Physiol., 31 May 2019. Volume 10 - 2019. [CrossRef]
- Ramírez Maluendas C, Valdez, F. 2017. Veech groups of infinite-genus surfaces. Algebraic & Geometric Topology 17 529–560. [CrossRef]
- Randecker, A. 2018. Wild translation surfaces and infinite genus. Algebraic & Geometric Topology 18, 2661–2699. [CrossRef]
- Rereddy, S K; A C Cao, B Blackwell, R Poling-Skutvik, P E Arratia, N Mirza. 2023. Rheology of saliva in health and disease. Biorheology. 2023;59(1-2):19-27. [CrossRef]
- Schuller, A.P.; Wojtynek, M.; Mankus, D. et al. The cellular environment shapes the nuclear pore complex architecture. Nature 598, 667–671 (2021). [CrossRef]
- Schwarz, WH. 1987. The rheology of saliva. J Dent Res. 1987 Feb:66 Spec No:660-6. [CrossRef]
- Sivakumar, T. ; A. Hand, M. Mednieks. 2009. Secretory proteins in the saliva of children. Journal of Oral Science. [CrossRef]
- Syed Musa SMS, Md Noorani, MS, Abdul Razak, F., et al. Using persistent homology as preprocessing of early warning signals for critical transition in flood. Sci Rep 11, 7234 (2021). [CrossRef]
- Thayer, CT. 1995. Higher-genus Chen-Gackstatter surfaces and the Weierstrass representation for surfaces of infinite genus. Experiment. Math. 4 (1) 19 - 39.
- Thompson DW. Ed. 1942. On Growth and Form. Dover Pubns; Revised ed, 1992. ISBN-13 : 978-0486671352.
- Tozzi A, Peters JF, Fingelkurts AA, Fingelkurts AA, Marijuán PC. 2017. Topodynamics of metastable brains. Physics of Life Reviews, 21, 1-20. [CrossRef]
- Tozzi A, Papo, D. 2020. Projective mechanisms subtending real world phenomena wipe away cause effect relationships. Progress in Biophysics and Molecular Biology. 151:1-13. [CrossRef]
- Tozzi A, Yurkin A, Peters JF. 2021. A Geometric Milieu Inside the Brain. Found Sci. [CrossRef]
- Twarock, R.; Luque, A. 2019. Structural puzzles in virology solved with an overarching icosahedral design principle. Nat Commun 10, 4414. [CrossRef]
- Ucar, H.; Watanabe, S.; Noguchi, J. et al. Mechanical actions of dendritic-spine enlargement on presynaptic exocytosis. Nature 600, 686–689 (2021). [CrossRef]
- Valdez, F. 2009 Infinite genus surfaces and irrational polygonal billiards. Geom Dedicata 143, 143 (2009). [CrossRef]
- Vutukuri, H.R.; Hoore, M.; Abaurrea-Velasco, C. et al. Active particles induce large shape deformations in giant lipid vesicles. Nature 586, 52–56 (2020). [CrossRef]
- Williamson R, Janos, L. 1987. Construction metrics with the Heine-Borel property. Proc. AMS. 100 (3): 567–573. [CrossRef]
- Wu, Katie P; Jyh-Yuh Ke, Chia-Ying Chung, Chia-Ling Chen, Tsong-Long Hwang, et al. 2008. Relationship between unstimulated salivary flow rate and saliva composition of healthy children in Taiwan. Chang Gung Med J. 2008 May-Jun;31(3):281-6.
- Zarrin, P.S.; Zahari, F.; Mahadevaiah, M.K. et al. 2020. Neuromorphic on-chip recognition of saliva samples of COPD and healthy controls using memristive devices. Sci Rep 10, 19742 (2020). [CrossRef]
- Zając, S.; Geary, C.; Andersen, E.S. et al. Genus trace reveals the topological complexity and domain structure of biomolecules. Sci Rep 8, 17537 (2018). [CrossRef]
- Zhang Y, Yu J, Wang X, Durachkosulin DM, Zhang S, Cosgrove DJ. 2021. Molecular insights into the complex mechanics of plant epidermal cell walls. Science. Vol 372, Issue 6543, pp. 706-711. [CrossRef]
- Zheng, H.; Xie, W. The role of 3D genome organization in development and cell differentiation. Nat Rev Mol Cell Biol 20, 535–550 (2019). [CrossRef]
Figure 1.
Intersecting salivary islands (saliva surface subsets). The Figure illustrates some of the topological relationships occurring between a mucin aggregate (left) and the salivary medium (right).
Figure 1.
Intersecting salivary islands (saliva surface subsets). The Figure illustrates some of the topological relationships occurring between a mucin aggregate (left) and the salivary medium (right).
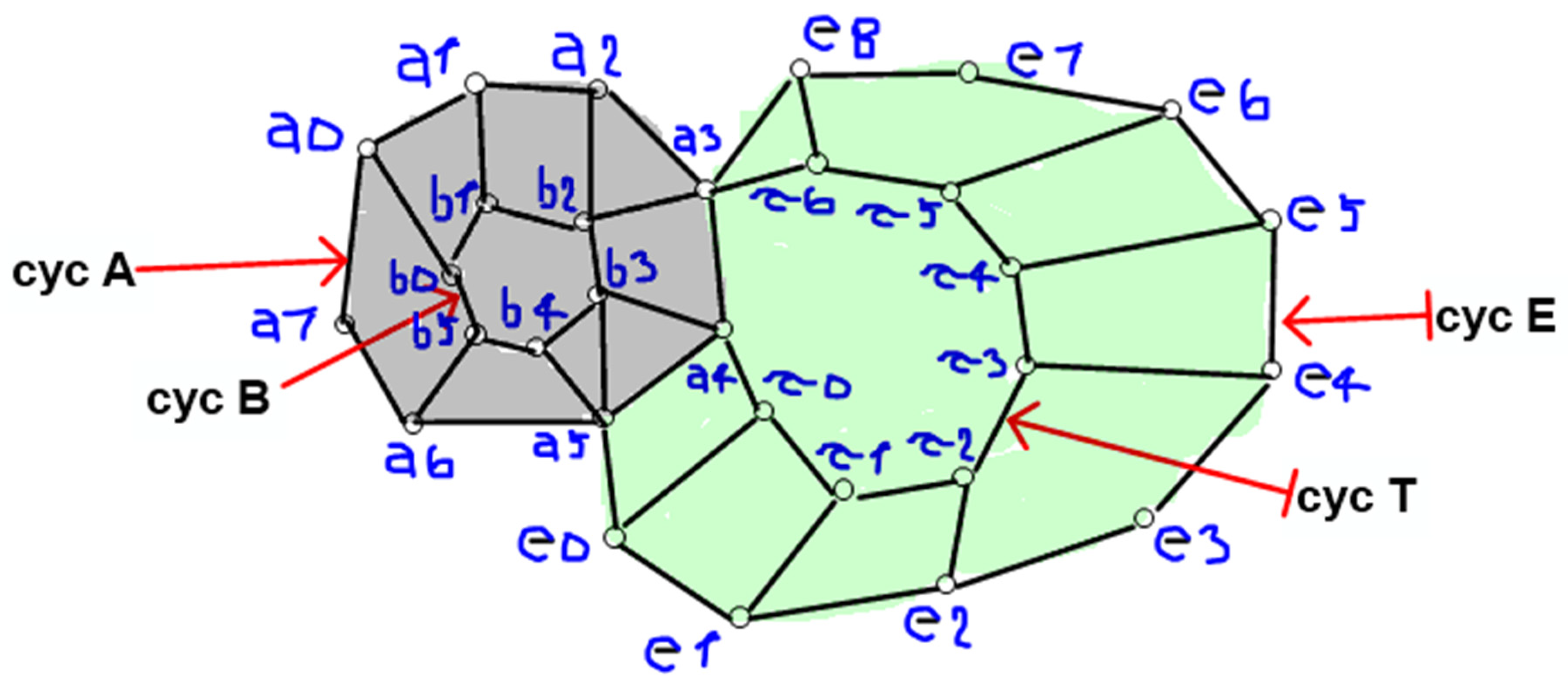
Figure 2.
Simulation of Hilbert (red) envelope curves on the peaks of a salivary signal (black). In this case, the salivary signal stands for the Fourier transform of the salivary temperatures that have been detected in a collected sample. .
Figure 2.
Simulation of Hilbert (red) envelope curves on the peaks of a salivary signal (black). In this case, the salivary signal stands for the Fourier transform of the salivary temperatures that have been detected in a collected sample. .
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






