Prerpints.org logo
Preprint
Communication

Design for Ultrafast Raster Photography with Large Amount of Spatio-Temporal Information

Altmetrics

Downloads

102

Views

37

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

01 December 2023

Posted:

04 December 2023

You are already at the latest version

Alerts
Abstract
Due to the lack of theoretical research on the amount of spatio-temporal information in the high-speed photography technologies, obtaining an optimized system with a best amount of spatio-temporal information remains a challenge, resulting in insufficient effective information and observation accuracy for ultrafast events. The paper presents an ultrafast raster imaging (URI) system with a large amount of spatio-temporal information based on the all-optical raster principle in single-shot. Specifically, we derive the optimal equation of spatial resolution and the expression for the maximum amount of spatio-temporal information that can achieve excellent performance for an URI system. It serves as a general guideline for getting a large amount of information design in the URI system. Compared to the existing URI systems, the advanced URI system exhibits an improvement of nearly 1 order of magnitude in the amount of spatio-temporal information, and more than twofold in spatial resolution. It shows a great potential for capturing intricate and non-repetitive ultrafast events on the femtosecond time scale.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

High-speed photography, which extends the temporal resolution beyond that of the human eye, is a time-amplified technique for blurring-free observations of transient processes. It is an indispensable tool for exploring fundamental mechanisms in physics, chemistry, and biology, and has been widely applied in industries, energy, and medicine [1,2,3,4,5]. It is strongly established that imaging techniques with different temporal resolutions are needed to study transient processes with different characteristic times. The traditional film-based cameras [6] and high-speed framing cameras based on digital memory [7] can get movies with frame interval time as short as 10 ps [7], but they are insufficient for observing transient dynamics on the atomic time scale (1ps ∼10 fs) due to the limitations of mechanical mechanisms and the electronic readout speed of detectors. Fortunately, with the generation and development of ultrashort pulse lasers, the temporal resolution of imaging based on pump-probe technology has been advanced to the attosecond region [8,9], which can effectively observe repeated ultrafast events. To realize measurements of non-repetitive processes, various single-shot ultrafast imaging techniques with a frame rate of up to trillion frames per second (Tfps) have been developed, including ultrafast compressed photography (CUP) [10,11,12,13,14,15] by passive detection and photography by active detection [16,17] which based on space division [18,19,20], angle division [21,22,23], wavelength division [24,25,26,27,28], spatial frequency division [29,30], or polarization division [31]. However, due to the lack of theoretical research on the amount of spatio-temporal information in the imagers, obtaining an optimized system with the best amount of large amo-amount of spatio-temporal information remains a challenge, resulting in insufficient effective information and observation accuracy for ultrafast events.
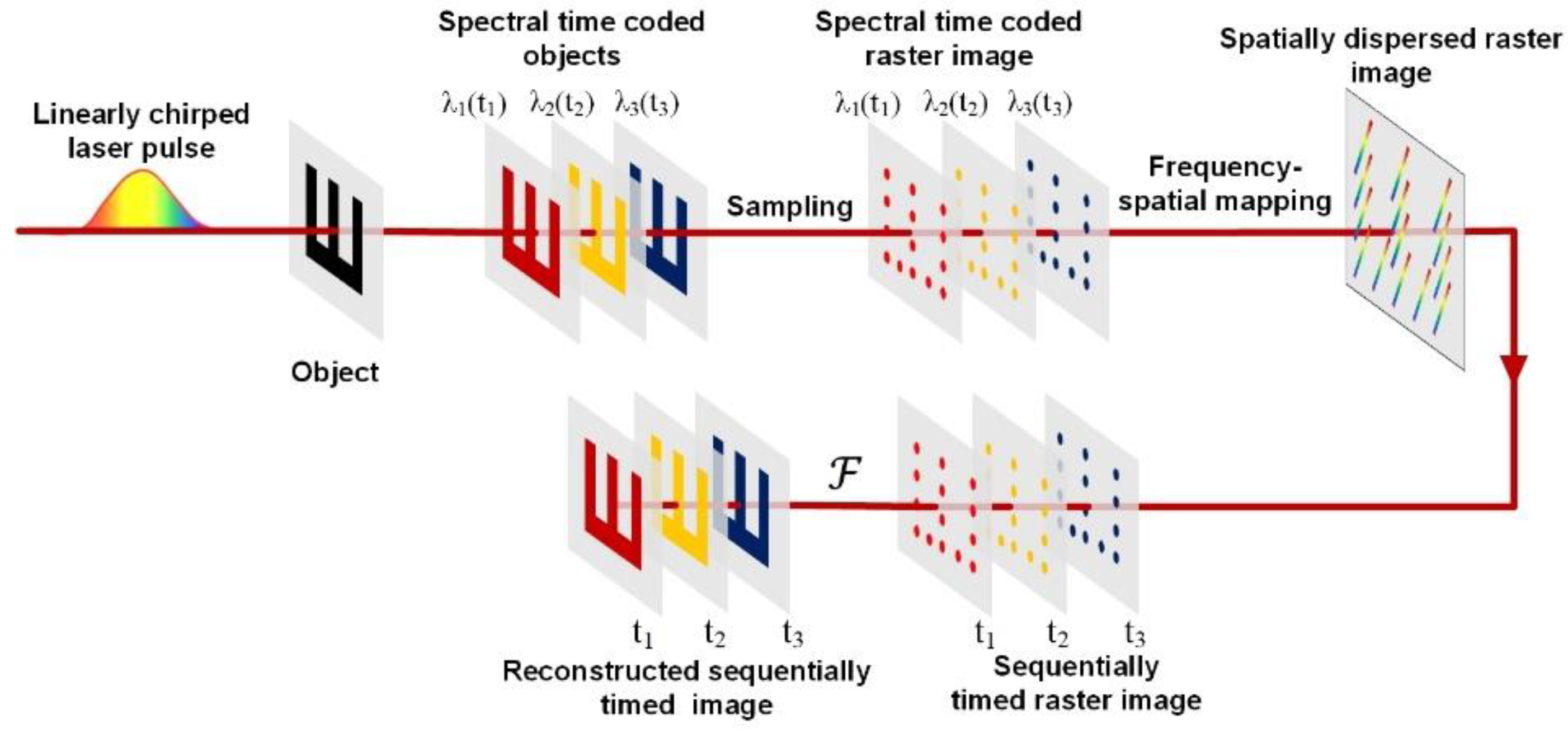
In this letter, we propose an ultrafast raster imaging system with a large amount of spatio-temporal information based on the all-optical raster principle in single-shot. The URI system is designed based on the Nyquist sampling theorem and frequency-time mapping method. Specifically, as shown in Figure 1, the object (transient scenes) is illuminated by a linearly chirped laser pulse. After sampling (e.g., using a microlens array) and imaging, raster images with spectrally time-coded are formed, and they pass through a frequency-spatial mapping device (a 4f optical system and a diffraction grating placed in the Fourier plane), resulting in a spatially dispersed raster image on the detection plane. Here, raster images of different wavelengths are located at different positions on the detector. After that, we extract each single-wavelength raster image by system calibration and reconstruct the object by performing the Fourier transform algorithm based on the Nyquist sampling theorem. In our previous work, the UIR system [32] has gotten 12-frame images with an intrinsic spatial resolution of 10-line pairs per millimeter (lp/mm). The frame rate and the temporal resolution are 2 Tfps and 460 fs, respectively. However, there is still a lot of room for optimizing the main parameters of spatial resolution, temporal resolution, frame rate, and frame number. Therefore, here we derive the optimal equation of spatial resolution and the expression for the best amount of spatio-temporal information that can achieve excellent performance for an URI system with improved the amount of spatio-temporal information by nearly 1 order of magnitude greater than the previous work [32]. It serves as a general guideline for getting a large amount of information design in the URI system, which renowned for its high spatial-temporal resolution and high frame rate, exhibits great potential for capturing intricate and non-repetitive ultrafast events on the femtosecond time scale.

2. The amount of information on high-speed photographic systems

For high-speed photography systems, the key goal is to obtain more effective information of the dynamic processes. The equation for the amount of spatio-temporal information in the imaging system can be expressed as [33,34,35].
I = I R I T = S · R 2 · ln κ · f · g 2 / 3 I R = S · R 2 · ln κ I T = f · g 2 / 3
Here, I represents the total amount of spatio-temporal information, which refers to the number of bits transmitted and recorded by a high-speed camera per unit of time (bit/s). It covers both time and space information: the amount of temporal information, denoted as IT, and the amount of temporal information, denoted as IR, so it is an important indicator for comprehensively evaluating the performance of high-speed cameras.
The frame rate f, which is the reciprocal of the frame interval time τf, is a fundamental parameter that characterizes the camera's temporal resolution capability. The modified temporal qualify factor g2/3 can be determined by the ratio of the frame interval time τf to the effective exposure time τ. In order to avoid information blurring caused by overlapping between the adjacent frames, the optimization condition is set to g2/3=1.
The space information amount IR is the product of the spatial bandwidth product (S·R2) of a single frame and the information capacity (ln κ) of a single pixel. Here, κ denotes the number of information levels and usually indicates the signal-to-noise ratio. S and R correspond to the area and spatial resolution of the image, respectively. I ​is usually used to evaluate the quality of a high-speed camera, which reflects not only the ability of the camera to record spatio-temporal information but also the level of design and manufacturing of the high-speed camera.

3. Analysis and discussion

3.1. Characterization of the spatial resolution and frame number

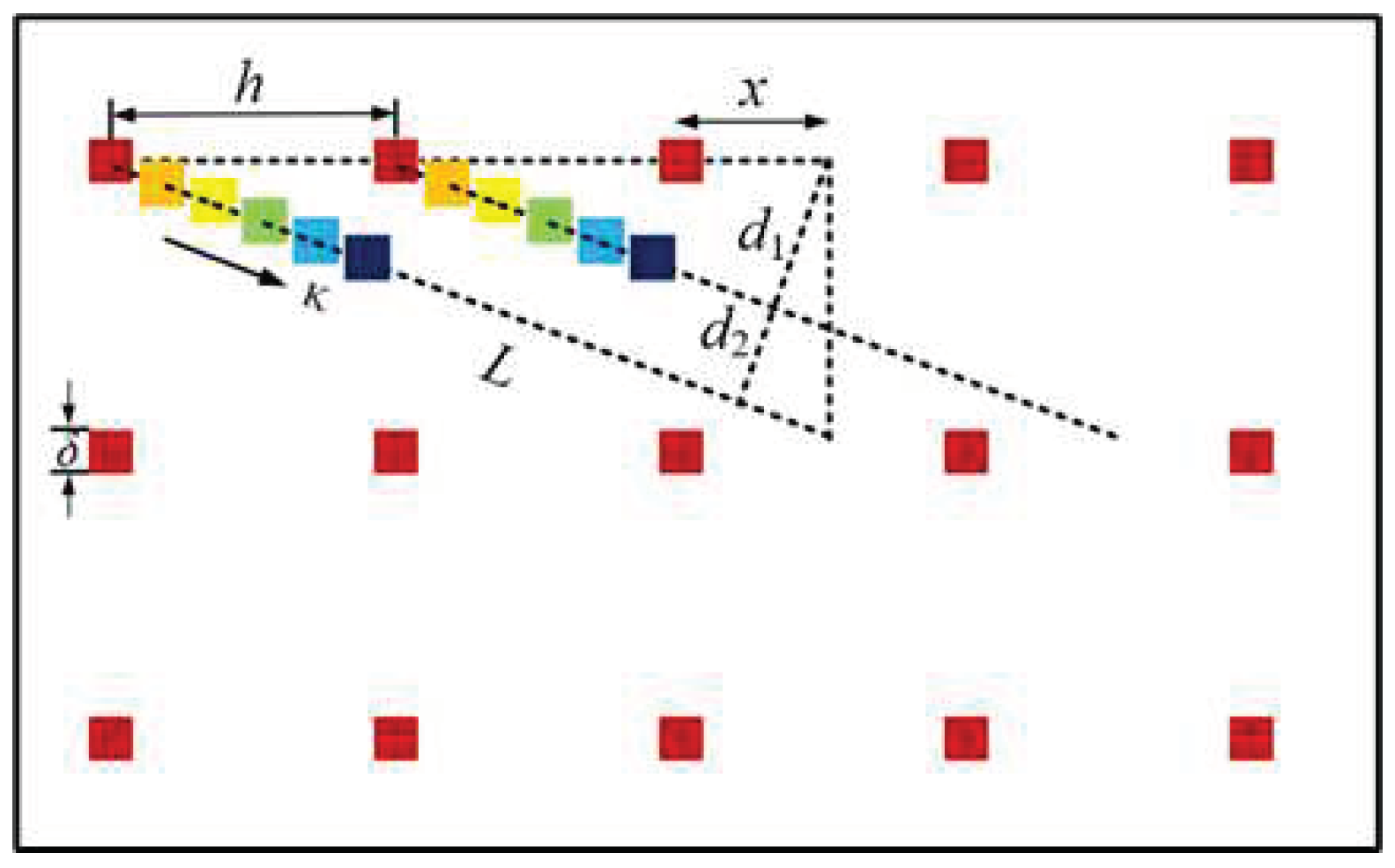
Spatial resolution (R) is a key parameter in high-speed photography. For URI system, the spatial resolution (intrinsic spatial resolution) is mainly decided by the pitch (h) of sampling points of the raster image. The sampling and framing of the URI are depicted in Figure 2. The red squares represent the raster sampling points after sampling the 2D image, the size is δ. Framing of the raster image along the time direction (K), while raster images of different wavelengths (colors) are located at different positions on the detector. L is the maximum length of spatially dispersive raster sampling points along the time direction (K), and d2 is the distance between two adjacent spatially dispersed sampling points of the raster image. The geometric relation between the parameters is given by
(2h+x) h=(d1+d2) L
Substituting equation (h+x)/h=d1/d2 into equation (2), after simplification, we obtain the relation h2=d2•L, Considering the framing of the raster image sampling points by sampling points, the value of L should be the product of the size of sampling points δ and the frame number n i.e., L=(n+1) δ. When d2=δ, the relationship between the pitch h of sampling point and the frame number n can be mathematically formulated
n=h2/δ2-1
Theoretically, R is inversely proportional to h of sampling points, that is, N=1/2h, combining equation (3), it can be expressed as
R = 1 2 1 （ n + 1 ) δ
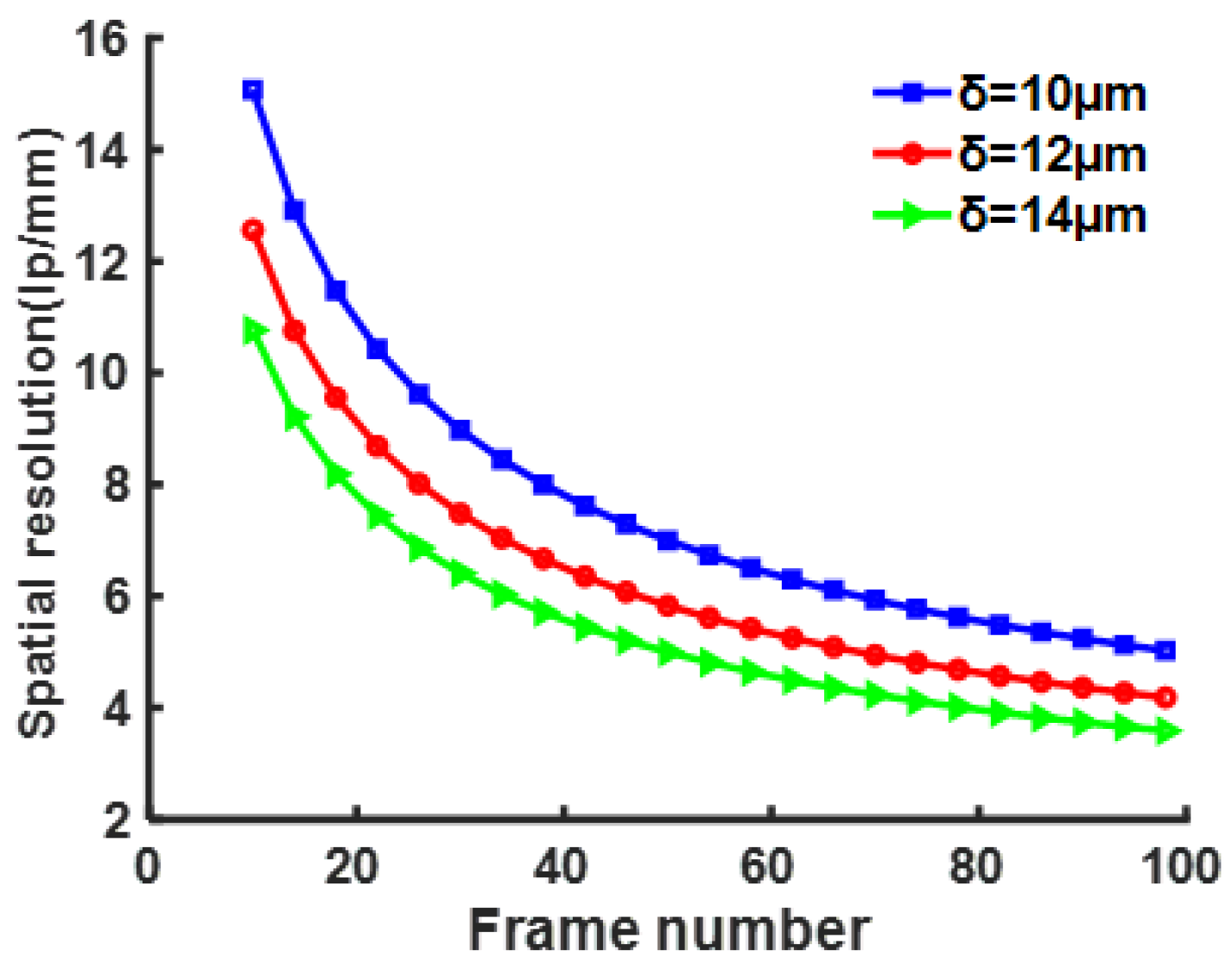
In URI, the size of sampling point of raster image δ is mainly modulated by the entrance pupil of an objective of the imaging system. Here, we consider the relationship between the spatial resolution and the frame number in the case of δ=10μm, 12μm, and 14μm, as illustrated in Figure 3. It is evident that there exists a trade-off between spatial resolution and frame number, that is, we can get more frames at the cost of an obvious decline in spatial resolution. But, on the brighter side, reducing the size of the sampling point of the raster image can potentially improve either spatial resolution or the frame number.

3.2. Frame rate and the spatial resolution

Frame rate f is another critical parameter in high-speed photography. To effectively capture ultrafast events on atomic time scale, frame rate should be performed at the femtosecond level. For an URI system, the frame rate is determined by the duration T of a probe laser pulse and the size of sampling point of raster image. the size of sampling point can be adjusted by the entrance pupil of the objective of the optical system. By combining equation (4) with the relationship Tf=L/δ=n, the relationship between the spatial resolution and the frame rate is given by
f = 1 T ( 1 4 R 2 δ 2 − 1 )
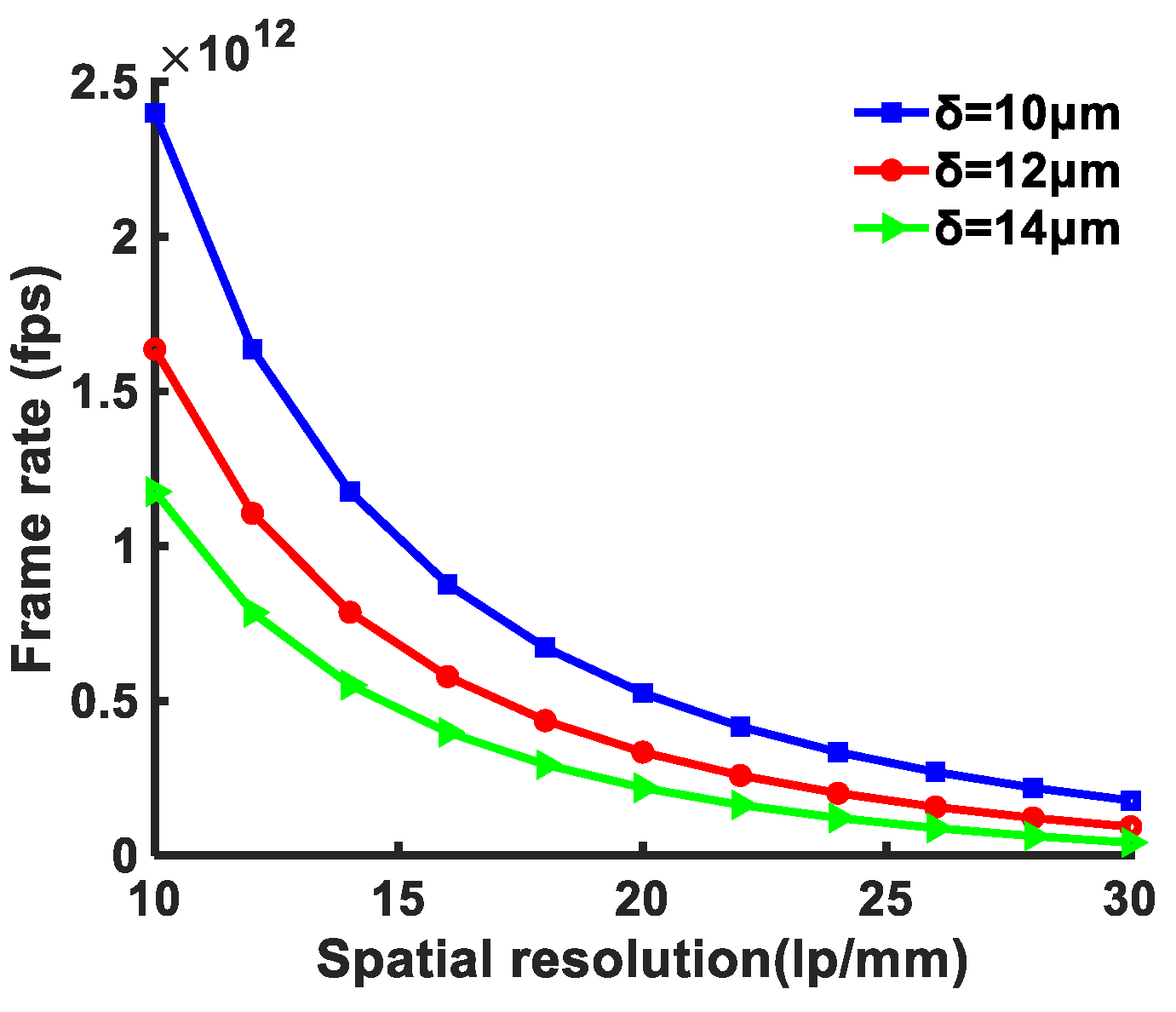
Figure 4 illustrates the relationship between frame rate and spatial resolution. Here, we consider the cases T=10ps and δ=10μm, 12μm, and 14μm. Obviously, the frame rate is inversely proportional to the square of the spatial resolution. Notably, by reducing the size of sampling point of the raster image, both of the frame rate and spatial resolution of an URI system can be effectively improved.

3.3. Optimal temporal resolution and spatial resolution equation for an URI

The temporal resolution of the URI system mainly relies on the duration of original Fourier-transform limit femtosecond pulse and the linearly chirped pulse. The equation τ = t T 0 indicates an optimal temporal resolution [36], where t0 is the Fourier-limited duration of the original femtosecond pulse, and the time window T is the FWHM (full width at half maximum) of the chirped laser pulse. Therefore, a shorter Fourier-limited duration femtosecond pulse source can further improve the temporal resolution of the URI system, the FWHM of the chirped pulse should cover the duration of the ultra-fast process. Here, to ensure the optimal temporal degree of freedom (DOF) and avoid information blurring caused by overlapping between the adjacent frames, the modification factor g 2 / 3 is set to 1. That is, the frame interval ( Δ t ) equals the effective exposure time τ. Therefore, the optimal frame number is denoted by n max = T / τ = T / t 0 , which should be a constant for a given light source system and the time window of the observation.
For a high-speed imaging system, equation (1) indicates that improving the spatial resolution can effectively improve the amount of spatio-temporal information. In URI, in a static situation, spatial resolution is time-independent. However, at the femtosecond scale, the frame number n = T / t 0 should be given based on the case of optimal temporal resolution, and then substituting it into equation (4). So, we can get the time-dependent spatial equation
R = 1 2 1 （ T / t 0 + 1 ) δ
According to the previous analysis and discussion, we know that reducing the size of sampling point of raster image is the key to improving the spatial resolution and frame rate. As we known, the size of sampling point of raster image should be equal to a shifting size ( Δ x ) of adjacent frames, i.e., δ = Δ x = ( f l / Λ ) Δ λ , here Λ and fl are the grating period and the focal length of the lens in the 4f optical system, respectively, and Δ λ is the corresponding wavelength difference, which should be greater than or equal to the spectral resolution of URI system, the spectral resolution ( δ λ ) can be denoted by δ λ = λ 0 Λ / S ′ , where S ′ is the probe beam width on the grating (given by S ′ = f l d / f m , here d , f m are the diameter and focal length of each lens in the microlens array, respectively). Therefore, the spectral resolution δ λ can be expressed as δ λ = λ 0 Λ f m / f l d , Considering that Δ λ ≥ δ λ , we can get δ ≥ λ 0 f m / d . Meanwhile, since one microlens corresponds to one sampling point, the size of sampling point must be greater than or equal to the diffraction limit of the microlens, that is, δ ≥ 1 . 22 λ 0 f m / d ,where λ 0 is the center wavelength of the probe laser pulses. Obviously, when δ min = 1.22 λ 0 f m / d , it follows that Δ λ > δ λ , Therefore, we obtain the optimally time-dependent spatial resolution
R o p t = 1 2 d 1.22 （ T / t 0 + 1 ) λ 0 f m
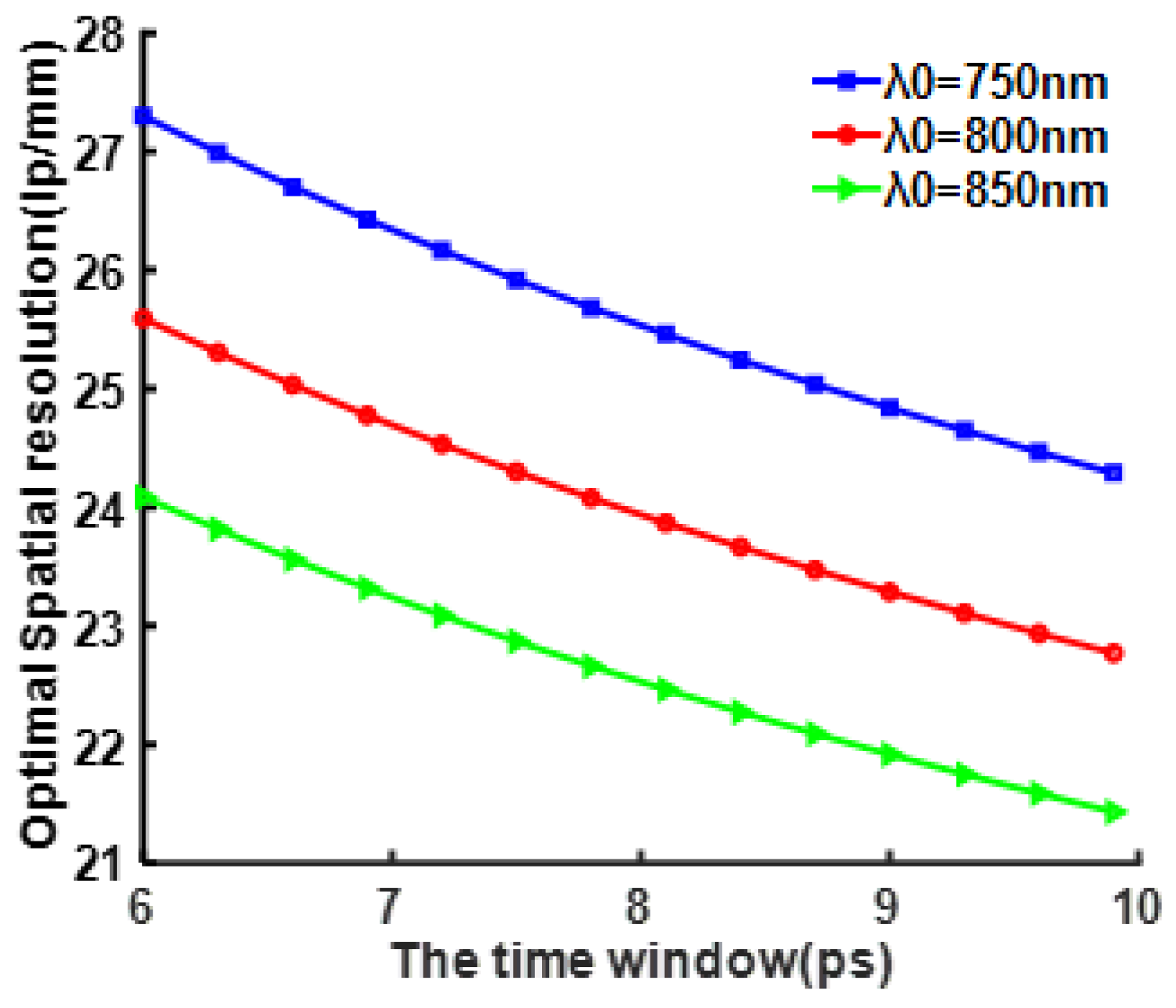
Figure 5 shows the relation between the time window and the spatial resolution in the case of δ = δ min for previous URI systems .When the designed time window T = 6 ps , it follows that n = 13 ,   f ≈ 2.2 × 10 12 fps , the spatial resolution is approximately improved to 26lp/mm.Therefore, compared with the existing URI systems, the spatial resolution of the optimized URI systems has been significantly improved by 2.6 times. In addition, we can get a higher spatial resolution will be obtained by a shorter central wavelength of the probe laser pulse.

3.4. The maximum amount of information of an URI system

According to equation (1) above, combining the expressions of the spatial resolution and frame rate, the amount of spatio-temporal information of an URI system is given by
I = S 4 T · n ( n + 1 ) δ 2 · ln κ · g 2 / 3
Here, S = a × b , is the area of the image, where a and b are the length and width, respectively. By substituting the optimal parameters into equation (8), we obtain the expression of maximum amount of spatio-temporal information
I max ≈ S 2 T · T / t 0 ( T / t 0 + 1 ) λ 0 2 · ( d f m ) 2
Equation (9) shows that for a given light source system of an URI, which provides the expression for designing the optimal URI. Here, the time window should be designed to cover the duration of the ultrafast process. Next, design suitable relative aperture ( d / f m ) of a microlens based on the current manufacturing level of the microlens array. Finally, we design the optimal sampling points pitch h of the URI system. 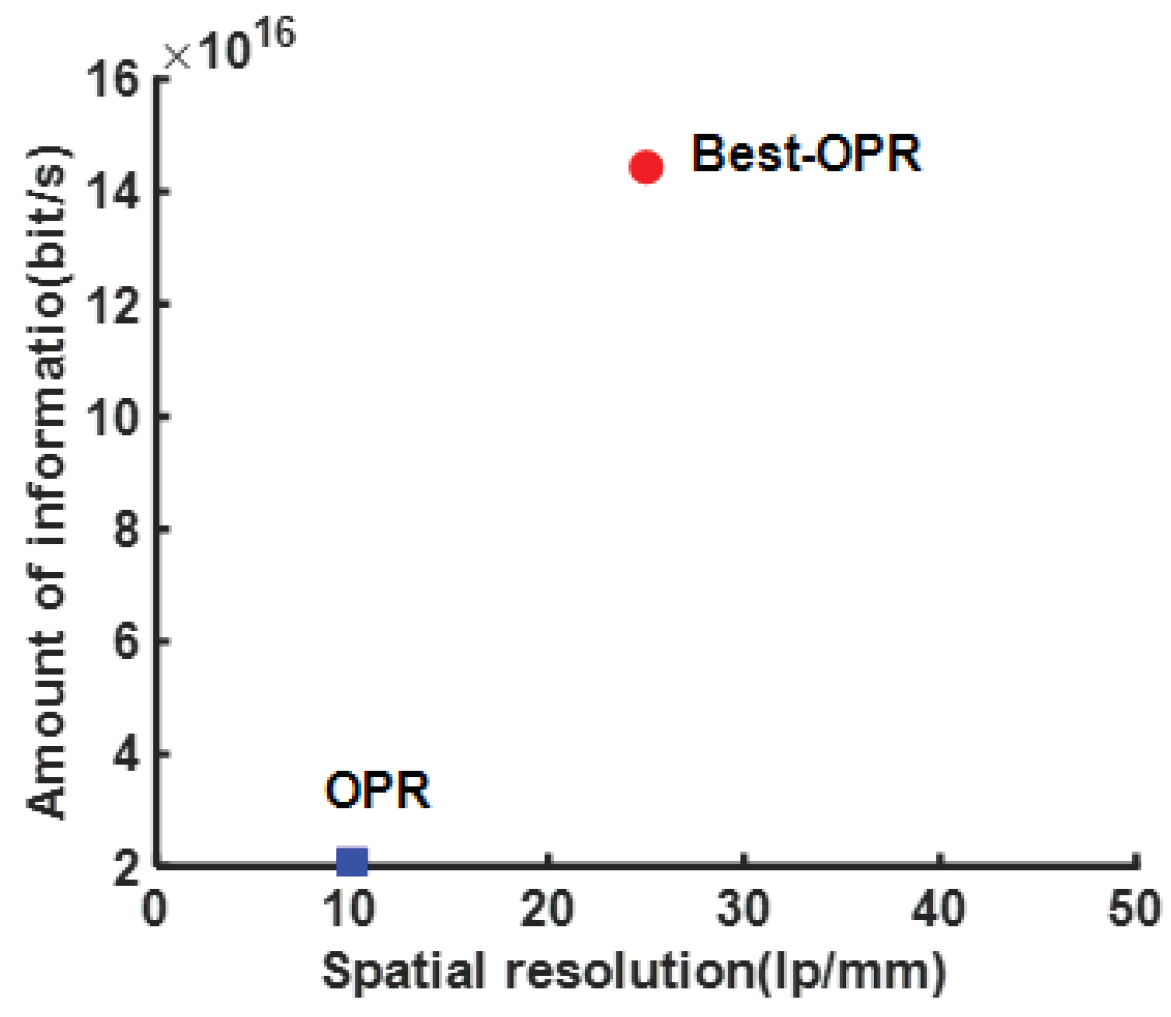As shown in Figure 6, after optimizing the existing URI system, namely Best-URI, the maximum amount of spatio-temporal information will reach 1.4×1017 bit/s. Meanwhile, it is evident from Figure 7 that the maximum amount of spatio-temporal information of Best-URI is close to 1 order of magnitude greater than that of 2.1×1016 bit/s in the existing URI system.

4. Conclusion

This paper presents a formula regarding the amount of spatio-temporal information based on the all-optical raster principle to realize an ultrafast imaging system with a large amount of spatio-temporal information. We derived the spatial resolution expression of the system by considering the pitch of sampling points, the size of the sampling point, and the frame number, as well as the relationship between spatial resolution and frame rate. Furthermore, we have also obtained the optimal time-dependent spatial resolution and the maximum amount of information of the system operating at the femtosecond time scale. Compared to the existing URI systems, an optimized URI system designed based on the maximum amount of information exhibits the improvement of nearly 1 order of magnitude in the amount of spatio-temporal information, and more than twofold in spatial resolution. The optimized URI system, renowned for its large amount of spatio-temporal information and high spatio-temporal resolution, exhibits greater potential for capturing intricate and non-repetitive ultrafast events on the femtosecond time scale.

Author Contributions

Conceptualization, Y.Z., X.Z. and J.L.; methodology, Y.Z.; software, Y.Z.; validation, Y.Z. and W.L.; Investigation, Y.Z., X.Z. and J.L.; Resources, W.L., X.Z. and J.L.; data curation, J.Y. and L.Z.; Writing—review and editing, Y.Z.; Supervision, Y.X. Z. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by National Major Instruments and Equipment Development Project of National Natural Science Foundation of China (61827815), National Natural Science Foundation of China (62075138, 62275163, 62205224),Natural Science Foundation of Guangdong Province, China (2021A1515011909), Shenzhen Science and Technology Program, China (JCYJ20210324-095213037), The 2023 Key Talent Project of Gansu Province: The Innovation Team Building of Integrated Circuit Packaging and Testing; Science and technology major special project of Gansu Provincial(22ZD6GE016).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Betti, R.; Hurricane, O. A. Inertial-confinement fusion with lasers. Nat. Phys. 2016, 12, 435–448. [Google Scholar] [CrossRef]
  2. Zewail, A.H. Femtochemistry: Atomic-Scale Dynamics of the Chemical Bond. J. Phys. Chem. A 2000, 104, 5660–5694. [Google Scholar] [CrossRef]
  3. Corkum, P.B.; Krausz, F. Attosecond Science. Nat. Phys. 2007, 3, 381. [Google Scholar] [CrossRef]
  4. Hassan, M.T.; Luu, T.T.; Moulet, A.; Raskazovskaya, O.; Zhokhov, P.; Garg, M.; Karpowicz, N.; Zheltikov, A.M.; Pervak, V.; Krausz, F.; Goulielmakis, E. Optical Attosecond Pulses and Tracking the Nonlinear Response of Bound Electrons. Nature 2016, 530, 66. [Google Scholar] [CrossRef]
  5. Bowlan, P.; Fuchs, U.; Trebino, R.; Zeitner, U. D. Measuring the spatiotemporal electric field of tightly focused ultrashort pulses with sub-micron spatial resolution. Opt. Express 2008, 16, 13663–13675. [Google Scholar] [CrossRef] [PubMed]
  6. Fuller, P. W. W. An introduction to high-speed photography and photonics. Imaging Sci. J. 2009, 57, 293–302. [Google Scholar] [CrossRef]
  7. Liang, J.; Wang, L. V. Single-shot ultrafast optical imaging. Optica 2018, 5. 1113-1127.
  8. Thomann, I.; Bahabad, A.; Liu, X.; Trebino, R.; Murnane, M.; Kapteyn, H. Characterizing Isolated Attosecond Pulses from Hollow-Core Waveguides Using Multi-Cycle Driving Pulses. Opt. Express 2009, 17, 4611–4633. [Google Scholar] [CrossRef]
  9. Lopez, R., et al. Characterization of high-order harmonic radiation on femtosecond and attosecond timescales. Appl. Phys. B 2004, 78, 835-838.
  10. Gao, L.; Liang, J.; Li, C.; Wang, L. V. Single-shot compressed ultrafast photography at one hundred billion frames per second. Nature 2014, 516, 74–77. [Google Scholar] [CrossRef] [PubMed]
  11. Liang, J.; Zhu, L.; Wang, L. V. Single-shot real-time femtosecond imaging of temporal focusing. Light Sci. Appl. 2018, 7, 42. [Google Scholar] [CrossRef]
  12. Qi, D. , et al. Single-shot compressed ultrafast photography: a review. Adv. Photon. 2020, 2, 014003. [Google Scholar]
  13. Yang, C. , et al. Hyperspectrally compressed ultrafast photography. Phys. Rev. Lett. 2020, 124, 023902. [Google Scholar] [PubMed]
  14. Haocheng, T.; Ting, M.; Xianglei, L.; Yaodan, H.; Jingqin, S.; Yanlei, Z.; Ping, L.; Liang, J.; Downer, M. C.; Zhengyan, L. Singleshot compressed optical field topography. Light Sci. Appl. 2022, 11, 244. [Google Scholar]
  15. Wang, P.; Wang, L. V. Single-Shot Reconfigurable Femtosecond Imaging of Ultrafast Optical Dynamics. Adv. Sci. 2023, e2207222. [Google Scholar] [CrossRef]
  16. Yao, J.; Qi, D.; Liang, H.; He, Y.; Yao, Y.; Jia, T.; Zhang, S. Exploring femtosecond laser ablation by snapshot ultrafast imaging and molecular dynamics simulation. Ultrafast Sci. 2022, 1–11. [Google Scholar] [CrossRef]
  17. Liang, J.; Wang, L. V. Single-shot ultrafast optical imaging. Optica 2018, 5, 1113–1127. [Google Scholar] [CrossRef] [PubMed]
  18. Zeng, X.; Lu, X.; Wang, C.; Wu, K.; Cai, Y.; Zhong, H.; Lin, Q.; Lin, J.; Ye, R.; Xu, S. Review and prospect of single-shot ultrafast optical imaging by active detection. Ultrafast Sci. 2023, 3, 0020. [Google Scholar] [CrossRef]
  19. Chen, G. H.; Li, J. F.; Peng, Q. X.; Liu, S. X.; Liu, J. All-optical coaxial framing photography using parallel coherence shutters. Opt.Lett. 2017, 42, 415–418. [Google Scholar]
  20. Sawashima, Y.; Yamanaka, D.; Takamoto, I.; Matsunaka, A.; Awatsuji, Y.; Nishio, K. Extending recordable time of light-in-flight recording by holography with double reference light pulses. Opt.Lett. 2018, 43, 5146–5149. [Google Scholar] [CrossRef]
  21. Zeng, X.; Zheng, S.; Cai, Y.; Lin, Q.; Liang, J.; Lu, X.; Li, J.; Xie, W.; Xu, S. High-spatial-resolution ultrafast framing imaging at 15 trillion frames per second by optical parametric amplification. Adv. Photon. 2020, 2, 53–63. [Google Scholar] [CrossRef]
  22. Huang, H.Y.; Guo, C.S. Simple system for realizing single-shot ultrafast sequential imaging based on spatial multiplexing in-line holography. Opt. Express 2022, 30, 41613–41623. [Google Scholar] [CrossRef]
  23. Sheinman, M.; Erramilli, S.; Ziegler, L.; Hong, M.K.; Mertz, J. Flatfield ultrafast imaging with single-shot non-synchronous array photography. Opt. Lett. 2022, 47, 577. [Google Scholar] [CrossRef] [PubMed]
  24. Zhu, Q.; Cai, Y.; Zeng, X.; Long, H.; Chen, H.; Zeng, L.; Zhu, Y.; Lu, X.; Li, J. FISI: Frequency domain integration sequential imaging at 1.26×10^13 frames per second and 108 lines per millimeter. Opt. Express 2022, 30, 27429–27438.
  25. Nakagawa, K.; Iwasaki, A.; Oishi, Y.; Horisaki, R.; Tsukamoto, A.; Nakamura, A.; Hirosawa, K.; Liao, H.; Ushida, T.; Goda, K.; Kannari, F.; Sakuma, I. Sequentially timed all-optical mapping photography (STAMP). Nat. Photon. 2014, 8, 695–700. [Google Scholar] [CrossRef]
  26. Yuan, X.; Li, Z.; Zhou, J.; Liu, S.; Wang, D.; Lei, C. Hybrid-plane spectrum slicing for sequentially timed all-optical mapping photography. Opt. Lett. 2022, 47, 4822–4825. [Google Scholar] [CrossRef]
  27. Lu, Y.; Wong, T.W.; Chen, F.; Wang, L. Compressed ultrafast spectral-temporal photography. Phys. Rev. Lett. 2019, 122, 193904. [Google Scholar] [CrossRef] [PubMed]
  28. Ding, P.; Jin, C.; Wu, X.; Deng, L.; Jia, T.; Huang, F.; Liang, J.; Sun, Z.; Zhang, S. Single-shot real-time ultrafast imaging of femtosecond laser fabrication. ACS Photonics 2021, 8, 738–744. [Google Scholar]
  29. Yi, Y.; et al. Single-shot spatiotemporal plasma density diagnosis using an arbitrary time-wavelength-encoded biprism interferometer. Opt. Lasers Eng. 2023, 168, 107647. [Google Scholar] [CrossRef]
  30. Ehn, A.; Bood, J.; Li, Z.; Berrocal, E.; Alden, M.; Kristensson, E. FRAME: Femtosecond videography for atomic and molecular dynamics. Light Sci. Appl. 2017, 6, e17045. [Google Scholar] [CrossRef] [PubMed]
  31. Moon, J.; Yoon, S.; Lim, Y.-S.; Choi, W. Single-shot imaging of microscopic dynamic scenes at 5 THz frame rates by time and spatial frequency multiplexing. Opt. Express 2020, 28, 4463. [Google Scholar] [CrossRef] [PubMed]
  32. Gao, G.; He, K.; Tian, J.; Zhang, C.; Zhang, J.; Wang, T.; Chen, S.; Jia, H.; Yuan, F.; Liang, L.; et al. Ultrafast all-optical solid-state framing camera with picosecond temporal resolution. Opt. Express 2017, 25, 8721–8729. [Google Scholar] [CrossRef]
  33. Zhu, Y.; Zeng, X.; Cai, Y.; Lu, X.; Zhu, Q.; Zeng, L.; He, T.; Li, J.; YY, M.; Zheng, S.; Xu, S.; Li, J. All-optical high spatial-temporal resolution photography with raster principle at 2 trillion frames per second. Opt. Express 2021, 29, 27298–27308. [Google Scholar] [CrossRef]
  34. Li, J.Z.; Jin, S.R. Relation of degrees of freedom of an image with modulation transfer function. Acta Photon. Sin. 1997, 26, 379–383. [Google Scholar]
  35. Li, J.Z.; Tan, X.X.; Gong, X.D.; et al. Studies on degree of freedom for high-speed photography. In Proceedings of the SPIE, USA, March 2005, Vol. 5580, pp. 805–810.
  36. SCHARDIN, H. Uber die Grenzen der Hochfrequenz Kinematographik. In Proceedings of the 6th International Congress on High-Speed Photography (ICHSP), Rio de Janeiro, Brazil, 14-17 August 1963. [Google Scholar]
  37. Sun, F. G.; Jiang, Z. Analysis of terahertz pulse measurement with a chirped probe beam. Appl. Phys. Lett. 1998, 73, 2233–2235. [Google Scholar] [CrossRef]
Preprints 92034 g001
Figure 1. The principle of URI, F , Fourier reconstruction algorithm.
Figure 1. The principle of URI, F , Fourier reconstruction algorithm.
Preprints 92034 g001
Preprints 92034 g002
Figure 2. Demonstration of sampling and framing of URI.
Figure 2. Demonstration of sampling and framing of URI.
Preprints 92034 g002
Preprints 92034 g003
Figure 3. The relationship between the spatial resolution and frame number of URI.
Figure 3. The relationship between the spatial resolution and frame number of URI.
Preprints 92034 g003
Preprints 92034 g004
Figure 4. The relationship between spatial resolution and frame rate of URI.
Figure 4. The relationship between spatial resolution and frame rate of URI.
Preprints 92034 g004
Preprints 92034 g005
Figure 5. The relationship between the optimal spatial resolution and the time window.
Figure 5. The relationship between the optimal spatial resolution and the time window.
Preprints 92034 g005
Preprints 92034 g006
Figure 6. The relationship between the maximum amount of information and the time window.
Figure 6. The relationship between the maximum amount of information and the time window.
Preprints 92034 g006
Preprints 92034 g007
Figure 7. Comparison of the amount of information in URI and Best-URI.
Figure 7. Comparison of the amount of information in URI and Best-URI.
Preprints 92034 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated