Prerpints.org logo
Preprint
Article

Real-Time 2D Orthomosaic Mapping from Drone-Captured Images Using Feature-Based Sequential Image Registration

Altmetrics

Downloads

206

Views

134

Comments

0

Submitted:

04 December 2023

Posted:

04 December 2023

You are already at the latest version

Alerts
Abstract
This study presents a method for the rapid and accurate generation of two-dimensional (2D) orthomosaic maps using selected image data collected by drone-captured video. The focus is on developing a real-time method capable of creating maps more quickly than image selection. The scale-invariant feature transform (SIFT) algorithm is applied to drone images to extract features in various scale regions. For feature point matching, a matching method based on the fast library for approximate nearest neighbors (FLANN) was adopted. A comparison of the computational speed of the FLANN with that of the k-nearest neighbors (KNN) and brute force matcher during the matching process revealed FLANN's superior capability for real-time data processing. The random sample consensus (RANSAC) algorithm was employed to enhance the accuracy of the matching by removing outliers, effectively identifying and eliminating mismatches, and reinforcing the reliability of feature point matching. The combination of SIFT, FLANN, and RANSAC algorithms demonstrates the capacity to process drone-captured image data in real time, facilitating the generation of precise 2D orthomosaic maps. The proposed method was assessed and validated using imagery obtained as the drone executed curvilinear and straight flight paths, confirming its accuracy and operational efficiency concurrently with the image capture process.
Keywords: 
Subject: Engineering  -   Architecture, Building and Construction

1. Introduction

1.1. Research Objectives

The advancement of drone technology, marked by its integration with high-resolution imaging and geometrical measurement tools, has innovatively enhanced the capability to capture detailed topographical and shape information quickly across extensive areas. Drones are acknowledged as efficient tools for collecting accurate spatial data, even in areas characterized by complex terrains or where access is challenging [1,2]. This capability underscores the expanding adoption of drones in various sectors, including military applications, bridge and civil construction, disaster response, and the management of marine structures, where the need for real-time information is critical.
In intelligence, surveillance, and reconnaissance missions using drones, the ability to accurately recognize ground terrain is critical. This study describes a method in which a drone creates an orthomosaic map by overlapping and adjusting multiple high-resolution photographs taken from separate locations to form a continuous, distortion-free image. The focus is on using drone images to analyze spatial information quickly and extract feature points from two-dimensional (2D) images to create orthomosaic maps in real time. Numerous studies have been conducted on the superposition and registration of images obtained through segmentation [3,4]. The task of correlating two images, whether they are from the same location captured from different positions or overlapping images from varied points, continues to be a significant challenge [5]. In a typical image registration problem, the challenge is rapidly registering drone-captured images with reference images, which entails the rapid detection of feature points and efficient matching between the extracted feature points. Several studies have already successfully presented algorithms that can solve image feature point extraction and matching and image registration [6,7,8].
Recently, advances in artificial intelligence and deep learning technology have propelled research in image processing and pattern recognition. Notably, algorithms based on neural networks have demonstrated high accuracy and efficiency in object recognition, topographic analysis, and image stitching with drone-captured images. These technological advances offer significant potential for producing orthomosaic maps using drones. Open-source solutions, such as OpenDroneMap, are available to generate orthomosaic maps, point clouds, 3D models, and other data types [9,10]. Nevertheless, selecting the most appropriate combination of algorithms for a specific problem and choosing one that ensures accuracy and rapid registration are characterized by empirical trials and errors.
Based on these technological advancements and limitations, this study focuses on a method for the real-time generation of orthomosaic maps with distortion-free and continuous images by integrating high-resolution images captured by drones in various locations. The primary objective of this study is to analyze the spatial information contained in the drone image rapidly and optimize the extraction of the feature points from 2D images to enhance the efficiency and accuracy of real-time orthomosaic map production. Given these techniques, this paper concentrates on the processes of extracting feature points, matching these feature points, and registering the images.

1.2. Overview of Applied Methods

The process of integrating multiple drone-captured images into a single continuous orthomosaic map involves image feature extraction, matching, and image registration stages.

1.2.1. Image Feature Extraction

Image feature extraction serves as a fundamental element in the field of image processing and object recognition. Several algorithms have been advanced in this discipline to enhance the precision and efficiency of these processes. Notable among these are the Harris corner detection, scale-invariant feature transform (SIFT), speeded-up robust features (SURF), features from the accelerated segment test (FAST), and oriented FAST and rotated binary robust independent elementary features (BRIEF) (ORB), each contributing distinct methods and innovations to the field.
The Harris corner detection algorithm is a prominent method for extracting corners from images. However, it has several drawbacks, including problems with scale invariance, vulnerability to rotation, and the need for parameter optimization (e.g., the window size and response threshold) depending on the variety of images and situations. Additionally, this method suffers from a slower computational speed [11,12,13,14,15]. The SIFT algorithm offers feature points invariant to scale and rotation and demonstrates robust matching performance, as its descriptors effectively encapsulate local information within images. It is highly reliable due to extensive testing in a variety of environments [16,17,18,19,20]. The SURF algorithm improves computational efficiency based on the fundamental concepts of SIFT [21,22,23,24,25,26]. Other methods, such as FAST and ORB, also have the advantage of outstanding computational speed [27,28].
Tareen and Saleem (2018) compared the feature extraction and feature matching time of various feature-detector-descriptors, including SIFT (128D), SURF (64D), SURF (128D), and ORB (1000). The terms 128D and 64D refer to the size of the descriptors. Their analysis revealed that ORB is the most efficient feature detector and descriptor, with the lowest computational cost, whereas SURF (128D) and SURF (64D) exhibited higher computational efficiency than SIFT (128D). Additionally, compared to SIFT, SURF (64D) required less computation time for feature matching, demonstrating that the feature matching time of SURF (64D) is shorter than that of SIFT (128D). However, although SURF (128D) took longer in feature matching compared to SIFT (128D), the SIFT algorithm was proposed as the superior feature detector and descriptor in terms of accuracy against scale, rotation, and affine transformations. Their review also ascertained that all matching algorithms involve a computation time of less than 100 s per feature point, indicating similar computational efficiency [29]. Considering that the resolution of the images applied in this study is 1920 × 1080, SIFT was chosen to balance efficiency and accuracy.

1.2.2. Image Matching

After extracting feature points between images, the points must be matched by comparing images to identify feature points corresponding to the same object or scene. A process is required to discover the transformation matrix between images and convert it into a single coordinate system. Through this procedure, multiple images are merged into a large image to create an orthomosaic map. Among the traditional matching algorithms are the fast library for approximate nearest neighbors (FLANN), k-nearest neighbors (KNN), and brute force (BF) matcher, each exhibiting unique advantages and disadvantages based on their specific characteristics [30, 31].
The FLANN-based matcher offers a rapid matching time but can have lower accuracy than the BF or KNN matcher [32,33,34,35]. The KNN matcher determines feature points based on the nearest neighbors, providing robust matching. However, it has a high computational cost [36,37]. Recently, deep learning methods, such as the learned invariant feature transform, super point, super glue, and LoFTR, have been employed in image matching [38,39,40]. These approaches, grounded in deep learning, are capable of robust performance even with various transformations and disturbances by learning and accounting for the intricate patterns and relationships within images. However, they necessitate training data and involve complex learning processes. Additionally, they can be characterized by prolonged execution times and significant resource requirements. Given that this study focuses on matching 2D images, the disadvantages associated with deep learning methods are not sufficiently counterbalanced by their benefits.
Compared to deep learning, traditional image matching methods, such as the FLANN-based matcher, KNN matcher, and BF matcher, are intuitive and can execute matches quickly without a complex learning process. Numerous academic studies and practical applications have demonstrated the effectiveness of these methods. This effectiveness stems from the ability of the algorithms to understand relationships between images based on feature points and perform matches using simple mathematical operations in the presence of image translation, rotation, and scaling. Thus, these algorithms enable rapid registration. Therefore, for the objective of real-time 2D orthomosaic map generation, methods that are simple and fast are deemed appropriate.

1.3. Paper Overview

In this study, considering these contexts, SIFT was used for feature point extraction, and the FLANN, KNN, and BF matchers were applied to feature point matching to identify the optimal combination. The focus was on addressing a balanced integration of optimization and efficiency through a selected combination of algorithms. The contents in the subsequent sections is introduced as follows:
  • Section 2 outlines the methodology for extracting feature points from images and generating a 2D orthomosaic map.
  • Section 3 explores the algorithms used for feature point matching and registration.
  • Section 4 evaluates the efficiency of the selected algorithms using validation examples of drone-captured images.

2. Procedure for 2D Orthomosaic Map Generation

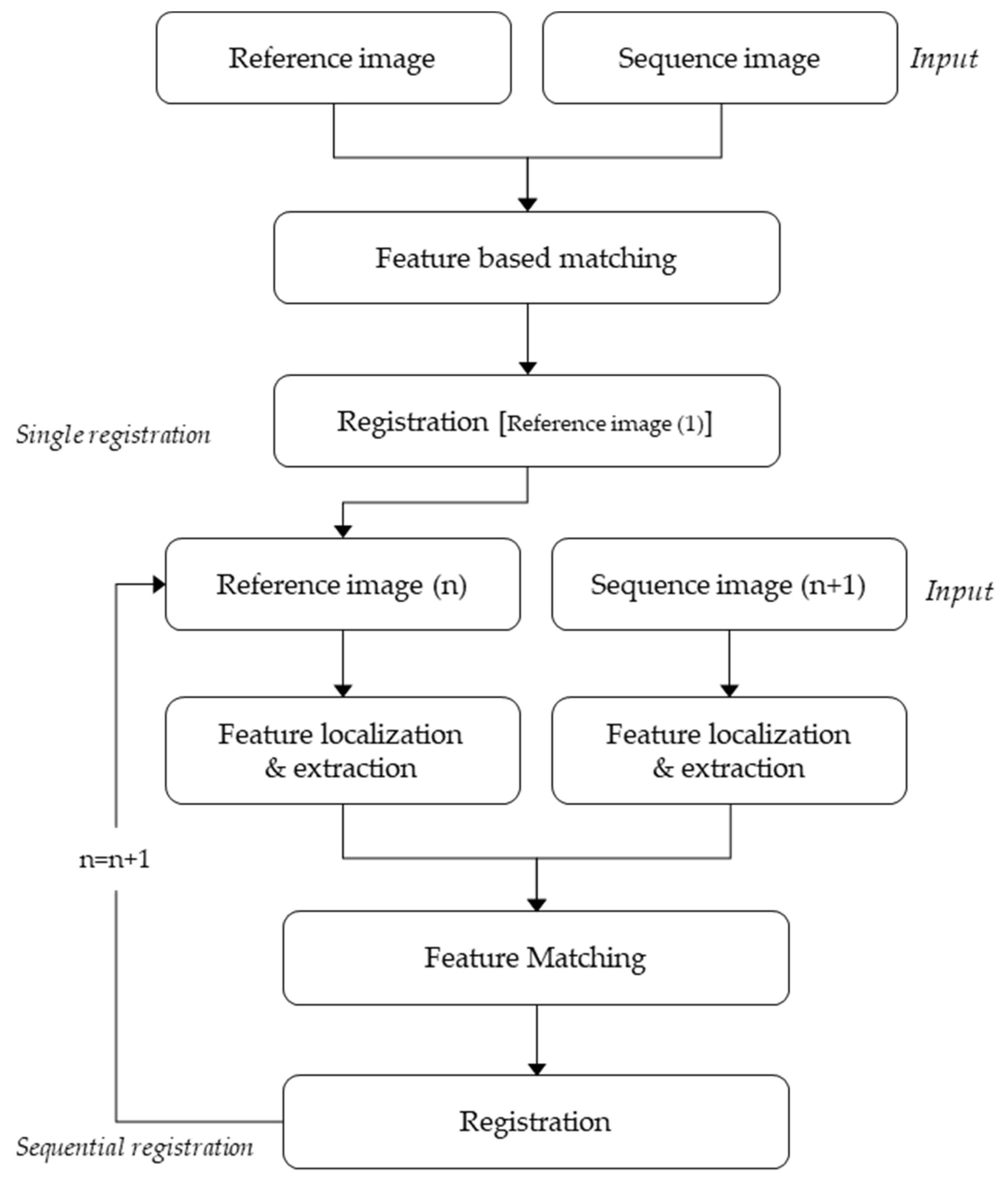
This study rigorously examines a method for the precise real-time registration of images captured by drones. In the first step, the drone-captured image is dissected into individual frames. In the second step, the SIFT extracts feature points from an initial reference image and subsequent sequential images. Then, FLANN matching is employed to identify and align matching feature points. In the third step, the aligned image becomes the new reference image. This process of feature point extraction, matching, and alignment is iteratively applied to each subsequent sequential image and is repeated for all images extracted from the drone until a comprehensive orthomosaic map is complete. Figure 1 visually represents this process, illustrating the steps to generate the 2D orthomosaic map from the drone images.

2.1. Images Extracted from Drone-Captured Video Frames

Drones are extensively employed for capturing nadir (vertical with the horizon) images in geographic information collection and analysis. When acquiring nadir images, image information is typically obtained from drones equipped with global positioning systems, cameras, and various sensors. However, in real-time environments, interruptions or delays in sensor data collection or transmission often occur due to weather conditions, obstacles, electromagnetic interference, and other technical problems. This study delves into the method of real-time 2D map generation to address these challenges, using only the directly saved image information from drones. Figure 2 and Figure 3 illustrate three example images extracted at 300 frame intervals (5 s) from nadir images acquired during a drone flight at an altitude of approximately 200 m. These drone images were captured at a resolution of 1920×1080 pixels, and the extracted images maintained the same resolution as the video.

2.2. Images Feature Extraction

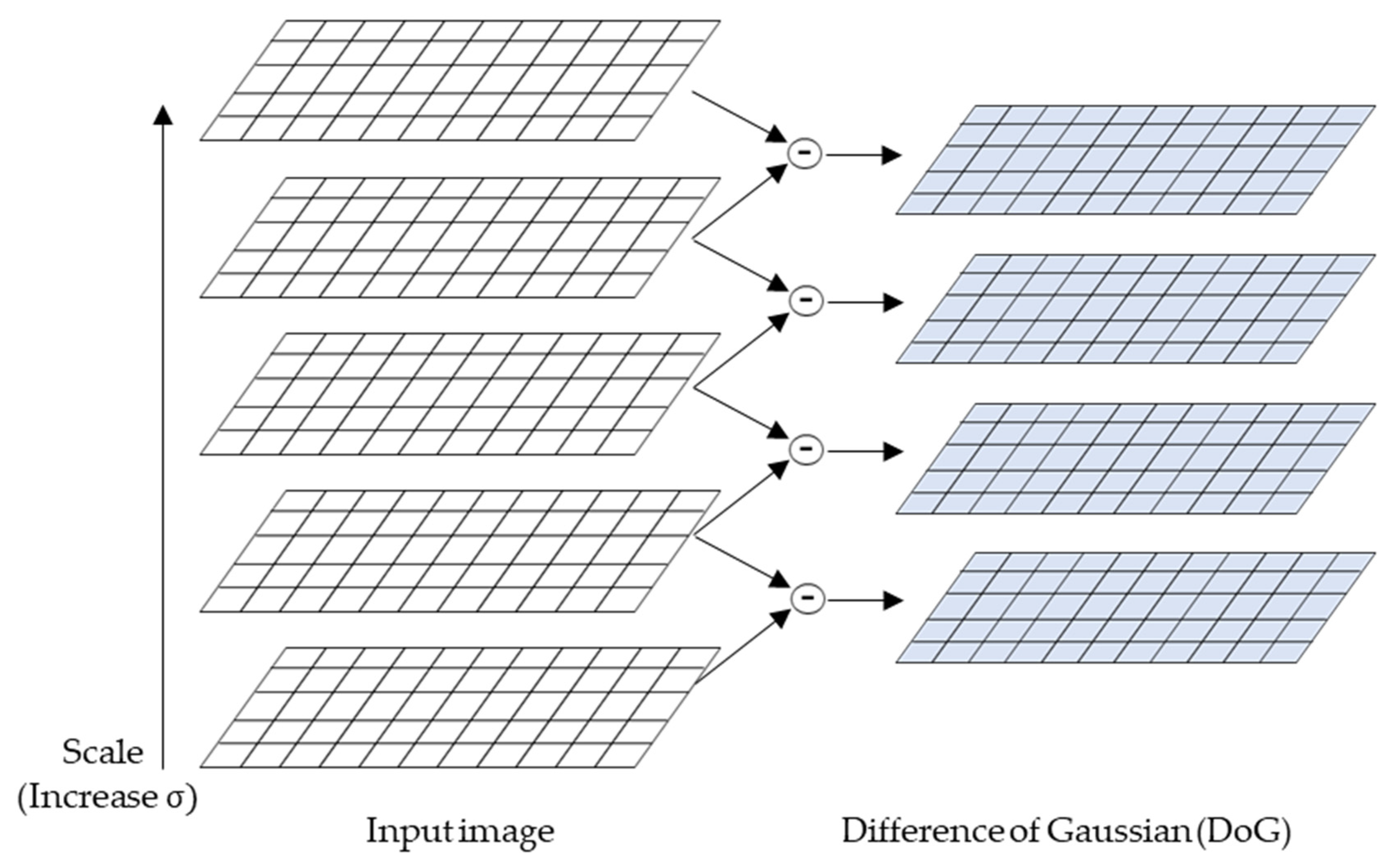
Various image feature extraction methods, such as SIFT, SURF, and ORB, are widely recognized and effectively employed in image analysis. The performance of each algorithm varies depending on its characteristics in various environments and conditions. Lowe (2004) introduced the SIFT, leading to advancements in object recognition and image feature extraction. This algorithm can extract features robustly across various scales, rotations, and viewpoints. Particularly, SIFT overcame the limitations of the Harris corner detection technique, which is sensitive to scale changes in images. The SIFT detector is based on approximating the Laplacian-of-Gaussian using the difference-of-Gaussians (DoG) operator. This detector searches for local maxima by applying DoG at various scales of the target image, creating a scale space. It computes DoG to identify local maxima values, selecting keypoint candidates. Gaussian blur is used to reduce image noise and decrease image complexity while emphasizing critical features. In the subsequent keypoint localization phase, meaningful keypoints are selected from candidates, and noisy and unstable points are eliminated. Extrema are detected using the generated DoG. If the coordinates are determined to be local minima or maxima, they are classified as keypoint candidates and compared to the surrounding pixel values to verify their status as extrema. In the orientation assignment phase, directions are assigned to each keypoint based on their gradient direction and magnitude, ensuring orientation invariance for keypoints, enabling them to be consistently detected even when the image is rotated. Unique feature descriptors are created using information from the vicinity of each keypoint. These descriptors contain local gradient information about the keypoints and are used to match keypoints with the same objects or scenes in other images. The descriptor ( D ( x , y , σ ) ) extracts a 16x16 neighborhood around each detected feature point, subdivides this region into subblocks, and calculates 128D. Equation (1) represents the convolution of the difference between two Gaussians (computed at different scales) with the image I ( x , y ) :
D ( x , y , σ ) = ( G ( x , y , k σ ) − G ( x , y , σ ) ) × I ( x , y ) ,
where G represents the Gaussian function, and k is a constant that defines the ratio between the sizes (or scales) of the consecutive Gaussian filters when constructing the scale space in SIFT. In SIFT, k is typically set to 2 and generates multiple Gaussian filter sizes to evenly distribute keypoints across various image scales. In addition, σ represents the standard deviation of the Gaussian filter. A higher σ value blurs the image over a wider area, whereas a lower σ value creates a sharper image by considering a narrower area. In SIFT, when σ values are given, multiple Gaussian filters are created based on them. These two values are crucial in extracting keypoints at various scales of the image within the SIFT algorithm, as presented in Figure 4.
The SURF algorithm relies on the analysis of the Gaussian scale space in an image [21]. The SURF detector is based on the determinant of the Hessian matrix and uses integral images to improve the feature detection speed. Its 64-byte descriptor describes each detected feature based on the distribution of Haar wavelet responses within a specific neighborhood. The SURF features are invariant to rotation and scale but lack affine invariance. However, the descriptor can be extended to 128-byte values to manage more extensive viewpoint changes. One of the significant advantages of SURF over SIFT is its lower computational cost. Equation (2) represents the Hessian matrix ( H ( X , s ) ) at point X = ( x , y ) at a scale of σ :
H H ( X , s ) = L L x x x x   ( X , s ) L L y x   ( X , s ) L L L x y   ( X , s ) L L y y   ( X , s ) ,
where L x x x x ( X , s ) represents the convolution of the Gaussian second-order derivative with the image I at point x , and similarly for L L L x y   ( X , s ) , and L y y   ( X , s ) . In SURF, a simplified box filter in the form of a Gaussian filter is employed to determine the extrema while increasing the scale of the filter. Therefore, the SURF method achieves a speed three times faster than that of the SIFT method by enlarging the filter size while searching, reducing the image size compared to the SIFT method. However, despite its speed advantage, the SURF algorithm is constrained by patent restrictions in OpenCV; therefore, it was excluded from consideration in this study.
The ORB algorithm is a blend of modified FAST detection and direction-normalized BRIEF description methods. In addition, FAST corners are detected at each layer of the scale area, and the quality of the detected points is evaluated using the Harris corner score, followed by top-quality points filtering. Due to the inherent instability of BRIEF descriptors under rotation, a modified version of the BRIEF descriptor is used. The ORB features are invariant to scale, rotation, and limited affine transformations.
Additionally, the KAZE and binary robust invariant scalable keypoints (BRISK) algorithms are also known for their excellent performance as feature extractors. The KAZE algorithm provides robust keypoints against brightness variations and rotations through nonlinear diffusion filtering, excelling in complex textures. In addition, BRISK achieves fast matching speeds while offering robust keypoints against rotation and scale changes using binary descriptors. The mentioned algorithms (i.e., SIFT, ORB, KAZE, and BRISK) were applied to two images, and the time required for feature point extraction was compared. Table 1 summarizes the OpenCV hyperparameters applied for feature point extraction algorithms.
Figure 5 presents two drone-captured images (resolution 1920×1080 pixels) as the subjects for feature point extraction with each algorithm. Figure 6 displays the results of key point extraction for each algorithm, and Table 2 summarizes the performance of each algorithm. Although the number of key points extracted varies among algorithms, despite exhibiting slightly slower performance than ORB, SIFT demonstrated sufficient computational efficiency. Furthermore, as mentioned in Section 1.2, SIFT is a feature detector and descriptor known for its relative excellence in terms of accuracy regarding scale, rotation, and affine transformations. Therefore, SIFT was selected to strike a suitable balance between efficiency and accuracy, considering the computational efficiency and characteristics of the 2D images emphasized in this study.

3. Image Feature Matching and Registration

3.1. Feature Matching

Feature point matching within images is crucial for identifying correspondences between images. In this study, we compared the performance of feature point matching using three methods: the FLANN, KNN, and BF matchers. The FLANN is a library that efficiently searches for approximate nearest neighbors within large datasets, outperforming traditional nearest-neighbor search methods in terms of speed and matching accuracy. In addition, FLANN achieves its optimized search through various combinations of algorithms and data structures, such as k-dimensional (KD) trees and hierarchical k-means. The KNN algorithm identifies the k closest neighbors of each data point within a given dataset based on distance metrics (e.g., Euclidean distance). This method is widely used in classification or regression problems and feature point matching, allowing it to rapidly identify the k most similar feature points to a given feature point. The BF matcher identifies nearest neighbors by computing the distances between all combinations of feature points. This approach is computationally intensive but provides high accuracy. In small datasets, the BF matcher can yield highly accurate matching results. Considering the characteristics of these three methods, we aimed to determine the most effective combination by applying the FLANN, KNN, and BF matchers to feature point matching after extracting the feature points.
For the performance comparison of these three methods, we extracted feature points using SIFT from two drone-captured images with a resolution of 1920×1080 pixels (Figure 5). Detailed settings and results for each method are provided as follows:
  • FLANN-based matcher: Five trees were constructed using the KD tree indexing method provided by OpenCV. The check count for searches was set to 50, and the test ratio between keypoints was set to 0.7. Matches were considered suitable matches only when the ratio of distances between the first- and second-nearest matches was less than this value. Thus, 569 matching points were extracted, and the matching time was measured at 0.056 s.
  • KNN matcher: For each feature point, k was set to 2 to determine the two nearest feature points, and the test ratio was set to 0.75. Consequently, 640 matching points were extracted, and the matching time was measured at 0.059 s.
  • BF matcher: The Euclidean distance between each matching point vector was calculated using OpenCV’s NORM_L2 function. The BF method performs searches on all keypoints; thus, the matching time for 4,792 keypoints was measured at 0.124 s.
Table 3 provides a comparison of each matching method in terms of the computed matching points, average distances between keypoints, and matching times. Figure 7 displays the matched keypoints for each method.
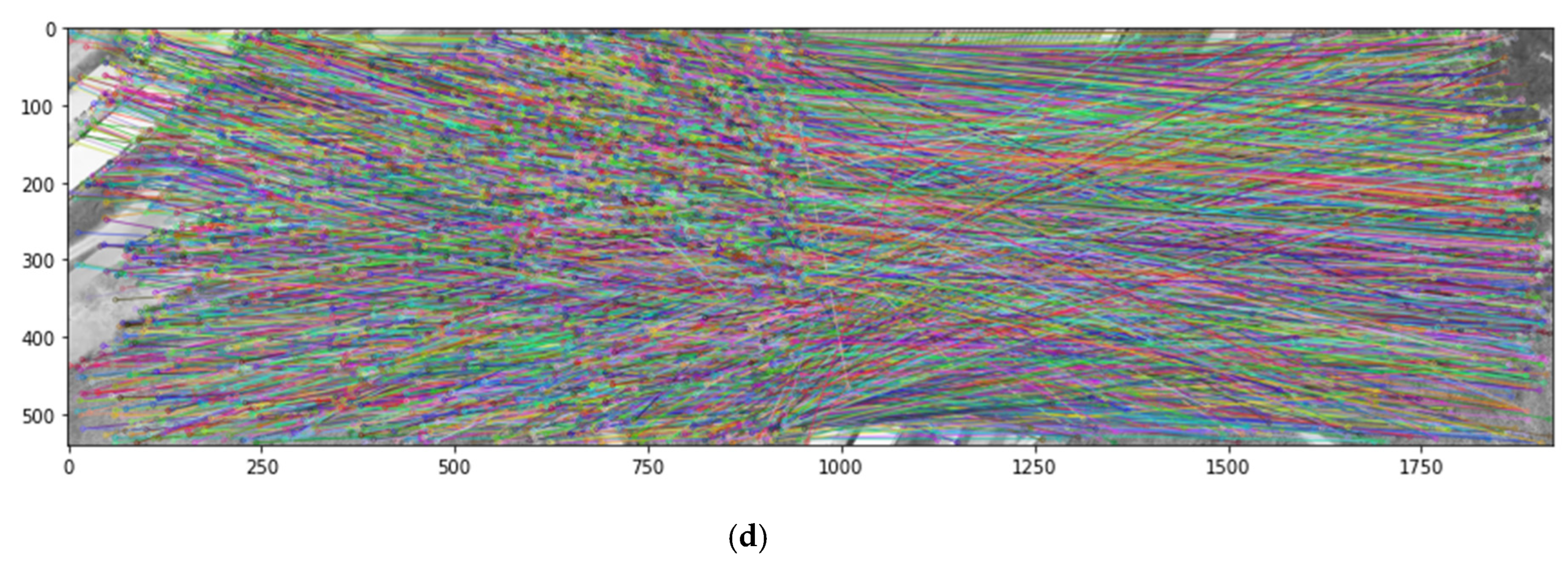
In summary, the FLANN and KNN matchers outperformed the BF matcher in selecting more suitable matching points for 2D orthomosaic map generation. The FLANN matcher exhibited relatively better performance; therefore, FLANN was chosen as the key-point-matching method in this study.

3.2. Feature Matching Refined by Random Sample Consensus

For registration of the 2D images, feature points were extracted using SIFT and matched using the FLANN method. The FLANN matcher compares feature points between two images and determines the nearest neighbors for each feature point. In this matching process, the KNN method is applied, referring to the KNN data points based on the distances between the descriptors of each feature point. However, it is not guaranteed that only accurate matching is always achieved during the KNN matching process, and outliers may be included. The random sample consensus (RANSAC) algorithm was applied to remove such outliers and ensure accurate matching. The RANSAC algorithm identifies and eliminates outliers and estimates the optimal model using the remaining points in the dataset [41]. This method iteratively estimates the model using randomly selected subsets of the data and selects the model that best matches the most data points. The critical advantage of this technique is its ability to estimate an accurate model from the data even when there are many outliers.
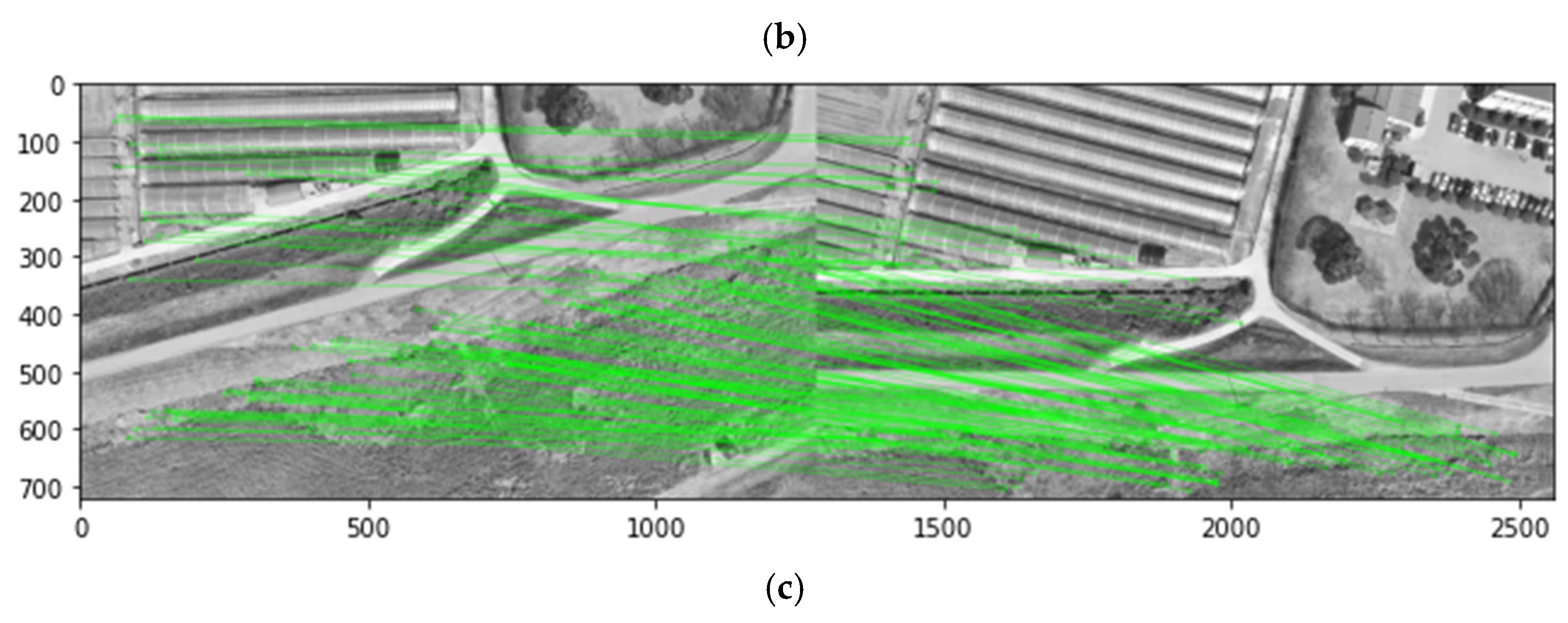
Consequently, this technique successfully allowed the calculation of the transformation matrix between the two images. Figure 8 visually compares the situation of feature point matching before and after the application of RANSAC in drone-captured images with a resolution of 1920×1080 pixels. To achieve successful results with RANSAC, the find homography function provided by OpenCV was used, with a defined tolerance of 5.0, and the number of iterations was determined automatically.

3.3. Registration (Projective Transformations by the 2D Homography Matrix)

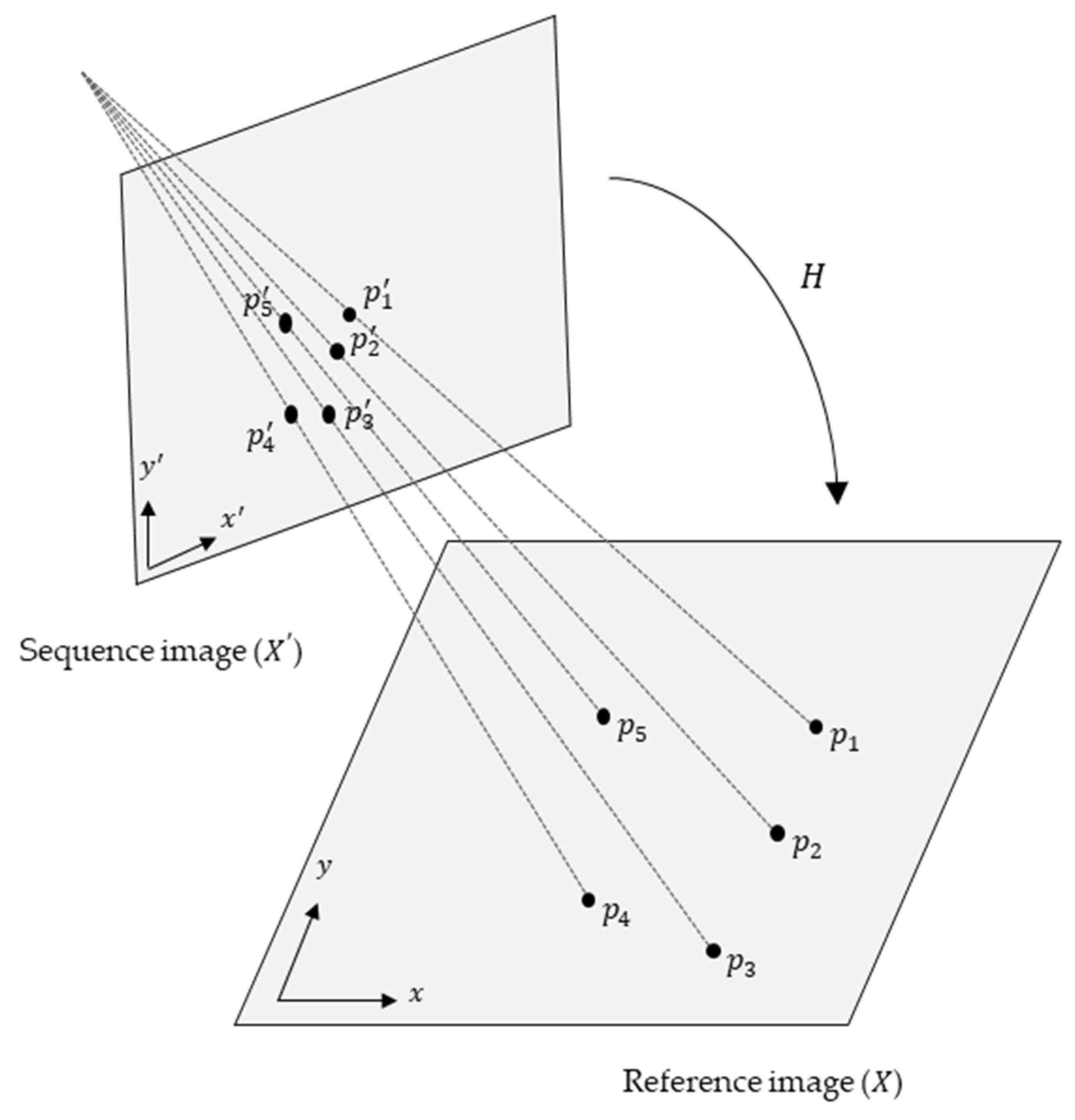
The extracted feature points from the images were used to determine corresponding points through the FLANN-based matcher. The homography matrix ( H ) between the reference image ( X ) and sequential image ( X ' ) is computed based on these correspondences. This homography matrix represents the projective transformation (i.e., plane projection relationship) between two 2D images. Equation (3) represents the transformation of the reference image ( X ) to the sequential image ( X ' ), and Figure 9 illustrates the geometric transformation (plane projection) between the two 2D images.
X = H X '
The sequential image is warped to align with the same plane as the reference image using the homography matrix. The boundaries of the warped image are smoothly blended, and unnecessary border regions are removed to create a final, perfectly aligned image. The two images are accurately aligned through this process around the area where the feature points match, resulting in a registered image. Figure 10 illustrates two examples of a precisely registered image created from two drone images with a resolution of 1920×1080 pixels. These images undergo SIFT feature point extraction, FLANN matching, and the registration process.

4. Two-dimensional Orthomosaic Map Generation Results

4.1. Drone-Captured Video

The outlined procedures and methods enabled extracting feature points from the drone-captured videos, performing feature matching and registration processes, and creating 2D orthomosaic maps. The map images were generated from two videos with a resolution of FHD (1920×1080 pixels), which were captured by a drone while flying in a circular path at a height of approximately 200 m above agricultural land with roads and structures. The first video (Drone Video 1) was captured as the drone flew in a circular path over the terrain with a road, with a recording duration of approximately 60 s. The second video (Drone Video 2) was captured as the drone flew in circular and straight paths over an area with roads and structures, with a recording duration of approximately 160 s. Table 4 summarizes the details of these two videos.

4.2. Real-time Two-dimensional Orthomosaic Map Generation

Drone-captured images were continuously extracted at intervals of 400 frames (approximately 6.66 s) from two video examples. Each image was categorically selected as either a reference or sequential image. The SIFT was employed for feature extraction, and the FLANN matcher was used to select matching points. Image registration was accomplished by computing a 2D homography matrix. All image registration tests were conducted on a workstation equipped with an Intel Core i9-10900K central processing unit (CPU) and 128 GB of RAM.
Figure 11 and Figure 12 depict individual frames extracted at 400-frame intervals (approximately 6.66 s) and the real-time 2D orthomosaic maps generated from Drone Video 1, respectively. Table 5 lists the CPU time spent at each step in the registration process, including the extraction of SIFT keypoints, utilization of the FLANN matcher, and the computation of image transformation matrices. While the time required increases at each stage due to the growing size of the reference image, all image registrations are completed in less time than it takes to extract the images. This efficiency, attributable to the quicker registration process compared with the image extraction time, underscores the capability to generate 2D orthomosaic maps in real time from the collected videos.
Figure 13 and Figure 14 similarly display individual frames extracted at 400-frame intervals (approximately 6.667 s) and the real-time 2D orthomosaic maps generated from Drone Video 2, respectively. Table 5 indicates a continuous increase in registration time for Drone Video 2 results, attributable to the enlarged size of the reference image at each registration stage. Although the image registration for Drone Video 2 was completed more swiftly than the frame extraction time from the drone footage, a limitation in real-time orthomosaic map generation was observed as the reference image size increased. Consequently, the generation of segmented orthomosaic maps at fixed time intervals may be necessary, depending on the characteristics of the collected drone-captured video.

5. Conclusion

This study explored the process of generating a real-time 2D orthomosaic map from videos collected using a drone. The primary focus of the research was to minimize the time required to extract images frame by frame from the video and efficiently align them. Feature points were extracted using SIFT, and during the feature point matching process, the FLANN-based, KNN, and BF matcher methods were compared. The FLANN matcher performed image feature point matching faster. The extracted and matched feature points were swiftly aligned using homography matrices. The real-time 2D orthomosaic map can be created faster than the time required for image extraction. A real-time and accurate 2D orthomosaic image can be successfully generated through the iterative application of images from drone flight patterns, such as circling and straight-line flight. However, as the registration process progresses, the increasing size of the reference image inevitably leads to a rise in CPU time. This increase imposes a constraint on the continuous, real-time generation of orthomosaic maps.
Consequently, a need for generating segmented orthomosaic maps at predetermined intervals was identified. Additionally, supplementary techniques are necessary to effectively connect each segmented orthomosaic map. Nevertheless, the suggested method in this study is expected to contribute to various fields in image processing using drones, which demand high efficiency and precision. In future research, a more in-depth exploration of video characteristics, image extraction intervals, shooting areas, and other related factors could lead to the development of even faster and more accurate algorithms for 2D orthomosaic map generation.

Author Contributions

Conceptualization and methodology, S.-Y.H. and J.H.L.; validation, formal analysis, investigation, S.-Y.H. and J.H.L.; data curation, M.Y; writing, S.-Y.H. and J.H.L.; project administration and funding acquisition, C.S.H. and J.H.C. All authors have read and agreed to the published version of the manuscript.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

This research was supported by the Challengeable Future Defense Technology Research and Development Program through the Agency for Defense Development (ADD), funded by the Defense Acquisition Program Administration (DAPA) in 2023 (No. 915027201).

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Rusnák, M.; Sládek, J.; Kidová, A.; Lehotsky, M. Template for high-resolution river landscape mapping using UAV technology. Measurement 2018, 115, 139–151. [Google Scholar] [CrossRef]
  2. Giordan, D.; Adams, M.S.; Aicardi, I.; Alicandro, M.; Allasia, P.; Baldo, M.; De Berardinis, P.; Dominici, D.; Godone, D.; Hobbs, P.; et al. The use of unmanned aerial vehicles (UAVs) for engineering geology applications. B Eng Geol Environ 2020, 79, 3437–3481. [Google Scholar] [CrossRef]
  3. Zhang, X.Y.; Leng, C.C.; Hong, Y.M.; Pei, Z.; Cheng, I.R.E.; Basu, A. Multimodal Remote Sensing Image Registration Methods and Advancements: A Survey. Remote Sens-Basel 2021, 13. [Google Scholar] [CrossRef]
  4. Audette, M.A.; Ferrie, F.P.; Peters, T.M. An algorithmic overview of surface registration techniques for medical imaging. Med Image Anal 2000, 4, 201–217. [Google Scholar] [CrossRef]
  5. Hwang, Y.S.; Schlüter, S.; Park, S.I.; Um, J.S. Comparative Evaluation of Mapping Accuracy between UAV Video versus Photo Mosaic for the Scattered Urban Photovoltaic Panel. Remote Sens-Basel 2021, 13. [Google Scholar] [CrossRef]
  6. Zheng, Q.; Chellappa, R. A computational vision approach to image registration. IEEE T Image Process 1993, 2, 311–326. [Google Scholar] [CrossRef]
  7. Thirion, J.P. New feature points based on geometric invariants for 3D image registration. Int J Comput Vision 1996, 18, 121–137. [Google Scholar] [CrossRef]
  8. Hsieh, J.W.; Liao, H.Y.M.; Fan, K.C.; Ko, M.T.; Hung, Y.P. Image registration using a new edge-based approach. Comput Vis Image Und 1997, 67, 112–130. [Google Scholar] [CrossRef]
  9. Vacca, G. Overview of Open Source Software for Close Range Photogrammetry. Int Arch Photogramm 2019, 42-4, 239–245. [Google Scholar] [CrossRef]
  10. Vithlani, H.N.; Dogotari, M.; Lam, O.H.Y.; Prüm, M.; Melville, B.; Zimmer, F.; Becker, R. Scale Drone Mapping on K8S: Auto-scale Drone Imagery Processing on Kubernetes-orchestrated On-premise Cloud-computing Platform. Proceedings of the 6th International Conference on Geographical Information Systems Theory, Applications and Management (Gistam) 2020, 318-325. [CrossRef]
  11. Harris, C.; Stephens, M.J. A Combined Corner and Edge Detector. In Proceedings of the Alvey Vision Conference, 1988; pp. 147–152. [CrossRef]
  12. Pei, Y.; Wu, H.; Yu, J.; Cai, G. Effective image registration based on improved harris corner detection. In Proceedings of the 2010 International Conference on Information, Networking and Automation (ICINA), 2010; pp. V1-93-V91-96.
  13. Ye, Z.; Pei, Y.; Shi, J. An improved algorithm for Harris corner detection. In Proceedings of the 2009 2nd International Congress on Image and Signal Processing, 2009; pp. 1-4.
  14. Chen, J.; Zou, L.-h.; Zhang, J.; Dou, L.-h. The Comparison and Application of Corner Detection Algorithms. Journal of multimedia 2009, 4. [Google Scholar] [CrossRef]
  15. Ram, P.; Padmavathi, S. Analysis of Harris corner detection for color images. In Proceedings of the 2016 International Conference on Signal Processing, Communication, Power and Embedded System (SCOPES), 2016; pp. 405-410.
  16. Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
  17. Meng, Y.; Tiddeman, B. Implementing the scale invariant feature transform (sift) method. Department of Computer Science University of St. Andrews 2006. [Google Scholar]
  18. Tao, Y.; Xia, Y.; Xu, T.; Chi, X. Research Progress of the Scale Invariant Feature Transform (SIFT) Descriptors. Journal of Convergence Information Technology 2010, 5, 116–121. [Google Scholar]
  19. Lakshmi, K.D.; Vaithiyanathan, V. Image Registration Techniques Based on the Scale Invariant Feature Transform. Iete Tech Rev 2017, 34, 22–29. [Google Scholar] [CrossRef]
  20. Burger, W.; Burge, M.J. Scale-invariant feature transform (SIFT). In Digital Image Processing: An Algorithmic Introduction; Springer: 2022; pp. 709-763.
  21. Bay, H.; Tuytelaars, T.; Van Gool, L. SURF: Speeded Up Robust Features. In Lecture Notes in Computer Science, 2006, Volume 3951, pp. 404–417.
  22. Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-Up Robust Features (SURF). Comput Vis Image Und 2008, 110, 346–359. [Google Scholar] [CrossRef]
  23. Abedin, M.Z.; Dhar, P.; Deb, K. Traffic Sign Recognition Using SURF: Speeded Up Robust Feature Descriptor and Artificial Neural Network Classifier. Int C Comp Elec Eng 2016, 198–201. [Google Scholar]
  24. Verma, N.K.; Goyal, A.; Vardhan, A.H.; Sevakula, R.K.; Salour, A. Object matching using speeded up robust features. In Proceedings of the Intelligent and Evolutionary Systems: The 19th Asia Pacific Symposium, IES 2015, Bangkok, Thailand, November 2015, Proceedings, 2016; pp. 415-427.
  25. Prinka; Wasson, V. An efficient Content Based Image Retrieval Based on Speeded up Robust Features (SURF) with Optimization Technique. 2017 2nd Ieee International Conference on Recent Trends in Electronics, Information & Communication Technology (Rteict) 2017, 730-735.
  26. Wang, R.; Shi, Y.; Cao, W. GA-SURF: A new speeded-up robust feature extraction algorithm for multispectral images based on geometric algebra. Pattern Recognition Letters 2019, 127, 11–17. [Google Scholar] [CrossRef]
  27. Xu, J.; Chang, H.-w.; Yang, S.; Wang, M. Fast feature-based video stabilization without accumulative global motion estimation. IEEE Transactions on Consumer Electronics 2012, 58, 993–999. [Google Scholar] [CrossRef]
  28. Sun, R.; Qian, J.; Jose, R.H.; Gong, Z.; Miao, R.; Xue, W.; Liu, P. A flexible and efficient real-time orb-based full-hd image feature extraction accelerator. IEEE Transactions on Very Large Scale Integration (VLSI) Systems 2019, 28, 565–575. [Google Scholar] [CrossRef]
  29. Tareen, S.A.K.; Saleem, Z. A comparative analysis of SIFT, SURF, KAZE, AKAZE, ORB, and BRISK. In Proceedings of the 2018 IEEE International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), Sukkur, Pakistan, 3–4 March 2018; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar]
  30. Liu, Z.; Guo, Y.; Feng, Z.; Zhang, S. Improved rectangle template matching based feature point matching algorithm. In Proceedings of the 2019 Chinese Control And Decision Conference (CCDC), 2019; pp. 2275-2280.
  31. Antony, N.; Devassy, B.R. Implementation of image/video copy-move forgery detection using brute-force matching. In Proceedings of the 2018 2nd International Conference on Trends in Electronics and Informatics (ICOEI), 2018; pp. 1085-1090.
  32. Muja, M.; Lowe, D.G. FLANN, fast library for approximate nearest neighbors. In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP’09), 2009; pp. 1-21.
  33. Wang, S.; Guo, Z.; Liu, Y. An image matching method based on sift feature extraction and FLANN search algorithm improvement. In Proceedings of the Journal of Physics: Conference Series, 2021; p. 012122.
  34. Gupta, M.; Singh, P. An image forensic technique based on SIFT descriptors and FLANN based matching. In Proceedings of the 2021 12th International Conference on Computing Communication and Networking Technologies (ICCCNT), 2021; pp. 1-7.
  35. Vijayan, V.; Kp, P. FLANN based matching with SIFT descriptors for drowsy features extraction. In Proceedings of the 2019 Fifth International Conference on Image Information Processing (ICIIP), 2019; pp. 600-605.
  36. Cao, M.-W.; Li, L.; Xie, W.-J.; Jia, W.; Lv, Z.-H.; Zheng, L.-P.; Liu, X.-P. Parallel K nearest neighbor matching for 3D reconstruction. IEEE Access 2019, 7, 55248–55260. [Google Scholar] [CrossRef]
  37. Gao, S.; Cai, T.; Fang, K. Gravity-matching algorithm based on k-nearest neighbor. Sensors 2022, 22, 4454. [Google Scholar] [CrossRef] [PubMed]
  38. Yi, K.M.; Trulls, E.; Lepetit, V.; Fua, P. Lift: Learned invariant feature transform. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, October 11-14, 2016, Proceedings, Part VI 14, 2016; pp. 467-483.
  39. DeTone, D.; Malisiewicz, T.; Rabinovich, A. Superpoint: Self-supervised interest point detection and description. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition workshops, 2018; pp. 224-236.1.
  40. Sun, J.; Shen, Z.; Wang, Y.; Bao, H.; Zhou, X. LoFTR: Detector-free local feature matching with transformers. In Proceedings of the Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2021; pp. 8922-8931.
  41. Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
Preprints 92172 g001
Figure 1. Procedure of image registration for two-dimensional orthomosaic map generation.
Figure 1. Procedure of image registration for two-dimensional orthomosaic map generation.
Preprints 92172 g001
Preprints 92172 g002
Figure 2. Nadir image Set 1 extracted from a drone-captured video at 60-frame intervals: (a) Frame 1; (b) Frame 2; (c) Frame 3.
Figure 2. Nadir image Set 1 extracted from a drone-captured video at 60-frame intervals: (a) Frame 1; (b) Frame 2; (c) Frame 3.
Preprints 92172 g002
Preprints 92172 g003aPreprints 92172 g003b
Figure 3. Nadir image Set 2 extracted from a drone-captured video at 60-frame intervals: (a) Frame 1; (b) Frame 2; (c) Frame 3.
Figure 3. Nadir image Set 2 extracted from a drone-captured video at 60-frame intervals: (a) Frame 1; (b) Frame 2; (c) Frame 3.
Preprints 92172 g003aPreprints 92172 g003b
Preprints 92172 g004
Figure 4. Schematic representation of the internal difference of Gaussian in the scale-invariant feature transform (SIFT).
Figure 4. Schematic representation of the internal difference of Gaussian in the scale-invariant feature transform (SIFT).
Preprints 92172 g004
Preprints 92172 g005
Figure 5. Drone-captured images for feature point extraction: (a) original; (b) gray-scale images.
Figure 5. Drone-captured images for feature point extraction: (a) original; (b) gray-scale images.
Preprints 92172 g005
Preprints 92172 g006aPreprints 92172 g006b
Figure 6. Extracted feature points from the drone images: (a) SIFT; (b) ORB; (c) KAZE; (d) BRISK.
Figure 6. Extracted feature points from the drone images: (a) SIFT; (b) ORB; (c) KAZE; (d) BRISK.
Preprints 92172 g006aPreprints 92172 g006b
Preprints 92172 g007aPreprints 92172 g007b
Figure 7. Matching results by algorithm: (a) Gray-scale image; (b) fast library for approximate nearest neighbors; (c) k-nearest neighbors (KNN); (d) brute force (BF).
Figure 7. Matching results by algorithm: (a) Gray-scale image; (b) fast library for approximate nearest neighbors; (c) k-nearest neighbors (KNN); (d) brute force (BF).
Preprints 92172 g007aPreprints 92172 g007b
Preprints 92172 g008aPreprints 92172 g008b
Figure 8. Results of applying the random sample consensus (RANSAC) algorithm: (a) Gray-scale images; (b) Before RANSAC application; (c) After RANSAC application.
Figure 8. Results of applying the random sample consensus (RANSAC) algorithm: (a) Gray-scale images; (b) Before RANSAC application; (c) After RANSAC application.
Preprints 92172 g008aPreprints 92172 g008b
Preprints 92172 g009
Figure 9. Transformation by the two-dimensional homography matrix based on the identified corresponding keypoints.
Figure 9. Transformation by the two-dimensional homography matrix based on the identified corresponding keypoints.
Preprints 92172 g009
Preprints 92172 g010
Figure 10. Registration results of the two-dimensional captured images (1920×1080 pixels): (a) Example 1; (b) Example 2.
Figure 10. Registration results of the two-dimensional captured images (1920×1080 pixels): (a) Example 1; (b) Example 2.
Preprints 92172 g010
Preprints 92172 g011
Figure 11. Extracted frame-by-frame images from Drone Video 1 per 400 frames (6.667 s).
Figure 11. Extracted frame-by-frame images from Drone Video 1 per 400 frames (6.667 s).
Preprints 92172 g011
Preprints 92172 g012
Figure 12. Sequentially registered two-dimensional orthomosaic map image of Drone Video 1.
Figure 12. Sequentially registered two-dimensional orthomosaic map image of Drone Video 1.
Preprints 92172 g012
Preprints 92172 g013
Figure 13. Extracted frame-by-frame images from Drone Video 2 per 400 frames (6.667 s).
Figure 13. Extracted frame-by-frame images from Drone Video 2 per 400 frames (6.667 s).
Preprints 92172 g013
Preprints 92172 g014
Figure 14. Sequentially registered two-dimensional orthomosaic map image of Drone Video 2.
Figure 14. Sequentially registered two-dimensional orthomosaic map image of Drone Video 2.
Preprints 92172 g014
Table 1. Hyperparameter and descriptor sizes for image keypoint extraction (OpenCV).
Table 1. Hyperparameter and descriptor sizes for image keypoint extraction (OpenCV).
Algorithms Hyperparameter (OpenCV) Descriptor size
SIFT n features: 500, n octave layers: 3,
contrast threshold: 0.04, edge threshold: 10,
sigma: 1.6, 		128 bytes
ORB n features: 500, scale factor: 1.2,
n levels: 8, edge threshold: 31,
first level: 0, WTA_K: 2,
patch size: 31, fast threshold: 20		 32 bytes
KAZE extended: false (64), upright: false,
threshold: 0.001, n octaves: 4,
n octave layers: 4, diffusivity: 1		 64 floats
BRISK thresh: 30, octaves: 3, pattern scale: 1.0 64 bytes
Table 2. Number of key points extracted and extraction time from two images.
Table 2. Number of key points extracted and extraction time from two images.
Algorithms Image 1 Image 2
No. of keypoints
[EA]		 Computation time [s] No. of keypoints
[EA]		 Computation time
[s]
SIFT 4792 0.06 6682 0.07
ORB 500 0.01 500 0.01
KAZE 1382 0.18 1734 0.18
BRISK 10670 0.11 8993 0.10
Table 3. Performance comparison of the proposed matching methods.
Table 3. Performance comparison of the proposed matching methods.
Method Matching points [EA] Avg. Distance Processing Time [s]
FLANN 569 151.748 0.056
KNN 640 157.272 0.059
BF 4792 272.515 0.124
Table 4. Drone videos for two-dimensional orthomosaic map generation.
Table 4. Drone videos for two-dimensional orthomosaic map generation.
Size [Pixels] Recoding time [s] Flight path
Drone Video 1 1920 × 1080 60 Circling
Drone Video 2 1920 × 1080 160 Circling, straight
Table 5. Time required to generate a two-dimensional orthomosaic map image from drone videos.
Table 5. Time required to generate a two-dimensional orthomosaic map image from drone videos.
CPU time per registration steps [s] Max. registration time [s]
Drone Video 1 (1) 0.209, (2) 0.803, (3) 1.303,
(4) 1.634, (5) 2.134, (6) 2.447,
(7) 2.975, (8) 3.160		 3.160
Drone Video 2 (1) 0.189, (2) 0.484, (3) 0.682, (4) 0.682
(5) 1.104, (6) 1.666, (7) 1.955, (8) 2.245
(9) 2.534, (10) 2.824, (11) 3.113, (12) 3.403
(13) 3.692, (14) 3.982, (15) 4.271, (16) 4.561
(17) 4.850, (18) 5.140, (19) 5.429, (20) 5.719
(21) 5.719, (22) 6.008, (23) 6.309		 6.309
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated