Prerpints.org logo
Preprint
Article

A Twin Frequency Control DC-DC Buck Converter Using Accurate Load Current Sensing Technique

Altmetrics

Downloads

87

Views

28

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

04 December 2023

Posted:

04 December 2023

You are already at the latest version

Alerts
Abstract
In this paper, a buck DC-DC converter with the proposed twin frequency control scheme (TFCS) and accurate load current sensing (ALCS) have been designed and implemented with 0.18µm CMOS technology for a supply voltage ranging from 2.0-3.0V which is compatible with state-of-the-art batteries (NiCd/NiMH: 1.1-2V, Li-Ion: 2.5-4.2V). The proposed converter yields a peak efficiency of about 92.7% with a load current of 30mA. Furthermore, it only occupies a silicon area of 1.3mm2. The proposed buck converter is dedicated for smartphone applications whereby it spends most of its time in idle, low load conditions.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Modern 4G smartphones are embedded with a high-speed multi-core processor, gigabytes of flash memory, high resolution color display, 3G/4G and Bluetooth wireless communication devices [1]. Therefore, the quiescent power consumption of a smartphone is comparable to a laptop or a handheld tablet. Furthermore, new modern applications such as live video streaming require a constant utilization of LED backlight display or cloud computing services which will no doubt increase the total power consumption drastically [2]. All the above enhanced functionalities of a 4G smartphone will heighten the pressure on the battery lifetime and escalate the urgency for a more efficient power management system [3]. However, the widely used NiCd/NiMH and Li-Ion batteries, providing the source of power is very limited in supplying the energy and power demands for the wide variety of applications found in a smartphone. This is supported by a recent research study which has shown that its energy density has only doubled over the past decade from 300 to 600Whr/liter [4]. Hence, the viable solution is to reduce the overall battery power consumption by improving the power efficiency of the power management unit (PMU) in a smartphone.
For the past few years, there have been numerous interesting research works [5,6] which have presented various power consumption usage models for 3G/4G smartphone. Modern power management systems in smartphone [7] are used to generate constant or variable output voltage supply from battery sources which have a wide input range variation e.g., NiCd/NiMH: 1.1-2V, Li-Ion: 2.5-4.2V [8,9]. Power converters (buck/boost) are indispensable building blocks found in a part of the power management unit (PMU) of a smartphone as shown in Figure 1. Their objectives are to supply a well-regulated supply voltage to the different group core modules [1] found in the smartphone. A full illustration of the PMU of a smartphone can be found here [10].
The key to prolonging the battery lifetime is to improve the power efficiency of the DC-DC converter. Since the smartphone spends most of its time in the low load condition [2], numerous research works [11,12,13,14] have already targeted at improving the light-load efficiency as its core priority. Though the new circuit implementation is novel, improvement in power efficiency is minimal and proposed circuit techniques are relatively complex. One of the more interesting works proposed [15] include a width-switching scheme whereby the width of the respective power transistors can be altered according to the load current demand. However, the light load efficiency falls below 80% for < 20mW of load power. In another literature [16], pulse-skipping modulation (PSM) is added in between PWM and PFM to ensure a seamless transition of the power efficiency curve from low to high load current. This technique is well-known as the tri-hybrid mode converter which can deliver high efficiency for a wide load range. On the other hand, it does have its drawbacks too. Whenever it transits to PSM mode, load regulation is always sacrificed, and power conversion efficiency is only maximized at several load conditions. Lastly, tri-hybrid mode control requires several modulators with complex-mode switching circuits which may lead to stability issue e.g., inductor runaway.
Hence, in this current research work, a twin frequency control scheme (TFCS), together with an accurate load current sensing block (ALCS), are proposed to achieve high efficiency at low load condition (<50mW) regardless of process/power transistor variation as well as source voltage or load current variation. This is compatible with the fact that smartphones drive these range of power load levels during their idle condition.
For proof of concept, a monolithic buck converter with the proposed TFCS and ALCS are implemented and tested. Furthermore, a conventional PWM/PFM buck controller is implemented as well to give a good comparison with our proposed work. The design and measurement details are presented in this paper in the following organization. Section II discusses the operation of the system and block level design. Section III presents the experimental results followed by a discussion and comparison with the state of the art works as summarized in Table 1. Finally, the conclusion will be shown in Section IV.

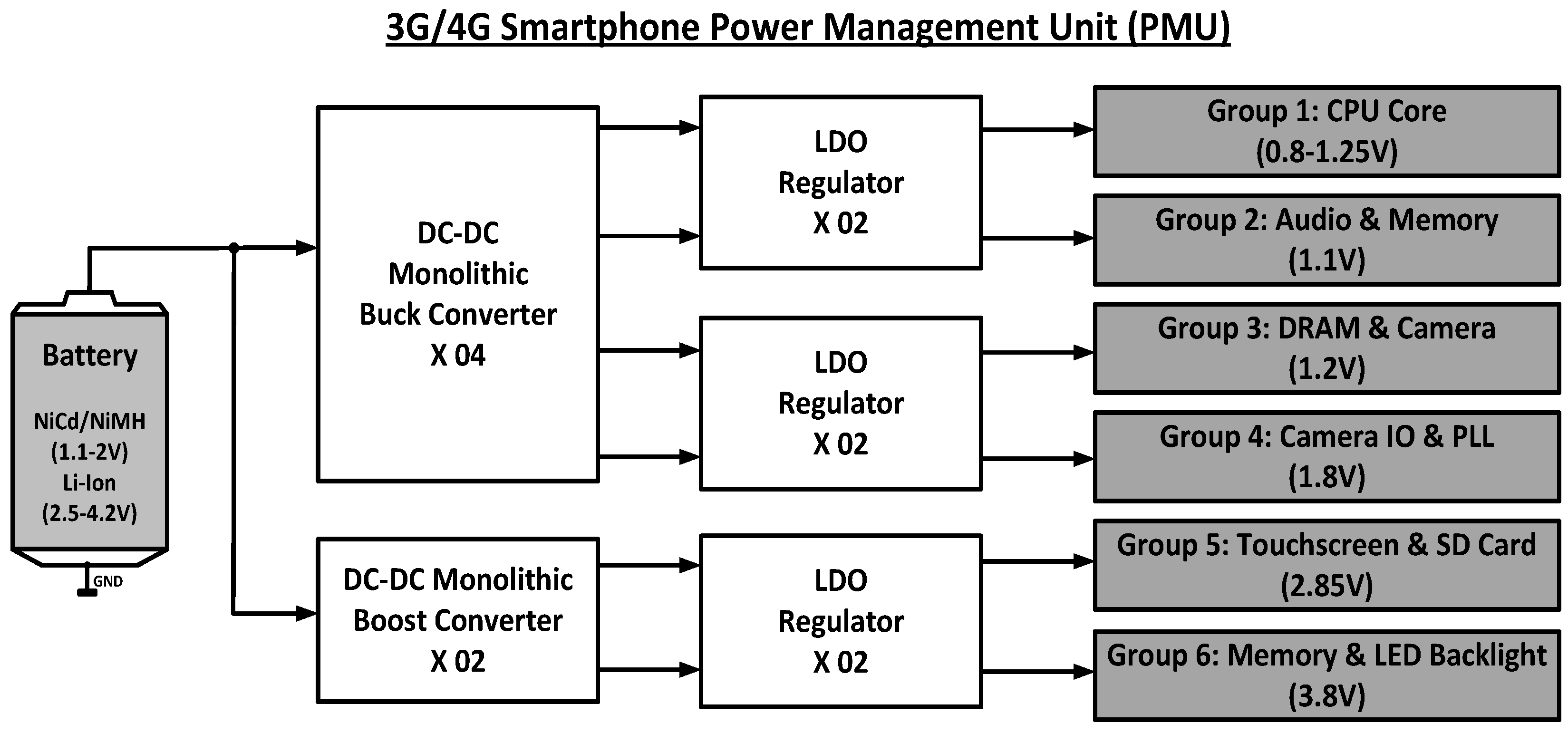
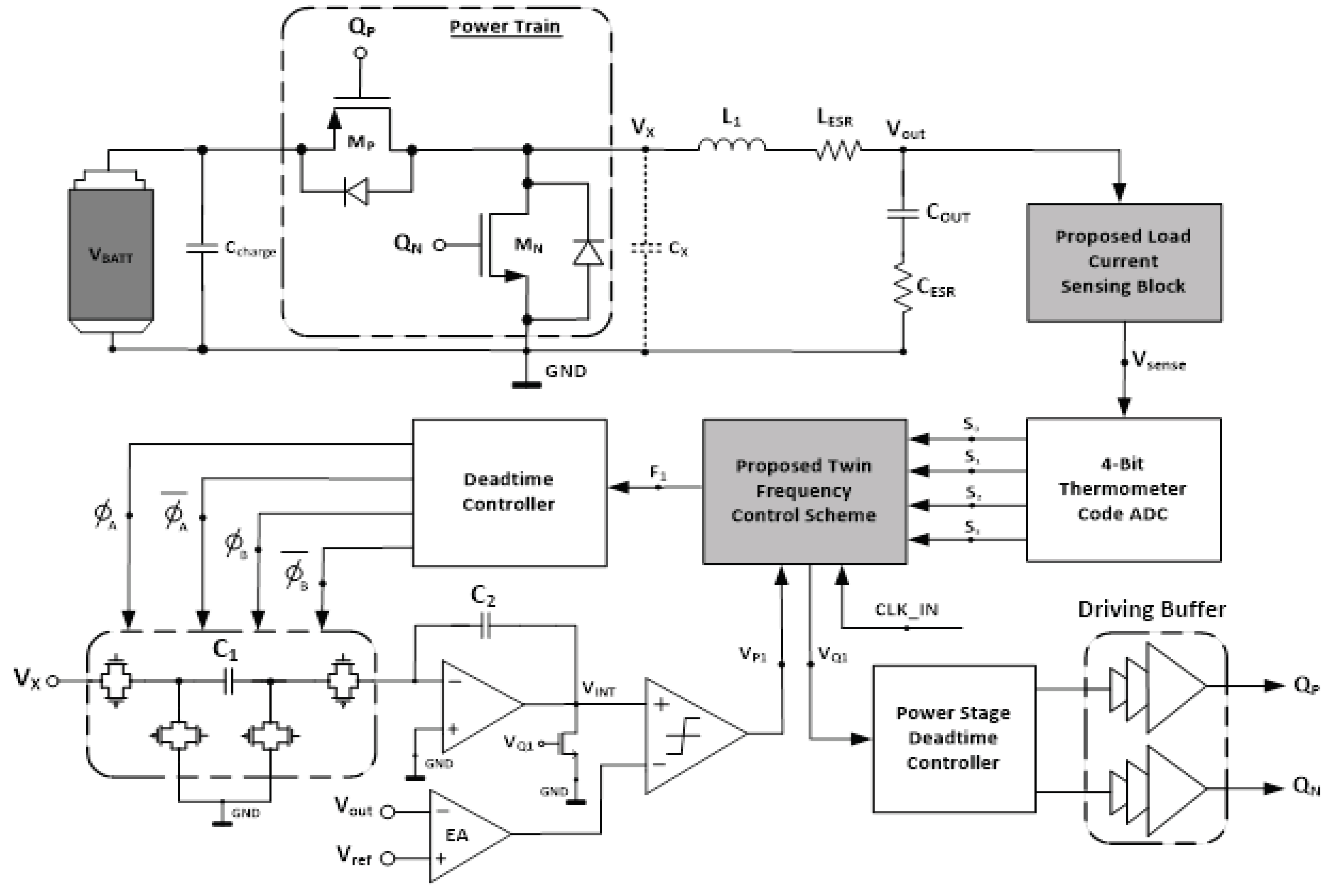
2. Proposed Twin Frequency Control DC-DC Buck Converter

Our proposed work, shown in Figure 2, consists of a twin frequency control scheme (TFCS), an accurate load current sensing (ALCS) block, a switched capacitor (SC) integrator, two deadtime controller and the power train stage. In general, the output voltage, Vout, gives important information about the load current and this will be sensed by the proposed load current sensing block to produce a sensing voltage, Vsense. Furthermore, this voltage in turn gets compared with a 4-bit thermometer code ADC to produce a 4-bit signal (S0, S1, S2 and S3). This gives an accurate indication of the load current level drawn by the output of the DC-DC converter. The 4-bit signal goes through the TFCS which yields two non-overlapping clocks to control the switches in the switched-capacitor integrator and also a clock frequency to reset the integration cycle. In other words, it is meant to define the switching period of the buck converter. The integrated voltage, Vint, monitors Vx which gives an indication of the output load current and its corresponding voltage level. The integrated voltage, Vint, can be derived as:
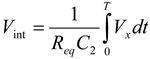Preprints 92208 i001 (1)
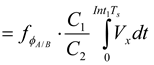Preprints 92208 i002 (2)
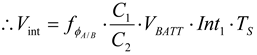Preprints 92208 i003 (3)
where Vint is the integrated voltage and also the output of the SC integrator. f ∅ A / B   is the frequency of the switches in the SC integrator and C 1 C 2 is the ratio of the capacitor which gives the gain of the amplifier. V B A T T   refers to the input voltage of the DC-DC buck converter. I n t 1   and Ts refer to the integration and switching period of the converter respectively.
With reference to equation (3), it is evident that the ratios of capacitors are a constant under any circumstances such as heavy or light load. The remaining parameters, except V B A T T , are variables which will change according to the DC load power drawn by the output of the converter. Specifically, at light load condition, the above mentioned 4-bit signal (S0, S1, S2 and S3) will activate the proposed TFCS. This will alter the switching frequency of the DC-DC converter and the corresponding switches in the SC integrator. Hence, the switching losses of the buck converter will be significantly reduced at low current load condition. This will improve the power efficiency for the load range (<50mW) where the smartphone is idling.

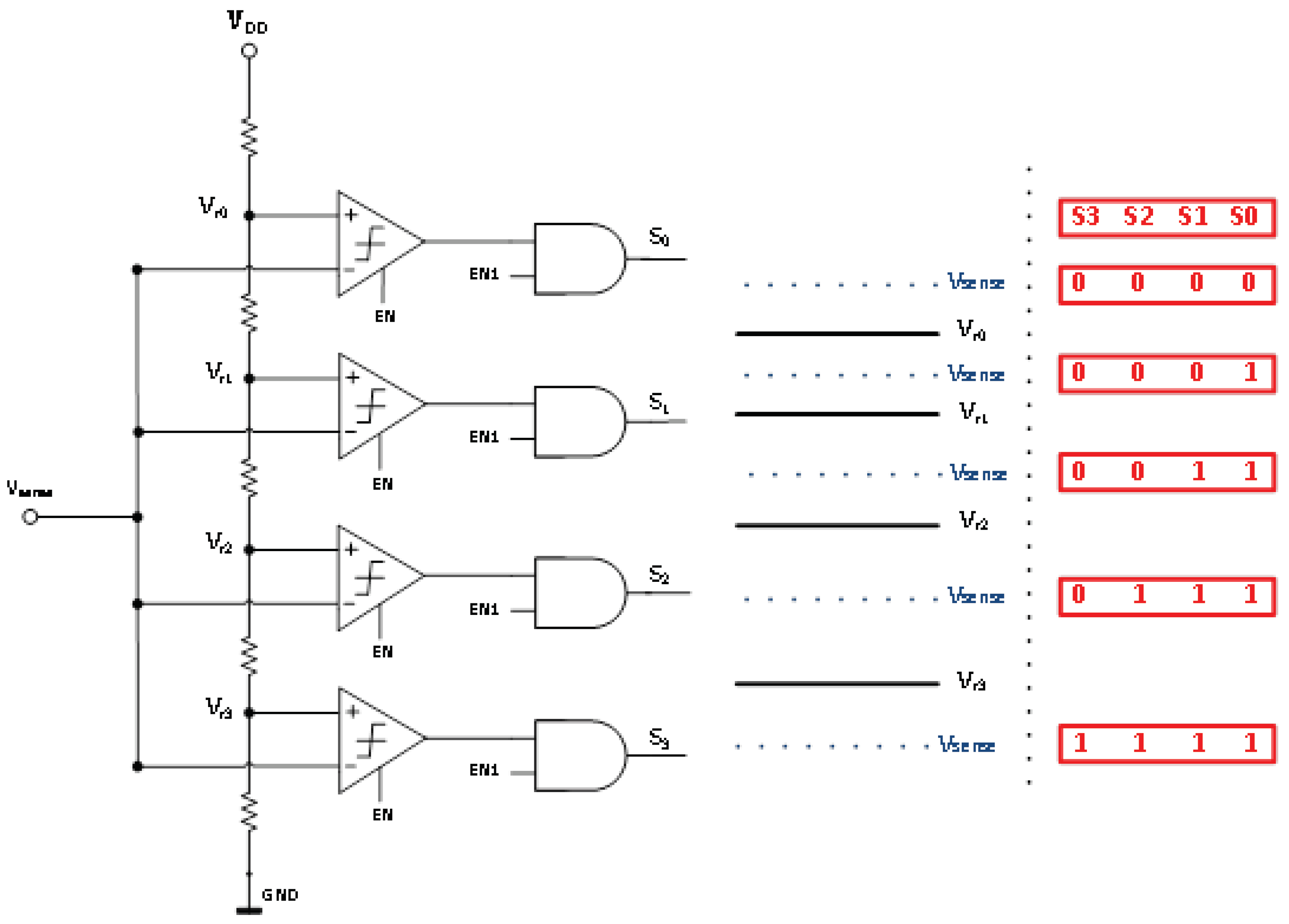
1.1. Proposed Accurate Load Current Sensing (ALCS) Block

The proposed ALCS, shown in Figure 3, is an extension and improvement to prior work [17]. A more in-depth analysis with regard to prior work of current sensing techniques will be presented in the Appendix. It is used to sense the load current and gives an output sense voltage, Vsense via the sensing resistor, Rsense. This voltage level is proportional to the load current level. Transistors MP1-MP4 and MN1-MN3 form a current conveyor structure where negative feedback is employed which forces the node voltage V1 to be equal to V2 at a balanced state equilibrium. If the node V2 increases, the drain voltage of MP3/gate voltage of MP1 will increase since transistor MN1 will force the mirrored current going through MN3 to be the same. This action allows a larger net current going through MP2, which gets mirrored over to MP3. Hence, the gate voltage of MP3 decreases which pulls node voltage V3 down. This constitutes a negative feedback and forces V2 to be equal to V1. At the same time, the cascode pair MP5 and MP6 is included to increase the output impedance of the current mirror formed by MP7 and MP8. This will ensure a more accurate mirroring of current, behaving more like an ideal current source. Thus, transistors MN6-MN7 are stacked on top of MN4-MN5 to form a diode-connected configuration. This is at the expense of MN4-MN5 being biased in the linear triode region, with a larger value of transistor length.
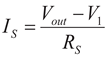Preprints 92208 i004 (4)
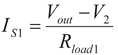Preprints 92208 i005 (5)
Assume V1 to be equal to V2:
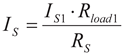Preprints 92208 i006 (6)
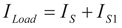Preprints 92208 i007 (7)
Substitute equation (6) into (7),
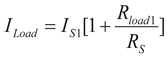Preprints 92208 i008 (8)
The output voltage, Vout, can be derived as:
Preprints 92208 i009 (9)
If the ratio of the resistance Rload1/RS << 1, equation (8) becomes:
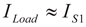Preprints 92208 i010 (10)
At the same time, equation (9) is simplified as:
Preprints 92208 i011 (11)
whereby Rload, total = Rload1 + Rload2.
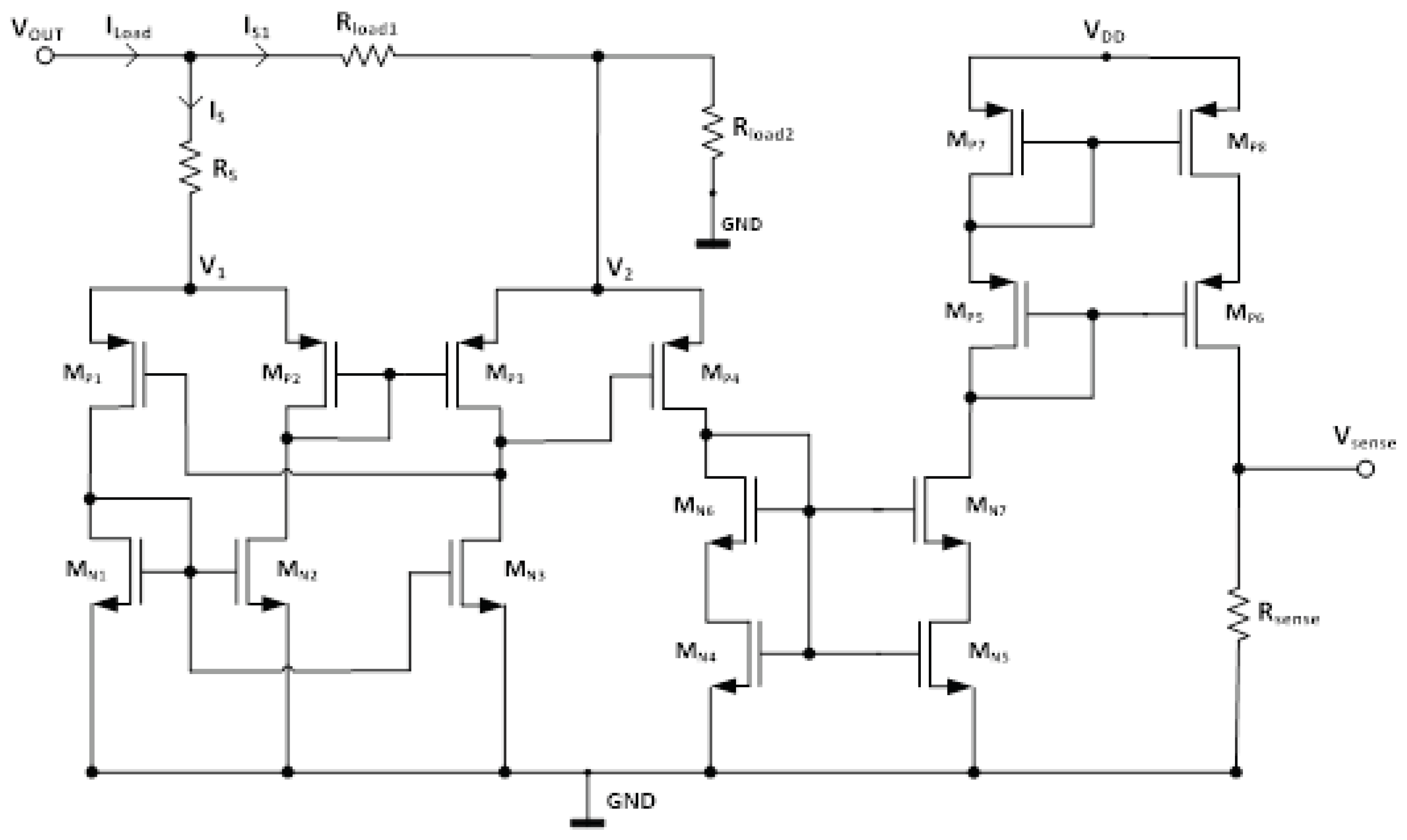
Preprints 92208 g003
Figure 3. Accurate Load Current Sensing (ALCS) Block.
Figure 3. Accurate Load Current Sensing (ALCS) Block.
Preprints 92208 g003
The above derivation proves that the two passive resistors Rload1 and Rload2 contribute to the total load resistance without excessive power dissipation which will degrade the power efficiency of the overall DC-DC buck converter. Furthermore, the current, Is, going through Rs is negligible, having minimal impact on the overall power efficiency. Hence, the sense voltage, Vsense can be derived to be:
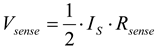Preprints 92208 i012 (12)
Substitute equation (6) into (12),
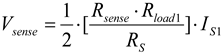Preprints 92208 i013 (13)
If the ratio of the resistance Rload1/RS = N 1 ,
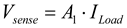Preprints 92208 i014 (14)
where Preprints 92208 i024 is a constant.
The above derivation of sense voltage, Vsense can be used to provide a voltage that is proportional to the load current. The power dissipation across the passive sensing resistor, Rsense is negligible as the current, Is, going through it is minimal. However, this sensing technique may have some drawbacks.
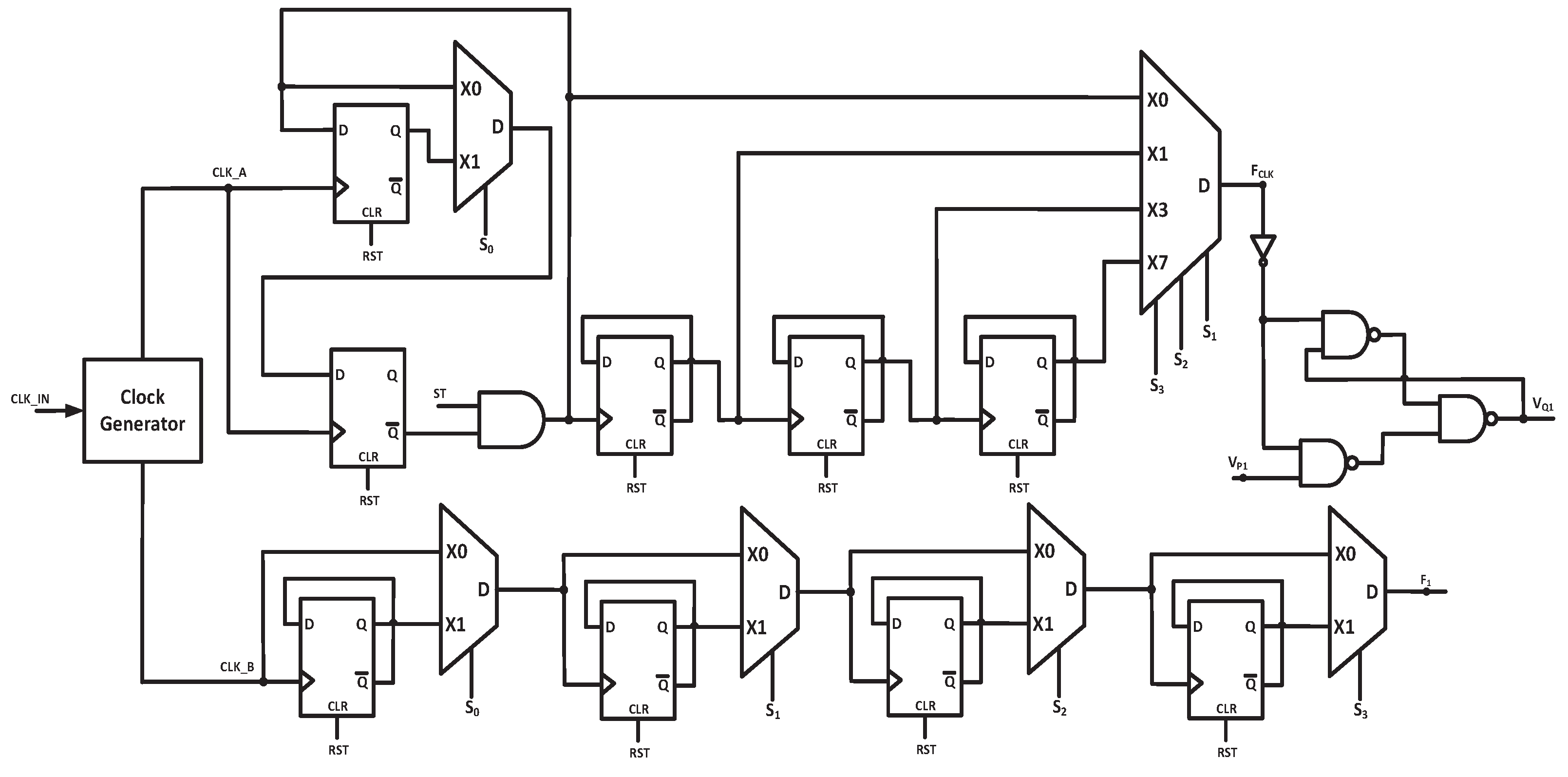
The above derivation and working operation assumes that the output voltage, Vout, is a constant value. But, in fact, there are some AC ripples riding on it. This is caused by the product of the inductor current ripple and the ESR of the output filtering capacitor. Thus, to ensure a more accurate load current sensing capability, the inductor value is made relatively larger to reduce the ripples riding on the output voltage. Furthermore, trimming techniques are employed for the resistor, Rsense as its value may differ by ±20% after the process of die fabrication. Therefore, careful consideration has to be taken into account when designing the next block as the resistor’s value due to process, voltage supply and temperature (PVT) variation should never exceed the 1-bit resolution of the ADC stage.
1.2. 4-Bit Thermometer Code ADC
The 4-Bit thermometer code ADC, shown in Figure 4, is employed to compare the sense voltage, Vsense, with 4 voltage levels (Vr0, Vr1, Vr2 and Vr3) to generate a 4-bit thermometer code signal (S0, S1, S2 and S3). This gives vital information about the current load level. There are basically 4 different levels (0001, 0011, 0111 and 1111) which correspond to 4 different light load conditions. The resolution of the load current level can be improved at the expense of increasing the no. of comparators in the ADC which will increase conduction and switching losses that may degrade power efficiency. Hence, there exist a tradeoff between better resolution and power efficiency.

1.3. Proposed Twin Frequency Control Scheme (TFCS)

The proposed TFCS, shown in Figure 5, is used to progressively alter the switching frequency of the buck controller and the integration cycle according to the load current which is embedded in the 4-bit signal level (S0, S1, S2 and S3). There are only 4 possible signal levels (0001, 0011, 0111 and 1111) which corresponds to 4 different load current level at light, idle condition of a smartphone (<40mA). As mentioned, the resolution of the load current level can be improved further but at the expense of increased power consumption. Hence, there exists an optimum value for the no. of levels of load current associated with the signal generated by the thermometer code ADC.

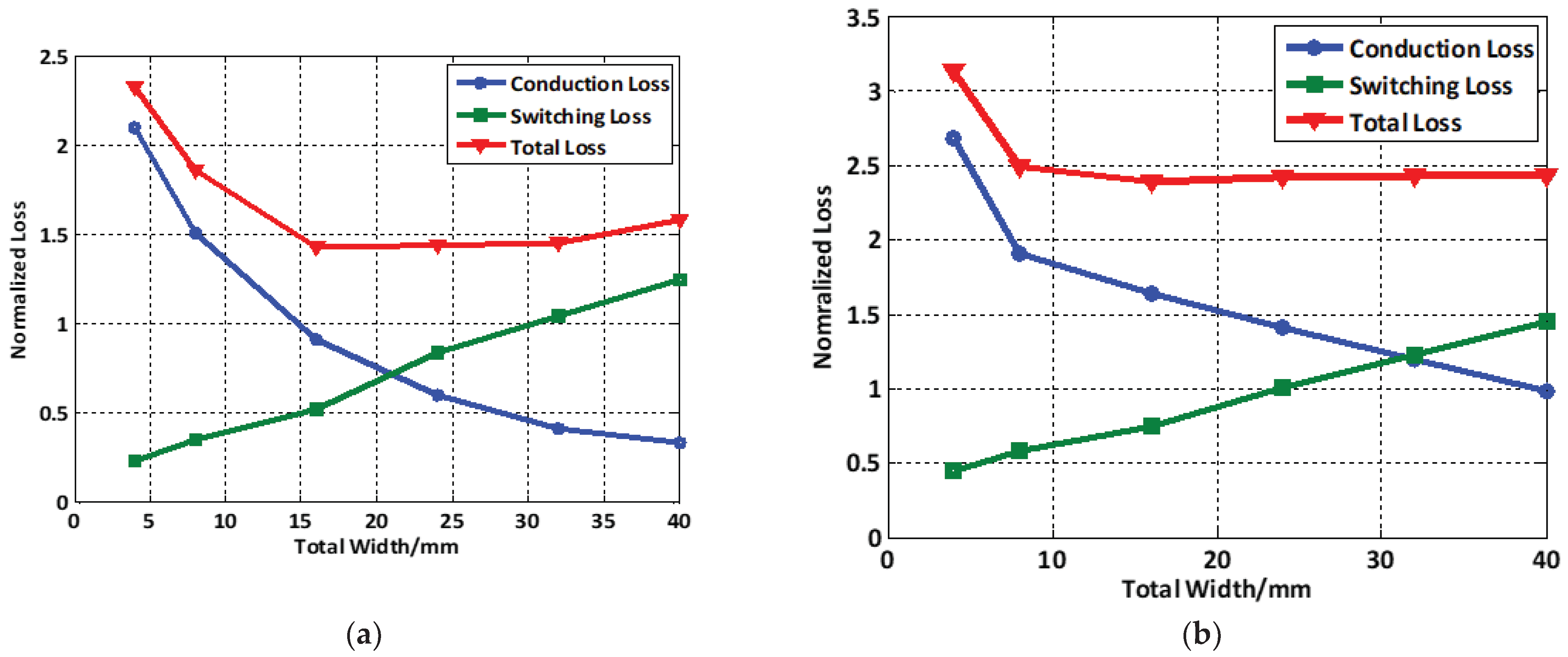
1.4. Power Train

The power train consists of one PMOS (MP) and NMOS (MN) device, as shown in Figure 2. Both are 3.3V transistors which have a thicker gate oxide and occupy a much larger area than a regular transistor. Considering the power NMOS transistor MN, the total power loss comprises of the sum of the switching and conduction loss as follow:
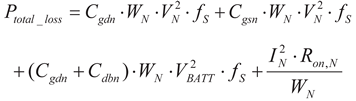Preprints 92208 i015 (15)
whereby Cgdn, Cgsn, Cdbn refers to the respective parasitic capacitance per unit width of the device, VBATT is the input voltage to the buck converter, fs refers to the switching frequency of the power train, Ron,N/WN is the on-resistance per unit width, IN refers to its RMS current and VN is the gate voltage of the power NMOS transistor. Thus, the optimum width, Wopt,N, can be calculated when the switching loss is equal to the conduction loss, given by:
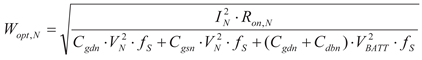Preprints 92208 i016 (16)
The optimized width for both the power NMOS and PMOS is shown in Figure 6 where the graph of the switching loss intersects the conduction loss. The graph plot is based on the highest load current of 40mA and at a switching frequency of 1MHz. The aspect ratio and the on-resistance of the power transistors are shown in Table 1. In addition, the on-resistance and input parasitic capacitance required to calculate the conduction and switching loss respectively, is the sum of simulation results and a theoretical calculation of the resistance/capacitance of metal routing/contact/via and the silicon area occupied by the layout of the power train. Since the optimized width has been finalized, it is now vital to find the best layout structure of the power train for our research application.
The efficiency of the power train is vital and depends largely on the layout structure which is a compromise between the total gate charge (Qg) and the on-resistance (Ron) of the power transistors [18]. This is because the area (W•L) of the power transistor is proportional to the total gate capacitance but inversely proportional to the on-resistance of the power transistor. Recent research [19] proves that power transistors, which do not take into account of the resistance and parasitic capacitance of metal routing, will have an error variation of more than 50% in the calculation of Qg and Ron. This is because the impact of the parasitic capacitance and resistance from layers of metal interconnection is extremely dependent upon the layout style of the power transistors and the positioning of its external source/drain connections. At the same time, the Ron is greatly affected by the distributed parasitic resistance associated with metal interconnects to the source and drain terminals. There are many past research efforts [20,21,22] aim at improving and optimizing the layout of power transistor to minimize parasitic resistance and capacitance.
Traditionally, power transistors are designed with multi-finger layout structure to maximize the channel width per unit area which will increase the current handling capability. On the other hand, regular waffle layout structure was introduced [21] to further optimize the width per area ratio by having four neighboring transistors, enclosing a centralized localized one. However, the above-mentioned layout structure does not yield the best optimum tradeoff between total gate capacitance (Qg) and the on-resistance (Ron). Thus, in recent research work, there is an interesting proposal for a hybrid waffle layout structure [23,24] which proves that it can best optimize tradeoff between area, total gate charge and on-resistance.
However, in this research work, the above-mentioned hybrid waffle layout may not be suitable as this buck converter is not operating at extremely high frequency (>100MHz). Hence, our proposed layout is a tapered/matrix structure, as shown in Figure 7, as it can provide a more uniform distribution of DC current among the fingers of the transistor. In addition, the fingers of the power transistor are designed in a diagonal way which will reduce the on-resistance and equalize the flow of current on opposite side of the device. Furthermore, the no. of fingers and multipliers for each power transistor are optimized, shown in Table. I, so as to balance the trade-off between total gate charge and parasitic interconnection resistance. One of the drawbacks is that there is a "hotspot" at the corner, furthest away from the centre of the power train. During measurement testing, this "hotspot" may increase the on-resistance of the power transistor, leading to an increase in the heat dissipation and ultimately degrading the power efficiency. Therefore, the die package must be thermally enhanced to avoid overheating of the silicon die chip or create other reliability issues. However, for our work, it focuses on a smartphone idling state (low load power) hence the above mentioned drawback may not be significant.

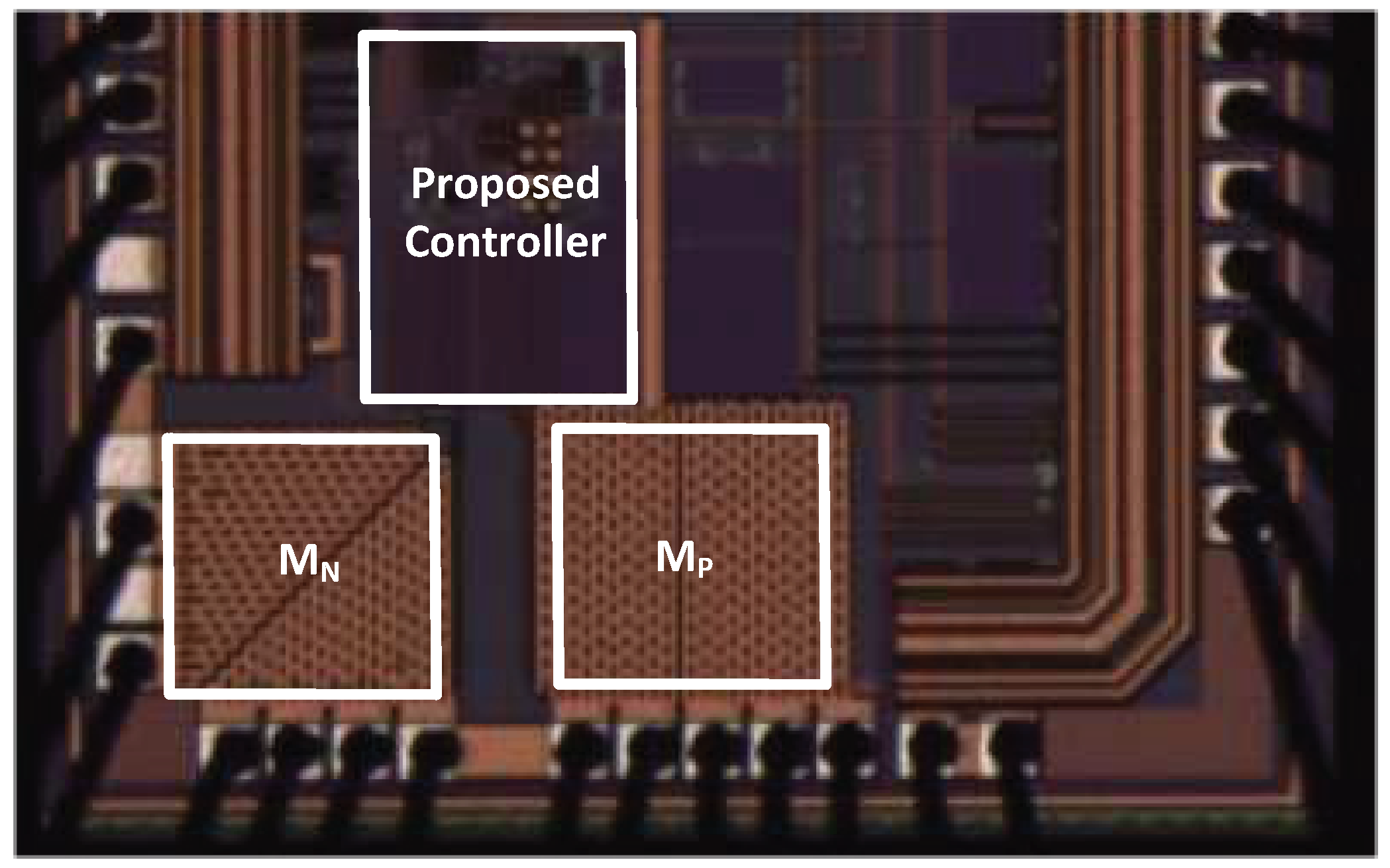
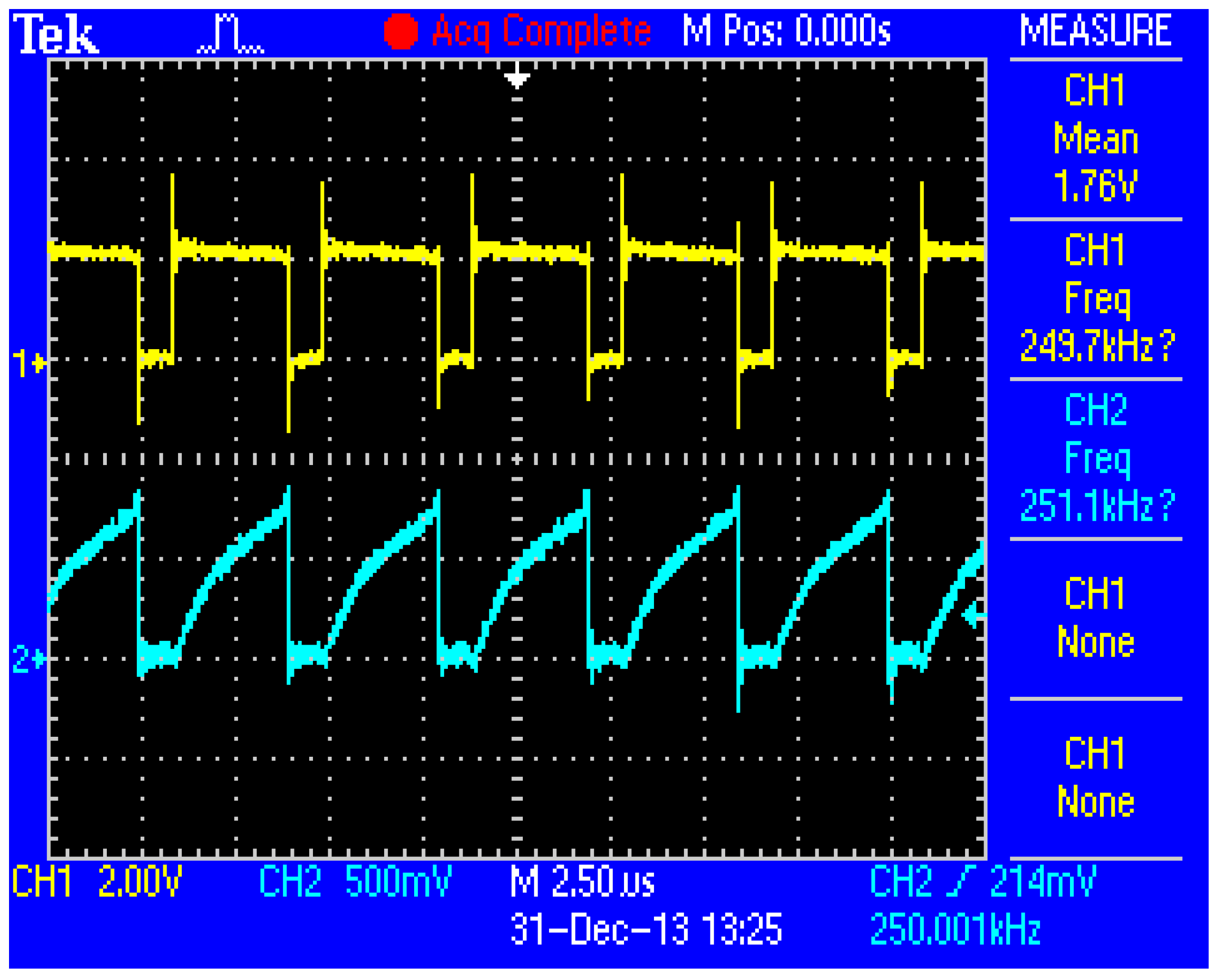
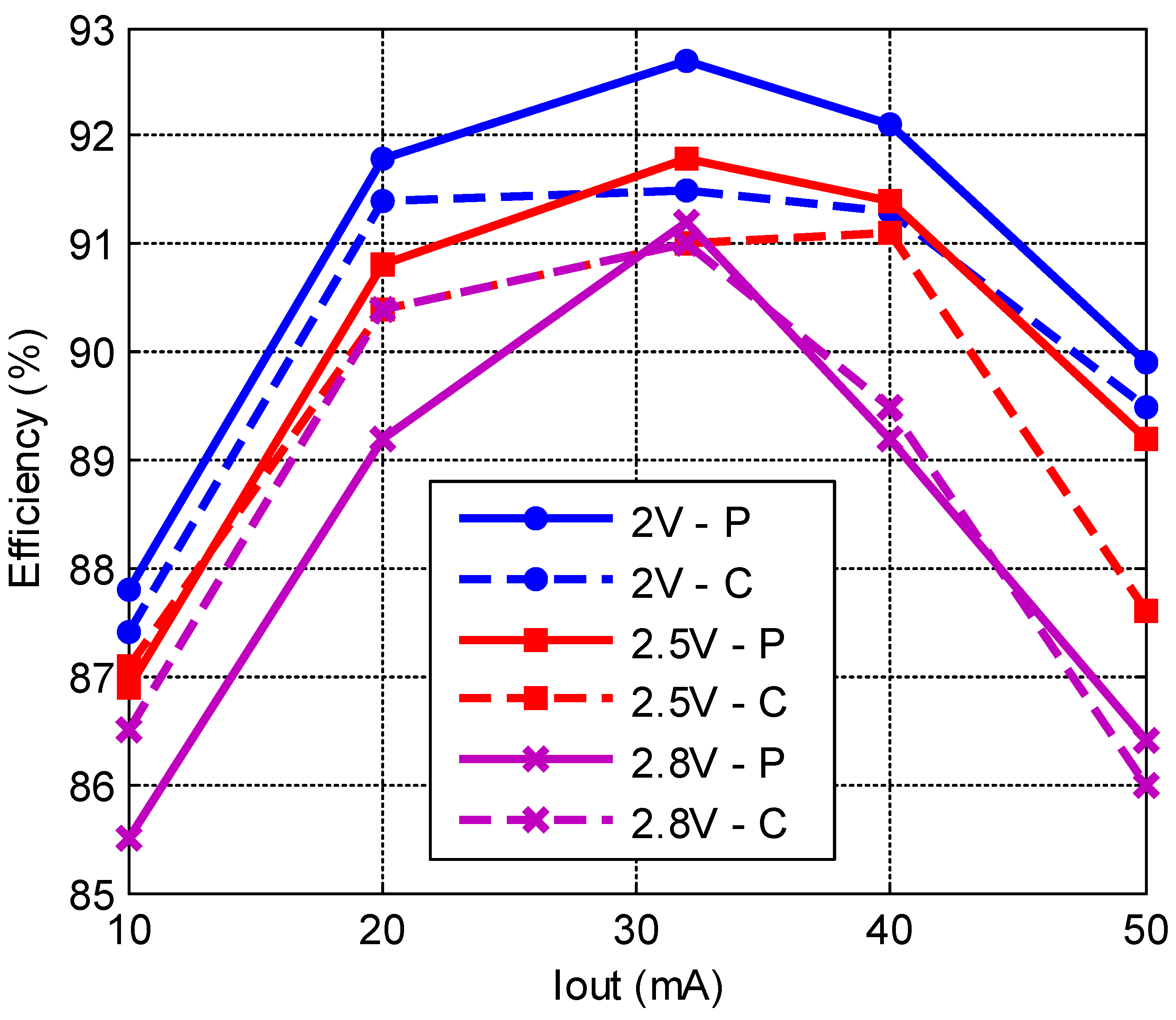
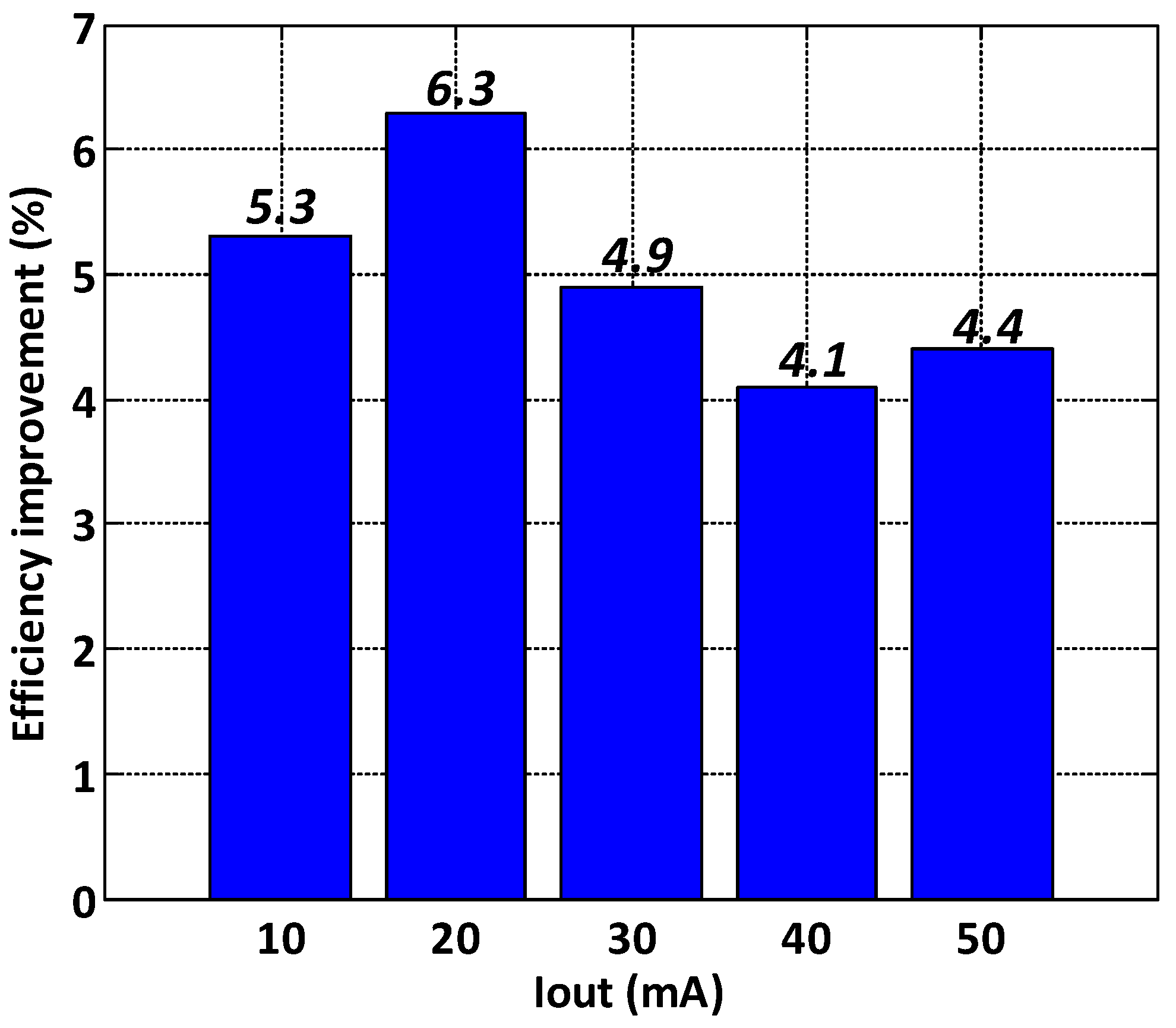
3. Experimental Results

A buck DC-DC converter with the proposed TFCS and ALCS has been implemented with 0.18µm 1P6M CMOS technology with an area of 1.3mm2. The micrograph of the chip is shown in Figure 7. The 2~3V input and 1.25V output buck converter utilizes an off-chip SMD 47µH inductor (Coilcraft Shielded 1812PS Series) with a DCR of <1.0Ω and a self-resonant frequency (SRF) of 17MHz. A relatively larger value of inductor value is selected to reduce the inductor ripple to <50% of the maximum load current. Furthermore, an output off-chip SMD ceramic 10µF filtering capacitor (AVX Hi-Cap MLCC) with an estimated ESR of ~0.5Ω. The capacitor type is chosen to be SMD ceramic capacitor since it is the most inexpensive as compared to tantalum or aluminum electrolytic. However, the trade-off comes with the relative larger value of ESR which will lead to a larger peak to peak ripple riding on the output voltage of the buck converter. Thus, a relatively larger value of inductor and capacitor is chosen so as to mitigate the ripple problem. Furthermore, this helps to yield a more accurate sensing of the load current as previously mentioned. Do take note that the choice for the type of capacitor does vary, depending on the application specification. A prototype of the buck converter with the TFCS and ALCS chip is also presented in Figure 8. It can be observed that our proposed work uses DIP package with 48 Leads. During testing, this is held tightly by the adjustable socket shown in Figure 8.
The performance evaluation is carried out in three general steps: 1) Performance of our proposed TFCS and ALCS at light loading conditions, 2) Comparison of the power efficiency between our proposed work and the conventional PWM/PFM controller and 3) Design specification and performance comparison are summarized in Table I. The proposed TFCS and ALCS allow the frequency to be reduced at different low load conditions. It achieves a peak efficiency of 92.7%, operating at 250kHz with VBATT = 2V, VOUT = 1.25V and ILOAD = 30mA, as shown in Figure 9. The top waveform is the voltage Vx while the bottom one shows the integrated voltage Vint. This proves that our proposed TFCS and ALCS buck converter is stable and achieved high efficiency at low load condition. However, taking a closer observation at the Vx waveform, there is a significant interval whereby there are body diode conduction losses which degrades the power efficiency. This is because our proposed buck converter uses a fixed deadtime controller. One of our current and future works has therefore included a novel deadtime controller. Furthermore, from Figure 9, it is evident that our proposed controller does not enter DCM operation at light load. The rationale is that for DCM operation, the node VX will oscillate when both the power transistors are idling. This is due to the existence of the LC tank formed by the inductor and the parasitic capacitance at that node. Thus, this will incur additional power losses. Recent research efforts have included another free-wheeling switch [9,25,26] to dampen the sub-harmonic oscillation. However, this will incur additional silicon area as the aspect ratio of the additional switch is comparable to the size of a power transistor. Furthermore, it adds complexity to the circuit design as another control signal has to be included to determine the turning on/off of this free-wheeling switch. Therefore, our proposed work uses a relatively larger inductor value to reduce the ripple at the output voltage of the buck converter while operating in CCM mode. This will allow the proposed ALCS to work ideally as any undesirable voltage ripple will cause inaccuracies in the sense voltage, Vsense. This can be considered a minimal trade-off for our proposed TFCS and ALCS buck converter as compared to other research literature.
Figure 10 shows the power efficiency between our proposed TFCS and ALCS converter and a conventional PWM/PFM controller at varying load conditions. A peak efficiency of about 92.7% can be achieved when our proposed buck converter is operating at 250kHz with 2.0V input voltage and 30mA load current. It can be observed that the efficiency degrades when the input voltage is higher. This is because the buck converter has to dissipate more energy to step it down to the same output voltage.
The efficiency improvement graph, shown in Figure 11, compares our proposed work with the latest state of the art work [25]. This shows that our improvement in power efficiency ranges from 4~6% across 10~50mA of load current. Our proposed specification and performance are summarized in Table I. It clearly shows that the proposed TFCS and ALCS technique yields an improvement in power efficiency (4~6%) as compared to some of the latest state of the art research work [25,27,28]. However, one drawback is the fact that the external inductor and capacitor are relatively larger in our proposed work so as to achieve a smaller peak to peak output voltage ripple for a more accurate sensing of the load current.
One area of improvement is to use the MOSFET segmentation technique as proposed in [29] which can help to further improve the power conversion efficiency. At the same time, our proposed work is not optimized for deadtime control; hence there is an ongoing current research into designing a deadtime controller to minimize body diode conduction loss which will improve efficiency. This ongoing work into deadtime control is continuity to this proposed work. In addition, the simulation results for the power efficiency of our proposed work is about 2~3% better than our testing results. The rationale for this margin is due to the power loss in the resistance of the Au (Gold) wire bonding, DIP package leads and the resistance in the traces of the PCB board. Careful consideration, recommended by [30], have been taken into account when designing the PCB board so that important power/ground lines have as short but as wide a trace as possible to minimize unnecessary power losses. Overall, our proposed TFCS and ALCS indeed yield an efficiency improvement over some of the latest research works though having a relatively larger external inductor and filtering capacitor.

4. Conclusions

A buck DC-DC converter with the proposed TFCS and ALCS has been designed and implemented with 0.18µm 1P6M CMOS technology, occupying an area of 1.3mm2. It yields a peak efficiency of about 92.7% when the buck converter is operating at 250kHz with 2.0V input voltage, 1.25V output voltage with a load current of 30mA. The proposed buck converter is implemented and dedicated for smartphone application whereby it spends most of its time in idle, low load conditions.

Acknowledgments

Our team would like to appreciate our deepest gratitude to Global Foundries and Singapore Economic Development Board (EDB) for supporting our research work.

6. Appendix

Sensing the inductor current in a buck converter is an important function of the DC-DC controller. Its current-sensing circuit should be easy to implement without increasing the form factor. Furthermore, the current sensor have to be fast for high switching frequency DC-DC converter in order to reduce the inductor size. The past research works yield many interesting current sensing techniques. One of them is to sense the on-resistance of the power transistor directly [31] but the drawback lies in the fact that the resistance value may change significantly by ± 30% due to PVT variation during the fabrication of the die. Hence, this technique is unreliable. Another work [32] instead proposed a novel self-learning technique to sense the instantaneous induct current via the parasitic resistance (DCR) of the inductor. One of the benefits include minimal power losses and thus applicable to varying loading conditions. In addition, it completely eliminates unnecessary losses by not introducing any additional passive components in the power line. However, it requires a very complex circuit implementation which occupies a large silicon area overhead.
At the same time, the more widely used approach is based on the sensing of the current [33,34,35] that passes through the power transistor. It employs the use of matched current mirrors and high gain amplifier to mirror a fraction of the current going through the respective power transistor to the sensing transistor. However, one of its disadvantage is that its accuracy is poor as it depends heavily on the matching performance of the current mirror in the ohmic region. Furthermore, channel-length modulation and process mismatch will induce an error of >15% [36]. On the other hand, there is a proposed use of an current offset cancellation technique [37] to further improve the accuracy of current sensing. However, one of its minor drawback is the relatively larger quiescent current required to provide the driving capability which leads to a degradation of power efficiency. Hence, it suffers an imminent trade-off between speed and accuracy. Some other techniques employ the advantage of the availability of bipolar transistor in BiCMOS process [38] to enhance the accuracy of its current sensing capability. This, however, proves to be too costly to implement.
There is also a filter approach which senses current in a continuous mode [39] by applying a inductor voltage across a tuned low-pass filter and sensing the filter current. One of its advantages is that it has minimal switching noise but its inherent accuracy is highly dependent on the DCR of the inductor and the tuning accuracy of the filter which may lead to a variation of >   ± 20%.
However, in our proposed TFCS and ALCS DC-DC buck converter, it employs a very accurate ALCS circuit which is an extension and improvement to the prior work [17]. It is able to achieve high accuracy of current sensing at the tradeoff of a slightly higher quiescent power consumption and a larger inductor value so as to minimize the output voltage ripple which will lead to inaccuracies in the sensing voltage, Vsense.

References

  1. W. J. Lee, Y. Z. Wang, D. H. Shin, N. H. Chang, and M. Pedram, "Power conversion efficiency characterization and optimization for smartphones," in Int. Symp. on Low Power Electronics and Design, 2012, pp. 103–108.
  2. A. Carrol and G. Heiser, "An Analysis of Power Consumption in a Smartphone," Proc. of the USENIX Annual Technical Conference, pp. 271–284, June 2010.
  3. Y. Huh, "Future direction of power management in mobile devices," in Proc. IEEE Asian Solid State Circuits Conf. (ASSCC), 2011, pp. 1–4.
  4. H. Kim, "Trends of R&D on Lithium Secondary Batteries for Electricial Vehicles," Smart Battery/Cell Forum, June 2011, Seoul, Korea.
  5. M. Dong and L. Zhong, "Self-constructive high-rate system energy modeling for battery-powered mobile systems," in 9th Int. Conf. on Mobile Systems, 2011, pp. 335–348.
  6. Z. Lide, B. Tiwana, R. P. Dick, Q. Zhiyun, Z. M. Mao, W. Zhaoguang, and Y. Lei, "Accurate online power estimation and automatic battery behavior based power model generation for smartphones," in IEEE Int. Conference on Hardware/Software Codesign and System Synthesis, 2010, pp. 105–14.
  7. D. Ma and R. Bondade, "Enabling Power-Efficient DVFS Operations on Silicon," IEEE Circuits Syst. Mag., vol. 10, pp. 14–30, 2010. [CrossRef]
  8. S. Chester, "Characteristics of Rechargeable Batteries," Texas Instruments Appl. Rep. no. "SNVA533", 2011.
  9. B. Sahu and G. A. Rincon-Mora, "A high-efficiency, dual-mode, dynamic, buck-boost power supply IC for portable applications," in 18th Int. Conf. on VLSI Design, 2005, pp. 858–861.
  10. T. Instruments. Handset: Smartphone [Online]. Available: http://www.ti.com/solution/handset_smartphone.
  11. B. Sahu and G. A. Rincon-Mora, "An Accurate, Low-Voltage, CMOS Switching Power Supply With Adaptive On-Time Pulse-Frequency Modulation (PFM) Control," IEEE Trans. Circuits Syst. I, vol. 54, pp. 312–321, 2007. [CrossRef]
  12. M. D. Mulligan, B. Broach, and T. H. Lee, "A constant-frequency method for improving light-load efficiency in synchronous buck converters," IEEE Trans. Power Electron Lett., vol. 3, pp. 24–29, 2005. [CrossRef]
  13. H. Lee and S.-R. Ryu, "An Efficiency-Enhanced DCM Buck Regulator With Improved Switching Timing of Power Transistors," IEEE Trans. Circuits Syst. II, Exp. Briefs, vol. 57, pp. 238–242, Mar. 2010. [CrossRef]
  14. Z. C. Sun and L. Siek, "A novel ripple controlled modulation for high efficiency DC-DC converters," in 13th Int. Symp. on Integrated Circuits (ISIC), 2011, pp. 238–241.
  15. S. Musunuri and P. L. Chapman, "Improvement of light-load efficiency using width-switching scheme for CMOS transistors," IEEE Trans. Power Electron Lett., vol. 3, pp. 105–110, 2005. [CrossRef]
  16. H.-W. Huang, K.-H. Chen, and S.-Y. Kuo, "Dithering Skip Modulation, Width and Dead Time Controllers in Highly Efficient DC-DC Converters for System-On-Chip Applications," IEEE J. Solid-State Circuits, vol. 42, pp. 2451–2465, 2007. [CrossRef]
  17. Y. H. Lam, W. H. Ki, C. Y. Tsui, and D. Ma, "Integrated 0.9 V charge-control switching converter with self-biased current sensor," in IEEE Int'l Midwest Symp. on Ckts. & Sys., pp. 305–308, Jul. 2004.
  18. A. J. Stratakos, S. R. Sanders, and R. W. Brodersen, "A low-voltage CMOS DC-DC converter for a portable battery-operated system," in Proc. IEEE Power Electron. Specialist Conf., Jun. 1994, pp. 619–626.
  19. Y. Katayama, M. Edo, T. Denta, T. Kawashima, and T. Ninomiya, "Optimum design method of CMOS IC for DC-DC converter that integrates power stage MOSFETs," in Proc. IEEE Power Electron. Specialist Conf., 2004, pp. 4486–4491.
  20. Y. Chen, Y. Fu, X. Cheng, T. X. Wu, and Z. J. Shen, "Modeling and Analysis of Metal Interconnect Resistance of Power IC's," in Proc. IEEE Int. Symp. Power Semiconductor Devices and IC's, 2007, pp. 253–256.
  21. L. Baker, R. Currences, S. Law, M. Le, C. Lee, S. T. Lin, and M. Teene, "A `waffle' layout technique strengthens the ESD hardness of the NMOS output transistor," in Proc. Symp. on Electrical Overstress/Electrostatic Discharge, 1989, pp. 175–81.
  22. A. V. d. Bosch, M. S. J. Steyaert, and W. Sansen, "A high density matched hexagonal transistor structure in standard CMOS technology for high speed applications," in Proc. IEEE Int. Conf. Microelectronic Test Structures, 1999, pp. 212–215.
  23. A. Yoo, M. Chang, O. Trescases, and W. T. Ng, "High Performance Low-Voltage Power MOSFETs with Hybrid Waffle Layout Structure in a 0.25µm Standard CMOS Process," in Proc. IEEE Int. Symp. Power Semiconductor Devices and IC's, 2008, pp. 95–98.
  24. A. Yoo, "Design, Implementation, Modeling, and Optimization of Next Generation Low-Voltage Power MOSFETs," Ph.D. dissertation, Department of Materials Science and Engineering, University of Toronto, Canada, 2010.
  25. Z. C. Sun, K. W. R. Chew, H. Tang, and L. Siek, "Adaptive Gate Switching Control for Discontinuous Conduction Mode DC-DC Converter," IEEE Trans. Power Electron., vol. 29, no. 3, pp. 1311–1320, March 2014. [CrossRef]
  26. T.-H. Kong, Y.-J. Woo, S.-W. Wang, S.-W. Hong, and G.-H. Cho, "Zero-order control of boost DC-DC converter with transient enhancement using residual current " in IEEE ISSCC Dig. Tech. Papers, 2011, pp. 390–392.
  27. T. Y. Man, P. K. T. Mok, and M. J. Chan, "A 0.9-V Input Discontinuous-Conduction-Mode Boost Converter With CMOS-Control Rectifier," IEEE J. Solid-State Circuits, vol. 43, no. 9, pp. 2036–2046, Sept. 2008. [CrossRef]
  28. W. Yan, W. Li, and R. Liu, "A Noise-Shaped Buck DC-DC Converter With Improved Light-Load Efficiency and Fast Transient Response," IEEE Trans. Power Electron., vol. 26, no. 12, pp. 3908–3924, Dec. 2011. [CrossRef]
  29. O. Trescases, G. Wei, A. Prodic, and W. T. Ng, "Predictive Efficiency Optimization for DC-DC Converters With Highly Dynamic Digital Loads," IEEE Trans. Power Electron., vol. 23, pp. 1859–1869, Jul. 2008. [CrossRef]
  30. K. Wong, "Parasitics can Hinder Switching Regulator and LDO Designs," Texas Instruments Appl. Rep. no. "SNVA689", May. 2013.
  31. T. A. Smith, S. Dimitrijev, and H. B. Harrison, "Controlling a DC-DC converter by using the power MOSFET as a voltage controlled resistor," IEEE Trans. Circuits and Syst. I, vol. 47, no. 3, pp. 357–362, Mar. 2000. [CrossRef]
  32. H. P. Forghani-Zadeh and G. A. Rincon-Mora, "An Accurate, Continuous, and Lossless Self-Learning CMOS Current-Sensing Scheme for Inductor-Based DC-DC Converters," IEEE J. Solid-State Circuits, vol. 42, no. 3, pp. 665–679, Mar. 2007. [CrossRef]
  33. C. Y. Leung, P. K. T. Mok, K. N. Leung, and M. Chan, "An integrated CMOS current-sensing circuit for low-Voltage current-mode buck regulator," IEEE Trans. Circuits Syst. II, vol. 52, no. 7, pp. 394–397, Jul. 2005. [CrossRef]
  34. C. Y. Leung, P. K. T. Mok, and K. N. Leung, "A 1-V integrated current-mode boost converter in standard 3.3/5-V CMOS technologies," IEEE J. Solid-State Circuits, vol. 40, no. 11, pp. 2265–2274, Nov. 2005. [CrossRef]
  35. C. F. Lee and P. K. T. Mok, "A monolithic current-mode CMOS DC-DC converter with on-chip current-sensing technique," IEEE J. Solid-State Circuits, vol. 39, no. 1, pp. 3–14, Jan. 2004. [CrossRef]
  36. P. Drennan and C. McAndrew, "Understanding MOSFET mismatch for analog design," IEEE J. Solid-State Circuits, vol. 38, no. 3, pp. 450–456, Mar. 2003. [CrossRef]
  37. H. Y. H. Lam, W. H. Ki, and D. Ma, "Loop gain analysis and development of high-speed high-accuracy current sensors for switching converters," in Proc. IEEE Int. Symp. Circuits and Syst. May 2004, pp. 828–831.
  38. M. Corsi, "Current sensing schemes for use in BiCMOS integrated circuits," in Proc. IEEE Bipolar/BiCMOS Circuits and Technology Meeting, Oct. 1995, pp. 55–57.
  39. E. Dallago, M. Passoni, and G. Sassone, "Lossless current sensing in low-voltage high-current DC/DC modular supplies," IEEE Trans. Ind. Electron. vol. 47, pp. 1249–1252, Dec 2000. [CrossRef]
Preprints 92208 g001
Figure 1. A Vital Part of the 3G/4G Smartphone Power Management Unit (PMU).
Figure 1. A Vital Part of the 3G/4G Smartphone Power Management Unit (PMU).
Preprints 92208 g001
Preprints 92208 g002
Figure 2. Proposed Twin Frequency Control DC-DC Buck Converter Using Accurate Load Current Sensing Technique.
Figure 2. Proposed Twin Frequency Control DC-DC Buck Converter Using Accurate Load Current Sensing Technique.
Preprints 92208 g002
Preprints 92208 g004
Figure 4. 4-Bit Thermometer Code ADC.
Figure 4. 4-Bit Thermometer Code ADC.
Preprints 92208 g004
Preprints 92208 g005
Figure 5. Proposed Twin Frequency Control Scheme (TFCS).
Figure 5. Proposed Twin Frequency Control Scheme (TFCS).
Preprints 92208 g005
Preprints 92208 g006
Figure 6. Optimized sizing of: (a) NMOS power transistor; (b) PMOS power transistor.
Figure 6. Optimized sizing of: (a) NMOS power transistor; (b) PMOS power transistor.
Preprints 92208 g006
Preprints 92208 g007
Figure 7. Die Photo of the buck converter with proposed TFCS and ALCS.
Figure 7. Die Photo of the buck converter with proposed TFCS and ALCS.
Preprints 92208 g007
Preprints 92208 g008
Figure 8. Prototype of a buck converter with proposed TFCS and ALCS.
Figure 8. Prototype of a buck converter with proposed TFCS and ALCS.
Preprints 92208 g008
Preprints 92208 g009
Figure 9. Peak Efficiency Achieved - Waveform of VX and VINT (VBATT = 2V, VOUT = 1.25V, Freq = 250kHz and ILOAD = 30mA).
Figure 9. Peak Efficiency Achieved - Waveform of VX and VINT (VBATT = 2V, VOUT = 1.25V, Freq = 250kHz and ILOAD = 30mA).
Preprints 92208 g009
Preprints 92208 g010
Figure 10. Power Efficiency of the proposed TFCS and ALCS buck converter & the conventional PWM/PFM controller at different loading conditions (P - Proposed Work, C - Conventional Work).
Figure 10. Power Efficiency of the proposed TFCS and ALCS buck converter & the conventional PWM/PFM controller at different loading conditions (P - Proposed Work, C - Conventional Work).
Preprints 92208 g010
Preprints 92208 g011
Figure 11. Efficiency improvement of the proposed TFCS and ALCS buck converter as compared to the latest state of the art work [25].
Figure 11. Efficiency improvement of the proposed TFCS and ALCS buck converter as compared to the latest state of the art work [25].
Preprints 92208 g011
Table 1. Performance Summary and Comparison.
Table 1. Performance Summary and Comparison.
Units JSSC [27] TPEL [28] TPEL [25] This Work
Year - 2008 2011 2013 2013
Technology µm 0.35 0.35 0.18 0.18
Input Voltage V 0.9~1.2 2.7~4.2 0.9~1.4 2.0~3.0
Output Voltage V 2.5 0.9 2.5 1.25
Peak Efficiency @ Load Current % 87@80mA 89@55mA 88@40mA 92.7@30mA
External Inductor µH 1.0 2.2 1.0 47.0
External Capacitor µF 4.7 4.7 10.0 10.0
Frequency kHz 670 200 800 250
Chip Silicon Area mm2 3.0 1.4 1.5 1.3
Power Transistors Implemented in this work:
Size Units MN         21168 µ m 0.35 µ m MP 35672 µ m 0.30 µ m
Finger Width µm 19.6 - 19.6 -
No. of. Finger - 60 - 91 -
Multiplier - 18 - 20 -
Channel Resistance mΩ Ron,n 80 Ron,p 95
Bonding Wire Resistance1 mΩ Rbond,n 200 Rbond,p 200
Total resistance2 mΩ Roverall,n 280 Roverall,p 295
Total Gate Capacitance3 pF Cgn 477.8 Cgp 574.3
1Wire Bonding performed by A*STAR IME - Au(Gold) Wire (1 mil diameter & 650mA/cm)
2Impedance and inductance for a bonding wire per unit cm is 1Ω and 10nH respectively
3Post Layout Extraction, including bond pads (Performed by Calibre)
Other Remarks: Process has 6 metal layers (EMI: M1-M5 -> 1mA/µm, M6 -> 5.34mA/µm at 30°C)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated