Educational Status as a Mediator of Intergenerational Social Mobility in Europe: A Positional Analysis Approach

Preprint

Article

Educational Status as a Mediator of Intergenerational Social Mobility in Europe: A Positional Analysis Approach

Altmetrics

Downloads

146

Views

106

Comments

A peer-reviewed article of this preprint also exists.

Glykeria Stamatopoulou,

Eva Tsouparopoulou

Maria Symeonaki^*

Glykeria Stamatopoulou,

Eva Tsouparopoulou

Maria Symeonaki^*

This version is not peer-reviewed

Submitted:

04 December 2023

Posted:

04 December 2023

You are already at the latest version

Alerts

Abstract

This paper investigates the transmission of educational attainment from parents to offsprings as a mediator of intergenerational class mobility in Europe. The study covers the last two decades with data drawn from a cross-national large scale sample survey, namely the European Social Survey (ESS), for the years 2002 - 2018. Interest has focused on the question of persistence of inequality of educational opportunities by examining attainment of nominal levels of education and the association between the educational attainment of the parent with the highest level of education and their descendants. The study covers also new trends in social mobility which consider education as a ‘positional good’ and a novel method of incorporating educational expansion into the transition probabilities is proposed, providing answers to whether the rising accessibility of educational qualifications attenuates the association between social origin and educational attainment. Therefore, the concept of positionality is taken into account in the estimation of intergenerational transition probabilities and to complement the analysis mobility measures are provided for both methods, nominal and positional. The proposed positional method is validated through a correlation analysis between the upward mobility scores (nominal and positional) with the Education Expansion Index (EEI) for the respective years. The upward mobility scores estimated via the positional method are higher correlated with the EEI for all years indicating a better alignment with the broader trends in educational participation and achievement.

Keywords:

Subject: Social Sciences - Sociology

1. Introduction

Intergenerational mobility encapsulates the societal transitions spanning generations and diverse socio-economic strata. It delineates individuals' progressions and achievements in comparison to their family's social, occupational, educational, and economic heritage, serving as a gauge for evaluating social justice and equal opportunities. Education stands as a pivotal factor in measuring social mobility, key in curbing the perpetuation of disparities through generations and acting as a mediator between socio-economic classes. Literature has substantiated the prominence of education in understanding and quantifying intergenerational mobility. Education is considered a significant factor due to its enduring impact on subsequent generations, in contrast to income or occupation, which can be more transient. Moreover, education's consistent data collection in various studies enables a more comprehensive analysis of intergenerational mobility. The association of education with concepts of social justice and equal opportunity further amplifies its significance in societal structures. Notably, numerous studies, such as those by Breen and Goldthorpe [1] and Blanden et al. [2], examine the persistent influence of education across generations and its role in shaping social mobility. These studies emphasise the importance of education in understanding and measuring intergenerational mobility. Moreover, Blanden et al. [2], draw attention to the relationship between education and social mobility, highlighting the enduring impact of educational opportunities on upward mobility, while Corak [3] explores intergenerational mobility from a multidimensional perspective, acknowledging the significance of education among other factors. Cunha and Heckman [4] examine the intergenerational transmission of both cognitive and noncognitive skills, illustrating how education acts as a channel for their transfer across generations. Blanden and Machin [5] investigate the relationship between education and intergenerational mobility, discussing the role of education in either facilitating or impeding social mobility. Moreover, Symeonaki and Stamatopoulou [6], Symeonaki et al. [7], Stamatopoulou et al. [8], Stamatopoulou and Symeonaki [9] estimate intergenerational educational mobility across European countries, allowing for a comparative study of discrepancies among countries in social mobility, leveraging diverse large-scale European databases, while Symeonaki and Tsinaslanidou [10] studied intergenerational educational mobility across countries of different welfare regimes.

In most studies concerning intergenerational educational mobility, the focal point has long been on the relationship between individuals' social backgrounds and their educational achievements, estimating intergenerational educational mobility in absolute terms, i.e., measuring education with the same nominal categories across all cohorts (e.g., using the International Standard Classification of Education (ISCED) levels and distinguishing categories of low (ISCED levels 0-2), medium (ISCED levels 3-4), and high (ISCED levels 5-8) for both parents and offsprings), with subsequent results implying that the effects of social origins on educational attainment have declined in several countries [9,11,12]. However, as Goldthorpe [13] suggests, it can be questioned how far the finding of a weakening effect of social origins, based on the nominal categories of educational qualification, does indeed indicate a reduction in class inequalities in education. He suggests that when education is valued as a positional good, people try to surpass their peers in the competition over the highest relative education. The term positionality refers to the idea that the value of educational credentials is attributable, in part, to their relative scarcity in the population. The term derives from the concept of positional good which was coined by Hirsch [14]. The fiercer the competition for educational success, the more likely it is to be affected by the resources that are available to the affluent and educated social strata. Therefore, inequality between strata in educational attainment may remain intact when education is viewed as a positional good, even if inequality of educational opportunity might have declined in nominal terms. In short, the question of whether education is a positional (relative) or nominal (absolute) good has important implications for temporal trends in inequality of educational opportunity. Recent studies have examined intergenerational educational mobility considering education as a positional good capturing the effect of educational expansion. Rotman et al. [15] present evidence suggesting divergent conclusions in Israel regarding trends in educational stratification between relative and absolute measures. Analysis of nominal education and years of schooling suggests consistent or decreased educational inequality, while positional measures show an increase in educational disparity. Fujihara and Ishida's [16] research in Japan reveals differing trends in educational inequality based on whether education is measured in relative or absolute terms. Using absolute measures, they note a reduced disparity between respondents with fathers of different educational levels. However, with relative measures, they observe a widening gap between respondents from distinct paternal education backgrounds. Both studies consider position in the educational distribution or economic returns for their assessments. Triventi et al. [17] present a consistent trend of declining educational inequality in Italy, irrespective of the measurement—absolute or relative—used for education. Unlike studies in Britain, Israel, and Japan, their findings indicate a consistent decrease in educational disparity over time. While their measures of relative education differ from the other studies, the overarching theme of assessing education in relative terms sparks inquiry into the differing trends among these countries. Moreover, Di Stasio et al. [18] analyse education as a positional good, contrasting country contexts to identify where education holds positional value. They find that strong vocational systems relate to lower overeducation instances, suggesting reduced positional value in these settings. Their study categorises countries based on overeducation and its returns, connecting these groupings to various models of the education-occupation relationship.

The present study aims to investigate both nominal (absolute) and relative (positional) patterns of intergenerational educational mobility in Europe by analysing transitions across the educational levels of respondents and their parents in Europe using raw data drawn from the European Social Survey (ESS) from the year 2002 and onwards. The objective is to reveal challenges faced by particular social strata in progressing upward within the educational framework using and comparing both nominal and positional methods. To our knowledge this is the first attempt to incorporate positionality in the estimation process of the transition probabilities. To validate the proposed methodology for measuring mobility we compare the correlations of upward probability measures both nominal and positional with the Educational Expansion Index (EEI) used in Araki [19]. Correlation coefficients are examined, and the positional approach is identified as superior, as it consistently exhibits higher correlations for all years.

The paper is outlined as follows. Section 2 reveals all the necessary information concerning the proposed methodology and the ESS data that are utilised in order to estimate intergenerational educational mobility in absolute and relative terms. Section 3 presents the measurement results of intergenerational educational mobility, nominal and positional, and the validation tests performed. Section 4 gives the conclusions of the study and provides the reader with the discussion concerning the comparison of absolute and positional intergenerational mobility and aspects of future work.

2. Materials and Methods

In the present analysis, data is drawn from the European Social Survey (ESS), a survey spanning over 40 countries since 2002, designed to track European public attitudes and values, and furnish European social and attitudinal indicators. The present study measures nominal and positional intergenerational educational mobility in Europe, making use of 5 rounds of ESS spanning a period of over 16 years (i.e., ESS1, ESS3, ESS5, ESS7, ESS9). To ensure comparability, the work specifically includes European countries that have participated in all rounds of the ESS, i.e., Belgium, Finland, France, Germany, Hungary, Ireland, the Netherlands, Norway, Poland, Portugal, Spain, Sweden, Switzerland, Slovenia, and the UK. Due to the different data collection methods used in ESS10 (face-to-face interviews, self-completion questionnaire), the variable of parental education was not measured, consequently the most recent trends of mobility are not included in this analysis. The study also aims to provide aggregated measures for these European countries.

Table 1 presents the socio-demographic characteristics of the respondents per round. The realized samples sizes and basic socio-demographic characteristics of the samples are presented in Table 1. As shown, most of the respondents for all the under-investigation countries were women, with mean age from 41.90 (Ireland, ESS1) to 49.14 (Portugal, ESS7) years, at least 39.03% (Ireland, ESS5) to 61.36% (Sweden, ESS3) were in paid job, while the respective percentage for participants in education, as main activity the last seven days, range from 7.46% (United Kingdom, ESS1) to 15.33% (Slovenia, ESS1).

Within the ESS, cross-national educational attainment variables for both parents and individuals have been generated from country specific variables in order to be standardised and to align with the latest International Standard Classification of Education (ISCED11). ¹ To facilitate the analysis, educational attainment was transformed into three educational categories using the transformation utilised by EUROSTAT, i.e. ISCED levels 0-2 = Low, ISCED levels 3-4 = Medium and ISCED levels 5-8 = High. For parents, the maximum educational level is taken into consideration for the analysis, assuming that the highest educational level between parents will positively affect children's educational attainments. Because of the lack of the harmonised variable for highest level of education for specific counties in the datasets of ESS1 and ESS7, we do not display results for Norway (2002) and for Hungary (2014). Table 2 outlines the ISCED levels and the categorisation.

Data weighting was performed using analysis weight (anweight). This specific weight is suitable for all types of analysis as it corrects for differential selection probabilities within each country as specified by sample design, for nonresponse, for noncoverage, and for sampling error related to the four post-stratification variables and takes into account differences in population size across countries².

Using raw data drawn from the ESS we first measure intergenerational educational mobility in absolute terms, using the same educational levels both for parents and offsprings. We define parental education as the educational level of either the father or the mother, based on the higher educational attainment between them. Mobility measures are estimated, namely upward and downward mobility indices, immobility index [20,21] and Prais-Shorrocks index [22,23].³

Shifting from an absolute to a relative perspective in the evaluation of educational attainment presents a notable challenge since “there is no obvious ‘one best way’ of producing a relative measure” [24]. We aim to incorporate positionality into the measurement of transition probabilities following the subsequent methodology.

The proposed method is comparable to that implemented by Triventi et al. [17] for calculating the cumulative advantage associated with each educational level. To understand how positionality has influenced educational attainment we estimate the proportions of individuals at all educational levels using EUROSTAT’s data available for the last two decades and the classification described in Table 2. A logarithmic transformation of the proportions is equal to the Educational Competitive Advantage Score (ECAS) used in Triventi et. al [17] which “attributes to each educational level a measure of its competitive advantage on the basis of how many individuals attained at least that qualification in a given year”. Rather than employing the actual ECAS, we opt for using the proportions of individuals in various educational levels as weights, denoted by

w_{1}

w_{2}

and

w_{3}

, to maintain the stochastic properties of the transition probability matrices. Thus, the proportion of individuals having low, medium, and high education at the time of the survey is treated as a set of weights reflecting the relative prevalence or importance of each educational category in the population. The transition probabilities are then calculated by considering not only the likelihood of moving from one educational level to another but also by incorporating the prevalence of individuals in each category as a weight. The weights act as a scaling factor, influencing the contribution of each educational category to the overall transition probabilities and serve as weights assigned to each (absolute) transition probability based on the factor of competitive advantage. Thus, we apply proportional scaling to adjust the transition probabilities based on the proportions, using the following equation to estimate the positional transition probabilities

p_{i j} (t)

{p p}_{i j} (t) = \frac{w_{j} (t) p_{i j} (t)}{\sum_{j} w_{j} (t) p_{i j} (t)}

(1)

The applied weights stem from the proportional representation of individuals within various educational tiers across distinct time frames. These adjustments accommodate the transition probabilities, ensuring alignment with the evolving educational landscape over recent years. Through these weights, the impact of current educational distributions on projected transitions is highlighted, preserving the overall structure of transition probabilities. Accounting for these educational distribution shifts can substantially refine the precision of the analysis, enabling a more accurate and a positional representation of intergenerational educational mobility.

To substantiate the proposed methodology, the upward mobility scores were subjected to correlation analysis with the Education Expansion Index (EEI) for the corresponding years, as computed using EUROSTAT’s data. The Educational Expansion Index is defined as the percentage of individuals aged between 15 to 64 that possess tertiary degrees [19] and serves as a metric encompassing the comprehensive expansion of educational attainment across a population, offering insights into alterations in educational participation and achievement. Examining the correlation between the upward mobility scores, calculated using both absolute and relational approaches, and the Educational Expansion Index (EEI) facilitates an evaluation of the extent to which the proposed measure aligns with the broader shifts in educational participation and achievement over the specified timeframe. The anticipation is that the two upward mobility scores, nominal and positional, will exhibit a strong correlation. The preferred methodology would be the one generating a higher correlation coefficient between the upward mobility scores and the Education Expansion Index (EEI) for the respective years.

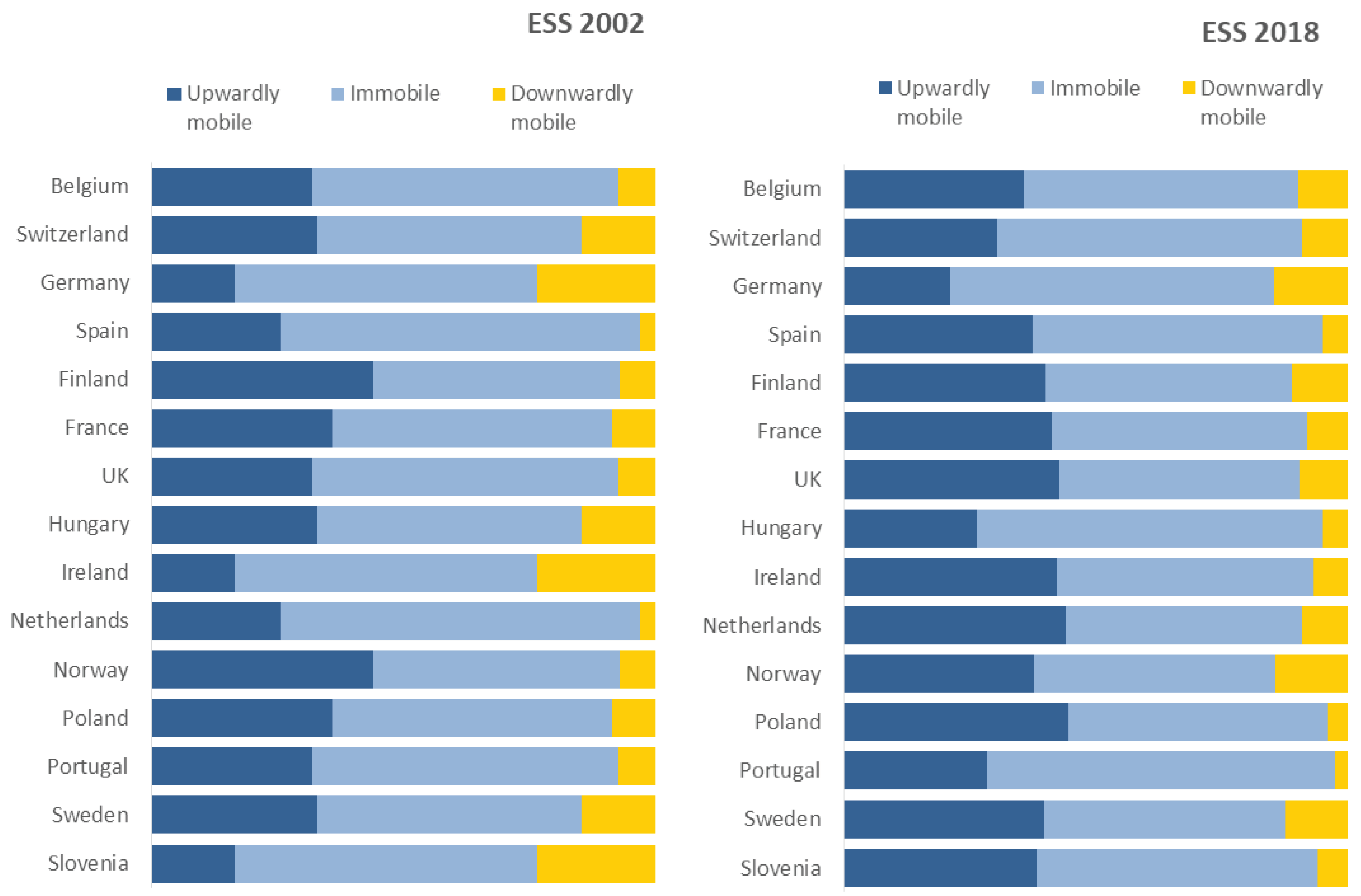
3. Results

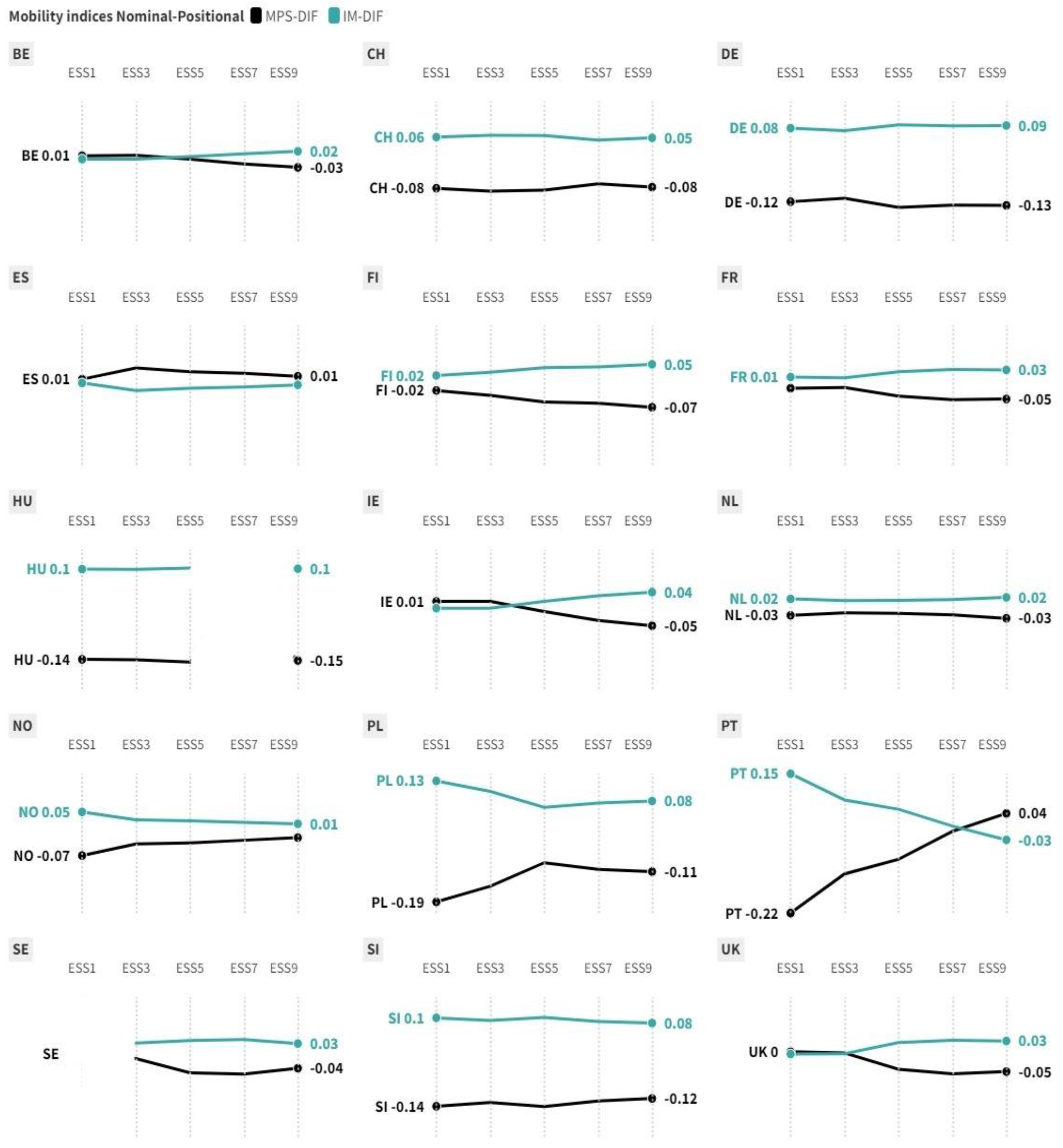
3.1. Nominal/absolute transition probabilities

In this section we estimate the transition probability matrices to portray the shifts between educational categories for both parent and respondent, encapsulating the movement between the same educational stages. Each element

p_{i j} (t)

\forall i, j = 1,2, 3

of the matrix

P (t)

describes the probability of an individual to move from state

i

(educational level of origin according to the highest level of education between mother and father) to state

j

(the respondent’s educational level) at time t. The elements found off the main diagonal of matrix

P (t)

give the total movements of individuals, while

p_{i i} (t)

\forall i = 1,2, 3

denotes the probabilities of individuals, being totally immobile (see also [6,7,25,26]).

Table A.1 in the Appendix presents the nominal transition probability matrices for all countries and ESS rounds, as well as the respective mobility indices. From the results, it is obvious that individuals from low educated background tend to gain better education than their parents, although they have considerably fewer chances to complete tertiary education compared to those originated from medium or highly educated origins. Indeed, the access to tertiary education seems unequal between people from different educational background in the majority of the sample, as parents’ educational profile seems to matter in all countries. However, it is notable that the upward movements predominate over the downward mobility, while the immobility rates decrease over time.

Figure 1 provides a more comprehensive overview of the transitions between educational categories, illustrating the percentages of individuals moving upward, downward, or remaining in the same educational category as their parents across all surveyed countries from 2002 to 2018. The figure reveals variations in educational flows across countries, with Finland and Belgium displaying a steady trend of upward movement through ESS. Besides, a noticeable increase in percentages of upwardly mobile individuals over time is detected in the majority of the countries, and especially in Ireland and Slovenia, where the values of the upward mobility index have risen sharply from 2002 to 2018. Some exceptions also exist, such as Switzerland and Hungary, where a decrease in the overall mobility is recorded from 2002 to 2018.

The values of both the Prais-Shorrocks and immobility indices validate the observed trend from 2002 to 2018 depicted in Figure 2, showing variations between countries and years. In particular, Norway and the Netherlands seem to be steadily the most mobile in the sample, while Hungary, Portugal and Switzerland show higher values of immobility, even though a notable decrease is indicated from 2002 to 2018.

3.2. Education as a ‘positional good’: Estimating positional transition probabilities

In order to estimate the positional transition probabilities, the respective weights were estimated. Figure 3 depicts the proportions of individuals belonging to the three educational levels based on the data provided by EUROSTAT with the use of the EU-Labour Force Survey (EU-LFS). The depicted trend in the proportions highlights intriguing shifts in educational categories over this period (2002-2018). The proportions of low educated individuals (ISCED 0-2), display a steady fall which suggests a decline in the prevalence of lower educational levels over time and a diminishing number of individuals with lower educational qualifications. On the contrary, the proportions of medium educated individuals (ISCED 3-4) exhibit relatively modest changes, suggesting stability rather than cumulative advantages. Meanwhile, the rising trend in the proportions of highly educated individuals (ISCED 5-8) implies a diminishing competitive advantage associated with higher educational levels and a rather decreasing prominence or influence of higher educational qualifications over the observed period.

Since transition probability matrices need to maintain their stochastic property, we opted for the incorporation of proportions in the weighting scheme adhering to this principle. Using Equation (1), the respective weights presented in Figure 3 and the nominal transition probability matrices (Table A.1), the positional transition probability matrices

P (t) = [p_{i j} (t)], \forall i, j = 1,2, 3

were estimated for the participating countries and years. Based on these positional transition probabilities, the upward and downward mobility indices are reconstructed and calculated in order to be compared with the nominal results. The rest of the mobility indices are estimated as aforementioned [20,21,22,23]. The respective matrices are exhibited in Table A.1 in the Appendix. In general, from the results it is evident that concerning the transition probabilities the relative measure of mobility is more robust than the absolute counterpart. In particular, for the majority of the countries,

p_{12}

takes higher values in the positional matrices compared to the nominal ones, and

p_{11}

seems to be overrated in the nominal results. Thus, shifting from a nominal to a relative perspective, people with low educational background appear to have greater chances of moving upwards and attaining medium level of education. However, a reversed pattern is detected in Spain and Portugal. Likewise, the observed mobility appears to overestimate the chances of people from high educated background attaining tertiary education, since transition probabilities

p_{33}

are considerably lower after applying the weights. A noticeable example of this trend is the case of Hungary, where

p_{33}

falls from 0.569 to 0.292 (ESS3) after the adjustment. However, Belgium and Ireland show no significant differences between nominal and positional transition matrices.

Figure A1 presents the differences in upward mobility indices before and after the adjustment. As shown, in all countries (except Germany) this difference between nominal and positional results takes positive values, which indicates that the nominal measure seems to exaggerate the upward movements compared to each relative measure. Between the countries, the Netherlands and France show greater differences when nominal and positional upward rates are compared, while the results for Switzerland, Norway and UK show no significant variations between the rates. On the other hand, smaller differences are observed for the case of Prais–Shorrocks and Immobility indices, in the comparison of nominal and positional mobility (Figure A2). This trend might be attributed to the fact that both

M_{P S}

and

I M

have been constructed based on the chances of people moving upwards or downwards in the social space and not on the actual flows, and for that reason it better reflects the relative mobility. However, Poland, Hungary and Slovenia seem to be exceptions to this trend, as the difference in

M_{P S}

takes significant higher values for these countries. Also, an interesting trend is detected for Portugal, where the difference in mobility rates has been reduced over time, reaching convergence, probably because of the changes that occurred in the participation of Portuguese in the different levels of education through the years 2002-2018 (as shown also in Figure 3).

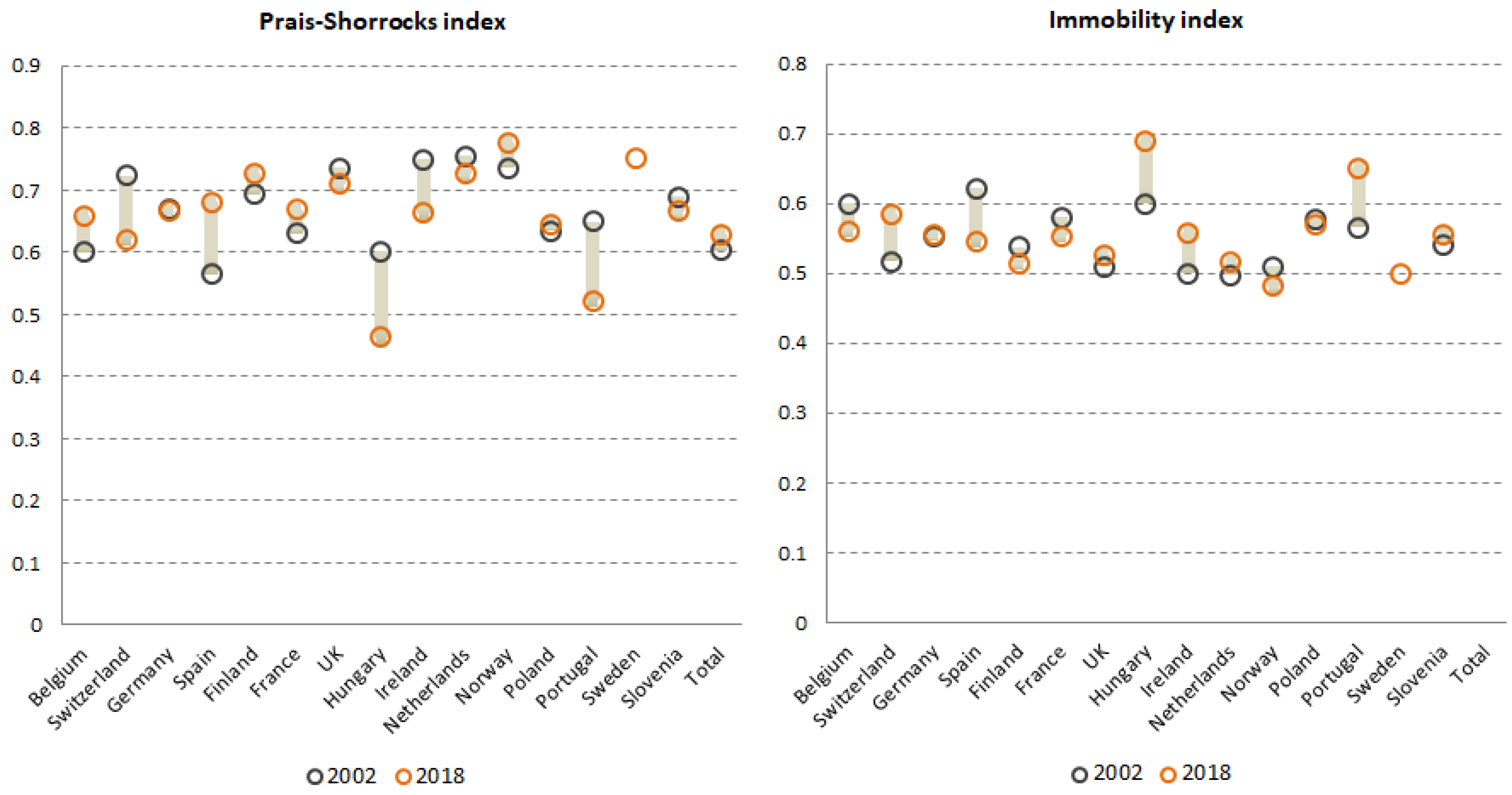
3.3. Validation

To validate the proposed methodology, the upward mobility scores underwent correlation analysis with the Education Expansion Index (EEI) calculated using EUROSTAT’s data for the corresponding years. Evaluating the correlation between the upward mobility scores, computed through both nominal and positional approaches, and the Educational Expansion Index (EEI) enables an assessment of the alignment of the proposed measure with broader shifts in educational participation and achievement over the specified period. Table 3 presents the Pearson’s correlation coefficient between nominal and positional upward mobility and Table 4 the respective correlations amongst nominal and positional upward mobility and EEI for the respective year. The two upward mobility indices exhibit a strong correlation as anticipated. Notably, positional upward mobility demonstrates a higher correlation with EEI, indicating a better alignment with the broader trends in educational participation and achievement.

4. Discussion

The present section interprets the presented results and provides insights into the patterns of intergenerational educational mobility, considering both nominal and positional perspectives. The aim was to examine the relationship between parental and individuals’ educational outcome in relative terms, in order to better understand the influence of education across generations. In this context, the proposed methodology is based on the concept of positionality, where the educational expansion and the rising accessibility of educational qualifications are taken into account. It is assumed that this novel additional element in the measurement of mobility would produce a more reliable picture of the educational inequalities. In order to explore this hypothesis, raw data are drawn from the European Social Survey for the 15 participated in all rounds of the survey countries to capture trends in educational transitions from 2002 to 2018.

The analysis of nominal transition probability matrices reveals distinct tendencies in educational mobility across European countries. More specifically, individuals from lower-educated backgrounds show a propensity to attain higher education than their parents, although access to tertiary education appears unequal. As upward mobility surpasses downward movements, a decline in immobility rates over time suggests a notable enhancement in educational opportunities. This trend signifies a propensity for individuals to progressively distance themselves from their parents' educational level. Notable exceptions, such as Switzerland and Hungary, exhibit a decrease in overall mobility. The examination of specific countries, including Finland and Belgium, underscores diverse trends in upward mobility.

The novel approach of incorporating positionality in transition probabilities enhances the understanding of mobility patterns. Weighted positional matrices demonstrate the robustness of relative measures compared to absolute ones. Low-educated individuals exhibit greater upward mobility chances, challenging conventional findings. However, Spain and Portugal deviate from this trend. Discrepancies in the likelihood of highly educated individuals attaining tertiary education emerge after adjustment, exemplified by Hungary's notable shift.

To validate the proposed methodology, correlations between upward mobility indices and the Educational Expansion Index (EEI) were examined. The positional approach exhibits stronger alignment with broader trends in educational participation and achievement, as indicated by higher correlations with EEI for all examined ESS rounds. Differences between nominal and positional measures vary across countries, emphasising the need for a nuanced understanding of mobility patterns.

Apparently, the observed trends hold implications for policymakers and researchers. Acknowledging education as a positional good necessitates tailored policy interventions to address relative mobility. Future research should investigate the subtle dynamics driving educational shifts, considering socio-economic, cultural, and policy-related factors. Furthermore, longitudinal analyses can offer a more profound insight into the changing patterns of mobility, complementing the aforementioned findings with new results deriving from the intermediate ESS rounds (e.g. ESS round 2). The presented findings contribute to the discourse on intergenerational educational mobility, offering valuable insights for policymakers aiming to foster equitable educational opportunities.

Author Contributions

Conceptualization, G.S., E.T. and M.S.; methodology, G.S., E.T. and M.S.; statistical analysis with IBM SPSS v.29, G.S., E.T. and M.S.; validation, G.S., E.T. and M.S.; formal analysis, G.S., E.Τ. and M.S.; investigation, G.S., E.Τ. and M.S.; data curation, G.S., E.Τ. and M.S.; writing—original draft preparation, G.S. and M.S.; writing—review and editing, G.S., E.Τ. and M.S.; visualization, G.S. and E.T. ; supervision, M.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Raw data that support the findings of this study are available from the European Social Survey at https://ess-search.nsd.no/en/study/bdc7c350-1029-4cb3-9d5e-53f668b8fa74.

Acknowledgments

We acknowledge use of raw data from: ESS Round 1: European Social Survey Round 1 Data (2002). Data file edition 6.6. Sikt - Norwegian Agency for Shared Services in Education and Research, Norway – Data Archive and distributor of ESS data for ESS ERIC. https://doi.org/10.21338/NSD-ESS1-2002, ESS Round 3: European Social Survey Round 3 Data (2006). Data file edition 3.7. Sikt - Norwegian Agency for Shared Services in Education and Research, Norway – Data Archive and distributor of ESS data for ESS ERIC. https://doi.org/10.21338/NSD-ESS3-2006, ESS Round 5: European Social Survey Round 5 Data (2010). Data file edition 3.4. Sikt - Norwegian Agency for Shared Services in Education and Research, Norway – Data Archive and distributor of ESS data for ESS ERIC. https://doi.org/10.21338/NSD-ESS5-2010, ESS Round 7: European Social Survey Round 7 Data (2014). Data file edition 2.2. Sikt - Norwegian Agency for Shared Services in Education and Research, Norway – Data Archive and distributor of ESS data for ESS ERIC. https://doi.org/10.21338/NSD-ESS7-2014, European Social Survey European Research Infrastructure (ESS ERIC). (2023), ESS9 - integrated file, edition 3.2 [Data set]. Sikt - Norwegian Agency for Shared Services in Education and Research. https://doi.org/10.21338/ess9e03_2. The study also makes use of the EUROSTAT’s data Population by educational attainment level, sex and age (%) - main indicators: Online data code: edat_lfse_03.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Table A1. Transition probabilities and mobility indices for both nominal and positional mobility, by country and ESS1(2002), ESS3(2006), ESS5(2010), ESS7(2014), ESS9(2015) rounds.

P_(YEAR)	Nominal mobility				Positional mobility				Nominal mobility				Positional mobility				Nominal mobility				Positional mobility
	Transition probabilities				Transition probabilities				Transition probabilities				Transition probabilities				Transition probabilities				Transition probabilities
	$M_{P S}$	$I M$	$U M$	$D M$	$M_{P S}$	$I M$	$U M$	$D M$	$M_{P S}$	$I M$	$U M$	$D M$	$M_{P S}$	$I M$	$U M$	$D M$	$M_{P S}$	$I M$	$U M$	$D M$	$M_{P S}$	$I M$	$U M$	$D M$
	Βelgium				Βelgium				Finland				Finland				France				France
P₍₂₀₀₂₎	$[\begin{matrix} 0.630 & 0.251 & 0.118 \\ 0.176 & 0.462 & 0.361 \\ 0.073 & 0.220 & 0.707 \end{matrix}]$				$[\begin{matrix} 0.687 & 0.234 & 0.079 \\ 0.222 & 0.498 & 0.80 \\ 0105 & 0.270 & 0.625 \end{matrix}]$				$[\begin{matrix} 0.456 & 0.333 & 0.211 \\ 0.125 & 0.531 & 0.344 \\ 0.047 & 0.326 & 0.628 \end{matrix}]$				$[\begin{matrix} 0.404 & 0.427 & 0.168 \\ 0.104 & 0.639 & 0.257 \\ 0.043 & 0.435 & 0.522 \end{matrix}]$				$[\begin{matrix} 0.568 & 0.316 & 0.116 \\ 0.260 & 0.468 & 0.272 \\ 0.095 & 0.202 & 0.703 \end{matrix}]$				$[\begin{matrix} 0.520 & 0.389 & 0.091 \\ 0.231 & 0.560 & 0.209 \\ 0.097 & 0.279 & 0.624 \end{matrix}]$
	0.600	0.599	0.319	0.073	0.595	0.603	0.198	0.199	0.693	0.538	0.439	0.070	0.717	0.522	0.284	0.194	0.630	0.580	0.359	0.085	0.648	0.568	0.230	0.202
P₍₂₀₀₆₎	$[\begin{matrix} 0.562 & 0.300 & 0.138 \\ 0.184 & 0.463 & 0.354 \\ 0.029 & 0.183 & 0.788 \end{matrix}]$				$[\begin{matrix} 0.576 & 0.314 & 0.110 \\ 0.197 & 0.506 & 0.297 \\ 0.035 & 0.224 & 0.741 \end{matrix}]$				$[\begin{matrix} 0.430 & 0.364 & 0.206 \\ 0.107 & 0.533 & 0.360 \\ 0.052 & 0.310 & 0.638 \end{matrix}]$				$[\begin{matrix} 0.336 & 0.486 & 0.178 \\ 0.075 & 0.644 & 0.281 \\ 0.040 & 0.412 & 0.548 \end{matrix}]$				$[\begin{matrix} 0.528 & 0.356 & 0.116 \\ 0.205 & 0.423 & 0.371 \\ 0.070 & 0.231 & 0.700 \end{matrix}]$				$[\begin{matrix} 0.515 & 0.408 & 0.077 \\ 0.215 & 0.519 & 0.266 \\ 0.085 & 0.330 & 0.585 \end{matrix}]$
	0.594	0.604	0.354	0.071	0.588	0.608	0.240	0.152	0.699	0.534	0.435	0.080	0.736	0.509	0.315	0.176	0.675	0.550	0.404	0.077	0.691	0.540	0.251	0.210
P₍₂₀₁₀₎	$[\begin{matrix} 0.554 & 0.300 & 0.146 \\ 0.151 & 0.436 & 0.413 \\ 0.038 & 0.221 & 0.740 \end{matrix}]$				$[\begin{matrix} 0.538 & 0.328 & 0.134 \\ 0.147 & 0.476 & 0.377 \\ 0.039 & 0.253 & 0.708 \end{matrix}]$				$[\begin{matrix} 0.409 & 0.478 & 0.113 \\ 0.118 & 0.614 & 0.268 \\ 0.049 & 0.415 & 0.537 \end{matrix}]$				$[\begin{matrix} 0.279 & 0.618 & 0.103 \\ 0.072 & 0.710 & 0.218 \\ 0.031 & 0.506 & 0.462 \end{matrix}]$				$[\begin{matrix} 0.511 & 0.418 & 0.071 \\ 0.129 & 0.650 & 0.221 \\ 0.032 & 0.314 & 0.654 \end{matrix}]$				$[\begin{matrix} 0.457 & 0.491 & 0.052 \\ 0.111 & 0.733 & 0.156 \\ 0.032 & 0.421 & 0.547 \end{matrix}]$
	0.635	0.577	0.356	0.084	0.639	0.574	0.280	0.146	0.720	0.520	0.415	0.092	0.775	0.483	0.313	0.203	0.593	0.605	0.378	0.061	0.632	0.579	0.233	0.188
P₍₂₀₁₄₎	$[\begin{matrix} 0.504 & 0.385 & 0.112 \\ 0.152 & 0.544 & 0.304 \\ 0.065 & 0.259 & 0.676 \end{matrix}]$				$[\begin{matrix} 0.450 & 0.440 & 0.110 \\ 0.128 & 0.588 & 0.284 \\ 0.057 & 0.290 & 0.653 \end{matrix}]$				$[\begin{matrix} 0.365 & 0.505 & 0.130 \\ 0.114 & 0.568 & 0.318 \\ 0.035 & 0.368 & 0.596 \end{matrix}]$				$[\begin{matrix} 0.211 & 0.658 & 0.130 \\ 0.059 & 0.658 & 0.283 \\ 0.019 & 0.438 & 0.544 \end{matrix}]$				$[\begin{matrix} 0.435 & 0.493 & 0.072 \\ 0.129 & 0.634 & 0.237 \\ 0.025 & 0.291 & 0.684 \end{matrix}]$				$[\begin{matrix} 0.327 & 0.611 & 0.061 \\ 0.090 & 0.726 & 0.185 \\ 0.020 & 0.376 & 0.604 \end{matrix}]$
	0.638	0.574	0.365	0.093	0.655	0.564	0.278	0.158	0.735	0.510	0.430	0.100	0.793	0.471	0.357	0.172	0.623	0.584	0.399	0.074	0.672	0.552	0.286	0.162
P₍₂₀₁₈₎	$[\begin{matrix} 0.486 & 0.341 & 0.173 \\ 0.103 & 0.461 & 0.436 \\ 0.075 & 0.189 & 0.736 \end{matrix}]$				$[\begin{matrix} 0.401 & 0.403 & 0.196 \\ 0.076 & 0.485 & 0.439 \\ 0.055 & 0.200 & 0.745 \end{matrix}]$				$[\begin{matrix} 0.369 & 0.500 & 0.131 \\ 0.108 & 0.554 & 0.338 \\ 0.014 & 0.362 & 0.623 \end{matrix}]$				$[\begin{matrix} 0.192 & 0.664 & 0.144 \\ 0.049 & 0.633 & 0.319 \\ 0.006 & 0.410 & 0.583 \end{matrix}]$				$[\begin{matrix} 0.400 & 0.494 & 0.107 \\ 0.106 & 0.650 & 0.244 \\ 0.042 & 0.345 & 0.613 \end{matrix}]$				$[\begin{matrix} 0.284 & 0.615 & 0.102 \\ 0.068 & 0.724 & 0.208 \\ 0.029 & 0.411 & 0.560 \end{matrix}]$
	0.659	0.561	0.356	0.099	0685	0.544	0.346	0.110	0.727	0.515	0.399	0.111	0796	0.469	0.376	0.155	0.623	0.584	0.399	0.074	0.716	0.523	0.308	0.010
	Germany				Germany				Hungary				Hungary				Ireland				Ireland
P₍₂₀₀₂₎	$[\begin{matrix} 0.553 & 0.389 & 0.058 \\ 0.179 & 0.662 & 0.158 \\ 0.069 & 0.485 & 0.446 \end{matrix}]$				$[\begin{matrix} 0.365 & 0.605 & 0.030 \\ 0.096 & 0.838 & 0.066 \\ 0044 & 0.732 & 0.224 \end{matrix}]$				$[\begin{matrix} 0.538 & 0.403 & 0.058 \\ 0.149 & 0.698 & 0.153 \\ 0.060 & 0.380 & 0.560 \end{matrix}]$				$[\begin{matrix} 0.426 & 0.557 & 0.017 \\ 0.104 & 0.855 & 0.041 \\ 0.064 & 0.710 & 0.226 \end{matrix}]$				$[\begin{matrix} 0.549 & 0.228 & 0.222 \\ 0.147 & 0.265 & 0.588 \\ 0.094 & 0.219 & 0.688 \end{matrix}]$				$[\begin{matrix} 0.622 & 0.241 & 0.137 \\ 0.206 & 0.345 & 0.449 \\ 0.139 & 0.303 & 0.558 \end{matrix}]$
	0.669	0.554	0.165	0.233	0.787	0.475	0.234	0.291	0.602	0.599	0.312	0.088	0.746	0.502	0.205	0.293	0.749	0.501	0.408	0.066	0.738	0.508	0.276	0.216
P₍₂₀₀₆₎	$[\begin{matrix} 0.520 & 0.409 & 0.071 \\ 0.155 & 0.664 & 0.181 \\ 0.038 & 0.359 & 0.603 \end{matrix}]$				$[\begin{matrix} 0.347 & 0.614 & 0.039 \\ 0.087 & 0.831 & 0.082 \\ 0.051 & 0.682 & 0.267 \end{matrix}]$				$[\begin{matrix} 0.532 & 0.399 & 0.069 \\ 0.131 & 0.701 & 0.169 \\ 0.038 & 0.400 & 0.563 \end{matrix}]$				$[\begin{matrix} 0.376 & 0.597 & 0.027 \\ 0.077 & 0.869 & 0.054 \\ 0.031 & 0.709 & 0.259 \end{matrix}]$				$[\begin{matrix} 0.476 & 0.217 & 0.307 \\ 0.130 & 0.261 & 0.609 \\ 0.044 & 0.178 & 0.778 \end{matrix}]$				$[\begin{matrix} 0.500 & 0.241 & 0.260 \\ 0.146 & 0.308 & 0.547 \\ 0.052 & 0.219 & 0.729 \end{matrix}]$
	0.669	0.554	0.195	0.201	0.778	0.482	0.245	0.273	0.603	0.598	0.294	0.101	0.748	0.502	0.226	0.272	0.743	0.505	0.447	0.062	0.732	0.512	0.349	0.139
P₍₂₀₁₀₎	$[\begin{matrix} 0.444 & 0.495 & 0.061 \\ 0.113 & 0.732 & 0.155 \\ 0.031 & 0.392 & 0.576 \end{matrix}]$				$[\begin{matrix} 0.249 & 0.716 & 0.035 \\ 0.052 & 0.873 & 0.075 \\ 0.019 & 0.616 & 0.365 \end{matrix}]$				$[\begin{matrix} 0.503 & 0.450 & 0.047 \\ 0.093 & 0.725 & 0.182 \\ 0.015 & 0.415 & 0.569 \end{matrix}]$				$[\begin{matrix} 0.322 & 0.657 & 0.021 \\ 0.049 & 0.883 & 0.068 \\ 0.011 & 0.696 & 0.292 \end{matrix}]$				$[\begin{matrix} 0.511 & 0.385 & 0.103 \\ 0.070 & 0.577 & 0.352 \\ 0.050 & 0.300 & 0.650 \end{matrix}]$				$[\begin{matrix} 0.467 & 0.426 & 0.107 \\ 0.060 & 0.598 & 0.342 \\ 0.043 & 0.316 & 0.641 \end{matrix}]$
	0.624	0.584	0.219	0.120	0.757	0.496	0.275	0.229	0.601	0.599	0.305	0.082	0.752	0.499	0.249	0.252	0.631	0.580	0.415	0.045	0.647	0.569	0.291	0.140
P₍₂₀₁₄₎	$[\begin{matrix} 0.443 & 0.494 & 0.063 \\ 0.119 & 0.725 & 0.156 \\ 0.042 & 0.528 & 0.430 \end{matrix}]$				$[\begin{matrix} 0.227 & 0.735 & 0.038 \\ 0.050 & 0.874 & 0.076 \\ 0.020 & 0.736 & 0.244 \end{matrix}]$				NA				NA				$[\begin{matrix} 0.485 & 0.426 & 0.089 \\ 0.089 & 0.557 & 0.354 \\ 0.048 & 0.190 & 0.762 \end{matrix}]$				$[\begin{matrix} 0.373 & 0.519 & 0.108 \\ 0.058 & 0.576 & 0.366 \\ 0.031 & 0.194 & 0.775 \end{matrix}]$
	0.701	0.533	0.200	0.158	0.828	0.448	0.283	0.269	NA	NA	NA	NA	NA	NA	NA	NA	0.598	0.601	0.428	0.045	0.638	0.575	0.331	0.094
P₍₂₀₁₈₎	$[\begin{matrix} 0.452 & 0.499 & 0.049 \\ 0.101 & 0.723 & 0.175 \\ 0.027 & 0.481 & 0.492 \end{matrix}]$				$[\begin{matrix} 0.235 & 0.732 & 0.033 \\ 0.043 & 0.862 & 0.095 \\ 0.013 & 0.673 & 0.314 \end{matrix}]$				$[\begin{matrix} 0.546 & 0.392 & 0.062 \\ 0.051 & 0.751 & 0.198 \\ 0.016 & 0.210 & 0.774 \end{matrix}]$				$[\begin{matrix} 0.314 & 0.648 & 0.038 \\ 0.021 & 0.891 & 0.088 \\ 0.011 & 0.416 & 0.573 \end{matrix}]$				$[\begin{matrix} 0.425 & 0.425 & 0.150 \\ 0.068 & 0.534 & 0.398 \\ 0.041 & 0.245 & 0.714 \end{matrix}]$				$[\begin{matrix} 0.291 & 0.515 & 0.194 \\ 0.039 & 0.536 & 0.426 \\ 0.022 & 0.238 & 0.740 \end{matrix}]$
	0.666	0.556	0.211	0.145	0.794	0.470	0.287	0.243	0.464	0.691	0.263	0.050	0.611	0.593	0.258	0.149	0.663	0.558	0.423	0.069	0.717	0.522	0.378	0.100
	TheNetherlands				TheNetherlands				Norway				Norway				Poland				Poland
P₍₂₀₀₂₎	$[\begin{matrix} 0.481 & 0.382 & 0.137 \\ 0.196 & 0.472 & 0.332 \\ 0.107 & 0.356 & 0.537 \end{matrix}]$				$[\begin{matrix} 0.471 & 0.448 & 0.081 \\ 0.204 & 0.588 & 0.209 \\ 0.125 & 0.496 & 0.379 \end{matrix}]$				$[\begin{matrix} 0.384 & 0.491 & 0.125 \\ 0.143 & 0.546 & 0.311 \\ 0.075 & 0.328 & 0.597 \end{matrix}]$				$[\begin{matrix} 0.188 & 0.708 & 0.104 \\ 0.063 & 0.705 & 0.233 \\ 0.036 & 0.469 & 0.495 \end{matrix}]$				$[\begin{matrix} 0.386 & 0.550 & 0.064 \\ 0.103 & 0.715 & 0.182 \\ 0.019 & 0.352 & 0.629 \end{matrix}]$				$[\begin{matrix} 0.213 & 0.773 & 0.014 \\ 0.052 & 0.912 & 0.037 \\ 0.016 & 0.767 & 0.217 \end{matrix}]$
	0.755	0.497	0.410	0.102	0.781	0.479	0.246	0.275	0.736	0.509	0.356	0.148	0.806	0.462	0.348	0.189	0.635	0.577	0.437	0.052	0.874	0.447	0.275	0.278
P₍₂₀₀₆₎	$[\begin{matrix} 0.446 & 0.371 & 0.183 \\ 0.199 & 0.482 & 0.319 \\ 0.093 & 0.327 & 0.580 \end{matrix}]$				$[\begin{matrix} 0.430 & 0.440 & 0.130 \\ 0.194 & 0.578 & 0.228 \\ 0.100 & 0.437 & 0.463 \end{matrix}]$				$[\begin{matrix} 0.371 & 0.510 & 0.119 \\ 0.105 & 0.648 & 0.248 \\ 0.034 & 0.379 & 0.586 \end{matrix}]$				$[\begin{matrix} 0.303 & 0.604 & 0.093 \\ 0.082 & 0.732 & 0.186 \\ 0.030 & 0.478 & 0.492 \end{matrix}]$				$[\begin{matrix} 0.403 & 0.561 & 0.036 \\ 0.073 & 0.713 & 0.214 \\ 0.017 & 0.542 & 0.441 \end{matrix}]$				$[\begin{matrix} 0.188 & 0.800 & 0.012 \\ 0.030 & 0.906 & 0.063 \\ 0.009 & 0.834 & 0.157 \end{matrix}]$
	0.746	0.503	0.427	0.101	0.765	0.490	0.266	0.244	0.698	0.535	0.379	0.114	0.737	0.509	0.294	0.197	0.722	0.519	0.412	0.057	0.874	0.417	0.292	0.291
P₍₂₀₁₀₎	$[\begin{matrix} 0.441 & 0.420 & 0.138 \\ 0.126 & 0.533 & 0.341 \\ 0.056 & 0.364 & 0.580 \end{matrix}]$				$[\begin{matrix} 0.402 & 0.488 & 0.110 \\ 0.114 & 0.616 & 0.270 \\ 0.055 & 0.452 & 0.493 \end{matrix}]$				$[\begin{matrix} 0.396 & 0.448 & 0.157 \\ 0.121 & 0.560 & 0.319 \\ 0.029 & 0.261 & 0.710 \end{matrix}]$				$[\begin{matrix} 0.296 & 0.560 & 0.143 \\ 0.083 & 0647 & 0.270 \\ 0.022 & 0.327 & 0.651 \end{matrix}]$				$[\begin{matrix} 0.561 & 0.333 & 0.107 \\ 0.141 & 0.450 & 0.409 \\ 0.045 & 0.153 & 0.802 \end{matrix}]$				$[\begin{matrix} 0.306 & 0.631 & 0.063 \\ 0.066 & 0.729 & 0.205 \\ 0.031 & 0.369 & 0.600 \end{matrix}]$
	0.723	0.518	0.445	0.078	0.703	0.504	0.289	0.207	0.667	0.555	0.370	0.107	0.703	0.532	0.324	0.144	0.594	0.604	0.392	0.048	0.683	0.545	0.300	0.155
P₍₂₀₁₄₎	$[\begin{matrix} 0.394 & 0.448 & 0.158 \\ 0.108 & 0.432 & 0.460 \\ 0.071 & 0.336 & 0.593 \end{matrix}]$				$[\begin{matrix} 0.328 & 0.536 & 0.136 \\ 0.090 & 0.516 & 0.394 \\ 0.061 & 0.414 & 0.525 \end{matrix}]$				$[\begin{matrix} 0.311 & 0.508 & 0.182 \\ 0.115 & 0.607 & 0.279 \\ 0.025 & 0.325 & 0.650 \end{matrix}]$				$[\begin{matrix} 0.224 & 0.584 & 0.192 \\ 0.077 & 0.649 & 0.274 \\ 0.017 & 0.347 & 0.637 \end{matrix}]$				$[\begin{matrix} 0.552 & 0.354 & 0.094 \\ 0.149 & 0.471 & 0.380 \\ 0.030 & 0.187 & 0.783 \end{matrix}]$				$[\begin{matrix} 0.265 & 0.666 & 0.069 \\ 0.058 & 0.716 & 0.227 \\ 0.015 & 0.373 & 0.612 \end{matrix}]$
	0.791	0.473	0.502	0.072	0.816	0.456	0.355	0.188	0.716	0.522	0.374	0.126	0.745	0.503	0.350	0.147	0.597	0.602	0.403	0.047	0.704	0.531	0.320	0.149
	$[\begin{matrix} 0.403 & 0.425 & 0.172 \\ 0.103 & 0.502 & 0.394 \\ 0.036 & 0.321 & 0.643 \end{matrix}]$				$[\begin{matrix} 0.313 & 0.519 & 0.169 \\ 0.074 & 0.567 & 0.359 \\ 0.026 & 0.373 & 0.601 \end{matrix}]$				$[\begin{matrix} 0.259 & 0.536 & 0.205 \\ 0.105 & 0.564 & 0.331 \\ 0.054 & 0.323 & 0.624 \end{matrix}]$				$[\begin{matrix} 0.179 & 0.598 & 0.223 \\ 0.069 & 0.593 & 0.338 \\ 0.035 & 0.335 & 0.630 \end{matrix}]$				$[\begin{matrix} 0.500 & 0.347 & 0.154 \\ 0.092 & 0.442 & 0.466 \\ 0.016 & 0.217 & 0.767 \end{matrix}]$				$[\begin{matrix} 0.214 & 0.653 & 0.133 \\ 0.031 & 0.653 & 0.316 \\ 0.006 & 0.379 & 0.615 \end{matrix}]$
P₍₂₀₁₈₎	0.726	0.516	0.439	0.091	0.760	0.494	0.349	0.158	0.777	0.482	0.376	0.145	0.799	0.467	0.386	0.146	0.646	0.570	0.446	0.041	0.759	0.494	0.367	0.139
	Portugal				Portugal				Slovenia				Slovenia				Spain				Spain
P₍₂₀₀₂₎	$[\begin{matrix} 0.867 & 0.074 & 0.059 \\ 0.444 & 0.333 & 0.222 \\ 0.222 & 0.278 & 0.500 \end{matrix}]$				$[\begin{matrix} 0.978 & 0.015 & 0.007 \\ 0.842 & 0.114 & 0.044 \\ 0.685 & 0.155 & 0.160 \end{matrix}]$				$[\begin{matrix} 0.484 & 0.468 & 0.048 \\ 0.140 & 0.684 & 0.175 \\ 0.091 & 0.455 & 0.455 \end{matrix}]$				$[\begin{matrix} 0.305 & 0.681 & 0.014 \\ 0.078 & 0.877 & 0.045 \\ 0.067 & 0.777 & 0.156 \end{matrix}]$				$[\begin{matrix} 0.737 & 0.126 & 0.137 \\ 0.251 & 0.318 & 0.430 \\ 0.036 & 0.149 & 0.814 \end{matrix}]$				$[\begin{matrix} 0.859 & 0.076 & 0.065 \\ 0.425 & 0.279 & 0.295 \\ 0.081 & 0.175 & 0.744 \end{matrix}]$
	0.650	0.567	0.132	0.025	0.650	0.418	0.022	0.560	0.689	0.541	0.323	0.108	0.831	0.446	0.247	0.307	0.565	0.623	0.256	0.029	0.559	0.627	0.145	0.227
P₍₂₀₀₆₎	$[\begin{matrix} 0.813 & 0.110 & 0.076 \\ 0.118 & 0.353 & 0.529 \\ 0.208 & 0.208 & 0.583 \end{matrix}]$				$[\begin{matrix} 0.955 & 0.030 & 0.015 \\ 0.411 & 0.287 & 0.302 \\ 0.592 & 0.138 & 0.270 \end{matrix}]$				$[\begin{matrix} 0.426 & 0.492 & 0.082 \\ 0.121 & 0.652 & 0.227 \\ 0.000 & 0.471 & 0.529 \end{matrix}]$				$[\begin{matrix} 0.241 & 0.723 & 0.036 \\ 0.061 & 0.850 & 0.089 \\ 0.000 & 0.748 & 0.252 \end{matrix}]$				$[\begin{matrix} 0.651 & 0.168 & 0.181 \\ 0.155 & 0.280 & 0564 \\ 0.056 & 0.260 & 0.684 \end{matrix}]$				$[\begin{matrix} 0.793 & 0.092 & 0.115 \\ 0.271 & 0.219 & 0.510 \\ 0.105 & 0.221 & 0.673 \end{matrix}]$
	0.625	0.583	0.188	0.016	0.744	0.504	0.116	0.380	0.696	0.536	0.347	0.111	0.828	0.448	0.283	0.270	0.693	0.538	0.335	0.042	0.657	0.562	0.239	0.199
P₍₂₀₁₀₎	$[\begin{matrix} 0.791 & 0.126 & 0.083 \\ 0.222 & 0.389 & 0.389 \\ 0.136 & 0.409 & 0.455 \end{matrix}]$				$[\begin{matrix} 0.938 & 0.042 & 0.020 \\ 0.540 & 0.264 & 0.195 \\ 0.396 & 0.332 & 0.272 \end{matrix}]$				$[\begin{matrix} 0.417 & 0.550 & 0.033 \\ 0.069 & 0.736 & 0.194 \\ 0.000 & 0.545 & 0.455 \end{matrix}]$				$[\begin{matrix} 0.209 & 0.775 & 0.016 \\ 0.030 & 0.890 & 0.080 \\ 0.000 & 0.777 & 0.223 \end{matrix}]$				$[\begin{matrix} 0.653 & 0.193 & 0.154 \\ 0.173 & 0.271 & 0.556 \\ 0.049 & 0.219 & 0.732 \end{matrix}]$				$[\begin{matrix} 0.758 & 0.137 & 0.106 \\ 0.259 & 0.248 & 0.492 \\ 0.080 & 0.217 & 0.703 \end{matrix}]$
	0.683	0.545	0.212	0.026	0.763	0.491	0.086	0.423	0.696	0.536	0.343	0.077	0.839	0.440	0.291	0.269	0.672	0.552	0.322	0.041	0.646	0.570	0.245	0.185
P₍₂₀₁₄₎	$[\begin{matrix} 0.732 & 0.168 & 0.100 \\ 0.239 & 0.283 & 0.478 \\ 0.088 & 0.294 & 0.618 \end{matrix}]$				$[\begin{matrix} 0.873 & 0.085 & 0.042 \\ 0.454 & 0.229 & 0.318 \\ 0.205 & 0.292 & 0.503 \end{matrix}]$				$[\begin{matrix} 0.383 & 0.567 & 0.050 \\ 0.080 & 0.693 & 0.227 \\ 0.000 & 0.417 & 0.583 \end{matrix}]$				$[\begin{matrix} 0.175 & 0.794 & 0.031 \\ 0.032 & 0.845 & 0.123 \\ 0.000 & 0.617 & 0.383 \end{matrix}]$				$[\begin{matrix} 0.618 & 0.202 & 0.180 \\ 0.151 & 0.354 & 0.495 \\ 0.098 & 0.279 & 0.622 \end{matrix}]$				$[\begin{matrix} 0.723 & 0.127 & 0.150 \\ 0.217 & 0.274 & 0.508 \\ 0.142 & 0.217 & 0.641 \end{matrix}]$
	0.684	0.544	0.269	0.041	0.698	0.535	0.148	0.317	0.670	0.553	0.367	0.075	0.742	0.505	0.315	0.180	0.703	0.531	0.350	0.055	0.681	0.546	0.357	0.192
P₍₂₀₁₈₎	$[\begin{matrix} 0.711 & 0.162 & 0.127 \\ 0.082 & 0.479 & 0.438 \\ 0.000 & 0.235 & 0.765 \end{matrix}]$				$[\begin{matrix} 0.829 & 0.105 & 0.067 \\ 0.151 & 0.487 & 0.363 \\ 0.000 & 0.274 & 0.726 \end{matrix}]$				$[\begin{matrix} 0.368 & 0.579 & 0.053 \\ 0.051 & 0.684 & 0.266 \\ 0.000 & 0.385 & 0.615 \end{matrix}]$				$[\begin{matrix} 0.154 & 0.808 & 0.038 \\ 0.018 & 0.816 & 0.166 \\ 0.000 & 0.545 & 0.455 \end{matrix}]$				$[\begin{matrix} 0.582 & 0.224 & 0.194 \\ 0.172 & 0.333 & 0.495 \\ 0.091 & 0.186 & 0.723 \end{matrix}]$				$[\begin{matrix} 0.660 & 0.157 & 0.183 \\ 0.217 & 0.261 & 0.522 \\ 0.112 & 0.142 & 0.745 \end{matrix}]$
	0.522	0.652	0.284	0.024	0.479	0.680	0.178	0.142	0.666	0.556	0.383	0.060	0.787	0.475	0.337	0.188	0.681	0.546	0.374	0.050	0.667	0.555	0.287	0.157
	Sweden				Sweden				Switzerland				Switzerland				United Kingdom				United Kingdom
P₍₂₀₀₂₎	NA				NA				$[\begin{matrix} 0.377 & 0.474 & 0.149 \\ 0.118 & 0.611 & 0.271 \\ 0.061 & 0.374 & 0.566 \end{matrix}]$				$[\begin{matrix} 0.239 & 0.677 & 0.084 \\ 0.068 & 0.793 & 0.139 \\ 0.043 & 0.600 & 0.357 \end{matrix}]$				$[\begin{matrix} 0.639 & 0.101 & 0.260 \\ 0.285 & 0.203 & 0.512 \\ 0.167 & 0.146 & 0.687 \end{matrix}]$				$[\begin{matrix} 0.658 & 0.126 & 0.215 \\ 0.302 & 0.261 & 0.437 \\ 0.186 & 0.197 & 0.617 \end{matrix}]$
	NA	NA	NA	NA	NA	NA	NA	NA	0.723	0.518	0.329	0.146	0.805	0.463	0.300	0.237	0.736	0.510	0.298	0.077	0.732	0.512	0.260	0.228
P₍₂₀₀₆₎	$[\begin{matrix} 0.352 & 0.444 & 0.205 \\ 0.125 & 0.529 & 0.346 \\ 0.055 & 0.404 & 0.541 \end{matrix}]$				$[\begin{matrix} 0.265 & 0.587 & 0.148 \\ 0.090 & 0.669 & 0.240 \\ 0.043 & 0.552 & 0.405 \end{matrix}]$				$[\begin{matrix} 0.426 & 0.467 & 0.108 \\ 0.107 & 0.619 & 0.274 \\ 0.038 & 0.359 & 0.603 \end{matrix}]$				$[\begin{matrix} 0.254 & 0.672 & 0.074 \\ 0.056 & 0.780 & 0.164 \\ 0.024 & 0.542 & 0.434 \end{matrix}]$				$[\begin{matrix} 0568 & 0.108 & 0.325 \\ 0.265 & 0.178 & 0.557 \\ 0.156 & 0.099 & 0.745 \end{matrix}]$				$[\begin{matrix} 0.531 & 0.164 & 0.305 \\ 0.238 & 0.261 & 0.501 \\ 0.147 & 0.151 & 0.702 \end{matrix}]$
	0.789	0.474	0.464	0.117	0.803	0.447	0.325	0.228	0.676	0.549	0.345	0.110	0.766	0.489	0.303	0.207	0.754	0.497	0.328	0.078	0.753	0.498	0.323	0.179
P₍₂₀₁₀₎	$[\begin{matrix} 0.329 & 0.525 & 0.145 \\ 0.118 & 0.624 & 0.258 \\ 0.044 & 0.374 & 0.582 \end{matrix}]$				$[\begin{matrix} 0.223 & 0.666 & 0.111 \\ 0.075 & 0.740 & 0.185 \\ 0.031 & 0.499 & 0.469 \end{matrix}]$				$[\begin{matrix} 0.375 & 0.554 & 0.071 \\ 0.102 & 0.726 & 0.172 \\ 0.037 & 0.352 & 0.611 \end{matrix}]$				$[\begin{matrix} 0.212 & 0.734 & 0.054 \\ 0.050 & 0.836 & 0.114 \\ 0.022 & 0.488 & 0.490 \end{matrix}]$				$[\begin{matrix} 0.555 & 0.330 & 0.116 \\ 0.218 & 0.465 & 0.317 \\ 0.082 & 0.399 & 0.519 \end{matrix}]$				$[\begin{matrix} 0.423 & 0.461 & 0.116 \\ 0.147 & 0.574 & 0.280 \\ 0.055 & 0.490 & 0.455 \end{matrix}]$
	0.732	0.512	0.446	0.098	0.784	0.478	0.321	0.202	0.644	0.571	0.306	0.096	0.731	0.512	0.301	0.187	0.731	0.513	0.358	0.113	0.774	0.484	0.286	0.230
P₍₂₀₁₄₎	$[\begin{matrix} 0.325 & 0.556 & 0.119 \\ 0.078 & 0.609 & 0.313 \\ 0.025 & 0.425 & 0.550 \end{matrix}]$				$[\begin{matrix} 0.199 & 0.693 & 0.108 \\ 0.044 & 0.695 & 0.261 \\ 0.015 & 0.507 & 0.478 \end{matrix}]$				$[\begin{matrix} 0.358 & 0.570 & 0.073 \\ 0.115 & 0.692 & 0.193 \\ 0.048 & 0.302 & 0.651 \end{matrix}]$				$[\begin{matrix} 0.183 & 0.752 & 0.065 \\ 0.051 & 0.797 & 0.152 \\ 0.024 & 0.395 & 0.581 \end{matrix}]$				$[\begin{matrix} 0.476 & 0.343 & 0.181 \\ 0.134 & 0.498 & 0.368 \\ 0.081 & 0.289 & 0.630 \end{matrix}]$				$[\begin{matrix} 0.306 & 0.510 & 0.183 \\ 0.072 & 0.617 & 0.310 \\ 0.046 & 0.384 & 0.570 \end{matrix}]$
	0.758	0.495	0.420	0.112	0.814	0.458	0.354	0.188	0.650	0.567	0.314	0.105	0.720	0.520	0.323	0.157	0.698	0.535	0.390	0.101	0.753	0.498	0.335	0.167
	$[\begin{matrix} 0.290 & 0.543 & 0.167 \\ 0.100 & 0.568 & 0.332 \\ 0.033 & 0.327 & 0.641 \end{matrix}]$				$[\begin{matrix} 0.173 & 0.650 & 0.177 \\ 0.055 & 0.623 & 0.322 \\ 0.018 & 0.359 & 0.622 \end{matrix}]$				$[\begin{matrix} 0.441 & 0.487 & 0.072 \\ 0.075 & 0.697 & 0.228 \\ 0.063 & 0.316 & 0.620 \end{matrix}]$				$[\begin{matrix} 0.235 & 0.681 & 0.084 \\ 0.031 & 0.760 & 0.209 \\ 0.028 & 0.368 & 0.604 \end{matrix}]$				$[\begin{matrix} 0.381 & 0.422 & 0.197 \\ 0.125 & 0.508 & 0.366 \\ 0.048 & 0.261 & 0.691 \end{matrix}]$				$[\begin{matrix} 0.230 & 0.531 & 0.238 \\ 0.065 & 0.553 & 0.382 \\ 0.025 & 0.275 & 0.700 \end{matrix}]$
P₍₂₀₁₈₎	0.751	0.499	0.397	0.123	0.791	0.473	0.383	0.144	0.621	0.586	0.305	0.091	0.700	0.533	0.324	0.142	0.710	0.527	0.427	0.096	0.759	0.494	0.384	0.122
	Total				Total
P₍₂₀₀₂₎	$[\begin{matrix} 0.600 & 0.252 & 0.148 \\ 0.182 & 0.605 & 0.213 \\ 0.097 & 0.314 & 0.589 \end{matrix}]$				$[\begin{matrix} 0.596 & 0.318 & 0.087 \\ 0.169 & 0.714 & 0.117 \\ 0.115 & 0.472 & 0.413 \end{matrix}]$
	0.603	0.598	0.290	0.110	0.603	0.574	0.174	0.252
P₍₂₀₀₆₎	$[\begin{matrix} 0.547 & 0.280 & 0.173 \\ 0.151 & 0.595 & 0.253 \\ 0.093 & 0.282 & 0.625 \end{matrix}]$				$[\begin{matrix} 0.596 & 0.318 & 0.087 \\ 0.169 & 0.714 & 0.117 \\ 0.115 & 0.472 & 0.413 \end{matrix}]$
	0.616	0.589	0.326	0.101	0.642	0.572	0.212	0.216
P₍₂₀₁₀₎	$[\begin{matrix} 0.549 & 0.343 & 0.108 \\ 0.128 & 0.648 & 0.225 \\ 0.047 & 0.320 & 0.633 \end{matrix}]$				$[\begin{matrix} 0.475 & 0.443 & 0.082 \\ 0.099 & 0.748 & 0.153 \\ 0.043 & 0.443 & 0.514 \end{matrix}]$
	0.585	0.610	0.327	0.081	0.631	0.579	0.226	0.195
P₍₂₀₁₄₎	$[\begin{matrix} 0.505 & 0.368 & 0.126 \\ 0.125 & 0.630 & 0.245 \\ 0.056 & 0.349 & 0.595 \end{matrix}]$				$[\begin{matrix} 0.553 & 0.355 & 0.093 \\ 0.148 & 0.658 & 0.194 \\ 0.073 & 0.403 & 0.523 \end{matrix}]$
	0.635	0.577	0.345	0.094	0.633	0.578	0.214	0.208
P₍₂₀₁₈₎	$[\begin{matrix} 0.400 & 0.494 & 0.107 \\ 0.106 & 0.650 & 0.244 \\ 0.042 & 0.345 & 0.613 \end{matrix}]$				$[\begin{matrix} 0.344 & 0.505 & 0.151 \\ 0.064 & 0.712 & 0.224 \\ 0.029 & 0.384 & 0.587 \end{matrix}]$
	0.669	0.554	0.411	0.081	0.678	0.548	0.293	0.159

Figure A1. The differences in upward mobility index between nominal and positional mobility, by country and ESS round (ESS1, ESS3, ESS5, ESS7, ESS9).

Figure A2. The differences in Μ_PS and IM between nominal and positional mobility, by country and ESS round (ESS1, ESS3, ESS5, ESS7, ESS9).

References

Breen, R.; Goldthorpe, J. H. Explaining Educational Differentials: towards a formal rational action theory. Rationality and Society 1997, Volume 9(3), pp. 275-305. [CrossRef]
Blanden, J.; Gregg, P.; Machin S. Intergenerational Mobility in Europe and North America (A Report Supported by the Sutton Trust). London: Centre for Economic Performance, 2005. http://cep.lse.ac.uk/about/news/IntergenerationalMobility.pdf.
Corak, M. Income Inequality, Equality of Opportunity, and Intergenerational Mobility. The Journal of Economic Perspectives 2013, Volume 27(3), pp. 79–102. http://www.jstor.org/stable/41955546.
4. Cunha, F; Heckman, J. The Technology of Skill Formation. American Economic Review 2007, Volume 97(2), pp. 31-47.
Blanden, J.; Machin, S. Recent Changes in Intergenerational Mobility in Britain. Sutton Trust Report, 2007, pp. 1-34, http://www.suttontrust.com/reports/mainreport.pdf.
Symeonaki M.; Stamatopoulou, G. Exploring the transition to Higher Education in Greece: issues of intergenerational educational mobility. Policy Futures in Education 2014, Volume 12(5), pp. 681-69. [CrossRef]
Symeonaki, M.; Stamatopoulou, G.; Michalopoulou C. Intergenerational educational mobility in Greece: Transitions and social distances. Communication in Statistics – Theory and Methods 2015, Volume 45(6), pp. 1710-1722. [CrossRef]
Stamatopoulou G.; Symeonaki M.; Michalopoulou C. Occupational and educational gender segregation in southern Europe. In Stochastic and Data Analysis Methods and Applications in Statistics and Demography; Bozeman, J.R., Oliveira T., Skiadas C.H. Eds.; Springer 2016, pp. 611-619.
Stamatopoulou G.; Symeonaki M. Intergenerational social mobility in Europe: Findings from the European Social Survey. In The Springer Series on Demographic Methods and Population Analysis, 2023.
Symeonaki, M.; Tsinaslanidou, P. Assessing the Intergenerational Educational Mobility in European Countries Based on ESS Data: 2002–2016. The Springer Series on Demographic Methods and Population Analysis Quantitative Methods in Demography 2022, pp. 359-372. [CrossRef]
Breen, R.; Luijkx, R.; Müller, W.; Pollak, R. Nonpersistent inequality in educational attainment: Evidence from eight European countries. American journal of sociology 2009, Volume 114(5), pp. 1475-1521. [CrossRef]
Breen, R.; Luijkx, R.; Müller, W.; Pollak, R. Long-term trends in educational inequality in Europe: Class inequalities and gender differences. European sociological review 2010, Volume 26(1), pp. 31-48. [CrossRef]
Goldthorpe, J. H. Analysing Social Inequality: A Critique of Two Recent Contributions from Economics and Epidemiology. European Sociological Review 2009, Volume 26, pp. 731–44. [CrossRef]
Hirsch, F. Social limits to growth. Harvard University Press, 1976.
Rotman, A.; Shavit, Y.; Shalev, M. Nominal and positional perspectives on educational stratification in Israel. Research in Social Stratification and Mobility 2016, Volume 43, pp. 17-24. [CrossRef]
Fujihara, S.; Ishida, H. The absolute and relative values of education and the inequality of educational opportunity: Trends in access to education in postwar Japan. Research in Social Stratification and Mobility 2016 Volume 43, pp. 25-37. [CrossRef]
Triventi, M.; Panichella, N.; Ballarino, G.; Barone, C.; Bernardi, F. Education as a positional good: implications for social inequalities in educational attainment in Italy, Research in social stratification and mobility 2016, Volume 43, pp. 39-52. https://hdl.handle.net/1814/61503.
Di Stasio, V.; Bol, T.; Van de Werfhorst, H.G. What makes education positional? Institutions, overeducation and the competition for jobs. Research in Social Stratification and Mobility 2016, Volume 43, pp. 53-63. [CrossRef]
Araki, S. Educational Expansion, Skills Diffusion, and the Economic Value of Credentials and Skills. American Sociological Review 2020, Volume 85(1), pp.128-175. [CrossRef]
Bibby, J. Methods of measuring mobility. Quality & Quantity: International Journal of Methodology, Springer 1975, Volume 9(2), pp. 107-136.
Goldthorpe, J.H.; Jackson, M. Intergenerational class mobility in contemporary Britain: political concerns and empirical findings. The British Journal of Sociology 2007, Volume 58, pp. 525-546. [CrossRef]
Prais, S. Measuring social mobility. Journal of the Royal Statistical Society 1955 Series A, Volume 118, pp. 56-66.
Shorrocks, A. The measurement of social mobility. Econometrica 1978, Volume 46, pp. 1013-1024.
Bukodi, E.; Goldthorpe, J.H. Educational attainment - relative or absolute - as a mediator of intergenerational class mobility in Britain. Research in Social Stratification and Mobility 2016, Volume 43, pp. 5-15. [CrossRef]
Bartholomew, D.J.; Forbes, A.F.; McClean, S.I. Statistical techniques for manpower planning, 2nd ed.; Wiley, 1991.
Vassiliou, P. Asymptotic behavior of Markov systems. Journal of Applied Probability 1982, Volume 19(4), pp. 851-857. [CrossRef]

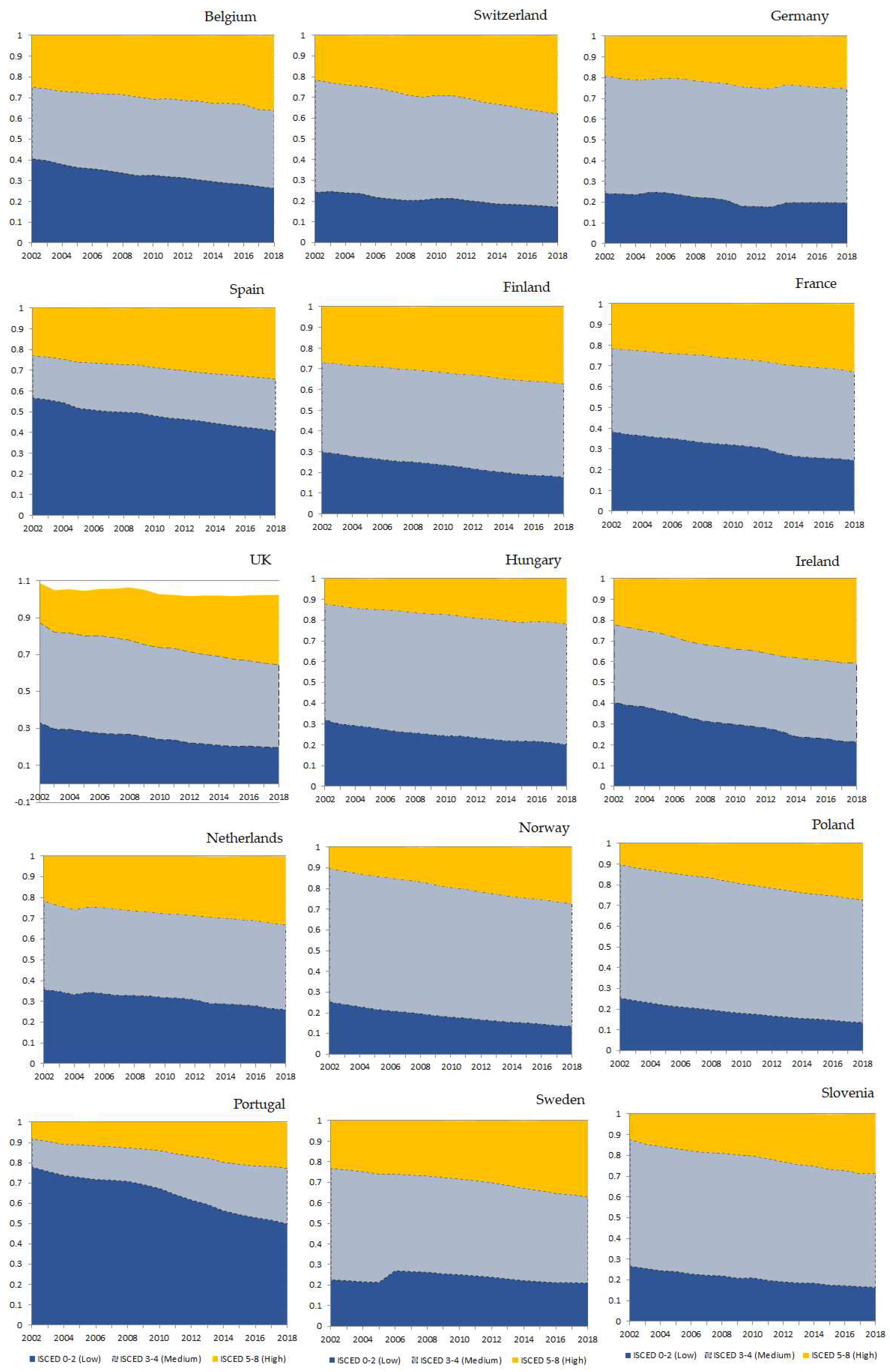
1	The production of the generated harmonised educational variable is particularly dependent on the availability of sufficiently detailed country specific education variables. For rounds ESS 5-9, the 7-category variable ‘es-isced’ is used in the analysis for both respondents and parents. For rounds ESS 1-4, the same variable has not been produced for all parents and/or for all countries. Thus, for these rounds we use the previous harmonised 5-category variable ‘edulvlva’ in order to classify both respondents and parents into the educational categories.
2	https://www.europeansocialsurvey.org/methodology/ess_methodology/data_processing_archiving/weighting.html
3	For a more detailed presentation of the indices see Symeonaki et al. [7].
4	https://www.europeansocialsurvey.org/methodology/ess_methodology/data_processing_archiving/weighting.html
5	For a more detailed presentation of the indices see Symeonaki et al. [7].

Figure 1. The percentages of people who move upward, downward or have the same education as their parents, by country, according to: (a) ESS1 dataset; (b) ESS9 dataset.

Figure 2. Changes in mobility rates by county, 2002 and 2018 (nominal mobility).

Figure 3. Country-wise distribution of proportions in educational attainment levels, 2002-2020 (EUROSTAT, based on the EU-LFS data).

Table 1. Socio-demographic characteristics of the sample, per ESS round (2002, 2006, 2010, 2014 and 2018).

			Country
Round		Characteristics	BE	CH	DE	ES	FI	FR	HU	IE	NL	NO	PL	PT	SE	SI	UK

ESS1	N		1,899	2,040	2,919	1,729	2,000	1,503	1,685	2,046	2,364	2,036	2,110	1,511	1,999	1,519	2,052
(2002)		Mean age (SD)	46.01 (19.07)	44.85(18.28)	47.22(18.72)	45.29(19.02)	45.75(18.35)	45.32(18.72)	45.03(18.46)	41.90(17.59)	44.10(17.15)	45.33(17.81)	43.08(18.52)	44.98(18.81)	45.85(18.13)	44.23(18.61)	45.60(18.41)
		Male (%)	48.39	48.34	48.34	48.83	48.22	47.94	47.13	49.19	49.54	49.14	47.72	47.17	49.08	48.50	48.48
		In paid job* (%)	45.25	54.24	43.98	45.19	52.97	44.32	43.57	53.09	50.19	59.77	40.10	51.75	60.11	42.00	54.83
		In education* (%)	7.70	10.51	10.15	8.44	13.30	12.23	10.15	11.73	10.12	9.20	13.05	11.12	12.95	15.33	7.46

ESS3	N		1,798	1,804	2,916	1,876	1,896	1,986	1,518	1,800	1,889	1,750	1,721	2,222	1,927	1,476	2,394
(2006)		Mean age (SD)	46.19 (19.09)	46.47 (18.62)	47.39 (18.95)	46.06 (18.90)	46.75 (18.98)	46.19 (18.52)	46.08(18.55)	42.67 (17.83)	45.81 (17.48)	45.79 (18.68)	43.53 (18.44)	46.63 (18.91)	46.56 (18.51)	45.41 (18.65)	45.90 (18.80)
		Male (%)	48.51	48.56	48.31	49.21	48.28	47.67	46.50	49.54	49.14	49.06	47.62	47.93	49.22	48.84	48.51
		In paid job* (%)	45.98	54.49	45.09	55.10	52.30	50.34	46.54	52.63	52.97	59.14	45.27	50.95	61.36	44.71	55.70
		In education* (%)	9.89	8.81	10.57	7.56	12.90	10.14	8.82	10.53	8.04	11.29	12.59	10.10	12.08	14.12	7.55

ESS5	N		1,704	1,506	3,031	1,885	1,878	1,728	1,561	2,576	1,829	1,548	1,751	2,150	1,497	1,403	2,422
(2010)		Mean age (SD)	46.85(19.26)	48.55(19.03)	48.31 (18.68)	45.91 (19.14)	47.51(19.29)	46.98(19.31)	46.39 (18.69)	42.68(18.13)	46.34(17.78)	45.90(18.98)	44.81 (18.77)	47.39(19.27)	46.86(19.27)	46.30(18.39)	45.42(18.91)
		Male	48.61	48.11	48.86	48.93	48.43	47.64	46.60	49.15	49.16	49.24	47.51	47.45	49.55	49.43	49.60
		In paid job* (%)	46.67	55.32	48.48	47.54	47.64	48.51	46.89	39.03	54.77	55.73	48.81	44.24	55.86	47.76	51.70
		In education* (%)	10.11	8.36	9.26	10.13	14.16	10.98	9.03	14.53	9.47	13.99	11.40	10.42	14.29	13.06	8.77

ESS7	N		1,769	1,532	3,045	1,925	2,087	1,917	1,698	2,390	1,919	1,436	1,615	1,265	1,791	1,224	2,264
(2014)		Mean age (SD)	47.48(19.34)	46.95(18.86)	48.88(19.92)	47.94(18.53)	48.65(19.56)	47.46(18.93)	47.72(18.91)	44.30(17.81)	46.80(18.42)	45.80(19.05)	46.29(18.61)	49.14(19.36)	47.78(20.14)	47.67(18.51)	46.96(18.70)
		Male	48.49	49.06	48.82	48.78	48.68	47.77	46.86	49.03	49.21	51.56	47.88	46.99	50.25	49.43	48.72
		In paid job* (%)	46.55	55.99	48.63	46.78	46.93	47.69	51.80	47.08	50.22	55.98	49.92	45.18	53.51	45.98	52.62
		In education* (%)	8.94	9.24	11.41	10.31	12.72	9.88	8.51	12.26	12.05	15.31	9.16	9.35	14.04	10.34	7.51

ESS9	N		1,767	1,542	2,358	1,668	1,755	2,010	1,661	2,216	1,673	1,406	1,500	1,055	1,539	1,318	2,204
(2018)		Mean age (SD)	47.69	47.71	49.10	48.8	49.06	48.50	48.64	45.57	46.41	45.92	47.44	49.44	45.46	49.08	47.45
			(19.35)	(18.98)	(19.21)	(18.54)	(19.86)	(19.58)	(19.03)	(18.13)	(19.15)	(19.26)	(18.58)	(18.90)	(19.15)	(18.83)	(18.57)
		Male (%)	49.05	49.17	49.26	48.61	48.92	47.82	47.13	49.09	49.31	51.95	47.75	46.67	50.78	49.43	48.95
		In paid job* (%)	49.36	58.10	48.85	50.33	48.59	49.14	56.95	49.74	51.36	54.61	53.56	49.21	58.14	50.57	57.67
		In education* (%)	7.73	8.10	10.18	9.67	12.36	10.23	8.15	12.89	13.01	15.90	8.53	10.18	15.32	9.66	6.33
*The reference period is during the last seven (7) days.

Table 2. ISCED levels and educational categories.

ISCED levels	Description	Recoded educational levels
ISCED level 0	Early childhood education (Primary education not completed)	Low
ISCED level 1	Less than lower secondary
ISCED level 2	Lower secondary
ISCED level 3	Lower tier upper secondary/Upper tier upper secondary	Medium
ISCED level 4	Advanced vocational, sub-degree	Medium
ISCED level 5	Short-cycle tertiary education (lower tertiary education)	High
ISCED level 6	Bachelor’s degree or equivalent
ISCED level 7	Master’s degree or equivalent
ISCED level 8	PhD degree or equivalent

Table 3. Pearson’s correlations coefficients among nominal upward mobility

{U P}_{N}

and positional upward mobility

{U P}_{P}

per ESS round.

Table 3. Pearson’s correlations coefficients among nominal upward mobility

{U P}_{N}

and positional upward mobility

{U P}_{P}

per ESS round.

ESS 1	ESS 3	ESS 5	ESS 7	ESS 9
r=.650**, p=.006	r=.715**, p=.003	r=.604*, p=.013	r=.599*, p=.018	r=.846**, p<.001

** Correlation significant at the .001 level. * Correlation significant at the .05 level.

Table 4. Pearson’s correlations coefficients among nominal upward mobility

{U P}_{N}

, positional upward mobility

{U P}_{P}

and the respective Educational Expansion Index (EEI) per ESS round.

Table 4. Pearson’s correlations coefficients among nominal upward mobility

{U P}_{N}

, positional upward mobility

{U P}_{P}

and the respective Educational Expansion Index (EEI) per ESS round.

	ESS 1	ESS 3	ESS 5	ESS 7	ESS 9
${U P}_{N} * E E I$	r=.373	r=.580*	r=.593*	r=.516*	r=.718**
${U P}_{P} * E E I$	r=.521*	r=.707**	r=.604*	r=.697**	r=.773**

** Correlation significant at the .001 level. * Correlation significant at the .05 level.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Educational Status as a Mediator of Intergenerational Social Mobility in Europe: A Positional Analysis Approach

Abstract

1. Introduction

2. Materials and Methods

3. Results

3.1. Nominal/absolute transition probabilities

3.2. Education as a ‘positional good’: Estimating positional transition probabilities

3.3. Validation

4. Discussion

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

Appendix A

References

MDPI Initiatives

Important Links

Subscribe