Prerpints.org logo
Preprint
Article

Blast-resistant Performance of Steel Petrochemical Control Room with 3D-Kagome Sandwich Wall

Altmetrics

Downloads

97

Views

14

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

04 December 2023

Posted:

05 December 2023

You are already at the latest version

Alerts
Abstract
As the control brain of the petrochemical plant, blast resistant performance requirements of the petrochemical control room should be guaranteed when the vapor cloud explosion occurs in the petrochemical production process. 3D-Kagome truss core sandwich structure is a kind of blast resistant material with high energy absorption. Considering the influence factors of the radius of the truss core rod and thickness of the upper and lower panels, in this paper, blast resistant performance of a real steel petrochemical control room with 3D-Kagome truss core sandwich wall is analyzed. With the optimization goal of plastic deformation energy and panel displacement, the optimal wall thickness and radius of the truss core rode are obtained. The optimized blast resistant wall is assembled, and the dynamic response of the steel petrochemical control room with the 3D-Kagome truss core sandwich blast resistant wall is analyzed. The simulation results show that the truss core layer does not dissipate the blast energy effectively when the radius ratio of the truss core rod is larger than 2.7% of the total thickness of the wall; with the increase of the thickness of the upper and lower panels, the proportion of plastic deformation energy of the truss core layer increases gradually and then tends to be a stable proportion value, that is about 90%; When the thickness ratio of the panel is 6.7% of the total one of the wall and the radius ratio of the truss core rod is 2.7% of the total thickness of the wall, the optimal blast resistant 3D-Kagome sandwich wall is determined.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

The petrochemical industry is the basis for the development of various industries and has been developing rapidly in recent years. In petrochemical plants, the petrochemical control room is the center of the entire production process, controlling the operating status of the petrochemical plant, and is also a place where more staff gathers. At the present stage, the petrochemical plants shows the development trend of the large-scale, centralized and intensive, and the risk of explosion accidents in petrochemical plants is also rising rapidly, leading to devastating consequences such as structural damage, casualties, and substantial economic losses [1].
Past accidents serve as stark reminders of the potential dangers that loom in petrochemical plants, for instance, the ExxonMobil Torres Refinery accident in Texas, USA (2005), where the loss of 15 lives and over 170 injuries occurred [2]. The vapor cloud explosion in Buncefield (UK) (2005) caused significant blast damage to surrounding commercial buildings and industrial equipment [3].The BP refinery explosion in Texas City, also in 2005, marked one of the worst industrial disasters in the history of the United States, claiming 15 lives and injuring 180 people [4]. Furthermore, the Yanshan Petrochemical Company accident in Beijing, China (2013) resulted in at least 5 deaths and multiple injuries [5]. These accidents underscore the pressing need to enhance the blast resistance and energy absorption capacity of petrochemical control room structures. In light of such potential risks, the development of an innovative structural system for petrochemical control rooms becomes indispensable.
Petrochemical control rooms typically require highly complex structural design specifications, including provisions for seismic, wind, and blast resistance. Additionally, these control rooms utilize high-strength and durable building materials and must adhere to specialized design requirements, such as protection against chemical corrosion and precise control of temperature and humidity. These factors contribute to differing structural responses and levels of damage between petrochemical control rooms and typical building structures when subjected to the same type of explosion. The TNT equivalent method, representing the effects of vapor cloud explosions as TNT equivalents, is widely used in structural specifications [6,7] to facilitate the implementation of the design procedure. The ASCE (2010) Design Guide comprehensively addresses methods for predicting blast overpressure resulting from accidental explosions in petrochemical plants, along with quantifying the effects of such blasts on structures [8]. This guide offers blast resistant design and structural reinforcement techniques to mitigate the hazards caused by unforeseen petrochemical explosions. Studies investigating damage for various structures caused by vapor cloud explosions have been conducted. Pritchard and Roberts [9] observed that the extent of damage of the structures depended on the distance from the center of the explosion. Clubley [10] performed full-scale experiments and finite element simulations to analyze the response of cylindrical shell structures subjected to high-power, prolonged explosions from sources such as hydrocarbon vapor clouds. Li et al. [11] examined the dynamic response of a reinforced concrete frame structure subjected to long-distance blast loading caused by an explosion, and their findings revealed that the cladding panels were particularly affected due to variations in blast forces acting on the structure. Blast-resistant walls, such as profiled/corrugated panels, are extensively utilized in the industry to provide safety barriers against hydrocarbon explosions for personnel, facilities, and critical equipment on offshore platforms. The response of blast-resistant walls under hydrocarbon explosions has been extensively analyzed using nonlinear finite element models, and these findings have been compared with design guidelines [12]. Furthermore, the response of steel profiled blast barriers without passive impact barrier systems and with passive impact barrier systems placed at specific offset locations behind the blast barriers under hydrocarbon explosions has been investigated [13]. Additionally, in scenarios involving terrorist attacks and accidental explosions in the petrochemical industry, the corresponding studies have shown that the protective walls or barriers is effective in minimizing blast effects and building damage [14]. Kiakojouri and his colleagues’ research emphasize the potential impact of progressive collapse on structures. They particularly focus on the pivotal role of strengthening and retrofitting techniques in mitigating such collapses, while also examining several parameters, including structural topology, the nature of triggering events, the initial collapse scale, collapse types, and seismic design requirements, and their influence on strengthening strategies [15,16].
Existing technologies for enhancing blast resistance in petrochemical control rooms mainly involve increasing the size of traditional reinforced concrete walls and columns. However, this conventional approach poses several challenges, especially in terms of cost-effectiveness and feasibility. Enlarging walls and columns significantly raises project expenses and becomes difficult to implement within existing space constraints [17]. Conversely, the use of lattice sandwich structures is gaining popularity in the construction sector due to their numerous benefits, including cost-effectiveness, lightweight properties, and thermal insulation. It is important to acknowledge that the sandwich panels with metal cores might encounter accidental industrial blast loads during their operational lifespan. Moreover, these sandwich panels have found widespread application in the aerospace, automotive, shipbuilding, defense industries, and others. Hence, conducting a thorough investigation into the performance of these structural panels under blast loading becomes imperative.
There are numerous studies in the literatures focusing on the resistance of composite plates subjected to impact or blast loading. Metallic honeycomb cores with random and periodic microstructures [18], such as metallic foams, honeycombs, and lattices, have shown potential for sandwich panels due to their excellent energy absorption capacity. Over the past decades, researchers have extensively investigated the plastic deformation, damage modes, and energy absorption behavior of sandwich panels with metal cores under explosive loading. Zhu et al. [19] conducted a study on the structural response of square metal sandwich panels with honeycomb cores under explosive loading using both experimental and numerical methods. The research provided insights into the deformation and damage modes, and highlighted that the large plastic deformation of the metal core effectively dissipates input energy. Furthermore, the effects of face sheet and core configurations on the structural response were also explored. Shen et al. [20] experimentally studied curved sandwich panels with aluminum foam cores under airburst loading. They found that the curvature of the panels altered the deformation/collapse pattern and improved blast resistance. Numerical and theoretical investigations have also been conducted to study the damage modes, blast resistance, and energy absorption of metallic cylindrical sandwich shells with closed-cell aluminum foam cores under blast loads and projectile impacts [21,22]. Furthermore, Chen and Hao [23] examined the performance of multi-arched bi-layered panels under uniform impact loads. Dharmasena et al. [24] demonstrated experimentally and numerically that a honeycomb metal core within a sandwich structure is a suitable choice for deflection-constrained design against air blast loads. Yang Yu et al. [25] investigated the low-velocity impact response of hybrid honeycomb sandwich panels and examined the effect of sandwich panel parameters on the response. The study showed that the energy absorption performance of hybrid honeycomb sandwich panels was better than that of conventional honeycomb sandwich panels.
The performance of lattice sandwich materials in response to blast loading is outstanding, and extensive studies have revealed several key advantages. Ashkan Vaziri et al. studied the deformation patterns of lattice sandwich structures under blast loading, including tensile deformation of the upper and lower panels, plastic deformation of the sandwich rods, and shear deformation between the core rods [26]. Similarly, Nan et al. investigated the mechanical properties of pyramidal kokomatsu sandwich panels under impact loads, providing a comprehensive analysis of rod diameter, aspect ratio, number of units, and plies, further showcasing the superiority of lattice sandwich materials [27]. Moreover, Guoqi Zhang et al. conducted experiments to evaluate the stress-strain curves and energy absorption mechanisms of a pyramidal truss sandwich structure composed of carbon fiber-reinforced polymer (CFRP) panels and an aluminum alloy core, demonstrating its excellent energy absorption performance [28]. The numerical study by Ubade Kemerli et al. verified the advantages of lattice sandwich materials, particularly highlighting the conjugate forced convective heat transfer effect in sandwich panels with Kagome truss cores. Their findings indicated that adjusting the length and diameter of stubs significantly improved the pressure drop and Nusselt number of fractional sandwich materials [29]. Parametric studies further reinforced the excellent performance of the lattice sandwich materials. By modeling seven combinations of outer layer thickness in ANSYS Workbench Explicit Dynamics, researchers evaluated the effects of continuous blast loading on sandwich panel performance. The results revealed that pyramidal lattice panels exhibited high energy dissipation capacity in all different configurations, achieving energy absorption ranging from 5% to 48% [30]. In summary, lattice sandwich materials offer great potential in the design of blast-resistant petrochemical control rooms, given their exceptional blast resistance, lightweight properties, superior thermal insulation, and remarkable energy absorption capabilities. These materials warrant further research and wider application in practical engineering projects within the petrochemical industry.
Considering the influence factors of the radius of the truss core rod and thickness of the upper and lower panels, in this paper, blast-resistant performance of a real steel petrochemical control room with 3D-Kagome truss core sandwich wall is analyzed. The study includes numerical modeling of the control room structure subjected to vapor cloud explosion loads, optimal blast-resistant design of the 3D-Kagome sandwich blast-resistant wall, and dynamic response analysis of the control room structure.

2. Geometry of 3D-Kagome sandwich panels

With the development of material manufacturing technologies, the truss lattice material as a porous material has received great attention from various fields, which has excellent multifunctional performances of light weight, high strength, blast resistance, heat insulation and sound absorption. For the truss core sandwich panel, it mainly includes three types, tetrahedral type, pyramid one and 3D-Kagome one, among which 3D-Kagome sandwich panel outperforms other two types on aforementioned multifunctional performances [31]. Therefore, the 3D-Kagome truss core sandwich structure is chosen in this paper. The structural model of this truss core sandwich panel is shown in Figure 1 and it consists of three parts: upper panel, middle truss core sandwich and lower panel.
It is observed from Figure 1 that the 3D-Kagome truss core sandwich panel is constituted by periodic arrangement of the same single cells. The truss core of the single cell structure is shown in Figure 2 in which Bc is the distance between different single cells, Hc is the height of the sandwich layer, Rc is the radius of the truss core rod, 2Lc is the length of the truss core rod, and ɷ is the angle between the truss core rod axis and the upper/ lower panels.
The relative density is one of the important parameters for the 3D-Kagome truss core sandwich panel, which consists of relative density of the truss core layer and ones of upper and lower sandwich panels. The relative density of the 3D-Kagome truss core sandwich panel is described by the following equations [32]:
sin ω = H c 2 L c
ρ ¯ c = ρ c ρ = 6 π L c H c ( R c B c ) 2 = 3 π sin ω R c B c 2
Substituting Eq.(1) into Eq.(2) will transfer them to the following form
ρ ¯ = 2 h B c 2 + 6 π R c   2 L c H c + 2 h B c 2
where ρ ¯   is the relative density of the truss core of single cell, ρ ¯ is the relative density of the sandwich structure of single cell, and h is the thickness of the upper and lower panels.
Under the blast load, the deformation of 3D-Kagome truss core sandwich panels mainly includes tensile deformation of upper and lower panels, plastic deformation of truss core layer and shear deformation between core layer and upper/lower panels. The blast energy is mainly absorbed by truss of core layer.

3. Finite element model (FEM) of petrochemical control room structure

To ensure the feasibility of the FEM of a real steel petrochemical control room with 3D-Kagome truss core sandwich wall, the following simplifications were made:
(1) The impact of doors and windows on the explosion load was not considered, and the structures were treated as fully enclosed.
(2) Interaction between the foundation and the upper structure of the petrochemical control room was not taken into account.
(3) Contact keywords were used to ensure that there was no relative sliding or separation at the connection points.
(4) The potential secondary effects of the explosion, such as fires, on the structure were not considered.
The real steel petrochemical control structure shown in Figure 3 is presented in this paper to testify the blast-resistant performance of new 3D-Kagome truss sandwich wall. The length of the structure is 35.7m, the width is 27.0m, and the height is 6.0m. The main members of the structure, such as the steel frame beam and column, are chosen with H section, and the cross-sectional size of each member is shown in Table 1.
The FEM of the steel petrochemical structure is shown in Figure 4, where all components of the structure are simulated by using solid units. Additionally, it should be noted that the model of the petrochemical control structure includes a perimeter of shear walls, strategically placed around the structure for enhanced stability and resistance to lateral forces. The connection node (welding or bolting) between the structural column and main beam is depicted in Figure 5, while the connection node between the main beam and secondary beam is shown in Figure 6. In the simulation, the column foot condition is represented by fixed constraints, and all contact units are defined as "CONTACT AUTOMATIC SURFACE TO SURFACE".
Johnson and Cook (1983) [33] proposed a concise model to characterize the plastic response of metals subjected to dynamic loading. The model establishes a relationship between the equivalent flow stress and the variables of strain, strain rate, and temperature. In this paper, the Johnson-Cook (J-C) material model and the GRUNEISEN state equation are used for the structure, and the yield stress of the structural steel is calculated according to the Eq.(4) [33]
σ y = A + B ε n 1 + C 1 ln ε ˙ 1 − T h M
where A is the baseline yield strength, B is the hardening factor of the yield strength, n is the hardening exponent, ε n is the effective plastic strain, ε ˙ is the strain rate, C1 is the strain rate sensitivity coefficient, T h is the reference temperature, and M is the temperature dependency index.
Johnson and Cook (1985) [34] expanded their basic model based on cumulative-damage, and the LS-DYNA implementation of the Johnson-Cook constitutive model includes this additional model feature. For the J-C failure model, the failure criterion is defined as
ε f = D 1 + D 2 exp ( D 3 P σ e f f ) ( 1 + D 4 ln ε ˙ ∗ ) ( 1 + D 5 T h )
where ε f is the failure strain, P is the stress, σ e f f is the effective stress, ε ˙ * is the plastic strain rate, and D 1 , D 2 , D 3 , D 4 , D 5 are the material parameters.
The GRUNEISEN state equation is described by [30]
p = r 0 C s 2 m 1 + ( 1 − g 0 2 ) m − α 2 m 2 1 − ( S 1 − 1 ) m − S 2 m 2 m + 1 − S 3 m 3 ( m + 1 ) 2 + ( g 0 + α m ) E 0
where p is pressure, m is the compression ratio, r 0 is the initial material density, Cs is the speed of sound, g0 is the Gruneisen parameter, α is the correction factor, E 0 is the internal energy, and S 1 , S 2 , S 3 are the parameters of the state equation.
The parameters of the J-C model and the GRUNEISEN state equation are shown in Table 2 and Table 3:
Avoiding the low efficiency of the traditional Arbitrary Lagrangian-Eulerian(ALE) algorithm for solving fluid-structure coupled problems, the CONWEP blast load model is used in which the blast load is calculated by defining the TNT charge, explosion surface, explosion location, explosion time and explosion pattern.

4. Optimal design of blast-resistant shearing-wall with 3D-Kagome sandwich materials

According to Code for design of blast resistant control building in petrochemical industry (GB50779—2012) [6], it is required for the blast-resistant structure to have the ability to bear a shock overpressure wave with 69 kPa which means the explosion with 1 ton of TNT occurs in the center of the structure at the blast distance of 30 meters. The width of the blast-resistant wall with the 3D-Kagome truss core sandwich structure is chosen as 1.5m with reference to the Chinese building design standard (14J938) [7], the length and thickness of the blast-resistant wall are chosen as 5.1m and 150mm according to the engineering background case.
The optimization design objectives of the blast-resistant wall with the 3D-Kagome truss core sandwich structure are the plastic deformation energy of the truss core of the sandwich layer, and the maximum displacement out of the panel plan for the sandwich structure.
According to Code for design of blast resistant control building in petrochemical industry (GB50779—2012) [6], the deformation limits for the steel structural members are shown in Table 4.
The FEM of 3D-Kagome truss core sandwich blast-resistant wall is shown in Figure 7, in which the angle ɷ between the truss core rod axis and the upper/ lower panels is chosen as 54.7º, that is, sin ω = 2 / 3 , the distance between the cells is 150mm, same J-C material model is used and all contact units are defined as “CONTACT AUTOMATIC SURFACE TO SURFACE”.

4.1. Influence analysis of radius of truss core rod

According to code for design of blast-resistant control building in petrochemical industry (GB50779—2012) [6], 1t TNT is chosen as the blast load, blast distance is 30m, thickness of sandwich blast-resistant wall is chosen as 150mm, the thickness of the upper and lower panels Hf is 5mm, and change the radius Rc of truss core rod from 2.5mm to 9mm. Plastic deformation energy curve of the truss core layer, the upper and lower panels for different truss core rod radius are shown in Figure 8. It is shown from Figure 8 the main blast energy is absorbed by truss core layer at first, and then the plastic deformation energy of the truss core layer is reduced with the increasing radius of the core layer rods. The plastic deformation energy of the upper panel and lower panels surpass one of the truss core layer at the rod radius of 0.7cm, which indicates the stiffness of the core layer is too large to absorb energy effectively.
The structural parameter ξ is defined as
ξ = deformation   energy   of   the   truss   core   layer   total   deformation   energy
The structural parameter ξ plays the role of the truss core layer on absorbing the blast energy, and the variation curve of parameter ξ for different radius of the truss core rod is shown in Figure 9. It is shown from Figure 9 that the parameter ξ values are reduced from 0.92 to 0.88 when the radius values of the truss core rod are increased from 0.25cm to 0.4cm, which indicates that the blast energy is mainly dissipated by plastic deformation of the core layer rod for the sandwich structure. However, the values of ξ . parameter are reduced from 0.3 to 0.16 when the radius values of the truss core rod are increased from 0.7cm to 0.9cm, which indicates that the truss core layer does not dissipate the blast energy effectively.
Displacement response of low panel with different truss core rod radius is shown in Figure 10. In Figure 10, it is shown that out-of-plane displacement of the sandwich panel is reduced with the increasing of the core rod radius, especially within 0.2-0.4cm radius of the rod. When the radius of the truss core rod is 0.9cm, the parameter ξ value is 0.16 in Figure 10, and it indicates that the plastic deformation energy of the truss core layer only accounts for 16% of the total plastic deformation energy of the sandwich blast-resistance wall. Out-of-plane displacement response of the sandwich blast-resistance wall is shown in Figure 11 for 0.9cm radius of core rod, and it is obvious that the panel of the sandwich blast-resistant wall become the main energy-consuming part.

4.2. Influence analysis of panel thickness

It is shown that the parameter ξ value is reduced rapidly when the radius of core rod is bigger than 0.5cm in Figure 9. Assuming that the radius of core rod is 0.25-0.5cm, variation of the parameter ξ for different panel thickness of the sandwich blast-resistant wall is shown in Figure 12. Assuming that the panel thickness is 1cm, the plastic deformation energy for different rod radius of the sandwich blast-resistant wall is shown in Figure 13.
In Figure 12, when the panel thickness is changed from 1cm to 3cm the parameter ξ value is about 0.9 for 0.25cm rod radius, 0.95 for 0.30 or 0.4cm rod radius. In Figure 13, when the thickness of the panel is 1cm, the plastic deformation energy curve of the sandwich blast-resistant wall has the same variation tendency as 0.5cm panel thickness. The plastic deformation energy of the truss core layer, the upper and lower panels are equal when the core rod radius is 0.8cm.
When the thickness of the upper and lower panels is changed, the out of plan displacement of the center point of the lower panel for different rod radius is shown in Figure 14. For 1cm panel thickness, the out of plan displacement of the center point of the lower panel for different core rod radius is shown in Figure 15.
It is observed from Figure 14 and Figure 15 that the out of plan displacement of the center point of the lower panel is reduced rapidly when the panel thickness is increased from 0.5cm to 3cm and the core rod radius is increased from 0.25cm to 0.4cm. The out of plan displacement of the center point of the lower panel is 7.6cm when the panel thickness is 1cm and core rod radius is 0.4cm, the corresponding displacement response history of the sandwich blast-resistance wall is shown in Figure 16, and the corresponding maximum θ=1.71which is less than the normative allowable deformation value [θ]. It is observed from Figure 12 that the parameter ξ is 0.85 when core rod radius is 0.4cm and the panel thickness is 1cm, and the corresponding plastic deformation energy response history of sandwich blast-resistant wall is shown in Figure 17. It is shown in Figure 17 that dissipation energy ability of the truss core layer is much greater than one of the upper or lower panel. As thus, it can be obtained that the optimal design parameters of the sandwich blast-resistance wall is 1cm panel thickness and 0.4cm core rod radius.

5. Dynamic response analysis of petrochemical control structure with optimal design parameters of 3D-Kagome sandwich blast-resistant wall

5.1. Assembly of sandwich blast- resistant wall

Based on the optimal design parameters of the sandwich blast-resistant wall, that is, 1cm panel thickness, 0.4cm truss core rod radius, the optimal sandwich blast-resistant wall is assembled with steel column of the petrochemical control structure, and shown in Figure 18. Here connection between the wall and steel column in the finite element model is described by using automatic face-to-face contact. Petrochemical control structural model with 3D-Kagome sandwich blast-resistant wall is shown in Figure.
In order to clearly describe the dynamic response of each sandwich blast-resistant wall under the blast load, the assembled blast-resistant walls are numbered to distinguish the location of the wall and a half of the whole wall model are shown in Figure 20.

5.2. Dynamic response analysis

The value and location of the explosion load in this section are satisfied with the “Code for design of blast-resistant control building in petrochemical industry” (GB50779-2012) [6], that is, 1 ton TNT, 30m blast distance from the control room structure. The specification establishes the criteria of a 30-meter blast distance and a 1-ton TNT explosion mass with the integration of engineering safety principles and scientific research in explosion mechanics. The specified values reflect the explosion risks inherent to specific industrial sectors and have been validated that meets the stringent safety requirements for blast-resistant control buildings. Considering the solution time as 0.2s, the displacement response clouds of the blast-front surface of the sandwich blast-resistant wall under the blast load are shown in Figure 21.
In Figure 21, it can be observed that as the blast shock wave reaches the front wall of the petrochemical control structure under the blast load, the deformation of sandwich blast-resistant wall (mainly KBQ4-1 and KBQ4-2) shown in Figure 21a occurs firstly near the center of wall. In Figure 21b–f, with the increase in time, it has the larger deformation at the center span and extends to KBQ4-3, and the deformation of near the center span of the blast wall is also increasing. Further, the KBQ4-2 and KBQ4-3 walls produce the largest deformations, and deformations of KBQ4-1 and KBQ4-4 walls began to decrease. In general, the maximum deformation of the sandwich blast-resistant wall subjected to the blast load is observed to occur in the middle span of the wall. Smaller deformations are observed at the two ends of the wall and at the connection parts between the wall and the column.
As it is known the maximum displacement occurs in the middle span of the wall, then the lower panels of the KBQ4-2, KBQ4-3, KBQ3-2, and KBQ3-3 walls are selected and the corresponding displacement response history are shown in Figure 22.
In Figure 22, maximum displacements of center points of the lower panels of KBQ4-2, KBQ4-3, KBQ3-2, KBQ3-3 walls are 7.89cm, 7.3cm, 7.1cm and 6.7cm, respectively. Meanwhile rebound phenomenon of the lower panel appears after reaching to the maximum deformation, and then reciprocal vibration occurs along center point of the lower panel. The nature of reciprocal vibration is due to the action of the blast load is instantaneous completion of the sandwich blast-resistant wall with inertial movement.
The displacement response clouds of the frame column under the blast load is shown in Figure 23, and the center point displacement response history of the middle span of the frame columns under the blast surface is shown in Figure 24. In Figure 23, it is evident that the location of the frame column plays a crucial role in its dynamic response. Specifically, the deformation initially manifests at the frame columns positioned on the explosion surface, denoted as A, B, C, and D, which serve as the corners of the blast-resistant face of the control room. Subsequently, it rapidly spreads to both sides. Finally, the deformation also occurs at the frame column positioned on the back surface of the explosion. Notably, the frame column in the middle span of the explosion surface exhibits the maximum deformation. Furthermore, in Figure 24, it illustrates the occurrence of a rebound phenomenon in the frame column.
According to Code for design of blast-resistant control building in petrochemical industry (GB50779—2012) [31], the safety of the structural design is mainly measured by the allowable deformation of each member of the structure subjected to the explosive load. In this paper, the support angle is used as the main measure criterion. The above modeling and solution by finite element software to obtain the dynamic response of the structure of 1 ton TNT at a blast distance of 30 m. Through the calculation, the center point maximum displacement and the bearing angle of the sandwich blast resistant walls at different locations of the blast surface are shown in Table 5, and maximum deformation and bearing angle of the frame column are shown in Table 6.
It is found from Table 5 and Table 6, deformations for different parts of the sandwich blast-resistant walls and frame column are smaller than allowable values of the petrochemical control structural design code.

6. Conclusions

In this paper, it focuses on studying the blast resistant performance of control room subjected to vapor cloud explosion load in the petrochemical industry. The blast-resistant performance of the steel control room with an assembled 3D-Kagome sandwich blast-resistant wall is investigated using the finite element analysis method. The study includes numerical modeling of the control room structure, optimal blast-resistant design of the 3D-Kagome sandwich blast-resistant wall, and dynamic response analysis of the control room structure. The simulation results show that:
1. Increasing the diameter of the core layer rods leads to a continuous decrease in plastic deformation energy of the core layer, while the one of the upper and lower panels continue to increase. When the rod radius is too large, the upper and lower panels become the main energy-absorbing components of the sandwich blast-resistant wall. Increasing the thickness of the upper and lower panels initially improves plastic deformation energy of the core layer. The plastic deformation energy of the core layer accounts for approximately 90% of the total, indicating that excessively thick panel thickness does not significantly enhance the blast resistant performance of the sandwich wall.
2. When the rod radius of the sandwich layer is 4mm, the thickness of upper/lower panel is 10mm, the plastic deformation energy of the sandwich layer accounts for 85% of the total. Additionally, the displacement at the center point of the lower panel meets the specified deformation requirements.
3. For the assembly of the blast-resistant wall subjected to a 1tTNT explosion at a distance of 30m, it experiences the highest displacement in the center of the blast wall. The displacement in the center spreads by a hemispherical manner to both sides. The displacement at the center point of the panel and the elasto-plastic corner displacement of different sections of the blast-resistant wall are compared with the specifications of design code.

Acknowledgements

This work was supported by the Key Technology Research and Development Program of Shaanxi Province of China under grant number 2019GY-079.

References

  1. E.S. Oran, G. Chamberlain, A. Pekalski. Mechanisms and occurrence of detonations in vapor cloud explosions. Progress in Energy and Combustion Science 2020; 77: 100804. [CrossRef]
  2. Q. Jia, G. Fu, X. Xie, S. Hu, Y. Wu, J. Li. LPG leakage and explosion accident analysis based on a new SAA method.Journal of Loss Prevention in the Process Industries 2017; 71: 104467. [CrossRef]
  3. G. Atkinson. Blast damage to storage tanks and steel clad buildings. Process. Saf. Environ 2011; 89(6): 382–390. [CrossRef]
  4. U.S. Chemical Safety and Hazard Investigation Board, Investigation Report, Refinery Explosion and Fire (15 Killed, 180 Injured) 2007. (Report No. 2005-04-I-TX).
  5. M. Z. Kamil, F. Khan, S. Z. Halim, P. Amyotte, S. Ahmed. A methodical approach for knowledge-based fire and explosion accident likelihood analysis. Process Safety and Environmental Protection 2023; 170: 339-355. [CrossRef]
  6. Standardization Administration of China (2012), GB50779—2012: Code for design of blast resistant control building in petrochemical industry. Beijing:China Planning Press.(In Chinese).
  7. Standardization Administration of China (2014), 14J938: Blast-resistant and Pressure-relief Doors, Windows, Roofs, and Wall Structures. Beijing: China Academy of Building Research. (In Chinese).
  8. ASCE, Design of Blast Resistant Buildings in Petrochemical Facilities, Second Edition, 2010.
  9. D. Pritchard, A. Roberts. Blast effects from vapour cloud explosions: a decade of progress. Saf. Sci.1993; 16 (3-4): 527–548. [CrossRef]
  10. S.K. Clubley. Non-linear long duration blast loading of cylindrical shell structures, Eng. Struct.2014; 59: 113–126. [CrossRef]
  11. B. Li, T.-C. Pan, A. Nair. A case study of the effect of cladding panels on the response of reinforced concrete frames subjected to distant blast loadings. Nucl. Eng. Des.2009; 239: 455–469. [CrossRef]
  12. L. Louca, J. Boh, Y. Choo. Design and analysis of stainless steel profiled blast barriers. J. Constr. Steel Res.2004; 60(12) : 1699–1723. [CrossRef]
  13. J. Boh, L. Louca, Y. Choo. Energy absorbing passive impact barrier for profiled blastwalls. Int. J. Impact Eng.2005; 31(8): 976–995. [CrossRef]
  14. D. Ambrosini, B.M. Luccioni. Reinforcedconcrete wall as protection against accidental explosions in the petrochemical industry. Struct. Eng. Mech.2009; 32(2): 213–233.
  15. F. Kiakojouri, V. De Biagi, B.Chiaia, & M. R. Sheidaii. Strengthening and retrofitting techniques to mitigate progressive collapse: A critical review and future research agenda. Engineering Structures 2022; 262:114274. [CrossRef]
  16. F. Kiakojouri, V. De Biagi, B.Chiaia, & M. R. Sheidaii. Progressive collapse of framed building structures: Current knowledge and future prospects. Engineering Structures 2020; 206: 110061. [CrossRef]
  17. D. G. Winget, K. A. Marchand, E. B. Williamson. Analysis and Design of Critical Bridges Subjected to Blast Loads. Journal of Structural Engineering 2005; 131(8): 1243. [CrossRef]
  18. F. Zhu, G. Lu, D. Ruan, Z. Wang. Plastic Deformation, Failure and Energy Absorption of Sandwich Structures with Metallic Cellular Cores. Int. J. Protective Struct.2010; 1(4): 507–541. [CrossRef]
  19. F. Zhu, L. Zhao, G. Lu, E. Gad. A numerical simulation of the blast impact of square metallic sandwich panels. Int. J. Impact Eng.2009; 36(5): 687–699. [CrossRef]
  20. J. Shen, G. Lu, Z. Wang, L. Zhao. Experiments on curved sandwich panels under blast loading. Int. J. Impact Eng.2010; 37(9): 960–970. [CrossRef]
  21. L. Jing, Z. Wang, L. Zhao. An approximate theoretical analysis for clamped cylindrical sandwich shells with metallic foam cores subjected to impulsive loading. Compos. Part B: Engineering 2014; 60: 150–157. [CrossRef]
  22. L. Jing, Z. Wang, L. Zhao. Dynamic response of cylindrical sandwich shells with metallic foam cores under blast loading—numerical simulations. Compos. Struct.2013; 99 : 213–223. [CrossRef]
  23. W. Chen, H. Hao. Experimental investigations and numerical simulations of multiarch double-layered panels under uniform impulsive loadings. Int. J. Impact Eng.2014; 63: 140–157. [CrossRef]
  24. K.P. Dharmasena, H.N.G. Wadley, Z. Xue, J.W. Hutchinson. Mechanical response of metallic honeycomb sandwich panel structures to high-intensity dynamic loading. Int. J. Impact Eng.2008; 35(9): 1063–1074. [CrossRef]
  25. Y. Yang, F. Tao. Dynamic response of the hybrid honeycomb sandwich panel with zero Poisson’s ratio under low-speed impact. Mechanics of Advanced Materials and Structures 2023; Pages 1-15.
  26. D. G. Winget, K. A. Marchand, E. B. Williamson. Analysis and Design of Critical Bridges Subjected to Blast Loads. Journal of Structural Engineering 2005; 131(8): 1243. [CrossRef]
  27. Vaziri, Zhenyu Xue, W. John. Performance and failure of metal sandwich plates subjected to shock loading. Journal of Mechanics of Materials and Structures 2007; 2(10): 1947-1963.
  28. F. Nan, W. Yang et al. Effect of structural parameters on mechanical properties of Pyramidal Kagome lattice material under impact loading. International Journal of Impact Engineering 2019; 132: 103313.
  29. G. Zhang, B. Wang, L. Ma, J. Xiong, L. Wu. Response of sandwich structures with pyramidal truss cores under the compression and impact loading. Composite Structures 2013; 100:451-463. [CrossRef]
  30. U. Kemerli, K. Kahveci. Conjugate forced convective heat transfer in a sandwich panel with a Kagome truss core: The effects of strut length and diameter. Applied Thermal Engineering 2020; 167: 114794. [CrossRef]
  31. R. M. Varghese, K. M. Varghese. Comparative study on the blast load response of woven and lattice core metallic sandwich panels. Materials Today: Proceedings 2022; 65:1343-1347. [CrossRef]
  32. H.N.G. Wadley, N.A. Fleck, A.G. Evans. Fabrication and structural performance of periodic cellular metal sandwich structures. Composites Science and Technology 2003;63(16): 2331– 2343. [CrossRef]
  33. 33. G.R. Johnson, and W.H. Cook. A Constitutive Model and Data for Metals Subjected to Large Strains, High Strain Rates, and High Temperatures. Proceedings 7th International Symposium on Ballistics, The Hague, 19-21 April 1983, 541-547.
  34. G.R. Johnson, W.H. Cook. Fracture Characteristics of Three Metals Subjected to Various Strains, Strain Rates, Temperatures and Pressures. Engineering Fracture Mechanics 1985；21(1): 31-48. [CrossRef]
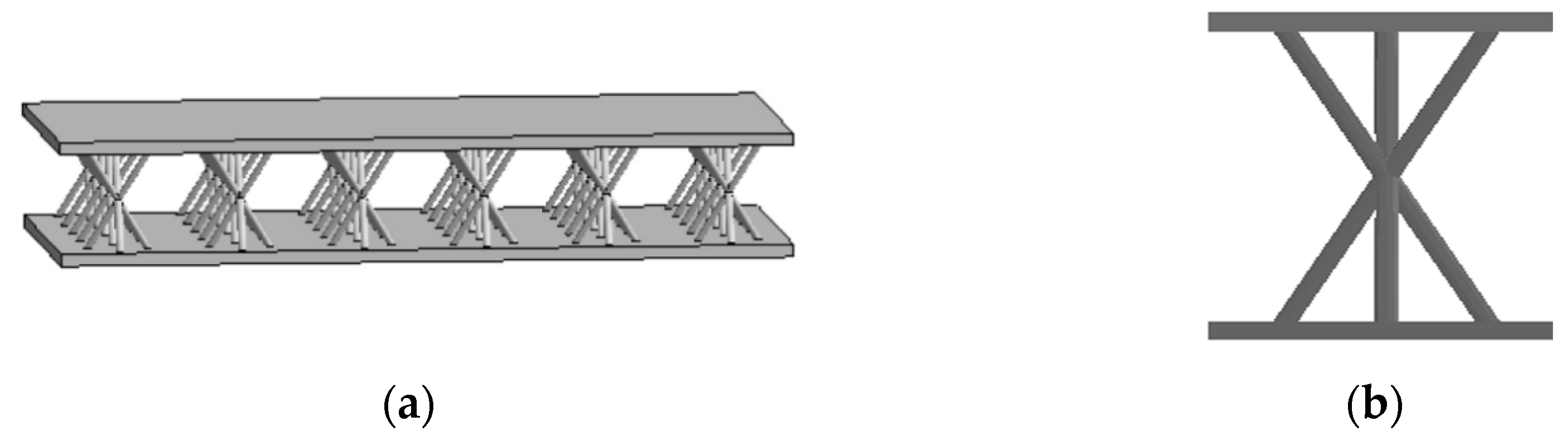
Preprints 92223 g001
Figure 1. 3D-Kagome sandwich structure: (a) 3D-Kagome truss core sandwich panel; (b) Single cell.
Figure 1. 3D-Kagome sandwich structure: (a) 3D-Kagome truss core sandwich panel; (b) Single cell.
Preprints 92223 g001
Preprints 92223 g002
Figure 2. Truss core of single cell.
Figure 2. Truss core of single cell.
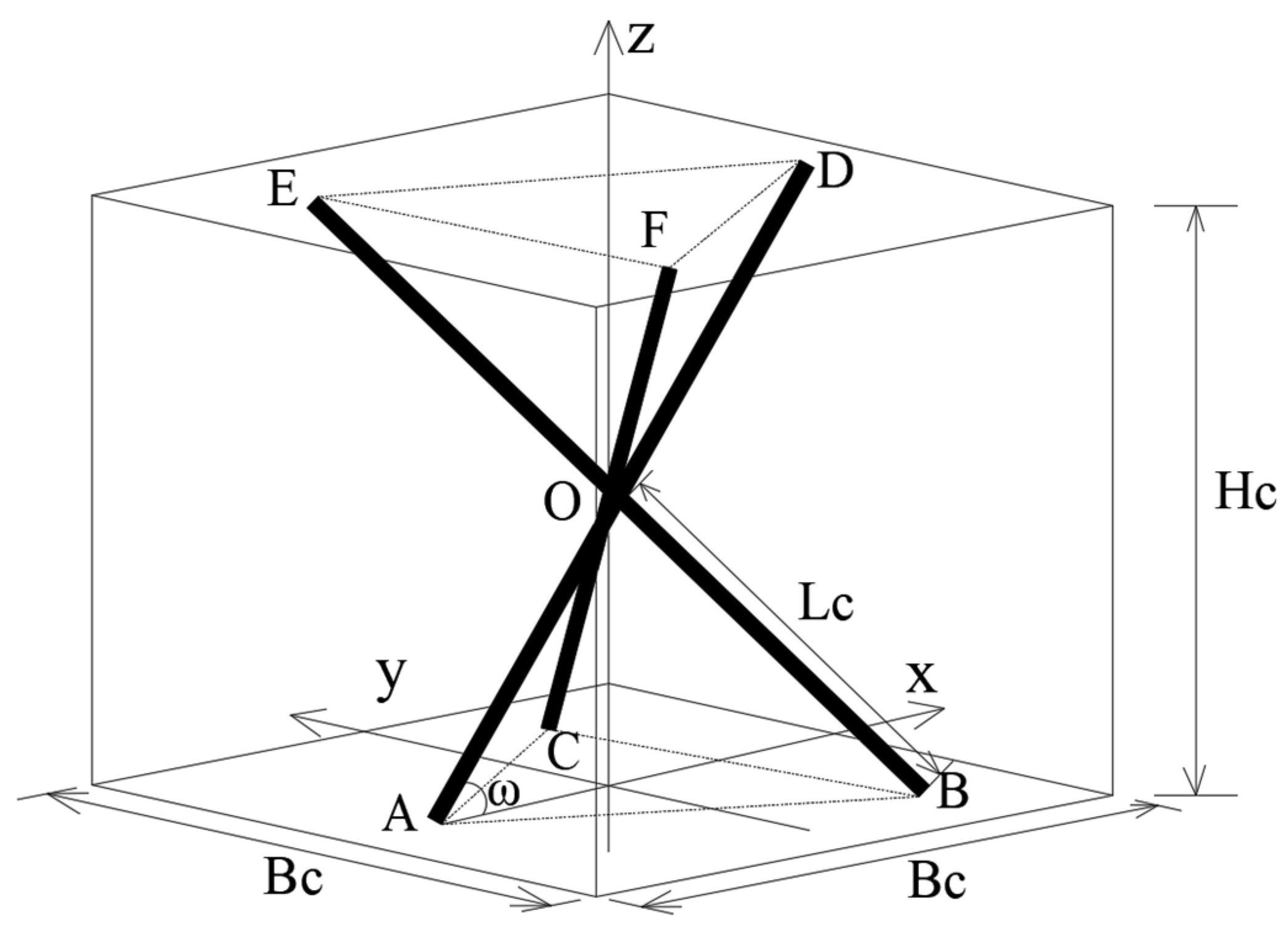
Preprints 92223 g002
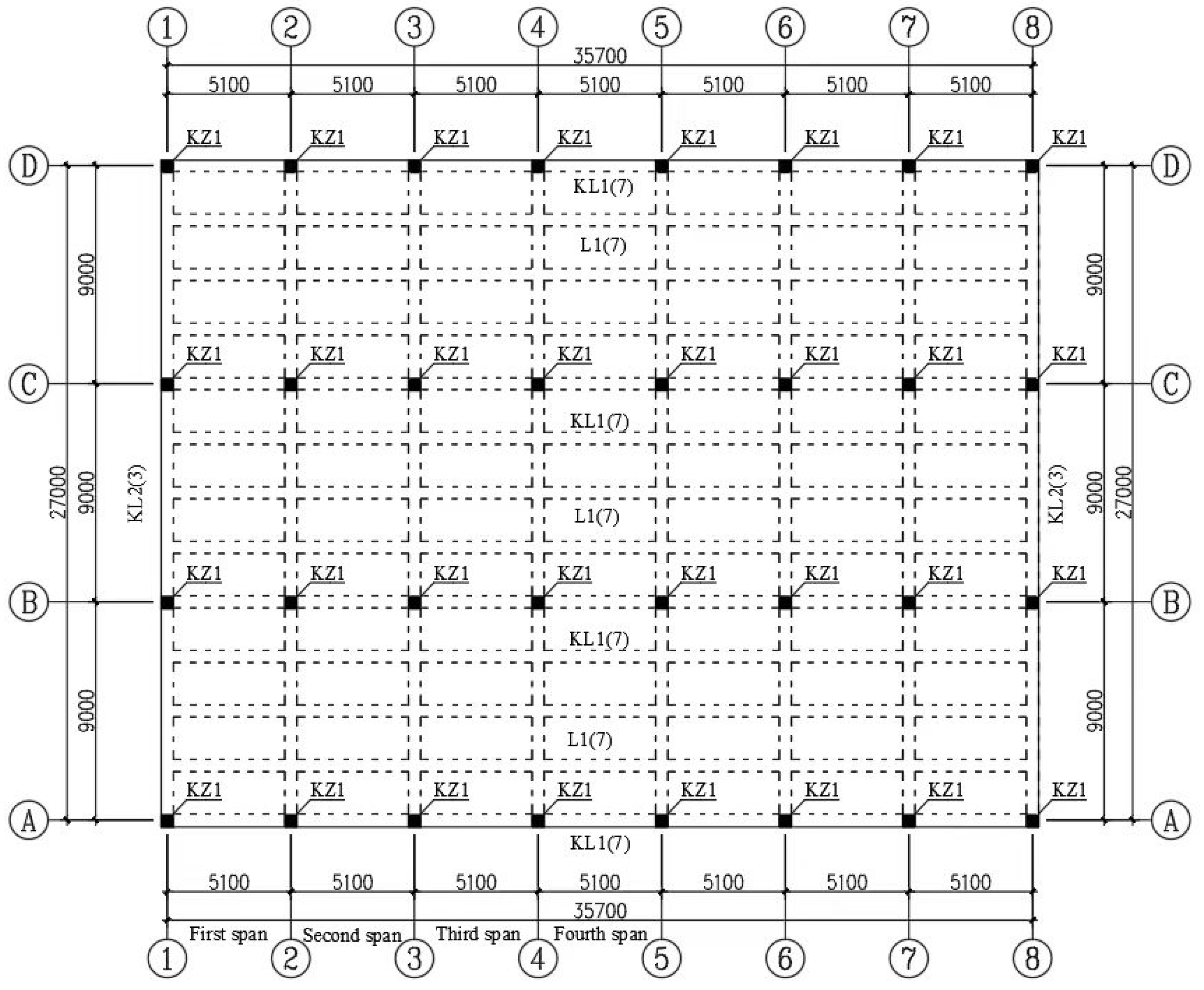
Preprints 92223 g003
Figure 3. Plan of steel petrochemical control structure.
Figure 3. Plan of steel petrochemical control structure.
Preprints 92223 g003
Preprints 92223 g004
Figure 4. Structural model of petrochemical control room.
Figure 4. Structural model of petrochemical control room.
Preprints 92223 g004
Preprints 92223 g005
Figure 5. Nodes between column and main beam.
Figure 5. Nodes between column and main beam.
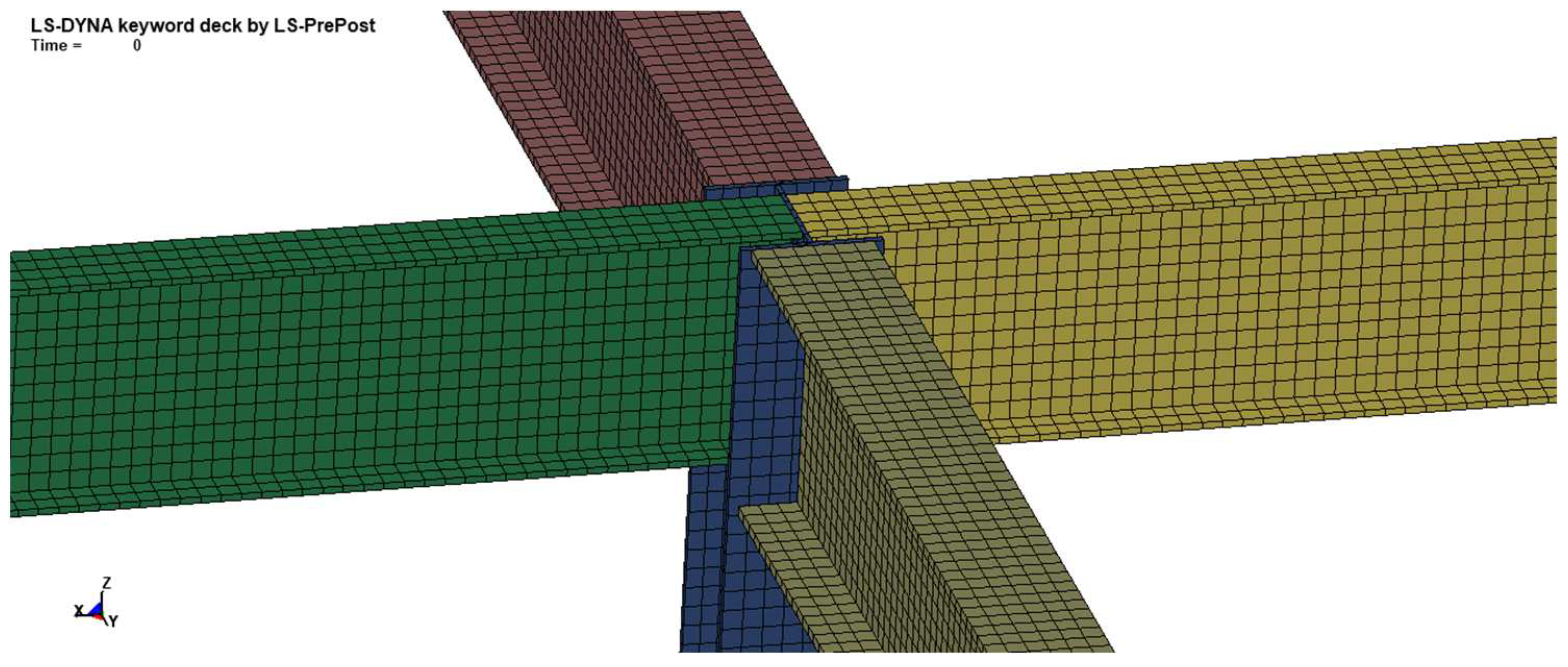
Preprints 92223 g005
Preprints 92223 g006
Figure 6. Nodes between main beam and secondary beam.
Figure 6. Nodes between main beam and secondary beam.
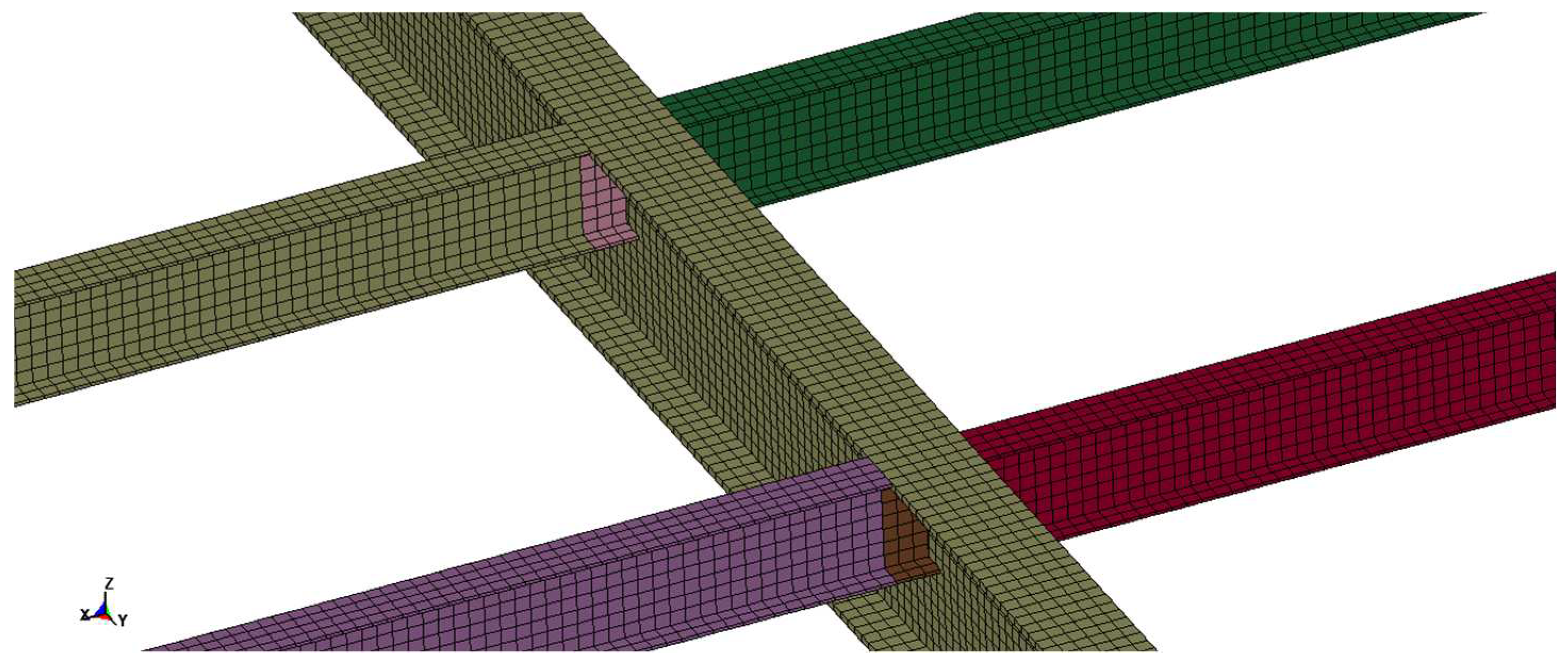
Preprints 92223 g006
Preprints 92223 g007
Figure 7. Quarter-scale model of a 3Daome truss core sandwich blast-resistant wall.
Figure 7. Quarter-scale model of a 3Daome truss core sandwich blast-resistant wall.
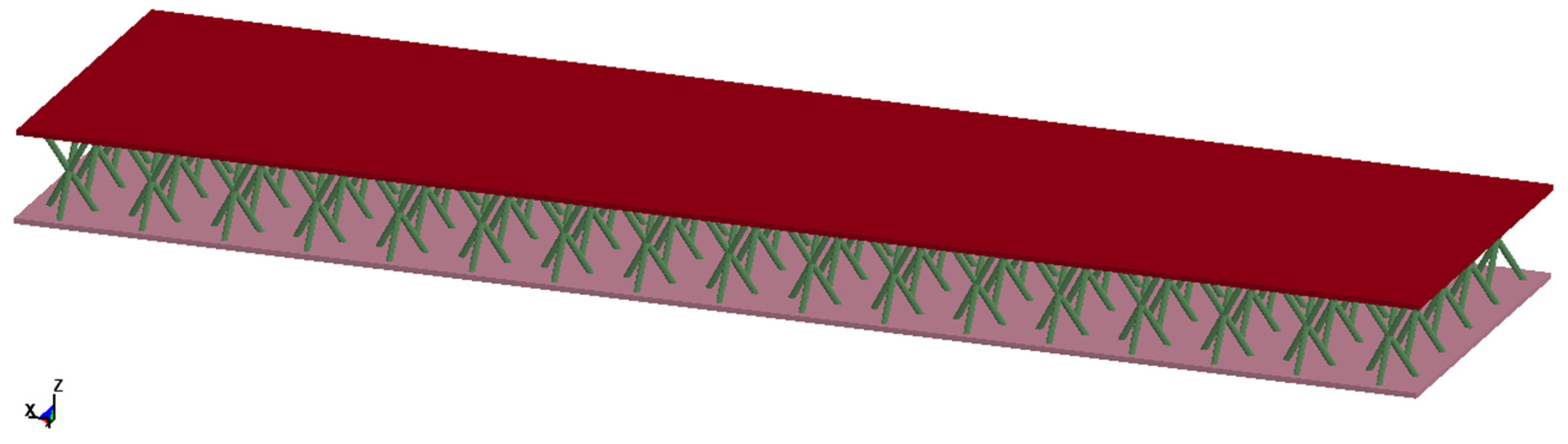
Preprints 92223 g007
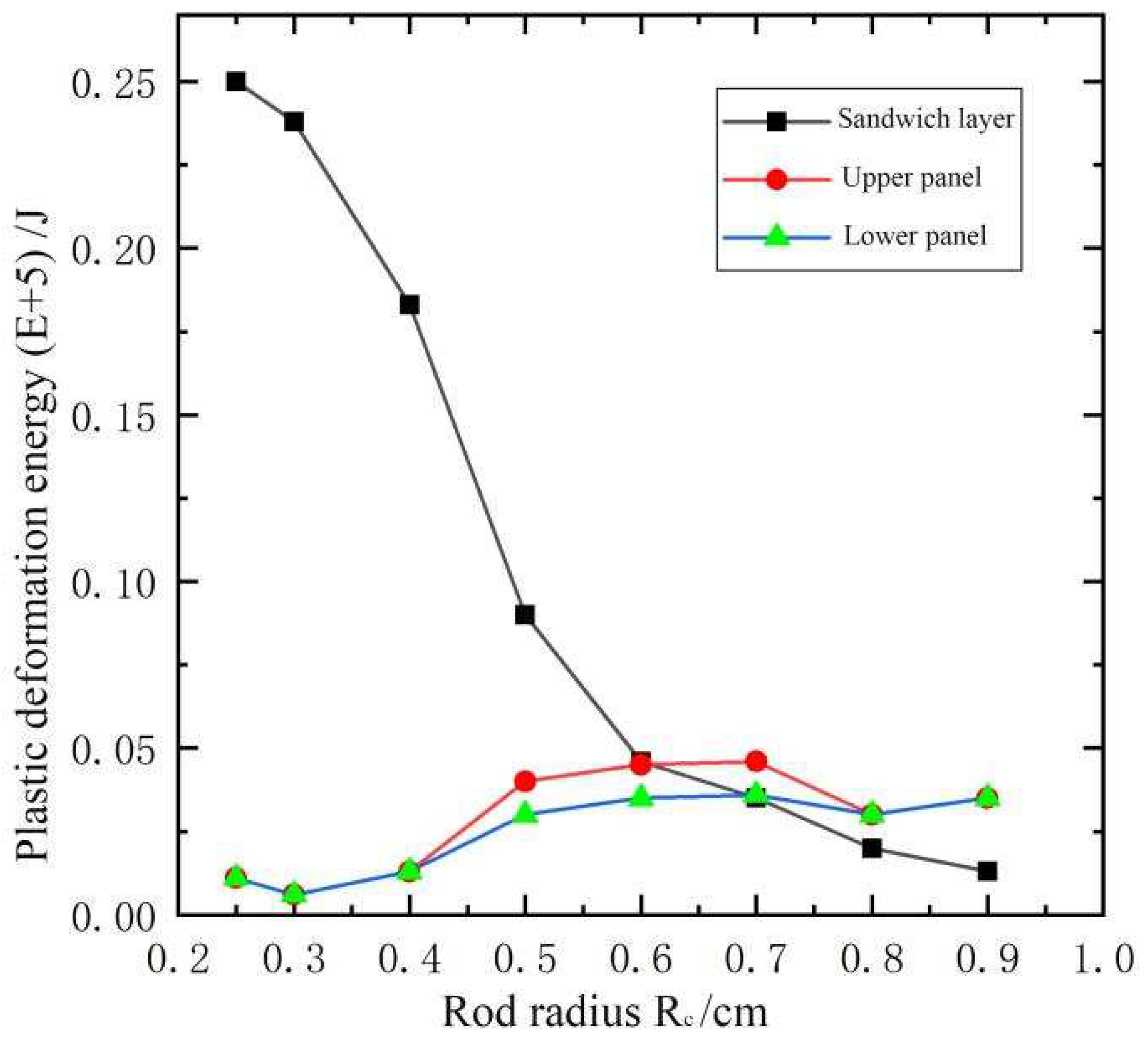
Preprints 92223 g008
Figure 8. Plastic deformation energy with different bar radii.
Figure 8. Plastic deformation energy with different bar radii.
Preprints 92223 g008
Preprints 92223 g009
Figure 9. ξ with different bar radii.
Figure 9. ξ with different bar radii.
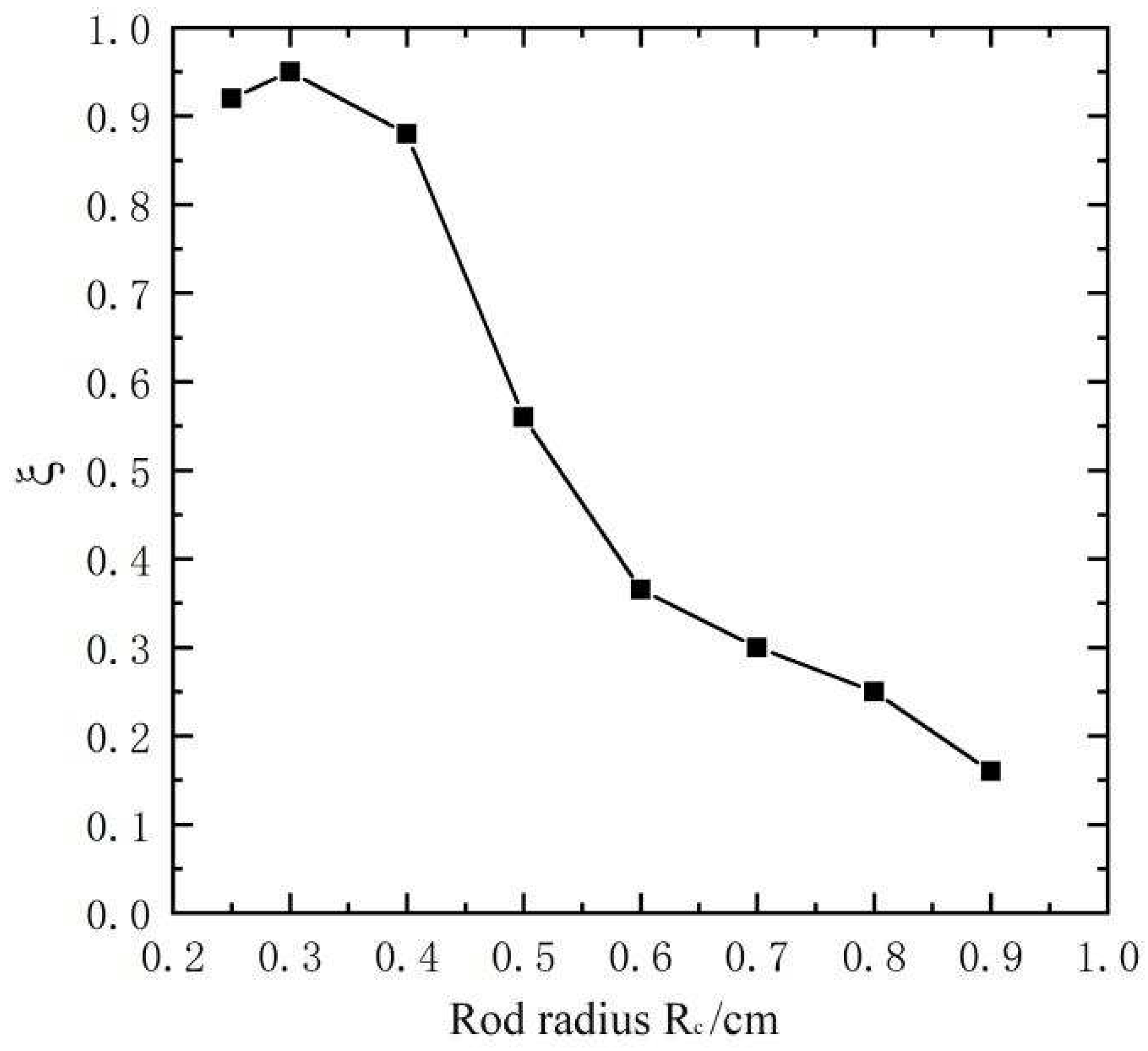
Preprints 92223 g009
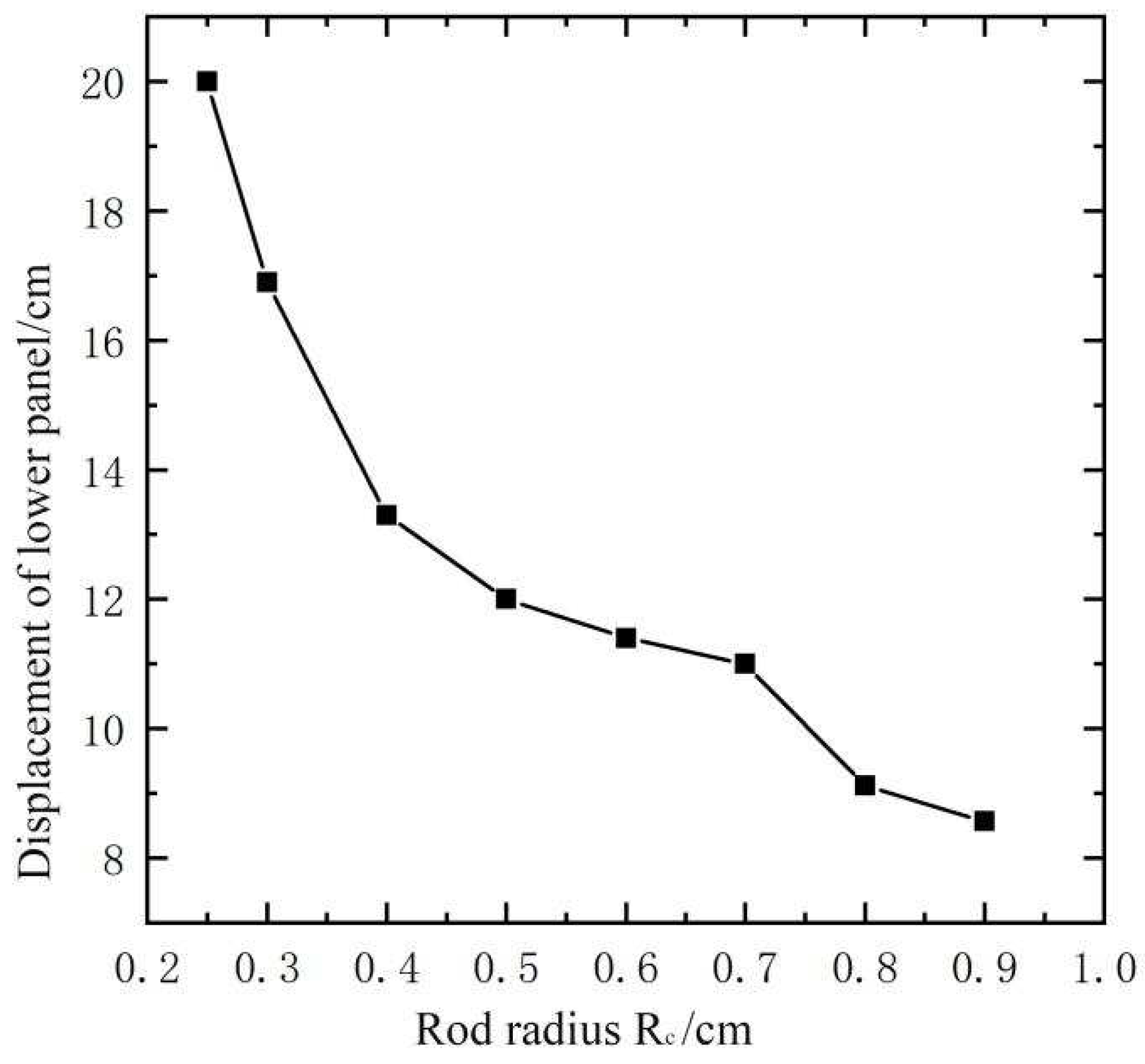
Preprints 92223 g010
Figure 10. Displacement variation of lower panel with different bar radii.
Figure 10. Displacement variation of lower panel with different bar radii.
Preprints 92223 g010
Preprints 92223 g011
Figure 11. Displacement of the sandwich wall along Z-axis with 0.9 cm radius of the truss core rod.
Figure 11. Displacement of the sandwich wall along Z-axis with 0.9 cm radius of the truss core rod.
Preprints 92223 g011
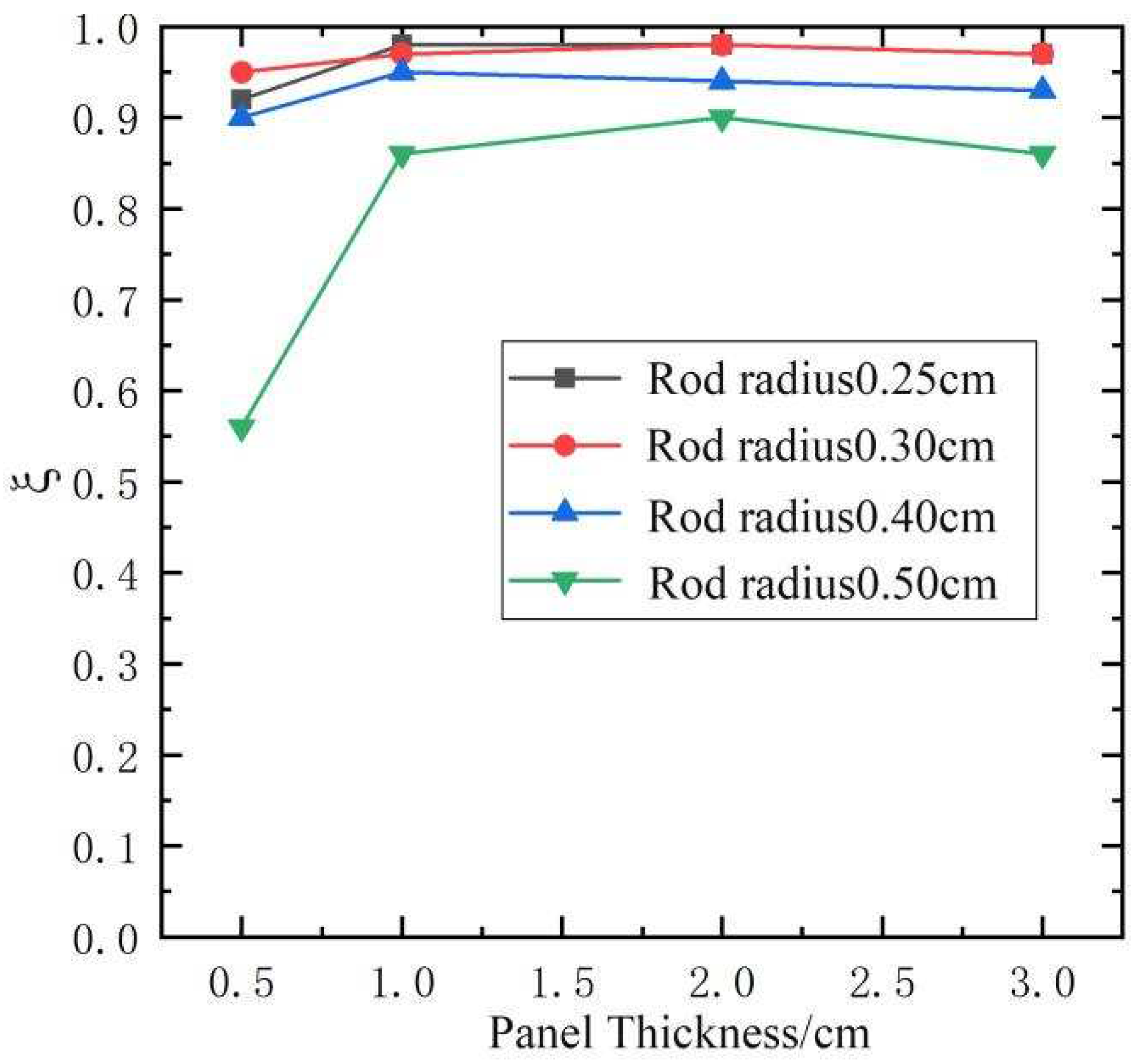
Preprints 92223 g012
Figure 12. Parameter ξ for different panel thickness.
Figure 12. Parameter ξ for different panel thickness.
Preprints 92223 g012
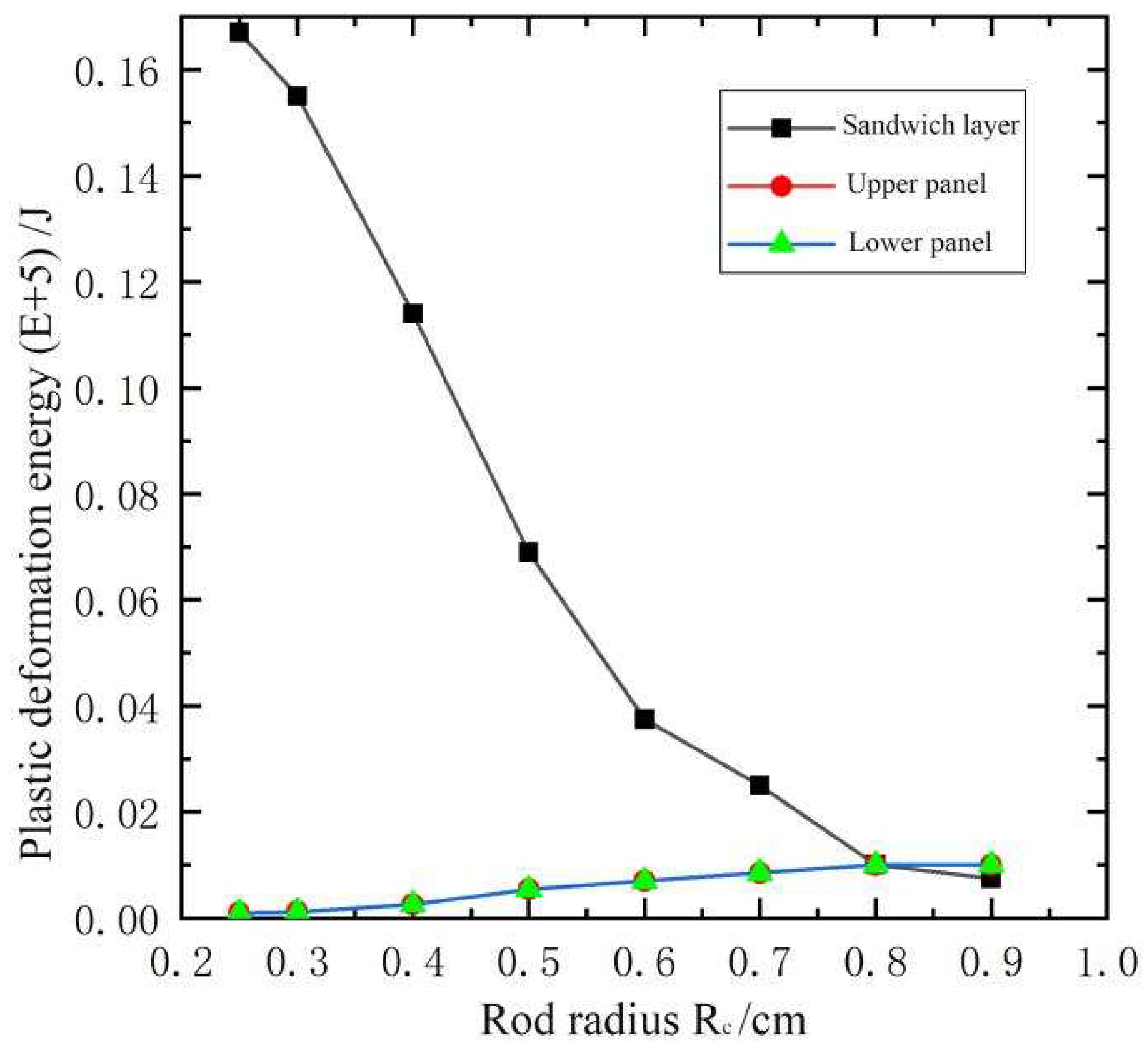
Preprints 92223 g013
Figure 13. Plastic deformation energy for different rod radius.
Figure 13. Plastic deformation energy for different rod radius.
Preprints 92223 g013
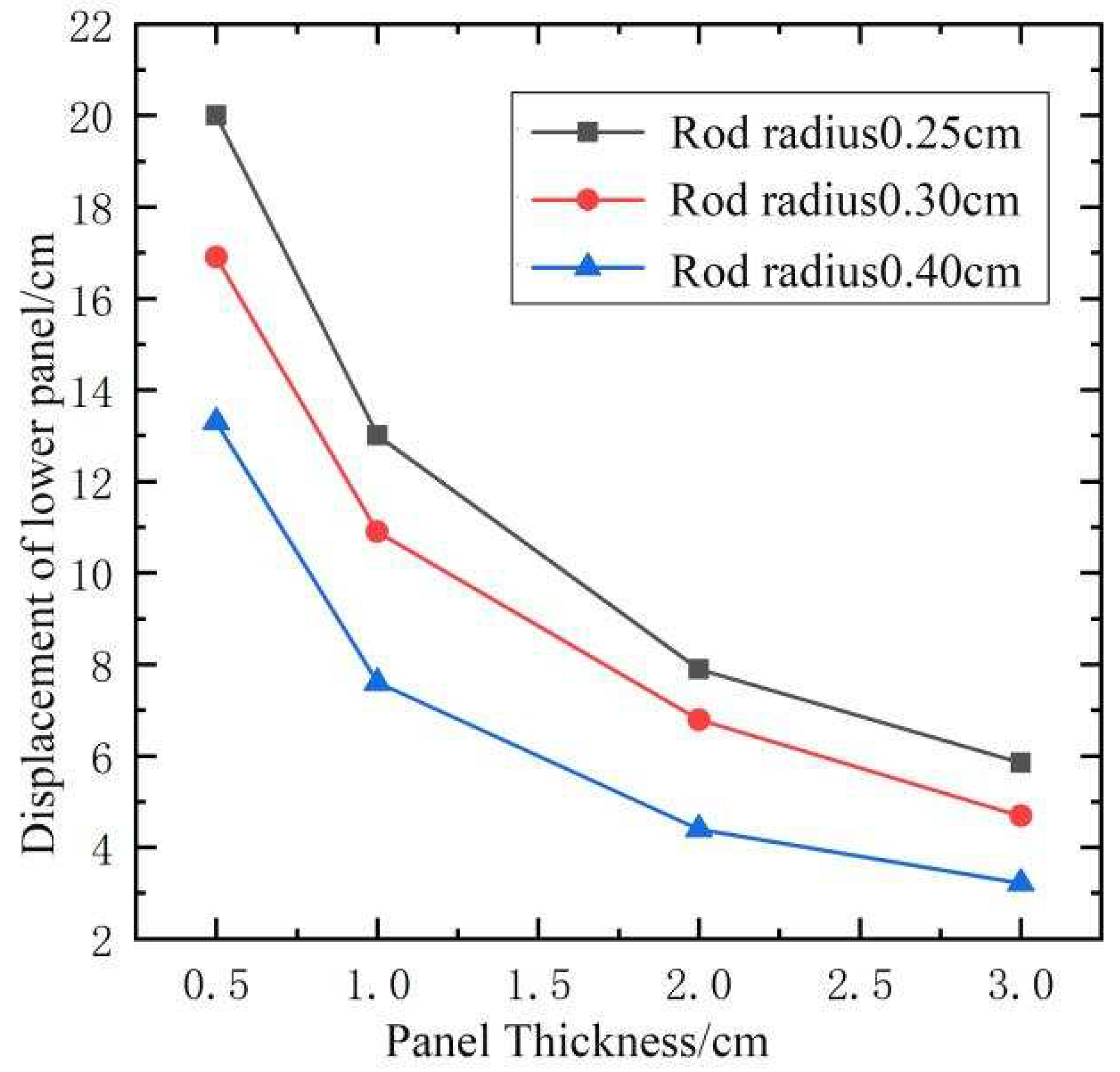
Preprints 92223 g014
Figure 14. Displacement curves of lower panel with different panel thickness.
Figure 14. Displacement curves of lower panel with different panel thickness.
Preprints 92223 g014
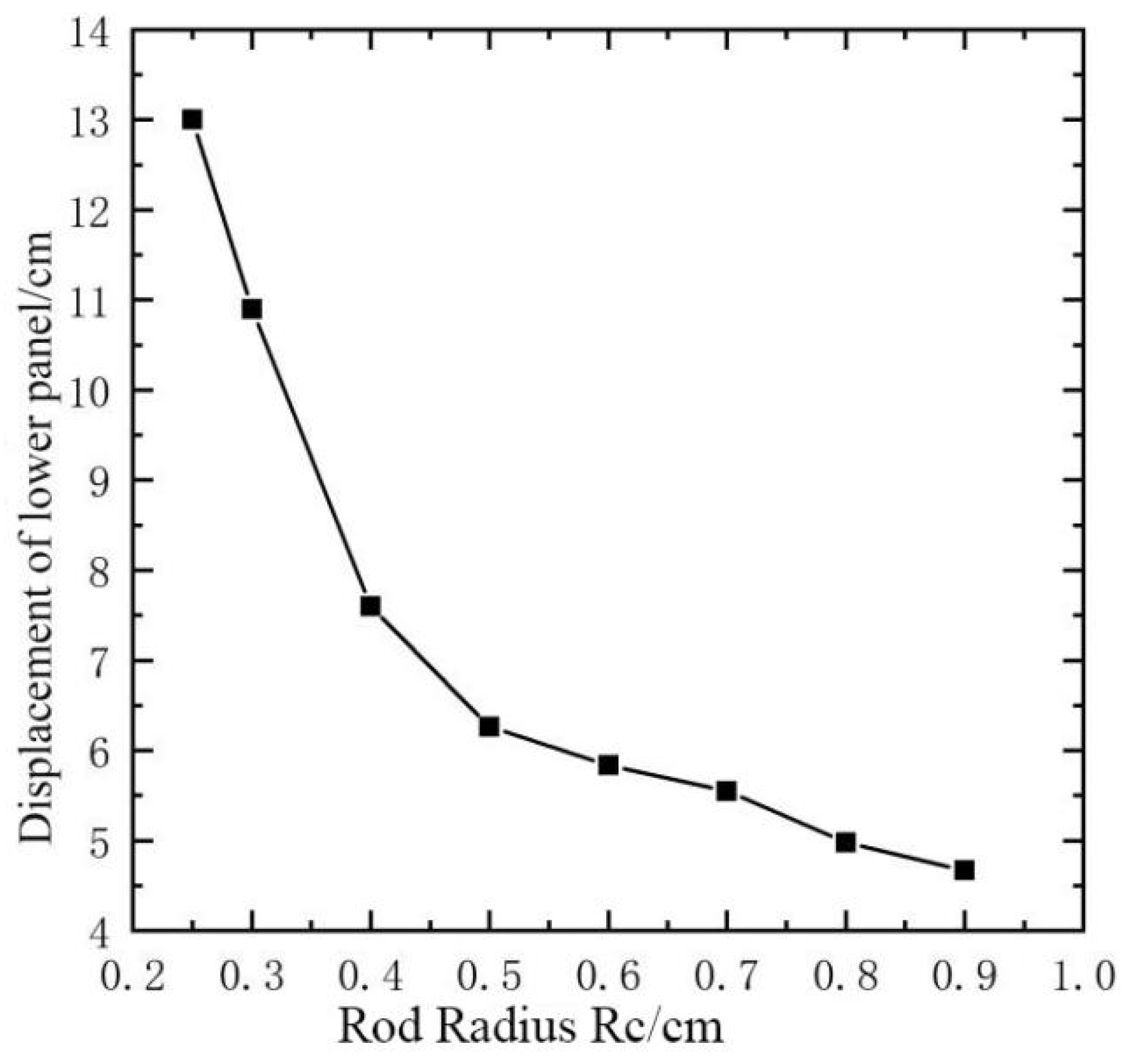
Preprints 92223 g015
Figure 15. Displacement curves of lower panel with different rod radius.
Figure 15. Displacement curves of lower panel with different rod radius.
Preprints 92223 g015
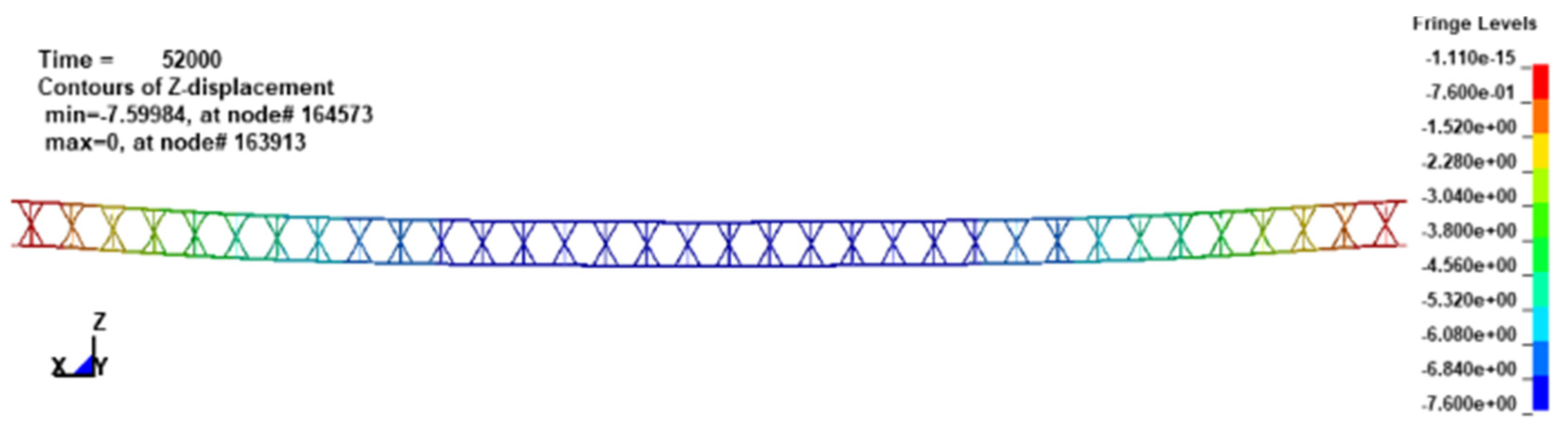
Preprints 92223 g016
Figure 16. Out of plan displacement of the sandwich blast-resistant wall with 0.4 mm radius of the core rod.
Figure 16. Out of plan displacement of the sandwich blast-resistant wall with 0.4 mm radius of the core rod.
Preprints 92223 g016
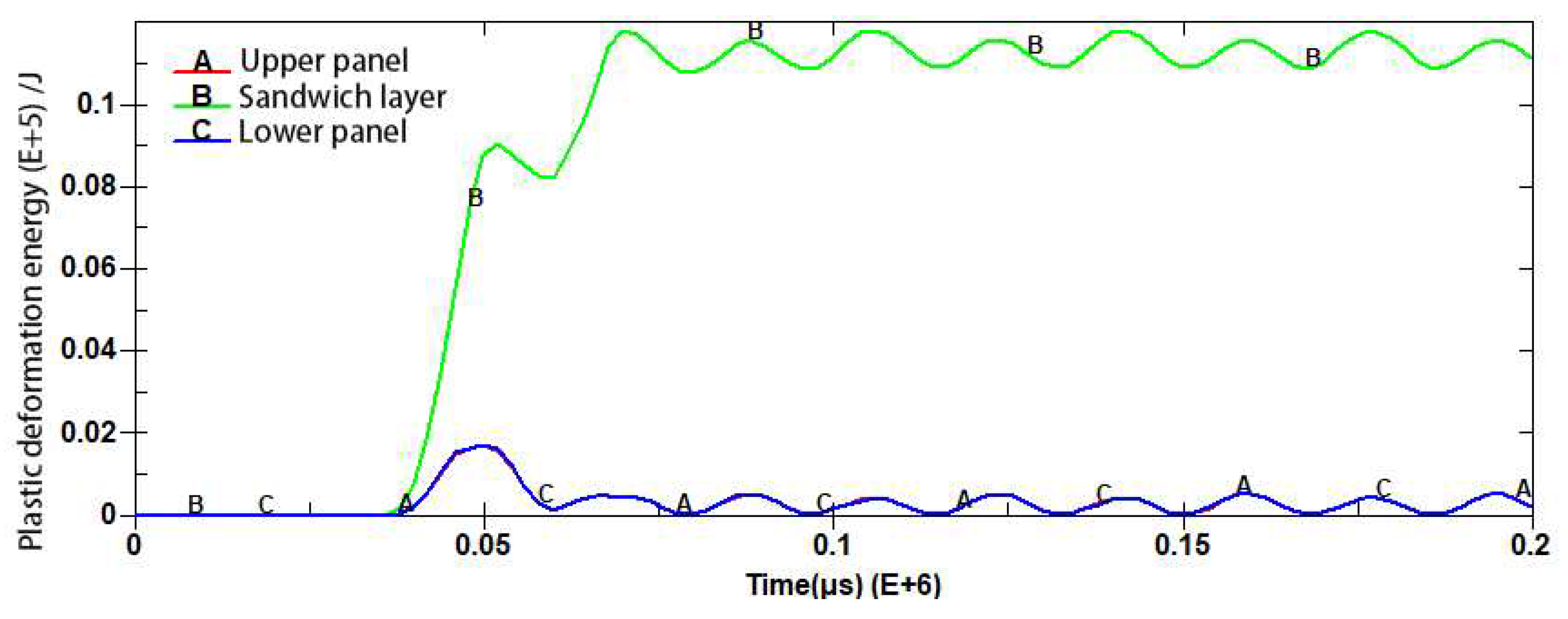
Preprints 92223 g017
Figure 17. Plastic deformation energy time curve with 0.4cm rod radius.
Figure 17. Plastic deformation energy time curve with 0.4cm rod radius.
Preprints 92223 g017
Preprints 92223 g018
Figure 18. Connection between sandwich panel blast-resistant wall and steel columns (top view).
Figure 18. Connection between sandwich panel blast-resistant wall and steel columns (top view).
Preprints 92223 g018
Preprints 92223 g019
Figure 19. petrochemical control structural model.
Figure 19. petrochemical control structural model.
Preprints 92223 g019
Preprints 92223 g020
Figure 20. sandwich blast-resistant walls number.
Figure 20. sandwich blast-resistant walls number.
Preprints 92223 g020
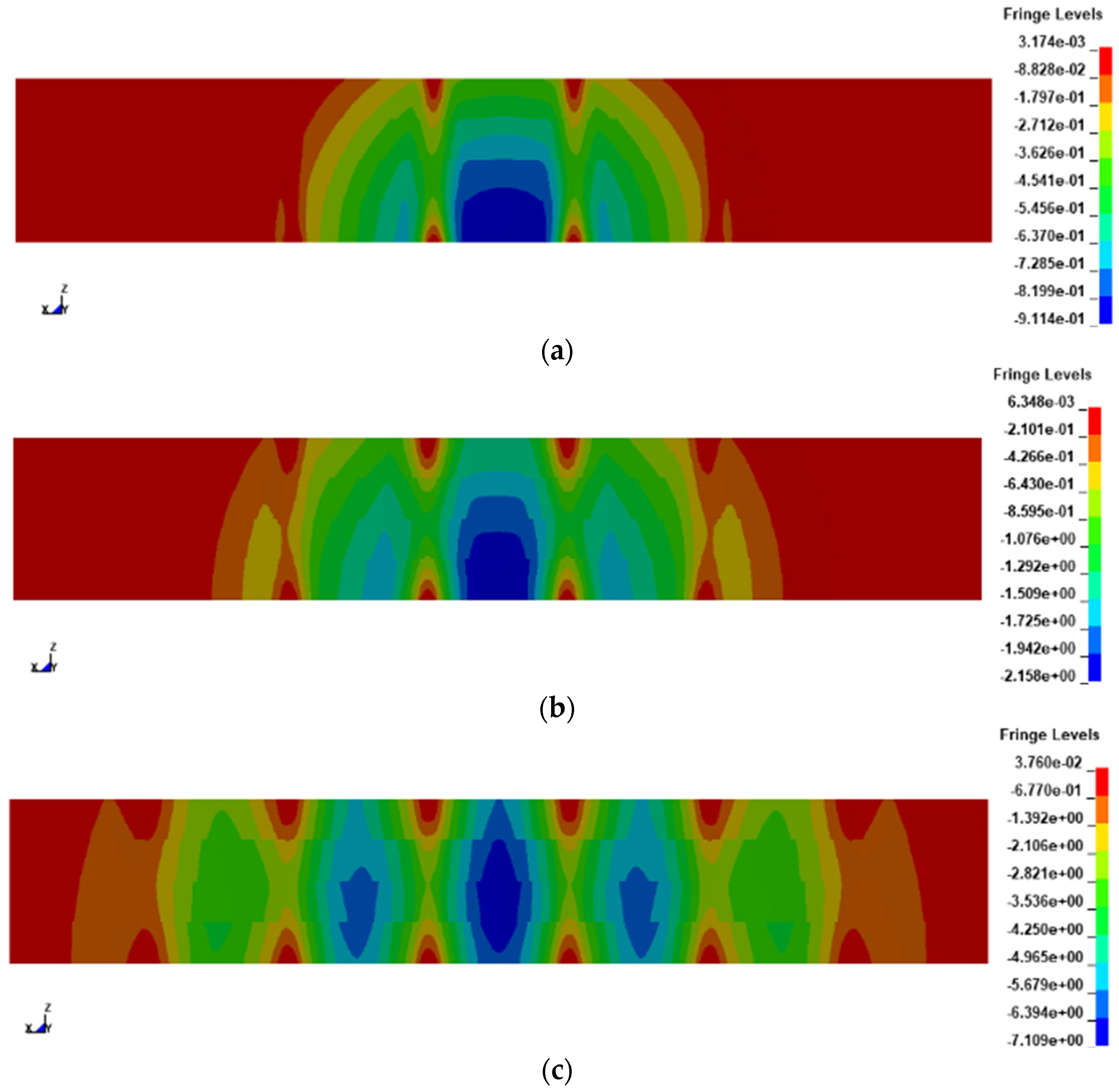
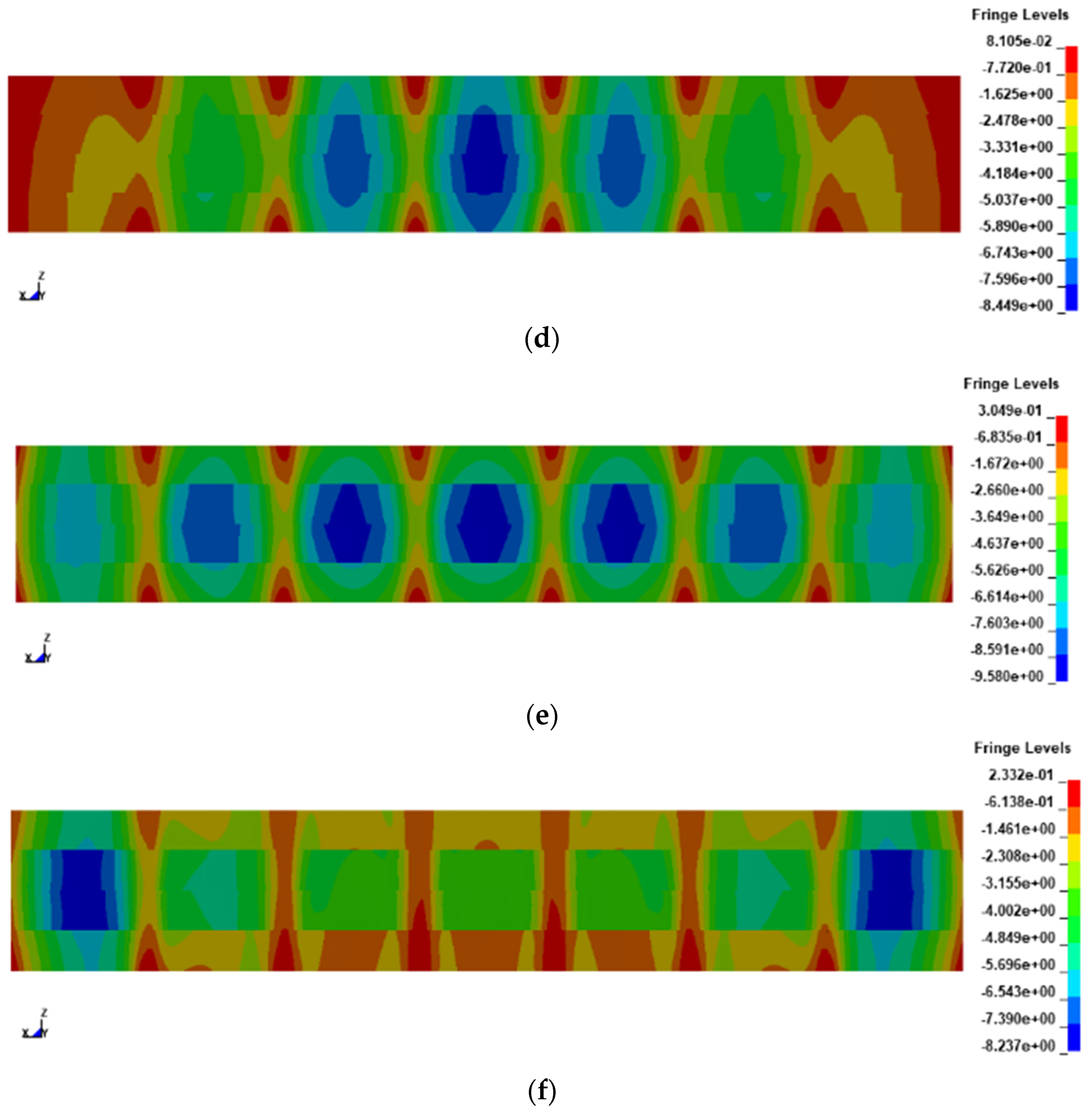
Preprints 92223 g021aPreprints 92223 g021b
Figure 21. Y-directional displacement clouds of the blast-resistant wall of the truss core sandwich panel at different moments (cm): (a) t=0.004s; (b) t=0.0046s; (c) t=0.05s; (d) t=0.054s; (e) t=0.062s; (f) t=0.07s.
Figure 21. Y-directional displacement clouds of the blast-resistant wall of the truss core sandwich panel at different moments (cm): (a) t=0.004s; (b) t=0.0046s; (c) t=0.05s; (d) t=0.054s; (e) t=0.062s; (f) t=0.07s.
Preprints 92223 g021aPreprints 92223 g021b
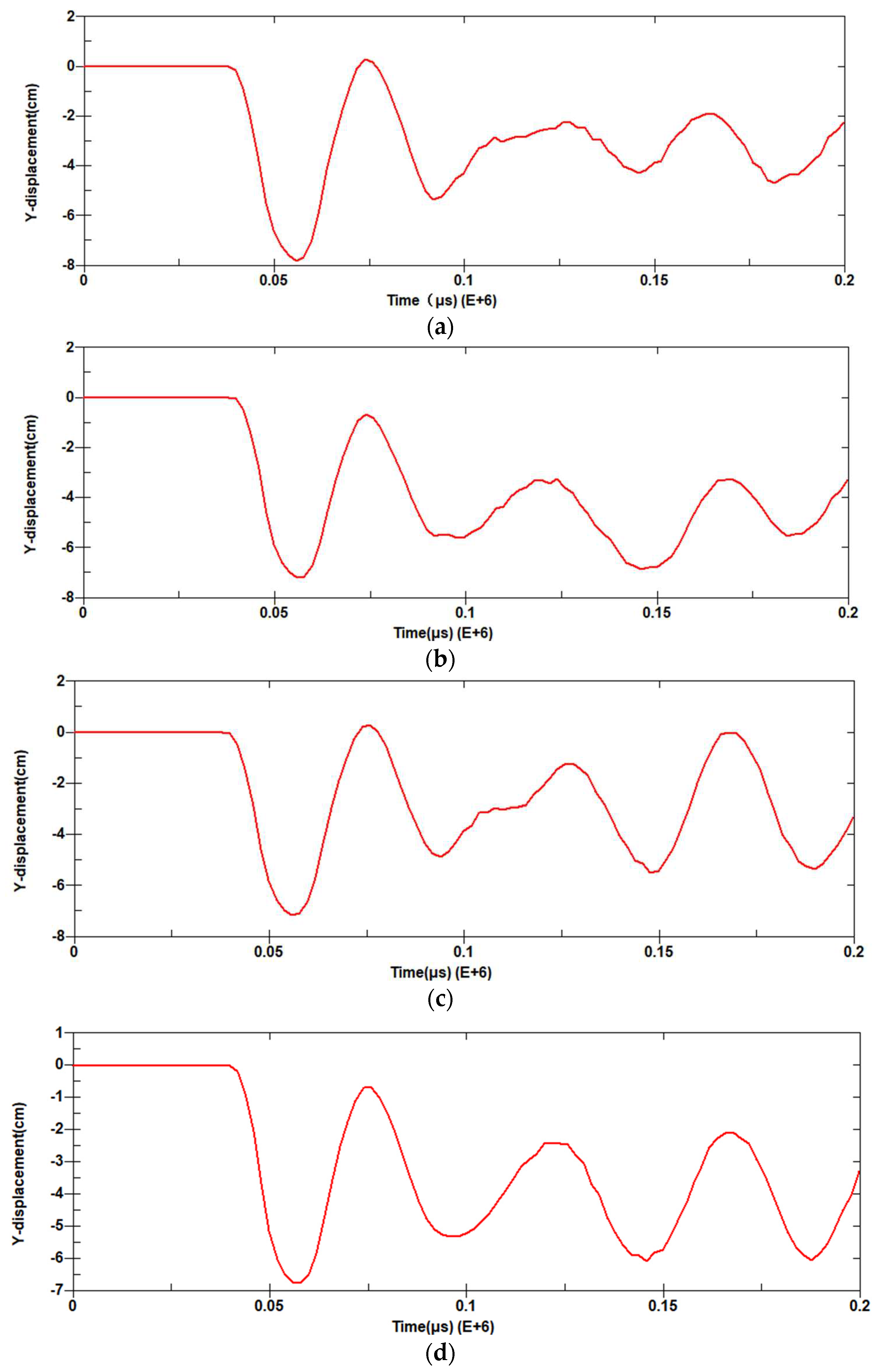
Preprints 92223 g022
Figure 22. Lower panel displacement response: (a) Lower panel displacement response of the center of KBQ4-2 wall; (b) Lower panel displacement response of the center of KBQ4-3 wall; (c) Lower panel displacement response of the center of KBQ3-2 wall; (d) Lower panel displacement response of the center of KBQ3-3 wall.
Figure 22. Lower panel displacement response: (a) Lower panel displacement response of the center of KBQ4-2 wall; (b) Lower panel displacement response of the center of KBQ4-3 wall; (c) Lower panel displacement response of the center of KBQ3-2 wall; (d) Lower panel displacement response of the center of KBQ3-3 wall.
Preprints 92223 g022
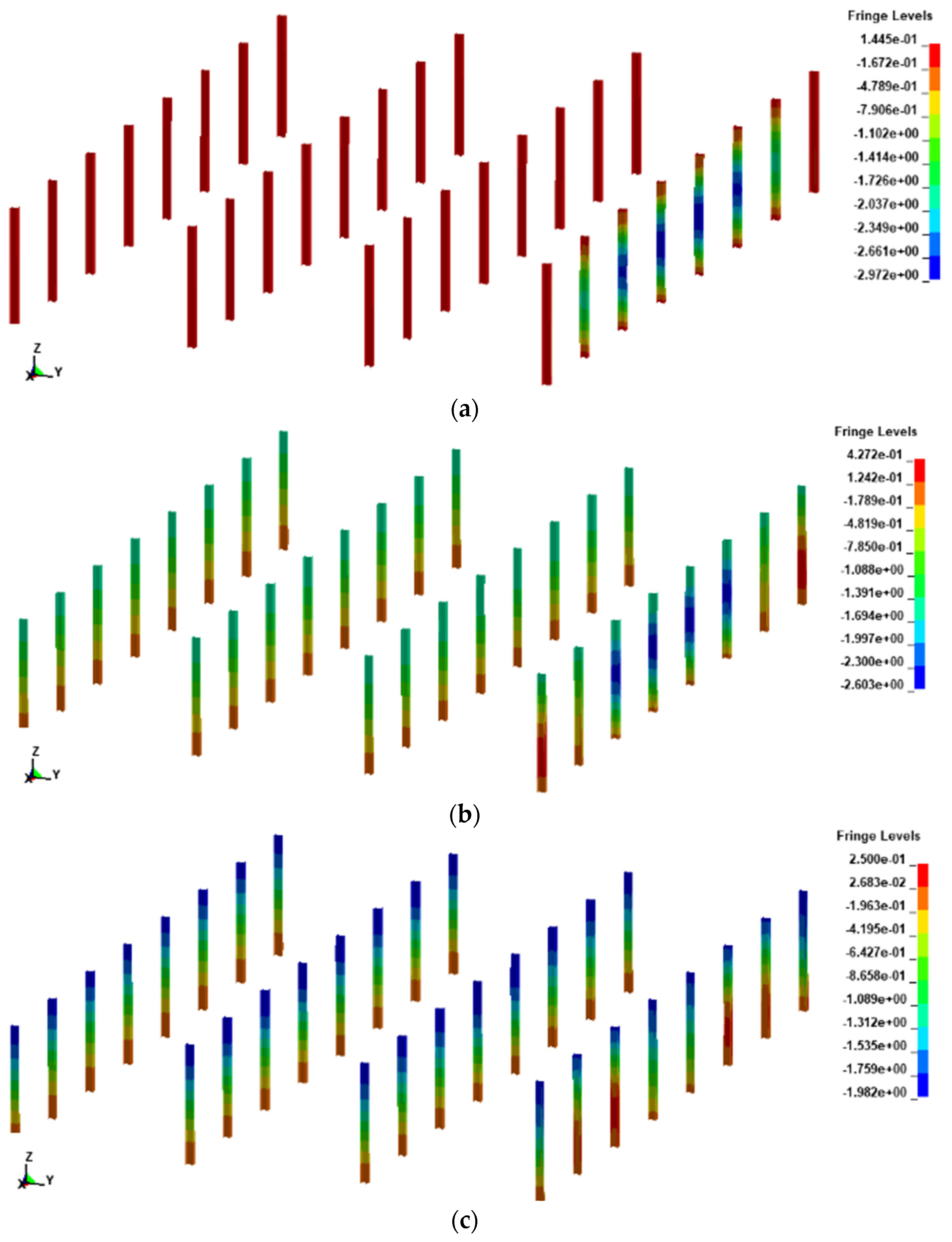
Preprints 92223 g023
Figure 23. Y-directional displacement clouds of frame columns at different time instants: (a) t=0.052s; (b) t=0.1s; (c) t=0.182s.
Figure 23. Y-directional displacement clouds of frame columns at different time instants: (a) t=0.052s; (b) t=0.1s; (c) t=0.182s.
Preprints 92223 g023
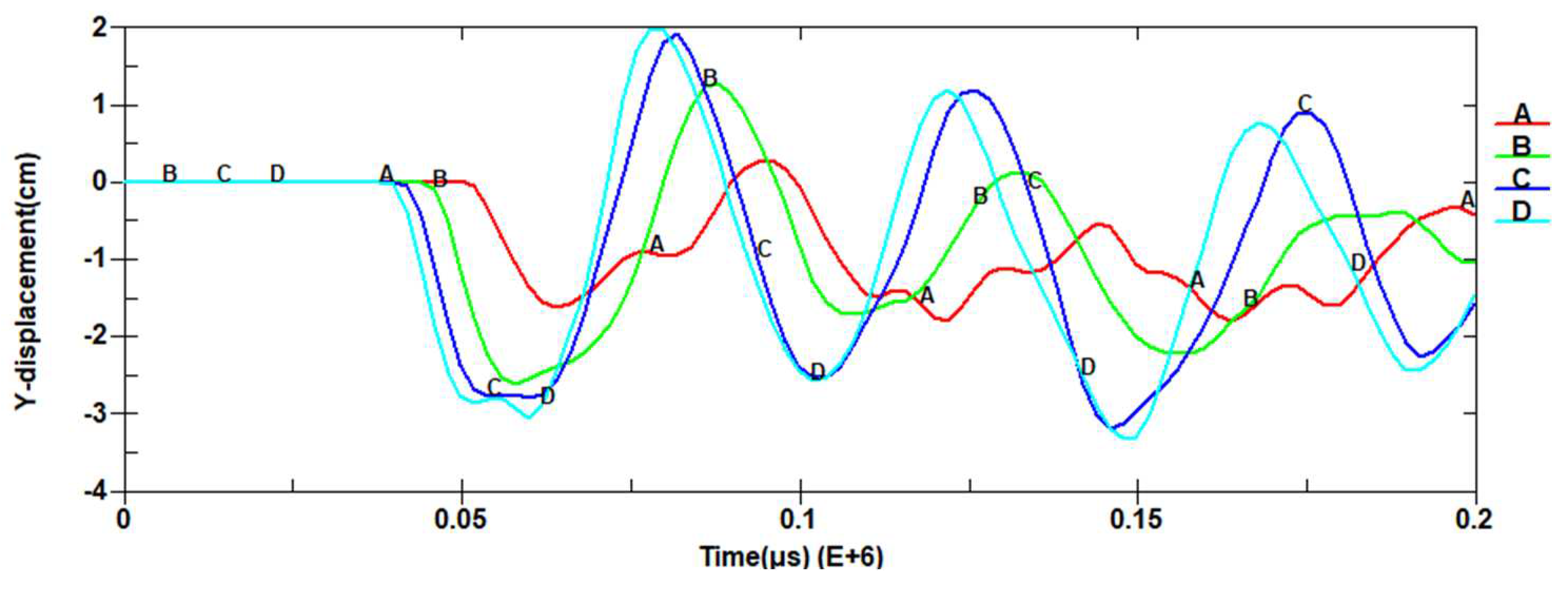
Preprints 92223 g024
Figure 24. Displacement curve of frame column of the control structure.
Figure 24. Displacement curve of frame column of the control structure.
Preprints 92223 g024
Table 1. Section sizes of the beam and column of the steel frame.
Table 1. Section sizes of the beam and column of the steel frame.
Type Symbol Cross-section size/mm
Column KZ1 350 × 350 × 12 × 19

Beam

Reinforced Concrete Slab		 KL1 700 × 300 × 13 × 24
KL2 700 × 300 × 13 × 24
L1
RCC Slab		 350 × 175 × 7 × 11
2000 × 1000 × 120
Table 2. J-C model parameters.
Table 2. J-C model parameters.
A B ε n C M
8E8 4.5E8 0.565 0.067 1.03
T h D 1 D 2 D 3 D 4
1793 0.0705 1.732 -0.54 -0.015
Table 3. GRUNEISEN state equation parameters.
Table 3. GRUNEISEN state equation parameters.
Cs S 1 S 2 S 3 E0
0.45 1.49 0.0 0.0 0.0
Table 4. Deformation limits of steel structural members.
Table 4. Deformation limits of steel structural members.
Structural elements θ
Main hot-rolled steel deck beam, secondary beam and purlin 6 ∘
Frame column, compression brace 1.5 ∘
Frame beam, tensile brace 2 ∘
Steel slab 6 ∘
Lattice beam 3 ∘
Cold-formed light steel panel (fixed end) 2 ∘
Cold-formed light steel panel (free end) 1.3 ∘
Secondary cold-formed light steel beam and purlin 3 ∘
Table 5. Center point displacement and bearing angle of sandwich blast-resistant walls.
Table 5. Center point displacement and bearing angle of sandwich blast-resistant walls.
Blast-resistant wall number Y - deformation ( Δ / m ) Corner ( θ / ∘ ) Blast-resistant wall number Y - deformation ( Δ / m ) Corner ( θ / ∘ )
KBQ1-1 0.055 1.24 KBQ3-1 0.063 1.42
KBQ1-2 0.058 1.30 KBQ3-2 0.071 1.59
KBQ1-3 0.060 1.35 KBQ3-3 0.067 1.50
KBQ1-4 0.054 1.21 KBQ3-4 0.061 1.37
KBQ2-1 0.055 1.24 KBQ4-1 0.070 1.57
KBQ2-2 0.062 1.39 KBQ4-2 0.079 1.77
KBQ2-3 0.064 1.44 KBQ4-3 0.073 1.64
KBQ2-4 0.052 1.17 KBQ4-4 0.068 1.53
Scope 0.052-0.064 1.17-1.44 0.061-0.079 1.37-1.77
Table 6. maximum deformation and bearing angle of the frame column.
Table 6. maximum deformation and bearing angle of the frame column.
Frame column number Y - directional   deformation ( Δ / m ) Corner ( θ / ∘ )
KZA 0.017 0.32
KZB 0.027 0.52
KZC 0.031 0.60
KZD 0.033 0.63
Scope 0.017-0.033 0.032-0.063
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated