SiaN-VO: Siamese Network for Visual Odometry

Despite advances in the reliability of sensory devices used by drones, the integrity of information from some devices is still considered an obstacle to ensuring successful flight plans. It is widely known that GNSS can suffer attacks or lose the signal from satellites, which can cause the drone to fail to complete its flight plan. In this context, we propose SiaN-VO, a Siamese network for visual odometry prediction. In our initial studies, this approach proved satisfactory for flights in static conditions (speed and height). Although interesting, these conditions do not reflect real flight conditions. In this sense, we have advanced our studies to propose the SiaN-VO, which fuses data from different sensors to enable displacement predictions to be made in dynamic flight conditions.

Keywords:

Subject: Engineering - Other

1. Introduction

Unmanned Aerial Vehicles (UAV) use the Global Navigation Satellite System (GNSS) signals as their primary location tool. Knowing the global position (latitude and longitude coordinates) allows the flight control system to be able to perform missions in outdoor environments. However, this system is susceptible to various types of attacks and also interruptions in signal reception [1,2].

During the aircraft’s flights, especially when the UAV is performing search and rescue (SAR) missions, it is important to estimate the position of the aircraft even if the GNSS information is not available [3]. Several approaches have been investigated, such as sensor fusion, Inertial Measurement Units (IMUs) and image-based inference. Image-based navigation use several strategies to estimate location: learning landmarks, optical flow, among other [4,5,6,7] Usually, these methods have high computational cost due to the use of consuming image processing pipelines.

We find in the literature works that propose image-based methods to estimate the displacement from a reference point (e.g., initial position) and avoid collision [8,9,10]. However, we did not find related work on using only Convolutional Neural Networks (CNN) and dataflow to estimate the global position of UAVs. The use of lightweight Artificial Neural Networks (ANN) models in image-based strategies can allow the decrease of the computational cost in the inference step.

Additionally, CNNs have achieved great success in computer vision pipelines, becoming the standard building block for image processing using machine learning techniques [11,12]. In comparison with traditional fully connected ANN layers, CNNs make better use of local spatial patterns observed in images, and require a much smaller number of parameters than the former [13].

In this regard, we present the Siamese Network for Visual Odometry (SiaN-VO) capable of inferring the displacement between a pair of sequential images captured by the drone. SiaN-VO is an evolved proposal of the method presented in a previous study [14]. The inferred displacement value is used in the haversine formula to calculate the new geographic coordinate (latitude and longitude) of the vehicle. We assume that the direction of flight and the height of the vehicle are obtained from sensors (e.g. compass and radio altimeter). This new method allows the inference of displacement to be carried out on flights with variations in altitude, overcoming the limitation of the previous proposal which required flights at a fixed altitude.

The remaining of this paper is organized as follows. Section 2, we describe the works found in the scientific literature close to the proposal. Section 3 details the proposed system. Section 4 details the methodology used to run the experiments, with information on the dataset, the training stage of the proposed method and the test stage. Section 5 details the results. Finally, Section 6 we present our conclusions and future work.

2. Scientific Literature

Numerous works in the literature highlight the importance of investigating methods and approaches for different vehicles (ground or air) to have location information without the dependency on external sources [8,9,10]. In general, these works investigate approaches that allow vehicles to move safely and reach their goal.

Visual approaches, such as visual odometry, have attracted attention for several reasons, among them price, accessibility, accuracy, and the independence on external signals, as in the case of GNSS-based methods [15,16]. Visual odometry is the process of estimating the motion of an agent (e.g., vehicle, human, and robot) using only the input from a single or multiple cameras [17].

There are works describing good results on merging visual odometry information with other information to achieve better accuracy in location inference [18,19]. The results show that merging information from visual odometry with other sensors can increase the accuracy of the positioning and movement information. Visual odometry commonly uses an important concept called optical flow.

Optical flow has been used to detect the motion of objects and scenery to help to autonomously drive vehicles and avoid collisions [20]. An example of this scenario can be seen in [21], where the proposed method (named LiteFlowNet2) is evaluated on datasets from different contexts. The MPI Sintel dataset is a dataset derived from the open source 3D animation short film, Sintel. In this setting the method receives a pair of sequential images and its output is a segmented image of the regions occupied by the characters’ movements in the time interval between the images received as input. Another dataset used is KITTI [20,22], which is a set of images captured by a car on urban routes. In this dataset, the method is evaluated for the goal of detecting the surrounding scenery in motion.

One can observe in the literature works that use the concepts above to estimate the movement of unmanned aerial vehicles [23,24]. The proposed methods can be used in outdoor and indoor environments.

However, it is common for navigation systems to use geographic coordinate information to manage UAV flight. Considering this context, we were not able to find works with the objective of inferring the geographic coordinate of UAVs during flight.

3. Siamese Network for Visual Odometry (SiaN-VO)

In this section, we describe the proposed new ANN model and its training procedure. It is important to emphasize that the proposed method presents the evolution of previously published work and the overcoming of the limitation on flight dynamics.

3.1. Network Architecture

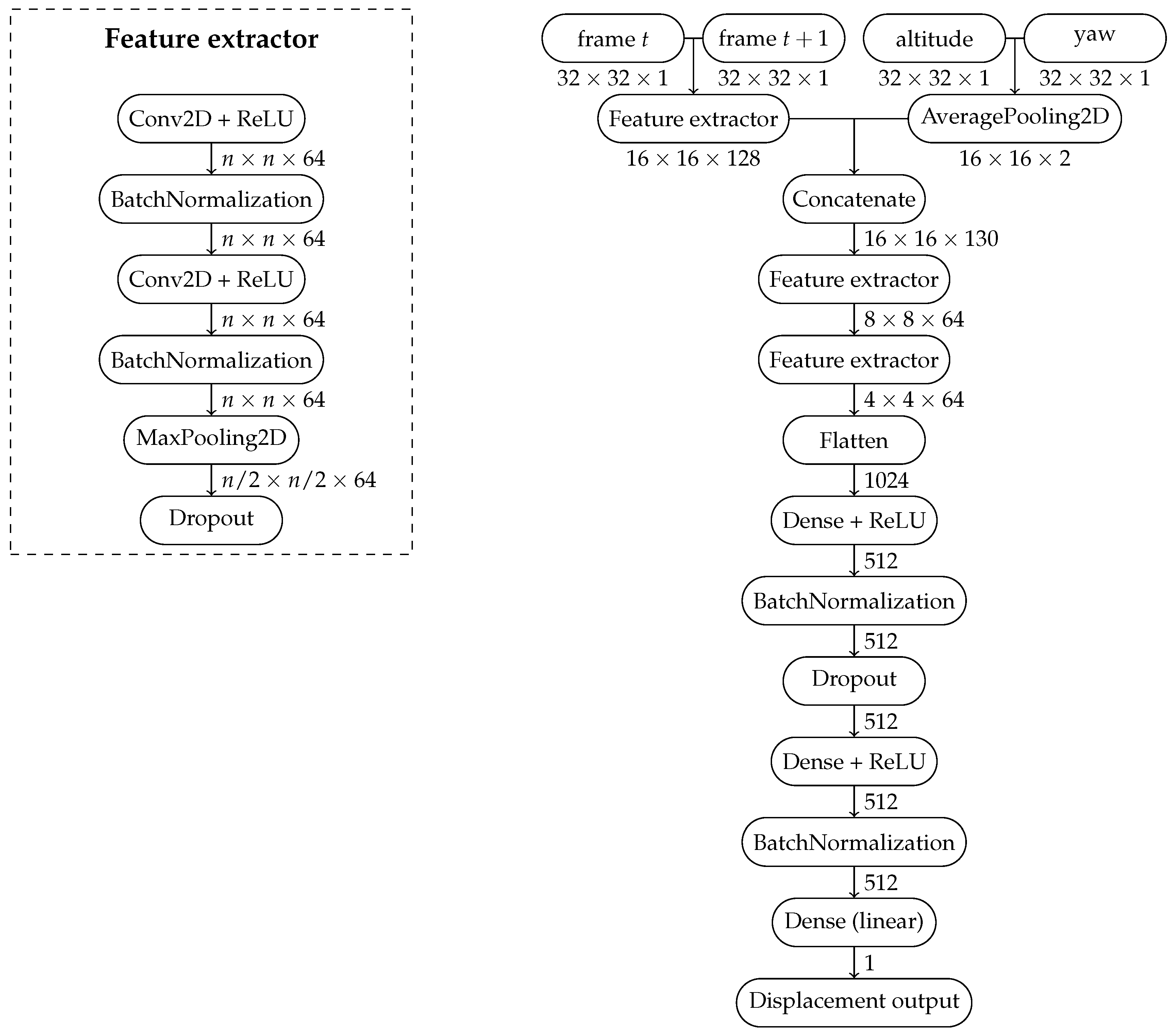
The proposed neural network model must be able to receive two images and two other matrices as input. One of them must contain the height value, while the other matrix must contain data from the yaw sensor1. The matrices have the same dimensions as the images and their values are repeated in all the cells. The transformation of the unit values into matrices with the value repeated in all the cells aims to provide stimulation similar to that of the images. This prevents the height and yaw data stimuli from being ignored because they are weak stimuli compared to the number of values in the image pair.

Pixel values are normalized between 0 and 1 for the image pairs. Yaw is also normalized between 0 and 1, where 0 represents where

0.5

means magnetic north, 0 means

- 180

degrees, and 1, 180 degrees. Altitude input that the aircraft flies with maximum height h from the ground. So, we divide the input by h so its maximum value is also 1.

Our network can be decomposed in two parts:

In the first part, we have a Siamese network, where the model receives a pair of images taken at consecutive time steps, and pass these images thorough identical neural network layers and weights. We chose the such a design assuming that the images can be processed independently. The neural network can find useful coarse patterns in them, like edges, before joining both images. Parallel to the Siamese network, there is an AveragePooling step that will adjust the dimensions of the height and yaw matrices to the same dimensions as the feature maps resulting from the Siamese network.
The results of the Siamese network and AveragePooling are concatenated, effectively overlaying the image maps and the two complementary data matrices. The concatenated feature maps then pass through a normal CNN pipeline, ending in a prediction head containing three fully connected layers, the last of which has only a single output — the displacement output.

During the search of the best hyperparameters for the neural network, we find that larger filter sizes work best for our problem, and we ultimately employ

7 \times 7

filters throughout the network. Apart from the filter size, our design choices took inspiration from the VGGNet architecture [25]: at every new set of convolutional layers we double the number of filters, as well as reducing by half the spatial dimensions of the image maps by means of applying MaxPooling layers with kernel size of

2 \times 2

. In summary, our model is composed by 6 convolutional layers (2 layers in the Siamese network and 4 sequential convolutional layers) and 3 fully connected layers. Dropout layers are set in 20%. In total, the neural network is 9 layers deep. The detailed architecture can be seen at Figure 1. It is important to note that the Siamese network is encapsulated in the figure within the “Feature extractor” element.

Once the model is to be employed in a small unmanned aircraft, computational power and storage are important restrictions. With this in mind, we design our neural network to receive gray-scale images of dimensions

32 \times 32

. The use of gray-scale images should suffice for the task of displacement prediction, once the color information transmitted by the red, green and blue channels should not give any significant insights about the movement of the vehicle. We would point out that we have reduced the size of the images used compared to the method proposed previously, allowing for a less computationally expensive execution.

4. Methodology for the experiments

In this section we will describe the dataset used and the methodology employed in the training and testing stages to evaluate SiaN-VO.

4.1. Dataset

In order to develop a large-scale simulated dataset to the task of UAV displacement estimation, we leverage the capabilities of AirSim [26], which is an open-source simulator for autonomous vehicles, including self-driving cars and drones.

We simulated drone flying in three different scenarios: a mountainous arctic region (mountains), a tropical forest (forest) and a city with green area (downtown). These scenarios include artifacts like lakes, rivers, different sizes of streets, buildings and vegetation. Besides the inherent heterogeneity of these choices of maps, we also varied the weather conditions, adding dust, mist and rain, creating a diversified range of settings. This variability in the scenarios are important if we want the machine learning model trained on this data to be able to generalize well to scenes never seen before, which is paramount once we employ these models in real-world applications. We also vary the flight dynamics, characteristics such as: height, acceleration, direction and environment. Figure 2 shows an example of the images in the dataset.

Table 1 shows details of the flights simulated in AirSim. The length of the flights varies, as do their maximum and minimum heights. It is important to note that the “map” column refers to the region in which the flight took place. So the environment may be forest, but in regions other than forest. It is important to note that in some cases the number of flights is less than the standard 50 flights. This is because the map we used was smaller and we didn’t want to use it to exhaustion.

The images taken from the drone have resolution of 720x480 pixels. Even though most applications may need smaller resolution, the operation of resizing in the data pipeline is very cheap, and on the plus side, the choice of a large resolution gives the user a choice to apply operations of data-augmentation, like random-cropping, that need an image larger than the input of the network. The use of data-augmentation operations in the preprocessing step can greatly increase the generalization ability of the models trained, as well as virtually increasing the dataset size.

The images are taken from a camera mounted under the vehicle, pointing vertically to the ground. In this configuration the captured images should obtain the maximum information about the drone movement in the horizontal plane. Additionally, the images are taken with approximately 3 frames per second, a slow rate but which is sufficient to obtain enough superposition between each pair of images, and which is easy to be replicated.

Unlike the previous work, the current study shows variation in the drone’s horizontal position and also in its height. In addition, the speed sampled for each flight segment comes from a uniform distribution.

Also, each image has an associated file with the ground truth information of the complete status of the drone in the instant the picture was taken, which includes linear and angular speeds, linear and angular accelerations, position, latitude and longitude, and attitude of the vehicle. We explicitly annotated the images with this set of information to the prediction of the vehicle displacement.

4.2. Training

For training our model, we employed ReLU activation functions throughout the network, except in the last layer, where we used a linear activation function. Additionally, we used batch-normalization layers after every weight layer, and dropout layers with probability

0.2

We trained the network on Tensorflow framework, and applied Adam optimizer with a learning rate of

0.001

. For our loss function, we used Mean Squared Error, and we trained the network for 30 epochs. At the end of each epoch during the training stage, the model is evaluated against a validation group. The model that shows an improvement in the value of the metric (considering the validation group) is saved as the best model found. This is the model used for the testing stage.

The data set is divided into three sets for training: training, validation and testing. To make up the test set, 1 flight made on each map of each environment is preserved with the complete sequence of images. In this way, the prediction and its impact during the flight can be evaluated. For the other sets,

80 %

was set aside for the training set and

20 %

for the validation set. In the training stage, the sets used are the training and validation sets. Thus, the training set is presented to the model and, at the end of each epoch, the model is evaluated on the validation set. If it shows an improvement in the value of the metric, the model is saved as the best model found so far.

Additionally, during training the image pairs were shuffled before been presented to the neural network: This assures that we do not feed correlated data to the model, once the image pairs seen in a single batch will not be all from the same flight or will not have been taken in a sequence by the camera mounted on the drone.

4.3. Test

The model generated in the training stage is evaluated in the test stage. In this stage, we use 1 route from each map (and from each environment) to predict displacement, considering execution during a flight. Table 2 shows the size of each route used in this stage. The name of the route was composed of the name of the environment and the conversion of the map into a numerical value (such as, A is 1 and B is 2).

Three levels of prediction were made for the final parts of each route. This approach allows us to better represent the negative impact of prediction on the completion of the mission. The three levels of prediction correspond to 20%, 40% and 60%. Finally, the flight was also predicted for the entire route, assuming that only the initial displacement coordinate was known.

It’s important to note that although the drone is subject to unknown influences (such as weather conditions) during flight, causing it to move in an undesired direction, we use the data from the yaw sensor to calculate the drone’s new geographical position. Thus, we use a sensor on the drone to estimate the direction of displacement. This approach allows us to avoid knowing the exact direction of movement, which could reduce the error of our proposal inadequately.

5. Results

We emphasize that we carried out the experiments in order to assess the ability of the proposed method to estimate the displacement based on the inputs received. Therefore, the method is used to infer the aircraft’s displacement and we calculate the new geographical coordinates (lat and long). It is important to mention that in this case study we consider that heading and height are obtained by other sensors, such as yaw and radio altimeter.

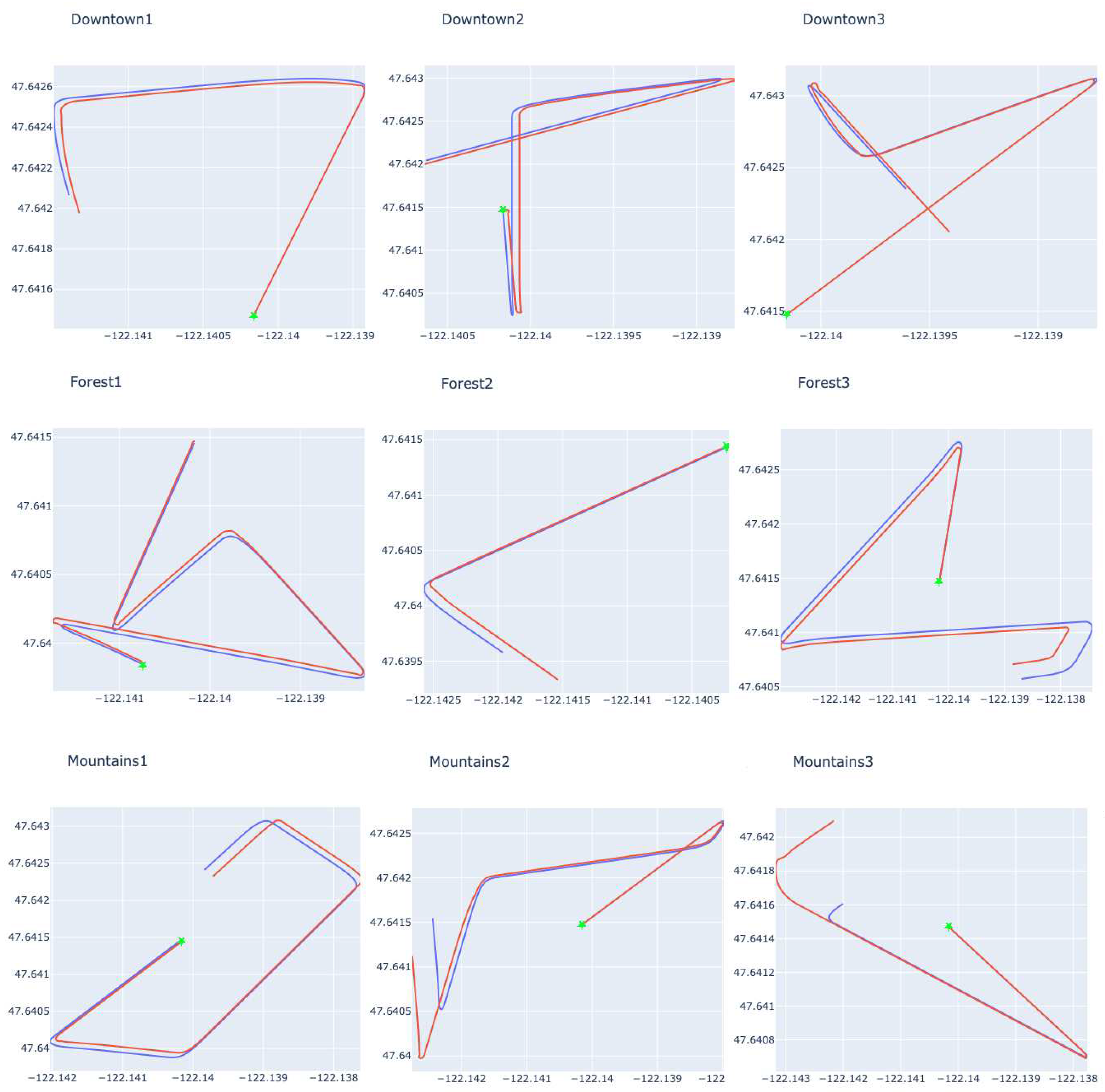
Firstly, Figure 3 shows the routes used in this test stage. The green dot on each route indicates the starting point of the flight. The expected route is outlined by the blue line, while the red line represents the route taken using the displacement estimation model. In the flights shown in this picture, doom was suffered in the final 20% of the flight. It’s important to note that the flights used speed variations, meaning that the distance covered during the prediction varied in size.

More details of the flights can be seen in Table 3, which summarizes the size of the route, the number of predictions made, the distance of the drone’s final position from the expected position and the average distance between each inferred and expected geographical position of the drone. It should be noted that this last piece of information is calculated based only on the period in which the displacement was inferred. The Table 4, Table 5 and Table 6 present similar information to the Table 3. This makes it possible to compare the changes that occurred at different points in the prediction.

In these results, it was not possible to find a clear link between the number of predictions and the metrics relating to the comparison between the final position and the average positional error during in-flight predictions. In other words, even if the number of predictions is higher on one flight than on another, it doesn’t mean that the errors will also be higher. This growth characteristic between the metrics mentioned cannot be affirmed when we analyze the increase in the prediction period considering isolated flights. This behavior occurs because apparently the errors are generated by a normal distribution with the center close to the expected value, causing predictions with positive (greater than expected) and negative (less than expected) error polarities. 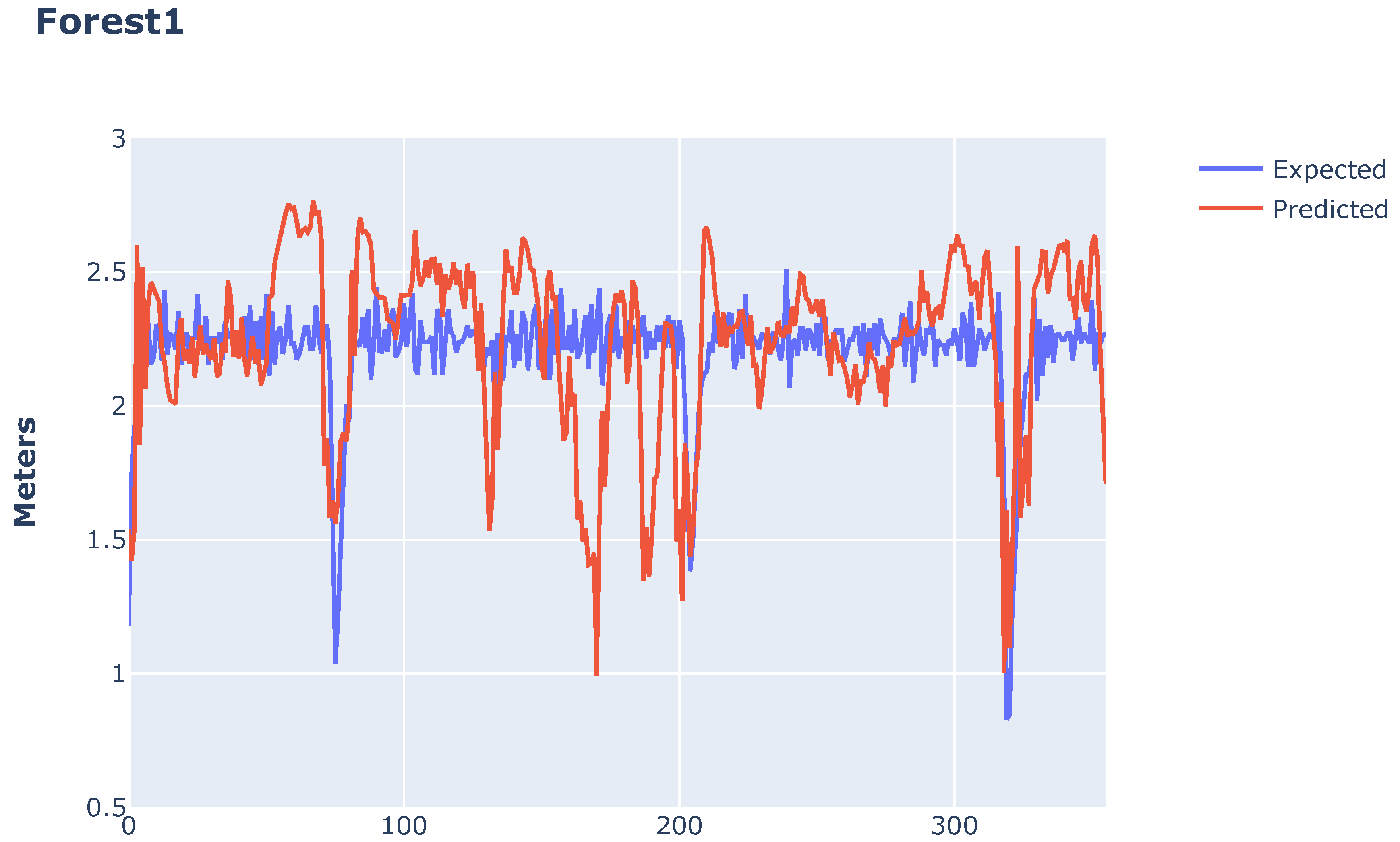Figure 4 makes it possible to compare the predicted values with the expected values, preserving the order in which the predictions were made during the flight.

With the variation in environments and routes used in the experiments presented, we believe that the SiaN-VO method is capable of predicting displacement in a variety of conditions (even with a change in height.) Another interesting feature presented by the method in the data set used is its ability not to accumulate noise in its prediction.

6. Conclusions

Inferring the position of a UAV with high accuracy without the use of GNSS is an obstacle with several studies in the scientific literature. The increasing evolution of UAVs and the high range of possible contexts in which they can be applied further highlights the need for independence from the GNSS signals for safe navigation.

The evolution provided by the proposed new architecture, giving rise to the SiaN-VO method, was able to infer the drone’s displacement and allow the value to be used to calculate the new geographical position. SiaN-VO makes the prediction based on a sequential pair of ground images, height and yaw data.

The results suggest that noise does not accumulate (or is imperceptible) in the predictions during flights on the routes described. Although we bear in mind that it is possible that noise accumulation becomes noticeable on long journeys and that this characteristic needs to be investigated further, we would like to emphasize that this characteristic is exciting and makes us believe that the SiaN-VO method is a promising approach in the field of visual odometry.

Furthermore, it is important to emphasize that the SiaN-VO method was able to overcome the obstacle of predicting drone displacement on routes with height variation. The successful prediction of displacement in these flight characteristics means that SiaN-VO surpasses the previous proposal, which exclusively uses images. Another point that surpasses the current approach is the possibility of using images with smaller dimensions (1/4 of the previous size), which allows for less computational processing.

In view of the results obtained in this work, we aim to advance our studies in the following directions:

Evaluate the performance of SiaN-VO with real flight data;
Evaluate SiaN-VO on long routes and with more variations in flight dynamics;
Measuring the performance of SiaN-VO in the face of data failures and inconsistencies;
Test our proposed model during a UAV flight.

Funding

This research was funded by Embraer.

Data Availability Statement

The source code for this work can be accessed at https://github.com/verri/sian-vo and the data set for training, validation and testing is available at http://doi.org/10.5281/zenodo.10140028.

Acknowledgments

The authors would like to thank Leonardo Silveira for his contribution to generating the dataset.

Conflicts of Interest

The authors declare no conflict of interest.

References

Oruc, A. Potential cyber threats, vulnerabilities, and protections of unmanned vehicles. Drone Syst. Appl. 2022, 10, 51–58. [Google Scholar] [CrossRef]
Moore, A.B.; Johnson, M. Geospatial Support for Agroecological Transition through Geodesign. Drones and Geographical Information Technologies in Agroecology and Organic Farming Contributions to Technological Sovereignty, CRC Press, 2022; 174–203. [Google Scholar]
Mohsan, S.A.H.; Khan, M.A.; Noor, F.; Ullah, I.; Alsharif, M.H. Towards the Unmanned Aerial Vehicles (UAVs): A Comprehensive Review. Drones 2022, 6. [Google Scholar] [CrossRef]
Braga, J.R.G.; Velho, H.F.C.; Conte, G.; Doherty, P.; Shiguemori, É.H. An image matching system for autonomous UAV navigation based on neural network. 2016 14th International Conference on Control, Automation, Robotics and Vision (ICARCV), 2016, pp. 1–6. 10.1109/ICARCV.2016.7838775.
da Penha Neto, G.; de Campos Velho, H.F.; Shiguemori, E.H. UAV Autonomous Navigation by Image Processing with Uncertainty Trajectory Estimation. Proceedings of the 5th International Symposium on Uncertainty Quantification and Stochastic Modelling; De Cursi, J.E.S., Ed.; Springer International Publishing: Cham, 2021; pp. 211–221. [Google Scholar]
Gupta, A.; Fernando, X. Simultaneous Localization and Mapping (SLAM) and Data Fusion in Unmanned Aerial Vehicles: Recent Advances and Challenges. Drones 2022, 6, 85. [Google Scholar] [CrossRef]
Noviello, C.; Gennarelli, G.; Esposito, G.; Ludeno, G.; Fasano, G.; Capozzoli, L.; Soldovieri, F.; Catapano, I. An Overview on Down-Looking UAV-Based GPR Systems. Remote Sensing 2022, 14. [Google Scholar] [CrossRef]
Rathnayake, B.S.S.; Ranathunga, L. Lane Detection and Prediction under Hazy Situations for Autonomous Vehicle Navigation. 2018 18th International Conference on Advances in ICT for Emerging Regions (ICTer), 2018, pp. 99–106. 10.1109/ICTER.2018.8615458.
Bergman, N.; Ljung, L.; Gustafsson, F. Terrain Navigation Using Bayesian Statistics. IEEE Control Systems 1999, 19, 33–40. [Google Scholar]
Titterton, D.H.; Weston, J.L. Strapdown Inertial Navigation Technology, 2nd ed.; 2004. [Google Scholar]
Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Advances in Neural Information Processing Systems; Pereira, F.; Burges, C.; Bottou, L.; Weinberger, K., Eds. Curran Associates, Inc.: 2012, Volume 25.
He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. CoRR 2015. [Google Scholar]
Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press, 2016. Available online: http://www.deeplearningbook.org.
Silveira, L.; Rodrigues, M.; Faiçal, B.S.; da Silva, A.S.Q.; Marcondes, C.; Maximo, M.R.O.A.; Verri, F.A.N. Navigation Aids Based on Optical Flow and Convolutional Neural Network. 2022 Latin American Robotics Symposium (LARS), 2022 Brazilian Symposium on Robotics (SBR), and 2022 Workshop on Robotics in Education (WRE), 2022; pp. 318–323. 10.1109/LARS/SBR/WRE56824.2022.9995889.
Aqel, M.O.; Marhaban, M.H.; Saripan, M.I.; Ismail, N.B. Review of visual odometry: types, approaches, challenges, and applications. SpringerPlus 2016, 5, 1–26. [Google Scholar] [CrossRef] [PubMed]
Yu, Y.; Hua, C.; Li, R.; Li, H. Pose Estimation Method Based on Bidirectional Recurrent Neural Network in Visual Odometry. Available at SSRN 415 5315. [CrossRef]
Scaramuzza, D.; Fraundorfer, F. Visual Odometry [Tutorial]. IEEE Robot. Autom. Mag. 2011, 18, 80–92. [Google Scholar] [CrossRef]
Rehder, J.; Gupta, K.; Nuske, S.; Singh, S. Global pose estimation with limited GPS and long range visual odometry. 2012 IEEE international conference on robotics and automation. IEEE: 2012; pp. 627–633.
Cai, G.S.; Lin, H.Y.; Kao, S.F. Mobile robot localization using gps, imu and visual odometry. 2019 International Automatic Control Conference (CACS). IEEE: 2019, pp. 1–6.
Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? the kitti vision benchmark suite. 2012 IEEE conference on computer vision and pattern recognition. IEEE: 2012, pp. 3354–3361.
W., H.; X., T.; Loy, C.C. W., H.; X., T.; Loy, C.C. A lightweight optical flow CNN—Revisiting data fidelity and regularization. IEEE Trans. Pattern Anal. Mach. Intell.
Menze, M.; Geiger, A. Object scene flow for autonomous vehicles. Proceedings of the IEEE conference on computer vision and pattern recognition, 2015, pp. 3061–3070.
Goppert, J.; Yantek, S.; Hwang, I. Invariant Kalman filter application to optical flow based visual odometry for UAVs. 2017 Ninth International Conference on Ubiquitous and Future Networks (ICUFN). IEEE: 2017; pp. 99–104.
Romero, H.; Salazar, S.; Santos, O.; Lozano, R. Visual odometry for autonomous outdoor flight of a quadrotor UAV. 2013 international conference on unmanned aircraft systems (ICUAS). IEEE: 2013, pp. 678–684.
Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. 2014. 10.48550/ARXIV.1409.1556.
Shah, S.; Dey, D.; Lovett, C.; Kapoor, A. AirSim: High-Fidelity Visual and Physical Simulation for Autonomous Vehicles. 2017. 10.48550/ARXIV.1705.05065.

Figure 1. Architecture of the Siamese Network for Visual Odometry (SiaN-VO).

Figure 2. Examples of images considering the environments in which the flights were simulated.

Figure 3. Example of expected routes (blue line) compared with routes that used prediction (red line) for 20% of the flight. The green dot signals the starting position of the flight.

Figure 4. Predicted and expected displacement values along the route Forest 1.

Table 1. Details of the flights that make up the simulated dataset.

Environment	Map	Number of routes
Downtown	A	50
Downtown	B	50
Downtown	C	50
Forest	A	12
Forest	B	10
Forest	C	50
Mountains	A	50
Mountains	B	50
Mountains	C	50

Table 2. Details of the name and size of each route used in the test stage.

Name	Flight size (m)
Downtown1	346.03
Downtown2	674.80
Downtown3	458.49
Forest1	783.77
Forest2	321.01
Forest3	1,001.24
Mountains1	906.62
Mountains2	784.24
Mountains3	569.84

Table 3. Summarization of results for flights with 20% predictions.

Route	Number of predictions	Distance between endpoints (m)	Average distance between expected and predicted position (m)
Downtown1	136	11.15	5.03
Downtown2	193	5.07	3.99
Downtown3	111	36.71	17.74
Forest1	72	1.17	6.28
Forest2	72	42.66	27.74
Forest3	83	19.14	21.17
Mountains1	197	13.32	21.17
Mountains2	275	52.84	43.68
Mountains3	195	55.71	48.33

Table 4. Summarization of results for flights with 40% predictions.

Route	Number of predictions	Distance between endpoints (m)	Average distance between expected and predicted position (m)
Downtown1	271	8.64	7.28
Downtown2	386	28.55	19.48
Downtown3	221	16.87	27.93
Forest1	143	1.00	5.94
Forest2	143	65.17	36.05
Forest3	166	36.05	23.79
Mountains1	393	22.46	23.33
Mountains2	550	94.10	56.95
Mountains3	390	58.78	34.87

Table 5. Summarization of results for flights with 60% predictions.

Route	Number of predictions	Distance between endpoints (m)	Average distance between expected and predicted position (m)
Downtown1	406	7.44	12.18
Downtown2	579	7.22	18.19
Downtown3	331	24.75	36.70
Forest1	214	15.96	16.82
Forest2	214	91.74	48.61
Forest3	249	34.53	19.67
Mountains1	589	28.07	32.06
Mountains2	825	129.05	69.73
Mountains3	585	49.05	49.85

Table 6. Summarization of results for flights with 100% predictions.

Route	Number of predictions	Distance between endpoints (m)	Average distance between expected and predicted position (m)
Downtown1	677	17.73	19.28
Downtown2	985	16.96	27.06
Downtown3	551	30.40	29.33
Forest1	357	15.58	12.23
Forest2	357	81.69	25.93
Forest3	415	48.94	28.81
Mountains1	981	22.82	15.31
Mountains2	1375	127.61	54.67
Mountains3	975	146.51	115.04

1	The angle at which the front of the drone is facing, based on magnetic north.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer