Preprint
Review
Artificial Populations in Agent-Based Modeling
Altmetrics
Downloads
180
Views
91
Comments
0
This version is not peer-reviewed
Advance in Cancer Pharmacoepidemiology
Preprints on COVID-19 and SARS-CoV-2
Submitted:
05 December 2023
Posted:
06 December 2023
You are already at the latest version
Alerts
Abstract
In the field of modeling social systems, the use of agent-based models (AM) has become a powerful tool for understanding processes occurring in society, in particular, for studying the spread of infections among the population. The agent model is based on a synthetic population consisting of agents, their interactions and sometimes the territory in which the interaction occurs. The choice of an appropriate method for creating such artificial populations and the selection of parameters becomes a key issue affecting the realism of the model and its ability to reflect real-world scenarios. This article delves into the interplay between agent-based modeling, synthetic population construction, and parameter selection, offering our insight into the complex process of modeling infectious disease dynamics. The review concludes with an exploration of extending the Covasim model [1] to experiments in computational epidemiology. Covasim, a dynamic transmission modeling tool, is known for its ability to adapt to different scenarios and offers predictive information critical for managing epidemiological situations. The Covasim model could include improvements to better simulate real-world epidemic conditions, including a revised transmission strategy to account for accumulation through daily contacts. In addition, we propose to add a module for intercity travel and a visualization package that will significantly expand the functionality of Covasim. These improvements make Covasim a more versatile and efficient tool for modeling and analyzing epidemic processes.
Keywords:
Subject: Biology and Life Sciences - Other
Introduction
In recent decades, the risk of large-scale viral outbreaks turning into epidemics and pandemics has increased significantly. A number of key viral outbreaks have already occurred since the early 2000s, including Severe Acute Respiratory Syndrome (SARS, 2002 - 2003), H1N1 Influenza or Swine Flu (2009), Middle East Respiratory Syndrome (MERS, 2012), Ebola virus outbreaks (from 2014 to 2016), Zika virus outbreak (2015–2016). The COVID-19 pandemic, caused by the novel coronavirus SARS-CoV-2, was first identified in late 2019 in Wuhan, China. It has spread rapidly throughout the world, causing significant morbidity and mortality, as well as significant social and economic disruption. As of November 12, 2023, 23,200,294 cases of COVID-19 were identified in the Russian Federation and 400,395 deaths were recorded. The novel coronavirus pandemic has taxed public health systems around the world, highlighting the importance of global cooperation and preparedness to respond to emerging infectious diseases.
Collecting comprehensive and accurate statistical data was already a difficult task, but during the COVID-19 pandemic, this problem has worsened and the primitiveness of monitoring and forecasting mechanisms has become apparent [2].
Although severe complications and deaths are the immediate consequences of outbreaks, their consequences also affect other aspects of society, affecting economic, social and psychological aspects. Research shows that viral outbreaks, such as the ongoing COVID-19 pandemic, result in significant economic losses [3]. The economic impacts include business closures, supply chain disruptions and changes in consumer behavior, affecting a variety of industries and livelihoods. Moreover, disease outbreaks can destabilize a society, contributing to an increase in civil unrest and various forms of crime. This complex interaction between health crises and social stability highlights the importance of understanding the broader socioeconomic context in which epidemics unfold. However, research also highlights that timely and well-coordinated interventions can significantly mitigate these economic costs, highlighting the critical role of proactive public health measures and policy responses [4].
Epidemiology and public health experts use a variety of tools to predict and respond to outbreaks and to conduct research into disease dynamics and the factors that influence them. One key tool is computer modeling, which can simulate complex systems with a large number of factors influencing the spread and impact of infectious diseases. Numerous studies have already been carried out in this area, and various approaches have been developed [5].
Computer modeling in epidemiology involves constructing mathematical representations of disease transmission dynamics, integrating variables such as population demographics [6,7,8], contact patterns [9], and intervention strategies [10,11]. These models provide a virtual laboratory that allows researchers to study hypothetical scenarios, evaluate the effectiveness of various measures, and anticipate potential outbreak trajectories. Such a method could play a key role in informing decision-making and public health policy.
Today, many different approaches to modeling are known. These approaches range from classical models such as the susceptible-infected-recovered (SIR) model [12] to more complex agent-based models that model the actions and interactions of individual agents within a population [8,9,13]. Two well-known paradigms, ordinary differential equations (ODE) [https://doi.org/10.1137/S00361445003719] and agent-based modeling (ABM, AM), represent the main approaches [14,15] that take into account various aspects of the complexity of understanding and disease transmission modeling.
ek, possible infection of medical personnel.
Models based on TACs operate at the population level of a population, dividing people into groups (for example, infected and uninfected) and quantifying changes in these groups over time. These mathematical equations describe how people transition between states, based on rate equations that take into account the current size of the population. By providing a macroscopic view of disease dynamics, ODE models effectively capture overall trends and calculate important indicators such as the basic reproductive number (R0). They are especially valuable when simplicity and computational efficiency are a priority. There are modifications that consider subpopulations - by age, etc. For example, in a study [16], the authors decided to take advantage of the fact that the mortality rate of the disease is high in older people, so they created a model taking into account age. The model also takes into account other signs: the number of beds needed, possible infection of medical personnel.
In contrast, AM views each individual in a population as an autonomous agent with distinctive traits, behaviors, and interactions. These agents operate at the micro level, engaging in local interactions that collectively shape population-level outcomes. AM is capable of capturing heterogeneity, allowing for a more detailed representation of individual behavior and interactions. This detailed approach can be used to study anti-epidemic measures [17,18,19], assess the impact on different population groups [20], and conduct sensitivity analysis of modeling results to changes in parameter values [21]. However, the detailed nature of AM adds complexity to the overall modeling task and, if not managed properly, can result in overly complex models with redundant parameters.
Although the flexibility of AM provides detailed insight into disease dynamics, it requires careful consideration during parameterization [22]. There is a high risk of introducing unnecessary parameters that do not make a significant contribution to the model results. Moreover, assigning realistic values to parameters in complex AMs can be challenging, potentially leading to information redundancy or hampering model interpretability. Finding the right balance in the choice of parameters and model complexity becomes important to ensure that the information obtained from the model is meaningful and consistent with the available empirical data.
The choice between ODE and AM depends on the research questions at hand and the level of detail required to obtain meaningful information [23,24]. While ODE models provide efficiency and ease in identifying trends at the population level, AM provides a more detailed representation of interactions at the individual level, allowing for more realistic depictions of complex systems. Effective modeling requires thoughtful consideration of the trade-offs between simplicity and detail, ensuring that the chosen approach is consistent with the objectives of the study and the available data.
Thus, computer modeling in epidemiology serves as an indispensable tool for understanding, predicting, and responding to disease outbreaks. The rich range of modeling approaches, from classical compartmental models to agent-based modeling, reflects the dynamic and evolving nature of research in this area. As technological capabilities advance and our understanding of disease dynamics deepens, the role of computational models in shaping public health strategies and policies will continue to grow.
Against this backdrop, our review article delves into the wide range of disciplines that can assist in epidemiological modeling. We have tried to cover a variety of representative topics.
What is modeling?
In this review, our focus is on the complex field of agent-based modeling, an area that has shown compelling results in computational epidemiology [25]. Our goal is to explain the technical details that are critical to obtaining the most accurate results. This entails the development and use of tools and methodologies capable of manipulating temporal state transitions for each agent in a population, coupled with an understanding of the factors that shape these outcomes. The information obtained through these tools serves as a valuable resource for analysts in various fields.
The creation and design of an agent model is preceded by a thorough analysis of the designed system [26,27]. This involves a comprehensive study of the factors contributing to the spread of infections and the underlying dynamics of transmission of the infectious agent. Formulating a formula for transition from one state to another requires a deep understanding of these complex processes.
The next step involves creating options for agent interaction [28]. The two main options are to either set which agent interacts with which (“social network”), or determine which places (locations) the agent visits during the day and calculate the interaction based on the simultaneous presence of agents in the same location. The first method is simpler, since it does not require specifying the characteristics of the locations (for example, the size of the room) and the agent’s daily routine. Explicitly specifying locations is suitable for studying how the mobility of agents affects the spread of infection and what measures to limit traffic are optimal.
The main goals of all these concerted efforts are to understand population behavior, quantify the effects of small changes in input data through sensitivity studies, evaluate the impact of large changes through parametric studies, identify the effects of various interventions, elucidate behavior and establish causality, and ultimately As a result, interpret the results in terms of the consequences of the measures taken.
Difficulties in creating an agent-based model and a synthetic population
Developing agent-based modeling (AM) systems presents many challenges, each of which requires thoughtful consideration and truly good solutions. First, a robust theoretical approach is needed to effectively describe the dynamic nature of disease in AM systems. To achieve this goal, graph-based dynamic or spatial systems are used [29], providing a framework for capturing the complex dynamics of disease spread and interactions within populations.
A major problem arises when constructing populations when data from different sources are combined. These datasets are inherently incomplete, often have varying degrees of detail, and may even contain conflicting information [30]. Integrating such heterogeneous data is a challenging task, requiring sophisticated techniques to ensure accuracy and consistency in the representation of synthetic populations.
Moreover, the very task of creating populations poses significant challenges, especially when working with big data. Populations in AM systems can include tens of millions or more agents, and the number of interactions within them can amount to hundreds of millions or even billions [31]. Managing and processing such large data sets requires advanced computational techniques, often using parallel computing. Parallel processing not only reduces execution time, but also facilitates the storage and retrieval of huge amounts of data at runtime, thereby overcoming the limitations imposed by the scale of the simulated population.
Another challenge is efficient modeling in AM systems. Given the scale and complexity of dynamic networks, implementing models that can accurately capture the nuances of disease dynamics requires both accuracy and efficiency. Achieving this balance is critical to the model's robustness and its ability to provide meaningful insight into infectious disease dynamics.
An essential aspect of dynamic assessment in AM systems involves sensitivity studies [32]. These studies aim to understand how changes in input parameters affect results, which requires multiple simulation runs. With significant population sizes, the need for rapid modeling becomes paramount. This requires the development of modeling methodologies that can quickly and accurately assess the impact of different parameters on outcomes, thereby increasing the value of the model for informing public health decisions and interventions.
Fundamentally, AM system development problems span theoretical aspects, data integration, computation, and modeling. Addressing these challenges requires an interdisciplinary approach that integrates ideas from epidemiology, computer science, and data analytics to create robust, scalable, and efficient AM systems for comprehensively studying the dynamics of infectious diseases in populations.
It is important to keep in mind that artificial population sizes typically range from tens or hundreds of millions of agents (nodes) to the size of cities/countries - and contain hundreds of millions or billions of connections. As a result, a significant number of agents/edges necessitates finding the most computationally efficient method.
Creation of a synthetic population
A synthetic population is a representation of a group of individuals, in our case humans. Groups can range from individual families to the entire population. The wide coverage of the size of such populations means there is a growing interest in using such populations in various fields [33,34,35,36,37,38,39,40]. These synthetic populations, often called “digital twins,” include agents modeled with different demographic attributes such as age, gender, location and housing, among others. They are often given an activity in which people visit certain places, if the geography is explicitly specified in the model, at certain times of day. There is often additional data associated with synthetic individuals. The specific data (attributed to synthetic individuals) depends on the needs and use of the population.
Figure 1.
Synthetic population includes agents with different demographic characteristics (Block A). These agents are assigned certain duties that they must perform in certain places and at certain times. This creates a network that connects agents to locations throughout the day, creating a Person-Location network (Block C). The Person-Person contact network (Block B) is developed based on the interactions obtained from the Person-Location graph.
Figure 1.
Synthetic population includes agents with different demographic characteristics (Block A). These agents are assigned certain duties that they must perform in certain places and at certain times. This creates a network that connects agents to locations throughout the day, creating a Person-Location network (Block C). The Person-Person contact network (Block B) is developed based on the interactions obtained from the Person-Location graph.
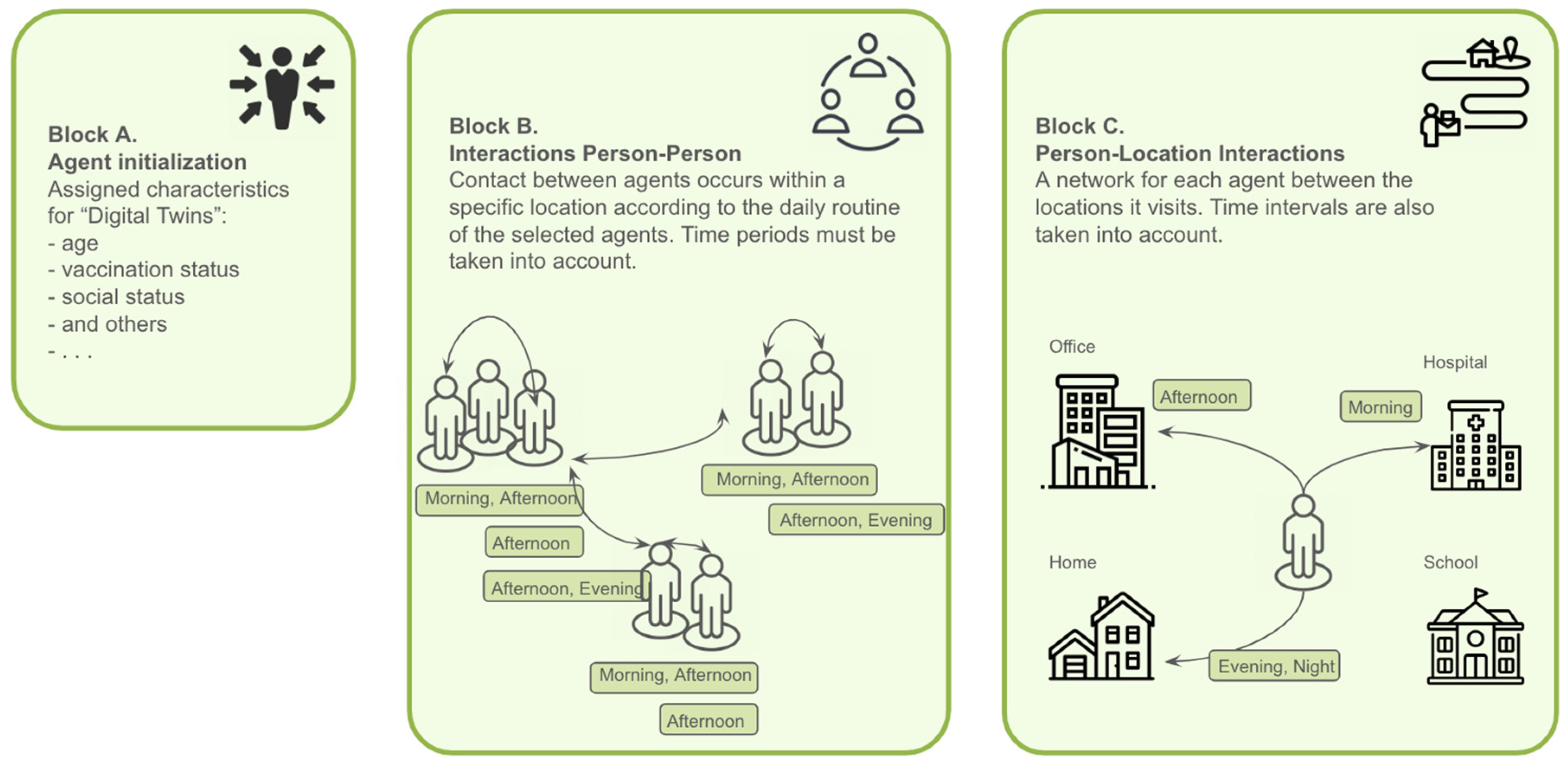
The essence of a synthetic population is its ability to reproduce the statistical characteristics observed in a particular region or country. Given the inherent heterogeneity of different regions, these synthetic populations are designed to mimic the diverse distribution of sociodemographic factors found in real populations [41,42,43,44]. Reproducing statistics within a synthetic population involves several steps. Data can be collected from various sources such as census data, population surveys. These data provide a basis for understanding the distribution of demographic characteristics such as age, gender, household size, income, occupation and other relevant characteristics within the target population. From the collected data, synthetic individuals are created, each assigned demographic attributes (e.g., age, gender) that reflect the observed distribution. For example, statistical distributions (eg, Gaussian, Poisson, or others) can be used to randomly assign attributes while preserving the overall observed statistical characteristics. Iterative proportional updating (IPU) is another effective method for generating synthetic populations by iteratively refining and updating digital twin attributes to match observed demographic characteristics [45].
As a result of the stochastic nature of the synthetic population creation process, each synthetic population typically represents a single instance or realization within a larger set or family of instances. This stochasticity allows for variability among different instances of synthetic populations, promoting the creation of a range of potential representations rather than a single final agent. This variability is critical to reflect the intrinsic diversity and complexity found in real populations, suggesting a range of possible scenarios and outcomes in the simulated environment. There is work assessing the variability of synthetic population specimens and contact networks in the United States. For example, [46] presented a statistical analysis to determine the appropriate level of model complexity and demonstrated its implementation on models used to create a synthetic population and contact network representing the population of the United States. The dispersion of all studied indicators (incidence rate, peak infection rate and time to reach the peak of the epidemic curve) has the inherent stochasticity of the epidemic process. To illustrate this, the authors argue that incidence rates appear to be more sensitive to the location of activity than to the timing of peak infection rates, and population synthesis has a greater impact on the resulting attack rate than the effect of activity type assignment.
To summarize, we can say that the process of creating a synthetic population consists of the following stages [47].
1) Creation of individuals and households. Individuals are formulated, each characterized by specific attributes such as age, gender and marital status. Households are then formed by aggregating individuals based on statistical data, such as the census.
2) Taking into account socio-economic factors. Integration of socioeconomic attributes beyond basic demographics such as education level, occupation, or health status. These factors greatly influence behavior patterns and decision-making processes among people.
3) Integration of the dynamics of the human condition. Introducing health-related attributes and behaviors to model the spread of disease or the impact of health interventions in a synthetic population. Measures related to infections, vaccinations, and health care-seeking behavior should be included.
4) Role assignment. Each synthetic person in the family is assigned a set of activities to engage in during the day. It is possible to add start and end times for these classes.
5) Distribution of locations, if locations are explicitly taken into account in the model. Determining suitable real-world locations for each activity within a synthetic population requires the right strategy. For example, one could use logic that favors locations closer to a person's home, but allows for less likely selection of more distant locations. Or, on the contrary, the opposite strategy may work in the case of large metropolitan areas. Cellular data sources can help in this process. A location can often be broken down into smaller units, such as laboratories, classrooms, and offices within a building.
6) Creation of interaction networks if locations are not explicitly taken into account. Connections between agents are specified, reflecting the possibility of their contact. Communications can be of different types (for example, within the family, within transport, work contact), reflecting the efficiency of transmission of
Simple random interaction networks
In the simplest case, a random graph of one of the types well studied in mathematics can be used as an interaction network. This approach allows us to build an abstract model that takes into account the most general features of human interaction, such as the presence of hubs - people with an extremely large number of contacts, potentially acting as super-spreaders.
A contact network is a graph in which agents are represented as vertices and their interactions as edges. The use of a social network of contacts can provide a deeper understanding of how diseases spread and epidemics occur. Despite the problems in obtaining data for such networks, the concept of these networks remains clear - it is physical contact that facilitates the transmission of an infectious agent.
With the increasing ability to model the behavior of large numbers of agents, the need to efficiently create large random networks has arisen. In this section, we will discuss several networking practices.
Contact networks are often approximated using various random network models, such as the Erdős-Rényi model, the preferential attachment model, the Chung-Lu model, and others. The Erdős-Rényi model [48] stands out as the most widely used due to its simplicity, but generates random networks with a binomial degree distribution, which is less commonly observed in real contact networks. On the other hand, the preferential attachment model produces networks [49] that display power-law degree distributions. The Chung-Lu model, a more general version, [50] allows the construction of a network from any given degree distribution, but also requires the introduction of a degree distribution, and the above models are controlled by a few simple parameters.
Other network generation methods used include the following [51]. The Watts-Strogatz model [52] simulates the small world phenomena observed in real networks by starting with a regular lattice and adding edges with a certain probability, balancing regularity and randomness. The Barabási-Albert (scale-free network) model produces scale-free networks [53,54,55] in which new nodes preferentially connect to existing high-degree nodes, resulting in a power-law degree distribution. Gilbert's model [56], also known as the random graph model, starts with nodes and connects them with a fixed probability, creating networks with varying degrees of connectivity. The wildfire model is designed to create graphs with a community structure [57], starting with a “burning” node, where each new node either joins an existing community or creates a new one. The configuration model generates random graphs [58] by defining degree sequences of nodes and randomly connecting edges based on these sequences. The stochastic block model [59] is used to generate block-structured graphs, where nodes belong to blocks and edge probabilities depend on block membership, effectively modeling community structures.
Epidemiological modeling
In this section, we take a closer look at the modeling system based on the conceptual representation of interactions presented in the earlier section.
To analyze how population behavior and the introduction of interventions by government organizations affect the spread of diseases, the EpiSimdemics model can be used [60]. The advantage of this model is the ability to integrate extensive interaction networks, which brings the model closer to more realistic processes in society. An interaction network can be represented as a labeled bipartite graph involving people and locations, called a person-location graph. Here, nodes are people and locations connected by edges that contain information about the type of activity and time of visit. Such a network is dynamic, it develops in response to changes in health status, the implementation of government policies (for example, the introduction of quarantine or a mask regime) or behavioral adjustments (limiting contacts among older people). The person-location graph is transformed into a person-person graph, where nodes represent agents and edges symbolize contacts between them, labeled by their duration. This system is also updated to reflect changes in a person's location graph.
Transmission and progression of infection in humans are considered to be interrelated but independently quantifiable processes. Transmission between people causes the infection to develop within a person, moving them from an uninfected state to an infected state. The progression of a disease in humans is controlled by probabilistic transitions, automata that provide probabilistic and synchronized state transitions. The system of probabilistic transitions and the network of contacts change in parallel and co-evolve. Essentially, an agent's contacts affect his health, and his health can affect his contacts. Coevolution may involve complex behavioral changes influenced by the exchange of information, the health of contacts, the lack of expected interaction, or demographic factors such as age that influence whether a group is at risk or not.
There are three important semantic points of the contagion propagation problem that lead to the EpiSimdemics algorithm.
- People can influence other people only through interactions that occur when they are in the same space and time.
- Changes in a person's health after infection can be predicted in advance.
- There is a minimum latency period. This is the amount of time that must pass between the time a person becomes infected and the opportunity to infect others. For most infectious diseases, there is an appropriate latency period that is determined by the biology of the infection. For influenza, this period is at least 24 hours.
The above observations led to a semantically oriented decomposition of the problem. Each iteration consists of the following four main steps.
- Each person determines the places he or she intends to visit based on regulatory schedules, government policies, individual behavior, and health conditions. The person sends a message to each location visited with details of the visit (time, duration and health status at the time of visit). This can be calculated in parallel for each person.
-
In each location, pairwise interactions occurring between the inhabitants of this location are calculated. Each interaction may or may not result in infection, depending on the stochastic model.A message is then sent to each infected person with detailed information about the infection (time of infection, infector and location). Again, each location can perform these calculations in parallel once it has information about all the people who will visit that location during the iteration.
- Each infected person updates their health status, entering the infected state. If a person is infected in several places, the earliest infection is selected.
-
Any global simulation states (i.e. total number of infected) are updated.Each iteration requires two synchronizations: between steps 1 and 2 and between steps 2 and 3.
COVASIM - a flexible epidemic modeling tool
In our understanding, the most suitable tool for constructing digital experiments in epidemiology is Covasim [13]. The development team created the Covasim software using an agent-based modeling approach to model epidemic dynamics taking into account disease characteristics, pharmaceutical interventions such as vaccination, and administrative measures such as physical restrictions and mask wearing. This software has played an important role in building scenarios for the COVID-19 epidemic, analyzing the dynamics of the pandemic, and assisting decision makers in many countries [61,62,63]. The Covasim model is a valuable tool in understanding and addressing the complexities of infectious disease spread, offering insights critical to developing effective strategies in the face of public health challenges.
In its basic version, Covasim is an open-source simulation framework adapted to study the dynamics of the COVID-19 pandemic. Covasim is built on the principles of agent-based modeling, where individuals (agents) correspond to an individual in a population, allowing for a more detailed representation of disease interactions and dynamics. The synthetic population embedded in Covasim represents people with a set of attributes, such as age, gender, health status, social status. When modeling the spread of infection, the model takes into account the frequency of contacts, the infectiousness of the virus, and the susceptibility of agents.
Using the open agent-based modeling environment Covasim, researchers are able to study different epidemic scenarios by adjusting infection parameters and various interventions such as social distancing, isolation, testing, contact tracing and vaccination campaigns. Considering the Covasim model as the most reliable tool for conducting computer epidemiological experiments and relying on the experience of the agent-based modeling approaches discussed above, we have introduced additional blocks that expand the adaptive capabilities of Covasim to real conditions, offering valuable predictive information to improve the management of epidemiological surveillance.
Implementation of a new virus transmission strategy. The Covasim model has been improved by implementing a cumulative strategy to more accurately model the dynamics of virus transmission. This new approach takes into account the accumulation of the virus during daily interactions between people. By taking into account the gradual accumulation of the virus during contacts throughout the day, the model now better reflects the subtleties and nuances of the actual dynamics of the spread of the virus, leading to more accurate epidemiological forecasts.
Enable agents to move between cities. A significant addition to the Covasim model is the inclusion of a module that simulates the movement of people between cities. This module promotes in-depth analysis of how the movement of people between different places, especially in relation to tourism flows, influences the development and progression of epidemics.
The user can set the intensity of passenger traffic, expressed in the average number of people moving daily from one location to another. After a random number of days, defined by a Poisson distribution with a mean of seven, have passed, the agents return to their original location.
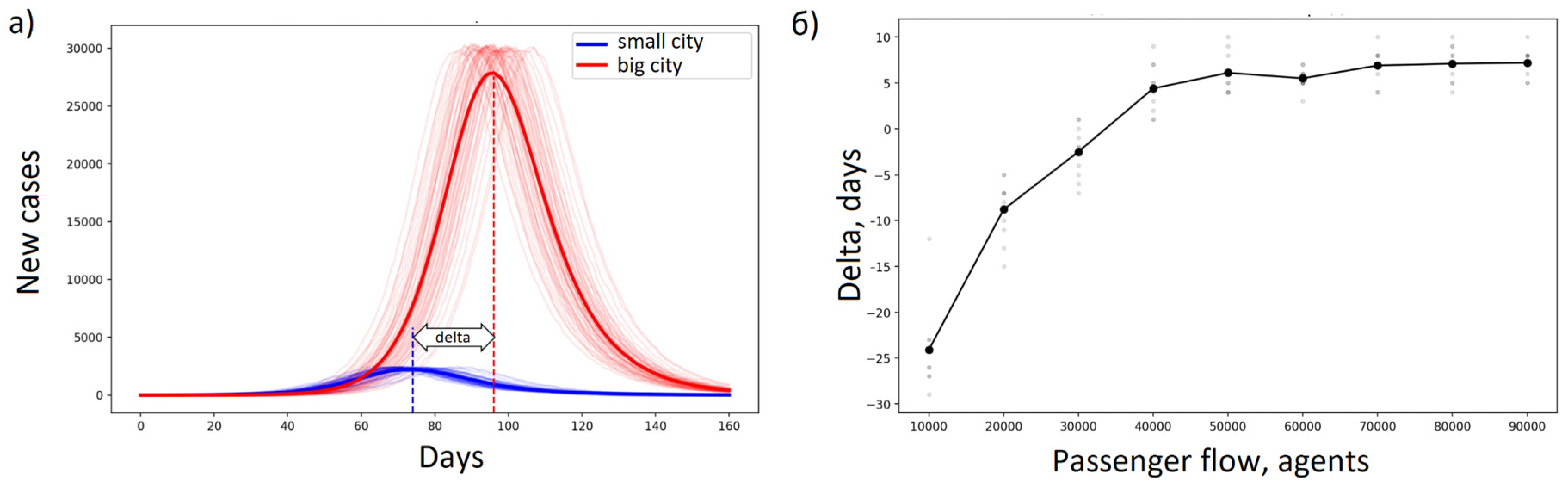
By examining different travel patterns between cities, this feature provides insight into how travel patterns influence the spread of infections. An example of using a modified version of Covasim, which includes a block for moving an agent between locations, is shown in Figure 2.
Integration of the visualization package. Another noteworthy improvement is the introduction of a visualization package to the Covasim model. This feature allows researchers to visualize and analyze the behavior and interactions of an artificial population in the context of various epidemiological scenarios. The visualization tools provided by this package help to understand complex modeling results, promoting a clearer understanding of how different variables and parameters affect the spread and control of diseases.
These improvements collectively enhance the capabilities of the Covasim model, allowing it to more accurately model, analyze and predict epidemic processes, thereby increasing its usefulness as a versatile and efficient tool for computational epidemiological experiments.
Conclusion
In conclusion, our study highlights the fundamental importance of agent-based models in analyzing social processes such as the spread of infectious diseases. Compared to widely used compartmental models, the construction of agent-based models, on the one hand, is simpler, since it describes reality in simple abstractions (agent, location, level of neutralizing antibodies) and does not require familiarity with differential equations. On the other hand, agent-based models, as a rule, contain a large number of parameters (for example, a matrix of contacts between different age groups, distribution of school sizes, etc.), the exact value of which is difficult or impossible to determine.
Building a synthetic population is an important step when creating an agent-based model, since population parameters can influence the trajectory of the modeled processes. The rational choice of parameters in these models becomes a decisive factor that directly affects the accuracy and relevance of the simulation results. Although the generated synthetic populations for chronic disease modeling using linked individual-, household-, and lifestyle-level data described using different approaches do not accurately reflect the original data, they are suitable for microsimulation and macrosimulation. By delving into the relationship between agent-based modeling, synthetic population generation, and detailed parameter selection, this article provides valuable insight into the process of modeling and interpreting infectious disease transmission dynamics.
The Covasim model is an innovative tool for modeling transmission dynamics and is noteworthy for its ability to adapt to different scenarios and provide valuable predictive data for better management of epidemiological situations. Expanding the functionality of the Covasim model could lead to a more powerful tool for implementing computational epidemiology experiments. Changes to the Covasim model may be made to improve its adaptability to real-life epidemic conditions. In particular, the introduction of a new virus transmission strategy that takes into account its accumulation during contacts throughout the day. Also adding a module for the movement of people between cities, which makes it possible to analyze the impact of tourist flows on the development of the epidemic under various configurations of movement between cities. Additionally, the introduction of a visualization package designed to analyze the behavior of an artificial population in the context of epidemiological scenarios. These changes significantly expand the functionality of Covasim, making it a more flexible and efficient tool for modeling and analyzing epidemic processes.
Funding
The work was supported by the Russian Science Foundation grant No. 21-15-00431 (review writing) and Rospotrebnadzor subsidy No. 141-02-2023-208 (modification of the agent model).
References
- Kerr C.C.,Stuart R.M.,Mistry D. et al.Covasim: An agent-based model of COVID-19 dynamics and interventions. PLOS Computational Biology. 2021;17;e1009149. [CrossRef]
- Heneghan C.J., and Jefferson T. Why COVID-19 modelling of progression and prevention fails to translate to the real-world. Advances in Biological Regulation. 2022;86;100914. [CrossRef]
- Shang Y., Li H., and Zhang R. Effects of Pandemic Outbreak on Economies: Evidence From Business History Context. Frontiers in Public Health. 2021;9;. [CrossRef]
- Parker C.F.,Nohrstedt D.,Baird J. et al. Collaborative crisis management: a plausibility probe of core assumptions. Policy and Society. 2020;39;510-529. [CrossRef]
- Lloyd-Smith J.O.,Mollison D.,Metcalf C.J.E. et al. Challenges in Modelling Infectious Disease Dynamics: Preface. Epidemics. 2015;10;iii-iv. [CrossRef]
- Kirkeby C.,Brookes V.J.,Ward M.P. et al. A Practical Introduction to Mechanistic Modeling of Disease Transmission in Veterinary Science. Frontiers in Veterinary Science. 2021;7;. [CrossRef]
- Hudson E., Brookes V., and Ward M. Demographic studies of owned dogs in the Northern Peninsula Area, Australia, to inform population and disease management strategies. Australian Veterinary Journal. 2018;96;487-494. [CrossRef]
- Glushchenko O.E.,Prianichnikov N.A.,Olekhnovich E.I. et al. VERA: agent-based modeling transmission of antibiotic resistance between human pathogens and gut microbiota. Bioinformatics. 2019;35;3803-3811. [CrossRef]
- Decelle A., Krzakala F., Moore C., and Zdeborová L. Asymptotic analysis of the stochastic block model for modular networks and its algorithmic applications. Physical Review E. 2011;84;066106. [CrossRef]
- Ackland G.J., Ackland J.A., Antonioletti M., and Wallace D.J. Fitting the reproduction number from UK coronavirus case data and why it is close to 1. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 2022;380;. [CrossRef]
- Creswell R.,Augustin D.,Bouros I. et al. Heterogeneity in the onwards transmission risk between local and imported cases affects practical estimates of the time-dependent reproduction number. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 2022;380;. [CrossRef]
- Shanta S.S., and Biswas M.H.A. The Impact of Media Awareness in Controlling the Spread of Infectious Diseases in Terms of SIR Model. Mathematical Modelling of Engineering Problems. 2020;7;368-376. [CrossRef]
- Kerr C.C.,Stuart R.M.,Mistry D. et al. Covasim: An agent-based model of COVID-19 dynamics and interventions. PLOS Computational Biology. 2021;17;e1009149. [CrossRef]
- Van Dyke Parunak H., Savit R., and Riolo R.L. Agent-Based Modeling vs. Equation-Based Modeling: A Case Study and Users’ Guide. Multi-Agent Systems and Agent-Based Simulation. 2010;1962;10-25. [CrossRef]
- Rahmandad H., and Sterman J. Heterogeneity and Network Structure in the Dynamics of Diffusion: Comparing Agent-Based and Differential Equation Models. Management Science. 2008;54;998-1014. [CrossRef]
- Bentout S., Tridane A., Djilali S., and Touaoula T.M. Age-Structured Modeling of COVID-19 Epidemic in the USA, UAE and Algeria. Alexandria Engineering Journal. 2020;60;401-411. [CrossRef]
- Gozzi N.,Tizzoni M.,Chinazzi M. et al. Estimating the effect of social inequalities on the mitigation of COVID-19 across communities in Santiago de Chile. Nature Communications. 2021;12;2429. [CrossRef]
- Squazzoni F.,Polhill J.G.,Edmonds B. et al. Computational Models That Matter During a Global Pandemic Outbreak: A Call to Action. Journal of Artificial Societies and Social Simulation. 2020;23;. [CrossRef]
- and Lux T. The social dynamics of COVID-19. Physica A: Statistical Mechanics and its Applications. 2021;567;125710. [CrossRef]
- Conte R., and Paolucci M. On agent-based modeling and computational social science. Frontiers in Psychology. 2014;5;. [CrossRef]
- Lux T., and Zwinkels R.C. Empirical Validation of Agent-Based Models ✶ ✶We gratefully acknowledge the very detailed and careful comments by three anonymous reviewers. Very useful feedback and comments have also been provided by Robert Axtell, Herbert Dawid, Cees Diks, and Blake LeBaron.. Handbook of Computational Economics. 2018;1962;437-488. [CrossRef]
- and Marks R.E. Validating Simulation Models: A General Framework and Four Applied Examples. Computational Economics. 2007;30;265-290. [CrossRef]
- Truong V.T.,Baverel P.G.,Lythe G.D. et al. Step-by-step comparison of ordinary differential equation and agent-based approaches to pharmacokinetic-pharmacodynamic models. CPT: Pharmacometrics & Systems Pharmacology. 2021;11;133-148. [CrossRef]
- Figueredo G.P.,Siebers P.,Owen M.R. et al. Comparing Stochastic Differential Equations and Agent-Based Modelling and Simulation for Early-Stage Cancer. PLoS ONE. 2014;9;e95150. [CrossRef]
- Tracy M., Cerdá M., and Keyes K.M. Agent-Based Modeling in Public Health: Current Applications and Future Directions. Annual Review of Public Health. 2018;39;77-94. [CrossRef]
- Grimm V.,Berger U.,Bastiansen F. et al. A standard protocol for describing individual-based and agent-based models. Ecological Modelling. 2006;198;115-126. [CrossRef]
- Khodabandelu A., and Park J. Agent-based modeling and simulation in construction. Automation in Construction. 2021;131;103882. [CrossRef]
- Zaplotnik Ž., Gavrić A., and Medic L. Simulation of the COVID-19 epidemic on the social network of Slovenia: Estimating the intrinsic forecast uncertainty. PLOS ONE. 2020;15;e0238090. [CrossRef]
- Démare T., Bertelle C., Dutot A., and Lévêque L. Modeling logistic systems with an agent-based model and dynamic graphs. Journal of Transport Geography. 2017;62;51-65. [CrossRef]
- Christen P., and Schnell R. Thirty-three myths and misconceptions about population data: from data capture and processing to linkage. International Journal of Population Data Science. 2023;8;. [CrossRef]
- Bhatele A.,Yeom J.,Jain N. et al. Massively Parallel Simulations of Spread of Infectious Diseases over Realistic Social Networks. 2017 17th IEEE/ACM International Symposium on Cluster, Cloud and Grid Computing (CCGRID). 2017;1962;. [CrossRef]
- Fonoberova M., Fonoberov V.A., and Mezić I. Global sensitivity/uncertainty analysis for agent-based models. Reliability Engineering & System Safety. 2013;118;8-17. [CrossRef]
- Bae J.W.,Paik E.,Kim K. et al. Combining Microsimulation and Agent-based Model for Micro-level Population Dynamics. Procedia Computer Science. 2016;80;507-517. [CrossRef]
- Heard D., Dent G., Schifeling T., and Banks D. Agent-Based Models and Microsimulation. Annual Review of Statistics and Its Application. 2014;2;259-272. [CrossRef]
- Prédhumeau M., and Manley E. A synthetic population for agent-based modelling in Canada. Scientific Data. 2023;10;148. [CrossRef]
- Xu Z.,Glass K.,Lau C.L. et al. A Synthetic Population for Modelling the Dynamics of Infectious Disease Transmission in American Samoa. Scientific Reports. 2017;7;16725. [CrossRef]
- Guo J.Y., and Bhat C.R. Population Synthesis for Microsimulating Travel Behavior. Transportation Research Record: Journal of the Transportation Research Board. 2008;2014;92-101. [CrossRef]
- Jiang N., Kavak H., Kennedy W.G., and Crooks A.T. Generation of Reusable Synthetic Population and Social Networks for Agent-Based Modeling. 2021 Annual Modeling and Simulation Conference (ANNSIM). 2021;1962;. [CrossRef]
- Jiang N.,Crooks A.T.,Kavak H. et al. A method to create a synthetic population with social networks for geographically-explicit agent-based models. Computational Urban Science. 2022;2;7. [CrossRef]
- Borysov S.S., Rich J., and Pereira F.C. How to generate micro-agents? A deep generative modeling approach to population synthesis. Transportation Research Part C: Emerging Technologies. 2019;106;73-97. [CrossRef]
- Lenormand M., and Deffuant G. Generating a Synthetic Population of Individuals in Households: Sample-Free Vs Sample-Based Methods. Journal of Artificial Societies and Social Simulation. 2015;16;. [CrossRef]
- Nicolaie M.A., Füssenich K., Ameling C., and Boshuizen H.C. Constructing synthetic populations in the age of big data. Population Health Metrics. 2023;21;19. [CrossRef]
- Agriesti S., Roncoli C., and Nahmias-Biran B. Assignment of a Synthetic Population for Activity-Based Modeling Employing Publicly Available Data. ISPRS International Journal of Geo-Information. 2022;11;148. [CrossRef]
- Wu G.,Heppenstall A.,Meier P. et al. A synthetic population dataset for estimating small area health and socio-economic outcomes in Great Britain. Scientific Data. 2022;9;19. [CrossRef]
- Gargiulo F., Ternes S., Huet S., and Deffuant G. An Iterative Approach for Generating Statistically Realistic Populations of Households. PLoS ONE. 2010;5;e8828. [CrossRef]
- Eubank S.,Barrett C.,Beckman R. et al. Detail in network models of epidemiology: are we there yet?. Journal of Biological Dynamics. 2010;4;446-455. [CrossRef]
- Barrett C.L.,Beckman R.J.,Khan M. et al. Generation and analysis of large synthetic social contact networks. Proceedings of the 2009 Winter Simulation Conference (WSC). 2010;1962;. [CrossRef]
- Erdös P., and Rényi A. On the evolution of random graphs. The Structure and Dynamics of Networks. 2017;1962;38-82. [CrossRef]
- Albert R., Jeong H., and Barabási A. Error and attack tolerance of complex networks. Nature. 2002;406;378-382. [CrossRef]
- Miller J.C., and Hagberg A. Efficient Generation of Networks with Given Expected Degrees. Lecture Notes in Computer Science. 2011;1962;115-126. [CrossRef]
- Bernovskiy M., and Kuzyurin N. Random graphs, models and generators of scale-free graphs. Proceedings of the Institute for System Programming of RAS. 2014;22;419-434. [CrossRef]
- Watts D.J., and Strogatz S.H. Collective dynamics of ‘small-world’ networks. Nature. 2002;393;440-442. [CrossRef]
- Barabási A., and Albert R. Emergence of Scaling in Random Networks. Science. 2002;286;509-512. [CrossRef]
- Barabási A., Albert R., and Jeong H. Scale-free characteristics of random networks: the topology of the world-wide web. Physica A: Statistical Mechanics and its Applications. 2002;281;69-77. [CrossRef]
- Albert R., Jeong H., and Barabási A. Diameter of the World-Wide Web. Nature. 2002;401;130-131. [CrossRef]
- and Gilbert E.N. Random Graphs. The Annals of Mathematical Statistics. 2007;30;1141-1144. [CrossRef]
- Leskovec J., Kleinberg J., and Faloutsos C. Graph evolution. ACM Transactions on Knowledge Discovery from Data. 2007;1;2. [CrossRef]
- Bender E.A., and Canfield E. The asymptotic number of labeled graphs with given degree sequences. Journal of Combinatorial Theory, Series A. 2004;24;296-307. [CrossRef]
- Decelle A., Krzakala F., Moore C., and Zdeborová L. Asymptotic analysis of the stochastic block model for modular networks and its algorithmic applications. Physical Review E. 2011;84;066106. [CrossRef]
- Barrett CL, Bisset KR, Eubank SG, Feng X, Marathe MV. Episimdemics: an efficient algorithm for simulating the spread of infectious disease over large realistic social networks. InSC'08: Proceedings of the 2008 ACM/IEEE Conference on Supercomputing 2008 Nov 15 (pp. 1-12). IEEE. [CrossRef]
- Panovska-Griffiths J.,Kerr C.C.,Stuart R.M. et al. Determining the optimal strategy for reopening schools, the impact of test and trace interventions, and the risk of occurrence of a second COVID-19 epidemic wave in the UK: a modelling study. The Lancet Child & Adolescent Health. 2020;4;817-827. [CrossRef]
- Kerr C.C.,Mistry D.,Stuart R.M. et al. Controlling COVID-19 via test-trace-quarantine. Nature Communications. 2021;12;2993. [CrossRef]
- Abeysuriya R.G.,Delport D.,Stuart R.M. et al. Preventing a cluster from becoming a new wave in settings with zero community COVID-19 cases. BMC Infectious Diseases. 2022;22;232. [CrossRef]
Figure 2.
Impact of passenger flow on the spread of infection between two cities. Two cities are simulated: a large one (a million agents) and a small one (one hundred thousand agents). On day 0, there are 30 infected agents in a small city, and 0 in a large city. We model the spread of infection in both cities with a certain passenger flow between them and measure the difference in days between the day of the “peak” of infection (the maximum number of new cases) in the small city and the large one . Several repeated simulations are carried out to level out the effects of randomness (a). The resulting relationship shows that the peak of infection can occur earlier in both small and large cities, depending on passenger flow (b).
Figure 2.
Impact of passenger flow on the spread of infection between two cities. Two cities are simulated: a large one (a million agents) and a small one (one hundred thousand agents). On day 0, there are 30 infected agents in a small city, and 0 in a large city. We model the spread of infection in both cities with a certain passenger flow between them and measure the difference in days between the day of the “peak” of infection (the maximum number of new cases) in the small city and the large one . Several repeated simulations are carried out to level out the effects of randomness (a). The resulting relationship shows that the peak of infection can occur earlier in both small and large cities, depending on passenger flow (b).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated




