Prerpints.org logo
Preprint
Article

From Local Energy Communities Towards National Energy System: A Grid-Aware Techno-Economic Analysis

Altmetrics

Downloads

107

Views

37

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

06 December 2023

Posted:

07 December 2023

You are already at the latest version

Alerts
Abstract
Energy communities are key actors in the energy transition since they optimally interconnect renewable energy capacities with the consumers. Despite versatile objectives, they usually aim at improving the self-consumption of renewable electricity within low voltage grids to maximize revenues. In addition, energy communities are an excellent opportunity to supply renewable electricity to regional and national energy systems. However, effective price signals have to be designed to coordinate the needs of the energy infrastructure with the interests of these local stakeholders. The aim of this paper is to demonstrate the integration of energy communities at the national level with a bottom-up approach. District energy systems with a building scale resolution are modelled in a mixed integer linear programming problem. The Dantzig-Wolfe decomposition is applied to reduce the computational time. The methodology lies within the framework of renewable energy hub, characterized by a high share of photovoltaic capacities. Both investments into equipment and its operation are considered. The model is applied on a set of five typical districts and weather locations representative of the Swiss building stock. The extrapolation to the national scale revealed a heterogeneous photovoltaic potential throughout the country. Present electricity tariffs promote a maximal investment into photovoltaic panels in every region, reaching an installed capacity of 67.2 GW and generating 80 TWh per year. Since the national PV capacity needed is forecast at 15.4 GW peak, coordinated investments between local and national actors are needed to prevent dispensable expenses. An uncoordinated design is expected to increase the total costs for residential energy systems by 43.2% and curtails 48.2% of local renewable electricity.
Keywords: 
Subject: Engineering  -   Energy and Fuel Technology

1. Introduction

In 2018, the European Parliament has emphasized the role of energy communities in the energy transition [2]. The reasons include the penetration of renewable energies, the reduction of energy poverty and the enhancement of technological acceptance [3]. Energy communities aim at supplying energy needs with high self-consumption of local energy sources. The reduction of the electricity grid reliance prevents costly grid reinforcements, therefore supporting a rapid electrification of heating and mobility services. In Switzerland, the electricity demand is expected to increase from 57 TWh/yr today to 95 TWh/yr in 2050, from which 33 TWh/yr is and will be supplied by hydropower [1,4]. Based on the cost-optimum scenario, the remaining electricity will be supplied by PV capacities (15.4 GW) and wind turbines (20 GW) [1]. The high investment into distributed capacities highlights the need for coordination between energy communities and grid utilities. The involvement of these actors in the decision-making dictates the energy flowing through the energy network, ultimately affecting the whole infrastructure.
The concept of an energy community is not strictly delimited but it can be described as a local energy system encompassing distributed sustainable energy conversion units, both on the supply and demand sides [3]. The concept of energy hub is usually used to model such systems. Multi-energy sources supply a multi-service demand with conversion units being optimally interconnected and operated. Extensive reviews have been carried out on this topic [5]. The scale considered varies from local energy hubs, such as a residential area to large scale systems including a whole country. Energy communities are usually deployed at the neighborhood scale since the proximity facilitates governance.
Due to its network structure, modeling an energy community at the district scale with a building resolution usually exceeds computational power [6]. Facing this problem, a popular method is to fix some degrees of freedom by making assumptions and scenarios based on expert knowledge (Table 1). As an example, half of the literature reviewed assumes energy demand profiles or predetermines the energy system configuration. The issue with such assumptions is the consideration of a fixed energy demand instead of energy services to be fulfilled. The change of approach is beneficial since it does not assume local investment decisions into energy capacities [7]. Therefore, it allows an optimal system design considering the interdependencies between subsystem components. An example within energy communities is the sharing of renewable energy capacities among buildings to maximize self-consumption. Another dimension is the coordination of the investments among subsystems to respect constraints at the district’s boundary, such as grid constraints. Modeling subsystems as entities embedded in a larger system reveals the interdependency of the decision-making. It also entails an ethical aspect, since the modeling should account for the interests of the actors concerned [7]. Therefore, assumptions and scenarios should be considered with care since they tend to oversimplify the view on the problem. Despite the extensive literature existing on the topic of energy communities, a holistic framework is usually not considered.
Besides the simplification of the problem statement, another research gap is the lack of generality of the results. Most of the literature considers a single case study on a neighborhood. Some authors investigated the broad impact of local residential systems but the scope relied on single building energy systems [8,9]. Therefore, the potential of energy communities to support the energy transition at the national level is an evident knowledge gap in the literature. Based on these research gaps, the present study aims at answering the following research questions:
  • Understanding the integration of renewable energy within local energy systems:
    • What are the investment and operation decisions within energy communities?
    • How does the decision-making change with geographic and urban context?
  • Impacts of the boundary conditions on local energy systems:
    • How does renewable electricity penetration change with electricity tariffs?
    • What is the impacts for energy communities to consider grid capacity constraints?

2. Methodology

The energy community is modelled as a renewable energy hub, being defined as a system optimally interconnecting multi-energy streams and conversion units [6]. Additionally, the energy hub is characterized by a high share of renewable energy and aims at maximizing self-consumption. The renewable energy hub is at the district scale within a low-voltage (LV) electricity grid deserved by a low to medium voltage (LV/MV) transformer. Service demands of each building, such as domestic hot water, domestic electricity and space heating, are supplied by conversion units and a gas and electricity utility. A mixed integer linear programming (MILP) formulation optimizes the investment into conversion units and the operation of the energy system. The conversion units include thermal units (air-water heat pumps, gas boilers, electrical heaters) and storage units (thermal tanks and lithium ion batteries). PV panels are the main source of renewable electricity. Their orientation on the roofs is a decision variable as described by Middelhauve et al. [6].
Energy and mass balances as well as heat cascade are the main constraints of the model. Electricity and natural gas balances are applied at the building and district scales, allowing synergies between buildings and between energy carriers. Equation (1a) shows the electricity balance between the buildings import and export E ˙ b , p , t g r and the LV/MV transformer exchanges E p , t t r . A positive symbol represents an import of energy and a negative one an export. In the equations, decision variables are highlighted with bold characters. Technical constraints are considered to model conversion units and to account for infrastructure specifications. For example, Constraint (1b) is applied to restrict the power exchanged on the LV/MV transformer to a specified value E ˙ t r , m a x . To reduce computational burdens time series are clustered into typical and extreme operating periods using the k-medoids algorithm. The typical day frequency is d p and the timesteps duration is d t . The model considers four sets: buildings B, typical periods P, timesteps T of each typical period and units U. More details on the formulation are given in the two theses [6,8].
∑ b ∈ B ( E ˙ b , p , t gr , + − E ˙ b , p , t gr , − ) · d p · d t = E p , t tr , + − E p , t tr , − ∀ p ∈ P , ∀ t ∈ T
E ˙ p , t tr , ± ≤ E ˙ t r , m a x ∀ p ∈ P , ∀ t ∈ T

2.0.1. Objective Functions

The objective functions are described in Equations (2a) to (2e). The total costs (TOTEX) encompass operating costs (OPEX) and capital costs (CAPEX). The OPEX correspond to the annual energy costs and revenues. The electricity and gas retail tariffs are respectively c e l , + and c n g , + and the feed-in tariff is c e l , − . The variables E t r and H g r , + correspond to the annual electricity and gas exchanges with the utility at the district level. The CAPEX (Eq.2c) consider investments and replacement costs of energy units. The costs are annualized over a n years horizon with an interest rate i. The investment costs C i n v are linearized with fixed ( i c 1 , u ) and variable ( i c 2 , u ) costs. The CAPEX is dictated by two decision variables, the binary decision to install a unit or not ( y u ) and the installed capacity ( f u ). When a conversion unit has a lifetime l u lower than the project horizon n, the replacement cost is given by the number of replacements R over the horizon n. Multi-objective optimization is performed to evaluate the solution space at the interplay of two conflicting objectives: OPEX and CAPEX. One objective is upper-bounded by an ϵ -constraint while the second objective is minimized. Pareto fronts are generated by varying the ϵ -constraints and by exchanging the objectives constrained and minimized.
TOTEX = OPEX + CAPEX
OPEX = c e l , + · E tr , + − c e l , − · E tr , − + c n g , + · H gr , +
CAPEX = i ( 1 + i ) ( 1 + i ) n − 1 ( C inv + C rep )
C inv = ∑ u = 1 U b u · ( i c 1 , u · y u + i c 2 , u · f u )
C rep = ∑ u = 1 U ∑ r = 1 R 1 ( 1 + i ) r · l u · ( i c 1 , u · y u + i c 2 , u · f u )

2.1. Decomposition

The energy community model has a building scale resolution. Due to the network structure and long computation time, the Dantzig-Wolfe decomposition is applied on the original MILP problem. The methodology is described in detail in [23]. Each building energy system represents a subsystem independent from other subsystems except for the resources balance (Eq. 1a) and capacity constraints (Eq. 1b), being linking constraints. The model is decomposed into distinct problems: a master problem (MP) and several sub problems (SPs). Linking constraints are included in the MP and represent the district energy system problem. The MP receives building energy system designs from the SPs and selects an optimal configuration of designs by a linear combination of the proposals. Each design accounts for an investment into conversion units and associated energy flows within the district LV grid. Once optimized, the MP calculates the dual values of the linking constraints that are inserted in the SPs objective function as Lagrangian multipliers. Within an iteration loop, the SPs find new design proposals based on price signals sent by the MP. The SPs are formulated as reduced costs, meaning that a solution with a negative value has the potential to improve the MP objective. The algorithm terminates when the SPs cannot find negative reduced costs or when the maximum number of iterations is reached.

2.2. Key Performance Indicators

Key performance indicators are used to quantify solutions performance. The self-consumption (SC) is the share of onsite electricity generation potential E p o t being consumed within the district. The self-sufficiency (SS) corresponds to the share of the electricity demand being supplied by onsite generated electricity. PV curtailment is the share of onsite electricity generation potential being neither self-consumed, nor sold to the grid. Finally, the PV penetration (PVP) is the proportion of the electricity demand that could be supplied by the onsite generated electricity with a SC of 100%.
SC = ( E p o t − E c u r t − E t r , − ) / E p o t
SS = ( E p o t − E c u r t − E t r , − ) / ( E p o t − E c u r t − E t r , − + E t r , + )
PVC = E c u r t / E p o t
PVP = E p o t / ( E p o t − E t r , − + E t r , + )

2.3. Typical Districts Identification

Gupta et al. estimated that Switzerland hosts 17’844 MV/LV transformers [24]. To handle this problem complexity, a k-medoids clustering algorithm is applied to find the most representative districts. The case study is implemented through a geographic information system to adequately describe the energy demands and sources. Clustering features consider real-estate characteristics (heating surface, roof area, service demands, building category, construction year) and geographic ones (annual solar irradiation, average temperature, infrastructure density). Typical Swiss weather profiles have been assessed for each district by Stadler et al. [8]. A principal component analysis is applied to reduce the dataset dimensionality [25]. The purpose is to restrain computational time while keeping the information variability from the dataset.
The k-medoids algorithm is run over 50 iterations to estimate the optimal number of clusters K o p t . The latter corresponds to the minimum number of clusters required to represent the initial dataset as faithfully as possible. Three indicators are used to assess the clustering quality: elbow, silhouette and Calinski-Harabasz (CH). The silhouette and CH indexes are two metrics of the clusters cohesion [26]. Therefore, the aim is to maximize their score. In contrast, the elbow method measures the distortion of the clusters and should be minimized. Figure 1 presents the mean score of the indicators. The trade-off between information loss and complexity reduction is clear for the CH and elbow index. Below 10 clusters, the marginal performance improvement of adding a new cluster is high. The value of K o p t is respectively 6 and 7 for the elbow and CH index. Regarding the silhouette index, K o p t reaches 4 clusters but the metric does not capture well the trade-off between information loss and complexity. While Figure 1 shows the mean score of the metrics over all iterations, Figure 2 represents the distribution of K o p t . The silhouette and elbow score are robust. However, the result of the CH metric is distributed over several K o p t , ranging from 12 to 19 clusters. Since K o p t is measured at the maximum of the CH score and since this maximum is located on a plateau, it makes K o p t difficult to locate. Therefore, the mean score interpretation is preferred. Based on this analysis, the optimal number of clusters is between 6 and 10. The exact value of K o p t depends on the level of detail needed for the case studies to accurately represent specific regions. This clustering algorithm allows considering versatile district typologies within a restricted set of case studies. In particular, it allows the contextualisation and extrapolation of local decisions to the national scale.

2.4. Case Study

Within this case study, 6 clusters are identified to represent the whole Swiss building stock (Figure 3). The Urban cluster is the largest one with a mix of single and multi-family dwellings, plus commercial centers. The Sub-urban one is represented by a compact village of 2-floors buildings. The Countryside and Mountain areas are both dominated by single family detached houses but with different densities. Finally, the Forest cluster is dominated by large farms converted into residential houses. The sixth cluster contains outliers and is not considered in the case study. It is characterised by forests, mountains and glaciers without any buildings. For extrapolation to the national level, the representative roof area of each typical district is used. Since the present study aims at analysing the impact of energy communities, it is assumed that each district in Switzerland can endorse the status of an energy community.
Most data are open source and provided by the Swiss government. The building characteristics, such as the height, heated areas or types of construction come from cantonal and federal Official Buildings Registry [27]. Energy standards such as the envelope heat transfer, building heat capacity and domestic electricity demand as well as the internal and external heat gains are calculated based on Swiss standard norms [28]. These data are used to build the thermal model of the buildings [29]. The outdoor temperature and solar irradiation come from Meteonorm [30]. These time series are clustered into ten typical periods of 24 hours and two extreme periods of one hour using k-medoids clustering. The project horizon is 20 years and the interest rate 2%. Electricity and gas retail tariffs are respectively 0.25 CHF/kWh and 0.10 CHF/kWh and the feed-in tariff is 0.14 CHF/kWh. These values are based on average energy tariffs in Switzerland for the years 2022-2023 [31]. The fixed investment cost for PV panels is 6556 CHF and the variable cost is 1300 CHF/kWpeak. More details on buildings, energy units and weather data are detailed in [6].

3. Results and Discussion

The discussion follows two axes. First, the decision-making trends within energy communities are analysed and contextualised with their geographic and urban characteristics. Then, the potential of energy communities to supply renewable electricity to the national infrastructure is analysed. The analysis considers grid constraints and confronts the cost and energy efficiency impacts of a coordinated or uncoordinated investment strategy between local investments and national energy needs.

3.1. Decision-making Trends within Energy Communities

A multi-objective optimization between the CAPEX and OPEX is performed to obtain the solution trends for each district. Figure 4 shows the progressive substitution of the principal energy source, natural gas, by renewable energy as investments are increased. Gas boilers deployment corresponds to the solution with lowest investment and highest operational cost. Then, it is substituted by investments into heat pumps and solar panels. The marginal PVP improvement decreases with investment since best roof orientations are activated first. The typical districts split into three decision-making trends. This behavior is mainly explained by the ratio η s between roof surfaces and heated surfaces. This ratio can be considered as an approximation of the PVP. With its large farms, the Forest cluster has the largest solar potential. However, it has as well the highest heated surface among the typical districts resulting in the lowest η s ratio ( η s = 0.57). The Urban and Sub-urban districts have similar building compactness ( η s = 0.80 and 0.86), even though they contain different building density and usage purposes. Finally, since clusters 3 and 5 mainly contain single-family dwellings, they have the largest roof area with respect to their energy demand ( η s = 1.26 and 1.42). However, since a large η s ratio usually represents small buildings, it means as well a low economy of scale. And as there is a fixed investment cost to install equipment, the investment to decarbonize the energy system increases together with η s .
Beside decarbonization, local investment decisions have as well an impact at the districts boundary with the upper energy system. Figure 5 presents the annual electricity flows at the LV/MV transformers. Electricity imports remain more or less constant since the installation of PV panels compensates for the electricity consumption of heat pumps. In District 4, heat pumps are deployed before PV panels, resulting in an increase of electricity imports in the low investment region. Electricity exports follow the same trend as the PVP, with the difference of exhibiting a constant slope of 9.4 k W h C H F , a value to be put in perspective with the feed-in tariff of 0.1 C H F k W h . It demonstrates the sensitivity of investments and energy flows to energy tariffs. Beside maximizing self-consumption, energy communities are able to move from passive consumers to renewable electricity suppliers. And this shift of role is predetermined based on price signals. A question still remains, do the grid operators provide the right incentives to perform the energy transition?

3.2. National-scale Impacts of Energy Communities

As seen in Figure 4, the marginal cost of PV panels is increasing with the investment allocated. The last economically feasible point is obtained once the investments into PV panels are break-even with the revenues over their lifetime [6]. Since the revenues vary with the electricity tariffs, the investments induced by the tariffs can be calculated assuming that local stakeholders would invest until they reach the last economically feasible point. Figure 6 and Figure 7 present these induced investments in the form of annual renewable electricity generated by energy communities in Switzerland for a range of feed-in and retail tariffs. Figure 6 is generated assuming that the investments were optimized for each building individually while Figure 7 represents the case of energy communities. Below a certain energy tariff, PV investments are not profitable due to the affordable electricity cost from the grid. The investment threshold is delimited by the lower black line. On the other side, the upper investment limit maps the region where the PV installed capacity reaches its maximum of 67.2 GW, representing an annual electricity generation of 80 TWh/yr. The extrapolation to the national scale assumes that 70% of the roofs are suitable for PV installations [32]. The PV potential calculated in this study is 14% higher than the one estimated by Swissolar (70 TWh/yr [32]). Since the PVP varies within and throughout typical districts, there exists a large spectrum of investments. Districts with high solar potential are firstly selected. Then investments with lower profitability are allocated as the price signals sent by the grid operators become more attractive. Present energy tariffs incite to invest into the maximum PV panels capacity, reaching a potential of 80 TWh/yr. However, Schnidrig et al. estimated that the cost-optimal PV deployment in Switzerland would lead to a 20 TWh/yr electricity generation from PV panels [1]. Therefore the price incentives should fall within the red-orange region. In conclusion, there is a discordance between the price signals sent by grid operators and the long-term needs of the infrastructure. This situation could result into costly grid reinforcements or local PV generation curtailment. In both cases, the solution is socially unfair since the former induces costs to end-users and the latter might render some investments unprofitable. In the remaining of the analysis, the impact of curtailment is analysed in terms of energy efficiency and costs.
To support the analysis, two scenarios are considered. In the first one (uncoordinated), an investment decision into PV panels and heat pumps is taken today. Then, peak shaving is applied on the energy system. The investment into storage units and their operation are optimized with fixed sizes of PV and heat pump units. In the second scenario (coordinated), all investment and operation decisions are taken considering peak shaving. Therefore, PV and heat pump capacities vary as the system is being constrained. The aim of these two scenarios is to assess the impact of peak shaving on the decision-making and to measure the importance of coordinating investments. Figure 8 shows the load duration curve of the electricity flows between energy communities and the national grid. The present electricity tariffs promote an energy system with a peak export power of 46.8 GW, exceeding by a factor three the existing capacity of the Swiss MV grid, being 15.8 GW [1]. The optimal PV capacity is represented on Figure 8 by the blue area and corresponds to a peak PV power of 15.4 ± 2 GW with a self-consumption of 5.8 GW at the time of the peak export. The curtailed system reduces by a third the maximum export power. The uncoordinated scenario exports more electricity and has a flat profile. Because of its large PV capacity, the energy system simply curtails the exceeding power. This outcome is beneficial for the grid operators since the export profile shows fewer variations. However, from the perspective of households, the PV investment is oversized since the optimal export profile would have been 29% lower (plain red line).
Figure 9 further details the energy efficiency and costs of the two scenarios. Each plot represents the impacts on energy communities as the peak export power is increasingly constrained, from 46.8 GW down to 5.1 GW as shown on Figure 8. In the uncoordinated scenario, an investment into batteries is allocated to increase self-consumption and self-sufficiency. Even though this strategy increases the energy performance, it is not sufficient to absorb the large amount of electricity generated onsite. Therefore, most of the peak shaving is performed by PV curtailment and 48.2% of the renewable electricity is simply not used. In contrast, under the consideration of peaks shaving, the coordinated scenario invests much less into PV panels. It reduces the self-sufficiency by 20%, but it mitigates curtailment with a PVC of 9.2% only. Beside low energy efficiency, non-coordination has a cost as well. The oversized PV capacity and PV curtailment induce a total cost difference of 43.2% between the two scenarios. The larger amount of electricity sold to the grid in the first scenario does not compensate for the high investment cost into PV panels, in contrast to the second scenario where the TOTEX are balanced between lower electricity revenues and lower investments.

4. Conclusion

The objective of this paper is to highlight the decisions-making trends within energy communities and their integration in the national energy infrastructure. The communities are modeled as renewable energy hubs considering operation and investments into energy conversion units. Five typical districts are considered and the energy system solutions are extrapolated to the national scale. Multi-objective optimization and grid constraints are applied to fulfill the national needs for local renewable electricity. The main outcomes of the study are as follows:
  • Investment trends are similar among the typical districts. However, their magnitude and solar potential differ based on the location and morphology of the buildings.
  • The PV potential of the Swiss building stock reaches 80 TWh/yr, a value that is close to the conclusion of previous studies [32]. The associated PV capacity is 67.2 GW.
  • Investment and operation decisions in energy communities are highly sensitive to electricity tariffs. Present price signals promote an excessive PV deployment into the energy system, with an installed capacity that could considerably exceed the forecast cost optimum of 15.4 GW [1].
  • Uncoordinated investments with respect to grid constraints could generate curtailment up to 48.2% and increase total costs by 43.2%. In contrast, a coordinated planning where energy communities adapt their equipment to the specifications of the infrastructure only curtails the PV generation potential by 9.2%.
The presented results contribute to a better understanding of the decision-making interdependency between local actors and national energy systems. A holistic approach encompassing various stakeholders within a single optimization favors a coordinated energy transition and increases acceptance for the decisions takers. Grid operators and national institutions should adopt a consensus on the appropriate price signals to send to local stakeholders to incentive renewables deployment while preventing flawed returns on investment. The extension of the work includes a better definition of the national infrastructure accounting for reinforcement costs. To this extent, bi-level and nested decomposition methods have a high potential at linking the various levels of decision-making.

Author Contributions

Conceptualization, Cédric Terrier; Data curation, Cédric Terrier, Joseph Loustau and Dorsan Lepour; Formal analysis, Cédric Terrier; Funding acquisition, François Maréchal; Investigation, Cédric Terrier; Methodology, Cédric Terrier, Joseph Loustau, Dorsan Lepour and François Maréchal; Project administration, François Maréchal; Resources, François Maréchal; Software, Cédric Terrier, Joseph Loustau and Dorsan Lepour; Supervision, François Maréchal; Validation, Joseph Loustau and Dorsan Lepour; Visualization, Cédric Terrier and Joseph Loustau; Writing – original draft, Cédric Terrier; Writing – review & editing, Joseph Loustau and Dorsan Lepour.

Funding

The research published in this report was carried out with the support of the Swiss Federal Office of Energy SFOE as part of the SWEET consortium SWICE. The authors bear sole responsibility for the conclusions and the results of the presented publication.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

Abbreviations

The following abbreviations are used in this manuscript:
LV/MV Low voltage / Medium voltage SP Sub Problem
CAPEX Capital cost PVP Photovoltaic penetration
OPEX Operating cost SC Self-Consumption
TOTEX Total cost SS Self-Sufficiency
MP Master Problem PVC Photovoltaic curtailment

References

  1. Schnidrig, J.; Cherkaoui, R.; Calisesi, Y.; Margni, M.; Maréchal, F. On the role of energy infrastructure in the energy transition. Case study of an energy independent and CO2 neutral energy system for Switzerland. Frontiers in Energy Research 2023, 11, 1164813. [Google Scholar] [CrossRef]
  2. Parliament, E. DIRECTIVE (EU) 2018/ 2001 OF THE EUROPEAN PARLIAMENT AND OF THE COUNCIL - of 11 December 2018 - on the promotion of the use of energy from renewable sources 2018. p. 128.
  3. Busch, H.; Ruggiero, S.; Isakovic, A.; Hansen, T. Policy challenges to community energy in the EU: A systematic review of the scientific literature. Renewable and Sustainable Energy Reviews 2021, 151, 111535. [Google Scholar] [CrossRef]
  4. of Energy, S.F.O. Perspectives énergétiques 2050. Technical report, 2013.
  5. Mohammadi, M.; Noorollahi, Y.; Mohammadi-ivatloo, B.; Yousefi, H. Energy hub: From a model to a concept – A review. Renewable and Sustainable Energy Reviews 2017, 80, 1512–1527. [Google Scholar] [CrossRef]
  6. Middelhauve, Luise. On the role of districts as renewable energy hubs. PhD thesis, EPFL, 2022.
  7. Bastholm, C.; Henning, A. The use of three perspectives to make energy implementation studies more culturally informed. Energy, Sustainability and Society 2014, 4, 3. [Google Scholar] [CrossRef]
  8. Stadler, P.M. Model-based sizing of building energy systems with renewable sources. PhD thesis, Lausanne, 2019.
  9. Kotzur, L.; Markewitz, P.; Robinius, M.; Cardoso, G.; Stenzel, P.; Heleno, M.; Stolten, D. Bottom-up energy supply optimization of a national building stock. Energy and Buildings 2020, 209, 109667. [Google Scholar] [CrossRef]
  10. Chakrabarti, A.; Proeglhoef, R.; Turu, G.B.; Lambert, R.; Mariaud, A.; Acha, S.; Markides, C.N.; Shah, N. Optimisation and analysis of system integration between electric vehicles and UK decentralised energy schemes. Energy 2019, 176, 805–815. [Google Scholar] [CrossRef]
  11. Murray, P.; Carmeliet, J.; Orehounig, K. Multi-Objective Optimisation of Power-to-Mobility in Decentralised Multi-Energy Systems. Energy 2020, 205, 117792. [Google Scholar] [CrossRef]
  12. Alhamwi, A.; Medjroubi, W.; Vogt, T.; Agert, C. Modelling urban energy requirements using open source data and models. Applied Energy 2018, 231, 1100–1108. [Google Scholar] [CrossRef]
  13. Kramer, M.; Jambagi, A.; Cheng, V. Bottom-up Modeling of Residential Heating Systems for Demand Side Management in District Energy System Analysis and Distribution Grid Planning 2017. p. 8.
  14. Wakui, T.; Hashiguchi, M.; Yokoyama, R. A near-optimal solution method for coordinated operation planning problem of power- and heat-interchange networks using column generation-based decomposition. Energy 2020, 197, 117118. [Google Scholar] [CrossRef]
  15. Reynolds, J.; Ahmad, M.W.; Rezgui, Y.; Hippolyte, J.L. Operational supply and demand optimisation of a multi-vector district energy system using artificial neural networks and a genetic algorithm. Applied Energy 2019, 235, 699–713. [Google Scholar] [CrossRef]
  16. Pickering, B.; Choudhary, R. District energy system optimisation under uncertain demand: Handling data-driven stochastic profiles. Applied Energy 2019, 236, 1138–1157. [Google Scholar] [CrossRef]
  17. Fazlollahi, S.; Becker, G.; Maréchal, F. Multi-objectives, multi-period optimization of district energy systems: II—Daily thermal storage. Computers & Chemical Engineering 2014, 71, 648–662. [Google Scholar] [CrossRef]
  18. Schütz, T.; Hu, X.; Fuchs, M.; Müller, D. Optimal design of decentralized energy conversion systems for smart microgrids using decomposition methods. Energy 2018, 156, 250–263. [Google Scholar] [CrossRef]
  19. Wirtz, M.; Heleno, M.; Moreira, A.; Schreiber, T.; Müller, D. 5th generation district heating and cooling network planning: A Dantzig–Wolfe decomposition approach. Energy Conversion and Management 2023, 276, 116593. [Google Scholar] [CrossRef]
  20. Wakui, T.; Hashiguchi, M.; Yokoyama, R. Structural design of distributed energy networks by a hierarchical combination of variable- and constraint-based decomposition methods. Energy 2021, 224, 120099. [Google Scholar] [CrossRef]
  21. Morvaj, B.; Evins, R.; Carmeliet, J. Optimization framework for distributed energy systems with integrated electrical grid constraints. Applied Energy 2016, 171, 296–313. [Google Scholar] [CrossRef]
  22. Silvente, J.; Kopanos, G.M.; Pistikopoulos, E.N.; Espuña, A. A rolling horizon optimization framework for the simultaneous energy supply and demand planning in microgrids. Applied Energy 2015, 155, 485–501. [Google Scholar] [CrossRef]
  23. Middelhauve, L.; Terrier, C.; Marechal, F. Decomposition Strategy for Districts as Renewable Energy Hubs. IEEE Open Access Journal of Power and Energy 2022, 9, 287–297. [Google Scholar] [CrossRef]
  24. Gupta, R.; Sossan, F.; Paolone, M. Countrywide PV hosting capacity and energy storage requirements for distribution networks: The case of Switzerland. Applied Energy 2021, 281, 116010. [Google Scholar] [CrossRef]
  25. Jolliffe, I.T.; Cadima, J. Principal component analysis: a review and recent developments. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 2016, 374, 20150202. [Google Scholar] [CrossRef]
  26. Arbelaitz, O.; Gurrutxaga, I.; Muguerza, J.; Pérez, J.M.; Perona, I. An extensive comparative study of cluster validity indices. Pattern Recognition 2013, 46, 243–256. [Google Scholar] [CrossRef]
  27. Office, F.S. Federal Register of Buildings and Dwellings 2019.
  28. SIA. SIA 380/1:2016 Heizwärmebedarf. Schweizerischer Ingenieur und Architektenverein 2016.
  29. Girardin, L. A GIS-based Methodology for the Evaluation of Integrated Energy Systems in Urban Area. PhD thesis, EPFL, 2012. [CrossRef]
  30. Remund, J.; Kunz, S.; METEOTEST.; of Energy, M.S.F.O. METEONORM - Global Meteorological Database for Engineers, Planners and Education, 2003.
  31. des producteurs d’énergie indépendants, A. Carte interactive des rétributions, 2023.
  32. Swissolar. Detailanalyse des Solarpotenzials auf Dächern und Fassaden 2020.
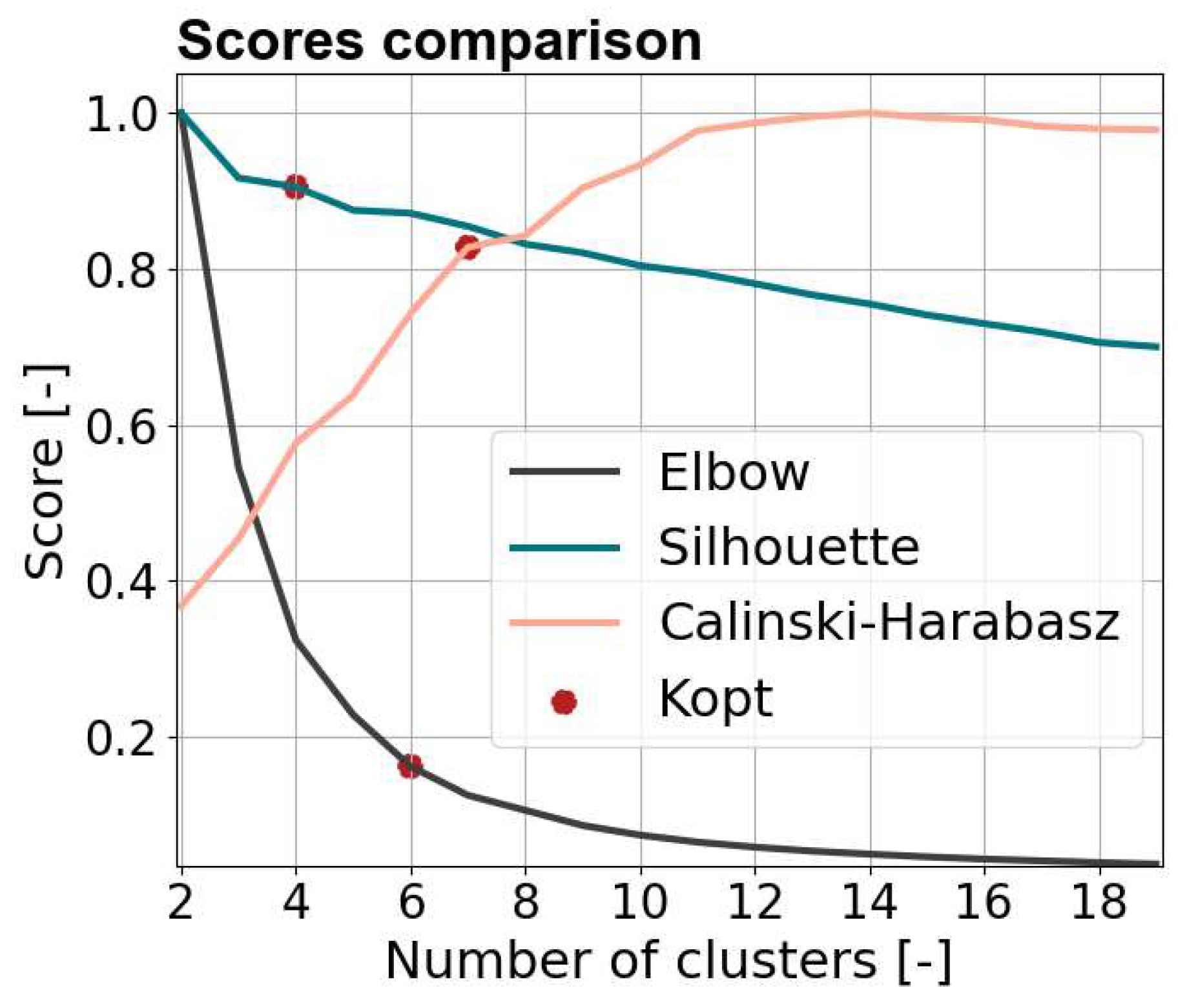
Preprints 92498 g001
Figure 1. Mean scores obtained for the three metrics over 50 iterations.
Figure 1. Mean scores obtained for the three metrics over 50 iterations.
Preprints 92498 g001
Preprints 92498 g002
Figure 2. Occurrences of the optimal number of clusters.
Figure 2. Occurrences of the optimal number of clusters.
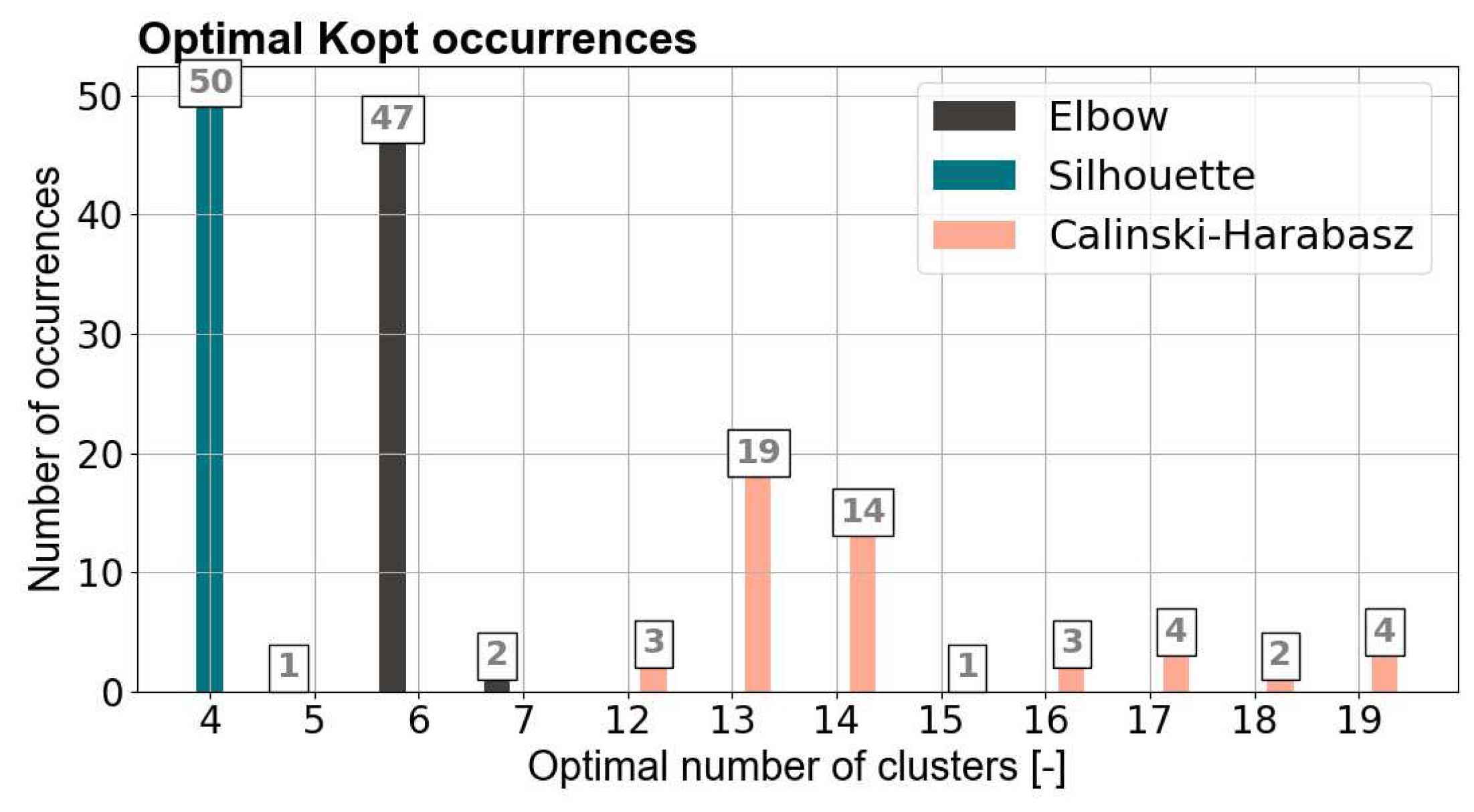
Preprints 92498 g002
Preprints 92498 g003
Figure 3. Typical districts distribution in Switzerland. The clusters differentiate the morphological and meteorological characteristics of the Swiss building stock.
Figure 3. Typical districts distribution in Switzerland. The clusters differentiate the morphological and meteorological characteristics of the Swiss building stock.
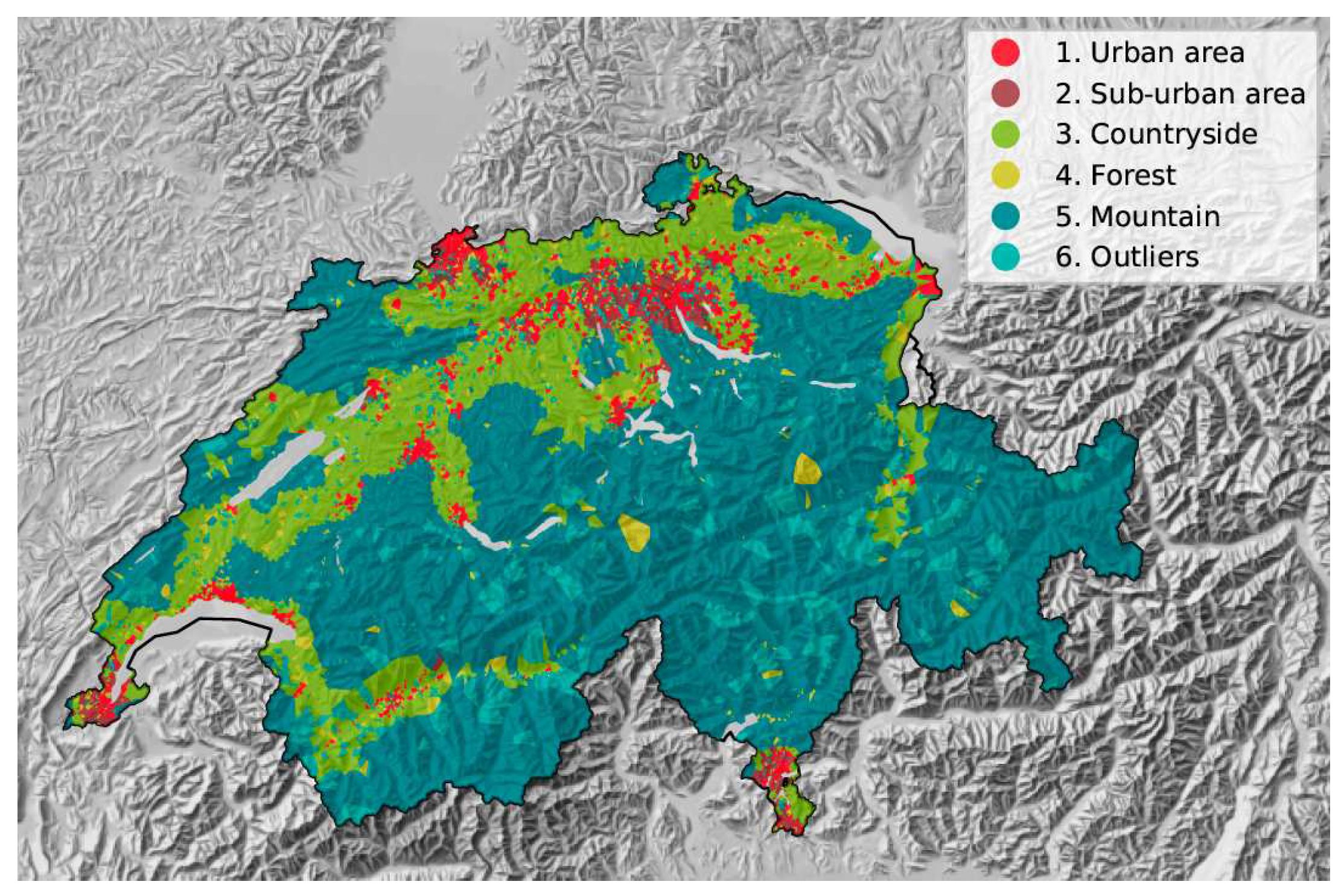
Preprints 92498 g003
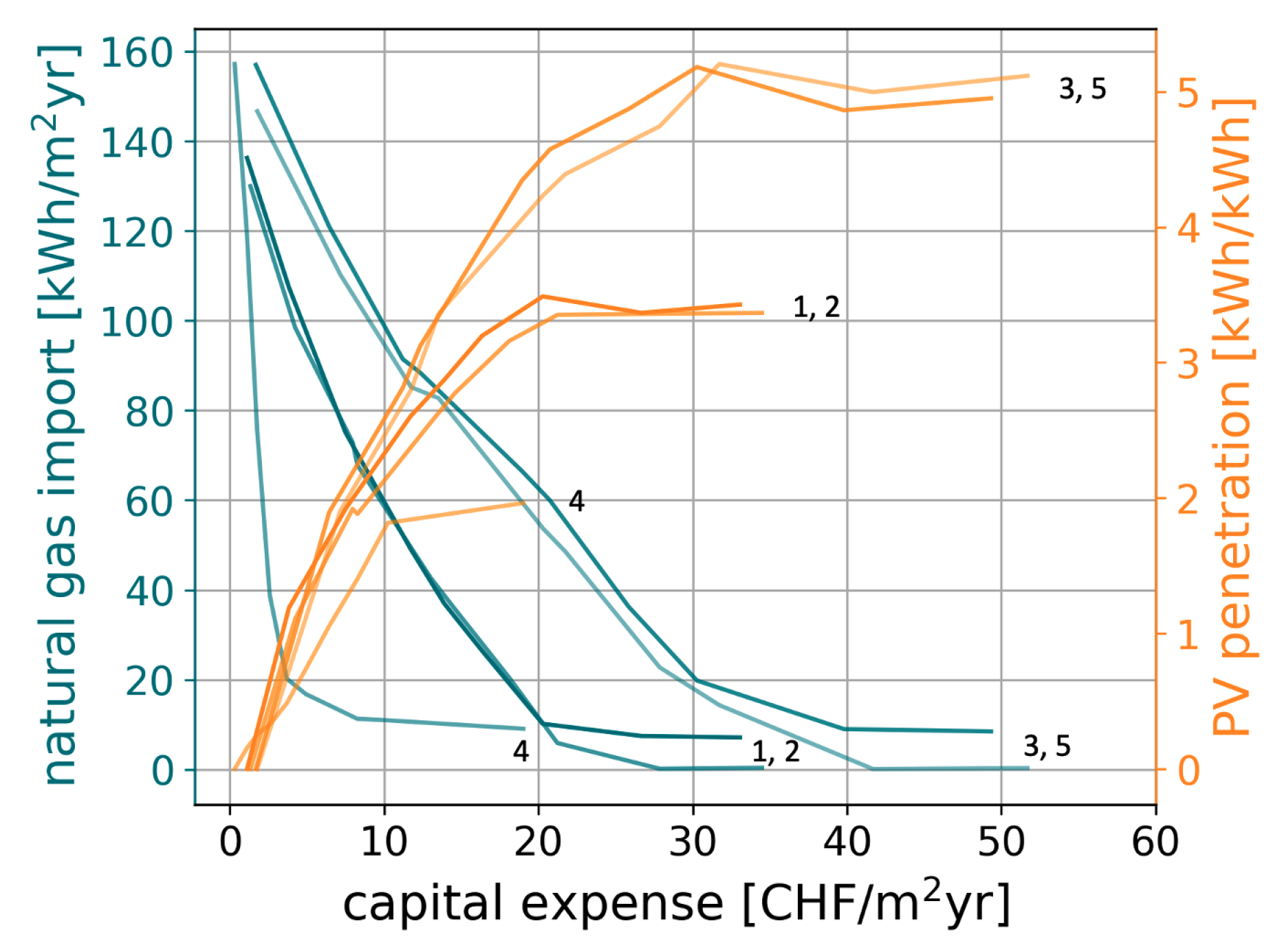
Preprints 92498 g004
Figure 4. Natural gas imports and renewable electricity generated onsite for each typical district.
Figure 4. Natural gas imports and renewable electricity generated onsite for each typical district.
Preprints 92498 g004
Preprints 92498 g005
Figure 5. Electricity flows at the districts LV/MV transformer, normalised by heated surface.
Figure 5. Electricity flows at the districts LV/MV transformer, normalised by heated surface.
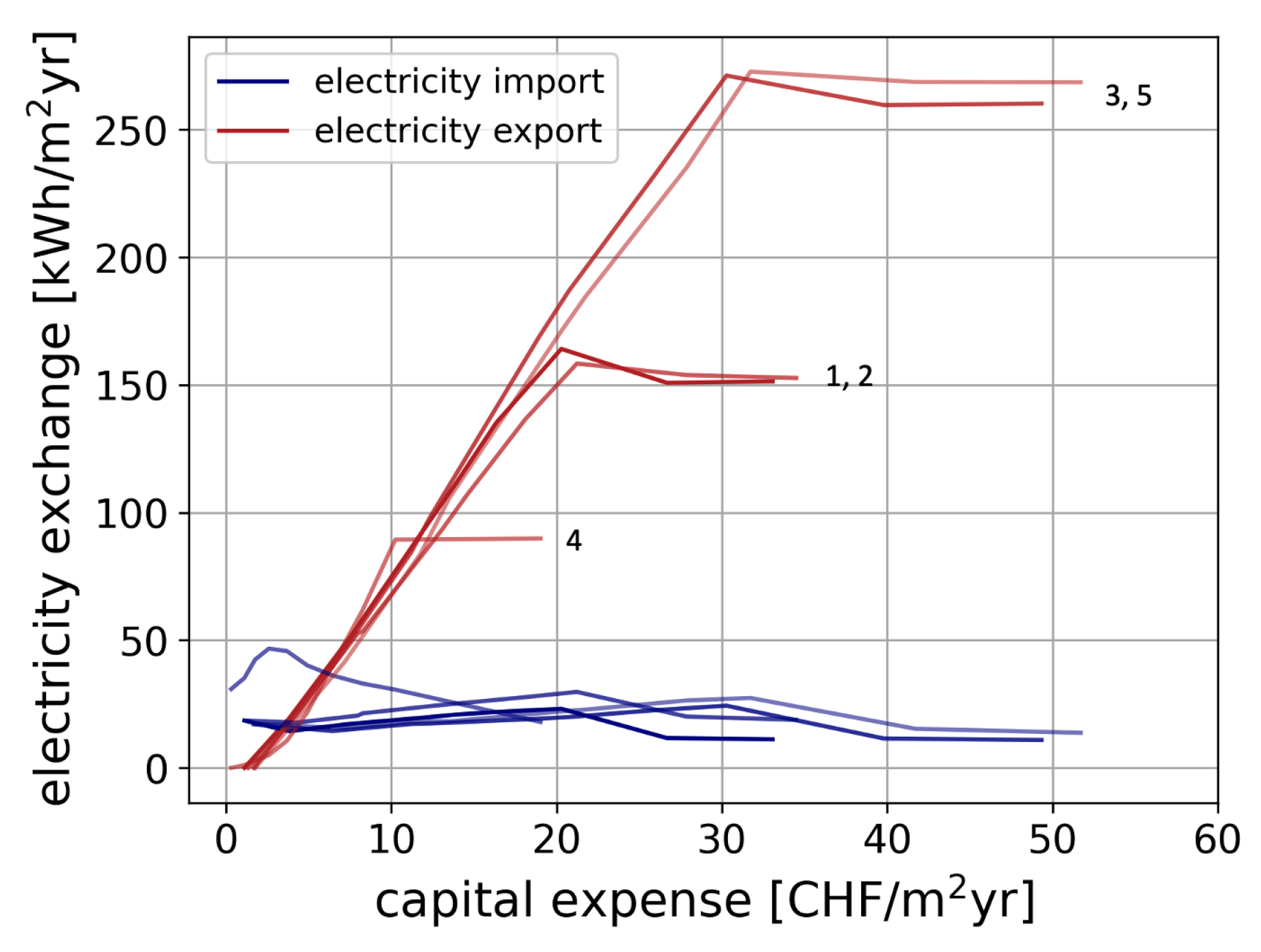
Preprints 92498 g005
Preprints 92498 g006
Figure 6. Optimal yearly renewable electricity generation based on building scale decisions.
Figure 6. Optimal yearly renewable electricity generation based on building scale decisions.
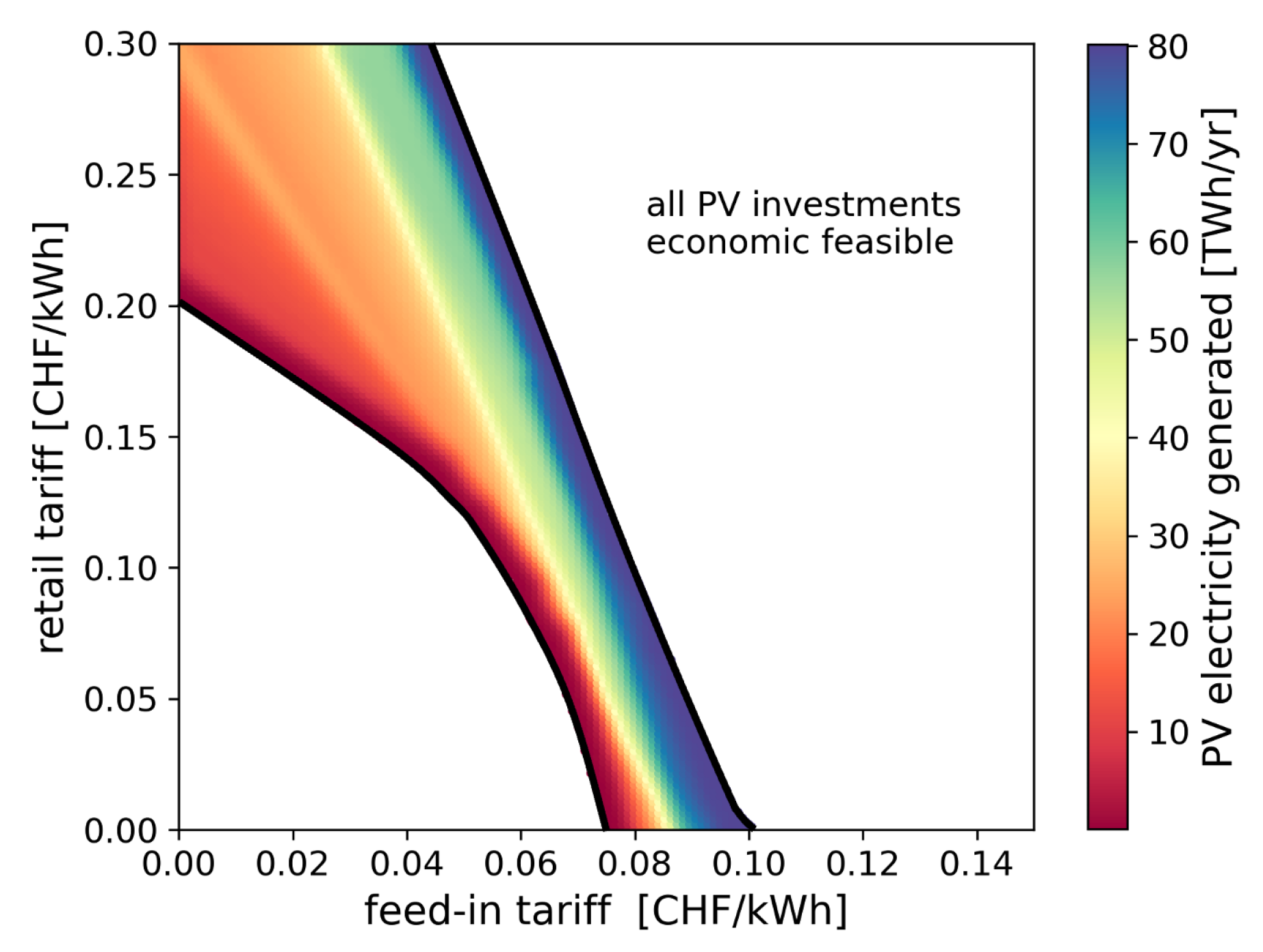
Preprints 92498 g006
Preprints 92498 g007
Figure 7. Optimal yearly renewable electricity generation based on energy communities.
Figure 7. Optimal yearly renewable electricity generation based on energy communities.
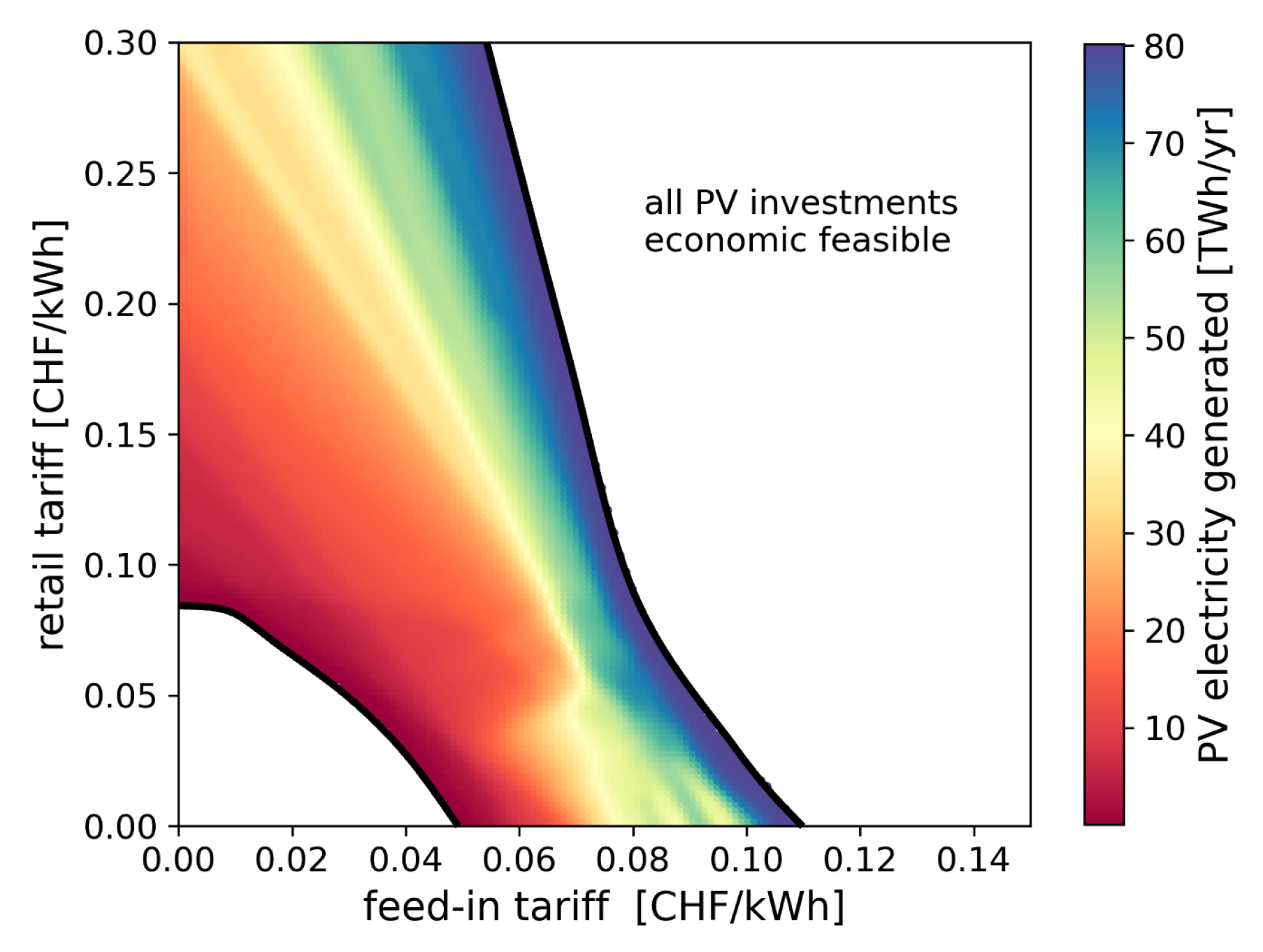
Preprints 92498 g007
Preprints 92498 g008
Figure 8. Load duration curve of electricity imports and exports for energy communities in Switzerland. The unconstrained solution is constrained to reduce the maximum power peaks by a factor three. Two design scenarios are considered, a coordinated one accounting for peak shaving in the investment decision and an uncoordinated one being imposed peak shaving after investment decision.
Figure 8. Load duration curve of electricity imports and exports for energy communities in Switzerland. The unconstrained solution is constrained to reduce the maximum power peaks by a factor three. Two design scenarios are considered, a coordinated one accounting for peak shaving in the investment decision and an uncoordinated one being imposed peak shaving after investment decision.
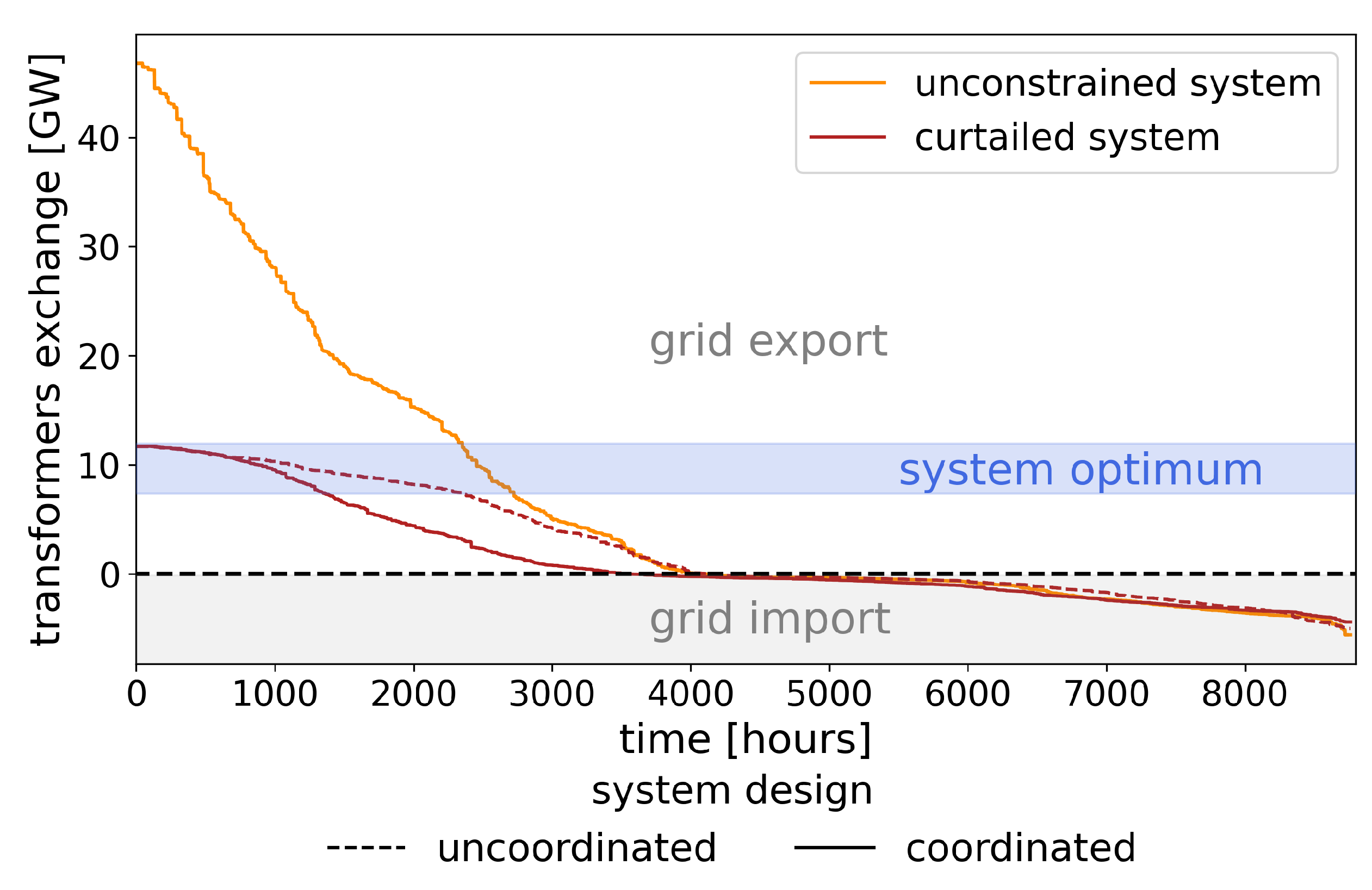
Preprints 92498 g008
Preprints 92498 g009
Figure 9. a) Energy performance and b) Cost impacts with respect to peak shaving. All values are given after extrapolation to the whole country. The cost metrics are normalised per heated surfaces.
Figure 9. a) Energy performance and b) Cost impacts with respect to peak shaving. All values are given after extrapolation to the whole country. The cost metrics are normalised per heated surfaces.
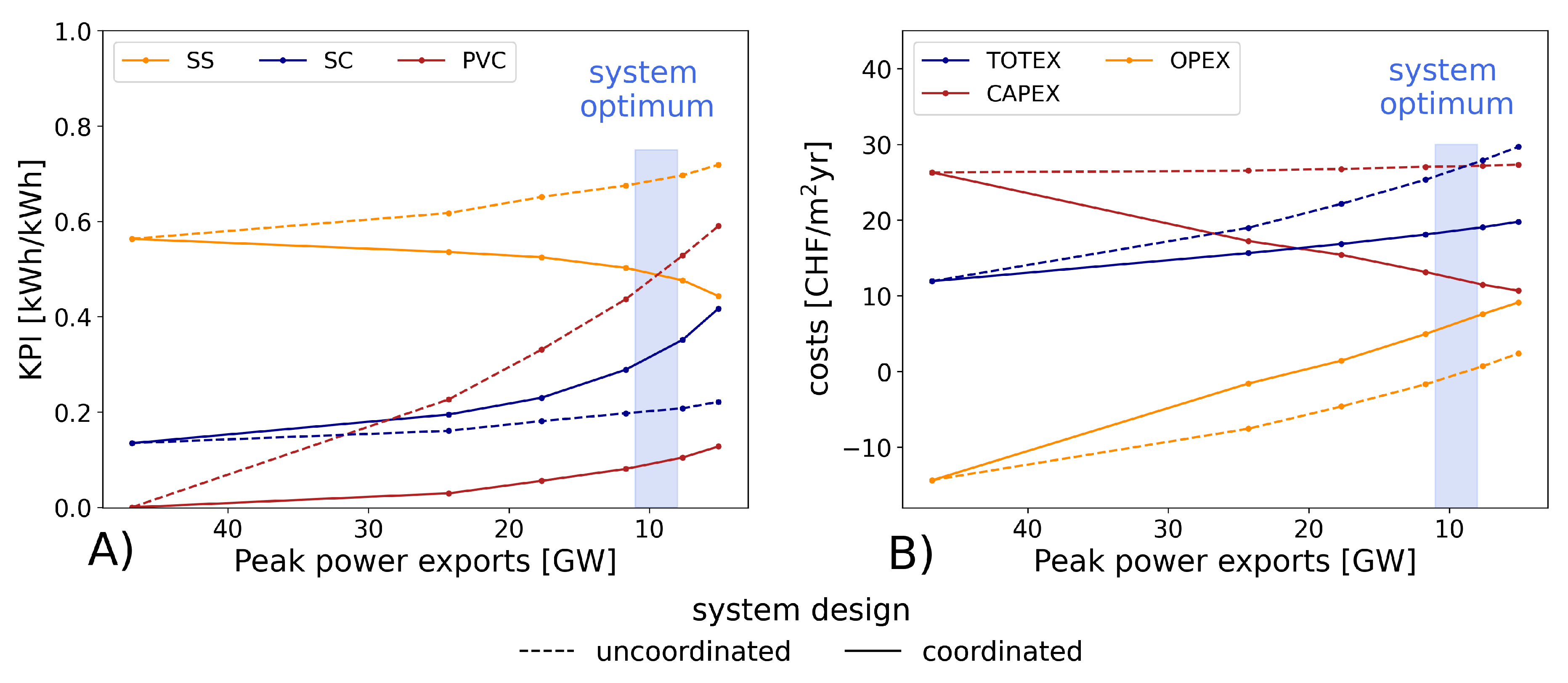
Preprints 92498 g009
Table 1. Literature review on energy communities: Sub problem and Main problem describe the resolution and scope of the studies. Approach shows the methodology used to handle problem complexity. Interdependent decisions highlights whether the authors considered decision-making interactions between buildings, and between the national and local scales. Finally, Systemic constraints refers to boundary constraints consideration, such as grid constraints.
Table 1. Literature review on energy communities: Sub problem and Main problem describe the resolution and scope of the studies. Approach shows the methodology used to handle problem complexity. Interdependent decisions highlights whether the authors considered decision-making interactions between buildings, and between the national and local scales. Finally, Systemic constraints refers to boundary constraints consideration, such as grid constraints.
Method Analysis
Sub problem Main problem Approach National
scope		 Interdependent
decisions		 Systemic
constraints		 Reference
Building Building Clustering ✓ ✗ ✗ [8]
Building Building Clustering ✓ ✗ ✗ [9]
Building District Pre-selection ✗ ✓ ✗ [10]
Building District Profiles ✗ ✗ ✓ [11]
Building District Pre-selection ✗ ✗ ✗ [12]
Building District Pre-selection ✗ ✗ ✗ [13]
Building District Dantzig-Wolfe ✗ ✓ ✗ [14]
District District Scenario ✗ ✗ ✗ [15]
Building District Scenario ✗ ✗ ✗ [16]
Building District Bi-level ✗ ✓ ✓ [17]
Building District Dantzig-Wolfe ✗ ✓ ✗ [18]
Building District Dantzig-Wolfe ✗ ✓ ✗ [19]
Building District Benders and
Dantzig-Wolfe		 ✗ ✓ ✗ [20]
Building District Bi-level ✗ ✓ ✓ [21]
District District Rolling horizons
+ pre-selection		 ✗ ✗ ✗ [22]
Building District Dantzig-Wolfe
+ clustering		 ✓ ✓ ✓ This paper
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated