Is the Special Relativity Compatible with Einstein’s Static Universe? Proposal for New “Generic” Transformations. The Twin Paradox.

Preprint

Article

Is the Special Relativity Compatible with Einstein’s Static Universe? Proposal for New “Generic” Transformations. The Twin Paradox.

Altmetrics

Downloads

122

Views

Comments

José Gabriel Ramírez^*

This version is not peer-reviewed

Submitted:

06 December 2023

Posted:

07 December 2023

You are already at the latest version

Alerts

Abstract

Albert Einstein, shortly after publishing his General Relativity Theory (GRT) applied it to the entire universe in a paper of 1917. Einstein assumed that such a universe was static in time and possessed a uniform distribution of matter on the largest scales, obtaining a static and finite universe of spherical spatial curvature of radius R. Although this model was refuted by Edwin Hubble's discovery of the expansion of the universe, it is still often studied as a theoretical framework for some problems, such as the twin paradox. This paper will show that Einstein's static universe model leads to a privileged frame of reference, so that any observer moving at the speed v will be able to measure speeds of light other than c depending on the direction of beam transmission. The above will refute the validity of the application to this closed and static universe of the Special Relativity Theory (SRT) proposed by Einstein in 1905 in his article . In addition, a new synchronization convention and new coordinate transformations will be deduced, the "generic" transformations, which will replace those of Lorentz. Finally, the twin paradox in this universe will be solved by making use of them.

Keywords:

Subject: Physical Sciences - Theoretical Physics

1. Introduction

It is known that when Einstein's Special Relativity – as it is currently understood – is applied to moving observers, it is necessary to resort to asymmetries that explain the results in correspondence with the observed phenomena. Think of the asymmetries (accelerations, for example) that are used when trying to break the reciprocity in time dilation by changing the point of view of observers at rest and in motion and, thus, solve most paradoxes about clocks, also known as twin paradoxes.

If we take Einstein's static universe that has a closed, positively curvatured geometry as the surface of a sphere, then we can assume that our 3-dimensional universe would be the surface of a three-dimensional hypersphere of radius R defined within a 4-dimensional space. However, in order to represent it graphically and make it more intuitive, we will limit ourselves to a 2-dimensional universe immersed in a three-dimensional space.

Figure 1. A 2-dimensional universe represented by the surface of a sphere immersed in three-dimensional space.

The fact that the universe is closed and static would imply that any observer moving at a velocity v, as well as any beam of light emitted in either direction of an equatorial geodesic, for example, would return to the starting point after the necessary time.

Figure 2. (a) Beam of light returning to the starting point. (b) Observer moving at velocity v returning to the point of departure.

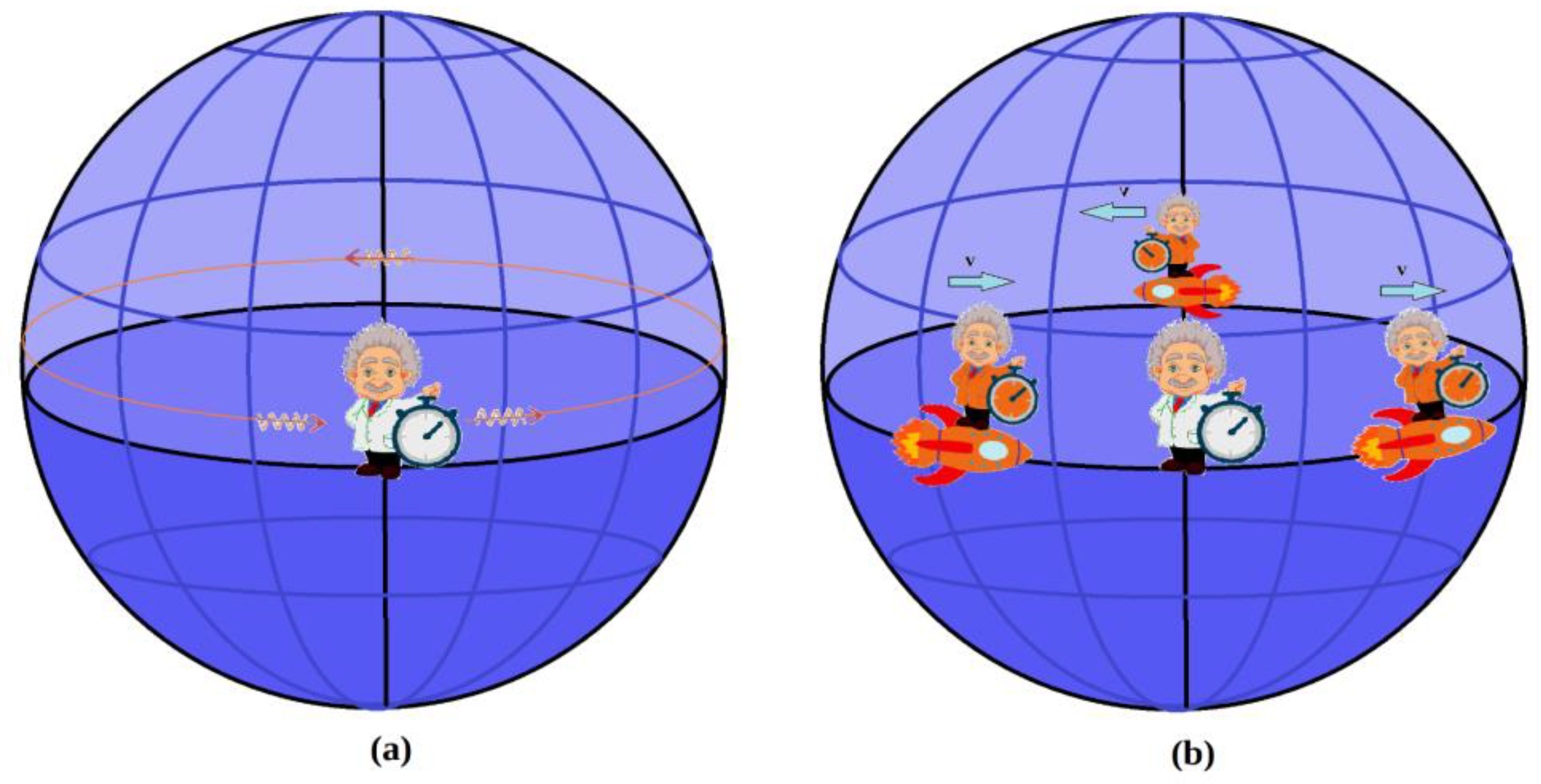
It is precisely the fact that a moving observer can return to the starting point that has revived the study of the twin paradox in this type of universe (see [3], [4], [5], [6] and [7]), since now, the traveling twin can meet his brother again moving at all times following the trajectory of a geodesic and, therefore, it is not possible to resort to the existence of accelerations to break the symmetry and be able to resolve the paradox. Now, in order to solve the paradox while saving the validity of Special Relativity, topological arguments or discontinuities in simultaneity are used to break the symmetry.

However, they do not seem to realize that having a closed universe with spherical symmetry causes the immediate appearance of a privileged frame of reference that contradicts the SRT since those observers who move with respect to it are able to detect different speeds of light for each of the directions in which the beam is sent. And it is the analysis of this incompatibility of Special Relativity in Einstein's universe that is the aim of this paper.

2. Metrics and Geodesics in Einstein's Universe

The metric for the hypersphere of the static universe that Einstein proposed can be written as:

{d s}^{2} = - c^{2} {d t}^{2} + R^{2} (d ξ^{2} + {s i n}^{2} ξ (d θ^{2} + {s i n}^{2} θ \cdot d ϕ^{2}))

(1)

It can be calculated (see [3]) that those addresses with the following coordinates:

ξ = θ = \frac{π}{2}

(2)

correspond to a geodesic of maximum length, the equatorial geodesic, which reduces the previous metric to the simplest two-dimensional form:

{d s}^{2} = - c^{2} {d t}^{2} + R^{2} d ϕ^{2}

(3)

where ϕ defined in the interval

ϕ ϵ [0, 2 π)

(4)

If, in addition, we do the coordinate change

x = R \cdot ϕ

(5)

then x will be defined in the interval

x ϵ [0, 2 π)

(6)

And since the universe is closed, we have that the position x = 0 is the same as the position x = 2πR. So, the above metric would be the most well-known form of:

{d s}^{2} = - c^{2} {d t}^{2} + {d x}^{2}

(7)

which is the Minkowski metric but with the x-coordinate limited to (4) and where L is the length of the universe:

L = 2 π R

(8)

Therefore, we will restrict ourselves to the specific case in which observers and light rays move over the equatorial geodesic (X-coordinate).

Since we assume that SRT is valid in this geodesic, then we will have to accept the Lorentz transformations as the coordinate-change expressions applicable between any two reference frames moving over it. But the acceptance of the SRT implies the validity of its postulates applied in a restricted way to this geodesic, i.e., equivalence of observers, constancy of the speed of light, contraction of lengths and time dilation. It is precisely this time dilation that is needed for the appearance and study of the twin paradox in this Einsteinian universe.

Since the SRT states that the speed of light in any direction is always equal to c, then there must be at least one observer, which we will call static or privileged, for whom two pulses emitted simultaneously in opposite directions must be received, after circling the universe, also simultaneously.

Figure 3. Simultaneous emission (a) and simultaneous reception (b) of two pulses of light in opposite directions.

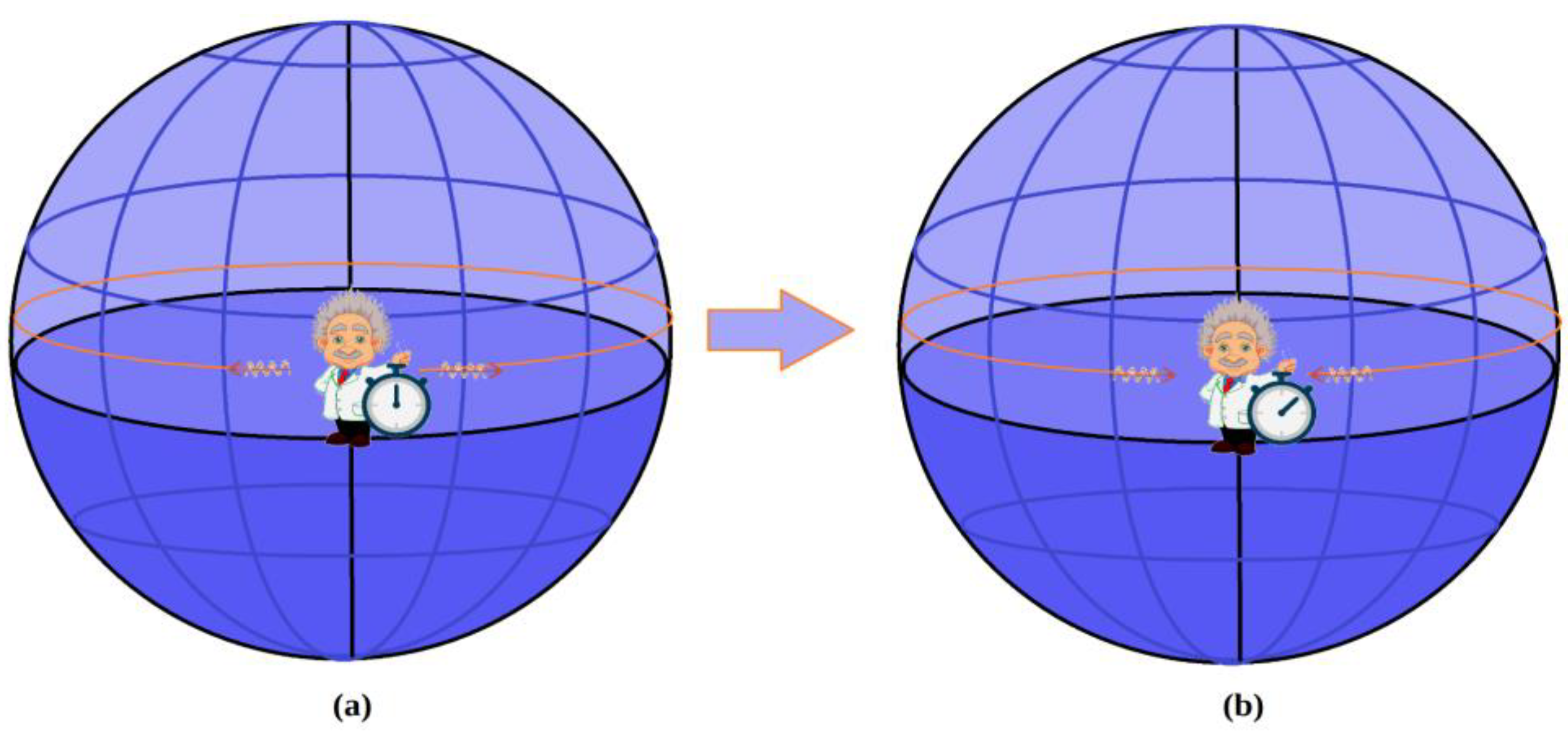
The constancy of c for said observer means that Einstein's synchronization convention is valid, allowing him to use it to synchronize his clocks and construct a reference system (see paragraph 0). In addition, this observer can calculate the length of the universe, L, just measuring time Δt it takes one pulse to return to the starting point and calculate:

L = 2 π R = c \cdot Δ t

(9)

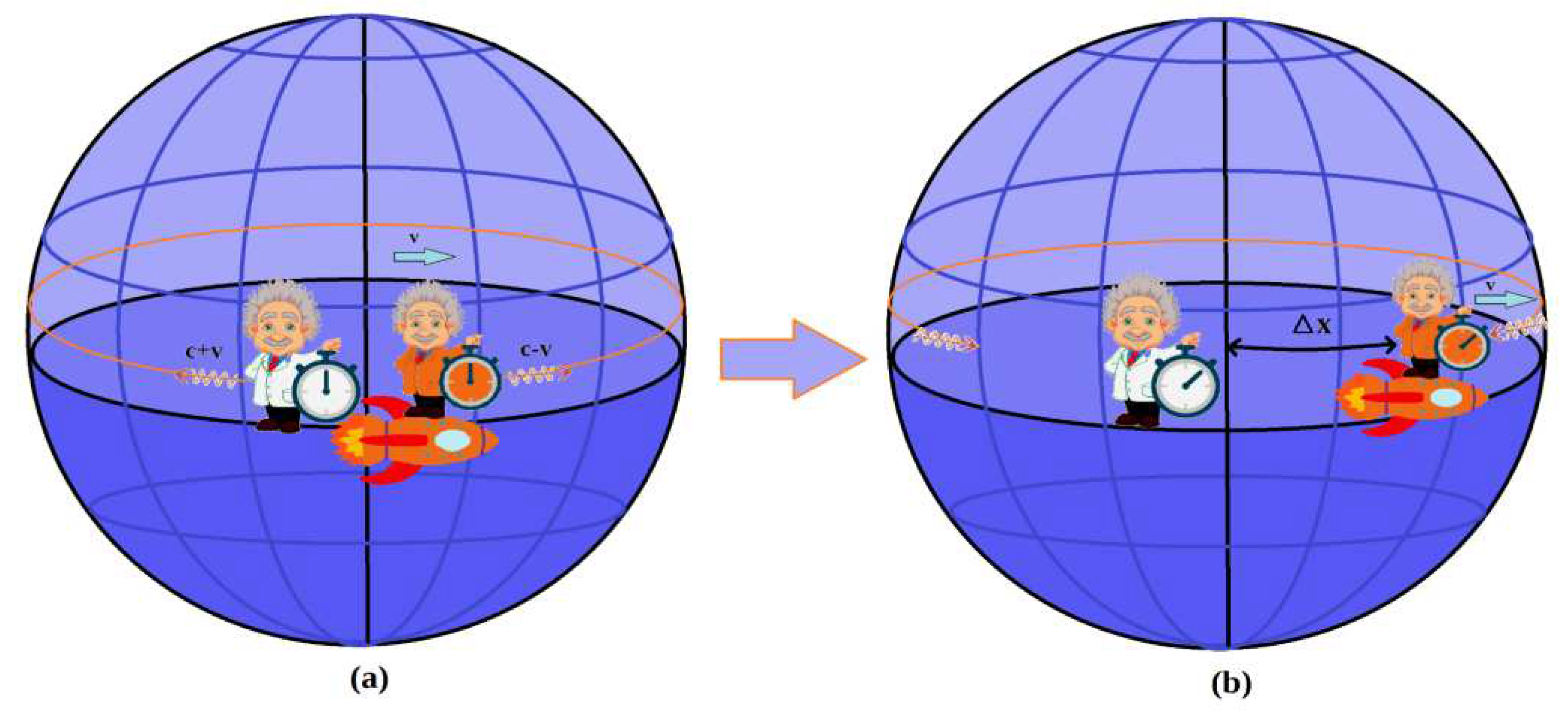
Once this static observer has been defined, it will be evident that for any other observer moving with velocity v with respect to him, the reception of pulses emitted simultaneously in opposite directions will no longer be simultaneous. Indeed, the beam of light sent in the opposite direction to the motion of the moving observer will have to travel a shorter distance Δx (the distance that the moving observer has moved during that time).

From the point of view of the static observer, the mobile observer is going in search of the beam sent in the opposite direction, while moving away from the pulse sent in the same direction of v. For the static observer, the effective velocities of the light pulses with respect to the moving observer will be c+v in the one case and c–v in the other.

The final result of the above is that, for the observer in motion, the reception of both pulses is no longer simultaneous and, therefore, this can be interpreted to mean that the speed of light has different values depending on the direction of transmission and, therefore, the principle of constancy of the speed of light is not valid for him.

Figure 4. Simultaneous emission (a) and non-simultaneous reception (b) for an observer moving at velocity v.

The above conclusion can also be obtained by plotting the space-time diagrams of both observers for the emission and reception of the pulses. The following figure shows these diagrams for the case of an observer moving at v = 0.5 c to the right, for which its time axis ct' is shown in orange. Figure 5a represents the time diagram of the pulse sent to the left, i.e., in the opposite direction to v, Figure 5b corresponds to the pulse sent in the same direction as v, and Figure 5c shows the two simultaneous processes. And, as can be seen from Figure 5c, for both observers there is a time difference in the reception of the light pulses, Δt in blue for the static observer and Δt' in red for the moving observer. (Recall that in this closed universe with x ϵ [0, 2πR = L), the point 0 and L are the same, so that everything that crosses to the right of point x = L will reappear to the point x = 0, and conversely, everything that crosses point x = 0 to the left will appear to point x = L).

Furthermore, as a consequence of the above, since c is not constant for the moving observer, it will not be possible for him to synchronize his clocks according to Einstein's convention (except at the local level, as we will see later), since, remember, Einstein's synchronization convention establishes by definition that the speed of light is c for both directions. Attempt by any mobile observer to synchronize their clocks will cause a discontinuity in their line of simultaneity, as we will demonstrate below. But to do so, let's return for a moment to Minkowski's infinite and flat universe.

3. Definition of simultaneity and reference system. Einstein’s synchronization convention

In his article [2] Einstein describes his convention of synchronization and how a reference frame based on it should be constructed: "If at the point A of space there is a clock, an observer at A can determine the time values of events in the immediate proximity of A by finding the positions of the hands which are simultaneous with these events. If there is at the point B of space another clock in all respects resembling the one at A, it is possible for an observer at B to determine the time values of events in the immediate neighborhood of B. But it is not possible without further assumption to compare, in respect of time, an event at A with an event at B. We have so far defined only an “A time" and a “B time." We have not defined a common “time" for A and B, for the latter cannot be defined at all unless we establish by definition that the “time" required by light to travel from A to B equals the “time" it requires to travel from B to A.".

Einstein's previous paragraph makes it very clear how coordinates are defined in a reference frame and how one should proceed to synchronize the clocks. This can be illustrated graphically with the following Figure 6:

in which we can imagine the X-axis replete with observers with synchronized clocks, so that when an event (the reception of lightning, for example) is claimed to have occurred at the coordinates (t, x) = (5 s, 2m) that means that the observer in x = 2 m saw the lightning strike in his position simultaneously with his clock striking 5 sec. As Einstein writes in [2] "the ‘time’ of an event is that which is given simultaneously with the event by a stationary clock located at the place of the event, this clock being synchronous, and indeed synchronous for all time determinations, with a specified stationary clock.".

On the other hand, attention should be drawn to the fact that Einstein's synchronization convention establishes by definition the constancy of the speed of light, c, in all directions. This means that any reference system whose clocks are synchronized according to this convention will always measure the same c-value.

4. Offsets Introduced by Einstein synchronization: relativity of simultaneity

Once it has been established how a frame of reference should be constructed, any observer can form his own, so that we can have several frame of reference, each with its own particular coordinates. But we need to know how, knowing the coordinates that an observer has obtained for an event, we can deduce the coordinates of the same event that another observer would get. In the case in which both reference frames move at a constant velocity (inertial reference frames) with a velocity v relative to each other, Einstein's Special Relativity Theory states that the equations that allow the transformation of the coordinates (t', x') of the moving observer in the increasing direction of the X-axis (to the right) and obtain the coordinates (x, t) of the "static" observer are the Lorentz Transformations (LT) whose expression has the form:

\begin{matrix} t = γ \cdot (t^{'} + \frac{v}{c^{2}} x^{'}) \\ x = γ \cdot (x^{'} + v \cdot t^{'}) \end{matrix}\}

(10)

where c is the speed of light in a vacuum (3x10⁸ m/s) and where

γ = \frac{1}{\sqrt{1 - v^{2} / c^{2}}}

(11)

Similarly, the inverse Lorentz transformations that allow the opposite coordinate change are given by the expressions:

\begin{matrix} t' = γ \cdot (t - \frac{v}{c^{2}} x) \\ x' = γ \cdot (x - v \cdot t) \end{matrix}\}

(12)

Now suppose a frame of reference K' is moving at a velocity v with respect to another static frame K. Suppose that at K' there are 3 clocks separated by a distance D'. We will consider the clock at x' = 0 as the coordinate origin of K' so that the other clocks must be synchronized with it. To do this, one possibility is that the observer at x' = 0 simultaneously sends two light pulses to the two clocks in their time t' = -D'/c so that, upon receiving these pulses, they must synchronize their clocks by assigning them the value t' = 0. After this process, the three clocks must be synchronized according to Einstein's convention.

Figure 7. Synchronization process in K' using light pulses.

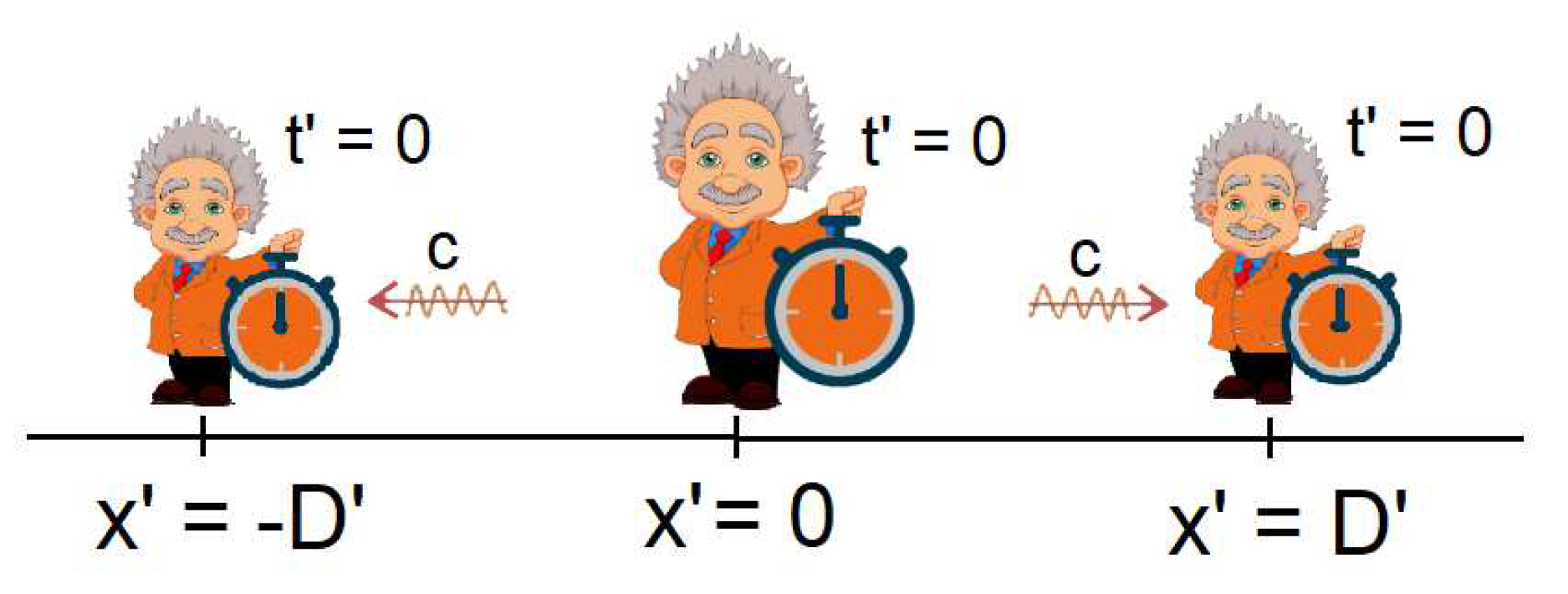
But the relativity of simultaneity implies that clocks that are synchronized in the system K' will not be synchronized for an external observer K. This begs the question of how the synchronization process of K' is viewed by another inertial observer who is at "rest" in K.

For K, since K' is moving with velocity v in the direction of the positive values of the X-axis, he will see that the clock at x' = -D' moves at the meeting of the pulse emitted from the coordinate origin, while the clock at x' = D' moves in the same direction as the light pulse "away" from it. Therefore, the synchronization light pulse will reach the clock x' = -D', which will be advanced, before the clock at x' = D' which will be delayed with respect to the clock at x' = 0.

The observer K can calculate this time lag simply by using the Lorentz transformations (10) for events in which photons hit the clocks and whose coordinates (ct',x') for K' will be (0,-D') and (0,D') respectively. Thus, for the clock at x' = D', the delay (sign "-") that K will measure will be:

Δ t_{D'} = 0 - γ \cdot (0 + D' \cdot \frac{v}{c^{2}}) = - γ \cdot D' \cdot \frac{v}{c^{2}}

(13)

and the advance (sign "+") of the clock at x' = -D' with respect to the clock at x' = 0 that will measure K will be:

Δ t_{- D'} = 0 - γ \cdot (0 - D' \cdot \frac{v}{c^{2}}) = γ \cdot D' \cdot \frac{v}{c^{2}}

(14)

If we now divide by Ɣ to compensate for the time dilation suffered by the clocks in K', the offset of the clocks in K' with respect to the central one that calculates K would be:

δ'_{S} = \mp D' \cdot \frac{v}{c^{2}}

(15)

What we have just calculated is nothing more than the consequence of the relativity of the simultaneity between inertial reference frames.

Figure 8. Synchronization process as seen by an external observer.

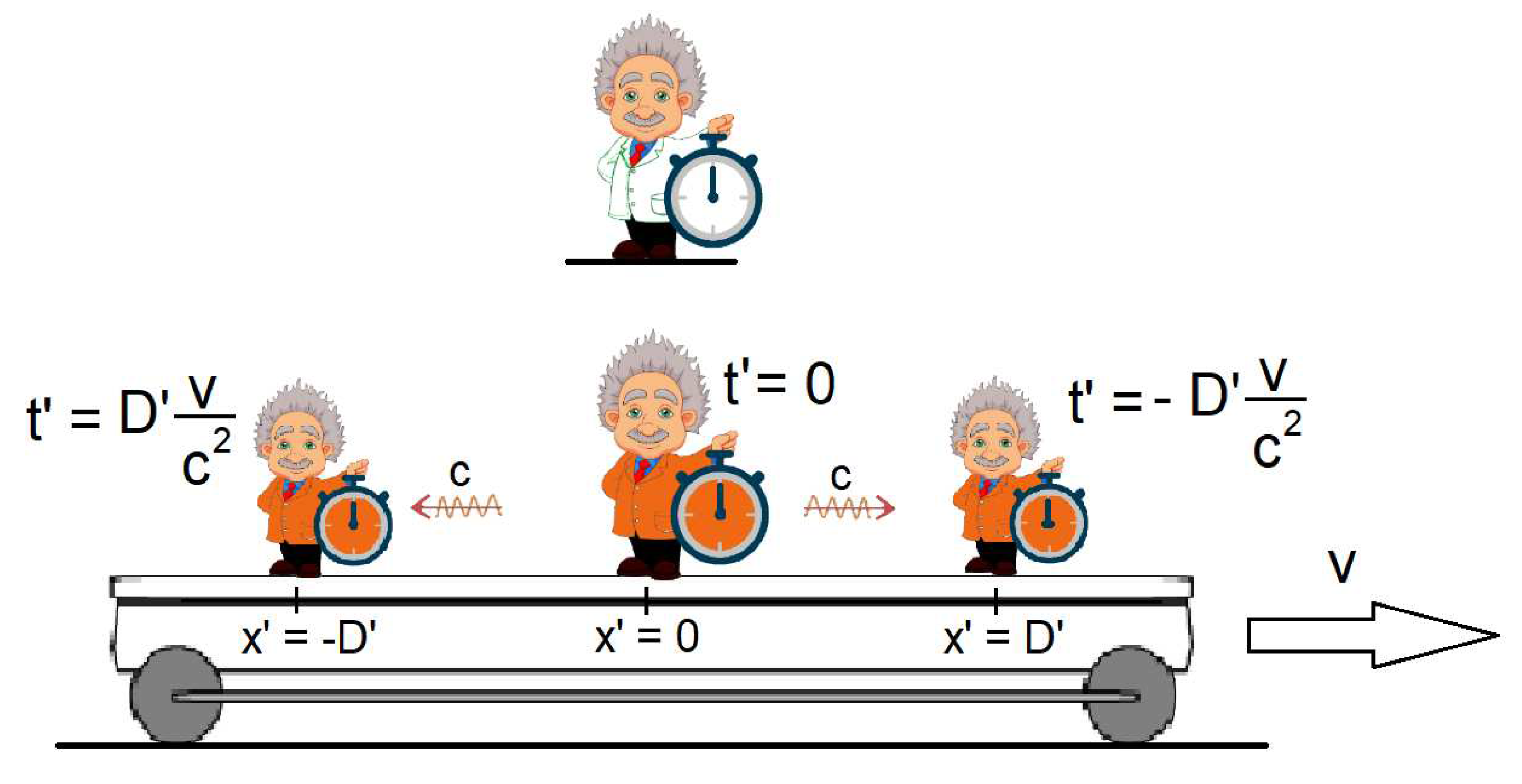
On the other hand, it should be noted that the value of the previous expression (15) corresponds to Sagnac corrections [8].

5. Einstein's synchronization in the closed and static Universe

The above for Minkowski's flat and infinite universe has its application to Einstein's universe. But in this case there are two peculiarities: we can choose the privileged observer as the external observer, and the geometry of the universe is closed.

Any moving observer with velocity v can locally synchronize their clocks using Einstein's convention. Imagine the case in which the mobile observer defines its X' coordinate between the boundaries (-L'/2, L'/2] and proceeds to synchronize two clocks located at the distance ±D' from the coordinate origin. Then, for the privileged observer, the offsets between these clocks will also comply with the expression (15).

Figure 9. Offset introduced by the synchronization process between clocks located at a distance D'.

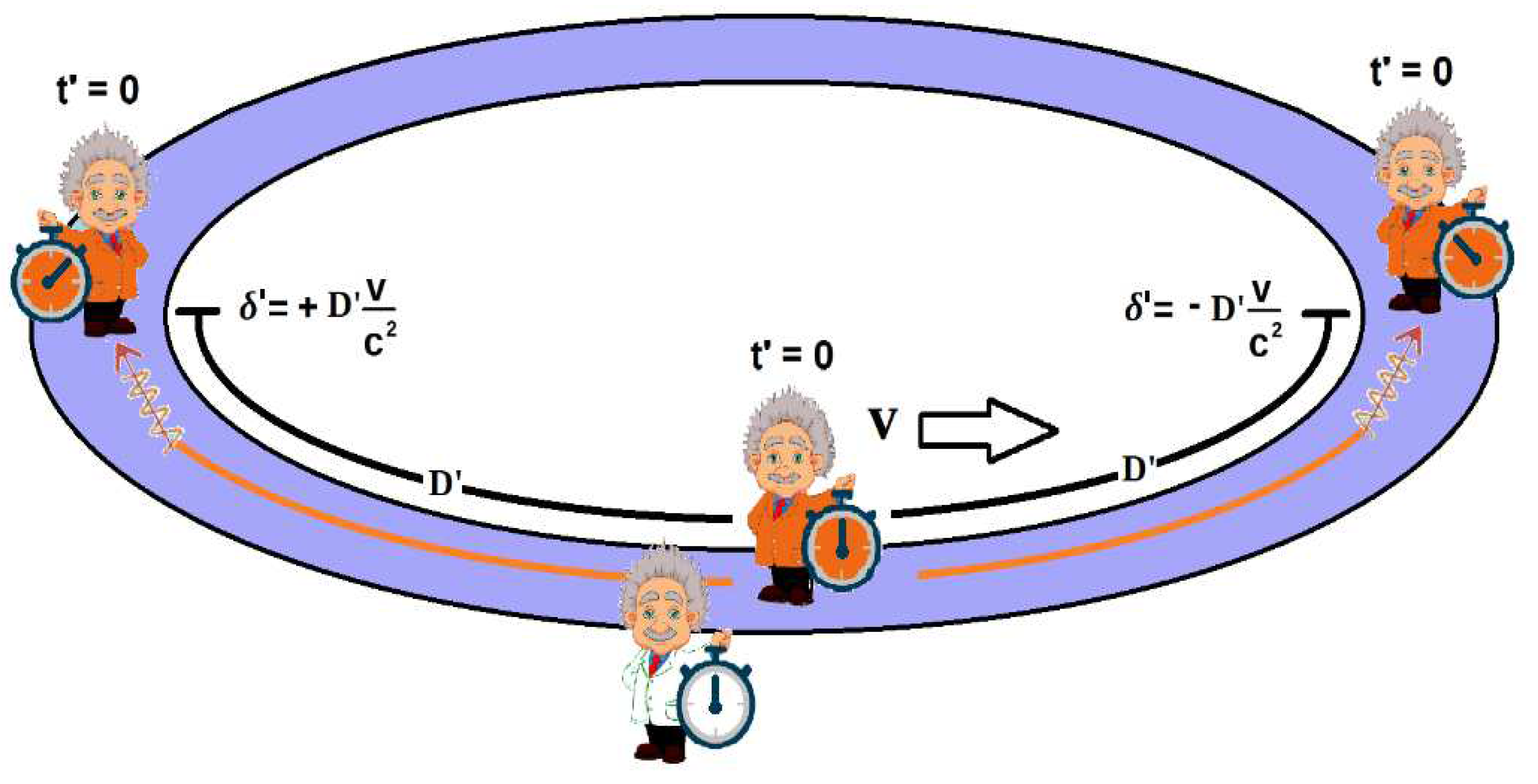
But what happens if we move the clocks away from the central one until they are both at the other end of the universe? It is now when the closed geometry of the universe comes into play, since, in that case, the two clocks will be together and at a distance L'/2 from the central one, so that, when the latter performs the synchronization process, the two will see that they are out of phase with each other in quantity:

Δ t' = \frac{L'}{2} \frac{v}{c^{2}} - \frac{- L'}{2} \frac{v}{c^{2}} = L' \frac{v}{c^{2}}

(16)

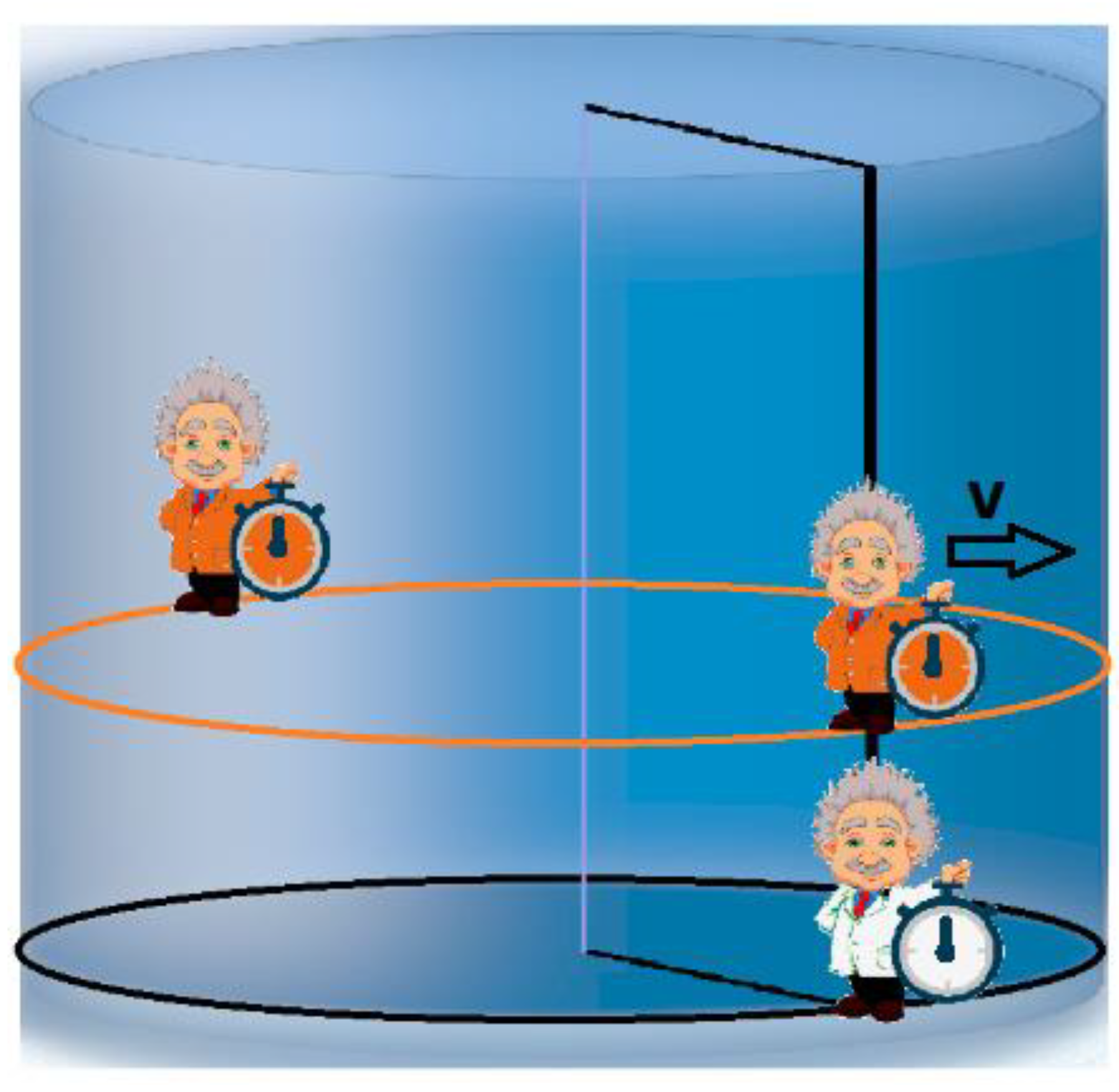
It is this time gap Δt' that some authors refer to as temporal discontinuity or discontinuity in simultaneity and which is usually represented in space-time diagrams (on cylinders to represent the temporal coordinate and spherical symmetry of the universe) as open spiral helices that move at velocity v, while for the static observer their lines of simultaneity correspond to closed circles:

But, as can be easily seen, the above figure corresponds exactly to the situation in Figure 10 from which the physical nonsense of this discontinuity is clearly deduced, the result of the attempt to maintain Einstein's synchronization convention and his SRT.

Despite all of the above, the mobile observer will be able to carry out the experiments he wishes while maintaining Einstein's synchronization and his results will be in correspondence with the SRT, as long as the experiment is not global, that is, as long as it is not necessary to "cross" the discontinuity.

At this point, the next question that arises is: is there a synchronization alternative that eliminates the offset between clocks Δt' above so that the lines of simultaneity of the moving observer also become closed circles? And the answer is easy to deduce by looking at Figure 10, since it is only necessary to cancel the offset with value (15) introduced between the clocks by Einstein's synchronization. But canceling that offset is equivalent to getting absolute simultaneity since, with it, all the clocks in Figure 10 will now read 0 s simultaneously. The same conclusion can also be reached by thinking that by doing c→∞, the value of (15) goes to 0.

But, although using superluminal signals is not physically possible, to cancel this lag it will be enough to modify Einstein's synchronization process so that, instead of c, the value of the speed of light ±c' obtained by the moving observer is used, where +c' is the speed of light emitted in the direction of the observer's motion and -c' the one issued in the opposite direction. This modification would make it possible to calculate the value of these ±c' values without more than imposing the compensation of the δ'_S offset introduced by Einstein's synchronization. To do this, we only have to use that, if before the observer at the coordinate origin wanted to synchronize a clock at a distance ±D' only had to send a pulse at its t' = 0 so that the clock synchronizes at t' = D'/c when it receives the beam, now, on the other hand, the synchronized clock will have to adjust its time t' to:

\frac{D'}{\pm c'} = \frac{D'}{c} \pm δ_{S} = \frac{D'}{c} \pm D' \frac{v}{c^{2}} = \frac{D'}{c} (1 \pm \frac{v}{c})

(17)

using +c' if the synchronization pulse is sent in the direction of v (right) and -c' if the pulse is sent in the opposite direction of v (left). And, now, we can clear the values:

\begin{matrix} + c' = \frac{c}{(1 + v / c)} \\ - c' = \frac{- c}{(1 - v / c)} \end{matrix}\}

(18)

Finally, once the new synchronization convention has been defined, we must deduce a new set of coordinate transformations between observers in such a way that they are compatible with this convention and which, in addition, must comply with the fact that the speeds of light obtained with them for a mobile observer with velocity v are those calculated in the previous expression (18).

6. New transformations between observers: the generic transformations

In this section we are going to deduce some new transformations that relate the distances and times measured by the static observer and with those of any other observer in motion with velocity v.

In order to distinguish these new transformations from those of Lorentz (LT) in the remainder of the document, we will call these new relationships generic transformations (GT) where the term "generic" has been chosen as opposed to the "special" term of the SRT.

On the other hand, we will call generic observers or reference systems (GO) those for which the new generic transformations are applicable and whose clocks are synchronized according to the new synchronization convention defined above.

For the deduction of GT, we will start from a usual linear coordinate change system of the type:

\begin{matrix} x = A \cdot x' + B \cdot t' \\ t = D \cdot x' + E \cdot t' \end{matrix}\}

(19)

in which the coordinates (ct, x) correspond to those of our reference frame K at rest, and the coordinates (ct', x') are those of a reference frame K' moving relative to the first at constant velocity v in the increasing direction of the X-axis, so that both X and X' axes are located on the equatorial geodesic (are parallel). Let's start with the time coordinate.

From what we have seen above, it is necessary to eliminate the offset introduced by the Einstein synchronization process by making δ'_S = 0. This is only possible if we eliminate the dependence of t on the position x'. That is, we must do D = 0.

On the other hand, if we want the new transformations to continue to provide the time dilation typical of SRT, we have no choice but to make E equal to the Lorentz factor, Ɣ. Therefore, we would have to

t = γ \cdot t' = \frac{t'}{\sqrt{1 - v^{2} / c^{2}}}

(20)

Now let's see what happens to the x-coordinate. To calculate the coefficient B, we can assume that the value B·t' corresponds to the position of the moving observer with respect to the static observer, i.e., that B·t' = v·t so x would be like this:

\begin{matrix} x = A \cdot x' + v \cdot t \\ t = γ \cdot t' \end{matrix}\}

(21)

On the other hand, we know that, as Einstein himself stated and as has been confirmed by a multitude of experiments, for every observer the speed of light in a round trip is a universal constant, c. Therefore, for the mobile observer, it must be verified that the time Δt' that it will take for the light to travel the distance L' for a round trip will be:

Δ t' = \frac{2 L'}{c}

(22)

The time that the privileged observer would measure for this round trip would be:

Δ t = \frac{L}{c - v} + \frac{L}{c + v} = γ^{2} \frac{2 L}{c}

(23)

And if we take into account (20) we will have to:

Δ t = γ Δ t' = γ^{2} \frac{2 L}{c}

(24)

then:

Δ t' = γ \frac{2 L}{c}

(25)

And if we want it to be fulfilled (22) there is no choice but to:

L' = γ L

(26)

that is, we must take A = 1/Ɣ and obtain the Lorentz length contraction. And, since t = Ɣ·t', we finally have to:

x = \frac{x'}{γ} + v \cdot t = \frac{x'}{γ} + v \cdot γ \cdot t' = \frac{x' + γ^{2} \cdot v \cdot t'}{γ}

(27)

Therefore, to recapitulate, the new generic transformations would be:

\begin{matrix} t = γ \cdot t' \\ x = \frac{x' + γ^{2} \cdot v \cdot t'}{γ} \end{matrix}\}

(28)

And clearing we get the inverse transformations:

\begin{matrix} t' = \frac{t}{γ} \\ x' = γ \cdot (x - v \cdot t) \end{matrix}\}

(29)

It should be noted here that the above generic transformations were first proposed by the American physicist F. R. Tangherlini in 1958 in his doctoral thesis [9]. However, Tangherlini did not deduce them using the procedure described here, nor did he apply them to Einstein's universe.

7. Immediate consequences of the new generic transformations

Observer asymmetry

The first and most obvious property of the new generic transformations, GT, is their total asymmetry between the direct and inverse forms. Unlike Lorentz transformations, in GT inverse transformations are not obtained from direct transformations by changing the sign of v to -v or vice versa. This asymmetry, obviously, means nothing more than the non-equivalence between the different observers. Therefore, the principle of relativity would be invalidated by the new transformations. It is now possible to distinguish between the two observers, the one who is "at rest or privileged" and the one who "moves" with respect to the first, as we had demanded.

Absolute simultaneity

The time independence of spatial coordinates implies that, unlike SRT, simultaneity is absolute, not relative. Any pair of simultaneous events in any one reference frame will also be simultaneous in all other generic reference frames (Δt = 0 = Δt').

In addition, as a consequence of the above, with the disappearance of the phase given by (15), it has now been possible for the open spiral of the moving observer to become closed circles as was already the case with the observer at rest or privileged.

Figure 12. Line of simultaneity of the moving observer after synchronizing their clocks.

Time dilation

Time dilation was one of the requirements imposed at the time of the deduction of the new GT. But unlike the symmetrical temporal dilation that emerges from SRT, with the new transformations temporal dilation is asymmetrical. That is, the observer at rest will see that the moving observer's clocks are running at a rate 1/Ɣ slower than his own. However, unlike LT, the moving observer will see that the clock of the resting observer is running at a faster speed than his own, with Ɣ being the proportionality factor.

This asymmetry in time dilation measured by both observers will resolve without any contradiction, as we will see later, the twin paradox.

If we assume two observers in motion at velocities v₁ and v₂ with respect to the observer at rest, the time relationship between the clocks of both observers would be, according to (20)

\frac{{t'}_{1}}{{t'}_{2}} = \frac{γ_{2}}{γ_{1}} = \sqrt{\frac{c^{2} - v_{1}^{2}}{c^{2} - v_{2}^{2}}}

(30)

In the above equation it must be taken into account that velocities are not relative, but absolute. That means that if v₂ = -v₁, i.e., both are moving at the same absolute speed but in opposite directions, then the clocks of both observers will be running at the same speed Δt₁' = Δt₂'.

Length contraction

The contraction of lengths with motion, or Lorentz contraction, is also a consequence of the new GT. But unlike the time dilation that was a requirement imposed in its deduction, the contraction of lengths arises after imposing such temporal dilation and the constancy of c on a round trip.

On the other hand, as with time dilation, the longitudinal contraction is also asymmetrical, so that, if two rulers at relative rest in each frame of reference have the same length L (proper length), for the privileged observer the ruler in motion will measure L/ɣ, while for the moving observer the stationary observer's rule will measure ƔL. This Lorentz contraction in length additionally assures the negative result in experiments such as the Michelson-Morley test [10].

In SRT, the effects of time dilation and longitudinal contraction could be attributed to the relativity of simultaneity. On the other hand, with the new GT in which simultaneity is absolute, it can be concluded that these effects are real and the result of the observer's state of motion. That is, the size of the "rulers" and the "rate" of the clocks actually vary depending on the speed.

New Generic Metric

If we assume that space is pseudo-Euclidean and that the Minkowski metric is valid for the observer at rest, then we have that for the observer in motion the form of the metric will be:

{d s}^{2} = c^{2} \cdot d t'^{2} - \frac{d x'^{2}}{γ^{2}} - 2 \cdot v \cdot d x' \cdot d t'

(31)

in which he highlights the existence of the cross-term that did not appear in Minkowski's metric:

g'_{t x} = g'_{x t} = e'_{t} \cdot e'_{x} = e'_{x} \cdot e'_{t} = - \frac{v}{c}

(32)

The expression (31) can be rewritten as follows

{d s}^{2} = c^{2} \cdot {(d t' - \frac{v}{c^{2}} \cdot d x')}^{2} - d x'^{2} = c^{2} \cdot d T'^{2} - d X'^{2}

(33)

in which with the change of variables:

\begin{matrix} T' = t' - \frac{v}{c^{2}} x' \\ X' = x' \end{matrix}\}

(34)

we return to Minkowski's metric and Lorentz transformations.

New velocity addition law

From the new GT, the equations that relate the values of the velocities u_x measured in the system at rest with the velocities u'_x measured by the observer in motion, respectively, are:

\begin{matrix} {u'}_{x} = γ^{2} \cdot (u_{x} - v) \\ u_{x} = \frac{{u'}_{x}}{γ^{2}} + v \end{matrix}\}

(35)

An immediate consequence of the above formulas is that, for the moving observer, u'_x can produce values greater than c. However, that will never happen for the privileged observer. That is, no object or light ray will be able to exceed c in the static frame of reference.

On the other hand, the relative speed with which each observer sees the other move is not the same, as it was with Lorentz transformations. If the static observer K sees the other observer K' moving at a velocity v, then K' will see K moving away from him at velocity v' = -Ɣ² ·v:

v' = γ^{2} \cdot (u_{x} - v) = γ^{2} \cdot (0 - v) = - γ^{2} \cdot v

(36)

Speed of light c

Using the new velocity transformation equations, let’s see what value for the speed of light, c', the moving observer of a light ray will measure in the increasing directions, +c', and decreasing, -c'. To do this, we only have to replace in (35) u_x with +c and -c, and operating we will get that:

\begin{matrix} + c' = γ^{2} \cdot (c - v) = \frac{c^{2}}{c + v} = \frac{c}{(1 + v / c)} \\ - c' = γ^{2} \cdot (- c - v) = \frac{- c^{2}}{c - v} = \frac{- c}{(1 - v / c)} \end{matrix}\}

(37)

Therefore, the new generic transformations provide different speeds of light for the round-trip senses, just as we wanted. In addition, in the event that the light ray moves in the opposite direction to the observer's motion, the speed of light that the observer will measure will be greater than c.

In extreme cases where the moving observer was moving at the speed of light v = c, the value of c' that would be measured would be:

\begin{matrix} + c' = \frac{c}{(1 + v / c)} = \frac{c}{2} \\ - c' = \frac{- c}{(1 - v / c)} = - \infty \end{matrix}\}

(38)

Finally, it should be noted that the values obtained in (37) coincide with the values advanced in (18), although at no time was this condition directly imposed in the deduction of the new GT.

8. New synchronization process

As mentioned above, the new synchronization convention will consist of modifying Einstein's convention so that, instead of c, use the speeds of light measured by the moving observer and given by (although there is the possibility of an external synchronization with the participation of the privileged observer, such synchronization will not be the subject of study in this document).

However, before a moving observer can proceed to synchronize his clocks, we must show that he can calculate the parameters he needs, i.e., the distance D' to the clock and the speed of light in the different directions +c' and -c', for which he will need to know the longitude of the universe L'.

Let us imagine that the observer in motion sends two pulses of light in opposite directions, right and left, and measures respectively the times t'_R and t'_L that it takes for each pulse to return to him after circling the universe. Both times, using the values of c' given by (37) will be:

\begin{matrix} t'_{R} = \frac{L'}{+ c'} = \frac{L'}{c} (1 + \frac{v}{c}) \\ t'_{L} = \frac{L'}{|- c'|} = \frac{L'}{c} (1 - \frac{v}{c}) \end{matrix}\}

(39)

from where adding the two values we have:

t'_{R} + t'_{L} = \frac{L'}{c} (1 + \frac{v}{c} + 1 - \frac{v}{c}) = 2 \frac{L'}{c}

(40)

and if we subtract we get:

t'_{R} - t'_{L} = \frac{L'}{c} (1 + \frac{v}{c} - 1 + \frac{v}{c}) = 2 L' \frac{v}{c}

(41)

From the above two expressions, and simply by measuring the times t'_R and t'_L the mobile observer can know the length of the universe, L', and the absolute velocity v at which it moves through it using:

L' = \frac{t'_{R} + t'_{L}}{2 c}

(42)

from where you can now calculate the speeds of light as

\begin{matrix} + c' = \frac{L'}{t'_{R}} \\ - c' = \frac{L'}{t'_{L}} \end{matrix}\}

(43)

Also, on the other hand, you can calculate the value of your absolute velocity v using

v = \frac{t'_{R} - t'_{L}}{t'_{R} + t'_{L}} \cdot c

(44)

To get the distance D' to the clock, you just have to, as you do with L', use that the round trip speed of the light is c and measure the time it takes the light to make the travel.

Obviously, for the resting or privileged observer, the above is consistent with the new generic transformations. For him, the times t_R and t_L that will be measured will be:

\begin{matrix} t_{R} = \frac{L}{c - v} \\ t_{L} = \frac{L}{c + v} \end{matrix}\}

(45)

and the sum of both times will have:

t_{r} + t_{L} = \frac{L}{c + v} + \frac{L}{c - v} = \frac{2 L c}{c^{2} - v^{2}} = 2 \frac{L}{c} γ^{2}

(46)

and by operating it is obtained that:

\frac{t_{r} + t_{L}}{γ} = 2 \frac{L γ}{c}

(47)

And if we take into account the temporal dilation and the contraction of lengths of the new generic transformations, we arrive at the following:

t'_{r} + t'_{L} = \frac{t_{r} + t_{L}}{γ} = 2 \frac{L γ}{c} = 2 \frac{L'}{c}

(48)

which is . And operating in the same way with the difference t_R - t_L will be obtained without difficulty (41).

Here it should be noted that, once the moving observer changes Einstein's synchronization convention to the newly proposed generic, local measurements of the speed of light in one direction will result in +c' and -c'. That is, these values will already be valid both globally and locally in the equatorial geodesic.

On the other hand, it is also not necessary for the moving observer to measure the speeds of light ±c' in order to synchronize their clocks. If you are able to know your absolute velocity v by any other procedure, you will only have to apply the expression (37) to derive ±c' or use (17) compensating for the offset δ_S introduced by Einstein's synchronization convention and thus synchronize your clocks. This is nothing more than applying Sagnac-type corrections to Einstein's synchronization.

9. Twin paradox in the closed universe

As we mentioned at the beginning of this paper, this type of closed universe has revived the study of the twin paradox. But after the previous analysis in which it has been shown that the Special Relativity is not globally applicable to the problem, the paradox disappears without the need to resort to temporal discontinuities or topological properties in order to maintain SRT. Now, thanks to the new generic transformations and their asymmetries in longitudinal contraction and time dilation, the paradox is resolved without leaving contradictions. See:

For the observer or static twin, the time it takes for its traveling twin to go around the entire universe at a velocity v will be:

t = \frac{L}{v}

(49)

and, by time dilation, the time he calculate has passed for his twin is

t' = \frac{t}{γ}

(50)

For the traveling twin his static twin moves, recall (36), at a velocity v' given by

v' = γ^{2} \cdot (u_{x} - v) = γ^{2} \cdot (0 - v) = - γ^{2} \cdot v

(36)

Then the time he needs to go around the universe completely until he meets him again will be:

t' = \frac{L'}{v'} = \frac{L'}{γ^{2} v}

(51)

And if we take into account the "contraction" of lengths, we finally obtain that:

t' = \frac{γ L}{γ^{2} v} = \frac{L}{γ v} = \frac{t}{γ}

(52)

As we expected, resolving the paradox without any contradiction: both observers agree that the traveling twin is the youngest.

10. Conclusions

In this paper we have shown that the use of a closed and static universe model such as the one proposed by Einstein in 1917 immediately gives rise to a privileged frame of reference and causes any observer moving at velocity v with respect to it to be able to measure different values of c for the speed of light as a function of the direction of transmission of the pulse. Both arguments, the existence of a privileged frame of reference together with the non-constancy of c, imply the immediate invalidity of Special Relativity globally, not locally, in that universe.

On the other hand, after analyzing the synchronization process according to Einstein's convention, which is also invalidated by the non-constancy of c, a new synchronization convention has been deduced and new transformations have been obtained, the generic transformations, which replace the Lorentz transformations of Special Relativity.

The consequences of these new GT can be summarized as follows:

Existence of a privileged observer for whom:

o

the speed of light is c either way

o

his metric is Minkowski's usual
Revocation of the principle of relativity and equivalence between inertial observers.
Elimination of the relativity of simultaneity. With the new generic transformations, simultaneity is absolute.
The effects of time dilation and contraction of lengths caused by motion, which are real and coincide with the values of Special Relativity, but which are dependent on the absolute speed at which the ruler or clock moves and, therefore, cease to be relative.
The speed of light for any observer moving relative to the privileged observer will have different values depending on the direction of motion.
The new generic transformations provide the same results for the main known kinematic effects (Doppler effects or stellar aberration). In the same way, they also explain the negative result of the Michelson-Morley experiment.

11. Discussions

After the analysis carried out in this paper, it is worth asking whether the new generic transformations would be applicable beyond Einstein's universe, so that they would also be valid for any other situation in which there was spherical symmetry and a privileged frame of reference. One such situation could be the Earth itself in which, as a privileged observer, the inertial observer at its center of gravity could be taken to be free from rotational motion. It would only be necessary to find an experiment with which to test this hypothesis and the validity of the generic transformations applied to its explanation. And that experiment could be the one carried out by Hafele-Keating in 1972 with macroscopic clocks and collected in [11]. It is immediately clear that the results of this experiment have an easy and clean explanation through the use of the new generic transformations, since this experiment is nothing more than an example of the application of the twin paradox to the Earth.

On the other hand, in the synchronization procedures used at the global level on Earth, the Sagnac-type effects of value (15) must be taken into account, which is nothing more than applying the same synchronization defined in this document. Therefore, shouldn't the new generic transformations be used on Earth instead of the Lorentz transformations?

References

Einstein, A. (1917) “Kosmologische Betrachtungen zur allgemeinen Relativitätstheorie”, Sitzungs. König. Preuss. Akad.: Sitzungsb. König. Preuss. Akad. 142-152.
Einstein, A. (1905) “On the Electrodynamics of Moving Bodies”, Annalen der Physik. Lpz. 17, 891.
García, J. (2022) “Paradoja de los Gemelos en el universo estático de Einstein ('Rodolfo Pérez Paradox'), Vídeo de Youtube https://youtu.be/vsjg2ybVcoM.
Weeks J. P. (2001). “The Twin Paradox in a Closed Universe”. The American Mathematical Monthly, No. 7 pp. 585-590. [CrossRef]
Brans C.H. and Stewart, D.R. (1973). “Unaccelerated-Returning-Twin Paradox in Flat Space-Time”. Physical Review D, Volume 8, Number 6. [CrossRef]
Dray, T. (1990), “The twin paradox revisited”, American Journal of Physics 58 (9): 822-825. [CrossRef]
Uzan, J.-P., Luminet, J.-P., Lehoucq, R. & Peter, P. (2002) “Twin Paradox and Space topology”, European Journal of Physics, 23:277-284. [CrossRef]
Wikipedia, “Sagnac Effect”, https://en.wikipedia.org/wiki/Sagnac_effect.
Tangherlini F. R. (1958), “The velocity of light in uniformly moving frame. A dissertation”, Stanford University.
Michelson, Albert A.; Morley, Edward W. (1887) "On the Relative Motion of the Earth and the Luminiferous Ether" . American Journal of Science. 34 (203): 333–345. [CrossRef]
Hafele, J. C.; Keating, R. E. (1972) "Around-the-World Atomic Clocks: Observed Relativistic Time Gains" (PDF). Science. 177 (4044): 168–170. [CrossRef]

Figure 5. Temporal diagrams of the transmission of pulses in opposite directions.

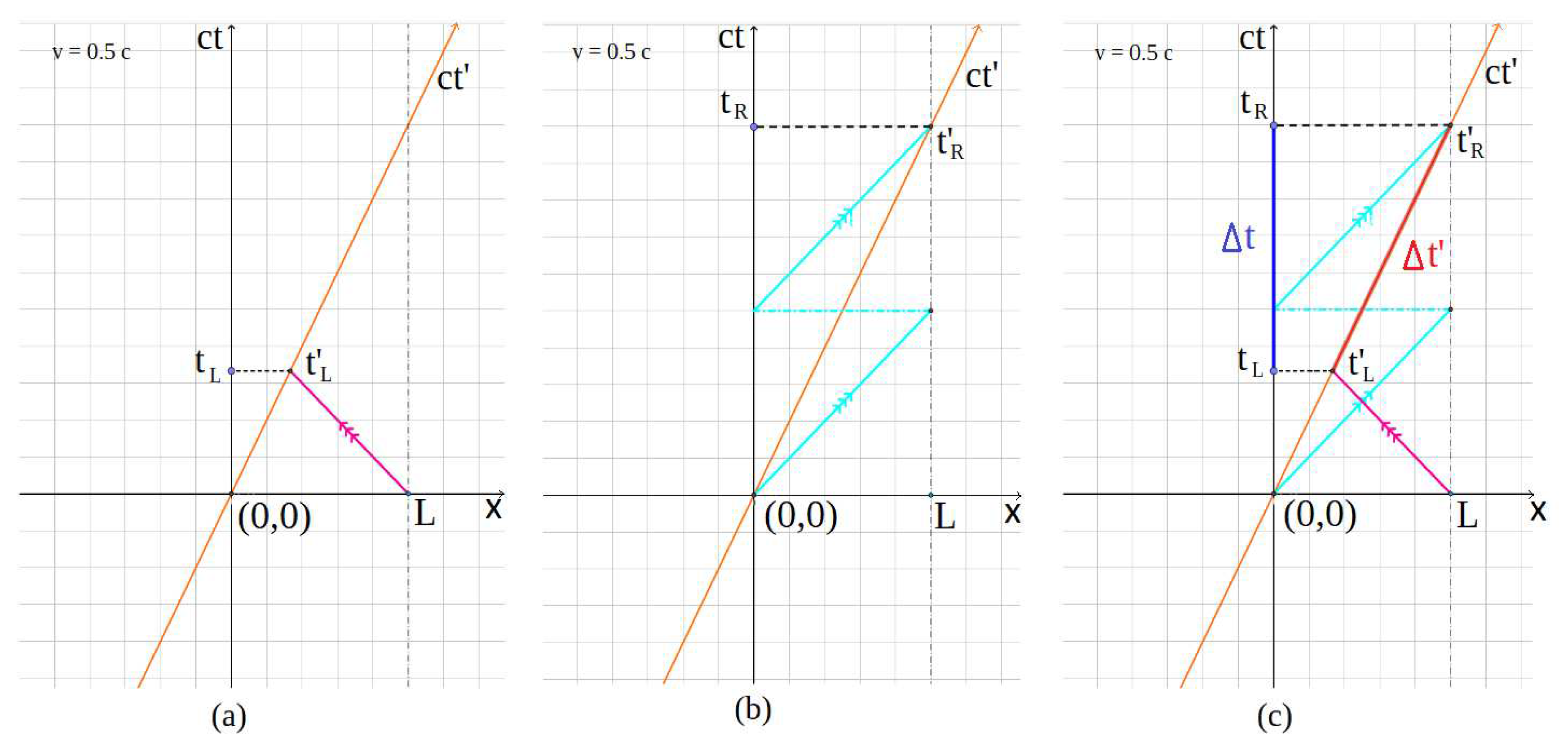
Figure 6. Construction of a reference system.

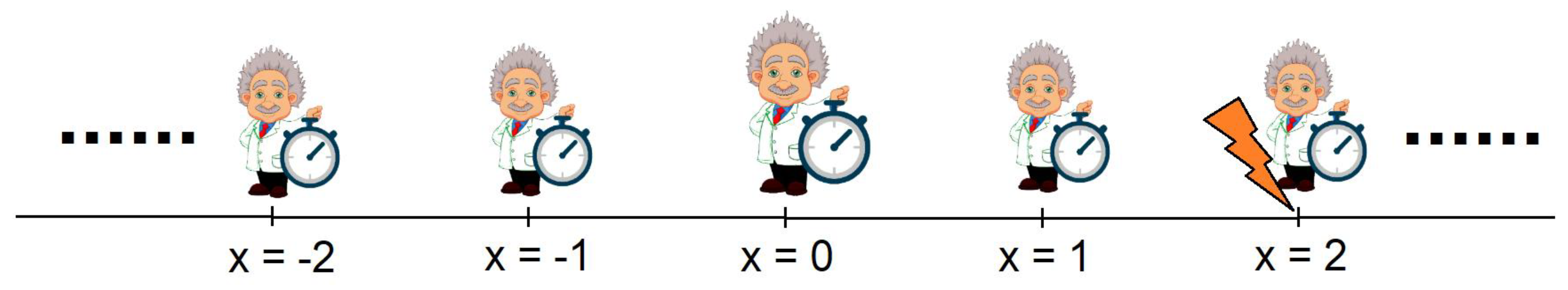
Figure 10. Offset introduced by synchronization between two clocks located together at the other end of the universe.

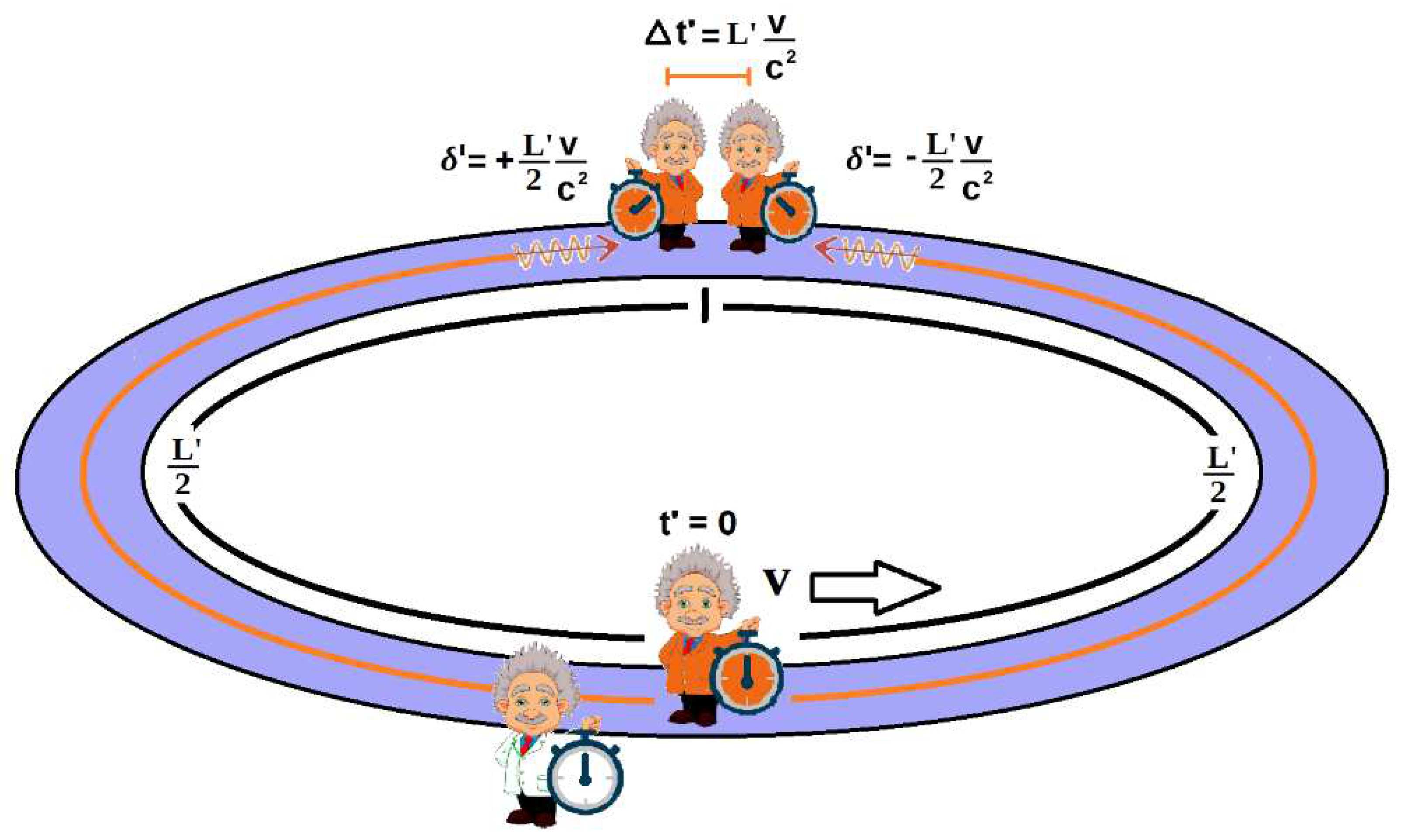
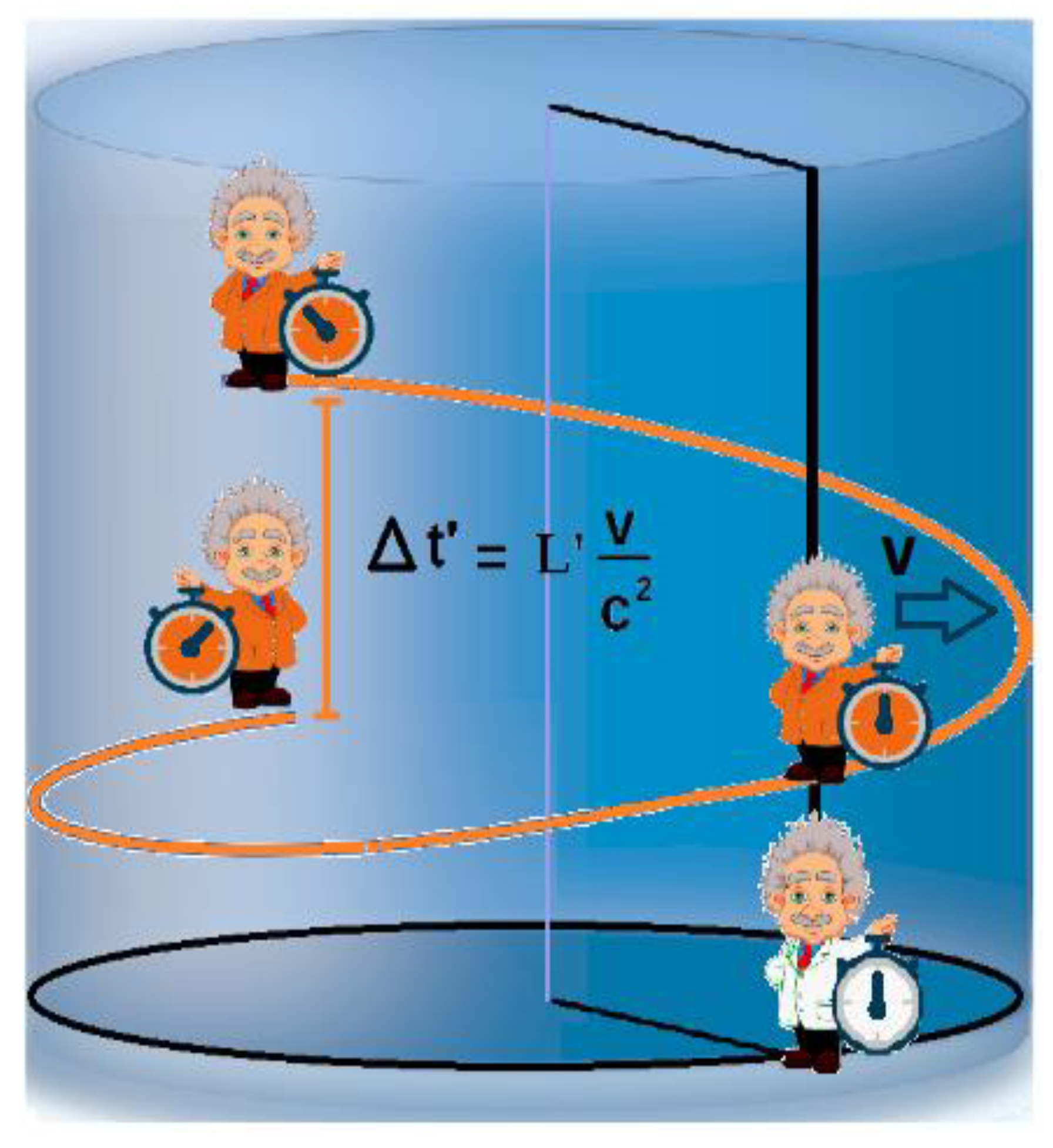
Figure 11. Representation of the lines of simultaneity over a cylinder-shaped space.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Is the Special Relativity Compatible with Einstein’s Static Universe? Proposal for New “Generic” Transformations. The Twin Paradox.

Abstract

1. Introduction

2. Metrics and Geodesics in Einstein's Universe

3. Definition of simultaneity and reference system. Einstein’s synchronization convention

4. Offsets Introduced by Einstein synchronization: relativity of simultaneity

5. Einstein's synchronization in the closed and static Universe

6. New transformations between observers: the generic transformations

7. Immediate consequences of the new generic transformations

Observer asymmetry

Absolute simultaneity

Time dilation

Length contraction

New Generic Metric

New velocity addition law

Speed of light c

8. New synchronization process

9. Twin paradox in the closed universe

10. Conclusions

11. Discussions

References

MDPI Initiatives

Important Links

Subscribe