Prerpints.org logo
Preprint
Article

IRS Backscatter Based Secrecy Enhancement against Active Eavesdropping

Altmetrics

Downloads

75

Views

13

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

06 December 2023

Posted:

07 December 2023

You are already at the latest version

Alerts
Abstract
This paper proposes to combat active eavesdropping by intelligent reflecting surface (IRS) backscatter techniques. To be specific, the source (Alice) sends the confidential information to the intended user (Bob), while the eavesdropper (Willie) transmits jamming signal to interrupt the transmission for more data interception. To enhance the secrecy, an IRS is deployed and connected with Alice through fiber to transform the jamming signal into the confidential signal by employing backscatter techniques. Based on the considered model, an optimization problem is formulated to maximize signal-to-interference-plus-noise ratio (SINR) at Bob under the constraints of the transmit power at Alice, the reflection vector at the IRS and the allowable maximum SINR at Willie. To address the optimization problem, an alternate optimization algorithm is developed. The simulation results verify the achievable secrecy gain of the proposed scheme.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

With the development of wireless communication technology, more and more private information is transmitted through public channels, which increases the risk of information leakage. Numerous studies have been conducted on physical layer security in wireless communication. However, the security rate of traditional secure communication methods is limited when the eavesdropper’s interference signal power is high [1]. To break this limit, intelligent reflecting surface (IRS) can be combined with backscatter technology and integrated into the wireless communication system. The integration of backscatter in IRS can enhance the communication security of the system by utilizing the power of interference signal emitted by active eavesdropper. The signal reflected by the IRS can reduce the impact of the eavesdropper’s interference signal and strengthen the required signal received by the legitimate user. This dual capability enhances the reliability of communication, fortifying the received signal quality for legitimate users in the system.
The IRS is capable of reflecting incident wireless signals, as a plane containing numerous passive reflecting elements constitutes it. As the demand for enhanced performance in various wireless communication systems continues to rise, there is a simultaneous increase in expectations for advanced wireless communication technologies. Beyond merely seeking improved performance, there is a growing demand for solutions that offer low deployment costs and minimal power consumption. In response to this demand, Intelligent Reflecting Surface (IRS) technology has emerged. This technology aims to effectively enhance the performance of wireless communication systems while adhering to the requirements of cost-effectiveness and energy efficiency. Each reflecting element of IRS has the capability to apply a phase shift to the incident signal, and when acting in unison, all reflective elements can jointly adjust their phase shifts [2]. The IRS is extensively used in wireless communications to enhance communication performance in various ways [3]. By adaptively adapting the amplitude and phase shift of the reflective elements, the IRS can reconfigure the wireless propagation environment and enhance desired signals [4,5,6], thereby effectively addressing channel fading and interference. Through the collaborative design of transmission beamforming at the transmitter and reflective beamforming at the IRS, communication systems assisted by IRS can achieve optimal transmission power [7,8] and maximum energy efficiency [9,10]. In practical application, the IRS stands out due to its light weight, low deformation, and flexible size adjustment. These characteristics simplify the installation and disassembly processes, allowing for easy and adaptable deployment. IRS can serve as an auxiliary device in wireless communication systems and can be flexibly integrated into it, with high compatibility.
The use of the IRS can increase the data rate of legitimate receivers while reducing the data rate of eavesdroppers, thereby enhancing the system’s security rate. The prevalent strategies for mitigating eavesdropping attacks such as artificial noise (AN) [11] and multi-antenna beamforming [12] suffer from high energy consumption, additional hardware costs or optimization difficulties due to the high correlation between legitimate and illegitimate links. To maximize the security rate, Yu et al. jointly optimized the transmitted information beam, artificial noise, and reflection coefficient [13]. Cui et al. investigated how to maximize the security rate of the communication system when the transmission power is fixed, and the reflection parameters set at the IRS are limited [1]. Shen et al. maximized the security rate of the multi-input single-output communication by joint majorization of the emission covariance at the source and the phase shift matrix at the IRS [14].
The uniqueness of the backscatter channel provides important insights into the physical layer security of communication systems [15]. In backscatter communication systems, a backscatter transmitter modulates and reflects received radio frequency (RF) signals to transmit data, rather than generating RF signals independently [16]. This unique mechanism presents distinct challenges and opportunities for securing information transmission. Backscatter communication is generally categorized into three types: monostatic backscatter communication, bistatic backscatter communication, and ambient backscatter communication [17]. Monostatic backscatter communication requires a dedicated RF source that is part of the same device and its commonly used in applications where a device needs to communicate with itself or in situations where a single device handles both transmission and reception. Bistatic backscatter communication requires a dedicated RF source that is separate from the receiving device and its used for scenarios where devices need to communicate over longer distances or when it is more practical to separate the transmitting and receiving functions. Ambient backscatter communication utilizes available ambient RF sources in the environment. The characteristics of backscatter channels can be utilised to generate security keys. The unique features of backscatter communication can be used to establish security keys and thus enhance the security of the communication system. A lightweight cryptography based approach to address the security of backscatter communication [18]. Ambient backscatter communication, which utilizes existing RF signals in the environment, can be leveraged for secure key generation. The randomness and variability in ambient signals can be used to generate cryptographic keys, enhancing the security of communication between devices. Although cryptography can achieve better security performance, it has limitations that rely on key generation, which can result in high communication overhead and computational complexity [15]. In order to break these limitations, research on physical layer security suitable for the characteristics of backscatter channels has been developed. The method of physical layer security is to utilize the characteristics of wireless channels to prevent eavesdroppers from obtaining information from transmitters. Physical layer security can be not only an alternative to cryptography but also a complement to enhance encryption technology. In addition, injecting artificially generated noise can deteriorate the eavesdropper’s channel conditions to enhance secure transmission [19].
Backscatter communication systems can use jamming to enhance security. The presence of interference in the backscatter channel can provide a diversity of communication paths, and the diversity of paths may make it more challenging for eavesdroppers to jam communications. Since backscatter devices utilize ambient signals or dedicated sources in the environment, they may not be as susceptible to traditional jamming techniques. This resilience contributes to the security of the communication link. The maximization of confidentiality in MIMO backscatter wireless systems is investigated by jointly optimizing the power supply of injected artificial noise and the precoding matrix [20]. An interference-based multi-tag scheduling method is proposed, which selects one tag for data transmission and another for artificial noise generation to have a deleterious effect on the eavesdropper [21]. Backscatter systems can be designed to be resilient to traditional eavesdropping methods, offering a more secure communication channel. Backscatter communication can be used for secure localization and authentication in applications where device positioning and identity verification are critical. Backscatter communication is well-suited for Internet of Things (IoT) applications where security and energy efficiency are crucial due to the low-power nature of backscatter devices. The researches of [22] provided an optimisation framework that maximizes the secrecy rate of backscatter communications in multi-cell NOMA networks and the reflection coefficients of the backscatter nodes are optimized for the presence of multiple eavesdroppers in each cell. To summarize, the inherent characteristics of backscatter communication systems, including their low power consumption, resistance to jamming, and adaptability to the RF environment, provide opportunities to enhance security in diverse applications, ranging from IoT networks to secure key generation. The combination of IRS and backscatter has been shown to have advantages in suppressing interference signals [23]. This combination scheme has not been further studied in secure communication. Therefore, our work aims to bridge this gap. Motivated by these studies, we propose a novel approach, called BackCom-IRS, that utilizes the combination of IRS and backscatter to improve secure communication and mitigate the effects of eavesdropping.
Specifically, our proposed approach, BackCom-IRS, leverages the power of interference signals through backscattering to improve the security communication rate, with higher eavesdropper power leading to greater benefits for secure communication. This paper proposes a method to enhance system security by limiting the signal-to-interference-plus-noise ratio (SINR) at the eavesdropper. Meanwhile, jointly optimize the IRS reflection coefficient and the source beamforming vector to maximize SINR at the legal user. The optimization problem is non-convex so it is challenging to solve the optimization problem. To solve the nonconvex optimization problem, we developed an alternation optimization algorithm. Transform the optimization problem into two convex problems and then optimize each of them alternatively. These two convex problems are positive semi-definite programs that can be solved using existing convex optimization solvers. The eavesdropper in this paper passively eavesdrops and sends interference signals. By leveraging the power of the interference signal through backscattering, the proposed scheme improves the legal user’s SINR. Simulation results prove the efficacy of the BackCom-IRS approach in enhancing communication system security.

2. System Model and Optimization Problem Formulation

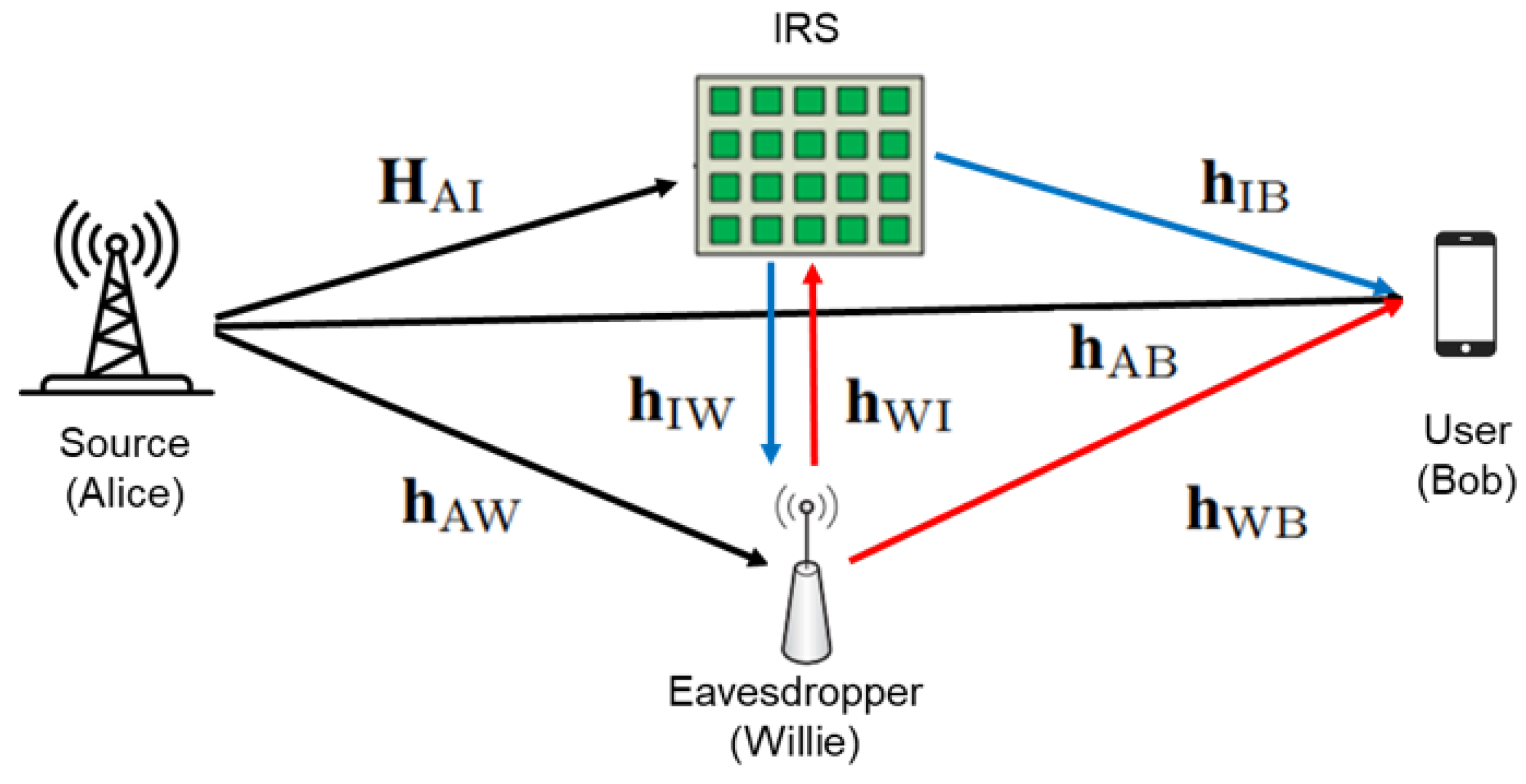
Consider an IRS-based backscatter wireless communication system countermeasure against active eavesdropping, as shown in Figure 1. A source (Alice), an IRS, a legitimate user (Bob), and an eavesdropper (Willie) constitute the communication system of this paper. In this system, Alice continuously transmits information to all directions. Willie is sending interference signals to prevent Bob from receiving the required signals to eavesdrop. Generally, the stronger the interference signals from an eavesdropper like Willie, the lower the communication system security is, which needs the IRS to enhancing this system’s security. The IRS, as a transmitter, aims to convert all received signals into desired signals through backscattering. The signal processed by IRS uses the interference signal from Willie to ensure the communication safety of legal user Bob. The number of antennas equipped by Alice is N, while Willie and Bob are equipped with one antenna each. IRS has L elements. It is assumed that all channels in the system experience quasi-static flat fading. Additionally, we consider that the channel state information (CSI) of all the involved channels in the system is precisely and accurately known in order to determine the limit of the security rate.
The channel gains from Alice to Bob, from the IRS to Bob, from Willie to Bob, from Willie to the IRS, from Alice to IRS, from the IRS to Willie, and from Alice to Willie are represented by the following notations: h AB ∈ C N × 1 , h IB ∈ C L × 1 , h WB ∈ C 1 × 1 , h WI ∈ C L × 1 , H AI ∈ C L × N , h IW ∈ C 1 × L , and h AW ∈ C 1 × N . The beamforming vector used by Alice to transmit the desired signal s is denoted by w ∈ C N × 1 , while the beamforming vector used by Willie to transmit the interference signal a is represented by v ∈ C 1 × 1 . The signals s and a represent the transmitted signals from Alice, the legitimate transmitter, and Willie, the eavesdropper, respectively. In addition, E [ | s | 2 ] = 1 and E [ | a | 2 ] = 1 . n B and n W represent the Gaussian white noise at Bob and Willie, respectively. These noises have zero mean and variances of σ B 2 and σ W 2 , respectively. The amplitude and phase shift incurred by the l-th reflective element of the IRS are represented by Θ = diag ( β 1 e j α 1 , β 2 e j α 2 , ⋯ , β L e j α L ) with α l = [ 0 , 2 π ] , l ∈ L = { 1 , 2 , ⋯ , L } and β l = [ 0 , 1 ] . In this model, we do not consider the interaction of IRS neighbouring reflective units and assume that each IRS reflective unit reflects the signal independently. Due to strong path loss, we overlook signals that reflected multiple times by the IRS. After the above design and construction of the whole system, the received signals at Bob and Willie can be respectively formulated as
y B = h AB H w s + h WB H v a + h IB H Θ ( h AI w s + h WI v a ) + n B ,
y W = h AW H w s + h IW H Θ ( H AI w s + h WI v a ) + n W .
In this system, the backscattering of signals through IRS does not need to distinguish the source signal s and interference signal a. The goal of this system is to maximize the SINR at Bob γ while we constrained Willie’s SINR ξ by setting the maximum value. The transmit powers at Alice and Willie are represented as P s and P a , respectively. Define θ = [ β 1 e j θ 1 , β 2 e j θ 2 , ⋯ , β L e j θ L ] H . The problem of this system is expressed as
max θ , w γ = h AB H w + h IB H Θ ( H AI w + h WI v ) 2 σ B 2 + h WB H v 2 ,
s . t . Tr ( w w H ) ≤ P s ,
θ l ≤ 1 , ∀ l ∈ L ,
ξ ≤ ε .
The SINR at Bob is primarily dependent on two key variables: the beamforming vector w used by Alice and the reflection coefficient vector θ utilized by the IRS. The SINR at Willie is formulated as
ξ = h AW H w + h IW H Θ ( H AI w + h WI v ) 2 σ W 2 .
The goal of this system model is to jointly optimize the transmission power of the transmitter and the reflection coefficient of the IRS to maximize the signal-to-interference-plus-noise ratio of the legitimate user Bob, while considering the constrain that the signal-to-interference-plus-noise ratio of the eavesdropper is below the threshold. The optimization problem in this model is non-convex. To solving this optimization problem involves transforming problem (3) into a quadratically constrained quadratic programming (QCQP) problem. Subsequently, finding a sub-optimal solution to problem (3) involves employing Alternating Optimization (AO) optimization methods.

3. Alternation Optimization

We develop an alternating optimization algorithm to solve the problem (3). Due to the coupling between the variables θ and w, directly solving the nonconvex problem (3) can be challenging. Specifically, we address this nonconvex problem by iteratively solving two sub-problems: sub-problem 1, which focuses on optimizing the beamforming vector w with a fixed reflection coefficient vector θ , and sub-problem 2, which focuses on optimizing θ with a fixed w.
Before optimizing these two sub-problems respectively, we need to convert the objective function equivalently. Since Θ = diag θ H , that expression can be converted to h AB H w + h IB H Θ ( H AI w + h WI v ) = h AB H w + θ H Φ w + θ H a , where Φ = diag h IB H H AI and a = diag h IB H h WI v . Transform the expression as h AB H w + θ H Φ w + θ H a = ( [ θ H , 1 ] [ Φ H , h AB ] H ) w + θ H a = θ ^ Φ ^ w + θ H a , letting θ ^ = [ θ H , 1 ] H and Φ ^ = [ Φ H , h AB ] H . Convet the expression to θ ^ Φ ^ w + θ H a = θ ^ Φ ^ w + [ θ H , 1 ] H [ a H , 0 ] H = θ ^ Φ ^ w + θ ^ a ^ , assuming a ^ = [ a H , 0 ] H . Letting w ^ = [ w H , 1 ] H , and Φ ˇ = [ Φ ^ , a ^ ] H , the expression can be transformed as θ ^ Φ ^ w + θ ^ a ^ = θ ^ ( Φ ^ w + a ^ ) = θ ^ Φ ˇ w ^ .
Therefore, the objective equation can be deduced as
h AB H w + h IB H Θ ( H AI w + h WI v ) 2 = θ ^ H Φ ˇ w ^ w ^ H Φ ˇ H θ ^ .
Similarly for the expression for SINR at Willie, we transform it in the same way. h AW H w + h IW H Θ ( H AI w + h WI v ) = θ ^ δ ˇ w ^ , letting δ ˇ = [ δ ^ , b ^ ] H , δ ^ = [ δ H , h AW ] H , b ^ = [ b H , 0 ] H , δ = diag h IW H H AI and b = diag h IW H h WI v .
Define W ^ = w ^ w ^ H , Θ ^ = θ ^ θ ^ H , rank ( W ^ ) = 1 , rank ( Θ ^ ) = 1 , W ^ ⪰ 0 , Θ ^ ⪰ 0 . The problem (3) is reformulated as
max Θ ^ , W ^ θ ^ H Φ ˇ w ^ w ^ H Φ ˇ H θ ^ = Tr ( W ^ Φ ˇ H Θ ^ Φ ˇ ) ,
s . t . Tr ( W ^ ) ≤ P s + 1 ,
W ^ N + 1 , N + 1 = 1 ,
Θ ^ l , l = 1 , l ∈ L or l = L + 1 ,
Θ ^ ⪰ 0 , rank ( Θ ^ ) = 1 ,
W ^ ⪰ 0 , rank ( W ^ ) = 1 ,
ξ ≤ ε .
We transform the problem (6) into its relaxed form by removing the constraints of rank ( W ^ ) = 1 and rank ( Θ ^ ) = 1 . Subsequently, the problem (6) is more tractable and can be solved using convex optimization techniques. This relaxation allows for a wider range of solutions. In addition, (6a) can be expressed as
Tr ( W ^ Φ ˇ H Θ ^ Φ ˇ ) = vec ( Φ ˇ ) H W ^ T ⊗ Θ ^ vec Φ ˇ .
The sub-problem 1 is transformed into optimizing W ^ under the condition of given Θ ^ . The sub-problem 2 is transformed into optimizing Θ ^ with fixed W ^ .
(sub-problem 1) When Θ ^ is given,
max W ^ Tr ( W ^ Φ ˇ H Θ ^ Φ ˇ ) ,
s . t . Tr ( W ^ ) ≤ P s + 1 ,
W ^ N + 1 , N + 1 = 1 ,
W ^ ⪰ 0 ,
ξ ≤ ε .
(sub-problem 2) When W ^ is given,
max Θ ^ Tr ( W ^ Φ ˇ H Θ ^ Φ ˇ ) ,
s . t . Θ ^ l , l = 1 , l ∈ L or l = L + 1 ,
Θ ^ ⪰ 0 ,
ξ ≤ ε .
The two subproblems resulting from the relaxation are convex. We can converge to an optimized solution for W ^ * and Θ ^ * , through iteratively solving the relaxed sub-problems 1 and 2 alternately. The above problem currently is a convex positive semi-definite program (SDP), and it can be efficiently solved using existing convex optimization solvers. If W ^ * and Θ ^ * are rank 1, restore w ^ * and θ ^ * using singular value decomposition (SVD). When using the SVD for rank reduction, we can choose to keep the first few largest singular values and set the others to zero. This will result in a lower rank approximation, but not usually a complete reduction to rank one. A rank-one solution is a special case and is unlikely to be realised in the general case. In other cases, recover the approximate solution w * and θ * using the standard Gaussian randomization method. This randomization method provides an approximate solution and is particularly useful when dealing with matrices of higher rank. The quality of the approximation depends on the properties of the original matrices and the size of the random matrix.
According to the above analysis, we recapitulate the overall algorithm for problem (3) as Algorithm 1. The objective value of optimizing problem (3) is represented by R ( k ) with variables Θ ^ ( k ) and W ^ ( k ) in the k-th iteration, while ϵ denotes a small threshold set to 0.001. Algorithm 1 always converges, as the objective value is non-decreasing over iterations and has a finite upper bound.
Algorithm 1 Algorithm for Sovling Problem (3)
1:
Initialization: Set k = 0 , θ ^ ( 0 ) = 1 L .  
2:
Compute Θ ^ ( 0 ) = θ ^ ( 0 ) H θ ^ ( 0 ) ;   R ( 0 ) = f ( W ^ ( 0 ) , Θ ^ ( 0 ) ) . 
3:
repeat 
4:
   Set k = k + 1 . 
5:
   With given Θ ^ ( k − 1 ) , optimize the sub-problem 1. 
6:
   With given W ^ ( k ) , optimize the sub-problem 2. 
7:
   Compute R ( k ) = f ( W ^ ( k ) , Θ ^ ( k ) ) . 
8:
until R ( k ) − R ( k − 1 ) R ( k ) < ϵ . 
9:
Recover w * and θ * .

4. Numerical Results

In order to evaluate the security of the proposed approach in this paper, numerical simulations were conducted on an IRS-assisted backscatter communication system. Additionally, for comparative analysis, this paper also provides several different schemes.
The first scheme considers the transmission scenario of a traditional wireless communication system that does not incorporate an IRS, which is expressed as Without-IRS. By comparing the performance of the IRS-assisted system against this Without-IRS scenario, we can evaluate the added benefits or improvements brought by the IRS. The optimization for this scheme is specifically for the beamformer w .Therefore, it may not take advantage of the additional capabilities that an IRS can offer in terms of enhancing communication links, mitigating interference, or improving overall system performance.
The second scheme is the wireless communication system assisted by passive reflection IRS, which is denoted by Reflection-IRS. This scheme involves the integration of an IRS into the wireless communication system. In this system, the IRS acts as a passive relay, reflecting signals to enhance communication links. This scheme jointly optimizes the IRS reflection coefficient θ and the source beamformer w . The optimization process considers both the reflection properties of the IRS and the beamforming at the source. In contrast, the difference in the scheme proposed in this paper is that the IRS in the backscatter system utilizes the interference from the eavesdropper to enhance the receiving power of the legitimate user. This scheme is used to compare the effects of backscatter technology for IRS assisted communication systems.
The third scheme involves only optimizing the reflection coefficient vector of the IRS using the maximum ratio transmission (MRT), referred to as MRT-IRS. In this approach, the beamforming vector of the source is not involved in optimization. The primary optimization in MRT-IRS scheme is directed towards the IRS reflection coefficient vector. The goal is to maximize the received signal power at the legal user by adjusting the IRS reflections. By optimizing only the IRS reflection coefficients and not involving the source beamforming vector, it provides a reference for evaluating the impact of IRS reflections alone on the system performance. This scheme simplifies the optimization process and could limit the overall performance compared to schemes that optimize both the source and the IRS.
The last scheme is a relay. By introducing a relay with a set number of antennas and specific transmit power, the performance of this relay-based system can be compared with the IRS-assisted system. This scheme employs a relay with four antennas in place of the IRS, and its position is set to be identical to the IRS in the BackCom-IRS approach for comparison purposes. This positioning ensures a fair and relevant comparison between the two approaches. Unlike the IRS-assisted system, which primarily reflects signals to enhance communication, the relay scheme actively amplifies and forwards signals. The transmit power of this relay is denoted by P r .
The link from Alice to Willie is modelled as a slow-fading Rayleigh channel. The channel gain from the IRS to Bob follows a Rician distribution with a Rician factor of 3 on a small scale. The path loss model for all channels in the system is denoted by P L = P L 0 − 10 l g ( d / d 0 ) dB. The path loss at the reference distance of d = d 0 and d 0 = 1 m is denoted by P L 0 = - 30 dB. The transmit power at Alice is P s = 9 dBW. The transmit power of relay is P r = 0.1 W. The noise variance is σ 2 = 10 − 5 . The distances from Alice to Bob, Alice to IRS, Alice to Willie, IRS to Bob, Willie to Bob, and Willie to IRS are d AB = 60 m, d AI = 55 m, d AW = 55 m, d IB = 15 m, d WB = 15 m, d WI = 15 m, respectivly.
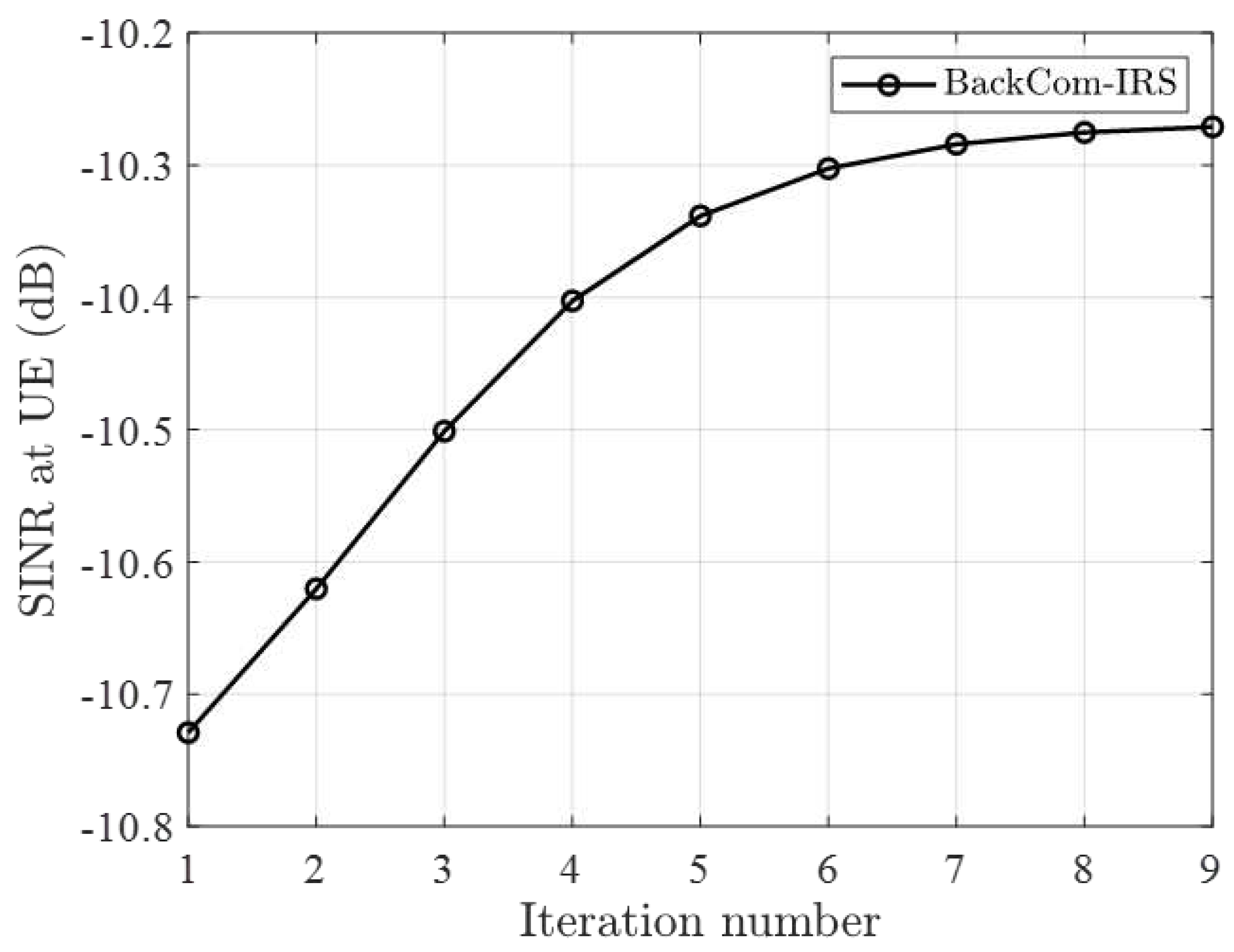
Figure 2 shows the SINR at user Bob in the BackCom-IRS scheme as a function of the iteration number t under randomly generated. It represents a typical result selected from several generating. In this case, P a = 9 dBW, L = 40 . As the iterations progress, the SINR at the legal user Bob tends to stabilize. It is evident that the proposed scheme exhibits good convergence behaviour.
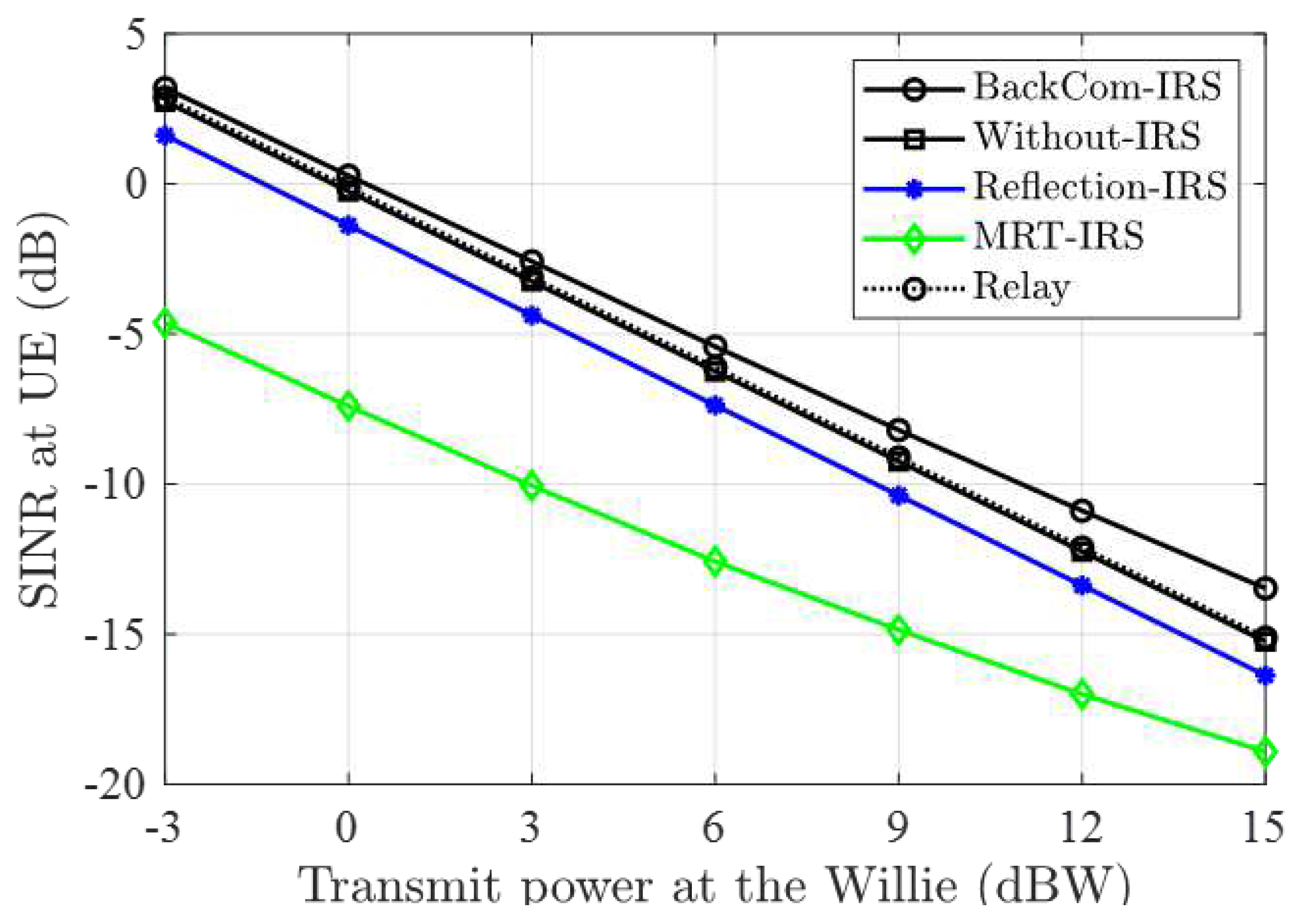
Figure 3 shows that the SINR at Bob changes with the transmission power of the eavesdropper Willie. It can be seen from this figure that SINR at Bob decreases as P a increases. Increasing the transmission power at the eavesdropper Willie is detrimental to the user’s received information. Higher transmission power of the eavesdropper negatively affects the communication link to user Bob. The proposed scheme outperforms the MRT-IRS scheme, traditional reflection IRS scheme, Relay scheme and Without-IRS scheme, as demonstrated in the simulation results. This implies that, even under conditions of increased eavesdropper power, the proposed scheme is more effective in maintaining a satisfactory SINR at user Bob. Especially in comparison to the conventional reflection-IRS, the IRS with integrated backscatter exhibits a more substantial difference in SINR as the eavesdropper’s transmit power increases. This implies that backscatter technology can enhance the security of IRS assisted communication systems.
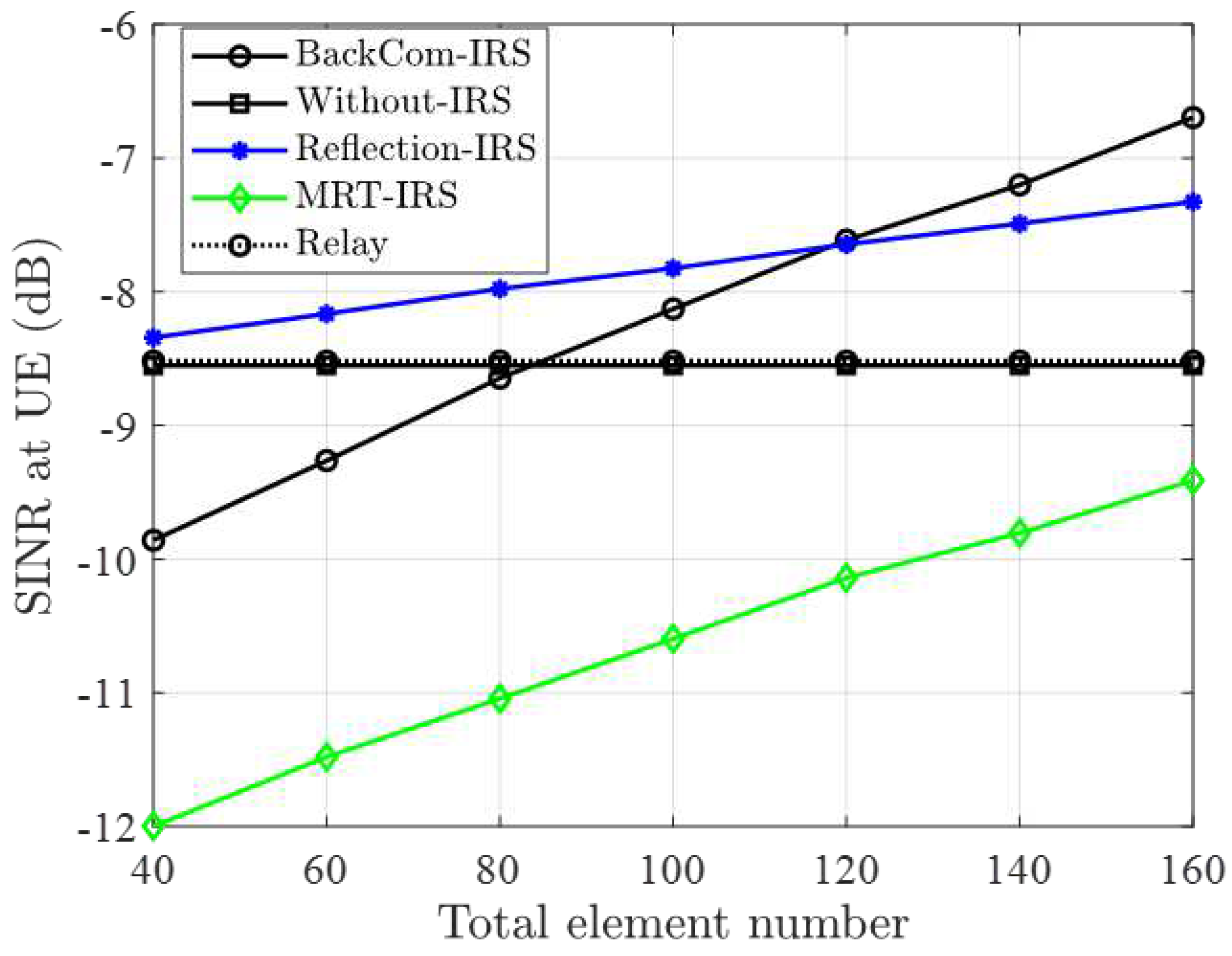
Figure 4 illustrates how the SINR at Bob is affected by the total number of reflective elements L at the IRS. This figure shows that the SINR at Bob increases as the number of elements L increases. The number of IRS elements does not affect the Without-IRS and relay scheme. At first, the relay scheme and the without-IRS scheme will be better than the scheme proposed in this paper. As the number of IRS components increases, the scheme proposed in this paper will achieve higher performance gains than other schemes. This implies that a larger number of elements in the IRS contributes positively to the security of the wireless communication system. When the number of reflecting elements is small, the received signal at legal user bob is dominated by the direct link other than the IRS assisted link. The performance differences between the proposed scheme and the MRT-IRS scheme increase with the reflecting elements of IRS. This indicates that as the number of reflective elements increases, the joint optimization of the beamforming vector of the source and the reflection coefficient of the IRS becomes more flexible, and the performance gain also becomes higher.

5. Conclusion

This paper proposed a scheme to realize secure communication using an IRS backscatter communication system. Under the constraint of the SINR of the eavesdropper, this paper obtained the maximum SINR of the user through the alternate optimization algorithm to solve the nonconvex objective problem. Alice’s beamforming vector and the IRS’s reflection coefficient are jointly optimized. The simulation results validate that the BackCom-IRS scheme outperforms other schemes such as MRT-IRS, reflection-IRS, without-IRS, and relay schemes. This work proved the research value of BackCom-IRS in secure communication. It demonstrates that the addition of the IRS can improve the security performance of communication systems and that IRS using backscattering can provide better security than traditional IRS used only for reflection, especially when the interference of the eavesdropper is significant. In the future, this work could be extended to multiple users or multiple eavesdropper communication systems or to investigate secure communication with BackCom-IRS under imperfect CSI.

Author Contributions

Conceptualization, Y.M. and J.Z.; methodology, Y.M.; software, Y.M.; formal analysis, Y.M., Y.S.; writing—original draft preparation, Y.M.; review and editing and validation, Y.S., and J.Z. All authors have read andagreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Cui, M.; Zhang, G.; Zhang, R. Secure wireless communication via intelligent reflecting surface. IEEE Wireless Commun. Lett. 2019, 8, 1410–1414. [Google Scholar] [CrossRef]
  2. Chu, Z.; Hao, W.; Xiao, P.; Shi, J. Intelligent reflecting surface aided multi-antenna secure transmission. IEEE Wireless Commun. Lett. 2020, 9, 108–112. [Google Scholar] [CrossRef]
  3. Wu, Q.; Zhang, S.; Zheng, B.; You, C.; Zhang, R. Intelligent reflecting surface-aided wireless communications: A tutorial. IEEE Trans. Commun. 2021, 69, 3313–3351. [Google Scholar] [CrossRef]
  4. Wu, C.; Yan, S.; Zhou, X.; Chen, R.; Sun, J. Intelligent reflecting surface (IRS)-aided covert communication with Warden’s statistical CSI. IEEE Wireless Commun. Lett. 2021, 10, 1449–1453. [Google Scholar] [CrossRef]
  5. Wu, Q.; Zhang, R. Towards smart and reconfigurable environment: Intelligent reflecting surface aided wireless network. IEEE Commun. Mag. 2020, 58, 106–112. [Google Scholar] [CrossRef]
  6. Gong, C.; Yue, X.; Wang, X.; Dai, X.; Zou, R.; Essaaidi, M. ; Intelligent reflecting surface aided secure communications for NOMA networks. IEEE Trans. Veh. Technol. 2022, 71, 2761–2773. [Google Scholar] [CrossRef]
  7. Wu, Q.; Zhang, R. Intelligent reflecting surface enhanced wireless network via joint active and passive beamforming. IEEE Trans. Wireless Commun. 2019, 18, 5394–5409. [Google Scholar] [CrossRef]
  8. Zhou, X.; Yan, S.; Wu, Q.; Shu, F.; Ng, D. W. K. Intelligent reflecting surface (IRS)-aided covert wireless communications with delay constraint. IEEE Trans. Wireless Commun. 2022, 21, 532–547. [Google Scholar] [CrossRef]
  9. Huang, C.; Zappone, A.; Alexandropoulos, G. C.; Debbah, M.; Yuen, C. Reconfigurable intelligent surfaces for energy efficiency in wireless communication. IEEE Trans. Wireless Commun. 2019, 18, 4157–4170. [Google Scholar] [CrossRef]
  10. Zhou, S.; Xu, W.; Wang, K.; Di Renzo, M.; Alouini, M. -S. Spectral and energy efficiency of IRS-assisted MISO communication with hardware impairments. IEEE Commun. Lett. 2020, 9, 1366–1369. [Google Scholar] [CrossRef]
  11. Li, W.; Ghogho, M.; Chen, B.; Xiong, C. Secure communication via sending artificial noise by the receiver: outage secrecy capacity/region analysis. IEEE Commun. Lett. 2012, 16, 1628–1631. [Google Scholar] [CrossRef]
  12. Zhou, X.; Ganti, R. K.; Andrews, J. G. Secure wireless network connectivity with multi-antenna transmission. IEEE Trans. Wireless Commun. 2010, 10, 425–430. [Google Scholar] [CrossRef]
  13. Yu, X.; Xu, D.; Sun, Y.; Ng, D. W. K.; Schober, R. Robust and secure wireless communications via intelligent reflecting surfaces. IEEE J. Sel. Areas Commun. 2020, 38, 2637–2652. [Google Scholar] [CrossRef]
  14. Shen, H.; Xu, W.; Gong, S.; He, Z.; Zhao, C. Secrecy rate maximization for intelligent reflecting surface assisted multi-antenna communications. IEEE Commun. Lett. 2019, 23, 1488–1492. [Google Scholar] [CrossRef]
  15. Saad, W.; Zhou, X.; Han, Z.; Poor, H. V. On the physical layer securityof backscatter wireless systems. IEEE Trans. Wireless Commun. 2014, 13, 3442–3451. [Google Scholar] [CrossRef]
  16. Kimionis, J.; Bletsas, A.; Sahalos, J. N. Bistatic backscatter radio for power-limited sensor networks. Proc. IEEE Glob. Commun. Conf. (GLOBECOM) 2013, 353–358. [Google Scholar]
  17. Van Huynh, N.; Hoang, D. T.; Lu, X.; Niyato, D.; Wang, P.; Kim, D. I. Ambient backscatter communications: A contemporary survey. IEEE Commun. Surveys Tuts. 2018, 20, 2889–2922. [Google Scholar] [CrossRef]
  18. Vahedi, E.; Ward, R. K.; Blake, I. F. Security analysis and complexity comparison of some recent lightweight RFID protocols. Proc. 4th Int. Conf. Comput. Intell. Security Inf. Syst. 2011, 6694, 92–99. [Google Scholar]
  19. Wang, H.-M.; Zheng, T.; Xia, X.-G. Secure MISO wiretap channels with multiantenna passive eavesdropper: Artificial noise vs. artificial fast fading. IEEE Trans. Wireless Commun. 2015, 14, 94–106. [Google Scholar] [CrossRef]
  20. Yang, Q.; Wang, H.-M.; Zhang, Y.; Han, Z. Physical layer security in MIMO backscatter wireless systems. IEEE Trans. Wireless Commun. 2016, 15, 7547–7560. [Google Scholar] [CrossRef]
  21. Han, J. Y.; Kim, M. J.; Kim, J.; Kim, S. M. Physical layer security in multi-tag ambient backscatter communications - Jamming vs. Cooperation. Proc. IEEE WCNC 2020, 1–6. [Google Scholar]
  22. Khan, W. U.; Liu, J.; Jameel, F.; Raza Khan, M. T.; Ahmed, S. H.; Jäntti, R. Secure backscatter communications in multi-cell NOMA networks: Enabling link security for massive IoT networks. Proc. IEEE INFOCOM 2020, 213–218. [Google Scholar]
  23. Xu, S.; Liu, J.; Zhang, J. Resisting undesired signal through IRS-based backscatter communication system. IEEE Commun. Lett. 2021, 25, 2743–2747. [Google Scholar] [CrossRef]
Preprints 92518 g001
Figure 1. An IRS-aided backscatter wireless communication system under active eavesdropper’s attack
Figure 1. An IRS-aided backscatter wireless communication system under active eavesdropper’s attack
Preprints 92518 g001
Preprints 92518 g002
Figure 2. Convergence of the BackCom-IRS scheme in a random observation
Figure 2. Convergence of the BackCom-IRS scheme in a random observation
Preprints 92518 g002
Preprints 92518 g003
Figure 3. SINR γ at Bob versus the transmit power P a at the Willie.
Figure 3. SINR γ at Bob versus the transmit power P a at the Willie.
Preprints 92518 g003
Preprints 92518 g004
Figure 4. SINR γ at Bob versus the total number of reflecting elements L at the IRS.
Figure 4. SINR γ at Bob versus the total number of reflecting elements L at the IRS.
Preprints 92518 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated