A Modification to the Remotely Sensed Active Layer Thickness (ReSALT) Algorithm to have Self-Consistency

Preprint

Article

A Modification to the Remotely Sensed Active Layer Thickness (ReSALT) Algorithm to have Self-Consistency

Altmetrics

Downloads

205

Views

145

Comments

Jatin Mathur^*

This version is not peer-reviewed

This preprints belongs to the Topic

Permafrost Dynamics and Impacts on the hydrology, Geomorphology, Ecosystem, and Infrastructure Based on Modeling, Observations, and Remote Sensing Products

Submitted:

30 June 2024

Posted:

02 July 2024

You are already at the latest version

Alerts

Abstract

Permafrost thaw is an important aspect of Earth’s carbon cycles. Initial estimates suggest that permafrost thaw could contribute anywhere between 20 to 500 Gt of CO2-eq by 2100. These estimates are all fundamentally centered around one number: active layer thickness (ALT). The deeper the ALT, the more emissions. Unfortunately, ALT is a highly spatially heterogeneous number and determined by numerous thermal, soil hydrology, and geomorphological effects. The remotely sensed active layer thickness (ReSALT) algorithm was introduced in 2010 to provide scientists with a way to model ALT heterogeneously at meter-scale resolution. However, upon inspection, this work shows that ReSALT’s modeling approach is self-inconsistent when using a variable soil porosity model. This work then introduces SCReSALT (Self-Consistent ReSALT) to solve that problem. Experimental comparisons to a past study in Utqiagvik (formerly Barrow), Alaska show significant improvement and suggest that SCReSALT should become a standard tool in permafrost thaw modeling. Code to reproduce all results can be found at https://github. com/jmathur25/permafrost-prediction.

Keywords:

Subject: Environmental and Earth Sciences - Remote Sensing

1. Introduction

Climate forecasting studies estimate that permafrost thaw could contribute anywhere between 20 to 500 Gt of CO₂-eq by 2100 ([1,2,3,4]). These estimates varied in the phenomenon they modeled, how that phenomenon was modeled, and assumptions of warming trends, therefore explaining the wide range of predictions. Regardless of these differences, a crucial variable in all forecasts is the active layer thickness (ALT), which describes the topmost layer of permafrost subject to annual freeze and thaw. Warmer temperatures lead to deeper active layers. Organic carbon is distributed throughout the soil column, meaning deeper active layers permit microbes to process more carbon and emit more greenhouse gases. Hence, there is a strong interest in developing modeling and forecasting algorithms for ALT. For more background on permafrost carbon cycles, refer to [5].

2. Background

2.1. ReSALT Description

The remotely sensed active layer thickness (ReSALT) algorithm was introduced to model ALT with broad spatial coverage while preserving heterogeneous predictive power [6]. Without remote sensing, permafrost thaw monitoring is constrained to sparse in-situ observations. Given the vast extent of permafrost, it would be incredibly useful if remote sensing could accurately monitor ALT. ReSALT leverages a technique known as interferometric synthetic aperture radar (InSAR) to create its predictions. For background information on InSAR, refer to [7]. Within the context of this paper, an InSAR measurement should be thought of as having three properties: i) the date of the reference SAR acquisition, ii) the date of the secondary SAR acquisition, and iii) a geocoded image containing ground subsidence1 per pixel. Specifically, if the ground position is measured as

δ

in an unchanging, earth-centered reference frame and the positive direction points towards the Earth’s center, then the image will consist of

D = δ_{r e f e r e n c e} - δ_{s e c o n d a r y}

per pixel.

ReSALT has been used in several studies since its conception ([6,8,9,10]). While it has demonstrated promising results, there is room for improvement. For example, the Permafrost Dynamics Observatory project reported a root mean square error (RMSE) of 15.18 cm in ReSALT predicted vs in-situ ALTs [10]. The in-situ data had an average ALT between 50 and 60 cm, making the RMSE somewhat large in magnitude. This error served as motivation for this paper.

ReSALT is based on two main phenomenon. The first is that thaw depth h is proportional to

\sqrt{A D D T}

, where

A D D T

stands for Accumulated Degree Days of Thaw. This is the well-known Stefan equation and is shown in (1).

h (t) = N \sqrt{A D D T (t)}

(1)

where N is a proportionality factor. This is derived in Appendix A. The second phenomenon is that when ice thaws into liquid water, the amount of volume reduces. This leads to ground subsidence as shown visually in Figure 1 and mathematically in (2).

δ (t) = \frac{ρ_{w} - ρ_{i}}{ρ_{i}} \int_{0}^{h (t)} P S d h = f (h (t))

(2)

where

ρ_{w}

is the density of water,

ρ_{i}

is the density of ice, P is the soil porosity, and S is the soil saturation. The integral captures the volumetric liquid water content. The ratio

\frac{ρ_{w} - ρ_{i}}{ρ_{i}}

captures the (positive) difference in volume height when liquid water phase transitions to solid ice.2 The ground subsidence can be computed by multiplying the two quantities, therefore arriving at (2). f is introduced as a convenience to compute subsidence from thaw depth.

Any particular InSAR image contains subsidence difference

D = δ (t_{i}) - δ (t_{j})

. Temperature is typically known at a coarse resolution. Hence, ReSALT strives to find a way to relate these two quantities and ultimately retrieve

h (t)

. It does so by posing the following least-squares inversion problem:

[\begin{matrix} D_{1} \\ ⋮ \\ D_{N} \end{matrix}] = [\begin{matrix} t_{2, 1} - t_{1, 1} & \sqrt{A D D T_{2, 1}} - \sqrt{A D D T_{1, 1}} \\ ⋮ & ⋮ \\ t_{2, N} - t_{2, N} & \sqrt{A D D T_{2, N}} - \sqrt{A D D T_{1, N}} \end{matrix}] [\begin{matrix} R \\ E \end{matrix}]

(3)

where

D_{i}

is the measured subsidence difference in the ith interferogram,

t_{2, i}

and

t_{1, i}

describe the times of the two SAR acquisitions that were used to create the ith interferogram,

A D D T

is the accumulated degree days of thaw, and

A D D T_{2, i}

and

A D D T_{1, i}

describe the

A D D T

’s at

t_{2, i}

and

t_{1, i}

. Note that all

D_{i}

refer to the same geographic location, but may differ in pixel location from image to image. R and E are the unknown variables and are solved for. R captures a long-term subsidence trend. More information can be found in [6,11]. E captures the relationship between

\sqrt{A D D T}

and subsidence difference, which can then be used to identify subsidence at any arbitrary time t via:

δ (t) = E \sqrt{A D D T (t)}

(4)

Then, (2) is inverted to obtain

h (t)

. More details on ReSALT’s derivation are shown in Appendix B.

2.2. ReSALT Inconsistency Description

In (3) and (4), subsidence is modeled as proportional to

\sqrt{A D D T}

. Using (1) and (2), it becomes evident that this only happens when P is constant with depth. Hence, any application of ReSALT that uses a non-constant porosity model is self-inconsistent. Examples of self-inconsistent applications of ReSALT are [8] and [9], which use the “mixed soil model” shown later in this paper.

3. Method

Observe that if R is ignored, the desired left-hand side (LHS) for (3) is thaw depth difference:

h (t_{i}) - h (t_{j}) = N (\sqrt{A D D T (t_{i})} - \sqrt{A D D T (t_{j})})

(5)

However, only subsidence difference and

A D D T

are measured. To see if subsidence difference can be related to thaw depth difference, (1) is analyzed as a ratio:

\frac{h (t_{i})}{h (t_{j})} = \sqrt{\frac{A D D T (t_{i})}{A D D T (t_{j})}}

(6)

h (t_{i}) = h (t_{j}) \sqrt{\frac{A D D T (t_{i})}{A D D T (t_{j})}}

(7)

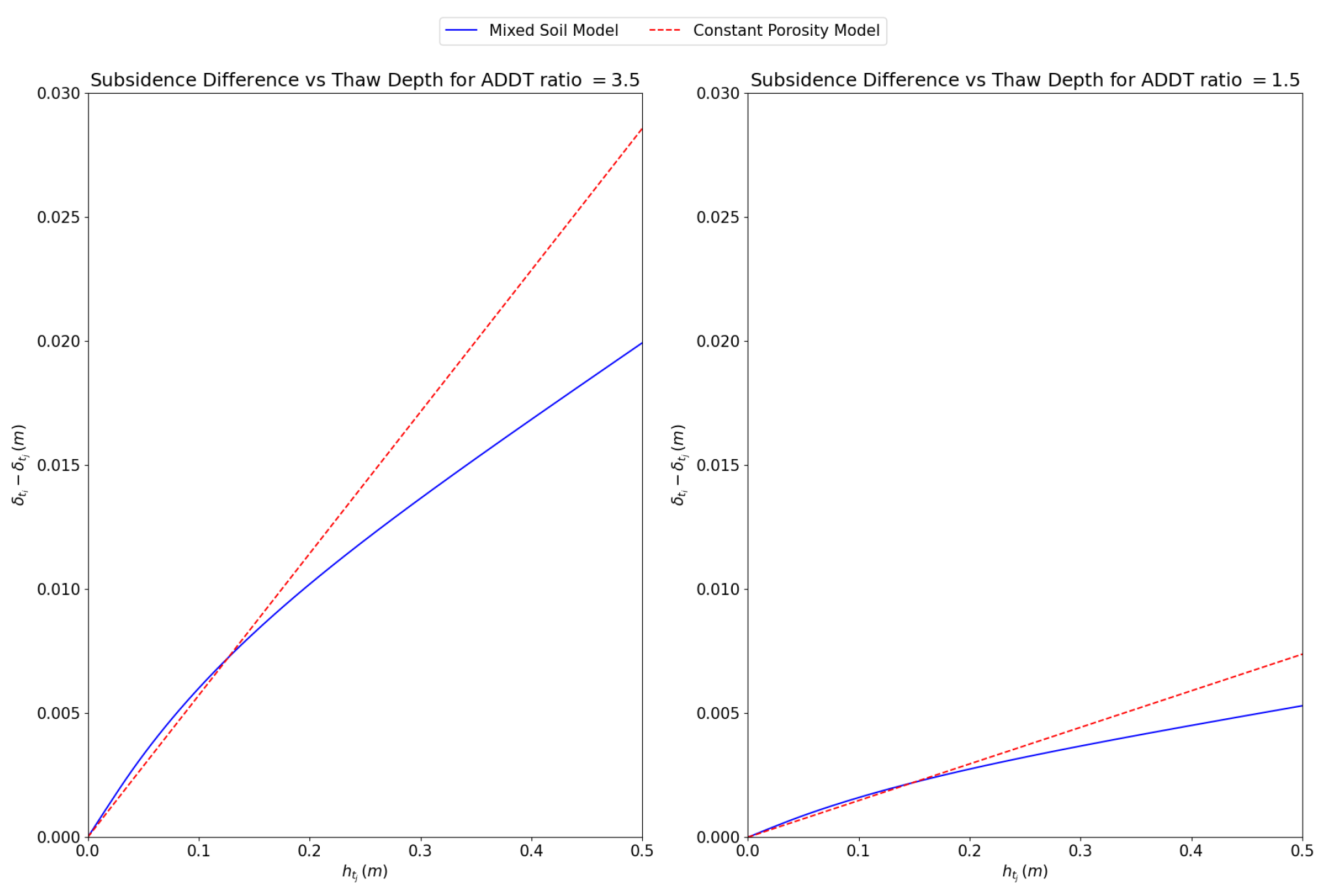
For convenience,

K : = \sqrt{\frac{A D D T (t_{i})}{A D D T (t_{j})}}

is introduced. Next, a list of candidate

h_{t_{j}}

on some large interval of possible thaw depths is generated, and corresponding

h_{t_{i}}

is computed using (7) for a fixed K. The subsidence for each candidate

h_{t_{j}}

and

h_{t_{i}}

can be computed using (2). A plot of candidate thaw depth differences and corresponding subsidence differences can then be constructed. See Figure 2 for examples of this plot for two soil porosity models. Each of these models is explained in [8]. As shown in the bottom two figures, a particular subsidence difference can unambiguously be mapped to a thaw depth difference. Intuitively, this is because (7) enables multiplicative growth of

h_{t_{i}}

with respect to

h_{t_{j}}

. Consequently, the hope is that (2) enables subsidence difference to grow strictly monotonically. Put another way, for each interferogram, K (which is known) acts as a constraint parameter that helps search the space of possible thaw depth pairs

h (t_{j})

and

h (t_{i})

. Corresponding subsidences can be computed and a graph can depict whether subsidence difference can be related to thaw depth difference. Of course, there is no guarantee this will work for all soil porosity models. A counterexample is discussed in Section 3.1. Also, note that in Figure 2 the bottom images demonstrate the effect of K on the method’s robustness. For the constant porosity model, there is no effect because the thaw depth difference is linearly related to the subsidence difference. For the “mixed soil model,” the slope is higher in the bottom-left image, making it easier to identify a particular thaw depth difference from a given subsidence difference. This is because larger K make the thaw depth pair have smaller values for the same thaw depth difference, which then exhibit larger subsidence gradients, as the top-right plot shows.

This method is summarized in Algorithm 1. (3) can be recast as:

[\begin{matrix} y_{1} \\ ⋮ \\ y_{N} \end{matrix}] = [\begin{matrix} \sqrt{A D D T_{2, 1}} - \sqrt{A D D T_{1, 1}} \\ ⋮ \\ \sqrt{A D D T_{2, N}} - \sqrt{A D D T_{1, N}} \end{matrix}] [\begin{matrix} N \end{matrix}]

(8)

Algorithm 1:Self-Consistent ReSALT LHS Retrieval

Require:: $K = \sqrt{\frac{A D D T_{t_{i}}}{A D D T_{t_{j}}}}$
Require:: $D = measured subsidence difference$
Require:: $N = number of samples$
Require:: $L = lower end of possible thaw depths$
Require:: $U = upper end of possible thaw depths$
1:: $s t e p \leftarrow \frac{U - L}{N - 1}$ ▹ Step size for linear spacing
2:: for $k = 1 \to N$ do
3:: $h_{k, j} \leftarrow L + (k - 1) \times s t e p$
4:: $h_{k, i} \leftarrow h_{k, j} \times K$
5:: $y_{k} \leftarrow h_{k, i} - h_{k, j}$
6:: $x_{k} \leftarrow f (h_{k, i}) - f (h_{k, j})$ ▹f is defined in (2)
7:: end for
8:: if not check_monotonically_changing $(x, y, K)$ then
9:: raise Error(“Fails SCReSALT requirement.”)
10:: end if
10:: This can be done with binary search, which enables fast solving for hundreds of pixels. Using a root-finding approach like Newton’s method would be slower.
11:: Find k such that $x_{k}$ is closest to D
12:: return $y_{k}$

where

y_{i}

is the best-matching thaw depth difference reported for each

D_{i}

via Algorithm 1. This now forms a self-consistent modeling of thaw, temperature, and ground subsidence under variable soil porosity models. Hence, this new method is called SCReSALT (Self-Consistent ReSALT). Least-squares inversion gives the best N. (1) can then be used to find the thaw depth at any point in the thaw season.

To extend the formulation to multiple years, the long-term trend R must be discounted from

D_{i}

before following the above approach. ReSALT jointly inverts for R and E, but a self-consistent model cannot do that. So, R must be estimated independently of and prior to N. Solving this is out-of-scope for this paper, but here are some ideas.

(i): Form interferograms across multiple years at the start of the thaw season, ideally when $A D D T = 0$ . Any observed subsidence can be attributed to R. Compute the best-fit R that solves all $D_{i} = R (t_{i} - t_{j})$ .
(ii): Compute an initial estimate of N by solving (8). N could be solved either per thaw season (which makes $R = 0$ ) or overall. Then, form interferograms across multiple years at the start of the thaw season and remove the subsidence contribution due to any initial thaw. This is known because the subsidence contribution due to initial thaw can be written as: $D_{h, i} = f (N_{s_{2, i}} \sqrt{A D D T_{2, i}}) - f (N_{s_{i, 1}} \sqrt{A D D T_{1, i}})$ . Note $N_{s_{2, i}}$ denotes N for the thaw season in the 2nd SAR image in the ith interferogram. $N_{s_{1, i}}$ means the same for the 1st SAR image. Compute the best-fit R that solves all $D_{i} - D_{h, i} = R (t_{i} - t_{j})$ .

Once R is known, the multi-year problem can be solved using (8) but instead of giving Algorithm 1 the observed subsidence difference

D_{i}

, give it

D_{i} - R (t_{i} - t_{j})

For completeness, it is worth noting that both ReSALT and SCReSALT do not need both SAR acquisitions to be during the thaw season. One acquisition could be before the thaw season, in which case

A D D T \approx 0

can be assumed for that acquisition. Hence, any measured subsidence difference can be modeled as the true subsidence at that point. ReSALT can directly use (3). SCReSALT would need a slight modification because it operates using ratios. Algorithm 1 could be modified such that if

A D D T_{t_{j}} < ϵ

, simply report

y = f^{- 1} (δ)

. Similarly, if

A D D T_{t_{i}} < ϵ

, report

y = f^{- 1} (- δ)

Lastly, in Appendix A, the Stefan equation is shown to also depend on a constant porosity model. Appendix D introduces SCReSALT-NS which relaxes this constraint. `NS’ stands for `non-Stefan’.

3.1. SCReSALT Counterexample Discussion

In Appendix C, a counterexample that does not meet the SCReSALT requirement is derived. Some possible solutions are described below.

(i): If a subsidence difference vs thaw depth difference graph can uniquely identify a subset of thaw depth differences, one could use the known thaw depth differences and the expectation that thaw depth only increases with time to select the right thaw depth.
(ii): Make sure to get a SAR acquisition before the thaw season starts. The measured subsidence difference is now true subsidence. Handling this was described earlier.

Note that any soil porosity model can be tested to see if it meets the SCReSALT requirement using Algorithm 1.

4. Experiments

To assess the practical improvement of SCReSALT, it is benchmarked against the results reported in [9]. [9] applies ReSALT to Utqiagvik (formerly Barrow), Alaska and uses the “mixed soil model” to predict ALT from 2006 to 2010. Metrics are extracted from the paper and the data product they release, which can be found at https://daac.ornl.gov/ABOVE/guides/ReSALT_InSAR_Barrow.html. [9] uses data from the U1 CALM3 plot. It uses L-band ALOS-PALSAR data and generates interferograms using the ISCE2 framework4. The paper defines the

χ^{2}

metric:

χ^{2} = \frac{{(A L T_{p r e d} - A L T_{g t})}^{2}}{e^{2}}

(9)

where e is the uncertainty in the measurement. In [9],

e = 7.9

cm. If

χ^{2} < 1.0

, it is called a “great match.” If the

A L T_{g t}

is within the uncertainty of

A L T_{p r e d}

, it is called a “good match." Otherwise, it is called a “bad match.” Uncertainty analysis is not described in this paper, but in brief, it could be computed by assigning an uncertainty distribution to each ReSALT/SCReSALT parameter and either analytically propagating that into a prediction uncertainty or more practically using numerical simulation. This work uses the fact that [9] stated that the ReSALT uncertainty is roughly twice that of the measurement uncertainty. Hence,

e_{R e S A L T} = e_{S C R e S A L T} = 15.8

cm. Other experimental details are described in Appendix E. Results are shown in Table 1.

5. Results

The metrics reported in [9] closely match the results computed from the data product. The “good match” category is a little worse because

e_{R e S A L T}

is not precisely known. That then influences the “bad match” category. Otherwise, the alignment is high, meaning there is high confidence in the derived Pearson R, mean absolute error (MAE), and RMSE values. The author also attempted to reproduce ReSALT but generally obtained worse numbers. It is difficult to get precise replication without source code, which is not available for [9]. Regardless, SCReSALT is shown to outperform ReSALT on virtually all metrics and handles outliers better given its reduced RMSE and

χ^{2}

. If compared to the reproduced ReSALT, SCReSALT’s improvement is even stronger. Furthermore, SCReSALT-NS demonstrates improvement over SCReSALT, suggesting that incorporating non-Stefan thaw dynamics can improve modeling accuracy. Also, the author was puzzled by the ReSALT data product’s low Pearson R. It is not clear why, but given the high measurement uncertainty, it is possible to have many “great matches” despite no correlation between predicted and ground-truth ALTs.

6. Conclusion

This work presents SCReSALT and SCReSALT-NS, two algorithms that modify ReSALT to enable self-consistent modeling of thaw, temperature, and ground subsidence in permafrost. It describes the conditions where SCReSALT can be used and shows its applicability to previously developed soil models. It is also shows that SCReSALT doesn’t work on all soil models. Possible solutions are discussed, but exploring them is left to future work. Experimentally, SCReSALT demonstrates significant improvement in estimating ALTs in Utqiagvik, Alaska. The author recommends that SCReSALT become a standard tool in permafrost thaw modeling.

Conflicts of Interest: The author declares no conflicts of interest.

Appendix A. Stefan’s Equation Derivation

First, Stefan’s equation is derived to understand the relationship between temperature and ground ice thaw. For a more rigorous discussion, refer to Section 1.4 and 1.5 of [12]. Figure A1 is provided to help visualize the relevant processes.

Figure A1. A diagram of a thawing soil column. h denotes the position of the thaw front. q is the (uniform) heat flux induced by

T_{t o p}

and

T_{b o t}

T_{t o p}

is the same as the temperature of the air. Brown circles denote soil particles. Anything that is not a soil particle is pore space. Note that any real soil would have a far more dense concentration of soil particles. Dark blue denotes liquid (thawed) water. Light blue denotes frozen (unthawed) water. If this is being viewed without color, the thawed water is above the middle small dashed rectangle, while the frozen water is below it. In this diagram, it is assumed that all pore space is filled with water. This does not have to be the case for Stefan’s equation to apply. A different bulk density

p_{p}

can capture the thaw dynamics of a variety of soil hydrology models.

Figure A1. A diagram of a thawing soil column. h denotes the position of the thaw front. q is the (uniform) heat flux induced by

T_{t o p}

and

T_{b o t}

T_{t o p}

p_{p}

can capture the thaw dynamics of a variety of soil hydrology models.

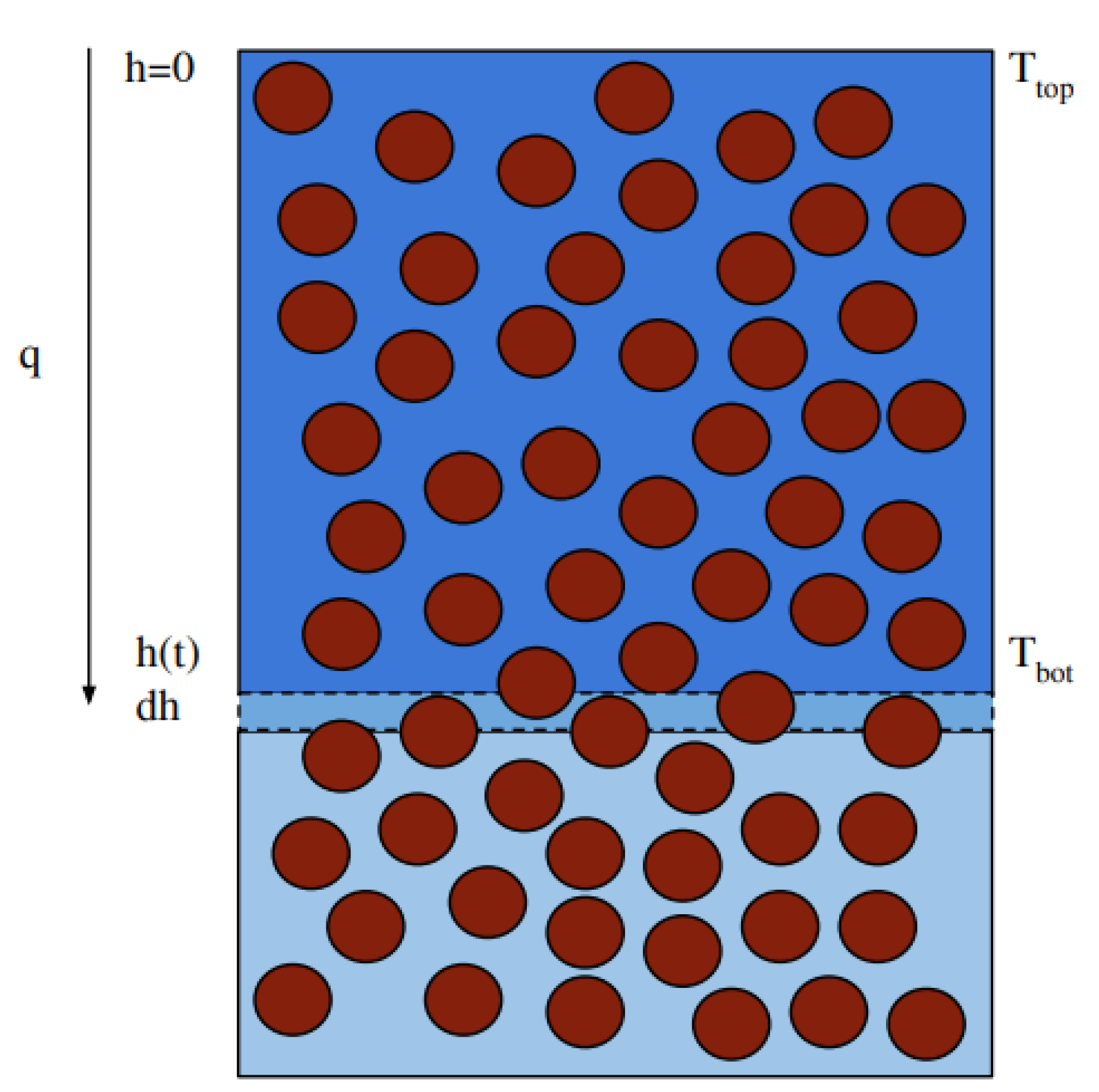
The derivation begins with Fourier’s Law:

q = - k_{p} \frac{d T}{d h}

(A1)

where q is the heat per unit area per unit time,

k_{p}

is the thermal conductivity of frozen soil, T is temperature, and h defines the position of the thaw front. Note that both T and h are functions of time t. Next, assume the temperature gradient is uniform throughout the column until the point of phase transition, after which it is constant.

\frac{d T}{d h} = \frac{(T_{b o t} - T_{t o p})}{h}

(A2)

Next, it is assumed that all heat at the boundary is absorbed as latent heat to facilitate phase change from ice to liquid water. Consequently, an infinitesimal change in thaw depth

d h

can be related to the amount of heat

d Q

required to do so by:

d Q = L p_{p} d h

(A3)

where

p_{p}

is the bulk density of ice in soil and L is the latent heat of fusion. Note that

p_{p} = ρ_{i} P_{f}

where

P_{f}

is the porosity of the soil with frozen5 water. Recall that this paper assumes the soil is fully saturated, meaning there is no need for an S term. Stefan’s equation assumes a homogeneous medium, meaning

P_{f}

and consequently

p_{p}

are assumed to be constant with depth. Evidently, using a non-constant porosity model with ReSALT is twice inconsistent! This new inconsistency will be revisited in Appendix D. Continuing with the derivation:

\frac{d Q}{d t} = L p_{p} \frac{d h}{d t} = q = - k_{p} \frac{T_{b o t} - T_{t o p}}{h}

(A4)

h can now be solved for:

h d h = - \frac{k_{p}}{p_{p} L} (T_{b o t} - T_{t o p}) d t

(A5)

\int_{h (t_{1})}^{h (t_{2})} h d h = - \frac{k_{p}}{p_{p} L} \int_{t_{1}}^{t_{2}} (T_{b o t} - T_{t o p}) d t

(A6)

Since

T_{b o t}

refers to the boundary of thawed/frozen soil, it is reasonable to assume

T_{b o t} \approx 0

6, in which case it can removed from (A6).

\int_{h (t_{1})}^{h (t_{2})} h d h = \frac{k_{p}}{p_{p} L} \int_{t_{1}}^{t_{2}} T_{t o p} d t

(A7)

Practically, once the thaw season begins

T_{t o p}

is typically larger than 0. Since

T_{t o p}

is measured on a daily basis (rather than continually), the right-hand side (RHS) can be replaced with:

\int_{h (t_{1})}^{h (t_{2})} h d h = \frac{k_{p}}{p_{p} L} (A D D T (t_{2}) - A D D T (t_{1}))

(A8)

where

A D D T

stands for the Accumulated Degree Days of Thaw. It is a standard number used in permafrost literature and is calculated at any day t by summing the temperatures larger than 0 of all days preceding and including t. Note that the use of

A D D T

implicitly assumes that the temperature stays above the freezing point (or more specifically, temperature always contributes to thaw in the time period under study). Continuing:

\int_{h (t_{1})}^{h (t_{2})} h d h = \frac{k_{p}}{p_{p} L} (A D D T (t_{2}) - A D D T (t_{1}))

(A9)

\frac{1}{2} (h {(t_{2})}^{2} - h {(t_{1})}^{2}) = \frac{k_{p}}{p_{p} L} (A D D T (t_{2}) - A D D T (t_{1}))

(A10)

h {(t_{2})}^{2} - h {(t_{1})}^{2} = \frac{2 k_{p}}{p_{p} L} (A D D T (t_{2}) - A D D T (t_{1}))

(A11)

Lastly, it is assumed that thaw begins when

A D D T

first exceeds 0°C-days. Hence, if

t_{s}

is the start of the thaw season,

h (t_{s}) = 0

and

A D D T (t_{s}) = 0

. The thaw depth at any time

t_{i}

can then be written as:

h {(t_{i})}^{2} - h {(t_{s})}^{2} = \frac{2 k_{p}}{p_{p} L} (A D D T (t_{i}) - A D D T (t_{s}))

(A12)

h {(t_{i})}^{2} = \frac{2 k_{p}}{p_{p} L} A D D T (t_{i})

(A13)

h (t_{i}) = \sqrt{\frac{2 k_{p}}{p_{p} L} A D D T (t_{i})}

(A14)

(1) is now derived (note that

N = \sqrt{\frac{2 k_{p}}{p_{p} L}}

). This is the same as equation (A4) in [13]. Note that in this derivation, the opposite sign convention is used. This derivation set

h = 0

at the ground and made h increase with depth. [13] does the opposite, hence flipping some signs in the above equations.

Appendix B. ReSALT Derivation

The derivation for ReSALT is now presented. InSAR gives measurements of ground subsidence

D = δ (t_{i}) - δ (t_{j})

as determined by two SAR acquisitions at

t_{i}

and

t_{j}

. ReSALT assumes the InSAR-measured subsidence is dominated by phase transition of ice to liquid water and can be modeled using (2). In general, P is not constant with depth. This means

δ (t_{i})

is not linearly proportional to

h (t_{i})

. However, because only

A D D T

and D are measured, ReSALT strives to find a way to relate the two. To do so, it assumes proportionality:

δ (t_{i}) \approx \frac{ρ_{w} - ρ_{i}}{ρ_{i}} P h (t_{i})

(A15)

This is the assumption, or self-inconsistency, that this paper solves. Continuing with the derivation, this is combined with (A14) to describe subsidence difference at arbitrary times:

\begin{matrix} δ (t_{i}) - δ (t_{j}) & = \frac{ρ_{w} - ρ_{i}}{ρ_{i}} P \sqrt{\frac{2 k_{p}}{p_{p} L}} \\ \times (\sqrt{A D D T (t_{i})} - \sqrt{A D D T (t_{j})}) \end{matrix}

(A16)

InSAR measures

δ (t_{i}) - δ (t_{j})

, and since the times of the two SAR acquisitions are known

A D D T (t_{i})

and

A D D T (t_{j})

can be determined. So, the coefficient

\frac{ρ_{w} - ρ_{i}}{ρ_{i}} P \sqrt{\frac{2 k_{p}}{p_{p} L}}

can be determined. If there are multiple InSAR images, (A16) can be posed as a least-squares inversion problem, leading to (3).

Appendix C. SCReSALT Counterexample Analysis

The mathematical condition of SCReSALT can be stated as follows: given an integrable function P for which

P (h) \in [0, 1]

, then for any ratio

K = \sqrt{\frac{A D D T_{i}}{A D D T_{j}}} = \frac{h_{t_{i}}}{h_{t_{j}}} \neq 1

h_{t_{i}} - h_{t_{j}}

can be uniquely identified by

δ_{t_{i}} - δ_{t_{j}}

. This can be restated as: if

f (K h_{0}) - f (h_{0}) = f (K h_{1}) - f (h_{1})

, then SCReSALT demands

h_{0} = h_{1}

. f is the same as in (2). The porosity can be written as:

P (h) = \frac{ρ_{i}}{ρ_{w} - ρ_{i}} f^{'} (h)

(A17)

There are constraints on P, and hence constraints on f, but for convenience P is initially ignored. To create a convincing failure case, the following is needed:

f (K h_{0}) - f (h_{0}) = f (K h_{1}) - f (h_{1})

(A18)

for some K and

h_{0} \neq h_{1}

. A simple way to analyze this is to consider a piecewise linear f:

f (h) = \{\begin{matrix} m_{0} h + b_{0} & for h_{0} \leq h \leq K h_{0} \\ m_{1} h + b_{1} & for h_{1} \leq h \leq K h_{1} \end{matrix}

(A19)

where

K h_{0} \leq h_{1}

. Other intervals of h are unspecified for simplicity. Substituting (A19) into (A18):

m_{0} K h_{0} - m_{0} h_{0} = m_{1} K h_{1} - m_{1} h_{1}

(A20)

m_{0} h_{0} (K - 1) = m_{1} h_{1} (K - 1)

(A21)

m_{0} h_{0} = m_{1} h_{1}

(A22)

This condition can certainly be constructed. A quadratic function can fit the ends of the piecewise linear function to ensure f is always differentiable. As long as i) the values and derivatives match at the intersection points and ii) a valid P can be constructed from f, the conditions are met. An example is shown below:

f (h) = \{\begin{matrix} 0.07 h & for h < 0.04 \\ - h^{2} + 0.15 h - 0.0016 & for 0.04 \leq h < 0.07 \\ 0.01 h + 0.0033 & for h \geq 0.07 \end{matrix}

(A23)

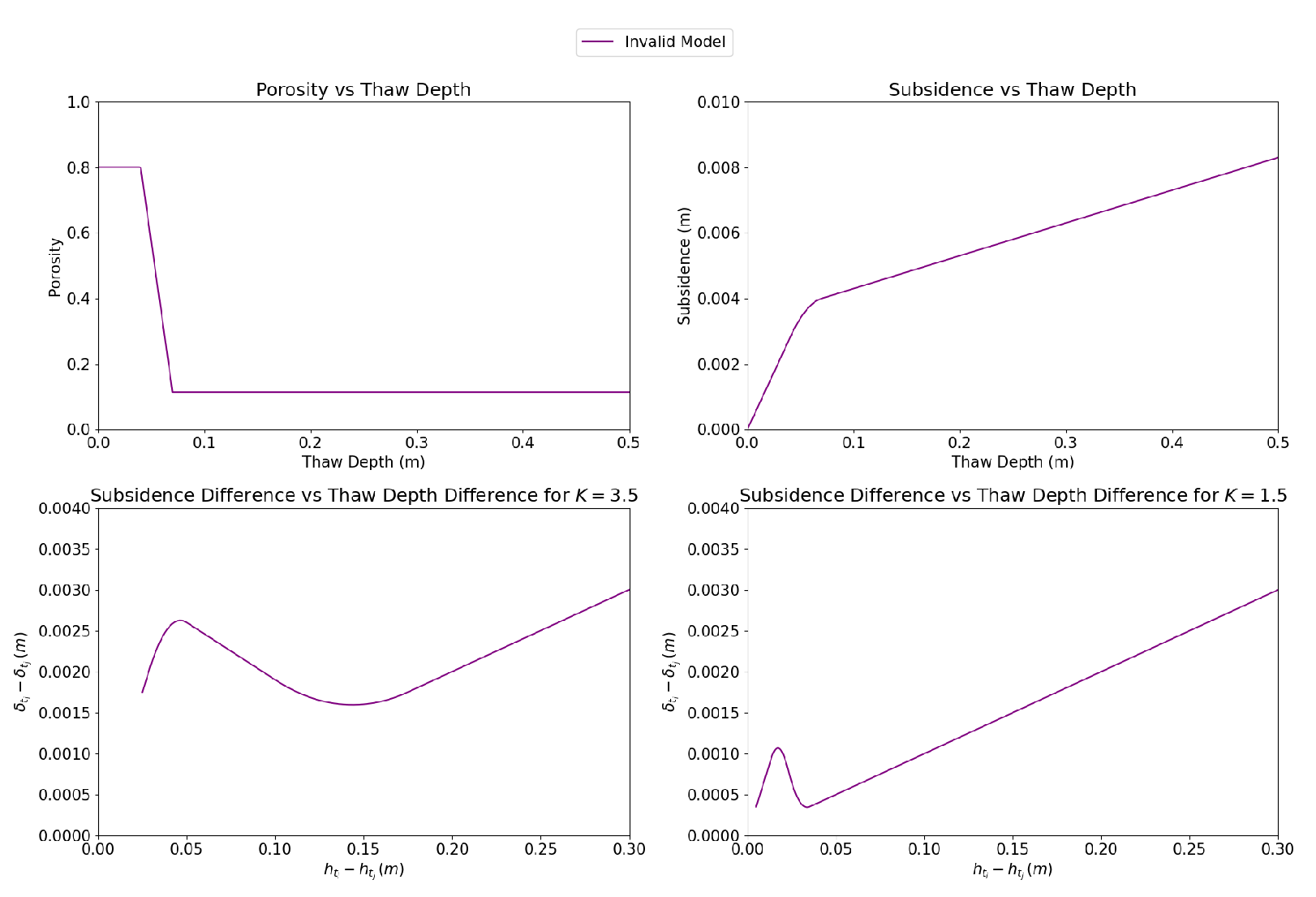
This was set up with

h_{0} = 0.01

m_{0} = 0.07

h_{1} = 0.07

, and

m_{1} = 0.01

in (A22). This example is scaled such that there is a valid corresponding P model, which can be computed using (A17). Both f and P are visualized in Figure A2, which demonstrates a potentially realistic soil porosity model that does not meet the SCReSALT requirement.

Figure A2. A diagram showing a physically realizable soil porosity model that fails the SCReSALT requirement. As shown in the bottom images, subsidence difference cannot always be mapped unambiguously to thaw depth difference.

Appendix D. Non-Stefan SCReSALT (SCReSALT-NS) Derivation

As shown in Appendix A, the Stefan equation assumes a homogeneous and hence constant porosity soil. The purpose of this paper is to derive an InSAR model that is self-consistent under a variable porosity model. Therefore, it is worth investigating whether the Stefan equation derivation can be modified to handle non-constant soil porosity, and whether that relationship can help derive a modification to SCReSALT.

The problem originates in (A5) because

p_{p} = ρ_{i} P_{f}

is a function of h and hence belongs on the LHS. Rewriting:

P_{f} h d h = - \frac{k_{p}}{ρ_{i} L} (T_{b o t} - T_{t o p}) d t

(A24)

The same logic that

T_{b o t} = 0

and

h (t_{s}) = A D D T (t_{s}) = 0

can be applied. Integrating:

\int_{0}^{h (t)} P_{f} h d h = \frac{k_{p}}{ρ_{i} L} A D D T (t)

(A25)

Assuming a fully saturated soil, no water loss, and no soil compression due to water freezing, P and

P_{f}

can be related as follows:

P_{f} = \frac{\frac{ρ_{w} P}{ρ_{i}}}{\frac{ρ_{w} P}{ρ_{i}} + 1 - P}

(A26)

To derive this, note that for an infinitesimal piece of soil

d h

P d h

captures the volume of water (per unit area), meaning

\frac{ρ_{w} P d h}{ρ_{i}}

captures the volume of ice. The volume of soil matter is

(1 - P) d h

and is assumed to be constant. This leads to the given expression for

P_{f}

. Continuing with the derivation, the LHS of (A25) will be referred to as the “porosity depth integration function” for the following discussion. Taking inspiration from (7), (A25) can be analyzed as a ratio:

\frac{\int_{0}^{h (t_{i})} P_{f} h d h}{\int_{0}^{h (t_{j})} P_{f} h d h} = \frac{A D D T (t_{i})}{A D D T (t_{j})}

(A27)

\int_{0}^{h (t_{i})} P_{f} h d h = \frac{A D D T (t_{i})}{A D D T (t_{j})} \int_{0}^{h (t_{j})} P_{f} h d h

(A28)

This suggests that a similar algorithm to Algorithm 1 can be employed. First, a list of candidate

h_{t_{j}}

on some large interval of possible thaw depths is generated. Corresponding

h_{t_{i}}

is computed using the (known) ratio

\frac{A D D T (t_{i})}{A D D T (t_{j})}

and inverting7 the porosity depth integration function. Since this function is strictly monotonic, the inverse should be a well-defined function. The subsidence for each candidate

h_{t_{j}}

and

h_{t_{i}}

can be computed using (2). Finally, a plot of candidate thaw depth

h (t_{j})

and corresponding subsidence differences can then be constructed. The hope is that subsidence difference can once again be related to a unique

h (t_{j})

(for which

h (t_{i})

is also known). Figure A3 shows that this is the case for the soil models discussed in this paper.

Figure A3. Plots showing the validity of SCReSALT-NS.

A least-squares inversion can be posed as follows:

[\begin{matrix} z_{1} \\ ⋮ \\ z_{N} \end{matrix}] = [\begin{matrix} A D D T_{2, 1} - A D D T_{1, 1} \\ ⋮ \\ A D D T_{2, N} - A D D T_{1, N} \end{matrix}] [\begin{matrix} M \end{matrix}]

(A29)

where

M = \frac{k_{p}}{ρ_{i} L}

and

z_{i}

is the difference in porosity depth integration function for the best-matching

h (t_{j})

and

h (t_{i})

for the measured

δ (t_{i}) - δ (t_{j})

. Specifically,

z = \int_{h (t_{j})}^{h (t_{i})} P_{f} h d h

(A30)

Upon obtaining M,

h (t)

for arbitrary t and known

A D D T (t)

can be found by inverting the porosity depth integration function. Results for this method are shown in Table 1. Interestingly, using P instead of

P_{f}

in (A25) obtained marginally better results, as shown in Table A1. It is unclear if this suggests a better model between P and

P_{f}

needs to be developed. More studies should be done to determine if there is modeling benefit to be gained here.

Table A1. Results for using P instead of

P_{f}

in (A25).

Table A1. Results for using P instead of

P_{f}

in (A25).

Metric	SCReSALT-NS-P
Avg $χ^{2}$	1.795
Great Match	0.614
Good Match	0.272
Bad Match	0.114
Bias (m)	0.0261
Pearson R	0.270
MAE (m)	0.080
RMSE (m)	0.106

Appendix E. Additional Experiments Info

Like [9], this paper uses node 61 of the U1 CALM plot as a reference or calibration node. In general, InSAR requires a calibration pixel where subsidence is known or can be assumed to calibrate the entire subsidence image. For example, exposed bedrock and gravel are typically assumed to have 0 subsidence. In [9], no pixel had known subsidence, so they instead formulated (3) as a delta subsidence difference with respect to the calibration node. They then scaled the best-fit E (really a delta E) by the

\sqrt{A D D T}

at measurement time, which is a valid operation under ReSALT formulation (but not SCReSALT). Then, they calculated the expected subsidence of the calibration node by evaluating (2) on the calibration node’s in-situ ALT. An offset is applied to make the calibration node E align with its expected subsidence. At this point, subsidence at measurement time is known per pixel. Finally, by inverting (2), ALT is estimated per pixel. SCReSALT handles the calibration node as follows:

SCReSALT is given the seasonal ALT of the calibration node as input. This is computed from the measured in-situ ALT and scaled to the end-of-season thaw depth according to (7). Note that $A D D T$ is known at both times, so this scaling is possible.
For a particular InSAR image, the seasonal ALT of the calibration node is scaled twice using (7), once using the $A D D T$ at the time of the reference image to get $h_{c a l, r e f}$ and another using the $A D D T$ at the time of the secondary image to get $h_{c a l, s e c}$ . Using (2), $δ_{c a l, r e f}$ and $δ_{c a l, s e c}$ are computed. Then, the expected subsidence difference can be computed as $δ_{c a l, r e f} - δ_{c a l, s e c}$ . This is used to apply a global offset to the InSAR image such that the calibration pixel has the expected subsidence difference.
SCReSALT operates with the calibrated subsidence difference image.

To be clear, the steps listed above only need to be followed when the calibration node is itself subsiding according to (2). If there was an exposed bedrock or gravel pixel, then a simple procedure would suffice where a global offset is applied to make the calibration pixel have 0 subsidence difference. SCReSALT ultimately needs an image in which subsidence difference is known. This is the same as ReSALT.

There are a few final experimental details that need mentioning:

The U2 plot was used in [9] but not in this paper. It accounted for a single pixel while U1 contributed 121 pixels (minus 6 unused pixels and 1 calibration pixel). This extra data point shouldn’t affect the analysis too much. Note that this would not affect the comparison between the ReSALT data product and SCReSALT in Table 1 because the ReSALT data product ALTs were only compared to U1 CALM ALTs.
Some interferograms were listed incorrectly in Table A1 of [9]. For example, rows 7 and 9 have the same granules but different dates. Duplicating granules does not make any sense, so this is a typographical error. The dates were used to infer the correct granules. The modified interferogram list is part of the publicly released codebase.
The 20th interferogram encountered a processing error with ISCE2. Given that this was just 1 interferogram out of 20, it is not expected to affect the analysis too much.

References

Schaefer, K.; others. Amount and timing of permafrost carbon release in response to climate warming. Tellus B 2011, 63, 165â180. doi:10.1111/j.1600-0889.2011.00527.x. [CrossRef]
Schneider von Deimling, T.; others. Observation-based modelling of permafrost carbon fluxes with accounting for deep carbon deposits and thermokarst activity. Biogeosciences 2015, 12. doi:10.5194/bg-12-3469-2015. [CrossRef]
Ruiz, S. $41M audacious grant will tackle permafrost thaw. Woodwell Climate, 2022. Available at: https://www.woodwellclimate.org/41-million-grant-for-permafrost-thaw-monitoring/.
Carbon emissions from Permafrost. 50x30, 2023. Available at: https://www.50x30.net/carbon-emissions-from-permafrost.
Miner, K.; others. Permafrost carbon emissions in a changing Arctic. Nature Reviews Earth & Environment 2022, 3. doi:10.1038/s43017-021-00230-3. [CrossRef]
Liu, L.; others. InSAR measurements of surface deformation over permafrost on the North Slope of Alaska. Journal of Geophysical Research: Earth Surface 2010, 115. doi:10.1029/2009JF001547. [CrossRef]
European Space Agency. InSAR Principles: Guidelines for SAR Interferometry Processing and Interpretation. Technical report, ESA Publications, 2007.
Liu, L.; others. Estimating 1992â2000 average active layer thickness on the Alaskan North Slope from remotely sensed surface subsidence. Journal of Geophysical Research: Earth Surface 2012, 117. doi:10.1029/2011JF002041. [CrossRef]
Schaefer, K.; others. Remotely Sensed Active Layer Thickness (ReSALT) at Barrow, Alaska Using Interferometric Synthetic Aperture Radar. Remote Sensing 2015, 7. doi:10.3390/rs70403735. [CrossRef]
Chen, R.; others. Permafrost Dynamics Observatory (PDO) â Part II: Joint Retrieval of Permafrost Active Layer Thickness and Soil Moisture from L-band InSAR and P-band PolSAR. Earth and Space Science 2023, 10. doi:10.1029/2022EA002453. [CrossRef]
Nixon, F.; Taylor, A. Regional active layer monitoring across the sporadic, discontinuous and continuous permafrost zones, Mackenzie Valley, northwestern Canada. Proceedings of the 7th International Conference on Permafrost. International Permafrost Association, 1998, pp. 815–820.
Yershov, E.D. General Geocryology; Cambridge University Press, 2004.
Michaelides, R.J.; others. Permafrost Dynamics ObservatoryâPart I: Postprocessing and Calibration Methods of UAVSAR LâBand InSAR Data for Seasonal Subsidence Estimation. Earth and Space Science 2021, 8. doi:10.1029/2020EA001630. [CrossRef]

1	InSAR measures subsidence in the line-of-sight (LOS) direction. Vertical deformation is obtained by using the incidence angle and projecting vertical deformation into the LOS direction.
2	[10] argues convincingly that the ReSALT formulation only works when $S = 1$ . If $S < 1$ , some open pore space will be filled by freeze/thaw before the ground subsides. At a critical threshold (characterized by the densities of liquid water and ice), freeze/thaw might lead to no ground subsidence. So, this work assumes $S = 1$ .
3	CALM is a long-running program that collects data on permafrost thaw. Data can be accessed at https://www2.gwu.edu/~calm/
4	https://github.com/isce-framework/isce2
5	In (2), P is the porosity when the soil water is liquid. $P \neq P_{f}$ . This will be discussed further in Appendix D.
6	At this point, the temperature must be in Celsius.
7	This inversion could be numerical or analytical, depending on whether the analytical expression for $P h$ lends itself to analytical integration and inversion. This paper used numerical integration when doing experiments.

Figure 1. The left box shows the soil column during winter when all water is frozen. The right box shows the soil column during summer when water is thawed up to the ALT. Subsidence

δ

occurs because ice takes up more volume than water for the same mass. Hence, under the assumptions of no water loss and fully saturated soil, ground subsidence is observed. Note that

h (t)

is typically measured with respect to the ground at the time of measurement.

δ (t)

is typically not measured.

Figure 1. The left box shows the soil column during winter when all water is frozen. The right box shows the soil column during summer when water is thawed up to the ALT. Subsidence

δ

occurs because ice takes up more volume than water for the same mass. Hence, under the assumptions of no water loss and fully saturated soil, ground subsidence is observed. Note that

h (t)

is typically measured with respect to the ground at the time of measurement.

δ (t)

is typically not measured.

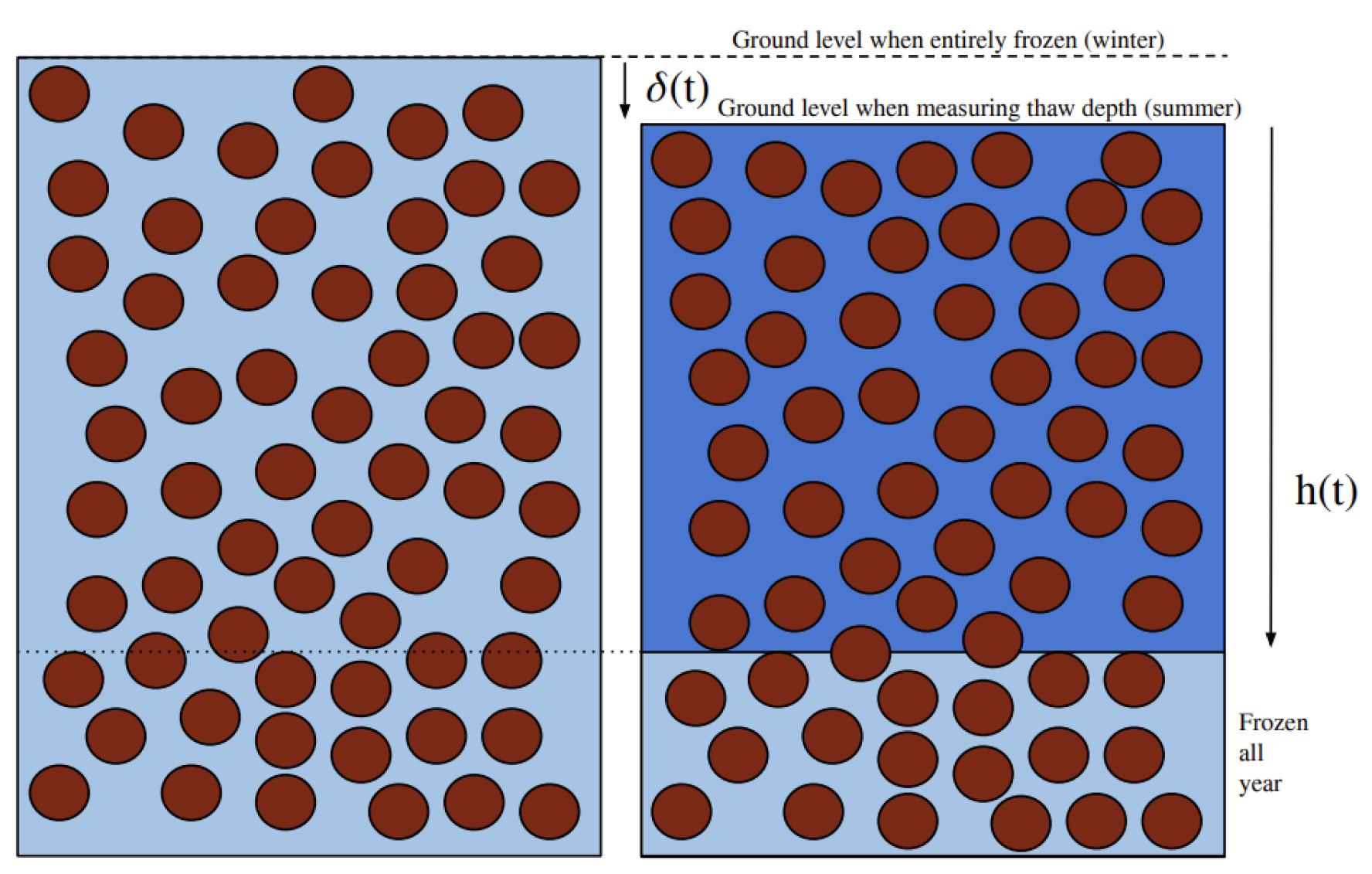
Figure 2. Plots showing the core idea of SCReSALT.

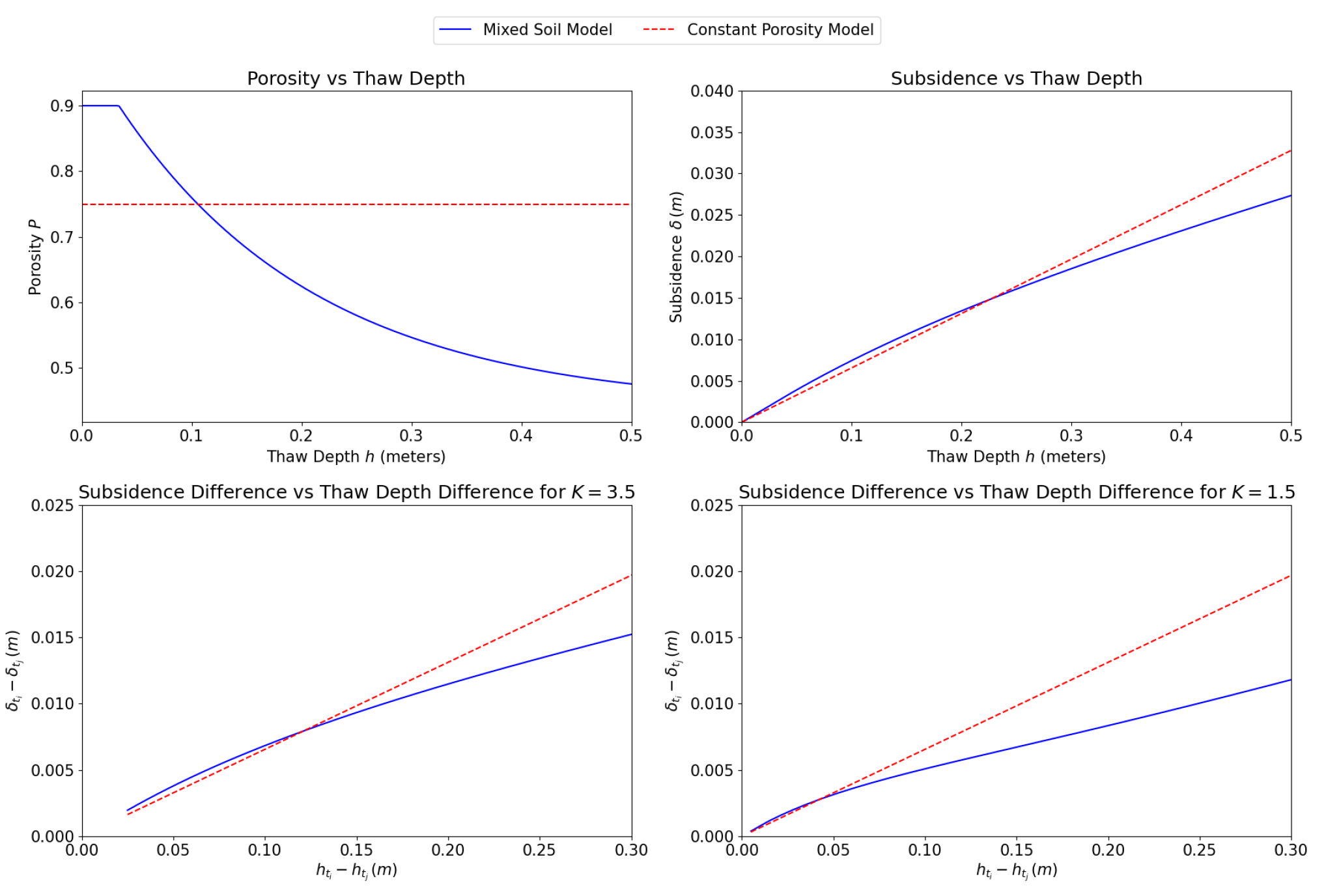
Table 1. Comparison of ReSALT vs. SCReSALT performance. The double line separates results from [9] and those produced by the author. For each metric the best score is bolded (except great/good/bad match because they are codependent). Also, two nodes had invalid predictions for the reproduced ReSALT (but not SCReSALT), so they were excluded when computing statistics for that column specifically.

Metric	ReSALT [9]	ReSALT (Data Product)	ReSALT (Reproduced)	SCReSALT	SCReSALT-NS
Avg $χ^{2}$	2.5	2.543	2.726	1.833	1.811
Great Match	0.62	0.623	0.527	0.570	0.614
Good Match	0.26	0.228	0.232	0.290	0.272
Bad Match	0.12	0.1491	0.241	0.140	0.114
Bias (m)	0.008	0.007	-0.067	-0.020	0.0261
Pearson R	-	-0.284	0.325	0.300	0.269
MAE (m)	-	0.087	0.101	0.084	0.080
RMSE (m)	-	0.126	0.130	0.107	0.106

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Modification to the Remotely Sensed Active Layer Thickness (ReSALT) Algorithm to have Self-Consistency

Abstract

1. Introduction

2. Background

2.1. ReSALT Description

2.2. ReSALT Inconsistency Description

3. Method

3.1. SCReSALT Counterexample Discussion

4. Experiments

5. Results

6. Conclusion

Appendix A. Stefan’s Equation Derivation

Appendix B. ReSALT Derivation

Appendix C. SCReSALT Counterexample Analysis

Appendix D. Non-Stefan SCReSALT (SCReSALT-NS) Derivation

Appendix E. Additional Experiments Info

References

MDPI Initiatives

Important Links

Subscribe