Prerpints.org logo
Preprint
Article

Development and Validation of a Compressible Reacting Gas-Dynamic Flow Solver for Supersonic Combustion

Altmetrics

Downloads

151

Views

219

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

06 December 2023

Posted:

07 December 2023

You are already at the latest version

Alerts
Abstract
An approach based on the OpenFOAM library has been developed to solve a high-speed, multicomponent mixture of a reacting, compressible flow. This work presents comprehensive validation of the newly developed solver called compressibleCentralReactingFoam with different supersonic flows, including shocks, expansion waves, and turbulence-combustion interaction. The comparisons of the simulation results with experimental and computational data confirm the fidelity of this solver for problems involving multicomponent high-speed reactive flows. The gas dynamics of turbulence-chemistry interaction are modeled using a partially-stirred reactor formulation and provide promising results to better understand the complex physics involved in supersonic combustors. A time-scale analysis based on local Damköhler numbers reveals different regimes of turbulent combustion. In the core of the jet flow, the Damköhler number is relatively high indicating that the reaction time scale is smaller than the turbulent mixing time scale. This means that the combustion is controlled by turbulent mixing. In the shear layer, where the heat release rate and the scalar dissipation rate have the highest value, the flame is stabilized due to finite rate chemistry with small Damköhler numbers and a high fraction of fine structure. This solver allows three-dimensional gas dynamic simulation of high-speed multicomponent reactive flows relevant to practical combustion applications.
Keywords: 
Subject: Engineering  -   Aerospace Engineering

1. Introduction

Supersonic airbreathing or supersonic combustion ramjet (scramjet) engine is the most promising technology for significant reduction flight times for long-distance civil flights and the first stages of space systems for putting payload into orbit. The future of access-to-space systems is faced with many technical and economic challenges. Designing and testing scramjet systems requires the ability to adequately understand and control the complex flow physics of these systems. The high-speed flow in the propulsion systems leads to many difficulties in achieving and maintaining combustion [1,2]. One of the significant features of the scramjet is the supersonic flow conditions in the combustor lead to very short residence times for fuel and air, typically of the order of milliseconds; therefore, the fuel must mix with the supersonic flow and burn entirely within a short time. Thus, future hypersonic propulsion systems' success will largely depend on efficient injection, mixing, and combustion processes inside the supersonic combustion chamber [1,3].
Computational fluid dynamics (CFD) and experimental testing have seen significant advances through the years in terms of reliability and accuracy. However, in the case of supersonic and hypersonic regimes, realistic high-enthalpy conditions can only be maintained and thus measured in experimental facilities for a very short period, in the order of milliseconds [4] which is insufficiently to provide a comprehensive analysis designing efficient scramjet engines. The numerical approach remains the primary analysis tool to cover the operating regimes of a scramjet consistently. CFD methods targeting the solution of the flow field inside supersonic engines are faced with the challenges of addressing internal flow dominated by complex shock wave patterns, shock wave boundary layer interaction with its separation, and most importantly, supersonic turbulence-combustion interaction, which, in many cases, is characterized by finite rate chemistry. Inaccurate prediction of shock position and separation locations can lead to unreliable results when reactions are activated, risking the success of the entire design process.
The computational approaches to simulate turbulent flows by solving compressible Navier-Stokes equations are Direct Numerical Simulation (DNS), Large Eddy Simulation (LES), and Reynolds Averaged Navier-Stokes (RANS). RANS is very useful in many real-world industrial applications because RANS simulations are computationally less expensive than DNS and LES. In RANS, fewer equations must be solved, and they are often solved with limited computational resources. However, because the turbulent flows using RANS are not fully resolved, turbulence-combustion interactions are also unresolved. Moreover, the reacting flow is highly nonlinear, unstable, and non-stationary. RANS will not adequately model turbulence-combustion interactions in scramjet [5] due to these constraints. The Direct Numerical Simulation (DNS) is a detailed computational approach that demands a fine grid to resolve all turbulent length scales and small time-steps comparable to chemical time scales. Hence, DNS would require tremendous computational resources for the simulations of the high-speed flows of practical interest. On the other hand, Large-Eddy Simulation (LES) resolves large scales of the turbulent flow, i.e., turbulent eddies larger than the smallest mesh size, while the smallest scales are modeled [6,7,8]. Thus, this feature of LES leads to a significant reduction in computational resources compared to DNS. During the past decade, LES, which is a compromise between the DNS [9] and the RANS [10] methods, has been extensively used to study high-speed combustion applications [11,12,13]. In LES, turbulence scales larger than the grid spacing are resolved, while subgrid scales and their effects on the large scales are modeled [14]. LES has been shown [15,16,17,18,19] to be computationally practical for modeling unsteady phenomena, including transient combustion events. One of the critical aspects of modeling unsteady turbulent combustion in high-speed jets is appropriately accounting for the influence of turbulence on the rate of chemical reactions. Transient turbulent combustion will also depend on accurately modeling the interaction between the jet mixing layer and the surrounding air.
DNS and LES of compressible turbulent reactive flows require highly accurate numerical schemes, which must capture shock waves, describe multicomponent mixtures and detailed chemical kinetics, and resolve a broad range of length scales. Numerical simulation of combustion in supersonic flow fundamentally differs from combustion in the subsonic regime. In supersonic combustion, chemical reactions occur under conditions of high pressure, temperature, and density. These conditions can significantly alter chemical kinetics and reaction rates, leading to different reaction pathways and species formation compared to subsonic conditions. Ignition and flame stabilization processes in supersonic combustion devices may differ significantly from those observed in the subsonic regime [3]. Combustion processes involve highly nonlinear chemical reactions and many species. Furthermore, turbulence increases the mixing of fuel and oxidizer and enhances combustion [20]. In turn, the combustion can intensify the turbulence via flow expansion [20]. As a result, the turbulent fluctuations can be very large [21].
Various CFD solvers in the literature are used to simulate high-speed airbreathing engines. These codes can be broadly categorized into three main categories: commercial, open-source, and in-house solvers, each with its own advantages and disadvantages. The commercial codes such as Fluent [22], StarCCM++ [23], NASA codes REACTMB [24], WIND-US [25], TAU-code code [26], VULCAN [27], SU2 [28] have been used successfully in solving the above-mentioned problems. Commercial solvers can be expensive, with limited access to the source code. Open-source solvers are typically freely available, with access to the source code, allowing for extensive customization and the development of user-specific models or algorithms. The open-source community often collaborates on code development. Among the open-source codes, the OpenFOAM library is a well-established open platform in the scientific community [29]. It is noteworthy that there are several in-house codes reported in the literature for high-speed compressible reacting flows [13,14,30,31,32,33,34,35,36,37]. These codes have been used to solve many problems involving turbulence-combustion interactions. Some of them are built on the OpenFOAM foundation. However, none of these codes are readily and freely available, i.e., they are not yet fully open-source [38].
The OpenFOAM library has high-fidelity reactive flow solvers (e.g., reactingFoam) that were validated for a variety of turbulent combustion applications under subsonic conditions [10]. As this solver lacks appropriate model construction for high-speed flows, a density-based compressible flow solver, namely rhoCentralFoam, was developed for high-speed flow modeling based on the central-upwind schemes of Kurganov and Tadmor [39,40]. Greenshields et al. [41] detailed this solver and validation against standard test cases. The solver was validated for compressible gas flow, including shocks and wave expansion. However, the rhoCentralFoam is limited to non-reacting flows. Therefore, in the current work, an in-house code, compressibleCentralReactingFoam, was developed by combining rhoCentralFoam with reactingFoam in the latest version of the OpenFOAM (i.e., v2306 [42]), to simulate high-speed compressible multicomponent reactive flows.
The challenges of scramjet simulation are due to multiscale (in terms of space and time) phenomena of non-steady, non-equilibrium turbulent combustion in the supersonic flow. Thus, the model needs to account for complex mixing phenomena, non-equilibrium transfer of turbulence energy, and the interaction between turbulence, and chemical kinetics. This paper demonstrates a physics-based methodology/computational tool, namely the compressibleCentralReactingFoam solver, to model the complex physical phenomena of reactive multicomponent gas flow at high Mach numbers. Moreover, the present work aims to quantitatively assess the accuracy and applicability of the newly developed solver in modeling supersonic combustion. A set of validation test cases are presented to demonstrate the capabilities of the solver ranging from simple one-dimensional shock-tube problems to complex three-dimensional scramjet combustor. In addition, three popular subgrid models - Smagorinsky model (SMG) [43,44], the Localized Dynamic k-equation Model (LDkEqn) [45,46], and Wall Adapted Local Eddy-Viscosity (WALE) [47] are evaluated for simulating supersonic turbulent combustion at conditions relevant to scramjet operation. Below, the short descriptions of these models are provided.
Subsection 2.1 presents the governing equations of supersonic multicomponent gas flow with chemical reactions and the basic approach to closure turbulent combustion equations. In Subsubsection 3.1.1, validations of 1D shock tube problems are solved. Subsubsection 3.1.2 presents simulations of 3D problems showing comparisons with experiments. The problem of turbulence-combustion interactions in the model scramjet combustor is presented in Subsubsection 3.1.3. Section 4 presents conclusions.

2. Materials and Methods

2.1. Governing Equations and Computational Solver of OpenFOAM Library

The governing equation of a reactive multicomponent mixture of gases consists of the continuity, the momentum, the energy balance, and the balance of mass fraction equations. A LES formulation is used to solve the equations for turbulent fluid flow. After Favre filtering, these equations can be written as [14,48]
∂ t ρ ¯   + ∇ · ρ ¯ u ˜ = 0 ,
∂ t ρ ¯ u ˜ + ∇ · ρ ¯ u ˜ ⊗ u ˜ = − ∇ p ¯ + ∇ · S ¯ − B ,
∂ t ρ ¯ h ˜ s + ∇ · ρ ¯ u ˜ h ˜ s = S ¯ · ∇ u ˜ + ∂ t p ¯ + ∇ p ¯ · u ˜ + ∇ · h ¯ − b h +   ω ˙ ¯ T ,
∂ t ρ ¯ Y ˜ i + ∇ · ρ ¯ u ˜ Y ˜ i = ∇ · j ¯ i − b i + ω ˙ ¯ i   .
Here, the symbol “~” denotes Favre-filtered quantities, and “ − “indicates filtered quantities; ρ is the gas mixture density, u is the velocity vector, p is the pressure, S is the viscous stress tensor, h s = ∑ i Y i ∫ T 0 T C p , i d T is the sensible enthalpy, T is the temperature, h is the heat flux vector, Y i is the species mass fraction, ω ˙ T = − ∑ i = 1 M ω ˙ i Δ h f , i 0 is the combustion heat release, Δ h f , i 0 is the formation enthalpy of i t h species, ω ˙ i is the species reaction rate, j i is the species mass flux. Subgrid pressure fluctuations and dissipation terms will be neglected.
The subgrid flow physics is concealed in the subgrid stress tensor B = ρ   ¯ u · u ˜ − u ˜ · u ˜   and flux vectors b i = ρ   ¯ u Y i ˜ − u ˜ Y i ˜ , b h = ρ   ¯ u h s ˜ − u ˜ h ˜ s , which results from filtering the nonlinear convective terms. Following [2], one may postulate that the gas mixture behaves as linear viscous fluid with Fourier heat conditions and Fickian species diffusion, such as j ¯ i ≈ D i ∇ Y i ˜ , D i = μ / S c i is the species diffusivities, p ¯ ≈ ρ   ¯ R u T ˜ ∑ i = 1 M Y i / M i , R u is the universal gas constant, M i is the molar mass of i t h species, S ¯ ≈ 2 μ D ˜ D is the viscous stress tensor, μ is the dynamic viscosity which is modeled using Sutherland’s law μ = A s T / 1 + T s / T , where A s ,   T s are Sutherland’s coefficient and temperature[30], D ˜ D = ∇ u ˜ + ∇ u ˜ T / 2 − ∇ · u ˜ I /3 is the deviatoric part of the rate strain tensor, h ¯ ≈ κ ∇ T ˜ , κ =   μ / P r is the thermal diffusivity, S c i and P r are the Schmidt and Prandtl numbers, respectively.
The LES equation (1)-(4) is closed by providing submodels for B , b i , b h . The most common subgrid models used in this paper for high-speed reactive flows are class of Smagorinsky models [43,44] of the form B = − 2 μ k D ˜ D + 2 / 3 ρ   ¯ k I , where μ k is the subgrid viscosity and k is the subgrid kinetic energy, b i = − μ k / S c t ∇ Y ˜ i , and b h = − μ k / P r t   ∇ h ˜ s , where S c t ≈ 0.7 and P r t ≈ 0.8 are the turbulent Schmidt and Prandtl numbers, respectively. To closure k and μ k in the Smagorinsky model (SMG) [44], they are formulated as μ k = c D ρ   ¯ · 2 D ˜ and k = c l · 2 D ˜ 2 , where c D and c l are model coefficients.
The second subgrid model used in this work is the Local Dynamic k-equation (LDkEqn) [45,46]. The LDkEqn turbulent model is an advanced subgrid-scale (SGS) turbulence model used in Large Eddy Simulation to improve the prediction of turbulent flows. Instead of using fixed model coefficient constants (as in the SMG), the LDkEqn model calculates them dynamically, adjusting the model coefficients to match the resolved flow characteristics. This adaptability allows the model to capture variations in turbulence intensity and anisotropy better. The LDkEqn model exhibits a scale-adaptive behavior, which means it can adapt to different turbulence scales in the flow. This adaptability is particularly beneficial in LES, where a wide range of turbulent structures exists; also, the LDkEqn model is designed to provide better predictions near walls. For the LDkEqn, a modeled transport equation ∂ t ρ   ¯ k + ∇ · ρ   ¯ k u ˜ = − B · D ˜ + ∇ · μ k ∇ k − c ε ρ   ¯ k 3 / 2 / ·   is solved for k and subgrid viscosity is modeled as μ k = c k ρ   ¯ ·   k 1 / 2 . The model coefficients c k and c ε are evaluated dynamically using scale similarity.
The third subgrid model used in this work is the Wall Adapted Local Eddy-Viscosity (WALE) subgrid model [47]. The WALE model is designed to improve the accuracy of LES by providing a more accurate representation of the subgrid-scale turbulence in the near-wall region, where traditional SGS models may struggle to capture complex flow phenomena. The WALE model is specifically designed to address the near-wall region of turbulent flows. In this region, small-scale turbulence structures are not well-resolved on the computational grid, and traditional SGS models may introduce excessive dissipation or fail to capture these structures accurately. The WALE model computes a subgrid-scale turbulent viscosity ( ν t ) that varies spatially and temporally based on the local flow characteristics. The specific coefficients used in the WALE model are C k = 0.094 ; C e = 1.048 ; C w = 0.325 .
Finally, to completely close the LES equations (1)-(4), the filtered reaction rates. ω ˙ ¯ i , incorporating the turbulence chemistry interactions, must be provided. The reaction rate provides the effect of combustion chemistry on the flow and how the turbulence affects the combustion chemistry. The LES Finite Rate Chemistry model (LES-FRC), specifically the LES Partially Stirred Reactor (LES-PaSR) model [48], is to be used in this work.
This study adopts the PaSR subgrid combustion model for the sequential and simultaneous processes of micro-mixing and chemical reactions. It is based on the conjecture that any turbulent flow can be divided into the fine structure ∗ and surrounding structure 0 , interacting through the balance equations [49,50]. Most dissipation and mixing, as well as chemical reactions, occur in the fine structure, where reactants are mixed at the molecular level. Therefore, each LES cell can be viewed as a partially stirred reactor containing a fine structure, ideally regarded as a Perfectly Stirred Reactor (PSR), exchanging mass and energy with surroundings. The filtered reaction rates for PSR are defined as ω ˙ i * ¯ = M i ∑ j = 1 M P i j ω j ˙ ^ ¯ , where ω j ˙ ^ = k f j ∏ k = 1 M X k P k j ′ − k r j ∏ k = 1 M X k P k j ″ , P i j = P i j ″ − P i j ′ are the stochiometric coefficients, X k = ρ Y k / M k is molar concentration, k f j and k r j being the Arrhenius forward and reverse rates of the j t h reaction step, k f j = A f j T β j exp − T a , j / T   , β j and T a , j are the Arrhenius parameters. The resulting rates in the PaSR model are [51], ω ˙ ¯ i = γ * ω ˙ i * ¯ + 1 − γ * ω ˙ i 0 ¯ , which can be simplified as ω ˙ ¯ i ≈ γ * ω ˙ i * ¯ , since ω ˙ i 0 ¯ are most negligible outside of the fine structure regions, where the fraction of reactive zone (fine structure) γ * is calculated based on geometrical analysis [2] γ * ≈ τ c / τ * + τ c , τ c is a global representative of chemical time step and τ * = μ e f f / ρ ¯ ε ˜ is the turbulent mixing time that is implemented in the OpenFOAM, μ e f f is the sum of laminar and turbulent dynamic viscosity, ε ˜ is the turbulent dissipation rate.

3. Results

3.1. Solver Validation

The capability of compressibleCentralReactingFoam to solve compressible flows with multicomponent reacting gas mixtures will be demonstrated for various problems. These include 1D shock tube problems, 2D and 3D geometries involving underexpanded jet formation, and 2D turbulent reacting gas flow in a scramjet combustor.

3.1.1. Shock Tube Problem.

Shock tube is a well-known benchmark problem (also known as Sod shock tube problem [52]) for the validation of compressible codes. It is an attractive test case for model validation due to the simple one-dimensional geometry of computational area and the possibility to simulate a wide range of flow physics, including shock and rarefaction waves, contact discontinuities, and complex wave interactions. The available analytical and computational solutions in the literature allow for the assessment of the code's accuracy and reliability. The shock tube problem for two cases have been solved: (1) a shock tube with an inert multicomponent gas mixture, and (2) a shock tube with a chemically reactive multicomponent gas mixture. In these validations, the initial discontinuity of the gas in the shock tube is decayed into different gas configurations such as shock waves, contact discontinuous, and rarefaction waves spreading into different directions (See Figure 1).
  • Inert Multicomponent Shock Tube
The first validation case is a multicomponent inert shock tube simulation without the chemical source term in order to avoid shock-induced autoignition of the gas mixture. A homogeneous premixed gas mixture of 20%H2/10%O2/70%Ar (in mole%) is used in the simulation to verify the numerical accuracy of the model implementations for thermal and mass transport of multicomponent mixture. The shock tube is 0.10 m in length, and it is discretized with 400 uniform elements. The time step is equal to Δ t = 10 − 7   s . In the middle of the tube is a fixed diaphragm that separates the gas between the left side ( T l   =   400   K and P l   =   8000   P a ) and the right side ( T r   =   1200   K and P r   =   80 , 000   P a ). At time t = 0 , the diaphragm is eliminated, and the shock wave starts to propagate from right to left and expansion wave moves in the opposite direction. The initial configuration of the gas mixture generates the propagation of shock and discontinuous waves to the left (low-pressure) and a rarefaction (expansion) wave to the right side (high-pressure) of the tube. Figure 2 shows the current simulation results (solid line) compared with the simulation results of Huang et al. [53]. The modeling results have good agreement. It is noteworthy that the compressibleCentralReactingFoam solver's accuracy is 2nd order for both time and spatial convective terms.
  • Reactive Multicomponent Shock Tube
A reactive multicomponent gas mixture in the shock tube is also modeled using the conditions of Martínez-Ferrer et al. [34] for comparison. The molar composition of the gas mixture is 20% H2/10% O2/70% Ar. The length of the tube is equal to L = 0.12   m with the initial conditions corresponding to the left and right sides as follows: ρ l , u l , p l = 0.072 ,     0 ,     7173 and ρ r , u r , p r = 0.18075 ,     − 487.34 ,     35   594 , where ρ ,   u   ,   and   p are measured in ( k g / m 3 ), ( m / s ), and ( P a ), respectively. The length of the tube is discretized by 400 uniform elements with 0.01 μ s timestep. The simulation used the reaction mechanism of Conaire et al. [54] for hydrogen which consists of nine (9) chemical species (H2, O2, H, O, OH, HO2, H2O2, H2O, A r ), and 18 elementary reactions. A wall boundary condition is implemented on the left side of the tube, and on the right side, a non-reflected boundary condition is implemented. The initial configuration of non-stable discontinuity is decayed into a shock propagated to the tube's left side. The solutions of spreading discontinuities in the shock tube for velocity, mass fraction of H , and temperature: U x , Y H , and T are shown in Figure 3 for 230 μ s simulation time. Comparisons of current solution (solid lines) in Figure 3 with computational data of Martínez-Ferrer et al. [34] (symbols) show good agreement. The visible discrepancies are seen in the vicinities of local maximums around x = 0.06 m at 230 μ s that is explained of using by Martínez-Ferrer et al. [34] a seventh-order accurate Weighted Essentially Non-Oscillatory (WENO) scheme to discretize the non-linear advective terms.
The decay process of the initial multicomponent gas mixture, and how the shock wave propagate in the tube was investigated in detail by comparing the profiles of inert and reactive mixture of H2/O2/Ar. Figure 4 shows the simulation results for the temperature profiles of inert and reactive mixture at various simulation times.
The shock starts to propagate from its initial position in the middle of the tube from right to left toward the wall (i.e., x = 0) with a velocity v r l = 8100 m/s and reaches the wall around 75 μ s . After reflection from the wall, the shock moves in the opposite direction from left to right. The reflected shock moves with a velocity of 4500 m/s that is almost half of v r l as the gas flows right to left with a velocity of 490 m/s. Due to the interaction of the shock with the wall, the temperature of the reflected shock is increased from 750 K to 1200 K for both inert and reactive cases. As seen in Figure 4b, the shock-induced autoignition starts to occur (i.e., a slight increase in temperature at x = 0) at 120 μ s for the reactive case as the simulation time is longer than the chemical induction time to generate combustion radicals. Due to the combustion heat release, the gas temperature increases to 2100 K as the simulation time is increased to 150 μ s . The gas temperature approaches equilibrium state as the simulation time is further increased to 220 μ s .

3.1.2. Simulation of Ladenburg Jet Problem.

Simulation of a well-known experiment of underexpanded jet problem by Ladenburg et al. [55] is conducted to verify code accuracy for the shock formation of supersonic jets. Two-dimensional axisymmetric simulation of the problem using rhoCentralFoam was reported previously [41,56]. In the current work, 3D simulation of the Ladenburg experiment is performed with the compressibleCentralReactingFoam solver. As the maximum temperature of the experiment is no more than 300 K, the chemical reactions will be at frozen state and hence, the gas mixture is considered be inert. The computational 3D mesh (see Figure 5) has 5 mm inlet radius, 10 mm free surface radius, and 30 mm length. The following inlet conditions for pressure, axial velocity and temperature are used to ensure a sonic condition with Mach number of one (1) at the inlet surface: 2.72 x 10 5   P a , 316.6   m / s and 247.1   K . The conditions at the free stream surface are: 1.01 x 10 5   P a , 0   m / s and 297   K . Non-reflected boundary conditions are used at the outlet. The simulations are performed using a mesh with total hexahedral elements equal to 1.72 million. The sketch showing wave structures and the simulation flow of Mach number contours is shown in Figure 6a. The pressure at the inlet of the computational region is the pressure of the reservoir, which is greater than the ambient pressure; thus, the flow is defined as underexpanded. When air accelerates from high inlet pressure to the atmosphere, the gas flow declines due to its expansion and acceleration. The gas jet expands to the atmospheric pressure through an expansion fan (Figure 6a). It is seen in Figure 6b in the free jet boundary above which the gas flow is at rest (i.e., M=0). In Figure 6a, numbers 1-5 in the circles indicate different gas structures, such as expansion and shock waves. The expansion waves (denoted by 1) are reflected from the free boundary as compression waves. The accumulated compression waves at a point then form an oblique shock wave, shown by the solid line (denoted by 2). The formed oblique shock waves are again reflected off the center line of the flow. This reflection causes the formation of a Mach reflection before the intersection point with the centerline, producing a triple shock point where the compression waves, oblique shock, and centerline coincide. The incoming oblique shock wave (denoted by 2) is the first Mach reflection. The second shock (denoted by 3) is a Mach reflection, perpendicular to the centerline termed a normal (Mach disk) shock. The third Mach reflection (denoted by 4) is another oblique shock wave that is reflected off the constant pressure-free air-jet boundary as an expansion fan (denoted by 5). The escalation of the pressure and temperature occurs as the flow passes through the normal shock or Mach disk. So, the Mach disk is the high-pressure region in an underexpanded air jet that is formed through shock waves and expansion waves created by the vast difference between the inlet pressure and the ambient pressure.
Figure 7 shows the comparison of the current simulation with experimental data of Ladenburg et al. [55] for density iso-lines. The simulation results have a good agreement with the experimental data, especially the location and height of the Mach disk. The experimental results show that a weak shock is produced due to the expansion of air from the nozzle orifice (close to density 3.8   k g / m 3 ) and then extends toward the nozzle axis. Thus, it creates a Mach disk feature and a triple point (i.e., the intersection of Mach disk, barrel shock and reflected shock). The experimental data in Figure 7 (i.e., lower panel) shows that the position of the triple point is at 1.7 mm radial distance and 13.3 mm axial distance. The computed radial and axial distance of the triple point are 1.65 mm and 13.5 mm, respectively. Thus, the computational results yield less than 3% error compared to the experimental data. In summary, the computational results are in good agreement with the experimental data as well as the physics of the shock formation, expansion wave behavior, and their interactions with jet boundary and slip lines.

3.1.3. Simulation of DLR Scramjet Combustor

The combustion experiment of the Waidmann et al. [57] is selected to validate the compressibleCentralReactingFoam solver to model the turbulence combustion interactions in a scramjet combustor. The experimental data were obtained for hydrogen combustion using the Scramjet test facility at the German Aerospace Center (DLR) at Mach number two. The experimental system was modeled using 2D and 3D computational studies by Oevermann [58] and Haung et al. [35], respectively. Oevermann [58] used RANS (i.e., k-ε turbulence model) with laminar flamelet whereas Huang et al. [35] used LES with PaSR sub-grid scale combustion model to simulate the Scramjet. Both computational studies produced reasonable agreement with the experimental data. In the current work, 2D LES simulation is conducted with PaSR sub-grid scale combustion model to validate compressibleCentralReactingFoam solver. Although the two-dimensional assumption may introduce some uncertainty when directly comparing it to the experiment, the 2D computational study will help to verify the accuracy of the model implementation in compressibleCentralReactingFoam qualitatively.
Figure 8 shows the geometry of DLR test rig. The combustor has a height of 50   mm and width of 45   mm at air inflow. The divergence angle of the upper wall is 3 0 to compensate for the expansion of the boundary layer. The following boundary conditions for air are established to ensure the Mach number M air ≈ 2 : u air = 730   m / s , T air = 340   K , p air = 10 5 Pa with the mass rate of airflow m ˙ air ≈ 1.0   kg / s . The injector of fuel ( H 2 ) is a slot in the center of the wedge-shaped strut with a height Δ y H 2 = 0.26   mm that gives the surface area of injection Δ s H 2 = 11.7   mm 2 . The following boundary conditions are used to establish fuel injector Mach number M H 2 ≈ 1 : u H 2 = 1200   m / s , T H 2 = 250   K , p H 2 = 10 5 Pa with the hydrogen mass flow m ˙ H 2 ≈ 1.26   g / s . The no-slip boundary conditions are implemented on the solid walls. The computational region is discretized on 100,000 hexahedrons (See Figure 9). A detailed kinetic mechanism for hydrogen combustion with 9 species and 18 elementary reactions [59] is used.
  • Simulation of Cold Flow DLR Combustor
Initially, the cold flow is simulated. Figure 10 shows a Schlieren photograph of the channel flow and computational data of density gradient contours corresponding to the experiment. Comparisons of these two pictures show that the current compressible solver is able to accurately capture the aerodynamics features such as shock waves, expansion waves, interaction, and reflection of these structures from the walls and jet-shear layer. The computational results shown in Figure 10b also identify various flow characteristics with labels 1 to 7. Label (1) shows the leading shocks formed on the tip of the edge (see Figure 10). Label (2) refers to the expansion waves due to the supersonic flow past the corners of the edge. Label (3) is the reflected shock of (1) from the upper wall whereas label (4) refers to the shocks formed due to collision of gas flow passing through the corner of the edge. Label (5) is an oblique shock formed from merging of the reflected shock and shocks in (4). Lebel (6) is a reflected from the upper wall oblique shock whereas label (7) is the jet shear-layer formed from the Kelvin-Helmholtz instability. The oblique shocks that are reflected from the upper and lower walls interact with the jet shear layer to get reflected again without penetration as shown Figure 10b.
Figure 11a shows the normalized contours of density gradient | ∇ ρ / ρ max |. Figure 11b shows the Mach numbers of the cold flow. Shocks are generated from the tip of the wedge and are further reflected from the lower and upper walls of the combustor. Also, the expansion wave on the upper wall at the starting divergence is seen. Gas flow passing the corners of the wedge are subjected to expansion by forming two expansion waves. The jet vortex structure arises from the Kelvin-Helmholtz instability of the jet-shear layer [14]. It is noteworthy that the simulation with the k − ε turbulent model did not generate shear-layer instabilities as reported by Oevermann [58]. This finding confirms that R A N S models are limited when predicting such phenomena and L E S models are more appropriate in scramjet combustor simulations.
Figure 12 compares the cold flow simulation results for pressure distributions with the experimental measurements of Waidmann et al. [57]. Figure 12a show the distribution of pressure on the lower (solid line) and upper (dashed line) walls along with experimental data obtained on the lower wall (symbols). Figure 12b compares the pressure along the center line with the experimental data. The model predictions are able to capture the pressure profiles observed experimentally.
  • Simulation of Reacting Flow DLR Combustor
Simulations were performed for reactive flow with detailed hydrogen kinetic mechanism for experimental conditions of Waidmann et al. [57]. Combustion was initiated with the help of an igniter during the test as no autoignition was observed experimentally. Our initial simulation also showed that combustion did not occur without an external ignition source. Hence, ignition zones at the two corners of the strut with temperature T i g n = 1500 K are implemented. Figure 13 compares Schlieren's photograph of the reactive flow with the computational data for the density contours obtained in the current work for the experimental condition of Waidmann et al. [57]. The comparison shows similar gas dynamic features such as shock waves, expansion waves, interaction, and reflection of the flow structures from the walls and jet-shear layer. Significant gas dynamic differences can be seen between cold flow (Figure 10) and hot flow (Figure 13). For example, expansion waves (i.e., labeled 2 in Figure 10) at the corners of the wedge in cold flow are replaced with the shocks generated due to the combustion in Figure 13. It should be noted that a considerable subsonic region is developed behind the hydrogen injection for reactive flow.
  • Influence of Turbulent Models on Scramjet Combustion
A discussion on the influence of different turbulent models on supersonic combustion is presented in this section. Scramjet simulations for the DLR Scramjet experiment [57] are performed with the following turbulent models described in Subsection 2.1: SMG, LDkEqn, and WALE. Figure 14 compares the experimental data for temperature at three cross sections along the combustor with the simulation results obtained with three turbulent models. The figure also shows the location of the temperature measurements in the DLR Scramjet combustor. The simulation results close to the strut (i.e., x = 62 mm) show that LDkEqn and WALE models have similar profiles. Further downstream (i.e., x = 216 mm), all three models have similar profiles. Overall, WALE model has slightly better agreement with the experimental data.
Figure 15 compares the current WALE model simulation results with other DLR Scramjet simulation data reported in the literature [12,30,58,60]. Modeling result of Berglund and Fureby, [60] closely follow the experimental profile except at x = 62 mm. Overall, the present model has better agreements with the experimental data at all locations, but it does show relatively higher diffusivity at downstream locations (i.e., x = 108 mm and 216 mm).
  • Analysis of Turbulence-Combustion Interaction in Scramjet Combustor
Based on the analysis of different turbulent models, the WALE model is selected as the most suitable for Scramjet simulation. The effect of turbulence-combustion coupling on gas dynamics and flame structure is discussed in this section using the DLR Scramjet simulation results obtained with WALE model. Figure 16 shows the Mach number (Ma), rate of heat release per unit volume (Qdot), instantaneous temperature (T), and normalized contour lines of densities’ gradient ( | ∇ ρ / ρ max |) obtained from the simulation. The shock structure, shown in Figure 16a,d, is characterized by strong interaction with the shear layers characterized by large density gradients. Behind the strut, a central recirculation bubble is generated with a subsonic region. The formation of the recirculation zone is very important for flame holding and, hence, stabilizing the flame in the scramjet combustor. The rate of heat release contours in Figure 16b show that combustion is intensive within the thin shear layers. The combustion is initiated within the shear layers separated by the recirculation zone close to the edges of the strut. This observation is supported by the temperature data presented in Figure 14a.
The direction of diffusive spreading of fuel and oxidizer helps to analyze turbulence-chemistry interactions. It can be estimated by the interaction between the gradients of fuel ( ∇ Y F ) and oxygen ( ∇ Y O ) mass fractions. Takeno and co-workers [61] suggested the use of a flame index (known as the Takeno Flame Index - TFI) based on scalar productions of the gradients of the fuel and oxidizer mass fraction, which help to distinguish between the premixed and non-premixed zones [61]. The TFI is defined as G F O = ∇ Y F · ∇ Y O / ∇ Y F   ∇ Y O . Positive and negative values of TFI indicate non-premixed or premixed modes, respectively [61]. Figure 17 shows the TFI calculated for the DRL Scramjet conditions. Pockets of non-premixed zones shown in red are surrounded by large premixed zone shown in dark blue.
Figure 18 shows the species mass fraction contours for O H , H , H O 2 and H 2 O . It is observed [9] that the OH field is far from uniform in the mixture due to turbulence, which would have been expected from fast chemistry arguments. High OH regions are found where the mixture fraction iso-surfaces are highly convoluted, and low values are in the areas where the mixture fraction iso-surfaces are stretched and not wrinkled. The mass fraction of OH is relatively small at the beginning, while it is most prominent in the downstream regions, especially in the transition zone. The OH radical represents the existence of a flame front which correlates with heat release rate. Field of H2O correlates with the field of instantaneous temperature while the field of HO2 correlates with OH and Qdot on the shear layer.
Figure 19 shows mixture fraction ( Z ) and scalar dissipation rate ( χ ) . The mixture fraction measures the local fuel/oxidizer ratio, and calculated as Z = φ · Y F / Y F 0 − Y O / Y O 0 + 1 / φ + 1 where φ is equivalence ratio. The scalar dissipation rate is calculated as χ = 2 D ∇ Z · ∇ Z , where D is the mixture diffusion coefficient. The scalar dissipation rate is essentially the rate of mixing between fuel and oxidizer [9] and represents the local mixing rate at the molecular level [62]. The scalar dissipation rate is critical for modeling the effect of turbulence on reaction rates as it has significant influence on non-premixed combustion. It often provides the connection between the molecular mixing and the combustion. In turbulent flows, the scalar dissipation is seen as a scalar energy dissipation. Its role is to destroy (dissipate) scalar variance (scalar energy) analogous to the dissipation of the turbulence. Unlike the kinetic energy dissipation, most of the scalar dissipation occurs at the finest scales. The scalar dissipation has higher values near the strut and decreases further downstream as shown in Figure 19b.
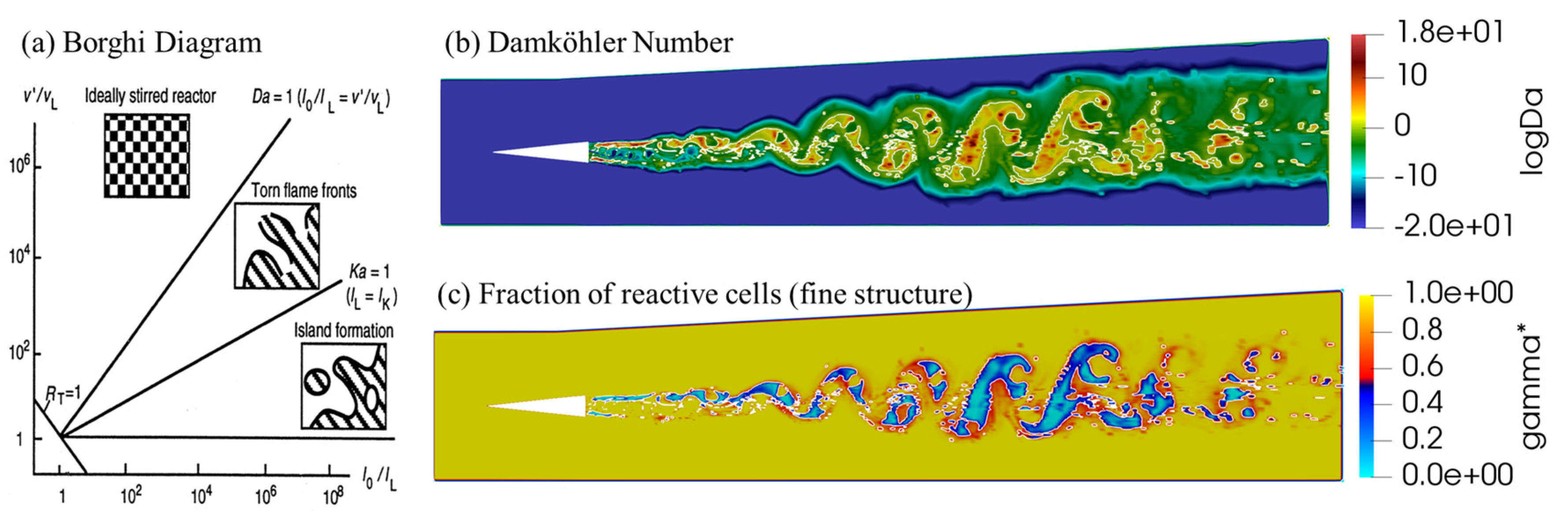
A time-scale analysis based on the estimation of the local Damköhler Number (Da) is also calculated to examine the reactive zones in more detail. The Da number, quantified as the ratio between the turbulent mixing time scale τ * and the chemical time scale τ c : D a = τ * / τ c [63,64]. The Borghi diagram [63] shown in Figure 20a helps to recognize different regimes of turbulent combustion. Figure 20b,c show the Damköhler number (Da) on a logarithmic scale and the fraction of fine structure ( γ * ), respectively. The bright white lines indicate the locations where D a = 1 . The Damköhler number is relatively high ( D a ≫ 1 ) in the core of the jet flow. This indicates that the time scale of chemical reaction is smaller than the turbulent mixing time scale which means combustion regime with fast chemistry. Thus, the fraction of reactive cells ( γ * ) (see Section 0 for details) is mostly small in this zone. In contrast, in the shear layer where the rate of the heat release (see Figure 16b) and the scalar dissipation rate (see Figure 19b) have the highest values, the flame is controlled by finite rate chemistry with D a ≪ 1 and γ * ≈ 1.   In the core flow, it is also seen small pockets where D a ≪ 1 indicating the combustion zone is in the “island formation” regime as shown in Figure 20a. These zones are characterized by the combustion regime with a finite rate chemistry with a rather high fraction of reactive cells ( γ * ~ 1 ) and are called partially-stirred reactor.

4. Conclusions

A computational validation of a new compressibleCentralReactingFoam code for modeling combustion in supersonic flows is presented. The validation cases include various complexities of high-speed flows with shocks, wave expansion, and turbulence-combustion interactions. Comparisons of the simulation results with the literature data demonstrated the numerical fidelity of the solver for reactive multicomponent gas mixtures at supersonic conditions. Moreover, detailed analysis on gas dynamics and turbulence-combustion interaction under supersonic conditions is presented to gain a deeper understanding of the complex physical-chemical phenomena involved. A comparative analysis on the influence of three turbulent subgrid models on scramjet combustion is presented. The comparison of simulation results with the experimental data shows that WALE subgrid scale is most suitable for Scramjet modeling. Moreover, the DLR Scramjet simulation results show that the flame is mainly stabilized in the combustor due to the forming of a subsonic bubble behind the strut. The supersonic flame structure is investigated through a comprehensive analysis of chemical species formation, scalar dissipation rate, flame index, heat release rate, fine structure, and Damköhler number. A time-scale analysis based on the local Damköhler number reveals different regimes of turbulence combustion in the Scramjet. In the core of the jet flow, the Da number is relatively high ( D a ≫ 1 ) indicating that the chemical time scale is smaller than the turbulent mixing time scale. This means that the combustion regime is dominated by fast chemistry. The results also show that the heat release rate and the scalar dissipation rate have the highest values in the shear layer, and the flame is stabilized due to finite rate chemistry with D a ≪ 1 and γ * ≈ 1 . Thus, the new solver presented in this paper can be used for high-speed simulation of multicomponent reactive gas mixtures in supersonic combustors.

Author Contributions

Conceptualization, A.G., P.G. and M.S.K.; methodology, A.G.; software, A.G.; validation, A.G.; formal analysis, A.G., P.G. and M.S.K.; investigation, A.G.; resources, A.G.; data curation, A.G.; writing—original draft preparation, A.G.; writing—review and editing, A.G., P.G. and M.S.K.; visualization, A.G.; supervision, P.G. and M.S.K.; project administration, A.G., P.G. and M.S.K.; funding acquisition, M.S.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. J. Urzay, “Supersonic Combustion in Air-Breathing Propulsion Systems for Hypersonic Flight,” Annual Review of Fluid Mechanics, vol. 50, no. 1, pp. 593–627, 2018, doi: 10.1146/annurev-fluid-122316-045217. [CrossRef]
  2. C. Fureby, “Large eddy simulation modelling of combustion for propulsion applications,” Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, vol. 367, no. 1899, pp. 2957–2969, Jul. 2009, doi: 10.1098/rsta.2008.0271. [CrossRef]
  3. G. A. Q. Abdulrahman, N. A. A. Qasem, B. Imteyaz, A. M. Abdallah, and M. A. Habib, “A review of aircraft subsonic and supersonic combustors,” Aerospace Science and Technology, vol. 132, p. 108067, Jan. 2023, doi: 10.1016/j.ast.2022.108067. [CrossRef]
  4. S. O’Byrne, M. Doolan, S. R. Olsen, and A. F. P. Houwing, “Measurement and imaging of supersonic combustion in a model scramjet engine,” Shock Waves, vol. 9, no. 4, pp. 221–226, Aug. 1999, doi: 10.1007/s001930050159. [CrossRef]
  5. S. Menon, V. Sankaran, and C. Stone, “Subgrid Combustion Modeling for the Next Generation National Combustion Code,” CCL-02–003, Apr. 2003. Accessed: Nov. 30, 2023. [Online]. Available: https://ntrs.nasa.gov/citations/20030038812.
  6. S. Menon and C. Fureby, “Computational Combustion,” in Encyclopedia of Aerospace Engineering, John Wiley & Sons, Ltd, 2010. doi: 10.1002/9780470686652.eae063. [CrossRef]
  7. Pierre Sagaut, Large Eddy Simulation for Incompressible Flows. in Scientific Computation. Berlin/Heidelberg: Springer-Verlag, 2006. doi: 10.1007/b137536. [CrossRef]
  8. T. Echekki and E. Mastorakos, Eds., Turbulent Combustion Modeling: Advances, New Trends and Perspectives, vol. 95. in Fluid Mechanics and Its Applications, vol. 95. Dordrecht: Springer Netherlands, 2011. doi: 10.1007/978-94-007-0412-1. [CrossRef]
  9. E. R. Hawkes, R. Sankaran, J. C. Sutherland, and J. H. Chen, “Direct numerical simulation of turbulent combustion: fundamental insights towards predictive models,” J. Phys.: Conf. Ser., vol. 16, no. 1, p. 65, Jan. 2005, doi: 10.1088/1742-6596/16/1/009. [CrossRef]
  10. L. F. Gutiérrez, Universidad Nacional de Córdoba-IDIT(CONICET), J. Tamagno, Univeridad Nacional de Córdoba, S. A. Elaskar, and Univeridad Nacional de Córdoba-CONICET, “RANS Simulation of Turbulent Diffusive Combustion using Open Foam,” JAFM, vol. 9, no. 2, pp. 669–682, Mar. 2016, doi: 10.18869/acadpub.jafm.68.225.24104. [CrossRef]
  11. A. Ingenito and C. Bruno, “Physics and Regimes of Supersonic Combustion,” AIAA Journal, vol. 48, no. 3, pp. 515–525, 2010, doi: 10.2514/1.43652. [CrossRef]
  12. F. Génin and S. Menon, “Simulation of Turbulent Mixing Behind a Strut Injector in Supersonic Flow,” AIAA Journal, vol. 48, no. 3, pp. 526–539, Mar. 2010, doi: 10.2514/1.43647. [CrossRef]
  13. C. Fureby, K. Nordin-Bates, K. Petterson, A. Bresson, and V. Sabelnikov, “A computational study of supersonic combustion in strut injector and hypermixer flow fields,” Proceedings of the Combustion Institute, vol. 35, no. 2, pp. 2127–2135, Jan. 2015, doi: 10.1016/j.proci.2014.06.113. [CrossRef]
  14. C. Fureby, G. Sahut, A. Ercole, and T. Nilsson, “Large Eddy Simulation of Combustion for High-Speed Airbreathing Engines,” Aerospace, vol. 9, no. 12, Art. no. 12, Dec. 2022, doi: 10.3390/aerospace9120785. [CrossRef]
  15. P. Gokulakrishnan et al., “LES-PDF Modeling of Flame Instability and Blow-out in Bluff-Body Stabilized Flames,” in 45th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, in Joint Propulsion Conferences. , American Institute of Aeronautics and Astronautics, 2009. doi: 10.2514/6.2009-5409. [CrossRef]
  16. P. Gokulakrishnan, R. Bikkani, M. Klassen, R. Roby, and B. Kiel, “Influence of Turbulence-Chemistry Interaction in Blow-out Predictions of Bluff-Body Stabilized Flames,” in 47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, in Aerospace Sciences Meetings. , American Institute of Aeronautics and Astronautics, 2009. doi: 10.2514/6.2009-1179. [CrossRef]
  17. A. Dasgupta, E. Gonzalez-Juez, and D. C. Haworth, “Flame simulations with an open-source code,” Computer Physics Communications, vol. 237, pp. 219–229, Apr. 2019, doi: 10.1016/j.cpc.2018.11.011. [CrossRef]
  18. E. D. Gonzalez-Juez, A. Dasgupta, S. Arshad, M. Oevermann, and D. Lignell, “Effect of the turbulence modeling in large-eddy simulations of nonpremixed flames undergoing extinction and reignition,” in AIAA SciTech Forum - 55th AIAA Aerospace Sciences Meeting, 2017. doi: 10.2514/6.2017-0604. [CrossRef]
  19. E. D. Gonzalez-Juez, A. R. Kerstein, R. Ranjan, and S. Menon, “Advances and challenges in modeling high-speed turbulent combustion in propulsion systems,” Progress in Energy and Combustion Science, vol. 60, pp. 26–67, May 2017, doi: 10.1016/j.pecs.2016.12.003. [CrossRef]
  20. N. Peters, Turbulent Combustion, 1st edition. Cambridge: Cambridge University Press, 2000.
  21. S. B. Pope, “Small scales, many species and the manifold challenges of turbulent combustion,” Proceedings of the Combustion Institute, vol. 34, no. 1, pp. 1–31, Jan. 2013, doi: 10.1016/j.proci.2012.09.009. [CrossRef]
  22. S. Huang, Q. Chen, Y. Cheng, J. Xian, and Z. Tai, “Supersonic Combustion Modeling and Simulation on General Platforms,” Aerospace, vol. 9, no. 7, Art. no. 7, Jul. 2022, doi: 10.3390/aerospace9070366. [CrossRef]
  23. M. Piasecka, A. Piasecki, and N. Dadas, “Experimental Study and CFD Modeling of Fluid Flow and Heat Transfer Characteristics in a Mini-Channel Heat Sink Using Simcenter STAR-CCM+ Software,” Energies, vol. 15, no. 2, Art. no. 2, Jan. 2022, doi: 10.3390/en15020536. [CrossRef]
  24. J. R. Edwards and J. A. Fulton, “Development of a RANS and LES/RANS Flow Solver for High-Speed Engine Flowpath Simulations,” in 20th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, in International Space Planes and Hypersonic Systems and Technologies Conferences. , American Institute of Aeronautics and Astronautics, 2015. doi: 10.2514/6.2015-3570. [CrossRef]
  25. C. Nelson, “An Overview of the NPARC Alliance’s Wind-US Flow Solver,” in 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, in Aerospace Sciences Meetings. , American Institute of Aeronautics and Astronautics, 2010. doi: 10.2514/6.2010-27. [CrossRef]
  26. J. Steelant, A. Mack, K. Hannemann, and A. Gardner, “Comparison of Supersonic Combustion Tests with Shock Tunnels, Flight and CFD,” in 42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, in Joint Propulsion Conferences. , American Institute of Aeronautics and Astronautics, 2006. doi: 10.2514/6.2006-4684. [CrossRef]
  27. J. P. Drummond, P. M. Danehy, R. L. Gaffney, S. A. Tedder, A. D. Cutler, and D. Bivolaru, “Supersonic Combustion Research at NASA,” presented at the 2007 Fall Technical Meeting - Eastern States Section of the Combustion Institute, Charlotesville, VA, Oct. 2007. Accessed: Nov. 30, 2023. [Online]. Available: https://ntrs.nasa.gov/citations/20080013391.
  28. F. Palacios et al., “Stanford University Unstructured (SU 2 ): Open-source Analysis and Design Technology for Turbulent Flows,” 2014. Accessed: Nov. 30, 2023. [Online]. Available: https://www.semanticscholar.org/paper/Stanford-University-Unstructured-(SU-2-)%3A-Analysis-Palacios-Economon/3b6dd8951b4d1e30fca73c8e737585ec920d81b0.
  29. H. G. Weller, G. Tabor, H. Jasak, and C. Fureby, “A tensorial approach to computational continuum mechanics using object-oriented techniques,” Computers in Physics, vol. 12, no. 6, pp. 620–631, Nov. 1998, doi: 10.1063/1.168744. [CrossRef]
  30. H. Zhang, M. Zhao, and Z. Huang, “Large eddy simulation of turbulent supersonic hydrogen flames with OpenFOAM,” Fuel, vol. 282, p. 118812, Dec. 2020, doi: 10.1016/j.fuel.2020.118812. [CrossRef]
  31. M. Chapuis, E. Fedina, C. Fureby, K. Hannemann, S. Karl, and J. Martinez Schramm, “A computational study of the HyShot II combustor performance,” Proceedings of the Combustion Institute, vol. 34, no. 2, pp. 2101–2109, Jan. 2013, doi: 10.1016/j.proci.2012.07.014. [CrossRef]
  32. N. Droeske, K. Makowka, P. Nizenkov, J. J. Vellaramkalayil, T. Sattelmayer, and J. von Wolfersdorf, “Validation of a Novel OpenFOAM Solver using a Supersonic, Non-reacting Channel Flow,” in 19th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, in AIAA AVIATION Forum. , American Institute of Aeronautics and Astronautics, 2014. doi: 10.2514/6.2014-3088. [CrossRef]
  33. K. Makowka, N. Droeske, J. J. Vellaramkalayil, T. Sattelmayer, and J. von Wolfersdorf, “Unsteady RANS Investigation of a Hydrogen-Fueled Staged Supersonic Combustor with Lobed Injectors,” in 19th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, in AIAA AVIATION Forum. , American Institute of Aeronautics and Astronautics, 2014. doi: 10.2514/6.2014-3215. [CrossRef]
  34. Martínez-Ferrer, P.J., R. Buttay, G. Lehnasch, and A. Mura, “A detailed verification procedure for compressible reactive multicomponent Navier–Stokes solvers,” Computers & Fluids, vol. 89, pp. 88–110, Jan. 2014, doi: 10.1016/j.compfluid.2013.10.014. [CrossRef]
  35. Z. Huang, G. He, F. Qin, and X. Wei, “Large eddy simulation of flame structure and combustion mode in a hydrogen fueled supersonic combustor,” International Journal of Hydrogen Energy, vol. 40, no. 31, pp. 9815–9824, Aug. 2015, doi: 10.1016/j.ijhydene.2015.06.011. [CrossRef]
  36. C. J. Arisman and C. T. Johansen, “Nitric Oxide Chemistry Effects in Hypersonic Boundary Layers,” AIAA Journal, vol. 53, no. 12, pp. 3652–3660, 2015, doi: 10.2514/1.J053979. [CrossRef]
  37. D. Zhou, S. Zou, and S. Yang, “An OpenFOAM-based fully compressible reacting flow solver with detailed transport and chemistry for high-speed combustion simulations,” in AIAA Scitech 2020 Forum, in AIAA SciTech Forum. , American Institute of Aeronautics and Astronautics, 2020. doi: 10.2514/6.2020-0872. [CrossRef]
  38. J.-J. O. Hoste, V. Casseau, M. Fossati, I. J. Taylor, and R. Gollan, “Numerical Modeling and Simulation of Supersonic Flows in Propulsion Systems by Open-Source Solvers,” in 21st AIAA International Space Planes and Hypersonics Technologies Conference, in International Space Planes and Hypersonic Systems and Technologies Conferences. , American Institute of Aeronautics and Astronautics, 2017. doi: 10.2514/6.2017-2411. [CrossRef]
  39. A. Kurganov and E. Tadmor, “New High-Resolution Central Schemes for Nonlinear Conservation Laws and Convection–Diffusion Equations,” Journal of Computational Physics, vol. 160, no. 1, pp. 241–282, May 2000, doi: 10.1006/jcph.2000.6459. [CrossRef]
  40. A. Kurganov, S. Noelle, and G. Petrova, “Semidiscrete Central-Upwind Schemes for Hyperbolic Conservation Laws and Hamilton--Jacobi Equations,” SIAM J. Sci. Comput., vol. 23, no. 3, pp. 707–740, Jan. 2001, doi: 10.1137/S1064827500373413. [CrossRef]
  41. C. J. Greenshields, H. G. Weller, L. Gasparini, and J. M. Reese, “Implementation of semi-discrete, non-staggered central schemes in a colocated, polyhedral, finite volume framework, for high-speed viscous flows,” International Journal for Numerical Methods in Fluids, vol. 63, no. 1, pp. 1–21, 2010, doi: 10.1002/fld.2069. [CrossRef]
  42. 2306.
  43. J. Smagorinsky, “General Circulation Experiments with the Primitive Equations,” Monthly Weather Review, vol. 91, p. 99, Jan. 1963, doi: 10.1175/1520-0493(1963)091<0099:GCEWTP>2.3.CO;2. [CrossRef]
  44. G. Erlebacher, M. Y. Hussaini, C. G. Speziale, and T. A. Zang, “Toward the large-eddy simulation of compressible turbulent flows,” Journal of Fluid Mechanics, vol. 238, pp. 155–185, May 1992, doi: 10.1017/S0022112092001678. [CrossRef]
  45. W.-W. Kim and S. Menon, “A new dynamic one-equation subgrid-scale model for large eddy simulations,” in 33rd Aerospace Sciences Meeting and Exhibit, in Aerospace Sciences Meetings. , American Institute of Aeronautics and Astronautics, 1995. doi: 10.2514/6.1995-356. [CrossRef]
  46. S. Huang and Q. S. Li, “A new dynamic one-equation subgrid-scale model for large eddy simulations,” International Journal for Numerical Methods in Engineering, vol. 81, no. 7, pp. 835–865, 2010, doi: 10.1002/nme.2715. [CrossRef]
  47. F. Nicoud and F. Ducros, “Subgrid-Scale Stress Modelling Based on the Square of the Velocity Gradient Tensor,” Flow, Turbulence and Combustion, vol. 62, no. 3, pp. 183–200, Sep. 1999, doi: 10.1023/A:1009995426001. [CrossRef]
  48. M. Berglund, E. Fedina, C. Fureby, J. Tegnér, and V. Sabel’nikov, “Finite Rate Chemistry Large-Eddy Simulation of Self-Ignition in Supersonic Combustion Ramjet,” AIAA Journal, vol. 48, no. 3, pp. 540–550, Mar. 2010, doi: 10.2514/1.43746. [CrossRef]
  49. V. Sabelnikov and C. Fureby, “Extended LES-PaSR model for simulation of turbulent combustion,” in Progress in Propulsion Physics, EDP Sciences, 2013, pp. 539–568. doi: 10.1051/eucass/201304539. [CrossRef]
  50. E. Baudoin, R. Yu, Bai, K. J. Nogenmur, X.-S. Bai, and C. Fureby, “Comparison of LES Models Applied to a Bluff Body Stabilized Flame,” in 47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, American Institute of Aeronautics and Astronautics. doi: 10.2514/6.2009-1178. [CrossRef]
  51. B. Magnussen, “On the structure of turbulence and a generalized eddy dissipation concept for chemical reaction in turbulent flow,” in 19th Aerospace Sciences Meeting, American Institute of Aeronautics and Astronautics. doi: 10.2514/6.1981-42. [CrossRef]
  52. G. A. Sod, “A survey of several finite difference methods for systems of nonlinear hyperbolic conservation laws,” Journal of Computational Physics, vol. 27, no. 1, pp. 1–31, Apr. 1978, doi: 10.1016/0021-9991(78)90023-2. [CrossRef]
  53. Z. Huang, M. Zhao, Y. Xu, G. Li, and H. Zhang, “Eulerian-Lagrangian modelling of detonative combustion in two-phase gas-droplet mixtures with OpenFOAM: Validations and verifications,” Fuel, vol. 286, p. 119402, Feb. 2021, doi: 10.1016/j.fuel.2020.119402. [CrossRef]
  54. M. Ó Conaire, H. J. Curran, J. M. Simmie, W. J. Pitz, and C. K. Westbrook, “A comprehensive modeling study of hydrogen oxidation,” International Journal of Chemical Kinetics, vol. 36, no. 11, pp. 603–622, 2004, doi: 10.1002/kin.20036. [CrossRef]
  55. R. Ladenburg, C. C. Van Voorhis, and J. Winckler, “Interferometric Studies of Faster than Sound Phenomena. Part II. Analysis of Supersonic Air Jets,” Phys. Rev., vol. 76, no. 5, pp. 662–677, Sep. 1949, doi: 10.1103/PhysRev.76.662. [CrossRef]
  56. M. Talukdar, “Numerical simulation of underexpanded air jet using OpenFOAM,” Master thesis, University of Stavanger, Norway, 2015. Accessed: Nov. 30, 2023. [Online]. Available: https://uis.brage.unit.no/uis-xmlui/handle/11250/302085.
  57. F. Alff, U. Brummund, W. Clauss, M. Oschwald, J. Sender, and W. Waidmann, Experimental Investigation of the Combustion Process in a Supersonic Combustion Ramjet (SCRAMJET) Combustion Chamber. 1994, p. 638.
  58. M. Oevermann, “Numerical investigation of turbulent hydrogen combustion in a SCRAMJET using flamelet modeling,” Aerospace Science and Technology, vol. 4, no. 7, pp. 463–480, Oct. 2000, doi: 10.1016/S1270-9638(00)01070-1. [CrossRef]
  59. U. Maas and J. Warnatz, “Ignition processes in hydrogenoxygen mixtures,” Combustion and Flame, vol. 74, no. 1, pp. 53–69, Oct. 1988, doi: 10.1016/0010-2180(88)90086-7. [CrossRef]
  60. M. Berglund and C. Fureby, “LES of supersonic combustion in a scramjet engine model,” Proceedings of the Combustion Institute, vol. 31, no. 2, pp. 2497–2504, Jan. 2007, doi: 10.1016/j.proci.2006.07.074. [CrossRef]
  61. H. Yamashita, M. Shimada, and T. Takeno, “A numerical study on flame stability at the transition point of jet diffusion flames,” Symposium (International) on Combustion, vol. 26, no. 1, pp. 27–34, Jan. 1996, doi: 10.1016/S0082-0784(96)80196-2. [CrossRef]
  62. R. W. Bilger, “Some Aspects of Scalar Dissipation,” Flow, Turbulence and Combustion, vol. 72, no. 2, pp. 93–114, Jun. 2004, doi: 10.1023/B:APPL.0000044404.24369.f1. [CrossRef]
  63. J. Warnatz · U. Maas · R.W. Dibble, Combustion. Springer Berlin Heidelberg, 2006. doi: 10.1007/978-3-540-45363-5. [CrossRef]
  64. T. Poinsot and D. Veynante, Theoretical and Numerical Combustion, Second Edition, 2nd edition. Philadelphia: R T Edwards Inc, 2005.
Preprints 92549 g001
Figure 1. Shock tube and spreading shock wave (red), the contact surface (black), and expansion fan (blue).
Figure 1. Shock tube and spreading shock wave (red), the contact surface (black), and expansion fan (blue).
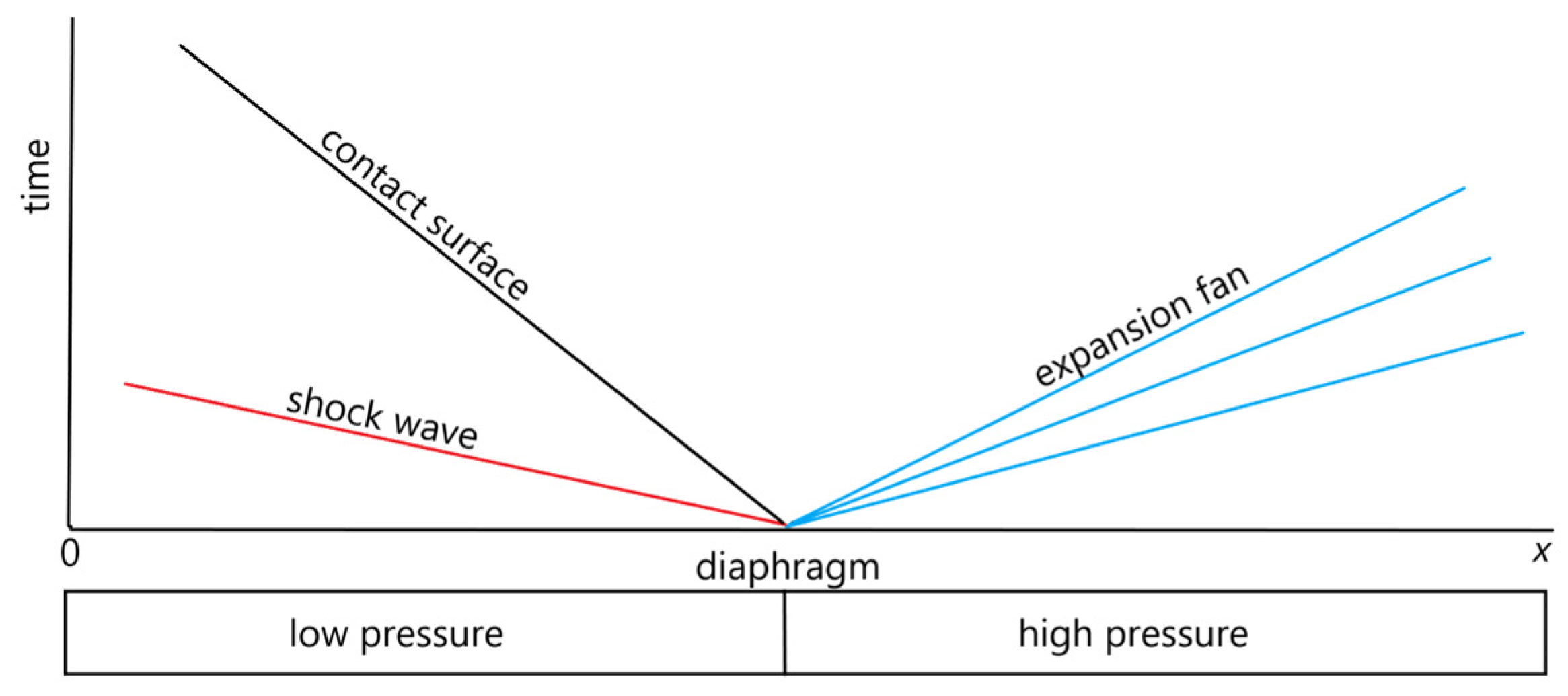
Preprints 92549 g001
Preprints 92549 g002
Figure 2. Multicomponent inert shock tube profiles of H2/O2/Ar mixture at 40 μs. Keys: solid line – current simulation; symbols – simulation of Huang et al. [53].
Figure 2. Multicomponent inert shock tube profiles of H2/O2/Ar mixture at 40 μs. Keys: solid line – current simulation; symbols – simulation of Huang et al. [53].
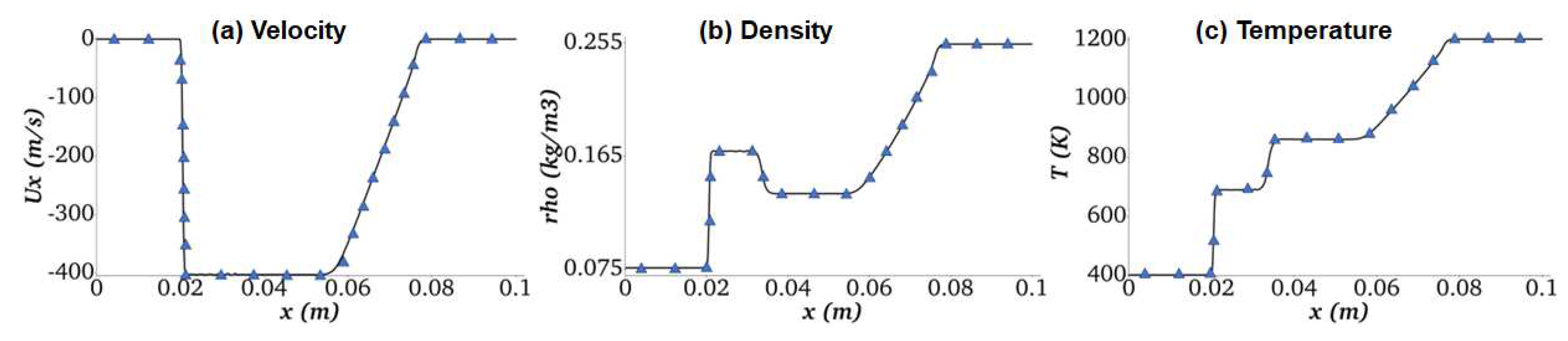
Preprints 92549 g002
Preprints 92549 g003
Figure 3. Multicomponent reactive shock tube profiles of H2/O2/Ar mixture at 230 μs. Keys: solid line – current simulation; symbols - Martínez-Ferrer et al. [34].
Figure 3. Multicomponent reactive shock tube profiles of H2/O2/Ar mixture at 230 μs. Keys: solid line – current simulation; symbols - Martínez-Ferrer et al. [34].
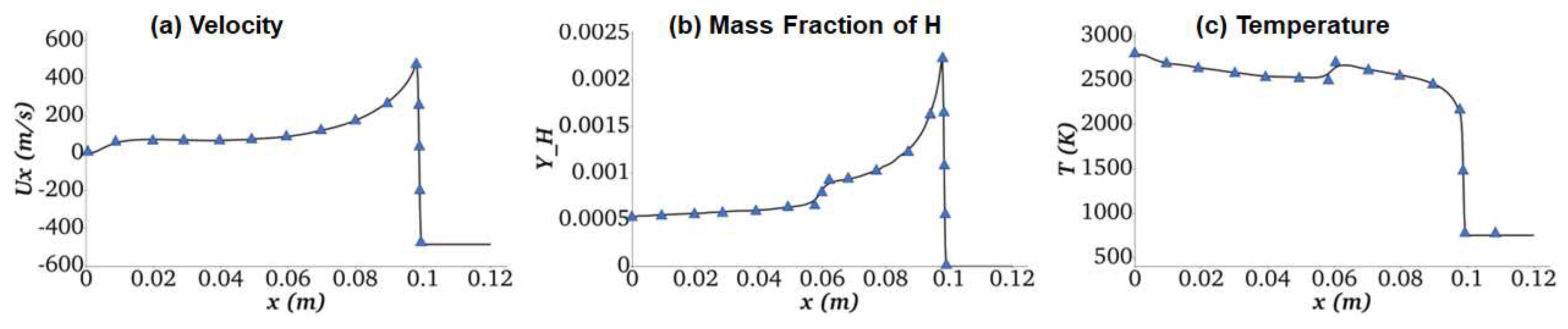
Preprints 92549 g003
Preprints 92549 g004
Figure 4. Temperature profiles of shocks/detonation wave for (a) inert and (b) reactive mixture at various times.
Figure 4. Temperature profiles of shocks/detonation wave for (a) inert and (b) reactive mixture at various times.
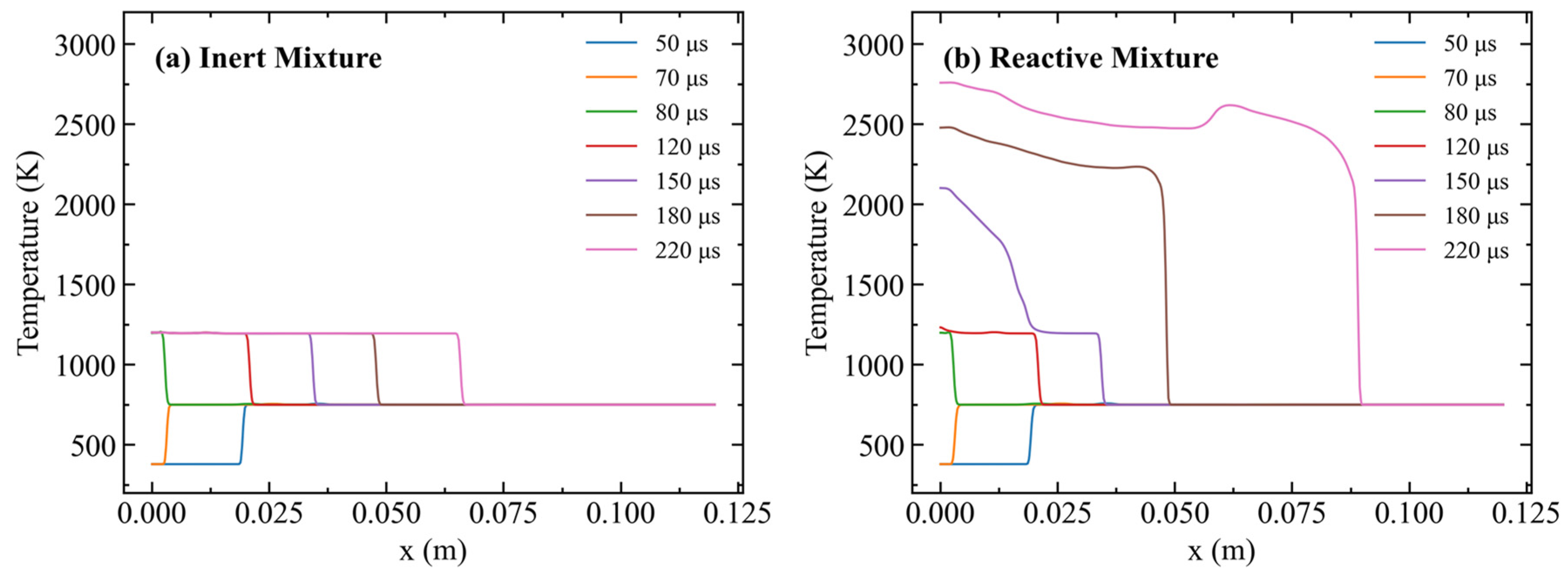
Preprints 92549 g004
Preprints 92549 g005
Figure 5. Computational 3D mesh for simulation of underexpanded jet of Ladenburg experiment. Inflow is shown by the yellow surface, the free stream inlet surface is violet, and the free stream surface is red.
Figure 5. Computational 3D mesh for simulation of underexpanded jet of Ladenburg experiment. Inflow is shown by the yellow surface, the free stream inlet surface is violet, and the free stream surface is red.
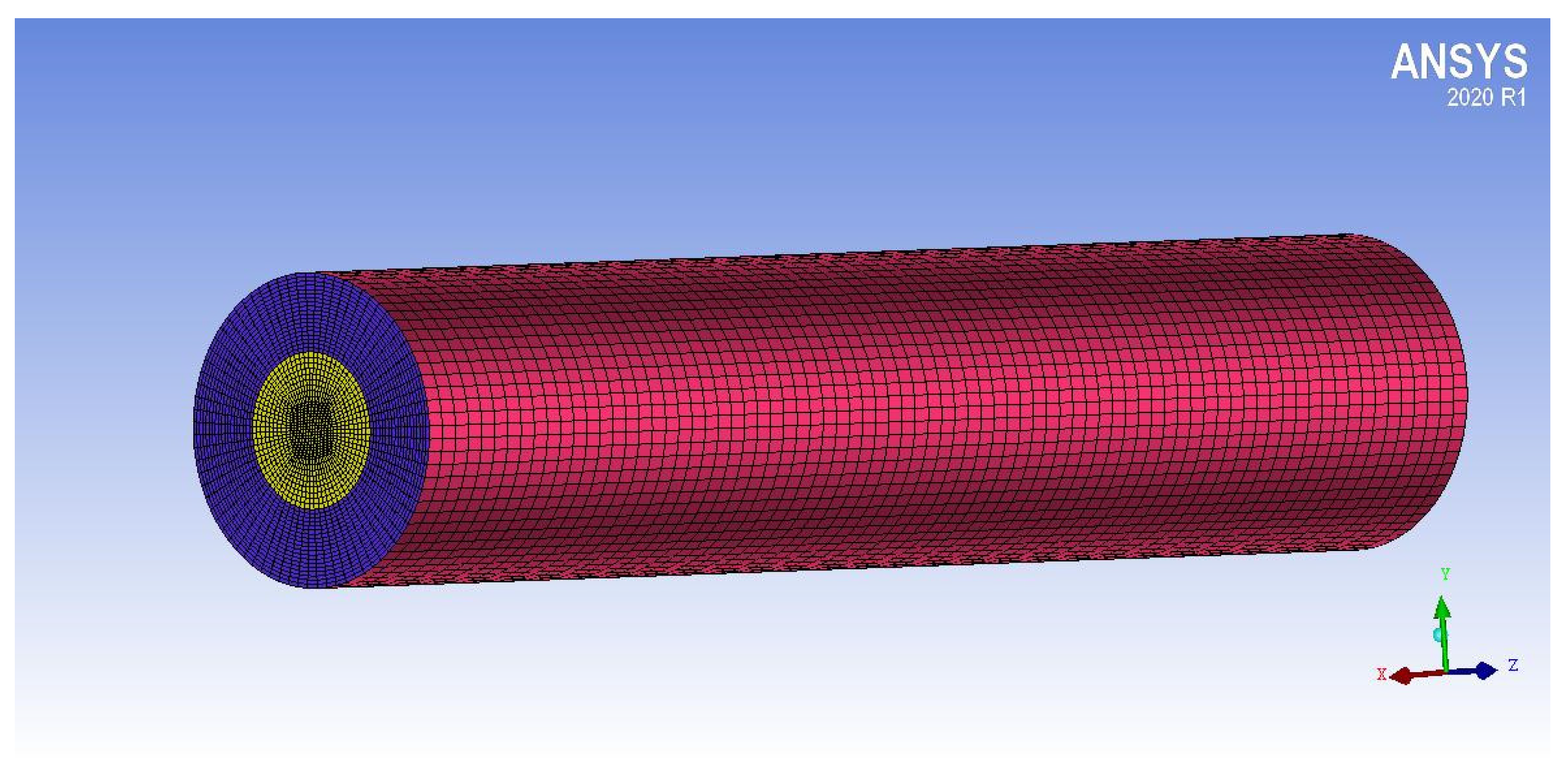
Preprints 92549 g005
Preprints 92549 g006
Figure 6. (a) Schematics of an underexpanded air jet. Keys: 1-expansion waves, 2-oblique shock, 3- normal shock, 4- reflected shock, 5-reflected expansion waves. (b) Contours of Mach numbers at the plane through the center of computational domain (see Figure 5).
Figure 6. (a) Schematics of an underexpanded air jet. Keys: 1-expansion waves, 2-oblique shock, 3- normal shock, 4- reflected shock, 5-reflected expansion waves. (b) Contours of Mach numbers at the plane through the center of computational domain (see Figure 5).
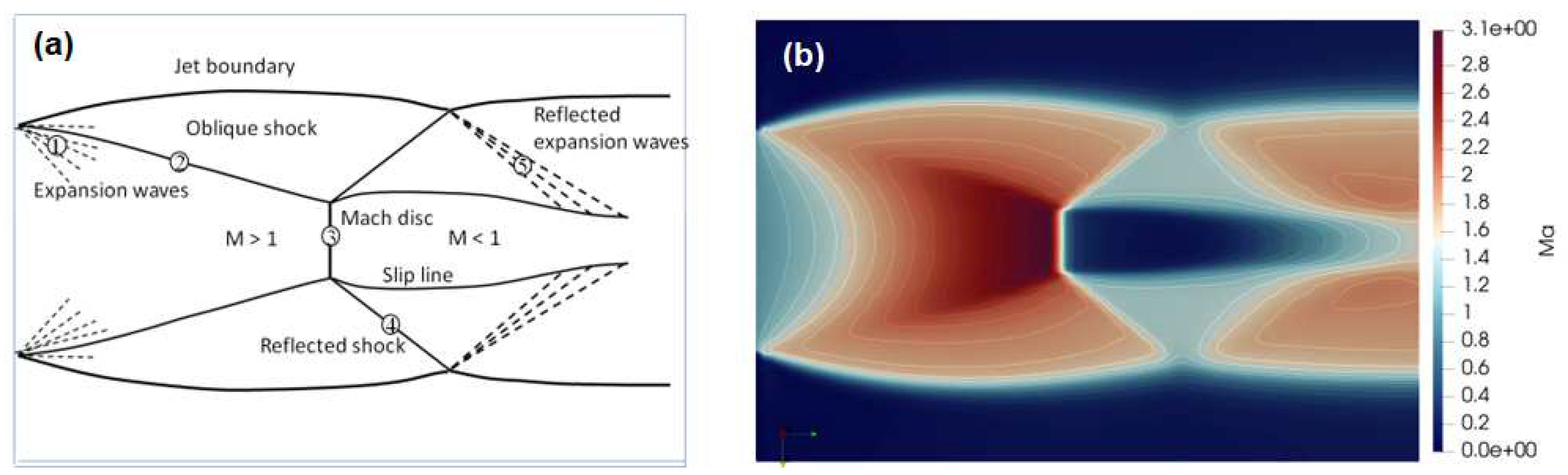
Preprints 92549 g006
Preprints 92549 g007
Figure 7. Density distribution of the supersonic jet measured by Ladenburg [55] (lower panel) compared with current computational results (upper panel). The values of the density contours are provided in kg/m3.
Figure 7. Density distribution of the supersonic jet measured by Ladenburg [55] (lower panel) compared with current computational results (upper panel). The values of the density contours are provided in kg/m3.
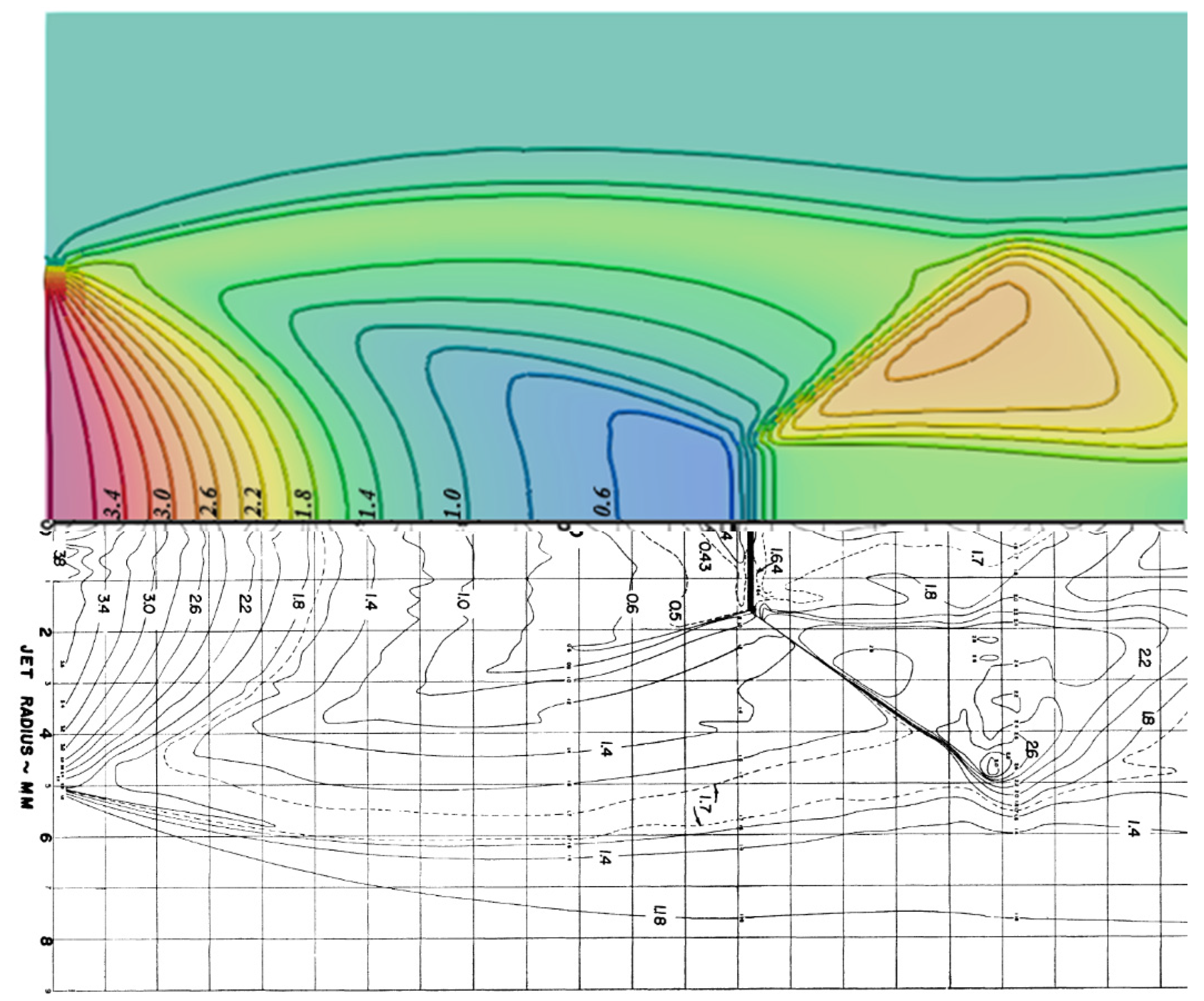
Preprints 92549 g007
Preprints 92549 g008
Figure 8. Geometry of DLR experiment [57]. The 12° wedge provides a stagnation zone for flame holding.
Figure 8. Geometry of DLR experiment [57]. The 12° wedge provides a stagnation zone for flame holding.
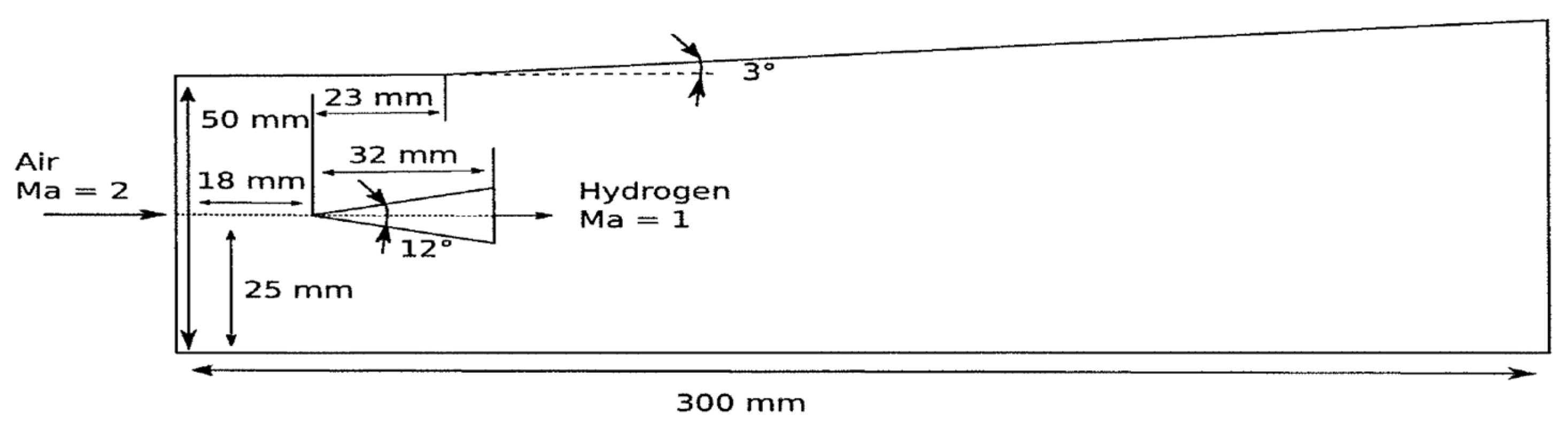
Preprints 92549 g008
Preprints 92549 g009
Figure 9. Computational 2D mesh for simulation of turbulence combustion in DLR.
Figure 9. Computational 2D mesh for simulation of turbulence combustion in DLR.
Preprints 92549 g009
Preprints 92549 g010
Figure 10. (a) Cold flow Schlieren photograph of the channel flow with hydrogen injection [57]; (b) Computational density gradient contours corresponding to the experimental in (a). Labels 1 to 7 in (b) refer to various flow structures discussed in the text.
Figure 10. (a) Cold flow Schlieren photograph of the channel flow with hydrogen injection [57]; (b) Computational density gradient contours corresponding to the experimental in (a). Labels 1 to 7 in (b) refer to various flow structures discussed in the text.
Preprints 92549 g010
Preprints 92549 g011
Figure 11. (a) Normalized density gradient contour; (b) Mach numbers for cold flow.
Figure 11. (a) Normalized density gradient contour; (b) Mach numbers for cold flow.
Preprints 92549 g011
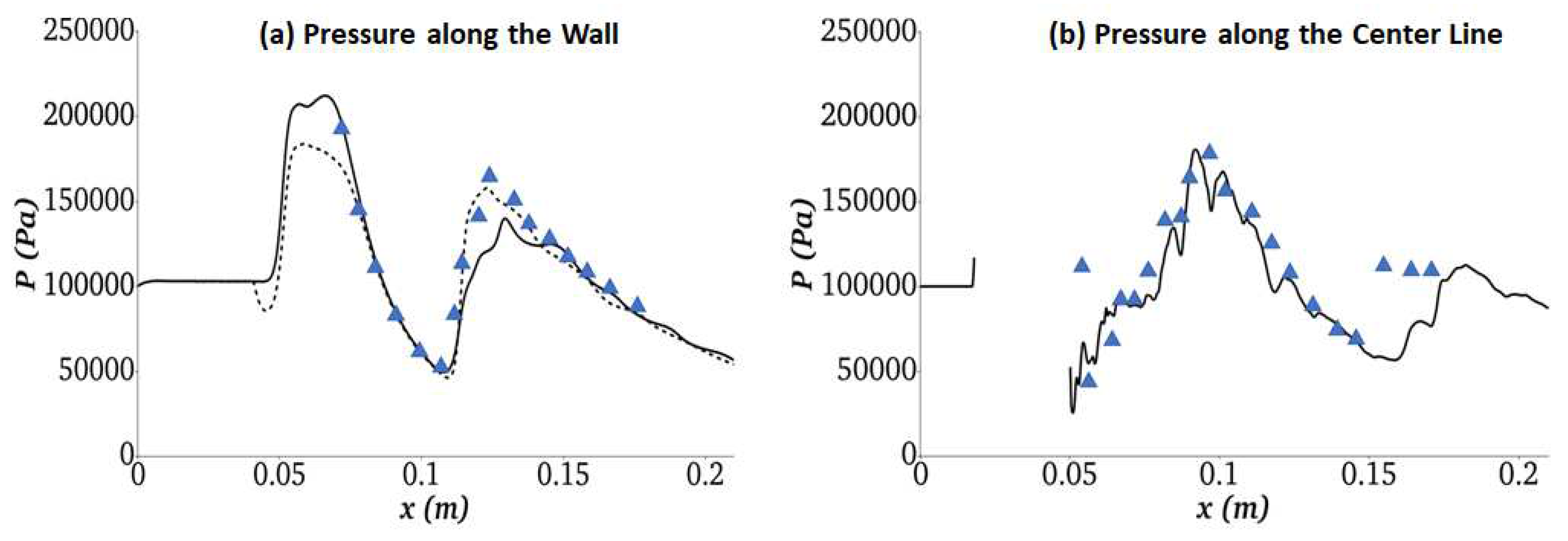
Preprints 92549 g012
Figure 12. (a) Pressure distribution along channel walls. Keys: symbols – experimental data for lower wall [57]; lines – current simulation (solid - lower wall; dashed - the upper wall); (b) Pressure distribution along the centerline. Keys; symbols – experimental data [57]; line – current simulation.
Figure 12. (a) Pressure distribution along channel walls. Keys: symbols – experimental data for lower wall [57]; lines – current simulation (solid - lower wall; dashed - the upper wall); (b) Pressure distribution along the centerline. Keys; symbols – experimental data [57]; line – current simulation.
Preprints 92549 g012
Preprints 92549 g013
Figure 13. (a) Schlieren photograph of the channel flow with hydrogen injection (source: Waidmann et al. [57]); (b) computational density gradient contours corresponding to the experimental conditions of Waidmann et al. [57].
Figure 13. (a) Schlieren photograph of the channel flow with hydrogen injection (source: Waidmann et al. [57]); (b) computational density gradient contours corresponding to the experimental conditions of Waidmann et al. [57].
Preprints 92549 g013
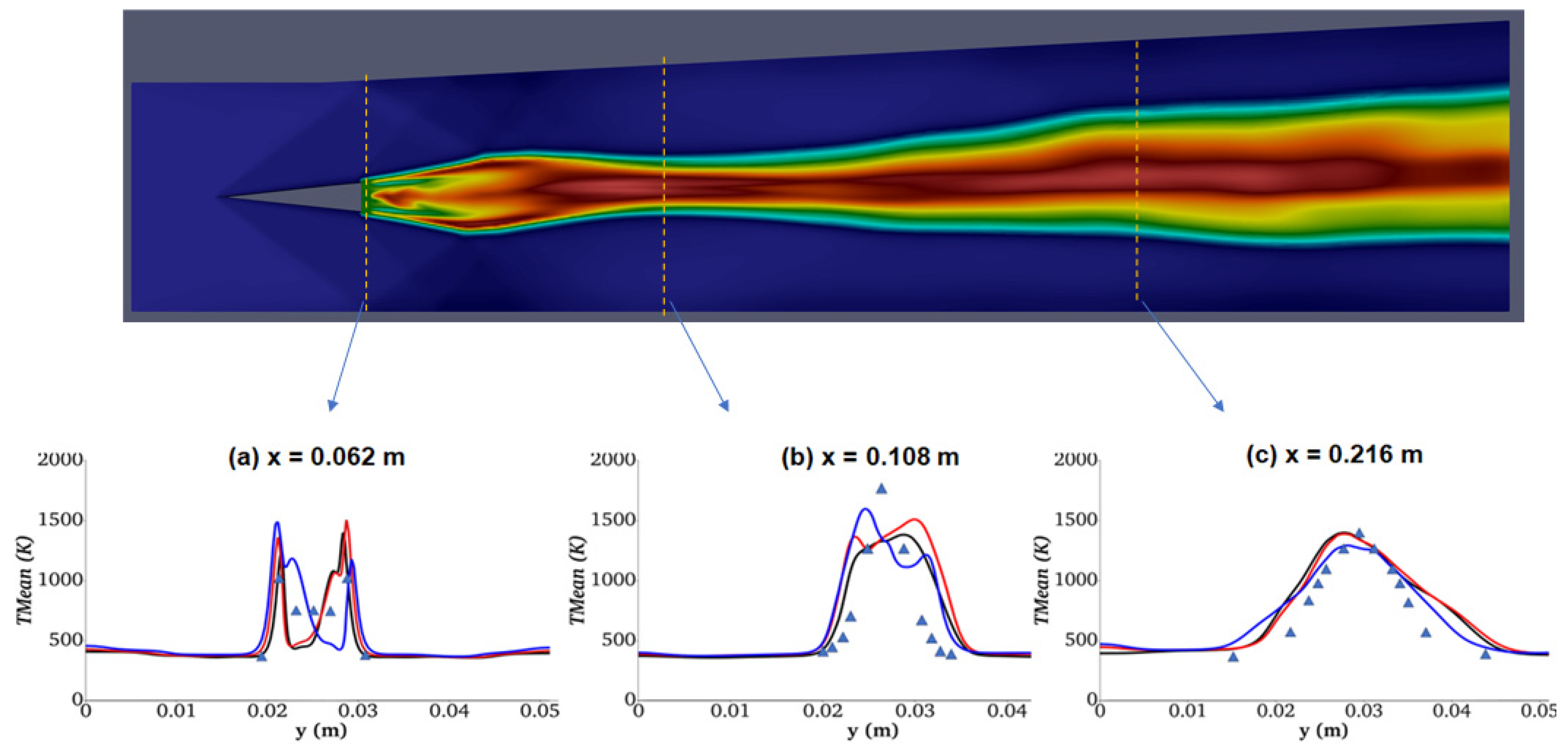
Preprints 92549 g014
Figure 14. Mean temperature at the three cross sections with different turbulence models. Keys: symbols – experimental data [57]; lines – simulation. Color keys: red – WALE; blue – SMG; green – LDkEqn.
Figure 14. Mean temperature at the three cross sections with different turbulence models. Keys: symbols – experimental data [57]; lines – simulation. Color keys: red – WALE; blue – SMG; green – LDkEqn.
Preprints 92549 g014
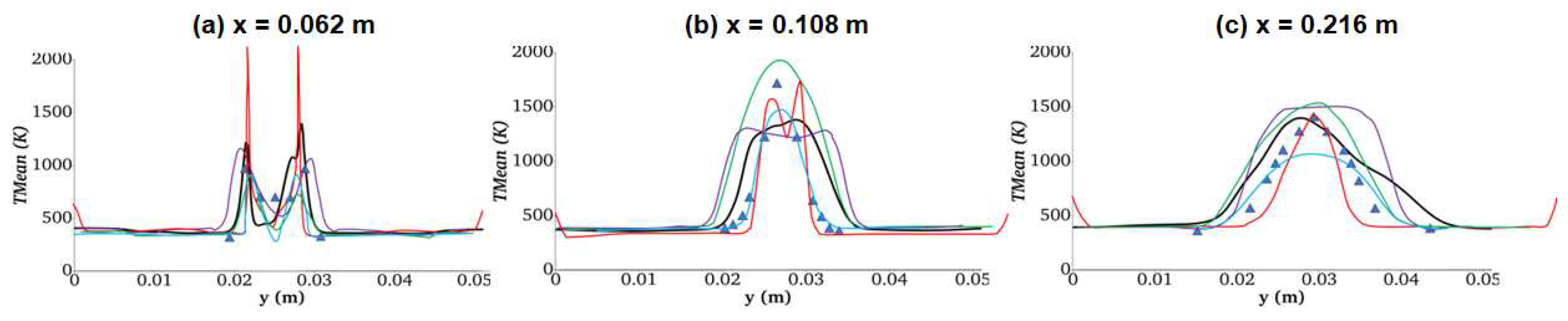
Preprints 92549 g015
Figure 15. Mean temperature at three cross-sections compared with literature simulation data. Keys: symbols – experimental data [57]; lines – simulation. Color keys: black - current simulation with WALE model; red - Berglund and Fureby [60]; green - Genin and Menon [12]; blue - Zhang et al. [30]; purple – Oevermann [58].
Figure 15. Mean temperature at three cross-sections compared with literature simulation data. Keys: symbols – experimental data [57]; lines – simulation. Color keys: black - current simulation with WALE model; red - Berglund and Fureby [60]; green - Genin and Menon [12]; blue - Zhang et al. [30]; purple – Oevermann [58].
Preprints 92549 g015
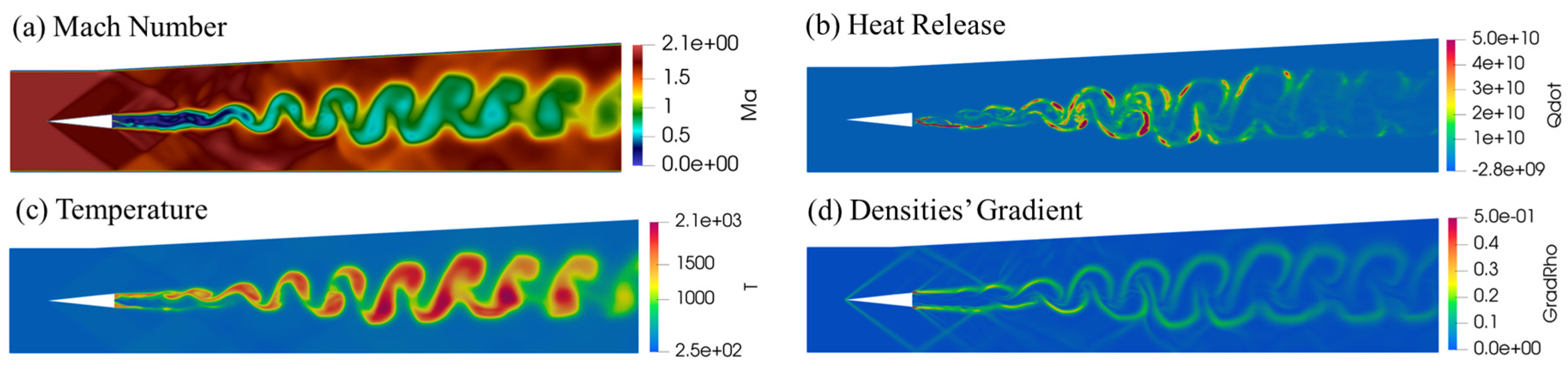
Preprints 92549 g016
Figure 16. Instantaneous distribution of: (a) Mach number; (b) heat release rate per unit volume Q d o t J / s   m 3 ; (c) temperature; (d) normalized contour lines of density gradient.
Figure 16. Instantaneous distribution of: (a) Mach number; (b) heat release rate per unit volume Q d o t J / s   m 3 ; (c) temperature; (d) normalized contour lines of density gradient.
Preprints 92549 g016
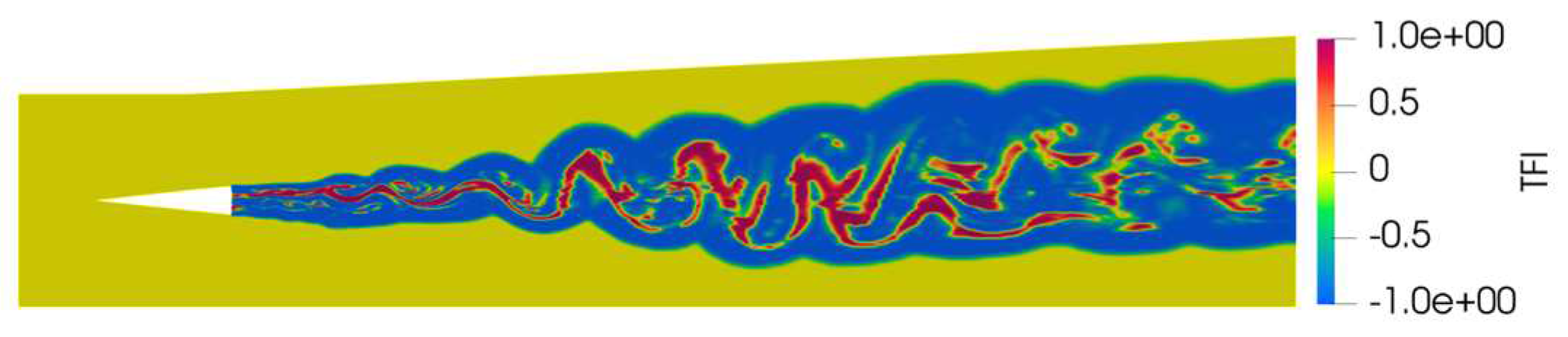
Preprints 92549 g017
Figure 17. Takeno Flame Index (TFI) [59].
Figure 17. Takeno Flame Index (TFI) [59].
Preprints 92549 g017
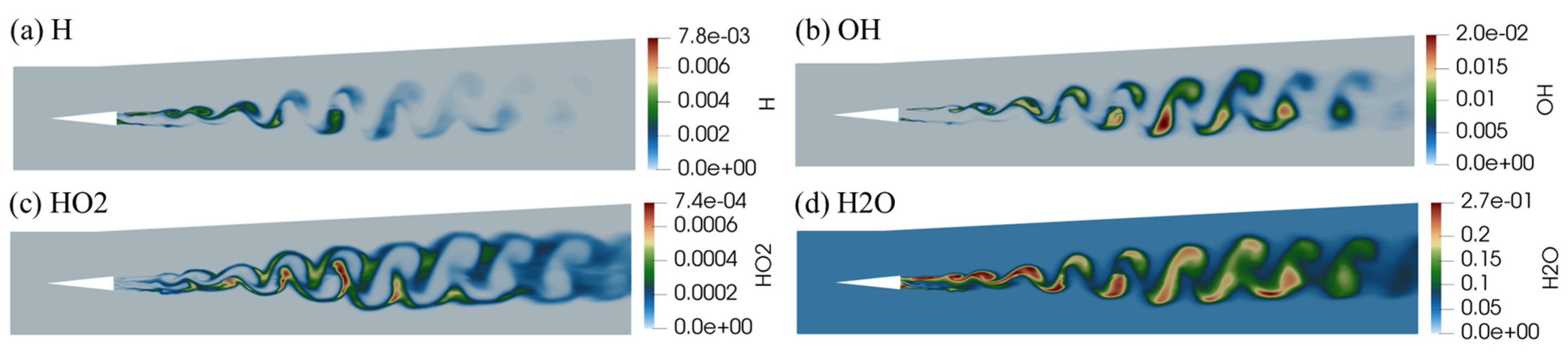
Preprints 92549 g018
Figure 18. Instantaneous distribution of species mass fraction. (a) H ; (b) O H ; (c) H O 2 ; (d) H 2 O .
Figure 18. Instantaneous distribution of species mass fraction. (a) H ; (b) O H ; (c) H O 2 ; (d) H 2 O .
Preprints 92549 g018
Preprints 92549 g019
Figure 19. Instantaneous distribution of: (a) mixture fraction; (b) scalar dissipation rate χ (in the log scale).
Figure 19. Instantaneous distribution of: (a) mixture fraction; (b) scalar dissipation rate χ (in the log scale).
Preprints 92549 g019
Preprints 92549 g020
Figure 20. (a) Borghi diagram [63]; (b) Damköhler number (Da in logarithmic scale); (c) fraction of reactive cells ( γ * ). The white lines indicate locations where D a = 1 .
Figure 20. (a) Borghi diagram [63]; (b) Damköhler number (Da in logarithmic scale); (c) fraction of reactive cells ( γ * ). The white lines indicate locations where D a = 1 .
Preprints 92549 g020
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated