Prerpints.org logo
Preprint
Article

Crystallization Behavior of Na2O-GeO2-P2O5 Glass System: (Micro)Structural, Electrical, and Dielectric Study

Altmetrics

Downloads

110

Views

36

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.pdf (719.28KB )

Submitted:

07 December 2023

Posted:

07 December 2023

You are already at the latest version

Alerts
Abstract
Sodium-phosphate-based glass-ceramics (GCs) are promising materials for a wide range of applications, including solid-state sodium-ion batteries, microelectronic packaging substrates, and humidity sensors. This study investigates the impact of 24-hour heat-treatments at varying temperatures on Na-Ge-P glass, with a focus on (micro)structural, electrical, and dielectric properties of prepared GCs. Various techniques such as powder X-ray diffraction (PXRD), infrared spectroscopy-attenuated total reflection (IR-ATR), and scanning electron microscopy-energy dispersive spectroscopy (SEM-EDS) are employed. With the elevation of heat-treatment temperature, crystallinity progressively rises; at 450 °C, the microstructure retains amorphous traits featuring nanometric grains, whereas at 550 °C, heat-treatment results in fully crystallized structures characterized by square-shaped micron-scale grains of NaPO3. The insight into the evaluation of electrical and dielectric properties is provided by Solid-State Impedance Spectroscopy (SS-IS), revealing a strong correlation with the conditions of controlled crystallization and observed (micro)structure. The glass-ceramic heat-treated at 450 °C achieves the highest DC conductivity of 2.30×10–8 Ω–1 cm–1 at 393 K. As the heat-treatment temperature rises, the crystallization of the NaPO3 phase depletes the glass matrix of mobile Na+ ions, resulting in a reduction in DC conductivity. Dielectric parameters also decrease with rising heat-treatment temperature, with the glass-ceramic heat-treated at 550 °C displaying the lowest permittivity of 19.37 and the dielectric loss of 0.008. This research uncovers the intricate relationship between heat-treatment conditions and material properties, emphasizing that controlled crystallization allows for precise modifications to microstructure and phase composition within remaining glassy phase, ultimately facilitating fine-tuning of material properties.
Keywords: 
Subject: Chemistry and Materials Science  -   Ceramics and Composites

1. Introduction

The ever-expanding energy demands arising from modern lifestyles and rapid advancements within the electronics sector underscore the need for the development of novel, sustainable, and renewable materials specifically tailored for integration into electronic devices and circuits. This necessity covers a wide range of applications, from solid-state batteries (SSB) [1] and capacitors [2] to microelectronic packaging substrates [3] and humidity sensors [4,5]. In the pursuit of high-efficiency materials, considerable efforts have been channeled towards exploring inorganic materials, with a notable focus on oxide glasses and glass-ceramics (GC). These materials garner significant interest in electrical technologies due to their dense and uniform microstructures, marked by a low grain boundary effect, along with their inherent capability for precise adjustment to achieve optimal properties, including robust mechanical and thermal stability, as well as exceptional electrical and dielectric properties [6,7,8]. In contrast to oxide glass, where physicochemical properties are primarily determined by chemical composition, glass-ceramics offer a unique advantage in a way that their properties are influenced not only by composition or crystallographic structure but also by microstructure and the precise type and quantity of crystalline phase(s) within the residual glassy phase. The latter can be precisely controlled by adjusting heat-treatment (HT) conditions, including temperature and duration.
One property that exhibits a strong dependence on the controlled crystallization process is ionic conductivity, and multiple studies have consistently confirmed a significant enhancement in ionic conductivity in the resulting glass-ceramic [6]. Amongst the studied systems, NASICON-type phosphates have received particular attention owing to their exceptional conductivity, reaching levels on the order of 10–3 S cm–1 [9]. Within this group, the LiGe2(PO4)3-based systems have been subject of extensive investigation [10,11,12,13,14,15,16], showcasing promise as solid electrolyte materials [17,18]. Thorough research into this system has persistently demonstrated that precise control over crystallization leads to a notable enhancement in ionic conductivity, with temperature and HT duration emerging as pivotal factors not only in the formation of conductive crystal phases but also in determining the size of resulting crystal grains and the porosity of the samples [12,13,14,15,16]. Although it has been recognized that increased conductivity is often associated with nanocrystallization [6], a study of the LiAlGePO4 system by Cruz et al. [12] revealed that nanometric grain sizes don't necessarily promote electrical conductivity, and the highest conductivity values were achieved in a GC sample with micrometric grain size and porous microstructure. Besides Li-Ge-P-based GC systems, their sodium counterparts, like the one from NaSnGePO4 system [19], have been gaining growing interest due to their potential use in sodium SSB, which are increasingly recognized as a safer, cost-effective, and environmentally friendly alternative to Li-based SSBs [20,21]. Beyond their role as electrolyte materials, sodium phosphate compounds have emerged as highly prospective candidates for ionically conducting inorganic binders in electrode materials, further enhancing their potential in battery technology [22].
Besides their use in SSBs, glasses-(ceramics) with low dielectric constants are sought-after as substrate materials for high-speed microelectronic packaging [3,23]. Reducing the dielectric constant of these materials typically involves utilizing less polarizable lighter elements like Na, P, and O, primarily due to the influence of factors such as atom size and electron number density. Another effective approach for achieving a lower dielectric constant is increasing porosity, and controlled crystallization thus provides a convenient means to modify the dielectric properties of these materials. On the other hand, porous GCs can also demonstrate favorable humidity-sensing properties, as water molecules have the capacity to physically adsorb on the grain surface within the pores, depending on the relative humidity [24,25]. An example of such a system are the Na-Mo-P GCs from our prior research, where it was demonstrated that specifically the samples with a porous microstructure exhibit outstanding humidity-sensing capabilities [26]. Building upon our research group's prior work, which demonstrated the efficacy of Solid-State Impedance Spectroscopy (SS-IS) for the comprehensive analysis of electrical and dielectric properties in phosphate-based glasses [27,28,29,30] and GC materials [26,31,32,33,34], including its utility in studying dielectric relaxation phenomena, assessing the dielectric loss factor, and distinguishing between bulk and grain boundary contributions, we have chosen to investigate the electrical and dielectric properties of GCs prepared from the 40Na2O-xGeO2-(60-x)P2O5 glass system described in [29].
This study investigates the impact of HT temperature on the (micro)structural, electrical, and dielectric properties of GCs produced through the controlled crystallization of an initial glass with a nominal composition of 40Na2O-10GeO2-50P2O5 whose structural, thermal and electrical properties are detailed in [29]. The structural and microstructural properties of the prepared GCs are examined through powder X-ray diffraction (PXRD), infrared spectroscopy-attenuated total reflection (IR-ATR), and scanning electron microscopy-energy dispersive spectroscopy (SEM-EDS). The findings reveal that as the HT temperature rises, there is a gradual increase in crystallinity. Moreover, the microstructure undergoes a transition, evolving from a primarily amorphous glass matrix with nanometric crystalline grain sizes in the NGP@450 GC to a fully crystallized microstructure featuring large grains with micron-scale dimensions in the NGP@550 GC. Solid-State Impedance Spectroscopy (SS-IS) is employed to study the electrical and dielectric properties, and the results underscore their strong correlation with the (micro)structural characteristics. In crystallized samples, the DC conductivity experiences a decline in comparison to the initial glass. Among the GCs under examination, the NGP@450 stands out with the highest DC conductivity, measuring 2.30×10–8 Ω–1 cm–1 at 393 K. On the other hand, with an increase in the HT temperature to 550°C, a GC sample NGP@550 is produced, which exhibits the lowest values for dielectric parameters, including a dielectric permittivity of 19.37 and a dielectric loss of 0.008. This research elucidates the intricate relationship between HT temperature and material properties, arising from the changes in the microstructure, emphasizing the vast potential of these materials across various technological applications.

2. Materials and Methods

Within the glass series 40Na2O-xGeO2-(60-x)P2O5 described in [29], a glass with the composition 40Na2O-10GeO2-50P2O5 (referred to as the initial glass and denoted in mole fractions of individual oxides) is chosen for the study of the crystallization process and the impact of (micro)structural changes on the electrical and dielectric properties of the prepared glass-ceramics (GCs). The starting glass, labeled as NGP, is prepared from raw materials through the melt quenching technique according to the procedure described in [29]. The conditions for the controlled crystallization of NGP glass are selected based on the results of the differential thermal (DTA) analysis [29], and the heat-treatment (HT) is performed for 24 hours at temperatures of 450 °C, 500 °C, and 550 °C. As a result, three distinct GCs, named NGP@450, NGP@500 and NGP@550, are synthesized. GCs formed through processing @450 °C and @500 °C exhibit a whitish/brown-whitish colour and maintain their structural integrity after thermal treatment. These samples are compact and easily prepared for structural analysis and electrical measurements. However, the GC obtained @550°C deforms during the HT process, resulting in an exceptionally thin and fragile sample that presents challenges when preparing it for electrical measurements.
The structure of the glass and glass-ceramic samples is examined using IR-ATR spectroscopy with a Thermo Fisher Nicolet iS50 FT-IR instrument. The crystalline phases formed during thermal treatment and their weight percentages are determined via powder X-ray diffraction (PXRD) analysis using Bruker D8 Discover diffractometer (Bruker AXS GmbH, Karlsruhe, Germany) with a LYNXEYE XE-T detector. PXRD patterns are recorded in the range of 10° ≤ 2θ ≤ 70° with CuKα radiation (1.5418 Å). Rietveld structure refinement is conducted using the HighScore X’pert Plus program 3.0 (Malvern Panalytical, Almelo, The Netherlands). Scanning electron microscopy with energy dispersive X-ray spectroscopy (SEM-EDS) analysis is performed with a Jeol 7000 FE-SEM to gain detailed insights into the morphology and composition of prepared samples. Gold electrodes are deposited on both sides of the samples using a Sputter Coater SC7620. The electrical and dielectric properties of both the initial glass and the prepared GCs are examined using Solid-State Impedance Spectroscopy (SS-IS). Complex impedance, Z*(ω), is measured across a wide frequency range (0.01 Hz–1 MHz) and temperature range (273–523 K) with an impedance analyzer (Novocontrol Alpha – AN dielectric spectrometer). Complex electrical conductivity, σ*(ω), permittivity, ε*(ω), and electrical modulus, M*(ω), are calculated from the experimental values of real and imaginary components of complex impedance, along with sample geometry.

3. Results and Discussion

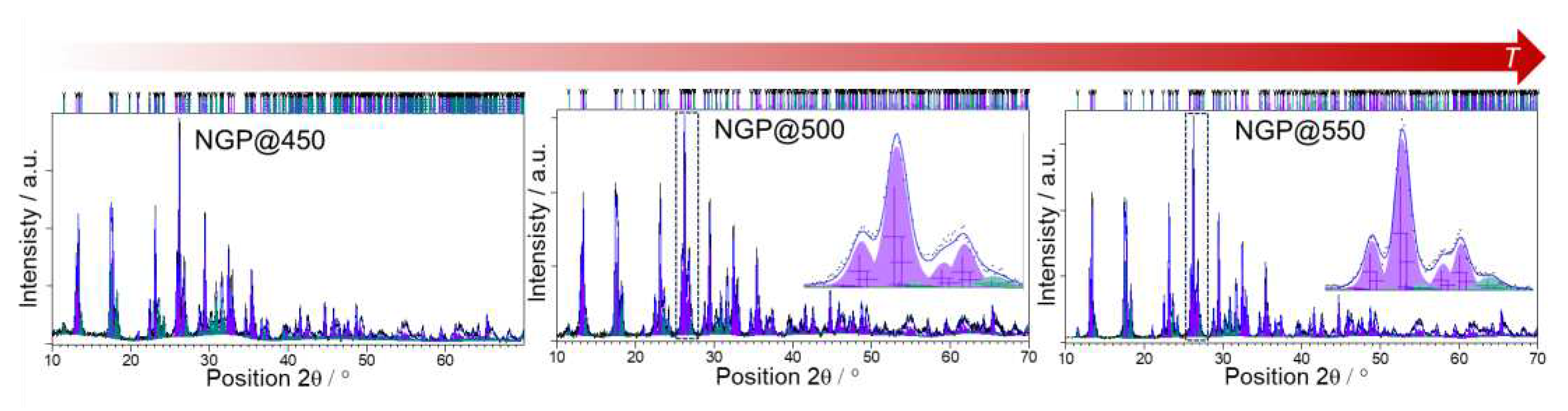
3.1. Structural and microstructural analysis

3.1.1. PXRD analysis

The PXRD analysis shows that all three GCs contain identical crystalline phases, namely NaPO3 (ICSD-18139) [35] and GeP2O7 (ICSD-74876) [36], seeFigure 1. In contrast to the PXRD pattern of NGP@450, the PXRD patterns of NGP@500 and NGP@550 do not exhibit the typical amorphous halo, usually observed between 20–30°. This absence indicates a minimal, if not negligible, presence of any remaining amorphous phase.
Quantitative phase analysis performed with Rietveld refinement showed NaPO3 to be the dominant crystal phase in all three samples, with GeP2O7 being the minor one. In the NGP@450 sample, the weight fraction of the NaPO3 crystal phase is 75.0(8)%, and the GeP2O7 crystal phase constitutes 25.0(9)%. Furthermore, in the NGP@500 sample, the weight fraction of the NaPO3 is 76.4(7)%, while GeP2O7 crystal constitutes 23.5(9) %. At the highest temperature, the ratio of two crystal phases remains similar, with 74.3(8)% of NaPO3 and 25.7(9) % of GeP2O7. These results indicate that elevating the crystallization temperature has a negligible impact on the quantitative composition i.e., the ratio of crystalline phases. However, it can be observed that amorphous halo, quite pronounced at 450 °C, diminishes at higher temperatures while the width of diffraction lines becomes narrower. These observations are further reinforced by the IR-ATR spectroscopy results, as illustrated in Figure S1(a) in the Supplementary Materials (SM). It's noteworthy that the IR-ATR spectroscopic results of the initial NGP glass closely align with prior findings from Raman spectroscopy [29], indicating a predominance of metaphosphate structure with traces of pyrophosphate units [37,38]. In the case of NGP@450, these results reveal a significant presence of the glass matrix, coupled with subtle changes in band shapes that signal the initial stages of crystallization. In contrast, the spectra of NGP@500 and NGP@550 exhibit remarkable similarity, characterized by sharp signals typically associated with crystalline materials, indicating a notably high degree of crystallinity. These findings are in alignment with the PXRD analysis. Moreover, when the IR-ATR spectra of the prepared samples are compared to the spectrum of the NaPO3 crystal phase from the SpectraBase®, it reveals a notable agreement, providing additional support for the PXRD analysis results that emphasize the prevalence of the NaPO3 crystal phase.

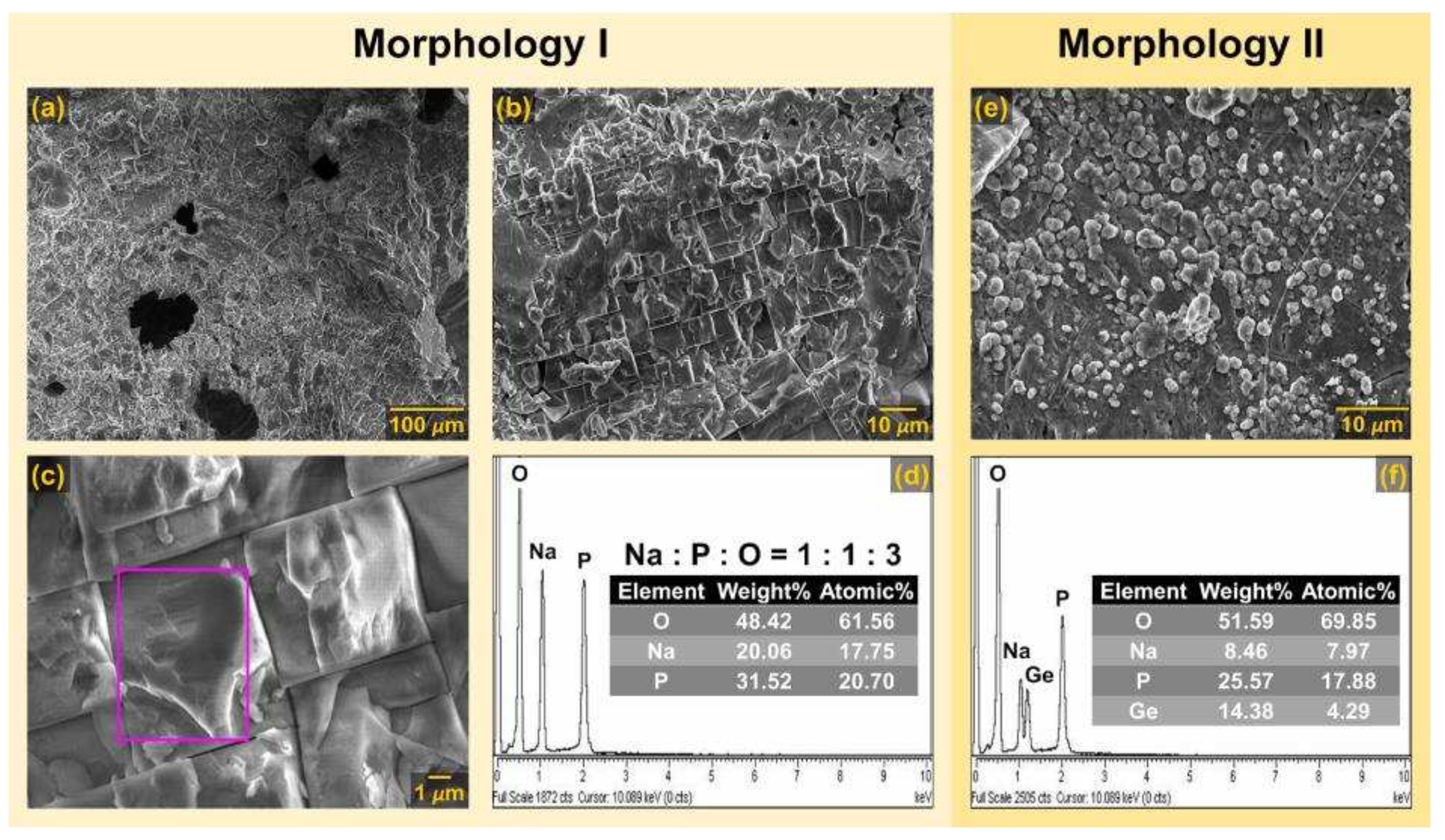
3.1.2. SEM-EDS analysis

Upon examining the acquired SEM micrographs, it becomes apparent that the surface of NGP@450 lacks visible crystals when observed at lower magnifications (X5k), see Figure S2(a) in the SM. Instead, aggregates resembling phase separations within the amorphous matrix are observed at higher magnifications (X25k), see Figure 2(a) and Figure S2(b) in the SM. However, at the highest magnifications of X30k, randomly dispersed nanosized grains are distinguished, measuring less than 50 nm, growing on the predominant amorphous glass matrix's surface, see Figure 2(b) and Figure S2(c) in the SM.
The observed grains can be attributed to the prevalent NaPO3 crystalline phase, as supported by the PXRD results for NGP@450, see Figure 1. Additionally, the EDS analysis results indicate that the GC obtained through HT at the lowest temperature of 450 °C predominantly consists of an amorphous matrix, with germanium detected on all analyzed surfaces, see Figure S2 in the SM. Upon raising the crystallization temperature to 500 °C, the surface of NGP@500 exhibits randomly scattered grains with sizes ranging from 100 to 500 nm, lacking a distinct morphology, as shown in Figure 2(c,d). The EDS analysis of grains on the surface of NGP@500 reveals an approximate Na:P:O ratio of 1:1:3, see Figure S3 in the SM, providing further validation to the PXRD and IR-ATR analysis results, which indicate the presence of the dominant crystalline phase, NaPO3. Unlike the previous two GC samples, the NGP@550 displays conspicuous surface features: large crystalline grains with micron-scale dimensions, as depicted in Figure 3(a-c). These grains have well-defined shape, predominantly appearing as regular squares (Morphology I), see Figure 3(c). In this region, EDS analysis exclusively detects Na, P, and O elements, with a Na:P:O ratio of 1:1:3, see Figure 3(d), thus unequivocally confirming that the square-shaped crystalline grains are indeed of the NaPO3 phase, which constitutes the majority of the NGP@550, as evidenced by PXRD and IR-ATR.
However, a different crystal morphology (Morphology II) in the shape of smaller spherical grains is also evident, as shown in Figure 3(e). The results of EDS analysis conducted in this region reveal a significant presence of Ge, alongside Na, P, and O elements, see Figure 3(f), suggesting that Morphology II may be associated with the minor GeP2O7 crystalline phase.
It is noteworthy that the EDS analysis results reveal a similarity in elemental compositions between NGP@500 and NGP@550 samples with dominant crystalline NaPO3 phase. However, while the grains in the NGP@500 lack a regular shape, the GC obtained at the higher crystallization temperature of 550°C exhibits a distinct, well-defined square shape. On the other side, while Ge is present on all analyzed surfaces of the NGP@500, it is either absent or found in minimal quantities in the NGP@550. This may be attributed to the reduced presence of a glass matrix or to its absence in the latter sample. The SEM-EDS analysis hence clearly demonstrates the progressive increase in crystallinity and the decrease in the amount of the residual amorphous phase in the prepared samples as the HT temperature rises. It is noteworthy that raising the HT temperature from 500 to 550 °C has no discernible impact on the composition and amount of crystalline phases. However, it does significantly influence the microstructure of the resulting GCs, a factor that will be discussed further due to its significant effect on electrical transport.

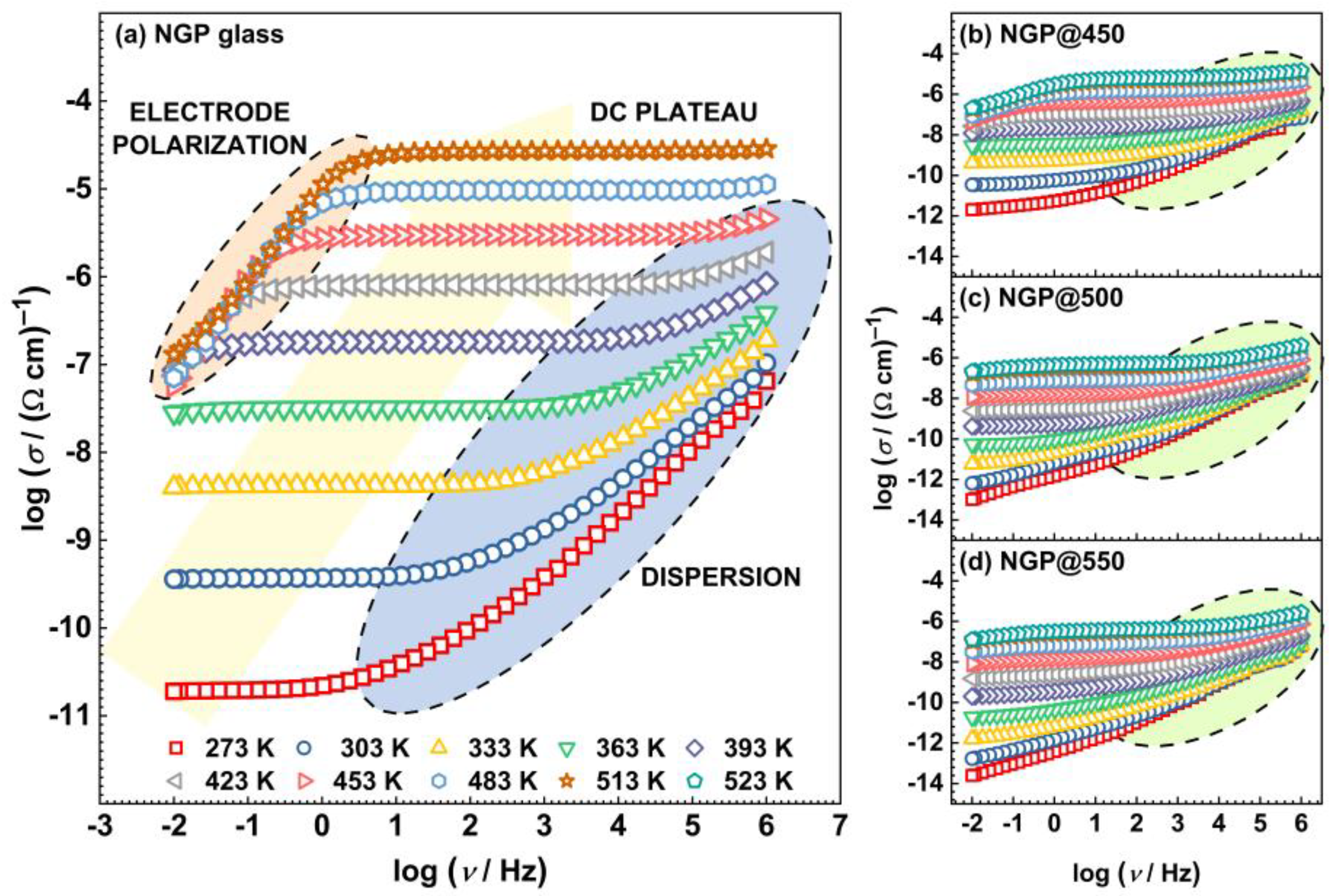
3.2. Electrical analysis

3.2.1. Electrical conductivity

Figure 4 shows the conductivity spectra of the initial NGP glass and all prepared GC samples. In the presented spectra for the initial glass, see Figure 4(a), three different areas are distinguished. At low temperatures and frequencies, conductivity demonstrates a frequency-independent behavior due to long-range ion motion, resulting in a constant value referred to as the DC plateau, σDC. Conversely, at low frequencies and higher temperatures, conductivity decreases due to electrode polarization (EP), which is a consequence of Na+ ion accumulation on gold electrodes. At high frequencies, a dispersion region emerges, indicating short-range ion motion. The difference in the shape of the spectra of the initial glass, see Figure 4(a), and GCs, see Figure 4(b-d), is most pronounced in the dispersion part of the curves and is caused by the different contributions (amorphous phase, crystalline grains, grain boundaries, etc.) to the total conductivity.

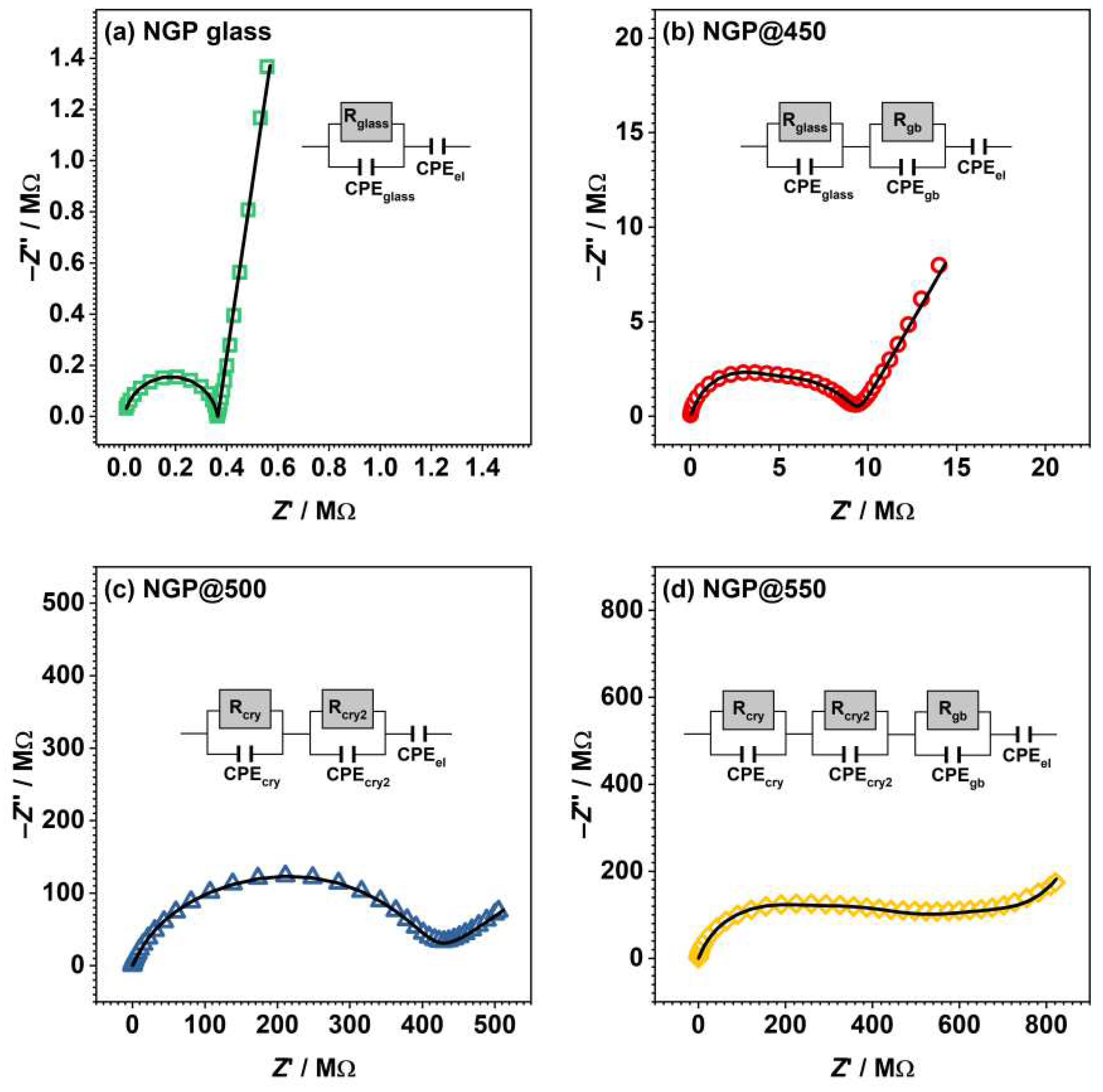
3.2.2. Complex impedance plane

In order to illuminate the various contributions to total conductivity, the experimental results are presented in the form of Nyquist plots, see Figure 5. The complex impedance spectra of the investigated samples undergo substantial changes as the initial glass crystallizes during the HT process, progressing from 450°C to 550°C. The initial glass displays a single depressed semicircle with a noticeable EP effect, while crystallized products reveal two or more depressed semicircles, and the influence of EP gradually wanes with rising HT temperature. Since the shape of each complex impedance spectrum is directly affected by various processes and effects, such as the presence of crystal and/or amorphous phases (glass matrix), crystal grain boundaries, and EP, the distinct shapes in the complex impedance spectra result from the impact of HT on the microstructure of the obtained GCs. By employing modeling with the appropriate electrical equivalent circuit (EEC), the resulting fitting parameters, specifically resistance and capacitance, can be linked to each process or effect, thus assigning a physical significance to them [39]. The EECs used for modeling the samples from this study are presented in Figure 5, and the corresponding fitting parameters are listed in Table S1 in the Supplementary Materials.
As mentioned earlier, the spectrum of the initial NGP glass is characterized by a single high-frequency semicircle representing the bulk conductivity of the glass sample and a low-frequency linear segment, indicative of EP which is a signature of ionic conductivity, see Figure 5(a). The corresponding EEC model describing the experimental impedance spectrum comprises a parallel R-CPE circuit, where R stands for resistance, CPE represents the constant-phase element, and EP is represented through a series-connected CPE. Conversely, the complex impedance spectrum of the NGP@450 is represented by an EEC model incorporating two R-CPE circles and an additional series-connected CPE, as depicted in Figure 5(b). The capacity values of the high-frequency semicircle are on the order of ~10–12 F, see Table S1, indicating its association with the predominant glass matrix phase. Furthermore, the low-frequency semicircle, with a capacity on the order of ~10–11 F, is correlated with the grain boundary effect, which emerges due to the beginning of crystallization observed in this sample. This correlation is substantiated by findings from PXRD, SEM-EDS, and IR-ATR analyses. The identical EEC model is utilized for interpreting the complex impedance spectrum of NGP@500 sample. Nonetheless, as this sample is primarily composed of two crystalline phases, NaPO3 and GeP2O7, with NaPO3 being the prevailing phase, the first contribution is ascribed to the dominant crystalline phase NaPO3, while the second contribution can be attributed to the less prominent crystalline phase, GeP2O7. This is further corroborated by the similar capacity values of the two contributions, both falling within the order of magnitude of ~10–11 F, see Table S1.
Increasing the HT temperature to 550 °C brings about an intriguing change in the shape of the complex impedance spectrum. To analyze the spectrum of NGP@550 sample, a model featuring three R-CPE circuits with an additional series-connected CPE element is applied, as depicted in Figure 5(d). While this sample maintains nearly the same composition, with identical crystal phases and similar relative proportions as NGP@500, its impedance spectrum reveals an extra semicircle. Based on the capacitance values acquired through EEC modeling, which are approximately in the order of 10–12 F, 10–11 F, and 10–9 F, the first contribution is ascribed to the prevailing NaPO3 crystal phase, the second one is assigned to the minor GeP2O7 phase, and the third one is a result of the crystal grain boundary. The distinct contributions from the crystal grain boundary and crystalline phases in this GC sample emerge due to the formation of clearly defined crystal grains and sharp grain boundaries, see Figure 3(a-c). This pronounced change in morphology profoundly influences the electrical transport within the prepared GC samples. Aside from the observed modifications in the shape of the depressed semicircles and the number of distinct contributions due to microstructural changes, it is also intriguing to note the impact of the HT temperature on the extent of electrode polarization (EP), which is linked to sodium ion mobility. It can be observed that EP gradually decreases with increasing HT temperature, indicating a reduction in sodium ion mobility within the prepared GC. This can be attributed to the promoted crystallization of the dominant NaPO3 crystalline phase, which leads to a reduction of mobile Na+ ions within the remaining glass matrix. This aspect will be further discussed in the following chapters.

3.2.3. DC conductivity and activation energy

From the obtained conductivity spectra, see Figure 5, the values of DC conductivity, σDC, are determined from the DC plateau, and where it is not possible to determine them from experimental data, they are calculated from the value of the total resistance, Rtot, obtained by modelling the impedance spectra in the complex impedance plane. The activation energy for DC conductivity, EDC, is calculated for all samples according to Equation (1):
σDCT = σ0*exp(–EDC/kBT),
where T is the temperature, σ0* pre-exponential factor, and kB Boltzmann's constant. The dependence of σDC on T is shown in Figure 6(a), while the values of σDC at 393 K, and EDC are listed in Table 1 and their dependence on the crystallization temperature is shown in Figure 6(b).
As the crystallization temperature increases, σDC continuously decreases, whereas the activation energy demonstrates the expected opposite trend. As previously explained, the observed trends are likely a consequence of the enhanced crystallization of the NaPO3 phase, depleting the remaining glass matrix of mobile Na+ ions. Nonetheless, the crystal grains are not connected enough to achieve an increase in conductivity by creating easy conduction pathways at the grain boundaries.
As the GC samples from this study predominantly consist of the NaPO3 crystalline phase, it is intriguing to compare the measured values of σDC and EDC with those of crystalline NaPO3. The crystalline NaPO3 demonstrates an ionic conductivity of 6.1×10−11 Ω−1 cm−1 at 60 °C, with and activation energy of 0.66 eV [22]. This closely aligns with the σDC and EDC values observed in the studied GC samples, where the conductivity spans from 4.10×10−10 for NGP@450 to 1.58×10−12 Ω−1 cm−1 for NGP@550 at 60 °C, and the activation energy is within the range of 0.79–1.11 eV.

3.3. Dielectric analysis

3.3.1. Complex permittivity

The dielectric properties of the prepared GCs are thoroughly analyzed using complex permittivity, ε*(ω), as defined by Equation (2):
ε*(ω) = 1/(iωC0Z*) = ε’(ω) – iε’’(ω),
where ε’(ω) and ε’’(ω) are the real and imaginary parts of the complex permittivity. The real component, ε’(ω), is commonly known as the dielectric constant. The frequency dependences of ε’(ω) and ε’’(ω) for the NGP@500 sample as representative of all the studied samples are shown in Figure 7(a,b).
The frequency-dependent behavior of ε’(ω), which represents the dielectric permittivity, reveals two distinct characteristics stemming from electrode polarization and bulk permittivity. Electrode polarization manifests in the highest ε’(ω) values observed at the lowest frequencies and highest temperatures, and it is a consequence of sample polarization induced by the presence of blocking gold electrodes. As the frequency increases, ε’(ω) exhibits a stepwise decline due to dipole relaxation, driven by the alignment of dipoles under the applied field. At the highest frequencies and lowest temperatures, ε’(ω) stabilizes at a constant value, as fast polarization processes take place within the glass under the applied field. In contrast, ε’’(ω) exhibits a decreasing trend with increasing frequency, attributed to translational diffusion, i.e. the long-range movement of mobile ions associated with DC conductivity [40]. The values of ε’(ω) measured at 303 K and 10 kHz for the investigated glass and GCs can be found in Table 1. Notably, GC samples exhibit an increase in ε’(ω) if compared to the initial glass. However, a rise in the temperature of HT results in a gradual decrease of ε’(ω), with the NGP@450 GC displaying the highest value among the studied samples.
Another important parameter that can be extracted from the permittivity data is the loss factor, known as tan δ. This factor quantifies the phase difference resulting from energy dissipation within the sample at a specific frequency and is calculated as tan δ = ε’(ω)/ε’’(ω). Generally, dielectric losses are notably lower at higher frequencies compared to lower frequencies and specific temperatures. This frequency-dependent behaviour of tan δ is typically associated with conduction losses and aligns with the observations made in the glass-(ceramic) samples examined in this study, as illustrated in Figure 7(b). The measured tan δ values for all samples at 303 K and 10 kHz are listed in Table 1, and the Inset in Figure 7(b) illustrates how the loss factor varies with the HT temperature. All samples exhibit low values of dielectric loss, with the NGP@550 having the lowest value. Interestingly, the dependence of tan δ on the HT temperature closely mirrors the trend in σDC, see Figure 6(b), with the NGP@550 one displaying the lowest value, which is linked to its lower conductivity. These findings highlight the clear impact of HT temperature on ε’(ω) and tan δ, along with their correlation with σDC, in line with prior research results [31,34].

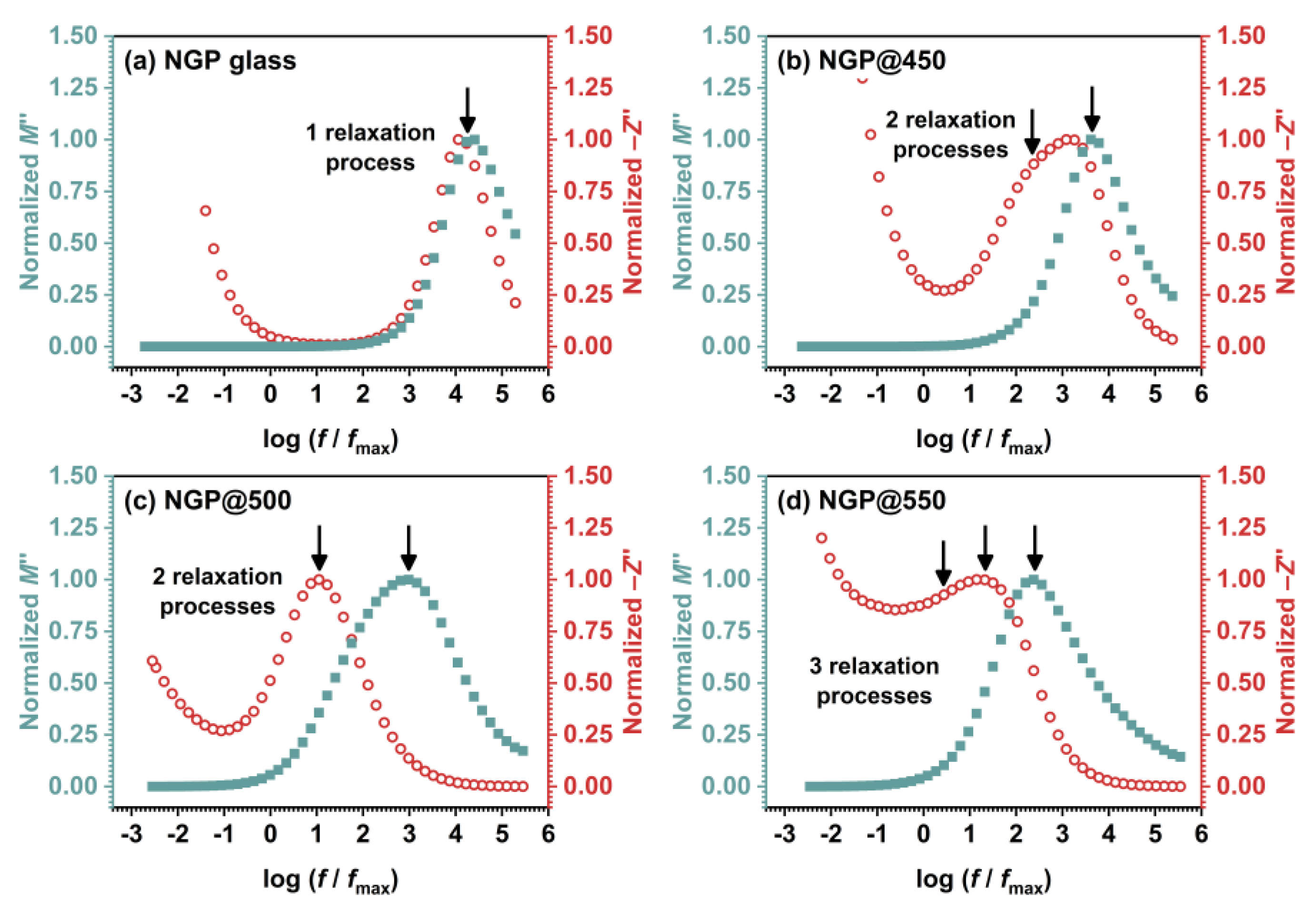
3.3.2. Electric modulus

Another way to observe and interpret dielectric relaxation is to display the results of impedance spectroscopy using the complex electric modulus, M*(ω). The modulus is the reciprocal of the value of the complex dielectric permittivity, ε*(ω), and is defined according to Equation (3):
M*(ω) = 1/ ε*(ω) = M’(ω) + iM’’(ω),
The main advantage of using this formalism lies in reducing the effect of electrode polarization. Figure S4 in the SM shows the imaginary modulus for the starting NGP glass and GCs. A detailed analysis can also contribute to the understanding of electrical transport in GCs. The different processes present in crystallized samples are visible and easy to separate based on the value of resistance and capacity, i.e. relaxation time, using a graphic display of the frequency-dependent electrical modulus, M’’(ω), and imaginary component of the impedance, Z’’(ω). Both of these displays reveal one or more distinct maxima at specific frequencies, describing the corresponding relaxation process, which shifts towards higher frequencies with an increase in temperature. The frequency values of these relaxations can be correlated with the separation of the different contributions of individual phases to the total conductivity, which provides an insight into the mechanisms of conductivity in the investigated GCs and the influence of crystallization on the transfer of Na+ ions as charge carriers.
For an investigation into whether the observed peaks in the frequency-dependent M’’(ω) and Z’’(ω) curves correspond to the same relaxation process, the curves are normalized, as demonstrated in Figure 8.
It is indeed observed that the maxima in both the M’’(ω) and Z’’(ω) curves are closely aligned for the initial NGP glass, as can be seen in Figure 8(a). This alignment suggests a non-localized relaxation process of the Debye type with a single relaxation time which implies that the observed phenomenon is a manifestation of the same underlying process, i.e. ionic conductivity. In contrast to the initial glass, the GC samples, which constitute heterogeneous systems comprising uniformly distributed crystalline grains within a glassy matrix, exhibit distinct characteristics. This is evident in the shape of the Z’’(ω) curve for NGP@450 sample, which displays two overlapped maxima. In contrast, a single maximum is observed in the M’’(ω) curve, and it closely matches the second of the two maxima in the Z’’(ω) curve, see Figure 8(b). Since M’’(ω) reflects processes associated with reduced capacitance values, the presence of just one peak in the M’’(ω) curve implies that the prevailing process at higher frequencies is characterized by diminished capacitance values when compared to the process at lower frequencies. Given the substantial weight fraction of the remaining glassy matrix in NGP@450 sample, the high-frequency contribution is ascribed to the predominant amorphous phase, while the lower-frequency process might be associated with a grain boundary effect. This is further corroborated by the EEC modeling, see Figure 5(b). Furthermore, the frequency dependence of M’’(ω) for NGP@500 sample reveals contributions from two separate relaxation processes, which overlapp due to similar relaxation frequencies. Conversely, a single peak is observed in Z’’(ω) curve, closely aligning with the first of the two maxima in the M’’(ω) curve, as depicted in Figure 8(c). Considering that Z’’(ω) reflects processes characterized by higher resistance values, the presence of only one maximum in Z’’(ω) curve suggests that the process occurring at a lower frequency exhibits higher resistance values compared to the process observed at a higher frequency, effectively masking the latter. Taking into account weight fractions of two crystalline phases in NGP@500 GC, the high-frequency contribution is attributed to the majority NaPO3 crystalline phase, while the lower-frequency process may be linked to the minority GeP2O7 crystalline phase, as previously depicted in Figure 5(c). In the case of NGP@550, both the M’’(ω) and Z’’(ω) curves exhibit distinct individual contributions, much like those observed for NGP@500, see Figure 8(d). Intriguingly, despite NGP@550 GC having nearly equal weight fractions of two crystalline phases, NaPO3 and GeP2O7, as the NGP@500 GC, their M’’(ω) and Z’’(ω) curves exhibit differing shapes, a phenomenon also observed in their complex impedance planes, see Figure 5(c,d). Namely, the Z’’(ω) curve of NGP@550 GC is broader compared to the Z’’(ω) curve of NGP@500 GC, which can be explained by the third contribution observed at the lowest frequencies. However, the three relaxation maxima overlap, making it challenging to separate them. On the other hand, in the M’’(ω) curve, the most prominent contribution is at the highest frequencies, and it can be attributed to the majority NaPO3 phase (74.3%). Therefore, the processes characterized by the highest resistance appear to be a result of the presence of the additional GeP2O7 crystal phase and contributions from the grain boundary. As previously explained, the distinct contributions of the crystal grain boundary and the crystalline phases in NGP@550 GC emerge due to the formation of well-defined crystal grains and sharp grain boundaries. Elevated HT temperature may as well contribute to the sintering of crystal grains and reduce the specific surface area. As a result, the morphology of NGP@550 GC appears significantly more compact, as shown in Figure 3, in contrast to NGP@500 GC, whose microstructure exhibits a more porous structure, as depicted in Figure 2(c,d).

4. Conclusions

This study investigates the impact of 24-hour heat-treatments at different temperatures on the (micro)structural, electrical, and dielectric properties of initial glass with the composition 40Na2O-10GeO2-50P2O5. The results obtained from PXRD, IR-ATR and SEM-EDS analyses demonstrate a progressive increase in crystallinity with rising heat-treatment temperatures, from 450 °C, across 500 °C, to 550 °C. In all three glass-ceramics, the primary crystalline phase is identified as NaPO3, with an additional crystalline phase, GeP2O7, emerging @500 °C and @550 °C HT samples. SEM-EDS findings reveal that @450 °C glass-ceramic sample is primarily composed of an amorphous glass matrix with nanometric crystalline grains. In contrast, HT @500 °C leads to randomly scattered crystalline grains lacking distinct morphology, with sizes ranging from 100 to 500 nm. Remarkably, even though glass-ceramic sample prepared by HT @550 °C possesses a composition nearly identical to the one HT @500 °C, it exhibits striking surface features, larger crystalline grains in the micron-scale range, and a distinctive square-shaped morphology of NaPO3 grains. Furthermore, the results of impedance spectroscopy reveal a strong correlation between the evaluated electrical and dielectric properties and the conditions of controlled crystallization. The electrical properties of the prepared glass-ceramics are thoroughly investigated by modeling complex impedance spectra using the appropriate electrical equivalent circuit, enabling the assignment of physical significance to each contribution to the overall conductivity. The primary contribution to the overall conductivity in sample HT @450 °C is attributed to the dominant glass matrix phase, while the low-frequency contribution is associated with the grain boundary effect, which arises as a result of the initial stages of crystallization observed in this sample. Conversely, within sample HT @500 °C, comprising primarily of two crystalline phases, namely NaPO3 as the predominant phase and GeP2O7 as the secondary phase, the main contribution is linked to the former crystalline phase, while the low-frequency contribution corresponds to the latter one. Glass-ceramic HT at highest temperature (@550 °C) demonstrates a distinct alteration in the complex impedance spectrum shape with an additional contribution. In this sample, three contributions are identified: the primary one associated with the prevailing NaPO3 crystal phase, the second with the minor GeP2O7 phase, and the third originating from crystal grain boundaries. These conspicuous contributions from the grain boundaries and crystalline phases are a result of the formation of well-defined crystal grains and sharp boundaries, as evidenced by SEM-EDS. Nonetheless, the increase in HT temperature is associated with a decline in DC conductivity. This trend is attributed to the increasing fraction of the NaPO3 phase, which, during crystallization, depletes the glass matrix of mobile Na+ ions. An examination of dielectric properties discloses a progressive decline in both dielectric permittivity and dielectric loss as the heat-treatment temperature increases. Notably, HT @550 °C results in glass-ceramic with the lowest values of dielectric permittivity and dielectric loss. Furthermore, the dielectric relaxation mechanisms within the crystallized samples are examined by analyzing the imaginary components of the complex electric modulus and complex impedance. These findings align seamlessly with the equivalent circuit modeling of the corresponding complex impedance spectra. This research unravels the intricate relationship between heat-treatment temperature and material characteristics, underscoring that controlled crystallization offers meticulous control over microstructure and the composition of crystalline phases within the residual glassy phase, ultimately facilitating the fine-tuning of material properties.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org.

Author Contributions

Conceptualization, A.M.M., Ž.S., L.P.; methodology, P.M., L.K., J.P., Ž.S., L.P.; software, S.M., M.R., Ž.S. L.P.; validation, S.M., M.R., P.M., L.K., Ž.S.; formal analysis, S.M., M.R., K.S.K., P.M., L.K., J.P., Ž.S., L.P.; investigation, S.M., M.R., K.S.K., P.M., L.K., J.P., Ž.S., L.P.; writing—original draft preparation, Ž.S., L.P.; writing—review and editing, S.M., M.R, P.M., L.K., J.P., A.M.M., Ž.S., L.P.; visualization, S.M., M.R, Ž.S., L.P.; supervision, J.P., L.P.; project administration, A.M.M., Ž.S., L.P.; funding acquisition, A.M.M., L.P. All authors have read and agreed to the published version of the manuscript.

Funding

This work is supported by the Croatian Science Foundation, EL-Trass-Ceram project IP-2014-09-5863. L.P. thanks for the donation from the Croatian Academy of Science and Arts (HAZU) 2019.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available from the corresponding author upon request.

Acknowledgments

J.P. and Ž.S. acknowledge the support of project CIuK (Grant KK.01.1.1.02.0016) and CeNIKS (Grant No. KK.01.1.1.02.0013), respectively, co-financed by the Croatian Government and the European Union through the European Regional Development Fund-Competitiveness and Cohesion Operational Programme. The authors are pleased to acknowledge Marijan Marciuš from Ruđer Bošković Institute, Zagreb, Croatia, for recording SEM images and Kristina Sklepić for help in electrical characterization.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Baniya, A.; Pathak, R.; Norris, B.; Li, H.; Rozyyev, V.; Elam, J.W.; Qiao, Q. 1 - Next-Generation Battery Technology Based on Solid-State Electrolytes. In Green Sustainable Process for Chemical and Environmental Engineering and Science; Smirnova, A., Numan-Al-Mobin, A., Inamuddin, Eds.; Elsevier, 2023; pp. 1–46 ISBN 978-0-323-90635-7.
  2. Yuan, Q.; Chen, M.; Zhan, S.; Li, Y.; Lin, Y.; Yang, H. Ceramic-Based Dielectrics for Electrostatic Energy Storage Applications: Fundamental Aspects, Recent Progress, and Remaining Challenges. Chem. Eng. J. 2022, 446, 136315. [Google Scholar] [CrossRef]
  3. Kumta, P.N.; Yong Kim, J. Chapter 2 - Low Dielectric Constant Glasses and Glass-Ceramics for Electronic Packaging Applications. In Handbook of Low and High Dielectric Constant Materials and Their Applications; Singh Nalwa, H., Ed.; Academic Press: Burlington, 1999; pp. 73–140. ISBN 978-0-12-513905-2. [Google Scholar]
  4. Arman Kuzubasoglu, B. Recent Studies on the Humidity Sensor: A Mini Review. ACS Appl. Electron. Mater. 2022, 4, 4797–4807. [Google Scholar] [CrossRef]
  5. Ku, C.-A.; Chung, C.-K. Advances in Humidity Nanosensors and Their Application: Review. Sensors 2023, 23, 2328. [Google Scholar] [CrossRef] [PubMed]
  6. Pietrzak, T.K.; Wasiucionek, M.; Garbarczyk, J.E. Towards Higher Electric Conductivity and Wider Phase Stability Range via Nanostructured Glass-Ceramics Processing. Nanomaterials 2021, 11, 1321. [Google Scholar] [CrossRef] [PubMed]
  7. Davis, M.J.; Zanotto, E.D. Glass-Ceramics and Realization of the Unobtainable: Property Combinations That Push the Envelope. MRS Bull. 2017, 42, 195–199. [Google Scholar] [CrossRef]
  8. Deubener, J.; Allix, M.; Davis, M.J.; Duran, A.; Höche, T.; Honma, T.; Komatsu, T.; Krüger, S.; Mitra, I.; Müller, R.; et al. Updated Definition of Glass-Ceramics. J. Non-Cryst. Solids 2018, 501, 3–10. [Google Scholar] [CrossRef]
  9. Dias, J.A.; Santagneli, S.H.; Messaddeq, Y. Methods for Lithium Ion NASICON Preparation: From Solid-State Synthesis to Highly Conductive Glass-Ceramics. J. Phys. Chem. C 2020, 124, 26518–26539. [Google Scholar] [CrossRef]
  10. Reddy, Ch.K.K.; Rao, R.B.; Reddy, Ch.G. The Role of Crystallization on Microstructural and Electrical Studies of Lithium Germanium Phosphate Glass-Ceramic Electrolytes. Ionics 2015, 21, 967–979. [Google Scholar] [CrossRef]
  11. Rohde, M.; Cui, Y.; Ziebert, C.; Seifert, H.J. Thermophysical Properties of Lithium Aluminum Germanium Phosphate with Different Compositions. Int. J. Thermophys. 2020, 41, 31. [Google Scholar] [CrossRef]
  12. Cruz, A.M.; Ferreira, E.B.; Rodrigues, A.C.M. Controlled Crystallization and Ionic Conductivity of a Nanostructured LiAlGePO4 Glass–Ceramic. J. Non-Cryst. Solids 2009, 355, 2295–2301. [Google Scholar] [CrossRef]
  13. Yan, B.; Zhu, Y.; Pan, F.; Liu, J.; Lu, L. Li1.5Al0.5Ge1.5(PO4)3 Li-Ion Conductor Prepared by Melt-Quench and Low Temperature Pressing. Solid State Ion. 2015, 278, 65–68. [Google Scholar] [CrossRef]
  14. Zhu, Y.; Zhang, Y.; Lu, L. Influence of Crystallization Temperature on Ionic Conductivity of Lithium Aluminum Germanium Phosphate Glass-Ceramic. J. Power Sources 2015, 290, 123–129. [Google Scholar] [CrossRef]
  15. Cui, Y.; Mahmoud, M.M.; Rohde, M.; Ziebert, C.; Seifert, H.J. Thermal and Ionic Conductivity Studies of Lithium Aluminum Germanium Phosphate Solid-State Electrolyte. Solid State Ion. 2016, 289, 125–132. [Google Scholar] [CrossRef]
  16. Santagneli, S.H.; Baldacim, H.V.A.; Ribeiro, S.J.L.; Kundu, S.; Rodrigues, A.C.M.; Doerenkamp, C.; Eckert, H. Preparation, Structural Characterization, and Electrical Conductivity of Highly Ion-Conducting Glasses and Glass Ceramics in the System Li1+xAlxSnyGe2-(x+y)(PO4)3. J. Phys. Chem. C 2016, 120, 14556–14567. [Google Scholar] [CrossRef]
  17. Das, A.; Goswami, M.; Illath, K.; Ajithkumar, T.G.; Arya, A.; Krishnan, M. Synthesis and Characterization of LAGP-Glass-Ceramics-Based Composite Solid Polymer Electrolyte for Solid-State Li-Ion Battery Application. J. Non-Cryst. Solids 2021, 558, 120654. [Google Scholar] [CrossRef]
  18. Zallocco, V.M.; Freitas, J.M.; Bocchi, N.; Rodrigues, A.C.M. Electrochemical Stability of a NASICON Solid Electrolyte from the Lithium Aluminum Germanium Phosphate (LAGP) Series. Solid State Ion. 2022, 378, 115888. [Google Scholar] [CrossRef]
  19. Gandi, S.; Chinta, S.R.; Ojha, P.K.; Surendra Babu, M.S.; Ravuri, B.R. High Na-Ion Conducting Na1+x[SnxGe2−x(PO4)3] Glass-Ceramic Electrolytes: Structural and Electrochemical Impedance Studies. J. Am. Ceram. Soc. 2018, 101, 167–177. [Google Scholar] [CrossRef]
  20. Lannerd, A.; Ly, K.; Smirnova, A. 8 - Beyond Lithium: Solid-State Sodium-Ion Batteries and Their Potential Applications. In Green Sustainable Process for Chemical and Environmental Engineering and Science; Smirnova, A., Numan-Al-Mobin, A., Inamuddin, Eds.; Elsevier, 2023; pp. 223–262 ISBN 978-0-323-90635-7.
  21. Gandi, S.; Chidambara Swamy Vaddadi, V.S.; Sripada Panda, S.S.; Goona, N.K.; Parne, S.R.; Lakavat, M.; Bhaumik, A. Recent Progress in the Development of Glass and Glass-Ceramic Cathode/Solid Electrolyte Materials for next-Generation High Capacity All-Solid-State Sodium-Ion Batteries: A Review. J. Power Sources 2022, 521, 230930. [Google Scholar] [CrossRef]
  22. Trivedi, S.; Pamidi, V.; Fichtner, M.; Reddy, M.A. Ionically Conducting Inorganic Binders: A Paradigm Shift in Electrochemical Energy Storage. Green Chem. 2022, 24, 5620–5631. [Google Scholar] [CrossRef]
  23. K. Arya, S.; S. Danewalia, S.; Singh, K. Frequency Independent Low- k Lithium Borate Nanocrystalline Glass Ceramic and Glasses for Microelectronic Applications. J. Mater. Chem. C 2016, 4, 3328–3336. [CrossRef]
  24. Kulwicki, B.M. Humidity Sensors. J. Am. Ceram. Soc. 1991, 74, 697–708. [Google Scholar] [CrossRef]
  25. Traversa, E. Ceramic Sensors for Humidity Detection: The State-of-the-Art and Future Developments. Sens. Actuators B Chem. 1995, 23, 135–156. [Google Scholar] [CrossRef]
  26. Foucaud, M.; Renka, S.; Klaser, T.; Popović, J.; Skoko, Ž.; Mošner, P.; Koudelka, L.; Šantić, A. Sodium-Ion Conductivity and Humidity-Sensing Properties of Na2O-MoO3-P2O5 Glass-Ceramics. Nanomaterials 2022, 12, 240. [Google Scholar] [CrossRef] [PubMed]
  27. Moguš-Milanković, A.; Sklepić, K.; Blažanović, H.; Mošner, P.; Vorokhta, M.; Koudelka, L. Influence of Germanium Oxide Addition on the Electrical Properties of Li2O–B2O3–P2O5 Glasses. J. Power Sources 2013, 242, 91–98. [Google Scholar] [CrossRef]
  28. Sklepić, K.; Banhatti, R.D.; Tricot, G.; Mošner, P.; Koudelka, L.; Moguš-Milanković, A. Insights from Local Network Structures and Localized Diffusion on the Ease of Lithium Ion Transport in Two Mixed Glass-Former Systems. J. Phys. Chem. C 2017, 121, 17641–17657. [Google Scholar] [CrossRef]
  29. Sklepić, K.; Tricot, G.; Mošner, P.; Koudelka, L.; Moguš-Milanković, A. Sodium Ion Conductivity in Mixed Former Na2O–P2O5–GeO2 and Na2O–B2O3–P2O5–GeO2 Glasses. J. Phys. Chem. C 2021, 125, 10593–10604. [Google Scholar] [CrossRef]
  30. Marijan, S.; Razum, M.; Klaser, T.; Mošner, P.; Koudelka, L.; Skoko, Ž.; Pisk, J.; Pavić, L. Tailoring Structure for Improved Sodium Mobility and Electrical Properties in V2O5–Nb2O5–P2O5 Glass(Es)-(Ceramics). J. Phys. Chem. Solids 2023, 181, 111461. [Google Scholar] [CrossRef]
  31. Pavić, L.; Sklepić, K.; Skoko, Ž.; Tricot, G.; Mošner, P.; Koudelka, L.; Moguš-Milanković, A. Ionic Conductivity of Lithium Germanium Phosphate Glass-Ceramics. J. Phys. Chem. C 2019, 123, 23312–23322. [Google Scholar] [CrossRef]
  32. Pavić, L.; Nikolić, J.; Graça, M.P.F.; Costa, B.F.O.; Valente, M.A.; Skoko, Ž.; Šantić, A.; Moguš-Milanković, A. Effect of Controlled Crystallization on Polaronic Transport in Phosphate-Based Glass-Ceramics. Int. J. Appl. Glass Sci. 2020, 11, 97–111. [Google Scholar] [CrossRef]
  33. Bafti, A.; Kubuki, S.; Ertap, H.; Yüksek, M.; Karabulut, M.; Moguš-Milanković, A.; Pavić, L. Electrical Transport in Iron Phosphate-Based Glass-(Ceramics): Insights into the Role of B2O3 and HfO2 from Model-Free Scaling Procedures. Nanomaterials 2022, 12, 639. [Google Scholar] [CrossRef]
  34. Marijan, S.; Pavić, L. Solid-State Impedance Spectroscopy Studies of Dielectric Properties and Relaxation Processes in Na2O–V2O5–Nb2O5–P2O5 glass system. Int. J. Miner. Metall. Mater. 2023. [Google Scholar] [CrossRef]
  35. Ondik, H.M. The Structure of Anhydrous Sodium Trimetaphosphate Na3P3O9, and the Monohydrate, Na3P3O9.H2O. Acta Crystallogr. 1965, 18, 226–232. [Google Scholar] [CrossRef]
  36. Kaiser, U.; Glaum, R. Beiträge zum thermischen Verhalten und zur Kristallchemie wasserfreier Phosphate. XI. Darstellung und Kristallstruktur einer triklinen Modifikation von GeP2O7. Z. Für Anorg. Allg. Chem. 1994, 620, 1755–1759. [Google Scholar] [CrossRef]
  37. Moustafa, Y.M.; El-Egili, K. Infrared Spectra of Sodium Phosphate Glasses. J. Non-Cryst. Solids 1998, 240, 144–153. [Google Scholar] [CrossRef]
  38. Sahar, M.R.; Hussein, A.W.M.A.; Hussin, R. Structural Characteristic of Na2O-P2O5-GeO2 Glass Systems. J. Non-Cryst. Solids 2007, 353, 1134–1140. [Google Scholar] [CrossRef]
  39. Sinclair, D.C. Characterization of Electro-materials using ac Impedance Spectroscopy. Bol. Soc. Esp. Cerámica Vidr. 1995, 34, 55–65. [Google Scholar]
  40. Schönhals, A.; Kremer, F. Analysis of Dielectric Spectra. In Broadband Dielectric Spectroscopy; Kremer, F., Schönhals, A., Eds.; Springer: Berlin, Heidelberg, 2003; pp. 59–98. ISBN 978-3-642-56120-7. [Google Scholar]
Preprints 92610 g001
Figure 1. Rietveld refinement of prepared glass-ceramics. Experimental data are given by black lines while the calculated profiles are shown in blue. Diffraction lines belonging to NaPO3 phase are colored purple while GeP2O7 lines are shown in teal. The insets in NGP@500 and NGP@550 patterns demonstrate the differences in the integral line breadths with the increase in temperature.
Figure 1. Rietveld refinement of prepared glass-ceramics. Experimental data are given by black lines while the calculated profiles are shown in blue. Diffraction lines belonging to NaPO3 phase are colored purple while GeP2O7 lines are shown in teal. The insets in NGP@500 and NGP@550 patterns demonstrate the differences in the integral line breadths with the increase in temperature.
Preprints 92610 g001
Preprints 92610 g002
Figure 2. SEM micrographs of the (a-c) NGP@450 and (d-f) NGP@500 glass-ceramic surface.
Figure 2. SEM micrographs of the (a-c) NGP@450 and (d-f) NGP@500 glass-ceramic surface.
Preprints 92610 g002
Preprints 92610 g003
Figure 3. SEM micrographs and EDS spectra of the 10GeO2@550 glass-ceramic surface.
Figure 3. SEM micrographs and EDS spectra of the 10GeO2@550 glass-ceramic surface.
Preprints 92610 g003
Preprints 92610 g004
Figure 4. Conductivity spectra of the initial NGP glass (a) and prepared glass-ceramics (b-d).
Figure 4. Conductivity spectra of the initial NGP glass (a) and prepared glass-ceramics (b-d).
Preprints 92610 g004
Preprints 92610 g005
Figure 5. Experimental and theoretical impedance spectra shown in the complex impedance plane for samples of starting glass (a) and prepared glass-ceramics obtained by the crystallization of starting glass at (b) 450 °C, (c) 500 °C and (d) 550 °C, measured at 150 °C.
Figure 5. Experimental and theoretical impedance spectra shown in the complex impedance plane for samples of starting glass (a) and prepared glass-ceramics obtained by the crystallization of starting glass at (b) 450 °C, (c) 500 °C and (d) 550 °C, measured at 150 °C.
Preprints 92610 g005
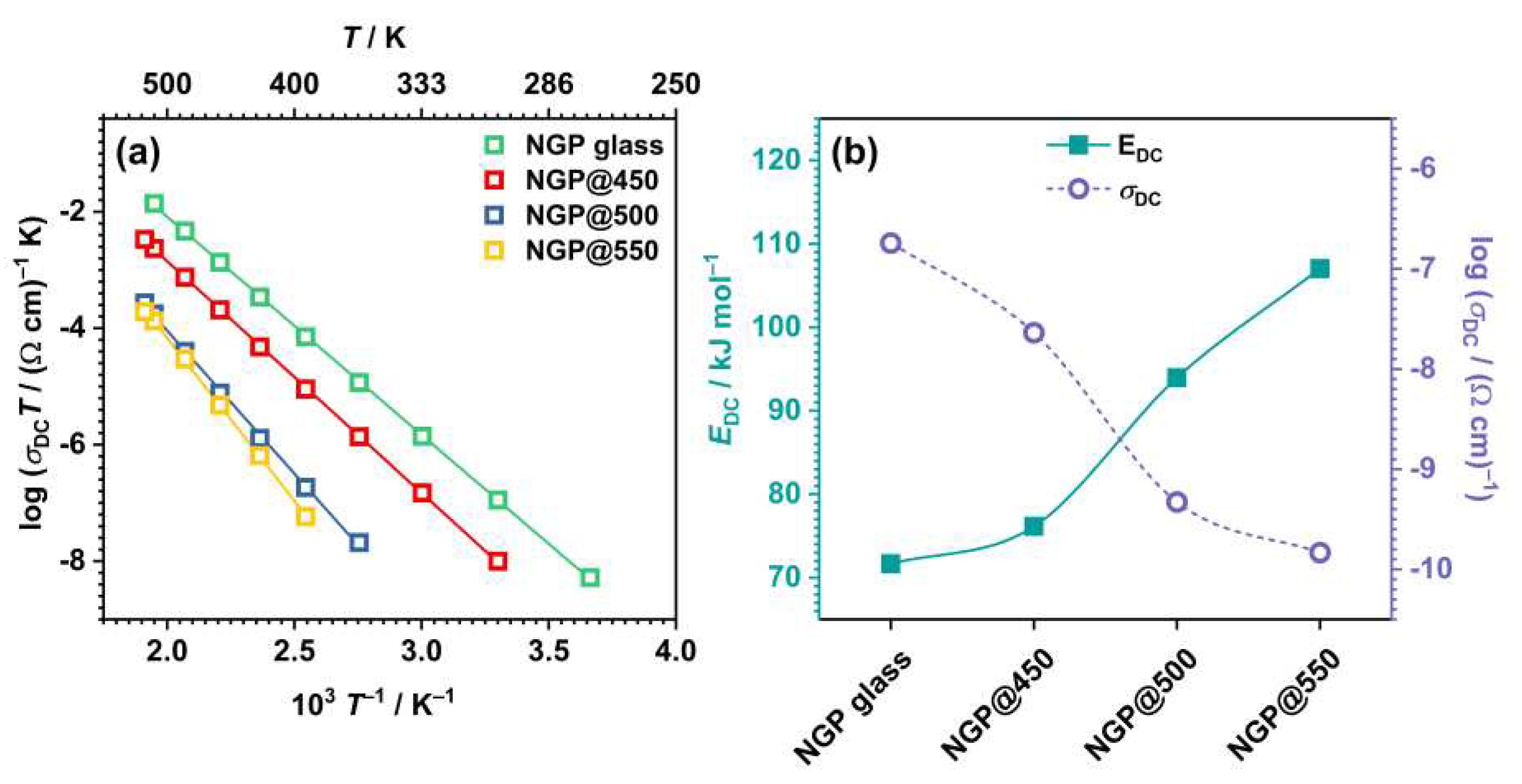
Preprints 92610 g006
Figure 6. Dependence of (a) log(σDC) vs 103/T and (b) EDC and σDC @393K on the crystallization temperature for all prepared samples.
Figure 6. Dependence of (a) log(σDC) vs 103/T and (b) EDC and σDC @393K on the crystallization temperature for all prepared samples.
Preprints 92610 g006
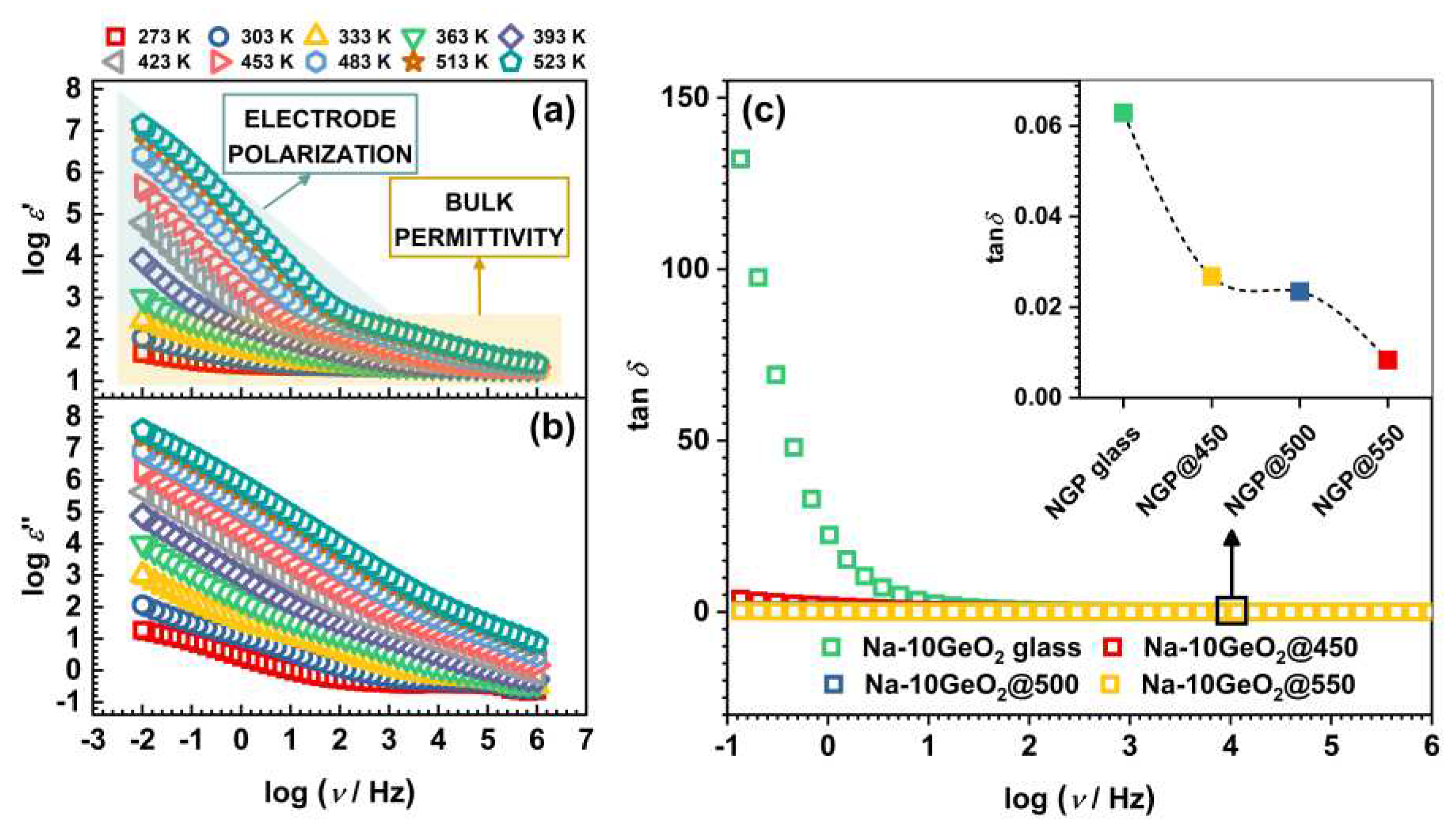
Preprints 92610 g007
Figure 7. Frequency dependence of (a) real, ε’(ω), and (b) imaginary, ε’’(ω), parts of the complex permittivity at different temperatures for the NGP@500 glass-ceramic, (c) the loss factor, tan δ, for all samples @303 K. Inset: Compositional dependence of tan δ for all samples @303 K and 10 kHz. The lines connecting data points are a guide to the eye.
Figure 7. Frequency dependence of (a) real, ε’(ω), and (b) imaginary, ε’’(ω), parts of the complex permittivity at different temperatures for the NGP@500 glass-ceramic, (c) the loss factor, tan δ, for all samples @303 K. Inset: Compositional dependence of tan δ for all samples @303 K and 10 kHz. The lines connecting data points are a guide to the eye.
Preprints 92610 g007
Preprints 92610 g008
Figure 8. Frequency dependence of normalised M′′(ω) and Z′′(ω) curves for all samples at 423 K.
Figure 8. Frequency dependence of normalised M′′(ω) and Z′′(ω) curves for all samples at 423 K.
Preprints 92610 g008
Table 1. DC conductivity, σDC, activation energy for DC conductivity, EDC, and selected dielectric properties for all studied samples.
Table 1. DC conductivity, σDC, activation energy for DC conductivity, EDC, and selected dielectric properties for all studied samples.
Sample σDC (Ω–1 cm–1)a EDC (kJ mol–1) ε’(ω) tanδb
NGP glass 1.81×10–7 71.7 13.24 0.063
NGP@450 2.30×10–8 76.1 22.82 0.027
NGP@500 4.70×10–10 94.0 20.98 0.023
NGP@550 1.47×10–10 107.0 19.37 0.008
a at 393K b at 303K and 10kHz.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated