1. Introduction
In view of the relentless explorations and investigations conducted by researchers and scientists over the span of past few decades, the tantalizing aspect of invisibility is no longer an imaginary concept. Remarkably, the advent of metamaterials and metasurfaces facilitated development of electromagnetic invisibility, especially with regard to antennas as one of its most successful applications. We know that phased array antennas are growing in popularity due to numerous appealing aspects such as high gain, high directivity, beam control, ease of manufacturing, among others. Naturally, antenna arrays are expected to play a critical part in fulfilling the ever-increasing demand for channel requirement in radar and wireless communications services, which may require deployment of crowded array systems in a very compact area. But, contrary to our expectation, such a dense system may exhibit performance degradation, owing to the cross-coupling between the antennas jammed so close together. Consequently, several approaches were developed in the last few decades to achieve electromagnetic cloaking. To rise up to this challenge, the concept of electromagnetic invisibility has been extensively investigated, especially with respect to antennas, to make it undetectable to the surrounding sensors, and thus immune to electromagnetic interference over a desired frequency range. Various techniques that have been reported include plasmonic cloaking [
1,
2,
3,
4,
5,
6], transformation-based cloaking [
7,
8,
9,
10,
11], transmission-line networks [
12,
13,
14], among others. Now, each of these prominent cloaking techniques have been shown to successfully induce electromagnetic invisibility; however, they have their own set of pros and cons. An important limitation of the transformation-based and transmission line cloaking methods is that they are based on the electro-magnetic isolation of the cloaked object (the concealed object is unable to transmit or receive electromagnetic energy), which means they are impractical for sensing or antenna applications. In addition, these techniques are known to utilize bulk volumetric metamaterials and so might prove cumbersome for systems with minimal space capacity. As a possible solution to this hurdle, mantle cloaking method, which utilizes simple, ultra-thin patterned metallic surfaces to bring about cancellation of the dominant scattering mode, was put forth at microwave frequencies [
15,
16,
17,
18]. Also, it is important to note that mantle cloaks tend to induce electromagnetic invisibility by employing metasurfaces that cancel out the fields scattered by the intended object. This implies that the concealed object, in fact, is not electromagnetically isolated from the surrounding environment, which makes mantle cloaking method, a perfect candidate for sensing and/or antenna applications. A detailed and extensive review of the most renowned techniques for obtaining electromagnetic invisibility is presented in [
19]. Implementation of mantle cloaking approach has also been carried out at low-terahertz (THz) frequencies using graphene-based metasurfaces [
20,
21]. A vital application of mantle cloaking method has been presented in [
22,
23], wherein the cloaks are demonstrated to overcome the mutual blockage between tightly placed antennas. The application of mantle cloaks to various cylindrical configurations facilitated cloaking of freestanding strip dipoles [
24], planar microstrip monopole antennas [
25], and very recently, slot antennas [
26]. These specially modeled mantle cloaks also bring about cloaking effect amongst the neighboring antennas, such that they do not perceive each other [
27,
28]. In a similar fashion, at low-THz frequencies, graphene-based metasurface cloaks are used to reduce mutual interactions between planar antennas [
29]. Additionally in [
30,
31], wideband cloaking using mantle cloaks has been achieved for microstrip monopoles. Furthermore, circuit-loaded metasurfaces have been shown to achieve waveform-selective invisibility in [
32,
33,
34]. Here, the waveform-selective cloaking devices either make an antenna invisible or visible for either short pulses or continuous waves; thus leading to novel invisibility devices with advanced functionalities. The mantle cloaking approach has also been deployed for cloaking of electrically large objects [
35] and recently, a novel cloaking technique was proposed in [
36], wherein, a planar metasurface for cloaking free-standing bow-tie antenna and its various array configurations is presented. The relative simplicity of the metasurface design and the fact that it is capable of cloaking the entire surface of the bow-tie antennas (half-wavelength structure) galvanized us to possibly protract this cloaking principle to other half-wavelength antennas, for instance, simple patch antenna configurations. As a part of our recently published works, in [
37], we have successfully demonstrated (through simulation results) cloaking of equilateral triangle patch antennas and its array structures.
In this paper, we have targeted the very popular and widely used microstrip patch antenna systems - rectangular and circularly shaped patch antennas along with their array configurations. And so, taking inspiration from the design methodology in [
36], we have devised a metasurface structure that facilitates cloaking of these practical patch antennas. For each of the commonly shaped microstrip antennas, firstly, we establish the decoupling and cloaking effects for two patches placed in close vicinity. We demonstrate that when the top surface of each patch antenna is coated by the specially tailored metasurface, they are decoupled (the effects of mutual coupling are nullified) from each other and restoration of their radiation patterns are also observed as if they were functioning in an isolated fashion (despite the two patches being confined close to each other). We then extend the cloak design to one-dimensional linear interleaved array configuration of these patches and effectively demonstrate efficient array performance, which means that the dimensional area initially established for one array, is now perfectly capable of accommodating two separate phased arrays, possibly leading to applications with compact space utilization. We would like to emphasize on the novelty of our design that sets it apart from other metasurface based cloaking devices. To the best of our knowledge, in the reported literatures [
22,
23,
24,
25,
26,
27], the cloaking structures employ dielectric substrates that are either circular or elliptical in shape and the metallic elements are embedded periodically along the circumference of these substrates. It is an extremely arduous task to fabricate these metasurfaces, making the practical realization and the experimental verifications of such designs much more difficult. Also, these reported metasurfaces are required to maintain sub-wavelength cross-sectional dimensions as an important design constraint and cannot be used to cloak large antenna surface. Our proposed structure, on the other hand, is a simple planar design placed directly on top of the patch antennas, which makes it a more practical construct and hence more favorable from fabrication point of view. Another important distinguishing characteristic of our design is that it covers (is coated on) the entire patch antenna surface area (whose resonant length is half the wavelength for a particular frequency in the dielectric medium), essentially achieving cloaking for an electrically large antenna surface. The design modeling, along with the numerical full-wave simulation results presented here are obtained with the CST Microwave Studio [
38].
The paper is sectioned as follows:
Section 2 consists of the schematic figures and describes the design process for a module of two rectangular patch antennas designed to operate at different frequencies (uncloaked as well as the cloaked structures); followed by
Section 3, which details the simulation results, showcasing the decoupling and cloaking effects of the coated metasurface for the two rectangular microstrip antennas.
Section 4 deals with the schematic configurations and simulation results for the interleaved rectangular patch arrays. In this section, we also highlight each array’s efficient beam scanning capabilities. In
Section 5, we introduce circular patch antenna systems and demonstrate the decoupling and cloaking effects of the corresponding coated cloak structures for the two patches placed in close vicinity. Furthermore, we exhibit the cloaking functionality of the metasurfaces on the one-dimensional interleaved array of the circular patches. Finally, we present the conclusion and the references for our work.
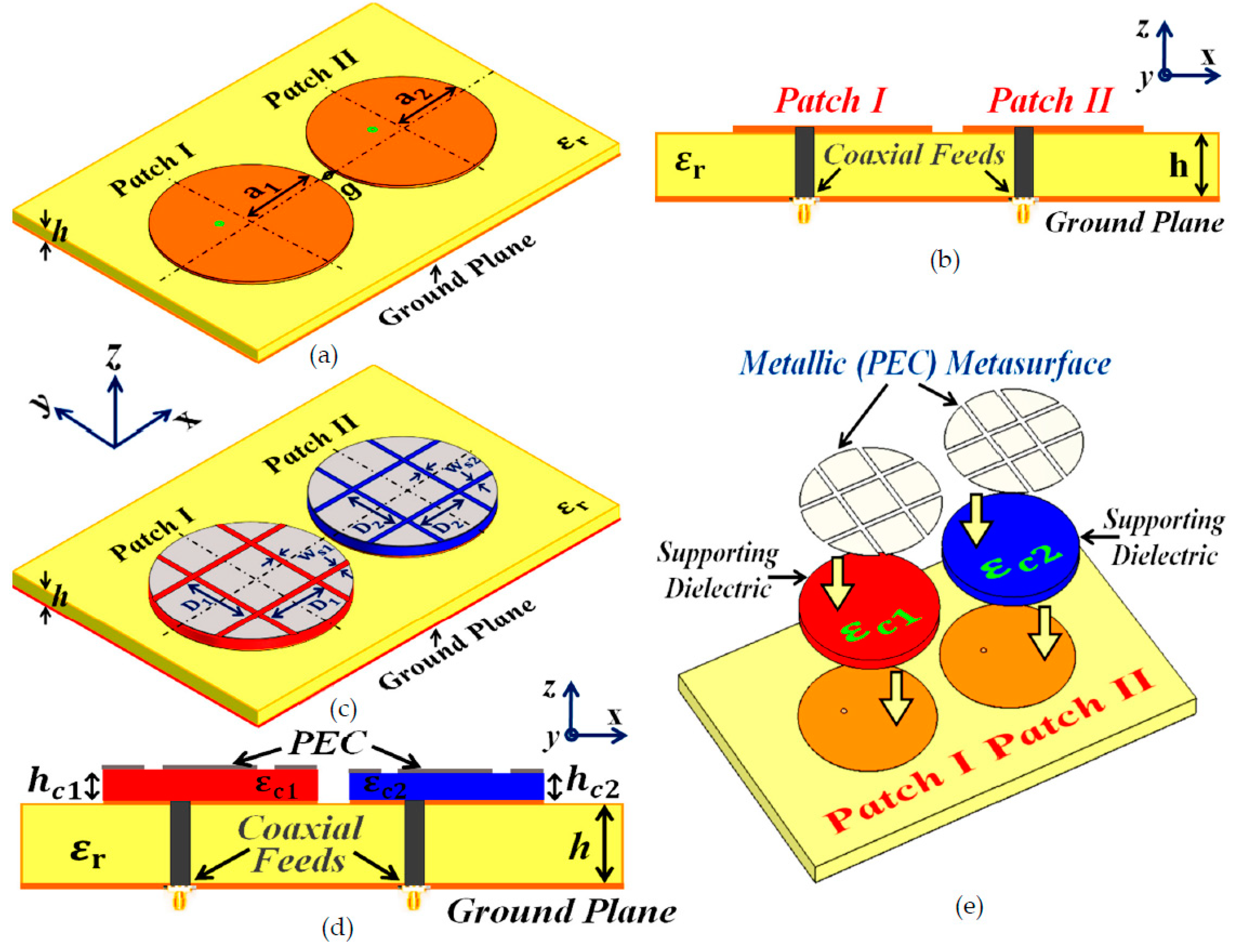
2. Design of Planar Coated Metasurfaces for Rectangular Patch Antennas
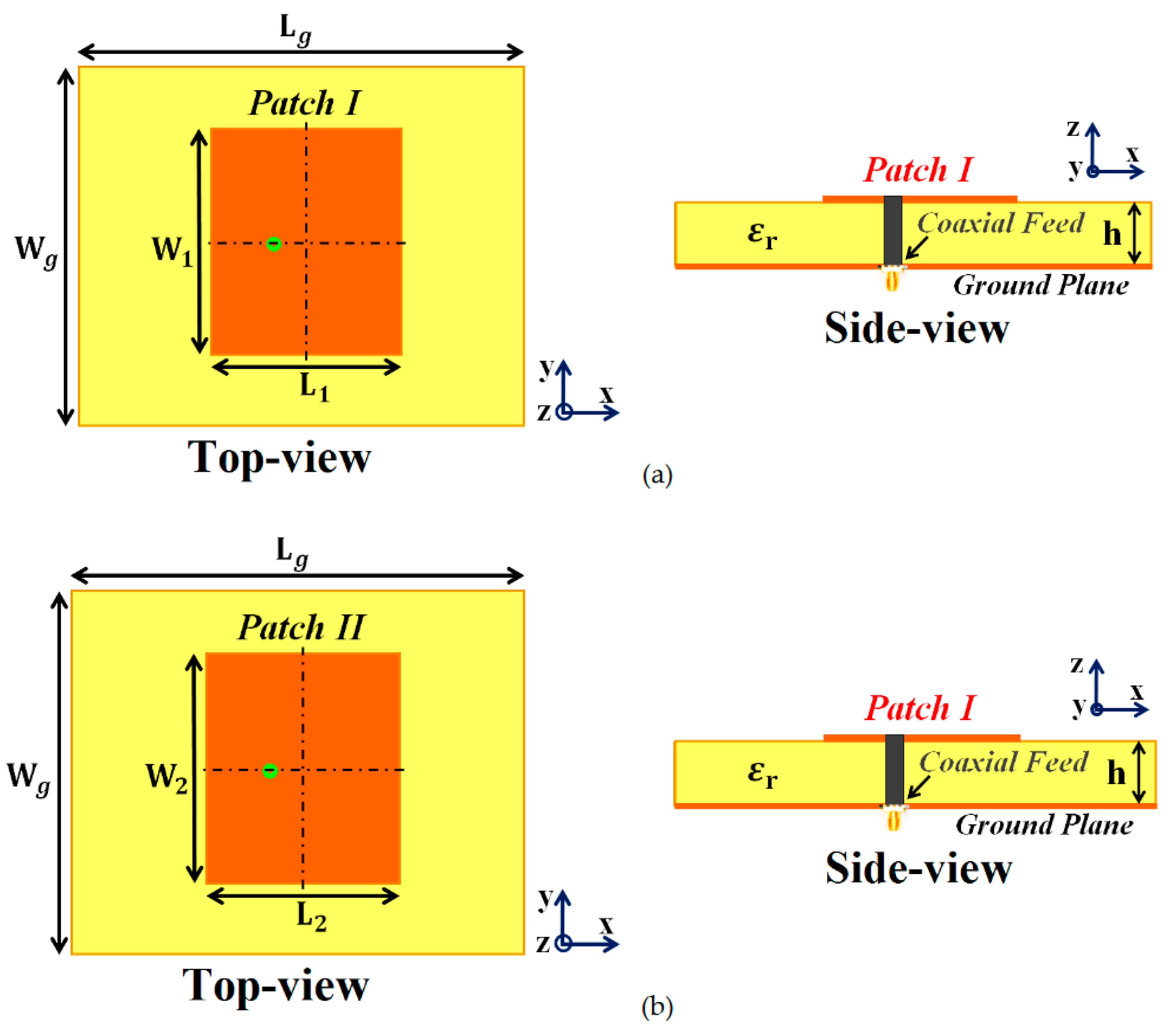
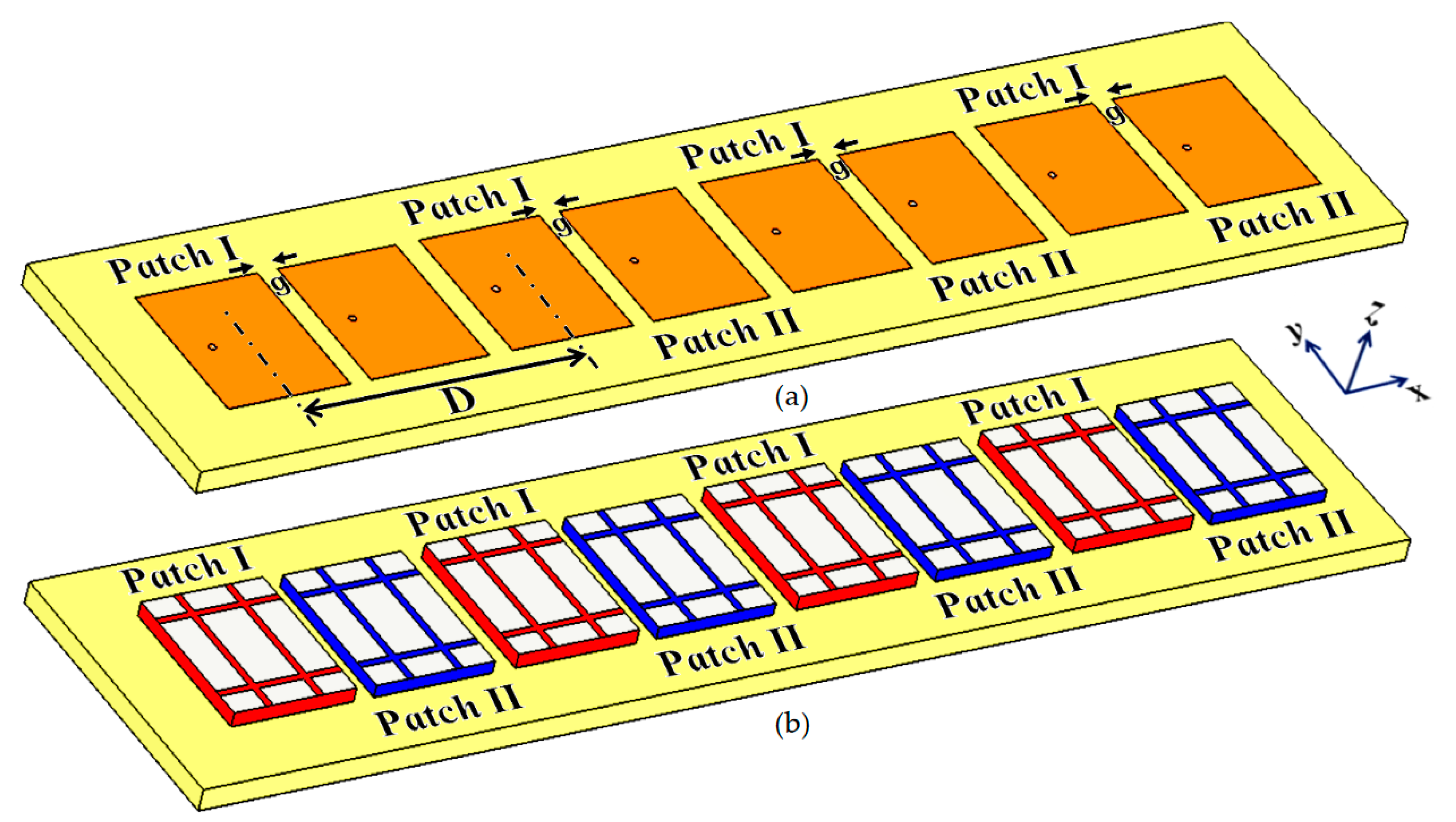
Our ultimate goal is to develop an interleaved system of two distinct phased arrays (wherein the elements of each array are placed in an extremely close vicinity) without compromising either of the array’s performance. To achieve this, we initiate our investigation by considering a single module of two simple, coaxially fed patch antennas–Patch I and II, operating at frequencies
GHz and
GHz, respectively. These patch antennas are embedded on a dielectric substrate (length
mm and width
mm) with thickness
mm and permittivity
(Rogers RT5880 was employed), backed by a ground plane. We should emphasize the reason for choosing two different frequencies for the patches. It is a well-known fact that the detrimental mutual interference effects are predominantly observed between closely placed antenna elements with different resonance frequencies; the closer the frequency values, the more apparent is the destructive interference (hence the reason for choosing operating frequencies of the patches merely 300 MHz apart. Also, C-band frequencies are targeted so that our designed antenna systems could be utilized for 5G applications). Firstly, we design and examine each patch antenna separately and record their matching and radiation performances (see
Figure 1 (a) and (b) for the schematic figures). As a result, we term this as the
isolated case and use the simulation results obtained from these scenarios as a template for comparison with the other cases. The parameters characterizing the patch antennas are:
mm,
mm,
mm, and
mm. After cataloging the results obtained with the isolated patches, we proceed on to situate the rectangular patches very close together on a single substrate (see
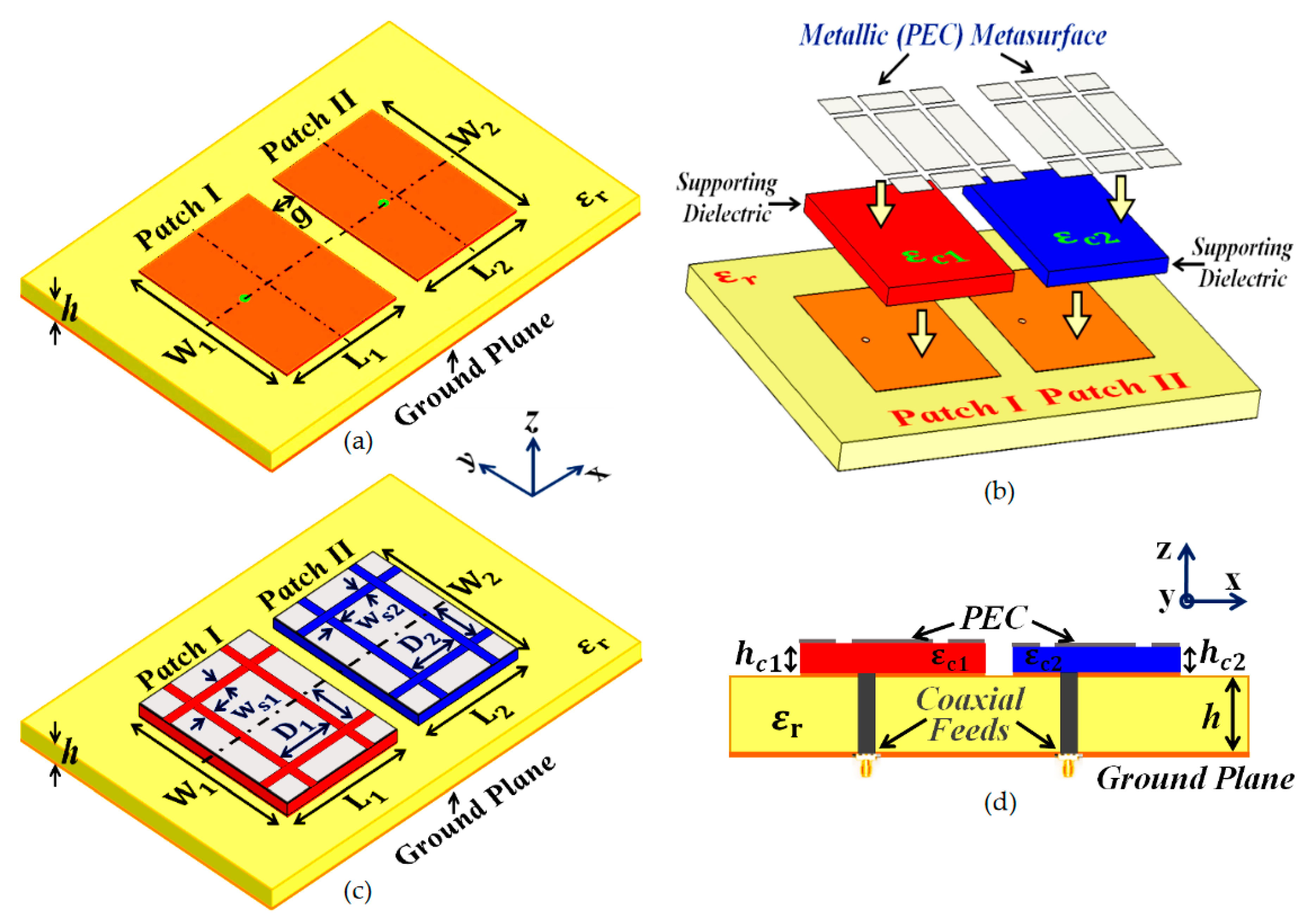
Figure 2 (a), sub-wavelength separation is employed such that
mm
; where
is the free space wavelength in relation to the frequency
). Since the separation
between them is extremely small, an undeniably strong mutual interference is caused in the near-field as well as the far-field of the structure, thereby resulting in the deterioration of the radiation properties of both the patches (simulation results are included in
Section 3). Notice that in
Figure 2 (a), the patch antennas aren’t covered with their corresponding cloaks yet and the mutual coupling effects are rampant in this particular scenario, thus we term this as
coupled uncloaked case.
To address and curtail the detrimental impacts of mutual coupling, we devised a metasurface structure (also referred to as
cloaks) for each patch antenna (refer to
Figure 2 (b), (c), and (d)). It is our claim that these specifically engineered metasurface cloaks eradicate the adverse effects of mutual coupling (as will be corroborated by the results shown in
Section 3), essentially
decoupling the rectangular patch antennas; therefore we aptly refer to this scenario as the
decoupled cloaked case. Despite being a finite and non-periodic structure, the rationale behind using the term ‘metasurface’ for our proposed construct is that it is a 2D structure, wherein the dimensions of perfect electric conductor (PEC) patches as well as the gaps between these elements are sub-wavelength which rather fits in the description of a metasurface. In addition to this, our proposed structure when integrated with the corresponding patch antenna, conveniently reduces its total radar cross-section (RCS) at the desired frequency (results are discussed in
Section 3), thereby controlling and/or redirecting scattered electromagnetic fields around the said antenna, thus demonstrating one of the many typical behaviors of a metasurface. We also refer to our structure as a ‘cloak’ owing to the fact that when the patch antenna is covered by it, the structure effectively makes that antenna ‘invisible’ to the electromagnetic fields at a particular frequency (an extremely narrowband frequency range, to be precise). We claim that the coated antenna becomes ‘invisible’, because at the intended frequency, it does not reflect waves back to the source (as seen from the total radar cross-section plots in the following section) and also does not scatter waves in other directions. The deployment of our proposed metasurface cloaks entails the following steps. The top surface area of each patch antenna is first coated with a thin layer (sub-wavelength thickness) of high dielectric constant supporting materials (thickness
mm,
mm, and relative permittivity
,
for Patch I and Patch II, respectively), wherein the surface of each dielectric conforms thoroughly to the corresponding patch antenna.
A PEC surface is then placed directly on top of each of these dielectrics. Note that thin slots are incorporated into this PEC surface, so that the resulting surface resembles an assembly of 2D sub-wavelength PEC patches, separated by extremely small gaps (slot widths are
mm and spacing between the slots are
mm and
mm). The thought process behind choosing this particular design for our metasurface can be explained in the following argument. An important characteristic of the metasurface is that it does not perturb the radiation characteristic of its corresponding patch at the antenna’s operating frequency (resonance frequency). This indicates that the metasurface should be chosen such that it will mimic the behavior of the current on the patch antenna at the resonance frequency. And so, metallic (PEC) patches are a natural choice. At the same time, we are concerned with making the metasurface ‘frequency selective’, such that the scattering cancellation behavior is apparent only at a required specific frequency (termed as the cloaking frequency, which is essentially the operating frequency of the neighboring patch antenna). For this purpose, small gaps are introduced between the PEC patches to create a situation similar to periodic arrangement of metallic elements. Even though the construct itself is pretty straight forward, the design process is not analytically trivial. We have endeavored to find ways and means to support our design with some form of analytical modelling in order to offer more rigorous theoretical explanations. In this regard, one of the sophisticated and popular means that we looked into, is the ‘generalized sheet transition conditions’ (GSTCs) for modelling of metasurfaces in reference to cloaking. But, we quickly realized that there are certain restrictions in applying GSTCs to our design. First and foremost, this approach requires the metasurface to be electrically large (several wavelengths); however the metasurface in our design is restricted to the dimensions of its corresponding patch antenna (resonant length of the patch antenna is half the operating wavelength in the dielectric medium). Additionally, in our designs, we observed that the patch antenna itself is strongly coupled to the metasurface, mainly because of the deeply sub-wavelength separation between the antenna and the metasurface. This involves higher-order mode coupling which further complicates the matter as far as theoretical and analytical modelling are concerned. As such, even though there are pretty sophisticated analysis available in the modelling of metasurfaces, we have not been able to discern a satisfactory analytical model for our design. Nevertheless, we are still looking at it as a part of future work. Considering the fact that, at present, we do not have a clear analytical model for our structure, parameterization is required in our design. That is why, rigorous parametric analysis was carried out to determine an optimum set of design parameters (i.e., varying one design parameter at a time within a certain range)
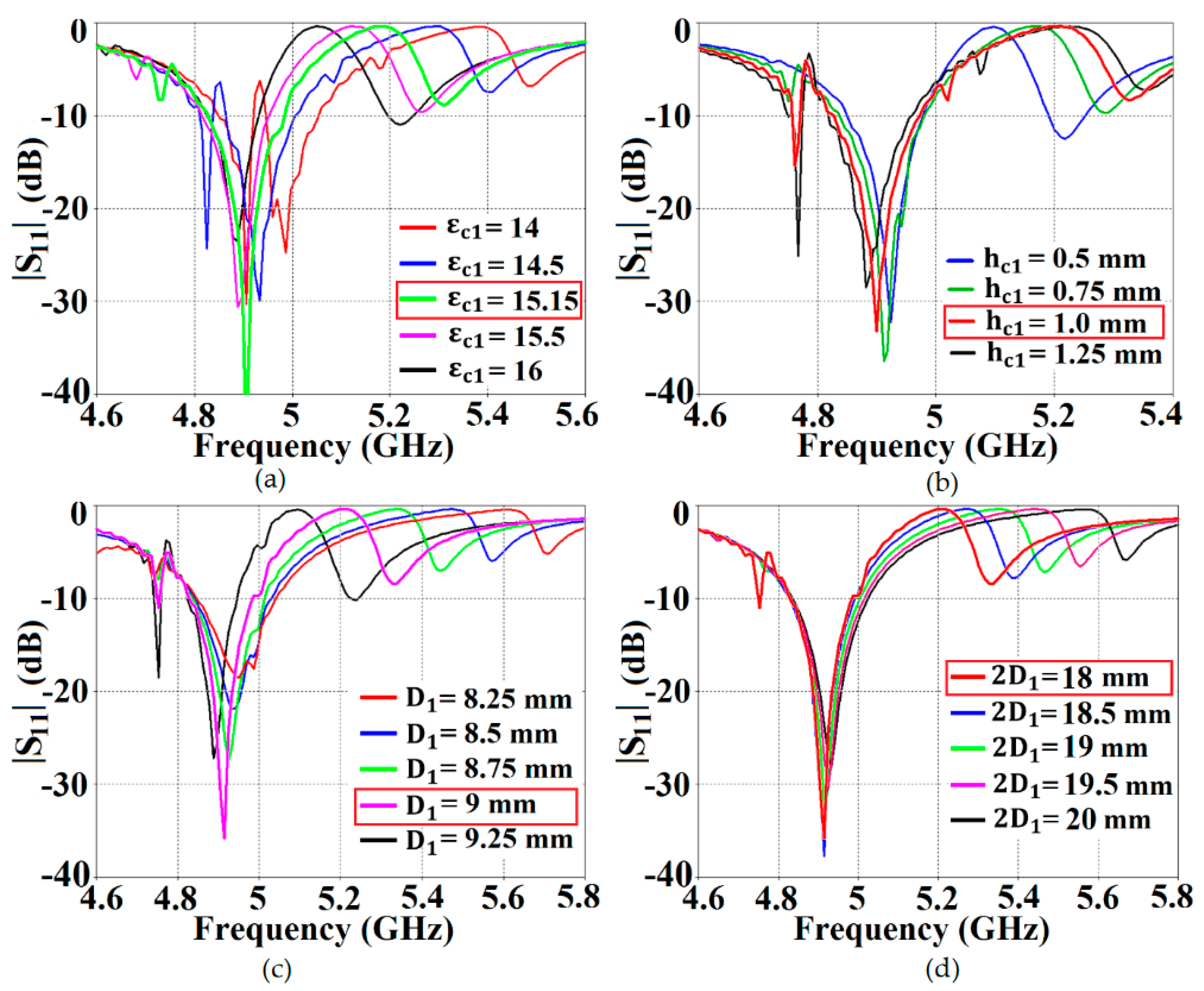
. To provide an insight into the steps undertaken to determine the cloak design constraints, several results are demonstrated through reflection coefficient plots (
) in
Figure 3, showing the parametric study of the design specifications that are paramount to our metasurface configuration. Through the comprehensive analysis, we quickly detected that among the many design parameters, the relative permittivity value of the supporting material (
Figure 3 (a)), thickness of these dielectric materials (
Figure 3 (b)) as well as the placement of the vertical and horizontal slots (
Figure 3 (c) and (d), respectively) on the PEC plays a crucial role in bringing about the decoupling and cloaking effects at an intended frequency. For the sake of brevity, we have only included analysis for the cloak design of Patch I. Here, we should remark that there are two frequencies of interest, which are taken into consideration when designing a cloak for its corresponding patch antenna – namely,
resonance frequency and
cloaking frequency (these frequency terminologies have been used throughout the article). The resonance frequency is the frequency where an antenna is well matched with its input impedance (the reflection coefficient
dB) and is generally a good radiator at this frequency. On the other hand, cloaking frequency indicates the frequency where we are interested in observing the decoupling and cloaking effects. Typically, the reflection coefficient
dB at the cloaking frequency; consequently the antenna ceases to be an efficient radiator at this frequency. In our configurations, cloaking frequency of one patch antenna is targeted at the resonance frequency of the other patch in its vicinity. For instance, let us consider Patch I; Patch I is designed to radiate at 4.9 GHz, thus the resonance frequency of Patch I is 4.9 GHz. Subsequently, the cloaking frequency for Patch I should be targeted at 5.2 GHz (which is the resonance frequency of Patch II). Similarly, the resonance and cloaking frequencies for Patch II are 5.2 GHz and 4.9 GHz, respectively. In general, from
Figure 3, we can see that although there are minimal deviations in the resonance frequency of Patch I (i.e.,
GHz), a more apparent tuning effect is observed for the frequencies where Patch I becomes unmatched (i.e.,
dB). In
Figure 3 (a), as the dielectric permittivity of supporting material for the metasurface increases, the cloaking frequency steadily shifts to lower values. With the increase in thickness of the supporting material, the cloaking frequency is seen to progress to higher values, apparent from
Figure 3 (b).
In regards to the placement of the slots on the PEC surface, cloaking frequency decreases with the increase in vertical slot separation; whereas it is seen to increase with the increase in horizontal slot separation (see
Figure 3 (c) and (d), respectively). As mentioned above, for Patch I, the frequency where we want to observe the decoupling and cloaking effects, i.e., the cloaking frequency, is set at
GHz. So, looking at the figures, following values were chosen for the cloak design of Patch I: Dielectric permittivity of the supporting material
, thickness
mm, vertical and horizontal slot separations
mm and
mm. Through similar parametric investigations, appropriate values for the cloak design of Patch II were determined. Based on our deductions, the specific arrangement of our metasurface, employing the abovementioned parameters, causes the surface currents on the PEC to be routed in the direction opposite to that of the currents on the patch antenna surface, basically giving rise to anti-phase surface currents. As an illustration, we have presented the cross-sectional view of the surface currents on an uncloaked and a cloaked antenna in
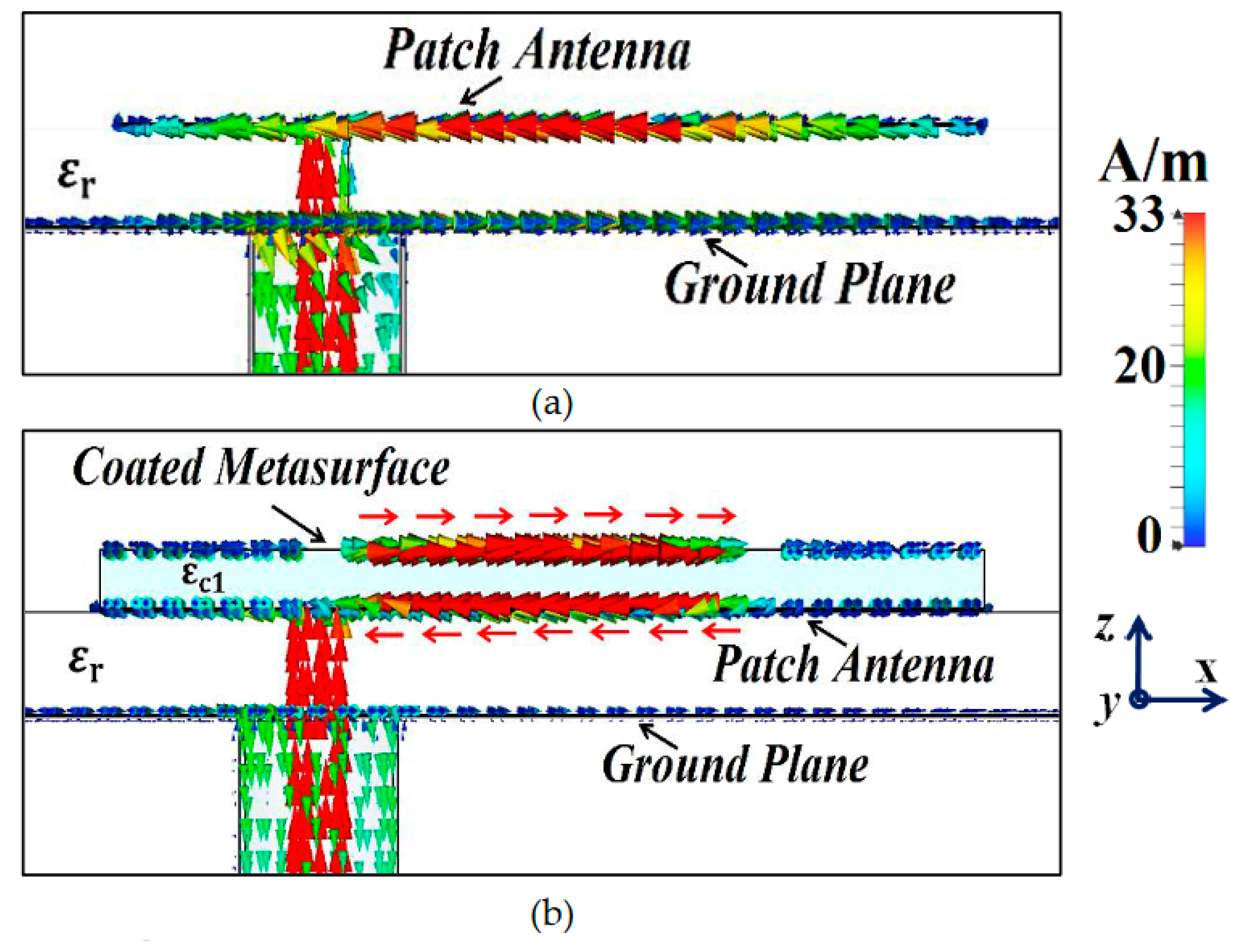
Figure 4 (in the illustrated figure, we have considered uncloaked and cloaked Patch I). It is obvious from
Figure 4 (b) that the direction of currents on the planar coated metasurface is opposite to that of the surface currents on the patch antenna (to provide a clearer view, we have highlighted the routes of currents on both the surfaces with red arrows). An analogous behavior of the surface currents is observed in case of Patch II (results are not presented to avoid repetitiveness). We believe that the fields induced by these anti-phase currents are ultimately responsible for the cancellation of the scattered fields by the targeted antenna at the intended cloaking frequency, in turn, achieving the desired decoupling and cloaking effects.
A significant feature of our metasurface design is the use of high dielectric constant supporting materials (
and
). The justification for exploiting such high dielectric permittivity values is given through the following observations and arguments. Firstly, in our proposed design, the PEC elements placed on the supporting dielectric materials act as a reactive load, effectively shifting the resonance frequency of the respective patch antenna to a slightly higher value. Now, the dielectric material for the metasurface acts as a superstrate to the patch antenna. The function of a superstrate is such that it marginally lowers the resonance frequency of the antenna. Thus, the higher permittivity supporting materials balance out the frequency tuning caused by the PEC elements of the metasurface, essentially making sure that the resonance frequency of the respective patch antenna remains unaltered. Another interesting observation related to higher permittivity materials is at the cloaking frequency of a patch (in terms of reflection coefficient,
dB at this frequency). As seen from
Figure 3 (a), higher the relative permittivity, lesser is the cloaking frequency. Here, the cloaking frequency for Patch I is set at 5.2 GHz, and to achieve decoupling and cloaking effects at this frequency, higher permittivity value is essential. If the cloaking effects were to be accomplished at some other higher frequency level, lower dielectric constant materials could have been be employed. As to what role dielectric permittivity plays in achieving the decoupling effects at a particular cloaking frequency, can be understood as follows. We have mentioned before that the proposed metasurface generates an anti-phase current on its surface. Now, the metallic (PEC) elements in our metasurface definitely have a reactive surface impedance associated with it and in order to produce the desired anti-phase surface currents, these metallic elements must acquire an appropriate surface impedance value at the intended frequency. We perceive that this is where the supporting dielectric material comes into picture; a specific dielectric constant is required to achieve the necessary surface impedance of the metasurface so as to bring about the cloaking effects at a particular frequency.
We realize that the investigations presented in this article are predominantly simulation based. However, as a way of assuring the reliability of our results, we have presented the analysis of our cloak’s functionality from two fundamentally different perspectives – One as an ‘antenna problem’, wherein we scrutinize the performance of the uncloaked and cloaked antennas in terms of their radiation properties, matching characteristics as well as the total efficiencies (all of which are presented in section III); while the other we perceive as a ‘scattering problem’ in presence of a plane wave excitation. We investigate the behavior of the cloaked antennas through total radar cross-section (RCS) plots and the electric field (E-field) contour plots at the respective cloaking frequencies of the rectangular patches (shown in section III). In the near future, to further support our claims, it is our endeavor to gather experimental verifications for our proposed design. As indicated above, the dielectrics used as supporting materials in the metasurface cloak design, possess high permittivity values. At the moment, to be able to fabricate such substrates with low loss tangents, we are scoping out reliable materials that can suffice the high permittivity requirement and are considering the use of polymers infilled with ceramic materials so as to form a polymer composite. The predicament is that ceramic material compositions pose several difficulties such as high costs for tools and challenging implementation like requirement of high temperature processing to achieve desired structural integrity and also agreeable dielectric properties. As an alternative, we are also considering ‘additive manufacturing’, also known as 3D printing, and striving to gain access to a sophisticated industrial grade 3D printing machine. A few options have been considered; the versatile FFF (fused filament fabrication) printer ‘Industry F421’ by 3DGENCE, the SLA (stereo lithography appearance) 3D printer ‘Lite600’ by UnionTech, among others. However, at present, we do not have access to such a sophisticated and expensive machine. We are working on securing funds for the same. We are also researching on the optimum printing strategy with regards to a printer’s reliability in generating dielectric materials. The main process parameters like printing speed, layer height and material infill are crucial in determining the impact on the relative permittivity values and loss tangents of the resulting printed samples [
39], so as to avoid discrepancies in the measured results. Although, currently, this is proving to be an impediment from the fabrication point of view, we are confident that in the near future, we will be able to manufacture reliable high dielectric constant materials that are paramount to our designs, which in turn will facilitate experimental verifications for our configurations. As a side note, in our simulation models, we have employed supporting dielectric materials with a loss tangent (tan δ) of
, and thermal conductivity as low as
. Through simulations, we observed that materials with tan δ as high as
were still found to be tolerable but further increase in the loss tangents destroyed the decoupling and cloaking behavior of the metasurface. Also, since we have considered sub 6 GHz frequency range, the polarization effects of the dielectric materials are negligible and does not affect the permittivity values.
3. Simulation Results Showcasing Decoupling and Cloaking of Two Rectangular Patch Antennas
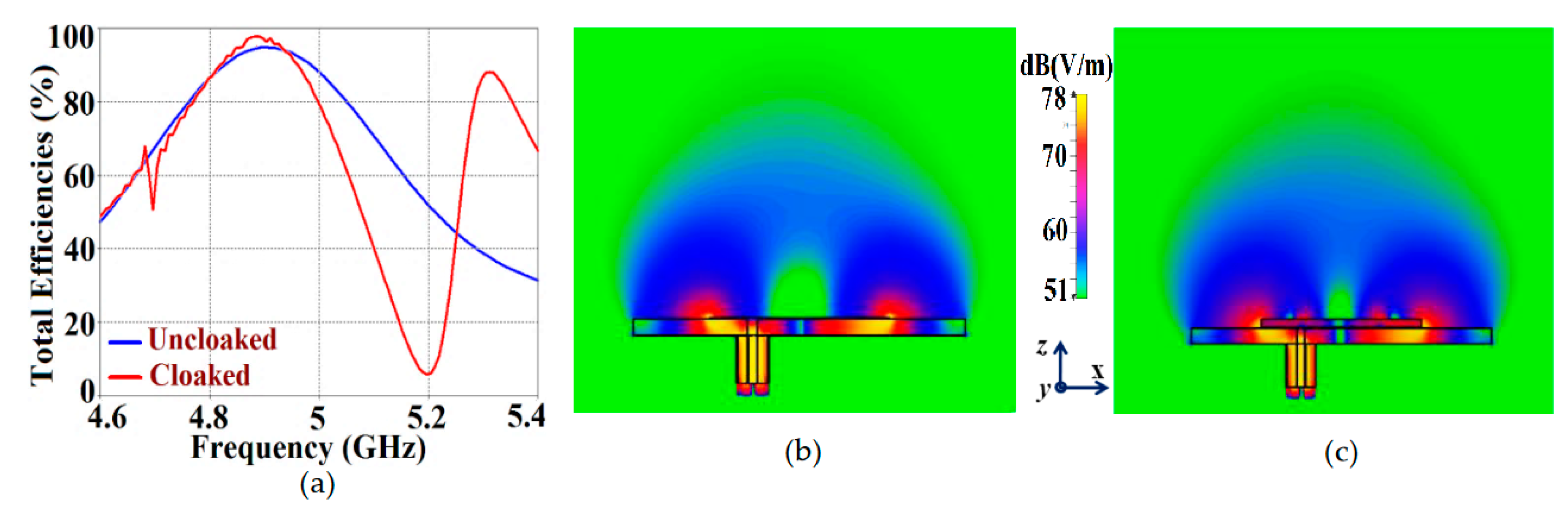
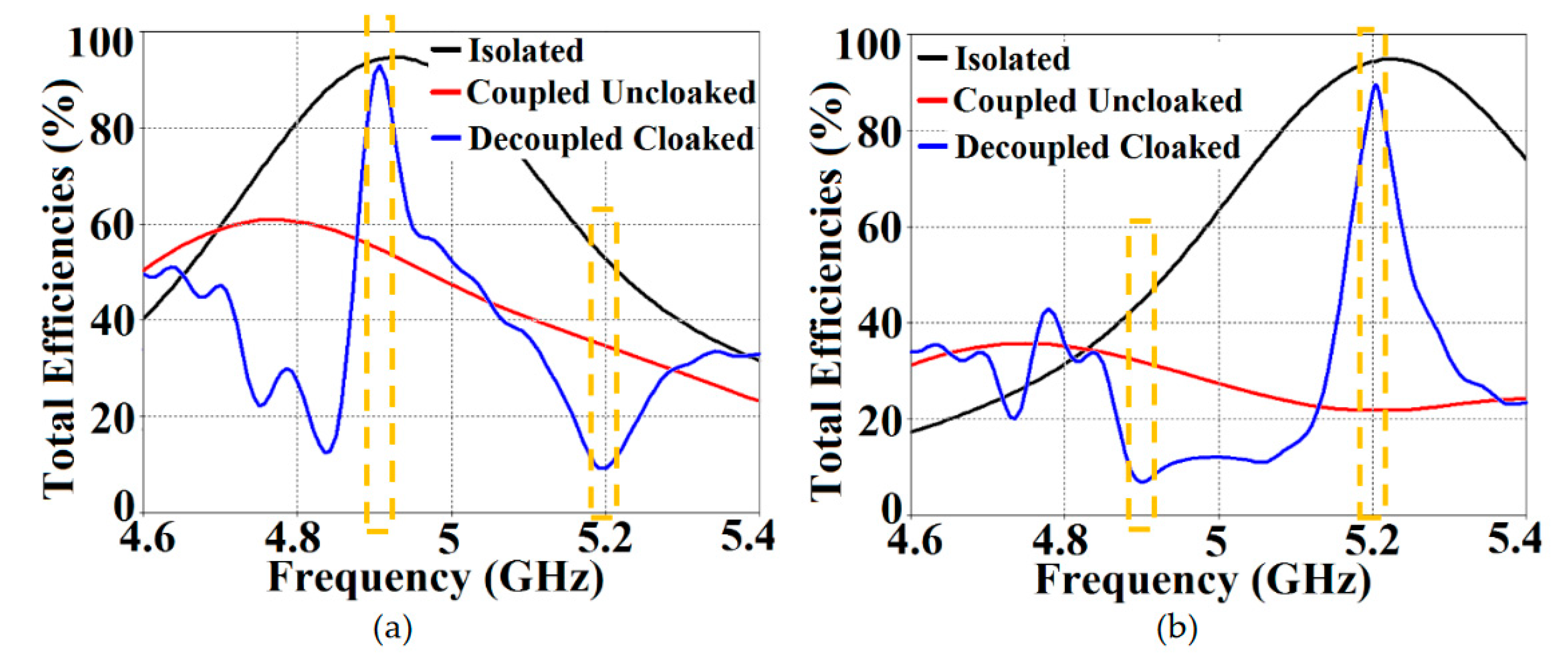
First and foremost, we would like to highlight one of the most important traits of our proposed structures. It is amazing to see that the metasurface coated on to a patch does not affect any of the radiation characteristics at the resonance frequency of the antenna it is integrated to, instead its effects are observed on the frequency of the neighboring patch antenna. To better explain this phenomenon, we have plotted the total efficiencies and E-field distributions for uncloaked and cloaked Patch I in
Figure 5. Let’s observe
Figure 5 (a); both the blue (for uncloaked Patch I) and red (for cloaked Patch I) curves show peak values of total efficiency at
GHz (resonance frequency for Patch I). It is also seen from the red curve that the minimum value of approximately 6 % occurs at
GHz (cloaking frequency for Patch I). Thus, we effectively show that even though Patch I is cloaked, it is still a very efficient radiator at its resonance frequency. However, the cloaked Patch I becomes an extremely poor radiator at its cloaking frequency. Also, comparing the E-field plots in
Figure 5 (b) and (c), we can clearly see that the radiation behaviors of both the uncloaked and cloaked Patch I are almost identical Consequently, we infer that the cloak construct coating Patch I allows unaltered radiation of the antenna at 4.9 GHz but suppresses any scattering/radiation emanating at 5.2 GHz (simply put, Patch I is made electromagnetically invisible at its cloaking frequency, i.e., 5.2 GHz). Again, for the sake of brevity, we have not included the plots for Patch II, but a very similar behavior is recorded for Patch II at its resonance and cloaking frequencies.
As mentioned in the previous section, we have analyzed our design configurations from two different perspectives. So, in the following analysis, we have focused our investigations on the ‘antenna problem’ perspective (basically implicating that we regard our structures as active devices), and have remarked on the matching and far-field radiation aspects of the proposed system. As a part of this analysis, we have presented the S-parameter plots in
Figure 6, along with the plots for total efficiencies in
Figure 7, followed by the E-field distribution contours in
Figure 8 for tightly arranged rectangular patches (both uncloaked and cloaked configurations) to demonstrate the decoupling and cloaking effects of the coated metasurface. Recall that the coupled uncloaked case refers to the scenario when the two patches are situated in a tight spatial arrangement (
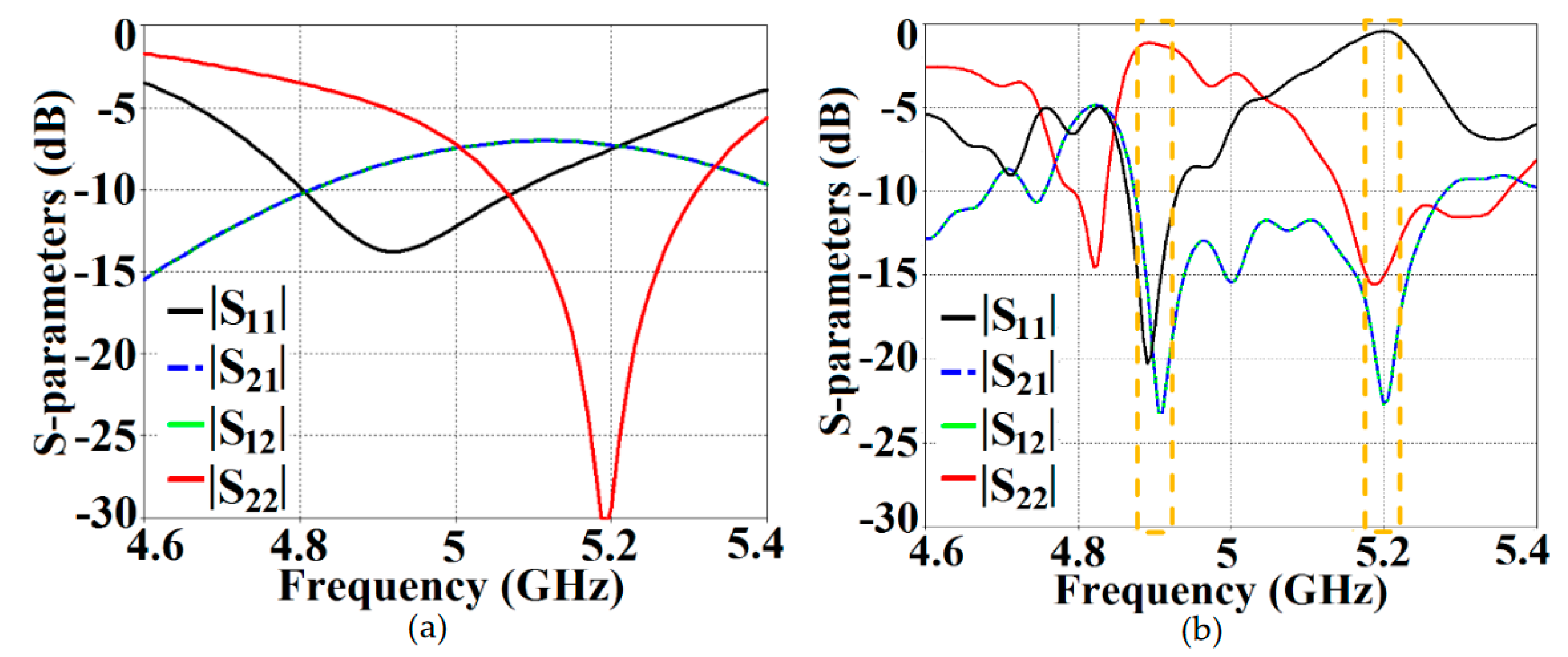
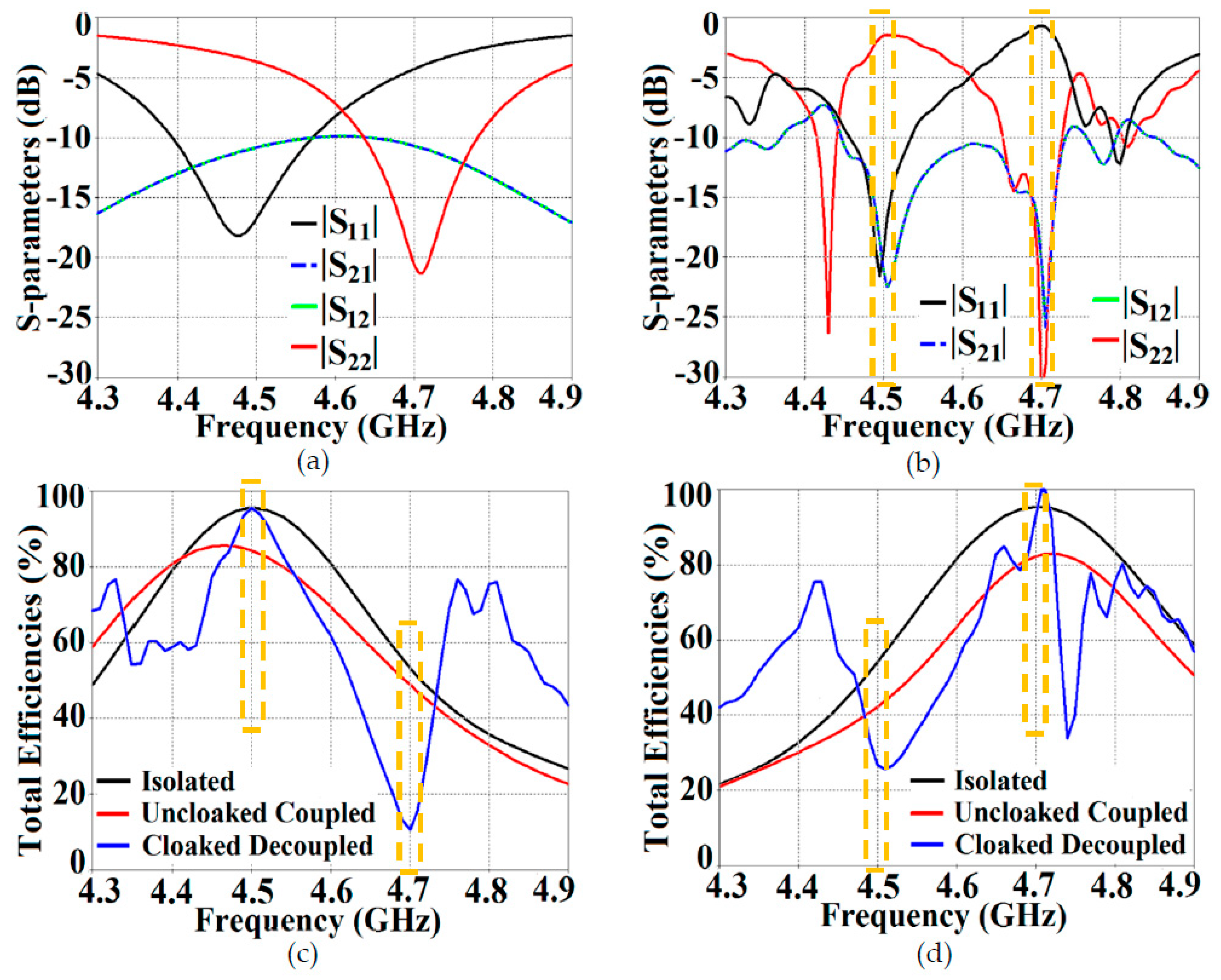
mm) and neither of the patches are coated with the metasurface cloaks. Naturally, the close proximity of the patch antennas introduces a considerable amount of mutual coupling between Patch I and II. This is evident from
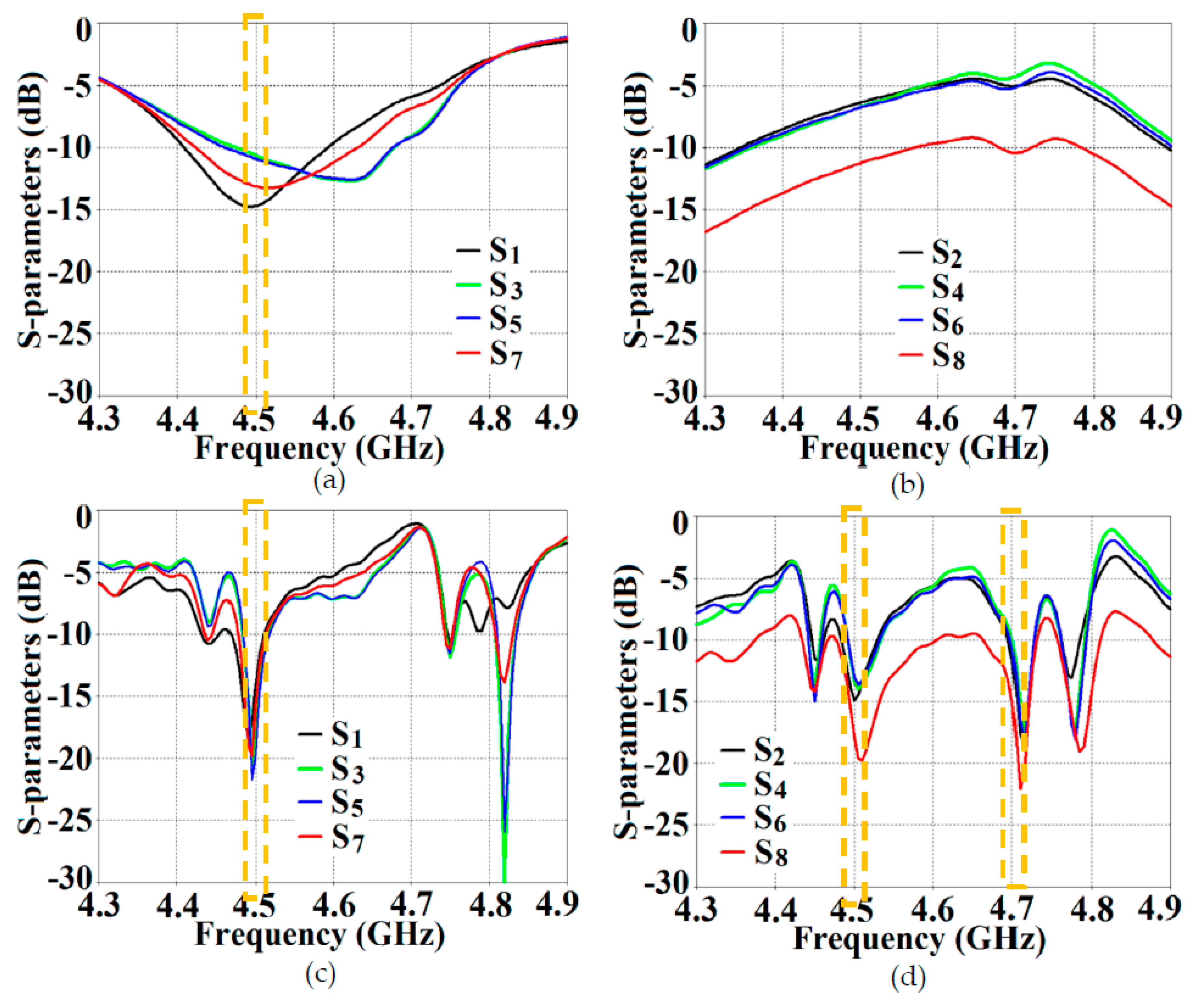
Figure 6 (a), where the coupling coefficients
dB at both
and
. Please note that the green and dotted blue curves, indicating the mutual coupling levels in
Figure 6, have overlapped completely and so they tend to appear as a single plot instead of the two curves that have been plotted. Accordingly, from
Figure 6 (b), we can see that when the individual patches are cloaked by their respective metasurfaces, the magnitudes of coupling coefficients (
and
) clearly decrease; a reduction of almost 15 dB in
and
is recorded at
as well as
. Additionally, from
Figure 6 (b), notice that
dB at frequency
and increases to
dB at frequency
, indicating that Patch I is perfectly matched and therefore, a good radiator at
, but is completely unmatched and hence, a poor radiating device at
). In a similar fashion,
dB at frequency
and then reaches
dB at frequency
, indicating that Patch II radiates excellently at
, however, it becomes a poor radiator at
. We have also displayed the plots for total efficiencies of the rectangular patch antennas in the isolated, coupled uncloaked and decoupled cloaked cases in
Figure 7. The following expression for the total efficiency (as calculated by CST) takes into consideration the impedance matching characteristics (signified by involvement of the reflection coefficient in the expression, i.e., either
or
from the S-parameter plots) along with the radiation properties (in terms of radiation efficiency) of the antennas. The total efficiency is computed as:
, where
signifies the total efficiency, Γ denotes the reflection coefficient (
or
), and
stands for radiation efficiency.
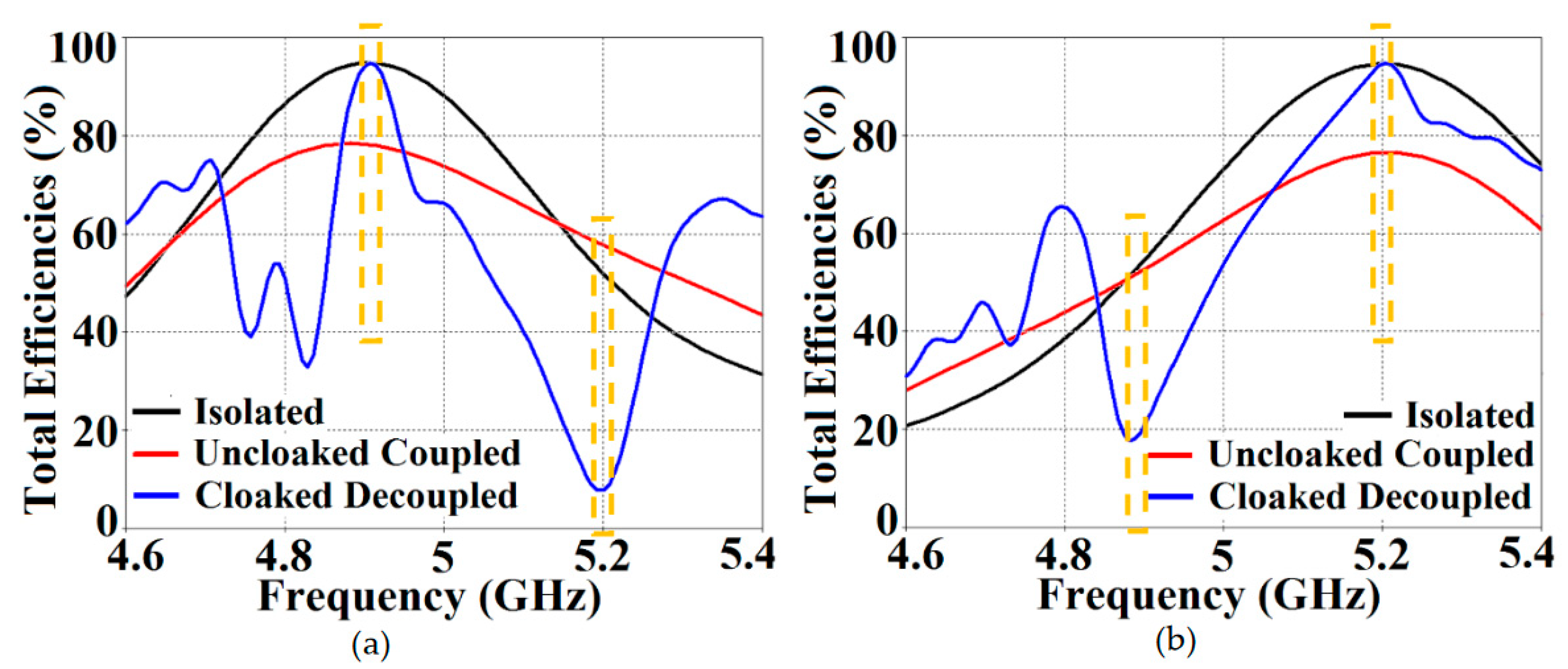
Due to the presence of mutual coupling between the uncloaked patches, the total efficiency drops by approximately 18% and 20% for Patch I and II, respectively, at their corresponding resonance frequencies (compare the red curves in
Figure 7 (a)–(b) with the black curves to spot the decrease in the efficiency levels).
On the other hand, for the cloaked scenario (illustrated by the blue curves in
Figure 7 (a)–(b)), the total efficiencies of each of the patches are seen to have recovered. It is worthwhile to notice that the restored efficiency levels are equal to the efficiencies recorded for the isolated cases, denoted by black curves in
Figure 7; and although the total efficiency of a cloaked patch antenna stays unchanged at its own resonance frequency, it reduces significantly at the resonance frequency of the neighboring patch antenna. This supports our previous assertion that the patterned metasurfaces do not change the radiation aspects of the patch antenna on which it is coated; instead its effect is evident at the cloaking frequency (which is the operating frequency of the other patch in its vicinity). Moreover, in
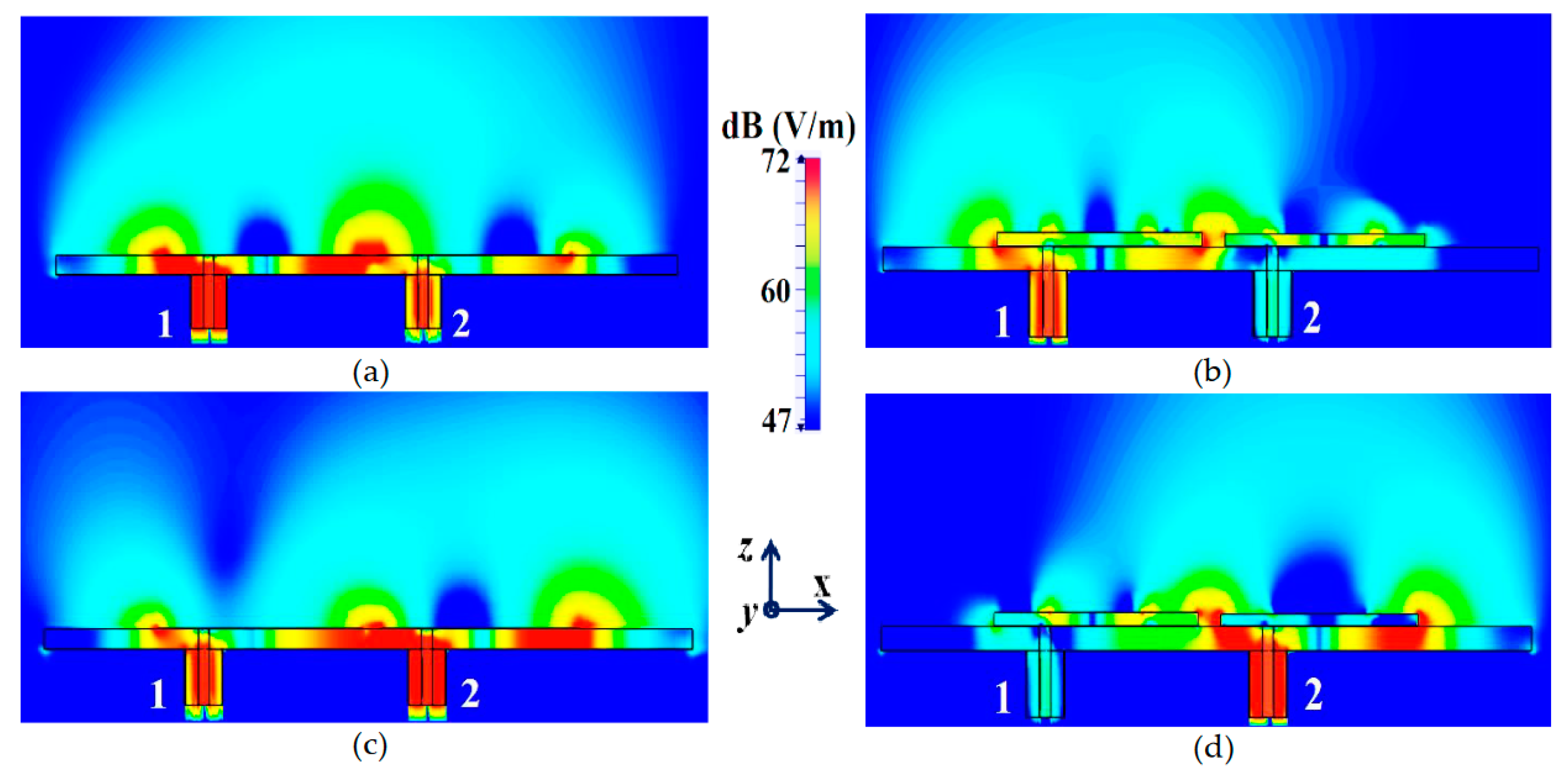
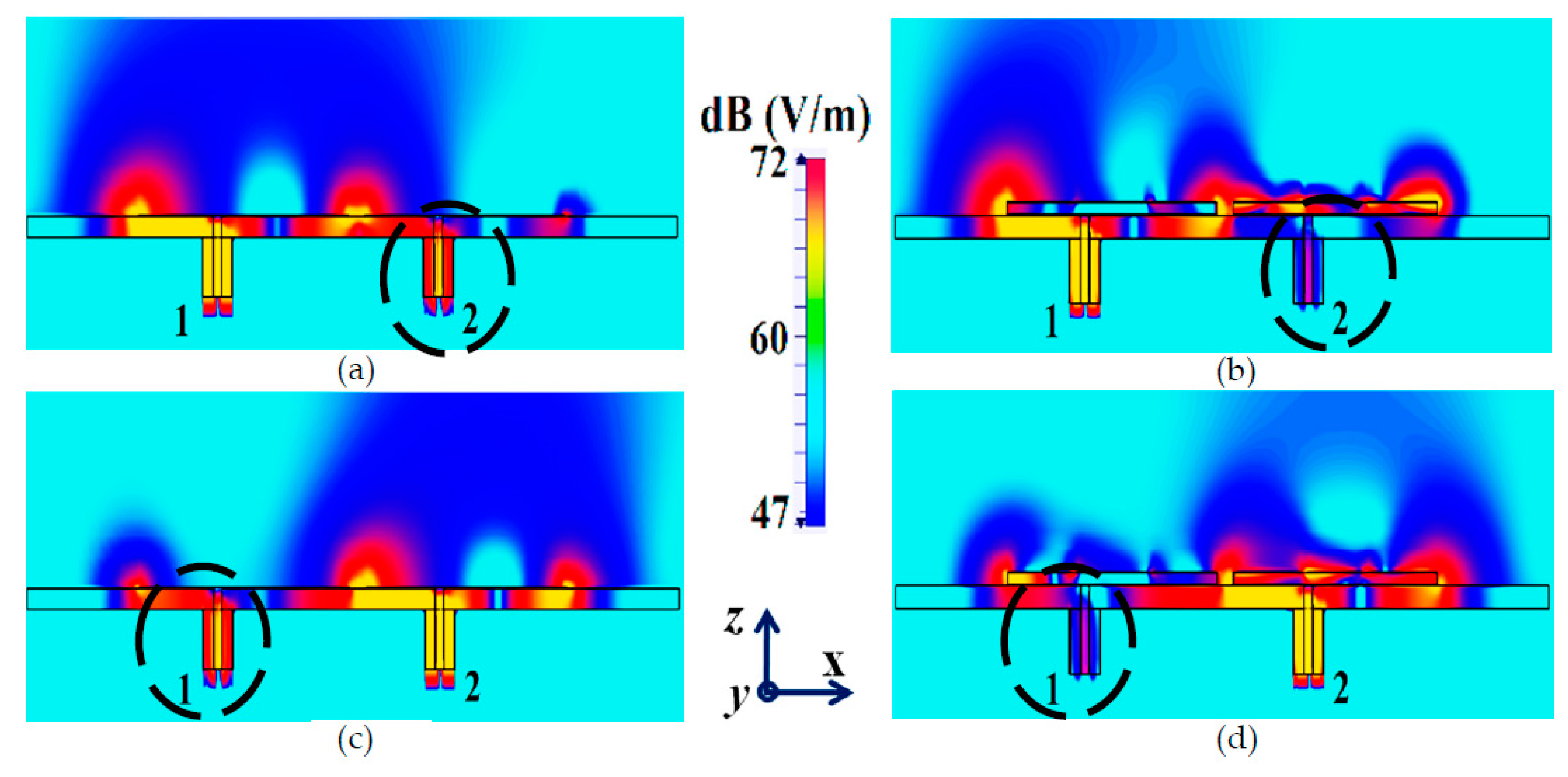
Figure 8, we have presented an exploded view of the E-field plots for the closely placed rectangular patches (with and without cloaks). Through the E-field plots, we endeavor to visually represent the effects of mutual coupling on the corresponding ports and also on each antenna’s radiation behavior, in their uncloaked form. Subsequently, we show that when the patch antennas are coated by the planar metasurfaces (cloaked cases), the coupling effects are considerably minimized. In
Figure 8 (a) and (b), Patch I (resonance frequency,
GHz) is excited, keeping Patch II (resonance frequency,
GHz) inactive.
Now, observe
Figure 8 (a), for the uncloaked antenna models, mutual interference is obvious in the sense that power is seen to be coupled from the input port of Patch I (denoted as 1) to the neighboring patch antenna port (denoted as 2); this is deduced based on high concentration of fields seen at port 2 (evident by the red colored region), despite the fact that Patch II is not active. On the other hand, when the metasurfaces are employed (cloaked case, see
Figure 8 (b)), power coupling from Port 1 to 2 is greatly minimized, thus highlighting the decoupling behavior of the cloak structure. Similarly,
Figure 8 (c)–(d) correspond to the uncloaked and cloaked cases, respectively, when Patch II is excited and Patch I is passive. Following the above argument, analogous deductions can be made for Patch II. To further manifest that the coated metasurfaces not only decouple the two antennas, but are also capable of restoring the far-field radiation behavior of individual patches, we present the polar plots for realized gain patterns in
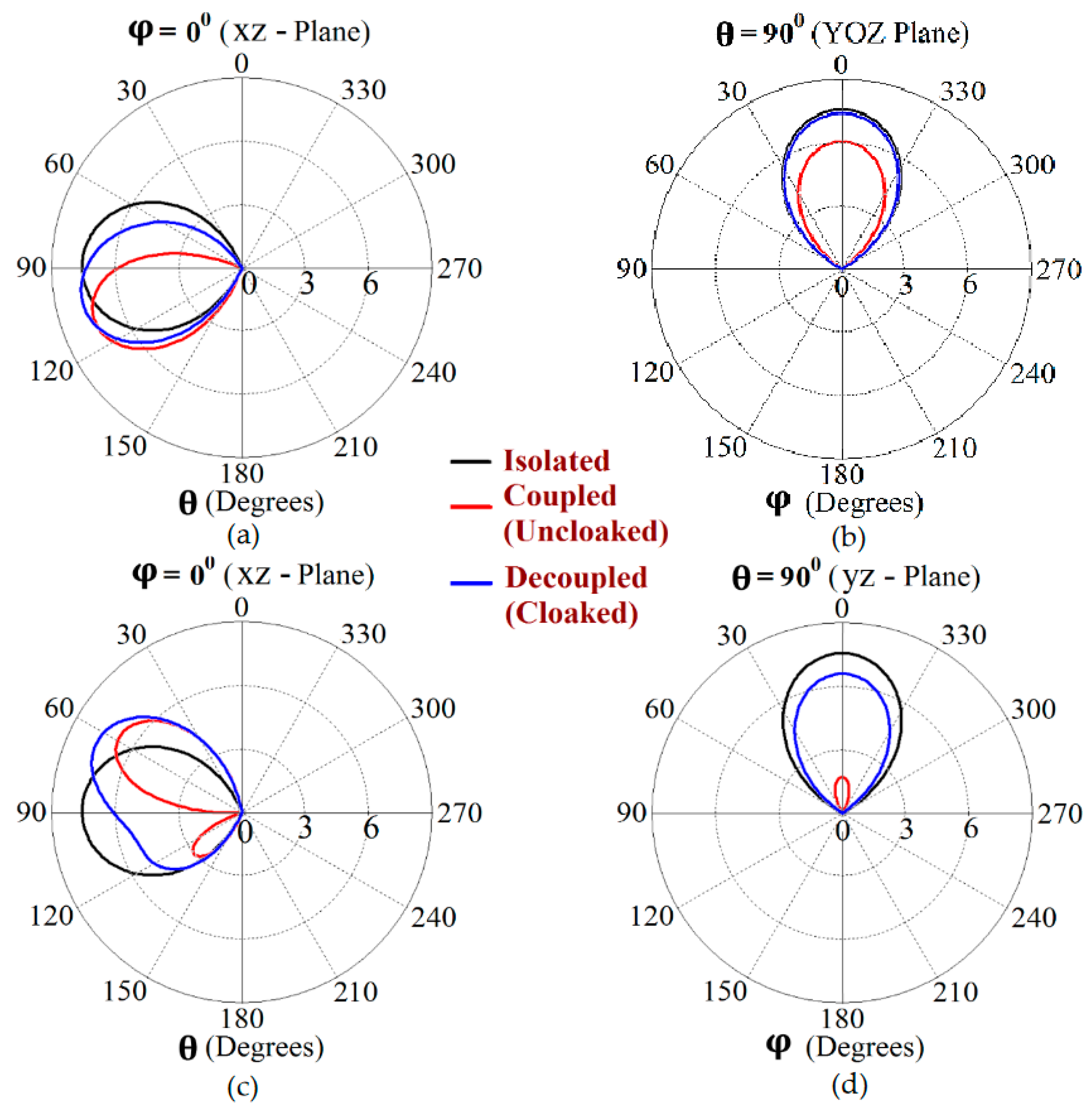
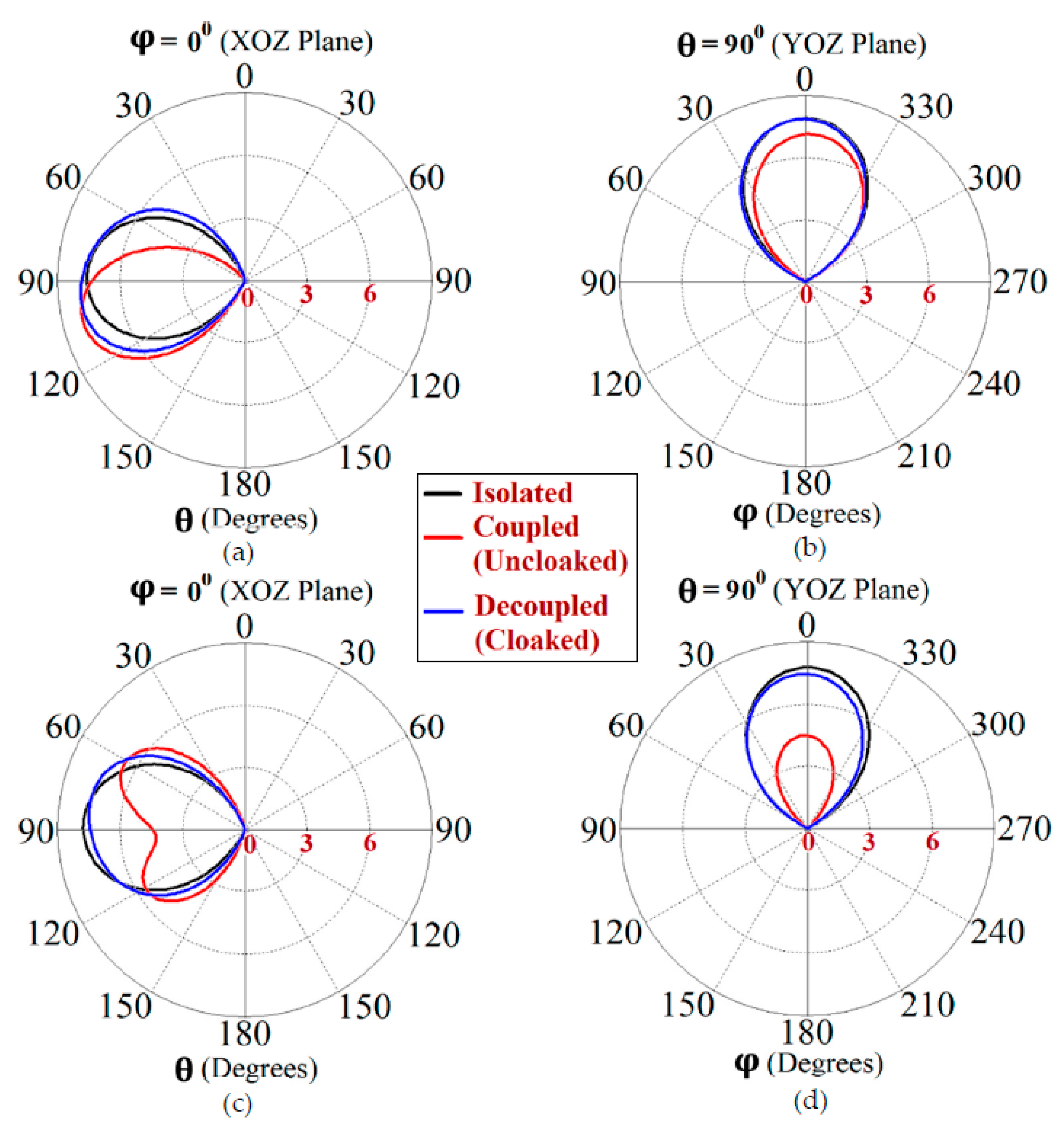
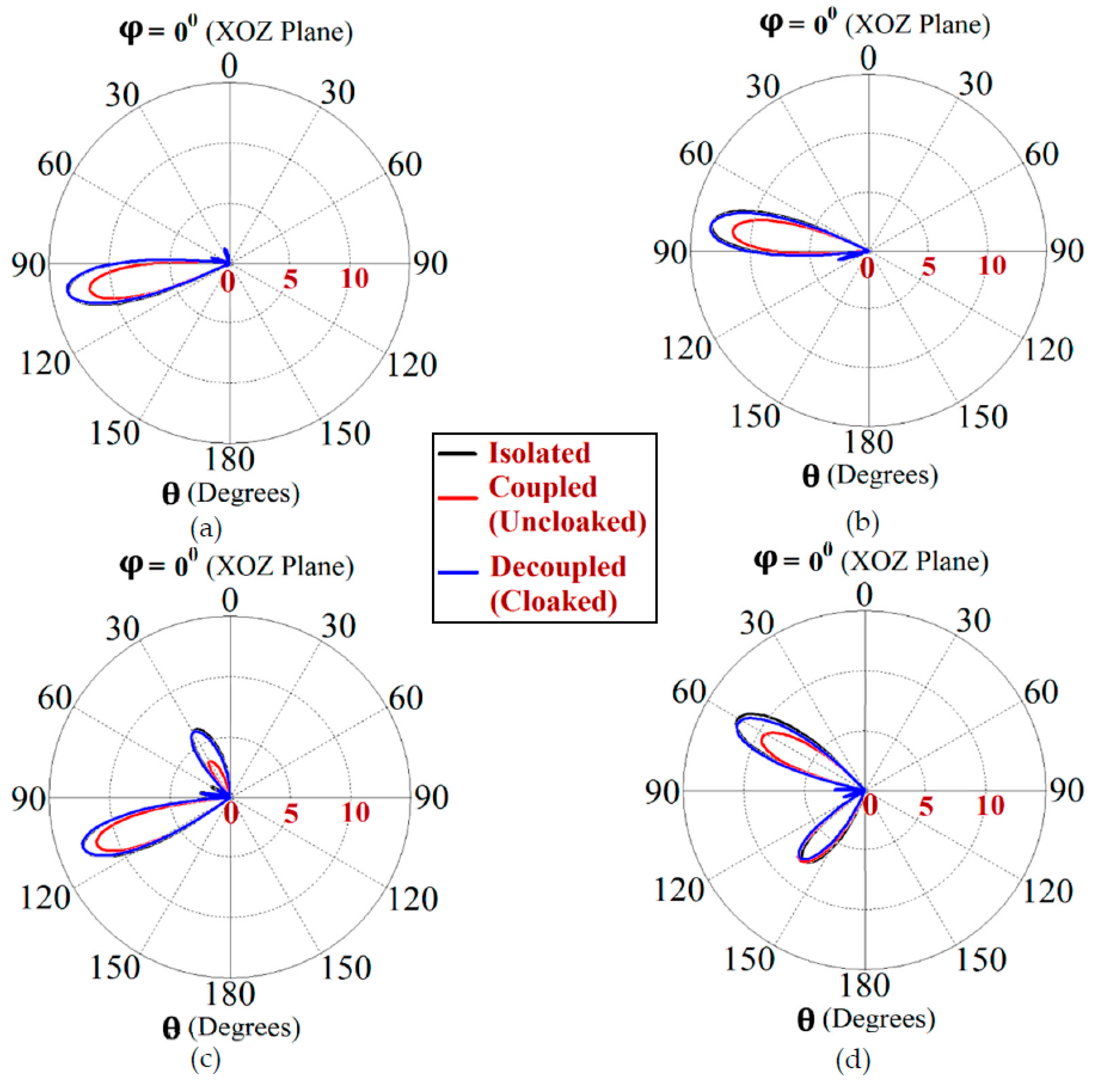
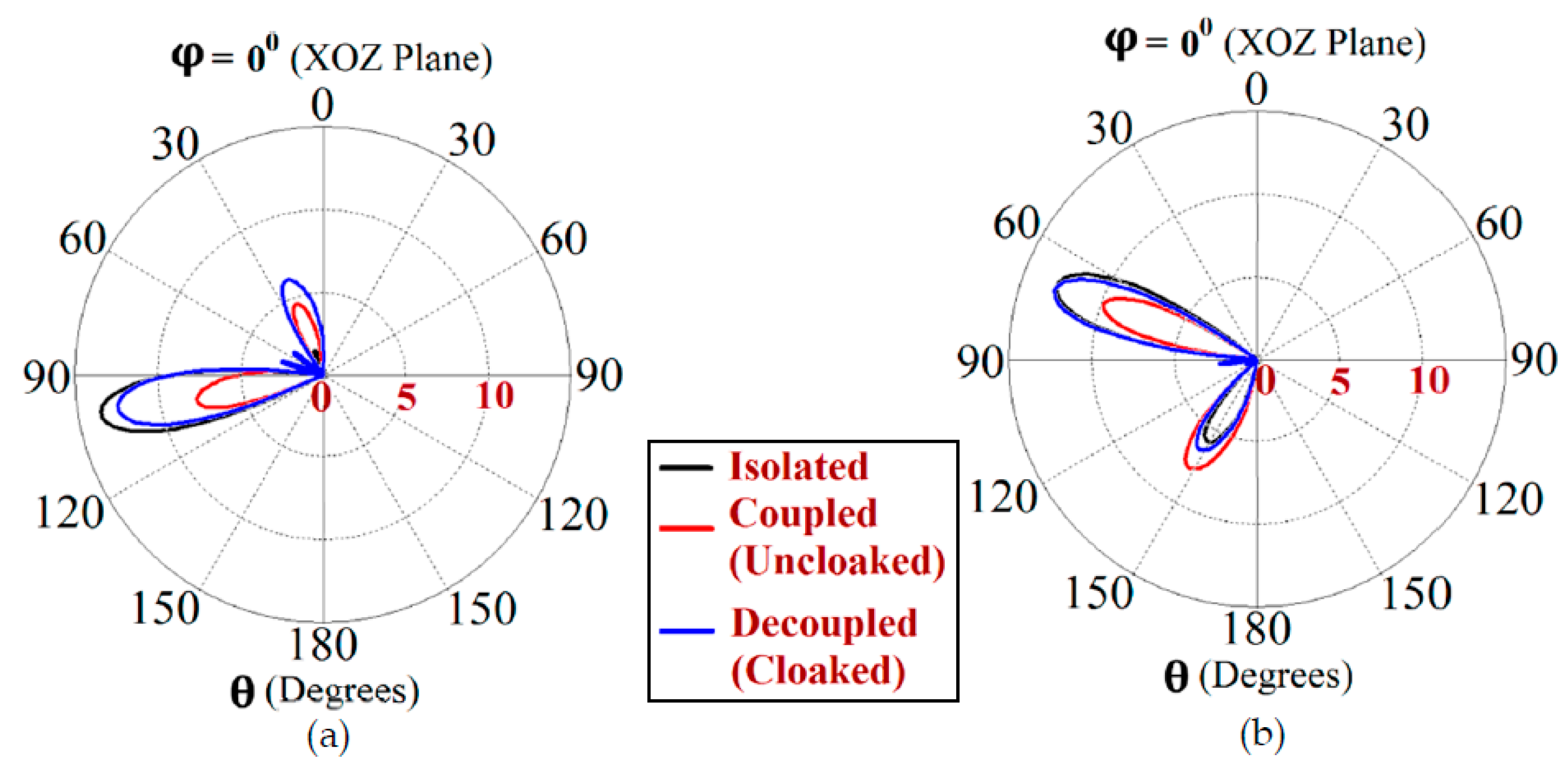
Figure 9. The simulated main lobe gain of both the patches in the isolated scenario is around 7.5 dBi (recall that isolated scenario represents the condition where measurement for each patch is carried out in the absence of the other and the radiation patterns for the same can be regarded as the ideal cases). We then compare the polar plots for the realized gain of the coupled (uncloaked) and decoupled (cloaked) patches. In
Figure 9, the radiation patterns are plotted in the xz (also denoted as
) and yz (also denoted as
) planes of reference for the patch antennas I and II at their corresponding resonance frequencies, i.e.,
GHz and
GHz, respectively. For the coupled (uncloaked) case, a considerable distortion in the gain patterns for both Patch I and Patch II is apparent (observe the solid red curves in
Figure 9). Nevertheless, it is obvious that the specifically tailored metasurfaces faithfully reinstate the gain patterns for both the patches (refer to the decoupled cloaked case shown by the solid blue curves in
Figure 9), at both the planes of reference.
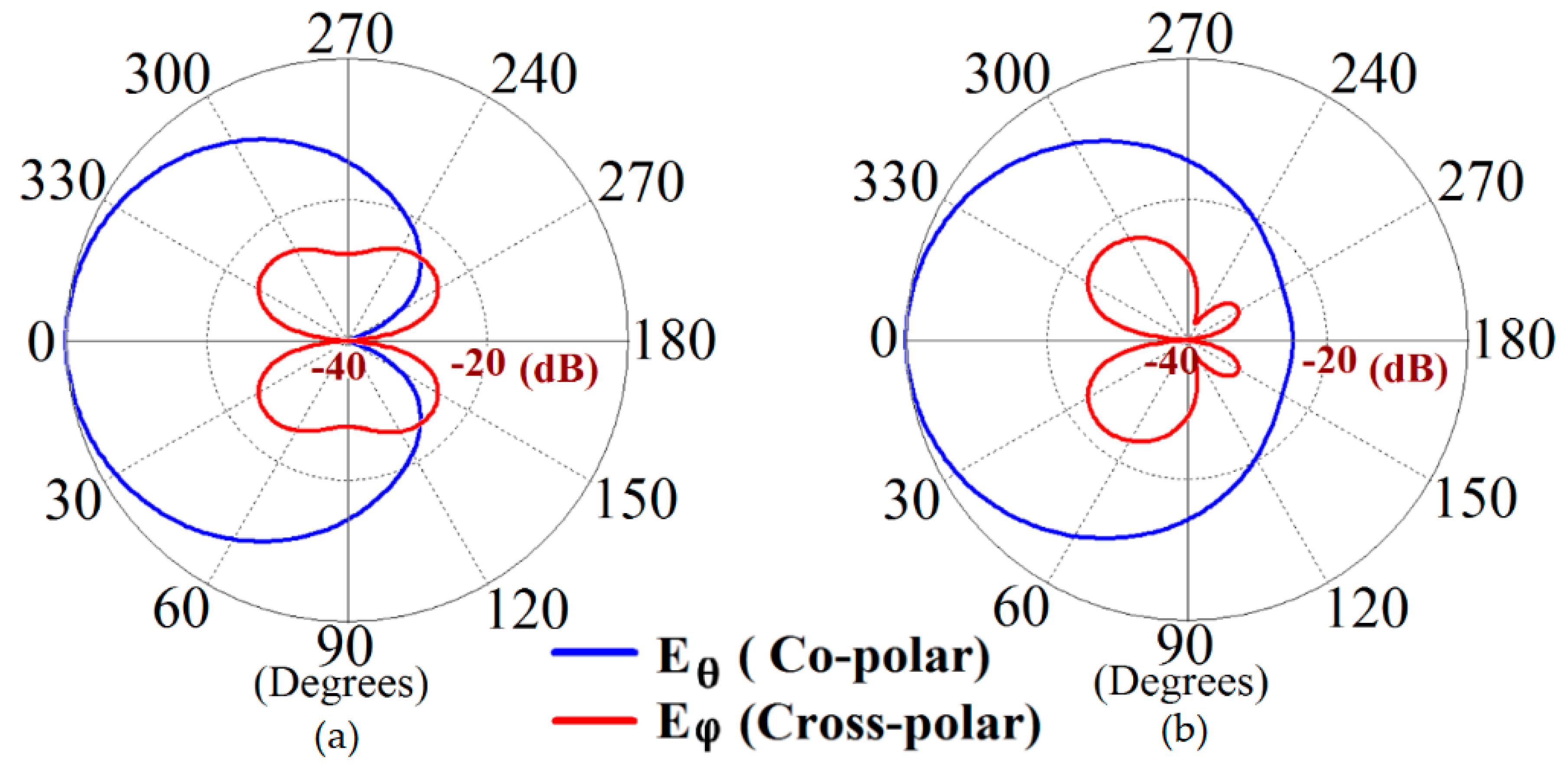
Furthermore, we would like to comment on the cross-polarization levels of our rectangular patch antennas.
On the basis of our design configurations, the rectangular antennas are horizontally polarized, and our observations indicate that patch antennas I and II show cross polarizations of approximately
dB and
dB at their respective resonance frequencies. Even when they are cloaked, the cross polarization levels are maintained at
dB and
dB, for Patch I and II, respectively. This accentuates the fact that the metasurface cloak does not interfere with the polarization levels of the antennas it is coated on. We have presented the co-polar and cross-polar E-field radiation in the following
Figure 10 for the cloaked Patch I and II at their respective resonance frequencies. Through the numerous simulation results demonstrated above, we have emphasized the decoupling effect of our metasurface in the near-field and also highlighted that the metasurface cloaks restore the far-field radiation patterns of each of the antennas, thereby emphasizing on the cloaking behavior of the proposed structures. We now proceed on to investigate the system as a ‘scattering problem’. Here, the patches coated with the cloak structures are essentially treated as passive devices and are bombarded by plane waves to study the scattering behavior of a patch antenna, with and without the cloak. For this purpose, we consider a transverse magnetic (TM) polarized plane wave and impinge it upon our design configurations to analyze their scattering performance. The detailed scattering aspects of Patch I is exhibited in
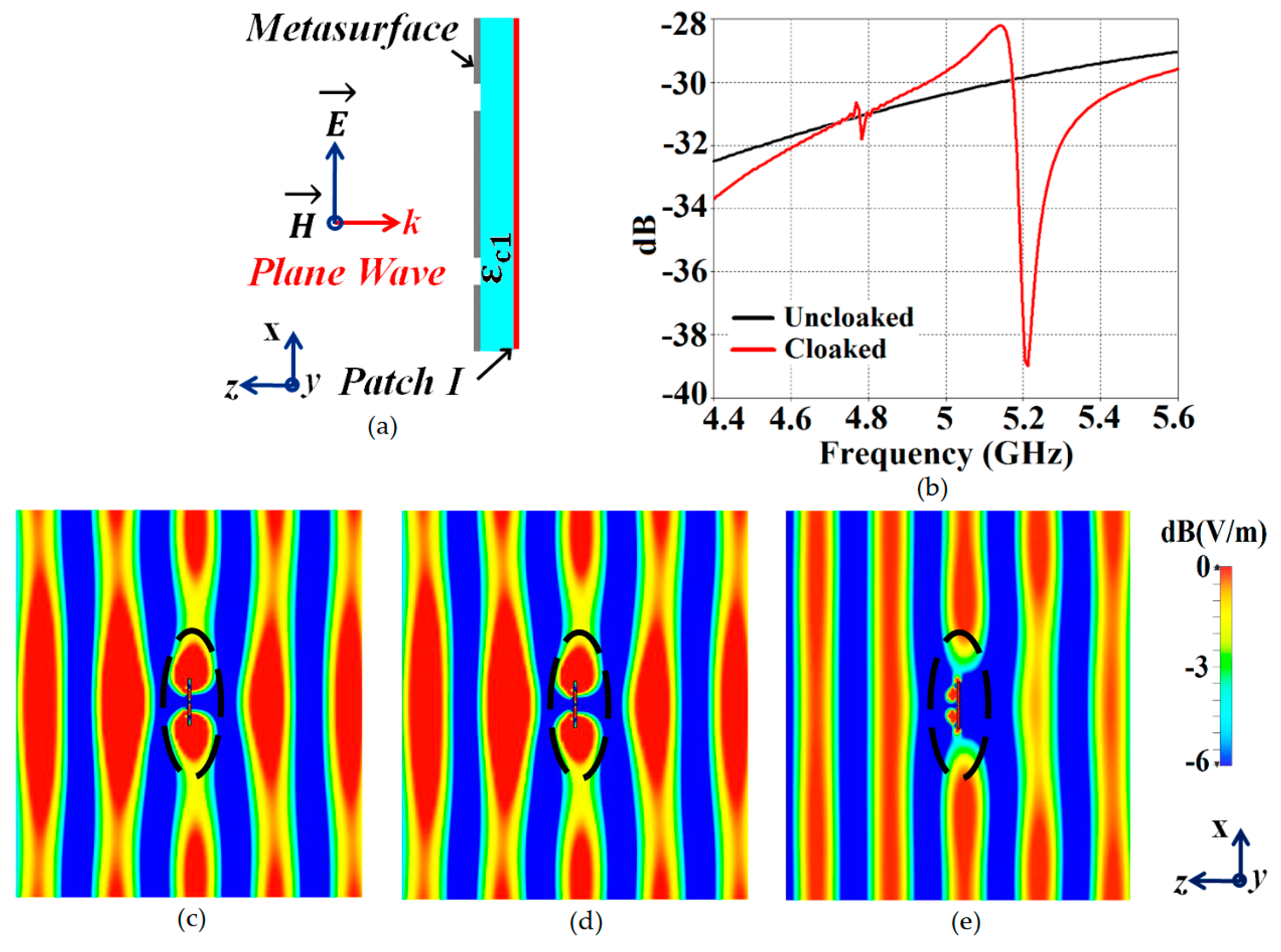
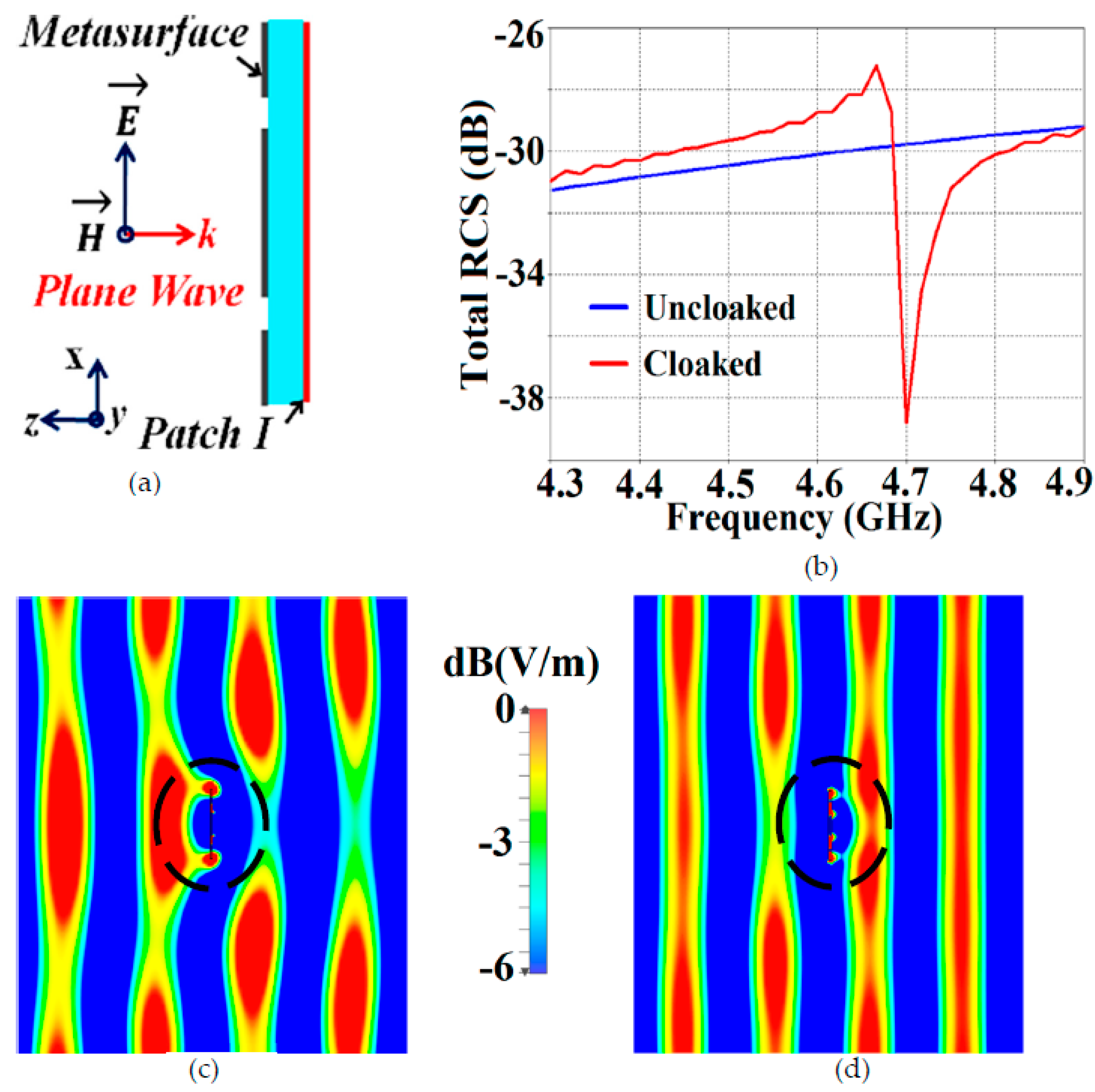
Figure 11 (the design set up for the integrated system of patch antenna coated with its corresponding metasurface in presence of a plane wave excitation, is depicted in
Figure 11 (a)).
Through the total RCS plot in
Figure 11 (b), we demonstrate the scattering cancellation action of our proposed metasurface. Comparing the black and red curves for uncloaked and cloaked Patch I, respectively, we see a significant decrease in the scattering width, which is evident from the 9 dB drop (approximately) recorded at Patch I’s cloaking frequency (i.e.,
GHz). Next, let us observe the behavior of E-field around the uncloaked Patch I; considerable scattering is seen around the edges, shown by the red colored region in
Figure 11 (c). Let’s compare this to the E-field plots for the cloaked Patch I.
Figure 11 (d) depicts E-field contour plots for cloaked Patch I at its resonance frequency (i.e.,
GHz). We can clearly see the scattering of E-field around the cloaked structure (evident by the concentration of red colored region around the patch edges), and notice that this scattering behavior is almost identical to that illustrated in
Figure 11 (c), for the uncloaked patch. This is an added confirmation that the designed metasurface do not harm or alter the radiation/ scattering behavior of the patch antenna at its resonating frequency. However, let’s pay attention to what happens at the cloaking frequency of Patch I (
GHz), as illustrated in
Figure 11 (e). At this frequency, the metasurface completely eliminates the scattering around Patch I (evident by the absence of red colored regions around the patch edges) and an almost smooth passage of the E-fields through the patch is observed, as if the electromagnetic fields cannot ‘see’ it. Thus, we deduce that Patch I is compelled to become
electromagnetically invisible at
GHz. Similar arguments can be advocated for the case of cloaked Patch II, however the corresponding results are not included in the paper for conciseness and to avoid repetition.
We summarize that the specifically designed cloaks not only improves the near-field characteristics (which basically entails decoupling of the antennas, and in this section, the decoupling behavior is depicted through S-parameter plots, total efficiencies and near-field E-field distribution plots), but also reinstate and improve the radiation properties of the antenna in the far-field (which we have demonstrated through the various polar plots). In addition, we have also showcased the total RCS plots and E-field plots, in presence of a TM polarized plane wave excitation source, to highlight the scattering cancellation capability of the cloaks, which essentially accentuates the far-field cloaking functionality of the proposed metasurface. In the following section, we have extended our metasurface design configuration to a linearly arranged, interleaved array of the two rectangular patches.
4. Cloaking of the Interleaved Rectangular Patch Arrays
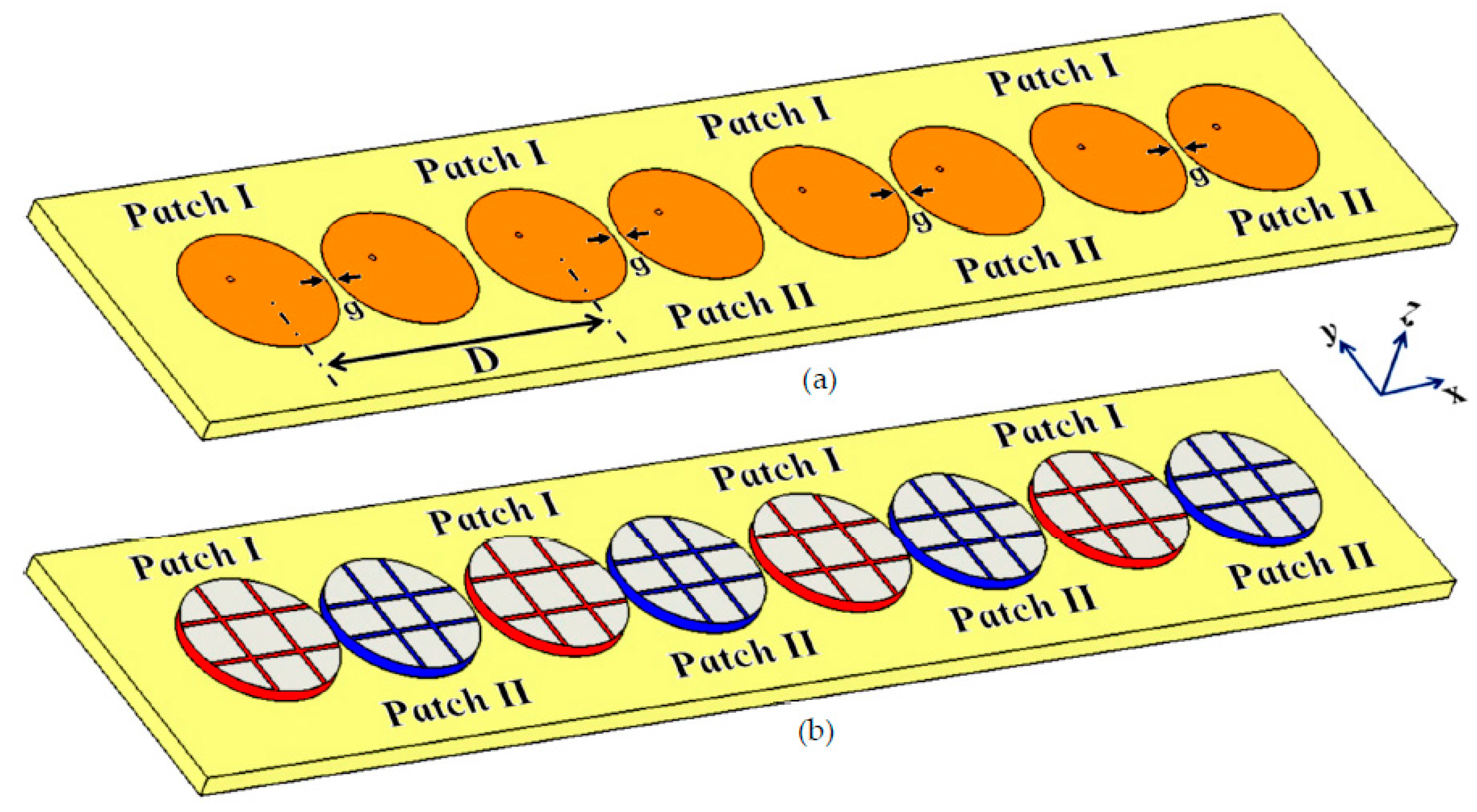
The cloak design specified in the aforementioned section is further protracted to an interleaved array of the patch antennas, wherein the module of the two patches (as described in Section II) is linearly repeated in the direction of the x-axis and are mounted on a single substrate with thickness
mm and permittivity
(i.e., Rogers RT5880 substrate is utilized). Refer to the design configuration shown in
Figure 12. Accordingly, there are four elements each for Patch I and Patch II in the array system. All the Patch I elements form one array, which is why they are excited simultaneously and will be referred to as Array I, henceforth. In a similar fashion, all the Patch II elements form the second array, which we term as Array II. Each element of Array I is spatially separated by a distance of
mm, whereas the elements of Array II are positioned right next to the elements of Array I at distance of
mm. Consequently, we have designed an interleaved system of two distinct arrays, essentially utilizing the same dimensional area that would have been employed for a single array. As is typical, when the antennas are without their cloaks, such close proximity of all these patch elements causes a strong interference, which destroys the matching as well as radiation aspects of both the arrays. As such, when these two arrays are so closely packed, the neighboring antenna elements are strongly coupled, deteriorating the total efficiency as well as the gain of each participating array. And so, contrary to the expected behavior of an array system, efficacy of each array in this case actually degrades. To improve the productivity of these arrays, we deploy the planar coated cloaks, as discussed in section II, to the respective rectangular patch antenna elements in our array configuration (illustrated in
Figure 12 (b)).
With the intention to effectively demonstrate that the arrays are decoupled from each other, we have presented the isolation parameters (coupling coefficients) for the cloaked arrays and compared it with their uncloaked counterparts (
Figure 13 and
Figure 14). Additionally, we also show the reflection coefficients at the respective ports. Consider
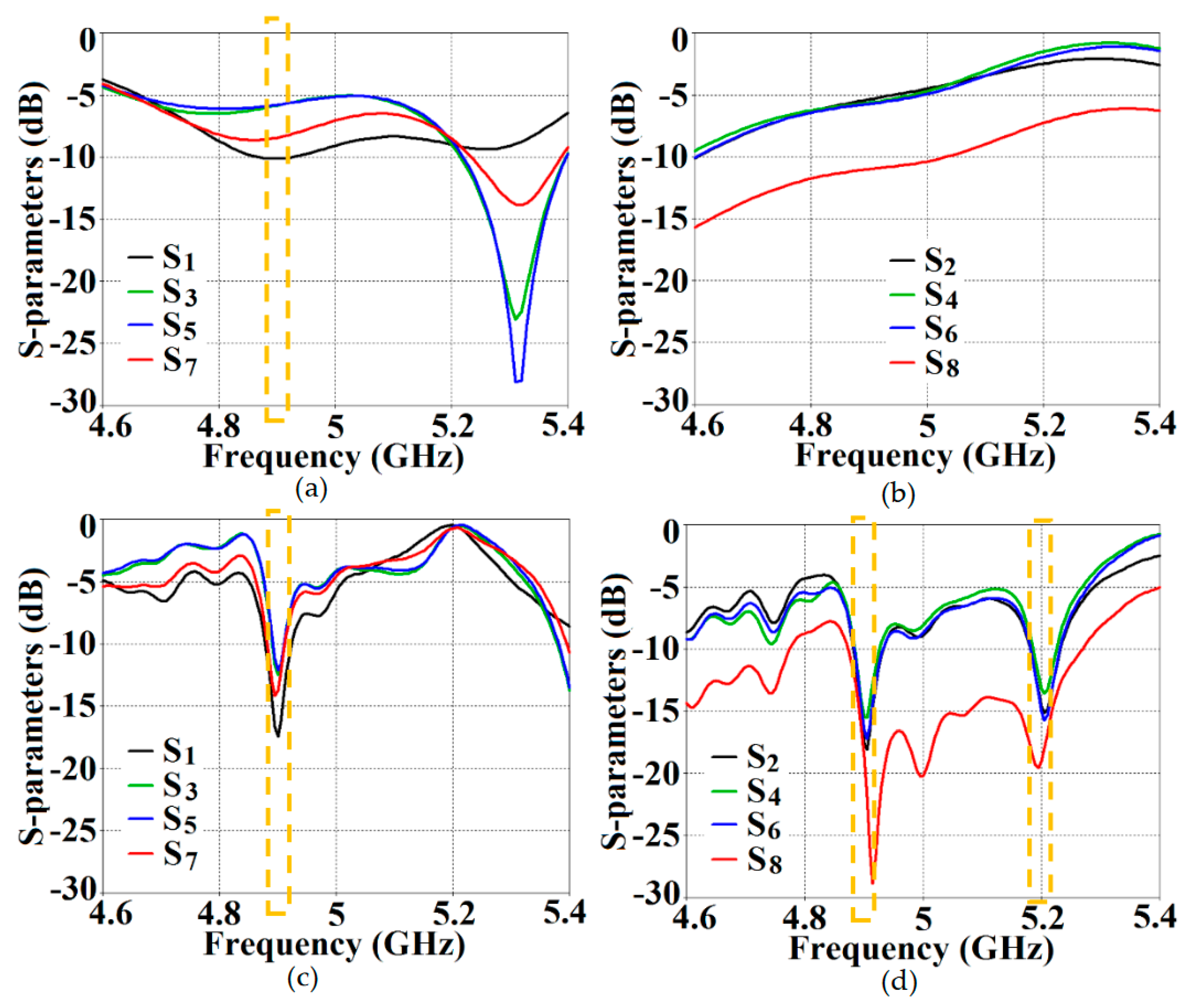
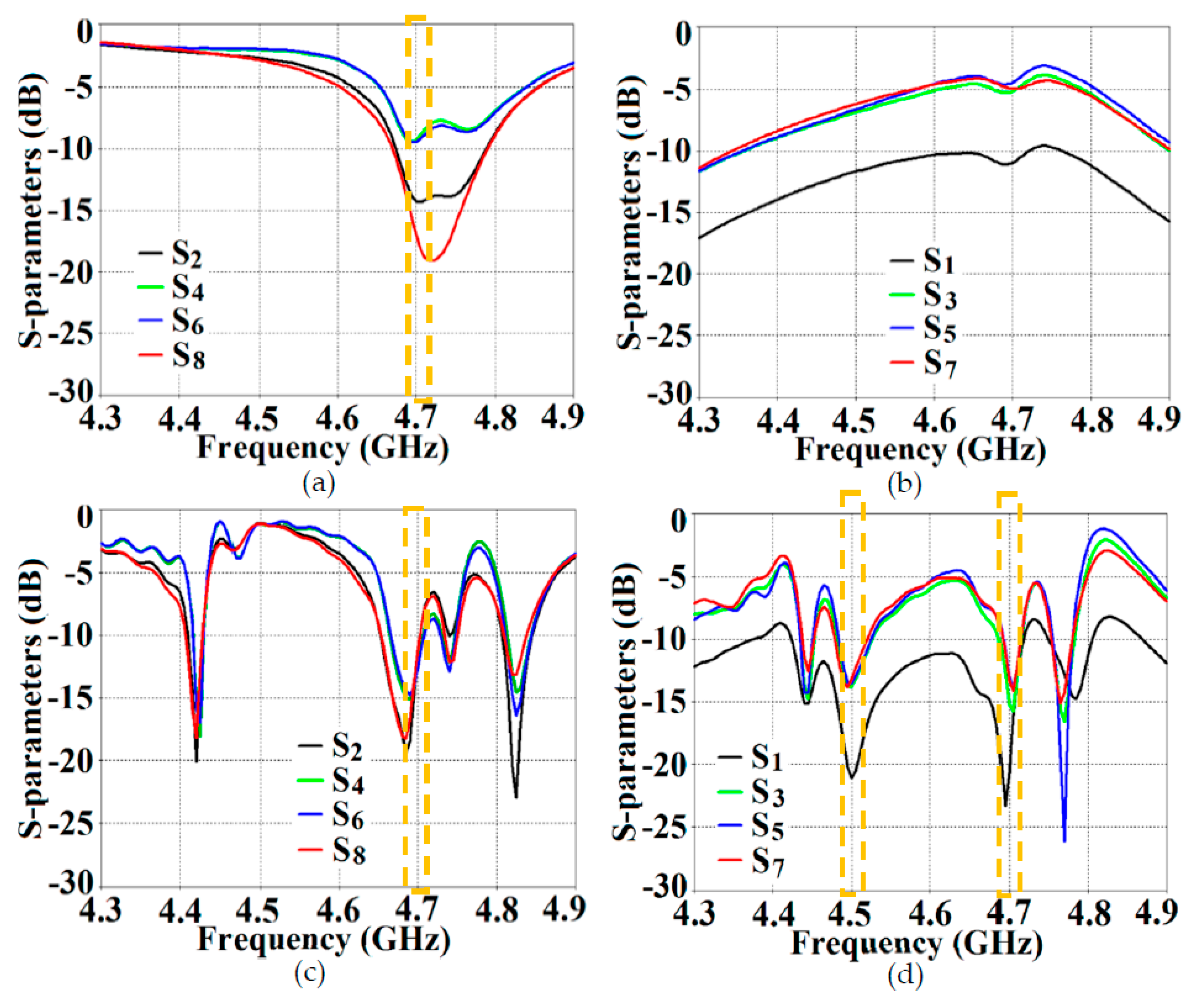
Figure 13; it depicts the isolation and reflection coefficients for uncloaked and cloaked versions of Array I (resonance frequency of this array is
4.9 GHz). When Array I is made active, it means that ports 1, 3, 5, and 7 are excited. Therefore, when Array I is activated, the active reflection coefficients are observed at the ports 1, 3, 5, and 7 (denoted as:
,
,
, and
); whereas the active coupling coefficients are studied at the ports 2, 4, 6, and 8 (denoted as:
,
,
, and
). Evidently, from
Figure 13 (a), matching characteristics for uncloaked Array I is completely destroyed at the resonance frequency
4.9 GHz. This is predominantly attributed to the high levels of mutual coupling arising due to the neighboring antenna elements; the isolation parameters shown in
Figure 13 (b) make this abundantly clear. It is fascinating to see that Array I (in the uncloaked form) not only becomes a non-radiator at its own resonance frequency but a tremendous amount of power coupling is evident at the neighboring array ports. On the other hand, when the arrays are coated with our proposed metasurface design, Array I elements are seen to be perfectly matched at 4.9 GHz in
Figure 13 (c). Along with this, Array I is effectively unmatched at the neighboring array’s frequency, i.e., at
5.2 GHz. This is credited to the fact that the coated metasurfaces greatly reduce the mutual coupling magnitudes (see
Figure 13 (d)) at each resonance frequency, essentially decoupling the neighboring array elements. Similar arguments and observations can be made when Array II is active. In this case, ports 2, 4, 6, and 8 are excited, which means that the active reflection coefficients (denoted as:
,
,
, and
) are plotted at these ports and the isolation coefficients (denoted as:
,
,
, and
) are plotted at the ports 1, 3, 5, and 7 (refer to
Figure 14). The decoupling and cloaking effects of our metasurface structures are also apparent in the plots for total efficiencies and the E-field distributions, portrayed in
Figure 15 and
Figure 16, respectively. The total efficiencies are plotted for each array in the isolated scenario, coupled uncloaked and decoupled cloaked conditions.
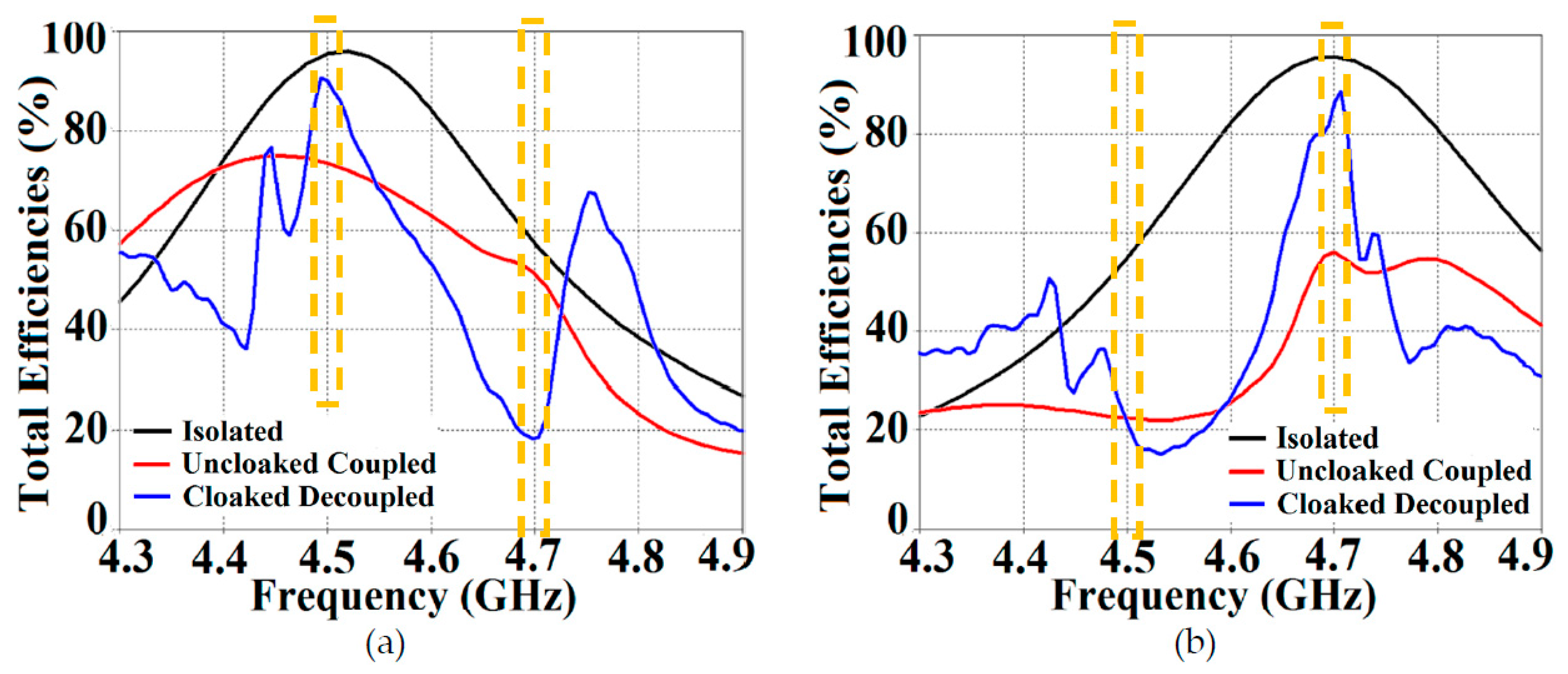
Referring to
Figure 15 (a) and (b), it is clear that the total efficiency decreases remarkably for the uncloaked arrays, especially in case of Array II (depicted by the solid red curves). A drop of approximately
is recorded for Array I and a whopping
reduction is seen for Array II, which means that the matching and radiation aspects of Array II are utterly destroyed. For the cloaked arrays, however, the total efficiencies are vastly recovered at their respective resonance frequencies (illustrated by the solid blue curves), almost emulating the efficiency values of the corresponding array in the isolated scenario (indicated by black curves). Once again, along with improving total efficiencies of each array at their respective resonance frequencies, the efficiency values attain negligible levels at the respective cloaking frequencies of the arrays (nearly reaching
at
GHz for Array I, and
at
GHz for Array II). The E-field contour plots for our array arrangement are presented in
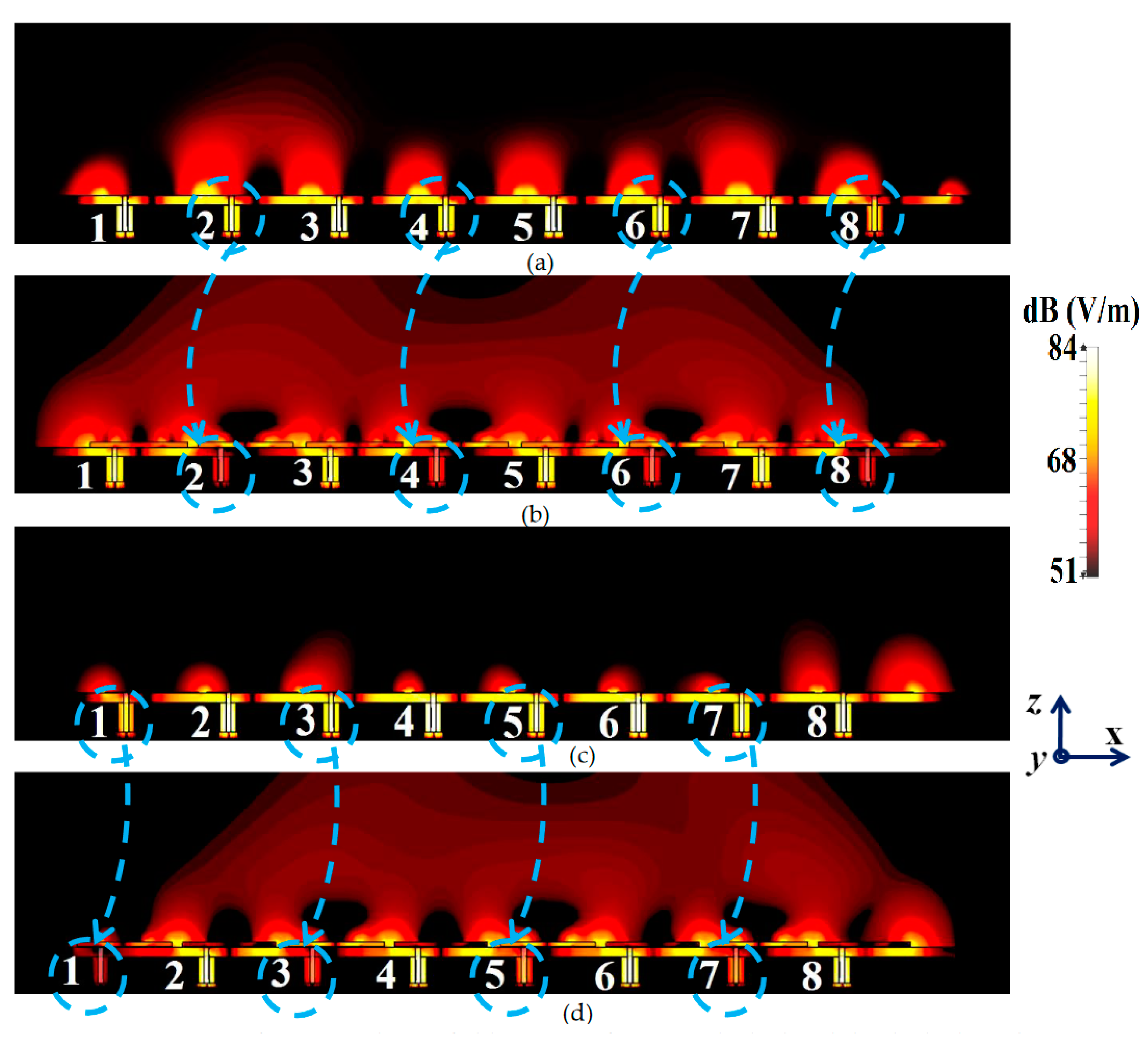
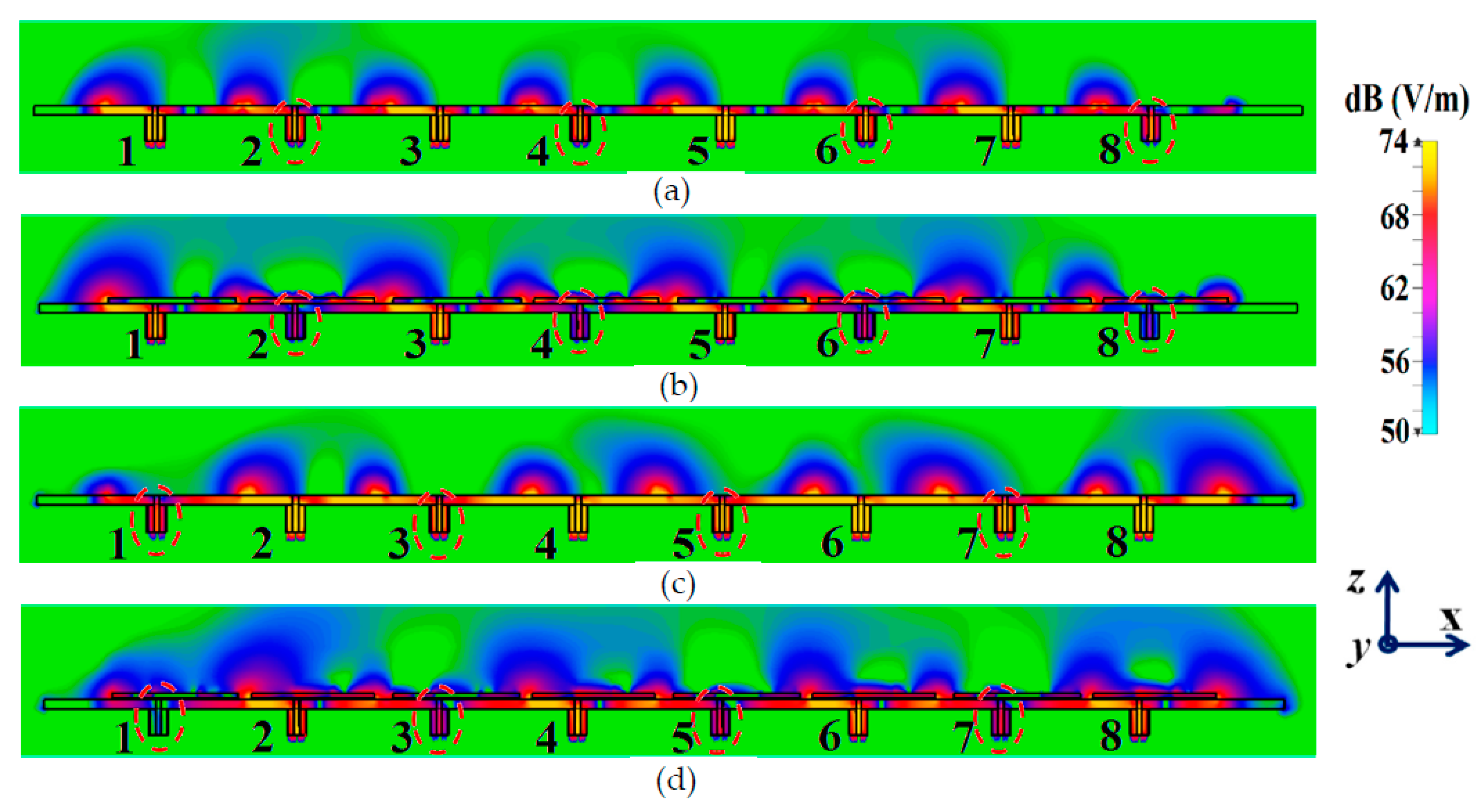
Figure 16; it serves to provide additional validation of the decoupling functionality of the metasurface constructs. In
Figure 16 (a) and (b), comparison of field plots are shown for the uncloaked and cloaked scenarios, respectively, when Array I is active (ports 1, 3, 5 and 7 are excited simultaneously) and Array II is kept inactive. Similarly, field plots when Array II is active (ports 2, 4, 6 and 8 are excited), and Array I passive, are shown in
Figure 16 (c) and (d). For the uncloaked coupled scenario, an unmistakable coupling is apparent between the neighboring elements of the interleaved arrays, ultimately inhibiting the far-field radiation efficacies of each array. For instance, consider
Figure 16 (a)–(b); here Array I is active. Despite this, for the uncloaked case (
Figure 16 (a)), power coupling is noticeable at the input ports of Patch II, i.e., at ports 2, 4, 6 and 8. Nonetheless, in
Figure 16 (b), the coupling becomes almost negligible when the array elements are cloaked by planar metasurfaces.
Ports 2, 4, 6 and 8 are marked in
Figure 16 (a) and (b) to highlight the decrease in power coupling at these input ports, in turn, ensuring reduction of the unwanted mutual interference between the neighboring elements of the two arrays. A very similar behavioral pattern can be deduced from
Figure 16 (c) and (d), where Array II is active. Therefore, we reiterate that by employing the specialized planar cloaks onto the respective patch element, the coupling effects are significantly diminished in the near-field. Along with this, restoration of the radiation patterns is noticed in the far-field, leading to a vast improvement in the overall radiation properties of each array.
4.1. Beam Scanning
The coated metasurfaces are definitely engineered with the sole purpose of enhancing the properties of each array such that they are comparable with the isolated array performance, which definitely increases the productivity of the array system as a whole, in spite of the crowded arrangement of the antenna elements. It is achieved by ensuring that all the elements of one array is made invisible to (decoupled from) all the elements of the neighboring array, in turn, manifesting that the two arrays can operate as if they were isolated (operating independently) from each other. This forms the basis for enabling efficient beam scanning at various scan angles. We know that by exciting the corresponding port of a targeted array with proper phase shifts, a desired beam angle can be achieved (we used the well-known formula for calculating required phase shift for the excitation signal that serves as an input for particular antenna elements of an array). Furthermore, we also determined the estimated range of beam scanning angles for our array configurations. It follows that both the designed arrays (Array I and II)) have the ability to scan the beam from
to
(a total of approximately
beam scan is available) in the xz-plane or also written as
plane of reference. To emphasize on the efficacy of the coated metasurfaces in enabling decoupling of the arrays at various beam scan angles, we demonstrate the active VSWR plots and isolation parameter plots for the uncloaked and cloaked Array I in
Figure 17 and
Figure 18 at scan angles
and
, respectively. As mentioned above, when Array I is excited, the mutual coupling coefficients (isolation parameters) are observed at the ports 2, 4, 6, and 8; and are denoted as:
,
,
, and
. Whereas, the active VSWR are plotted at the ports 1, 3, 5, and 7 (denoted as VSWR 1, VSWR 3, VSWR 5, and VSWR 7).
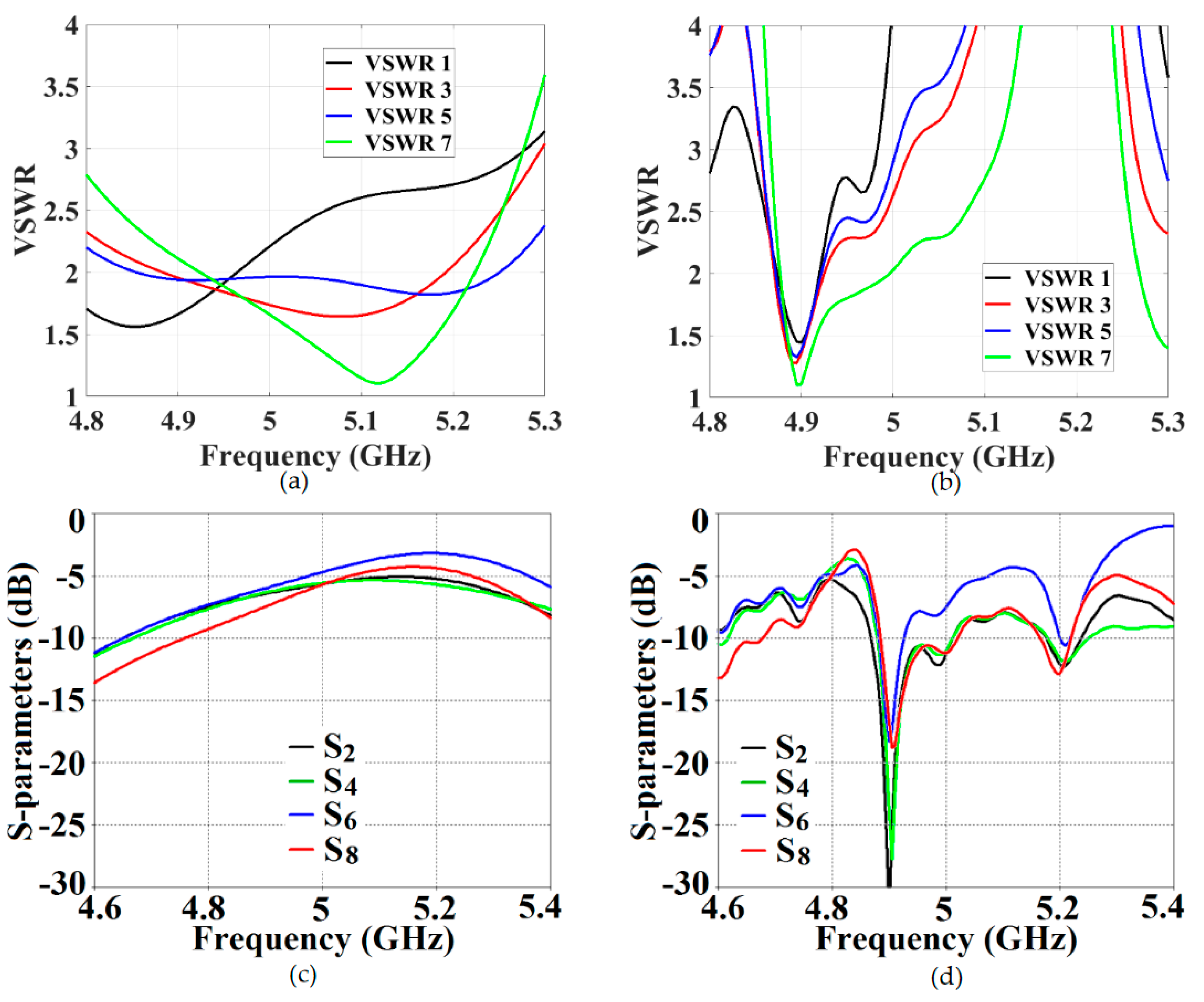
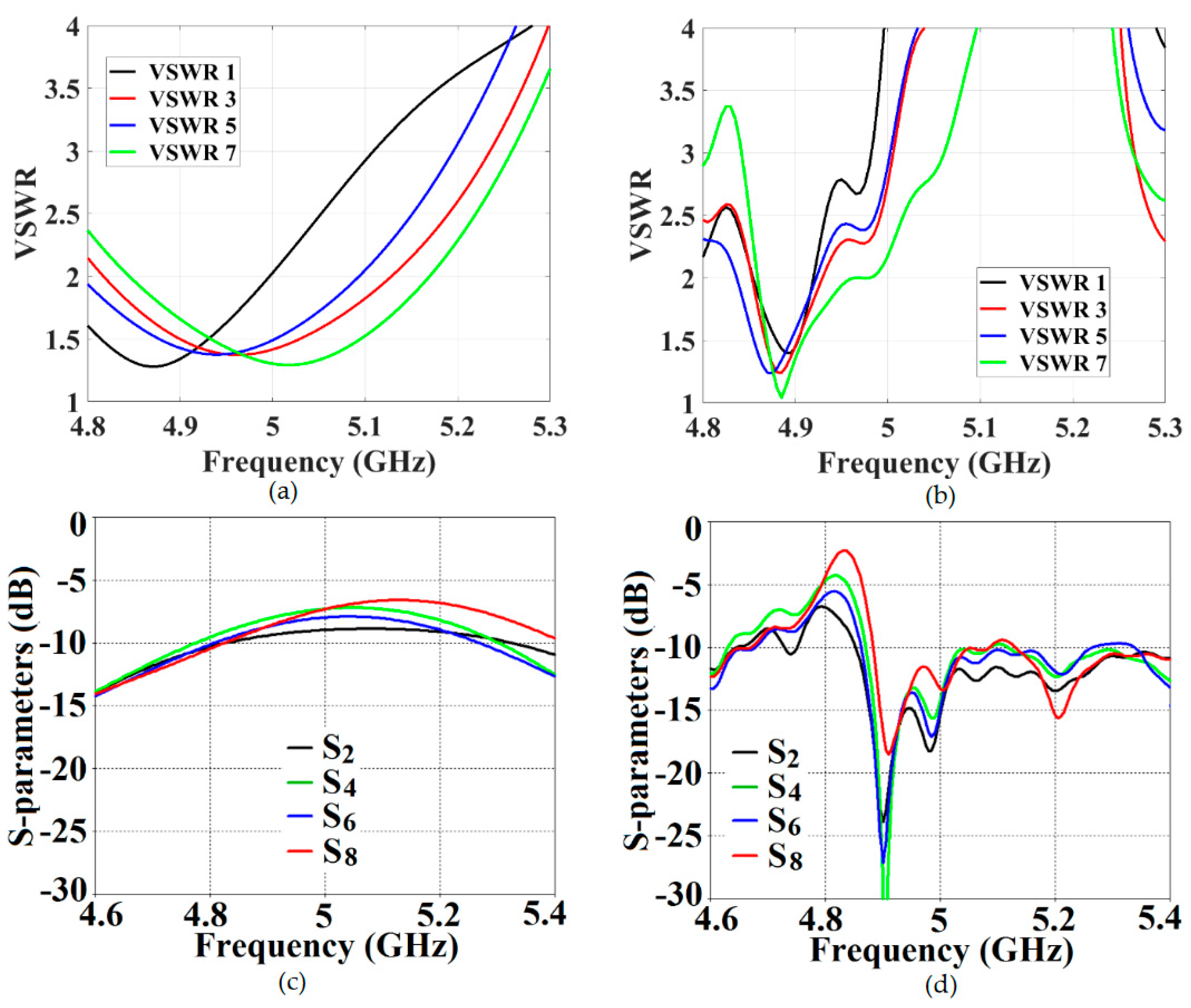
It is clear from the following figures that for the uncloaked coupled Array I (see
Figure 17 (a), (c) and
Figure 18 (a), (c)), at each of the scan angles, the VSWR plots show degradation in the matching characteristics, and the active isolation coefficients depict high values of coupling levels, at the resonance frequency
GHz. Again, this is a clear indication of tremendous mutual coupling present between the two uncloaked arrays. From the active VSWR plots and the isolation plots for the cloaked Array I (see
Figure 17 (b), (d) and
Figure 18 (b), (d)), at each of the scan angles, it is revealed that the array shows good matching properties and a considerable reduction of mutual coupling at the desired resonance frequency.
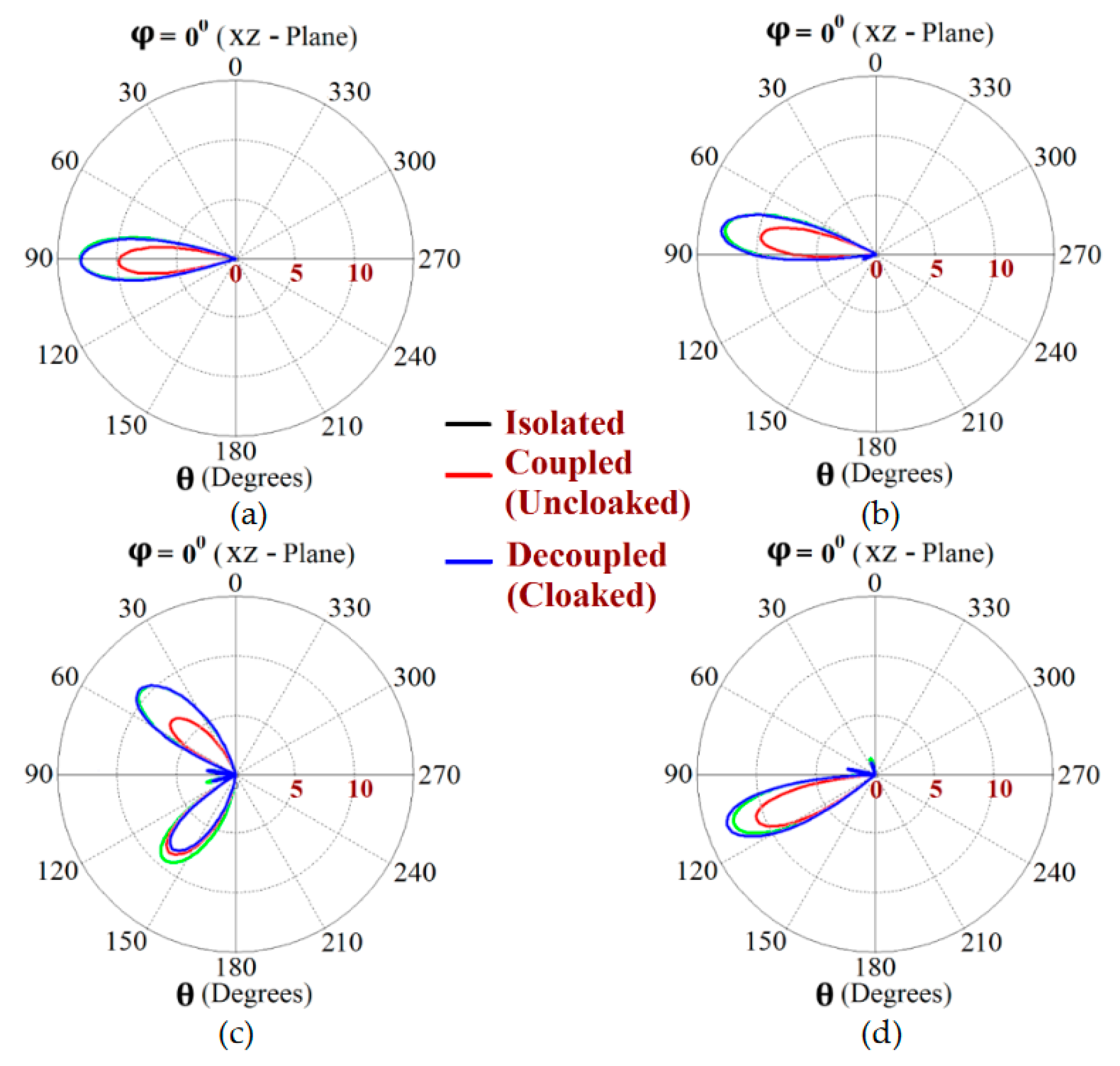
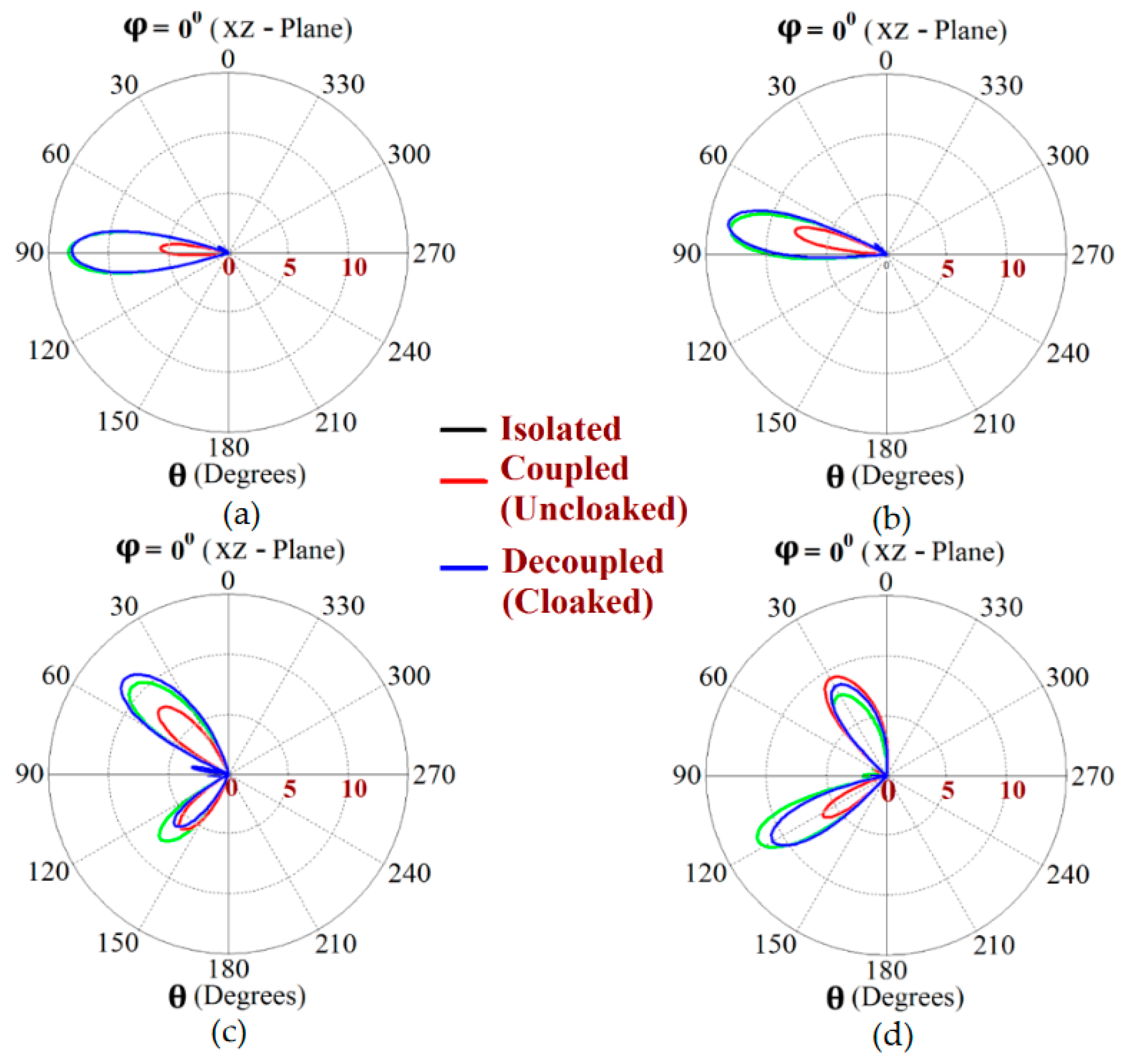
This indicates that the coated metasurface cloaks effectively decouple the two arrays. We have further presented the polar plots for various beam scanning angles for both Array I and Array II in
Figure 19 and
Figure 20. It is apparent from the polar plots for both arrays that in the uncloaked (coupled) condition (observe the solid red curves depicted in
Figure 19 and
Figure 20), reduction in the main lobe gain as well as some distortion in the pattern itself is present. On the other hand, in the cloaked (decoupled) case (solid blue curves), the metasurface cloaks coating the antenna elements of the arrays are shown to faithfully rehabilitate the realized gain patterns at all the illustrated beam angles. We should comment upon the side lobes that seem to emerge as the beam steers toward its extreme angles (especially at
and
). Even though the side lobes are present, it should not affect the main lobe radiation much, since considerable magnitude of gain is still concentrated in the main lobe at that particular angle.
Figure 1.
Design configurations: (a) Isolated Patch I and (b) Isolated Patch II.
Figure 1.
Design configurations: (a) Isolated Patch I and (b) Isolated Patch II.
Figure 2.
Schematics for (a) Uncloaked Patch I and II, (b) unfolded view of the cloak design for the patches, (c) Cloaked Patch I and II, and (d) side-view of the cloaked rectangular patches, detailing the structural parameters of the coated metasurfaces.
Figure 2.
Schematics for (a) Uncloaked Patch I and II, (b) unfolded view of the cloak design for the patches, (c) Cloaked Patch I and II, and (d) side-view of the cloaked rectangular patches, detailing the structural parameters of the coated metasurfaces.
Figure 3.
Parametric analysis using the reflection coefficients () for (a) Relative permittivity of the supporting dielectric material, (b) thickness of the dielectric , (c) vertical slot placement , and (d) horizontal slot placement for the cloak design of Patch I.
Figure 3.
Parametric analysis using the reflection coefficients () for (a) Relative permittivity of the supporting dielectric material, (b) thickness of the dielectric , (c) vertical slot placement , and (d) horizontal slot placement for the cloak design of Patch I.
Figure 4.
Cross-sectional view of the surface currents: (a) Uncloaked, (b) Cloaked Patch I at the cloaking frequency.
Figure 4.
Cross-sectional view of the surface currents: (a) Uncloaked, (b) Cloaked Patch I at the cloaking frequency.
Figure 5.
Plots for (a) total efficiencies and electric field contours at GHz for (b) uncloaked, (c) cloaked Patch I.
Figure 5.
Plots for (a) total efficiencies and electric field contours at GHz for (b) uncloaked, (c) cloaked Patch I.
Figure 6.
S-parameter plots for (a) Coupled uncloaked (b) Decoupled cloaked rectangular patch antennas.
Figure 6.
S-parameter plots for (a) Coupled uncloaked (b) Decoupled cloaked rectangular patch antennas.
Figure 7.
Total efficiencies when (a) Patch I is active and (b) Patch II is active.
Figure 7.
Total efficiencies when (a) Patch I is active and (b) Patch II is active.
Figure 8.
Electric field contours for the two rectangular patches placed close together: (a) Coupled Uncloaked (without cloaks), (b) Decoupled Cloaked (with cloaks) cases, when Patch I ( GHz) is active, and similarly for (c) Uncloaked, (d) Cloaked cases, when Patch II ( GHz) is active.
Figure 8.
Electric field contours for the two rectangular patches placed close together: (a) Coupled Uncloaked (without cloaks), (b) Decoupled Cloaked (with cloaks) cases, when Patch I ( GHz) is active, and similarly for (c) Uncloaked, (d) Cloaked cases, when Patch II ( GHz) is active.
Figure 9.
Realized gain patterns at (a), (b) for Patch I (at frequency GHz), and at (c), (d) for Patch II (at frequency GHz).
Figure 9.
Realized gain patterns at (a), (b) for Patch I (at frequency GHz), and at (c), (d) for Patch II (at frequency GHz).
Figure 10.
E-field plots showing co-polar and cross-polar radiations for the cloaked configurations of (a) Patch I at GHz and (b) Patch II at GHz.
Figure 10.
E-field plots showing co-polar and cross-polar radiations for the cloaked configurations of (a) Patch I at GHz and (b) Patch II at GHz.
Figure 11.
(a) Cross-sectional view of Patch I coated with the metasurface cloak, (b) total RCS plot for Patch I, and E-field plots for (c) uncloaked Patch I at GHz, (d) cloaked Patch I at GHz, and (e) cloaked Patch I at GHz in presence of a normally incident TM polarized plane wave.
Figure 11.
(a) Cross-sectional view of Patch I coated with the metasurface cloak, (b) total RCS plot for Patch I, and E-field plots for (c) uncloaked Patch I at GHz, (d) cloaked Patch I at GHz, and (e) cloaked Patch I at GHz in presence of a normally incident TM polarized plane wave.
Figure 12.
Schematic configurations of (a) uncloaked and (b) cloaked rectangular patch antenna arrays.
Figure 12.
Schematic configurations of (a) uncloaked and (b) cloaked rectangular patch antenna arrays.
Figure 13.
(a) Active reflection coefficients, (b) Active coupling coefficients for uncloaked (coupled) Array I, (c) Active reflection coefficients, and (d) Active coupling coefficients for cloaked (decoupled) Array I (resonance frequency GHz).
Figure 13.
(a) Active reflection coefficients, (b) Active coupling coefficients for uncloaked (coupled) Array I, (c) Active reflection coefficients, and (d) Active coupling coefficients for cloaked (decoupled) Array I (resonance frequency GHz).
Figure 14.
(a) Active reflection coefficients, (b) Active coupling coefficients for uncloaked (coupled) Array II, (c) Active reflection coefficients, and (d) Active coupling coefficients for cloaked (decoupled) Array II (resonance frequency GHz).
Figure 14.
(a) Active reflection coefficients, (b) Active coupling coefficients for uncloaked (coupled) Array II, (c) Active reflection coefficients, and (d) Active coupling coefficients for cloaked (decoupled) Array II (resonance frequency GHz).
Figure 15.
Plots for total efficiencies: (a) Array I (resonance frequency GHz) active and (b) Array II (resonance frequency GHz) active.
Figure 15.
Plots for total efficiencies: (a) Array I (resonance frequency GHz) active and (b) Array II (resonance frequency GHz) active.
Figure 16.
Electric field contours for (a) uncloaked and (b) cloaked patch antenna arrays when Array I (operating frequency, GHz) is active; (c) uncloaked, (d) cloaked patch antenna arrays when Array II (operating frequency, GHz) is active.
Figure 16.
Electric field contours for (a) uncloaked and (b) cloaked patch antenna arrays when Array I (operating frequency, GHz) is active; (c) uncloaked, (d) cloaked patch antenna arrays when Array II (operating frequency, GHz) is active.
Figure 17.
Active VSWR plots for (a) uncloaked coupled, (b) cloaked decoupled Array I ( GHz), and Isolation parameter plots for (c) uncloaked coupled, (d) cloaked decoupled Array I, at scan angle = .
Figure 17.
Active VSWR plots for (a) uncloaked coupled, (b) cloaked decoupled Array I ( GHz), and Isolation parameter plots for (c) uncloaked coupled, (d) cloaked decoupled Array I, at scan angle = .
Figure 18.
Active VSWR plots for (a) uncloaked coupled, (b) cloaked decoupled Array I ( GHz), and Isolation parameter plots for (c) uncloaked coupled, (d) cloaked decoupled Array I, at scan angle = .
Figure 18.
Active VSWR plots for (a) uncloaked coupled, (b) cloaked decoupled Array I ( GHz), and Isolation parameter plots for (c) uncloaked coupled, (d) cloaked decoupled Array I, at scan angle = .
Figure 19.
Realized gain plots for Array I ( GHz) showing beam-scanning at scan angles: (a) , (b) , (c) , and (d) .
Figure 19.
Realized gain plots for Array I ( GHz) showing beam-scanning at scan angles: (a) , (b) , (c) , and (d) .
Figure 20.
Realized gain plots for Array II ( GHz) showing beam-scanning at angles: (a) , (b) , (c) , and (d) .
Figure 20.
Realized gain plots for Array II ( GHz) showing beam-scanning at angles: (a) , (b) , (c) , and (d) .
Figure 21.
Schematics for (a) uncloaked circular Patch I and II, (b) cross-sectional side view of the uncloaked coupled patches, (c) cloaked Patch I and II, (d) side-view of the cloaked circular patches, detailing the structural parameters of the coated metasurfaces, and (e) unfolded view of the cloak design.
Figure 21.
Schematics for (a) uncloaked circular Patch I and II, (b) cross-sectional side view of the uncloaked coupled patches, (c) cloaked Patch I and II, (d) side-view of the cloaked circular patches, detailing the structural parameters of the coated metasurfaces, and (e) unfolded view of the cloak design.
Figure 22.
Plots for S-parameters: (a) Uncloaked coupled (b) Cloaked decoupled patch antennas, and plots for total efficiencies: (c) Patch I is active, and (d) Patch II is active.
Figure 22.
Plots for S-parameters: (a) Uncloaked coupled (b) Cloaked decoupled patch antennas, and plots for total efficiencies: (c) Patch I is active, and (d) Patch II is active.
Figure 23.
Electric field contours for, (a) Uncloaked coupled, (b) Cloaked decoupled cases, when Patch I is active ( GHz), and (c) Uncloaked coupled, (d) Cloaked decoupled cases, when Patch II is active ( GHz).
Figure 23.
Electric field contours for, (a) Uncloaked coupled, (b) Cloaked decoupled cases, when Patch I is active ( GHz), and (c) Uncloaked coupled, (d) Cloaked decoupled cases, when Patch II is active ( GHz).
Figure 24.
Realized gain patterns at (a), (b) for Patch I (at GHz), and at (c), (d) for Patch II (at GHz).
Figure 24.
Realized gain patterns at (a), (b) for Patch I (at GHz), and at (c), (d) for Patch II (at GHz).
Figure 25.
(a) Cross-sectional side-view, (b) Total RCS plot for cloaked Patch I, and E-field distributions for cloaked Patch I at (c) GHz, (d) GHz in presence of a normally incident TM polarized plane wave.
Figure 25.
(a) Cross-sectional side-view, (b) Total RCS plot for cloaked Patch I, and E-field distributions for cloaked Patch I at (c) GHz, (d) GHz in presence of a normally incident TM polarized plane wave.
Figure 26.
Schematic configurations of (a) uncloaked and (b) cloaked interleaved circular patch antenna arrays.
Figure 26.
Schematic configurations of (a) uncloaked and (b) cloaked interleaved circular patch antenna arrays.
Figure 27.
Plots for total efficiencies: (a) Array I ( GHz) active and (b) Array II ( GHz) active.
Figure 27.
Plots for total efficiencies: (a) Array I ( GHz) active and (b) Array II ( GHz) active.
Figure 28.
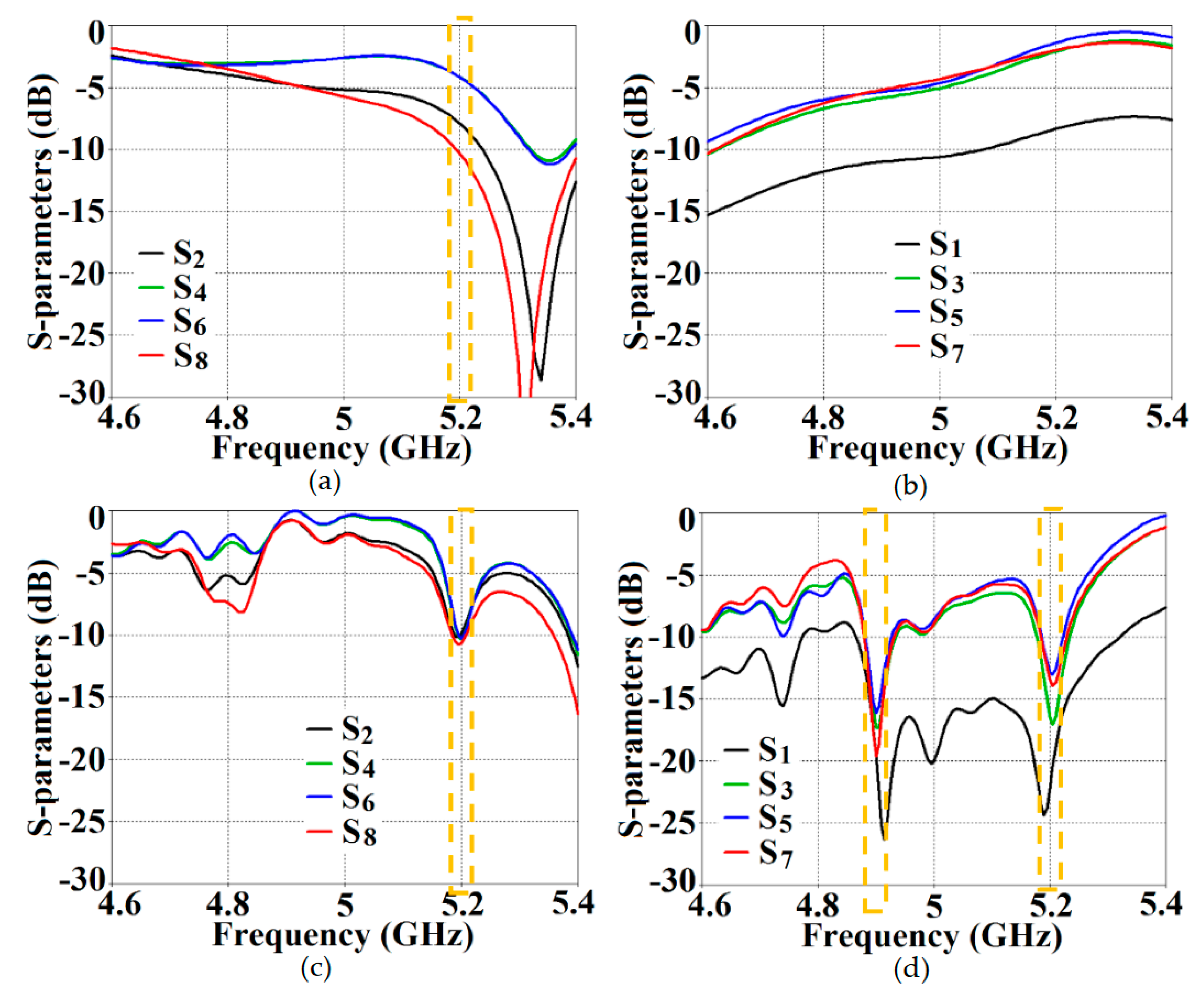
(a) Active reflection coefficients, (b) Active coupling coefficients for uncloaked (coupled) Array I, (c) Active reflection coefficients, and (d) Active coupling coefficients for cloaked (decoupled) Array I (resonance frequency – GHz).
Figure 28.
(a) Active reflection coefficients, (b) Active coupling coefficients for uncloaked (coupled) Array I, (c) Active reflection coefficients, and (d) Active coupling coefficients for cloaked (decoupled) Array I (resonance frequency – GHz).
Figure 29.
(a) Active reflection coefficients, (b) Active coupling coefficients for uncloaked (coupled) Array II, (c) Active reflection coefficients, and (d) Active coupling coefficients for cloaked (decoupled) Array II (resonance frequency – GHz).
Figure 29.
(a) Active reflection coefficients, (b) Active coupling coefficients for uncloaked (coupled) Array II, (c) Active reflection coefficients, and (d) Active coupling coefficients for cloaked (decoupled) Array II (resonance frequency – GHz).
Figure 30.
E-field contours: (a) uncloaked, (b) cloaked patch antenna arrays when Array I is active and (c) uncloaked, (d) cloaked patch antenna arrays when Array II is active.
Figure 30.
E-field contours: (a) uncloaked, (b) cloaked patch antenna arrays when Array I is active and (c) uncloaked, (d) cloaked patch antenna arrays when Array II is active.
Figure 31.
Realized gain polar plots for Array I ( GHz) at scan angles: (a) , (b) , (c) , and (d) .
Figure 31.
Realized gain polar plots for Array I ( GHz) at scan angles: (a) , (b) , (c) , and (d) .
Figure 32.
Realized gain polar plots for Array II ( GHz) at scan angles: (a) and (b) .
Figure 32.
Realized gain polar plots for Array II ( GHz) at scan angles: (a) and (b) .