Discrete-Time Adaptive Control for Uncertain Scalar Multiagent Systems with Coupled Dynamics: A Lyapunov-Based Approach

Preprint

Article

Discrete-Time Adaptive Control for Uncertain Scalar Multiagent Systems with Coupled Dynamics: A Lyapunov-Based Approach

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Islam A. Aly,

Kadriye Merve Dogan^*

Islam A. Aly,

Kadriye Merve Dogan^*

This version is not peer-reviewed

Submitted:

07 December 2023

Posted:

08 December 2023

You are already at the latest version

Alerts

Abstract

Discrete-time architectures offer a distinct advantage over their continuous counterparts, as they can be seamlessly implemented on embedded hardware without the necessity for discretization processes. Yet, because of the difficulty of ensuring Lyapunov difference expressions, their designs, which are based on quadratic Lyapunov-based frameworks, are highly complex. As a result, various existing continuous-time results using adaptive control methods to deal with system uncertainties and coupled dynamics in agents of a multiagent system cannot be directly applied to the discrete-time context. Furthermore, compared to their continuous-time equivalent, discrete-time information exchange based on periodic time intervals is more practical in the control of multiagent systems. In this paper, we first introduce a discrete-time adaptive control architecture designed for uncertain scalar multiagent systems without coupled dynamics as a preliminary result. We then introduce another discrete-time adaptive control approach for uncertain multiagent systems in the presence of coupled dynamics. Our approach incorporates observer dynamics to manage unmeasurable coupled dynamics, along with a user-assigned Laplacian matrix to induce cooperative behaviors among multiple agents. Our solution includes Lyapunov analysis with logarithmic and quadratic Lyapunov functions for guaranteeing asymptotic stability with both controllers. To demonstrate the effectiveness of the proposed control architectures, we provide an illustrative example.

Keywords:

Subject: Engineering - Control and Systems Engineering

1. Introduction

1.1. Literature Review

The exploration of multiagent systems has seen a growing interest due to their effective and adaptable solutions for tackling intricate real-world tasks. Over the past decade, they have left a significant mark on a diverse range of fields, including scientific, civilian, and military applications such as environmental monitoring, exploration, in/on-space assembly, maintenance and manufacturing, traffic management, and payload and passenger transportation. A key attribute of multiagent systems is their capacity to collaboratively execute missions by operating in specified formations. In the existing literature, the primary focus of general research lies in the development of distributed control algorithms that enable operations with local interactions [1,2,3,4]. The presence of uncertainties, such as unknown coefficients from modeling, disturbances, and unknown friction effects, along with coupled dynamics in rigid systems with flexible components or slung load dynamics, can negatively impact the performance and stability of sole agents and/or the overall multiagent system. As a result, systems with coupled dynamics and uncertainty become critical for guaranteeing the entire system’s stability [5,6,7,8]. To address the challenge posed by uncertainty, effective solutions are presented in continuous-time adaptive and robust control architectures as discussed in [9,10,11,12,13,14,15]. Subsequently, in [16,17,18], the focus shifts to the examination of continuous-time adaptive architectures tailored for managing uncertain multiagent systems characterized by coupled dynamics, particularly in a leader-follower framework. The continuous adaptive control formulations introduced in [16,17,18] are specifically designed to address various challenges in uncertain multiagent systems with coupled dynamics. Basically, the designs in [16,17] aim to achieve boundedness of the tracking error when dealing with uncertain multiagent systems in the presence of coupled dynamics only and coupled and actuator dynamics together, respectively. The design in [18] aims to achieve asymptotic convergence of the tracking error when dealing with uncertain multiagent systems in the presence of coupled dynamics. Furthermore, the results in [16,17,18] for a leader-follower setting with a classical command tracking approach (i.e., where all agents converge to the position specified for the leader agent(s) only).

The majority of networked multiagent control systems currently in use are limited in their capacity for creating cooperative behaviors, such that they use the classical command tracking approach. Recognizing the significance of diversifying agent positions in military and civilian applications, one effective strategy involves assigning user-defined positions to each agent, thereby facilitating the creation of continuous-time formations. This can be achieved by manipulating matrices associated with graph theory, employing user-assigned nullspace, and introducing a novel representation for the Laplacian matrix in undirected and connected graphs [19,20,21,22,23,24]. Specifically, in [19,20], a novel Laplacian matrix is introduced by modifying the degree matrix, while in [21], another novel Laplacian matrix is introduced by modifying the degree matrix to create complex behaviors, but former ones’ formulation necessitates precise knowledge of neighboring agent states and none of the controllers in [19,20,21] can create a robust result when faced with unknown terms. Addressing the robustness, the authors of [22,23] proposed a distributed controller featuring a user-defined Laplacian matrix that is used in [21], offering increased flexibility to agents in the presence of coupled dynamics and actuator dynamics, respectively. Note that all of the controllers are designed in [19,20,21,22,23,24] are continuous-time algorithms.

Discretizing continuous-time algorithms to apply in embedded code may cause stability margins to be lost [25]. Furthermore, compared to their continuous-time equivalent, discrete-time information exchange based on periodic time intervals is practically more practicable in the control of multiagent systems. Yet, because of the complexity of the resulting Lyapunov difference expressions, discrete-time control designs, which are based on Lyapunov-based frameworks, are highly complex. This issue arises because the controlled physical system’s Lyapunov stability cannot be guaranteed by the Lyapunov difference expressions since they cannot be made negative-definite [26,27,28,29,30]. To ensure asymptotic stability for sole systems, the authors in [29,30,31,32,33,34,35,36] solve this issue by logarithmic Lyapunov functions in the Lyapunov analysis. In the context of the multiagent systems, the authors of [4] cover optimal discrete-time cooperative control in multiagent systems, the authors of [37] design adaptive fault-tolerant tracking control for discrete-time multiagent systems via reinforcement learning algorithm, the authors of [38] propose cooperative adaptive optimal output regulation of nonlinear discrete-time multi-agent systems, and the authors of [39] study discrete-time control of multiagent systems with a misbehaving agent.

Note that none of the above results are considered a discrete-time setting for an uncertain multiagent system with coupled dynamics while having the capability of assigning different positions for each agent to achieve complex tasks. To this end, in this paper, discrete-time adaptive control algorithms are designed for an uncertain multiagent system with and without unmeasurable coupled dynamics that ensures asymptotic stability using a Lyapunov candidate composed of logarithmic and quadratic functions and adopts user-assigned Laplacian matrix nullspace yielding flexibility in positioning. Finally, preliminary conference versions of this paper are considered as [40], where this paper goes beyond the conference version by providing detailed proofs of all the results and detailed simulation studies with related discussions.

1.2. Organization

The structure of this paper is as follows. In Section 2, for completeness, the stability analysis of the discrete-time controller for the uncertain multiagent system in the absence of coupled dynamics is presented. In Section 3, the stability analysis of the first proposed discrete-time controller for the uncertain dynamical system with coupled dynamics is presented, which guarantees asymptotic convergence of the tracking error. Section 4 validates the theoretical contributions with an illustrative numerical example. In Section 5, concluding remarks are given.

1.3. Notation and Mathematical Preliminaries

A general notation and a graph theoretical notation are used in this paper. We refer to Table 1 for the general notation used in this paper, and the graph theoretical notation is given below.

Consider an undirected connected graph

G

is defined by set of nodes (i.e.,

V_{G} = {1, \dots, n}

) and set of edges (i.e.,

E_{G} \subset V_{G} \times V_{G}

). A graph

G

is then considered as a connected graph with a path between any pair of distinct nodes, where a path

i_{0} i_{1} \dots i_{L}

is a finite sequence of nodes (i.e.,

i_{k - 1} \sim i_{k}

k = 1, \dots, L

), and when the nodes i and j are neighbors (i.e.,

(i, j) \in E_{G}

i \sim j

denotes the neighboring relation. In addition, the degree matrix is denoted by

D (G) ≜ diag (d) \in R^{n \times n}

with

d = {[d_{1}, \dots, d_{n}]}^{T}

with a degree of a node

d_{i}

being equal to the number of its neighbors, the adjacency matrix is denoted by

A (G) \in R^{n \times n}

with

{[A (G)]}_{i j} ≜ 1

(i, j) \in E_{G}

and

{[A (G)]}_{i j} ≜ 0

otherwise, and the Laplacian matrix of a graph

G

denoted by

L (G) ≜ D (G) - A (G)

,41,42].

Finally, for the definition of the modified version of the Laplacian matrix that allows to assign different positions to each node, let

ω = {[ω_{1}, \dots, ω_{n}]}^{T} \in R^{n}

being a vector with entries

ω_{i} \in R_{+}, i = 1, \dots, n

, where

ω

represents the user-assigned nullspace [21]. Next, consider the modified degree matrix given by

\bar{D} (G, ω) ≜ diag (A (G) ω) {(diag (ω))}^{- 1} = diag (\bar{d}) \in R^{n \times n}

with

\bar{d} = {[{\bar{d}}_{1}, \dots, {\bar{d}}_{n}]}^{T} \in R^{n}

. Here,

A (G)

is the standard adjacency matrix. Then the modified Laplacian matrix of a graph

G

can be represented as

L (G, ω) ≜ \bar{D} (G, ω) - A (G)

Lemma 1.

In the context of a leader-follower setting, one can define

K = diag ([κ_{1}, . . ., κ_{n}]) \in R^{n \times n}

with

κ_{i} \in {0, 1}

for all

i = 1, . . ., n

, where at least one

κ_{i}

being equal to 1 (for a leader agent

κ_{i} = 1

, otherwise it is 0). That further yields a modified Laplacian matrix of the leader-following setting that allows assigning different positions that is

F (G, ω) ≜ L (G, ω) + K

2. Preliminary Results: Adaptation For Agent-Based Uncertainty

In this section, a discrete-time adaptive controller is designed that allows one to assign different positions for each agent in the presence of agent-based uncertainties only. To this end, consider the uncertain multiagent system in the absence of the coupled dynamics consisting of n agents given by

\begin{matrix} x_{i} (k + 1) & = & x_{i} (k) + Δ_{i} σ_{i} (x_{i} (k)) + u_{i} (k), x_{i} (0) = x_{i 0}, i = 1, \dots, n, k \in N . \end{matrix}

(1)

Here,

x_{i} (k) \in R

represents the agent state,

u_{i} (k) \in R

represents the control input of agent i,

Δ_{i} \in R

represents an unknown weight uncertainty, and

σ_{i} (x_{i} (k)) \in R

represents a basis function of agent i, where its bound can be represented as

∥ σ (x_{i} (k)) ∥_{2} \leq l_{c i} + l_{i} {∥ x_{i} (k) ∥}_{2}

, with

l_{c i} \in R_{+}

and

l_{i} \in R_{+}

as standard in the literature [35].

The control objective of this section is ensuring the states of the agents to track states of the reference model without getting affected by the presence of the uncertainties and able to assign nullspaces to the overall system for creating complex behaviors. Thus, consider the reference model to track given by

\begin{matrix} x_{r_{i}} (k + 1) & = & x_{r_{i}} (k) - ϵ \sum_{i \sim j} (\frac{ω_{j}}{ω_{i}} x_{r_{i}} (k) - x_{r_{j}} (k)) - ϵ κ_{i} (x_{r_{i}} (k) - c (k)), x_{r_{i}} (0) = x_{r_{i 0}}, k \in N, \end{matrix}

(2)

where

x_{r_{i}} (k) \in R

and

x_{r_{j}} (k) \in R

are the ideal reference state of agent i and agent j respectively, and

c (k) \in R

is a bounded command available only to leader agent(s) and

c (k) = v (k) ω_{i}

with a bounded

v (k) \in R_{+}

. In (2),

ϵ < \frac{1}{max ({\bar{d}}_{i}) + 1}

, where modified degree value,

{\bar{d}}_{i}

, ensures that the eigenvalues of

I - ϵ F (G, ω)

remains within the unit circle.

To overcome the given tracking objective of this section, we propose the below discrete-time adaptive controller

\begin{matrix} u_{i} (k) & = & - ϵ \sum_{i \sim j} (\frac{ω_{j}}{ω_{i}} x_{i} (k) - x_{j} (k)) - ϵ κ_{i} (x_{i} (k) - c (k)) - {\hat{Δ}}_{i} (k) σ_{i} (x_{i} (k)), \end{matrix}

(3)

where

{\hat{Δ}}_{i} (k) \in R

stands for an estimate of unknown weight uncertainty

Δ_{i}

(details below).

Then, using the proposed adaptive control law given by (3) in the uncertain multiagent system given by (1) yields

\begin{matrix} x_{i} (k + 1) & = & x_{i} (k) - ϵ \sum_{i \sim j} (\frac{ω_{j}}{ω_{i}} x_{i} (k) - x_{j} (k)) - ϵ κ_{i} (x_{i} (k) - c (k)) - {\tilde{Δ}}_{i} (k) σ_{i} (x_{i} (k)), k \in N . \end{matrix}

(4)

Here,

{\tilde{Δ}}_{i} (k) ≜ {\hat{Δ}}_{i} (k) - Δ_{i} \in R

is the weight estimation error.

Next, the tracking error can be defined as

e_{i} (k) ≜ x_{i} (k) - x_{r_{i}} (k) \in R

an error between the agent state and its reference model, where its dynamics can be rewritten as

\begin{matrix} e_{i} (k + 1) & = & e_{i} (k) - ϵ \sum_{i \sim j} (\frac{ω_{j}}{ω_{i}} e_{i} (k) - e_{j} (k)) - ϵ κ_{i} e_{i} (k) - {\tilde{Δ}}_{i} (k) σ_{i} (x_{i} (k)), k \in N . \end{matrix}

(5)

Then, the error dynamics can be written in a combined form for an overall multiagent system as

\begin{matrix} e (k + 1) & = & (I - ϵ F) e (k) - {\tilde{Δ}}^{T} (k) σ (x (k)) . \end{matrix}

(6)

Here,

e (k) = {[e_{1} (k), \dots, e_{n} (k)]}^{T} \in R^{n}

σ (x (k)) = {[σ_{1} (x_{1} (k)), \dots, σ_{n} (x_{n} (k))]}^{T} \in R^{n}

, and

\tilde{Δ} (k) = diag

([{\tilde{Δ}}_{1} (k), \dots, {\tilde{Δ}}_{n} (k)]) \in R^{n}

. In (5),

(I - ϵ F)

is Schur, it follows from converse Lyapunov theory [43] that there exists a unique

P \in P^{n}

satisfying the discrete-time Lyapunov equation given by

\begin{matrix} 0_{n} = {(I - ϵ F)}^{T} P (I - ϵ F) + R - P \end{matrix}

(7)

with

R \in P^{n}

Next, the combined adaptive control inputs with a weight update law can be written as

\begin{matrix} u (k) & = & - ϵ F x (k) + ϵ K c (k) - {\hat{Δ}}^{T} (k) σ (x (k)) \\ \hat{Δ} (k + 1) & = & \hat{Δ} (k) + [\frac{γ}{1 + μ e^{T} (k) P e (k)} (e (k + 1) - (I - ϵ F) e (k) {)σ^{T} (x (k))]}^{T}, \end{matrix}

(8)

\begin{matrix} \hat{Δ} (0) ≜ {\hat{Δ}}_{0}, k \in N . \end{matrix}

(9)

Here,

u (k) = {[u_{1} (k), \dots, u_{n} (k)]}^{T} \in R^{n}

x (k) = {[x_{1} (k), \dots, x_{n} (k)]}^{T} \in R^{n}

\hat{Δ} (k)

diag ([{\hat{Δ}}_{1} (k), \dots,

{\hat{Δ}}_{n} (k)]) \in R^{n}

μ \in R_{+}

is a design variable, and

γ \in R_{+}

is a learning rate. Then, using (9), weight estimation error dynamics that will be used in the stability analysis of next theorem can be obtained as

\begin{matrix} \tilde{Δ} (k + 1) & = & \tilde{Δ} (k) + [\frac{γ}{1 + μ e^{T} (k) P e (k)} (e (k + 1) - (I - ϵ F) e (k) {)σ^{T} (x (k))]}^{T}, \\ \tilde{Δ} (0) ≜ {\hat{Δ}}_{0} - Δ = {\tilde{Δ}}_{0}, k \in N . \end{matrix}

(10)

Theorem 1.

Consider the uncertain multiagent system given by (1) and the agent reference model given by (2), then the discrete-time adaptive control architecture given by (8) along with the weight update law given by (8) guarantees the Lyapunov stability of the closed-loop system given by (6) and (10) (i.e., boundedness of the

(e (k), \tilde{Δ} (k))

. Moreover, one can conclude the asymptotic tracking error convergence that is

\begin{matrix} lim_{k \to \infty} e (k) = 0 . \end{matrix}

(11)

Proof.

To show the Lyapunov stability of the closed-loop system given by (6) and (10) (i.e., boundedness of the

(e (k), \tilde{Δ} (k))

, one can consider the Lyapunov function candidate composed of logarithmic and quadratic functions given by

\begin{matrix} V (e, \tilde{Δ}) & ≜ & \underset{V_{1}}{\underset{︸}{ι^{- 1} ln (1 + μ e^{T} P e)}} + \underset{V_{2}}{\underset{︸}{α^{- 1} tr ({\tilde{Δ}}^{T} \tilde{Δ})}}, \end{matrix}

(12)

where

ι \in R_{+}

, and

α \in R_{+}

. Note that

V (0, 0) = 0

and

V (e, \tilde{Δ}) > 0

for all

(e, \tilde{Δ}) \neq (0, 0)

Then, first, taking the Lyapunov difference of

V_{1} (\cdot)

and using the error dynamics given by (6) yields

\begin{matrix} Δ V_{1} ≜ V_{1} (e (k + 1)) - V_{1} (e (k)) \\ = ι^{- 1} ln (1 + μ e^{T} (k + 1) P e (k + 1)) - ι^{- 1} ln (1 + μ e^{T} (k) P e (k)) \\ = ι^{- 1} ln (1 + μ {[(I - ϵ F) e (k) - {\tilde{Δ}}^{T} (k) σ (x (k))]}^{T} P [(I - ϵ F) e (k) - {\tilde{Δ}}^{T} (k) σ (x (k))]) \\ - ι^{- 1} ln (1 + μ e^{T} (k) P e (k)) . \end{matrix}

(13)

Note that using natural logarithm property

ln a - ln b = ln (a / b)

and by adding and subtracting “

\frac{μ e^{T} (k) P e (k)}{1 + μ e^{T} (k) P e (k)}

” to the above equality

Δ V_{1}

can be rewritten as

\begin{matrix} Δ V_{1} & = & ι^{- 1} ln (1 + μ (\frac{{[(I - ϵ F) e (k) - {\tilde{Δ}}^{T} (k) σ (x (k))]}^{T} P [(I - ϵ F) e (k) - {\tilde{Δ}}^{T} (k) σ (x (k))]}{1 + μ e^{T} (k) P e (k)} \\ - \frac{e^{T} (k) P e (k)}{1 + μ e^{T} (k) P e (k)})) . \end{matrix}

(14)

Then, using the discrete-time Lyapunov equation given by (7) and another natural logarithmic operator property given by

ln (1 + a) \leq a

when

a \geq - 1

[44], an upper bound for (14) can be obtained as

\begin{matrix} Δ V_{1} & \leq & \frac{ι^{- 1} μ}{1 + μ e^{T} (k) P e (k)} (- e^{T} (k) R e (k) + σ^{T} (x (k)) \tilde{Δ} (k) P {\tilde{Δ}}^{T} (k) σ (x (k)) \\ - 2 σ^{T} (x (k)) \tilde{Δ} (k) P (I - ϵ F) e (k)) . \end{matrix}

(15)

Second, taking the Lyapunov difference of

V_{2} (\cdot)

along with the weight uncertainty error dynamics given by (10) and using (6) in the dynamics yields

\begin{matrix} Δ V_{2} & ≜ & V_{2} (\tilde{Δ} (k + 1)) - V_{2} (\tilde{Δ} (k)) \\ = & α^{- 1} tr ({\tilde{Δ}}^{T} (k + 1) \tilde{Δ} (k + 1)) - α^{- 1} tr ({\tilde{Δ}}^{T} (k) \tilde{Δ} (k)) \\ = & α^{- 1} tr (({\tilde{Δ}}^{T} (k) + \frac{γ}{1 + μ e^{T} (k) P e (k)} (- {\tilde{Δ}}^{T} (k) σ (x (k)) σ^{T} (x (k)))) \\ \cdot (\tilde{Δ} (k) + \frac{γ}{1 + μ e^{T} (k) P e (k)} (- σ (x (k)) σ^{T} (x (k)) \tilde{Δ} (k)) - α^{- 1} tr ({\tilde{Δ}}^{T} (k) \tilde{Δ} (k)) . \end{matrix}

(16)

Using the trace operator property

a^{T} b = tr (b a^{T})

in (16) and simplifying (16) yields

\begin{matrix} Δ V_{2} & = & \frac{α^{- 1} γ}{1 + μ e^{T} (k) P e (k)} σ^{T} (x (k)) \tilde{Δ} (k) (- 2 + \frac{γ σ^{T} (x (k)) σ (x (k))}{1 + μ e^{T} (k) P e (k)}) {\tilde{Δ}}^{T} (k) σ (x (k)), \end{matrix}

(17)

Note that the bound for

∥ \frac{σ^{T} (x (k)) σ (x (k))}{1 + μ e^{T} (k) P e (k)} ∥_{2}

with

{∥ σ (x (k)) ∥}_{2} \leq l_{c} + l {∥ x (k) ∥}_{2}

l_{c} \in R_{+}

, and

l \in R_{+}

yields

∥ \frac{σ^{T} (x (k)) σ (x (k))}{1 + μ e^{T} (k) P e (k)} ∥_{2} \leq η

(see Appendix A for details), where

η \in R_{+}

. Then setting

γ = ρ_{γ} η^{- 1}

ρ_{γ} \in (0, 1)

, and

α^{- 1} γ = ι^{- 1} μ ρ_{1}

with

ρ_{1}

being a free variable that will be designed later, an upper bound for (17) can be written as

\begin{matrix} Δ V_{2} & \leq & \frac{ι^{- 1} μ}{1 + μ e^{T} (k) P e (k)} (σ^{T} (x (k)) \tilde{Δ} (k) (- 2 ρ_{1} + ρ_{γ} ρ_{1}) {\tilde{Δ}}^{T} (k) σ (x (k))) . \end{matrix}

(18)

Next, using (15) and (18) to compute

Δ V (\cdot) ≜ Δ V_{1} (\cdot) + Δ V_{2} (\cdot)

, and defining the augmented errors as

{\tilde{q}}^{T} (k) = [\begin{matrix} e^{T} (k), & σ^{T} (x (k)) \tilde{Δ} (k) \end{matrix}]

, the Lyapunov difference equation can be written as

\begin{matrix} Δ V_{1} + Δ V_{2} & \leq & \frac{ι^{- 1} μ}{1 + μ e^{T} (k) P e (k)} (- e^{T} (k) R e (k) + σ^{T} (x (k)) \tilde{Δ} (k) [P - 2 ρ_{1} + ρ_{γ} ρ_{1}] {\tilde{Δ}}^{T} (k) σ (x (k)) \\ - 2 σ^{T} (x (k)) \tilde{Δ} (k) P (I - ϵ F) e (k)) \\ = & \frac{ι^{- 1} μ}{1 + μ e^{T} (k) P e (k)} (e^{T} (k) [- R + β {(I - ϵ F)}^{T} P (I - ϵ F)] e (k) \\ + σ^{T} (x (k)) \tilde{Δ} (k) [P + \frac{1}{β} P - 2 ρ_{1} + ρ_{γ} ρ_{1}] {\tilde{Δ}}^{T} (k) σ (x (k))) \\ - \frac{ι^{- 1} μ}{1 + μ e^{T} (k) P e (k)} {\tilde{q}}^{T} (k) \underset{M \geq 0}{\underset{︸}{[\begin{matrix} β {(I - ϵ F)}^{T} P (I - ϵ F) & (P (I - ϵ F))^{T} \\ P (I - ϵ F) & \frac{1}{β} P \end{matrix}]}} \tilde{q} (k) . \end{matrix}

(19)

Note that M is a positive semi-definite matrix, and with a small value of

β \in R_{+}

, one can satisfy

- \bar{R} = - R + β {(I - ϵ F)}^{T} P (I - ϵ F) < 0

. Then, taking an upper bound of (19) yields

\begin{matrix} Δ V & \leq & \frac{ι^{- 1} μ}{1 + μ e^{T} (k) P e (k)} (- e^{T} (k) \bar{R} e (k) \\ - σ^{T} (x (k)) \tilde{Δ} (k) \underset{N > 0}{\underset{︸}{[ρ_{1} (2 - ρ_{γ}) - (1 + \frac{1}{β}) P]}} {\tilde{Δ}}^{T} (k) σ (x (k))) . \end{matrix}

(20)

Note that N is positive definite (see Appendix B for details); hence, an upper bound for (20) can be written as

\begin{matrix} Δ V & \leq & \frac{l_{0}^{- 1} μ}{1 + μ e^{T} (k) P e (k)} (- e^{T} (k) \bar{R} e (k)), \end{matrix}

(21)

which proves the boundedness of the

(e (k), \tilde{Δ} (k))

. It then follows from [Theorem 13.10, [43] that

{lim}_{k \to \infty} (e (k)) = 0

. □

3. Adaptation For Both Agent-Based Uncertainty and Coupled Dynamics

In this section, a discrete-time adaptive controller is designed that allows one to assign different positions for each agent in the presence of agent-based uncertainties and coupled dynamics. Specifically, consider a multiagent system consisting of n agents given by

\begin{matrix} x_{i} (k + 1) & = & x_{i} (k) + Δ_{i} σ_{i} (x_{i} (k)) + p_{u i} (k) + u_{i} (k), x_{i} (0) = x_{i 0}, \end{matrix}

(22)

\begin{matrix} ξ_{i} (k + 1) & = & f_{u i} ξ_{i} (k) + g_{u i} x_{i} (k), \end{matrix}

(23)

\begin{matrix} p_{u i} (k) & = & h_{u i} ξ_{i} (k) i = 1, \dots, n k \in N . \end{matrix}

(24)

Here,

p_{u i} (k) \in R

is the output of the coupled dynamics,

ξ_{i} (k) \in R

is the state of the coupled dynamics, and

f_{u i} \in R

g_{u i} \in R

, and

h_{u i} \in R

are variables related to coupled dynamics, where

f_{u i} \in (- 1, 1)

that is standard consideration in the literature [16].

The objective here is to achieve asymptotic convergence of the tracking error in the presence of not only agent-based uncertainties but also coupled dynamics. To this end, an observer dynamics is used to estimate the state of the unmeasurable coupled dynamics. Specifically, the adaptive controller is now designed as

\begin{matrix} u_{i} (k) & = & - ϵ \sum_{i \sim j} (\frac{ω_{j}}{ω_{i}} x_{i} (k) - x_{j} (k)) - ϵ κ_{i} (x_{i} (k) - c (k)) - {\hat{Δ}}_{i} (k) σ_{i} (x_{i} (k)) - h_{u i} {\hat{ξ}}_{i} (k), \end{matrix}

(25)

where

{\hat{ξ}}_{i} (k) \in R

stands for an estimate of the coupled dynamics of agent i with the estimation dynamics given by

\begin{matrix} {\hat{ξ}}_{i} (k + 1) & = & f_{u i} {\hat{ξ}}_{i} (k) + g_{u i} x_{i} (k), \hat{ξ} (0) = {\hat{ξ}}_{0}, k \in N, \end{matrix}

(26)

\begin{matrix} {\hat{p}}_{u i} (k) & = & h_{u i} {\hat{ξ}}_{i} (k) . \end{matrix}

(27)

Here,

{\hat{p}}_{u i} (k) \in R

is the estimated output of the coupled dynamics.

Then, using the proposed adaptive control law given by (25) in the uncertain multiagent system with coupled dynamics given by (22) yields

\begin{matrix} x_{i} (k + 1) & = & x_{i} (k) - ϵ \sum_{i \sim j} (\frac{ω_{j}}{ω_{i}} x_{i} (k) - x_{j} (k)) - ϵ κ_{i} (x_{i} (k) - c (k)) - {\tilde{Δ}}_{i} (k) σ_{i} (x_{i} (k)) - h_{u i} \tilde{ξ} (k) . \end{matrix}

(28)

Here,

{\tilde{Δ}}_{i} (k) ≜ {\hat{Δ}}_{i} (k) - Δ_{i} \in R

is the weight estimation error, and

{\tilde{ξ}}_{i} (k) ≜ {\hat{ξ}}_{i} (k) - ξ (k) \in R

coupled dynamics estimation error.

Next, the tracking error dynamics can be rewritten as

\begin{matrix} e_{i} (k + 1) & = & e_{i} (k) - ϵ \sum_{i \sim j} (\frac{ω_{j}}{ω_{i}} e_{i} (k) - e_{j} (k)) - ϵ κ_{i} e_{i} (k) - {\tilde{Δ}}_{i} (k) σ_{i} (x_{i} (k)) - h_{u i} \tilde{ξ} (k), k \in N . \end{matrix}

(29)

Then, the error dynamics can be written in a combined form for an overall multiagent system as

\begin{matrix} e (k + 1) & = & (I - ϵ F) e (k) - {\tilde{Δ}}^{T} (k) σ (x (k)) - H \tilde{ξ} (k) . \end{matrix}

(30)

Here,

\tilde{ξ} (k) = {[{\tilde{ξ}}_{1} (k), \dots, {\tilde{ξ}}_{n} (k)]}^{T} ≜ \hat{ξ} (k) - ξ (k) \in R^{n}

is the coupled dynamics combined observer error with

ξ (k) = {[ξ_{1} (k), \dots, ξ_{n} (k)]}^{T} \in R^{n}

and

\hat{ξ} (k) = {[{\hat{ξ}}_{1} (k), \dots, {\hat{ξ}}_{n} (k)]}^{T} \in R^{n}

. In addition, in (30),

H = diag ([h_{u 1},

\dots, h_{u n}]) \in R^{n \times n}

Next, the combined adaptive control input can be written as

\begin{matrix} u (k) & = & - ϵ F x (k) + ϵ K c (k) - {\hat{Δ}}^{T} (k) σ (x (k)) - H \hat{ξ} (k) \end{matrix}

(31)

with the same augmented weight update law given in (9) and the below augmented observer dynamics

\begin{matrix} \hat{ξ} (k + 1) & = & F \hat{ξ} (k) + G x (k), \hat{ξ} (0) = {\hat{ξ}}_{0}, k \in N, \end{matrix}

(32)

\begin{matrix} {\hat{p}}_{u} (k) & = & H \hat{ξ} (k), \end{matrix}

(33)

where

F = diag ([f_{u 1}, \dots, f_{u n}]) \in R^{n \times n}

G = diag ([g_{u 1}, \dots, g_{u n}]) \in R^{n \times n}

, and

{\hat{p}}_{u} (k) = [{\hat{p}}_{u 1} (k), \dots,

{\hat{p}}_{u n} {(k)]}^{T} \in R^{n}

. In (32), F is Schur, it follows from converse Lyapunov theory [43] that there exists a unique

S \in P^{n}

satisfying the discrete-time Lyapunov equation given by

\begin{matrix} 0_{n} = F^{T} S F + R_{F} - S \end{matrix}

(34)

with

R_{F} \in P^{n}

Finally, weight estimation error dynamics that will be used in the stability analysis of next theorem satisfies the dynamics given by

\begin{matrix} \tilde{ξ} (k + 1) & = & F \tilde{ξ} (k), \tilde{ξ} (0) = {\tilde{ξ}}_{0}, k \in N . \end{matrix}

(35)

Theorem 2.

Consider the uncertain agent system given by (22) subject to the unmeasurable coupled dynamics given by (23) and (24), and the agent reference model given by (2), then the discrete-time adaptive control architecture given by (31) along with the weight update law given by (9) and the observer dynamics given by (26) and (27) guarantees the Lyapunov stability of the closed-loop system given by (30), (10), and (35) (i.e., boundedness of the

(e (k), \tilde{Δ} (k), \tilde{ξ} (k))

. Moreover, one can conclude the asymptotic tracking error convergence that is

\begin{matrix} lim_{k \to \infty} e (k) = 0 . \end{matrix}

(36)

Proof.

To show the Lyapunov stability of the closed-loop system given by (30), (10), and (35) (i.e., boundedness of the

(e (k), \tilde{Δ} (k), \tilde{ξ} (k))

, one can consider the Lyapunov function candidate composed of logarithmic and quadratic functions given by

\begin{matrix} V (e, \tilde{Δ}, \tilde{ξ}) & ≜ & \underset{V_{1}}{\underset{︸}{ι^{- 1} ln (1 + μ e^{T} P e)}} + \underset{V_{2}}{\underset{︸}{α^{- 1} tr ({\tilde{Δ}}^{T} \tilde{Δ})}} + \underset{V_{3}}{\underset{︸}{ν^{- 1} {\tilde{ξ}}^{T} S \tilde{ξ}}}, \end{matrix}

(37)

where

ν \in R_{+}

. Note that

V (0, 0, 0) = 0

and

V (e, \tilde{Δ}, \tilde{ξ}) > 0

for all

(e, \tilde{Δ}, \tilde{ξ}) \neq (0, 0, 0)

Then, first, taking the Lyapunov difference of

V_{1} (\cdot)

and using the error dynamics given by (30) yields

\begin{matrix} Δ V_{1} & ≜ & V_{1} (e (k + 1)) - V_{1} (e (k)) \\ = & ι^{- 1} ln (1 + μ e^{T} (k + 1) P e (k + 1)) - ι^{- 1} ln (1 + μ e^{T} (k) P e (k)) \\ = & ι^{- 1} ln (1 + μ {[(I - ϵ F) e (k) - {\tilde{Δ}}^{T} (k) σ (x (k)) - H \tilde{ξ} (k)]}^{T} \\ \cdot P [(I - ϵ F) e (k) - {\tilde{Δ}}^{T} (k) σ (x (k)) - H \tilde{ξ} (k)]) - ι^{- 1} ln (1 + μ e^{T} (k) P e (k)) . \end{matrix}

(38)

Note that using natural logarithm property

ln a - ln b = ln (a / b)

and by adding and subtracting “

\frac{μ e^{T} (k) P e (k)}{1 + μ e^{T} (k) P e (k)}

” to the above equality

Δ V_{1}

can be rewritten as

\begin{matrix} Δ V_{1} & = & ι^{- 1} ln (1 + μ ({[(I - ϵ F) e (k) - {\tilde{Δ}}^{T} (k) σ (x (k)) - H \tilde{ξ} (k)]}^{T} \\ \cdot \frac{P [(I - ϵ F) e (k) - {\tilde{Δ}}^{T} (k) σ (x (k)) - H \tilde{ξ} (k)]}{1 + μ e^{T} (k) P e (k)} - \frac{e^{T} (k) P e (k)}{1 + μ e^{T} (k) P e (k)})) . \end{matrix}

(39)

using another natural logarithmic operator property

ln (1 + a) \leq a

when

a \geq - 1

[44], an upper bound for (39) can be obtained as

\begin{matrix} Δ V_{1} & \leq & \frac{ι^{- 1} μ}{1 + μ e^{T} (k) P e (k)} (- e^{T} (k) R e (k) + σ^{T} (x (k)) \tilde{Δ} (k) P {\tilde{Δ}}^{T} (k) σ (x (k)) + {\tilde{ξ}}^{T} (k) H^{T} P H \tilde{ξ} (k) \\ - 2 σ^{T} (x (k)) \tilde{Δ} (k) P (I - ϵ F) e (k) - 2 {\tilde{ξ}}^{T} (k) H^{T} P (I - ϵ F) e (k) + 2 σ^{T} (x (k)) \tilde{Δ} (k) P H \tilde{ξ} (k)), \end{matrix}

(40)

where “

- R ≜ {(I - ϵ F)}^{T} P (I - ϵ F) - P \in R_{-}^{n \times n}

” given by (7) is used.

Second, taking the Lyapunov difference of

V_{2} (\cdot)

along with the weight uncertainty error dynamics given by (10) and using (30) in the dynamics yields

\begin{matrix} Δ V_{2} & ≜ & V_{2} (\tilde{Δ} (k + 1)) - V_{2} (\tilde{Δ} (k)) \\ = & α^{- 1} tr ({\tilde{Δ}}^{T} (k + 1) \tilde{Δ} (k + 1)) - α^{- 1} tr ({\tilde{Δ}}^{T} (k) \tilde{Δ} (k)) \\ = & α^{- 1} tr (({\tilde{Δ}}^{T} (k) + \frac{γ}{1 + μ e^{T} (k) P e (k)} (- {\tilde{Δ}}^{T} (k) σ (x (k)) σ^{T} (x (k)) - H \tilde{ξ} (k) σ^{T} (x (k)))) \\ \cdot (\tilde{Δ} (k) + \frac{γ}{1 + μ e^{T} (k) P e (k)} (- σ (x (k)) σ^{T} (x (k)) \tilde{Δ} (k) - σ (x (k)) {\tilde{ξ}}^{T} (k) H^{T}) \\ - α^{- 1} tr ({\tilde{Δ}}^{T} (k) \tilde{Δ} (k)) . \end{matrix}

(41)

Then using the trace operator property

a^{T} b = tr (b a^{T})

and simplifying (41) yields

\begin{matrix} Δ V_{2} & = & \frac{α^{- 1} γ}{1 + μ e^{T} (k) P e (k)} σ^{T} (x (k)) \tilde{Δ} (k) (- 2 + \frac{γ σ^{T} (x (k)) σ (x (k))}{1 + μ e^{T} (k) P e (k)}) {\tilde{Δ}}^{T} (k) σ (x (k)) \\ + \frac{α^{- 1} γ^{2} σ^{T} (x (k)) σ (x (k))}{{(1 + μ e^{T} (k) P e (k))}^{2}} {\tilde{ξ}}^{T} (k) H^{T} H \tilde{ξ} (k) \\ + \frac{α^{- 1} γ}{1 + μ e^{T} (k) P e (k)} {\tilde{ξ}}^{T} (k) H^{T} (- 2 + 2 \frac{γ σ^{T} (x (k)) σ (x (k))}{1 + μ e^{T} (k) P e (k)}) {\tilde{Δ}}^{T} (k) σ (x (k)) . \end{matrix}

(42)

Note that using

∥ \frac{σ^{T} (x (k)) σ (x (k))}{1 + μ e^{T} (k) P e (k)} ∥_{2} \leq η

, and setting

γ = ρ_{γ} η^{- 1}

and

α^{- 1} = ι^{- 1} μ ρ_{1} γ^{- 1}

an upper bound for (42) can be written as

\begin{matrix} Δ V_{2} & \leq & \frac{ι^{- 1} μ}{1 + μ e^{T} (k) P e (k)} (σ^{T} (x (k)) \tilde{Δ} (k) (- 2 ρ_{1} + ρ_{γ} ρ_{1}) {\tilde{Δ}}^{T} (k) σ (x (k)) + ρ_{γ} {\tilde{ξ}}^{T} (k) H^{T} H \tilde{ξ} (k)) \\ + \frac{ι^{- 1} μ}{1 + μ e^{T} (k) P e (k)} {\tilde{ξ}}^{T} (k) H^{T} (- 2 ρ_{1} + 2 γ η ρ_{1}) {\tilde{Δ}}^{T} (k) σ (x (k)) . \end{matrix}

(43)

Third, taking the Lyapunov difference of

V_{3} (\cdot)

and using the error in observer dynamics (35) yields

\begin{matrix} Δ V_{3} & ≜ & V_{3} (\tilde{ξ} (k + 1)) - V_{3} (\tilde{ξ} (k)) \\ = & ν^{- 1} {\tilde{ξ}}^{T} (k + 1) S \tilde{ξ} (k + 1) - ν^{- 1} {\tilde{ξ}}^{T} (k) S \tilde{ξ} (k) \\ = & ν^{- 1} {\tilde{ξ}}^{T} (k) F^{T} S F \tilde{ξ} (k) - ν^{- 1} {\tilde{ξ}}^{T} (k) S \tilde{ξ} (k) \\ = & - ν^{- 1} {\tilde{ξ}}^{T} (k) (S - F^{T} S F) \tilde{ξ} (k) \\ = & - ν^{- 1} {\tilde{ξ}}^{T} (k) R_{F} \tilde{ξ} (k) . \end{matrix}

(44)

Setting

R_{F} = H^{T} R_{H} H

with

R_{H} \in P^{n}

, and

ν = ι μ^{- 1} ρ_{2}^{- 1}

with

ρ_{2}

being a free variable that will be designed later, an upper bound for (44) can be written as

\begin{matrix} Δ V_{3} & \leq & - \frac{ι^{- 1} μ}{1 + μ e^{T} (k) P e (k)} {\tilde{ξ}}^{T} (k) H^{T} ρ_{2} R_{H} H \tilde{ξ} (k) . \end{matrix}

(45)

Then, using (40), (43), and (45) to compute

Δ V (\cdot) ≜ Δ V_{1} (\cdot) + Δ V_{2} (\cdot) + Δ V_{3} (\cdot)

, and defining

{\tilde{q}}_{1}^{T} (k) = [\begin{matrix} e^{T} (k), & σ^{T} (x (k)) \tilde{Δ} (k), & {\tilde{ξ}}^{T} (k) H^{T} \end{matrix}]

, the combined Lyapunov difference equation can be written as

\begin{matrix} Δ V_{1} + Δ V_{2} + Δ V_{3} \\ \leq & \frac{ι^{- 1} μ}{1 + μ e^{T} (k) P e (k)} (- e^{T} (k) R e (k) + σ^{T} (x (k)) \tilde{Δ} (k) [P - 2 ρ_{1} + ρ_{γ} ρ_{1}] {\tilde{Δ}}^{T} (k) σ (x (k)) \\ + {\tilde{ξ}}^{T} (k) H^{T} [P - R_{H} ρ_{2} + ρ_{γ} ρ_{1}] H \tilde{ξ} (k) - 2 σ^{T} (x (k)) \tilde{Δ} (k) P (I - ϵ F) e (k)) \\ - 2 {\tilde{ξ}}^{T} (k) H^{T} P (I - ϵ F) e (k) + 2 σ^{T} (x (k)) \tilde{Δ} (k) [P - ρ_{1}] H \tilde{ξ} (k) + σ^{T} (x (k)) \tilde{Δ} (k) [2 ρ_{1} γ η]H \tilde{ξ} (k)) \end{matrix}

\begin{matrix} = & \frac{ι^{- 1} μ}{1 + μ e^{T} (k) P e (k)} (e^{T} (k) [- R + β {(I - ϵ F)}^{T} P (I - ϵ F)] e (k) \\ + σ^{T} (x (k)) \tilde{Δ} (k) [P + \frac{1}{β} P - 2 ρ_{1} + ρ_{γ} ρ_{1}] {\tilde{Δ}}^{T} (k) σ (x (k)) \\ + {\tilde{ξ}}^{T} (k) H^{T} [2 P - R_{H} ρ_{2} + ρ_{γ} ρ_{1}] H \tilde{ξ} (k) + σ^{T} (x (k)) \tilde{Δ} (k) [2 ρ_{1} γ η]H \tilde{ξ} (k)) \\ - \frac{ι^{- 1} μ}{1 + μ e^{T} (k) P e (k)} {\tilde{q}}_{1}^{T} (k) \underset{\bar{F} \geq 0}{\underset{︸}{[\begin{matrix} β {(I - ϵ F)}^{T} P (I - ϵ F) & (P (I - ϵ F))^{T} & (P (I - ϵ F))^{T} \\ P (I - ϵ F) & \frac{1}{β} P & (- P + ρ_{1})^{T} \\ P (I - ϵ F) & - P + ρ_{1} & P \end{matrix}]}} {\tilde{q}}_{1} (k) . \end{matrix}

(46)

Note that setting

ρ_{1} = (1 + \frac{1}{β}) P \in P^{n}

one can show the

\bar{F}

matrix is positive semi-definite as shown in Appendix C. Then using

- \bar{R} = - R + β {(I - ϵ F)}^{T} P (I - ϵ F) < 0

, and taking an upper bound of (46) yields

\begin{matrix} Δ V & \leq & \frac{ι^{- 1} μ}{1 + μ e^{T} (k) P e (k)} (- e^{T} (k) \bar{R} e (k) - σ^{T} (x (k)) \tilde{Δ} (k) \underset{ρ_{3}}{\underset{︸}{[(1 + \frac{1}{β}) P - (1 + \frac{1}{β}) ρ_{γ} P]}} {\tilde{Δ}}^{T} (k) σ (x (k)) \\ - {\tilde{ξ}}^{T} (k) H^{T} \underset{ρ_{4}}{\underset{︸}{[- 2 P + R_{H} ρ_{2} - ρ_{γ} ρ_{1}]}} H \tilde{ξ} (k) + σ^{T} (x (k)) \tilde{Δ} (k) [2 ρ_{1} γ η]H \tilde{ξ} (k)), \\ \leq & \frac{ι^{- 1} μ}{1 + μ e^{T} (k) P e (k)} (- e^{T} (k) \bar{R} e (k)) - \frac{ι^{- 1} μ}{1 + μ e^{T} (k) P e (k)} {\tilde{q}}_{2}^{T} (k) \underset{ρ_{5} \geq 0}{\underset{︸}{[\begin{matrix} ρ_{3} & - ρ_{1} ρ_{γ} \\ - ρ_{1} ρ_{γ} & ρ_{4} \end{matrix}]}} {\tilde{q}}_{2} (k), \end{matrix}

(47)

where

{\tilde{q}}_{2}^{T} (k) = [\begin{matrix} σ^{T} (x (k)) \tilde{Δ} (k) & {\tilde{ξ}}^{T} (k) H^{T} \end{matrix}]

. In (47),

γ = ρ_{γ} η^{- 1}

is used. One can then show positive definiteness of

ρ_{5}

as shown in Appendix D. Finally, one can obtain an upper bound for (47) that is

\begin{matrix} Δ V & \leq & \frac{l_{0}^{- 1} μ}{1 + μ e^{T} (k) P e (k)} (- e^{T} (k) \bar{R} e (k)), \end{matrix}

(48)

which proves the boundedness of the

(e (k), \tilde{Δ} (k), \tilde{ξ} (k))

. It then follows from [Theorem 13.10, [43] that

{lim}_{k \to \infty} (e (k)) = 0

. □

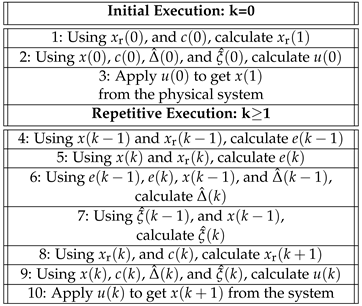
Remark 1.

The given proposed discrete-time adaptive control architecture can be sequentially executed in embedded code. Table 2 presents one possible sequential operation of this architecture. Note that no knowledge of any signal from step

(k + 1)

is required to execute the architecture.

4. Illustrative Numerical Examples

In order to illustrate the efficacy of the proposed discrete-time control architecture, consider a group of 5 agents on a line graph with the third agent being a leader. See Figure 1 for the graph formation chosen for the illustrative numerical examples of this paper. For the simulations, we select the uncertain weights as

Δ = [0.075, 0.05, 0.015, 0.0375, 0.0606]

and the coupled dynamics matrices as

f_{u i} = [- 0.1, - 0.05, - 0.02, - 0.15, - 0.2]

g_{u i} = [0.6, 0.5, 0.4, 0.3, 0.2]

, and

h_{u i} = [1.3, 1.2, 1, 0.9, 0.7]

Here, we choose the nullspace

ω = [1; 2; 3; 2; 1]

and use the command

c (k) = v (k) w_{3} = 1.5

(i.e.,

v (k) = 0.5

) such that

{lim}_{k \to \infty} x (k) = v (k) ω

. Thus, the expectation for convergences is that the first agent should converge to

0.5

, the second agent should converge to 1, the third (the leader) agent should converge to

1.5

, the fourth agent should converge to 1, and the fifth agent should converge to

0.5

Regarding the update law, we calculated weight update law with

γ = 0.43

and

μ = 1

, where the known basis functions are selected as

σ_{1} (x_{1} (k)) = x_{1}^{2} (k)

σ_{2} (x_{2} (k)) = cos x_{2} (k)

σ_{3} (x_{3} (k)) = x_{3} (k)

σ_{4} (x_{4} (k)) = sin x_{4} (k)

, and

σ_{5} (x_{5} (k)) = x_{5}^{3} (k)

. We set the time step

Δ t

0.2

, the control parameter

ϵ

1 / 6

, and Lyapunov equation matrices R to

0.1 I

, and

R_{F}

2 I

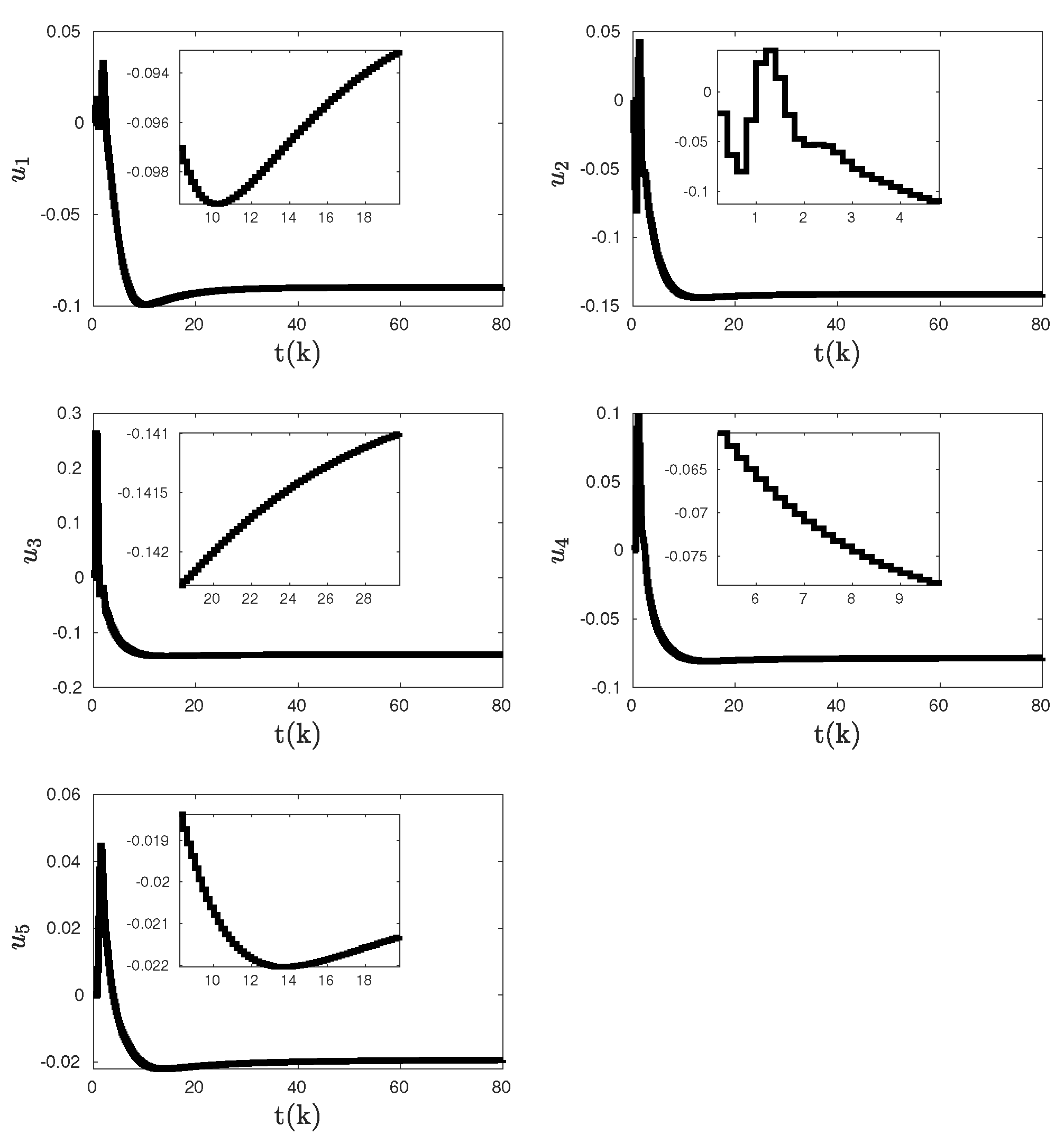
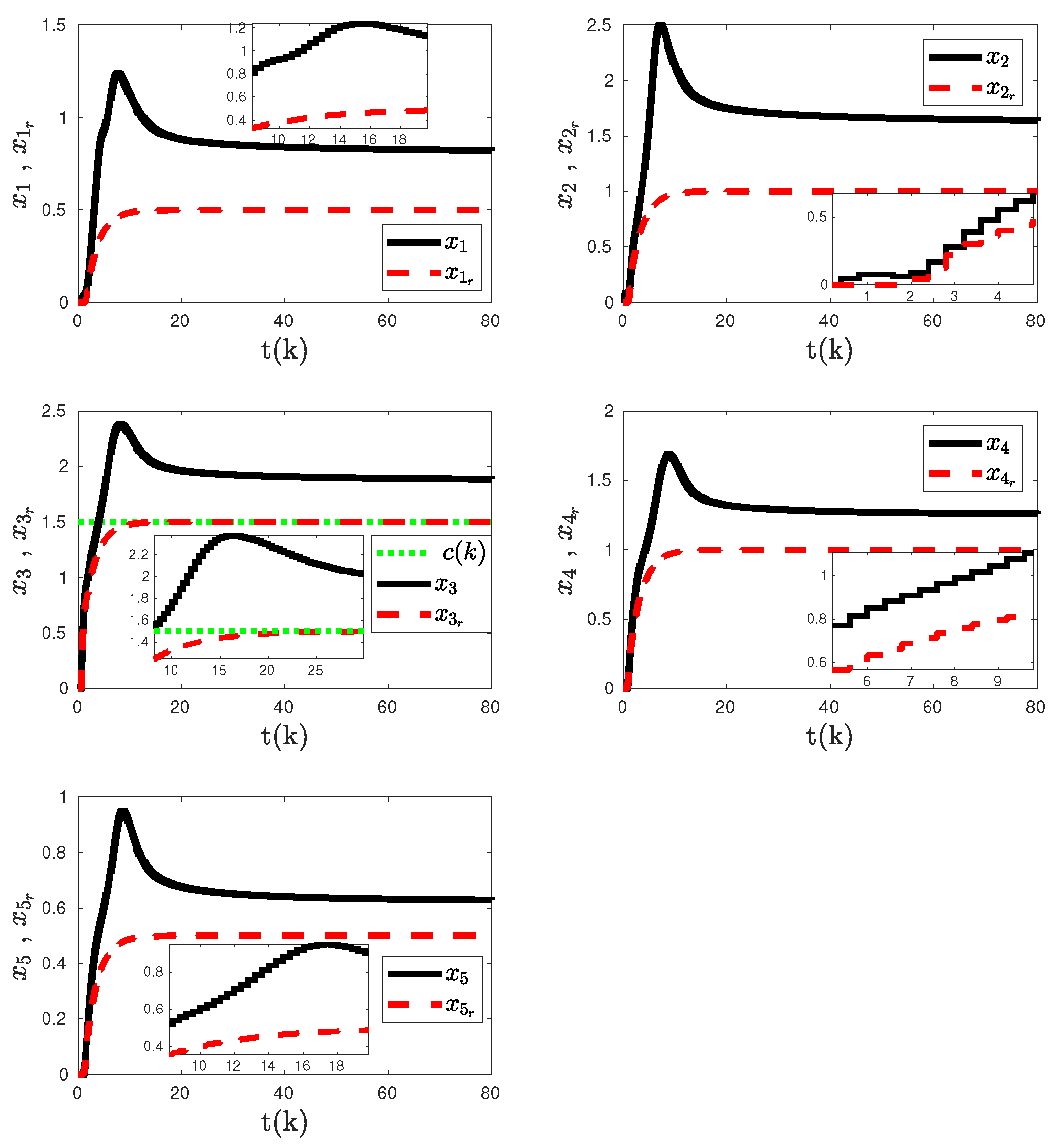
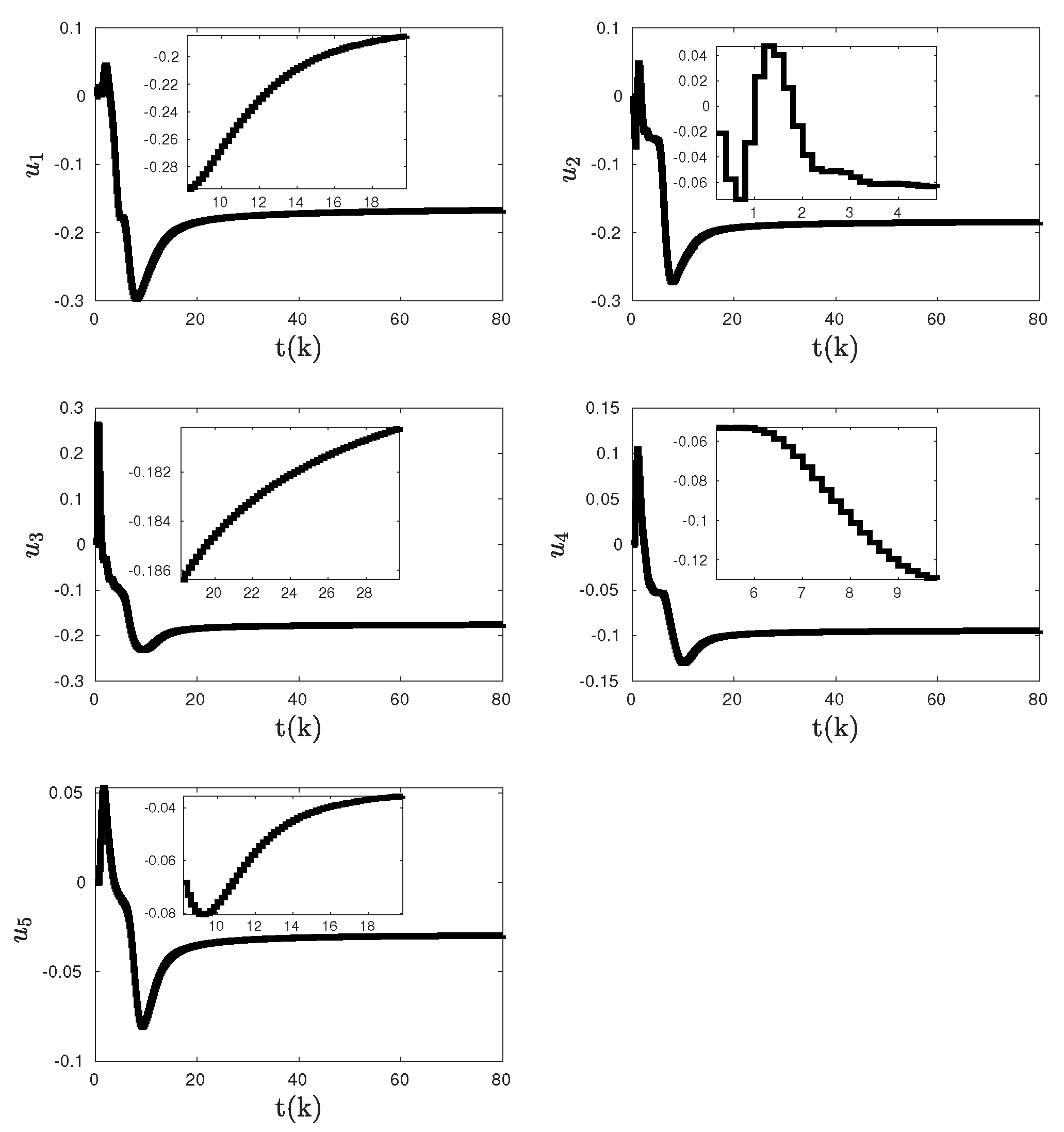
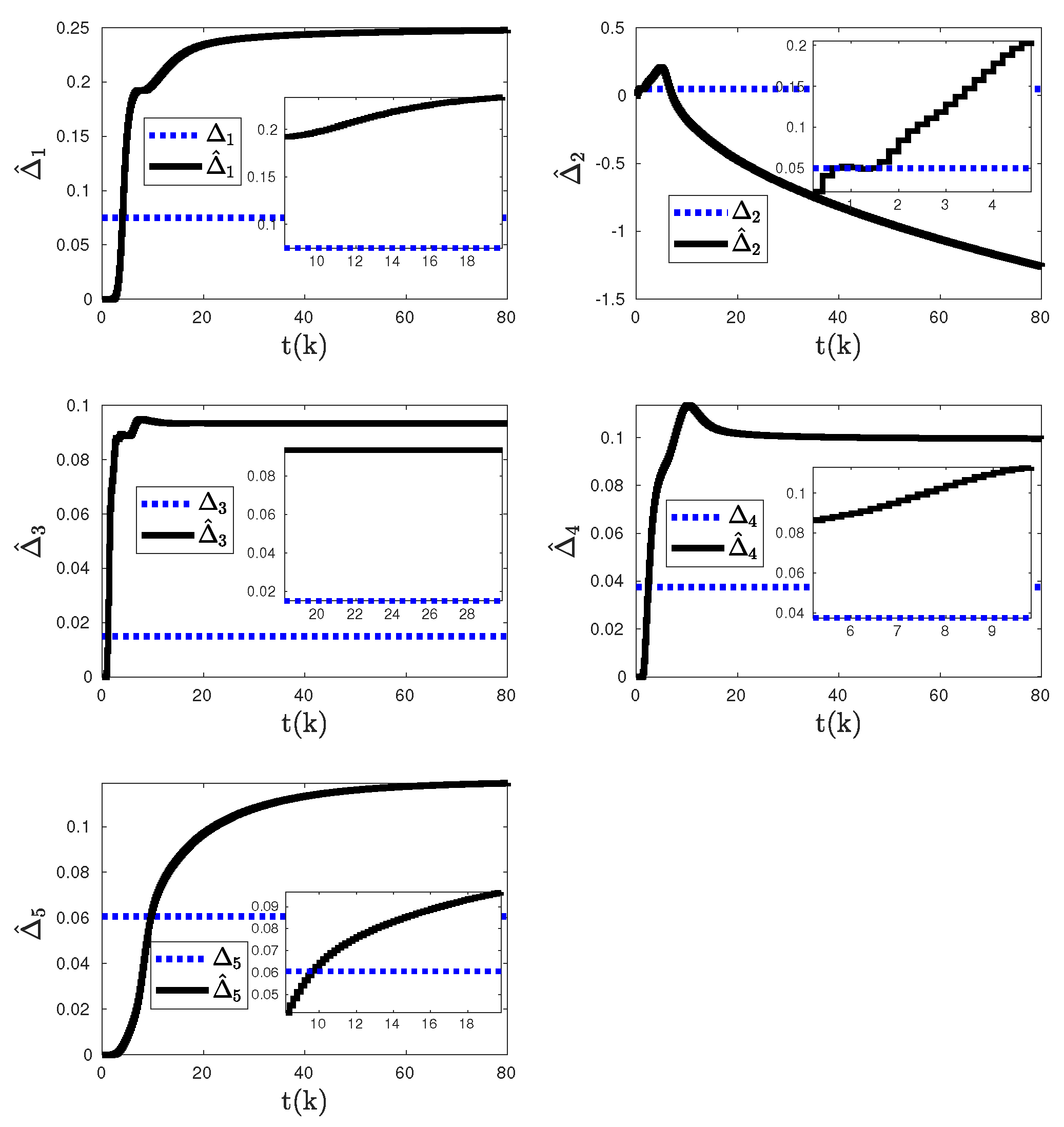
For motivating the necessity of the controller that is proposed in Section 3, we first simulated the uncertain multiagent system in the presence of the unmeasurable coupled dynamics with the proposed controller of Section 2. Figure 2, Figure 3, and Figure 4 show the closed-loop system response with the proposed discrete-time adaptive control architecture given in Section 2. These are tracking response, control input, and unknown weight estimates, respectively. As you see from Figure 2, Figure 3, and Figure 4, convergence to the assigned position cannot be achieved.

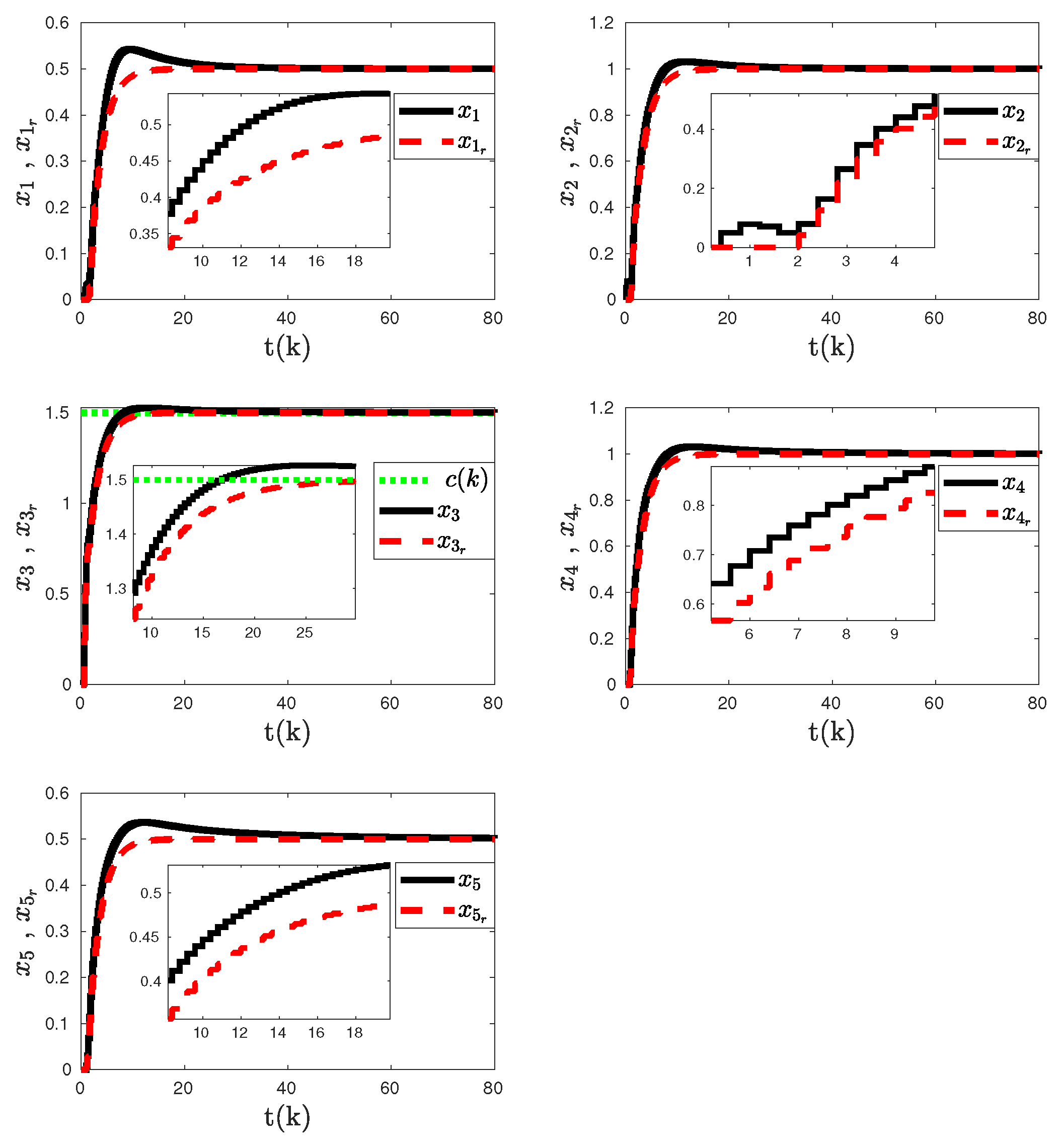
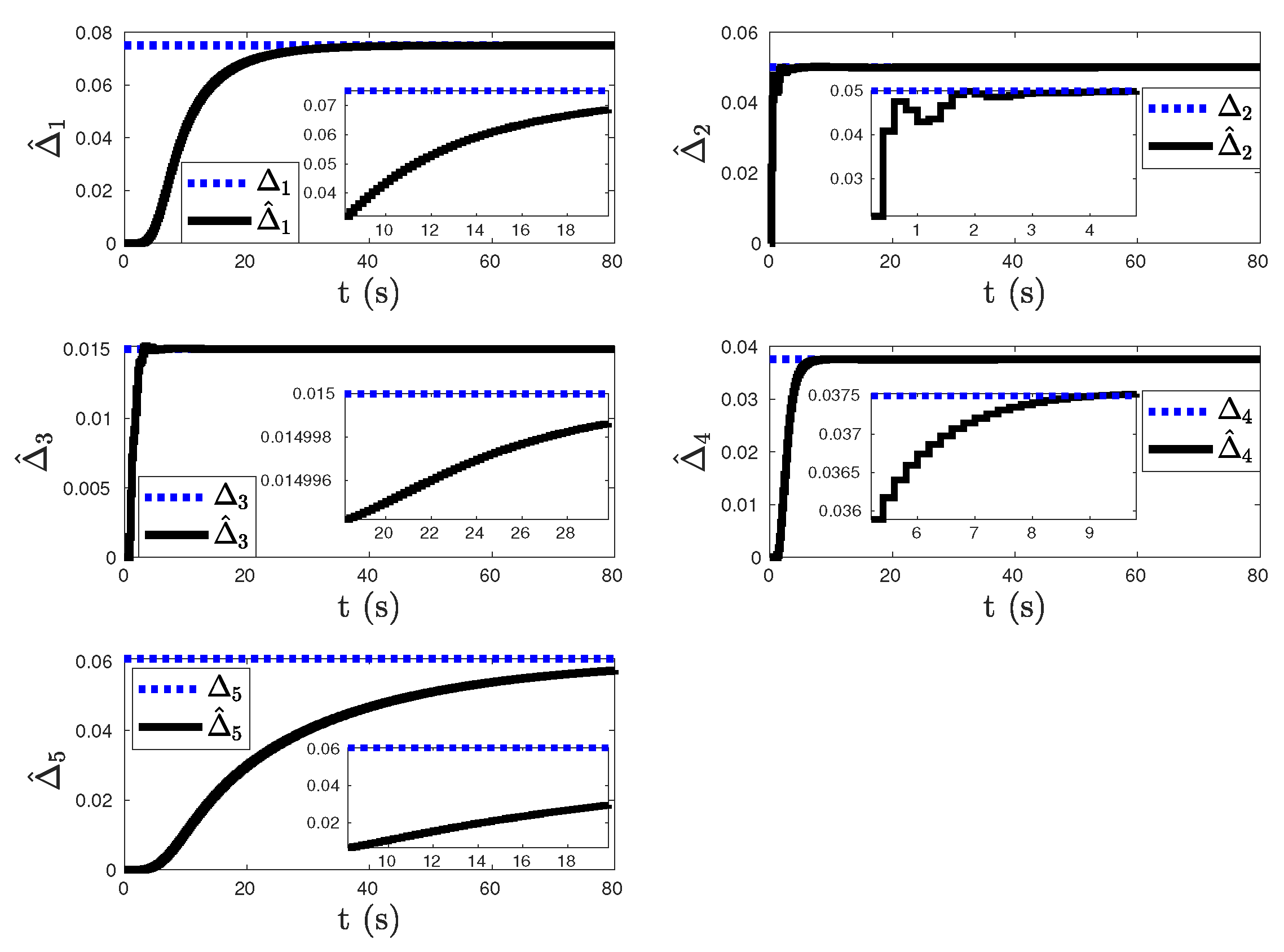
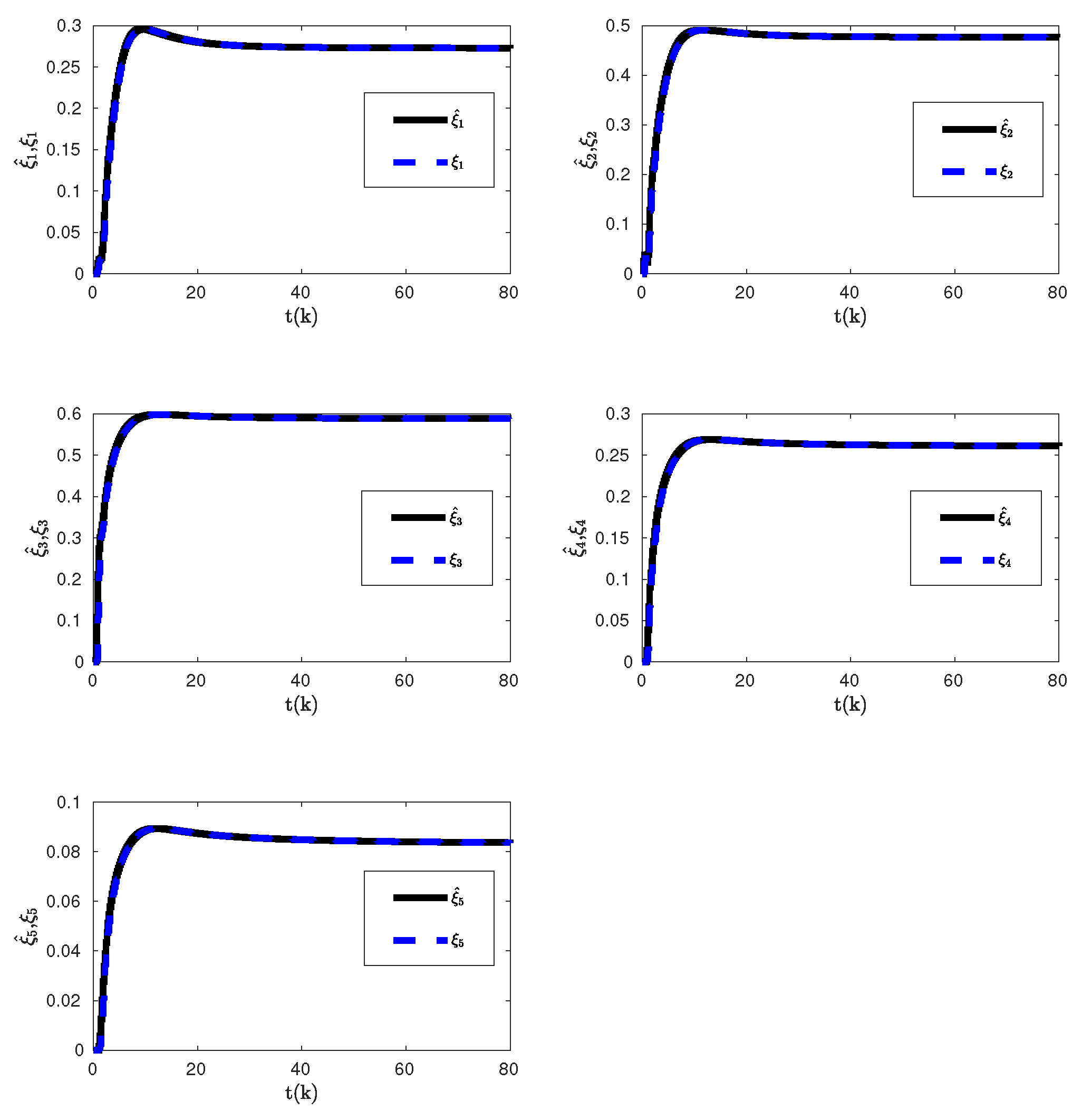
Figure 5, Figure 6, Figure 7, and Figure 8 then show the closed-loop system response, control input, unknown weights estimates, and observer state, respectively, for each agent in the presence of the agent-based uncertainty and the coupled dynamics with the proposed discrete-time adaptive control architecture given in Section 3, where the effects of system uncertainties and coupled dynamics are suppressed successfully while achieving the convergence to the assigned position.

Figure 2. Uncertain multiagent system response in the presence of coupled dynamics with the proposed discrete-time adaptive control method given in Section 2.

Figure 3. Control inputs with the proposed discrete-time adaptive control method given in Section 2.

Figure 4. Agent-based uncertainty estimations of the proposed discrete-time adaptive control method given in Section 2.

Figure 5. Uncertain multiagent system response in the presence of coupled dynamics with the proposed discrete-time adaptive control method given in Section 3.

Figure 6. Control inputs with the proposed discrete-time adaptive control method given in Section 3.

Figure 7. Agent-based uncertainty estimations of the proposed discrete-time adaptive control method given in Section 3.

Figure 8. Agent-based coupled dynamics of the proposed discrete-time adaptive control method given in Section 3.

5. Conclusion

This paper addresses the challenges and complexities associated with discrete-time architectures in the context of multiagent systems with uncertain scalar dynamics and coupled interactions. The paper introduces discrete-time adaptive control architecture with observer dynamics for managing unmeasurable coupled dynamics. Additionally, a user-assigned Laplacian matrix is incorporated to induce cooperative behaviors among multiple agents. The proposed control architecture is accompanied by Lyapunov analysis employing logarithmic and quadratic Lyapunov functions to guarantee asymptotic stability. Through an illustrative example, the paper demonstrates the effectiveness of the introduced control architecture, showcasing its ability to address uncertainties and coupled dynamics in multiagent systems. These contributions open avenues for further research in the development and application of adaptive control strategies in discrete-time scenarios. The future research direction can include adding actuator dynamics and unknown control degradation to the multiagent system model as well as experimentally validating the theoretical results of this paper with the system with multiple robots.

Appendix A

In this appendix, the upper bound for

∥ \frac{σ^{T} (x (k)) σ (x (k))}{1 + μ e^{T} (k) P e (k)} ∥_{2} \leq η

is obtained. Given that

{∥ x (k) ∥}_{2} \leq {∥ e (k) ∥}_{2} + x_{r}^{*}

{∥ σ (x (k)) ∥}_{2} \leq l_{c} + l {∥ x (k) ∥}_{2}

, and setting

d^{*} = l_{c} + l x_{r}^{*}

then the bound on

σ^{T} (x (k)) σ (x (k))

can be written as

\begin{matrix} ∥ σ^{T} {(x (k)) σ (x (k)) ∥}_{2} & \leq & {(l_{c} + l {∥ x (k) ∥}_{2})}^{2} \\ = & l_{c}^{2} + 2 l l_{c} {(∥ e (k) ∥}_{2} + x_{r}^{*}) + l^{2} {∥ x (k) ∥}_{2}^{2} \\ = & l_{c}^{2} + 2 l l_{c} {(∥ e (k) ∥}_{2} + x_{r}^{*}) + l^{2} {(∥ e (k) ∥}_{2}^{2} + 2 x_{r}^{*} {∥ e (k) ∥}_{2} + x_{r}^{*^{2}}) \\ = & l_{c}^{2} + 2 l (l_{c} + l x_{r}^{*}) ∥ e (k) ∥_{2} + 2 l (l_{c} + l x_{r}^{*}) x_{r}^{*} - l^{2} x_{r}^{*^{2}} + l^{2} {∥ e (k) ∥}_{2}^{2} \\ = & l_{c}^{2} + 2 l d^{*} {∥ e (k) ∥}_{2} + 2 l d^{*} x_{r}^{*} - l^{2} x_{r}^{*^{2}} + l^{2} {∥ e (k) ∥}_{2}^{2} \\ = & l^{2} {∥ e (k) ∥}_{2}^{2} + 2 l d^{*} {∥ e (k) ∥}_{2} + d^{*^{2}} - 2 l^{2} x_{r}^{*^{2}} - 2 l l_{c} x_{r}^{*} + 2 l d^{*} x_{r}^{*} \\ = & {(l ∥ e (k) ∥}_{2} + d^{*})^{2} . \end{matrix}

Then an upper bound for

∥ \frac{σ^{T} (x (k)) σ (x (k))}{1 + μ e^{T} (k) P e (k)} ∥_{2}

can be written as

\begin{matrix} ∥ \frac{σ^{T} (x (k)) σ (x (k))}{1 + μ e^{T} (k) P e (k)} ∥_{2} & \leq & {(\frac{l}{\sqrt{μ \underset{̲}{λ} (P)}} + d^{*})}^{2} \\ = & \frac{l^{2}}{μ \underset{̲}{λ} (P)} + d^{*^{2}} + \frac{2 l d^{*}}{\sqrt{μ \underset{̲}{λ} (P)}} \\ \leq & \frac{2 l^{2}}{μ \underset{̲}{λ} (P)} + 2 d^{*^{2}} = η, \end{matrix}

where the Young’s inequality “

2 x y \leq \frac{x^{2}}{2} + \frac{y^{2}}{2}

” is used at the last step.

Appendix B

In this appendix, the below N is proven to be positive definite

\begin{matrix} N ≜ ρ_{1} (2 - ρ_{γ}) - (1 + \frac{1}{β}) P . \end{matrix}

Note that setting

ρ_{1} ≜ \frac{1 + β}{β} P

yields

\begin{matrix} N ≜ (1 + \frac{1}{β}) P (2 - ρ_{γ}) - (1 + \frac{1}{β}) P . \end{matrix}

Recall that

ρ_{γ} \in (0, 1)

; and hence, “

(2 - ρ_{γ}) > 1

”. That concludes the positive definiteness of

\begin{matrix} N ≜ (1 + \frac{1}{β}) P (1 - ρ_{γ}) > 0 . \end{matrix}

Appendix C

In this appendix, the below

\bar{F}

matrix is proven to be positive semi-definite

\begin{matrix} \bar{F} ≜ [\begin{matrix} β {(I - ϵ F)}^{T} P (I - ϵ F) & (P (I - ϵ F))^{T} & (P (I - ϵ F))^{T} \\ P (I - ϵ F) & \frac{1}{β} P & (- P + ρ_{1})^{T} \\ P (I - ϵ F) & - P + ρ_{1} & P \end{matrix}] \geq 0 . \end{matrix}

To prove the positive semi-definiteness of the above matrix, one needs to prove that the minors of the matrix are positive semi-definite [45]. Let

p_{1}

p_{2}

,and

p_{3}

be the minors of

\bar{F}

given by

\begin{matrix} p_{1} & = & β {(I - ϵ F)}^{T} P (I - ϵ F) > 0, \\ p_{2} & = & {(I - ϵ F)}^{T} P (I - ϵ F) P - {(I - ϵ F)}^{T} P (I - ϵ F) P = 0, \\ p_{3} & = & {(I - ϵ F)}^{T} P (I - ϵ F) (P^{T} P - β P^{T} P + 2 β ρ_{1} P - β ρ_{1}^{2}) \\ - {(I - ϵ F)}^{T} P (I - ϵ F) (P^{T} P + P^{T} P - ρ_{1} P) \\ + {(I - ϵ F)}^{T} P (I - ϵ F) (- P^{T} P + ρ_{1} P - \frac{1}{β} P^{T} P) \\ = & {(I - ϵ F)}^{T} P (I - ϵ F) (- β P^{T} P + 2 β ρ_{1} P - β ρ_{1}^{2} - 2 P^{T} P + 2 ρ_{1} P - \frac{1}{β} P^{T} P) \\ = & {(I - ϵ F)}^{T} P (I - ϵ F) (- β P^{T} P - 2 P^{T} P - \frac{1}{β} P^{T} P) \\ + {(I - ϵ F)}^{T} P (I - ϵ F) (ρ_{1} (2 β P + 2 P) - β ρ_{1}^{2}) \\ = & {(I - ϵ F)}^{T} P (I - ϵ F) (\frac{- {(β + 1)}^{2}}{β} P^{T} P) \\ + {(I - ϵ F)}^{T} P (I - ϵ F) (2 ρ_{1} P (β + 1) - β ρ_{1}^{2}) \end{matrix}

where

p_{1}

is positive definite since

β \in R_{+}

and

P \in P_{+}

, and

p_{2} = 0

. To prove

p_{3} = 0

, one needs to use

ρ_{1} ≜ \frac{1 + β}{β} P

that is defined in Appendix B. Then one can conclude

p_{3} = 0

\begin{matrix} p_{3} & = & {(I - ϵ F)}^{T} P (I - ϵ F) (\frac{- {(1 + β)}^{2}}{β} P^{T} P) + {(I - ϵ F)}^{T} P (I - ϵ F) (2 \frac{{(1 + β)}^{2}}{β} P^{T} P - \frac{{(1 + β)}^{2}}{β} P^{T} P) = 0 \end{matrix}

This concludes the proof that the matrix

\bar{F}

is positive semi-definite.

Appendix D

In this appendix, the below

ρ_{5}

matrix is proven to be positive definite

\begin{matrix} ρ_{5} = [\begin{matrix} ρ_{3} & - ρ_{1} ρ_{γ} \\ - ρ_{1} ρ_{γ} & ρ_{4} \end{matrix}] \end{matrix}

with

ρ_{1} ≜ \frac{1 + β}{β} P

ρ_{3} ≜ [(1 + \frac{1}{β}) P - (1 + \frac{1}{β}) ρ_{γ} P] = (1 - ρ_{γ}) ρ_{1}

, and

ρ_{4} ≜ [- 2 P + R_{H} ρ_{2} - ρ_{γ} ρ_{1}]

. To prove the positive definiteness of the above matrix, one needs to prove that the minors of the matrix are positive semi-definite [45]. Let

p_{1}

and

p_{2}

be the minors of

ρ_{5}

given by

\begin{matrix} p_{1} & = & ρ_{3} = (1 - ρ_{γ}) ρ_{1}, \\ p_{2} & = & ρ_{3} ρ_{4} - ρ_{γ}^{2} ρ_{1} ρ_{1} \\ = & (1 - ρ_{γ}) ρ_{1} (- 2 P + R_{H} ρ_{2} - ρ_{γ} ρ_{1}) - ρ_{γ}^{2} ρ_{1} ρ_{1} \\ = & ρ_{1} (- 2 P + (1 - ρ_{γ}) R_{H} ρ_{2} - ρ_{γ} ρ_{1} + 2 ρ_{γ} P) . \end{matrix}

Here,

p_{1}

is positive definite since

ρ_{γ} \in (0, 1)

. Then setting

ρ_{2} ≜ \frac{1}{\underset{̲}{λ} (R_{H})} {(1 - ρ_{γ})}^{- 1} (2 P + ρ_{γ} ρ_{1} - 2 ρ_{γ} P)

yields

\begin{matrix} p_{2} & = & ρ_{1} (\frac{R_{H}}{\underset{̲}{λ} (R_{H})} - R_{H}) (2 P + ρ_{γ} ρ_{1} - 2 ρ_{γ} P) \\ p_{2} & = & ρ_{1} \underset{> 0}{\underset{︸}{(\frac{R_{H}}{\underset{̲}{λ} (R_{H})} - R_{H})}} \underset{> 0}{\underset{︸}{(2 P (1 - ρ_{γ})}} + ρ_{γ} ρ_{1}) . \end{matrix}

This concludes the proof that the matrix

ρ_{5}

is positive definite.

References

Olfati-Saber, R.; Fax, J.A.; Murray, R.M. Consensus and cooperation in networked multi-agent systems. Proceedings of the IEEE 2007, 95, 215–233. [CrossRef]
Ren, W.; Atkins, E. Distributed multi-vehicle coordinated control via local information exchange. International Journal of Robust and Nonlinear Control 2007, 17, 1002–1033. [CrossRef]
Mesbahi, M.; Egerstedt, M. Graph Theoretic Methods in Multiagent Networks; Princeton University Press, 2010. [CrossRef]
Lewis, F.L.; Zhang, H.; Hengster-Movric, K.; Das, A. Cooperative control of multi-agent systems: optimal and adaptive design approaches; Springer Science & Business Media, 2013. [CrossRef]
Rohrs, C.; Valavani, L.; Athans, M.; Stein, G. Robustness of continuous-time adaptive control algorithms in the presence of unmodeled dynamics. IEEE Transactions on Automatic Control 1985, 30, 881–889. [CrossRef]
Nguyen, N.; Urnes, J. Aeroelastic modeling of elastically shaped aircraft concept via wing shaping control for drag reduction. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, 2012. [CrossRef]
Nobleheart, W.; Chakravarthy, A.; Nguyen, N. Active wing shaping control of an elastic aircraft. IEEE American Control Conference 2014, pp. 3059–3064. [CrossRef]
Pequito, S.D.; Kar, S.; Aguiar, A.P.; et al. A Framework for Structural Input/Output and Control Configuration Selection in Large-Scale Systems. IEEE Trans. Automat. Contr. 2016, 61, 303–318. [CrossRef]
Hou, Z.G.; Cheng, L.; Tan, M. Decentralized robust adaptive control for the multiagent system consensus problem using neural networks. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics) 2009, 39, 636–647. [CrossRef]
Das, A.; Lewis, F.L. Distributed adaptive control for synchronization of unknown nonlinear networked systems. Automatica 2010, 46, 2014–2021. [CrossRef]
Yucelen, T.; Egerstedt, M. Control of multiagent systems under persistent disturbances. American Control Conference 2012, pp. 5264–5269. [CrossRef]
Yucelen, T.; Johnson, E.N. Control of multivehicle systems in the presence of uncertain dynamics. International Journal of Control 2013, 86, 1540–1553. [CrossRef]
Wang, W.; Wen, C.; Huang, J. Distributed adaptive asymptotically consensus tracking control of nonlinear multi-agent systems with unknown parameters and uncertain disturbances. Automatica 2017, 77, 133–142. [CrossRef]
Sarsilmaz, S.B.; Yucelen, T. A Distributed Adaptive Control Approach for Heterogeneous Uncertain Multiagent Systems. AIAA Guidance, Navigation, and Control Conference 2018. [CrossRef]
Dogan, K.M.; Gruenwald, B.C.; Yucelen, T.; Muse, J.A.; Butcher, E.A. Distributed adaptive control and stability verification for linear multiagent systems with heterogeneous actuator dynamics and system uncertainties. Int. Journal of Control 2018, pp. 1–19. [CrossRef]
Dogan, K.M.; Yucelen, T.; Ristevki, S.; Muse, J.A. Distributed adaptive control of uncertain multiagent systems with coupled dynamics. In Proceedings of the 2020 American Control Conference (ACC). IEEE, 2020, pp. 3497–3502. [CrossRef]
Dogan, K.M.; Yucelen, T.; Muse, J.A. Stability verification for uncertain multiagent systems in the presence of heterogeneous coupled and actuator dynamics. In Proceedings of the AIAA Scitech 2021 Forum, 2021, p. 0530. [CrossRef]
Aly, I.A.; Dogan, K.M. Uncertain multiagent system in the presence of coupled dynamics: An asymptotic approach. In Proceedings of the AIAA SCITECH 2022 Forum, 2022, p. 0359. [CrossRef]
DeVries, L.D.; Kutzer, M.D. Kernel design for coordination of autonomous, time-varying multi-agent configurations. In Proceedings of the 2016 American Control Conference. IEEE, 2016, pp. 1975–1980. [CrossRef]
DeVries, L.; Sims, A.; Kutzer, M.D. Kernel Design and Distributed, Self-Triggered Control for Coordination of Autonomous Multi-Agent Configurations. Robotica 2018, 36, 1077–1097. [CrossRef]
Tran, D.; Yucelen, T. On new Laplacian matrix with a user- assigned nullspace in distributed control of multiagent systems. In Proceedings of the ACC, 2020. [CrossRef]
Dogan, K.M.; Yucelen, T. Distributed Adaptive Control for Uncertain Multiagent Systems with User-Assigned Laplacian Matrix Nullspaces. In Proceedings of the CCTA 2021, 2021. [CrossRef]
Kurttisi, A.; Aly, I.A.; Dogan, K.M. Coordination of Uncertain Multiagent Systems with Non-Identical Actuation Capacities. In Proceedings of the 2022 IEEE 61st Conference on Decision and Control (CDC). IEEE, 2022, pp. 3947–3952. [CrossRef]
Aly, I.A.; Kurttisi, A.; Dogan, K.M. An Observer-Based Distributed Adaptive Control Algorithm for Coordination of Multiagent Systems in the Presence of Coupled Dynamics. In Proceedings of the 2023 American Control Conference (accepted). [CrossRef]
Santillo, M.A.; Bernstein, D.S. Adaptive control based on retrospective cost optimization. Journal of Guidance, Control, and Dynamics 2010, 33, 289–304. [CrossRef]
Goodwin, G.; Ramadge, P.; Caines, P. Discrete-time multivariable adaptive control. IEEE Transactions on Automatic Control 1980, 25, 449–456. [CrossRef]
Kanellakopoulos, R. A discrete-time adaptive nonlinear system. In Proceedings of the Proc. American Control Conference, 1994, pp. 867–869. [CrossRef]
Venugopal, R.; Rao, V.; Bernstein, D. Lyapunov-based backward-horizon discrete-time adaptive control. Adaptive Contr. Sig. Proc. 2003, 17, 67–84. [CrossRef]
Hayakawa, T.; Haddad, W.M.; Leonessa, A. A Lyapunov-based adaptive control framework for discrete-time non-linear systems with exogenous disturbances. International Journal of Control 2004, 77, 250–263. [CrossRef]
Akhtar, S.; Venugopal, R.; Bernstein, D.S. Logarithmic Lyapunov functions for direct adaptive stabilization with normalized adaptive laws. Int. Journal of Control 2004, 77, 630–638. [CrossRef]
Johansson, R. Global Lyapunov stability and exponential convergence of direct adaptive control. International Journal of Control 1989, 50, 859–869. [CrossRef]
Johansson, R. Supermartingale analysis of minimum variance adaptive control. Control-Theory and Advanced Technology 1995, 10, 993–1013. [CrossRef]
Haddad, W.M.; Hayakawa, T.; Leonessa, A. Direct adaptive control for discrete-time nonlinear uncertain dynamical systems. In Proceedings of the Proc. American Control Conference, 2002, pp. 1773–1778. [CrossRef]
Hoagg, J.B.; Santillo, M.A.; Bernstein, D.S. Discrete-time adaptive command following and disturbance rejection with unknown exogenous dynamics. IEEE Transactions on Automatic Control 2008, 53, 912–928. [CrossRef]
Dogan, K.M.; Yucelen, T.; Haddad, W.M.; Muse, J.A. Improving transient performance of discrete-time model reference adaptive control architectures. International Journal of Adaptive Control and Signal Processing 2020, 34, 901–918. [CrossRef]
Dogan, K.M.; Kurttisi, A.; Yucelen, T.; Koru, A.T. A Projection Operator-Based Discrete-Time Adaptive Architecture for Control of Uncertain Dynamical Systems With Actuator Dynamics. IEEE Control Systems Letters 2022, 6, 3343–3348. [CrossRef]
Li, H.; Wu, Y.; Chen, M. Adaptive fault-tolerant tracking control for discrete-time multiagent systems via reinforcement learning algorithm. IEEE Transactions on Cybernetics 2020, 51, 1163–1174. [CrossRef]
Jiang, Y.; Fan, J.; Gao, W.; Chai, T.; Lewis, F.L. Cooperative adaptive optimal output regulation of nonlinear discrete-time multi-agent systems. Automatica 2020, 121, 109149. [CrossRef]
Yildirim, E.; Yucelen, T. Discrete-Time Control of Multiagent Systems with a Misbehaving Node. In Proceedings of the 2022 American Control Conference (ACC). IEEE, 2022, pp. 48–53. [CrossRef]
Aly, I.A.; Dogan, K.M. Discrete-Time Adaptive Control Algorithm for Coordination of Multiagent Systems in the Presence of Coupled Dynamics. IEEE/RSJ International Conference on Intelligent Robots, Detroit, Michigan 2023. [CrossRef]
Mesbahi, M.; Egerstedt, M. Graph theoretic methods in multiagent networks; Princeton University Press, 2010. [CrossRef]
Godsil, C.D.; Royle, G. Algebraic graph theory; Springer, New York, 2001. [CrossRef]
Haddad, W.M.; Chellaboina, V. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach; Princeton University Press: Princeton, NJ, 2008. [CrossRef]
Topsok, F. Some bounds for the logarithmic function. Inequality Theory and Applications 2006, 4, 137.
Bhatia, R. Positive definite matrices; Princeton university press, 2009. [CrossRef]

Figure 1. Directed graph representation for an undirected line graph with five agents, where the third agent is the leader.

Table 1. Notation

$N$	set of non-negative integers
$R$	set of real numbers
$R_{+}$	set of positive real numbers
$R^{n}$	set of $n \times 1$ real column vectors
$R^{n \times m}$	set of $n \times m$ real matrices
$P^{n}$	set of $n \times n$ positive definite real matrices
≜	equality by definition
${(\cdot)}^{T}$	transpose of a matrix
${(\cdot)}^{- 1}$	inverse of a matrix
$tr (\cdot)$	Trace operator
$\ln (\cdot)$	Natural logarithm
${∥ \cdot ∥}_{2}$	Euclidean norm
$λ (A)$	eigenvalues of the real matrix $A \in R^{n \times n}$
$\bar{λ} (A)$	maximum eigenvalue of the real matrix $A \in R^{n \times n}$
$\underset{̲}{λ} (A)$	minimum eigenvalue of the real matrix $A \in R^{n \times n}$
$I_{n}$	$n \times n$ identity matrix
$0_{n}$	$n \times n$ zero matrix
diag(·)	diagonalized vector

Table 2. Sequential Operation

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Discrete-Time Adaptive Control for Uncertain Scalar Multiagent Systems with Coupled Dynamics: A Lyapunov-Based Approach

Abstract

1. Introduction

1.1. Literature Review

1.2. Organization

1.3. Notation and Mathematical Preliminaries

2. Preliminary Results: Adaptation For Agent-Based Uncertainty

3. Adaptation For Both Agent-Based Uncertainty and Coupled Dynamics

4. Illustrative Numerical Examples

5. Conclusion

Appendix A

Appendix B

Appendix C

Appendix D

References

MDPI Initiatives

Important Links

Subscribe