A Perfect Load Forecasting Strategy (PLFS) for Smart Grids Based on Artificial Intelligence

Preprint

Article

A Perfect Load Forecasting Strategy (PLFS) for Smart Grids Based on Artificial Intelligence

Altmetrics

Downloads

112

Views

Comments

A peer-reviewed article of this preprint also exists.

Asmaa Hamdy Rabie,Ahmed I. Saleh,

Said H. Abd Elkhalik,

Ali E. Takieldeen^*

Asmaa Hamdy Rabie,Ahmed I. Saleh,

Said H. Abd Elkhalik,

Ali E. Takieldeen^*

This version is not peer-reviewed

Submitted:

08 December 2023

Posted:

08 December 2023

You are already at the latest version

Alerts

Abstract

Recently, the application of Artificial Intelligence (AI) in many areas of life has allowed raising the efficiency of systems and converting them into smart ones, especially in the field of energy. Integrating AI with power systems allows electrical grids to be smart enough to predict the future load, which is known as Intelligent Load Forecasting (ILF). Hence, suitable decisions for power system planning and operation procedures can be taken accordingly. Moreover, ILF can play a vital role in electrical demand response, which guarantees a reliable transitioning of power systems. This paper introduces a Perfect Load Forecasting Strategy (PLFS) for predicting future load in smart electrical grids based on AI techniques. The proposed PLFS consists of two sequential phases, which are; Data Preprocessing Phase (DPP) and Load Forecasting Phase (LFP). In the former phase, input electrical load dataset is prepared before the actual forecasting takes place through two essential tasks, namely feature selection and outlier rejection. Feature selec-tion is done using Advanced Leopard Seal Optimization (ALSO) as a new natural inspired opti-mization technique, Citation: To be added by editorial staff during production. Academic Editor: Firstname Last-name Received: date Revised: date Accepted: date Published: date Copyright: © 2023 by the authors. Submitted for possible open access publication under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/). While outlier rejection is accomplished through Interquartile Range (IQR) as a measure of statis-tical dispersion. On the other hand, actual load forecasting takes place in LFP using a new pre-dictor called; Weighted K-Nearest Neighbor (WKNN) algorithm. The proposed PLFS has been tested through excessive experiments. Results have shown that PLFS outperforms recent load forecasting techniques as it introduces the maximum prediction accuracy with the minimum root mean square error.

Keywords:

Subject: Engineering - Other

1. Introduction

Electrical load forecasting is an important process in Smart Electrical Grids (SEGs) [1,2,3]. That is because it can improve the performance of SEGs, stability, reliability, safety, and can reduce the power costs. In SEGs, load forecasting plays an instrumental role in other sectors such as customer demand forecasting and power generation sectors as it provides them with information about the amount of energy needed in the future [4,5]. Electrical companies pay attention to provide continuous and reliable service to their customers [1]. Indeed, higher electrical loads increase the complexity in designing SEGs. Hence, load forecasting is an important process to accurately determine the amount of energy needed in the future. Traditional load forecasting models cannot provide quick and perfect results, therefore, it is important to find a fast and accurate load forecasting model based on artificial intelligence techniques.

Artificial Intelligence (AI) technology plays a major role in many different sectors such as civil sector, medical sector, telecommunication sector, electricity sector, …..etc.. In SEGs, AI can be used to introduce a perfect load forecasting model that gives quick and more accurate results [4,5]. There are several AI techniques that can be used to estimate how much power will be required in the future such as Artificial Neural Networks (ANNs), K-Nearest Neighbors (KNN), Fuzzy Logic (FL), Support Vector Machine (SVM), Naïve Bayes (NB), and Decision Tree (DT) [6]. Despite the effectiveness of these techniques in current research, these techniques cannot reach optimal results in the least possible time. Hence, it is essential to improve these techniques to give fast and accurate predictions. To provide perfect results, preprocessing processes called outlier rejection and feature selection should be performed before using the forecasting model to enable the forecasting model to provide fast and accurate results [6]. That is because irrelevant features and bad items may prevent load forecasting model to provide accurate results and also may take a long time during training.

Feature selection process selects the most important features that have an effect on the load and removes irrelevant features [4,5]. It reduces overfitting and give load forecasting model the ability to give fast and more accurate results. Feature selection methods are categorized to wrapper, filter, and hybrid [6]. Filter methods are fast but less accurate methods while wrapper methods are accurate but slow methods. Hybrid methods combines filter and wrapper methods to quickly and accurately select the best features. Outlier rejection process eliminates bad items that have a bad effect on the load forecasting model. It enable load forecasting model to correctly learn and provide accurate results. There are three main categories to classify outlier rejection methods called distance-based methods, cluster-based methods, and statistical-based methods [4,6].

In this paper, a new load forecasting strategy called Perfect Load Forecasting Strategy (PLFS) has been introduced to accurately and quickly forecast loads. PLFS contains two main phases called Data Pre-processing Phase (DPP) and Load Forecasting Phase (LFP). In DPP, two main processes called feature selection and outlier rejection have been applied to prepare the input electrical dataset before learning the load forecasting model. Feature selection process has been performed using a new optimization technique named Advanced Leopard Seal Optimization (ALSO). On the other hand, outlier rejection process has been performed using statistical-based method called Interquartile Range (IQR). In LFP, a new load forecasting algorithm called Weighted K-Nearest Neighbor (WKNN) will be applied to provide perfect predictions based on the prepared dataset after removing outliers and irrelevant features. Results ensured that the proposed PLFS outperforms recent techniques according to accuracy, error, and execution time metrics.

The structure of this paper is arranged as follows; section 2 introduces the previous work about recent load forecasting techniques. Section 3 discusses the proposed perfect load forecasting strategy in detail and section 4 provides the experimental results. Finally, conclusions and future works have been presented in section 5.

2. Related Work

Through this section, the most recent load forecasting techniques will be described. As presented in [1], three deep learning models called Gated Recurrent Units (GRU), Long Short-Term Memory (LSTM), and Recurrent Neural Networks (RNN) algorithms were applied as load forecasting models. Experimental results showed that GRU outperformed LSTM and RNN in terms of R-squared, mean square error, and mean absolute error. Although GRU is effective, it should be able to predict loads based on new features. Additionally, it should be trained on online dataset collected from smart meters. Feature selection and outlier rejection methods were not used before applying prediction model. In [2], Hybrid Forecasting Model (HFM) was proposed to forecast loads and prices. In fact, HFM consists of two main methods called Bidirectional Long Short-Term Memory with Attention Mechanism (BiLSTM-AM) technique and Ensemble Empirical Mode Decomposition (EEMD) technique. Results showed that the proposed HFM is suitable, reliable, and has a high performance. On the other hand, HFM should be tested on many datasets of different size and diversity. Feature selection and outlier rejection methods were not used before applying prediction model.

According to [3], two load forecasting methods called Artificial Neural Network (ANN) and Auto Regressive Integrated Moving Average (ARIMA) were used. Results ensured that ANN can handle non-linear load data but ARIMA cannot. Hence, ANN is better than ARIMA for predicting loads. Although the accuracy of ANN, it takes a long time to be trained. Feature selection and outlier rejection methods were not used before applying prediction model. In [7], four prediction methods were used after preparing data by selecting the best features. These methods are called Support Vector Regression based on Polynomial function, Support Vector Regression based on Radial Basis (SVR-RB) function, Support Vector Regression based on linear function, and ANN. Experimental results proved that SVR-RB results were better than other three methods based on six features. Although SVR-RB provides high accuracy, it should be combined with other machine learning algorithms such as deep learning to provide more accurate results. Additionally, outlier rejection method should be used before using prediction model to provide more accurate results.

Related to [8], Hybrid Prediction Technique (HPT) was introduced to accurately provide short term load predictions. HPT consists of three techniques called thermal exchange optimization algorithm, radial basis function network, and wavelet transform decomposition. Results illustrated that HPT outperformed other load prediction techniques as it can provide accurate results. However, HPT took a large amount of execution time to be implemented. As shown in [9], six AI techniques were used in parallel to predict the loads. These techniques are LSTM, support vector regression, multilayer perceptron, random forest, temporal convolutional network, and extreme gradient boosting. Through experimental results, it is proved that LSTM can provide the best results compared to other five techniques. Although the effectiveness of the used techniques, there are many drawbacks such as the implementation of techniques took a long amount of time and also the techniques depended on a limited number of hyperparameters. Additionally, feature selection and outlier rejection methods were not used before applying the prediction method to give more accurate results. A comparison between these recent load forecasting techniques is presented in Table 1.

3. The Proposed Perfect Load Forecasting Strategy (PLFS)

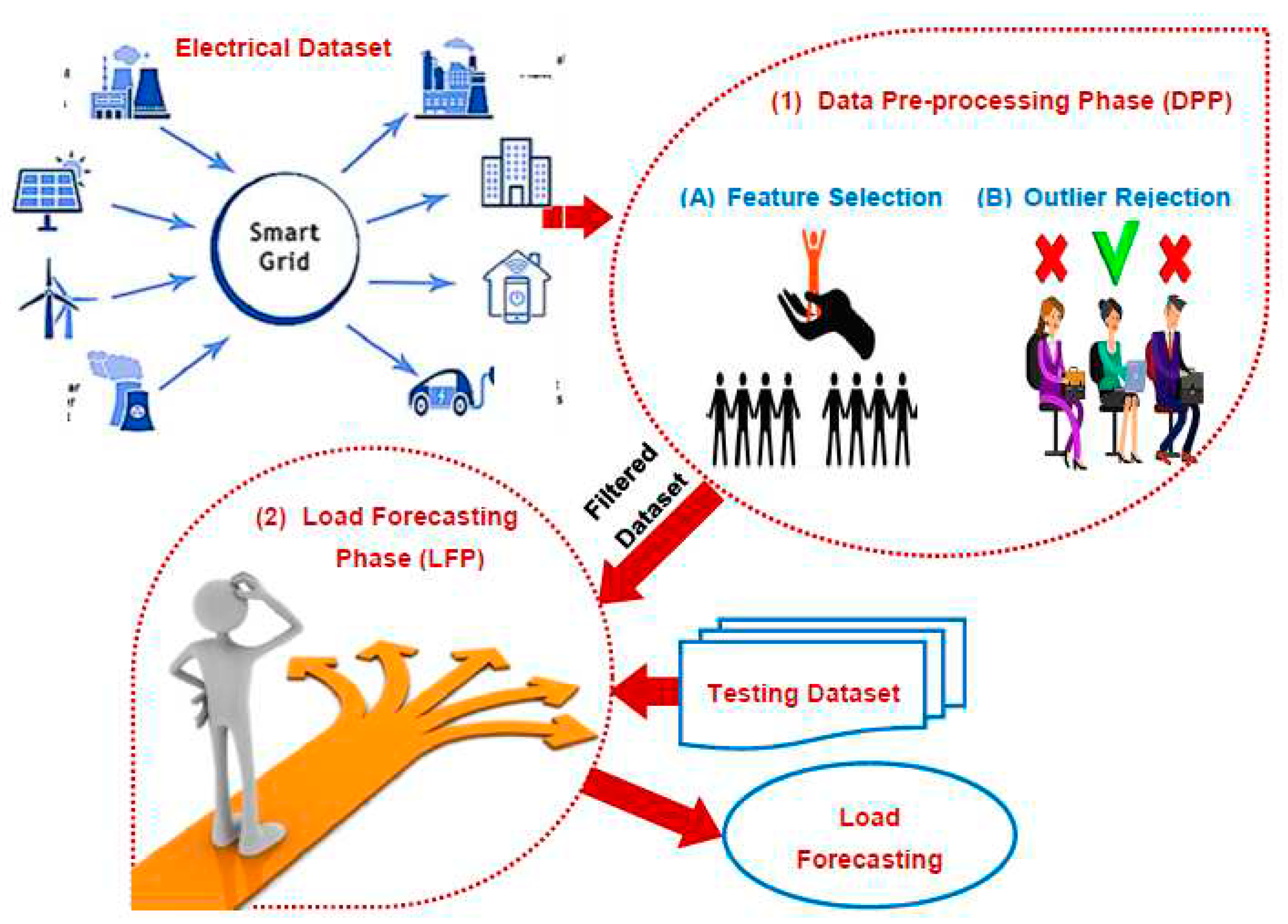
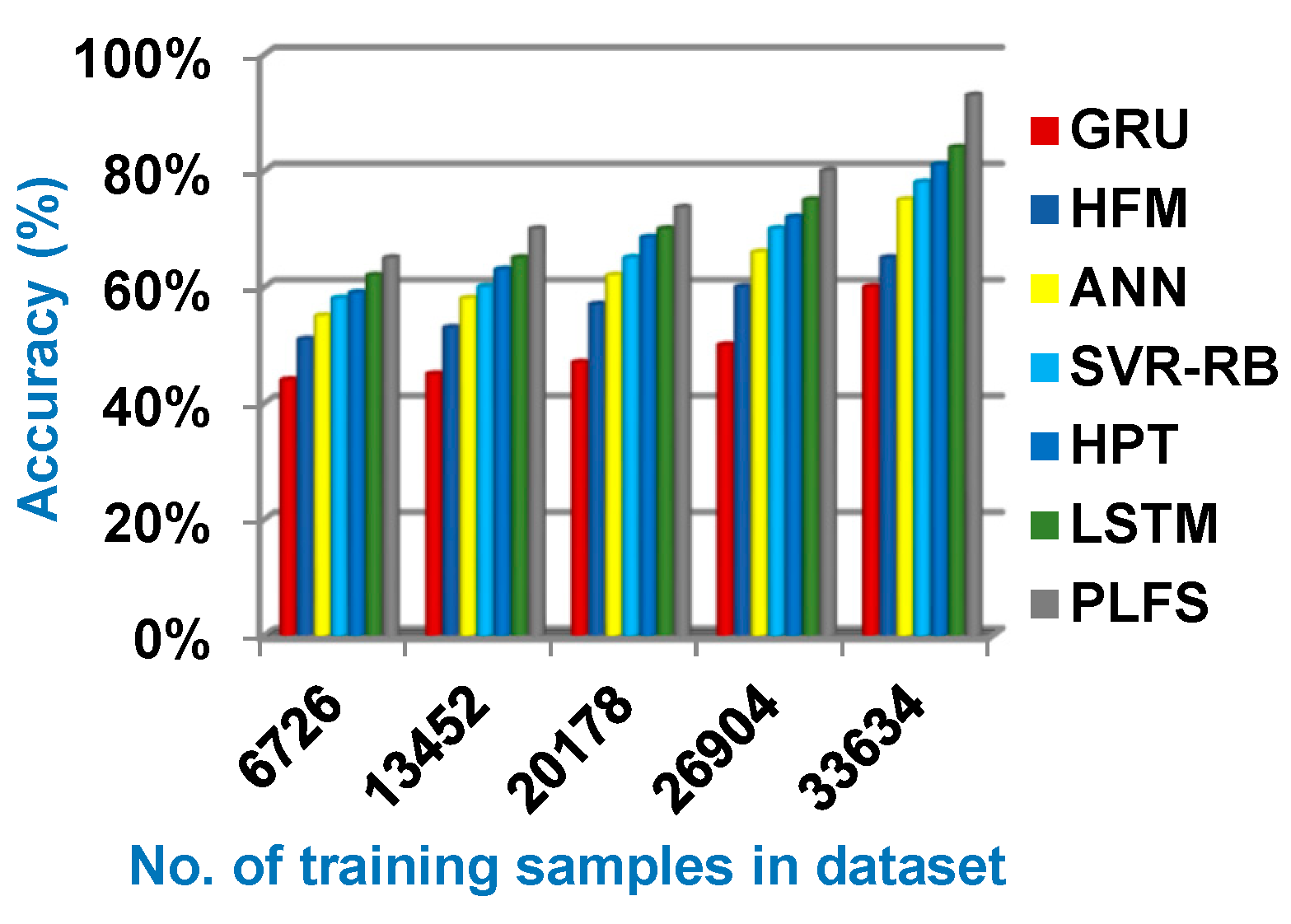
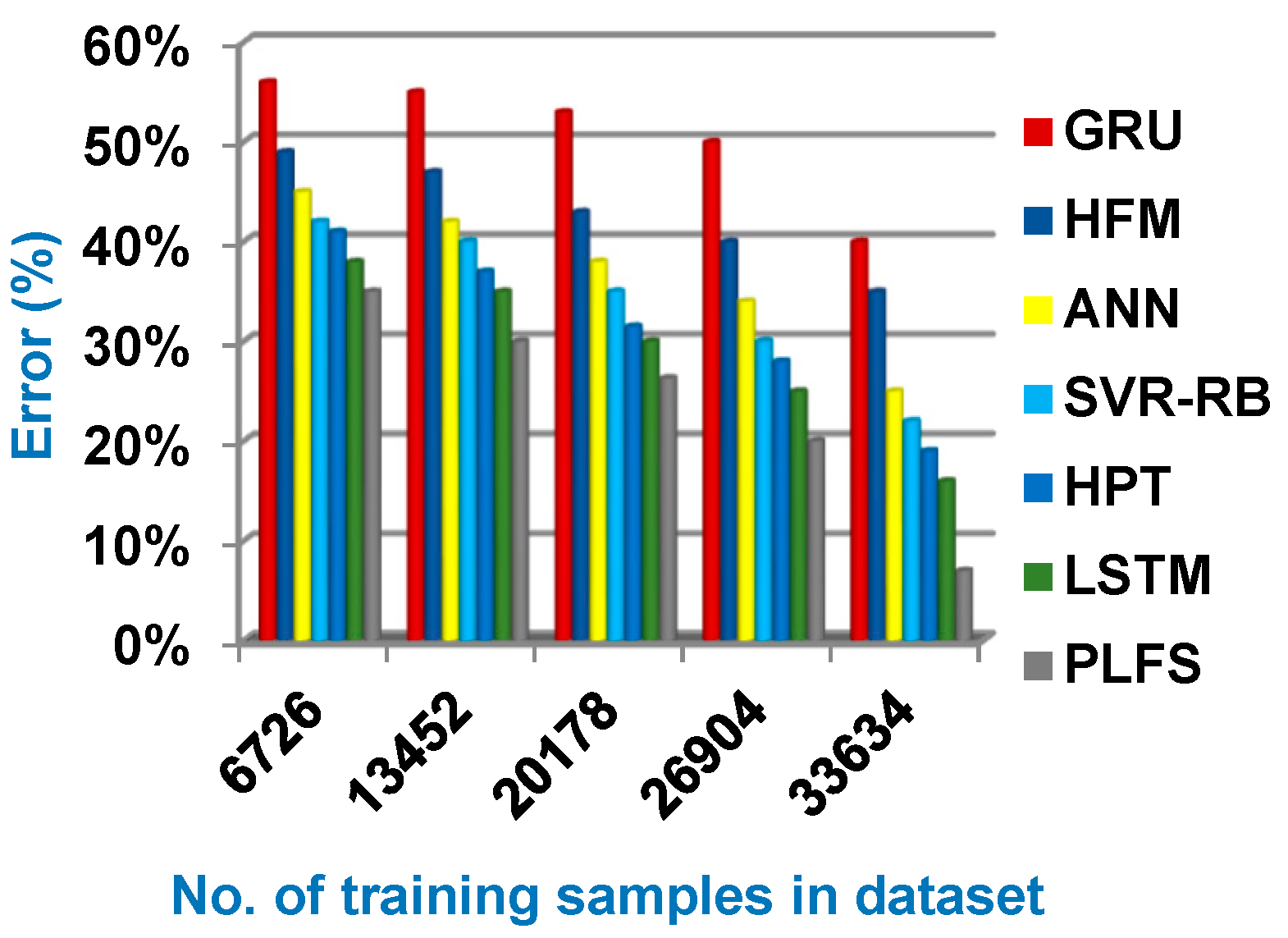
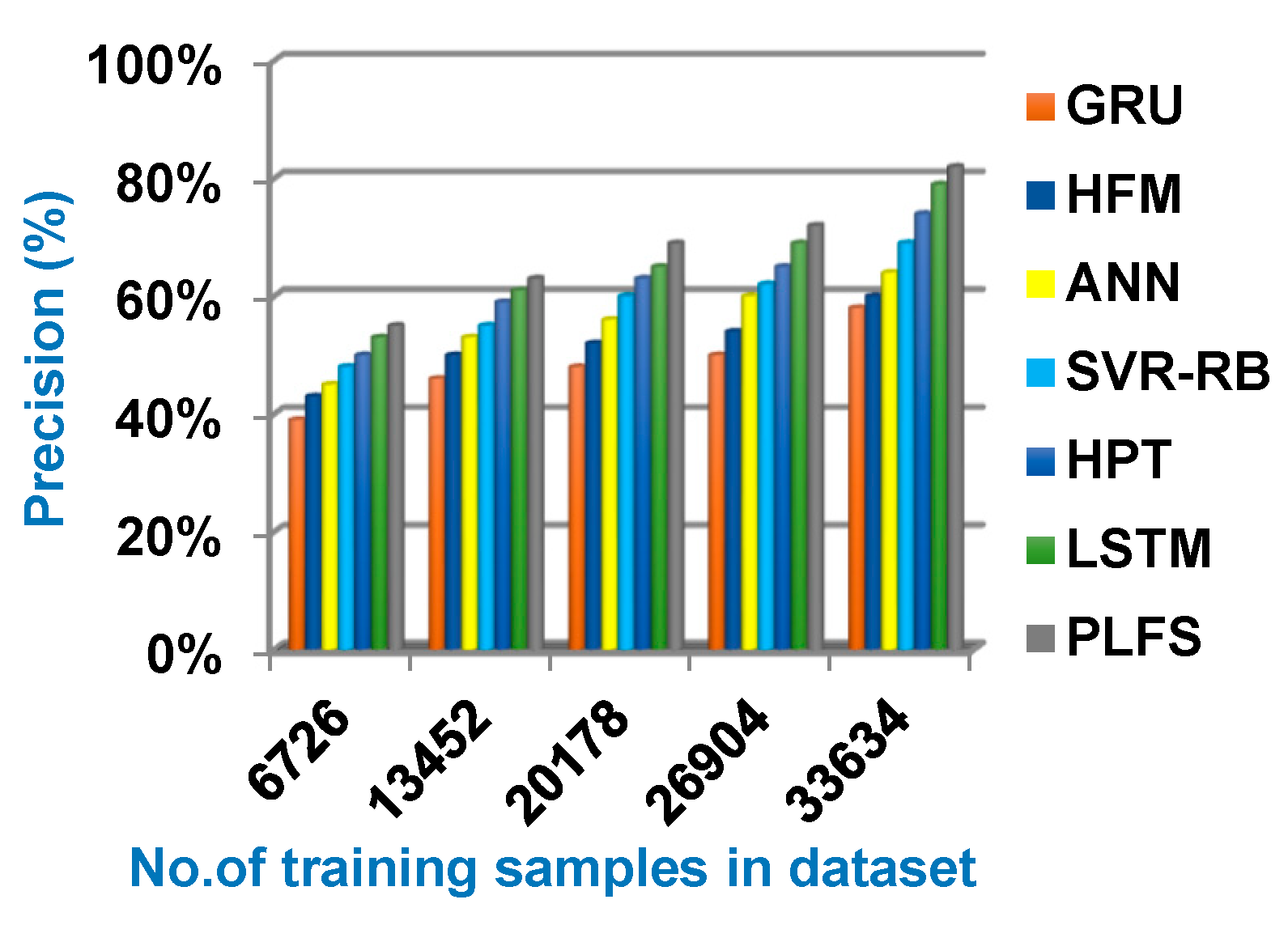
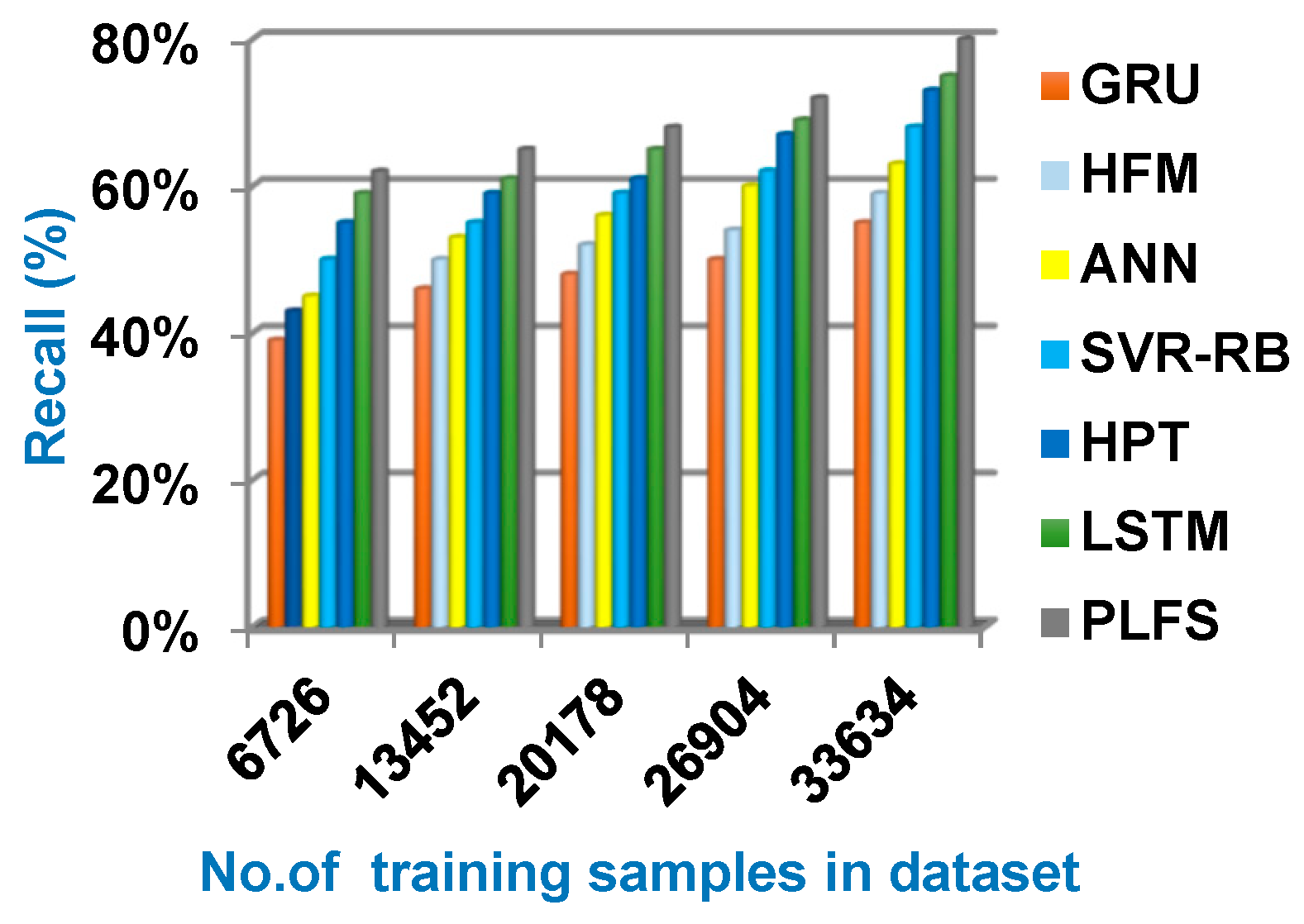
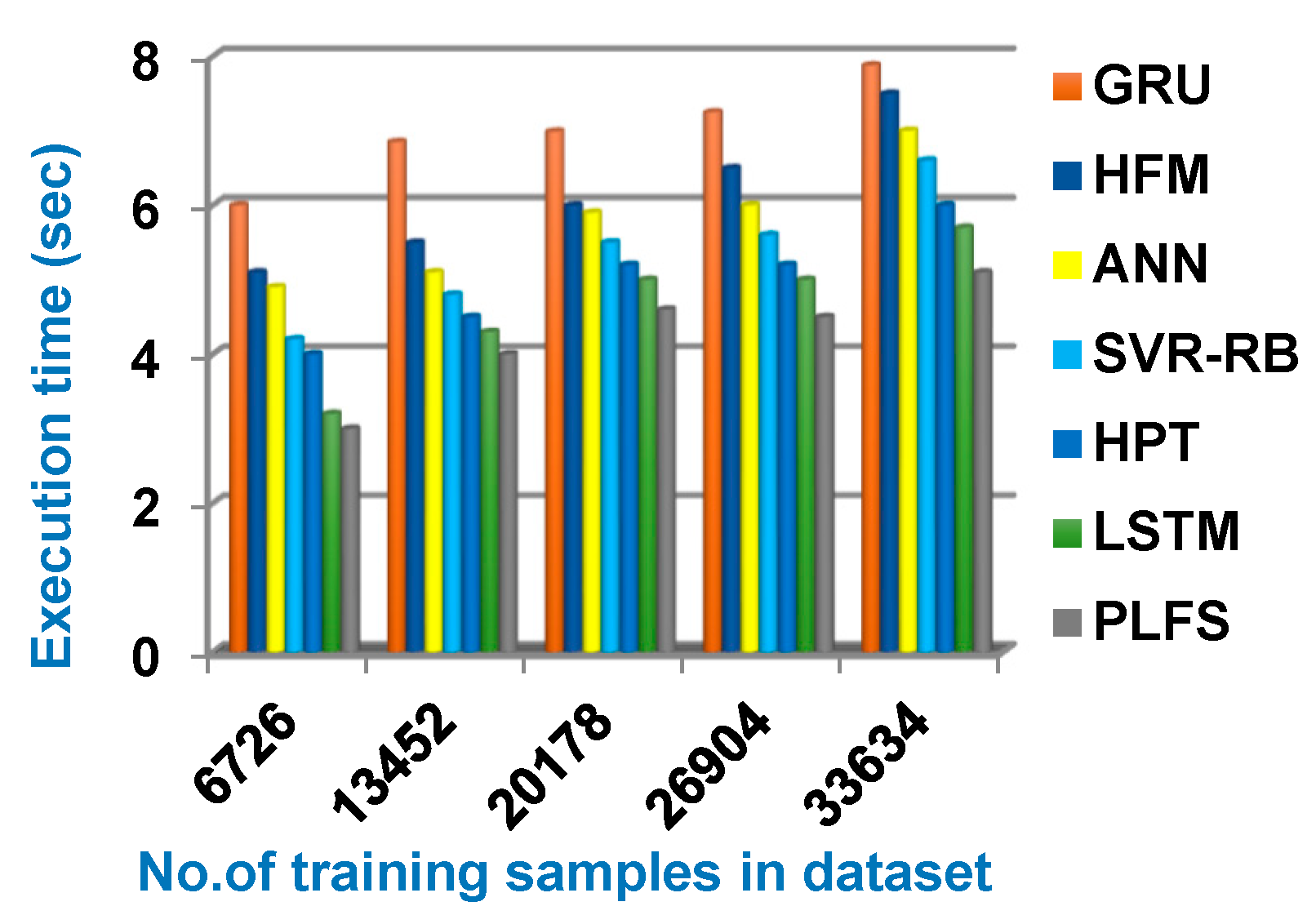
In this section, Perfect Load Forecasting Strategy (PLFS) as a new forecasting strategy is introduced to accurately estimate the amount of electricity required in the future. PLFS consists of two sequential phases called Data Pre-processing Phase (DPP) and Load Forecasting Phase (LFP) as presented in Figure 1. DPP aims to filter dataset from irrelevant features and outliers to contain valid data. Then, LFP aims to provide a perfect load forecasting based on valid dataset passed from DPP. In DPP, two main processes called feature selection and outlier rejection will be applied to filter the electrical dataset before learning the load forecasting model in LFP to provide perfect results. While feature selection removes non informative features, outlier rejection removes invalid items in the dataset to prevent overfitting problem and to enable the forecasting model to provide accurate results. At the end, the proposed load forecasting model in LFP will be used to give a perfect results. In this work, feature selection process will be performed using a new selection method called Advanced Leopard Seal Optimization (ALSO). Then, Interquartile Range (IQR) will be used to detect outliers. Finally, Weighted K-Nearest Neighbor (WKNN) algorithm will be used to provide fast and accurate forecasts.

3.1. The Advanced Leopard Seal Optimization (ALSO)

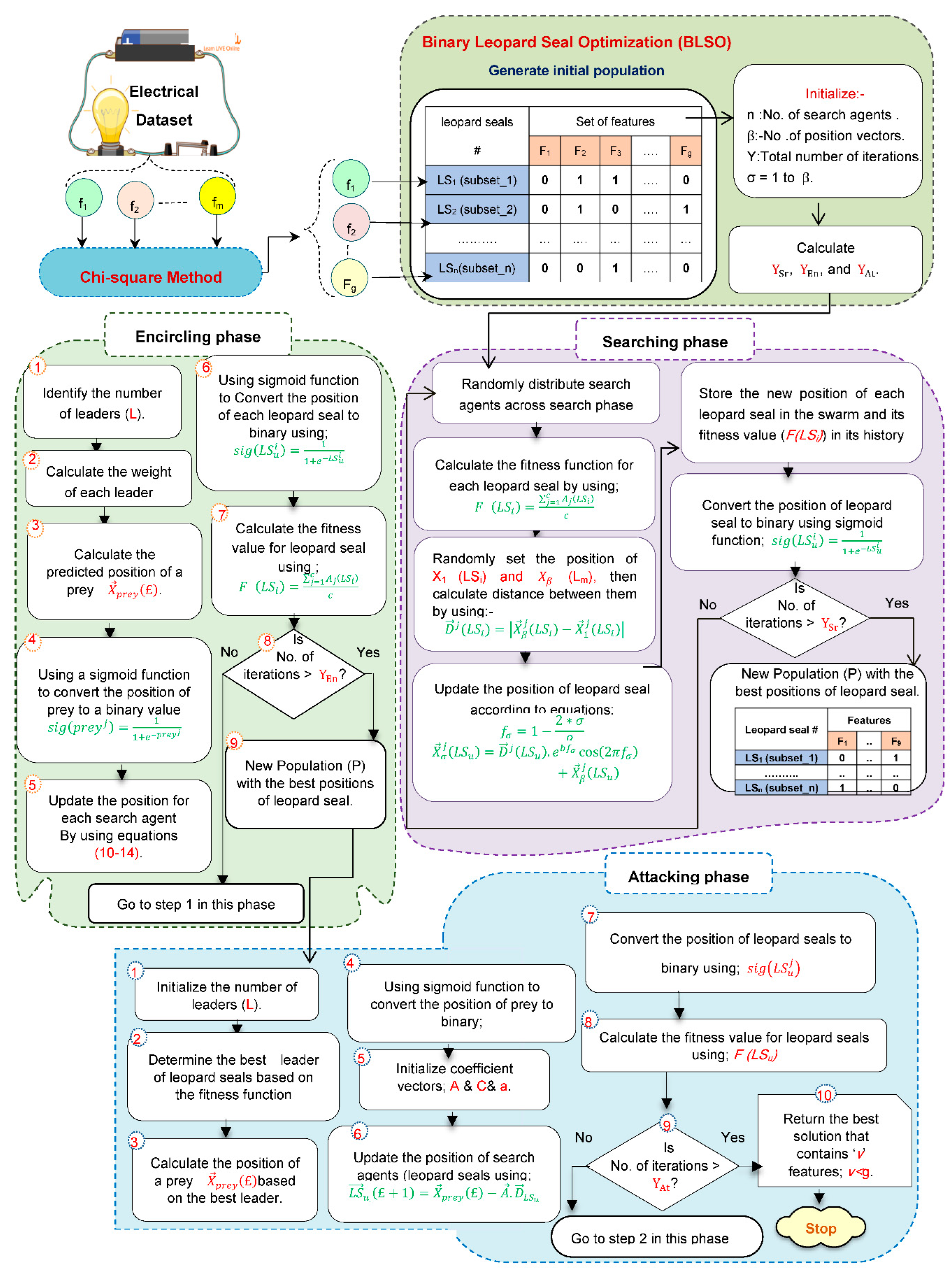
In this subsection, a new feature selection method called Advanced Leopard Seal Optimization (ALSO) that combines both filter and wrapper approaches will be discussed in detail. While filter approaches can quickly select a set of features, wrapper approaches can accurately select the best features. Hence, ALSO includes Chi-square as a filter method [10] and Binary Leopard Seal Optimization (BLSO) as a wrapper method [11]. While Chi-square is a fast but inaccurate method, BLSO is an accurate but slow method. Accordingly, ALSO contains both different methods for their cooperation together, so that each of them compensates for the problems of the other to determine the optimal set of features. The implementation of ALSO is represented in many steps as shown in Figure 2. At first, the collected dataset from smart electrical grids is followed to Chi-square to quickly select a set of informative features. Then, this set of features is followed to BLSO to accurately select the most significant features on electrical load forecasting. BLSO begins with create initial Population (P) including many leopard seals called search agents. It is assumed that P includes ‘n’ Leopard Seals (LS); LS = {LS1, LS2, ……, LSn}. Each LS in P is represented in binary form where zero denotes a useless feature while one denotes a useful feature. After creating search agents in P, these agents will be evaluated using the average accuracy value from ‘c’ classifiers as a fitness function to prove that a set of features selected can enable any classifier to give the best load forecasting. According to ‘c’ classifiers, the fitness function for i^th leopard seal (LSi) can be measured by (1).

F ({L S}_{i}) = \frac{\sum_{j = 1}^{c} A_{j} ({L S}_{i})}{c}

(1)

Where the fitness value for ith leopard seal is F(LSi), the classifiers number that is used to calculate the fitness value of the selected features in each seal is c, and the accuracy of jth classification according to the chosen features in ith leopard seal is Aj(LSi). To illustrate the idea, it is supposed that there are two seals in P; n=2 and three classifiers; c=3, applied to measure the fitness value of the selected features in every seal as illustrated in Table 2. Related to Table 2, it is supposed that the applied classifiers are Support Vector Machine (SVM) [6,11], K-Nearest Neighbors (KNN) [4,12], and Naïve Bayes (NB) [4,5]. According to the accuracy of these classifiers, SVM and NB provide that the best seal is LS2 while KNN provides that LS1 is the best seal. At the last, the average accuracy value proved that the best seal is LS2. Hence, evaluating seals based on single classifier cannot give the best set of features that can enable any classifier to give the best results.

According to the fitness values, the highest fitness value indicates to the best solution (seal) where the essential aim of the selection process is to provide the maximum average accuracy value. In fact, it is a necessary to assign the iterations number (Y) and also the position vectors number of the agents through its movement according to each iteration (£). Accordingly, the number of iterations for three phases called searching, encircling, and attacking based on the Y values will be calculated by (2-4) [2].

Y_{S r} = ⌊\frac{Y}{3}⌋

(2)

Y_{E n} = ⌊\frac{Y}{3}⌋

(3)

Y_{A t} = (Y - 2 * ⌊\frac{Y}{3}⌋)

(4)

Where YSr, YEn,, and YAt are the number of iterations for three phases called searching, encircling, and attacking respectively. To execute BLSO, three phases called searching, encircling, and attacking will be sequentially implemented based on YSr, YEn,, and YAt as shown in Figure 2. Initially, the steps of searching phase will be executed until the number of iterations (YSr) is terminated. In the case if the YSr is not met, the position vectors of each agent will be modified using (5).

{\vec{X}}_{σ}^{j} ({L S}_{u}) |_{\forall σ \in {2,3, 4, \dots, β - 1}} = {\vec{D}}^{j} ({L S}_{u}) . e^{b f_{σ}} \cos (2 π f_{σ}) + {\vec{X}}_{β}^{j} ({L S}_{u})

(5)

Where the modified

σ

’s position of LSu at jth iteration is

{\vec{X}}_{σ}^{j} ({L S}_{u})

, positions of LSu from 2 to

β

-1 is

σ

;

σ

{2, 3, 4,….,

β

-1}, and

{\vec{D}}^{j} ({L S}_{u})

is the distance between the search agent and the prey that can be computed by (6). b is the logarithmic spiral shape, the angle scaling factor for the

σ

’s position of the agent is

f_{σ}

computed by (7), and the modification of the last position (

β

’s position) of LSu at jth iteration is

{\vec{X}}_{σ}^{j} ({L S}_{u})

{\vec{D}}^{j} ({L S}_{u}) = |{\vec{X}}_{β}^{j} ({L S}_{u}) - {\vec{X}}_{1}^{j} ({L S}_{u})|

(6)

f_{σ} = 1 - \frac{2 * σ}{β}

(7)

Where the modified 1st position of LSu at jth iteration is

{\vec{X}}_{1}^{j} ({L S}_{u})

, the total positions number is β, and the current position of LSu is

σ

. After updating the positions of agents, these new positions should be changed to a binary value by using function called a sigmoid function (8) [11].

{L S}_{b_u}^{i} (£ + 1) = \{\begin{matrix} 1 if r (0,1) \geq sig ({L S}_{u}^{i}) \\ 0 otherwise \end{matrix}

(8)

Where

{L S}_{b_u}^{i} (£ + 1)

is the binary value of uth agent at ith bit in

£ + 1

that represents the next iteration; i=1,2,...,f and

s i g ({L S}_{u}^{i})

is the sigmoid function that will be calculated by (9) [10,11]. Furthermore, r(0,1) is a random value between 0 and 1.

s i g ({L S}_{u}^{i}) = \frac{1}{1 + e^{- L_{u}^{i}}}

(9)

Where the base of the natural logarithm is e. In P, the new position of each seal

{L S}_{b_u}^{i} (£ + 1)

will be evaluated by (1). Through searching for a prey, each agent in P will keep updated position and fitness values. In fact, the procedures of searching phase will be continued until the YSr is terminated. Then, the best position in P for each agent will be assigned based on the maximum evaluation value through their search for prey after searching phase is completed. Related to the best agents in P generated by the searching phase, the steps of the encircling phase will be implemented until the iterations number (YEn) is terminated. At first, the best leaders will be determined based on the calculations of evaluation function. Then, Weighted Leaders Prey Allocation (WLPA) method will be used for prey allocation [11]. The leopard seals will update their positions depending on the prey’s position using (10-14).

{\vec{D}}_{{L S}_{u}}^{j} = |\vec{C .} {\vec{X}}_{p r e y}^{j} - {\vec{X}}_{{L S}_{u}}^{j}|

(10)

{\vec{X}}_{{L S}_{u}}^{j + 1} = {\vec{X}}_{p r e y}^{j} - \vec{A} . {\vec{D}}_{{L S}_{u}}^{j}

(11)

\vec{A} = 2 . \vec{a} . \vec{r_{1}} - \vec{a}

(12)

\vec{C} = 2 . \vec{r_{2}}

(13)

a = 2 - j * \frac{2}{Y_{E n}}

(14)

Where the uth agent’s position at iteration j is

{\vec{X}}_{{L S}_{u}}^{j}

, the forecasted position of the prey at the jth iteration is

{\vec{X}}_{p r e y}^{j}

, and the distance between the uth agent and the prey is

{\vec{D}}_{{L S}_{u}}^{j}

. Additionally, random vectors belonging to [0,1] are

\vec{r_{1}}

and

\vec{r_{2}}

, coefficient vectors are

\vec{A}

and

\vec{C}

calculated by (12) and (13), the number of iterations in encircling phase is YEn calculated by (3). A vector that decrements linearly from two to zero over iterations is

\vec{a}

computed by (14). In the encircling phase, the new position of leopard will be in between the current position of leopard and the prey’s position depending on

\vec{A}

that includes a random value in [-1,1]. In the case if the YEn is not met, leopard seals will update their positions based on prey’s position by (10-14). At the last of the encircling phase, each leopard in P will assign its new position by calculating the distance between the leopard and prey applying (10). After that, the new position of leopard is calculated applying (11) and then is evaluated using the evaluation (fitness) function for determining the best solutions (leaders). Then, the sigmoid function should be applied to change all positions to be in binary form using (8).

The last phase called attacking phase receives the last information from the previous phase called encircling phase. Initially, the best leopard seals (alpha) will be determined and their positions will be used for determining the location of the target prey

{\vec{X}}_{p r e y} (£)

. Then, the positions of leopard seals will be converted into binary using the sigmoid function. In the case if YAt is not terminated, the leopard seals will modify their positions and then will test them by using the fitness function. At the end, the optimal solution will be the fittest leopard seal that contains the best set of features.

3.2. Interquartile Range (IQR) Method

In this section, the Interquartile Range (IQR) method will be used as an outlier rejection method to detect and then remove outliers. To use IQR, the dataset is divided into four equal parts or segments. To define the IQR, the distances between the quartiles are used. In the case if data point is more than 1.5×IQR below the first segment or above the third segment, then this data point is considered as outlier. Accordingly, all data points that are above Q3+1.5×IQR and below Q1-1.5×IQR are outliers, where Q3 is the third segment and Q1 is the first segment as shown in Figure 3. To calculate IQR, subtract the first segment from the third segment; IQR= Q3 – Q1.Then, IQR can be used to determine outliers by using many sequential steps; (i) the interquartile range (IQR) will be calculated for the data, (ii) the interquartile range (IQR) will be multiplied by 1.5, (iii) the maximum allowed normal value will be determined; H=Q3+1.5×(IQR). Accordingly, outliers are points that are greater than H, (vi) the minimum allowed normal value will be determined; L=Q1-1.5×(IQR). Accordingly, outliers are points that are lower than L.

3.3. The Proposed Weighted K-Nearest Neighbor (WKNN) Algorithm

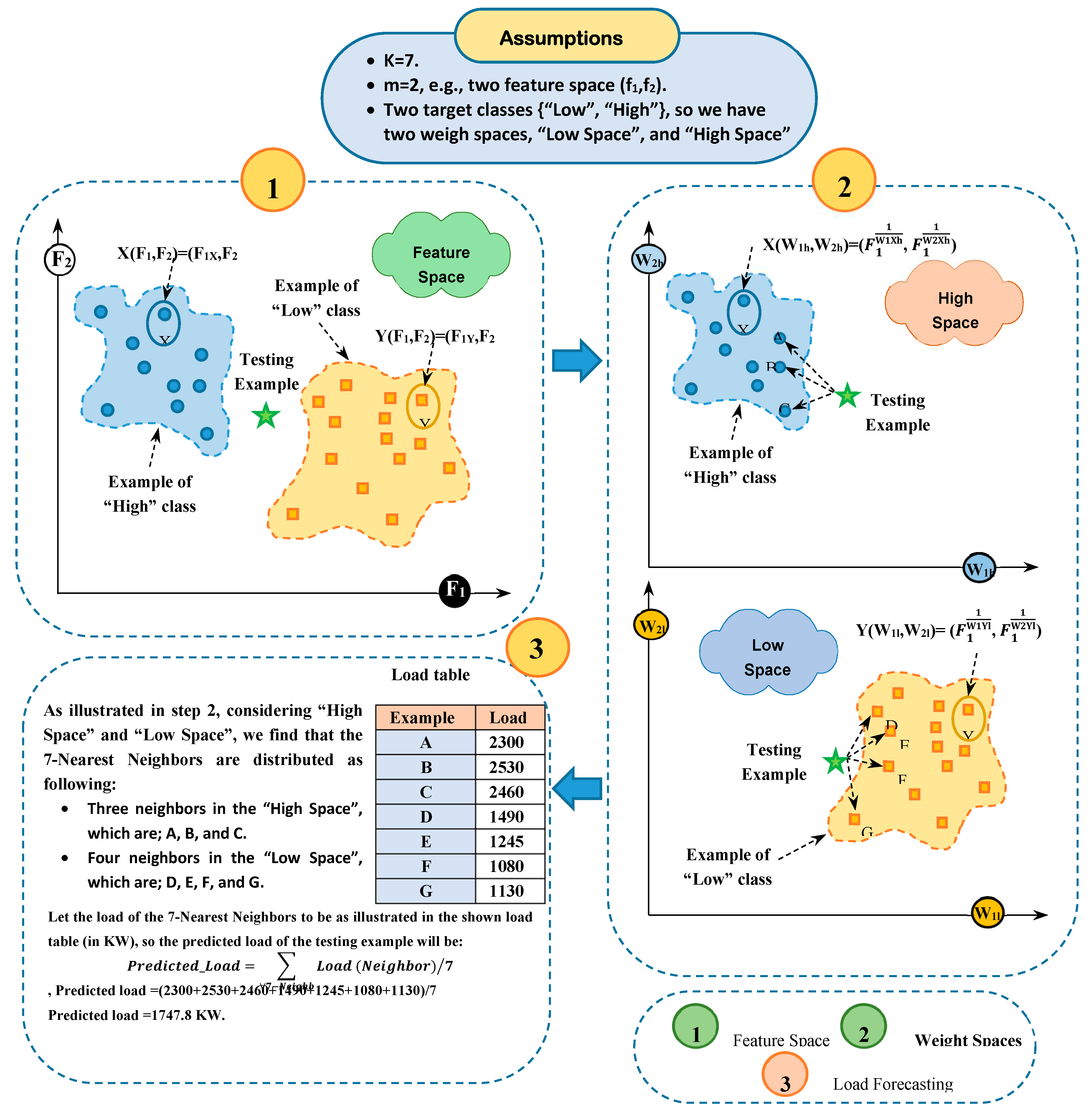
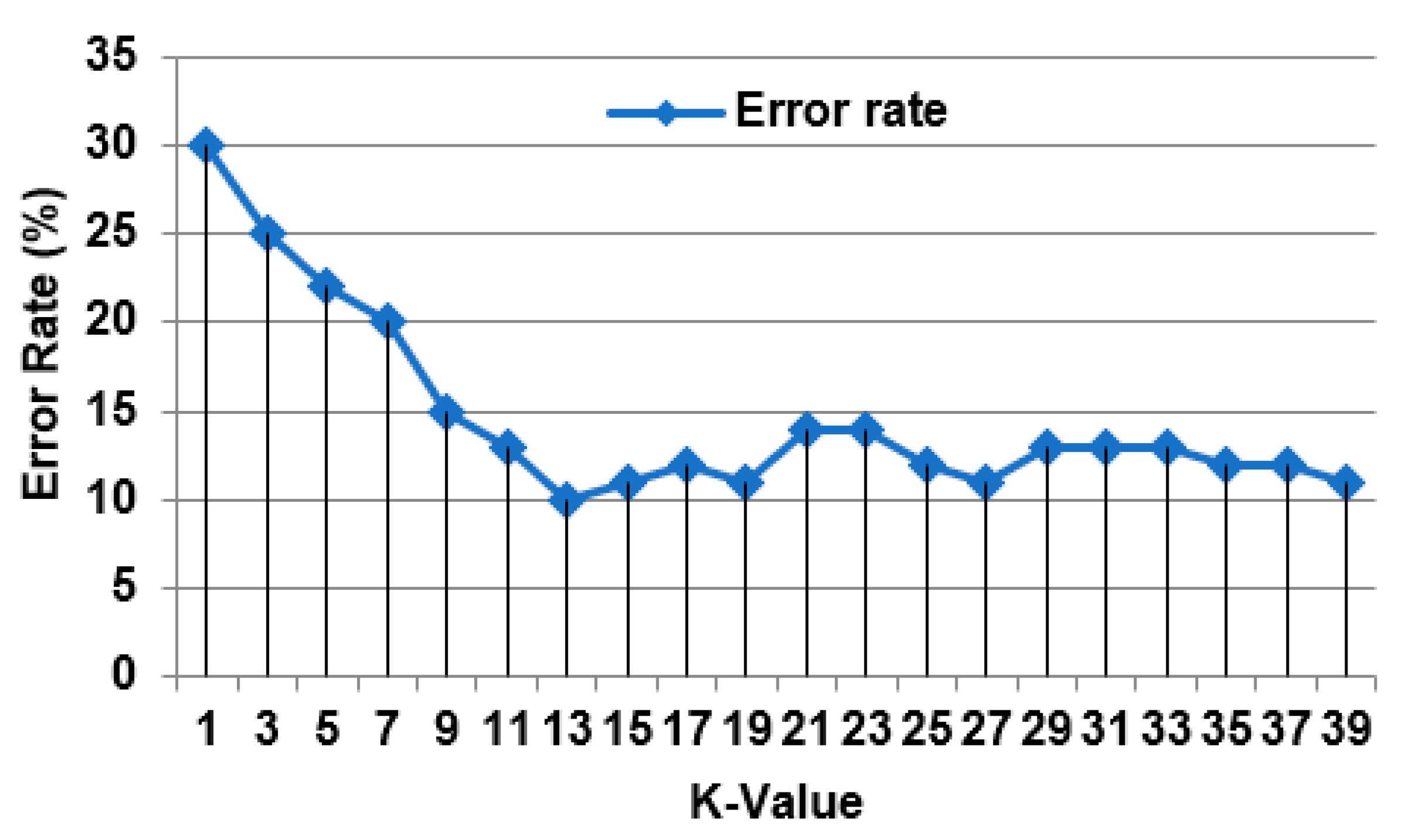
In this section, a new forecasting model called Weighted K-Nearest Neighbor (WKNN) will be explained in detail. WKNN consists of two main methods called Naïve Bayes (NB) as a feature weighting method [6] and K-Nearest Neighbor (KNN) as a load forecasting method based on the weighted features [4,6]. In fact, the traditional KNN is a simple and straightforward method that can be easily implemented. On the other hand, KNN is based on measure the distance between the features of each testing item and every training item separately without taking the impact of features on the class categories. Hence, NB is used as a weighting method to measure the impact of features on the class categories. Thus, a feature space will be converted into a weight space. Then, KNN will be implemented in weight space instead of feature space. In other words, the distance between any testing item and every training item will be implemented in a weight space using Euclidean distance [6].

Let testing item is represented as E={

f_{E}^{1}

f_{E}^{2}

,…..,

f_{E}^{v}

} and training item is represented as Q={

f_{Q}^{1}

f_{Q}^{2}

,…..,

f_{Q}^{v}

}, where

f_{E}^{i}

is the i^th feature value at E testing item and

f_{Q}^{i}

is the i^th feature value at Q training item; i={1, 2, …, v}. Then, WKNN starts with calculating the Euclidean distance between each testing item in testing dataset and every training item in training dataset in v-dimension weight space using (15).

D (E, Q) |_{c l a s s = c} = \sqrt{\sum_{i = 1}^{v} {({{(f}_{E}^{i})}^{\frac{1}{w_{c E}^{f i}}} - {{(f}_{Q}^{i})}^{\frac{1}{w_{c Q}^{f i}}})}^{2}}

(15)

Where

D (E, Q) |_{c l a s s = c}

is the Euclidean distance between E and Q items at class category c in a weight space.

w_{c E}^{f i}

is weight of ith feature at E item that belongs to c class while

w_{c E}^{f i}

is the weight of ith feature at Q item that belongs to c class using (16) and (17).

w_{c E}^{f i} = P (c E| f_{i}) = P (c E) . P (f_{i}| c E)

(16)

w_{c Q}^{f i} = P (c Q| f_{i}) = P (c Q) . P (f_{i}| c Q)

(17)

Where the probability that feature

f_{i}

is in items of class

c E

P (c E| f_{i})

and the probability that feature

f_{i}

is in items of class

c Q

P (c Q| f_{i})

. Also,

P (c E)

the probability of occurrence of class

c E

and

P (c Q)

are the probability of occurrence of class

c Q

P (f_{i}| c E)

is the probability of generating the feature

f_{i}

given the class

c E

and

P (f_{i}| c Q)

is the probability of generating the feature

f_{i}

given the class

c Q

. After calculating the distance (D) between each testing item and every training items separately using (15), distances should be in ascending order. Then, the k items that have the lowest distance values should be determined to take the average of their loads as a predicted load value for the testing or new item using (18).

P r e d i c a t e d_L o a d (E) = \frac{\sum_{j = 1}^{k} l o a d (Q_{j})}{k}

(18)

Where

P r e d i c a t e d_L o a d (E)

is the predicted load of testing item

E

l o a d (Q_{j})

is the load of the jth nearest training item, and k is the number of nearest neighbors. Figure 4 presents an illustrative example to illustrate the idea of implementing WKNN algorithm.

4. Experimental Results

Through this section, the proposed Perfect Load Forecasting Strategy (PLFS) that consists of two phases called Data Pre-processing Phase (DPP) and Load Forecasting Phase (LFP) will be executed. In DPP, feature selection process using Advanced Leopard Seal Optimization (ALSO) and outlier rejection process using Interquartile Range (IQR) will be implemented. Then, the filtered dataset will be passed to Weighted K-Nearest Neighbor (WKNN) algorithm in LFP to provide fast and accurate predictions. The proposed PLFS will be implemented using electricity load forecast dataset [13]. Confusion matrix performance metrics will be used to test the effectiveness of the proposed PLFS [4,6,12]. These metrics are accuracy, error, precision, and recall. Additionally, execution time will be measured to test the speed of the proposed PLFS. The used parameters values are presented in Table 3. Actually, K value is determined experimentally. To execute KNN algorithm, many different values are applied using 1000 samples in the electricity load forecast dataset. 800 samples represent training dataset and 200 samples represent testing dataset. According to K value, error value of KNN is assigned to find the optimal value of K that can give KNN the ability to introduce the minimum error values. In this work, K value belongs to 1 and 40; K∈[1,40]. The minimum error value is assigned at K =13. Accordingly, the optimal value of K is 13 as shown in Figure 5. Through the next experiments, the used value of K is 13.

4.1. Electricity Load Forecast Dataset Description

Electricity dataset is an internet dataset that consists of 16 features and 48048 samples [13,14]. It is a short-term electricity load forecasting dataset that records data at every hour. This dataset is collected from 3-1-2015 (01:00:00 AM) to 27-6-2020 (12:00:00 AM). The dataset contains historical electricity load that is available on daily post-dispatch reports and collected from the grid operator (CND). Through this dataset, historical weekly forecasts are available on weekly pre-dispatch reports, both from CND. Additionally, this data includes calendar information that related to school periods, from Panama's Ministry of Education and also includes calendar information that related to holidays, from "When on Earth?" website. The dataset includes also weather variables such as relative humidity, temperature, wind speed, and precipitation. This dataset is divided into training and testing with 70% and 30% respectively. Hence, training dataset includes 33634 samples and testing dataset includes 14.414 samples.

4.2. Testing the Proposed Perfect Load Forecasting Strategy (PLFS)

Through this section, the proposed PLFS will be tested against other load forecasting methods. These methods are GRU [1], HFM [2], ANN [3], SVR-RB [7], HPT [8] and LSTM [9] as presented in Table 1. Figure 6, Figure 7, Figure 8 and Figure 9 illustrate accuracy, error, precision, and recall of PLFS against other load forecasting methods. Additionally, figure 10 showed the execution time of PLFS against other load forecasting methods. Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 ensure that PLFS can provide accurate results at the minimum execution time.

Figure 6, Figure 7, Figure 8 and Figure 9 show that PLFS provides the maximum accuracy, precision, and recall values but it provides the minimum error and execution time values according to the number of training samples. Related to figure 6, the accuracy of GRU, HFM, ANN, SVR-RB, HPT, LSTM, and PLFS are 60%, 65%, 75%,78%, 81%, 84%, and 93% respectively at the maximum training samples number. Figure 7 shows that the error of GRU, HFM, ANN, SVR-RB, HPT, LSTM, and PLFS are 40%, 35%, 25%, 22%, 19%, 16%, and 7% respectively at the maximum training samples number. Accordingly, PLFS provides the best accuracy and error values while GRU provides the worst values. According to figure 8, the precision of GRU, HFM, ANN, SVR-RB, HPT, LSTM, and PLFS are 58%, 60%, 64%, 69%, 74%, 79%, and 82% respectively at the maximum training samples number. Hence, the maximum precision value is provided by PLFS but the minimum value is provided by GRU.

Figure 9 illustrates that the recall of PLFS is better than GRU, HFM, ANN, SVR-RB, HPT, and LSTM with values are 80%, 55%, 59%, 63%, 68%, 73%, and 75% respectively at the maximum training samples number. According to figure 10, the minimum execution time is provided by PLFS but the maximum execution time is provided by GRU with values are 5.1 sec. and 7.88 sec. respectively at the maximum training samples number. The execution time of HFM, ANN, SVR-RB, HPT, and LSTM are 7.5, 7, 6.6, 6, and 5.7 respectively at the maximum training samples number. Thus, Figures (6→10) proved that the proposed PLFS can provide the best results compared to other load forecasting methods called GRU, HFM, ANN, SVR-RB, HPT, and LSTM.

5. Conclusions

In this paper, a new load forecasting strategy called Perfect Load Forecasting Strategy (PLFS) has been introduced to provide fast and accurate results. PLFS consists of two phases called Data Pre-processing Phase (DPP) and Load Forecasting Phase (LFP). Two main processes called feature selection and outlier rejection have been used in DPP to prepare and filter dataset from irrelevant features and outliers. Feature selection has been performed using Advanced Leopard Seal Optimization (ALSO) while outlier rejection has been performed using Interquartile Range (IQR). Next, Weighted K-Nearest Neighbor (WKNN) algorithm has been used as load forecasting method in LFP based on the prepared dataset to quickly provide accurate results. Experimental results showed that the proposed PLFS provides the maximum accuracy, precision, and recall values but the minimum error and execution time with values equal 93%, 82%, 80%, 7%, and 5.1 sec. respectively at the maximum training samples number. At the end, the proposed PLFS can provide fast and accurate predictions.

References

M. Abumohsen, A. Owda, and M. Owda, “Electrical Load Forecasting Using LSTM, GRU, and RNN Algorithms,” Energies, Volume 16, Issue 5, 2023, PP. 1-31.
W. Gomez,F. Wang, and Z. Amogne, “Electricity Load and Price Forecasting Using a Hybrid Method Based Bidirectional Long Short-Term Memory with Attention Mechanism Model,” International Journal of Energy Research, Hindawi, Volume 2023, 2023, PP. 1-18. [CrossRef]
C. Tarmanini, N. Sarma, C. Gezegin, et. al., “Short term load forecasting based on ARIMA and ANN approaches,” Energy Reports, Elsevier,Volume 9, issue 3, 2023, PP. 550-557. [CrossRef]
A. Rabie, S. Ali, A. Saleh, and H. Ali, “A fog based load forecasting strategy based on multi-ensemble classification for smart grids,” Journal of Ambient Intelligence and Humanized Computing, Springer, Volume 11, Issue 1, 2020, PP. 209-236. [CrossRef]
A. Rabie, A. Saleh, and H. Ali, “Smart electrical grids based on cloud, IoT, and big data technologies: state of the art,” Journal of Ambient Intelligence and Humanized Computing, Springer, Volume 12, 2021, PP. 9450-9478.
A. Saleh, A. Rabie, and K. Abo-Al-Ezb, “A data mining based load forecasting strategy for smart electrical grids,” Advanced Engineering Informatics, Elsevier, Volume 30, Issue 3, 2016, PP.422- 448. [CrossRef]
A. Alrashidi and A. Qamar, “Data-Driven Load Forecasting Using Machine Learning and Meteorological Data,” Computer Systems Science and Engineering, Volume 44, Issue 3, 2023, PP. 1973-1988. [CrossRef]
S. Khan, “Short-Term Electricity Load Forecasting Using a New Intelligence-Based Application,” Sustainability, Volume 15, Issue 16, 2023, PP. 1-12. [CrossRef]
M. Cordeiro-Costas, D. Villanueva, P. Eguía-Oller, et. al., “Load Forecasting with Machine Learning and Deep Learning Methods,” Applied Sciences, Volume 13, Issue 13, 2023, PP. 1-25. [CrossRef]
A. Rabie, A. Saleh, and N. Mansour, “A Covid-19’s integrated herd immunity (CIHI) based on classifying people vulnerability,” Computers in Biology and Medicine, Elsevier, Volume 140, 2022, PP. 1-29. [CrossRef]
A. Rabie, N. Mansour, A. Saleh, and Ali E. Takieldeen "Expecting individuals’ body reaction to Covid-19 based on statistical Naïve Bayes technique." Pattern Recognition 128 (2022): 108693.
W. Shaban, A. Rabie, A. Saleh, and M. Abo-Elsoud, “A new COVID-19 Patients Detection Strategy (CPDS) based on hybrid feature selection and enhanced KNN classifier,” Knowledge-Based Systems, Elsevier, Volume 205, 2020, PP.1-18. [CrossRef]
https://www.kaggle.com/datasets/saurabhshahane/electricity-load-forecasting.
Lin, Faa-Jeng, Chao-Fu Chang, Yu-Cheng Huang, and Tzu-Ming Su. "A Deep Reinforcement Learning Method for Economic Power Dispatch of Microgrid in OPAL-RT Environment." Technologies 11, no. 4 (2023): 96. [CrossRef]

Figure 1. The main steps of the proposed Perfect Load Forecasting Strategy (PLFS).

Figure 2. Steps of implementing the ALSO.

Figure 3. The boxplot that represents the Interquartile Range (IQR) method as an outlier rejection method.

Figure 4. Load forecasting using WKNN algorithm.

Figure 5. Error rate VS K-value.

Figure 6. Accuracy of load forecasting methods.

Figure 7. Error of load forecasting methods.

Figure 8. Precision of load forecasting methods.

Figure 9. Recall of load forecasting methods.

Figure 10. Execution time of load forecasting methods.

Table 1. A comparison between the recent load forecasting techniques.

Technique	Advantages	Disadvantages
Gated Recurrent Units (GRU) [1]	GRU is an accurate method.	It cannot predict loads based on new features. It does not trained on online dataset collected from smart meters. Feature selection and outlier rejection methods were not used before applying prediction model.
Hybrid Forecasting Model (HFM) [2]	HFM is suitable, reliable, and has a high performance.	HFM does not be tested on many datasets of different size and diversity. Feature selection and outlier rejection methods were not used before applying prediction model.
Artificial Neural Network (ANN) [3]	ANN is an accurate method.	ANN takes a long time to be trained. Feature selection and outlier rejection methods were not used before applying prediction model.
Support Vector Regression based on Radial Basis (SVR-RB) function [7]	SVR-RB provides high accuracy.	outlier rejection method should be used before using prediction model to provide more accurate results.
Hybrid Prediction Technique (HPT) [8]	HPT provides accurate results.	HPT took a large amount of execution time to be implemented
Long Short-Term Memory (LSTM) [9]	LSTM is an accurate method.	LSTM depended on a limited number of hyperparameters. Feature selection and outlier rejection methods were not used before applying the prediction method to give more accurate results.

Table 2. Identify the best seal according to every classifier and average accuracy.

Classifier #	Accuracy of every seal		The best seal
Classifier #	LS₁	LS₂	The best seal
C₁ =SVM	0.75	0.75	LS₂
C₂ =KNN	0.9	0.8	LS₁
C₃ =NB	0.7	0.9	LS₂
Average accuracy	0.767	0. 816	LS₂

Table 3. The used parameters values through experiments.

Parameter	Description	Applied value
b	A number that defines the movement shape of logarithmic spiral in the encircling phase	3
u	No. of alpha leopard seals	7
R	The maximum number of iterations	100
r	Random value that is needed in the sigmoid function	Random in [0,1]
K	The number of nearest neighbors used in KNN method	1≤K≤40

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Perfect Load Forecasting Strategy (PLFS) for Smart Grids Based on Artificial Intelligence

Abstract

1. Introduction

2. Related Work

3. The Proposed Perfect Load Forecasting Strategy (PLFS)

3.1. The Advanced Leopard Seal Optimization (ALSO)

3.2. Interquartile Range (IQR) Method

3.3. The Proposed Weighted K-Nearest Neighbor (WKNN) Algorithm

4. Experimental Results

4.1. Electricity Load Forecast Dataset Description

4.2. Testing the Proposed Perfect Load Forecasting Strategy (PLFS)

5. Conclusions

References

MDPI Initiatives

Important Links

Subscribe