Prerpints.org logo
Preprint
Article

Research on Convolutional Neural Network Inference Acceleration and Performance Optimization for Edge Intelligence

Altmetrics

Downloads

80

Views

17

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

08 December 2023

Posted:

11 December 2023

You are already at the latest version

Alerts
Abstract
In recent years, Edge Intelligence (EI) has emerged, combining edge computing with AI, specifically deep learning, to run AI algorithms directly on edge devices. In practical applications, EI faces challenges related to computational power, power consumption, size, and cost, with the primary challenge being the trade-off between computational power and power consumption. This has rendered traditional computing platforms unsustainable, making heterogeneous parallel computing platforms a crucial pathway for implementing EI. In our research, we leveraged the Xilinx Zynq 7000 heterogeneous computing platform, employed High-Level Synthesis (HLS) for design, and implemented two different accelerators for LeNet-5 using loop unrolling and pipelining optimization techniques. The experimental results show that when running at a clock speed of 100 MHz, the PIPELINE accelerator, compared to the UNROLL accelerator, experiences an 8.09% increase in power consumption but speeds up by 14.972 times, making the PIPELINE accelerator superior in performance. Compared to the CPU, the PIPELINE accelerator reduces power consumption by 91.37% and speeds up by 70.387 times, while compared to the GPU, it reduces power consumption by 93.35%.This study provides two different optimization schemes for edge intelligence applications through design and experimentation, and demonstrates the impact of different quantization methods on FPGA resource consumption. These experimental results can provide a reference for practical applications, thereby providing a reference hardware acceleration scheme for edge intelligence applications.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

In 2017, AlphaGo's consecutive victories against human players brought AI into the public eye, sparking a wave of interest. Today, AI has found widespread applications in various fields such as small object detection [1], speech recognition [2], image classification g [3], and more. Currently, most AI computational tasks rely on deployment on cloud and other large-scale computing platforms, but the significant physical distance between these resource-intensive platforms and smart endpoints limits the convenience of AI. This has given rise to the idea of integrating Edge Computing (EC) with AI, leading to the emergence of Edge Intelligence (EI) [4,5]. EI enables the transfer of AI technologies from central clouds to the edge, closer to data sources, facilitating low-latency, distributed, and highly reliable services [6].
Convolutional Neural Networks (CNNs) [7], as one of the typical deep learning algorithms, have achieved significant success compared to other AI algorithms such as Support Vector Machines (SVM) and Decision Trees [8] in various computer vision fields, including image classification, semantic segmentation, and object detection [9]. They have been widely applied in various domains, including smart cities [10], the industrial Internet of Things (IoT) [11]. Due to the large number of parameters and computational complexity of CNNs, research in Edge Intelligence (EI) has led to the emergence of a series of network lightweighting techniques such as network pruning [12], model distillation [13], parameter quantization [14], and Once-For-All [15]. These techniques aim to reduce the model's memory and computational requirements, making it suitable for use on low-power and resource-constrained edge devices. In addition to network lightweighting, there is a widespread focus on achieving a balance between computational power and power consumption through hardware acceleration techniques. Traditional computing platforms primarily include CPUs, GPUs, FPGAs, and ASICs. Among these, GPU [16], FPGA [17,18], and ASIC [19] excel in parallel implementations and can be applied to edge-side inference. To better adapt to deep learning intelligent algorithms while considering power constraints on edge devices, the core processor chips of computing platforms often adopt heterogeneous forms. Many single-chip solutions also use customized heterogeneous approaches to further improve energy efficiency [20], mitigating the trade-off between computational power and power consumption.
This article is based on the Zynq device (hardware environment), Vivado HLS 2018.3, and Vivado 2018.3 (software environment). In edge computing devices, in addition to pursuing high performance, reducing power consumption is of vital significance for prolonging device life and reducing heat generation. In this article, we test and compare two different accelerators designed specifically for the high computational complexity of CNN convolution calculations on FPGA platforms, namely the low-performance, low-power UNROLL accelerator and the high-performance, high-power PIPELINE accelerator. We compare the two accelerators in terms of power consumption and resource performance, and analyze the reasons. Additionally, we compared the throughput and power consumption performance of CNN running on CPU and GPU platforms with the performance of CNN running on the FPGA platform in our experiments. The contributions of this article are as follows:
  • Designed energy-efficient accelerators for the LeNet-5 network using Vivado High-Level Synthesis (HLS), implementing convolutional calculations, activation, pooling, and fully connected operations on the PL side.
  • Applied Gaussian filtering and histogram equalization algorithms on the PS side to perform noise filtering on images, enhancing the differentiation between target characters and background noise, highlighting character details for improved recognition by the Lenet-5 convolutional neural network on the FPGA platform.
  • Quantized weight parameters and analyzed resource consumption for different data types to determine the optimal solution. Transformed fixed-point quantization into parameterized quantization to ensure compatibility with various FPGA platforms.
  • Designed two different optimization schemes for convolution calculations and compared experimental results, demonstrating that the designed accelerators achieve faster speeds and lower power consumption compared to platforms like CPU.
The remaining sections of this paper are organized as follows: Section two provides an introduction to relevant work related to this research. Section three offers a detailed exposition of image processing algorithms, model optimization strategies, and CNN hardware acceleration approaches. Section four describes the system architecture and hardware implementation of the accelerator. Section five explores the analysis of experimental results with different accelerators and compares them with other platforms. Section six provides a comprehensive summary of the entire work, emphasizing the design's limitations and future optimization directions.

2. Related work

Since Apple proposed OpenCL for heterogeneous computing in 2008, research on using FPGA-based hardware platforms and ARM+FPGA heterogeneous approaches to accelerate CNN has become increasingly rich [21]. However, many challenges still exist. CNN computations primarily focus on convolutional layer operations, and Multiply-Accumulate (MAC) operations are the basic building blocks of fully connected layers and convolutional layers. Therefore, a significant amount of research is concentrated on how to implement new lightweight convolutional operation architectures that ensure computational precision while improving the efficiency of convolutional operations. Current research directions mainly revolve around the following aspects.
Acceleration is achieved through optimizing network structures and quantizing and compressing model parameters. Li et al. [22] introduced an inference engine that can determine the optimal weight quantization bit-width for the LeNet network. This engine allows most of the data in the network's computation process to be quantized using 8 bits and employs 16-bit computation for a small portion of the data, resulting in significant hardware resource savings. Wei et al. [23] explored different approaches for storing network parameters. To minimize external RAM access time, on-chip BRAM was chosen for storing network parameters, and the entire network's parameters, except for the input and output layers, were binarized. The result achieved a throughput of 0.4 FPS and a power consumption of 2.8 W. Huang et al. [24] proposed deep deformable convolution on the CenterNet network architecture to reduce resource consumption, and used ShuffleNet V2 [25] as the network backbone to conduct experiments on the Pascal VOC dataset, achieving a throughput of 26 FPS and a power consumption of 5.6 W.
To accelerate convolutional layer calculations. Zhang [26] and Guan [27] used traditional sliding window convolution algorithms to design deep learning accelerators based on FPGAs. Ahmad and Pasha [28] designed pipeline and parallel convolution computation engines to improve the throughput of convolution calculations while reducing the overall system's computational complexity and power consumption. Accelerators based on fast algorithms like Winograd and FFT [29,30] achieve rapid convolution computations at the algorithmic level. In [31], a comparison between Winograd and FFT algorithms was made, highlighting that FFT algorithms require more memory due to complex numbers. Under similar parameter configurations, Winograd exhibited better acceleration compared to FFT algorithms.
Furthermore, Chen Zhang and his colleagues [32] have implemented a deep pipelined multi-FPGA architecture to overcome the resource constraints of a single FPGA board. They used a cluster of FPGAs to extend the design space efficiently for accelerating convolutional neural networks. They connected 7 FPGA boards using high-speed serial links and proposed a dynamic programming algorithm to deploy the layers of convolutional neural networks effectively across different FPGA boards in the cluster. They successfully implemented AlexNet and VGG-16 neural networks in the FPGA cluster, and the results showed that their approach improved energy efficiency by 21 times and 2 times compared to optimized multi-core CPUs and GPUs, respectively.

3. Methodology

3.1. Optimization of the LeNet-5 Model

The structure of the LeNet-5 neural network is shown in Figure 1. This network consists of convolutional layers, pooling layers, and fully connected layers. The input feature map is a grayscale image, meaning it has only one channel, and the dimensions of the image are both 28x28. The size of the feature map can be represented as 28x28x1, with a total of 784 pixels.
In this study, the classic LeNet-5 model is optimized by introducing Dropout into the fully connected layer calculation. Compared with the original algorithm, the optimized algorithm reduces the complexity of the network and is suitable for implementation on FPGA platforms.
A schematic diagram comparing the network structure before and after adding Dropout in the fully connected layer during forward propagation is shown in Figure 2. Dropout randomly deactivates a portion of neurons with a certain probability P during the forward propagation phase. The purpose of Dropout is to prevent network overfitting, enhance the network's generalization performance, and improve recognition accuracy.
Furthermore, using the compression function can lead to the phenomenon of gradient vanishing in images, resulting in the loss of image features. Therefore, in this study, an activation function is used. The expression is shown in Equation (1).
r e l u x = x 0   i f i f   x > 0 x ≤ 0
The R e l u function mimics the biological principle that neurons are activated only when the input exceeds a certain threshold. Its main characteristic is unilateral inhibition, which can sparsify the model, enhance feature extraction capability, reduce inter-parameter dependencies, and maintain stable convergence speed, addressing the issue of gradient vanishing. The image is shown in Figure 3.
The LeNet-5 neural network, as shown in Table 1, has an input data size of 784 (28*28*1) without padding. The total number of weights in the convolutional layers is the sum of the weights in conv1 and conv2, where conv1 has 6*1*5*5 = 150 weights, and conv2 has 16*6*5*5 = 2400 weights. So, the total number of weights in both convolutional layers is 150 + 2400 = 2550.
This 1*400 matrix is then fed into the neural network model, which consists of three layers: 256*120, 120*84, and 84*10. The total number of weights in the neural network is the sum of the weights in these three layers. FC1 has 256*120 = 30720 weights, FC2 has 120*84 = 10080 weights, and FC3 has 84*10 = 840 weights. Therefore, the total number of weights in the LeNet-5 network is 30720 + 10080 + 840 + 2550 = 44190.The calculated result implies that 250KB of SRAM is sufficient to store all the weight data of this model, making it suitable for deployment on Zedboard.

3.2. Convolution calculation

During the operation of the convolutional computation module, the first step is to load the input weight data. Next, the input image data is loaded, and the data enters the row buffer for waiting for convolution computation. Then, the convolution calculation is performed in a sliding window manner, where multiplication and accumulation operations are performed as the window slides. After the computation is complete, the output channels are integrated. The convolution calculation formula is shown as Equation (2).
G x , y = 1 2 π σ 2 e − x 2 + y 2 2 σ 2
In the equation, G x , y is the Gaussian function, σ is the standard deviation of the Gaussian function, and x , y represents the coordinates of the two-dimensional point within the Gaussian function.
The principle of Gaussian filtering is to scan the entire image with a window. Whenever the center of the window scans a pixel in the image, the calculation result within the neighborhood of that window is used to replace the pixel. Gaussian filtering can avoid the ringing effect and is superior to the ideal filter. If a filter has a sudden change in the frequency domain, it will cause the resulting image to become blurry at the edges.

3.3. Image Enhancement Algorithms

The histogram equalization algorithm adjusts the grayscale distribution of the target image based on the theory that an image is clearest when its grayscale distribution is uniform. The probability calculation formula for the grayscale histogram is shown in Equation (3).
P k = n k n , k = 0 , 1 , … , L − 1
In the equation, P k is the probability of the k-th grayscale level's grayscale distribution, n is the total number of image pixels, and n k is the number of pixels in the k-th grayscale level.
The sum of probabilities for all grayscale levels equals 1, as shown in Equation (4).
∑ k = 0 L − 1 P k = 1
In the equation, P k is the probability of the k-th grayscale level's grayscale distribution, and L is the total number of grayscale levels.
Histogram equalization is an algorithm that achieves the purpose of image enhancement by transforming the histogram to achieve a uniform grayscale distribution. Its basic principle is to adjust the grayscale distribution of the target image so that the grayscale distribution of the resulting image is as uniform as possible. This can improve the clarity of the recognition target, facilitating the subsequent detection by the LeNet-5 convolutional neural network.
The formula for calculating the grayscale level in the histogram equalization algorithm is as shown in Equation (5).
S k = ∫ 0 k P r d r
In the equation, S k is the cumulative distribution function, k stands for the first k grayscale levels in the image, and P r represents the probability of the r-th grayscale level.
After applying the grayscale level equalization algorithm, the grayscale distribution of the original image becomes more uniform, making the image clearer. The mapping formula for grayscale level equalization is shown in Equation (6).
f k = L − 1 ∗ S k
In the equation, f k is the grayscale mapping function, and L is the number of grayscale levels.
Histogram equalization algorithm is fast in execution speed and has a simple implementation principle, making it suitable for deployment on embedded devices.

3.4. CNN Accelerator Strategy

Because the convolutional layer's computations account for over 90% of the entire network model [33], in order to accelerate the inference process of convolutional neural networks, this paper adopts a strategy of loop unrolling and tiling, optimizing the convolutional layer operations within the network model.

3.4.1. Loop unrolling

To improve the computation speed of neural networks [34], weight parameters and intermediate results are stored in Block RAM (BRAM) with high-speed read/write characteristics. Since BRAM used for data storage only has two input/output ports and cannot access all data needed for convolutional operations at once, to overcome the limitation of memory ports and accelerate the inference process of convolutional neural networks, a strategy of loop unrolling for output feature maps can be employed to optimize the convolutional layer operations in the network model.
Loop unrolling for output feature maps is achieved by parallelizing the computation of N convolutional kernel weight parameter values and the pixel values from one input feature map, performing multiply-accumulate operations in each clock cycle, as illustrated in Figure 4 ( N = 2 ).

3.4.2. Pipeline design

The core of pipeline design lies in dividing a combinatorial logic system into multiple stages, inserting registers between each stage to temporarily store intermediate data. Each small module can execute in parallel, resulting in an increase in operating frequency and data throughput. Pipeline design is typically introduced when the circuit design has tight timing constraints and requires a high operating frequency. The pipeline design shortens the data path length within one clock cycle, increases data throughput, and improves the clock cycle. However, it also introduces data delay and significantly increases resource usage. It is a design approach that trades resources for speed.
As shown in Figure 5(a), it represents a basic loop with M operations and N iterations. If each operation in the loop takes one clock cycle, the total latency of the entire loop is M*N cycles. This structure uses the fewest resources but has the longest execution time. Figure 5(b) illustrates an ideal pipeline structure with N stages. The pipeline stages can work simultaneously, but it requires a certain amount of storage resources. The throughput of this pipeline architecture D is calculated as shown in Equation (7).
D = N T = N ∑ i = 1 M + N − 1 t i
In the equation, where N represents the number of iterations, M is the total number of computations, and T is the total time spent on all computations. t i is the maximum processing time spent on the i-th computation process.

3.4.3. Adder Tree

To speed up the network's computation speed as much as possible, an adder tree has been incorporated into the fully connected layer to improve data throughput. Since expanding all 256 loops would be resource-intensive on the Zedboard, the 256 loops are split into two sets of 16 loops each. Only one set of 16 loops is expanded, allowing for increased code parallelism in a resource-limited environment.
In Figure 6, we can observe that 16 data points are being added. In the add0 layer, 16 data points are paired and summed in pairs using 8 adders, resulting in 8 values. Then, 8 data points are paired and added in pairs using 4 adders, resulting in 2 values. Finally, these 2 values are added together using a single adder to obtain the final result sum.

4. Accelerator Implementation

4.1. Hardware Accelerator Architecture

This project is based on the development of Zynq, which consists of two parts: the PS (Processing System) side and the PL (Programmable Logic) side. The overall architecture design is shown in Figure 7. From the diagram, it can be seen that image data is stored in the DDR3 memory on the PS side, while the entire LeNet-5 convolutional neural network is implemented in the PL side. The LeNet neural network is further divided into convolution modules, pooling modules, and fully connected modules. The flow of image data starts from the PS side and is transmitted to the PL side. To obtain the prediction results, the PL side needs to transmit the prediction results to the PS side for display. This approach deploys the entire LeNet-5 neural network's logic and various layers in the PL, significantly reducing data transfer and computation time, thus reducing the overall prediction time of the neural network. The resources available on the PL side of the Zedboard are sufficient to implement the LeNet neural network, which is why this method was adopted in this design to maximize network performance.

4.2. UNROLL Accelerator

In this approach, UNROLL statements are added to unroll the for loop. After unrolling the for loop, due to the limited input and output ports of BRAM used for storing data, it's not possible to retrieve all the data needed for convolution operations at once. To overcome this memory port limitation, ARRAY_PARTITION statements can be used to partition arrays into multiple arrays based on the actual requirements. This increases the data read ports, facilitating faster data retrieval and significantly improving data throughput.
After unrolling the for loop, to address the limitation of reading only one operand in a single clock cycle and make full use of FPGA's parallel processing capabilities, the following optimization statement can be used to further partition the input array in the first convolution operation. In the statement, "#pragma HLS" indicates the use of optimization directives, and "variable" specifies which variable to partition. The optimization statement:
#pragma HLS ARRAY_PARTITION variable=Kw complete dim=1
#pragma HLS ARRAY_PARTITION variable=Kw complete dim=2
#pragma HLS ARRAY_PARTITION variable=Kb complete dim=1
#pragma HLS ARRAY_PARTITION variable=out complete dim=3
In the 6th line of code in Table 2, the UNROLL optimization statement is used to unroll the innermost for loop of the convolution operation. The C synthesis tool will generate 6 multipliers and perform parallel computation of these 6 multiplication operations, as illustrated in Figure 8. In the first operation, all 6 elements of the first convolution kernel are taken at once, and they are multiplied by the value of the first pixel point in_0_0 in the input feature map. In the second operation, all the first row's second elements of the 6 convolution kernels are taken and multiplied by the pixel value of the second pixel in the first row of the input feature map, and so on. After 14,400 operations, all the pixel points in the input feature map have undergone multiplication operations. The output feature map size of the first convolutional layer is 24*24*6, and each convolution kernel has 25 elements, so the last multiplication operation on the input feature map's last pixel with the last element of the convolution kernel is located at 24*24*25=14,400. The code optimization principle in the 12th line of Table 2 is the same, but it performs addition operations on each pixel point in the output feature map instead of multiplication. The same optimization approach is used for the convolution computation in the C3 layer.

4.3. PIPELINE Accelerator

The PIPELINE optimization statement instructs the compiler to pipeline the code within the specified for loop, enabling multiple iterations to be executed in parallel. The II (Initiation Interval) parameter determines the number of clock cycles needed between iterations, i.e., the interval before the current loop can accept new data. If not explicitly set, the default value is 1, indicating fully pipelined operation. The PIPELINE optimization statement allows we to set the II parameter to control the interval between iterations. When II=1, it optimizes the code according to the most efficient standard. If the code cannot complete within one clock cycle with II=1, the system will automatically increase II, incrementally, until the condition is satisfied. This helps balance performance and resource utilization in FPGA designs by adjusting the pipeline initiation interval as needed.
The code optimized using PIPELINE for the first convolutional layer is as shown in Table 3. Due to the "#pragma HLS PIPELINE" statement, the for loop in line 6 will be unrolled, and the code in line 7 will be pipelined. The effect is the same for line 11. The second convolutional layer is also optimized using the same method. Similarly, to increase BRAM read/write ports and speed up data access, we need to partition the array using the same statement.

4.4. Fixed-Point Parameters

In order to conserve resources on the Zedboard and reduce both the parameter count and computational complexity of CNNs, as well as the hardware resource requirements during algorithm implementation, researchers often perform quantization or fixed-point representation [51] of parameters such as weights and biases in the CNN inference process, while ensuring algorithm accuracy. The IEEE 754 standard defines the single-precision floating-point number format as shown in Equation (8).
V = − 1 s × M × 2 E − 127
In the equation, s is used to control the sign bit. When s is 1, V is negative, and when s is 0, V is positive. M represents the fractional part after the decimal point, and E is the exponent part, also known as the bias value. For double-precision floating-point numbers, we can change E − 127 to E − 1023 and leave everything else unchanged. As for single-precision floating-point numbers, their data format consists of 32 binary bits. The highest bit is the sign bit, followed by an 8-bit exponent part, and the final 23 bits are the fractional part. In contrast, the decimal point in fixed-point numbers can be changed and adjusted within the program based on design requirements.
To explore the impact of different data types on FPGA resource consumption, we conducted independent experiments using fully connected layers, defining the weight parameters as floating point numbers, integers, and fixed-point numbers. Defining integers refers to taking only the integer part of the weight parameter, ignoring the decimal part. The fixed-point numbers we used are represented using a 16-bit fixed-point notation, where 8 bits represent the integer part and the remaining bits represent the decimal part. Table 4 shows the resource consumption when weight parameters are defined as floating-point numbers, integers, and fixed-point numbers. It is evident that among these three data types, floating-point numbers consume the most FPGA internal resources, with the number of DSPs exceeding the total resources inside Zedboard by a large margin. Next is fixed-point numbers, which, compared to floating-point numbers, reduce BRAM consumption by 23%, DSP consumption by 29%, FF consumption by 11%, and LUT consumption by 40%. While the number of DSPs consumed also exceeds the total number of internal DSPs in the device, it is possible to adjust the number of decimal places used to represent fractions to reduce DSP resource consumption based on actual circumstances. Therefore, choosing fixed-point numbers to define weight parameters is the most suitable method, although precision may decrease slightly, the degree of decrease is relatively small and can be negligible.
When performing fixed-point quantization on neural network parameters, the resource consumption can vary depending on the FPGA model used. Different FPGAs have varying numbers of internal resources, and using a fixed fixed-point quantization scheme for the accelerator may not be compatible with other FPGA models or may not optimize the accelerator's performance to the fullest. To facilitate portability across different FPGA models, this design optimizes fixed-point quantization to parameterized fixed-point quantization. During the accelerator design process, the data's fixed-point length is defined as N using macros. With this optimization, when porting the accelerator to other FPGA platforms, you only need to modify the parameter N before synthesis to maximize the accelerator's performance based on the platform's resource constraints.

5. Experimental Evaluation

This study utilized Xilinx's Vivado HLS 2018.3 to implement three different LeNet-5 accelerators as IP cores: unoptimized, UNROLL-optimized, and PIPELINE-optimized. These accelerators were deployed on the Xilinx Zedboard FPGA platform, as shown in Figure 9. The Zedboard platform features the Zynq XC7Z020-CLG484-1 as its main chip, equipped with 512 MB of DDR and 220 DSP units. In this chapter, the effectiveness of the proposed optimization techniques will be analyzed. Each optimization method will be evaluated for resource utilization, and performance metrics, including computation speed and power consumption, will be compared with other computing platforms.
Table 5 presents the performance and resource consumption of different approaches. It is quite evident that compared to the unoptimized accelerator, the UNROLL-optimized accelerator experiences a 25.64% increase in BRAM usage, a 1020% increase in DSP usage, a 401.99% increase in FF usage, and a 316.67% increase in LUT usage. For the PIPELINE-optimized accelerator, BRAM usage increases by 30.77%, DSP usage increases by 1670%, FF usage increases by 557.67%, and LUT usage increases by 500.44%. In terms of performance, the PIPELINE-optimized accelerator is 15.97 times faster than the UNROLL-optimized accelerator while increasing power consumption by 0.164 watts. This improvement is due to the PIPELINE-optimized accelerator's approach of enhancing code parallelism on top of loop unrolling. It employs multiple DSP units in parallel to perform computations simultaneously, effectively breaking down a large task into many smaller subtasks allocated to DSP units for collaborative execution, which is akin to pipelining operations [35,36]. Registers are inserted between these subtasks, allowing intermediate data to be stored in these registers, thereby significantly improving data throughput.
Figure 10 demonstrates the data processing process of the for loop after using UNROLL and PIPELINE optimization statements. Variables ending with "_load" on the left represent data read operations, while the corresponding values on the right indicate the time required for the read operation. Figure 10(a) illustrates the data processing process after UNROLL optimization, which reveals a time gap of more than three cycles between the read operations of data c1_w_0 and c1_w_1. Conversely, Figure 10(b) presents the data processing process after PIPELINE optimization, indicating that data read operations from BRAM occur simultaneously. Hence, compared to UNROLL optimization, the PIPELINE optimized accelerator exhibits lower latency.
We also developed test and validation software programs on the CPU. In our related work, we compared the time and power consumption for predicting a single image in the MNIST test set (10,000 images). Table 6 shows that, under the same design functionality, the PIPELINE-optimized accelerator is 70.387 times faster than the i7-10875H CPU @2.30GHz using Matlab computations, and it reduces power consumption by 91.37%. Table 6 also presents results from previous studies on GPUs, which indicates that the PIPELINE-optimized accelerator reduces power consumption by 93.35% compared to Nvidia GTX 840M using cuDNN [37], with only a slight decrease in speed (0.83ms). This comparison demonstrates that FPGA platforms have significantly lower power consumption compared to CPUs and GPUs, resulting in substantial energy savings while maintaining excellent acceleration performance.

6. Conclusions

In this paper, we focused on the LeNet-5 model, investigating its structural principles and hardware implementation. We proposed a lightweight, fully programmable SOC platform design based on the ZYNQ 7000 series Zedboard. In this work, we introduced two optimization strategies for CNN and compared their performance. We achieved the deployment of the LeNet-5 CNN on the Zedboard through collaborative software-hardware optimization. Experimental results demonstrated that the PIPELINE-optimized accelerator had excellent performance, with a prediction time of only 1.07ms, an error rate of 0.99%, and power consumption of 2.193w. Compared to the i7-10875H CPU, the accelerator showed a 98.6% increase in throughput and a 91.37% reduction in power consumption. This design achieves strong performance with lower power consumption and hardware resource usage, making it highly significant for the edge deployment of CNNs with limited resources.
While this research has achieved the expected results, there are some limitations in the current design that need further refinement and improvement in future work. These limitations and areas for improvement include:
  • The separation of network training on a CPU platform and network inference acceleration on an FPGA platform can be improved for a more integrated system. Future work should focus on accelerating the backpropagation process to enhance the system's completeness.
  • Most FPGA platforms operate at frequencies ranging from 100 to 300MHz. In this design, a frequency of 100MHz was used to ensure correct data transfer. Optimizations can be applied to data transfer to increase clock frequencies.
  • Exploring the fusion of multiple FPGAs, where multiple FPGAs collaborate, is an area that hasn't been extensively studied in this work. Many planning and allocation issues need to be addressed in this direction, making it a potential future research area.

Author Contributions

Conceptualization, J.T.; data curation, Y.L. and Z.X.; simulation, Z.Y. and Z.C.; writing—original draft preparation, Z.C. and J.T.; writing—review and editing, Z.Y. and Y.L.; supervision, J.T. All authors have read and agreed to the published version of the manuscript.

Funding

This work was financially supported by the Science and Technology Program of Guangxi, China (Nos. 2018AD19184), the Project of Guangxi Education Department of China (Nos. 2018KY0258) and the Project of the Guilin University of Technology (Nos.GLUTQD2017003).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Yu, G.; Wang, T.; Guo, G.; Liu, H. SFHG-YOLO: A Simple Real-Time Small-Object-Detection Method for Estimating Pineapple Yield from Unmanned Aerial Vehicles. Sensors 2023, 23(22), 9242. [Google Scholar] [CrossRef] [PubMed]
  2. Slam, W.; Li, Y.; Urouvas, N. Frontier Research on Low-Resource Speech Recognition Technology. Sensors 2023, 23(22), 9096. [Google Scholar] [CrossRef] [PubMed]
  3. Li, H.; Wang, Q.; Ling, L.; Lv, Z.; Liu, Y.; Jiao, M. Research on Recognition of Coal and Gangue Based on Laser Speckle Images. Sensors 2023, 23(22), 9113. [Google Scholar] [CrossRef] [PubMed]
  4. Wang, X.; Han, Y.; Wang, C.; Zhao, Q.; Chen, X.; Chen, M. In-edge ai: Intelligentizing mobile edge computing, caching and communication by federated learning. Ieee Network 2019, 33(5), 156–165. [Google Scholar] [CrossRef]
  5. Li, E.; Zhou, Z.; Chen, X. In Edge intelligence: On-demand deep learning model co-inference with device-edge synergy, Proceedings of the 2018 Workshop on Mobile Edge Communications, 2018; pp 31-36. [CrossRef]
  6. Wang, X.; Han, Y.; Leung, V. C.; Niyato, D.; Yan, X.; Chen, X. Convergence of edge computing and deep learning: A comprehensive survey. IEEE Communications Surveys & Tutorials 2020, 22(2), 869–904. [Google Scholar] [CrossRef]
  7. Benardos, P.; Vosniakos, G.-C. Optimizing feedforward artificial neural network architecture. Engineering applications of artificial intelligence 2007, 20(3), 365–382. [Google Scholar] [CrossRef]
  8. Qifang, B.; E, G. K.; Joshua, K.; Justin, L. What is Machine Learning? A Primer for the Epidemiologist. American journal of epidemiology 2019, 188(12). [Google Scholar] [CrossRef]
  9. Tang, Z.; Shao, K.; Zhao, D.; Zhu, Y. Recent progress of deep reinforcement learning: from AlphaGo to AlphaGo Zero. Control Theory & Applications 2017, 34(12), 1529–1546. [Google Scholar] [CrossRef]
  10. Zeng, L.; Chen, X.; Zhou, Z.; Yang, L.; Zhang, J. Coedge: Cooperative dnn inference with adaptive workload partitioning over heterogeneous edge devices. IEEE/ACM Transactions on Networking 2020, 29(2), 595–608. [Google Scholar] [CrossRef]
  11. Zhang, W.; Yang, D.; Peng, H.; Wu, W.; Quan, W.; Zhang, H.; Shen, X. Deep reinforcement learning based resource management for DNN inference in industrial IoT. IEEE Transactions on Vehicular Technology 2021, 70(8), 7605–7618. [Google Scholar] [CrossRef]
  12. Guo, X.-t.; Xie, X.-s.; Lang, X. Pruning feature maps for efficient convolutional neural networks. Optik 2023, 281, 170809. [Google Scholar] [CrossRef]
  13. Liu, Z.; Li, J.; Shen, Z.; Huang, G.; Yan, S.; Zhang, C. In Learning efficient convolutional networks through network slimming, Proceedings of the IEEE international conference on computer vision, 2017; pp 2736-2744.
  14. Qin, H.; Gong, R.; Liu, X.; Shen, M.; Wei, Z.; Yu, F.; Song, J. In Forward and backward information retention for accurate binary neural networks, Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2020; pp 2250-2259.
  15. Chen, K.; Tao, W. Once for all: a two-flow convolutional neural network for visual tracking. IEEE Transactions on Circuits and Systems for Video Technology 2017, 28(12), 3377–3386. [Google Scholar] [CrossRef]
  16. Hinton, G. E.; Salakhutdinov, R. R. Reducing the dimensionality of data with neural networks. science 2006, 313(5786), 504–507. [Google Scholar] [CrossRef]
  17. Jiang, J.; Jiang, M.; Zhang, J.; Dong, F. A CPU-FPGA Heterogeneous Acceleration System for Scene Text Detection Network. IEEE Transactions on Circuits and Systems II: Express Briefs 2022, 69(6), 2947–2951. [Google Scholar] [CrossRef]
  18. Zhai, J.; Li, B.; Lv, S.; Zhou, Q. FPGA-based vehicle detection and tracking accelerator. Sensors 2023, 23(4), 2208. [Google Scholar] [CrossRef]
  19. Zhang, J.-F.; Lee, C.-E.; Liu, C.; Shao, Y. S.; Keckler, S. W.; Zhang, Z. In SNAP: A 1.67—21.55 TOPS/W sparse neural acceleration processor for unstructured sparse deep neural network inference in 16nm CMOS, 2019 Symposium on VLSI Circuits, IEEE: 2019; pp C306-C307. [CrossRef]
  20. Venkat, A.; Tullsen, D. M. Harnessing ISA diversity: Design of a heterogeneous-ISA chip multiprocessor. ACM SIGARCH Computer Architecture News 2014, 42(3), 121–132. [Google Scholar] [CrossRef]
  21. Huang, K.-Y.; Juang, J.-C.; Tsai, Y.-F.; Lin, C.-T. Efficient FPGA Implementation of a Dual-Frequency GNSS Receiver with Robust Inter-Frequency Aiding. Sensors 2021, 21(14), 4634. [Google Scholar] [CrossRef]
  22. Li, Z.; Wang, L.; Guo, S.; Deng, Y.; Dou, Q.; Zhou, H.; Lu, W. L. In An 8-bit fixed-point CNN hardware inference engine, Proceedings of the 2017 IEEE International Symposium on Parallel and Distributed Processing with Applications and 2017 IEEE International Conference on Ubiquitous Computing and Communications (ISPA/IUCC), Guangzhou, China, 2017; pp 12-15. [CrossRef]
  23. Wei, K.; Honda, K.; Amano, H. In An implementation methodology for Neural Network on a Low-end FPGA Board, 2020 Eighth International Symposium on Computing and Networking (CANDAR), IEEE: 2020; pp 228-234. [CrossRef]
  24. Huang, Q.; Wang, D.; Dong, Z.; Gao, Y.; Cai, Y.; Li, T.; Wu, B.; Keutzer, K.; Wawrzynek, J. In Codenet: Efficient deployment of input-adaptive object detection on embedded fpgas, The 2021 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, 2021; pp 206-216. [CrossRef]
  25. Ma, N.; Zhang, X.; Zheng, H.-T.; Sun, J. In Shufflenet v2: Practical guidelines for efficient cnn architecture design, Proceedings of the European conference on computer vision (ECCV), 2018; pp 116-131.
  26. Zhang, X.; Wang, J.; Zhu, C.; Lin, Y.; Xiong, J.; Hwu, W.-m.; Chen, D. In AccDNN: An IP-based DNN generator for FPGAs, 2018 IEEE 26th Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), IEEE: 2018; pp 210-210. [CrossRef]
  27. Guan, Y.; Liang, H.; Xu, N.; Wang, W.; Shi, S.; Chen, X.; Sun, G.; Zhang, W.; Cong, J. In FP-DNN: An automated framework for mapping deep neural networks onto FPGAs with RTL-HLS hybrid templates, 2017 IEEE 25th Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), IEEE: 2017; pp 152-159. [CrossRef]
  28. Ahmad, A.; Pasha, M. A. In Towards design space exploration and optimization of fast algorithms for convolutional neural networks (CNNs) on FPGAs, 2019 Design, Automation & Test in Europe Conference & Exhibition (DATE), IEEE: 2019; pp 1106-1111. [CrossRef]
  29. Liang, Y.; Lu, L.; Xiao, Q.; Yan, S. Evaluating fast algorithms for convolutional neural networks on FPGAs. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems 2019, 39(4), 857–870. [Google Scholar] [CrossRef]
  30. Bao, C.; Xie, T.; Feng, W.; Chang, L.; Yu, C. A power-efficient optimizing framework fpga accelerator based on winograd for yolo. Ieee Access 2020, 8, 94307–94317. [Google Scholar] [CrossRef]
  31. Podili, A.; Zhang, C.; Prasanna, V. In Fast and efficient implementation of convolutional neural networks on FPGA, 2017 IEEE 28Th international conference on application-specific systems, architectures and processors (ASAP), IEEE: 2017; pp 11-18. [CrossRef]
  32. Zhang, C.; Wu, D.; Sun, J.; Sun, G.; Luo, G.; Cong, J. In Energy-efficient CNN implementation on a deeply pipelined FPGA cluster, Proceedings of the 2016 International Symposium on Low Power Electronics and Design, 2016; pp 326-331. [CrossRef]
  33. Qiu, J.; Wang, J.; Yao, S.; Guo, K.; Li, B.; Zhou, E.; Yu, J.; Tang, T.; Xu, N.; Song, S. In Going deeper with embedded FPGA platform for convolutional neural network, Proceedings of the 2016 ACM/SIGDA international symposium on field-programmable gate arrays, 2016; pp 26-35. [CrossRef]
  34. Ajili, M. T.; Hara-Azumi, Y. Multimodal Neural Network Acceleration on a Hybrid CPU-FPGA Architecture: A Case Study. IEEE Access 2022, 10, 9603–9617. [Google Scholar] [CrossRef]
  35. Lammie, C.; Olsen, A.; Carrick, T.; Azghadi, M. R. Low-Power and High-Speed Deep FPGA Inference Engines for Weed Classification at the Edge. IEEE Access 2019, 7, 51171–51184. [Google Scholar] [CrossRef]
  36. Medus, L. D.; Iakymchuk, T.; Frances-Villora, J. V.; Bataller-Mompeán, M.; Rosado-Muñoz, A. A Novel Systolic Parallel Hardware Architecture for the FPGA Acceleration of Feedforward Neural Networks. IEEE Access 2019, 7, 76084–76103. [Google Scholar] [CrossRef]
  37. Chetlur, S.; Woolley, C.; Vandermersch, P.; Cohen, J.; Tran, J.; Catanzaro, B.; Shelhamer, E. cudnn: Efficient primitives for deep learning. arXiv 2014, arXiv:1410.0759. [Google Scholar] [CrossRef]
  38. Hu, X.; Zhang, P. Accelerated Design of Convolutional Neural Network based on FPGA. International Core Journal of Engineering 2021, 7(7), 195–201. [Google Scholar]
  39. Park, S.-S.; Park, K.-B.; Chung, K.-S. In Implementation of a CNN accelerator on an Embedded SoC Platform using SDSoC, Proceedings of the 2nd International Conference on Digital Signal Processing, 2018; pp 161-165. [CrossRef]
  40. Bjerge, K.; Schougaard, J. H.; Larsen, D. E. A scalable and efficient convolutional neural network accelerator using HLS for a system-on-chip design. Microprocessors and microsystems 2021, 87, 104363. [Google Scholar] [CrossRef]
Preprints 92686 g001
Figure 1. LeNet-5 network architecture.
Figure 1. LeNet-5 network architecture.
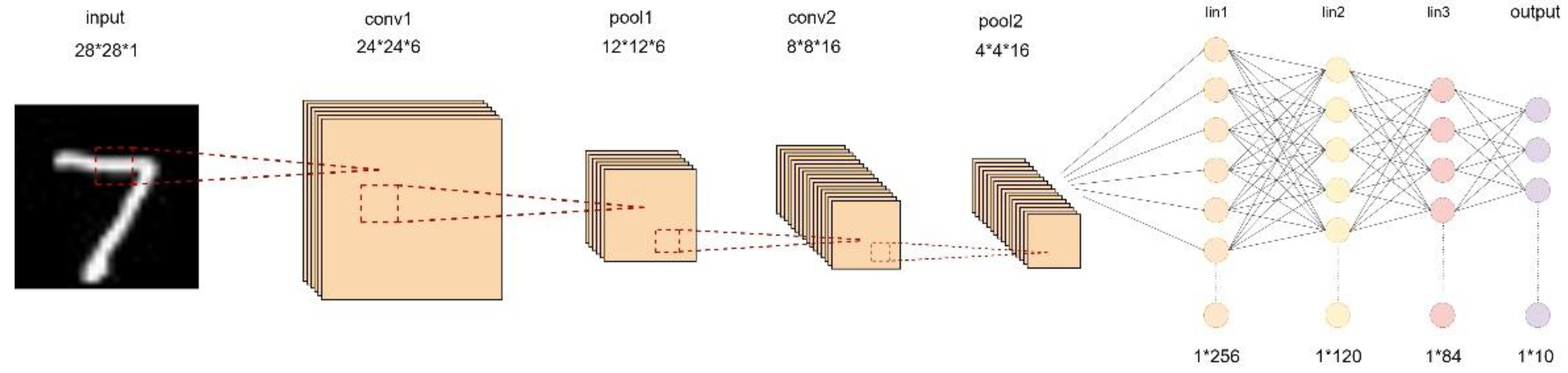
Preprints 92686 g001
Preprints 92686 g002
Figure 2. Comparative diagram of the FC network structure before and after adding Dropout.
Figure 2. Comparative diagram of the FC network structure before and after adding Dropout.
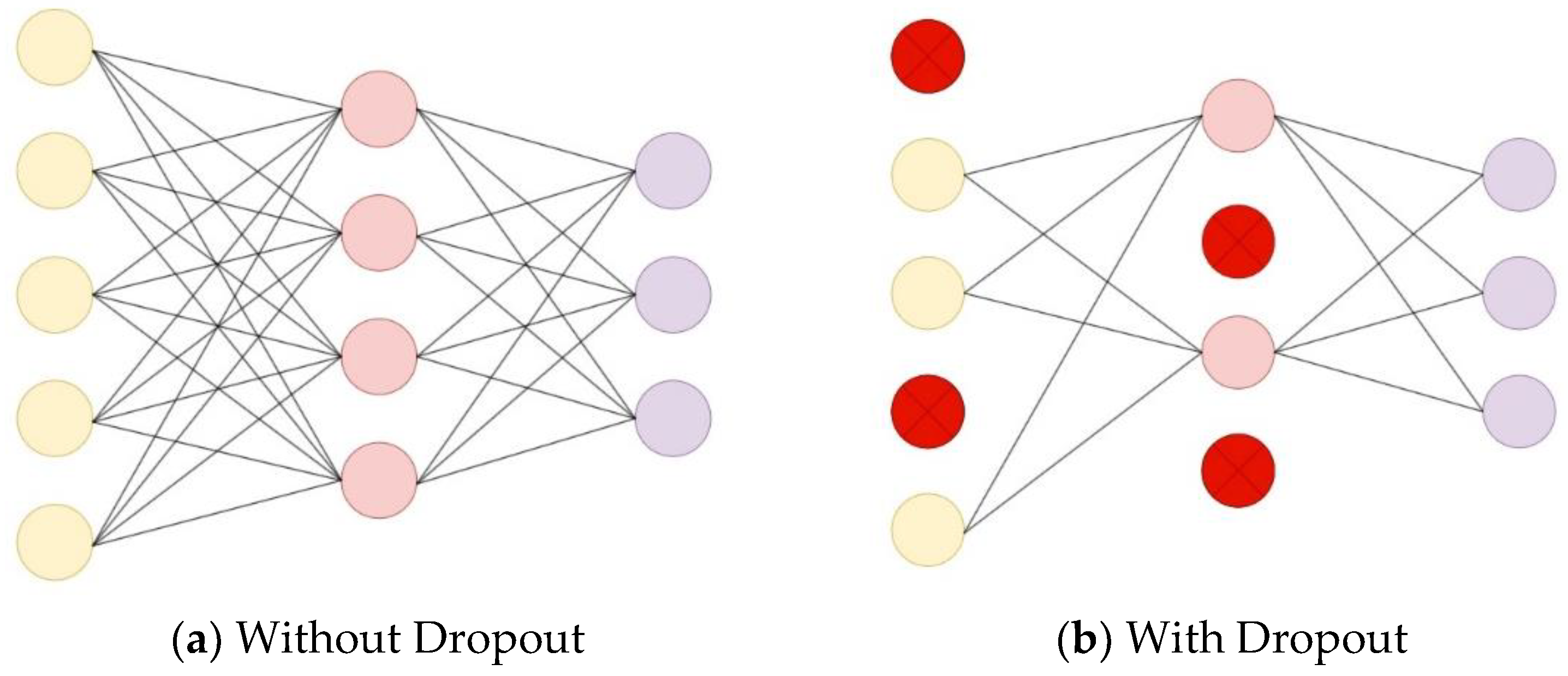
Preprints 92686 g002
Preprints 92686 g003
Figure 3. Activation function image.
Figure 3. Activation function image.
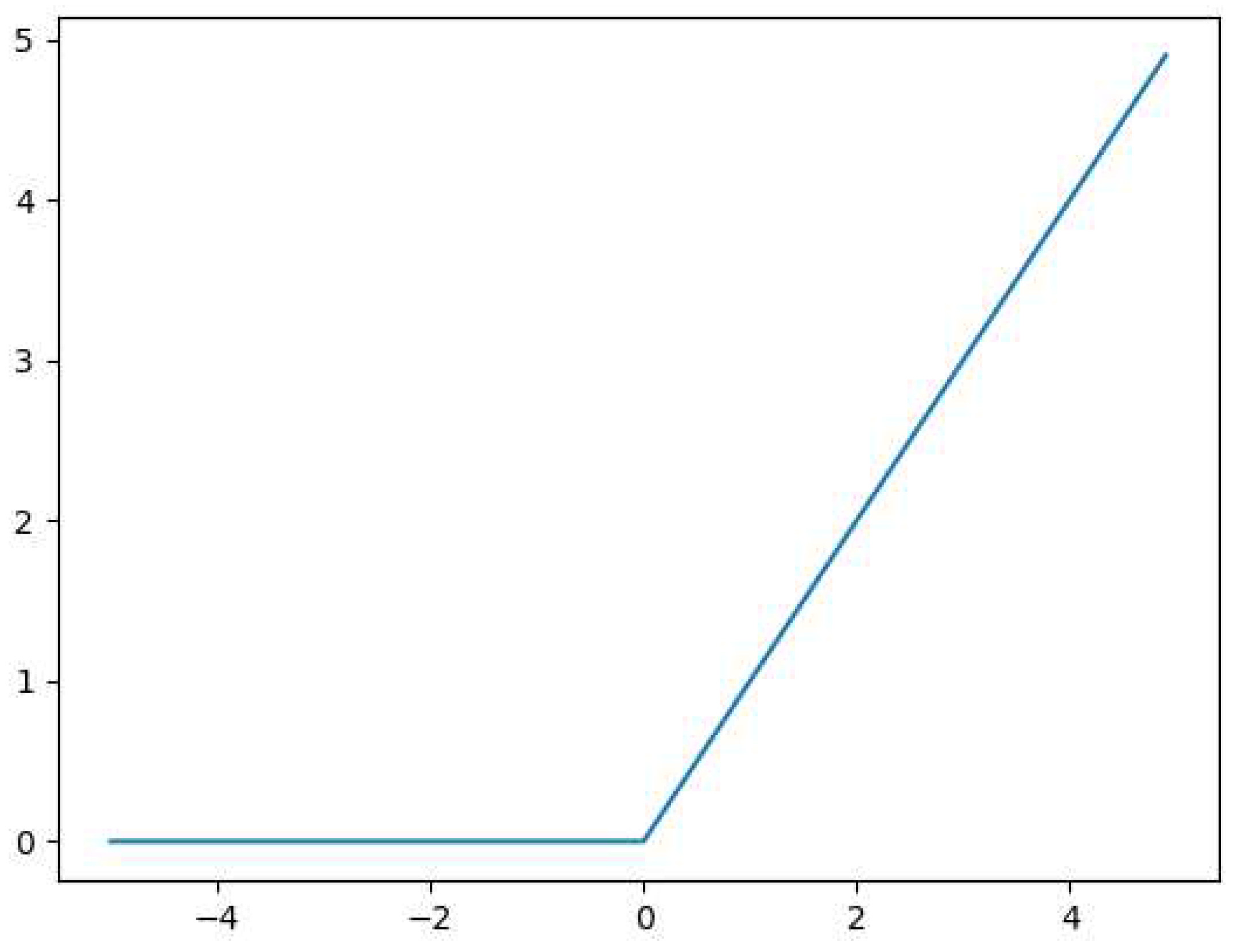
Preprints 92686 g003
Preprints 92686 g004
Figure 4. Schematic Diagram of Loop Unrolling for Output Feature Maps.
Figure 4. Schematic Diagram of Loop Unrolling for Output Feature Maps.
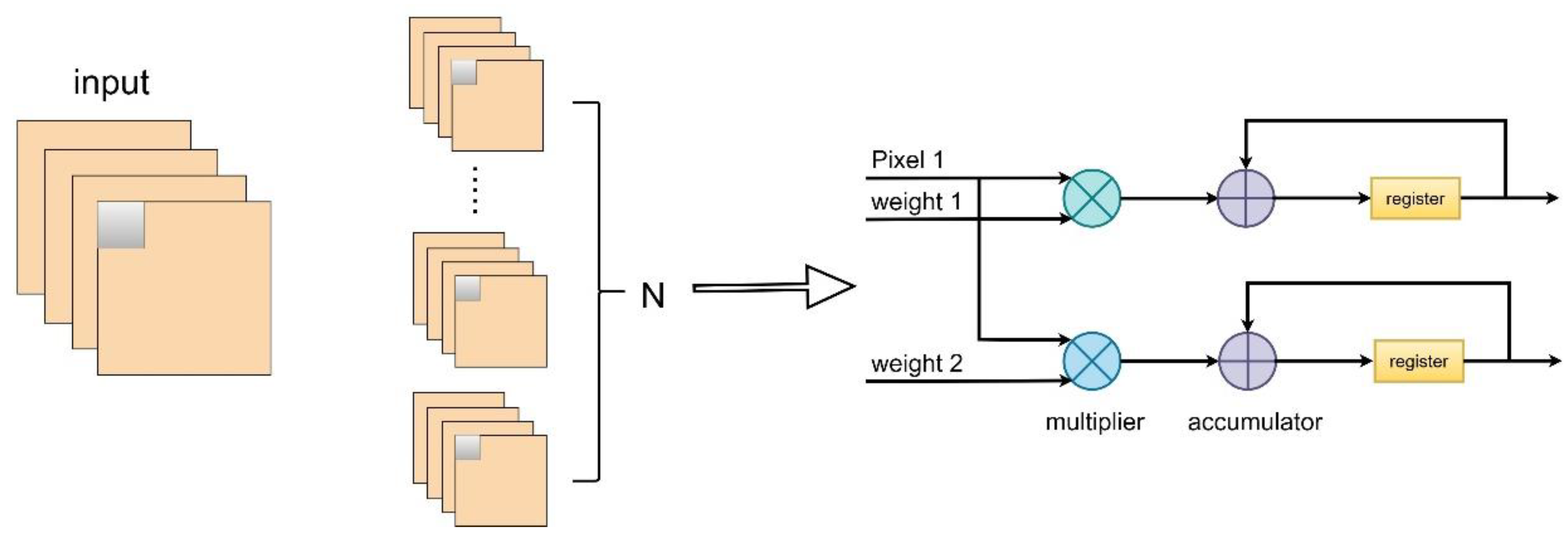
Preprints 92686 g004
Preprints 92686 g005
Figure 5. Comparison between before and after adding the pipeline.
Figure 5. Comparison between before and after adding the pipeline.
Preprints 92686 g005
Preprints 92686 g006
Figure 6. Schematic diagram of the fully connected layer's addition tree.
Figure 6. Schematic diagram of the fully connected layer's addition tree.
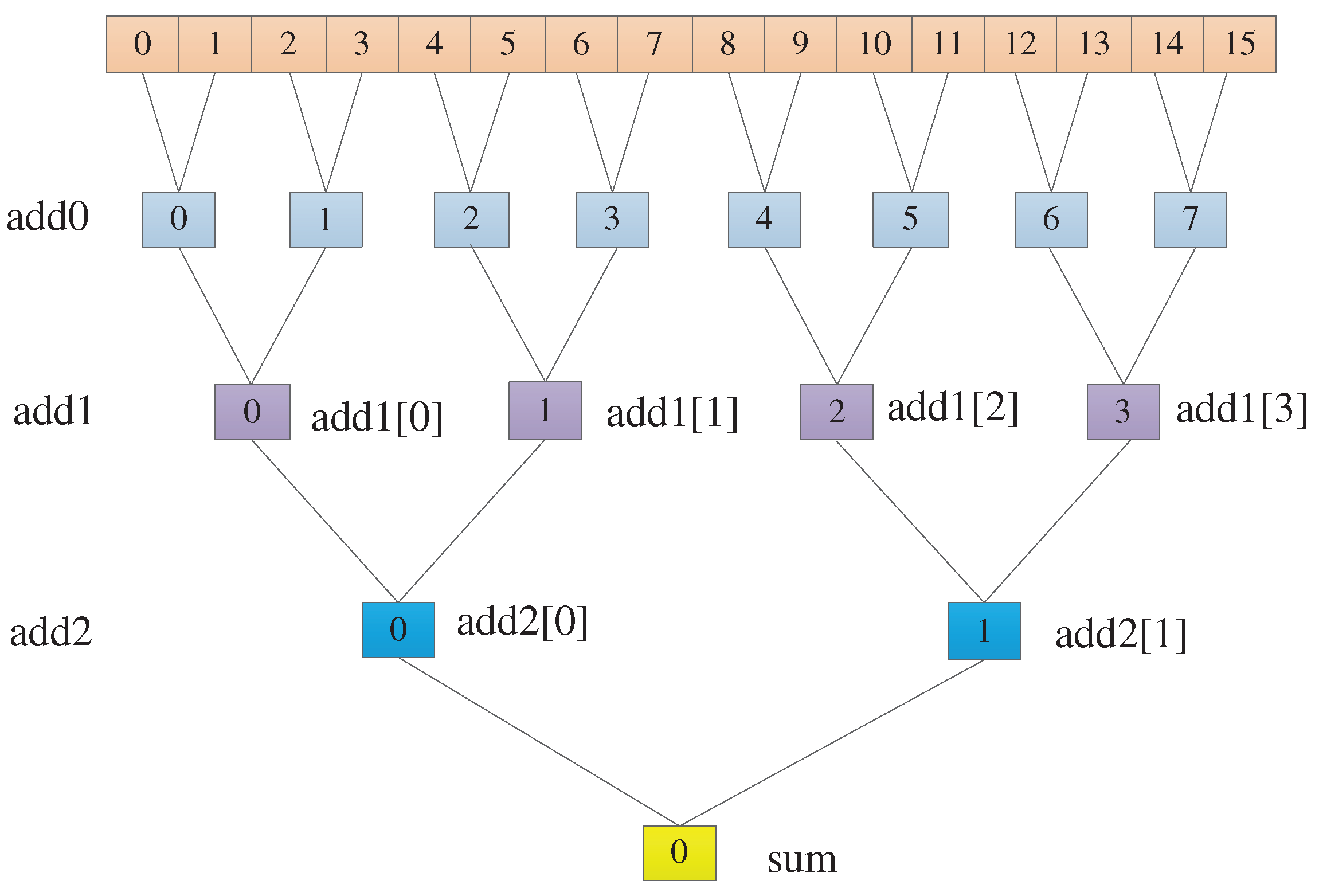
Preprints 92686 g006
Preprints 92686 g007
Figure 7. Hardware Accelerator Architecture Diagram.
Figure 7. Hardware Accelerator Architecture Diagram.
Preprints 92686 g007
Preprints 92686 g008
Figure 8. The operations after unrolling the for loop in the C1 layer.
Figure 8. The operations after unrolling the for loop in the C1 layer.
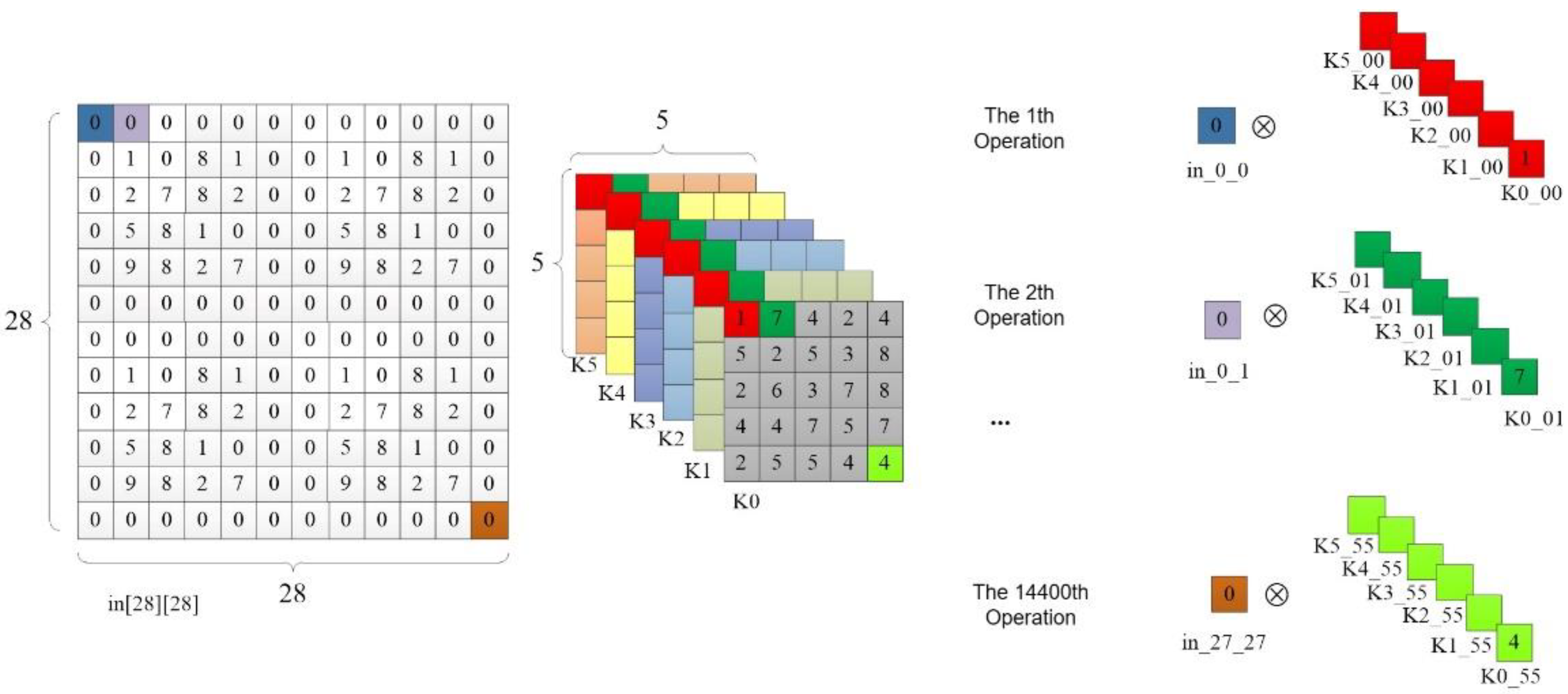
Preprints 92686 g008
Preprints 92686 g009
Figure 9. The experimental results of the accelerator.
Figure 9. The experimental results of the accelerator.
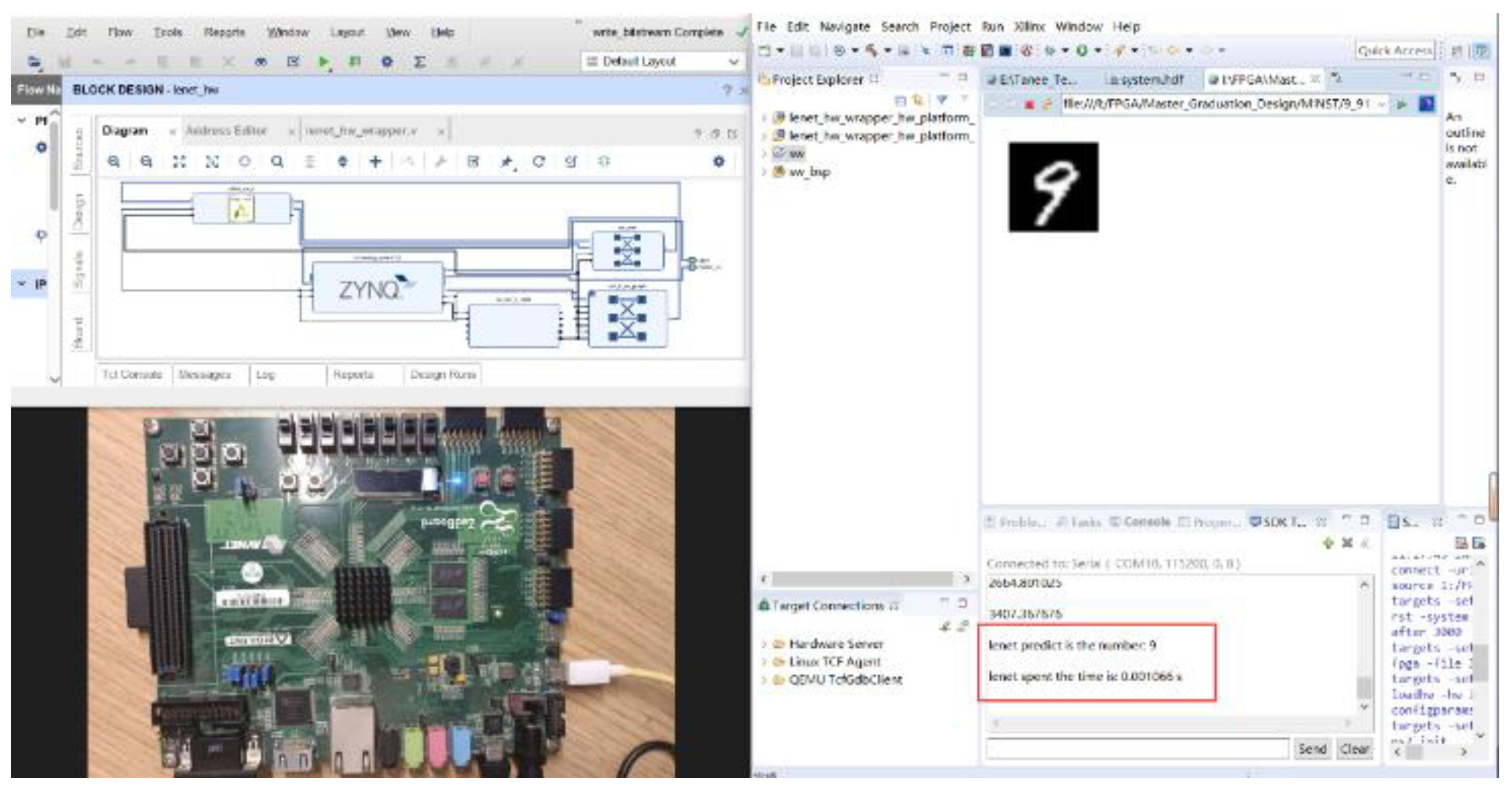
Preprints 92686 g009
Preprints 92686 g010
Figure 10. Data loading after using different optimization statements.
Figure 10. Data loading after using different optimization statements.
Preprints 92686 g010
Table 1. The structure of the LeNet-5 neural network.
Table 1. The structure of the LeNet-5 neural network.
Layer Type Input Output Kernel Stride
Conv 28*28*1 24*24*6 5*5 1
Pool 24*24*6 12*12*6 2*2 2
Conv 12*12*6 8*8*16 5*5 1
Pool 8*8*16 4*4*16 2*2 2
FC 1*256 1*120 256*120 -
FC 1*120 1*84 120*84 -
FC 1*84 1*10 84*10 -
Table 2. Code for the First Convolutional Layer.
Table 2. Code for the First Convolutional Layer.
Rows Codes
1 for(int i=0;i<24;i++){
2  for(int j=0;j<24;j++){
3  for(int y=0;y<5;y++){
4  for(int x=0;x<5;x++){
5 #pragma HLS PIPELINE
6  for(int k=0;k<6;k++){
7  out[i][j][k] += in[i+y][j+x]*Kw[k][y][x];
8  }}}}}
9 for(int i=0;i<24;i++){
10  for(int j=0;j<24;j++){
11 #pragma HLS PIPELINE
12  for(int k=0;k<6;k++){
13  out[i][j][k]+=Kb[k];
14 }}}
Table 3. Code for the First Convolutional Layer.
Table 3. Code for the First Convolutional Layer.
Rows Codes
1 for (int i=0;i<120;i++){
2  sum=0;
3  for(int j_set=0;j_set<16;j_set++){
4 #pragma HLS PIPELINE
5   for(int j=0;j<16;j++){
6    tmp[j] = in[j+j_set*16]*fc1_w[i][j+j_set*16];
7   }
8   for(int k=0;k<8;k++){
9    add0[k]=tmp[k*2]+tmp[k*2+1];
10   }
11   for(int k=0;k<4;k++){
12    add1[k]=add0[k*2]+add0[k*2+1];
13   }
14   for(int k=0;k<2;k++){
15    add2[k]=add1[k*2]+add1[k*2+1];
16  }
17  sum += add2[0]+add2[1];
18  }
19  out[i]=sum;
20 }
Table 4. FPGA Resource Consumption.
Table 4. FPGA Resource Consumption.
FPGA Resource BRAM DSP FF LUT
Available Quantity 1090 900 437200 218600
Defined as Floating-Point 260 1282 134701 202357
Defined as Integer 0 256 17049 5523
Defined as Fixed-Point 0 1024 86264 114800
Defined as Floating-Point 260 1282 134701 202357
Table 5. Performance Comparison of Accelerators.
Table 5. Performance Comparison of Accelerators.
Design Unoptimized UNROLL PIPELINE
BRAM 78 98 102
DSP 10 112 177
FF 3461 17374 22762
LUT 6569 27371 39443
Power 1.874w 2.029w 2.193w
Time 20.37ms 16.02 ms 1.07 ms
Table 6. Performance Comparison Across Different Platforms.
Table 6. Performance Comparison Across Different Platforms.
Device Time Power Error Rate
PIPELINE 1.07ms 2.193w 0.99%
UNROLL 16.02ms 2.029w 0.99%
xc7z020 [38] 59.4ms 4.2w -
Zynq zc706 [39] 1.607ms 10.98w -
Ultra96 [40] 4.6ms 3.55w -
Intel Core i7 2.30GHz 75ms 25.43w 0.99%
NVidia GTX 840M [37] 0.24ms 33w 1.09%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated