Preprint
Article
A Complete Pipeline for Heart Rate Extraction from Infant ECG
Altmetrics
Downloads
116
Views
104
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
07 December 2023
Posted:
08 December 2023
You are already at the latest version
Alerts
Abstract
Infant electrocardiograms (ECG) and heart rates (HR) are very useful biosignals for psychological research and clinical work, but can be hard to analyze properly, particularly long form (≥5 minutes) recordings taken in naturalistic environments. Infant HRs are typically much faster than adult HRs, and so some of the underlying frequency assumptions made about adult ECGs may not hold for infants. However, the bulk of publicly available ECG approaches focus on adult data. Here, existing open-source ECG approaches are tested on infant datasets. The best performing open-source method is then modified to maximize its performance on infant data (e.g., including a 15Hz high pass filter, adding local peak correction). The HR signal is then subsequently analyzed, developing an approach for cleaning data with separate sets of parameters for the analysis of cleaner and noisier HR. A Signal Quality Index (SQI) for HR is also developed, providing insight into where a signal is recoverable and where it is not, allowing for more confidence in analysis performed on naturalistic recordings. The tools developed and reported in this paper provide a base for future analysis of infant ECG and related biophysical characteristics. Of particular importance, the proposed solutions outlined here can be efficiently applied to real-world large datasets.
Keywords:
Subject: Computer Science and Mathematics - Signal Processing
1. Introduction
Measures of the cardiovascular system provide a good window into the activity of the autonomic nervous system (ANS), reflecting innervations from both the sympathetic and parasympathetic branches [1]. Variations in heart period and heart rate variability have been linked to important cognitive functions, such as attention, memory, and information processing, as well as changes in arousal and regulatory abilities [2,3,4,5]. ANS activity measurement has been fruitful in understanding both typical and atypical development, with atypical ANS shown in manifestations of autism spectrum disorders [6,7], attention deficit and hyperactivity disorders [8], conduct disorders [9], as well as the emergence of other neuropsychiatric conditions [10]. Cardiovascular measures are particularly useful for the study of cognitive and emotional development beginning with the first days of life since both the cardiovascular and autonomic systems are well developed at birth [11], and electrocardiography (ECG) recordings can be obtained in non-invasive fashion. In the context of infants’ limited behavioural repertoire, reduced motor development, and lack of verbal communication abilities, non-invasive methods that can give insights into cognitive and emotion functions, are essential for understanding how these develop within the critical first 1000 days of life. With advances in wearable sensing technology, ECG can be more easily obtained outside the laboratory as well, allowing dense recordings over hours and days [12,13]. This opens unprecedented opportunities for studying the development in the natural environment, allowing us to understand the complexity of factors that can contribute to typical and atypical outcomes [14].
Although ECG has been used for studying infant cognitive and emotional development for several decades, there currently are few evaluations of complete open-access pipelines, especially focussed on infant ECG recorded in naturalistic environments. Children, and in particular infants, have a much higher heart rate (HR) than adults [15], and so algorithms tailored to process adult heart signals might not be the optimal choice for processing the signals recorded from the infant heart. In addition to the higher heart rate, there are many other factors (e.g., differing ECG complex shapes that occur) that should be considered when using ECGs from infants and children [16]. Free movement during typical activities and lengthy recordings can produce more motion-induced noise, such as baseline wander and motion artefacts [17], which can be particularly problematic when cardiac activity is recorded from infants in naturalistic settings (e.g., their everyday home environment). This is in addition to other forms of ECG noise (such as power line interference and signal processing artefacts [18,19] that must be accounted for in ECG processing. Building on and extending our previous work [12], the primary aim of the current study is to propose a complete open-source processing pipeline for long infant ECG recordings (≥5 minutes) and validate it under a range of conditions (including naturalistic conditions) against open-source state-of-the-art approaches. Compared to our previous work, we increase dataset sizes, include ECG data recordings from a range of devices recorded at a range of sampling rates, and present a deeper validation of the different steps of the pipeline.
During typical functioning, the depolarization of the heart ventricles produces a short and characteristic spike of electric signal, often referred to as the QRS complex, with the peak of the QRS complex referred to as the R-peak (Figure 1). When detected, the time between consecutive R peaks (ΔR-R) can be used to calculate the instantaneous HR in beats per minute (see Equation 1). This gives a precise beat-by-beat HR measurement derived from the ECG.
HR = 60/(ΔR-R)
There are many pre-established open-source methods designed to preprocess ECG data and then extract the R-peaks [20,21,22,23,24,25,26,27,28,29,30,31,32,33]. While some comparative analyses have been previously carried out [19,21], no analysis exists evaluating the effectiveness of these methodologies on infants and young children ECGs. Many of these methods also investigate other ECG complexes such as T-waves and P-waves, as well as the QRS complex as a whole (see Figure 1). In the present paper, only the R-peak detection is analysed.
For the ECG preprocessing step, usually a decision must be made as to whether the signal is of sufficient quality for further processing and analysis. Noise can be reduced by a frequency-filtering approaches, with low pass filters (LPF) for removing aspects such as white noise, high pass filtering (HPF) used for aspects such as baseline drift, bandpass filtering (BPF) to remove low-frequency and high-frequency noise, and notch filtering for mains interference. Alternatively, other approaches such as wavelets and Empirical Mode Decomposition have also been used [34,35,36].
Typical ECG pipelines will only encompass the preprocessing of the ECG signal and then the R-peak detection. Given the inherent noise level in infant and young children ECG, and particularly ECG recordings in the natural environment, this paper aims to encapsulate the ECG to HR process as a complete open-access pipeline, also accounting for any HR cleaning and HR signal quality measurements. First pre-existing open-access ECG pipelines from literature were evaluated. The best performing method was then chosen as the basis to develop our new open-source pipeline for the infant ECG and subsequent infant HR signal. A range of additional preprocessing options were evaluated, along with some ECG post-processing steps. To account for the high levels of noise in infant ECG, additional HR processing steps and a HR signal quality index (SQI) to help automatically reject areas of unrecoverable signal were incorporated to form a complete pipeline (Figure 2).
2. Materials and Results
In this section, existing ECG pipelines will be applied to datasets containing infants and toddlers. Then, we propose an adapted ECG pipeline (including two novel preprocessing approaches). Finally, we propose a HR pipeline designed specifically to deal with longform and noisy recordings.
2.1. Datasets
Three infant ECG datasets (Table 1) were used to develop the pipeline and test the existing approaches. Datasets A, B, and C were all captured using different devices with different sampling rates in different environments. Dataset A and B are characterised by relatively low levels of noise and will be used to evaluate the ECG pipeline and initial HR processing. Some of the recordings in Dataset A have gaps in recording due to Bluetooth dropout from the BiosignalPlux device (a subset of the recordings in Dataset A were the object of analyses in our previous work [12]). Dataset C contains the noisiest ECG (including areas of non-signal) and will be used for HR quality analysis. Further details on these datasets can be found in the Appendix B. The distribution of recording time and ages for each dataset is illustrated in Figure 3.
A consistent issue across datasets was the range of ECG morphologies detected, such as double R-peaks and distorted T-waves. As infants are much smaller and less compliant than adults, ECG devices were often placed at a range of angles, and occasionally upside-down, therefore ECGs had to be evaluated individually to determine if the signal was inverted. The devices used often had very narrow electrodes, which made a traditional ECG notation (e.g., 12 lead analysis) difficult to apply.
All datasets were recorded from subjects recruited from urban areas in the North-East of England. Families received remuneration commensurate with the specific study they were involved in and an age-appropriate book as a token of participation. The research procedures were approved by the Ethic Committee of the Department of Psychology at University of York. Participants’ caregivers signed an informed consent prior to the beginning of the research procedure.
2.2. The ECG Pipeline
The main focus of the ECG pipelines analysed here is to accurately extract a set of R-peak locations from an ECG signal, identifying the peak within QRS complexes (known as peak detection). Some pipelines may also search for other ECG complexes, which will not be analysed here. A pipeline typically starts with preprocessing, a mathematical manipulation of the ECG signal to allow the QRS complex to be more easily identifiable.
Once the signal has gone through preprocessing, the resulting preprocessed ECG will contain R-peak locations that differ slightly from the raw ECG, due to the mathematical operations that occur during preprocessing. In order to readjust the peaks back to the original location on the raw ECG (i.e., the R-peak location on the raw ECG, rather than the R-peak location on the preprocessed ECG), we are introducing a “local peak correction” operation. Additionally, we introduce a square-wave specific filter for those devices where it is appropriate.
2.2.1. Existing ECG Approaches
Firstly, 12 open-source pre-existing ECG methods (Table 2) were applied to Datasets A and B. These approaches represent the available open-source methods for R-peak extraction. Three separate Python packages that contain all or a subset of these methods were initially considered - HeartPy, Neurokit2, and py-ecg-detectors. However, all ECG methods in py-ecg-detectors were found to contain matching implementations in Neurokit2, without the flexibility to implement preprocessing and peak-detection of a method separately. This reduced the selection of ECG methods to those found in the HeartPy and Neurokit2 packages - the default HeartPy method, and 11 other approaches from the Neurokit2 package (including the default Neurokit2 approach). The open-source nature of the Neurokit2 means that some methods may match more closely than others to the authors’ original intentions. For example, the method by Gamboa [33] did not appear to work at all, which is unlikely to match the original author’s intentions. As such, this analysis is strictly representative of the implementation of these methods in readily available open-source Python software. It is acknowledged that proprietary measures for measuring infant ECG may well exist as part of commercial innovation and research.
The specificity, sensitivity and Positive Predictive Value (PPV) of the methods were then compared against a ground truth set of labels (Figure 4 and Figure 5). Specificity penalises incorrect peak selection, and PPV identifies the ratio of correctly identified peaks out of all peaks identified for a given method. Given the sparsity of peaks within a signal, both measures tend to be preferable due to their inclusion of False Positives within the denominator. The sensitivity is also important but can be falsely inflated by a method identifying many false peaks, and so must be considered in the context of the other two metrics. These methods all require precise detection of peak location.
Specificity = (True Negatives) / (True Negatives + False Positives)
Sensitivity = (True Positives) / (True Positives + False Negatives)
Positive Predictive Value = (True Positives) / (True Positives + False Positives)
The distributions of results are shown in violin plots, with black dots representing each individual result. The median and interquartile ranges (IQR) are also shown as dotted lines. Collectively, this visualisation allows for evaluation of both the summative statistics and the general metric distribution. In cases where results of some methods fell far beyond the range of the best performing methods, visualisations have been truncated to preserve a clearer comparison between the core performances. For each method their conventional preprocessing has been applied, although local peak correction was used after labelling to allow fair comparison between the different methods. The datasets used are Datasets A & B, which are both clean enough to have a reliable ground truth. A visualisation of the algorithmically-labelled peaks by different methods in sample infant ECG without local peak correction is shown in Figure 6, with the labels shown on both the preprocessed ECG.
The range of successes that different current methods have for dealing with infant ECG are shown for Dataset A (Figure 4) and Dataset B (Figure 5). The Figure 6 visualisation shows the effect of different preprocessing methods on the raw heart rate, and that some approaches label other complexes in the ECG instead of the QRS.
The inbuilt methods for both packages [23,28] outperformed the implementation of all other pre-existing methods, with the Neurokit2 method performing best overall. This is true both when considering their respective full distribution, median and interquartile ranges (IQR). Out of the remaining methods, Martínez et al.’s wavelet-based method [24] and Rodrigues et al.’s approach [27] were 3rd and 4th best. Martinez had good specificity and fairly good PPV but worse sensitivity, indicating the peaks that were detected were accurate, but many peaks were missing. Rodrigues was able to adapt better than most methods to the fast heart rate and noisy signals, but still had some worst-case subjects that it was unable to adapt to, especially in Dataset B.
Nabian et al.’s method [25] appeared 5th-best overall, narrowly outperforming the sensitivity of the Martinez method for Dataset A but had more results with poorer for specificity and PPV. Zong’s approach [29] did next best for Dataset A but fell apart completely on Dataset B. Engelse and Zeelenberg’s method [23,26] had a low false peaks detection rate, but also did not detect enough of the true peaks for accurate HR calculation. Christov’s method [20] seemed to work well with some of the signals but would need altering of its internal threshold factors to properly adapt to children’s ECG.
All other approaches tested [21,26,30,32] did not perform well with the datasets and had lower median specificity/sensitivity/PPV values than the other methods. They would likely need some fundamental changes to be suited to the ECG of a young child, as many of these methods contained time constraints which work very well for adults but were too rigid for the faster heart rate of a child, falsely rejecting too many R-peaks or identifying other complexes in the ECG over the QRS complex.
2.2.2. Proposed ECG Preprocessing
We developed two separate preprocessing approaches by adapting the best performing pre-existing approach (Neurokit2). These two approaches were a frequency-preprocessing approach and an Empirical Mode Decomposition (EMD) approach, which are both then tested and compared against the existing approaches. The frequency-based approach applies filters that attenuate the energy of a signal occurring at a given frequency. Low-pass filters remove high-frequency detail, only allowing smooth changes in the signal to pass through. High-pass filters (HPF) do the opposite, removing smooth signal trends to leave more rapidly altering complexes in the signal. Bandpass filters (BPF) remove some of the high frequency and low frequency information, whereas notch filters only remove signal energy at a given frequency. One problem with frequency filters is that they do not discriminate between two separate signal sources that share a frequency band. EMD is an adaptive technique that decomposes the signal into Intrinsic Mode Functions (IMFs) - characteristic signals that can have overlapping frequency information [40]. If noise or non-QRS complexes can be completely captured in an IMF, they can be removed without affecting the QRS. This same logic can also be applied to wavelet filtering [34,41,42].
A recent study [43] found that a 0.05-150Hz BPF preprocessing approach outperformed a 1-17Hz BPF approach on a study investigating peak detection in children - but the study only tested those two specific filters. As such, it was considered worth evaluating a range of 5th-order Butterworth BPFs and HPFs applied before R-peak detection.
We chose the Neurokit2 algorithm for peak detection due to its high performance across all categories (see Figure 4 and Figure 5) as well as the simplicity of the initial baseline Neurokit2 preprocessing (a 0.5Hz HPF with a 50Hz band stop filter). A variety of different frequency filters were applied in addition to the standard Neurokit2 preprocessing to determine the best frequency-preprocessing approach. Dataset A and Dataset B were both used to test the frequency ranges (Figure 7). An upper frequency bound of 20, 30, 50, 100, and “None” was used (with the “None” option indicating no upper bound, i.e., an HPF). A range of lower bounds were also tested, with 0.5, 2, 5, 8, 10, 15, and 20Hz lower bounds shown in Figure 7. In general, the high pass filters had better median specificity/sensitivity/PPV than the bandpass filters, as well as overall improved distributions. However, the improvement in results is marginal when compared to the 50Hz/100Hz upper bounds. For Dataset A, the 15Hz HPF approach was marginally better than similar filter approaches when considering median and IQR, although an upper bound of 50Hz and any lower bound between 8-20Hz produce fairly similar results. For Dataset B, the lower IQR had perfect specificity, sensitivity, and PPV for 5-15Hz HPF, with the only distinguishing factor being how well the worst-case results were processed. However, the 20Hz HPF results were a lot worse for Dataset B.
During the assessment of the ECG preprocessing options, elevated T-waves were observed in some of the subjects in the recordings. T-waves typically overlap in frequency with QRS waves [44], which can cause some problems in R-peak detection. An approach using EMD could remove the T-waves while preserving the QRS complex. Here, we remove any signals with >50% of the signal power between 0.5-8Hz, given that T-wave content is reported to lie in the 0-10Hz range [44], and the QRS is reported to lie in the 8-20Hz range [21]. The EMD approach is also used with standard Neurokit2 preprocessing and peak detection.
A comparison between the proposed 15Hz HPF filter and the EMD approach with the best-performing pre-existing approaches is shown in Figure 8 (Dataset A) and Figure 9 (Dataset B). The HeartPy, Neurokit2, Martinez and Rodrigues results display the same characteristics as in Figure 4 and Figure 5. The 15Hz HPF approach improves on the EMD and all pre-existing methods in terms of worst-case labelling and median, IQR statistics for Dataset A. Specifically, the 15Hz HPF median specificity, sensitivity, and PPV (0.999989, 0.9958, 0.9975) outperformed the median results of all other methods, the closest pre-existing method being Neurokit2 (0.999975, 0.9863, 0.9938). If we interpret these median results on the average signal length (30.5 minutes, 4180 peaks), it would mean: 13 fewer peaks labelled incorrectly (10 vs 23), 39 fewer peaks missed (18 vs 57) and only 0.25% of peaks that were identified were labelled incorrectly (vs 0.72% for Neurokit2). While the EMD approach does improve on the other pre-existing approaches, for Dataset A, for Dataset B, the EMD approach performs much worse overall, with a few worst-case labels performing very poorly.
Average heart rate varies as a function of age [15], so a sub-analysis visualizing the performance of the methods at different age boundaries on Dataset A was also carried out (Figure 10). Age-divisions were chosen as a balance between keeping a large enough cohort size for valid analysis, and to recognise natural groupings that arose within the datasets (see Figure 3). Dataset B age-based analysis contained far fewer participants, especially when split into cohorts, and is included in Appendix C for completeness. The results for 15Hz HPF on Dataset A were worst in the 8-10 month range, but still outperformed all other methods at all age ranges (Figure 10).
2.2.3. ECG Peak Detection
R-peak detection is the process by which an algorithm finds the R-peak within the QRS complex, for all QRS complexes in an ECG signal. By testing all the pre-existing methods, it was clear that Neurokit2 was one of the best suited to these datasets (Figure 4 and Figure 5) and works well with the proposed preprocessing approaches of 15Hz HPF or EMD filtering (Figure 7 and Figure 8). The Neurokit2 peak detection is used in the proposed ECG pipeline without alteration in this specific step.
2.2.4. Local Peak Correction
Stronger frequency filtering applied during the preprocessing step has a stronger impact on peak location, shifting R peaks (and other peaks) in the ECG (see Figure 6). To counteract the shifting-peaks effects, we implemented a novel local correction relative to the unfiltered signal. This correction iteratively searches for the largest peak ± 0.01s either side of the peak location on the processed ECG to check for a larger local peak within the raw unprocessed ECG, until no larger peak is found within the search limit. To distinguish this technique from “peak detection”, it will be referred to as “peak correction”. This peak correction only has a small impact on peak location but preserves variation between peaks and allows for more accurate comparison of specificity/sensitivity/positive predictive value measures (see Appendix D). In instances where multiple indices could be labelled for a given peak, the closest peak to the preprocessed ECG was used (see Appendix E).
It was also observed that the first and last beat of an ECG were liable to be missed under certain methods. This was addressed by a one-second artificial extension of the signal at the start and the end. The first/last values of the preprocessed ECG were as used as the constant value for the extensions at each end. While this will only have a small impact for long recordings, it could be very impactful for shorter recordings.
2.2.5. Square Wave Peak Correction
While filter-based preprocessing will deal with many sources of noise, any periodic non-ECG signal is likely to be preserved with the frequency-processing and EMD methods. Square waves were occasionally observed when recording was started prior to attaching the device to a subject. The nature of square waves is very likely dependent on the device, and square wave removal is highly recommended in these recordings. For the EgoActive device responsible for Dataset C, a median filter with a 101-sample width was used to exclude blocks of signal that were within 0.5% of a local maximum/minimum. The precise filter width and max/min margin will depend on the gain and sampling rate of the device used. This correction was applied post peak detection, to remove any peaks deemed to occur during these periods. Square wave correction was not required for Datasets A and B.
2.3. The HR Pipeline
2.3.1. Calculate Raw Heart Rate
Once a set of R-peaks is detected, the heart rate can be calculated as described by Equation 1. This is an instantaneous heart rate calculation reflecting beat-to-beat changes. For some research questions, an average heart rate (collected over a few beats) will be preferred and will likely reduce the impact of noise in the calculation. Here, only instantaneous heart rate is considered. Even with good R-peak detection methods, a peak can be missed, or a non-R-peak can be incorrectly labelled. This will lead to an erroneous heart rate measurement, which can be detected through filtering.
2.3.2. Correction for Missing and Additional Beats
A missing R-peak will cause two true measurements to be replaced by a single false measurement of approximately half value (Figure 11a), while an additional peak will cause one true measurement to be replaced by two roughly double false measurements (Figure 11b), although the proximity of the additional peak to existing peaks will alter the amplification ratio of the subsequent heart rate.
To detect beats which vary above/below a local median by more than a given proportional threshold, we used a median filter. The effects of the specific filter width and threshold are illustrated in Figure 12. The identified incorrect measurements are removed, and then estimated by local linear interpolation. If precise beat-to-beat comparisons are not required, a more liberal threshold over a wider beat-window can robustly account for noise. The first evaluation (Figure 12a) examines a clean ECG against a ground truth, and only deals with missing beats. The second evaluation (Figure 12b) compares the residual heart rate from a filter applied to the output of the ECG pipeline against a ground truth and represents the approach that should be taken with a less clean initial ECG.
Two metrics are used to ascertain the ideal filter width and proportional threshold for HR processing. The first metric is used to evaluate the median approach applied to a clean set of R-peak labels that only contains a few errors. The second metric is used to evaluate the median approach applied to a realistically processed ECG.
Dataset A (N=97) was captured using a BiosignalPlux device that recorded the ECG through Bluetooth. Across the 97 recordings, occasional disconnections would occur, leading to gaps in signal (23 in total). Additionally, the noise arising from infant motion would also lead to small periods where no QRS complex could be identified (323). These gaps in the ground truth R-peak list result in drops in the derived HR signal. The optimal median filter approach will identify these gaps, without removing any real signal. The expected number of gaps to interpolate over is recorded for each participant. The absolute difference between interpolations made by the filter and the expected number of interpolations is used to evaluate the optimal parameters for a clean environment. Figure 12a shows the variation in these results with different parameter choices.
Next, the output from the proposed ECG pipeline (15Hz HPF preprocessing, Neurokit2 peak detection) is used to represent a realistically preprocessed signal. The residual heart rate between the median-filtered ECG and a ground truth (with gaps interpolated over) is used to demonstrate the optimal parameters from a noisier baseline (Figure 12b).
For the clean ECG test (Figure 12a), a high activation threshold (e.g., 1.7 or 1.8) combined with a narrow filter width (e.g., 7-21) produced a very low number of incorrect adjustments (<3% compared to total number of adjustments, or <0.0015% compared to every potential adjustment e.g., every single heart rate beat). Almost all these incorrect adjustments were due to arrhythmias in the heart rate, causing a longer than expected gap between detected beats. A very conservative threshold combined with very few beats needed to accurately determine the incorrect label makes sense given the cleanness of the ground truth. For the test with the processed ECG (Figure 12b), a much more liberal activation threshold (e.g., 1.2 or 1.3) with a much wider filter width (15-31) provided the optimal parameters for reducing the heart rate residual with this dataset. This accounts for the higher level of uncertainty in underlying truth in the processed heart rate.
2.3.3. Correction for Shifted Beats
Wrongly located R-peaks can remain undetected by the median filter approach described above. A useful observation is that an early-labelled beat will lead to a much greater heart rate rise followed by a much steeper heart rate drop than would typically appear within a natural signal (Figure 11c). A late-labelled beat will do the opposite. The proposed algorithm searches for the presence of three consecutive sign changes concurrently with a large variation in the heart rate difference (>15bpm for the first and third heart rate gaps, >25bpm for the middle gap), thus identifying the mislabelled beats within a signal, provided the neighbouring beats are correct. Areas with large amounts of mislabelled beats are likely to be caught by the algorithm for missing/additional beats and are likely one reason for the more conservative thresholds present in the processed HR tests.
2.3.4. Signal Quality Index Calculation
In addition to developing methods to correct R-peak labels for longform infant ECG, it is important to identify time periods that have many (consecutive) incorrect labels due to noisy measurements. Local linear interpolation will be unable to accurately reflect the underlying HR for these periods, and so they may need to be excluded from further data analyses. Thus, we developed an algorithm optimized for longform infant ECG to help identify regions in which a data recovery approach is inadvisable.
Pre-existing methods for HR quality assessment were not found to be suitable for long heart rates. Kramer et al. [45] use non-stationary signal, viable heart-rate range, and high signal-to-noise ratio (SNR), but require the signal to be rejected/accepted in full. Rodrigues et al. [17] extracted shapes and behaviours of the signal to group ECG samples by an agglomerative clustering approach, an approach that becomes computationally inefficient for longer recordings. It is also worth noting that many ECG methods implicitly try to reject areas of high noise directly in the ECG [46], with the HeartPy method [28] able to explicitly reject peaks which create a beat interval >30% above or below of the mean interval time of the whole signal. Additionally, Zhao & Zhang [47] proposed a noise detection algorithm based on agreement from different ECG algorithms. However, given the results in this paper showing the poor performance of most algorithms on infant ECG (see Figure 4 and Figure 5), this approach was not explored here.
The beat correction algorithm for missed/additional beats was used as a baseline measure of signal quality, with additional steps added to fine-tune the quality algorithm further. Figure 2 highlights that correctly labelled R-peaks will typically fall inside the expected bounds, whereas incorrectly labelled R-peaks are likely going to either cause a steep decrease or increase in heart rate (for missing or additional labels, respectively). By calculating the proportion of “wrong” labels within a given filter width, a rolling measure of heart rate signal quality is calculated. If a small number of incorrect labels are present, a close approximation to the original heart rate can be recovered. If many measurements are incorrect, then the heart rate cannot be reliably approximated. A filter width of 31 and an adaptive threshold of 1.3 was used (Figure 12b).
A moving-median approach was used to create the base of a binary Signal Quality Index (SQI) vector [12]. At each time point (i.e., heartbeat measurement), the percentage of local beats within the filter width that deviated by a multiplicative factor of 1.3 above or below the local median was calculated (i.e., the local median indicates the existence of poor signal within the sliding window, and for a median HR of 100bpm the proportion of beats outside 77-130bpm was calculated). If the percentage of poor beats was ≤25%, then SQI=1 (high signal quality) at that time point. Otherwise, SQI=0 (low signal quality). The sliding window was then moved to the next time point.
To make the SQI more accurate, additional manipulations were used to account for the specific location of the high-deviation beats. First, the regions of good SQI were then extended (i.e., set to SQI=1) according to whether the beats just beyond the boundary of the good SQI region were within the local median range. Second, continuous regions >3.5s long of high-deviation beats (>1.3 beats from local median) were set to SQI=0, as were any gaps in heart rate longer than 2.5s. Lastly, any remaining good regions <5s long were set to SQI=0, to leave regions of a reasonable size. These parameters could be tailored depending on the length of the useful heart rate region for a given research question, and how precise a heart rate is required to be.
The Boolean SQI vector can then be applied to the heart rate to either set areas of bad signal to 0bpm, or to cut those regions from the signal.
2.3.5. SQI-Filtered Heart Rate
The SQI-step of the pipeline was evaluated using the specificity and sensitivity metrics (Equations (2) and (3)) applied to Dataset C, a very longform dataset (length ≥ 50 minutes) captured outside of a lab environment, taken at 250Hz. These factors combined to give high levels of noise in the dataset, while still being clean enough to have areas of signal that should be preserved. A set of filtering parameters that minimised the residual error in the processed HR (AT: 1.3, FW: 31) were used as the base for the SQI algorithm (Figure 12B). An example visualisation of the SQI algorithm applied to a noisy HR is shown in Figure 13, with the results of the analysis shown in Figure 14.
As seen in Figure 13, the SQI algorithm is not designed to label HR as poor when only individual beats are missing. However, when multiple peaks are missing and the underlying median filter is more unreliable, the HR is designed to be labelled as not usable. Figure 14 shows the general success rate of the SQI algorithm when applied to noisy datasets. Overall, the SQI has a high true positive rate, meaning almost no clean signal is excluded from the recording. The SQI does have a higher false positive rate for some of the recordings, meaning some noisy signal may make it into the final analysis, which may require these recordings to be excluded. However, this does represent a significant improvement over the baseline of including all HR signal and is also shown to work very well for the cleaner signals (top left of Figure 14).
2.3.6. Cleaned and Filtered Heart Rate
The end result is a heart rate signal that has been corrected in areas of small mislabelling, and is discounted in areas of large noise where the signal is unrecoverable.
3. Discussion
Until now, there has been limited freely available research on ECG R-peak detection methods which are adequate for infants. In this paper, existing open-source ECG methods were tested on infant datasets acquired in a range of conditions (including naturalistic conditions), and the best performing method was adapted into a high-performing novel pipeline that contains all necessary steps from raw ECG preprocessing to HR calculation. Our proposed approach includes alterations to the preprocessing and local peak correction steps, explicitly outlying a guide for when to interpolate missing/additional beats, and introduces an SQI vector designed to detect unreliable areas of HR measurements that can be adapted around for further data analysis steps. This is particularly relevant for real-world large data sets collected in the natural environment, where manual rejection of unreliable areas of HR measurements would not be feasible.
Both the HeartPy and Neurokit2 packages are highly useful open-source scientific tools that collectively provide a wide range of options for ECG analysis. They both provide a wide range of functionality beyond R-peak detection in ECG, although that is all that is focussed on here. It is worth acknowledging that there are many methods that exist outside of the open-source domain which are not evaluated here. While many of the methods in Neurokit2 were open source originally some were written in different languages and have had to be adapted into Python, with both the translation issues and the inherent nature of open-source collaborative approaches meaning that some imperfections in implementation can arise. The analysis in this paper focuses on the available open-source implementation of these methods, rather than necessarily the methods themselves.
The HeartPy, and Neurokit2 default show the best results with Dataset A and Dataset B overall, with both performing particularly well on Dataset B. The Rodrigues method performed well on Dataset A, and Martinez shows good specificity and a reasonably good PPV IQR on Dataset A and a good overall performance on Dataset B. All four approaches were quick to run and had ECGs that they labelled to a very high standard, although all of them also had ECGs that were not labelled as accurately as our proposed pipeline later managed.
The inbuilt Neurokit2 method was chosen as a candidate for further fine tuning due to the high performance and simple initial preprocessing. Many existing methods contain several hard-coded parameters that have been developed to work with adult ECGs. Neurokit2’s inbuilt method only used a notch filter tuned at mains frequency and a fairly unrestrictive high-pass filter of 0.5Hz. The Neurokit2 preprocessing was applied before all frequency-processing testing, but the specific notch filter could be altered depending on the ECG device and the 0.5Hz HPF could also be removed given that a stronger HPF is likely to be optimal for infant ECG.
In developing a new pipeline, it was found that a 15Hz high-pass filter provided an approximate best filter for infant ECG preprocessing (Figure 7), which is very different to the 8-20Hz BPF commonly suggested for preprocessing in adults [21]. This held for two different devices with different amounts of subject motion and different sampling rates (Figure 8 and Figure 9). It also improved on other methods at a range of age ranges (Figure 10). While the specific bands were slightly different for the two datasets (e.g., a 20Hz HPF worked well for Dataset A but not Dataset B), the 15Hz HPF fell within a good range both times. This gives us confidence that it is a more robust methodology for infants. It would be interesting for a future study to test the age range at which the optimal HPF begins to drop for older children. The precise frequency bounds used could vary slightly depending on the specific device used and sample population. These results indicate that any upper bound of 50Hz or higher and any lower bound of 8-15Hz appear to have very similar levels of performance across both tested datasets.
The proposed EMD preprocessing approach improved the default Neurokit2 method slightly in Dataset A but did not out-perform the optimal frequency-processing filter. In Dataset B there were a few worst-case scenarios that caused the EMD approach to have low specificity and PPV. Additionally, there is a dramatically increased run-time when applying EMD processing. As such, it is not recommended to use this approach.
One section of major contribution that the new pipeline brings is the novel local peak correction. The 0.01s threshold was determined heuristically to balance overcoming high frequency noise while minimising false peak detection. This allows for much heavier filtering without compromising on the R-peak label locations, as well as comparative analysis between R-peak detection for the different methods. The start/end peak detection had a very minimal reactive effect, and the start/end of ECGs are often discarded. However, in pure detection terms, it was found to improve all the open-source algorithms evaluated here at very little computational cost, and so is recommended for future inclusion. The square wave filtering was very device-specific, as two thirds of the devices detected did not tend to exhibit square wave noise, and so square wave filtering would only succeed in subtracting noise from the signal. However, for the device that did exhibit square wave noise, it greatly improved detection.
Where either precise beat detection is required or a heart is suspected to contain arrhythmias, the heart rate filtering proposed here may not be appropriate. However, it was found to do a good job at preserving the overall shape of the heart rate, and subsequently serve as a good way to detect noisy periods when also combined with the SQI. It was found that a much more conservative activation threshold (1.7/1.8) and thinner width of median filter (7-15) were optimal for cleaner ECGs, but that more liberal thresholds (1.2/1.3) and wider filters (15-31) would produce lower residual heart rates when applied to the detected heart rate (Figure 12). While it is recommended to view some raw ECG along with the processed heart rate to ascertain the underlying level of noise, a choice of 1.7/11 or 1.3/31 activation threshold/filter width for cleaner and noisier signals respectively can serve as a fair initial parameter choice (with the former being recommended for short lab-based ECGs with no motion, and the latter being recommended for any other forms of ECG).
Neither Dataset A nor B were sufficiently noisy to test the SQI analysis properly. As such, Dataset C was the only one used for this purpose. The sensor used for Dataset C was the EgoActive sensor, a lightweight wearable device designed for much longer recordings in the natural environment, while being as unobtrusive as possible to the child to ensure comfort and allow free moving. The lower ECG sampling rate was chosen to maximise the duration of a continuous recording [12]. The SQI approach to determine noisy periods of HR serves as a good first step towards a robust noise-detection algorithm. The SQI-mediated HR allows for the analysis of long recordings, which can contain large amounts of noise. While the SQI method serves as a good automatic way to identify unreliable heart rate calculations, the specific parameters used will depend on the research question. For example, more noise-averse analysis such as standard-deviation based HRV require stricter noise thresholds. Analysis concerned with general HR rises/falls or average HRs can use a looser threshold to capture more data. The SQI calculation did work very well on recordings with easily discernible noise, being particularly good at separating non-HR periods from HR periods but struggling a bit more with noisy HR vs clean HR. Understanding and automatically detecting which types of noise cause poorer performance could make it more robust in future. The specific parameters used in the SQI are dependent on how much noise is tolerable for a given research problem, meaning it will likely have to be double-checked if parameters are altered.
The proposed pipeline was very computationally efficient. The ECG pipeline was applied to all of Dataset A (N=97, sampling rate=500Hz, Mrecording=32 minutes, 94,089,683 data points) and took 111.33s in total (1.15s per ECG). The total preprocessing and peak labelling time was 20.75s (0.21s per ECG) and the local peak correction took 90.59s (0.93s per ECG). The HR pipeline is also computationally efficient, as a combination of median filters and difference functions provide the backbone for both the SQI and the beat-cleaning algorithms. By applying the SQI to the heart rate, the size of the vectors processed are greatly reduced compared to an ECG (1-3Hz sample density for HR compared to 250-1000Hz for ECG). An N=63 set of noisy HR signals collectively covering 92 hours (comprising 559,612 beats in total) took only 6.68s total processing time. This includes both the time to filter the heart rate with a moving-median filter, and create the SQI vector. All calculations were done consecutively using an 11th Gen Intel(R) Core (TM) i5-1145G7 @ 2.60GHz, and do not include the loading times required to import the data into Python initially.
Future Research
Since adaptations are shown to improve the Neurokit2 pipeline, it is very possible that other methods could also be adapted to process infant ECG. Some exploratory analysis on the HeartPy and Pan-Tompkins methods was carried out and was not initially encouraging (though was not in depth enough to draw concrete conclusions). Additionally, while the computational inefficiency of the EMD approach was a concern for longform ECGs, many studies focus on shorter infant ECG signals where processing time will be less of a factor. Given the strong performance of the approach on Dataset A, it is very possible that small alterations to the EMD methodology (such as the criteria for IMF rejection) could prove to be a positive avenue for future research.
The datasets captured here lay the grounding for a future infant-specific approach for the R peaks, especially for machine-learning approaches. Additionally, there could also be great future use in infant-specific analysis of the remaining ECG morphology.
Finally, sensor orientation and position, particularly for small wearable sensors, can have a big impact on different infant ECG complexes. A general analysis creating a consistent set of guidelines for wearable infant ECG could prove of great use to the scientific community, as could further validation of different aspects of this pipeline on data collected at specific sensor orientations and positions.
4. Conclusions
In this work, we evaluate existing open-source ECG pipelines on longform infant datasets, before improving on the state-of-the art approach to develop our own pipeline. We also develop a HR pipeline to clean up the signal and identify areas which are too noisy to process. Collectively, these form a full, computationally efficient pipeline to turn raw infant ECG signals into cleaned and processed HR signals. This process is designed to even work on naturalistic recordings, although it also outperforms existing methods in short lab-based recordings of infants as well.
Author Contributions
Conceptualization, H.T.M., E.G., M.I.K., S.S.; methodology, H.T.M., E.G., M.I.K., S.S., Q.C.V.; software, H.T.M.; validation, H.T.M., A.P.M.-C., M.C.G.-d-S.; formal analysis, H.T.M.; investigation, A.P.M.-C., M.C.G.-d-S., E.G.; resources, E.G., S.S.; data curation, H.T.M., A.P.M.-C., M.C.G.-d-S., E.G; writing—original draft preparation, H.T.M., E.G., M.I.K., Q.C.V.; writing—review and editing, all authors; visualization, H.T.M.; supervision, E.G., M.I.K., Q.C.V., S.S.; project administration, E.G..; funding acquisition, E.G., M.I.K., Q.C.V., All authors have read and agreed to the published version of the manuscript.
Funding
This work presented in this manuscript received funding from the Wellcome Leap, the 1 kD Program.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Ethics Committee of the Department of Psychology, University of York, for studies involving humans.
Informed Consent Statement
Informed consent was obtained from all subjects involved in this study.
Data Availability Statement
All data and software will be made available upon reasonable request sent to Elena Geangu (elena.geangu@york.ac.uk).
Acknowledgments
We would like to express our gratitude to all families who dedicated their time to donate data in the study. The authors would also like to thank Nicoleta Gavrila, Lauren Charters, Aastha Mishra, Emily Clayton, and Brigita Ceponyte for additional help in data collection, and David Mullineaux for help in verifying the code used in the project.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
-
The following additional resources will be made available to researchers upon request:
- a
- Datasets A, B, and C, with each file including
- b
- Raw ECG
- c
- ECG timeseries corresponding to a.
- d
- Labelled true R-Peaks indices (datasets A and B only)
- e
- Detected R-Peaks indices from our 15Hz HPF pipeline, post correction
- f
- Raw HR generated from d.
- g
- HR timeseries corresponding to e.
- h
- Moving-median-filtered HR example
- i
- HR SQI (Dataset C only)
- j
- Labelled SQI truth (Dataset C only)
- Python source code for applying the entire ECG and HR pipeline to raw ECG signal
Appendix B. Further Dataset Information
Dataset A served as the main dataset to develop the ECG-processing and early HR-processing section of the pipeline (everything except HR signal quality). It comprised 97 separate ECG signals of children aged 3-42 months (total recording time: 52 hours 20 minutes, Mduration: 32 minutes, min: 11 minutes, max: 52 minutes, distribution of age and recording duration shown in Figure 3A). ECGs in Dataset A were collected using a BiosensorPlux device (PLUX Biosignals, Lisbon, Portugal) with a sampling rate of 500Hz. ECGs were trimmed at the start and end prior to any analysis to exclude any non-recording period (e.g. the trimmed periods are not included in the recording times above). There are 23 recording gaps in total in the dataset due to Bluetooth dropout from the BiosignalsPlux device. These recordings occurred while infants engaged in free-play in a semi naturalistic setting in a lab (i.e., play room).
In Dataset A R-peaks were hand-labelled, and any R-peaks where the ground truth was difficult to ascertain due to signal morphology or noise levels were counted for all ECGs. ECGs with a more than 1 uncertain peak in 400 were excluded from the analysis, leaving 97 ECGs. Note that due to the exclusion criteria allowing for some level of peak-labelling uncertainty, this will follow through into some uncertainty in the subsequent metrics calculated. The worst case and average uncertainties for each subject in Dataset A were as follows. Specificity: worst case=-1.12x10-5, mean=-3.03x10-6. Sensitivity: worst case=-2.44x10-3, mean=-7.02x10-4. PPV: worst case=-2.43x10-3, mean=-7.01x10-4. These values are sufficiently small (even assuming the worst case error for each individual subject in the dataset) that they do not affect any final conclusions drawn.
Dataset B serves as a validation set by using a different sampling rate and sensor. Dataset B comprises 25 ECG signals from 19 infants aged 5-13 months (the ECGs from the 6 infants who supplied two recordings were taken at least 2 months apart). The total recording time was 3 hours 34 minutes (Mduration: 8min 36s, min: 4min 50s, max: 17min 31s), distribution of age and recording duration shown in Figure 3B). This dataset has higher signal quality than Dataset A (higher sampling frequency, less noise, shorter duration), but is a smaller dataset. The ECGs were collected across 19 subjects, with 6 subjects providing double recordings taken at least 2 months apart. ECGs were collected using a Physio16 box for the Geodesic EEG System (GES) 400 device with a sampling rate of 1000Hz. ECGs were trimmed at the start and end to exclude any non-recording period. These recordings occurred in a lab, and the infant remained mostly stationary throughout. There are a maximum of 2 uncertain peak labels in a subject (and only 4 uncertain labels across all subjects), which has a vanishingly minimal effect on subsequent calculations.
Dataset C served as a test set for the HR signal quality. 12 ECGs with a longer recording time and lower sampling rate (250Hz) were gathered using the EgoActive body sensor [12], and were deliberately selected for a high noise level from a larger selection of recordings. Children in these recordings were between 5-11 months (see Figure 3C). These 12 naturalistic recordings were taken from a larger dataset recorded in the subject’s home, with the device often containing periods of high movement and also being left on post-recording. Quality labelling was done on a beat–by-beat basis on the calculated HR signal. Any areas of “good” signal shorter than 5s was marked as bad, to ensure a minimum length of heart rate. Mduration=90 minutes long for the total signal lengths (min: 55 mins, max: 120 minutes), or Mduration=79 minutes when accounting for non-signal at the start and end of the recording (min: 50 mins, max: 112 mins). The latter value is the one shown in Table 1. ECGs were lightly trimmed to avoid processing >2 hours of signal, but aimed to include both HR and non-HR portions of signal where possible.
Appendix C. Age-Based Analysis for Dataset B
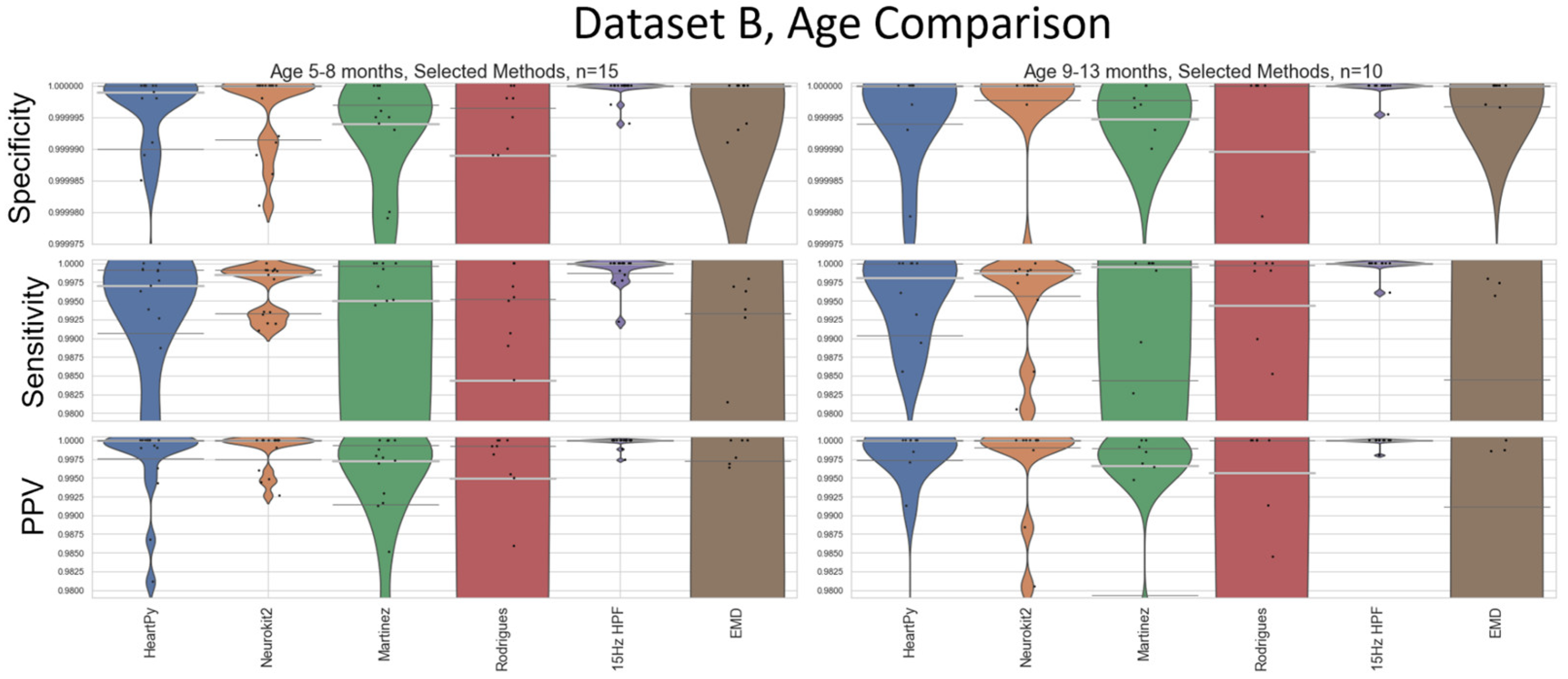
The smaller dataset size of Dataset B (N=25) compared to Dataset A (N=97) made any sub-analysis less reliable, as fewer outlier results are needed to sway the median and IQRs. While acknowledging the reduced statistical power, it is worth noting that the 15Hz HPF approach proposed by our pipeline did still outperform all other methods after the age-breakdown was applied, with the IQR and medians still indicating perfect specificity/sensitivity/PPV in all cases except the lower IQR value for sensitivity in the 5-8 months cohort (Figure A1). The HeartPy and Neurokit2 default methods both had very good median specificity/PPV and reasonably good median sensitivity. There were enough results in the cohorts to start to distinguish the general trends of the methods, and no results were recorded to counteract the main age-related conclusions drawn in Figure 9 (while accounting for the different overall performances of the different methods between Datasets A and B).
Figure A1.
An age-based breakdown of Figure 9. A different age bracket is shown in each quadrant. The median is shown as a thick, light grey bar, and the IQR is shown as thin dark grey bars. Each black dot represents one result.
Figure A1.
An age-based breakdown of Figure 9. A different age bracket is shown in each quadrant. The median is shown as a thick, light grey bar, and the IQR is shown as thin dark grey bars. Each black dot represents one result.
Appendix D. Results without Local Peak Correction
In many of the results in the main text, local peak correction was used to realign the R peak labelled on a preprocessed ECG with the R peak on the original unprocessed ECG. Prior to developing this methodology, either each method would have to be labelled by hand, or allowing peaks within a margin of error (e.g. 0.01s either side of the true label) would have to be used. Naive uses of specificity/sensitivity/PPV analysis without local corrections of error margins is shown in Figure A2 and Figure A3 for Datasets A and B respectively. The improvement shown by using local correction is shown in Figure A4 and Figure A5 (relative to Figure 4 and Figure 5). The Local Peak Correction improved the Sensitivity and PPV for all methods, showing an improvement in the ratio of True Positives to both False Negatives and False Positives. The EngZee method performed the best without this correction, likely due to the very minimal preprocessing required by the approach. Interestingly, the specificity did drop slightly for Pan-Tompkins, Hamilton, Christov and Rodrigues, and more dramatically for Kalidas and Elgendi. This could be due to the reduced number of True Negatives and/or an increase in the number of False Positives (see Equation (2)).
Figure A2.
Violin plots showing the specificity, sensitivity, and positive predictive values for the pre-existing ECG approaches applied to Dataset A, with no local peak correction.
Figure A2.
Violin plots showing the specificity, sensitivity, and positive predictive values for the pre-existing ECG approaches applied to Dataset A, with no local peak correction.
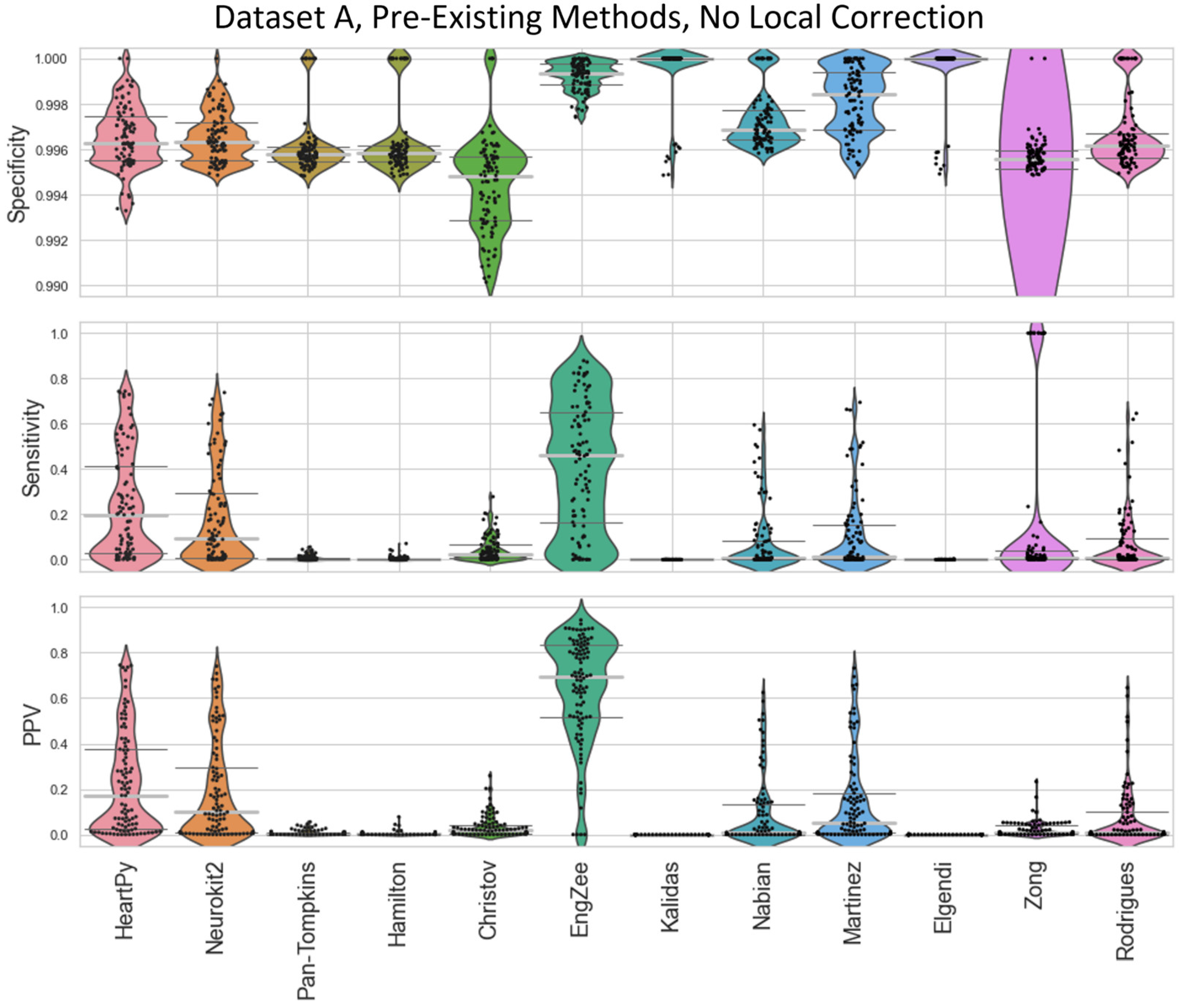
Figure A3.
Violin plots showing the specificity, sensitivity, and positive predictive values for the pre-existing ECG approaches applied to Dataset B, with no local peak correction.
Figure A3.
Violin plots showing the specificity, sensitivity, and positive predictive values for the pre-existing ECG approaches applied to Dataset B, with no local peak correction.
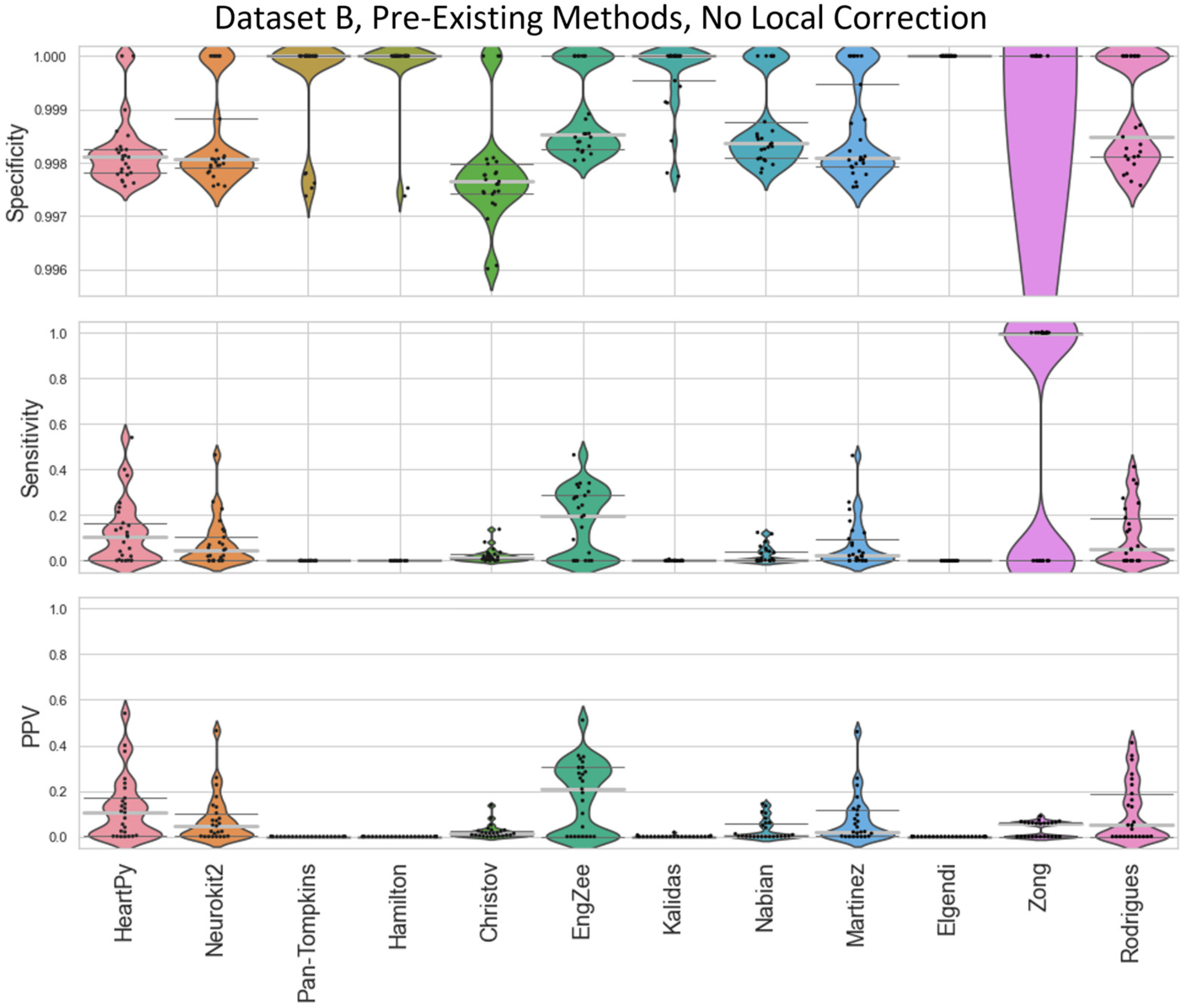
Figure A4.
Violin plots showing the improvement in specificity, sensitivity, and positive predictive values for the pre-existing ECG approaches applied to Dataset A, after local peak correction is applied. A negative improvement indicates that a metric got worse.
Figure A4.
Violin plots showing the improvement in specificity, sensitivity, and positive predictive values for the pre-existing ECG approaches applied to Dataset A, after local peak correction is applied. A negative improvement indicates that a metric got worse.
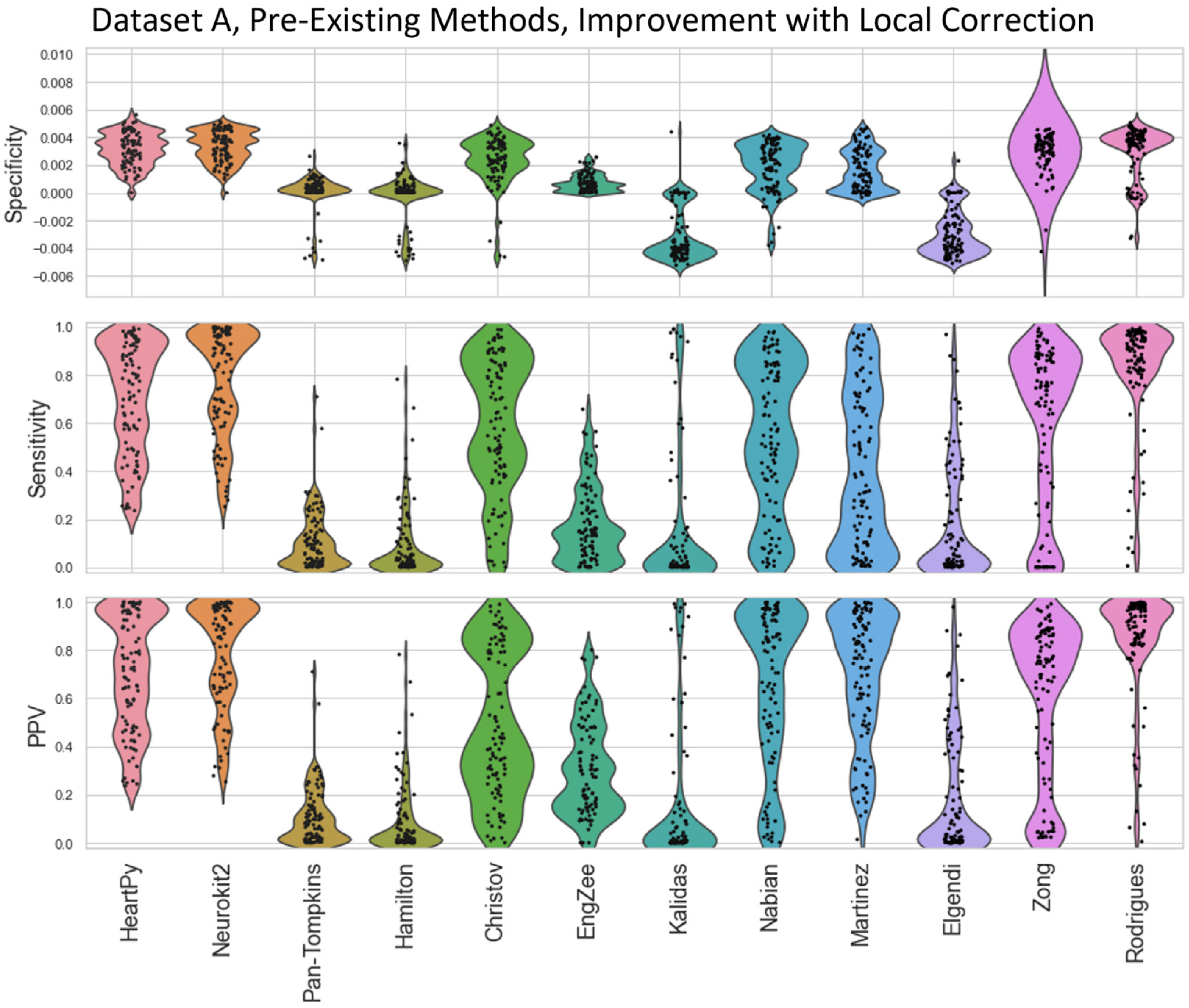
Figure A5.
Violin plots showing the improvement in specificity, sensitivity, and positive predictive values for the pre-existing ECG approaches applied to Dataset B, after local peak correction is applied. A negative improvement indicates that a metric got worse.
Figure A5.
Violin plots showing the improvement in specificity, sensitivity, and positive predictive values for the pre-existing ECG approaches applied to Dataset B, after local peak correction is applied. A negative improvement indicates that a metric got worse.
Appendix E. Labelling Uncertainty
ECG is an analogue signal recorded with digital devices. A digital device recording analogue voltages that are very close in value being digitised to be exactly the same, due to discretization and gain issues. If this issue occurs during a QRS complex it means that there are multiple timestamps that could define an R-peak within a given QRS complex (see Figure A6), as the digital device will be unable to discern the difference between these values. Any method which finds one of these peaks should be considered to have found a “true” peak, but could be marked as incorrect if the “truth” label is on one of the other identical values in that QRS complex. Since the preprocessed ECG is typically smooth, local peak correction will naturally fall on the closest valid peak to the peak labelled on the preprocessed ECG. The R-peak on the raw ECG closest to the peak on the preprocessed ECG is used in all cases to ensure that if any of these peaks are arrived at by local peak correction they will be marked as “true” for a given method.
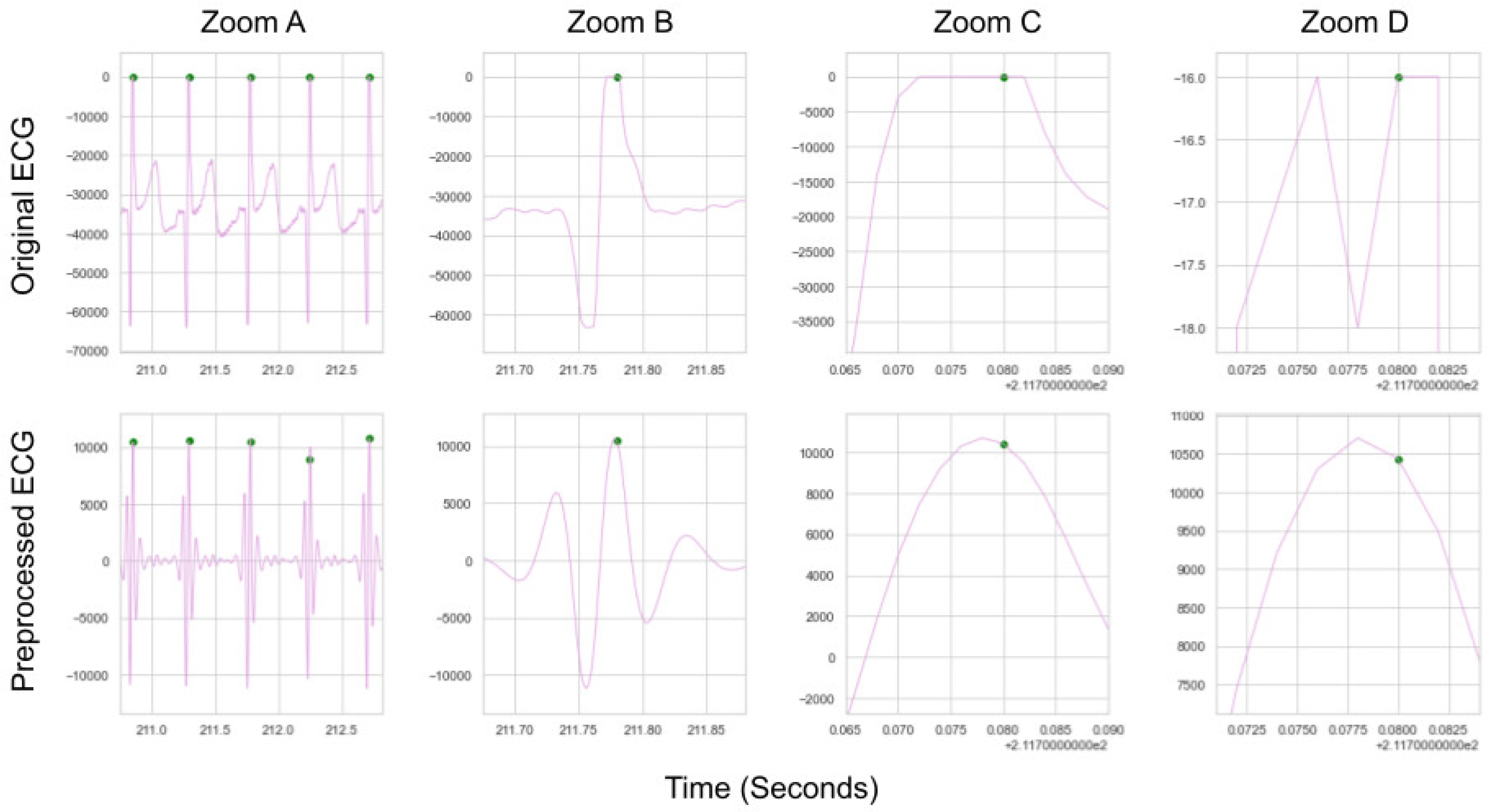
Figure A6.
A demonstration of why local adjustment is needed where peaks need to be aligned perfectly. Zoom A, B, C, and D all show the same central peak. Zoom D shows that 3 specific indexes could all be labelled as the truth on the original ECG, due to the sensitivity of the sensor recording 3 values as “-16”. All three indexes (at 211.776s, 211.780s, 211.782s) are very close in value and could serve as a “true” label.
Figure A6.
A demonstration of why local adjustment is needed where peaks need to be aligned perfectly. Zoom A, B, C, and D all show the same central peak. Zoom D shows that 3 specific indexes could all be labelled as the truth on the original ECG, due to the sensitivity of the sensor recording 3 values as “-16”. All three indexes (at 211.776s, 211.780s, 211.782s) are very close in value and could serve as a “true” label.
References
- Fox, N.A.; Schmidt, L.A.; Henderson, H.A.; Marshall, P.J. Developmental Psychophysiology: Conceptual and Methodological Issues. In Handbook of Psychophysiology, Cacioppo, J.T., Tassinary, L.G., Berntson, G.G., Eds.; Cambridge: Cambridge University Press: 2007; pp. 453–481. [CrossRef]
- Porges, S.W.; Raskin, D.C. Respiratory and heart rate components of attention. J. Exp. Psychol. 1969, 81, 497–503. [Google Scholar] [CrossRef] [PubMed]
- Richards, J.E.; Casey, B.J. Heart Rate Variability During Attention Phases in Young Infants. Psychophysiology 1991, 28, 43–53. [Google Scholar] [CrossRef] [PubMed]
- Zantinge, G.; van Rijn, S.; Stockmann, L.; Swaab, H. Physiological Arousal and Emotion Regulation Strategies in Young Children with Autism Spectrum Disorders. J. Autism Dev. Disord. 2017, 47, 2648–2657. [Google Scholar] [CrossRef] [PubMed]
- Zantinge, G.; van Rijn, S.; Stockmann, L.; Swaab, H. Psychophysiological responses to emotions of others in young children with autism spectrum disorders: Correlates of social functioning. Autism Res. 2017, 10, 1499–1509. [Google Scholar] [CrossRef] [PubMed]
- Gomez, I.N.; Flores, J.G. Diverse Patterns of Autonomic Nervous System Response to Sensory Stimuli Among Children with Autism. Curr. Dev. Disord. Rep. 2020, 7, 249–257. [Google Scholar] [CrossRef]
- Heilman, K.J.; Harden, E.R.; Zageris, D.M.; Berry-Kravis, E.; Porges, S.W. Autonomic regulation in fragile X syndrome. Dev. Psychobiol. 2011, 53, 785–795. [Google Scholar] [CrossRef] [PubMed]
- Imeraj, L.; Antrop, I.; Roeyers, H.; Swanson, J.; Deschepper, E.; Bal, S.; Deboutte, D. Time-of-day effects in arousal: disrupted diurnal cortisol profiles in children with ADHD. J. Child Psychol. Psychiatry 2012, 53, 782–789. [Google Scholar] [CrossRef] [PubMed]
- Van Goozen, S.H.; Matthys, W.; Cohen-Kettenis, P.T.; Buitelaar, J.K.; VAN Engeland, H. Hypothalamic-Pituitary-Adrenal Axis and Autonomic Nervous System Activity in Disruptive Children and Matched Controls. J. Am. Acad. Child Adolesc. Psychiatry 2000, 39, 1438–1445. [Google Scholar] [CrossRef] [PubMed]
- Mulkey, S.B.; Plessis, A.D. The Critical Role of the Central Autonomic Nervous System in Fetal-Neonatal Transition. Semin. Pediatr. Neurol. 2018, 28, 29–37. [Google Scholar] [CrossRef] [PubMed]
- Groome, L.J.; Swiber, M.J.; Atterbury, J.L.; Bentz, L.S.; Holland, S.B. Similarities and Differences in Behavioral State Organization during Sleep Periods in the Perinatal Infant Before and After Birth. Child Dev. 1997, 68, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Geangu, E.; Smith, W.A.P.; Mason, H.T.; Martinez-Cedillo, A.P.; Hunter, D.; Knight, M.I.; Liang, H.; Bazan, M.d.C.G.d.S.; Tse, Z.T.H.; Rowland, T.; et al. EgoActive: Integrated Wireless Wearable Sensors for Capturing Infant Egocentric Auditory–Visual Statistics and Autonomic Nervous System Function ‘in the Wild’. Sensors 2023, 23, 7930. [Google Scholar] [CrossRef] [PubMed]
- Maitha, C.; Goode, J.C.; Maulucci, D.P.; Lasassmeh, S.M.S.; Yu, C.; Smith, L.B.; Borjon, J.I. An open-source, wireless vest for measuring autonomic function in infants. Behav. Res. Methods 2020, 52, 2324–2337. [Google Scholar] [CrossRef] [PubMed]
- Dahl, A. Ecological Commitments: Why Developmental Science Needs Naturalistic Methods. Child Dev. Perspect. 2016, 11, 79–84. [Google Scholar] [CrossRef] [PubMed]
- Fleming, S. et al. Normal ranges of heart rate and respiratory rate in children from birth to 18 years of age: A systematic review of observational studies. Lancet 2011, 377, 1011–1018. [CrossRef] [PubMed]
- Tipple, M. Interpretation of electrocardiograms in infants and children. Images Paediatr. Cardiol. 1999, 1, 3–13. Available online: http://www.ncbi.nlm.nih.gov/pubmed/22368537.
- Rodrigues, J.; Belo, D.; Gamboa, H. Noise detection on ECG based on agglomerative clustering of morphological features. Comput. Biol. Med. 2017, 87, 322–334. [Google Scholar] [CrossRef]
- Clifford, G.D. ECG Statistics, Noise, Artifacts, and Missing Data. In Advanced Methods and Tools for ECG Data Analysis; Artech. House Inc.: London, UK, 2006. [Google Scholar]
- Friesen, G.M.; Jannett, T.C.; Jadallah, M.A.; Yates, S.L.; Quint, S.R.; Nagle, H.T. A comparison of the noise sensitivity of nine QRS detection algorithms. IEEE Trans. Biomed. Eng. 1990, 37, 85–98. [Google Scholar] [CrossRef] [PubMed]
- Christov, I.I. Real time electrocardiogram QRS detection using combined adaptive threshold. Biomed. Eng. Online 2004, 3, 28. [Google Scholar] [CrossRef] [PubMed]
- Elgendi, M.; Jonkman, M.; DeBoer, F. Frequency bands effects on QRS detection. In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing, June 2010; pp. 428–431. [Google Scholar] [CrossRef]
- Hamilton, P.S. Open Source ECG Analysis. Comput. Cardiol. 2002, 29, 101–104. [Google Scholar]
- W. A. H. Engelse and C. Zeelenberg, Single Scan Algorithm for QRS-Detection and Feature Extraction. In Computers in Cardiology; 1979; pp. 37–42.
- Kalidas, V.; Tamil, L. Real-time QRS detector using stationary wavelet transform for automated ECG analysis. In Proceedings of the 2017 IEEE 17th Int. Conf. Bioinforma. Bioeng. BIBE 2017, vol. 2018-January, pp. 457–461.
- Gamboa, H. Multi-Modal Behavioral Biometrics Based on HCI and Electrophysiology. Universidade Tecnica de Lisboa, 2008.
- Lourenço, A.; Silva, H.; Leite, P.; Lourenço, R.; Fred, A. Real time electrocardiogram segmentation for finger based ECG biometrics. In Proceedings of the BIOSIGNALS 2012 Int. Conf. Bio-Inspired Syst. Signal Process. 2012; pp. 49–54. [CrossRef]
- Makowski, D.; Pham, T.; Lau, Z.J.; Brammer, J.C.; Lespinasse, F.; Pham, H.; Schölzel, C.; Chen, S.H.A. NeuroKit2: A Python toolbox for neurophysiological signal processing. Behav. Res. Methods 2021, 53, 1689–1696. [Google Scholar] [CrossRef] [PubMed]
- Martinez, J.; Almeida, R.; Olmos, S.; Rocha, A.; Laguna, P. A Wavelet-Based ECG Delineator: Evaluation on Standard Databases. IEEE Trans. Biomed. Eng. 2004, 51, 570–581. [Google Scholar] [CrossRef]
- Nabian, M.; Yin, Y.; Wormwood, J.; Quigley, K.S.; Barrett, L.F.; Ostadabbas, S. An Open-Source Feature Extraction Tool for the Analysis of Peripheral Physiological Data. IEEE J. Transl. Eng. Heal. Med. 2018, 6, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.; Tompkins, W.J. A Real-Time QRS Detection Algorithm. IEEE Trans. Biomed. Eng. 1985, 32, 230–236. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, T.; Samoutphonh, S.; Silva, H.; Fred, A. A low-complexity R-peak detection algorithm with adaptive thresholding for wearable devices. In Proceedings of the Int. Conf. Pattern Recognit., no. January 2021; pp. 9967–9974. [CrossRef]
- van Gent, P.; Farah, H.; van Nes, N.; van Arem, B. HeartPy: A novel heart rate algorithm for the analysis of noisy signals. Transp. Res. Part F: Traffic Psychol. Behav. 2019, 66, 368–378. [Google Scholar] [CrossRef]
- Zong, W.; Moody, G.; Jiang, D. A robust open-source algorithm to detect onset and duration of QRS complexes. Comput. Cardiol. 2003, 2003, 737–740. [Google Scholar] [CrossRef]
- Li, C.; Zheng, C.; Tai, C. Detection of ECG characteristic points using wavelet transforms. IEEE Trans. Biomed. Eng. 1995, 42, 21–28. [Google Scholar] [CrossRef] [PubMed]
- Pal, S.; Mitra, M. Empirical mode decomposition based ECG enhancement and QRS detection. Comput. Biol. Med. 2012, 42, 83–92. [Google Scholar] [CrossRef]
- A. Velayudhan and S. Peter. Noise Analysis and Different Denoising Techniques of ECG Signal—A Survey. IOSR J. Electron. Commun. Eng. (IOSR-JECE) 2016, 3, 40–44. [Google Scholar]
- P. van Gent. Python Heart Rate Analysis Toolkit Documentation. 2020.
- Sadhukhan, D.; Mitra, M. R-Peak Detection Algorithm for Ecg using Double Difference And RR Interval Processing. Procedia Technol. 2012, 4, 873–877. [Google Scholar] [CrossRef]
- Gutierrez-Rivas, R.; Garcia, J.J.; Marnane, W.P.; Hernandez, A. Novel Real-Time Low-Complexity QRS Complex Detector Based on Adaptive Thresholding. IEEE Sensors J. 2015, 15, 6036–6043. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. London Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Peng, Z.; Wang, G. A Novel ECG Eigenvalue Detection Algorithm Based on Wavelet Transform. BioMed Res. Int. 2017, 2017. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zhu, J.; Yan, T.; Yang, L. A new modified wavelet-based ECG denoising. Comput. Assist. Surg. 2019, 24, 174–183. [Google Scholar] [CrossRef] [PubMed]
- Hirokawa, J.; Hitosugi, T.; Miki, Y.; Tsukamoto, M.; Yamasaki, F.; Kawakubo, Y.; Yokoyama, T. The influence of electrocardiogram (ECG) filters on the heights of R and T waves in children. Sci. Rep. 2022, 12. [Google Scholar] [CrossRef] [PubMed]
- Tereshchenko, L.G.; Josephson, M.E. Frequency content and characteristics of ventricular conduction. J. Electrocardiol. 2015, 48, 933–937. [Google Scholar] [CrossRef] [PubMed]
- Kramer, L.; Menon, C.; Elgendi, M. ECGAssess: A Python-Based Toolbox to Assess ECG Lead Signal Quality. Front. Digit. Heal. 2022, 4. [Google Scholar] [CrossRef] [PubMed]
- D’aloia, M.; Longo, A.; Rizzi, M. Noisy ECG Signal Analysis for Automatic Peak Detection. Information 2019, 10. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, Y. SQI Quality Evaluation Mechanism of Single-Lead ECG Signal Based on Simple Heuristic Fusion and Fuzzy Comprehensive Evaluation. Front. Physiol. 2018, 9, 1–13. [Google Scholar] [CrossRef] [PubMed]
Figure 1.
A visualisation of the different complexes with an ECG. ΔR-R represents the time between R peaks, as depicted in Equation (1).
Figure 1.
A visualisation of the different complexes with an ECG. ΔR-R represents the time between R peaks, as depicted in Equation (1).
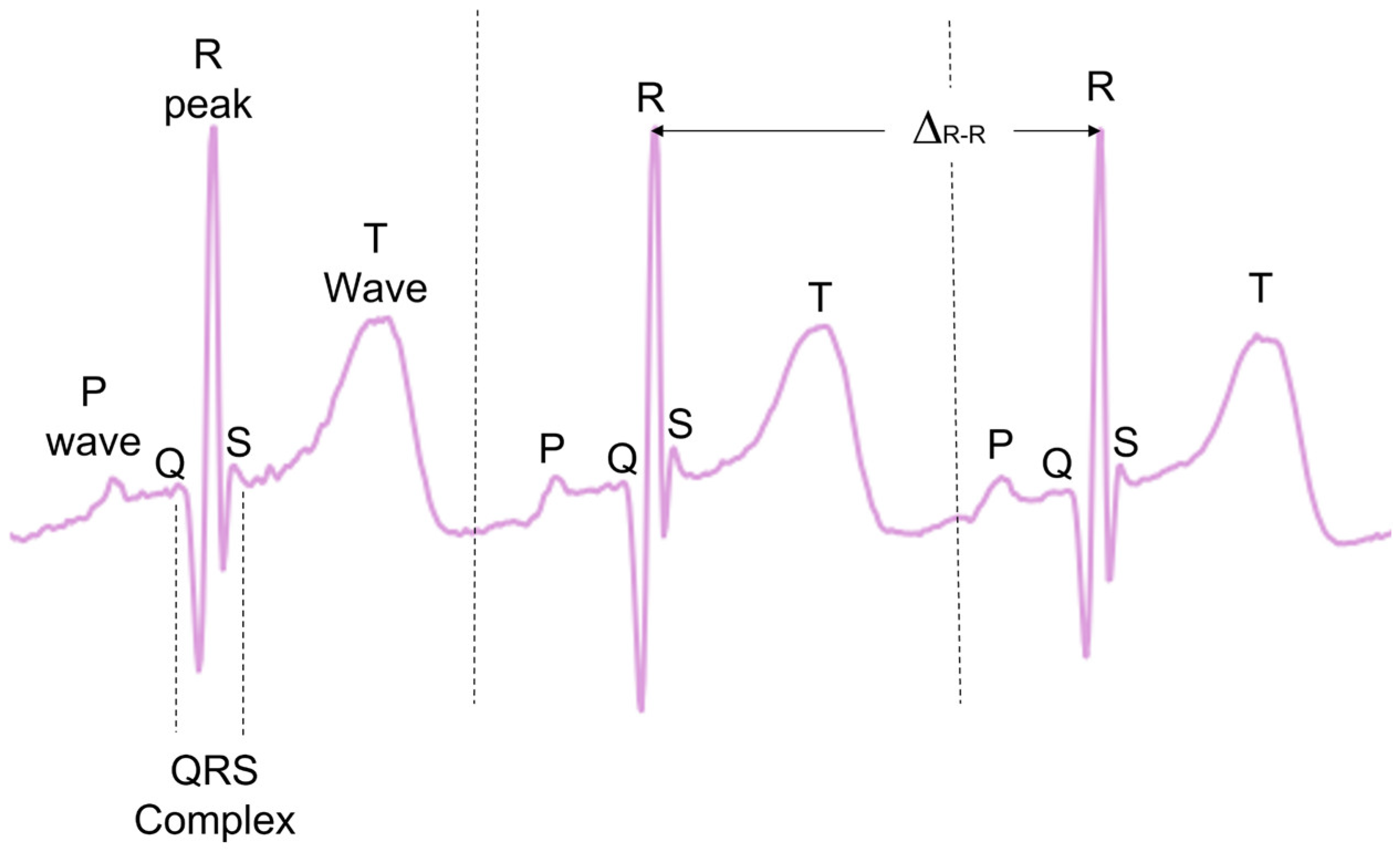
Figure 2.
The proposed new pipeline for processing infant ECG into a usable heart rate. The ECG pipeline (top row, blue boxes) takes raw ECG and applies preprocessing. The preprocessed ECG is then passed into the peak detection step, and then the novel steps of local peak correction and square wave correction (where required by the device appropriate). The HR pipeline (bottom row, red boxes) extracts a raw heart rate from the detected ECG peaks, and corrects for any obvious mislabelling, while carrying out an SQI calculation to determine quality of the signal. Adapted from Geangu et al. [12] to represent an infant-specific pipeline.
Figure 2.
The proposed new pipeline for processing infant ECG into a usable heart rate. The ECG pipeline (top row, blue boxes) takes raw ECG and applies preprocessing. The preprocessed ECG is then passed into the peak detection step, and then the novel steps of local peak correction and square wave correction (where required by the device appropriate). The HR pipeline (bottom row, red boxes) extracts a raw heart rate from the detected ECG peaks, and corrects for any obvious mislabelling, while carrying out an SQI calculation to determine quality of the signal. Adapted from Geangu et al. [12] to represent an infant-specific pipeline.
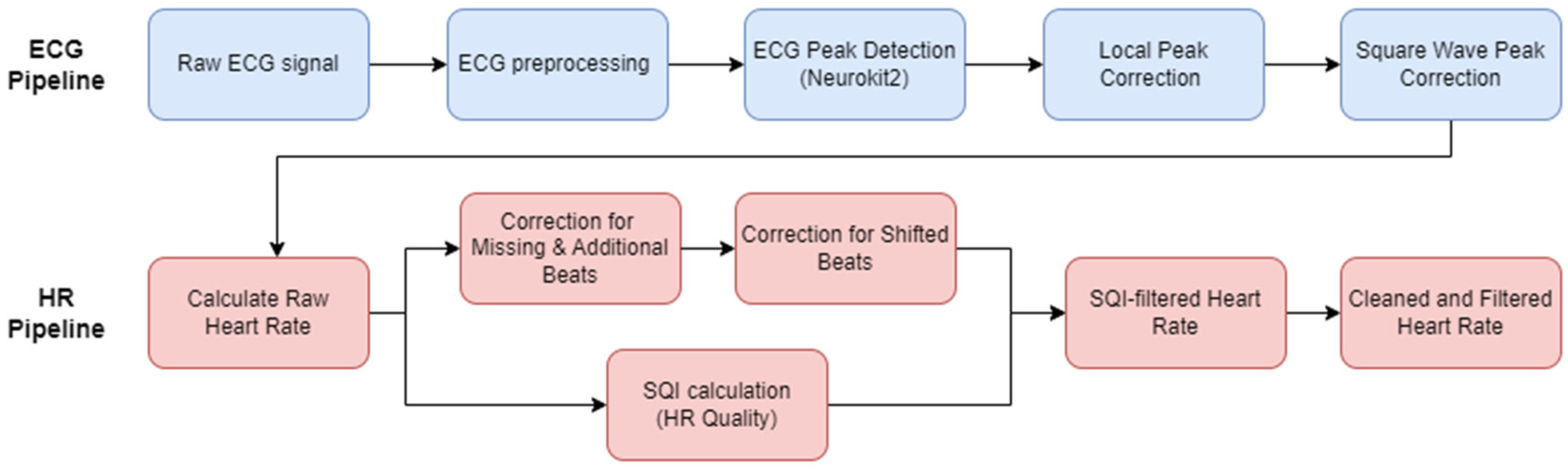
Figure 3.
Plot age of participant vs length of recording. (a) Dataset A: the recordings have been roughly grouped into cohorts of 2.9-7.9 months (N =25, Mage=5.8 m.o.), 8-10.9 months (N=15, Mage=9.3 m.o.), 11-19.9 months (N=23, Mage=13.4 m.o.), and 20-42.3 months (N=34, Mage=30.8 m.o.). (b) Dataset B: The recordings are grouped into cohorts of 5-6.9 months (N=7, Mage=6.0 m.o.), 7-8.9 months (N=9, Mage=8.0 m.o.), 9-10.9 months (N=6, Mage=9.9 m.o.) and 11-13.9 months (N=4, Mage=12.0 m.o.). (c) Dataset C: The recordings are grouped into cohorts of 5-7.9 months (N=7, Mage=5.8 m.o.) and 8-11 months (N=5, Mage=9.5 m.o.). All y-axes and x-axes have different scales. A consistent colour-scale for age has been used in all subplots.
Figure 3.
Plot age of participant vs length of recording. (a) Dataset A: the recordings have been roughly grouped into cohorts of 2.9-7.9 months (N =25, Mage=5.8 m.o.), 8-10.9 months (N=15, Mage=9.3 m.o.), 11-19.9 months (N=23, Mage=13.4 m.o.), and 20-42.3 months (N=34, Mage=30.8 m.o.). (b) Dataset B: The recordings are grouped into cohorts of 5-6.9 months (N=7, Mage=6.0 m.o.), 7-8.9 months (N=9, Mage=8.0 m.o.), 9-10.9 months (N=6, Mage=9.9 m.o.) and 11-13.9 months (N=4, Mage=12.0 m.o.). (c) Dataset C: The recordings are grouped into cohorts of 5-7.9 months (N=7, Mage=5.8 m.o.) and 8-11 months (N=5, Mage=9.5 m.o.). All y-axes and x-axes have different scales. A consistent colour-scale for age has been used in all subplots.
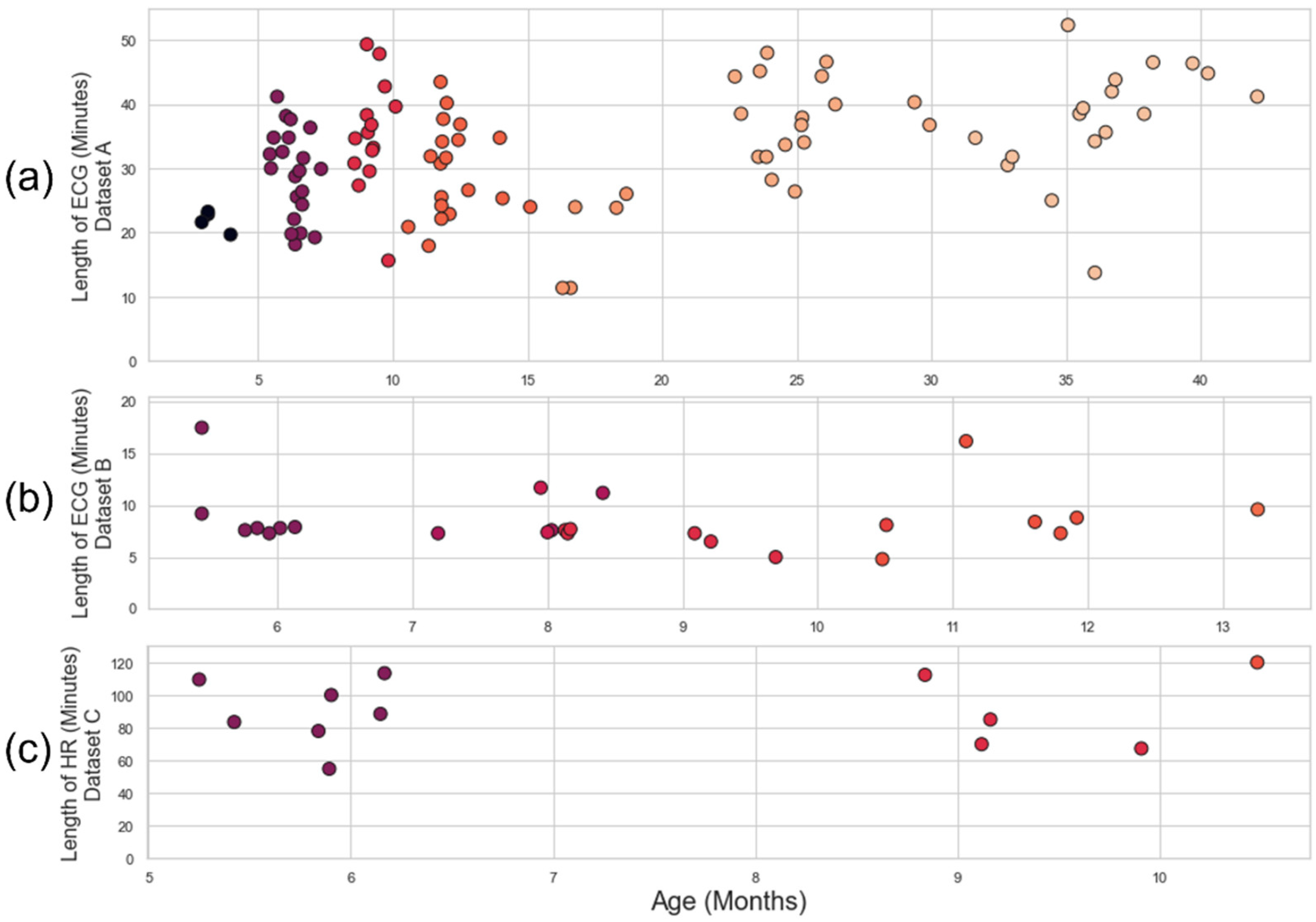
Figure 4.
Violin plots showing the specificity, sensitivity and positive predictive values for the pre-existing ECG approaches applied to Dataset A, with local peak correction applied to allow for cross-method comparison. The thin dark-grey lines represent interquartile values, the thick light-grey line represents the median. Each dot represents a single result in the dataset, with the “violin” helping visualise the distribution. HeartPy, Neurokit2, Rodrigues and Martinez are shown in more detail in Figure 8.
Figure 4.
Violin plots showing the specificity, sensitivity and positive predictive values for the pre-existing ECG approaches applied to Dataset A, with local peak correction applied to allow for cross-method comparison. The thin dark-grey lines represent interquartile values, the thick light-grey line represents the median. Each dot represents a single result in the dataset, with the “violin” helping visualise the distribution. HeartPy, Neurokit2, Rodrigues and Martinez are shown in more detail in Figure 8.
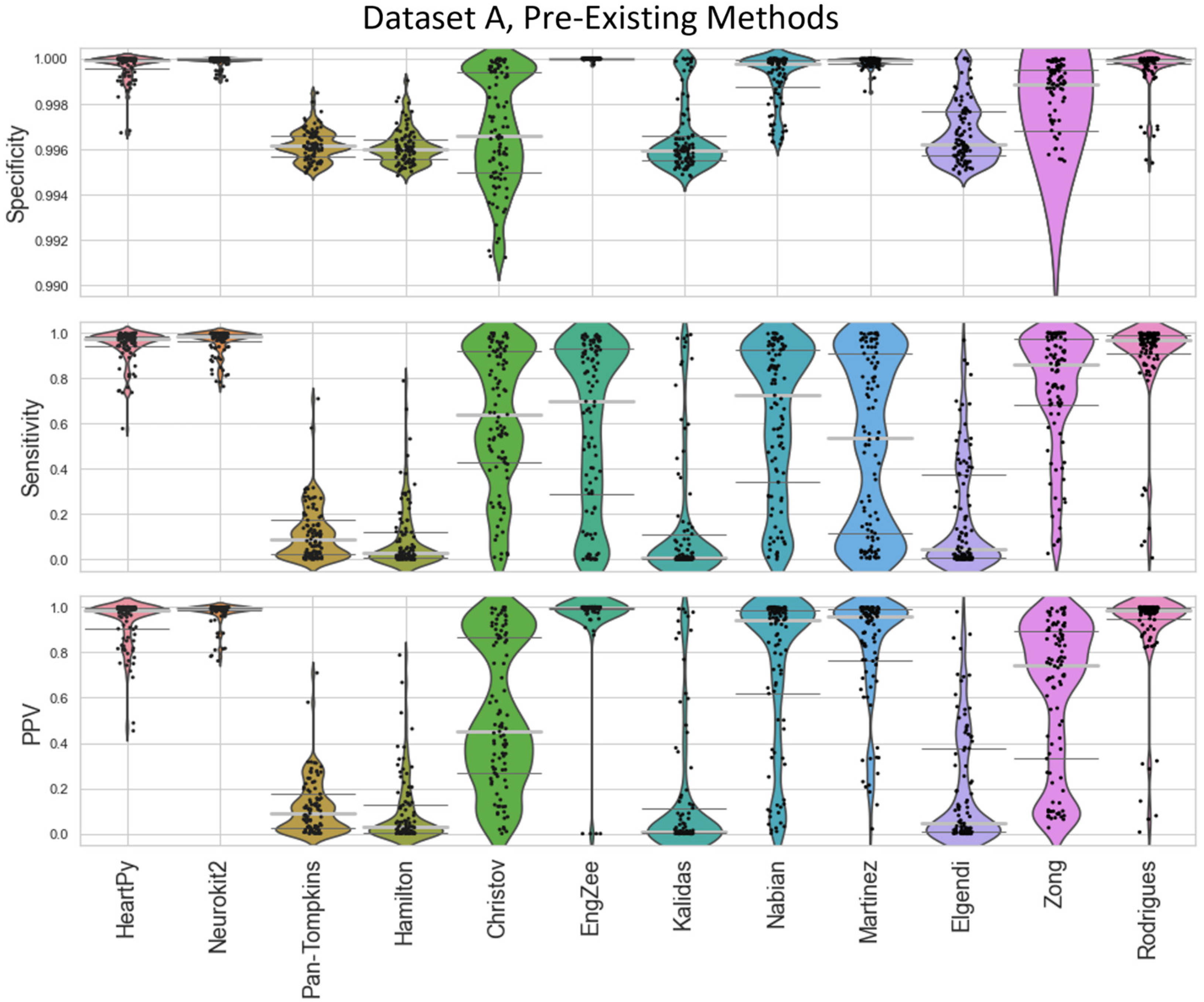
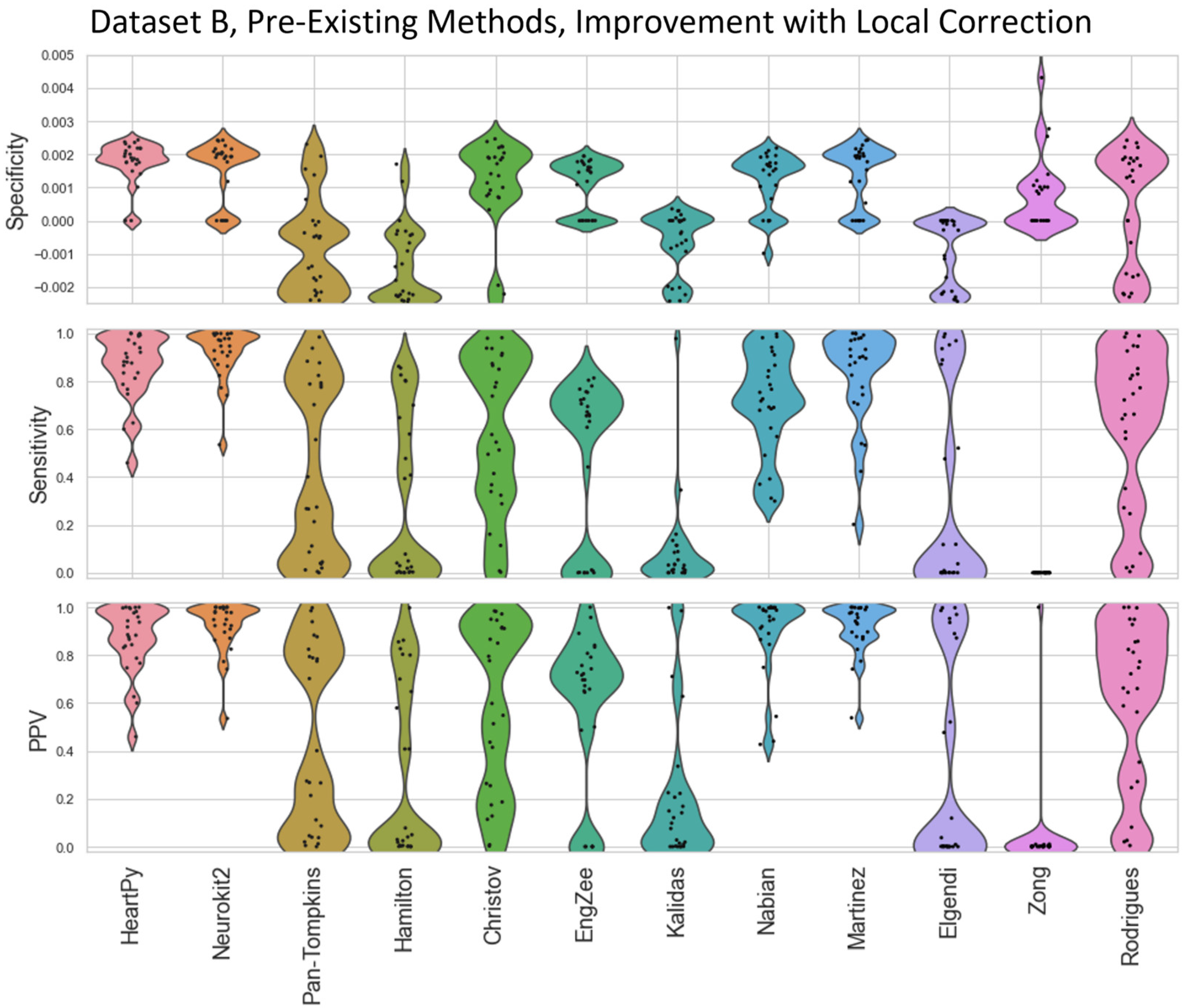
Figure 5.
Violin plots showing the specificity, sensitivity, and positive predictive values for the pre-existing ECG approaches applied to Dataset B, with local peak correction applied to allow for cross-method comparison. HeartPy, Neurokit2, Rodrigues and Martinez are shown in more detail in Figure 9.
Figure 5.
Violin plots showing the specificity, sensitivity, and positive predictive values for the pre-existing ECG approaches applied to Dataset B, with local peak correction applied to allow for cross-method comparison. HeartPy, Neurokit2, Rodrigues and Martinez are shown in more detail in Figure 9.
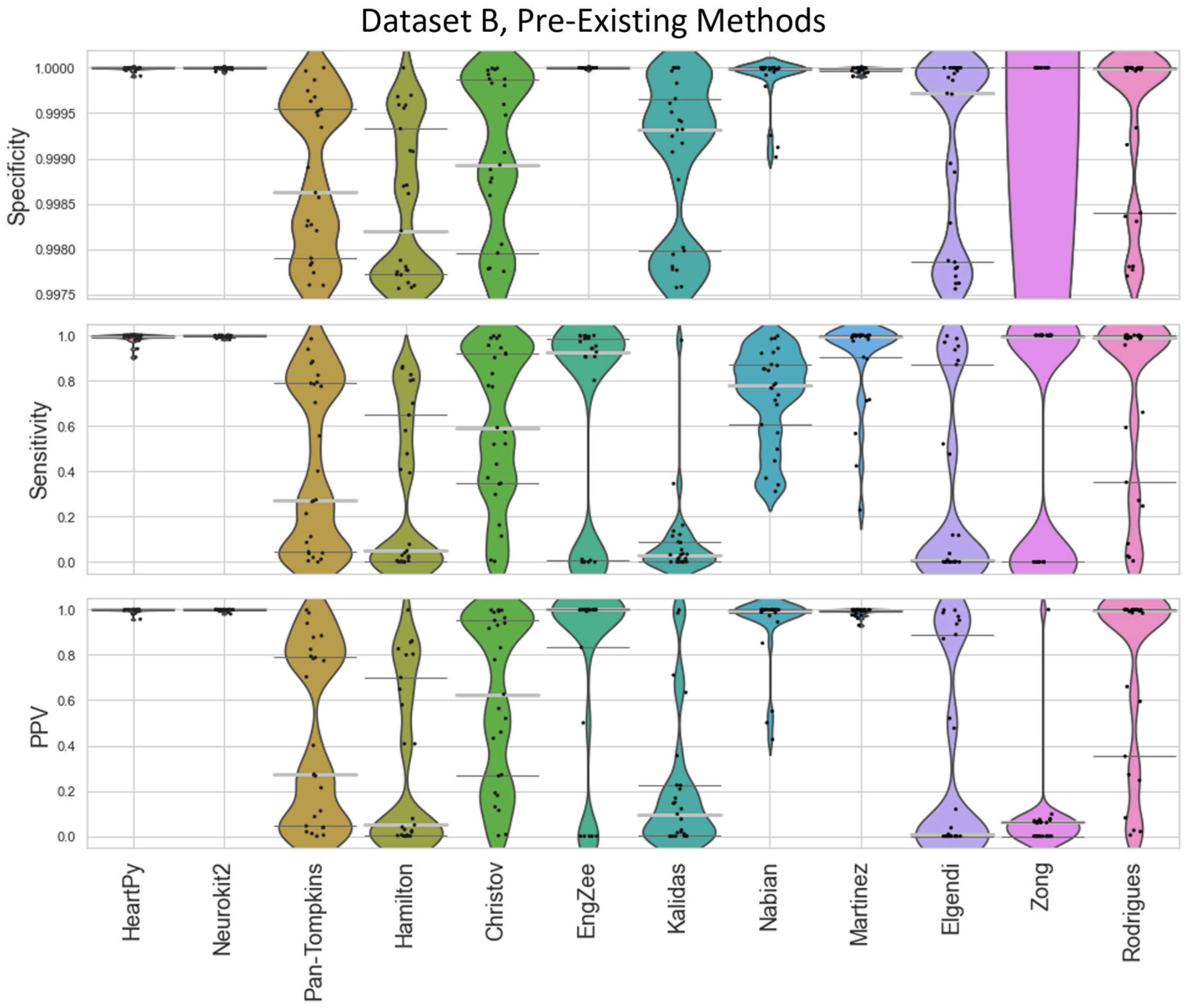
Figure 6.
A visualization of the peak detection for the pre-existing methods on a 12-month-old from Dataset A. The raw ECG and ground truth are shown left. All other approaches show the preprocessed ECG and original detected R-peak location for that method.
Figure 6.
A visualization of the peak detection for the pre-existing methods on a 12-month-old from Dataset A. The raw ECG and ground truth are shown left. All other approaches show the preprocessed ECG and original detected R-peak location for that method.
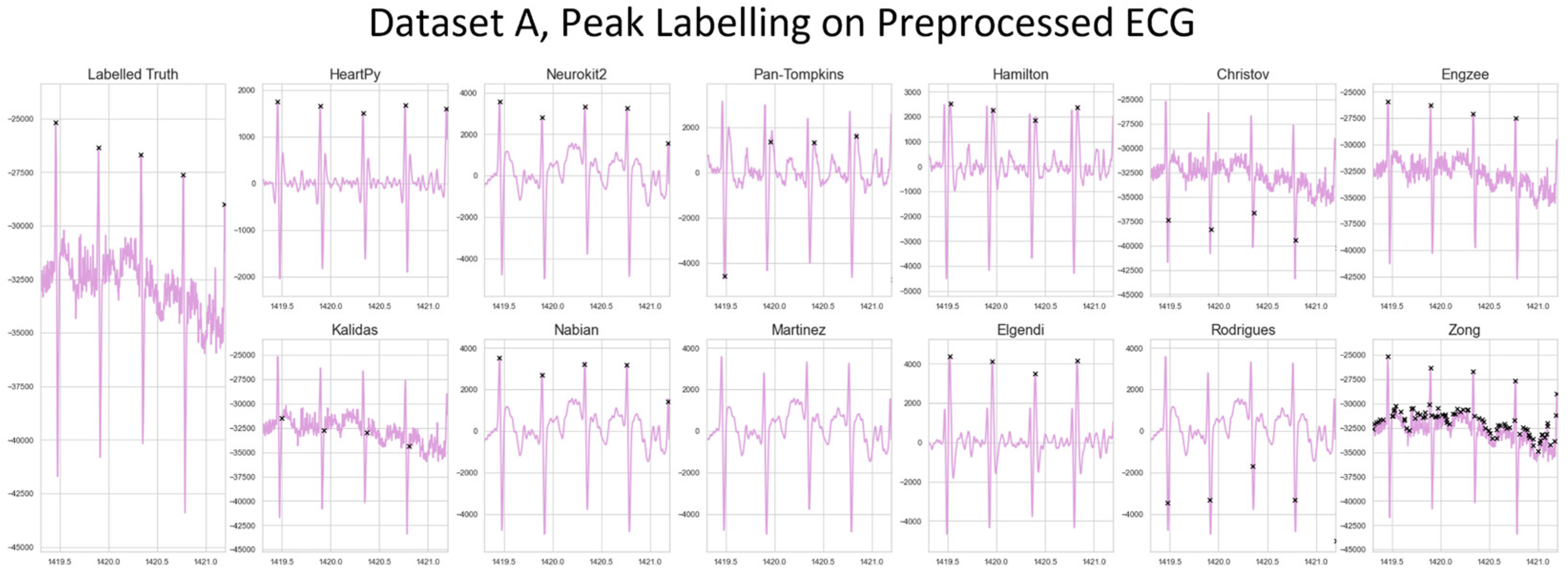
Figure 7.
The Specificity, Sensitivity, and PPV (columns 1, 2, and 3) results shown as violin plots for a selection of frequency-preprocessing methods applied to (a) Dataset A, and (b) Dataset B. In all subplots, the median is shown as a thick, light grey bar, and the IQR is shown as thin dark grey bars. Each black dot represents one result. The lower frequency bounds are shown on the y-axis, the upper frequency bounds on the x-axis (with the right-most column of each subplot indicating no upper bound, i.e., an HPF). Results are all shown at a consistent scale, violin plots which go to the edge of the graph may have results outside the visualized range.
Figure 7.
The Specificity, Sensitivity, and PPV (columns 1, 2, and 3) results shown as violin plots for a selection of frequency-preprocessing methods applied to (a) Dataset A, and (b) Dataset B. In all subplots, the median is shown as a thick, light grey bar, and the IQR is shown as thin dark grey bars. Each black dot represents one result. The lower frequency bounds are shown on the y-axis, the upper frequency bounds on the x-axis (with the right-most column of each subplot indicating no upper bound, i.e., an HPF). Results are all shown at a consistent scale, violin plots which go to the edge of the graph may have results outside the visualized range.
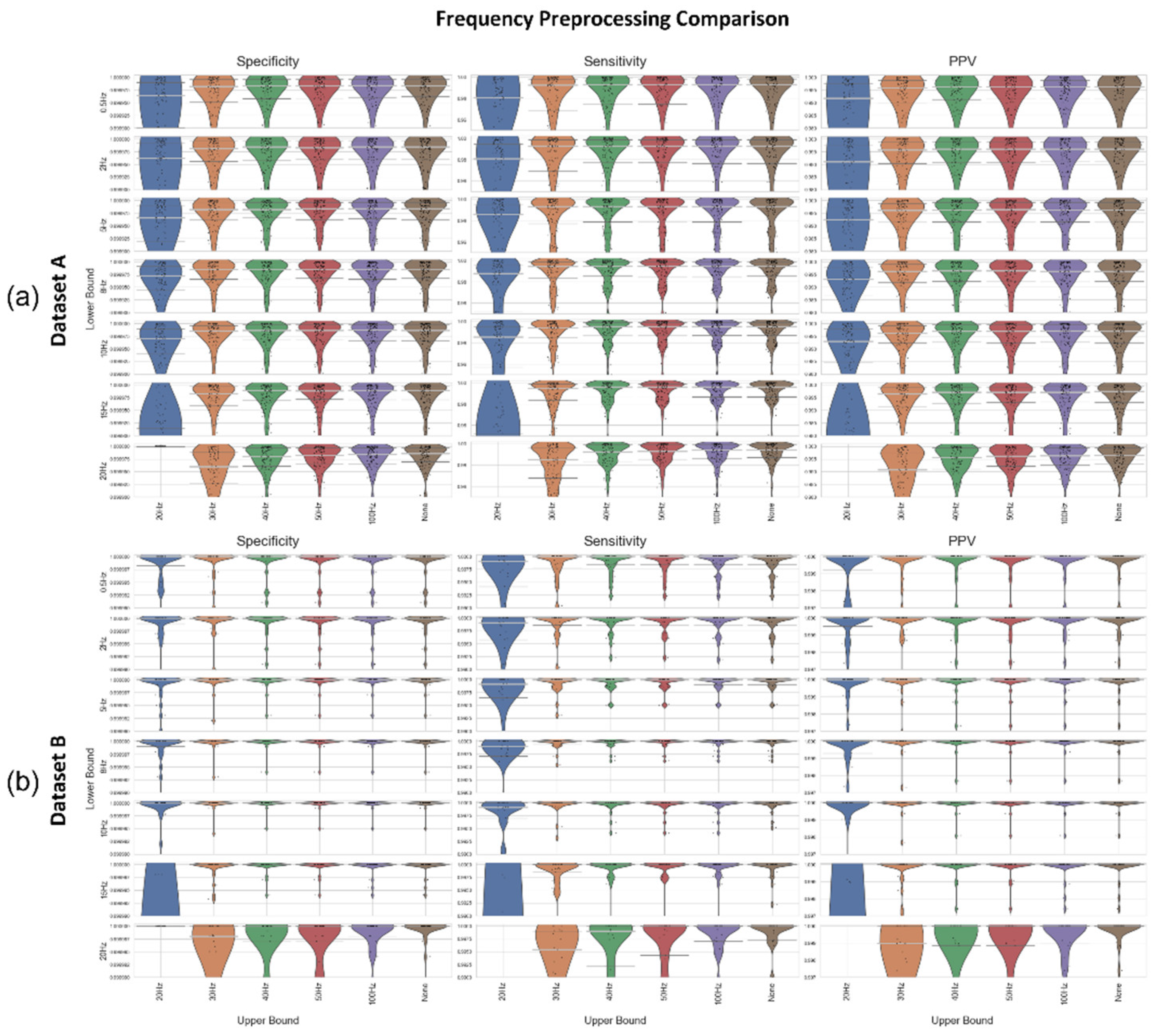
Figure 8.
Violin plots for the best approaches for Dataset A. The median is shown as a thick, light grey bar, and the IQR is shown as thin dark grey bars. Each black dot represents one result. The HeartPy, Neurokit2, Martinez and Rodrigues results are the same as in Figure 4, but with a greater y-axis zoom. The EMD and 15Hz HPF approaches are new ones evaluated by this paper.
Figure 8.
Violin plots for the best approaches for Dataset A. The median is shown as a thick, light grey bar, and the IQR is shown as thin dark grey bars. Each black dot represents one result. The HeartPy, Neurokit2, Martinez and Rodrigues results are the same as in Figure 4, but with a greater y-axis zoom. The EMD and 15Hz HPF approaches are new ones evaluated by this paper.
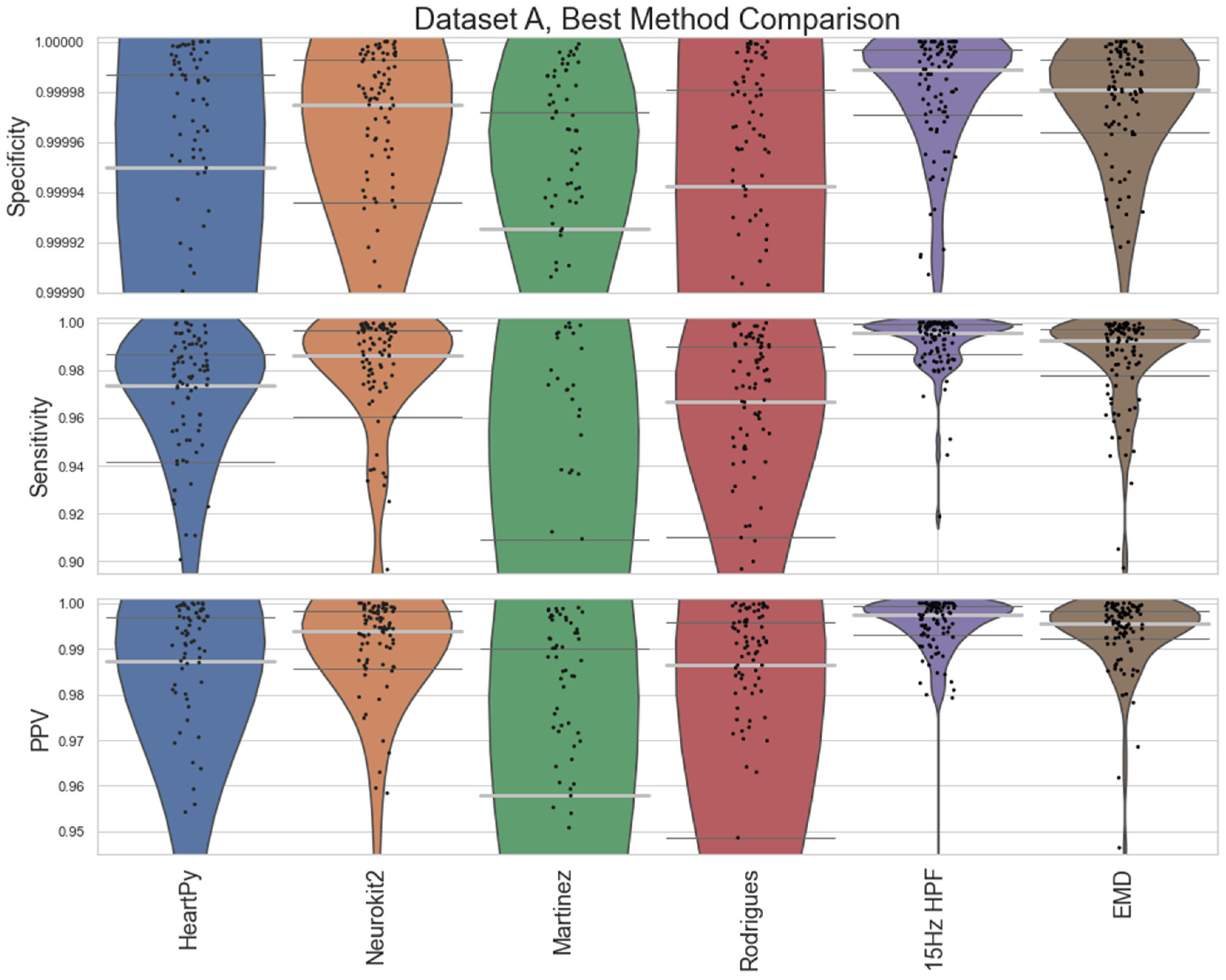
Figure 9.
Violin plots for the best approaches for Dataset B. The median is shown as a thick, light grey bar, and the IQR is shown as thin dark grey bars. Each black dot represents one result. The HeartPy, Neurokit2, Martinez and Rodrigues results are the same as in Figure 5, but with a greater y-axis zoom.
Figure 9.
Violin plots for the best approaches for Dataset B. The median is shown as a thick, light grey bar, and the IQR is shown as thin dark grey bars. Each black dot represents one result. The HeartPy, Neurokit2, Martinez and Rodrigues results are the same as in Figure 5, but with a greater y-axis zoom.
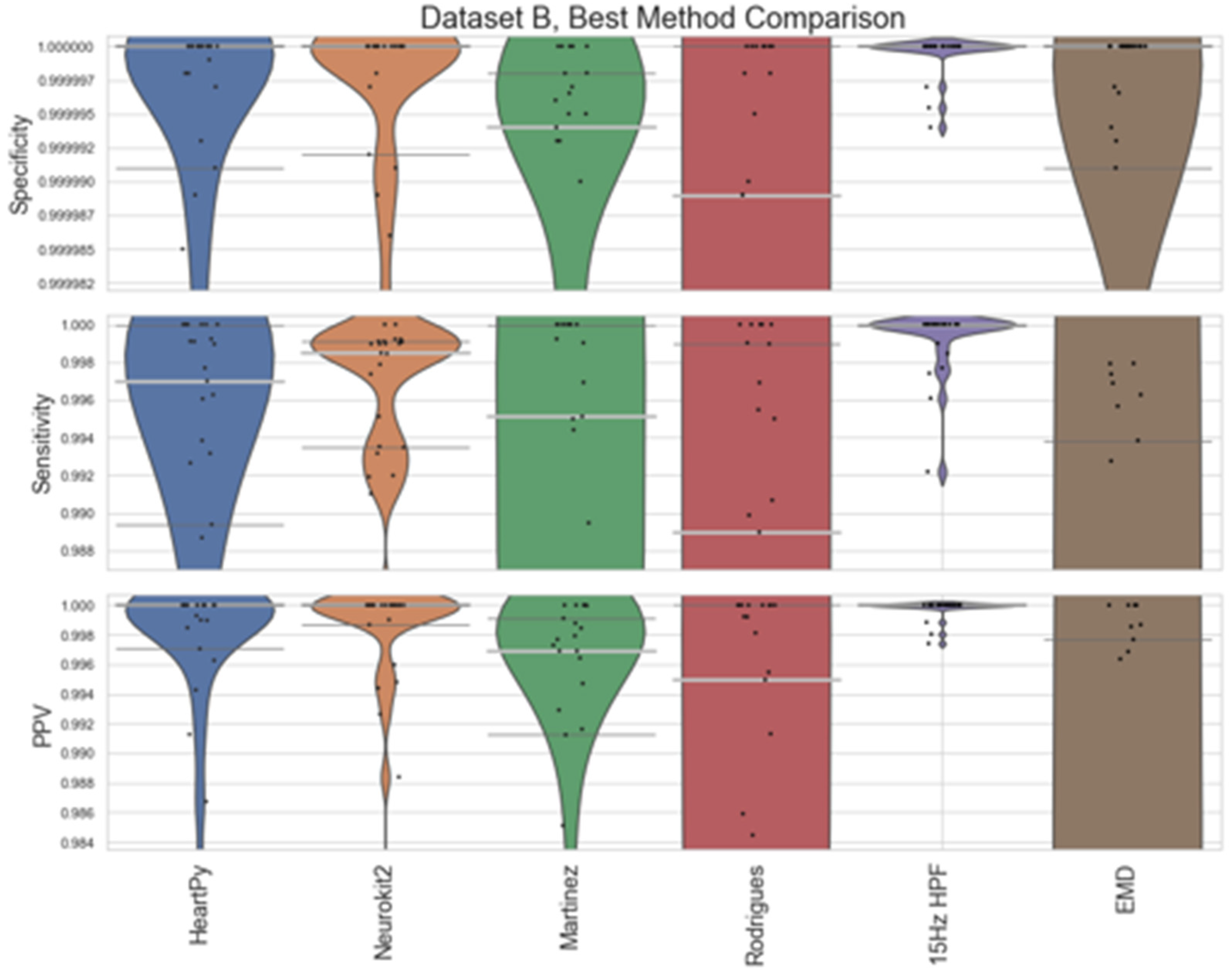
Figure 10.
An age-based breakdown of Figure 8. A different age bracket is shown in each quadrant. The median is shown as a thick, light grey bar, and the IQR is shown as thin dark grey bars. Each black dot represents one result.
Figure 10.
An age-based breakdown of Figure 8. A different age bracket is shown in each quadrant. The median is shown as a thick, light grey bar, and the IQR is shown as thin dark grey bars. Each black dot represents one result.
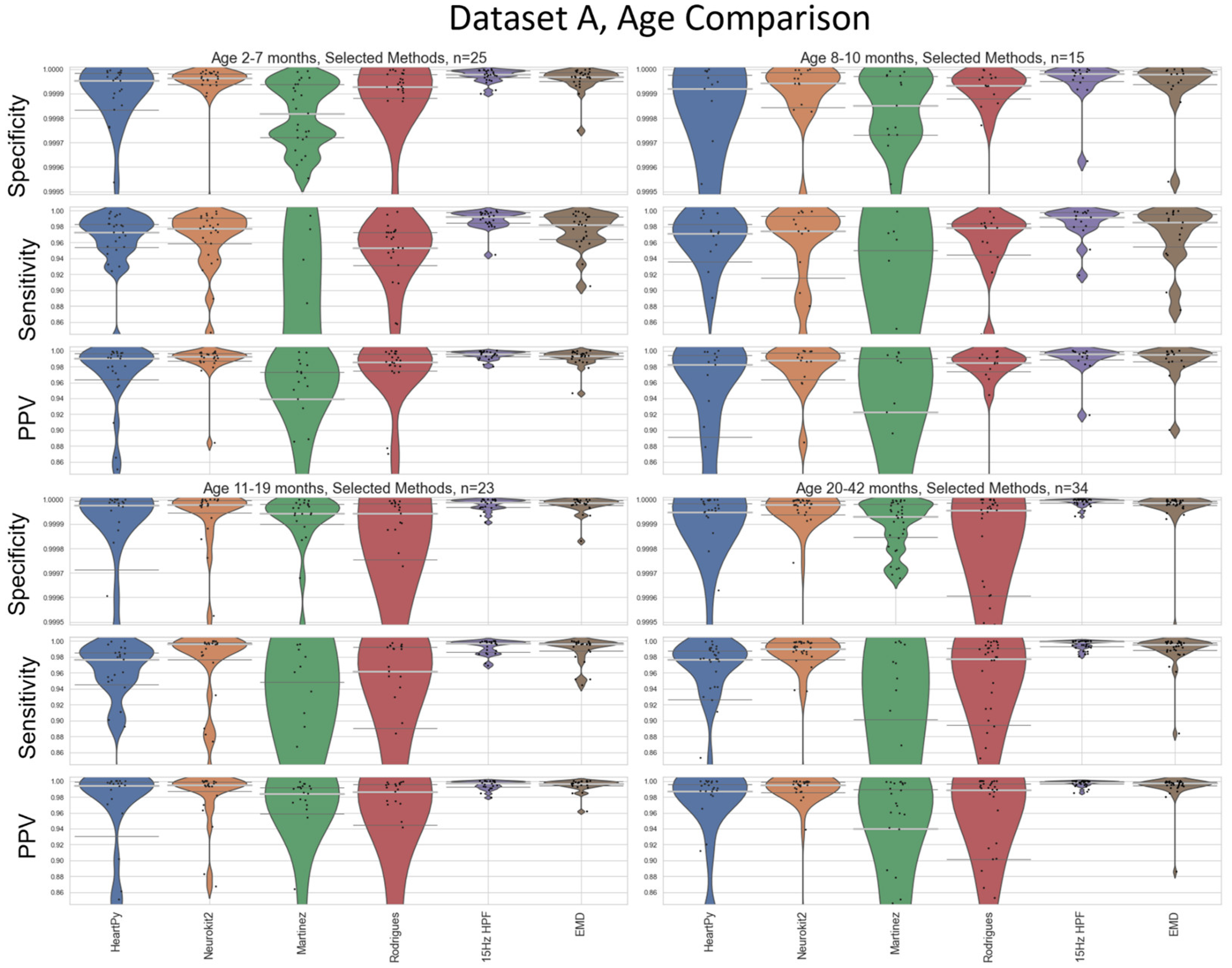
Figure 11.
A demonstration of potential inaccuracies arising in R-peak labelling algorithms. Each QRS complex should contain one R-peak label. The left column shows an ECG signal (purple) and peak labels. The black “x”s show the underlying true peak labels. The blue “+”s and red “o”s show incorrect labelling. The right column shows the corresponding instantaneous heart rate, calculated through Equation 1. (a) A single lower heart rate measurement due to missing a beat; (b) Two raised heart rate measurements due to an additional beat; (c) Two incorrect heart rate measurements, one higher and one lower, with the order depending on the direction the beat is shifted. (c) is adapted from Geangu et al. [12].
Figure 11.
A demonstration of potential inaccuracies arising in R-peak labelling algorithms. Each QRS complex should contain one R-peak label. The left column shows an ECG signal (purple) and peak labels. The black “x”s show the underlying true peak labels. The blue “+”s and red “o”s show incorrect labelling. The right column shows the corresponding instantaneous heart rate, calculated through Equation 1. (a) A single lower heart rate measurement due to missing a beat; (b) Two raised heart rate measurements due to an additional beat; (c) Two incorrect heart rate measurements, one higher and one lower, with the order depending on the direction the beat is shifted. (c) is adapted from Geangu et al. [12].
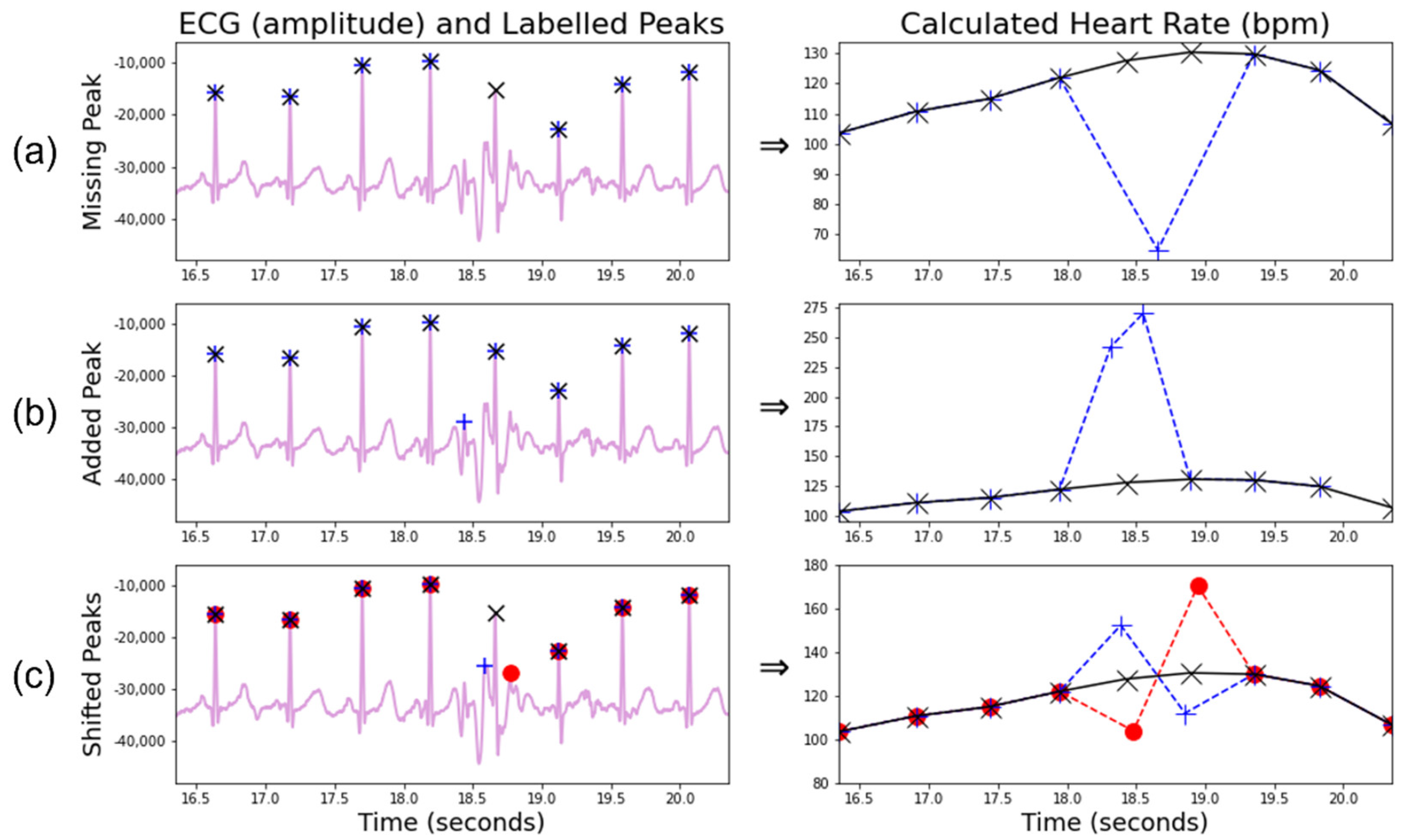
Figure 12.
The result of parameter variation for selecting different Filter Widths (FW) and Activation Thresholds (AT) with a local moving-median filter. (a) The total number of errors in interpolation for the moving-median applied to a clean dataset, with 346 the expected number of interpolations across the dataset. One 12-month infant with a mildly arrhythmic heart rate accounts for 4 of the incorrect interpolations in the optimal parameter choices. (b) The heart rate residual shows the difference between the interpolated heart rate and the true heart rate for the moving-median applied to a realistically processed dataset. A trade-off is then made between how strict the threshold is in removing incorrect peak labels compared to preserving the original signal. (b) is adapted from Geangu et al. [12], with additional data and labels added.
Figure 12.
The result of parameter variation for selecting different Filter Widths (FW) and Activation Thresholds (AT) with a local moving-median filter. (a) The total number of errors in interpolation for the moving-median applied to a clean dataset, with 346 the expected number of interpolations across the dataset. One 12-month infant with a mildly arrhythmic heart rate accounts for 4 of the incorrect interpolations in the optimal parameter choices. (b) The heart rate residual shows the difference between the interpolated heart rate and the true heart rate for the moving-median applied to a realistically processed dataset. A trade-off is then made between how strict the threshold is in removing incorrect peak labels compared to preserving the original signal. (b) is adapted from Geangu et al. [12], with additional data and labels added.
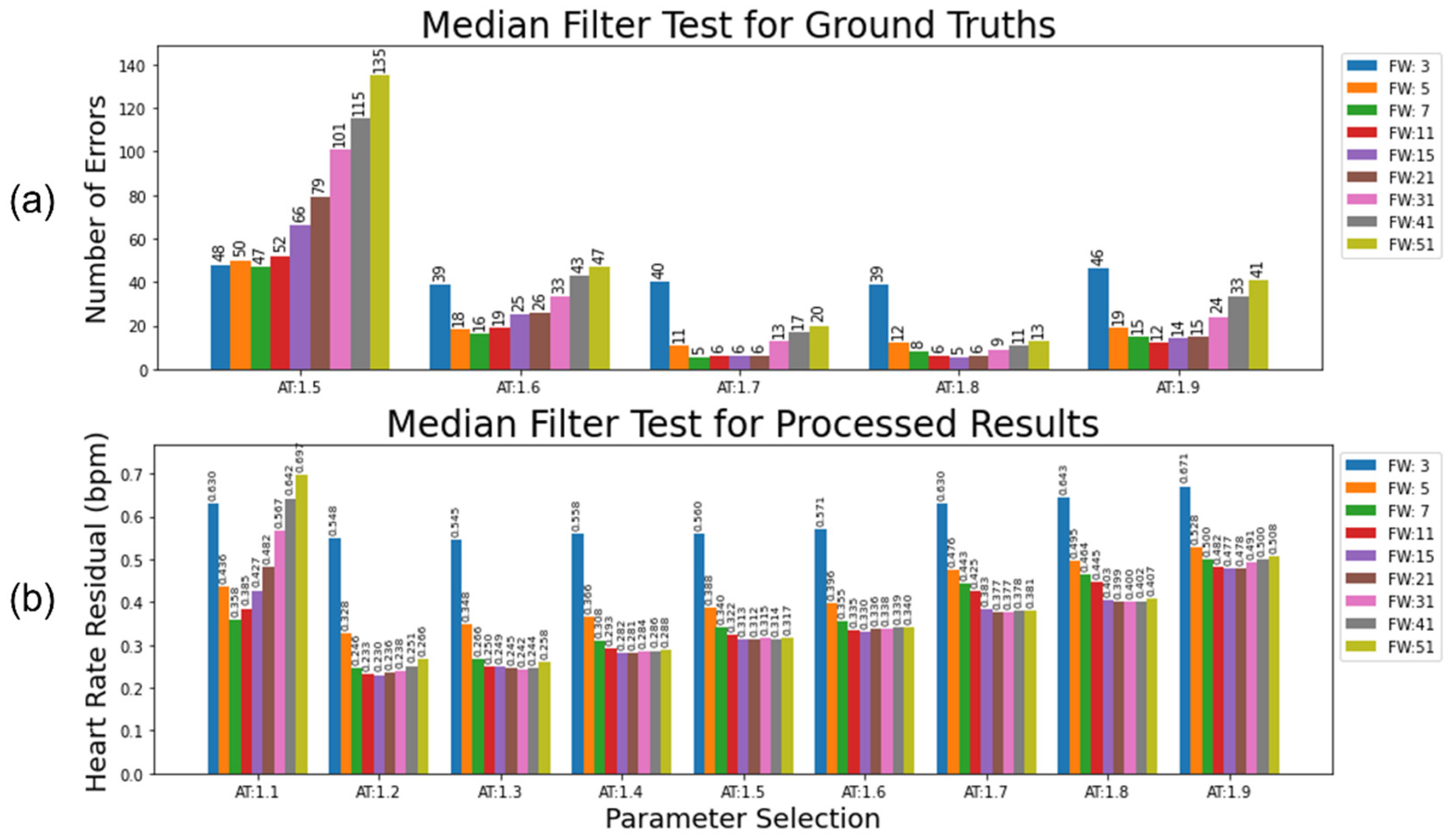
Figure 13.
A demonstration of SQI on dataset C. Top: The derived HR signal. Brown and green lines represent the raw HR. Brown HR is HR that falls within a local median, while green HR falls outside the local median. The red HR line represents the HR following local linear interpolation to remove outlier HR points. The purple line represents the SQI vector indicating whether a time point has good (=1) or poor (=0) signal quality. This vector indicates a noisy period when the HR data can be considered unreliable and thus excluded from further analyses. Bottom: The corresponding ECG signal (light purple), with the detected R-peaks shown as green dots. Individual missing peaks can be approximated by interpolation, but a noisier period (SQI=0) becomes harder to recover and so is considered unreliable.
Figure 13.
A demonstration of SQI on dataset C. Top: The derived HR signal. Brown and green lines represent the raw HR. Brown HR is HR that falls within a local median, while green HR falls outside the local median. The red HR line represents the HR following local linear interpolation to remove outlier HR points. The purple line represents the SQI vector indicating whether a time point has good (=1) or poor (=0) signal quality. This vector indicates a noisy period when the HR data can be considered unreliable and thus excluded from further analyses. Bottom: The corresponding ECG signal (light purple), with the detected R-peaks shown as green dots. Individual missing peaks can be approximated by interpolation, but a noisier period (SQI=0) becomes harder to recover and so is considered unreliable.
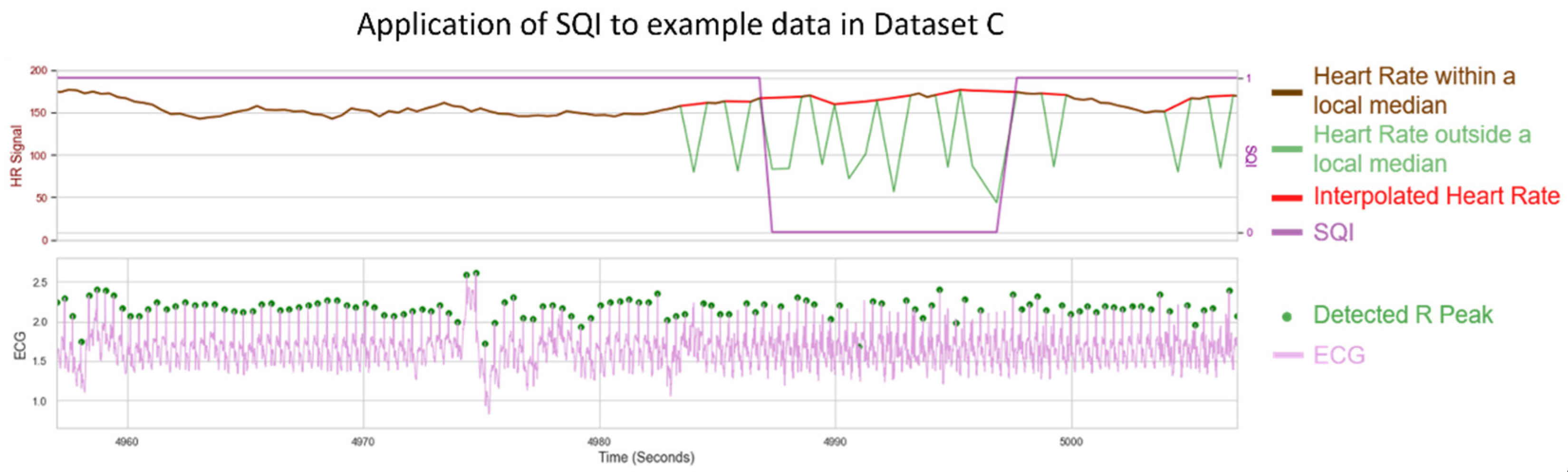
Figure 14.
A demonstration of the SQI algorithm on a noisy dataset. Each dot represents one recording. The algorithm has a very good true positive rate (sensitivity), but a slightly worse false positive rate (1-specificity), implying it will often identify good areas, but may not reject areas of bad HR as often as it should.
Figure 14.
A demonstration of the SQI algorithm on a noisy dataset. Each dot represents one recording. The algorithm has a very good true positive rate (sensitivity), but a slightly worse false positive rate (1-specificity), implying it will often identify good areas, but may not reject areas of bad HR as often as it should.
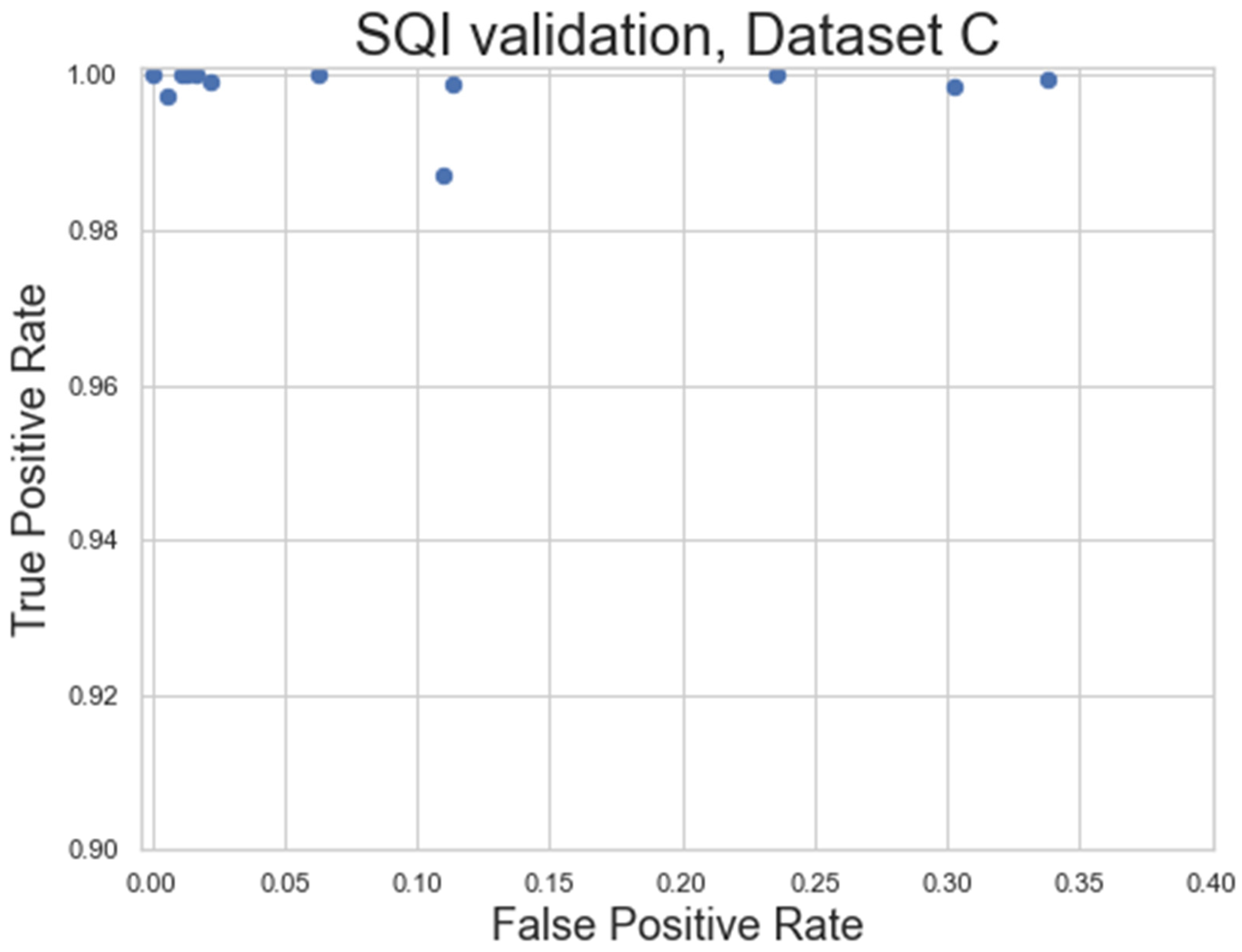
Table 1.
The infant dataset information for the three datasets used in this paper. Age column shows the range and mean ± standard deviation.
Table 1.
The infant dataset information for the three datasets used in this paper. Age column shows the range and mean ± standard deviation.
| Dataset | Device | Sampling Rate (Hz) | Environment | N | Age(months) | Total Recording | Mean Duration |
|---|---|---|---|---|---|---|---|
| A | Biosignal Plux |
500 | Free play in infant play area of research lab | 97 | 2.9-42.1 (Mage=16.9 ± 11.2) | 52 hrs, 20 min |
32 min, 22 sec |
| B | Geodesic EEG System | 1000 | Experimental lab condition (sitting on lap) | 25 | 5.6-13.0 (Mage=8.5 ± 2.1) | 3 hr, 34 min |
8 min, 36 sec |
| C | EgoActive sensor | 250 | Home environment | 12 | 5.3-10.4 (Mage=7.3 ± 1.9) | 15 hrs, 45 min |
78 min, 46 sec |
Table 2.
A guide to the pre-existing ECG pipelines tested in this paper.
| ECG Method | Method Description |
|---|---|
| HeartPy [28,37] | An approach designed to work with noisy data for both photoplethysmogram and ECG data. It uses baseline wander removal, a 0.05Hz notch filter, and a 0.003-20Hz bandpass filter in preprocessing. Peak detection is done through an adaptive threshold, followed by outlier detection and rejection. HeartPy does allow for user customization, although the only alteration made here was to raise the maximum allowed heart rate to 220bpm. |
| Neurokit2 [23] | A method which only uses a 0.5Hz HPF and a 50Hz notch filter in preprocessing. It uses gradients to detect the QRS complex, then detects the R-peak within the QRS. |
| Pan-Tompkins [26] | One of the first ECG peak detection methods to use preprocessing and properly account for noise. It uses a 5-15Hz BPF for preprocessing before taking a derivative, squaring, and integrating with a moving window to isolate the R-Peak, which is detected via a series of thresholds. |
| Hamilton [30] | This approach is an adaptation of Pan-Tompkins which uses an 8-16Hz BPF, rectification instead of squaring, and also a smaller integration window. |
| Christov [20] | A method that uses two self-adjusting algorithms to detect the current beat and the interval between beats, self-adjusting for different sampling frequencies. It is particularly designed for multi-lead analysis |
| EngZee [31] (Engelse & Zeelenberg) |
The oldest method tested, although the method used in Neurokit2 is an updated version from Lourenço et al. [22]. It uses a 48-52Hz notch filter, before differentiating the signal and passing it through an adaptive LPF, finally using an adaptive threshold analysis (inspired by Christov’s approach) to detect the peak. |
| Kalidas [32] | This method resamples the signal to 80Hz, before using Daubechies 3 wavelets as the basis set for stationary wavelet transforms. The signal is then squared and a moving window average is applied to enhance the R-peaks, which are then detected using threshold-based peak detection. |
| Nabian [25] | This approach is contained within a greater physiological signal toolbox, which aims to detect P, Q, R, S, and T points in the ECG. The R-peak detection is derived from Pan-Tompkins. A sliding window is used to detect a liberal initial R-peak list before culling the list down. |
| Martinez [24] | This approach also aims to identify multiple ECG complexes. Building off Li et al.’s approach [34], it uses a quadratic spline wavelet transform to identify the QRS peak. |
| Elgendi [21] | This approach uses an 8-20Hz BPF as optimal for identifying QRS complexes in adult ECGs. This choice is based on comparing a wide range of 2nd order Butterworth BPFs, along with moving window integration and thresholding to detect the R-peaks. |
| Zong [29] | Uses a LPF, a non-linear scaling factor to enhance the QRS complex and reduce noise, and then adaptive thresholds to determine the onset and duration of the QRS complex. The non-linear scaling factor reduces low frequency noise, eliminating the need for a HPF as well as the LPF. In the Neurokit2 implementation, the LPF is set at the Nyquist frequency (half the sampling rate), whereas in the paper Zong et al. appear to recommend a 16Hz LPF. |
| Rodrigues [27] | Uses a double derivative, square, and moving window integration in preprocessing to enhance the QRS complex. The R-Peak is then detected using a finite state machine which enhances the R-peak position [38] and uses an adaptive exponential decaying threshold for detection [39]. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






