Preprint
Article
Ridge-Type Pretest and Shrinkage Estimation in Spatial Error Model: An Application to Housing Cost Data
Altmetrics
Downloads
119
Views
38
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
07 December 2023
Posted:
11 December 2023
You are already at the latest version
Alerts
Abstract
Spatial regression models have garnered significant attention across several disciplines, including functional magnetic resonance imaging analysis, econometrics, home price analysis, and many other domains. The phenomenon of sparsity is often found in nature, when a limited number of factors contribute significantly to the overall variation. Spatial regression models frequently use sparsity to indicate less complex computational and more superficial covariance structures. The spatial error model is a significant spatial regression model that focuses on the geographical dependence present in the error terms rather than the response variable. This study proposes an effective approach for estimating the vector of regression coefficients in the spatial error model, taking into consideration of the prior knowledge that some coefficients are insignificant and there is multicollinearity among the regressors. It also introduces pretest and shrinkage ridge estimators for spatial error regression models, evaluating their performance compared to traditional maximum likelihood estimators. It also assesses their efficacy using real-world data and bootstrapping techniques for comparison purposes.
Keywords:
Subject: Computer Science and Mathematics - Probability and Statistics
1. Introduction
Data collected over a geographic region may generally show some dependence, whereby nearby observations are more similar than those made at significant distances. The incorporation of a covariance structure into conventional statistical models allows for the modeling of this phenomenon. Spatial regression models, incorporating various spatial dependencies, are increasingly utilized in various disciplines like geology, epidemiology, disease surveillance, urban planning, and econometrics.
Autoregressive models in the context of time-series reflect the data at time t as a linear combination of the most recent observations. Similarly, in the spatial framework, these models represent the data from a certain spatial place as a function of data from neighboring locations. The collection of data is often associated with a geographical location known as a site, and a metric of distance is used to define the notion of proximity between these sites.
One of the most used autoregressive models is the Spatial error(SE) model in which a linear regression with a spatially lagged autoregressive error component is used to model the spatial response variable’s mean. [20] investigated the quantile regression estimation for the SE model with potentially variable coefficients. They established the proposed estimators’ asymptotic properties. [27] applied the SE model to examine the existence of spatial clustering and correlation between neighboring counties for the data from Egypt’s 2006 census. [38] used the SE model in order to evaluate the Social Disorganization Theory. [33] used the combined application of SE model and Spatial Lag Model based on cross-section data of 20 districts in Chengdu. They found that the haze had a negative impact on both the selling and rental prices of houses. [43] proposed a robust estimation method based on SE models, demonstrating reduced bias, a more stable empirical influence function, and robustness to outliers through simulation. More information about the spatial autoregressive models can be found in [15,18,19,25,42], among others.
In frequentist statistics, we use sample information to establish inferences about unknown parameters, while we columbine the sample information with some uncertain prior information (UPI) which is also known as non-sample information to draw conclusions about the unknown parameters in Bayesian statistics. It is possible that such subjective UPI is not always available. However, procedures for model selection such as Akaike’s Information Criterion (AIC), Bayesian Information Criterion (BIC), or model selection techniques could still be used to provide the UPIs.
One of the Initial trails to incorporate the sample information and the UPI used to estimate the regression parameters by using sample information and the UPI is referred to as pretest estimation. Pretest estimator relies on determining whether some of the regression coefficients are significant, after which the pretest selects either the full model estimator or the revised model estimator, which has fewer number of coefficients. Obviously, the pertest chooses the full or sub model estimators based on a binary weights. A new modification of the pretest estimator that uses a smooth wights between the full and sub model estimators is known as shrinkage estimator, it shrinks the estimator of the regression coefficients in the direction of a target value impacted by the UPI. Nevertheless, the modified shrinkage estimator suffers sometimes from an over shrinkage phenomenon. Later on an improved version of this estimator is proposed that controls the over shrinkage issue, which is known as positive shrinkage estimator.
The concept of using pretest and shrinkage estimating methodologies has received considerable attention by many researchers, for example, [6] introduced an efficient estimation using the pretest and shrinkage methods to estimate the regression coefficients vector of the marginal model in case of multinomial responses. [32] developed different shrinkage and penalty estimation strategies for the negative binomial regression model when an over fitting and uncertainty information exist about the subspace. [35] proposed shrinkage estimation for the parameter vector of the linear regression model with heteroscedastic errors, and extended their study to the high-dimensional heteroscedastic regression model. More details about the pretest and shrinkage can be found in [1,4,21], among other references.
The mulicolinearity is a major issue when fitting a multiple linear regression model using the ordinary least squares method (OLS) that appears when some of the regressor variables are correlated, especially when the correlation between any two is high. There are several techniques discussed in the literature to reduce the risk of this issue. [28] introduced the concept of ridge regression as a solution for nonorthogonal problems.They showed the estimator improve the mean square error of estimation. [30] introduced a new biased estimator and demonstrated theoretically and numerically the improvement of the new one. [31] proposed a new version of Liu estimator for the vector of parameters in a linear regression model based on some prior information.
Using the idea of shrinkage, [7] introduced an improved form of Liu-type estimator. Analytical and numerical results were used to demonstrate the proposed method’s superiority. [13] suggested the pretest and shrinkage ridge estimation for the linear regression model and showed the benefit of using the recommended estimators in conjunction with certain penalty estimators. [9] defined Liu-type rank-based estimators for robust regression, analyzed their asymptotic behavior, established biasing parameter superiority criteria, and supported their findings with numerical computations. [14] introduced the pretest and shrinkage approaches based on generalized ridge regression estimation. Later on, [8] suggested the use of the ridge estimator as a suitable approach for handling high-dimensional multicollinear data. Further, [11] proposed an enhanced ridge method for genome regression modeling and used a rank ridge estimator to estimate parameters and make predictions in the presence of multicollinearity and outliers within the data set. Recently, [3] proposed a novel pretest and shrinkage estimate technique, known as the Liu-type approach, developed for the conditional autoregressive model. For more information, we advice the reader to consult the following references [22,23].
In this article, we aim to propose the ridge-type pretest and shrinkage estimation strategy for the regression coefficients vector in the SE model when some prior information is available about the irrelevant coefficients. We will partition the vector as , where is a vector that contains the coefficients of the main effect, and is a vector of irrelevant coefficients, with . Mainly, we focus in estimating the vector when the UPI indicates that is ineffective, which can be achieved by testing a statistical hypothesis of the form . In some instances, the estimator of the full model may exhibit considerable variability and provide challenges in terms of interpretation. Conversely, the estimator of the sub model may yield a significantly biased and under-fitted estimate. To tackle this matter, we have taken into account the pretest, shrinkage, and positive shrinkage ridge estimators for the vector .
In accordance with our goal the paper is organized as follows. Section 2 offers an overview of the SE model. The discussion of the maximum likelihood estimators for the parameters of the SE model are discussed in Section 3. In Section 4, we proposed the pretest and shrinkage ridge estimators. Asymptotic analysis of the proposed estimators and some theoretical results are presented in Section 5. The set of estimators are compared numerically using simulated and real data example in Section 6. Some concluding remarks are given in Section 7. An appendix containing some proofs is given at the end of this manuscript.
2. Spatial Error Model
Let represents a set of spatial sites (frequently known as locations, regions, etc.). The set forms what is commonly referred to as a lattice, and the set of nearby sites for , denoted by is defined as: , . A neighborhood structure can be determined using a predefined adjacency metric. In regular lattices, if two sites just share edges, they are rook-based neighbors; if they also share borders and/or corners, they are queen-based neighbors.
Let be a vector of observations collected at sites , and be the matrix of covariates. Following Cressie and Wikle [19], the SE model models the response at the site as:
where be the vector of unknown regression parameters, known as the large-scale effect, is noise vector that has a Gaussian distribution with mean and covariance matrix . The parameters are used to model the spatial dependencies among the errors , with . Let , and assume that is invertible, where is the identity matrix, then by ignoring the spatial indices, the SE in (1) can be rewritten in matrix format as:
Nature exhibits sparsity in many situations, which means that a small number of factors can account for the majority of the observed variability. Sparsity is frequently used in spatial regression models to imply covariance structures that are easier to compute. Consequently, by setting , and , where is the variance component, is the spatial dependance parameter, and is the weight or proximity known matrix with a main diagonal of zeros, and off diagonal entices if the location j is neighbor to location i, otherwise , the preceding model yields a straightforward and frequently used version. Usually, the weight matrix is normalized as . So, The SE regression model can be rewritten as follows
3. Maximum Likelihood Estimation
Let , the maximum likelihood estimator (MLE) of may be acquired by the use of a two-step profile-likelihood method see [18]. At first we fix and find the MLEs of as a function of , which are given below
Then, we plug and into the log-likelihood and obtain the MLE of by maximizing the profile log-likelihood function. Finally, the MLEs of and are computed by replacing by in equations (6) and (7), respectively. [34] proved that is a consistent estimator of , and asymptotically has normal distribution. This finding makes it simple to demonstrate that is asymptotically normal and consistent. The significance of regression coefficients can often be determined subjectively or through certain model selection techniques in various situations. As a result of this information, the regression coefficients vector is divided into two sub vectors as , where is a vector of important coefficients and is a vector of unimportant coefficients with . Similarly, the matrix of covariates is also partitioned as , where and are consisting of the first and the last columns of the design matrix of dimensions and , respectively. Consequently, the SE full model in (3) can be rewritten as:
For the full model in (8), we can obtain the MLEs of using the same technique employed in model (4), see [5]. The MLEs are as follows
and has an identical formula as by exchanging the indices 1 and 2 in the above two equations. The full model estimation may be prone to significant variability and may be difficult to interpret. Our primary goal is on estimating when does not sufficiently account for the variation in the response variable, which can be achieved by formulating a linear hypothesis as follows:
Assuming the null hypothesis in (10) is true, the updated model based on this assumption of the model given (8) becomes
We will refer to the model in (11) as the restricted SE model. Let be the MLE of of the model in(11), then
Obviously, will have a better performance than if the null hypothesis in (10) is true, while the opposite occurs when begins to move away from the null space. Yet, the restricted strategy method can provide under-fitted and highly biased model. To dominate the large bias, we propose the ridge-type estimation strategy of the full, and reduced models, then improve the two estimators using the pretest and shrinkage estimation idea.
4. Materials and Methods: Developing Pretest and Shrinkage Ridge Estimation Strategies
In this section we propose a set of estimators for the SE model parameters vector in (11). Following [28], The ridge estimator of for the model given in (4) is defined as
where is known as the ridge parameter. Clearly, when , the ridge estimator reduces to the MLE of , but if , the ridge estimator .
4.1. Full and Reduced Models Ridge Estimators
The unretracted full model ridge estimator of , denoted by is defined as follows
where is the ridge parameter for unretracted full model estimator . Assuming the null hypothesis in (10) is true, the restricted ridge estimator of for the model in (11), denoted by is given by
where is the ridge parameter for restricted model estimator . When the null hypothesis in (10) is accurate or almost accurate (i.e., when is close to zero), is generally a more effective estimator than . Nevertheless, as deviates from the zero space, becomes inefficient in comparison with the unrestricted estimator . In addition to the gain obtained by employing the idea of ridge estimation to the MLE of , we also aim to find estimators that are functions of and and intended to lessen the dangers connected with any of these two estimators over the majority of the parameter space. The pretest and shrinkage estimators, which will be built in the following subsection, can help with this.
4.2. Pretest, Shrinkage, and Positive Shrinkage Ridge Estimators
In line with testing the null hypothesis in (10), the pretest estimator selects either the full model estimator if is rejected or the restricted ridge estimator if not. An appropriate test statistics to test the hypothesis in (10) is:
where is defined in a similar manner as , , and , which is a consistent estimator of , and the statistic follows asymptotically a chi-square distribution with degrees of freedom under the null hypothesis. Hence, the pretest estimator, denoted by , is given by
where is an indicator function, and is the upper quantile of the chi-square distribution with degrees of freedom. The pretest estimator depends on the level of the significance , and selects if the null hypothesis is rejected, and otherwise based on a binary weights. These drawbacks can be improved using smoother weights of the two estimators and instead, which is known as the shrinkage estimator. It is denoted by, , and given by
The shrinkage estimator may experience an over-shrinkage in which negative coordinates may be produced whenever . The positive shrinkage estimator, a modified version of , resolves this issue. It is denoted by , and given by
where It is easy to see that all the pronounced shrinkage estimators satisfy the following general form
Simply, for , , and , the corresponding functions are given by , , and respectively.
5. Asymptotic Analysis
In this section, we will study the asymptotic performance of all estimators based on their asymptotic quadratic risks. Our goal is to investigate the behaviour of the set of estimators near the null space, so we consider a sequence of local alternatives given by
Obviously, when , the local alternatives in (20) may be simplified to the null hypothesis given in (10). Assuming that represents the cumulative distribution function of any estimator of , say , then: . Thus for any positive definite matrix , the weighted quadratic loss function is defined as
where is the trace of the matrix . Define , then if , where denotes to the convergence in distribution, then the asymptotic (distributional) quadratic risk (ADQR) of , denoted by , is given by
The asymptotic (distributional) bias (ADB) of can be obtained via
For the purpose of deriving asymptotic distributional properties, in addition to the first four assumptions of [34], we set the following regularity conditions:
- (A1)
- , as , where is the ith row of .
- (A2)
- Let . Then, , where is positive definite matrix.
- (A3)
-
LetThen, , where for .
In sequel, we call the above assumptions as the “named regularity condition (NRC)".
The primary tool to derive expressions of the asymptotic quadratic risks for the proposed estimators is to find the asymptotic distribution of the unrestricted full model ridge estimator and the restricted ridge estimator . To this end, we make use of the following lemma. The proof is provided in the Appendix.
Lemma 1.
Assume the NRC. If , then
where denotes convergence in distribution. Indeed, Lemma 1 enables us to give some asymptotic distributional results about the estimators and , presented in the following theorem, which are easy to prove. See [21] for similar results.
Theorem 1.
Let , , and . Assume the local alternatives in (20) and NRC. Then, as we have
- (1)
- (2)
- (3)
- (4)
- (5)
- (6)
- E
- (7)
- , where is the cumulative distribution function of a non-central chi-square distribution with q degrees of freedom and non-centrality parameter Δ.
where , , .
With Lemma 1 in hand, it is pretty straightforward to reach the asymptotic distributional properties of the shrinkage estimators. Through the subsequent theorems, we will give the asymptotic bias and weighted quadratic risk functions.
Theorem 2.
Under the assumptions of Lemma 1, the asymptotic distributional bias of the shrinkage estimators are given by
For the proof, refer to Appendix.
The following result reveals the expressions for the ADQR of the proposed shrinkage estimators.
Theorem 3.
Under the assumptions of Lemma 1, the asymptotic distributional quadratic risk of the shrinkage estimators are given by
where is a positive definite weight matrix,
For the proof, refer to the Appendix.
6. Numerical Analysis
To demonstrate our theoretical findings, we first use Monte Carlo simulation experiments, then apply the set of proposed estimators to a real data set. The Monte Carlo simulation is used to investigate the performance of the ridge-type set of estimators in comparison to the MLE given in (9) via the simulated mean square error of each estimator.
6.1. Simulation Experiments
In this section, we compare the set of ridge-type estimators with respect the MLE using Monte Carlo simulation experiments based on their simulated mean squared errors. In each one of theses experiments, we consider an square lattices using with the corresponding sample sizes of , respectively. To show the performance of the proposed estimators when a multicollinearity exits, we generate the design matrix from multivariate normal distribution with mean , and a variance-covariance matrix with first order autoregressive structure in which and apply it for , while the error term is generated from another multivariate normal with mean and a SE variance matrix with . We set . For the weight matrix , a queen-based contiguity neighborhood was used. The set of values for is . We partitioned the vector of coefficients as where is a vector of ones, and , is a zero vector of dimension , and , where is the Euclidian norm of , and represents the non-centrality parameter. The range of values for is set to be from 0 to 2. Then we fitted the model in (8) using the spautolm function within the R-package spdep [16], obtain the values of all estimators considered in our study, and computed the simulated mean square error (SMSE) of each estimator as . The simulated relative efficiency (SRE) of any estimator, say , with respect to the MLE is calculated as:
where is any of the estimators . It is evident that when the is greater than one, it signifies that this estimate outperforms the MLE of the full model, and vice versa. We run the simulation for , and use for testing the hypothesis in (20). No statistically significant change was seen while altering the spatial dependency parameter. Therefore, we have chosen to simply exhibit the graphs for . Figure 1, Figure 2 and Figure 3 show the results of the SRE against various values of . The findings support the following conclusions:
- (i)
- Across all values, the ridge-type full model estimator consistently outperforms the traditional MLE estimator. Furthermore, as increases, so does its efficiency for fixed values of and . Additionally, when the multicollinearity among the explanatory variables in the design matrix becomes stronger, efficiency increases as expected.
- (ii)
- The Ridge-type sub-model estimator outperforms all other estimators when . Since the null hypothesis is correct, it is expected. However, once begins to depart from the null space, the estimator’s SRE drops precipitously and approaches to zero, making it less effective than the other estimators.
- (iii)
- The SRE values grow while holding other parameters constant as the correlation coefficient increases among the explanatory factors.
- (iv)
- As the number of zero coefficients increase , all estimators SRE also increase.
- (v)
- The ridge-type positive shrinkage estimator uniformly prevails over the competing estimators.
6.2. Data Example
In 1970, [26] examined the use of housing market data for census tracts in the Boston Statistical Metropolitan Area. Their major objective was to establish a relationship between a set of (15) variables and the median cost of owner-occupied residences in Boston. [24] offered a corrected version of the data set along with new spatial data. The data set is accessible through the R-Package spdep. There are 506 observations in the data, each of which relates to a single census tract. The variables in the data include the tract identification number (TRACT), median owner-occupied housing prices in US dollars (MEDV), corrected median owner-occupied housing prices in US dollars (CMEDV), percentages of residential land zoned for lots larger than 2500 square feet per town (constant for all Boston tracts) (ZN), percentages of non-retail business areas per town (INDUS), average room sizes per home (RM), the percentage of owner-occupied homes built before 1940 (AGE), a dummy variable with two levels that is 1 if the tract borders the Charles River and 0 otherwise (CHAS), crime rate per capita (CRIM), weighted distance to main employment centers (DIS), nitrogen oxides concentration (parts per 10 million) per twon (NOX), an accessibility index to radial highway per town (constant for all Boston tracts) (RAD), property tax rate per town ($10,000)(constant for all Boston tracts) (TAX), percentage of the lower-class population (LSTAT), pupil-teacher ratios per town (constant for all Boston tracts) (PTRATIO), and the variable , where b is the proportion of blacks (B). [37] added the location of each tract in latitude (LAT), and longitude (LON) variables.
Assuming a SE model, we can predict the response variable log(CMEDV) using all available variables, that will be referred to as full SE model. For these data, a variety of selection techniques were used to determine the submodel. One submodel that was used by [5] is the model obtained by adaptive LASSO algorithm, which will be referred as our SE submodel. The two models are summarized in Table 1.
Figure 4 displays a coloured plot of the correlation coefficients for each variable. When a strong linear relationship is present, the color seems dark; when a weak linear relationship is present, the color shifts to light or may even vanish. The CMEDV and a few other factors have a strong linear relationship, as seen in the plot. This plot is useful for examining the strength of linearity between the original response CMEDV and any other variable, if exists. The selected variables by adaptive LASSO algorithm appear to have a strong, medium and weak relationship with the response variable. Moreover, some variables exhibit collinearity, and this issue will show how really the ridge-type estimators will show up the high performance in comparison with the MLE estimator.
To assess the effectiveness of the suggested estimators we employed a bootstrapping technique suggested by [41], computing the mean squared prediction error (MSPE) for any estimator as follows:
- 1.
- Fit a SE full and sub models as appear in Table 1 using the spautolm function and get the MLEs of , , the spatial dependance parameter , the covariance matrix .
- 2.
-
As the columns of the two matrices and are not orthogonal, and the sample size is large, we followed Philip S. et al [17] to estimate the tuning ridge parameters for the two estimators and which are, respectively, given by:, and .
- 3.
- Use the Cholesky decomposition method in order to express the matrix in a decomposed form as , where is an lower triangular matrix.
- 4.
- Let , where , and define the centered residual as , then select with replacement a sample of size form to get .
- 5.
- Calculate the bootstrapping response value as , then use it to fit the full and sub models and obtain bootstrapping estimated values of all estimators.
- 6.
- Calculate the predicted value of the response variable using each estimator as follows: , where represents any of the estimators in the set .
- 7.
- For the bootstrapping sample, calculate the square root of the mean square prediction error (MSPE) aswhere B is the number of bootstrapping samples.
- 8.
- Calculate the relative efficiency (RE) of any estimator with respect to the MLE as follows:where is any of the ridge-types proposed estimators. We apply the bootstrapping technique times.
Table 2 summarizes the results of the relative efficiencies, where a number greater than one of the relative efficiency implies the superior performance of the estimator in the denominator.
The table illustrates the better performance of the submodel ridge-type estimator compared to all other estimators. It is then followed by the pretest estimator , demonstrating the correctness of the submodel that was selected. Also, the ridge positive shrinkage estimator performs better than the shrinkage one. Furthermore, all ridge-type estimators outperformed the MLE of .
7. Conclusion
This paper discusses the pretest, shrinkage, and positive shrinkage ridge-type estimators of the parameter vector for SE model when there is a previous suspicion that certain coefficients are insignificant, and the muticolinearity presents between two or more regressor variables. To obtain the proposed set of estimators for the main effect vector of coefficients , we test the hypothesis . The proposed estimators were compared analytically via their asymptotic distributional quadratic risks, and numerically by simulation experiments and a real data example.
Our results, showed that there is no significant effect of the spatial dependence parameters , while the performance of the ridge estimators increases when the correlation among the regressor variables increase. Moreover, the performance of the ridge estimators always better than the MLE. In addition, the estimator dominates all estimators under the null hypothesis or when near the null space and delivers higher efficiency than the other estimators. However, the proposed positive shrinkage ridge estimators performs better than the MLE in all seniors. Further, we apply the set of estimators to a real data example, and used a bootstrapping technique to evaluate their performance based on the relative efficacy of square root of the mean squared prediction error.
Author Contributions
The author initiated the research, designed the study, proposed estimators, established a methodology, simulated data, analyzed findings, wrote a manuscript, underwent critical revision, and received final approval. The coauthor meticulously stages the research, from design to final approval, ensuring accuracy, clarity, and coherence of findings through an iterative process.
Funding
This study is self-funded.
Data Availability Statement
The data set is accessible through the R-Package “spdep.”
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
In this section, we give proofs of the main results.
Proof of Lemma 1: For the proof, we follow the approach of Yuzbasi et al [44], with a slight modification. Let and define
where . Following [36],
with finite-dimensional convergence holding trivially. Also
Thus with the finite-dimensional convergence holding trivially. Since is convex and has a unique minimum, it follows that
It concludes
Proof of Theorem 2: Because all of the pronounced estimators are special cases , we give the bias of this estimator here. Then the proof follows by applying relevant function in each estimator. Hence, we have
Using part one of Lemma 1, . Further using part three of Lemma 1 along with Theorem 1 in Appendix B of [29], we get
Therefore, the asymptotic bias of the general shrinkage estimator is given by
The proof is complete considering the expressions for given in Table A1.
Proof of Theorem 3: Similar to the proof of Theorem 2, we provide the ADQR of the shrinkage estimator here. Then the proof follows by applying relevant function in each estimator. Hence, we have
From Lemma 1, we have
From Lemma 1
References
- Ahmed SE.(2014). Penalty, shrinkage and Pretest Strategies Variable Selection and estimation. Cham: Springer International Publishing 2014.
- Ahmed SE, Bahadir Y. (2016). Big Data Analytics: Integrating Penalty Strategies. Big Data Analytics: Integrating Penalty Strategies. 11(2), 105–115.
- Al-Momani M.(2023). Liu-type pretest and shrinkage estimation for the conditional autoregressive model. PLOS ONE. 18(4). [CrossRef]
- Al-Momani M, Dawod AB.(2022). Model selection and post selection to improve the estimation of the arch model. Journal of Risk and Financial Management. 15(4), 174.
- Al-Momani M, Hussein AA, Ahmed SE.(2016). Penalty and related estimation strategies in the spatial error model. Statistica Neerlandica. 71(1), 4–30.
- Al-Momani M, Riaz M, Saleh MF. (2022). Pretest and shrinkage estimation of the regression parameter vector of the marginal model with multinomial responses. Statistical Papers. [CrossRef]
- Arashi M, Kibria BMG, Norouzirad M, Nadarajah S.(2014). Improved preliminary test and Stein-rule Liu estimators for the ill-conditioned elliptical linear regression model. Journal of Multivariate Analysis. (126), 53–74.
- Arashi M, Norouzirad M, Ahmed SE., Bahadir Y.(2018). Rank-based Liu Regression. Computational Statistics. 33(3),1525–1561.
- Arashi M, Norouzirad M, Roozbeh M, Khan NM.(2021). A high-dimensional counterpart for the ridge estimator in multicollinear situations. Mathematics. 9(23),3057.
- Arashi M, Roozbeh M.(2016). Some improved estimation strategies in high-dimensional semiparametric regression models with application to riboflavin production data. Statistical Papers. 60(3), 667–686.
- Arashi M, Roozbeh M, Hamzah NA, Gasparini M.(2021). Ridge regression and its applications in genetic studies. PLOS ONE. 16(4). [CrossRef]
- Bahadir Y, Ahmed SE, Ahmed F. (2023). Post-shrinkage strategies in statistical and machine learning for high dimensional data. S.l.: CRC PRESS 2023.
- Bahadir Y, Ahmed SE, and Gungor M. (2017). Robust estimation approach for spatial error model. REVSTAT-Statistical Journal. 15 (2),251–276.
- Bahadir Y, Arashi M, Ahmed SE.(2020). Shrinkage estimation strategies in Generalised Ridge Regression Models: Low/high-dimension regime. International Statistical Review. 88(1),229–251.
- Baltagi BH, Lesage JP, Pace RK.(2017). Spatial econometrics: Qualitative and limited dependent variables. Bingley, UK: Emerald Group Publishing Limited. 2017.
- Bivand R. (2022). R packages for Analyzing Spatial Data: A comparative case study with Areal Data. Geographical Analysis. 54 (3),488–518.
- Boonstra PS, Mukherjee B, Taylor JM.(2015). A small-sample choice of the tuning parameter in ridge regression. Statistica Sinica. [CrossRef]
- Cressie N. (1993). Statistics for Spatial Data. Nashville, TN: John Wiley & Sons 1993.
- Cressie N, Wikle CK.(2011). Statistics for Spatio-Temporal Data. Chichester, England: Wiley-Blackwell 2011.
- Dai X, Li E, Tian M.(2019). Quantile regression for varying coefficient spatial error models. Communications in Statistics - Theory and Methods. 50 (10),2382–2397.
- Ehsanes S A K M. (2006). Theory of preliminary test and Stein-type estimation with applications. Hoboken (N.J.): Wiley-Interscience. 2006.
- Ehsanes S A K M, Arashi M, Golam K B M (2019). Tank-based methods for shrinkage and selection: With application to machine learning. Hoboken (N.J.):John Wiley & amp; Sons, Inc. 2019.
- Ehsanes S A K M, Arashi M, Saleh R A, Norouzirad M. (2022). Theory of ridge regression estimation with applications. Hoboken (N.J.):John Wiley & amp; Sons, Inc. 2019.
- Gilley OW, Pace RK.(1996). On the Harrison and Rubinfeld data. Journal of Environmental Economics and Management. 31 (3),403–405.
- Haining R. (2003). Spatial Data Analysis: Theory and Practice. Cambridge: Cambridge University Press; 2003.
- Harrison D, Rubinfeld DL.(1978). Hedonic housing prices and the demand for Clean Air. Journal of Environmental Economics and Management. 5 (1),81–102.
- Higazi SF, Abdel-Hady DH, Al-Oulfi SA.(2013). Application of spatial regression models to income poverty ratios in Middle Delta contiguous counties in Egypt. Pakistan Journal of Statistics and Operation Research. . 9 (1),93.
- Hoerl AE, Kennard RW.(1970). A new Liu-type estimator in linear regression model. Technometrics. 12 (1),55–67.
- Judge, George G., and M. E. Bock. (1970). The Statistical Implications of Pre-Test and Stein-Rule Estimators in Econometrics. North-Holland Pub. Co.. 1978.
- Kejian L.(1993). A new class of blased estimate in linear regression. Communications in Statistics - Theory and Methods. 22 (2),393–402.
- Li Y, Yang H.(2010). A new Liu-type estimator in linear regression model. Statistical Papers. 53 (2),427-437.
- Lisawadi S, Ahmed SE, Reangsephet O.(2020). Post estimation and prediction strategies in negative binomial regression model. International Journal of Modelling and Simulation. 41 (6),463–477.
- Liu R, Yu C, Liu C, Jiang J, Xu J.(2018). Impacts of haze on housing prices: An empirical analysis based on data from Chengdu (China). International Journal of Environmental Research and Public Health. 15 (6),1161.
- Mardia KV, Marshall RJ. (1984). Maximum likelihood estimation of models for residual covariance in spatial regression. Biometrika. 71 (1),135–146.
- Nkurunziza S, Al-Momani M, Lin EY. (2016). Shrinkage and lasso strategies in high-dimensional heteroscedastic models. Communications in Statistics - Theory and Methods. 45 (15),4454–4470.
- Wenjiang Fu and Keith Knight. (2000). Asymptotics for lasso-type estimators. The Annals of Statistics. 28 (5), 1356–1378.
- Pace R K, Gilley, O W. (1997). Using the Spatial Configuration of the Data to Improve Estimation. Journal of Real Estate Finance and Economics. (14),333–340.
- Piscitelli A. (2019). Spatial Regression of Juvenile Delinquency: Revisiting Shaw and McKay. International Journal of Criminal Justice Sciences. 14 (2),132–147.
- Roozbeh M, Babaie–Kafaki S, Aminifard Z.(2021). Two penalized mixed–integer nonlinear programming approaches to tackle multicollinearity and outliers effects in linear regression models. Journal of Industrial and Management Optimization. 17 (6),3475.
- Roozbeh M, Babaie-Kafaki S, Manavi M.(2022). A heuristic algorithm to combat outliers and multicollinearity in regression model analysis. Iranian Journal of Numerical Analysis and Optimization. 12 (1),173–186.
- Solow AR. (1985). Bootstrapping correlated data. Journal of the International Association for Mathematical Geology. 17 (7),769–775.
- Waller LA, Gotway CA. (2004). Applied Spatial Statistics for Public Health Data. Hoboken (N.J.):Wiley-Interscience. 2004.
- Yildirim V, Mert K Y. (2020). Robust estimation approach for spatial error model. Journal of Statistical Computation and Simulation. 90 (9),1618–1638.
- Yuzbasi, B., Arashi, M., and Ahmed, S. E. (2020). Shrinkage estimation strategies in generalized ridge regression models under low/high-dimension regime. International Statistical Review. 88 (1), 229-251.
Figure 1.
SRE of the suggested estimators with respect to the MLE () for , , , and .
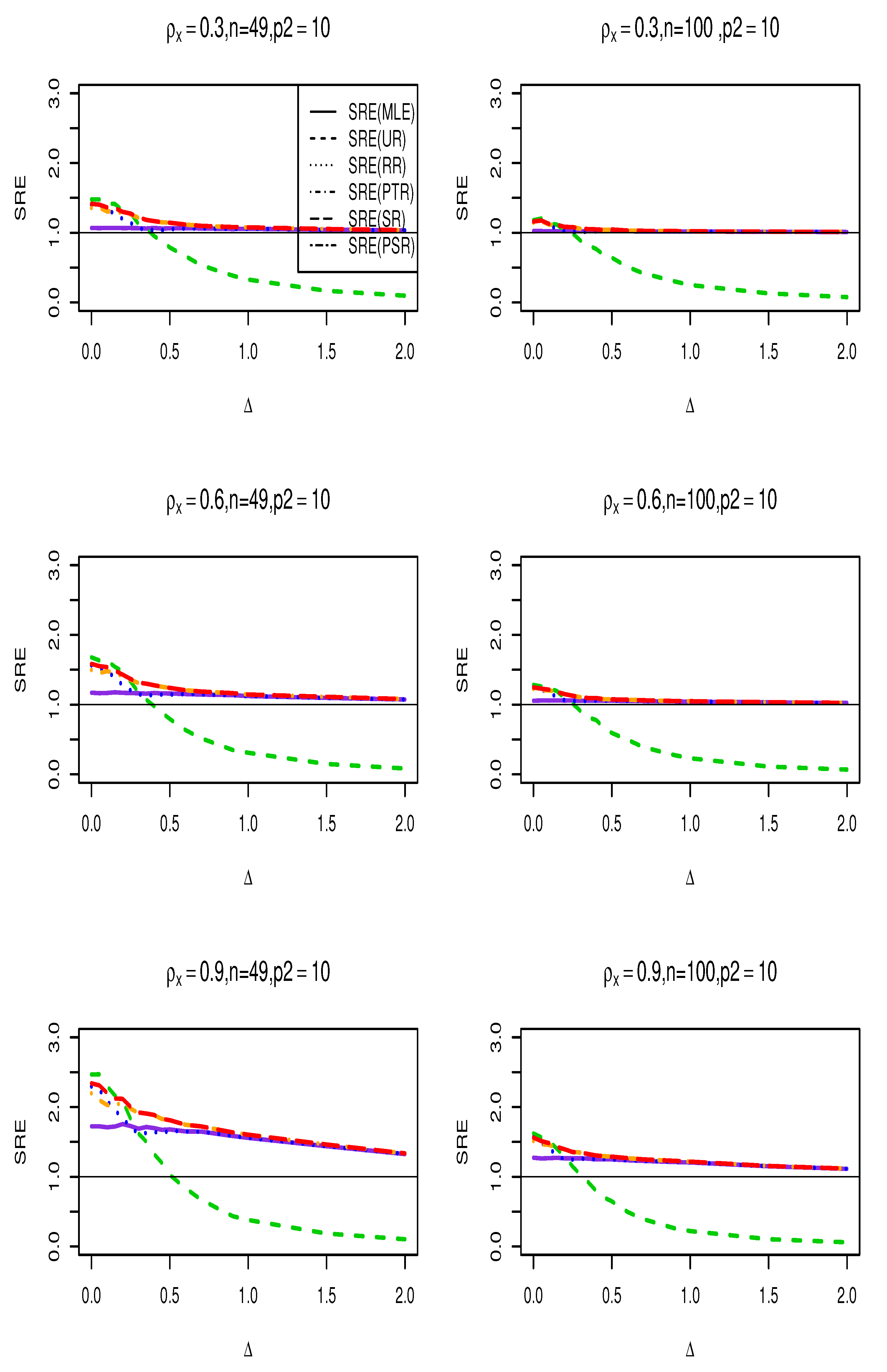
Figure 2.
SRE of the suggested estimators with respect to the MLE () for , , , and .
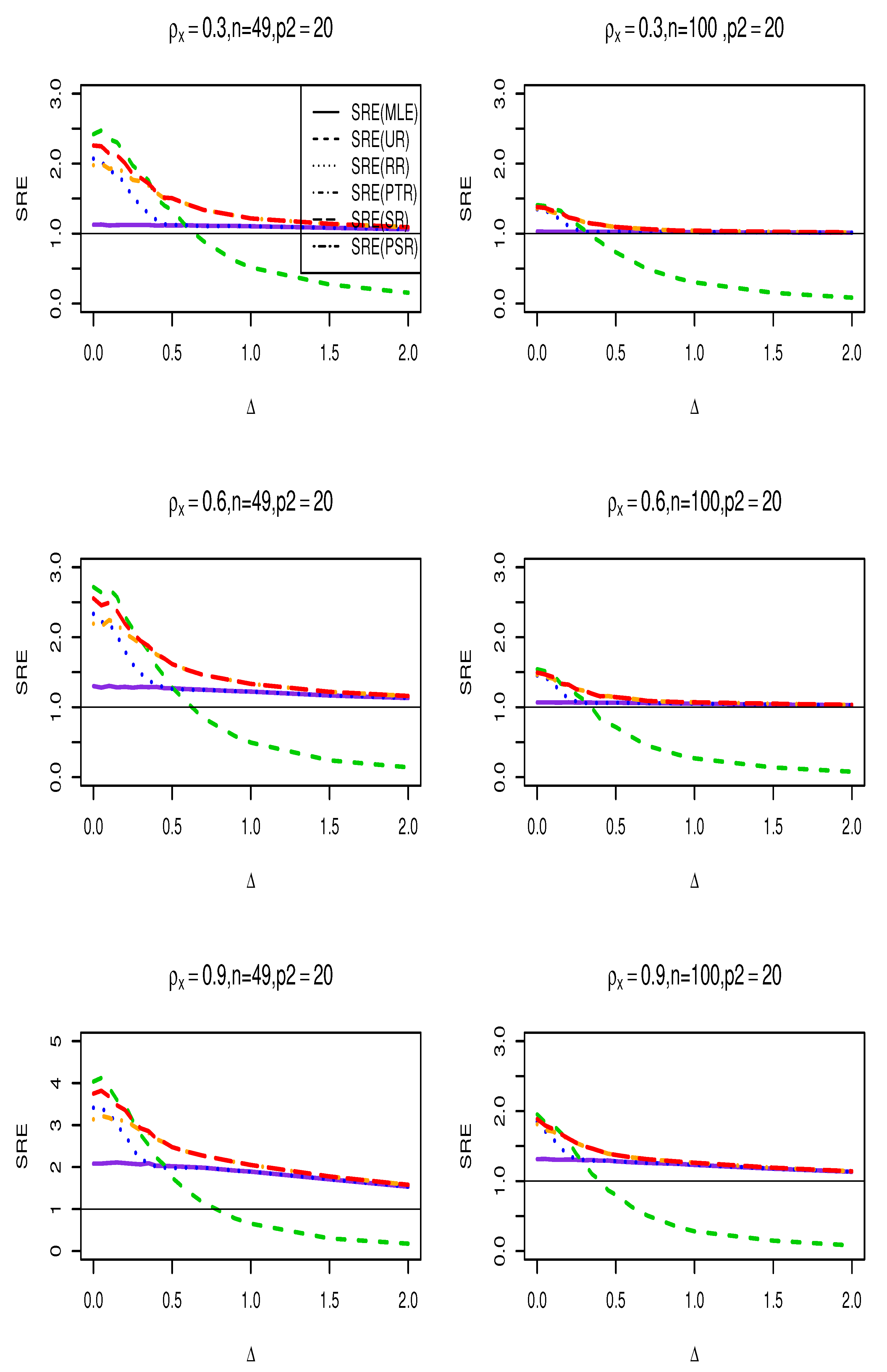
Figure 3.
SRE of the suggested estimators with respect to the MLE () for , , , and .
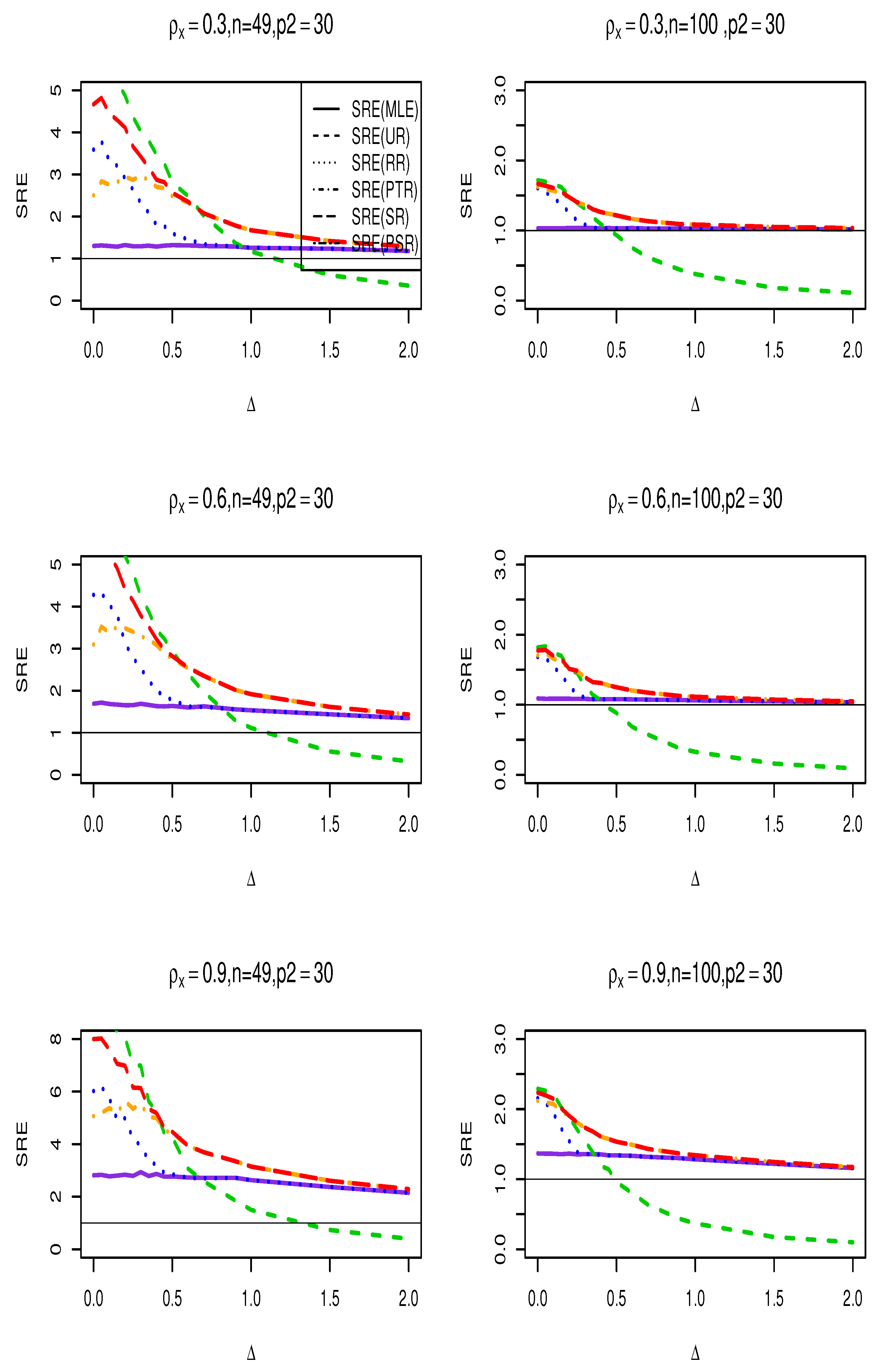
Figure 4.
Correlation Matrix for the Boston Housing Data.
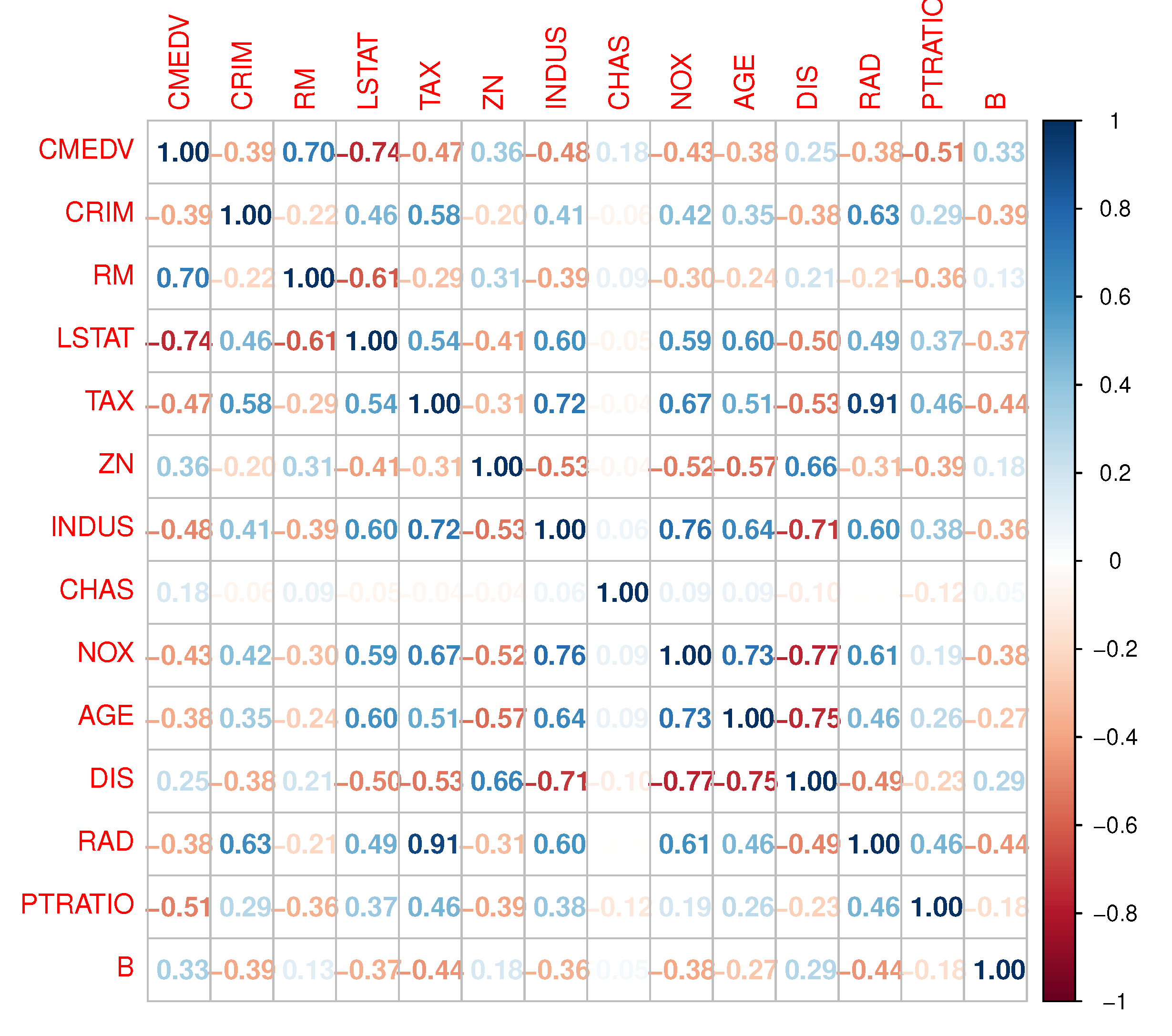
Table 1.
Full and Submodel
| Selection Criterion | Model |
|---|---|
| Full | log(CMEDV) = log(LSTAT)+I(RM^2) + TAX |
| +B +log(RAD) + CHAS +CRIM + PTRATIO | |
| + AGE+ LAT+ LON+log(RAD)+ I(NOX^2) | |
| + log(DIS) + ZN+ INDUS | |
| Submodel | log(CMEDV) = log(LSTAT)+ I(RM^2)+ TAX+ B+ CRIM |
| + PTRATIO |
Table 2.
RE of the proposed estimators
| Estimator | |||||
| 1.0198 | 2.9468 | 2.8624 | 2.3070 | 2.3287 |
Table A1.
Expressions for the corresponding functions in the proposed shrinkage estimators
| Shrinkage estimator | function | |
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







