Prerpints.org logo
Preprint
Article

A Longitudinal Study on the Development of Executive Function and Calibration

Altmetrics

Downloads

165

Views

47

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

08 December 2023

Posted:

11 December 2023

Read the latest preprint version here

Alerts
Abstract
This longitudinal study aimed to examine the development of executive function and calibration accuracy in pre-adolescents. Two hundred sixty two students(127 females) from grades 4 (n = 91), 5 (n = 89) and 6 (n = 82) took measures of executive function and performance calibration in a sport task, three times within a period of 20 months. A latent growth curve modeling analysis showed a significant relation between the rates of change of executive function and calibration. Further, the results showed a dynamic interplay in the development of executive function and calibration. There were significant inter-individual differences in the estimated population means both in executive function and calibration and in the rate of change of executive function, but not in the rate of change for calibration. The age of the participants had a positive effect only on the estimated population mean of executive function. Overall, although the development of executive function and calibration in pre-adolescence presents a pattern of improvement, it is also characterized by large inter-intividual differences.
Keywords: 
Subject: Social Sciences  -   Cognitive Science

1. Introduction

In the course of development, children acquire several important mental qualities that allow them to intentionally regulate their behavior and thinking. These, for example, include, among others, the abilities to assess accurately the difficulty of a task to be undertaken, to stay focused on it despite external or internal distractions, to detect errors and revise accordingly and to search for alternative solutions to a problem. These qualities are referred to as “higher order cognitive processes”. These encompass two groups of processes: metacognitive ones and executive functions (EF).
The development and the relation of these processes to effective functioning in every-day tasks, including academic tasks, have been extensively examined [1,2]. However, despite the strong conceptual links between these two groups of processes [3], these have often been studied independently. As a consequence “there is limited evidence on the nature of their relationship and how this extends developmentally” [4] (p. 1). The present study aimed to add in the limited research base that charted simultaneously the development of metacognitive processes and executive functions. In particular, the study focused on the developmental relations of executive functions and the metacognitive process of performance estimations.

1.1. Executive functions

Executive functions are theorized as higher-order cognitive processes that facilitate the cognitive adaptability and flexibility of goal-oriented behaviour. These are assumed to be triggered in novel, challenging, and complex situations when concentration and attention are needed [5]. Based mainly on Miyake’s et al. [6] work, most theorists endorse that there are three core executive functions, namely inhibition, working memory, and cognitive flexibility [5].
Following Diamond [5], inhibition allows students to block habitual thoughts and actions and to control their attention, behavior, thoughts, and emotions, thus enabling them to focus on the task at hand and take the most appropriate actions. Working memory refers to the short-term storage and handling of information. It enables the interrelation and reorganisation of pieces of information or the incorporation of new information into action plans. Cognitive flexibility, or shifting, allows students to change approaches when solving a problem while shifting attention between task demands and to adjust to new demands, rules, or priorities [5].
Health, quality of life and success in school and life have been positively linked to EF ([1]. For example, studies by Alloway and Alloway [7], Roebers et al. [8] and Cantin et al. [9] have shown the positive effects of executive functions on school success and academic achievement while sport performance has also been linked to executive functions [10,11,12].

1.2. The metacognitive process of calibration of performance

The concept of metacognition (MC) was introduced by Flavell [13] who defined metacognition as cognition of cognition that serves two basic functions, namely, the monitoring and control of cognition. Since then, three facets of MC have been theorized: metacognitive knowledge which refers to declarative knowledge regarding tasks, strategies and goals: metacognitive experiences which denote the person’s awareness of his/her feelings and perceptions when coming across a task and metacognitive skills that refer to the deliberate use of strategies in order to control cognition [14].
Calibration refers to the degree of the fit between individuals’ judgements of performance and their actual performance [15]. Therefore, calibration is the difference between one’s estimated performance and actual performance on specific tasks [16]. Calibration involves awareness of internal processes [17] including monitoring of what students know about a topic or skill and judging this knowledge with a criterion task. Thus, calibration can be considered a metacognitive experience since “metacognitive experiences are what the person is aware of and what she or he feels when coming across a task and processing the information related to it” [14] (p. 279). These are resulting from conscious processing related to instructions and task characteristics [18].
Well-calibrated students can realize their actual level of performance focusing on aspects of the tasks that they have not mastered yet [19]. In contrast, miscalibrated students may set unrealistic or rather easy goals which may prohibit them from trying to improve their performance [20]. Miscalibrated students may also be less responsive to external feedback (i.e., how to improve skills) and may not take responsibility for their development due to inaccurate self-feedback regarding their learning.
Research in academic settings has shown that students usually overestimate their performance [21,22]. Similarly, in physical education, students overestimated their performance in sport tasks including basketball chest-pass, basketball shooting, and soccer pass [23,24].

1.3. Development of executive functions, metacognition and calibration

Theorists have noted a conceptual similarity between EF and MC [3,25]. These concepts are theorized as higher-order cognitive processes that allow individuals to function and adapt effectively to new and demanding tasks. Further, they are theorized to be initiated and controlled by the individual. Moreover, both involve sub-procedures (e.g., shifting, updating, and inhibition for EF, monitoring and control for MC). Additionally, both concepts refer to the ability of individuals to monitor and control their thinking and behavior. Given the theoretical overlap between these two concepts, it is somewhat surprising that their development has been examined independently.
Regarding the development of EF, an earlier review of [26] indicated that inhibition shows a rapid and large improvement during the preschool years and slower improvement later on. Working memory shows a linear and longer improvement in the time period between pre-school and adolescence while shifting “follows a protracted development through adolescence” [26] (p. 1652) and is developed later than the other two core EFs as it is based on these [27]. More recent longitudinal studies generally confirmed the assertions of Best and Miller [26]. For example Lee et al., [28] reported that working memory showed a steady increase from 6 to 15 years, while Brydges et al., [29] reported improvements in all three EFs from 8 to 10 years.
As for the development of calibration, research evidence has indicated an improvement in calibration accuracy with age [30]. For example, kindergartners showed a stronger overconfidence compared to second graders in computer-based learning tasks [31] and early primary schoolers overestimate themselves in comparison to older children [32,33]. In sport settings, a positive relationship between age and prediction accuracy was found among runners, with older runners showing better calibration accuracy compared to younger ones [34]. In physical education, sixth-grade students were more accurate compared to the fifth-grade students [35]. Although the evidence of these cross-sectional studies has indicated an improvement in calibration accuracy with age, there are not any related longitudinal studies to chart the development of this metacognitive experience. To this end, an earlier call by Chen and Bembenutty [18] for related longitudinal studies with regard to authentic school tasks is still relevant.
Roebers [3] summarized the results of studies on the development of EF and MC. For EF, she concluded that a significant improvement in inhibition and working memory appears between the third and fourth year of life, while continuous improvement of these EFs as well as in shifting takes place in middle childhood and adolescence. Similarly, regarding MC, remarkable improvements are observed around the fourth year of age, although several actions, including making performance predictions, are still difficult for upper – elementary school children [36].
Given the theoretical overlap between these two concepts, and developmental findings which denoted a rapid improvement of both in early years and a continuous improvement in school years, it would be informative to study how their relationship progresses developmentally. Respective information would “provide knowledge regarding which concept precedes other in order to better understand developmental mechanisms” [37] p. 99). However, studies that have focused on the development of both EF and MC are rare. In such an effort, Howard et al. [4] assessed children’s EF and metacognitive abilities at three time points: at the beginning of children’s final preschool year; at end of the final preschool year and at the end of the first year of school. Their results showed bi-directional associations between EF and MC in a cross-lagged panel model. Spiess et al. [37] measured executive functions and metacognitive control twice within 8 months, in eight-year-old children. Their results showed an improvement of both EF and MC, although, in contrast to Howard, et al. [4] the longitudinal links between EF and MC were not significant. However, this result may be due to stability of the constructs in the relative short period of this study. Finally, in a study with 1st graders, Roebers et al. (2012) reported that executive functions were significantly related to metacognition both cross-sectionally and longitudinally.
The present study aimed to add in the limited studies that examined concurrently the development of EF and MC. In particular, the present longitudinal study enriches the limited pool of these studies in three important aspects: First, by the employment of latent growth modeling, it assessed the rates of change in EF and the metacognitive skill of calibration as well as the magnitude of the relationship between the two rates. Further, the present study examined potential individual differences in these developmental trajectories. Second, the study focused on 10 to 12 year-old- students as both EF and MC are still developing and the specific metacognitive skill of performance prediction is under-developed [36]. Finally, an authentic school sport task was employed instead of a cognitive task [37].

2. Materials and Methods

2.1. Design

The study involved a longitudinal design with two measures across three time points. Students were assessed on EF and calibration regarding a sport task at three times: At the beginning of the academic year (T1), at the end of the academic year (T2) and one year later at the end of the next academic year (T3).

2.2. Participants

Two hundred sixty two (127 females) grade 4 (91), grade 5 (89) and grade 6 (82) students took part in the study at T1. Out of these, 249 students took part at T2 (grade 4: n = 87, grade 5: n= 82, grade 6: n = 80) while 233 students took part at T3 (grade 4: n = 82, grade 5: n = 80, grade 6: n = 71). Students at T3 were attending the next grade than at T1 and T2.

2.3. Measures

2.3.1. Executive function.

The design fluency test [38] was used to assess students’ EF. This is part of the Delis-Kaplan Executive Function System, which is a standardized test battery with satisfactory psychometric properties including test-retest reliability, convergent and discriminant validity [39]. The test consists of three conditions with one minute allowed for each condition. In each of these, a sheet with 35 square boxes with unstructured arrays of dots is used. In condition 1, each box contains five solid dots students generate as many novel designs as possible using four consecutive straight lines. In condition 2, each box contains five solid and five blank dots, and students have to generate as many novel designs as possible, using four consecutive straight lines connecting only blank dots. In condition 3, each box contains five solid and five blank dots, and students have to generate as many novel designs as possible, using four consecutive straight lines alternating between connecting a solid and a blank dot (starting either from a solid or a blank dot). The number of correct and unique designs is the students’ scores in each condition of the test. The first condition evaluates fluency in generating visual patterns, the second condition assesses inhibition, and the third cognitive flexibility (switching). A total score of students’ scores in the three test conditions served as a measure of executive function.

2.3.2. Sport task.

A basketball shooting test [40] was employed. This test has demonstrated a satisfactory test-retest reliability .92. Students had to shoot, without time limit, 10 shots in front of the basket from a distance of 2.5m. Students’ score in this test was their number of successful shots.

2.3.3. Calibration

Before taking the basketball shooting test, students answered the following question: “How many of your shots out of 10 will be successful from this position in the following test?” Students’ answers in this question were their scores in the estimation of their shooting performance. The calibration accuracy index (i.e., absolute values of the difference between estimated and actual performance) [16] was used. Scores of this index closer to zero indicate higher calibration accuracy.

2.4. Procedures

The study was approved by the Institution’s Ethics Review Committee. Parental written consent was secured and the students were assured for the anonymity of their responses.The students completed the design fluency test in their classrooms. For each condition of the test, the experimenter provided respective instructions and demonstrated one trial on the classroom blackboard. Students performed a practice trial including three boxes of dots before proceeding to each condition of the test. The experimenter used a stopwatch to monitor the time allocated to each test condition. Next, students provided estimations for their performance on the basketball test and took the test individually at the basketball court of their schools.

2.5. Statistical Analysis

A latent growth modeling analysis was performed on the data using Mplus version 8.1 statistical software [41] Preliminary analyses involved descriptive statistics and correlations for the three time points, examination of the univariate kurtosis and checking whether missing data were completely missing at random.

3. Results

3.1. Preliminary analyses

The kurtosis values across the three measures were 2, 0.82 and 1.18 for accuracy and 0.21, 0.30 and 0.21 for executive function. Although, these univariate kurtosis values were in acceptance levels, following a suggestion by Byrne [42] the latent growth modeling analyses were performed both with the ML estimator of Mplus which is more sensitive to multivariate kurtosis and with the MLM estimator which provides more robust results in the case of multivariate kurtosis. Given that the χ2 results of the two analyses did not differ substantially, following Byrne [42], it is reasonable to infer that the data set had multivariate normality. Since the ML estimator uses all cases for the analysis including those with missing data, in contrast to the MLM estimator which uses only the cases with complete data, we present results provided by the ML estimator.
Regarding the type of missing data, students with complete data on the three measures did not differ significantly on accuracy and executive function at T1 to those that had missing data on these two variables either on T2 or T3 or on T2 and T3 (Wilks’ lamda = .994, F(2, 259) = .837, p > .01. Therefore, data from all 262 students were used in subsequent analyses.

3.2. Sample descriptives and correlations

Descriptive statistics for the sample of participants are presented in Table 1 while correlations between the variables of the study are presented in Table 2. Descriptives denoted small improvements both in accuracy and in EF across the three measures while small correlations were observed between accuracy and EF.

3.3. Latent growth curve modeling

Latent growth modeling provides for the estimation of latent factors termed intercepts and slopes as well for their means and variances. Intercepts denote the individual’s score at a specified time of measurement while slopes represent the rate of change over the period of interest. The means of these latent factors represent estimations of the population scores at the time of interest (intercept) and the population’s trajectory of “true” change within the period of measurements (slope), while their variances reflect population inter-individual differences [42]. We defined a dual-domain linear growth model (Figure 1). It involved six measured variables (total score on design fluency test and calibration measured at three time points), four latent factors (intercept and slope for each domain) as well as covariances between the latent factors. We centered the model at T3 to examine the estimated population mean and variance at that time.
Latent growth modeling provides for the estimation of latent factors termed intercepts and slopes as well for their means and variances. Intercepts denote the individual’s score at a specified time of measurement while slopes represent the rate of change over the period of interest. The means of these latent factors represent estimations of the population scores at the time of interest (intercept) and the population’s trajectory of “true” change within the period of measurements (slope), while their variances reflect population inter-individual differences [42]. We defined a dual-domain linear growth model (Figure 1). It involved six measured variables (total score on design fluency test and calibration measured at three time points), four latent factors (intercept and slope for each domain) as well as covariances between the latent factors. We centered the model at T3 to examine the estimated population mean and variance at that time.
This model had non-acceptable fit indices (Table 3: Model 1). A revision of this model involved the addition of two covariances between two pairs of error variances (based on the modification indices) and the elimination of the non-significant covariance between the accuracy intercept and the accuracy slope. This revised model presented acceptable fit (Table 3: Model 2, Figure 2).
Table 4 presents covariances between the latent factors (Model 2). Both within-domain (intercept of accuracy with slope of accuracy) and between-domains (intercept of accuracy with slope of executive function) significant covariances were observed
Table 5 presents means and variances of the latent factors. The estimated rate of improvement of calibration accuracy was not significant. On the contrary, an improvement of 2.43 between T1 and T3 resulted in an estimated population mean of 27.67 at T3 for executive function.
Given the high variability of 3 out of four latent factors, denoting high inter-individual variability, we examined whether the inclusion of grade as a predictor variable could explain this variability (Model 3, Figure 3). Goodness-of-fit statistics (Table 3) for this model were adequate. The results denoted a significant effect of grade on the intercept of EF.

4. Discussion

This study examined the parallel development of executive function and calibration accuracy through latent growth curve modeling. This approach can provide insights regarding the change of constructs over time including the relation between the rates of change, as well as evidence regarding inter-individual variability in the growth of the constructs.
Regarding the relation of the rates of change between EF and calibration accuracy, the results showed a significant relationship which indicates that those students who progressed in one of the constructs did so in the other one as well. Another noteworthy aspect of the results is the interrelationships between rates of change and the intercepts of EF and calibration. The rate of change (slope) of EF related to the intercept of calibration. Given that calibration was centered at Time 3, this result denotes that students with better calibration scores at Time 3, had a higher rate of change in EF. Conversely, the significant relationship of the intercept of EF with the rate of change (slope) of calibration indicates that students with higher EF scores at Time 3 had a higher rate of change in calibration. These results suggest that these two concepts are not only interlinked but they also affect the development of each other. These results are in congruence with those of Howard et al. [4] but not with those of Spiess et al. [37]. The present results are also in partial agreement with those of Roebers et al. [8] who tested and reported only a longitudinal direct influence of EF to metacognition. The different age of the participants in the current study than the age of participants in the previous studies, as well as the difference in the metacognitive aspect examined and in the tasks that were employed may account for the diverse findings.
The results also indicated a strong relation between the intercepts of EF and calibration accuracy. This shows that at T3 students with higher EF scores had also better calibration scores. Generally, previous correlational studies with children showed low relationships between executive functions and aspects of metacognition [43,44]. Similarly, in a study with six-year-olds, [45] reported no associations between executive functions and calibration accuracy. On the contrary, when structural equation modeling statistical procedures were employed, results showed a substantial relation between executive function and aspects of metacognition in children [8,37]. The results of the present study which also employed such an approach indicated a significant respective relation. As such, structural equation modeling procedures may provide the “true” shared variance between metacognitive processes and executive functions in relative studies [3].
A third point of interest is the individual variability in the intercepts and slopes of the latent factors. Specifically, significant variances emerged for the latent factors of the intercepts of EF and calibration and the rate of change (slope) of EF. These significant variances suggest that there are significant inter-individual differences at Time 3, both for EF and calibration, as well as for the rate of change of EF. The addition of age, as a possible factor which may account for these inter-individual differences showed that only EF at T3 was affected. Thus at T3, the estimated population means for EF was positively affected by students’ grade, with students of higher grades having higher EF scores. As the rate of change was not affected by students’ age, this can be attributed to inter-individual variability.
The rate of change for calibration, as well as its variability, was non-significant. Also, this rate was not affected by students’ grade. These results imply that during the period of the study, students’ mean calibration did not change significantly with no signs of inter-individual differences. Although a recent meta-analysis [46] indicated that children's self-overestimation gradually decreases with age, from early to late childhood, this was based on cross-sectional studies. On the contrary, the present longitudinal results show that for the specific age-range, overestimation remains relatively stable.
Overall, the results of the present study add to the limited studies that have examined concurrently the development of EF and aspects of metacognition (Howard et al. 2021; Spiess et al., 2016). The present study showed a dynamic interplay in the development of EF and calibration in 10-to-12 year old students. Given that previous respective studies (Howard et al., 2021; Spiess et al., 2016) used different measurement tools both for EF and for metacognitive aspects, no definite conclusions can be drawn regarding the developmental interaction of EF and metacognitive processes.
A limitation of the study regards the instrument used for the measurement of EF. The design fluency test, does not provide for working memory but instead only for inhibition and switching. Therefore, future respective studies may use EF tests that measure working memory.

Author Contributions

For research articles with several authors, a short paragraph specifying their individual contributions must be provided. The following statements should be used “Conceptualization, M.G. and A.K.; methodology, M.G and A.K.; validation, E.S.; investigation, E.S; resources, M.G.; , E.S.; writing—original draft preparation, M.G. and E.S.; writing—review and editing, A.K.; supervision, M.G.; project administration, M.G.; funding acquisition, M.G. and E.S. All authors have read and agreed to the published version of the manuscript.”.

Funding

This research was supported by a grant from the Hellenic Foundation for Research and Innovation (H.F.R.I.) under the “1st Call for H.F.R.I. Research Projects to support Faculty Members & Researchers and the Procurement of High-and the procurement of high-cost research equipment grant” (Project Number: 1041) to the first author, and by a scholarship from the Greek State Scholarship Foundation to the second author.

Institutional Review Board Statement

The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Ethics Committee of DEPARTMENT OF PHYSICAL EDUCATION AND SPORT SCIENCE, UNIVERSITY OF THESSALY (1522, 5/6/2019).

Informed Consent Statement

Written informed consent was obtained from all subjects involved in the study.

Data Availability Statement

The data underlying the results presented in the study are part of a research program and are available on request from the first author (M.G.; mgoudas@pe.uth.gr).

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Diamond, A.; Ling, D. Review of the evidence on, and fundamental questions about, efforts to improve executive functions, including working memory. In Cognitive and Working Memory Training: Perspectives from Psychology, Neuroscience,and Human Development; Novick, J.M., Bunting, M.F., Dougherty, M.R., Engle, R.W., Eds.; Oxford University Press: Oxford, UK, 2020; pp. 145–389. [Google Scholar] [CrossRef]
  2. Gutierrez de Blume, A. P. Calibrating calibration: A meta-analysis of learning strategy instruction interventions to improve metacognitive monitoring accuracy. J. Ed. Psych. 2023, 114, 681–700. [Google Scholar] [CrossRef]
  3. Roebers, C. M. Executive function and metacognition: Towards a unifying framework of cognitive self-regulation. Developmental Review 2017, 45, 31–51. [Google Scholar] [CrossRef]
  4. Howard, S.J.; Vasseleu, E.; Neilsen-Hewett, C.; de Rosnay, M.; Chan, A.Y.C.; Johnstone, S; Mavilidi, M.; Paas, F.; Melhuish, E.C. Executive function and self-regulation: Bi-directional longitudinal associations and prediction of early academic skills. Front. Psychol. 2021, 12(733328). [Google Scholar] [CrossRef]
  5. Diamond, A. Executive functions. Ann Rev Psych. 2013, 64, 135–168. [Google Scholar] [CrossRef] [PubMed]
  6. Miyake, A.; Friedman, N. P.; Emerson, M. J.; Witzki, A. H.; Howerter, A.; Wager, T. D. The unity and diversity of executive functions and their contributions to complex “frontal lobe” tasks: A latent variable analysis. Cogn. Psych. 2000, 41, 49–100. [Google Scholar] [CrossRef]
  7. Alloway, T. P.; Alloway, R. G. Investigating the predictive roles of working memory and IQ in academic attainment. J. Exp. Child Psych. 2010, 106, 20–29. [Google Scholar] [CrossRef] [PubMed]
  8. Roebers, C. M.; Cimeli, P.; Röthlisberger, M.; Neuenschwander, R. Executive functioning, metacognition, and self-perceived competence in elementary school children: An explorative study on their interrelations and their role for school achievement. Metacogn. Learn. 2012, 7(3, 151–173. [Google Scholar] [CrossRef]
  9. Cantin, R. H.; Gnaedinger, E. K.; Gallaway, K. C.; Hesson-McInnis, M. S.; Hund, A. M. Executive functioning predicts reading, mathematics, and theory of mind during the elementary years. J. Exp. Child Psych. 2016, 146, 66–78. [Google Scholar] [CrossRef]
  10. Contreras-Osorio, F.; Campos-Jara, C.; Martínez-Salazar, C.; Chirosa-Ríos, L.; Martínez-García, D. Effects of sport-based interventions on children’s executive function: A systematic review and meta-analysis. Brain Sci. 2021, 11, 755. [Google Scholar] [CrossRef]
  11. Heilmann, F.; Weinberg, W.; Wollny, R. The impact of practicing open- vs. closed-skill sports on executive functions—An updated meta-analytic review with focus on characteristics of sports. Brain Sci. 2022, 12, 1071. [Google Scholar] [CrossRef] [PubMed]
  12. Vestberg, T.; Reinebo, G.; Maurex, L.; Ingvar, M.; Petrovic, P. Core executive functions are associated with success in young elite soccer players. PloS One 2017, 12, e0170845. [Google Scholar] [CrossRef] [PubMed]
  13. Flavell, J. H. Metacognition and cognitive monitoring: A new area of cognitive– developmental inquiry. Am. Psych. 1979, 34, 906–911. [Google Scholar] [CrossRef]
  14. Efklides, A. (2008). Metacognition: Defining its facets and levels of functioning in relation to self-regulation and co-regulation. Eur. Psych. 2008; 13, 277–287. [Google Scholar] [CrossRef]
  15. Keren, G. Calibration and probability judgements: Conceptual and methodological issues. Acta Psych. 1991, 77, 217–273. [Google Scholar] [CrossRef]
  16. Schraw, G. A conceptual analysis of five measures of metacognitive monitoring. Metacog. Learn. 2009, 4, 33–45. [Google Scholar] [CrossRef]
  17. Pieschl, S. Metacognitive calibration - an extended conceptualization and potential applications. Metacogn. Learn. 2009, 4, 3–31. [Google Scholar] [CrossRef]
  18. Chen, P.P.; Bembenutty, H. Calibration of performance and academic delay of gratification: Individual and group differences in self-regulation of learning. In Handbook of self-regulation of learning and performance, 2nd ed.; Schunk, D.H., Greene, J.A., Eds.; Routledge: New York, USA, 2018; pp. 407–420. [Google Scholar]
  19. Efklides, A. How does metacognition contribute to the regulation of learning? An integrative approach. Psych. Topics, 2014, 23, 1–30. https://psycnet.apa.org/record/2014-25618-001.
  20. Chen, P.; Rossi, P. D. Utilizing calibration accuracy information with adolescents to improve academic learning and performance. In Applications of self-regulated learning across diverse disciplines: A tribute to Barry J. Zimmerman, Bembenutty, H.; Cleary, T. J.; Kitsantas, A., Eds., Information Age, USA, 2013, pp.263-297.
  21. Hacker, D. J.; Bol, L.; Bahbahani, K. Explaining calibration accuracy in classroom contexts: The effects of incentives, reflection, and explanatory style. Metacog. Learn. 2008, 3, 101–121. [Google Scholar] [CrossRef]
  22. Xia, M.; Poorthuis, A. M. G.; Zhou, Q.; Thomaes, S. Young children’s overestimation of performance: A cross-cultural comparison. Child Dev. 2022, 93, 207–221. [Google Scholar] [CrossRef]
  23. Kolovelonis, A.; Goudas, M. The relation of physical self-perceptions of competence, goal orientation,and optimism with students’ performance calibration in physical education. Learn. Ind. Diff. 2018, 61, 77–86. [Google Scholar] [CrossRef]
  24. Kolovelonis, A.; Goudas, M. Does performance calibration generalize across sport tasks? A multiexperiment study in physical education. J. Sport Exer. Psych. 2019, 41, 333–344. [Google Scholar] [CrossRef]
  25. Roebers, C. M.; Feurer, E. Linking executive functions and procedural metacognition. Child Dev. Persp. 2016, 10, 39–44. [Google Scholar] [CrossRef]
  26. Best, J.R. Effects of physical activity on children’s executive function: Contributions of experimental research on aerobic exercise. Dev. Rev. 2010, 30, 331–551. [Google Scholar] [CrossRef]
  27. Hoyle, R.H.; Dent, A.L. Developmental trajectories of skills and abilities relevant for self-regulation of learning and performance. In Handbook of self-regulation of learning and performance, 2nd ed.; Schunk, D.H, Greene, J.A., Eds.; Routledge: New York, USA, 2018; pp. 49–63. [Google Scholar]
  28. Lee, K.; Bull, R.; Ho, R. M. Developmental changes in executive functioning. Child Dev. 2013, 84, 1933–1953. [Google Scholar] [CrossRef]
  29. Brydges, C. R.; Fox, A. M.; Reid, C. L.; Anderson, M. The differentiation of executive functions in middle and late childhood: A longitudinal latent-variable analysis. Intelligence, 2014; 47, 34–43. [Google Scholar] [CrossRef]
  30. Franchak, J. M. Development of affordance perception and recalibration in children and adults. J. Exper. Child Psych. 2019, 183, 100–114. [Google Scholar] [CrossRef]
  31. Wacker, S.; Roebers, C. M. Stop and think: Additional time supports monitoring processes in young children. PLoS ONE, 2022, 17: e0274460. [CrossRef]
  32. Cottini, M.; Basso, D.; Pieri, A.; Palladino, P. Metacognitive monitoring and control in children's prospective memory. J. Cognin. Devel. 2021, 22, 619–639. [Google Scholar] [CrossRef]
  33. Was, C. A., & Al-Harthy, I. S. (2018). Persistence of overconfidence in young children: Factors that lead to more accurate predictions of memory performance. Eur. J. Develop. Psych. 2015, 15, 156–171. [CrossRef]
  34. Liverakos, K.; McIntosh, K.; Moulin, C.J.A.; O’Connor, A.R. How accurate are runners’ prospective predictions of their race times? PLoS ONE, 2018, 13(8): e0200744. [CrossRef]
  35. 35. Kolovelonis, A,; Goudas, M.; Dermitzaki, I. Students’ performance calibration in a basketball dribbling task in elementary physical education. Int. Elect. J. Elem. Educ. 2012; 4, 507–517.
  36. van Loon, M.H.; de Bruin, A.B.H.; van Gog, T.; van Merriënboer, J.J.G. Activation of inaccurate prior knowledge affects primary-school students’ metacognitive judgments and calibration. Learn. Instr. 2013, 24, 15–25. [Google Scholar] [CrossRef]
  37. Spiess, M.; Meier, B.; Roebersm, C. M. Development and longitudinal relationships between children’s executive functions, prospective memory, and metacognition. Cogn. Devel. 2016, 38, 99–113. [Google Scholar] [CrossRef]
  38. Delis, D. C.; Kaplan, E.; Kramer, J. H. Delis-Kaplan executive function system (D-KEFS). The Psychological Corporation, San Antonio, USA, 2004. [CrossRef]
  39. Delis, D. C.; Kramer, J. H.; Kaplan, E.; Holdnack, J. Reliability and validity of the Delis-Kaplan executive function system: An Update. J. Intern. Neuropsych. Soc. 2004, 10, 301–303. [Google Scholar] [CrossRef]
  40. Pojskić, H.; Šeparović, V.; Užičanin, E. Reliability and factorial validity of basketball shooting accuracy tests. Sport Sci. Prac. Asp. 2011, 8, 25–32. http://www.sportspa.com.ba/images/june2011/full/rad5.pdf.
  41. Muthén, L.K.; Muthén, B.O. Mplus Statistical Software, v. 8.1. Muthén &Muthén, Los Angeles, USA, 2021.
  42. Byrne, B. M. Structural equation modeling with Mplus. Routledge, NY, USA, 2012.
  43. Bryce, D.; Whitebread, D.; & Szűcs, D. The relationships among executive functions, metacognitive skills and educational achievement in 5 and 7 year-old children. Metacogn. Learn. 2014, 10, 181–198. [CrossRef]
  44. Geurten, M.; Catale, C.; Meulemans, T. Involvement of executive functions in children's metamemory. Appl. Cogn. Psych. 2016, 30, 70–80. [Google Scholar] [CrossRef]
  45. Destan, N.; Roebers, C. M. What are the metacognitive costs of young children’s overconfidence? Metacogn. Learn. 2015, 10, 347–374. [Google Scholar] [CrossRef]
  46. Xia, M; Poorthuis A. M. G.; Thomaes, S. Children's overestimation of performance across age, task, andhistorical time: A meta-analysis. Child Dev. 2023, 00:1–22. [CrossRef]
Preprints 92748 g001
Figure 1. The hypothesized model (Model 1).
Figure 1. The hypothesized model (Model 1).
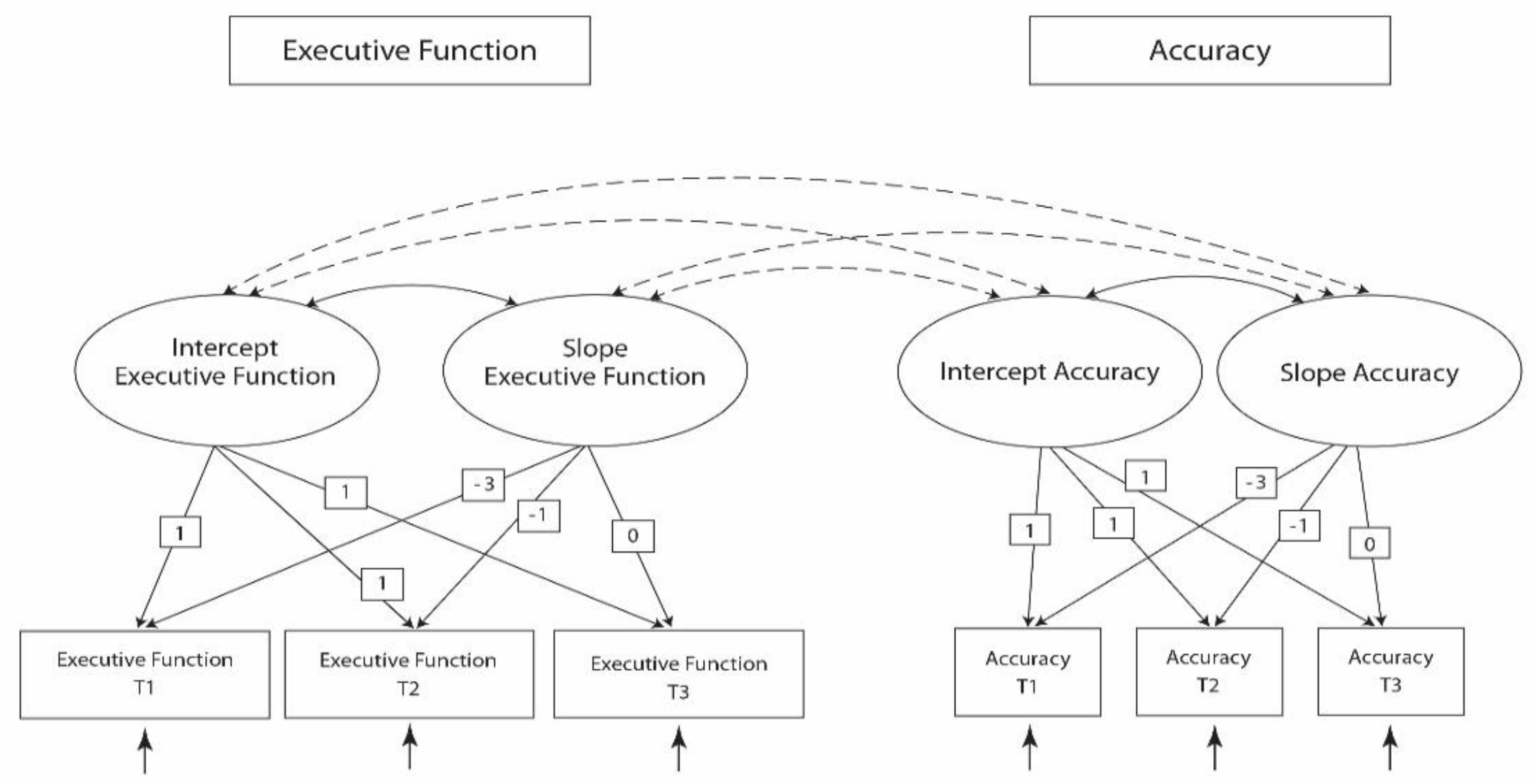
Preprints 92748 g001
Preprints 92748 g002
Figure 2. The revised model (Model 2).
Figure 2. The revised model (Model 2).
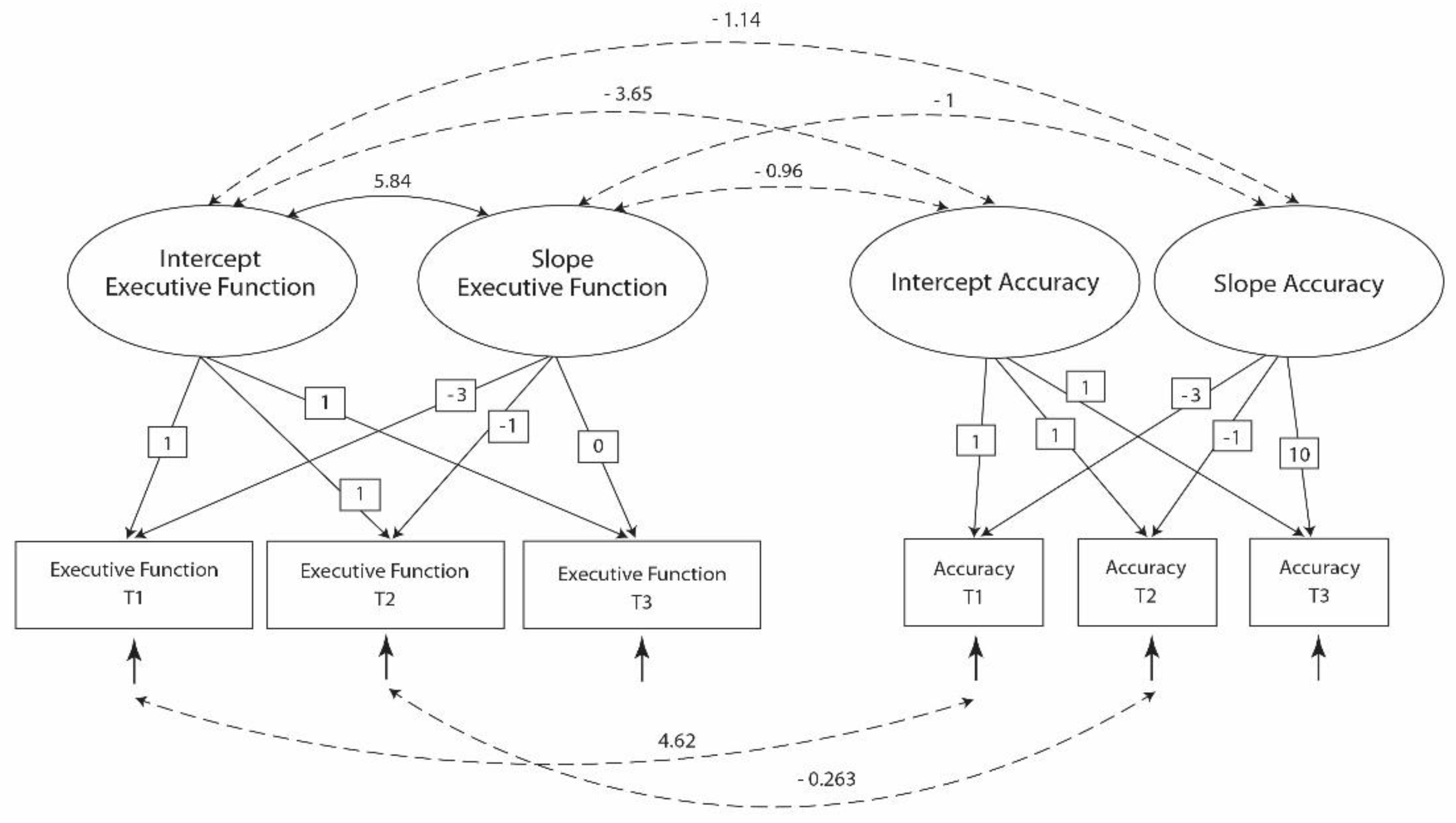
Preprints 92748 g002
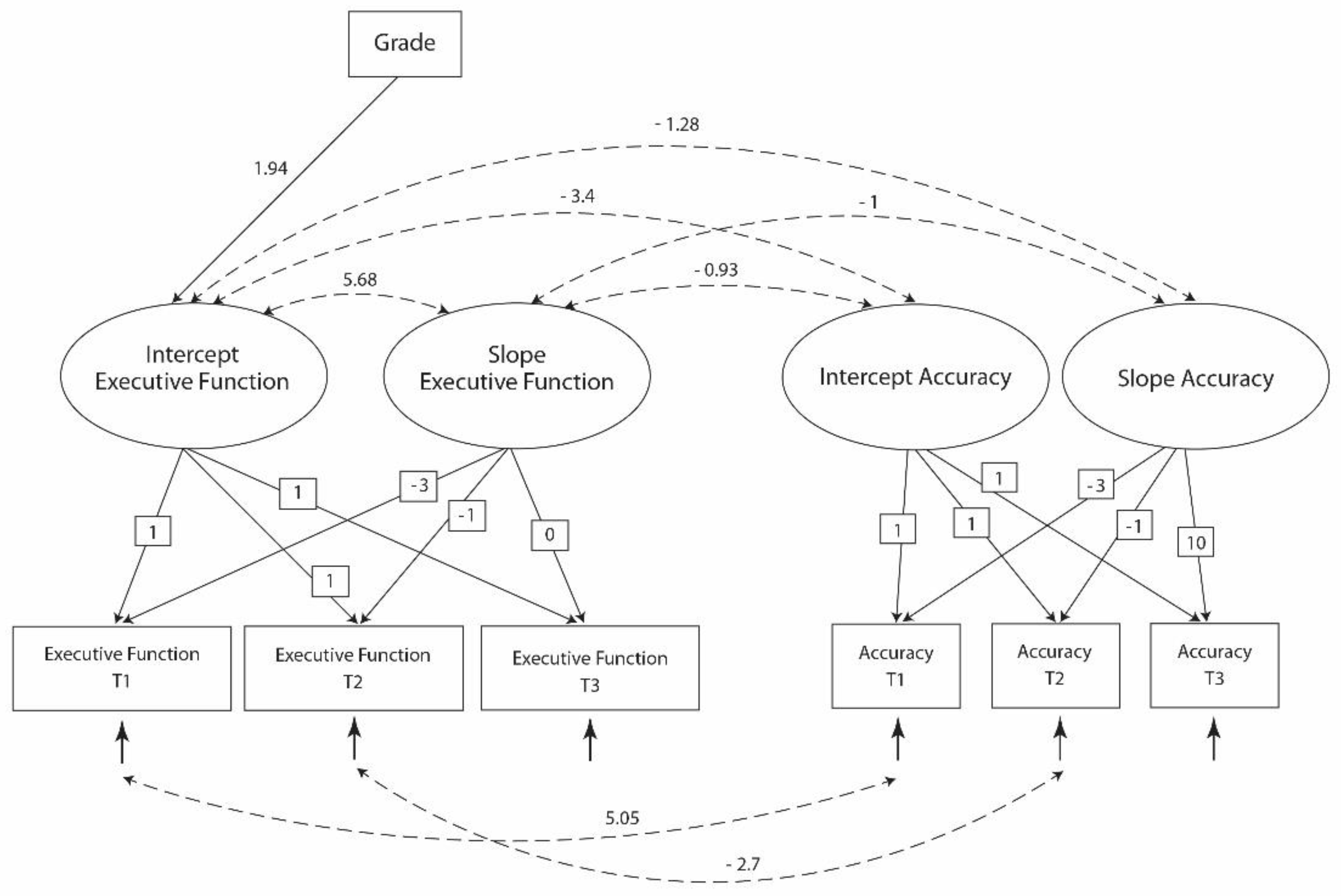
Preprints 92748 g003
Figure 3. The model with grade as predictor (Model 3).
Figure 3. The model with grade as predictor (Model 3).
Preprints 92748 g003
Table 1. Descriptive statistics of the observed variables of the study.
Table 1. Descriptive statistics of the observed variables of the study.
T1 T2 T3
Μ SD M SD M SD
Total sample
Calibration accuracy 2.21 1.76 2.15 1.81 2.06 1.68
Executive function 20.30 7.23 26.10 8.23 27.02 8.61
Grade 4
Calibration accuracy 2.86 2.16 2.31 1.97 2.21 1.95
Executive function 19.19 6.91 25.47 7.56 24.21 7.33
Grade 5
Calibration accuracy 1.89 1.55 2.33 1.81 2.09 1.53
Executive function 20.87 7.27 25.38 8.06 28.63 8.95
Grade 6
Calibration accuracy 1.83 1.22 1.80 1.58 1.85 1.48
Executive function 20.93 7.47 27.53 9.00 28.46 8.88
Table 2. Correlations between executive function and calibration.
Table 2. Correlations between executive function and calibration.
T1 T2 T3
Total sample
-.14* -.35** -.25**
Grade 4
-.29** -.45** -.19
Grade 5
-.00 -.39** -.41**
Grade 6
.01 -.18 -.14
*p<.05, **p<.001.
Table 3. Goodness-fit-indices.
Table 3. Goodness-fit-indices.
χ2/df CFI TLI RMSEA SRMR
Model 1 3.59 .91 .80 .1 .05
Model 2 1.91 .97 .93 .06 .04
Model 3 1.59 .98 .94 .05 .04
CFI: Comparative Fit Index, TLI: Tucker-Lewis Fit Index, RMSEA: Root Mean Square Error of Approximation, SRMR: Standardized Root Mean Square Residual.
Table 4. Covariances between latent factors.
Table 4. Covariances between latent factors.
1 2 3
1.Intercept accuracy
2.Intercept executive function -3.65**
3.Slope accuracy - -1.14*
4.Slope executive function -.96** 5.85* -1**
*p<.05, **p<.001.
Table 5. Estimated means and variances of latent factors.
Table 5. Estimated means and variances of latent factors.
Mean Variance
Estimate SE Estimate SE
Intercept accuracy 2.1** .1 .44* .16
Slope accuracy -.06 .5 .12 .07
Intercept executive function 27.67** .52 39.24** 6.67
Slope executive function 2.43** .19 4.94* 1.80
*p<.05, **p<.001.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated