Prerpints.org logo
Preprint
Article

Impact of Crustacean Morphology on Metachronal Propulsion: A Numerical Study

Altmetrics

Downloads

81

Views

35

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.zip (95.50MB )

This version is not peer-reviewed

Submitted:

08 December 2023

Posted:

11 December 2023

You are already at the latest version

Alerts
Abstract
Metachrony is defined as coordinated asynchronous movement throughout multiple appendages, such as the cilia of cells and swimmerets of crustaceans. We investigate the process of metachronal propulsion, notably used by species of crustaceans and microscopic cells to move through fluid. A rigid crustacean model with paddles moving in symmetric strokes was created to simulate metachronal movement. Coupled with the surrounding fluid domain, we employ the immersed boundary method to analyze fluid-structure interactions. To explore the effect of nonlinear morphology on the efficiency of metachronal propulsion, we generate and simulate a range of crustacean body shapes, from upward curves to downwards curves. We found that the highest propulsion velocity is achieved when the crustacean model morphology follows a downwards curve, specifically a parabola of leading coefficient k=−0.4. This curved morphology results in 4.5% higher velocity compared to the linear model. As k deviates from −0.4, the propulsion velocity decreases with increasing magnitude, forming a concave downward trend. The impact of body shape on propulsion velocity is shown by how the optimal velocity with k=−0.4 is 71.5% larger than the velocity at k=1. Overall, this study suggests that morphology has a significant impact on metachronal propulsion.
Keywords: 
Subject: Computer Science and Mathematics  -   Applied Mathematics

1. Introduction

Animals have developed diverse methods of moving in aquatic environments. Most species of fish undulate varying parts of their bodies to create thrust and swim. The locomotion of fish is often further propelled or controlled by median fins [1]. Jet propulsion is another such approach to movement, used by cephalopods like octopuses and jellyfish. In this process, animals forcefully eject a jet of water to propel themselves in the opposite direction [2]. Microscopic ciliates use densely packed arrays of cilia to propel themselves, while crustaceans use pleopods, or swimmerets, to swim forward. Curiously, cilia and pleopods both move in a metachronal rhythm [3,4].
In biology, metachronal motion describes asynchronous yet coordinated movement in multiple similar appendages. These motions are asynchronous because they are performed at different times, one after another in a cyclic pattern. Research has suggested that synchronous oscillation produces no propulsion, while metachronal oscillation enables forward movement, achieving the act of swimming [5]. Further, asynchronous appendage motion results in superior performance over synchronous movement in both efficiency and velocity [6,7,8].
Metachronal propulsion can be classified into symplectic and antiplectic types. Also described as head-to-tail, symplectic metachrony occurs when the first appendage begins its movement, followed by the remaining ‘arms’ in sequence. Antiplectic metachrony, or tail-to-head, starts with the last appendage and propagates forward. Symplectic and antiplectic metachrony have inverse effects on motion; antiplectic movement causes an increase in net flow of surrounding fluid while symplectic movement leads to a decrease [9].
Thus, a significant factor that affects the behavior of metachronal propulsion is phase difference, which is the lag between the motions of adjacent legs [10]. In this study, we attribute antiplectic metachrony with a positive phase difference and symplectic metachrony with a negative phase difference.

1.1. Metachronal Propulsion in Crustaceans

Crustaceans use metachrony in their swimmerets, which are small appendages used for swimming [11]. Swimmeret motion can be divided into the power stroke (PS) and the return/recovery stroke (RS), where PS propels the crustacean forward and the RS returns the appendage to the appropriate position [12]. There are generally four to five rows consisting of a pair of swimmerets; each pair of swimmerets beats synchronously, but each row is asynchronous [13].
A qualitative justification behind the use of metachronal propulsion in crustaceans is that the minuscule lengths between their swimmerets are prone to causing interference in synchronous movement [14]. Therefore, applying a phase shift on swimmeret cycles can help mitigate inefficiency or produce beneficial effects [15].
Using a drag-based mechanic model, metachronal motion in the swimmerets has been shown to increase body velocity, leading to the result that metachrony produced velocity about 10% larger than synchronous movement [16]. However, the drag-based model fails to consider fluid-structure effects, which turn out to significantly impact propulsion.
Iterating over this flaw, the immersed boundary method was used to simulate models of crustaceans varying in paddle number over a range of phase differences and Reynolds numbers from 0 to 100 [13]. In this range, the researchers discovered that the average flux over these Reynolds numbers follows the same trend from a phase difference of -0.2 to 0.2, varying more as the phase difference approaches the endpoints of -0.5 and 0.5. By testing different numbers of paddles sharing the same spacing as before, [13] found that the correlation between efficiency and the number of paddles reversed as Re was increased from 0.1 to 100. However, the model with 4 paddles was 85%-90% efficient over the range, showing that possessing four paddles is a reasonable assumption for the low Reynolds number used in this study.

1.2. Impact of Body Structure on Propulsion

Since the rigid crustacean body is attached to its appendages, this boundary has significant effect on the fluid flow from metachronal propulsion. Depending on the shape, the body structure can either limit or promote fluid movement, directly correlated to the effectiveness of crustacean locomotion. Additionally, this study allows crucial insight into the evolutionary motivations for a crustacean’s morphology, opening up discussions of optimality. For these reasons, exploring the effect of body shapes on metachronal propulsion is significant.
Following previous research, we model the crustacean’s power and return stroke as symmetric identical movements [13]. The return stroke features additional drag asymmetry due to a changing paddle size, which has been previously modeled with porous paddles [15]. This simplification was made to isolate the mechanics of metachronal propulsion’s improved efficiency over other propulsion methods, rather than convolute the experiment with an additional source of forward movement.

1.3. Methods of Investigating Metachronal Propulsion

Previously, researchers have used many methods to analyze the mechanics of metachronal propulsion through videos, robotic models, and fluid simulations. Video analysis explores metachrony through biological observations, while modeling via robot or software aims to simulate metachronal motion.

1.3.1. Video Analysis

Videos of metachronal locomotion can be analyzed frame-by-frame, noting the movement of the organism’s legs as the video progresses [6,14,17]. Particle image velocimetry can be used in tandem to acquire information on the organism’s kinematics [18]. This method is most convenient if the studied organism is commonly available and visible to the human eye.

1.3.2. Robotic Modeling

Another method of examining metachrony is through robotic implementations, in which a mechanical setup is used to mimic a biological equivalent. For example, magnetically-actuated ciliary arrays can be used to simulate the cilia in cells [8,19]. Through this method, it has been discovered that antiplectic metachronal motion in cilia leads to an increased net flow and formation of vortices [9,20]. Another application of robotics can be seen with a robotic crustacean model [4,21,22]. In the aspect of isolating a mechanism’s effect, robotic modeling proves advantageous over video analysis.

1.3.3. Fluid Simulations

Computational fluid dynamics (CFD) can be employed without biological samples or mechanical equipment, making it an accessible method of simulation and analysis. CFD includes a wide variety of applications, such as observing factors like temperature, velocity, pressure, and drag in a design [23,24,25,26]. Applying CFD to metachronal motion in cilia shows that it is beneficial, leading to increased size range of accessible food particles, optimized mucus transport, and optimized flow [27,28,29].
One facet of CFD relevant to metachronal propulsion is simulating fluid-structure interactions, which directly address how structures performing metachronal propulsion shape surrounding flows. Like robotic modeling, CFD simulations can exclude the impact of unwanted factors. A particular framework, the immersed boundary method, has been prevalent in modeling fluid-structure interactions by uses Lagrangian points to model the structure and Eulerian coordinates to represent the surrounding fluid [30].

1.4. Goals

Although [13,21,22] explored the effects of phase difference, number, and length to spacing ratio in appendages, their analyses were conducted under the simplifying assumption of a linear morphology. For the first time, we run and assess simulations to examine the effect of nonlinear morphology on metachronal propulsion.

2. Methods

The 2-dimensional crustacean model consists of four mobile paddles below a curved wall, representing the swimmerets and the body, respectively. Mirroring a crustacean’s biology, both these structures are modeled as rigid boundaries immersed in a fluid.
The curved body of the model was designed to recreate biological equivalents. In Figure 1, a common American prawn demonstrates an arched anatomy during metachronal locomotion. In Figure 2, many key aspects of the crustacean model are displayed, as well as an example of antiplectic metachronal propulsion. While the rightmost paddle is executing the return stroke, the others are still finishing power strokes in sequence.
For our use of a flow with low Reynolds number, where inertial forces are less significant, we have decided to use four paddles to perform our study [31]. Research has also been done on the effect of appendage spacing on metachronal propulsion, but for the purposes of isolating one change, the fluid simulation for our research assumes a constant, common spacing length of 0.2 m [21].
While crustaceans feature multiple joints that assist the power and return stroke, the paddles in this study are modeled as single joints to observe the isolated effect of metachronal motion. Both mechanisms aid the crustacean in achieving propulsion, but we chose to primarily examine metachronal motion and therefore simplified the movement into a singular paddle without joints. To avoid collisions between adjacent paddles, we have modeled the paddle length to be 0.1 m.

2.1. Paddle Movement

The paddles are indexed i = 1, 2, 3, 4 from left to right, attached to the body at points p i , with coordinate pair ( h i , k i ) . In the swimmer’s Lagrangian structure, joined endpoints with a stiffness constant form the paddle structure. Let a i , j denote the jth point in paddle i, with x-coordinate x i , j and y-coordinate y i , j . Then, the movement of point a i , j can be modeled by the original parametric equations
( x i , j , y i , j ) = ( h i + r cos ( θ 1 + 2 t T ( θ 2 − θ 1 ) ) , k i + r sin ( θ 1 + 2 t T ( θ 2 − θ 1 ) ) ) , t ≤ T 2 ( h i + r cos ( θ 2 + 2 t T ( θ 1 − θ 2 ) ) , k i + r sin ( θ 2 + 2 t T ( θ 1 − θ 2 ) ) ) , t ≥ T 2
where θ 1 and θ 2 describe the starting and ending positions of the paddle in radians. For our model, θ 1 = 5 π 4 and θ 2 = 7 π 4 , shown in Figure 1 by the gray range around the first paddle. These θ values were chosen to best provide a general stroke range for crustaceans, comparable to values used in prior studies [13]. r represents the radius of motion, obtained by using the distance formula between a i , j and p i . T represents the combined period of the power and return stroke, and the two cases in the expression symbolize the PS and RS, respectively. Δ ϕ , the phase difference between adjacent paddles in seconds, is incorporated in the expression through t. Representing the current time in period T, t is formulated with the following original equation.
t = t 1 − Δ ϕ ( 4 − i ) mod T
Here, t 1 represents the time since the start of the simulation, where t can be conceptualized as denoting the current progression through T . It is worth noting that this formulation describes tail-to-head motion; paddle 4 does not experience any phase shift, and the leftmost paddles are shifted the most. Altogether, the parametric expression describes a circular motion around a circle with center ( h i , k i ) , creating a periodic oscillation between angles θ 1 and θ 2 . This forms the power stroke and return stroke patterns.

2.2. Crustacean Morphology

To mimic the natural arch of a crustacean during metachronal propulsion, we used a parabolic formula to describe its body shape. The parabolic body’s vertex is halfway between paddle 2 and 3, providing a symmetric curve over the four paddles. Such points on the body are described by the equation
y = k ( x − 0.5 ) 2 + 0.3 ,
where 0.5 describes the x-coordinate of the vertex and 0.3 describes the body’s highest or lowest point. This formulation ensures that for − 1 ≤ k ≤ 1 , the full range of motion for all paddles is contained in the fluid domain. In the fluid simulation, this parabolic morphology is represented by short line segments that collectively approximate the parabola.

2.3. Model Configuration

For this model, the horizontal spacing s between paddles is held at a constant of 0.2 meters, and each paddle is 0.1 meters long. The main motivation behind this choice is that it allows the paddles ample room to create flow, yet still promotes fluid interaction. A fixed horizontal spacing allows for increased ease of coordinate formulation, so that h i is simply 0.2 ∗ i . k i follows the parabolic equation of the curved body. The domain of the immersed boundary solver is 3 meters wide and 0.6 meters tall, capturing the crustacean model and fluid behind it.
Period T is set to 0.05 seconds, so the symmetric PS and RS both take 0.025 s to execute. The value of T does not affect any results as long as the total simulation time is adjusted to include five full periods for every paddle. We consider the range 0 ≤ Δ ϕ ≤ 0.025 to examine the optimal phase-difference for our crustacean model, and then set Δ ϕ to a constant to consider the effect of body shape on propulsion. We choose not to examine Δ ϕ < 0 , as research indicates that symplectic motion leads to decreased net flow [9]. Also, we do not simulate 0.025 < Δ ϕ < 0.050 to create a comparison with the precedents set by [9,13].
A constant of 10 points make up an outline of the crustacean’s body. Both the paddles and the body are assigned stiffness values of 10 9 N m − 1 , where stiffness k describes the ratio of the applied force to resulting displacement. In a similar study of jellyfish propulsion, [36] used a stiffness of 10 7 to represent the deformable jellyfish bell. With a stiffness constant 2 orders of magnitude above 10 7 , the deformation of the legs becomes negligible. The stability of the legs is demonstrated in the supplementary materials, where the limbs are not impacted by surrounding flows.

2.4. Fluid Theory

Aside from the crustacean model, the behavior of the surrounding incompressible fluid is governed by the Navier-Stokes equation, which is
ρ ( ∂ V ∂ t + V · ∇ V ) = − ∇ p + μ Δ V + F , ∇ · V = 0 ,
where V → = { u , v , w } , μ is the dynamic viscosity, ρ is the fluid density, and F is the force exerted on the fluid by the paddles. Overall, the first equation states that momentum’s rate of change is equal to the sum of the pressure gradient, viscous forces, and external forces exerted by the paddles. The second equation describes continuity. The gravity term in the standard Navier-Stokes equation is neglected because there is single phase flow with constant density and temperature.
The Reynolds number (Re) of a fluid is significant in determining the flow regime. A smaller Reynolds number describes a flow where viscous effects dominate behavior, and a higher Reynolds number implies that inertial effects preside instead. This dimensionless quantity can be calculated using the formula
R e = ( ρ c L c ) / μ ,
where c is the characteristic velocity and L c is the characteristic length. Setting c to the maximum speed of the paddle tip and L c to the paddle length results in R e = 0.03 . This low Reynolds number was chosen to focus on the effects of metachronal propulsion rather than increasing the resulting vorticity.

2.5. Immersed Boundary Software

In this study, we utilize the immersed boundary method for analyzing metachronal propulsion in crustaceans for the reason of improved universality over video analysis and ease over robotic modeling. Furthermore, the ability to accurately model fluid-structure interactions is paramount for capturing the optimal configurations for metachrony.
While 3-dimensional models are possible, this study uses 2-dimensional models for the purpose of simulation. We model the side view of a crustacean, capturing a cross-section where the body and appendages are visible. While 3D models can encapsulate more realistic details of the crustacean, a 2D model preserves forward locomotion, the most significant aspect, while reducing computation time exponentially. Using a 2D model has many precedents in effectively studying metachronal propulsion, from both simulating cilia and crustaceans [13,28].
The immersed boundary method is performed via IB2d, a software specifically developed for simulating 2-dimensional fluid-structure interactions. The IB2d software offers both a MATLAB and a Python implementation of the solver, including mesh generation and useful structures like springs, beams, targets, and more [32,33,34]. In our study, target points were extensively used to model the prescribed motion of the paddles. We chose IB2d over other CFD tools like IBAMR and Ansys due to ease of installation and usage. IB2d is similar to another software, IBAMR, in performance and method, but the former’s installation requires no additional downloading of other libraries. While the Ansys Suite allows for fluid-structure interaction through system coupling and motion through user-defined functions (UDFs), the required setup is much more complex. Also, IB2d allows for more flexibility than commercial software by being open source, allowing for user edits. A specific feature of IB2d is that it does not require external driving forces to model fluid-structure interactions, isolating the effects of propulsion [32]. This software has precedents of successful use in multiple studies involving fluid dynamics and solid-fluid interactions [35,36].

2.6. Immersed Boundary Configuration

The domain that we are solving over consists of decoupled Eulerian coordinates and Lagrangian points, essential for the immersed boundary method. The 100 by 20 Eulerian grid defines the fluid domain, where Navier-Stokes equations take effect. Lagrangian points outline the crustacean model, with 3 points marking the endpoints of each leg and 10 points describing the body. At each time step, the motion of the paddles is translated into forces, which are then interpolated to affect the fluid flow. This occurs every 10 μ s for 0.25 s. This ensures that the last paddle experiences five full periods of motion, but since the other paddles start in the middle of a stroke, they will not necessarily undergo five full periods even though they move at the same speed as the last paddle.

2.7. Performance Metrics

To analyze the performance of metachronal propulsion, we average the horizontal velocity across all Eulerian points and times. For every time step, we iterated through the 100 by 20 Eulerian grid and averaged the horizontal velocity at every point. Then, we took the average of this average horizontal velocity over all time steps from 0 s to 0.25 s. Since the model aims to swim forward or right-to-left, as shown in Figure 3, a positive velocity represents forward metachronal propulsion.

2.8. Convergence Analysis

We performed a spatial grid convergence test to determine how the computational domain’s size affected results. To isolate width, we preserve the grid spacing and height of the Eulerian grid. We investigated the case where k = 0 , Δ ϕ = 0.010 with a computational domain of height L y = 0.6 m and a varying width L x = { 3 , 3.3 , 3.6 , . . . , 6 } . To ensure that Eulerian points are equally spaced in the domain, we adjust the points per row proportionally to L x .
Figure 3 displays the propulsion velocity for the range of considered grid widths. As grid width approaches 6, the graph increases less and begins to plateau. Examining the differences between propulsion velocities in the tested range of L x , the simulated velocity using L x = 3 was varied less than 1 % from the resulting velocity with L x = 6 . Between the cases L x = 5.7 and L x = 6.0 , the relative error diminishes to less than 0.1 % .
We chose to run the following simulations with L x = 3 to decrease the time required for simulation while preserving more than a 99 % accuracy to larger widths like L x = 6 .

2.9. Validation Test

To ensure that our MATLAB implementation functions properly, we run two confirmation tests on specific phase differences. First, we ran the simulation with a phase-shift of 0. Without any meaning phase-shift, the crustacean model moves synchronously. Given that the power stroke and return stroke were modeled identically, the expected time-averaged velocity in the x direction is 0. Similarly, for a phase-shift of 0.025 s, or half the period of an entire stroke, the opposing movements of the 4 paddles should all cancel out, resulting in V x = 0 . Finally, a third sample simulation was done in order to establish a sense of magnitude for the results of the two previous simulations. For this run, we chose a phase-shift of 0.01 s. We created Table 1 exhibiting the results of these three simulations.
These values reveal that between Δ ϕ = 0.01 and Δ ϕ = 0.025 , their corresponding propulsion velocities are more than 3 orders of magnitude apart. This suggests that V x at Δ ϕ = 0.025 is distinctly smaller than Δ ϕ = 0.01 . The horizontal velocity at Δ ϕ = 0 is not as low as the velocity at Δ ϕ = 0.025 , but is still distinguishable from the larger velocity at Δ ϕ = 0.01 . However, the difference between simulated velocity and expected velocity at Δ ϕ = 0 may arise from the reasons below. An explanation for this phenomenon is that more fluid-structure interactions occur with Δ ϕ = 0 than 0.025 . With a phase difference of 0.025, we note that fluid domain forces are nullified every period. This is because adjacent paddles repeatedly exert the same amount of force into each other, leaving little possibility for fluid-structure interactions to develop. However, with Δ ϕ = 0 , the generated waves are propelled in the same direction, mixing and interacting with the crustacean. With more unpredictable fluid-structure interactions, we expect a propulsion velocity with some error. This validation test verifies the accuracy of our implementation of metachronal propulsion.

3. Results

We conduct simulations on the impact of phase difference ( Δ ϕ ) and morphology (k) on metachronal velocity.

3.1. Effect of Phase Difference on Velocity

We simulate the 2D crustacean model with immersed boundary with varying phase differences. Since we wish to isolate the effect of Δ ϕ on V x , we fix k at 0, resulting in a linear crustacean model.

3.1.1. Experimentation

The simulation was performed over a range of phase differences between 0 and 0.025 s with the configuration outlined in Section 2. An increment of 0.0025 s between trials was used. The average horizontal propulsion velocities for each phase difference is shown below in Figure 4.
Figure 5 depicts six frames of the crustacean model’s metachronal motion with ϕ = 0 , taken in increments of 0.010 seconds over one full period. From t=0s to t=0.025s, all paddles undergo the power stroke, and from t=0.025s to t=0.050s, they undergo the return stroke. This shift in direction is shown by the velocity vectors of the surrounding fluid, as they switch in direction from t=0.020s to t=0.030s. Since the phase shift is 0 seconds, Figure 5 shows synchronous motion, which has all four paddles moving in unison. Figure 6 shows six frames of metachronal motion with ϕ = 0.010 between paddles, which is asynchronous motion because the paddles are not at the same phase at the same time. As discussed later in Section 4.1 , the difference between the resulting velocities of synchronous and asynchronous motion are significant because asynchronous motion causes a large increase in propulsion when compared to synchronous motion.

3.2. Effect of Body Morphology on Velocity

We simulate the 2D crustacean model via IB2d with varying body morphologies. To do so, we adjust the value of k and therefore the body shape while holding Δ ϕ constant at 0.01 s .
With the methodology outlined in Section 2, the simulation was performed over a range of body morphologies, represented by the interval − 1 ≤ k ≤ 1 and shown in Figure 7. Due to the behavior of parabolas, the crustacean body will assume an upwards curve (convex) when k > 0 and a downwards curve (concave) when k < 0 . We incremented k by 0.1 between trials to obtain a comprehensive graph with 21 data points.
Figure 8 presents the relation between k and V x . As k increases from -1, the propulsion velocity steadily rises with negative concavity, peaking when k equals -0.4. Then, V x steadily decreases as k increases to 1. The results show that propulsion velocity is maximized when k = − 0.4 , when the crustacean’s body is a slight downward curve described by the equation y = − 0.4 ( x − 0.5 ) 2 + 0.3 .
Figure 9 depicts six frames of the crustacean model’s metachronal motion with k = − 0.4 , taken in increments of 0.010 seconds over one full period. Since k is negative here, the crustacean morphology resembles a downwards curve. Figure 10 shows six frames of metachronal motion with k = 0.4 , which yields an upward curve. Both of these flow diagrams are simulated with ϕ = 0.010 , the phase shift that optimizes horizontal velocity.

4. Discussion

The results reveal that a curved downwards morphology achieves superior metachronal propulsion.

4.1. Effect of Phase Difference

The phase difference of metachronal locomotion heavily impacts the resulting propulsion velocity, optimized at Δ ϕ = 0.01 as shown in Figure 4. While metachronal motion with Δ ϕ = 0.020 produced a velocity of 0.016m/s, metachronal motion with Δ ϕ = 0.010 achieved velocities upwards of 0.192m/s, a increase of more than 1200% in speed. Adjustments of phase shift in the interval from 0 to 0.025 is shown to yield a wide range of velocities, including negative, zero, and positive. As the phase difference increases from 0, the propulsion velocity steadily grows before plateauing at 0.01, decreasing gradually until reaching zero at Δ ϕ = 0.025 . The results show that V x is maximized at Δ ϕ = 0.01 seconds, or when each swimmeret differs by 20% of the period in motion. This trend agrees with the figures and results introduced in [9,13,15] for antiplectic metachronal propulsion. Additionally, the negative propulsion velocity from a phase difference of 0.0225 has been previously produced by [13]. Thus, creating a phase difference between appendages enhances velocity and efficiency in crustaceans and cilia. To visually see video difference between synchronous and asynchronous movement, please refer to the fluid simulations S1 and S2 in the Supplemental Materials.

4.2. Effect of Morphology

Our results show the significance of morphology on velocity from metachronal propulsion. By comparing the propulsion velocities over a range of different nonlinear morphologies, we found that a downwards parabola with a leading coefficient of -0.4 maximizes propulsion velocity, achieving a time-averaged mean 4.5% larger than the velocity of the linear model. Shown in Figure 8, adjusting the coefficient k resulted in a range of different propulsion velocities. Over the range of − 1 to 1 in increments of 0.1 , the value of k influenced the propulsion velocity, as shown by how V x at k = 1 varied by 39% from V x at k = 0 . Overall, Figure 8 resembles a wide downward curve that achieves maximum propulsion velocity at k = − 0.4 , which corresponds to a downward parabola. Compared to the linear morphology, when k = 0 , a nonlinear morphology with k = − 0.4 results in a 4.53 % increase in velocity. While not necessarily optimal, morphologies with k values between − 0.1 and − 0.7 outperform the linear morphology in terms of propulsion velocity as well.
Comparing the flow diagram between Figure 9 and Figure 10 at t = 0.020 seconds and 0.030 seconds, the waves created by paddles interact differently. With a downwards morphology of k = − 0.4 , the movement of the last paddle carries the wave backwards in a downwards manner at time = 0.020 seconds, while the upwards morphology of k = 0.4 results in the wave being carried in a higher direction. At t = 0.030 seconds, the last paddle in the morphology with k = 0.4 creates a wave below the preexisting wave, while the last paddle in the morphology with k = − 0.4 creates a wave around the same height as the preexisting wave. These differences occur throughout the fluid simulations for Figure 9 and Figure 10, which can be accessed as Video S3 and Video S4. These examples show how the favorable orientation and interaction of waves in the morphology with k = − 0.4 contributes to its higher propulsion velocity.
Another explanation for the superior performance of the downwards parabola is that the curved border allows for improved wave propagation and fluid transport. The additional space provided by the morphology might reduce interference for metachronal waves, which then creates increased propulsion.

5. Conclusion

In both CFD and robotic models, previous research simplifies simulating metachronal movement by implementing a linear body. However, this is not the case for cilia or crustaceans; cilia extend off a curved cell surface and crustaceans do not swim perfectly straight. By introducing a way of altering morphology, we bring an additional dimension of biological accuracy to research in metachronal propulsion. In this study, we assessed the impact of phase difference and morphology on metachronal propulsion. The simulations on phase difference show that propulsion is maximized at Δ ϕ = 0.01 . Additionally, it can be concluded that the phase shift plays a significant role in determining the efficiency of metachronal movement, capable of yielding speeds 800% of those from non-metachronal movement. Simulations for nonlinear morphologies reveal that the downwards parabolic curve with variable k = 0.4 yields optimal metachronal propulsion, 4.5% larger than its nonlinear equivalent. Further, within the interval − 1 < k < 1 , corresponding morphologies have large effects on metachronal propulsion. One such curved morphology resulted in 30% less velocity than the linear model, given that the phase shift is constant. These results contribute to the body of knowledge in bio-inspired fluid mechanics and metachronal movement. Comprehension of this topic can lead to development of new nanotechnology or marine exploration technology by introducing a new method of efficient swimming.

6. Future Research

The techniques and models used in this study can benefit from future iterations and extensions. A generalized parabola equation was used to generate morphologies. Future research may look into methods of generating a larger variety of morphologies, or creating an adaptive method to find the optimal shape for metachronal propulsion. Another consideration for future studies in morphology and metachrony is investigating the best way to position paddles on different morphologies. This study placed paddles at x-coordinates of 0.2 , 0.4 , 0.6 , 0.8 regardless of body shape. This method of keeping paddle-body intersection points constant could alter more variables than expected. For example, the spacing between crustacean appendages is altered, increasing between paddle 1 and 2 but decreasing between paddle 2 and 3. Implementing additional walls for the crustacean body and flexible paddles will allow for more realistic configurations. The development of flexible paddles is especially pivotal, as the movement of crustaceans is altered by the jointed nature of the swimmerets. Our method features a simple process of generating paddle coordinates, but more research could yield a standardized procedure for placing paddles on nonlinear morphologies. Expanding the results of this study from 2-D simulations to 3-D simulations will allow for the modeling of more complex and realistic crustacean biology, as well as improving visualization.

Supplementary Materials

The following supporting information can be downloaded at this link (This is a temporary link for the convenience of the reviewers and editors; if the paper is accepted for publication, this link will be replaced by one to our supplemental materials). Video S1: Fluid simulation for the crustacean morphology with k = 0 and phase change = 0s. Video S2: Fluid simulation for the crustacean morphology with k = 0 and phase change = 0.010s. Video S3: Fluid simulation for the crustacean morphology with k = -0.4 and phase change = 0.010s. Video S4: Fluid simulation for the crustacean morphology with k = 0.4 and phase change = 0.010s.

Author Contributions

Conceptualization, E.C. and Z.J.K.; Data curation, E.C.; Formal analysis, E.C.; Investigation, E.C. and Z.J.K.; Methodology, E.C. and Z.J.K.; Project administration, E.C.; Resources, E.C. and Z.J.K.; Supervision, Z.J.K.; Validation, E.C. and Z.J.K.; Visualization, E.C. and Z.J.K.; Writing – original draft, E.C. and Z.J.K.; Writing – review & editing, E.C. and Z.J.K.

Funding

This research received no external funding.

Acknowledgments

We gratefully acknowledge three anonymous reviewers for their careful reading of our initial manuscript and for offering constructive and insightful critique that allowed us to significantly improve the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
CFD Computational Fluid Dynamics
Re Reynolds Number
PS Power Stroke
RS Return/Recovery Stroke

References

  1. Lauder, G.V. Fish Locomotion: Recent Advances and New Directions. Annual Review of Marine Science 2015, 7, 521–545. [Google Scholar] [CrossRef] [PubMed]
  2. Zhu, Q. Physics and applications of squid-inspired jetting. Bioinspiration and Biomimetics 2022, 17, 041001. [Google Scholar] [CrossRef] [PubMed]
  3. Purcell, E.M. Life at low Reynolds number. American Journal of Physics 1977, 45, 3–11. [Google Scholar] [CrossRef]
  4. Ford, M.P.; Lai, H.K.; Samaee, M.; Santhanakrishnan, A. Hydrodynamics of metachronal paddling, effects of varying Reynolds number and phase lag. Royal Society Open Science 2019, 6, 191387. [Google Scholar] [CrossRef] [PubMed]
  5. Hayashi, R.; Takagi, D. Metachronal Swimming with Rigid Arms near Boundaries. Fluids 2020, 5, 24. [Google Scholar] [CrossRef]
  6. Kohlhage, K.; Yager, J. An analysis of swimming in remipede crustaceans. Philosophical Transactions of the Royal Society B: Biological Sciences 1994, 346, 213–221. [Google Scholar]
  7. Lim, J.L.; DeMont, M.E. Kinematics, hydrodynamics and force production of pleopods suggest jet-assisted walking in the American lobster (Homarus americanus). Journal of Experimental Biology 2009, 212, 2731–2745. [Google Scholar] [CrossRef] [PubMed]
  8. Elgeti, J.; Gompper, G. Emergence of metachronal waves in cilia arrays. Proceedings of the National Academy of Sciences 2013, 110, 4470–4475. [Google Scholar] [CrossRef]
  9. Milana, E.; Zhang, R.; Vetrano, M.R.; Peerlinck, S.; Volder, M.D.; Onck, P.R.; Reynaerts, D.; Gorissen, B. Metachronal patterns in artificial cilia for low Reynolds number fluid propulsion. Science Advances 2020, 6, eabd2508. [Google Scholar] [CrossRef]
  10. Byron, M.L.; Murphy, D.W.; Katija, K.; Hoover, A.P.; Daniels, J.; Garayev, K.; Takagi, D.; Kanso, E.; Gemmell, B.J.; Ruszczyk, M.; Santhanakrishnan, A. Metachronal Motion across Scales: Current Challenges and Future Directions. Integrative and Comparative Biology 2021, 61, 1674–1688. [Google Scholar] [CrossRef]
  11. Mulloney, B.; Smarandache-Wellmann, C. Neurobiology of the crustacean swimmeret system. Progress in Neurobiology 2012, 96, 242–267. [Google Scholar] [CrossRef]
  12. Laverack, M.S.; Macmillan, D.L.; Neil, D.M. A comparison of beating parameters in larval and post-larval locomotor systems of the lobster Homarus gammarus (L.). Philosophical Transactions of the Royal Society B: Biological Sciences 1976, 274, 87–99. [Google Scholar]
  13. Grazier-Nakajima, S.; Guy, R.D.; Zhang-Molina, C. A Numerical Study of Metachronal Propulsion at Low to Intermediate Reynolds Numbers. Fluids 2020, 5, 86. [Google Scholar] [CrossRef]
  14. Murphy, D.W.; Webster, D.R.; Kawaguchi, S.; King, R.; Yen, J. Metachronal swimming in Antarctic krill: gait kinematics and system design. Marine Biology 2011, 158, 2542–2554. [Google Scholar] [CrossRef]
  15. Zhang, C.; Guy, R.D.; Mulloney, B.; Zhang, Q.; Lewis, T.J. Neural mechanism of optimal limb coordination in crustacean swimming. Proceedings of the National Academy of Sciences 2014, 111, 13840–13845. [Google Scholar] [CrossRef] [PubMed]
  16. Alben, S.; Spears, K.; Garth, S.; Murphy, D.; Yen, J. Coordination of multiple appendages in drag-based swimming. Journal of the Royal Society Interface 2010, 7, 1545–1557. [Google Scholar] [CrossRef] [PubMed]
  17. Alexander, D.E. Kinematics of swimming in two species of Idotea (Isopoda: Valvifera). Journal of Experimental Biology 1988, 138, 37–49. [Google Scholar] [CrossRef]
  18. Daniels, J.; Aoki, N.; Havassy, J.; Katija, K.; Osborn, K. Metachronal Swimming with Flexible Legs: A Kinematics Analysis of the Midwater Polychaete Tomopteris. Integrative and Comparative Biology 2021, 61, 1658–1673. [Google Scholar] [CrossRef]
  19. Hanasoge, S.; Hesketh, P.; Alexeev, A. Metachronal Acutation of Microscale Magnetic Artificial Cilia. American Chemical Society Applied Materials & Interfaces 2020, 12, 46963–46971. [Google Scholar]
  20. Khaderi, S.N.; den Toonder, J.M.J.; Onck, P.R. Microfluidic propulsion by the metachronal beating of magnetic artificial cilia: a numerical analysis. Journal of Fluid Mechanics 2011, 688, 44–65. [Google Scholar] [CrossRef]
  21. Ford, M.P.; Santhanakrishnan, A. Closer Appendage Spacing Augments Metachronal Swimming Speed by Promoting Tip Vortex Interactions. Integrative and Comparative Biology 2021, 61, 1608–1618. [Google Scholar] [CrossRef] [PubMed]
  22. Ford, M.P.; Ray, W.K.; DiLuca, E.M.; Patek, S.N.; Santhanakrishnan, A. Hybrid Metachronal Rowing Augments Swimming Speed and Acceleration via Increased Stroke Amplitude. Integrative and Comparative Biology 2021, 61, 1619–1630. [Google Scholar] [CrossRef] [PubMed]
  23. Wang, A.X.G.; Kabala, Z.J. Body Morphology and Drag in Swimming: CFD Analysis of the Effects of Differences in Male and Female Body Types. Fluids 2022, 7, 332. [Google Scholar] [CrossRef]
  24. Sun, H.; Ding, W.; Zhao, X.; Sun, Z. Numerical Study of Flat Plate Impact on Water Using a Compressible CIP–IBM–Based Model. J. Mar. Sci. Eng. 2022, 10, 1462. [Google Scholar] [CrossRef]
  25. Jiang, H. Numerical Simulation of Self-Propelled Steady Jet Propulsion at Intermediate Reynolds Numbers: Effects of Orifice Size on Animal Jet Propulsion. Fluids 2021, 6, 230. [Google Scholar] [CrossRef]
  26. Kim, D.-H.; Park, J.-C.; Jeon, G.-M.; Shin, M.-S. CFD Simulation for Estimating Efficiency of PBCF Installed on a 176K Bulk Carrier under Both POW and Self-Propulsion Conditions. Processes 2021, 9, 1192. [Google Scholar] [CrossRef]
  27. Ding, Y.; Kanso, E. Selective particle capture by asynchronously beating cilia. Physics of Fluids 2015, 27, 121902. [Google Scholar] [CrossRef]
  28. Chateau, S. Why anti-plectic metachronal cilia are optimal to transport bronchial mucus. Physical Review E 2019, 100, 042405. [Google Scholar] [CrossRef]
  29. Brennen, C. An oscillating-boundary-layer theory for ciliary propulsion. Journal of Fluid Mechanics 1974, 65, 799–824. [Google Scholar] [CrossRef]
  30. Peskin, C.S. Flow patterns around heart valves: A numerical method. Journal of Computational Physics 1972, 10, 252–271. [Google Scholar] [CrossRef]
  31. Lauga, E.; Powers, T.R. The hydrodynamics of swimming microorganisms. Annual Review of Fluid Mechanics 2009, 41, 105–139. [Google Scholar] [CrossRef]
  32. Battista, N.A.; Baird, A.J. , Miller, L.A. A Mathematical Model and MATLAB Code for Muscle-Fluid-Structure Simulations. Integrative and Comparative Biology 2015, 55, 901–911. [Google Scholar] [CrossRef] [PubMed]
  33. Battista, N.A.; Strickland, W.C.; Miller, L.A. IB2d: a Python and MATLAB implementation of the immersed boundary method. Bioinspiration and Biomimetics 2016, 12, 036003. [Google Scholar] [CrossRef] [PubMed]
  34. Senter, D.M.; Douglas, D.R.; Strickland, W.C.; Thomas, S.G.; Talkington, A.M.; Miller, L.A.; Battista, N.A. A semi-automated finite difference mesh creation method for use with immersed boundary software IB2d and IBAMR. Bioinspiration and Biomimetics 2021, 16, 016008. [Google Scholar] [CrossRef] [PubMed]
  35. Battista, N.A.; Strickland, W.C.; Barrett, A.; Miller, L.A. IB2d Reloaded: A more powerful Python and MATLAB implementation of the immersed boundary method. Mathematical Methods in the Applied Sciences 2017, 41, 8455–8480. [Google Scholar] [CrossRef]
  36. Miles, J.G.; Battista, N.A. Naut Your Everyday Jellyfish Model: Exploring How Tentacles and Oral Arms Impact Locomotion. Fluids 2019, 4, 169. [Google Scholar] [CrossRef]
Preprints 92804 g001
Figure 1. A marsh grass shrimp (Palaemonetes vulgaris) performing metachronal swimming. This figure is displayed under the Creative Commons CC BY-SA 3.0 License. Image courtesy of Nils Tack/University of South Florida.
Figure 1. A marsh grass shrimp (Palaemonetes vulgaris) performing metachronal swimming. This figure is displayed under the Creative Commons CC BY-SA 3.0 License. Image courtesy of Nils Tack/University of South Florida.
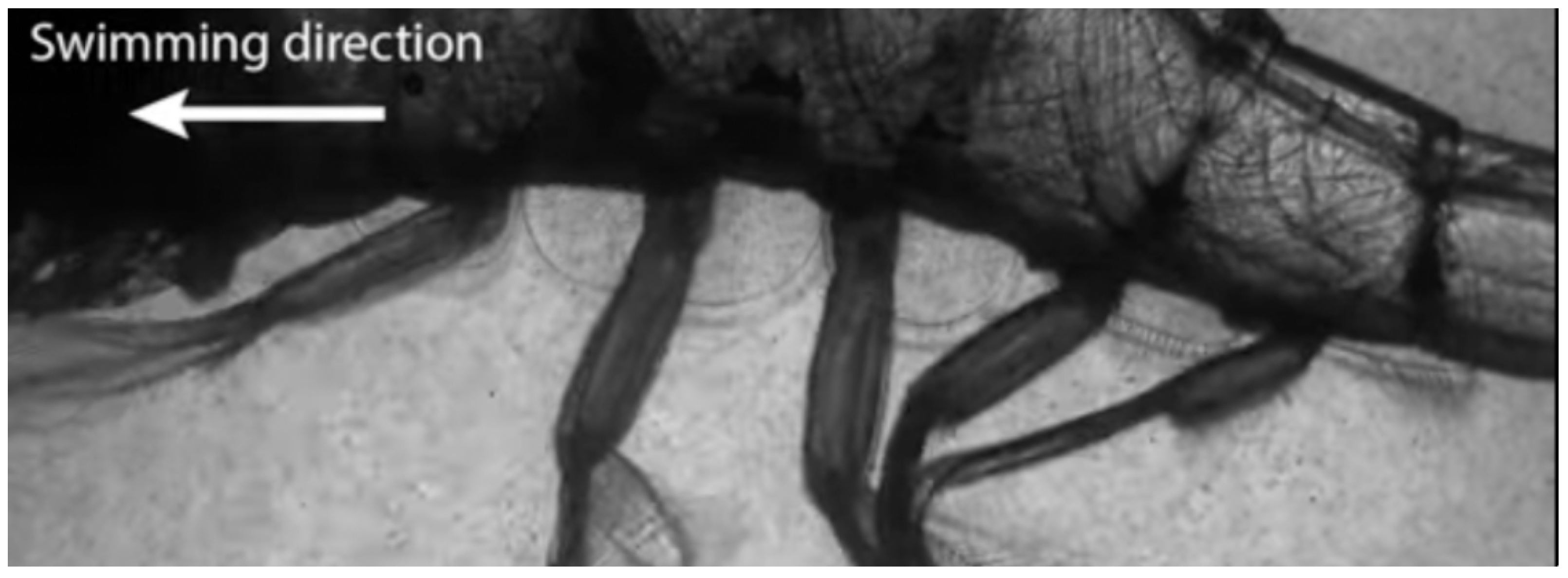
Preprints 92804 g001
Preprints 92804 g002
Figure 2. A schematic of a sample crustacean model. Some indicated features include labeled power strokes and return strokes, the swimming direction, paddle spacing, and each paddle’s range of motion.
Figure 2. A schematic of a sample crustacean model. Some indicated features include labeled power strokes and return strokes, the swimming direction, paddle spacing, and each paddle’s range of motion.
Preprints 92804 g002
Preprints 92804 g003
Figure 3. A comparison between the grid width, L x , and the simulated propulsion velocity.
Figure 3. A comparison between the grid width, L x , and the simulated propulsion velocity.
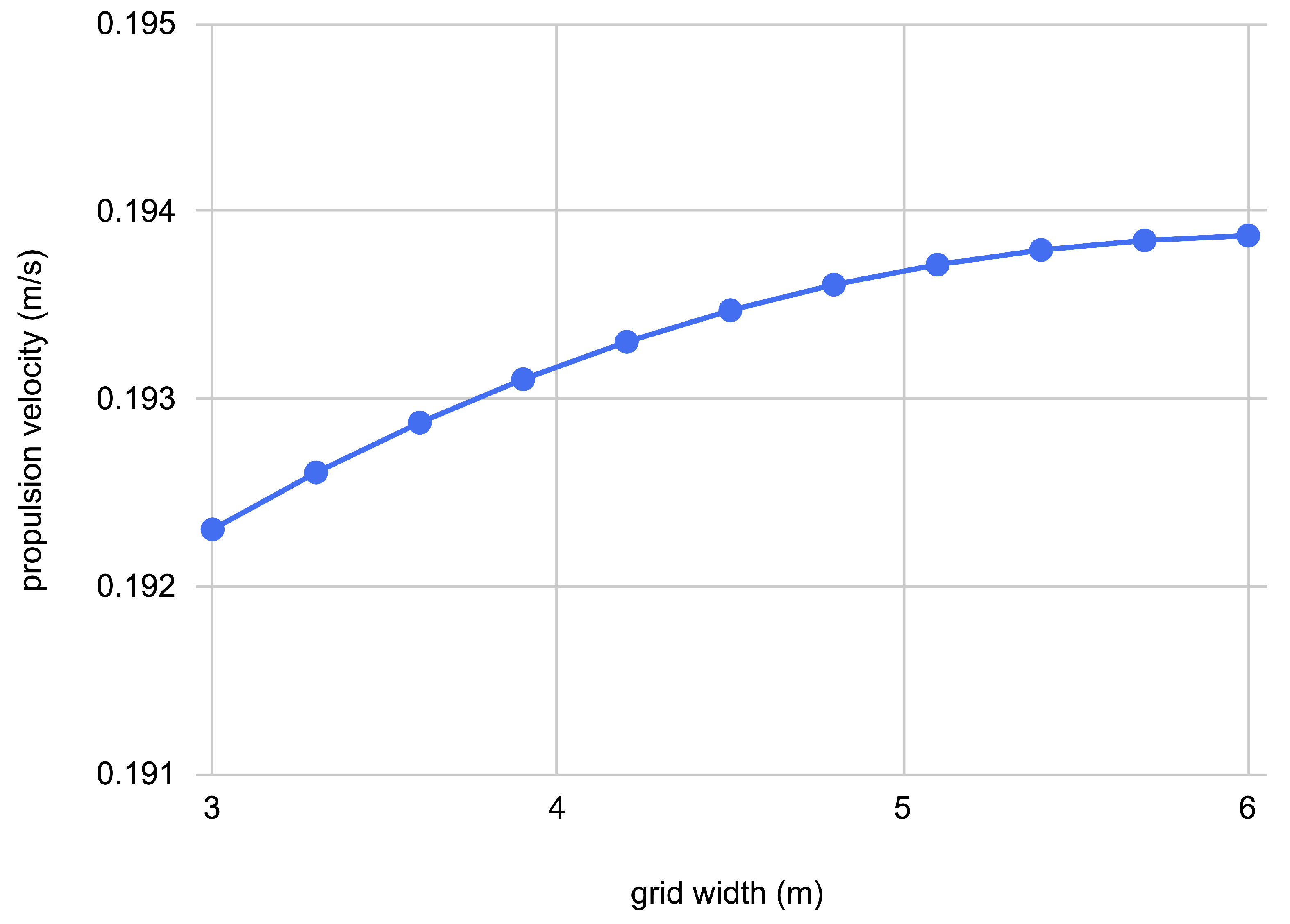
Preprints 92804 g003
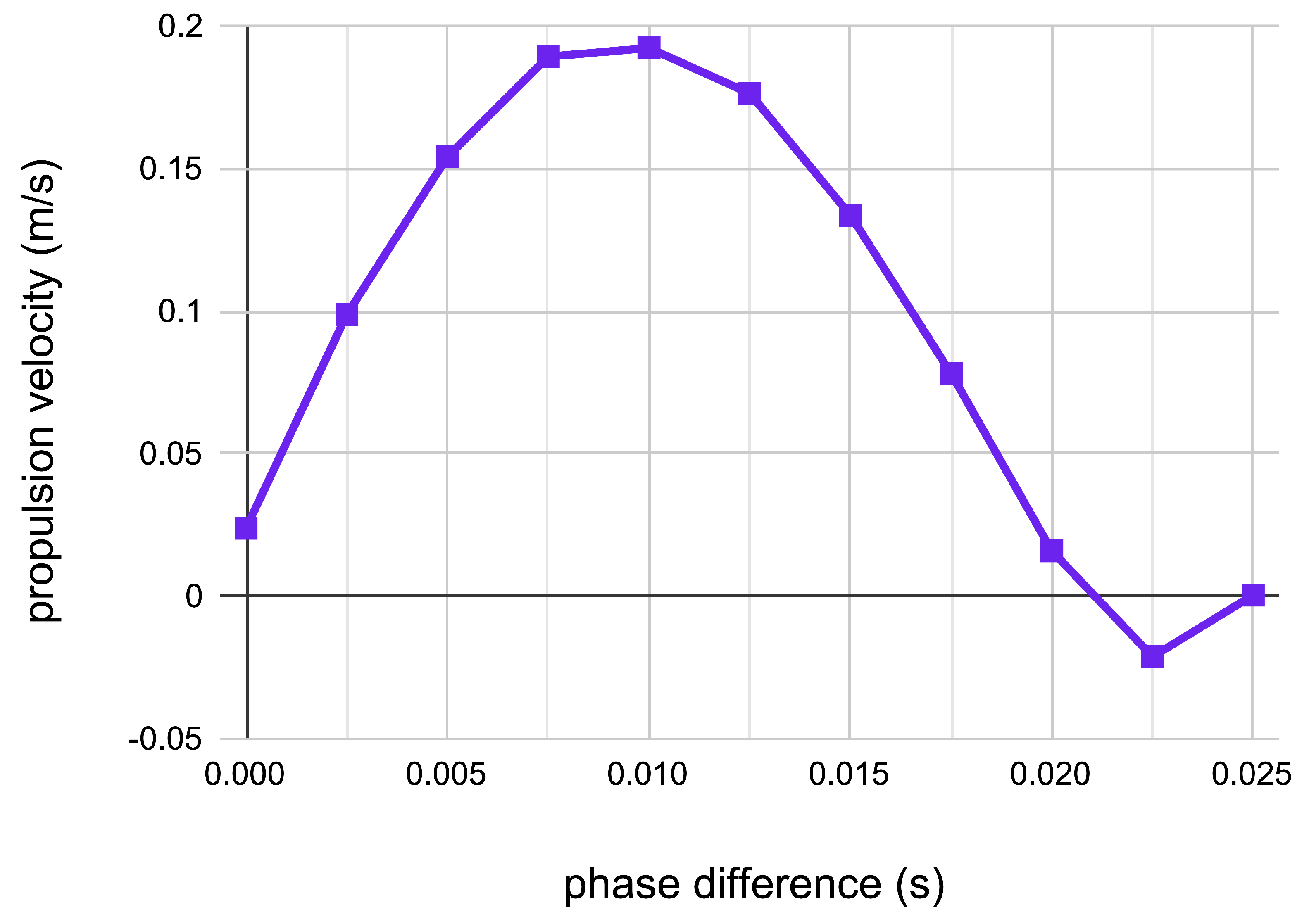
Preprints 92804 g004
Figure 4. The effect of phase difference ( Δ ϕ ) on propulsion velocity ( V x ) over a range of 0 ≤ Δ ϕ ≤ 0.025 .
Figure 4. The effect of phase difference ( Δ ϕ ) on propulsion velocity ( V x ) over a range of 0 ≤ Δ ϕ ≤ 0.025 .
Preprints 92804 g004
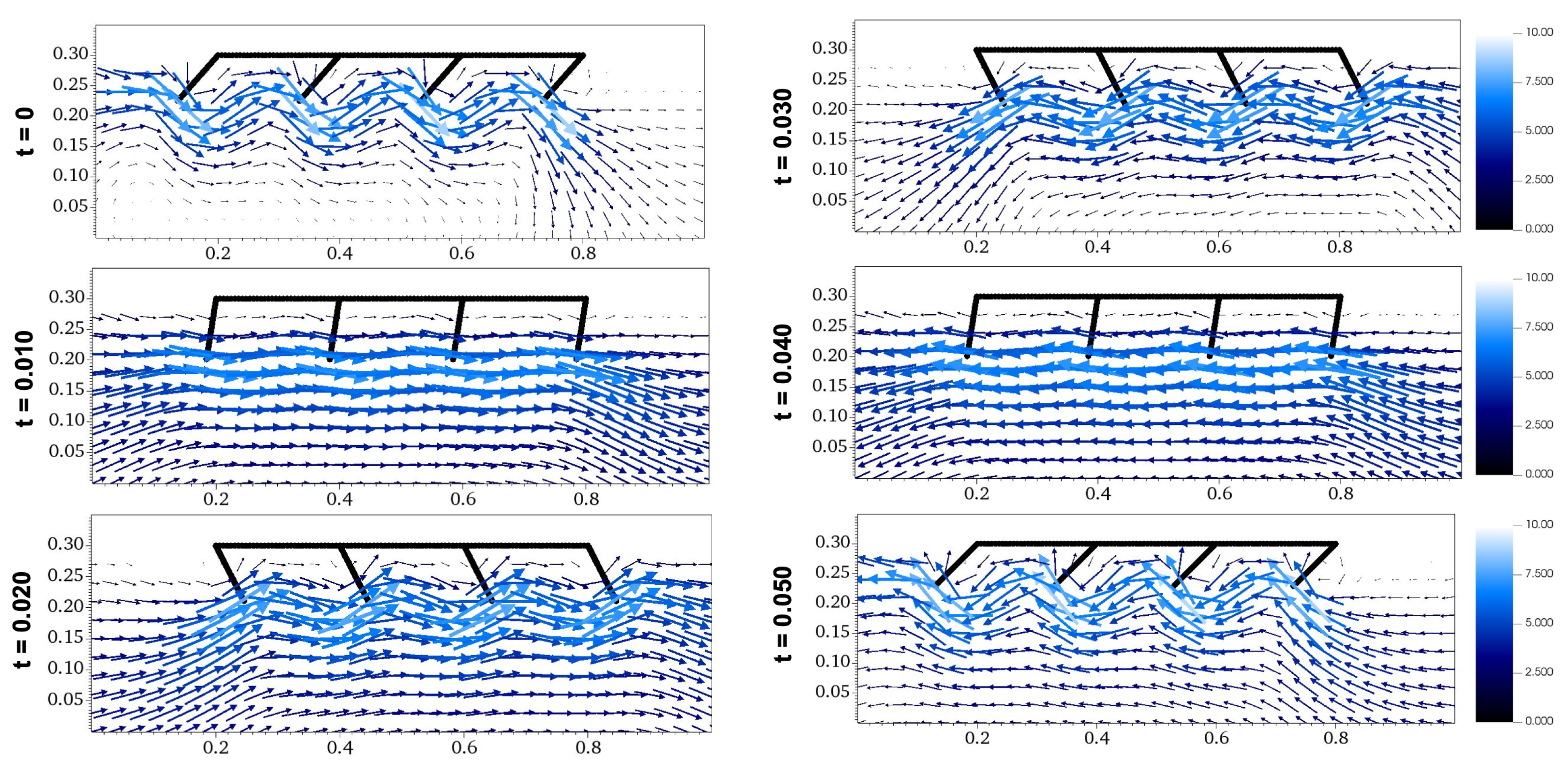
Preprints 92804 g005
Figure 5. Flow diagrams of metachronal propulsion with ϕ = 0 , a synchronous paddle motion.
Figure 5. Flow diagrams of metachronal propulsion with ϕ = 0 , a synchronous paddle motion.
Preprints 92804 g005
Preprints 92804 g006
Figure 6. Flow diagrams of metachronal propulsion with ϕ = 0.010 , an asynchronous paddle motion.
Figure 6. Flow diagrams of metachronal propulsion with ϕ = 0.010 , an asynchronous paddle motion.
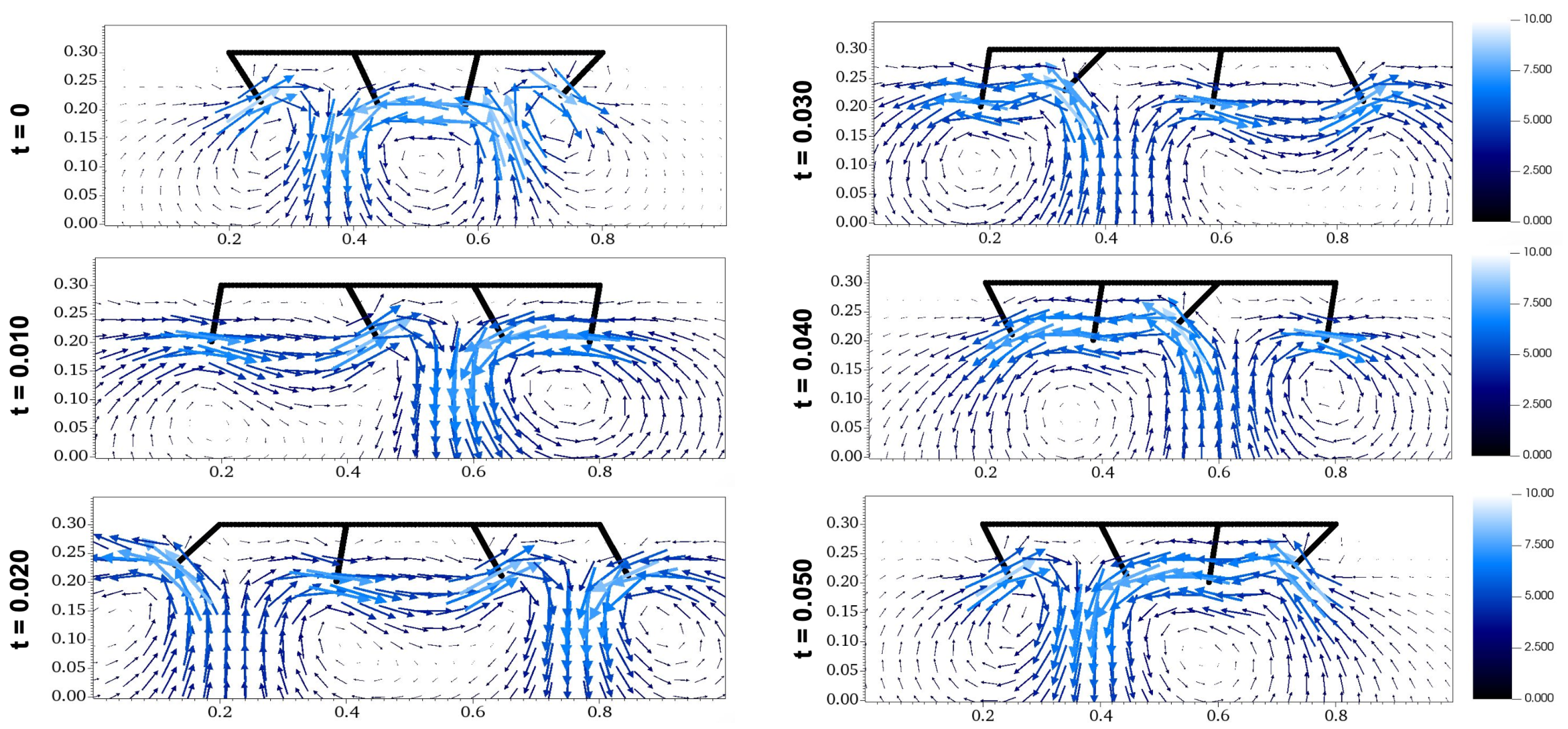
Preprints 92804 g006
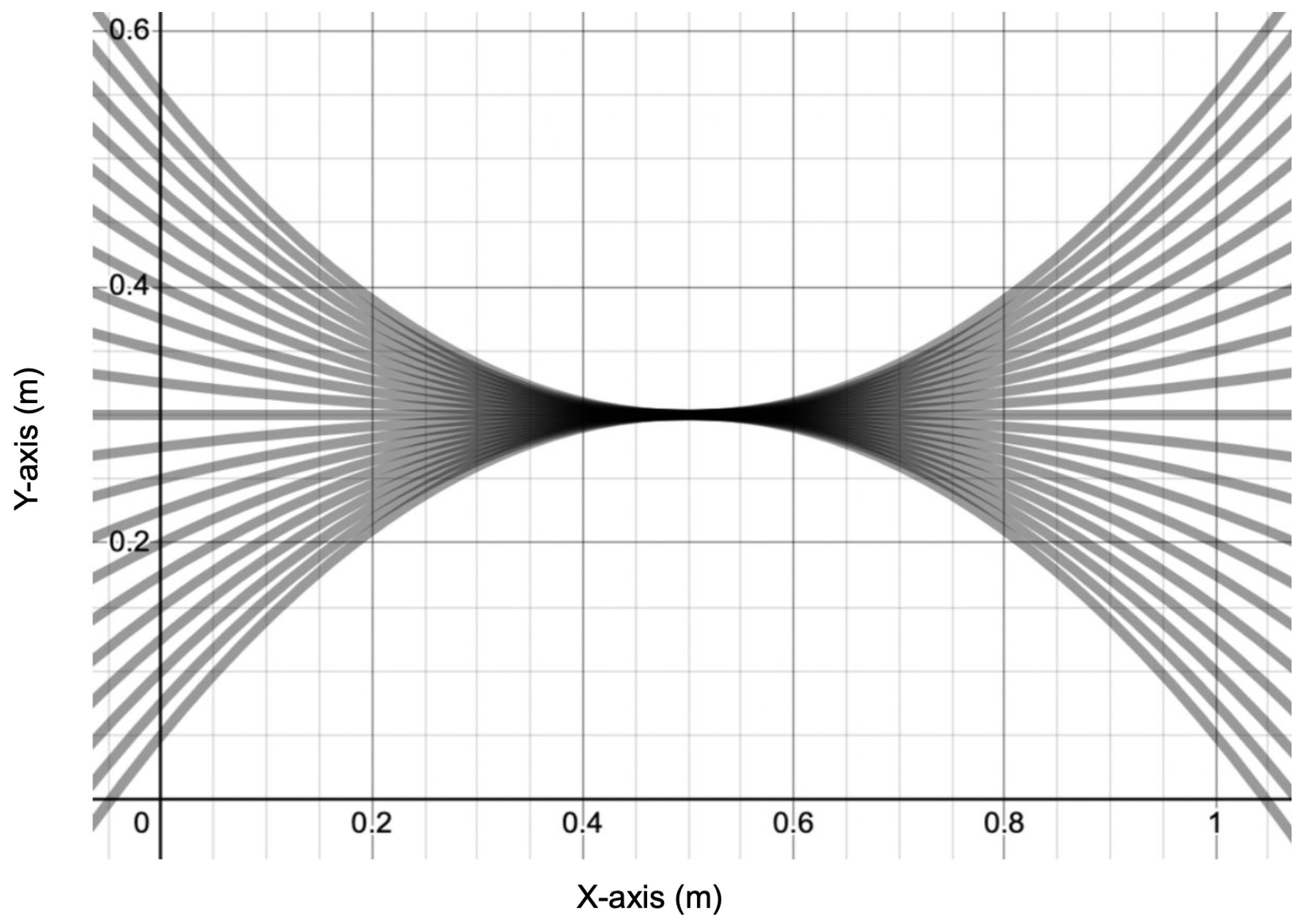
Preprints 92804 g007
Figure 7. A graphical representation of the tested range of crustacean morphology, with − 1 ≤ k ≤ 1 .
Figure 7. A graphical representation of the tested range of crustacean morphology, with − 1 ≤ k ≤ 1 .
Preprints 92804 g007
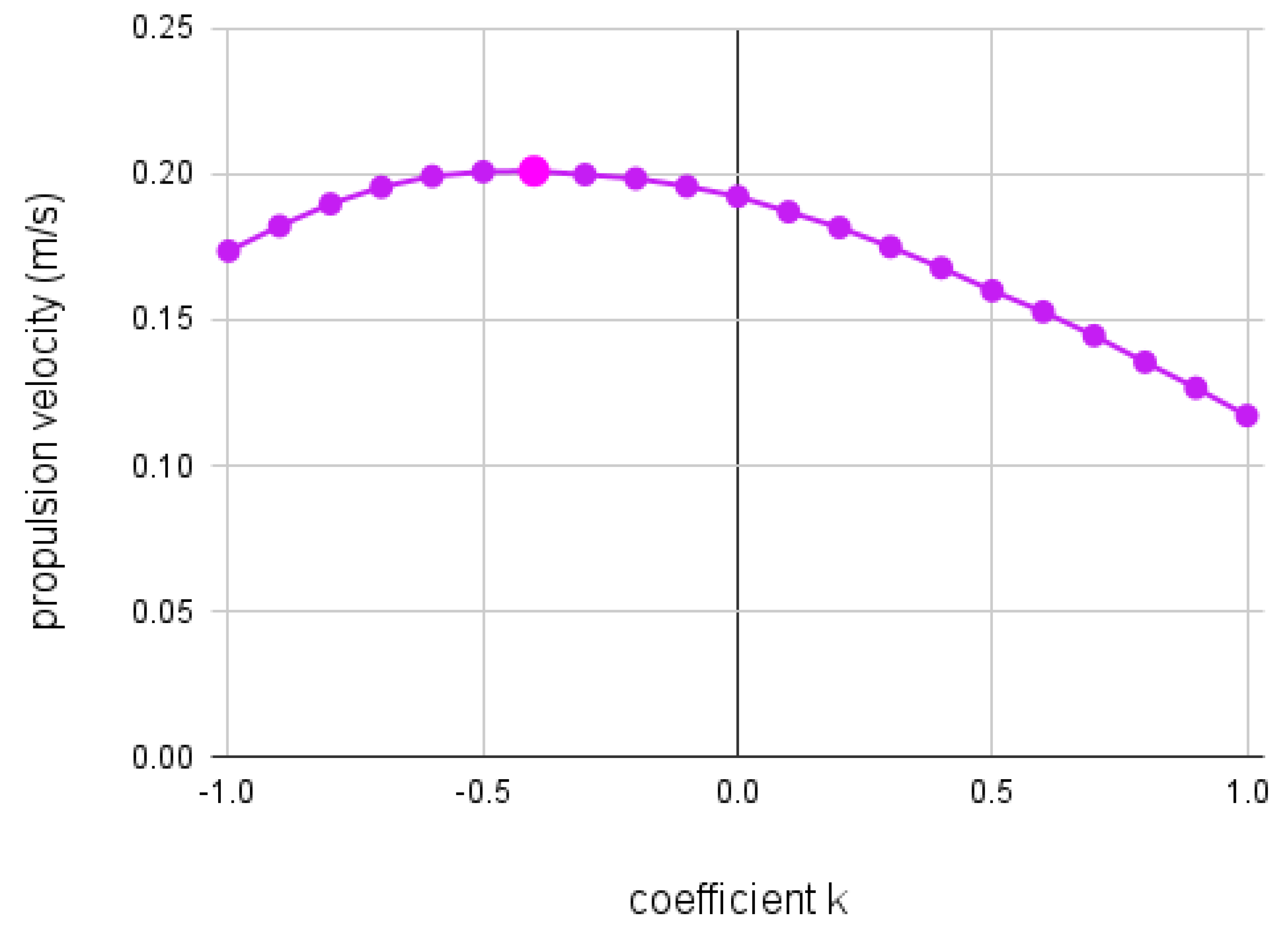
Preprints 92804 g008
Figure 8. The effect of coefficient k on propulsion velocity ( V x ) over a range of -1 ≤ k ≤ 1.
Figure 8. The effect of coefficient k on propulsion velocity ( V x ) over a range of -1 ≤ k ≤ 1.
Preprints 92804 g008
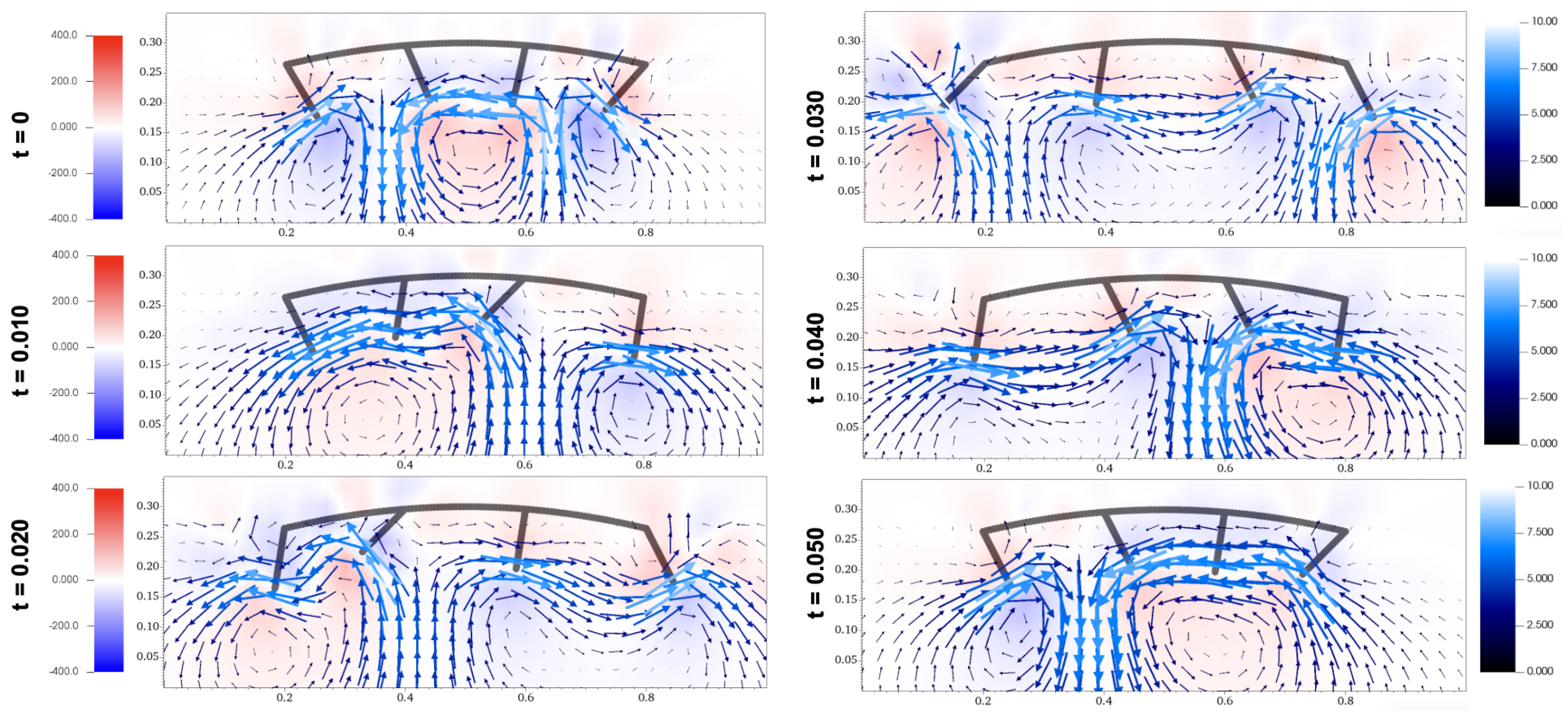
Preprints 92804 g009
Figure 9. Flow diagrams of metachronal propulsion including vorticity with k = − 0.4 , which assures maximum V x .
Figure 9. Flow diagrams of metachronal propulsion including vorticity with k = − 0.4 , which assures maximum V x .
Preprints 92804 g009
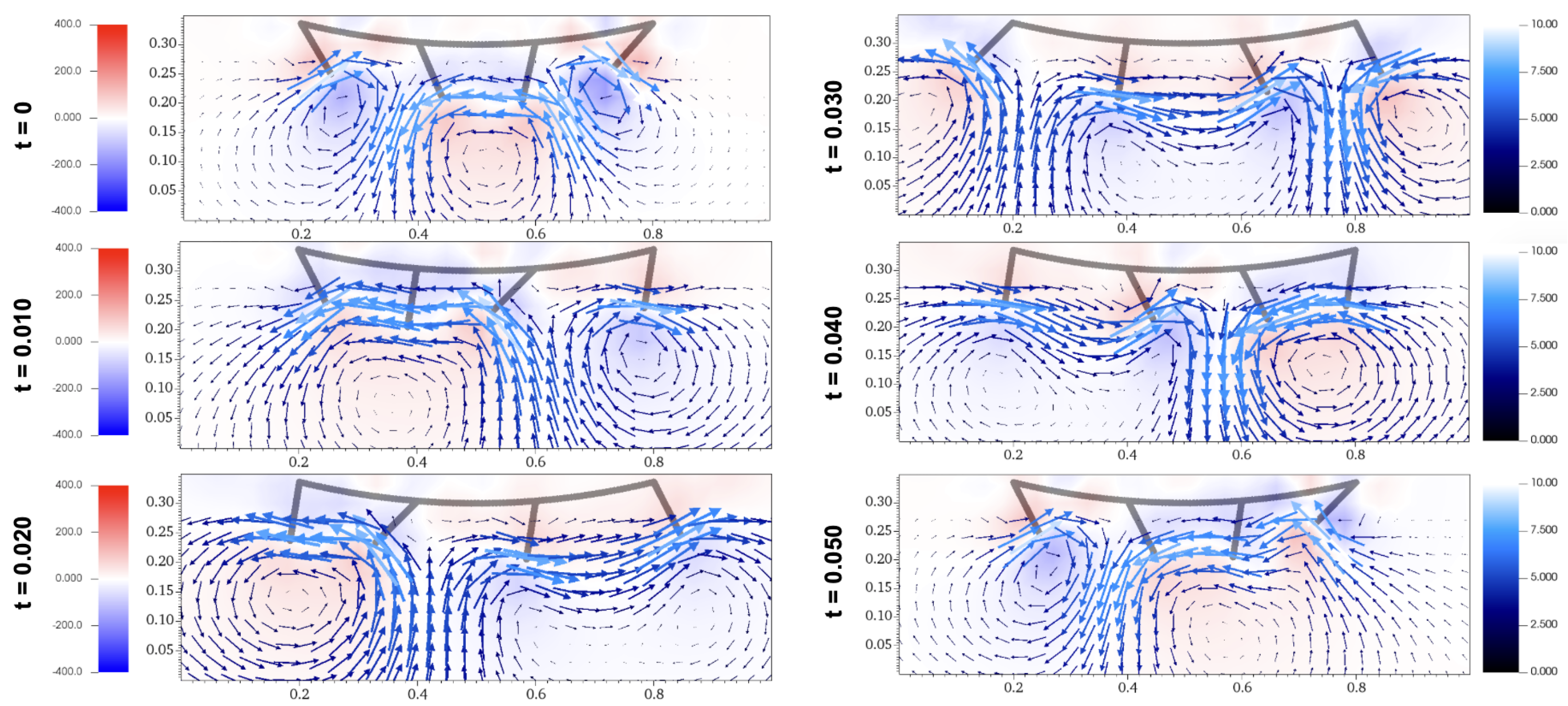
Preprints 92804 g010
Figure 10. Flow diagrams of metachronal propulsion including vorticity with k = 0.4 .
Figure 10. Flow diagrams of metachronal propulsion including vorticity with k = 0.4 .
Preprints 92804 g010
Table 1. The effect of confirmatory phase difference values on propulsion velocity.
Table 1. The effect of confirmatory phase difference values on propulsion velocity.
Δ ϕ ( s ) V x ( m . s − 1 )
0 0.0238
0.01 0.1539
0.025 0.0004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Impact of Crustacean Morphology on Metachronal Propulsion: A Numerical Study

Enbao Cao

et al.

,

2023

Underwater Vehicle CFD Analyses and Reusable Energy Inspired by Biomimetic Approach

Andra-Teodora Nedelcu

et al.

,

2018

Investigations on Motion Responses of Suspended Submersible in Internal Solitary Wave Field

Zhenyang He

et al.

,

2024

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated