Prerpints.org logo
Preprint
Article

Optimization of Rebar Usage and Sustainability Based on Special-Length Priority: A Case Study on Mechanical Couplers in Diaphragm Wall

Altmetrics

Downloads

230

Views

14

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

09 December 2023

Posted:

11 December 2023

You are already at the latest version

Alerts
Abstract
The construction industry generates significant CO2 emissions, and rebar is a major contributor to this environmental impact. Extensive research has been conducted to address this issue. Recent advancements have introduced algorithms to reduce rebar waste and consumption, demonstrating the feasibility of achieving near-zero rebar cutting waste (N0RCW) by considering special-length rebars. However, conventional lap splices, the most common rebar joint method, consistently consume excessive rebar quantities despite extending beyond their mandated zones. Conversely, couplers eliminate rebar lengths required for lapping splices, reducing the usage of rebar. Applying special lengths and couplers in heavily loaded structures like diaphragm walls can significantly reduce rebar usage and cutting waste, consequently reducing CO2 emissions and associated costs. This study aims to optimize rebar consumption and sustainability in diaphragm wall structures by integrating mechanical couplers with a special-length rebar approach. A case study confirmed a substantial reduction in purchased rebar usage (17.95% and 5.38%) and carbon emissions (15.24% and 2.25%) compared to the original design and previous study, respectively. Broadly implementing the proposed method across various buildings and infrastructure projects could further multiply these benefits, fostering the achievement of SDGs adopted by the United Nations for sustainable construction.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Steel reinforcement bar has a high embodied carbon footprint, about 9.2 times that of concrete [i], making it one of the major contributors to greenhouse gases (GHG) emissions. The US Environmental Protection Agency [ii] denotes that GHGs comprise 79.4% CO2, 11.5% CH4 (methane), 6.2% N2O (nitrous oxide), and 3% fluorinated gases. It is reported that in 2020 the global consumption of concrete reached 14 billion m3 [iii]. This amount corresponds to 1.078 billion tons of rebar, a cutting waste of 53.9 million tons, wasting 188.92 million tons of CO2. Improperly managed cutting waste can end up in landfills, occupying valuable limited space of landfill and contributing to the production of landfill gas (LFG). LFG mainly constituted 40-50% CO2 and 50-60% CH4 [iv], with trace amounts of H2S (hydrogen sulfide) [v]. Methane is a powerful GHG and is estimated to have a GWP (Global Warming Potential) of 27-30 over 100 years [2]. It has been discovered that rebar and concrete can significantly contribute to acid rain formation [vi]. Acid rain forms when harmful gases such as sulfur dioxide (SO2) and nitrogen dioxide (NO2) react with water vapor in the atmosphere [vii]. Acid rain causes significant harm to the environment, particularly to the soil. In addition, steel and rebar production may contribute to mercury emissions besides carbon emissions, leading to ecotoxicity [viii]. Mercury emissions can adversely impact the environment by polluting water bodies, harming wildlife, and posing a risk to human health.
Conventional lap splicing, the prevailing method for connecting rebars, is also a major contributor to rebar waste and CO2 emissions in the construction industry, especially in large-scale projects like diaphragm walls, due to the long overlapping lengths of rebar required. Lap splice-based rebar waste depends on rebar diameter, required lap length, and cutting pattern.
One challenge in reducing rebar waste is adhering to lap splice regulations mandated by building codes. Lap splice length is typically derived from the bonding strength between concrete and steel rebar, considering the safety factor. Thus, the structural design provides a safe sufficient lap splice length. However, the lap splice position or region regulations mandated by the building codes and stock-length rebar usage restrict the reduction of rebar usage and cutting waste as per various studies [ix, x, xi, xii], ranging from 7.2% to 10.6%, exceeding the common range of 3-5% [xiii]. Nonetheless, it is difficult to adhere to these regulations on-site, and thus lap splice positions are often not followed in practice [xiv]. This approach continuously consumes a greater quantity of rebars, even when not adhering to mandated regulations. Researchers proposed special length rebars as one of the solutions to the high rebar consumption and waste issue. Investigations confirmed that special-length rebar enables further reduction in cutting waste to below 3% [xv, xvi].
Massive substructures such as diaphragm walls could illustrate the issue. The case study found that purchasing stock-length rebars for reinforcement in a total of 293 diaphragm wall panels resulted in 2173 tons (9.62%) of cutting waste [15], as large-diameter rebars (32 mm and 40 mm) were required to resist the massive lateral forces such as an earthquake in addition to the pressure of soil. The study additionally revealed that the utilization of special length rebars in diaphragm walls results in the consumption of 19,582 tons of rebar and the generation of 0.77% of cutting waste. Consequently, the adverse environmental impact due to high rebar usage remains evident. Furthermore, the ACI building code [xvii] prohibits lap splices for rebar sizes with a diameter of 36 mm and larger due to long overlapping lengths. Mechanical couplers can be used instead of lap splices to effectively transfer the tensile strength of rebar while maintaining structural integrity and stability. Couplers eliminate the need for lap splices, which further reduces required rebar, associated cutting waste, and environmental impact.
Prior studies have primarily focused on columns [xviii, xix], beams [18], and shear walls [10] for rebar cutting waste optimization, neglecting an essential structural component: diaphragm walls. Diaphragm walls play a pivotal role as the foundation backbone of building structures [xx], serving to connect various structural elements. Comprising multiple wall panels with similar reinforcement, the unique characteristic of diaphragm wall rebar lies in its prefabrication into rebar cages. A significant reduction in rebar usage and carbon emissions is expected by performing detailed reinforcement design and optimizing for special lengths.

1.1. Rebar usage and cutting waste issues

Global concrete volume reached 14 billion m3 in 2020 [3]. Converting this amount with a rebar-to-concrete consumption ratio of 0.077 tons/m3 [1] indicates that 1.078 billion tons of rebar are used. Assuming a 5% cutting waste rate, this results in 53.9 million tons of rebar-cutting waste and 188.92 million tons of carbon emission. Cutting steel reinforcement bars (rebar) is unavoidable in reinforced concrete (RC) structure construction and generates cutting waste and considerable carbon emissions [xxi]. Considering a rebar price of USD 900/ton [xxii], a unit of rebar-carbon emissions of 3.505-ton-CO2/ton [xxiii], and a carbon price of USD 75/ton-CO2 [xxiv], implies a loss of USD 62.68 billion for the industry. This condition urges stronger efforts to reduce rebar usage and cutting waste, contributing to environmental sustainability.
Rebar usage and cutting waste issues have been the concerns of the Sustainable Development Goals (SDGs) [xxv] created by the United Nations in 2015, especially SDGs 12, 13, and 15. SDG 12 aims to ensure sustainable consumption and production patterns; SDG 13 aims to take serious action to combat climate change and its impacts; finally, SDG 15 aims to protect and restore land, as well as halt land degradation. Reducing rebar usage and its impact will accelerate the achievement of the SDGs in the civil engineering and construction sector.
Most studies conducted rebar waste minimization on stock length rebars [xxvi, 10, 11, 12]. Some investigations [9, 10] explored the lap splice position optimization with stock-length rebar to reduce rebar cutting waste. These approaches, however, still produced a high cutting waste rate. Special-length rebar concepts are then introduced for cutting pattern combinations and have been confirmed to significantly reduce cutting waste [13, 18, xxvii]. Special lengths can be customized in 0.1 m intervals and have certain order requirements such as maximum and minimum special lengths, minimum ordered quantity, and preorder time. Rachmawati et al. [15] proposed a three-step algorithm to minimize rebar cutting waste in diaphragm walls by considering special lengths and lap splice position adjustments. The algorithm generated 0.77% rebar cutting waste from 293 panels of diaphragm wall, saving 10,399 tons of CO2 emissions and USD 3,480,108 in costs.

1.2. Mechanical couplers

The use of mechanical couplers has increased in construction due to their advantages which solve the limitations of conventional lap splices. Table 1 summarizes the limitations of conventional lap splices identified by various studies. Furthermore, several investigations [xxviii, xxix, xxx] have emphasized that the application of lap splices may over-reinforce the structural section, reduce ductility, and alter the deformation capacity.
A mechanical coupler, also known as a mechanical splice or rebar coupler, is a device used for connecting two rebars, eliminating the lapping length, and ensuring the structural stability and strength of RC structures. In seismic applications, the coupler length should be less than 15 times the rebar diameter [xxxiv]. Rebars with different diameters can be connected laterally or vertically by using couplers. Mechanical coupler utilization can significantly reduce rebar congestion and also offer prefabrication of reinforcement on-site for precast concrete structures [xxxv]. Mechanical couplers have been shown to offer several benefits [31]: (1) reduced rebar congestion, (2) significant reduction in rebar waste and consumption, (3) effective control of concrete crack propagation, (4) improved structural continuity between bars, ensuring better integrity, (5) reduced labor required and construction costs, and (6) feasibility of connecting rebars of different lengths and diameters.
In the current construction industry, various types of couplers are employed. The five types of couplers which are readily available are (1) shear screw couplers, (2) headed bar couplers, (3) grouted sleeve couplers, (4) threaded couplers, and (5) swaged couplers [34]. The most prevalent type is the threaded coupler, characterized by its short length and ease of installation [xxxvi, xxxvii]. Four types of threaded couplers are commonly used: parallel threaded couplers (PTC), taper threaded couplers (TTC), upset-headed couplers (UHC), and rib thread couplers (RTC) [xxxviii].

1.3. Research objective

Rapid urbanization and the construction of high-rise buildings are reducing the availability of urban land [xxxix]. This has led to an increase in the construction of underground and buried structures in metropolitan cities [xl], such as diaphragm walls. Population growth and urbanization are driving demand for construction, which is depleting natural resources used in construction materials and harming the environment [xli].
Given the considerable demand for steel rebars in diaphragm wall construction, it represents an exemplary case study for optimizing rebar usage and environmental sustainability. The primary objective of this research is to assess the effectiveness of mechanical couplers in optimizing rebar usage and cutting waste of diaphragm walls and improving sustainability by integrating mechanical couplers with a special-length priority approach. A comprehensive analysis of rebar usage and cutting waste, considering the environmental and economic implications, is presented in this research. To identify the effectiveness and novelty of the proposed method, a comparative analysis will be undertaken against the conventional lap splice method of the original design and the recent study [15]. This comparison will encompass rebar usage, cutting waste, cost, and the CO2 emissions associated with cutting waste. Furthermore, this research will analyze the cost comparison between using couplers and the conventional method of overlapping rebar. This research provides the construction industry with new insights into optimizing rebar usage and sustainability while maintaining structural integrity and addressing the environmental impact of rebar. Furthermore, it also accelerates sustainable and green construction practices and the achievement of the Sustainable Development Goals (SDGs).

2. Characteristics of diaphragm wall

Diaphragm walls are underground reinforced concrete structures that extend vertically or at a slight angle, commonly used in underground construction, foundation systems, and retaining walls to provide lateral support. Diaphragm walls resist lateral forces from soil and water pressure, and transfer lateral loads induced by seismic events or other dynamic forces to the foundation of a building [20, 40]. A diaphragm wall system is generally composed of multiple wall panels. Main vertical rebars resist vertical and bending loads generated by lateral loads from soil, water pressure, and seismic activity. Horizontal (space) rebars distribute loads evenly along the length of the wall. Transverse shear, shear link, or tie reinforcement resists shear forces caused by lateral loads.
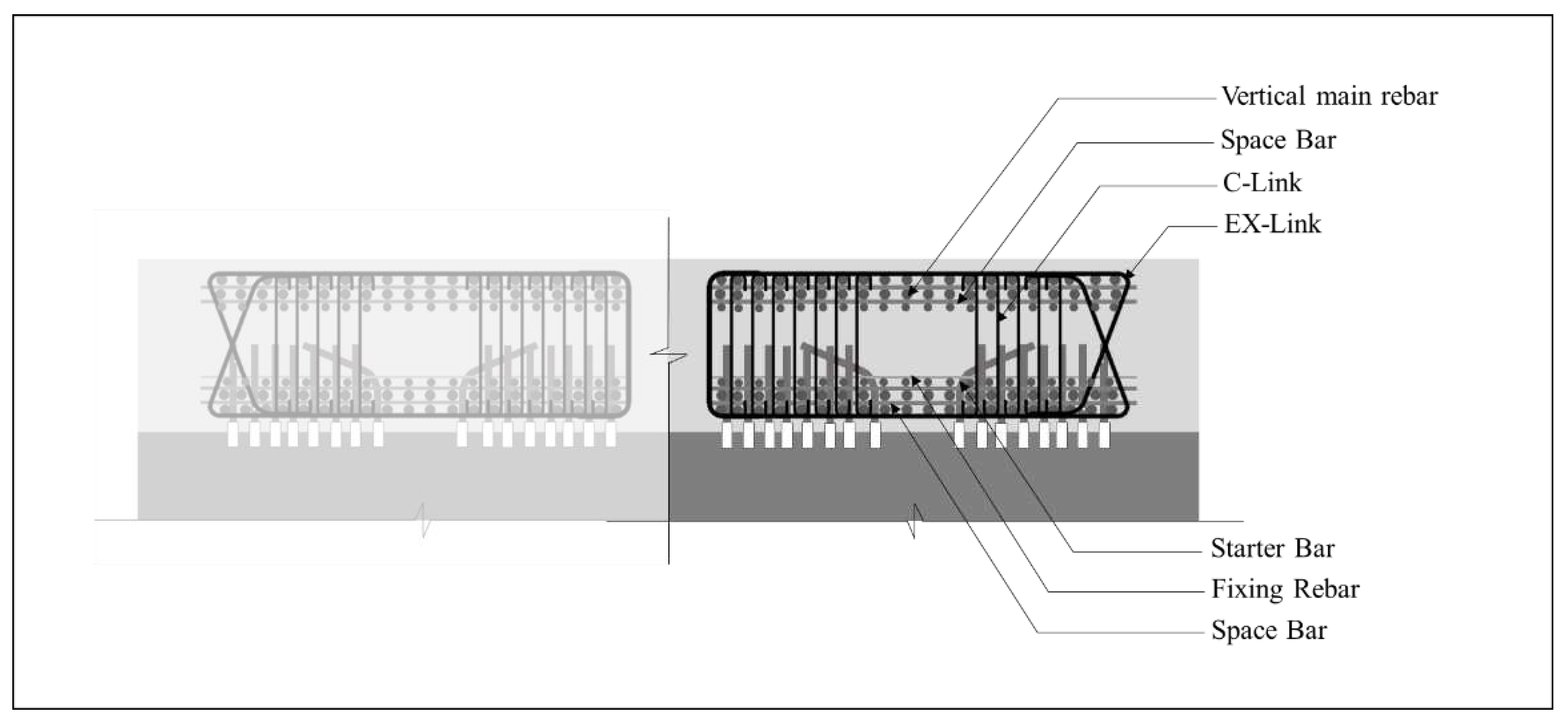
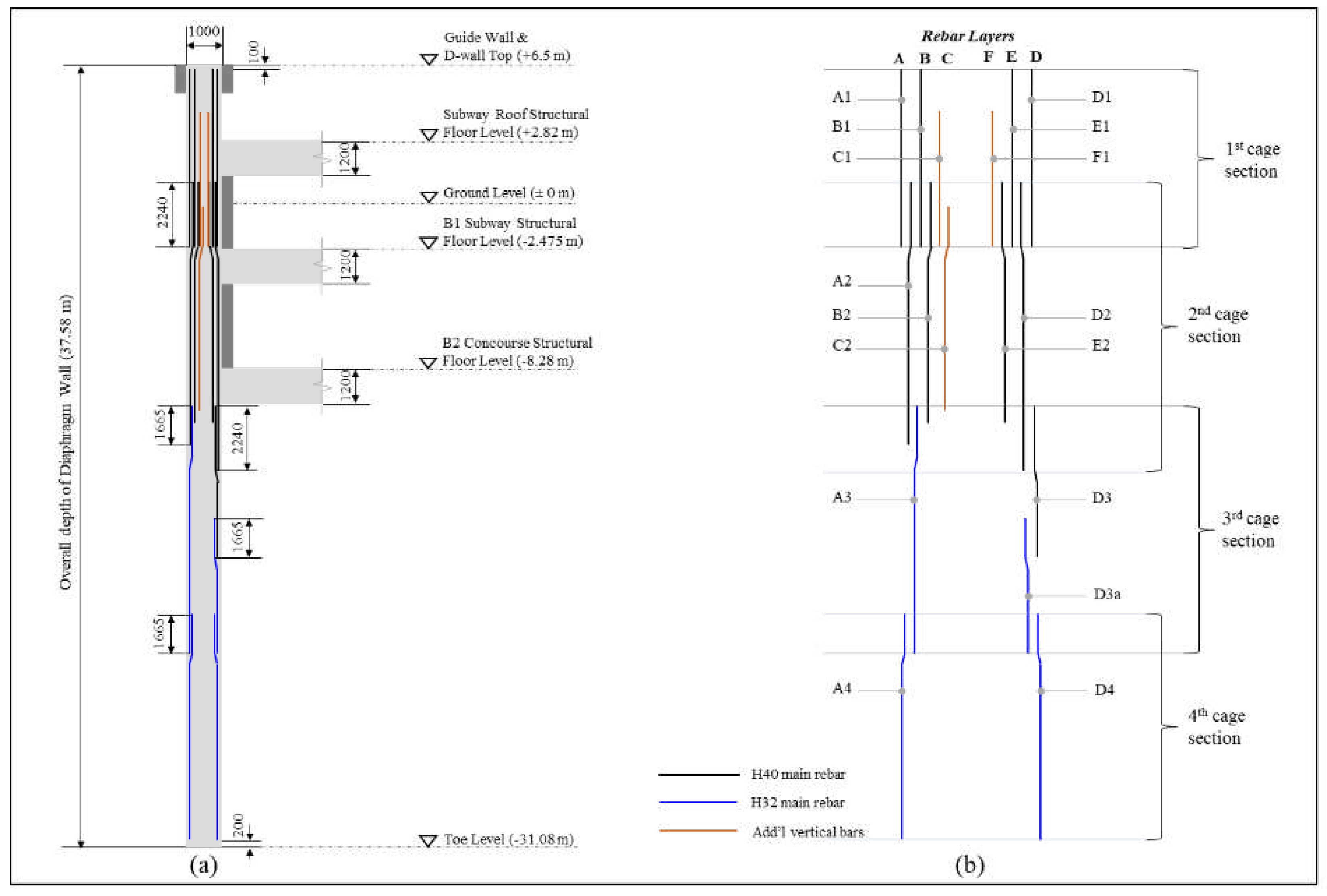
Diaphragm walls require a substantial amount of steel reinforcement bars to withstand lateral soil forces. This reinforcement is prefabricated into rebar cages and divided into three or more sections depending on the wall’s depth. Fabricated cages are inserted section by section into the excavated ground. Starter bars anchor the diaphragm wall reinforcement at every floor slab to ensure structural integrity. A typical diaphragm wall panel consists of two rebar cages. Each rebar cage can be divided into three groups of reinforcement: main vertical rebars, space bars, and horizontal ties or links. Additional rebars for various purposes, such as spacers, fixing rebars, stiffeners, hanging bars, suspension hooks, and lifting rebars, are also incorporated to strengthen the cage and aid in the installation process. The main vertical rebars in the cage are held in position by horizontal links such as EX-links and C-links, which serve a similar function to hoops in column reinforcement. Figure 1 illustrates the rebar arrangement of the rebar cage.
Diaphragm wall construction typically follows four steps: (1) constructing a guide wall, (2) excavating the soil and filling the space with slurry, (3) installing rebar cages, and (4) pouring concrete using a tremie pipe. The guide wall is temporarily constructed to ensure the alignment of wall continuity and to assist in the installation of rebar cages. The dimensions of a wall panel depend on geological conditions and structural designs [40]. Diaphragm wall construction begins with the construction of primary wall panels, followed by secondary panels. Special joints with water stop connect the wall panels, with the specific type of joint varying depending on the contractor's preference or excavating equipment used.

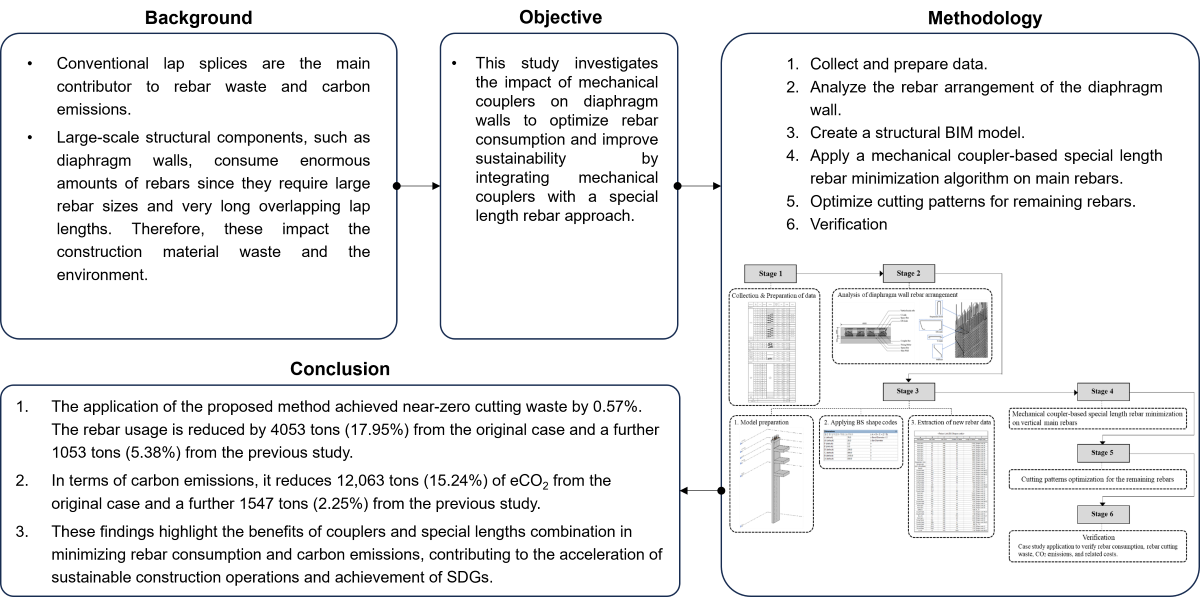
3. Methodology

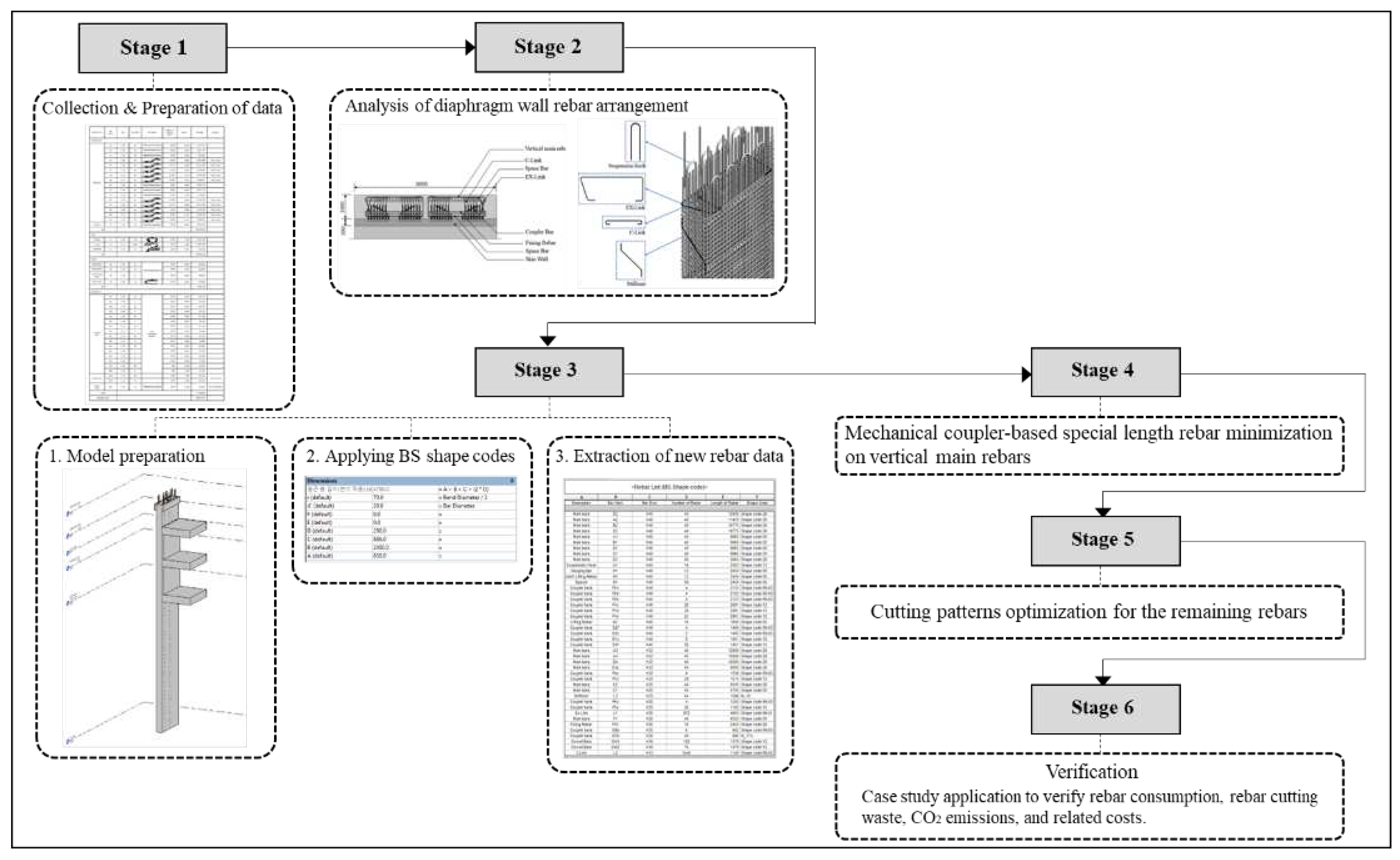
Figure 2 illustrates the flowchart of the proposed study. This outlines the process and validation procedure of our proposed approach, analyzing the impact of mechanical rebars on diaphragm wall rebar consumption.
  • Stage 1: Collect structural analysis results to obtain information about the location of structural members and rebar properties, including bar length, diameter, shape, quantity, and location.
  • Stage 2: Analyze the rebar arrangement within a diaphragm wall panel.
  • Stage 3: Create a Building Information Modeling (BIM) structural model and apply BS shape codes to retrieve the rebar list.
  • Stage 4: Implement a mechanical coupler-based special length rebar minimization algorithm on vertical main rebars.
  • Stage 5: Combine all the remaining rebars in a cutting pattern optimization algorithm using special lengths.
  • Stage 6: Analyze rebar consumption, rebar cutting waste, carbon emissions, and related costs to validate the proposed algorithm. Then compare the results of the proposed algorithm to those of the original design, which used the conventional lap splice method, with stock length rebars, and to the findings of the previous study [15], which also employed the lap splice method and incorporated special length rebars. Consequently, the impact of couplers is investigated through rebar cutting waste, costs, and generated amount of CO2 emissions.

3.1. Mechanical coupler-based special-length-priority optimization algorithm

The objectives and constraints for this study have been established for the optimization of special lengths considering mechanical couplers. The objective is to minimize rebar cutting waste to less than 1% by incorporating special lengths and couplers for the main vertical rebars. The constraints for the special length order include a minimum length of 6 meters, a maximum length of 12 meters, a minimum ordered quantity of 50 tons for each special length, and a pre-order lead time of two months [13].
Since the rebar cage of the diaphragm wall is arranged with rebars of different diameters, the deeper the wall panel, the smaller the rebar, the total length is calculated by combining all the rebars with the same diameter that are arranged in the same layer, as shown in Equation (1), which is adopted from the study by Rachmawati et al. [15].
L t o t a l = ∑ i = 1 l L r e b a r _ i
in which, L t o t a l is the total length of wall rebar in the same diameter; and L r e b a r _ i is the length of rebar i.
To obtain the number of required rebar in each total length, the continuous total rebar length is divided by the optimal reference length as in Equation (2), adopted from the study by Rachmawati et al. [15]. The optimal reference length is assumed to be 12 m in this study. The generated number is rounded up for a whole number.
n r e b a r = L t o t a l L r e f
in which, n r e b a r is the number of required rebars; and L r e f is the optimal reference length available in the market.
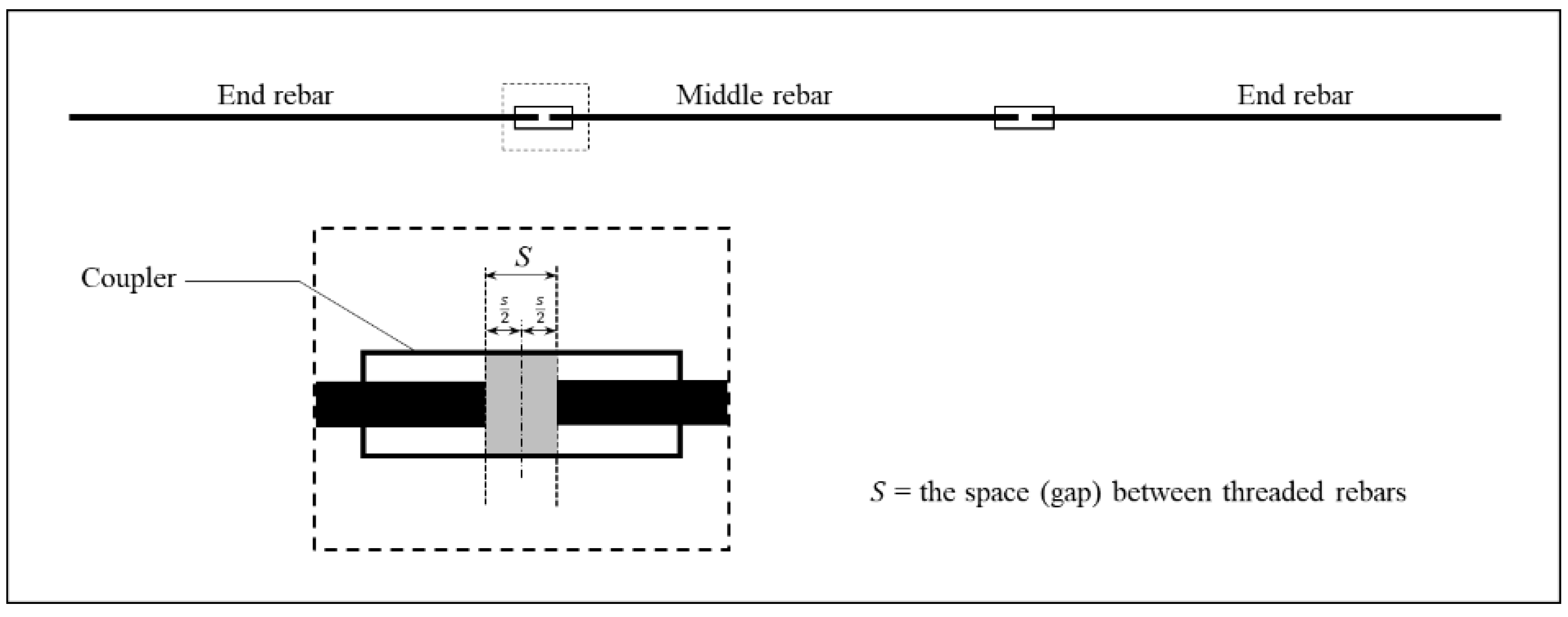
Then, to determine the special length of the rebar, Equation (3) is used considering the total length, the number of rebars required, and the gap between the threaded rebars. A threaded coupler typically includes a gap between the rebars to facilitate installation in case of misaligned threads and for grouting purposes [xlii]. To obtain the exact length, this gap must be deducted from the rebars. As illustrated in Figure 3, half of the gap is subtracted from the end rebar, while the entire gap is subtracted from the middle rebar. Since the special length is ordered in 0.1 m increments, the generated value is rounded up to one decimal place.
L s p e c i a l = L t o t a l n r e b a r − s 2   for   end   rebar , L t o t a l n r e b a r − s   for   middle   rebar
in which, L s p e c i a l is the special length; and s is the space between the threaded rebars.

3.2. Cutting pattern optimization algorithm

After special lengths are generated from the optimization of main rebars considering the couplers, all the remaining rebars are combined into special length cutting patterns, which produce the minimum cutting waste. Equation (4) is adopted from the study by Lee et al. [13] for the minimization of rebar cutting waste.
M i n i m i z e   f X i = ∑ i = 1 N L s p i n i − l i n i L s p i n i
in which, L s p i is the special length cutting pattern; l i is the length of cutting pattern i obtained by combining required lengths; and n i represents the number of rebar combinations with the same cutting pattern i.

4. Case study and Verification

4.1. Case study application

The proposed study was verified on the diaphragm wall of an interchange station, provided by the shop drawing set of a primary wall panel. The case diaphragm wall was comprised of multiple panels, including 293 primary wall panels, each measuring 6 m in length and 1m in width. The overall depth of the panel is 37.58 m; 31.08 m underground and 6.5 m above the ground level. All the wall panels were connected to the three floors of the interchange station: B2 concourse structural floor level, B1 subway structural floor level, and subway roof structural floor level. The depth of each floor slab is 1200 mm. Skin walls with 300 mm thickness were located between each floor. In this case study project, high tensile bar grade 500 MPa was employed for all the reinforcement. In addition, the diameter of the high tensile rebar symbolized as ‘H’ in the shop drawings, was also adopted in this study. The attributes of the case study diaphragm wall panel are summarized in Table 2.
The case wall panel was reinforced with two similar rebar cages, each comprised of four rebar cage sections, as demonstrated in Figure 4(b). The reinforcement comprised vertical main rebars, horizontal EX-links, C-links, and additional rebars for lifting and aligning purposes. In each cage section, vertical main rebars were held in place by two EX-links. C-links anchored main rebars by sandwiching the EX-links. The 1st cage section employed six layers of main rebars which were separated by space bars, as shown in Figure 1. Stiffeners were used to strengthen the cage section and to prevent the cage from deformation. Starter bars were used to anchor the floor reinforcement to the rebar cages and were separated by fixing rebars to maintain the positions. For the lifting process, hanging bars and lifting bars were used for the lower cages from second to fourth, and suspension hooks were additionally employed for the first cage section.
The rebar marks from the original shop drawing were used. The letter in the rebar mark indicates the rebar layer and the number indicates the location of the rebar. As shown in Figure 4(b), the rebar mark "A1" indicates the vertical rebar in layer A of the 1st rebar cage section. The rebar layers A and D extended along the rebar cage from the 1st to the 4th section, while layers B and E were located only in the 1st and 2nd sections. The mechanical coupler-based special-length-priority optimization algorithm was applied to the vertical main rebars of the diaphragm wall panel, and all the remaining rebars were optimized in cutting patterns. The rebar layers C and F, located in the upper two sections were much smaller than the main rebars in both length and diameter, so they were included in the remaining rebars.
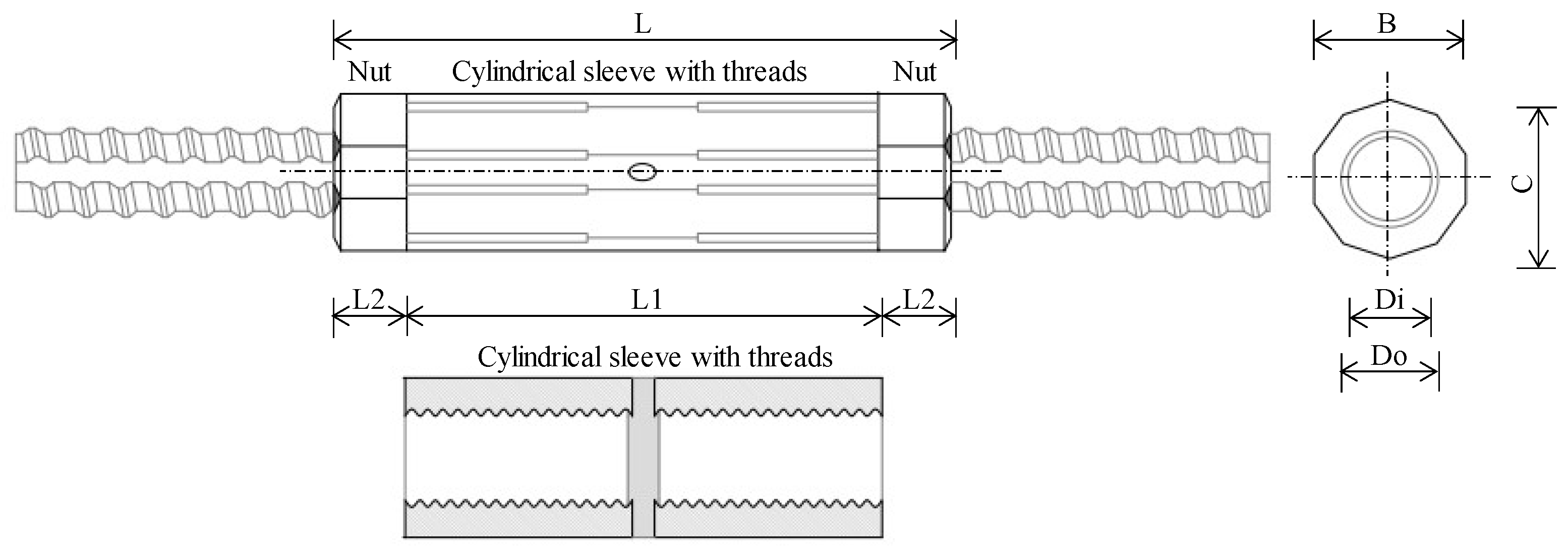
Regarding the coupler usage, this study considered rib thread couplers, which generally consist of a cylindrical sleeve with threads onto which rebar ends are securely threaded and fastened with nuts (see Figure A1 in the Appendix A). Table A1 in the Appendix provides the dimensions of threaded rebar couplers by Tokyo Tekko [xliii]. As shown in Figure A1, the coupler and threaded rebar have a gap between the threads, enabling construction even if the threads are misaligned. The gap is typically 20 mm for rebar sizes H16 to H29 and 30 mm for rebar sizes above H32 [42]. The coupler also provides a permissible tolerance for the rebar length inserted in the center, ensuring rebar connection even if the threaded rebars have a cutting length error.

4.1.1. Mechanical coupler-based special-length rebar minimization on main vertical rebars

The case application was conducted according to the stages described in the flowchart of the methodology, Figure 2. First and foremost, fundamental information about the diaphragm wall panel and its reinforcing bars was gathered from the case study project shop drawings. The original rebar list for the diaphragm wall is displayed in Appendix A Table A2. Subsequently, a structural BIM model was created after analyzing the arrangement of rebar within the diaphragm wall and eliminating the lap lengths since the proposed study considered mechanical couplers. In addition, all rebars in the model were assigned BS shape codes. The revised rebar list obtained from this model is presented in Appendix A Table A3, serving as the primary data source for this study.
The main vertical rebars of layers A, B, D, and E, as shown in Figure 4(b), were optimized in special lengths considering mechanical couplers instead of lap splices. Equations (1) to (3) were used to calculate the special length for the main rebars. In rebar layer A, H40 and H32 rebars were used as main vertical rebars. The optimization was conducted individually on the same diameter rebars. Therefore, rebars A1 and A2 were combined as the total length and divided by the optimal reference length of 12 m, resulting in the number of required rebars. Then the total length was again divided by the number of rebars to obtain the exact required length of rebars that are connected by couplers. Additionally, since a minimum of 30 mm gap was suggested between the threads for couplers’ sizes above H32 [42], 15 mm was subtracted from each end rebar and 30 mm from each middle rebar for the required lengths. Table 3 summarizes the results of the mechanical coupler-based special length rebar minimization according to rebar layers. It was observed that rebar D3 was reduced from rebar layer D due to the minimization algorithm.

4.1.2. Cutting patterns optimization for the remaining rebars

Consequently, the remaining rebars in the diaphragm wall panel’s rebar cage were combined in cutting pattern optimization using special lengths to generate minimal rebar cutting waste. Table 4 provides the results of cutting pattern optimization. From the table, the available market lengths of 12 m and 11 m were found to be the most efficient lengths for H32 and H13 rebars, respectively, in terms of minimizing cutting waste. However, since special lengths are purchased in 0.1 m intervals, these lengths were considered to be special lengths for the purpose of this study.

4.1.3. Analysis of the results by the algorithm

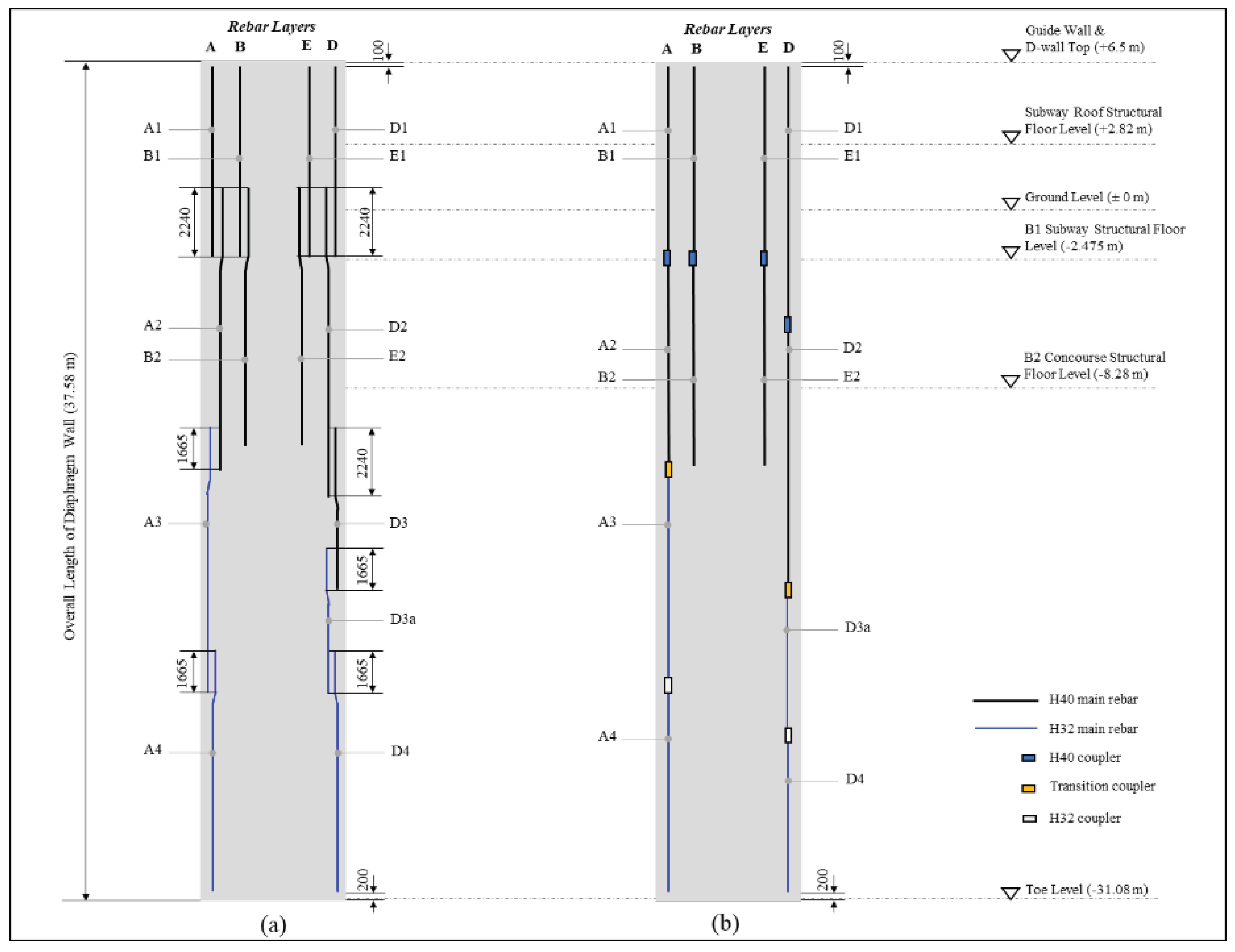
Figure 5(a) demonstrates the original arrangement of the main rebars; 1st and 2nd cage sections were arranged with H40 rebars. The 3rd cage section included both H40 and H32, in which bar mark D3 rebar was H40, and the rest were H32. The 4th cage section was arranged with H32 rebars. After special length rebar minimization based on mechanical couplers, the rebar cage was arranged with new special length rebars in each layer, as demonstrated in Figure 5(b). In rebar layer D, the number of rebars was reduced from three to two.
Table 5 summarizes the required rebar quantity, ordered rebar quantity, and cutting waste after applying the proposed algorithm. The unit weights of rebars (H20, H16, and H13) are slightly different for these three cases. In the original case and the previous study [15], the unit weight of each rebar size was obtained from the information provided in the case study project. However, in the coupler case, both the rebars and couplers were purchased from the same company. Therefore, the unit weights were obtained from the company’s specifications [44, 45]. It has been confirmed that the proposed algorithm considering mechanical couplers only generated 0.358 tons of rebar cutting waste with a 0.57% loss rate (less than 1%) in one diaphragm wall panel.

4.2. Verification of the algorithm

The calculation was expanded to 293 panels of diaphragm wall. To verify the effectiveness of the algorithm, rebar quantities by the proposed algorithm were compared to the original case and the previous study by Rachmawati et al. [15] in terms of rebar quantities, carbon quantities, and associated costs. Since all the rebar length necessary for overlapping was eliminated, rebar usage for one panel was reduced by 17.95% from the original case which employed conventional lap splices and stock length rebars. The rebar quantities of the original case are shown in Appendix A Table A4.
Table 6 shows the rebar quantities of the original case, the previous case, and the coupler case. The RCW rate of the original case was 9.62%, while the previous study and the coupler case achieved N0RCW by 0.77% and 0.57% respectively.
The rebar quantities were converted into carbon emissions to analyze the differences between each case. The carbon emission factors of rebar and coupler were referenced and interpolated based on the data from the study by Ghayeb et al. [23]. The factor of 3.505 ton-CO2 per rebar ton was used to calculate the carbon quantity of rebars. The carbon emission of the H32 coupler was 19.490 kg-CO2-e/pcs and that of the H40 coupler is recalculated based on H32 data through the regression method, resulting in 23.978 kg-CO2-e/pcs. A total of 70,320 H40 couplers were required for 293 diaphragm wall panels, emitting 1686 tons of carbon emission. Additionally, a total of 23,440 H32 couplers produced 457 tons of carbon emissions.
Subsequently, the total carbon emissions were converted to carbon price by USD 75 per ton of CO2 [24]. The rebar cost was computed based on the inflation rate [xlvi], resulting in USD 908 per ton of rebar [22]. The material costs and processing costs of rebars and couplers are shown in Appendix A Table A6. The processing cost is the expense incurred for the installation process of each lap splice or coupler. The processing cost was considered the same for lap splices and couplers. It was calculated to reflect the current inflation rate [46], using the data from the study by Kwon et al. [1]. In addition, a transition coupler is required to connect rebars with different diameters. In this study, the price of the transition coupler required to join H40 and H32 rebars was assumed to be the same as the H40 coupler’s price. An amount of USD 868,452 was required to purchase H40 and transition couplers, and USD 197,834 for H32 couplers.
Table 7 summarizes the comparison of the original case and coupler case in terms of rebar quantities, carbon emissions, and associated costs, including rebar cost, coupler cost, processing cost, and carbon price. It has been observed that the proposed algorithm reduced 4053 tons (17.95%) of the purchased rebar quantity from the original case which used only stock length rebars by eliminating lap splices and using couplers instead. A total carbon emissions amount of 12,063 tons (15.24%) were saved. Furthermore, a total cost reduction of USD 3,734,348 (13.91%) was achieved, including rebar cost, labor cost, and carbon price. The processing cost was significantly reduced by USD 215,850 (53.86%).
Table 8 depicts the comparison between the previous study [15] and the coupler case in terms of rebar usage, carbon emissions, and associated costs. Since the lap splices were substituted by couplers, rebar usage was saved by 1053 tons (5.38%). The overall cost was reduced further by USD 27,646 and the processing cost was further reduced by USD 22,109 (10.68%) from the previous study [15]. This shows that mechanical couplers are significantly effective for the rebar minimization in the case study diaphragm wall, maintaining sustainability in construction.

5. Discussion

Conventional lap splicing is the most common method for rebar connection due to its simplicity and cost-effectiveness. However, it requires adherence to the lapping zone recommended by building codes [17]. Conventional lap splicing is also prone to errors, such as improper lap length or incorrect installation, which can compromise its performance. Additionally, conventional lap splices require more and longer rebar as the diameter increases. ACI [17] prohibits their use for rebar connections larger than 36 mm. Furthermore, lap splices can be difficult to inspect and repair. An alternative to the lap splice is the welded joint or splice method, which consumes less rebar but requires higher costs and skilled labor to execute. However, welded joints emit flames and smoke that could potentially harm surrounding construction works, and the gas used to weld the rebars is not completely environmentally safe. Additionally, welded joints can be vulnerable to cracking if not properly executed.
Conversely, mechanical couplers offer speed and ease of installation, which can save time and costs for construction projects. Mechanical joints enable the connection of adjacent rebars without lapping, requiring less rebar and thus less cutting waste. Additionally, a sharp rise in rebar prices and a shortage of labor have resulted in the increasing use of couplers. Furthermore, the cost of couplers is gradually decreasing over time as their usage becomes more prevalent. Through this study, a 17.95% reduction in rebar usage and a 95.41% in cutting waste was achieved for diaphragm wall structures, demonstrating a near-zero cutting waste. In comparison to the findings of the previous study [15], a further reduction in rebar usage of 5.38% was observed, demonstrating the potential of couplers in promoting accelerated sustainable construction practices.
Despite these benefits, mechanical couplers have not been widely adopted in the construction industry. This is due to a combination of factors, such as the higher initial costs associated with couplers, the absence of standardized design guidelines for their use, and a general lack of awareness among construction professionals.
A wide variety of couplers are available on the market, some suitable for use in non-seismic regions and others designed to withstand lateral forces. Nevertheless, the selection of the right coupler is crucial to reducing rebar usage, cutting waste, and maintaining structural integrity. Furthermore, couplers are generally only used in new construction, with a few exceptions for retrofitting buildings, where existing reinforcement is already in place. These issues should be addressed in future investigations.
Since couplers are easy to install, they improve construction site productivity. Therefore, couplers require systematic planning and supply chain management (SCM) throughout the construction process to maintain and enhance the productivity of the construction site. Future studies could further explore the planning and development of an SCM strategy that emphasizes couplers, in addition to coupler selection, including the prefabricated rebar cage practices and devices that could be used to aid the prefabricated process. Nonetheless, the broad application of couplers and special length rebars to various construction projects, including buildings, bridges, tunnels, and subways, can significantly reduce rebar usage, saving construction costs, accelerating the construction phase, and reducing the environmental impacts (CO2 emissions) associated with rebars. Moreover, the reduction of rebar usage and waste aligns with the Sustainable Development Goals (SDGs) proposed by the United Nations, particularly SDGs 12, 13, and 15, which emphasize sustainable production and consumption patterns. This reduction in rebar usage alleviates the environmental burden associated with its production and disposal, contributing to a more sustainable construction industry.

6. Conclusion

This study aims to assess the capabilities of mechanical couplers in optimizing rebar usage in large structural components that require the use of large rebar sizes and improving sustainability with integrated mechanical couplers and a special-length rebar approach. The proposed method was implemented in a case study involving a diaphragm wall reinforced with H32 and H40 diameter rebars. The impact of the proposed method was assessed by comparing its results to those of the conventional lap splices approach. Through this study, several notable findings can be found as follows:
  • The proposed method required 18,530 tons of rebar to be purchased, reducing the rebar usage significantly by 4053 tons (17.95%) compared to the original case with the conventional lap splice approach.
  • The proposed method resulted in a rebar cutting waste rate of 0.57%, presenting the achievement of near-zero cutting waste. The method also reduces the related waste rate by 95.41%.
  • The remarkable impact of the coupler and special-length rebar combination on the environment and construction is demonstrated by the reduction of carbon emissions by 12,063 tons of eCO2 (15.24%) and a decrease in the total cost by USD 3,734,348 (13.91%) over the original design.
  • Compared to previous findings [15], the rebar usage was further reduced by 1053 tons (5.38%), leading to a reduction in carbon emissions by 1547 tons of eCO2 (2.25%).
  • These findings highlight the noteworthy capabilities of the couplers and special length rebars combination on exceptionally reducing the rebar usage and rebar cutting waste, contributing to the acceleration of sustainable construction operations, as well as achievement of SDGs. The findings also demonstrate a method for substantially decreasing construction materials, costs, and environmental impact without jeopardizing the structural integrity of diaphragm walls. However, mechanical couplers have not been widely adopted in the construction industry due to several reasons, including the high initial costs and lack of awareness of the engineers and practitioners.
Future investigations should focus on developing systematic planning and supply chain management (SCM) strategies specifically tailored to the integration of couplers and special length rebars, including prefabricated rebar and associated auxiliary devices as these are essential for improving construction site efficiency. This study showcases the potential of the proposed method to significantly reduce rebar usage and cutting waste within a large-scale construction project. Implementing the proposed method across various buildings and infrastructure projects could further multiply these benefits, fostering the rapid adoption of more sustainable and green construction operations.

Author Contributions

Conceptualization, S.K., K.Y.K.; methodology, S.K., K.Y.K.; validation, S.K., D.D.W., L.P.K., K.Y.K.; formal analysis, D.D.W. and L.P.K.; investigation, D.D.W. and L.P.K.; resources, S.K.; data curation, L.P.K.; writing—original draft preparation, D.D.W. and L.P.K.; writing—review and editing, S.K., D.D.W. and L.P.K.; supervision, S.K.; project administration, K.Y.K.; funding acquisition, S.K. All authors have read and agreed to the published version of the manuscript.

Funding

This study was supported by the National Research Foundation of Korea (NRF) grants funded by the Korea government (MOE) (No. 2022R1A2C2005276).

Data Availability Statement

The data that support the findings of this study are available from the corresponding authors upon reasonable request.

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A

Preprints 92810 g0a1
Figure A1. Rib thread coupler details (Tokyo Tekko).
Figure A1. Rib thread coupler details (Tokyo Tekko).
Preprints 92810 g0a1
Table A1. Specifications for the rib thread coupler in mm unit (Tokyo Tekko).
Table A1. Specifications for the rib thread coupler in mm unit (Tokyo Tekko).
Bar Size Outside diameter of the coupler Length Dimension of thread
Coupler Nut Total Pitch Inside diameter Root diameter
B C L1 L2 L P Di Do
20 31 32.6 110 20 150 8 19.6 23.1
25 40 42.1 140 20 180 10 24.8 29.0
32 50 52.6 190 30 250 13 31.4 36.6
40 64 67.3 220 30 280 16 39.0 45.4
Table A2. Original rebar list of the diaphragm wall.
Table A2. Original rebar list of the diaphragm wall.
Serial No. Description Bar Mark Size No. of Rebar Length of rebar (m) Unit weight Kg/m Total (Kg) Total (Ton)
1 Main Bars D2 H40 40 12.000 9.864 4734.720 4.735
2 A2 40 11.425 4507.848 4.508
3 B2 40 10.775 4251.384 4.251
4 E2 40 10.775 4251.384 4.251
5 A1 40 8.865 3497.774 3.498
6 B1 40 8.865 3497.774 3.498
7 D1 40 8.865 3497.774 3.498
8 E1 40 8.865 3497.774 3.498
9 D3 40 5.665 2235.182 2.235
10 A3 H32 40 12.000 6.313 3030.240 3.030
11 A4 40 10.560 2666.611 2.667
12 D4 40 10.560 2666.611 2.667
13 D3a 40 8.000 2020.160 2.020
14 Suspension Hook U1 H40 16 2.750 9.864 434.016 0.434
15 Spacer S1 58 2.450 1401.674 1.402
16 Hanging Bar H1 12 2.450 290.002 0.290
17 Add'l Lifting Bar H3 12 2.450 290.002 0.290
18 Starter Bars P1c 28 2.160 596.575 0.597
19 P2c 4 2.160 85.225 0.085
20 P1d 28 2.160 596.575 0.597
21 P2d 4 2.160 85.225 0.085
22 P1e 24 2.160 511.350 0.511
23 P2e 4 2.160 85.225 0.085
24 Lifting Rebar H2 16 1.800 284.083 0.284
25 Starter Bars G1c 8 1.520 119.946 0.120
26 G2c 2 1.520 29.987 0.030
27 G1f 28 1.520 419.812 0.420
28 G2f 4 1.520 59.973 0.060
29 P3c H32 28 1.570 6.313 277.519 0.278
30 P4c 4 1.570 39.646 0.040
31 Add'l vertical bars C2 H25 40 9.335 3.854 1439.084 1.439
32 C1 40 5.785 891.816 0.892
33 Stiffener L3 44 1.820 308.628 0.309
34 Starter Bars P5c 28 1.225 132.192 0.132
35 P6c 4 1.225 18.885 0.019
36 EX-Link L1 H20 972 4.766 2.470 11,442.403 11.442
37 Fixing Rebar FR1 16 2.450 96.824 0.097
38 Starter Bars G7b 48 0.700 82.992 0.083
39 G8b 6 0.700 10.374 0.010
40 Add'l vertical bars F1 40 4.320 426.816 0.427
41 Dowel Bars SW1 H16 152 1.395 1.580 335.023 0.335
42 SW2 76 1.395 167.512 0.168
43 C-Link L2 H13 3440 1.214 1.040 4343.206 4.343
Table A3. A new rebar list extracted from the BIM model after applying BS shape codes.
Table A3. A new rebar list extracted from the BIM model after applying BS shape codes.
Main Rebars
Serial No. Description Bar Mark Size No. of Rebar Length of rebar Weight (Ton) BS Shape code
1 Main Bars D2 H40 40 9.760 3.851 26
2 B2 40 8.535 3.368 26
3 E2 40 8.535 3.368 26
4 A2 40 9.185 3.624 26
5 A1 40 8.865 3.498 00
6 B1 40 8.865 3.498 00
7 D1 40 8.865 3.498 00
8 E1 40 8.865 3.498 00
9 D3 40 3.425 1.351 26
10 A3 H32 40 10.335 2.610 26
11 A4 40 8.895 2.246 26
12 D4 40 8.895 2.246 26
13 D3a 40 6.335 1.600 26
Remaining  Rebars
Serial  No. Description Bar  Mark Size No.  of Rebar Length  of rebar Weight  (Ton) BS  Shape code
1 Suspension Hook U1 H40 16 2.518 0.397 13
2 Spacer S1 58 2.450 1.402 00
3 Hanging Bar H1 12 2.450 0.290 00
4 Add'l Lifting Bar H3 12 2.450 0.290 00
5 Coupler Bars P2c 4 2.160 0.085 99-03
6 P2d 4 2.160 0.085 99-03
7 P2e 4 2.160 0.085 99-03
8 P1c 28 2.052 0.567 12
9 P1d 28 2.052 0.567 12
10 P1e 24 2.052 0.486 12
11 Lifting Rebar H2 16 1.800 0.284 00
12 Coupler Bars G2c 2 1.520 0.030 99-03
13 G2f 4 1.520 0.060 99-03
14 G1c 8 1.412 0.111 12
15 G1f 28 1.412 0.390 12
16 Coupler Bars P4c H32 4 1.570 0.040 99-03
17 P3c 28 1.483 0.262 12
18 Add'l vertical bars C2 H25 40 8.741 1.348 26
19 C1 40 5.191 0.800 00
20 Stiffener L3 44 1.820 0.309 26
21 Coupler Bars P6c 4 1.225 0.019 99-03
22 P5c 28 1.158 0.125 12
23 EX-Link L1 H20 972 4.766 11.442 99-01
24 Add'l vertical bars F1 40 4.320 0.427 00
25 Fixing Rebar FR1 16 2.450 0.097 00
26 Coupler Bars G7b 48 0.700 0.083 99-04
27 G8b 6 0.700 0.010 99-03
28 Dowel Bars SW1 H16 152 1.362 0.327 12
29 SW2 76 1.362 0.164 12
30 C-Link L2 H13 3440 1.214 4.343 99-02
Table A4. Rebar quantities of the original lap splice case (293 panels).
Table A4. Rebar quantities of the original lap splice case (293 panels).
Bar Diameter (mm) Stock length (m) No. of rebar Actual rebar quantity (ton) Ordered rebar quantity (ton) Cutting waste (ton) Loss rate (%)
H40 12 103,136 11,503.56 12,208.00 704.45 5.77%
H32 12 46,880 3135.33 3551.44 416.11 11.72%
H25 12 18,752 817.65 867.24 49.60 5.72%
H20 12 148,258 3533.41 4394.37 860.96 19.59%
H16 12 8497 147.24 161.10 13.86 8.60%
H13 12 112,219 1272.56 1400.49 127.93 9.13%
20,409.74 22,582.65 2172.91 9.62%
Table A5. Rebar quantities of the previous lap splice case (293 panels) [17].
Table A5. Rebar quantities of the previous lap splice case (293 panels) [17].
Description H40 H32 H25 H20 H16 H13 Total
Required quantity (ton) 12,208.00 3,551.44 867.24 4,394.37 161.10 1,400.49 22,582.65
Ordered quantity (ton) 10,882.29 2,929.94 778.03 3,564.13 144.25 1,283.79 19,582.43
Cutting waste (ton) 1,325.71 621.50 89.21 830.24 16.85 116.71 3000.22
Loss rate (%) 10.9% 17.5% 10.3% 18.9% 10.5% 8.3% 13.3%
Table A6. Material cost and processing cost of rebars and couplers.
Table A6. Material cost and processing cost of rebars and couplers.
Description Material cost Processing cost
Rebar (USD/ton) Coupler (USD/pcs) Lap splice (USD/m) Coupler (USD/m)
H40 908 12.35 2.09 2.09
H35 908 11.50 1.75 1.75
H32 908 8.44 1.62 1.62
H29 908 6.90 1.32 1.32
H25 908 6.14 1.05 1.05
H22 908 5.37 0.80 0.80
H19 908 4.22 0.59 0.59
The data of H40 was interpolated based on H32 by regression method.

References

  1. Kwon, K.; Kim, D.; and Kim, S. Cutting waste minimization of rebar for sustainable structural work: A systematic literature review. Sustainability 2021, 13, 5929. [Google Scholar] [CrossRef]
  2. United States Environmental Protection Agency. Overview of Greenhouse Gases. 2023. Available online: https://www.epa.gov/ghgemissions/overview-greenhouse-gases (accessed on 23 November 2023).
  3. Global Cement and Concrete Association. Cement and Concrete around the World. 2023. Available online: https://gccassociation.org/concretefuture/cement-concrete-around-the-world/ (accessed on 23 November 2023).
  4. Hanson, J. L.; Manheim, D. C.; Yeşiller, N. Geoenvironmental Assessment of Climate Impacts from Landfill Gas Emissions. Soils and Foundation 2023, 63, 101279. [Google Scholar] [CrossRef]
  5. Malmir, T.; Lagos, D.; Eicker, U. Optimization of Landfill Gas Generation based on A Modified First-Order Decay Model: A Case Study in the Province of Quebec, Canada. Environ Syst Res 2023, 12, 6. [Google Scholar] [CrossRef]
  6. Assadolahfardi, G.; Panahandeh, A.; Khalvati, A.A.; Sekhavati, A. Life cycle assessment of construction phase of monorail project in Qom, Iran. Pollution 2017, 3, 81–99. [Google Scholar] [CrossRef]
  7. Hu, C.; Zhou, Z.; Luo, Y.; Yan, X. Effect of Acid Rain on Mechanical Properties and Aging Mechanism of Asphalt. J. Mater. Civ. Eng 2023, 35, 04023137. [Google Scholar] [CrossRef]
  8. Gomes, F.; Brière, R.; Feraille, A.; Habert, G.; Lasvaux, S. , Tessier, C. Adaptation of environmental data to national and sectorial context: application for reinforcing steel sold on the French market. The International Journal of Life Cycle Assessment, 2013; 18, 926–938. [Google Scholar] [CrossRef]
  9. Chen, Y.; Yang, T. Lapping Pattern, Stock Length, and Shop Drawing of Beam Reinforcements of an RC Building. Journal of Computing in Civil Engineering 2015, 29, 04014028. [Google Scholar] [CrossRef]
  10. Nadoushani, Z. S. M.; Hannad, A. W.; Xiao, J.; Akbarnezhad, A. Minimizing cutting wastes of reinforcing steel bars through optimizing lap splicing within reinforced concrete elements. Construction and Building Materials 2018, 185, 600–608. [Google Scholar] [CrossRef]
  11. Zheng, C.; Yi, C.; Lu, M. Integrated optimization of rebar detailing design and installation planning for waste reduction and productivity improvement. Automation in Construction 2019, 101, 32–47. [Google Scholar] [CrossRef]
  12. Khondoker, M. T. H. Automated reinforcement trim waste optimization in RC frame structures using building information modeling and mixed integer linear programming. Automation in Construction 2021, 124. [Google Scholar] [CrossRef]
  13. Lee, D.; Son, S.; Kim, D.; Kim, S. Special-Length-Priority Algorithm to Minimize Reinforcing Bar-Cutting Waste for Sustainable Construction. Sustainability 2020, 12, 5950. [Google Scholar] [CrossRef]
  14. Widjaja, D. D.; Rachmawati, T. S. N.; Kwon, K.; Kim, S. Investigating Structural Stability and Constructability of Buildings Relative to the Lap Splice Position of Reinforcing Bars. Journal of The Korea Institute of Building Construction, 2023; 23, 315–326. [Google Scholar] [CrossRef]
  15. Rachmawati, T. S. N.; Lwun P., K.; Lim, J.; Lee, J.; Kim, S. Optimization of lap splice positions for near-zero rebar cutting waste in diaphragm walls using special-length-priority algorithms. Journal of Asian Architecture and Building Engineering 2023. [Google Scholar] [CrossRef]
  16. Widjaja, D. D.; Kim, S. Reducing rebar cutting waste and rebar usage of beams: A two-stage optimization algorithm. Buildings 2023, 13, 2279. [Google Scholar] [CrossRef]
  17. ACI Committee 318. Building Code Requirements for Structural Concrete (ACI 318-19); and Commentary (ACI 318R-19); American Concrete Institute: Farmington Hills, MI, USA, 2019. [Google Scholar]
  18. Porwal, A.; Hewage, K. N. Building information modeling based analysis to minimize the waste rate of structural reinforcement. Journal of Construction Engineering and Management 2012, 138, 943–954. [Google Scholar] [CrossRef]
  19. Nadoushani, Z. S.; Hammad, A. W. A.; Akbarnezhad, A. A. Framework for Optimizing Lap Splice Positions within Concrete Elements to Minimize Cutting Waste of Steel Bars. In Proceedings of the 33rd International Symposium on Automation and Robotics in Construction (ISARC), Auburn, USA; 2016. [Google Scholar]
  20. ugli Makhmudov, J. I.； ugli Sobirov, O. K. SEISMIC RESILIENCE THROUGH DIAPHRAGM WALL CONSTRUCTION. GOLDEN BRAIN 2023, 1, 11–21. [Google Scholar]
  21. Datta, S. D.; Rana, Md. J.; Assafi, M. N.; Mim, N. J.; Ahmed, S. Investigation on the generation of construction wastes in Bangladesh. International Journal of Construction Management 2023, 23, 2260–2269. [Google Scholar] [CrossRef]
  22. Construction Association of Korea. Construction on hold as material prices go through the roof. Retrieved October 11 2023. Available online: https://koreajoongangdaily.joins.com/2022/04/22/business/industry/Inflation/20220422165447730.html.
  23. Ghayeb, H. H.; Razak, H. A.; Sulong, N.H.R. Evaluation of the CO2 emissions of an innovative composite precast concrete structure building frame. Journal of Cleaner Production 2020, 242, 118567. [Google Scholar] [CrossRef]
  24. IMF. Why countries must cooperate on carbon prices. Retrieved October 11, 2023. 2022. Available online: https://www.imf.org/en/Blogs/Articles/2022/05/19/blog-why-countries-must-cooperate-on-carbon-prices.
  25. United Nations Development Programme. The SDGs in Action. 2023. Available online: https://www.undp.org/sustainable-development-goals (accessed on 23 November 2023).
  26. Zubaidy, D. S.; Dawood, S. Q.; Khalaf, I. D. Optimal utilization of rebar stock for cutting processes in housing project. IARJSET 2016, 3, 189–193. [Google Scholar] [CrossRef]
  27. Kim, D.; Lim, C.; Liu, Y.; Kim, S. Automatic Estimation System of Building Frames with Integrated Structural Design Information (AutoES). Iranian Journal of Science and Technology, Transactions of Civil Engineering 2020, 44, 1145–1157. [Google Scholar] [CrossRef]
  28. Shokrzadeh, M. R.; Nateghi, A. F.; Mansoori, M. R.; Pasha, P. Failure area evaluation of the coupler with threaded bar: Experimental and Numerical study. International Journal of Advanced Structural Engineering 2022, 12, 531–543. [Google Scholar] [CrossRef]
  29. Bompa, D. V.; Elghazouli, A. Y. Monotonic and cyclic performance of threaded reinforcement splices. Structures 2018, vol. 16, 358–372. [Google Scholar] [CrossRef]
  30. Nateghi-Alahi, F.; Shokrzadeh, M. R. Behavior considerations for mechanical rebar couplers. In Proceedings of the University of Tokyo International Congress on Science and Engineering, Tokyo, Japan, 14-15 October 2019; pp. 30–41. [Google Scholar]
  31. Singh, R.; Himanshu, S. K.; Bhalla, N. Reinforcement Couplers As An Alternative To Lap Splices: A Case Study. International Journal of Engineering Research & Technology. [CrossRef]
  32. Chiari, V. G.; Moreno, J. A. L. Experimental evaluation of coupler behavior for mechanical rebar splices in reinforced concrete structures. IBRACON Structures and Materials Journal 2018, 11, 1326–1353. [Google Scholar] [CrossRef]
  33. Damsara, K.D.P.; Kulathunga, D.D.T.K. Analysis on Effectiveness of Rebar Couplers in Splicing of Reinforcement Bars. Proceedings of International Symposium on Advances in Civil and Environmental Engineering Practices for Sustainable Development (ACEPS-2018), Galle, Sri Lanka, 15 March 2018; Available online: https://www.researchgate.net/publication/325818277_Analysis_on_Effectiveness_of_Rebar_Couplers_in_Splicing_of_Reinforcement_Bars.
  34. Tazarv, M.; Saiidi, M. S. Seismic design of bridge columns incorporating mechanical bar splices in plastic hinge regions. Engineering Structures 2016, 124, 507–520. [Google Scholar] [CrossRef]
  35. Bompa, D. V.; Elghazouli, A. Y. Ductility considerations for mechanical reinforcement couplers. Structures 2017, vol. 12, 115–119. [Google Scholar] [CrossRef]
  36. Moka, V. T. K.; Rajendran, S. C. Role of coupler in structural behavior of RC elements. Materials Today: Proceedings 2022, 64, 1035–1042. [Google Scholar] [CrossRef]
  37. Chidambaram, R. S.; Agarwal, P. Performance evaluation of innovative hybrid rebar coupler in reinforced concrete beams subjected to monotonic loading. Structural Concrete 2018, 19, 892–903. [Google Scholar] [CrossRef]
  38. Qing, Y.; Wang, C. L.; Meng, S.; Zeng, B. Experimental study on the seismic performance of precast concrete columns with thread-bolt combination couplers. Engineering Structures 2022, 251, 113461. [Google Scholar] [CrossRef]
  39. Yousheng, D.; Keqin, Z.; Wenjie, L.; Qian, S.; Erli, M. Optimization of beam parameters for coupling beam pile structure foundations under vertical loading. The Structural Design of Tall and Special Buildings 2007, 32, e2007. [Google Scholar] [CrossRef]
  40. Mironov, D.A.; Osokin, A.I.; Loseva, E.S.; Kuzhelev, A.I. Specific features of diaphragm wall construction. In IOP Conference Series: Materials Science and Engineering; IOP Publishing, 2020; Volume 775, 012051. [Google Scholar]
  41. Alsakka, F.; Haddad, A.; Ezzedine, F.; Salami, G.; Dabaghi, M.; Hamzeh, F. Generative design for more economical and environmentally sustainable reinforced concrete structures. Journal of Cleaner Production 2023, 387, 135829. [Google Scholar] [CrossRef]
  42. Proposed Reinforced Pre-assembly Method for Tokyo Steel Co., Ltd. Presentation.
  43. Tokyo Tekko Company Ltd., Threaded Rebar Joint, ACE-Joint. Available online: https:// www.tokyotekko.co.jp/en/prd/tekko/nsts/nsts04/main/04/teaserItems1/0/linkList/0/link/31.Catalogue_Ace-Joint.pdf (accessed on 23 November 2023).
  44. Tokyo Tekko Company Ltd., Neji-Tetsu-Con (Hot rolled threaded rebar). Available online: https://www.tokyotekko.co.jp/en/prd/tekko/tc/tc01/main/03/teaserItems1/00/linkList/0/link/30.Catalogue_Neji-Tetsu-Con.pdf (accessed on 23 November 2023).
  45. Tokyo Tekko Company Ltd., Neji-Tetsu-Con (Hot rolled threaded rebar). Available online: https://www.tokyotekko.co.jp/en/prd/tekko/tc/tc01/main/03/teaserItems1/00/linkList/0/link/30.Catalogue_Neji-Tetsu-Con.pdf (accessed on 23 November 2023).
  46. World Economic Outlook, Navigating Global Divergences, October 2023. Available online: https://www.imf.org/en/Publications/WEO/Issues/2023/10/10/world-economic-outlook-october-2023 (accessed on 23 November 2023).
Preprints 92810 g001
Figure 1. Rebar arrangement of a rebar cage
Figure 1. Rebar arrangement of a rebar cage
Preprints 92810 g001
Preprints 92810 g002
Figure 2. Flowchart of the methodology.
Figure 2. Flowchart of the methodology.
Preprints 92810 g002
Preprints 92810 g003
Figure 3. Illustration of end rebar and middle rebar.
Figure 3. Illustration of end rebar and middle rebar.
Preprints 92810 g003
Preprints 92810 g004
Figure 4. Vertical rebar arrangement of a diaphragm wall panel. (a) Cross-section. (b) Rebar cage sections. (Adapt from: Rachmawati et al. [4]).
Figure 4. Vertical rebar arrangement of a diaphragm wall panel. (a) Cross-section. (b) Rebar cage sections. (Adapt from: Rachmawati et al. [4]).
Preprints 92810 g004
Preprints 92810 g005
Figure 5. Diaphragm wall vertical rebar arrangement. (a) Before special length optimization. (b) After special length optimization.
Figure 5. Diaphragm wall vertical rebar arrangement. (a) Before special length optimization. (b) After special length optimization.
Preprints 92810 g005
Table 1. Conventional lap splice limitations.
Table 1. Conventional lap splice limitations.
Author(s) Description
Singh et al. [xxxi] Time-consuming in design and installation.
Increased rebar congestion probability.
Increased amount of rebar used.
Chiari and Junior [xxxii] Limited use in structural restoration.
Limited allowable rebar diameters for splicing.
Shokrzadeh et al. [28] Increased rebar consumption and cost, especially for bars with a diameter greater than 30 mm.
Rebar congestion issue due to lap splicing.
Damsara and Kulathunga [xxxiii] Rebar congestion issue due to lap splicing.
Significant rebar waste due to the longer lap lengths required for larger diameter rebars.
Table 2. Attributes of the diaphragm wall panel.
Table 2. Attributes of the diaphragm wall panel.
Description Contents
Length of D-wall
Width of D-wall
Overall depth of D-wall
Thickness of skin wall
Depth of floor slab
Top concrete cover
Bottom concrete cover
Strength of rebars
Concrete strength
Length of ordered rebar, l o r d e r (m)		 6 m
1 m
37.58 m
300 mm
1200 mm
100 mm
200 mm
SHD500
24 MPa
6 ≤   l o r d e r   ≤ 12
Table 3. Mechanical coupler-based special length rebar minimization on vertical main rebars.
Table 3. Mechanical coupler-based special length rebar minimization on vertical main rebars.
Bar mark Bar size (mm) Unit weight (kg/m) [[xliv], [xlv]] No. of rebar Required length (m) Special length (m) Required rebar quantity (ton) Ordered rebar quantity (ton) Loss rate (%)
A1 H40 9.864 40 9.010 9.1 3.555 3.590 0.99%
A2 H40 9.864 40 8.995 9.0 3.549 3.551 0.06%
B1 H40 9.864 40 8.685 8.7 3.427 3.433 0.17%
B2 H40 9.864 40 8.685 8.7 3.427 3.433 0.17%
E1 H40 9.864 40 8.685 8.7 3.427 3.433 0.17%
E2 H40 9.864 40 8.685 8.7 3.427 3.433 0.17%
D1 H40 9.864 40 11.010 11.1 4.344 4.380 0.81%
D2 H40 9.864 40 10.995 11.0 4.338 4.340 0.05%
A3 H32 6.313 40 9.585 9.6 2.420 2.424 0.16%
A4 H32 6.313 40 9.600 9.6 2.424 2.424 0.00%
D3a H32 6.313 40 7.585 7.6 1.915 1.919 0.20%
D4 H32 6.313 40 7.600 7.6 1.919 1.919 0.00%
38.172 38.279 0.28%
Table 4. Cutting pattern optimization for the remaining rebars.
Table 4. Cutting pattern optimization for the remaining rebars.
Bar size (m) Unit weight (kg/m) [44, 45] Special length (m) No. of rebar Required rebar quantity (ton) Ordered rebar quantity (ton) Loss rate (%)
H40 9.864 10.3 51 5.129 5.182 1.01%
H32 6.313 12 4 0.302 0.303 0.41%
H25 3.854 10.6 65 2.600 2.655 2.08%
H20 2.466 9.6 513 12.040 12.145 0.86%
H16 1.560 8.2 38 0.484 0.486 0.34%
H13 0.995 11 383 4.155 4.192 0.87%
24.711 24.963 1.01%
Table 5. Rebar quantities and cutting waste after applying the proposed algorithm (one panel).
Table 5. Rebar quantities and cutting waste after applying the proposed algorithm (one panel).
Description H40 H32 H25 H20 H16 H13 Total
Required quantity (ton) 34.623 8.981 2.600 12.040 0.484 4.155 62.884
Ordered quantity (ton) 34.774 8.990 2.655 12.145 0.486 4.192 63.241
Cutting waste (ton) 0.151 0.009 0.055 0.105 0.002 0.037 0.358
Loss rate (%) 0.43% 0.10% 2.08% 0.86% 0.34% 0.87% 0.57%
Table 6. Rebar quantities of the original case, the previous case, and the coupler case (293 panels).
Table 6. Rebar quantities of the original case, the previous case, and the coupler case (293 panels).
Description Required quantity (ton) Ordered quantity (ton) Cutting waste (ton) Loss rate (%)
Original case 20,409.74 22,582.65 2172.91 9.62%
Previous case [15] 19,432.05 19,582.36 150.31 0.77%
Coupler case 18,424.88 18,529.69 104.81 0.57%
Table 7. Comparison of the original case and the coupler case in terms of rebar quantities, carbon emissions, and associated costs (293 panels).
Table 7. Comparison of the original case and the coupler case in terms of rebar quantities, carbon emissions, and associated costs (293 panels).
Description Original case (O) Coupler case (C) Reduction (O-C) Reduction rate (O-C)/O
Ordered quantity (ton) 22,582.65 18,529.69 4052.96 17.95%
Carbon emissions (ton) 79,152.19 67,089.54 12,062.64 15.24%
Rebar cost (USD) 20,505,045 16,824,959 3,680,086 17.95%
Coupler cost (USD) - 1,066,286 - -
Processing cost (USD) 400,791 184,942 215,850 53.86%
Carbon price (USD) 5,936,414 5,031,716 904,698 15.24%
Overall cost (USD) 26,842,251 23,107,902 3,734,348 13.91%
The costs except the carbon price were converted from KRW to USD using the current exchange rate [46].
Table 8. Comparison of the previous case [15] and the coupler case in terms of rebar quantities, carbon emissions and associated costs (293 panels).
Table 8. Comparison of the previous case [15] and the coupler case in terms of rebar quantities, carbon emissions and associated costs (293 panels).
Description Previous case (P) Coupler case (C) Reduction (P-C) Reduction rate (P-C)/P
Ordered quantity (ton) 19,582.36 18,529.69 1052.67 5.38%
Carbon emissions (ton) 68,636.18 67,089.54 1546.63 2.25%
Rebar cost (USD) 17,780,785 16,824,959 955,826 5.38%
Coupler cost (USD) - 1,066,286 - -
Processing cost (USD) 207,050 184,942 22,109 10.68%
Carbon price (USD) 5,147,713 5,031,716 115,998 2.25%
Overall cost (USD) 23,135,549 23,107,902 27,646 0.12%
The costs except the carbon price were converted from KRW to USD using the current exchange rate [46].
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated