Preprint
Article
Predictive Quality Analytics of Surface Roughness in Turning Operation Using Polynomial and Artificial Neural Network Models
Altmetrics
Downloads
60
Views
27
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
11 December 2023
Posted:
12 December 2023
You are already at the latest version
Alerts
Abstract
The variability of the material properties of steel from different suppliers causes problems in achieving the required surface quality after turning. Therefore, the manufacturer needs to be able to estimate the resulting quality before starting production, especially if it is an expensive, small-batch production from stainless steel. Predictive models will make it possible to estimate the surface roughness from the mechanical properties of steel in the Mill Test Certificate (MTC) and thus support decision-making about the supplier selection or the acceptance of a material supply. Multivariate second-order polynomial model and feedforward back-propagation Artificial Neural Network (ANN) model were used to enhance the methodological robustness in formulating the decision if the predicted surface roughness is outside the required range, even before accepting the delivery. Both models can accurately predict surface roughness, while the ANN model is more accurate than the polynomial model; however, the predictive model is sensitive to the accuracy of the input data, and the model’s prediction is valid only under precisely defined conditions. The prediction model is used in a step-by-step decision-making procedure, which enables the trained staff to make a quick decision.
Keywords:
Subject: Engineering - Industrial and Manufacturing Engineering
1. Introduction
The selection and evaluation of suppliers are two of the most critical activities of a company and significantly affect the quality of the final products. Today, there are several tools to support decision-making in the selection of suppliers and to predict the responses of machining processes, which combine traditional methods with the technological advances of Industry 4.0. Küpper et al. [1] found that participants of the Boston Consulting Group study identified predictive analytics, sensors and tracking, and electronic feedback loops as the most impactful technologies. Data analytics has started gathering the interest of quality researchers and practitioners who investigate approaches, algorithms, and methods for supporting manufacturing quality procedures in the context of Industry 4.0 [2].
Considering the Industry 4.0 requirements, the supplier’s selection is essential in promoting collaborative strategies between suppliers and manufacturers [3]. Industry 4.0 affects all industry sectors, and the steel supply chain is no exception. There are many opportunities that the steel industry can benefit from adopting a Quality 4.0 approach [4]. For example, quality control enables complete and instant traceability of the data. By using technologies such as blockchain, every step in the supply chain can be traced and reviewed for quality specifications. It is also difficult to ensure transparency within the entire supply chain without Quality 4.0 tools, which guarantee that no data in the system can be changed unless all parties agree to do it. This means that no more fake Mill Test Certificates (MTC) or signatures can be made [5]. Therefore, collaboration across the supply chain is essential [6].
Polynomial models and Artificial Neural Network (ANN) are frequently used tools of Quality 4.0. They can also predict the results of the steel product machining process. Routara et al. [7], Wang and Feng [8], and Vasanth et al. [9] predicted surface roughness using polynomial models. Pal [10] and Vasanth et al. [9] used neural network models to predict surface roughness for the turning process. Çaydaş and Ekici [11] used the ANN model to estimate the surface roughness values of AISI 304 austenitic stainless steel in CNC turning operation. Predicting allows manufacturing companies to make predictions about the quality of the manufactured product based on data obtained before and during the process. This ability was called predictive quality [2]. According to [12], predictive quality analytics refers to analyzing incoming data to recognize and solve problems in advance. This emerging category of artificial intelligence (AI) enables manufacturers to decrease losses in both quality and waste by identifying root causes efficiently and preventing losses ahead of time.
According to Tercan et al. [13], the general approach to predictive quality involves three main steps: the collection and aggregation of process and quality data, the training of a predictive model, and the use of the model for real-time predictions as a basis for decisions on measures to be taken in the process.
The possibility to rely on MTC is important for the customer as the certificate credibility significantly influences the decision-making process and, according to [14], has a significant effect on machining cost as it is measured as an index of quality. When purchasing steel round bars from different suppliers without a long-term contractual relationship, customers cannot always be sure that the same product quality will be made from the supplied steel belonging to the declared grade. Currently, the trends of predictive modelling of turning processes using machine learning methods are still actual and also concern smaller companies that deal with piece production or production in small batches.
The research aims to propose a surface roughness prediction model and methodology for deciding whether to accept or reject a specific supply of stainless steel round bars for products manufactured for the food industry. The input variables are the main difference between the proposed and already published prediction models. While most models have input variable machining parameters (speed, depth of cut, feed rate), the presented model uses the material properties available from MTC.
Lean Six Sigma Small Mixed Batch (LSS-SMB) research methods, which were developed in previous research using a polynomial model and ANN tools in the Analyze and Control phase of the DMAIC (Define, Measure, Analyze, Improve control) method, help companies without an established quality management system according to ISO 9001:2015 or without an agreement with the supplier on supply acceptance sampling according to ISO 28598-1:2017 and ISO 3951-2:2013 to decide whether to purchase steel from an unverified supplier.
2. Context of the Study
The research was carried out in an organization producing equipment for the food industry in small long-term batches and follows on from the findings from the previous stage of the research presented in [15]. The organization is not certified according to ISO 9001 and chooses steel suppliers based on previous experience and the lowest price offered in the surrounding market.
These facts lead to the organization sometimes having a problem maintaining the required surface roughness after fine turning in the case of some deliveries of AISI 304 and AISI 304L grades. In our case, AISI 304 and AISI 304L stainless steel cylinder shafts are considered working samples on which hard and fine turning operations were performed. Cylinders are one of the most important and expensive components of produced equipment. Cylinders consist of a tube, side flange and shaft, machined by turning on the CNC center MAZAK QTN 350. Product volume is about 1800 pcs per year in 271 design variants. The common feature of variants is the same grade of steel, machined on the same CNC center, using the same cutting fluid and tool. Large pieces are machined in one clamping during two shifts. We can consider this production as a small batch as each step starts and finishes before proceeding to the next one as defined in ISO 7870-8, 2017 and [16]. The resulting Critical-to-Quality (CTQ) characteristic is a shaft precise diameter with tolerance h6 and center line average roughness Ra with specification from 0.6 až 1.1 µm, measured after hard and finish turning of stainless steel bars from ∅25h9 to ∅80h9. A coated cemented carbide cutting tool (CVD TICN+AL2O3+TIN), manufactured by Sandvik, Sweden, and Zubora 65 H Extra cooling lubricant, is used for finish turning. The new cutting tool plates are used for each workpiece.
We ended the first stage of the research with the prediction ANN model and found that surface roughness and dimensional deviation can be predicted with regard to the supplier and the attached Mill Test Certificate (MTC) of the steel.
In this paper, the research continued by expanding the database with new measurements and MTC of used steels. With the new certificates, we found that in some cases, not all the data was legible, or the steel manufacturer was not mentioned, which called into question the credibility of the supplier. We did not include these MTCs in further research.
3. Materials and Methods
3.1. Materials
In our case, AISI 304 (EN 1.4301) (X5CrNi18-10) and AISI 304L EN 1.4307 (X2CrNi18-9) stainless steel round bars are considered working samples on which hard and fine turning operations were performed. Round bars are purchased from European (EUR) or Asian (ASI) suppliers with MTC.
Austenitic chromium-nickel steel AISI 304 is the most widely used type of stainless steel with good corrosion resistance, cold formability and weldability. It is resistant to water, water vapor, air humidity, edible acids, and weak organic and inorganic acids. It is well polishable and malleable by deep drawing, bending and rounding. AISI 304 stainless steel is a typical difficult-to-machine material [17], so the cutting parameters should be selected reasonably [18]. When machining, it is necessary to work with sharp tools made of high-alloy, high-speed steel, carbide, or carbide alloys due to the tendency to hardening. It is used in the engineering and nuclear industry, architecture, transport equipment, the food industry, the pharmaceutical and cosmetic industry, the construction of chemical apparatus and motor vehicles, in the production of surgical instruments, sanitary equipment, objects and devices for the household and objects of art.
Austenitic chromium-nickel steel AISI 304L has increased resistance to intercrystalline corrosion (extremely low carbon content). The material is weldable, very well polished and well cold formable. Machining conditions are similar to AISI 304. Temperature stress is up to 400 °C. It is used similarly to the AISI 304 material, but the possibility of cold processing is better.
3.2. Methods
Mathematical modeling is used to describe the relationship between steel material properties and the roughness of a surface after finish turning. We selected two models, namely multivariate second order polynomial and Artificial Neural Network models.
The polynomial model has long been used in many areas of science and technology. The second order model for n input variables takes the form:
where y is the output variable (Roughness Ra), n is the number of input variables, b is the polynomial model coefficients to be estimated, and ε represents the noise or error observed in the response y. The coefficients of the model were determined using the ordinary least squares method.
Artificial neural network models are machine learning models that approximate complex functions by learning from data. We use a feedforward neural network with a Levenberg-Marquardt backpropagation learning algorithm with ten neurons in the hidden layer, as was recommended in our previous research [15].
We can consider the polynomial model and the artificial neural network as backbox models that do not require prior knowledge about modelled data. The residual values calculated after model fitting serve for the identification of possible outliers in analyzed data and the following metrics were used for model accuracy comparison:
- Coefficient of Determination (R²)
- Mean Absolute Error (MAE)
- Maximum absolute Error (MaAE)
- Root Mean Squared Error (RMSE)
4. Results and Discussion
4.1. Model Validity Check
The multivariate polynomial model and the model with an ANN presented in [15] fairly accurately predicted the surface roughness from the material properties listed in the MTC, namely Yield Strength Rp0.2, Elongation, and Hardness. The accuracy of the prediction was verified using samples omitted from the model calculation. However, it is important that the models are able to predict roughness for other products in the future. Therefore, we proceeded to verify the correctness of the model on other samples that were produced later. Material properties, measured roughness and polynomial and ANN model predictions for three new samples are presented in Table 1. It is clear from the table that the predictions are wrong, especially for the polynomial model. Finding the reasons for this result was the subject of the analysis presented below.
Figure 1 shows the space of input variables of the model, where the value of Yield Strength Rp0.2 is on the x-axis, the Elongation value is on the y-axis, and the Hardness value is on the z-axis. The figure shows the training set of samples (Model Training Set) from [15] and the set of new samples (New Samples). It is clear from the figure that the input variable space of new samples 2 and 3 is far from the training set of samples. The value of the Yield Strength of the new samples is twice, and the value of Elongation is half that of the samples from the training set. With the new sample 1, there will probably be another reason why the models are unable to predict the roughness. Upon further investigation, it was found that sample 1 was produced with machine setup values for feed rate and depth of cut different from the training set.
The presented results of the analysis show:
- The polynomial and ANN models cannot predict values for samples that are very far from the training set of samples (new samples 2 and 3).
- It is crucial to ensure the accuracy and reliability of the data collected during production, as the models only apply to the defined machining parameters (new sample 1).
Based on the conclusions from the analysis, we examined both the original and new samples (hardness measurement, MTC, machine setup), and for further investigation of the use of prediction models, we excluded suspicious samples.
4.2. Prediction Models Calculated from Revised and New Data
After the revision of the original and new samples, a data set of 26 samples was created (Appendix A, Table A1). The value of Tensile Strength Rm was added to the input variables because several sources [19] and [20] state that none of the values of Rm and Rp0.2 alone are sufficiently informative. Multivariate polynomial models and ANN models were created for the new data set. Polynomial models had three input variables (Yield Strength Rp0.2, Elongation, and Hardness) as in the article [15] and four inputs (Tensile Strength Rm, Yield Strength Rp0.2, Elongation, and Hardness). The other two models are ANNs with four inputs. Calculating coefficients of polynomial models takes approximately 10 seconds, and the training time of ANN is approximately 2.5 minutes in Matlab Cloud service.
Table 2 contains model performance expressed as R2, MAE, MaAE, and RMSE values for four polynomial models and two ANN models. Models 1, 3, and 5 were trained with all samples. Then, the sample with a maximum value of residual was excluded from the training set for models 2, 4, and 6. Figure 2 shows Roughness measurement, prediction and residuals for polynomial models 2 and 4 and ANN model number 6.
From Table 2, we can see that models with four inputs outperform models with three inputs. Their value of the coefficient of determination R2 is greater, and the errors are smaller than for the three input models. Even model 3, without excluding the outlier sample, is better than the most accurate three input model 2 with excluded sample 24. However, the most reliable is ANN model 6 with excluded outlier 1. Figure 3 compares predictions of the best ANN model and the best polynomial model.
A graphical comparison of the ANN and the polynomial model is shown in Figure 4. The ANN model is significantly better in the mean absolute error (MAE) and root mean square error (RMSE) values. The Maximum absolute Error (MaAE) of the ANN model and the polynomial model is almost the same, but the ANN model is slightly better.
We compared the performance of the proposed prediction models with several similar models from the literature (Table 3). The table is incomplete because different authors give different coefficients. The values of the coefficients of the proposed models are comparable to or better than for the models from the literature.
Table 4 contains the advantages and disadvantages of the presented ANN and polynomial models and a recommendation for dealing with the disadvantages.
4.3. Using a Prediction Model
The presented roughness prediction models can be used in different ways. Table 5 lists some of them. However, the correct use of the model conditions the achievable benefits. First, the model must be accurate enough to serve the abovementioned purposes. Figure 5 shows the revised control scheme from our previous research [15], where the Learning loop with the Machine learning algorithm regularly updates the model. This is done after each roughness measurement, and the reason for the deviation of the prediction from reality needs to be investigated. The cause for the deviation can be:
- incorrect input data, either measurement of surface roughness or MTC,
- a change in the turning process that is not part of the model (see Model extension loop in Figure 6),
- the model does not give accurate results for the given steel. Our research has shown that the model can be extended while remaining consistent with older measurements.
This last section of the using a prediction model describes a step-by-step decision making procedure for acceptance or rejection of a particular shipment of stainless steel round bars (Table 6).
5. Conclusions
In the context of purchasing, supplier selection and evaluation methods are crucial for ensuring quality, cost, and delivery performance. The supplier’s selection is essential in promoting collaborative strategies between suppliers and manufacturers. Maintaining strong relationships with suppliers is the key to success, especially in small-batch and piece production.
This paper describes a predictive model for determining surface roughness after fine turning to support decisions about supplier selection or acceptance and rejection of a particular steel round bar supply. Multivariate second order polynomial and Artificial Neural Network models can accurately predict surface roughness, while the ANN model is more accurate than the polynomial one. Expanding the model inputs with Tensile Strength Rm increased the accuracy of the prediction. Both models are sensitive to the accuracy of the input data. Therefore, a well-defined procedure for using the model is required. This includes checking the accuracy of the measured roughness data and the reliability of the MTC from which the input data comes. The model’s prediction is valid under precisely defined conditions. The existing model is tied to the type of machining center, the machine setup and the cutting tools used.
The prediction model is used in a step-by-step decision making procedure to accept or reject a particular batch of stainless steel round bars. The defined procedure will enable the trained staff to make a quick decision. The model applies to a specific CNC center MAZAK QTN 350 and AISI 304 and 304L grade steel. The model can potentially be used for other machining centers, machine setup and steels. For this purpose, in the future, it will be necessary to create software applications and gather data from other MTCs and measurements.
Author Contributions
Conceptualization, K.Z. and P.B.; methodology, P.B.; software, P.B.; validation, K.Z., P.B. and M.C.; investigation, M.C.; resources, M.C.; data curation, M.C. and M.M.; writing—original draft preparation, K.Z and P.B.; writing—review and editing, P.B. and K.Z; supervision, M.M. All authors have read and agreed to the published version of the manuscript.
Data Availability Statement
Data supporting the results of this study are available from the corresponding authors upon request.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Table A1.
Inputs, measured hardness, and predicted hardness from models 4 and 6.
| Sample | Tensile Strength Rm (MPa) | Yield Strength Rp0.2 (MPa) | Elongation A (%) | Hardness HBW |
Roughness Ra (µm) | Prediction Ra (µm) | |
|---|---|---|---|---|---|---|---|
| Polynom. model 4 | ANN model 6 |
||||||
| 1 | 585 | 235 | 55 | 168 | 0.832 | 1.0028 | 0.9914 |
| 2 | 583.62 | 276.05 | 54 | 158 | 0.808 | 0.8079 | 0.8086 |
| 3 | 573.58 | 270.13 | 54 | 156 | 0.802 | 0.8077 | 0.8016 |
| 4 | 581 | 292 | 58 | 174 | 0.99 | 0.9462 | 0.9453 |
| 5 | 580 | 284 | 57 | 176 | 0.941 | 0.9451 | 0.9393 |
| 6 | 584 | 286 | 59 | 176 | 0.941 | 0.9517 | 0.9423 |
| 7 | 579.15 | 290.53 | 53 | 158 | 0.898 | 0.8820 | 0.8909 |
| 8 | 586 | 286 | 73 | 175 | 0.90 | 0.8960 | 0.8997 |
| 9 | 579.45 | 290.53 | 53 | 158 | 0.87 | 0.8813 | 0.8775 |
| 10 | 580 | 284 | 72 | 176 | 0.945 | 0.9519 | 0.9500 |
| 11 | 608 | 318 | 57.5 | 170 | 0.94 | 0.9155 | 0.9394 |
| 12 | 585 | 235 | 55 | 168 | 0.992 | 1.0028 | 0.9914 |
| 13 | 581 | 292 | 58 | 174 | 0.90 | 0.9462 | 0.9453 |
| 14 | 573 | 239 | 58 | 167 | 0.931 | 0.9057 | 0.9315 |
| 15 | 707 | 565 | 37 | 210 | 1.229 | 1.2280 | 1.2295 |
| 16 | 608 | 291 | 55 | 160 | 0.691 | 0.7147 | 0.6912 |
| 17 | 635 | 332 | 48 | 165 | 0.6262 | 0.6262 | 0.6265 |
| 18 | 634 | 320 | 43 | 163 | 0.5848 | 0.5707 | 0.5840 |
| 19 | 630 | 328 | 44 | 161 | 0.5604 | 0.5917 | 0.5599 |
| 20 | 628 | 325 | 46 | 156 | 0.6196 | 0.5765 | 0.6257 |
| 21 | 630 | 332 | 47 | 161 | 0.6106 | 0.6469 | 0.6096 |
| 22 | 630 | 325 | 46 | 161 | 0.6146 | 0.5965 | 0.6137 |
| 23 | 625 | 322 | 47 | 155 | 0.5966 | 0.6059 | 0.5912 |
| 24 | 608 | 270 | 58.5 | 160 | 0.5906 | 0.5879 | 0.5906 |
| 25 | 729 | 607 | 41 | 216 | 1.28 | 1.2815 | 1.2798 |
| 26 | 637 | 397 | 49 | 188 | 1.019 | 1.0140 | 1.0192 |
References
- Küpper, D.; Knizek, C.; Ryeson, D.; Noecker, J. Quality 4.0 Takes More Than Technology. Available online: https://www.bcg.com/publications/2019/quality-4.0-takes-more-than-technology (accessed on 20 8 2019).
- Bousdekis, A.; Lepenioti, K.; Apostolou, D.; Mentzas, G. Decision Making in Predictive Maintenance: Literature Review and Research Agenda for Industry 4.0, IFAC-PapersOnLine 2019, 52(13), 607-612. [CrossRef]
- Resende, C.; Geraldes, C.; Lima, F. R. Decision Models for Supplier Selection in Industry 4.0 Era: A Systematic Literature Review. Procedia Manufacturing 2021, 55, 492–499. [Google Scholar] [CrossRef]
- Santos, G.; Sá, J.C.; Félix, M.J.; Barreto, L.; Carvalho, F.; Doiro, M.; Zgodavová, K.; Stefanović, M. New Needed Quality Management Skills for Quality Managers 4.0. Sustainability 2021, 13, 6149. [Google Scholar] [CrossRef]
- Andreatti, A.; Quality 4.0 Opportunities in the Steel Supply Chain. SteelTrace. Available online: https://steeltrace.co/quality4_opportunities/ (accessed on 20 10 2023).
- Kauppila, O.; Välikangas, K.; Majava, J. Improving supply chain transparency between a manufacturer and suppliers: a triadic case study. Management and Production Engineering Review, 2020, 11, 84-91. [CrossRef]
- Routara, B.C.; Bandyopadhyay, A.; Sahoo, P. Roughness modeling and optimization in CNC end milling using response surface method: effect of workpiece material variation. Int J Adv Manuf Technol 2009, 40, 1166–1180. [Google Scholar] [CrossRef]
- Wang, X.; Feng, C. X. Development of Empirical Models for Surface Roughness Prediction in Finish Turning. The International Journal of Advanced Manufacturing Technology, 2020, 20, 348–356. [Google Scholar] [CrossRef]
- Vasanth, X. A.; Paul, P.S.; Varadarajan, A.S. neural network model to predict surface roughness during turning of hardened SS410 steel. Int J Syst Assur Eng Manag, 2020, 11, pp. 704–715. [CrossRef]
- Pal, S.K.; Chakraborty, D. Surface roughness prediction in turning using artificial neural network. Neural Comput & Applic 2005, 14, 319–324. [Google Scholar] [CrossRef]
- Çaydaş, U.; Ekici, S. Support vector machines models for surface roughness prediction in CNC turning of AISI 304 austenitic stainless steel. J Intell Manuf 2012, 23, 639–650. [Google Scholar] [CrossRef]
- Matics, Predictive Quality in Manufacturing. Glossary terms. https://matics.live/glossary/predictive-quality-in-manufacturing/#:~:text=Predictive%20quality%20analytics%20refers%20to,preventing%20losses%20ahead%20of%20time.
- Tercan, H.; Meisen, T. Machine learning and deep learning based predictive quality in manufacturing: a systematic review, Journal of Intelligent Manufacturing 2022, 33(7), 1879-1905. [CrossRef]
- Dubey, V.; Sharma, A.K.; Pimenov, D.Y. Prediction of Surface Roughness Using Machine Learning Approach in MQL Turning of AISI 304 Steel by Varying Nanoparticle Size in the Cutting Fluid. Lubricants 2022, 10, 81. [Google Scholar] [CrossRef]
- Zgodavova, K.; Bober, P.; Majstorovic, V.; Monkova, K.; Santos, G.; Juhaszova, D. Innovative Methods for Small Mixed Batches Production System Improvement: The Case of a Bakery Machine Manufacturer. Sustainability 2020, 12, 6266. [Google Scholar] [CrossRef]
- Cliftonsteel. Tensile Strength of Steel vs Yield Strength of Steel. Clifton Steel, https://www.cliftonsteel.com/education/tensile-and-yield-strength. Accessed 21 October 2023.
- ZwickRoell. “Yield strength and offset yield Rp 0.2.” ZwickRoell, 2023, https://www.zwickroell.com/industries/materials-testing/tensile-test/yield-point/. Accessed 21 October 2023.
- Khair, R. Small Batch Production: Pros, Cons, & Everything You Need to Know https://ventrify.ca/design/small-batch-production/ Posted on: November 4, 2021.
- Sansmachining. “Turning Of AISI304 Stainless Steel.” SANS Machining, 16 August 2022, https://www.sansmachining.com/turning-of-aisi304-stainless-steel/. Accessed 21 October 2023.
- Dubovská, R.; Majerík, J. Experimental Investigation and Analysis of Cutting Forces When Machining X5CrNi18-10 Stainless Steel. Manufacturing Technology 2015, 15, 322–329. [Google Scholar] [CrossRef]
Figure 1.
Model input space for samples used for model calculation (Model Training Set) and new samples.
Figure 1.
Model input space for samples used for model calculation (Model Training Set) and new samples.
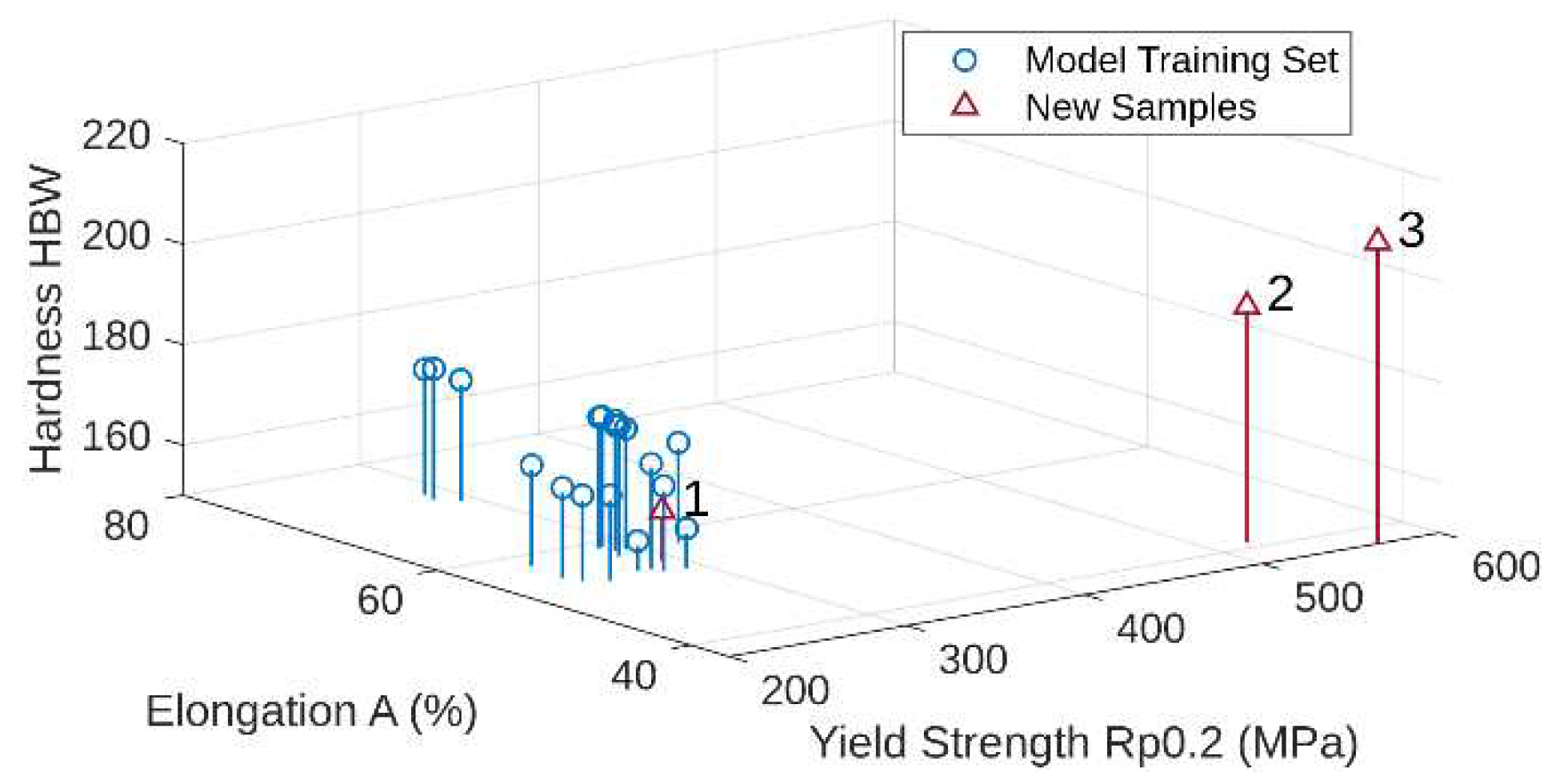
Figure 2.
Measurement, prediction and residuals for models number 2 (a,b), 4 (c,d), and 6 (e,f).
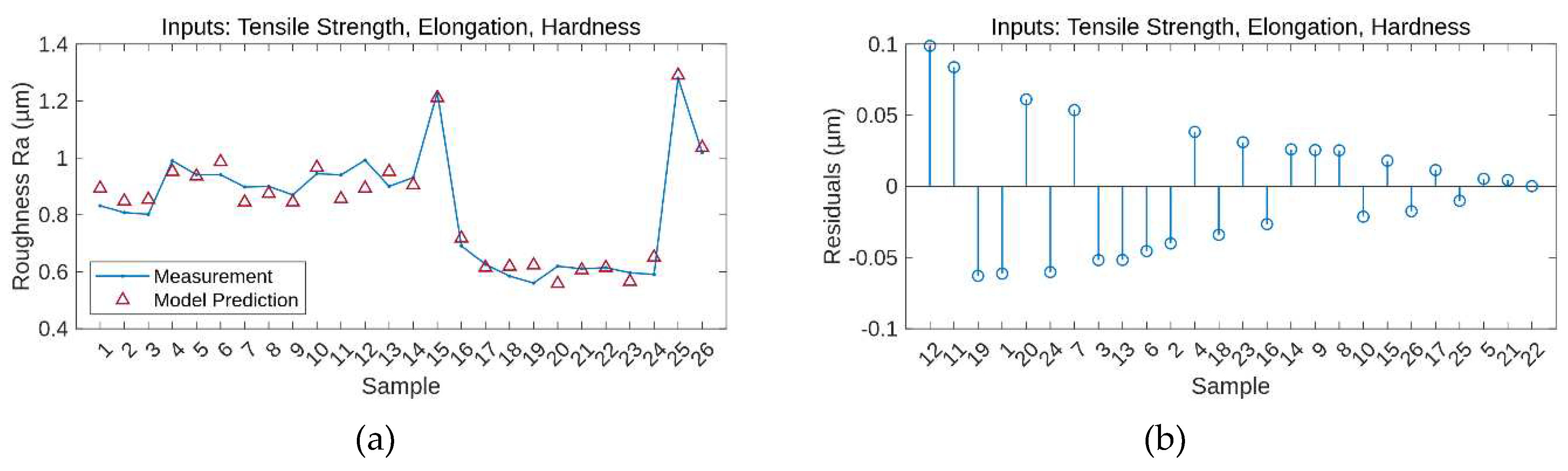
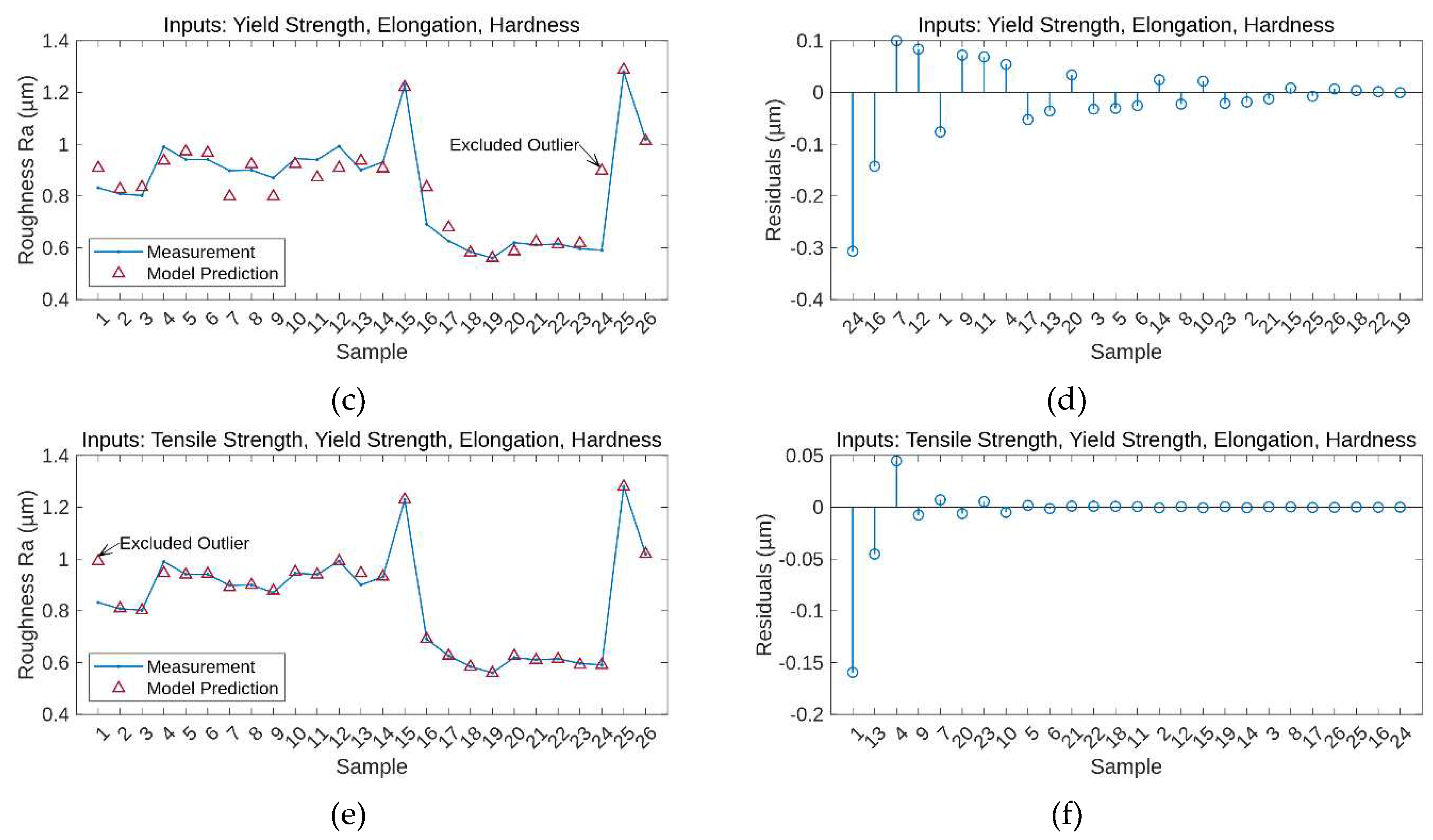
Figure 3.
Comparison of best ANN and Polynomial model predictions.
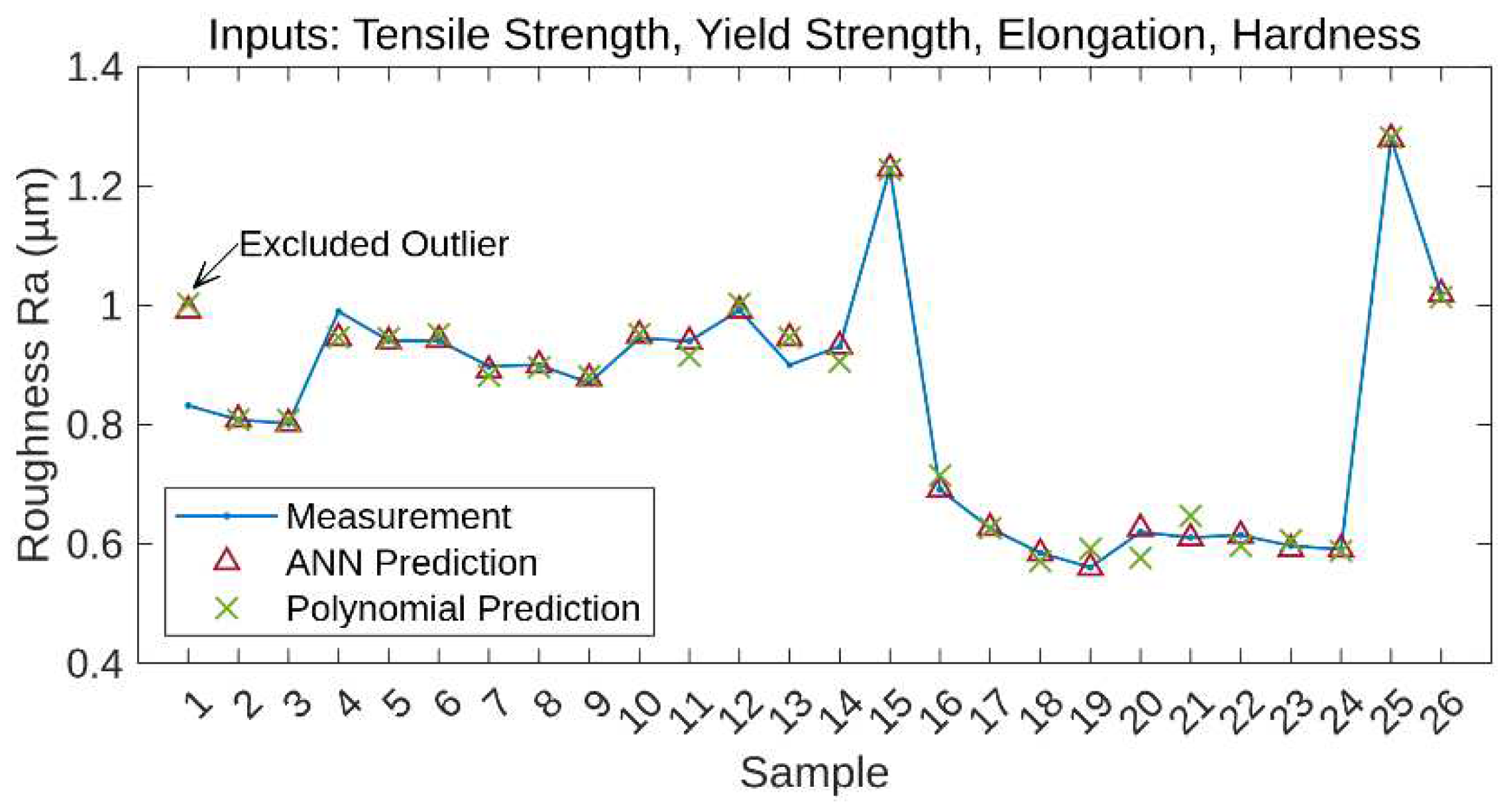
Figure 4.
Comparison of coefficients Mean Absolute Error (MAE), Maximum absolute Error (MaAE), Root Mean Squared Error (RMSE), and Coefficient of Determination (R²) for best ANN and polynomial models.
Figure 4.
Comparison of coefficients Mean Absolute Error (MAE), Maximum absolute Error (MaAE), Root Mean Squared Error (RMSE), and Coefficient of Determination (R²) for best ANN and polynomial models.
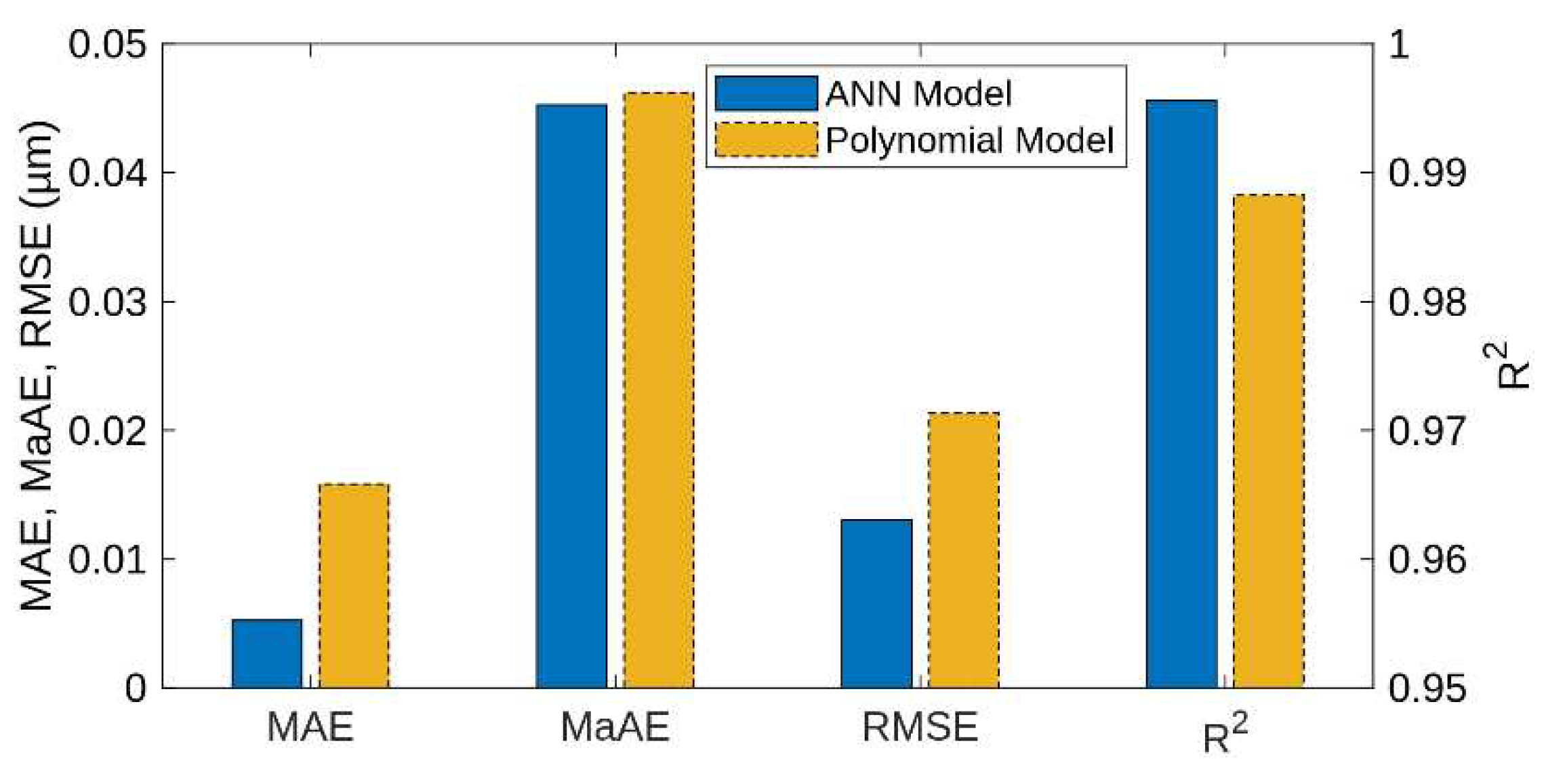
Figure 5.
Revised control scheme using the roughness prediction model.
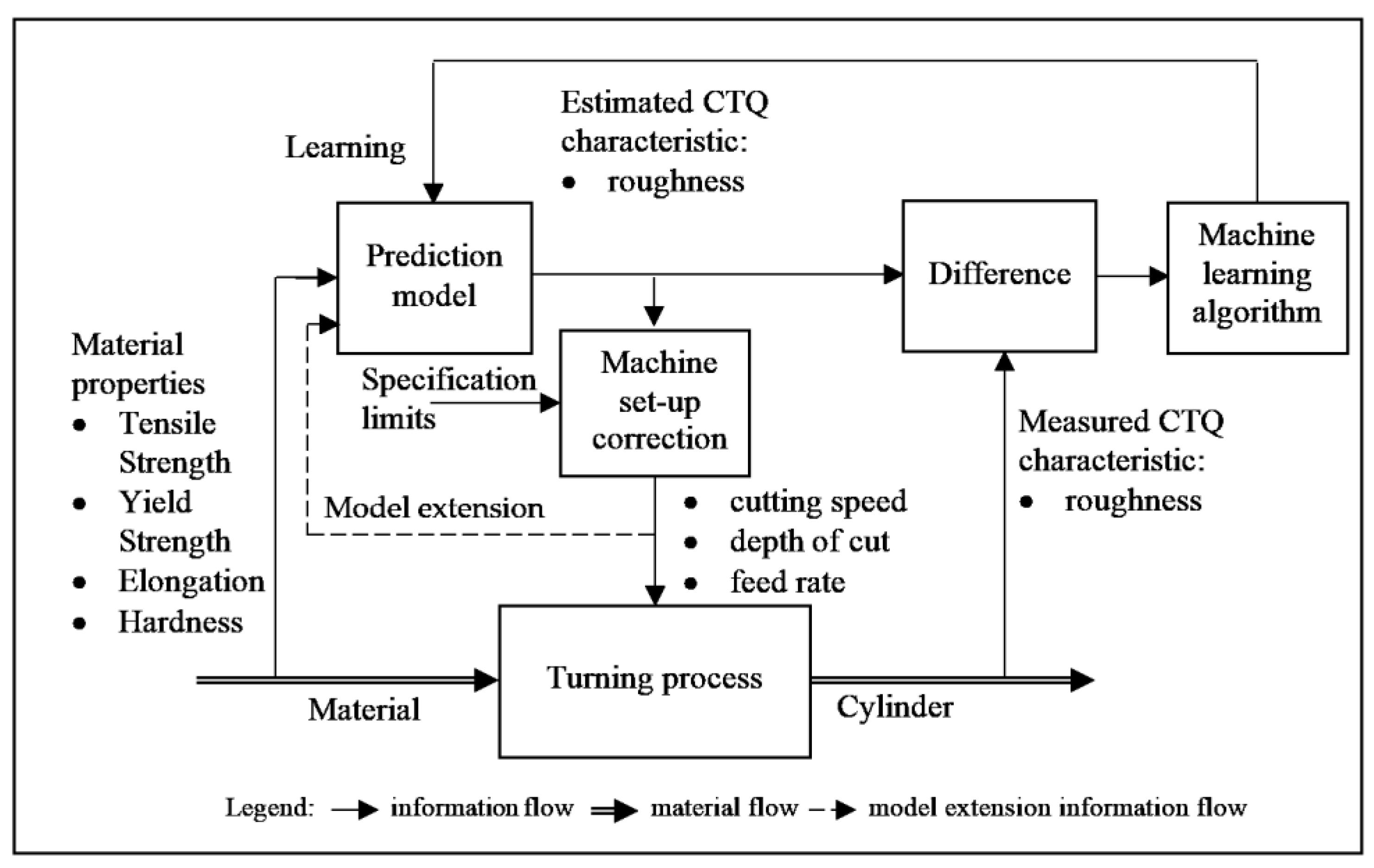
Table 1.
Sample data, measured roughness, and predicted roughness by polynomial and ANN models.
| New Sample | Inputs | Outputs | Roughness prediction (µm) | |||
|---|---|---|---|---|---|---|
| Yield Strength Rp0.2 (MPa) | Elongation A (%) | Hardness HBW |
Roughness Ra (µm) | Polynomial model | ANN model |
|
| 1 | 291 | 55 | 160 | 0.552 | 0.9292 | 0.9706 |
| 2 | 520 | 41 | 197 | 1.265 | -5.819 | 0.9249 |
| 3 | 565 | 37 | 210 | 0.909 | -10.530 | 0.9251 |
Table 2.
Model performance R2, MAE, MaAE, and RMSE.
| No | Model type | Inputs x1, x2, x3, (x4) | Excluded outlier |
R2 | MAE | MaAE | RMSE | |
|---|---|---|---|---|---|---|---|---|
| 1 | Polynomial model | Yield Strength, Elongation, Hardness | - | 0.8579 | 0.0524 | 0.2325 | 0.0728 | |
| 2 | 24 | 0.9268 | 0.0383 | 0.1427 | 0.0516 | |||
| 3 | Tensile Strength, Yield Strength, Elongation, Hardness | - | 0.9725 | 0.0229 | 0.0898 | 0.0321 | ||
| 4 | 1 | 0.9883 | 0.0158 | 0.0462 | 0.0462 | |||
| 5 | ANN model | Tensile Strength, Yield Strength, Elongation, Hardness | - | 0.9822 | 0.0114 | 0.0801 | 0.0257 | |
| 6 | 1 | 0.9956 | 0.0053 | 0.0453 | 0.0131 |
The best polynomial and ANN model is shown in bold.
Table 3.
Comparison of performance of presented prediction models and models from the literature.
| Model | R2 | RMSE |
|---|---|---|
| Presented polynomial model 4 | 0.9883 | 0.0213 |
| Presented ANN model 6 | 0.9956 | 0.0131 |
| Routara (2009), polynomial | - | 0.08518 |
| Pal (2005), ANN, different configurations | - | 0.0486 - 0.185 |
| Vasanth (2020): | ||
|
0.95701 | 0.0307 |
|
0.96994 | - |
|
0.96870 | - |
|
0.994 | - |
| Wang (2002), polynomial | 0.923 | - |
Table 4.
Advantages and disadvantages of using presented prediction models.
| Advantage | Explanation |
|---|---|
| The model is valid for a wide spectrum of AISI 304 and 304L grade steels. | The existing training set contains various materials. Tensile Strength ranges from 573 to 729 MPa, Yield Strength from 235 to 607 MPa, Elongation from 37 to 73%, and Hardness from 155 to 216 HBW. |
| The model can identify errors in the measurement or the MTC. | If the input variables of the new sample are within the valid range of the model, but the measured roughness has a large deviation from the prediction, then it is necessary to investigate whether there was an error in the measurement, a different machine setup or whether the MTC is credible. |
| The model is valid across different manufacturers. | The data was obtained from different manufacturers, and the model is still consistent. |
| The model is open to future extension. | The model has the potential to determine the machine setup for the desired roughness if measurements at different setups are available. |
| Disadvantage | Explanation |
| The model is sensitive to the accuracy of the input data. | A well-defined procedure for using the model is required. People must be trained and regularly checked to ensure they follow the procedures. There must be a procedure to verify the credibility of MTC. |
| The model’s prediction is valid under precisely defined conditions. | The existing model is tied to the type of machining center, the machine setup and the cutting tools used. However, it can be retrained for new conditions if measurements are available. |
Table 5.
Use case of the prediction model.
| Use case | Description |
|---|---|
| Choose the supplier, and choose the steel grade on the market. | If the predicted roughness is within the CTQ specification limit, this supplier/steel grade can be contracted. |
| Acceptance or rejection of a particular steel shipment. | The prediction model allows the reduction of the variation of output quality by controlling the input. In this case, a particular steel shipment is rejected if the predicted roughness is not within the CTQ specification limit. |
| Machine setup correction. | The prediction model allows the reduction of the variation of the output quality by adjusting the production process if the predicted roughness is not within the CTQ specification limit. |
| Checking the credibility of the supplier | The difference between predicted and measured roughness can lead to questioning the credibility of a MTC. |
Table 6.
Decision making procedure using a predictive model.
| Step | Question / Decision / Next step | |
|---|---|---|
| 1 | Is a Mill Test Certificate (MTC) available for the shipment? | |
| YES | Go to step 2 | |
| NO | Decision REJECT, end of procedure The absence of an MTC raises questions about the quality of the product and its compliance with the required standards. The quality after turning cannot be guaranteed. |
|
| 2 | Does the MTC contain all the required data? | |
| YES | Go to step 3 | |
| NO | Decision procedure not applicable, end of procedure. A procedure based on a predictive model cannot be used for decision making if input data are unavailable. It is necessary to proceed differently. |
|
| 3 | Are required input values in the valid range of the model? | |
| YES | Go to step 4 | |
| NO | Decision procedure not applicable, end of procedure. A procedure based on a predictive model cannot be used for decision making If the input data is outside the scope of the model. |
|
| 4 | Is predicted hardness from the model within the CTQ decision limits?* | |
| YES | Decision ACCEPT, end of procedure. | |
| NO | Go to step 5 | |
| 5 | Is there a verified machine setup for this material? | |
| YES | Decision ACCEPT, end of procedure. This branch of the decision tree will make it possible to expand the validity area of the model by including a new sample in the training set. |
|
| NO | Decision REJECT, end of procedure. The quality after turning cannot be guaranteed. |
|
* The decision limits are usually stricter than the specification limits.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







