Prerpints.org logo
Preprint
Article

AE-Qdrop: Towards Accurate and Efficient Low-bit Post-training Quantization for Convolutional Neural Network

Altmetrics

Downloads

100

Views

32

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

11 December 2023

Posted:

12 December 2023

You are already at the latest version

Alerts
Abstract
Post-training quantization is pivotal in deploying convolutional neural networks for mobile applications. Block-wise reconstruction with adaptive rounding, as employed in prior works like BrecQ and Qdrop, facilitates acceptable 4-bit quantization accuracy. However, adaptive rounding is time-intensive, and its constraint on weight optimization space curtails the potential for quantization performance. The optimality of block-wise reconstruction hinges on the quantization status of subsequent network blocks. In this investigation, we delve into the theoretical underpinnings of the limitations inherent in adaptive rounding and block-wise reconstruction. Our exploration leads to the development of a post-training quantization methodology, designated as AE-Qdrop. This algorithm operates in two distinct phases: block-wise reconstruction and global fine-tuning. The block-wise reconstruction phase introduces a progressive optimization strategy, superseding adaptive rounding, which not only augments quantization precision but also significantly improves quantization efficiency. To mitigate the risk of overfitting, we introduce a random weighted quantized activation mechanism. During the global fine-tuning phase, we account for interdependencies among quantized network blocks. The weight of each network block will be corrected with logit matching and feature matching. Extensive experiments validate that AE-Qdrop achieves high-precision and efficient quantization. For instance, in the case of 2-bit MobileNetV2, AE-Qdrop outperforms Qdrop by achieving a 6.26% enhancement in quantization accuracy and quintupling the quantization efficiency.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

In recent years, Convolutional Neural Networks (CNNs) have demonstrated outstanding performance across various computer vision tasks. However, the large-scale parameters and high computational complexity of CNNs pose challenges to devices in terms of storage, power consumption, and computational capabilities. In resource-constrained mobile applications such as intelligent wearable devices, unmanned aerial vehicles, and smart robots, CNNs quickly deplete storage, memory, battery, and computational units. Therefore, reducing the parameter amount and computational complexity of CNNs are crucial objectives for their effective deployment in mobile applications.
Researchers have proposed a range of CNN compression and acceleration techniques, which include knowledge distillation [1,2], neural network architecture search [3,4], pruning [5,6], low-rank decomposition [7], and quantization [8]. Knowledge distillation employs a larger model as a ’teacher’ to guide the training of a smaller ’student’ model. Neural network architecture search employs methods such as hyperparameter tuning and reinforcement learning to identify the most optimal network structure and parameter scale. Pruning involves removing redundant components from the original network, which often necessitates retraining due to changes in the network structure. Low-rank decomposition aims to reduce parameter size while maintaining the original network structure, although its decompression process might lead to increased computational overhead. Quantization involves converting floating-point (FP) network parameters into lower-bit parameters, retaining the network structure. This reduction in data bit-width can directly decrease power consumption and storage requirements, and improve computational speed. For example, the power consumption and area requirements of a FP adder are 30 and 100 times greater, respectively, than those of an 8-bit adder [9]. Therefore, quantization is a highly effective technique for model compression.
Due to the introduction of quantization noise through rounding and truncation operations in quantization computations, quantization often compromises the performance of neural networks. Quantization techniques primarily consist of Quantization-Aware Training (QAT) and Post-Training Quantization (PTQ). QAT, which relies on complete training data and labels, retrains network weights and quantization parameters through back-propagation. Although it can achieve high quantization accuracy, this method incurs a significant time cost. In contrast, PTQ quantizes the network based on a small set of samples without retraining. However, it faces challenges in terms of accuracy. At 8 bits, PTQ can achieve nearly lossless accuracy, so recent research has predominantly focused on low-bit quantization (<=4 bits). Among these techniques, AdaRound [10] has significantly improved 4-bit quantization accuracy by optimizing weight rounding and layer-wise reconstruction. BrecQ [11] has posited that block-wise reconstruction is a more effective optimization objective, suggesting the use of the Fisher matrix as an approximation for the Hessian matrix. Qdrop [12] posits that activation quantization can be regarded as a form of weight perturbation. It concurrently quantizes weights and activations during the block-wise reconstruction process, employing a random dropout quantized activation scheme to alleviate overfitting. This approach ultimately achieves acceptable 4-bit quantization accuracy.
However, Qdrop still exhibits certain shortcomings. On one hand, the adaptive rounding technique used in Qdrop limits the optimization space of weight elements to a binary set, which compromises its quantization performance, especially at lower bit-widths. Additionally, the time-intensive nature of adaptive rounding diminishes the overall efficiency of the quantization process. For lightweight networks like MobileNetV2, which are frequently deployed on mobile devices, Qdrop requires approximately 40 minutes to complete the quantization. On the other hand, Qdrop quantizes each network block individually (block-wise reconstruction), overlooking the impact of subsequent network blocks on the current one, which can lead to suboptimal solutions.
To address the aforementioned challenges, this paper introduces AE-Qdrop, a post-training quantization algorithm that is both highly precise and efficient. AE-Qdrop is comprised of two phases: block-wise reconstruction and global fine-tuning. During the block-wise reconstruction phase, we propose a progressive optimization strategy. This strategy, which replaces adaptive rounding, progressively tightens constraints on the optimization space for weights, thereby achieving superior quantization accuracy and efficiency. Concurrently, we develop a random weighted quantized activation scheme to mitigate the issue of over-fitting. Global fine-tuning further enhances quantization accuracy by correcting network weights through logit matching and feature matching. Our contributions can be summarized as follows:
  • We perform a theoretical analysis of the shortcomings associated with adaptive rounding and block reconstruction.
  • We introduce AE-Qdrop, a two-stage algorithm that includes block-wise reconstruction and global fine-tuning. This algorithm combines a progressive optimization strategy with random weighted quantization activation, enhancing the accuracy and efficiency of block-wise reconstruction. Subsequently, global fine-tuning is applied to further optimize the weights, thereby improving the overall quantization accuracy.
  • Extensive experiments are conducted to evaluate the quantization results of mainstream networks, demonstrating the superior performance of AE-Qdrop, particularly at low bit widths.
The subsequent content of this paper is organized as follows: Section 2 provides a brief overview of the related work on neural network quantization. In Section 3, we elucidate the limitations of adaptive rounding and block-wise reconstruction through theoretical analysis. Section 4 expounds on the specific details of AE-Qdrop. Section 5 delves into an in-depth analysis and discussion of the experimental results. Ultimately, the conclusions are presented in Section 6.

2. Related Work

2.1. Quantization-aware Training

QAT retrained quantized networks based on fully labeled training datasets to mitigate quantization noise. The straight-through estimator (STE) [13] addressed the zero-gradient issue during backpropagation resulting from rounding operations. Throughout the training process, Google [14] employed exponential moving averages to smooth the activation ranges. LSQ [15] treated the quantization scale factor as a trainable parameter, while LSQ+ [16] introduced a learnable quantization zero-point. Both DSQ [17] and N2UQ [18] optimized the gradient estimation of rounding operations through an approximate function, thus alleviating gradient mismatch issues. Binary/Ternary networks [19,20] were also focal points of QAT research. Although QAT achieved lower-bit quantization and competitive results, it required complete datasets and sufficient training time.

2.2. Post-training Quantization

PTQ requires only a small amount of data. In comparison to QAT, PTQ is more efficient and convenient, leading to its broader application in the industry. Early PTQ focused on minimizing the quantization error of network parameters through techniques such as optimizing quantization factor scale [21,22], bias correction [23], piecewise linear quantization [24,25], and outlier separation [26,27]. For instance, Nvidia’s TensorRT [28], a widely used quantization tool, searches for optimal quantization factor scale by minimizing the Kullback-Leibler (KL) distance between FP activation and quantized activation. Similarly, EasyQuant [29] optimizes the quantization scaling factor based on the cosine similarity metric. Although early PTQ achieved near-lossless 8-bit quantization accuracy, these schemes would fail at low bit widths. This failure can be attributed to the fact that minimizing the quantization error of network parameters does not necessarily equate to optimal quantization.
Subsequently, LAPQ [30] proposed solving the quantization scaling factor by minimizing the loss function. Inspired by this, AdaRound introduced an adaptive rounding technique to align the outputs of FP network layers with quantized network layers, significantly enhancing PTQ performance. Through theoretical investigations and assumptions about second-order losses, BrecQ posits that minimizing block output errors is a more rational optimization objective. Furthermore, Qdrop points out that BrecQ neglects the impact of activation quantization in weight optimization and argues that activation quantization noise can be transformed into a form of weight perturbation. It devises a block-wise reconstruction with random dropout of quantized activations, making the quantized weights more robust to the noise induced by quantized activations.

3. Background and Theoretical Analysis

3.1. Quantizer

For a FP tensor (activation or weight) x, we can map it to an integer tensor q according to the following equation:
q = clip round x s + z , q min , q max s = x max − x min 2 b − 1 z = q min − round x min s x q = s ( q − z )
clip ( · ) and round ( · ) respectively denote the truncation and rounding operations. s represents the quantization scaling factor, reflecting the proportional relationship between FP values and integers. The variable z is defined as the offset corresponding to the zero point. The maximum value in the vector is denoted by x max , while x min represents the minimum value. The quantization range, specified by q min , q max , is determined by the bit width b. We consider only uniform unsigned symmetric quantization, as this is the most widely used quantization setting. Consequently, q min is equal to 0, and q max equals 2 b − 1 . Non-linear quantization is not considered due to its unfriendly nature towards hardware deployment. x q refers to the FP tensor, also known as the fake-quantized tensor. In the FP domain, the quantizer discretizes the continuous FP values into 2 b FP values. The difference between x q and x is defined as the parameter quantization error.

3.2. AdaRound

AdaRound reexamines the effect of weight quantization on the loss function using a second-order Taylor expansion. For the l t h layer of the network f l ( · ) , the change in the loss function L ( · ) due to weight quantization is defined as:
L f n ( f n − 1 … f l ( x f , w q ) ) ) − L f n ( f n − 1 … f l ( x f , w f ) ) ) = L x f , w f + ▵ w − L x f , w f ≈ Δ w T g w x f , w f + 1 2 Δ w T H w x f , w f Δ w ≈ 1 2 Δ w T J y : w T x f , w f H y x f , w f J y : w x f , w f ▵ w = 1 2 ▵ y T H y x f , w f ▵ y ≈ 1 2 ▵ y T I ▵ y = 1 2 ∥ Δ y ∥ 2
where L ( · ) is equal to L f n ( f n − 1 … f l ( · ) ) , g w x f , w f represents the gradient matrix and H w x f , w f represents Hessian matrix. Considering that the FP model has converged, g w x f , w f is approximately 0. By introducing the network layer output y and the Jacobian matrix J y : w x f , w f of y with respect to w, H w x f , w f can be decomposed into J y : w T x f , w f H y x f , w f J y : w x f , w f . ▵ y = J y : w x f , w f ▵ w = y − y q is the difference in network layer output before and after weight quantization. By approximating the Hessian matrix H w x f , w f with the identity matrix I , the change in the loss function caused by weight quantization is approximately equal to the change in the output of the network layer. Therefore, the optimization goal of weight quantization can be defined as layer-wise reconstruction:
min ▵ w L x f , w f + ▵ w − L x f , w f → min ▵ w ∥ Δ y ∥ 2
AdaRound introduces the trainable tensor v with the same dimension as w into the weight quantizer to indirectly optimize ▵ w :
q w = clip floor w f s w + h ( v ) ) + z , q min , q max h ( v ) = clip 1.2 1 + exp ( − v ) − 0.1 , 0 , 1 ▵ w = w f − s w ( q w − z )
This scheme is called adaptive rounding. To ensure that h v converges to 0 or 1, AdaRound introduces a regularization term for equation (3). Therefore, the final optimization goal is:
min v ∥ Δ y ∥ 2 + λ ∑ 1 − 2 h v − 1 β
where β and λ are parameters governing the regularization. If w f contains M elements, then adaptive rounding provides Δ w ( w q ) with a solution space of size 2 M . Nearest neighbor rounding is only one set of solutions, but there may be better solutions that minimize Equation (3). Therefore, adaptive rounding can effectively improve quantization accuracy.

3.3. Drawbacks of Adaptive Rounding

Considering that weight and activation are quantized simultaneously, equation (2) can be generalized as:
L f n ( f n − 1 … f l ( x q , w q ) ) ) − L f n ( f n − 1 … f l ( x f , w f ) ) ) = L x f + Δ x , w f + Δ w − L x f , w f ≈ ▵ x T g x x f , w f + 1 2 ▵ x T H x x f , w f ▵ w + ▵ w T g w x f , w f + 1 2 ▵ w T H w x f , w f ▵ w + ▵ x T H x w x f , w f ▵ w ≈ 1 2 ▵ x T H x x f , w f ▵ x + 1 2 ▵ w T H w x f , w f ▵ w + Δ x T H x w x f , w f ▵ w = 1 2 ▵ x T J y : x T x f , w f H y x f , w f J y : x x f , w f ▵ x + 1 2 ▵ w T J y : w T x f , w f H y x f , w f J y : w x f , w f ▵ w + ▵ x T J y : x T x f , w f H y x f , w f J y : w x f , w f ▵ w = 2 · ▵ y T H y x f , w f ▵ y ≈ 2 · ▵ y T I ▵ y
Qdrop demonstrates that the impact of activation quantization on the loss function can be converted into weight perturbation τ ( x ) , that is:
L x f + Δ x , w f + Δ w − L x f , w f = L x f , ( w f + Δ w ) ⊙ ( 1 + τ ( x ) − L x f , w f = L x f , w f + Δ w + w f ⊙ τ ( x ) + Δ w ⊙ τ ( x ) − L x f , w f
Considering f l ( · ) as the l-th network block, Equation (6) can be generalized for block-wise reconstruction [11]. The optimization goal for block-wise reconstruction can be derived based on Equations (6) and (7):
min Δ w f L x f , w f + Δ w + w f ⊙ τ ( x ) + Δ w ⊙ τ ( x ) ︸ ( Δ w f ) − L x f , w f → min Δ w f ∥ Δ y ∥ 2
In Qdrop, the optimization of Equation 8 is conducted through adaptive rounding, which constrains the optimization space of each element in w q to a binary set. As the quantization bit width decreases, the weight perturbation τ ( x ) gradually increases. Consequently, the binary set might not offer the optimal Δ w f , thereby limiting the quantization performance. A simple example is illustrated in Figure 1. As observed, the FP output y f = 0.98 , the optimal quantized output y q ada achievable with adaptive rounding is 0.85 , but the actual optimal quantized output y f best is 0.95 . Furthermore, optimizing weight rounding through the addition of regularization terms requires extensive iterative cycles, which increases the time cost of network quantization. Last but not least, an adversarial relationship exists between the regularization terms and the reconstruction error, hindering the optimization of the reconstruction error.

3.4. Drawbacks of Block-wise Reconstruction

The derivation of Equation (6) actually relies on the assumption that the network blocks from the l t h to the n t h are not quantized. If all network blocks are quantized, then the optimization objective for the l t h network block can be transformed into:
min Δ w f L f n q ( f n − 1 q … f l ( x q , w q ) ) ) − L f n ( f n − 1 … f l ( x f , w f ) ) )
It is evident that the optimal quantization of the l t h network block is correlated with subsequent quantized network blocks. Whether the optimal solution for Equation (8) is applicable to Equation (13) depends on the discrepancy between f n q ( f n − 1 q … f l ( · ) ) and f n ( f n − 1 … f l ( · ) ) . Consequently, block-wise quantization disregards the influence of subsequent quantized network blocks, leading to suboptimal quantization of each network block.

4. AE-Qdrop

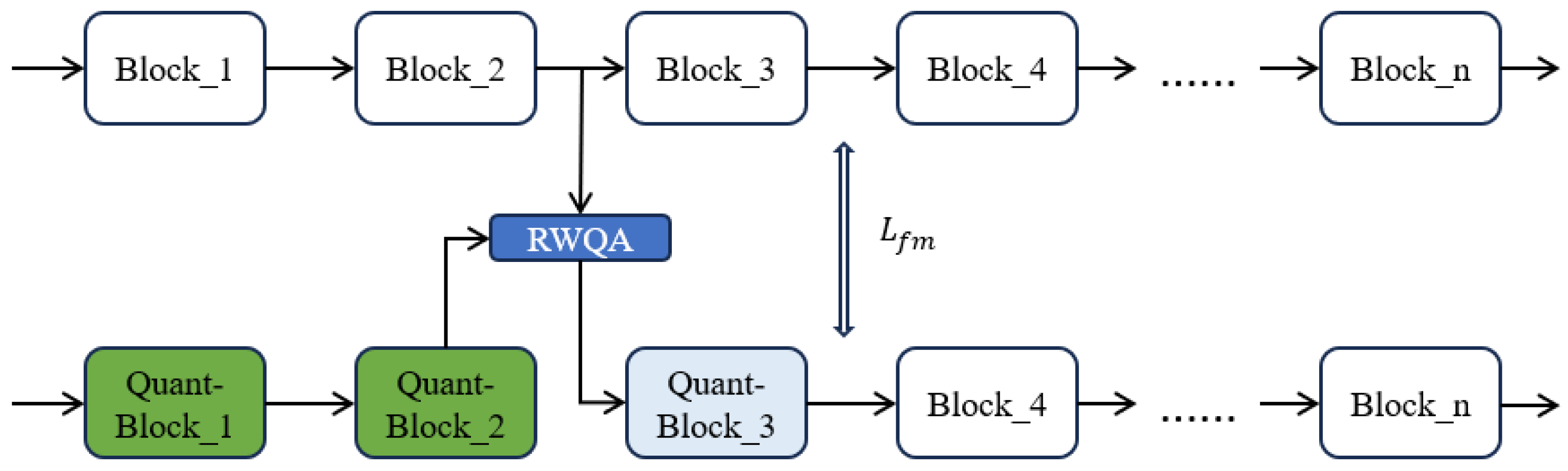
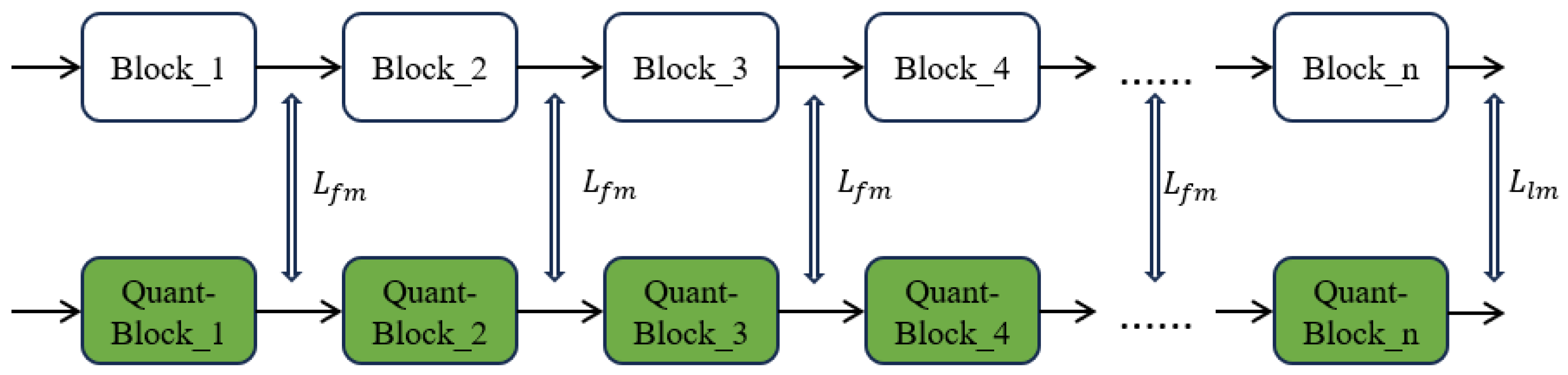
AE-Qdrop is a two-stage post-training quantization algorithm, consisting of block-wise reconstruction and global fine-tuning. In the block reconstruction phase (as depicted in Figure 2), a progressive optimization strategy is adopted, replacing the adaptive rounding. This approach, devoid of the inherent drawbacks of adaptive rounding, achieves high-precision and efficient quantization. The random weighted quantized activation is utilized to enhance the diversity of activation, effectively improving the generalization performance of the quantized model. Block-wise reconstruction provides a pre-quantized model for global fine-tuning. Global fine-tuning (as shown in Figure 3) aims to correct the suboptimal weights of the pre-quantized model via feature matching and logit matching. It must be noted that the limited unlabeled calibration samples render a single-stage global fine-tuning insufficient for achieving a high-precision quantized model. Hence, block-wise reconstruction is crucial and indispensable.

4.1. Block-wise Reconstruction: Progressive Optimization Strategy

AE-Qdrop indirectly optimizes Δ w f by adjusting w f . However, this optimization process faces several challenges. On one hand, the gradient mismatch problem of the straight-through estimator becomes prominent when weights and activations are quantized to low bit-widths, potentially causing confusion in the optimization direction. On the other hand, a limited number of calibration samples can easily lead to overfitting. To address these challenges, we propose a progressive optimization strategy.
At first, we quantize the activation but do not quantize the weight. The weight w f can be updated along the correct gradient direction since the straight-through estimator is not required. It is worth noting that the updated weight can absorb the weight perturbation generated by activation quantization, i.e., w f ← w f ⊙ ( 1 + τ ( x ) ) .
Next, the new weight is quantized. Considering that the previous optimization has significantly reduced weight perturbation, Equation (8) will be close to Equation (3). Therefore, we only optimize the weight rounding direction to avoid overfitting. Different from AdaRound, We achieve optimal rounding by setting the upper and lower bounds of w f :
w f * ∈ [ s w ( clip floor w f s w + z , q m i n , q m a x − z ) , s w ( clip floor w f s w + 1 + z , q m i n , q m a x − z ) ]
If the updated weight w f * ≥ s w ( clip floor w f 1 s w + 0.5 + z , q m i n , q m a x − z ) , rounding up is the best rounding. On the contrary, rounding down is the best rounding. This scheme does not introduce additional optimization tensors to the weight quantizer and does not require additional regularization terms. It focuses entirely on minimizing the reconstruction error. Since the rounding operation is a step function, small weight updates cannot be reflected in the next calculation in time, thus increasing the difficulty of rounding optimization. For this reason, in the early stage of rounding optimization, We keep the truncation operation of the weight quantizer, but cancel the rounding operation. Weight updates of any magnitude can be reflected in the calculation results in time, thus accelerating the convergence of weight in the rounding direction.
In conclusion, progressive optimization divides block-wise reconstruction into three stages:
  • Quantize activation while keeping weight unquantized. Optimize w f to absorb weight perturbations caused by activation quantization and then set the upper and lower bounds of w f according to the equation (10) to achieve rounding optimization.
  • Quantize activation and maintain truncation calculation of the weight quantizer but disable the rounding calculation.
  • Quantize both activation and weight.
In the first stage, the weights are not quantized; hence, w q = w f . The optimization space of Δ w f is free of any constraints. During the second stage, as the bounds for w f are set and rounding operations are not considered, the optimization space for w q and Δ w f is confined within a continuous numerical range. In the final stage, each element of Δ w f is restricted to a binary set. Compared to AdaRound, the progressive optimization strategy offers a larger optimization space and higher optimization efficiency.

4.2. Block-wise Reconstruction: Random weighted Quantized Activation

Considering the limited number of samples available for post-training quantization, Qdrop introduces a random dropout quantized activation (RDQA) scheme to alleviate overfitting in block-wise reconstruction:
q y ← y 1 + u ( y ) q y − y y
Here, u ( y ) is a binary tensor randomly sampled from the Bernoulli distribution B ( 1 , 0.5 ) with the same dimension as y. Similar to the Dropout mechanism [31], RQQA is only employed during the quantization phase and is not applied during the inference stage, which can also be regarded as a data augmentation scheme.
Inspired by Mixup [32], We proposes random weighted quantized activation (RWQA) in AE-Qdrop:
q y ← t ( y ) q y + ( 1 − t ( y ) ) y = y ( 1 + t ( y ) q y − y y )
Here, t ( y ) is a FP tensor sampled from a uniform distribution U ( 0 , 1 ) with the same dimensions as y. In comparison to RQQA, RWAQ offers a more diverse set of feature inputs for block reconstruction, further enhancing the generalization capability of the quantization model.

4.3. Global Fine-tuning

Block-wise reconstruction produces a pre-quantized model. The analysis presented in Section 3.3 reveals that each quantized network layer still has the potential for further optimization. As a result, AE-QDrop introduces global fine-tuning. We further analyze the optimization the l t h network block in the pre-quantized model:
L f n q ( f n − 1 q . . . f l ( x q l , w q l ) ) ) − L f n ( f n − 1 . . . f l ( x f l , w f l ) ) ) = L f n q ( f n − 1 q . . . f l ( x q l , w q l ) ) ) − L f n q ( f n − 1 q . . . f l ( x f l , w f l ) ) ) + L f n q ( f n − 1 q . . . f l ( x f l , w f l ) ) ) − L f n ( f n − 1 . . . f l ( x f l , w f l ) ) ) ≈ ▵ x l T g x ( q , l ) x f l , w f l + ▵ w l T g w ( q , l ) x f l , w f l + 2 · ▵ y l T I ▵ y l + L f n q ( f n − 1 q . . . f l + 1 ( x q l + 1 , w q l + 1 ) ) ) − L f n ( f n − 1 . . . f l + 1 ( x f l + 1 , w f l + 1 ) ) ) ≈ ∑ i = l n ▵ x i T g x ( q , i ) x f i , w f i + ∑ i = l n ▵ w i T g w ( q , i ) x f i , w f i + 2 ∑ i = l n ▵ y i T I ▵ y i
Therefore, global fine-tuning aims to minimize ∑ i = 1 n ▵ y i T I ▵ y i , g x ( q , i ) and g w ( q , i ) . ∑ i = 1 n ▵ y i T I ▵ y i can be calculated directly, indicating that the output of each quantized network block should simultaneously match the output of the FP network block. We refer to this as feature matching. However, g x ( q , i ) and g w ( q , i ) cannot be calculated directly because the label of the sample is unknown.
If the quantized network has converged just like the FP network, g x ( q , i ) and g w ( q , i ) will be approximately equal to 0. Qualitatively speaking, for the same input sample, if the output of the quantized network aligns with that of the FP network, it is posited that the quantized network is also in a state of convergence. Therefore, we optimize ∑ i = l n ▵ x i T g x ( q , i ) x f i , w f i and ∑ i = l n ▵ w i T g w ( q , i ) x f i , w f i based on the perspective of knowledge distillation. The FP model is regarded as the teacher, while the quantized model is perceived as the student. The KL distance between the output z of the FP network and the output z q of the quantized network will be minimized, which is called logit matching. In order to avoid overfitting, we only correct the rounding direction of the weight. To sum up, the loss function L g f of global fine-tuning is defined as:
L f m i = ▵ y i T I ▵ y i = ∥ y q i − y i ∥ 2 L l m = ∑ i = 1 m p i z ; T log p i z ; T p i z q ; T , p i z ; T = e z i / T ∑ j m e z j / T L g f = L l m + θ n ∑ i = 1 n L f m i
where T and θ represent the distillation temperature and hyperparameter respectively.

5. Experimental Result

5.1. Experimental setup

We conduct extensive experiments on various network architectures and demonstrate the top1 classification accuracy of AE-Qdrop in the Imagenet dataset. Our code is based on the open source implementation of Qdrop. Quantized networks include ResNet18 (Res18), ResNet50 (Res50), MobileNetV2 (MV2), RegNet-600MF (Reg600M), RegNet-3.2GF (Reg3.2G) and MnasNetx2 (MNx2). All experiments are based on GeForce RTX 3090 Ti GPU, Intel(R) Core(TM) i7-7700K CPU hardware platform. The calibration dataset consists of 1024 randomly selected images from the ImageNet training set.
In block reconstruction, each network block undergoes optimization iterations totaling 2000. The iterative counts for the three phases of progressive weight optimization are distributed as [800, 400, 800]. The Adam optimizer is employed, starting with an initial learning rate of 4 × 10 − 4 , and varies according to a cosine decay strategy. The global fine-tuning iteration count is 2000, with a distillation temperature T = 20 and a hyperparameter θ = 0.1 . The SGD optimizer is utilized, commencing with an initial learning rate of 1 × 10 − 6 , and also follows a cosine decay strategy.

5.2. Comprehensive Comparison

In Table 1, the quantization accuracy of AE-Qdrop is compared with several mainstream PTQ methods. Under 4w4a, LAPQ optimizes only the quantization scale factors without adjusting the weights, resulting in the poorest quantization performance. Adaround is based on layer-wise reconstruction and ignores inter-layer dependencies, so its accuracy is lower than that of Brecq. The Brecq method, not considering the weight perturbations caused by activation quantization, exhibits notably lower quantization accuracy than Qdrop and AE-Qdrop. The drawbacks of adaptive rounding and block-wise reconstruction are not apparent at 4-bit, hence the performance of AE-Qdrop and Qdrop is comparable. However, as the bit-width decreases, AE-Qdrop shows a significant accuracy advantage over Qdrop, especially for lightweight networks like MV2 and MNx2. For instance, at 2w2a, the quantization accuracy of AE-Qdrop surpasses that of Qdrop by 6.49% (MV2) and 3.22% (MNx2). Lightweight networks have larger parameter distribution ranges and smaller parameter sizes. The former will lead to larger quantization errors, increasing the difference between the optimal solutions of Equation (7) and Equation (8), while the latter weakens the optimization ability of adaptive rounding. Notably, at 4w2a, AE-Qdrop’s performance advantage is most pronounced, exceeding Qdrop by 12.07% (MV2) and 8.36% (MNx2). Compared to 2-bit weights, 4-bit weights represent more information. The progressive weight optimization strategy in AE-Qdrop relaxes the constraints on weights, allowing the 4-bit weights to fully utilize their representational capacity to minimize quantization error. Therefore, AE-Qdrop achieves its greatest accuracy advantage at 4w2a.
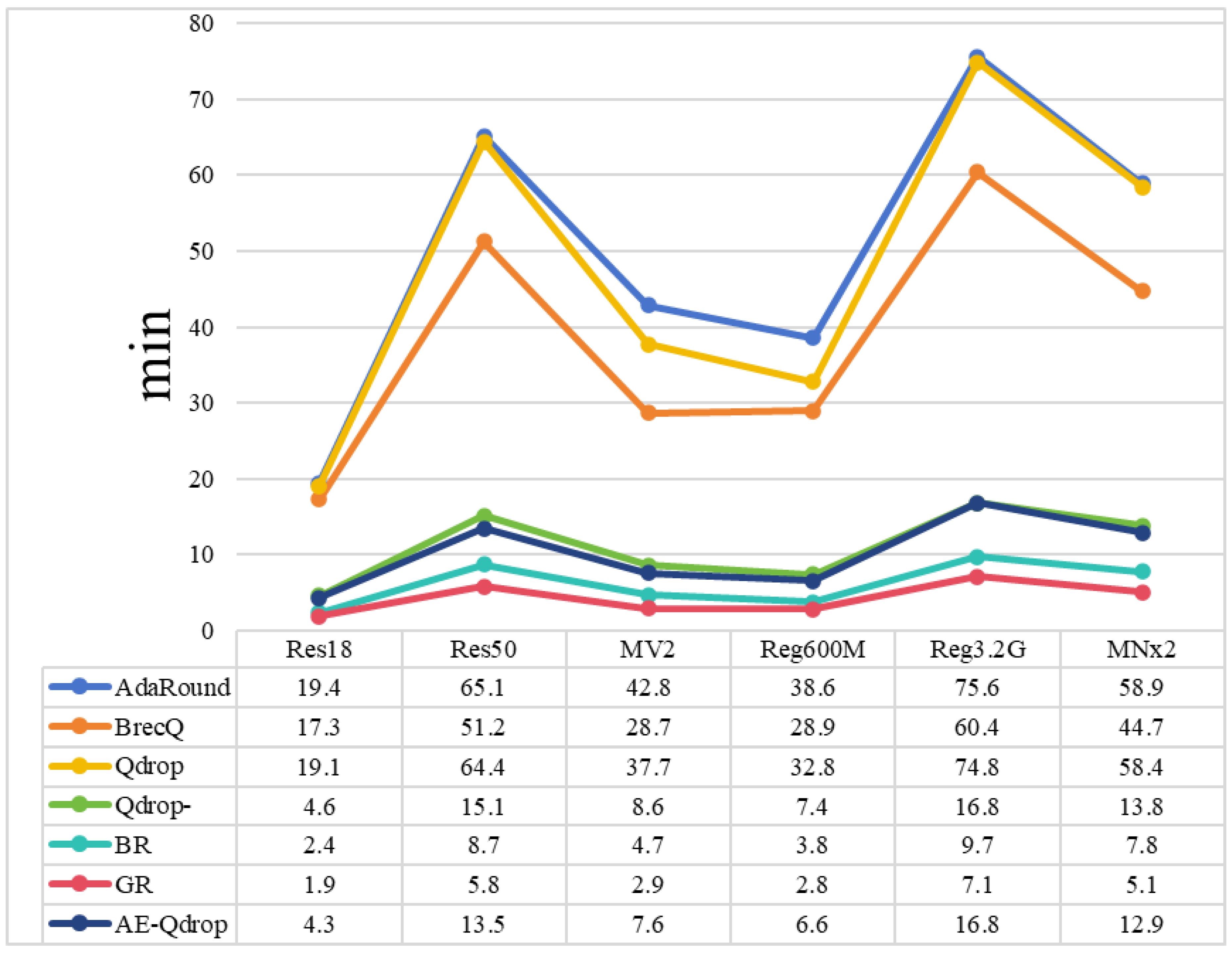
Figure 4 depicts the time required to perform AE-Qdrop compared to other PTQ methods. Among them, Adaround has the lowest quantization efficiency. Despite Brecq having a slight advantage over Qdrop in terms of quantization efficiency, it does not make up for its poor quantization accuracy. For MV2, which is widely deployed in mobile applications, AE-Qdrop only needs 7.7 minutes for quantization (with blockwise reconstruction and global fine-tuning taking 4.7 minutes and 2.9 minutes, respectively). Its quantization efficiency is five times that of Qdrop and achieves higher quantization accuracy, effectively demonstrating that AE-Qdrop is a high-precision and efficient quantization scheme. Qdrop- represents the quantization result when the number of adaptive rounding iterations in Qdrop is set to 4000. Although the quantization efficiency of Qdrop- is close to AE-Qdrop, the reduction in iteration count leads to a noticeable decrease in quantization accuracy. As shown in Table 1, under 2w2a, the accuracy of Qdrop- drops by 3.79% to 8.01% compared to Qdrop, and by 6.06% to 11.06% compared to AE-Qdrop.

5.3. Ablation Study

In Table 2, we explore the impact of various design components on quantization performance under 2w2a. The baseline denotes the results of block reconstruction without the use of progressive optimization strategies and data augmentation. Few calibration samples make block reconstruction prone to overfitting; thus, the performance gains from data augmentation are quite significant, especially for larger networks like ResNet and RegNet, with an accuracy improvement of over 3.6%. Compared to RDQA proposed in Qdrop, RWQA offers a performance gain of 0.6% to 3.7%. POS shows more pronounced effects on MV2 and MNx2, with quantization accuracy improvements of 4.66% and 4.77%, respectively. Combining RWQA and POS with the Baseline results in single-stage block reconstruction. This combination enhances performance by 5.3% to 13.15%, reaffirming the effectiveness of RWQA and POS. After block-wise reconstruction, executing global finetune yields the quantization results for AE-Qdrop. As observed, GF significantly improves the quantization accuracy for MV2, MNx2, and Reg600M. The larger parameter volume of ResNet and Reg3.2G imparts robustness against quantization noise, which reduces the discrepancy between f q n ( f q n − 1 … f l ( · ) ) and f n ( f n − 1 … f l ( · ) ) ; thus, the gains from global finetune are limited.
In Table 3, we explore the quantization results achieved solely through single-stage global fine-tuning. Mean Squared Error (MSE) represents an early approach to post-training quantization, which does not involve weight adjustment. It determine quantization scale factors by minimizing the L2 norm of parameter quantization errors. In recent works and in AE-Qdrop, MSE is utilized to provide a pre-quantized network for block-wise reconstruction. under 4w4a, although the quantization results of MSE in significant accuracy loss, the quantized models retain some image recognition capability. Global fine-tuning significantly enhances performance, but there is a notable disparity compared to the results of Brecq and Qdrop. As quantization bit-width decreases, especially at 2w2a, the MSE-derived quantized model completely fails, and global fine-tuning offers no benefits, indicating that global fine-tuning alone cannot retrain a quantized network via just 1024 calibration samples. Therefore, for optimal quantization performance, the block-wise reconstruction phase in AE-Qdrop is indispensable, providing a favorable initial state for global fine-tuning.

6. Conclusion

This paper theoretically analyzes the shortcomings of adaptive rounding and block reconstruction and introduces a novel post-training quantization algorithm, AE-Qdrop. The progressive optimization strategy provides a larger optimization space for block reconstruction. Random weighted quantized activation introduces more diverse activations to the network layer. Global fine-tuning takes into account dependencies between network blocks and further improves quantization accuracy through feature matching and logit matching. Numerous experiments demonstrate that AE-Qdrop is a high-precision and efficient post-training quantization algorithm. Currently, there is still a significant accuracy gap between low-bit (<4bit) PTQ and full-precision networks. In future work, we will explore combining AE-Qdrop with other techniques such as bias correction, outlier separation, etc., to achieve better quantization performance.

Author Contributions

Conceptualization, Methodology, Software, Writing original draft preparation, Jixing Li; Conceptualization, Methodology, Gang Chen; Resources, Supervision, Funding acquisition, Min Jin. Validation, Investigation, Wenyu Mao; Supervision, Project administration, Huaxiang Lu. All authors have read and agreed to the published version of the manuscript

Funding

This research was supported in part by the National Natural Science Foundation of China 92364202 and in part by the CAS Strategic Leading Science and Technology Project XDA18040400, XDB44000000.

Data Availability Statement

Imagenet Dataset: https://image-net.org/. Other data will be made available on request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Zhu, A.; Wang, B.; Xie, J.; Ma, C. Lightweight Tunnel Defect Detection Algorithm Based on Knowledge Distillation. Electronics 2023, 12, 3222. [Google Scholar] [CrossRef]
  2. Gou, J.; Yu, B.; Maybank, S.J.; Tao, D. Knowledge distillation: A survey. International Journal of Computer Vision 2021, 129, 1789–1819. [Google Scholar] [CrossRef]
  3. Baymurzina, D.; Golikov, E.; Burtsev, M. A review of neural architecture search. Neurocomputing 2022, 474, 82–93. [Google Scholar] [CrossRef]
  4. Song, Y.; Wang, A.; Zhao, Y.; Wu, H.; Iwahori, Y. Multi-Scale Spatial–Spectral Attention-Based Neural Architecture Search for Hyperspectral Image Classification. Electronics 2023, 12, 3641. [Google Scholar] [CrossRef]
  5. Li, Y.; Adamczewski, K.; Li, W.; Gu, S.; Timofte, R.; Van Gool, L. Revisiting random channel pruning for neural network compression. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2022; pp. 191–201. [Google Scholar]
  6. Shen, W.; Wang, W.; Zhu, J.; Zhou, H.; Wang, S. Pruning-and Quantization-Based Compression Algorithm for Number of Mixed Signals Identification Network. Electronics 2023, 12, 1694. [Google Scholar] [CrossRef]
  7. Schotthöfer, S.; Zangrando, E.; Kusch, J.; Ceruti, G.; Tudisco, F. Low-rank lottery tickets: finding efficient low-rank neural networks via matrix differential equations. Advances in Neural Information Processing Systems 2022, 35, 20051–20063. [Google Scholar]
  8. Gholami, A.; Kim, S.; Dong, Z.; Yao, Z.; Mahoney, M.W.; Keutzer, K. A survey of quantization methods for efficient neural network inference. In Low-Power Computer Vision; Chapman and Hall/CRC, 2022; pp. 291–326.
  9. Krishnamoorthi, R. Quantizing deep convolutional networks for efficient inference: A whitepaper. arXiv 2018, arXiv:1806.08342 2018. [Google Scholar]
  10. Nagel, M.; Amjad, R.A.; Van Baalen, M.; Louizos, C.; Blankevoort, T. Up or down? adaptive rounding for post-training quantization. In Proceedings of the International Conference on Machine Learning. PMLR; 2020; pp. 7197–7206. [Google Scholar]
  11. Li, Y.; Gong, R.; Tan, X.; Yang, Y.; Hu, P.; Zhang, Q.; Yu, F.; Wang, W.; Gu, S. BRECQ: Pushing the Limit of Post-Training Quantization by Block Reconstruction. In Proceedings of the 9th International Conference on Learning Representations, ICLR 2021, Virtual Event, Austria, 3-7 May 2021. OpenReview.net, 2021. [Google Scholar]
  12. Wei, X.; Gong, R.; Li, Y.; Liu, X.; Yu, F. QDrop: Randomly Dropping Quantization for Extremely Low-bit Post-Training Quantization. In Proceedings of the the Tenth International Conference on Learning Representations, ICLR 2022, Virtual Event, 25-29 April 2022. OpenReview.net, 2022. [Google Scholar]
  13. Bengio, Y.; Léonard, N.; Courville, A. Estimating or propagating gradients through stochastic neurons for conditional computation. arXiv 2013, arXiv:1308.3432 2013. [Google Scholar]
  14. Jacob, B.; Kligys, S.; Chen, B.; Zhu, M.; Tang, M.; Howard, A.; Adam, H.; Kalenichenko, D. Quantization and training of neural networks for efficient integer-arithmetic-only inference. In Proceedings of the IEEE conference on computer vision and pattern recognition; 2018; pp. 2704–2713. [Google Scholar]
  15. Esser, S.K.; McKinstry, J.L.; Bablani, D.; Appuswamy, R.; Modha, D.S. Learned Step Size quantization. In Proceedings of the 8th International Conference on Learning Representations, ICLR 2020, Addis Ababa, Ethiopia, 26-30 April 2020. OpenReview.net, 2020. [Google Scholar]
  16. Bhalgat, Y.; Lee, J.; Nagel, M.; Blankevoort, T.; Kwak, N. Lsq+: Improving low-bit quantization through learnable offsets and better initialization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops; 2020; pp. 696–697. [Google Scholar]
  17. Gong, R.; Liu, X.; Jiang, S.; Li, T.; Hu, P.; Lin, J.; Yu, F.; Yan, J. Differentiable soft quantization: Bridging full-precision and low-bit neural networks. In Proceedings of the IEEE/CVF international conference on computer vision; 2019; pp. 4852–4861. [Google Scholar]
  18. Liu, Z.; Cheng, K.T.; Huang, D.; Xing, E.P.; Shen, Z. Nonuniform-to-uniform quantization: Towards accurate quantization via generalized straight-through estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2022; pp. 4942–4952. [Google Scholar]
  19. Li, Z.; Ni, B.; Li, T.; Yang, X.; Zhang, W.; Gao, W. Residual quantization for low bit-width neural networks. IEEE Transactions on Multimedia 2021. [Google Scholar] [CrossRef]
  20. Xu, W.; Li, F.; Jiang, Y.; Yong, A.; He, X.; Wang, P.; Cheng, J. Improving extreme low-bit quantization with soft threshold. IEEE Transactions on Circuits and Systems for Video Technology 2022, 33, 1549–1563. [Google Scholar] [CrossRef]
  21. Shin, S.; Hwang, K.; Sung, W. Fixed-point performance analysis of recurrent neural networks. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP); IEEE, 2016; pp. 976–980. [Google Scholar]
  22. Banner, R.; Nahshan, Y.; Soudry, D. Post training 4-bit quantization of convolutional networks for rapid-deployment. Advances in Neural Information Processing Systems 2019, 32. [Google Scholar]
  23. Nagel, M.; Baalen, M.v.; Blankevoort, T.; Welling, M. Data-free quantization through weight equalization and bias correction. In Proceedings of the IEEE/CVF International Conference on Computer Vision; 2019; pp. 1325–1334. [Google Scholar]
  24. Fang, J.; Shafiee, A.; Abdel-Aziz, H.; Thorsley, D.; Georgiadis, G.; Hassoun, J.H. Post-training piecewise linear quantization for deep neural networks. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part II 16. Springer, 2020; pp. 69–86. [Google Scholar]
  25. Park, D.; Lim, S.G.; Oh, K.J.; Lee, G.; Kim, J.G. Nonlinear depth quantization using piecewise linear scaling for immersive video coding. IEEE Access 2022, 10, 4483–4494. [Google Scholar] [CrossRef]
  26. Zhao, R.; Hu, Y.; Dotzel, J.; De Sa, C.; Zhang, Z. Improving neural network quantization without retraining using outlier channel splitting. In Proceedings of the International conference on machine learning. PMLR; 2019; pp. 7543–7552. [Google Scholar]
  27. Zhao, M.; Ning, K.; Yu, S.; Liu, L.; Wu, N. Quantizing Oriented Object Detection Network via Outlier-Aware Quantization and IoU Approximation. IEEE Signal Processing Letters 2020, 27, 1914–1918. [Google Scholar] [CrossRef]
  28. Jeong, E.; Kim, J.; Tan, S.; Lee, J.; Ha, S. Deep learning inference parallelization on heterogeneous processors with tensorrt. IEEE Embedded Systems Letters 2021, 14, 15–18. [Google Scholar] [CrossRef]
  29. Wu, D.; Tang, Q.; Zhao, Y.; Zhang, M.; Fu, Y.; Zhang, D. EasyQuant: Post-training Quantization via Scale Optimization. arXiv 2006, arXiv:2006.16669. [Google Scholar]
  30. Nahshan, Y.; Chmiel, B.; Baskin, C.; Zheltonozhskii, E.; Banner, R.; Bronstein, A.M.; Mendelson, A. Loss aware post-training quantization. Machine Learning 2021, 110, 3245–3262. [Google Scholar] [CrossRef]
  31. Baldi, P.; Sadowski, P.J. Understanding dropout. Advances in neural information processing systems 2013, 26. [Google Scholar]
  32. Verma, V.; Lamb, A.; Beckham, C.; Najafi, A.; Mitliagkas, I.; Lopez-Paz, D.; Bengio, Y. Manifold mixup: Better representations by interpolating hidden states. In Proceedings of the International conference on machine learning. PMLR; 2019; pp. 6438–6447. [Google Scholar]
Preprints 92912 g001
Figure 1. A simple calculation example to illustrate that adaptive rounding can not provide an optimal solution.
Figure 1. A simple calculation example to illustrate that adaptive rounding can not provide an optimal solution.
Preprints 92912 g001
Preprints 92912 g002
Figure 2. The block-wise reconstruction stage of AE-Qdrop.
Figure 2. The block-wise reconstruction stage of AE-Qdrop.
Preprints 92912 g002
Preprints 92912 g003
Figure 3. The global fine-tuning stage of AE-Qdrop.
Figure 3. The global fine-tuning stage of AE-Qdrop.
Preprints 92912 g003
Preprints 92912 g004
Figure 4. Quantization execution time.
Figure 4. Quantization execution time.
Preprints 92912 g004
Table 1. Quantization accuracy comparison results.
Table 1. Quantization accuracy comparison results.
Method Bits(W/A) Res18 Res50 MV2 Reg600M Reg3.2G MNx2
FP32 32/32 71.01 76.63 72.62 73.52 78.46 76.52
LAPQ 4/4 60.30 70.00 49.70 57.71 55.89 65.32
AdaRound 67.96 73.88 61.52 68.20 73.85 68.86
BrecQ 68.16 72.95 62.08 68.94 73.94 71.01
Qdrop- 69.05 74.79 67.72 70.60 76.21 72.57
Qdrop 69.16 74.91 67.86 70.95 76.45 72.81
AE-Qdrop 69.24 74.98 67.93 70.83 76.54 72.68
AdaRound 4/2 0.44 0.17 0.29 2.14 0.10 0.93
BrecQ 31.19 16.95 0.28 4.22 3.47 6.34
Qdrop- 56.46 61.87 10.26 46.68 59.58 16.71
Qdrop 58.10 63.26 17.03 49.78 61.87 33.96
AE-Qdrop 58.48 64.53 29.10 52.71 64.29 42.32
AdaRound 2/2 0.39 0.13 0.12 0.79 0.11 0.40
BrecQ 25.91 8.26 0.19 2.49 1.72 0.38
Qdrop- 46.12 48.81 6.18 31.30 48.38 16.37
Qdrop 51.55 55.21 9.97 39.31 53.88 24.21
AE-Qdrop 52.24 55.55 16.46 40.58 54.56 27.43
Table 2. Under 2w2a, the impact of various design components on quantization performance.
Table 2. Under 2w2a, the impact of various design components on quantization performance.
Method Res18 Res50 MV2 Reg600M Reg3.2G MNx2
Baseline 46.40 47.90 6.44 27.73 41.17 15.72
Baseline+RDQA 50.00 52.29 7.52 36.29 52.89 16.64
Baseline+RWQA 51.05 52.89 8.78 36.92 53.51 20.35
Baseline+POS 47.12 49.55 11.10 28.75 41.74 20.49
Baseline+RWQA+POS 51.73 55.36 13.33 39.06 54.32 24.61
Baseline+RWQA+POS+GF 52.24 55.55 16.46 40.58 54.56 27.43
Table 3. The quantization results achieved solely through single-stage global fine-tuning.
Table 3. The quantization results achieved solely through single-stage global fine-tuning.
Method Res18 Res50 MV2 Reg600M Reg3.2G MNx2
4w4a MSE 49.75 65.54 22.40 51.70 66.75 49.71
MSE+GF 65.05 69.10 36.69 60.05 70.24 56.68
4w2a MSE 9.33 4.35 0.11 1.9 2.01 0.27
MSE+GF 25.18 6.98 0.18 3.3 4.43 0.28
2w2a MSE 0.08 0.16 0.11 0.15 0.11 0.10
MSE+GF 0.08 0.10 0.09 0.16 0.17 0.10
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated