Prerpints.org logo
Preprint
Article

3D Magnetization Textures: Toroidal Magnetic Hopfion Stability in Cylindrical Samples

Altmetrics

Downloads

116

Views

60

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

11 December 2023

Posted:

12 December 2023

You are already at the latest version

Alerts
Abstract
Topologically non-trivial magnetization configurations in ferromagnetic materials on the nanoscale, such as hopfions, skyrmions, vortices, etc., attract considerable attention of researchers during the last years. In this article applying the theory of micromagnetism, I demonstrate that the toroidal hopfion magnetization configuration is a metastable state of a thick cylindrical ferromagnetic nanodot or a nanowire of a finite radius. Existence of this state is a result of the competition of the exchange, magnetostatic, and magnetic anisotropy energies. The Dzyaloshinskyi-Moriya exchange interaction and surface magnetic anisotropy are of the second importance for the hopfion stabilization. The toroidal hopfion metastable magnetization configuration may be reached in the process of the sample re-magnetizing by applying an external magnetic field along the cylindrical axis.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

Topologically non-trivial two- (2D) and three- (3D) dimensional magnetization configurations in ferromagnetic materials, such as hopfions, skyrmions, vortices and domain walls, attract considerable attention of researchers during the last years [1]. Stability of 3D magnetization configurations and the role of 3D (Hopf index), 2D (skyrmion number) topological charges and gyrovector in their dynamics are still far from complete understanding. Nowadays 3D magnetization configurations in ferromagnetic materials on the nanoscale can be observed experimentally using electron holography or X-ray magnetic circular dichroism [2, 3, 4].
The important question is stability of the different 3D magnetization configurations. The standard approach to consider stability and dynamics of magnetization configurations in magnetically ordered media is micromagnetism and the Landau-Lifshitz equation of motion of the magnetization field. It was established in the field theory [5, 6] that any physical system with the second spatial derivatives in the Lagrange-Euler equation or squared gradient field term in the Lagrangian has no stable, time-independent, localized solutions in 3D case for any form of the potential. Now this statement is referred to as the Hobard—Derrick theorem. However, stable localized solutions (localized solitons) can exist if there are any energy contributions linear with respect to spatial derivatives or with higher-order spatial derivatives of the field [7, 8]. Prominent example of the energy terms with the first derivatives are the so called Lifshitz invariants accounting for the Dzyaloshinskii-Moriya interactions (DMI) in magnetic materials with broken inversion symmetry. It was proved theoretically that such terms stabilize quasi two-dimensional localized structures in the form of magnetic skyrmions [9]. Other opportunity to get stable 3D field configurations is accounting for the higher-order spatial derivatives in the Lagrangian. The terms quartic in spatial derivatives were suggested by Skyrme [10] and Faddeev [11] within the classical field theory. It was shown that the Faddeev-Skyrme Lagrangian has stable 3D localized soliton solutions in the form of toroidal hopfions [12, 13]. The toroidal hopfions are some kinds of the localized topological solitons and are characterized by non-zero values of 3D topological charge (Hopf index) [14, 15]. It was shown recently [16] that the classical Heisenberg model with competing long-range exchange interactions can result in the terms quadratic in the second spatial derivatives of magnetization field. Although such model is beyond the standard theory of micromagnetism, it may result in stabilization of the toroidal magnetic hopfions. The question is: whether is it possible to stabilize the magnetic hopfions in a ferromagnet within the standard exchange approach (avoid exotic exchange interactions) due to non-zero DMI terms and/or magnetostatic energy? Such energy contributions are beyond the field theory and applicability of the Hobart-Derrick theory to the evaluation of stability of the magnetic field configurations should be reconsidered. The simple scaling analysis accounting for the DMI terms was conducted in Ref. [17]. However, this analysis ignored the magnetostatic interaction (which is unavoidable in real ferromagnetic samples) and the finite sample sizes. The non-local magnetostatic interaction is usually not considered in the theory of magnetic skyrmions and hopfions or accounted in a simplified form. The skyrmions are considered either in the bulk magnetic crystals without inversion symmetry or in ultrathin films. In both cases the magnetostatic interaction is reduced to a local form of some extra contribution to the magnetic anisotropy energy. Accounting for the magnetostatic interaction in relatively thick magnetic dots [18] allows to stabilize quasi-2D skyrmions without presence of any DMI, if a small out-of-plane magnetic anisotropy is included to the energy functional. The magnetostatic interaction was not included to the energy functional in Refs. [19 - 21] describing the magnetic hopfions in thick cylindrical dots without explanations of its importance. We note that the magnetostatic interaction can also lead to stabilization of other kinds of complicated magnetization textures: the Bloch point hopfions with non-zero Hopf index or half-hedgehog (3D quasi-skyrmion) magnetization textures even in soft magnetic materials with no DMI [22-24].
In this article, I consider the magnetic energy functional consisting of the exchange, magnetostatic, Dzyaloshinskii-Moriya and magnetic anisotropy energies. I show that the magnetostatic energy is crucial for the toroidal hopfion stability (metastability) in a cylindrical ferromagnetic nanodots and nanowires. The DMI energy term also supports the stabilization of the magnetic toroidal hopfions. However, the DMI energy is of second importance in comparison with the magnetostatic energy and the hopfion can be stable in soft magnetic materials with no DMI.

2. Materials and Methods

In this section, I give a definition of the 3D topological charge (Hopf index) of a magnetization texture and present explicit equations describing magnetization of the toroidal magnetic hopfion. Then, I analyze the energy and stability of the magnetic hopfion in magnetic cylindrical nanodots and nanowires, using the methods of the theory of micromagnetism and determine the main magnetic and geometrical parameters of existence of the stable hopfion configurations in the restricted cylindrical geometry.
The Hopf index of a 3D magnetization texture is calculated as an integral over the system volume from the dot product of the emergent magnetic field vector potential and the emergent magnetic field A · B [15, 25]. A general expression of the Hopf invariant for the mapping of the 3D space (r) to the unit sphere m r 2 = 1 of the magnetization field is
Q H = 1 4 π 2 ∫ d V A · B .
We use the general definition of the emergent electromagnetic field tensor (in the units of ℏ / 2 e ) resulting from an inhomogeneous spin texture m r in the form F μ ν m = m · ∂ μ m × ∂ ν m , where m r = M r / M s is the unit magnetization vector, M s is the saturation magnetization, ∂ μ = ∂ / ∂ x μ denote spatial derivatives and the indices μ ,   ν corresponds to the components of 3D radius-vector r in an orthogonal coordinate system. The field tensor is related to the emergent field vector potential A as F μ ν m = ∂ μ A ν m − ∂ ν A μ m . The emergent magnetic field B = ∇ × A can be defined as in the standard electrodynamics B λ m = ε λ μ ν F μ ν m / 2 [26, 27].
The emergent magnetic field B is unambiguously defined for any given magnetization texture m r . However, to calculate the Hopf index we need to find the emergent field vector potential A in a proper gauge as shown recently in Ref. [27]. Alternative approach to find the Hopf index is using of the Hopf mapping. The definition of the Hopf mapping of the 3D coordinate space R 3 (represented by the unit radius hypersphere S 3 in the 4D space) to the unit sphere 𝑆2(𝒎) is [28] m = Z + σ Z [28], where σ = σ x , σ y , σ z are the Pauli matrices and Z = Z 1 , Z 2 T is a spinor composed from the hypersphere coordinates X i , i = 1, 2, 3, 4 satisfying the condition ∑ i = 1 4 X i 2 = 1 . The spinor components are Z 2 = X 1 + i X 2 , Z 1 = X 4 + i X 3 , and their normalization is Z 1 2 + Z 2 2 = 1 . The Hopf index (3D topological charge) can be then represented as triple dot product
Q H = 1 4 π 2 ∫ d V Z + ∇ Z · ∇ Z + × ∇ Z ,
in the form similar to the skyrmion number (2D topological charge).
The radius vector r can be described in the different orthogonal coordinate systems. However, the hopfion magnetization m r is the simplest in the toroidal coordinates r η , β , φ [12, 13]. There is the connection between the cylindrical ρ , φ , z (or Cartesian (x, y, z)) and toroidal η , β , φ coordinates [29] ρ = a s i n h η / τ , z = a s i n β / τ , φ = φ ,   τ = c o s h η − c o s β , where the toroidal parameter η varies from 0 to ∞ , the poloidal angle β varies from − π to π , the azimuthal angle φ varies from 0 to 2 π , and a is a scale parameter having sense of the hopfion radius. The z-component of the hopfion magnetization [27] is
m z η = p 1 − c o s h 2 m η t a n h 2 n η 1 + c o s h 2 m η t a n h 2 n η ,
where p = m z η = 0 is the hopfion polarity, p = ± 1 .
Other magnetization components in the toroidal coordinates can be found from the expression
m x r + i m y r = 1 − m z 2 η e x p i n φ + m β .           ( 3 ' )
For the particular case n = 1 and m = 1 , the function m z η is reduced to the well-known simple form m z η = p 1 − 2 t a n h 2 η . The Hopf index Q H = m n p of the toroidal magnetic hopfion is integer for an infinite sample. The Hopf index (3D topological charge) is proportional to the product of the poloidal m and azimuthal n vorticities and does not depend on the details of the hopfion magnetization profile m z η . Below we consider the simplest hopfion with n = 1 , m = 1 and Q H =1, which is assumed to be the lowest energy toroidal hopfion.
The physical system under consideration is a thick cylindrical ferromagnetic dot or cylindrical nanowire of radius R and thickness (length) L. The limit of an infinite cylinder R → ∞ and L → ∞ is assumed because the hopfion magnetization given by Equations (3), (3´) is derived for infinite space. The toroidal hopfion magnetization field (3), (3´) has the simplest representation in the toroidal coordinates. However, to consider a cylindrical ferromagnetic sample we need to change the toroidal coordinates to the cylindrical ones. The energy functional consists of the contributions of the exchange, DMI, uniaxial anisotropy and magnetostatic energies
E m = ∫ d 3 r A ∑ α ∇ m α 2 + D m · r o t m + K 1 − m z 2 − 1 2 M s m · H m r ,
where A is the exchange stiffness constant, D is the DMI parameter and the magnetostatic field H m r is calculated with the magnetostatic Green function formalism [30], H m r = M s ∫ d 3 r ´ G ^ r , r ´ m r ´ , G ^ r , r ´ α β = − ∂ 2 / ∂ x α ∂ x β 1 / r − r ´ .
The idea is to calculate the magnetic energy functional E m as a function of the hopfion radius E a substituting to E m the toroidal hopfion magnetization given by Equations (3), (3´). To calculate the different contributions to the magnetic energy (4) we use the angular parameterization for the magnetization m r components via spherical angles Θ , Φ :   m z = c o s Θ , m x + i m y = s i n Θ e x p i Φ , and the cylindrical coordinates r ρ , φ , z for the radius-vector r. The magnetization spherical angles are functions of the radius-vector, Θ = Θ r , Φ = Φ r . Following the theory of 2D magnetic solitons (vortices and skyrmions) [31], it is naturally to choose the hopfion magnetization spherical angles in axially symmetric form, Θ r = Θ ρ , z , Φ r = n φ + γ ρ , z . The angle γ ρ , z = m β ρ , z is the variable hopfion helicity. The in-plane hopfion magnetization components are m ρ = sin ⁡ Θ cos ⁡ γ and m φ = sin ⁡ Θ sin ⁡ γ . The explicit form of the functions η ρ , z and β ρ , z in the cylindrical coordinates ρ , φ , z is given by the expressions η ρ , z = a t a n h 2 a ρ / ρ 2 + z 2 + a 2 , β ρ , z = a t a n 2 a z / ρ 2 + z 2 − a 2 . These expressions allow to rewrite the hopfion magnetization (3) for p = +1 in the cylindrical coordinates as m z ρ , z = 1 − 8 ρ 2 a 2 / a 2 + ρ 2 + z 2 2 . The toroidal hopfions can be approximately interpreted as twisted skyrmion strings with their centers located in the xOy plane (z=0) and described by the equation ρ = a . The poloidal angle β describes the twist angle around the ring ρ = a . However, there is important difference between the twisted skyrmion string and hopfion magnetization configuration. The string magnetization in its center is directed along ρ ^ direction ( m = ± ρ ^ ) , whereas for the toroidal hopfion the magnetization m at the ring ρ = a is directed along z-axis oppositely to the magnetization in the hopfion center, m = − p z ^ .
We express the spatial coordinates ρ , z in the units of the hopfion radius a , which has sense of the scale parameter. Then, substituting the hopfion magnetization m r components (3) to the energy (4) and accounting for the expression m · r o t m = − s i n 2 Θ ∂ γ / ∂ z for the even on z part of the DMI energy one can find explicitly the local exchange and DMI energies for an infinite sample in the form:
E e x = 32 π 2 A a ,                 E D = − 64 π D I d a 2 ,  
where I d is some integral which was evaluated numerically to be I d = 0.26 for the hopfion angles Θ ρ , z and γ ρ , z .
The uniaxial magnetic anisotropy contribution E a = 2 π K ∫ d ρ ρ ∫ d z s i n 2 Θ and the magnetostatic contribution diverge increasing the sample radius R as approximately ~ l n R (R is the upper limit of the integration over the polar radius vector ρ). Although the toroidal hopfion is a localized soliton and the far-field magnetization is asymptotically trivial, m r → m 0 (unform magnetization background) at r → ∞ , the degree of the soliton localization in the radial ρ-direction is not sufficient to get finite anisotropy and magnetostatic energies at R → ∞ .
Therefore, we use a finite in-plane sample size R calculating the energy contributions defined by Equation (4) by using the toroidal hopfion magnetization given by Equations (3), (3´). Although these equations describe the hopfion in an infinite sample, we use them below as trial functions to find the hopfion magnetic energy in a finite cylindrical sample of radius R assuming that R is large enough. The cylinder thickness (wire length) L can be finite or infinite.
The magnetic anisotropy term can be written as
E a = 4 π 2 M s 2 Q I a R a a 3 ,  
where Q = K / 2 π M s 2 , I a x = 2 ∫ 0 x d ρ ρ ∫ 0 z m d z s i n 2 Θ , z m = β x / 2 , β = L / R .
To calculate the components of the Green´s function tensor we use the Coulomb kernel 1 / r − r ´ decomposition via the Bessel functions of the first kind J μ x :
1 r − r ´ = ∫ 0 ∞ d k e x p − k z − z ´ ∑ μ = − ∞ ∞ J μ k ρ J μ k ρ ´ e x p i μ φ − φ ´ .
The hopfion magnetization m r components in the cylindrical coordinates do not depend on the azimuthal angle φ . Therefore, we can average the dipolar field H m r over φ . This leads to the axially symmetric field in the form H m r = H m ρ ρ , z , 0 , H m z ρ , z . The magnetostatic field is related to the magnetization components via the averaged Green´s functions g α β ρ , ρ ´ , z , z ´ = ∫ 0 2 π d φ ∫ 0 2 π d φ ´   G ^ r , r ´ α β / 2 π . The components g α β are equal to zero if at least one of the indices α , β is equal to φ . Only the components g ρ ρ ,   g ρ z ,   g z ρ ,   g z z are not equal to zero. The contribution of the components g ρ z ,   g z ρ to the magnetostatic energy disappears due to the system cylindrical symmetry and the hopfion axial symmetry. Therefore, the non-local magnetostatic energy can be written as
E m = − π M s 2 ∫ d ρ ρ ∫ d z ∫ d ρ ´ ρ ´ ∫ d z ´ g ρ ρ m ρ ρ , z m ρ ρ ´ , z ´ + g z z m z ρ , z m z ρ ´ , z ´ .
The hopfion magnetostatic energy is sum of two contributions, ρ ρ and z z , which depend on the hopfion magnetization components m ρ and m z , respectively. The first contribution can be expressed as
E m ρ ρ = 2 π 2 M s 2 I m ρ R a a 3
where the integral I m ρ x is defined as I m ρ x = ∫ d z ∫ d z ´ I ρ z , k , x I ρ z ´ , k , x , I ρ z , k , x = − k ∫ 0 x d ρ ρ J 1 k ρ m ρ ρ , z , m ρ ρ . z = s i n Θ ρ , z c o s γ ρ , z , J 1 x is the Bessel function of the first kind. The upper and lower limits in the integral over the thickness coordinates z , z ´ are ± ∞ for magnetic wires. However, the limits are finite and equal ± β x / 2 for the magnetic dots or finite length wires with the aspect ratio β = L / R .
The integral in Equation (8) cannot be calculated analytically/numerically and is too complicated to operate with. We note that the function e x p − k z − z ´ in the definition of I m ρ x has a sharp maximum at z = z ´ , therefore, we can substitute I ρ z ´ , k , x to I ρ z , k , x under the integral sign. Then, the integral is essentially simplified to be I m ρ x = 2 ∫ − z m z m d z ∫ 0 ∞ d k k − 1 1 − e x p − k z m c o s h ⁡ ( k z ) ( I ρ z , k , x ) 2 , z m = β x / 2 It can be shown that within the limit β ≫ 1 (cylindrical wire) the integral is reduced to the simple expression, I m ρ x = 4 ∫ 0 β x / 2 d z ∫ 0 x d ρ ρ m ρ ρ , z 2 . It has the form of an effective hard axis magnetic anisotropy in ρ -direction, normal to the cylinder side surface. This anisotropy is analogous to the shape anisotropy of uniformly magnetized wire along its length.
The second, z z contribution to the magnetostatic energy can be presented in the form similar to Equation (8)
E m z z = 2 π 2 M s 2 I m z R a a 3 ,
where in the local approximation the integral I m z x = 2 ∫ − z m z m d z ∫ 0 ∞ d k k e x p − k z m c o s h ⁡ ( k z ) ( I z z , k , x ) 2 , I z z , k , x = ∫ 0 x d ρ ρ J 0 k ρ m z ρ , z .
Using the energy contributions described by Equations (5), (6) and (7) we can write the total dimensionless magnetic energy ε m = E m / 4 π M s 2 l e 3 of the toroidal hopfion in the cylindrical dot/wire in the units of 4 π M s 2 l e 3 ,
ε a = 16 π 2 a − 16 d I d a 2 + π Q I a R a a 3 + π 2 I m ρ R a a 3 + π 2 I m z R a a 3 ,
where l e = A / 2 π M s 2 is the material exchange length, d = D / M s 2 l e is reduced DMI parameter, and the hopfion radius a is presented in the units of l e .
Although the exchange and DMI energies in Eq. (10) have finite limit at R → ∞ , we need to rewrite them for finite values of the ratio R / a , similar to the magnetic anisotropy and magnetostatic energies. We use the expressions
ε e x a = π a I e x R a ,         ε D a = − 1 2 d a 2 I D R a ,  
where I e x x = ∫ 0 x d ρ ρ ∫ − z m z m d z ∇ m z 2 / s i n 2 Θ + s i n 2 Θ ∇ γ 2 + 1 / ρ 2 , and I D x = ∫ 0 x d ρ ρ ∫ − z m z m d z s i n 2 Θ ∂ γ / ∂ z . The limiting values are I e x x → ∞ = 16 π and I D x → ∞ = 32 I d in agreement with Equation (5).
Generalizing Equation (10) for a finite value of the cylindrical dot/wire radius R and arbitrary value L of the dot thickness (wire length), the total normalized magnetic energy of the toroidal hopfion is
ε a , R = π a I e x R a − 1 2 d a 2 I D R a + π Q I a R a a 3 + π 2 I m ρ R a a 3 + π 2 I m z R a a 3 .
We note that the hopfion energy (12) is essentially more complicated than the simple scaling polynomial equations in Ref. 17 due to presence of the magnetostatic interaction and finite system size R. The magnetic anisotropy and magnetostatic terms should be taken at finite value of R due to their divergence at R → ∞ . The hopfion energy depends not only on the scale parameter (hopfion radius) a, but also on the sample radius R and the aspect ratio β .

3. Results and discussion

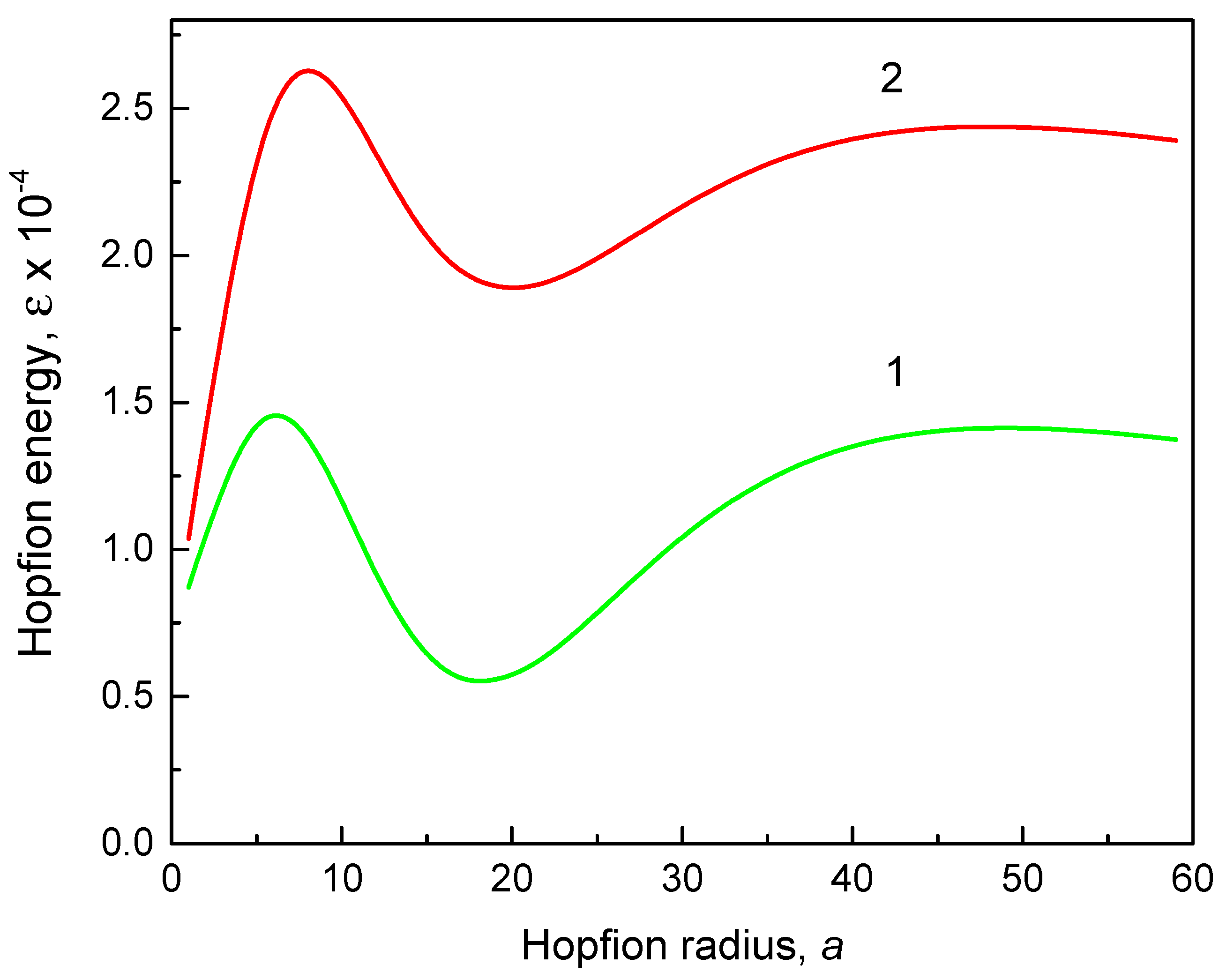
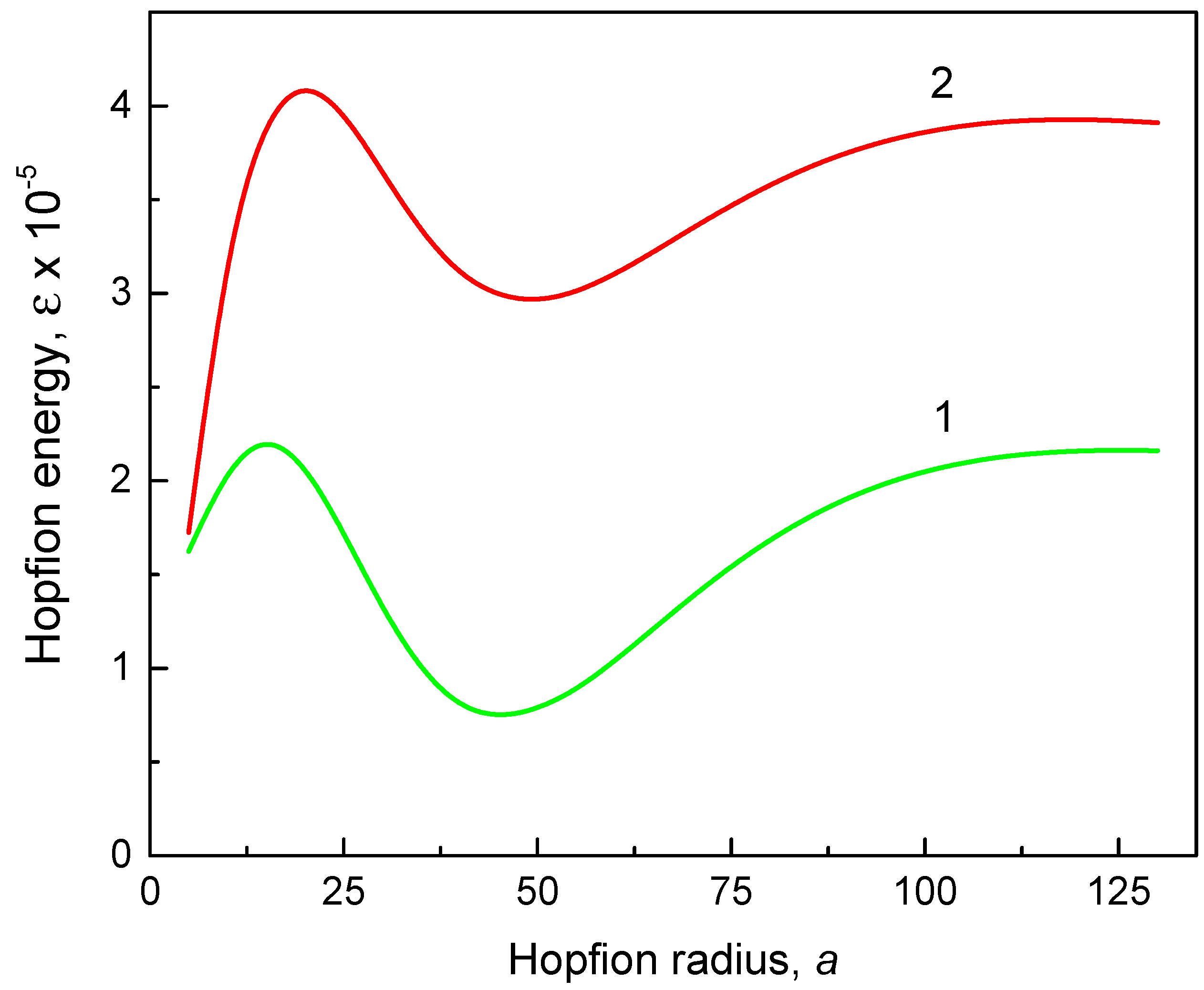
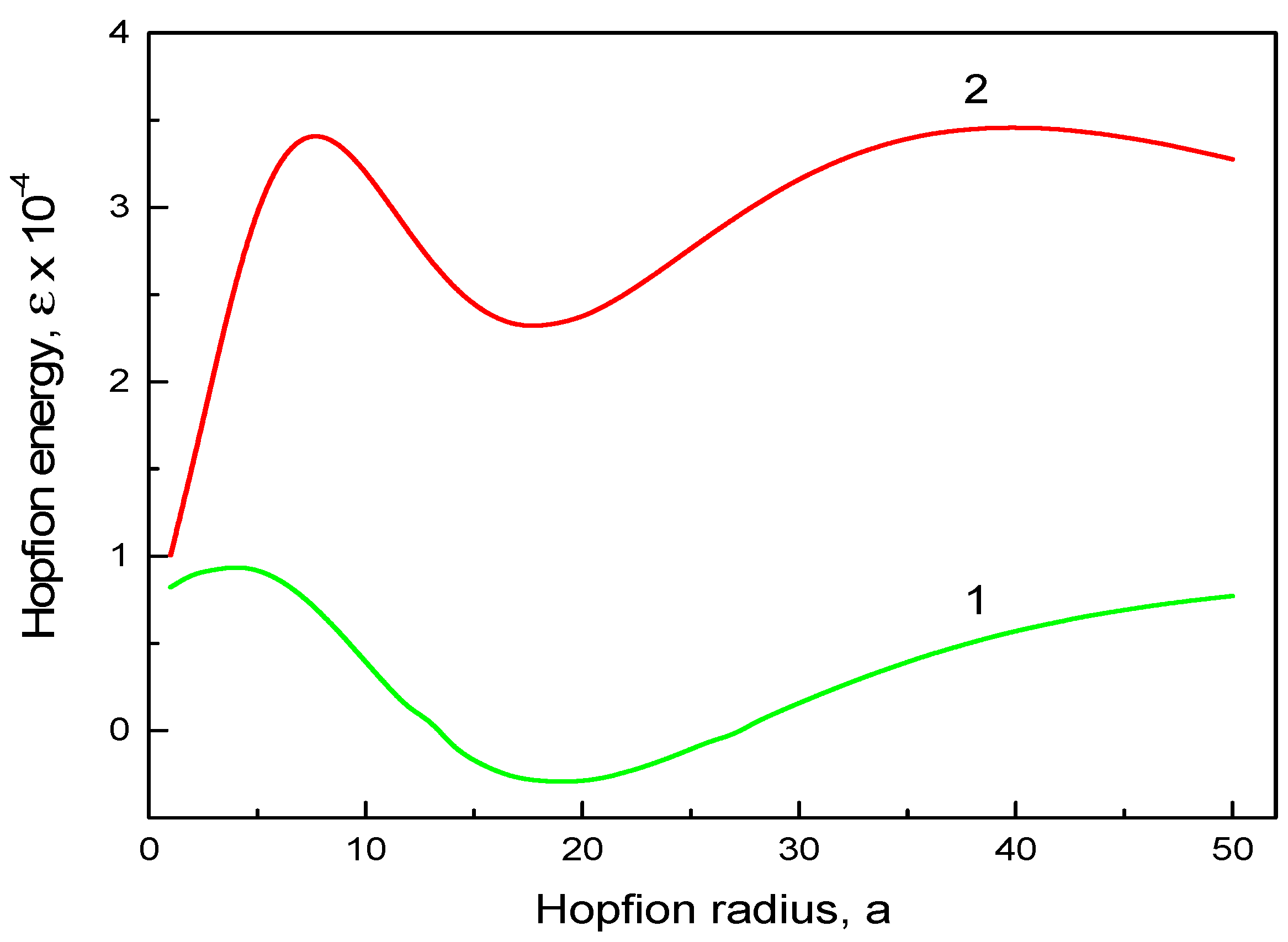
The hopfion magnetic energy ε a , R (12) vs. the hopfion radius a is plotted in Figure 1 and Figure 2. To plot Figures 1, 2 we used the set of the magnetic material parameters A = 11 pJ/m, Ms = 837 kA/m, K=0, which are typical for the soft magnetic material such as Ni80Fe20 alloy (permalloy). However, we used finite values of the magnetic anisotropy constant K to plot Figure 3. There is a pronounced minimum of the magnetic energy at finite values of the hopfion radius a, which corresponds to the hopfion stable state.
The magnetostatic terms in Equation (12) are mainly responsible for the appearance of the minimum of the hopfion energy ε a , R at a 0 ≈ 0.90 ÷ 0.92 R in soft magnetic materials ( K = 0 ). The reduced equilibrium hopfion radius a 0 / R is approximately equal to 0.9 and weekly depends on the sample magnetic and geometrical parameters. The magnetostatic energy contributions given by Equations (8), (9) are functions only on x = R / a and β . Therefore, the reduced equilibrium value of a 0 / R depends only on β if only the magnetostatic energy is accounted. The weak dependence a 0 / R = f β , R , d on other sample parameters reflects small contributions of the exchange and DMI energies to the total magnetic energy of the toroidal hopfion. However, the equilibrium skyrmion radius a 0 depends on the magnetic anisotropy constant, especially at high values of the cylinder aspect ratio β .
The uniaxial magnetic anisotropy energy in Equation (12) influences strongly the hopfion stability and the value of the equilibrium hopfion radius. It re-normalizes in some sense the magnetostatic contribution, which can be approximately treated as an effective hard axis magnetic anisotropy in the in-plane ρ -direction. The magnetic anisotropy destabilizes the hopfion state at K > 0 (¨easy axis¨ anisotropy), or stabilize it for K < 0 (¨easy plane¨ anisotropy), see Figure 3. The positive magnetic anisotropy energy at K > 0 increases influence of the positive magnetostatic energy contribution. The energy minimum becomes shadow and disappears at large values of K. The negative ¨easy plane¨ anisotropy energy ( K < 0 ) competes with the magnetostatic energy. This leads to the negative magnetic hopfion energy and more deep energy minimum at moderate values of K , see Figure 3. The ¨easy axis¨ (¨easy plane¨) magnetic anisotropy leads to a decrease (increase) of the equilibrium skyrmion radius a 0 .
It is reasonable to use in the calculations of the hopfion energy the cylinder aspect ratio β ≥ 2 due to strong localization of the hopfion in the z-direction. The DMI term at typical value of d ~ 1 ( D ~ 1 mJ/m2) is essentially smaller than the magnetostatic term and results in a small modification of the hopfion magnetic energy. I.e., to stabilize the toroidal hopfion in a cylindrical dot/wire we can ignore DMI and consider the hopfion stabilization in strong ferromagnets. The hopfion energy value at the minimum ε a 0 in soft magnetic materials (K = 0) and magnetic materials with an ¨easy axis¨ ( K > 0 ) magnetic anisotropy is typically higher than the energy ε S D of the out-of-plane single domain (SD) state, especially at large values of β . Therefore, the toroidal hopfion is not ground state of the cylindrical dot or wire with zero or positive uniaxial magnetic anisotropy constant. The ground state is longitudinally magnetized dot/wire with almost uniform magnetization configuration ( m z = ± 1 ), for which in good approximation the magnetic energy is ε S D = π / 2 R / l e 3 β N z z β − Q , where N z z β = 2 β − 1 ∫ 0 ∞ d k k − 2 J 1 2 k 1 − e x p − β k is the cylinder deaminization factor along axial z-direction [32], and Q = K / 2 π M s 2 . The SD state energy can be obtained from the hopfion energy given by Equation (12) within the limit a → 0 . The situation is drastically changed for the ¨easy plane¨ anisotropy K < 0 (Figure 3). The hopfion energy ε a 0 can be negative at the moderate values of K (the value K = 0.22 MJ/m3 was used to plot Figure 3), and, therefore, ε a 0 < ε S D . However, there is no guaranty that the toroidal hopfion is the ground state of the cylindrical dot/wire with the ¨easy plane¨ anisotropy K < 0 because other inhomogeneous magnetic configurations may have lower energy than the hopfion energy ε a 0 .
We note that there is an essential energy barrier between the hopfion magnetization state ε a 0 and single-domain state ε S D , a → 0 . The hopfion energy ε a given by Equation (12) goes asymptotically to the value of ε S D at the hopfion radius increasing a / R → ∞ . Apparently, this limit also describes the cylindrical dot/wire single domain state with the magnetization along the cylindrical dot/wire axis. The SD magnetization configuration limits a → 0 and a → ∞ correspond to the hopfion collapse or infinite extension in the radial direction, correspondingly. The energy minimum at a finite value of a = a 0 is separated from the longitudinal SD state a → ∞ by a huge energy barrier. The energy barriers for the transitions from the finite radius a 0 hopfion configuration to the SD state ( a 0 → 0 ,   a 0 → ∞ ) are much bigger than the thermal energy at k B T room temperature (assuming that T is much lower than the Curie temperature T c , where M s T c → 0 and the barriers disappear). Therefore, the energy barriers out of interest for the hopfion thermostability on the long-time scale. The hopfion energy minimum is very deep and the hopfion magnetization configuration is thermostable.
We note that for the finite cylindrical samples other hopfion ansatz was suggested [19] and used in Ref. [21]. This ansatz is a good approximation to minimize the hopfion energy if the magnetostatic energy contribution is ignored and a strong surface out-of-plane magnetic anisotropy is introduced by enforcing the boundary conditions m = z ^ at the dot top/bottom faces z = ± L / 2 . The magnetostatic interaction is accounted numerically in Refs. [33, 34]. However, the authors of these papers believe that the strong out-of-plane magnetic anisotropy (K = 0.8 MJ/m3 in the surface layers [33] or the surface anisotropy Ks = 0.5 mJ/m2 [34]) along with DMI are necessary for the hopfion stabilization in the cylindrical dots or infinite films. Calculation of the surface magnetic anisotropy contribution to the hopfion energy showed that it is negligible small for the surface anisotropy values Ks order of 1 mJ/m2. We demonstrated in Figure 1, Figure 2 and Figure 3 that the main contribution to the hopfion energy comes from the magnetostatic interaction, which is unavoidable present for all inhomogeneous magnetization textures in the restricted geometry (the cylindrical thick magnetic dots and wires). Although DMI and uniaxial out-of-plane surface magnetic anisotropy may be accounted in the energy functional, they are of the second importance for the toroidal hopfion stabilization.
The toroidal hopfion metastable magnetization configuration may be reached in the process of the sample re-magnetizing by applying the magnetic field along the cylindrical axis Oz as an intermediate metastable state in the low-field part of the hysteresis loop M z H z = V − 1 ∫ d V M z r , H z . Using the hopfion magnetization (3) we can find the volume averaged reduced magnetization μ z a , β = m z ρ , z at zero magnetic field H z = 0 , which has sense of the hopfion remanent magnetization. The equilibrium remanent magnetization μ z a 0 , β is increasing function of the cylinder aspect ratio β saturating at β ≫ 1 , μ z a 0 , β ≫ 1 → 1 . We note that at the fixed value of the cylinder aspect ratio β , the remanent magnetization μ z a , β in soft magnetic materials has a minimum at the hopfion radius a m approximately equal to the hopfion equilibrium radius a 0 , a m ≈ a 0 , for any value of β ≥ 2 .

4. Conclusions

It is demonstrated that the toroidal hopfion magnetization configuration is a metastable state of a thick cylindrical ferromagnetic nanodot or a nanowire of a finite radius R. Existence of this state in soft magnetic materials is a result of the competition of the exchange and magnetostatic energies. The reduced equilibrium hopfion radius a 0 / R is approximately equal to 0.9 and weekly depends on the sample magnetic end geometrical parameters. The uniaxial ¨easy axis¨ magnetic anisotropy (the anisotropy constant K > 0 ) destabilizes the hopfion state, whereas the ¨easy plane¨ magnetic anisotropy ( K < 0 ) facilitates the hopfion stabilization. The Dzyaloshinskyi-Moriya exchange interaction and the out-of-plane surface magnetic anisotropy are of the second importance for the hopfion stabilization. The toroidal hopfion metastable magnetization configuration may be reached in the process of the sample re-magnetizing by applying an external magnetic field along the cylindrical axis. The hopfion magnetization configuration corresponds to a deep magnetic energy minimum and is stable with respect to the thermal fluctuations.

Author Contributions

There is a single author of the manuscript.

Funding

K.G. acknowledges support by IKERBASQUE (the Basque Foundation for Science). The research of K.G. was funded in part by the Spanish Ministry of Science and Innovation grants PID2019-108075RB-C33 /AEI/10.13039/501100011033, PID2022-137567NB-C21/AEI/10.13039/ 501100011033 and by the Basque Country government under the scheme “Ayuda a Grupos Consolidados” (Ref. IT1670-22). The APC was funded by XXX.

Data Availability Statement

Not applicable.

Acknowledgments

The author thanks to O. Chubykalo-Fesenko (Institute for Materials Science, Madrid, Spain) for stimulating discussion of the inhomogeneous magnetization states in magnetic nanostructures.

Conflicts of Interest

Not applicable.

References

  1. Fernandez-Pacheco, A.; Streubel, R.; Fruchart, O.; Hertel, R.; Fischer, P.; Cowburn, R.P. Tree-dimensional nanomagnetism. Nat. Commun. 2017, 8, 15756. [Google Scholar] [CrossRef]
  2. Donnelly, C.; Scagnoli, V. Imaging three-dimensional magnetic systems with X-rays. J. Phys. Cond. Mat. 2020, 32, 213001. [Google Scholar] [CrossRef] [PubMed]
  3. Donnelly, C.; Metlov, K.L.; Scagnoli, V.; Guizar-Sicairos, M.; Holler, M.; Bingham, N.S.; Raabe, J.; Heyderman, L.J.; Cooper, N.R.; Gliga, S. Experimental observation of vortex rings in a bulk magnet. Nat. Phys. 2021, 17, 316–321. [Google Scholar] [CrossRef]
  4. Kent, N.; Reynolds, N.; Raftrey, D.; Campbell1, I.T.G.; Virasawmy, S.; Dhuey, S.; Chopdekar, R.V.; Hierro-Rodriguez, A.; Sorrentino, A.; Pereiro, E.; Ferrer, S.; Hellman, F.; Sutcliffe, P.; Fischer, P. Creation and observation of Hopfions in magnetic multilayer systems. Nat. Commun. 2021, 12, 1562. [Google Scholar] [CrossRef] [PubMed]
  5. Hobart, R.H. On the instability of a class of unitary field models, Proc. Phys. Soc. 1963, 82, 201–203. [Google Scholar] [CrossRef]
  6. Derrick, G.H. Comments on nonlinear wave equations as models for elementary particles, J. Math. Phys. 1964, 5, 1252–1254. [Google Scholar] [CrossRef]
  7. Dzyaloshinskii, I. E. Theory of helicoidal structures in antiferromagnets. Sov. Phys. JETP 1964, 19, 960–971. [Google Scholar]
  8. Bogdanov, A.N.; Yablonskii, D.A. Thermodynamically stable “vortices” in magnetically ordered crystals. The mixed state of magnets. Sov. Phys. JETP 1989, 68, 101–103. [Google Scholar]
  9. Bogdanov, A. Hubert, The stability of vortex-like structures in uniaxial ferromagnets. J. Magn. Magn. Mat. 1999, 195, 182–192. [Google Scholar] [CrossRef]
  10. Skyrme, T. H. A non-linear field theory. Proc. R. Soc. 1961, A 260, 127–138. [Google Scholar] [CrossRef]
  11. Faddeev, L. D. Some comments on the many-dimensional solitons. Lett. Math. Phys. 1976, 1, 289–293. [Google Scholar] [CrossRef]
  12. Gladikowski J, Hellmund M. Static solitons with nonzero Hopf number. Phys. Rev. D 1997, 56, 5194–5199. [CrossRef]
  13. Hietarinta J, Salo P. Ground state in the Faddeev-Skyrme model. Phys. Rev. D 2000, 62, 081701. [Google Scholar] [CrossRef]
  14. Hopf, H. Über die Abbildungen der dreidimensionalen Sphäre auf die Kugelfläche. Math. Analen 1931, 104, 637–665. [Google Scholar] [CrossRef] [PubMed]
  15. Whitehead, J.H.C. An expression of Hopf ’s invariant as an integral. Proc. Natl. Acad. Sci. U.S.A. 1947, 33, 117–123. [Google Scholar] [CrossRef] [PubMed]
  16. Rybakov, F.N.; Kiselev, N.S.; Borisov, A.B.; Doering, L.; Melcher, C.; Bluegel, S. Magnetic hopfions in solids. APL Mater. 2022, 10, 111113. [Google Scholar] [CrossRef]
  17. Bogdanov, A. New localized solutions of the nonlinear field equations. JETP Lett. 1995, 62, 247–251. [Google Scholar]
  18. Guslienko, K.Y. Skyrmion State Stability in Magnetic Nanodots with Perpendicular Anisotropy, IEEE Magn. Lett. 6, 4000104 (2015). [CrossRef]
  19. Sutcliffe, P. Hopfions in chiral magnets. J. Phys. A Math. Theor. 2018, 51, 375401. [Google Scholar] [CrossRef]
  20. Tai, J.S.B.; Smalyukh, I.I. Static Hopf solitons and knotted emergent fields in solid - state non -centrosymmetric magnetic nanostructures. Phys. Rev. Lett. 2018, 121, 187201. [Google Scholar] [CrossRef]
  21. Göbel, B.; Akosa, C.A.; Tatara, G.; Mertig, I. Topological Hall signatures of magnetic hopfions. Phys. Rev. Res. 2020, 2, 013315. [Google Scholar]
  22. Tejo, F.; Hernández Heredero, R.; Chubykalo-Fesenko, O.; Guslienko, K.Y. The Bloch point 3D topological charge induced by the magnetostatic interaction, Sci. Rep. 2021, 11, 21714. [Google Scholar] [CrossRef] [PubMed]
  23. Berganza, E.; Jaafar, M.; Fernandez-Roldan, J.A.; Goiriena-Goikoetxea, M.; Pablo-Navarro, J.; García-Arribas, A.; Guslienko, K.; Magén, C.; De Teresa, J.M.; Chubykalo-Fesenko, O.; Asenjo, A. Half-hedgehog spin textures in sub-100 nm soft magnetic nanodots. Nanoscale 2020, 12, 18646–18653. [Google Scholar] [CrossRef]
  24. Berganza, E.; Fernandez-Roldan, J.A.; Jaafar, M.; Asenjo, A.; Guslienko, K.; Chubykalo-Fesenko, O. 3D quasi-skyrmions in thick cylindrical and dome-shape soft nanodots, Sci. Rep. 2022, 12, 3426. [Google Scholar] [CrossRef] [PubMed]
  25. Faddeev, L.; Niemi, A.J. Stable knot-like structures in classical field theory. Nature 1997, 387, 58–61. [Google Scholar] [CrossRef]
  26. Guslienko, K.Y. Gauge and emergent electromagnetic fields for moving magnetic topological solitons, EPL 2016, 113, 67002. [CrossRef]
  27. Guslienko, K.Y. Emergent magnetic field and vector potential of the toroidal magnetic hopfions, Chaos, Solitons & Fractals 2023, 174, 113840. [CrossRef]
  28. Wilczek, F.; Zee, A. Linking number, spin and statistics of solitons. Phys. Rev. Lett. 1983, 51, 2250–2252. [Google Scholar] [CrossRef]
  29. Moon, P.H.; Spencer, D.E. Toroidal Coordinates (η, θ, ψ). Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions; New York, Springer Verlag 1988; pp. 112-115.
  30. Guslienko, K.Y.; Slavin, A.N. J. Magn. Magn. Mat. 2011, 323, 2418-2424. [CrossRef]
  31. Kosevich, A.M.; Ivanov, B.A.; Kovalev, A. S. Magnetic solitons. Phys. Rep. 1990, 194, 117–238. [Google Scholar] [CrossRef]
  32. Joseph, R.I. , Ballistic Demagnetizing Factor in Uniformly Magnetized Cylinders, J. Appl. Phys. 1966, 37, 4639–4643. [Google Scholar] [CrossRef]
  33. Wang, X.S.; Qaiumzadeh, A.; Brataas, A. Current-driven dynamics of magnetic hopfions. Phys. Rev. Lett. 2019, 123, 147203. [Google Scholar]
  34. Liu, Y.; Lake, R.K.; Zang, J. Binding a hopfion in a chiral magnet nanodisk. Phys. Rev. B 2018, 98, 174437. [Google Scholar] [CrossRef]
Preprints 93019 g001
Figure 1. The hopfion energy ε a , R vs. the hopfion radius, a (in units of the exchange length). The dot radius R = 20 l e , the DMI parameter d = 1, the exchange length l e = 5 nm. (1) the cylindrical dot aspect ratio height/radius β = 2, (2) the cylindrical wire aspect ratio length/radius β = 8.
Figure 1. The hopfion energy ε a , R vs. the hopfion radius, a (in units of the exchange length). The dot radius R = 20 l e , the DMI parameter d = 1, the exchange length l e = 5 nm. (1) the cylindrical dot aspect ratio height/radius β = 2, (2) the cylindrical wire aspect ratio length/radius β = 8.
Preprints 93019 g001
Preprints 93019 g002
Figure 2. The hopfion energy ε a , R vs. the hopfion radius, a (in units of the exchange length) The dot radius R = 50 l e , the DMI parameter d = 1, the exchange length l e = 5 nm. (1) the cylindrical dot aspect ratio height/radius β = 2, (2) the cylindrical wire aspect ratio length/radius β = 10.
Figure 2. The hopfion energy ε a , R vs. the hopfion radius, a (in units of the exchange length) The dot radius R = 50 l e , the DMI parameter d = 1, the exchange length l e = 5 nm. (1) the cylindrical dot aspect ratio height/radius β = 2, (2) the cylindrical wire aspect ratio length/radius β = 10.
Preprints 93019 g002
Preprints 93019 g003
Figure 3. The hopfion energy ε a , R vs. the hopfion radius, a (in units of the exchange length) The dot radius R = 20 l e , the cylindrical dot aspect ratio height/radius β = 2, the DMI parameter d = 1, the exchange length l e = 5 nm. (1) the ¨easy plane¨ magnetic anisotropy K / 2 π M s 2 = − 0.5 ; (2) the ¨easy axis¨ magnetic anisotropy K / 2 π M s 2 = 1 .
Figure 3. The hopfion energy ε a , R vs. the hopfion radius, a (in units of the exchange length) The dot radius R = 20 l e , the cylindrical dot aspect ratio height/radius β = 2, the DMI parameter d = 1, the exchange length l e = 5 nm. (1) the ¨easy plane¨ magnetic anisotropy K / 2 π M s 2 = − 0.5 ; (2) the ¨easy axis¨ magnetic anisotropy K / 2 π M s 2 = 1 .
Preprints 93019 g003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated