Prerpints.org logo
Preprint
Article

Feature Representation Learning for Few-Shot Fine-Grained Image Classification: A Comprehensive Review

Altmetrics

Downloads

230

Views

93

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

12 December 2023

Posted:

12 December 2023

You are already at the latest version

Alerts
Abstract
Few-shot fine-grained image classification (FSFGIC) methods refer to machine learning methods which aim to classify images (e.g., bird species, flowers, and airplanes) belonging to subordinate object categories of the same entry-level category with only a few samples. It is worth to note that feature representation learning is used not only to represent training samples, but also to construct classifiers for performing various FSFGIC tasks. In this paper, starting from the definition of FSFGIC, a taxonomy of feature representation learning for FSFGIC is proposed. According to this taxonomy, we discuss key issues on FSFGIC (including data augmentation, local or/and global deep feature representation learning, class representation learning, and task specific feature representation learning). The existing popular datasets and evaluation standards are introduced. Furthermore, a novel classification performance evaluation mechanism is designed with a 0.95 confidence interval for judging whether the classification accuracy obtained by a certain specified method is good or bad. Moreover, current challenges and future trends of feature representation learning on FSFGIC are elaborated.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Few-shot fine-grained image classification (FSFGIC) methods [1] refer to machine learning methods which aim to classify images (e.g., birds [2], flowers [3], and airplanes [4]) belonging to subordinate object categories of the same entry-level category with only a few samples. As illustrated in Figure 1, The researchers indicated that a two-year-old child can classify different categories of objects after looking at a few images, but the child may be confused about fine-grained categories with a limited number of samples [5,6], due to the following reasons: (1) Objects for FSFGIC are obtained from sub-categories of one category, making them visually very similar; (2) The fine-grained characteristics also bring small inter-class changes caused by highly similar sub-categories, as well as large intra-class changes in pose, scale, and rotation of object. Since the objects in different sub-categories of the same entry-level category are very similar to each other, a key consideration in FSFGIC is how to effectively learn discriminative features from extremely limited training samples, which makes FSFGIC a very challenging research problem. Furthermore, the labelling of fine-grained images is time-consuming and expensive, because fine-grained objects have to be accurately labeled by domain experts.
Recently, with the growing attention on FSFGIC, various FSFGIC methods have been proposed. Many few-shot learning methods have also been applied to handle FSFGIC tasks with impressive results. Currently, there lacks a survey about FSFGIC. This paper aims to fill this gap. It is worth to note that the quality of feature representation learning directly affects the classification performance on FSFGIC. The reason is that feature representation learning is used not only to represent training samples, but also to construct classifiers for performing FSFGIC tasks. In this way, a taxonomy of feature representation learning for FSFGIC is proposed. According to this classification, we discuss different types of FSFGIC methods in depth. It is worth to note that those few-shot image classification algorithms (e.g., [7,8]) that have achieved good classification performance in some FSFGIC datasets are also introduced in this survey.
The contributions of this survey comprise following aspects. This is the first work to review FSFGIC under a taxonomy of feature representation learning. And then different types of feature representation learning techniques for FSFGIC are reviewed. Meanwhile, the relationships among different FSFGIC methods are presented. Furthermore, a novel classification performance evaluation mechanism is designed for judging whether the classification accuracy obtained by a certain specified method is good or bad. Combining with representative existing FSFGIC techniques, the main unresolved issues on FSFGIC are discussed.

2. Problem, datasets, and categorization of FSFGIC methods

In this section, the problem formulation of FSFGIC, categorization of FSFGIC methods, and representative benchmark datasets for FSFGIC are presented.

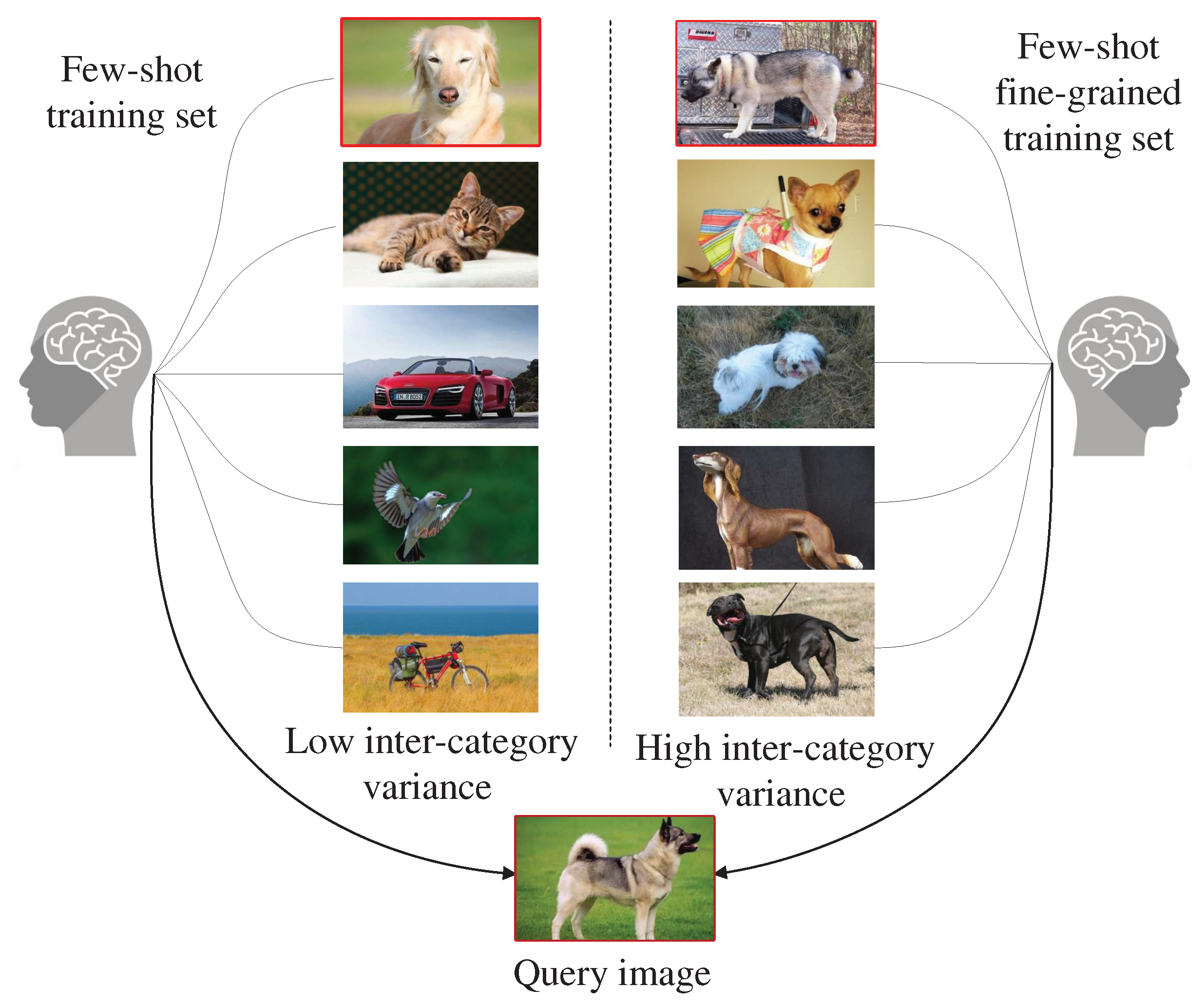
2.1. Problem formulation

For a FSFGIC task, the target dataset D contains two parts: a support set S and a query set Q . The small support set S includes C unseen classes, and each of which has K labeled samples. The query set Q contains J unlabeled samples.
D = { S = { ( x i , y i ) i = 1 C × K } ∪ Q = { ( x j ) j = 1 J } } ,
where S ∩ Q = ∅ , x i and x j denote fine-grained samples and ( x i , x j ) ∈ C , and y i ∈ C represents the ground truth label of x i . The goal of FSFGIC is to successfully classify x j into its corresponding class in C from S . Thus, the problem is denoted as a C-way K-shot task.
It is worth to note that the training samples of each class in FSFGIC are too limited to effectively learn transferable knowledge [8,9] for performing FSFGIC tasks. Then, an episodic training paradigm [10] with an auxiliary set A , which has similar data distribution with D , is applied for tackling the aforementioned problem as follows
A = { E = { ( u i , v i ) i = 1 N } ∪ F = { ( u j , v j ) j = 1 M } } ,
where u i and u j are fine-grained images, v i and v j are their corresponding labels; E ∩ F = ∅ , D ∩ A = ∅ . The auxiliary set A contains plenty of classes and labeled samples which are far larger than C and K respectively.
In each round of training, A is randomly separated into two parts: an auxiliary support set G = { ( u i , v i ) i = 1 C × K } and an auxiliary query set H = { ( u j , v j ) j = 1 J } . Since N ≫ C × K , E can mimic the composition of S in each iteration. Then A is employed to learn prior knowledge for training S .

2.2. A taxonomy of the existing feature representation learning for FSFGIC

According to the difference of contents and representations of learned features, the existing feature representation learning techniques for FSFGIC can be divided into three categories: local or/and global deep feature representation learning based FSFGIC methods [11,12], class representation learning based FSFGIC methods [13,14], and task specific feature representation learning based FSFGIC methods [15,16]. According to different types of feature representation learning paradigms, a summary of feature representation learning for FSFGIC methods is illustrated in Figure 2.
Local or/and global deep feature representation based FSFGIC methods utilize the degree of difference of the local or/and global deep feature representations between query and support samples for performing FSFGIC tasks. Class feature representation learning based FSFGIC methods utilize deep feature representations from all training samples in a class to construct a class feature representation (e.g., class-level graph [17] or class-level local deep feature representation [7]) for this class. And then class feature representation is used to perform FSFGIC tasks. Task specific feature representation learning based FSFGIC methods utilize deep feature representations from all training images in a task (i.e., one training episode) to construct a task specific feature representation (e.g., task-level graph relationship representation [18] or task-level local deep feature representation [8]) for this task and to perform FSFGIC tasks.
It is worth to note that after feature representation is learned, most meta-learning based techniques, which can be divided into two branches (i.e., optimization-based techniques and metric-based techniques), are utilized for performing FSFGIC tasks. Optimization-based techniques aim to converge the model to novel tasks which learns how to update the parameters of a given initial model with only a few training samples for each category. Metric-based techniques aim to learn a transferable feature knowledge and obtain a distribution based on similarity metrics between different samples. In this way, for each type of feature representation learning, both optimization-based and metric-based techniques used for FSFGIC will be reviewed in detail.

2.3. Benchmark datasets

Datasets have become one of the most critical roles in the development of FSFGIC, not only as a means for evaluating the classification accuracy of different FSFGIC methods, but also for greatly promoting the development of the field of FSFGIS (e.g., solving more complex, practical, and challenging problems). Currently, the representative datasets for training and evaluation on FSFGIC are CUB200-2011 [2], Stanford Dogs [19], Stanford Cars [20], FGVC-Aircraft [4], NABirds [21], SUN397 [22], and Oxford 102 Flowers [3]. The number of images and the number of categories corresponding to these datasets are shown in Table 1.
A detailed description of the datasets available on FSFGIC can be accessed at https://paperswithcode.com/task/fine-grained-image-classification. Furthermore, some ultra-fine-grained image datasets (i.e., Cottons and Soybeams [23]) have been introduced. Compared with the current widely used FSFGIC datasets (e.g., CUB200-2011 [2]), the inter-class differences among ultra-fine-grained images are much smaller which put forward greater requirements on the design of FSFGIC algorithms.

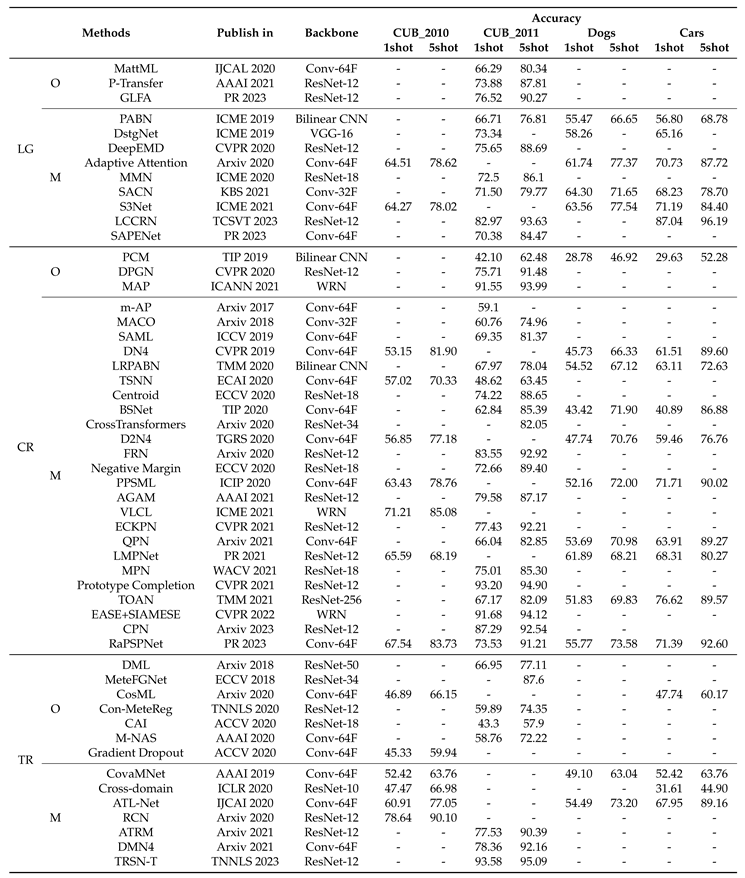
3. Methods on FSFGIC

In this section, we first review the data augmentation techniques for FSFGIC. And then local or global deep feature representation learning based FSFGIC methods, class representation learning based FSFGIC methods, and task specific feature representation learning based FSFGIC methods are introduced in detail. Furthermore, the relationships among the classification methods for different types of FSFGIC techniques are also introduced.

3.1. Data augmentation techniques for FSFGIC

Data augmentation techniques aim to enhance both the quantity and diversity of training data, thus alleviating overfitting and improving generalization ability. Currently, two types of data augmentation techniques are widely used on FSFGIC. The first type of data augmentation techniques (e.g., random horizontal flipping [24,25], jittering [26,27], scaling [1], random cropping [6], translation [28], zooming [28], and random rotation [29,30]) are used as a basic image manipulation in FSFGIC methods.
The second type of data augmentation techniques [31,32,33,34] are based on deep learning mechanisms which aim to mimic the characteristics of real data. For example, in [31], generative adversarial networks (GAN) are utilized to generate realistic samples from a given dataset. In [35], a feature encoder-decoder was used to augment the dataset by generating feature representations. In [36], a pre-trained GAN without discriminator was applied to generate subtle features of fine-grained images. And in [37], GAN was used to generate hallucination images. In [38], a self-training strategy was developed with unlabeled data for augmenting data, and in [39], they applied self-taught learning strategy to measure the credibility of each pseudo-labeled instance. In [40], a fully annotated auxiliary dataset which has similar distribution with the target dataset was used to train a meta learner which can transfer knowledge from an auxiliary dataset to a target dataset. In [41] a diversity transfer network (DTN) was proposed to learn to transfer latent diversities from training data to testing data. Xu et al. [33] first proposed a variational auto encoder (VAE)-based feature disentanglement method on FSL problem to generate images. Δ -encoder [42] utilized a auto-encoder to find deformations between different samples of the same category, then generated new samples for the other categories. [43] proposed a method of foreground extraction and posture transformation, which can extract foreground from base classes and generate additional samples for novel sub-classes to realize data expansion. Inspired by the hypothesis that language can help learn new visual objects [? ], auxiliary semantic modalities (e.g., attribute annotations [24,44]) are applied for the support set while ignoring the query set. In addition, other data augmentation techniques will be described in detail in the following review of FSFGIC methods.

3.2. Local or/and global deep feature representation learning based FSFGIC methods

In the field of FSFGIC, some scholars consider that local deep feature representations have the ability to recognize the discriminative regions for distinguishing subtle differences of fine-grained features. Some scholars argue that combining global and local deep feature representation learning can effectively improve the capability of deep feature representation. Currently, there are two main research directions (i.e., optimization-based techniques and metric-based techniques) which utilize local or global deep feature representations for performing FSFGIC tasks as illustrated in the following.

3.2.1. Optimization-based local or/and global deep feature representation learning

In FSFGIC, learning to fine-tune methods aim to fine-tune the model with few training samples by integrating the fine-tuning process in the meta-training stage. Traditional feature generation networks fail to capture the subtle difference between fine-grained categories, to address this problem, a feature composition framework was proposed in [45] to generate fine-grained features for novel classes. In training stage, they proposed a dense attribute-based attention to compute attention features for all attributes and then aligned them with attribute semantic vectors to obtain similarity score. After that, they apply these attribute features to construct features of novel classes.
Learning to fine-tune. In order to distinguish subtle and local parts in fine-grained categories, a multi-attention meta-learning (MattML) method [6] was proposed for FSFGIC. Attention mechanisms are applied on the designed base learner and task learner to capture local deep feature representations and to fine-tune the initialized classifier for performing FSFGIC tasks. It was indicated in [46] that some knowledge in the base data may be biased against the new class, so transferring the entire knowledge in the base data to the new class may not obtain a good meta learner or classifier. An evolutionary search strategy is proposed for transferring partial knowledge by fine-tuning particular layers in the base model after obtaining deep feature representations through feature extractor. First, several fine-tuning strategies are randomly generated and their corresponding classification accuracies on the validation set are obtained. K strategies with the highest accuracy are selected as parents. Second, with the help of gene mutation and gene crossover as in an evolutionary algorithm, off-spring vectors are obtained and their corresponding classification accuracies are calculated. By repeating this process in iterations, the best fine-tuning strategy can be obtained. This proposed evolutionary search strategy can be embedded into a metric-based method [47] and an optimization-based method [48] for performing FSFGIC tasks. [49] proposed a global- and local-aware feature augmentation method to augment features in terms of improving the diversity of the augmented samples and alleviating the overfitting problem.

3.2.2. Metric-based local or/and global deep feature representation learning

Metric-based local or/and global deep feature representation learning methods can be classified into three categories: attention mechanism, metric strategy for improving class representation, and multimodel learning.
Attention mechanism. Following the idea that a self-attention mechanism has the ability to indicate the discriminative regions in an image [50], an image saliency regions incorporation strategy [51] was designed. Local deep feature representations from training samples and their corresponding saliency maps obtained from [52] are combined for improving the classification performance on FSFGIC. Following the idea of object localization strategy [53], a meta-reweighting strategy [54] was designed to extract and exploit local deep feature representations of support samples. Furthermore, an adaptive attention mechanism based on the meta-reweighting model is designed to localize the region of interest in query samples. The aim of the designed adaptive attention mechanism is to match query image and support image to highlight relevant regions of interest for obtaining more discriminative local deep feature representations. A trilinear spatial-awareness network (S3Net) [55] was proposed to strength the spatial representation of each local descriptor by adding a global relationship feature with self-attention. They construct the multi-scale features to enhance rich representation in global features. Finally, a local loss and a global loss are combined to learn the discriminative features. In [56], they proposed a attention based pyramid structure to weight the different areas of the feature maps and produce multi-scaled features. [57] proposed a fusion spatial attention method that performs spatial attention simultaneously in both the image and the embedded space. [58] proposed a self-attention based prototype enhancement network (SAPENet) to obtain a more representative prototype for each class.
Metric strategy for improving class representation. The DeepEMD method [59] formalized the problem of image classification as an optimal image matching problem. And then earth mover’s distance (EMD) is applied to select local discriminative feature representations for finding optimal matching between query samples and support samples. In [60], a two stage comparison strategy is proposed to mine hard examples which correspond to the top 2 relation scores outputted by the first relation network and then are inputed into a second relation network to distinguish similar classes. A subtle difference module [55] is proposed to classify confused or near-duplicated samples based on the cooperation of local and global similarities between query image and the prototype of each class. [61] used the Sinkhorn distance to find an optimal matching between images, mitigating the object mismatch caused by misaligned position. Meanwhile, they propose the intraimage and interimage attentions as the bilateral normalization on the Sinkhorn distance to suppress the object mismatch caused by background clutter.
Multimodel learning. In [62], Zhao et al. argued that cross-modal external knowledge will help improve the classification performance on FSFGIC. In this way, a mirror mapping network (MMN) is designed to map multimodal features (i.e., external knowledge and global and local feature representations) into the same semantic space. The external knowledge which is extracted from textual descriptions and knowledge graph are utilized to generate global and local features for training samples. Finally, global and local feature representations from samples and external knowledge are combined for performing FSFGIC tasks.
Feature distribution Sun et al. [63], proposed a domain-specific FSFGIC task of marine organisms. They design a feature fusion model to focus on the key regions. Specifically, the framework consists of a ConvNet-based feature ectractor, a feature fusion model and a classifier. As the key component, the feature fusion model utilizes the focus-area location and high-order integration to generate feature representations which contain more identifiable information.
Semantic alignment. Huang et al. [40]proposed a novel pairwise bilinear polling to recognize the subtle difference of fine-grained images. Specifically, they design a fine-grained features extractor which contains a alignment loss regularization and a pair-wise bilinear pooling layer. The alignment loss aims to match the features of the same position and pair-wise bilinear pooling layer is able to capture comparative features from pairs of images. [64] proposed a bi-directional local alignment strategy, which complements the forward and backward distance by convex combination and strengthens the effective alignment between contextual semantic information.
Multi-scale representation. Different from the single-scale representation, multi-scale can enhance the representation of global features because large-scale with larger receptive fields contains more rich information [65,66,67,68,69,70,71,72]. In [55], a structural pyramid descriptor is constructed by exploiting the pyramid pooling of the global feature with different scales. Then, multi-scale features are magnified into the same size and fused together by the bilinear intepolations. Ruan et al. [56] proposed a spatial attentive comparison network (SACN) for FSFG task. They contrust a selective-comparison similarity module (SCSM) based on pyramid structure and attention machanism to assign different weights to the background and target which aims to produce multi-scaled features maps for classification. In [73], Zhang et al. proposed a multi-scale second-order relation network (MsSoSN), which equipps second-order pooling and a scale selector to create multi-scale second-order representations. They propose a scale and discrepancy discriminator to reweight multi-scale features, which is trained by a self-supervision way. In [74], they proposed a new hierarchical residual-like block which is applicable to lightweight ResNet structures such as ResNet-10, and they are the first one trying to integrate the idea of multi-scale representation into cross-domain few-shot classification problem.

3.3. Class representation learning based FSFGIC methods

The authors of class representation learning based methods argue that local or/and global deep feature representations learned from extremely limited training samples cannot effectively represent a novel class, and class representations (e.g., class-level graph [17] or class-level local deep feature representation [7]) can be used to alleviate the phenomenon of over-fitting and effectively represent a novel class.

3.3.1. Optimization-based class representation learning

The existing optimization-based class representation learning can be divided into two categories: (1) learning a model-based methods which aim to design network architectures to efficiently adapt to target tasks through only several gradient descent steps; (2) learning to fine-tune-based methods.
Learning a model. In [75], an optimization-based FSFGIC method was proposed which includes two modules: a bilinear feature learning module and a classifier mapping module. Class-level feature representations are obtained from the bilinear feature learning module [76]. Furthermore, a novel “piecewise mappings” strategy is proposed which aims to map each sub-vector in class-level feature representations into its corresponding sub-classifier, and then to combine these sub-classifiers together to generate a class-level classifier. Meta Variance Transfer methods [34] is proposed to learn to augment from the others by observing variations of real data (e.g. geometric deformation, background changes, simple noise) which could hint on unseen variations in other classes. Then the model learns to transfer the variance in the feature space by selecting the variations that could be helpful in simulating the unseen test examples for the target class. In order to combine distribution-level and instance-level relation, Yang et al. [77] proposed distribution propagation graph network (DPGN). The features of support images and query images are fed into a dual complete graph network, they apply a point-to-distribution aggregation a strategy to aggregate instance similarities to construct distribution representations. And a distribution-to-point aggregation strategy is applied to calculate similarity with both distribution-level and instance-level relations. Inspired by the compositional representation of objects in humans, [78] proposed a neural network architecture that explicitly represents objects as a dictionary of shared components and their spatial composition.
Learning to fine-tune. A weight imprinting strategy was proposed in [79] which aimed to set weights directly of a ConvNet classifier for new categories. They applied a normalization layer with a scaling factor in the classifier which aims to transform the features of new category samples into activation vectors as the weights of the normalization layer. In [80] a transfer-based method was proposed to generate class representations. They applied a power transform mechanism to preprocess support features to make them closer to the Gaussian distribution. According to the gaussian-like distribution, they applied maximum a posteriori probability to find the estimates of each class center which is similar to the minimization of Wasserstein distance. then a iterative algorithm based on a Wasserstein distance to estimate the optimal transport from the initial distribution of the features to its the Gaussian distribution to update the center. In [81], they proposed an Adaptive Distribution Calibration (ADC) method for FSL, which can adaptively transfer distribution information from related base classes to calibrate the biased distributions of novel classes.

3.3.2. Metric-based class representation learning

Many techniques have been put forward for effective metric-based class representations which can be broadly divided into five categories: feature distribution, attention mechanism, metric strategy for improving class representation, semantic alignment, and multimodal learning.
Feature distribution. It was demonstrated in [82] that GANs based feature generator [83] suffers from the issue of mode collapse. To address this problem, variational autoencoder (VAE) [84] and GANs are combined together to form a conditional feature generation model [32] which aims to learn the conditional distribution of image features on the labeled class data and the marginal distribution of image features on the unlabeled class data. Alternatively, a multi-mixed feature distribution can be learned for represent each category in RepMet [85] and perform FSFGIC tasks. Davis et al. [27] extended DeepEMD method [59] by reconstructing each query sample as a weighted sum of components from the same class for obtaining class-level feature distribution. [86] proposed a re-abstraction and perturbing support pair network (RaPSPNet) for FSFGIC. Specifically, they first design a feature re-abstraction embedding (FRaE) module which can not only effectively amplify the difference between the feature information from different categories but also better extract the feature information from images. Furthermore, a novel perturbing support pair (PSP) based similarity measure module is designed which evaluates the relationships of feature information among a query image and two different categories of support images (a support pair) at the same time for guiding the designed FRaE module to find salient feature information from the same category of query and support images and find distinguishable feature information from the different categories of query and support images.
Afrasiyabi [25] proposed two distribution alignment strategy to align the novel categories to the related base categories which aims to obtain better class respresentations. A centroid alignment strategy and an adversarial alignment strategy based on Wasserstein distance is designed to enforce intra-class compactness. Das et al. proposed a non-parametric approach [87] to address the problem that only base-class prototypes are available. They considered that all class prototype distributions are arranged on a manifold. They first estimate the novel-class prototypes by calculating the mean of the prototypes which are near the noval samples. A graph is structured with all the class prototypes and an induced absorbing Markov-chain is applied to complete classification task. Inspired by the fact that humans can use learned concepts or components to help them recognize novel classes, [88] proposed Compositional Prototypical Networks (CPN) to learn a transferable prototype for each human-annotated attribute, which we call a component prototype. In order to learn fine-grained structure in the feature space, Luo et al. proposed a two-path network to adaptively learn the views [89]. One path is label-guided classification, the support features belong to same class are aggregated into a prototype and the similarities are calculated between the prototypes and query images. Another path is instance-level classification which aims to produce different views for an image, then mapping them into feature space to construct a better fine-grained semantic structure. [90] proposed to combine the frequency features with routine features. In addition to a regular CNN module, a discrete cosine transformation is applied to generate frequency feature representations. Then, two kinds of feaures are concatenated as the final features. In order to explore intra-class distribution information, [91] proposed improved prototypical networks (IPN). Compared to the prototype network, IPN adds a weight distribution module to weight different samples belong to same category. And a distance scaling module is applied to maximize the inter-class difference while minimize the intra-class difference via distance measurement at different scales. To gain Gaussian-like distributions, [92] proposed a transfer-based method to process features belong to same class. They introduce transforms to adjust the distribution of features, and a Wasserstein distance based iterative algorithm to calculate prototype for each class. Similarly, [93] proposed optimal-transport algorithm to tansform features into Gaussian-like distributions and estimate best class centres.
Attention mechanism. Attention strategy aims to select discriminative feature or region from the extracted feature space for effective class-level feature representation. In [50], an attention mechanism [94] was applied to locate and reweight semantically relevant local region pairs between query and support samples which aims to strength discriminative objects and suppress the background. He et al. [95] indicated that object localization (using local discriminative regions) can provide great help for FSFGIC. Then a self-attention based complementary module which utilize channel attention and spatial attention was designed for performing weakly supervised object localization and finding their corresponding discriminative regions. Alternatively, [96] utilize channel attention and spatial attention to find discriminative regions from query and support samples for improving the classification performance of FSFGIC. Alternatively, a novel transformer based neural network architecture called CrossTransformers [97] was designed which applies a cross attention mechanism to find coarse spatial correspondence between the query and support labeled samples in a class. In [24], an attention mechanism was proposed to mix two modalities (i.e., semantic and visual modalities) and ensure that the representations of attributes are in the same space with visual representation.
Single prototype-based methods may fail to capture the subtle information of a class. To address this problem, Huang et al. [98] proposed a descriptor-based multi-prototype network (LMPNet) to learn multi-prototype. They design an attention mechanism to weight all channels in each spatial position of all samples adaptively to obtain local descriptors, and construct multiple prototypes based on these descriptors which contain more complete information of a class.
Metric strategy for improving class representation. To obtain discriminative class representations for FSFGIC, image-to-class metric strategies have been proposed. Deep nearest neighbor neural network (DN4) [7] was proposed which aims to learn optimal class-level local deep feature representation of a class space based on the designed image-to-class similarity measure strategy in the case of extremely limited training samples. A discriminative deep nearest neighbor neural network (D2N4) [99] extended the DN4 method [7] by adding a center loss function [100]. And then class-level local and global feature representations are learned for improving the quality discriminability features in the framework of the DN4 method [7]. In [26], Li et al. argued that if samples can be well classified by two different similarity measures at the same time, then the samples in a class can be more compactly distributed in a smaller feature space and a more discriminative feature map can be obtained. In this way, a bi-similarity network (BSNet) [26] was proposed that the learned class-level feature representations from query and support samples are obtained by using two different similarity measures. In [38], Zhu et al. argued that a large number of unlabeled data has the high potential to improve the classification performance in FSFGIC tasks. A progressive point to set metric learning (PPSML) [38] was presented for semi-supervised FSFGIC tasks. The aim of a self-training strategy is to select local and global feature representations from a mixture of labeled and unlabeled samples. Then point to set similarity measure is applied to obtain class-level local or global feature representation for performing FSFGIC tasks. To avoid overfitting and calculate a robust class representation under the condition of extremely limited training samples, a deep subspace network (DSN) [101] was introduced to transform class representation into an adaptive subspace and generate a corresponding classifier. And then testing samples are classified according to the nearest subspace classifier. That is to assign the query sample to the class which has the shortest Euclidean distance between the query and its projection onto the class-specific subspace.
Triantafillou et al. propose a mean average precision (m-AP) [102] which aims to learn similarity metric based on information retrieval. They extended the work of that optimizes for AP in order to account for all possible choices of query among the batch points. They then use the frameworks of SSVM (Structural Support Vector Machine) and DLM (Direct Loss Minimization) for optimization of m-AP.
Liu et al. [103] introduced a negative margin loss to reduce inter-class variance and generate more efficient decision boundaries. They integrate the margin parameter to softmax loss and apply negative margin to softmax loss which aims to improve both the discriminability on training classes and the transferability to novel classes of the learned metrics. Hilliard et al.[28] proposed a metric-agnostic conditional embeddings (MACO) network. MACO contains four stages, the feature stage is used to obtaining features, the relational stage produces a single veter as the class respresentation of each class. The conditioning stage connects the class representations to query image features which aims to learn the class representation that is more relevant to the query image and the classifier makes the final prediction.
Semantic alignment. It was indicated in [104] that people tend to compare similar objects thoroughly in a pairwise manner, e.g., comparing the heads of two birds first, then their wings and feet. In this manner, it is natural to enhance feature information during the comparison process. A low-rank pairwise bilinear pooling operation network [104] was designed for obtaining class-level deep feature representation between query and support samples in terms of the way that people compare similar objects. It was indicated in [50] that the dominant object can be located anywhere in the image. In this way, directly calculating the distance between query and support samples may cause ambiguity. To address this problem, semantic alignment metric learning (SAML) [50] was proposed to align the semantically related local regions on samples by a “collect and select” strategy. On the one hand, the similarities of all local region pairs from query samples and support class in a relation matrix are calculated and obtained. On the other hand, an attention mechanism [94] was applied to “select” the semantically relevant pairs. Li et al. [96] extended the method in [50], and a convolutional block attention module [105] was applied to capture discriminative regions. To eliminate the influence of noise and improve the efficiency of a similarity measure, query-relevant regions from support samples are selected for semantic alignment. And then multi-scale class-level feature representations are utilized to represent discriminative regions of the query and support samples in a class and perform FSFGIC tasks. In [25] a centroid associative alignment strategy was proposed to enforce intra-class compactness and obtain better class representations.
Alternatively, an end-to-end graph-based approach called explicit class knowledge propagation network (ECKPN) [17] was proposed which aims to learn and propagate the class representations explicitly. First, a comparison module is used to explore the relationship between paired samples for learning sample representations in instance-level graphs. Secondly, a squeeze strategy is proposed to make the instance-level graph to generate the class-level graph which can help obtain class-level visual representation. Third, the class-level visual representations are combined with the instance-level sample representations for performing FSFGIC tasks.
Multimodel learning. Inspired by the prototypical network [48], a multimodal prototypical network [106] was designed for mapping text data into the visual feature space by using GANs. In [24], Huang et al. indicated that some methods which apply auxiliary semantic modalities into a metric learning framework only augment the feature representations of samples with available semantics and ignore the query samples, which may lose the potential for the improvement of classification performance and may lead to a shift between the modalities combination and the pure-visual representation. To address this issue, an attributes-guided attention module (AGAM) is proposed which aims to make more effective use of human-annotated attributes and learn more discriminative class-level feature representations. An attention alignment mechanism is designed to distill knowledge from attribute guidance to the pure visual feature selection process, so that it can learn to pay attention to more semantic features without using the restriction of attribute annotation. To better align the visual and language feature distributions that describe the same object class, [107] proposed a cross-modal distribution alignment module, in which they introduce a vision-language prototype for each class to align the distributions, and adopt the Earth Mover’s Distance (EMD) to optimize the prototypes.
Gu et al. [108] proposed a two-stream neural network (TSNN), which not only learns features from RGB images, but also focus on steganalysis features via a steganalysis rich model filter layer. The RGB stream aims to distinguish the diference between support images and query images based on the global-level features and calculate the representations of each support class, the steganalysis stream extracts steganalysis features to locate critical regions. An extractor and fusion module is used to fusion the two-stream features by a general convolutional block. An image-to-class deep metric is applied to produce the similarity scores.
Zhang et al. [109] introduced fine-grained attributes into prototype network and proposed a prototype completion network (ProtoComNet). In meta-training stage, ProtoComNet will extracts representative attribute features as priors. They applied a attention-based aggregator to aggregate the attribute features and prototype to obtain completed prototype. In addition, a Gaussian-based prototype fusion strategy was designed to learn mean-based prototypes from unlabeled samples, and applied the Bayesian estimation to fuse the two kinds of prototypes which aims to produce more representative prototypes.

3.4. Task specific feature representation learning based FSFGIC methods

Task specific feature representation learning based FSFGIC methods aim to overcome the problem of overfitting and poor generalization and utilize deep feature representation from all training samples in a task (i.e., one training episode) to construct a task specific feature representation (e.g., task-level graph relationship representation [18] or task-level local deep feature representation [8]) for this task.

3.4.1. Optimization-based task specific feature representation learning

The existing optimization-based task specific feature representation learning methods can be divided into two categories: learning a model and learning to fine-tune.
Learning a model. In [110], a task embedding network was presented to learn task specific feature representations via a Fisher information matrix [111] for exploring the nature of the target task and its relationship to other tasks. Meanwhile, the learned task specific feature representations can also show the similarity between two different tasks. It was indicated in [112] that the existing optimization based methods learn to equally utilize meta-knowledge in each task without considering the diversity of each task. To address this problem, they extended the model-agnostic meta-learning method [113] to deal with the imbalance of the number of samples in each task instance and out-of-distribution tasks, but complex data set encoding and calculation of balance variables for each task increase the computational complexity of the algorithm. To effectively obtain a task-specific architecture for each new task, a meta neural architecture search method [114] (M-NAS) was proposed. Specifically, an auto-encoder is designed to generate a task-aware model architecture which has the ability to tailor the globally shared meta-parameters. It was indicated in [115] that meta-learning models are prone to overfitting in a new task with limited samples. In this way, a gradient dropout regularization is proposed to efficiently adapt to a new task. The key idea is to impose uncertainty to the meta-training stage via adding a noise gradient to parameters for improving the generalization of the model. [116] proposed hierarchically cascaded transformers that exploit intrinsic image structures through spectral tokens pooling and optimize the learnable parameters through latent attribute surrogates.
In order to improve the representation ability of mate-learning methods, a deep meta-learning (DEML) method [117] was proposed to generate high-level concepts for each images in a task. These concepts can guide the meta-learner adapt quickly to new tasks. Moreover, a concept discriminator is designed to to recognize different images. Tian et al. [118] propose a new consistent meta-regularization (Con-MetaReg) to enhance the learning ability of meta-learning model. Specifically,a base learner trains on the support set, then another learner trains on a novel query set. Con-MetaReg is proposed to align the two learner by the Frobenius norm of the difference between parameters to eliminate the data discrepancy for better meta-knowledge. In [119], a label-free loss function called Self-Critique and Adapt (SCA) was proposed. SCA can be added to a base model to learn knowledge with an unsupervised loss from a critic loss network. The features learnded form the base model will be send to the critic network to create a loss for target task.
Learning to fine-tune. In order to overcome overfitting and the poor generalization ability caused by limited training samples, an effective scheme [1] for selecting samples from the auxiliary data was proposed. According to a given classifier with shared parameters, some samples with similar feature distributions as some given target samples are selected from an auxiliary dataset with rich samples. The selected samples from an auxiliary dataset and the given target samples are sent into the classifiers to pre-train a weight initialization. Finally the remaining target samples are used to fine-tune the parameters corresponding to the classifiers for quickly adapting to target tasks.
In order to improve the generalization on the novel domain, [120] proposed a combining domain-specific meta-learners (CosML) method. CosML pre-training a set of meta-learners on different domains to learn domain-specific parameters. CosML generates task and domain prototypes to represent each task and domain in the feature space. For novel domain, they inirialize a subnetwork with the domain-specific meta-parameters which are weighted by the similarity of these domains and the novel domain. In the optimizing phase, properties in an image that are not related to the target task will interfere the optimization results. A context-agnostic (CA) [30] method is proposed to abandon the additional properties in training data. In training task, they apply a context-adversarial network to generate another object without extra information to the base network to initialize context-agnostic weights.

3.4.2. Metric-based task specific feature representation learning

The existing metric-based task specific feature representation learning methods can be classified into three categories: feature distribution, attention mechanism, and metric strategy for improving task representation.
Feature distribution. In [121], a covariance metric network (CovaMNet) was proposed which aims to obtain task-level covariance representations and a covariance metric between query and support samples. Furthermore, a novel deep covariance metric is designed to measure the consistency of distributions between query and support samples for performing FSFGIC tasks.
The metric function may be failed to generalize due to the discrepancy between the feature distributions of the base and novel domains in a task. To address this problem, Tseng et al. [122] proposes a cross-domain approach which applies a feature-wise transformation layer to simulate the feature distributions of different domains. In the train stage, the feature-wise transformation layer is inserted into the feature encoder and optimized by two hyper-parameters via a learning-to-learn strategy. [123] proposed a unsupervised embedding adaptation mechanism called early-stage feature reconstruction (ESFR). ESFR contains a feature-level reconstruction training stage and a dimensionality-driven early stopping stage which aim to find out more generalizable features.
Attention mechanism. In [8], an adaptive episodic attention module was designed to select and weight key regions among the entire task. Alternatively, attention strategy has also been used in graph neural networks (GNNs) for effectively obtaining task-level relation representations. Guo et al. indicated in [18] that existing GNN-based FSFGIC methods focus on the sample-to-sample relation while neglecting task level relationships. And then a GNN based sample-to-task FSFGIC method named attention-based task level relation module (ATRM) was proposed to consider the specificity of different tasks. In ATRM, task relation representations between the embedding features of a target sample and the embedding features of all samples in the task are obtained by calculating the absolute difference between target sample and all samples in the task. And then an attention mechanism is used to learn task specific relation representations for each task.
Metric strategy for improving task representation. It was indicated in [8] that the existing image-to-image similarity measure [54] or image-to-class similarity measure [7] cannot make full use of local deep feature representations. To address this problem, an adaptive task-aware local representations network (ATL-Net) is designed to select local descriptors with learned thresholds and assign selected local representations different weights based on episodic attention for improving the local deep feature representations. In [124], a region comparison network was proposed which aims to reveal how FSFGIC works in neural networks. In order to explore more fine-grained information and find the critical regions, each support sample is divided into several parts, and task-level local deep feature representations between each region in a support sample and each query sample are used to calculate their feature similarities and their corresponding region weights. And then an explainable network is designed to find the critical regions related to the final classification results. A discriminative mutual nearest neighbor neural network (DMN4) [125] extended the DN4 method [7] and a mutual nearest neighbor mechanism [126] was applied to obtain task-level local feature representations between query and support samples for performing FSFGIC tasks. Li et al. extended a triplet network [127] into a deep K-tuplet network [128] for learning a task level local deep feature representation by utilizing the relationship among the input samples in an training episode.
Table 2. Comparative FSFGIC results of three categories.
Table 2. Comparative FSFGIC results of three categories.
Preprints 93061 i001
LG: Local or/and global deep feature representation learning. CR: Class representation learning. TR: Task specific feature representation learning. O: Optimization-based. M: Metric-based.

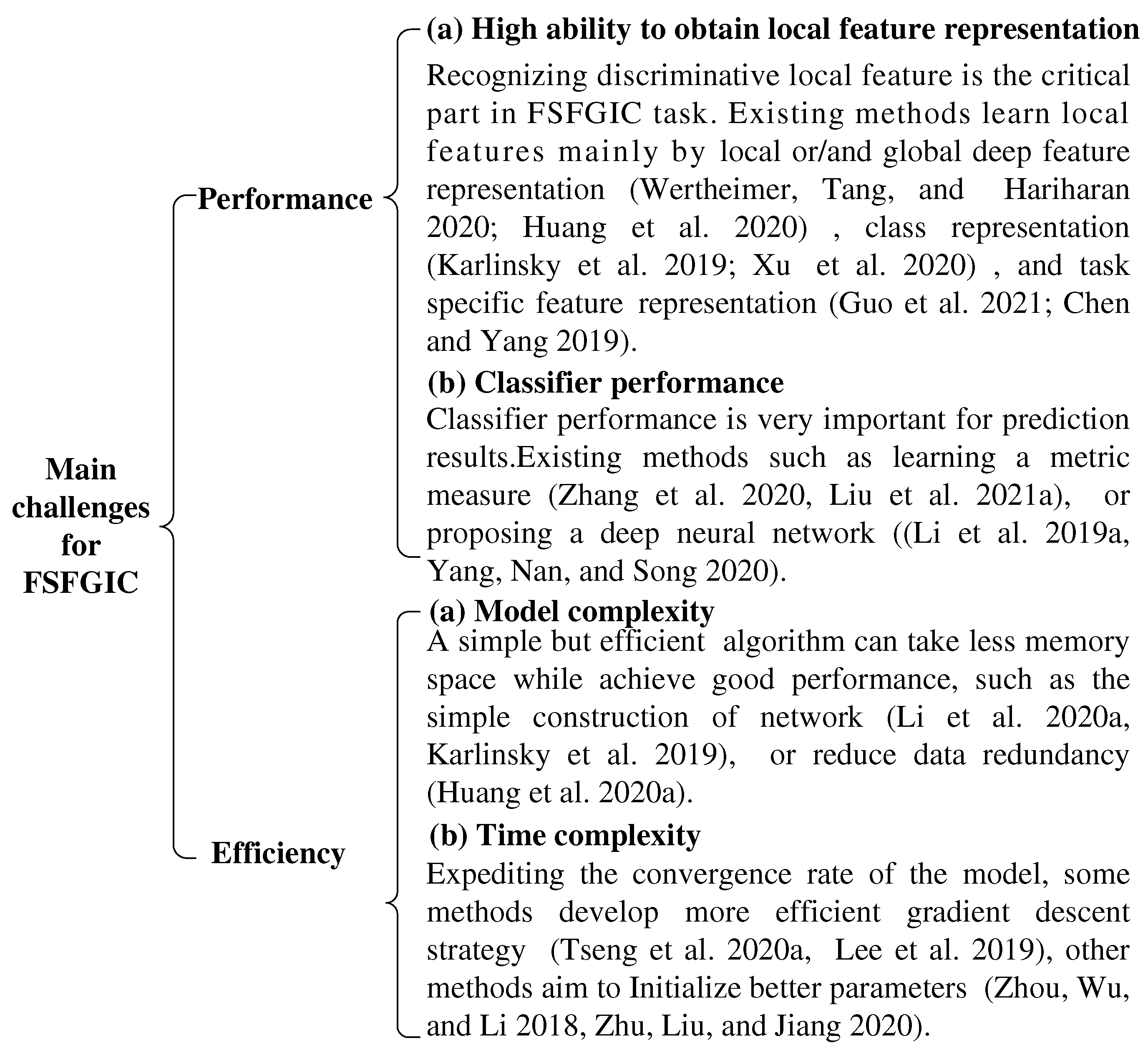
4. Summary and discussions

Our investigation indicates that the existing FSFGIC methods have made great process in FSFGIC tasks, but there are still some important challenges on FSFGIC that need to be dealt with in the future.
Trade-off between the problem of overfitting and the ability of image feature representation. Our investigation indicates that the existing FSFGIC algorithms are still at the stage of theoretical exploration and cannot be used in practical applications. Currently, data augmentation, regularization, and modeling of the feature extraction process can effectively alleviate the overfitting problem caused by extremely limited training samples and can also enhance the ability of feature representation, but there is still a trade-off between overcoming the over-fitting problem and enhancing the ability of image feature representation. On the one hand, image feature representation is used not only to represent train samples, but also to construct classifiers for performing FSFGIC tasks. In this manner, the quality of feature representation directly affects the classification performance on FSFGIC. On the other hand, due to the extremely limited number of training samples on FSFGIC, the existing FSFGIC methods utilize a relatively simple network as a backbone (e.g., Conv-64F [10]) for alleviating the overfitting problem. Our investigation indicates that the existing simple networks cannot effectively learn discriminative features from training samples compared with the existing large networks (e.g., ResNet50 [129]). Therefore, how to balance the problem of overfitting and the ability of image feature representation is one of the most important challenges on FSFGIC.
Generalization in FSFGIC. There exists two main challenges on generalization in FSFGIC methods. On the one hand, an ideal FSFGIC algorithm should have the ability to handel various learning tasks with different complexity and diversity of data. Our investigation indicates that, currently, the number of tasks and datasets available for FSFGIC training is very limited (much less than the number of instances available in few-shot learning). Most of the existing FSFGIC methods are over-designed for specific benchmark tasks and data sets which may weaken the applicability of the existing FSFGIC methods for dealing with more general FSFGIC tasks. On the other hand, our investigation indicates that most of the existing FSFGIC researches focus on common application scenarios with small scale tasks and large scale labeled auxiliary data. However, the actual FSFGIC tasks that need to be solved may be dynamic and the labeled auxiliary data is not available. Therefore, it is necessary to generalize the technique of feature representation learning to effectively perform cross-domain or multi-domain FSFGIC tasks.
Theoretical research. In essence, all FSFGIC solutions are designed by specific techniques to obtain feature representations that can be used to accurately represent samples and to perform FSFGIC tasks. Although the quality of feature representation directly affects the classification performance of FSFGIC, our investigation indicates that no one has considered how to establish a theoretical approach to measure whether the feature representation learned from training samples can correctly reflect the inherent characteristics of the training samples. Therefore, constructing the a systematic theory for FSFGIC from the perspective of improving the accuracy of feature representations obtained from training samples can bring new inspiration to FSFGIC researchers.
Preprints 93061 g003
Figure 3. Comparison of few-shot image classification and few-shot fine-grained image classification.
Figure 3. Comparison of few-shot image classification and few-shot fine-grained image classification.
Preprints 93061 g003

5. Conclusion

In this paper, we presented a comprehensive review on feature representation learning for FSFGIC. A taxonomy for FSFGIC is proposed. In terms of this taxonomy, different issues on FSFGIC methods are discussed. The main unresolved problems related to feature representation learning for FSFGIC are identified and discussed. We hope that this survey can help newcomers and practitioners position themselves this evolving field, and the survey highlights future research opportunities.

Author Contributions

Conceptualization, Methodology, and Writing—Review and Editing: Jie Ren, Weichuan Zhang, and Changming Sun;Investigation, Writing Original Draft: Jie Ren, Changmiao Li, and Yaohui An; Supervision: Weichuan Zhang. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Shaanxi natural science basic research project under Grant 2022JM-394 and the Scientific Research Program funded by Shaanxi Provincial Education Department, under Grant 23JY029.

Data Availability Statement

Data are contained within the article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Zhang, Y.; Tang, H.; Jia, K. Fine-grained visual categorization using meta-learning optimization with sample selection of auxiliary data. In Proceedings of the European Conference on Computer Vision, 2018, pp. 233–248.
  2. Wah, C.; Branson, S.; Welinder, P.; Perona, P.; Belongie, S. The caltech-ucsd birds-200-2011 dataset 2011.
  3. Nilsback, M.E.; Zisserman, A. Automated flower classification over a large number of classes. In Proceedings of the Indian conference on computer vision, graphics & image processing, 2008, pp. 722–729.
  4. Maji, S.; Rahtu, E.; Kannala, J.; Blaschko, M.; Vedaldi, A. Fine-grained visual classification of aircraft. arXiv preprint arXiv:1306.5151 2013.
  5. Smith, L.B.; Slone, L.K. A developmental approach to machine learning? Frontiers in psychology 2017, 8, 2124. [CrossRef]
  6. Zhu, Y.; Liu, C.; Jiang, S. Multi-attention Meta Learning for Few-shot Fine-grained Image Recognition. In Proceedings of the International Joint Conference on Artificial Intelligence, 2020, pp. 1090–1096. [CrossRef]
  7. Li, W.; Wang, L.; Xu, J.; Huo, J.; Gao, Y.; Luo, J. Revisiting local descriptor based image-to-class measure for few-shot learning. In Proceedings of the IEEE conference on computer vision and pattern recognition, 2019, pp. 7260–7268. [CrossRef]
  8. Dong, C.; Li, W.; Huo, J.; Gu, Z.; Gao, Y. Learning task-aware local representations for few-shot learning. In Proceedings of the Proceedings of the Twenty-Ninth International Conference on International Joint Conferences on Artificial Intelligence, 2021, pp. 716–722. [CrossRef]
  9. Zhang, W.; Liu, X.; Xue, Z.; Gao, Y.; Sun, C. NDPNet: A novel non-linear data projection network for few-shot fine-grained image classification. arXiv preprint arXiv:2106.06988 2021. [CrossRef]
  10. Vinyals, O.; Blundell, C.; Lillicrap, T.; Wierstra, D.; et al. Matching networks for one shot learning. Advances in neural information processing systems 2016, 29.
  11. Cao, S.; Wang, W.; Zhang, J.; Zheng, M.; Li, Q. A few-shot fine-grained image classification method leveraging global and local structures. International Journal of Machine Learning and Cybernetics 2022, 13, 2273–2281. [CrossRef]
  12. Abdelaziz, M.; Zhang, Z. Learn to aggregate global and local representations for few-shot learning. Multimedia Tools and Applications 2023, pp. 1–24. [CrossRef]
  13. Zhu, H.; Koniusz, P. EASE: Unsupervised discriminant subspace learning for transductive few-shot learning. In Proceedings of the IEEE conference on computer vision and pattern recognition, 2022, pp. 9078–9088.
  14. Li, Y.; Bian, C.; Chen, H. Generalized ridge regression-based channelwise feature map weighted reconstruction network for fine-grained few-shot ship classification. IEEE Transactions on Geoscience and Remote Sensing 2023, 61, 1–10. [CrossRef]
  15. Hu, Z.; Shen, L.; Lai, S.; Yuan, C. Task-adaptive Feature Disentanglement and Hallucination for Few-shot Classification. IEEE Transactions on Circuits and Systems for Video Technology 2023. [CrossRef]
  16. Zhou, Z.; Luo, L.; Zhou, S.; Li, W.; Yang, X.; Liu, X.; Zhu, E. Task-Related Saliency for Few-Shot Image Classification. IEEE Transactions on Neural Networks and Learning Systems 2023. [CrossRef]
  17. Chen, C.; Yang, X.; Xu, C.; Huang, X.; Ma, Z. Eckpn: Explicit class knowledge propagation network for transductive few-shot learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2021, pp. 6596–6605.
  18. Guo, Y.; Ma, Z.; Li, X.; Dong, Y. Atrm: Attention-based task-level relation module for gnn-based fewshot learning. arXiv preprint arXiv 2021, 2101.
  19. Khosla, A.; Jayadevaprakash, N.; Yao, B.; Li, F.F. Novel dataset for fine-grained image categorization: Stanford dogs. In Proceedings of the CVPR Workshop on Fine-Grained Visual Categorization. Citeseer, 2011, Vol. 2.
  20. Krause, J.; Stark, M.; Deng, J.; Fei-Fei, L. 3D object representations for fine-grained categorization. In Proceedings of the IEEE international conference on computer vision workshops, 2013, pp. 554–561. [CrossRef]
  21. Van Horn, G.; Branson, S.; Farrell, R.; Haber, S.; Barry, J.; Ipeirotis, P.; Perona, P.; Belongie, S. Building a bird recognition APP and large scale dataset with citizen scientists: The fine print in fine-grained dataset collection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2015, pp. 595–604. [CrossRef]
  22. Xiao, J.; Hays, J.; Ehinger, K.A.; Oliva, A.; Torralba, A. Sun database: Large-scale scene recognition from abbey to zoo. In Proceedings of the IEEE computer society conference on computer vision and pattern recognition. IEEE, 2010, pp. 3485–3492. [CrossRef]
  23. Yu, X.; Zhao, Y.; Gao, Y.; Xiong, S.; Yuan, X. Patchy image structure classification using multi-orientation region transform. In Proceedings of the AAAI Conference on Artificial Intelligence, 2020, Vol. 34, pp. 12741–12748. [CrossRef]
  24. Huang, S.; Zhang, M.; Kang, Y.; Wang, D. Attributes-guided and pure-visual attention alignment for few-shot recognition. In Proceedings of the AAAI Conference on Artificial Intelligence, 2021, Vol. 35, pp. 7840–7847. [CrossRef]
  25. Afrasiyabi, A.; Lalonde, J.F.; Gagné, C. Associative alignment for few-shot image classification. In Proceedings of the European Conference on Computer Vision, 2020, pp. 18–35. [CrossRef]
  26. Li, X.; Wu, J.; Sun, Z.; Ma, Z.; Cao, J.; Xue, J.H. BSNet: Bi-similarity network for few-shot fine-grained image classification. IEEE Transactions on Image Processing 2020, 30, 1318–1331. [CrossRef]
  27. Wertheimer, D.; Tang, L.; Hariharan, B. Few-shot classification with feature map reconstruction networks. In Proceedings of the IEEE conference on computer vision and pattern recognition, 2021, pp. 8012–8021.
  28. Hilliard, N.; Phillips, L.; Howland, S.; Yankov, A.; Corley, C.D.; Hodas, N.O. Few-shot learning with metric-agnostic conditional embeddings. arXiv preprint arXiv:1802.04376 2018.
  29. Zhang, M.; Wang, D.; Gai, S. Knowledge distillation for model-agnostic meta-learning. In European Conference on Artificial Intelligence; 2020; pp. 1355–1362.
  30. Perrett, T.; Masullo, A.; Burghardt, T.; Mirmehdi, M.; Damen, D. Meta-learning with context-agnostic initialisations. In Proceedings of the Asian Conference on Computer Vision, 2020.
  31. Pahde, F.; Nabi, M.; Klein, T.; Jahnichen, P. Discriminative hallucination for multi-modal few-shot learning. In Proceedings of the IEEE International Conference on Image Processing, 2018, pp. 156–160. [CrossRef]
  32. Xian, Y.; Sharma, S.; Schiele, B.; Akata, Z. f-vaegan-d2: A feature generating framework for any-shot learning. In Proceedings of the IEEE conference on computer vision and pattern recognition, 2019, pp. 10275–10284. [CrossRef]
  33. Xu, J.; Le, H.; Huang, M.; Athar, S.; Samaras, D. Variational feature disentangling for fine-grained few-shot classification. In Proceedings of the IEEE International Conference on Computer Vision, 2021, pp. 8812–8821. [CrossRef]
  34. Park, S.J.; Han, S.; Baek, J.W.; Kim, I.; Song, J.; Lee, H.B.; Han, J.J.; Hwang, S.J. Meta variance transfer: Learning to augment from the others. In Proceedings of the International Conference on Machine Learning, 2020, pp. 7510–7520.
  35. Luo, Q.; Wang, L.; Lv, J.; Xiang, S.; Pan, C. Few-shot learning via feature hallucination with variational inference. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, 2021, pp. 3963–3972.
  36. Tsutsui, S.; Fu, Y.; Crandall, D. Meta-reinforced synthetic data for one-shot fine-grained visual recognition. Advances in Neural Information Processing Systems 2019, 32.
  37. Pahde, F.; Jähnichen, P.; Klein, T.; Nabi, M. Cross-modal hallucination for few-shot fine-grained recognition. arXiv preprint arXiv:1806.05147 2018.
  38. Zhu, P.; Gu, M.; Li, W.; Zhang, C.; Hu, Q. Progressive point to set metric learning for semi-supervised few-shot classification. In Proceedings of the IEEE International Conference on Image Processing, 2020, pp. 196–200.
  39. Wang, Y.; Xu, C.; Liu, C.; Zhang, L.; Fu, Y. Instance credibility inference for few-shot learning. In Proceedings of the IEEE conference on computer vision and pattern recognition, 2020, pp. 12836–12845.
  40. Huang, H.; Zhang, J.; Zhang, J.; Wu, Q.; Xu, J. Compare more nuanced: Pairwise alignment bilinear network for few-shot fine-grained learning. In Proceedings of the IEEE International Conference on Multimedia and Expo, 2019, pp. 91–96.
  41. Chen, M.; Fang, Y.; Wang, X.; Luo, H.; Geng, Y.; Zhang, X.; Huang, C.; Liu, W.; Wang, B. Diversity transfer network for few-shot learning. In Proceedings of the AAAI Conference on Artificial Intelligence, 2020, Vol. 34, pp. 10559–10566. [CrossRef]
  42. Schwartz, E.; Karlinsky, L.; Shtok, J.; Harary, S.; Marder, M.; Kumar, A.; Feris, R.; Giryes, R.; Bronstein, A. Delta-encoder: An effective sample synthesis method for few-shot object recognition. Advances in Neural Information Processing Systems 2018, 31.
  43. Wang, C.; Song, S.; Yang, Q.; Li, X.; Huang, G. Fine-grained few shot learning with foreground object transformation. Neurocomputing 2021, 466, 16–26. [CrossRef]
  44. Tokmakov, P.; Wang, Y.X.; Hebert, M. Learning compositional representations for few-shot recognition. In Proceedings of the IEEE International Conference on Computer Vision, 2019, pp. 6372–6381.
  45. Huynh, D.; Elhamifar, E. Compositional fine-grained low-shot learning. arXiv preprint arXiv:2105.10438 2021.
  46. Shen, Z.; Liu, Z.; Qin, J.; Savvides, M.; Cheng, K.T. Partial is better than all: revisiting fine-tuning strategy for few-shot learning. In Proceedings of the AAAI Conference on Artificial Intelligence, 2021, Vol. 35, pp. 9594–9602. [CrossRef]
  47. Chen, W.Y.; Liu, Y.C.; Kira, Z.; Wang, Y.C.F.; Huang, J.B. A closer look at few-shot classification. arXiv preprint arXiv:1904.04232 2019.
  48. Snell, J.; Swersky, K.; Zemel, R. Prototypical networks for few-shot learning. Advances in neural information processing systems 2017, 30.
  49. Shi, B.; Li, W.; Huo, J.; Zhu, P.; Wang, L.; Gao, Y. Global-and local-aware feature augmentation with semantic orthogonality for few-shot image classification. Pattern Recognition 2023, 142, 109702. [CrossRef]
  50. Hao, F.; He, F.; Cheng, J.; Wang, L.; Cao, J.; Tao, D. Collect and select: Semantic alignment metric learning for few-shot learning. In Proceedings of the IEEE international Conference on Computer Vision, 2019, pp. 8460–8469.
  51. Flores, C.F.; Gonzalez-Garcia, A.; van de Weijer, J.; Raducanu, B. Saliency for fine-grained object recognition in domains with scarce training data. Pattern Recognition 2019, 94, 62–73. [CrossRef]
  52. Tavakoli, H.R.; Borji, A.; Laaksonen, J.; Rahtu, E. Exploiting inter-image similarity and ensemble of extreme learners for fixation prediction using deep features. Neurocomputing 2017, 244, 10–18. [CrossRef]
  53. Zhang, X.; Wei, Y.; Feng, J.; Yang, Y.; Huang, T.S. Adversarial complementary learning for weakly supervised object localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 1325–1334. [CrossRef]
  54. Jiang, Z.; Kang, B.; Zhou, K.; Feng, J. Few-shot classification via adaptive attention. arXiv preprint arXiv:2008.02465 2020.
  55. Wu, H.; Zhao, Y.; Li, J. Selective, structural, subtle: Trilinear spatial-awareness for few-shot fine-grained visual recognition. In Proceedings of the IEEE International Conference on Multimedia and Expo, 2021, pp. 1–6.
  56. Ruan, X.; Lin, G.; Long, C.; Lu, S. Few-shot fine-grained classification with spatial attentive comparison. Knowledge-Based Systems 2021, 218, 106840. [CrossRef]
  57. Song, H.; Deng, B.; Pound, M.; Özcan, E.; Triguero, I. A fusion spatial attention approach for few-shot learning. Information Fusion 2022, 81, 187–202. [CrossRef]
  58. Huang, X.; Choi, S.H. Sapenet: Self-attention based prototype enhancement network for few-shot learning. Pattern Recognition 2023, 135, 109170. [CrossRef]
  59. Zhang, C.; Cai, Y.; Lin, G.; Shen, C. Deepemd: Few-shot image classification with differentiable earth mover’s distance and structured classifiers. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2020, pp. 12203–12213.
  60. Chen, Q.; Yang, R. Learning to distinguish: A general method to improve compare-based one-shot learning frameworks for similar classes. In Proceedings of the IEEE International Conference on Multimedia and Expo, 2019, pp. 952–957.
  61. Liu, Y.; Zhu, L.; Wang, X.; Yamada, M.; Yang, Y. Bilaterally normalized scale-consistent sinkhorn distance for few-shot image classification. IEEE Transactions on Neural Networks and Learning Systems 2023. [CrossRef]
  62. Zhao, J.; Lin, X.; Zhou, J.; Yang, J.; He, L.; Yang, Z. Knowledge-based fine-grained classification for few-shot learning. In Proceedings of the IEEE International Conference on Multimedia and Expo, 2020, pp. 1–6. [CrossRef]
  63. Sun, X.; Xv, H.; Dong, J.; Zhou, H.; Chen, C.; Li, Q. Few-shot learning for domain-specific fine-grained image classification. IEEE Transactions on Industrial Electronics 2020, 68, 3588–3598. [CrossRef]
  64. Zheng, Z.; Feng, X.; Yu, H.; Li, X.; Gao, M. BDLA: Bi-directional local alignment for few-shot learning. Applied Intelligence 2023, 53, 769–785. [CrossRef]
  65. Zhang, W.; Sun, C. Corner detection using second-order generalized Gaussian directional derivative representations. IEEE Transactions on Pattern Analysis and Mchine Intelligence 2019, 43, 1213–1224. [CrossRef]
  66. Zhang, W.; Sun, C.; Gao, Y. Image intensity variation information for interest point detection. IEEE Transactions on Pattern Analysis and Machine Intelligence 2023, 45, 9883–9894. [CrossRef]
  67. Jing, J.; Liu, S.; Wang, G.; Zhang, W.; Sun, C. Recent advances on image edge detection: A comprehensive review. Neurocomputing 2022. [CrossRef]
  68. Zhang, W.; Zhao, Y.; Breckon, T.P.; Chen, L. Noise robust image edge detection based upon the automatic anisotropic Gaussian kernels. Pattern Recognition 2017, 63, 193–205. [CrossRef]
  69. Jing, J.; Gao, T.; Zhang, W.; Gao, Y.; Sun, C. Image feature information extraction for interest point detection: A comprehensive review. IEEE Transactions on Pattern Analysis and Machine Intelligence 2023, 45, 4694–4712. [CrossRef]
  70. Zhang, W.; Sun, C.; Breckon, T.; Alshammari, N. Discrete curvature representations for noise robust image corner detection. IEEE Transactions on Image Processing 2019, 28, 4444–4459. [CrossRef]
  71. Zhang, W.; Sun, C. Corner detection using multi-directional structure tensor with multiple scales. International Journal of Computer Vision 2020, 128, 438–459. [CrossRef]
  72. Shui, P.L.; Zhang, W.C. Corner detection and classification using anisotropic directional derivative representations. IEEE Transactions on Image Processing 2013, 22, 3204–3218. [CrossRef]
  73. Zhang, H.; Torr, P.; Koniusz, P. Few-shot learning with multi-scale self-supervision. arXiv preprint arXiv:2001.01600 2020.
  74. Chen, Y.; Zheng, Y.; Xu, Z.; Tang, T.; Tang, Z.; Chen, J.; Liu, Y. Cross-domain few-shot classification based on lightweight Res2Net and flexible GNN. Knowledge-Based Systems 2022, 247, 108623. [CrossRef]
  75. Wei, X.S.; Wang, P.; Liu, L.; Shen, C.; Wu, J. Piecewise classifier mappings: Learning fine-grained learners for novel categories with few examples. IEEE Transactions on Image Processing 2019, 28, 6116–6125. [CrossRef]
  76. Lin, T.Y.; RoyChowdhury, A.; Maji, S. Bilinear CNN models for fine-grained visual recognition. In Proceedings of the IEEE International Conference on Computer Vision, 2015, pp. 1449–1457. [CrossRef]
  77. Yang, L.; Li, L.; Zhang, Z.; Zhou, X.; Zhou, E.; Liu, Y. DPGN: Distribution propagation graph network for few-shot learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2020, pp. 13390–13399.
  78. He, J.; Kortylewski, A.; Yuille, A. CORL: Compositional representation learning for few-shot classification. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, 2023, pp. 3890–3899.
  79. Qi, H.; Brown, M.; Lowe, D.G. Low-shot learning with imprinted weights. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 5822–5830.
  80. Hu, Y.; Gripon, V.; Pateux, S. Leveraging the feature distribution in transfer-based few-shot learning. In Proceedings of the International Conference on Artificial Neural Networks, 2021, pp. 487–499.
  81. Liu, X.; Zhou, K.; Yang, P.; Jing, L.; Yu, J. Adaptive distribution calibration for few-shot learning via optimal transport. Information Sciences 2022, 611, 1–17. [CrossRef]
  82. Arjovsky, M.; Bottou, L. Towards principled methods for training generative adversarial networks. arXiv preprint arXiv:1701.04862 2017.
  83. Xian, Y.; Lorenz, T.; Schiele, B.; Akata, Z. Feature generating networks for zero-shot learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 5542–5551. [CrossRef]
  84. Verma, V.K.; Arora, G.; Mishra, A.; Rai, P. Generalized zero-shot learning via synthesized examples. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 4281–4289.
  85. Karlinsky, L.; Shtok, J.; Harary, S.; Schwartz, E.; Aides, A.; Feris, R.; Giryes, R.; Bronstein, A.M. Repmet: Representative-based metric learning for classification and few-shot object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2019, pp. 5197–5206. [CrossRef]
  86. Zhang, W.; Zhao, Y.; Gao, Y.; Sun, C. Re-abstraction and perturbing support pair network for few-shot fine-grained image classification. Pattern Recognition 2023, p. 110158. [CrossRef]
  87. Das, D.; Moon, J.; George Lee, C. Few-shot image recognition with manifolds. In Proceedings of the Advances in Visual Computing: International Symposium, 2020, pp. 3–14. [CrossRef]
  88. Lyu, Q.; Wang, W. Compositional Prototypical Networks for Few-Shot Classification. arXiv preprint arXiv:2306.06584 2023. [CrossRef]
  89. Luo, X.; Chen, Y.; Wen, L.; Pan, L.; Xu, Z. Boosting few-shot classification with view-learnable contrastive learning. In Proceedings of the IEEE International Conference on Multimedia and Expo, 2021, pp. 1–6.
  90. Chen, X.; Wang, G. Few-shot learning by integrating spatial and frequency representation. In Proceedings of the Conference on Robots and Vision, 2021, pp. 49–56.
  91. Ji, Z.; Chai, X.; Yu, Y.; Pang, Y.; Zhang, Z. Improved prototypical networks for few-shot learning. Pattern Recognition Letters 2020, 140, 81–87. [CrossRef]
  92. Hu, Y.; Pateux, S.; Gripon, V. Squeezing backbone feature distributions to the max for efficient few-shot learning. Algorithms 2022, 15, 147. [CrossRef]
  93. Chobola, T.; Vašata, D.; Kordík, P. Transfer learning based few-shot classification using optimal transport mapping from preprocessed latent space of backbone neural network. In Proceedings of the AAAI Workshop on Meta-Learning and MetaDL Challenge, 2021, pp. 29–37.
  94. Zagoruyko, S.; Komodakis, N. Paying more attention to attention: Improving the performance of convolutional neural networks via attention transfer. arXiv preprint arXiv:1612.03928 2016.
  95. He, X.; Lin, J.; Shen, J. Weakly-supervised Object Localization for Few-shot Learning and Fine-grained Few-shot Learning. arXiv preprint arXiv:2003.00874 2020.
  96. Li, Y.; Li, H.; Chen, H.; Chen, C. Hierarchical representation based query-specific prototypical network for few-shot image classification. arXiv preprint arXiv:2103.11384 2021.
  97. Doersch, C.; Gupta, A.; Zisserman, A. Crosstransformers: spatially-aware few-shot transfer. Advances in Neural Information Processing Systems 2020, 33, 21981–21993.
  98. Huang, H.; Wu, Z.; Li, W.; Huo, J.; Gao, Y. Local descriptor-based multi-prototype network for few-shot learning. Pattern Recognition 2021, 116, 107935. [CrossRef]
  99. Yang, X.; Nan, X.; Song, B. D2N4: A discriminative deep nearest neighbor neural network for few-shot space target recognition. IEEE Transactions on Geoscience and Remote Sensing 2020, 58, 3667–3676. [CrossRef]
  100. Wen, Y.; Zhang, K.; Li, Z.; Qiao, Y. A discriminative feature learning approach for deep face recognition. In Proceedings of the European Conference on Computer Vision, 2016, pp. 499–515. [CrossRef]
  101. Simon, C.; Koniusz, P.; Nock, R.; Harandi, M. Adaptive subspaces for few-shot learning. In Proceedings of the IEEE conference on computer vision and pattern recognition, 2020, pp. 4136–4145. [CrossRef]
  102. Triantafillou, E.; Zemel, R.; Urtasun, R. Few-shot learning through an information retrieval lens. Advances in Neural Iformation Processing Systems 2017, 30.
  103. Liu, B.; Cao, Y.; Lin, Y.; Li, Q.; Zhang, Z.; Long, M.; Hu, H. Negative margin matters: Understanding margin in few-shot classification. In Proceedings of the European Conference on Computer Vision, 2020, pp. 438–455. [CrossRef]
  104. Huang, H.; Zhang, J.; Zhang, J.; Xu, J.; Wu, Q. Low-rank pairwise alignment bilinear network for few-shot fine-grained image classification. IEEE Transactions on Multimedia 2020, 23, 1666–1680. [CrossRef]
  105. Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision, 2018, pp. 3–19.
  106. Pahde, F.; Puscas, M.; Klein, T.; Nabi, M. Multimodal prototypical networks for few-shot learning. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, 2021, pp. 2644–2653. [CrossRef]
  107. Wang, R.; Zheng, H.; Duan, X.; Liu, J.; Lu, Y.; Wang, T.; Xu, S.; Zhang, B. Few-Shot Learning with Visual Distribution Calibration and Cross-Modal Distribution Alignment. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2023, pp. 23445–23454.
  108. Gu, Q.; Luo, Z.; Zhu, Y. A Two-Stream Network with Image-to-Class Deep Metric for Few-Shot Classification. In ECAI 2020; 2020; pp. 2704–2711.
  109. Zhang, B.; Li, X.; Ye, Y.; Huang, Z.; Zhang, L. Prototype completion with primitive knowledge for few-shot learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2021, pp. 3754–3762. [CrossRef]
  110. Achille, A.; Lam, M.; Tewari, R.; Ravichandran, A.; Maji, S.; Fowlkes, C.C.; Soatto, S.; Perona, P. Task2vec: Task embedding for meta-learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2019, pp. 6430–6439.
  111. Jaakkola, T.; Haussler, D. Exploiting generative models in discriminative classifiers. Advances in Neural Information Processing Systems 1998, 11.
  112. Lee, H.B.; Lee, H.; Na, D.; Kim, S.; Park, M.; Yang, E.; Hwang, S.J. Learning to balance: Bayesian meta-learning for imbalanced and out-of-distribution tasks. arXiv preprint arXiv:1905.12917 2019.
  113. Finn, C.; Abbeel, P.; Levine, S. Model-agnostic meta-learning for fast adaptation of deep networks. In Proceedings of the International Conference on Machine Learning, 2017, pp. 1126–1135.
  114. Wang, J.; Wu, J.; Bai, H.; Cheng, J. M-nas: Meta neural architecture search. In Proceedings of the AAAI Conference on Artificial Intelligence, 2020, Vol. 34, pp. 6186–6193.
  115. Tseng, H.Y.; Chen, Y.W.; Tsai, Y.H.; Liu, S.; Lin, Y.Y.; Yang, M.H. Regularizing meta-learning via gradient dropout. In Proceedings of the Asian Conference on Computer Vision, 2020.
  116. He, Y.; Liang, W.; Zhao, D.; Zhou, H.Y.; Ge, W.; Yu, Y.; Zhang, W. Attribute surrogates learning and spectral tokens pooling in transformers for few-shot learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2022, pp. 9119–9129.
  117. Zhou, F.; Wu, B.; Li, Z. Deep meta-learning: Learning to learn in the concept space. arXiv preprint arXiv:1802.03596 2018.
  118. Tian, P.; Li, W.; Gao, Y. Consistent meta-regularization for better meta-knowledge in few-shot learning. IEEE Transactions on Neural Networks and Learning Systems 2021, 33, 7277–7288. [CrossRef]
  119. Antoniou, A.; Storkey, A.J. Learning to learn by self-critique. Advances in Neural Information Processing Systems 2019, 32.
  120. Peng, S.; Song, W.; Ester, M. Combining domain-specific meta-learners in the parameter space for cross-domain few-shot classification. arXiv preprint arXiv:2011.00179 2020.
  121. Li, W.; Xu, J.; Huo, J.; Wang, L.; Gao, Y.; Luo, J. Distribution consistency based covariance metric networks for few-shot learning. In Proceedings of the AAAI conference on artificial intelligence, 2019, Vol. 33, pp. 8642–8649. [CrossRef]
  122. Tseng, H.Y.; Lee, H.Y.; Huang, J.B.; Yang, M.H. Cross-domain few-shot classification via learned feature-wise transformation. arXiv preprint arXiv:2001.08735 2020.
  123. Lee, D.H.; Chung, S.Y. Unsupervised embedding adaptation via early-stage feature reconstruction for few-shot classification. In Proceedings of the International Conference on Machine Learning, 2021, pp. 6098–6108.
  124. Xue, Z.; Duan, L.; Li, W.; Chen, L.; Luo, J. Region comparison network for interpretable few-shot image classification. arXiv preprint arXiv:2009.03558 2020.
  125. Liu, Y.; Zheng, T.; Song, J.; Cai, D.; He, X. Dmn4: Few-shot learning via discriminative mutual nearest neighbor neural network. In Proceedings of the AAAI Conference on Artificial Intelligence, 2022, Vol. 36, pp. 1828–1836. [CrossRef]
  126. Gowda, K.; Krishna, G. The condensed nearest neighbor rule using the concept of mutual nearest neighborhood. IEEE Transactions on Information Theory 1979, 25, 488–490. [CrossRef]
  127. Ye, M.; Guo, Y. Deep triplet ranking networks for one-shot recognition. arXiv preprint arXiv:1804.07275 2018.
  128. Li, X.; Yu, L.; Fu, C.W.; Fang, M.; Heng, P.A. Revisiting metric learning for few-shot image classification. Neurocomputing 2020, 406, 49–58. [CrossRef]
  129. He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016, pp. 770–778. [CrossRef]
Preprints 93061 g001
Figure 1. Comparison of few-shot image classification and few-shot fine-grained image classification.
Figure 1. Comparison of few-shot image classification and few-shot fine-grained image classification.
Preprints 93061 g001
Preprints 93061 g002
Figure 2. Classification of feature representation learning techniques in existing FSFGIC methods.
Figure 2. Classification of feature representation learning techniques in existing FSFGIC methods.
Preprints 93061 g002
Table 1. Representative benchmark datasets for FSFGIC.
Table 1. Representative benchmark datasets for FSFGIC.
Dataset name Class images categories
SUN397 Scenes 130,519 397
Oxford 102 Flowers Flowers 8,189 102
CUB200-2011 Birds 11,788 200
Stanford Dogs Dogs 20,580 120
Stanford Cars Cars 16,185 196
FGVC-Aircraft Aircrafts 10,000 100
NABirds Birds 48,562 555
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated