1. Introduction

The problem with a quantum version of general relativity is that the calculations that would describe interactions of very energetic gravitons — the quantized units of gravity — would have infinitely many infinite terms. You would need to add infinitely many counterterms in a never-ending process. Renormalization would fail. Because of this, a quantum version of Einstein’s general relativity is not a good description of gravity at very high energies. It must be missing some of gravity’s key features and ingredients.

However, we can still have a perfectly good approximate description of gravity at lower energies using the standard quantum techniques that work for the other interactions in nature. The crucial point is that this approximate description of gravity will break down at some energy scale — or equivalently, below some length.

Above this energy scale, or below the associated length scale, we expect to find new degrees of freedom and new symmetries. To capture these features accurately we need a new theoretical framework.

– Sera Cremonii, theoretical physicist at Lehigh University, specializing on string theory, quantum gravity, and cosmology, as quoted by Natalie Wolchover [118]

2. Time Dispersion in Quantum Mechanics

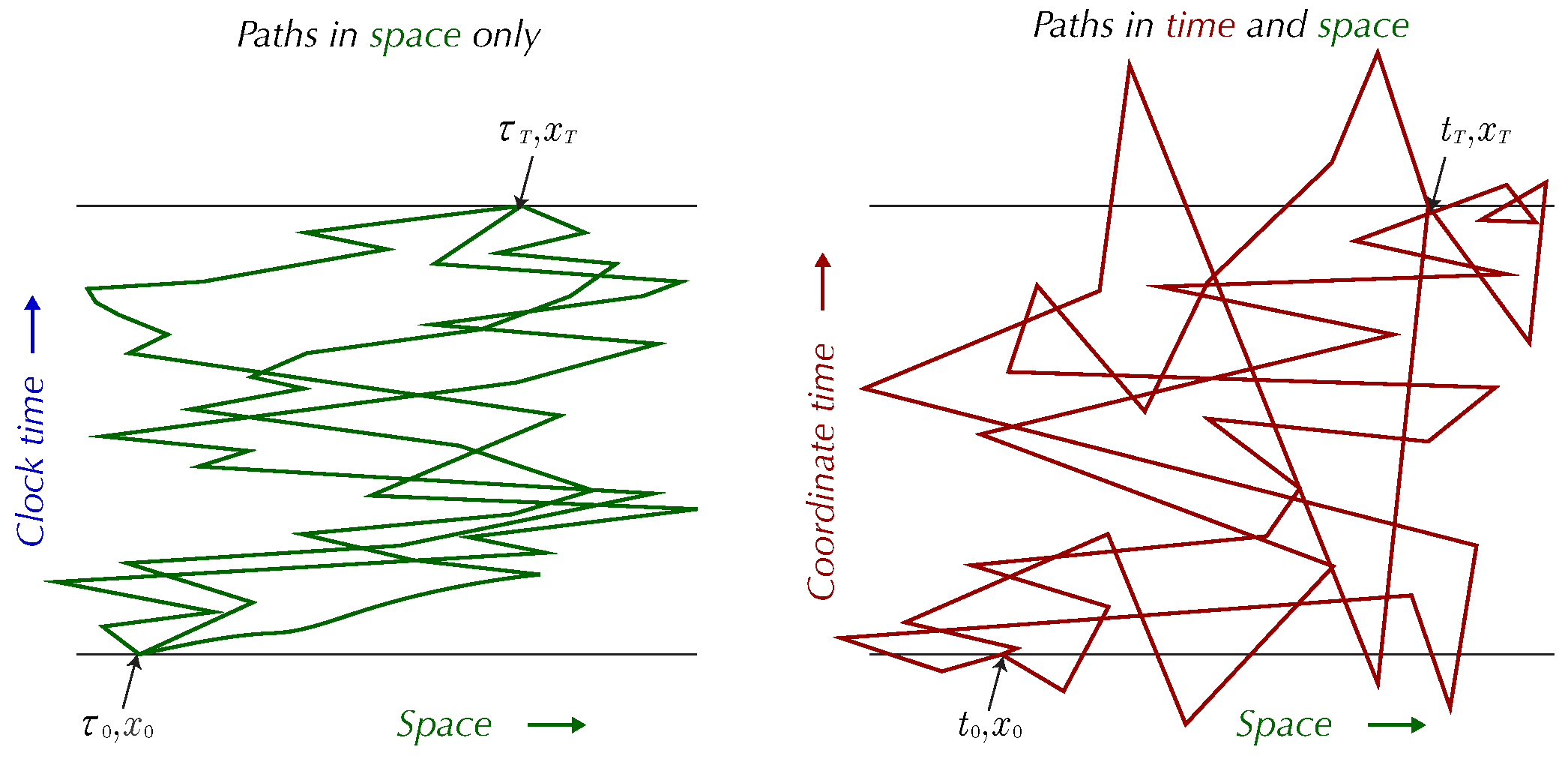
Figure 2.1. Paths in space; paths in time and space

Figure 2.1. Paths in space; paths in time and space

“Wheeler’s often unconventional vision of nature was grounded in reality through the principle of radical conservatism, which he acquired from Niels Bohr: Be conservative by sticking to well-established physical principles, but probe them by exposing their most radical conclusions.” – K. S. Thorne [108]

2.3. Spin Zero Fields

While most of the key ideas show up in the single particle case, we can’t, as noted get to falsifiability without extending the work to QFT, specifically QED. We worked primarily with the spin zero case, as the simplest. From the spin zero case, the generalization to QED was relatively straightforward.

For this step, it proved simpler to start with the FS/T equation and generalize it to high energies. We started with the single particle solutions, albeit with an extension in coordinate time as well as in space. We used the single particle solutions of the FS/T equation to define a Fock space. And with the free solutions and the creation and annihilation operators for the Fock space, we derived the Feynman propagators as the time-ordered vacuum expectation products in the usual way.

SQM propagators

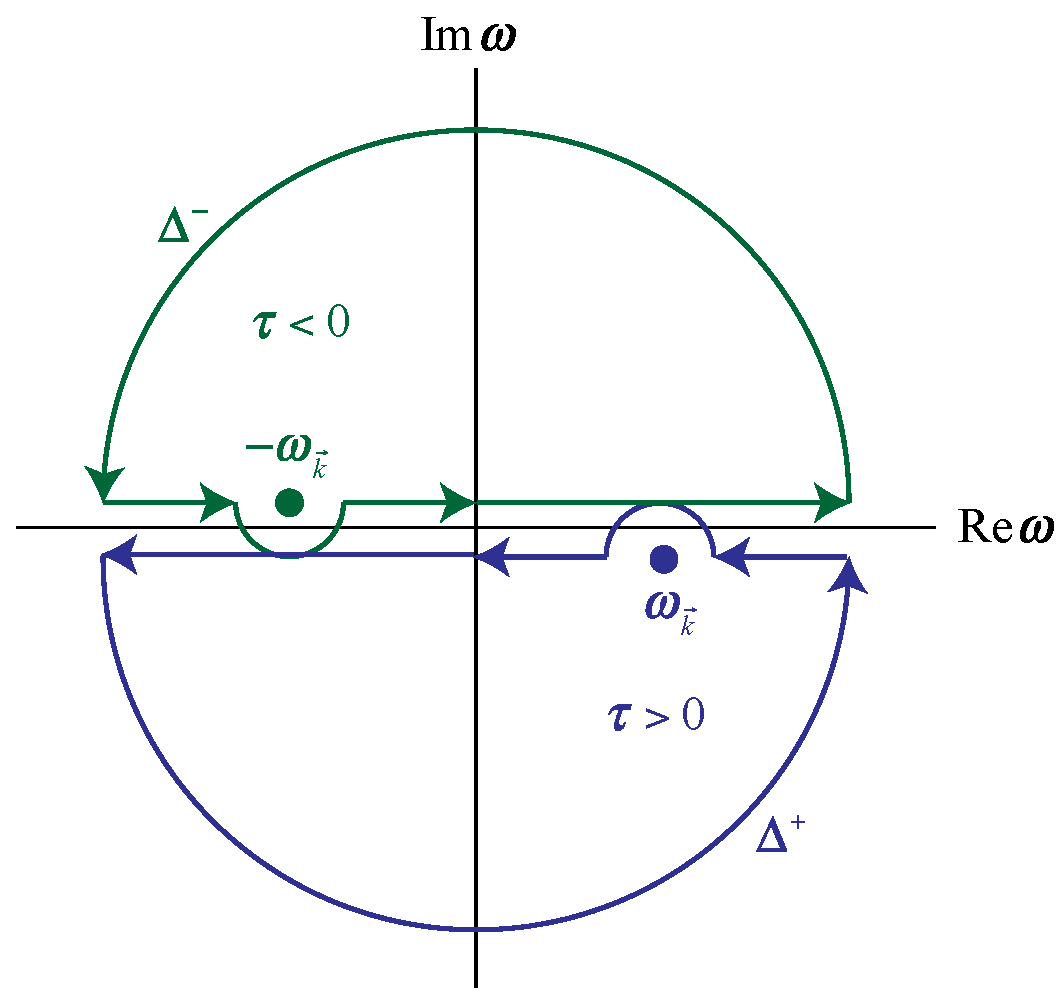
Figure 2.2. Contour integral for propagator.

Figure 2.2. Contour integral for propagator.

To ground the development of the TQM propagators we did a careful examination of the development of the SQM propagators. Tracking in particular Klauber’s line-by-line treatment, we noted there is one place where we start with three dimensional single particle wave functions, but then rewrite the $\frac{1}{2{\omega }_{\overrightarrow{k}}}$ normalization factor as a contour integral over $\omega$.

This is done in a way that folds in the Feynman boundary conditions.

The specific value of ${\omega }_{\overrightarrow{k}}$ appears as the residue of the pole in the complex plane. This means that while we seem to be doing an integral over all possible values of $\omega$, the only one which will actually have an effect on the final result is the on-shell value:

$${\omega }_{\overrightarrow{k}}\equiv \sqrt{{\overrightarrow{k}}^2+m^2}$$

(2.14)

The effect of this maneuver is to give us a manifestly covariant propagator which gives formal covariance, as well as a considerable simplification of the QED integrals. But the off-shell energies are not being explored. The virtual particles are in fact virtual. We can think of TQM as SQM with the virtual particles replaced by real ones.

Details 

We start with the free SQM wave functions:

$${\varphi }_k\left(x\right)=\frac{1}{\sqrt{\mathsf{V}}}\frac{1}{\sqrt{\left|2{\omega }_{\overrightarrow{k}}\right|}}exp\left(-ı{\omega }_{\overrightarrow{k}}\tau +ı\overrightarrow{k}·\overrightarrow{x}\right),{\omega }_{\overrightarrow{k}}\equiv \sqrt{{\overrightarrow{k}}^2+m^2}$$

(2.15)

These are the basis for the SQM Fock space, which consists of appropriately symmetrized products of these. We define the creation and annihilation operators by their effects on this Fock space:

$$a_{\overrightarrow{k}}\left|n_{\overrightarrow{k}}\right.〉=\sqrt{n_{\overrightarrow{k}}}\left|n_{\overrightarrow{k}}-1\right.〉,a_{\overrightarrow{k}}^{†}\left|n_{\overrightarrow{k}}\right.〉=\sqrt{n_{\overrightarrow{k}}+1}\left|n_{\overrightarrow{k}}+1\right.〉$$

(2.16)

with the 3D commutators being:

$$\left[a_{\overrightarrow{k}},a_{\overrightarrow{k^{\prime }}}^{†}\right]={\delta }^3\left(\overrightarrow{k}-\overrightarrow{k^{\prime }}\right)$$

(2.17)

Note there is no mention of harmonic oscillators here; the creation and annihilation operators are defined by entirely by their effects on Fock space.

Now we build up the spin zero field operators as sums over the free single particle solutions in the interaction picture. We have the sums over the positive frequency components on the left and negative frequency components on the right:

$${\varphi }_{\tau }^S\left(\overrightarrow{x}\right)=\sum _{\overrightarrow{k}}\frac{1}{\sqrt{2V{\omega }_{\overrightarrow{k}}}}\left(a_{\overrightarrow{k}}{e}^{-ı{\omega }_{\overrightarrow{k}}\tau +ı\overrightarrow{k}·\overrightarrow{x}}+a_{\overrightarrow{k}}^{†}{e}^{ı{\omega }_{\overrightarrow{k}}\tau -ı\overrightarrow{k}·\overrightarrow{x}}\right)$$

(2.18)

We mark SQM parts with a superscript S. The normalization factor $\frac{1}{\sqrt{2{\omega }_{\overrightarrow{k}}}}$ corresponds to the convention of normalizing beams to energy/volume (see for instance Feynman [40]). The $\frac{1}{\sqrt{\mathsf{V}}}$ represents box normalization, used when we are summing over a discrete set of wave vectors; to compute the propagator we shift to integrating over a continuous set of wave vectors, so we take $\frac{1}{\sqrt{V}}\to \frac{1}{\sqrt{{\left(2\pi \right)}^3}}$.

The propagator is defined in terms of time ordered products of the free wave functions:

$$ı{\mathsf{\Delta }}_{21}^S\left(\overrightarrow{x}-\overrightarrow{y}\right)\equiv 〈0\left|T\left\{{\varphi }_2^S\left(\overrightarrow{x}\right),{\varphi }_1^S\left(\overrightarrow{y}\right)\right\}\right|0〉$$

(2.19)

We are marking the clock time for the x particle with ${\tau }_2$ or just a 2; the clock time for the y particle with a ${\tau }_1$ or just a 1. With the time-ordered wave functions between in sandwich only those terms with a creation operator on the left and an annihilation operator on the right will have an effect. The result, after rather a bit of algebra is:

$$ıS_{\tau }\left(k\right)=\frac{ı}{{\left(2\pi \right)}^3}\left(\frac{e^{-ı{\omega }_{\overrightarrow{k}}\tau }}{2{\omega }_{\overrightarrow{k}}}\theta \left(\tau \right)+\frac{e^{ı{\omega }_{\overrightarrow{k}}\tau }}{2{\omega }_{\overrightarrow{k}}}\theta \left(-\tau \right)\right)$$

(2.20)

These are Feynman boundary conditions; as noted, excellent for S matrix calculations.

The next step in the derivation is to replace the positive time branch with a contour integral:

$$\frac{e^{-ı{\omega }_{\overrightarrow{k}}\tau }}{2{\omega }_{\overrightarrow{k}}}\theta \left(\tau \right)=\frac{ı}{2\pi }\underset{-\infty }{\overset{\infty }{\int }}d\omega \frac{e^{-ı\omega \tau }}{\left(\omega -{\omega }_{\overrightarrow{k}}+ı\epsilon \right)\left(\omega +{\omega }_{\overrightarrow{k}}\right)}$$

(2.21)

and the negative time with a similar contour integral. Combined, they give us the familiar expression for the propagator:

$$ı{\mathsf{\Delta }}_{\omega }^S\left(\overrightarrow{k}\right)=\frac{ı}{{\omega }^2-{\overrightarrow{k}}^2-m^2+ı\epsilon }$$

(2.22)

So the variable $\omega$ is not free. It is slotted to be reduced to its on-shell value when the contour integral is actually done.

TQM Propagators

We start with the FS/T. To extend to the relativistic case we promote the bare mass to the relativistic mass: $m\to w$:

$$ı2w\frac{\partial }{\partial \tau }\psi =-\left(w^2-{\overrightarrow{k}}^2-m^2\right)\psi$$

(2.23)

The promotion of the mass to the relativistic energy is an obvious generalization and may be treated as a reasonable Ansatz, one that works for massless and massive particles both. We provided in paper C a more sophisticated justification where we assumed that the foreground particle is surrounded by a quantum vacuum of the same kind of particles. The requirement that both the foreground particle and the background particles obey the KG equation and that they are in equilibrium forced the promotion from bare mass to relativistic mass.

Free Wave Functions

With the FS/T equations we have their corresponding free solutions by inspection.

TQM free wave function:

$${\varphi }_k\left(x\right)=\frac{1}{\sqrt{\mathsf{TV}}}\frac{1}{\sqrt{\left|2w\right|}}exp\left(-ı{\varpi }_k\tau -ıkx\right),{\varpi }_k\equiv -ı\frac{w^2-{\overrightarrow{k}}^2+m^2}{2w}$$

(2.24)

The changes are:

• Three vectors go to four vectors: $\overrightarrow{k}·\overrightarrow{x}\to kx$. Obvious.
• Energy normalization goes from on-shell energy to free energy: $w_{\overrightarrow{k}}\to w$. The shift from the on-shell energy to the unconstrained energy is an aspect of the shift from time as parameter (constrained) to time as observable (unconstrained).
• Box normalization goes to hyper box normalization: $\mathsf{V}\to \mathsf{TV}$. We assume periodic boundary conditions. We can think of this as a box in time large enough to contain the entire interaction of interest. The use of box normalization is a great help with dimension checking. Once the dimension checking is done, it is often simpler to work with continuous normalization. In this case the factors ${\left(2\pi \right)}^3$ go to ${\left(2\pi \right)}^4$.

As with SQM, we define the Fock space in terms of sums of the appropriately symmetrized free wave functions. The creation and annihilation operators are defined by their effects in Fock space:

$$a_k\left|n_k\right.〉=\sqrt{n_k}\left|n_k-1\right.〉,a_k^{†}\left|n_k\right.〉=\sqrt{n_k+1}\left|n_k+1\right.〉$$

(2.25)

with 4D commutators:

$$\left[a_k,a_{k^{\prime }}^{†}\right]={\delta }^4\left(k-k^{\prime }\right)$$

(2.26)

All other commutators are zero. Again, we make no use of the usual interpretation in terms of harmonic oscillators.

Propagators in TQM can be handled the same way, but with four dimensions in play rather than three:

$$ı{\mathsf{\Delta }}_{21}\left(x-y\right)=〈0\left|T\left\{{\varphi }_2\left(x\right),{\varphi }_1\left(y\right)\right\}\right|0〉$$

(2.27)

We again use Feynman boundary conditions, to keep the development in parallel with SQM. But we stop the derivation just before the trick with the contour integral:

$$ı{\mathsf{\Delta }}_{\tau }\left(x-y\right)=\frac{1}{{\left(2\pi \right)}^4}\int d^{4}k\frac{e^{-ı{\varpi }_k{\tau }_{xy}-ık\left(x-y\right)}}{2w}\theta \left(\tau \right)-\frac{e^{-ı{\varpi }_k{\tau }_{xy}-ık\left(x-y\right)}}{2w}\theta \left(-\tau \right)$$

(2.28)

in momentum space:

$$ı{\mathsf{\Delta }}_{\tau }\left(k\right)=\frac{1}{{\left(2\pi \right)}^4}\left(\frac{e^{-ı{\varpi }_k\tau }}{2w}\theta \left(\tau \right)-\frac{e^{-ı{\varpi }_k\tau }}{2w}\theta \left(-\tau \right)\right)$$

(2.29)

Note that the second term in TQM differs from the second term in SQM by the overall sign, by the sign of the clock frequency term, and by taking $2\pi$ to the 4th rather than 3rd power.We can see that the w integral is real; that off-shell values will contribute to the result. Effectively we have moved from virtual fluctuations in energy to real ones. This is what changing time from parameter to observable means in the context of propagators.

To understand the relationship of this to the SQM propagator we focus on the left hand term, the retarded part of the propagator. We expect:

$$\begin{array}{c}w\approx {\omega }_{\overrightarrow{k}}\\ t\approx \tau \\ {\varpi }_k\approx 0\end{array}$$

(2.30)

With this we have in TQM:

$$\begin{array}{c}exp\left(-ıwt\right)\approx exp\left(-ı{\omega }_{\overrightarrow{k}}\tau \right)\\ exp\left(-ı{\varpi }_k\tau \right)\approx 1\end{array}$$

(2.31)

so in TQM the time dependence seen in the SQM picture is carried by the coordinate time/coordinate energy factor instead.

3. Time Dispersion in Gravity

3.4. Three Graviton Vertex

To promote the vertexes from QGR to TGR we can use the same procedure as for the spin zero case earlier (subSection 2.4.1).

Unfortunately the original graviton/graviton interactions are extremely complex. And as QGR is a non-linear gauge theory we have to include ghost terms in the action, which adds considerably to the complexity. DeWitt [23] notes there are 171 terms in the three point vertex, 2850 terms in the four point vertex – although he goes on to reassure us that with appropriate symmetrizations these may be reduced to 11 and 28 respectively.

We confine ourselves to the three vertex case here.

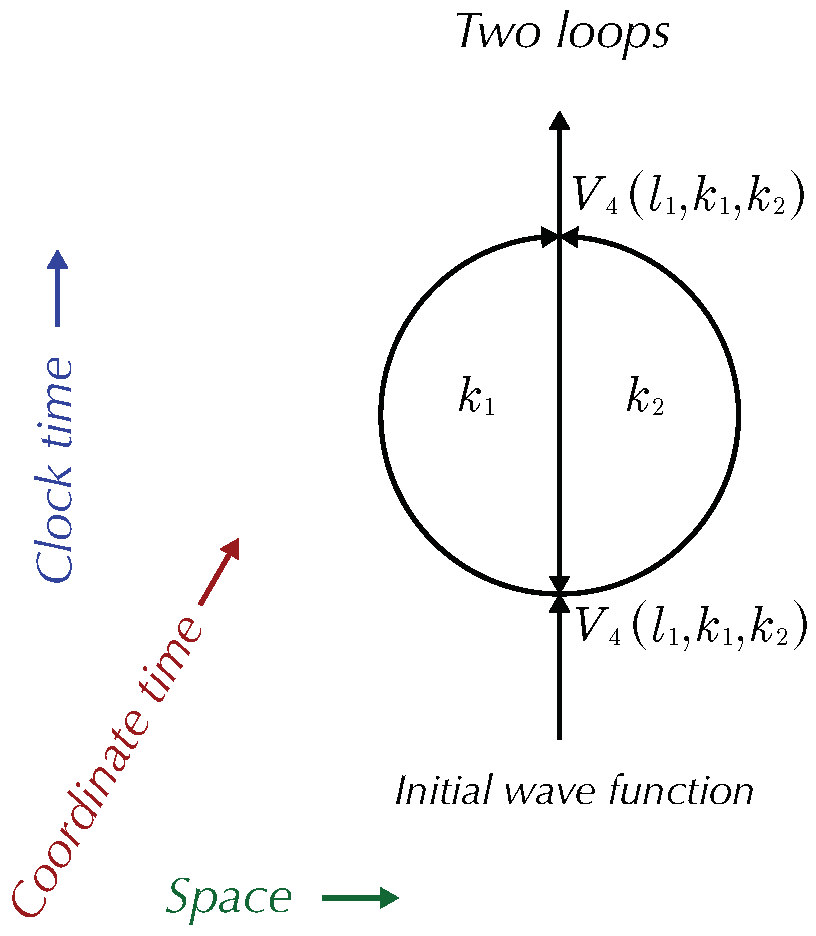
Figure 3.1. Three graviton vertex.

Figure 3.1. Three graviton vertex.

We are tracking the derivation in Jakobsen. We are assuming the metric is locally flat. And that there is no nearby matter to complicate things. We are skipping the steps used to reduce the EH Lagrangian to a sum of products of powers of the metric and its first derivatives. We are using the QGR form of the action to derive the three graviton vertex. Once we have the vertex in QGR we promote it to a three graviton vertex in TGR using the rule in subSection 2.4.1.

For the three graviton vertices in de Donder gauge, the ghost contribution is zero. Therefore in this specific case we need only the $h^3$ term in the EH action. To get this, we read off the $h^3$ terms in:

$$S_{EH}=\int d\tau \int d\overrightarrow{x}\sqrt{-g}\frac{1}{4}\left(2g^{\sigma \gamma }{g}^{\rho \delta }{g}^{\alpha \beta }-g^{\gamma \delta }{g}^{\alpha \beta }{g}^{\rho \sigma }-2g^{\sigma \alpha }{g}^{\gamma \rho }{g}^{\delta \beta }+g^{\rho \sigma }{g}^{\alpha \gamma }{g}^{\beta \delta })g_{\alpha \beta ,\rho }{g}_{\gamma \delta ,\sigma }\right)$$

(3.25)

Using:

$$\sqrt{-g}\approx 1+h_{\nu }^{\nu },h\equiv h_{\nu }^{\nu }$$

(3.26)

$$g^{\mu \nu }\approx {\eta }^{\mu \nu }-h^{\mu \nu }$$

(3.27)

We can expand the action in powers of h keeping only those with exactly three powers of h. There are sixteen such, four from the determinant and twelve from the remaining terms.

We define U by:

$$S_{EH}=\frac{1}{2}\int d\tau \int d\overrightarrow{x}{U}^{\mu \nu \alpha \beta \rho \lambda \delta \sigma }{h}_{\mu \nu }{h}_{\alpha \beta ,\rho }{h}_{\gamma \delta ,\sigma }$$

(3.28)

With this we have:

$$\begin{array}{c}{U}^{\mu \nu \alpha \beta \rho \lambda \delta \sigma }{h}_{\mu \nu }{h}_{\alpha \beta ,\rho }{h}_{\gamma \delta ,\sigma }=\frac{1}{2}{h}_{\nu }^{\mu }{h}_{,\mu }{h}^{,\nu }-\frac{1}{4}{hh}_{,\rho }{h}^{,\rho }+h_{\nu }^{\mu }{h}_{\mu ,\rho }^{\nu }{h}^{,\rho }\\ -h_{\nu }^{\mu }{h}_{\mu }^{\nu ,\sigma }{h}_{\sigma ,\rho }^{\rho }+\frac{1}{4}{hh}_{\nu ,\rho }^{\mu }{h}_{\mu }^{\nu ,\rho }-h_{\mu }^{\nu }{h}_{\sigma ,\nu }^{\mu }{h}^{,\sigma }\\ -h_{\nu }^{\mu }{h}^{,\nu }{h}_{\mu ,\rho }^{\rho }+\frac{1}{2}{hh}_{\sigma ,\rho }^{\rho }{h}^{,\sigma }-h_{\nu }^{\mu }{h}_{\mu ,\sigma }^{\rho }{h}_{\rho }^{\nu ,\sigma }\\ -\frac{1}{2}{hh}_{\nu ,\rho }^{\mu }{h}_{\mu }^{\rho ,\nu }+h^{\mu \nu }{h}_{\mu ,\rho }^{\sigma }{h}_{\nu ,\sigma }^{\rho }-\frac{1}{2}{h}_{\nu }^{\mu }{h}_{\sigma ,\mu }^{\rho }{h}_{\rho }^{\sigma ,\nu }\\ +2h_{\nu }^{\mu }{h}_{\rho }^{\sigma ,\nu }{h}_{\mu ,\sigma }^{\rho }\end{array}$$

(3.29)

In SQM each vertex is accompanied by a $\delta$ function in three momentum plus a $\delta$ function in clock energy reflecting the fact that it is normal to take the limit as $\tau \to \pm \infty$ in QGR. It is at this point in the derivation that we promote the vertex from QGR to TGR. Using the convention that all momenta are inward bound we have:

$${\delta }^4\left(l_1+l_2+l_3\right)$$

(3.30)

The vertex is given (in Jakobsen’s notation) by:

$$2ı\kappa V_{h^3}^{\mu \nu \alpha \beta \gamma \delta }\left(l_1,l_2,l_3\right)$$

(3.31)

We have one pair of indices – $\left(\mu \nu \right)\left(\alpha \beta \right)\left(\gamma \delta \right)$ – for each of the three incoming gravitons. The vertex may be expanded out in terms of “U” functions. The U functions are extremely complicated but not functions of the momenta; they are eight dimensional constant matrices. In a certain sense the U function appears only once here; the second and third terms are symmetrized versions of the first. Each of the three terms gives up six of its eight indexes to the incoming gravitons, leaving the other two to pair with all three possible pairs of the graviton momenta.

$$V_{h^3}^{\mu \nu \alpha \beta \gamma \delta }\left(l_1,l_2,l_3\right)=-\left(U^{\mu \nu \alpha \beta \rho \gamma \delta \sigma }{l}_{\left(2\right)\sigma }{l}_{\left(3\right)\rho }+U^{\alpha \beta \gamma \delta \rho \mu \nu \sigma }{l}_{\left(3\right)\sigma }{l}_{\left(1\right)\rho }+U^{\gamma \delta \mu \nu \rho \alpha \beta \sigma }{l}_{\left(1\right)\sigma }{l}_{\left(2\right)\rho }\right)$$

(3.32)

Note that the vertex is completely symmetric in its three inputs. And that there are two powers of $l^2$ present. It is these two powers of $l^2$ which are at the heart of the renormalization problem: they are what make the SQM loops for QGR hard to renormalize. In a self-energy loop there are two of these $l^2$ vertexes. So the integrals go as:

$$L\sim {\kappa }^2\int \frac{d^{4}l{l}^4}{l^4}\sim {\mathsf{\Lambda }}^4$$

(3.33)

where $\mathsf{\Lambda }$ is a cutoff in momentum.

4. Self-Energy Feynman Diagrams

“The shell game that we play … is technically called ’renormalization’. But no matter how clever the word, it is still what I would call a dippy process! Having to resort to such hocus-pocus has prevented us from proving that the theory of quantum electrodynamics is mathematically self-consistent. It’s surprising that the theory still hasn’t been proved self-consistent one way or the other by now; I suspect that renormalization is not mathematically legitimate.” - Richard P. Feynman p128 [42]

• We first examine loops for fixed times. This helps to clarify why they are a problem for SQM and why they are not for TQM.
• We use the Fourier transform to extend the fixed time analysis to the traditional infinite time case.
• We include energy-dependent coupling – this is what is make makes the SQM loops in QG hard or unrenormalizable past the first loop. In TQM the energy dependence of the coupling produces merely minor corrections.
• We discuss various implications and extensions.

4.1. Self-Energy Loop for Fixed Clock Time

Figure 4.1. Self-energy loop for fixed clock time.

Figure 4.1. Self-energy loop for fixed clock time.

We will look at a simpler case of the basic problem. We look at a loop that starts at clock time 0, ends at clock time $\tau$. We will look first at the SQM case, then at TQM.

4.1.1. SQM

As noted, QFT is not normally used for short time intervals. The heart of the loop is the calculation:

$$L\sim \int d^{4}k\frac{ı}{k^2+ıϵ}\frac{ı}{{\left(l-k\right)}^2+ıϵ}$$

(4.1)

However to calculate the loop for short times we have to use the “unpacked” form of the propagators. This keeps the SQM integrals explicitly on-shell. We have:

$$L\sim \int d\overrightarrow{k}\frac{exp\left(-ı{\omega }_{l_1-k}\mathsf{\Delta }\tau \right)}{2{\omega }_{l_1-k}}\frac{exp\left(-ı{\omega }_{\mathrm{k}}\mathsf{\Delta }\tau \right)}{2{\omega }_k}$$

(4.2)

$${\omega }_{l_1-k}=\sqrt{{\left(\overrightarrow{l_1}-\overrightarrow{k}\right)}^2},{\omega }_k=\left|\overrightarrow{k}\right|$$

(4.3)

at large momentum we have:

$${\omega }_{l_1-k},{\omega }_k\to \left|\overrightarrow{k}\right|$$

(4.4)

in either case.

The integral then goes as:

$$L\to \int {\left|\overrightarrow{k}\right|}^{2}d\mathsf{\Omega }d\overrightarrow{k}\frac{exp\left(-2ı\left|\overrightarrow{k}\right|\mathsf{\Delta }\tau \right)}{4{\left|\overrightarrow{k}\right|}^2}=4\pi \underset{0}{\overset{\infty }{\int }}dkexp\left(-2ı\left|\overrightarrow{k}\right|\mathsf{\Delta }\tau \right)$$

(4.5)

This is not convergent. Divergence is logarithmic, as expected. So the problem is not associated with the virtual particles, Feynman boundary conditions, or even the limit as clock time goes to infinity, and so on. This is a very minimalist divergence.

The program of renormalization boils down to tossing out the $k\to \infty$ bit in a clean way and hoping that whatever dependence on high frequency we are tossing out at the same time does not have a detectable influence on the results.

And, so far, this has been true.

4.1.2. TQM

We will start, as always in TQM, with a GTF:

$${\phi }_0\left(l_1\right)=\sqrt[4]{\frac{1}{{\pi }^{4}det\left(\widehat{\mathsf{\Sigma }}\right)}}{e}^{ı{\left(l_1-l_0\right)}_{\mu }{x}_0^{\mu }-{\left(l_1-l_0\right)}^{\mu }\frac{1}{2{\widehat{\mathsf{\Sigma }}}^{\mu \nu }}{\left(l_1-l_0\right)}^{\nu }}$$

(4.6)

With dispersion:

$$\widehat{\mathsf{\Sigma }}\equiv \left(\begin{array}{cccc}{\widehat{\sigma }}_t& 0& 0& 0\\ 0& {\widehat{\sigma }}_x^2& 0& 0\\ 0& 0& {\widehat{\sigma }}_x^2& 0\\ 0& 0& 0& {\widehat{\sigma }}_z^2\end{array}\right)$$

(4.7)

For convenience, we will assume that the initial beam is narrow in momentum. This is normally true in scattering experiments.

The loop integral looks like:

$$L_{\tau }=\int d^{4}k{d}^4{l}_1{K}_{\tau }\left(l_1-k\right)K_{\tau }\left(k\right){\phi }_0\left(l_1\right)$$

(4.8)

The kernels are given by:

$$\begin{array}{c}{K}_{\tau }\left(l_1-k\right)=\frac{exp\left(-ı{\varpi }_{l-k}\tau \right)}{2\left(w_1-w\right)},{\varpi }_{l-k}=-\frac{{\left(l_1-k\right)}^2}{2\left(w_1-w\right)}\\ K_{\tau }\left(k\right)=\frac{exp\left(-ı{\varpi }_k\tau \right)}{2w},{\varpi }_k=-\frac{k^2}{2w}\end{array}$$

(4.9)

The integrals are non-trivial. We can simplify this with use of some physical intuition. We know that the two loop gravitons are completely symmetric. Therefore the average frequency for each is:

$$\overline{w}\equiv \frac{w_0}{2}$$

(4.10)

To lowest order we can replace the frequencies in the denominators with the average:

$$\frac{1}{2\left(w_1-w\right)},\frac{1}{2w}\to \frac{1}{2\overline{w}}$$

(4.11)

(For future reference, we note that the loop integral can now be expressed as the product of four separate integrals, one for each dimension. )

We are looking at a convolution. We can replace this with a product in coordinate space. The kernels are now simple enough to do the Fourier transform explicitly:

$$K_{\tau }\left(x^{\prime };x\right)=-ı\frac{{\overline{w}}^2}{4{\pi }^2{\tau }^2}{e}^{-ı\overline{w}\frac{{\left(x\prime -x\right)}^2}{2\tau }}$$

(4.12)

The product equals a single coordinate space kernel:

$$K_{\tau }^{\left(2\overline{w}\right)}\left(x^{\prime };x\right)=-ı\frac{{\left(2\overline{w}\right)}^2}{4{\pi }^2{\tau }^2}exp\left(-ı\frac{2\overline{w}}{2\tau }{\left(x^{\prime }-x\right)}^2\right)$$

(4.13)

with a modified mass $2\overline{w}$ and an additional prefactor $-ı\frac{{\left(\overline{w}\right)}^2}{16{\pi }^2{\tau }^2}$.

The original wave function in coordinate space is:

$${\phi }_0\left(x\right)=\sqrt[4]{\frac{1}{{\pi }^{4}det\left(\mathsf{\Sigma }\right)}}exp\left(-ıl_{0}x-\frac{{\left(x-x_0\right)}^2}{2\mathsf{\Sigma }}\right),\mathsf{\Sigma }={\widehat{\mathsf{\Sigma }}}^{-1}$$

(4.14)

The loop term in coordinate space is (without prefactor):

$$L_{\tau }^{\prime }\left(x^{\prime }\right)=\int d^{4}x{K}_{\tau }^{\left(2\overline{w}\right)}\left(x^{\prime };x\right){\phi }_0\left(x\right)$$

(4.15)

This is just the integral to advance a wave function of mass $2\overline{w}$ a distance $\tau$ in time, so we have:

$$L_{\tau }^{\prime }\left(x^{\prime }\right)={\phi }_{\tau }^{\left(2\overline{w}\right)}\left(x^{\prime }\right)$$

(4.16)

We have a correction that shows a spread in time, but at the slightly slower rate associated with the larger mass $2\overline{w}$. The full correction is greater at shorter clock times, as one would expect. Now we transform back to momentum space:

$$\begin{array}{c}{L^{\prime }}_{\tau }\left(l^{\prime }\right)=\int d^{4}l{K}_{\tau }^{\left(2\overline{w}\right)}\left(l^{\prime };l\right){\phi }_0\left(l\right)\\ K_{\tau }^{\left(2\overline{w}\right)}\left(l^{\prime };l\right)=exp\left(ı\frac{l^2}{4\overline{w}}\tau \right){\delta }^4\left(l^{\prime }-l\right)\end{array}$$

(4.17)

The loop correction for fixed clock time (folding back in the prefactor) is:

$$L_{\tau }\left(l_1\right)=-ı\frac{{\left(\overline{w}\right)}^2}{16{\pi }^2{\tau }^2}exp\left(ı\frac{l_1^2}{4\overline{w}}\tau \right){\widehat{\phi }}_0\left(l_1\right)$$

(4.18)

At this point the value of the loop correction at a particular value of $l_1$ is independent of the specific shape of the incoming wave function. We are therefore free to drop the initial wave function from the analysis. We rewrite the loop without the initial wave function:

$$L_{\tau }\left(l_1\right)=-ı\frac{w_0^2}{16{\pi }^2{\tau }^2}exp\left(ı\frac{l_1^2}{2w_0}\tau \right)$$

(4.19)

4.4. Discussion

Figure 4.2. Self-energy diagram with two loops.

Figure 4.2. Self-energy diagram with two loops.

“A certain exhaustion however prevents us from further investigation, for the time being.” t’Hooft and Veltman [105]

We can extend this approach to more complex diagrams. For instance in the two loop self-energy diagram with a pair of four graviton vertexes, we can represent the momenta by:

$$l_1=\frac{p_0}{3}+k_{1,}{l}_2=\frac{p_0}{3}-k_1-k_2,l_3=\frac{p_0}{3}+k_2$$

(4.38)

which will let again combine the three loop kernels into one. And we can employ multiple differentiating factors:

$$exp\left(-ıa_{\mu }{k}_1^{\mu }\right),exp\left(-ıb_{\nu }{k}_2^{\nu }\right),exp\left(-ıc_{\nu }{l}_1^{\nu }\right)$$

(4.39)

to pull down the necessary powers of the loop momenta. The convergence is provided by the dispersion in the initial GTF and by the entanglement of the initial GTF with loops.

Including the polarizations is an obvious extension. A preliminary exploration has suggested that Shoshany’s OGRe package [97] is the logical tool. However the complexity of the vertex calculations has made clear that this is a separate project.

And of course we still have to normalize; no measurement happens in isolation but always in reference to others. And the calculational complexity of diagrams in TQM is significantly greater: the initial wave functions must be GTFs, so their dispersions must be included. And each propagator and vertex has one more dimension to manage.

5. Discussion

• The single particle solutions extend in time in the same way they extend in space (very desirable in a description of General Relativity).
• The loop diagrams are complex (as expected) but finite.

References

1. Ronald Adler, Maurice Bazin, and Menahem Schiffer. Introduction to General Relativity. McGraw-Hill, New York, 1965.
2. John Ashmead. Morlet wavelets in quantum mechanics. Quanta, 1(1), 2012.
3. John Ashmead. Time dispersion in quantum mechanics. Journal of Physics: Conference Series, 1239:012015, May 2019. [CrossRef]
4. John Ashmead. Does the Heisenberg uncertainty principle apply along the time dimension? Journal of Physics: Conference Series, 1956(1):012014, 2021. arXiv:2101.10512.
5. John Ashmead. Time dispersion in quantum electrodynamics. Journal of Physics: Conference Series, 2482(1):012023, may 2023. [CrossRef]
6. Markus Aspelmeyer. How to avoid the appearance of a classical world in gravity experiments. ArXiv e-prints, 03 2022. arXiv:2203.05587.
7. Gennaro Auletta. Foundations and Interpretation of Quantum Mechanics: In the Light of a Critical-Historical Analysis of the Problems and of a Synthesis of the Results. World Scientific Publishing Co. Pte. Ltd., Singapore, 2000.
8. Yu. V. Baryshev. Energy-momentum of the gravitational field: Crucial point for gravitation physics and cosmology. ArXiv e-prints, 2008. arXiv:0809.2323.
9. N. E. J. Bjerrum-Bohr. Quantum Gravity as an Effective Field Theory. Cand. Scient. Thesis, Univ. of Copenhagen, 2001.
10. N. E. J. Bjerrum-Bohr, Poul H. Damgaard, Guido Festuccia, Ludovic Planté, and Pierre Vanhove. General relativity from scattering amplitudes. Phys. Rev. Lett., 121:171601, 2018. arXiv:1806.04920.
11. J. D. Bjorken and S. D. Drell. Relativistic Quantum Fields. McGraw Hill, New York, 1965.
12. J. D. Bjorken and S. D. Drell. Relativistic Quantum Mechanics. McGraw Hill, New York, 1965.
13. Tobias Bothwell, Colin J. Kennedy, Alexander Aeppli, Dhruv Kedar, John M. Robinson, Eric Oelker, Alexander Staron, and Jun Ye. Resolving the gravitational redshift across a millimetre-scale atomic sample. Nature, 602(7897):420–424, 2022. [CrossRef]
14. Craig Callender. What Makes Time Special? Oxford University Press, 2017.
15. Craig Callender and Nick Huggett. Physics meets Philosophy at the Planck scale: Contemporary Theories in Quantum Gravity. Cambridge University Press, New York, 2001.
16. Daniel Carney, Philip C. E. Stamp, and Jacob M. Taylor. Tabletop experiments for quantum gravity: a user’s manual. Classical and Quantum Gravity, 36(3), 07 2019. arXiv:1807.11494.
17. Sean Carroll. Something Deeply Hidden: Quantum Worlds and the Emergence of Spacetime. Dutton, 2022.
18. Sean M. Carroll. Spacetime and geometry: an introduction to General Relativity. Addison Wesley, San Francisco, 2019.
19. Marios Christodoulou, Andrea Di Biagio, Richard Howl, and Carlo Rovelli. Gravity entanglement, quantum reference systems, degrees of freedom. Classical and Quantum Gravity, 40(4):047001, Jan 2023. [CrossRef]
20. John Collins. Renormalization: An Introduction to Renormalization, the Renormalization Group, and the Operator-Product Expansion. Cambridge University Press, Cambridge, 1984.
21. Bryce S. DeWitt. Quantum theory of gravity. i. the canonical theory. Phys. Rev., 160:1113–1148, Aug 1967. [CrossRef]
22. Bryce S. DeWitt. Quantum theory of gravity. ii. the manifestly covariant theory. Phys. Rev., 162:1195–1239, Oct 1967. [CrossRef]
23. Bryce S. Dewitt. Quantum theory of gravity. iii. applications of the covariant theory. Physical Review, 162(5):1239–1256, October 1967. [CrossRef]
24. Bryce S. Dewitt. Quantum theory of gravity. i. the canonicál theory – errata. Physical Review, 171(5):1834–1834, July 1968. [CrossRef]
25. P. A. M. Dirac. General Principles of Quantum Mechanics. International series of monographs on physics. Oxford, Clarendon Press, 4th edition edition, 1958.
26. P. A. M. Dirac. General Theory of Relativity. Princeton University Press, 1996.
27. John F. Donoghue. General relativity as an effective field theory: the leading quantum corrections. Phys. Rev. D, 50:3874–3888, Sep 1994. [CrossRef]
28. John F. Donoghue. The ideas of gravitational effective field theory. In XXVIII International Conference on High Energy Physics, ICHEP94, Glasgow, 1994.
29. John F. Donoghue. Introduction to the effective field theory description of gravity. In Advanced School on Effective Field Theories, Almunecar, Spain, 1995.
30. I. D. Faddeev and V. N. Popov. Covariant quantization of the gravitational field. Sov Phys Usp, 162:777–788, 1974. [CrossRef]
31. John R. Fanchi. Parameterized Relativistic Quantum Theory, volume 56 of Fundamental Theories of Physics. Kluwer Academic Publishers, 1993.
32. John R. Fanchi. Review of invariant time formulations of relativistic quantum theories. Found. Phys., 23(3), 1993. [CrossRef]
33. John R. Fanchi. Manifestly covariant quantum theory with invariant evolution parameter in relativistic dynamics. Found Phys, 41:4–32, 2011. [CrossRef]
34. John R. Fanchi and R. Eugene Collins. Quantum mechanics of relativistic spinless particles. Found Phys, 8(11/12):851–877, 1978. [CrossRef]
35. Richard P. Feynman. Space-time approach to non-relativistic quantum mechanics. Rev. Mod. Phys., 20:367–387, Apr 1948. [CrossRef]
36. Richard P. Feynman. Space-time approach to quantum electrodynamics. Phys Rev, 76:769–789, 1949. [CrossRef]
37. Richard P. Feynman. The theory of positrons. Phys Rev, 76:749–759, 1949. [CrossRef]
38. Richard P. Feynman. Mathematical formulation of the quantum theory of electromagnetic interaction. Physical Review, 80:440–457, 1950. [CrossRef]
39. Richard P. Feynman. Quantum Electrodynamics. W. A. Benjamin, Inc, New York, 1961.
40. Richard P. Feynman. Quantum Electrodynamics. Advanced Book Classics. Addison-Wesley, New York, 1961, 1998.
41. Richard P. Feynman. Quantum theory of gravity. Acta Phys Polon, 24:697–722, 1963.
42. Richard P. Feynman. QED: the Strange Theory of Light and Matter. Penguin Books, 1990.
43. Richard P. Feynman, Albert R. Hibbs, and Daniel F. Styer. Quantum Mechanics and Path Integrals. Dover Publications, Mineola, N.Y., 2010.
44. Richard P. Feynman and Alfred R. Hibbs. Quantum Mechanics and Path Integrals. McGraw-Hill, 1965.
45. Richard P. Feynman, Fernando B. Morínigo, William G. Wagner, and Brian F. Hatfield. Feynman Lectures on Gravitation. Addison-Wesley, Reading, Mass., 1995.
46. Partha Ghose. Testing Quantum Mechanics on New Ground. Cambridge University Press, Cambridge, 1999.
47. Herbert Goldstein. Classical Mechanics Second Edition. Addison-Wesley, Reading, MA, 1980.
48. Walter Greiner. Relativistic Quantum Mechanics: Wave Equations. Springer, Berlin, 3rd ed edition, 2000.
49. Walter Greiner and J Reinhardt. Quantum Electrodynamics. Springer-Verlag, Berlin, 2nd corrected edition, 1994.
50. H. W. Hamber. Quantum Gravitation: the Feynman Path Integral Approach. Springer, Berlin, 2009.
51. James B. Hartle. Gravity: An Introduction to Einstein’s General Relativity. Pearson Education, 2006.
52. W. Heisenberg. The Physical Principles of the Quantum Theory. University of Chicago Press, Chicago, 1930.
53. Lawrence P. Horwitz. On the significance of a recent experiment demonstrating quantum interference in time. Physics Letters A, 355:1–6, 2006. arXiv:quant-ph/0507044.
54. Lawrence P. Horwitz. Relativistic Quantum Mechanics. Fundamental Theories of Physics. Springer, 2015.
55. Lawrence P. Horwitz. Concepts in Relativistic Dynamics. World Scientific, 2023.
56. Lawrence P. Horwitz and C. Piron. Relativistic dynamics. Helvetica Physica Acta, 46(3), 1973.
57. Kerson Huang. Quantum Field Theory: from Operators to Path Integrals. Wiley, New York, 1998.
58. Nick Huggett, Niels Linnemann, and Mike Schneider. Quantum gravity in a laboratory? ArXiv e-prints, 2022. arXiv:2205.09013.
59. C. J. Isham, Roger Penrose, and Dennis William Sciama. Quantum Gravity: an Oxford Symposium. Clarendon Press, Oxford, 1975.
60. Claude Itzykson and Jean Bernard Zuber. Quantum Field Theory. Dover Publications, Mineola, N.Y., 2005.
61. Armas Jácome. Conversations on Quantum Gravity. Cambridge University Press, 2021.
62. Gustav Uhre Jakobsen. General relativity from quantum field theory. ArXiv e-prints, 10 2020. arXiv:2010.08839.
63. Michio Kaku. Quantum Field Theory: a Modern Introduction. Oxford University Press, New York, 1993.
64. Youka Kaku, Tomohiro Fujita, and Akira Matsumura. Enhancement of quantum gravity signal in an optomechanical experiment. ArXiv e-prints, 06 2023. arXiv:2306.02974.
65. T. Kashiwa, Y. Ohnuki, and M. Suzuki. Path Integral Methods. Clarendon Press; Oxford University Press, 1997.
66. D. C. Khandekar, S. V. Lawande, and K. V. Bhagwat. Path-integral Methods and their Applications. World Scientific Publishing Co. Pte. Ltd., Singapore, 1993.
67. H. Y. Kim, M. Garg, S. Mandal, L. Seiffert, T. Fennel, and E. Goulielmakis. Attosecond field emission. Nature, 613(7945):662–666, 2023. [CrossRef]
68. Robert D. Klauber. Student Friendly Quantum Field Theory. Sandtrove Press, 2nd edition, 2013.
69. Hagen Kleinert. Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets. World Scientific, New Jersey, 2009.
70. Steve K. Lamoreaux. A review of the experimental tests of quantum mechanics. Intl. J. of Mod. Physics, 7:6691–6762, 1992. [CrossRef]
71. Tom Lancaster and Stephen Blundell. Quantum Field Theory for the Gifted Amateur. Oxford University Press, first edition, 2014.
72. M. C. Land and L. P. Horwitz. Off-shell quantum electrodynamics. ArXiv e-prints, 1996. arXiv:hep-th/9601021v1.
73. David McMahon. Quantum Field Theory Demystified. McGraw-Hill, New York, N.Y., 2008.
74. Charles W. Misner, Kip S. Thorne, and John Archibald Wheeler. Gravitation. W. H. Freeman and Company, 1973.
75. Subhendra Mohanty. Gravitational Waves from a Quantum Field Theory Perspective. Lecture Notes in Physics. Springer, 2023.
76. Stavros Mougiakakos. Scattering Amplitudes in Effective Gravitational Theories. Theses, Université Paris-Saclay, December 2021.
77. Stavros Mougiakakos and Pierre Vanhove. The Schwarzschild-Tangherlini metric from scattering amplitudes in various dimensions. Phys. Rev. D, 103:026001, 2021. arXiv:2010.08882.
78. J. G. Muga, R. Sala Mayato, and I. L. Egusquiza. Time in Quantum Mechanics. Springer, Berlin; New York, 2002.
79. J. G. Muga, R. Sala Mayato, and I. L. Egusquiza. Time in Quantum Mechanics - Vol 2. Springer-Verlag, Berlin; New York, 2008.
80. Daniele Oriti and Louis A. Duhring Fund. Approaches to Quantum Gravity: toward a new Understanding of Space, Time and Matter. Cambridge University Press, Cambridge, 2009.
81. M. Ossiander, F. Siegrist, V. Shirvanyan, R. Pazourek, A. Sommer, T. Latka, A. Guggenmos, S. Nagele, J. Feist, J. Burgdörfer, R. Kienberger, and M. Schultze. Attosecond correlation dynamics. Nature Physics, 13:280, 11 2016. [CrossRef]
82. Wolfgang Pauli. General Principles of Quantum Mechanics. Springer-Verlag, 1980.
83. Roger Penrose and C. J. Isham. Quantum Concepts in Space and Time. Clarendon Press; Oxford University Press, 1986.
84. Michael Edward Peskin and Daniel V. Schroeder. An Introduction to Quantum Field Theory. Addison-Wesley, Reading, Mass., 1995.
85. Pierre Ramond. Field theory. Addison Wesley, 1990.
86. R. J. Rivers. Path Integral Methods in Quantum Field Theory. Cambridge University Press, New York, 1987.
87. Tony Rothman and Stephen Boughn. Can gravitons be detected? Foundations of Physics, 36(12):1801–1825, 2006. arXiv:gr-qc/0601043.
88. Carlo Rovelli. Quantum Gravity. Cambridge University Press, Cambridge, UK ; New York, 2004.
89. Carlo Rovelli. General Relativity: The Essentials. Cambridge University Press, 2021.
90. J. J. Sakurai. Advanced Quantum Mechanics. Addison-Wesley, 1967.
91. L. S. Schulman. Techniques and Applications of Path Integrals. John Wiley and Sons, Inc., New York, 1981.
92. L. S. Schulman. Time’s Arrows and Quantum Measurement. Cambridge University Press, New York, 1997.
93. Bernard F Schutz. A First Course in General Relativity. Cambridge University Press, 1990.
94. Matthew D. Schwartz. Quantum Field Theory and the Standard Model. Cambridge University Press, 2014.
95. Jakob Schwichtenberg. No-Nonsense Quantum Field Theory. No-Nonsense Books, 2020.
96. Alfred Shapere and Frank Wilczek. Classical time crystals. Phys. Rev. Lett., 109:160402, Oct 2012. [CrossRef]
97. Barak Shoshany. OGRe: An object-oriented general relativity package for Mathematica. Journal of Open Source Software, 6(65):3416, 2021. arXiv:2109.04193.
98. Lee Smolin. Three Roads to Quantum Gravity. Basic Books, 2001.
99. Mark Allen Srednicki. Quantum field theory. Cambridge University Press, New York, 2007.
100. E. C. G. Stueckelberg. La signification du temps propre en mécanique ondulatoire. Helv. Phys. Acta., 14:322–323, 1941.
101. E. C. G. Stueckelberg. Un nouveau modèle de l’électron ponctuel en théorie classique. Helv. Phys. Acta., 14:51, 1941. [CrossRef]
102. Leonard Susskind and André Cabannes. General Relativity: The Theoretical Minimum. Basic Books, 2023.
103. Leonard Susskind and James Lindesay. An Introduction to Black Holes, Information and the String Theory Revolution: The Holographic Universe. World Scientific, 2004.
104. Mark Swanson. Path Integrals and Quantum Processes. Academic Press, Inc., 1992.
105. G. ’t Hooft and M. Veltman. One-loop divergencies in the theory of gravitation. Annales de L’Institut Henri Poincare Section (A) Physique Theorique, 20(1):69–94, January 1974.
106. David Joshua Tannor. Introduction to Quantum Mechanics: a Time-Dependent Perspective. University Science Books, Sausalito, Calif., 2007.
107. Kip Thorne and Lia Halloran. The Warped Side of Our Universe: An Odyssey Through Black Holes, Wormholes, Time Travel, and Gravitational Waves. Liveright Publishing Corporation, 2023.
108. Kip S. Thorne. John Archibald Wheeler (1911-2008). Science, 320:1603, 2009. [CrossRef]
109. David Tong. Lectures on General Relativity. 2019. Available online: https://www.damtp.cam.ac.uk/user/tong/gr.html.
110. Martin J. G. Veltman. Quantum theory of gravitation. In R. Balian and J. Zinn-Justin, editors, Methods in Field Theory, LesHouches, Session XXVIII, chapter 5. North-Holland Publishing Co., 1975.
111. Matt Visser. Lorentzian Wormholes: From Einstein to Hawking. Springer-Verlag, New York, 1996.
112. Robert M Wald. General Relativity. University of Chicago Press, Chicago, 1984.
113. Robert M. Wald. Quantum Field Theory in Curved Spacetime and Black Hole Thermodynamics. University of Chicago Press, Chicago & London, 1994.
114. Steven Weinberg. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity. John Wiley and Sons, Inc., New York, 1972.
115. Steven Weinberg. Quantum Theory of Fields: Foundations, volume I. Cambridge University Press, 1995.
116. Steven Weinberg. Quantum Theory of Fields: Modern Applications, volume II. Cambridge University Press, 1995.
117. F. Wilczek. Quantum time crystals. Phys. Rev. Lett, 109(15):160401, Oct 2012. [CrossRef]
118. Natalie Wolchover. Why gravity is not like the other forces. June 2020. Available online: https://www.quantamagazine.org/why-gravity-is-not-like-the-other-forces-20200615/.
119. A. Zee. Quantum Field Theory in a Nutshell. Princeton University Press, Princeton, N.J., 2010.
120. Anthony Zee. Einstein Gravity in a Nutshell. Princeton University Press, 2013.
121. H. D. Zeh. The Physical Basis of the Direction of Time. Springer-Verlag, Berlin, 2001.
122. Jean Zinn-Justin. Path Integrals in Quantum Mechanics. Oxford University Press, Oxford, 2005.