Prerpints.org logo
Preprint
Article

A comprehensive Study for Predicting the Geometrical Characteristics of an Inclined Negatively Buoyant Jet Using Group Method of Data Handling (GMDH) Neural Network

Altmetrics

Downloads

116

Views

56

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

08 December 2023

Posted:

12 December 2023

You are already at the latest version

Alerts
Abstract
A new approach for predicting the geometrical characteristics of the mixing behavior of an inclined dense jet for angles ranging from 15° to 85° is proposed in this study. This approach is called group method of data handling (GMDH) which is based on the artificial neural network (ANN) technique. The proposed model was trained and tested using existing experimental data reported in literature. The model was then evaluated using statistical indices as well as compared with analytical models from previous studies. The results of the coefficient of determination (R2) indicate a high accuracy of the proposed model with values of 0.9719 and 0.9513 for training and testing for the dimensionless of the distance from the nozzle to the return point xr/D, and 0.9454 and 0.9565 for training and testing for the dimensionless of the terminal rise height yt/D . Moreover, four previous analytical models were used to evaluate the GMDH model. The results showed the superiority of the proposed model in predicting the geometrical characteristics of the inclined dense jet for all tested angles. Finally, the standard error of estimate (SEE) was applied to demonstrate which model performed the best in terms of getting closer to the actual data. The results illustrate that all fitting lines of the GMDH model performed very well for all geometrical parameter predictions and was the best model with approximately 10% error, which was the lowest value of error among the models. Therefore, this study confirms that the GMDH model can be used to predict the geometrical properties of the inclined negatively buoyant jet with high performance and accuracy.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

The unwanted wastewater produced from seawater desalination plants is normally discharged back into the coastal water body adjacent to the plants. This is done with a submerged pipe creating a buoyant effluent jet. This effluent (brine) has a high concentration of salinity which causes negative impacts on the marine ecosystem, particularly in the near-field zone of the discharge point [1,2]. The discharged effluent is either a positively buoyant jet (lighter than the receiving water) or a negatively buoyant jet (denser than the receiving water), depending on the method used in the desalination plant. The dense jet (negatively buoyant jet) has highly adverse effects on the marine environment. Commonly, desalination plants that use a Reverse Osmosis (RO) system use submerged discharges, which formed a negatively buoyant jet, to ensure a high dilution of this effluent in order to minimize the adverse impacts on the marine environment.
A large body of previous research has focused on laboratory studies of the mixing of the negatively buoyant jet either alone or in combination with modeling efforts [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]. Less effort, however, has been given to numerical modeling and developing an analytical solution and to predict the behaviors and geometric characteristics of inclined dense jets [27,28,29,30], which still requires further investigation. Therefore, more studies using numerical modeling as an efficient tool can be useful for predicting the behaviors of brine discharges into seawater.
As known, there are two hypotheses for developing models either based on the entrainment or jet spreading, which are being developed and studied previously. In 2003, Lee and Chu [27] developed a model called JETLAG/VISJET in order to predict the mixing of the near-field zone of an inclined round buoyant jet. This model is a combination of two approaches, i.e., entrainment and jet spreading, and presents empirical correlations for the dilution of the geometrical characteristics. In 2004, Jirka [28] developed an integrated numerical model (CORJET) that can predict negatively buoyant jets for a wide range of angles (0° to 90°) discharged into ambient water with slop or flat bottom. A few years later, Kikkert et al. [29] presented an analytical method to predict the behavior of an inclined dense jet using experimental data reported from previous studies to validate their model. Their model has limitations as it can be valid for angles ranging from 0° to 75° and for densimetric Froude numbers ( F r d ), the ratio of inertia to buoyancy, ranging from 14 to 99. In the same manner as of Kikkert et al. [29], Oliver et al. [30] developed a modified integral model called the Reduced Buoyancy Flux (RBF) model to predict the behavior of negatively buoyant jets in near-fields. One of the advantages of this modified model is its ability to predict the effects of the additional mixing noted in previous studies.
In recent years, efforts in different areas of the engineering science field have focused on the use of Artificial Neural Network (ANN) methods. One of these methods is the group method of data handling (GMDH), which is used for solving nonlinear engineering problems and providing explicit equations for modeling the hydraulic and hydrological phenomena. Using this method has shown accurate results compared to those of other methods [31,32,33,34,35,36,37,38,39,40], for example, Alitaleshi and Daghbandan [32] conducted a study to evaluate the quality of treated water in a water treatment plant using GMDH-type neural network. The results showed the success of the model used (GMDH) for prediction as the results of the determination coefficient were higher than 0.97. Naeini et al. [33] developed a model using GMDH to estimate the Elasticity modulus ( E s ) of clayey deposits that is used to predict the elastic settlement of foundations. The results obtained were compared with the previous empirical equations. They found that the GMDH model showed higher performance (32 to 42% improvement) with respect to the other correlations. Another study was conducted by Gholami et al. [35] to study the ability of the GMDH model for predicting the geometric variables of stable channels (width, depth, and slope). The results showed that the GMDH model performed well. Moreover, they compared the result obtained from GMDH with those from previous theoretical equations (based on regression analysis), and this comparison showed the ability of GMDH model to predict the geometric variables of channels better than other theoretical equations. Najafzadeh et al. [39] used GMDH to predict scour depth around a vertical pile exposed regular waves and compared their results with the result of different previous methods. They concluded that the use of GMDH model provided the most accurate prediction of scour depth compared to other models.
Recently, Alfaifi et al. [41] have used a GMDH model to predict the geometrical characteristics of inclined dense jets for angles 15° and 52°. It is believed that this is the first time this new approach has been used in the field of mixing jet behavior. These researchers have established empirical equations for estimating the geometrical characteristics of inclined buoyant jets. The GMDH results gave an accurate prediction for the parameters tested compared to the other analytical models.
Therefore, the goal of the present study is to examine the superiority of the GMDH model in predicting the main geometrical characteristics of inclined negatively buoyant jets by performing a comprehensive study for a wide range of angles ranging from 15° up to 85°. Moreover, the performance of the GMDH model is assessed by comparing its results to those of other analytical and numerical methods. To the best of the authors’ knowledge, this study with use of the GMDH method has not been used before for predictions for inclined negatively buoyant jets.

2. Methodology

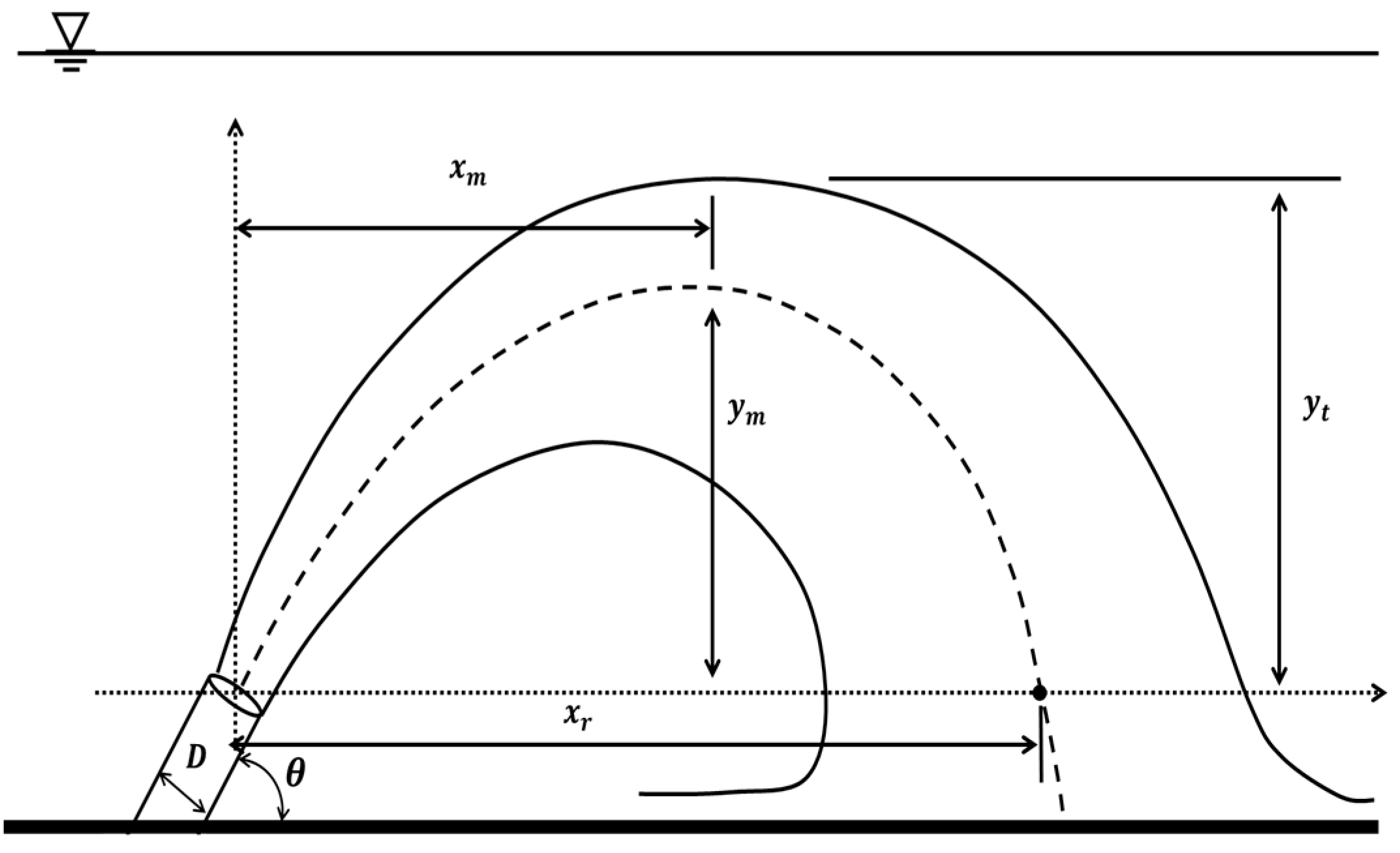
2.1. Analysis of an Inclined Negatively Buoyant Jet

In Figure 1, an inclined turbulent round dense jet being discharge into a body of stagnant water body is illustrated (the ambient velocity is, U a = 0 ). The port (jet) for the discharge has a diameter D and is positioned at an angle ( θ ) compared to the horizontal plane. The ambient water into which the jet is being expelled is an unstratified and has a constant density ρ a . This water is deep enough to allow the jet to fully develop below the water surface without any effects from water surface. The initial discharge velocity of the jet is U 0 and it has a density ρ a ( ρ a < ρ 0 ).
The four crucial characteristics of the mixing of the jet with regard to geometry are: its terminal rise height ( y t ); the horizontal distance from the point of maximum height of the centerline to the nozzle ( x m ); its centerline height ( y m ), and its return point ( x r ), i.e., the distance horizontally from where the jet’s centerline returns to the same elevation as the tip of the nozzle (Figure 1). The distribution pattern of a jet being discharged into a homogeneous and stagnant ambient fluid can be affected by various parameters known as the source angle θ , D , U 0 and the initial density difference ( ∆ ρ = ρ 0 − ρ a ) between the ambient fluid and the discharge fluid. In addition, the inclined dense jets can be characterized by its discharge volume flux Q 0 = U 0 π D 2 / 4 , momentum flux M 0 = U 0 2 D 2 π / 4 , and buoyancy flux B 0 = g 0 ′   U 0 π D 2 / 4 , where g ′ =   g ( ρ 0 − ρ a ) / ρ a , which defined as the effective gravitational acceleration and g is the gravitational acceleration. Two length scales can be formed from these fluxes: the momentum length scale L M = M 0 3 / 4 / B 0 1 / 2 , which determines the distance over which the buoyancy of the jet is less important than its momentum, and the source length scale L Q = Q 0 / M 0 1 / 2 , which determines the distance over which the source discharge is important. These two length scales are employed to determine the mixing and geometric characteristics of a turbulent buoyant jet. The equation defining the jet densimetric Froude number ( Fr d ) is as follows:
F r d = U 0 g ′ D ,
The terminal rise height of an inclined dense jet can be written in terms of the length scales as:
y t L M = f L M L Q , θ ,
Instead of the length scales, y t can also be alternatively expressed by using the jet’s densimetric Froude number and nozzle diameter as:
y t F r d D = C y t θ ,
Similarly, the other geometric parameters of the jet (i.e. x r , x m , and y m ) can be derived by using the coefficient values ( C x r , C x m , and C y m ), which can be established through experiments.

2.2. The GMDH Method

Several researchers in various engineering fields have used artificial neural network methods to address a wide-range of applications, such as multigene genetic-programming (MGGP) technique, genetic algorithm artificial neural network (GAA),the genetic programming (GP), Gene Expression Programming (GEP), and the GMDH. These approaches were used for solving nonlinear engineering problems while providing an explicit equation for predicting and modeling each phenomenon. Their studies have shown accurate results compared to those of other methods [32,35,36,37,38,39,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57]. Therefore, regarding the outcomes obtained from previous studies, it is worth implementing some of those methods to predict the geometrical characteristics of inclined buoyant jets.
The group method of data handling (GMDH) was first proposed by Ivakhnenko [58], and is a computer program-based algorithm. This type of algorithm is often used to model problems that involve data series for multi-input-single-output systems. Second-order polynomials are used in the GMDH as network functions, and the main advantage of the GMDH, as opposed to traditional neural networks, is its use in establishing mathematical models for a given procedure.
The concept of the GMDH of selection and hybridization corresponds to the genetic algorithm. Like other types of neural networks, the GMDH can have one or more hidden layers. More information regarding GMDH processing is provided in a recently published article by the same authors in Alfaifi et al. [41].

2.2.1. GMDH Modeling Setup

To use the GMDH method for prediction of the geometrical characteristics of a negatively buoyant dense jet, the output variables were set to be the dimensionless of jet characteristics (i.e., x m / D , y m / D , x r / D , and y t / D ) by using one output variable for each run. For all cases, the Fr d and θ parameters were used as input variables. The explicit equations for the GMDH were developed using the GMDH Shell software [59]. The dataset used covered all discharge angles presented in previous studies ranging from 15° to 85°. Obtaining a good prediction from the GMDH model is based on the preparation of the dataset, and therefore the observed dataset used in this study was randomly divided into two groups one for training and one for testing. For each case, the GMDH model was trained using 70% to 80% of the dataset, while the remaining data were used for testing the model. In this study, the layers were limited to a maximum of two layers in order to ensure the simplicity of the model. The developed models were used to calculate the dimensionality of the jet geometrics as a function of Fr d and θ for the training dataset. The optimal models were then selected and used to perform additional calculations for the testing dataset. Finally, the performances of these models were evaluated.
For the training dataset, the models developed were used to determine the dimensionless of the jet geometrics as a function of Fr d and θ , with the optimal models being selected. After that, the models selected were used to perform additional calculations for the testing dataset, and then their performance was evaluated.

3. Results and Discussion

In this section, the results of the proposed model (GMDH) are presented. The predicted results of the GMDH are compared with the observed data obtained from previous studies for angles ranging from 15° to 85°. For brevity, only the results of x r / D and y t / D are shown in this section. The results of the dimensionless geometrical parameters x r / D and y t / D for the actual data for training and testing are plotted versus the predicted values of the GMDH model, as shown in Figure 2a,b. In order to evaluate the performance of the GMDH model, a linear fit with the coefficient of determination ( R 2 ) was added to each Figure to show the accuracy of the proposed model in predicting and fitting the actual data. From these Figures, it can be seen that the R 2 values show an excellent prediction for the proposed model (GMDH) where 0.9719 and 0.9513 were for training and testing for x r / D and 0.9454 and 0.9565 were for training and testing for y t / D . The testing results for both parameters show a good prediction of the model. Although there was a decrease in the value of the R 2 for x r / D for the testing model compared to the training model, the accuracy remains high and acceptable. This indicates that all fitting lines pass through most of the data and the proposed model is highly accurate and satisfactory.
Figure 3a,b, shows a detailed depiction of the performance of the GMDH model for x r / D (Figure 3a) and y t / D (Figure 3b) as well as how the model was trained and tested by the data index. In Figure 3a, the model was trained by 75% of the data, while in Figure 3b, it was trained by 70% of the data. As mentioned previously, the model was trained by between 70% and 80% of the data. Therefore, the key to influencing the change of training ratio is to obtain a simple model with high accuracy.
The equations extracted from the GMDH method for all geometrical parameters are presented in Table 1. These equations were used to predict the geometrical parameters in this study. As can be seen, all of the equations in Table 1 are functions of the F r d and the θ . These equations are valid for F r d ranging from 10 to 100. All of the equations presented in Table 1 can be used for predicting the geometrical parameters for the inclined dense jet for any angles located between 15° and 85°. All of these equations are presented in dimensionless geometric parameters, which depend on the same input variables: F r d and θ .

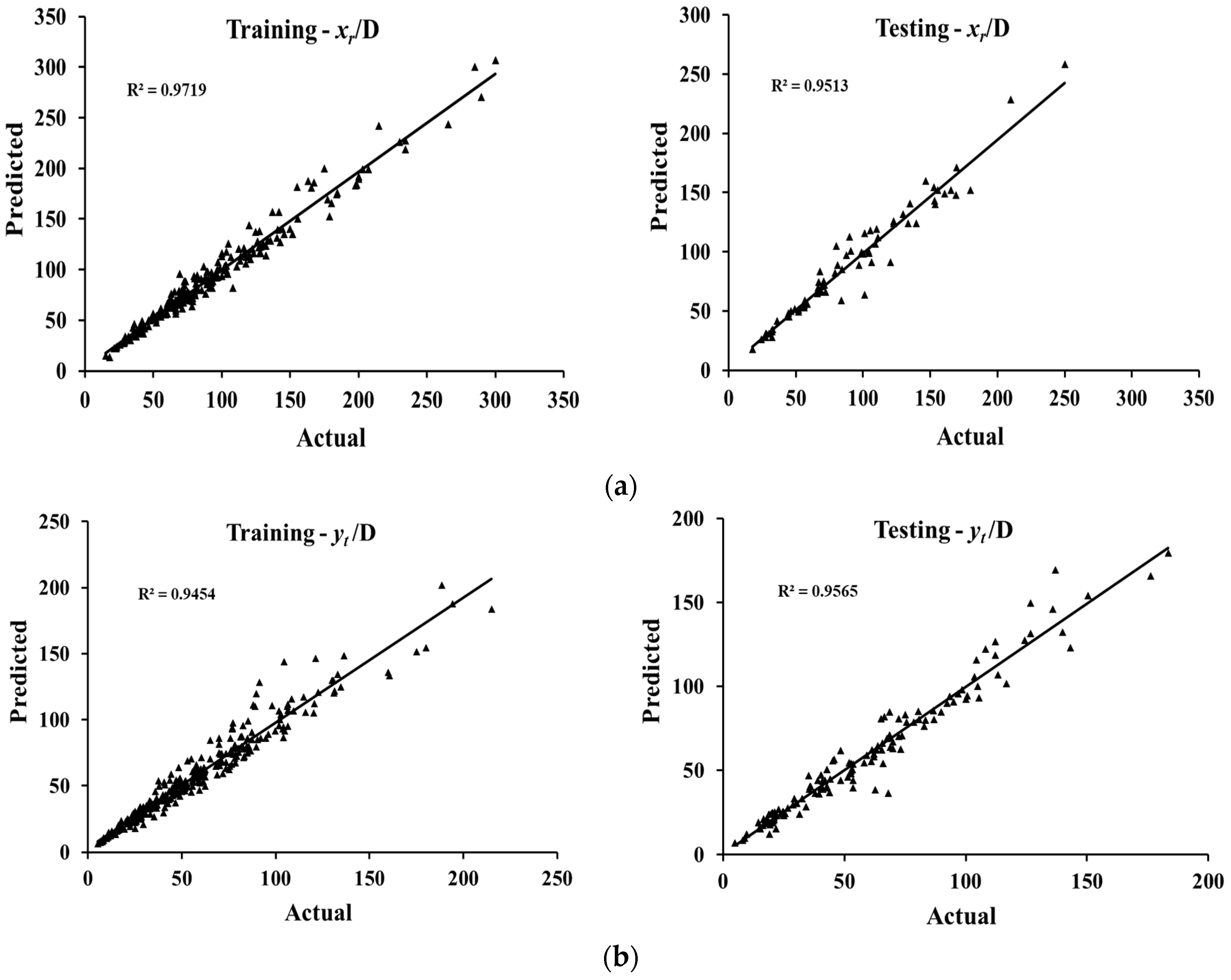
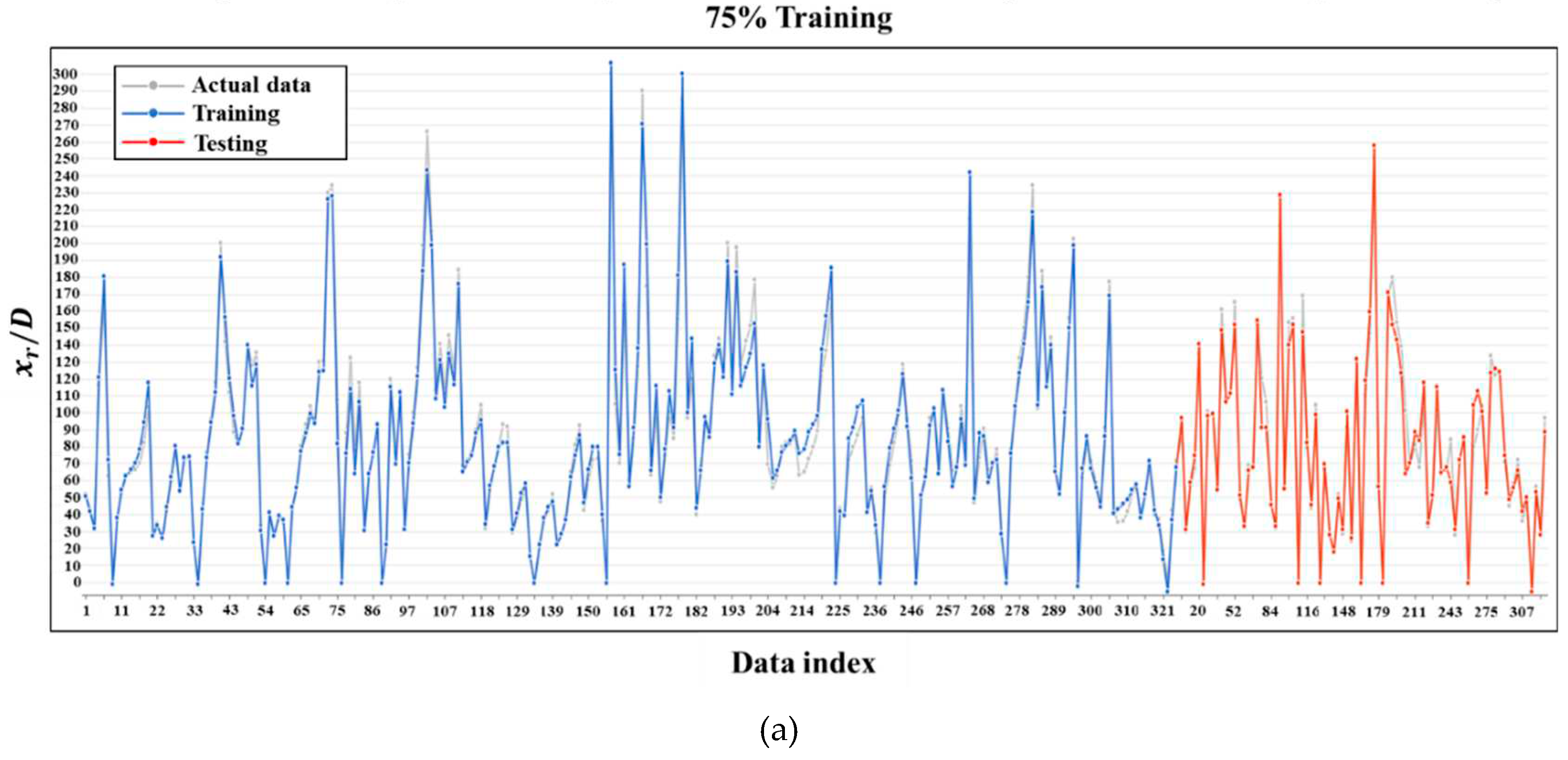
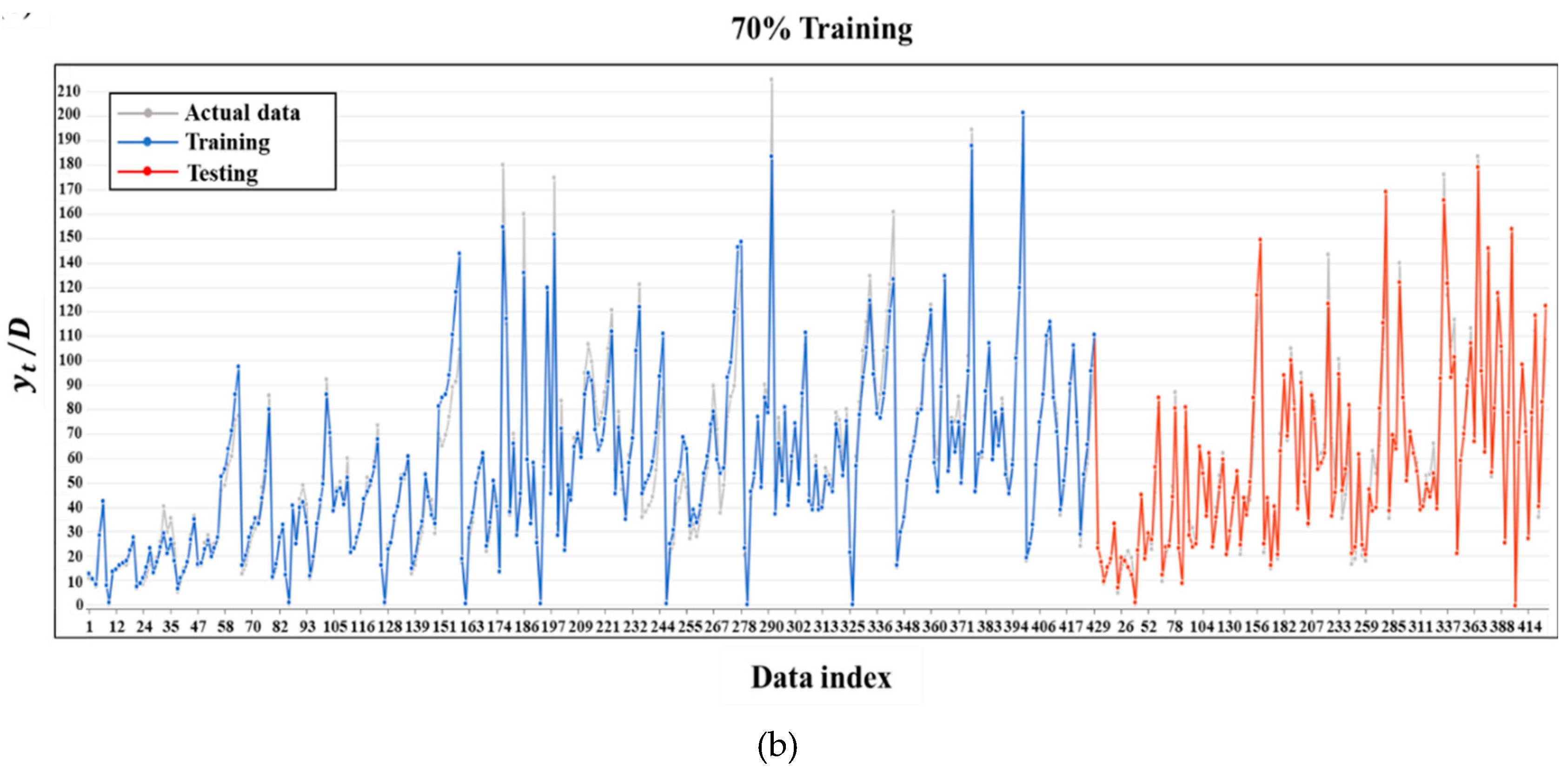
3.1. Assessment of the model performance statistically

Some of the most commonly used statistical indices are presented in this study to evaluate the performance of the GMDH model. These indices can clearly show the accuracy of the proposed model as it is commonly used in literature. In the present study, the three most important types of statistical indices were used: the coefficient of determination ( R 2 ), Root Mean Squared Error (RMSE), and Mean Absolute Error (MAE), which are defined as follows:
R 2 = 1 − ∑ ( y ^ − y ¯ ) 2 ∑ ( y − y ¯ ) 2
MAE = ∑ i = 1 n y ^ − y n
RMSE = ∑ i = 1 n y ^ − y 2 n
where y ^ is the predicted values of the GMDH model, y ¯ is the mean of the actual data, y is the actual data, and n is the number of actual data. As known, the low values of these parameters (except R 2 ) indicate the high accuracy of the model. The statistical results obtained for the GMDH model from these Equations (i.e., 8-10) are presented in Table 2. The results of the GMDH model used for predicting the geometrical characteristics of the inclined jet show a high accuracy of the prediction, as shown from the R 2 results. All geometrical results are higher than 0.94, which means that the model proposed produced excellent predicting results. The highest value of the R 2 was 0.967 for x r / D , while the lowest value for the same index was for x m / D , which was 0.948. The most interesting finding from Table 2 are the testing results, which are the results that evaluate the accuracy of the proposed model. For MAE, the lowest value was noted for the y m / D (4.458), while the lowest value for the RMSE was found for the x m / D (6.861). On the other hand, the highest value for MAE was shown for x m / D (6.809), while for the RMSE, the highest value was found for x r / D (10.143). Generally, all the results obtained for the statistical indices in Table 2 show excellent agreement between the dataset observed and the proposed model (GMDH) which can be used for predicting the geometrical parameters of the inclined dense jets with highly accurate results.

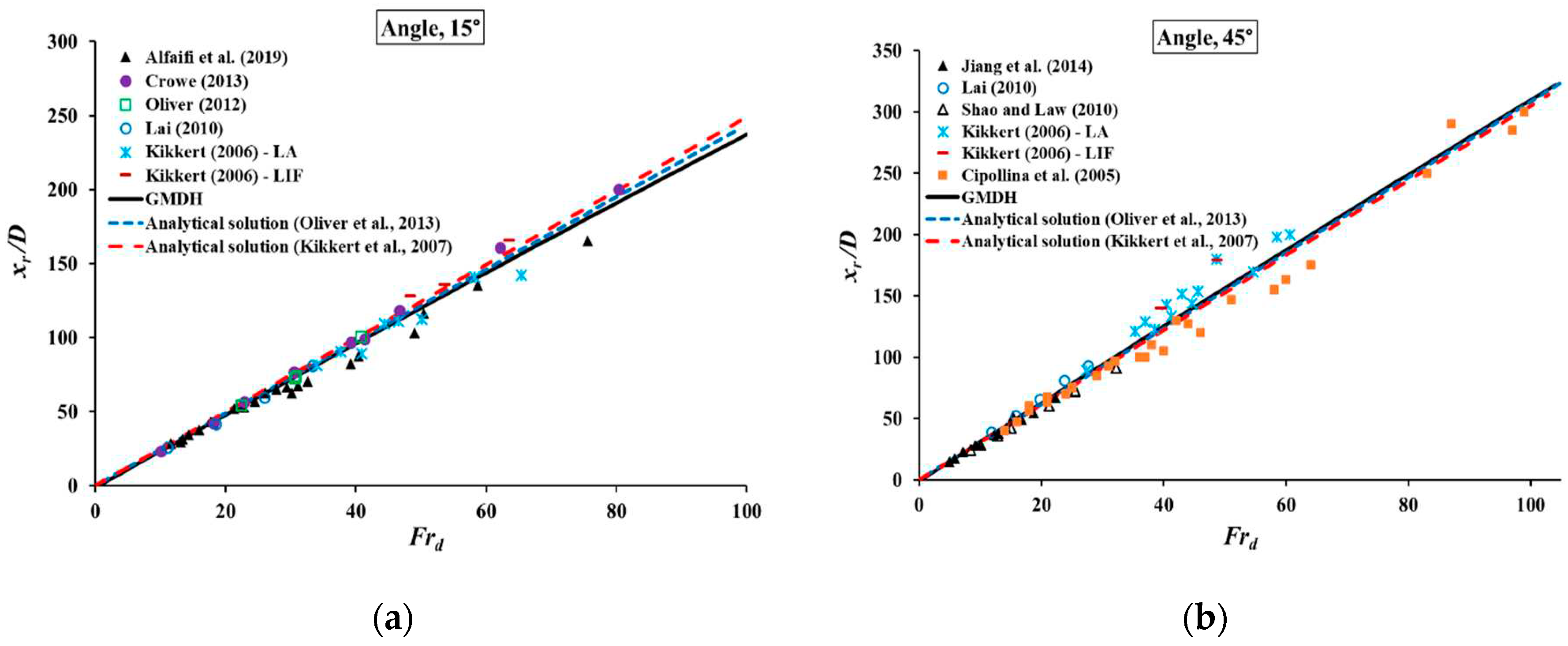
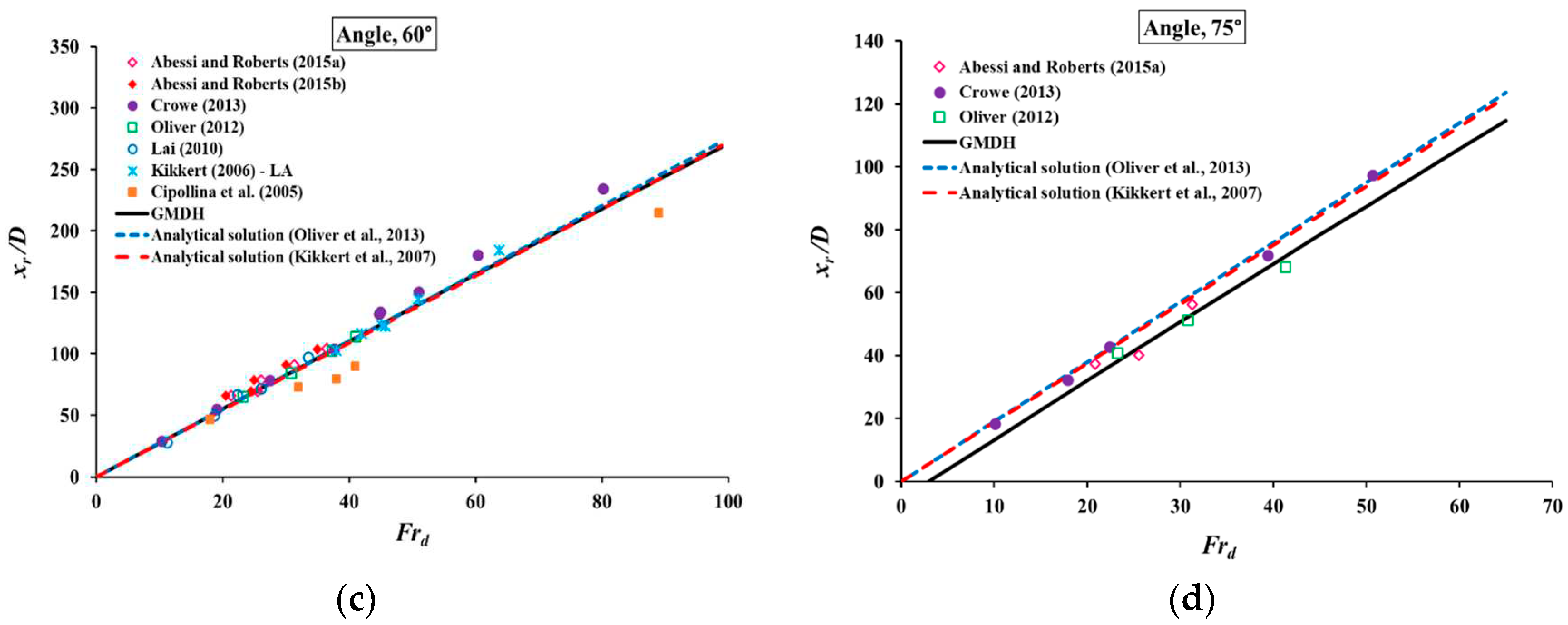
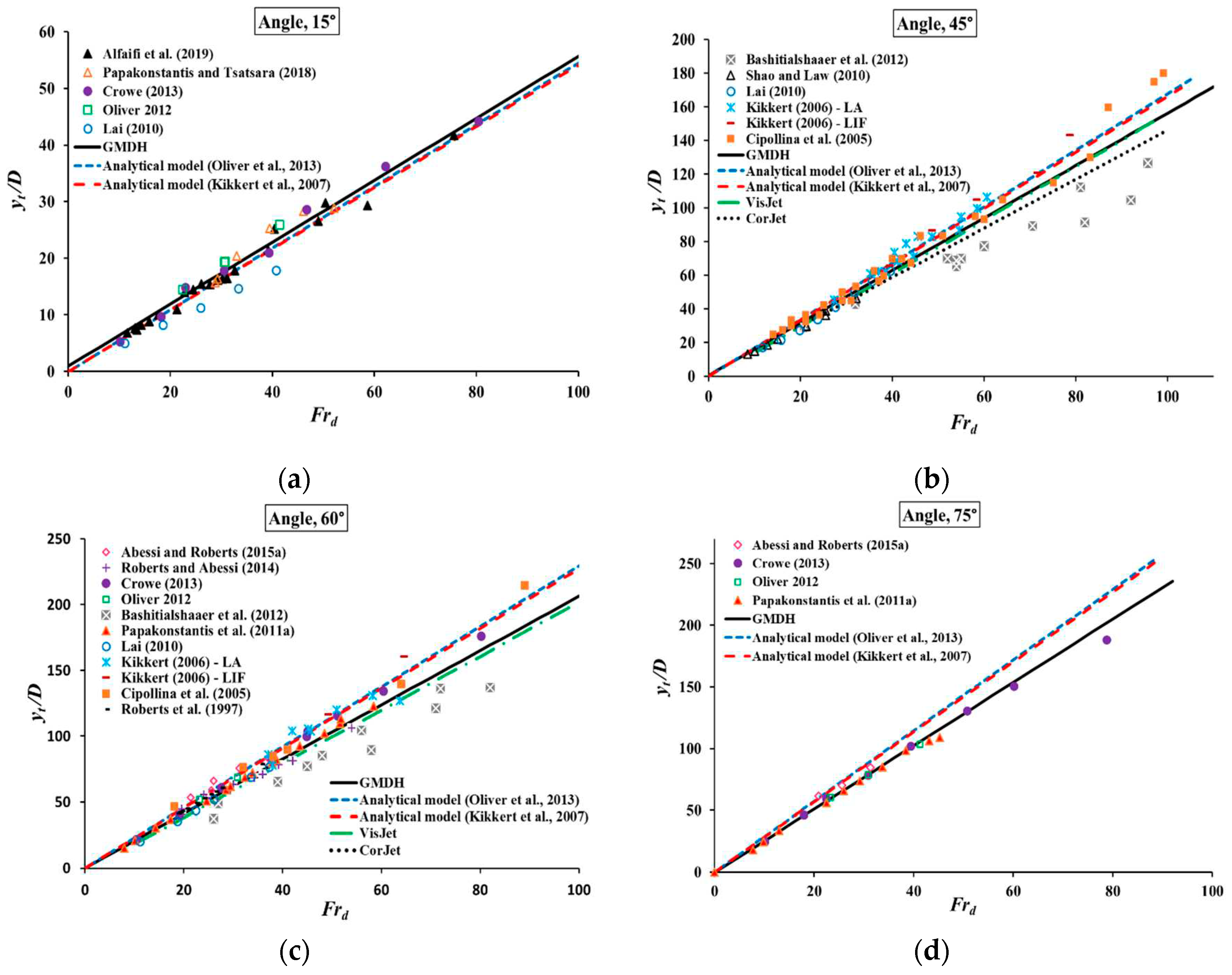
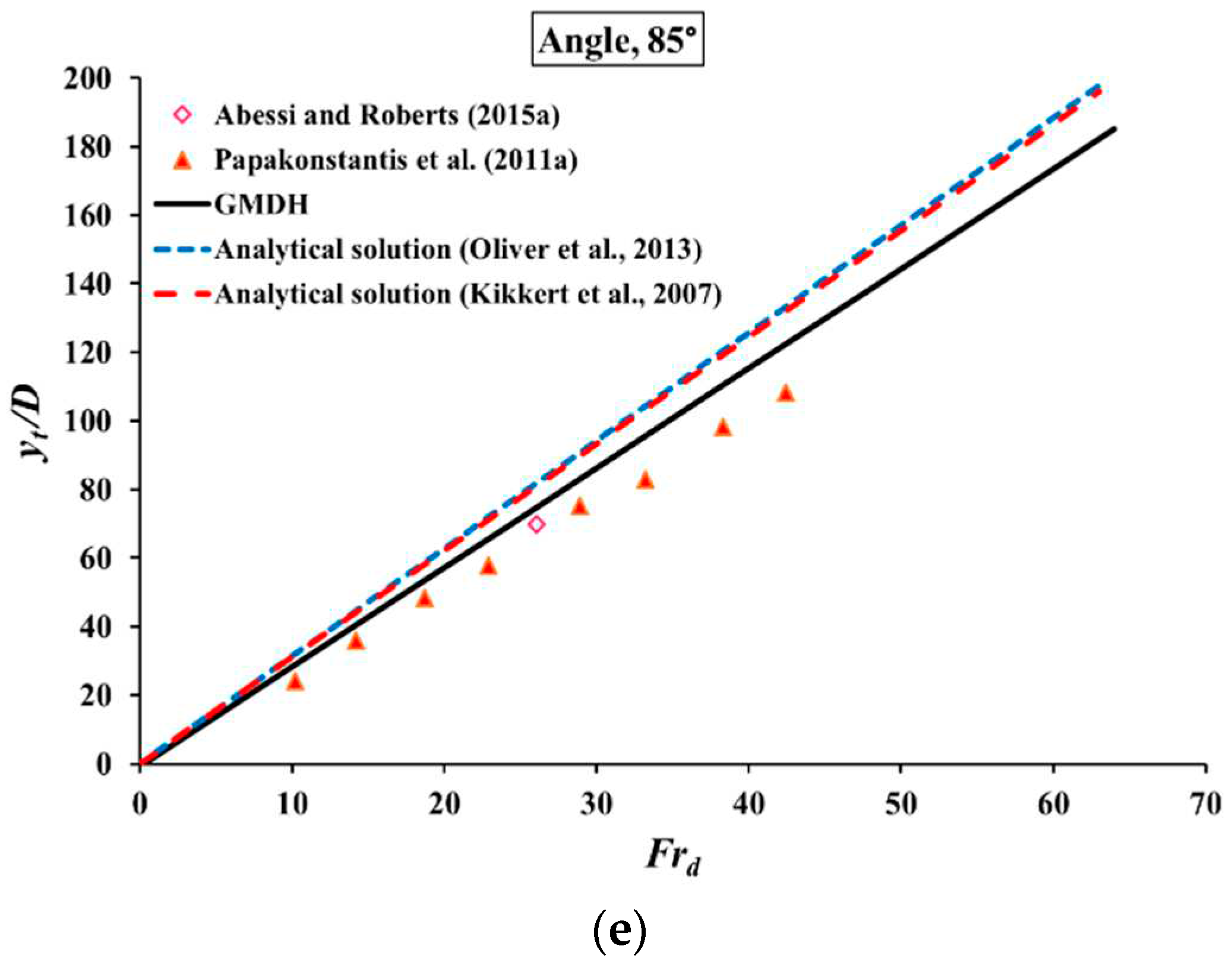
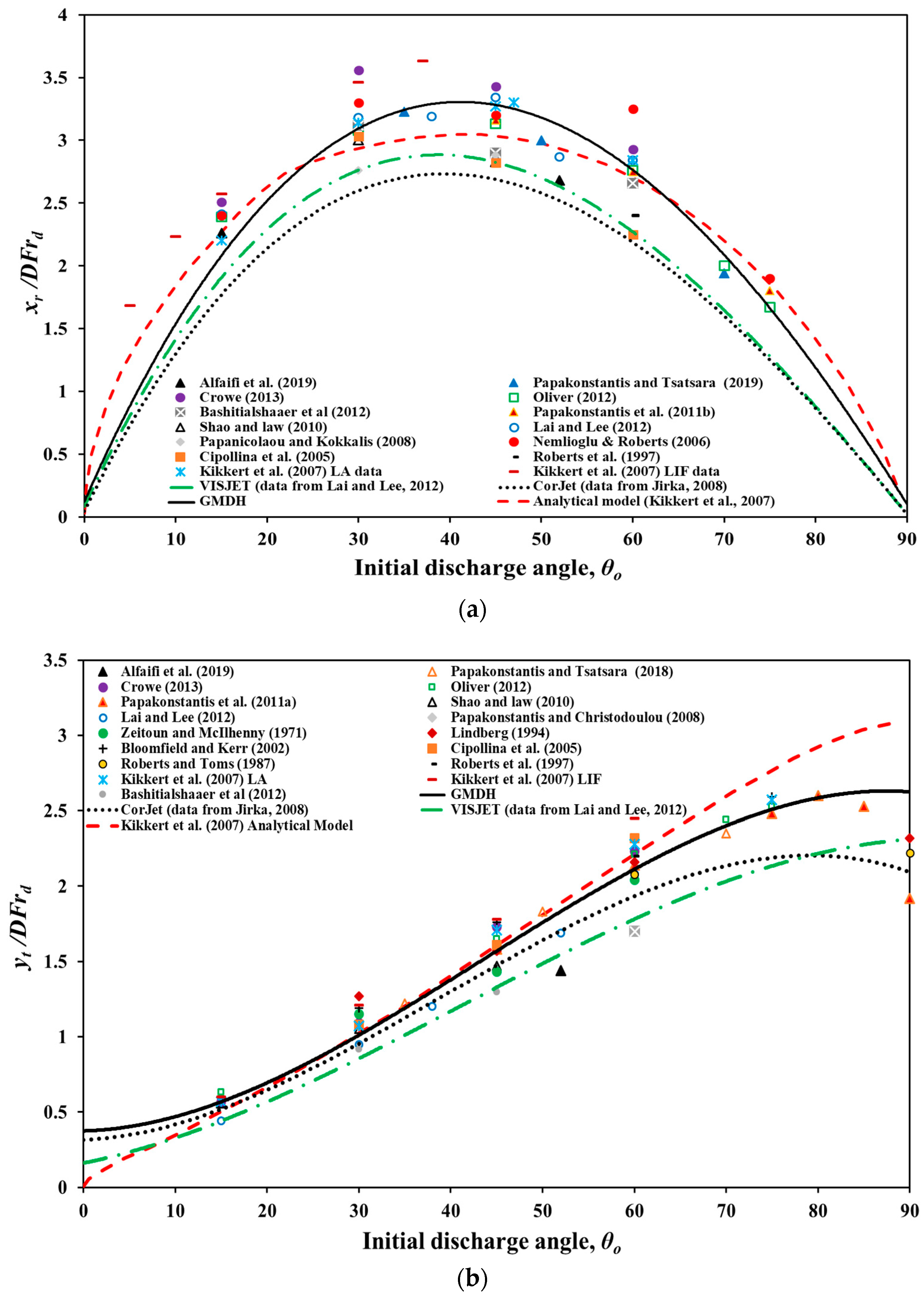
3.2. Comparing GMDH results with previous models

In this study, another evaluation for the performance of the GMDH model has been done by comparing it with several analytical and numerical models reported on in previous studies. Four analytical models explained in the literature were selected. These analytical solution models were CORJET for Jirka [60], Kikkert et al. [29], VISJET for Lee and Chu [27], and Oliver et al. [61]. The results of the GMDH model for dimensionless geometrical characteristics of x r / D and y t / D versus the F r d are shown in Figure 4 and Figure 5, along with the previous analytical models. For brevity, the results of four angles (i.e., 15°, 45°, 60°, and 75°) for x r / D , and five angles (i.e., 15°, 45°, 60°, 75°, and 85°) for y t / D , are presented in this study. The existing dataset found that the highest angle in the literature was 75° for x r / D , while 85° was the highest for y t / D . Due to a lack of previous data for some of the geometrical parameters, results of only two analytical models (CORJET and VESJET) were shown in several pictures. As shown in Figure 4, the GMDH model predicted results are presented in black lines and more effectively demonstrate predictions compared to the observed data obtained from the previous experiments compared to other analytical models (see Figure 4a,c). It is clear that the GMDH model shows accurate predictions and its results are almost identical and overlap with the previous analytical model for some angles (i.e., 45° and 60°), see Figure 4b,c.
Another comparison for the GMDH predicted results for y t / D is presented in Figure 5a,b,c,d, and e. A fifth angle was added for the y t / D comparison (i.e., 85°) to test the predictive capability of the proposed model. In these Fig.s, two other models were added to the comparison (i.e., CORJET and VISJET). The proposed model (GMDH) showed a good prediction of all angles. It should be noted that it is in a neutral position for the data scatter. In addition, there is a convergence of the GMDH and VISJET models presented by Lee and Chu [27] in Figure 5b,c. The predicted results of other analytical models (i.e., Kikkert et al. [29]; Oliver et al. [61]) were seen slightly higher than other models as the inclination angle increased, while the predicted results of the CORJET model were lowest in terms of comparing to the actual data and other models.
To quantify the variations of the results obtained from these models (proposed and previous models) with the actual data, the statistical index equation called Standard Error of the Estimate (SEE) can be used to see which model is preferred and gave a more precise prediction of the actual data. The low value of the SEE, the more accurate of the model. The SEE equation is defined as follows:
SEE = 1 n ∑ ( y ^ − y ) 2
The results of the model predictions for geometrical parameters for all angles are summarized in Table 3. The results of the standard error show that the GMDH model performed better and is much more accurate than other models. All results of the SEE for the GMDH model were the lowest values for all angles for both geometrical parameters except for angle 45° for x r / D where the result of Oliver et al.’s model was the lowest. Therefore, the SEE results illustrate that all fitting lines of the GMDH model performed well for all geometrical parameter predictions, as the scattered data are closely located around the fitting lines with approximately 10% error around the lines. As a result, the GMDH model is the most accurate model among those tested.
Accordingly, this provides evidence that the GMDH model is considered a reliable model for predicting the geometrical parameters of the near-field mixing zone of the inclined dense jets.
Figure 6a,b, shows the results of the constant values for the normalized forms ( x r / D F r d ) and ( y t / D F r d ) for the GMDH model plotted against the initial discharge angle along with the data reported in previous studies. Third-order polynomial fittings were obtained for all models in both Figures. Despite the large dispersion in the actual data, the fitting curve of the proposed model is considered the best prediction compared to the other models in terms of being close to most of the actual data. Moreover, the results obtained from the GMDH model are consistent with what was previously stated by [6], which shows that the horizontal distance of the return point increases with an increasing angle up to approximately 40° and then the distance begins to decrease. For Figure 6b, the results show that the terminal rise height gradually increases as the angle of the jet increases until reaching approximately angle 85°, at which point the fitting curve stays almost constant without any change. In this Figure, the GMDH model was in good agreement with the observed data. Generally, it can be seen that the GMDH predictive model shows better results with the observed data than the other models.

3.3. Uncertainty analysis

Uncertainty analysis is crucial to assess the confidence in the results obtained and evaluate the proposed GMDH models. Therefore, to measure the uncertainty of the prediction of the geometrical characteristics obtained from the GMDH models, several explicit statistics were employed such as, the prediction error ( E i ), Mean Prediction Error ( M P E ), Standard Deviation ( s d ), and Width of Uncertainty Band ( W U B ). These parameters are calculated for the whole dataset employed in this study. The negative and positive values of the M P E demonstrate that the models are underestimating or overestimating the observed values, respectively. These parameters are as follows [44]:
E i = P r e d i c t i o n i − A c t u a l i ,
E ¯ = ∑ i = 1 n E i / n ,
M P E = ∑ i = 1 n ( P r e d i c t i o n − A c t u a l ) n ,
s d = ∑ i = 1 n E i − E ¯ 2 n − 1 ,
W U B = 1.96 s d n
where n is the sample size. Moreover, a confidence band was defined around the prediction error values for M P E and s d by using Wilson score method without a continuity correction. The difference between the low and high uncertainty bands is defined as the WUB. The model can be considered highly accurate when the value of the WUB is smaller. Therefore, a confidence band of 95% was achieved using ±1.96 s d / n values [62].
Results of the uncertainty analysis obtained for the GMDH models predictions of the x m / D , x r / D , y m / D , and y t / D are presented in Table 4 along with the mean prediction errors, the width of uncertainty band and 95% Prediction Error Interval ( P E I ).
Based on the results shown in Table 4, the lowest values for the mean prediction error was for the non-dimensional y t / D , while the lowest value of the s d , W U B , and 95 %   P E I is obtained for the y m / D which indicates that it is the most accurate model compared to other models. On the other hand, the least accurate predicted model in this study was found to be for the non-dimensional geometrical parameters of x m / D and x r / D with the higher values of the s d , W U B , and 95 %   P E I , respectively. For the M P E , it can be seen that the largest value was for the x m / D , i.e., + 0.29 . Although both x r / D and y m / D had almost the same value of the M P E , but considering the W U B and 95 %   P E I values the predicted model of y m / D is more accurate. The larger value of the W U B was noted for the x r / D where was ranging from − 1.04 to + 1.04 , which is inaccurate compared to other predicted models. As a result, the non-dimensional values of the geometrical characteristic y m / D predicted by the model showed the lowest values of the mean prediction error, smallest uncertainty bandwidth, and confidence band of 95% prediction error interval, therefore, validating the accuracy of this GMDH methodology.

4. Conclusions

Discharge of the brine water produced from desalination plants back into the coastal ocean using a submerged pipe is a common method widely used in engineering practices. Therefore, studying the mixing behavior of this discharge in the near-field zone has become a research priority to reduce the impact of this water on the marine environment. The discharged water can be formed as an inclined negatively buoyant jet when its density is higher than the density of the receiving water. Therefore, predicting the geometrical characteristics of this jet is crucial important for improving the understanding of the mixing behavior of this type of discharging and its dilution. In this study, the geometrical characteristics of the inclined negatively buoyant jet for angles ranging from 15° to 85° was modeled and predicted using a type of artificial neural network (ANN) called group method of data handling (GMDH). Results of this model were evaluated statistically and compared with a number of other analytical models previously studied. The results show that this model, while being efficient, is more accurate and is better able to accurately predict the geometrical characteristics of the negatively buoyant jet compared to the others.

Author Contributions

Conceptualization, All; methodology All; data curation, H.A.; writing—original draft preparation, H.A.; writing—review and editing, All; supervision, H.B. All authors have read and agreed to the published version of the manuscript.

Funding

This work was funded by King Abdulaziz City for Science and Technology (KACST), Saudi Arabia.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The first author would like to acknowledge King Abdulaziz City for Science and Technology (KACST) for their scholarship and financial support during his PhD study.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Petersen, L. K.; Heck, N.; Reguero, G. B.; Potts, D.; Hovagimian, A.; Paytan, A. Biological and Physical Effects of Brine Discharge from the Carlsbad Desalination Plant and Implications for Future Desalination Plant Constructions. Water 2019, 11 (2). [CrossRef]
  2. Bombar, G.; Dölgen, D.; Alpaslan, M. N. Environmental impacts and impact mitigation plans for desalination facilities. Desalination and Water Treatment 2016, 57 (25), 11528-11539. [CrossRef]
  3. Cipollina, A.; Brucato, A.; Grisafi, F.; Nicosia, S. Bench-Scale Investigation of Inclined Dense Jets. Journal of Hydraulic Engineering 2005, 131 (11), 1017-1022. [CrossRef]
  4. Kikkert, G. A. Buoyant jets with two and three-dimensional trajectories. Doctor of Philosophy, University of Canterbury, Christchurch, New Zealand, 2006. https://ir.canterbury.ac.nz/items/30cdc6c9-3174-479c-9470-30a248cb11c4.
  5. Zeitoun, M. A.; McIlhenny, W. F. 1971. Conceptual Designs of Outfall Systems for Desalination Plants. In Proceedings of the Offshore Technology Conference, Houston, Texas. 2006. OTC-1370-MS. [CrossRef]
  6. Abessi, O.; Roberts, P. J. W. Dense Jet Discharges in Shallow Water. Journal of Hydraulic Engineering 2015, 142 (1), 04015033. [CrossRef]
  7. Papakonstantis, I. G.; Christodoulou, G. C. Discussion of “Inclined Negatively Buoyant Discharges” by G. A. Kikkert, M. J. Davidson, and R. I. Nokes. Journal of Hydraulic Engineering 2008, 134 (12), 1782-1784. [CrossRef]
  8. Abessi, O.; Roberts, P. J. W. Effect of Nozzle Orientation on Dense Jets in Stagnant Environments. Journal of Hydraulic Engineering 2015, 141 (8), 06015009. [CrossRef]
  9. Bashitialshaaer, R.; Larson, M.; Persson, K. M. An Experimental Investigation on Inclined Negatively Buoyant Jets. Water 2012, 4 (3), 720-738. [CrossRef]
  10. Nemlioglu, S.; Roberts, P. J. W. 2006. Experiments on dense jets using three-dimensional laser-induced fluorescence (3DLIF). In MWWD 2006 -The 4th international conference on marine waste water disposal and marine environment, Antalya, Turkey, November 6-10/2006.
  11. Lindberg, W. R. Experiments on Negatively Buoyant Jets, with and without Cross-Flow. In Recent Research Advances in the Fluid Mechanics of Turbulent Jets and Plumes, Davies, P. A., Neves, M. J. V. Eds.; Springer Netherlands, 1994; pp 131-145.
  12. Roberts Philip, J. W.; Toms, G. Inclined Dense Jets in Flowing Current. Journal of Hydraulic Engineering 1987, 113 (3), 323-340. (acccessed 2023/11/27). [CrossRef]
  13. Papakonstantis, I. G.; Christodoulou, G. C.; Papanicolaou, P. N. Inclined negatively buoyant jets 1: geometrical characteristics. Journal of Hydraulic Research 2011, 49 (1), 3-12. [CrossRef]
  14. Papakonstantis, I. G.; Christodoulou, G. C.; Papanicolaou, P. N. Inclined negatively buoyant jets 2: concentration measurements. Journal of Hydraulic Research 2011, 49 (1), 13-22. [CrossRef]
  15. Crowe, A. Inclined negatively buoyant jets and boundary interaction. Doctor of Philosophy, University of Canterbury, Christchurch, New Zealand, 2013. http://hdl.handle.net/10092/7895.
  16. Bloomfield, L. J.; Kerr, R. C. Inclined turbulent fountains. Journal of fluid mechanics 2002, 451, 283-294. [CrossRef]
  17. Shao, D.; Law, A. W.-K. Mixing and boundary interactions of 30° and 45° inclined dense jets. Environmental Fluid Mechanics 2010, 10 (5), 521-553. [CrossRef]
  18. Papakonstantis, I. G.; Tsatsara, E. I. Mixing Characteristics of Inclined Turbulent Dense Jets. Environmental Processes 2019, 6 (2), 525-541. [CrossRef]
  19. Roberts, P. J. W.; Ferrier, A.; Daviero, G. Mixing in Inclined Dense Jets. Journal of Hydraulic Engineering 1997, 123 (8), 693-699. [CrossRef]
  20. Jiang, B.; Law, A. W.-K.; Lee, J. H.-W. Mixing of 30° and 45° Inclined Dense Jets in Shallow Coastal Waters. Journal of Hydraulic Engineering 2014, 140 (3), 241-253. [CrossRef]
  21. Chung Kei Chris, L. Mixing of inclined dense jets. Master thesis, the University of Hong Kong, Pokfulam, Hong Kong, 2009. http://hdl.handle.net/10722/65319.
  22. Lai, C. C. K.; Lee, J. H. W. Mixing of inclined dense jets in stationary ambient. Journal of Hydro-environment Research 2012, 6 (1), 9-28. [CrossRef]
  23. Abessi, O.; Roberts, P. J. W. Multiport Diffusers for Dense Discharges. Journal of Hydraulic Engineering 2014, 140 (8), 04014032. [CrossRef]
  24. Oliver, C. Near field mixing of negatively buoyant jets. Doctor of Philosophy, University of Canterbury, Christchurch, New Zealand, 2012. http://hdl.handle.net/10092/6300.
  25. Papakonstantis, I. G.; Tsatsara, E. I. Trajectory Characteristics of Inclined Turbulent Dense Jets. Environmental Processes 2018, 5 (3), 539-554. [CrossRef]
  26. Papanicolaou, P. N.; Kokkalis, T. J. Vertical buoyancy preserving and non-preserving fountains, in a homogeneous calm ambient. International Journal of Heat and Mass Transfer 2008, 51 (15), 4109-4120. [CrossRef]
  27. Lee, J. H. W.; Chu, V. H. Turbulent jets and plumes: a Lagrangian approach; Springer: New York, NY, USA, 2003. [CrossRef]
  28. Jirka, G. H. Integral Model for Turbulent Buoyant Jets in Unbounded Stratified Flows. Part I: Single Round Jet. Environmental Fluid Mechanics 2004, 4 (1), 1-56. [CrossRef]
  29. Kikkert, G. A.; Davidson, M. J.; Nokes, R. I. Inclined Negatively Buoyant Discharges. Journal of Hydraulic Engineering 2007, 133 (5), 545-554. [CrossRef]
  30. Oliver, C. J.; Davidson, M. J.; Nokes, R. I. Predicting the near-field mixing of desalination discharges in a stationary environment. Desalination 2013, 309, 148-155. [CrossRef]
  31. Zaji, A. H.; Bonakdari, H. Robustness lake water level prediction using the search heuristic-based artificial intelligence methods. ISH Journal of Hydraulic Engineering 2019, 25 (3), 316-324. [CrossRef]
  32. Alitaleshi, F.; Daghbandan, A. Using a multi-objective optimal design of GMDH type neural networks to evaluate the quality of treated water in a water treatment plant. Desalination and Water Treatment 2019, 139, 123-132. [CrossRef]
  33. Naeini, S. A.; Moayed, R. Z.; Kordnaeij, A.; Mola-Abasi, H. Elasticity modulus of clayey deposits estimation using group method of data handling type neural network. Measurement 2018, 121, 335-343. [CrossRef]
  34. Parsaie, A.; Haghiabi, A. H. Improving Modelling of Discharge Coefficient of Triangular Labyrinth Lateral Weirs Using SVM, GMDH and MARS Techniques. Irrigation and Drainage 2017, 66 (4), 636-654. (acccessed 2023/11/27). [CrossRef]
  35. Gholami, A.; Bonakdari, H.; Ebtehaj, I.; Shaghaghi, S.; Khoshbin, F. Developing an expert group method of data handling system for predicting the geometry of a stable channel with a gravel bed. Earth Surface Processes and Landforms 2017, 42 (10), 1460-1471. (acccessed 2023/11/27). [CrossRef]
  36. Najafzadeh, M.; Zahiri, A. Neuro-Fuzzy GMDH-Based Evolutionary Algorithms to Predict Flow Discharge in Straight Compound Channels. Journal of Hydrologic Engineering 2015, 20 (12), 04015035. [CrossRef]
  37. Najafzadeh, M.; Barani, G.-A.; Hessami-Kermani, M.-R. Evaluation of GMDH networks for prediction of local scour depth at bridge abutments in coarse sediments with thinly armored beds. Ocean Engineering 2015, 104, 387-396. [CrossRef]
  38. Ebtehaj, I.; Bonakdari, H.; Zaji, A. H.; Azimi, H.; Khoshbin, F. GMDH-type neural network approach for modeling the discharge coefficient of rectangular sharp-crested side weirs. Engineering Science and Technology, an International Journal 2015, 18 (4), 746-757. [CrossRef]
  39. Najafzadeh, M.; Barani, G. A.; Hessami-Kermani, M. R. Group method of data handling to predict scour depth around vertical piles under regular waves. Scientia Iranica 2013, 20 (3), 406-413. [CrossRef]
  40. Madandoust, R.; Bungey, J. H.; Ghavidel, R. Prediction of the concrete compressive strength by means of core testing using GMDH-type neural network and ANFIS models. Computational Materials Science 2012, 51 (1), 261-272. [CrossRef]
  41. Alfaifi, H.; Abdolmajid, M.; Bonakdari, H. Experimental Investigation and Model Development of Geometric Characteristics of Negatively Buoyant Jets Inclined at 15° and 52° using GMDH Method. Journal of Coastal Research 2020, 36 (3), 636-653. [CrossRef]
  42. Rostami, A.; Hemmati-Sarapardeh, A.; Karkevandi-Talkhooncheh, A.; Husein, M. M.; Shamshirband, S.; Rabczuk, T. Modeling heat capacity of ionic liquids using group method of data handling: A hybrid and structure-based approach. International Journal of Heat and Mass Transfer 2019, 129, 7-17. [CrossRef]
  43. Azimi, H.; Bonakdari, H.; Ebtehaj, I. A Highly Efficient Gene Expression Programming Model for Predicting the Discharge Coefficient in a Side Weir along a Trapezoidal Canal. Irrigation and Drainage 2017, 66 (4), 655-666. (acccessed 2023/11/28). [CrossRef]
  44. Bonakdari, H.; Mohammadian, A. Evolutionary prediction of an inclined dense jet in shallow water. Desalination and Water Treatment 2019, 155, 32-47. [CrossRef]
  45. Yan, X.; Mohammadian, A.; Ao, R.; Liu, J.; Yang, N. Two-dimensional convolutional neural network outperforms other machine learning architectures for water depth surrogate modeling. Journal of Hydrology 2023, 616, 128812. [CrossRef]
  46. Yang, J.; Singh, H.; Hines, E. L.; Schlaghecken, F.; Iliescu, D. D.; Leeson, M. S.; Stocks, N. G. Channel selection and classification of electroencephalogram signals: An artificial neural network and genetic algorithm-based approach. Artificial Intelligence in Medicine 2012, 55 (2), 117-126. [CrossRef]
  47. Morshed, J.; Kaluarachchi, J. J. Application of artificial neural network and genetic algorithm in flow and transport simulations. Advances in Water Resources 1998, 22 (2), 145-158. [CrossRef]
  48. Chatterjee, S.; Mahapatra, S. S.; Lamberti, L.; Pruncu, C. I. Prediction of welding responses using AI approach: adaptive neuro-fuzzy inference system and genetic programming. Journal of the Brazilian Society of Mechanical Sciences and Engineering 2022, 44 (2), 53. [CrossRef]
  49. Zhang, W.; Rennie, C. D.; Nistor, I. A new model developed by multigene genetic programming for the temporal evolution of bridge pier scour. Canadian Journal of Civil Engineering 2023, 50 (7), 549-559. [CrossRef]
  50. Yan, X.; Mohammadian, A. Prediction of a rosette dense jet group in crossflow ambient conditions using multi-gene genetic programming. Desalination and Water Treatment 2020, 190, 440-448. [CrossRef]
  51. Bahreini Toussi, I.; Mohammadian, A.; Kianoush, R. Prediction of Maximum Pressure at the Roofs of Rectangular Water Tanks Subjected to Harmonic Base Excitation Using the Multi-Gene Genetic Programming Method. Mathematical and Computational Applications 2021, 26 (1), 6. [CrossRef]
  52. Yan, X.; Wang, Y.; Mohammadian, A.; Liu, J. Simulations of the Concentration Fields of Rosette-Type Multiport Buoyant Discharges Using Combined CFD and Multigene Genetic Programming Techniques. Journal of Marine Science and Engineering 2021, 9 (11), 1311. [CrossRef]
  53. Yan, X.; Mohammadian, A.; Khelifa, A. Modeling spatial distribution of flow depth in fluvial systems using a hybrid two-dimensional hydraulic-multigene genetic programming approach. Journal of Hydrology 2021, 600, 126517. [CrossRef]
  54. Yan, X.; Mohammadian, A. Multigene Genetic-Programming-Based Models for Initial Dilution of Laterally Confined Vertical Buoyant Jets. In Journal of Marine Science and Engineering, 2019; Vol. 7.
  55. Ebtehaj, I.; Bonakdari, H.; Khoshbin, F.; Bong, C. H. J.; Ghani, A. A. Development of group method of data handling based on genetic algorithm to predict incipient motion in rigid rectangular storm water channel. Scientia Iranica 2017, 24 (3), 1000-1009. [CrossRef]
  56. Najafzadeh, M.; Saberi-Movahed, F. GMDH-GEP to predict free span expansion rates below pipelines under waves. Marine Georesources & Geotechnology 2019, 37 (3), 375-392. [CrossRef]
  57. Daghbandan, A.; Khalatbari, S.; Abbasi, M. M. Applying GMDH-type neural network for modeling and prediction of turbidity and free residual aluminium in drinking water. Desalination and Water Treatment 2019, 140, 118-131. [CrossRef]
  58. Ivakhnenko, A. G. Polynomial Theory of Complex Systems. IEEE Transactions on Systems, Man, and Cybernetics 1971, SMC-1 (4), 364-378. [CrossRef]
  59. GMDH Inc. 2019. GMDH Shell DS (version 3.8.9). GMDH Inc. https://gmdhsoftware.com/.
  60. Jirka, G. H. Improved Discharge Configurations for Brine Effluents from Desalination Plants. Journal of Hydraulic Engineering 2008, 134 (1), 116-120. [CrossRef]
  61. Oliver, C. J.; Davidson, M. J.; Nokes, R. I. Removing the boundary influence on negatively buoyant jets. Environmental Fluid Mechanics 2013, 13 (6), 625-648. [CrossRef]
  62. Shaghaghi, S.; Bonakdari, H.; Gholami, A.; Ebtehaj, I.; Zeinolabedini, M. Comparative analysis of GMDH neural network based on genetic algorithm and particle swarm optimization in stable channel design. Applied Mathematics and Computation 2017, 313, 271-286. [CrossRef]
Preprints 92786 g001
Figure 1. Dimensional parameters of the inclined round dense jet in stagnant ambient water.
Figure 1. Dimensional parameters of the inclined round dense jet in stagnant ambient water.
Preprints 92786 g001
Preprints 92786 g002
Figure 2. The scatter plot with fitting lines of the actual and GMDH predicted results for angles from 15° to 85°: (a) x r / D and (b) y t / D .
Figure 2. The scatter plot with fitting lines of the actual and GMDH predicted results for angles from 15° to 85°: (a) x r / D and (b) y t / D .
Preprints 92786 g002
Preprints 92786 g003aPreprints 92786 g003b
Figure 3. The performance of GMDH model in the training and testing stage.
Figure 3. The performance of GMDH model in the training and testing stage.
Preprints 92786 g003aPreprints 92786 g003b
Preprints 92786 g004aPreprints 92786 g004b
Figure 4. A comparison of GMDH predicted results with previous analytical solutions for x r / D for angles: (a) 15°, (b) 45°, (c) 60°, and (d) 75°.
Figure 4. A comparison of GMDH predicted results with previous analytical solutions for x r / D for angles: (a) 15°, (b) 45°, (c) 60°, and (d) 75°.
Preprints 92786 g004aPreprints 92786 g004b
Preprints 92786 g005aPreprints 92786 g005b
Figure 5. A comparison of GMDH predicted results with previous analytical solutions for y t / D for angles: (a) 15°, (b) 45°, (c) 60°, (d) 75° and (e) 85°.
Figure 5. A comparison of GMDH predicted results with previous analytical solutions for y t / D for angles: (a) 15°, (b) 45°, (c) 60°, (d) 75° and (e) 85°.
Preprints 92786 g005aPreprints 92786 g005b
Preprints 92786 g006
Figure 6. Results of various nozzle angles compared with previous observed data and analytical models for: (a) horizontal distance of return point; (b) Terminal rise height.
Figure 6. Results of various nozzle angles compared with previous observed data and analytical models for: (a) horizontal distance of return point; (b) Terminal rise height.
Preprints 92786 g006
Table 1. Nonlinear equations extracted from GMDH for dimensionless geometrical parameters.
Table 1. Nonlinear equations extracted from GMDH for dimensionless geometrical parameters.
Geometrical GMDH proposed equations
x m / D = -   31.538 + 1.94873 θ   -   0.0234242   θ 2 +   1.63203   Fr d (4)
x r / D = -   0.35311 + 2.9030   Fr d + 0.065091   Fr d N 3   -   0.13909   Fr d 2   -   0.005735   N 3 2 N 3 = -   47.2107 + 2.77506   θ   -   0.0340387   θ 2 + 2.82939   Fr d (5)
y m / D = 2.37956   -   0.139279   θ + 0.0263993   θ   Fr d + 0.0026574   θ 2 + 0.113531   Fr d (6)
y t / D = 1.00174 + 0.0336764   θ Fr d   -   0.000250209   θ 2 + 0.0418149   Fr d (7)
Table 2. Results of statistical indices for training and testing of the GMDH model.
Table 2. Results of statistical indices for training and testing of the GMDH model.
Geometrical
parameter 		R2 MAE RMSE R2 MAE RMSE
training testing
x m / D 0.948 5.911 8.239 0.936 6.809 9.192
x r / D 0.971 6.052 8.556 0.951 6.499 10.143
y m / D 0.962 4.009 5.711 0.947 4.458 6.861
y t / D 0.945 5.471 8.298 0.956 5.236 7.804
Table 3. Results of the standard error of the estimate for all models.
Table 3. Results of the standard error of the estimate for all models.
Geometrical
parameter 		Angle GMDH
model 		CORJET VISJET Kikkert et al.
(2007) 		Oliver et al. (2013)
x r / D 15° 6.39 - - 7.94 6.86
45° 10.82 - - 11.72 10.77
60° 9.42 - - 12.29 9.51
75° 4.35 - - 20.80 4.99
y t / D 15° 3.35 - - 3.72 3.66
45° 11.13 12.16 11.31 15.71 12.44
60° 9.81 12.17 10.96 18.72 12.31
75° 3.93 - - 12.00 12.95
85° 9.06 - - 15.53 16.39
Table 4. Uncertainty analysis for GMDH prediction models of the geometrical characteristics.
Table 4. Uncertainty analysis for GMDH prediction models of the geometrical characteristics.
GMDH model for the geometrical characteristic Number of
sample size 		MPE s d WUB 95% PEI
x m / D 309 +0.29 8.58 ±0.96 -0.66 to +1.25
x r / D 305 -0.11 9.29 ±1.04 -1.15 to +0.93
y m / D 341 -0.10 6.11 ±0.65 -0.75 to +0.55
y t / D 420 -0.03 8.25 ±0.79 -0.82 to +0.76
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
A comprehensive Study for Predicting the Geometrical Characteristics of an Inclined Negatively Buoyant Jet Using Group Method of Data Handling (GMDH) Neural Network

Hassan Alfaifi

et al.

,

2023

Design of a Cyclone Separator Critical Diameter Model based on a Machine Learning and CFD

Donggeun Park

et al.

,

2020

Transfer Learning with Deep Neural Network toward the Prediction of Wake Flow Characteristics of Containerships

Min-Kyung Lee

et al.

,

2023

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated