Prerpints.org logo
Preprint
Article

Design and Analysis of a Linear Electric Generator for Harvesting Vibration Energy

Altmetrics

Downloads

100

Views

29

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

12 December 2023

Posted:

12 December 2023

You are already at the latest version

Alerts
Abstract
This paper provides a proof of concept for a linear electric generator that can be used to harvest energy from various sources of linear motion, such as vibrations, free-piston engines and wave energy. The generator can be used to power small electronic devices, such as sensors, or charge household batteries. Literature was reviewed to develop an understanding about the applications, control methods, excitation methods and mechanics of rotating and linear electric machines. A bidirectional, two-sided linear machine was designed with two stator cores and a single mover core. The stator windings and mover winding can be independently excited, allowing for three modes: no mover excitation, DC excited mover, and AC excited mover. Simulations results showed that the magnetic flux generated by DC excited stator cores were concentrated in the centre of the mover core. The use of two stator cores eliminates lateral flux in the mover core when it is not excited, minimising attraction and repulsion forces. Parametric analysis showed that flux cutting occurred in all operation modes, verifying that the generator will produce power when operating. Hardware tests produced an output current when the machine is electrically and mechanically excited, verifying the proposed design.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

1.1. Background

Currently, electricity production relies on fossil fuels as its main source of energy. In Australia, as of 2018, coal, oil and gas are used to produce 93 . 8 % of the electricity consumed while renewable sources only account for 6 . 2 % [1]. Burning of fossil fuels to produce electricity results in the release of large amounts of carbon dioxide into the atmosphere, which leads to global warming. Additionally, the world’s fossil fuel reserves are depleting which has led to a global energy crisis [2]. The combination of these two have led to the development of methods of harvesting energy from renewable sources such as solar, wind and wave energy. The electricity generated by these methods can be fed into the grid to supplement or replace fossil fuel energy production.
Energy can also be harvested from sources with wasted vibration energy, thermal energy or pressure energy. These sources are present in small quantities less than 100 W . While not suitable for providing power to the grid, these sources could be used to power small devices such as electronics and sensors located in rural areas or areas not powered by the distribution network [3]. This energy can also be used to power electronics carried on a person that would otherwise use a battery. Devices such as pacemakers can be powered by piezoelectric-based vibration harvesters using body movements, breathing or heartbeats as their source of mechanical excitation [4]. Examples of vibration sources that can be harvested are automotive, civil structures such as buildings and railways, and industrial machines [5].
Vibrations have a wide variety of forms based on their displacement waveforms and frequencies. Vibrations with a sinusoidal waveform do not require an end stop force as the vibration velocity naturally reduces to zero, while non-sinusoidal waveforms do require an end stop force. The end stop force may be produced by a physical barrier, however this usually results in abrupt changes in speed and may result in mechanical wear. Alternatively, the end stop force may be produced by electromagnetic means, but this results in a large drop in generated energy [6]. Due to this reason, this project will focus on harvesting energy from mechanical excitation sources that do not require an end stop force.
Various machine designs have been proposed in literature to harvest energy from sources of vibrations. Piezoelectric converters can be used to harvest energy but are only efficient at their resonance frequency and have a small bandwidth [7,8]. Additionally, piezoelectric converters are limited in the output power. The harmonic frequency of piezoelectric harvesters is limited a range of 1 to 20 H z [9]. A cantilever design is effective at amplifying the displacement amplitude experienced at the electromechanical converter but has a large overall size due to the cantilever arm [10]. Adaptive pneumatic vibration isolations platforms can use a series of wedges and rollers to vary the stiffness of the machine and decrease the resonance frequency and amplitude. However, this design experiences jumps between resonance and non-resonance based on the initial conditions of the system [11].
Vibration harvesting generators can be used to harvest energy from human motion to power wearable electronics. These tend to function at low frequencies due to the nature of their excitation source, resulting in a power output on the scale of mW. A linear generator was designed in [12] using a magnet suspended between to ring magnets using levitation. This setup replaced the conventional mechanical springs with magnetic springs. A non-linear generator was proposed in [13] which utilised a magnetic ball moving along a two-dimensional surface to harvest in-plane vibration. A bowl-shaped housing with a saddle was used to contain and constrain the motion of the ball. The design allowed a bi-stable orbit to be produced by vibrations in any direction within the plane to influence the motion of the ball around a central saddle.
Reviewed literature contains designs of linear electric machines to harvest energy from a range of sources of mechanical motion. Linear electric generators have been extensively studied as a method of harvesting energy from free-piston engines due to their variable stroke length which improves response time and thermal efficiency [14,15]. Similar designs have also been proposed as method of harvesting energy from other types of engines such as Stirling engines [16]. Linear electric generators have been tested as a means of extracting wave energy. These designs use a float connected to the mover of the generator to produce power. The low number of moving parts and direct coupling between the source and generator make these designs more reliable than the equivalent rotating machine which typically uses a turbine or lift-arm [6,17].
Different excitation sources need to be considered when designing an electric machine as these produce the magnetic field patterns. Permanent magnets can produce high thrust at low speeds but typically have higher flux leakage and cogging forces [18]. DC excitation is comparable to permanent magnets in thrust if the supplied current is high enough, although this may cause magnetic saturation leading to increased core losses [19,20].
The magnetic reluctance of a machine can be reduced by using stator and translator cores that do not have sharp edges [21]. This improves the distribution of flux through the core and increases the field strength. The improved flux distribution reduces core saturation and hysteresis losses. This results in an increase in the induced voltage and output power.
Reducing the mass of the mover results in an increase in velocity and output power [22]. The mass of the mover can be reduced by having both the excitation and output windings on the stator and replacing the mover with a split mover and secondary stator [23]. This design increases the efficiency of the machine when compared to a similar machine of the same power output.
Cogging forces are often observed in linear electric machines and tend to increase ripple in force and speed. These can be reduced by utilising a fractional pole pitch [17]. Resonance occurs in a linear generator when the mechanical natural frequency of the electric generator matches that of the mechanical excitation source [24]. Mechanical resonance is typically achieved through the use of tension and compression springs. It is also possible to use a gas filled bounce chamber if the applied mechanical force only acts in one direction [25]. Damping force depends on the load and the magnetic field strength of the generator. Increasing the mover mass will decrease electromagnetic damping [8]. Controlling the output current will vary the electronic stiffness of the machine, affecting the resonance frequency and reducing the spring stiffness required [26].
Various control methods can be used to improve performance in the steady-state and transient state and remove undesired characteristics. Some control methods found are sliding mode control which can reduce ripple in force and speed while increasing stability [27], barrier function based adaptive control which reduces chattering and improves resistance to perturbation [28], and neuro-fuzzy vector control which can improve the transient and steady-state performance while adjusting the active and reactive power output [29].
A linear generator design in [30] was capable of harvesting vibrations at 50 H z with displacements less than 1 m m . The housing of the machine was secured to the vibration source. Tension and compression springs were used to transfer vibrations from the housing to the mover and provide mechanical resonance during operation. The excitation current was controlled as the vibration displacement could not be controlled. The designed generator lacked a complete shaft or guide. Applying a lateral or rotational force to the generator would result in collision between the mover and the housing of the generator.

1.2. Motivations and Contributions

The hardware options for extracting energy directly from linearly oscillating objects is limited without the use of mechanisms to transform linear motion to rotating motion. The linear generator is desired in this application due to the lack of transforming mechanics which would represent potential energy losses within the system. The existing designs for linear generators proposed in literature are typically limited in their applications to oscillating motion with a displacement less than 10 m m . This limits their applications to very small vibrations or to harvesting energy from human motion. The design of a linear generator with a larger stroke would significantly increase the possible applications for energy harvesting. The lack of transforming mechanics would reduce the machine size to maintain portability of the generator. Such a device could be used for powering nearby electronics in locations unsuitable for connection to the main power grid.
This paper provides a proof of concept of a new bi-directional, two-sided linear electric generator to harvest energy from a range of linear mechanical excitation sources, in particular, vibration energy. The aims of the design are to harvest energy from a source with linear displacement amplitude of approximately 30 m m at less than 10 H z . The main contributions of this paper include:
  • Detailed theoretical finite element modelling and simulation using Flux by Cedrat. The magnetic flux within and between the stator and mover cores was modelled to analyse machine reluctance. Air gap reluctance was reduced through the use of flanges on the stator teeth.
  • Simulation studies were performed for various excitation modes in both static and parametric analysis. The modes studied include no mover coil excitation, a DC excited mover coil, and an AC excited mover coil.
  • Construction and design of a practical linear generator were performed once the proposed design was verified. Calculations for the mechanical properties of the machine were undertaken to obtain the spring rate which would provide the desired resonant frequency.
  • Verification and analysis of the hardware through the use of empirical testing with the use of a pneumatic actuator.
The proposed design provides the framework for further work involving the construction of similar machines to harvesting of energy from large vibration sources such as carriageways and transformers.

1.3. Paper Structure

The paper is organised as follows. Section II outlines theoretical aspects associated with the proposed design. Section III provides details of the proposed machine design. Section IV describes the simulation process and highlights the main findings from simulation results. Section V outlines the design of a prime mover describes the hardware tests performed. Finally, Section VI provides a brief conclusion to the paper.

2. Theoretical Aspects

2.1. Electromagnetism

The magnetic field produced by an electric current in a coil is given in Ampere’s Law (1), where N is the number of turns, I n e t is the electric current and l c is the mean path length that the magnetic flux travels along the core.
H = N i / l c
The magnetic flux density is described using (2), where μ is the magnetic permeability of the material which can be specified as a ratio of the magnetic permeability of free space, μ 0 = 4 π × 10 − 7 H / m , assuming the material is homogenous and isotropic.
B = μ H = μ R μ 0 H
The total magnetic flux is found using (3), assuming the flux density and cross-sectional area, A, are constant.
ϕ = B A
Faraday’s Law (4) describes the electromotive force (EMF) produced in a closed circuit due to a changing magnetic flux. The generated EMF is negative according to Lenz’s law which states that a generated current must flow in a direction to oppose the change in magnetic flux that produced it. This can be manipulated for a moving conductor in a constant magnetic field to produce an induced voltage, e i n d (5), with v for the conductor velocity and l for the conductor length.
E M F = − N d ϕ d t
e i n d = ( v × B ) · l

2.2. Mechanics

Translational mechanical system components can be categorised into three groups: masses, dampers and springs, based on their interaction with applied forces. The net force of a translational mechanical system as a function of displacement is given in (6), where m is the mass, c is the damping factor, k is the spring constant. x, x ˙ and x ¨ are the displacement, velocity and acceleration, respectively.
F = m x ¨ + c x ˙ + k x
Hooke’s Law, given in (7), in describes the force exerted by spring as a function of displacement. The spring will always tend to return to its free length.
F = − k x
Mechanical resonance is achieved through the use of springs, resulting in simple harmonic motion of a spring-mass system. The angular frequency of a spring-mass system with no external force is given in (8).
ω = k m
The electromagnetic forces generated in linear machines attempt to align the magnetic fields of the stator and mover to reduce the energy stored in the magnetic field. The forces generated have two main components. The thrust force acts along the length of the machine in the direction of motion. The attraction or repulsion force acts perpendicular to the direction of motion and is typically not desired as it tends to change the air gap length. Cogging forces may be produced by the interaction between the excitation source and the teeth of other cores. These are observed as a tangential force and result in vibrations and speed ripple. Cogging forces can be reduced in permanent magnet linear generators by using bevelled magnets instead of rectangular magnets [31]. Thrust fluctuations occur during operation of linear electric motors. These arise from changes in the reluctance of the machine due to the relative position of the mover and stator teeth throughout the stroke. Thrust fluctuations can be reduced by using skewed slots, skewed poles or unequal pole pitches in the stator and mover cores [32].

3. Machine design

The proposed design is a two-sided bi-directional linear electric generator consisting of two identical stator cores and a single mover core.
The stator cores each have thirteen teeth and twelve slots, with the outer teeth having a size equal to half of the inner teeth. They are comprised of laminations of approximately 0 . 65 m m thick to reduce the losses due to generated eddy currents. Flanges on the teeth reduce the magnetic reluctance at the air gap by increasing the surface area used to transfer flux. The two stator cores are positioned opposite each other and face inwards. The stator cores each have a single-phase winding around the inner eleven teeth which are wound so that they face the air gap. Each winding has 20 turns per slot using a copper wire with a diameter of 0 . 53 m m , with the two stator cores being individually energised.
The mover core has eleven teeth and consists of laminations of 40 m m wide for the teeth and 20 m m wide for the slots. A fractional pole pitch equal to four thirds the pole pitch of the stator core is used to reduce cogging forces. The mover core is mounted between them on a shaft and oscillates when mechanically excited. The machine is designed such to harvest energy from mechanical oscillations of an amplitude less than 30 m m and a frequency of less than 10 H z , matching those of the vibration source to be harvested. The mover core has two separate windings which are independent, allowing for the machine to operate as a single-phase system or a two-phase system. The winding consists of 24 turns of copper wire of diameter 1 m m per slot, wound axially.
The symmetrical geometry of the generator minimises attraction and repulsion forces generated between the mover core and stator cores. Both the stator cores and mover core are made from silicone steel, a form of electrical steel, which has a relative permeability of approximately 4000.
The housing components of the machine are made from aluminium as it is not a magnetic material. This is required to reduce the amount of flux that escapes the cores when excited. The bolts, nuts and threaded rods are made of steel but do not form a complete magnetic circuit external to the iron cores. The air gap between each stator cores and the mover core can be adjusted independently up to a maximum of 25 m m . The housing allows for a maximum stroke length of 56 m m . The springs used had a spring rate of 8 . 81 m m . These springs have a free length of 79 . 5 m m and a minimum length of 43 . 4 m m . This corresponds to a compression of 36 . 1 m m , which is over 20 % greater than what is required. The mover mass was measured to be 5 . 92 k g . The resulting resonant frequency, calculated using (8) is 6 . 1397 H z if one spring was used on either side of the machine, and 8 . 6828 H z if two springs are used on either side.
The assembled generator with both stator cores, mover core and housing is shown in Figure 1. Parameters and dimensions of the generator cores are given in Table 1.

4. Simulations

4.1. Modelling of the generator

Finite element analysis was performed in Flux by Cedrat to simulate and analyse the magnetic flux generated by the machine. Flux 2D was used due to the reduced computational power and time required. This was considered suitable as the machine has a uniform cross-section along its width. Only the stator cores and mover core were modelled as it is assumed that the magnetic flux would not propagate significantly into the rest of the machine. An air gap of 1 m m is used in the model.

4.2. Magnetostatic analysis

The first simulation has the same current directions in the two stator cores. This results in the flux in the stator teeth opposite each other to flow in the same direction. The purpose of this simulation is to determine how well flux could be transmitted through the air gaps and mover core as the flux. The results of this simulation are shown in Figure 2a and Figure 2b. A magnetic flux density of 1 . 45 T was shown in the stator cores with vector potentials at ± 3 . 9 W b / m around the stator windings.
The second simulation used opposite current directions in the two stator cores, such that the flux from the stator cores mirror each other. This results in flux being generated in the stator, passing into the mover, then back to the same stator through a different tooth. The results of this simulation are shown in Figure 3a and Figure 3b. The flux magnitude is similar to that of the first simulation while the vector potentials differ significantly from those of the first simulation.
Figure 4a and Figure 4b show the isolines along with the flux arrows at the boundary of the stator cores and mover cores, respectively. The flux travels in opposite directions on adjacent stator teeth. These figures also show the flux entering the mover core and exiting the mover core on the same side. The mover core slots are surrounded by magnetic flux. This suggests that moving the mover core will cause the mover coils to cut flux lines. This, in turn, will induce a voltage in the mover winding and produce an output. This verifies the ability of the proposed design to act as an electric generator.
Figure 4a shows that very little flux exits the stator cores through the back of the cores. Fringing flux is apparent at the top and bottom tooth of each stator core. In Figure 4b, flux is lost through the of the mover core outside the stator core region. However, this flux is of low strength.
The excitation currents in the stator slots were modified to reflect what was found in the electrical circuit of the physical model. The stator slot currents were changed so that adjacent slots were given currents of equal magnitude but in opposite directions. This corrects an issue in the previous simulations, in which the current in adjacent slots was in the same direction. The magnitude of the currents were changed to reflect the actual currents in the windings when given a 12 V DC excitation. The magnetic flux and vector potential throughout the machine cores are shown in Figure 5a. It can be seen that the flux density in the teeth of the stator cores differ significantly from the previous simulations. The flux density in the teeth at the ends of the stator cores is very high while the flux density in the teeth in the middle of the cores is very low. The flux is much stronger in the centre of the mover as it is concentrated here. The flux lines show that the fields generated by each stator repel each other. Figure 5b shows the graphs of the magnetic flux density through the centre of the mover core. The x-component of the magnetic flux is close to zero. The y-component of the magnetic flux gradually increases from zero at the ends of the core to over 1 . 35 T at the centre of the core.

4.3. Parametric analysis

The linear generator was simulated while the mover position was varied from − 15 m m to + 15 m m , resulting in a total stroke length of 30 m m . Step sizes of 1 m m were used. This step size provided sufficient detail without causing simulation time and the number of generated frames to be exceptionally large. A smaller step size of 0 . 2 m m was also tested but resulted in an excessively long simulation time. The results of these simulations are used to generate images which are then compiled into videos to display the change in flux throughout the stroke.
The excitation currents for the stator and mover windings were found experimentally when supplied with a 12 V excitation. The current is dependent on the resistance of the windings. As time cannot be used as an input parameter, an alternating current must instead be found using another changing variable. The simulations run define any alternating currents as functions of the current position of the mover. The period and phase shift of the current could be adjusted.

4.3.1. No mover excitation

The linear electric machine was first simulated with a DC excitation current to the stator and no excitation current to the mover. This simulates an induction generator. The flux fields and vector potential are symmetrical between the left and right side of the machine. No fringing flux or flux leakage is observed in this operation mode. The magnetic flux density through the centre of the mover core is shown in Figure 6 and has only a y-component. The flux peaks at over 1 . 3 T , being at its greatest at the midpoint of the stator cores. This causes the generated magnetic field to remain stationary relative to the stator cores but move relative to the mover core. This relative movement between mover slots and the magnetic field causes flux cutting to occur in the mover leading to the generation of an output current.

4.3.2. DC excited mover

The generator was simulated with DC excitation currents to both the stator cores and the mover core. The x-component and y-component of the magnetic flux density through the centre of the mover core are shown in Figure 7a and Figure 7b, respectively. The y-component of the flux is comparable the simulation with no mover excitation current. The x-component of the flux consists of a linear gradient with a peak that moves as the mover position changes. The flux in the middle of the mover core remains at above 1 T throughout the entire stroke.

4.3.3. AC excited mover

The generator was simulated with an AC excitation current to the mover windings with a DC excitation to the stator windings. The AC current was assigned as a function of the current mover core position to produce a period of stroke cycle. The x-component and y-components of the magnetic flux density in the centre of the mover are shown in Figure 8a and Figure 8b, respectively. The y-component of the magnetic flux density is comparable to that of the previous simulations. However, the x-component has significant peaks.

5. Hardware tests

Empirical testing of the hardware was performed to verify that the machine could produce a current. A force of up to 265 . 05 N was applied by a pneumatic actuator connected to a solenoid valve to allow for oscillating motion. A DC supply was used to provide a voltage of 14 . 56 V to the stator windings, giving it a current of 3 . 00 A . An output current was observed from both mover windings when the mover housing was mechanically excited. This verifies that the proposed machine can operate as an electric generator. It can also be concluded that magnetic flux passes from the stator cores to the mover core via the air gap.
Control side electronics are required to perform further experimentation on the linear generator. This controller will provide variable frequency AC to the excitation circuit dependent on the frequency, stroke length and speed of the mover core. The required circuitry and control was not completed at the time of writing, and therefore could not be used to perform further hardware experimentation. Additionally, no suitable mechanical excitors were available to provide controllable motion, further limiting hardware experimentation.

6. Conclusion

This paper proposed the a novel design for a linear generator consisting of two stator cores and a single mover core to harvest vibration energy. Simulations were performed in to model the propagation of magnetic flux throughout the machine and showed that the flux generated from the stator cores propagated into the mover core where they combined to increase their magnitude to over 1 . 35 T . Parametric analysis showed that the magnetic flux generated by the stator cores did not move relative to the stator cores but moved relative to the mover core throughout the stroke of the machine. This shows that there is a change in flux around the windings as the machine operates, leading to the generation of a current in the mover windings.
Empirical hardware tests were performed with a pneumatic prime mover to verify that an output current is generated when in motion. An output current was observed when the stator cores were supplied with a DC current and the mover was mechanically excited. Future work will include the required control side electronics that are necessary to provide a suitable current for the excitation circuit according to the motion of the mover core, as well as as controllable mechanical excitation source for variable motion.
The proposed design will be used as a test model for further experimentation of control systems and hardware. An inverter can be added to the input and output circuits of the system. At the input side, the inverters will provide a variable alternating current to provide control over oscillation frequency and end stop force. At the output side, the inverter will be used in conjunction with a rectifier to filter the output waveform, ensuring the output is sinusoidal with no harmonics. Control schemes can be implemented to improve response time to changing loads, increase stability, and reduce voltage ripple and harmonic distortion. Further work will examine the mechanical forces experienced by the machine, including cogging forces and end effects. The effect of the fractional pole pitch and flanged cores will be analysed to determine if they are suitable for improving vibration harvesting.

References

  1. A. Ball, J. Billing, C. McCluskey, P. Pham, O. Pittman, S. Lawson, S. Ahmad, A. Starr, J. Rousseau and N. Lambert, “Australian Energy Statistics,” Australian Government Department of Environment and Energy, 2018.
  2. M. Höök and X. Tang, “Depletion of fossil fuels and anthropogenic climate change—A review,” Energy Policy, vol. 52, pp. 797–809, 2013. [CrossRef]
  3. S. S. Kulkarni and R. K., “A Comprehensive Review of Energy Harvesting Techniques and its Potential Applications,” International Journal of Computer Applications, vol. 139, pp. 14–19, 2016.
  4. A. Ballo, M. Bottaro and A. D. Grasso, “A Review of Power Management Integrated Circuits for Ultrasound-Based Energy Harvesting in Implantable Medical Devices," Applied Sciences, vol. 11, 2021. [CrossRef]
  5. Z. Hadas, V. Vetiska, J. Vetiska and J. Krejsa, “Analysis and efficiency measurement of electromagnetic vibration energy harvesting system,” Microsystem Technologies, vol. 22, pp. 1767–1779, 2016. [CrossRef]
  6. M. H. Aliabadi, S. H. Hosseinian, S. J. Moghani and M. Abedi, “Multisided linear induction generator, analytical modeling, 3-D finite element analysis and experimental test,” Elektronika ir Elektrotechnika, vol. 19, pp. 8–14, 2013.
  7. Z. Li, Z. Yang, H. Naguib and J. Zu, “Design and Studies on a Low-Frequency Truss-Based Compressive-Mode Piezoelectric Energy Harvester,” IEEE/ASME Transactions on Mechatronics, vol. 23, pp. 2849–2858, 2018. [CrossRef]
  8. C. K. Thein, F. M. Foong and Y. C. Shu, “Damping ratio and power output prediction of an electromagnetic energy harvester designed through finite element analysis,” Sensors and Actuators, A Physical, vol. 286, pp. 220–231, 2019. [CrossRef]
  9. S. Zhou, J. Cao, D.J. Inman, J. Lin, S. Liu and Z. Wang, “Broadband tristable energy harvester: Modeling and experiment verification,” Applied Energy, vol. 133, pp. 33–39, 2014. [CrossRef]
  10. C. K. Thein, F. M. Foong and Y. C. Shu, “Spring amplification and dynamic friction modelling of a 2DOF/2SDOF system in an electromagnetic vibration energy harvester – Experiment, simulation, and analytical analysis,” Mechanical Systems and Signal Processing, vol. 132, pp. 232–252, 2019.
  11. N. Y. P. Vo, and T. D. Le, “Adaptive pneumatic vibration isolation platform,” Mechanical Systems and Signal Processing, vol. 133, 2019. [CrossRef]
  12. H. Tri Nguyen, D.A. Genov, H. Bardaweel, “Vibration energy harvesting using magnetic spring based nonlinear oscillators: Design strategies and insights," Applied Energy, vol. 269, 2020. [CrossRef]
  13. Y. Gu, W. Liu, C. Zhao, P. Wang, “A goblet-like non-linear electromagnetic generator for planar multi-directional vibration energy harvesting,” Applied Energy, vol. 266, 2020. [CrossRef]
  14. W. R. Cawthorne, P. Famouri, J. Chen, N. N. Clark, T. I. McDaniel, R. J. Atkinson, S. Nandkumar, C. M. Atkinson and S. Petreanu, “Development of a linear alternator-engine for hybrid electric vehicle applications,” IEEE Transactions on Vehicular Technology, vol. 48, pp. 1797–1802, 1999. [CrossRef]
  15. U. Ngwaka, B. Jia, C. Lawrence, D. Wu, A. Smallbone and A. P. Roskilly, “The characteristics of a Linear Joule Engine Generator operating on a dry friction principle,” Applied Energy, vol. 237, pp. 49–59, 2019. [CrossRef]
  16. I. Boldea, S. A. Nasar, Linear Electric Actuators and Generators, 1997. [CrossRef]
  17. J. Prudell, M. Stoddard, E. Amon, T. K. A. Brekken and A. Von Jouanne, “A permanent-magnet tubular linear generator for ocean wave energy conversion,” IEEE Transactions on Industry Applications, vol. 46, pp. 2392–2400, 2010. [CrossRef]
  18. J. S. Shin, R. Watanabe, T. Koseki, and H. J. Kim, “Practical design approach of a transverse flux linear synchronous motor for compact size, small mover weight, high efficiency, and low material cost," IEEE Transactions on Magnetics, vol. 51, 2015.
  19. Y. Tang, J. J. H. Paulides, T. E. Motoasca and E. A. Lomonova, “Flux-switching machine with DC excitation," IEEE Transactions on Magnetics, vol. 48, pp. 3583–3586. 2012. [CrossRef]
  20. J. Li, W. Li, R. Li and Z. Ming, “A Five-Phase Doubly Fed Doubly Salient HTS Linear Motor for Vertical Transportation," IEEE Transactions on Applied Superconductivity, vol. 28, 2018. [CrossRef]
  21. O. Farrok, M. R. Islam, Y. Guo, J. Zhu and W. Xu, “A Novel Design Procedure for Designing Linear Generators," IEEE Transactions on Industrial Electronics, vol. 65, pp. 1846–1854, 2018. [CrossRef]
  22. O. Farrok, M. R. Islam, M. R. I. Sheikh, Y. Guo and J. G. Zhu, “Design and Analysis of a Novel Lightweight Translator Permanent Magnet Linear Generator for Oceanic Wave Energy Conversion," IEEE Transactions on Magnetics, vol. 53, pp. 1–4, 2017. [CrossRef]
  23. O. Farrok, M. R. Islam, M. R. I. Sheikh, Y. Guo and J. G. Zhu, “A Split Translator Secondary Stator Permanent Magnet Linear Generator for Oceanic Wave Energy Conversion," IEEE Transactions on Industrial Electronics, vol. 65, pp. 7600–7608, 2018. [CrossRef]
  24. J. Jun, Y. Shin and J. H. Kim, “Linear electric generator with Halbach array to self-charge a smartphone," Journal of Vibroengineering, vol. 18, pp. 587–594, 2016.
  25. U. J. Seo, B. Riemer, R. Appunn and K. Hameyer, “Design considerations of a linear generator for a range extender application," Archives of Electrical Engineering, vol. 64, pp. 581–592, 2015. [CrossRef]
  26. M. F. Iacchetti, R. Shuttleworth and M. Zhang, “Volt-ampere ratings in electronically tuned linear alternators for thermoacoustic engines," IET Renewable Power Generation, vol. 12, pp. 1256–1262, 2018. [CrossRef]
  27. A. Benamor, M. T. Benchouia, K. Srairi and M. E. H. Benbouzid, “A novel rooted tree optimization apply in the high order sliding mode control using super-twisting algorithm based on DTC scheme for DFIG," International Journal of Electrical Power & Energy Systems, vol. 108, pp. 293–302, 2019. [CrossRef]
  28. T. S. L. V. Ayyarao, “Modified vector controlled DFIG wind energy system based on barrier function adaptive sliding mode control,” Protection and Control of Modern Power Systems, vol. 4, 2019. [CrossRef]
  29. H. M. Jabr, D. Lu and N. C. Kar, “Design and implementation of neuro-fuzzy vector control for wind-driven doubly-fed induction generator,” IEEE Transactions on Sustainable Energy, vol. 2, pp. 404–413, 2011. [CrossRef]
  30. S. J. Cho and J. H. Kim, “ Linear electromagnetic electric generator for harvesting vibration energy at frequencies more than 50 Hz," Advances in Mechanical Engineering, vol. 9, 2017. [CrossRef]
  31. N. M. Kimoulakis, A. G. Kladas and J. A. Tegopoulos, “Cogging force minimization in a coupled permanent magnet linear generator for sea wave energy extraction applications,” IEEE Transactions on Magnetics, vol. 45, pp. 1246–1249, 2009. [CrossRef]
  32. Y. Wang, K. Zhang and M. Zhou, “Suppression of thrust fluctuation of doubly-fed linear motor,” Journal of Modern Transportation, vol. 20, pp. 103–107, 2012. [CrossRef]
Preprints 93057 g001
Figure 1. The assembled generator.
Figure 1. The assembled generator.
Preprints 93057 g001
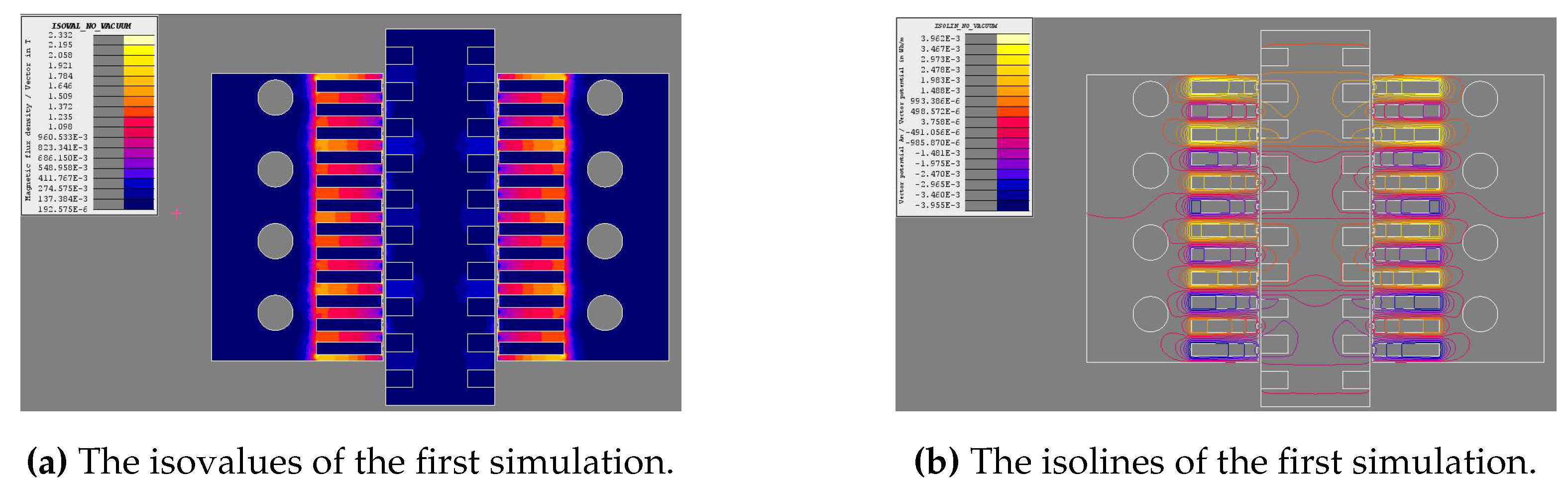
Preprints 93057 g002
Figure 2. Magnetic field during the first simulation.
Figure 2. Magnetic field during the first simulation.
Preprints 93057 g002
Preprints 93057 g003
Figure 3. Magnetic field during the second simulation.
Figure 3. Magnetic field during the second simulation.
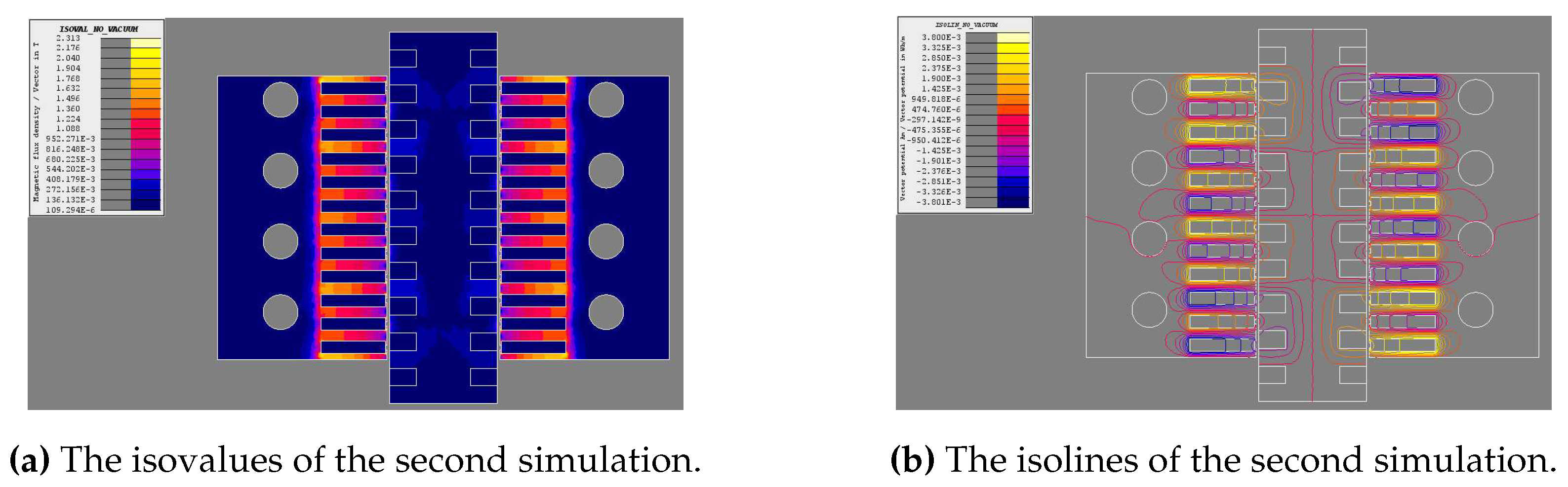
Preprints 93057 g003
Preprints 93057 g004
Figure 4. The flux arrows of the stator and mover cores.
Figure 4. The flux arrows of the stator and mover cores.
Preprints 93057 g004
Preprints 93057 g005
Figure 5. Magnetic flux with corrected excitation current.
Figure 5. Magnetic flux with corrected excitation current.
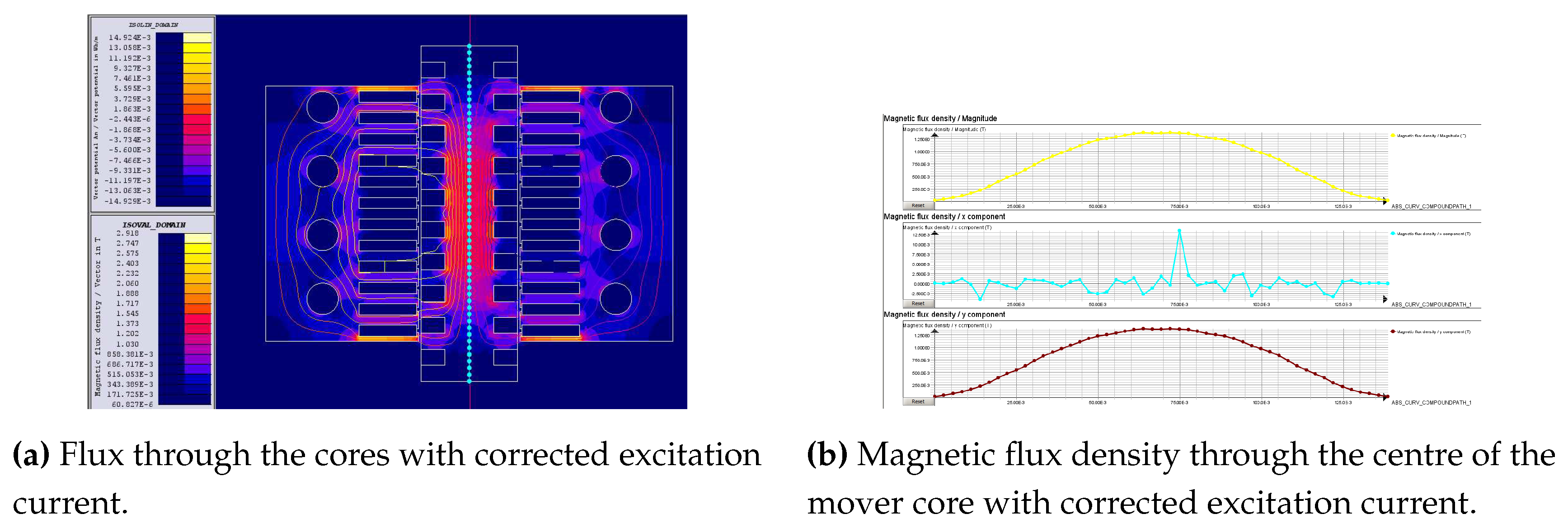
Preprints 93057 g005
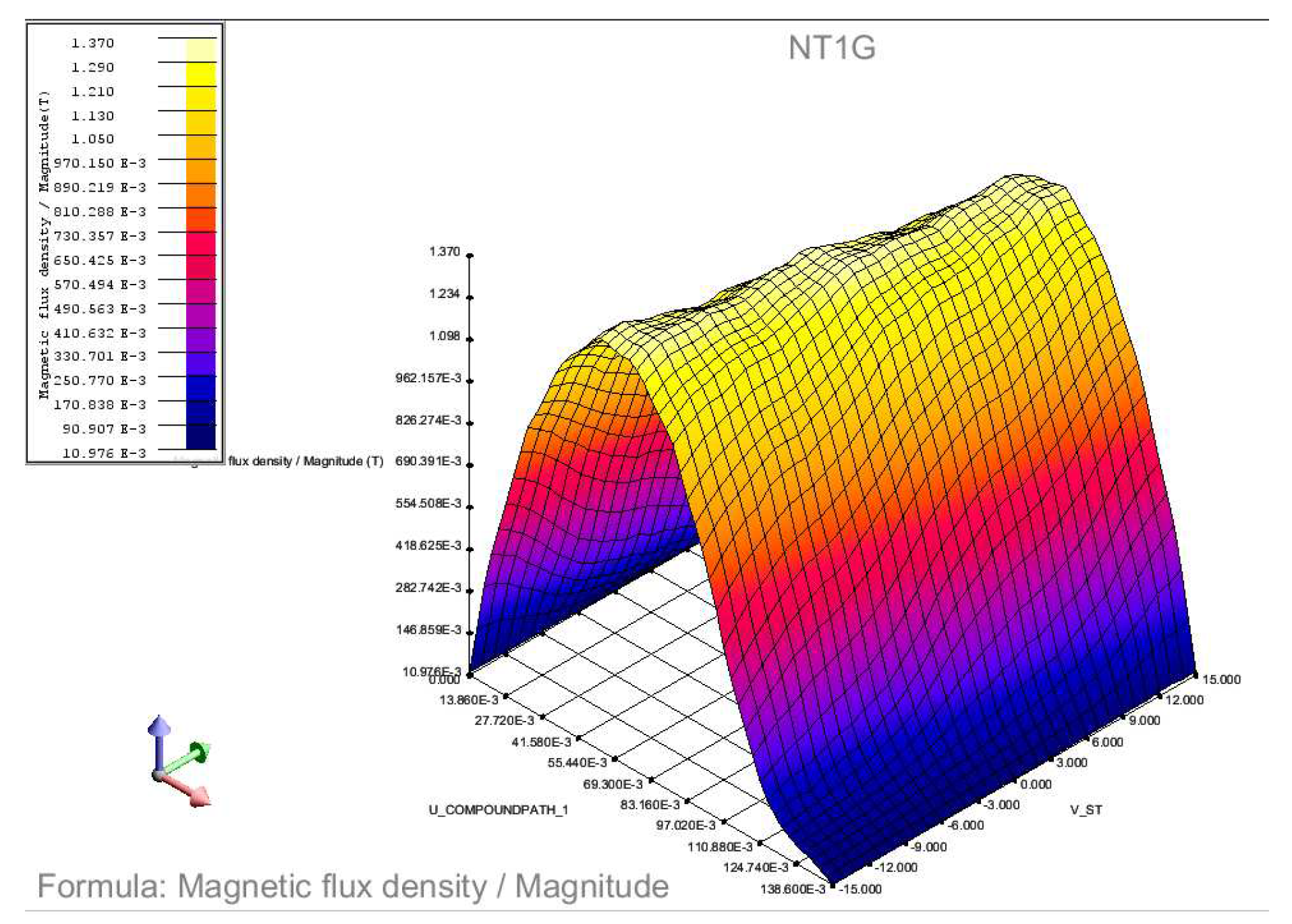
Preprints 93057 g006
Figure 6. Magnetic flux density through the mover core without mover excitation.
Figure 6. Magnetic flux density through the mover core without mover excitation.
Preprints 93057 g006
Preprints 93057 g007
Figure 7. Magnetic flux density resultd with DC mover excitation.
Figure 7. Magnetic flux density resultd with DC mover excitation.
Preprints 93057 g007
Preprints 93057 g008
Figure 8. Magnetic flux density results with AC mover excitation.
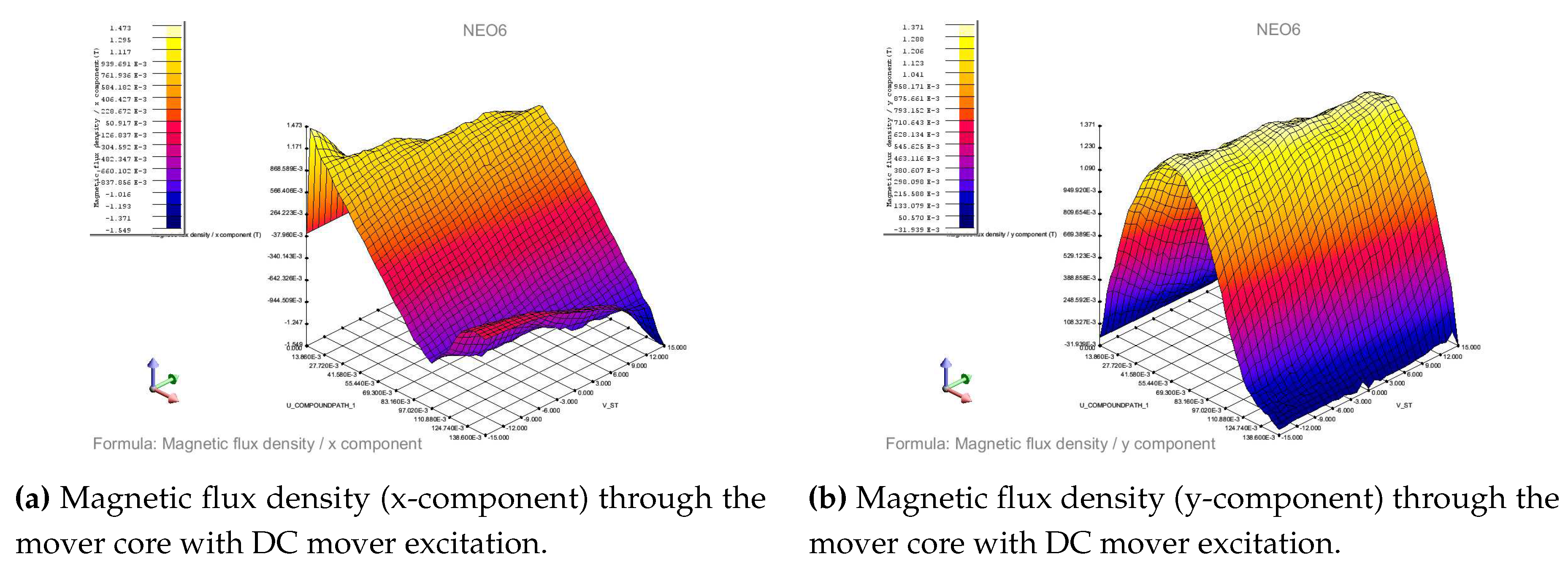
Figure 8. Magnetic flux density results with AC mover excitation.
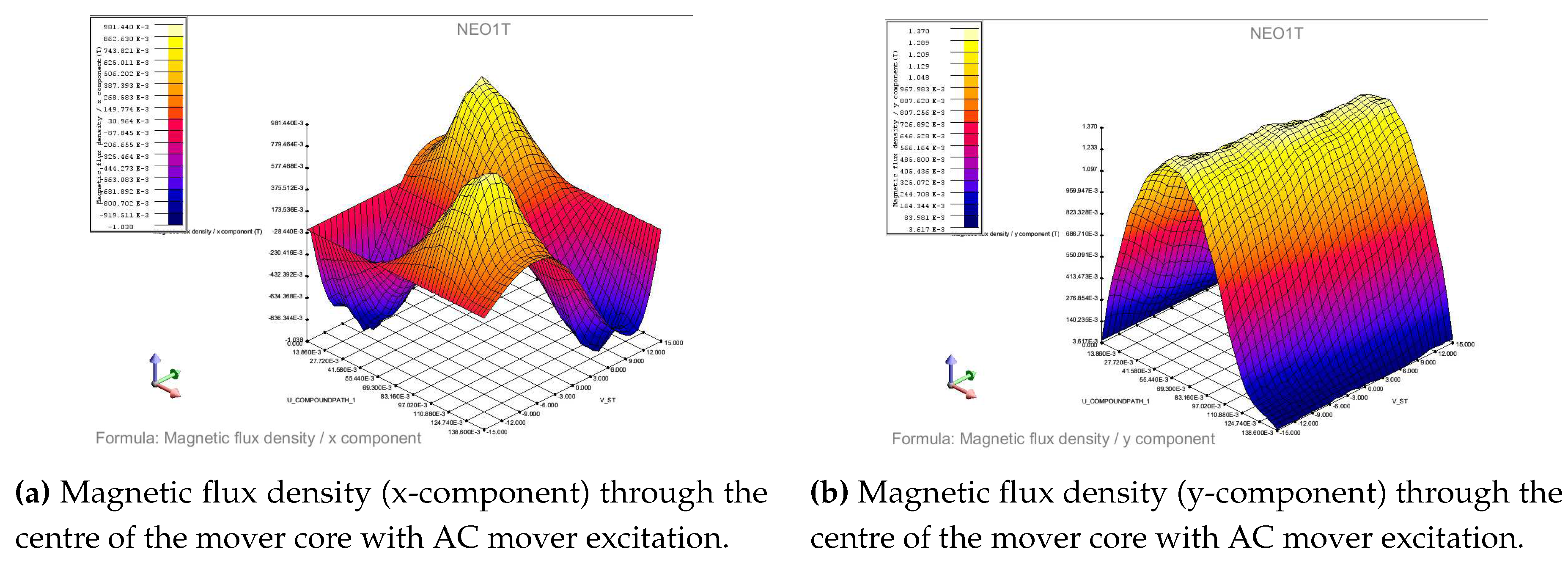
Preprints 93057 g008
Table 1. Core parameters
Table 1. Core parameters
Parameter Value Unit
Number of stator teeth 13
Number of stator slots 12
Stator pole pitch 8.8 mm
Depth of stator slot 24 mm
Number of mover teeth 11
Number of mover slots 10
Mover pole pitch 13.2 mm
Width of mover tooth 6.6 mm
Width of mover slot 6.6 mm
Depth of mover slot 10 mm
Mover length 138.6 mm
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated