Prerpints.org logo
Preprint
Review

Review of Generative Models in Generating Synthetic Attack Data for Cybersecurity

Altmetrics

Downloads

154

Views

53

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

11 December 2023

Posted:

12 December 2023

You are already at the latest version

Alerts
Abstract
The ability of deep learning to process vast data and uncover concealed malicious patterns has spurred the adoption of deep learning methods within the cybersecurity domain. Nonetheless, a notable hurdle confronting cybersecurity researchers today is the acquisition of a sufficiently large dataset to train deep learning models effectively. Privacy and security concerns associated with using real-world organization data have made cybersecurity researchers seek alternative strategies, notably focusing on generating synthetic data. Generative Adversarial Networks (GANs) have emerged as a prominent solution, lauded for their capacity to generate synthetic data spanning diverse domains. Despite their widespread use, the efficacy of GANs in generating realistic cyber attack data remains a subject requiring thorough investigation. Moreover, the proficiency of deep learning models trained on such synthetic data to accurately discern real-world attacks and anomalies poses an additional challenge that demands exploration. This paper delves into essential aspects of generative learning, scrutinizing their data generation capabilities, and conducts a comprehensive review to address the above questions. Through this exploration, we aim to shed light on the potential of synthetic data in fortifying deep learning models for robust cybersecurity applications.
Keywords: 
Subject: Computer Science and Mathematics  -   Security Systems

1. Introduction

The use of machine learning for cyber security has become increasingly prominent over recent years, as it offers a way to defend against constantly evolving cyber threats. However, one of the significant challenges of applying machine learning methods in anomaly or intrusion detection systems is the need for more realistic cyber attack datasets. Given privacy and security concerns, real-world organizations cannot share their data. Thus, most cybersecurity datasets are created using simulated attacks conducted by red-blue teams or hackathons. These simulations can provide some attack data, but the attack scenarios are often limited and specific to the simulation environment. The attack data must be more diverse and realistic to train models and estimate system security. To effectively defend against a constantly changing threat landscape, there is a need for automated methods of generating diverse and realistic attack data without impacting the regular operation of an organization’s production environment. One possible approach for automating the generation of diverse and realistic attack data is using generative models to generate synthetic data.
Generative Adversarial Networks (GAN) have been widely used to generate synthetic data, especially image generation and text manipulation. GANs can fool the defender into believing that the synthetic data is the actual data [1,2]. The success of adversarial networks in different domains [3] has intrigued the cybersecurity research community to use GANs in cybersecurity. GANs have been used in cybersecurity in different ways. The most common application is to improve the intrusion detection and security of the systems. There is also research to explore how adversarial systems can use GANs to spoof security systems like fingerprints, passwords, face detection, etc. [4,5]. GANs are also used to generate malware, and cyber attack data [6]. While the development of GAN-based privacy and security methods seems promising and has opened new research avenues [5], the quality of synthetic attack data generated by GANs needs to be determined. It is still unclear whether the artificial attack data is realistic as the actual cyber attack data and whether it contains the signature attack vector. Also, when the intrusion detection systems and deep learning models are trained on the synthetically generated attack data, there is a need to analyze further whether these models can detect new or unseen real-world attacks. In this paper, we did a survey and critical analysis on the application of GANs in generating cyber attack data while making the following contributions:
  • We explored the critical features of generative learning and the capabilities of generative models, highlighting their effectiveness in creating new data compared to discriminative models [7]. This comparison is further enriched by a detailed examination of how generative models operate.
  • We provide a concise overview of GANs, focusing on their data generation capabilities and architecture. It includes examining various models and techniques that generate diverse image and text data across domains using GANs.
  • Next, we comprehensively review various methods for generating synthetic cyber attack data using GANs.
  • Finally, we assess the value of synthetically generated attack data by conducting experiments with the NSL-KDD dataset. Specifically, we examine the characteristics of DoS attacks and gauge how well GAN-generated data can improve the training of intrusion detection systems for real-world cyber-attack mitigation.
The paper is organized as follows. The next section discusses the different modeling techniques and generative models.The GAN architecture is presented in Section 3. Section 4 overviews models and techniques for generating synthetic data in images and text. In Section 5, we present a detailed literature survey of methods to generate cyber attack data using GANs. Further, in Section 6, we present a critical analysis of GANs capability to generate realistic attack data and the usefulness of this synthetic attack data in training intrusion detection classifiers. Finally, we provide the discussion in Section 7 and conclude the paper in Section 8.

2. Modeling Techniques

In this section, we will discuss the various modeling techniques, with a specific focus on an in-depth examination of the crucial facets of generative learning [8]. We also analyze the mechanisms through which generative models adeptly generate data. The modeling techniques are of two types, generative and discriminative modeling [9]. The below subsections give a brief overview of each modeling type.

2.1. Generative models

Generative modeling is a type of modeling that has been widely used in statistics. When applied to machine learning it has been useful in various fields like natural language processing, visual recognition, speech recognition and data generation tasks [10]. Naive Bayes [11], Bayesian networks [12], Markov Random fields [13], Hidden Markov Models [14] and Linear Discriminant Analysis (LDA) [15] are some of those generative modeling techniques. The advent of Deep Learning [16] has sparked the development of the deep generative models like Boltzmann machines [17], Restricted Boltzmann Machines [18], Deep Belief Networks [19], Deep Boltzmann Machines [20] including graphical models like Sigmoid Belief Networks [21], Differentiable Generator Networks [22], Variational Autoencoders [23] etc. Generative Adversarial Network [1], popular as GAN, is a type of generative model that received massive attention in the past few years due to their remarkable success in generating synthetic data [24].

2.2. Discriminative models

Discriminative models, as their name indicates, are capable of understanding the boundaries amongst the given data points using probability estimates, and thus are widely used in classification approaches. The supervised learning [25] approaches such as Logistic regression [26], Support Vector Machine [27], Neural networks [28], Nearest Neighbor [29] are based on discriminative modeling. When provided with sufficient labeled data, these methods have succeeded in classification tasks [30]. They can learn to discriminate between different types of data and output the instance that belongs to a particular class.

2.3. Difference between Generative and Discriminative Models

The generative and discriminative modeling differs in their approach to solving the learning tasks [31]. The discriminator plays more of a classifier role by creating the decision boundary between the different classes. It does not attempt to learn the actual distribution of the data but tries to learn the mapping between the data vector and the label vector, given enough labeled mapping samples. The generative family handles it more challenging by modeling the data distribution and suggesting how likely an example belongs to a distribution. Since the model knows the data and its distribution, it is generative and can produce new examples. It is also possible for them to model a distribution by producing convincingly “fake" data that looks like been drawn from that distribution.
Mathematically, any classifier must estimate the function f : x → y , or p ( y | x ) for a given dataset x with corresponding labels y. The discriminative models [32] use the conditional probability and model the posterior p ( y | x ) directly or learn a direct mapping from input, x to the class labels, y. Whereas, the generative models [33] learn the distribution of the input x and the label y, or just p ( x ) , if there are no labels, from the joint probability p ( x , y ) . They estimate the parameters of p ( x | y ) and p ( y ) directly from the training data and make the predictions by using Bayes’ rules to calculate p ( y | x ) and pick the most likely label y.

2.4. Why Generative models?

Generative models have a significant role to play. When it comes to tasks like generating new data examples, determining how likely it is for any event to occur, or handling missing values by making use of available unlabeled data, or the ability to infer information from related activities, the discriminative models or the supervised learning algorithms requires a considerable amount of labeled data to perform such tasks with reasonable accuracy. It is usually tough and expensive to label the data; in fields like cyber security [34], where the data is limited, it is even harder to train the model. The most likely approaches used in such situations are the unsupervised [35] and semi-supervised [36] learning. However, only some have achieved the level of accuracy as the supervised algorithms. The unsupervised algorithms have to deal with the high dimensionality of random variables. It enforces both the statistical and computational challenges to generalize the number of configurations and solve a problem in a tractable way as the number of dimensions grows exponentially. One of the ways to deal with the high dimensionality of intractable computations is to approximate them or design them in a way that does not require such computations. Generative modeling techniques have proved promising [37] in providing the latter design approach.

2.5. How Generative Models work?

Given the training data and the set of parameters, θ , a model can be built to estimate probability distribution. The likelihood is the probability that a model assigns to the training data for a dataset containing m samples of x ( i ) ,
∏ i = 1 m p m o d e l ( x ( i ) ; θ )
The maximum likelihood provides a way to compute the parameters, θ , that can maximize the likelihood of the training data. To simplify θ , log is taken in Equation (1) to express the probabilities as a sum rather than the product,
θ * = a r g max θ ∑ i = 1 m l o g p m o d e l ( x ( i ) ; θ )
If p d a t a lies within the family of distributions of p m o d e l ( x ; θ ) , the model can precisely find the p d a t a . In the real world, there is no access to p d a t a , and only the training data is available for modeling. The models must define their density function and find the p m o d e l ( x ; θ ) that maximizes the likelihood. The generative models which can explicitly represent the probability distribution of the data are called explicit density models [38]. The Fully Visible Belief Networks (FVBNs) [39] and nonlinear independent component analysis [40] are a few such explicit density models which can successfully optimize directly on the log-likelihood of the training dataset. However, their use is limited to solving simple problems and imposing design restrictions. As the data gets complex and the dimensionality of the data grows, it gets computationally intractable to find the maximum likelihood. Then approximations are made on the maximum likelihood, either by using deterministic approximations, as in variational methods like Variational AutoEncoder (VAE) [23], or by using stochastic approximations such as Monte Carlo methods [41] The variational autoencoder is one of the popular semi-supervised generative modeling technique, but it suffers from low-quality samples.
Another family of deep generative nets, called implicit density models [42], do not explicitly represent the probability distribution over the space where data lies but provide some indirect way to interact with the probability distribution p m o d e l . In indirect ways, they can draw samples from the distribution. One of the methods used by implicit density models is Markov Chain [43] to stochastically draw samples from p m o d e l distribution and transform an existing sample to obtain another sample from the same distribution. Another strategy is to generate the samples in a single step directly from the distribution represented by the model. The generative model in GANs is based on implicit density models and uses the latter strategy to generate the samples directly from the distribution represented by the model.

2.6. How Generative Models generate data?

Any information can be processed if it is represented well. In the case of machine learning tasks, it is critical to represent the information so that the model can perform subsequent learning tasks efficiently [44]. The choice of representation varies as per the learning strategy of the model. For instance, a feedforward network trained using supervised learning criteria learns specific properties at every hidden layer. The network’s last layer is usually a softmax layer, which is a linear classifier. The features in the input may not represent linearly separable classes, but they may eventually become separable until the last hidden layer. Also, the choice of the classifier in the output layer impacts the properties learned by the last hidden layer. The supervised learning methods do not explicitly pose any condition on the intermediate features that the network should learn. Whereas, in cases where the model wants to estimate density, the representation should be designed to make density estimation easier. In such a case, it may be appropriate to consider the distributed representations, which are independent and can be easily separated from each other. Representation learning [45] plays an integral role in the unsupervised and semi-supervised models, which try to learn from unlabeled data by capturing the shape of the input distribution. A good representation would be one that can help the learning algorithm identify the different underlying factors causing variations in data and help them separate these factors from each other. It would result in the different features or directions in the feature space corresponding to different causes disentangled by the representation. In the classic case of supervised learning, the label y presented with each observation x is at least one of the essential factors directly providing variation. In the case of unlabeled data, as in unsupervised and semi-supervised [46], the representation needs to use other indirect hints about these factors. The learning algorithm can be designed to represent these hints in the form of implicit prior beliefs to guide the learner. For a given distribution p ( x ) , let h represent many of the underlying causes of the observed x and let the output y be one of the most silent causes of x. The p ( x ) and p ( y | x ) should be firmly tied, and a good representation would allow us to compute p ( y | x ) . Once it is possible to obtain the underlying explanations, i.e., h for the observed x, it is easy to separate the features or directions in feature space corresponding to the different causes and consequently easier to predict y from h.
The true generative process would be,
p ( h , x ) = p ( x | h ) p ( h )
and, the marginal probability for data, x, can be computed from the expectation of h, as:
p ( x ) = E h p ( x | h )
If the representation is made in such a way that it is possible to recover h, then it is easy to predict y from such representation and by using Bayes’ rule, it is possible to find p ( y | x ) ,
p ( y | x ) = p ( x | y ) p ( y ) p ( x )
The marginal probability, p ( x ) , is tied to conditional probability, p ( y | x ) , and the knowledge of the structure of p ( x ) would help us learn p ( y | x ) . Here, latent factors are the underlying causes h of the observed x. The latent factors or variables are the variables that are not directly observed but rather inferred from other variables that are directly measured. The latent variables are meaningful but not observable. The latent variables can capture the dependencies between different observed variables, x. They help reduce the dimensionality of data and provide different ways of representing the data. So they can give a better understanding of the data.
Many probabilistic models, like linear factor models, use latent variables and compute the marginal probability of data, p ( x ) , as described in Equation (4). A linear factor model can be defined as a stochastic linear decoder function that can generate x by adding noise to a linear transformation of h. It is possible to find some explanatory independent factors h, which have a similar joint distribution and are sampled from the given distribution like h p ( h ) , where p ( h ) is a factorial distribution, with
p ( h ) = ∏ i p ( h i )
Then the real-valued observable variables can be sampled as,
x = W h + b + noise
where, W is the weight matrix and noise is Gaussian and diagonal, which means it is independent of dimensions.
The unsupervised learning algorithm would try to learn a representation that captures all the underlying factors of variation and then try to disentangle them from each other. A brute force solution may not be feasible to find all or most of such factors, so a semi-supervised approach can be used to determine the most relevant factors of variation and encode only those salient factors. The autoencoder and generative models can be trained to optimize fixed criteria like the mean square error to determine which ’causes’ or factors should be considered salient. For instance, if a group of pixels follows a highly recognizable or distinct pattern, that pattern could be considered extremely salient. However, the models trained on mean square error have limited performance and failed to reconstruct the images completely [47].
Another method to identify features’ salience is using GANs [48]. In this approach, a generative model is trained to fool a classifier which is a discriminative model. The classifier should recognize all the samples from training data as accurate and the samples from the generative model as fake. Any structured pattern recognized by the discriminator can be considered salient, which makes the generative adversarial networks better at finding which factors should be represented.
Thus, summarizing the above discussion, there are two essential aspects that make the generative way of learning powerful. First, they try to learn the underlying causal factors from cause-effect relationships via the hidden factors that can explain the data. Secondly, they use the distributed representations to identify these factors, which are independent and can be set separately from each other. Each direction in the distributed representation space can correspond to a different underlying causal factor, helping the system identify the salient features.
The advantage of learning the underlying causal factors [49] is that if the exact generative process learns to model from x being the effect and y as the cause, then p ( x | y ) is adaptive to change in p ( y ) . Also, the causal relationships are invariant to any change in the problem domain, type of tasks, or any non-stationary temporal variations in the dataset. The learning strategy of generative models attempting to recover the causal factors, h and p ( x | h ) , is robust and generalizes to any feature changes. Various regularization strategies have been suggested in the literature to find the underlying factors of variations [50]. Some of the popular strategies used by different learning algorithms are smoothness, linearity, multiple explanatory factors, depth or hierarchical organization of explanatory factors, shared factors across tasks, manifolds, natural clustering, sparsity, simplicity of factor dependencies, temporal and spatial coherence, etc. but causal factors [51] is most advantageous for the semi-supervised learning and makes the model more robust to any change in the distribution of underlying causes or while using the model for a new task [52].
The second advantage of the underlying causal factors is that the distributed representations are more potent in representing the underlying causal factors than the symbolic factors. The symbolic or one-hot representations are non-distributed, representing only n mutually exclusive regions, whereas distributed representations can represent 2 n configurations for a vector of n binary features. Each direction in the representation space can correspond to the value of a different underlying configuration variable.
Different learning algorithms like k-means clustering [53], k-nearest neighbors [54], decision trees [55], gaussian mixtures, kernel machine with the gaussian kernel [56], and language or translation models based on n-grams [57] are based on non-distributed representations. These algorithms break the input space into different regions with a separate set of parameters for each region. Suppose there are enough examples in the dataset that represents each different region. In that case, the learning algorithm can fit the training data set well without solving any complicated optimization problem. However, these models suffer as the number of dimensions grows and if there are insufficient examples in the dataset to represent each dimension. They fail miserably if the number of parameters exceeds the number of examples that explain each region. Also, the non-distributed representation needs a different degree for each region that does not allow them to generalize to new regions when target functions are not smooth and may increase or decrease several times in many different regions.
On the other hand, the distributed representations [58] use the shared attributes and introduce the concept of similarity space by representing the inputs as semantically close if they are close in the distance. They can compactly represent complicated structures using a small number of parameters and generalize better over shared attributes. For example, a ’truck’ and ’car’ both have common attributes like " n u m b e r _ o f _ t y r e s " and " h a s _ s t e e r i n g " and many other things that are valid for cars and generalizations to trucks, as well.
The distributed representation uses separate directions in the representation space to capture the variations between different underlying factors [59]. These features are discovered automatically by the network and are not required to be fixed beforehand or labeled. The generative models learn from the distributed representation to disentangle the various features, even when the model has never seen the feature before. Each direction or vector represents a new feature. Adding or subtracting these representation vectors is possible to generate new features. For instance, in the famous example of generating new images using GAN [60], the distributed representation disentangles the concept of gender from the concept of wearing glasses. Given the image of a man with glasses, if the representation vector of the man is subtracted and the representation of a woman without glasses is added, it would give the vector representation of the woman with glasses, and a generative model can correctly generate the image corresponding to the resulting representation vector. Therefore, it is successfully able to generate new unseen synthetic data.
Table 1. Comparison between Generative and Discriminative modeling techniques.
Table 1. Comparison between Generative and Discriminative modeling techniques.
Generative Models Discriminative Models
Learn the underlying data distribution Learn the decision boundary between different classes of the data
Model the joint probability distribution between the input and output data Model the conditional probability distribution of the output given the input
Can generate new data from the learned distribution Cannot generate new data from the learned decision boundary
Used for tasks such as image and audio synthesis, text generation, and anomaly detection Used for tasks such as classification, regression, and object recognition
Make no assumptions about the data Use prior assumptions about the data
Examples include VAE, GAN, and RBM Examples include Logistic Regression, SVM, and Neural Networks

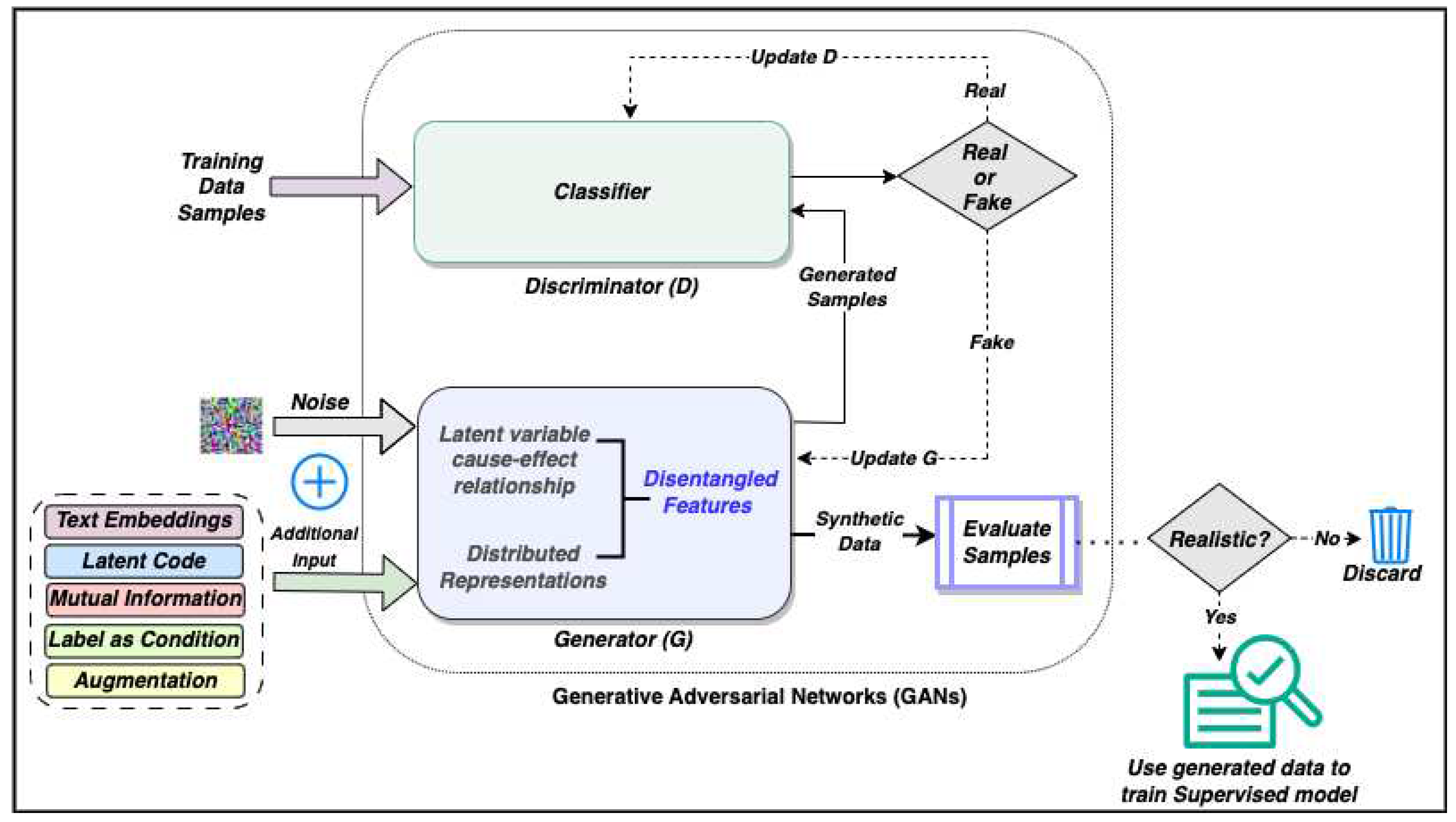
3. Generative Adversarial Networks (GANs)

In this section we give a detailed description of GANs and their training process. The Generative Adversarial Networks or GANs [1] are the type of generative models based on differentiable generator networks [61]. The differentiable generator networks are the class of networks that either trains only a generator network or pair a generator network with any other network. For example, variational autoencoders can have a pair of generators with an inference network. Similarly, in GANs, there is a pair of a generator network with a discriminator network, which is a discriminative model.
The two networks in GAN compete like adversaries in a two-player game. The generator network produces samples that intend to come from the training data distribution. The discriminator tries to correctly classify if the sample is drawn from the training data or the generator. The generator can win the game only when it has learned to create samples as if they were drawn from the same distribution as training data, whereas the discriminator should learn to distinguish if the sample is real or fake.

3.1. Construction of Networks

The generator network is the parameterized generative model designed to generate samples. The model can be a simple neural network that transforms the sample of latent variables z to training sample x or to a distribution of training samples over x, using a differentiable function. The network architecture provides the choice of possible distributions from which samples can be drawn, and the parameters select the desired distribution from within that family. The network can be represented by a function, G, which is differentiable for its input z and has parameters θ ( G ) . When z is sampled from some prior distribution, G ( z ) yields a sample of x drawn from p m o d e l . The generator network thus produces the samples, x = G ( z ; θ ( G ) ) where the dimensions of z are at least as large as the dimensions of x.
The discriminator network is the traditional supervised classifier, and it can be represented by a function D that takes input x, parameterized by θ ( D ) . The discriminator outputs a probability D ( x ; θ ( D ) ) , which is the probability that x is a real training example rather than a fake sample drawn from the generator model.

3.2. Cost Function

The cost function, J for both networks can be defined in terms of the parameters of each. The discriminator tries to minimize J ( D ) ( θ ( D ) , θ ( G ) ) while it can control only its own parameters θ ( D ) . At the same time, generator tries to minimize J ( G ) ( θ ( D ) , θ ( G ) ) but has control only over θ ( G ) .
This framework is designed like a zero-sum game where minimax technique is applied, and both players compete for a fixed and limited pool of total resources. These resources can be denoted by a value function, V ( G , D ) . Each makes a move such that the player’s best move is disadvantageous for the opponent. Both the generator and discriminator try to minimize their cost, which depends on the other’s parameters, while they have no control over it. Both try to improve and make the best move to win such that at least all the neighboring costs are greater or equal to their cost. One is trying to minimize the value function, and the other is trying to maximize it. The goal is to make both of them as good as possible so that both reach their peak ability and there is no winner. This state is called Nash Equilibrium [62], where each network is at its best for the other. So the Nash equilibrium will be the tuple ( θ ( D ) , θ ( G ) ) for a local minimum of J ( D ) with respect to θ ( D ) and a local minimum of J ( G ) with respect to θ ( G ) . After certain epochs, both distributions should gradually converge.
The cost of the discriminator, J ( D ) , here can be computed as the standard cross-entropy cost minimized for a standard binary classifier with a sigmoid output
J ( D ) ( θ ( D ) , θ ( G ) ) = − 1 2 E x ∼ p d a t a [ log ( D ( x ) ) ]                                       − 1 2 E z ∼ p m o d e l [ log ( 1 − D ( G ( z ) ) ) ]
To formulate the zero-sum game for these two players, the generator and discriminator, the sum of the total cost should be set to zero.
J ( G ) + J ( D ) = 0
J ( G ) = − J ( D )
Now, for discriminator, the reward or the pay-off is given by, V ( θ ( D ) , θ ( G ) ) ,
V ( θ ( D ) , θ ( G ) ) = J ( D ) ( θ ( D ) , θ ( G ) )
whereas, the generator receives − V ( θ ( D ) , θ ( G ) ) as its pay-off
V ( θ ( D ) , θ ( G ) ) = − J ( D ) ( θ ( D ) , θ ( G ) )
Each player tries to maximize its pay-off, so using the minimax technique, the solution can be given by minimizing the generator and maximizing the discriminator value,
θ ( G ) * = a r g min θ ( G ) max θ ( D ) V ( θ ( D ) , θ ( G ) )

3.3. Training of Networks

Both the generator and discriminator networks can be defined by multi-layer perception neural networks and trained using backpropagation. There is no constraint on the form that any of the two networks should take; they do not need to be of the same form. A support vector machine ( S V M ) [63] can be used for both the generator and discriminator or S V M for the generator and a neural network for the discriminator. However, using anything other than neural networks may increase the bias of the model [64].
Say, if stochastic gradient descent (SGD) is performed on mini-batch of m samples of data from distribution p d a t a ( x ) and m samples of noise from distribution p m o d e l ( z ) then for every iteration, the loss functions of generator and discriminator can be defined as below:
The generator is updated by decreasing its gradient,
L o s s g = Δ θ g 1 m ∑ log ( 1 − D ( G ( z ) ) )
The discriminator is updated by increasing its gradient,
L o s s d = Δ θ d 1 m ∑ [ log D ( x ) + log ( 1 − D ( G ( z ) ) ) ]
Here, the log is again taken as it is numerically more stable and it simplifies the computation.
During training, there can be following scenarios:
  • False Negative - The input is real but the discriminator gives the output as fake: The real data is given to the discriminator. The generator is not involved in this step. The discriminator makes a mistake and classifies the input as fake. This is a training error and the weights of the discriminator are updated using backpropagation.
  • True Negative - The input is fake and the discriminator gives the output as fake: The generator generates some fake data from random noise in latent space. If the discriminator recognizes this as fake, there is no need to update the discriminator. The weights of the generator should be updated using backpropagation using the loss function value.
  • False Positive - The input is fake but the discriminator gives the output as real. The discriminator should be updated. The loss function is used to update the weights of discriminator.
The generator produces the fake distribution p m o d e l ( x ) , and the actual distribution from the sample data p d a t a ( x ) is known. There is an associated divergence between the two because they are not identical distributions, so our loss function is non-zero. This divergence can be computed by minimizing either the Jensen-Shannon [65] or KL (Kullback-Leibler)-divergence) [66], between the data and the model distribution, and updating the policy of both the players till they reach convergence.
The discriminator training aims to estimate the ratio of densities at every point x. When the discriminator gets the input from the generated and the true distribution, if it can classify correctly, the loss function value is propagated to the generator, and the generator weights are updated. However, if the discriminator cannot correctly distinguish between the two distributions, then the discriminator weights are updated.
p d a t a ( x ) p m o d e l ( x )
At a time, only one of the networks is trained. Although the two compete as adversaries, they can also be seen as cooperative since the discriminator shares the estimated ratio with the generator, allowing it to improve. Both the networks continue till the generated distribution gets close to the true distribution, and the networks reach the NASH equilibrium.

4. Generating Data using GANs

The goal of unsupervised learning is not to provide a mapping between the inputs and targeted output but rather to learn the structure of the input data. Most of the unsupervised methods do that to make use of the unlabeled data to improve the accuracy of supervised learning methods.
GANs are one such generative networks that can discover the structure of the data and generate realistic samples. As discussed in Section 2, the generative models use cause-effect relationships via the latent factors and distributed representations to disentangle the independent features to discover the data structure. GANs can exploit these properties of generative models to identify the salient features and learn the representations. They can represent the learned features as vectors which can be manipulated using vector arithmetic to generate new data samples with different semantics.

4.1. Different techniques in GAN for generating data

GANs have made a significant impact in generating synthetic data, especially in the field of computer vision. They have also been successful in generating tabular and structured data. This section discusses the various techniques and frameworks used to generate different data types. The process of generating synthetic data in GAN models is illustrated in Figure 1.

4.2. Generating images

GANs were able to produce realistic images [1,67]. The framework, Deep Convolution generative adversarial networks (DCGAN) [60] demonstrated the capability of GANs to learn reusable feature representations of an image. In DCGAN, both the generator and discriminator were able to learn the hierarchy of feature representations. GAN can be first used to build any image representation, while the discriminator does the classification task, parts of generator and discriminator can act as feature extractors. The convolution GANs were trained to build a good image representation for unlabeled data. It used salient features or filters learnt by the generator to draw specific objects. In DCGAN, vector arithmetic manipulation was applied to the latent space results to generate new images and to transfer styles between images by adding or removing new objects.
While GANs could generate synthetic images, the images’ quality may sometimes be low. It may take a long time to map the complex relationship between the latent space and generated images, often resulting in low-quality images. As the generator begins from random noise, it may start generating a random image from a domain. Sometimes, the generator needs help exploring the possible solution space to find the real solution. It is one of the limitations of basic GANs, called mode collapse [1]. To improve the training stability of GANs, conditional generative adversarial networks (CGANs) [68] were introduced as an extension of GANs. They suggested that instead of randomly generating samples from noise with no control over the data mode, applying a condition on the generator and discriminator by feeding some additional information, y, to the network is possible. This conditioning could be based on any auxiliary information, such as class labels or data from other modalities. In the generator, the prior input noise p z ( z ) and y are combined in joint hidden representation as l o g ( 1 − D ( G ( z | y ) ) ) , whereas, in the discriminator, the x and y are given as inputs to the discriminative function, l o g ( D ( x | y ) ) . CGANs have been widely used in improving the quality of new examples, but they could be used only for labeled datasets.
Different variants of GANs have been proposed lately, especially in computer vision, to improve image quality. LAPGAN [69] was a kind of conditional GAN which used the laplacian pyramid framework to produce high-resolution image samples. The laplacian pyramid [70] is a technique for image encoding equivalent to sampling the image with laplacian operators of many scales. In LAPGAN, a series of generative convolution network models were used. At each level of the Laplacian pyramid, a separate generative convnet was trained using conditional GAN. Each level would capture the image structure at a particular scale of the laplacian pyramid, generating samples coarse-to-fine, commencing on a low-frequency residual image. LAPGAN breaks the original problem into a sequence of more manageable stages, each subsequent stage conditioning the output from the previous scale on the sampled residual until the final level is reached. They successfully generated high-resolution, realistic images of CIFAR10 [71] and Large-scale Scene Understanding (LSUN) [72] datasets. The generated images were evaluated by estimating log-likelihoods which were high on both datasets. Also, sample images were drawn from the model, and they were found to be slightly sharper than the original images. The human-user study did a quantitative measure of the quality of samples to see if participants could distinguish the samples from real images and were also compared against the images generated by the standard GANs [1]. The results from the study showed that the LAPGAN models produced images far more realistic than the standard GANs.
Similarly, the Progressive Growing of GANs (PGGAN) [67] was suggested to produce high-quality synthetic images. The PGGAN starts with low-resolution images and adds new layers to the generator and the discriminator as training progresses. The resolution increases as the growing network models the fine details. This kind of architecture allows the network to learn the large-scale structure of the image distribution and then gradually focus on finer-scale details instead of learning all the scales at once. PGGAN proved to be a more stable and balanced network regarding training speed and output concerning quality and variations in generated images. The experiments were conducted on CIFAR10 and CelebA [73] datasets, and the quality of images generated was evaluated using multi-scale statistical similarity [74] to see if the local image structure of the generated image is similar to the training set over all scales. PGGANs were also used in augmenting training data to derive synthetic images similar to actual images in the field of medical imaging [75].
RenderGAN [76] was proposed to generate realistic labeled data to eliminate the need for cost and time extensive manual labeling. The framework was used in the BeesBook project [77] to analyze the social behavior of honeybees. A barcode-like marker is used to identify honeybees with limited labeled data, and it is hard to annotate the new barcode markers. The labeled data generated from RenderGAN was of high quality. It was used to train a supervised deep convolution neural network (DCNN) to predict the labels from input data. A 3D model which can generate a simple image of the tag based on position, orientation, configuration, etc., was embedded into the generator network of RenderGAN to produce samples from corresponding input labels. Now, the generated samples may lack many factors of the actual data, such as blurring, lighting, background, etc., so a series of augmentation functions were introduced for the generator to adapt and learn the image characteristics from unlabeled data. Five million tags were generated using the RenderGAN framework, which was indistinguishable from actual data for a human observer.
StackGANs [78] was another type of GANs proposed to generate images from a text description. The StackGAN synthesized high-quality photo-realistic images conditioned on a text description. They used two stages. The first stage sketches the primary object’s shape and colors based on the text description and produces low-resolution images. The second stage takes the results of the first stage and the given text description as input and generates high-resolution images with realistic photo details. The text description is first encoded by an encoder, giving a text embedding [79]. The text embedding needs to be transformed to generate latent conditioning variables as input of the generator. The latent space for text embedding may grow into a high dimensional space, so conditional augmentation was used to produce an additional conditioning variable, c ^ , which supports a smooth latent data manifold by using a small number of image-text pairs and generates images from a linearly interpolated sentence embedding. The noise vector, z, is fixed, so the generated image is only inferred from the given text description. The StackGAN framework was used to generate images for CUB [80], COCO [81], and Oxford-102 [82] datasets to generate the images of birds species using the five to ten text descriptions given for each. The generated images were evaluated using inception score (IS) [83], a metric commonly used to assess the quality of images produced by GANs. The IS measures the diversity and quality of generated images by comparing their predicted class probabilities to those of real images using a pre-trained image classifier, such as Inception-v3 [84]. The IS is obtained by calculating the KL divergence between the two distributions and then exponentiating the result. Human evaluation was also conducted, and their observations correlated with the IS.
Another exciting variant, InfoGAN [85], was suggested to improve the interpretation and representations learned by a regular GAN. InfoGAN used the mutual information between a small subset of latent variables and the observations to disentangle the feature representations in an unsupervised manner. The latent information or latent code, c, was provided to the network to give some semantically meaningful information about the factors of variation. For example, when generating images from MNIST digits (0-9) dataset [86], two continuous variables that represent the digit’s angle and thickness of the digit’s stroke were used; pose information for CelebA; and background digits for housing number images, Street View House Number(SVHN) dataset [87], were used as a latent code. The mutual information, I, between the noise, z, and the latent code, c, was maximized; the generator becomes a function of G ( z , c ) , and the mutual information, I ( c ; G ( z , c ) ) should be high. The images generated by InfoGAN showed that this modification in the architecture helped the generator to disentangle variations like the presence or absence of glasses, hairstyles, and emotions, demonstrating that the model acquired a certain level of visual understanding without any supervision.

4.3. Generating tabular synthetic data

The above discussion shows that various frameworks of GANs, with or without some modifications, could successfully generate realistic image data. Though in many real-world business applications, the data combine categorical and numerical features with missing or unknown values, making it more challenging to use GANs. Different approaches were proposed to adapt to such data types and generate realistic synthetic data, which can be used to train a supervised classifier. Two of the popular approaches are discussed below:

4.3.1. Airline Passenger Name Record (PNR) generation

The passenger name records (PNR) airlines store traveler information. They can be a good data source for building commercial business applications such as client segmentation and adaptive product pricing [88]. The paper on airlines PNR generation [89] showed that the passenger record data could be synthetically generated using GANs and used this data to predict clients and nationality. Access to PNR data is limited, as it contains personally identifiable information (PII), and it falls under EU General Data Protection Regulation (GDPR) [90] strict data privacy regulations. In this situation, synthetic data, which has the original data structure and follows the same distribution, should be sufficient to train the supervised classifier.
A variant of GANs, called Cramer GANs [91] with a generator/critic architecture that combines feedforward layers with the Cross-Net architecture [92] was used. Cramer GANs were suggested as an improvement over original GANs [1] and Wasserstein GANs (WGANs) [93]. The original GAN model used Jensen-Shannon divergence (JSD) or KL-divergence, which finds the similarity between the probability distributions of data and the model. It keeps updating the generator and discriminator till they converge. The Wasserstein GANs (WGANs) use the Wasserstein distance, which is the Earth Mover (EM) distance, and it computes the distance between two probability distributions. It produces better sample quality than the original GANs. When batch training uses stochastic gradient descent (SGD) based methods, WGANs suffer from biased gradients [94]. They may converge to the wrong minimum while estimating Wasserstein distance from batch samples. To overcome this problem and provide unbiased sample gradients, the Cramer Distance [95], which measures the energy distance between the two distributions, is used to build the GAN networks. In the Cramer GANs [91], the discriminator, also called critic, has a trainable loss function, which combines the energy distance with the transformation function to map the input space to the hyper-parameter space. The critic or discriminator seeks to maximize the energy. In contrast, the generator tries to minimize the energy of the transformed variables and is designed to penalize the functions with a high gradient.
The PNR data contains numerical, categorical, and date data. It has missing or NaN values. The input embedding layer was used to process the categorical features in PNR data. In GANs, the generator is differentiable, so it cannot generate discrete data such as one-hot encoded values or character representations [1]. Either the discrete or categorical columns need to be encoded into numerical columns [1] or represented as continuous vectors [96]. The latter method is called embedding. It reduces the dimensionality of categorical variables and meaningfully represents the categories in the transformed space. The weighted average of the embedded representation was used, and the embedding layer was shared between the generator and the discriminator, ensuring a fully-differentiable process. The embedding layers increase the representational power, so different layers were used per each categorical feature.
All the missing values in numerical features were filled by some random value taken from the same column. For all the categorical features, the missing values were replaced with a dummy new level, ’UNK.’ Then, a new binary column was added, whose values are 1 for all the filled-in rows and 0 otherwise. One such column was added per numerical column with missing values. These auxiliary binary columns were treated as categorical columns and encoded using the embedding process. Multiple feed-forward neural networks were used to learn the complex feature interactions. Both the generator and discriminator were composed of fully connected layers, and N cross-layers were stacked [92] to automatically compute up to N-degree cross-feature interactions.
The quality of synthetic data generated was evaluated by computing the multivariate measure using Jensen-Shannon divergence (JSD) to see how the two empirical distributions of actual and synthetic data differ. Then a classifier was trained to discriminate the difference between the real and the generated samples, labeling the actual samples 0 and the synthetic ones 1. Also, the Euclidean distance between each generated point and its nearest neighbor in the training and test data was calculated to determine if the generative model is learning the original distribution and not simply memorizing and reproducing the training data. The distribution of distances was compared using the Kolmogorov-Smirnov (KS) [97] two-sample test to determine if they differ. The results [89] showed that the models trained on synthetic data could successfully classify for both the business cases, client segmentation, and product pricing.

4.3.2. Synthesizing fake tables

Tabular data is the most common structured data type, which can be clearly defined using rows and columns and conforms to the data for models. Some of the tabular data sets like employee, hospital, or travel datasets contain private information, like social security numbers (SSN), salary, health conditions, or other personally identifiable information (PII), which may raise a security concern, if data is shared with partners or made publicly available to train the models. Anonymization techniques can be used to remove sensitive information. However, they are prone to attacks and can be recovered by adversaries if they possess other users’ background information. Secondly, these modifications negatively impact the usability of data.
To overcome these challenges, table-GANs [98] were proposed to synthetically generate fake tables statistically similar to the original table structure. Four types of datasets from different domains, LACity dataset [99] containing records of Los Angeles government employees (salary, departments, etc.), Adult dataset [100] with personal records (nationality, education level, occupation, etc.), Health dataset [101] with information such as blood test results, diabetes, etc., and Airline dataset [102] with passenger travel information, were considered. All these datasets contain categorical, discrete, and continuous values.
The table-GANs were designed to have three convolutional neural networks (CNN), compared to two networks in original GANs, a discriminator to distinguish between the actual and synthetic records, a generator to generate realistic records, and a classifier to increase the semantic integrity of synthetic records. The classifier was added to determine if the synthetic records were correct and close to the real-world scenario. For example, a person with a low cholesterol level may not be diagnosed with diabetes, and there will be no such record in the original table. The classifier discards all such records generated by the generator.
In addition to the original GAN objective loss function, two other additional loss functions, information loss and classification loss, were computed. The information loss finds the discrepancy between the statistical characteristics, the mean, and the standard deviation of synthetic and original record features by using the L-2 norm or Euclidean distance. Suppose the value of this difference is zero. In that case, the actual and synthetic records have statistically the same features, and the discriminator may not be able to distinguish whether the inputs are from training data or synthetically generated. The classification loss is used to check the semantic integrity and balance the privacy and usability of synthetic data generated. It finds the discrepancy between the label of a generated record and the label predicted by the classifier for that record and will remove the semantically incorrect records.
The security and privacy concerns were addressed as the entire table was generated synthetically by the table-GANs, and none of the actual records were directly disclosed. These synthetic tables are strong against the re-identification attack and attribute disclosure issues, as attackers can not reveal any original identification.
The adversary’s access may be limited to black-box queries that return the model’s output on a given input. The adversary may train many attack models as shadow models based on the generator’s behavior by making inferences about the members of the synthetic tables. This attack is called membership inference attack [103]. The table-GAN was attacked with various hinge-loss configurations to evaluate the impact of the membership attack. Hinge loss slightly disturbs the training process of table-GAN, so it converges to the point that balances synthesis quality and the possibility of being attacked. The paper showed that the attack performance decreased by increasing the hinge loss. Finally, model compatibility, which is the difference in the performance of data trained on actual and synthetic data, was used to assess the quality of the generated data. The models trained using the synthetic tables exhibited similar performance to those trained using the original table.
The Table 2 gives a summary of different techniques and methods used to generate image and tabular data.

5. Generating Cyber Attack data using GAN

Cyber security is one of the major business concerns today for the organizations world-wide. With systems being internet-connected and Internet of Things (IoT) emerging as the latest technology, there is a need to protect the networks, systems and programs, from the digital attacks. Every industry like telecommunication, manufacturing, healthcare, education, finance, government etc., are being exposed to cyber attacks. These cyber attacks are usually designed to access, change or destroy sensitive information; to extort money from users; or disrupt usual business processes. There are different ways of attacking a system. For instance, a Denial of Service (DoS) attack attempts to restrict the access of resources for the host or prevent the utilization of resources. Other attacks like vulnerability exploitation obtain privileged access to a host network by taking advantage of known vulnerabilities. The unauthorized attempt or threat to deliberately access or manipulate information, or disable the system is defined as intrusions, and the methods used to monitor and detect this aberration, are called as intrusion detection systems (IDS) [104].
The IDS tries to find exceptional patterns in network traffic that do not conform to the expected normal behavior. These non-conforming patterns are usually referred to as anomalies or outliers. The IDS monitors the network for such malicious acts or security protocol violations, and raises an alarm or sends an alert to the administrator if any anomaly is detected. Though the IDS may not necessarily take any other action. There are two types of IDS, Network Intrusion Detection Systems (NIDS), which monitor network packets moving in and out of the network, and Host Intrusion Detection Systems (HIDS), which monitor the activities of a single host such as a computer or clients connected to that computer. The IDS algorithms are classified based on their detection approach, with signature-based detection and anomaly-based detection being the two main categories.
Signature-based detection is a traditional method that relies on a pre-programmed list of known attack behaviors. It uses a database of previously identified bad patterns to report an attack and is only as effective as its database of known signatures. On the other hand, anomaly-based detection techniques use statistical and machine learning methods to detect malicious behaviors that deviate from known normal behaviors. These approaches have gained widespread attention from researchers over the past decade, and several models have been proposed in literature to detect intrusions into the network [105,106,107]. However, the increasing complexity of attacks and attackers’ skills have made these models only as good as the datasets on which they were developed. Obtaining a complete and real dataset is challenging in the realm of cybersecurity, as the information needed to develop models is held in various logs and network traffic of an organization that faced a cyber attack. Additionally, these logs and network traffic carry private information of the organization and cannot be released to the public. Even when a realistic dataset is obtained, it captures only one of the several possible attacks for that organization’s topology and is therefore incomplete.
Alternative approaches to creating a dataset have been proposed in literature, including semi-synthetic and synthetic data generation techniques. In the semi-synthetic data generation approach, a network is set up, simulating a realistic network topology, and human penetration testers penetrate into the network. The dataset is then built by capturing the normal user behavior and the simulated attack behavior, followed by appropriately labeling those behaviors for developing statistical and machine learning models. Synthetic data generation techniques do not require any humans to penetrate into the network; rather, the attack data is simulated by models that learn how attacks can be performed. Synthetic data generation approaches, specifically using GANs, have been gaining increasing attention over the past few years due to their applicability to different types of topologies and the possibility of creating a dataset that can represent different attack sets on a given topology.
Various approaches, including supervised, semi-supervised, and unsupervised learning, have been used for anomaly detection [108]. In semi-supervised techniques, the model is trained using only the normal training dataset, and the likelihood of the test dataset is compared against the learned model. However, these algorithms assume that normal instances are more frequent than anomalies in the test data, which can lead to false alarms or blocking of normal data packets as anomalies. Moreover, these methods may not be suitable for dynamic and sequential responses to new or deformed cyber threats.
On the other hand, supervised anomaly classifiers learn from labeled datasets that contain normal or anomaly classes. In network systems, the dataset consists of recorded samples with pre-assigned labels in the form of a feature vector of network features. The supervised learning algorithm’s goal is to learn from the labeled dataset and predict whether a new instance is normal or an anomaly, and to raise an alert when an anomaly is detected. Although state-of-the-art supervised algorithms can be applied well to solve this type of problem, they face several challenges. The datasets are highly imbalanced, with a low number of anomalous packets, and prediction accuracy is generally reported to be low, while training time is very high. In addition, large datasets with high variance are required to train these algorithms to build robust intrusion detection systems. The available datasets are often limited and outdated, or they may have missing ground truth values. The manual labeling of real networks containing millions to billions of flows is also a challenging task for security experts. Additionally, most organizations do not want to disclose their network traffic and attack data information, making it difficult to collect or label such datasets.
Unsupervised learning methods, on the other hand, do not require labeled data for training, making them suitable for anomaly detection when labeled data is scarce. However, they have some limitations in the context of cybersecurity. Unsupervised methods are based on the assumption that anomalies are rare events and can be identified as deviations from normal data distribution. However, in cybersecurity, it is often challenging to define what is normal behavior, as cyber threats are constantly evolving and changing. Moreover, unsupervised methods may not be able to completely exploit the spatial-temporal correlation and multiple variable dependencies, which are essential for accurately detecting anomalies in complex cyber systems. Ideally, it would be best if such datasets could be synthetically generated, as explained in Section 4. In this situation, GAN can be of great use for anomaly detection. Section 2 illustrates how GANs have been used recently to generate synthetic data in variety of domains. In this section, we discussed the different methods proposed by researchers for generating various type of cyber attacks using GANs.

5.1. Flow-based Network Traffic Generation

To develop, analyze, and evaluate secure networks and cyber monitoring systems like IDS, network traffic flows are essential. However, obtaining real network traffic that is appropriate for such purposes is challenging due to privacy and security concerns. Publicly available real traffic is often inconsistent, insufficient, or incomplete, making it less useful. Therefore, synthetic traffic generation techniques have been developed [109,110,111]. These techniques involve extracting key features from real traffic and using them to create similar network traffic flows. Various traffic generation techniques have been developed over time and GANs have emerged as a promising approach in synthetic traffic generation.
Ring et. al. [112] proposed a GAN model to generate synthetic flow-based network traffic to evaluate an NIDS. The Wasserstein GANs (WGANs) [93] were used to generate the synthetic flow-based network data based on CIDDS-001 [113] dataset. The flow-based network traffic contains header information about the network connections between two end-point devices like servers, workstation computers or mobile phones. Each flow is an aggregated information containing source IP address, source port, destination IP address, destination port and transport protocols of the transmitted network packets. Most of these attributes like IP address, ports and transport protocols are categorical and can not be processed by GANs, since the generator is differentiable [1]. These attributes need to be encoded into numerical or continuous vectors. IP2Vec [114], based on Word2Vec method [115], was used to transform IP addresses into a continuous feature space such that the standard similarity measures can be applied. IP2Vec was extended to learn the embeddings for other attributes, like ports, transport protocols, duration, bytes and packets and a neural network based on backpropagation was used to train the embedding layer. For preprocessing of these attributes, other alternatives such as numeric and binary transformations were also experimented. The results showed that although numeric transformations were straightforward and easy to implement but they were not able to truly represent the distributions and capture the similarities. The binary transformation of these categorical and numerical attributes of flow-based data did pretty well and were able to capture the internal structure of the traffic and subnet, except a few cases. On an average, the embeddings based on IP2Vec transformations gave the best results.
To evaluate the quality of data generated by GAN, approaches like Inception Score (IS) can not be used for flow-based data, as inception score is based on Inception Net v3 [84] and can classify only the images. There is no standard method to evaluate the quality of network traffic so different methods were proposed to assess the quality from different views. To evaluate the diversity and distribution of the generated data, the temporal distributions of generated flows for each week’s traffic were visually analysed to see if they represented the internal structure of the original traffic and subnets. Secondly, the distribution of the generated and real traffic data in each attribute, was compared independently by computing the euclidean distance between the probability distributions of the generated and weekly traffic input for each attribute. Thirdly, the domain knowledge checks were used to assess the intrinsic quality of the generated data. Some heuristics based on the properties of flow-based network data were tested to check the sanity and see if the generated data is realistic or not. For instance, if the transport protocol is UDP, then the flow must not have any TCP flags; if the multi-or broadcast IP address appears in the flow, then it must be the destination IP address. The flows generated by both the binary and IP2Vec embeddings transformation were realistic and showed good results for all the evaluation methods.
Cheng et al. [116] proposed and developed a novel GAN model called PAC-GAN, which generates realistic network traffic at the IP packet level. PAC-GAN encodes each network packet into a grey scale image and generates IP packets using CNN GANs. The network traffic generator uses an encoding scheme that converts and maps network traffic data into images using image-based matrix representations. By learning and manipulating the byte values of data packets, the PAC-GAN can generate realistic variants of different types of network traffic, such as ICMP pings, DNS queries, and HTTP get requests, that can be transmitted through real networks.
Shahid et al. [117] proposed a method for generating synthetic traffic sequences that closely resemble actual bidirectional flows in IoT networks. They combined an autoencoder with a Wasserstein GAN to learn latent vectors that can be decoded into realistic sequences of packet sizes. The generated bidirectional flows mimic the characteristics of genuine ones, which can deceive anomaly detectors into identifying them as real. However, the quality of synthetic traffic sequences depends heavily on the training data used. During the training phase, the generator can only reproduce sequences that were observed in the training data. The authors tested their model using a small amount of data, which may have led to overfitting. Yin et al. [118] have developed an end-to-end framework, NetShare for generating test traffic using GANs which focus on tackling the fidelity, scalability, and privacy challenges and tradeoffs in existing GAN based approaches [110].

5.2. Cyber Intrusion Alert Data Synthesis

Cyber intrusion alert data plays an important role in detecting and profiling anomalous activities and behaviors, as well as identifying network vulnerabilities. However, the cyber attack data is highly imbalanced as the intrusions are rare events and often hard to identify [119]. Moreover, the absence of ground truth and organizations’ reluctance to share such data further hinder experimentation and research . Additionally, these datasets exhibit non-homogeneous characteristics, further complicating the analysis and development of effective defense mechanisms. Given the complex and dynamic nature of cyber attacks, innovative approaches are required to generate realistic and diverse data that accurately captures the intricacies of real-world intrusions.
GANs have demonstrated their capacity to learn intricate data distributions, aiming to generate data that is progressively more realistic and aligns with the underlying patterns and characteristics of real intrusion alerts [120]. The generator part of the GAN learns to generate synthetic intrusion alerts, while the discriminator part evaluates the authenticity of the generated alerts. Using GANs to generate synthetic cyber intrusion alerts helps address the challenges posed by imbalanced and non-homogeneous data in cybersecurity. These generated alerts not only aid in characterizing intrusion features but also complement the existing data, ensuring a more diverse and representative dataset for robust analysis and defense against cyber threats.
Recent work by Sweet et al. [120,121] have investigated the effectiveness of GANs in generating synthetic intrusion alerts by learning the sparsely distributed categorical features from samples of malicious network intrusions. Their proposed framework for synthetic cyber-intrusion alert data utilizes Wasserstein GAN models [93] with some modifications. Two variants were investigated: WGAN with Gradient Penalty (WGAN-GP) [122] and WPGAN-MI [123], which integrates gradient penalty with Mutual Information constraint. WGAN-GP incorporates a gradient penalty term in the discriminator loss function, enhancing the utility of gradients and improving training stability. WPGAN-MI, on the other hand, introduces a mutual information term in the generator’s loss, aiming to approximate the mutual information between the generator’s noise input and the generated output samples. To estimate mutual information, a neural network is employed to compute the Donsker-Varadhan (DV) representation of KL-divergence. As discussed in section IV, the InfoGANs [85] also used the mutual information constraint, which helped the generator to explore the full domain of the data while generating new samples.
To evaluate their framework, Sweet et al. [120] utilized datasets from the National Collegiate Penetration Testing Competition (CPTC) [124] held in 2017 and 2018. These datasets encompassed malicious actions performed by participating teams as they attempted to compromise the target networks. The features included source and destination IP addresses, port numbers, attack categories, attack signatures, and alerts. The alerts were categorized based on the destination IP address, capturing unique attack behaviors for each target. The fidelity of the generated data was assessed using Histogram Intersection and Conditional Entropy measures, both demonstrating the potential of GANs to generate diverse artificial attack data reflective of the behaviors observed in the ground truth dataset. The GAN models were trained to learn the distribution of input data on a per-target IP basis. The evaluation utilized the histogram intersection score between the ground truth and generated alerts to assess the GANs’ ability to capture the latent behavior and feature dependencies of the dataset. The analysis revealed that WPGAN-GPMI, with its mutual information constraint, outperformed the WGAN-GP model by synthesizing alerts pertaining to more attack stages and accurately recreating the target-based cyber-alert data from the malicious alert datasets.

5.3. Generating Attack Data using Adversarial Examples

Machine learning models are commonly employed for detecting spams, malware, anomalies, network intrusions, and other illegal activities. However, ML models including Deep Neural Networks (DNNs) have recently been found to be vulnerable to adversarial attacks, which compromises their robustness [125,126,127]. This vulnerability poses a significant threat to the reliability of machine learning in security-sensitive domains. Adversarial attacks involve the deliberate creation of malicious inputs by adversaries with the aim of deceiving the system. These inputs, known as adversarial examples, are carefully crafted to manipulate the predictions made by the machine learning model, resulting in erroneous outputs. Even a minor modification to the input can cause the neural network to misclassify the data, and these alterations are often imperceptible to the human eye [125].
GANs have been employed to generate synthetic cyber attacks that can bypass security defenses or exploit vulnerabilities in systems, such as intrusion detection systems or malware detection models. In this setup, the generator network is trained to produce adversarial examples capable of deceiving or evading the target system’s defenses, while the discriminator network learns to differentiate between real and adversarial examples. GANs play a crucial role in assessing the robustness and effectiveness of security systems, as well as in developing improved defenses against cyber attacks.
Adversarial attacks can be classified into two types: white box attacks and black box attacks. In white box attacks [128], the adversary has complete knowledge of the model architecture, learning algorithms, parameters, and access to the training dataset. This allows them to manipulate the feature vector in the test dataset to cause misclassification. On the other hand, in black box attacks [127], the adversary has no knowledge of the model architecture, learning parameters, or access to the training dataset. In this scenario, the attacker can only observe the labels or class outputs of the model when interacting with it remotely, such as through an API. By continually modifying the input and observing the corresponding output, the attacker establishes a relationship between the changes in inputs and outputs. The remote DNN model that the adversary is observing is commonly referred to as an ‘Oracle’.
To overcome the lack of knowledge in black box attacks, the adversary can train a local substitute DNNs with a synthetic dataset. The inputs are synthetic and generated by the adversary, whereas the outputs are the labels assigned by the Oracle or remote DNN when the adversary was querying the DNN with their synthetic inputs. The substitute model is designed with similar decision boundaries, and the adversary crafts the adversarial examples to misclassify the substitute model. These same adversarial examples can then be used to misclassify the target DNN. Two models, MalGAN [129] and IDSGAN [130] were proposed to use GANs to generate the synthetic adversarial examples against the detection system. In this context, we further explore the construction and evaluation of the capabilities of these models in generating realistic adversarial attack examples.

5.3.1. MalGAN: Generating Malware Adversarial Examples using GAN

MalGAN, proposed by Hu et al. [129], focuses on creating adversarial examples for malware detection systems. These detection systems are like black boxes to attackers, meaning they don’t know their internal workings. So, the attackers can only perform black-box attacks to understand the features used by the malware detection algorithm. The key idea behind MalGAN is to trick the malware detection system into misclassifying benign programs as malware. It uses a dataset of programs with API features represented as binary vectors. MalGAN incorporates a black-box detection model (Oracle) in the discriminator and generator. The generator creates adversarial examples, while the discriminator tries to imitate the Oracle. The adversarial examples successfully bypass the black-box detector, showing transferability [131] across different classifiers. However, when the detector is retrained with adversarial examples, it becomes more robust against these attacks.
The advantage of MalGAN is that it can generate new adversarial malware examples, making the detector more robust without needing to collect a large number of actual malware samples and label them manually. This makes the malware detection system more effective and helps improve its performance against adversarial attacks.

5.3.2. IDSGAN: Generating Adversarial Examples against Intrusion Detection System

IDSGAN [130] another GAN model proposed to create adversarial attacks that deceive and evade the IDS. Similar to MalGAN, IDSGAN treats the IDS as a black box and aims to deceive it with adversarial attacks. The IDS is built using a classifier like DNN or SVM on a cyber security dataset like NSL-KDD. IDSGAN uses a generator and discriminator, where the discriminator emulates the behavior of the black-box IDS. The generator produces adversarial examples by applying small perturbations only to non-functional features of the attack data. IDSGAN successfully generates adversarial examples that bypass the black-box IDS, leading to lower detection rates and higher evasion rates. This indicates that the generated adversarial examples can effectively fool the IDS.
The main difference between MalGAN and IDSGAN lies in the types of attacks they generate, the features of their respective datasets (binary feature vector for MalGAN and a sequence of features for IDSGAN), and the treatment of constructing adversarial examples. IDSGAN’s dataset includes both numeric and non-numeric discrete features, which are categorized into four sets: intrinsic, content, time-based, and host-based features. When creating adversarial examples, IDSGAN applies random noise only to the non-functional features of each attack, while keeping the functional features unchanged to maintain the attack’s nature. This ensures the attack remains intact and doesn’t break during perturbation.
MalGAN used malware API dataset consisting of binary feature vector, the NSL-KDD dataset used in IDSGAN, is a sequence of 41 features describing the normal and the malicious network traffic records. There are 9 discrete and 32 continuous features. The non numeric discrete features are one-hot encoded to do numeric conversion. As per the meaning of the features, they are categorized into four sets. The features, like d u r a t i o n , p r o t o c o l t y p e , s e r v i c e , f l a g , s o u r c e b y t e s , d e s t i n a t i o n b y t e s are ’intrinsic’ as they show the characteristics of connection in a network. Similarly, the ’content’ features are the ones which mark the content of connections and show the behavior related to attack if it exist in the traffic. The ’time-based’ features check for the connections which have the same destination host or same service as the current, in past 2 seconds. The ’host-based’ traffic features monitor similar connections in the past 100 connections. The malicious data consists of four type of attacks, probe, U2R, DoS and R2L. Each category of the attack has some functional features which represents the basic function of the attack.
While making small perturbations, no change is made in the functional features of each attack. Otherwise, the attack will be broken. The random noise is added only to the nonfunctional features to generate adversarial examples. The generator is a simple neural network with five linear layers and the update to the parameters of the network is made based on the feedback from the discriminator.
Here various machine learning algorithms like, Support Vector Machine (SVM), Logistic Regression (LR), Multilayer Perceptron (MLP), K-Nearest Neighbor (KNN), Random Forest, Decision Trees, were used to train the black-box IDS to test the transferability of the adversarial samples. To show the robustness of IDS model, detection rate was measured. The detection rate gives the proportion of correctly detected malicious traffic records to the total attack records detected by the black-box IDS. The original detection rate and the adversarial detection rates were computed. To show the ability of IDS, another metrics, called the evasion increase rate was used. It is the rate of increase in the undetected adversarial malicious traffic by the IDS as compared to the original malicious traffic examples. IDSGAN model showed lower detection rate and high evasion rate which means more malicious traffic could evade the IDS, showing that the adversarial examples generated by IDSGAN are realistic and the generator was able to successfully fool the black-box IDS.
Yang et al. [132] introduced a novel technique for identifying previously unknown attacks by utilizing a GAN-based approach to learn the hidden distribution of original data. Their method involves using a DNN for classification and evaluating performance metrics on two distinct datasets. Meanwhile, Lee and Park [133] addressed the negative impact of imbalanced data on attack classification by generating new virtual data that is similar to the existing data using GAN. They were able to achieve better results with RandomForest using the newly generated data compared to the original data. Huang and Lei [134] presented a three-step approach to overcome the negative effects of labeled imbalanced data in datasets. They first performed feature extraction using FeedForward neural network (FNN), then generated virtual data using GAN, and evaluated the classification performance of the resulting data on three different datasets using CNN. Shahriar et al. [135] proposed attack detection in cyber physical systems (CPS) and suggested a fix for imbalanced and missing data using the generative adversarial network (GAN) based intrusion detection system (G-IDS), where GAN generates synthetic samples, and IDS gets trained on them along with the original ones.

6. Analysis of GAN generated Synthetic Attack Data

The effectiveness of GAN-generated data in cybersecurity remains an open question. Real-world cyber-attacks often involve complex contexts, such as the timing of Distributed Denial of Service (DDoS) attacks or the intricate patterns of lateral movements in system breaches. These attacks usually exhibit signatures across multiple traffic units, presenting a significant challenge for GANs to replicate accurately. Nonetheless, more straightforward, isolated attack vectors like SQL Injection, Application Scanning, and Port Scanning have distinct network flow signatures that GANs can potentially mimic. While GAN-generated data can augment Intrusion Detection System (IDS) training datasets or aid in creating simulated attack scenarios, it often includes considerable noise. This noise can lead to trained models under performing in real-world situations.
In this section, we delve into an analysis to evaluate the fidelity of GAN-generated cyber-attack data. Our study focuses on three key aspects: the similarity of GAN-generated attack data features to actual attacks, whether GANs preserve the original data distribution, and the response of classifiers trained on authentic data when exposed to a mix of original and GAN-generated data. This comprehensive approach provides insights into the potential and limitations of using GANs for cybersecurity. We have chosen a DoS attack from the NSL-KDD dataset for our analysis. Table 3 presents the different attack categories the NSL-KDD dataset has. With 41 features, of which 9 are discrete values, and 32 are continuous values, the dataset has both normal and malicious traffic. Using domain knowledge and the information given by the dataset as depicted in Table 3, we first identified features that are reflective of a DoS attack, followed by performing statistical analysis to obtain the range and standard deviation of those identified features across various DoS and normal traffic.
Figure 2 shows the features we identify corresponding to various attack categories in the NSL-KDD dataset. We then performed statistical analysis to find a correlation between those different features using Pearson’s coefficient. GAN-generated attack traffic can represent DoS traffic only if the distribution of the data in those identified features and the correlation among those features is preserved. To this end, we built a conditional GAN model where the discriminator was trained only on the attack samples. At the same time, the generator was set to challenge the discriminator until the discriminator could identify the attack traffic accurately. To evaluate the generated attack data, we built a 1) white-box-model, supervised model using FNN (Feed-forward neural network) trained on NSL-KDD dataset’s train data constituting both normal and attack data and 2) anomaly-detector: a semi-supervised model that is trained only on the normal data within the NSL-KDD’s train data and 3) performed a Statistical Analysis: We calculated the expected standard deviation (SD) of the features identified in our feature analysis that are reflecting a DoS attack. We then tested the performance of the resulting white-box model and the anomaly detector against the NSL-KDD dataset’s test data to ensure its performance meets the accuracy requirements. As expected, the accuracy prediction obtained was over 99% on the white-box model’s test data, and the anomaly-detector model could distinguish between normal and attack traffic with an accuracy of over 81%.
We then used the white-box model to detect the normal and attack traffic in our GAN-generated attack data. The white box could report the GAN-generated attack data as not normal accurately; however, it classified the attack data into one of the attack categories in Table 3. The anomaly-detector model accurately reported the GAN-generated attack data as not normal as part of static analysis in our evaluation. We measured the Euclidean distance between the standard deviation of the feature values from the NSL-KDD dataset and the standard deviation of the same features from GAN-generated attack data. We found most of the generated samples to have inconsistent feature values that neither correspond to normal traffic nor DoS traffic. Henceforth, our analysis and evaluation have concluded that while most of the GAN-generated attack data was not normal, it did not correspond to expected DoS traffic. Our static analysis of the features points out that those GAN-generated attacks reported as not normal by the trained models are neither normal nor attack traffic units as the expected feature correlations are missing and thus the data represents mere noise. Many solutions have claimed the ability of their GANs to generate attack data based on their white-box models or their anomaly detectors reporting them as not normal. However, we would like to point out that not-normal does not mean attack data; instead, as we provided evidence above, it is often mere noise and not an unknown attack or a new attack. We believe our analysis helps researchers continue developing GAN-based attack generation models capable of generating attack data that represents real-world attacks and thus address the concerns associated with obtaining real-world attack data due to privacy issues.

7. Discussion

GANs, with their unique architecture of a generator and discriminator working in tandem, have demonstrated remarkable proficiency in generating data that closely mimics real-world patterns. This capability is particularly advantageous in cybersecurity, where the availability of diverse and extensive datasets is paramount for the practical training of models. However, analyzing the authenticity of synthetic data generated by GANs in the context of cyber attacks is essential. While GANs can produce data statistically similar to real-world datasets, it is crucial to study this synthetic data adequately to analyze if it represents the complexities and nuances of cyber threats. Also, the reliability of deep learning models trained solely on synthetic data is still being determined. These models may not perform well when exposed to real-world attack scenarios, leading to potential vulnerabilities.
Our analysis of synthetic data generated for DoS attacks shows that while GAN-generated attack data often deviates from normal traffic, it does not align with typical DoS traffic patterns. Static analysis reveals that this data, flagged as abnormal by trained models, lacks the expected feature correlations, indicating it is neither normal nor genuine attack traffic but relatively just noise. Recognizing that abnormal data does not necessarily signify an attack; in many cases, it may be simply noise. Our work underscores the need to analyze the GAN-based models further to generate data that accurately reflects real-world attacks. Other works like Attack trees [136], popular graphical models to represent cyberattack scenarios, pose challenges for organizations due to the need for advanced security expertise and stakeholder engagement [137]. Current automation methods from system models or attack pattern libraries need more maturity for practical use [138]. Large Language Models (LLMs) like PAC-GPT [139] provide a potential solution by aiding in the automated synthesis of attack trees, leveraging their natural language generation capabilities [140].

8. Conclusion

This comprehensive review of generative models, particularly GANs, in generating synthetic attack data for cybersecurity underscores the potential and challenges of this approach. GANs have emerged as a powerful tool in addressing the scarcity of large, diverse datasets, crucial for training robust deep learning models in cybersecurity. The ability of these models to generate data that mirrors real-world scenarios can significantly enhance the training process, leading to more effective cybersecurity solutions. However, the effectiveness of models trained on synthetic data in accurately detecting and responding to real-world cyber threats is an area that requires further investigation. The findings of this review suggest a need for a balanced approach, combining both natural and synthetic data, to ensure the robustness and reliability of cybersecurity models. Moreover, the ethical and privacy considerations associated with using synthetic data in cybersecurity should be considered. Future research should address these challenges, ensuring that the development and deployment of these technologies are done responsibly and with due consideration of potential consequences.

References

  1. Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Advances in neural information processing systems, 2014, pp. 2672–2680.
  2. Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Communications of the ACM 2020, 63, 139–144.
  3. Shahriar, S. GAN computers generate arts? a survey on visual arts, music, and literary text generation using generative adversarial network. Displays 2022, p. 102237. [CrossRef]
  4. Yinka-Banjo, C.; Ugot, O.A. A review of generative adversarial networks and its application in cybersecurity. Artificial Intelligence Review 2020, 53, 1721–1736. [CrossRef]
  5. Cai, Z.; Xiong, Z.; Xu, H.; Wang, P.; Li, W.; Pan, Y. Generative adversarial networks: A survey toward private and secure applications. ACM Computing Surveys (CSUR) 2021, 54, 1–38.
  6. Hu, W.; Tan, Y. Generating adversarial malware examples for black-box attacks based on GAN. Data Mining and Big Data: 7th International Conference, DMBD 2022, Beijing, China, November 21–24, 2022, Proceedings, Part II. Springer, 2023, pp. 409–423.
  7. Jordan, A.; others. On discriminative vs. generative classifiers: A comparison of logistic regression and naive bayes. Advances in neural information processing systems 2002, 14, 841.
  8. Lee, H.W.; Lim, K.Y.; Grabowski, B.L. Generative learning: Principles and implications for making meaning. In Handbook of research on educational communications and technology; Routledge, 2008; pp. 111–124.
  9. Nallapati, R. Discriminative models for information retrieval. Proceedings of the 27th annual international ACM SIGIR conference on Research and development in information retrieval, 2004, pp. 64–71.
  10. Oussidi, A.; Elhassouny, A. Deep generative models: Survey. 2018 International Conference on Intelligent Systems and Computer Vision (ISCV), 2018, pp. 1–8. doi:10.1109/ISACV.2018.8354080.
  11. Webb, G.I. Naïve Bayes. Encyclopedia of machine learning 2010, 15, 713–714.
  12. Pearl, J. Bayesian networks; UCLA: Department of Statistics, UCLA, 2011.
  13. Clifford, P. Markov random fields in statistics. Disorder in physical systems: A volume in honour of John M. Hammersley 1990, pp. 19–32.
  14. Eddy, S.R. Hidden markov models. Current opinion in structural biology 1996, 6, 361–365.
  15. Izenman, A.J. Linear discriminant analysis. In Modern multivariate statistical techniques; Springer, 2013; pp. 237–280.
  16. LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. nature 2015, 521, 436–444.
  17. Fahlman, S.E.; Hinton, G.E.; Sejnowski, T.J. Massively parallel architectures for Al: NETL, Thistle, and Boltzmann machines. National Conference on Artificial Intelligence, AAAI, 1983.
  18. Fischer, A.; Igel, C. An introduction to restricted Boltzmann machines. Iberoamerican congress on pattern recognition. Springer, 2012, pp. 14–36.
  19. Hinton, G.E. Deep belief networks. Scholarpedia 2009, 4, 5947.
  20. Salakhutdinov, R.; Hinton, G. Deep boltzmann machines. Artificial intelligence and statistics. PMLR, 2009, pp. 448–455.
  21. Sutskever, I.; Hinton, G.E. Deep, narrow sigmoid belief networks are universal approximators. Neural computation 2008, 20, 2629–2636. [CrossRef]
  22. Bontrager, P.; Togelius, J. Fully differentiable procedural content generation through generative playing networks. arXiv preprint arXiv:2002.05259 2020.
  23. Kingma, D.P.; Welling, M.; others. An introduction to variational autoencoders. Foundations and Trends® in Machine Learning 2019, 12, 307–392.
  24. Nikolenko, S.I. Synthetic data for deep learning; Vol. 174, Springer, 2021.
  25. Caruana, R.; Niculescu-Mizil, A. An empirical comparison of supervised learning algorithms. Proceedings of the 23rd international conference on Machine learning, 2006, pp. 161–168.
  26. Wright, R.E. Logistic regression. Reading and Understanding Multivariate Statistics 1995, pp. 217–244.
  27. Joachims, T. Svmlight: Support vector machine. SVM-Light Support Vector Machine http://svmlight. joachims. org/, University of Dortmund 1999, 19.
  28. Kröse, B.; Krose, B.; van der Smagt, P.; Smagt, P. An introduction to neural networks; The University of Amsterdam, 1993.
  29. Peterson, L.E. K-nearest neighbor. Scholarpedia 2009, 4, 1883.
  30. Phyu, T.N. Survey of classification techniques in data mining. Proceedings of the international multiconference of engineers and computer scientists, 2009, Vol. 1.
  31. Bernardo, J.; Bayarri, M.; Berger, J.; Dawid, A.; Heckerman, D.; Smith, A.; West, M. Generative or discriminative? getting the best of both worlds. Bayesian statistics 2007, 8, 3–24.
  32. Minka, T. Discriminative models, not discriminative training. Technical report, Technical Report MSR-TR-2005-144, Microsoft Research, 2005.
  33. Theis, L.; Oord, A.v.d.; Bethge, M. A note on the evaluation of generative models. arXiv preprint arXiv:1511.01844 2015.
  34. Amit, I.; Matherly, J.; Hewlett, W.; Xu, Z.; Meshi, Y.; Weinberger, Y. Machine learning in cyber-security-problems, challenges and data sets. arXiv preprint arXiv:1812.07858 2018.
  35. Barlow, H.B. Unsupervised learning. Neural computation 1989, 1, 295–311.
  36. Zhu, X.; Goldberg, A.B. Introduction to semi-supervised learning. Synthesis lectures on artificial intelligence and machine learning 2009, 3, 1–130.
  37. Khosravi, P.; Choi, Y.; Liang, Y.; Vergari, A.; Broeck, G.V.d. On tractable computation of expected predictions. arXiv preprint arXiv:1910.02182 2019.
  38. Huang, C.W.; Touati, A.; Dinh, L.; Drozdzal, M.; Havaei, M.; Charlin, L.; Courville, A. Learnable explicit density for continuous latent space and variational inference. arXiv preprint arXiv:1710.02248 2017.
  39. Frey, B.J.; Hinton, G.E.; Dayan, P.; others. Does the wake-sleep algorithm produce good density estimators? Advances in neural information processing systems. Citeseer, 1996, pp. 661–670.
  40. Karhunen, J. Nonlinear independent component analysis. ICA: Principles and Practice 2001, pp. 113–134.
  41. Hammersley, J. Monte carlo methods; Springer Science & Business Media, 2013.
  42. Tran, D.; Ranganath, R.; Blei, D. Hierarchical implicit models and likelihood-free variational inference. Advances in Neural Information Processing Systems 2017, 30.
  43. Ching, W.K.; Ng, M.K. Markov chains. Models, algorithms and applications 2006.
  44. Wang, H.; Lei, Z.; Zhang, X.; Zhou, B.; Peng, J. Machine learning basics. Deep learning 2016, pp. 98–164.
  45. Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE transactions on pattern analysis and machine intelligence 2013, 35, 1798–1828.
  46. Arora, S.; Khandeparkar, H.; Khodak, M.; Plevrakis, O.; Saunshi, N. A theoretical analysis of contrastive unsupervised representation learning. arXiv preprint arXiv:1902.09229 2019.
  47. Hodson, T.O.; Over, T.M.; Foks, S.S. Mean squared error, deconstructed. Journal of Advances in Modeling Earth Systems 2021, 13, e2021MS002681. [CrossRef]
  48. Jiang, B.; Zhou, Z.; Wang, X.; Tang, J.; Luo, B. CmSalGAN: RGB-D salient object detection with cross-view generative adversarial networks. IEEE Transactions on Multimedia 2020, 23, 1343–1353. [CrossRef]
  49. Goudet, O.; Kalainathan, D.; Caillou, P.; Guyon, I.; Lopez-Paz, D.; Sebag, M. Causal generative neural networks. arXiv preprint arXiv:1711.08936 2017.
  50. Zhou, G.; Yao, L.; Xu, X.; Wang, C.; Zhu, L.; Zhang, K. On the opportunity of causal deep generative models: A survey and future directions. arXiv preprint arXiv:2301.12351 2023.
  51. Kügelgen, J.; Mey, A.; Loog, M.; Schölkopf, B. Semi-supervised learning, causality, and the conditional cluster assumption. Conference on Uncertainty in Artificial Intelligence. PMLR, 2020, pp. 1–10.
  52. Han, T.; Tu, W.W.; Li, Y.F. Explanation consistency training: Facilitating consistency-based semi-supervised learning with interpretability. Proceedings of the AAAI conference on artificial intelligence, 2021, Vol. 35, pp. 7639–7646. [CrossRef]
  53. Kanungo, T.; Mount, D.M.; Netanyahu, N.S.; Piatko, C.; Silverman, R.; Wu, A.Y. The analysis of a simple k-means clustering algorithm. Proceedings of the sixteenth annual symposium on Computational geometry, 2000, pp. 100–109.
  54. Kramer, O.; Kramer, O. K-nearest neighbors. Dimensionality reduction with unsupervised nearest neighbors 2013, pp. 13–23.
  55. De Ville, B. Decision trees. Wiley Interdisciplinary Reviews: Computational Statistics 2013, 5, 448–455.
  56. Cho, Y.; Saul, L. Kernel methods for deep learning. Advances in neural information processing systems 2009, 22.
  57. Sennrich, R. Modelling and optimizing on syntactic n-grams for statistical machine translation. Transactions of the Association for Computational Linguistics 2015, 3, 169–182. [CrossRef]
  58. Hinton, G.E. Distributed representations 1984.
  59. Hinton, G.E.; Ghahramani, Z. Generative models for discovering sparse distributed representations. Philosophical Transactions of the Royal Society of London. Series B: Biological Sciences 1997, 352, 1177–1190. [CrossRef]
  60. Radford, A.; Metz, L.; Chintala, S. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv preprint arXiv:1511.06434 2015.
  61. Li, T.; Ortiz, J.M. Generative Adversarial Network 1011.
  62. Ratliff, L.J.; Burden, S.A.; Sastry, S.S. Characterization and computation of local Nash equilibria in continuous games. 2013 51st Annual Allerton Conference on Communication, Control, and Computing (Allerton). IEEE, 2013, pp. 917–924.
  63. Sun, F.; Xie, X. Deep non-parallel hyperplane support vector machine for classification. IEEE Access 2023. [CrossRef]
  64. Zhang, X.Y.; Xie, G.S.; Li, X.; Mei, T.; Liu, C.L. A Survey on Learning to Reject. Proceedings of the IEEE 2023, 111, 185–215. [CrossRef]
  65. Chen, L.; Deng, Y.; Cheong, K.H. Permutation Jensen–Shannon divergence for Random Permutation Set. Engineering Applications of Artificial Intelligence 2023, 119, 105701. [CrossRef]
  66. Wildberger, J.; Guo, S.; Bhattacharyya, A.; Schölkopf, B. On the Interventional Kullback-Leibler Divergence. arXiv preprint arXiv:2302.05380 2023.
  67. Karras, T.; Aila, T.; Laine, S.; Lehtinen, J. Progressive growing of gans for improved quality, stability, and variation. arXiv preprint arXiv:1710.10196 2017.
  68. Mirza, M.; Osindero, S. Conditional generative adversarial nets. arXiv preprint arXiv:1411.1784 2014.
  69. Denton, E.L.; Chintala, S.; Fergus, R.; others. Deep generative image models using a laplacian pyramid of adversarial networks. Advances in neural information processing systems, 2015, pp. 1486–1494.
  70. Burt, P.; Adelson, E. The Laplacian pyramid as a compact image code. IEEE Transactions on communications 1983, 31, 532–540. [CrossRef]
  71. Krizhevsky, A.; Nair, V.; Hinton, G. Cifar-10 (canadian institute for advanced research). URL http://www. cs. toronto. edu/kriz/cifar. html 2010, 5.
  72. Song, F.Y.Y.Z.S.; Xiao, A.S.J. LSUN: Construction of a Large-scale Image Dataset using Deep Learning with Humans in the Loop. arXiv preprint arXiv:1506.03365 2015.
  73. Liu, Z.; Luo, P.; Wang, X.; Tang, X. Deep learning face attributes in the wild. Proceedings of the IEEE international conference on computer vision, 2015, pp. 3730–3738.
  74. Wang, Z.; Simoncelli, E.P.; Bovik, A.C. Multiscale structural similarity for image quality assessment. The Thrity-Seventh Asilomar Conference on Signals, Systems & Computers, 2003. Ieee, 2003, Vol. 2, pp. 1398–1402. [CrossRef]
  75. Bowles, C.; Chen, L.; Guerrero, R.; Bentley, P.; Gunn, R.; Hammers, A.; Dickie, D.A.; Hernández, M.V.; Wardlaw, J.; Rueckert, D. Gan augmentation: Augmenting training data using generative adversarial networks. arXiv preprint arXiv:1810.10863 2018.
  76. Sixt, L.; Wild, B.; Landgraf, T. Rendergan: Generating realistic labeled data. Frontiers in Robotics and AI 2018, 5, 66. [CrossRef]
  77. Wario, F.; Wild, B.; Couvillon, M.J.; Rojas, R.; Landgraf, T. Automatic methods for long-term tracking and the detection and decoding of communication dances in honeybees. Frontiers in Ecology and Evolution 2015, 3, 103. [CrossRef]
  78. Zhang, H.; Xu, T.; Li, H.; Zhang, S.; Wang, X.; Huang, X.; Metaxas, D.N. Stackgan: Text to photo-realistic image synthesis with stacked generative adversarial networks. Proceedings of the IEEE international conference on computer vision, 2017, pp. 5907–5915.
  79. Reed, S.E.; Akata, Z.; Mohan, S.; Tenka, S.; Schiele, B.; Lee, H. Learning what and where to draw. Advances in neural information processing systems, 2016, pp. 217–225.
  80. Wah, C.; Branson, S.; Welinder, P.; Perona, P.; Belongie, S. The caltech-ucsd birds-200-2011 dataset, 2011.
  81. Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft coco: Common objects in context. European conference on computer vision. Springer, 2014, pp. 740–755.
  82. Nilsback, M.E.; Zisserman, A. Automated flower classification over a large number of classes. 2008 Sixth Indian Conference on Computer Vision, Graphics & Image Processing. IEEE, 2008, pp. 722–729.
  83. Salimans, T.; Goodfellow, I.; Zaremba, W.; Cheung, V.; Radford, A.; Chen, X. Improved techniques for training gans. Advances in neural information processing systems, 2016, pp. 2234–2242.
  84. Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 2818–2826.
  85. Chen, X.; Duan, Y.; Houthooft, R.; Schulman, J.; Sutskever, I.; Abbeel, P. Infogan: Interpretable representation learning by information maximizing generative adversarial nets. Advances in neural information processing systems, 2016, pp. 2172–2180.
  86. LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proceedings of the IEEE 1998, 86, 2278–2324. [CrossRef]
  87. Netzer, Y.; Wang, T.; Coates, A.; Bissacco, A.; Wu, B.; Ng, A.Y. Reading digits in natural images with unsupervised feature learning. NIPS workshop on deep learning and unsupervised feature Learning, 2011.
  88. Vinod, B. The continuing evolution: Customer-centric revenue management. Journal of Revenue and Pricing Management 2008, 7, 27–39. [CrossRef]
  89. Mottini, A.; Lheritier, A.; Acuna-Agost, R. Airline passenger name record generation using generative adversarial networks. arXiv preprint arXiv:1807.06657 2018.
  90. Voigt, P.; Von dem Bussche, A. The eu general data protection regulation (gdpr). A Practical Guide, 1st Ed., Cham: Springer International Publishing 2017. [CrossRef]
  91. Bellemare, M.G.; Danihelka, I.; Dabney, W.; Mohamed, S.; Lakshminarayanan, B.; Hoyer, S.; Munos, R. The cramer distance as a solution to biased wasserstein gradients. arXiv preprint arXiv:1705.10743 2017.
  92. Wang, R.; Fu, B.; Fu, G.; Wang, M. Deep & cross network for ad click predictions. In Proceedings of the ADKDD’17; 2017; pp. 1–7.
  93. Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein gan. arXiv preprint arXiv:1701.07875 2017.
  94. Ajalloeian, A.; Stich, S.U. Analysis of SGD with Biased Gradient Estimators. arXiv preprint arXiv:2008.00051 2020.
  95. Székely, G.J. E-statistics: The energy of statistical samples. Bowling Green State University, Department of Mathematics and Statistics Technical Report 2003, 3, 1–18.
  96. Guo, C.; Berkhahn, F. Entity embeddings of categorical variables. arXiv preprint arXiv:1604.06737 2016.
  97. Lilliefors, H.W. On the Kolmogorov-Smirnov test for normality with mean and variance unknown. Journal of the American statistical Association 1967, 62, 399–402.
  98. Park, N.; Mohammadi, M.; Gorde, K.; Jajodia, S.; Park, H.; Kim, Y. Data synthesis based on generative adversarial networks. arXiv preprint arXiv:1806.03384 2018.
  99. LA.
  100. Adult. UCI Machine Learning Repository, 1996. [CrossRef]
  101. Health.
  102. Airline.
  103. Shokri, R.; Stronati, M.; Song, C.; Shmatikov, V. Membership inference attacks against machine learning models. 2017 IEEE Symposium on Security and Privacy (SP). IEEE, 2017, pp. 3–18.
  104. Bhuyan, M.H.; Bhattacharyya, D.K.; Kalita, J.K. Network anomaly detection: methods, systems and tools. Ieee communications surveys & tutorials 2013, 16, 303–336. [CrossRef]
  105. Khraisat, A.; Gondal, I.; Vamplew, P.; Kamruzzaman, J. Survey of intrusion detection systems: techniques, datasets and challenges. Cybersecurity 2019, 2, 1–22. [CrossRef]
  106. Ahmad, Z.; Shahid Khan, A.; Wai Shiang, C.; Abdullah, J.; Ahmad, F. Network intrusion detection system: A systematic study of machine learning and deep learning approaches. Transactions on Emerging Telecommunications Technologies 2021, 32, e4150. [CrossRef]
  107. Yang, Z.; Liu, X.; Li, T.; Wu, D.; Wang, J.; Zhao, Y.; Han, H. A systematic literature review of methods and datasets for anomaly-based network intrusion detection. Computers & Security 2022, p. 102675. [CrossRef]
  108. Bulusu, S.; Kailkhura, B.; Li, B.; Varshney, P.K.; Song, D. Anomalous Instance Detection in Deep Learning: A Survey. arXiv preprint arXiv:2003.06979 2020.
  109. Zhang, J.; Tang, J.; Zhang, X.; Ouyang, W.; Wang, D. A survey of network traffic generation 2015.
  110. Lin, Z.; Jain, A.; Wang, C.; Fanti, G.; Sekar, V. Using GANs for sharing networked time series data: Challenges, initial promise, and open questions. Proceedings of the ACM Internet Measurement Conference, 2020, pp. 464–483.
  111. Xu, S.; Marwah, M.; Arlitt, M.; Ramakrishnan, N. Stan: Synthetic network traffic generation with generative neural models. Deployable Machine Learning for Security Defense: Second International Workshop, MLHat 2021, Virtual Event, August 15, 2021, Proceedings 2. Springer, 2021, pp. 3–29.
  112. Ring, M.; Schlör, D.; Landes, D.; Hotho, A. Flow-based network traffic generation using generative adversarial networks. Computers & Security 2019, 82, 156–172. [CrossRef]
  113. Ring, M.; Wunderlich, S.; Grüdl, D.; Landes, D.; Hotho, A. Flow-based benchmark data sets for intrusion detection. Proceedings of the 16th European conference on cyber warfare and security, 2017, pp. 361–369.
  114. Ring, M.; Dallmann, A.; Landes, D.; Hotho, A. Ip2vec: Learning similarities between ip addresses. 2017 IEEE International Conference on Data Mining Workshops (ICDMW). IEEE, 2017, pp. 657–666.
  115. Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient estimation of word representations in vector space. arXiv preprint arXiv:1301.3781 2013.
  116. Cheng, A. PAC-GAN: Packet Generation of Network Traffic using Generative Adversarial Networks. 2019 IEEE 10th Annual Information Technology, Electronics and Mobile Communication Conference (IEMCON). IEEE, 2019, pp. 0728–0734.
  117. Shahid, M.R.; Blanc, G.; Jmila, H.; Zhang, Z.; Debar, H. Generative deep learning for Internet of Things network traffic generation. 2020 IEEE 25th Pacific Rim International Symposium on Dependable Computing (PRDC). IEEE, 2020, pp. 70–79.
  118. Yin, Y.; Lin, Z.; Jin, M.; Fanti, G.; Sekar, V. Practical gan-based synthetic ip header trace generation using netshare. Proceedings of the ACM SIGCOMM 2022 Conference, 2022, pp. 458–472.
  119. Myneni, S.; Chowdhary, A.; Sabur, A.; Sengupta, S.; Agrawal, G.; Huang, D.; Kang, M. DAPT 2020-constructing a benchmark dataset for advanced persistent threats. Deployable Machine Learning for Security Defense: First International Workshop, MLHat 2020, San Diego, CA, USA, August 24, 2020, Proceedings 1. Springer, 2020, pp. 138–163.
  120. Sweet, C.; Moskal, S.; Yang, S.J. On the Variety and Veracity of Cyber Intrusion Alerts Synthesized by Generative Adversarial Networks. ACM Transactions on Management Information Systems (TMIS) 2020, 11, 1–21. [CrossRef]
  121. Sweet, C.; Moskal, S.; Yang, S.J. Synthetic intrusion alert generation through generative adversarial networks. MILCOM 2019-2019 IEEE Military Communications Conference (MILCOM). IEEE, 2019, pp. 1–6.
  122. Gulrajani, I.; Ahmed, F.; Arjovsky, M.; Dumoulin, V.; Courville, A.C. Improved training of wasserstein gans. Advances in neural information processing systems, 2017, pp. 5767–5777.
  123. Belghazi, M.I.; Baratin, A.; Rajeswar, S.; Ozair, S.; Bengio, Y.; Courville, A.; Hjelm, R.D. Mine: mutual information neural estimation. arXiv preprint arXiv:1801.04062 2018.
  124. Munaiah, N.; Pelletier, J.; Su, S.H.; Yang, S.J.; Meneely, A. A Cybersecurity Dataset Derived from the National Collegiate Penetration Testing Competition. HICSS Symposium on Cybersecurity Big Data Analytics, 2019.
  125. Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing properties of neural networks. arXiv preprint arXiv:1312.6199 2013.
  126. Papernot, N.; McDaniel, P.; Jha, S.; Fredrikson, M.; Celik, Z.B.; Swami, A. The limitations of deep learning in adversarial settings. 2016 IEEE European symposium on security and privacy (EuroS&P). IEEE, 2016, pp. 372–387.
  127. Papernot, N.; McDaniel, P.; Goodfellow, I.; Jha, S.; Celik, Z.B.; Swami, A. Practical black-box attacks against machine learning. Proceedings of the 2017 ACM on Asia conference on computer and communications security, 2017, pp. 506–519.
  128. Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. arXiv preprint arXiv:1412.6572 2014.
  129. Hu, W.; Tan, Y. Generating adversarial malware examples for black-box attacks based on gan. arXiv preprint arXiv:1702.05983 2017.
  130. Lin, Z.; Shi, Y.; Xue, Z. Idsgan: Generative adversarial networks for attack generation against intrusion detection. arXiv preprint arXiv:1809.02077 2018.
  131. Papernot, N.; McDaniel, P.; Goodfellow, I. Transferability in machine learning: from phenomena to black-box attacks using adversarial samples. arXiv preprint arXiv:1605.07277 2016.
  132. Yang, Y.; Zheng, K.; Wu, B.; Yang, Y.; Wang, X. Network intrusion detection based on supervised adversarial variational auto-encoder with regularization. IEEE Access 2020, 8, 42169–42184. [CrossRef]
  133. Lee, J.; Park, K. GAN-based imbalanced data intrusion detection system. Personal and Ubiquitous Computing 2021, 25, 121–128. [CrossRef]
  134. Huang, S.; Lei, K. IGAN-IDS: An imbalanced generative adversarial network towards intrusion detection system in ad-hoc networks. Ad Hoc Networks 2020, 105, 102177. [CrossRef]
  135. Shahriar, M.H.; Haque, N.I.; Rahman, M.A.; Alonso, M. G-ids: Generative adversarial networks assisted intrusion detection system. 2020 IEEE 44th Annual Computers, Software, and Applications Conference (COMPSAC). IEEE, 2020, pp. 376–385.
  136. Schneier, B. Attack trees. Dr. Dobb’s journal 1999, 24, 21–29.
  137. Gadyatskaya, O.; Trujillo-Rasua, R. New directions in attack tree research: catching up with industrial needs. Graphical Models for Security: 4th International Workshop, GraMSec 2017, Santa Barbara, CA, USA, August 21, 2017, Revised Selected Papers 4. Springer, 2018, pp. 115–126.
  138. Wideł, W.; Audinot, M.; Fila, B.; Pinchinat, S. Beyond 2014: Formal Methods for Attack Tree–based Security Modeling. ACM Computing Surveys (CSUR) 2019, 52, 1–36.
  139. Kholgh, D.K.; Kostakos, P. PAC-GPT: A novel approach to generating synthetic network traffic with GPT-3. IEEE Access 2023. [CrossRef]
  140. Gadyatskaya, O.; Papuc, D. ChatGPT Knows Your Attacks: Synthesizing Attack Trees Using LLMs. International Conference on Data Science and Artificial Intelligence. Springer, 2023, pp. 245–260.
Preprints 92928 g001
Figure 1. Synthetic Data Generation Process in GANs.
Figure 1. Synthetic Data Generation Process in GANs.
Preprints 92928 g001
Preprints 92928 g002
Figure 2. Feature Mapping of NSL-KDD to Intrusion Patterns
Figure 2. Feature Mapping of NSL-KDD to Intrusion Patterns
Preprints 92928 g002
Table 2. Different models used to generate image and tabular synthetic data using GAN
Table 2. Different models used to generate image and tabular synthetic data using GAN
Data Type Model Method Generated Data Quality
Images DCGAN [60] Vector Arithmetic Manipulation Low, suffers from Mode Collapse
CGAN [68] Label as condition Improved Quality
LAPGAN [69] Conditional GAN with Laplacian Pyramid High-resolution Realistic Images
PGGAN) [67] Focus on finer-scale details High quality Synthetic Images
RenderGAN [76] Image Augmentation Realistic Labeled Images
StackGANs [78] Generate images from a text description using Text Embedding Good quality images, evaluated using Inception Score
InfoGAN [85] Use Mutual Information as condition Model can disentangle variations, improved generated images
Tabular PNR generation [89] Use Cramer GAN [91] Evaluated using Jensen-Shannon divergence (JSD), Realistic data generated
Table-GANs [98] Use 3 CNNs, additional classifier to increase synthetic records integrity Models trained using synthetic data performed well
Table 3. Attack Categories of NSL-KDD
Table 3. Attack Categories of NSL-KDD
DoS R2L U2R Probe
back ftp_write buffer_overflow ipsweep
land guess_passwd loadmodule nmap
pod imap perl portsweep
smurf multihop rootkit satan
teardrop phf
spy
warezclient
warezmaster
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated