Prerpints.org logo
Preprint
Article

A Mechanistic Model of Binding Characterizes the Interplay between Temporo-Spatial Binding Strength and Noise

Altmetrics

Downloads

69

Views

16

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

11 December 2023

Posted:

12 December 2023

You are already at the latest version

Alerts
Abstract
The temporo-spatial theory of consciousness postulates that the brain implements its own inner time and space for conscious processing of outside world. In line with this hypothesis, I present a mechanistic model of mutually connected processes that encode the inner space and time. The model is used to elaborate the binding mechanism between two sets of processes representing the inner space and time, respectively. Further, a stochastic version of the model is developed to investigate the interplay between the binding strength and noise. The spectral entropy is used to characterize the noise effects on the systems of processes when the binding strength is varied. The stochastic modeling results reveal that the spectral entropy values for strongly bound systems have similar entropy values for weakly bound or even decoupled systems. Thus, the analysis performed in this study allows to conclude that the binding mechanism is noise-resilient.
Keywords: 
Subject: Computer Science and Mathematics  -   Other

Introduction

A mechanism that provides a unified conscious representation of a scene that is characterized by different perceptual features is known as perceptual binding [1,2,3]. Thus, primary function of the binding mechanism is to unify the sensory information processed in different parts of the brain in order to give us a unitary conscious experience of an object or scene. Several mechanisms have been proposed to solve the binding problem. For example, the temporal neuronal synchrony models propose that different perceptual features are bound together when the firing activities of neurons processing these features are synchronized [2,3,4,5]. Similarly, Temporo-spatial Theory of Consciousness suggests that the temporal alignment permits binding between a stimulus and ongoing spontaneous neural activity [6,7]. Operational Architectonics suggests that binding is achieved with operational synchrony among neuronal processes occurring in different brain regions [8,9]. Other alternatives to the binding mechanisms based on temporal synchrony have been also proposed [10]. In this work, I present a stochastic mechanistic model of binding which is developed based on my previous works [11,12]. The model allows to quantify the interplay between noise and binding.
Noise in neurons may generate significant fluctuations in neuronal responses [13,14], yet sensory features represented by neuronal circuits remain stable [15]. For example, noise affects neuronal signals transmitted by sensory-motor system [14], operation of voltage-gated channels [16,17], synaptic activity [18,19], potential difference across nerve cell membrane [20], propagation of action potential [21] and spike train coding [22]. Further, noise can change the information-processing of sub-threshold periodic signals by helping these signals to cross the threshold. Such noise-induced transmission of information has been detected in cat visual neurons [23], rat [24], and crayfish [25]. The information capacity of neuronal networks also depends on noise [26]. Additive noise can increase the mutual information of threshold neurons [26,27,28]. Nevertheless, very little is known how phenomenal states and perceptual binding remain robust against noise despite ubiquitous noise sources in neural circuits. In my previous work, I have shown that entropy decreases with increase in the size of network that contains negative feedback loops interconnecting processes [12]. In this study, I investigate the interplay between noise and the binding strength using the same framework in which bound phenomenal states are encoded in relationships among processes. A phenomenal state (quale) is postulated to be a dynamic property of running processes and is isomorphic to the executed relationships among the processes [29,30].
Other theories of consciousness have also postulated that the emergence of a conscious experience is associated with a specific action or execution performed by the brain. Theory of Neuronal Group Selection (TNGS) postulates that qualia are high-dimensional discriminations of specific conscious scenes among a vast repertoire of different possible conscious scenes [31]. And, differences in qualia are determined by differences in the neural structure and dynamics. Similarly, in Integrated information theory (ITT), qualia arises from the reduction of uncertainty when a particular conscious state occurs out of a repertoire of alternative states [32]. Complex systems with larger numbers of possible states generate more information by reducing the greater uncertainty and thus can generate complex and vivid conscious experience. For example, consider the conscious experience of a spatial position of a point-like object (i.e. without shape or any other features except the location) in empty space. According to ITT, the conscious experience of the point location occurs when the brain reduces uncertainty by ruling out all possible different positions of that point in space. However, within this framework, it is not clear how the reduction of uncertainty can reoccur contentiously in time when the phenomenal state is retained conscious over time. By contrast, in the dynamical framework presented in my study, the continuous execution of processes is an inherent attribute of the framework. A phenomenal state arises from the execution of relationships among processes and is then isomorphic to the executed relationships. Therefore, the phenomenal state is a dynamic property that exists as long as the execution of this property by the system continues in time. In the above example with the spatial position, the phenomenal state isomorphic to a specific position in space would arise when the relationships among a process assigned to the specific position and other processes assigned to all other possible locations in space are executed. Further, the phenomenal state, in this case, would represent not a single point by itself but the point within the inner phenomenal space.
In this work, I present a mechanistic model that describes perceptual binding between system’s encoded space and time which are isomorphic to Euclidean space and time, respectively. The same framework can also be applied to other examples of perceptual binding [11]. The main goal of this work is to investigate how binding is affected by noise. The implication of noise on the system is quantified using spectral entropy. The results indicate that the binding mechanism is robust against noise.

Materials and Methods

The system of oscillating processes and relationships among processes are used to represent the physical carrier of phenomenal states. The system’s inner space and time are assumed to be encoded in relationships among the processes that are described by the following variables: P t → = p 1 t , p 2 t , … , p n t and Q t → = q 1 t , q 2 t , … , q m t respectively, where t is regular external time. There are n number of oscillating processes to encode space and m number of processes to encode time. The inner space and time are encoded in the relationships among processes which describe how the processes influence each other or interact. For the brain or neural networks such relationships would be set by the entrainment with external stimuli that are placed at different spatial positions and acting with varying time intervals. I assume that the system of processes is already entrained and thus each process is in specific relationships to all other processes as P → = A P → and Q → = B Q → , where the structure of A and B represents the memory which should be isomorphic to real space and time. The elements of matrices are independent of time. However, the relationships among processes encoded in A and B are continuously executed as all processes continuously oscillate in time. This is an important concept of this framework in which a phenomenal state (quale) is assumed to be a property of a dynamical system which emerges and exists when that property is realized or “happens”. Therefore, the relationships among processes must be continuously executed, yet the specific relationships among processes must be maintained over time as long as the experience of the corresponding phenomenal state is unchanged. Although, in general, the relationships among processes can be nonlinear (e.g., the relationships between two processes which are represented by a limit cycle in the phase plane), in the case of inner space and time the relationships are linear and isomorphic to Euclidean space. Therefore, Euclidean distance hollow matrices A and B are used to represent the relationships among processes:
p i = ∑ j = 1 n i − j 2 p j     q i = ∑ j = 1 m i − j 2 α q j ,
where ε and α are scaling parameters for the “distance and interval” measures between processes. If the processes representing inner space and time are independent then their dynamics are described by the following systems of ordinary differential equations:
d P → d t = A P → − X → + P →     d X → d t = P → d Q → d t = B Q → − Z → + Q →   d Z → d t = Q →
where
A = 0 ε ⋯ ( n − 1 ) 2 ε ε 0 ⋯ ( n − 2 ) 2 ε ⋮ ⋮ ⋱ ⋮ ( n − 1 ) 2 ε ( n − 2 ) 2 ε ⋯ 0 , B = 0 α ⋯ ( m − 1 ) 2 α α 0 ⋯ ( m − 2 ) 2 α ⋮ ⋮ ⋱ ⋮ ( m − 1 ) 2 α ( m − 2 ) 2 α ⋯ 0 .
System (2) has a solution P → = A P → and Q → = B Q → with oscillating P → = K → cos ( λ t ) + L → sin ( λ t ) and Q → = H → cos () η t ) + R → sin ( η t ) , where K → , L → , H → , R → are sets of amplitude values and λ and η are frequencies. Also, X t → = x 1 t , x 2 t , … , x n t and Z t → = z 1 t , z 2 t , … , z m t are sets of auxiliary processes. If the processes representing inner space and time are bound then the equations in System (2) must be coupled. Different coupling schemes have been investigated in my previous study [11]. Here, the number of modeled processes is reduced to simplify the analysis of the stochastic effects on the coupled systems. A dynamical system that contains a set of two processes P t → = p 1 t , p 2 t representing the inner space bound to two processes Q t → = q 1 t , q 2 t representing the inner time can be described by the following system of the coupled equations:
d p 1 d t = ε p 2 − p 1 − x 1 + ω f 1 q 1 , q 2 d p 2 d t = ε p 1 − p 2 − x 2 + ω f 2 q 1 , q 2 d x 1 d t = p 1 ,   d x 2 d t = p 2 d q 1 d t = α q 2 − q 1 − z 1 + ω g 1 p 1 , p 2 d q 2 d t = α q 1 − q 2 − z 2 + ω g 2 p 1 , p 2 d z 1 d t = q 1 ,   d z 2 d t = q 2
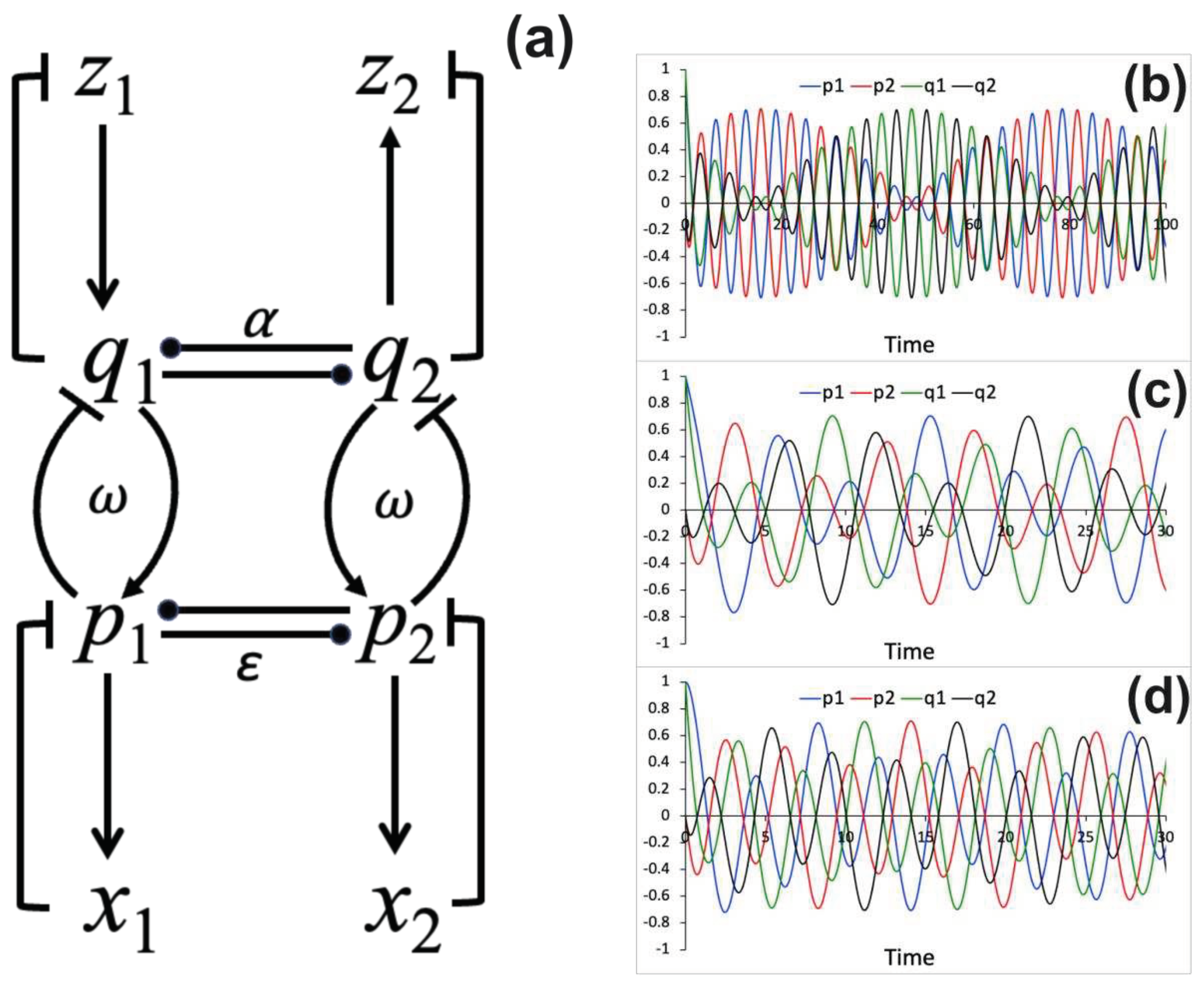
The binding interaction between p 1 , p 2 , x 1 , x 2 and q 1 , q 2 , z 1 , z 2 sets of processes is described by f 1 q 1 , q 2 , f 1 q 1 , q 2 and g 1 p 1 , p 2 , g 1 p 1 , p 2 functions. For System (3), the functions are set as: f 1 q 1 , q 2 = q 1 , f 2 q 1 , q 2 = q 2 , g 1 p 1 , p 2 = − p 1 , g 2 p 1 , p 2 = − p 2 . This interaction scheme is shown in Figure 1a. The binding strength between p i and q i processes depends on the parameter ω. The sign of parameter ε determines whether p 1 and p 2 processes are mutually activating (ε > 0 ) or inhibiting (ε < 0 ) each other. Similarly, the sign of parameter α determines whether q 1 and q 2 processes are mutually activating ( α > 0 ) or inhibiting ( α < 0 ) each other. Although, this interaction scheme with a fixed coupling constant ω = 1 and an alternative wiring: f 1 q 1 , q 2 = q 1 − q 2 , f 2 q 1 , q 2 = q 2 − q 1 , g 1 p 1 , p 2 = p 2 − p 1 , g 2 p 1 , p 2 = p 1 − p 2 have been investigated in my previous study [11], in this work, the dynamic behavior of the system is analyzed as a function of coupling strength constant ω. As an example, numerical solutions of System (3) for P t → = p 1 t , p 2 t and Q t → = q 1 t , q 2 t processes obtained for three different binding strength parameter values (ω = 0.1, 0.5 and 1) are shown in Figures 1b-d.
Preprints 92898 g001
Figure 1. The interaction diagram and dynamical relationships among processes. (a). The diagram that shows interaction among processes. (b-d) Numerical solutions for the time evolution of P t → = p 1 t , p 2 t and Q t → = q 1 t , q 2 t processes computed using different values of the coupling constant: (b) ω = 0.1 , (c) ω = 0.5 , (d) ω = 1 . In all simulations, ε = − 1 and α = − 1 thus representing the mutual inhibition between p 1 and p 2 processes and between q 1 and q 2 processes. The following initial conditions are used: P 0 → = 1 , 0 , X 0 → = 0 , 0 and Q 0 → = 1 , 0 , Z 0 → = 0 , 0 .
Figure 1. The interaction diagram and dynamical relationships among processes. (a). The diagram that shows interaction among processes. (b-d) Numerical solutions for the time evolution of P t → = p 1 t , p 2 t and Q t → = q 1 t , q 2 t processes computed using different values of the coupling constant: (b) ω = 0.1 , (c) ω = 0.5 , (d) ω = 1 . In all simulations, ε = − 1 and α = − 1 thus representing the mutual inhibition between p 1 and p 2 processes and between q 1 and q 2 processes. The following initial conditions are used: P 0 → = 1 , 0 , X 0 → = 0 , 0 and Q 0 → = 1 , 0 , Z 0 → = 0 , 0 .
Preprints 92898 g001
Next, System (3) is converted into a stochastic model using Gillespie’s method. For the system S → = p 1 , p 2 , x 1 , x 2 , q 1 , q 2 , z 1 , z 2 , the states are updated using the following general Gillespie’s scheme [33]:
  • Initialize the process state vector, S → , and set the initial time at 0.
  • Calculate the propensities, a k S → .
  • Generate a uniform random number, r 1 .
  • Compute the time for the next event, τ = − 1 ∑ k a k S → ln r 1 .
  • Generate a uniform random number, r 2 .
  • Find which event is next, I = i , if ∑ k = 1 i − 1 a k S → ∑ k a k S → ≤ r 2 < ∑ k = 1 i a k S → ∑ k a k S →
  • Update state vector, S → → S → + y i .
  • Update time, t → t + τ .
  • Repeat (2)-(8).
The stochastic model is used to characterize the interplay between the binding strength ω and noise. All numerical solutions of System (3) are obtained by using XPP/XPPAUT software (http://www.math.pitt.edu/~bard/xpp/xpp.html, accessed on 4th November 2023). XPP codes that are sufficient to reproduce all results presented in this work are provided in Appendix A. The code A is used to generate results for the deterministic model described by Equations (3) and the code B is used to perform stochastic simulation and produce the corresponding model results.
The spectrum analysis and spectral entropy are used to quantify noise effects on the system. The spectral analysis is a common tool in signal processing and in neurophysiological studies [34–37]. Spectral entropy is based on Shannon's entropy formalism that is a foundational concept of information theory [38]. The entropy metric is an important component of information integration theory of consciousness [39,40]. I have used spectral analysis tools to study noise effects on systems of different sizes which are described by uncoupled equations (2) [12]. Here, I use the same method to compute spectral entropy for two systems of bound processes to characterize the interplay between binding strength and noise.
The spectral entropy value H is computed using the following equation:
H = − k ∑ j = 1 2048 P S D j ^ Log 2 P S D ^ j ,
where k = 1 Log 2 2048 ≈ 0.1 and P S D ^ is the normalized power spectral density that is computed by dividing the power spectral density by the total power [41]. The power spectral density is computed from the fast Fourier transform (FFT) obtained for each process trajectory p i t that is simulated using code B in Appendix A. The Fourier Analysis function in Excel’s Analysis ToolPak is used to obtain the corresponding signal p i f in the frequency domain. 4096 points are used to compute p i f , which corresponds to a total average simulation time of ~930 arb. u. where the period of oscillations ranges between ~4-7 arb. u. The sampling frequency, f , is obtained by dividing the number of points by the time interval, Δ t . The frequency magnitudes are computed using Excel’s IMABS function. The power spectral density is calculated using the following formula: P S D j = p f j 2 / 2 Δ f . 2048 data points are used to compute spectral densities and the corresponding spectral entropy value from Equation (4). Finally, the coupling parameter ω is varied to characterize the effect of the binding strength on system’s spectral entropy values. For each fixed value of the coupling parameter ω, simulations are repeated ten times. Then, these ten spectral entropy values are used to compute the average spectral entropy value and the corresponding standard deviation from mean.

Results

In my previous work [11], the deterministic mathematical model described by System (3) has been successfully applied to study the perceptual binding between the location of a stimulus at two possible positions and presence or absence of a light stimulus at these positions. However, the binding strength ω has been assumed to be the largest: ω = 1 . It has been shown that System (3) exhibit different regimes of modulated oscillations depending on ε and α parameter values [11]. By contrast, in this study, ε and α are fixed and the binding strength ω is varied. Further, the model is used to describe the possible binding mechanism between encoded space and time. Thus, the model allows to investigate how the encoding signals may change if the binding strength between encoded space and time is varied. It is assumed that the space and time could be perceived independently as well as together. This assumption follows from the assumption that entrainment of the subsystem that encodes inner space can be performed either simultaneously with or independently from entrainment of the subsystem that encodes inner time. In addition, stochastic simulations of the model are performed to characterize robustness of the binding mechanism against noise.
When two oscillatory systems are coupled, they modulate each other and thus the oscillatory dynamics of the coupled system is altered. The modulation depends on the parameter ω that describes the binding strength between two oscillatory systems, see Figure 1a. Figures 1b-d demonstrate how the binding strength parameter influences the modulation of two coupled oscillatory systems. To characterize robustness of the coupled system against noise, stochastic simulations are performed. The results of stochastic model simulations are shown in Figure 2. The stochastic model is simulated using different values of the binding strength parameter ω. Figures 2a, d, g present the stochastic trajectories for P t → = p 1 t , p 2 t and Q t → = q 1 t , q 2 t processes obtained for the following binding strength parameter values ω = 0.1, 0.5 and 1. These results can be compared to numerical results of the deterministic model shown in Figures 1b-d which are obtained for the same ω parameter values. Although, the initial conditions used for simulation results in Figures 1 and 2 are different. Figures 2b, e, h show distribution histograms for process p 1 obtained from trajectories recorded over much larger time frames (>1000 arb. u.) than shown in Figures 2a, d, g. Also, for p 2 and q 1 , 2 processes the corresponding histograms (not shown) look similar to those shown in Figures 2a, d, g. Normalized power spectral densities are also computed from trajectories as described in Method section. Alteration of the normalized power spectral densities for process p 1 as a function of varied binding strength parameter values is demonstrated in Figures 2c, f, i. There is a shift of normalized power spectrum peaks to higher frequencies as the binding strength ω increases.
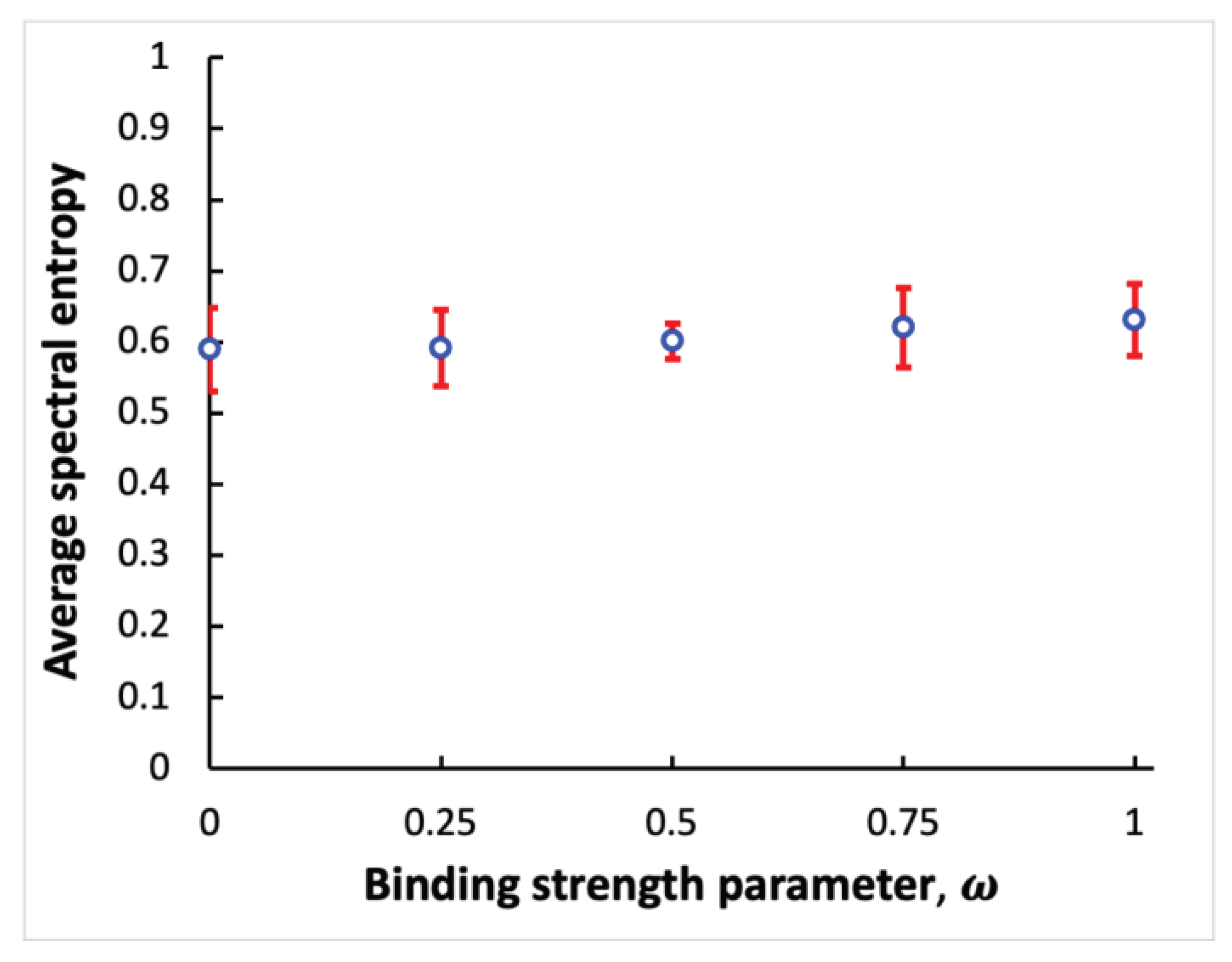
Next, spectral entropy is calculated using the power spectra to quantify sensitivity of the coupled systems of processes to noise. For cases shown in Figure 2, the spectral entropy values ≈ 0.55, 0.57 and 0.55 obtained using the power spectra shown in Figures 2c, f, i with binding strength parameter values ω = 0.1, 0.5 and 1, respectively. Because the spectral entropy values do not change significantly with alteration of the binding strength parameter, it can be concluded that strongly and weakly bound oscillatory systems are equally robust against noise. To test this hypothesis in a more systematic way, fifty independent simulation experiments for the coupled systems of processes are performed, with ten simulation experiments for each of five different values of the binding strength parameter: ω = 0, 0.25, 0.5, 0.75 and 1. In each independent simulation, the spectral entropy value is computed. Then, the average over ten spectral entropy values is calculated for each specific ω parameter value. Figure 3 shows the average spectral entropy values plotted versus the binding strength parameter. The error bars represent standard deviation values. The result indicates that the robustness of the coupled systems against noise does not vary significantly when the binding strength changes. Therefore, the binding mechanism used to couple two oscillatory systems is resilient to noise.

Discussion

In this work, I present a mechanistic stochastic model of perceptual binding between two percepts. I embrace the assumption proposed in the temporo-spatial theory of consciousness, that the brain implements its own inner time and space for conscious processing of outside world [6,7]. Thus, I use my model to investigate the possible binding mechanism between encoded space and time. Specifically, the model is used to investigate how the oscillating processes that encode the inner space and time are modulated when the binding strength between them is varied. Although, the inner space and time could be always strongly integrated, unified and represented by inseparable sets of processes, in this study the main assumption is that the inner space and time can be perceptually represented independently or weakly/strongly bound. Therefore, spatial pattern variations and temporal changes could be in principle perceived as separable events. Further, the model can be applied to describe binding mechanism between any two percepts that can be represented by two systems of oscillating processes, as has been demonstrated in my previous work [11].
Stochastic simulations of the model show that the binding mechanism is robust against inherent noise. Therefore, the model results provide some explanation why perceptual experiences and perceptual binding can be retained robustly unchanged despite ubiquitous noise sources in neuronal circuits. Further, in my previous work it has been shown that large systems that involve more interconnected oscillating processes are less noise sensitive than small systems with fewer processes [12]. Noise is suppressed in the large systems by negative feedback loops that are involved in the network of interconnected processes. Also, the peaks of power spectral densities have been shifted from low to high frequency values with increase of the number of processes [12]. Figures 2c, f, i also show a shift of normalized power spectrum peaks to higher frequencies as the binding strength increases. This shift to higher frequencies occurs because the binding mechanism involves negative feedback loops, see Figure 1a. Similar observations have been reported for gene regulatory networks with negative feedback loops [42,43].
In this study, the interplay between binding strength and noise is characterized using power spectral density and spectral entropy values. The spectral analysis has been often used to analyze electroencephalograms to study neurophysiology of sleep [34], predict changes in memory performance [41], detect differences in brain activities of subjects under different conditions [35,36,37]. Because the same spectral analysis tools are used in this work, it should be relatively easy to compare results and validate conclusions derived from the model simulations with results obtained in neurophysiological experiments.
Overall, the mechanistic model allows us to better understand how binding can alter dynamics of neural-like oscillatory systems. The stochastic version of the model gives us a useful tool to study noise effects on systems that involve binding. Therefore, we can better understand mechanisms with which the brain suppresses or employs inherent noise to make our perceptual binding and experiences sturdy.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable

Conflicts of Interest

The author declares no conflict of interest.

Appendix A

The XPPAUT code A is used to simulate results in Figures 1b-d.
# code A
init p1=1, p2=0, x1=0, x2=0, q1=1, q2=0, y1=0, y2=0
par eps=-1.0, alpha=-1.0, w=1.0
p1'=eps*p2-p1-x1+w*q1
x1'=p1
p2'=eps*p1-p2-x2+w*q2
x2'=p2
q1'=alpha*q2-q1-z1-w*p1
z1'=q1
q2'=alpha*q1-q2-z2-w*p2
z2'=q2
@ dt=.025, total=100, xplot=t, yplot=p1
@ xmin=0, xmax=100, ymin=-1, ymax=1
done
The XPPAUT code B is used to generate trajectories and histograms in Figure 2.
# code B
init p1=1000, p2=0, x1=0, x2=0, q1=1, q2=0, z1=0, z2=0
par eps=-1.0, alpha=-1.0, w=1
# compute the cumulative event
x11=abs(eps*p2)
x12=x11+abs(eps*p1)
x13=x12+abs(alpha*q2)
x21=x13+abs(alpha*q1)
x22=x21+abs(p1)
x23=x22+abs(p2)
x31=x23+abs(q1)
x32=x31+abs(q2)
x33=x32+abs(x1)
x41=x33+abs(x2)
x42=x41+abs(z1)
x43=x42+abs(z2)
#binding
x44=x43+abs(w*p1)
x51=x44+abs(w*p2)
x52=x51+abs(w*q1)
x53=x52+abs(w*q2)
# choose a random event
s2=ran(1)*x53
y1=(s2<x11)
y2=(s2<x12)&(s2>=x11)
y3=(s2<x13)&(s2>=x12)
y4=(s2<x21)&(s2>=x13)
y5=(s2<x22)&(s2>=x21)
y6=(s2<x23)&(s2>=x22)
y7=(s2<x31)&(s2>=x23)
y8=(s2<x32)&(s2>=x31)
y9=(s2<x33)&(s2>=x32)
y10=(s2<x41)&(s2>=x33)
y11=(s2<x42)&(s2>=x41)
y12=(s2<x43)&(s2>=x42)
y13=(s2<x44)&(s2>=x43)
y14=(s2<x51)&(s2>=x44)
y15=(s2<x52)&(s2>=x51)
y16=(s2>=x52)
# time for the next event
tr'=tr-log(ran(1))/x53
p1'=p1+sign(eps)*sign(p2)*y1-sign(p1)*y5-sign(x1)*y9+sign(q1)*y15
p2'=p2+sign(eps)*sign(p1)*y2-sign(p2)*y6-sign(x2)*y10+sign(q2)*y16
q1'=q1+sign(alpha)*sign(q2)*y3-sign(q1)*y7-sign(z1)*y11-sign(p1)*y13
q2'=q2+sign(alpha)*sign(q1)*y4-sign(q2)*y8-sign(z2)*y12-sign(p2)*y14
x1'=x1+sign(p1)*y5
x2'=x2+sign(p2)*y6
z1'=z1+sign(q1)*y7
z2'=z2+sign(q2)*y8
@ bound=100000000,meth=discrete,total=10000000,njmp=1000
@ xp=tr,yp=p1
@ xlo=0,ylo=-1000,xhi=40,yhi=1000
done

References

  1. Roskies, A.L. , The binding problem. Neuron, 1999. 24(1): p. 7-9, 111-25.
  2. von der Malsburg, C. , The what and why of binding: the modeler's perspective. Neuron, 1999. 24(1): p. 95-104, 111-25. [CrossRef]
  3. von der Malsburg, C. , Binding in models of perception and brain function. Curr Opin Neurobiol, 1995. 5(4): p. 520-6. [CrossRef]
  4. Gray, C.M. , The temporal correlation hypothesis of visual feature integration: still alive and well. Neuron, 1999. 24(1): p. 31-47, 111-25. [CrossRef]
  5. Singer, W. , Neuronal synchrony: a versatile code for the definition of relations? Neuron, 1999. 24(1): p. 49-65, 111-25. [CrossRef]
  6. Northoff, G. , What the brain's intrinsic activity can tell us about consciousness? A tri-dimensional view. Neuroscience and Biobehavioral Reviews, 2013. 37(4): p. 726-738. [CrossRef]
  7. Northoff, G. and Z.R. Huang, How do the brain's time and space mediate consciousness and its different dimensions? Temporo-spatial theory of consciousness (TTC). Neuroscience and Biobehavioral Reviews, 2017. 80: p. 630-645. [CrossRef]
  8. Fingelkurts, A.A. and A.A. Fingelkurts, Mind as a nested operational architectonics of the brain. Physics of Life Reviews, 2012. 9(1): p. 49-50.
  9. Fingelkurts, A.A., A. A. Fingelkurts, and C.F.H. Neves, Phenomenological architecture of a mind and Operational Architectonics of the brain: the unified metastable continuum Journal of New Mathematics and Natural Computing, 2009. 5(1): p. 221-244.
  10. O'Reilly, R.C., R. Busby, and R. Soto, Three forms of binding and their neural substrates: Alternatives to temporal synchrony, in The Unity of Consciousness, A. Cleeremans, Editor. 2003, Oxford University Press. p. 168--192.
  11. Kraikivski, P. , A Dynamic Mechanistic Model of Perceptual Binding. Mathematics, 2022. 10(7). [CrossRef]
  12. Kraikivski, P. , Implications of Noise on Neural Correlates of Consciousness: A Computational Analysis of Stochastic Systems of Mutually Connected Processes. Entropy, 2021. 23(5): p. 583. [CrossRef]
  13. Azouz, R. and C.M. Gray, Cellular mechanisms contributing to response variability of cortical neurons in vivo. J Neurosci, 1999. 19(6): p. 2209-23. [CrossRef]
  14. Faisal, A.A., L. P. Selen, and D.M. Wolpert, Noise in the nervous system. Nat Rev Neurosci, 2008. 9(4): p. 292-303. [CrossRef]
  15. Mainen, Z.F. and T.J. Sejnowski, Reliability of spike timing in neocortical neurons. Science, 1995. 268(5216): p. 1503-6. [CrossRef]
  16. Steinmetz, P.N. , et al., Subthreshold voltage noise due to channel fluctuations in active neuronal membranes. J Comput Neurosci, 2000. 9(2): p. 133-48. [CrossRef]
  17. White, J.A., J. T. Rubinstein, and A.R. Kay, Channel noise in neurons. Trends Neurosci, 2000. 23(3): p. 131-7. [CrossRef]
  18. Calvin, W.H. and C.F. Stevens, Synaptic noise and other sources of randomness in motoneuron interspike intervals. J Neurophysiol, 1968. 31(4): p. 574-87. [CrossRef]
  19. Fellous, J.M. , et al., Synaptic background noise controls the input/output characteristics of single cells in an in vitro model of in vivo activity. Neuroscience, 2003. 122(3): p. 811-29. [CrossRef]
  20. Jacobson, G.A. , et al., Subthreshold voltage noise of rat neocortical pyramidal neurones. J Physiol, 2005. 564(Pt 1): p. 145-60. [CrossRef]
  21. Faisal, A.A. and S.B. Laughlin, Stochastic simulations on the reliability of action potential propagation in thin axons. PLoS Comput Biol, 2007. 3(5): p. e79. [CrossRef]
  22. van Rossum, M.C., B. J. O'Brien, and R.G. Smith, Effects of noise on the spike timing precision of retinal ganglion cells. J Neurophysiol, 2003. 89(5): p. 2406-19. [CrossRef]
  23. Longtin, A., A. Bulsara, and F. Moss, Time-interval sequences in bistable systems and the noise-induced transmission of information by sensory neurons. Phys Rev Lett, 1991. 67(5): p. 656-659. [CrossRef]
  24. Collins, J.J., T. T. Imhoff, and P. Grigg, Noise-enhanced information transmission in rat SA1 cutaneous mechanoreceptors via aperiodic stochastic resonance. J Neurophysiol, 1996. 76(1): p. 642-5. [CrossRef]
  25. Douglass, J.K. , et al., Noise enhancement of information transfer in crayfish mechanoreceptors by stochastic resonance. Nature, 1993. 365(6444): p. 337-40. [CrossRef]
  26. Bulsara, A.R. and A. Zador, Threshold detection of wideband signals: A noise-induced maximum in the mutual information. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics, 1996. 54(3): p. R2185-R2188. [CrossRef]
  27. Kosko, B. and S. Mitaim, Stochastic resonance in noisy threshold neurons. Neural Netw, 2003. 16(5-6): p. 755-61. [CrossRef]
  28. Mitaim, S. and B. Kosko, Adaptive stochastic resonance in noisy neurons based on mutual information. IEEE Trans Neural Netw, 2004. 15(6): p. 1526-40. [CrossRef]
  29. Kraikivski, P. , Building Systems Capable of Consciousness. Mind & Matter, 2017. 15: p. 185-195.
  30. Kraikivski, P. , Systems of Oscillators Designed for a Specific Conscious Percept. New Mathematics and Natural Computation, 2020. 16: p. 73–88. [CrossRef]
  31. Edelman, G.M. , Naturalizing consciousness: a theoretical framework. Proc Natl Acad Sci U S A, 2003. 100(9): p. 5520-4. [CrossRef]
  32. Balduzzi, D. and G. Tononi, Integrated information in discrete dynamical systems: motivation and theoretical framework. PLoS Comput Biol, 2008. 4(6): p. e1000091. [CrossRef]
  33. Gillespie, D.T. , Exact stochastic simulation of coupled chemical reactions. The Journal of Physical Chemistry, 1977. 81(25): p. 2340-2361. [CrossRef]
  34. Prerau, M.J. , et al., Sleep Neurophysiological Dynamics Through the Lens of Multitaper Spectral Analysis. Physiology (Bethesda), 2017. 32(1): p. 60-92. [CrossRef]
  35. Tuominen, J. , et al., Segregated brain state during hypnosis. Neurosci Conscious, 2021. 2021(1): p. niab002. [CrossRef]
  36. Thilakavathi, B. , et al., EEG power spectrum analysis for schizophrenia during mental activity. Australasian Physical & Engineering Sciences in Medicine, 2019. 42(3): p. 887-897. [CrossRef]
  37. Helakari, H. , et al., Spectral entropy indicates electrophysiological and hemodynamic changes in drug-resistant epilepsy - A multimodal MREG study. Neuroimage Clin, 2019. 22: p. 101763. [CrossRef]
  38. Shannon, C.E. , A mathematical theory of communication. The Bell System Technical Journal, 1948. 27(3): p. 379-423.
  39. Tononi, G. , An information integration theory of consciousness. BMC Neuroscience, 2004. 5: p. 42. [CrossRef]
  40. Seth, A.K. , et al., Theories and measures of consciousness: An extended framework. PNAS, 2006. 103(28): p. 10799 –10804. [CrossRef]
  41. Tian, Y. , et al., Spectral Entropy Can Predict Changes of Working Memory Performance Reduced by Short-Time Training in the Delayed-Match-to-Sample Task. Front Hum Neurosci, 2017. 11: p. 437. [CrossRef]
  42. Austin, D.W. , et al., Gene network shaping of inherent noise spectra. Nature, 2006. 439(7076): p. 608-11. [CrossRef]
  43. Simpson, M.L., C. D. Cox, and G.S. Sayler, Frequency domain analysis of noise in autoregulated gene circuits. Proc Natl Acad Sci U S A, 2003. 100(8): p. 4551-6. [CrossRef]
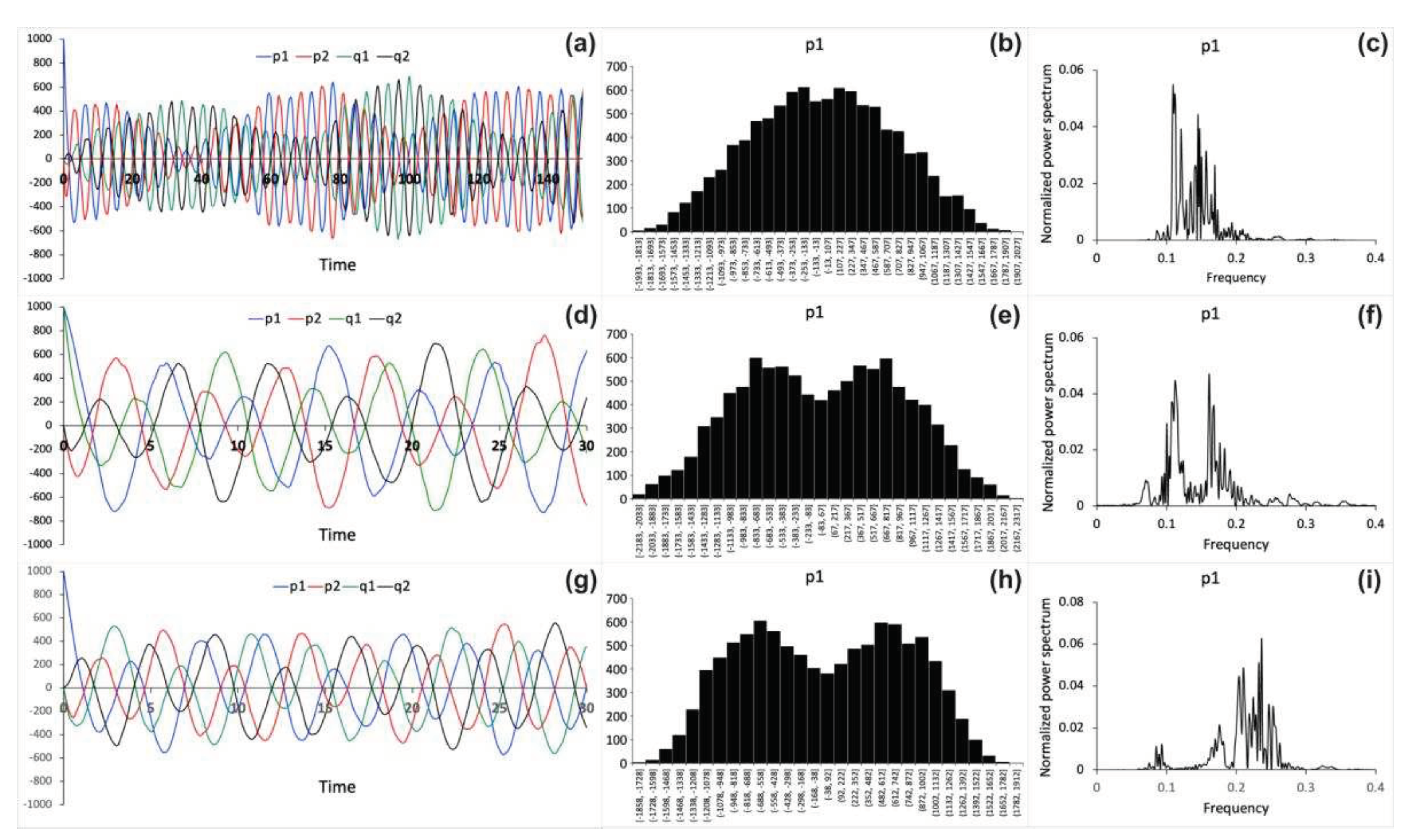
Preprints 92898 g002
Figure 2. Numerical stochastic simulation results obtained using the following binding strength parameter values: (a, b, c) ω = 0.1, (d, e, f) ω = 0.5 and (g, h, i) ω = 1. (a, d, g) Stochastic trajectories for P t → = p 1 t , p 2 t and Q t → = q 1 t , q 2 t processes. Time is shown in arbitrary units. The following initial conditions are used: P 0 → = 1000 , 0 , X 0 → = 0 , 0 , Q 0 → = 1 , 0 , Z 0 → = 0 , 0 in (a), (g) and P 0 → = 1000 , 0 , X 0 → = 0 , 0 , Q 0 → = 1000 , 0 , Z 0 → = 0 , 0 in (d). (b, e, h) Distribution histograms for process p 1 , computed using trajectories recorded over (b) 1580 arb. u., (e) 1120 arb. u., and (h) 1071 arb. u time frames. (c, f, i) Normalized power spectral densities for process p 1 .
Figure 2. Numerical stochastic simulation results obtained using the following binding strength parameter values: (a, b, c) ω = 0.1, (d, e, f) ω = 0.5 and (g, h, i) ω = 1. (a, d, g) Stochastic trajectories for P t → = p 1 t , p 2 t and Q t → = q 1 t , q 2 t processes. Time is shown in arbitrary units. The following initial conditions are used: P 0 → = 1000 , 0 , X 0 → = 0 , 0 , Q 0 → = 1 , 0 , Z 0 → = 0 , 0 in (a), (g) and P 0 → = 1000 , 0 , X 0 → = 0 , 0 , Q 0 → = 1000 , 0 , Z 0 → = 0 , 0 in (d). (b, e, h) Distribution histograms for process p 1 , computed using trajectories recorded over (b) 1580 arb. u., (e) 1120 arb. u., and (h) 1071 arb. u time frames. (c, f, i) Normalized power spectral densities for process p 1 .
Preprints 92898 g002
Preprints 92898 g003
Figure 3. Dependence of spectral entropy on the coupling strength between two bound oscillatory systems. Open circles represent the average spectral entropy values obtained using different values of the binding strength parameter ω. Error bars provide standard deviation values.
Figure 3. Dependence of spectral entropy on the coupling strength between two bound oscillatory systems. Open circles represent the average spectral entropy values obtained using different values of the binding strength parameter ω. Error bars provide standard deviation values.
Preprints 92898 g003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated