Prerpints.org logo
Preprint
Technical Note

LeafArea Package: A Tool for Estimating Leaf Area in Andean Fruit Species

Altmetrics

Downloads

85

Views

41

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

11 December 2023

Posted:

12 December 2023

You are already at the latest version

Alerts
Abstract
Leaf area estimation is a critical component in the study of plant growth and productivity within agricultural systems. This research introduces the LeafArea package, a specialized tool designed to calculate the leaf area of six distinct Andean fruit species: S. quitoense, S. betaceum, P. peruviana, R. fruticosus, P. ligularis and P. edulis. Leveraging response variables such as species type, leaf length and width, the package employs advanced machine learning algorithms to estimate leaf area accurately. The primary focus of the study is to identify the most effective model for describing the relationship between leaf width, length, and area for each plant species. Currently, the LeafArea package utilizes four different machine learning algorithms, namely generalized linear model (GLM), generalized linear mixed model (GLMM), Random Forest and XGBoost. Among these, XGBoost stands out as a top-performing algorithm, exhibiting exceptional predictive accuracy. The evaluation metrics employed in the program provide valuable insights for researchers, aiding in informed decision-making. Specifically, XGBoost demonstrates significantly lower prediction errors and approaches a near-perfect R2 value, emphasizing its potential to enhance predictive accuracy. These results underscore the efficacy of machine learning techniques, as a compelling choice for researchers seeking precise and robust predictions in leaf area estimation. The LeafArea package thus represents a valuable tool for advancing our understanding of plant growth dynamics, resource allocation, and overall productivity within agricultural ecosystems.
Keywords: 
Subject: Biology and Life Sciences  -   Agricultural Science and Agronomy

1. Introduction

Leaf area estimation serves as a vital parameter in various agricultural practices, including crop management, yield prediction, and the optimization of resource utilization [1]. Recognizing this significance, our study introduces the LeafArea package available on GitHub (https://github.com/velasquez-vasconez/LeafArea), a sophisticated tool tailored for the precise calculation of leaf area in six distinct Andean fruit species: Solanum quitoense, Solanum betaceum, Physalis peruviana, Rubus fruticosus, Passiflora ligularis and Passiflora edulis.
This prominent fruit species play important roles in the economy and traditional culture of the Andean region. These fruits are not only integral to the ecological diversity of the Andean region but also play pivotal roles in the local economy and cultural traditions [2]. Their cultivation and utilization have been deeply intertwined with the livelihoods of Andean communities for generations.
Andean fruit species have gained global recognition for their nutritional value, unique flavors, and potential health benefits [2,3,4]. Exotic fruits continue to grow worldwide, understanding the growth and productivity of these species becomes increasingly relevant. Accurate leaf area estimation, as studied in this research, provides a crucial foundation for optimizing cultivation practices, resource allocation, and ultimately enhancing the yield and quality of these valuable fruits [5]. By delving into the intricate relationships between leaf traits and area, this study not only contributes to the scientific understanding of plant growth but also offers practical insights that can benefit both farmers and researchers working to maximize the potential of Andean fruit species.
Our primary objective centers on identifying the most effective model for elucidating the intricate relationship between leaf width, length, and area specific to each plant species. The LeafArea package computes leaf area using the best GLM and GLMM described in this study. Additionally, it incorporates two robust machine learning algorithms, namely Random Forest and XGBoost, demonstrating its potential to revolutionize leaf area estimation practices.
Accurate and reliable models for estimating leaf area based on easily measurable leaf traits are invaluable tools for both researchers and farmers. This innovative approach not only ensures accurate leaf area estimations but also propels the study into the forefront of modern research methodologies in plant science. The LeafArea package emerges as a transformative tool, facilitating advancements in our understanding of Andean fruit plants growth and provides valuable tools for researchers and farmers to optimize plant breeding practices and enhance productivity in the region.

2. Materials and Methods

This The growth patterns of leaves from various plant species were evaluated, including blackberry (R. fruticosus), tamarillo (S. betaceum), sweet granadilla (P. ligularis), lulo (S. quitoense), goldenberry (P. peruviana) and passion fruit (P. edulis). The plants were planted in experimental plots that were established in six municipalities of the department of Nariño such as Arboleda, Sandoná, La Florida, El Peñol, Providencia and Ipiales. To calculate plant leaf area using the ImageJ program v1.4.3 [6]. Digital images of the plant leaves were captured under proper scale and lighting. Subsequently, these images were imported into ImageJ, where the user selects the region of interest by tracing the outline of each leaf. ImageJ then calculates the area of the selected the region of interest, providing an accurate measurement of the leaf area in pixels. To convert this measurement to a physical unit, such as square centimeters, a scale calibration was performed using a reference object of known dimensions within the image. Finally, the software provides the calculated leaf area in the desired unit, allowing for precise and efficient analysis of plant leaf size. We initiated our analysis by conducting a pairwise scatter plot matrix, which provided insights into the relationships between leaf area, leaf length, and leaf width. To address the observed non-linear relationship between leaf area and its predictors, we employed a square root transformation (sqrt) on the response variable. This transformation was applied to enhance the functional form of the variable and to achieve better data symmetry. A high degree of correlation between the leaf length and width variables indicated the presence of multicollinearity issues. Variance inflation factors (vif) exceeded 15 for the leaf dimension variables, suggesting potential problems in statistical analysis. To mitigate these issues, we adopted a common practice of retaining the predictor variable that demonstrated the best model fit. Subsequently, we decided to eliminate the leaf width variable, which reduced multicollinearity in the final model. As an additional strategy, we introduced a synthetic variable, denoted as ‘Length_width’, which was computed as the square root of the product of leaf length and width. In addition to deterministic models, we assessed machine learning techniques such as Random Forest and XGBoost. These methods provided a holistic perspective on predictive capabilities, revealing a hierarchy of predictive power. The data was then split into training and testing sets with a random seed set to ensure reproducibility. The split ratio was 80:20 for training and testing sets, respectively. The Random Forest and XGBoost model was implemented using the ‘rf’ and ‘xgbTree’ method, respectively, from the ‘caret’ package [7]. The performance of four models was evaluated on the test and training sets. Metrics such as RMSE, MAE, MAPE, and R2 were calculated and reported for each model. Finally, the best models were implemented in the LeafArea package to predict the LeafArea for the entire dataset, and the predictions were added as new variables to the original dataset. All statistical procedures were performed using the R software v4.2.3 [8].

Results and discussion

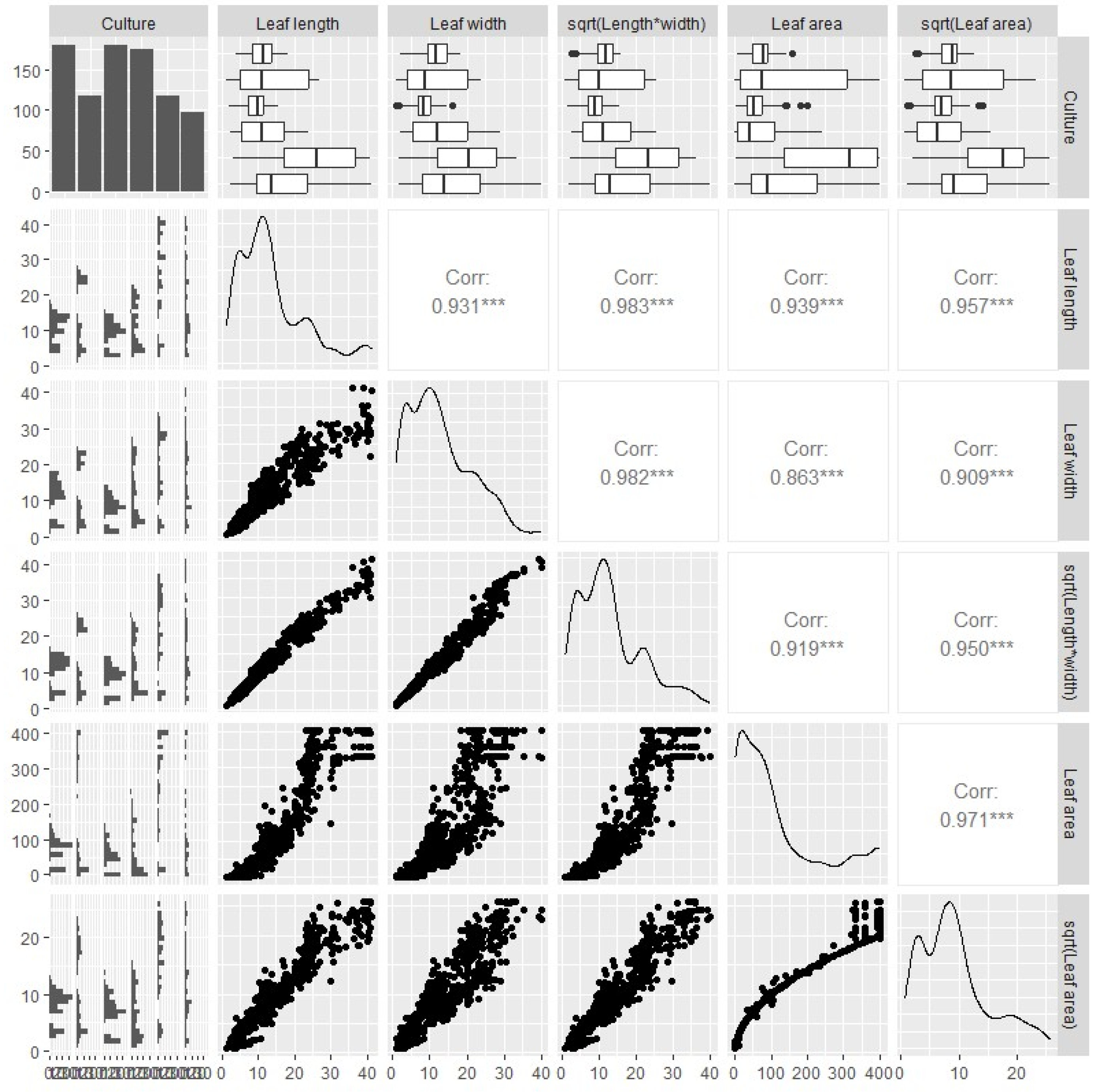
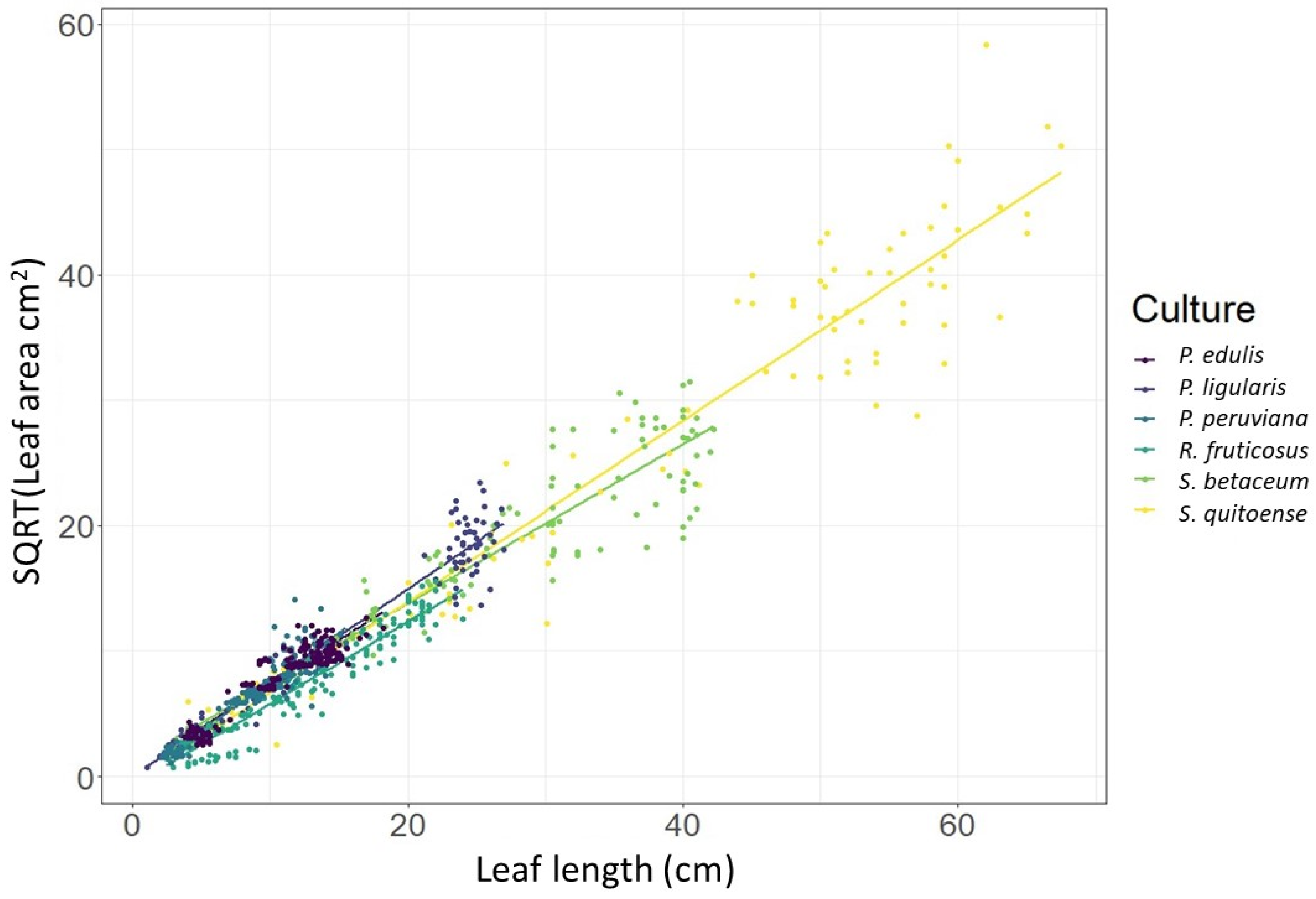
Pairwise scatter plot matrix revealed that leaf area revealed a significant positive correlation (p<0.001) with both leaf length and width (Figure 1). As expected, the expansion of the leaf surface demonstrates exponential growth in relation to the independent variables (Figure 1). The leaf continues to grow, especially in terms of both width and length, the rate at which its area increases accelerate significantly. To address the observed non-linear relationship between leaf area and its predictors, we applied a square root transformation (sqrt) to the response variable. The square root transformation improved the functional form of the variable and the symmetry of the data, as evident from the distribution of points and the boxplots (Figure 1). Furthermore, the correlation coefficient with the predictor variables improved by up to four points (Figure 1). This statistical technique is effective in cases where the data exhibits a right-skewed distribution or when the relationship between variables is curvilinear, meaning that the rate of change is not constant [9]. The square root transformation is one of the power transformations used to stabilize variances and linearize relationships [10].
The high degree of correlation between the variables Leaf length and width indicated the presence of multicollinearity problems. Variance inflated (vif) values were found to be greater than 15 for the leaf dimension variables (Figure S1). Multicollinearity can create problems in statistical analysis, as it becomes challenging to disentangle the unique contributions of each predictor variable to the dependent variable [11,12,13]. To mitigate the multicollinearity problems, a common practice is to retain the predictor variable that demonstrated the best model fit and the lowest RMSE values. It was decided to eliminate the leaf width variable that generated the models with the lowest fit to reduce multicollinearity in the final model. As an additional strategy, we introduced a synthetic variable, denoted as ‘Length_width’, which was computed as the square root of the product of the leaf length and width. The composed variable was identified as the most suitable representation of leaf expansion and played an important role in producing the most effective GLM and GLMM models (Figure 2), as suggested by Favero [14] and Freedman [15].
The GLMM models are better suited for data with hierarchical or clustered structures, where observations are not necessarily independent [16]. The highest Log-likelihood value was from the GLM3 model provides the best overall fit among the GLM and GLMM models (Figure 2). Among the GLM models, GLM3 has the highest Log-likelihood value. The obtained results emphasize the significance of the synthetic variable ‘Length_width’ as a more predictive factor compared to the individual variables that were independently evaluated. Synthetic variables are often created by combining or transforming multiple individual variables to better represent complex underlying relationships in the data [17]. On the other hand, GLMMs were better suited to capture the intricate relationships often encountered in real-world datasets (Figure 3). By doing so, they enhance predictive accuracy and model performance [18]. This collective evidence underscores the importance of adopting comprehensive modeling approaches, such as GLMMs and composite variables, when seeking a deeper understanding of complex datasets and striving for more robust predictive capabilities.
In addition to deterministic models, we evaluated machine learning techniques such as Random Forest and XGBoost. The evaluation of performance metrics offered a holistic perspective on their predictive capabilities (Table 1). Notably, the results revealed a clear hierarchy of predictive power (Table 1). Among the GLMs and GLMMs, GLM3 and GLMM3 emerged as the strongest contenders, showcasing lower prediction errors and higher R2 values. However, the machine learning models, particularly XGBoost, surpassed all others, exhibiting remarkably lower RMSE, MAE, MAPE, and highest R2. This outcome underscores the remarkable potential of machine learning techniques in enhancing predictive accuracy and highlights XGBoost as a standout performer, making it a compelling choice for tasks that demand precise and robust predictions.
The comparison of performance metrics across various modeling techniques reveals a striking contrast, particularly with the introduction of machine learning methods like Random Forest and XGBoost into the analysis. While the traditional GLMs and GLMMs offer reasonably good predictive performance, it becomes evident that these models have certain limitations when striving for highly accurate predictions. However, with the advent of machine learning techniques, we observe a significant leap in predictive power. This remarkable outcome underscores the transformative potential of machine learning in enhancing predictive accuracy. XGBoost precision and robustness position it as a standout performer, making it an exceptionally compelling choice for tasks demanding the utmost accuracy and reliability in predictions [19]. These results not only validate the effectiveness of machine learning but also emphasize the importance of selecting the right modeling approach to achieve superior predictive outcomes, particularly when working with complex or high-dimensional data.
The LeafArea package has undergone a meticulous model selection process, resulting in the identification of the optimal GLM and GLMM for calculating leaf area across six distinct species of fruit plants. These selected models have been incorporated into a dedicated function within the package, ensuring accurate and reliable leaf area predictions (calculate_LeafArea_glm and calculate_LeafArea_glmm, respectively). Moreover, specialized functions have been developed to compute leaf area using state-of-the-art machine learning techniques, specifically XGBoost and Random Forest models (calculate_LeafArea_rf and calculate_LeafArea_xgb, respectively). The four functions not only provide leaf area estimates but also furnish comprehensive predictive power evaluation metrics. These metrics empower users to make informed decisions by comparing and selecting the model that best aligns with their specific requirements, thus enhancing the versatility and usability of the LeafArea package.
The four functions have been implemented in the R package LeafArea to calculate leaf area, currently for six plant species. We encourage researchers to provide sufficient data to expand both the number of species and the number of observations, thereby continually enhancing the predictive power of our models. This includes broadening the range of plant species that can be studied. The LeafArea package is open-source (https://github.com/velasquez-vasconez/LeafArea), and any contributions to the database or code will be greatly appreciated.

Conclusions

The LeafArea package introduces four invaluable functions for precise leaf area estimation in six Andean fruit species. It incorporates the optimal GLM and GLMM models, alongside the powerful Random Forest and XGBoost algorithms, resulting in a robust and versatile approach. The exceptional performance of XGBoost underscores its potential to revolutionize leaf area estimation practices, exhibiting outstanding predictive accuracy. GLMMs prove effective in capturing complex relationships, while machine learning techniques, particularly XGBoost, surpass all models, offering superior predictive accuracy. The LeafArea package actively encourages collaborative contributions to its database and code, fostering a collective effort to advance our comprehension of plant growth dynamics and productivity.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org.

Author Contributions

For research articles with several authors, a short paragraph specifying their individual contributions must be provided. The following statements should be used Conceptualization, PAV-V and DAD; methodology, PAV-V and DAD; software, PAV-V, validation, PAV-V and DAD; formal analysis, PAV-V; investigation, PAV-V and DAD; resources, DAD; data curation, PAV-V; writing—original draft preparation, PAV-V; writing—review and editing, PAV-V and DAD; visualization, PAV-V; supervision, DAD; project administration, DAD; funding acquisition, DAD. All authors have read and agreed to the published version of the manuscript.

Funding

The study was supported by Ministerio de Ciencia Tecnología e Innovación, Colombia (MINCIENCIAS). Research project: “ESTUDIO DE SISTEMAS DE CULTIVO ASOCIADOS A LOS FRUTALES ANDINOS ESTRATEGIA INNOVADORA PARA LA REACTIVACIÓN ECONÓMICA DE LOS MUNICIPIOS DE SANDONÁ, LA FLORIDA, ARBOLEDA, PROVIDENCIA Y EL PEÑOL” CON CÓDIGO BPIN 2020000100677”.

Acknowledgments

The authors would like to extend their heartfelt gratitude to Johana M. Belalcazar, Jenifer B. Vargas, Laura M. Pantoja, Luisa F. Vallejo, Javier M. Chamorro, Carlos Charfuelan, Tania M. Pantoja, for their invaluable support and dedication in collecting and organizing the data for this study, their contributions are deeply appreciated. Deeply grateful to Dra. Martha I. Cabrera Otalora and Dr. Juan S. Chirivi Salomon for their invaluable support and guidance.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Zheng, C.; Abd-Elrahman, A.; Whitaker, V.M.; Dalid, C. Deep Learning for Strawberry Canopy Delineation and Biomass Prediction from High-Resolution Images. Plant Phenomics 2022, 2022, . [CrossRef]
  2. Fischer, G.; Parra-Coronado, A.; Balaguera-López, H.E. Altitude as a Determinant of Fruit Quality with Emphasis on the Andean Tropics of Colombia. A Review. Agron. Colomb. 2022, 40, . [CrossRef]
  3. Bautista-Montealegre, L.G.; DEantonio-Florido, L.Y.; Cardona, W.A.; Bolaños-Benavides, M.M.; Fischer, G. Mineral Nutrition and Tolerance to Colletotrichum Spp. of Andean Blackberry (Rubus Glaucus Benth.) in Nursery. Agron. Mesoam. 2022, 48655, . [CrossRef]
  4. Muñoz-Ordoñez, F.J.; Gutiérrez-Guzmán, N.; Hernández-Gómez, M.S.; Fernández-Trujillo, J.P. The Climactic Conditions Limit Fruit Production and Quality in Gulupa (Passiflora Edulis Sims f. Edulis) under Integrated Fertilization. South African J. Bot. 2023, 153, 147–156, . [CrossRef]
  5. Jiang, J.; Johansen, K.; Stanschewski, C.S.; Wellman, G.; Mousa, M.A.A.; Fiene, G.M.; Asiry, K.A.; Tester, M.; McCabe, M.F. Phenotyping a Diversity Panel of Quinoa Using UAV-Retrieved Leaf Area Index, SPAD-Based Chlorophyll and a Random Forest Approach. Precis. Agric. 2022, 23, 961–983, . [CrossRef]
  6. Abramoff, M.; Magalhaes, P.; Ram, S. Biophotonics International. Image Processing with ImageJ; LAURIN, 2004;
  7. Kuhn, M. Building Predictive Models in R Using the Caret Package. J. Stat. Softw. 2008, 28, 1–26.
  8. R Core Team R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria 2020.
  9. Asghari, M.; Fathollahi-Fard, A.M.; Mirzapour Al-e-hashem, S.M.J.; Dulebenets, M.A. Transformation and Linearization Techniques in Optimization: A State-of-the-Art Survey. Mathematics 2022, 10, 283, . [CrossRef]
  10. Noel, D.D. Normality Assessment of Several Quantitative Data Transformation Procedures. Biostat. Biometrics Open Access J. 2021, 10, . [CrossRef]
  11. Chan, J.Y.-L.; Leow, S.M.H.; Bea, K.T.; Cheng, W.K.; Phoong, S.W.; Hong, Z.-W.; Chen, Y.-L. Mitigating the Multicollinearity Problem and Its Machine Learning Approach: A Review. Mathematics 2022, 10, 1283, . [CrossRef]
  12. Davino, C.; Romano, R.; Vistocco, D. Handling Multicollinearity in Quantile Regression through the Use of Principal Component Regression. Metron 2022, 80, 153–174, . [CrossRef]
  13. Gokmen, S.; Dagalp, R.; Kilickaplan, S. Multicollinearity in Measurement Error Models. Commun. Stat. - Theory Methods 2022, 51, 474–485, . [CrossRef]
  14. Fávero, L.P.; Belfiore, P. Manual de Análise de Dados: Estatística e Modelagem Multivariada Com Excel®, SPSS® e Stata®; 2017;
  15. Freedman, D. Statistical Models: Theory and Practice; 2009;
  16. Schielzeth, H.; Dingemanse, N.J.; Nakagawa, S.; Westneat, D.F.; Allegue, H.; Teplitsky, C.; Réale, D.; Dochtermann, N.A.; Garamszegi, L.Z.; Araya-Ajoy, Y.G. Robustness of Linear Mixed-effects Models to Violations of Distributional Assumptions. Methods Ecol. Evol. 2020, 11, 1141–1152, . [CrossRef]
  17. Scutari, M.; Denis, J.-B. Bayesian Networks: With Examples in R.; Press, C., Ed.; 2021;
  18. Carvalho, A.M.X. de; Mendes, F.Q.; Borges, P.H. de C.; Kramer, M. A Brief Review of the Classic Methods of Experimental Statistics. Acta Sci. Agron. 2022, 45, e56882, . [CrossRef]
  19. Rao, G.S.; Dangeti, S.; Amiripalli, S.S. An Efficient Modeling Based on XGBoost and SVM Algorithms to Predict Crop Yield. In; 2022; pp. 565–574.
Preprints 92938 g001
Figure 1. Pairwise scatter plot matrix and correlation analysis between the variables. The leaf area exhibits a significant positive correlation (p<0.001) with both leaf length and width. The leaf area was subjected to a square root transformation (sqrt) in response to the observed non-linear relationship. A synthetic variable was created by the square root of the product of the leaf length and width.
Figure 1. Pairwise scatter plot matrix and correlation analysis between the variables. The leaf area exhibits a significant positive correlation (p<0.001) with both leaf length and width. The leaf area was subjected to a square root transformation (sqrt) in response to the observed non-linear relationship. A synthetic variable was created by the square root of the product of the leaf length and width.
Preprints 92938 g001
Preprints 92938 g002
Figure 2. Comparing Log-likelihood between generalized linear models (GLMs) and generalized linear mixed models (GLMMs). The parameter ‘Length_width’ represents the composed variable obtained from SQRT(Length * Width).
Figure 2. Comparing Log-likelihood between generalized linear models (GLMs) and generalized linear mixed models (GLMMs). The parameter ‘Length_width’ represents the composed variable obtained from SQRT(Length * Width).
Preprints 92938 g002
Preprints 92938 g003
Figure 3. Relationship between square root of leaf area and Leaf Length in a generalized linear mixed model across six fruit species.
Figure 3. Relationship between square root of leaf area and Leaf Length in a generalized linear mixed model across six fruit species.
Preprints 92938 g003
Table 1. Comparison of performance metrics across generalized linear models (GLMs) and generalized linear mixed models (GLMMs).
Table 1. Comparison of performance metrics across generalized linear models (GLMs) and generalized linear mixed models (GLMMs).
Models RMSE MAE MAPE R2
GLM1 1.8141 1.3980 22.0732 0.9053
GLM2 1.5440 1.0946 18.5890 0.9314
GLM3 1.4840 1.0651 16.7689 0.9366
GLMM1 1.6140 1.1470 16.0398 0.9240
GLMM2 1.4316 1.0130 15.7745 0.9390
GLMM3 1.3946 0.9614 13.7895 0.9410
Random Forest 1.2099 0.9578 10.7773 0.9655
XGBoost 0.3043 0.1801 1.4751 0.9990
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated