Prerpints.org logo
Preprint
Article

A Mathematical Structure Underlying Sentences and Its Connection with Short–Term Memory

Altmetrics

Downloads

73

Views

11

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

11 December 2023

Posted:

12 December 2023

You are already at the latest version

Alerts
Abstract
The mathematical structure underlying a sentence is made of two independent processing units in series. The conditional probability density function of sentence length (measured in words) recordable in the extended short–term memory (E–STM) buffer made of CF cells is Gaussian. The number of sentences that authors of Italian and English Literatures have written is compared to that theoretically available to them. The multiplicity factor α describes this comparison. α>1 is more likely than α<1 and often α≫1, therefore the same sentence pattern is reused many times. These texts are easier to read. Very few novels show α<1. In these cases, there are enough diverse sentence patters to convey meaning, but most of them are not used. Texts are more difficult to read, as measured by a universal readability index GU. A mismatch index IM synthetically describes the process. α, GU. and IM increase with year of publication. Future work will concern other literatures – including ancient ones as Greek and Latin – to confirm what, in our opinion, is general feature of human mind.
Keywords: 
Subject: Computer Science and Mathematics  -   Other

1. Introduction: Two short–term memory processing units in series

Recently [1], we have proposed a well–grounded conjecture that a sentence – read or pronounced, the two activities are similarly processed by the brain [2] – is elaborated by the short–term memory (STM) with two independent processing units in series, with similar buffer size. The clues for conjecturing this model has emerged by considering many novels belonging to the Italian and English Literatures. We have shown that there are no significant mathematical/statistical differences between the two literary corpora, according to surface deep–language variables. In other words, the mathematical surface structure of alphabetical languages – a creation of human mind – is deeply rooted in humans, independently of the particular language used.
A two–unit STM processing can be justified according to how a human mind seems to memorize “chunks” of information written in a sentence. Although simple and related to the surface of language, the model seems to describe mathematically the input–output characteristics of a complex mental process largely unknown.
The first processing unit is linked to the number of words between two contiguous interpunctions, variable indicated by I p – termed word interval (Appendix A lists the mathematical symbols used in the present paper) – approximately ranging in Miller’s 7 ± 2 law range [3,4,5,6,7,8,9,10,11,12]. The second unit is linked to the number M F of I p ’s contained in a sentence, referred to as the extended STM, or E–STM, ranging approximately from 1 to 6. We have shown that the capacity (expressed in words) required to process a sentence ranges from 8.3 to 61.2 words, values that can be converted into time by assuming a reading speed. This conversion gives the range 2.6 ~ 19.5 seconds for a fast–reading reader [13], and 5.3 ~ 30.1 seconds for a common reader of novels, values well supported by experiments reported in the literature [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29].
The E–STM must not be confused with the intermediate memory [30, 31]. It is not modelled by studying neuronal activity, but by studying surface aspects of human communication, such as words and interpunctions, whose effects writers and readers have experienced since the invention of writing.
The modeling of the STM processing by two units in series has never been considered in the literature before Reference [32] and [1]. The reader is very likley aware that the literature on the STM and its various aspects is very large and multidisciplinary, but nobody, as far as we know, has never considered the connections we have found and discussed in References [32, 1]. Moreover, a sentence conveys meaning, therefore the theory we are further developing might be a starting point to arrive at the Information Theory that includes meaning.
Today, some attempts are being made by many scholars trying to arrive at a “semantic communication” theory or “semantic information” theory, but results are still, in our opinion, in their infancy [33,34,35,36,37,38,39,40,41]. These theories, as those concerning the STM, have not considered the main “ingredients” of our theory as a starting point for including meaning, still a very open issue.
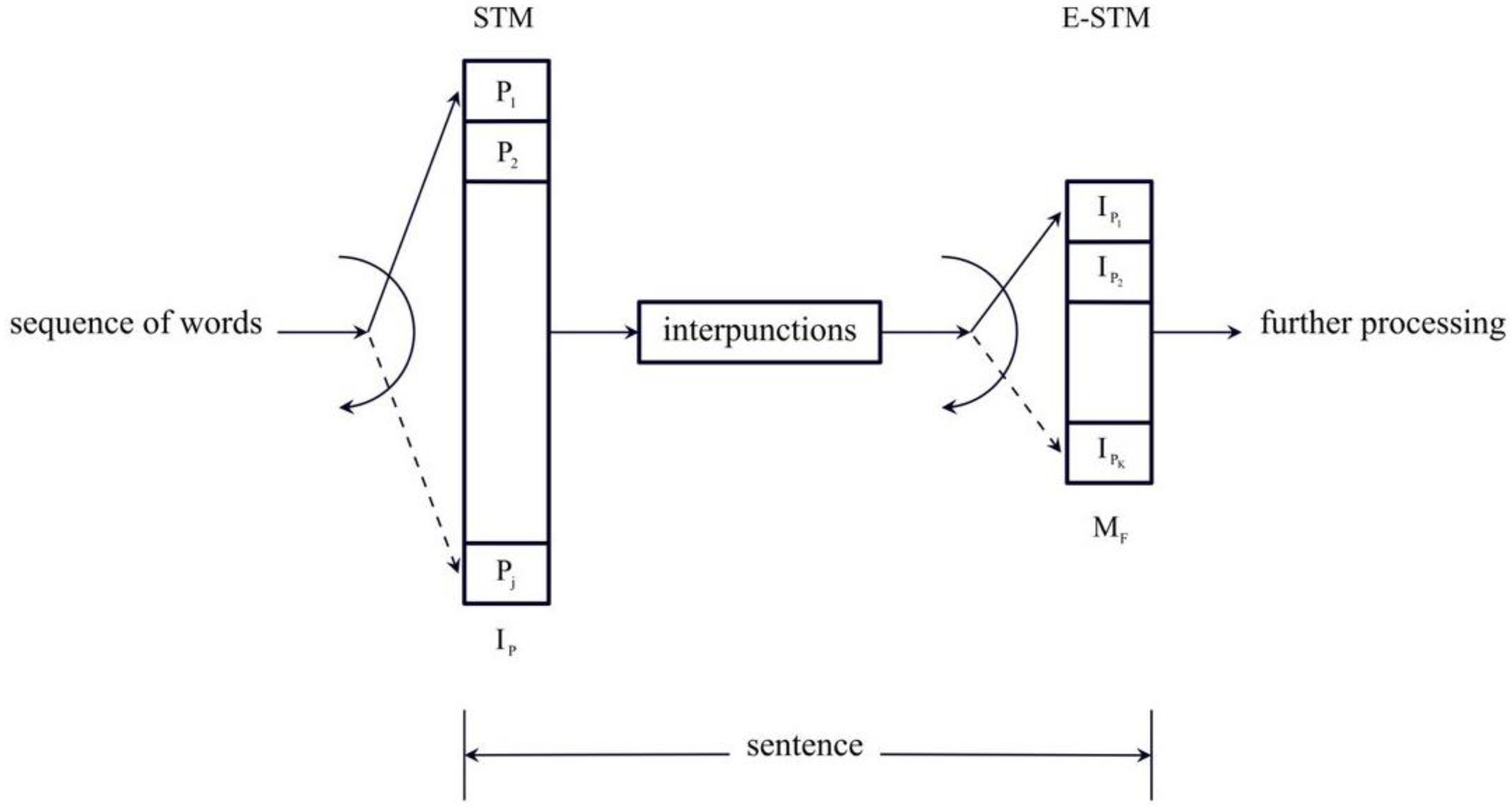
Figure 1 sketches the flow–chart of the two processing units [1]. The words p 1 , p 2 ,… p j are stored in the first buffer up to j items, approximately in Miller’s range, until an interpunction is introduced to fix the length of I P . The word interval I P is then stored in the second buffer up to k items, from about 1 to 6, until the sentence ends. The process is then repeated for the next sentence.
The purpose of the paper is to further investigate the mathematical structure underlying sentences, first theoretically and secondly experimentally, by considering the novels previously mentioned [1], listed in Tables B.1 for Italian Literature and in Table B.2 for English Literature.
After this Introduction, in Section 2 we study the probability distribution function (PDF) of sentence size – measured in words – recordable by an E–STM buffer made of C F cells (this parameter plays the role of M F ). In Section 3 we study the number of sentences, with the same number of words, that C F cells can process. In Section 4, we compare the number of sentences that authors of Italian and English Literatures actually wrote for a novel to the number of sentences theoretically available to them, by defining a multiplicity factor. In Section 5 we define a mismatch index, which synthetically measures to what extent a writer uses the number of sentences theoretically available of Section 5. In Section 6 we show that the parameters studied increase with the year of novel publication. Finally, in Section 7, we summarize the main results and propose future work.

2. Probability distribution of sentence length versus E–STM buffer size

First, we study the conditional PDF of sentence length, measured in words W – i.e. the parameter which in long texts, as chapters, gives P F for each chapter – recordable in an E–STM buffer made of C F cells – i.e. the parameter which gives M F in chapters. Secondly, we study the overlap of the PDFs because this overlap gives interesting indications.

2.1. Probability distribution of sentence length

To estimate the PDF of sentence length, we run a Monte Carlo simulation based on the PDF of I P obtained in [1] by merging the two literatures recalled in the in the Introduction.
In Reference [1], we have shown that the PDF of I P , P F and M F – as just recalled, these averages refer to single chapters of the novels – can be modelled with a three–parameter log–normal density function (natural logs):
f x = 1 2 π σ x x − 1 exp − 1 2 ln x − 1 ) − μ x σ x 2
In Eq. (1), μ x and σ x are, respectively, the mean value and the standard deviation the log–normal PDF. Table 1 reports these values for the three deep–language variables.
The Monte Carlo simulation steps are the following.
  • Consider a buffer made of C F cells. The sentence contains C F word intervals: for example, if C F = 3 , the sentence contains two interpunctions followed by a full stop, or a question mark, or an exclamation mark.
  • Generate C F independent values of I P according to the log–normal model given by Equation (1) and Table 1. The independence of I P from a cell to another cell is reasonable [1].
  • Add the number of words contained in the C F cells to obtain W :
    W = ∑ i = 1 C F I p , i
  • Repeat steps 1 to 3 many times (we did it 100,000 times, i.e., we simulated 100,000 sentences of different length) to obtain a stable conditional PDF of W .
  • Repeat steps 1 to 4 for another C F and obtain another PDF.
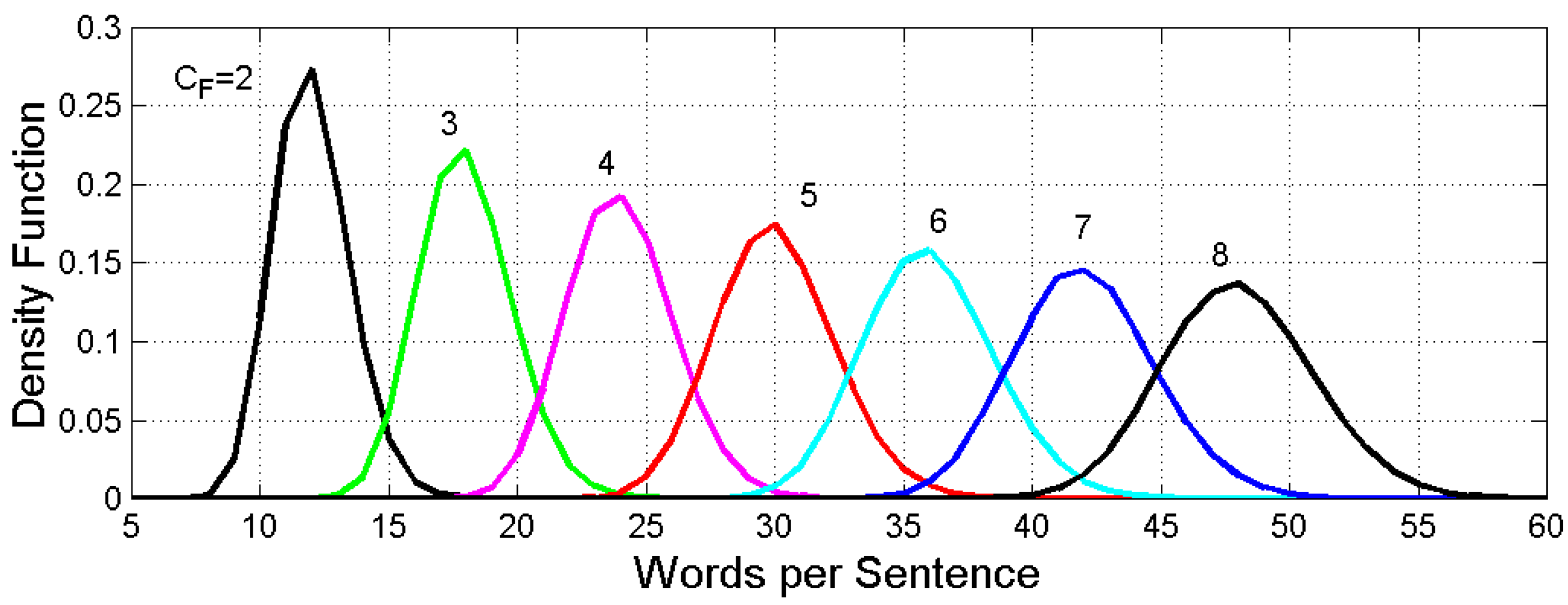
Figure 2 shows the conditional PDF for several C F . Each PDF can be very well modelled by a Gaussian PDF f C F x because the probability of getting unacceptable negative values is negligible in any of the PDFs shown in Figure 2. For example, for C F = 3 the mean value and the standard deviation are, respectively, m 3 = 18.00 words and s 3 = 1.79 words.
In general terms, the mean value of Equation (2) is given by:
m C F = W = ∑ i = 1 C F I p , i = ∑ i = 1 C F I P , i = C F I p
Therefore, m C F is proportional to C F . As for the standard deviation of W , if the I p , i ' s are independent – as we assume – then the variance s C F 2 of W is given by:
s C F 2 = ∑ i = 1 C F σ I P , i 2 = C F × σ I P 2
Therefore, the standard deviation s C F is proportional to C F . Finally, according to the central limit theory [42], in a significant range about the mean the PDF can be modelled as a Gaussian PDF.
In conclusion, the Monte Carlo simulation produces a Gaussian PDF with mean value proportional to C F and standard deviation proportional to C F . These findings are clearly evident in the PDF’s shown in Figure 2 in which m C F and s C F increase as theoretically expected, therefore, mean values and standard deviations of the other PDF’s can be calculated by scaling the values found for C F = 3 . For example, for C F = 6 , m 6 = 2 × 18.00 = 36.00 words and s 6 = 2 × 1.79 = 2.53 words.
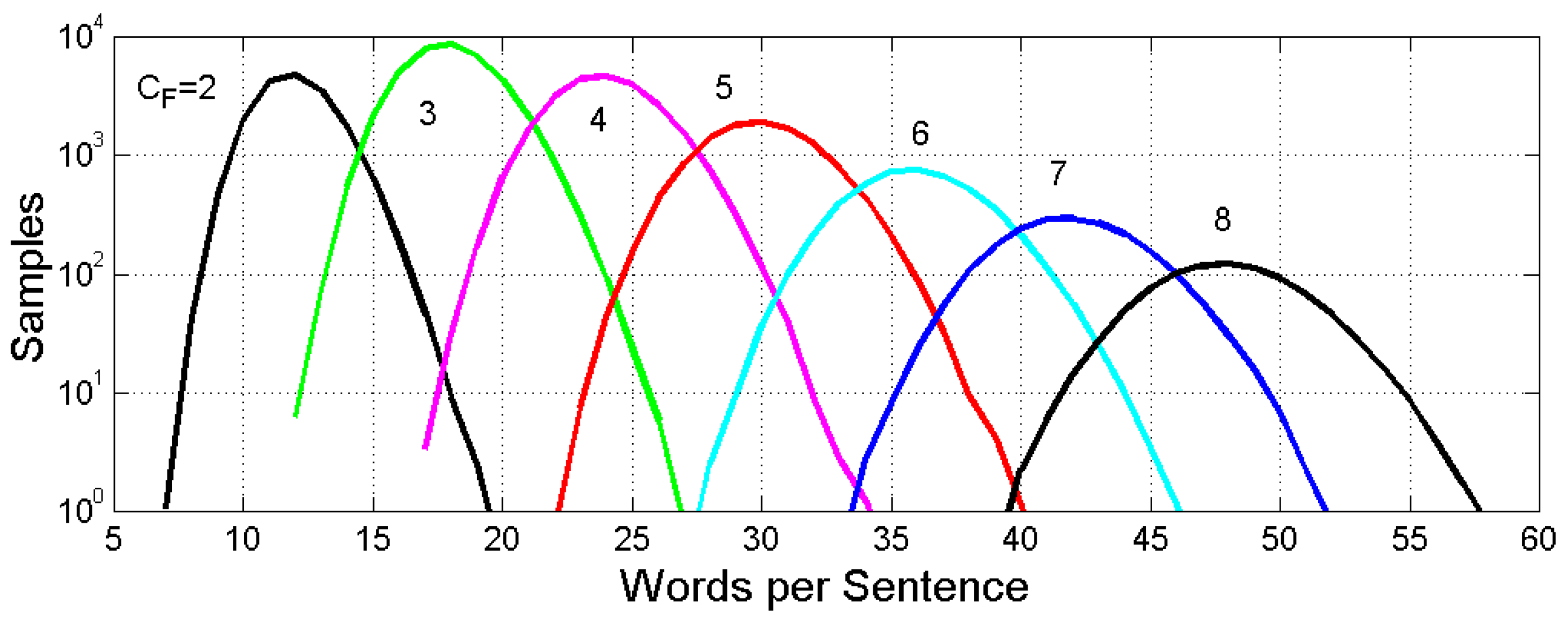
Figure 3 shows the histograms corresponding to Figure 2. The number of samples for each conditional PDF, out of 100,000 considered in the Monte Carlo simulation, are obtained by distributing the samples according to the PDF of M F given by Eq. (1) and Table 1. The case C F = 3 gives the largest sample size.
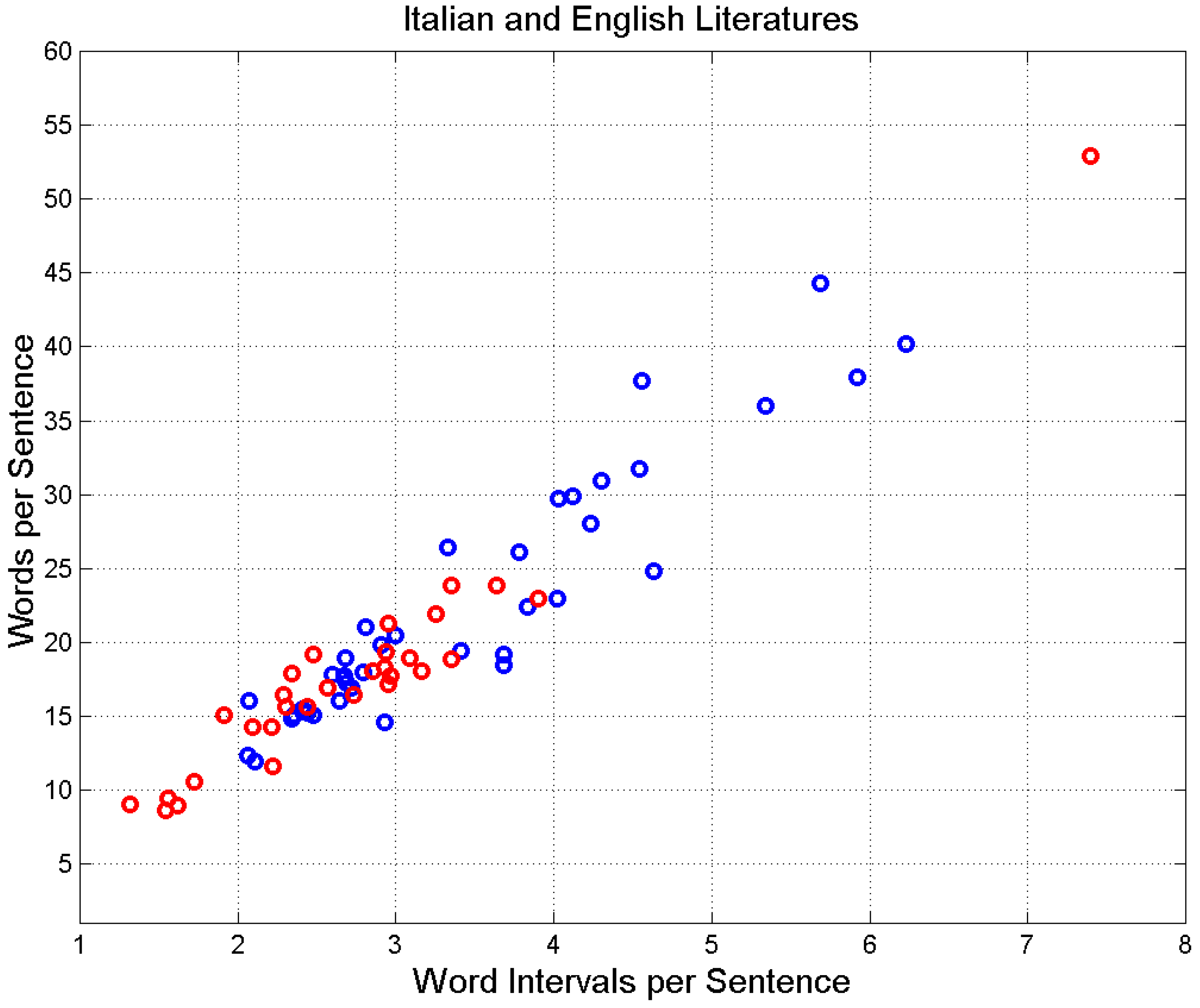
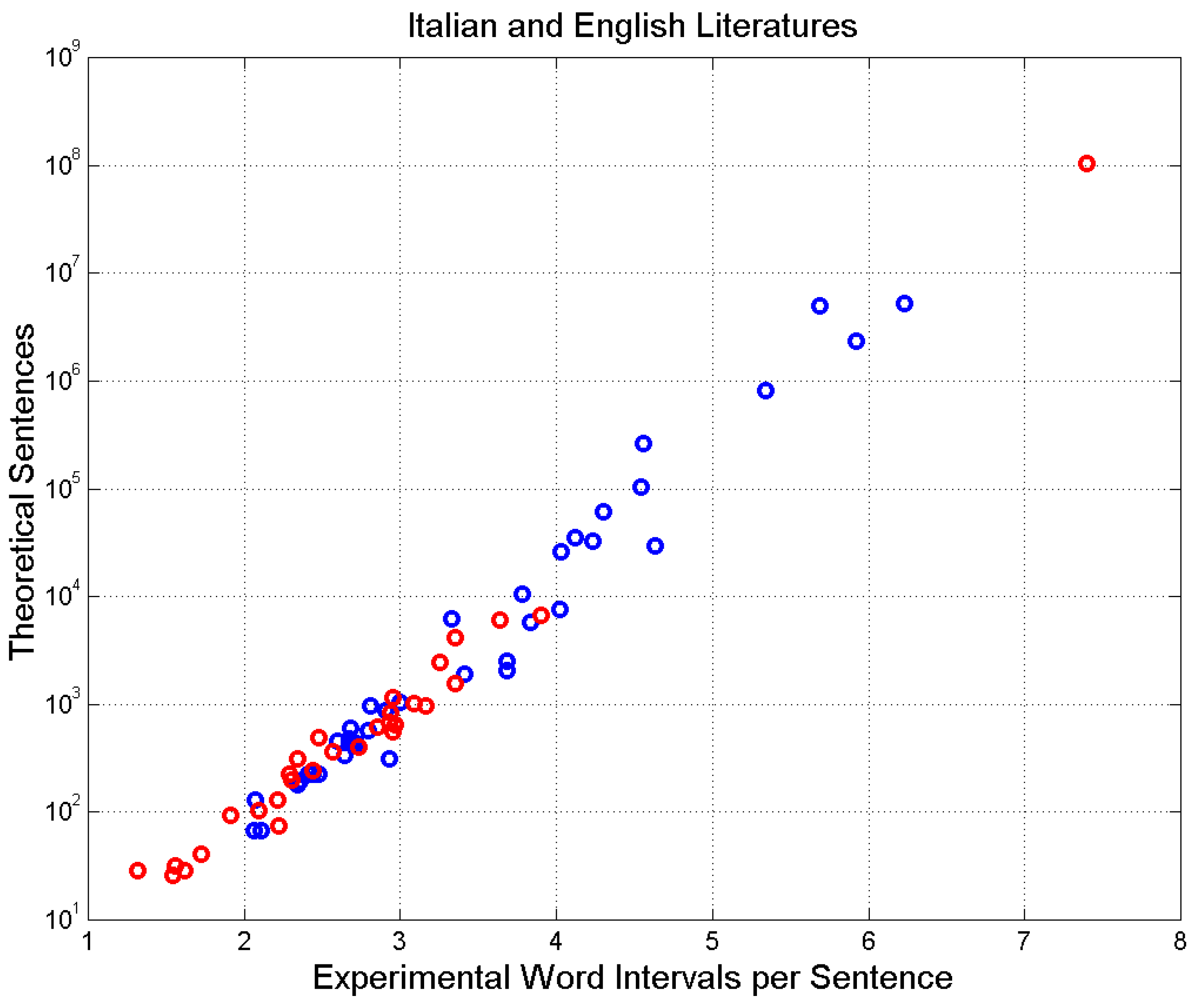
The results shown above have an experimental basis because the relationship between P F – average of words per sentence for the entire novel, calculated by averaging the P F of single chapters, by weighting single chapters with the fraction of novel total word, as discussed in [32] – versus < M F > – average of M F of a novel calculated as P F – is linear, as Figure 4 shows by drawing P F versus M F concerning the novels mentioned above.

2.2. Overlap of the conditional probability distributions

Figure 2 shows that the conditional PDFs overlap, therefore some sentences can be processed by buffers of diverse C F size, either larger or smaller. Let us define the probability of these overlaps.
Let W t h be the intersection of two contiguous Gaussian PDFs, for example f C F − 1 x and f C F x , therefore the probability p H L that a sentence length can be found in the nearest lower Gaussian PDF (going from C F → C F − 1 ) is given by:
p H L = ∫ − ∞ W t h f C F x d x ≈ ∫ 0 W t h f C F x d x
Similarly, the probability that a sentence length can be found in the nearest higher Gaussian PDF (going from C F − 1 → C F ) is given by:
p L H = ∫ W t h ∞ f C F − 1 x d x
For example, the threshold value between f C F = 3 x and f C F = 4 x is W t h = 20.9 words and p H L = 6.6 % , p L H = 5.5 % .
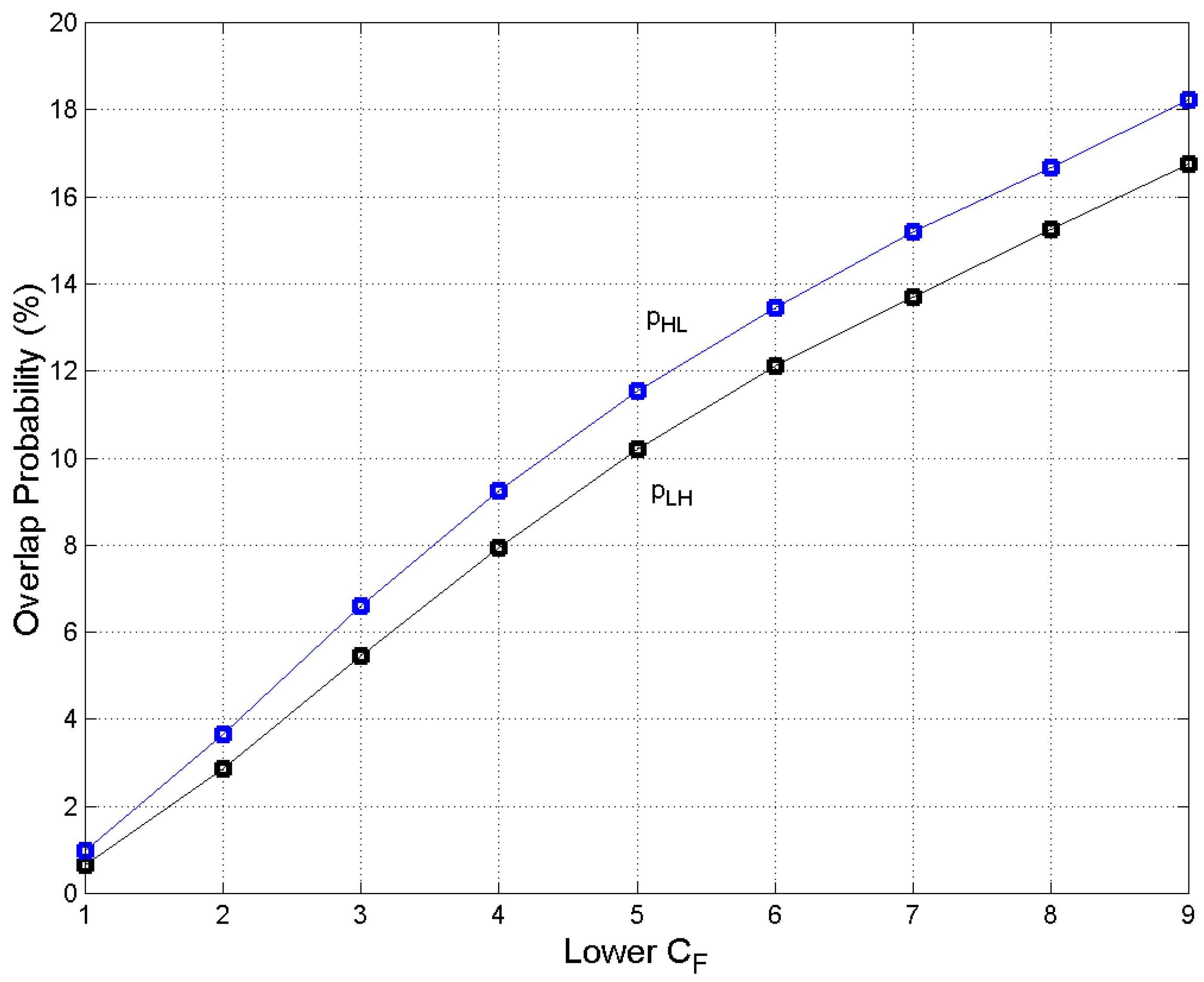
Figure 5 draws these probabilities (%) versus C F − 1 (lower V F ). Because s C F increases with C F , therefore p H L > p L H . however, this is not only a mathematically obvious result, but it also meaningful because it indicates that: a) a human mind can process sentences of length belonging to the contiguous lower or higher M F – the probability of going to more distant PDFs is negligible – and b) the number of these sentences is larger in the case C F → C F − 1 , which just means that an E–STM buffer can process to a larger extent data matched to a smaller capacity buffer than data matched to a larger capacity buffer.
In general, there is continuity in the length of sentences that a human mind can process as the PDF of P F shows according to Equation (1), therefore each writer/reader can change the buffer size in a range within the larger range of the log–normal PDF.
Finally, notice that each sentence conveys meaning – theoretically any sequence of words might be meaningful, although this may not be the case, but we do not know their proportion – therefore the PDFs found above are also the PDFs associated with meaning. Moreover, the same numerical sequence of W words can carry different meanings, according to the words used. Multiplicity of meaning, therefore, is “built–in” in a sequence of W words. We will further explore this issue in the next sections by considering the number of sentences that authors of Italian and English Literatures actually wrote.
So far, we have explored the processing of the words of a sentence by simulating sentences of diverse length, conditioned to the E–STM buffer size. In the next section we explore the complementary processing concerning the number of sentences that contain the same number of words.

3. Theoretical number of sentences recordable in C F cells

We study the number of sentences of W words that an E–STM buffer, made of C F cells, can process. In synthesis, we ask the following question: how many sentences S W C F containing the same number of words W , Equation (2), can be theoretically written in C F cells?
Table 2 reports these numbers as a function of W and C F . We calculated these data first by running a code and then by finding the mathematical recursive formula that generates them, given by:
S W C F = S W − 1 C F + S W − 1 C F − 1
For example, if W = 20 words and C F = 4 , we read S 19 C F = 4 = 816 , S 19 C F − 1 = 3 = 153 , therefore S 20 C F = 4 = 816 + 153 = 969 .
(columns) recordable in an E–STM buffer made of C F cells with the same number of words (items) indicated in the first column.
Words W (items storeable) E–STM buffer made of C F cells
1 2 3 4 5 6 7 8
1 1 0 0 0 0 0 0 0
2 1 1 0 0 0 0 0 0
3 1 2 1 0 0 0 0 0
4 1 3 3 1 0 0 0 0
5 1 4 6 4 1 0 0 0
6 1 5 10 10 5 1 0 0
7 1 6 15 20 15 6 1 0
8 1 7 21 35 35 21 7 1
9 1 8 28 56 70 56 28 8
10 1 9 36 84 126 126 84 36
11 1 10 45 120 210 252 210 120
12 1 11 55 165 330 462 462 330
13 1 12 66 220 495 792 1254 792
14 1 13 78 286 715 1287 2046 2046
15 1 14 91 364 1001 2002 3333 4092
16 1 15 105 455 1365 3003 5335 7425
17 1 16 120 560 1820 4368 8338 12760
18 1 17 136 680 2380 6188 12706 21098
19 1 18 153 816 3060 8568 18894 33804
20 1 19 171 969 3876 11628 27462 52698
21 1 20 190 1140 4845 15504 39090 80160
22 1 21 210 1330 5985 20349 54594 119250
23 1 22 231 1540 7315 26334 74943 173844
24 1 23 253 1771 8855 33649 101277 248787
25 1 24 276 2024 10626 42504 134926 350064
26 1 25 300 2300 12650 53130 177430 484990
27 1 26 325 2600 14950 65780 230560 662420
28 1 27 351 2925 17550 80730 296340 892980
29 1 28 378 3276 20475 98280 377070 1189320
30 1 29 406 3654 23751 118755 475350 1566390
31 1 30 435 4060 27405 142506 594105 2041740
32 1 31 465 4495 31465 173971 768076 2635845
33 1 32 496 4960 35960 205436 973512 3403921
34 1 33 528 5456 40920 241396 1178948 4377433
35 1 34 561 5984 46376 282316 1461264 5556381
36 1 35 595 6545 52360 328692 1789956 7017645
37 1 36 630 7140 58905 381052 2118648 8807601
38 1 37 666 7770 66045 439957 2499700 10926249
39 1 38 703 8436 73815 506002 2939657 13425949
40 1 39 741 9139 82251 579817 3519474 16365606
41 1 40 780 9880 91390 662068 4099291 19885080
42 1 41 820 10660 101270 753458 4761359 23984371
43 1 42 861 11480 111930 854728 5514817 29499188
44 1 43 903 12341 123410 966658 6369545 35014005
45 1 44 946 13244 135751 1090068 7336203 41383550
46 1 45 990 14190 148995 1225819 8426271 48719753
47 1 46 1035 15180 163185 1374814 9652090 58371843
48 1 47 1081 16215 178365 1537999 11026904 68023933
49 1 48 1128 17296 194580 1716364 12564903 79050837
50 1 49 1176 18424 211876 1910944 14281267 91615740
51 1 50 1225 19600 230300 2122820 16192211 105897007
52 1 51 1275 20825 251125 2353120 18315031 122089218
53 1 52 1326 22100 273225 2604245 20668151 140404249
54 1 53 1378 23426 296651 2877470 23272396 161072400
55 1 54 1431 24804 320077 3174121 26149866 184344796
56 1 55 1485 26235 344881 3494198 29323987 210494662
57 1 56 1540 27720 371116 3839079 32818185 239818649
58 1 57 1596 29260 398836 4210195 36657264 272636834
59 1 58 1653 30856 428096 4609031 40867459 309294098
60 1 59 1711 32509 458952 5037127 45476490 350161557
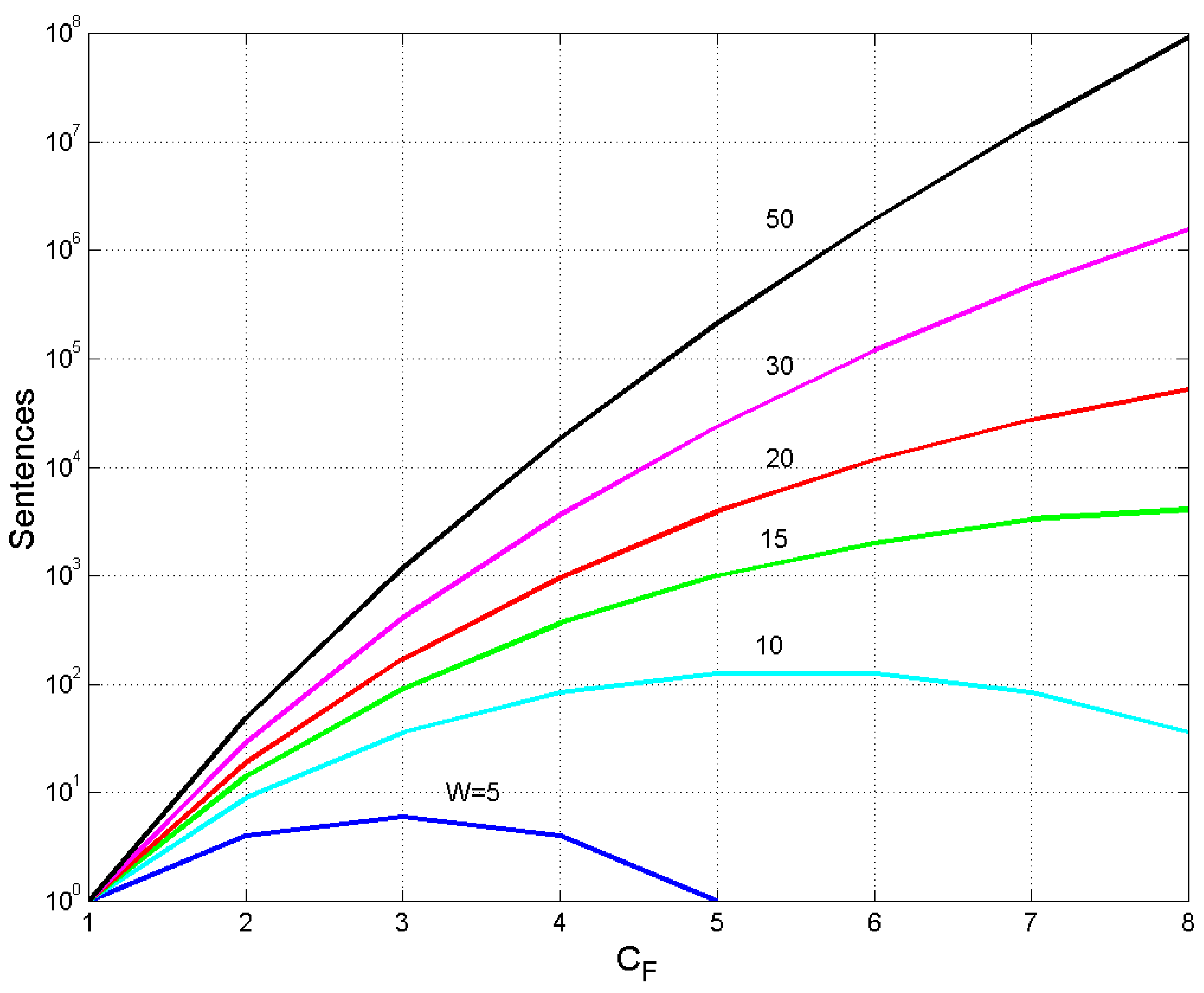
Figure 6 draws the data reported in some lines of Table 2 for a quick overview. We see how fast the number of sentences changes with C F , for constant W . For example, if W = 20 words, then S W = 20 ranges from 1 ( C F = 1 ) to 52,698 sentences ( C F = 8 ) . Maxima are clearly visible for W = 5 and W = 10 words at C F = 3 and C F = 5 or 6 , respectively. Values become fantastically large for larger W and C F , well beyond the ability and creativity of single writers, as we will show in Section 4.
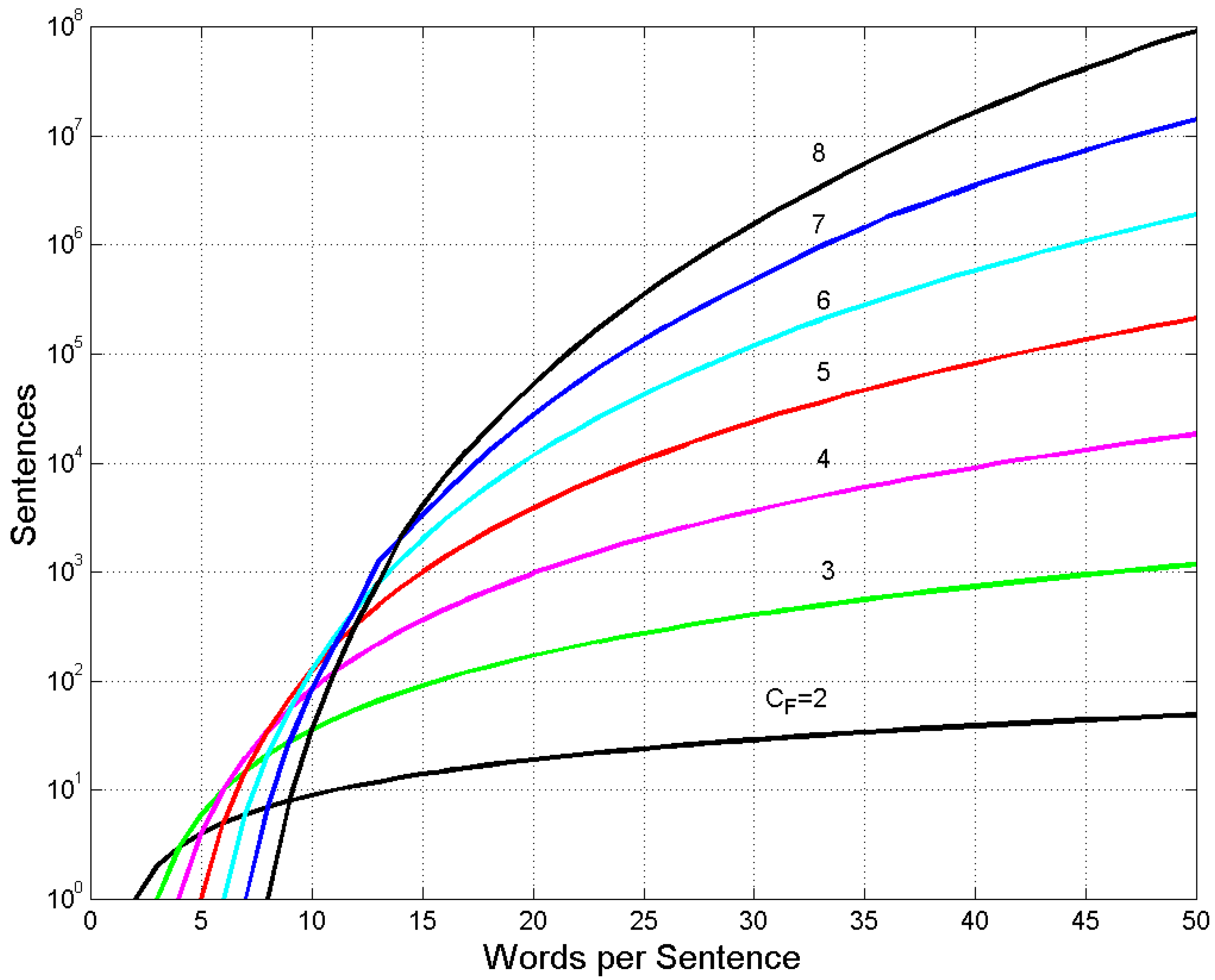
Figure 7 draws the data reported in some columns of Table 2, i.e. the number of sentences S W C F versus W , for fixed C F . In this case, it is useful to adopt an efficiency factor ε , defined as the ratio between S W C F and W , for a given C F :
ε = S W C F W
This factor says, synthetically, how a buffer of C F cells is efficient in providing sentences with a given number of words, its units being sentences per word.
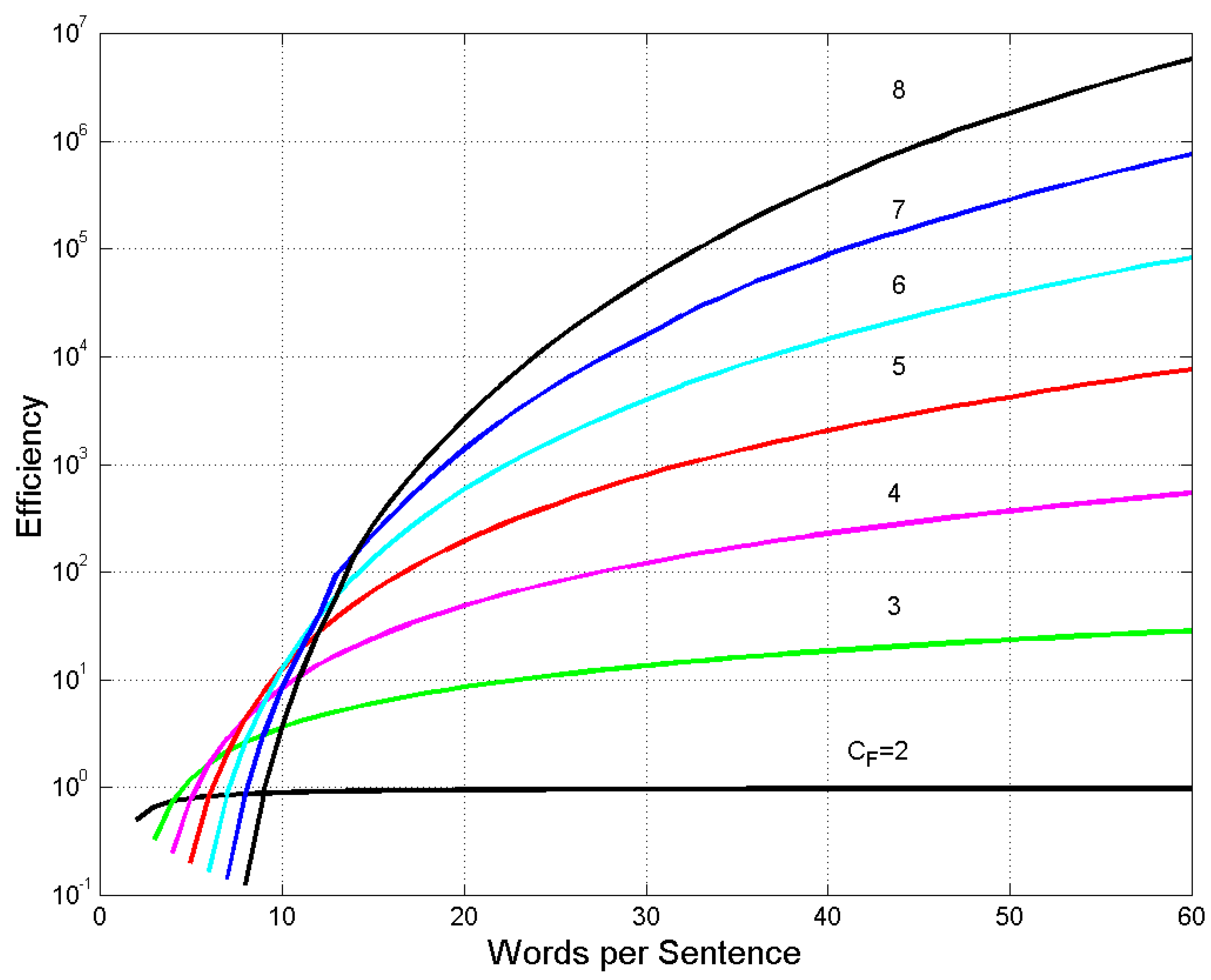
Figure 8 shows ε versus W . It is interesting to notice that for W ≲ 10 words, the buffer C F = 2 can be more efficient than the others. Beyond W = 10 , the larger buffers become very efficient, with very large ε .
If a writer uses short buffers – e.g., deliberately because of his/her style, or necessarily because of reader’s E–STM memory size – then he/she has to repeat the same numerical sequence of words many times, according to the number of meanings conveyed. For example, if C F = 2 and W = 10 the writer has only 9 different choices, or patterns of two numbers whose sum is 10 (Table 2). Therefore, Table 2 gives the minimum number of meanings that can be conveyed. The larger C F , the larger is the variety of sentences that can be written with W words.
, Equation (8), of an E–STM buffer of C F cells versus words per sentence W .
Now, the following question naturally arises: How many sentences authors do write in their texts, compared to the theoretical number available to them? In the next section we will compare these two sets of data by studying the novels taken from the Italian and English Literatures listed in Appendix B, by assuming their average values P F and M F and by defining a multiplicity factor.

4. Experimental multiplicity factor of sentences

We compare the number of sentences that authors of Italian and English Literatures actually wrote for each novel to the number of sentences theoretically available to them, according to P F , M F of each novel. In this analysis, we do not consider the values of P F and M F of each chapter of a novel because the detail would be so fine to miss the general trend given, on the contrary, by the average values P F , M F of the complete novel.
As is well known, the average value and the standard deviation of integers very likely are not integers – as is always the case for the linguistic parameters – therefore, to apply the mathematical theory of the previous sections, we must do some interpolations and only at the end of the calculation consider integers.
Let us compare the experimental number of sentences S P F M F of a novel, reported in Tables B.1 and B.2 to the theoretical number S W C F available to the author, according to the experimental values < P F > (which plays the role of W ) and < M F > (which plays the role of C F ) of the novel.
By referring to Figure 7, the interpolation between the integers of Table 2 to find the curve of constant C F – given by the real number M F – is linear along both axes. At the intersection of the vertical line (corresponding to the real number P F ) and the new curve (corresponding to the real number M F ), we find the theoretical S W C F by rounding the value to the nearest integer towards zero. For example, for David Copperfield, in Table B.2 we read S P F M F = 19 , 610 and the interpolation gives S W C F = 1 , 553 . Figure 9 shows the result of this exercise. We see that S W C F increases rapidly with M F . The most displaced (red) circle is due to Robinson Crusoe.
The comparison between S P F M F and S W C F is done by defining a multiplicity factor α , defined as the ratio between S P F M F (experimental value) and S W C F (theoretical value):
α = S P F M F S W C F
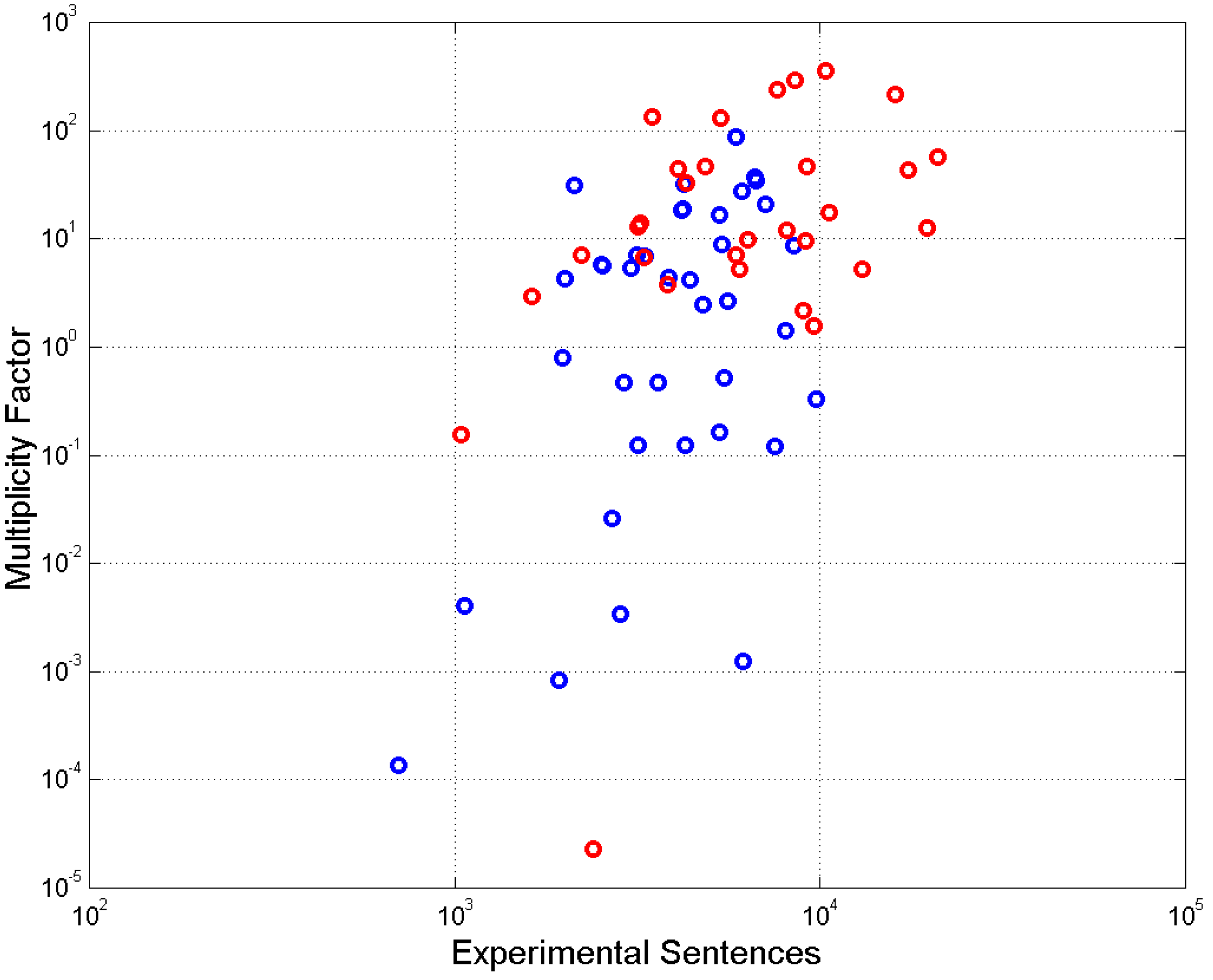
The values of α for each novel are reported in Tables B.1, B.2. For example, for David Copperfield α = 19 , 610 / 1 , 553 = 12.63 . Figure 10 shows α versus S P F M F . We notice a fair increasing trend of α with S P F M F .
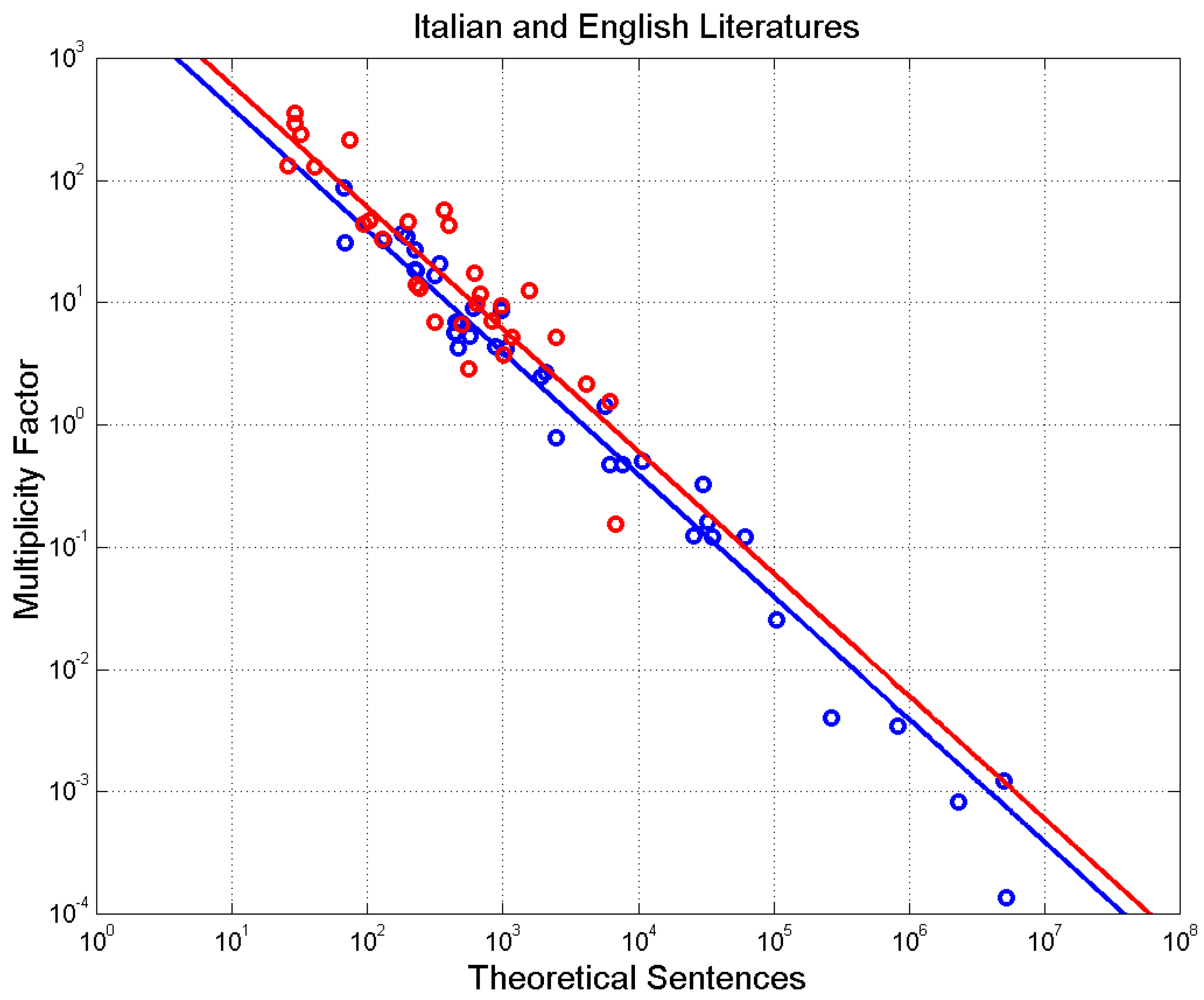
Figure 11 shows α versus S W C F . An inverse relation power law is a good fit:
α = 3886 / S W C F     Italian
α = 6028 / S W C F     English
The correlation coefficient of log values is − 0.9873. for Italian and − 0.9710. for English.
From Equations (10)(11) α = 1 when S W C F = 3886 for Italian and S W C F = 6028 for English, therefore, novels with sentences in the range 4000 ~ 6000 use, on the average, the number of sentences theoretically available for their averages P F and M F .
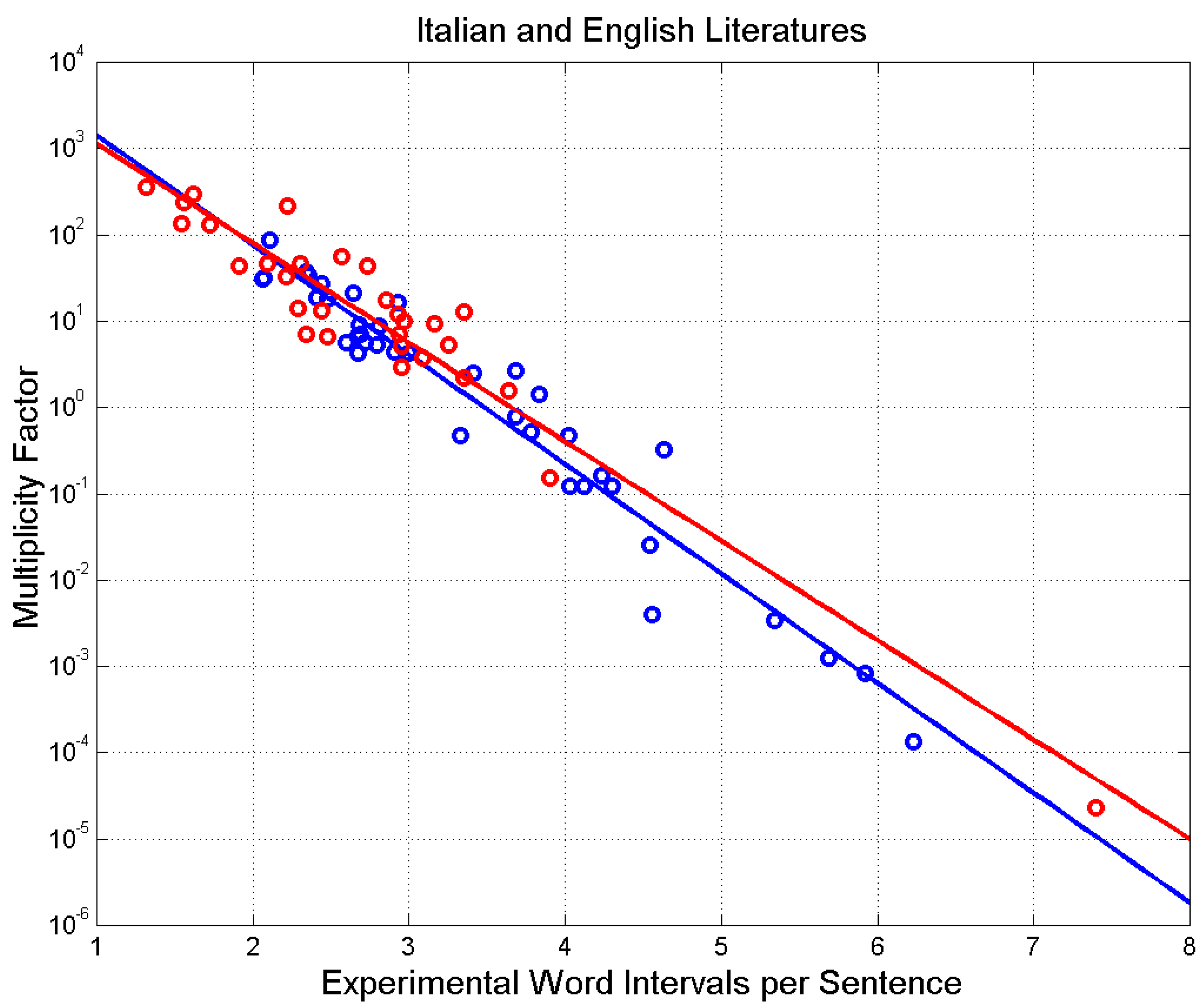
Figure 12 shows α versus < M F > . In this case, an exponential law is a good fit:
α = 26 , 027 × e − 2.923 × M F     Italian
α = 15 , 855 × e − 2.649 × M F     English
For Italian Literature (correlation coefficient of linear–log values is − 0.9697 ) α = 1 when M F = 3.48 , for English Literature (correlation coefficient of linear–log values is − 0.9603 ) α = 1 when M F = 3.65 . Therefore, novels with sentences in the range 4000 ~ 6000 use, on the average, the same E–STM buffer size M F ≈ 3.5 cells.
From Figure 10, Figure 11 and Figure 12, we can draw the following conclusion. In general, α > 1 is more likely than α < 1 and often α ≫ 1 . When α ≫ 1 , the writer reuses many times the same pattern of number of words. The multiplicity factor, therefore, indicates also the minimum multiplicity of meaning conveyed by an E–STM, besides, of course, the many diverse meanings conveyed by the same sequence of I p ' s obtainable by only changing words. Few novels show α < 1 . 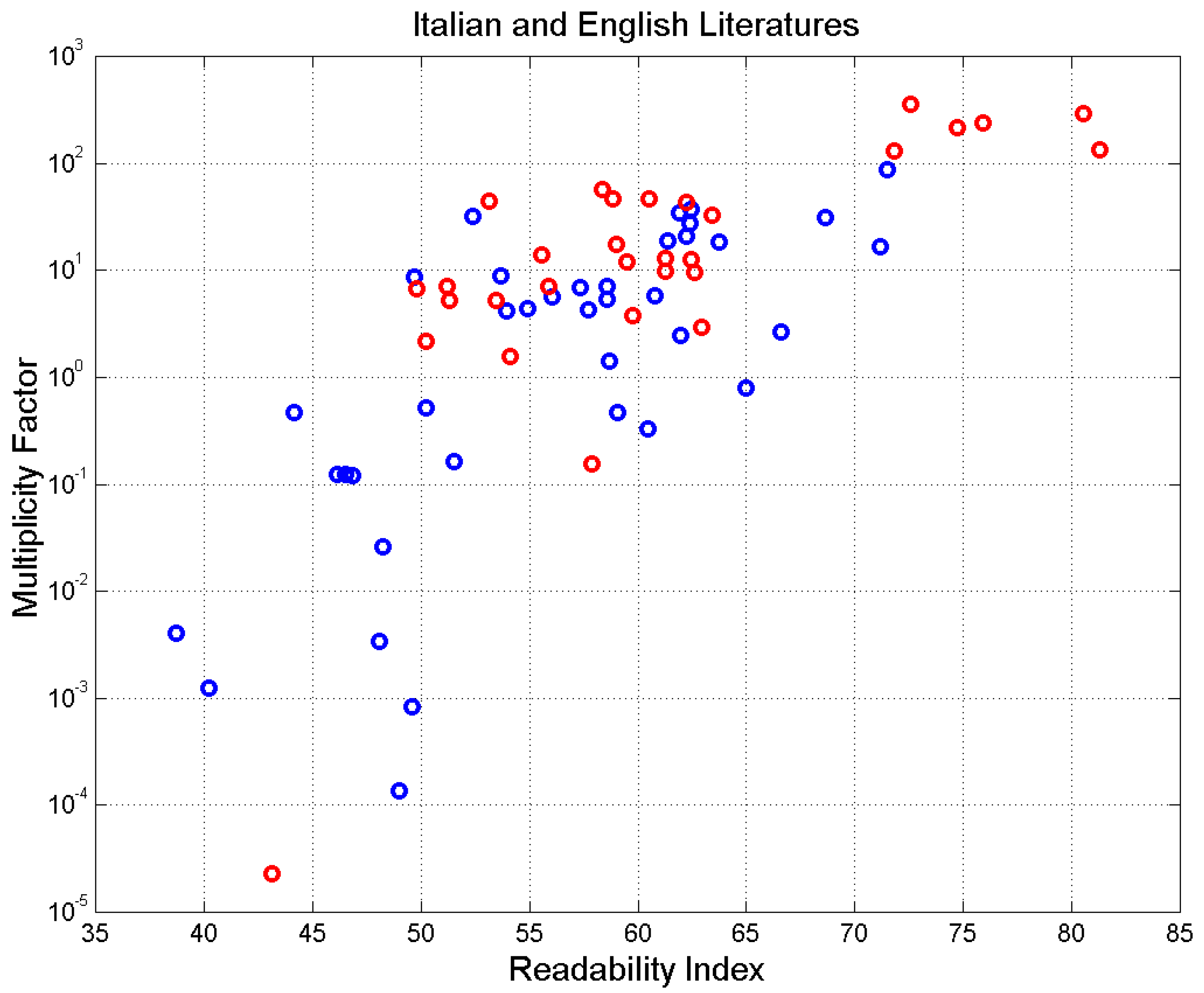In these cases, the writer has enough diverse patters to convey meaning but most of them are not used.
Finally, it is interesting to relate α to a universal readability factor G U , which is a function of both P F and I P [43]. Figure 13 shows α versus G U . Since readability of a text increases as G U increases, we can see that the novels with α < 1 tend to be less readable than those with α > 1 . The less readable novels have in general large values of P F and, therefore, may contain more E–STM cells (large M F ).
In conclusion, if a writer does use the full variety of sentence patterns available, or even overuses them, then he/she writes texts that are easier to read. On the other hand, if a writer does not use the full variety of sentence patterns available, then he/she tends to write texts more difficult to read. In the next section we define a useful index, the mismatch index, which synthetically describes these cases.

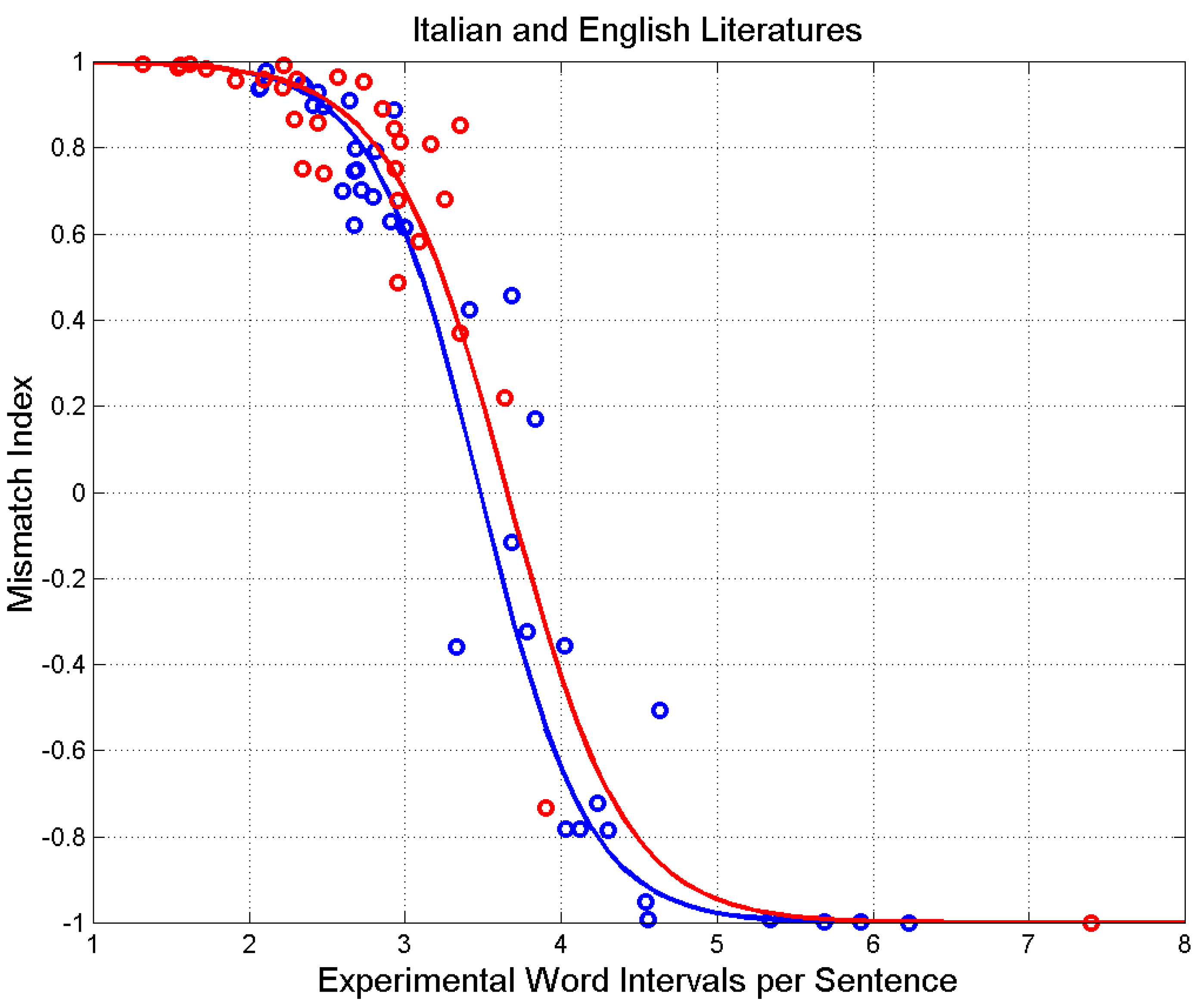
5. Mismatch index

We define a useful index, the mismatch index, which measures to what extent a writer uses the number of sentences theoretically available, according to the averages P F and M F of the novel. For this purpose, we define the mismatch index:
I M = S P F M F − S W C F S P F M F + S W C F = α − 1 α + 1
According to Equation (14), I M = 0 when S P F M F = S W C F , hence α = 1 and in this case experiment and theory are perfectly matched. They are over matched when I M > 0 ( α > 1 ) and under matched when I M < 0 ( α < 1 ) .
Figure 14 shows the scatterplot of I M versus M F . The mathematical models drawn are calculated by substituting Equations (12) (13) in Equation (14). We can reiterate that when I M > 0 (over matching, M F ≲ 3.5 ) the writer repeats sentence patterns because there are not enough diverse patterns to convey all meanings. Texts are easier to read. When I M < 0 (under matching, M F ≳ 3.5 ) the writer has theoretically many sentence patters to choose from, but he/she uses only few or very few of them. Texts are more difficult to read.
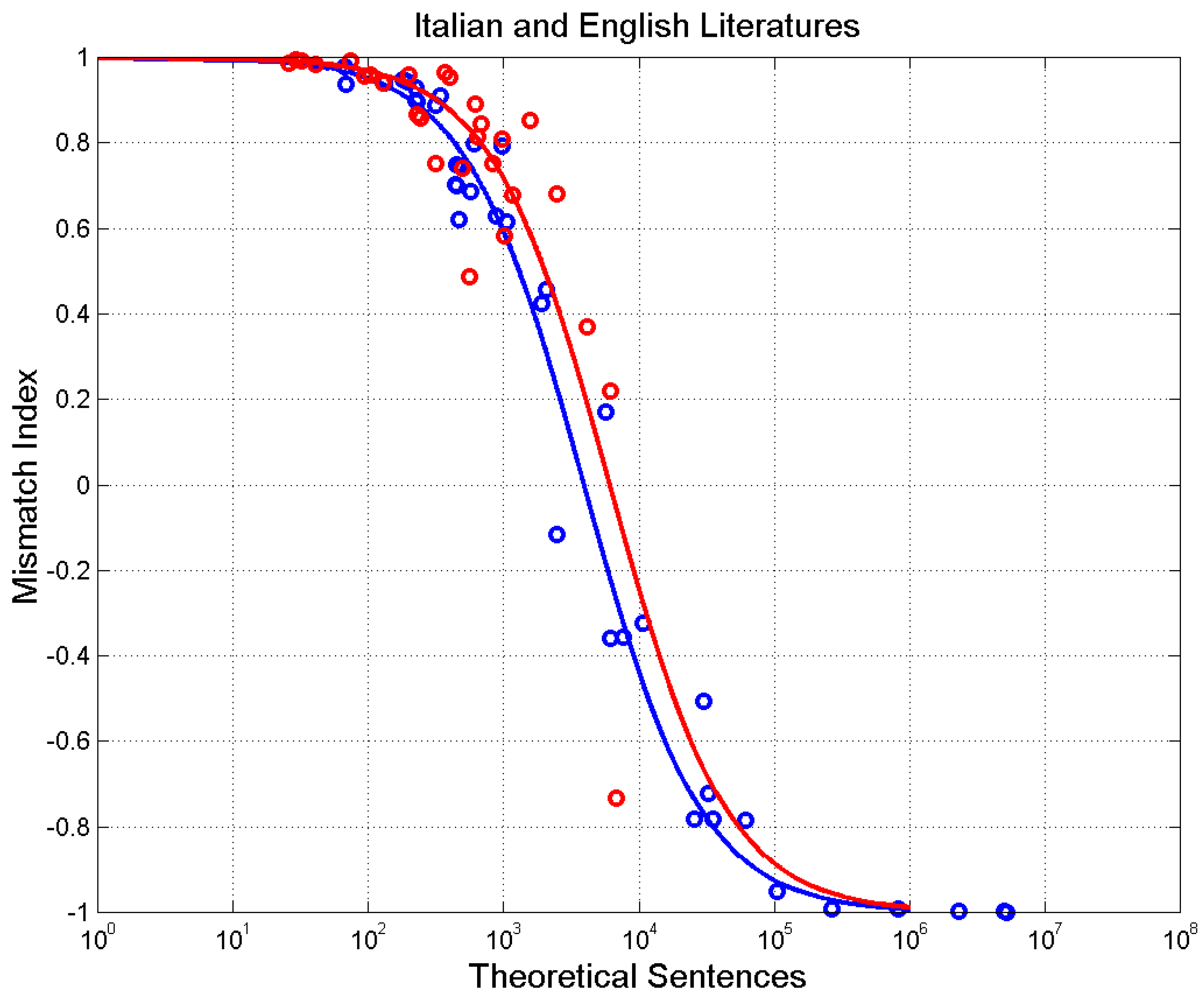
Figure 15 shows the scatterplot of I M versus S W C F . The mathematical models drawn are calculated by substituting Equations (10) (11) in Equation (14). Over matching is found for S W C F < 3886 for Italian and S W C F < 6028 for English.
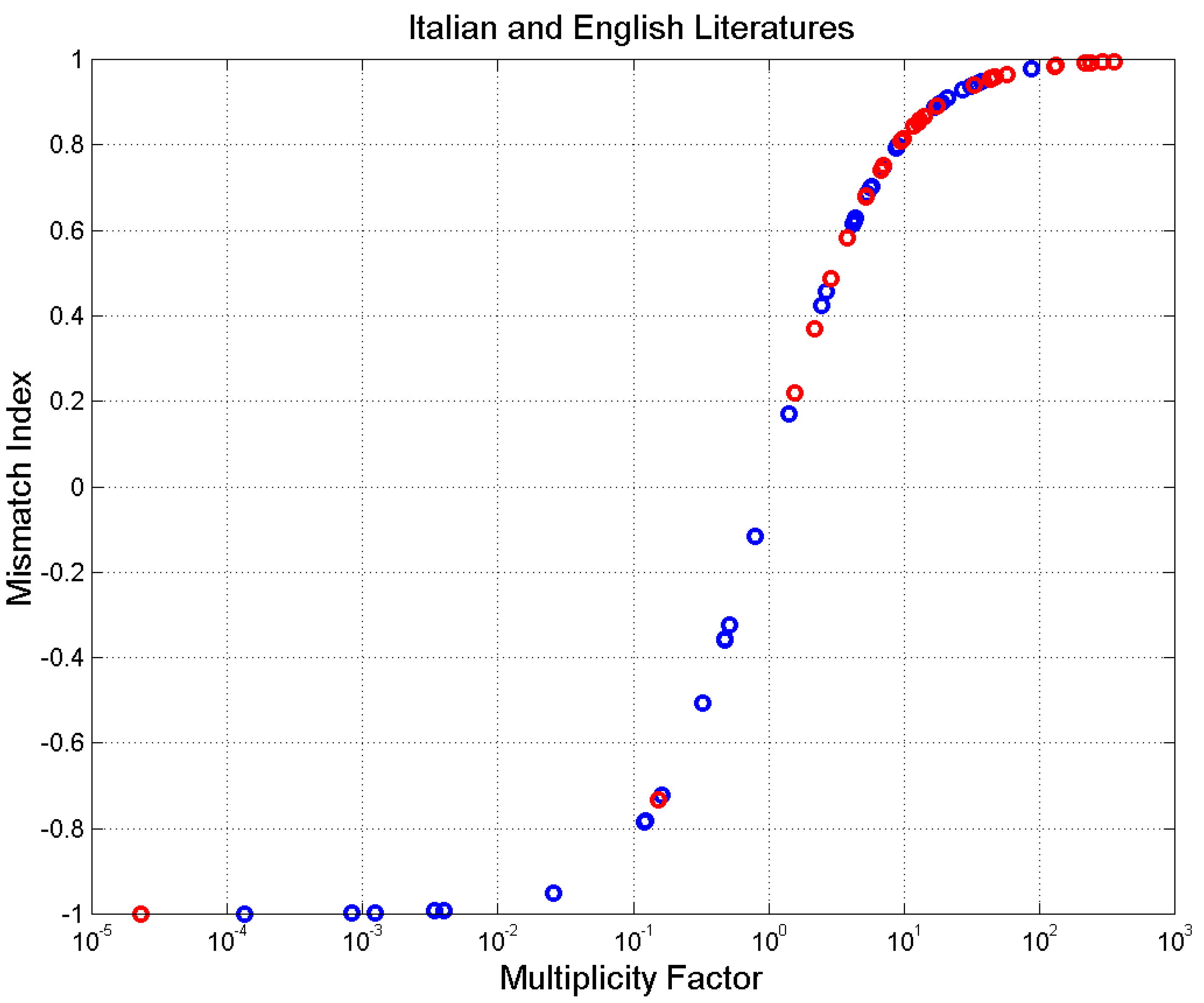
Finally Figure 16 shows I M versus α , Equation (14), a synthetic picture that summarizes the entire analysis of mismatch.
versus the multiplicity factor I M for Italian (blue circles) and English (red circles) novels.
As we can realize by reading the year of publication in Tables B.1, B.2, the novels span a long period. Do the parameters studied depend on time? In the next section we show that the answer to this question is positive.

6. Time dependence

The novels considered in Tables B.1, B.2 were published in a period spanning several centuries. We show that the multiplicity factor α and the mismatch index I M do depend on time.
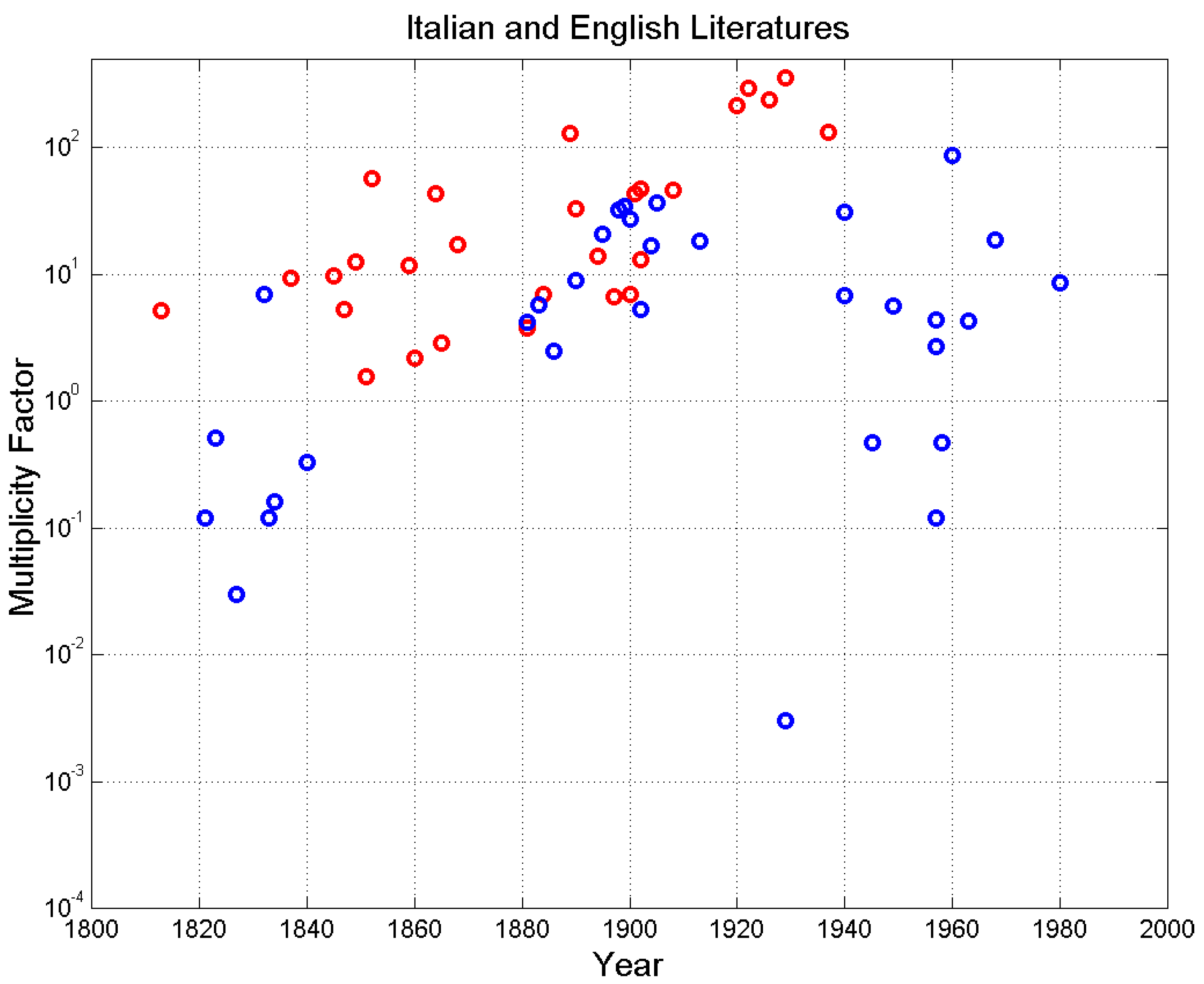
Figure 17 shows the multiplicity factor versus year of publication of the novel since 1800. It is evident that writers tend to use larger values of α – therefore E–STM buffers of small size – as we approach the present epoch, and a possible saturation at I M ≈ 100 . English shows a stable increasing pattern while Italian seems to contain samples coming from two diverse sets of data, one evolving in agreement with English, the other (given by the novels labelled with “*” in Table B.1), always increasing with time, but with diverse slope.
versus year of novel publication, for Italian (blue circles) and English (red circles) novels.
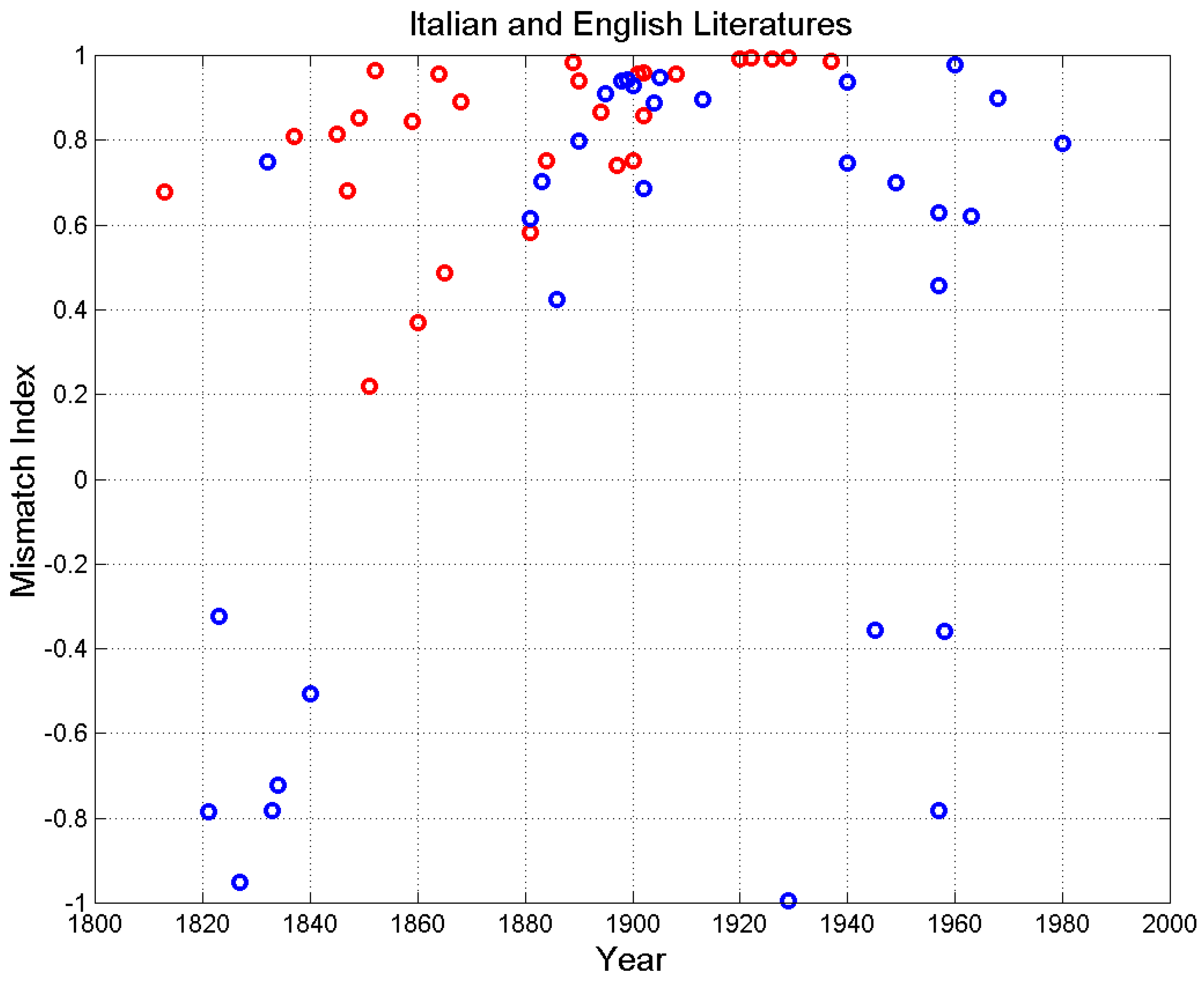
Figure 18 shows the mismatch index versus year of novel publication.
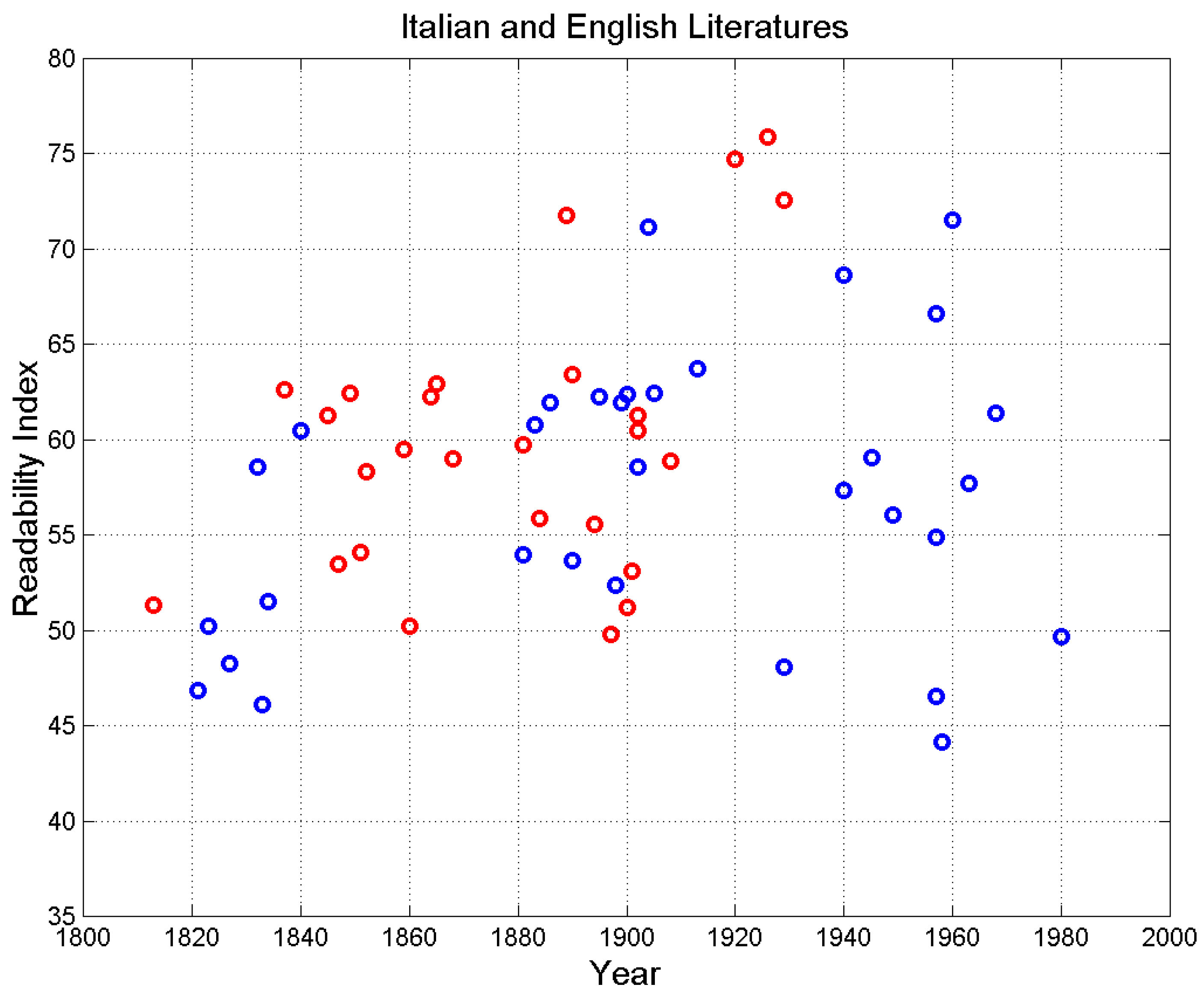
Figure 19 shows the universal readability index versus time. In both figures we can notice the same trends shown in Figure 17, therefore reinforcing the conjecture that: (a) writers are partially changing their style with time by making their novels more readable, i.e. more matched to less educated readers, according to the relationship between G U and the schooling years in Italian school system, as discussed in [43]; (b) a saturation seems to occur in all parameters in the novels written in the second half of the XX century, at least according to the novels of Appendix B.

7. Summary and future work

We have investigated the mathematical structure underlying sentences, first theoretically and secondly experimentally by studying a large number of novels of Italian and English Literatures, written down several centuries.
We have studied the conditional PDF of sentence length – measured in words – allowed by an E–STM buffer made of C F cells, with a Monte Carlo simulation based on the log–normal PDF of the word interval I P . The simulation produces a conditional Gaussian PDF with mean value proportional to C F and standard deviation proportional to C F . These PDFs overlap, indicating, therefore, that some sentences can be processed by buffers of diverse M F size, either larger or smaller, and that the number of sentences is larger in the overlap case C F → C F − 1 than in the case C F − 1 → C F . This means that an E–STM buffer can process to a larger extent data matched to a smaller buffer capacity than data matched to a larger buffer capacity,
We have also studied the number of sentences with equal number of words that the E–STM buffer of C F cells can theoretically process. We have then compared this number to the number of sentences that authors of Italian and English Literatures actually wrote for each novel, by defining the multiplicity factor α . In general, α > 1 is more likely than α < 1 and often α ≫ 1 . When α ≫ 1 the writer reuses many times the same pattern of number of words in a sentence. The multiplicity factor, therefore, indicates also the minimum multiplicity of meanings conveyed. Few novels show α < 1 . In these cases, the writer has enough diverse patters to convey meaning but most of them are not used.
We have then defined the mismatch index − 1 ≤ I M ≤ + 1 , which measures to what extent a writer uses the number of sentences theoretically available. When I M = 0 the match is perfect, the number of sentences theoretically available equals that written in a novel. When I M > 0 (referred to as over matching) the writer repeats sentence patterns because there are not enough diverse patterns to convey all meanings. Texts, however, are easier to read as the universal readability index G U increases. When I M < 0 (under matching) the writer has theoretically many sentence patterns to choose from, but he/she uses only few of them. Texts are more difficult to read, G U decreases.
We have shown that α , I M and G U increase with year of novel publication. Writers are partially changing their style with time by making their novels more readable, i.e. more matched to less educated readers.
Future work should consider other literatures to confirm what, in our opinion, is general because connected to human mind. The same analysis done on ancient languages, such as Greek and Latin – for which there is a large literary corpus – would show whether these ancient writers/readers displayed similar E–STM.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The author wishes to thank the many scholars who, with great care and love, maintain digital texts available to readers and scholars of different academic disciplines, such as Perseus Digital Library and Project Gutenberg.

Conflicts of Interest

The author declares no conflict of interest.

Appendix A. List of mathematical symbols

Symbol Definition
C F Cells of E–STM buffer
G U Universal readability index
I M Mismatch index
I p Word interval
M F Word intervals in a sentence, chapter average
M F Word intervals in a sentence, novel average
P F Words in a sentence, chapter average
< P F > Words in a sentence, novel average
S P F M F Experimental sentences
S W C F Theoretical sentences written in C F cells
W Words in a sentence
f x Three-parameter log-normal density function
f C F x Gaussian PDF
m C F Mean value of Gaussian PDF
s C F standard deviation of Gaussian PDF
α Multiplicity factor
ε Efficiency factor
μ x Mean value of log–normal PDF
σ x standard deviation of log–normal PDF

Appendix B. List of the novels from Italian and English Literatures considered

Tables B.1 and B.2 list author, title of novel and year of publication of Italian and English Literatures considered in the paper, with deep-language average statistics, multiplicity factor α and mismatch index I M . The averages < C P > , < P F > , < I P > < M F > have been calculated by weighting each chapter value with its fraction of total number of words of the novel, as described in [32].
Table B.1. Authors of the novels of the Italian Literature. Number of total sentences (sentences ending with full–stop, question mark, exclamation mark), average number of characters per word 〈CP〉, average number of words pr sentence, 〈PF〉, average number of word intervals, 〈IP〉, average number word intervals per sentence, 〈MF〉, multiplicity factor α, mismatch index IM.
Table B.1. Authors of the novels of the Italian Literature. Number of total sentences (sentences ending with full–stop, question mark, exclamation mark), average number of characters per word 〈CP〉, average number of words pr sentence, 〈PF〉, average number of word intervals, 〈IP〉, average number word intervals per sentence, 〈MF〉, multiplicity factor α, mismatch index IM.
Author (Literary Work, Year) Sentences < C P > < P F > < I P > < M F > α I M
Anonymous (I Fioretti di San Francesco, 1476) 1064 4.65 37.70 8.24 4.56 0.004 -0.99
Bembo Pietro (Prose, 1525) 1925 4.37 37.91 6.42 5.92 0.001 -1.00
Boccaccio Giovanni (Decameron, 1353) 6147 4.48 44.27 7.79 5.69 0.001 -1.00
Buzzati Dino (Il deserto dei tartari, 1940) 3311 5.10 17.75 6.63 2.67 6.90 0.75
Buzzati Dino (La boutique del mistero, 1968*) 4219 4.82 15.45 6.37 2.41 18.83 0.90
Calvino (Il barone rampante, 1957*) 3864 4.63 19.87 6.73 2.91 4.37 0.63
Calvino Italo (Marcovaldo, 1963*) 2000 4.74 17.60 6.59 2.67 4.28 0.62
Cassola Carlo (La ragazza di Bube, 1960*) 5873 4.48 11.93 5.64 2.11 87.66 0.98
Collodi Carlo (Pinocchio, 1883) 2512 4.60 16.92 6.19 2.72 5.74 0.70
Da Ponte Lorenzo (Vita, 1823) 5459 4.71 26.15 6.91 3.78 0.51 -0.32
Deledda Grazia (Canne al vento, 1913, Nobel Prize 1926) 4184 4.51 15.08 6.06 2.48 18.35 0.90
D’Azeglio Massimo (Ettore Fieramosca, 1833) 3182 4.64 29.77 7.36 4.03 0.12 -0.78
De Amicis Edmondo (Cuore, 1886) 4775 4.55 19.43 5.61 3.41 2.48 0.42
De Marchi Emilio (Demetrio Panelli, 1890) 5363 4.70 18.95 7.06 2.68 8.95 0.80
D’Annunzio Gabriele (Le novelle delle Pescara, 1902) 3027 4.91 17.99 6.38 2.79 5.35 0.68
Eco Umberto (Il nome della rosa, 1980*) 8490 4.81 21.08 7.46 2.81 8.70 0.79
Fogazzaro (Il santo, 1905) 6637 4.79 14.84 6.33 2.34 37.08 0.95
Fogazzaro (Piccolo mondo antico, 1895) 7069 4.79 16.08 6.10 2.64 20.98 0.91
Gadda (Quer pasticciaccio brutto… 1957*) 5596 4.76 18.43 4.98 3.68 2.69 0.46
Grossi Tommaso (Marco Visconti, 1834) 5301 4.59 28.07 6.56 4.23 0.16 -0.72
Leopardi Giacomo (Operette morali, 1827) 2694 4.70 31.78 6.90 4.54 0.03 -0.95
Levi Primo (Cristo si è fermato a Eboli, 1945*) 3611 4.73 22.94 5.70 4.02 0.47 -0.36
Machiavelli Niccolò (Il principe, 1532) 702 4.71 40.17 6.45 6.23 0.0001 -1.00
Manzoni Alessandro (I promessi sposi, 1840) 9766 4.60 24.83 5.30 4.63 0.33 -0.51
Manzoni Alessandro (Fermo e Lucia, 1821) 7496 4.75 30.98 7.17 4.30 0.12 -0.78
Moravia Alberto (Gli indifferenti, 1929*) 2830 4.81 36.00 6.74 5.34 0.003 -0.99
Moravia Alberto (La ciociara, 1957*) 4271 4.56 29.93 7.28 4.12 0.12 -0.78
Pavese Cesare (La bella estate, 1940) 2121 4.54 12.37 5.97 2.06 31.19 0.94
Pavese Cesare (La luna e i falò, 1949*) 2544 4.47 17.83 6.83 2.60 5.64 0.70
Pellico Silvio (Le mie prigioni, 1832) 3148 4.80 17.27 6.50 2.69 7.00 0.75
Pirandello Luigi (Il fu Mattia Pascal, 1904, Nobel Prize 1934) 5284 4.63 14.57 4.94 2.93 16.72 0.89
Sacchetti Franco (Trecentonovelle, 1392) 8060 4.37 22.43 5.82 3.83 1.41 0.17
Salernitano Masuccio (Il Novellino, 1525) 1965 4.40 19.20 5.14 3.68 0.79 -0.12
Salgari Emilio (Il corsaro nero, 1899) 6686 4.99 15.09 6.36 2.36 34.46 0.94
Salgari Emilio (I minatori dell’Alaska, 1900) 6094 5.01 15.24 6.25 2.44 27.21 0.93
Svevo Italo (Senilità, 1898) 4236 4.86 16.04 7.75 2.07 32.34 0.94
Tomasi di Lampedusa (Il gattopardo, 1958*) 2893 4.99 26.42 7.90 3.33 0.47 -0.36
Verga (I Malavoglia, 1881) 4401 4.46 20.45 6.82 3.00 4.21 0.62
Table B.2. Authors of the novels of the English Literature. Number of total sentences, average number of characters per word 〈CP〉, average number of words pr sentence, 〈PF〉, average number of word intervals, 〈IP〉, average number word intervals per sentence, 〈MF〉, multiplicity factor α, mismatch index IM. Notice that for Dicken’s novels, Table 1 of [44] reported the number of sentences ending only with full–stop; sentences ending with question mark and exclamation mark were not reported, contrarily to all othe literary texts there (and here) reported. Moreover, the analysis conducted in Reference [44] was done by considering only the sentences ending with full–stop, that is why the values of 〈PF〉 and 〈MF〉 there reported are larger (upper bounds) than those listed below.
Table B.2. Authors of the novels of the English Literature. Number of total sentences, average number of characters per word 〈CP〉, average number of words pr sentence, 〈PF〉, average number of word intervals, 〈IP〉, average number word intervals per sentence, 〈MF〉, multiplicity factor α, mismatch index IM. Notice that for Dicken’s novels, Table 1 of [44] reported the number of sentences ending only with full–stop; sentences ending with question mark and exclamation mark were not reported, contrarily to all othe literary texts there (and here) reported. Moreover, the analysis conducted in Reference [44] was done by considering only the sentences ending with full–stop, that is why the values of 〈PF〉 and 〈MF〉 there reported are larger (upper bounds) than those listed below.
Literary Work (Author, Year) Sentences < C P > P F < I P > M F α I M
The Adventures of Oliver Twist (C. Dickens, 1837–1839) 9,121 4.23 18.04 5.70 3.16 9.46 0.81
David Copperfield (C. Dickens, 1849–1850) 19,610 4.04 18.83 5.61 3.35 12.63 0.85
Bleak House (C. Dickens, 1852–1853) 20,967 4.23 16.95 6.59 2.57 56.98 0.97
A Tale of Two Cities (C. Dickens, 1859) 8,098 4.26 18.27 6.19 2.93 11.89 0.84
Our Mutual Friend (C. Dickens, 1864–1865) 17,409 4.22 16.46 6.03 2.73 43.41 0.95
Matthew King James (1611) 1,040 4.27 22.96 5.90 3.90 0.15 -0.73
Robinson Crusoe (D. Defoe, 1719) 2,393 3.94 52.90 7.12 7.40 0.00002 -1.00
Pride and Prejudice (J. Austen, 1813) 6,013 4.40 21.31 7.16 2.95 5.20 0.68
Wuthering Heights (E. Brontë, 1845–1846) 6,352 4.27 17.78 5.97 2.97 9.83 0.82
Vanity Fair (W. Thackeray, 1847– 1848) 13,007 4.63 21.95 6.73 3.25 5.26 0.68
Moby Dick (H. Melville, 1851) 9,582 4.52 23.82 6.45 3.64 1.56 0.22
The Mill On The Floss(G. Eliot, 1860) 9,018 4.29 23.84 7.09 3.35 2.17 0.37
Alice's Adventures in Wonderland (L. Carroll, 1865) 1,629 3.96 17.19 5.79 2.95 2.90 0.49
Little Women (L.M. Alcott, 1868–1869) 10,593 4.18 18.09 6.30 2.85 17.34 0.89
Treasure Island (R. L. Stevenson, 1881–1882) 3,824 4.02 18.93 6.05 3.09 3.79 0.58
Adventures of Huckleberry Finn (M. Twain, 1884) 5887 3.85 19.39 6.63 2.94 7.05 0.75
Three Men in a Boat (J.K. Jerome, 1889) 5,341 4.25 10.55 6.14 1.72 130.27 0.98
The Picture of Dorian Gray (O. Wilde, 1890) 4,292 4.19 14.30 6.29 2.21 33.02 0.94
The Jungle Book (R. Kipling, 1894) 3,214 4.11 16.46 7.14 2.29 14.10 0.87
The War of the Worlds (H.G. Wells, 1897) 3,306 4.38 19.22 7.67 2.48 6.72 0.74
The Wonderful Wizard of Oz (L.F. Baum, 1900) 2,219 4.017 17.90 7.63 2.34 7.02 0.75
The Hound of The Baskervilles (A.C. Doyle, 1901–1902) 4,080 4.15 15.07 7.83 1.91 43.87 0.96
Peter Pan (J.M. Barrie, 1902) 31,77 4.12 15.65 6.35 2.44 13.07 0.86
A Little Princess (F.H. Burnett, 1902–1905) 4,838 4.18 14.26 6.79 2.09 46.97 0.96
Martin Eden (J. London, 1908–1909) 9,173 4.32 15.61 6.76 2.30 46.33 0.96
Women in love (D.H. Lawrence, 1920) 16,048 4.26 11.62 5.22 2.22 216.86 0.99
The Secret Adversary (A. Christie, 1922) 8,536 4.28 8.97 5.52 1.62 294.34 0.99
The Sun Also Rises (E. Hemingway, 1926) 7,614 3.92 9.43 6.02 1.56 237.94 0.99
A Farewell to Arms (H. Hemingway,1929) 10,324 3.94 9.05 6.80 1.32 356.00 0.99
Of Mice and Men (J. Steinbeck, 1937) 3,463 4.02 8.63 5.61 1.54 133.19 0.99

References

  1. Matricciani, E. Is Short–Term Memory Made of Two Processing Units? Clues from Italian and English Literatures Down Several Centuries. Information, 2023; to be published. Available at: Preprints 2023, 2023101661. [Google Scholar] [CrossRef]
  2. Deniz, F.; Nunez–Elizalde, A.O.; Huth, A.G.; Gallant Jack, L. The Representation of Semantic Information Across Human Cerebral Cortex During Listening Versus Reading Is Invariant to Stimulus Modality 2019, J. Neuroscience, 39, 7722–7736.
  3. Miller, G.A. The Magical Number Seven, Plus or Minus Two. Some Limits on Our Capacity for Processing Information, 1955, Psychological Review, 343−352.
  4. Crowder, R.G. Short–term memory: Where do we stand?, 1993, Memory & Cognition, 21, 142–145.
  5. Lisman, J.E. , Idiart, M.A.P. Storage of 7 ± 2 Short–Term Memories in Oscillatory Subcycles, 1995, Science, 267, 5203,. 1512– 1515.
  6. Cowan, N. , The magical number 4 in short−term memory: A reconsideration of mental storage capacity, Behavioral and Brain Sciences, 2000, 87−114.
  7. Bachelder, B.L. The Magical Number 7 2: Span Theory on Capacity Limitations. Behavioral and Brain Sciences 2001, 24, 116–117. [Google Scholar] [CrossRef]
  8. Saaty, T.L. , Ozdemir, M.S., Why the Magic Number Seven Plus or Minus Two, Mathematical and Computer Modelling, 2003, 233−244.
  9. Burgess, N. , Hitch, G.J. A revised model of short–term memory and long–term learning of verbal sequences, 2006, Journal of Memory and Language, 55, 627–652.
  10. Richardson, J.T. E, Measures of short–term memory: A historical review, 2007, Cortex, 43, 5, 635–650.
  11. Mathy, F. , Feldman, J. What’s magic about magic numbers? Chunking and data compression in short−term memory, Cognition, 2012, 346−362.
  12. Gignac, G.E. The Magical Numbers 7 and 4 Are Resistant to the Flynn Effect: No Evidence for Increases in Forward or Backward Recall across 85 Years of Data. Intelligence, 2015; 48, 85–95. [Google Scholar] [CrossRef]
  13. Trauzettel−Klosinski, S., K. Dietz, K. Standardized Assessment of Reading Performance: The New International Reading Speed Texts IreST, IOVS 2012, 5452−5461.
  14. Melton, A.W. , Implications of Short–Term Memory for a General Theory of Memory, 1963, Journal of Verbal Learning and Verbal Behavior, 2, 1–21.
  15. Atkinson, R.C. , Shiffrin, R.M., The Control of Short–Term Memory, 1971, Scientific American, 225, 2, 82–91.
  16. Murdock, B.B. Short–Term Memory, 1972, Psychology of Learning and Motivation, 5, 67–127.
  17. Baddeley, A.D. , Thomson, N., Buchanan, M., Word Length and the Structure of Short−Term Memory, Journal of Verbal Learning and Verbal Behavior, 1975, 14, 575−589.
  18. Case, R. , Midian Kurland, D., Goldberg, J. Operational efficiency and the growth of short–term memory span, 1982, Journal of Experimental Child Psychology, 33, 386–404.
  19. Grondin, S. A temporal account of the limited processing capacity, Behavioral and Brain Sciences, 2000, 24, 122−123.
  20. Pothos, E.M. , Joula, P., Linguistic structure and short−term memory, Behavioral and Brain Sciences, 2000, 138−139.
  21. Conway, A.R.A. , Cowan, N., Michael F. Bunting, M.F., Therriaulta, D.J., Minkoff, S.R.B, A latent variable analysis of working memory capacity, short−term memory capacity, processing speed, and general fluid intelligence . Intelligence, 2002; 163–183. [Google Scholar]
  22. Jonides, J. , Lewis, R.L., Nee, D.E., Lustig, C.A., Berman, M.G., Moore, K.S., The Mind and Brain of Short–Term Memory, 2008 Annual Review of Psychology, 69, 193–224.
  23. Barrouillest, P. , Camos, V., As Time Goes By: Temporal Constraints in Working Memory, Current Directions in Psychological Science, 2012, 413−419.
  24. Potter, M.C. 2012; Frontiers in Psychology. [CrossRef]
  25. Jones, G, Macken, B., Questioning short−term memory and its measurements: Why digit span measures long−term associative learning, Cognition, 2015, 1−13.
  26. Chekaf, M. , Cowan, N., Mathy, F., Chunk formation in immediate memory and how it relates to data compression, Cognition, 2016, 155, 96−107.
  27. Norris, D. , Short–Term Memory and Long–Term Memory Are Still Different, 2017, Psychological Bulletin, 143, 9, 992–1009.
  28. Houdt, G.V. , Mosquera, C., Napoles, G., A review on the long short–term memory model, 2020, Artificial Intelligence Review, 53, 5929–5955.
  29. Islam, M. , Sarkar, A., Hossain, M., Ahmed, M., Ferdous, A. Prediction of Attention and Short–Term Memory Loss by EEG Workload Estimation. Journal of Biosciences and Medicines, 2023; 304–318. [Google Scholar] [CrossRef]
  30. Rosenzweig, M.R. , Bennett, E.L., Colombo, P.J., Lee, P.D.W. Short–term, intermediate–term and Long–term memories,, Behavioral Brain Research, 1993, 57, 2, 193–198.
  31. Kaminski, J. Intermediate–Term Memory as a Bridge between Working and Long–Term Memory, The Journal of Neuroscience, 2017, 37(20), 5045–5047.
  32. Matricciani, E. Deep Language Statistics of Italian throughout Seven Centuries of Literature and Empirical Connections with Miller’s 7 ∓ 2 Law and Short–Term Memory. Open Journal of Statistics 2019, 9, 373–406. [Google Scholar] [CrossRef]
  33. Strinati E., C. , Barbarossa S. 6G Networks: Beyond Shannon Towards Semantic and Goal–Oriented Communications, 2021, Computer Networks, 190, 8, 1–17.
  34. Shi, G. , Xiao, Y, Li, Xie, X. From semantic communication to semantic–aware networking: Model, architecture, and open problems, 2021, IEEE Communications Magazine, 59, 8, 44–50.
  35. Xie, H. , Qin, Z., Li, G.Y., Juang, B.H. Deep learning enabled semantic communication systems, 2021, IEEE Trans. Signal Processing, 69, 2663–2675.
  36. Luo, X. , Chen, H.H., Guo, Q. Semantic communications: Overview, open issues, and future research directions, 2022, IEEE Wireless Communications, 29, 1, 210–219.
  37. Wanting, Y. , Hongyang, D, Liew, Z. Q., Lim, W.Y.B., Xiong, Z., Niyato, D., Chi, X., Shen, X., Miao, C. Semantic Communications for Future Internet: Fundamentals, Applications, and Challenges, 2023, IEEE Communications Surveys & Tutorials, 25, 1, 213–250.
  38. Xie, H. , Qin, Z., Li, G.Y., Juang, B.H. Deep learning enabled semantic communication systems, 2021, IEEE Trans. Signal Processing, 69, 2663–2675.
  39. Bellegarda, J.R. , Exploiting Latent Semantic Information in Statistical Language Modeling, 2000, Proceedings of the IEEE, 88, 8, 1279–1296.
  40. D’Alfonso, S. On Quantifying Semantic Information. 2011; Information, 2, 61–101. [Google Scholar] [CrossRef]
  41. Zhong, Y. , A Theory of Semantic Information, 2017, China Communications, 1–17.
  42. Papoulis Papoulis, A. Probability & Statistics; Prentice Hall: Hoboken, NJ, USA, 1990. [Google Scholar]
  43. Matricciani, E. Readability Indices Do Not Say It All on a Text Readability. Analytics 2023, 2, 296–314. [Google Scholar] [CrossRef]
  44. Matricciani, E. Capacity of Linguistic Communication Channels in Literary Texts: Application to Charles Dickens’ Novels. Information 2023, 14, 68. [Google Scholar] [CrossRef]
Preprints 92971 g001
Figure 1. Flow–chart of the two processing units of a sentence. The words p 1 , p 2 ,… p j are stored in the first buffer up to j items to complete a word interval I P , approximately in Miller’s range, when an interpunction is introduced. I P is then stored in the E–STM buffer. up to k items, i.e. in M F cells, approximately 1 to 6, until the sentence ends.
Figure 1. Flow–chart of the two processing units of a sentence. The words p 1 , p 2 ,… p j are stored in the first buffer up to j items to complete a word interval I P , approximately in Miller’s range, when an interpunction is introduced. I P is then stored in the E–STM buffer. up to k items, i.e. in M F cells, approximately 1 to 6, until the sentence ends.
Preprints 92971 g001
Preprints 92971 g002
Figure 2. Conditional PDFs of words per sentence versus E–STM buffer of C F cells from 2 to 8. Each PDF can be modelled with a Gaussian PDF fCF(x) with mean value proportional to CF and standard deviation proportional to C F .
Figure 2. Conditional PDFs of words per sentence versus E–STM buffer of C F cells from 2 to 8. Each PDF can be modelled with a Gaussian PDF fCF(x) with mean value proportional to CF and standard deviation proportional to C F .
Preprints 92971 g002
Preprints 92971 g003
Figure 3. Conditional histograms of words per sentence versus E–STM buffer of C F cells from 2 to 8, obtained from Figure 1, by simulating 100,000 sentences weighted with the PDF of MF.
Figure 3. Conditional histograms of words per sentence versus E–STM buffer of C F cells from 2 to 8, obtained from Figure 1, by simulating 100,000 sentences weighted with the PDF of MF.
Preprints 92971 g003
Preprints 92971 g004
Figure 4. Scatterplot of < P F > versus MF of Italian novels (blue circles) and English novels (red circles).
Figure 4. Scatterplot of < P F > versus MF of Italian novels (blue circles) and English novels (red circles).
Preprints 92971 g004
Preprints 92971 g005
Figure 5. Overlap probability (%) versus C F − 1 (lower CF, pHL and pLH are given by Equations (5) and (6).
Figure 5. Overlap probability (%) versus C F − 1 (lower CF, pHL and pLH are given by Equations (5) and (6).
Preprints 92971 g005
Preprints 92971 g006
Figure 6. Number of sentences S W C F made of W words versus E–STM buffer capacity CF.
Figure 6. Number of sentences S W C F made of W words versus E–STM buffer capacity CF.
Preprints 92971 g006
Preprints 92971 g007
Figure 7. Number of sentences S W C F recordable in a E–STM buffer capacity CF versus words per sentence.
Figure 7. Number of sentences S W C F recordable in a E–STM buffer capacity CF versus words per sentence.
Preprints 92971 g007
Preprints 92971 g008
Figure 8. Efficiency ε Equation (8), of an E–STM buffer of CF cells versus words per sentence W.
Figure 8. Efficiency ε Equation (8), of an E–STM buffer of CF cells versus words per sentence W.
Preprints 92971 g008
Preprints 92971 g009
Figure 9. Theoretical number of sentences S W C F versus MF for Italian (blue circles) and English (red circles) novels.
Figure 9. Theoretical number of sentences S W C F versus MF for Italian (blue circles) and English (red circles) novels.
Preprints 92971 g009
Preprints 92971 g010
Figure 10. Multiplicity factor versus S P F M F for Italian (blue circles) and English (red circles) novels.
Figure 10. Multiplicity factor versus S P F M F for Italian (blue circles) and English (red circles) novels.
Preprints 92971 g010
Preprints 92971 g011
Figure 11. Multiplicity factor α versus theoretical number of words S W C F for Italian (blue circles and blue line) and English (red circles and red line) novels.
Figure 11. Multiplicity factor α versus theoretical number of words S W C F for Italian (blue circles and blue line) and English (red circles and red line) novels.
Preprints 92971 g011
Preprints 92971 g012
Figure 12. Multiplicity factor α versus MF for Italian (blue circles and blue line) and English (red circles and red line) novels.
Figure 12. Multiplicity factor α versus MF for Italian (blue circles and blue line) and English (red circles and red line) novels.
Preprints 92971 g012
Preprints 92971 g013
Figure 13. Multiplicity factor α versus readability index GU for Italian (blue circles) and English (red circles) novels.
Figure 13. Multiplicity factor α versus readability index GU for Italian (blue circles) and English (red circles) novels.
Preprints 92971 g013
Preprints 92971 g014
Figure 14. Mismatch index I M versus MF for Italian (blue circles and blue line) and English (red circles and red line) novels.
Figure 14. Mismatch index I M versus MF for Italian (blue circles and blue line) and English (red circles and red line) novels.
Preprints 92971 g014
Preprints 92971 g015
Figure 15. Mismatch index I M versus theoretical number of sentences S W C F < 3886 for Italian (blue circles and blue line) and English (red circles and red line) novels.
Figure 15. Mismatch index I M versus theoretical number of sentences S W C F < 3886 for Italian (blue circles and blue line) and English (red circles and red line) novels.
Preprints 92971 g015
Preprints 92971 g016
Figure 16. Mismatch index I M versus the multiplicity factor IM for Italian (blue circles) and English (red circles) novels.
Figure 16. Mismatch index I M versus the multiplicity factor IM for Italian (blue circles) and English (red circles) novels.
Preprints 92971 g016
Preprints 92971 g017
Figure 17. Multiplicity factor I M versus year of novel publication, for Italian (blue circles) and English (red circles) novels.
Figure 17. Multiplicity factor I M versus year of novel publication, for Italian (blue circles) and English (red circles) novels.
Preprints 92971 g017
Preprints 92971 g018
Figure 18. Mismatch factor α versus year of novel publication, for Italian (blue circles) and English (red circles) novels.
Figure 18. Mismatch factor α versus year of novel publication, for Italian (blue circles) and English (red circles) novels.
Preprints 92971 g018
Preprints 92971 g019
Figure 19. Universal readability index G U versus year of novel publication, for Italian (blue circles) and English (red circles) novels.
Figure 19. Universal readability index G U versus year of novel publication, for Italian (blue circles) and English (red circles) novels.
Preprints 92971 g019
Table 1. Mean value μ x and standard deviation σx of the log–normal PDF of the indicated variable [1].
Table 1. Mean value μ x and standard deviation σx of the log–normal PDF of the indicated variable [1].
μ x σ x
I P 1.689 0.180
P F 3.038 0.441
M F 0.849 0.483
Table 2. Theoretical number of sentences S W C F (columns) recordable in an E–STM buffer made of CF cells with the same number of words (items) indicated in the first column.
Table 2. Theoretical number of sentences S W C F (columns) recordable in an E–STM buffer made of CF cells with the same number of words (items) indicated in the first column.
Words W (items storeable) E–STM buffer made of C F cells
1 2 3 4 5 6 7 8
1 1 0 0 0 0 0 0 0
2 1 1 0 0 0 0 0 0
3 1 2 1 0 0 0 0 0
4 1 3 3 1 0 0 0 0
5 1 4 6 4 1 0 0 0
6 1 5 10 10 5 1 0 0
7 1 6 15 20 15 6 1 0
8 1 7 21 35 35 21 7 1
9 1 8 28 56 70 56 28 8
10 1 9 36 84 126 126 84 36
11 1 10 45 120 210 252 210 120
12 1 11 55 165 330 462 462 330
13 1 12 66 220 495 792 1254 792
14 1 13 78 286 715 1287 2046 2046
15 1 14 91 364 1001 2002 3333 4092
16 1 15 105 455 1365 3003 5335 7425
17 1 16 120 560 1820 4368 8338 12760
18 1 17 136 680 2380 6188 12706 21098
19 1 18 153 816 3060 8568 18894 33804
20 1 19 171 969 3876 11628 27462 52698
21 1 20 190 1140 4845 15504 39090 80160
22 1 21 210 1330 5985 20349 54594 119250
23 1 22 231 1540 7315 26334 74943 173844
24 1 23 253 1771 8855 33649 101277 248787
25 1 24 276 2024 10626 42504 134926 350064
26 1 25 300 2300 12650 53130 177430 484990
27 1 26 325 2600 14950 65780 230560 662420
28 1 27 351 2925 17550 80730 296340 892980
29 1 28 378 3276 20475 98280 377070 1189320
30 1 29 406 3654 23751 118755 475350 1566390
31 1 30 435 4060 27405 142506 594105 2041740
32 1 31 465 4495 31465 173971 768076 2635845
33 1 32 496 4960 35960 205436 973512 3403921
34 1 33 528 5456 40920 241396 1178948 4377433
35 1 34 561 5984 46376 282316 1461264 5556381
36 1 35 595 6545 52360 328692 1789956 7017645
37 1 36 630 7140 58905 381052 2118648 8807601
38 1 37 666 7770 66045 439957 2499700 10926249
39 1 38 703 8436 73815 506002 2939657 13425949
40 1 39 741 9139 82251 579817 3519474 16365606
41 1 40 780 9880 91390 662068 4099291 19885080
42 1 41 820 10660 101270 753458 4761359 23984371
43 1 42 861 11480 111930 854728 5514817 29499188
44 1 43 903 12341 123410 966658 6369545 35014005
45 1 44 946 13244 135751 1090068 7336203 41383550
46 1 45 990 14190 148995 1225819 8426271 48719753
47 1 46 1035 15180 163185 1374814 9652090 58371843
48 1 47 1081 16215 178365 1537999 11026904 68023933
49 1 48 1128 17296 194580 1716364 12564903 79050837
50 1 49 1176 18424 211876 1910944 14281267 91615740
51 1 50 1225 19600 230300 2122820 16192211 105897007
52 1 51 1275 20825 251125 2353120 18315031 122089218
53 1 52 1326 22100 273225 2604245 20668151 140404249
54 1 53 1378 23426 296651 2877470 23272396 161072400
55 1 54 1431 24804 320077 3174121 26149866 184344796
56 1 55 1485 26235 344881 3494198 29323987 210494662
57 1 56 1540 27720 371116 3839079 32818185 239818649
58 1 57 1596 29260 398836 4210195 36657264 272636834
59 1 58 1653 30856 428096 4609031 40867459 309294098
60 1 59 1711 32509 458952 5037127 45476490 350161557
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated