Prerpints.org logo
Preprint
Article

Numerical Simulation of CdTe Crystal Growth by VGF Technique Assisted by Axial Low-Frequency Oscillations of the Melt

Altmetrics

Downloads

126

Views

25

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.pdf (243.95KB )

Submitted:

12 December 2023

Posted:

13 December 2023

You are already at the latest version

Alerts
Abstract
The problem of intensification of melt crystal growth process has been analyzed using CdTe as an actual material. Numerical simulation of 100 mm diameter CdTe crystal growth by VGF technique has been carried out. The heat-mass transfer was controlled by introducing of low-frequency oscillating baffle into the melt, so called axial vibrational control (AVC) technique. The baffle configuration has been optimized to destroy solid «tails», which were formed near the crucible walls at high cooling rates due to the low thermoconductivity and the corresponding latent heat. Analysis of CdTe homogeneity range showed that during fast crystal cooling Te micro precipitations were formed resulting from decay of oversaturated Cd-riched nonstoichiometric solid solution at Bridgman crystal growth technique. A VGF grown CdTe crystal after full crystallization stays inside the phase field of the high temperature wurtzite polymorph. This makes it possible to go through the polymorph transition without Te micro-precipitating using the advantages of VGF specific feature of very slow cooling.
Keywords: 
Subject: Engineering  -   Chemical Engineering

1. Introduction

The problem of increasing the efficiency of industrial crystal growing processes has been of concern to both scientists and businesses for the last 30 years due to the growing volume of single crystal production. Moreover, over 90% of industrial crystals are grown from the liquid phase. In turn, more than 50% of these crystals are obtained by directional crystallization of melts (Figure 1a). This applies to 90% of semiconductor crystals, which are mainly obtained by the Czochralski, Bridgman, VGF, TNM methods and their variations (Figure 1b).
The impressive achievements of the VGF method for production of perfect structure GaAs crystals with a diameter of up to 200 mm are associated with the implementation of a multi-crucible configuration of the growth installation [1]. In this installation, even despite the low growth rate of the VGF process, it was possible to implement a highly profitable industrial process [2]. However, these achievements are inextricably linked with an increase in the chemical purity of the starting material to a purity of 7-8N [3,4,5].
Semiconductor crystals of cadmium telluride (CdTe) and its solid solutions (CdxZn1-xTe) are the best materials for room-temperature X-ray and gamma-ray detection systems [6], which are widely used in medicine, security systems, and scientific technology. Therefore, interest in these materials has a steady growth trend [7].
To date, the industrial production of high-quality CdZnTe crystals with a diameter of up to 100 mm has been carried out using the THM method [8,9]. This method made it possible to overcome the problem of high-temperature polymorph transition and reduce the concentration of non-stoichiometric defects to the required level [9]. Lowered growth temperatures, low segregation of Zn, and the ability to use the seed crystal are advantages of THM. Achieved mobility-lifetime product, leakage current, and resistivity for growth crystals are compared with the best available CdZnTe crystals [11]. However, from a commercial point of view, the THM method remains low-profit due to the low growth rate and the complexity of preparing a polycrystalline seed of variable composition.
The growth of structurally perfect CdTe and CdZnTe crystals with a diameter of 100 mm due to the low thermal conductivity of the material by the Bridgman method is accompanied by a number of problems, one of which is a concave front at a relatively high crystallization rate [12,13]. It is formed, on the one hand, due to the extremely low thermal conductivity of cadmium telluride, which entails very slow radial heat transfer. On the other hand, during the CdTe crystallization, a large amount of latent heat is released, and taking into account natural convection in the melt, this leads to its uneven distribution along the crystallization front, which also leads to its sagging.
In Ref [14] it was shown, that the use of the AVC (axial vibrational control) technique made it possible to solve the above problems by creating a controlled forced laminar flows in the melt using a submerged inert oscillating disk. However, the authors also declared that in a real experiment, the use of a cylindrical disk eventually led to the formation of a gas bubble along the surface, especially in viscous liquids, which over time caused the turbulence of the flow due to the chaotic movement of the gas bubble. It is assumed that this is due to the compressibility effect during crystallization. In the case of free access of the melt to the surface of the forming crystal, hydrodynamic equilibrium is established, and bubble formation does not occur. However, if access of the melt to the surface is limited, which occurs with the introduction of oscillations through a cylindrical disk due to the small distance between the periphery of the disk and the crucible wall at a high frequency of oscillations, a gradual formation of cadmium vapor occurs [15], which forms a stable bubble on the surface of the oscillating disk account of surface tension forces.
This problem can be solved by configuring an oscillating body that is capable of both effectively leveling the crystallization front and providing free access of the melt to the surface of the crystal being grown. In this work, a cylindrical ring is presented as an oscillating baffle for calculating the growth of CdTe crystal using the VGF method, which satisfies all the above requirements. In the present research, we analyzed the configuration of low-frequency oscillating ring-baffle and its influence on heat-mass-transfer at VGF crystal growth of CdTe crystals.

2. Mathematical model

Modeling of the crystallization front in the melt was carried out in the approximation of an incompressible linearly viscous fluid in a gravity field, which is described by the Navier-Stokes equation supplemented by the continuity equation:
ρ 0 ∂ v ¯ ∂ t + v ¯ · ∇ v ¯ = μ ρ 0 ∇ 2 v ¯ − 1 ρ 0 ∇ p + f ¯ g + f ¯ c r ;
∇ · v ¯ = 0 .
The fluid density and the gravity force in the Navier-Stokes equation was determined by the Boussinesq approximation:
ρ T = ρ 0 − ρ 0 β T − T m ;
f ¯ g = − ρ − ρ 0 g ¯ = − ρ 0 β T − T m g ¯ .
The law of energy conservation for an incompressible fluid, taking into account crystallization, is written in the enthalpy-porosity formulation [16]:
∂ ρ H ∂ t + ∇ ρ v ¯ H = − ∇ · k ∇ T .
Neglecting kinetic energy, the enthalpy of the melt is determined as
H = ε ∆ H m + ∫ T r e f T C p d T .
Enthalpy-porosity formulation describes the crystallization process as a change in the “porosity” of the medium ε, or a change in the fraction of liquid, which for two-phase systems with unlimited solubility is defined as
ε = 1 ,                                                               T ≥ T l ;   T − T s T l − T s ,                               T s < T < T l ;     0 ,                                                               T ≤ T s ,  
where T is temperature, T s is solidus temperature, Tl is liquidus temperature. When crystallizing a phase without decomposition, Ts = Tl, and the authors [19] propose using a different formulation for ε, however, to increase the stability of the numerical model, we adopted
T s = T m − ∆ T ,             T l = T m + ∆ T ,           ∆ T = 0,01   K ,
here Tm is CdTe melting temperature.
The drop in the fluid velocity at ε < 1 (transition to the crystalline phase) is due to the term f ¯ c r . The use of the modified Kozeny-Carman equation is widespread:
f ¯ c r = − C v ¯ = − A 1 − ε 2 ε 3 + 0,001 v ¯ ,
where coefficient A is selected manually, and the larger it is, the sharper the change in speed will be, but the less stable the numerical model becomes. In this work, for all calculations we used A = 10 6 .

3. Numerical model parameters

Numerical simulation was carried out in a two-dimensional axisymmetric approximation for CdTe melt in a crucible with an inner diameter of 100 mm without an oscillating body and with it (Figure 2). A cylindrical ring with sharp edges was attached to the central rod using cylindrical spokes. Previously, it was demonstrated that cylindrical body [17] as well as a plane disk with rounded edges [18] did not cause flows when oscillating in isothermal fluid. So, the above-described ring-baffle constructed from dense graphite was used as an oscillating body in our numerical simulation.
Grid models with an average cell size of 0.5 mm were constructed. For the near-wall layers, additional grinding was applied. For the model with an oscillating ring-baffle, the mesh was also refined with a minimum cell size of 5 μm with a smooth change in size. The calculation was carried out using the ANSYS 14.5 package. If necessary, the adaptive mesh refinement method was used to further refine the mesh during the calculation process. The specific features of the mesh model at AVC application are described in details in Ref. [14].
The CdTe and dense graphite properties used for the numerical simulation are presented in Table 1.
It should be noted that the public domain contains conflicting data on the heat capacity and thermal conductivity of molten cadmium telluride. In Ref. [22], devoted to the growth of cadmium telluride crystals by the Bridgman method, the thermal diffusivity coefficients α near the melting point were experimentally determined. Then from the definition of thermal diffusivity:
k = α ρ C p ,
one can determine the thermal conductivity of cadmium telluride near its melting point. The calculated thermal conductivity coefficients are presented in Table 1.
The heat capacity of the CdTe melt was taken constant and calculated from the equation for the solid state at the melting temperature of the substance [15]. To correctly calculate the enthalpy of CdTe, the heat capacity equation in the solid state was adjusted taking into account the change in its density in the solid state [20]:
k C p s ′ = ρ s ρ l C p s .
The boundary conditions for the temperature along the crucible walls were determined from the equation
T x , t = T 0 + d T d x · x − d T d t · t = T 0 + τ x x − τ t t ,
where T0 is the temperature that determines the initial position of the crystallization front, τx is the temperature gradient along the height of the crucible, τt is the temperature gradient over time (linear crystallization rate).
v x t = A ω cos ⁡ ω t ; v y = 0 .
Here A is the amplitude of oscillations, ω = 2 π f is the angular frequency of oscillations, f is the frequency of oscillations.
The equations were solved using the finite volume method. The gradients were discretized using the least squares method. The continuity and Navier-Stokes equations were solved jointly using the Coupled scheme; pressure discretization was carried out using the PRESTO scheme. Discretization of speed and energy was carried out using second-order schemes in the calculation without a ring and using first-order schemes - with a ring. Time discretization was carried out according to a first-order scheme.
We paid particular attention to relaxation coefficients. The crystallization model in the enthalpy-porosity formulation is extremely unstable, so it is necessary to introduce small relaxation coefficients for almost all variables and increase the number of internal iterations when calculating the time step. The relaxation and accuracy coefficients for the absolute discrepancy, at which constant values of the variables were achieved, are indicated in Table 2.

4. Results and discussion

4.1. Effect of linear crystallization rate

Calculations were carried out in a crucible at linear crystallization rates τt = 0.2, 1 and 5 K/hour in unsteady mode. The initial approximation was specified using a stationary calculation under boundary conditions T0 = 1363 K, which corresponds to the position of the crystallization front before reaching the conical expansion of the crucible, i.e. position of the seed crystal.
The value of τx in the VGF method is chosen to be constant and small enough to ensure minimal thermal stress, which affects the structural perfection of the crystal. It is technologically possible to provide a linear gradient τx = 1 K/cm, which was adopted for all calculations.
In the resulting sections of the crystallization fields (Figure 3), one can observe how, during the crystal growth process, the crystallization front bends from the crucible axis to the wall.
Two parts of the crystallization front can be distinguished: central and peripheral. Note that they have different curvature, and this is explained by the influence of the thermal effect of crystallization. Indeed, if we imagine that crystallization occurs without a thermal effect, then the curvature of the crystallization front is determined solely by the ratio of thermal conductivities in the melt and crystal (see Ref. [22]). However, taking into account the crystallization heat significantly increases the sagging of the front, and leads to the appearance of a linear “tail” part of the crystal at the periphery of the crucible. In Figure 4 shows the velocity field in a logarithmic scale (on the left) and the temperature field (on the right) with the “tails” positioned at a height of 8 cm from the bottom of the crucible. Similar fields are shown in Figure 5 at a distance of 14 cm from the bottom of the crucible.
They clearly show how, at different crystallization rates, an isothermal region is established, which has been formed due to the heat of crystallization. In this region, thermal equilibrium is established, and the melt flow rate in it drops to almost zero. This means that the convective part of equation (5) also tends to zero, and the temperature distribution, and therefore the shape of the front, is determined only by the time term and the thermal conductivity of cadmium telluride in the liquid and solid phases.
In the near-wall region, the axial temperature gradient predominates, which is determined by the boundary condition (12). Towards the center of the crucible the axial temperature gradient decreases to zero due to the heat of crystallization. On the one hand, this leads to the formation of “tails” and the establishment of a linear front, on the other hand to a stationary thermal regime closer to the crucible axis, which determines the concave front profile due to the difference in thermal conductivity coefficients.
Consequently, to straighten the crystallization front, it is necessary to ensure the distribution of the heat of crystallization over the crucible due to the convective term in equation (5), that is, to introduce a sufficient flow rate into the isothermal region.
The complete results of the crystallization process as movies are presented in Supplementary section.
The use of the AVC technique involves the creation of a laminar controlled flow, but at high frequencies and amplitudes of vibrations a transition to a turbulent regime occurs. It can be seen that at τt = 0.2 K/hour, the bending of the crystallization front is the smallest, the size of the “tails” is small, and the total crystallization time is approximately three days, which is acceptable for the technology of growing high-quality single crystals. Consequently, vibrational parameters will be selected for this mode, at which it will be possible to align the crystallization front

4.2. Unsteady calculation of crystallization assisted by axial low-frequency vibrations

The oscillation amplitude of a ring-baffle (Figure 2) was 0.1 mm, the oscillation frequency was 50 Hz. Calculation of oscillatory motion requires the choice of a minor step size for accurate calculation of the velocity field. In our calculation, its size was 1/400 of the oscillation period (5×10–5 s), optimized for AVC technique earlier [18]. The calculation was carried out until a stationary temperature distribution in the liquid was achieved, which took 60 s.
The oscillatory motion of a baffle in the form of cylindrical ring in a viscous liquid in an unlimited volume leads to the formation of a flow velocity field that is sinusoidal in time and solenoidal in space. Complication of this model by taking into account the geometric dimensions of the crucible and thermal convection leads to a change in the flow velocity and deformation of the flow shape. In a viscous fluid, the AVC flows generate two regions (Figure X).
Preprints 93102 g006
Figure 6. Velocity field colored by magnitude after 9×104 s of CdTe VGF crystal growth at AVC action with 50 Hz frequency and 0.1 mm amplitude.
Figure 6. Velocity field colored by magnitude after 9×104 s of CdTe VGF crystal growth at AVC action with 50 Hz frequency and 0.1 mm amplitude.
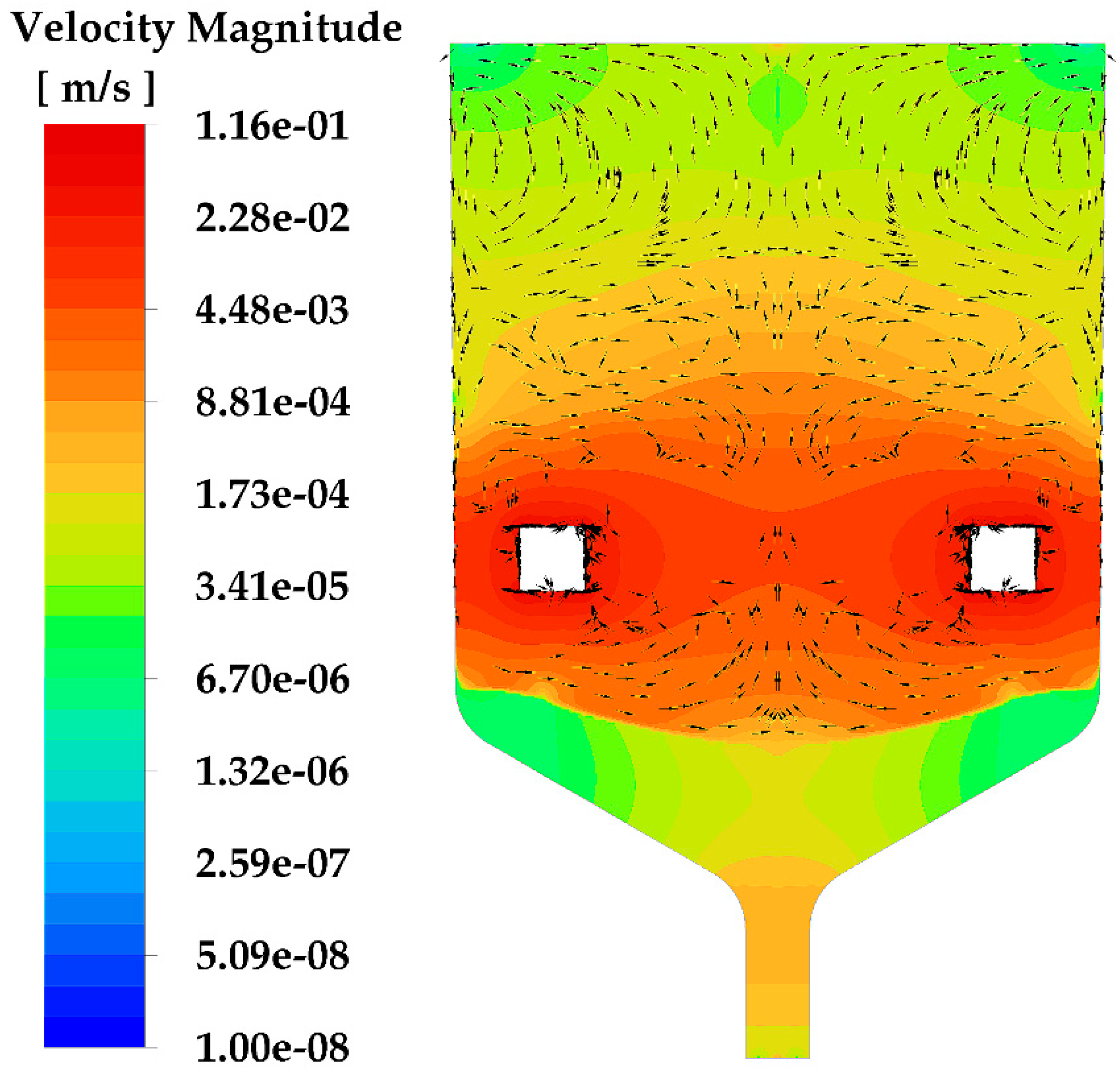
Preprints 93102 g006
The primary region is adjacent to the ring. The secondary region is flowing around the ring. The formation of the primary region is a consequence of viscous dissipation of velocity from the surface of the ring. While the formation of the secondary region is a consequence of the flow around the body (movement of the fluid mass) during its movement. The primary region is quite small, so the energy distribution in the system is determined primarily by the secondary flow.
Preprints 93102 g007
Figure 7. Crystallized parts of the melt at VGF growth of CdTe at cooling rates 0.2 K/h without (a) and with the ring-baffle oscillating with 50 Hz frequency and 0.1 mm amplitude (b).
Figure 7. Crystallized parts of the melt at VGF growth of CdTe at cooling rates 0.2 K/h without (a) and with the ring-baffle oscillating with 50 Hz frequency and 0.1 mm amplitude (b).
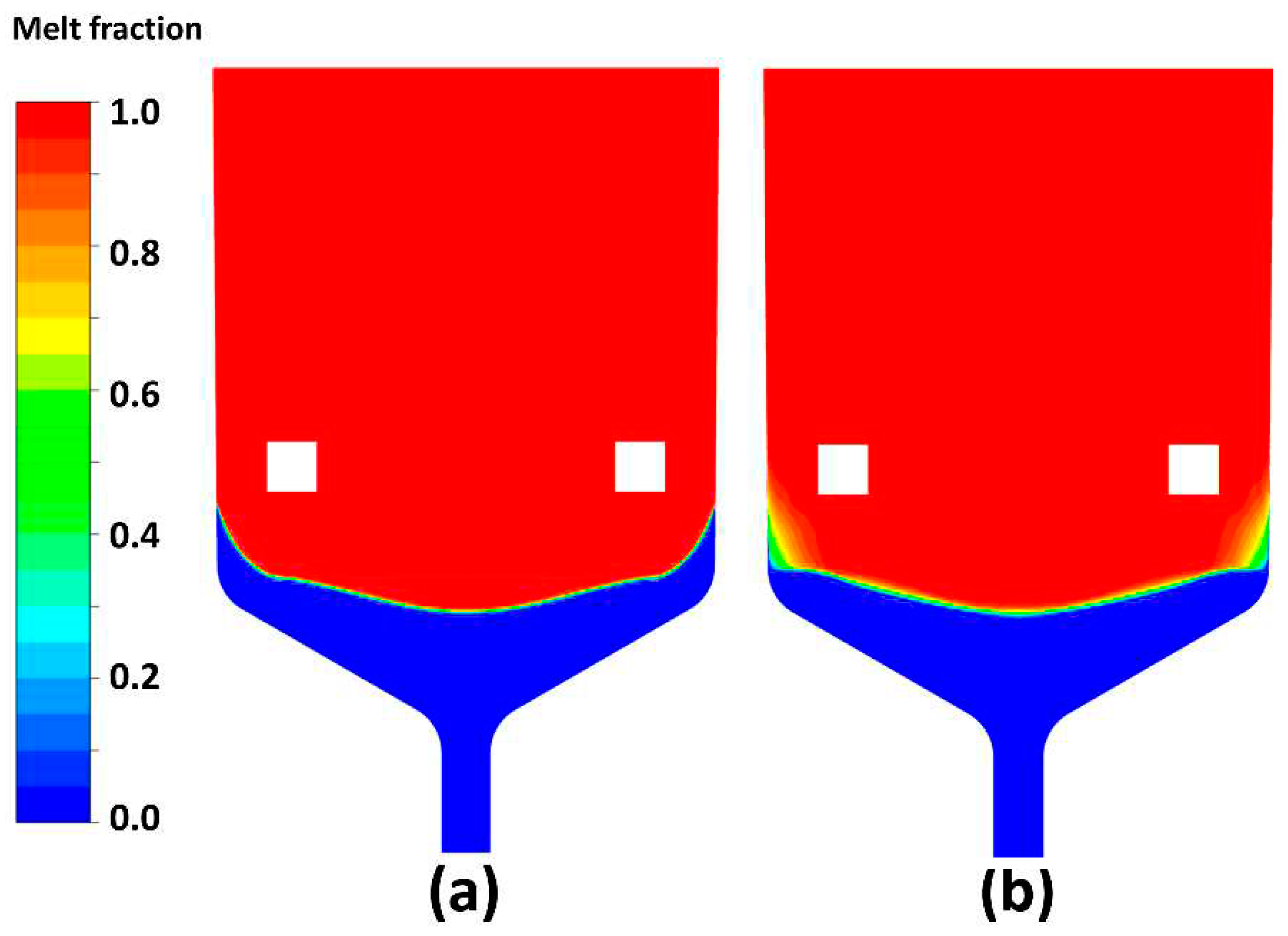
Preprints 93102 g007
The hot AVC flows, as expected, gradually dissolve the solidified “tail”. Note that the “blurring” of the crystallization front is a specific feature of the “mushy zone” model which is used in FLUENT software for solidification processing. Consequently, the exact shape of the front is plotted by the deep-blue region where liquid fraction is equal to zero.
Melting of the solid “tail” occurs due to the transfer of a colder mass of the melt to a hotter region of the melt when the ring-baffle moves downwards, followed by the movement of a warmer melt to the crystallization front - when the ring-baffle moves up (Figure 8).
Besides, at AVC action, a uniform redistribution of the enthalpy of crystallization occurs, followed by the expansion of the isothermal region. The position of the ring closer to the crucible wall also plays a significant role - a more intense sinusoidal axial flow occurs above the “tail” due to the presence of a narrower cylindrical split than in the center, thereby more intense heat and mass transfer. Finally, the ring itself has a high coefficient of thermal conductivity, which allows it to serve as an additional source of heat, which is shown in the temperature distribution when the disk oscillates resulting to further intensification of heat transfer. This is reflected in the appearance of an additional bend of the crystallization front, where the section between the “tail” and the central part of the front is parallel to the surface of the disk.
Preprints 93102 g009
Figure 9. Velocity fields colored by magnitude without (a) and with the ring-baffle oscillating with 50 Hz frequency and 0.1 mm amplitude (b).
Figure 9. Velocity fields colored by magnitude without (a) and with the ring-baffle oscillating with 50 Hz frequency and 0.1 mm amplitude (b).
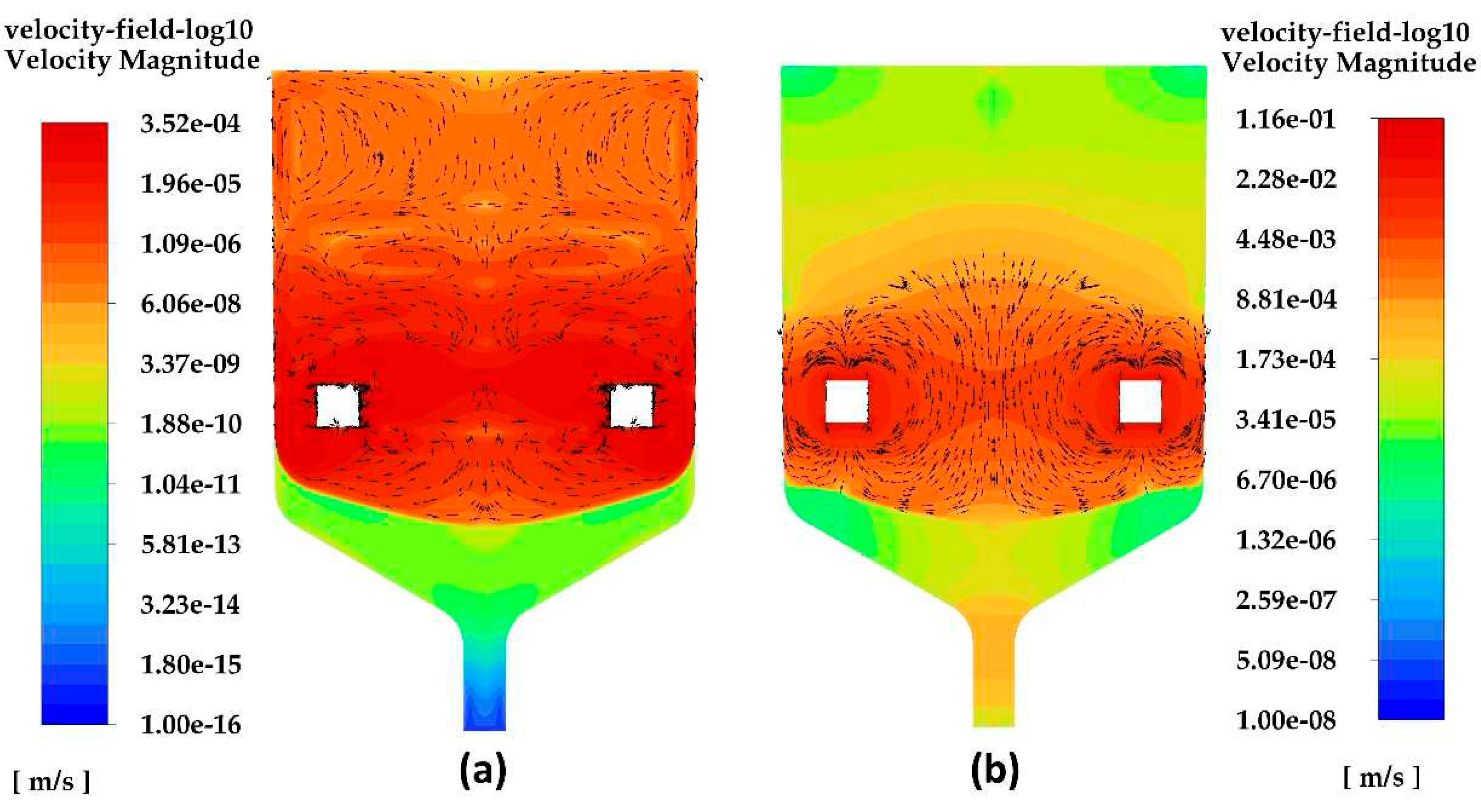
Preprints 93102 g009
The introduction of axial low-frequency vibrations through the disk with sharp edges leads to the breakdown of clusters in the melt [24], improving the structural perfection of the grown crystal. The integral power of viscous dissipation was determined using the expression
P = ∫ V   μ ∂ v x ∂ y + ∂ v y ∂ x 2 d V
In the case of the disk with sharp edges maximum of P value reached 8×106 W/m3, while the momentum Pw in the whole melt volume reached 0.2 W [24].
The maximum power of viscous dissipation during our ring-baffle oscillation (Figure 10), however, does not allow achieving the required indicators. This value was more than in order less (1.4×105 W/m3) than in the case of a plane disk. This is explained by the fact that the movement of the melt when the ring-baffle oscillates is freer than when the plane disk oscillates. The friction between the layers of the moving liquid is much less, because the mass transfer of the liquid melt when the disk oscillates only through the area between the melt and the wall, which leads to an increase in energy viscous dissipation.

4.3. The role of high temperature phase transition for CdTe crystal growth at congruent crystallization

The high temperature wurzite-sphalerite phase transition in CdTe is a controversial issue for the last 30 years [26,27,28,29,30,31]. In Ref. [32], using the systematic approach to the analysis of homogeneity ranges of cadmium and zinc chalcogenides we demonstrated that for CdTe there is a polymorph transition at 1210-1270 K depending on nonstoichiometry (Figure 12). In the case of CdTe direct crystallization from the Cd-saturated melt in the range of polymorphic transition one observed Te precipitation (see insertion in Figure 11), which resulted from compensation of nonstoichiometric composition passing through the polymorph transition at fast cooling specific for Bridgman technique. The quantitative analysis showed that the amount of Te precipitation within the experimental accuracy coincided with the ΔXTe of phase transition from a high temperature wurzite CdTe to a low-temperature sphalerite CdTe.
Comparing Bridgman and VGF processes (Figure 11) due to the very low crystallization rate of the VGF technique the grown CdTe crystal after the full crystallization will be in the feild of w-CdTe (see the insertion Figure 12). At the further slow cooling it is possible to go through the polymorph transition achieving the equilibrium state by moving sequentially from point (1) to point (2) and then to point (3) followed by the further crystal annealing. Whereas at Bridgman technique at comparatively fast cooling rate and high temperature gradient (20 K/cm [12]) we move from point (1') to point (2') and at the further the crystal cooling Te micro precipitations are forming resulting from decay of oversaturated Cd-riched nonstoichiometric solid solution.
On the other hand, we can adjust the raw ingots composition to the green points (see Figure 12) by preliminary annealing and go through the polymorph transition without ΔX deviation very close to the stoichiometric composition. Unfortunately, to the date an exact CdTe phase diagram near the polymorph transition needs refinement. Furthermore, we hope to do this in the nearest future.

5. Conclusions

Analysis of possible application of VGF technique to the CdTe crystal growth let us conclude that in spite of very low thermal conductivity of CdTe it is possible to realize the crystal growth with appropriate rates specific for the conventional VGF applied to GaAs crystal growth. However, in the case of CdTe we need to use AVC technique to suppress the formation of solid «tails» near the crucible walls. The «tails» play a negative role by creating tensions in growing crystal resulting to the generation a large number of dislocations. Besides they provokate the formation of twins.
Due to the low crystallization rate, the VGF method assisted by the AVC technique is a promising tool for growth of large diameter CdTe crystals with adjusted nonstoichiometry. Moreover, application of liquid B2O3 as an encapsulated agent [12] for CdTe growth, similar to GaAs growth opens the opportunity to control total pressure and to suppress the cadmium vaporization from Cd-riched melt. The latter let us adjust the nonstoichiometry of VGF grown CdTe crystals.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org.

Author Contributions

Conceptualization, O.N. and A.D.; methodology, V.K. and D.B.; software, O.N., A.D. and V.K.; validation, I.A. and E.M..; formal analysis, E.M.; investigation, O.N., A.D., V.K. and E.M.; resources, I.A. and D.B; data curation, E.M.; writing—original draft preparation, I.A. and A.D.; writing—review and editing, O.N. and A.D.; visualization, E.M.; supervision, V.K.; project administration, I.A.; funding acquisition, A.D. All authors have read and agreed to the published version of the manuscript

Funding

This research was funded by the Ministry of Science and Higher Education of Russia through the project FSSM-2022-0005.

Data Availability Statement

Not applicable.

Acknowledgments

The authors are grateful to the Mendeleev Center for the Collective Use of Scientific Equipment for the optical measurements.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Stefan Eichler, Thoмas Binger, Michael Butter, Rico Rihмann, M. S. Arrangement and Method for Producing a Crystal from the Melt of a Raw Material and Single Crystal. Patent DE 10 2007 026 298 A1, 2008.
  2. Dropka, N.; Holena, M.; Thieme, C.; Chou, T. Development of the VGF Crystal Growth Recipe: Intelligent Solutions of Ill-Posed Inverse Problems Using Images and Numerical Data. Cryst. Res. Technol. 2023; 58, 11. [Google Scholar] [CrossRef]
  3. Balbaşı, Ö. B.; Ünal, M.; Genç, A. M.; Çelik, G.; Parlak, M.; Turan, R. Investigation of Seeded Vertical Gradient Freeze (VGF) Growth of CdZnTe Bulk Crystals. J. Cryst. Growth 2022, 584, 126573. [Google Scholar] [CrossRef]
  4. Friedrich, J.; Müller, G. Erlangen—An Important Center of Crystal Growth and Epitaxy: Major Scientific Results and Technological Solutions of the Last Four Decades. Cryst. Res. Technol. 2020; 55, 2. [Google Scholar] [CrossRef]
  5. Shkir, M.; Ganesh, V.; AlFaify, S.; Black, A.; Dieguez, E.; Bhagavannarayana, G. VGF Bulk Growth, Crystalline Perfection and Mechanical Studies of CdZnTe Single Crystal: A Detector Grade Materials. J. Alloys Compd. 2016, 686, 438–446. [Google Scholar] [CrossRef]
  6. Prokesch, M.; Soldner, S. A.; Sundaram, A. G. CdZnTe Detectors for Gamma Spectroscopy and X-Ray Photon Counting at 250 × 106 Photons/(Mm2 S). J. Appl. Phys. 2018, 124(4). [Google Scholar] [CrossRef]
  7. Available online: https://www.linkedin.com/pulse/cdznte-crystal-market-share-amp-new-trends-analysis-report-lwgec/ (accessed on 2 December 2023).
  8. Roy, U. N.; Weiler, S.; Stein, J. Growth and Interface Study of 2in Diameter CdZnTe by THM Technique. J. Cryst. Growth 2010, 312(19), 2840–2845. [Google Scholar] [CrossRef]
  9. Ünal, M., Turan, R. (2023). A Path to Produce High-Performance CdZnTe Crystals for Radiation Detection Applications: Crystal Growth by THM, Surface Preparation, and Electrode Deposition. In: Abbene, L., Iniewski, K.(. (eds) High-Z Materials for X-ray Detection. Springer, Cham. [CrossRef]
  10. Roy, U. N.; Burger, A.; James, R. B. Growth of CdZnTe Crystals by the Traveling Heater Method. J. Cryst. Growth 2013, 379, 57–62. [Google Scholar] [CrossRef]
  11. Ünal, M.; Turan, R. A Path to Produce High-Performance CdZnTe Crystals for Radiation Detection Applications: Crystal Growth by THM, Surface Preparation, and Electrode Deposition. In High-Z Materials for X-ray Detection; Springer International Publishing: Cham, 2023; pp. 227–243. [Google Scholar] [CrossRef]
  12. Stelian, C.; Calestani, D.; Velázquez, M.; Zappettini, A. Numerical and Experimental Investigation of CdZnTe Growth by the Boron Oxide Encapsulated Vertical Bridgman Method. Int. J. Heat Mass Transf. 2021, 176, 121490. [Google Scholar] [CrossRef]
  13. Zhang, N.; Yeckel, A.; Derby, J. J. Maintaining Convex Interface Shapes during Electrodynamic Gradient Freeze Growth of Cadmium Zinc Telluride Using a Dynamic, Bell-Curve Furnace Profile. J. Cryst. Growth 2012, 355(1), 113–121. [Google Scholar] [CrossRef]
  14. Avetissov, I.; Kostikov, V.; Meshkov, V.; Sukhanova, E.; Grishechkin, M.; Belov, S.; Sadovskiy, a. Modeling of Axial Vibrational Control Technique for CdTe VGF Crystal Growth under Controlled Cadmium Partial Pressure. J. Cryst. Growth 2014, 385, 88–94. [Google Scholar] [CrossRef]
  15. Brebrick, R. F. The Cd–Te Phase Diagram. Calphad 2010, 34(4), 434–440. [Google Scholar] [CrossRef]
  16. Voller, V. R.; Swaminathan, C. R. Eral source-based method for solidification phase change. Numer. Heat Transf. Part B Fundam. 1991, 19(2), 175–189. [Google Scholar] [CrossRef]
  17. Lyubimov, D. V.; Cherepanoy, A. A.; Lyubimova, T. P.; Roux, B. The Flows Induced by a Heated Oscillating Sphere. Int. J. Heat Mass Transf. 1995, 38(11), 2089–2100. [Google Scholar] [CrossRef]
  18. Avetissov, I. C.; Sadovskii, A. P.; Sukhanova, E. A.; Zharikov, E. V. Single Crystal Growth by Axial Vibrational Control Technique in Czochralski Configuration. J. Cryst. Growth 2011, 318(1), 979–982. [Google Scholar] [CrossRef]
  19. Voller, V. R.; Prakash, C. A Fixed Grid Numerical Modelling Methodology for Convection-Diffusion Mushy Region Phase-Change Problems. Int. J. Heat Mass Transf. 1987, 30(8), 1709–1719. [Google Scholar] [CrossRef]
  20. Glazov, V. M.; Pavlova, L. M. Volumetric Effects of ZnTe, CdTe and HgTe Compounds at Melting and Subsequent Heating. Scand. J. Metall. 2001, 30(6), 379–387. [Google Scholar] [CrossRef]
  21. Regel, A.P.; Glazov, V.M. Physical properties of electron melts. Moscow, Nauka, 1980, 206 p.
  22. Sen, S.; Konkel, W. H.; Tighe, S. J.; Bland, L. G.; Sharma, S. R.; Taylor, R. E. Crystal Growth of Large-Area Single-Crystal CdTe and CdZnTe by the Computer-Controlled Vertical Modified-Bridgman Process. J. Cryst. Growth, 1988; 86, 1–4, 111–117. [Google Scholar] [CrossRef]
  23. Avetissov, I. C.; Zharikov, E. V.; Zinovjev, a. Y.; Sadovskiĭ, a. P. A New Method of Heat and Mass Transfer Control in the Melt at Crystal Growth by Czochralski Technique. Dokl. Phys. 2009, 54(9), 410–412. [Google Scholar] [CrossRef]
  24. Avetissov, I. C.; Sadovskiy, A.; Belov, S.; Khomyakov, A.; Rekunov, K.; Kostikov, V.; Sukhanova, E. Thermodynamic Features of Axial Vibrational Control Technique for Crystal Growth from the Melt. CrystEngComm 2012, 2213–2219. [Google Scholar] [CrossRef]
  25. Avetissov, I. C.; Sukhanova, E. a.; Khomyakov, a. V.; Zinovjev, a. Y.; Kostikov, V. a.; Zharikov, E. V. Simulation and Crystal Growth of CdTe by Axial Vibration Control Technique in Bridgman Configuration. J. Cryst. Growth 2011, 318(1), 528–532. [Google Scholar] [CrossRef]
  26. Triboulet Robert and Siffert Paul. CdTe and Related Compounds; Physics, Defects, Hetero-and Nano-Structures, Crystal Growth, Surface and Applications. Part II; 2010. ISBN: 9780080965130. [CrossRef]
  27. Greenberg, J. H.; Guskov, V. N.; Fiederle, M.; Benz, K.-W. Experimental Study of Non-Stoichiometry in Cd1−xZnxTe1±δ. J. Electron. Mater. 2004, 33(6), 719–723. [Google Scholar] [CrossRef]
  28. Ivanov, Y. M.; Polyakov, A. N.; Kanevsky, V. M.; Pashaev, E. M.; Horvath, Z. J. Detection of Polymorphous Transformations in CdTe by Dilatometry. Phys. status solidi 2003, No. 3, 889–892. [Google Scholar] [CrossRef]
  29. Avetisov, I. C.; Ivanov, Y. M.; Zorin, A. V. The Polymorphous Transition in CdTe. Poverkhnost'. Rentgenovskie, Sinkhrotronnye i Nejtronnye Issledovaniya; ISSN 1028-0960; Worldcat; No. 10, 82-88.
  30. Greenberg, J. H.; Guskov, V. N.; Lazarev, V. B.; Shebershneva, O. V. Vapor Pressure Scanning of Non-Stoichiometry in Cadmium Telluride. Mater. Res. Bull. 1992, 27(7), 847–854. [Google Scholar] [CrossRef]
  31. Mozhevitina, E. N.; Levonovich, B. N.; Avetisov, I. C. CdTe Homogeneity Region. Inorg. Mater. 2013, 49(5), 439–444. [Google Scholar] [CrossRef]
  32. Avetissov, I.; Mozhevitina, E.; Khomyakov, A.; Avetisov, R. Nonstoichiometry of A II B VI Semiconductors. Cryst. Res. Technol. 2015, 50(1), 115–123. [Google Scholar] [CrossRef]
Preprints 93102 g001
Figure 1. Distribution by mass of grown crystals of the main methods for the most popular crystals (a) and various technologies for growing semiconductor crystals (b).
Figure 1. Distribution by mass of grown crystals of the main methods for the most popular crystals (a) and various technologies for growing semiconductor crystals (b).
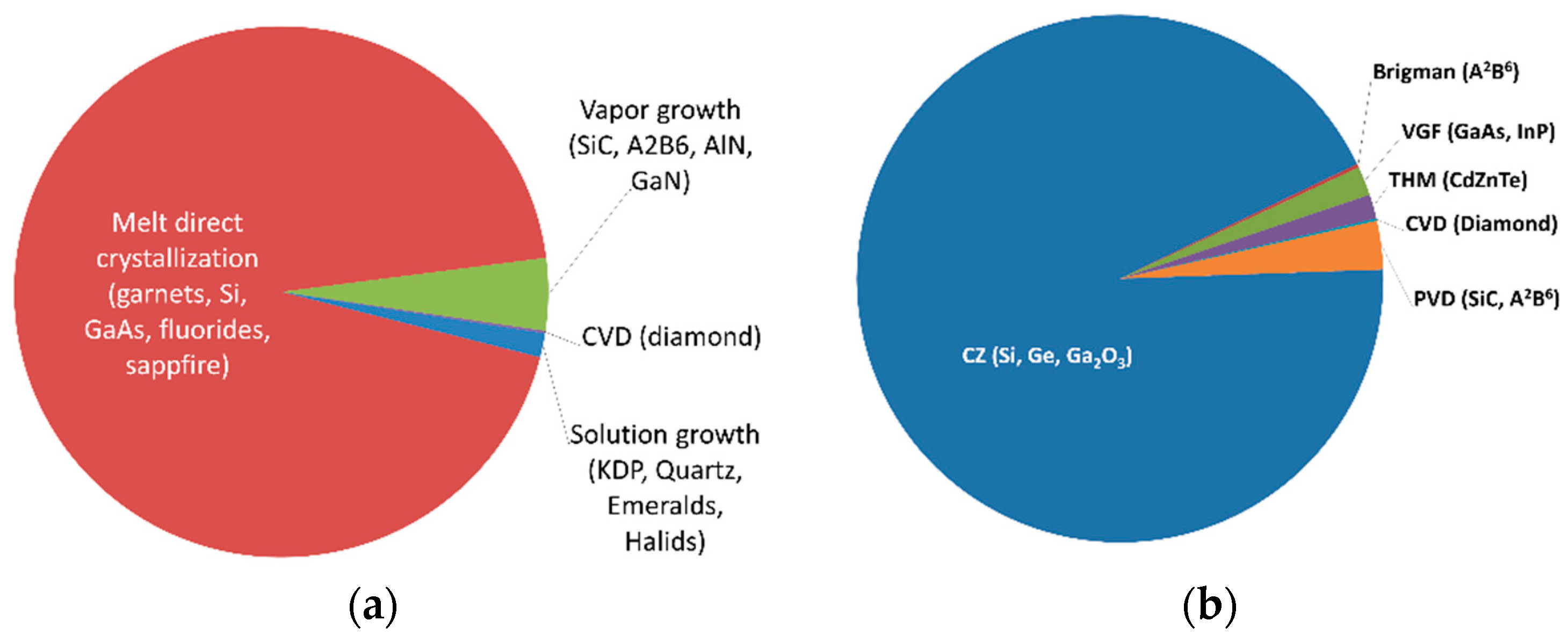
Preprints 93102 g001
Preprints 93102 g002
Figure 2. Geometrical model of the crucible with the oscillating ring-baffle inside the CdTe melt and the fragment of the grid using for numerical calculations (for dimension details see Table S1).
Figure 2. Geometrical model of the crucible with the oscillating ring-baffle inside the CdTe melt and the fragment of the grid using for numerical calculations (for dimension details see Table S1).
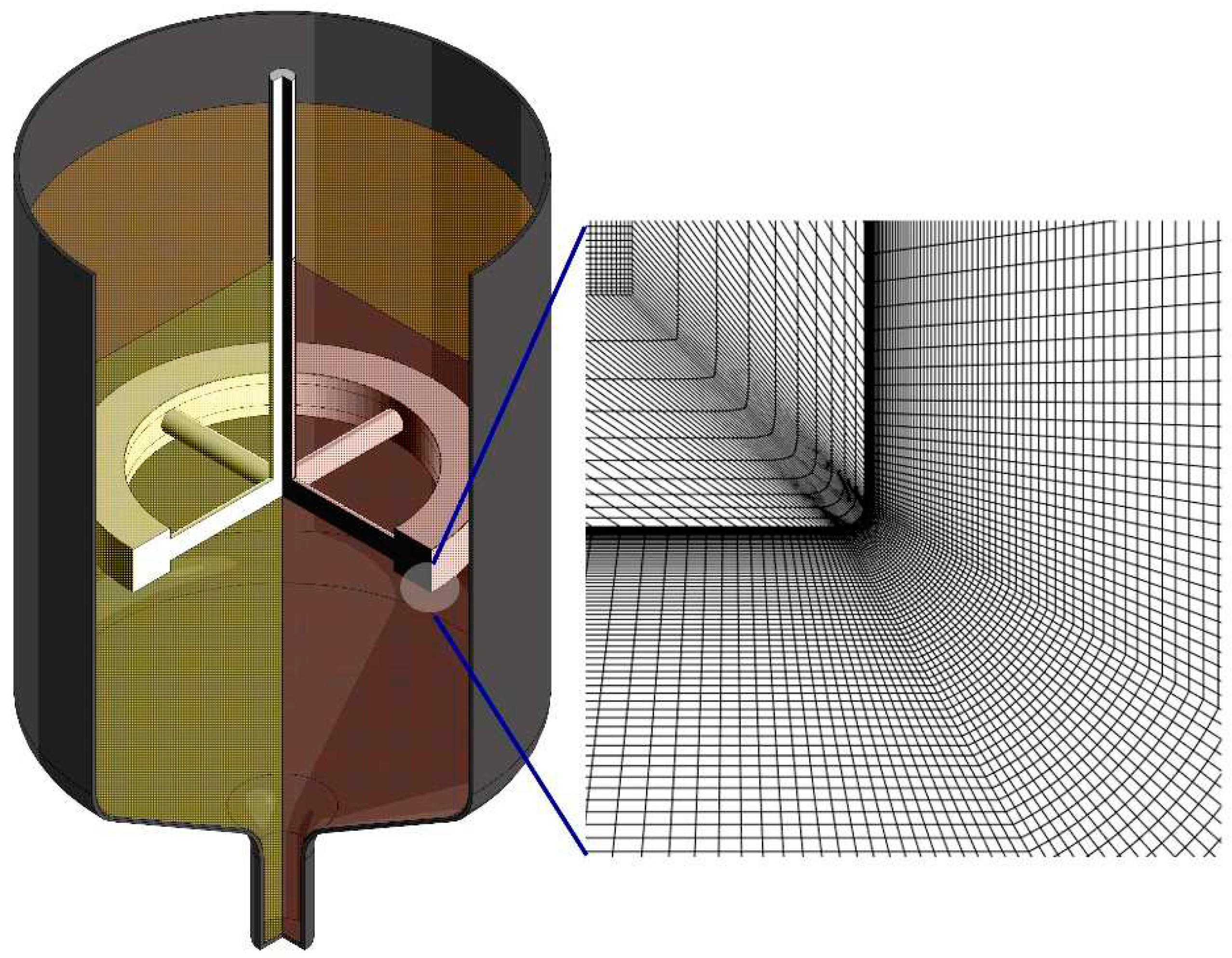
Preprints 93102 g002
Preprints 93102 g003
Figure 3. Crystallized part of the melt at VGF growth of CdTe at cooling rates 0.2 K/h (a); 1.0 K/h (b); 5.0 K/h (c), when the «tails» reached 8 cm height from the crucible bottom.
Figure 3. Crystallized part of the melt at VGF growth of CdTe at cooling rates 0.2 K/h (a); 1.0 K/h (b); 5.0 K/h (c), when the «tails» reached 8 cm height from the crucible bottom.
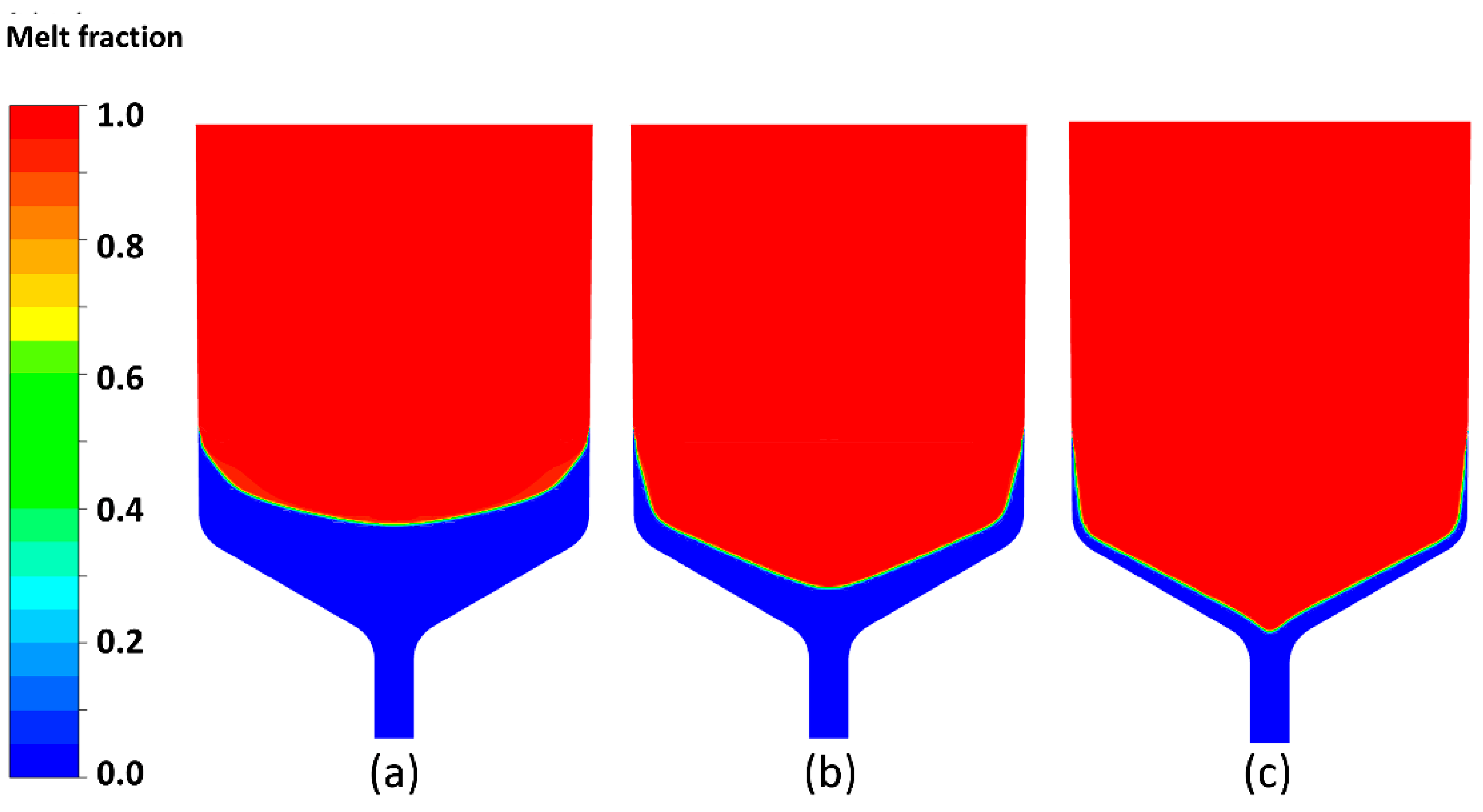
Preprints 93102 g003
Preprints 93102 g004
Figure 4. Velocity fields (left parts) and temperature distribution (right) colored by magnitude after 2.2×104 s of CdTe VGF crystal growth at 0.2 K/h (a), 0.5 K/h (b), 1.0 K/h (c) cooling rate when the «tails» reached 8 cm height from the crucible bottom.
Figure 4. Velocity fields (left parts) and temperature distribution (right) colored by magnitude after 2.2×104 s of CdTe VGF crystal growth at 0.2 K/h (a), 0.5 K/h (b), 1.0 K/h (c) cooling rate when the «tails» reached 8 cm height from the crucible bottom.
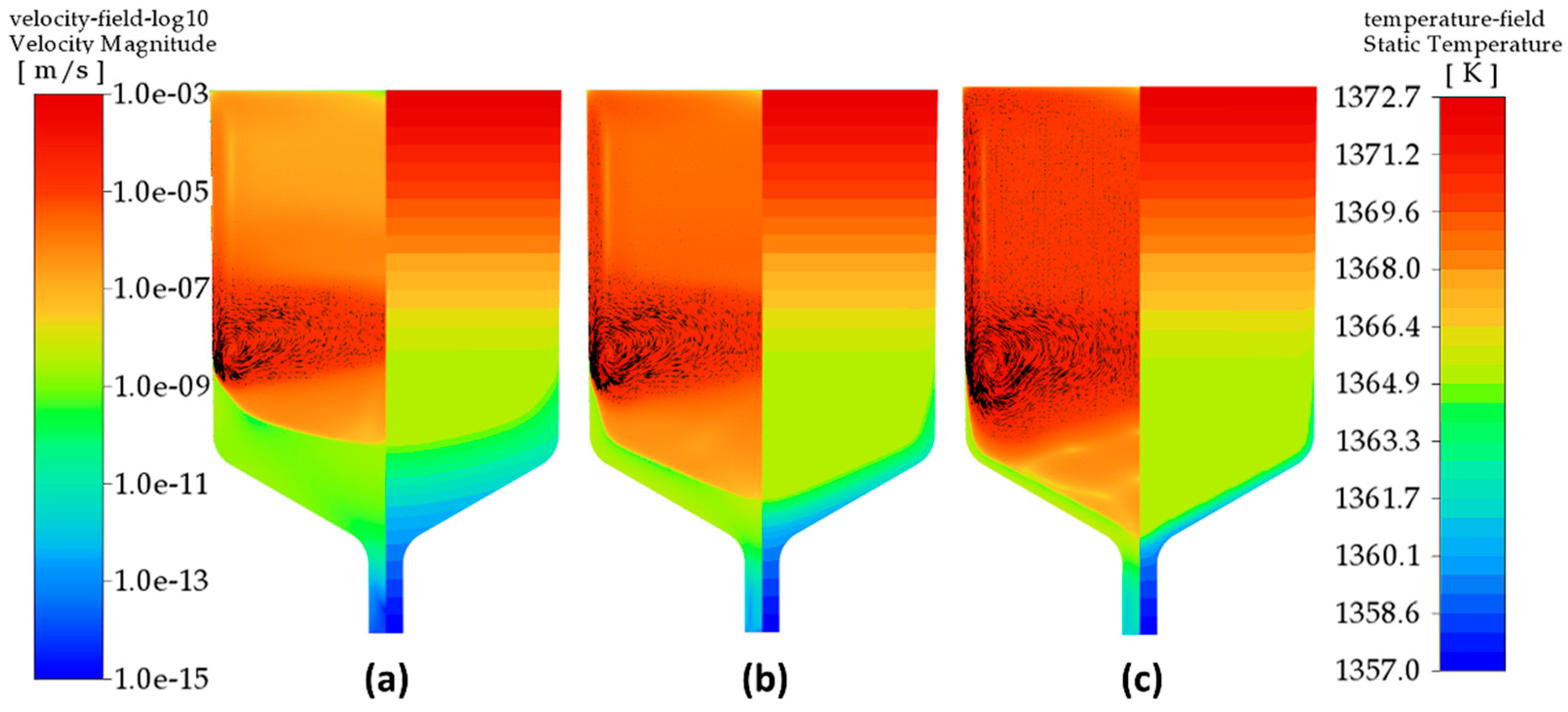
Preprints 93102 g004
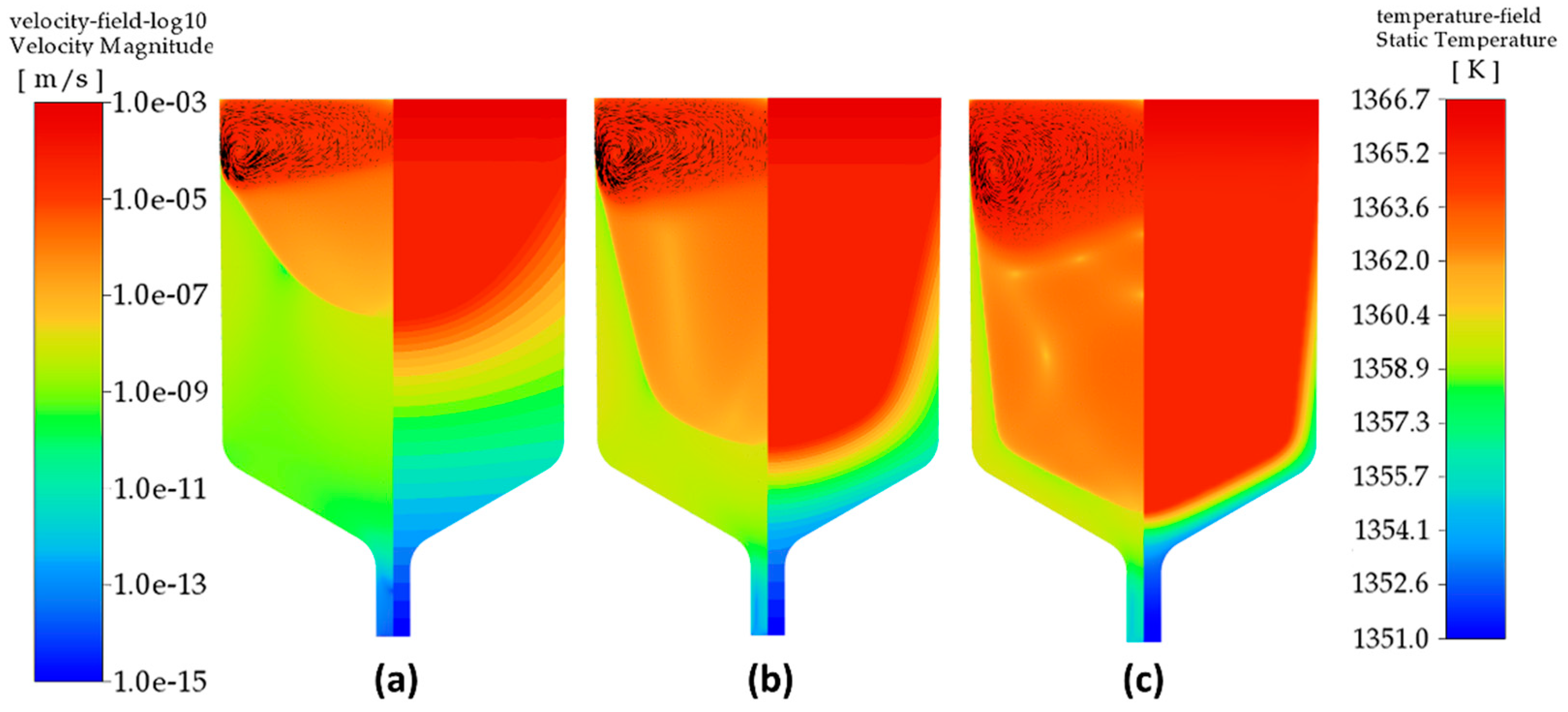
Preprints 93102 g005
Figure 5. Velocity fields (left parts) and temperature distribution (right) colored by magnitude after 2.2×104 s of CdTe VGF crystal growth at 0.2 K/h (a), 0.5 K/h (b), 1.0 K/h (c) cooling rate when the «tails» reached 18 cm height from the crucible bottom.
Figure 5. Velocity fields (left parts) and temperature distribution (right) colored by magnitude after 2.2×104 s of CdTe VGF crystal growth at 0.2 K/h (a), 0.5 K/h (b), 1.0 K/h (c) cooling rate when the «tails» reached 18 cm height from the crucible bottom.
Preprints 93102 g005
Preprints 93102 g008
Figure 8. Static temperature fields in the melt at VGF growth of CdTe at cooling rates 0.2 K/h without (a) and with the ring-baffle oscillating with 50 Hz frequency and 0.1 mm amplitude (b).
Figure 8. Static temperature fields in the melt at VGF growth of CdTe at cooling rates 0.2 K/h without (a) and with the ring-baffle oscillating with 50 Hz frequency and 0.1 mm amplitude (b).
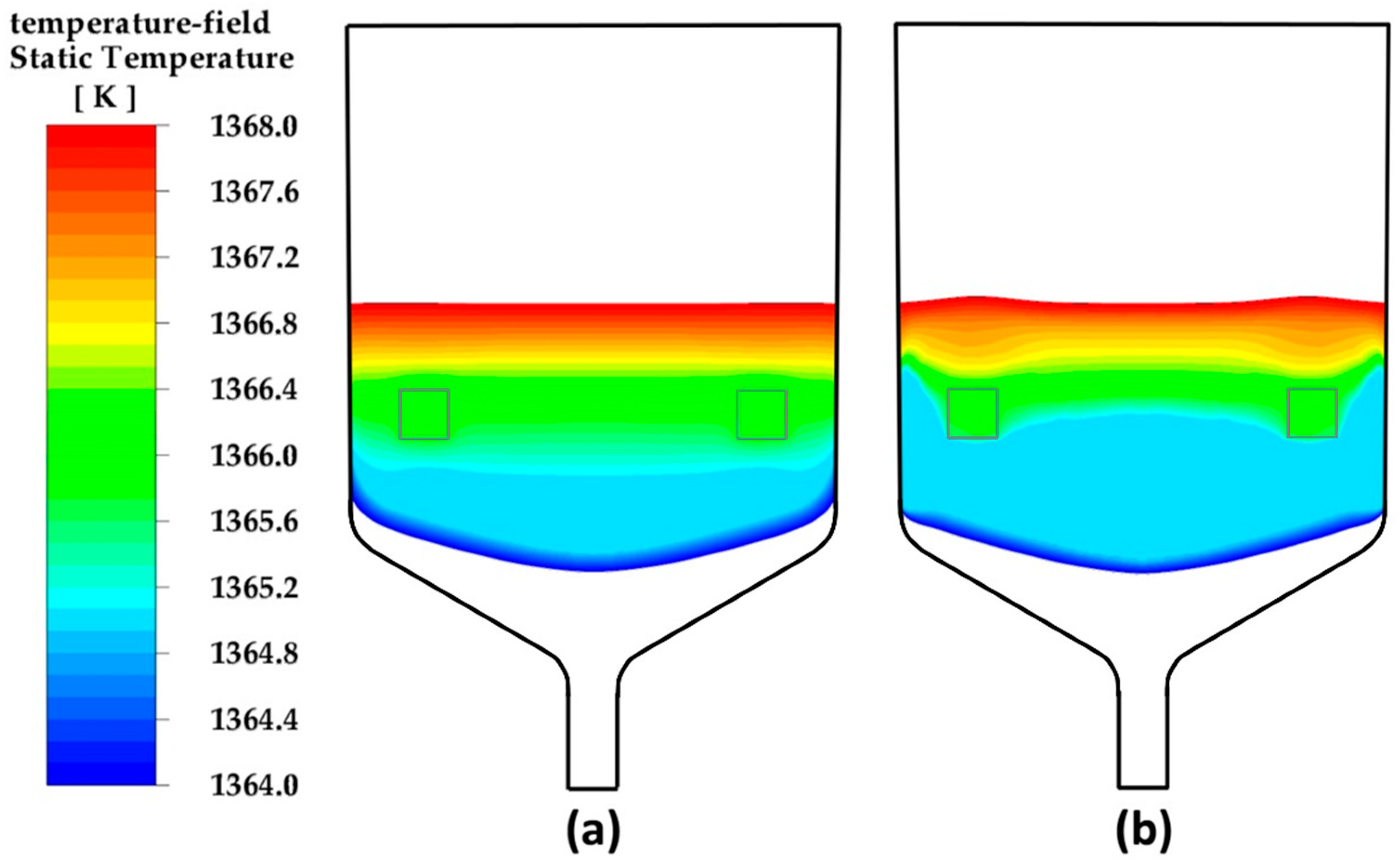
Preprints 93102 g008
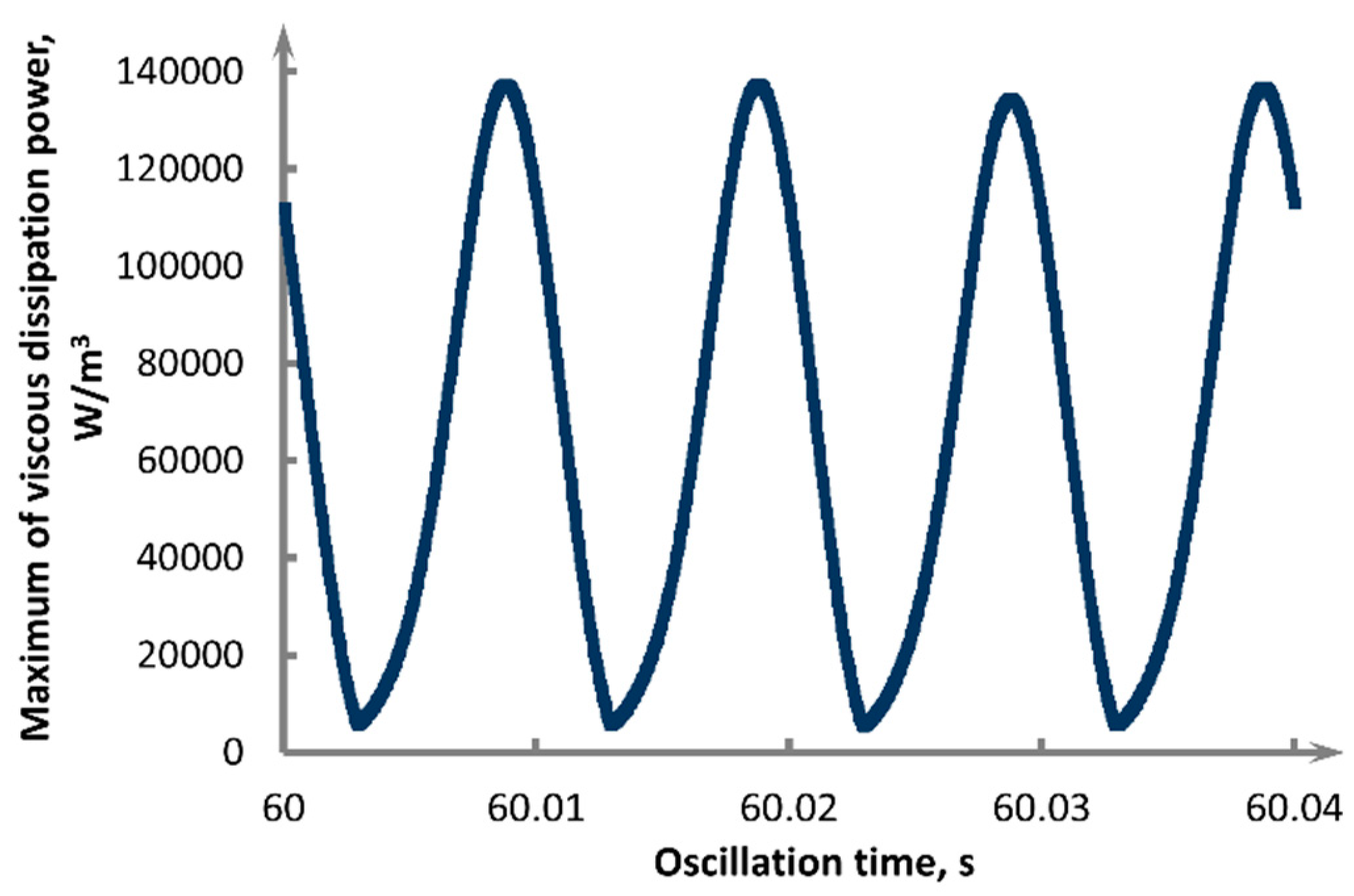
Preprints 93102 g010
Figure 10. Convergence history of specific viscous dissipation rate (w) at the ring-baffle right angle (a) at disk oscillation of 25 Hz frequency and 0.3 mm amplitude.
Figure 10. Convergence history of specific viscous dissipation rate (w) at the ring-baffle right angle (a) at disk oscillation of 25 Hz frequency and 0.3 mm amplitude.
Preprints 93102 g010
Preprints 93102 g011
Figure 11. Homogeneity range of CdTe with pathway of Cd-riched melt crystallization at conventional Bridgman growth. Literature data on homogeneity range are presented in Ref. [32].
Figure 11. Homogeneity range of CdTe with pathway of Cd-riched melt crystallization at conventional Bridgman growth. Literature data on homogeneity range are presented in Ref. [32].
Preprints 93102 g011
Preprints 93102 g012
Figure 12. Fragment of CdTe homogeneity range close to polymorph transition from Cd-riched side and possible pathways of crystallization at Bridgman (red dots and black dash lines) and VGF (green dots and blue dash lines) crystal growth. In the insertion, the VGF crystallized CdTe and its temperature profile.
Figure 12. Fragment of CdTe homogeneity range close to polymorph transition from Cd-riched side and possible pathways of crystallization at Bridgman (red dots and black dash lines) and VGF (green dots and blue dash lines) crystal growth. In the insertion, the VGF crystallized CdTe and its temperature profile.
Preprints 93102 g012
Table 1. Properties of CdTe and graphite using for numerical simulation.
Table 1. Properties of CdTe and graphite using for numerical simulation.
Parameter Value Temperature range, K Approximation type Reference
CdTe
Melting temperature, K 1365 [15]
Enthalpy of crystallization, J∙kg-1 209200 [20]
Density CdTe melt, kg∙m-3 5663,6 1300-1400 Boussinesq [20]
Thermal expansion, K-1 6,3952∙10-5
Dynamic viscosity, Pa∙s 8.3215 · 10 − 3 − 4.3729 · 10 − 6 · T 1365-1400 Piecewise-linear [21]
Heat capacity (solid), J∙kg-1∙K-1 198.63 + 0.0392 · T 298.15-1365 Piecewise-linear
Heat capacity (liquid), J∙kg-1∙K-1 251.1831 1365-1400
Thermal conductivity (solid), W∙m-1∙K-1 11.304 − 7.3152 · 10 − 3 · T 1300-1365 Piecewise-linear [22]
Thermal conductivity (liquid), W∙m-1∙K-1 7.8909 − 4.6318 · 10 − 3 · T 1365-1400
Graphite
Density, kg∙m-3 1700
Heat capacity (solid), J∙kg-1∙K-1 2148.3
Thermal conductivity (solid), W∙m-1∙K-1 44.165
Table 2. Relaxation factors and absolute residual criteria using for numerical simulation.
Table 2. Relaxation factors and absolute residual criteria using for numerical simulation.
Relaxation factors Value Absolute residualcriteria Value
CFL 9 Continuity 10-9 without the ring
Pressure 0.25 10-7 with the ring
Momentum 0.25 Velocities 10-9 without the ring
Body Forces 0.5 10-6 with the ring
Volume Fraction 0.1-0.5 Energy 10-6
Energy 1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated