Prerpints.org logo
Preprint
Article

PSO based Unconstrained Polygonal Fitting of 2D Shapes

Altmetrics

Downloads

88

Views

32

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

11 December 2023

Posted:

13 December 2023

You are already at the latest version

Alerts
Abstract
In this paper, we present a general version of polygonal fitting problem called Unconstrained Polygonal Fitting (UPF). Our goal is to represent a given 2D shape S with an N-vertex polygonal curve P with a known number of vertices, so that the Intersection over Union (IoU) metric between S and P is maximized without any assumption or prior knowledge of the object structure and the location of the N-vertices of P that can be placed anywhere in the 2D space. The search space of the UPF problem is a superset of the classical polygonal approximation (PA) problem, where the vertices are constrained to belong in the boundary of the given 2D shape. Therefore, the resulting solutions of the UPF may better approximate the given curve than the solutions of the PA problem. For a given number of vertices N, a Particle Swarm Optimization (PSO) method is used to maximize the IoU metric, which yields almost optimal solutions. Furthermore, the proposed method has also been implemented under the equal area principle so that the total area covered by P is equal to the area of the original 2D shape to measure how this constraint affects IoU metric. The quantitative results obtained on more than 2,800 2D shapes included in two standard datasets quantify the performance of the proposed methods and illustrate that their solutions outperform baselines from the literature.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Vision and Graphics

1. Introduction

Polygonal shape fitting is a key problem in computer vision and computer graphics with several applications including object recognition, computational cartography, signal summarization, and compression [1,2,3,4]. When curves are modeled, straight-line segments are usually preferred due to their simplicity. The polygonal fitting process saves memory space, reduces rendering time on graphics applications, and gives a more compact representation of the original shape.
According to the classical polygonal approximation problem of a 2D shape, the goal is to compute an N-vertex polygonal curve P that approximates the boundary B of the original shape S according to a predefined error criterion. In the classical polygonal approximation, the vertices of P are an ordered sub-sequence of the boundary points B [1]. The classical polygonal shape fitting provides poor results, especially when the number of vertices is low and the shape complexity is high. In this work, we study a general version of polygonal fitting called Unconstrained Polygonal Fitting (UPF) problem to provide better solutions with the same number of vertices. According to UPF, the N-vertices of P can be placed anywhere in the 2D space. Therefore, the search space of UPF problem is a superset of the classical polygonal approximation (PA) problem, where the vertices are constrained to belong in the boundary of the given 2D shape. This means that the resulting solutions of UPF may better approximate the given curve than the PA problem solutions. This theoretically interesting computer vision problem has compact and easy-to-grasp description, but a very high algorithmic complexity due to the large search space. Even if just a triangle ( N = 3 ) is used, there does not exist any trivial method to compute the optimal solution of UPF problem.
Different error criteria have been proposed for shape fitting - polygonal approximation problems. In this research, the Intersection over Union (IoU) metric between S and P is maximized given a fixed number of polygonal vertices N, without any assumption or prior knowledge of the object structure. IoU metric can be easily replaced by any other segmentation metric, for example, accuracy and dice coefficient ( D I C E ) without any change in the proposed methodology. Another problem instance, that we experimentally study is to define the problem under the Equal Area constraint which states that the area covered by the polygonal curve P should be equal to the area of the given shape S.
Figure 1 shows two example outputs of the classical polygonal approximation using the Douglas-Peucker algorithm [5] (left) and the unconstrained polygonal fitting using the proposed method (right) for N = 4 vertices. In both cases, it holds that the solution of the UPF problem provides higher IoU, DICE values compared with the results of Douglas-Peucker algorithm. In the first example with an apple, the Douglas-Peucker algorithm yields D I C E = 79.6 % , I o U = 66.1 % (Figure 1a), while the proposed method yields D I C E = 90.8 % , I o U = 83.2 % (Figure 1b). In the second example with a building, the Douglas-Peucker algorithm yields D I C E = 88.9 % , I o U = 80.1 % (Figure 1c), while the proposed method yields D I C E = 97.5 % , I o U = 95.1 % (Figure 1d). There exists several examples where there exists significant differences in performance between the optimal solutions of the two problems, especially for lower values of N where the optimal solutions of UPF space may be far from the shape boundary.
In summary, the major contributions of our work are the following: To the best of our knowledge, this is the first work to define and solve the UPF problem. The proposed method solves the UPF problem via Particle Swarm Optimization (PSO) [6] that quickly explore the search space. The proposed framework suggests solutions that outperform baselines in quantitative terms, even if are not necessarily optimal due to the PSO. Especially in a low-dimensional search space, that is true for low number of vertices, the proposed method clearly outperforms baselines of classical PA, since even the optimal solutions of the classical PA problem usually fail to obtain high performance results due to the limited search space (shape boundary) of PA problem.

2. Related Work

The problem of shape fitting - polygonal approximation has been studied extensively during the last five decades [1,4,5,7]. The methods that have been developed solve the problem by approximating the original shape S by a polygonal curve P under the constraint that the P vertex sequence is an ordered sub-sequence of the vertices along shape boundary. The polygonal approximation problem can be formulated in two ways [1,7]:
  • The problem of better fitting, where the approximation error is minimized or the fitting accuracy is maximized given the number of vertices N.
  • The problem of minimum number of vertices, where the approximation error or the fitting accuracy is bounded and the goal is to find the minimum number of vertices that satisfy the given bound.
The polygonal approximations algorithms can be classified as (1) optimal or non-optimal and (2) supervised or unsupervised algorithms [7]. The non-optimal algorithms do not guarantee any kind of optimum as optimal algorithms but can find reasonable polygonal approximations faster than the optimal ones. The supervised algorithms take into account parameters to generate polygonal approximations, while the unsupervised algorithms generate the polygonal approximations without parameters. Yin [8] presents a polygonal approximation approach based on the discrete particle swarm optimization (PSO) algorithm. Each particle represented as a binary vector corresponds to a candidate solution to the polygonal approximation problem. A swarm of particles is initiated and fly through the solution space for targeting the optimal solution. In [9], the authors proposes a non-optimal and unsupervised algorithm for generation of polygonal approximations based on the convex hull of the 2D closed curves or contours. The significance levels of the contour points are computed using a symmetric version of the well-known Douglas-Peucker algorithm and, finally, a thresholding process is applied to obtain the vertices or dominant points of the polygonal approximation.
In the case of 2D shape fitting, a 2D binary image is given with foreground points representing the shape to be modeled. This image can be the result of any object detection or image segmentation method (e.g., [10,11,12]). Several models can be used to solve the 2D shape fitting problem. In the literature, there exists several approaches that fit a set of ellipses to the given 2D shape based on (a) the Hough Transform,(b) Genetic and Optimization Algorithms and (c) edge-following [12,13]. In [12], a framework has been proposed to represent a given 2D shape with an automatically determined number of ellipses based on expectation maximization criterion, so that the total area covered by the ellipses is equal to the area of the original shape. The method has been successfully applied to cell [14] and tree detection [15] problems. In [4], an algorithm is proposed to extract and vectorize objects in images with low-complexity polygons based on local merging and splitting of cells. Departing from a polygonal partition that oversegments an image into convex cells, the algorithm refines the geometry of the partition while labeling its cells by a semantic class. The authors applied their method to a variety of scenes, from organic shapes to man-made objects through floor maps and line-drawing sketches.
Concerning the metrics that have been used to measure the performance on shape fitting problem can be classified into :
  • Boundary based metrics that compares the distance between the boundary of given shape and the approximated curve. Some of the most most metrics are the root mean square error ( R M S E ) between the two curves and the maximum error between the boundary S and their corresponding subcurves of P. These metrics have the advantage that can also be applied on given curves (non closed contours) but are sensitive to boundary noise [1,7].
  • Region based metrics that compares the region of the approximated shape and the given shape. Region-based metrics are more tolerant to noise since they do not restrict themselves to the boundaries of shapes but rather take into account all shape points [12]. Common metrics of this category are the Intersection over Union (IoU) and the Dice coefficient (DICE), which is defined by twice the area of the shapes’ intersection divided by the sum of the areas of each shape. Both of them have been also used to measure the performance of image segmentation methods [16].

3. Unconstrained Polygonal Fitting

3.1. Problem Formulation

We assume a binary image I that represents a 2D shape S. A pixel p of I belongs either to the foreground S ( I ( p ) = 1 ) or to the background ( I ( p ) = 0 ). The area A of the 2D shape is given by
A ( S ) = ∑ p ∈ S I ( p ) .
We also assume a closed polygonal curve P with N vertices P i , i ∈ { 1 , . . . , N } , which belong in the 2D space (not necessary on the boundary of S). The binary image I P is also defined so that I P ( p ) = 1 at points p that are inside any of the polygonal curve P and I P ( p ) = 0 , otherwise. Then, the Intersection over Union I o U ( P ) metric between the 2D shape S and P is calculated as follows:
I o U ( P ) = ∑ p ∈ S I P ( p ) ∑ p ∈ I m a x ( I ( p ) , I P ( p ) ) .
Essentially, I o U ( P ) is the percentage of the 2D shape points that are under polygonal curve P divided by the number of 2D points that belong to shape S either polygonal curve P. The optimal solution of Unconstrained Polygonal Fitting problem is the closed polygonal curve P that maximizes the I o U ( P ) .
P * = a r g m a x P I o U ( P )

3.2. Equal Area Principle

The equal area principle (constraint) has been used in [12,14] restricting the area of P to be equal with the area of the given shape. This is a reasonable constraint in the sense that we except in many cases that the optimal solutions of the UPF problem have almost the same area with the given shape S. So, by adding this extra constraint, we reduce the search space of the problem without mainly affecting the performance of the method. Additionally, some applications may also include this requirement. Let A ( P ) denote the areas of polygonal curve P, A ( P ) = ∑ p ∈ I I P ( p ) . According to the Equal Area constraint it holds that the area of polygonal curve P is equal with the area of shape S meaning that A ( P ) = A ( S ) . Therefore the optimal solution of Unconstrained Polygonal Fitting problem under equal area principle is the closed polygonal curve P that maximizes the I o U ( P ) under equal area principle.
P * = a r g m a x P I o U ( P ) , A ( P ) = A ( S )
Hereafter, we describe a simple procedure that applies the equal area principle on a polygonal curve P, yielding a new polygonal curve P ¯ so that A ( P ¯ ) = A ( S ) . Let C be the centroid of S1 and P ¯ i be the i vertex of polygonal curve P ¯ , i ∈ { 1 , . . . , N } .
C = 1 A ( S ) ∑ p ∈ S p
P ¯ i = C + A ( S ) A ( P ) · ( P i − C )

3.3. UPF-PSO Algorithm

In this work, we cast the search for a single polygonal curve as a stochastic optimization problem that is solved based on Particle Swarm Optimization (PSO) [6]. PSO is a derivative-free optimization method that handles multi-modal, discontinuous objective functions with several local minima. Optimization is performed through the evolution of particles (candidate solutions) of a population (swarm). Particles lie in the parameter space of the objective function to be optimized and evolve through a limited number of generations (iterations) according to a policy which emulates “social interaction”. The main parameters of PSO are the number of particles and generations, the product of which determines its computational budget (i.e., the number of objective function evaluations). PSO achieves near-optimal solutions and has been successfully applied in several challenging optimization problems in computer vision and pattern recognition such as classification, clustering, prediction, image segmentation, video co-segmentation, object tracking [17,18].
The proposed Unconstrained Polygonal Fitting based on Particle Swarm Optimization Algorithm (UPF-PSO) optimizes IoU metric (see Eq. 3) for different polygonal curves that are directly represented by PSO particles. The input to UPF-PSO is the binary image I representing the given shape S and the number of vertices N of the polygonal closed curve that will be fitted to S. The UPF-PSO method quickly explores the search space starting from random solutions. Iteratively, PSO searches for a polygonal curve that maximizes the IoU metric.
We represent each particle by a 2 · N vector with the 2D coordinates of the N points of the polygonal curve. In order to simplify the search space, we assume that the vertices are in clockwise order; otherwise, in the evolution process we correct the order of vertices of each particle according to this hypothesis. The fitness (objective function) of the particle is directly given by the IoU metric of the particle (see Eq. 2). The UPF-PSO Algorithm is analytically described hereafter.
Initially, we create a population of M (e.g. M = 20 ) particles that are located in random positions around the centroid of the shape S under the Equal Area Principle (see Section 3.2) to be in valid positions of the search space. In the evolution process, PSO finds the current optimal solution in order to update the best global solution. Additionally, the best local solution of each particle is also updated, where the IoU of the particle reaches a better solution. The method terminates when the number of iterations of the evolution process exceeds the given number of generations, e.g. 100.

4. Experimental Evaluation

The evaluation of the proposed approach was based on two standard datasets from the literature. More specifically, we employ:
  • MPEG-7 [19], which consists of 1,400 binary shapes organised in 70 categories with 20 shapes per category. This dataset has been extensively used in shape tasks [12,14,20].
  • A subset of LEMS [21], that is, 1,462 shapes that come from the following categories of the original database: Buildings, Containers, Fish, Fruit and vegetables, Misc Animal, People, Robots, Toddlers, and Turtles [14].
Figure 2 shows twelve sample images form the MPEG-7 dataset and LEMS dataset.
We compared the proposed Unconstrained Polygonal Fitting based on Particle Swarm Optimization Algorithm (UPF-PSO) and UPF-PSO under equal area principle (UPF-PSO-EA) methods2 with the Douglas-Peucker algorithm (DP) [5] and Douglas-Peucker algorithm under equal area principle (DP-EA) [5]. Additionally, we have implemented a sequential baseline method of classical Polygonal Approximation that maximizes IoU. This method uses an initial polygonal curve that is given by the execution of the Douglas-Peucker algorithm (DP) with high number of vertices (e.g. 50 > > N ). In each step, it sequentially removes the vertex of the polygonal curve so that the IoU of the resulting polygonal curve is maximized. The method terminates when the number of vertices are reduced to N. This baseline method is called Sequential Maximization of IoU (SM). After the execution of SM, the equal area principle can be applied yielding the SM-EA method.
In our experiments, we have evaluated the methods for different values of N. Since, our framework makes sense to be applied for low values of N, where the difference in performance between the solutions of UPF and PA usually is significant, we have fitted polygonal curves with 3 ≤ N ≤ 10 (eight cases). According to the formulation of the UPF problem, we have compared the performance of UPF-PSO, UPF-PSO-EA, DP, DP-EA, SM and SM-EA on the IoU metric. For a given dataset, we also compute P r ( m / I o U ) , where m is a method in {UPF-PSO, UPF-PSO-EA, DP, DP-EA, SM, SM-EA}. P r ( m / I o U ) is quantified as the percentage of shapes of the datasets where the method m clearly outperforms the two others under the IoU. This also means that the value 100 % − ∑ m P r ( m / I o U ) gives the percentage of images for which there is no clear winner method.
Table 1 and Table 2 present the average IoU, DICE and Pr(m/IOU) metrics computed on all images from the MPEG7 and LEMS datasets, respectively. It holds that UPF-PSO and UPF-PSO-EA clearly outperform the rest methods in any dataset. UPF-PSO slightly outperforms UPF-PSO-EA. UPF-PSO or UPF-PSO-EA outperform all the rest methods in about 80 % of shapes under MPEG-7 and LEMS datasets. SM or SM-EA outperform all the rest methods in about 17 % of shapes under MPEG-7 dataset and LEMS dataset. DP or DP-EA outperform all the rest methods in about 3 % of shapes under MPEG-7 and LEMS datasets.
Figure 3 depicts the average IoU of UPF-PSO, UPF-PSO-EA, DP, DP-EA, SM and SM-EA computed for different values of N ∈ { 3 , . . . , 10 } in the two datasets used. UPF-PSO and UPF-PSO-EA clearly outperform the rest methods under any dataset and N ≤ 8 . As expected, the lower N, the better outer-performance of the proposed methods compared to the classical PA methods. For high values of N ( N > 8 ), the problem search space increases, so it is more difficult for the PSO to find near-optimal solutions. At the same time, when N obtains high values, the solutions of classical PA significantly better approximate the given shape, reducing the gap from the UPF methods. Theoretically, it holds that as N tends to infinity, the optimal solution of both problems (classical PA and UPF) converges to the initial shape having IoU equal to one ( l i m N → ∞ I o U = 1 ). When equal area principle is applied it holds that the results are similar under any method. Usually, the equal area principle provides better results for low values of N where the fitting polygon is less complex. The results under DICE metric depicted in Figure 4 agree with the results of Figure 3.
Figure 5 illustrates the Pr(m/IoU), m ∈ {UPF-PSO, UPF-PSO-EA, DP, DP-EA, SM, SM-EA} over the 1,400 images of MPEG-7 dataset (Figure 5(a)) the 1,462 of LEMS dataset Figure 5(b). The results agree with the results of Figure 3. If we sum the cases where UPF-PSO or UPF-PSO-EA outperforms all the rest methods, it holds that for N ≤ 8 is more than 70 % and 68 % under MPEG-7 dataset and LEMS dataset. As it was expected, when N = 3 , UPF-PSO or UPF-PSO-EA clearly outperform the rest method on more than 98 % of shapes and any dataset.
Finally, Figure 6, Figure 7 and Figure 8 depict several output examples of the proposed methods and baselines to further study their behaviour. The DICE-IoU metrics and the used method-N are depicted in the title and caption of each result, respectively. These figures depict results for N = 3 , 6 , 9 vertices on a turtle, bat and horse shapes from MPEG 7 and LEMS datasets. The results of N = 3 , N = 6 and N = 9 , corresponds to low, middle and high values of N according to the proposed framework. In most of the cases the proposed methods outperform the baselines. As it was expected, the difference in performance between the proposed methods and baselines is higher for low value of N ( N = 3 ), due to the limited classical polygonal approximation problem - search space that is restricted on the shape boundary. PSO based methods yield high performance results, when it is more possible to find near-optimal solutions, which is true under low values of N and less complex given shapes. On other cases (high values of N and complex shapes), the PSO based methods may fail to provide high performance solutions due to the complicated and high dimensional search space. For example, in the case of N = 9 and horse shape (see Figure 8) that is the most complex shape, the results of UPF-PSO and UPF-PSO-EA underperform the SM method. However, it should be noticed that under this complex shape, when N = 3 or N = 6 it seems that the proposed methods outperform all baselines. Concerning, the other two simpler shapes, it holds that UPF-PSO or UPF-PSO-EA outperform any other method even when N = 9 , showing that the proposed methods are able to provide high performance results even for high values of N.

5. Conclusions

In this work, a novel PSO based polygonal fitting algorithm (UPF-PSO) has been proposed to solve a general version of the polygonal fitting problem called Unconstrained Polygonal Fitting (UPF). An N-vertex polygonal curve P with known number of vertices is fitted to a given 2D shape S so that the Intersection over Union is maximized. I o U metric can be easily replaced by any other segmentation metric e.g. Accuracy/Dice coefficient without any change in the proposed methodology. According to the UPF-PSO algorithm, the location of the N-vertices of P that can be placed anywhere in the 2D space generally provides better solutions compared to those of the classical polygonal approximation problem, where the vertices are restricted to belong in the boundary of the given 2D shape. In our experimental results, we have also compared the proposed UPF-PSO with several baselines in two standard datasets of 2D shapes of more than 2,800 images showing the high performance of the proposed framework. As it was expected, when the number of vertices is low, the difference in performance between UPF-PSO and the rest baseline methods increases as the solutions of classical polygonal approximation problem generally fails to provide well fitting results. In ongoing and future work, our aim is to study more unconstrained fitting problems and to provide better solutions especially for high values of N by relaxing the constraint that the new shape border should be a subset of the given shape boundary. Additionally, we plan to consider extensions of UPF-PSO towards handling more complex shapes than polygons. Finally, we plan to extend the proposed framework on 3D shape and to explore real applications that the proposed proposed system may be useful.

Author Contributions

The author confirms contribution to the paper as follows: Conceptualization, C.P..; Funding acquisition, C.P.; Investigation, C.P.; Methodology, C.P.; Software, C.P.; Validation, C.P.; Supervision, G.C. and H.P.; Data Curation, C.P.; Writing – original draft, C.P.; Writing – review & editing, C.P.. C.P. reviewed the results and approved the final version of the manuscript.

Institutional Review Board Statement

Not applicable

Informed Consent Statement

Not applicable

Data Availability Statement

The associated code and datasets are developed for the project can be shared publicly after the paper acceptance. The sharing of parts of the code or datasets could be approved, at the authors’ discretion, upon request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Panagiotakis, C.; Tziritas, G. Any dimension polygonal approximation based on equal errors principle. Pattern recognition letters 2007, 28, 582–591. [CrossRef]
  2. Panagiotakis, C.; Doulamis, A.; Tziritas, G. Equivalent key frames selection based on iso-content principles. IEEE Transactions on circuits and systems for video technology 2009, 19, 447–451.
  3. Kyriazis, N.; Argyros, A. Scalable 3D Tracking of Multiple Interacting Objects. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2013, pp. 3430–3437.
  4. Li, M.; Lafarge, F.; Marlet, R. Approximating shapes in images with low-complexity polygons. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2020, pp. 8633–8641.
  5. Douglas, D.H.; Peucker, T.K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature. Cartographica: the international journal for geographic information and geovisualization 1973, 10, 112–122. [CrossRef]
  6. Kennedy, J.; Eberhart, R. Particle swarm optimization. Proceedings of ICNN’95-international conference on neural networks. IEEE, 1995, Vol. 4, pp. 1942–1948.
  7. Fernández-García, N.L.; Martínez, L.D.M.; Carmona-Poyato, Á.; Madrid-Cuevas, F.J.; Medina-Carnicer, R. Assessing polygonal approximations: A new measurement and a comparative study. Pattern Recognition 2023, 138, 109396.
  8. Yin, P.Y. A discrete particle swarm algorithm for optimal polygonal approximation of digital curves. Journal of visual communication and image representation 2004, 15, 241–260. [CrossRef]
  9. García, N.L.F.; Martínez, L.D.M.; Poyato, Á.C.; Cuevas, F.J.M.; Carnicer, R.M. Unsupervised generation of polygonal approximations based on the convex hull. Pattern Recognition Letters 2020, 135, 138–145. [CrossRef]
  10. Panagiotakis, C.; Papadakis, H.; Grinias, E.; Komodakis, N.; Fragopoulou, P.; Tziritas, G. Interactive image segmentation based on synthetic graph coordinates. Pattern Recognition 2013, 46, 2940–2952. [CrossRef]
  11. Yang, X.; Gao, X.; Tao, D.; Li, X.; Li, J. An efficient MRF embedded level set method for image segmentation. IEEE Transactions on Image Processing 2015, 24, 9–21.
  12. Panagiotakis, C.; Argyros, A. Parameter-free modelling of 2D shapes with ellipses. Pattern Recognition 2016, 53, 259–275. [CrossRef]
  13. Mai, F.; Hung, Y.; Zhong, H.; Sze, W. A hierarchical approach for fast and robust ellipse extraction. Pattern Recognition 2008, 41, 2512–2524. [CrossRef]
  14. Panagiotakis, C.; Argyros, A. Region-based Fitting of Overlapping Ellipses and its application to cells segmentation. Image and Vision Computing 2020, 93, 103810. [CrossRef]
  15. Markaki, S.; Panagiotakis, C. Unsupervised Tree Detection and Counting via Region-Based Circle Fitting. BMVC, 2023.
  16. Jin, L.; Yang, J.; Kuang, K.; Ni, B.; Gao, Y.; Sun, Y.; Gao, P.; Ma, W.; Tan, M.; Kang, H.; others. Deep-learning-assisted detection and segmentation of rib fractures from CT scans: Development and validation of FracNet. EBioMedicine 2020, 62. [CrossRef]
  17. Papoutsakis, K.; Panagiotakis, C.; Argyros, A.A. Temporal action co-segmentation in 3d motion capture data and videos. Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 6827–6836.
  18. Gad, A.G. Particle swarm optimization algorithm and its applications: a systematic review. Archives of computational methods in engineering 2022, 29, 2531–2561.
  19. Latecki, L.J.; Lakamper, R.; Eckhardt, T. Shape descriptors for non-rigid shapes with a single closed contour. IEEE Conference on Computer Vision and Pattern Recognition. IEEE, 2000, Vol. 1, pp. 424–429.
  20. Bai, X.; Yang, X.; Latecki, L.J.; Liu, W.; Tu, Z. Learning context-sensitive shape similarity by graph transduction. Pattern Analysis and Machine Intelligence, IEEE Transactions on 2010, 32, 861–874. [CrossRef]
  21. Kimia, B. A Large Binary Image Database, LEMS Vision Group at Brown University, 2002. http://www.lems.brown.edu/~dmc/.
1
The centroid of P can be also used. The centroid of S is more preferable for stability reasons in an iterative process.
2
In each execution, the PSO based methods may yields slightly different results due to Particle Swarm Optimization, so we have executed 10 times each PSO based method (UPF-PSO, UPF-PSO-EA) getting the average IoU.
Preprints 92921 g001
Figure 1. Example outputs of the proposed classical polygonal approximation (left) and unconstrained polygonal fitting (right) for N = 4 vertices.
Figure 1. Example outputs of the proposed classical polygonal approximation (left) and unconstrained polygonal fitting (right) for N = 4 vertices.
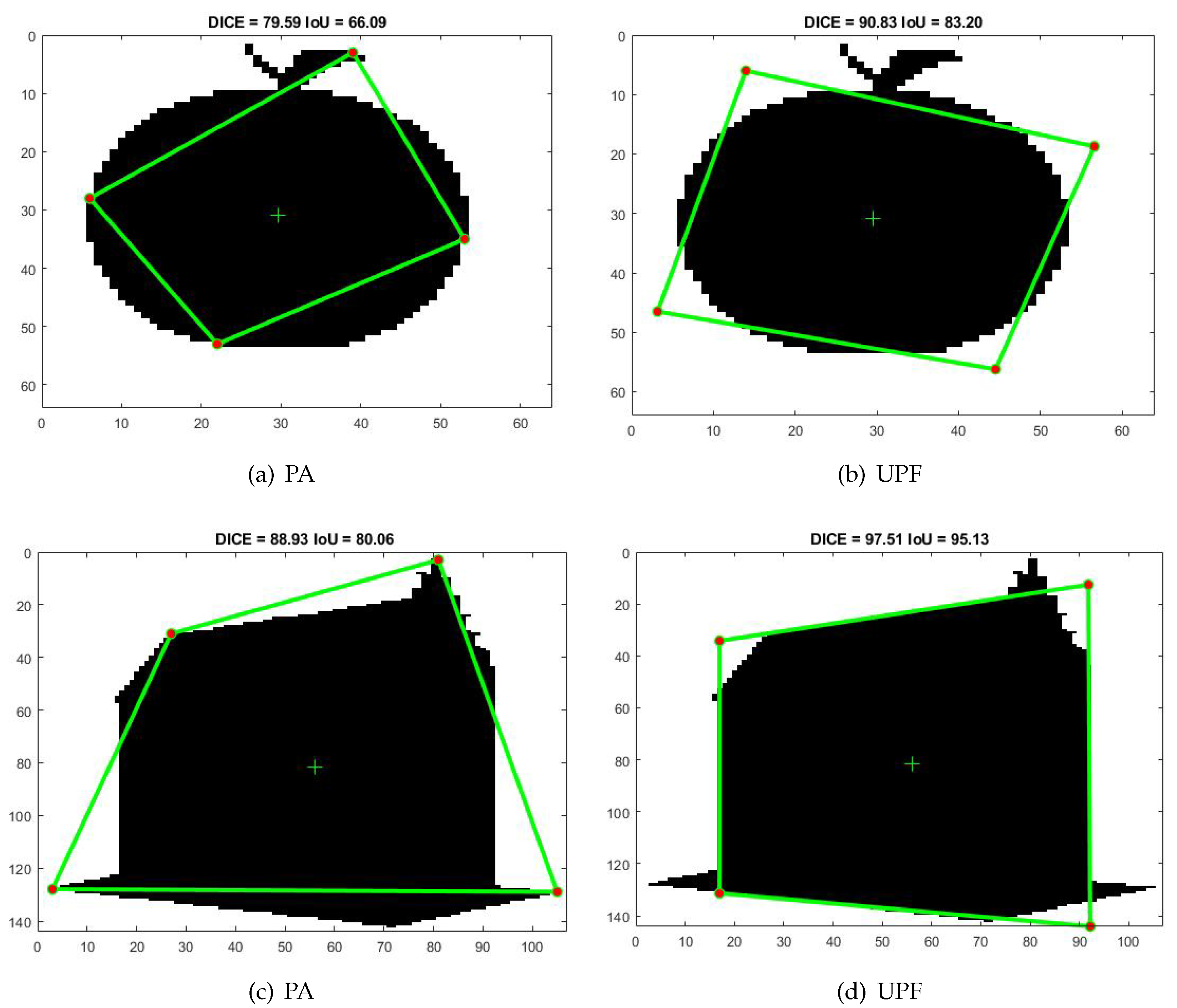
Preprints 92921 g001
Preprints 92921 g002
Figure 2. Twelve sample images form (a) the MPEG-7 dataset and (b) the LEMS dataset.
Figure 2. Twelve sample images form (a) the MPEG-7 dataset and (b) the LEMS dataset.
Preprints 92921 g002
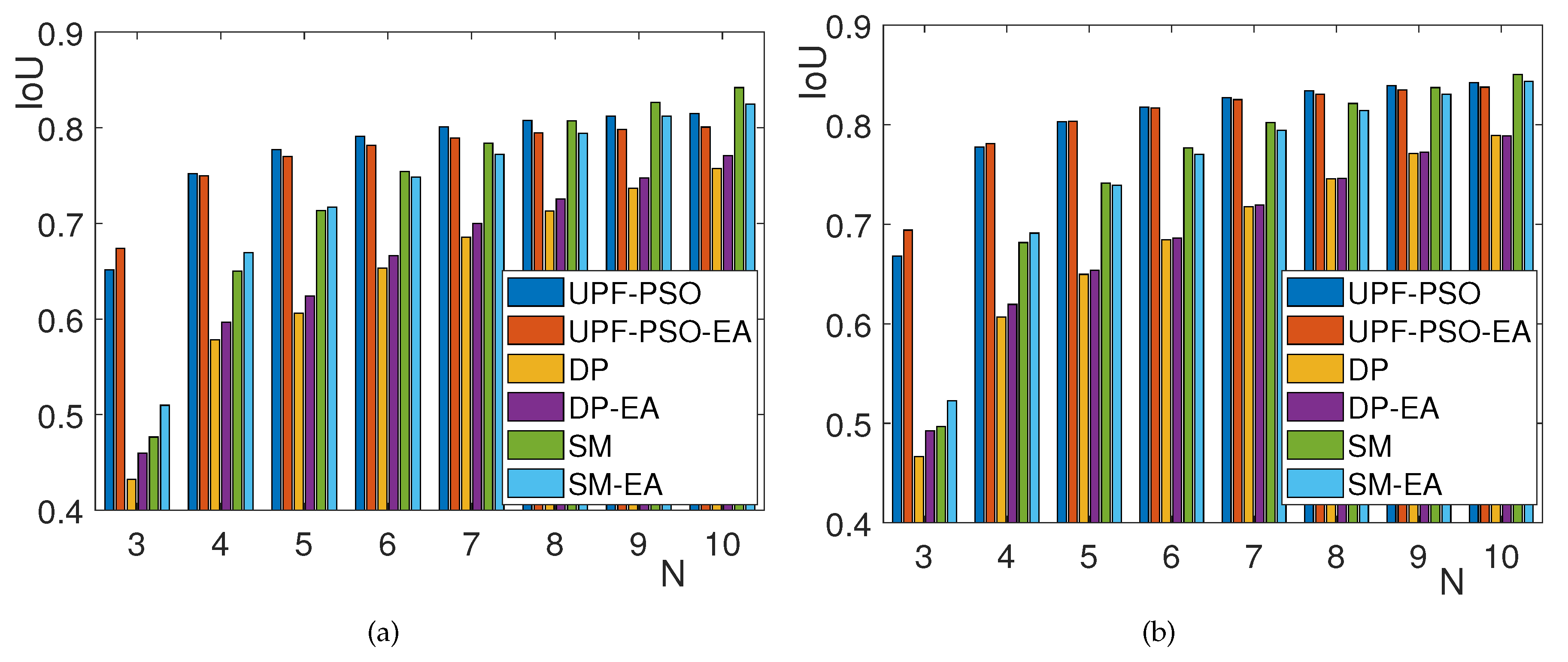
Preprints 92921 g003
Figure 3. (a) The IoU metric of UPF-PSO, UPF-PSO-EA, DP, DP-EA, SM, SM-EA methods over (a) the 1,400 images of MPEG-7 dataset and (b) the 1,462 of LEMS dataset.
Figure 3. (a) The IoU metric of UPF-PSO, UPF-PSO-EA, DP, DP-EA, SM, SM-EA methods over (a) the 1,400 images of MPEG-7 dataset and (b) the 1,462 of LEMS dataset.
Preprints 92921 g003
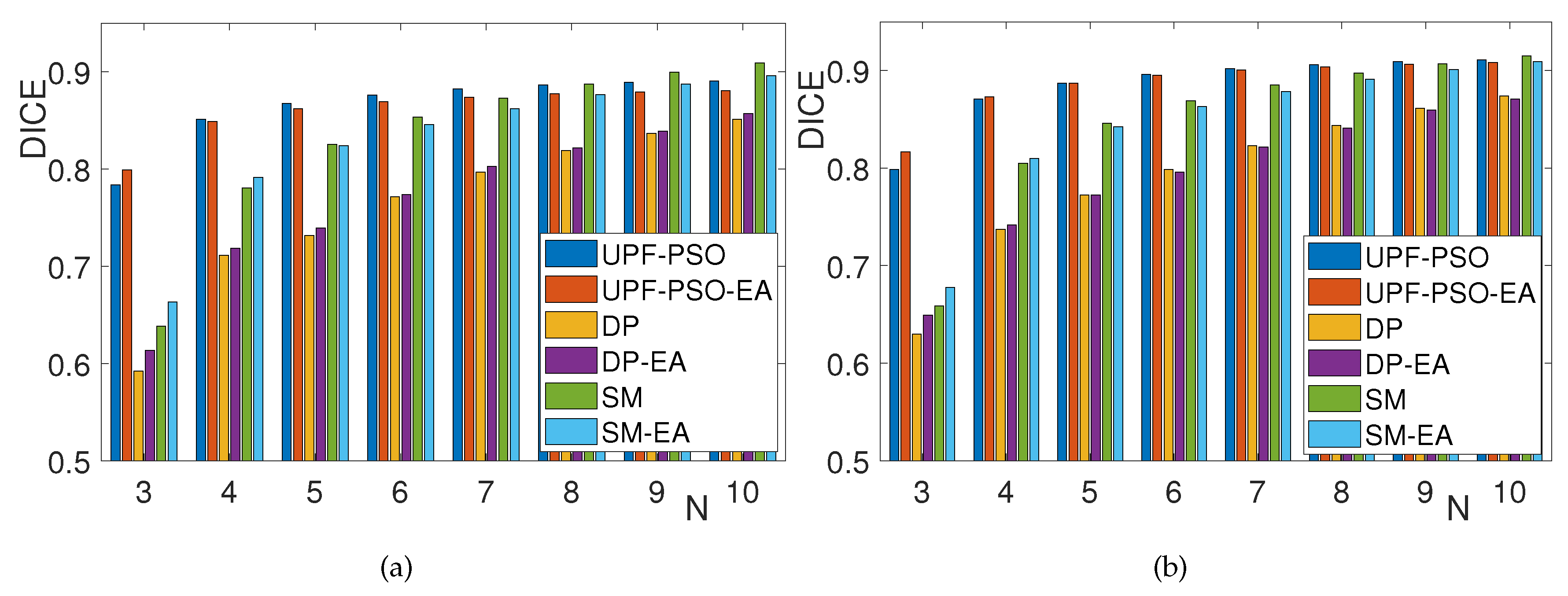
Preprints 92921 g004
Figure 4. (a) The DICE metric of UPF-PSO, UPF-PSO-EA, DP, DP-EA, SM, SM-EA methods over (a) the 1,400 images of MPEG-7 dataset and (b) the 1,462 of LEMS dataset.
Figure 4. (a) The DICE metric of UPF-PSO, UPF-PSO-EA, DP, DP-EA, SM, SM-EA methods over (a) the 1,400 images of MPEG-7 dataset and (b) the 1,462 of LEMS dataset.
Preprints 92921 g004
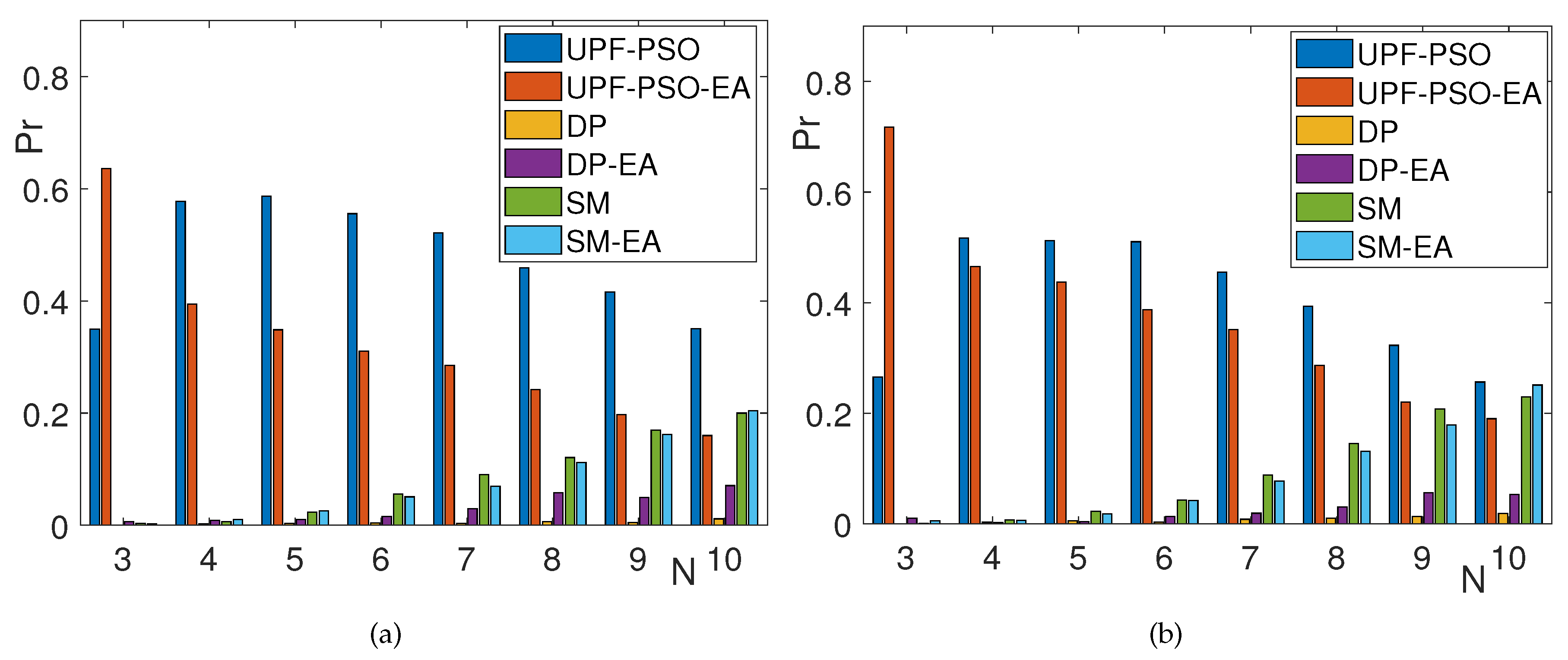
Preprints 92921 g005
Figure 5. (a) The Pr(m/IoU), m ∈ {UPF-PSO, UPF-PSO-EA, DP, DP-EA, SM, SM-EA} over the (a) 1,400 images of MPEG-7 dataset and (b) the 1,462 of LEMS dataset.
Figure 5. (a) The Pr(m/IoU), m ∈ {UPF-PSO, UPF-PSO-EA, DP, DP-EA, SM, SM-EA} over the (a) 1,400 images of MPEG-7 dataset and (b) the 1,462 of LEMS dataset.
Preprints 92921 g005
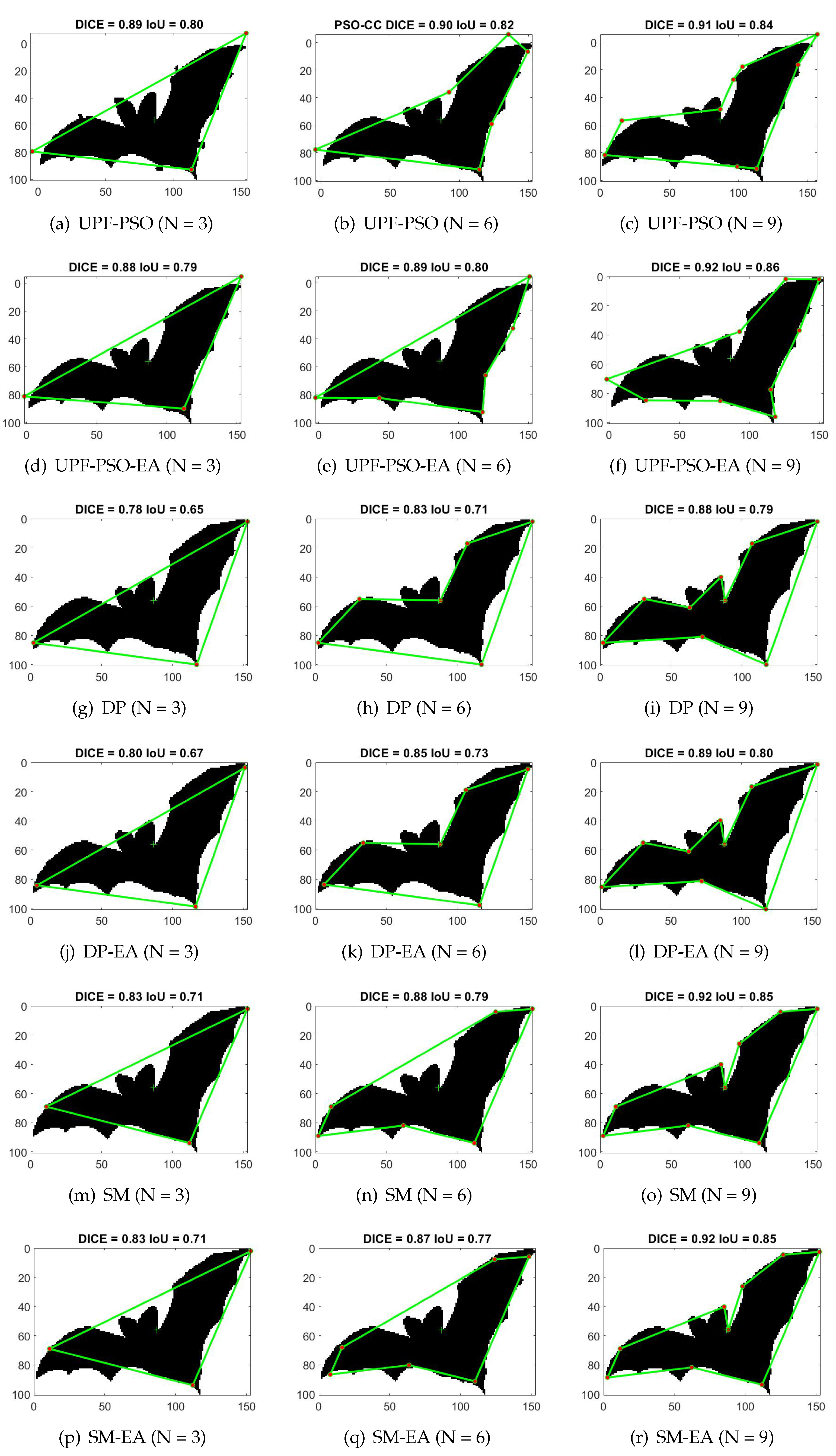
Preprints 92921 g006
Figure 6. Results of the proposed methods and baselines for N = 3 , 6 , 9 vertices on a bat shape from MPEG7 dataset.
Figure 6. Results of the proposed methods and baselines for N = 3 , 6 , 9 vertices on a bat shape from MPEG7 dataset.
Preprints 92921 g006
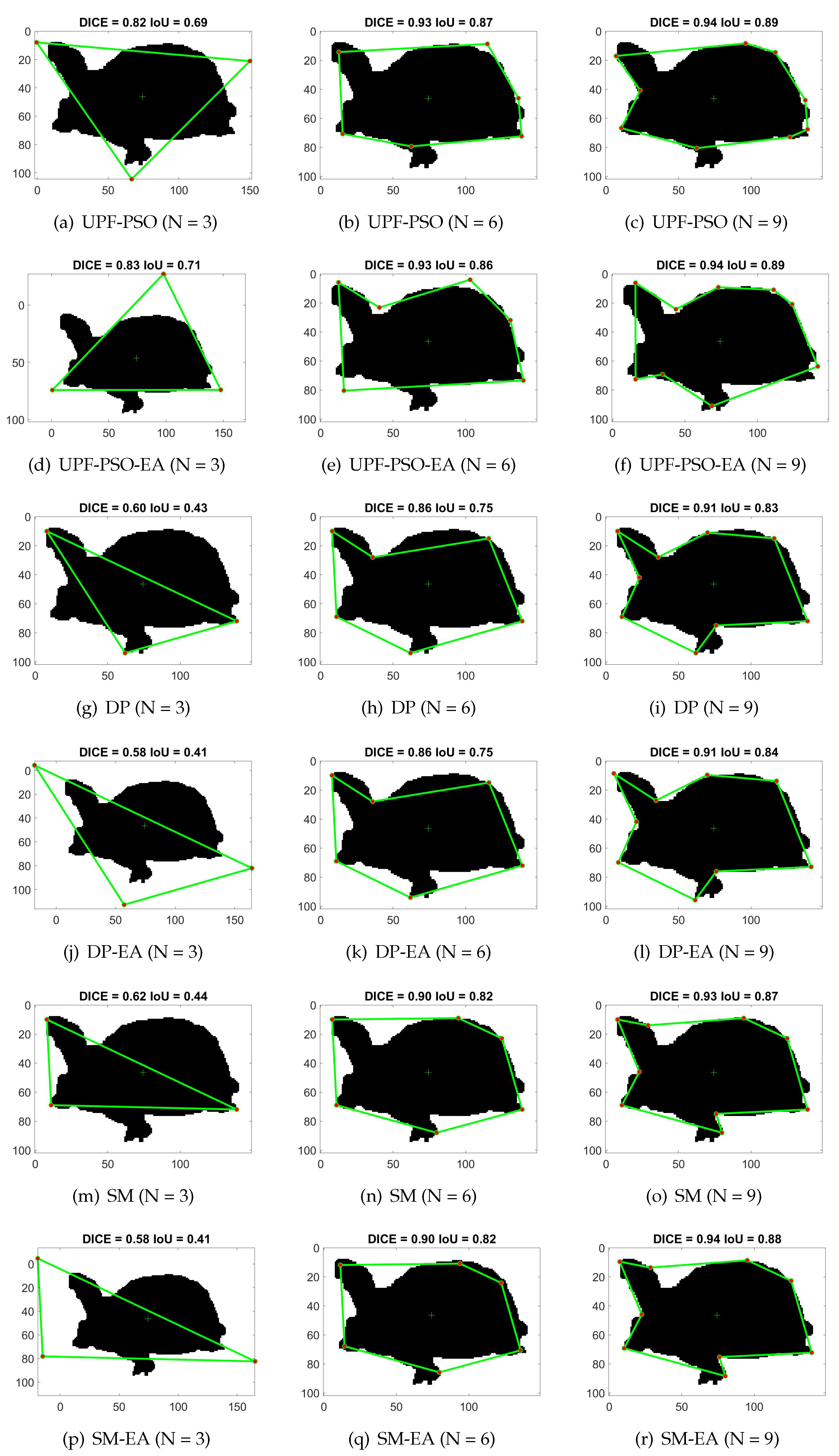
Preprints 92921 g007
Figure 7. Results of the proposed methods and baselines for N = 3 , 6 , 9 vertices on a turtle shape from LEMS dataset.
Figure 7. Results of the proposed methods and baselines for N = 3 , 6 , 9 vertices on a turtle shape from LEMS dataset.
Preprints 92921 g007
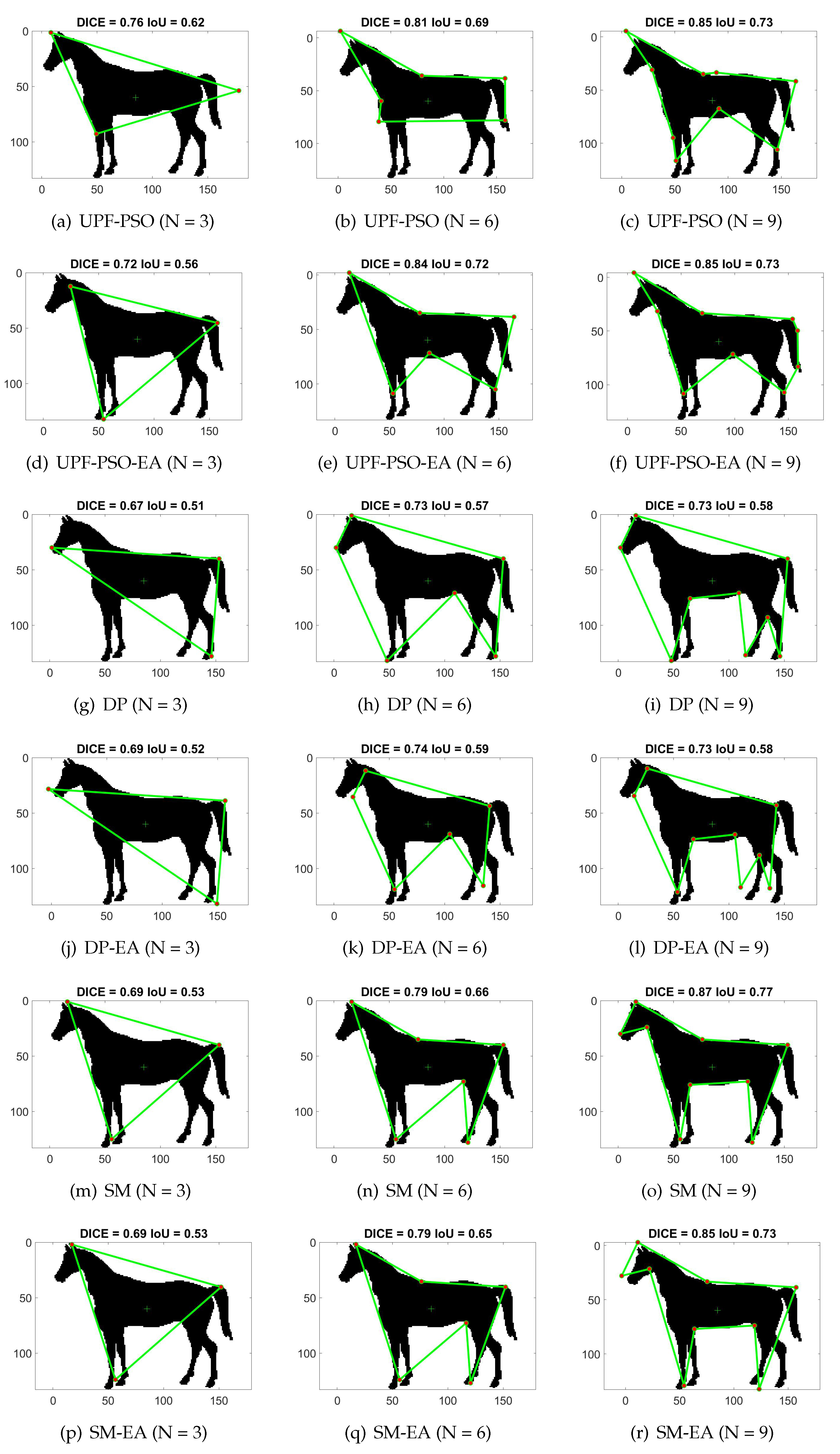
Preprints 92921 g008
Figure 8. Results of the proposed methods and baselines for N = 3 , 6 , 9 vertices on a horse shape from LEMS dataset.
Figure 8. Results of the proposed methods and baselines for N = 3 , 6 , 9 vertices on a horse shape from LEMS dataset.
Preprints 92921 g008
Table 1. The average IoU, DICE, Pr(m/IOU), UPF-PSO, UPF-PSO-EA, DP, DP-EA, SM, SM-EA methods computed on all images of MPEG7 dataset.
Table 1. The average IoU, DICE, Pr(m/IOU), UPF-PSO, UPF-PSO-EA, DP, DP-EA, SM, SM-EA methods computed on all images of MPEG7 dataset.
Methods IoU DICE Pr(m/IOU)
UPF-PSO 0.776 0.866 0.477
UPF-PSO-EA 0.770 0.861 0.322
DP 0.645 0.764 0.005
DP-EA 0.661 0.771 0.031
SM 0.732 0.833 0.084
SM-EA 0.731 0.831 0.080
Table 2. The average IoU, DICE, Pr(m/IOU), of the methods UPF-PSO, UPF-PSO-EA, DP, DP-EA, SM, SM-EA methods computed on all images of LEMS dataset.
Table 2. The average IoU, DICE, Pr(m/IOU), of the methods UPF-PSO, UPF-PSO-EA, DP, DP-EA, SM, SM-EA methods computed on all images of LEMS dataset.
Methods IoU DICE Pr(m/IOU)
UPF-PSO 0.801 0.885 0.404
UPF-PSO-EA 0.803 0.886 0.382
DP 0.679 0.793 0.008
DP-EA 0.685 0.794 0.024
SM 0.751 0.848 0.093
SM-EA 0.751 0.847 0.089
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated