Submitted:
13 December 2023
Posted:
14 December 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Literature Review
3. Railyard routing graph
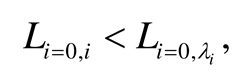
3.1. Traditional routing graph
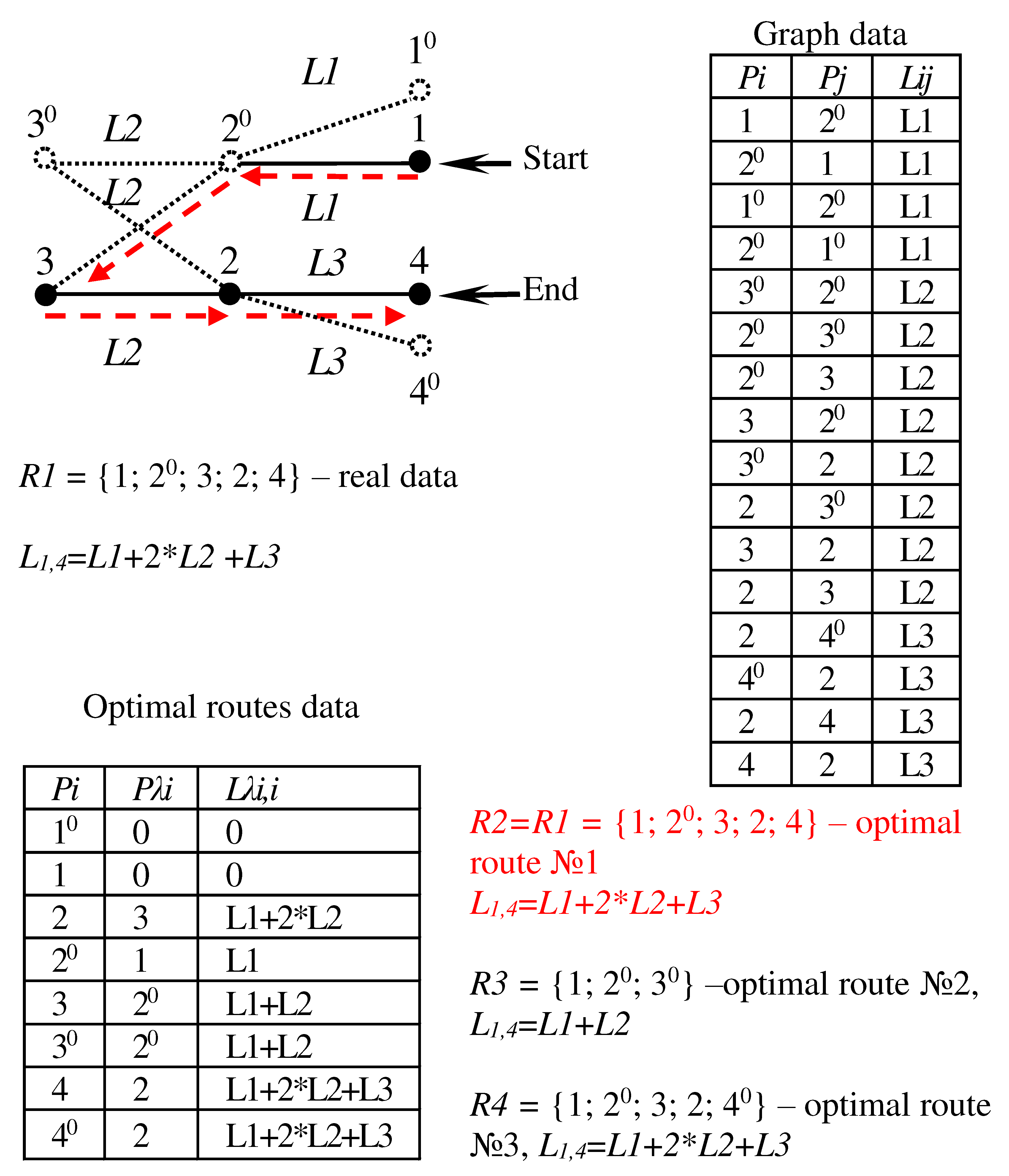
3.2. Double Vertex Graphs for the representation of the raylway track
3.3. Connectivity graph for the representation of the railway track train shunting
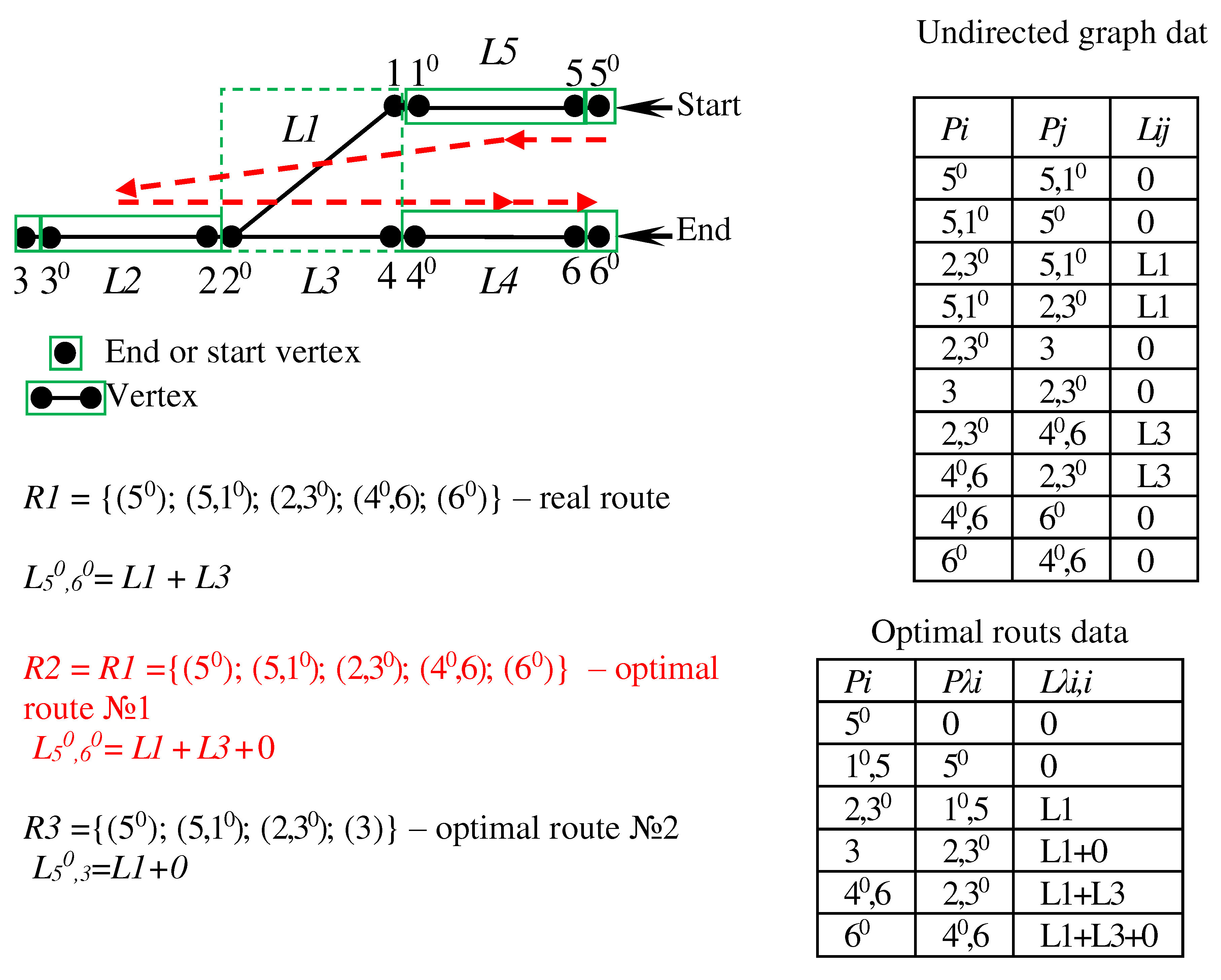
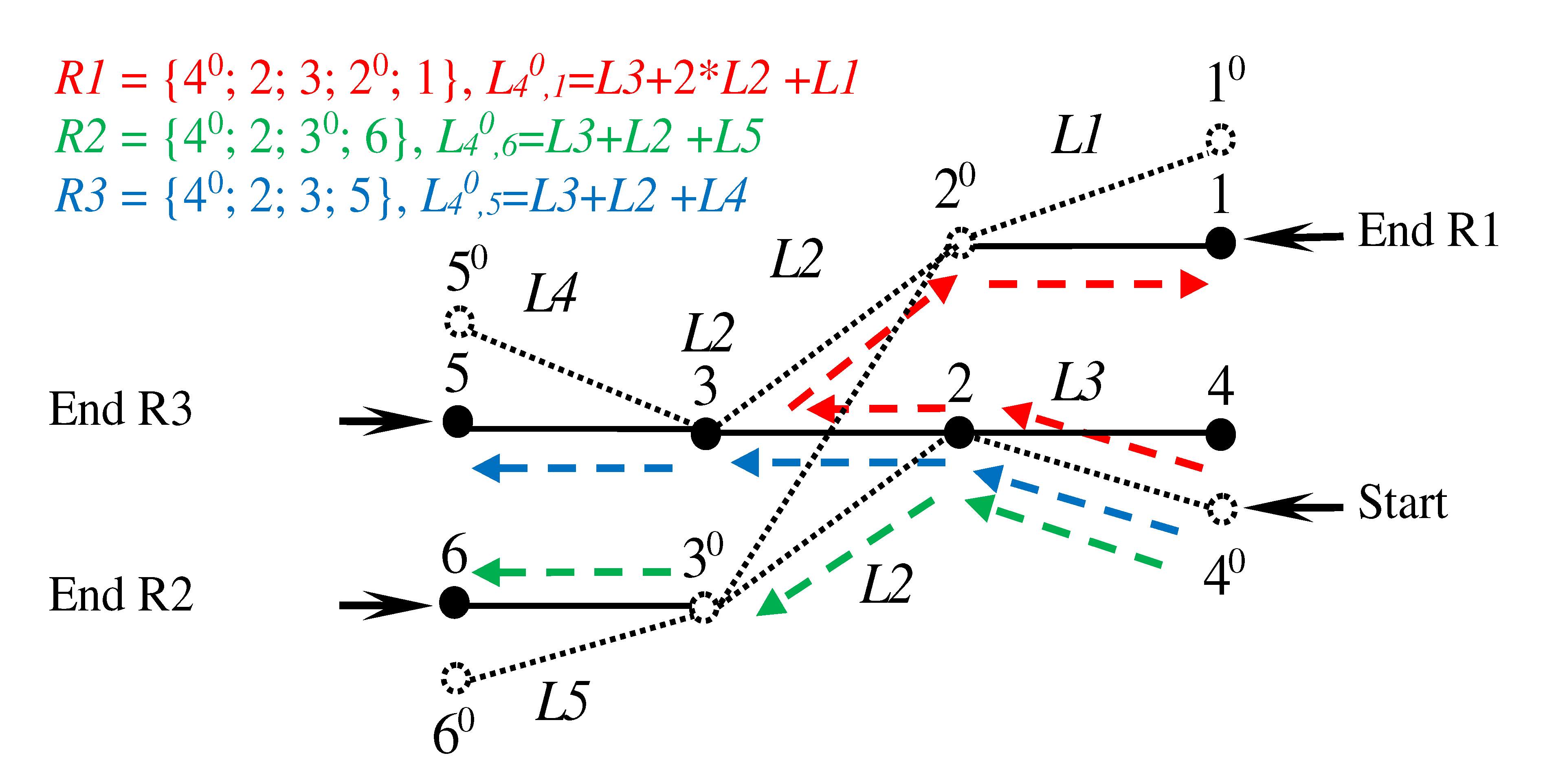
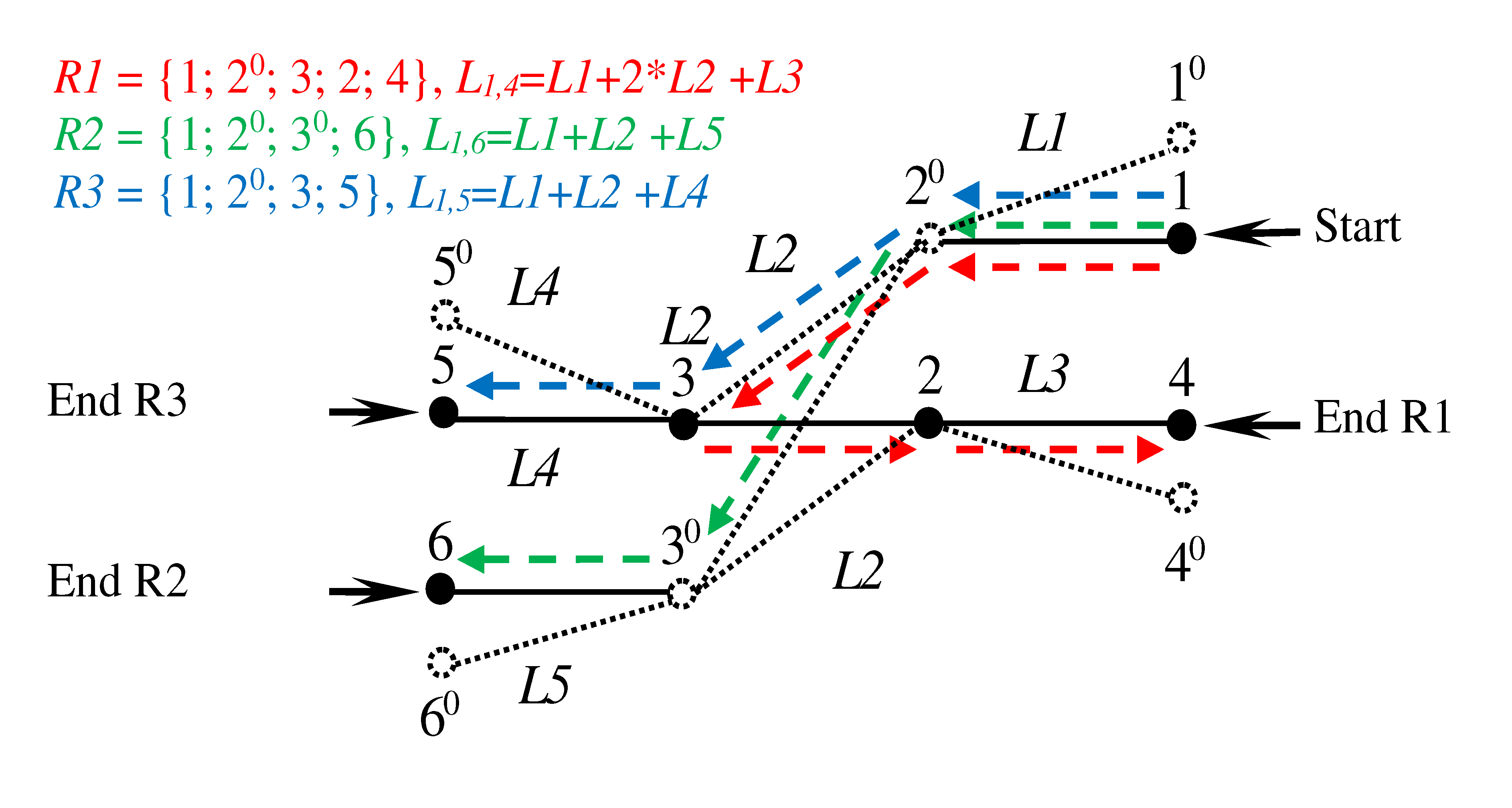
3.4. Proposed Double Vertex Graphs for representation of the draw-out track
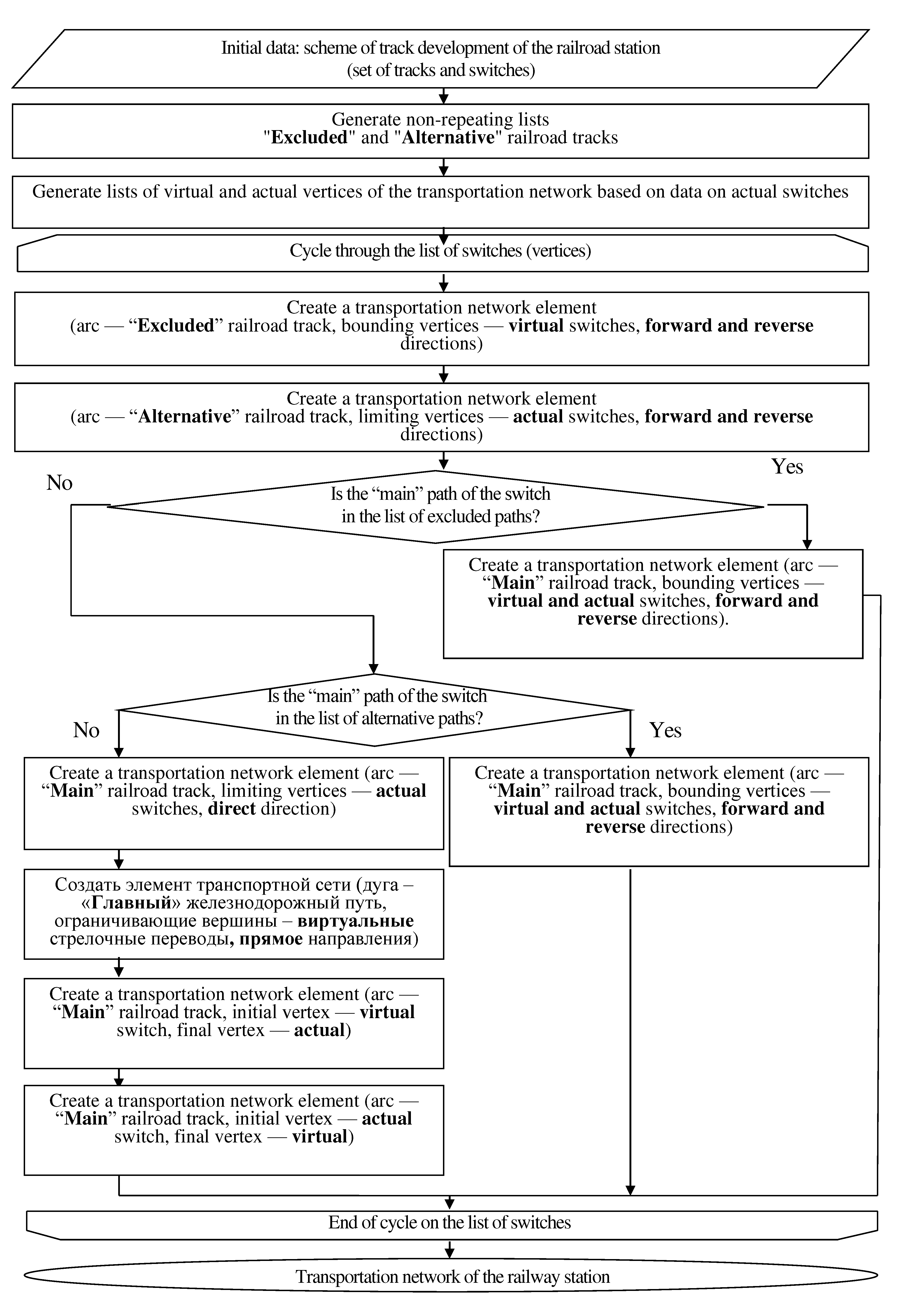
4. Algorithm of forming railyard transport network
5. Simulation experiment
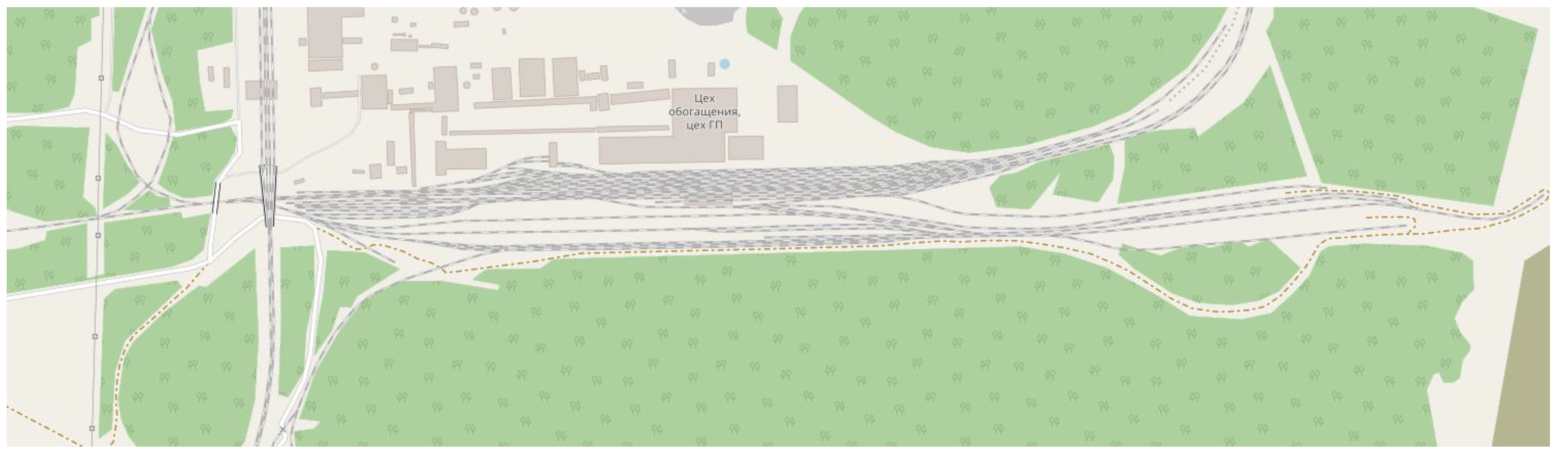
5.1. Description of the test object
 |
5.2. Simulation results
6. Conclusion
References
- Euler, L. Solutio problem at is ad geometriam situs pertinentis. Commentarii Academia Scientiarum Petropolitanae 1741, 8, 128–140. [Google Scholar]
- Richard, J. Trudeau. Introduction to Graph Theory. - Corrected, enlarged republication. - New York, 1993. -С. 76. ISBN 978-0-486-67870-2.
- Dijkstra E., W. A note on two problems in connexion with graphs. Numer. Math / F. Brezzi- Springer-Verlag, 1959. - Vol. 1, Iss. 1. - P. 269-271. 0029. [Google Scholar] [CrossRef]
- Dreyfus S., E. An appraisal of some shortest-path algorithms. Operations Research. 1969, 17, 395–412. [Google Scholar] [CrossRef]
- El-Sherbeny, Nasser A. (2014): The Algorithm of the Time-Dependent Shortest Path Problem with Time Windows. In AM 05 (17), pp. 2764-2770. [CrossRef]
- Ahuja, R., Magnanti. Network Flows: Theory, Algorithms, and Applications. Prentice-Hall, Upper Saddle River. ISBN, 1993; ISBN 9780136175490. [Google Scholar]
- Clarke, G. Scheduling of vehicles from a central depot to a number of delivery points / G. Clarke, J.W. Wright. Operations Research. 1964, 12, 568–581. [Google Scholar] [CrossRef]
- Lin, S. Computer solutions of the traveling salesman problem. Bell System Technical Journal. 1965, 44, 2245–2269. [Google Scholar] [CrossRef]
- Christofides INT The vehicle routing problem. In N. Christofides, A. Christofides INT The vehicle routing problem. . , Combinatorial Optimization, N. Christofides, A. Mingozzi, P. Toth, Ed.; Wiley, Chichester, 1979; 315–338. [Google Scholar]
- Gillett, B.E. A heuristic algorithm for the vehicle dispatch problem / B.E. Gillett, L.R. Miller. Operations Research. 1974, 22, 340–349. [Google Scholar] [CrossRef]
- Wren, A. Computers in Transport Planning and Operation. — Ian Allan, London, 1971.
- Wren, A. Computer scheduling of vehicles from one or more depots to a number of delivery points / A. Wren and A. Holliday. Operational Research Quarterly. 1972, 23, 333–344. [Google Scholar] [CrossRef]
- Orda and, R. Rom. Shortest-path and minimum delay algorithms in networks with time-dependent edge-length. Journal of the ACM 1990, 37, 607–625. [Google Scholar] [CrossRef]
- K. Nachtigall. Time depending shortest-path problems with applications to railway networks. European Journal of Operational Research 1995, 83, 154–166. [Google Scholar] [CrossRef]
- X. Cai, T. Kloks, and C. K. Wong. Time-varying shortest path problems with constraints. Networks 1997, 29, 141–150. [Google Scholar] [CrossRef]
- H. D. Sherali, K. Ozbay, and S. Subramanian. The time-dependent shortest pair of disjoint paths problem: Complexity, models, and algorithms. Networks 1998, 31, 259–272. [Google Scholar] [CrossRef]
- Chabini. Discrete dynamic shortest path problems in transportation applications: Complexity and algorithms with optimal run time. Transportation Research Record: Journal of the Transportation Research Board 1998, 1645, 170–175. [Google Scholar] [CrossRef]
- E. Kanoulas, Y. E. Kanoulas, Y. Du, T. Xia, and D. Zhang. Finding fastest paths on a road network with speed patterns. In Proceedings of the 22st International Conference on Data Engineering (ICDE), 2006.
- B. Ding, J. X. B. Ding, J. X. Yu, and L. Qin. Finding timedependent shortest paths over large graphs. In Proceedings of the 11th International Conference on Extending Database Technology: Advances in Database Technology, pages 205-216. ACM, 2008.
- B. C. Dean. Continuous-time dynamic shortest pathalgorithms. Master’s thesis, Massachusetts Instituteof Technology, 1999.
- Foschini, Luca; Hershberger, John; Suri, Subhash (2014): On the Complexity of Time-Dependent Shortest Paths. In Algorithmica 68 (4), pp. 1075-1097. [CrossRef]
- Gilbert Laporte, Stefan Ropke, and Thibaut Vidal. Chapter 4: Heuristics for the Vehicle Routing Problem, pages 87-116. 2014. [CrossRef]
- Anand Subramanian, Eduardo Uchoa, and Luiz Satoru Ochi. A hybrid algorithm for a class of vehicle routing problems. Computers & Operations Research, 40(10):2519-2531, 2013. ISSN 0305-0548. [CrossRef]
- Florian Arnold and Kenneth Sorensen. Knowledge-guided local search for the vehicle routing problem. Computers & Operations Research, 105:32-46, 2019. ISSN 0305-0548. [CrossRef]
- Thibaut Vidal, Teodor Gabriel Crainic, Michel Gendreau, Nadia Lahrichi, and Walter Rei. A hybrid genetic algorithm for multidepot and periodic vehicle routing problems. Operations Research, 60(3):611-624, 2012. [CrossRef]
- Jan Christiaens and Greet Vanden Berghe. Slack induction by string removals for vehicle routing problems. Transportation Science 1998, 54, 417–433, 2020. [Google Scholar]
- Luca Accorsi and Daniele Vigo. A fast and scalable heuristic for the solution of large-scale capacitated vehicle routing problems. Technical report, University of Bologna, 2020.
- Marcus Poggi and Eduardo Uchoa. Chapter 3: New exact algorithms for the capacitated vehicle routing problem. In Vehicle Routing: Problems, Methods, and Applications, Second Edition, pages 59-86. SIAM, 2014.
- Luciano Costa, Claudio Contardo, and Guy Desaulniers. Exact branch-price-and-cut algorithms for vehicle routing. Transportation Science 2019, 53, 946–985. [Google Scholar] [CrossRef]
- Diego Pecin, Artur Pessoa, Marcus Poggi, and Eduardo Uchoa. Improved branch-cut-and-price for capacitated vehicle routing. In Jon Lee and Jens Vygen, editors, Integer Programming and Combinatorial Optimization, pages 393-403, Cham, 2014. Springer International Publishing. ISBN 978-3-319-07557-0.
- Artur Pessoa, Ruslan Sadykov, Eduardo Uchoa, and Fran_cois Vanderbeck. A generic exact solver for vehicle routing and related problems. Mathematical Programming, 183(1):483-523, Sep 2020. ISSN 1436-4646. [CrossRef]
- Laetitia Jourdan, Matthieu Basseur, and E-G Talbi. Hybridizing exact methods and metaheuristics: A taxonomy. European Journal of Operational Research 2009, 199, 620–629. [Google Scholar] [CrossRef]
- Claudia Archetti and, M. Grazia Speranza. A survey on matheuristics for routing problems. EURO Journal on Computational Optimization 2014, 2, 223–246 ISSN 2192. [Google Scholar]
- Valeria Leggieri and Mohamed Haouari. A matheuristic for the asymmetric capacitated vehicle routing problem. Discrete Applied Mathematics, 2018, 234, 139–150, Special Issue on the Ninth International Colloquium on Graphs and Optimization (GO IX), 2014. [CrossRef]
- Dynamic optimization of wagon flows /, P.N. Mishkurov, A.N. Rakhmangulov. - Moscow: RUSAINS, 2017. - 110 P.
- Li, Shengdong; Lv, Hongxia; Xu, Changan; Chen, Tao; Zou, Congcong (2020): Optimized Train Path Selection Method for Daily Freight Train Scheduling. In IEEE Access 8, pp. 40777-40790. [CrossRef]
- Osintsev, N.A.; Rakhmangulov, A.N. Wagon flow management in industrial transportation systems. Vestnik of Nosov Magnitogorsk State Technical University. 2013, 1, 16–20. [Google Scholar]
- Rakhmangulov, Aleksandr; Sładkowski, Aleksander; Osintsev, Nikita; Mishkurov, Pavel; Muravev, Dmitri (2017): Dynamic Optimization of Railcar Traffic Volumes at Railway Nodes. In Aleksander Sładkowski (Ed.): Rail Transport-Systems Approach, vol. 87. Cham: Springer International Publishing (Studies in Systems, Decision and Control), pp. 405-456.
- Aleksandrov, A.E.; Surin, A.V.; Shipulin, A.V. Use of the simulation models in the operational planning of the train work (in Russian). Vestnik of Rostov State University of Railway Communication. 2015, 4, 65–72. [Google Scholar]
- Pascariu, Bianca; Samà, Marcella; Pellegrini, Paola; D’Ariano, Andrea; Rodriguez, Joaquin; Pacciarelli, Dario (2022): Performance Evaluation of a Parallel Ant Colony Optimization for the Real-Time Train Routing Selection Problem in Large Instances. In Leslie Pérez Cáceres, Sébastien Verel (Eds.): Evolutionary Computation in Combinatorial Optimization, vol. 13222. Cham: Springer International Publishing (Lecture Notes in Computer Science), pp. 46–61.
- Yang, Zhonggao; Xiang, Dan; Cheng, Yili (2020): VR Panoramic Technology in Urban Rail Transit Vehicle Engineering Simulation System. In IEEE Access, p. 1. [CrossRef]
- Rakhmangulov, A.N. Railway transport-technological systems: organization of functioning: monograph / A.N. Rakhmangulov, P.N. Mishkurov, O.A. Kopylova. Kopylova. - Magnitogorsk: Nosov Magnitogorsk State Technical University, 2014. 300 P.
- Khabarov, V. I. Creation of the simulation model of the train movement using the multi-agent and discrete event approaches on the example of the West Siberian railroad. Izvestiya Transsiba. 2017, 3, 143–154. [Google Scholar]
- Kalinina, A.R. Development of the simulation model of the nodal technical station. Transport of the Asia-Pacific Region. 2015, 2, 39–46. [Google Scholar]
- Merkulov, A.V. , Godyaev A.I. Some aspects of simulation modeling of the railway section infrastructure. Bulletin of the Pacific State University. 2015, 4, 109–116. [Google Scholar]
- Chislov, O. , Zadorozhniy V., Lomash D., Chebotareva E., Solop I., Bogachev T. (2020) Methodological Bases of Modeling and Optimization of Transport Processes in the Interaction of Railways and Maritime Transport. In: Macioszek E., Sierpiński G. (eds) Modern Traffic Engineering in the System Approach to the Development of Traffic Networks. TSTP 2019. Advances in Intelligent Systems and Computing, vol 1083. Springer, Cham. [CrossRef]
- Kolokolnikov, V.S. , Slobodyanyuk I.G. Technology of macromodeling of polygons. Transport of the Urals. 2019, 3, 48–51. [Google Scholar] [CrossRef]
- Shmulevich, M.I. , Starikov A.E. Features of shunting work rationing in the simulation model of the station. World of Transport and Transportation. 2015, 5, 198–212. [Google Scholar]
- V¨olz, W.D. , Ermittlung der Leistungsf¨ahigkeit von Knotenpunkten spurgef¨uhrter Verkehrssysteme mittels Graphentheorie. PhD thesis, Lehrstuhl und Institut f¨ur Verkehrswesen, Eisenbahnbau und -betrieb; Technische Universit¨at Hannover, Hannover, 1976.
- Montigel, M. Formal Representation of Track Topologies by Double Vertex Graphs.. Computers in Railways III / T. Murthy [and others]. Washington, DC, 1992. pp. 359-370.
- G’ely, L. , Dessagne, G. & Pesneau, P., A multi scalable model based on a connexity graph representation. Computers in Railways XII, Beijing, China, volume 1, pp. 193–204, 2010.
- Montigel, M. : Time-triggered exchange of train route data between train control systems. 8th International Conference on Computer Aided Design, Manufacture and Operation in the Railway and Other Advanced Mass Transit Systems (COMPRAIL). Lemnos, Greece, Southampton, 2002. pp. 33-41.
- Scheidt, M. Proposal for a railway layer model / WIT Transactions on the Built Environmentthis link is disabled. 2018. [Google Scholar]
- Shekhar, S. , Singh A., Belur M. N., Rangaraj N. Development of a railway junction simulator for evaluation of control strategies and capacity utilization optimization. 2019 Fifth Indian Control Conference (ICC). New Delhi, India: IEEE, 09.01.2019 - 11.01.2019, 260-265.
- Mishkurov, P.N. , Rakhmangulov A.N., Fridrikhson O.V. Methodology of formation of the transportation network of the railway station. Bulletin of the Ural State University of Railway Transport. 2021, 3, 50–64. [Google Scholar] [CrossRef]
- Kuzmin D. V., V. , Baginova V. V. V., Krasnobaev D. A., Musatov D. V. Development of the simulation discrete event model of the transport infrastructure using optimization tools. T-Comm: Telecommunications and transport. 2023, 17, 42–48. [Google Scholar] [CrossRef]
- Abar, S. , Theodoropoulos G. K., Lemarinier P., O’Hare G. M. Agent Based Modelling and Simulation tools: A review of the state-of-art software. Computer Science Review. 2017, 24, 13–33. [Google Scholar] [CrossRef]
- Mishkurov, P. N. , Rakhmangulov A. N. Features of building an agent-based simulation model of a railway station. Modern problems of Russian Transport Complex. 2021, 11, 29–40. [Google Scholar] [CrossRef]
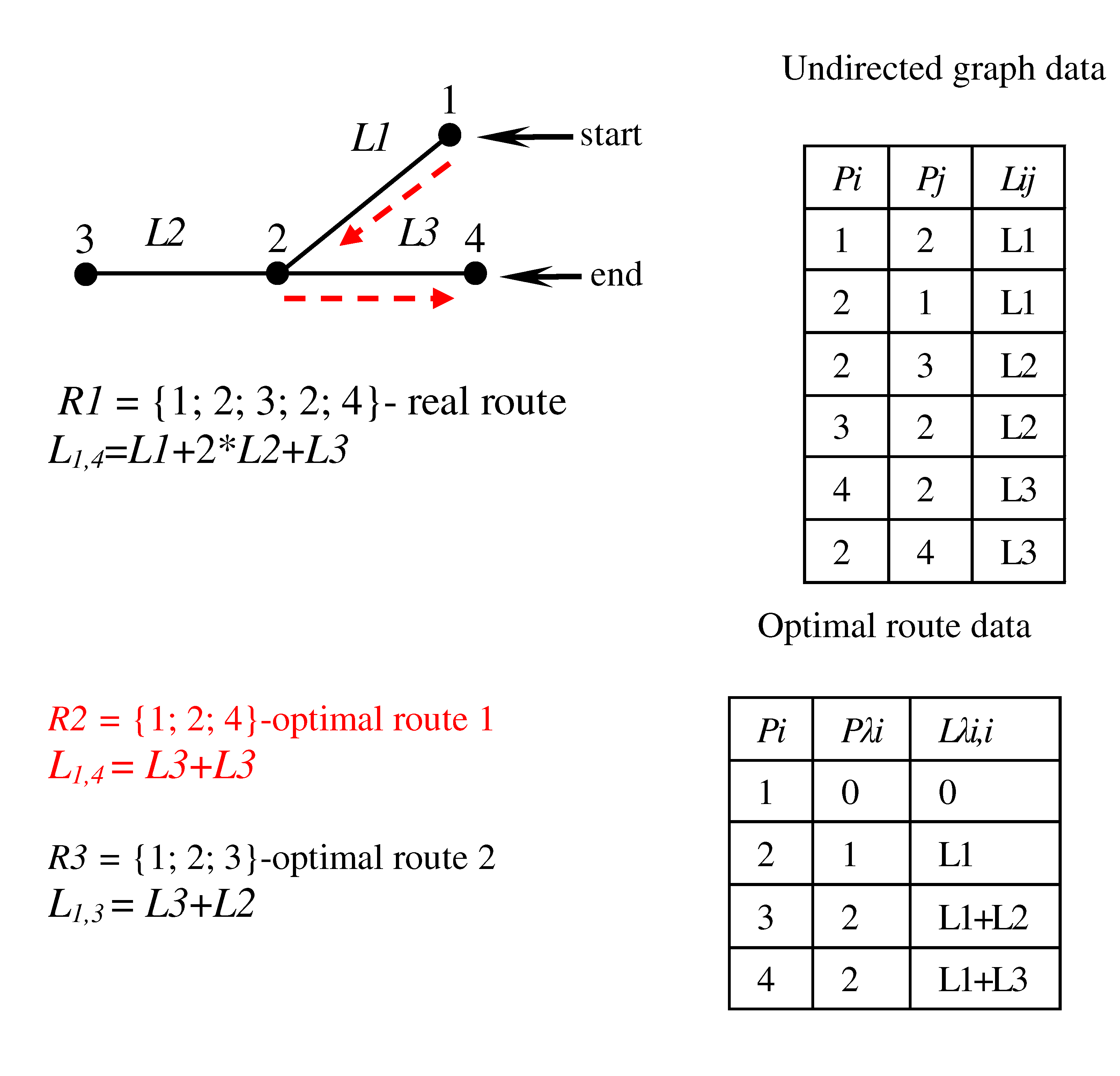

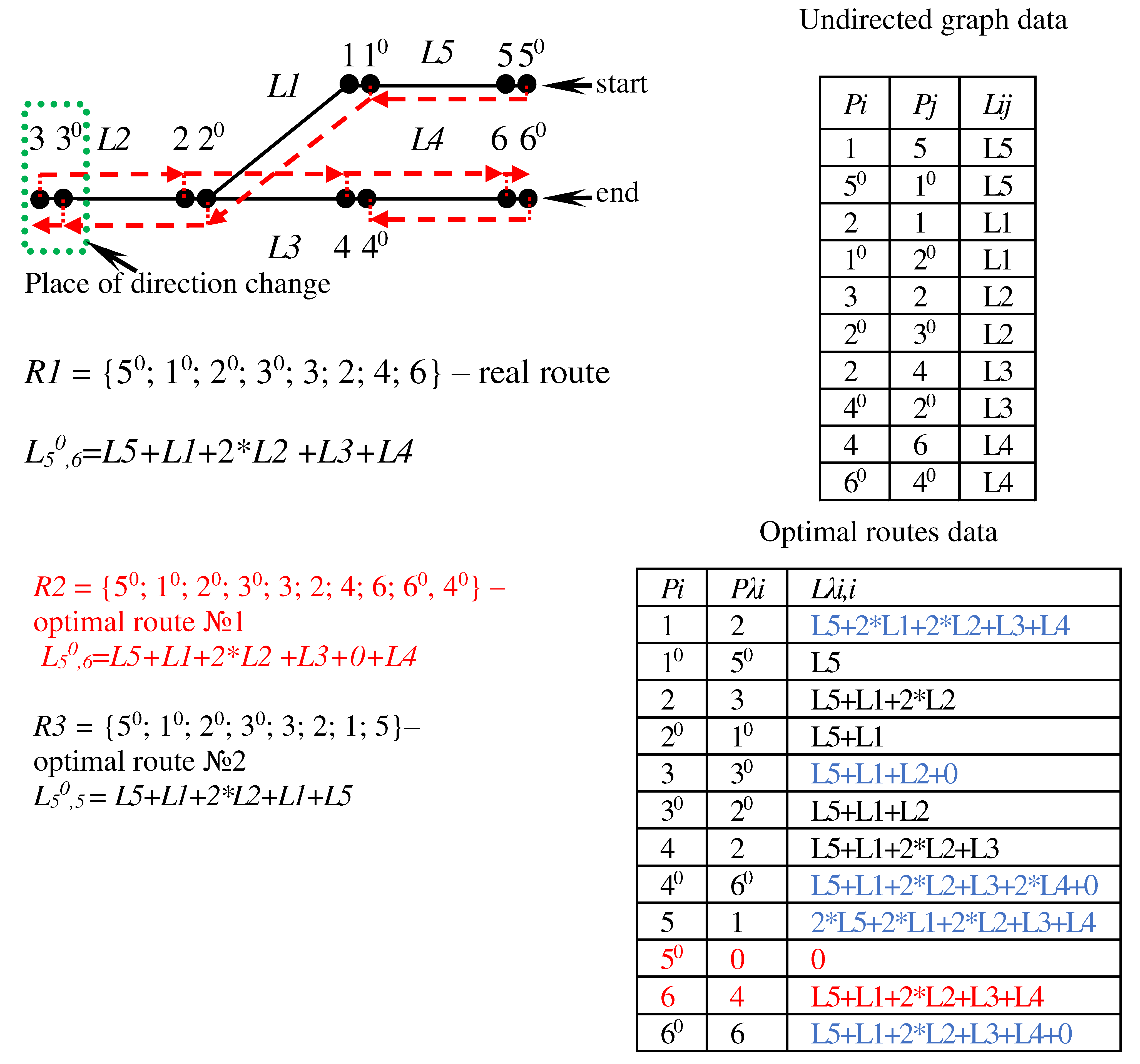
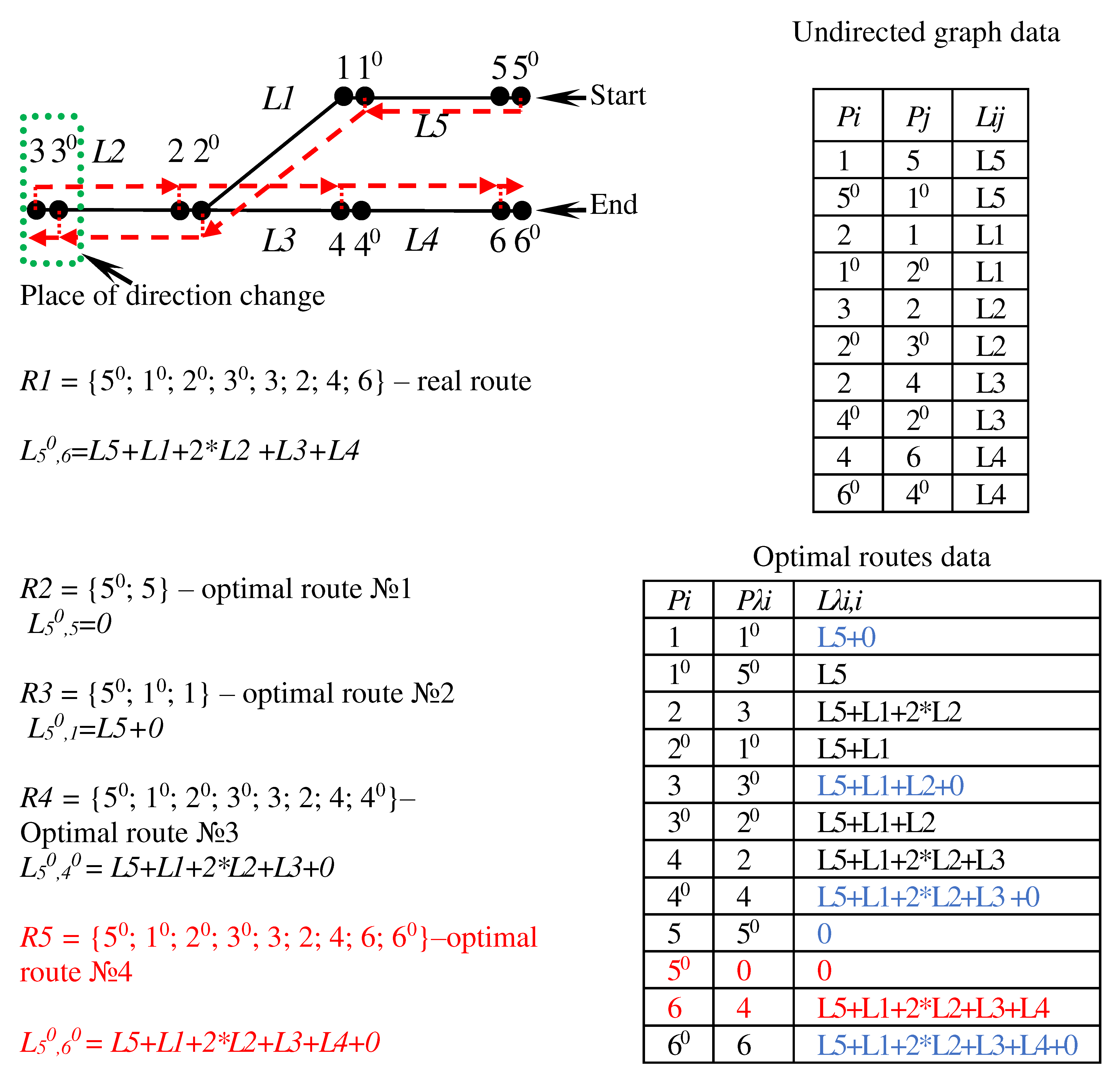
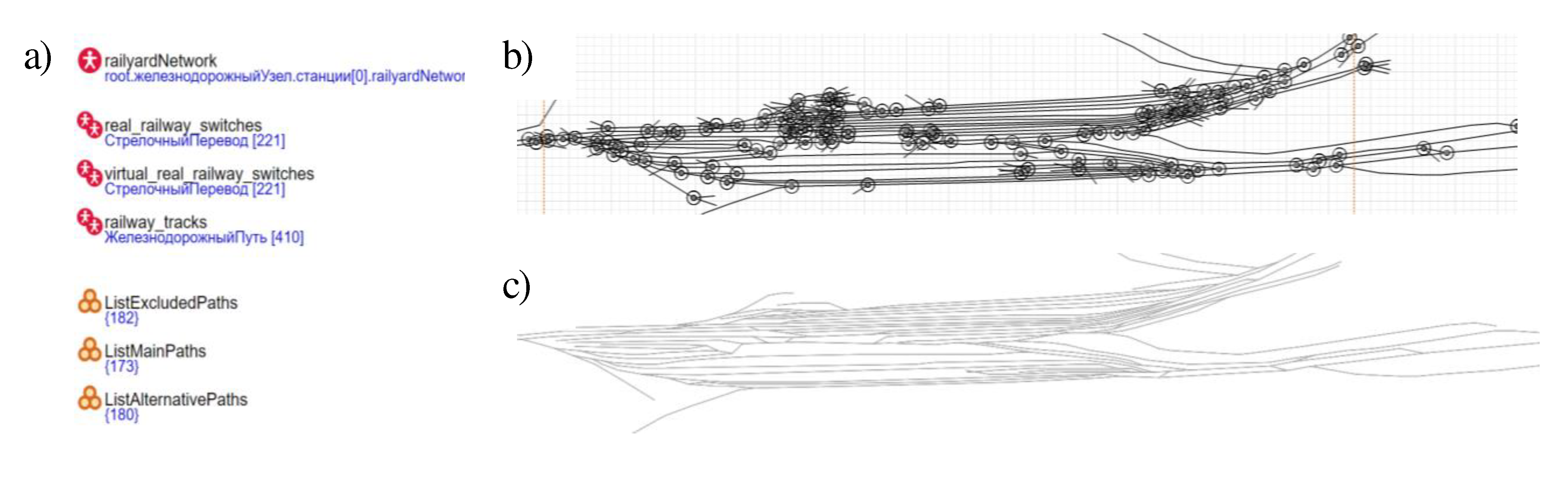
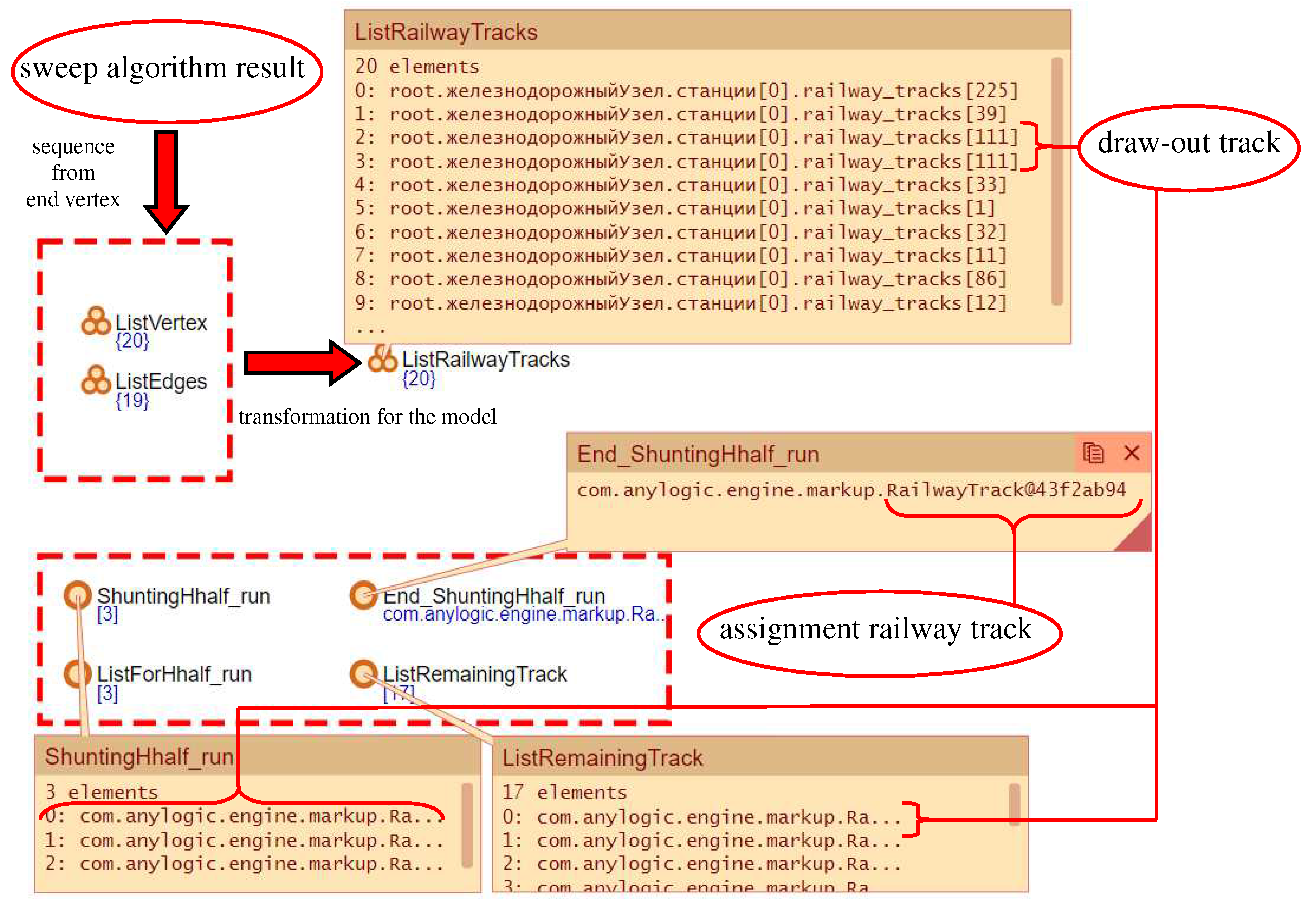
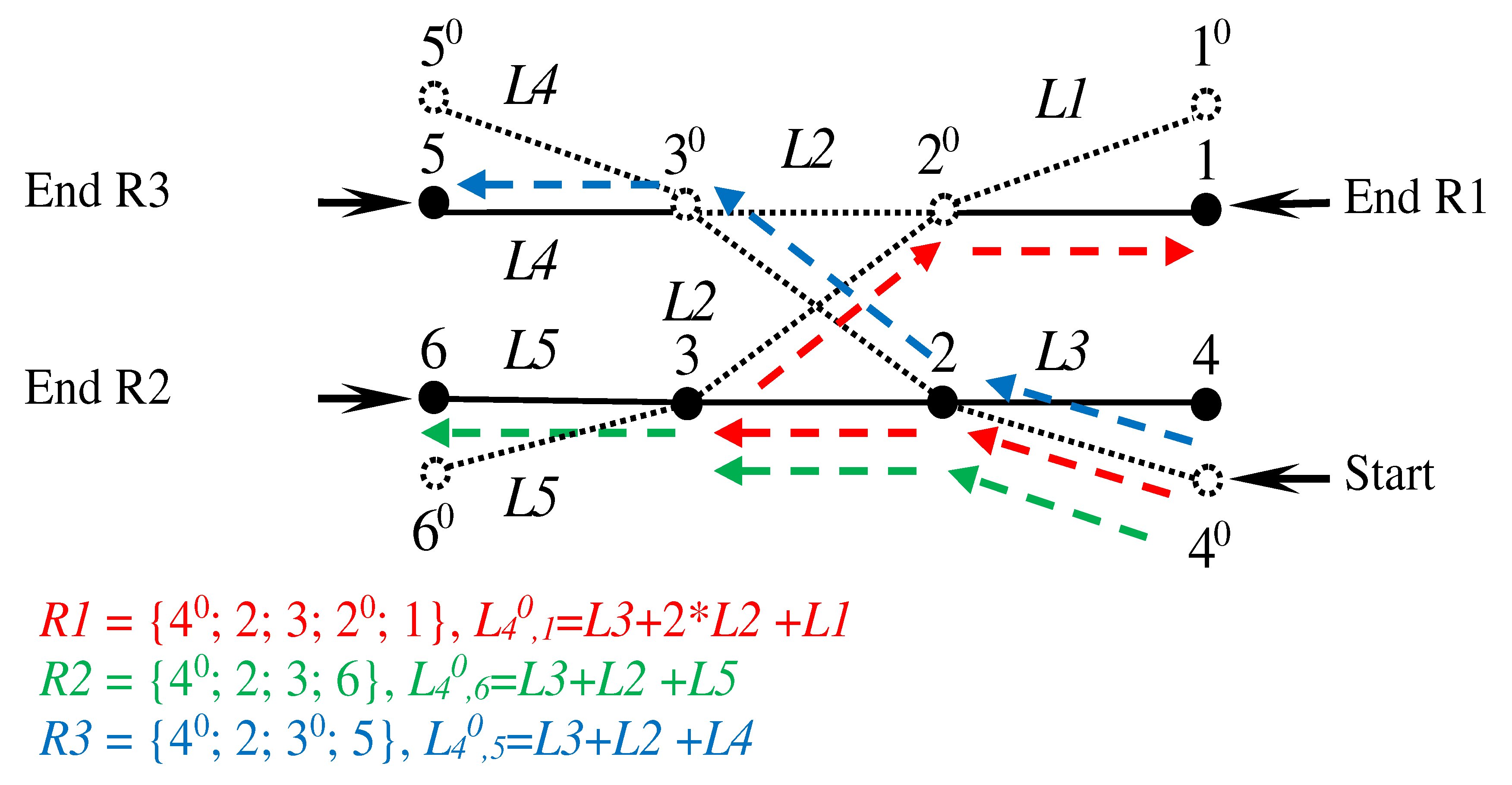
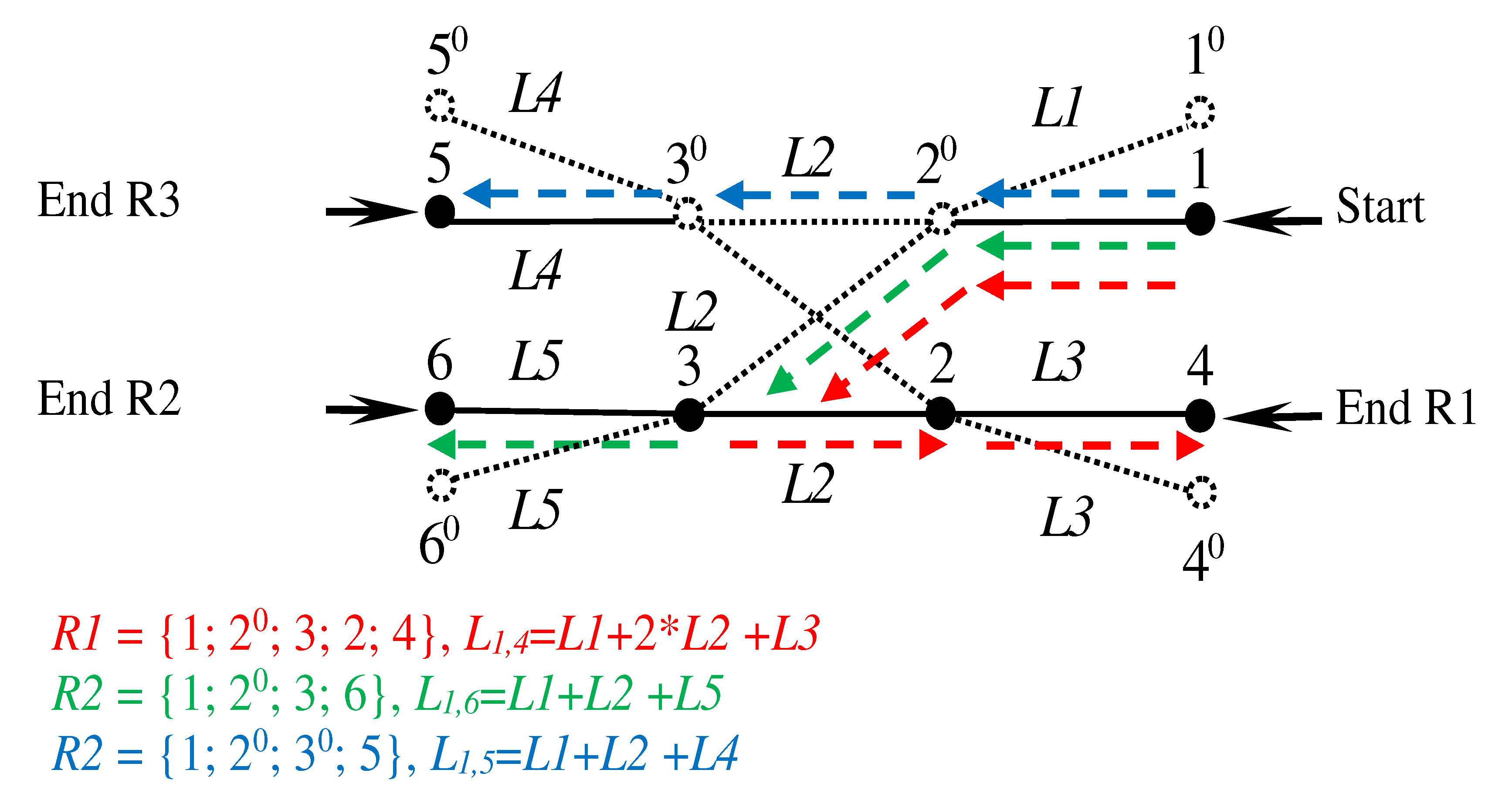
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





