Prerpints.org logo
Preprint
Article

Fully Automatic Segmentation Framework for FL Biometric Measurement in Foetal Ultrasound Images

Altmetrics

Downloads

117

Views

68

Comments

0

Submitted:

13 December 2023

Posted:

14 December 2023

You are already at the latest version

Alerts
Abstract
Femur length (FL) is a biometric measurement of ultrasound images used to identify the growth patterns and abnormalities of the foetus. Automatic segmentation of FL can improve the efficiency and convenience of inexperienced users. The femur region in a low-cost ultrasound image is a small area with low contrast intensity compared with the non-femur region. This study proposed a fully automated framework for segmenting and measuring the FL in a portable ultrasound image. We utilized statistical modeling, employing Gaussian mixture functions for thresholding to extract the femur area from the background. We also used the localizing region-based active contour method to segment the femur region accurately. We also proposed a refinement step in this framework to obtain a more accurate femur area in the ultrasound image. Because the length and position of the femur are the main factors affecting foetal biometric measurement accuracy, we not only evaluated segmentation results using region-based methods, such as sensitivity, specificity, and dice similarity. We also applied the FL measurement approach to evaluate the angle and length accuracy relative to the ground truth. In terms of region-based segmentation performance, the proposed method provided the best average performance with a sensitivity of 0.78, specificity of 0.87, and dice similarity of 0.81. For FL measurement performance, the proposed framework achieved an average angle accuracy of 0.99, distance accuracy of 0.88, and length accuracy of 0.93.
Keywords: 
Subject: Computer Science and Mathematics  -   Mathematical and Computational Biology

1. Introduction

Ultrasonography is a noninvasive imaging modality that is used for routine prenatal care and for providing essential information that enables doctors or midwives to ensure foetal development and a possible diagnosis of the problem. Emerging advances have introduced portable ultrasound devices that are small and inexpensive [1,2,3,4]. Mobile ultrasound devices are a helpful modality, especially in developing countries. Nevertheless, this device has many shortcomings, particularly with regard to the image quality. However, the development of research in the medical image diagnostic field has enabled more accessible and accurate analysis techniques for portable ultrasound images.
Femur length (FL) is a biometric measure used to estimate foetal weight. FL is an essential alternative when other biometric measurements such as biparietal diameter and abdominal circumference cannot be obtained. FL can be combined with different biometric sizes or used alone [5,6]. Automatic biometric analysis of the foetus can improve efficiency, reduce the time required, and provide convenience to inexperienced users [7,8,9]. In general, the automatic FL segmentation method consists of four main steps: pre-processing, femur region extraction, segmentation of femur bones, and post-processing. One of the essential steps is to extract the femur area, which is aimed at separating the femur area from the background.
The thresholding approach is often implemented in the femur-extraction step. Thresholding techniques have been proposed for femur segmentation. [10] proposed entropy-based thresholding to obtain an intensity value with the maximum number of entropies from two distribution classes, that is, the object class and background class. However, the entropy-based method does not always produce good accuracy and thus [10] provided an alternative way to increase the intensity and sharpness of the region features. [11] also proposed an entropy function for image segmentation. In multilevel Otsu thresholding, which applies the principle of the Otsu technique to separate the object from the background, the image is divided into more than two levels, with an ordered threshold value [12,13]. [12] implemented 4-level image thresholding and then selected a threshold value for binary segmentation. The weakness of multilevel Otsu thresholding is that we have to precisely determine the thresholding levels to obtain the greyscale range of the region of interest. [14] proposed a multilevel set approach that was based the Likelihood Region to segment bone in a lumbar ultrasound image. The multilevel thresholding also implemented for segmentation purpose in the other modality such as MRI [15]. In the statistical thresholding technique, [16] used the threshold value calculated based on the mean and standard deviation of the intensities in a specific image area. The particular area was a sub-image in the top middle of the half-size image. The result of the femur extraction using the statistical thresholding technique was influenced by the average contrast of the input ultrasound image. If the average contrast is too low, the region of interest will merge with other areas.
Such machine learning and deep learning approaches were applied for ultrasound image segmentation. [17] compared two hybrid learning approaches, the SegNet network and random forest regression model. As stated in the study, SegNet is more promising for overcoming the problem of bright structural interference, similar to the femoral region. [18] trained eight segmentation architecture in deep learning using EffientNetB0 network to segment the fetal head biometric. U-Net architecture model was used for fetal head segmentation by [19]. However, the deep learning approaches require sufficient training data. In addition, research [20] shows that the traditional segmentation approach is more precise than the deep learning segmentation approach.
The femur ultrasound image captured by portable ultrasound has low contrast and brightness, as shown in Figure 1(a). The distribution of the intensity histogram was unimodal and tended to accumulate in the low-intensity areas (Figure 1(b)). Therefore, the problem is how to extract the femur region with a small area and intensity that is not significantly different from the background area.
According to [21], traditional thresholding methods such as the Otsu thresholding method makes it difficult to extract objects from their background on a unimodal histogram distribution, especially for small regions with low contrast against the background area. A statistical modeling approach that uses the probability distribution of intensity values is efficient and adaptable for separating objects from the background. One that applies this approach is the Gaussian mixture model method that implements the expectation maximization (EM) method to estimate the number of modes of the histogram [21]. The disadvantage of this approach, however, is that the computation time is large and sometimes does not fit the data used.
Therefore, we propose a new approach to image thresholding based on a statistical modeling approach to extract a small area in the ultrasound image, in this case, for FL segmentation. In this approach, we assume that the histogram is bimodal. The first and second distribution models are measured using a Gaussian mixture function. The threshold value is determined by the intensity value, which gives the local minimum of the mixture model’s weight. The proposed approach searches for the threshold value around a predefined initial value or traces a local optimum to reduce the computational time.
Despite many femur segmentation studies, this paper provides a comprehensive automatic FL measurement framework that includes steps to remove speckle noise and refinement steps that result in the best segmentation performance. Moreover, we propose a line measurement technique to evaluate FL segmentation performance. We applied a hybrid denoising approach [22] to reduce speckle noise. In the second step, we extracted the femur region using the proposed thresholding method. Femur object candidates were selected based on some characteristics of the femur, such as its location and size. Next, the pixel in the selected femur object with the highest intensity was chosen as the starting point of the localizing region-based active contour (LRAC) segmentation method implemented in [23]. Segmentation results using the LRAC method sometimes exceed the region of interest. Hence, we proposed a refinement step for merging distinct subregions on a straight line. The remainder of this paper is organized as follows. Section 2 describes the data used in the experiment and explains the proposed method and its implementation in automatic FL segmentation. This section describes automatic femur segmentation, statistical model-based thresholding, object selection, femur segmentation, FL measurement method, and evaluation performance. Section 3 discusses the experimental results obtained by comparing the proposed and existing techniques. Section 4 presents the conclusions of the experiment.

2. Materials and Methods

2.1. Data

Ultrasound images used for automatic FL segmentation and measurement were collected from pregnant women with gestational ages of 15-36 weeks. The image sizes employed in this study varied. The data of 31 femur images were recorded using a Sonostar™ Ubox-10 ultrasound scanner by a midwife in Indonesia. The ultrasound images example used in the segmentation experiment are shown in Figure 2, with properties that presented in Table 1. All sample ultrasound images have a low quality and a small region of interest. The femur area indicated by the red circle in each image has a varying position and orientation. In all cases in Table 1, the femur exhibits an inclination that forms a diagonal line.

2.2. Proposed Femur Segmentation Framework

The framework of the automatic femur segmentation is shown in Figure 3. First, the preprocessing step aims to remove speckle noise from the foetal ultrasound image. We implemented a hybrid speckle noise-reducing method that integrates anisotropic diffusion and multiresolution bilateral filtering. The second step is femur region extraction which has two sub-steps: thresholding and object selection. We applied the proposed statistical model-based thresholding approach to obtain the femur area. The next step is object selection, which aims to remove objects that are too small or too large, and eliminate the curvilinear-shaped beam on the top of each image and the acoustic artefacts located at the bottom of the image. The pixel with the highest intensity value was selected from the remaining object. The pixel becomes the starting point for the femur area when using the localising region-based active contour method. If the segmentation results exceed the region of interest, then we refine the area using two sub-steps: object thresholding and sub-region connecting. Suppose object thresholding results in more than one object, and the sub-objects on the straight line are merged. The last stage of the segmentation process smoothens the outline boundaries of an object. After the femur was obtained, FL was measured based on the maximum distance of the points at both ends of the femur.

2.3. Image Thresholding

The proposed image thresholding, named the Localizing Gaussian Mixture Model (LGMM) method aims to segment an image with a small object with low contrast from the background based on the Gaussian mixture model function. The principle of the thresholding method is to obtain the minimum local value of the Gaussian mixture model function of the pixel intensity distribution. Unlike the thresholding method based on the Gaussian mixture model proposed in [21], the proposed technique does not apply the EM algorithm to estimate the Gaussian mixture value and its parameters.
The proposed thresholding method uses the conditional density principle p(y|x) which refers to the probability distribution of the pixel intensity for a given class of x (e.g. background or object). The density is often modelled as a normal distribution, as in the following equation 1 [24]:
p ( y | x ) = 1 2 π σ x exp ⁡ − y − μ x 2 2 σ x 2
where μx and σx refer to the mean and standard deviation of pixel intensity in class x
For the problem of two-class segmentation (object and background), a Gaussian mixture model, h(y), adjusts variable y to meet the best fit, as in the following equation 2 [24]:
h ( y ) = 1 2 π σ o b j exp ⁡ − y − μ o b j 2 2 σ o b j 2 + 1 2 π σ b a c k exp ⁡ − y − μ b a c k 2 2 σ b a c k 2
The threshold T is achieved using the following equation 3:
T = x m i n = arg ⁡ min x ∈ S ⊆ G ⁡ h ( x )
where S⊆G represents the intensity levels of an image.
Because the value of p(y|x) shows the probability of a y-pixel in the x-class, the smaller the p-value, the farther the y-pixel from the x-class distribution; and vice versa, the greater the p-value, the closer the y-pixel is to the x-class distribution. Suppose that there is a histogram, as in Figure 4, depicting the distribution of the pixel values in an image; then, the optimal threshold, T, which separates the two classes, that is, the object (R1) and the background (R2), is the minimum value of the Gaussian mixture model function, h(T).
The main step used in the proposed thresholding algorithm is shown in Figure 5, where the T-value is obtained from the local minimum value of h(T) in its histogram distribution. Because the h(T) calculation for each grey value requires considerable computation time, an initial value T is given to accelerate the process of finding the smallest value of h(T). The search for the lowest value of h(T) is performed around T by comparing h(T) with h(T-1) and h(T+1). If h(T) is the smallest of the two values, then T is the selected threshold value. If the cost of h(T-1) or h(T+1) is lower, the search is done by shifting T to the left (T = T-1) or right (T = T + 1).

2.4. Femur Selection

To obtain the actual femur area, it is necessary to select an object that matches the characteristics of the femur. The femur has a long and thin shape. [10] proposed an object density and height-to-width ratio of objects to determine the femur region. The ratio was measured using a bounding box around the object. Density measurements require intact and connected areas that are strongly influenced by the quality of the ultrasound image input. Based on [10], the density d of an object can be formulated as follows 4:
d = ∑ i = 1 M ∑ j = 1 N b w ( i , j ) M ∗ N , i f   b w ( i , j ) = 1
where M and N are the bounding-box dimensions of each candidate region. The region image, bw, is a black-white image that has a grey level of 1 for object pixels and 0 for backgrounds. If the candidate object is horizontal, where N > M, then the femur region is chosen to satisfy the following equation 5:
M N > ( β − 0.1 ) ∧ N M > ( 2 α ) ∧ d > ( 0.5 γ )
If the candidate object is almost vertical, indicated by M > N, the equation is modified as follows 6:
M N > 2 α ∧ N M > ( β − 0.1 ) ∧ d > ( 0.5 γ )
Where α,β and γ are determined based on the values given in research [10].

2.5. Femur Segmentation

From the obtained femur area, the object was segmented using the localising region-based active contour method [23]. This process begins by determining a starting point which is then expanded using the active contour technique, until the convergent conditions are met. The starting point was chosen based on the most significant intensity value in the femur region.

2.6. Segmentation Refinement

If the segmentation result has more than one object, the femur region lies on a straight line, and the object selection and the region merging process are required. Areas smaller than 60 pixels are removed.
To investigate the regions lying on a straight line, we applied a linear regression approach, as shown in Figure 6. Suppose there are N regions that are R1, R2, ... RN; first, there are two different consecutive regions, for example, R1 consisting of n1 pixels and R2 containing n2 pixels. If (x1i, y1i) ∈ R1, i = 1,2, ...,n1 and (x2j, y2j) ∈ R2, j = 1,2, ...,n2, then (xk, yk) ∈ (R1∪R2) where k = 1,2,...,(n1 + n2). A line equation formed from these (xk, yk) points is expressed as 7:
y = gx + b
where g is the gradient of the line and b is a constant. Using equation 7, the values of y1' and y2' are determined for each x1 and x2 value. If y1' ∈ y1 and y2' ∈ y2, then regions R1 and R2 are merged. If y1' ∈ y1 and y2' ∉ y2, then region R1 is selected and R2 is discarded, and vice versa; if y2' ∈ y2 and y1' ∉ y1, then region R2 is selected and R1 is removed. Therefore, the number of N regions is reduced by one compared to the N-1 regions. The checking and merging processes were repeated until a single region remained.

2.7. FL Measurement

After the femur region was extracted, the line detection and measurement techniques were executed, as shown in Figure 7. The bold line indicates the bounding box. The cross lines represent intersection points. The thin lines represent the distances between the intersection points. First, a bounding box was created automatically around the femur region. Subsequently, the points which are the intersection results between the points along the femur boundary and the points on the minor side of the box were specified. The FL was measured by the maximum distance between the intersection points on both minor sides. The maximum distance value is chosen as the FL for foetal weight prediction because the segmented femur area is not precisely square and the femur width is relatively small.

2.8. Quantitative Performance

Two measurements, that is, region-based measurement, such as precision, sensitivity, specificity, and Dice similarity [25,26] and line-based measurement [27] are used to quantify the performance of the proposed method. The region-based metric evaluates the precision and accuracy segmentation results compared to the manual segmentation result as the ground truth. Assuming that RD is the detected region and RG is the ground truth region, the precision (P) in 8, sensitivity or true positive (TP) in 9, specificity or true negative (TN) in 10, and dice similarity (D) in 11 are defined by the following equations respectively [28].
P = R D ∩ R G R D ∪ R G
T P = R D ∩ R G R G
T N = R D ∪ R G ¯ R G ¯
D = 2 ∗ R D ∩ R G R D + R G
The line-based metric measures the accuracy of a detected FL line compared with manual measurements. Three matching criteria, that is, the angle between two lines, line-to-line distance, and FL distance, are defined as shown in Figure 8. Suppose that the line segment L =(x1, y1, x2, y2) connected two-point (x1, y1) and (x2, y2) has a centroid point, m = (x, y), the orientation of the L-line is determined as 12:
θ ( L ) = tan − 1 ⁡ y 2 − y 1 x 2 − x 1
Figure 8 shows that the horizontal line in the middle of the object, the LG-line, is the FL obtained manually or the ground truth and a horizontal line above it, the LD-line, is the detected line. The angle between the LG-line and the LD-line is defined as 13 [27].
α ( L G , L D ) = θ ( L G ) − θ ( L D ) , 180 − θ ( L G ) − θ ( L D ) , i f θ ( L G ) − θ ( L D ) ≤ 9 0 ∘ o t h e r w i s e
The angle accuracy of two lines is expressed as 14.
α L G , L D = θ L G − θ L D , 180 − θ L G − θ L D , i f θ L G − θ L D ≤ 9 0 ∘ o t h e r w i s e 1 − α ( L G , L D ) 18 0 ∘
The line-to-line distance is defined by the equation 15 [27].
d ( L G , L D ) = p d ( m D , L G ) + p d ( m G , L D ) 2
where LD is the detected line, LG is the ground truth line, mD is the centroid point of the identified line (LD), pd(mD, LG) is the point-line distance between the mD-point and the ground truth line (LG), and pd(mG, LD) is the point line distance between the mG-point and the detected line (LD). The point-line distance between the m-point of the first line and second L-line is defined as 16:
p d ( m , L ) = ( x 2 − x 1 ) ∗ y − ( y 2 − y 1 ) ∗ x   −   ( y 1 x 2 − y 2 x 1 ) ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2
The line distance accuracy is computed by the equation 17.
a c c = 1 − d ( L G , L D ) d m a x | | , i f d ( L G , L D ) d m a x       0 , o t h e r w i s e
where dmax is the minor-axis length of the femur region, as shown in Figure 8. FL was measured using the Euclidean distance between the two endpoints of the line segment. The accuracy of the FL was determined using the equation 18:
1 − | l L G − l L D | l L G
where lLG is the length of the ground truth line and lLD is the length of the detected line.

3. Results and Discussion

We conducted two experiments and compared them with several methods to test the proposed methods. The first experiment will use images commonly employed in image thresholding research to assess the strengths and weaknesses of each applied approach. The second experiment will use ultrasound images, followed by automatic extraction of the femur area.

3.1. Performance Evaluation on General Images

In this evaluation, we used four general images, namely Coins, Blocks, Potatoes, and Hand X-ray images, with various modal histograms: bimodal, nearly bimodal, unimodal, and multimodal. We implemented a thresholding method to segment these images into two values (binary image) with the proposed method LGMM and the thresholding method in the state of the art, which includes multilevel Otsu threshold [12,13] with k=2, the entropy-based [10], and statistical-based thresholding method [16].
The segmentation results on the Coins image (first row of Figure 9) displaying a bimodal histogram showed a similarity between the proposed and multilevel Otsu methods. Both methods' threshold values effectively separated the bimodal distribution into two components, as depicted in Figure 10(a). However, the threshold values derived from the statistical-based method tended to skew towards the right, excluding numerous intensity values belonging to the coins' object. Conversely, the threshold values from the entropy-based process leaned towards the left, favoring lower-intensity regions and capturing more parts of the object.
The segmentation outcomes on the Blocks image (second row of Figure 9) exhibiting a multi-modal histogram revealed a close resemblance between the proposed and statistical-based methods. The threshold values derived from both methods effectively divided between the second and third modes, characterized by higher intensities, as depicted in Figure 10(b). In contrast, the threshold values generated by the multilevel Otsu method are divided between the first and second modes, including numerous intensity values belonging to the Blocks object. Conversely, the threshold values from the entropy-based method tended to lean towards the left of the boundary between the second and third modes, causing a portion of the second mode to be captured as part of the object along with the third mode.
Different segmentation outcomes are depicted in the Potatoes image (third row of Figure 9), showcasing a bimodal histogram (Figure 10 (c)) where the first mode is significantly more dominant than the second mode. The proposed method yielded small object segments within the second mode. In contrast, both the multilevel Otsu and statistical-based methods tended to divide the first mode into two sections. However, the entropy-based method, somewhat surprisingly, produced a threshold above the second mode, resulting in fewer segments captured from the object.
The histogram shape of the Hand X-ray image is nearly bimodal (Figure 10 (d)). Both the proposed and entropy-based methods successfully segmented it into two parts at the boundary between modes one and two. Conversely, the other two methods provided threshold values that leaned toward the left and right sides of the histogram distribution.
The proposed method demonstrated its strengths across various images. In the Coins image, it aligned closely with the multilevel Otsu method, effectively segmenting the bimodal histogram into distinct components. While the statistical-based method tended to exclude crucial intensity values by skewing towards the right and the entropy-based method captured more object details leaning to the left, the proposed method maintained a balanced approach, effectively capturing both intensity regions. In the Blocks image, it behaved similarly to the statistical-based method, effectively distinguishing between higher intensity modes. This contrasts the multilevel Otsu method, which included undesired intensities from the first mode, and the entropy-based method, which unintentionally included the second mode within the object boundary. Moreover, in the Potatoes image, the proposed method delineated smaller object segments within the dominant first mode, showcasing its ability to capture nuanced details.

3.2. Femur Region Extraction

In the proposed thresholding method, the threshold values are initially determined by the rules of the global thresholding algorithm, where the initial threshold value determination depends heavily on the image histogram distribution used [29]. If the background area and the object area of comparison are almost identical, a good initial value for T is the average grey level of the image. If the object area is small compared to the background area or vice versa, the one-pixel group dominates the histogram; therefore, the middle value between the maximum and minimum grey levels is a good initial choice for T.
Figure 11(a) shows a unimodal histogram of an image that the bins tend to accumulate on the low intensity and only a few bins are on the right. The femur object lies on the right bins of the histogram. The dashed line is the GMM function, h(y), as written in equation 2. The threshold value is equal to the smallest amount of h(y) or on the local minima. The initial threshold is derived from the distribution of intensities at the midpoint. The search for the threshold values starts from the initial threshold to the right until the local minimum is found. Figure 11(b) is another example of the image histogram that has the intensity distribution of two regions, objects and backgrounds, close to normal distribution. The shape of the histogram is bimodal. In the second example, the local minima are located on the initial threshold.
To evaluate the proposed threshold method, we compared it with other thresholding techniques implemented to segment femur ultrasound images, that is, the entropy-based [10], multilevel Otsu threshold [12,13], and statistical-based thresholding method [16]. The ultrasound images used in the segmentation experiment are shown in Figure 2. A comparison of the thresholding results is shown in Figure 12. The circle indicates the location of the femur. From the figure, it is known that the proposed thresholding method is not only suitable for images with a unimodal histogram distribution with small objects and low contrast to the background, but is also more suitable for recognising the femur region. The entropy-based method shown in Figure 12(a) results in a small area and can hardly be observed. Conversely, the multilevel approach provides a broader region, which makes it challenging to identify the region of interest, as shown in Figure 12(b). The segmentation result of the statistical method was smaller than that of the multilevel Otsu method. Nevertheless, some regions are incorporated into undesirable areas. Figure 13 shows the position of the threshold value of the histogram where the multilevel thresholding method has the smallest threshold value, followed by the statistical-based approach, the proposed method (LGMM), and the entropy-based method.

3.3. Region Selection, Segmentation and Refinement

As already shown in the discussion of thresholding, low-quality input images cannot provide a complete femur segmentation result, therefore, density measurement will cause errors in the selection of femur objects. To solve this problem, we implemented a selection technique to choose an object that is not too large or too small and not attached to the top or bottom edge. Based on both empirical data and the specific needs of our tasks, we carried out a meticulous iterative process to achieve the best possible parameters, the lowest limit, and the highest limit of the candidate femur area. Regions containing pixels amounting to less than 0.03% or more than 1,4% of the image size are removed. Objects that are bright and connected to the top or bottom edges are indicated as artefacts owing to improper scanner positioning. The candidate femur area is also determined by the ratio between the length and width as well as the size of the density that defines a long and thin region. An example of the femur object selection result for a low-quality ultrasound image is shown in Figure 14.
From the area remaining after the object selection process, the object is segmented using the localising region-based active contour (LAC) method with the most significant intensity value as the initial iteration point. The LAC method proposed by [30] implements an active contour method using local image statistics. A small ball is used to divide the area along the contour into interior and exterior areas, and the shape is determined by local statistical information regarding the interior and exterior areas. The internal energy was measured by the specific strength proposed by [31] which is referred to as the uniform modeling energy. The primary step of this method consists of two parts: initialisation and updates. Initialisation was implemented to minimise the energy in the local region. Based on this specified point, we set a mask with 1-intensity in the area of 2 × 2 pixels around the selected location and set other pixel locations with the 0-value. The signed distance map function is updated by subtracting the intensity value of each pixel and the bins of a histogram in the interior region; then, the subtraction result is added to the same bin of the histogram in the exterior region. Both the initialisation and updating steps were performed as a given number of iterations. Figure 15 shows the areas based on the active contour process for the initial iteration (Figure 15(a)) and after 350 iterations (Figure 15(b)).
Femur segmentation results are not always exact in the area of interest. Segmentation of the femur region which has a weak edge, provides an over-segmenting result, as shown in Figure 16. Hence, the thresholding technique is applied once more to obtain the actual femur in an over-segmentation area. The ratio of the minor axis length to the major axis length was computed to distinguish the over-segmentation area from the others. Ratios greater than 0.2 are used to identify the long and slim object and to determine the over-segmentation region.
If the segmentation result has more than one object, as shown in Figure 17, in which the femur region lies on a straight line, then object selection and region merging are required. Regions containing pixels amounting to 0.02% of the image size are removed, as shown in Figure 17(b).
The merging process is performed by determining the shortest path that connects the boundary pixels of the first and second regions, as shown in Figure 18(a). The gap is filled with a small circular blob that has a radius equal to one-third of the minor-axis average of the regions to connect the separate objects. The gap-filling step is illustrated in Figure 18(b) – Figure 18(e). The final result of object merging is shown in Figure 18(f).
The final step is the object boundary smoothing process using the Savitzky-Golay sliding polynomial filter which is commonly used to smooth noisy signals [32], as shown in Figure 19. Figure 20 shows the results of the oversegmentation approach for the example images in Figure 16.

3.4. FL Measurement and Performance Comparison

Using the dataset in this research, the performance of the proposed thresholding method is compared with the approaches proposed in previous studies, with some modifications in the object selection stage. In particular, for the entropy-based thresholding method which produces a small object, we do not utilise the object selection step. For the multilevel Otsu thresholding method and the statistical-based thresholding method, large objects with areas larger than 1,4% of image size pixels are not cut out because the thresholding results tend to be broader objects. However, the objects attached to the edge of the image were removed. Figure 21 shows the outcome of the segmentation and measurement of the FL for each image in Figure 2. After the region was obtained, FL was measured based on the line length.
Some femur detection failures of other methods are shown in Figure 22. Failure of the entropy method occurs because the threshold result is only a few pixels and is in the upper boundary area of the image. Thus, the point is detected as the starting point of the segmentation of the femur object, as shown in Figure 22(a). The error of the Otsu multilevel method, as shown in Figure 22(b), is due to the broader thresholding results from the top to the lower end. Therefore, at the object selection stage, the area was discarded because the femur was not indicated, and the object of the femur was a smaller object. In statistical-based methods, femur errors occur at a gestational age of approximately 15 weeks, when the size of the femur is small, and an ultrasound probe still exposes the foetal sac. The outer area of the sac had an intensity value higher than that of the femur bone, so that the region was recognised as a femur object, as shown in Figure 22(c).
Table 2 presents a comparative analysis of region-based segmentation performance metrics across various thresholding methods. The table includes mean values and standard deviations for precision, sensitivity, specificity, and Dice similarity for each method. The Entropy-Based and Multilevel Otsu methods exhibit lower mean values across all metrics, suggesting comparatively poorer segmentation performance with higher variability, as indicated by relatively higher standard deviations. In contrast, the Statistical Based method demonstrates higher mean values, signifying better overall performance and relatively lower variability. However, the Proposed Thresholding Method surpasses all other methods, showcasing the highest mean values for precision, sensitivity, specificity, and Dice similarity, coupled with notably lower standard deviations. This implies superior segmentation accuracy and consistency, positioning the proposed method as an optimal choice for reliable region-based segmentation in this context.
Table 3 displays the line-based performance averages of FL detection and measurement across different thresholding methods. The table includes metrics for angle accuracy, distance accuracy, and length accuracy. The angle, distance, and length accuracies were measured using equation 14, equation 17 dan equation 18. The Entropy-Based and Multilevel Otsu methods exhibit moderate performance across all metrics, with higher standard deviations implying variability in FL measurement accuracy. The Statistical Based method demonstrates relatively higher mean values across all metrics, indicating better overall FL measurement accuracy with moderate variability. Notably, the Proposed Thresholding Method outperforms all other methods, showcasing significantly higher mean values for angle accuracy, distance accuracy, and length accuracy, coupled with notably lower standard deviations. This suggests superior accuracy and consistency in FL measurements, positioning the proposed method as highly precise and reliable for FL assessment in this context.
Collectively, both tables underscore the superiority of the Proposed Thresholding Method, showcasing its exceptional performance in both segmentation accuracy and FL measurement precision across various evaluation metrics.

4. Conclusion

Localizing Gaussian mixture modeling-based thresholding is proposed to segment the femur area in the ultrasound image, especially for images of low-cost portable ultrasound devices that have low brightness and contrast. In general images experiment, the proposed method consistently demonstrated a balanced segmentation approach, effectively capturing relevant intensity values across diverse histogram shapes compared to other methods that exhibited biases or limitations towards specific intensity regions. From the experiments of FL segmentation and measurement, this proposed thresholding method provides the best quantitative performance when compared to the multilevel Otsu thresholding method, entropy-based thresholding method, and statistical-based thresholding method. This technique is also robust in recognising FL at various gestational ages and positions of the ultrasound probe. In this study, an automatic FL segmentation and measurement technique is proposed for ultrasound images. The entire process consists of the speckle noise reduction step, the thresholding stage, the object selection stage, the region segmentation stage, and the stage that is applied to overcome over-segmenting and to smooth the region boundary curve. This approach will be developed to segment the femoral area in 3D ultrasound images.

Author Contributions

Conceptualization, Handayani Tjandrasa and Nanik Suciati; methodology, Fajar Astuti Hermawati, Elsen Ronando, and Dwi Harini Sulistyowati.; software, Fajar Astuti Hermawati, Elsen Ronando, and Dwi Harini Sulistyowati.; validation, Fajar Astuti Hermawati, Elsen Ronando, and Dwi Harini Sulistyowati.; formal analysis, Elsen Ronando.; investigation, Elsen Ronando.; resources, Dwi Harini Sulistyowati.; data curation, Dwi Harini Sulistyowati.; writing—original draft preparation, Fajar Astuti Hermawati.; writing—review and editing, Handayani Tjandrasa and Nanik Suciati.; visualization, Elsen Ronando.; supervision, Handayani Tjandrasa and Nanik Suciati.; project administration, Fajar Astuti Hermawati.; funding acquisition, Fajar Astuti Hermawati.

Funding

This research was funded by Directorate General of Higher Education, Research and Technology Ministry of Education, Culture, Research and Technology, Indonesia, grant number 159/E5/P6.02.00.PT/2022.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

This study did not require written consent to participate in accordance with national law and institutional requirements. Written permission was waived as this was a retrospective study with no potential risk to the patient.

Data Availability Statement

Data will be made available on request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Amoah, B.; Anto, E.A.; Crimi, A. Automatic Fetal Measurements for Low-Cost Settings by Using Local Phase Bone Detection. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS; 2015; Volume 2015-Novem, pp. 161–164. [Google Scholar] [CrossRef]
  2. Baran, J.M.; Webster, J.G. Design of Low-Cost Portable Ultrasound Systems : Review. 2009, 53706, 792–795. [Google Scholar]
  3. Hermawati, F.A.; Sugiono. Evonda Ultrasound Image Formation from Doppler Transducer. In Advanced Materials Techniques, Physics, Mechanics and Applications; Chang, S.-H., Parinov, I.A., Jani, M.A., Eds.; Springer International Publishing, 2017; pp. 535–543. [Google Scholar]
  4. Maraci, M.A.; Napolitano, R.; Papageorghiou, A.; Noble, J.A. Fetal Head Detection on Images from a Low-Cost Portable USB Ultrasound Device. In Proceedings of the Conference Proc. of Medical Image Understanding and Analysis (MIUA) 2013; 2013; pp. 1–6. [Google Scholar]
  5. Papageorghiou, A.T.; Sarris, I.; Ioannou, C.; Todros, T.; Carvalho, M.; Pilu, G.; Salomon, L.J. Ultrasound Methodology Used to Construct the Fetal Growth Standards in the INTERGROWTH-21 St Project. 2013, 27–32. [Google Scholar] [CrossRef]
  6. Stirnemann, J.; Villar, J.; Salomon, L.J.; Ohuma, E.; Ruyan, P.; Altman, D.G.; Nosten, F.; Craik, R.; Munim, S.; Cheikh Ismail, L.; et al. International Estimated Fetal Weight Standards of the INTERGROWTH-21 St Project. Ultrasound in Obstetrics & Gynecology 2017, 49, 478–486. [Google Scholar] [CrossRef]
  7. Carneiro, G.; Georgescu, B.; Good, S. Knowledge-Based Automated Fetal Biometrics Using Syngo Auto OB Measurements Knowledge-Based Automated Fetal Biometrics. Whitepaper ACUSON S2000TM Ultrasound System 2008. [Google Scholar]
  8. Espinoza, J.; Good, S.; Russell, E.; Lee, W. Does the Use of Automated Fetal Biometry Improve Clinical. Journal of Ultrasound in Medicine 2013, 32, 847–850. [Google Scholar] [CrossRef] [PubMed]
  9. Pramanik, M.; Gupta, M.; Banerjee, K. Enhancing Reproducibility of Ultrasonic Measurements by New Users. In Proceedings of the Proc. of SPIE, Medical Imaging 2013: Image Perception, Observer Performance, and Technology Assessment; 2013; Volume 8673, pp. 1–6. [Google Scholar]
  10. Wang, C. Automatic Entropy-Based Femur Segmentation and Fast Length Measurement for Fetal Ultrasound Images. In Proceedings of the International Conference on Advanced Robotics and Intelligent Systems, 2014; ARIS 2014. 2014; pp. 5–9. [Google Scholar]
  11. Yang, Y.; Hou, X.; Ren, H. Accurate and Efficient Image Segmentation and Bias Correction Model Based on Entropy Function and Level Sets. Inf Sci (N Y) 2021, 577, 638–662. [Google Scholar] [CrossRef]
  12. Mukherjee, P.; Swamy, G.; Gupta, M.; Patil, U.; Banerjee, K. Automatic Detection and Measurement of Femur Length from Fetal Ultrasonography. In Proceedings of the Proc. of SPIE, Medical Imaging 2010: Ultrasonic Imaging, Tomography, and Therapy; 2010; Volume 7629, pp. 1–9. [Google Scholar]
  13. Ponomarev, G. V.; Gelfand, M.S.; Kazanov, M.D. A Multilevel Thresholding Combined with Edge Detection and Shape-Based Recognition for Segmentation of Fetal Ultrasound Images. In Proceedings of the Proceedings of Challenge US: Biometric Measurements from Fetal Ultrasound Images ISBI 2012; 2012; pp. 13–15. [Google Scholar]
  14. Umamaheswari, V.; Venkatasai, P.M.; Poonguzhali, S. A Multi-Level Set Approach for Bone Segmentation in Lumbar Ultrasound Images. IETE J Res 2022, 68, 977–989. [Google Scholar] [CrossRef]
  15. Sharma, S.R.; Alshathri, S.; Singh, B.; Kaur, M.; Mostafa, R.R.; El-Shafai, W. Hybrid Multilevel Thresholding Image Segmentation Approach for Brain MRI. Diagnostics 2023, 13. [Google Scholar] [CrossRef] [PubMed]
  16. Khan, N.H.; Tegnander, E.; Dreier, J.M.; Eik-nes, S.; Torp, H.; Kiss, G. Automatic Detection and Measurement of Fetal Biparietal Diameter and Femur Length — Feasibility on a Portable Ultrasound Device. Journal of Obstetrics and Gynecology 2017, 7, 334–350. [Google Scholar] [CrossRef]
  17. Zhu, F.; Liu, M.; Wang, F.; Qiu, D.; Li, R.; Dai, C. Automatic Measurement of Fetal Femur Length in Ultrasound Images: A Comparison of Random Forest Regression Model and SegNet. Mathematical Biosciences and Engineering 2021, 18, 7790–7805. [Google Scholar] [CrossRef]
  18. Alzubaidi, M.; Agus, M.; Shah, U.; Makhlouf, M.; Alyafei, K.; Househ, M. Ensemble Transfer Learning for Fetal Head Analysis: From Segmentation to Gestational Age and Weight Prediction. Diagnostics 2022, 12. [Google Scholar] [CrossRef] [PubMed]
  19. Nagabotu, V.; Namburu, A. Precise Segmentation of Fetal Head in Ultrasound Images Using Improved U-Net Model. ETRI Journal 2023. [Google Scholar] [CrossRef]
  20. Hermawati, F.A.; Tjandrasa, H.; Suciati, N. Phase-Based Thresholding Schemes for Segmentation of Fetal Thigh Cross-Sectional Region in Ultrasound Images. Journal of King Saud University - Computer and Information Sciences 2022, 34, 4448–4460. [Google Scholar] [CrossRef]
  21. Huang, Z.; Chau, K. A New Image Thresholding Method Based on Gaussian Mixture Model. Appl Math Comput 2008, 205, 899–907. [Google Scholar] [CrossRef]
  22. Hermawati, F.A.; Tjandrasa, H.; Suciati, N. Hybrid Speckle Noise Reduction Method for Abdominal Circumference Segmentation of Fetal Ultrasound Images. International Journal of Electrical and Computer Engineering (IJECE) 2018, 8, 1747–1757. [Google Scholar] [CrossRef]
  23. Hermawati, F.A.; Tjandrasa, H.; Sugiono; Sari, G.I.P.; Azis, A. Automatic Femur Length Measurement for Fetal Ultrasound Image Using Localizing Region-Based Active Contour Method. J Phys Conf Ser 2019, 1230, 0–10. [Google Scholar] [CrossRef]
  24. Solomon, C.; Breckon, T. Fundamentals of Digital Image Processing : A Practical Approach with Examples in Matlab; John Wiley & Sons, Ltd, 2011; ISBN 9780470689783. [Google Scholar]
  25. Udupa, J.K.; LeBlanc, V.R.; Zhuge, Y.; Imielinska, C.; Schmidt, H.; Currie, L.M.; Hirsch, B.E.; Woodburn, J. A Framework for Evaluating Image Segmentation Algorithms. Computerized Medical Imaging and Graphics 2006, 30, 75–87. [Google Scholar] [CrossRef]
  26. Hermawati, F.A.; Tjandrasa, H.; Suciati, N. Phase-Based Thresholding Schemes for Segmentation of Fetal Thigh Cross-Sectional Region in Ultrasound Images. Journal of King Saud University - Computer and Information Sciences 2021. [Google Scholar] [CrossRef]
  27. Kong, B.; Phillips, I.T.; Halarick, R.M.; Prasad, A.; Kasturi, R. A Benchmark: Performance of Dashed-Line Detection Algorithms. In Graphics Recognition Methods and Applications. GREC 1995. Lecture Notes in Computer Science, vol 1072; Kasturi, R., Tombre, K., Eds.; Springer: Berlin, Heidelberg, 1995; pp. 270–286. [Google Scholar]
  28. Rueda, S.; Fathima, S.; Knight, C.L.; Yaqub, M.; Papageorghiou, A.T.; Rahmatullah, B.; Foi, A.; Maggioni, M.; Pepe, A.; Tohka, J.; et al. Evaluation and Comparison of Current Fetal Ultrasound Image Segmentation Methods for Biometric Measurements : A Grand Challenge. IEEE Trans Med Imaging 2014, 33, 797–813. [Google Scholar] [CrossRef]
  29. Gonzalez, R.C.; Woods, R.E.; Scott, A.H.; Hall, P.P. Digital Image Processing; Pearson Education, Inc, 2008; ISBN 9780131687288. [Google Scholar]
  30. Lankton, S.; Tannenbaum, A. Localizing Region-Based Active Contours. IEEE Trans Image Process. 2009, 17, 2029–2039. [Google Scholar] [CrossRef]
  31. Chan, T.F.; Vese, L.A. Active Contours Without Edges. IEEE Transaction on Image Processing 2001, 10, 266–277. [Google Scholar] [CrossRef] [PubMed]
  32. Gander, W.; Hrebicek, J. Solving Problems in Scientific Computing Using Maple and MATLAB®; Fourth; Springer: Berlin, Heidelberg, 2004; ISBN 9783540211273. [Google Scholar]
Preprints 93254 g001
Figure 1. (a) An example of a femoral ultrasound image obtained from a portable scanner and (b) its histogram.
Figure 1. (a) An example of a femoral ultrasound image obtained from a portable scanner and (b) its histogram.
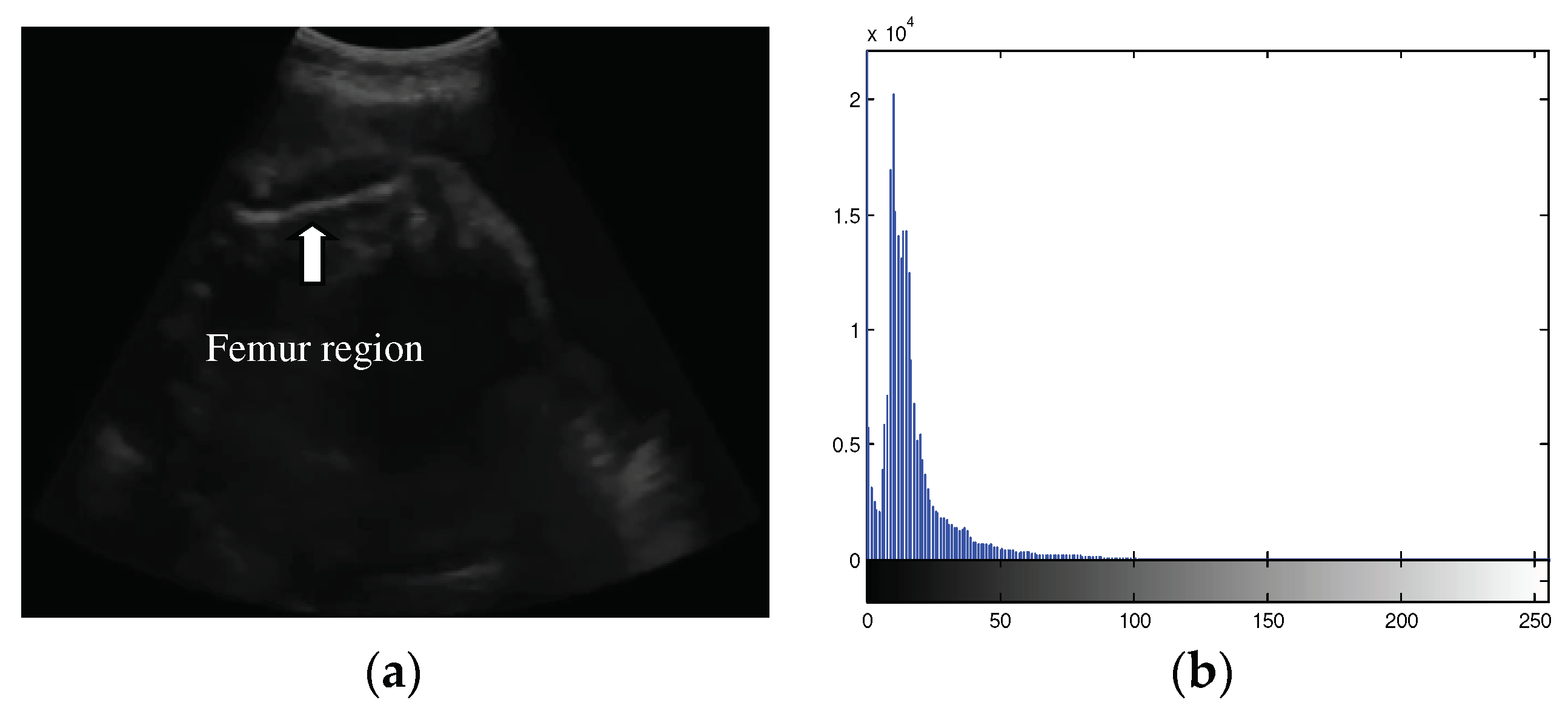
Preprints 93254 g001
Preprints 93254 g002
Figure 2. Example of femur ultrasound images for segmentation experiment.
Figure 2. Example of femur ultrasound images for segmentation experiment.
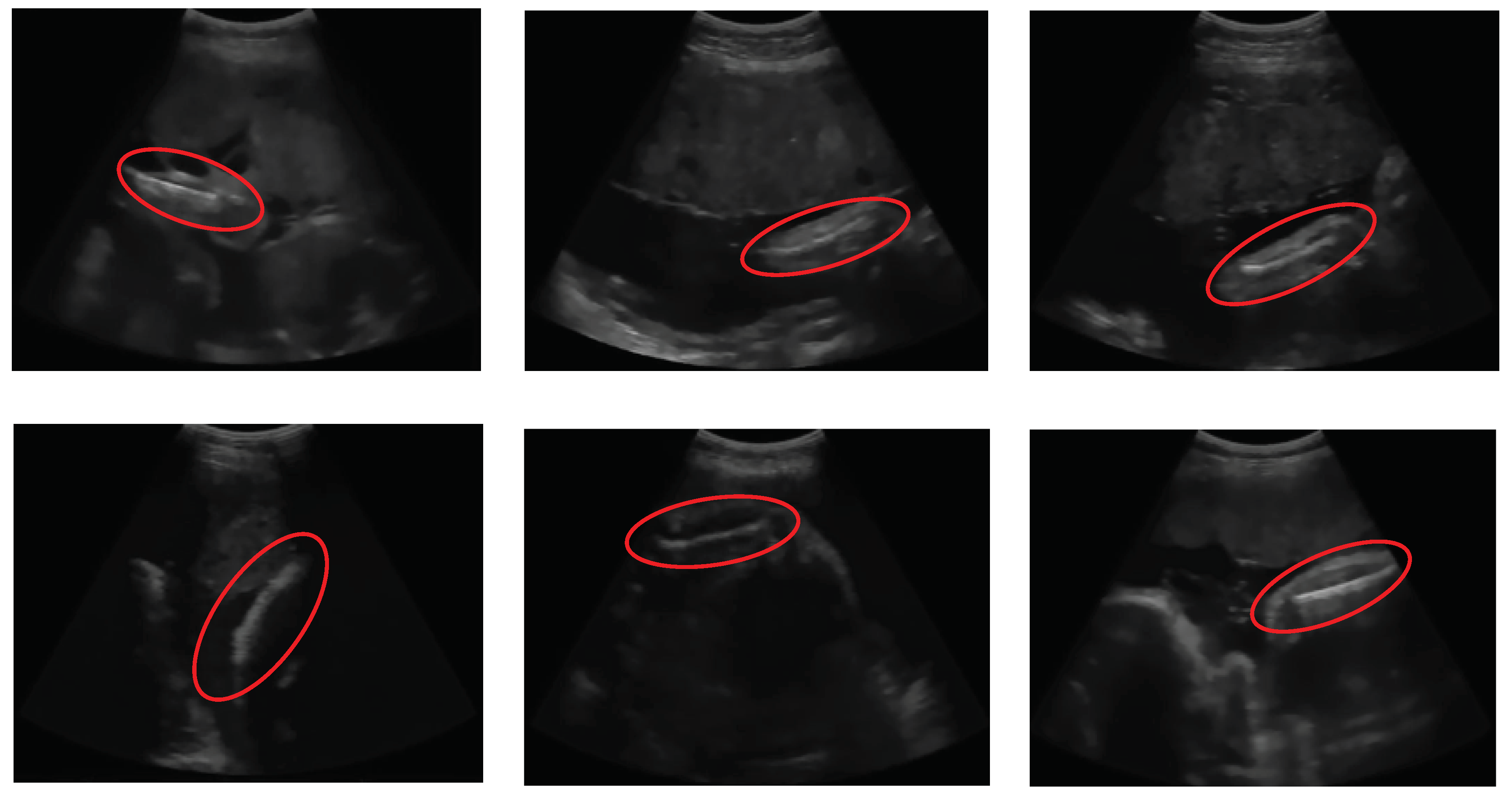
Preprints 93254 g002
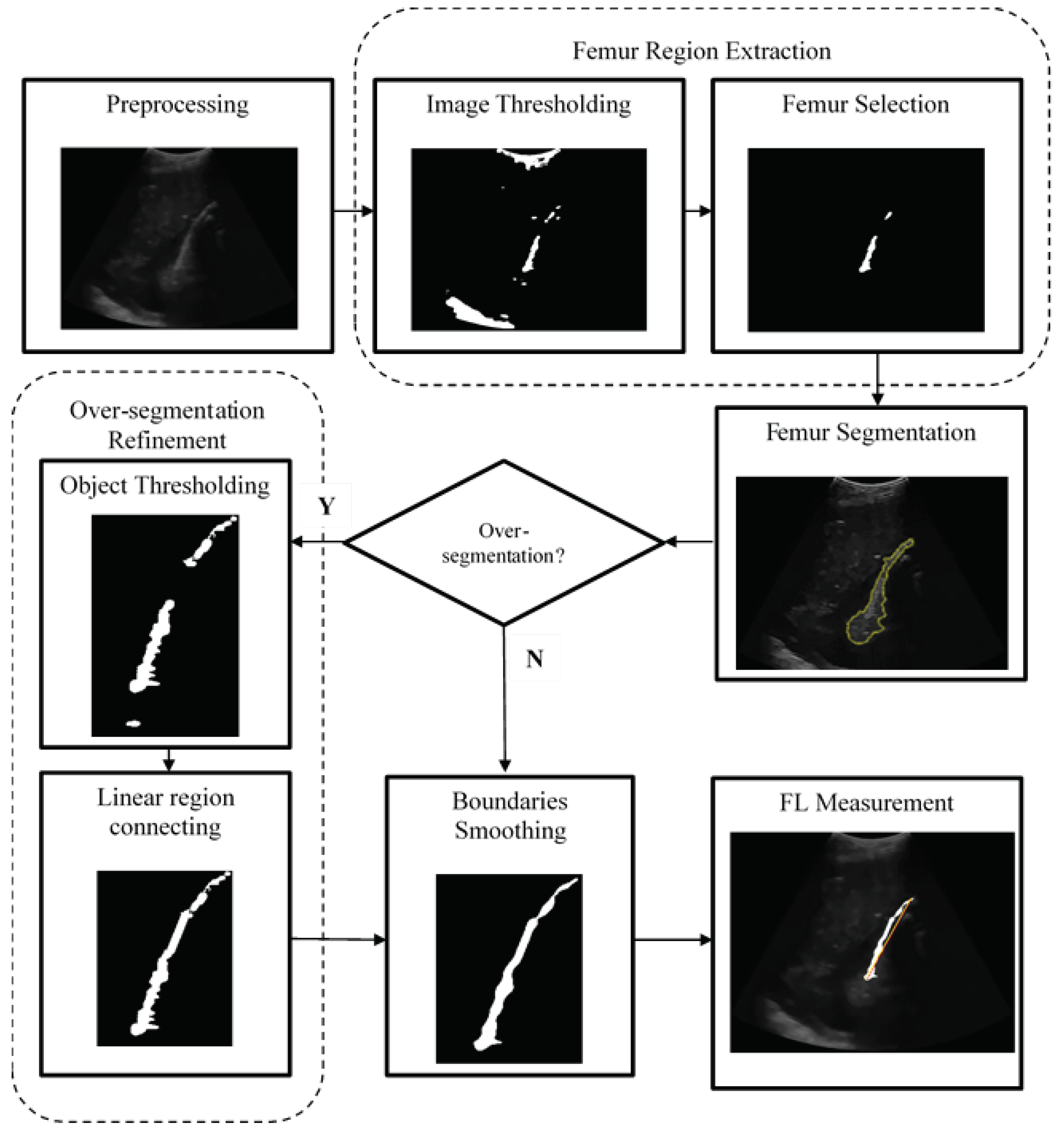
Preprints 93254 g003
Figure 3. Block diagram of the automatic femur segmentation method.
Figure 3. Block diagram of the automatic femur segmentation method.
Preprints 93254 g003
Preprints 93254 g004
Figure 4. Image histogram with object and background split.
Figure 4. Image histogram with object and background split.
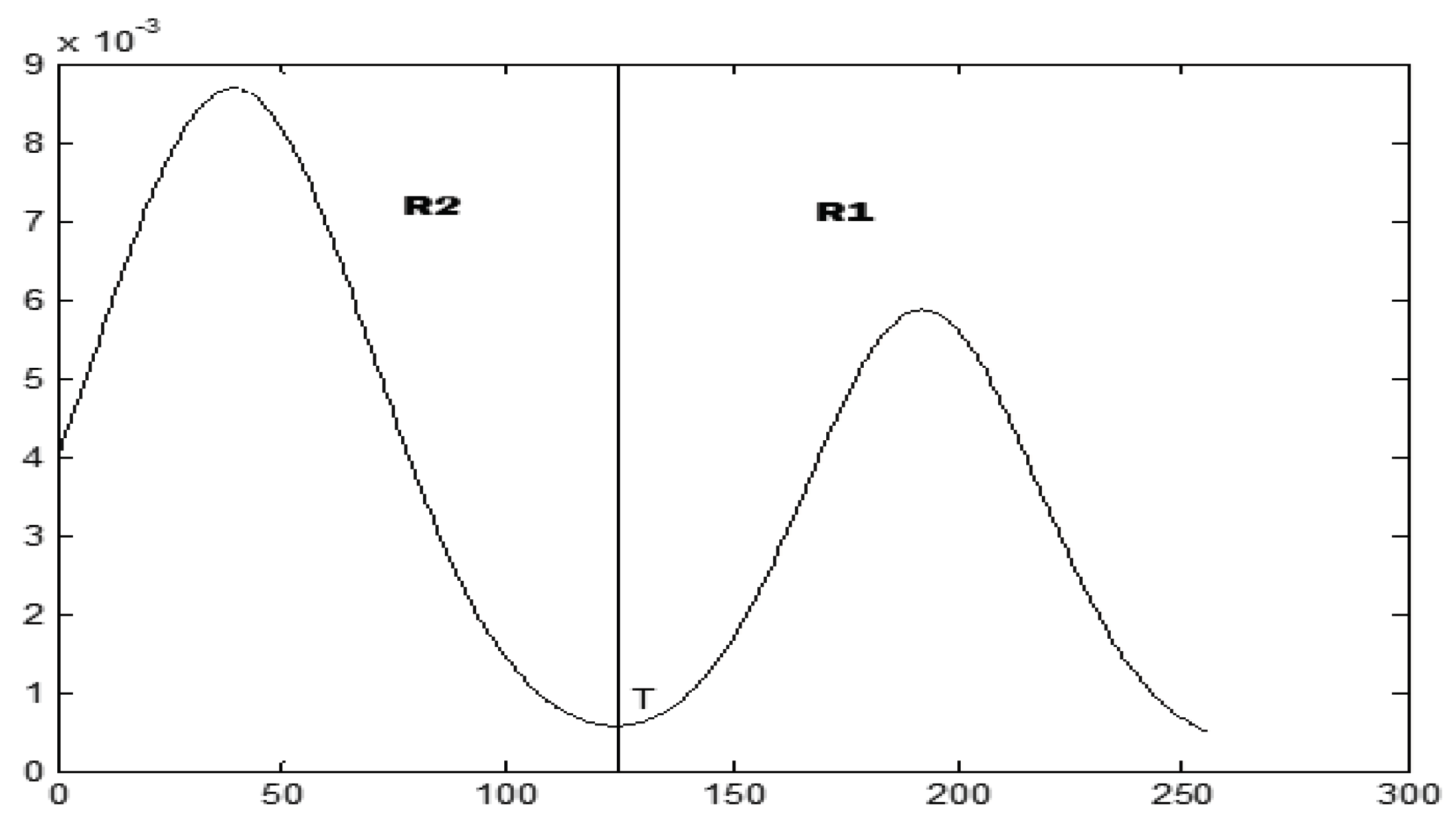
Preprints 93254 g004
Preprints 93254 g005
Figure 5. Flowchart of proposed thresholding algorithm.
Figure 5. Flowchart of proposed thresholding algorithm.
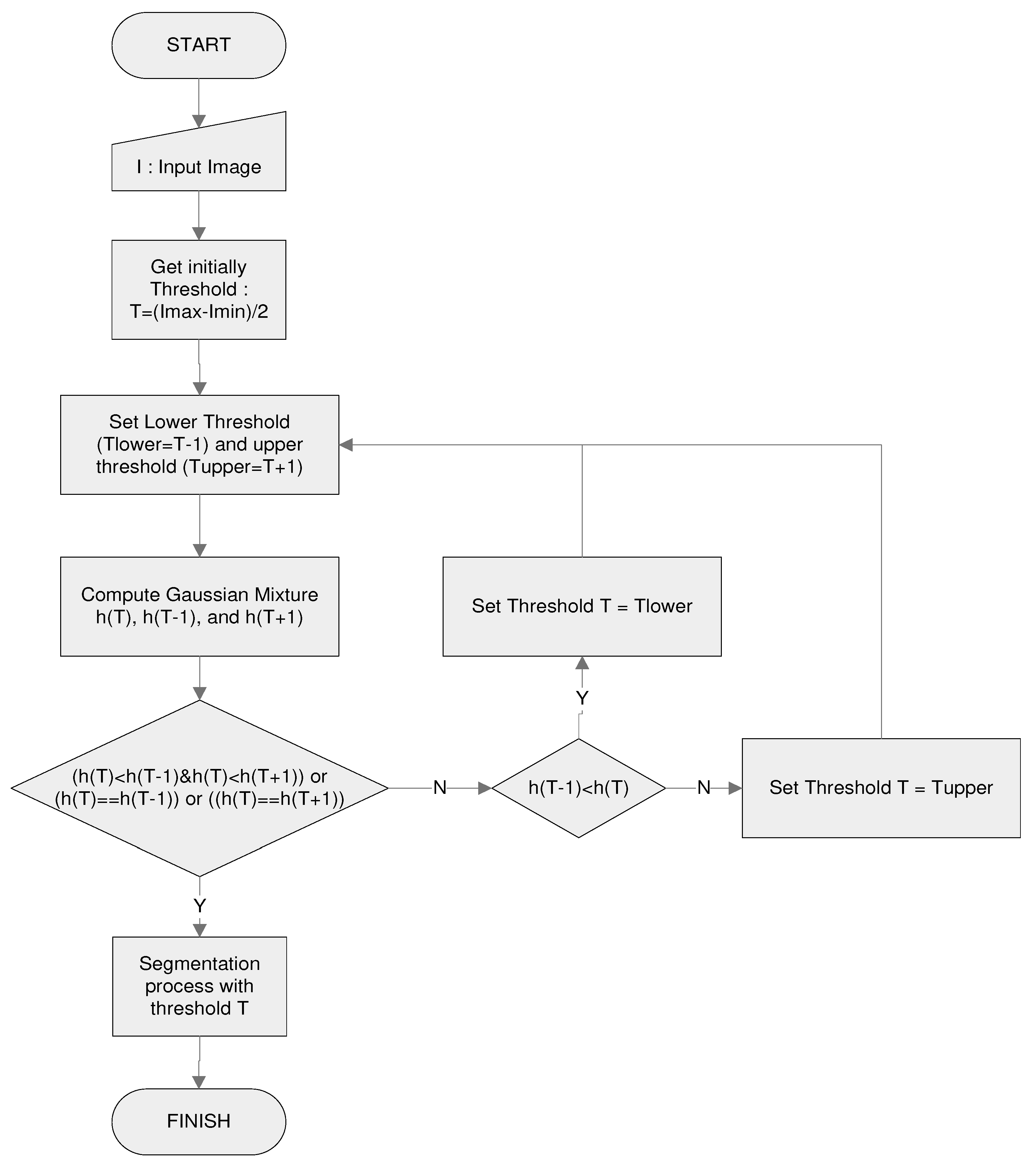
Preprints 93254 g005
Preprints 93254 g006
Figure 6. The plot of regression between (a) two linear regions (b) two less linear regions.
Figure 6. The plot of regression between (a) two linear regions (b) two less linear regions.
Preprints 93254 g006
Preprints 93254 g007
Figure 7. Illustration of the FL measurement.
Figure 7. Illustration of the FL measurement.
Preprints 93254 g007
Preprints 93254 g008
Figure 8. Line based metric of the FL measurement.
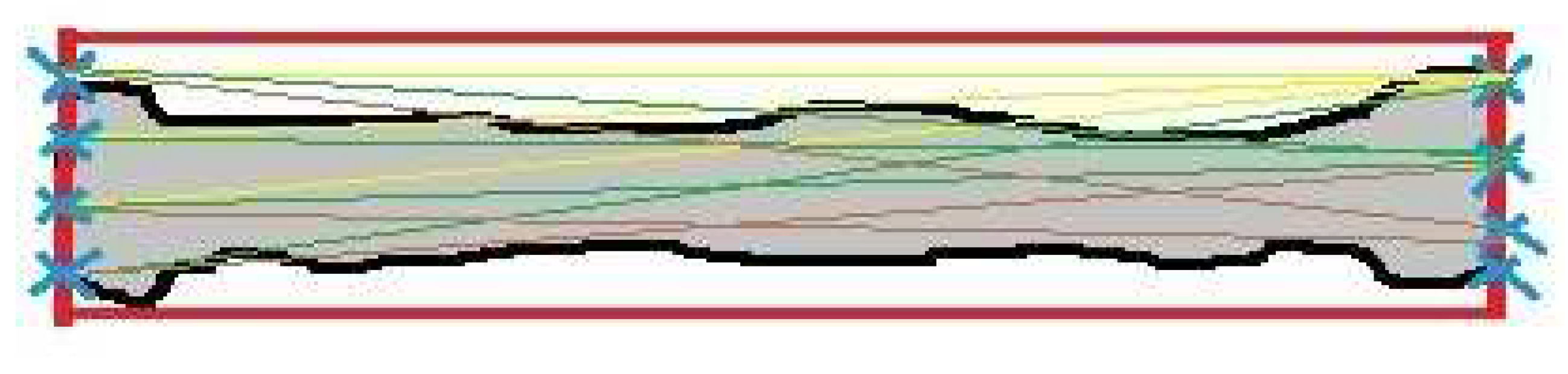
Figure 8. Line based metric of the FL measurement.
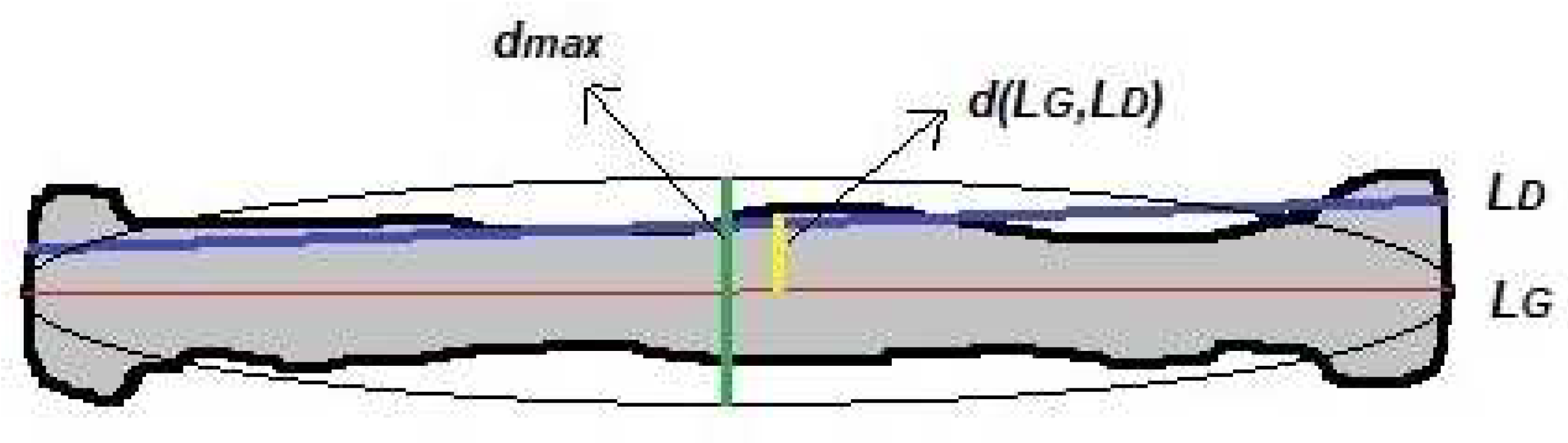
Preprints 93254 g008
Preprints 93254 g009
Figure 9. Comparison of thresholding results in (a) Coins, Blocks, Potatoes, and Hand X-ray images, respectively using (b) proposed thresholding method (c) Otsu multilevel thresholding method with k=2 (d) statistical-based method (e) entropy-based method.
Figure 9. Comparison of thresholding results in (a) Coins, Blocks, Potatoes, and Hand X-ray images, respectively using (b) proposed thresholding method (c) Otsu multilevel thresholding method with k=2 (d) statistical-based method (e) entropy-based method.
Preprints 93254 g009
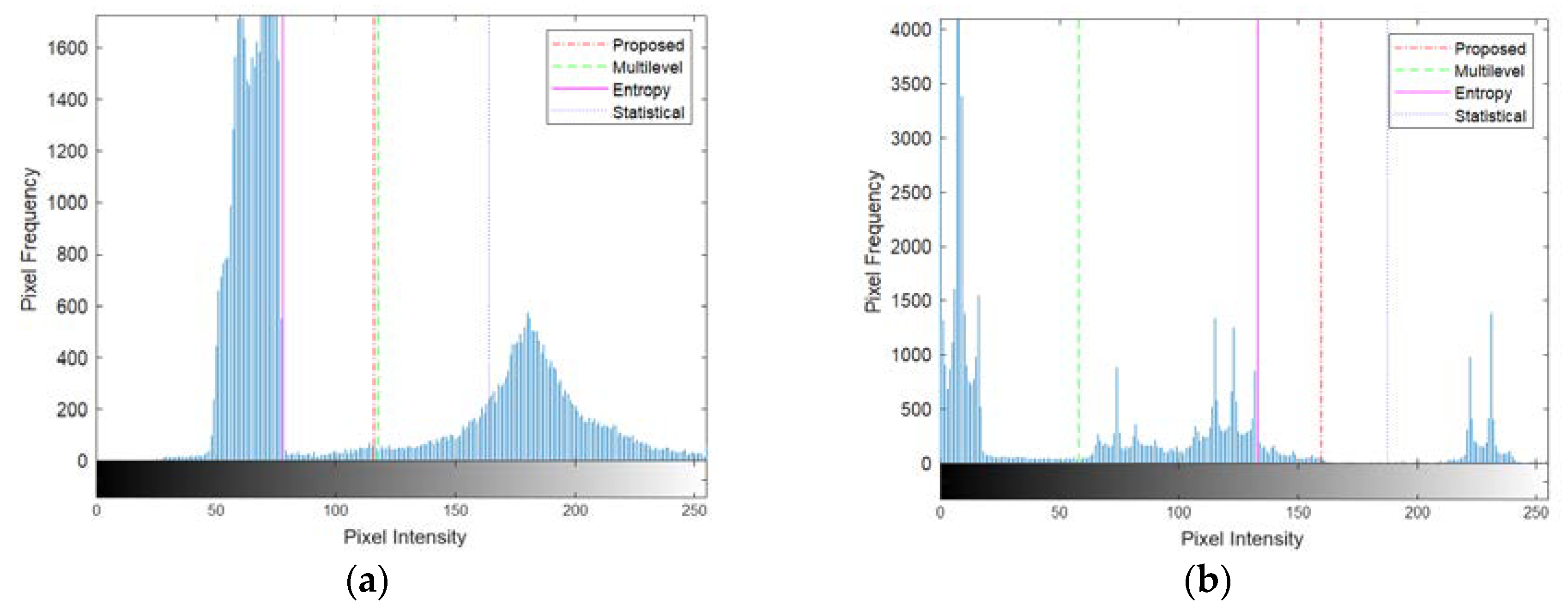
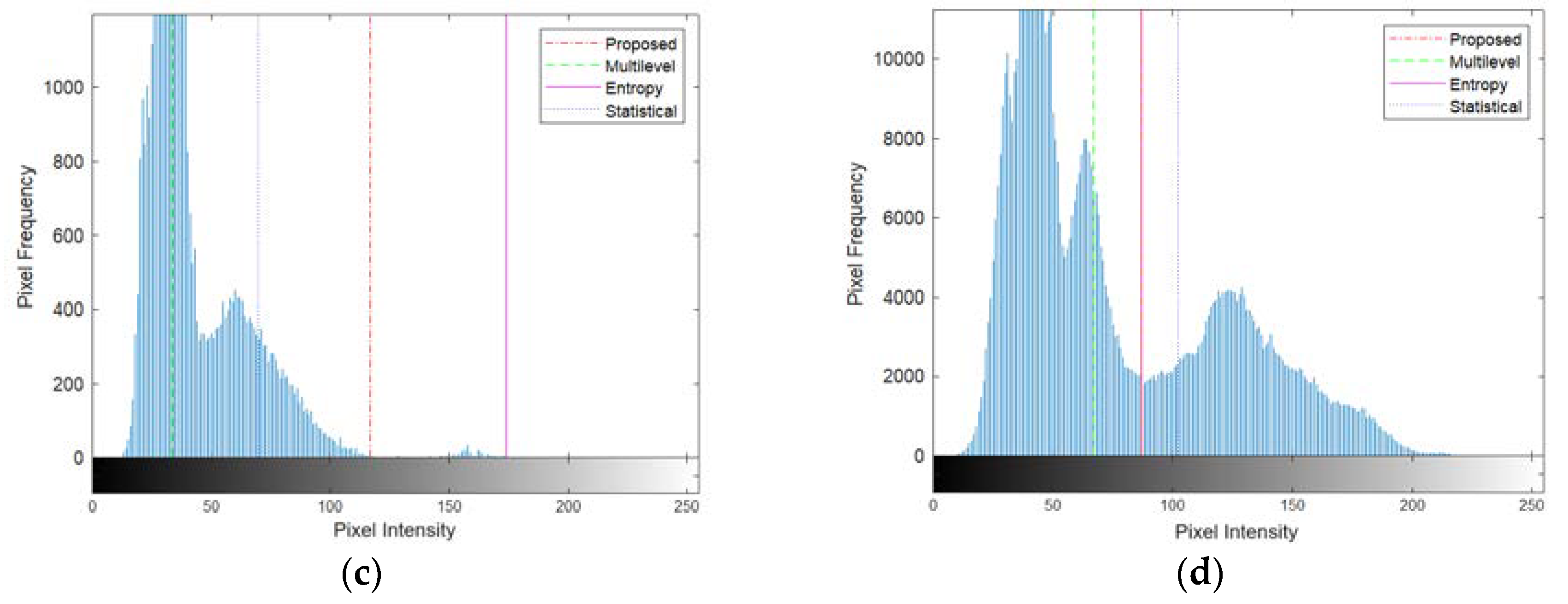
Preprints 93254 g010aPreprints 93254 g010b
Figure 10. Histograms and threshold values of the general images, respectively, from top left to bottom right: (a) Coins (b) Blocks (c) Potatoes (d) Hand X-ray.
Figure 10. Histograms and threshold values of the general images, respectively, from top left to bottom right: (a) Coins (b) Blocks (c) Potatoes (d) Hand X-ray.
Preprints 93254 g010aPreprints 93254 g010b
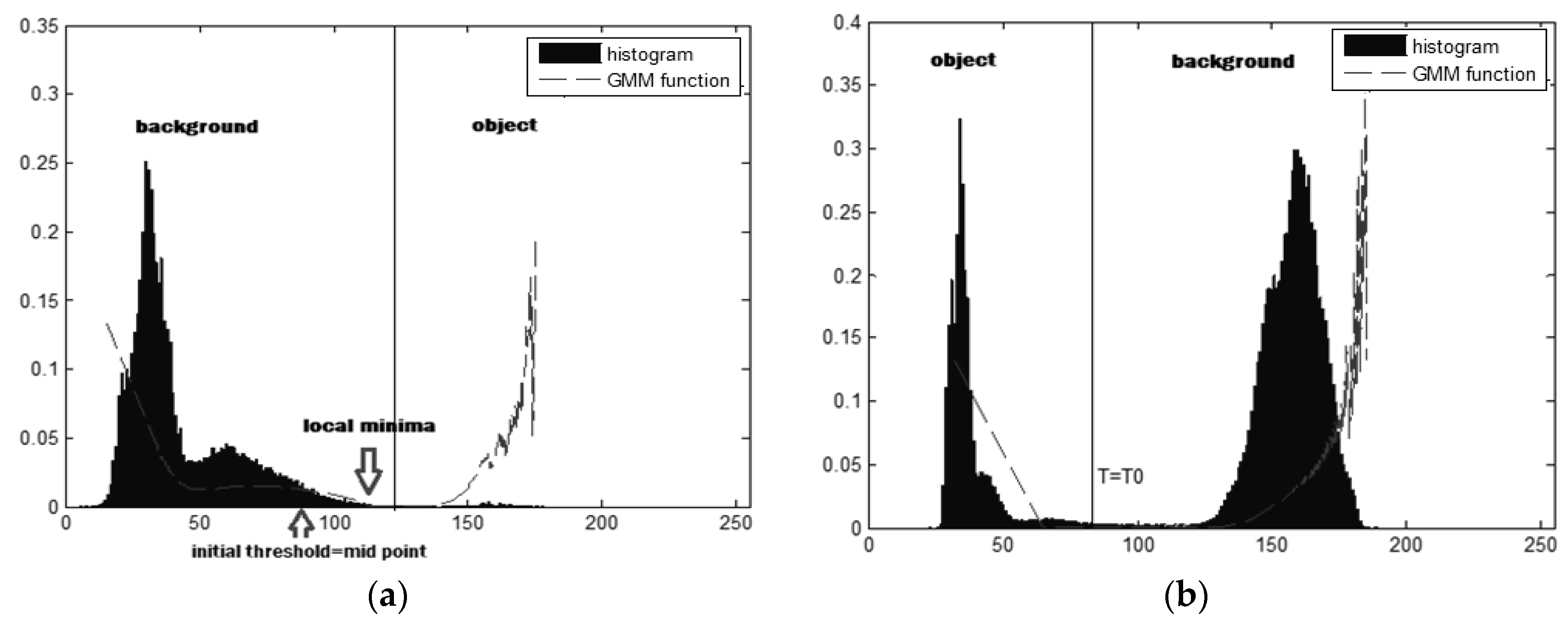
Preprints 93254 g011
Figure 11. (a) Example of the unimodal histogram and its Gaussian mixture function (b) Example of the bimodal histogram and its Gaussian mixture function.
Figure 11. (a) Example of the unimodal histogram and its Gaussian mixture function (b) Example of the bimodal histogram and its Gaussian mixture function.
Preprints 93254 g011
Preprints 93254 g012aPreprints 93254 g012b
Figure 12. Comparison of thresholding results using (a) entropy-based method (b) Otsu multilevel thresholding method (c) statistical-based method (d) proposed thresholding method.
Figure 12. Comparison of thresholding results using (a) entropy-based method (b) Otsu multilevel thresholding method (c) statistical-based method (d) proposed thresholding method.
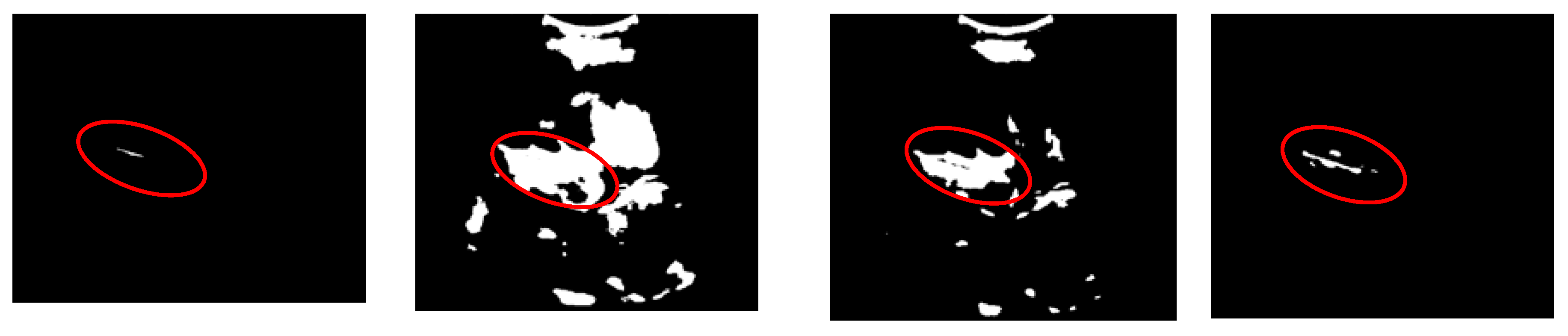
Preprints 93254 g012aPreprints 93254 g012b
Preprints 93254 g013aPreprints 93254 g013b
Figure 13. Histograms and threshold values of the example images.
Figure 13. Histograms and threshold values of the example images.
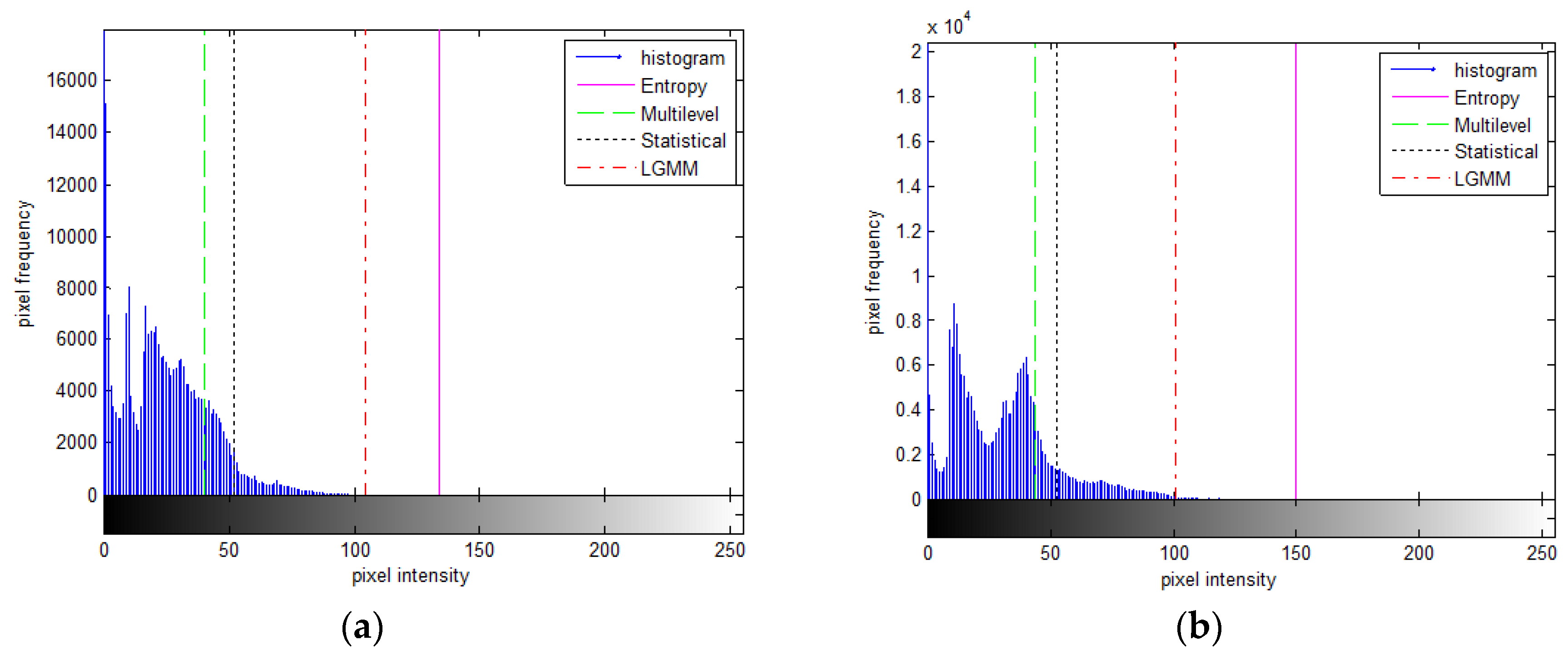
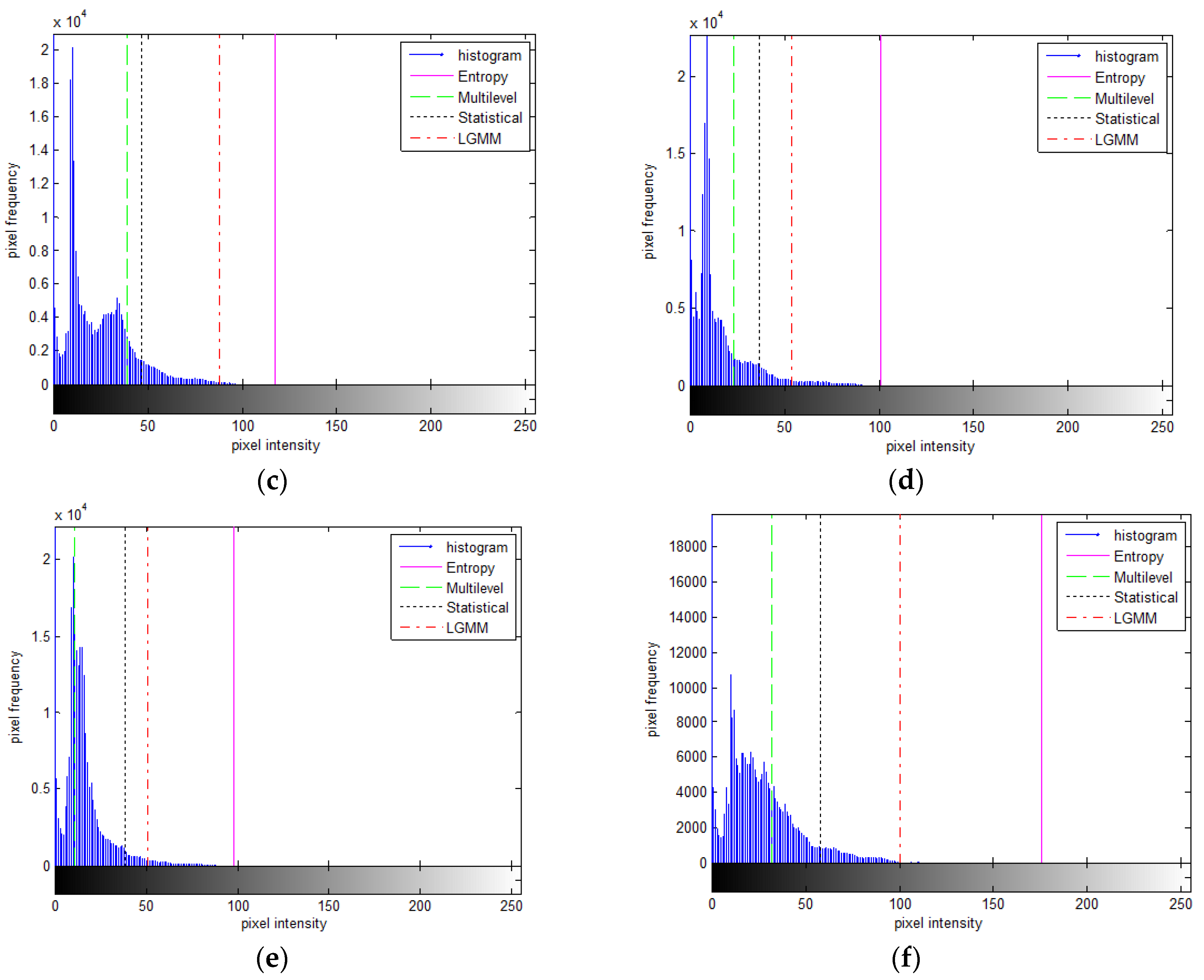
Preprints 93254 g013aPreprints 93254 g013b
Preprints 93254 g014
Figure 14. (a) Before object selection (b) After object selection.
Figure 14. (a) Before object selection (b) After object selection.
Preprints 93254 g014
Preprints 93254 g015
Figure 15. Example of localizing region-based active contour process at (a) initial iteration using the most significant intensity value (b) after 350 iterations.
Figure 15. Example of localizing region-based active contour process at (a) initial iteration using the most significant intensity value (b) after 350 iterations.
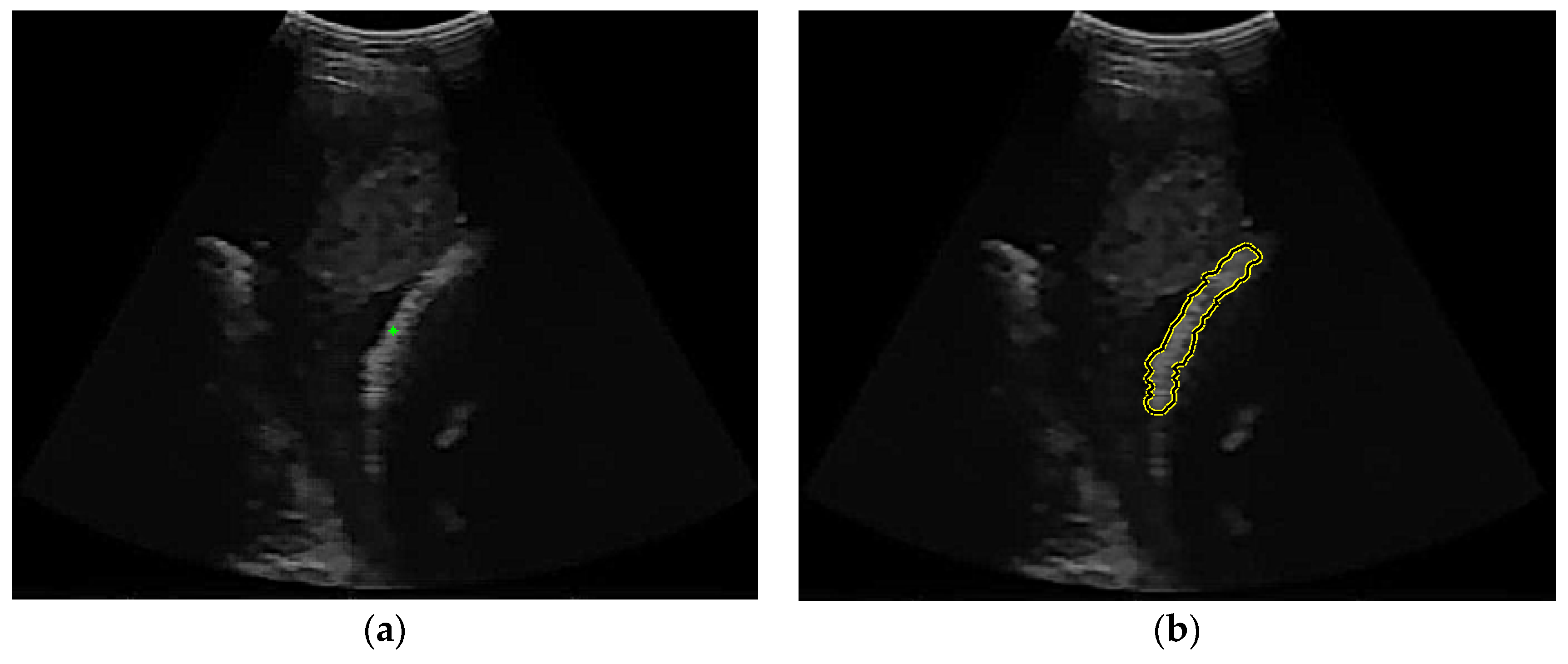
Preprints 93254 g015
Preprints 93254 g016
Figure 16. Examples of over-segmentation femur region.
Figure 16. Examples of over-segmentation femur region.
Preprints 93254 g016
Preprints 93254 g017
Figure 17. Thresholding result of the over-segmentation area (a) before removing the object (b) after removing the object.
Figure 17. Thresholding result of the over-segmentation area (a) before removing the object (b) after removing the object.
Preprints 93254 g017
Preprints 93254 g018
Figure 18. The region merging process: (a) the shortest path between two boundaries, (b)-(e) the gap filling stage, and (f) the merging result.
Figure 18. The region merging process: (a) the shortest path between two boundaries, (b)-(e) the gap filling stage, and (f) the merging result.
Preprints 93254 g018
Preprints 93254 g019
Figure 19. The process of boundary smoothing: (a) before refinement, (b) after refinement, and (c) smoothing result.
Figure 19. The process of boundary smoothing: (a) before refinement, (b) after refinement, and (c) smoothing result.
Preprints 93254 g019
Preprints 93254 g020
Figure 20. Final result of the object segmentation.
Figure 20. Final result of the object segmentation.
Preprints 93254 g020
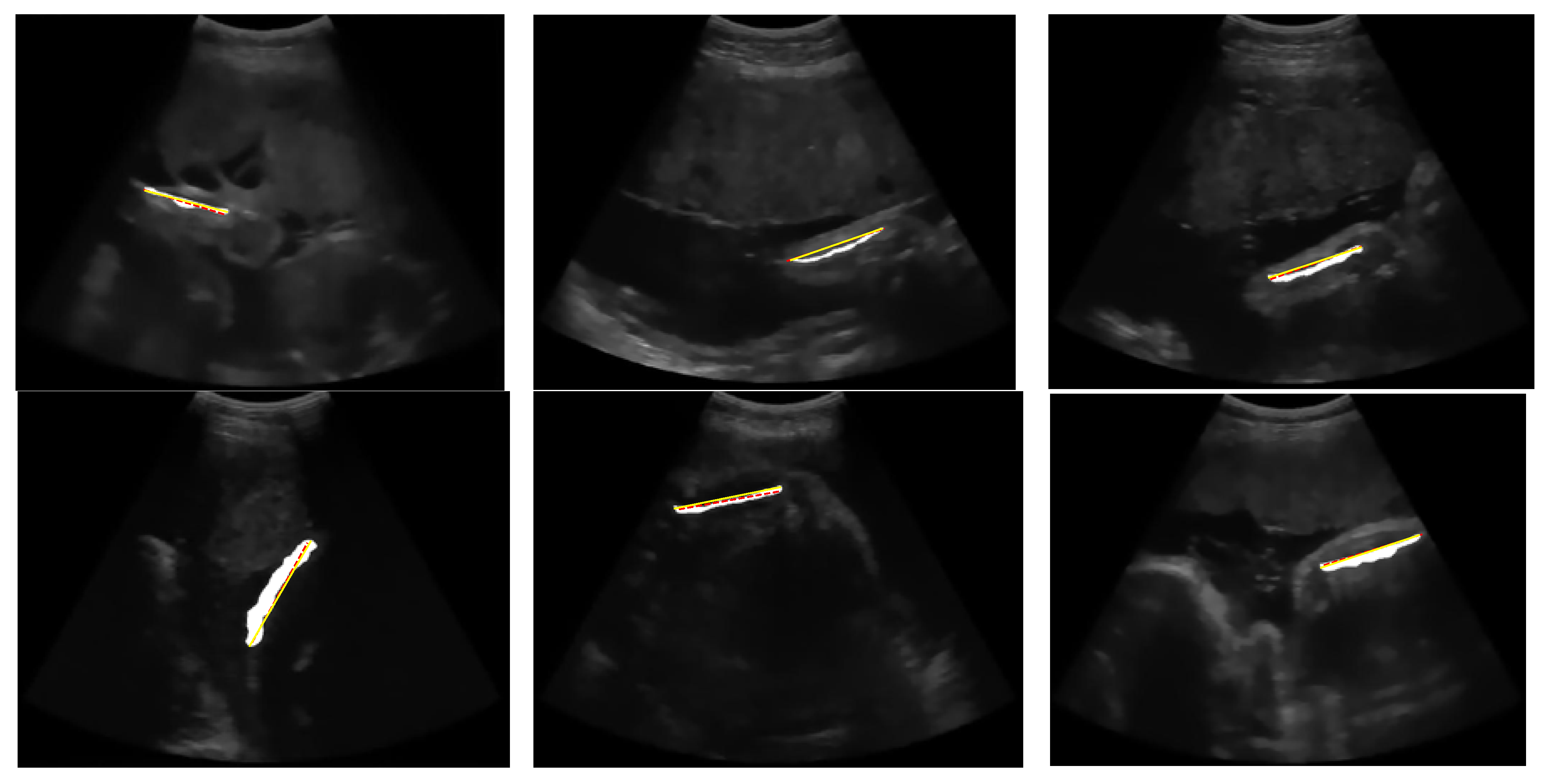
Preprints 93254 g021
Figure 21. The result of the automatic FL segmentation and measurement where the white region is a femur area, the red line is ground truth of FL, and the yellow line is the detected FL.
Figure 21. The result of the automatic FL segmentation and measurement where the white region is a femur area, the red line is ground truth of FL, and the yellow line is the detected FL.
Preprints 93254 g021
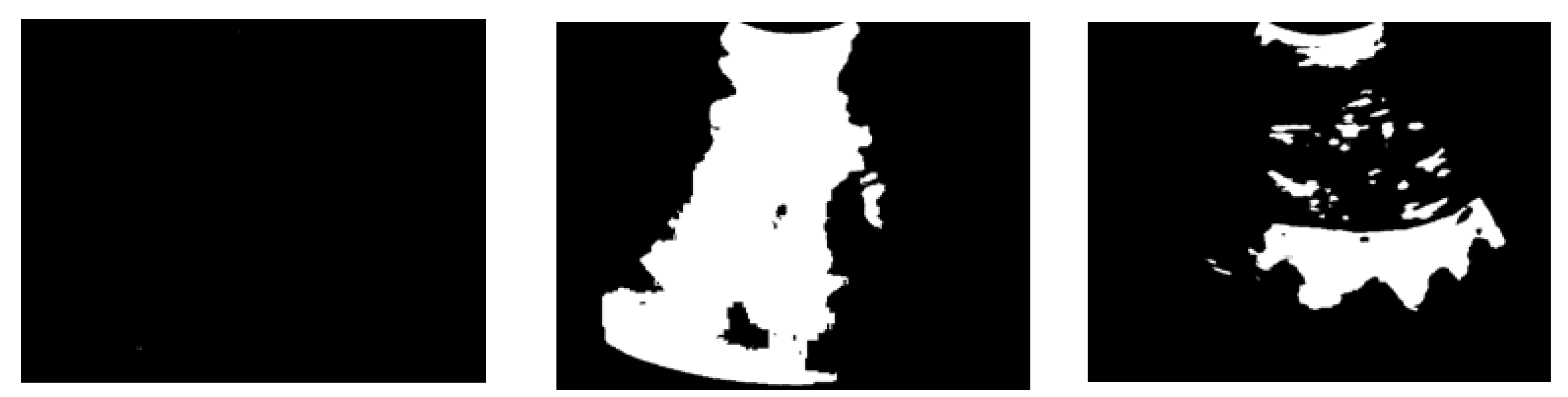
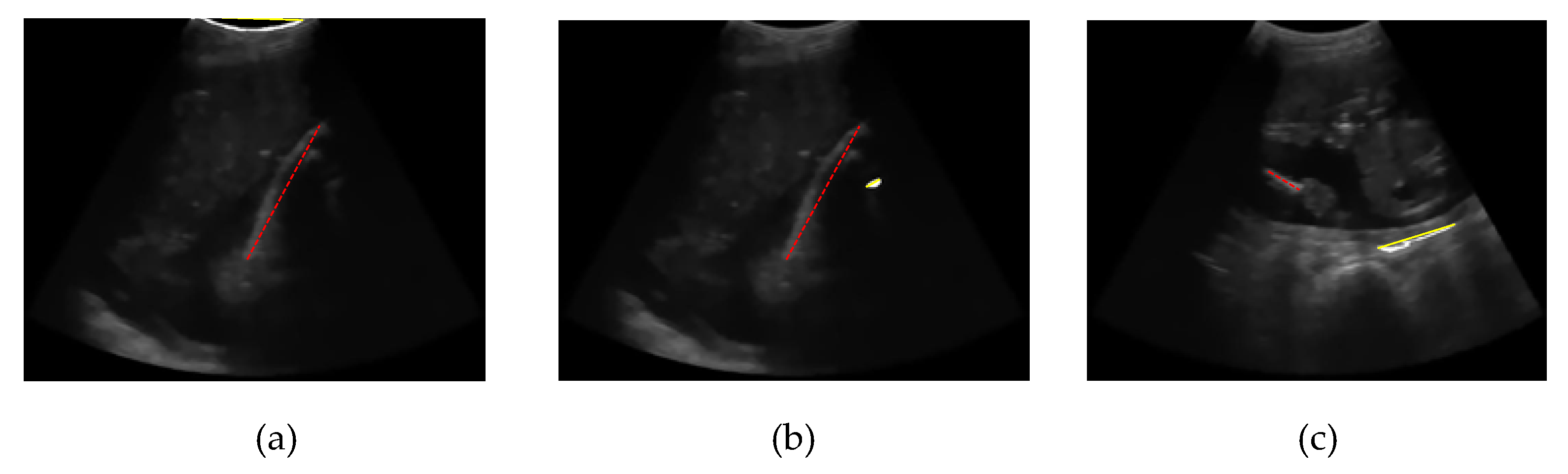
Preprints 93254 g022aPreprints 93254 g022b
Figure 22. Failures result of (a) entropy-based method, (b) multilevel Otsu method, (c) statistical-based method, where the dash line is the ground truth, and the straight line is a detected FL.
Figure 22. Failures result of (a) entropy-based method, (b) multilevel Otsu method, (c) statistical-based method, where the dash line is the ground truth, and the straight line is a detected FL.
Preprints 93254 g022aPreprints 93254 g022b
Table 1. Properties of The Ultrasound Image Examples in Figure 2.
Table 1. Properties of The Ultrasound Image Examples in Figure 2.
Image Id Image Size Femur Orientation
FL-15-01 670x537 negative slope approaching horizontal
FL-21-01 677x529 positive slope approaching horizontal
FL-21-02 681x527 positive slope approaching horizontal
FL-23-02 687x532 positive slope approaching vertical
FL-32-01 687x531 positive slope approaching horizontal
FL-41-02 674x524 positive slope approaching horizontal
Table 2. Mean and standard deviation of region-based segmentation performance.
Table 2. Mean and standard deviation of region-based segmentation performance.
Thresholding Method Precision Sensitivity Specificity Dice Similarity
Entropy-Based [10] 0,40±0,35 0,47±0,42 0,62±0,41 0,47±0,42
Multilevel Otsu [12,13] 0,35±0,37 0,41±0,43 0,59±0,41 0,41±0,43
Statistical Based [16] 0,58±0,28 0,67±0,33 0,78±0,28 0,69±0,32
Proposed Thresholding method 0,68±0,07 0,78±0,12 0,87±0,13 0,81±0,05
Table 3. Mean and standard deviation of FL measurement performance.
Table 3. Mean and standard deviation of FL measurement performance.
Thresholding Method Angle Accuracy Distance Accuracy Length Accuracy
Entropy-Based [10] 0,89 ± 0,14 0,52 ± 0,46 0,80 ± 0,27
Multilevel Otsu [12,13] 0,69 ± 0,43 0,45 ± 0,47 0,50 ± 0,47
Statistical Based [16] 0,95 ± 0,08 0,73 ± 0,36 0,79 ± 0,33
Proposed Thresholding method 0,99± 0,01 0,88± 0,10 0,93± 0,07
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated