Preprint
Article
Entropy of Difference
Altmetrics
Downloads
62
Views
18
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
24 November 2023
Posted:
14 December 2023
You are already at the latest version
Alerts
Abstract
{Here, we propose a new tool to estimate the complexity of a time series: the entropy of difference (ED). The method is based solely on the sign of the difference between neighbouring values in a time series. This makes it possible to describe the signal as efficiently as prior proposed parameters such as permutation entropy (PE) or modified permutation entropy (mPE), but (1) reduces the size of the sample that is necessary to estimate the parameter value, and (2) enables the use of the Kullback-Leibler divergence to estimate the "distance" between the time series data and random signals.
Keywords:
Subject: Computer Science and Mathematics - Applied Mathematics
1. Introduction
Permutation entropy (PE), introduced by Bandt and Pompe [1], as well as its modified version [2], are both efficient tools to measure the complexity of chaotic time series. Both methods propose to analyze time series: by first choosing an embedding dimension m to split the original data in a subset of m-tuples: , then to substitute to the m-tuples values by the rank of the values, resulting in a new symbolic representation of the time series. For example, consider the time series . Choosing, for example, an embedding dimension , will split the data in a set of 4-tuples: . The Bandt-Pompe method will associate the rank of the value with each 4-tuples. Thus, in the lowest element is in position 2, the second element is in position 1, is in position 4 and finally is in position 3. Thus the 4-tuple is rewritten as . This procedure thus results in each to be rewritten as a symbolic list:. Each element is then a permutation of the set . Next, the probability of each permutation in is then computed: , and finally the PE for the embedding dimension m, is defined as . The modified permutation entropy (mPE) just deals with those cases in which equal quantities may appear in the m-tuples. For example for the m-tuple , computing PE will produce while computing mPE will associate . Both methods are widely used due to their conceptual and computational simplicity [3,4,5,6,7,8]. For random signals, PE leads to a constant probability (for white Gaussian noise), which does not make it possible to evaluate the “distance" between the probability found in the signal: and the probability produced by a random signal: , with the Kullback-Leibler (KL) divergence [9,10]: . Furthermore, the number of m-tuples are for PE and even greater for mPE [2], thus requiring then a large data sample to perform significant statistical estimation of .
2. Entropy of difference-method
The entropy of difference (ED) method proposes to substitute to the m-tuples with strings s containing the sign (“+" or “-"), representing of the difference between subsequent elements in the m-tuples. For the same : this leads to the representation: . For an m value, we have strings s from to . Again we compute, in the time series, the probability distribution of these strings s and define the entropy of difference of order m as: . The number of elements: to be treated, for an embedding m, are smaller for ED compared with the number of permutations in PE or to the elements in mPE (see Table 1).
Furthermore the probability distribution for a string s, in a random signal: is not constant and could be computed through the recursive equation. Indeed let’s be the probability density for the signal variable at time t, and let’s the corresponding cumulative distribution function (). Let’s make the hypothesis that the signal is not correlated in time, which means that the join probability is just the product of probability: . Under these conditions, we can easily evaluate the . For example for , we have 4 probabilities: and . These give respectively:
and
This result is totally independent of the probability density provided that the signal is not correlated in time. We can proceed in the same way for any and thus obtain a recurrence on the 1 (in the following equations x and y are strings made of “+" and “-"):
leading to a complex probability distribution for the . For example for we have strings with the highest probability for the string (and its symmetric ): (see Figure 1). These probabilities could then be used to determine the KL-divergence between the time series probability and the random uncorrelated signal.
To each string s we can associate an integer number, it’s binary representation, through the substitutions , . So, for we have , , , and so on up to .
Table 3.
values, for different m-embedding.
| 1 | |
The recurrence gives some specific . To simplify the notations, let’s write a set of a successive “+". For example the second and third rules gives
then
We can also write
This equation is also valid when so for (with ) or for . We can continue in this way and determine the general values of and so on.
In the case where the data are integers, we can avoid the situation where two successive data are equal () by adding a small amount of random noise. For example, we take the first decimal of (and we add a small noise ) and we have:
Table 4.
values for , for different m-embedding.
| 0.982 | 2.01 | 2.01 | 0.991 | |||||||||
| 0.924 | 3.00 | 5.05 | 3.00 | 3.00 | 5.05 | 3.00 | 0.960 | |||||
| 0.756 | 3.86 | 9.10 | 5.92 | 9.23 | 16.0 | 11.0 | 4.03 | 3.86 | 11.1 | 16.2 | 9.10 | |
| 5.78 | 9.22 | 4.03 | 0.768 |
Table 5.
values for , for different m-embedding.
Despite the complexity of , the Shannon entropy for a random signal: increases linearly with m (see Figure 2): . If the m-tuples where equiprobable it will leads to .
3. Periodic signal
Let’s see what happens with a period 3 data . To evaluate the we only have 3 types of 2-tuples. For example for we have , , . We have only two possible string “+" or “-", so the probabilities mustt be or . For again we have only 3 types of 3-tuples: , , . We have possible string , , and . The consistency of the inequalities between , and reduces the number of possible strings to 3. For example, if gives , then must be and must be . Due to period 3 these will appear times. To evaluate we have again only 3 types of 4-tuples: , , and again these will appear times in the data. This reasoning can be generalised to a signal of period p: , consequently and remains constant for . Obviously, since we are only using the differences between the ’s, the periodicity in terms of signs , may be smaller than the periodicity p of the data, so .
4. Chaotic logistic map example
Let us illustrate the use of ED on the well know logistic map [13] driven by the parameter .
It is obvious that for a range of values of where the time series reaches a periodic behavior (any cyclic oscillation between n different values), the ED will remain constant. The evaluation of the ED could thus be used as a new complexity parameter to determine the behavior of the time series (see Figure 3).
For we know that the data are randomly distributed with a probability density given by [14]
But the logistic map produce correlations in the data, so we expect a deviation from the uncorrelated random .
We can then compute exactly the ED for an m-embedding, and the KL-divergence from a random signal. For example, for , we can determine the and by solving the inequality and respectively which implies that and , and then
In this case the logistic map produces a signal that contains twice as many increasing pairs than decreasing pairs . So:
For we can perform the same calculation, we have respectively:
Graphically we have:
Effectively the logistic map with forbids the string “- -" where . For strings of length 3 we have:
The probability of difference for some string length m versus s the string binary value, where “+" and “-", give us the “spectrum of difference" for the distribution q (see Figure 4).
5. divergences versus m on real data and on maps
The manner in which the evolves with m is another parameter of the complexity measure. measures the loss of informations when the random distribution is used to predict the distribution . Increasing m introduces more bits information in the signal and the behavior versus m shows how the data diverges from a random distribution.
The graphics (see Figure 6) shows the behavior of versus m for two different chaotic maps and for real financial data [15]: the opening value of the nasdaq100, bel20 everyday from 2000 to 2013. For maps, the logarithmic map and logistic map are shown (see Figure 6 for the logarithmic map).
For maps the simulation starts with a random number between 0 and 1, then first iterate 500 times to avoid transients. Starting with that seeds, 720 iterates where kept on which the where computed. It can be seen that the Kullback-Leibler divergence from the logistic map at to the random signal is fitted by a quadratic function of m: (p-value for all the parameter), while the logarithmic map behavior is linear in the range . Financial data are also quadratic , with a higher curvature than the logistic map due to the fact that the spectrum of the probability is compatible with a constant distribution (see Figure 6) rendering the prediction of increase or decrease signal completely random, which is not the case in any true random signal.
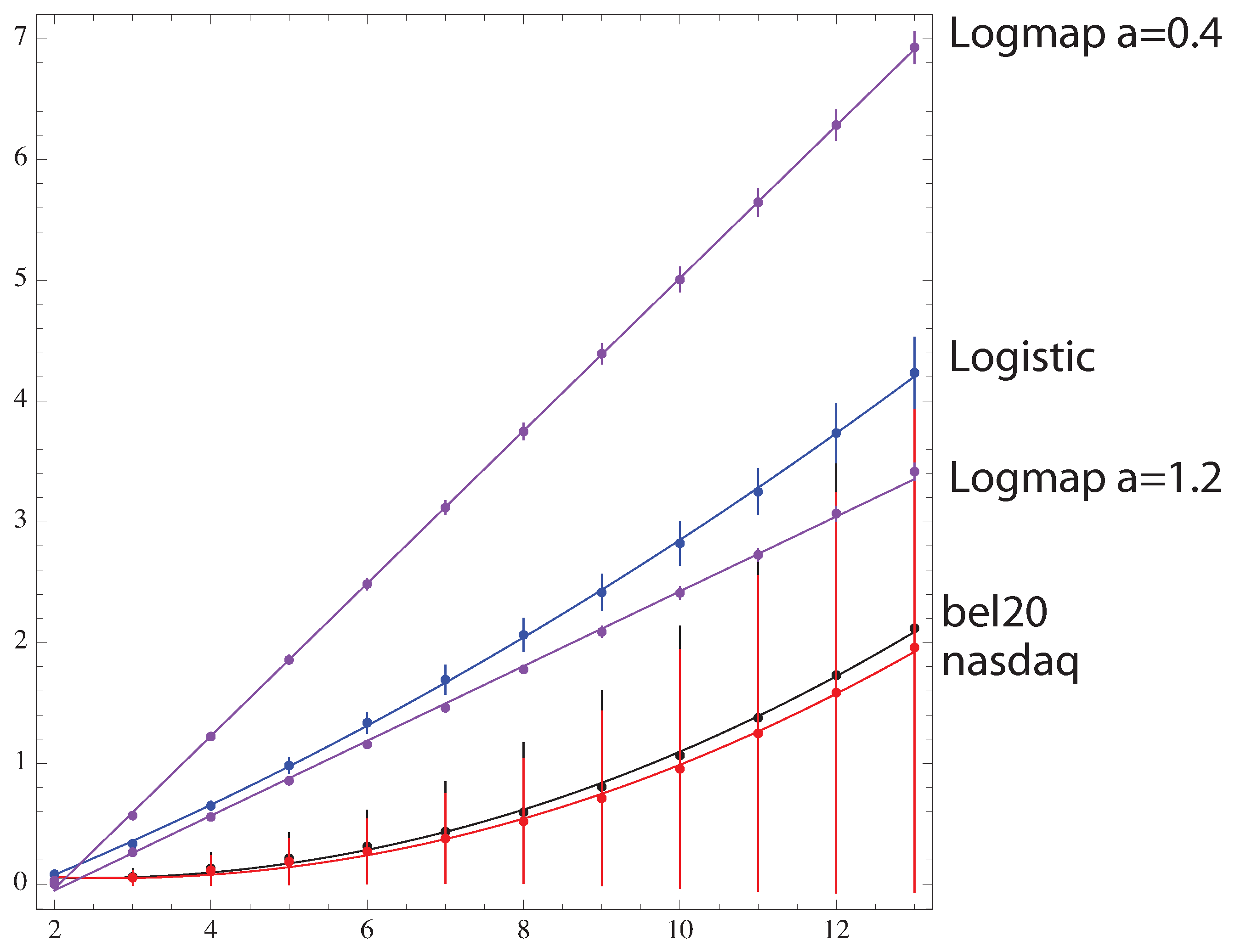
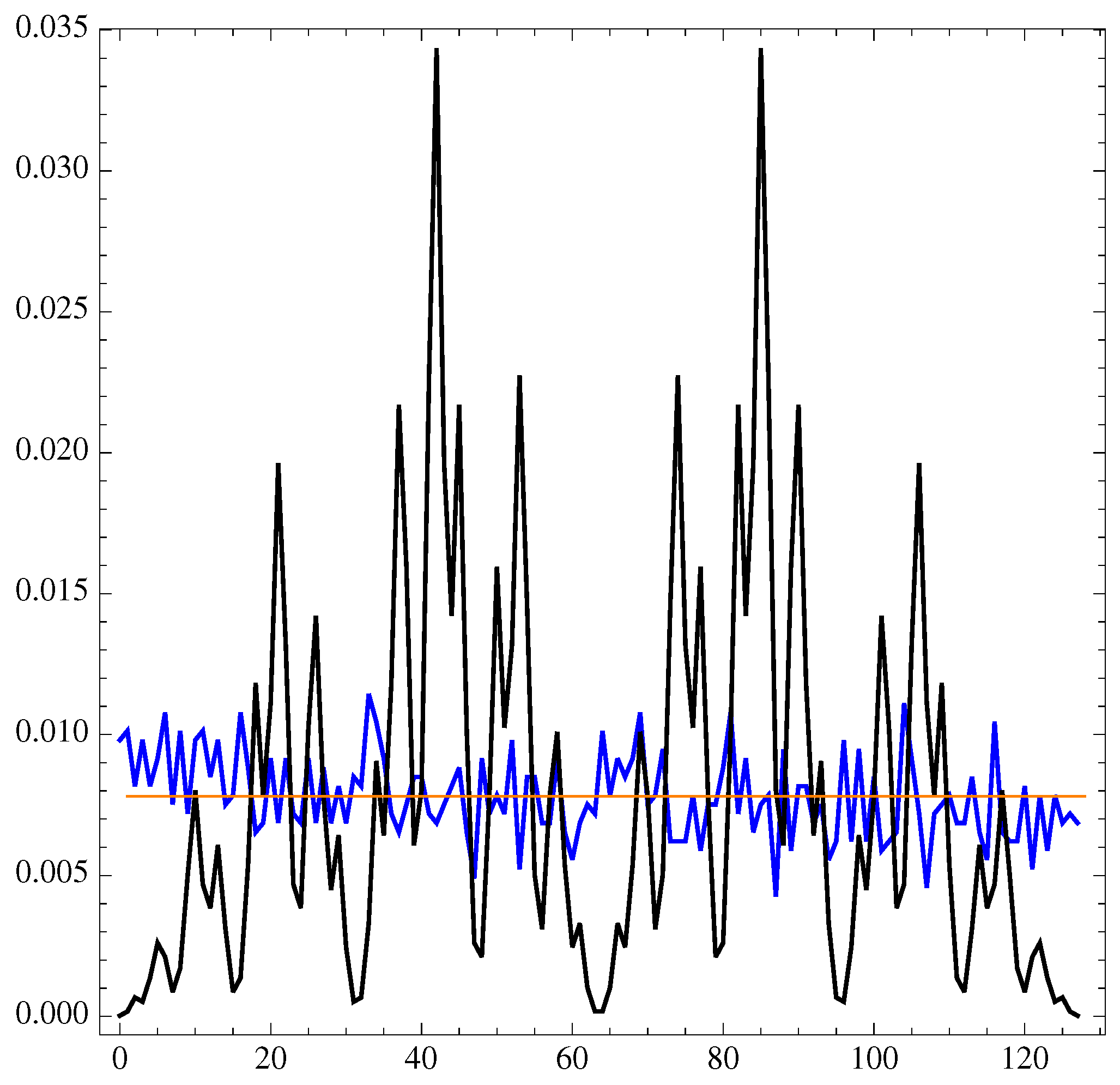
Figure 8.
The KL-divergence for the data.

Figure 9.
The spectrum of versus the string binary value (from 0 to ) for the bel20 financial data.

6. Conclusions
The simple property of increases or decreases in a signal makes it possible to introduce the entropy of difference as a new efficient complexity measure for chaotic time series. The probability distribution of string for random signal is used to evaluate the Kullback-Leibler divergence versus the number of data m used to build the difference string. This shows different behavior for different types of signal and can also be used also to characterize the complexity of a time series.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
P["+"]= P["-"] = 1/2;
P["-", x__] := P[x] - P["+", x];
P[x__, "-"] := P[x] - P[x, "+"];
P[x__, "-", y__] := P[x] P[y] - P[x, "+", y];
P[x__] :=1/(StringLength[StringJoin[x]] + 1)!
References
- C. Bandt and B. Pompe, Phys. Rev. Lett. 88, 174102 (2002).
- Chunhua Bian, Chang Qin, Qianli D. Y. Ma and Qinghong Shen Phys. Rev. E 85, 021906 (2012).
- L. Zunino, D. G. Pérez, M. T. Martín, M. Garavaglia, A. Plastino, and O. A. Rosso, Phys. Lett. A 372, 4768 (2008).
- X. Li, G. Ouyang, and D. A. Richards, Epilepsy Res. 77, 70 (2007).
- X. Li, S. Cui, and L. J. Voss, Anesthesiology 109, 448 (2008).
- B. Frank, B. Pompe, U. Schneider, and D. Hoyer, Med. Biol. Eng. Comput. 44, 179 (2006).
- E. Olofsen, J. W. Sleigh, and A. Dahan, Br. J. Anaesth. 101, 810 (2008).
- O. A. Rosso, L. Zunino, D. G. Perez, A. Figliola, H. A. Larrondo, M. Garavaglia, M. T. Martin and A. Plastino, Phys. Rev. E 76, 061114 (2007).
- S. Kullback and R. A. Leibler Ann. Math. Statist., 22, 1, 79, (1951).
- Édgar Roldán and Juan M. R. Parrondo Phys. Rev. E, 85, 3, 031129, (2012).
- F. Ginelli, P. Poggi, A. Turchi, H. Chate, R. Livi, and A. Politi Phys. Rev. Lett. 99, 130601 (2007).
- J. Theilerb and P. E. Rapp, Electroencephalography and Clinical Neurophysiology, 98, 3, 213 (1996).
- R.M. May, Nature 261, 459 (1976).
- M. Jakobson,Communications in Mathematical Physics, 81, 39-88 (1981).
- data are provided by http://www.wessa.net/.
| 1 | See Appendix A
|
Figure 1.
The values for the probability of , from to .
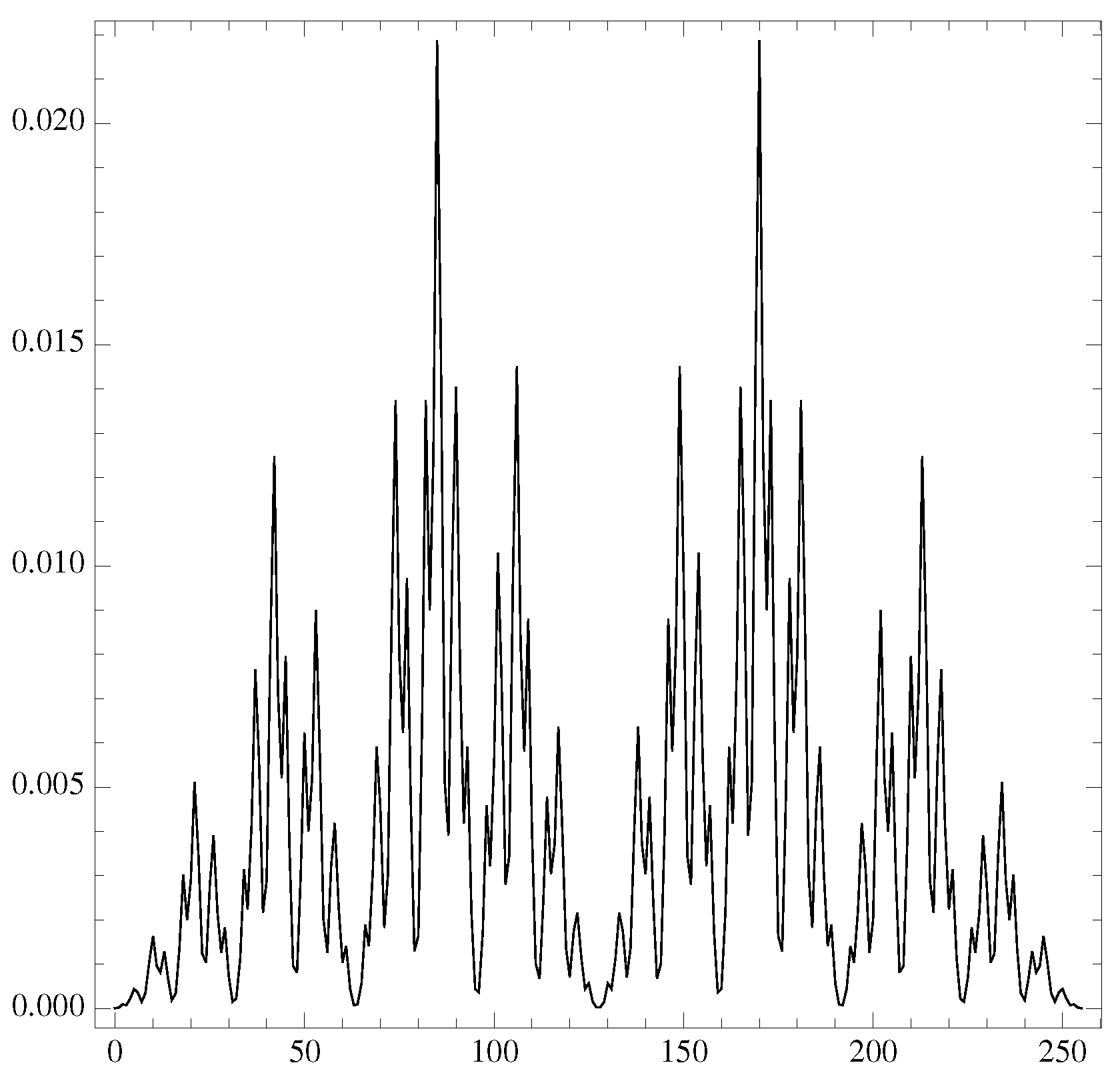
Figure 2.
The values for the probability of , for decimal (blue) and for a random distribution (red).
Figure 2.
The values for the probability of , for decimal (blue) and for a random distribution (red).
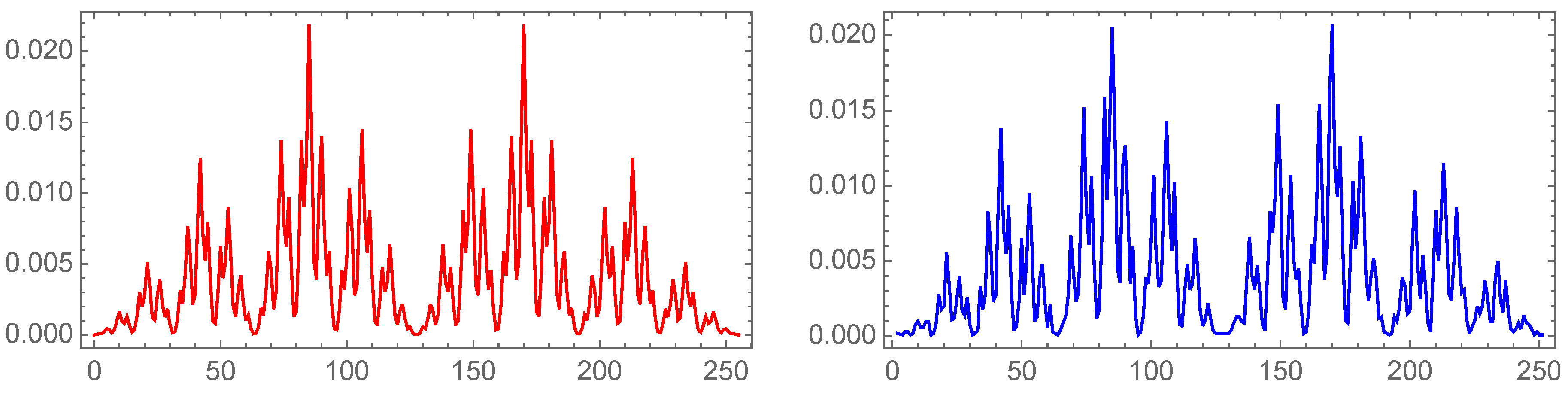
Figure 3.
The Shannon entropy of : , increases linearly with m, the fit gives a sum of squared residuals of and a p-value= and on the fit parameter respectively.
Figure 3.
The Shannon entropy of : , increases linearly with m, the fit gives a sum of squared residuals of and a p-value= and on the fit parameter respectively.
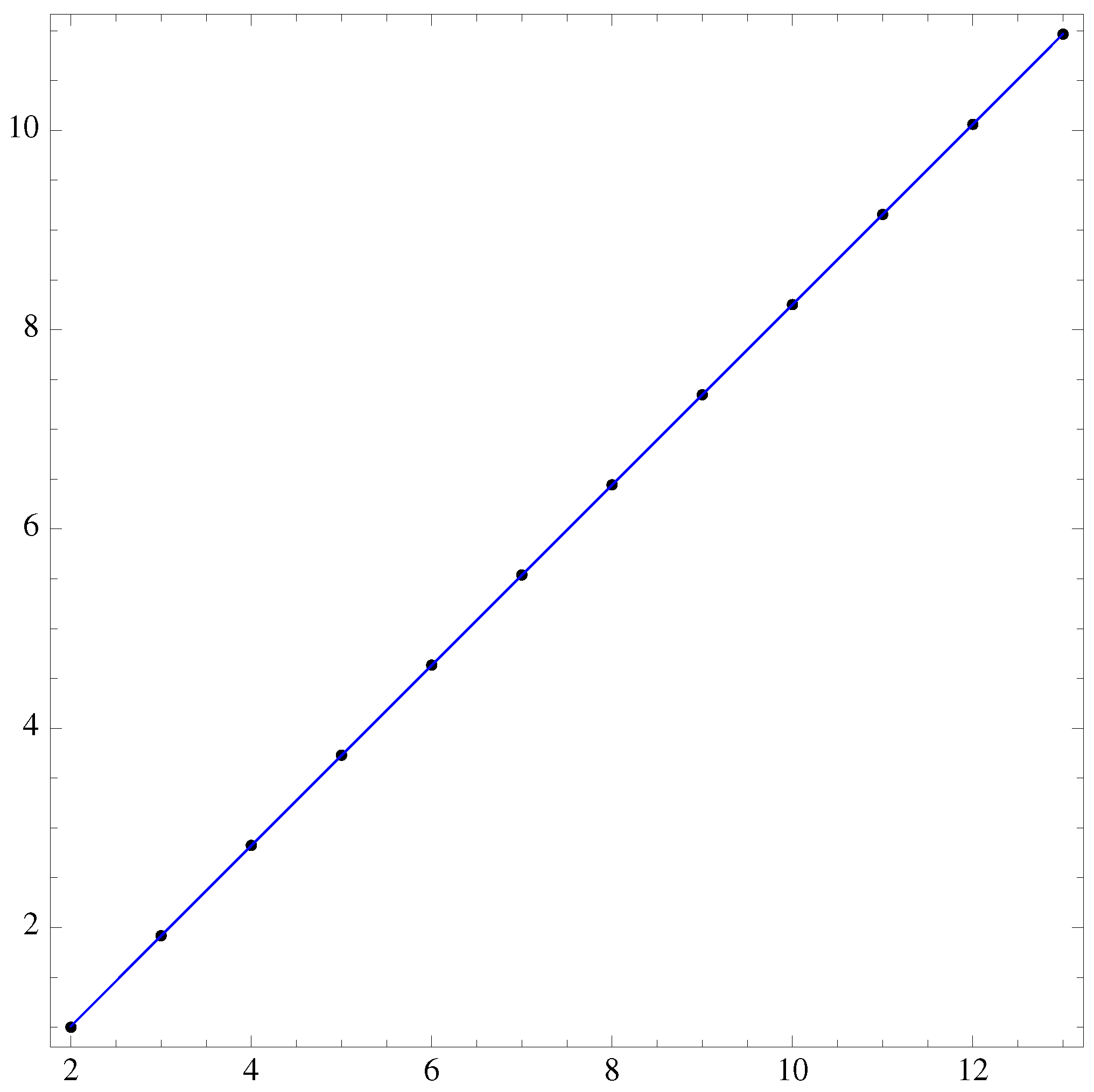
Figure 4.
The (strings of length 12) is plotted versus , with the bifurcation diagram, and the value of the Lyapunov exponent respectively. The constant value appears when the logistic map enters into a periodic regime.
Figure 4.
The (strings of length 12) is plotted versus , with the bifurcation diagram, and the value of the Lyapunov exponent respectively. The constant value appears when the logistic map enters into a periodic regime.
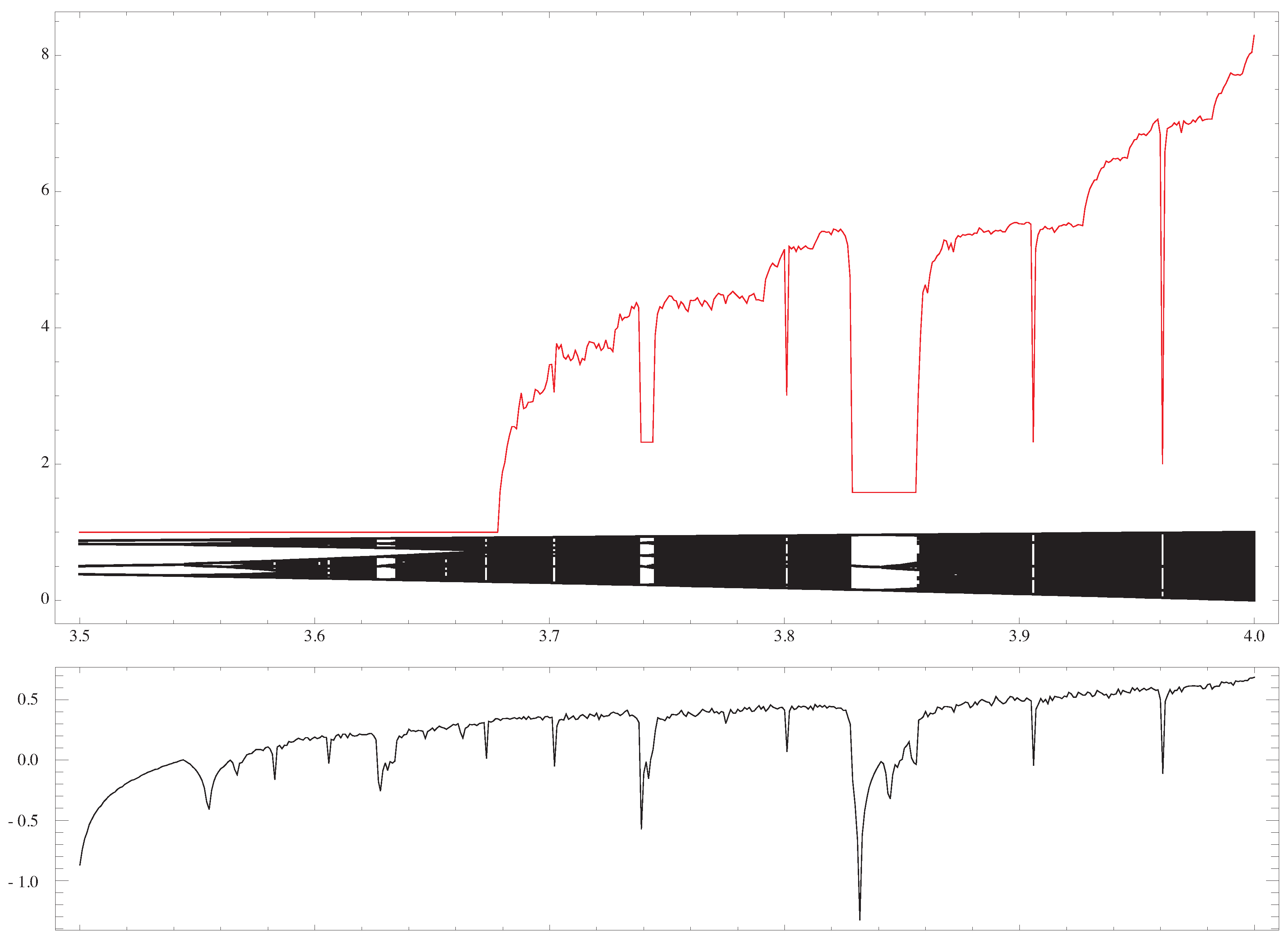
Figure 5.
From (blue), the first iteration of logistic map (gray) gives and second iteration (black) gives , the respective positions of allow us to determine .
Figure 5.
From (blue), the first iteration of logistic map (gray) gives and second iteration (black) gives , the respective positions of allow us to determine .
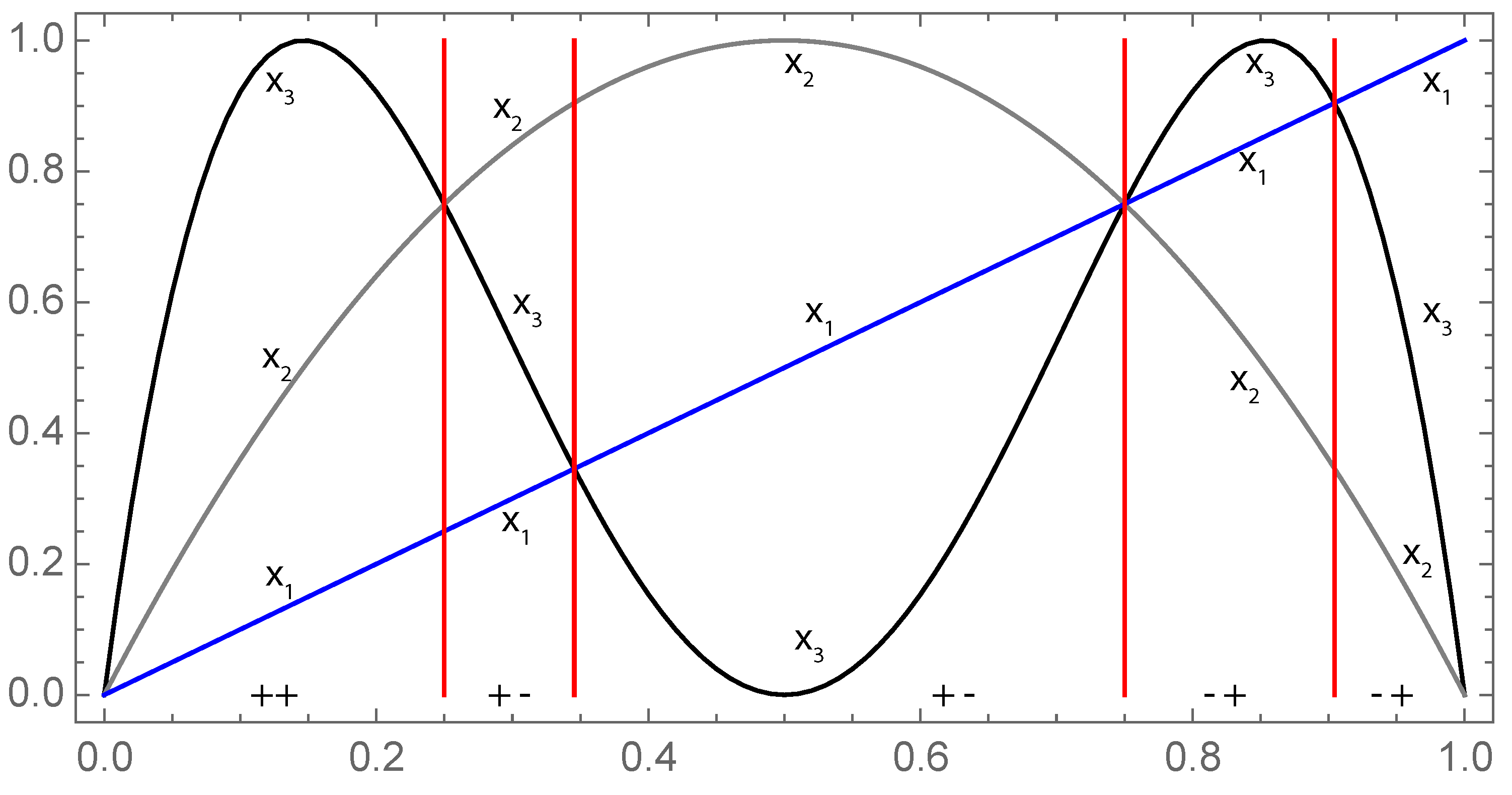
Figure 6.
The spectrum of (black) versus the string binary value (from 0 to ) for the logistic map at and the one from a random distribution (red).
Figure 6.
The spectrum of (black) versus the string binary value (from 0 to ) for the logistic map at and the one from a random distribution (red).
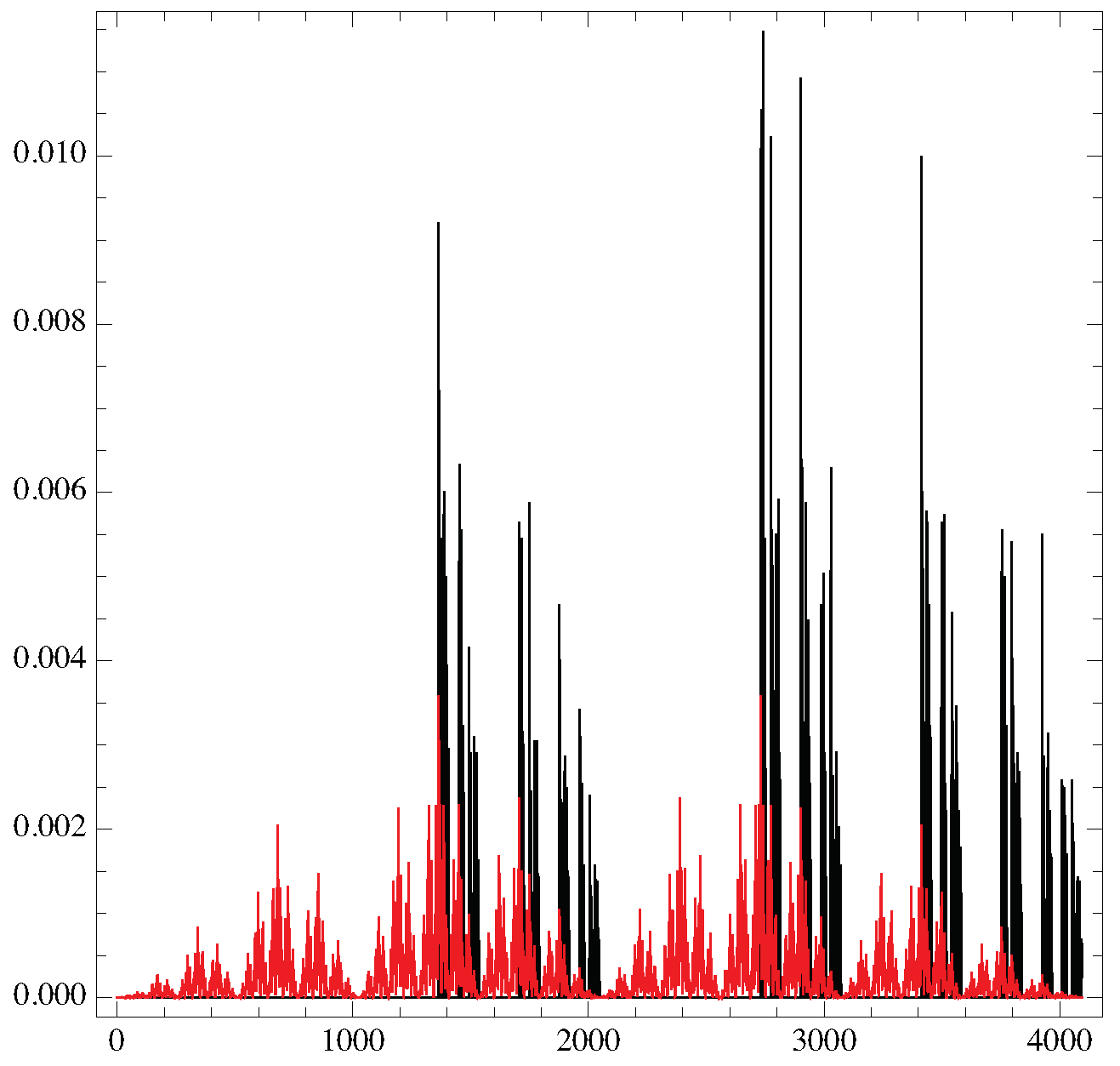
Figure 7.
The versus a for the logarithm map .
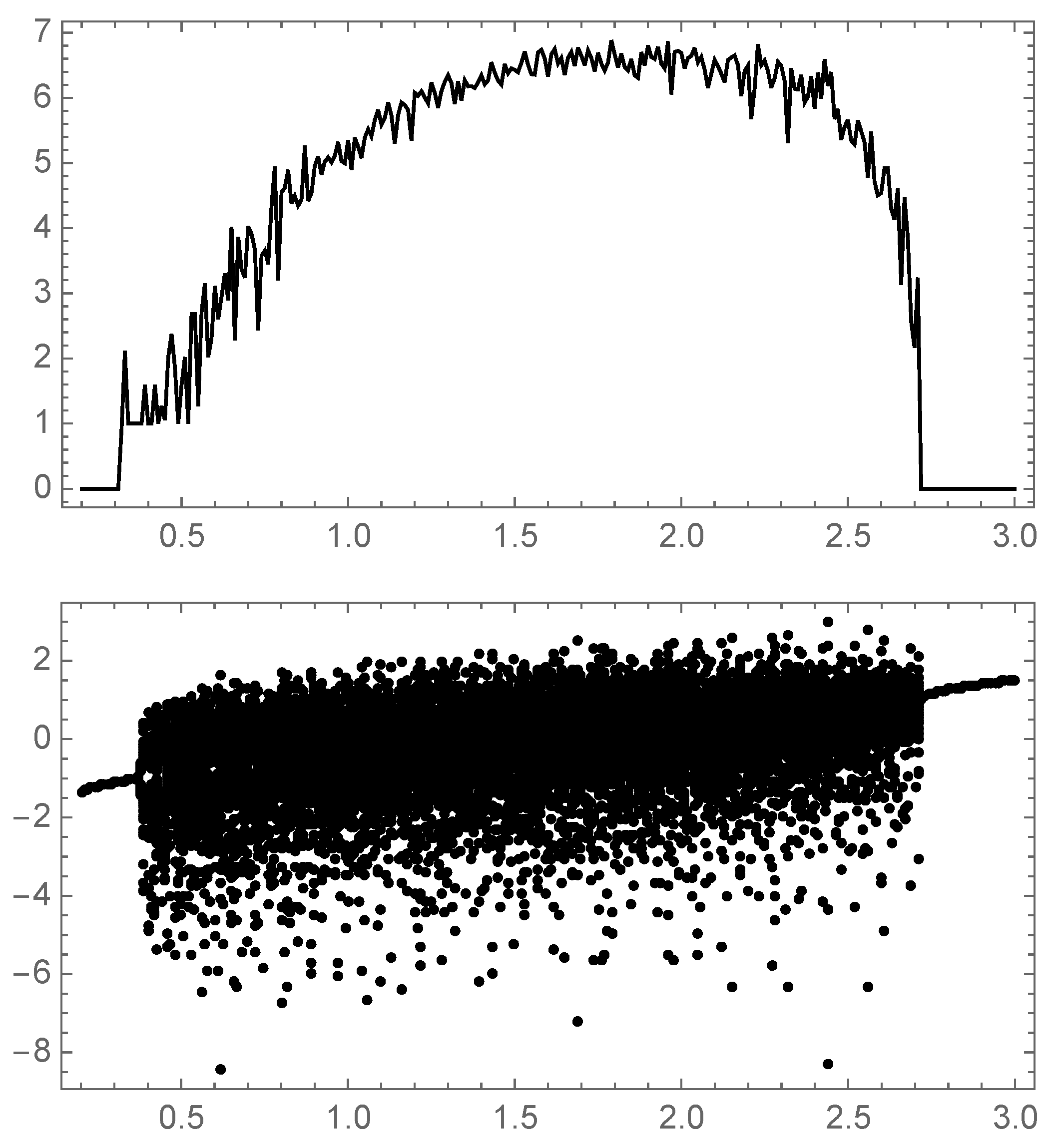
Table 1.
K values, for different m-embedding.
| m | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|
| 6 | 24 | 120 | 720 | 5040 | |
| 13 | 73 | 501 | 4051 | 37633 | |
| 4 | 8 | 16 | 32 | 64 |
Table 2.
values, for different m-embedding, ordered by the binary representation of the string.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| 1 | 2 | 2 | 1 | |||||||||||||
| 1 | 3 | 5 | 3 | 3 | 5 | 3 | 1 | |||||||||
| 1 | 4 | 9 | 6 | 9 | 16 | 11 | 4 | 4 | 11 | 16 | 9 | 6 | 9 | 4 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






