Prerpints.org logo
Preprint
Article

Production systems with parallel heterogeneous servers of limited capacity: accurate modeling and performance analysis

Altmetrics

Downloads

91

Views

54

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

13 December 2023

Posted:

15 December 2023

You are already at the latest version

Alerts
Abstract
Heterogeneous systems of limited capacity have general applications in manufacturing, but also for logistic or service systems, due to the differences in server or workstation performance or work assignment, in close relationship with system flexibility, where saturation and blocking are ordinary situations of systems with high demand and limited capacity, so accurate loss quantification is essential for performance evaluation. Multi-class systems of limited capacity have been studied much less than parallel homogeneous systems (Erlang models). In this context, accurate models for parallel heterogeneous ordered-entry systems are developed: without any prior queue, M/Mi/c/c, and with a k capacity queue M/Mi/c/c+k. These new matrix models give an exact state formulation, and their accuracy is verified through discrete event simulation and comparison with literature results. Also, the effect of queue capacity is studied in relationship with the pattern of service rates. Next, the heterogeneous recirculating system model is also developed with good approximation results. Finally, the proposed models are applied to evaluate systems with non-exponential service times, through a new hybrid methodology by combining the Markovian model and the Monte Carlo Method (MCM) for normal or lognormal service times that also yield useful good approximations to the simulated system.
Keywords: 
Subject: Engineering  -   Industrial and Manufacturing Engineering

1. Introduction

Parallel server systems with limited capacity are present in many operational situations of interest in manufacturing [1], but also in transportation or traffic [2], service [3], or computer systems [4]. Their study through Markovian network models requires accurate loss quantification to evaluate properly their performance and the ordinary model of these systems consists of enumerating all the states for the size of the system, in order to calculate the state probabilities that sum the unit. Among them, there is interest in the probability of the full and empty states that allow estimating the maximum expected capacity or idleness. In particular, the analysis of the parallel systems with homogeneous or identical servers facilitates analytical explicit expressions of the state probabilities. Therefore, based on the PASTA property [5], the probability of the full-size system is established in manuals as the estimation of the arrival rate percentage that becomes lost due to blocking when the system is busy, so the effective throughput is the difference with the offered load rate. For parallel systems with identical servers, the Erlang systems of Poisson arrivals and service rates are well-known and of great interest for service systems like call centers [6]. In addition, the important property of performance equivalence of M/G/c/c and M/M/c/c [3] gives extra opportunities for the analysis and decision-making with service time distributions other than the exponential one.
Even when parallel homogeneous systems have been studied in depth (Erlang models), many real systems have heterogeneous servers, where non-uniform human behavior [7], or task variety is present. The discipline of ordered entry is work assignment upon arrival to the first server idle in the order of arrangement. This is a frequent natural assignation, for instance in conveyor systems or call centers. In this context, some former studies are in more direct connection with the present work: Initial research of parallel heterogeneous systems can be found in [8], who analyzed ordered entry with the heterogeneous systems with the random discipline of service. His work assumed no queue in front of the servers, M/Mi/n. His error analysis of the heterogeneous vs. homogeneous system concluded that a heterogeneous system cannot be replaced by one of the equal servers whose mean service rate is the average of the mean service rate of each server. [9,10] studied the parallel system with homogeneous servers and ordered entry and with application to conveyor systems. Singh (1970, 1971) [11,12] compared homogeneous and heterogeneous Markovian queuing systems and obtained the steady-state probabilities of a heterogeneous with three servers system M/Mi/3. Later, some other researchers dealt with the analysis of the server arrangement for performance optimization. Elsayed (1983) [13] and Yao (1987) [14] studied the optimal allocation of buffers in front of the servers but without the quantification of blocking. Yao (1986) [15] or Saglam and Shahbazov (2007) [16] paid attention to minimizing the overflow of the system. Further extensions in parallel heterogeneous system studies can be found in Boxma et al. (1994) [17], who gave a comprehensive view of solution methods at the epoch. Isguder and Uzunoglu (2014) [18] dealt with the semi-Markov process of GI/M/n/0 and loss quantification; and more recently Melikov et al. (2020) [19] with an exact formulation, but approximate resolution for ordered entry. Specifically, systems under the ordered entry discipline can also be referred to the work of Cooper (1976) [20] that concludes the need for a multi-dimensional birth-and-death process to represent the system. Matsuy and Fukuta (1977) [21] studied the state probabilities of a parallel system of heterogeneous multi-servers (multichannel) with ordered entry discipline and no waiting line, M/Mi/n. With direct application to conveyor systems, they found that the optimal order for maximum throughput minimizing the overflow is the faster to slower server arrangement. Nath and Enns (1981) [22] proved that the overflow (loss) is minimal for M/Mi/c under the faster service rule. Pourbabai and Sonderman (1986) [23] studied approximate expressions of heterogeneous server G/G/n.
With the focus on heterogeneous systems with retrial, it can be remarked the surveys by Muth and White (1979) [24], and Nazzal and El-Nashar (2007) [25] for simulation works. Nawijn (1983, 1984) [26,27] studied the analytical model of two heterogeneous servers with recirculation, Pourbabai (1987) [28], the asymptotic performances of random access, and an ordered entry G/M/K/O with approximate expressions. Recently, Boysen et al. (2019) [29] have presented a revision focused on the operation and not on modeling. Even though, close-loop or recirculating systems have been studied much less than ordinary loss systems, the recirculating flow represents additional difficulties in system modeling. Using stochastic models Muth and White (1979) [24] analyzed a conveyor with one loading station. Soderman (1982) [30] modeled the recirculating conveyor systems with a single loading station and a single unloading station as GI/M/1/1, by superposition of recirculating rate with the new arrivals. He approximated joint interarrival distribution as hyperexponential with an iterative method. Schmidt and Jackman (2000) [31] modeled a recirculating system as a queue network based on an approximate method of solving tandem finite queues with blocking by Brandwajan and Jow (1988) [32]. Hsieh and Bozer (2005) [33] used conditional probabilities to approach the recirculating overflow and considered multiple unloading stations. Haghighi and Mishev (2006) [34] revised the formulation of Disney’s model in a two-station multiserver model with balking and reneging. Retrial queues or recirculating systems are also of particular interest in modeling service systems like call centers, Gans et al. (2003) [6] or in merging systems with recirculation, Van der Gaast et al. (2018) [35].
Together with the analytical models, time-consuming simulation allows the evaluation of system performance of complex systems dimming the difficulties of heterogeneous systems. Proper simulation can also provide experimental verification of analytical models. Today’s growing computing capabilities are paving an increasing use of simulation. Nevertheless, the possibilities of analytical models can be better valued in optimization analysis, transient behavior, or system control, in particular when quick solutions are better that long simulation runs, with a particular interest in the decision-making of evolving flexible systems.
Heterogeneous systems have no accurate analytical models available like homogenous ones. We contribute to reducing this gap in this paper with a set of new scalable models that gives accurate quantification of the loss of the parallel system with heterogeneous servers of limited capacity, and even including recirculation. It will allow the calculation of performance metrics based on the state probabilities solved from the transition matrix. We develop a detailed justification with a novel approach to evaluate the loss of the system applied to parallel heterogeneous servers and we also verify its agreement with simulation results with differences under 0.5%, followed by the analysis of system performance. The model contributes to overcoming the low accuracy of other loss estimations only based on the probability of a busy system from conventional transition state diagrams, which states only enumerates the size of the system. Its application to recirculating systems also gives a good approximation, under 1% across most of the arrival rate range. Finally, these good results have suggested approaching some more general heterogeneous systems with service rate distributions other than Poisson.
This paper is organized as follows: In Section 2, we present parallel systems of identical servers without a waiting line and the classical transition diagram of a loss system, Model A, where the PASTA property is applied for heterogeneous servers and only gives a rough approximation to the simulated system. Next, a new approach to evaluate loss is introduced in Model B. It is verified against former analytical calculations from literature and through experimental simulation, with very accurate results in both cases. It follows the detailed analysis of the loss and full-size probabilities of the system across the arrival rate range. Then, Section 3 introduces Model E, which includes a waiting queue of limited capacity in front of the servers, and the influence of the maximum queue size is analyzed for optimal configuration. In Section 4, the recirculating system is modeled by adapting Model E, and its performance is checked against simulation results. Next, in Section 5, the combined application of Model B with the Monte Carlo Method evaluates the use of the transition states matrix of Markovian chains to evaluate systems with non-exponential service time distributions. In the Conclusions section, a synthesis of contributions, results, and potential future works are outlined.

2. Loss parallel system without queue

We consider a workstation with a mean service rate μ with Poisson distribution (service interdeparture time of exponential distribution), with a total capacity of k units, in a queue of finite capacity k-1, and with an arrival flow rate λ. It is represented by the distribution of state probabilities of M/M/1/K equated by (1), with utilization ρ=λ/μ and inventory L, [1].
i = 0 , .. k ; p i = { ρ i ( 1 − ρ ) 1 − ρ k + 1           i f       ρ ≠ 1 1 k + 1                 i f       ρ = 1     }                       L = ∑ i = 0 k i ⋅ p i
If the server has infinite capacity, the departure rate will be equal to the arrival rate with the same distribution (Burke, 1956) [36]. Because of the finite capacity of the buffer queue, the effective input rate will be lower than λ, so when the system is full with k units, a new coming unit cannot enter the system and is lost or discarded from the arrival flow. Due to the memoryless property of the arrival rate of exponential time distribution, the loss does not modify the exponential interarrival time distribution, with an effective rate λeff lower than λ due to loss. The effective rate is λeff=λ(1-pk) based on the PASTA (Poisson Arrivals See Time Averages) property ([2] p. 128; [1] p. 14 & 102; [3] p. 73).
Next, we consider the model of homogeneous servers M/M/m/m, with the rate of arrivals λand of k identical parallel servers with the service rate μ that have all Poisson distribution (exponential interarrival time) with a k maximum size or capacity of the system. It is frequently named the Erlang first model and the probability of the full system is given by the well-known Erlang-B formula B(m,r) (2), where the traffic flow ratio is r=λ/μ and the utilization ρ=λ/(mμ). We have run the experimental simulation of the M/M/1/m and the Erlang systems through the discrete event simulation software Arena by Rockwell, in 30 regenerative replications of 1000 h, with a previous 1000 h warm-up period. It confirms the full agreement of the mean results from simulation and the analytical model always within 1% difference and inside the half-width interval of simulation variability that includes the 95% simulation shots, in all the regime ranges. The use of Little’s law based on this effective input rate allows the calculation of the waiting times or cycle time inside the system CT (queue and server) from L= λeff ⋅CT..
  p i = ( λ / μ ) n n ! ∑ i = 0 m ( λ / μ ) i i !   ;         i = 0 , ..     m ;       a n d       B ( m , r ) ≡ p m = r m m ! ∑ i = 0 m r i i ! ;     r = λ / μ

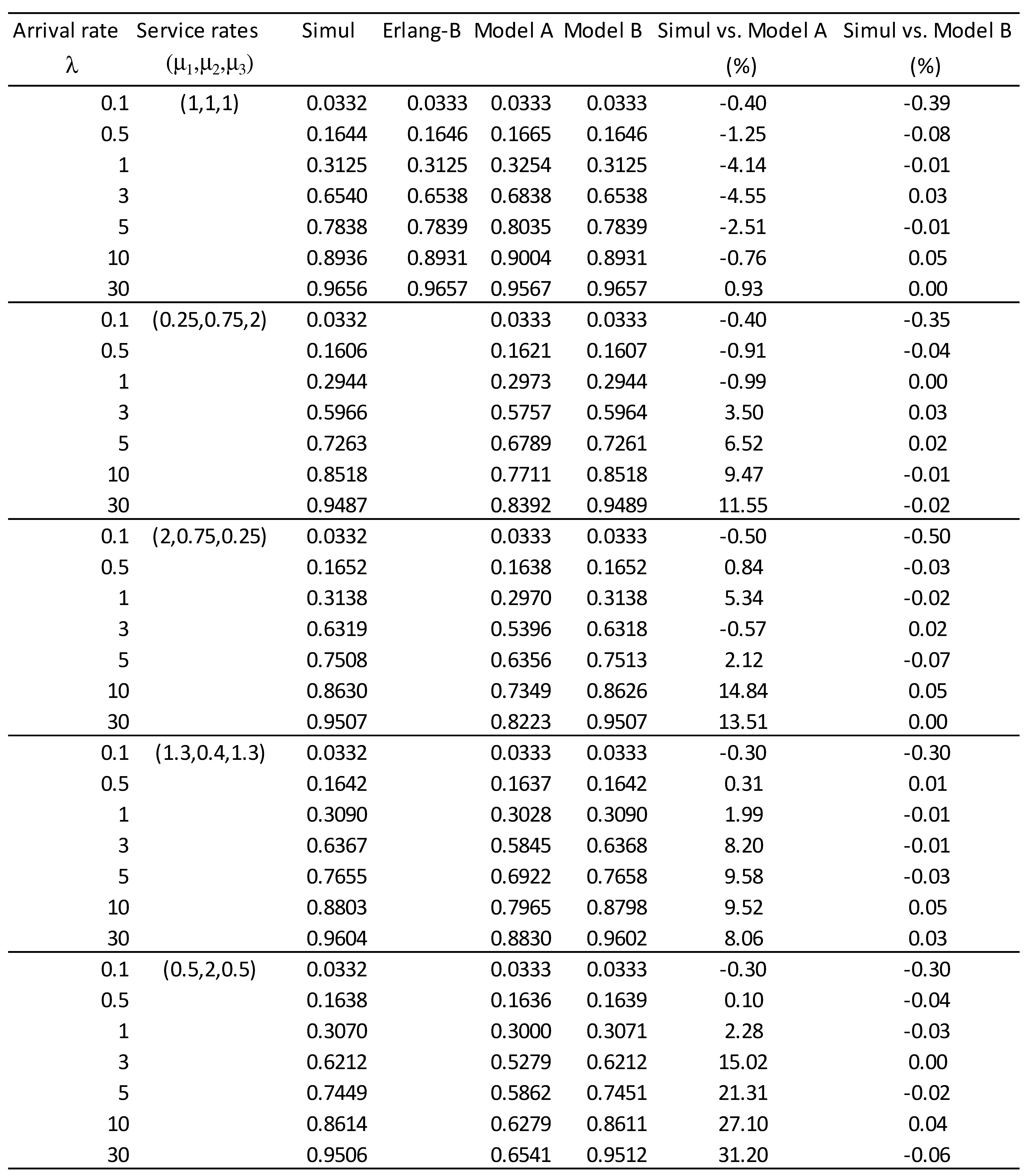
2.2. System of heterogeneous parallel servers

Next, we consider a multiclass or heterogeneous server system, with arrival rate λ with Poisson distribution. We consider a 3 parallel server system with service rates μ1, μ2, μ3, also with Poisson distribution. Parts or customers are serviced ordered entry. The state diagram of the system, Model A, is included in Figure 1. Each server can only allocate 1 unit and the 3-tuple indicate which server is in service (1) or empty (0), read from right to left, like a binary number. Thus, (110) denotes empty (0) the server 1 and in service servers 2 and 3. The state (1,1,1) is the state of the full system.
The resolution in the stationary regime of the Markovian chains system can be expressed by their state equations in the form of the transition matrix (3) and by solving the homogeneous linear system of equations. It is an ordinary alternative replacing the last equation with the product form condition of probabilities sum the unit, (3).
A ⋅ p = c [ − λ μ 1 μ 2 0 μ 3 0 0 0 λ − ( λ + μ 1 ) 0 μ 2 0 μ 3 0 0 0 0 − ( λ + μ 2 ) μ 1 0 0 μ 3 0 0 λ λ − ( λ + μ 1 + μ 2 ) 0 0 0 0 0 0 0 0 − ( λ + μ 3 ) μ 1 0 0 0 0 0 0 λ − ( λ + μ 1 + μ 3 ) 0 μ 2 0 0 0 0 0 0 − ( λ + μ 2 + μ 3 ) μ 1 1 1 1 1 1 1 1 1 ]     ⋅     [ p 000 p 001 p 010 p 011 p 100 p 101 p 110 p 111 ]     =     [ 0 0 0 0 0 0 0 1 ]
Model results and system simulations are included in Table 1, where R*=R/Σμ.. In the case μ1=μ2=μ3, it can be directly compared to the Erlang first model for k=3 by (2). The throughput is calculated for Model A by applying the PASTA property, so λeff =λ(1-p111)= λ(1-pf), where pf is the probability of the maximum size or full system.
There are significant differences between the experimentally simulated throughput and the calculated by Model A which mostly overestimates the throughput when arrival rates are high (saturation). Note that in this conventional transition diagram that enumerates the states of the servers, the probability of the full system with all busy servers estimates the probability of loss. The transition to the full system (111) happens at the rate λ (birth) from the size 2 of the system ‒states (110), (011) or (101)‒ and the system leaves (death) the full state from size 3 to 2 at rate Σμ
We also consider the homogeneous system M/M/m/m with m=3, so it is applicable the Erlang-B formula (2) for the calculation of the effective throughput λeff=λ(1-p111)= λ(1-B(3,r)), see Table 1. For the Erlang model, the results are completely in agreement with those from the simulation, thus the identical set of servers of M/M/m/m behaves with no difference with an ordered entry system, but since the servers are undistinguishable, the order becomes irrelevant and there would not be difference serving by ordered entry, random entry, or another service discipline [31].
Next, we consider a new formulation of the transition diagram, Model B. Different from Model A, when the system is full, the lost offered load is redirected to a virtual server with a queue of infinite capacity, herein called loss server, where arrivals enter when the real servers of the system are occupied, Figure 2. When arrivals are lost the busy system enters the state >111= b.
The transition matrix is given by (4), and the mean number of customers L in the system or the utilization U is calculated by (5). Note that when the system falls into the loss server, state >(111)=b, the 3-server subsystem is occupied, and the calculation of L in the servers by (5) is taken into account. In the transition diagram, the transition (birth) from the busy system (111) into the loss state happens at the rate λ, so the arrival goes into the loss server when servers are busy and the system leaves this loss state at the rate Σμ from size 3 to 2, as soon any server is available to serve, as represented.
A ⋅ p = c [ − λ μ 1 μ 2 0 μ 3 0 0 0 0 λ − ( λ + μ 1 ) 0 μ 2 0 μ 3 0 0 0 0 0 − ( λ + μ 2 ) μ 1 0 0 μ 3 0 0 0 λ λ − ( λ + μ 1 + μ 2 ) 0 0 0 0 μ 3 0 0 0 0 − ( λ + μ 3 ) μ 1 0 0 0 0 0 0 0 λ − ( λ + μ 1 + μ 3 ) 0 μ 2 μ 2 0 0 0 0 0 0 − ( λ + μ 2 + μ 3 ) μ 1 μ 1 0 0 0 λ 0 λ λ − ( λ + μ 1 + μ 2 + μ 3 ) 0 1 1 1 1 1 1 1 1 1 ]     ⋅     [   p 000 p 001 p 010 p 011 p 100 p 101 p 110 p 111 p 111 b ]   =   [   0 0 0 0 0 0 0 0 1 ]
  L = ∑ i = 0 k + 1 i ⋅ p i =     0 ⋅ p 000 +   1 ⋅ ( p 001 + p 010 + p 100 ) + 2 ⋅ ( p 110 + p 101 + p 011 ) + 3 ⋅ p f   + 3 ⋅ p b U = L / 3
The results of simulation in Table 1 have been obtained with Arena software by Rockwell Inc. λ=μi=1, also with a simulation run of 30 replications of 1000 hours, after 1000 hours warm-up for the stationary regime, where throughput is expressed dimensionless by divided into Σμi. The effective throughput rate is calculated by λeff=λ(1-pbusy). Where pbusy is the percentage of time the 3-server system is busy. In the Erlang model of identical servers pbusy pbusy =B(3,r) by (2), for Model A with 3 servers is pbusy =p111 = pf from (3), and in the case of Model B, with 3 servers and the loss server, is pbusy =p111+p>111= pf+pb from (4). Model A is a representation of a loss system that evaluates throughput from the offered load λ. The direct calculation based on the PASTA property with the effective offered load λeff=λ(1- pf), is only a rough approximation for heterogeneous parallel servers, as the experimental results in Table 1 show for Model A.
The results indicate that the description of the system states and their probabilities should take into account not only the states of the servers but the associated allocation of all the arrivals and the different independent states in order to be considered a product form set of state probabilities of sum unit. In addition to the servers’ busy state (111), the lost customers enter the loss server. In the transitions diagram of Model B, the >(111)=b is a state of full size for the servers. The system transits into the state >(111) with the rate λ when the arrivals overflow the servers, and the net input into the servers is λeff , while through the loss server is λ-λeff. Based on the PASTA property, the split of the Poisson rate for all the servers, including the loss server, remains Poisson [1]. Based on [36], the net output rate through the loss server, which includes a queue of infinite capacity, is also λ-λeff, as providing the service rate of the loss server is greater than λ-λeff. This loss server has infinite capacity and we can associate an arbitrarily sufficient high service rate>(λ- λeff), complying with it. Finally, the total output of the whole system is λ, the sum of the servers and loss server together.
The system transition into the loss server of probability pb with rate λ after the system is full (111), and the system leaves the state at the rate the sum of the service rates of the 3 servers, so as soon any server releases a customer after service the number of customers in the servers becomes m-1, as represented in the transition states diagram. Note that by including the loss server in Model B, the system is not a loss system anymore, so the calculation of the states associated with the offered rate is accurate. The probability of state >(111)=b is the percentage of time that the arrival rate falls into the loss server, but this happens always after the servers are occupied. In Model B the PASTA property is applied to the 3 real servers defined in the transition diagram: the offered rate to the servers is λ(1-p>111 )= λ(1-pb ) before the application of the PASTA property. After applying the PASTA property to the three servers input, the effective rate through the servers becomes λeff=λ(1–p>111–p111)= λ(1–pb –pf), by discounting the percentage of time the servers are occupied p111. The arrival net rate into the loss server is finally λ( pb+pf), which is an accurate account of the time percentage that the total arrival rate λ (offered load) does not enter into the servers, verified in the experimental through the accurate results of Table 1. There is a need of considering every single arrival in the probabilities that arises from the multi-dimensional queue nature of the ordered entry for heterogeneous systems. While Erlang systems of undistinguishable homogeneous servers do not require it.
In the timeline of the arrival rates, there are intervals of time when the servers are occupied and no arrivals trying to enter the system with probability pf, and others where the arrivals try to enter and are rejected to the loss server with probability pb. At both intervals, no entrance of customers into the server system is possible, so they are discounted to get the effective arrival rate into the servers. In Model B, the every arrival is included in the set of states for accurate accounting, so the system evaluates every customer destination. In general, an ordinary transition matrix that only enumerates the states of the servers, Model A, overestimates throughput (underestimates the probability of occupied servers) for high offered load by applying the PASTA property, see Table 1. In synthesis, including the time percentage of the loss state (loss server) provides accurate throughput calculation of systems of finite capacity, Model B.
The evolution of the probabilities or percentage of time for Model B of full servers pf, loss from blocking when servers are busy (blocking) pb, and the system occupied pocc= pb+pf are represented in Figure 3. In addition, the probability of an empty system p0 is represented in the results. While λ/Σμ < 1, the probability of system busy pb is lower than the probability of full servers pf. When λ/Σμ≈1 both are equally probable. It is remarkable that the probability of full servers pf continues to grow with increasing levels of arrival rate up to the point it reaches a maximum, at about λ/Σμ≈1.75. After that maximum, when some extra load is offered, goes directly to the loss server, and pf decreases while pb continuously grows. The percentage of time the servers are occupied with no customers trying to enter the servers, pf, decreases monotonically after that maximum, so for an infinite arrival rate, it is inferred that there is no chance of a full system without loss, so pf → 0 while the probability of loss from blocking pb continuous to grow. Thus, when an extremely high load is offered λ→∞, loss from blocking probability pb would become the only probable situation.
Also from the results of Figure 3, at low λ, the probability of empty system p0 is higher than the probability of occupied system pocc. At about λ/Σμ≈0.6 both are equally probable and when λ/Σμ >0.7 approx., the probability of empty system p0 becomes lower than the probability of occupied servers pf. In an attempt to maximize the utilization of servers, increasing the arrival rate λ over that point will increase the utilization. Nevertheless, if the increase of cost from losing a customer is higher than the reduction of cost by increasing utilization, operating the system over that point might be no convenient. Increasing the installed capacity to avoid customer loss instead of increasing server utilization might be a better option. Note that at λ/Σμ≈0.6 the perceived saturation of servers is low, so only about 18% of the time the servers would be observed full, pf, or empty, p0. Nevertheless, judging the service performance of a loss system based on the observed utilization of the servers seems to be clearly misleading: for instance, at a high offered load of λ/Σμ =4, less than 20% of the time the servers will be fully occupied pf, with the appearance of extra idle capacity, while in fact the system is saturated and the offered load loss pb is more than 60%.
Model B considers heterogeneous servers, whereas the Erlang model M/M/k/k just with k identical servers is a particular case. In this case, the full system state can be described properly by λeff=λ(1- pbusy), from (1) and (2), results included in Table 1. The results of Model B for (k=3, μ1=μ2=μ3=μ=1) of identical servers are also those of the Erlang-B formula. It results in pbusy = B(3,λ/μ) in Figure 3, but it has also been verified through the numerical values identical to 15 decimal places.
The calculations based on simulation confirm the accuracy of Model B, M/Mi/k/k, to describe the heterogeneous parallel server systems. From the former results, it is valuable the comparison the overflow results of M/Mi/k calculated from the analytical results by Matsui and Fukuta (1977) [21], and those got for the full system pbusy= pb+pf from Model B, Table 2. The probabilities are identical. Based on the independence of events of the exponential interarrival times, the results from the arrangement of arrivals in an infinite waiting queue or providing new arrivals after the loss are equivalent in terms of overflow or loss. Noteworthy, the M/Mi/k system has an infinite capacity queue in front of the servers. It is known that this system model is unstable when λ≥Σμ is unstable as the waiting line grows indefinitely. Meanwhile, the M/Mi/k/k by Model B redirects the overflow to the loss server without that limitation.

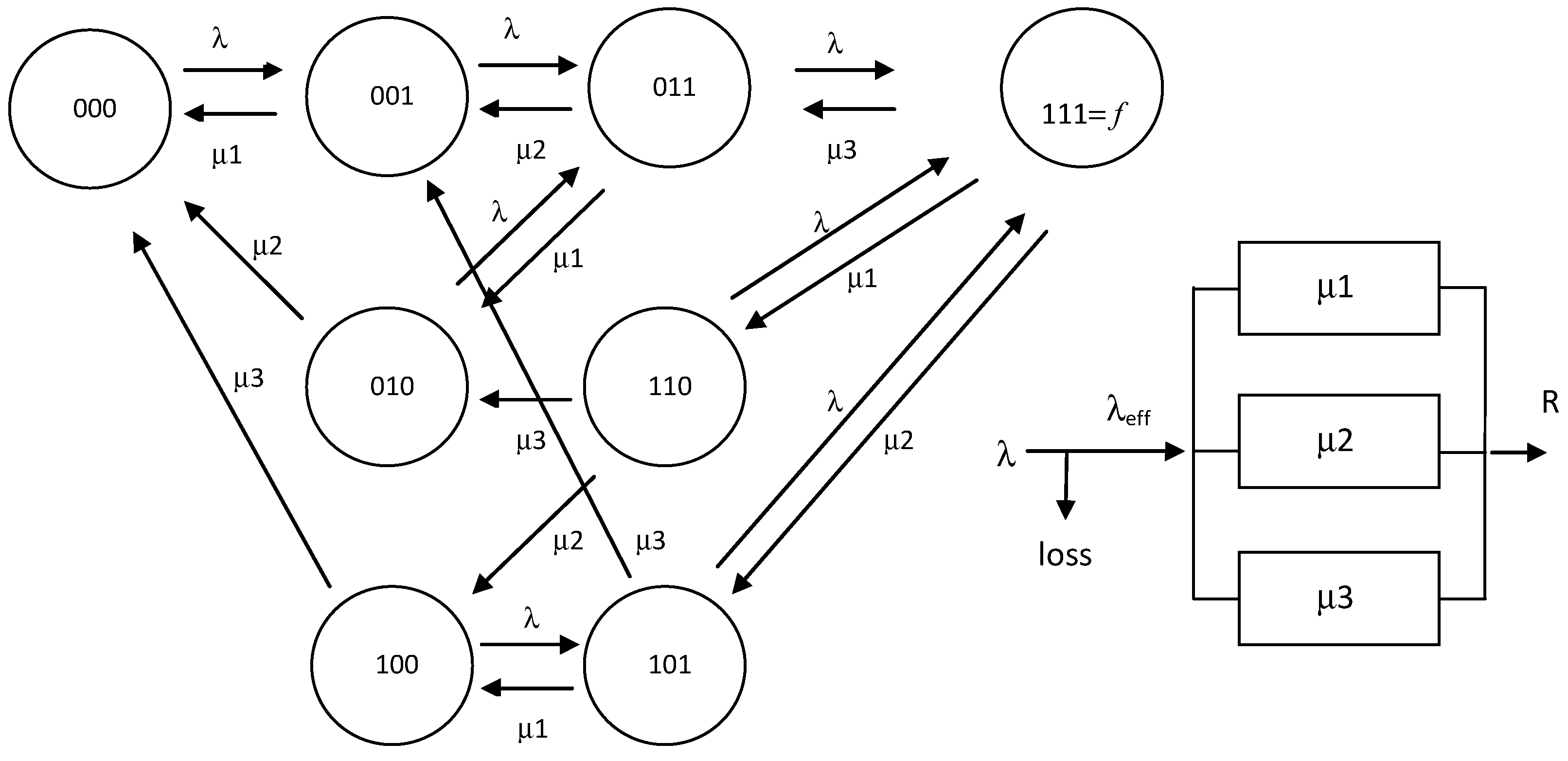
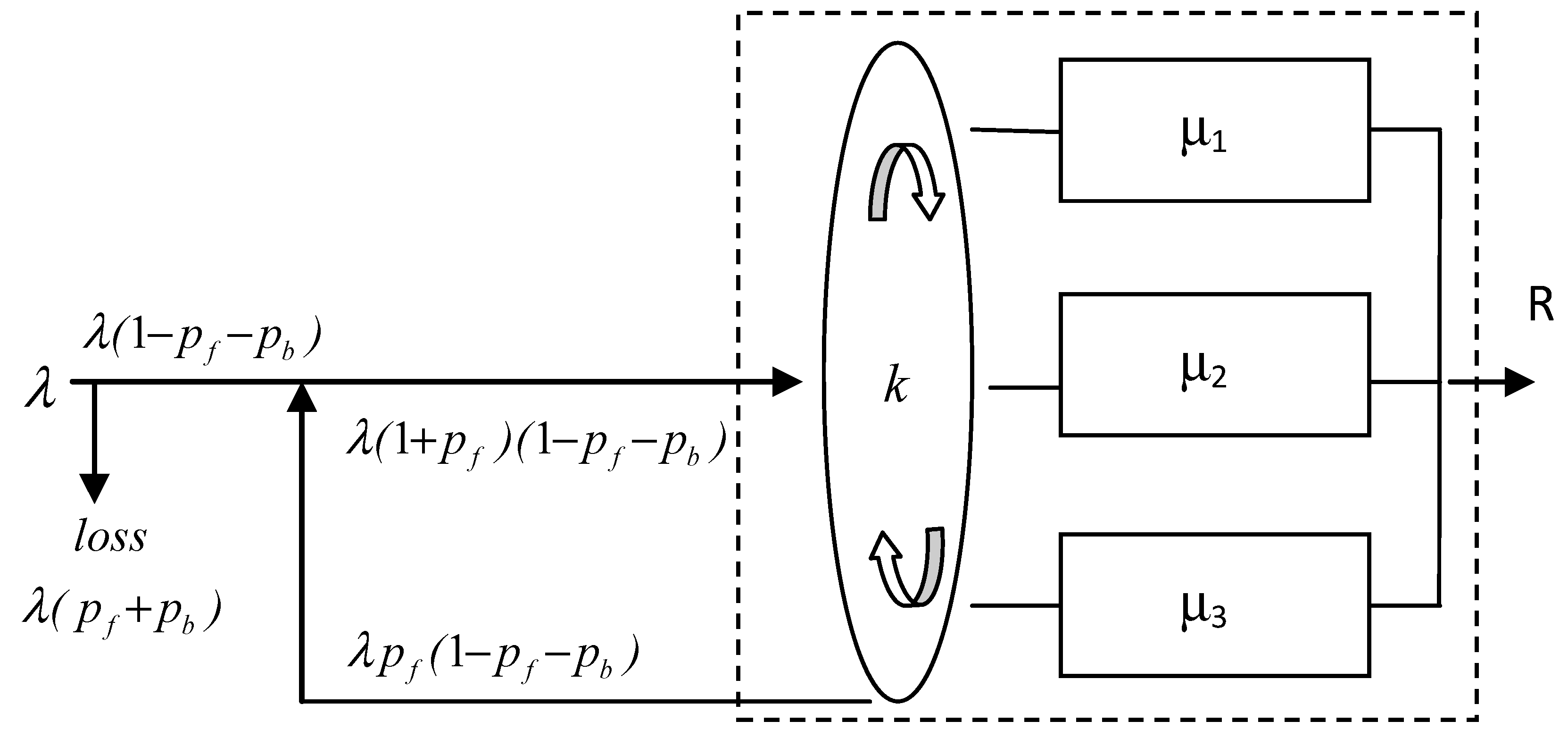
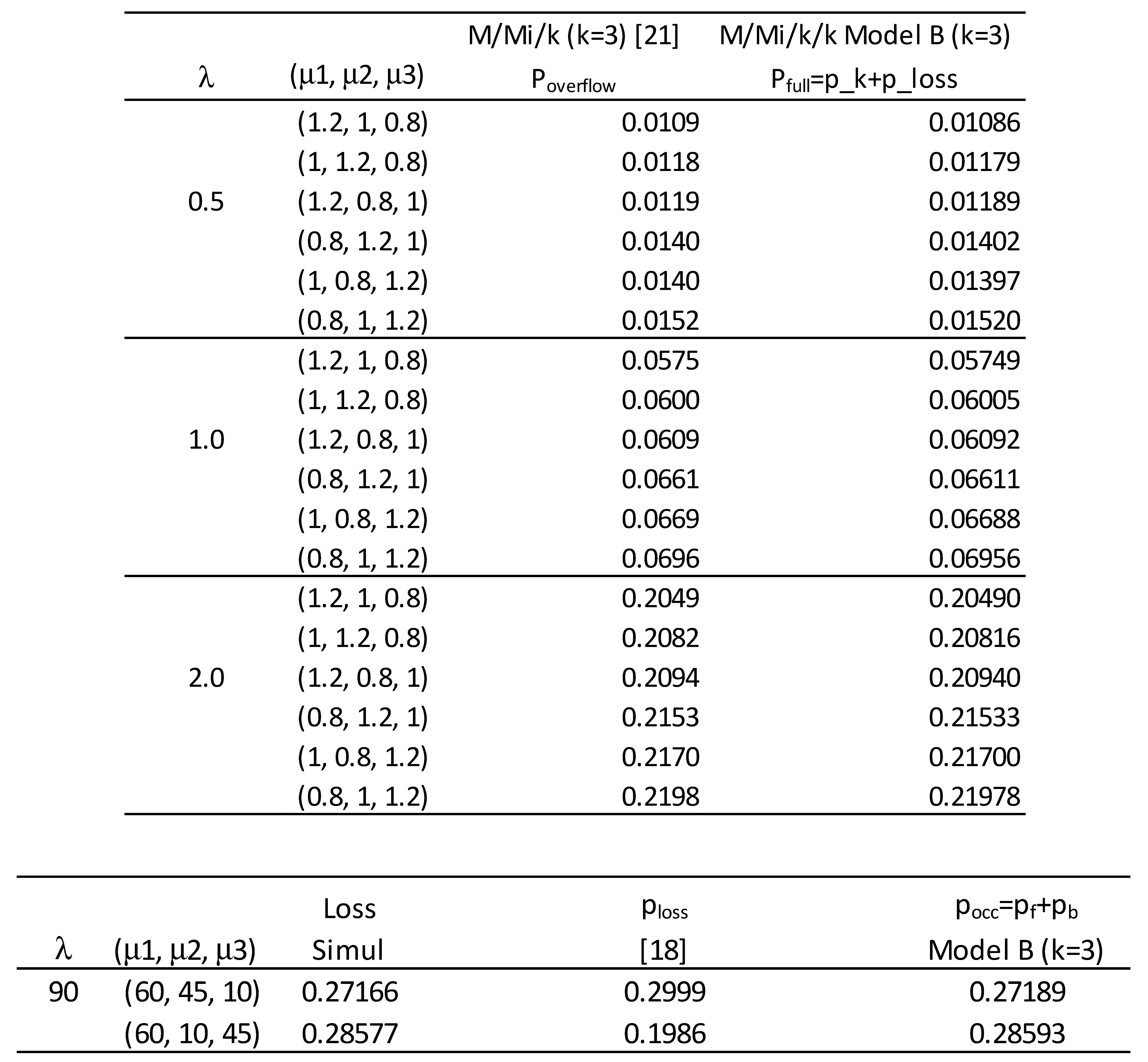
3. Parallel heterogeneous servers with a common waiting queue.

The Model B includes servers without any prior queue. Next, we consider Model E, Figure 4, where the servers have a common queue of limited capacity in front of them, so only when the queue is full the incoming arrivals are lost. The discipline of assignation is ordered entry. The whole system has a total capacity of m+k, where k is the capacity of the queue and m is the number of servers. For the case of m=3, the transition rate diagram of Figure 4 represents the states of the system, where the state >(3)+k is the state where loss probability is accounted, pb. In the birth and death transitions, the death of the state b falls into the (3)+k-1 state, because as soon as any customer is serviced in any server, a customer enters the server and a new allocation in the queue of capacity k becomes available. Its transition rate matrix k=3 is A in (6).
Preprints 93195 i006
In order to evaluate the performance of the model, Table 3 shows the comparison of the throughput of Model E vs. the simulation results, where the dimensionless throughput is R*=R/Σμ=λ(1-pf-pb)/Σμ. There is complete agreement in the results and the proper representation of the parallel loss system with buffer by Model E. The Model B and Model E of multiclass or heterogeneous servers have been presented for m=3 and they are accurate.
The accuracy of this methodology can be used for large systems M/Mi/m/m+k, at the cost of the description of intermediate states in the state transition matrix, because the size of the transition matrix is of the order 2m. Nevertheless, the construction for a higher queue capacity k is a much simple birth and death sequence of extra states in the queue. We have developed the algorithm to automate the generation of elements of the transition matrix for an arbitrary number of servers m. Even when the coding of the algorithm is out of the scope of this paper, it is worth mentioning some basic insights. The matrix is sparse and can be formulated as the sum of three rate matrices: rates out (negative) from the state (allocated in the diagonal of the matrix), rate into the state (positive) from the death of other states, and rate to the state (positive) from other state births. The states are also automatically enumerated from the binary number representation (m digits) of every server state (0-1, idle or busy). Even programmed in a matrix efficient code like Matlab, this exact transition matrix construction of size order 2m is heavy for moderate system size m.
For the sake of presenting the model generalization for any size of the system, Figure 5 includes the operating curves R* vs. offered arrival rate λ, calculated for parallel systems of m= 6, 8, and 10 servers, in each case with queue capacity k=m/2, and Σμ=8. The service rates are in descending arithmetic progression from the first server μ1=1.5(Σμ/m) for faster to slower (f-t-s) and ascending up to the last server with μm=1.5(Σμ/m) in the slower to faster (s-t-f) arrangement.
Now, we examine how the pattern of the servers influences the performance of the system, Figure 6. With slight unbalance, some extra throughput is obtained when the order from faster to slower is applied, but when the unbalance is high, see for instance (2, 0.75, 0.5), the benefit can be only obtained under medium to low utilization (low arrival rate). The system underperforms the balanced service rates (1,1,1) of the same average for high utilization. When utilization tends to saturation (see Figure 6 over 90% utilization), the throughput is quite similar, attenuating the effect of the server’s arrangement. Even though, for a given average arrival rate of mean service time, the maximum throughput is reached by homogenous servers (1,1,1) or slightly heterogeneous. A high unbalance in service rates punishes the throughput. In a rough estimation, reductions up to the order of 5% in R/∑μ can be observed in Figure 6, depending on the pattern of multiclass servers that makes significant heterogeneity for the performance and not only the average of service rates.
Next, the performance improvement by adding a queue is evaluated through Model E for different values of maximum queue capacity, Figure 7. For k=0, Model E is equivalent to Model B. The operative curves of Figure 7 show that the size of the buffer increases throughput, but more relevant, for heterogeneous service rates, the performance can reach higher results with unbalanced service rates arranged from slower to faster, (0.25,0.75,2), than the balanced distribution (1,1,1), as providing a buffer of enough capacity. In the case of heterogeneous servers without any queue, ordering the servers from faster to slower gives the best results in throughput.
When heterogeneous servers are combined with a prior queue, the performance is slightly better with assignation from slower to faster service rates when no queue (k=0), but in combination with a minimum queue the results become similar, and with sufficient capacity (k=4) the performance of heterogeneous and homogeneous systems are undistinguishable, see Figure 7. A properly dimensioned queue before the multiclass parallel servers can provide improvements in performance overwhelming the heterogeneity of service times. This applies to traffic problems like call centers where the use of interactive voice response to the arriving customers can handle a waiting queue to be serviced. Former research established priority on the faster agents in [37], also mentioned in [14] and [16], or in the problem of fair agents, [7]. Our results show that a proper queue or buffer can compensate for heterogeneity.
Conversely to manufacturing systems of tangible products, where the cycle time of customers in the system could be secondary after throughput, in service manufacturing or pure service systems, the sojourn time in the system could be a priority and fundamental metric. For the system under study with m=3, multiclass servers with a buffer of maximum size k before them, the time in the system, also called sojourn time or cycle time CT , is calculated by the Little’s law (7) and represented in Figure 8. At low λ, the better results (minimum CT) are obtained with faster-to-slower server priority, while in the rest of the range the better configuration is the homogeneous arrangement of servers. While queue capacity improves throughput by mitigating loss with a high offered load, it also increases CT.
  L ( m = 3 ,   k )   = ∑ i = 0 m + k + 1 i ⋅ p i =     0 ⋅ p 000 +   1 ⋅ ( p 100 + p 010 + p 010 ) + 2 ⋅ ( p 110 + p 101 + p 011 ) +     3 ⋅ p 111   + 4 ⋅ p 111 + 1 + ...   ( 3 + k ) ⋅ p f + ( 3 + k ) p f C T = λ e f / L = λ ( 1 − p 111 + k − p > 111 + k ) / L = λ ( 1 − p f − p f ) / L

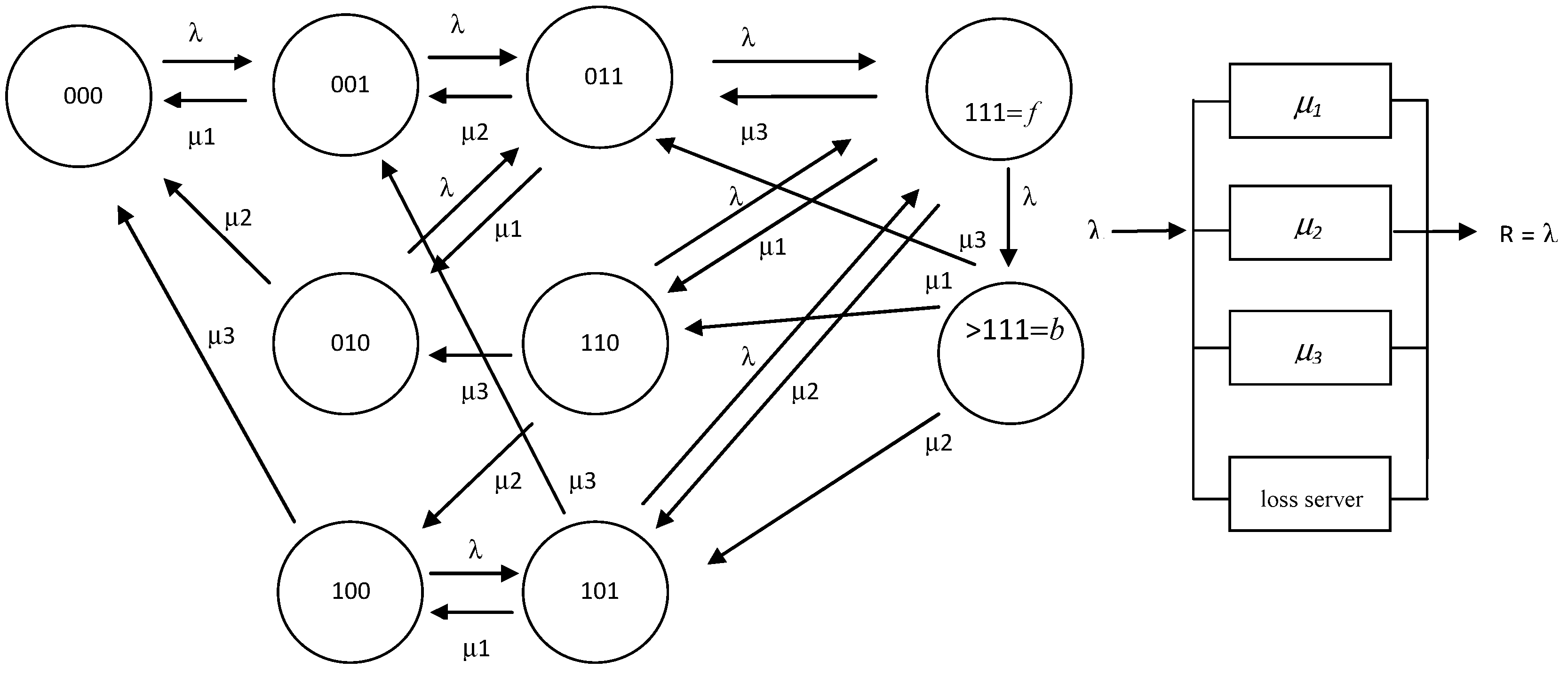
4. Parallel heterogeneous servers with a common waiting queue.

Next, we consider the case when the rejected arrival rate recirculates and merges with the offered input flow into the system, instead of blocking and direct loss. The system could represent a conveyor with recirculation or another system with retrial. The recirculating rate has priority over the external input and the system remains a loss system. In general, it is known that the merging input rate will not be Poisson [36]. Models B and E have demonstrated their accuracy to evaluate the overflow of a parallel system of limited capacity.
We modify Model E to include the recirculation flow as represented in Figure 9. When the conveyor recirculates the non-served arrivals, the offered load increases including the flow recirculated in the time percentage the system is full pf, so the expected recirculated rate is λpf, and the net offered load to the system becomes λr =λ(1+pf) instead of λ. Thus, considering the findings from Model B, the loss of this net offered load would be λr (pf+pb) =λ(1+pf) (pf+pb), but in fact, the loss of the recirculating fraction λ pf (pf + pb) doesn’t exit the system, but it remains in recirculation, so the net loss out of the system will be λ(1+pf)(pf+pb) - λ pf (pf+pb) =λ (pf+pb) that is consistent with the net balance with the external offered load λ, already verified in the Models B and E. In consequence, the output rate is expected to be λr(1-pf-pb)= λ(1+pf) (1-pf-pb). The recirculation does not generate any extra state in the transition state diagram of servers in Model E, see Figure 4, but increases the offered load to the servers. In general, the probabilities pf and pb with recirculation would reach different values than those without recirculation.
We formulate the recirculation model through the transition state matrix as a product form problem with the same states of Model E, so the size of the system provides a complete description of states with probability sum unit, but with the correction of the offered load at the entrance of the conveyor. Thus, the resulting matrix for the conveyor of maximum capacity 3, with 3 servers and ordered entry service is also (6), but the offered load is λr =λ(1+pf) instead of λ. The state probability is the solution of the A⋅p=c, where A=A(λ,μi,pf). The solution is obtained from the iteration on pf as a fix point problem that converges very quickly. In general, the expression of the effective rate offered and the recirculating rate through the conveyor involve conditional probabilities, but the proposed transition state diagram is complete by incorporating the loss server state, and the iteration as a fix point problem provides the state probabilities solution.
In Table 4, the results for the system of 3 servers with a queue (conveyor) of maximum capacity 3 are included, with and without recirculation. The output rate has been evaluated from the average result of simulation over 600,000 recirculating cycles with a warm-up of 60,000 cycles, with 10 independent replications. Model E with recirculation approaches simulation within 1% in most of the ranges of operation, with a maximum below 1.4%.

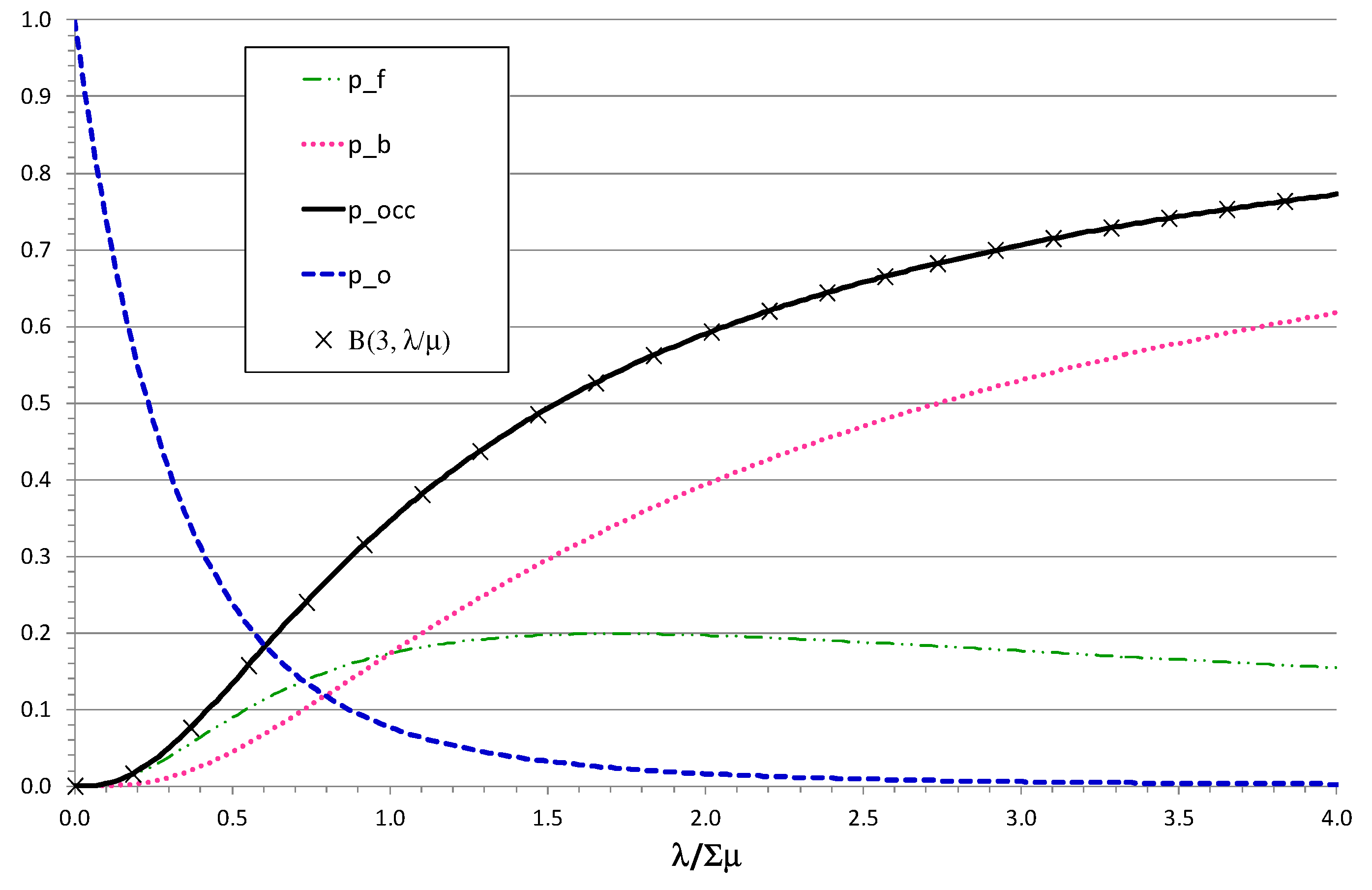
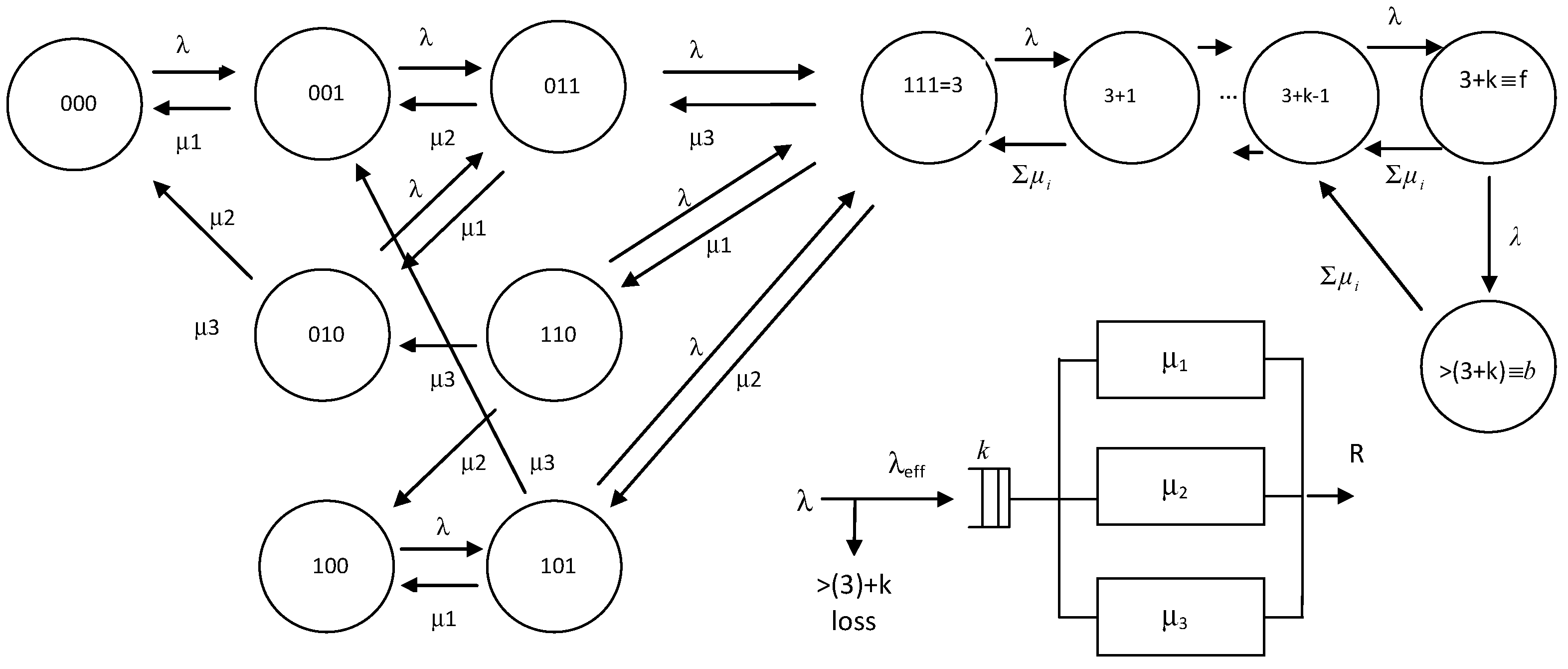
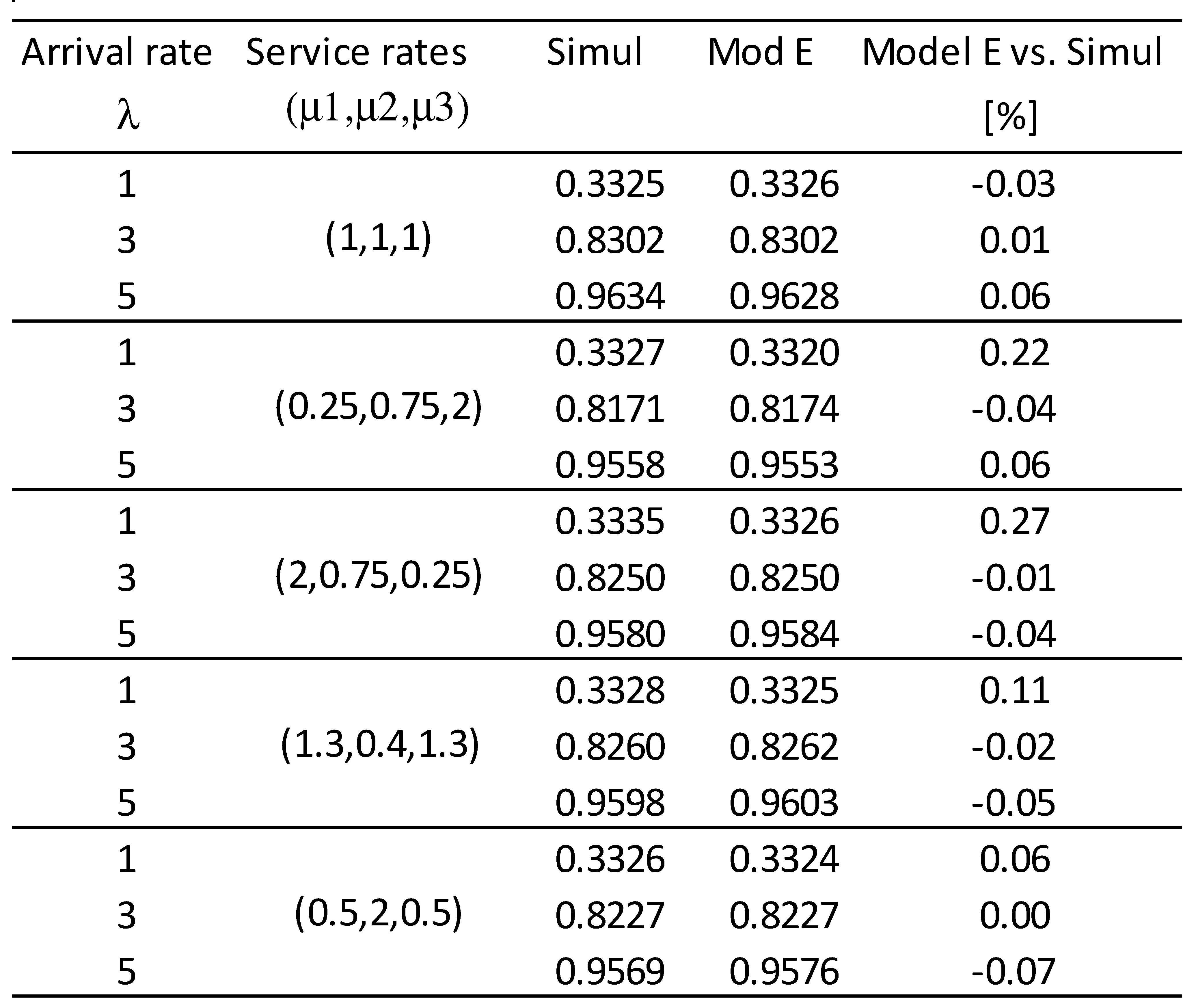
5. Hybrid modeling of heterogeneous servers with general service time distributions.

5.1. Uncertainty of the offered load

The stationary solution of the M/M/c/c+k system of identical servers has been studied analytically and is included in manuals of Markovian queues. The analytical multiclass, multichannel or heterogeneous servers Model E can be used to study the performance of M/Mi/3/3+k, but using the Monte Carlo Method (MCM) could be approaching M/Gi/3/3+k. The combination of MCM and Model E can offer the resulting distribution of the stationary solution for each system setup of mean arrival rate, and service rates Gi coming from general (non-exponential) distributions. Regardless of the distribution from which the service rates come, Model E offers one solution (stationary), so it could be assessed the variability effect of service rates under general distribution on performance by generating the resulting distribution of performance results.
We propose the use of the precise stationary solution from the transition matrix in combination with MCM to evaluate the effect of the uncertainty in the offered load or the service rates, approaching the solution of the system for other service distributions. The transition matrix is developed with the strong assumption of events independent or memoryless, so independent state probabilities are evaluated in a Markovian process. The MCM would offer the distribution of solutions from independent trials of shots to the non-exponential distributions of arrival and/or service rates. MCM is a standard method for uncertainty evaluation in other fields like metrology and its use together with the analytical Markovian model can bring benefits to evaluate the effect of service time variability or arrival rate uncertainty, without the time-consuming discrete-event simulation to get the stationary solution under general distributions. For instance, it might be of interest in facilitating system control or decision-making in logistic or manufacturing activities in cyberphysical systems. While the transition matrix gives the stationary solution of the temporal series, the output of the MCM is a distribution around the average stationary solutions that show the expected spread around the mean value under the ergodic assumption, due to the variation of the service times under different distributions.
Hybrid modeling of accurate Markovian chain models in combination with MCM could facilitate approximate studies by dimming the limitation of the distribution with memory that non-exponential distributions impose, because each shot in the MCM simulation will be calculated independently with the accurate stationary result (expected asymptotic mean in time of an ergodic process), and the resulting distribution from MCM will the convolution of stationary results generated from shots to the distribution of the arrival rate or the service rate. The alternative of direct discrete-event simulation would require to looking for the average solution when a simultaneous change of mean values and their variance, so the effect of mean and variance would be combined in every solution of the simulation run. In addition, real systems are better represented for decision-making by mean value of service time or demand in short-term periods with some uncertainty, but with a drift in longer temporal periods. The accurate transition rate matrix of Markovian chains combined with MCM simulation represents a convenient and controlled way of separating the variability in different time scales, dealing with the offered load uncertainty, or analyzing the mean effects on system performance for non-exponential service time distributions.
In Figure 10 are presented the results for Model B, with a standard deviation of 10% of the offered load, with mean service rate configurations (1,1,1) and (2,0.75,0.25) of the same average service rate 1. Each point in the Figure 10 is the result of 10,000 shots through MCM simulation. While the overall mean performance seems to be slightly higher for (1,1,1) across the range, depending on the particular level of offered load it could be reverse or simply undistinguishable due to the uncertainty of the arrival rate.

5.2. Application to non-exponential service time distributions

In Table 5, the results of simulation and Model B are compared for exponential service time and also normal or lognormal distributions. The normal distribution can be appropriated for logistic or manufacturing systems, where the coefficient of variation (CV) in the range from 0.2 to 0.5 is realistic [38]. A 0.3 value is set for this study. The lognormal distribution is found to fit properly some service times like call centers. Again the CV=0.3 has been used, based on [39]. For the application of MCM each point is obtained from 10,000 shots to the distribution.
We note that sampling service times from a normal distribution of a given mean provides a normal distribution of service times of the same mean. In the case of the lognormal distribution, in order to provide a mean service time m and coefficient of variation CV the sampling distribution must sample from the mean μ and standard deviation σ given by (8).
μ = ln [ m C V 2 + 1 ]   ;       σ = ln ( C V 2 + 1 )
As a consequence of non-exponential service times, the throughput does not vary in a significant way with respect to the exponential times of the same average, so the independence of exponential arrivals seems to dominate over the non-exponential service times. The average difference between the discrete events simulation of the system and Model B with MCM is 0.8% (ranging from -0.4% to 2.4%) for the normal distribution and 0.7% (ranging from -0.5% to 2.2%) for the lognormal. The pattern of homogeneous server rates (1,1,1) offers better throughput in all the cases under analysis. The difference with the solution of exponential service times for every server’s arrangement is very low, so these results would initially support the use of the transition matrix as a first approach to study non-homogeneous server systems M/Gi/k/k. Further testing would consolidate this possibility. While the equivalence of homogenous systems M/M/k/k and M/G/k/k is well established, the performance of heterogeneous systems seems also mainly influenced by the average values and with little dependence on the service time distribution.

6. Conclusions

We have presented the accurate analytical modeling of heterogeneous or multi-class parallel server systems of limited capacity through their transition rate matrix. The loss mechanisms have been modeled inside the system, so the transition rate matrix captures precisely the loss percentage, with accurate results checked with former analytical results and experimentally through simulation. Model B revises the usual application of the PASTA property to the offered load, by including the loss evaluation as a state in the transition state diagram. This state diagram construction has demonstrated its accuracy for heterogeneous server parallel systems, where the Erlang system is a particular case with homogeneous servers (B-Erlang formula). The addition of a queue of finite capacity in front of the servers can also be accurately modeled with the same methodology, Model E. The precise evaluation through the model is outstanding in all regimes, from low demand to leveled load/capacity or system oversaturation, which allows qualifying it as an exact model for the state probabilities in agreement with simulation also inside the intervals of confidence. It has been verified that a small queue approaches very quickly heterogeneous to homogenous performance of the same average service rate, with practical significance in logistic, manufacturing or service operations. The recirculating systems present higher difficulty to be assessed, even though the model has been developed successfully through the transition matrix as an open system with a modified offered load that includes recirculation. Even when the flow is strictly non-exponential, the iterative process of resolution as a product form problem includes all the state probabilities of every offered arrival, even the loss state that establishes continuity, as it provides a fair good approximation of the output rate from a simple and scalable model.
These models have allowed the easy analysis of performance in a full range of arrival rates, with insights into system behavior for ordered entry assignments. In real systems, the homogeneity of servers can be a rough assumption. Many problems of interest in logistics, manufacturing systems, call centers, or computer servers, among others, include heterogeneous service times across servers, so this analytical model of heterogeneous servers can evaluate their behavior better.
Based on this methodology, the hybrid modeling of the transition matrix along the application of the Monte Carlo Method (MCM) can be an intermediate practical technique in between analytical models and pure discrete-event simulation. The transition matrix gives a basic behavior structure under the assumptions of events independence in a Markovian chain, and the MCM allows the introduction of the variability around the stationary solution, for uncertainty estimation or for non-exponential service times. The initial test of normal and lognormal distributions shows useful approximations. Future works of hybrid modeling that combine transition matrix of limited complexity with MCM can be a useful starting point for further research, integrating available growing computation capabilities with simple structured models for the study of complex systems. In particular, in the dynamic situation of short-term changes of manufacturing system, where the stationary regime is less representative and the opportunities for system control in the transient regime could be better facilitated by the state transition matrix, instead of the stationary long-term solution of simulation. This is foreseen of particular interest for cyberphysical systems or digital twins of growing importance , where not only the massive data but appropriate structured models could provide analysis opportunities and benefits for decision-making.

Author Contributions

Conceptualization, R.C. ; methodology, R.C..; software, A.A.; validation, R.C. and A.A.; formal analysis, R.C.; investigation, A.A.; data curation, A.A.; writing—original draft preparation, A.A.; writing—review and editing, R.C.; visualization, A.A.; supervision, R.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

No new data were created in addition to those already included.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Curry:, G.L.; Feldman, R.M. Manufacturing systems modelling and analysis; Springer Science & Business Media, 2010. [Google Scholar]
  2. Smith, J.M. Introduction to Queuing Networks: Theory ∩ Practice. Springer, 2018.
  3. Shortle, J.F.; Thompson, J.M.; Gross, D.; Harris, C.M. Fundamentals of queueing theory. John Wiley & Sons, 2018.
  4. Efrosinin, D. Controlled queueing systems with heterogeneous servers. 2004. https://d-nb.info/971824401/34.
  5. Wolff, R.W. Poisson arrivals see time averages. Operations Research 1982, 30, 223–231. [Google Scholar] [CrossRef]
  6. Gans, N.; Koole, D.; Mandelbaum, A. Telephone call centers: Tutorial, review, and research prospects. Manufacturing Service Operations Management 2003, 5, 79–141. [Google Scholar] [CrossRef]
  7. Armony, M.; Ward, A.R. Fair dynamic routing in large-scale heterogeneous-server systems. Operations Research 2010, 58, 624–637. [Google Scholar] [CrossRef]
  8. Gumbel, H. Waiting lines with heterogeneous servers. Operations Research 1960, 8, 504–511. [Google Scholar] [CrossRef]
  9. Disney, R.L. Some multichannel queueing problems with ordered entry. Journal of Industrial Enginering 1962, 13, 46–48. [Google Scholar]
  10. Disney, R.L. Some Multichannel Queueing Problems with Ordered Entry-an Application to Conveyor Theory. Journal of Industrial Engineering 1963, 14, 105–108. [Google Scholar]
  11. Singh, W.S. Two-server Markovian queues with balking: Heterogeneous vs. homogeneous servers. Operations Research 1970, 18, 145–159. [Google Scholar] [CrossRef]
  12. Singh, V.S. Markovian queues with three heterogeneous servers. IIE Transactions 1971, 3, 45–48. [Google Scholar] [CrossRef]
  13. Elsayed, E.A. Multichannel queueing systems with ordered entry and finite source. Computers & Operations Research 1983, 10, 213–222. [Google Scholar] [CrossRef]
  14. Yao, D.D. . The arrangement of servers in an ordered-entry system. Operations Research 1987, 35, 759–763. [Google Scholar] [CrossRef]
  15. Yao, D.A. Convexity properties of the overflow in an ordered-entry system with heterogeneous servers. Operations Research Letters 1986, 5, 145–147. [Google Scholar] [CrossRef]
  16. Saglam, V.; Shahbazov, A. Minimizing loss probability in queuing systems with heterogeneous servers. Iranian Journal of Science and Technology, Transaction A, Science 2007, 31, 199–206. [Google Scholar]
  17. Boxma, O.J.; Koole, G.M.; Liu, Z. Queueing-theoretic solution methods for models of parallel and distributed systems. Centrum voor Wiskunde in Informatica, Department of Operations Research, Statistics, and System Theory. 1994. https://ir.cwi.nl/pub/5133.
  18. Isguder, H.O.; Uzunoglu-Kocer, U. Analysis of GI/M/n/n queueing system with ordered entry and no waiting line. Applied Mathematical Modelling 2014, 38, 1024–1032. [Google Scholar] [CrossRef]
  19. Melikov, A.Z.; Ponomarenko, L.A.; Mekhbaliyeva, E.V. Analyzing the models of systems with heterogeneous servers. Cybernetics and Systems Analysis 2020, 56, 89–99. [Google Scholar] [CrossRef]
  20. Cooper, R.B. Queues with ordered servers that work at different rates. Operations Research, 1976; 13, 69–78. [Google Scholar] [CrossRef]
  21. Matsui, M.; Fukuta, J. On a Multichannel Queueing System with Ordered Entry and Heterogeneous Servers. AIIE Transactions 1977, 9, 209–214. [Google Scholar] [CrossRef]
  22. Nath, G.B.; Enns, E.G. Optimal service rates in the multiserver loss system with heterogeneous servers. Journal of Applied Probability 1981, 18, 776–781. [Google Scholar] [CrossRef]
  23. Pourbabai, B.; Sonderman, D. Service utilization factors in queueing loss systems with ordered entry and heterogeneous servers. Journal of Applied Probability 1986, 23, 236–242. [Google Scholar] [CrossRef]
  24. Muth, E.J.; White, J.A. Conveyor theory: A survey. AIIE Transactions 1979, 11, 270–277. [Google Scholar] [CrossRef]
  25. Nazzal, D.; El-Nashar, A. Winter Simulation Conference - Survey of research in modeling conveyor-based automated material handling systems in wafer fabs 2007, 1781–1788. [CrossRef]
  26. Nawijn, W.M. A note on many-server queueing systems with ordered entry, with an application to conveyor theory. Journal of Applied Probability 1983, 20, 144–152. [Google Scholar] [CrossRef]
  27. Nawijn, W.M. On a two-server finite queuing system with ordered entry and deterministic arrivals. European Journal of Operations Research 1984, 18, 388–395. [Google Scholar] [CrossRef]
  28. Pourbabai, B. Markovian queueing systems with retrials and heterogeneous servers. Computers and Mathematics with Applications 1987, 13, 917–923. [Google Scholar] [CrossRef]
  29. Boysen, N.; Briskorn, D.; Fedtke, S.; Schmickerath, M. Automated sortation conveyors: A survey from an operational research perspective. European Journal of Operations Research 2019, 276, 796–815. [Google Scholar] [CrossRef]
  30. Sonderman, D. An analytical model for recirculating conveyors with stochastic inputs and outputs. International Journal of Production Research 1982, 20, 591–605. [Google Scholar] [CrossRef]
  31. Schmidt, L.C.; Jackman, J. Modeling recirculating conveyors with blocking. European Journal of Operations Research 2000, 124, 422–436. [Google Scholar] [CrossRef]
  32. Brandwajn, A.; Jow, Y. An approximation method for tandem queues with blocking. Operations Research 1988, 36, 73–83. [Google Scholar] [CrossRef]
  33. Hsieh, Y.J. Analytical modeling of closed-loop conveyors with load recirculation. In: International Conference on Computational Science and Its Applications. Springer, Berlin, Heidelberg, 2005. [CrossRef]
  34. Haghighi, A.M.; Mishev, D.P. A parallel priority queueing system with finite buffers. Journal of Parallel Distributed Computing 2006, 66, 379–392. [Google Scholar] [CrossRef]
  35. Van der Gaast, J.P.; De Koster, M.B.M.; Adan, I.J. Conveyor merges in zone picking systems: A tractable and accurate approximate model. Transportation Science 2018, 52, 1428–1443. [Google Scholar] [CrossRef]
  36. Burke, P.J. The output of a queuing system. Operations Research 1956, 4, 699–704. [Google Scholar] [CrossRef]
  37. Armony, M. Dynamic routing in large-scale service systems with heterogeneous servers. Queueing Systems 2005, 51, 287–329. [Google Scholar] [CrossRef]
  38. Pike, R.; Martin, G.E. The bowl phenomenon in unpaced lines. International Journal of Production Research 1994, 32, 483–499. [Google Scholar] [CrossRef]
  39. Bolotin, V. Telephone circuit holding time distributions. In: Proc. 14th International Teletraffic Congress. The fundamental role of teletraffic in the evolution of telecommunications networks, Labetoulle, J. and Roberts, J.W.(Ed). Elsevier, 2014.
Preprints 93195 g001
Figure 1. Model A transition rate diagram of 3-parallel heterogeneous entry-ordered servers..
Figure 1. Model A transition rate diagram of 3-parallel heterogeneous entry-ordered servers..
Preprints 93195 g001
Preprints 93195 g002
Figure 2. Model B transition rate diagram of 3-parallel heterogeneous ordered entry servers.
Figure 2. Model B transition rate diagram of 3-parallel heterogeneous ordered entry servers.
Preprints 93195 g002
Preprints 93195 g003
Figure 3. Model B (c=3, μ=μ1=μ2=μ3=1): evolution of occupied system pocc, loss from blocking pb, full system pf and empty system p0 probabilities.
Figure 3. Model B (c=3, μ=μ1=μ2=μ3=1): evolution of occupied system pocc, loss from blocking pb, full system pf and empty system p0 probabilities.
Preprints 93195 g003
Preprints 93195 g004
Figure 4. Model E transition rate diagram of 3 parallel heterogeneous entry-ordered servers with a waiting queue.
Figure 4. Model E transition rate diagram of 3 parallel heterogeneous entry-ordered servers with a waiting queue.
Preprints 93195 g004
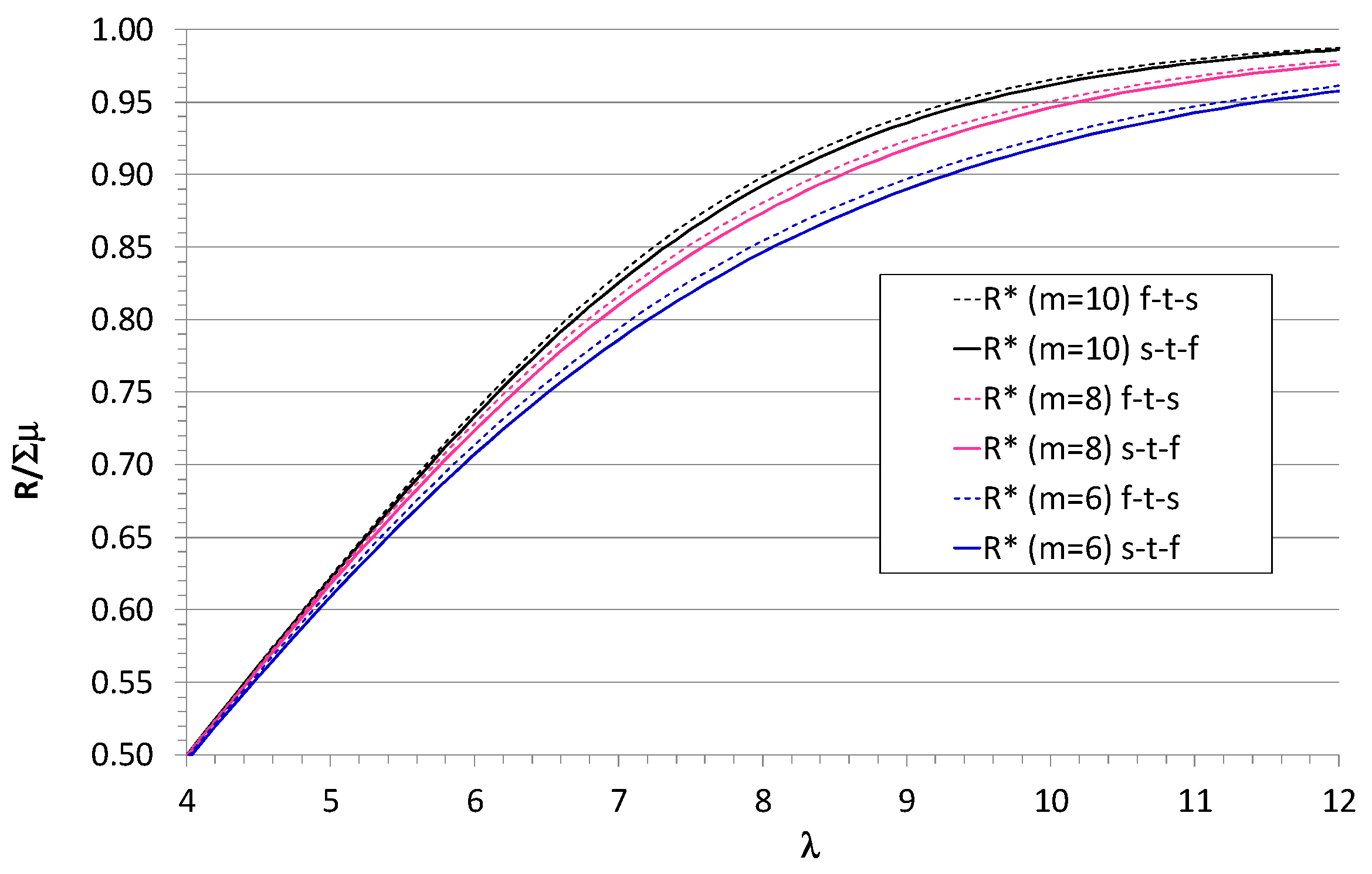
Preprints 93195 g005
Figure 5. Model E (k=m/2, Σμ=8) vs. throughput R*= R/Σμ; for different service rate patterns, faster to slower (f-t-s) and slower to faster (s-t-f).
Figure 5. Model E (k=m/2, Σμ=8) vs. throughput R*= R/Σμ; for different service rate patterns, faster to slower (f-t-s) and slower to faster (s-t-f).
Preprints 93195 g005
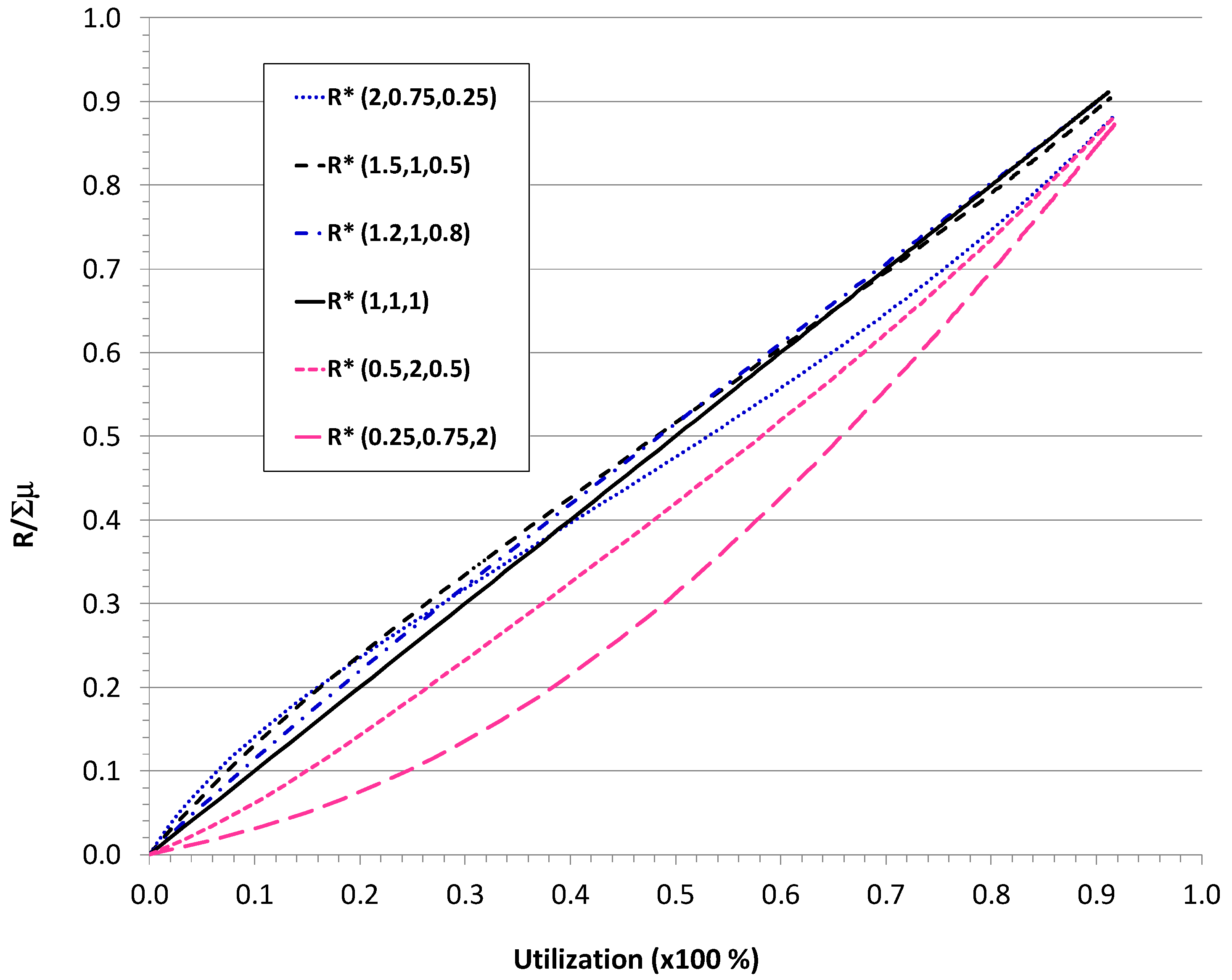
Preprints 93195 g006
Figure 6. Model B (m=3) utilization vs. throughput for different service rates patterns (μ1,μ2,μ3).
Figure 6. Model B (m=3) utilization vs. throughput for different service rates patterns (μ1,μ2,μ3).
Preprints 93195 g006
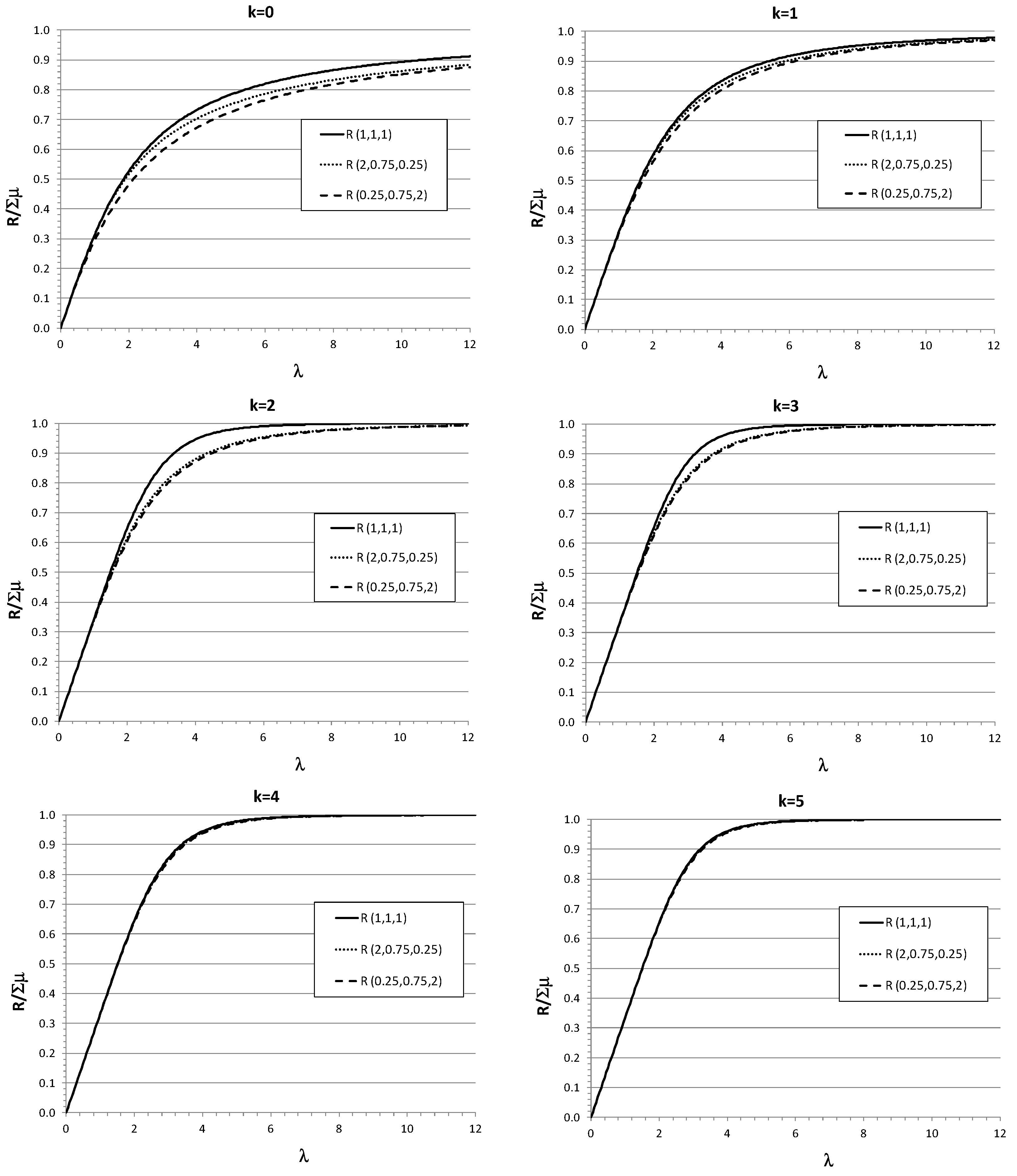
Preprints 93195 g007
Figure 7. Model E (m=3), arrival rate λ vs. throughput R/Σμ, for different service rates patterns (μ1,μ2,μ3) and buffer size k.
Figure 7. Model E (m=3), arrival rate λ vs. throughput R/Σμ, for different service rates patterns (μ1,μ2,μ3) and buffer size k.
Preprints 93195 g007
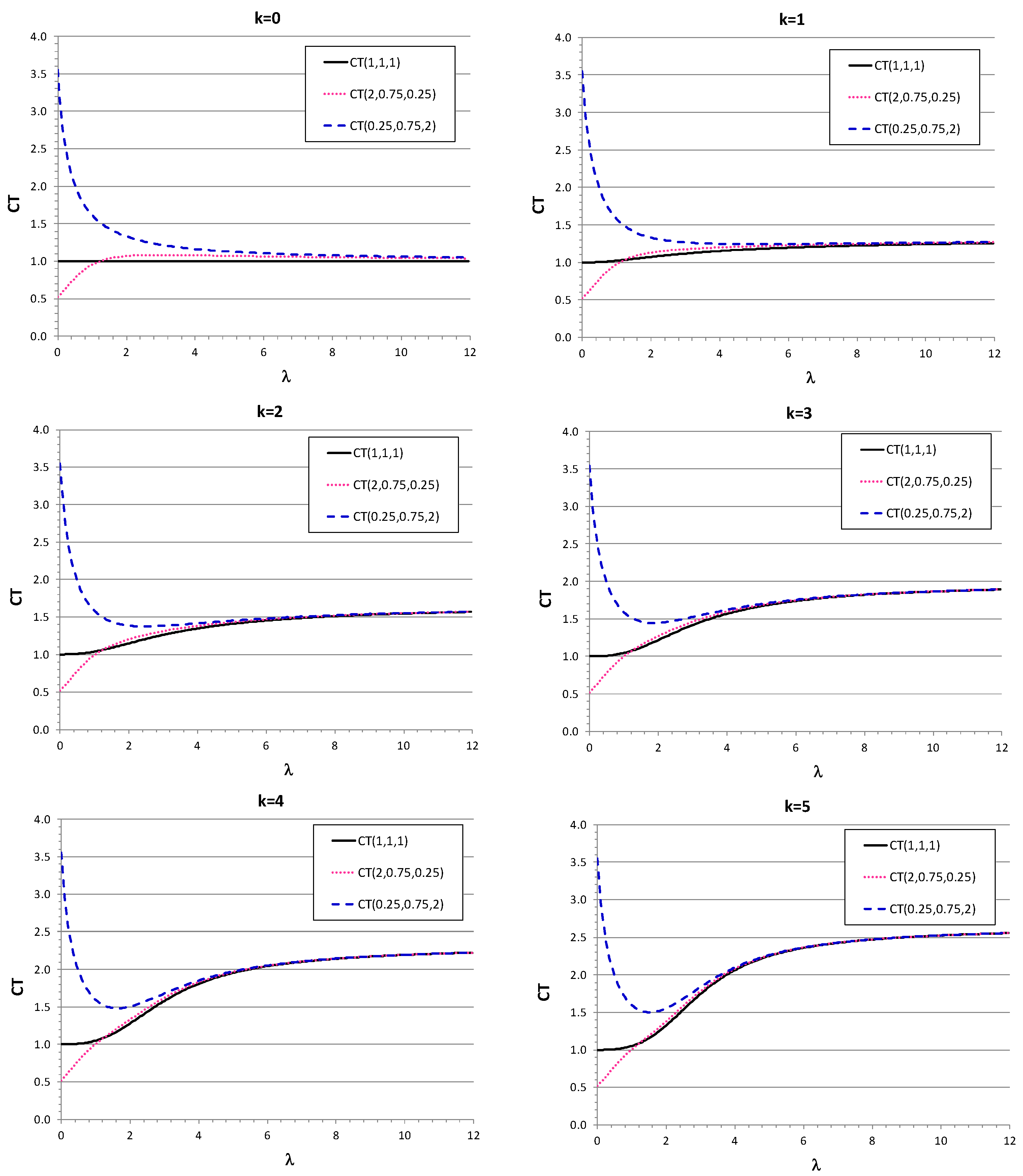
Preprints 93195 g008
Figure 8. Model E (m=3), arrival rate λ vs. sojourn time CT, for different service rates patterns (μ1,μ2,μ3) with average service rate 1 and buffer size k.
Figure 8. Model E (m=3), arrival rate λ vs. sojourn time CT, for different service rates patterns (μ1,μ2,μ3) with average service rate 1 and buffer size k.
Preprints 93195 g008
Preprints 93195 g009
Figure 9. Flow rates for Model E (m=3) with recirculation.
Figure 9. Flow rates for Model E (m=3) with recirculation.
Preprints 93195 g009
Preprints 93195 g010
Figure 10. Effect of arrival rate uncertainty in operating curve of Model B.
Figure 10. Effect of arrival rate uncertainty in operating curve of Model B.
Preprints 93195 g010
Table 1. Dimensionless throughput R* of three servers from Simulation, M/M/3/3 (Erlang-B), Model A, and Model B.
Table 1. Dimensionless throughput R* of three servers from Simulation, M/M/3/3 (Erlang-B), Model A, and Model B.
Preprints 93195 i001
Table 2. Loss probability comparison from analytical literature models to Model B.
Table 2. Loss probability comparison from analytical literature models to Model B.
Preprints 93195 i002
Table 3. Dimensionless throughput R* of Model E (m=3, k=3) vs. simulation.
Table 3. Dimensionless throughput R* of Model E (m=3, k=3) vs. simulation.
Preprints 93195 i003
Table 4. Throughput of Model E (m=3, k=3) vs. simulation, with and without recirculation.
Table 4. Throughput of Model E (m=3, k=3) vs. simulation, with and without recirculation.
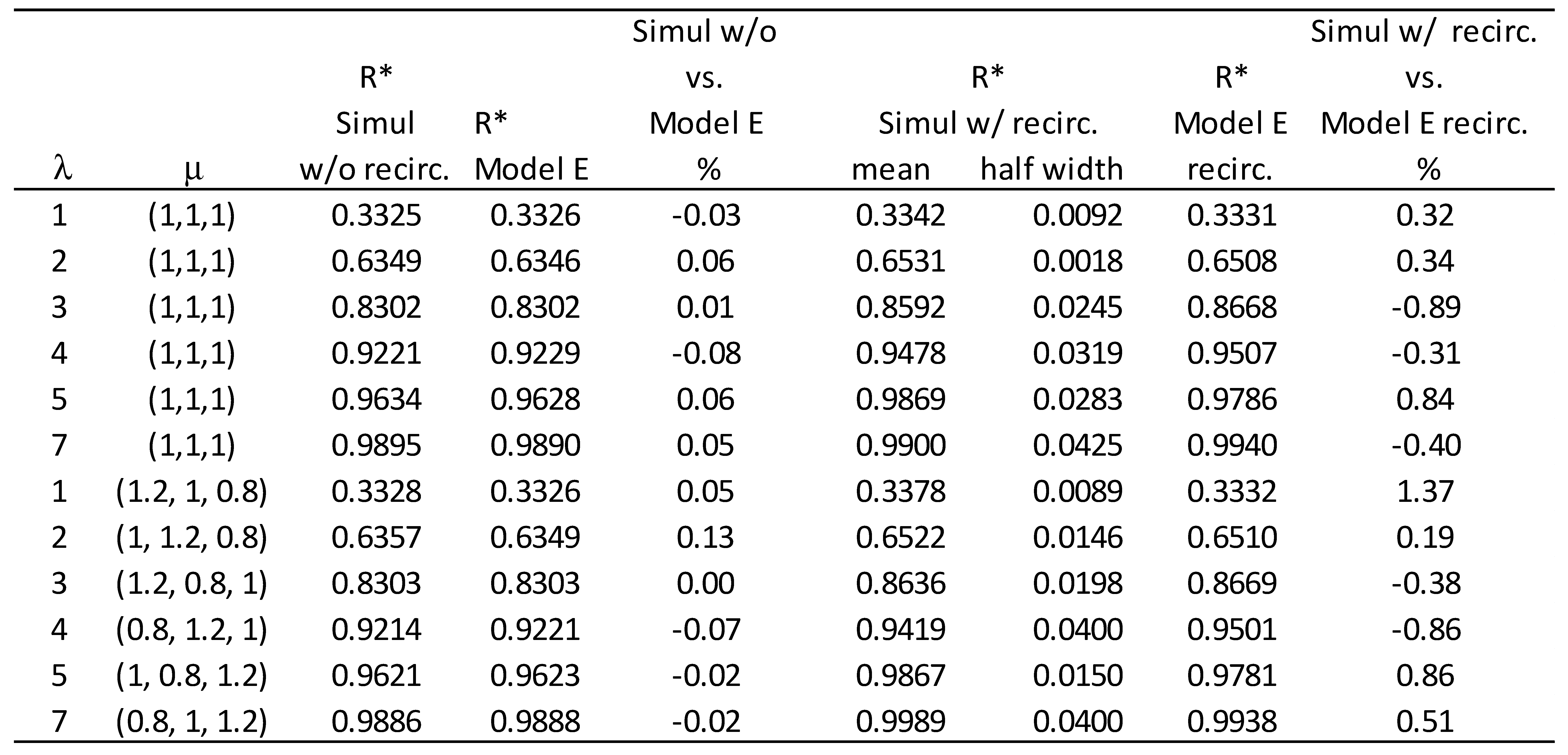Preprints 93195 i004
Table 5. Simulation and Model B throughput for 3 parallel server with exponential arrival rate and service rate distributions exponential, normal and lognormal.
Table 5. Simulation and Model B throughput for 3 parallel server with exponential arrival rate and service rate distributions exponential, normal and lognormal.
Preprints 93195 i005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated