Prerpints.org logo
Preprint
Article

Charge Storage and Magnetic Properties Nitrogen-containing Nanoporous Biocarbon

Altmetrics

Downloads

91

Views

26

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

14 December 2023

Posted:

15 December 2023

You are already at the latest version

Alerts
Abstract
The article presents a technology for producing nitrogen-containing nanoporous biocarbon with high degree of elemental composition homogeneity, confirmed by electron spectroscopy. The research explores the relationship among the electronic characteristics of supramolecular nanoporous carbon, its porous structure, and the capacitance at its interface with the electrolyte. The obtained biocarbon is characterized by micro and mesopores, as evidenced by the results of studies by the method of nitrogen adsorption/desorption. The specific area of the available porous surface was found to be 1247 m2/g. Comparing this result with the data of small-angle X-ray scattering, we conclude that micropores are open while mesopores remain closed. This material was found to have a saturation magnetization σs of 1.4 A∙m2∙kg-1 and a coercive force Hc of 10 kA/m. The impedance studies of electrochemical cells of supercapacitors made of the experimental biocarbon were carried out. Equivalent electrical circuits of the studied electrochemical processes were constructed and characterized.
Keywords: 
Subject: Chemistry and Materials Science  -   Electrochemistry

1. Introduction

The technology of the first supercapacitors (SC) was developed back in 1953, but scientists are still working to improve their efficiency. The main problem with these devices is their insufficient energy density, which is the basis for the fundamental contradiction between the growing needs of the latest circuitry and the capabilities of traditional technologies for autonomous energy generation and storage devices. The energy capacity of SC is being increased in two main ways: by increasing the specific capacitance of the active electrode material and by increasing the maximum operating voltage. The first task is to increase the capacity of the double electric layer of carbon materials, and the second is to use organic electrolytes and electrolytes based on ionic liquids [1,2].
Success in increasing the capacitance of carbon materials hinges on achieving an optimal combination of a porous structure and the corresponding electronic configuration of the material. Such a combination will facilitate unlocking the Helmholtz capacitance through the capacitance of the spatial charge region in a solid. For this purpose, carbon materials are modified by introducing ions of various impurities (atoms of O, N, B, S, P, Si, etc.) into their structure [3,4,5,6,7]. Nitrogen and oxygen are the most widely used. The effect of oxygen has been extensively examined due to its consistent presence in carbon materials. Oxygen functional groups can be readily incorporated into carbon materials through chemical reactions involving activating or oxidizing agents. They play a crucial role in the capacitive characteristics by altering the surface wettability, reactivity and electrical conductivity of the material. Meanwhile, nitrogen-functional groups are gaining growing interest as promising alternative options for modifying the carbon system. Their addition leads to an improvement in electrochemical behaviour, mainly through a contribution to the capacity of the double electric layer or to the pseudocapacitance [8,9,10,11], improved wettability [12,13], reduced reactivity of the material [14], and increased electron transfer rate [15,16]. Various techniques exist for introducing nitrogen-functional groups into nanoporous carbon materials. These include reaction with N-containing sources (NH3, NO, urea, etc.), carbonisation of N-containing precursor (such as melamine, pyridine, etc.), and the heat treatment of N-containing precursors infiltrated into the matrix [17,18,19,20,21,22,23,24,25]. Predominant nitrogen-functional groups include pyridine, pyrrole, and pyridine-N-oxide. The influence of nitrogen-functional groups on the supercapacitor performance was reported in [26]. It is highlighted that nitrogen-functional groups not only increase the capacity due to Faraday reactions but also elevate hydrophilicity and electron transfer rates. Consequently, this improvement contributes to enhanced capacitive characteristics of the supercapacitor [27]. There are reports on the production of nitrogen-containing porous carbon materials by simple synthesis methods [28,29]. Direct pyrolysis for the synthesis of porous carbon materials without further activation is considered the most promising method of large-scale production [30].
Expanding the operating voltage range is the second strategic direction for improving the performance of supercapacitors. Organic electrolytes find extensive use in industrial supercapacitors owing to their electrochemical stability at voltages of 2.5-3.2 V. However, organic electrolytes have a number of disadvantages, including high cost, toxicity, low electrical conductivity, flammability, and the necessity for establishing specific working conditions (such as dew point control and an inert environment). Therefore, there has been a growing interest in substituting organic electrolytes with aqueous alternatives. The primary strategy involves elevating the operational voltage, constrained by the water decomposition potential. Research [31,32,33] demonstrated that when using neutral electrolytes like Na2SO4 and Li2SO4, a symmetrical supercapacitor built with activated carbon and Na2SO4 as the electrolyte exhibits a robust stability voltage of 1.6 V along with intriguing characteristics. In [34], it is reported that a symmetrical supercapacitor based on activated carbon using an aqueous solution of Li2SO4 as an electrolyte is distinguished by a substantial cell voltage of 1.9 V and commendable capacity retention even after 10,000 cycles. The elevated cell voltages are linked to a considerable overpotential at the negative electrode for the electrochemical reaction of hydrogen production and high solvation energy of dissolved ions. Therefore, it is important to develop the technology for the synthesis of nanoporous carbon material with high superpotential values for oxygen and hydrogen release reactions in order to expand the cell voltage. Under the conditions of high environmental safety requirements, it is necessary to abandon the use of harmful substances as feedstocks for carbonisation and precursors for their modification.
The objective of this study is to acquire a nitrogen-containing environmentally friendly nanoporous carbon material by direct pyrolysis without further activation, to analyse its structure, composition, porosity, specific capacitive characteristics, and to assess the possibility of the obtained material operating in an extended operating voltage range with an aqueous solution of Na2SO4 as an electrolyte.

2. Conceptual Provisions and Experimental Methodology

Sample preparation

Direct pyrolysis was employed to create a nitrogen-containing nanoporous carbon material (NCNM). The carbon source utilized was glucose, sodium bicarbonate served as the activator (porogen), and urea was introduced as a nitrogen source for carbon doping (alloying). These precursors were dissolved in water in equal mass ratios to form a clear solution. The resulting solution was then subjected to drying in an air atmosphere at 100°C until a constant weight was achieved. The resulting product was subjected to pyrolysis in a tubular reactor at a suitable temperature for 2 h under an argon atmosphere. Pyrolysis was carried out at temperatures of 600 °C, 700 °C, and 800 °C. We considered it inappropriate to increase the carbonisation temperature above 800 °C, as graphitisation of carbon begins at such temperatures [35]. The process is accompanied by a decrease in the specific surface area due to a decrease in the micropore content, which will negatively affect the specific capacitive characteristics of SCs. The heating rate was 5 °C/min. The synthesized carbon material was washed in distilled water at room temperature to remove residual inorganic salts, then washed with ethanol and dried at 80 °C.

Research methods

The macroscopic features of the particles of the carbon material synthesized in this work were studied using a Phenom ProX scanning electron microscope (ThermoFisher Scientific, Waltham, Massachusetts, USA). The elemental composition of the studied coal was determined with the help of an additional EDS energy dispersive microanalysis module in this microscope.
The study of adsorption/desorption of gases by porous bodies is often used to estimate the parameters of the porous structure within certain models, such as specific surface area, total pore volume, pore size distribution, average pore radius, etc. In our studies, the automated analyzer Quantachrome NOVAtouch LX2 was used for such an assessment, which allowed us to determine the porous structure of the synthesized carbon material using nitrogen adsorption/desorption isotherms at a temperature of T = 77 K. The samples were preliminarily degassed in a vacuum at a temperature of 473 K. The duration of degassing was 16 hours.
The X-ray diffraction method was used for the raw materials and for the carbonaceous material synthesized from them (NCNM). Diffractograms were obtained using an automated X-ray diffractometer DRON-3. Monochromatic CuKα- radiation with a wavelength of λ = 0.15418 nm was used to irradiate the samples, and X-ray diffractograms were measured in a continuous scanning mode with an angular velocity of 2 degrees/min in the range of diffraction angles 2θ = 5 - 120°. The methodology for the study of powder samples is described in detail in the monograph [36].
Taking into account the complex structure of the synthesized NCNM carbon material, information about its structure from the X-ray diffraction analysis is insufficient. Therefore, an additional source of data is the small-angle X-ray scattering (SAXS) technique. Such scattering is caused by the formation of inhomogeneities in the electron density distribution in a substance, so it is one of the most effective methods for studying the atomic structure of a substance in the size range from 1 to 100 nm. An important advantage of the method is the ability to study completely disordered objects, which also include amorphous carbon materials. The SAXS spectra were measured on a DRON-3 automatic diffractometer with monochromatized CuKα radiation. Primary and scattered beam collimators were used to limit the parasitic scattering of the monocrystal monochromator, entrance slits, and to reduce the intensity of background scattering in air. During the study, the NCNM powder samples were placed in a 1.5 mm high cuvette with the inlet and outlet holes covered with a 50 μm thick polyethylene film. Correction for background scattering and collimation correction for the height of the detector receiving slit were made on the SAXS intensity curves before their analysis.
The magnetic characteristics (saturation magnetization, coercive force, etc.) of the material under study were calculated from the measured hysteresis loops. To obtain them, a vibration magnetometer was used [37], and measurements were performed at room temperature. The magnetometer was calibrated by comparison, using pure non-porous nickel with a density of ρ = 8,9 g cm-3 as a standard. The content of the magnetic phase in the obtained material was calculated based on the data of the saturation specific magnetization measurement. During measurements in magnetic fields with insufficient strength, the measured magnetization value is an ambiguous function of the amount of ferromagnetic phase in the sample. It also depends on the structure of the phase, its dispersion, stresses in it, etc. Therefore, quantitative measurements of saturation magnetization for phase analysis should be performed in strong fields sufficient for complete saturation. For the carbon materials under study, the saturation specific magnetization was measured in a magnetic field of 800 kA/m.
Electrochemical measurements were performed using a two-electrode scheme to investigate the behaviour of the synthesized carbon materials in a real supercapacitor. For this purpose, the materials under study with a binding agent (5 % polyvinylidene fluoride) were pressed onto a 0.5 cm2 nickel mesh. The weight of the active material did not exceed 3 mg. A 30 % aqueous solution of KOH and a 1 M aqueous solution of Na2SO4 were used as electrolytes.
The impedance measurements of the experimental electrochemical cells of supercapacitors were carried out in the frequency range of 10-2 ÷ 106 Hz using the measuring complex "AUTOLAB" by ECO CHEMIE (Netherlands), equipped with computer programs FRA-2 and GPES. The amplitude of the measuring signal was 5·10-3 V.

3. Results and Discussion

Galvanostatic studies

In order for activated carbon to be used as an active material for supercapacitor electrodes, it must have good electrical conductivity and high specific capacitance. The specific capacitance was determined by galvanostatic charging and discharging of a laboratory supercapacitor cell (Figure 1, a, b) using the formula:
С = 2 I ⋅ t U ⋅ m
where I represent the current, t stands for the discharge time, U denotes the voltage drop during discharge, m indicates the mass of the supercapacitor electrode.
The results of the calculation of the specific capacitance for each synthesised carbon are shown in Table 1. Each number in the table is an average value calculated from the study of three supercapacitors.
As can be seen from Table 1, NCNMs synthesised at 800 °C have the highest specific capacity. Therefore, all further studies were carried out for this carbon.
SC made from NCNMs have high coulombic efficiency at a given charge/discharge current density (97 % for the 30 % KOH electrolyte and 94 % for the 1 M Na2SO4 electrolyte). This means that the charge accumulation is mainly due to non-Faraday processes. Despite the lower capacity of NCNMs in 1 M Na2SO4 electrolyte, this electrochemical system accumulates 2.2 times more energy due to an increase in the charging limit voltage to 1.8 V.
SEM microphotography and surface elemental analysis.
The behaviour of the synthesised carbons in different electrolytes can be explained by referencing the outcomes of structural and porous structure studies.
The structure of the synthesized NCNM, as evident from the SEM images (Figure 2, a, b), is homogeneous, and no inclusions of other phases are visible in the images. Large macropores are not observed, which may indicate the presence of mainly meso-, micro- and nanoporous structure. The porous structure is spongy; the pores are cavities and channels in a continuous solid matrix (Figure 2, c). The pores were apparently formed during the synthesis process as a result of the decomposition of sodium bicarbonate to form carbon dioxide and water. The closed pore configuration commonly found in traditional activated carbons significantly restricts the accessibility of pores to electrolyte ions. Carbon materials characterized by open pores are preferred for application in supercapacitors. In Figure 2, d, one can see the gaps in the material that connect the pores to each other. The determination of the elemental composition of the synthesized NCNM showed the presence of three elements - C, N, O (Figure 3). The content of nitrogen and oxygen varies in different parts of the sample surface. Out of 10 measurements at different points, the lowest value of 2.88 % wt. and the highest value of 25.17 % wt. for nitrogen content and 3.26 % wt. and 11.11 % wt. for oxygen, respectively, were obtained.

Nitrogen adsorption/desorption porometry

The shape of the adsorption isotherm (Figure 4) can be described in a certain approximation as a type I isotherm with elements of a type II isotherm [38]. Type I isotherms are characteristic of porous solids in which micropores predominate and the volume of other pores is much smaller. Type II isotherms are characteristic of macroporous solids. The presence of a hysteresis loop on the isotherms indicates additional vapour absorption as a result of capillary condensation of the adsorbed gas, as well as irreversible retention of adsorbate molecules in pores nearly matching the size of nitrogen molecules. However, in our case, the hysteresis is quite insignificant, indicating the commendable reversibility of the adsorption/desorption process within the porous structure of the examined activated carbon sample.
Preprints 93379 g003
Figure 3. SEM images and analysis of NCNM energy dispersive X-ray spectroscopy.
Figure 3. SEM images and analysis of NCNM energy dispersive X-ray spectroscopy.
Preprints 93379 g003
According to the form of hysteresis, it can be described as H4 hysteresis [38]. H4-type hysteresis loops are characteristic of aggregated zeolite crystals, mesoporous zeolites, and micro-mesoporous carbon. Electron microscopic studies of activated carbon with an H4-type hysteresis loop in the isotherm [39] typically reveal a porous structure characterized by slit-shaped pores.
To determine the parameters of the synthesized NCNM, the acquired isotherm underwent analysis using the Quantachrome TouchWin software. According to the shape of the isotherm and the hysteresis loop, the synthesised carbon has a micro-mesoporous structure. To ascertain the specific surface area, the multipoint BET method [39] was employed, which fits the experimental data with a linear approximation in the range of relative pressures P/P0 = 0.05 ÷ 0.35. Since for microporous solids the BET method can give a large error in the calculation of the specific surface area, the BET Assistant subprogramme was used for correct calculations. This subprogramme allows calculations to be performed exclusively within the linearity range of the BET equation, which gives the most correct results. Table 2 displays the outcomes of the specific area calculation. The application of the BET model to simulate the adsorption curve revealed a relatively strong correlation coefficient between the model and the experimental data, as indicated in Table 2. Additionally, Table 2 presents the values for the specific pore volume and the average pore size.
Based on the isotherm’s configuration in Figure 4, it can be inferred that the synthesized sample primarily consists of micropores and mesopores with small radii. For mesoporous materials, the Barret-Joyner-Halenda (BJH) method, relying on the Kelvin equation, can be employed to ascertain the pore size distribution [40]:
l n P P 0 = 2 γ V L R T r m
where γ represents the surface tension of nitrogen at its boiling point, VL is the molar volume of liquid nitrogen, R denotes the universal gas constant, and rm signifies the pore radius.
The pore distribution was determined using this method by analyzing the desorption isotherm, which is closer to the genuine thermodynamic equilibrium (Figure 5).
Figure 5 shows that mesopores with a size of 2 nm make a minor contribution to the porous structure of the sample, but the micropore content is more important. This makes it possible to use the density functional theory (DFT) method for modelling. DFT relies on quantum mechanical calculations utilizing fundamental molecular parameters that characterize gas-gas and gas-solid interactions within an adsorption system. The calculation results are depicted in Figure 6. Based on Figure 6, it can be deduced that the porous structure is predominantly microporous, with the pore distribution exhibiting multiple maxima for micropores measuring approximately 1 nm or less in size.
Thus, the substantial quantity of micropores explains the rather high specific capacity of the synthesised NCNM. Micropores play a crucial role in charge accumulation and ion adsorption. Additionally, the existence of mesopores proves beneficial for facilitating the transport of ions from the electrolyte volume to the electrode/electrolyte interface.

X-ray diffraction analysis

The X-ray diffractogram of the NCNM sample (Figure 7) has features that are located in the region of small diffraction angles (2θ ≈ 1-15°). The diffractogram shows a maximum with an angular position of 2θ ≈ 5.5°. It corresponds to an interplanar distance of d≈1.6 nm, which is significantly higher than the interlayer distance in polycrystalline graphite (d = 0.335 nm).
Across a broad angular spectrum, the primary peak of the NCNM sample is localized near the diffraction angles of 2θ ≈ 22.5°, which corresponds to an interplanar distance d ≈ 0.395 nm. This position is displaced to the left in comparison to the diffraction peak of graphite (2θ ≈ 26.5°, d = 0.335 nm). It can be assumed that the appearance of this maximum is due to scattering from three-dimensional graphite-like clusters formed from parallel graphene layers. Note that the value d ≈ 0.395 nm corresponds to the characteristic distances between graphene layers. Along with the main maximum, the diffractogram shows blurred diffuse maxima localized at 2θ ≈ 42.5° and 2θ ≈ 78.5°, which are likely to be caused by scattering from individual isolated graphene layers.

Small-angle X-ray scattering

The porous structure of NCNM was also studied by SAXS technique. In contrast to the isothermal nitrogen adsorption/desorption method, this method allows us to detect not only open pores but also closed pores. Figure 8 shows the scattering intensity curve I(s) of X-rays by the examined
sample, subsequent to applying a collimation correction for the height of the detector receiving slit —specifically, the transition from slit to point collimation. The resulting spectrum takes the form of a curve that consistently diminishes across the entire range of studied scattering angles. This pattern signifies a random distribution of scattering irregularities (pores) and, consequently, the absence of correlation in their spatial arrangement. To compute the distribution functions of pore inertia radii, a method was employed that involves representing the scattering intensity curve as a composite of several curves. Each of these curves was characterized using the Guinier formula [41]:
I ( s ) = ∑ k I k ( 0 ) e − 1 3 s 2 R g k 2
Here I k ( 0 ) represents the square of the total scattering length, R g k denote the electronic radius of inertia of the k-th pore fraction, s = 4 π λ ⋅ s i n ( θ ) stands for the modulus of the scattering wave vector, and λ = 1.5418 Å is radiation wavelength.
To construct dependence (3), we use the method of tangents, which is based on the following provisions:
  • A tangent is drawn to the scattering curve constructed in Guinier coordinates [ s 2 , l n I ( s ) ] at the point of intersection with the ordinate axis.
  • The slope of the tangent determines the radius of inertia of the smallest particles Rg1, and the point of intersection of the tangent with the ordinate axis gives the value I1(0).
  • The contribution to the scattering intensity of the smallest particles is computed using the Guinier formula:
    I 1 ( s ) = I 1 ( 0 ) ⋅ e x p ( − 1 3 s 2 ⋅ R g 1 2 ) .
  • The difference scattering curve I 2 ( s ) = I ( s ) − I 1 ( s ) is calculated, and by performing similar calculations for this curve I2(s), the scattering invariants for the particles of the second fraction I2(0), Rg2 are determined.
  • Applying the above method iteratively, the scattering invariants for particles of all fractions are determined until the scattering intensity curve calculated by formula (3) coincides with the experimental curve.
We can determine the volume fraction of pores with a specific radius of inertia using the formula,
m k = I k ( 0 ) / R g k 3 ∑ k I k ( 0 ) / R g k 3 ,
considering that the contribution to the scattering volume from particles of the k-th fraction is proportional to I k ( 0 ) R g k 3 .
If the particle distribution is characterized by a Gaussian function with the assumption that the variance of the distribution is   Δ R g k ≈ R g k , the particle distribution function can be expressed as follows:
F ( R g ) = 2 R g k ∑ k m k R g k e x p [ − ( R g − R g k ) 2 R g k 2 ] .
By employing the formula ( R g s ) 3 = ∑ k = 1 N m k R g k 3 , where N is the number of pore fractions, we determined the average pore radius. For the assessment of the specific pore surface area, we computed integral characteristics of the scattering intensity curves, namely, the integral Porod invariant (Qp) and Porod constant (Kp). These values are directly proportional to the volume and surface area of the pores, respectively [42]:
σ = 16 ε 2 r 2 N π h a 0 e − 2 r / a 0 e − E a / k T .
Here, N is the number of trapping centres, r is the distance between them, ε is the material dielectric constant, a0 is the radius of wave-function localization, Ea is the activation energy, k is the Boltzmann constant, ћ is the Plank constant, and T is the temperature. Neglecting long-range interactions the wave-function for a system of two δ-wells separated by a distance r takes the form
Q p = ∫ 0 s m a x s 2 I ( s ) d s + K p s m a x ,
K p ≈ ∫ s m i n s m a x s 4 I s d s s m a x − s m i n .
Here s m i n ,   s m a x represent the minimum and maximum values of the wave vector.
The formula
S p = π K p Q p .
Was used to calculate the specific surface area Sp .
Figure 9 shows a graph of pore distribution by radius of inertia. From this figure, it is evident that the primary contribution to the pore volume comes from micropores with a maximum radius at 1.4 nm and mesopores with a maximum radius at 3.4 nm. Additionally, larger inhomogeneities with effective radii of inertia up to 50 nm are present in the sample.
The calculated values of the integral scattering invariants (the Porod invariant Qp and the Porod constant Kp), which are used to determine the specific pore surface area, are given in Table 3. Also in Table 3, we have the average value of the pore radius of inertia Rgs and the specific surface area Sp calculated per unit volume of the sample. If we take into account that the density of activated carbon is approximately 1.9 g/cm3, the calculated specific surface area is 1125 m2/g. This value is slightly lower than the value of 1247 m2/g obtained using the nitrogen adsorption/desorption method (Table 2). This difference may be due to the fact that the SAXS method uses a circular heterogeneity model for calculation, while the adsorption/desorption isotherms show a predominant content of slit-like pores. On the other hand, the average radius of inertia is almost twice as large as that calculated from the nitrogen adsorption/desorption isotherms. This observation suggests that the open micropores in the synthesized carbon are mainly micropores, with a limited number of mesopores remaining closed and inaccessible to nitrogen molecules.

Magnetometry

In the course of studying the magnetic properties of the synthesized NCNM, it was observed to exhibit ferromagnetic characteristics with a distinctive hysteresis in specific magnetization (Figure 10). The saturation specific magnetization of NCNM, measured in a magnetic field of 800 kA/m, is σs = 1.4 A∙m2∙kg-1, and the coercive force Hc = 10 kA/m.
Unlike previously studied magnetic carbon structures [43,44,45], NCNM does not contain ferromagnetic metal atoms. It is obvious that the mechanism of magnetism formation in the synthesized carbon structures is different. In the review analysis of experimental data of synthesized high-temperature ferromagnets without metal atoms [44,45], five main types of carbon magnetic structures were identified:
  • Chains of interacting radicals.
  • Carbon structures containing trivalent elements, such as P, N, B.
  • Structures that are a combination of sp2- and sp3- coordinated carbon atoms.
  • Graphite and nanographite.
  • Fullerenes.
In our case, subjecting a nitrogen-containing precursor to pyrolysis at relatively moderate temperatures (800 °C) results in the formation of a graphite-like material with a significant abundance of unpaired spins. This provides the potential for exchange interaction between these spins [46]. The material takes on a three-dimensional structure composed of both sp2- and sp3- carbon atoms.
Examinations of ferromagnetic materials derived from diverse nitrogen-containing substances have indicated that their structure typically exhibits amorphous and disordered characteristics. An unambiguous correspondence was found: a higher content of amorphous carbon corresponds to an increased spontaneous magnetization [46]. Another regularity of such materials is the close connection between magnetic properties and the presence of various radicals, particularly nitroxyl radicals, predominantly situated at the edges of graphite-like structures. It is assumed that ferromagnetic carbon material in its pure form has never been isolated, and that the ferromagnetic phase was present in the form of islands within a nonmagnetic matrix [47].
The inherent magnetism of carbon materials is theoretically explained by the presence of mixed carbon orbitals formed at the boundaries of impurities and defects [48,49]. These defects cause the appearance of quasi-localized states near the Fermi level, influencing the magnetic moment of the carbon atom network. The authors of [50] point out that it is possible to control the magnetization in carbon by controlled generation of defects and alloying. The analysis of the X-ray diffraction patterns in Figure 7 shows an expansion in the interlayer distance between graphene layers in graphite-like clusters compared to polycrystalline graphite. This is the cause of additional structural defects. The disordered arrangement of graphene layers also adds to the defects. Thus, a combination of structural defects and nitroxyl radicals is the most likely cause of ferromagnetic properties in the synthesized carbon material.

Impedance studies

The impedance spectroscopy method is commonly employed for investigating electrochemical processes at both the electrode/electrolyte interface and within the volume of the electrode material. This method makes it possible to conduct research across a broad frequency range. To elucidate the correlation between the structure and capacitive parameters of the examined carbon, the experimental impedance hodographs -Im Z = f(Re Z) are modelled by equivalent circuitry. Such circuits serve as a simplified model representing real processes in the system under examination. The primary criterion for selecting an equivalent circuit is the physical significance of all its structural elements under the condition of optimal approximation.
Experimental Nyquist diagrams and equivalent electrical circuits modelled on their basis are shown in Figure 11. As can be seen from these diagrams there are a small semicircular pattern in the high frequency domain for the Na2SO4-based electrolyte. This observation suggests the occurrence of processes of charge transfer and accumulation involving Faraday processes or pseudocapacitance. For a supercapacitor with a KOH-based electrolyte, such semicircular pattern is nearly negligible, signifying a substantial prevalence of double electric layer capacitance over capacitance attributed to redox reactions.
In the mid-frequency range, Nyquist diagrams look like a sloping straight line, indicating the course of diffusion processes in the system under study. At low frequencies, this line transitions to an almost vertical slope, suggesting the electrostatic capacitive accumulation of electric charge. The presented Nyquist diagrams are well modelled by the equivalent de Levie circuit, which is modified, in accordance with Voight’s approach [51], by the series connection of the parallel RSCCSC link. Here, RSC and CSC are, respectively, the resistance and capacitance of the spatial charge region (SCR) in the studied carbon. The calculated parameters of the equivalent electrical circuit, which are shown in the inset of Figure 11, are detailed in Table 4.
The element R1 encompasses the resistance of the electrolyte, lead wires, and contacts. Since the manufacturing technology of the supercapacitors was the same, we can see the higher resistance of the 1 M Na2SO4 electrolyte. The following elements of the circuit govern diffusion processes within the pores of the carbon material and the buildup of electric charges at the electrode/electrolyte interface. Specifically, the CRE1||R2 link is primarily manages diffusion processes in transport pores (macro- and mesopores), and the C2||R3 and C3||R4-C4 links handle charge accumulation in micropores. When modelling the impedance hodographs, the constant phase element of the CPE was used, whose impedance is determined according to equation [51]:
Z C P E = C P E T j ω − C P E P .
The CPEP parameter considers the phase deviation, reflecting the nature of the modeled process. Specifically, when the CPEP value is close to 1, this element characterises the capacitive behaviour of the system, and when CPEP is close to 0.5, it is diffusive. The incorporation of this element is attributed to the fractal structure of the carbon material [52] resulting in the heterogeneous distribution of charge carriers at the electrode/electrolyte interface. As can be seen from Table 4, as a result of modelling for the 1 M Na2SO4 electrolyte, the obtained value of the CPEP approaches 0.5, which indicates a significantly greater influence of diffusion processes than in the KOH-based electrolyte.
The total effective surface area, as determined by the BET method (Table 2), amounts to 1247 m2/g. Comparing this value with the measured specific capacitance, we find that the differential capacitance of the synthesised nanoporous carbon in a 30 % aqueous solution of KOH is ~ 14.4 μF/cm2, and in a 1 M aqueous solution of Na2SO4 ~ 9.6 μF/cm2.

4. Conclusions

  • A technology for synthesizing of nitrogen-containing biocarbon, NCNM, characterized by high degree of chemical composition homogeneity and a well-developed porous structure, has been introduced. This structure contributes to the superior energy performance of supercapacitors.
  • The correlation of the results obtained by the nitrogen adsorption/desorption method and small-angle X-ray analysis indicates the accessibility of pores for the electrolyte and their full contribution to the specific capacity for NCNM.
  • The NCNM exhibits specific saturation magnetization values of σs = 1.4 A∙m2∙kg-1 and coercive force Hc = 10 kA/m when measured in a magnetic field of 800 kA/m. These magnetic properties arise from a graphite-like material containing numerous unpaired spins, enabling exchange interactions. The material forms a three-dimensional structure comprising both sp2- and sp3-carbon atoms.
  • In a symmetrical electrochemical supercapacitor (SC), the specific capacitance reaches 180 F/g, surpassing existing market analogs by more than 50 %. The differential capacitance of the synthesized nanoporous carbon in a 30% aqueous solution of KOH is ~ 14.4 μF/cm2, and in a 1 M aqueous solution of Na2SO4 - 9.6 μF/cm2. According to the results of impedance spectroscopy, it was found that in the case of the 1 M Na2SO4 electrolyte, diffusion processes have a significantly greater influence on charge accumulation than in the KOH-based electrolyte.

Author Contributions

Conceptualisation, F.I., I.B. and A.B.; methodology, I.B., E.S., A.B and Y.K.; validation, F.I., I.B. and Z.K.; formal analysis, M.K., V.M.; investigation, E.S., V.M., A.B. and Y.K.; data curation, F.I., I.B. and E.S.; writing – original draft preparation, E.S., V.M., and A.B.; writing – review and editing, F.I., I.B.; theoretical modeling, M.K.; software, Z.K.; visualization, E.S., V.M.; supervision, F.I. and I.B.; project administration, F.I. and I.B.; funding acquisition, Z.K. All authors have read and agreed to the published version of the manuscript.

Funding

The findings presented herein are derived from a project supported by the European Union’s Horizon 2020 research and innovation program, as per the Marie Skłodowska-Curie grant agreement No 778156. Additionally, we acknowledge the support received from science resources allocated during the years 2018-2022 for the execution of the international co-financed project with the reference number W13/H2020/2018 (Dec. MNiSW 3871/H2020/2018/2).

Conflicts of Interest

Authors declare no conflicts of interest.

References

  1. Maksymych, V.; Całus, D.; Ivashchyshyn, F.; Pidluzhna, A.; Chabecki, P.; Shvets, R. Quantum energy accumulation in semiconductor < ionic liquid > layered clathrates. Applied Nanoscience. 2022, 12, 1147–1153. [Google Scholar] [CrossRef]
  2. Chabecki, P. Quantum Energy Storage in Dielectric[removed] Porous Clathrates. Energies. 2022, 15, 6069. [Google Scholar] [CrossRef]
  3. Hulicova-Jurcakova, D.; Puziy, A.M.; Poddubnaya, O.I.; Suárez-García, F.; Tascón, J.M.; Lu, G.Q. Highly stable performance of supercapacitors from phosphorus-enriched carbons. J. Am. Chem. Soc. 2009, 131, 5026–5027. [Google Scholar] [CrossRef] [PubMed]
  4. Deng, Y.; Xie, Y.; Zou, K.; Ji, X. Review on recent advances in nitrogendoped carbons: preparations and applications in supercapacitors. J. Mater. Chem. A. 2015, 4, 1144–1173. [Google Scholar] [CrossRef]
  5. Mostazo-López, M. J.; Ruiz-Rosas, R.; Morallón, E.; Cazorla-Amorós, D. Generation of nitrogen functionalities on activated carbons by amidation reactions and Hofmann rearrangement: chemical and electrochemical characterization. Carbon. 2015, 91, 252–262. [Google Scholar] [CrossRef]
  6. Xiang, S.; Yang, X.; Lin, X.; Chang, C.; Que, H.; Li, M. Nitrogen and sulfur co-doped polyurethane-based porous carbon materials as supercapacitors exhibit excellent electrochemical performance. J. Solid State Electrochem. 2017, 21, 1457–1465. [Google Scholar] [CrossRef]
  7. Inagaki, M.; Toyoda, M.; Soneda, Y.; Morishita, T. Nitrogen-doped carbon materials. Carbon. 2018, 132, 104–140. [Google Scholar] [CrossRef]
  8. Kwon, T.; Nishihara, H.; Itoi, H.; Yang, Q.-H.; Kyotani, T. Enhancement mechanism of electrochemical capacitance in nitrogen- /boron-doped carbons with uniform straight nanochannels. Langmuir. 2009, 25, 11961–11968. [Google Scholar] [CrossRef] [PubMed]
  9. Yang, X.; Wu, D.; Chen, X.; Fu, R. Nitrogen-enriched nanocarbons with a 3-D continuous mesopore structure from polyacrylonitrile for supercapacitor application. J. Phys. Chem. C. 2010, 114, 8581–8486. [Google Scholar] [CrossRef]
  10. Lei, Z.; Christov, N.; Zhang, L.L.; Zhao, X.S. Mesoporous carbon nanospheres with an excellent electrocapacitive performance. J. Mater. Chem. 2011, 21, 2274–2281. [Google Scholar] [CrossRef]
  11. Ornelas, O.; Sieben, J.M.; Ruiz-Rosas, R.; Morallón, E.; Cazorla-Amorós, D.; Geng, J.; Soin, N.; Siores, E.; Johnson, B. F. G. On the origin of the high capacitance of nitrogen-containing carbon nanotubes in acidic and alkaline electrolytes. Chem. Commun. 2014, 50, 11343–11346. [Google Scholar] [CrossRef] [PubMed]
  12. Wei, X.; Jiang, X. , Wei, J.; Gao, S.; Functional groups and pore size distribution do matter to hierarchically porous carbons as high-rate-performance supercapacitors. Chem. Mater. 2016, 28, 445–458. [Google Scholar] [CrossRef]
  13. Candelaria, S.L.; Garcia, B.B.; Liu, D.; Cao, G. Nitrogen modification of highly porous carbon for improved supercapacitor performance. J. Mater. Chem. 2012, 22, 9884–1889. [Google Scholar] [CrossRef]
  14. Salinas-Torres, D.; Shiraishi, S.; Morallón, E.; Cazorla-Amorós, D. Improvement of carbon materials performance by nitrogen functional groups in electrochemical capacitors in organic electrolyte at severe conditions. Carbon. 2015, 82, 205–213. [Google Scholar] [CrossRef]
  15. Seredych, M.; Hulicova-Jurcakova, D.; Lu, G.Q.; Bandosz, T.J. Surface functional groups of carbons and the effects of their chemical character, density and accessibility to ions on electrochemical performance. Carbon. 2008, 46, 1475–1488. [Google Scholar] [CrossRef]
  16. Wang, X.; Liu, C.-G.; Neff, D.; Fulvio, P.F.; Mayes, R.T.; Zhamu, A.; Fang, Q.; Chen, G.; Meyer, H. M.; Jang, B. Z.; Dai, S. Nitrogen-enriched ordered mesoporous carbons through direct pyrolysis in ammonia with enhanced capacitive performance. J. Mater. Chem. A. 2013, 1, 7920. [Google Scholar] [CrossRef]
  17. Raymundo-Piñero, E.; Cazorla-Amorós, D.; Linares-Solano, A.; Find, J.; Wild, U.; Schlögl, R. Structural characterization of N-containing activated carbon fibers prepared from a low softening point petroleum pitch and a melamine resin. Carbon. 2002, 40, 597–608. [Google Scholar] [CrossRef]
  18. Xia, Y.; Mokaya, R. Synthesis of ordered mesoporous carbon and nitrogen-doped carbon materials with graphitic pore walls via a simple chemical vapor deposition method. Adv. Mater. 2004, 16, 1553–1558. [Google Scholar] [CrossRef]
  19. Kruk, M.; Dufour, B.; Celer, E.B.; Kowalewski, T.; Jaroniec, M.; Matyjaszewski, K. Synthesis of mesoporous carbons using ordered and disordered mesoporous silica templates and polyacrylonitrile as carbon precursor. J. Phys. Chem. B. 2005, 2005. 109, 9216–9225. [Google Scholar] [CrossRef]
  20. Bleda-Martínez, M.J.; Peng, C.; Zhang, S.; Chen, G.Z.; Morallón, E.; CazorlaAmorós, D. Electrochemical methods to enhance the capacitance in activated carbon/polyaniline composites. J. Electrochem. Soc. 2008, 155, A672–A678. [Google Scholar] [CrossRef]
  21. Inagaki, M.; Konno, H.; Tanaike, O. Carbon materials for electrochemical capacitors. J. Power Sources. 2010, 195, 7880–7903. [Google Scholar] [CrossRef]
  22. Nishihara, H.; Kyotani, T. Templated nanocarbons for energy storage. Adv. Mater. 2012, 24, 4473–4498. [Google Scholar] [CrossRef] [PubMed]
  23. Shen, W.; Fan, W. Nitrogen-containing porous carbons: synthesis and application. J. Mater. Chem. A. 2013, 1, 999–1013. [Google Scholar] [CrossRef]
  24. Mostazo-López, M. J.; Ruiz-Rosas, R.; Morallón, E.; Cazorla-Amorós, D. Nitrogen doped superporous carbon prepared by a mild method. Enhancement of supercapacitor performance. International Journal of Hydrogen Energy. 2016, 41, 19691–19701. [Google Scholar] [CrossRef]
  25. Quílez-Bermejo, J.; González-Gaitán, C.; Morallón, E.; Cazorla-Amorós, D. Effect of carbonization conditions of polyaniline on its catalytic activity towards ORR. Some insights about the nature of the active sites. Carbon. 2017, 119, 62–71. [Google Scholar] [CrossRef]
  26. Zhao, J.; Lai, H.; Lyu, Z.; Jiang, Y.; Xie, K.; Wang, X.; Wu, Q.; Yang, L.; Jin, Z.; Ma, Y.; Liu, J.; Hu, Z. Hydrophilic hierarchical nitrogen-doped carbon nanocages for ultrahigh supercapacitive performance Adv. Mater. 2015, 27, 3541–3545. [Google Scholar] [CrossRef]
  27. Ostafiychuk, B.K.; Budzulyak, I.M.; Kuzyshyn, M.M.; Rachiy, B.I.; Zatorskiy, R.A.; Lisovskiy, R.P.; Mandzyuk, V.I. Nitrogen-Containing Nanoporous Coal for Electrodes of Supercapacitors. Journal of Nano and Electronic Physics. 2013, 5, 03049. [Google Scholar]
  28. Tian, W.; Zhang, H.; Sun, H.; Tadé, M.O.; Wang, S. Template-free synthesis of N-doped carbon with pillared-layered pores as bifunctional materials for supercapacitor and environmental applications. Carbon, 2017, 118, 98–105. [Google Scholar] [CrossRef]
  29. Zhu, C.; Li, H.; Fu, S.; Du, D.; Lin, Y. Highly efficient nonprecious metal catalysts towards oxygen reduction reaction based on three-dimensional porous carbon nanostructures. Chemical Society Reviews. 2016, 45, 517–531. [Google Scholar] [CrossRef]
  30. Puthusseri, D.; Aravindan, V.; Madhavi, S.; Ogale, S. 3D micro-porous conducting carbon beehive by single step polymer carbonization for high performance supercapacitors: the magic of in situ porogen formation. Energy Environ. Sci. 2014, 7, 728–735. [Google Scholar] [CrossRef]
  31. Bichat, M.P.; Raymundo-Piñero, E.; Béguin, F. High voltage supercapacitor built with seaweed carbons in neutral aqueous electrolyte. Carbon. 2010, 48, 4351–4361. [Google Scholar] [CrossRef]
  32. Demarconnay, L.; Raymundo-Piñero, E.; Béguin, F. A symmetric carbon/carbon supercapacitor operating at 1.6 V by using a neutral aqueous solution. Electrochem. Commun. 2010; 12, 1275–1278. [Google Scholar] [CrossRef]
  33. Chen, Y.; Zhang, J.; Li, M.; Yang, C.; Zhang, L.; Wang, C.; Lu, H. Strong interface coupling and few-crystalline MnO2/Reduced graphene oxide composites for supercapacitors with high cycle stability. Electrochim. Acta. 2018, 292, 115–124. [Google Scholar] [CrossRef]
  34. Gao, Q.; Demarconnay, L.; Pineroa, E.R.; Beguin, F. Exploring the large voltage range of carbon/carbon supercapacitors in aqueous lithium sulfate electrolyte. Energy Environ. Sci. 2012, 5, 9611–9617. [Google Scholar] [CrossRef]
  35. Inagaki, M. Structure and Texture of Carbon Materials. Carbons for Electrochemical Energy Storage and Conversion Systems. 2009, 37–76. [Google Scholar] [CrossRef]
  36. Pecharsky, V.K.; Zavalij, P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials. Springer: New York, NY, USA, 2009. [Google Scholar]
  37. Bordun, I.; Pidluzhna, A.; Ivashchyshyn, F.; Borysiuk, A.; Całus, D.; Chwastek, K. Structural and magnetic properties of Ni/C composites synthesized from beet pulp and corn stems. Magnetochemistry. 2021, 7, 31. [Google Scholar] [CrossRef]
  38. Thommes, M.; Kaneko, K.; Neimark, A.; Olivier, J.; Rodriguez-Reinoso, F.; Rouquerol, J.; Sing, K. Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC Technical Report). Pure and Applied Chemistry. 2015, 87, 1051–1117. [Google Scholar] [CrossRef]
  39. Rouquerol, J.; Rouquerol, F.; Llewellyn, P.; Maurin, G.; Sing, K. Adsorption by powders and porous solids: principles, methodology and applications. 2nd edition. Academic press, Oxford, 2014. [Google Scholar]
  40. Lozano-Castelló, D.; Suárez-Garsía, F.; Cazorla-Amoróz, D. Á. Linares-Solano, Porous texture of carbons. In Carbon for Electrochemical Energy Storage Systems (Beguin F. and Frackowiak E., Eds.). CRC Press, Taylor and Francis Group, Boca Raton, New York, 2002. [Google Scholar]
  41. Guinier, A.; Fournet, G. Small-angle scattering of X-rays. New York: Wiley, 1955. [Google Scholar]
  42. Porod, G. General theory. In: Glatter O, Kratky O, editors. Small-angle X-ray scattering. London: Academic, 1982. [Google Scholar]
  43. Soloviy, C.; Malovanyy, M.; Bordun, I.; Ivashchyshyn, F.; Borysiuk, A.; Kulyk, Y. Structural, magnetic and adsorption characteristics of magnetically susceptible carbon sorbents based on natural raw materials. Journal of Water and Land Development. 2020, 47, 160–168. [Google Scholar] [CrossRef]
  44. Makarova, T.L. Magnetic properties of carbon structures. Semiconductors. 2004, 38, 615–638. [Google Scholar] [CrossRef]
  45. Murata, K.; Ushijima, H.; Ueda, H.; Kawaguchi, K. A stable carbon-based organic magnet. Journal of the Chemical Society, Chemical Communications. 1992, 7, 567–569. [Google Scholar] [CrossRef]
  46. Ushijima, H.; Murata, K.; Ueda, H.; Kawaguchi, K. Preparation of amorphouslike carbons by pyrolysis of organic compounds and their magnetic properties. Molecular Crystals and Liquid Crystals Science and Technology. Section A. Molecular Crystals and Liquid Crystals. 1993, 233, 351–360. [Google Scholar] [CrossRef]
  47. Setnescu, R.; Jipa, S.; Setnescu, T.; Kappel, W.; Kobayashi, S.; Osawa, Z. IR and X-ray characterization of the ferromagnetic phase of pyrolysed polyacrylonitrile. Carbon. 1999, 37, 1–6. [Google Scholar] [CrossRef]
  48. Yazyev, O.V.; Helm, L. Defect-induced magnetism in graphene. Physical Review B - Condensed Matter and Materials Physics. 2007, 75, 125408. [Google Scholar] [CrossRef]
  49. Son, Y.W.; Cohen, M.L.; Louie, S.G. Half-metallic graphene nanoribbons. Nature. 2006, 444, 347–349. [Google Scholar] [CrossRef] [PubMed]
  50. Zhang, Y.; Talapatra, S.; Kar, S.; Vajtai, R.; Nayak, S.K.; Ajayan, P.M. First-principles study of defect-induced magnetism in carbon. Physical Review Letters. 2007, 99, 10720. [Google Scholar] [CrossRef] [PubMed]
  51. Barsoukov, E.; Macdonald, J.R. Impedance spectroscopy: theory, experiment, and applications. John Wiley & Sons Inc., New Jersey, 2018. [Google Scholar]
  52. Mandzyuk, V.I.; Myronyuk, I.F.; Sachko, V.M.; Rachiy, B.I.; Kulyk, Yu.O.; Mykytyn, I.M. Structure and Electrochemical Properties of Saccharide-derived Porous Carbon Materials. J. Nano- Electron. Phys. 2018, 10, 02018. [Google Scholar] [CrossRef]
Preprints 93379 g001
Figure 1. Galvanostatic charge-discharge cycles for the bio-carbon material NCNM synthesised at 800 °C in 30% KOH electrolyte (a) and in 1M Na2SO4 (b).
Figure 1. Galvanostatic charge-discharge cycles for the bio-carbon material NCNM synthesised at 800 °C in 30% KOH electrolyte (a) and in 1M Na2SO4 (b).
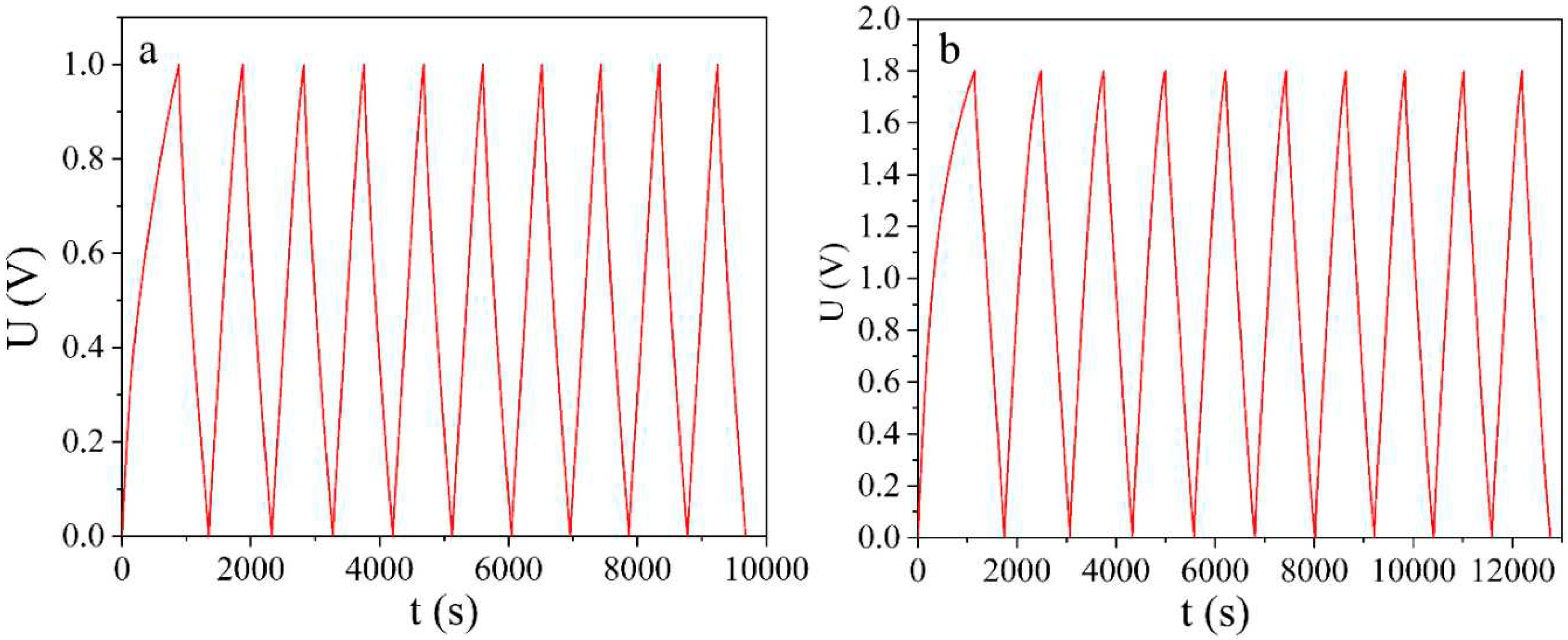
Preprints 93379 g001
Preprints 93379 g002
Figure 2. SEM images of NCNM at high magnification: 550х (a), 2250х (b), 9500х (c) and 9600х (d).
Figure 2. SEM images of NCNM at high magnification: 550х (a), 2250х (b), 9500х (c) and 9600х (d).
Preprints 93379 g002
Preprints 93379 g004
Figure 4. Nitrogen adsorption/desorption isotherm NCNM.
Figure 4. Nitrogen adsorption/desorption isotherm NCNM.
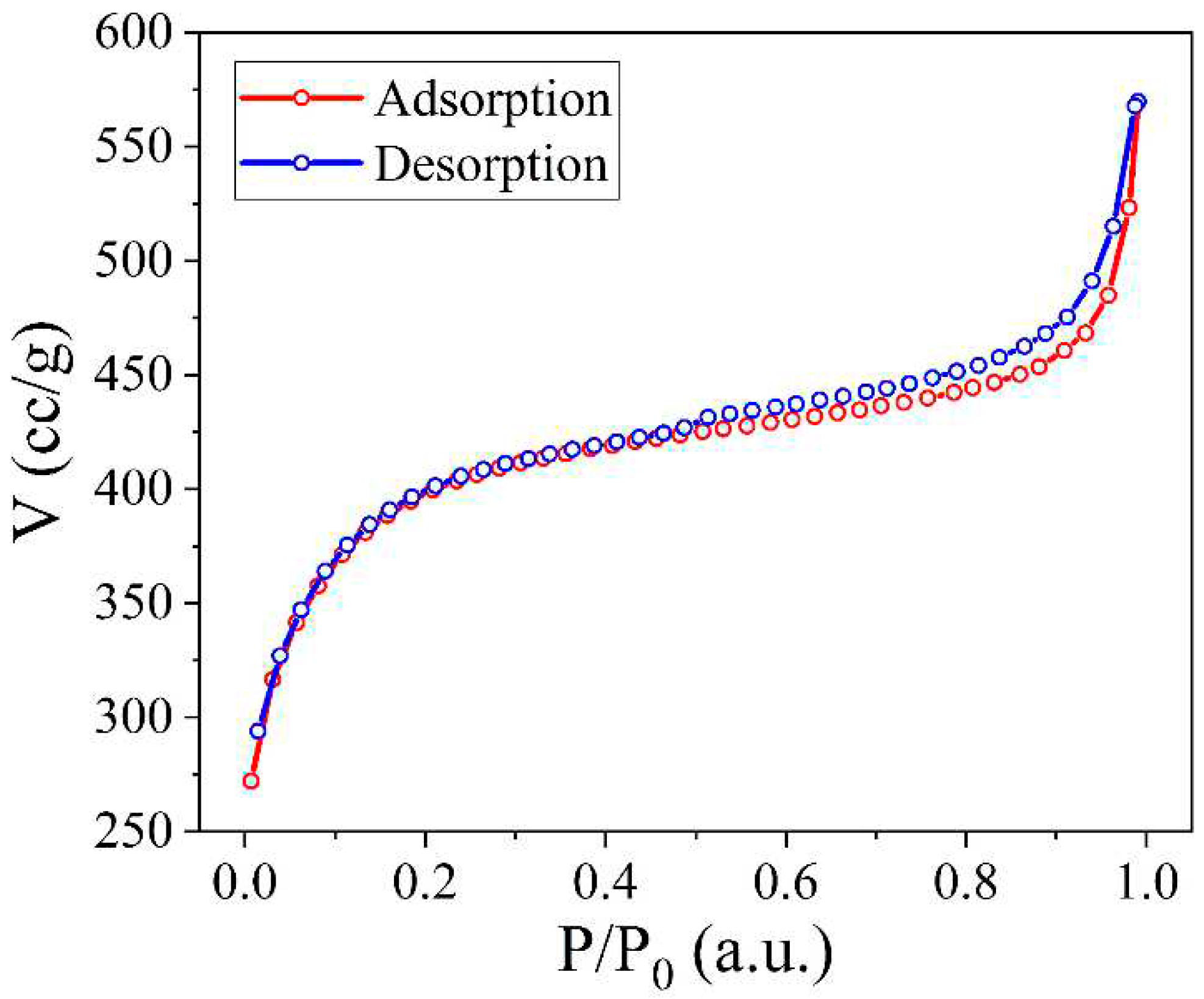
Preprints 93379 g004
Preprints 93379 g005
Figure 5. Pore size distribution for the synthesised NCNM calculated by the BJH method.
Figure 5. Pore size distribution for the synthesised NCNM calculated by the BJH method.
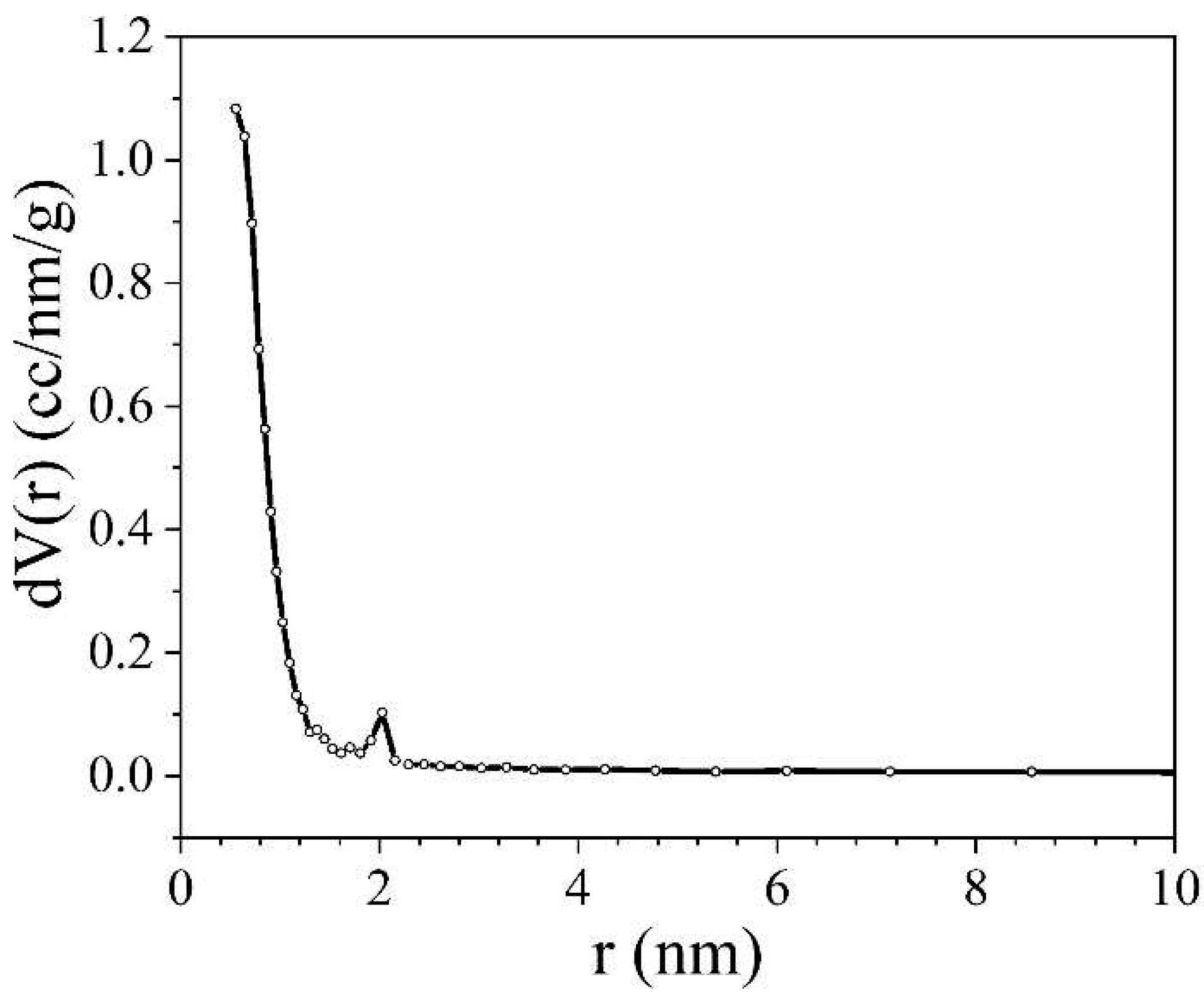
Preprints 93379 g005
Preprints 93379 g006
Figure 6. Pore size distribution for the synthesised NCNM calculated by the DFT method.
Figure 6. Pore size distribution for the synthesised NCNM calculated by the DFT method.
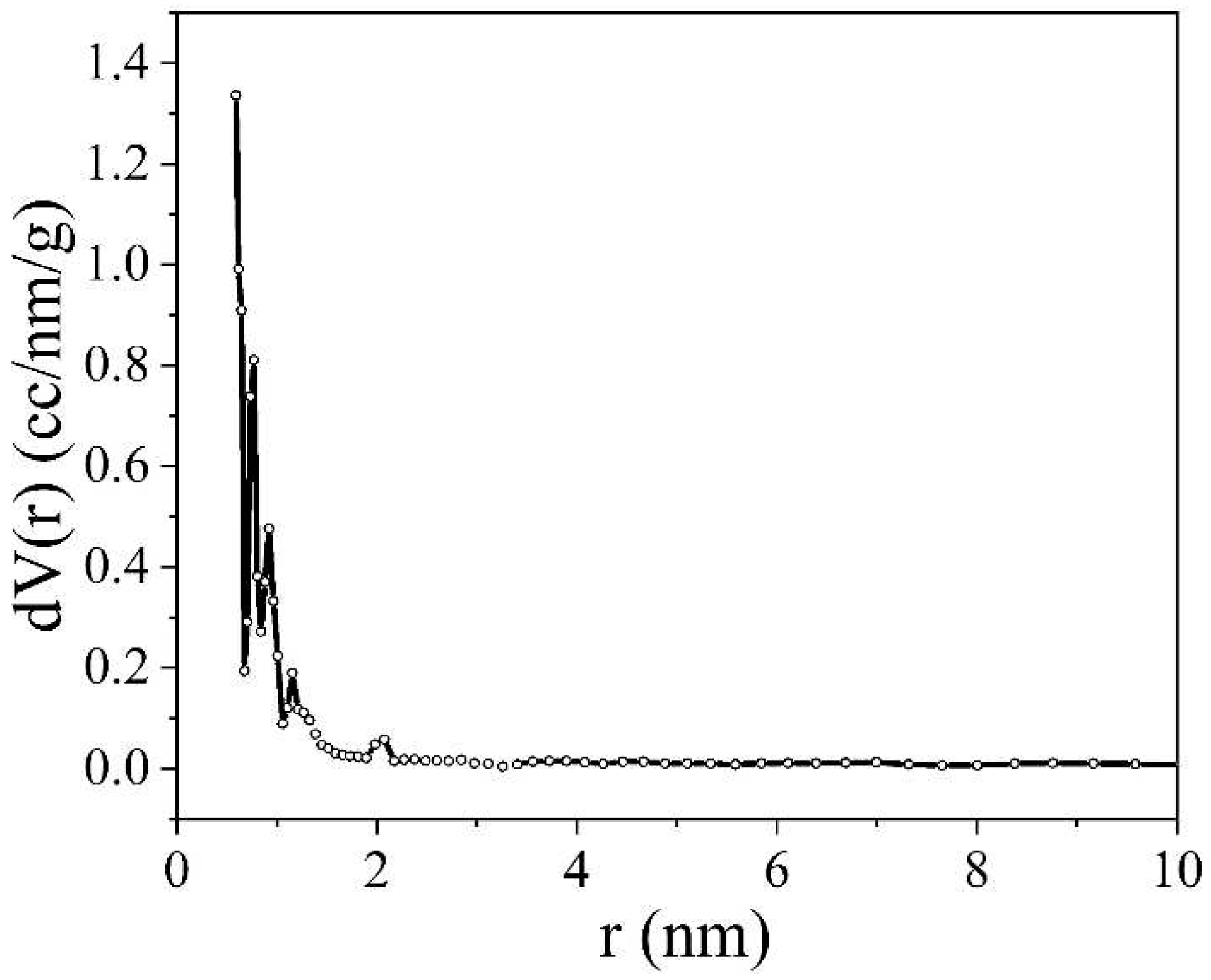
Preprints 93379 g006
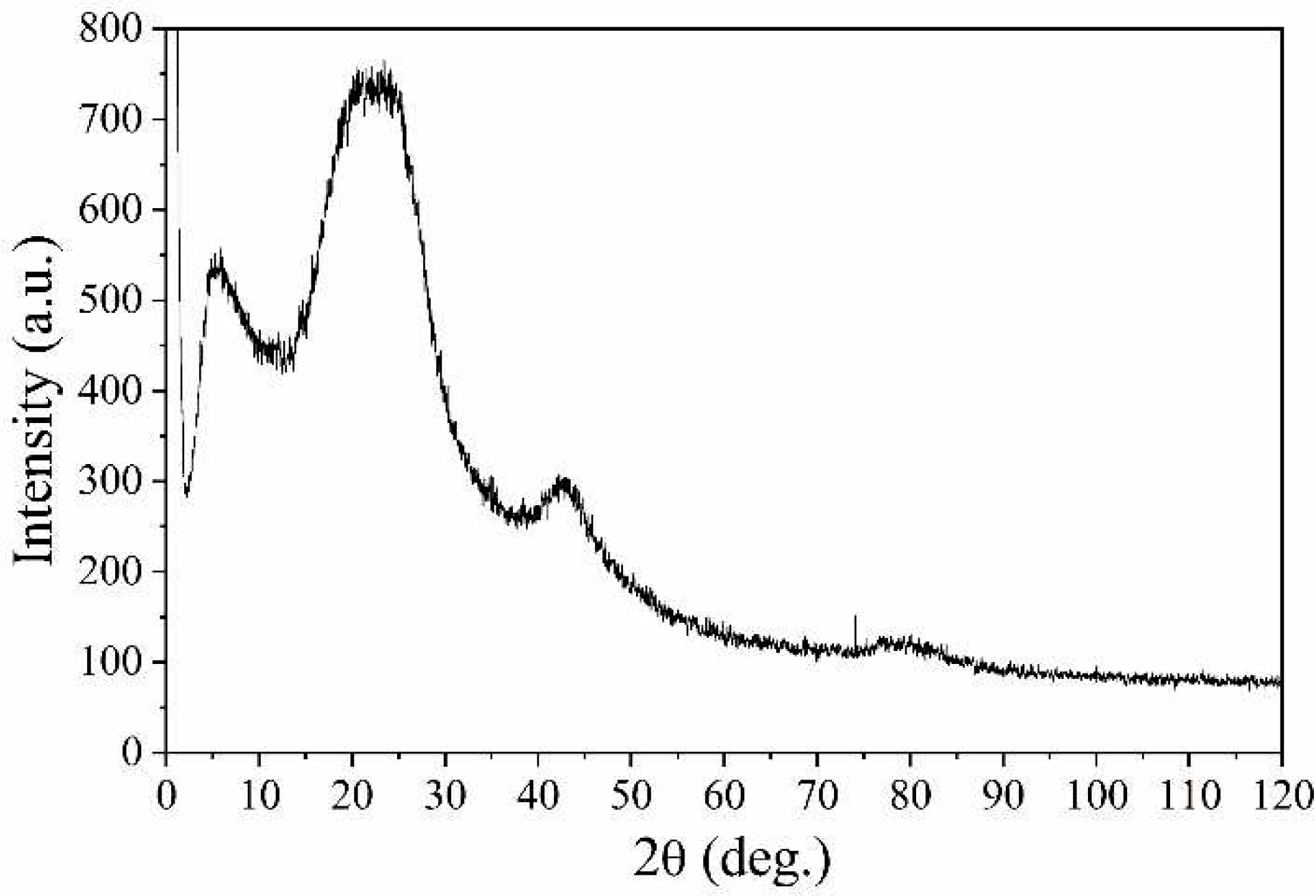
Preprints 93379 g007
Figure 7. X-ray diffractogram of NCNM sample.
Figure 7. X-ray diffractogram of NCNM sample.
Preprints 93379 g007
Preprints 93379 g008
Figure 8. Intensity curve of the NCNM small-angle scattering (dots - experimental data corrected for background scattering, solid curve - smoothing by spline approximation).
Figure 8. Intensity curve of the NCNM small-angle scattering (dots - experimental data corrected for background scattering, solid curve - smoothing by spline approximation).
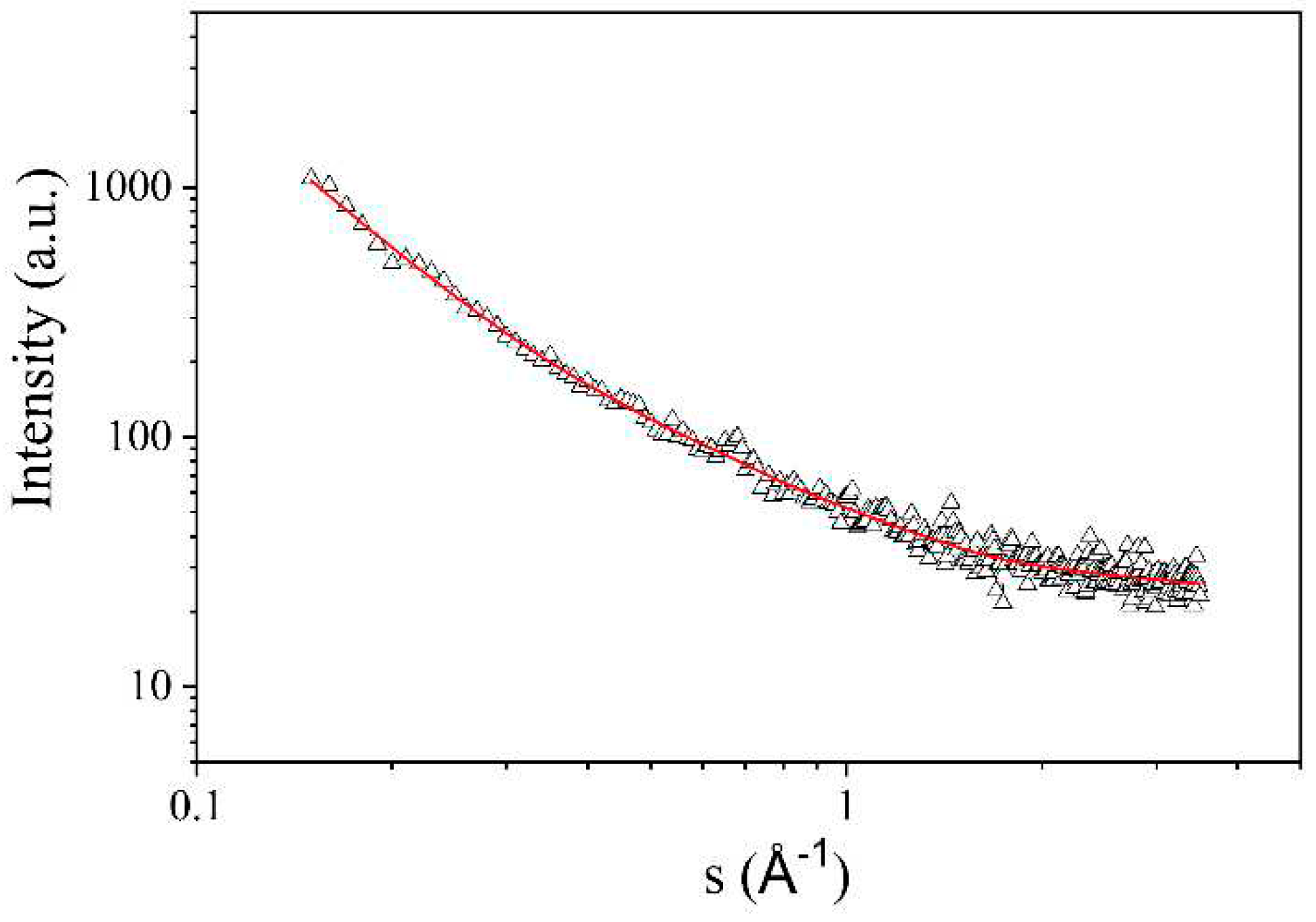
Preprints 93379 g008
Preprints 93379 g009
Figure 9. Volumetric functions of NCNM pore distribution by radii of inertia.
Figure 9. Volumetric functions of NCNM pore distribution by radii of inertia.
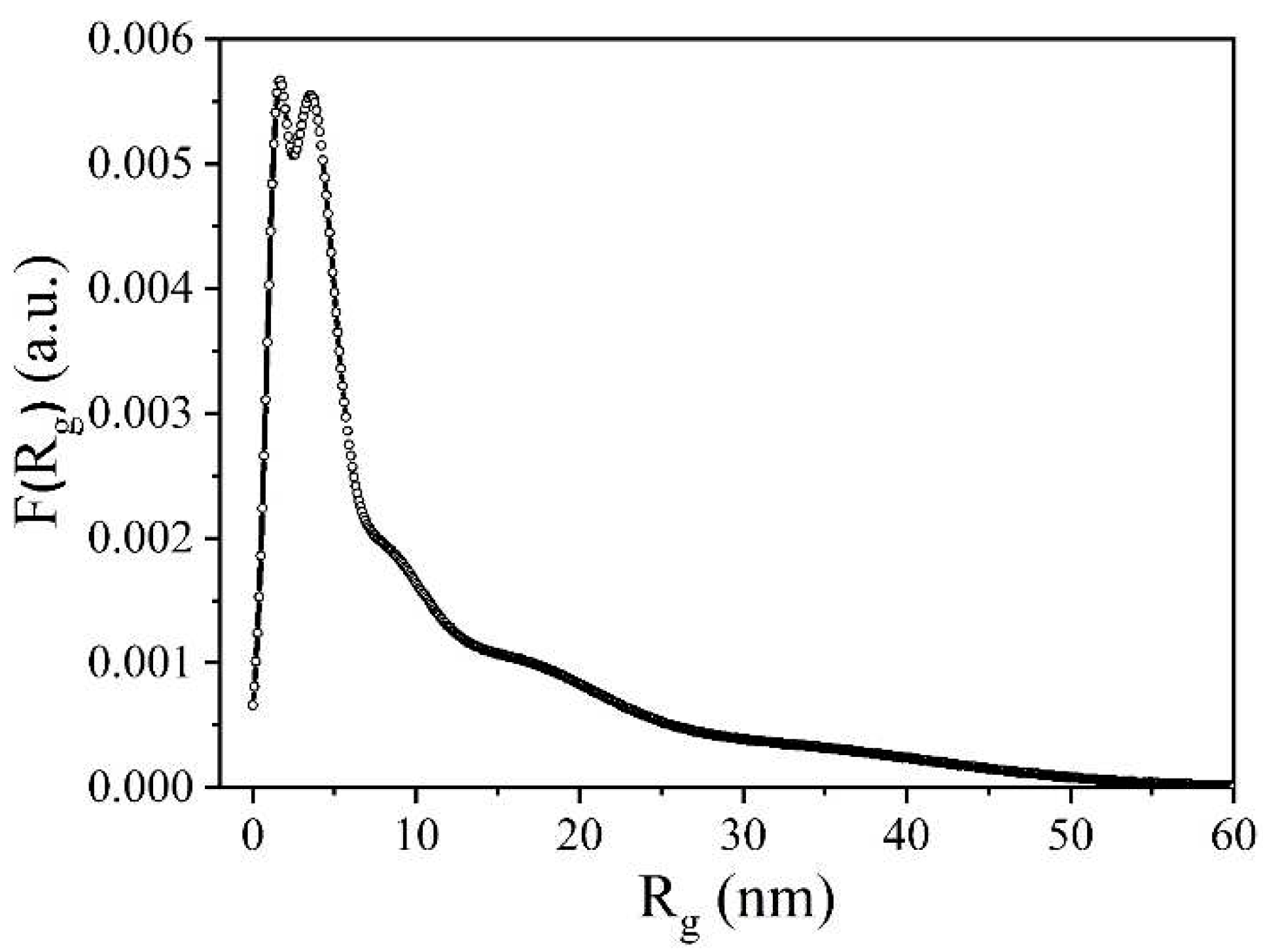
Preprints 93379 g009
Preprints 93379 g010
Figure 10. Magnetic moment hysteresis loop for NCNM.
Figure 10. Magnetic moment hysteresis loop for NCNM.
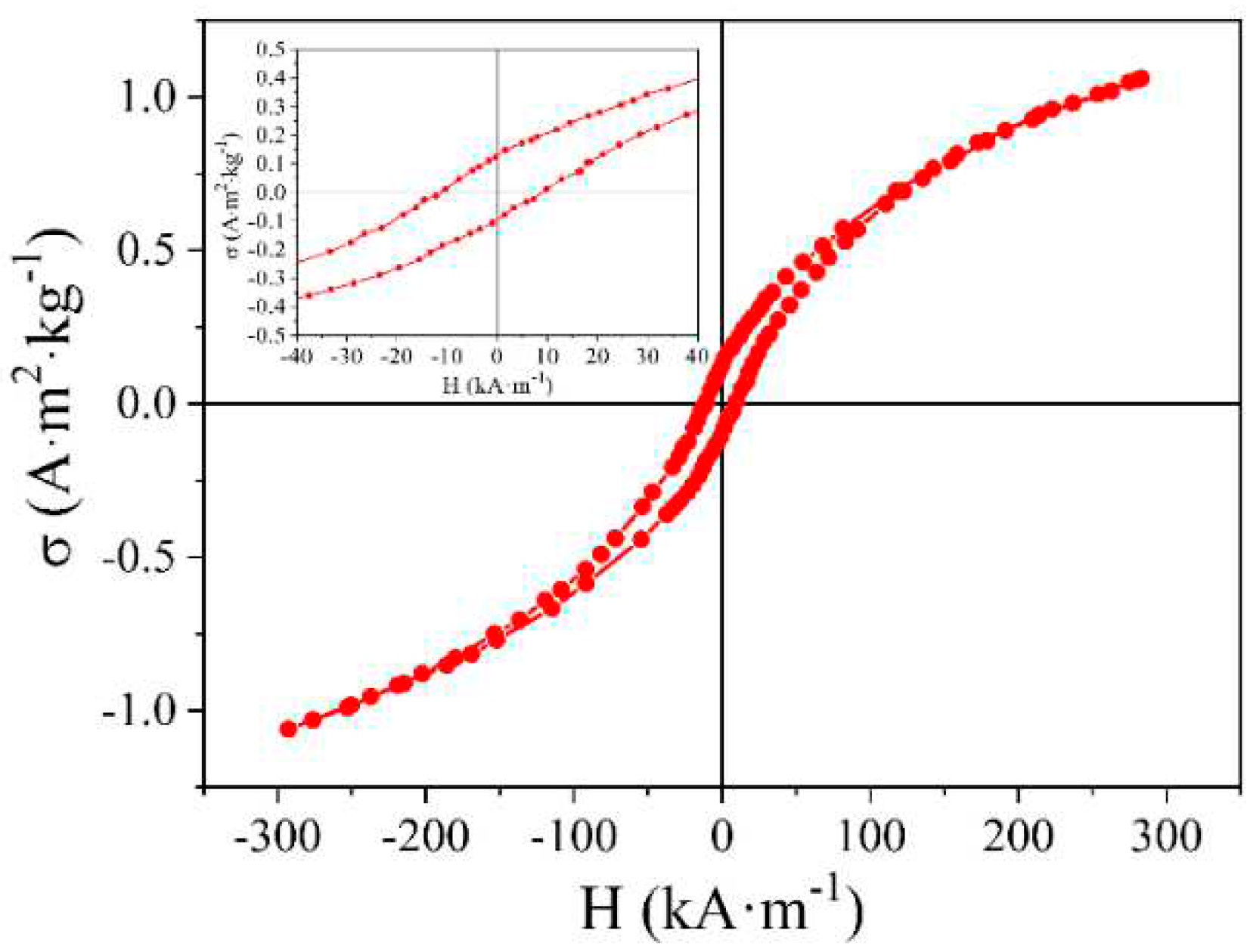
Preprints 93379 g010
Preprints 93379 g011
Figure 11. Nyquist diagram of synthesised bio-carbon from glucose in KOH electrolyte (a) and Na2SO4 electrolyte (b). The dots represent the experimental dependences, and the solid lines are modelled by the equivalent electrical circuits shown in the inset.
Figure 11. Nyquist diagram of synthesised bio-carbon from glucose in KOH electrolyte (a) and Na2SO4 electrolyte (b). The dots represent the experimental dependences, and the solid lines are modelled by the equivalent electrical circuits shown in the inset.
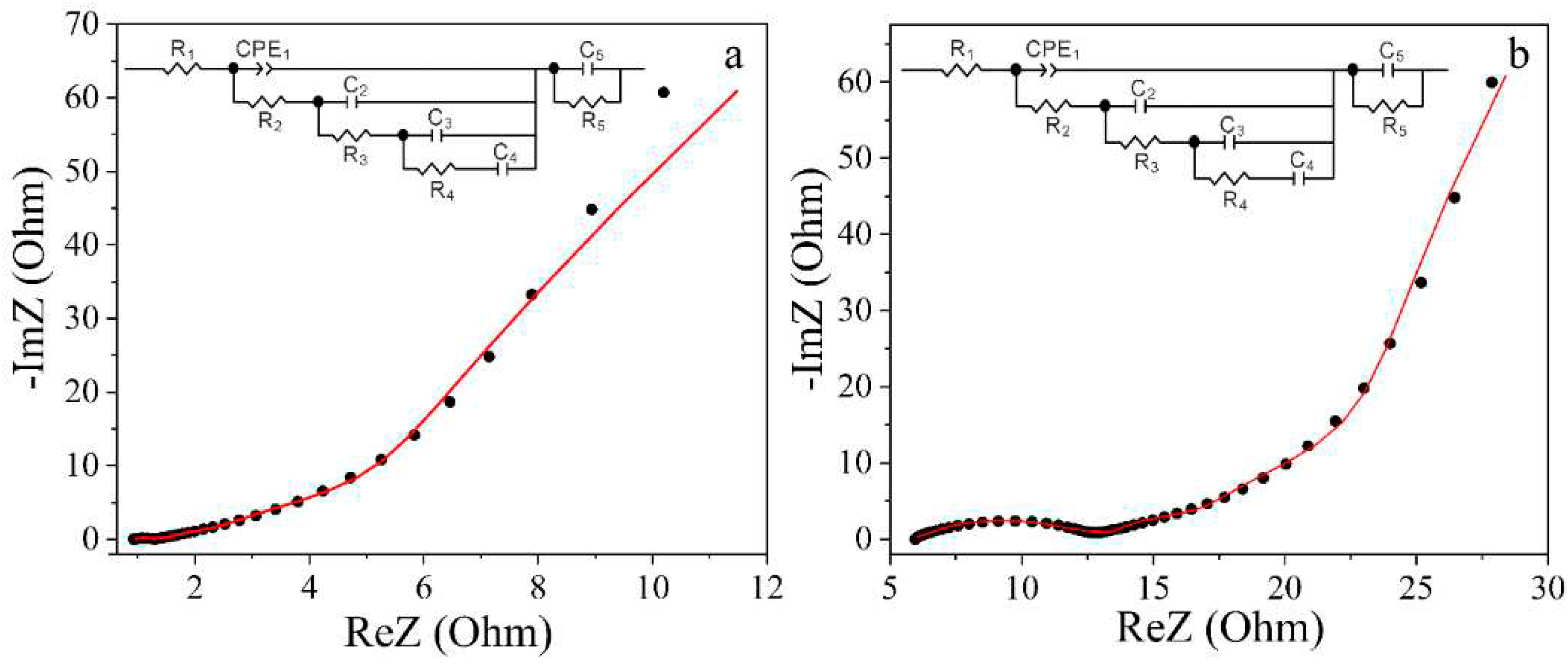
Preprints 93379 g011
Table 1. Specific capacity in F/g of synthesised carbon materials in different electrolytes (charge/discharge current density 0.5 A/g).
Table 1. Specific capacity in F/g of synthesised carbon materials in different electrolytes (charge/discharge current density 0.5 A/g).
Electrolyte Synthesis temperature NCNM, oС
600 700 800
30 % KOH 20 109 180
1 M Na2SO4 9 68 124
Table 2. Structural parameters of the studied carbon.
Table 2. Structural parameters of the studied carbon.
Sample S, m2/g V, cm3/g r ¯ , nm Correlation coefficient according to the BET model
NCNM 1247 0.88 1.42 0.996
Table 3. Structural characteristics of the investigated biocarbon using the SAXS method.
Table 3. Structural characteristics of the investigated biocarbon using the SAXS method.
Sample Kp·104, nm-4 Qp·103, nm-3 Rgs, nm Sp,
m2 / cm3
NCNM 0.883 49.5 2.95 592
Table 4. Parameters of the equivalent circuit for the investigated biocarbon.
Table 4. Parameters of the equivalent circuit for the investigated biocarbon.
Electrolyte R1, Оhm CPE1 R2, Оhm C2, F R3, Ohm C3, F R4, Оhm C4, F R5, Ohm C5, mF/g
T P
30 % КОН 0.958 0.052 0.785 0.84 0.037 3.839 0.066 23.7 0.063 0.315 0.131
1M Na2SO4 5.639 0.007 0.429 5.608 0.032 6.376 0.099 32 0.098 3.114 0.045
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated