Preprint
Article
Antiangiogenic Therapy Efficacy Can Be Tumor Size Dependent,as Mathematical Modeling Suggests
Altmetrics
Downloads
120
Views
28
Comments
0
A peer-reviewed article of this preprint also exists.
supplementary.cpp (54.65KB )
This version is not peer-reviewed
Submitted:
14 December 2023
Posted:
15 December 2023
You are already at the latest version
Alerts
Abstract
Antiangiogenic therapy (AAT) is an indirect oncological modality which is aimed at disruption of cancer cells nutrient supply. Invasive tumors have been shown to possess inherent resistant to this treatment, while compactly growing benign tumors react to it by shrinkage. It is generally accepted that AAT by itself is not curative. This study presents a mathematical model of non-invasive tumor growth with physiologically justified account of alteration of microvasculature and biomechanical aspects during tumor growth and AAT. In untreated setting the model reproduces tumor growth with saturation, where the maximum tumor volume depends on the level of angiogenesis. The outcomes of simulations of AAT depend on the tumor size at the moment of treatment initiation. If it is close to the stable size of avascular tumor grown in absence of angiogenesis, then the tumor is rapidly stabilized by AAT. Treatment of large tumors is accompanied by displacement of normal tissue due to the tumor shrinkage. During it, microvasculature undergoes distortion which degree depends on the displacement distance. As it affects tumor nutrient supply, the stable size of a tumor that undergoes AAT negatively correlates with its size at the beginning of treatment. For sufficiently large initial tumors, the long-term survival of tumor cells is compromised by competition with normal cells for severely limited inflow of nutrients, which makes AAT effectively curative.
Keywords:
Subject: Computer Science and Mathematics - Mathematical and Computational Biology
1. Introduction
1.1. Biological background
Cancer currently remains a major cause of morbidity and mortality worldwide [1]. New methods of its treatment, as a rule, have limited efficacy, target only a narrow range of cancer types and have limited availability to the general public due to their high cost. Therefore, an important challenge in oncology is optimization of the types of anticancer therapy that are already introduced into clinical practice.
Standard and long-established types of anticancer treatment, chemotherapy and radiotherapy, lead to eradication of actively proliferating cells subject to the therapeutic action. The non-selectivity of these treatments inevitably leads to the damage of healthy cells that are reached by chemotherapeutic drugs or are traversed by radiation beams. Recently, a group of radically different anticancer modalities have emerged, that perform indirect interference with the mechanisms sustaining the existence of cancer as a complex organ, embedded in a host organism [2]. Prominent examples of such approaches are immunotherapy and antiangiogenic therapy. Immunotherapy is an umbrella term for a group of medical interventions aimed at the disruption of the ability of cancer cells to evade immune surveillance [3]. The goal of antiangiogenic therapy (AAT) is breaking the process of tumor angiogenesis, i.e., formation of blood vessels, in particular capillaries that provide nutrient exchange [4]. These therapies are not devoid of side-effects, which are nevertheless usually more moderate and affect other organs than the standard treatments.
Enabling the process of tumor angiogenesis is a crucial step in cancer progression. In its absence tumors generally cannot grow beyond the size of 1-2 mm [5]. Further tumor growth is restricted by limited nutrient supply from capillaries located in normal tissues that are pushed away by growing tumor mass. Thus, an avascular tumor eventually reaches a stable state in which ongoing proliferation of its cells in the tumor periphery is compensated by the death of nutrient-deprived cells in its core.
One way for the tumor cells to overcome nutrient deficiency is to invade nearby tissues and co-opt existing capillaries. Enabling invasion is a crucial hallmark of malignant tumors [6]. However, it is a complex process that requires accumulation of a sufficient number of cell mutations [7]. Since the overall frequency of mutations correlates with the rate of tumor cell divisions, acquiring invasive phenotype is a long process for small tumors. Angiogenic switch is a faster process that generally manifests itself while a tumor is yet benign and lacking invasive properties.
In healthy tissues the process of angiogenesis takes place, e.g., during wound healing, and it leads to an ordered vascular system, finely tuned for each organ. Tumor cells, however, produce angiogenic molecules excessively, that results in the formation of chaotically organized and highly permeable capillary networks. AAT neutralizes the action of angiogenic molecules. This leads to the cessation of formation of new capillaries, to the normalization of structure of already formed tumor capillaries [8], to further normalization of the density of capillary network [9], and to alleviation of tumor-associated edema [10].
The restriction of nutrient supply caused by AAT limits the growth of tumor and can yield its shrinkage, but generally does not lead to tumor cure. That provides ground for the use of AAT in combination with another modalities. In clinical practice AAT is generally paired with chemotherapy (CT) [11]. There are multiple factors that influence the efficacy of AAT by itself and in combination with CT. In particular, AAT entails reduced inflow of chemotherapeutic drug in tumor, which was observed experimentally [12,13]. This renders the problem of optimization of AAT-based treatments in clinical practice a highly nontrivial task. Its solution is heavily compromised by the impossibility to test all the feasible treatment alterations due to the logistical and ethical reasons.
1.2. Mathematical background
A methodology that can point at the potential biomarkers of treatment efficacy and that can significantly narrow down the range of potentially effective therapeutic protocols is mechanistic mathematical modeling. It envisions the tumor and its microenvironment as a single complex system which, contrary to the real-life situation, can be reproduced under broad variation of parameters and treatment approaches.
There exist several methods of modeling tumor growth taking into account angiogenesis and AAT. The simplest method relies on the system of ordinary differential equations. The models of this kind generally include an equation for logistic growth of the tumor volume, with its maximum value being a variable depending on the concentration of antiangiogenic drug [14]. Although such phenomenological models can be convenient for preclinical and clinical studies, they clearly represent oversimplifications omitting spatial aspects and neglecting many physiological processes that can influence treatment outcome.
The most popular approach for modeling angiogenesis and AAT is agent-based modeling involving detailed reproduction of capillary networks and, frequently, explicit consideration of blood flow maps [15,16]. Such models can provide elegant visualizations of microvasculature remodeling and can yield useful insights. However, they require significant computational costs, which increase with the tumor size. That crucially limits the practical use of such models. Up to date, they have not been used to simulate an entire course of AAT.
The use of continuous spatially-distributed models based on partial differential equations can provide a compromise between computational cost and physiological validity [17,18]. Although such models are unable to reproduce the microscopic aspects of capillary network, they allow consideration of crucial dynamic features of tumor microvasculature under unperturbed tumor growth and under the course of therapy. However, the related models presented nowadays in literature are focused on invasive tumors, and they ignore the biomechanical aspects crucial for reproduction of the tumor response to the alterations of microvasculature.
On the other hand, there exists sufficient amount of modeling studies devoted to biomechanical aspects accompanying tumor growth and treatment, which do not account for dynamically changing tumor microvasculature. In particular, consideration of interstitial fluid dynamics and its influence on drug delivery is a well researched problem in case of static tumors [19,20,21]. In the case of a dynamic tumor that can both grow and shrink during therapy, a physiologically correct approach for modeling is simultaneous account for the stress arising in the solid phase of the tissue (cells and extracellular matrix) along with the dynamics of interstitial fluid, since they are closely interrelated. In particular, deformation of the solid component of the tissue affects fluid flow, while outflow of fluid from the tumor leads to its shrinkage and to the alleviation of stress exerted by the surrounding normal tissue.
The related works on mathematical modeling with account of solid stress are less numerous. The methods used in them range from relatively simple to complex ones. The complex methods are generally adapted from the area of solid mechanics, being based on multiplicative decomposition of the tissue strain gradient tensor into components corresponding to different physical processes [22,23]. The use of such methods is associated with great computational costs, but is justified, e.g., if quantitative agreement with experimental results is pursued. For qualitative studies, however, more practical approach is the use of simpler methods that regard tumor as a liquid-like or linearly elastic medium [24,25]. Such methods have been repeatedly proven to be able to qualitatively reproduce experimental observations, e.g., the decrease of maximum tumor size with the increase of applied external pressure [26] and the oozing of liquid from a large tumor due to the elevated pressure in its core [27].
The current study simultaneously considers both alterations of microvasculature and evolution of biomechanical aspects during tumor growth and antiangiogenic treatment. This study is based on our previous works on mathematical modeling of tumor angiogenesis and AAT [28,29,30] and on our works focused on biomechanical properties of tumor and normal tissues [31,32,33,34].
2. Model
2.1. Equations
The investigated model is presented in the system of Eqs. (1). It has nine partial differential equations controlling the dynamics of spatially distributed variables. The block scheme of the main model interactions is presented in Figure 1. For detailed description of the interactions of the model we refer the readers to our previous work [33]. The crucial model aspects are as follows.


The model reproduces spherically symmetric growth of a non-invasive tumor within a normal tissue. Under sufficient levels of glucose g, tumor cells maintain the proliferative state , in which their number grows exponentially. Cells use interstitial fluid f as the mass source. In the absence of glucose, they transit reversibly to the quiescent state . Under nutrient deficiency tumor cells die, which is reflected by their transition into dead state m. In it they gradually degrade transforming into interstitial fluid.
Tumor cells are surrounded by normal cells h, and they collectively constitute the porous solid phase fraction of the tissue, denoted as . The interstitial fluid represents its second phase, capable of viscous flow through the pores within the solid fraction. The tissue is assumed to be saturated and incompressible, which implies that the total density of cells and fluid together remains constant.
The rate of cell proliferation is influenced by both local glucose level and local solid stress, denoted as . The solid stress function is built on the assumption that the volume fraction of cells correlates with the average distance between them [35]. When the cell fraction is at its normal value (), interactions among cells result in zero solid stress. Cells in close proximity tend to repel each other, while cells at a distance tend to attract. With increasing distance the interaction strength eventually vanishes.
Interstitial fluid enters the tissue from capillaries, two types of which are taken into account: normal and abnormal . Abnormal capillaries possess increased permeability to fluid and glucose due to the influence of vascular endothelial growth factor (VEGF) v. It is produced by nutrient-deprived quiescent cells. It also stimulates formation of new capillaries in the abnormal state. At low VEGF concentrations capillaries normalize, which implies decrease of their permeability. Normalized excessive capillaries tend to return to their basal physiological density, which reflects the process of pruning of microvasculature in healthy tissues. Interstitial fluid drains into the lymphatic system, not considered explicitly, but assumed to have density proportional to that of normal cells. Consequently, lymphatic capillaries are absent within the tumor. Blood capillaries degrade within the tumor due to implicit factors such as rupture caused by their displacement as well as due to biochemical reasons [36].
We model the action of AAT as having the maximum theoretically possible efficacy. When the treatment begins, all the present VEGF is implied to become immediately bound to antiangiogenic drug and therefore neutralized. The following normalization of microvasculature, however, is not immediate. The dynamics of accompanying processes happens at physiologically justified rates, as described above.
2.2. Parameters
Parameters of the model were determined based on the outcomes of experiments of different nature presented in literature, if available, or estimated in order to reproduce the well-established features accompanying tumor growth otherwise. The basic set of parameters is provided in Table 1, where the following normalization parameters were used to obtain their model values: 1 h for time; cm for length; cells/mL for maximum cell density; mol/mL for VEGF concentration; 100 cm2/cm3 for capillary surface area density; 1 mg/mL for glucose concentration. The choice of the majority of model parameters is justified in our work [33].
2.3. Numerical solving
During the numerical simulation of Eqs. (1), intercellular fluid f was not explicitly taken into account, given the conservation law . The kinetic, diffusion, and advection equations for other variables were solved sequentially at each time step. The explicit Euler method was employed to solve the kinetic equations. The use of this straightforward approach is justified by the relatively small time steps which choice is guided for solving advective equations. For diffusion equations, the implicit Crank-Nicholson scheme was implemented. These classical methods are described, e.g., in the book [51]. To solve the advective equations, the conservative flux-corrected transport algorithm, incorporating an implicit antidiffusion stage, was used [52]. However, this method introduces a minor amount of uncorrectable diffusion, leading to an artificial invasion of the tumor into normal tissue. A similar challenge arises in modeling the normal tissue boundary. To address this issue, two additional floating points were introduced on the computational grid, marking the positions of the tumor-normal tissue interface and the normal tissue boundary. The coordinates of these points were computed by ensuring the conservation of total cell volume when solving advection equations at each time step.
The following initial conditions were used, that represent a spherical section of normal tissue of initial radius mm with a small spherical colony of tumor cells of radius mm located in its center, at :
Here, is the steady state value for the fraction of cells. It is only slightly smaller than , which corresponds to a minor stretching of the network of interconnected cells due to the pressure of surrounding fluid. The following boundary conditions were used, where is the changing radius of tumor and is the changing outer radius of normal tissue:
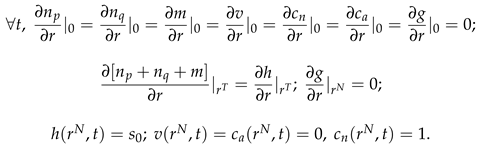
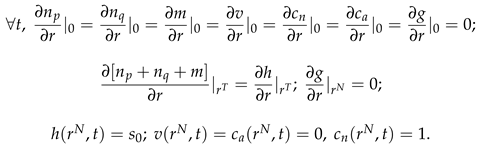
There are two separate advective motions in this model: denotes the absolute velocity of the fluid, and the velocity of the solid phase. By summing up of the equations of dynamics of all cells and assuming both flow velocities to be zero at , Eqs. (4) are obtained. They were used for defining advective velocities during numerical solution.
3. Results
3.1. Free tumor growth with and without angiogenesis
Figure 2 compares the cases of free tumor growth with and without initiation of angiogenesis, under the same values of model parameters, presented in Table 1. Initially, the tumor consists entirely of proliferating cells, with their number growing exponentially. However, within a few hours, some tumor cells start experiencing deficiency of nutrients, which are supplied to the tumor mass from surrounding capillaries pushed away by expanding tumor. Consequently, tumor growth slows down and tumor obtains a layered structure. Its inner core becomes predominantly occupied by quiescent cells and the outer rim by proliferating cells. This structure is characteristic of tumor spheroids in experimental settings and non-invasive tumors in vivo. As the total number of tumor cells keeps increasing, further exacerbation of nutrient deficiency results in appearance of dead cells in the tumor core. Their degradation turns them into viscous liquid, from the modeling point of view indistinguishable from the rest of interstitial fluid. Decreased number of tumor cells in the central part of the tumor implies stretching of the solid phase of the tumor tissue. That, in accordance with the biomechanical terms in Eqs. (1), underlies elevated fluid pressure in the tumor core, compared to it in the surrounding normal tissue. Therefore, fluid oozes from the tumor mass, contributing to further decrease of its growth rate. When the total rates of tumor cell proliferation and death equate, tumor reaches a stable state.
In the case without angiogenesis, the avascular tumor growth stops at mm radius. That is consistent with clinical observations [5]. In the presence of angiogenesis, the formation of new capillaries is stimulated by VEGF secreted by quiescent tumor cells. Capillaries influenced by VEGF have greater permeability, which along with the increase of microvascular density contributes to the increased inflow of glucose to the tumor. The vascularized tumor has larger pool of proliferating cells, which means that greater total rate of outflow of dead cells is required to compensate for it yielding the stable tumor. In the considered simulation, the corresponding maximum tumor radius is mm. This model is restricted with consideration of a homogeneous non-mutating tumor. In a more realistic scenario further tumor growth would be ensured in particular by continuous selection of cells that proliferate faster and are more tolerant to nutrient deficiency, as well as by initiation of tumor cell invasion into surrounding tissue accompanied by co-opting of capillaries located there.
Despite the variety of considered physiological processes and non-trivial pattern of distribution of model variables produced by this model, on the higher level of consideration the simulations of free tumor growth provide quite classical S-shaped growth curves [53]. Such curves by themselves can be qualitatively reproduced by much simpler models, based on a few ordinary differential equations. In the corresponding models, the dependence of tumor growth on angiogenesis is generally reproduced via introduction of the dependence of maximum tumor volume on the amount of secreted proangiogenic signals [14]. In such simpler approach the cessation of angiogenesis results in gradual decrease of tumor volume down to the value corresponding to the case of initially avascular tumor. The current model, however, yields more intricate pattern of tumor response to AAT, as discussed in further section.
3.2. Antiangiogenic therapy beginning at different moments of tumor growth
Figure 3 illustrates the non-trivial nature of tumor response to AAT under the variation of tumor radius at which the treatments begins. Elimination of VEGF for the 1 mm tumor yields its quick growth saturation. The capillary system that undergoes degradation within the tumor volume, normalization and pruning is eventually stabilized with a slightly greater total amount of capillaries than in the case of avascular tumor. Therefore, it can support the existence of a stable tumor slightly greater than 1 mm in radius.
AAT performed for larger tumors does not result in tumor stabilization at this radius. For 2 mm tumor the treatment yields the final tumor radius of 0.6 mm. For 3 mm and 4 mm tumors their sizes steadily decrease through the simulations tending to negligible values. Although from the modeling point of view tumor always has some finite radius, the interpretation of such qualitative results may imply complete tumor cure.
The reasons behind this non-trivial pattern of tumor response to AAT lie in the processes accompanying tumor shrinkage and consequent remodeling of displaced normal tissue and microvasculature. In case of a small vascularized tumor the displacement of capillary system is only minor. Therefore, the final tumor size is almost not affected by the physiological processes that happen along the tissue displacement. From the general mathematical point of view, the system state right before the antiangiogenic treatment is by itself close to the stable state that would be achieved under the absence of angiogenesis. Thus, the treatment imposes only a comparably small perturbation of the tumor dynamics.
In contrast, large vascularized tumors have evolved to the states significantly different from the stable state of initially avascular tumor. Rapid normalization of microvessel structure and density in response to the elimination of VEGF entails quick decrease of the total volume of proliferative tumor cells that can be sustained by microvasculature. In a short period, the overall tumor cell proliferation rate becomes unable to compensate for the rate of ongoing loss of tumor volume due to the outflow of dead cell remnants. As the difference between the absolute rates of these processes keeps increasing, tumor undergoes rapid shrinkage.
The displacement of the interface between tumor and normal tissue pulls the normal cells and microvasculature towards the center of the tumor, in accordance with the advection terms presented in Eqs. (1). The spherical geometry of the system means that this forced motion of capillaries is more active in the regions with greater curvature, i.e., near the tumor. As the normalized capillary system undergoes rupture and pruning, its overall volume continuously decreases. Eventually microvasculature system ends up in the state in which its density is close to its initial value at the outer side of normal tissue, but it falls down to negligible values towards the tumor surface. The total volume of a stable microvasculature depends on the degree of its displacement and remodeling that is has undergone in response to treatment. Therefore, initially larger tumors end up having smaller volumes of surrounding microvasculature.
The stable volume of tumor that can be supported by nutrient supply from the resulting microvasculature depends not only on the total volume of the latter, but also on its configuration within the normal tissue. The pool of normal cells represents active consumers of nutrients, and therefore competitors of tumor cells. Large gaps between the tumor surface and the areas with physiologically normal capillary density are detrimental for the tumor size, since the nutrients that are supplied from capillaries and that diffuse towards the tumor undergo active consumption by normal cells. In extreme cases, the level of glucose entering the tumor rim is by itself not sufficient to ensure tumor cells survival, which results in the steady decrease of tumor volume down to negligible values.
Overall, the complexity of the intertwined physiological processes results in the observed hysteresis effect, in which the final state of the tumor after AAT depends on the previous history of tumor progression.
3.3. Combining antiangiogenic therapy with chemotherapy
The above-described nature of tumor response to the cessation of angiogenesis should also affect the combined types of treatment involving AAT. Previously, we have hypothesized that in combination with chemotherapy (CT) the delay of administration of antiangiogenic drug can be beneficial compared to the case of simultaneous initiation of CT and AAT. The rationale behind this hypothesis was that such approach can exploit the increased permeability of the angiogenic capillary network in the peritumoral region, in contrast to the normalized network that forms in result of AAT. Thus, it should ensure enhanced penetration of the cytotoxic agent into the tumor. The account for biomechanical properties of the tissues, however, suggests that alternation of scheduling of combined AAT and CT may yield more non-trivial consequences.
To illustrate this idea, let’s consider an augmented version of the model expressed by Eqs. (1)-(4), that also considers intravenous injections of chemotherapeutic drug. Eqs. (5) list additional terms introduced in the model to account for the chemotherapeutic drug and its action. Chemotherapy is assumed to affect only proliferating cells. One newly introduced partial differential equation governs the distribution of chemotherapeutic agent in tissue, and a new ordinary differential equation governs its temporal dynamics in blood.


The term of drug injections represents the external control which increases the concentration of chemotherapeutic drug in blood by a normalized unit as designated moments. In this work we simulate a protocol with injections separated by three-week intervals. The beginning of CT takes place when tumor achieves 4 mm radius.
Additional model parameters are presented in Table 2. It is well-known that substances with low molecular weight move through the pores in capillaries walls by diffusion, while the process of advection dominates for high molecular weight agents [54]. The same reasoning applies for their movement through the tissue. Both physiological processes of diffusion and advection are accounted for herein. The estimation of corresponding parameters was performed in lines with our approach presented previously in [33], assuming a chemotherapeutic agent with 5 nm hydrodynamic radius. The sensitivity of cells to the drug corresponds to a moderate CT which by itself can not eradicate the tumor.
The following initial and boundary conditions were used for chemotherapeutic drug:
Figure 4 illustrates the tumor dynamics in the resulting system under treatment of a relatively large tumor by CT, AAT and their combination, with AAT taking place at different moments. Chemotherapy by itself results in significant tumor shrinking which, however, is followed by tumor regrowth after the treatment is halted. The case of mono-AAT has been already demonstrated above and it effectively results in the eradication of tumor.
Combination of CT and AAT starting simultaneously leads to faster shrinkage of tumor than mono-AAT. This happens since the tumor cells in this case are subject not only to the similar depletion of nutrients, but also to the direct cytotoxic action. However, the case of mono-CT initially leads to even faster shrinkage of tumor. This reflects the above-mentioned fact that the normalization of capillaries results in reduced decrease of cytotoxic agent into the tumor. In the case of high-molecular-weight chemotherapeutic agent, considered herein, this reduction is very well pronounced and is eventually reflected in these high-level tumor growth curves. However, in the long term the combination of simultaneously initiated CT and AAT proves to be more efficient than mono-CT due to the eventual critical shortage of nutrient supply to the tumor as their competition with normal cells exacerbates under the capillary network scarcity.
Delay of the beginning of AAT within its combination of CT allows to ensure faster initial shrinkage of tumor. The seeming benefit of such approach nevertheless is deceptive. At the moments of third and fifth injection of chemotherapeutic drug tumor has the radii of mm and mm correspondingly. In accordance with the simulations, presented in the previous section, AAT initiated for such tumors results in their stabilization at small but notable sizes. Thus, the delay of AAT administration in combination with CT compromises potential curative effect of the treatment.
4. Conclusions
This paper presented a mathematical modeling study of the non-invasive solid tumor response to antiangiogenic therapy (AAT), taking into account biomechanical aspects. The tumor in the considered model represents a compact object embedded in normal tissue. Increase of tumor volume and displacement of normal tissue are ensured by the gradients of solid stress that arise due to the tumor cell proliferation. Tumor pushes away microvasculature during its growth, compromising its own supply of nutrients, which are necessary for cell proliferation and survival. Degradation and outflow of dead cells eventually compensate for tumor proliferation, yielding stabilization of tumor growth.
Initiation of angiogenesis by tumor cells experiencing metabolic stress results in augmentation of microvasculature permeability and surface area. Resulting abnormal microvasculature can support existence of larger stable tumors.
Simulations of AAT show that the outcome of the elimination of proangiogenic factors depends on the proximity of current tumor size to the size of the stable avascular tumor grown without initiation of angiogenesis. For a tumor with close size, AAT yields minor perturbation of its dynamics and leads to its rapid stabilization. For greater tumors, however, the quick fall of nutrient supply significantly affects their dynamics. Domination of outflow of dead cell mass over cell proliferation causes the displacement of interface between tumor and normal tissue that pulls the normal cells and microvasculature towards the tumor core. As the capillary system undergoes rupture and pruning during this movement, the system eventually stabilizes at notably decreased volumes of capillary system, which density moreover falls towards the tumor surface. The degree of distortion of microvasculature depends on the distance of its displacement. Therefore, the stable sizes of tumors that underwent AAT negatively correlate with their sizes at the beginning of AAT. For sufficiently large initial tumors, the destruction of microvasculature is so crucial that eventually it is able to support the survival of only normal but not tumor cells. Thus, in such cases AAT is effectively curative, provided that it blocks all the possible mechanisms of angiogenesis.
The idea that AAT can be curative is an intriguing outcome of this study, however, to the best of our knowledge there are no clinical cases supporting it. The very possibility of obtaining such confirmation is significantly compromised by the fact that AAT is rarely used in mono-regime. It is generally combined with other modalities, including surgical removal of the tumor after its shrinkage caused by AAT. Moreover, the model used herein assumes compactly growing benign tumors, while invasive tumors have been numerously shown to possess inherent resistance to AAT due to the ability of motile cancer cells to actively escape nutrient-deficient regions [55]. Therefore, for invasive tumors the possibility of curative effect of AAT seems highly unlikely. It should be also noted, that in reality other signaling molecules than VEGF can be involved in stimulation of microvessel growth, although they are generally assumed to be much less important.
The designed approach considers in detail the physiological processes accompanying dynamics of tumor and its microenvironment during AAT. This dynamics largely determines the efficacy of delivery of concomitantly administrated drugs to the tumor. The consideration of tissue as a porous biphasic media with solid and liquid components is crucial for a physiologically adequate reproduction of the dynamics of high molecular weight drugs, which is dominated by advective motion. This study provides example simulations of AAT combined with chemotherapy (CT). One of the qualitative outcomes of administrating AAT simultaneously with CT, suggested by modeling, is the notable reduction of inflow of chemotherapeutic drug into the tumor, which compromises initial tumor shrinkage. Given these intriguing results, we will use the developed model as the basis for future studies on optimization of combined types of antitumor therapy with the use of antiangiogenic drugs.
Supplementary Materials
The C++ computational code can be downloaded at: Preprints.org.
Author Contributions
Conceptualization, M.K. and A.K.; methodology, M.K. and A.K.; software, M.K.; investigation, M.K.; writing—original draft preparation, M.K.; writing—review and editing, M.K. and A.K.; visualization, M.K.; supervision, A.K.; funding acquisition, M.K. and A.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Russian Science Foundation under grant 22-21-00835.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CT | chemotherapy |
| AAT | antiangiogenic therapy |
| VEGF | vascular endothelial growth factor |
References
- Siegel, R.L.; Miller, K.D.; Wagle, N.S.; Jemal, A. Cancer statistics, 2023. Ca Cancer J Clin 2023, 73, 17–48. [Google Scholar] [CrossRef] [PubMed]
- Hanahan, D.; Weinberg, R.A. Hallmarks of cancer: the next generation. cell 2011, 144, 646–674. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.S.; Mellman, I. Oncology meets immunology: the cancer-immunity cycle. immunity 2013, 39, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Jayson, G.C.; Kerbel, R.; Ellis, L.M.; Harris, A.L. Antiangiogenic therapy in oncology: current status and future directions. The Lancet 2016, 388, 518–529. [Google Scholar] [CrossRef] [PubMed]
- Naumov, G.N.; Akslen, L.A.; Folkman, J. Role of angiogenesis in human tumor dormancy: animal models of the angiogenic switch. Cell cycle 2006, 5, 1779–1787. [Google Scholar] [CrossRef] [PubMed]
- Lazebnik, Y. What are the hallmarks of cancer? Nature Reviews Cancer 2010, 10, 232–233. [Google Scholar] [CrossRef]
- Kalluri, R.; Weinberg, R.A.; others. The basics of epithelial-mesenchymal transition. The Journal of clinical investigation 2009, 119, 1420–1428. [Google Scholar] [CrossRef] [PubMed]
- Gee, M.S.; Procopio, W.N.; Makonnen, S.; Feldman, M.D.; Yeilding, N.M.; Lee, W.M. Tumor vessel development and maturation impose limits on the effectiveness of anti-vascular therapy. The American journal of pathology 2003, 162, 183–193. [Google Scholar] [CrossRef] [PubMed]
- Yuan, F.; Chen, Y.; Dellian, M.; Safabakhsh, N.; Ferrara, N.; Jain, R.K. Time-dependent vascular regression and permeability changes in established human tumor xenografts induced by an anti-vascular endothelial growth factor/vascular permeability factor antibody. Proceedings of the National Academy of Sciences 1996, 93, 14765–14770. [Google Scholar] [CrossRef]
- Jain, R.K.; Di Tomaso, E.; Duda, D.G.; Loeffler, J.S.; Sorensen, A.G.; Batchelor, T.T. Angiogenesis in brain tumours. Nature Reviews Neuroscience 2007, 8, 610–622. [Google Scholar] [CrossRef]
- Garcia, J.; Hurwitz, H.I.; Sandler, A.B.; Miles, D.; Coleman, R.L.; Deurloo, R.; Chinot, O.L. Bevacizumab (Avastin®) in cancer treatment: A review of 15 years of clinical experience and future outlook. Cancer treatment reviews 2020, 86, 102017. [Google Scholar] [CrossRef] [PubMed]
- Claes, A.; Wesseling, P.; Jeuken, J.; Maass, C.; Heerschap, A.; Leenders, W.P. Antiangiogenic compounds interfere with chemotherapy of brain tumors due to vessel normalization. Molecular cancer therapeutics 2008, 7, 71–78. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Pulfer, S.; Li, S.; Chu, J.; Reed, K.; Gallo, J.M. Pharmacodynamic-mediated reduction of temozolomide tumor concentrations by the angiogenesis inhibitor TNP-470. Cancer research 2001, 61, 5491–5498. [Google Scholar] [PubMed]
- Hahnfeldt, P.; Panigrahy, D.; Folkman, J.; Hlatky, L. Tumor development under angiogenic signaling: a dynamical theory of tumor growth, treatment response, and postvascular dormancy. Cancer research 1999, 59, 4770–4775. [Google Scholar] [PubMed]
- McDougall, S.R.; Anderson, A.R.; Chaplain, M.A. Mathematical modelling of dynamic adaptive tumour-induced angiogenesis: clinical implications and therapeutic targeting strategies. Journal of theoretical biology 2006, 241, 564–589. [Google Scholar] [CrossRef]
- Stéphanou, A.; McDougall, S.R.; Anderson, A.R.; Chaplain, M.A. Mathematical modelling of the influence of blood rheological properties upon adaptative tumour-induced angiogenesis. Mathematical and Computer Modelling 2006, 44, 96–123. [Google Scholar] [CrossRef]
- Swanson, K.R.; Rockne, R.C.; Claridge, J.; Chaplain, M.A.; Alvord Jr, E.C.; Anderson, A.R. Quantifying the role of angiogenesis in malignant progression of gliomas: in silico modeling integrates imaging and histology. Cancer research 2011, 71, 7366–7375. [Google Scholar] [CrossRef] [PubMed]
- Alfonso, J.C.L.; Köhn-Luque, A.; Stylianopoulos, T.; Feuerhake, F.; Deutsch, A.; Hatzikirou, H. Why one-size-fits-all vaso-modulatory interventions fail to control glioma invasion: in silico insights. Scientific reports 2016, 6, 37283. [Google Scholar] [CrossRef] [PubMed]
- Welter, M.; Rieger, H. Interstitial fluid flow and drug delivery in vascularized tumors: a computational model. PloS one 2013, 8, e70395. [Google Scholar] [CrossRef]
- Steuperaert, M.; Debbaut, C.; Carlier, C.; De Wever, O.; Descamps, B.; Vanhove, C.; Ceelen, W.; Segers, P. A 3D CFD model of the interstitial fluid pressure and drug distribution in heterogeneous tumor nodules during intraperitoneal chemotherapy. Drug delivery 2019, 26, 404–415. [Google Scholar] [CrossRef]
- Zhan, W. Convection enhanced delivery of anti-angiogenic and cytotoxic agents in combination therapy against brain tumour. European Journal of Pharmaceutical Sciences 2020, 141, 105094. [Google Scholar] [CrossRef] [PubMed]
- Stylianopoulos, T.; Martin, J.D.; Snuderl, M.; Mpekris, F.; Jain, S.R.; Jain, R.K. Coevolution of solid stress and interstitial fluid pressure in tumors during Pprogression: implications for vascular collapse evolution of solid and fluid stresses in tumors. Cancer research 2013, 73, 3833–3841. [Google Scholar] [CrossRef] [PubMed]
- Preziosi, L.; Ambrosi, D.; Verdier, C. An elasto-visco-plastic model of cell aggregates. Journal of theoretical biology 2010, 262, 35–47. [Google Scholar] [CrossRef] [PubMed]
- Byrne, H.M.; King, J.R.; McElwain, D.S.; Preziosi, L. A two-phase model of solid tumour growth. Applied Mathematics Letters 2003, 16, 567–573. [Google Scholar] [CrossRef]
- Franks, S.; King, J. Interactions between a uniformly proliferating tumour and its surroundings: Stability analysis for variable material properties. International journal of engineering science 2009, 47, 1182–1192. [Google Scholar] [CrossRef]
- Byrne, H.; Preziosi, L. Modelling solid tumour growth using the theory of mixtures. Mathematical medicine and biology: a journal of the IMA 2003, 20, 341–366. [Google Scholar] [CrossRef] [PubMed]
- Jain, R.K.; Tong, R.T.; Munn, L.L. Effect of vascular normalization by antiangiogenic therapy on interstitial hypertension, peritumor edema, and lymphatic metastasis: insights from a mathematical model. Cancer research 2007, 67, 2729–2735. [Google Scholar] [CrossRef] [PubMed]
- Kolobov, A.; Kuznetsov, M. Investigation of the effects of angiogenesis on tumor growth using a mathematical model. Biophysics 2015, 60, 449–456. [Google Scholar] [CrossRef]
- Kuznetsov, M.; Kolobov, A. Optimization of Combined Antitumor Chemotherapy with Bevacizumab by Means of Mathematical Modeling. Trends in Biomathematics: Modeling, Optimization and Computational Problems: Selected works from the BIOMAT Consortium Lectures, Moscow 2017 2018, pp. 347–363.
- Kuznetsov, M. Mathematical modeling shows that the response of a solid tumor to antiangiogenic therapy depends on the type of growth. Mathematics 2020, 8, 760. [Google Scholar] [CrossRef]
- Kuznetsov, M. Combined influence of nutrient supply level and tissue mechanical properties on benign tumor growth as revealed by mathematical modeling. Mathematics 2021, 9, 2213. [Google Scholar] [CrossRef]
- Kuznetsov, M.; Kolobov, A. Agent-Based Model for Studying the Effects of Solid Stress and Nutrient Supply on Tumor Growth. Mathematics 2023, 11, 1900. [Google Scholar] [CrossRef]
- Kuznetsov, M.; Kolobov, A. Optimization of size of nanosensitizers for antitumor radiotherapy using mathematical modeling. International Journal of Molecular Sciences 2023, 24, 11806. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsov, M.; Kolobov, A. Mathematical modelling for spatial optimization of irradiation during proton radiotherapy with nanosensitizers. Russian Journal of Numerical Analysis and Mathematical Modelling 2023, 38, 303–321. [Google Scholar] [CrossRef]
- Mascheroni, P.; Stigliano, C.; Carfagna, M.; Boso, D.P.; Preziosi, L.; Decuzzi, P.; Schrefler, B.A. Predicting the growth of glioblastoma multiforme spheroids using a multiphase porous media model. Biomechanics and modeling in mechanobiology 2016, 15, 1215–1228. [Google Scholar] [CrossRef] [PubMed]
- Holash, J.; Maisonpierre, P.; Compton, D.; Boland, P.; Alexander, C.; Zagzag, D.; Yancopoulos, G.; Wiegand, S. Vessel cooption, regression, and growth in tumors mediated by angiopoietins and VEGF. Science 1999, 284, 1994–1998. [Google Scholar] [CrossRef] [PubMed]
- Freyer, J.; Sutherland, R. A reduction in the in situ rates of oxygen and glucose consumption of cells in EMT6/Ro spheroids during growth. J Cell Physiol 1985, 124, 516–524. [Google Scholar] [CrossRef] [PubMed]
- Izuishi, K.; Kato, K.; Ogura, T.; Kinoshita, T.; Esumi, H. Remarkable tolerance of tumor cells to nutrient deprivation: possible new biochemical target for cancer therapy. Cancer research 2000, 60, 6201–6207. [Google Scholar] [PubMed]
- Netti, P.A.; Berk, D.A.; Swartz, M.A.; Grodzinsky, A.J.; Jain, R.K. Role of extracellular matrix assembly in interstitial transport in solid tumors. Cancer research 2000, 60, 2497–2503. [Google Scholar] [PubMed]
- Kelm, J.M.; Sanchez-Bustamante, C.D.; Ehler, E.; Hoerstrup, S.P.; Djonov, V.; Ittner, L.; Fussenegger, M. VEGF profiling and angiogenesis in human microtissues. Journal of biotechnology 2005, 118, 213–229. [Google Scholar] [CrossRef]
- Mac Gabhann, F.; Popel, A.S. Interactions of VEGF isoforms with VEGFR-1, VEGFR-2, and neuropilin in vivo: a computational model of human skeletal muscle. American Journal of Physiology-Heart and Circulatory Physiology 2007, 292, H459–H474. [Google Scholar] [CrossRef]
- Köhn-Luque, A.; De Back, W.; Yamaguchi, Y.; Yoshimura, K.; Herrero, M.; Miura, T. Dynamics of VEGF matrix-retention in vascular network patterning. Physical biology 2013, 10, 066007. [Google Scholar] [CrossRef] [PubMed]
- Dickson, P.V.; Hamner, J.B.; Sims, T.L.; Fraga, C.H.; Ng, C.Y.; Rajasekeran, S.; Hagedorn, N.L.; McCarville, M.B.; Stewart, C.F.; Davidoff, A.M. Bevacizumab-induced transient remodeling of the vasculature in neuroblastoma xenografts results in improved delivery and efficacy of systemically administered chemotherapy. Clinical cancer research 2007, 13, 3942–3950. [Google Scholar] [CrossRef] [PubMed]
- Stamatelos, S.K.; Kim, E.; Pathak, A.P.; Popel, A.S. A bioimage informatics based reconstruction of breast tumor microvasculature with computational blood flow predictions. Microvascular research 2014, 91, 8–21. [Google Scholar] [CrossRef] [PubMed]
- Dings, R.P.; Loren, M.; Heun, H.; McNiel, E.; Griffioen, A.W.; Mayo, K.H.; Griffin, R.J. Scheduling of radiation with angiogenesis inhibitors Anginex and Avastin improves therapeutic outcome via vessel normalization. Clinical Cancer Research 2007, 13, 3395–3402. [Google Scholar] [CrossRef] [PubMed]
- Casciari, J.; Sotirchos, S.; Sutherland, R. Mathematical modelling of microenvironment and growth in EMT6/Ro multicellular tumour spheroids. Cell proliferation 1992, 25, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Clough, G.; Smaje, L. Exchange area and surface properties of the microvasculature of the rabbit submandibular gland following duct ligation. The Journal of physiology 1984, 354, 445–456. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsov, M.B.; Kolobov, A.V. Transient alleviation of tumor hypoxia during first days of antiangiogenic therapy as a result of therapy-induced alterations in nutrient supply and tumor metabolism – Analysis by mathematical modeling. Journal of theoretical biology 2018, 451, 86–100. [Google Scholar] [CrossRef] [PubMed]
- Baker, P.G.; Mottram, R. Metabolism of exercising and resting human skeletal muscle, in the post-prandial and fasting states. Clinical science 1973, 44, 479–491. [Google Scholar] [CrossRef]
- Tuchin, V.; Bashkatov, A.; Genina, E.; Sinichkin, Y.P.; Lakodina, N. In vivo investigation of the immersion-liquid-induced human skin clearing dynamics. Technical Physics Letters 2001, 27, 489–490. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical recipes 3rd edition: The art of scientific computing; Cambridge university press, 2007.
- Boris, J.P.; Book, D.L. Flux-corrected transport. I. SHASTA, a fluid transport algorithm that works. Journal of computational physics 1973, 11, 38–69. [Google Scholar] [CrossRef]
- Kuznetsov, M.; Clairambault, J.; Volpert, V. Improving cancer treatments via dynamical biophysical models. Physics of Life Reviews 2021, 39, 1–48. [Google Scholar] [CrossRef] [PubMed]
- Herring, N.; Paterson, D.J. Levick’s introduction to cardiovascular physiology; CRC Press, 2018.
- Bergers, G.; Hanahan, D. Modes of resistance to anti-angiogenic therapy. Nature Reviews Cancer 2008, 8, 592–603. [Google Scholar] [CrossRef] [PubMed]
Figure 1.
Scheme of the main interactions of the model governed by Eqs. (1). Green arrows denote stimulating interactions, red lines show inhibiting interactions, white arrows correspond to transitions of variables.
Figure 1.
Scheme of the main interactions of the model governed by Eqs. (1). Green arrows denote stimulating interactions, red lines show inhibiting interactions, white arrows correspond to transitions of variables.
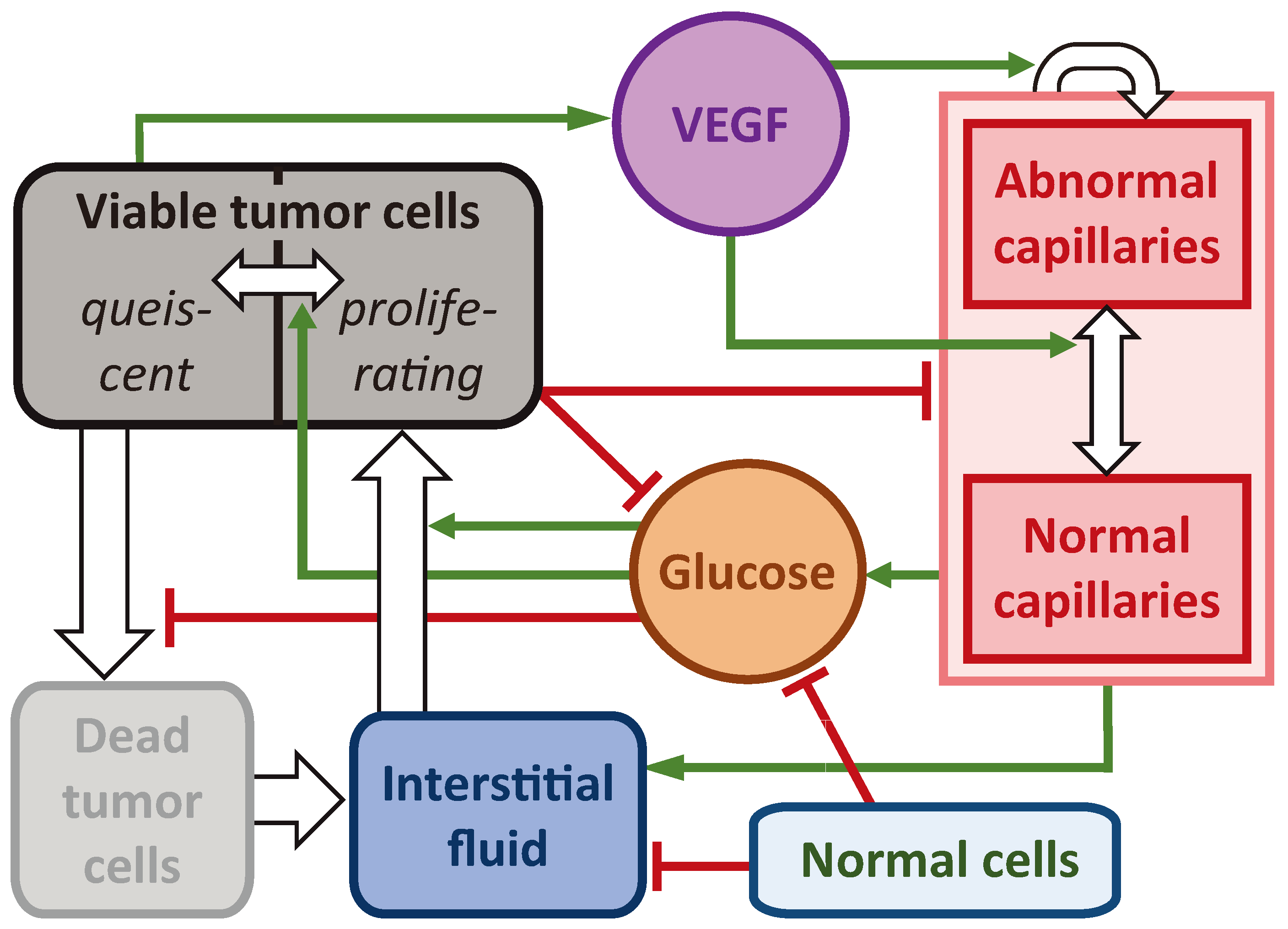
Figure 2.
Left: tumor growth curves produced by Eqs. (1)-(4) with and without angiogenesis. Middle and right: distributions of model variables for these simulations. Values of the variables for glucose, VEGF and capillaries are renormalized for better visualization.
Figure 2.
Left: tumor growth curves produced by Eqs. (1)-(4) with and without angiogenesis. Middle and right: distributions of model variables for these simulations. Values of the variables for glucose, VEGF and capillaries are renormalized for better visualization.
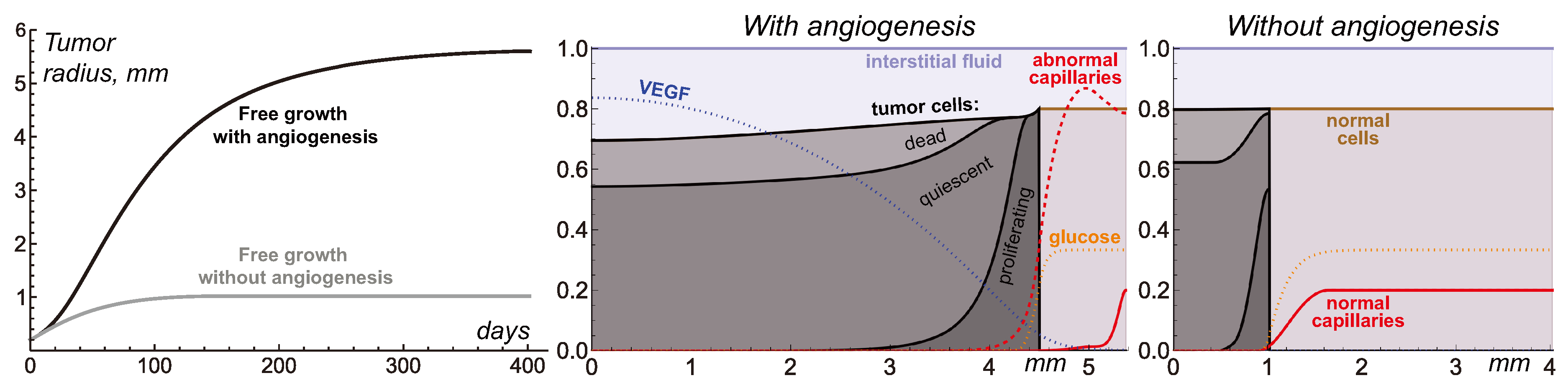
Figure 3.
Left: tumor growth curves produced by Eqs. (1)-(4) under free tumor growth and with antiangiogenic therapy (AAT) starting at four different moments. Middle and right: stable distributions of model variables for the simulations of AAT starting when tumor reaches 1 mm and 4 mm in radius. Values of the variables for glucose and capillaries are renormalized for better visualization.
Figure 3.
Left: tumor growth curves produced by Eqs. (1)-(4) under free tumor growth and with antiangiogenic therapy (AAT) starting at four different moments. Middle and right: stable distributions of model variables for the simulations of AAT starting when tumor reaches 1 mm and 4 mm in radius. Values of the variables for glucose and capillaries are renormalized for better visualization.

Figure 4.
Tumor growth curves produced by Eqs. (1)-(6) under free tumor growth, antiangiogenic therapy (AAT), chemotherapy (CT), and their combination with AAT starting at times of different injections of chemotherapeutic drug.
Figure 4.
Tumor growth curves produced by Eqs. (1)-(6) under free tumor growth, antiangiogenic therapy (AAT), chemotherapy (CT), and their combination with AAT starting at times of different injections of chemotherapeutic drug.
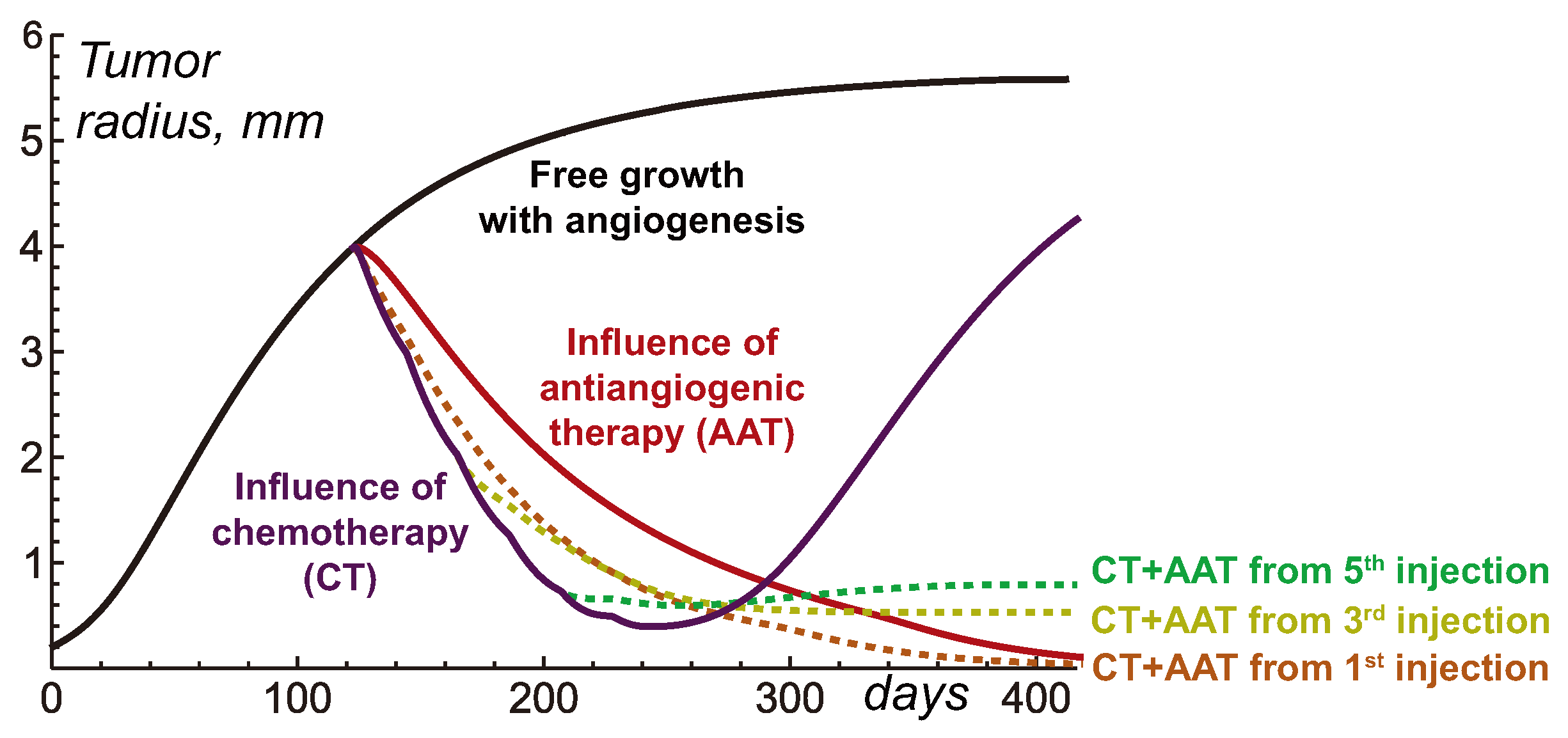
Table 1.
Model parameters.
| Parameter | Description | Value | Based on |
|---|---|---|---|
| Cells: | |||
| B | maximum rate of cell proliferation | 0.01 | [37] |
| critical stress for cell proliferation | 15 | [35] | |
| smoothing parameter of Heaviside function | 500 | [33] | |
| rate of death by starvation | 0.003 | [33,38] | |
| critical level of glucose for survival | 0.001 | [33] | |
| M | rate of degradation of dead cells | 0.01 | [33] |
| Stress: | |||
| k | solid stress coefficient | 500 | [33] |
| minimum fraction of interacting cells | 0.3 | [26] | |
| initial fraction of cells | 0.8 | [26] | |
| Interstitial fluid: | |||
| hydraulic conductivity of normal capillaries | 0.1 | [22] | |
| hydraulic conductivity of abnormal capillaries | 0.22 | [33] | |
| fluid pressure in capillaries | 4 | [22] | |
| hydraulic conductivity of lymphatic capillaries | 1300 | [22] | |
| lymph pressure | 0 | [22] | |
| K | tissue hydraulic conductivity | 0.1 | [39] |
| VEGF: | |||
| secretion rate | 1 | [40] | |
| internalization rate | 1 | [41] | |
| degradation rate | 0.01 | [42] | |
| diffusion coefficient | 21 | [42] | |
| Capillaries: | |||
| R | maximum rate of angiogenesis | 0.008 | [43] |
| maximum surface area density | 5 | [43] | |
| characteristic degradation rate | 0.03 | [43,44] | |
| coefficient of degradation in the tumor core | 2 | [43,44] | |
| normalization rate | 0.1 | [45] | |
| denormalization rate | 0.1 | [45] | |
| pruning rate | 0.002 | [45] | |
| Michaelis constant for VEGF action | 0.001 | [33] | |
| coefficient of active movement | 0.03 | [43,44] | |
| Glucose: | |||
| Michaelis constant for consumption | 0.01 | [46] | |
| permeability of normal capillaries | 4 | [47] | |
| permeability of abnormal capillaries | 10 | [48] | |
| parameter of consumption by proliferating cells | 1200 | [37] | |
| rate of consumption by normal tissue | 0.5 | [49] | |
| diffusion coefficient | 100 | [50] | |
Table 2.
Additional parameters of the model accounting for chemotherapy.
| Parameter | Description | Value |
|---|---|---|
| Cells: | ||
| sensitivity to chemotherapeutic agent | 0.05 | |
| Chemotherapeutic agent: | ||
| fraction of available pore cross-section area, normal capillaries | 0.09 | |
| fraction of available pore cross-section area, abnormal capillaries | 0.58 | |
| diffusive permeability, normal capillaries | 0.007 | |
| diffusive permeability, abnormal capillaries | 0.25 | |
| diffusion coefficient | 13 | |
| clearance rate | 0.0015 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






