Prerpints.org logo
Preprint
Article

Dynamic Correlations in Disordered Systems: Implications on High-Temperature Superconductivity

Altmetrics

Downloads

118

Views

23

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

14 December 2023

Posted:

15 December 2023

You are already at the latest version

Alerts
Abstract
Liquid and gas are distinct in their extent of dynamic atomic correlations; in gas atoms are almost uncorrelated whereas they are strongly correlated in liquid. This distinction applies also to electronic systems. Fermi liquids are actually gas-like, whereas strongly correlated electrons are liquid-like. Doped Mott insulators share characteristics with supercooled liquids. Such distinctions have important implications on superconductivity. We discuss the evolution of dynamic atomic correlations in liquid with temperature, and a possible effect of dynamic correlations on the high-temperature superconductivity in the cuprates.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

At ambient pressure liquid evaporates to gas through a first-order phase transition. Under high pressure, however, the change becomes continuous beyond the tri-critical point. Thus, the distinction between liquid and gas is not as obvious as it may appear. But, the critical difference can be found in the specific heat, CV. In ideal gas CV = (3/2)kB, whereas in liquid CV = 3 kB [1,2]. This is because atoms in gas interact with each other only through occasional collisions, so that the potential energy, <U>, is practically zero. Thus, specific heat originates only from the kinetic energy, <T>, and CV = (3/2)kB. On the other hand, atoms in liquid are always influencing each other through the interatomic potential. Thus, through the equipartition theorem <U> = <T>, resulting in CV = 3kB, known as Dulong-Petit law for solid. In other words, liquid is condensed matter, not high-density gas. Indeed, the physical density of liquid is almost as high as that of a solid [3]. In gas atom-atom interactions are collisional. In liquid atoms are held together by cohesive force just as solid, and atomic motions are vibrational [4].
In spite of such important differences between liquid and gas, many ideas and theories of liquid are based upon models of high-density gas. For instance, the hard-sphere (HS) model [5, 6] is a gas model with <U> = 0. Widely used concepts, such as free-volume [7] and jamming [8], stem from the HS model, thus assume liquid basically as high-density gas. The widely used Weeks-Chandler-Andersen (WCA) principle [9] states that at high temperatures only the repulsive part of the potential is relevant, thus the HS model is always justified. Here, the role of the potential is essentially neglected. However, as we discuss below, the potential energy plays a critical role in controlling the properties of liquid and supercooled liquid.
Because there are fundamental and qualitative differences between the gas model and the elastic liquid/solid model, we should start with an elastic model in which the harmonic interaction is assumed from the beginning, instead of starting with the gas model and increasing density to describe liquid. Such an approach, based on the concept of atomic-level stresses [10] and the density wave instability [11], had a major success in describing the evolution of the structure of liquid with temperature [12] and in elucidating the glass transition [13]. In this paper we briefly describe this theory, discuss the atomic dynamics in superfluid 4He observed by inelastic neutron scattering [14], and the possible implication on the high-temperature superconductivity in the cuprates [15].

2. Dynamic Correlation in Liquid and the Glass Transition

In 1952 Frank [16] suggested that icosahedral clusters of atoms (Figure 1) may exist in liquid, to explain the high degree of supercooling observed by Turnbull [17]. He argued that for the Lennard-Jones potential, the icosahedral cluster has a lower energy than the close-packed f.c.c. cluster, by 8.4%. The icosahedral cluster cannot be the basis of a simple crystalline phase because of the predominant five-fold symmetry, whereas it can exist as a short-range order (SRO) in an aperiodic structure of liquid. Frank argued that for this reason crystallization requires significant structural reorganization, and this presents the energy barrier for transformation [16]. Soon, Bernal discovered a high density of icosahedral clusters in his random-packed HS model [5]. Since then, the idea of regarding the icosahedral cluster, or similar high-symmetry clusters, as the building block to form a liquid structure became the standard approach to the structure of liquid [18,19,20,21,22,23,24]. However, this “bottom-up” approach cannot readily explain strong medium-range order (MRO) in the liquid structure.
The structure of liquid and glass is usually expressed in terms of the atomic pair-distribution function (PDF), g r , or G r = 4 π r ρ 0 g r − 1 , where ρ 0 is the atomic number density [6], given by
g r = 1 N ∑ i , j δ r − r i − r j .
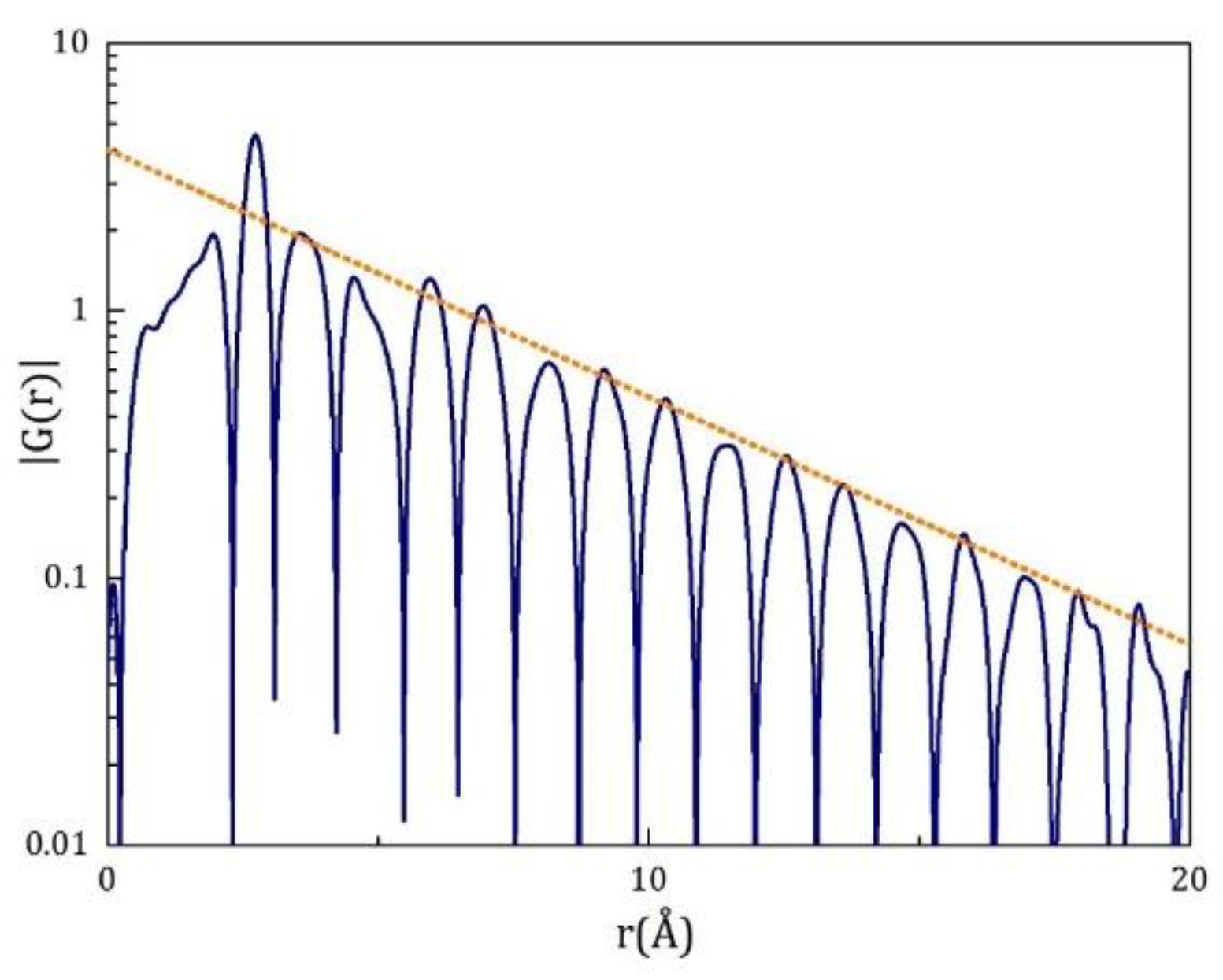
where r i is the position of the i-th atom and N is the total number of atoms. The PDF describes only the two-body correlation, whereas the full description of the real structure requires high-order correlations as well. However, the PDF can be directly determined by scattering experiment with x-ray or neutrons [25]. The PDF of metallic liquids and glasses show prominent exponentially decaying oscillations around the average density with a well-defined periodicity (Figure 2 [26]). The length-scale for the exponential decay, ξ s ,
G r = G 0 r e x p − r / ξ s ,
obeys the Curie-Weiss law in its temperature dependence [12,26],
ξ s T = C T − T I G .
This diverges at TIG, although it never happens because TIG < 0. The state reached by extrapolation to TIG is characterized by the long-range density wave correlation [11,26].
Preprints 93369 g002
Figure 2. The G r of Pd42.5Ni7.5Cu30P20 liquid at T = 600K, just above Tg [26].
Figure 2. The G r of Pd42.5Ni7.5Cu30P20 liquid at T = 600K, just above Tg [26].
Preprints 93369 g002
Equation (2) suggests that there is a driving force toward this state, the density wave (DW) state. The right theoretical framework to study this state is the density wave theory, in which the atomic density, ρ r , is given by,
ρ r = ∫ ρ q e i q · r d q .
Now, the Fourier-transform of the interatomic potential, ϕ r , is strongly dependent upon the diverging part of the potential close to r = 0. However, the diverging part is never relevant, because atoms do not come so close to each other. Therefore, we can remove the diverging part to define the pseudopotential, ϕ p p r . Its Fourier-transform, ϕ p p q , was found to have a strong minimum close to the wavenumber expected for the DW state, q D W . Thus, we theorize that ϕ p p q is driving the system to the DW state, resulting in the increase in ξ s as temperature is reduced [11,27,28]. However, the SRO of the DW state was found to be quite poor, with almost no icosahedral local structure [26]. Therefore, the DW state, obtained by minimizing the energy in q space, and the SRO, obtained by minimizing the energy in r space, are incompatible with each other. Also, local thermal fluctuations disrupt the long-range nature of the DW state. Our theory is that the compromise among these competing factors produces the MRO [11,27,28]. This approach elucidates the Curie-Weiss law, Equation (2), and the glass transition temperature [13] with high quantitative accuracy for metallic glasses, and provides reasonable explanation of other properties [29,30].

3. Dynamic Correlation in Superfluid 4He

We now turn our focus to the atomic dynamics in 4He which becomes superfluid due to the Bose-Einstein (BE) condensation. The BE condensation is well-defined for ideal gas, whereas He atoms interact through the Lennard-Jones potential. As a result, only about 7% of He atoms condense to the BE state [31]. Thus, the PDF of 4He determined by neutron scattering which shows the average interatomic distance of 3.6 Å [32] describes essentially the structure of uncondensed atoms. To determine the structure of the BE condensed atoms we measured the dynamic structure factor, S(q, E), of 4He by inelastic neutron scattering, and transformed it to the energy-resolved PDF, g(r, E) [14] defined by.
g r , E = 1 N ∑ i , j ∫ δ r − r i 0 − r j t e x p i ω t d t .
where r i t is the position of the i-th atom at time t and E = ћ ω .
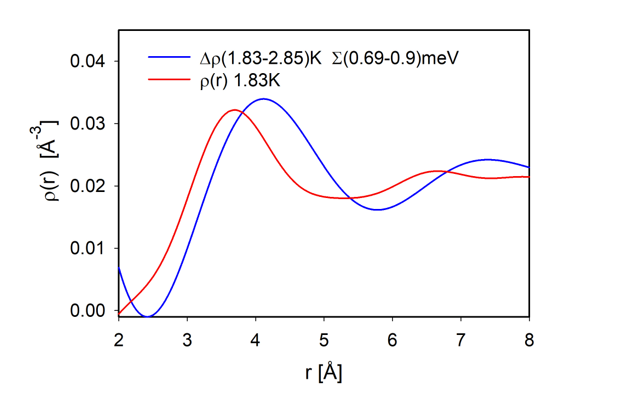
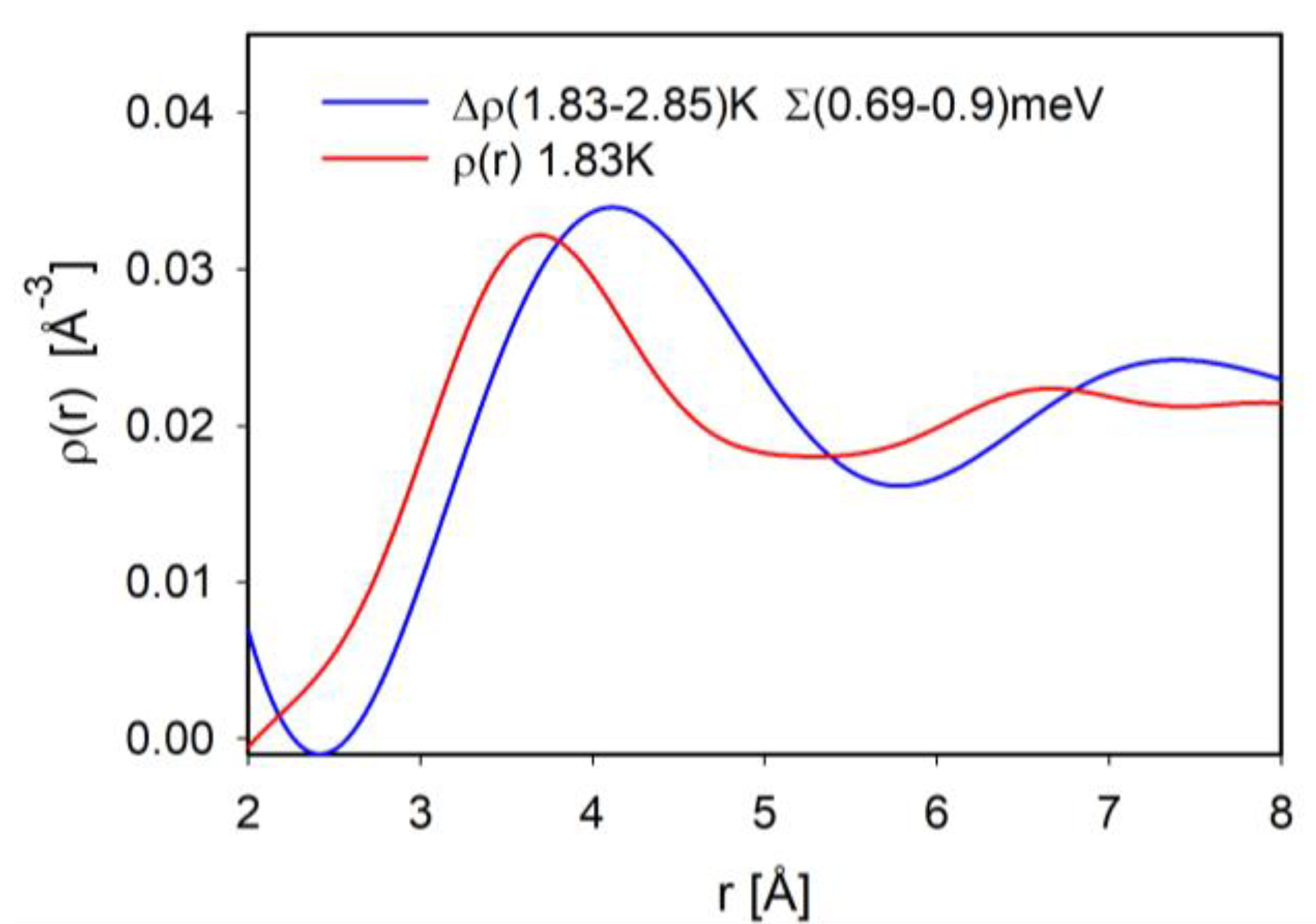
If we focus on the roton energy at 0.7 meV, we are primarily looking at condensed atoms. Particularly by comparing g(r, E) above and below the BE condensation temperature, TBE, we can extract the atomic correlations in the condensate. We discovered that the interatomic distance for the BE condensed atoms is 4 Å [14], much longer than that of the uncondensed atoms [32]. To illustrate this difference we compare the total PDF (in red) against the integral of g(r, E) from E = 0.69 to 0.9 meV (in blue) in Figure 3. It is clear that upon the BE condensation the first peak shifts outward by 0.3 Å or more. We explained this difference in terms of atomic wavefunction overlap [15]. In the condensed state the wavefunctions of different atoms cannot overlap, because it would lead to level-splitting. To allow such hybridization for each pair of atoms the ground state has to be a macroscopic resonant state, just as the resonant valence bond (RVB) state [33]. For bosons like 4He spin resonance into the spin singlet state is not required. However, slow dynamics will not allow the system to reach such a massive resonant ground state, just as the antiferromagnet stays in the Néel state even though the true quantum ground state is the resonant state [34]. The simplest alternative is to eliminate the wavefunction overlap by atoms becoming separated a little further. As a result, the interatomic distance is larger than in uncondensed state where small overlap is allowed, just as in the exchange hole compared to the correlation hole for electrons [35].

4. Dynamic Correlation among Electrons

Our method to observe dynamic correlations in real space and time using the energy-resolved PDF [14] and the Van Hove function [36,37],
G r , t = 1 N ∑ i , j δ r − r i 0 − r j t ,
can be applied to electrons to observe dynamic correlations among electrons. For atoms the classical interpretation of the correlation functions, eqs. (1), (5) and (6), are valid, but for electrons we have to be more careful about the quantum effect. The inelastic x-ray scattering cross-section of electrons is given by [38],
d σ d ω d Ω = σ 0 S q , ω = σ 0 2 π ∑ k . k ′ ∫ c k + t c k + q t c k ′ + q + 0 c k ′ 0 e − i ω t d t ,
where c k + t creates a fermion with the momentum k at time t, σ 0 = e 2 / m , e is the electron charge, m is the electron mass, and <…> denotes quantum and thermal average. Usually, the decoupling by random-phase approximation (RPA),
c k + t c k + q t c k ′ + q + 0 c k ′ 0 → c k + q t c k ′ + q + 0 c k + t c k ′ 0 ,
is applied and,
c k + q t c k ′ + q + 0 c k + t c k ′ 0 = δ k , k ′ 1 − n k + q n k δ ω − E k + q − E k / ħ e i ω t
where n k = c k + c k . Thus, the dynamic structure factor, S(q, ω), describes the excitation of electrons from below the Fermi level to above. It is also interpreted as the imaginary part of the dielectric response function [39].
However, the RPA decoupling in reciprocal space erases the phase relationship between the initial and final states in the transition, which contains the information on the real space correlations. To avoid this loss of phase information and to observe the correlation in real space, we introduce a real-space description,
c k + t = ∫ c + r ′ , t e − i k · r ′ d r ′ ,           c k + q t = ∫ c r ′ ′ , t e i k + q · r ′ ′ d r ′ ′ .
where c + r , t is a fermion creator at r and t. Then,
c k + t c k + q t c k ′ + q + 0 c k ′ 0 = ∫ c + r ′ , t c r ′ ′ , t c + r ′ ′ ′ , 0 c r ′ ′ ′ ′ , 0 × e x p i − k · r ′ + k + q · r ′ ′ − k ′ + q · r ′ ′ ′ + k ′ · r ′ ′ ′ ′ d r ′ d r ′ ′ d r ′ ′ ′ d r ′ ′ ′ ′ .
The intermediate scattering function [40],
F q , t = ∫ S q , ω e i ω t d ω ,
is given by,
F q , t = ∑ k , k ′ c k + t c k + q t c k ′ + q + 0 c k ′ 0 .
In the real space representation, Equation (11), the summation over k and k’ in Equation (13) yields r’ = r’’, r’’’ = r’’’’. Then,
          F q , t = ∫ c + r ′ , t c r ′ , t c + r ′ ′ ′ , 0 c r ′ ′ ′ , 0 e x p i q · r ′ − r ′ ′ ′ d r ’ d r ’ ’ ’ = ∫ ρ r ′ , t ρ r ′ ′ ′ , 0 e x p i q · r ′ − r ′ ′ ′ d r ’ d r ’ ’ ’ ,
where
ρ r , t = c + r , t c r , t
is the local density operator. Thus, the Van Hove function is expressed as the density correlation function in real space and time,
G r , t = ∫ F q , t e i q r d q = ∫ ρ ( r + r ′ , t ) ρ r ′ , 0 d r ′ .
This proves that the classical interpretation of the double-Fourier-transformation of S(q, E) as the Van Hove correlation function is valid, even for electrons. The energy-resolved PDF is given by,
g r , ω = 1 2 π ∫ G r , t e − i ω t d t .
We measured the electronic S(q, E) for polycrystalline beryllium by inelastic x-ray scattering with the incident energy of 11.32 keV and energy resolution of 0.7 eV at the Beamline 27ID-B of the Advanced Photon Source of Argonne National Laboratory. The preliminary result [41] shows the exchange-correlation hole of the size about 2 Å. Surprisingly, at the plasmon energy of about 20 eV the exchange-correlation hole is extended to about 5 Å. In plasmon electrons are dynamically correlated, resulting in larger separation among electrons than in electrons at large. This result demonstrates that the dynamic state affects electron correlations. The details of this observation will be reported elsewhere.

5. Implication on High-Temperature Superconductivity

The combination of the result on 4He and the observation of electron correlations by inelastic x-ray scattering have very significant implications on the high-temperature superconductivity of the cuprates. In the regular BCS superconductors electrons are in the Fermi-liquid state, and they are gas-like as discussed above. Electrons avoid each other by forming exchange-correlation holes, and the density functional theory (DFT) [42] works. The Cooper pairs are large and they B-E condensate at high temperatures of the order of 1000K. Thus, the pairing temperature determines the superconducting critical temperature, Tc. The Cooper pairs are large, up to 1000Å, and they are strongly overlapping with each other.
In contrast, in the cuprates electrons are strongly correlated, just as in liquid and supercooled liquid in which the potential energy is as important as the kinetic energy. For this reason, it is interesting to note that it was recently found that in the overdoped cuprates the periodicity of the charge density wave was independent of the Fermi momentum as the doping density was changed [43]. It is likely that the Coulomb repulsion energy is involved in the formation of the density waves, for instance through the pseudopotential discussed above [11,27,28].
Furthermore, in the cuprates the Cooper pairs are small, of the order of nm in size, and low in density. Thus, they are likely to be preformed above the superconducting transition temperature [44-46]. If that is the case, Tc is equal to TBE, and it is controlled by the BE condensation rather than by pairing. We speculate that as in the case of 4He the separation between Cooper pairs is longer in the BE condensate than in the normal state, to avoid wavefunction overlap. Then the Coulomb repulsion energy is reduced in the BE condensate compared to the normal state, adding to the driving force for the BE condensation [15]. The difference is similar to the case of exchange and correlation effects for fermions, so the energy difference must be related to the exchange constant. This effect is most likely negligible for 4He, because the interaction energy (van der Waals force) is small. However, for the cuprates a small change in the repulsion energy can have a very significant effect. Because the hole density is low, the energy associated with wavefunction overlap is a small percentage of U. Nevertheless, the on-site Coulomb repulsion, U, is nearly 10 eV at Cu [35], huge in contrast to kBTc ~ 10 meV. Although the value of U itself may not be influenced by the BE condensation, slight changes in the extent of the p-d hybridization due to the BE condensation can affect the total repulsion energy. Thus, a tiny change in the repulsion energy can have a major effect on Tc. So far, the effort to increase Tc focused on the pairing force. This new mechanism calls for a change in strategy, to increase Tc through the correlation effects.
To test this hypothesis we plan to measure the g(r, E) for doped holes in the superconducting cuprates with inelastic x-ray scattering. The measurement is quite difficult because of the low intensity of the signal due to the high energy-resolution (better than 10 meV) required to observe the energy gap, and due to low doping density. However, this is within the realm of feasibility with advanced facilities.

6. Conclusions

Gas and liquid are fundamentally different in the role of the interatomic potential. In gas atomic interactions are collisional and the average potential energy is negligibly small compared to the kinetic energy. In liquids the potential energy is as important as the kinetic energy. We suggest that this difference can be instructive in discussing the difference in dynamics between nearly free electrons and strongly correlated electrons. We point out that electron correlation can be influenced by the dynamic state of electrons. In particular, the Bose-Einstein condensation of Cooper pairs could affect electron correlation, giving rise to an additional driving force to increase the superconducting transition temperature.

Funding

This work was supported by the U. S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Science and Engineering Division.

Data Availability Statement

Data used in this work are available upon request from the corresponding author.

Acknowledgments

The author is grateful to Peter Fulde for encouragement.

Conflicts of Interest

The author declares no conflict of interest.

Notice of Copyright

This manuscript has been authored by UT-Battelle, LLC under Contract No. DE-AC05-00OR22725 with the U.S. Department of Energy. The United States Government retains and the publisher, by accepting the article for publication, acknowledges that the United States Government retains a non-exclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this manuscript, or allow others to do so, for United States Government purposes. The Department of Energy will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (http://energy.gov/downloads/doe-public-access-plan).

References

  1. Wallace, D.C. Statistical mechanics of monoatomic liquids. Phys. Rev. E 1997, 56, 4179–4186. [Google Scholar] [CrossRef]
  2. Wallace, D.C. Liquid dynamics theory of high-temperature specific heat. Phys. Rev. E 1998, 57, 1717–1722. [Google Scholar] [CrossRef]
  3. Egami, T. Understanding the Properties and Structure of Metallic Glasses at the Atomic Level. J. Metals 2010, 62, 2, 70–75. [Google Scholar] [CrossRef]
  4. Moon, J.; Lindsay, L.; Egami, T. Atomic dynamics in fluids: Normal mode analysis revisited. Phys. Rev. E 2023, 108, 014601. [Google Scholar] [CrossRef] [PubMed]
  5. Bernal, J.D. A geometrical approach to the structure of liquids. Nature 1959, 183, 141–147. [Google Scholar] [CrossRef]
  6. Finny, J. Random packing and the structure of simple liquids. I. The geometry of random close packing. Proc. Roy. Soc. Lond. A 1970, 319, 479–493. [Google Scholar]
  7. Cohen, M.H.; Turnbull, D. Molecular transport in liquids and glasses. J. Chem. Phys. 1959, 31, 1164–1169. [Google Scholar] [CrossRef]
  8. Liu, A.J.; Nagel, S.R. The jamming transition and the marginally jammed solid. Ann. Rev. Cond. Mat. 2010, 1, 347–369. [Google Scholar] [CrossRef]
  9. Weeks, J.D.; Chandler, D; Andersen, H.C. Role of repulsive forces in determining the equilibrium structure of simple liquids. J. Chem. Phys. 1971, 54, 5237–5247. [CrossRef]
  10. Egami, T. Atomic level stresses. Progr. Mater. Sci. 2011, 56, 637–653. [Google Scholar] [CrossRef]
  11. Egami, T.; Ryu, C.W. Structural principles in metallic liquids and glasses: Bottom-up or top-down. Frontiers in Materials 2022, 9, 874191. [Google Scholar] [CrossRef]
  12. Egami, T.; Ryu, C.W. Medium-range atomic correlation in simple liquid. II. Theory of temperature dependence. Phys. Rev. E 2021, 104, 064110. [Google Scholar] [CrossRef]
  13. Egami, T.; Poon, S.J.; Zhang, Z.; Keppens, V. Glass transition in metallic glasses: A microscopic model of topological fluctuations in the bonding network. Phys. Rev. B 2007, 76, 024203. [Google Scholar] [CrossRef]
  14. Dmowski, W.; Diallo, S.O.; Lokshin, K.; Ehlers, G.; Ferré, G.; Boronat, J.; Egami, T. Observation of dynamic atom-atom correlation in liquid helium in real space. Nature Commun. 2017, 8, 15294. [Google Scholar] [CrossRef] [PubMed]
  15. Egami, T. K. Alex Müller and superconductivity. Physica C 2023, 613, 1354345. [Google Scholar] [CrossRef]
  16. Frank, F.C. Supercooling of liquids. Proc. Roy. Soc. Lond. A 1952, 215, 43–46. [Google Scholar]
  17. Turnbull, D. Kinetics of solidification of supercooled liquid mercury droplets. J. Chem. Phys. 1952, 20, 411–424. [Google Scholar] [CrossRef]
  18. Sadoc, J.F. Use of regular polytopes for the mathematical description of the order in amorphous structures. J. Non-Cryst. Solids 1981, 44, 17–30. [Google Scholar] [CrossRef]
  19. Sethna, J.P. Frustration and curvature: Glasses and the cholesteric blue phase. Phys. Rev. Lett. 1983, 51, 2198–2201. [Google Scholar] [CrossRef]
  20. Nelson, D.R. Order, frustration, and defects in liquids and glasses. Phys. Rev. B 1983, 28, 5515–5535. [Google Scholar] [CrossRef]
  21. Steinhardt, P.J.; Nelson, D.R.; Ronchetti, M. Icosahedral bond order in supercooled liquids. Phys. Rev. Lett. 1981, 47, 1297–1300. [Google Scholar] [CrossRef]
  22. Tomida, T.; Egami, T. Molecular-dynamics study of orientational order in liquids and glasses and its relation to the glass transition. Phys. Rev. B 1995, 52, 3290–3308. [Google Scholar] [CrossRef] [PubMed]
  23. Miracle, D.B. A structural model for metallic glasses. Nature Mater. 2004, 3, 697–702. [Google Scholar] [CrossRef]
  24. Sheng, H.W.; Luo, W.K.; Alamgir, F.M.; Bai, J.M.; Ma, E. Atomic packing and short-to-medium-range order in metallic glasses. Nature 2006, 439, 419–425. [Google Scholar] [CrossRef] [PubMed]
  25. Warren, B.E. X-ray diffraction (Addison-Wesley, Reading, 1969).
  26. Ryu, C.W.; Dmowski, W.; Kelton, K.F.; Lee, G.W.; Park, E.S.; Morris, J.R.; Egami, T. Curie-Weiss behavior of liquid structure and ideal glass state. Scientific Reports 2019, 9, 18579. [Google Scholar] [CrossRef] [PubMed]
  27. Egami, T.; Ryu, C.W. World beyond the nearest neighbors. J. Phys: Condens. Matter. 2023, 35, 174002. [Google Scholar] [CrossRef] [PubMed]
  28. Egami, T.; Ryu, C.W. Origin of medium-range atomic correlation in simple liquid: Density wave theory. AIP Adv. 2023, 13, 085308. [Google Scholar] [CrossRef]
  29. Ryu, C.W.; Dmowski, W.; Egami, T. Ideality of liquid structure: A case study for metallic alloy liquids. Phys. Rev. E 2020, 101, 030601(R). [Google Scholar] [CrossRef]
  30. Ryu, C.W.; Egami, T. Origin of liquid fragility. Phys. Rev. E 2020, 102, 042615. [Google Scholar] [CrossRef]
  31. Glyde, H.R. Excitations in liquid and solid helium; Clarendon Press, Oxford, UK, 1994.
  32. Svensson, E.C.; Sears, V.F.; Woods, A.D.B.; Martel, P. Neutron-diffraction study of the static structure factor and pair correlations in liquid 4He. Phys. Rev. B 1980, 21, 3538–3651. [Google Scholar] [CrossRef]
  33. Anderson P.W. Science 1987, 235, 1196-1198.
  34. Keffer, F. Spin waves, in Handbuch der Physik, 18, pt. 2; Springer-Verlag, Berlin, GE, 1966.
  35. Fulde, P. Electron correlations in molecules and solids; Springer, Berlin, 2012.
  36. Van Hove, L. Correlation in space and time and Born approximation scattering in systems of interacting particles. Phys. Rev. 1954, 95, 249–262. [Google Scholar] [CrossRef]
  37. Egami, T.; Shinohara, Y. Perspective: Correlated atomic dynamics in liquid seen in real space and time. J. Chem. Phys. 2020, 153, 180902. [Google Scholar] [CrossRef] [PubMed]
  38. e. g., Platzman, P.M.; Tzor, N. X-ray scattering from electron gas. Phys. Rev. 1965, 139, A410–A413. [Google Scholar] [CrossRef]
  39. Abbamonte, P.; Finkelstein, K.D.; Collins, M.D.; Gruner, S.M. Imaging density disturbances in water with a 41.3-attosecond time resolution. Phys. Rev. Lett. 2004, 92, 237401. [Google Scholar] [CrossRef] [PubMed]
  40. Lovesey, S.W. Theory of neutron scattering from condensed matter; Oxford University Press, Oxford, UK, 1984.
  41. Bista, R.; Upton, M.; Shinohara, Y.; Egami, T. Direct observation of electron correlation in space by inelastic x-ray scattering. 2023, unpublished.
  42. Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
  43. Li, Q.; Huang, H.-Y.; Ren, T.; Weschke, E.; Ju, L.; Zou, C.; Zhang, S.; Qiu, Q.; Liu, J.; Ding, S.; Singh, A.; Prokhnenko, O.; Huang, D.-J.; Esterlis, I.; Wang, Y.; Xie, Y.; Peng, Y. Prevailing charge order in overdoped La2-xSrxCuO4 beyond the superconducting dome. Phys. Rev. Lett. 2023, 131, 116002. [Google Scholar] [CrossRef]
  44. Emery, V.J.; Kivelson, S.A. Importance of phase fluctuations in superconductors with small superfluid density. Nature 1995, 374, 434-437. [Google Scholar] [CrossRef]
  45. Uemura, Y.J. Bose-Einstein to BCS crossover picture for high-Tc cuprates. Physica C 1997, 282-287, 194-197.
  46. Xu, Z.A.; Ong, N.P.; Wnag, Y.; Kakeshita, T.; Uchida, S. Vortex-like excitations and the onset of superconducting phase fluctuation in underdoped La2-xSrxCuO4. Nature 2000, 406, 486–488. [Google Scholar] [CrossRef]
Preprints 93369 g001
Figure 1. An icosahedral cluster.
Figure 1. An icosahedral cluster.
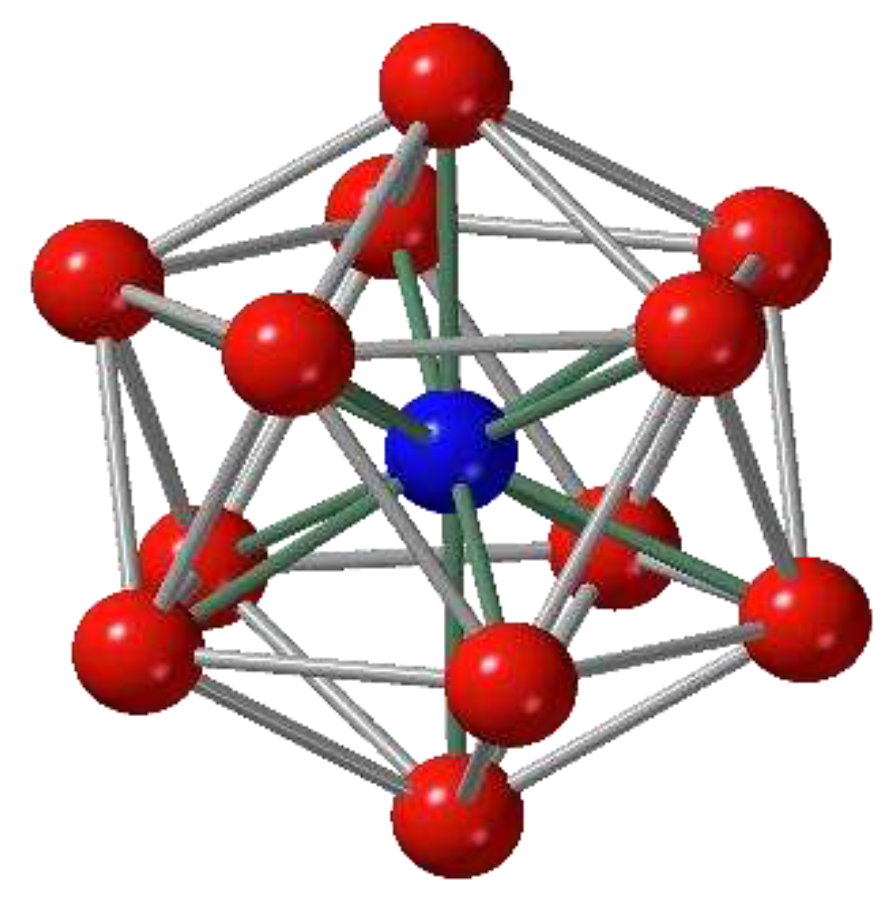
Preprints 93369 g001
Preprints 93369 g003
Figure 3. The total PDF (red) and the portion (0.69 – 0.9 meV) of the difference in the energy-resolved PDFs of 4He, Δg(r, E) = gT1(r, E) − gT2(r, E) (blue), for T1 = 1.83 K and T2 = 2.85 K [14].
Figure 3. The total PDF (red) and the portion (0.69 – 0.9 meV) of the difference in the energy-resolved PDFs of 4He, Δg(r, E) = gT1(r, E) − gT2(r, E) (blue), for T1 = 1.83 K and T2 = 2.85 K [14].
Preprints 93369 g003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated