Preprint
Article
Quaternion-Spin and Some Consequences
Altmetrics
Downloads
179
Views
84
Comments
0
This version is not peer-reviewed
Theoretical, Quantum and Computational Chemistry
Submitted:
15 December 2023
Posted:
18 December 2023
Read the latest preprint version here
Alerts
Abstract
Changing the symmetry of spin from SU(2) to the quaternion group, $Q_8$, has many ramifications. In this paper we first summarize the properties of Q-spin and then discuss some of those resulting changes.
Keywords:
Subject: Physical Sciences - Quantum Science and Technology
Introduction
Spin is regarded as a point particle of intrinsic angular momentum. First discovered in a Stern-Gerlach (SG) experiment [1], spin is characterized as a vector operator, , with one component, , being an eigenoperator on its states. Rather than , we use the Pauli spin vector, from so
These states of even parity and with unit vectors form the Bloch sphere. Based upon experimental data, spin is fully characterized by the state vectors and the algebra of its three Pauli spin components, along with the identity, form the SU(2) group. From Eq.(1) spin is always polarized with a value of either or . Here we challenge that result.
Whereas position-momentum, energy-time are complementary pairs defined in spaces that are the Fourier transforms of each other, no complementary property to spin angular momentum, , is known. Spin is universally considered to be the two state Dirac spin with vector polarization, , and nothing more. We define the complementary attribute of spin by introducing a bivector, so a spin is expressed as,
where the helicity operator is defined as a second rank totally anti-symmetric Cartesian tensor,
We generally refer to as quaternion or Q-spin. The two contributions, being complementary, cannot simultaneously manifest but the first term describes polarization and the second term describes the hyper-helicity, . The latter arises in the isotropy of free-flight and the former arises in a polarizing anisotropic environment.
The reason to introduce the hyper-helicity (or simply the helicity), is that there exists additional evidence for spin from coincidence photon experiments [2,3,4] revealed by the apparent violation of Bell’s Inequalities (BI) [5]. The conclusion of Bell’s Theorem, [5], is the violation is due to non-local connectivity, entanglement, between the two spins in an EPR pair. Here we find the extra correlation is due to quantum coherence, [6], which results from defining helicity using a bivector, , giving the complementary property to the spin vector polarization, .
There is no bivector in the Dirac equation so the helicity cannot be found from it. However, one is easily introduced by changing the Dirac field from the gamma matrix representations in Minkowski spacetime, , by multiplying one gamma matrix by the imaginary number i,7]. This changes the spin symmetry from SU(2) to the Quaternion group, . Then the spin spacetime field for one particle is , where . This is the only change made in the theory of Q-spin, but it is profound. Our description of Nature radically changes with many well established ideas taking on entirely different interpretations.
The subscript s denotes spin spacetime, , to distinguish it from Minkowski spacetime.
Changing the spin symmetry from SU(2) to , the quaternion group, changes the point particle description to one where a spin has a 2D structure. Rather than a polarized vector, say N-S, Q-spin is bent, like N-E.
Both Minkowski and SS have coordinate frames and these are related. The former has coordinates , defining the Laboratory Fixed Frame, (LFF), and SS has coordinates , defining a Body Fixed Frame (BFF) which orients a structured spin (2D) in Minkowski spacetime. We make the assumption that the spinning 2D spin in free-flight is coplanar to the polarizing filter. This sets as the axis of linear momentum which spins. The polarization components, are a rotation away from Minkowski spacetime.
This paper is based upon three which present the theory of Q-spin. The first introduces a Quantum Field Theory treatment of the Dirac equation under the quaternion group, [7]. In the second`paper the helicity is defined and shows it conserves the correlation from an EPR pair before and after separation, [8]. Finally in paper 3, [6] a simulation is presented which agrees with the experiment and explains the apparent violation of BI.
Q-spin structure
From this change of symmetry, spin acquires a 2D structure. Rather than a point particle of “intrinsic" angular momentum with two states of up and down, spin emerges as a two dimensional spinning disc with “extrinsic" angular momentum with not two, but four states: two polarized states similar to Eq.(1) [7], and two coherent helicity states of left and right, , Figure 1.
The structure of Q-spin is geometrically identical to a photon having two orthogonal fermionic axes analogous to the orthogonal electric and magnetic components of a photon. Each axis is a spin ½ with a magnetic moments of . In free-flight these two axes must couple to give a coherent or resonant spin 1 with a magnetic moment of , Figure 2. A boson is produced. This resonance between the two orthogonal axes stabilizes the 2D structure, and lowers its energy. The three spin axes shown are all perpendicular to the axis of linear momentum which is spun by its helicity, see Figure 1. Note the two spins precess oppositely and are in phase. The two axes are maintained as mirror images of each other, and, being a spinning disc, it is impossible to know which is the real spin and which is its reflection.
In an anisotropic polarizing field, the boson spin in free-flight decouples into its two axes [6]. One aligns with the filter axis while the second randomizes in the filtering process. That is, upon measurement, spin is our usual measured spin ½ that Dirac obtained from his equation with its two states, [9]. Q-spin is an anyon, [10] which allows both complementary fermionic and bosonic properties. Only 2D structures admit anyons. Point particles and 3D structures do not.
All of this follows by the simple change of introducing the imaginary rendering making Hermitian.
Here a Dirac electron is denoted, for a fermion of spin which in the solution to the Dirac equation, and is the usual two-state spin accepted today. The four state Q-spin electron is denoted for a boson which means the solution of the SS form of the Dirac equation, which is discussed below.
Decomposing the correlation
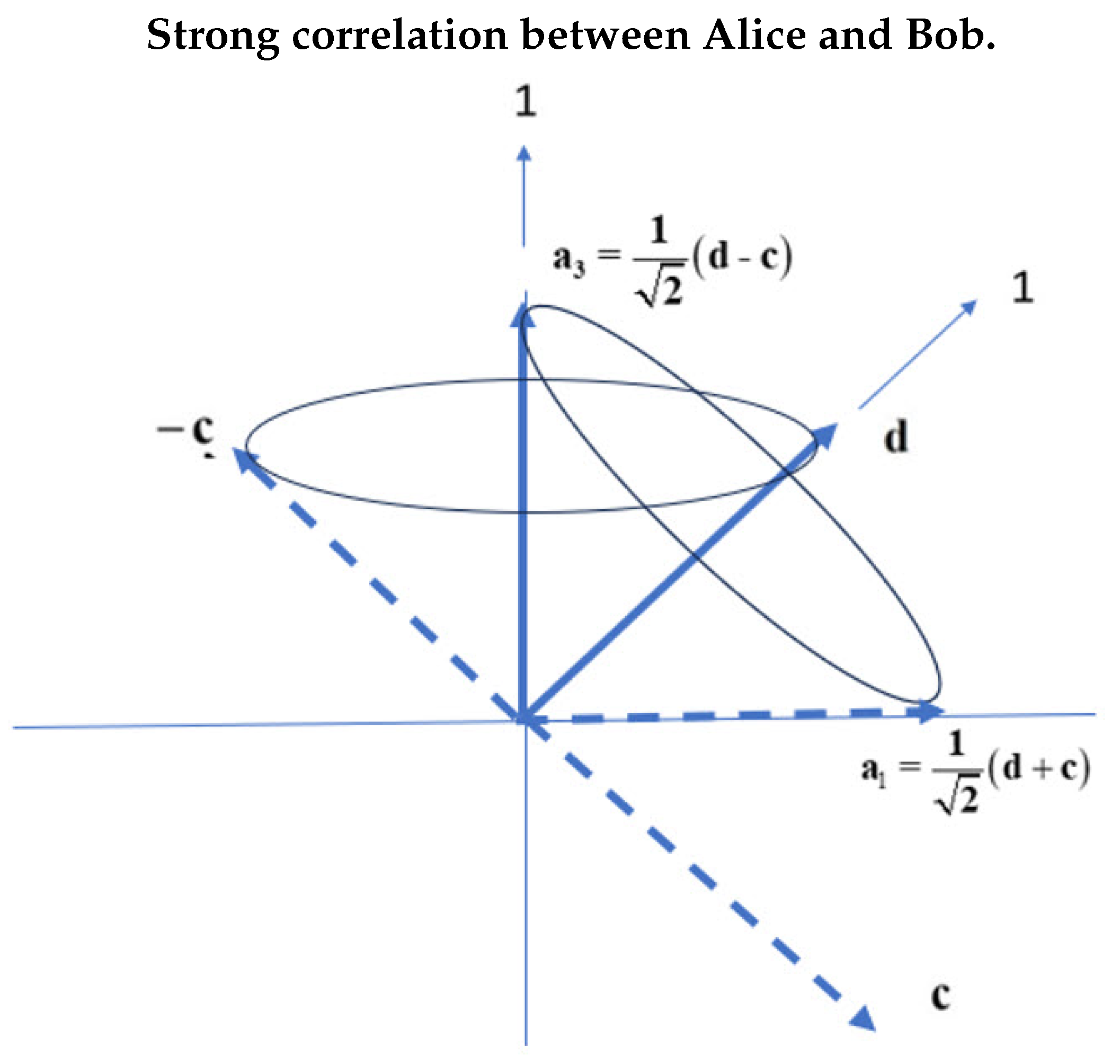
In reference [6] it is shown the violation of BI is due to the transition from a boson in free-flight to a fermion when measured. A simulation confirms this and generates the EPR correlation in Figure 3 which plots the correlation between EPR pairs versus their filter angle difference, . The cosine similarity curve is decomposed into two parts. The triangle is simulated from the product state polarization, whereas the French Mustache is purely coherence and is simulated by the decoupling of the boson into its fermionic components. The CHSH form of BI, [11], is 2 for polarization and 1 for the coherence, giving a total of 3. Although neither polarization nor coherence violate BI their sum does because EPR coincidence experiments cannot yet distinguish between clicks that are from polarization and coherence. All this we discussed below and the violation of the Tsirel’son bound, [12].
The Geometric Algebra foundation
The fundamental starting point of the theory is based upon the well know expression from Geometric Algebra, [13] for the geometric product of two Pauli spin components,
The first term is symmetric and gives the polarization. The second term is antisymmetric and gives the coherence. The two contributions are complementary since i cannot simultaneously be equal and not equal to j. From this the polarization and the helicity are defined as complementary attributes of spin.
Outline
In this paper we enlarge upon the ideas presented so far after which some of the consequences are presented. Some are speculative. Many question old and established beliefs. Here is the organization of the paper:
First we show that entanglement is due to coherence by dropping the off-diagonal terms of the singlet state. Doing this leaves only the polarization (with a CHSH of 2). Including the helicity, the contribution from coherence is calculated (with a CHSH of 1), leading to apparent violation of BI.
The extra correlation is from helicity and not from non-locality as Bell’s theorem asserts. This paper is not about Bell’s theorem which is not violated here. There are no Local Hidden Variables (LHV) and the only variable is which orients a spin on the Bloch sphere. These papers are about the formulation of Q-spin
The Dirac equation is modified by using which gives the Q-spin form of the Dirac equation. Since every spin is differently oriented, each has its own spin spacetime. These break up into two complementary spaces: a 2D spin spacetime for the polarization, and the 4D hypersphere, with four spatial dimensions. From this complementary space, helicity is described by a unit quaternion. We discuss these changes with most of the equations’ derivations given in detail in the Appendix.
By using the quaternion group rather than SU(2), Dirac’s two spin, matter-antimatter hypothesis, is replaced by one structured 2D spin in the 4D Dirac field. This change solves the negative energy problem faced by Dirac.
After showing that helicity obviates the need for non-locality, there are a number of fundamental differences from the point particle spin that Dirac found. Besides now displaying structure, rather than a point, Nature becomes local and real. We discuss the implications of this with respect to to Bell’s theorem. We give the mechanisms that are responsible for the violation of CHSH inequality as due to the transition from a boson to a fermion, thereby showing there is no quantum weirdness.
The field of quantum information theory, which rests entirely of Bell’s theorem, must be reassessed. Quantum teleportation and other quantum technologies fail. Qubits disappear in free-fight, with implications for quantum computing. Without entanglement, suggestions that spacetime has a lattice of entangled particles, [14], is replaced by an alternate construction.
We show that the local singlet state is an approximation giving a CHSH value of 2.828, whereas we argue the true value is from the simulation with a CHSH of 3.
In particle physics and the Standard Model, we show that neutrinos are unnecessary since in free-flight an electron is a boson, obviating the need for neutrinos. Additionally we suggest that the 1956 parity experiment of WU, [15], should be re-analyzed using Q-spin.
All this impacts upon the interpretation of QM as a theory of measurement, but not of Nature.
Motivation
Non-locality is firmly established in QM as evidenced from the 2022 Nobel Prize in Physics, [2,3,4]. However, there is no rational explanation, until now, for non-locality, leading to a large popular science literature with highly speculative suggestions which people assert must follow. The reason for this stems from the notion that, physically, instant-action-at-a-distance cannot be rationalized, and the term “quantum weirdness", [16] is simply revelation with no basis. Issac Newton rejected this as an “absurdity", [17] and Albert Einstein called it “spooky", [18]. Nonetheless, today it is an active research topic and the basis for the enormous field of quantum information theory which rests entirely of Bell’s Theorem, [5]. Quantum technologies of computing, [19], teleportation, [20,21] and cryptography, [22] are well known applications, which rely on “quantum channels" which connect distant formally entangled particles.
The view presented in this and companion papers, [6,7,8], is that the concept of non-locality is untenable and makes no physical sense, despite the large body of scientific evidence which suggests otherwise. Basically, the guiding principles are that if something does not make physical sense to us, it is probably wrong. This also assumes that we are capable of following the logic of Nature and the evidence we gather is not beyond the realm of our ability. It therefore follows that if the notion of non-locality is untenable, then there must be an objective alternative. We assert that Q-spin fills that requirement.
Coherence
EPR coincidence experiments, start, as usual, with an EPR pair entangled at the source and in a singlet state,
We prefer to work in state space which makes it easier to distinguish between the diagonal polarized states, , and the off-diagonal coherent states, . Moreover, the state operators here describe the pure state of particles, rather than a statistical ensemble over similarly prepared EPR pairs. Eventually we average over all the different spin orientations, , in the simulation. There is no statistical interference between EPR pairs and every pair produces a coincidence event.
The correlation between an EPR pair is defined by the quantum trace over the operators, given by[23],
Here the dagger denotes the adjoint operator. The spin operators for Alice and Bob are A and B while the pure state operator is .
The entangled singlet two particle state operator, , is found by taking the outer product of Eq.(5), (see the appendix),
written in two forms. First is the tensor product between the two identity matrices, and the scalar product between the two Pauli spin vectors. Expressed as a matrix, the two diagonal elements describe polarization, whereas the two off-diagonal elements describe coherence. (Note the four terms correspond to )
The coherent terms are responsible for the entanglement and preclude the product state. If those two coherent states are dropped, then the singlet state becomes a product state. We give the results found in [6],(see appendix),
in terms of the tensor product of the two single particle state operators, [24]
where .
Having the state operators for the singlet state and the product state, allows us to calculate the EPR correlation using Eq.(6). The entangled singlet, Eq.(7) gives the total correlation that can be obtained from a singlet state as, (all these are worked out in the Appendix) [8]
Here is the totally symmetric second rank Cartesian tensor. This obtains the usual term which is plotted in Figure 3 along with the simulated points. Notice the two curves differ with more correlation from the simulation. In Eq.(10) the unit vectors of and express the direction that the filters are set by Alice and Bob.
Likewise using Eq.(8) the product state gives,
The basis component, is chosen to be the usual LFF component Z, giving the two final cosine terms. The correlation from the product is the triangle shown in Figure 3, and which is confirmed by the simulation. This has a CHSH value of 2, not violating Bell’s theorem. Subtracting the correlation between the full singlet and the product states separates out the mustache function which also does not violate BI, although the sum does. We conclude the mustache function is a result of coherence and is responsible for the observed violation of BI. That is, the violation is not due to non-locality.
Upon separation, locality means the off-diagonal terms are dropped while non-locality means they are retained. Here we drop them so that after leaving the singlet, the state of an EPR pair is a product state, Eq.(8).
From EPR coincidence experiments, the observed correlation is not consistent with a product state, Eq.(11) but rather gives the full correlation displayed in Eq.(10). One of the many statements of the EPR paradox [25], is the conclusion that entanglement must be maintained over spacetime. This is justified by Bell’s Theorem, but, as mentioned above, how such non-local connectivity is maintained is not understood, and defies rational explanation, [26]. [27,28].
We can use the same product state Eq.(8) and calculate the correlation from the helicity, Eq.(3) [8],
Clearly adding the symmetric polarization, Eq.(11) and the coherence, Eq.(12) gives the full correlation observed, Eq.(10),
This is an example of the Law of Conservation of Geometric Correlation, [8] which states that in the separation process, no correlation is lost, but rather it is divided between the various symmetry modes from the decomposition of such entangled states. Entanglement is not necessary to preserve the correlation after separation.
In conclusion, if the quantum coherence terms are dropped when an EPR pair separates, the resulting product state, Eq.(11), does not agree with the experimental results. Including the coherent terms from helicity resolves this to give the full quantum correlation, Eq.(10). That is, the violation is a result of coherence rather than non-local connectivity.
Complementarity and EPR coincidences
We have proposed that polarization and helicity are complementary properties. It is widely and erroneously believed that orthogonal components of the Pauli spin vector, which do not commute, are complementary attributes. Even though they lead to the Heisenberg uncertainty relationship, these spin components are only incompatible since they are measured in the same apparatus which can be rotated at will to detect any component.
Pauli stated [29] “Intuitively, observables are complementary if the experimental arrangements allowing their unambiguous definitions are mutually exclusive."
Moreover, the definition of complementarity for angular momentum is,
The commutation relations of the sigma components do not obey the above but rather, . Also both spin components are angular momentum, whereas one component of complementary attributes must be a function of the angle, and not its derivative.
More evidence will be given below when the Dirac equation is summarized, but first we discuss the effect of complementarity. The treatment here is for pure states of single particles. As such, they can be represented as extreme points in a convex set with the mixed states being interior points, [30]. Interior points are mixtures of pure, extreme points.
However, incompatible complementary attributes are represented in inverse, dual, or complementary spaces which belong to different, exclusive, convex sets. This further rules out Pauli spin components which belong to the same convex set. Therefore, we assert coincidence experiments contain contributions from purely polarization and purely coherent events, but, because they exist in complementary spaces, each belongs to a different convex set. The origin of this is the geometric product, Eq.(4).
Despite having quoted Pauli that different apparatus are need to detect complementary attributes, we suggest that coincidence experiments are not sensitive to the different origin of polarization and coherence clicks. Therefore from these experiments, events are from two different complementary sources to which the experiment is blind.
We use the usual definition of EPR correlation between equal coincidence events (), , and unequal events(), given by,
and coincidence EPR experiments result in the minus cosine similarity, [2,3,4].
Usually when outputs are distributed between the two types of events, they are weighted by probabilities, and . We expect, however, events to arise from either polarization or from coherence, which cannot be mixed. With no mixed states, the probabilities are replaced by Boolean operators that ensure complementarity: that is, a click is either from pol (polarization), or from coh (coherence),
with or , with the sum of the contributions being the total number of events, .
Suppose that it is possible to filter the system such that the experiments can distinguish between the two, then we can write the total correlation as collecting the different events in two different bins,
The correlation from each is evaluated to obtain the full correlation as shown in Figure 3 being the sum of the two contributions. Note the value of a correlation is independent of the total number of clicks, so for the simulation calculation we did the following: first in Eq.(17) assume and and the polarization algorithm was used to give the triangle in Figure 3. Then we set and and calculated the mustache curve using the coherence algorithm. After this, the total correlation is their sum, Figure 3.
A filter, in principle, might be constructed by polarizing the beam at the source. Additionally, a filter might vary the strengths of the applied field to inhibit or promote decoupling
Dirac equation under Q
Spin emerges from the Dirac equation and here we summarize its changes when the symmetry is changed from SU(2) to Q. Equation (2) defines Q-spin, which modifies the usual vector on a Bloch sphere, to a spinning vector on the Bloch sphere. We have not yet reviewed the origin of this nor its structure shown in Figure 1, which we summarize here, [7].
The new equation in SS replaces which gives a non-Hermitian equation by virtue of ,
and we suppress the subscript s on the derivatives. The anti-commutation of the matrices ensures that energy is conserved and the Klein-Gordon equation is recovered. Note that the symmetry change also changes the signature of the Dirac field to,
The order of the components in SS is and the term is not a spatial component, but rather time-like and a frequency. This dimension is the origin of quantum coherence that leads to the formulation of helicity.
In free-flight the spin is in an isotropic environment, rendering the two axes indistinguishable. Therefore, permutation with the parity operator, does not change the dependence in Eq.(18), but the bivector, is anti-symmetric to 13 permutation. Therefore the above equations admits two solutions in left and right handed coordinate frames, which are mirror states, see Figure 4,31],
These reflective states are displayed in Figure 2 as oppositely in-phase precession of the two axes.
Figure 4 shows the mirror images of . Note that summing the two states cancels the bivector and subtracting them cancels the (1,3) polarizations, leading to states that are odd and even with respect to parity,
This separates the Dirac equation into two distinct and separate spaces which are the complementary spaces of Q-spin: the first is a 2D Dirac equation in the (1,3) plane, and the second is the Weyl equation for a massless spinor,
Spin spacetime separates into two distinct spaces: polarization spacetime, , Eq.(22); and coherent space (not spacetime) , Eq.(23). The Hermitian part, Eq.(22), is the same as the usual Dirac equation, but in two dimensions rather than three.
The bivector component, , describes a massless Weyl spinor in coherent space, Eq.(23). Within coherent space, , time does not exist beyond the constant frequency of its spinning. Time and rest mass remain in polarization space. Similar to the two complementary inverse spaces of position and momentum, here the two spin spaces carry the two complementary properties, polarization and coherence.
We discuss these solution more fully below.
Spin spacetime
The two solutions exist in complementary spaces shown in Figure 5 which relates Minkowski spacetime with coordinates , to the even parity, polarization component of Q-spin with coordinates . From Minkowski spacetime, spin is a spinning disc. From here on, we call the components (0,1,3), spin spacetime, SS, while the component (2), is the coherent space of quaternions from the Weyl equation. The polarization components, are a rotation away from Minkowski spacetime, where is the vector that orients a spin on the Bloch sphere,
The filter direction is also expressed in the LFF by,
showing the spinning disc and the polarizer are coplanar. Call the disc the 2D spin.
The solution to the Weyl equation, Eq.(23), is a unit quaternion, [7,13], which exists in the hypersphere with four spatial dimensions. These are beyond our spacetime and its role is to spin the axis and consequently the disc. Only the stereographic projection of spin polarization is projected into Minkowski spacetime. The quaternion is not observable but it is, nonetheless, an element of reality of spin in the different physical space of quaternions. Spin spacetime has a 2D space of polarization, and an inverse space, of quaternions, the hypersphere, depicted in Figure 5.
The 2D spin equation
The solution to the 2D Dirac equation is the same as the 3D Dirac equation and we can immediately write down,
where the even parity state is written as . Define a momentum vector which after transforming to the LFF using Eqs.(24) we find that, [7],
leading to the same Klein-Gordon equation in both Minkowski and SS,
The energies from the eigenvalues are,
which is the usual results but with the momentum from the two axes. We interpret these two energies as the opposite precessions of the axes as depicted in Figure 2.
Helicity
The helicity follows from the solution to the Weyl equation, Eq.(23). This is given in [7] and not repeated here.
Note that there is no linear time, in the Weyl equation so there can be no boosts, only rotations. This means the left and right solutions are identical, ,32]. Since the quaternion spins the disc, a boost in the 2D SS carries along the spinor in .
As a massless Weyl equation, its L and R precessions normally define chirality, a Lorentz invariant. However, here a unit quaternion spins the 2D polarization disk which carries mass. This, then, defines the helicity as the disc spins in free-flight which is not a Lorentz invariant. Susskind called such a structure a “world sheet", [14], from string theory, to contrast a “world line" from gravitational theory.
From particle physics, the helicity is defined as the projection of the spin polarization along the axis of linear momentum, . The helicity is R for a positive value and L for a negative value of the projection, or vice versa. Here the solutions of the Weyl equation are a unit quaternions, [7]
where is the frequency of the helicity. The two signs, ±, then define the helicity of Q-spin in free-flight. The complementary attribute to spin angular momentum is a quaternion, whose sole purpose is to spin the Y axis. Figs.(Figure 5) and Figure 1. There is correlation between the helicities of Alice and Bob. The decoupling of the boson in the presence of a field is illustrated in, see Figure 6. Depending on its sign, the aligned axis spins L or R, thereby determining the sign of the spin precession which can be measured as up or down by .
We do not go into the symmetry reduction of the Q-spin field determined by the gamma matrices, . We note, however, that the pseudo-scalar defines a helicity matrix,
showing that the L and R handed components of the quaternion Dirac field generates the two spatial gamma matrices, ,
and the helicity axis, . The matrix usually projects the R and L handed chiral states from a Dirac field. Here we define showing the odd and even parity states, Eq.(21), are projected from the mirror Q-spin states of Eq.(18),
In free-flight, the two spin axes on the same particle have equal but opposite energy, opposite magnetic moments, and constructively interfere to form the resonance boson of Q-spin.
This description, quite different from Dirac’s matter-antimatter interpretation, nonetheless, rests upon the same mathematical basis as the Dirac field.
The Problem with the Dirac field
When Dirac wrote down his equation, he was expecting the two state spin that is observed. His gamma matrices, however, were four dimensional, containing two SU(2) spins with two states, and each being the mirror image twin of the other.
The SU(2) description of Dirac spin shows it is a point particle with three spatial components, of , with its antimatter twin the opposite, , being the reflection, or mirror image, of its partner. In contrast, under Q, a Q-spin is one particle with four states, and represented by , displaying both L and R helicities via the .
The perplexing point for Dirac was the twin spin also had opposite, or negative, energies from its partner which went to minus infinity. Dirac resolved this by proposing a fermionic definition of a negative energy continuum, and added electrons according to the Pauli principle until he had filled the continuum. Holes of antimatter positrons are formed as electrons jumped to positive energy.
Dirac, seeing his second particle with opposite charge, believed this was a way antimatter can form. Eventually this interpretation took hold, but it has worrying details, such as issues with the negative energy of the antimatter twin, lepton decay in the standard model, [33], and parity violation, the tau-theta puzzle, [34].
Here we do not dispute the existence of antimatter, but question the Dirac interpretation of its production. The four dimensional field describes one, not two, particles. Since the two spins precess oppositely and in phase, Figure 2, the two energies must be equal and opposite. This interpretation resolves the negative energy problem Dirac encountered. Later we discuss the parity violation of beta decay.
From Figure 2, the two coupled axes that give the spin 1 boson, are mirror states. Normally two spins can form four states, the singlet and the triplet. In the triplet, the symmetric in-phase precession of the two spins can be in two directions by simultaneously reversing the precession of each, Figure 2. This generates the two magnetic components of . However, consistent with a photon, Q-spin has no component nor a singlet state because the mirror symmetry between the two axes cannot then be maintained.
We also note that the wave-particle duality of spin is dependent upon its environment. The polarization (particle), , and the coherence (wave), are manifest as complementary attributes such that the polarization exists only in an anisotropic environment as a fermion, whereas the coherence exists only in an isotropic environment as a boson,
By finding a 2D planar structure of an electron, it is no longer a point particle, whereas all the elementary particles in the Standard Model are point particles. We can only surmise that in the brief epoch after the Big Bang, electrons and positrons were formed in a two step process, with at first positrons having a charge of and electrons with . Call these pre-spins for now, and indeed are point particle vector quantities. Shortly thereafter, collisions resulted in either: 2D Q-spins (collisions between particles with the same charge), which are stabilized by the resonance of its boson spin, whereas collisions between particles with opposite charge are annihilated.
If such a two-step process occurred, then it can also reverse in collisions, which would resemble a matter-antimatter pair production, [35] but does not provide proof of Dirac’s interpretation.
Bell’s Theorem
The notion of non-locality rests upon the violation of BI, [5] which have nothing to do with quantum mechanics but provide a useful quantitative classical definition of the “Invisible Boundary” [36] between the microscopic and macroscopic. For the CHSH [11] form of Bell’s inequalities, the invisible boundary is 2. Here we accept Bell’s inequalities, but reject Bell’s Theorem which states in his own words [37],
“If [a hidden-variable theory] is local it will not agree with quantum mechanics, and if it agrees with quantum mechanics it will not be local."
We first point out that in the presentation here, there are no hidden variables and consequently there can be no loopholes. The only variable is the angle which orients a spin on the Bloch sphere (with an azimuthal component of zero).
Second Q-spin theory does not violate Bell’s theorem when viewed as two complementary sources of events. Each attribute obeys BI with a CHSH of two for polarization and one for coherence, from the simulation.
We do not question the mathematical rigor of the derivation of Bell’s theorem, [37]. Rather we assert that the theorem is only applicable to classical system, giving a CHSH bound of 2, which is never violated. Quantum systems display complementarity which Bell ignored. Simply stated, Bell’s theorem considered only polarized states and not coherence. His theorem’s proof shows that using classical systems, the only way to violate his classical bound was to invoke non-local connectivity. This, he proves cannot be due to Local Hidden Variables. The work here proves his conclusion wrong.
Non-locality vs. local realism
The immediate consequence of the inapplicability of Bell’s Theorem is that non-local connectivity is not viable. Out of the myriad descriptions we feel that Wikipedia sums up non-locality the best, [50]:
“The paradox is that a measurement made on either of the particles apparently collapses the state of the entire entangled system—and does so instantaneously, before any information about the measurement result could have been communicated to the other particle ... and hence assured the “proper" outcome of the measurement of the other part of the entangled pair."
Scholarpedia states [51], “Bell’s theorem asserts that if certain predictions of QM are correct then our world is non-local. “Non-local" here means that there exist interactions between events that are too far apart in space and too close together in time for the events to be connected even by signals moving at the speed of light."
Without Bell’s Theorem, these definitions cannot be supported.
The violation of BI now takes on entirely different meaning. Spin polarization and helicity both simultaneously exist as elements of reality; coincidence experiments are sensitive to both polarization and helicity Eq.(13); the experimental violation of Bell’s inequalities confirms local realism.
The diametrically opposite conclusion is reached in Bell-type experiments of which an enormous literature exists, see “The Big Bell test" [52]. The paper’s conclusion is incorrect claiming local realism is challenged. Rather their data shows just the opposite: evidence for local realism by the existence of elements of reality that account for the apparent violation.
Quantum teleportation
Quantum teleportation, [21], depends solely upon long range correlation between EPR pairs which cannot be justified in the absence of Bell’s Theorem. The opening paragraph in that paper confirms this, “The existence of long range correlations between Einstein-Podolsky-Rosen (EPR) pairs of particles raises the question of their use for information transfer."
Teleportation claims that non-locality is mediated by “Einstein, Podolsky, Rosen Channels", but nowhere are these “channels" formulated and there is no evidence they exist. Our work shows they do not exist. In particular the step from their Eq.(4) to Eq.(5), which is critical to quantum teleportation, cannot be justified. This requires swapping entanglement over spacetime separations. When Alice’s spin is far from Bob’s entangled pair, 23, then the following process is applied which is physically unfeasible:
Therefore their Eq.(5) is impossible and the notion of quantum teleportation collapses. Recall Longuet-Higgins [53] made the distinction between mathematical operations and feasible operations, like ammonia, NH, and methyl fluoride, FCH, both have inversion symmetry, but only for ammonia is it feasible. The concept of quantum teleportation is unfeasible, along with emerging technologies [20,22] that use it.
Quantum computing
We do not suggest that quantum computing is unfeasible, but it too partly rests upon Bell’s theorem and entirely rests on the persistence and stability of qubits. We suggest this needs to be re-examined since the polarized states of up and down that make a qubit, cannot persist in free-flight when the fermions change to bosons. Rather, the spacing between the gates must be carefully controlled to allow, in principle, the phase of the helicity to determine the polarized state when entering the next gate.
Entanglement decomposition
Entanglement, as Schrödinger famously said [54] was difference from classical systems. Without Bell’s theorem, persistence of entanglement between separated pairs is not possible. Therefore we accept entanglement as a vital property of QM but reject that it persists after separation, [8], to non-local situations. Whereas QM gives Tsirel’son’s bound, [12], of , the simulation gives a maximum violation with a CHSH of 3. The reason for this is that the singlet state, Eq.[5] is an approximation. We show this later in this paper.
The theory presented here agrees with the usual quantum result of without non-local “EPR channels", (see the appendix). The violation is due to correlation between the helicities.
The simulated value of CHSH = 3 is due to the modeling of Q-spin giving a CHSH value 1 per axis. Here we suggest the simulation gives a more accurate accounting for the correlation than from QM. Essentially the Q-spin treatment here supports the notion that polarization carries two axes while the coherence initially carries only one, being the coupled boson of spin 1, see Figure 6. The left and right parts of this figure show the two possible polarization axes after the boson has decoupled. The center part shows the coupled boson. These axes are attracted to the filter via two mechanisms. For polarized states, only the sign of the aligning vector determines the correlation and this is easily modeled by finding if the polarization vector is positive or negative. This generates the triangle correlation in Figure 3 with a CHSH value of 2.
Coherent states, in contrast, initially precess in a filter about the intact boson axis, see Figure 6. It must, however, eventually decompose into the fermionic axes the closer the boson gets to the filter. Since each axis carries opposite spin, it is important to know which axis aligns. To this end, first we determine which axis lies closer to the applied filter direction. We assume this closer axis is favoured to align. The click of is found again by determining if that closer axis is positive, plus click, or negative, minus click. This process generates the mustache function in Figure 3, which is closely fit by the following function which is plotted in Figure 7
We propose that the true correlation between the two spins is more accurately determined by this classical simulation than from QM.
The alignment and polarization of these axes is determined by their relative orientation with respect to the filter direction. Additionally the strength of the applied field relative to the spin-spin coupling between the two axes is also relevant. In Figure 8, the left panel shows the aligned coherent spin. At this orientation, and say up to 22.5 degrees on either side of the filter, the boson precesses and nutates intact with magnetic moment of , twice that of the two fermionic axes with a magnetic moment of each. Notice in Eq.(36) that the filter angle between Alice and Bob is which is consistent with a magnetic moment of and a spinning boson.
If the boson is offset from the filter to one direction by 45 degrees, second panel, then one of the fermionic axes aligns leading to the precession of the fermion with a magnetic moment of . The third panel shows the boson perpendicular to the field. In this case there is a competition between the two axes. One axis aligns with the positive direction of the filter, or the second axis is pulled to the negative direction along the filter. The panel on the right of Figure 8 shows that in a strong field, one quarter of the time Q-spin acts as a boson, and three quarters it acts as a fermion. We conclude that in a strong polarizing field, in some cases the boson is encountered intact and in others it decouples to the fermion.
Figure 9.
Displaying the maximum correlation from coherence. Alice sets her filter to and the boson spin of 1 aligns. Bob has two settings that will give the maximum violation by applying his filter either along or along at 45 degrees from . Alternately, Alice can set her filter angle to and Bob has two filter settings, and that lead to the maximum correlation. Note that a spin of magnitude 1 makes an angle of 45 degrees with filter directions.
Figure 9.
Displaying the maximum correlation from coherence. Alice sets her filter to and the boson spin of 1 aligns. Bob has two settings that will give the maximum violation by applying his filter either along or along at 45 degrees from . Alternately, Alice can set her filter angle to and Bob has two filter settings, and that lead to the maximum correlation. Note that a spin of magnitude 1 makes an angle of 45 degrees with filter directions.
Interpreting the maximum CHSH correlation
In the last section we showed how different orientations of Q-spins in a polarizing field favour fermions over bosons, or vice versa. In EPR coincidence experiments, we seek the correlation between two Q-spins for Alice and Bob at different settings.
Figure 10 top left shows the BFF of Q-spin whence each quadrant is bisected by a boson spin. At separation Alice and Bob share the same BFF so before filtering, both spins of the EPR pair are anti-parallel bosons. When Alice and Bob set their polarizers to be parallel, the anti-correlation is whereas if the polarizers are anti-parallel, the correlation is . Turning the applied filters to 90 degrees apart, gives no correlation. These four points are seen in Figure 3 at .
If we choose the filter setting of Alice and Bob to both lie at 45 degrees in the LFF, then both Alice and Bob simultaneously encounter their boson together in the same way as if the filters were applied along the Z axis. That is, since the two bosons are anti-parallel along any direction, the situation becomes identical to the anti-correlation of , already discussed for the Z direction.
If, however, the two filters are separated by increasing to , by moving Alice’s filter to 22.5 degrees from the bisector, to , and Bob’s down by 22.5 degrees to , then both still remain coupled bosons, Figure 10. Alice’s boson then aligns along and Bob’s aligns along , Figure 10. Both bosons are forced to align with their applied field along these two directions, for Alice and for Bob.
The BFF precesses with the helicity left or right in the LFF, so with fixed polarizer settings of , it can be shown that one quarter of the time, both bosons lie within that wedge without decoupling, which can be deduced by placing two panels, one for Bob and one for Alice, on top of each other in Figure 8. It is shown in the Appendix and [6] that for coherence correlation, both Alice and Bob spins must be bosons. This is the origin of factor in Eq.11. Three quarters of the time, the correlation is due to fermion polarization and one quarter of the time, the correlation is due to the boson coherence.
A similar situation occurs in the other quadrants of the BFF, as seen from the second, lower, wedge in the same figure. Alice’s boson then precesses about and Bob’s around . This is shown in Figure 9. Note that the angle a spin makes with its polarized direction differs from fermion to boson, given by . A spin precesses at the magic angle of 54.74 degrees while a spin 1 makes an angle of 45 degrees. In Figure 9 the 45 degree precession of the bosons is depicted, and this shows considerable correlation as the axes coincide as they precess. The 45 degrees precession angle supports the assumption that the bosons have not decoupled, and remain intact within the wedge.
Note also from Figure 10, that similar wedges occur so that is also strongly correlated to , and is strongly coupled to , and so forth around the 2D plane.
The maximum correlation from coherence for the S=CHSH inequality is determined by the filter setting that differ by , as shown in Figure 10, and giving,
We do not treat the dynamics of the 2D spin approaching the filter, but if the magnetic moment for each spin axis is , then the resonance spin of 1 has a Larmor precession proportional to before it decouples. The Larmor frequency of the resonance spin is twice that of the aligned or polarized spin .
The singlet state
Above we stated that the singlet state is an approximation. Here we summarize the treatment in [6]. A singlet state is usually expressed by opposing polarized states which are anti-symmetrized, , see Eq.(5). Here a spin has structure and we suggest a singlet state of an electron is more realistically expressed as shown in Figure 11 where the two magnetic axes are attracted which is balanced by the repulsion of the charges. The helicity now spins the axis as shown.
First the singlet state can be separated into the sum of eight product states if non-Hermitian states are used [56],
Each time an EPR pair separates, it does so randomly into only one of the eight non-hermitian terms. Each term represents a polarization direction and its helicity. That is why the states are non-Hermitian.
There are two product states in Eq.(38) for each BFF quadrant that can emerge, see Figure 10. One term describe left helicity and the other right helicity for each quadrant.
We suggest that after initial separation, each spin settles into a trajectory with the disc of polarization spinning along the axis of linear momentum, see Figure 1, governed by the Intermediate Axis theorem, [57].
Inserting the Pauli spin matrices and summing the eight terms reproduces the entangled singlet matrix shown in Eq.(7). In the sum, the outer coherent states cancel, and those, we suggest, are responsible for the difference between QM and the classical simulation.
To show this, each quadrant has two terms that are Hermitian conjugates of each other, describing L and R helicity. Upon separation, either the left or right handed helicity occurs. For the first quadrant, , adding the left and right , , Eq.(8), matrices leads to a Hermitian matrix from the two terms. That is, for each quadrant, at separation, the EPR pair is one of the eight products, for example for the first quadrant,
This shows Alice and Bob’s states with opposite polarization (diagonal elements), and opposite helicity, (off-diagonal elements) in the two by two matrices. Adding the Hermitian conjugate gives a Hermitian matrix for the state in the first quadrant,
Permutations of gives similar matrices for the other three quadrants. Finally summing over the quadrants gives the entangled singlet, Eq.(7). Notice the outer coherent terms cancel between quadrants, which is responsible for the difference in correlation between quantum, CHSH and the simulation, CHSH.
We conclude that use of the singlet state in QM, Eq.(5) is an approximation which misses these canceled terms. That is entanglement is a property of QM, but not of Nature. Entanglement simplifies calculation but missing correlation is the price.
Black holes and wormholes
Suggestions by Maldacena and Susskind [14] are expressed by the relationship ER=EPR where ER stands for Einstein-Rosen Bridges, (wormholes), [58], while the EPR [59], refers to QM and entanglement as a way to quantize spacetime [60]. Wormholes are solutions to the Einstein Field Equations [61] and are purely geometric distortions of spacetime, mathematically connecting different spacetime spaces. Maldacena and Susskind suggest that the wormholes are equivalent to, or created by, a pair of entangled black holes, with Alice at one and Bob at the other performing gedanken experiments with credible outcomes. Although non-local entanglement is not possible, [6], Q-spin presents an alternative that replaces non-locality. We point to [8,13],
as perhaps the smallest quantum entity which could be the building blocks of spacetime, with the LHS indicating the smallest component of quantum spin in free-flight, and the RHS indicating the connection to geometry,
The following construction is speculative: consider Minkowski spacetime as composed of a diffuse gas, a lattice, of particles in free-flight with spin . Each particle has a mass of at least a rest mass, and energy of at least a zero point. These particles attract each other according an inverse power law like Newton’s Law of gravity, but because space is so diffuse and the masses so small, there is little attraction between the particles. We are assuming that throughout the vastness of space, these particles form the microscopic fabric of spacetime. As mass increases, these particles pull closer and eventually they merge and coalesce into denser particles, increasing both mass and energy. For N coalesced points the structure is now , with Black Holes in the limit that . Examination of n-tuples of spin operators, [62], suggests the first step is to find the irreducible components under the Lorentz Group, and consider the quantization of the resulting structures. We have found a microscopic fermionic spin of magnitude with a microscopic dimensional hyperspace which carries a quantum of energy. Quantum gravity is a macroscopic force with a far reach. It is suggested to be mediated by a boson with spin of magnitude 2. Whereas we have found that reality must extend to the forth dimensional quaternion projective space, the hypersphere, one can only suggest that gravity is more complicated and likely extends to the next credible projective space of octonions in the hypersphere, or beyond. We do not know the nature of matter and energy in the dark regions of these vast hyperspaces beyond our visualization. All we can know are their stereographic projections into our dimension, and from these observations we must try to visualize what lies beyond our senses.
Standard Model
The success of the Standard Model, SU(3)⊗SU(2)⊗U(1), is marred by problems with the Weak Force, with Lepton number [55] and parity violations, [63]. Our work suggests replacing SU(2) with the quaternion group, . In this section we explore some consequences of this change on beta decay and parity violation.
Beta decay
Beta decay is fundamentally expressed as a neutron in a nucleus decaying into a proton by emitting a beta particle, a Fermi electron and an anti-neutrino,
The reason that Pauli, [29] and Fermi, [64] hypothesized neutrinos was because energy and angular momentum are not conserved by Fermi electrons. The neutrino was therefore hypothesized to be a fermion, without mass nor charge. This immediately revealed that neutrinos have no mirror image and therefore violated parity.
Quaternion spin in free-flight, however, is a boson which obviates the neutrino being a fermion (call it naked),
Although this restores parity to naked neutrinos, we are left with a particle which is the spinning of nothing. We assert this puts into doubt the existence of neutrinos. Rather we suggest that neutrinos are mistaken for the complementary property of spin, it’s helicity. Helicity of Q-spin in free-flight carries different quanta of energy from one interaction to another. This can lead to the observed distribution of beta decay energies which neutrinos were postulated to solve.
A naked neutrino is just the helicity of Q-spin which resides on the boson electron and is not a separate particle.
Initially, neutrinos were postulated to be massless, but later a tiny mass was assigned. Neutrino mass is needed to transform neutrinos to different flavours. If helicity replaces neutrinos, then they can have no mass. We can perhaps account for the proposed tiny given mass to neutrinos by the mass defect between fermion and boson electrons in Eqs.(43 and 44). The boson electron is likely energetically more stable than fermion electrons because the 2D structure is stabilized by its resonance boson,
Despite the enormous effort put into detecting neutrinos, the results are equivocal at best, [65,66]. One experiment detected only 500 events over 15 years that were interpreted as neutrinos. This from an estimated flux of about neutrinos per square centimeter passing the detector in that time period. Moreover, none of these events are the direct detection of neutrinos, but rather the proposed consequence of a neutrino collision with other particles.
Parity violation
Motivated by Yang and Lee, [34], the Wu experiment, conducted in 1956 by physicist Chien-Shiung Wu [15], tested the conservation of parity in weak nuclear interactions. Prior to this experiment, it was thought that the laws of physics were symmetric under parity. However, Wu’s experiment with the decay of cobalt-60 nuclei showed that weak interactions violate parity conservation.
First we modify the cobalt decay using boson electrons,
The goal of the experiment was to show that the beta decay is isotropic, which would be reflected in the (parity conserving) emission of the two gamma rays. Anisotropy in the gamma ray emission would be evidence for parity violation. The experiment, [15], polarized the cobalt atoms in a strong magnetic field which was immersed in a cryostat at 3 mK. Wu reported one experimental difficulty was placing the detectors inside the cryostat. This means that the beta electrons were measured in the presence of the magnetic field.
Figure 8 shows that the orientation of spins in a polarizing field determines if the boson spin is coupled or decoupled. Along the polar axis, the bosons remain coupled while along the equatorial axes, they uncouple into fermion spins. This difference was not considered by Wu.
Upon beta decay in the equatorial directions, boson electrons emerge into a strong polarizing field. These immediately decouple the boson so only fermion electrons impinge onto the detector. In contrast, in the polar directions the boson electrons remain intact and do not decouple.
There are a number of differences between boson and fermion electrons. First, in a field, the Larmor precession of the bosons is twice that of the fermion electrons. Second their energy is different, Eq.(45). Finally, the frequencies of the two gamma rays from nickel might differ depending on whether the boson or fermion emerge in Eq.(46).
Wu assumed that only fermion electrons emerged, and designed her detectors for them. Some polar events might then be missed. If so, this suggests her experiments favoured equatorial events over polar events. Indeed Fig(Figure 12) shows this to be true, which supports our hypothesis.
From EPR coincidence experiments, at 45 degrees the contribution to the correlation from the bosons is about that of polarized spins, see Figure 3. In the Wu experiment, Figure 12 at 3 mK the asymmetry due to the polar counts would be addressed also with about more polar events, yet this might just be a coincidence.
Nonetheless, we believe these differences are enough to justify a re-analysis of the Wu experiment to determine if, indeed, parity is violated by the weak force.
Interpretations of quantum mechanics
The existence of helicity sheds light on the Einstein-Bohr debates [25]. Position and momentum do not commute and therefore incompatible observables. Bohr claimed, contrary to Einstein, that only the measured property exists in his philosophy of complementarity [67]. A similar situation exists for spin. The coherence and polarization do not commute and are incompatible elements of reality. They influence each other. The spinor spins the polarization; the indistinguishably of the two polarization axes creates the parity for the helicity to know which way to spin. This structure is easily visualized, and evolves as one might intuitively expect.
Such an ontological description of spin is contrary to the Copenhagen interpretation, seen as particles manifesting differently in different spaces. Likewise, without Bell’s theorem, EPR are validated.
There are many other interpretations of QM, [68]. All focus on a specific aspect of the measurement problem. Only two are microscopic: the ensemble, [69] and de Broglie-Bohm, [70] interpretations. The latter is a Hidden Variable (HV) approach of Bohmian mechanics but in order to be successful its “quantum potential" must be non-local. The Ensemble approach, [69] is closest to the details of an experiment. It assumes the wavefunction is an ensemble of similarly prepared systems, consistent with the statistical mechanical view. Measurement is ensemble averaging. We have used von Neumann’s, [23], treatment of projective measure on a state operator by self-adjoint operators which are the observables, [8]. We have used the same approach to evaluate anti-Hermitian operators that are not observables yet are elements of reality. We suggest that all the other interpretations will evaporate with a QM that includes the higher dimensional spaces, and treats measurement according to some projection [23], onto our spacetime. Realizing now that Nature exists beyond our ability to measure, we must accept that information is lost upon measurement, [71], like determining which slit a particle passes. The epistemological question is to find methods to account for properties of Nature we cannot observe. This is not easy as spin taught us taking almost 100 years to find helicity is the complementary attribute to spin polarization. It is to Bell’s credit, [5] that he encapsulated a classical boundary that the quantum coherence exceeded, that gives the cryptic evidence for helicity. Quantum mechanics gives an incomplete description of the Nature. Its success is in its ability to encapsulate quantitatively what we can measure, giving vivid insight. With Bell’s Theorem gone nothing stands in the way of the conclusion of EPR [59]: QM is incomplete. Rather it is a theory of measurement and restricted to our spacetime.
Conclusions
Quaternions, [72], one of the many legacies of Hamilton, [73] are more than mathematical constructs that are defined in the hypersphere, with four spatial dimensions. Quaternions are elements of reality possessed by spin, complementary to its vector polarizations. Reality extends beyond our three spatial dimensions. The origin 1 of the unit quaternions coincides with origin of the Bloch sphere’s and extends it by adding helicity to each Bloch vector, and these spin either L or R with a constant frequency. Spin is not purely a vector quantity but includes the 4-dimensional hypersphere of unit quaternions, and only the 2x2 vector part of a spin, , is projected into our spacetime. This paper concludes QM is a theory of measurement, but not of Nature which is ontological and deterministic.
Coherence equations
Equations (5) is the usual singlet definition. Going from Eq.(6) to Eq.(7) is simply taking the outer product of the singlet which is entangled, Eq.(7). The singlet ket is expressed,
leading to the entangled state operator,
The entanglement can be removed by dropping the off-diagonal terms in the matrix, as shown in Eq.(8),
giving a product state in terms of the single pure spin state operator for a single spin, [24].
Calculate the correlations
Correlation from the entangled state
From the entangled singlet, Eq.(48)
Using
and
Correlation from the product state
From the product state for polarization, with no entanglement, Eq.(11)
Calculate the correlation from the product state for helicity, with no entanglement,
The shows that the full correlation from the entangled state is preserved between the polarization and coherent contributions with a product state,
which is an example of the Conservation of Geometric Correlation, [8].
Complementary equations
Here are three sets of complementary variables,
Until now the complementary property to angular momentum has not been discovered. It is the helicity. The commutator of angular momentum
differs from above. Moreover, the conjugate pairs in Eq.(56) are represented in different, inverse, spaces. The angular momentum pairs in Eq.(57) are represented in the same vector space, and so are not complementary pairs. Since they do not commute, Heisenberg Uncertainty holds for different J components, but since are both represented in the same vector space, they are only incompatible pairs.
The rest of this section is straightforward.
Dirac Equation equations
Q-spin correlation
In contrast to the state operator for polarized spin, Eq.(11), Q-spin has two orthogonal axes giving a state operator as
in the BFF. From this the expectation values are calculated for the spin axes, using both the symmetric and anti-symmetric contribution, Eq.(59),
using , and the vector products,
The two equations (59) describe the two orthogonal axes contracted with the filter direction. These are quaternions with the axis spun by the term, and the axis spun oppositely by the term, as seen in Figure 6 bottom left and right.
In free-flight, the angular momentum of the two axes constructively interferes to produce a purely resonance spin being a boson of magnitude 1,
formed from the sum of the two axes. Permutation of the signs, gives the bisectors of the quadrants as shown in the BFF in Figure 6, In the presence of a field, the boson aligns with the filter direction, Eq.(59), shown by being rotated up by 45 degrees and give being rotated up by 45 degrees so they coincide with their bisector,
Although the BFF makes it easier to visualize, the experiments are done in the LFF, so we use the transformation given Eq.24 to get the LFF expression with the filter vector also written in the LFF. Use of these leads to the following expressions which give the projections of the two axes into the LFF. The details are,
This can also be cast into quaternions,
These results are summarized below
The second equality separates the quaternion into a product of a geometric quaternion, and a field quaternion. From these, all correlation is obtains algebraically and for the simulation.
Correlation calculations
Upon separation, Alice and Bob’s spins are anti-correlated by requiring differs between Alice and Bob by , see Fig.(4) of [6]. The correlation in free-flight takes into account all orientations of the two anti-parallel spins and, by virtue of the product state having two terms, Eq.(49), we include its Hermitian conjugate, see Eq.(8). This ensures that both right and left handed helicities are retained. As expected, the anti-correlation is -1,
When approaching a polarization filter, the bosons at Alice Bob are polarized along the two fields giving the correlation
which is obtained from QM, but without any non-local connections.
An important point is that both Alice and Bob must both simultaneously be bosons. Taking only the scalar part of the quaternions in Eq.(67) gives
and only the product state survives in the correlation, even if one spin is coherent,
To get the full correlation, Eq.(67), Alice and Bob’s spins must both be Q-spins which means both must lie within the wedge. The lower part of Fig. Figure 10 depicts the situations described here. The L and R spins are polarized Dirac spins. Both polarization axes are present, but one is averaged by the spinning, Eq.(59). The center figure shows the Q-spin before decoupling.
References
- Gerlach, W., Stern, O. (1922). Das magnetische moment des silberatoms. Zeitschrift für Physik, 9(1), 353-355.
- Clauser, J. F. , Horne, M. A., Shimony, A., & Holt, R. A. (1969). Proposed experiment to test local hidden-variable theories. Physical review letters, 23(15), 880.
- Aspect, Alain, Jean Dalibard, and Gérard Roger. “Experimental test of Bell’s inequalities using time-varying analyzers.” Physical review letters 49.25 (1982): 1804.Aspect, Alain (15 October 1976). “Proposed experiment to test the non separability of quantum mechanics”. Physical Review D. 14 (8): 1944–1951.
- Weihs, G. , Jennewein, T., Simon, C., Weinfurter, H., Zeilinger, A. (1998). Violation of Bell’s inequality under strict Einstein locality conditions. Physical Review Letters, 81(23), 5039.
- Bell, John S. “On the Einstein Podolsky Rosen paradox." Physics Physique Fizika 1.3 (1964): 195.
- Sanctuary, B. Non-Local EPR Correlations using Quaternion Spin. Preprints 2023, 2023010570. [Google Scholar]
- Sanctuary, B. Extrinsic Quaternion Spin. Preprints.org 2023, 2023020055. [Google Scholar] [CrossRef]
- Sanctuary, B. Spin with Hyper-helicity. Preprints 2023, 2023010571. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The quantum theory of the electron. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character. 1928, 117, 610–624. [Google Scholar]
- Wilczek, F. Quantum mechanics of fractional-spin particles. Physical review letters 624, 49, 957. [Google Scholar] [CrossRef]
- Clauser, J.F.; Horne, M.A.; Shimony, A.; Holt, R.A. Proposed experiment to test local hidden-variable theories. Physical review letters 1969, 23, 880. [Google Scholar] [CrossRef]
- Tsirel’son, B.S. Quantum analogues of the Bell inequalities. The case of two spatially separated domains. Journal of Soviet Mathematics 1987, 36, 557–570. [Google Scholar] [CrossRef]
- Doran, C. , Lasenby, J., (2003). Geometric algebra for physicists. Cambridge University Press.
- Maldacena, J.; Susskind, L. Cool horizons for entangled black holes. Fortschritte der Physik 2013, 61, 781–811. [Google Scholar] [CrossRef]
- Wu, C. S., Ambler, E., Hayward, R. W., Hoppes, D. D., & Hudson, R. P. (1957). Experimental test of parity conservation in beta decay. Physical review, 105(4), 1413.
- Carroll, S. (2018). Alice and Bob Meet the Wall of Fire: The Biggest Ideas in Science from Quanta. MIT Press. [CrossRef]
- Original letter from Isaac Newton to Richard Bentley Author: Isaac Newton, Source: 189.R.4.47, ff. 7-8, Trinity College Library, Cambridge, UK: extract:“That gravity should be innate inherent and essential to matter so that one body may act upon another at a distance through a vacuum without the mediation of any thing else by and through which their action or force may be conveyed from one to another is to me so great an absurdity that I believe no man who has in philosophical matters any competent faculty of thinking can ever fall into it.".
- Born, M. , Born, H., Born, I., & Einstein, A. (1971). The Born-Einstein letters: correspondence between Albert Einstein and Max and Hedwig Born from 1916 to 1955. Walker.
- National Academies of Sciences, Engineering, and Medicine. (2019). Quantum computing: progress and prospects.
- Bashar, M. A., Chowdhury,M. A., Islam, R., Rahman, M. S., and Das,S. K. , “A Review and Prospects of Quantum Teleportation," 2009 International Conference on Computer and Automation Engineering, 2009, pp. 213-217. [CrossRef]
- Bennett, C. H., Brassard, G., Crépeau, C., Jozsa, R., Peres, A., Wootters, W. K. (1993). Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Physical review letters 1895, 70.
- Gisin, N. , Ribordy, G., Tittel, W., Zbinden, H., Quantum cryptography. Reviews of modern physics, 74(1), 145, 2002.
- Von Neumann, John. Mathematical foundations of quantum mechanics. Princeton university press, 1955.
- Fano, Ugo. “Description of states in quantum mechanics by density matrix and operator techniques. Reviews of modern physics 1957, 29, 74. [CrossRef]
- Jammer, M. (1974). Philosophy of Quantum Mechanics. the interpretations of quantum mechanics in historical perspective.
- Newton to Bentley, 25 February 1692/3, The Correspondence of Isaac Newton, ed. H. W. Turnbull (Cambridge: Cambridge University Press, 1961). C: Turnbull (Cambridge.
- Einstein, Albert. Born-Einstein Letters 1916-1955: Friendship, Politics and Physics in Uncertain Times. Palgrave Macmillan, 2014.
- Mullin, W. J. (2017). Quantum weirdness. Oxford University Press.
- Pauli, W. (1930). Pauli letter collection: letter to Lise Meitner (No. CERN-ARCH-PLC, pp. Letter-2412).
- Leonard, I. E., & Lewis, J. E. (2015). Geometry of convex sets. John Wiley & Sons.
- Okun, Lev B. “Mirror particles and mirror matter: 50 years of speculation and searching. Physics-Uspekhi, 2007; 50, 380.
- Peskin, M. E. Peskin, M. E., Schroeder, D. V. (1995). An Introduction To Quantum Field Theory (Frontiers in Physics), Boulder, CO.
- Bose, T., Boveia, A., Doglioni, C., Griso, S. P., Hirschauer, J., Lipeles, E., ... & Wang, L. T. (2021). Physics beyond the standard model.
- Lee, T.D.; Yang, C.N. Question of parity conservation in weak interactions. Physical Review 1956, 104, 254. [Google Scholar] [CrossRef]
- Anderson, E. K., Baker, C. J., Bertsche, W., Bhatt, N. M., Bonomi, G., Capra, A., ... & Wurtele, J. S. (2023). Observation of the effect of gravity on the motion of antimatter. Nature, 621(7980), 716-722. 621(7980), 716.
- Wick, David. The Infamous Boundary: Seven decades of heresy in quantum physics. Springer Science and Business Media, 2012.
- Bell, John S. (1987). Speakable and Unspeakable in Quantum Mechanics. Cambridge University Press. p. 65. ISBN 9780521368698. OCLC 15053677.
- Nordén, Bengt. “Quantum entanglement: facts and fiction–how wrong was Einstein after all? Quarterly reviews of biophysics 2016, 49.
- Hossenfelder, S.; Palmer, T. Rethinking superdeterminism. Frontiers in Physics 2020, 8, 139. [Google Scholar] [CrossRef]
- Hooft, Gerard T. “Ontology in quantum mechanics." arXiv preprint arXiv:2107.14191 (2021). arXiv:2107.14191 (2021).
- Hooft, Gerard T. Deterministic quantum mechanics: the mathematical equations. Frontiers in Physics 2020, 8, 253. [CrossRef]
- Cetto, A. M., Casado, A., Hess, K., & Valdés-Hernández, A. (2021). “Towards a Local Realist View of the Quantum Phenomenon." in Towards a Local Realist View of the Quantum Phenomenon, 4.
- Hess, Karl, “A critical review of works pertinent to the Einstein-Bohr debate and Bell’s Theorem" pre-print, November 2021.
- Khrennikov, A. Get rid of nonlocality from quantum physics. Entropy 2019, 21, 806. [Google Scholar] [CrossRef]
- Oaknin, D.H. The Bell theorem revisited: geometric phases in gauge theories. Frontiers in Physics 2020, 8(142). [Google Scholar] [CrossRef]
- De Raedt, H.; Jattana, M.S.; Willsch, D.; Willsch, M.; Jin, F.; ichielsen, K. Discrete-event simulation of an extended Einstein-Podolsky-Rosen-Bohm experiment. Frontiers in physics 2020, 8, 160. [Google Scholar] [CrossRef]
- Kupczynski, M. Is the Moon there if nobody looks: Bell Inequalities and Physical Reality. Frontiers in Physics 2020, 8, 273. [Google Scholar] [CrossRef]
- Christian, J. (2014). Disproof of Bell’s Theorem: Illuminating the Illusion of Entanglement. Universal-Publishers.
- Santos, E. “Local realistic interpretation of entangled photon pairs in the Weyl-Wigner formalism. Frontiers in Physics 2020, 8, 191. [Google Scholar] [CrossRef]
- See “Quantum entanglement" Wikipedia.
- Scholarpedia, see “Bell’s theorem".
- BIG Bell Test Collaboration. “Challenging local realism with human choices.". Nature 2018, 557, 212–216. [CrossRef]
- Longuet-Higgins, Hugh C. “The symmetry groups of non-rigid molecules.". Molecular Physics 1963, 6, 445–460. [CrossRef]
- Schrödinger, E. , “Discussion of probability relations between separated systems". Mathematical Proceedings of the Cambridge Philosophical Society. 31 (4): 555–563 (1935).
- Fonseca, R. M. (2020, August). Violation of lepton number in 3 units. In Journal of Physics: Conference Series (Vol. 1586, No. 1, p. 012003). IOP Publishing.
- Sanctuary, B. C. “Separation of Bell states." arXiv preprint arXiv:0705.3657 (2007).
- Poinsot, Louis. New theory of the rotation of bodies extracted from a memoir read at the Academy of Sciences of the Institute, May 19, 1834 by M. Poinsot.
- Einstein, Albert, and Nathan Rosen. “The particle problem in the general theory of relativity.". Physical Review 1935, 48, 73. [CrossRef]
- Einstein, A.; Podolsky, B.; Rosen, N. Can quantum mechanical description of physical reality be considered complete? Phys Rev 1935, 47, 777–780. [Google Scholar] [CrossRef]
- Van Raamsdonk, M. Building up spacetime with quantum entanglement. General Relativity and Gravitation, 2010; 42, 2323–2329. [Google Scholar]
- Carroll, S. M. (2019). Spacetime and geometry. Cambridge University Press.
- Sanctuary, B.C. Multipole operators for an arbitrary number of spins. The Journal of Chemical Physics, 1976; 64, 4352–4361. [Google Scholar]
- Schwartz, M. D. (2014). Quantum field theory and the standard model. Cambridge University Press.
- Fermi, E. (1934). Versuch einer Theorie der β-Strahlen. I. Zeitschrift für Physik, 88(3-4), 161-177.
- Waxman, E. (2007). Neutrino astrophysics: A new tool for exploring the universe. Science, 315(5808), 63-65.
- Mertens, S. (2016, May). Direct neutrino mass experiments. In Journal of Physics: Conference Series (Vol. 718, No. 2, p. 022013). IOP Publishing.
- Bohr, Niels. “Can quantum-mechanical description of physical reality be considered complete?." Physical review 48.8 (1935): 696.
- Wikipedia search interpretations of quantum mechanics.
- Ballentine, Leslie E. “The statistical interpretation of quantum mechanics." Reviews of Modern Physics 42.4 (1970): 358.
- Bohm, David (1952). “A Suggested Interpretation of the Quantum Theory in Terms of ’Hidden Variables’ I". Physical Review. 85 (2): 166–179.
- Braunstein, Samuel L., and Arun K. Pati. “Quantum information cannot be completely hidden in correlations: implications for the black-hole information paradox." Physical review letters 98.8 (2007): 080502.).
- Snygg, J. (1997). Clifford Algebra: A Computational Tool for Physicists. Oxford University Press on Demand.
- Gsponer, A.; Hurni, J.P. (2002). The physical heritage of Sir WR Hamilton. arXiv preprint math-ph/0201058.
Figure 1.
Two properties of Q-spin in free-flight: its polarization axes, and , are perpendicular to its helicity. These two fermionic axes couple to give a boson of spin 1. The helicity is in the direction of propagation and averages out the polarizations. Q-spin is geometrically identical to a photon in free-flight.
Figure 1.
Two properties of Q-spin in free-flight: its polarization axes, and , are perpendicular to its helicity. These two fermionic axes couple to give a boson of spin 1. The helicity is in the direction of propagation and averages out the polarizations. Q-spin is geometrically identical to a photon in free-flight.
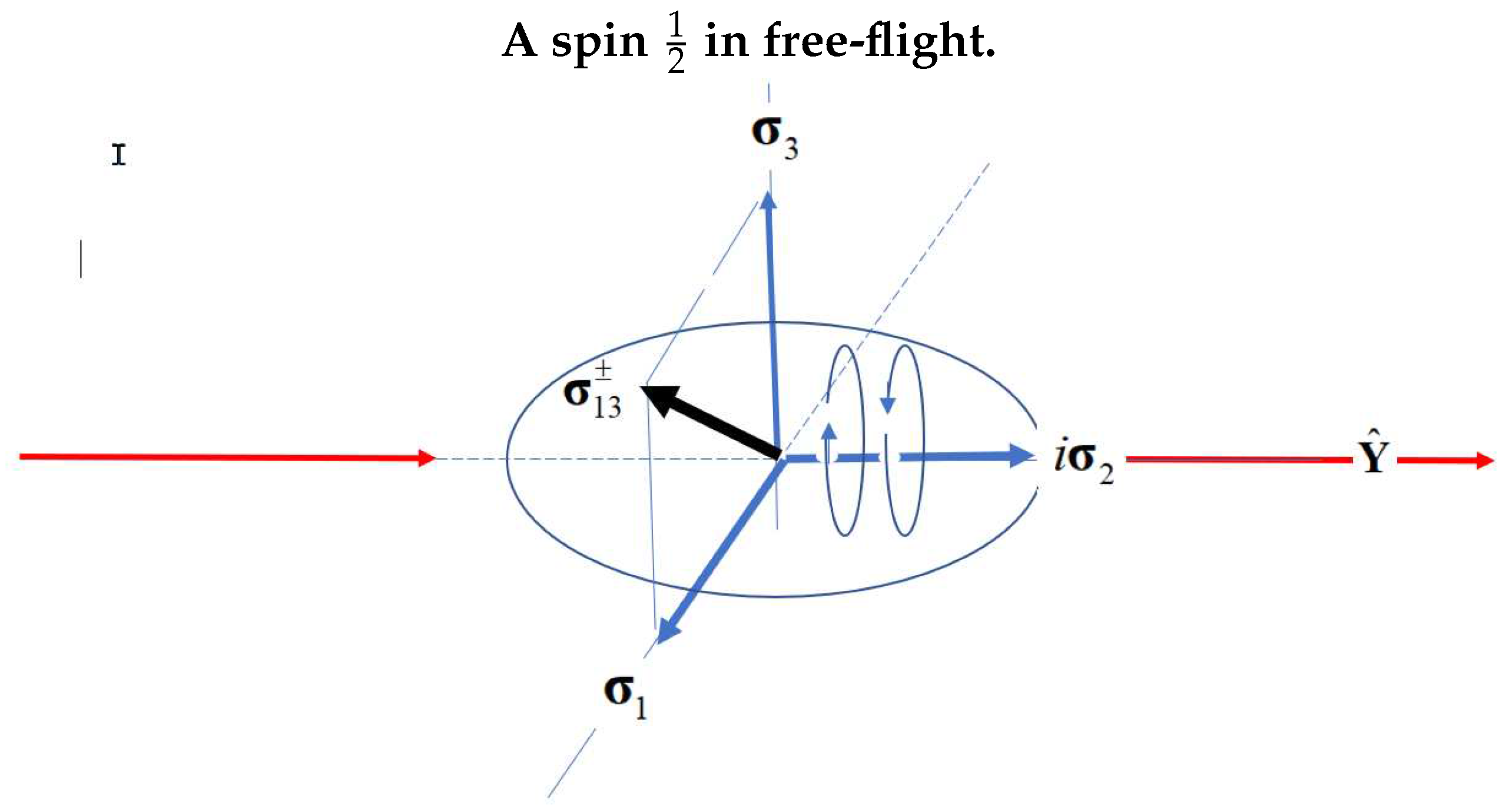
Figure 2.
Each of the two polarization axes are spins of . They are mirror states that couple to form Q-spin of even parity and spin magnitude 1.
Figure 2.
Each of the two polarization axes are spins of . They are mirror states that couple to form Q-spin of even parity and spin magnitude 1.
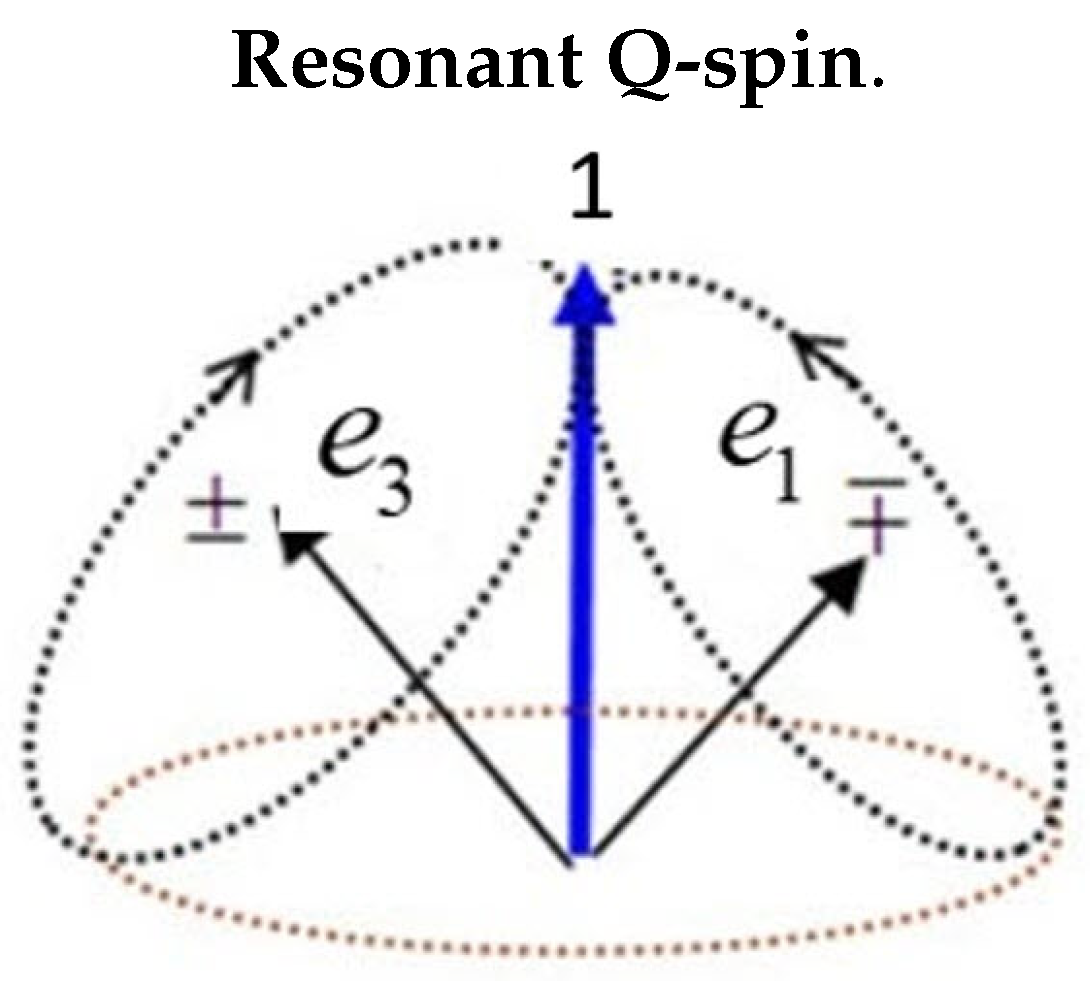
Figure 3.
Plotting intensity versus the angle difference . The results of the simulation are given by the points. The solid lines are from QM. The CHSH values are listed.
The full correlation is the sum of that from polarization, the triangle, and coherence, the mustache. Note the hardly discernible residual quaternion correlation along the horizontal axis.
Figure 3.
Plotting intensity versus the angle difference . The results of the simulation are given by the points. The solid lines are from QM. The CHSH values are listed.
The full correlation is the sum of that from polarization, the triangle, and coherence, the mustache. Note the hardly discernible residual quaternion correlation along the horizontal axis.
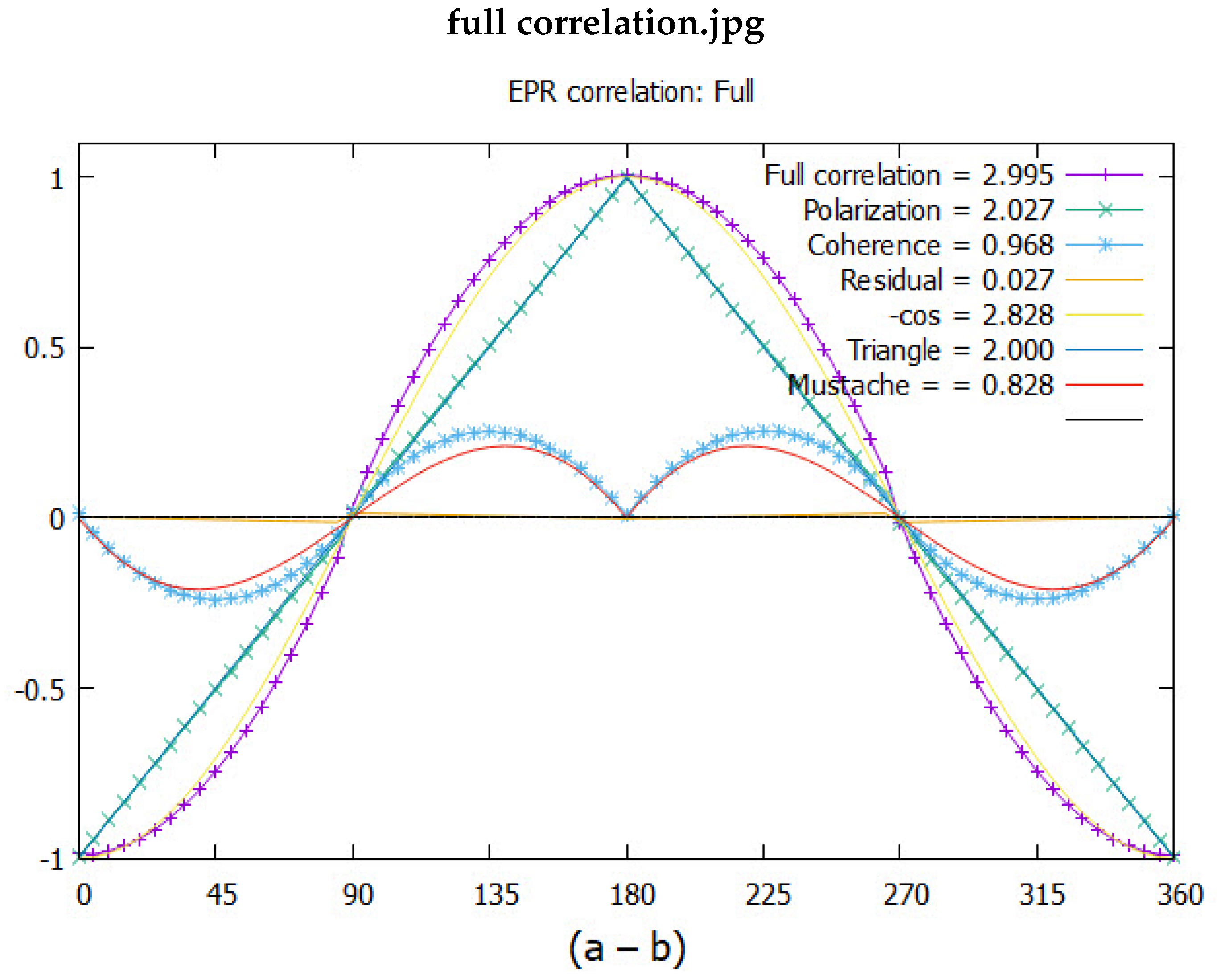
Figure 4.
The mirror states of a Q-spin with on the left and on the right. Note that adding these states is independent of and subtracting them is independent of and . Since we are blind to the imaginary axis, it is impossible to know which is the real object, or its reflection.
Figure 4.
The mirror states of a Q-spin with on the left and on the right. Note that adding these states is independent of and subtracting them is independent of and . Since we are blind to the imaginary axis, it is impossible to know which is the real object, or its reflection.
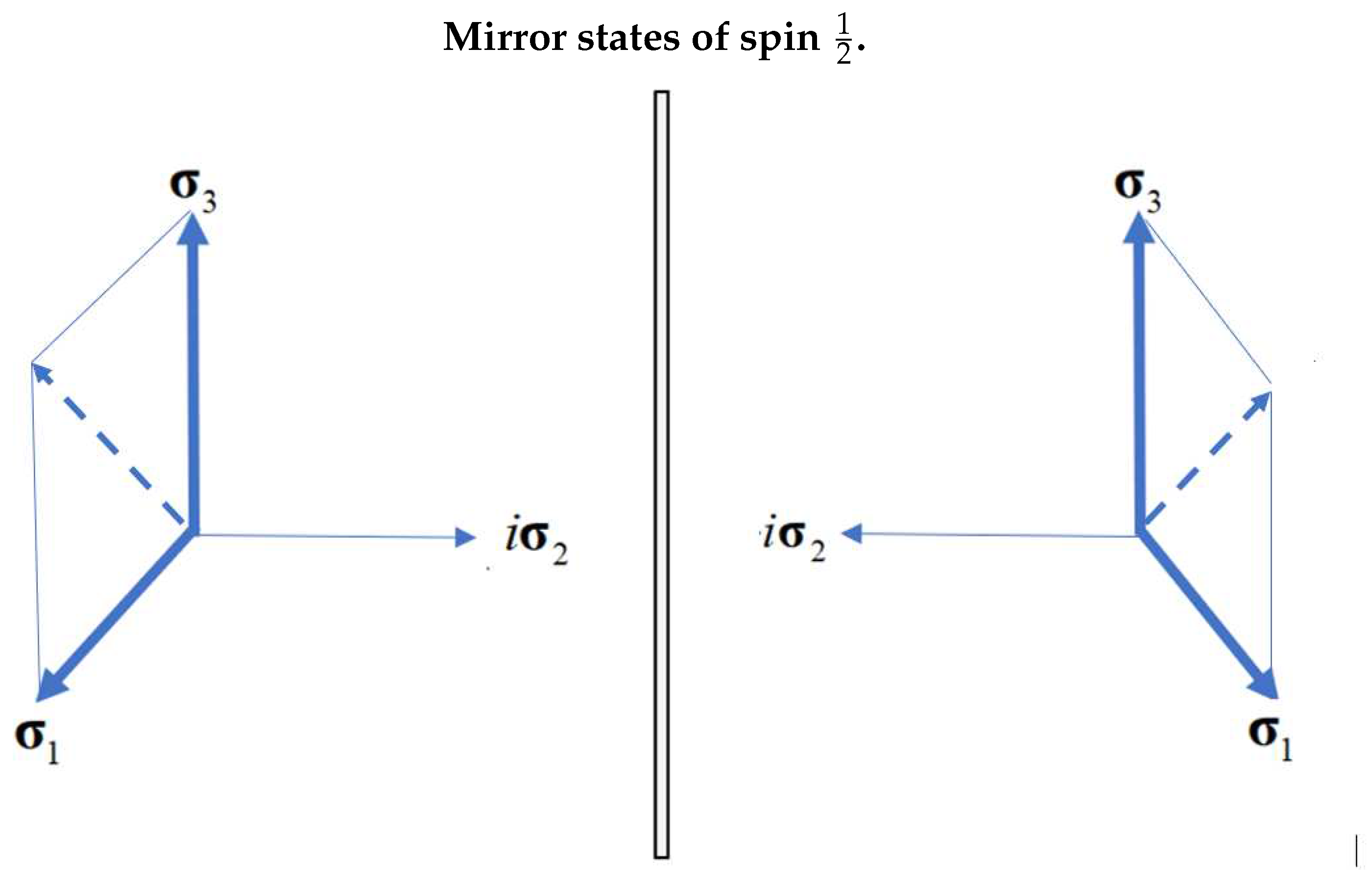
Figure 5.
A spin is oriented in spin spacetime by basis which spins about the axis so that in Minkowski spacetime, with components , only a smeared out image of the precessing spin is projected.
Figure 5.
A spin is oriented in spin spacetime by basis which spins about the axis so that in Minkowski spacetime, with components , only a smeared out image of the precessing spin is projected.
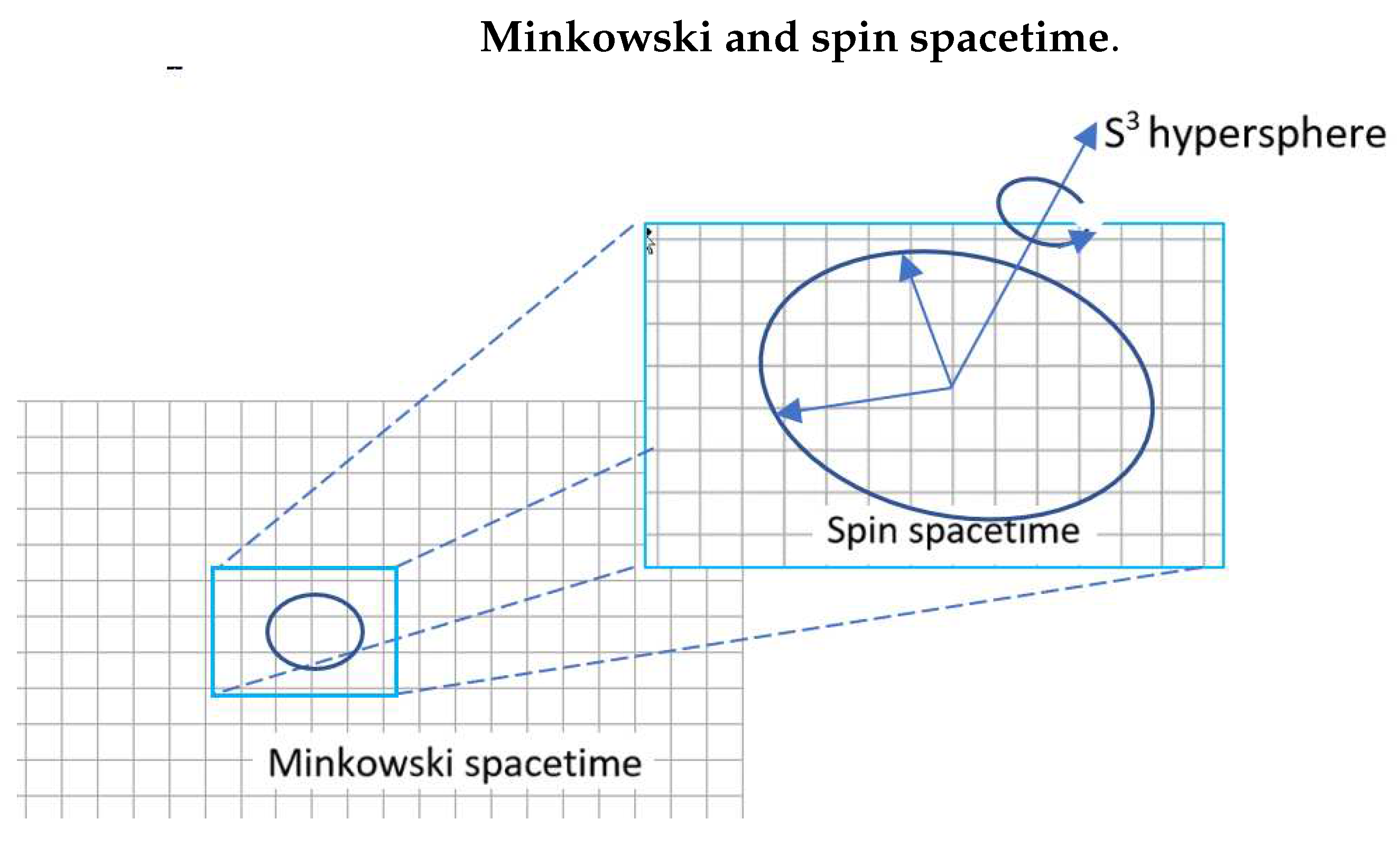
Figure 6.
The center part shows the fermionic axes coupled to give the boson in free-flight. In a polarizing field, one of the two axes aligns with the field and the other axis precesses perpendicular to the aligned axis. The direction of the spinning, and the sign of the spin, is determined by the helicity being transferred to the polarized axis.
Figure 6.
The center part shows the fermionic axes coupled to give the boson in free-flight. In a polarizing field, one of the two axes aligns with the field and the other axis precesses perpendicular to the aligned axis. The direction of the spinning, and the sign of the spin, is determined by the helicity being transferred to the polarized axis.
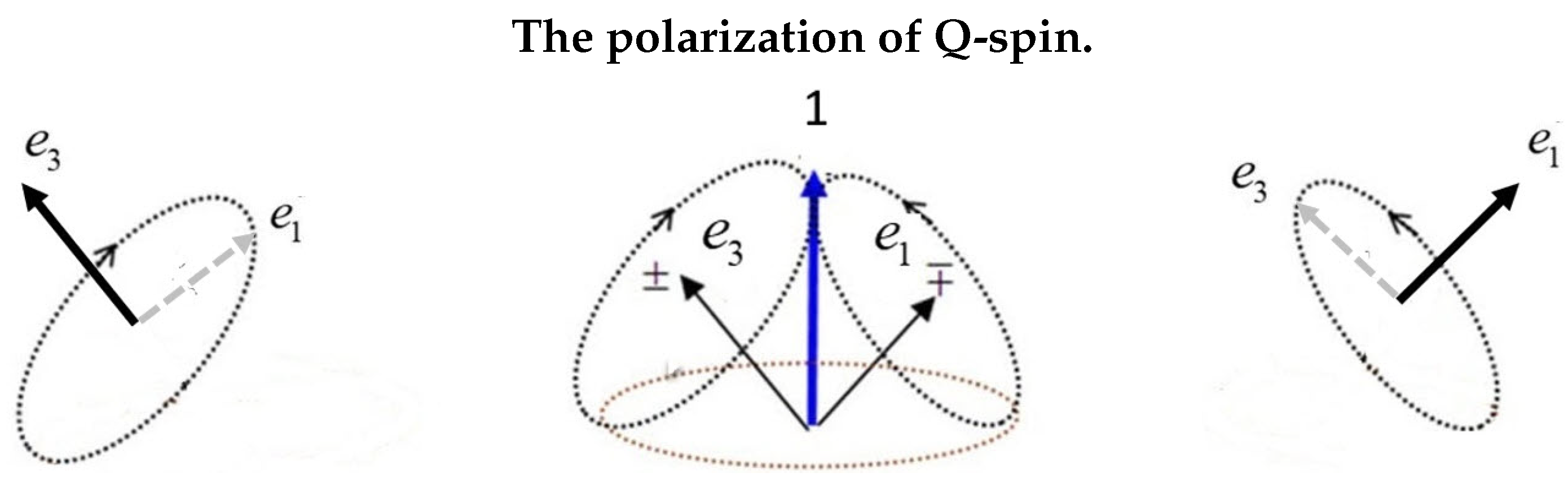
Figure 7.
The function given in Eq.(36) compared to the simulation. Also shown is the correlation from QM showing less correlation than the simulation.
Figure 7.
The function given in Eq.(36) compared to the simulation. Also shown is the correlation from QM showing less correlation than the simulation.
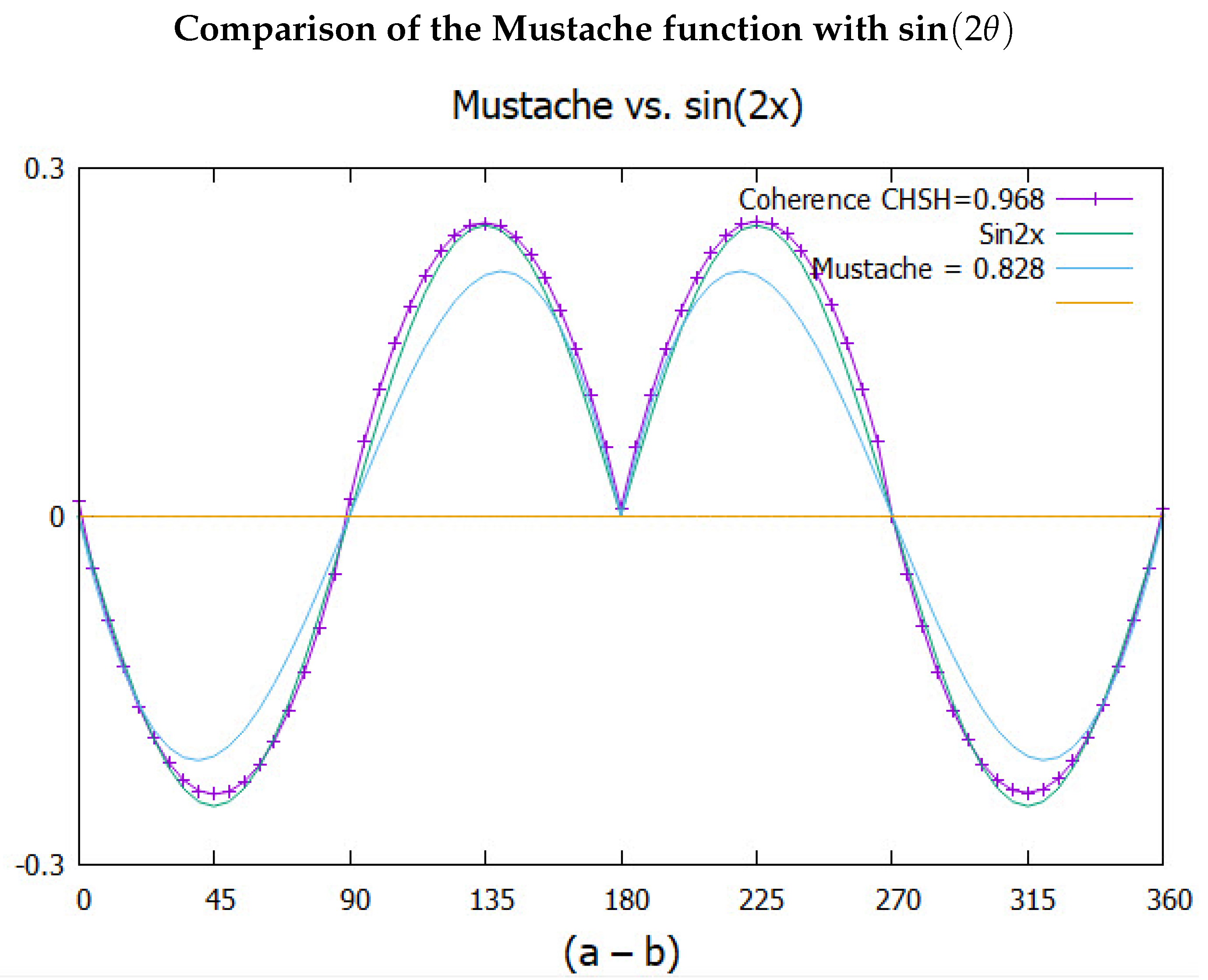
Figure 8.
The three circles express the filter plane with the filter axis in the vertical Z direction. The two orthogonal axes and their bisector have the same labels as Figure 6. The left panel shows that the boson spin is oriented along along the filter axis, while the other two show it rotated by 45 and 90 degrees from the filter. In some cases the boson persists and in others the fermion (see the text). The right panel summarized that boson spins are favoured along the polar or filter axis, making 45 degree wedges, while Fermi spins are favoured along the equatorial axes. One quarter of the time bosons are encountered and three quarters are fermions.
Figure 8.
The three circles express the filter plane with the filter axis in the vertical Z direction. The two orthogonal axes and their bisector have the same labels as Figure 6. The left panel shows that the boson spin is oriented along along the filter axis, while the other two show it rotated by 45 and 90 degrees from the filter. In some cases the boson persists and in others the fermion (see the text). The right panel summarized that boson spins are favoured along the polar or filter axis, making 45 degree wedges, while Fermi spins are favoured along the equatorial axes. One quarter of the time bosons are encountered and three quarters are fermions.
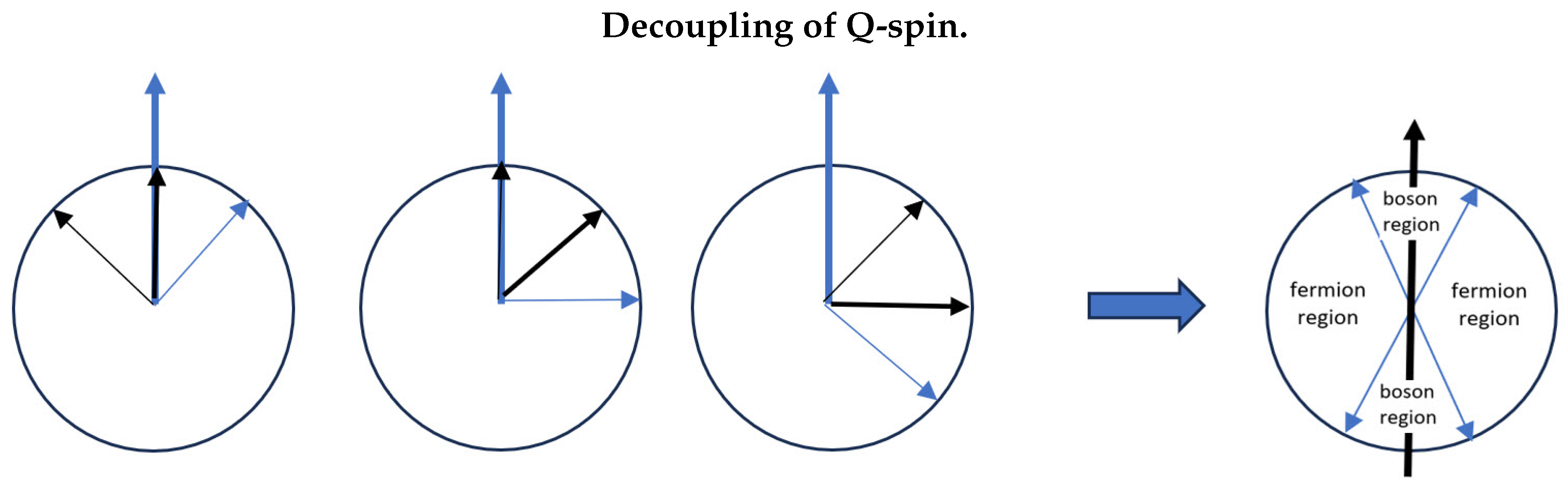
Figure 10.
Alice’s spin in the (1,1) quadrant) and Bob’s spin (in the (-1,-1) quadrant) are oriented anti-parallel in the BFF. All vectors are unit. The superposition of the two axes of spin , and creates the Q-spin of magnitude 1.
The heavy black lines indicate the filter settings at Alice and Bob that give the maximum violation of the CHSH inequality. The field wedge of on either side of the Q-spin means that both Alice and Bob are simultaneously probing the resonant Q-spin. Bottom: repeat of Figure 6.
Figure 10.
Alice’s spin in the (1,1) quadrant) and Bob’s spin (in the (-1,-1) quadrant) are oriented anti-parallel in the BFF. All vectors are unit. The superposition of the two axes of spin , and creates the Q-spin of magnitude 1.
The heavy black lines indicate the filter settings at Alice and Bob that give the maximum violation of the CHSH inequality. The field wedge of on either side of the Q-spin means that both Alice and Bob are simultaneously probing the resonant Q-spin. Bottom: repeat of Figure 6.
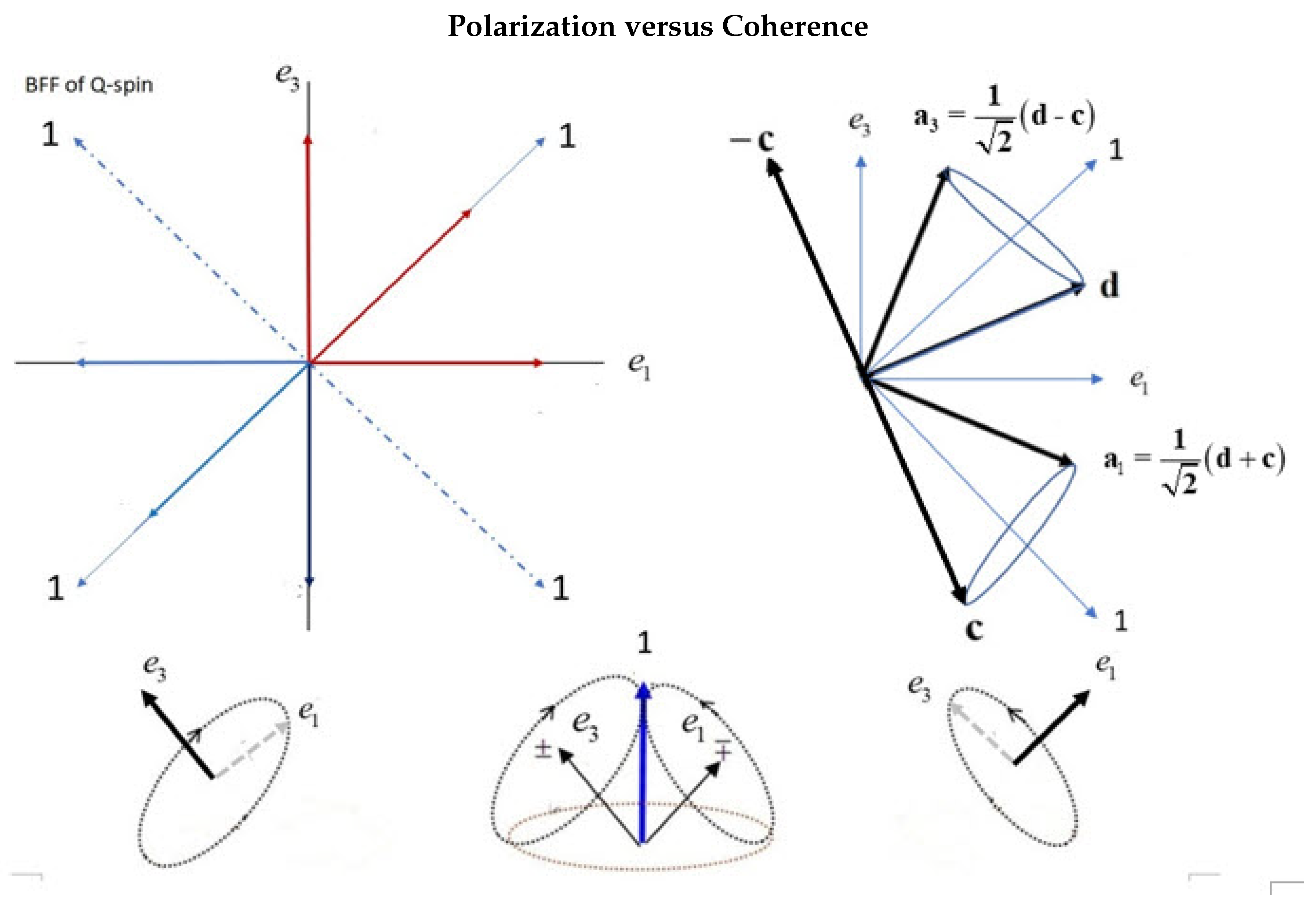
Figure 11.
A possible structure of the singlet with two electrons. While the electric charges repel, the magnetic moments attract. If one spin is in a LH frame, the other is in a RH frame. The helicities are opposite.
Figure 11.
A possible structure of the singlet with two electrons. While the electric charges repel, the magnetic moments attract. If one spin is in a LH frame, the other is in a RH frame. The helicities are opposite.
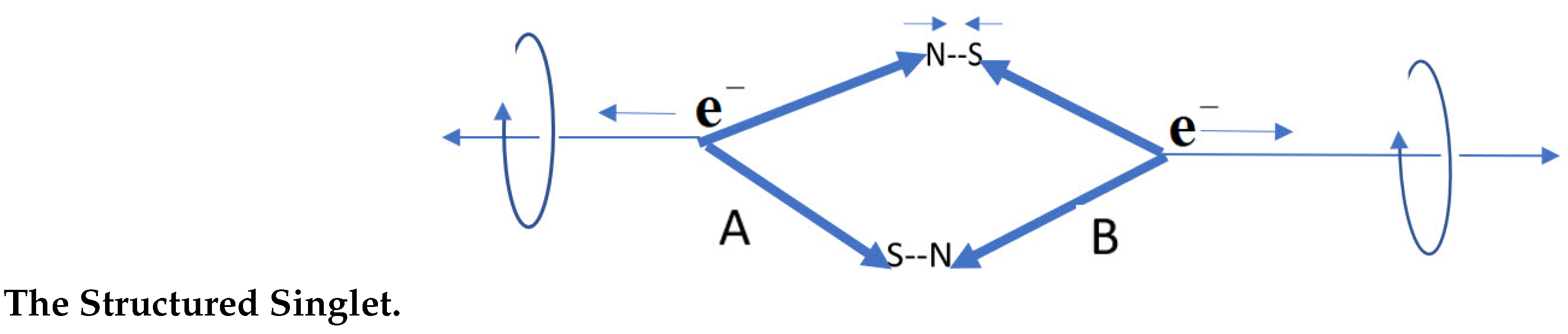
Figure 12.
The asymmetry of the gamma ray production between the polar and equatorial detectors in the Wu Parity Experiment
Figure 12.
The asymmetry of the gamma ray production between the polar and equatorial detectors in the Wu Parity Experiment
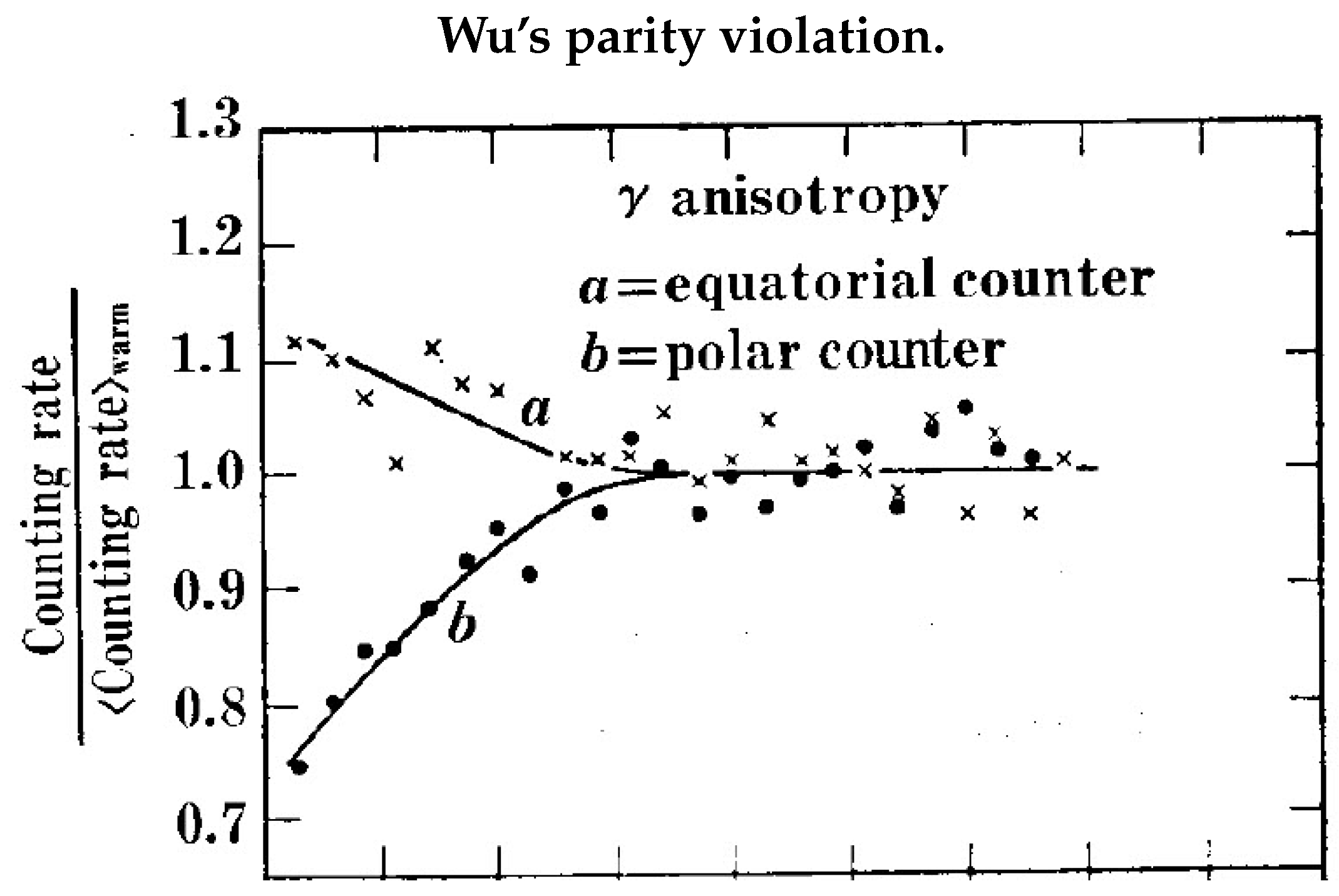
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





