Preprint
Article
Priority-aware Actuation Update Scheme in Heterogeneous Industrial Networks
Altmetrics
Downloads
75
Views
21
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
15 December 2023
Posted:
18 December 2023
You are already at the latest version
Alerts
Abstract
In the heterogeneous wireless networked control system (WNCS), age of information (AoI) of the actuation update and actuation update cost are important performance metrics. To reduce the monetary cost, the control system can wait for the availability of WiFi network of the actuator and then conduct the update by using WiFi network in an opportunistic manner, but it leads to the increased AoI of the actuation update. To assess this problem, this paper proposes a priority-aware actuation update scheme (PAUS) where the control system decides whether to deliver or delay the actuation update to the actuator by considering the control priority (i.e., robustness of AoI of the actuation update). For the optimal decision, we formulate a Markov decision process model and derive the optimal policy based on Q-learning. Simulation results demonstrate that PAUS outperforms the comparison schemes in terms of the expected reward.
Keywords:
Subject: Computer Science and Mathematics - Computer Networks and Communications
1. Introduction
According to Industry 4.0, wireless networked control systems (WNCSs) have been applied to industrial networks for various services such as industrial automation, smart manufacturing, and unmanned robot control [1,2]. WNCSs have been considered as a prominent solution in industrial networks to provide real-time and reliable actuation [3]. WNCSs generally consist of sensors, actuators, and a controller. Sensors collect the latest samples of environment states and deliver them to the controller. After the controller computes control decisions for actuators, it sends the control command to the actuators. In addition, as mobile actuators such as mobile robots and automated guided vehicles have recently been deployed, wireless control for mobile actuators has been actively deployed. During the general process of WNCSs, there are two principal updates: 1) status updates from sensors to the controller and 2) actuation updates from the controller to actuators, which need to be timely updated due to the time-critical-control applications in WNCSs.
Since timeliness is an important metric in WNCSs, age of information (AoI) has been introduced as a novel metric to quantify the freshness of information updates [4,5]. AoI is defined as the amount of elapsed time since the latest delivered information (i.e., updates in WNCS) was generated. It is based on the perspective of destinations and therefore it linearly increases with time until an update is received at a destination. Since WNCS requires timely and fresh updates to improve the control performance, AoI has been applied to WNCS as a key performance metric [6,7].
After AoI was introduced, the research on AoI for status updates in industrial networks or WNCSs has been maturely studied [2,7,8]. However, the research on AoI for actuation updates has not been focused yet even though it is critical for the control performance. For example, delayed actuation updates can result in production inefficiency, plant destruction, and casualties [2,8]. In other words, the timeliness of the actuation update should be controlled by the controller in WNCS. In addition, since there are different AoI requirements according to the control priorities for the actuators (i.e., robustness of AoI of the actuation update) [9,10], the priority needs to be considered when delivering the actuation update. For example, the priority can be defined to classify purposes concerning the criticality level at a particular moment [10].
Meanwhile, in industrial environments, heterogeneous wireless networks such as cellular (e.g., 5G new radio (NR)) and WiFi networks [11,12] have been deployed. Accordingly, the type of network available for mobile actuators varies depending on the location. In this scenario, the actuation updates via cellular network need the monetary cost while the updates via WiFi network are usually free to use. To reduce the monetary cost, the control system prefers to use WiFi network for the actuation updates. However, since WiFi network is not always available, it can increase AoI, which results in a critical situation, especially for high-priority control commands. Consequently, it is important to determine the appropriate actuation update policy considering both the monetary cost and AoI with priority.
To address the AoI control problem in heterogeneous networks, there have been several works [13,14,15,16,17,18]. Pan et al. [13] determined the scheduling policy over an unreliable but fast channel or a slow reliable channel to minimize AoI. Altman et al. [14] and Raiss-el-fenni et al. [15] introduced the receiver’s policy to decide whether to receive updates from cellular or WiFi networks to minimize the costs. Bhati et al. [16] provided the optimal average AoI considering heterogeneous multiple servers with different capabilities. Fidler et al. [17] showed the effect of independent parallel channels on AoI based on the queuing models. Xie et al. [18] formulated the generalized scheduling problem in multi-sensor multi-server systems to minimize AoI. However, there is no previous work to jointly consider the monetary cost and the priority from the system operator’s perspective.
To address these challenges, this paper proposes a priority-aware actuation update scheme (PAUS) that jointly considers the cost and AoI with priority. In PAUS, the control system determines whether to deliver or delay the actuation update to the actuator based on AoI with priority and cost. We formulate a Markov decision process (MDP) model and determine the optimal policy based on Q-learning (QL). Simulation results demonstrate that PAUS reduces the cost while satisfying the required AoI.
The main contribution of this paper is as follows: 1) to the best of our knowledge, this is the first work to jointly consider AoI with priority and cost; and 2) extensive simulation results present the performance of PAUS under various settings, which can be utilized as the guidelines for the control system operator.
The remainder of this paper is organized as follows. The system model and problem formulation are provided in Section 2 and Section 3, respectively. The QL-based algorithm is presented in Section 4. After simulation results are provided in Section 5, this paper is concluded with future works in Section 6.
2. System Model
Figure 1 presents the system model of this paper. It is assumed that a control system (i.e., controller) delivers the actuation update to the mobile actuator using either the cellular base station (CBS) or WiFi access point (WAP). It is also assumed that CBS is always available whereas WAP is only available when the actuator is close enough to WAP.
The monetary cost should be considered for actuation updates according to the network type. The use of the cellular network (i.e., via CBS) requires monetary costs based on the data plans of network operators. On the other hand, the use of WiFi networks (i.e., via WAP) is usually free. Therefore, the actuation update via WAP is efficient in terms of reducing the monetary cost for the system operator. However, WAPs are intermittently available [14]. Consequently, actuation updates using WAPs in an opportunistic manner can lead to increased AoI while it can reduce the monetary cost. Since increasing AoI leads to a critical situation (e.g., production inefficiency and casualties [2,8]), it is needed to maintain low AoI. Moreover, since there are control priorities in actuation updates, the priority should be considered when delivering the actuation updates. For example, the update of high priority has a strict AoI requirement than that of low priority, which is not relatively sensitive to AoI [10].
Therefore, it is important to determine the actuation update policy that can minimize the monetary cost while maintaining AoI below a desired value considering priority. To determine the optimal policy, this paper formulates an MDP problem in the next section.
3. Problem Formulation
In this section, we formulate an MDP model based on the timing diagram in Figure 2. In the formulated MDP model, the actuation update can be delivered via either CBS or WAP. Furthermore, if WAP is currently not available, the control system can delay the update with the expectation of future WAP contacts.
Whether to deliver the actuation update (i.e., via CBS or WAP) or delay the update is determined at each decision epoch according to the state at the decision epoch.
3.1. State Space
At each decision epoch, the state set can be defined as
where denotes the availability of WAP. In addition, and represent the current AoI and the existence of the actuation update with priority i, respectively.
First, can be defined as
where represents whether the actuator can receive the information from WAP or not. In other words, means that the actuator cannot connect WAP (i.e., can only connect to CBS) because there is no available WAP. Otherwise (i.e., ), the actuator can connect to WAP as well as CBS because WAP is close to the actuator.
Moreover, can be defined as
where denotes the current AoI of the actuation update with priority i and is the maximum AoI in the system model.
In addition, can be defined as
where denotes the existence of the actuation update with priority i. In other words, means that the actuation update with priority i exists at the control system and needs to be delivered to the actuator. Otherwise (i.e., ), the actuation update with priority i does not exist.
3.2. Action Space
At each decision epoch, the control system determines an action (i.e., deliver or delay). Consequently, let denote a global action space for the actuator, where is a local action space of the actuation update with priority i. can be defined as
where 0 and 1 stand for defined actions. Specifically, means that the control system delivers the update to the actuator. On the other hand, means that the control system delays the update.
3.3. Transition probability
The transition probability from the current state to the next state when the control system chooses the action a can be described as
because the availability of WAP is not dependent on the other states and determined action. In addition, the existence of the update is not dependent on the other states while current AoI is dependent on the existence of the update. Consequently, can be rearranged as
We assume that the duration of the disconnection (connection) between WAP and an actuator follows the exponential distribution with mean () [19]. Consequently, the probability that the actuator can connect to WAP during is . In addition, the actuator can disconnect with WAP during with probability . Therefore, and can be defined by
and
If the control system delays the actuation update when the update exists, current AoI increases until . If becomes , the control system should deliver the actuation update to the actuator. In this paper, AoI increases with different increasing rates according to the priority i. This is because, even if the same amount of time elapses, it can be perceived as relatively more time for the update with high priority (i.e., higher i) compared to that with low priority (i.e., lower i). In other words, the increasing rate of high-priority updates (e.g., high criticality level) is higher than that of low-priority updates (e.g., low criticality level) because increasing AoI of high-priority updates is much more critical compared to that of low-priority updates. Moreover, when the control system delivers the actuation update, the corresponding AoI becomes 0. Consequently, can be described as
and
where is an increasing function (e.g., a linear increasing function) as the priority i increases.
We assume that the probability that a new actuation update with priority i occurs follows the Poisson distribution with mean [20]. Consequently, the probability that the control system has a new actuation update with priority i during is . Therefore, can be described as
and
3.4. Reward and Cost Functions
For the reward and cost functions, we consider the monetary and delivery costs as well as the current AoI. Specifically, the total reward function, , is defined as
where is the reward function by means of AoI and is the cost function according to the monetary and delivery cost. Note that delivery cost denotes the additional cost caused by the delivery such as energy consumption or association overhead [14]. w () is a weight factor to balance and .
Specifically, can be obtained by
where is current AoI with priority i at the current time t and is target AoI which can be considered as a service requirement of the update with priority i. In addition, means the ramp function defined as:
In addition, can be represented as
where and are the monetary and delivery costs when the control system delivers the actuation update. These and are predefined constants that allow balancing the monetary cost and the delivery cost within the cost function and thus defining priorities.
4. QL-based Actuation Update Algorithm
To find the optimal policy in the formulated MDP model in Section 3, this paper proposes a QL-based algorithm. QL is a typical reinforcement learning algorithm to solve sequential decision problems [21]. QL uses a state-action value, , with given state s and taking action a. After is initialized to zero, can be updated at each subsequent iteration by
where , R, and denote the learning rate, instant reward, and discount factor, respectively. To balance between exploitation and exploration, the decaying -greedy approach can be used for iterative updates of . Specifically, the agent (i.e., control system) randomly selects the action with probability and selects the greedy action with maximum with probability 1-. In addition, gradually decreases during iterative updates to initially explore the environment and to finally exploit the greedy action. After converges to the optimal, the best action for every state can be selected as . Detailed steps for update is given in Algorithm 1.
| Algorithm 1: Steps for update |
|
5. Performance Analysis Results
To evaluate the performance, we conduct extensive simulations by means of a Python-based event-driven simulator where each simulation includes decision epochs, and the average values of 10 simulations are used for the average reward. We compare the proposed scheme (i.e, PAUS) with the following four schemes: 1) SEND where the control system delivers the actuation update immediately when a new actuation update occurs to minimize AoI, 2) TARGET where the control system delays the actuation update, and then delivers it right before exceeding the target AoI requirement, 3) PERIOD where the control system periodically delivers the actuation update, and 4) WAIT where the control system waits for WiFi to make the best use of WiFi.
The default parameter settings are as follows. The average probability of disconnection and connection between WAP and actuator is set to and , respectively. The default values of and w are set to 20 and , respectively. In addition, is assumed to be a linear function with a static coefficient (i.e., 1) according to i. Furthermore, we assume that there are 5 priorities where 1 is the lowest (i.e., less critical) and 5 is the highest (i.e., more critical). Moreover, , , and the period of PERIOD are set to 10, , and 10 decision epochs, respectively. It is assumed that and to use CBS are set to 4 and 1, respectively, while those to use WAP are set to 0 and 1, respectively.
Figure 3 shows the overall performance of the accumulated reward, AoI satisfaction ratio, and total monetary cost according to the simulation time. In Figure 3a, as the simulation time increases, the accumulated rewards for all schemes decrease because AoI and the monetary cost are accumulated. Among them, PAUS achieves the highest accumulated reward because it jointly considers AoI and the monetary cost. On the other hand, WAIT has the lowest accumulated reward because it waits for WiFi, which leads to increased AoI. Meanwhile, in Figure 3b, it is found that PAUS, SEND, and TARGET can guarantee the AoI requirement (i.e., satisfaction ratio) while PERIOD and WAIT cannot. This is because PERIOD and WAIT deliver the actuation update periodically and only at WiFi, respectively, without consideration of AoI. In addition, Figure 3c shows the accumulated cost among them. Among PAUS, SEND, and TARGET which have satisfaction ratio, it can be noted that PAUS has the lowest accumulated cost. This means that PAUS can minimize the monetary cost while maintaining AoI within the required value.
Figure 4 shows the average reward and AoI satisfaction ratio according to weight factor w. In Figure 4a, as w increases, the average rewards of PERIOD and WAIT decrease because of the increasing AoI. Between them, the average reward of WAIT is higher than that of PERIOD because it tries to reduce AoI whenever WiFi is available. On the other hand, as w increases, the expected rewards of SEND and TARGET increase due to the reduced AoI. Between them, the increasing rate of SEND is higher than that of TARGET because SEND can minimize AoI with increasing w. Meanwhile, PAUS achieves the highest average reward. This is because PAUS can reduce the monetary cost at lower w and AoI at higher w. In Figure 4b, it can be noted that PAUS cannot guarantee the AoI requirement at lower w. This is because PAUS aims to focus on reducing the monetary cost, which can increase AoI at lower w. Consequently, it is found that w needs to be set higher than to make AoI below the required value.
Figure 5 shows the average reward and AoI satisfaction ratio according to the actuation update arrival rate . In Figure 5a, as increases, the average rewards of all schemes decrease because increasing increases the number of deliveries, which can lead to monetary costs or delayed updates. Among them, the decreasing rate of SEND and PERIOD is higher than that of others. In the case of SEND, this is because as increases, the number of updates via CBS becomes higher, which increases the monetary cost. On the other hand, in the case of PERIOD, the periodical actuation update is still used even when increases, which results in delayed updates. Overall, PAUS achieves the highest average reward because it aims to minimize the cost jointly considering the monetary cost and AoI. In addition, from Figure 5b, even when increases, PAUS, SEND, and TARGET can guarantee the AoI requirement. On the other hand, PERIOD and WAIT cannot guarantee the AoI requirement because PERIOD still uses the periodical actuation update and WAIT delays the actuation update and waits for WiFi irrespective of changes.
Figure 6 shows the average reward and AoI satisfaction ratio according to the monetary cost . In Figure 6a, as increases, the average rewards of all schemes decrease because increased leads to higher monetary cost. Among them, the decreasing rate of SEND is higher than that of others because SEND immediately tries to deliver the actuation update even when CBS is only available. On the other hand, WAIT has the lowest decreasing rate because WAIT always prefers to use WAP. Overall, PAUS achieves the highest average reward. This is because PAUS can fully utilize either CBS at lower or WAP at higher . In Figure 6b, it can be noted that PAUS cannot guarantee the AoI requirement at higher . This is because PAUS reduces the monetary cost at higher , which can increase AoI, to maximize the total reward function defined in (17). Note that if the system operator needs to enhance AoI satisfaction ratio even at higher , the weight factor w in the total reward function can be adjusted.
Figure 7 shows the average reward and AoI satisfaction ratio according to the WAP connection probability . In Figure 7a, as increases, the expected rewards of all schemes increase because increased leads to lower monetary cost. Among them, the increasing rate of WAIT is higher than that of others because the increasing results in more opportunities to deliver updates via WAP, which can reduce AoI as also shown in Figure 7b. Overall, as presented in Figure 7a and Figure 7b, PAUS achieves the highest average reward while guaranteeing the AoI requirement. This is because PAUS can fully utilize either CBS at lower or WAP at higher .
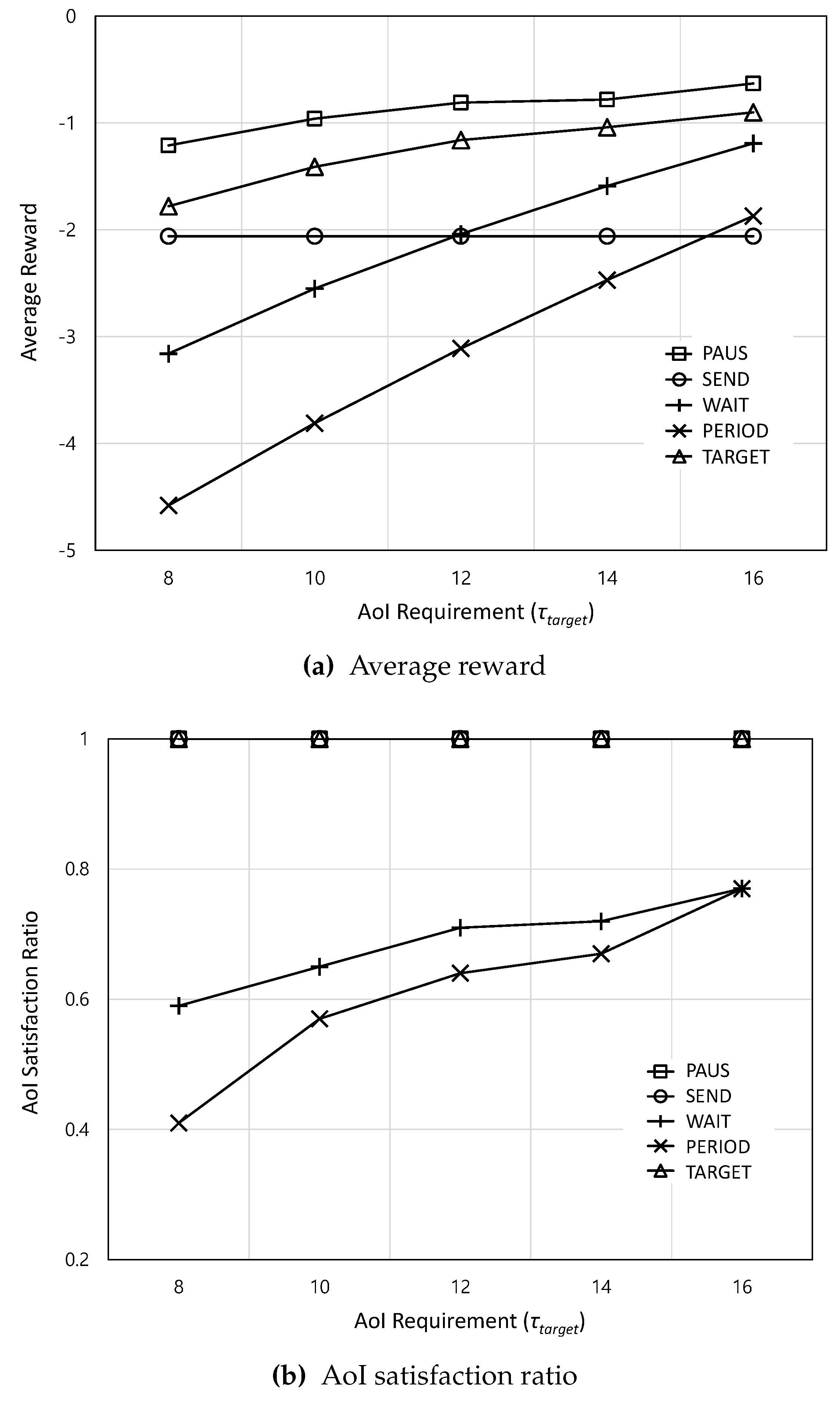
Figure 8 shows the average reward and AoI satisfaction ratio according to the AoI requirement . In Figure 8a, as increases, the average rewards of all schemes except for SEND (i.e., PAUS, WAIT, PERIOD, and TARGET) increase because there is enough time to wait for WiFi, which can reduce the monetary cost. However, because SEND delivers actuation updates irrespective of the AoI requirement, the average reward of SEND does not change according to the AoI requirement. From Figure 8b, although AoI satisfaction ratios of WAIT and PERIOD increase, they still cannot guarantee the AoI requirement.
6. Conclusion
This paper proposes a priority-aware actuation update scheme (PAUS) where the control system determines whether to deliver or delay the actuation update considering the monetary cost and AoI with priority. To find the optimal policy, this paper formulates an MDP model and provides a QL-based solution. Simulation results demonstrate that PAUS outperforms the comparison schemes in terms of the expected reward considering various operational environments. In our future work, we will validate the proposed scheme in the practical application scenarios.
Author Contributions
Conceptualization, Y.K.; methodology, H.K.; validation, Y.K.; formal analysis, J.S and T.S.. and Y.K.; investigation, J.S. and Y.K.; resources, J.S., H.K. and T.S.; data curation, Y.K. and Y.K.; writing—original draft preparation, Y.K.; writing—review and editing, Y.K. and Y.K.; visualization, Y.K.; supervision, T.S. and Y.K.; funding acquisition, Y.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the research grant of Kongju National University in 2023 and in part by "Regional Innovation Strategy (RIS)" through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (MOE)(2021RIS-003)
Institutional Review Board Statement
Not applicable
Informed Consent Statement
Not applicable
Data Availability Statement
Not applicable
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mansano, R.K.; Rodrigues, R.J.; Godoy, E.P.; Colon, D. A New Adaptive Controller in Wireless Networked Control Systems: Developing a Robust and Effective Controller for Energy Efficiency. IEEE Industry Applications Magazine 2019, 25, 12–22. [Google Scholar] [CrossRef]
- Wang, X.; Chen, C.; He, J.; Zhu, S.; Guan, X. AoI-Aware Control and Communication Co-Design for Industrial IoT Systems. IEEE Internet of Things Journal 2021, 8, 8464–8473. [Google Scholar] [CrossRef]
- Liu, W.; Popovski, P.; Li, Y.; Vucetic, B. Wireless Networked Control Systems With Coding-Free Data Transmission for Industrial IoT. IEEE Internet of Things Journal 2020, 7, 1788–1801. [Google Scholar] [CrossRef]
- Sun, Y.; Uysal-Biyikoglu, E.; Yates, R.D.; Koksal, C.E.; Shroff, N.B. Update or Wait: How to Keep Your Data Fresh. IEEE Transactions on Information Theory 2017, 63, 7492–7508. [Google Scholar] [CrossRef]
- Kaul, S.; Yates, R.; Gruteser, M. Real-time status: How often should one update? 2012 Proceedings IEEE INFOCOM, 2012, pp. 2731–2735. [CrossRef]
- Champati, J.P.; Al-Zubaidy, H.; Gross, J. Statistical Guarantee Optimization for AoI in Single-Hop and Two-Hop FCFS Systems With Periodic Arrivals. IEEE Transactions on Communications 2021, 69, 365–381. [Google Scholar] [CrossRef]
- Chang, B.; Li, L.; Zhao, G.; Meng, Z.; Imran, M.A.; Chen, Z. Age of Information for Actuation Update in Real-Time Wireless Control Systems. IEEE INFOCOM 2020 - IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), 2020, pp. 26–30. [CrossRef]
- Xu, C.; Xu, Q.; Wang, J.; Wu, K.; Lu, K.; Qiao, C. AoI-centric Task Scheduling for Autonomous Driving Systems. IEEE INFOCOM 2022 - IEEE Conference on Computer Communications, 2022, pp. 1019–1028. [CrossRef]
- Hazra, A.; Donta, P.K.; Amgoth, T.; Dustdar, S. Cooperative Transmission Scheduling and Computation Offloading With Collaboration of Fog and Cloud for Industrial IoT Applications. IEEE Internet of Things Journal 2023, 10, 3944–3953. [Google Scholar] [CrossRef]
- Chi, H.R.; Wu, C.K.; Huang, N.F.; Tsang, K.F.; Radwan, A. A Survey of Network Automation for Industrial Internet-of-Things Toward Industry 5.0. IEEE Transactions on Industrial Informatics 2023, 19, 2065–2077. [Google Scholar] [CrossRef]
- Cogalan, T.; Camps-Mur, D.; Gutiérrez, J.; Videv, S.; Sark, V.; Prados-Garzon, J.; Ordonez-Lucena, J.; Khalili, H.; Cañellas, F.; Fernández-Fernández, A.; Goodarzi, M.; Yesilkaya, A.; Bian, R.; Raju, S.; Ghoraishi, M.; Haas, H.; Adamuz-Hinojosa, O.; Garcia, A.; Colman-Meixner, C.; Mourad, A.; Aumayr, E. 5G-CLARITY: 5G-Advanced Private Networks Integrating 5GNR, WiFi, and LiFi. IEEE Communications Magazine 2022, 60, 73–79. [Google Scholar] [CrossRef]
- Hewa, T.; Braeken, A.; Liyanage, M.; Ylianttila, M. Fog Computing and Blockchain-Based Security Service Architecture for 5G Industrial IoT-Enabled Cloud Manufacturing. IEEE Transactions on Industrial Informatics 2022, 18, 7174–7185. [Google Scholar] [CrossRef]
- Pan, J.; Bedewy, A.M.; Sun, Y.; Shroff, N.B. Age-Optimal Scheduling Over Hybrid Channels. IEEE Transactions on Mobile Computing 2023, 22, 7027–7043. [Google Scholar] [CrossRef]
- Altman, E.; El-Azouzi, R.; Menasche, D.S.; Xu, Y. Forever Young: Aging Control For Hybrid Networks. Proceedings of the Twentieth ACM International Symposium on Mobile Ad Hoc Networking and Computing; Association for Computing Machinery: New York, NY, USA, 2019; Mobihoc ’19; pp. 91–100. [Google Scholar] [CrossRef]
- Raiss-el fenni, M.; El-Azouzi, R.; Menasche, D.S.; Xu, Y. Optimal sensing policies for smartphones in hybrid networks: A POMDP approach. 6th International ICST Conference on Performance Evaluation Methodologies and Tools, 2012, pp. 89–98. [CrossRef]
- Bhati, A.; Pillai, S.R.B.; Vaze, R. On the Age of Information of a Queuing System with Heterogeneous Servers. 2021 National Conference on Communications (NCC), 2021, pp. 1–6. [CrossRef]
- Fidler, M.; Champati, J.P.; Widmer, J.; Noroozi, M. Statistical Age-of-Information Bounds for Parallel Systems: When Do Independent Channels Make a Difference? IEEE Journal on Selected Areas in Information Theory 2023, 4, 591–606. [Google Scholar] [CrossRef]
- Xie, X.; Wang, H.; Liu, X. Scheduling for Minimizing the Age of Information in Multi-Sensor Multi-Server Industrial IoT Systems. IEEE Transactions on Industrial Informatics 2023, pp. 1–10. [CrossRef]
- Ko, H.; Kyung, Y. Performance Analysis and Optimization of Delayed Offloading System With Opportunistic Fog Node. IEEE Transactions on Vehicular Technology 2022, 71, 10203–10208. [Google Scholar] [CrossRef]
- Dong, Y.; Chen, Z.; Liu, S.; Fan, P.; Letaief, K.B. Age-Upon-Decisions Minimizing Scheduling in Internet of Things: To Be Random or To Be Deterministic? IEEE Internet of Things Journal 2020, 7, 1081–1097. [Google Scholar] [CrossRef]
- Marí-Altozano, M.L.; Mwanje, S.S.; Ramírez, S.L.; Toril, M.; Sanneck, H.; Gijón, C. A Service-Centric Q-Learning Algorithm for Mobility Robustness Optimization in LTE. IEEE Transactions on Network and Service Management 2021, 18, 3541–3555. [Google Scholar] [CrossRef]
Figure 1.
System model.
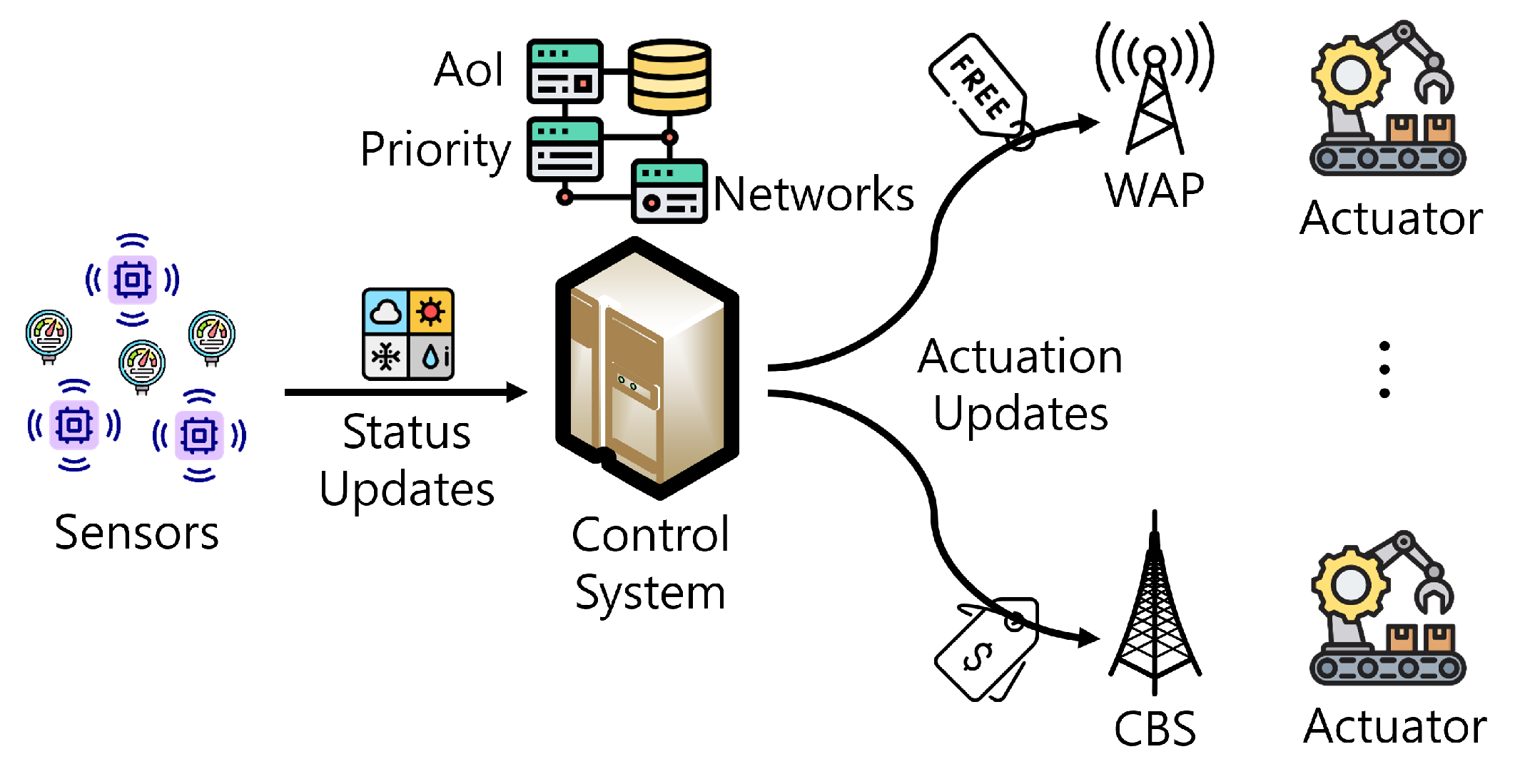
Figure 2.
Timing diagram for PAUS
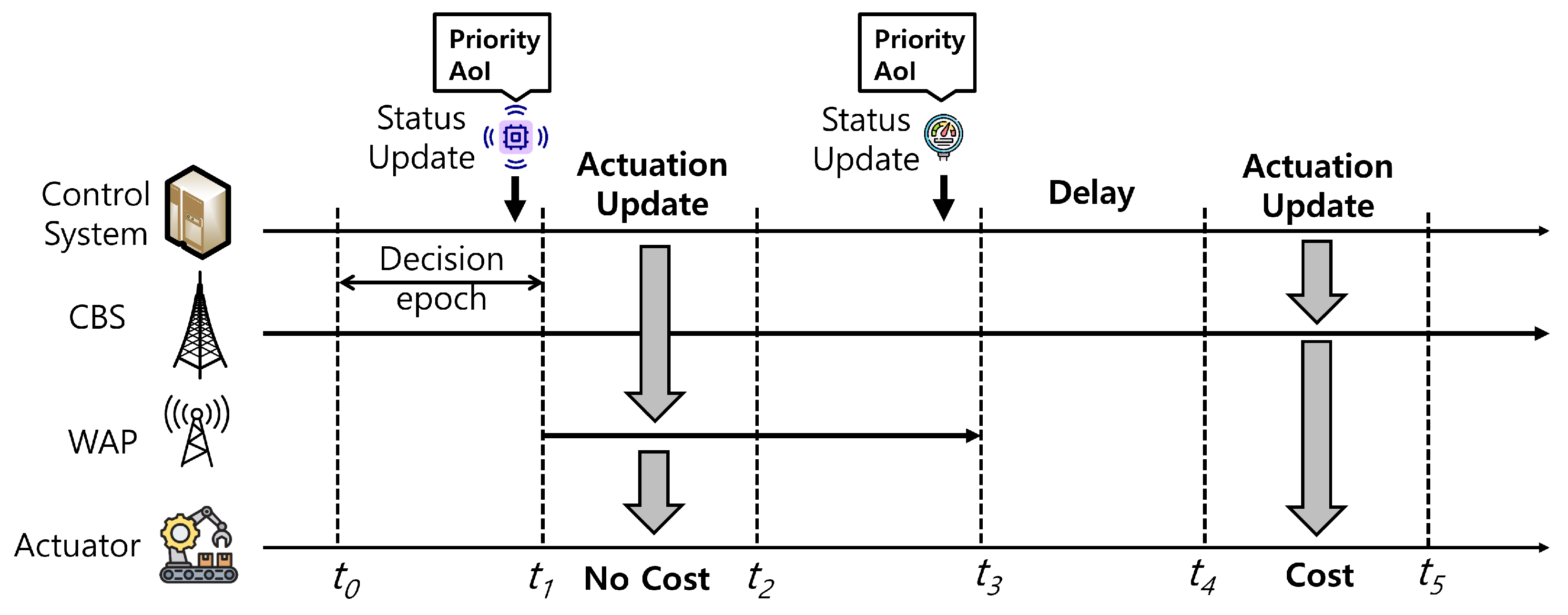
Figure 3.
Overall performance of the accumulated reward, AoI satisfaction ratio, and accumulated cost according to the simulation time
Figure 3.
Overall performance of the accumulated reward, AoI satisfaction ratio, and accumulated cost according to the simulation time

Figure 4.
The average reward and AoI satisfaction ratio according to weight factor w
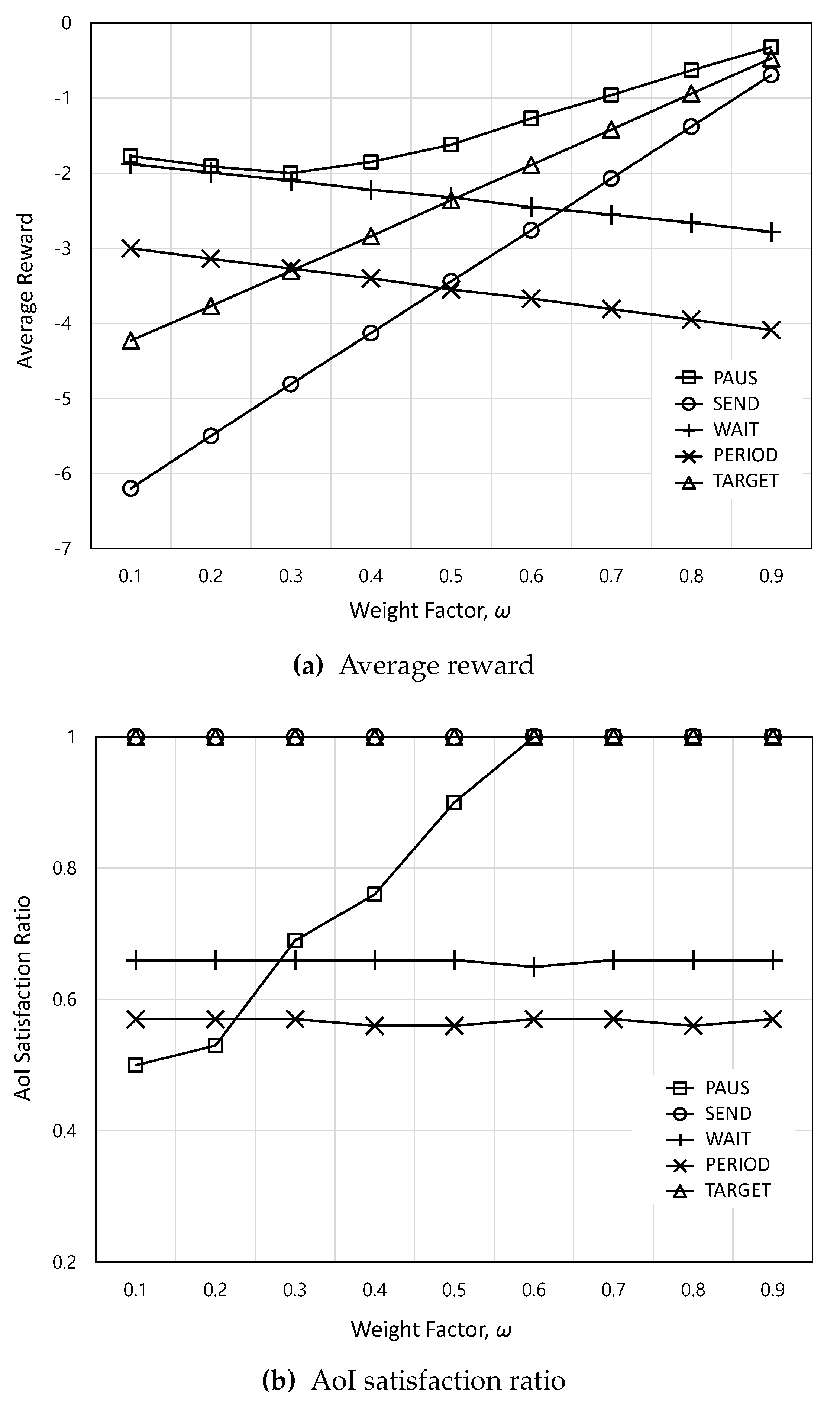
Figure 5.
The average reward and AoI satisfaction ratio according to the actuation update arrival rate
Figure 5.
The average reward and AoI satisfaction ratio according to the actuation update arrival rate
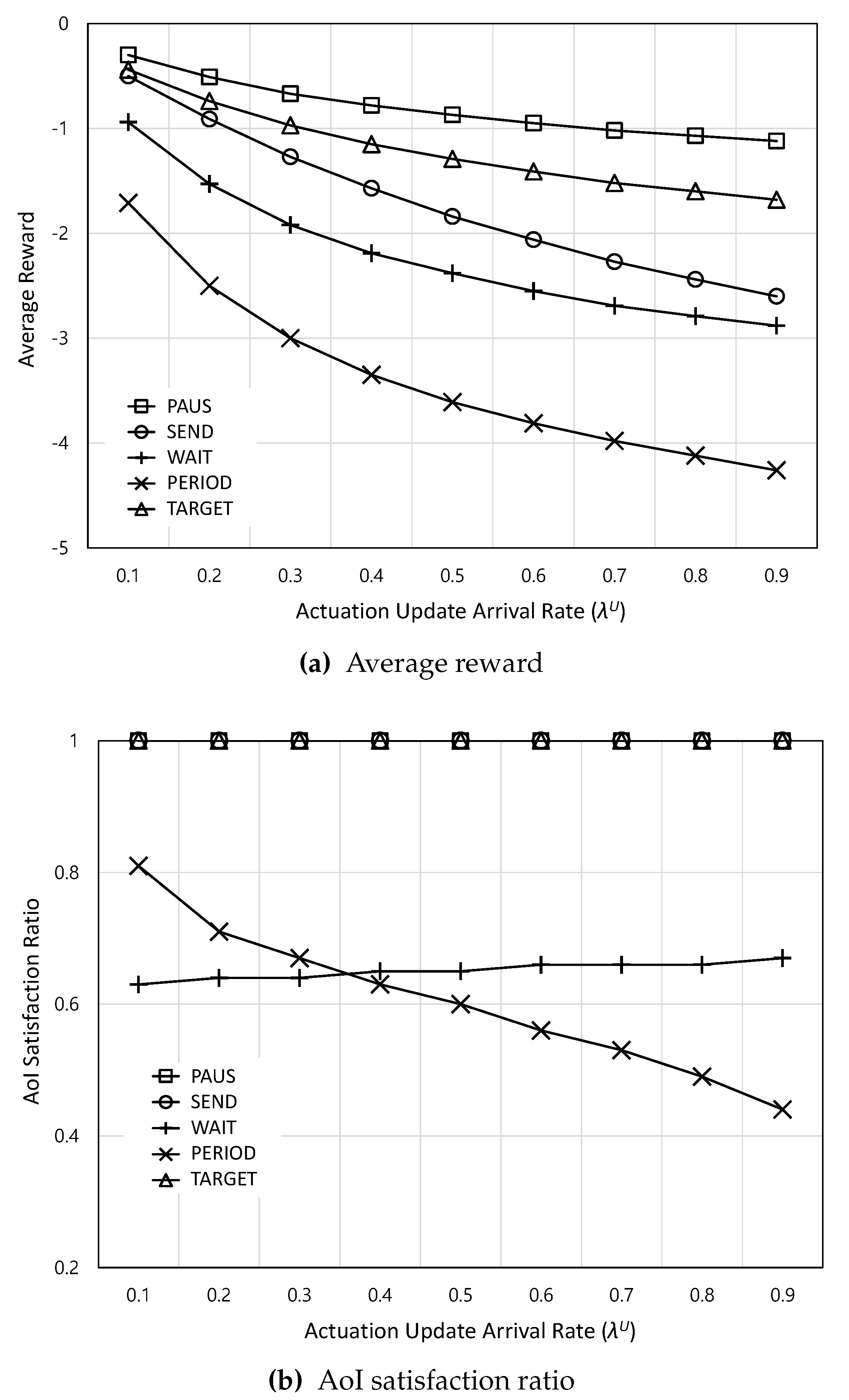
Figure 6.
The average reward and AoI satisfaction ratio according to the monetary cost
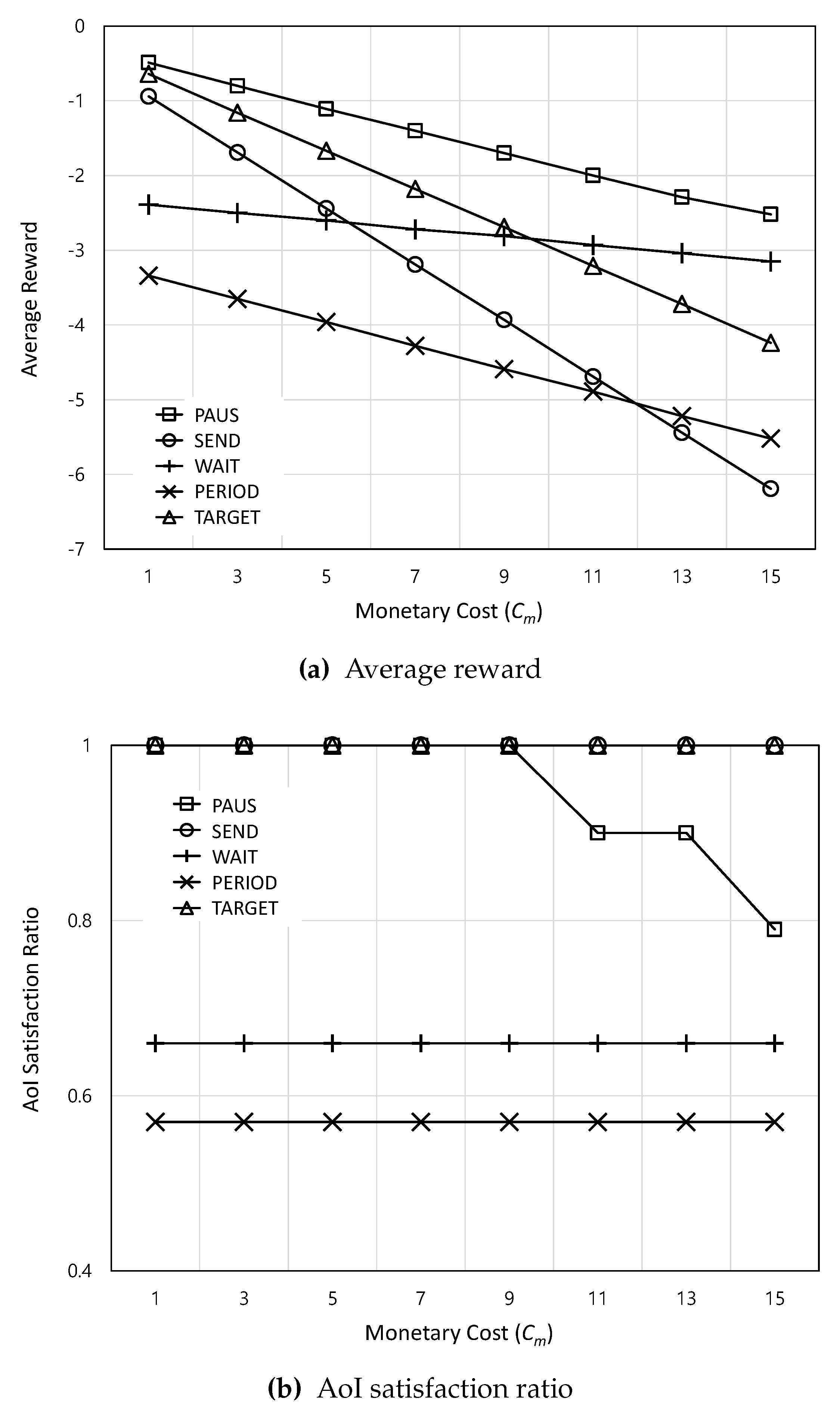
Figure 7.
The average reward and AoI satisfaction ratio according to the WAP connection probability
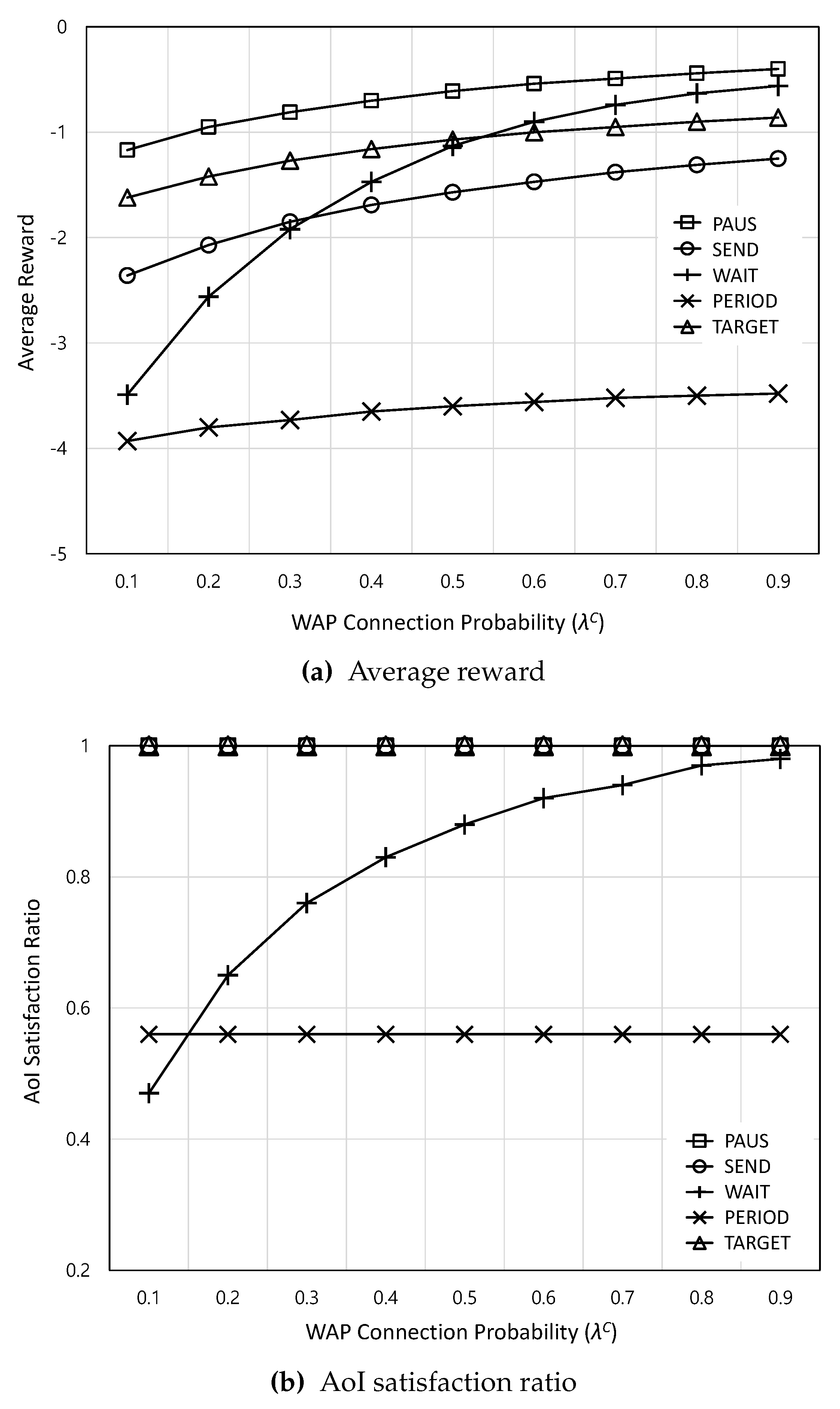
Figure 8.
The average reward and AoI satisfaction ratio according to the AoI requirement
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






